| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 2. ПРЕОБРАЗОВАНИЕ ХАРТЛИ
Общего одобрения достигнет тот, кто соединил приятное с полезным.
Гораций, Наука поэзии
В своей оригинальной статье, опубликованной в журнале Proceedings of the Institute of Radio Engineers в 1942 г., P. Хартли (1890-1970) подчеркнул строго взаимное соответствие пары интегральных формул, которые он ввел. В следующем разделе мы будем использовать обозначения автора и убедимся в полной симметрии этих формул. Однако со временем среди радиоинженеров установилась общепринятая теперь терминология, вследствие чего исходные определения Хартли приобрели несколько архаичную форму. Поэтому после точной записи соотношений в их исторически исходном виде мы перейдем к форме записи, согласующейся с практикой последних лет, и это преобразование в его современной форме будет определено как преобразование Хартли.
Исходная формулировка
Начнем рассмотрение с сигнала  , который является функцией времени и может представлять собой напряжение, формируемое в оконечных устройствах телефонной линии связи. Это колебание имеет частотный спектр, который может быть определен с помощью преобразования Фурье. Существует несколько научных школ, отличающихся разным представлением преобразования Фурье, и одна из этих школ, подходы которой будут проанализированы ниже, несмотря на ее почтенный возраст, представляет надежный базис для рассмотрения изначальной формы преобразования Хартли.
, который является функцией времени и может представлять собой напряжение, формируемое в оконечных устройствах телефонной линии связи. Это колебание имеет частотный спектр, который может быть определен с помощью преобразования Фурье. Существует несколько научных школ, отличающихся разным представлением преобразования Фурье, и одна из этих школ, подходы которой будут проанализированы ниже, несмотря на ее почтенный возраст, представляет надежный базис для рассмотрения изначальной формы преобразования Хартли.
Этот вариант преобразования Фурье  определяется выражением
определяется выражением

где  является комплексной функцией угловой частоты
является комплексной функцией угловой частоты  которая принимает только вещественные значения. Таким образом, для любого колебания
которая принимает только вещественные значения. Таким образом, для любого колебания  может быть определено преобразование Фурье
может быть определено преобразование Фурье  (или комплексный спектр), однозначно соответствующее этому колебанию.
(или комплексный спектр), однозначно соответствующее этому колебанию.
Дельта-функции. Здесь следует сделать небольшое отступление. Можно найти функции, для которых вышеприведенный интеграл не
существует, и множество математических исследований было посвящено решению очень сложных задач, которые могут при этом возникать. Существует два класса задач, к которым применимы эти рассуждения. Один из них включает функции, которые не могут описывать явления реального мира и которые, кроме того, имеют незначительный (если вообще имеют) физический интерес; другой класс включает дельта-функции и их производные, играющие важную роль при анализе физических явлений, даже если эти функции имеют сложное математическое описание. Тем не менее дельта-функции в ситуациях, где они возникают, являются одним из основных инструментов физического анализа. В данной работе мы не будем рассматривать первый класс задач, в которых функции обладают бесконечным числом неустранимых разрывов. Мы осознаем, что дельта-функции не являются функциями в обычном понимании, но принимаем термин «обобщенные функции» [М. J. Lighthill. An Introduction to Fourier Analysis and Generalized Functions, Cambridge Univ. Press, 1958 (Лайтхилл М. Д. Введение в анализ Фурье и обобщенные функции)] при анализе  представляющих собой единичный импульс и его производную.
представляющих собой единичный импульс и его производную.
Нулевые функции. Вопрос ставится следующим образом: может ли быть восстановлено исходное колебание  по заданной функции
по заданной функции  ? Ответ на этот вопрос звучит так: в основном может. Один из путей преодоления неопределенности этого заключения состоит в предварительном ограничении класса функций теми из них, для которых ответ однозначно утвердителен. Однако следует иметь в виду возможность такой неопределенности, что оказывается полезным для понимания вопросов, связанных с разрывными функциями, анализ которых часто приводит к дополнительным сложностям. Эти аспекты будут рассмотрены ниже.
? Ответ на этот вопрос звучит так: в основном может. Один из путей преодоления неопределенности этого заключения состоит в предварительном ограничении класса функций теми из них, для которых ответ однозначно утвердителен. Однако следует иметь в виду возможность такой неопределенности, что оказывается полезным для понимания вопросов, связанных с разрывными функциями, анализ которых часто приводит к дополнительным сложностям. Эти аспекты будут рассмотрены ниже.
На данном этапе достаточно объяснить понятие нулевой функции. Сама по себе следующая мысль может показаться несколько нелепой, но ее следует иметь в виду: нулевая функция есть функция, интеграл от которой равен нулю независимо от выбора пределов интегрирования. Естественно, что функция, в явном виде равная нулю, является нулевой функцией. Другим видом нулевой функции является функция  , которая по определению равна единице при
, которая по определению равна единице при  и нулю при всех других значениях
и нулю при всех других значениях  Еще одной функцией этого типа является функция
Еще одной функцией этого типа является функция  также представляющая практический интерес. Нулевые функции не зависят от чередования их положительных и отрицательных значений, что не определяет их нулевое значение; интеграл в бесконечных пределах от модуля пулевой функции равен нулю, т. е. если
также представляющая практический интерес. Нулевые функции не зависят от чередования их положительных и отрицательных значений, что не определяет их нулевое значение; интеграл в бесконечных пределах от модуля пулевой функции равен нулю, т. е. если  - нулевая функция, то
- нулевая функция, то 
Несмотря на то что нулевые функции представляются математически корректно даже в случае разрывных функций, они не играют значительной роли в физике. При наличии на входе механической системы воздействия  на ее выходе будет отсутствовать какая-либо реакция.
на ее выходе будет отсутствовать какая-либо реакция.
Ясно, что сумма  имеет такое же преобразование Фурье
имеет такое же преобразование Фурье  что и
что и  . Поэтому, когда осуществляется попытка обращения процесса, т. е. его восстановления по заданной функции
. Поэтому, когда осуществляется попытка обращения процесса, т. е. его восстановления по заданной функции  в общем случае оказывается невозможным восстановление полной структуры колебания
в общем случае оказывается невозможным восстановление полной структуры колебания  за исключением случая отсутствия нулевых функций. В отсутствие нулевых функций колебание
за исключением случая отсутствия нулевых функций. В отсутствие нулевых функций колебание  может быть восстановлено по заданной функции
может быть восстановлено по заданной функции  с помощью обратного преобразования Фурье
с помощью обратного преобразования Фурье 

Интегралы от функции  Хартли ввел пару формул
Хартли ввел пару формул

В этих соотношениях для функции  мы будем следовать определению автора, данному им в его оригинальной статье и в соответствии с которым эта функция представляет собой сумму косинуса и синуса одного и того же аргумента
мы будем следовать определению автора, данному им в его оригинальной статье и в соответствии с которым эта функция представляет собой сумму косинуса и синуса одного и того же аргумента

Таким образом, отсутствуют существенные отличия пары введенных интегралов от обычных интегральных формул преобразования Фурье, однако на практике эти различия значительны. Во-первых, функция  вещественна в отличие от функции
вещественна в отличие от функции  . Во-вторых, обратное преобразование для его реализации требует точно такой же процедуры интегрирования, как и прямое преобразование. Наконец,
. Во-вторых, обратное преобразование для его реализации требует точно такой же процедуры интегрирования, как и прямое преобразование. Наконец,  не является обычным преобразованием Фурье, и мы должны быть готовы к нетрадиционным характеру и свойствам этого преобразования. Значительная часть умозрительных построений относительно преобразования Фурье, а именно спектра колебания, являющегося функцией времени, непосредственно неприменима к
не является обычным преобразованием Фурье, и мы должны быть готовы к нетрадиционным характеру и свойствам этого преобразования. Значительная часть умозрительных построений относительно преобразования Фурье, а именно спектра колебания, являющегося функцией времени, непосредственно неприменима к  и значительная часть последующего материала посвящена выработке навыков, необходимых для уяснения различий и сходства вещественного и традиционного преобразований.
и значительная часть последующего материала посвящена выработке навыков, необходимых для уяснения различий и сходства вещественного и традиционного преобразований.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
- Глава 2. ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Преобразование Хартли
- Четная и нечетная составляющие
- Формулы связи
- Примеры
- Энергетический и фазовый спектры
- Глава 3. ТЕОРЕМЫ
- Свертка
- Соотношения между преобразованиями во временной и частотой областях
- Глава 4. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Физический смысл величин «тау» и v
- Четная и нечетная составляющие
- Примеры дискретных преобразований Хартли
- Степени свободы
- Другие вещественные ядра
- Теоремы
- Выводы
- Глава 5. ЦИФРОВАЯ ФИЛЬТРАЦИЯ ПОСРЕДСТВОМ СВЕРТКИ
- Циклическая свертка
- Дополнение нулями
- Обращение свертки
- Теорема о свертке
- Теорема о свертке в частотной области (спектральное сглаживание)
- Числовой пример свертки
- Коэффициент
- Числовой пример корреляционной функции
- Низкочастотная фильтрация
- Подчеркивание границ
- Свертка с использованием быстрого преобразования Хартли
- Способ без использования перестановок
- Свертка как умножение матриц
- Глава 6. Двумерные преобразования
- Двумерное преобразование Хартли
- Симметрия и антисимметрия
- Примеры
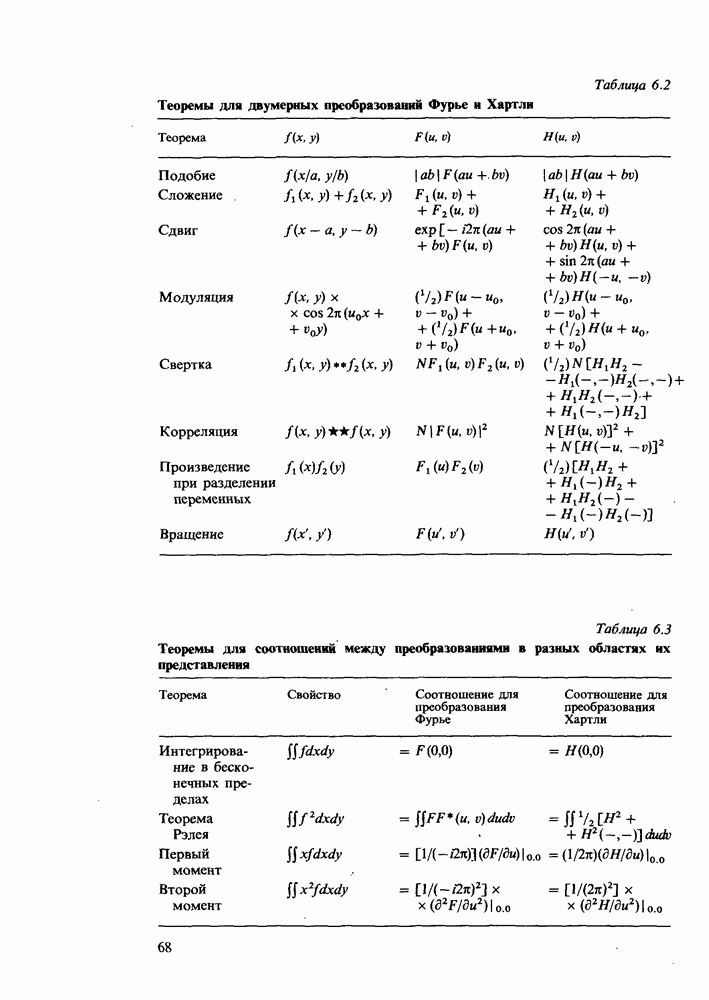
- Теоремы для двумерных преобразований
- Круговая симметрия
- Двумерная фильтрация
- Цикличность для двумерного случая
- Трехмерный случай
- Глава 7. ФАКТОРИЗАЦИЯ МАТРИЦЫ ПРЕОБРАЗОВАНИЯ
- Перестановка
- Перестановочные диаграммы
- Перестановочная матрица
- Ячеистая структура перестановочной диаграммы
- Каскадные матрицы
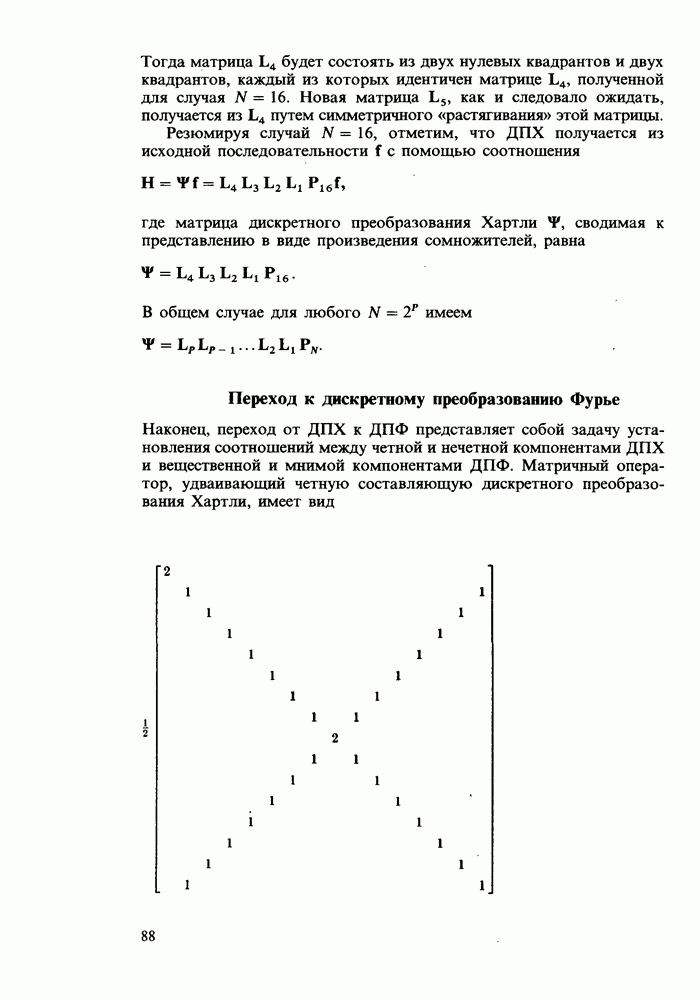
- Переход к дискретному преобразованию Фурье
- Глава 8. АЛГОРИТМ БЫСТРОГО ПРЕОБРАЗОВАНИЯ
- Свойство N log N
- Повторное разбиение последовательностей
- Преобразование с использованием разложения на подпоследовательности
- Общая формула разложения.
- Направленный сигнальный граф
- Вычисление с замещением
- Анализ временных затрат на вычисление с помощью полосковой диаграммы
- Степепи числа 2
- Тригонометрические функции
- Быстрое вычисление синусов
- Операция быстрого поворота
- Быстрая перестановка
- Преобразование для последовательностей с основанием 4 и другие модификации
- Ранее применявшиеся подходы к преобразованию вещественных данных
- Глава 9. ПРЕОБРАЗОВАНИЕ ХАРТЛИ В ОПТИКЕ
- Свойства симметрии
- Осуществление преобразования Хартли, использующее поляризацию
- Практическое осуществление
- Источник некогерентного излучения
- Пример
- Голография в плоскости Хартли
- Приложение 1. ПРОГРАММЫ ВЫЧИСЛЕНИЙ НА ЭВМ
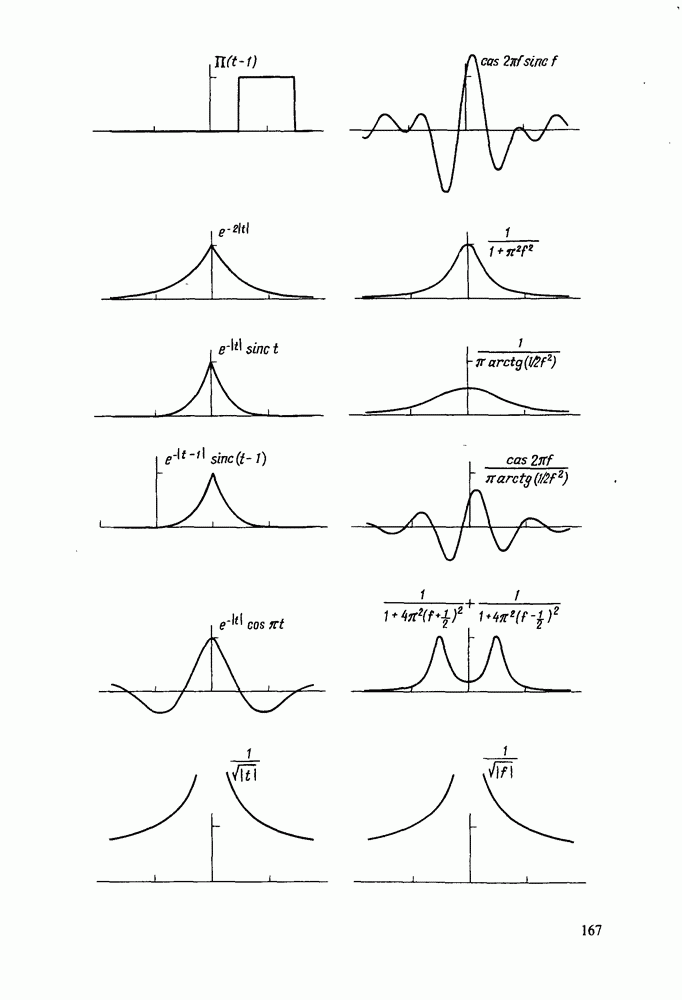
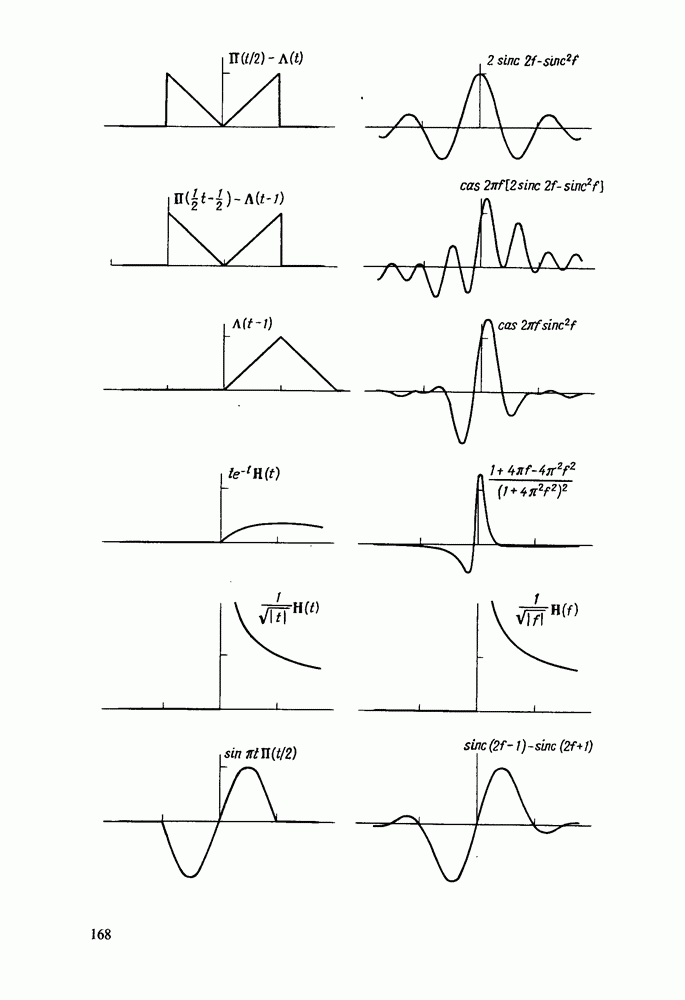
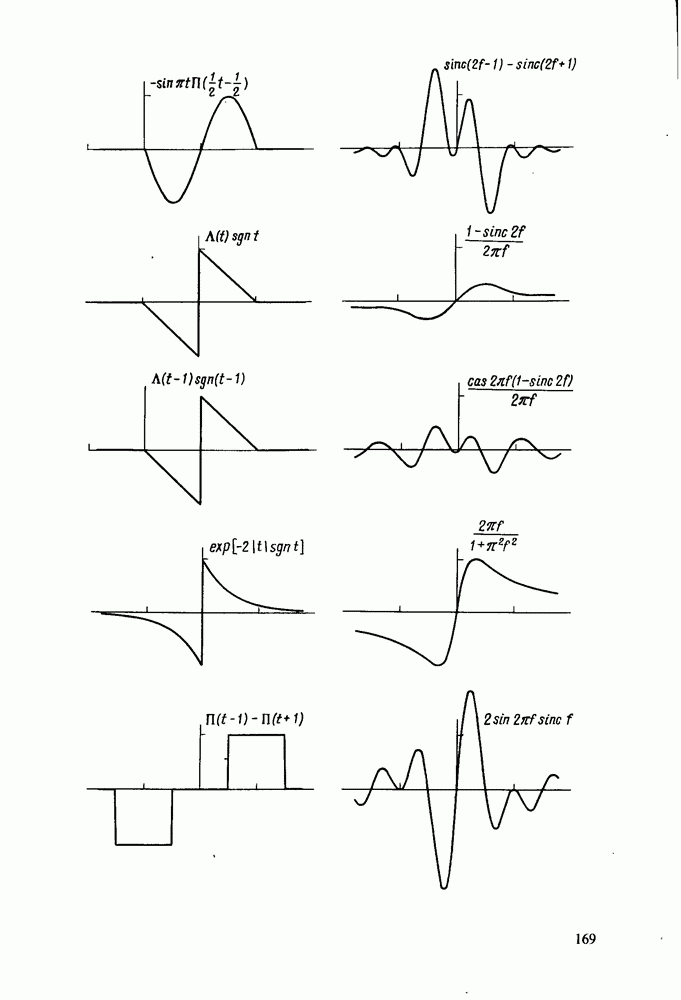
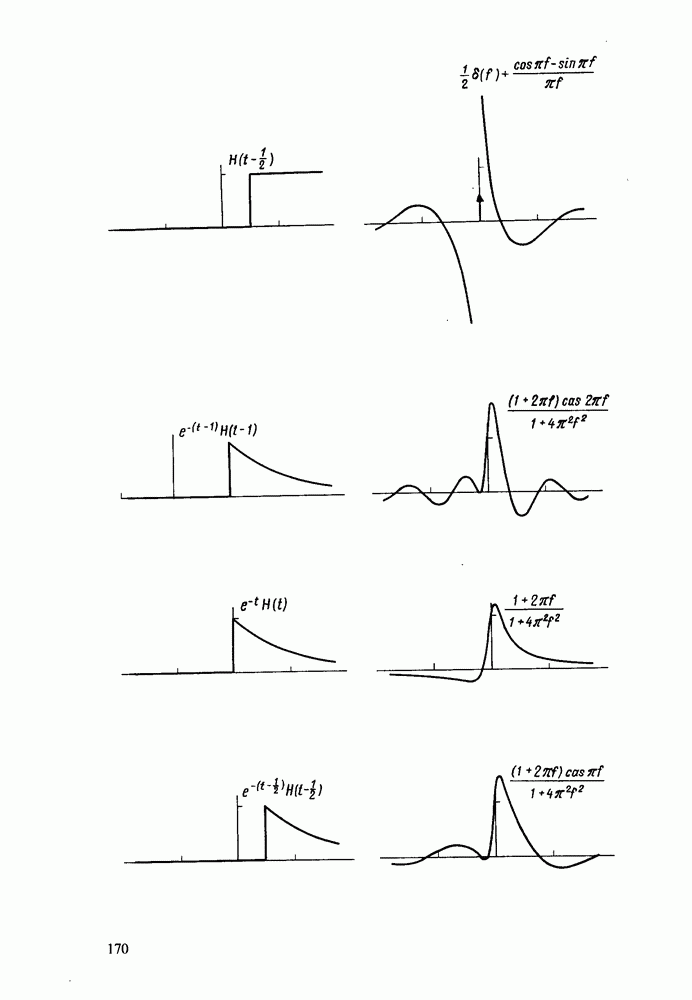
- Приложение 2. АТЛАС ПРЕОБРАЗОВАНИЙ ХАРТЛИ