| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Операция быстрого поворота
Внутри программы  (строки 6170, 6180) имеются две операции вида
(строки 6170, 6180) имеются две операции вида

которые, очевидно, представляют собой стандартные формулы поворота системы координат на угол  Для этого требуются четыре операции умножения и две операции сложения, а от эффективности их выполнения в силу частого обращения к этому блоку программы в значительной степени зависит суммарное машинное время. Ниже будет описан метод быстрого поворота, введенный Бьюнеманом (О. Випетап. Inversion of the Helmholtz (or Laplace-Poisson) Operator for Slab Geometry, J. Computational Phys., vol. 12, pp. 124-130, 1973-Обращение оператора Гельмгольца (Лапласа-Пуассона) для геометрии на плоскости). Посредством довольно удачного приема количество операций умножения уменьшено до трех. Число операций сложения возросло до трех, однако для многих ЭВМ, затрачивающих больше времени на выполнение операций умножения, чем на сложение, имеет место существенное сокращение машинного времени. Для пояснения алгоритма Бьюнемана рассмотрим рис. 8.7. При
Для этого требуются четыре операции умножения и две операции сложения, а от эффективности их выполнения в силу частого обращения к этому блоку программы в значительной степени зависит суммарное машинное время. Ниже будет описан метод быстрого поворота, введенный Бьюнеманом (О. Випетап. Inversion of the Helmholtz (or Laplace-Poisson) Operator for Slab Geometry, J. Computational Phys., vol. 12, pp. 124-130, 1973-Обращение оператора Гельмгольца (Лапласа-Пуассона) для геометрии на плоскости). Посредством довольно удачного приема количество операций умножения уменьшено до трех. Число операций сложения возросло до трех, однако для многих ЭВМ, затрачивающих больше времени на выполнение операций умножения, чем на сложение, имеет место существенное сокращение машинного времени. Для пояснения алгоритма Бьюнемана рассмотрим рис. 8.7. При

Рис. 8.7. Иллюстрация быстрого алгоритма Бьюнемана для поворота прямоугольной системы координат.
заданных координатах  точки Р мы получаем ее новые координаты
точки Р мы получаем ее новые координаты  в результате поворота исходных осей на угол
в результате поворота исходных осей на угол  и проектирования исходных координат на оси
и проектирования исходных координат на оси  . Таким образом, имеем
. Таким образом, имеем

В качестве альтернативного подхода отложим на оси  отрезок
отрезок  такой, что
такой, что  Тогда
Тогда  что представляет собой интересное соотношение, так как слагаемое
что представляет собой интересное соотношение, так как слагаемое  не имеет коэффициентов. В этом случае
не имеет коэффициентов. В этом случае  является горизонтальной проекцией отрезка
является горизонтальной проекцией отрезка  выражаемого в виде суммы отрезков
выражаемого в виде суммы отрезков  (одной из исходных координат) и
(одной из исходных координат) и  просто равного
просто равного  Следовательно,
Следовательно,

где 
Зная координату  можем выразить у в виде суммы
можем выразить у в виде суммы  и
и  . Таким образом, имеем
. Таким образом, имеем

 Вспомогательный линейный сегмент
Вспомогательный линейный сегмент  введение которого ускоряет выполнение рассматриваемой процедуры, является связующим звеном между исходными данными и искомым результатом и ниже обозначается
введение которого ускоряет выполнение рассматриваемой процедуры, является связующим звеном между исходными данными и искомым результатом и ниже обозначается  Таким образом, алгоритм, заменяющий общепринятые преобразования, имеет вид
Таким образом, алгоритм, заменяющий общепринятые преобразования, имеет вид

Данный метод, реализуемый в программе  требует наличия таблицы значений функции
требует наличия таблицы значений функции  которые, как было
которые, как было
отмечено в предыдущем разделе, могут быть также использованы для определения функции косинуса.
Вычисление тангенсов может быть осуществлено с помощью таблицы синусов посредством соотношения

Фрагмент программы, реализующий эту процедуру, имеет вид

где  - синус, а
- синус, а  - тангенс половинного угла.
- тангенс половинного угла.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
- Глава 2. ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Преобразование Хартли
- Четная и нечетная составляющие
- Формулы связи
- Примеры
- Энергетический и фазовый спектры
- Глава 3. ТЕОРЕМЫ
- Свертка
- Соотношения между преобразованиями во временной и частотой областях
- Глава 4. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Физический смысл величин «тау» и v
- Четная и нечетная составляющие
- Примеры дискретных преобразований Хартли
- Степени свободы
- Другие вещественные ядра
- Теоремы
- Выводы
- Глава 5. ЦИФРОВАЯ ФИЛЬТРАЦИЯ ПОСРЕДСТВОМ СВЕРТКИ
- Циклическая свертка
- Дополнение нулями
- Обращение свертки
- Теорема о свертке
- Теорема о свертке в частотной области (спектральное сглаживание)
- Числовой пример свертки
- Коэффициент
- Числовой пример корреляционной функции
- Низкочастотная фильтрация
- Подчеркивание границ
- Свертка с использованием быстрого преобразования Хартли
- Способ без использования перестановок
- Свертка как умножение матриц
- Глава 6. Двумерные преобразования
- Двумерное преобразование Хартли
- Симметрия и антисимметрия
- Примеры
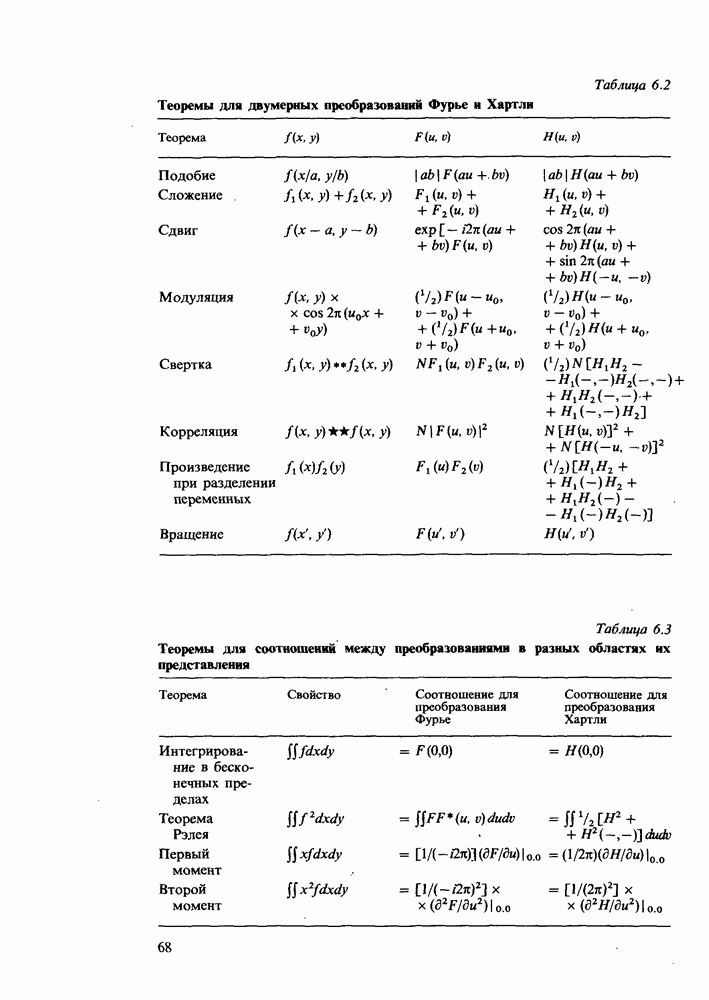
- Теоремы для двумерных преобразований
- Круговая симметрия
- Двумерная фильтрация
- Цикличность для двумерного случая
- Трехмерный случай
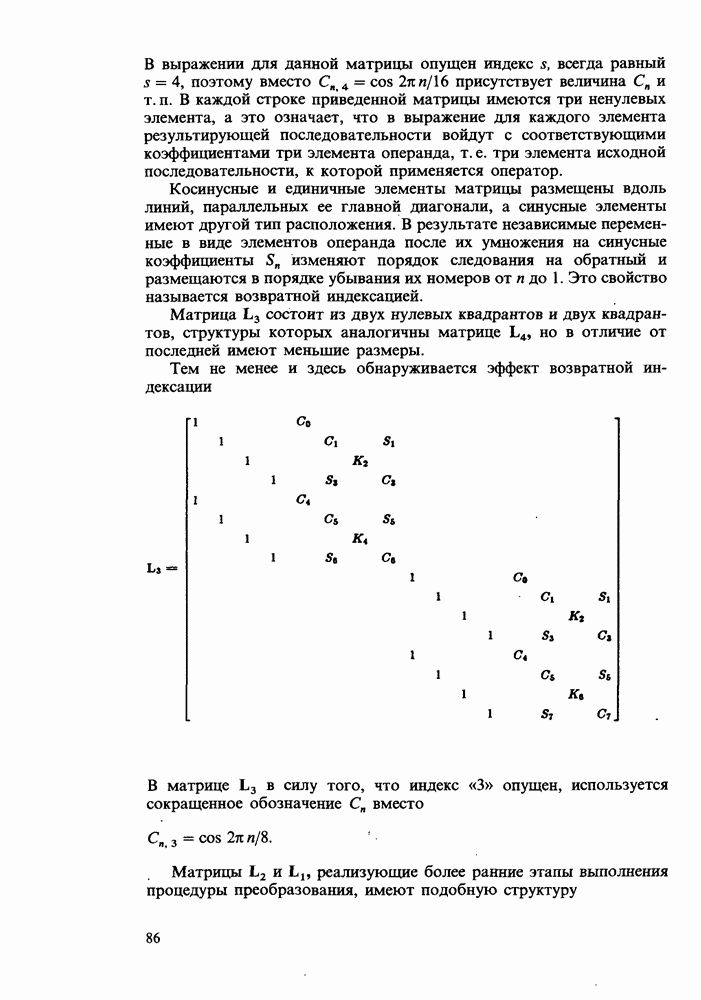
- Глава 7. ФАКТОРИЗАЦИЯ МАТРИЦЫ ПРЕОБРАЗОВАНИЯ
- Перестановка
- Перестановочные диаграммы
- Перестановочная матрица
- Ячеистая структура перестановочной диаграммы
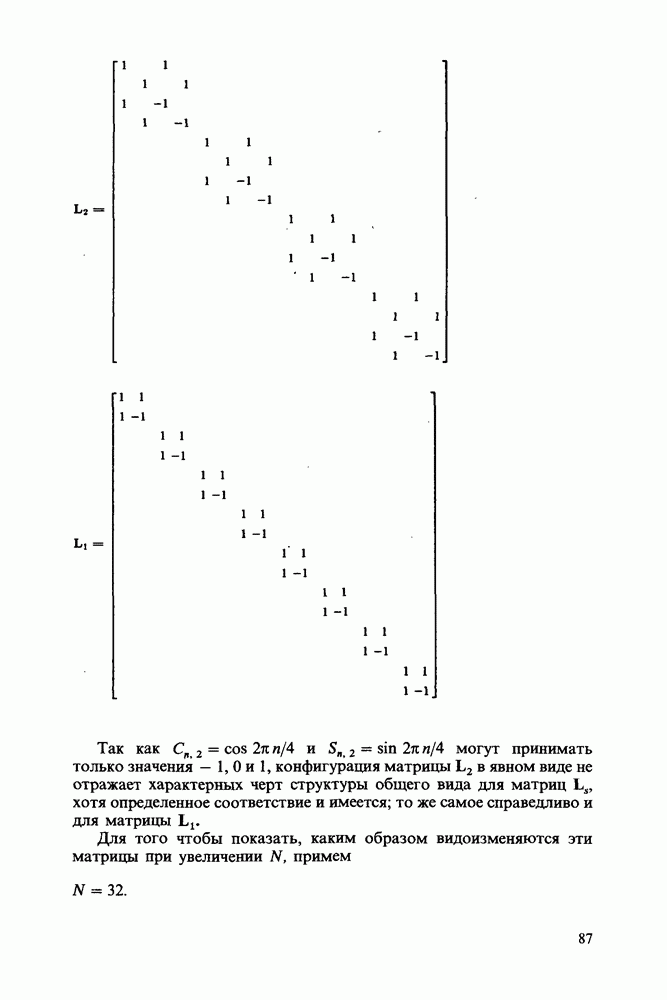
- Каскадные матрицы
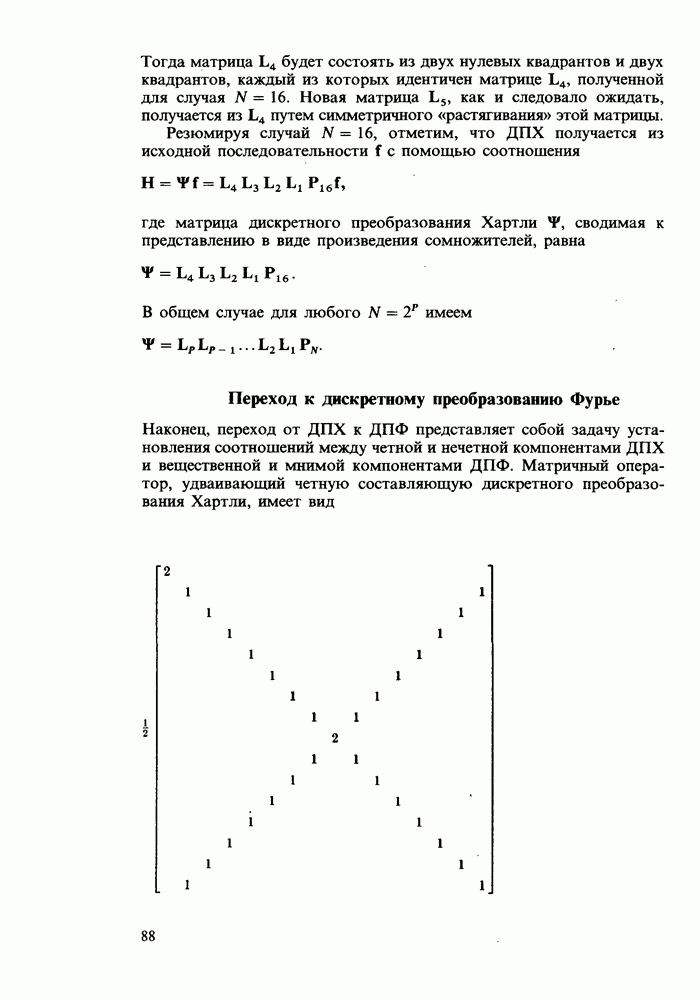
- Переход к дискретному преобразованию Фурье
- Глава 8. АЛГОРИТМ БЫСТРОГО ПРЕОБРАЗОВАНИЯ
- Свойство N log N
- Повторное разбиение последовательностей
- Преобразование с использованием разложения на подпоследовательности
- Общая формула разложения.
- Направленный сигнальный граф
- Вычисление с замещением
- Анализ временных затрат на вычисление с помощью полосковой диаграммы
- Степепи числа 2
- Тригонометрические функции
- Быстрое вычисление синусов
- Операция быстрого поворота
- Быстрая перестановка
- Преобразование для последовательностей с основанием 4 и другие модификации
- Ранее применявшиеся подходы к преобразованию вещественных данных
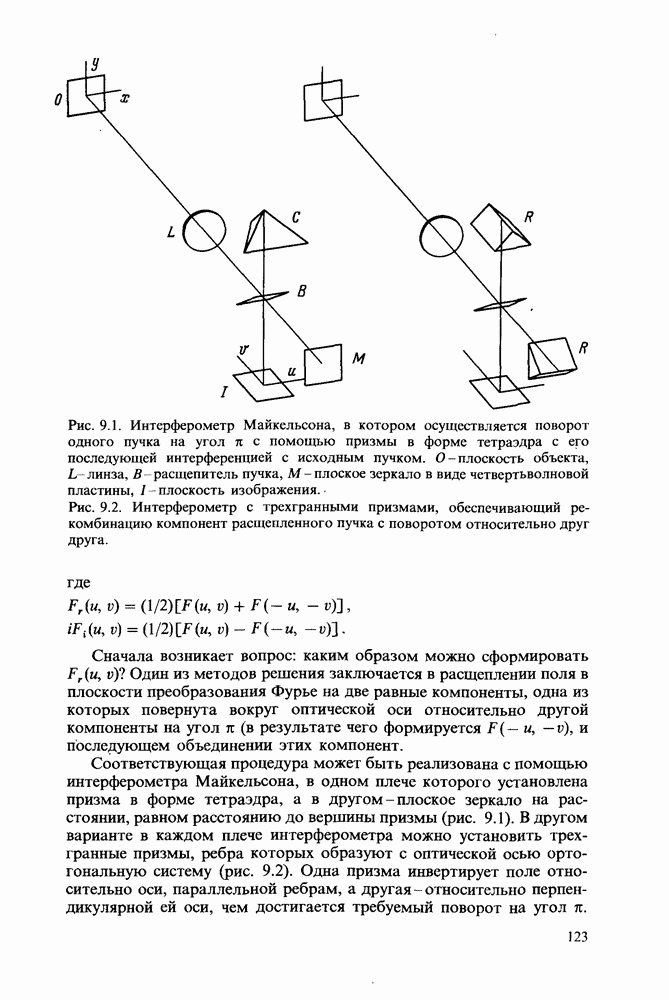
- Глава 9. ПРЕОБРАЗОВАНИЕ ХАРТЛИ В ОПТИКЕ
- Свойства симметрии
- Осуществление преобразования Хартли, использующее поляризацию
- Практическое осуществление
- Источник некогерентного излучения
- Пример
- Голография в плоскости Хартли
- Приложение 1. ПРОГРАММЫ ВЫЧИСЛЕНИЙ НА ЭВМ
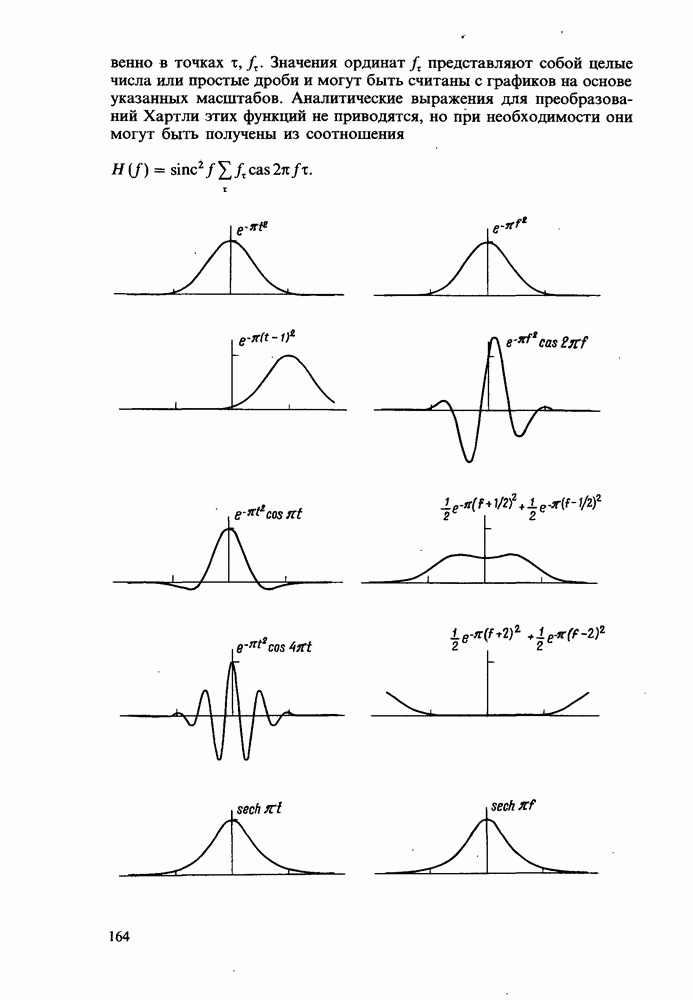
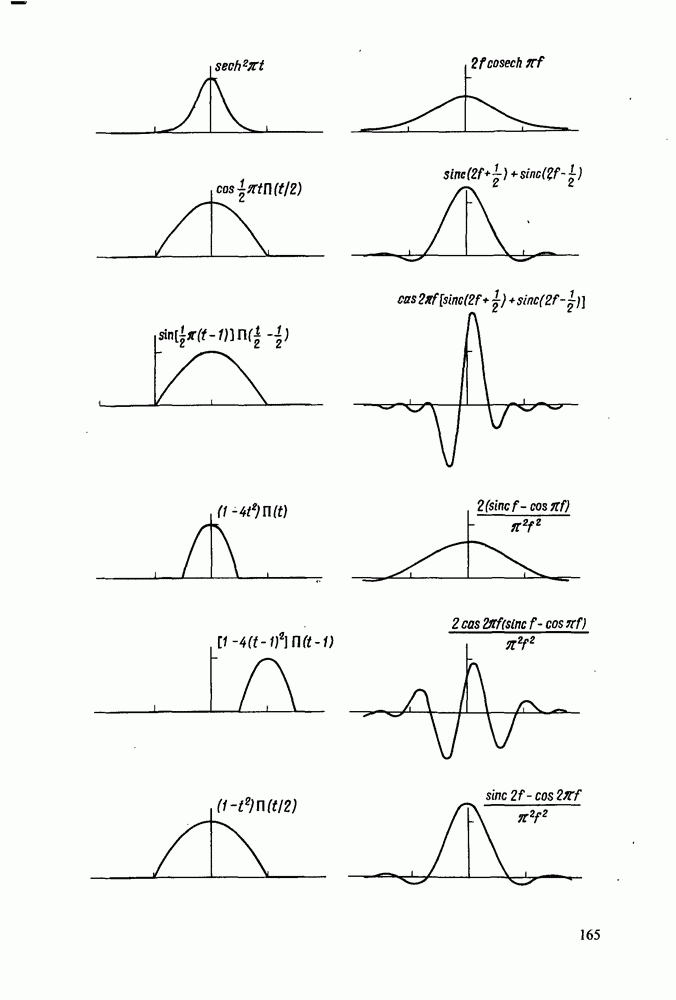
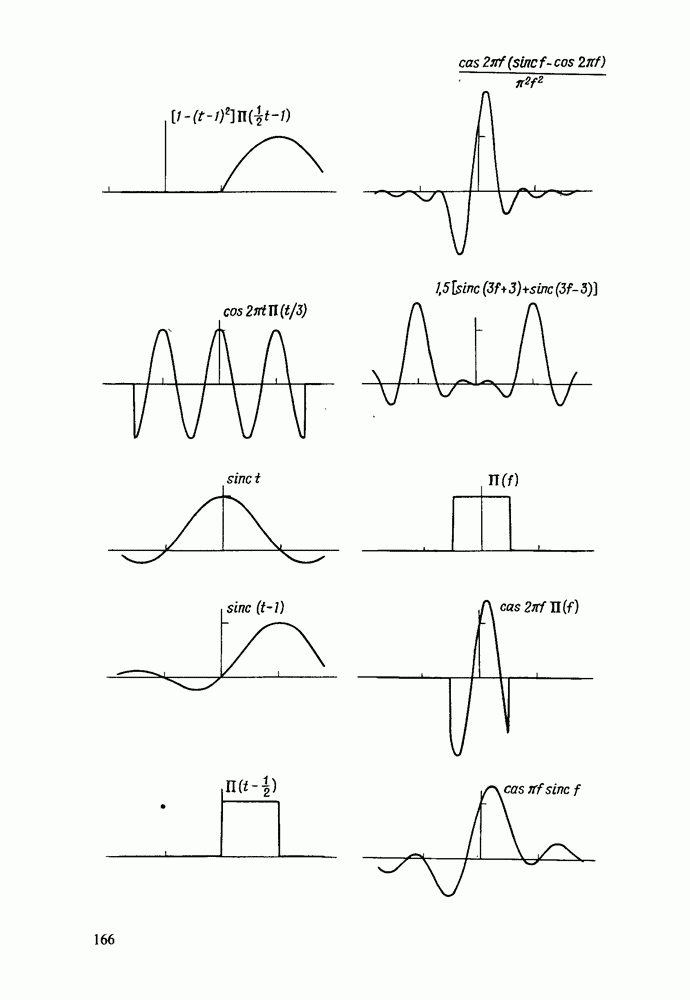
- Приложение 2. АТЛАС ПРЕОБРАЗОВАНИЙ ХАРТЛИ