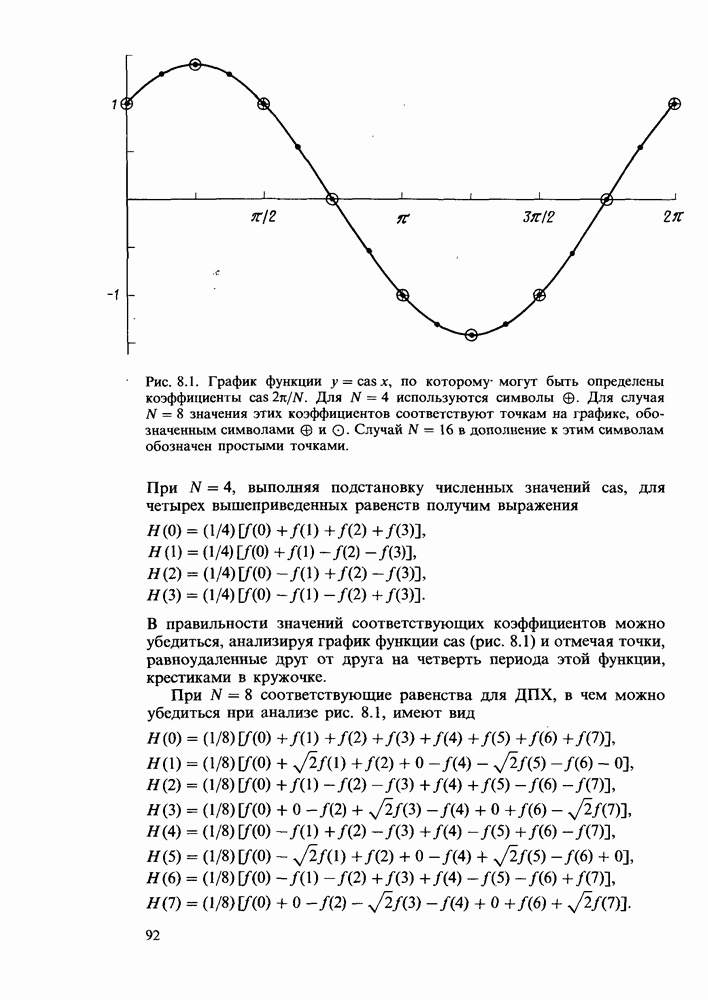
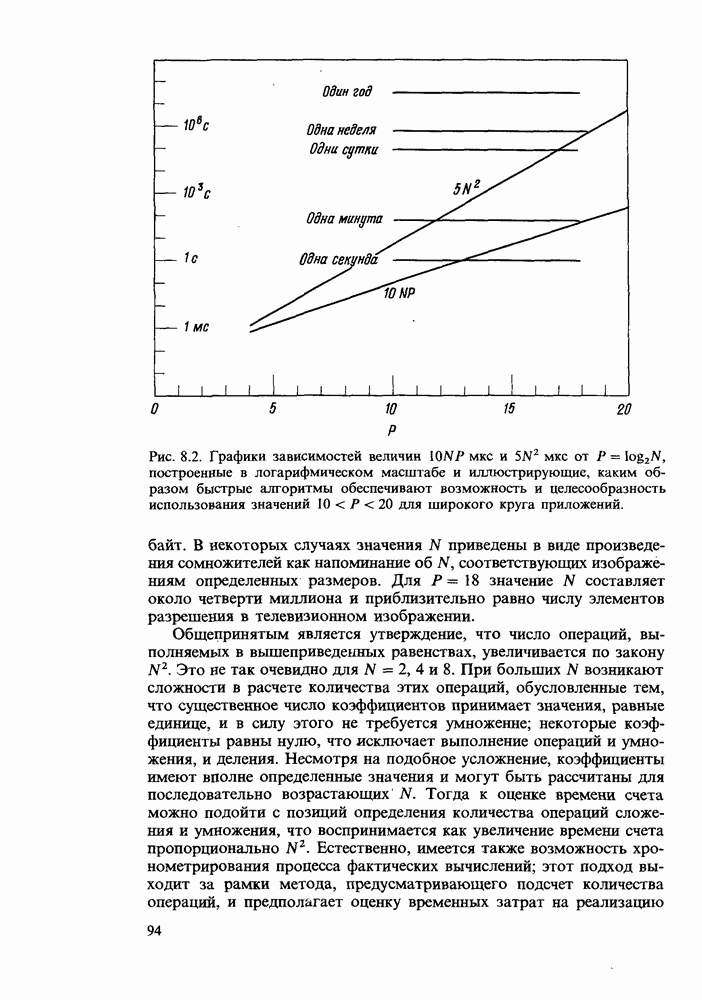
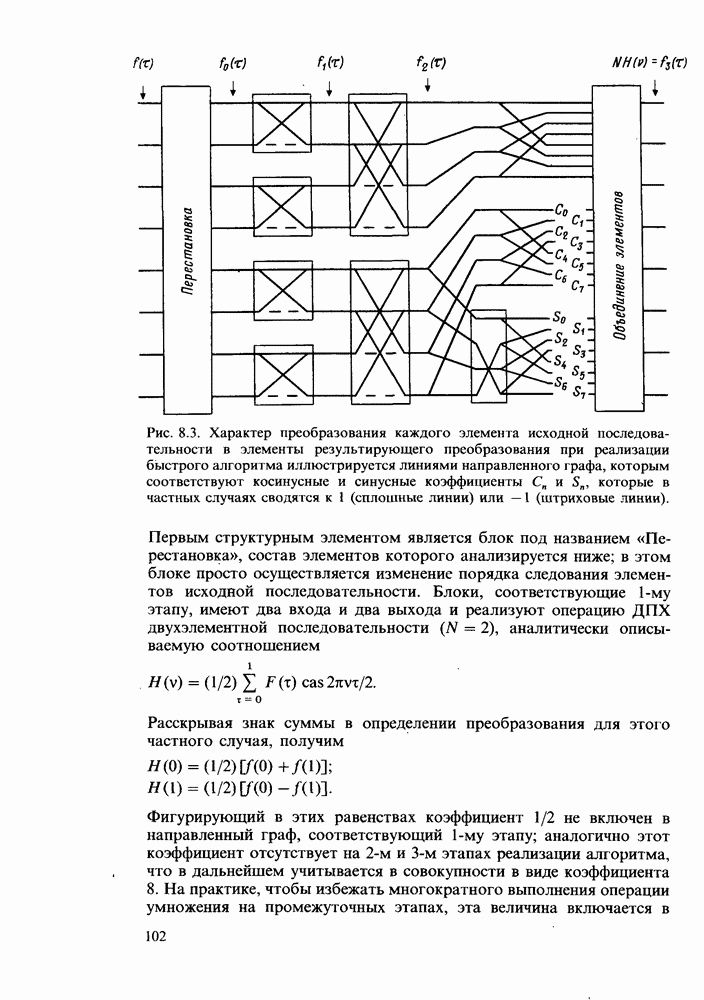
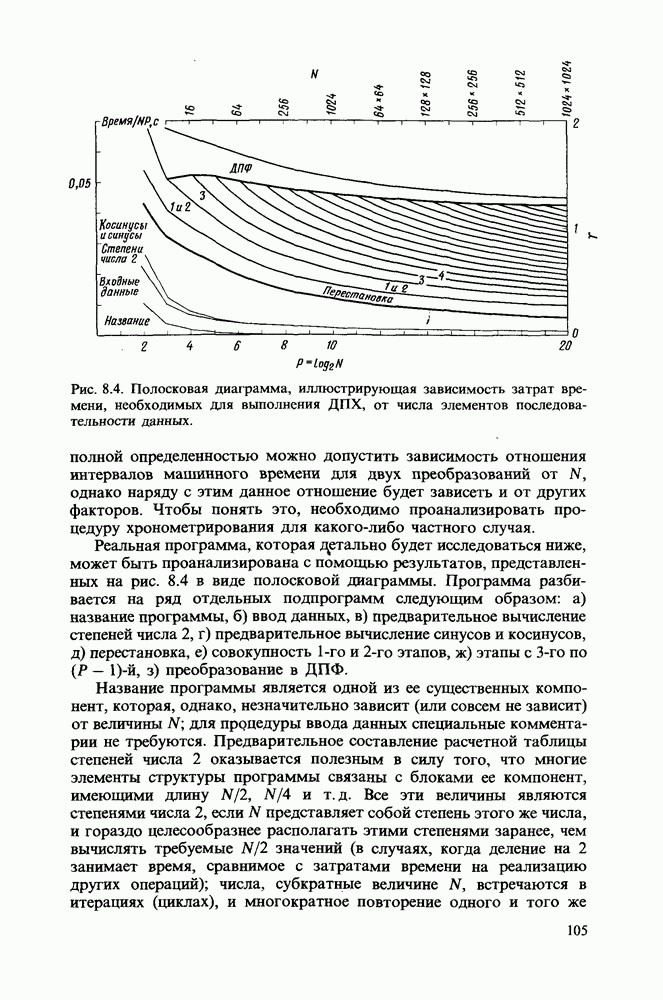
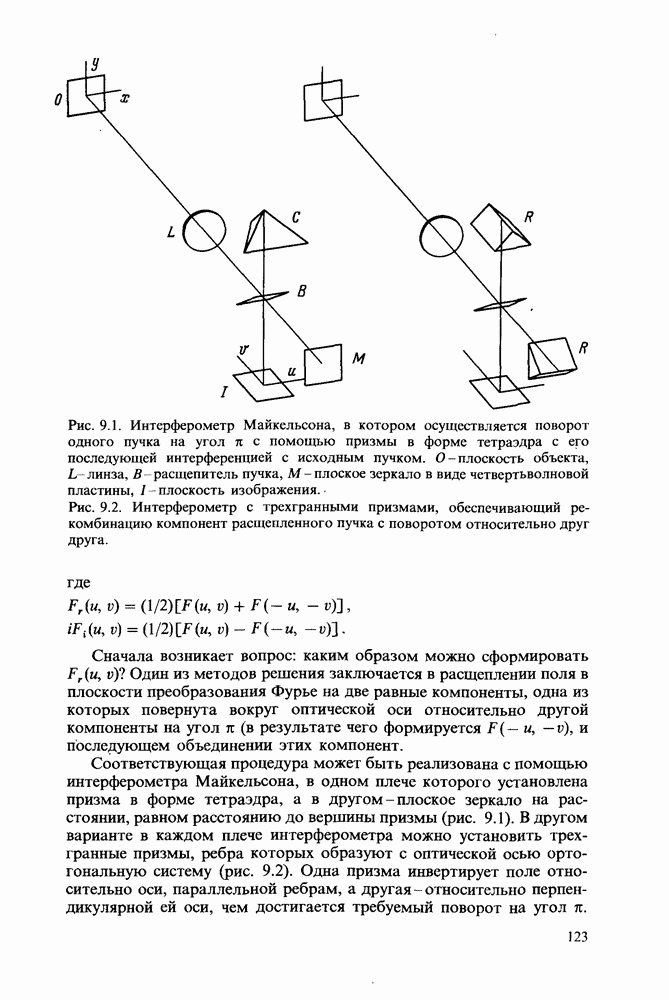
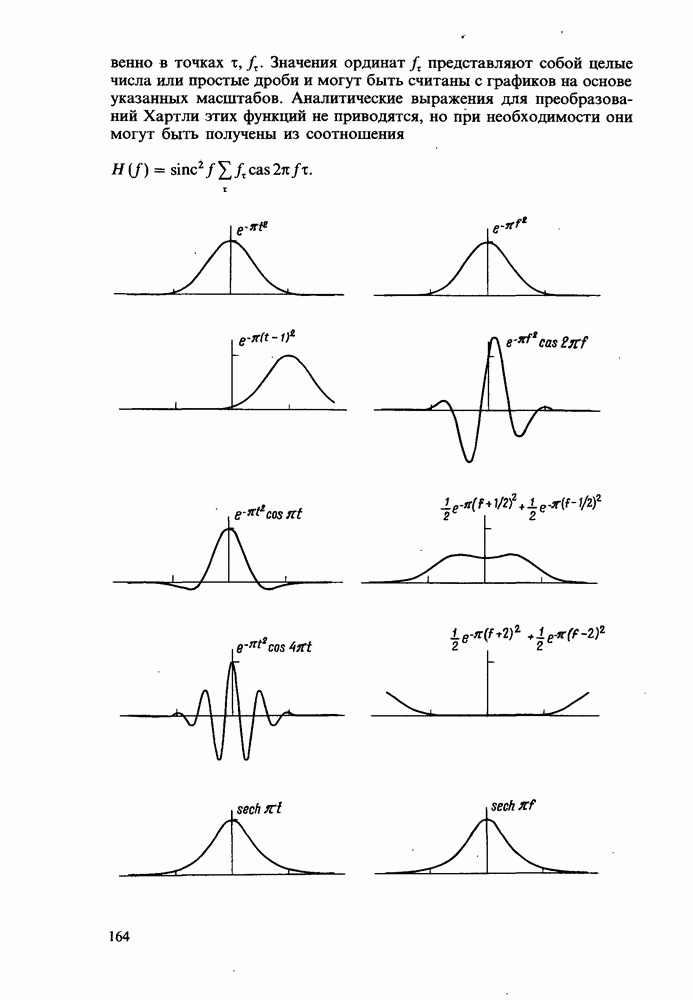
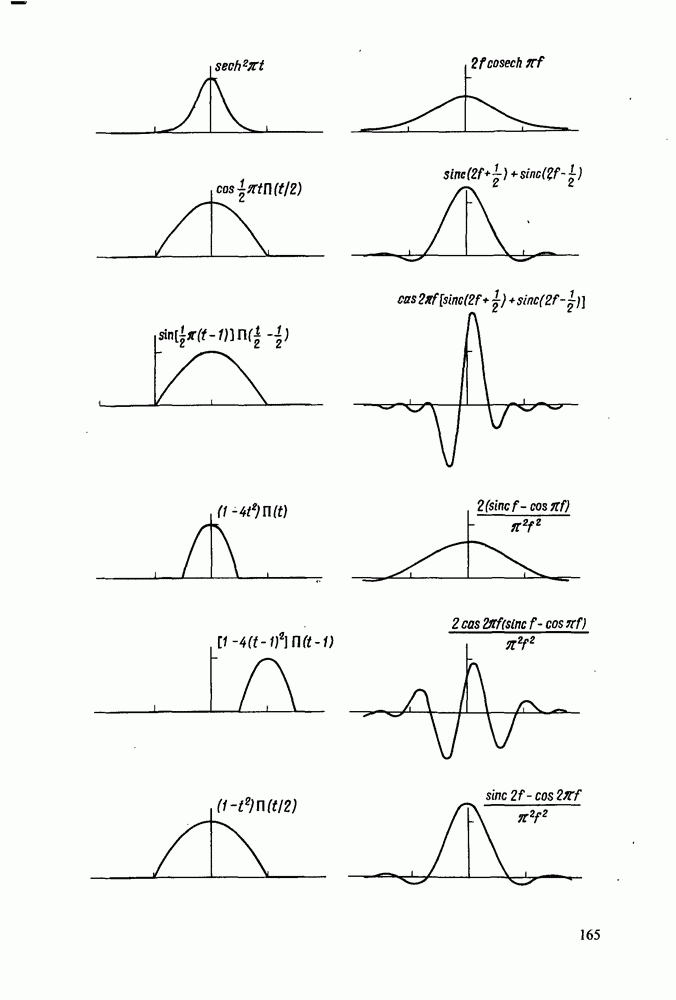
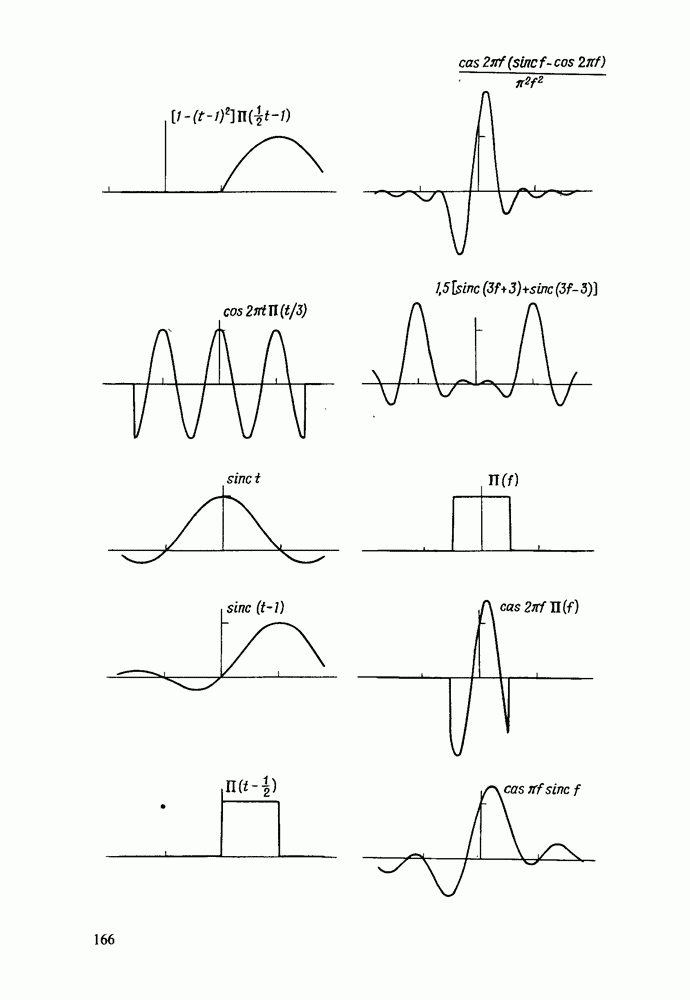
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
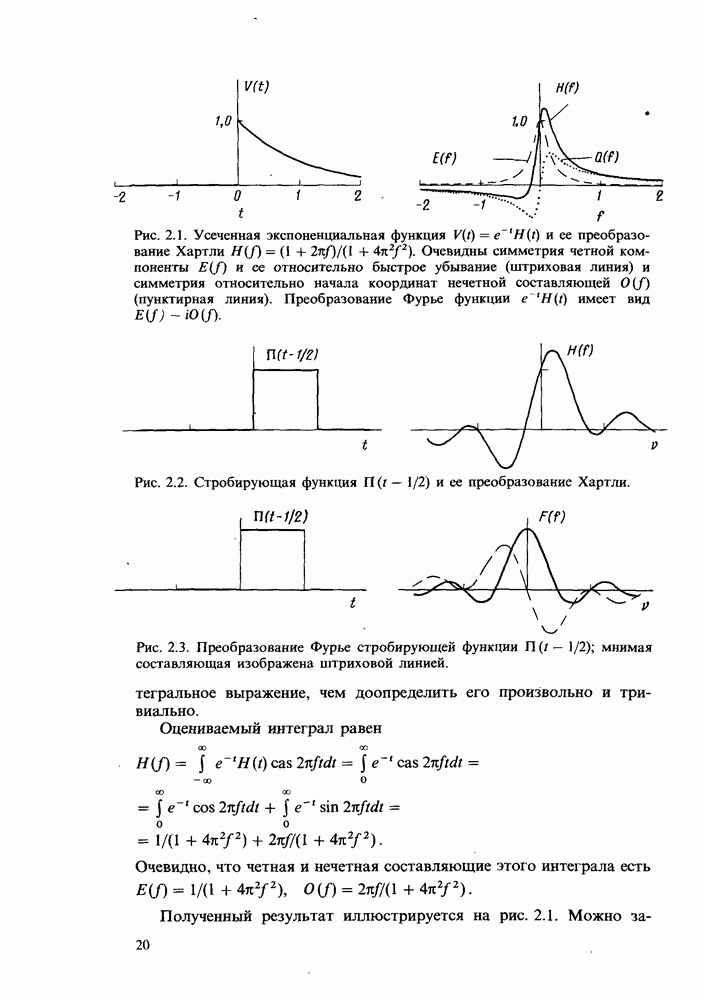
Преобразование Хартли
В определение Хартли для преобразования  в явном виде был включен коэффициент
в явном виде был включен коэффициент  для получения симметричного выражения. Если опустить этот коэффициент, то оба интеграла одновременно не могут быть корректными. Однако следует признать нецелесообразным сохранение пары таких специфических коэффициентов, особенно при выполнении численных расчетов. Многие авторы отреагировали на подобную ситуацию применительно к преобразованию Фурье рассмотрением функции
для получения симметричного выражения. Если опустить этот коэффициент, то оба интеграла одновременно не могут быть корректными. Однако следует признать нецелесообразным сохранение пары таких специфических коэффициентов, особенно при выполнении численных расчетов. Многие авторы отреагировали на подобную ситуацию применительно к преобразованию Фурье рассмотрением функции  вместо
вместо  . В результате коэффициент
. В результате коэффициент  исчезает в определении прямого преобразования Фурье, однако в формуле обратного преобразования Фурье появляется коэффициент
исчезает в определении прямого преобразования Фурье, однако в формуле обратного преобразования Фурье появляется коэффициент  . Таким образом, эти авторы намеренно жертвуют симметрией формул. Справедливо замечание, что это дополнительная нагрузка для памяти, так как приходится запоминать, какая из формул содержит величину
. Таким образом, эти авторы намеренно жертвуют симметрией формул. Справедливо замечание, что это дополнительная нагрузка для памяти, так как приходится запоминать, какая из формул содержит величину  Один способ запоминания состоит в том, что коэффициент
Один способ запоминания состоит в том, что коэффициент  стоит перед интегралом, в котором фигурирует дифференциал
стоит перед интегралом, в котором фигурирует дифференциал  что означает наличие величины вида
что означает наличие величины вида  т. е. циклической частоты
т. е. циклической частоты  Отсюда естественно возникает вопрос: почему непосредственно не иметь дело с частотой? Именно к этому выводу в течение многих лет склонялось мнение разных исследователей. Приверженцев использования коэффициента
Отсюда естественно возникает вопрос: почему непосредственно не иметь дело с частотой? Именно к этому выводу в течение многих лет склонялось мнение разных исследователей. Приверженцев использования коэффициента  в настоящее время практически уже нет, тогда как имеется достаточное количество сторонников правомерности записи
в настоящее время практически уже нет, тогда как имеется достаточное количество сторонников правомерности записи  но общепринятой практикой является применение множителя
но общепринятой практикой является применение множителя  под знаком экспоненты в интегралах для прямого и обратного преобразований. Данная процедура реализуется автоматически при использовании частоты
под знаком экспоненты в интегралах для прямого и обратного преобразований. Данная процедура реализуется автоматически при использовании частоты  вместо угловой частоты
вместо угловой частоты  При этом имеем
При этом имеем

Далее  будет рассматриваться как преобразование Хартли функции
будет рассматриваться как преобразование Хартли функции  которая в свою очередь является обратным преобразованием Хартли функции
которая в свою очередь является обратным преобразованием Хартли функции  Естественно, прямое и обратное преобразования неразличимы.
Естественно, прямое и обратное преобразования неразличимы.
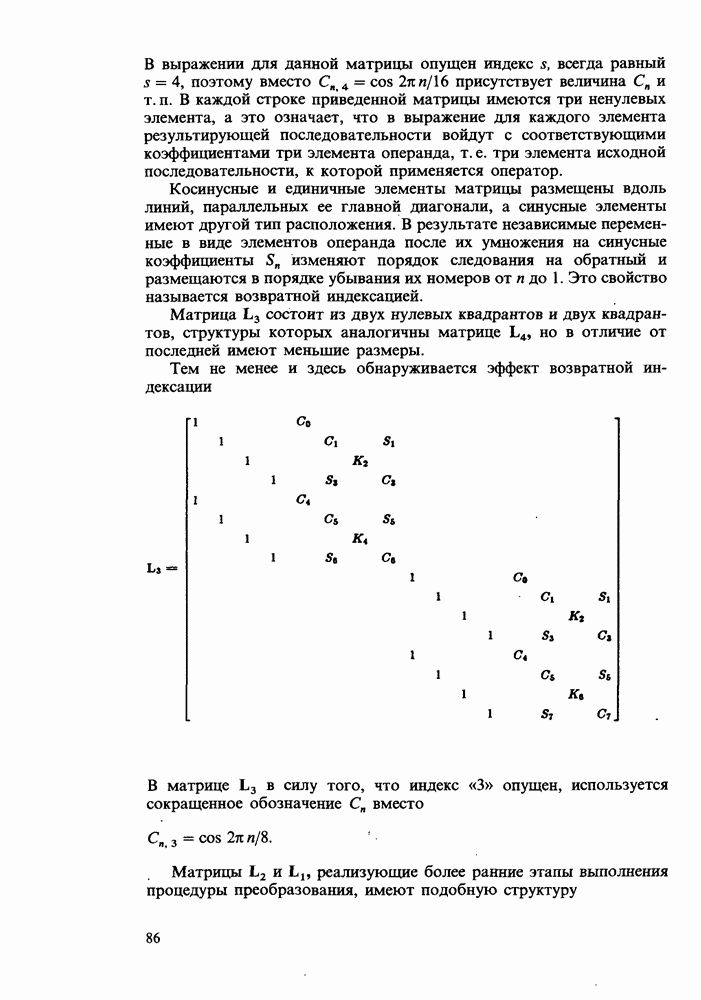
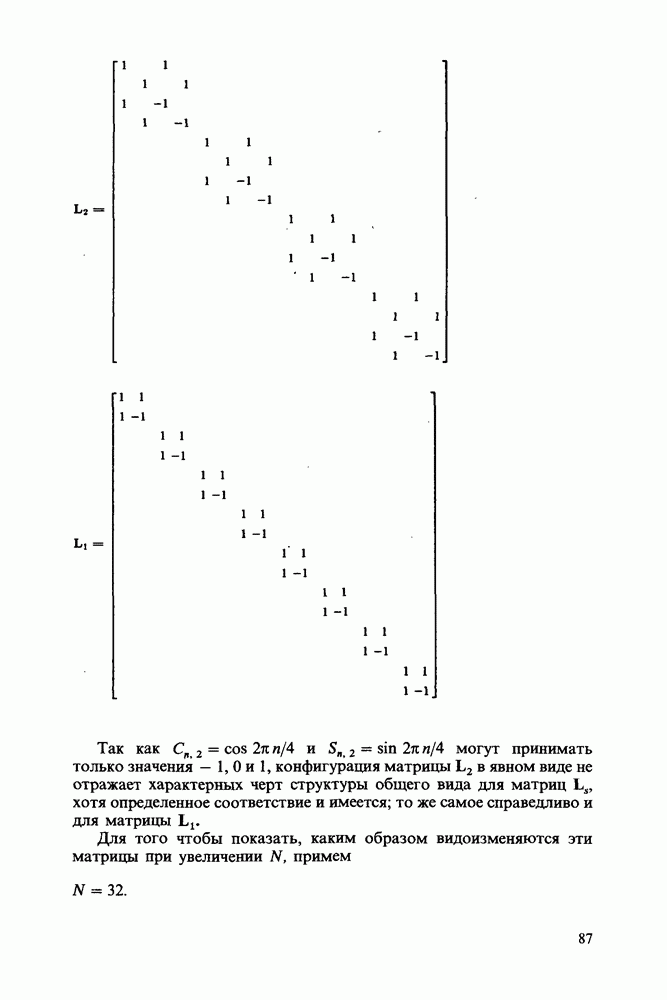
Определенное здесь преобразование Хартли несколько отлично от исходного преобразования Хартли  Однако, кроме как для исторической справки, вряд ли возникнет необходимость упоминать
Однако, кроме как для исторической справки, вряд ли возникнет необходимость упоминать  и вряд ли целесообразно именовать
и вряд ли целесообразно именовать  преобразованием Хартли. Видимо, такие терминологические различия - это все, что необходимо. Вводя новые обозначения, мы добиваемся согласования с общеупотребимыми терминами, используемыми в преобразовании Фурье, что далее будет распространено и на дискретные преобразования.
преобразованием Хартли. Видимо, такие терминологические различия - это все, что необходимо. Вводя новые обозначения, мы добиваемся согласования с общеупотребимыми терминами, используемыми в преобразовании Фурье, что далее будет распространено и на дискретные преобразования.
Для сравнения приведем соотношения для преобразований Фурье, записанных с помощью вышеупомянутых обозначений:

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
- Глава 2. ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Преобразование Хартли
- Четная и нечетная составляющие
- Формулы связи
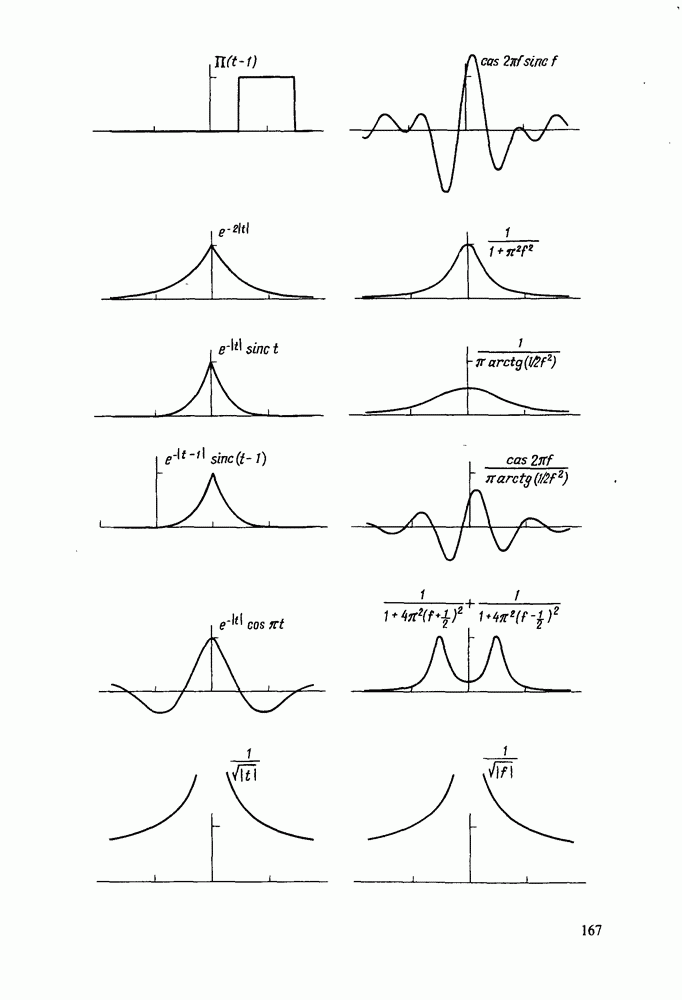
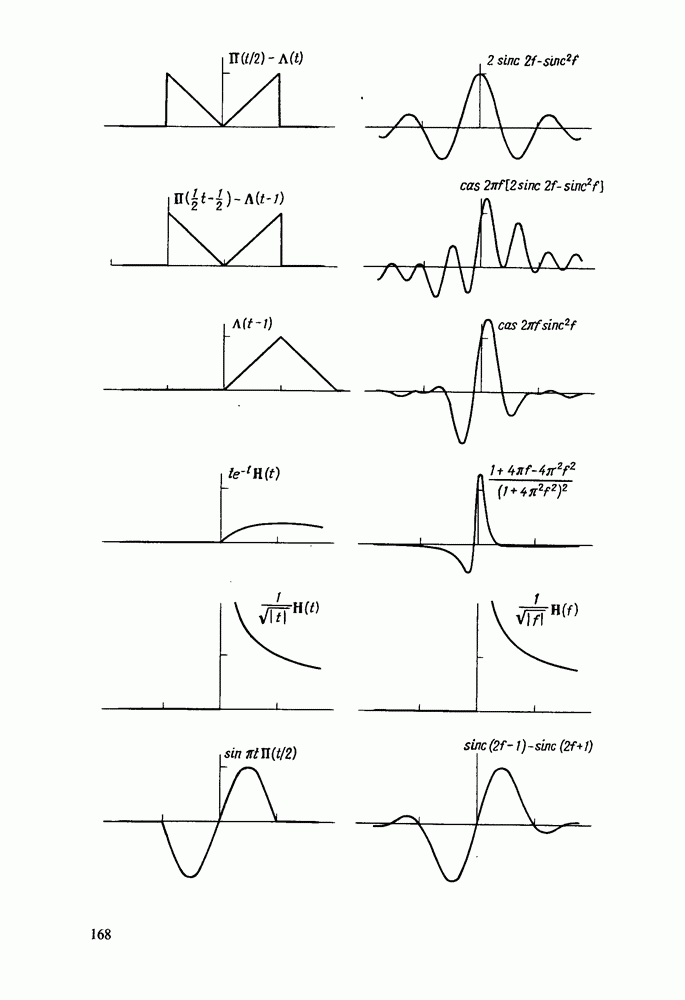
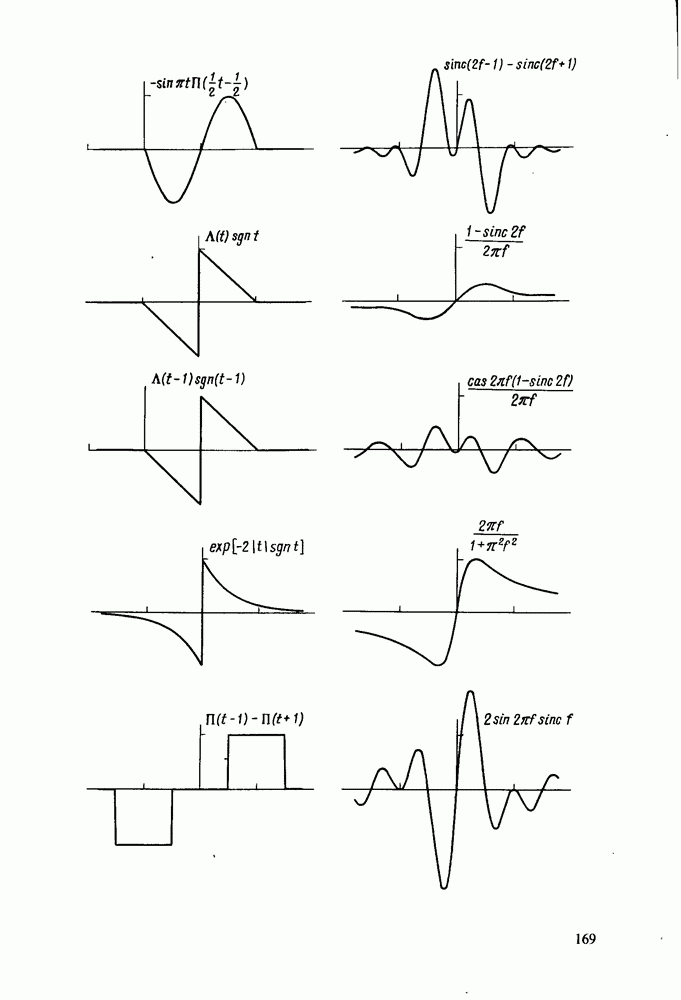
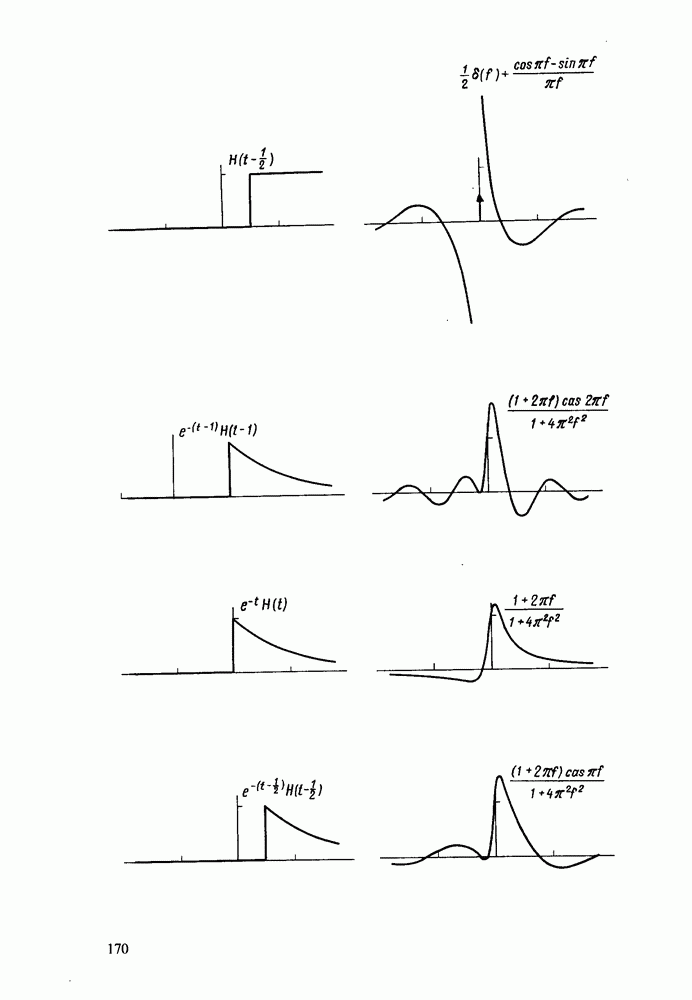
- Примеры
- Энергетический и фазовый спектры
- Глава 3. ТЕОРЕМЫ
- Свертка
- Соотношения между преобразованиями во временной и частотой областях
- Глава 4. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Физический смысл величин «тау» и v
- Четная и нечетная составляющие
- Примеры дискретных преобразований Хартли
- Степени свободы
- Другие вещественные ядра
- Теоремы
- Выводы
- Глава 5. ЦИФРОВАЯ ФИЛЬТРАЦИЯ ПОСРЕДСТВОМ СВЕРТКИ
- Циклическая свертка
- Дополнение нулями
- Обращение свертки
- Теорема о свертке
- Теорема о свертке в частотной области (спектральное сглаживание)
- Числовой пример свертки
- Коэффициент
- Числовой пример корреляционной функции
- Низкочастотная фильтрация
- Подчеркивание границ
- Свертка с использованием быстрого преобразования Хартли
- Способ без использования перестановок
- Свертка как умножение матриц
- Глава 6. Двумерные преобразования
- Двумерное преобразование Хартли
- Симметрия и антисимметрия
- Примеры
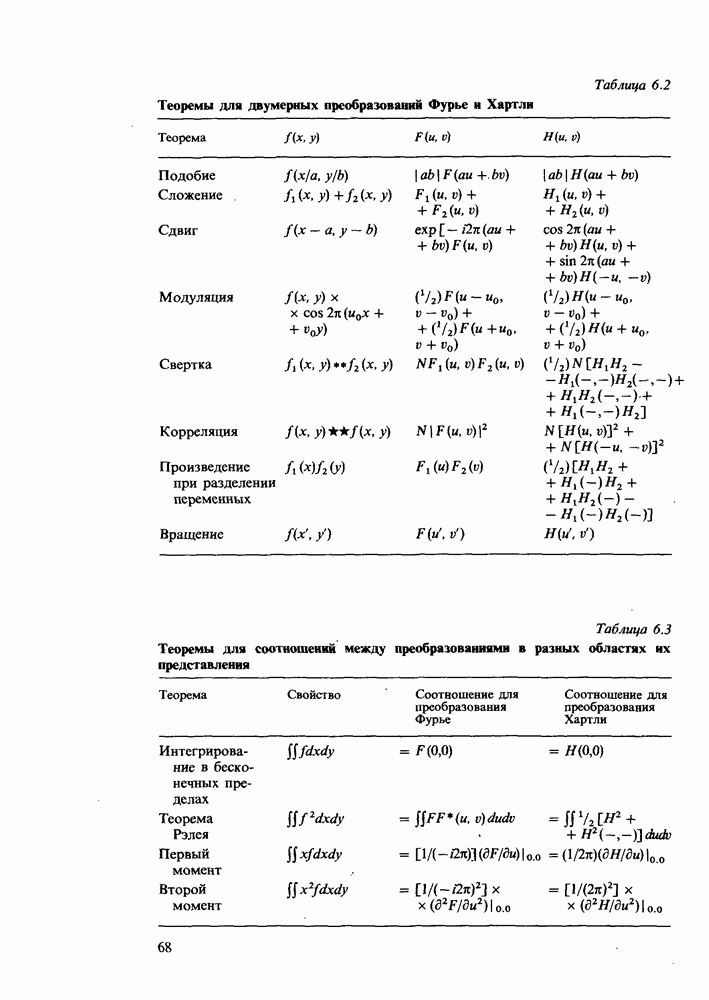
- Теоремы для двумерных преобразований
- Круговая симметрия
- Двумерная фильтрация
- Цикличность для двумерного случая
- Трехмерный случай
- Глава 7. ФАКТОРИЗАЦИЯ МАТРИЦЫ ПРЕОБРАЗОВАНИЯ
- Перестановка
- Перестановочные диаграммы
- Перестановочная матрица
- Ячеистая структура перестановочной диаграммы
- Каскадные матрицы
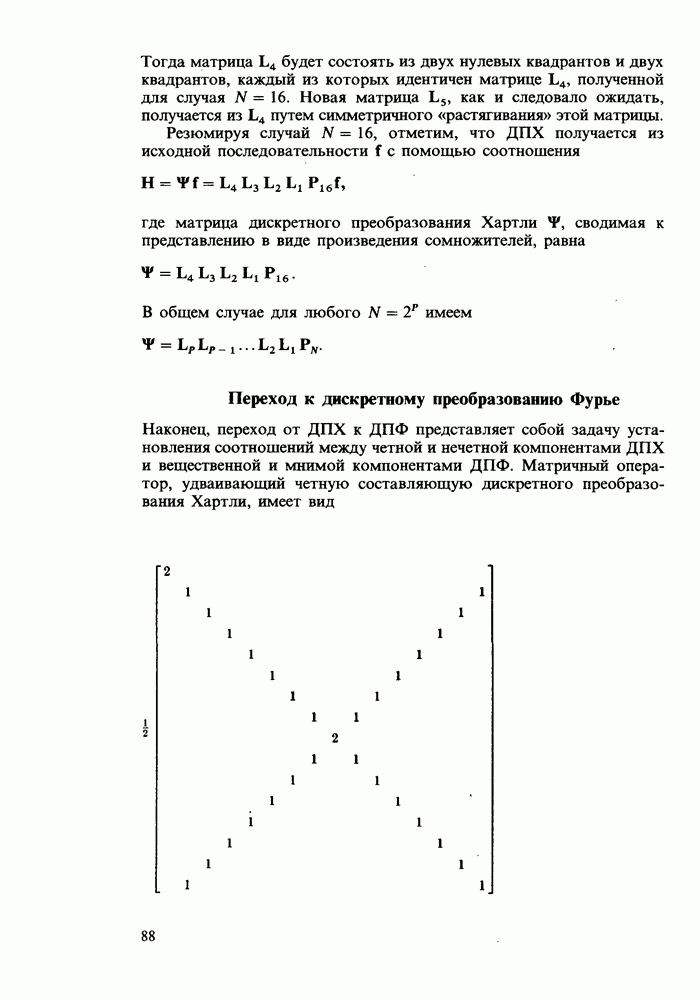
- Переход к дискретному преобразованию Фурье
- Глава 8. АЛГОРИТМ БЫСТРОГО ПРЕОБРАЗОВАНИЯ
- Свойство N log N
- Повторное разбиение последовательностей
- Преобразование с использованием разложения на подпоследовательности
- Общая формула разложения.
- Направленный сигнальный граф
- Вычисление с замещением
- Анализ временных затрат на вычисление с помощью полосковой диаграммы
- Степепи числа 2
- Тригонометрические функции
- Быстрое вычисление синусов
- Операция быстрого поворота
- Быстрая перестановка
- Преобразование для последовательностей с основанием 4 и другие модификации
- Ранее применявшиеся подходы к преобразованию вещественных данных
- Глава 9. ПРЕОБРАЗОВАНИЕ ХАРТЛИ В ОПТИКЕ
- Свойства симметрии
- Осуществление преобразования Хартли, использующее поляризацию
- Практическое осуществление
- Источник некогерентного излучения
- Пример
- Голография в плоскости Хартли
- Приложение 1. ПРОГРАММЫ ВЫЧИСЛЕНИЙ НА ЭВМ
- Приложение 2. АТЛАС ПРЕОБРАЗОВАНИЙ ХАРТЛИ