| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Быстрое вычисление синусов
Табулирование синусов, аргументы которых составляют долю окружности единичного радиуса, не является достижением сегодняшнего дня, а было достаточно развито еще 1800 лет назад Птолемеем. Более эффективная процедура вычисления синусов по сравнению с использованием встроенных программ, реализуемых разработчиками ЭВМ, может быть изучена исходя из опыта предыдущих столетий.
Идея Птолемея заключалась в переходе от грубого к точному разбиению окружности. Из теории правильных многоугольников известно, что длины хорд, стягивающих дуги с центральными углами 60 и 12°, соответственно равны  , где
, где  - длина хорды, стягивающей дугу с центральным углом
- длина хорды, стягивающей дугу с центральным углом  для окружности единичного радиуса. Согласно изящной теореме Птолемея, длина хорды, соответствующей разности заданных центральных углов, может быть получена из соотношения
для окружности единичного радиуса. Согласно изящной теореме Птолемея, длина хорды, соответствующей разности заданных центральных углов, может быть получена из соотношения

эквивалентного выражению

По известным значениям  Птолемей мог, таким образом, оценить
Птолемей мог, таким образом, оценить  , а также длины хорд для центральных углов, кратных 12°. Получающаяся при этом таблица эквивалентна таблице, составленной из синусов углов, кратных 6°.
, а также длины хорд для центральных углов, кратных 12°. Получающаяся при этом таблица эквивалентна таблице, составленной из синусов углов, кратных 6°.
В соответствии с теоремой Птолемея утверждается, что для четырехугольника  произвольной формы (рис. 8.6), вершины которого лежат на окружности с центром О, имеет место равенство
произвольной формы (рис. 8.6), вершины которого лежат на окружности с центром О, имеет место равенство  Для четырехугольника, имеющего прямоугольную форму, как частный случай получаем теорему Пифагора. При
Для четырехугольника, имеющего прямоугольную форму, как частный случай получаем теорему Пифагора. При  получаем теорему Птолемея для синуса разности углов.
получаем теорему Птолемея для синуса разности углов.
Табличные данные для угла 12° применительно к обозначениям, принятым в этой книге, соответствуют случаю  . Для перехода к более мелкому разбиению окружности Птолемей ввел в рассмотрение метод, эквивалёнтный методу определения длины хорды,
. Для перехода к более мелкому разбиению окружности Птолемей ввел в рассмотрение метод, эквивалёнтный методу определения длины хорды,

Рис. 8.6. Теорема Птолемея: AC•BD = AB•CD+AD•BC.
стягивающей половину дуги:

который позволил получить результаты вплоть до угла 0,75° и кратных ему значений, что соответствует N = 480. Этот метод не пригоден для углов, кратных 1°. Однако Птолемей исходил из неравенства

Таким образом,

С учетом того, что  из системы этих двух неравенств можно заключить:
из системы этих двух неравенств можно заключить:

Так как различие правой и левой частей начинает проявляться с шестого десятичного знака, это грубое приближение, но можно повысить точность вычислений, развив метод Птолемея.
Интересным представляется вывод для хорды, стягивающей дугу 1° (или для  ), дальнейшее применение правила разбиения на две равные части позволило Птолемею составить таблицу длин хорд для интервалов, следующих через 0,5° (для синуса - через каждые 0,25°), с точностью до пятого десятичного знака. Так как эта таблица соответствует случаю
), дальнейшее применение правила разбиения на две равные части позволило Птолемею составить таблицу длин хорд для интервалов, следующих через 0,5° (для синуса - через каждые 0,25°), с точностью до пятого десятичного знака. Так как эта таблица соответствует случаю  она отвечает требованиям программ вычисления БПФ, используемых в настоящее время.
она отвечает требованиям программ вычисления БПФ, используемых в настоящее время.
Если составление таблицы начать с элементов  т.е. для 0, следующих через интервалы 22,5°, то можно перейти к таблице, составленной из элементов, следующих через 11,25°, путем вычисления синусов каждого из промежуточных значений аргумента 0 исходя из определенных значений функции
т.е. для 0, следующих через интервалы 22,5°, то можно перейти к таблице, составленной из элементов, следующих через 11,25°, путем вычисления синусов каждого из промежуточных значений аргумента 0 исходя из определенных значений функции  Формула для разности имеет вид
Формула для разности имеет вид

Поправочный коэффициент  может быть получен из формулы, определяющей длину хорды, стягивающей половину первоначальной дуги; для этой формулы исходной величиной является:
может быть получен из формулы, определяющей длину хорды, стягивающей половину первоначальной дуги; для этой формулы исходной величиной является:  Таким образом:
Таким образом:

Эта реккурентная формула используется в программе  приведенной в приложении 1.
приведенной в приложении 1.
Составление таблицы косинусов представляет собой отдельный вопрос. В следующем разделе будет показано, что целесообразно располагать таблицей значений  При наличии такой таблицы косинусы могут быть получены из соотношения
При наличии такой таблицы косинусы могут быть получены из соотношения

Однако нет необходимости заранее вычислять косинусы в явном виде, так как вместо этого можно использовать тангенсы половинных углов, что и целесообразно осуществлять на практике.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
- Глава 2. ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Преобразование Хартли
- Четная и нечетная составляющие
- Формулы связи
- Примеры
- Энергетический и фазовый спектры
- Глава 3. ТЕОРЕМЫ
- Свертка
- Соотношения между преобразованиями во временной и частотой областях
- Глава 4. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Физический смысл величин «тау» и v
- Четная и нечетная составляющие
- Примеры дискретных преобразований Хартли
- Степени свободы
- Другие вещественные ядра
- Теоремы
- Выводы
- Глава 5. ЦИФРОВАЯ ФИЛЬТРАЦИЯ ПОСРЕДСТВОМ СВЕРТКИ
- Циклическая свертка
- Дополнение нулями
- Обращение свертки
- Теорема о свертке
- Теорема о свертке в частотной области (спектральное сглаживание)
- Числовой пример свертки
- Коэффициент
- Числовой пример корреляционной функции
- Низкочастотная фильтрация
- Подчеркивание границ
- Свертка с использованием быстрого преобразования Хартли
- Способ без использования перестановок
- Свертка как умножение матриц
- Глава 6. Двумерные преобразования
- Двумерное преобразование Хартли
- Симметрия и антисимметрия
- Примеры
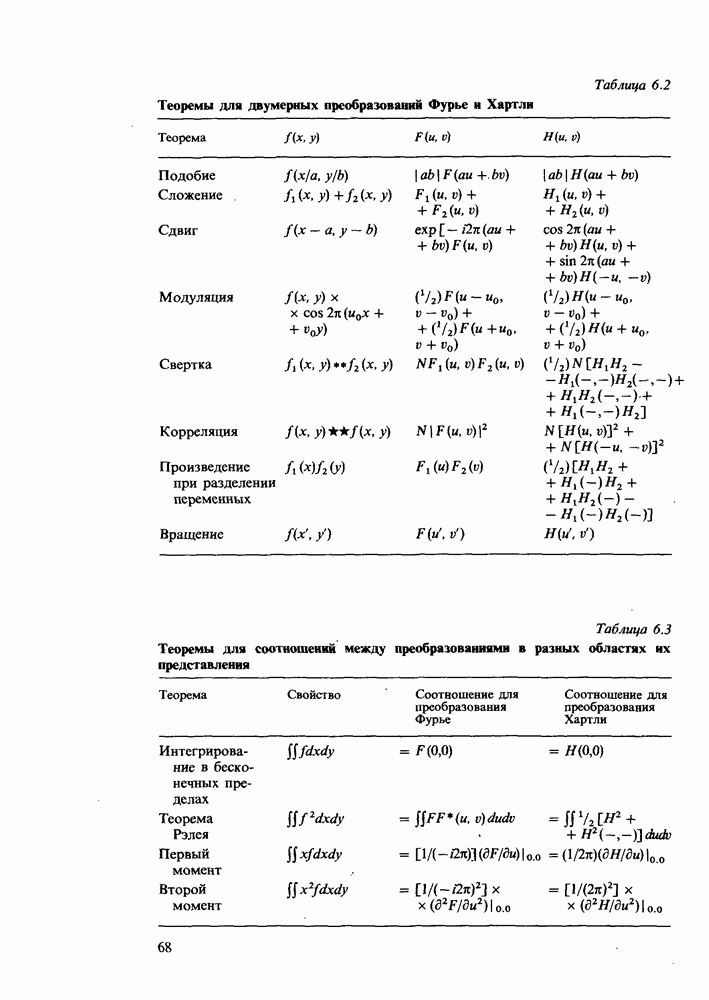
- Теоремы для двумерных преобразований
- Круговая симметрия
- Двумерная фильтрация
- Цикличность для двумерного случая
- Трехмерный случай
- Глава 7. ФАКТОРИЗАЦИЯ МАТРИЦЫ ПРЕОБРАЗОВАНИЯ
- Перестановка
- Перестановочные диаграммы
- Перестановочная матрица
- Ячеистая структура перестановочной диаграммы
- Каскадные матрицы
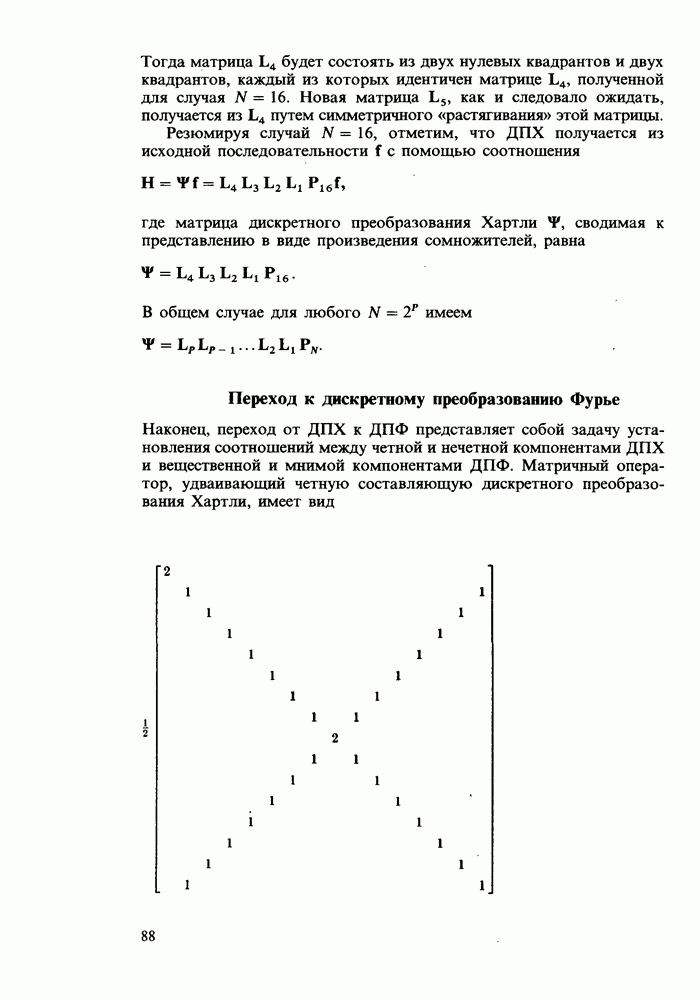
- Переход к дискретному преобразованию Фурье
- Глава 8. АЛГОРИТМ БЫСТРОГО ПРЕОБРАЗОВАНИЯ
- Свойство N log N
- Повторное разбиение последовательностей
- Преобразование с использованием разложения на подпоследовательности
- Общая формула разложения.
- Направленный сигнальный граф
- Вычисление с замещением
- Анализ временных затрат на вычисление с помощью полосковой диаграммы
- Степепи числа 2
- Тригонометрические функции
- Быстрое вычисление синусов
- Операция быстрого поворота
- Быстрая перестановка
- Преобразование для последовательностей с основанием 4 и другие модификации
- Ранее применявшиеся подходы к преобразованию вещественных данных
- Глава 9. ПРЕОБРАЗОВАНИЕ ХАРТЛИ В ОПТИКЕ
- Свойства симметрии
- Осуществление преобразования Хартли, использующее поляризацию
- Практическое осуществление
- Источник некогерентного излучения
- Пример
- Голография в плоскости Хартли
- Приложение 1. ПРОГРАММЫ ВЫЧИСЛЕНИЙ НА ЭВМ
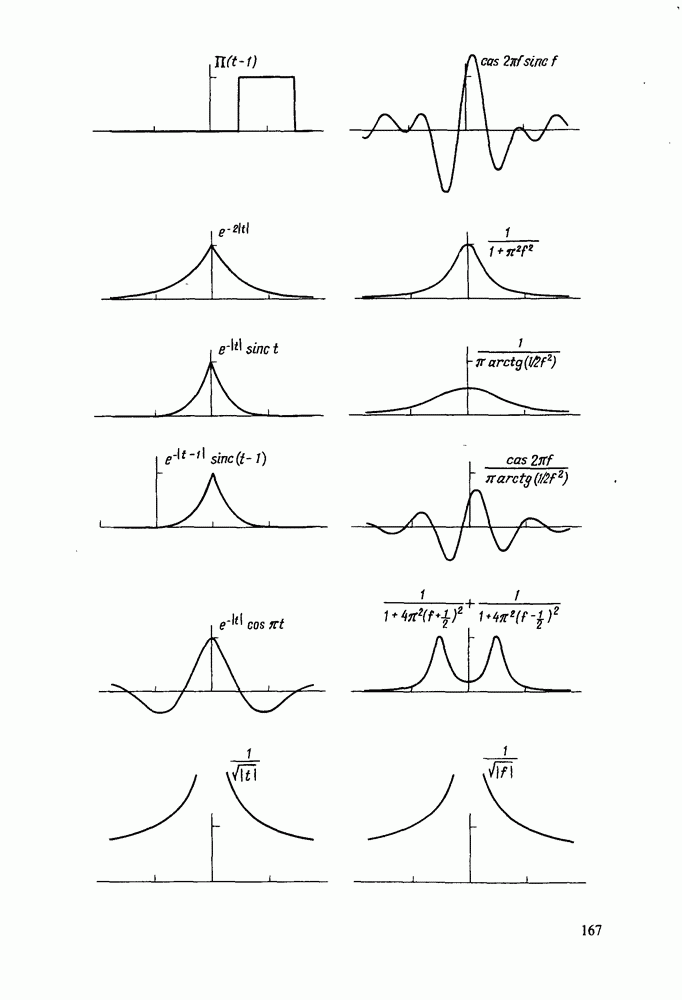
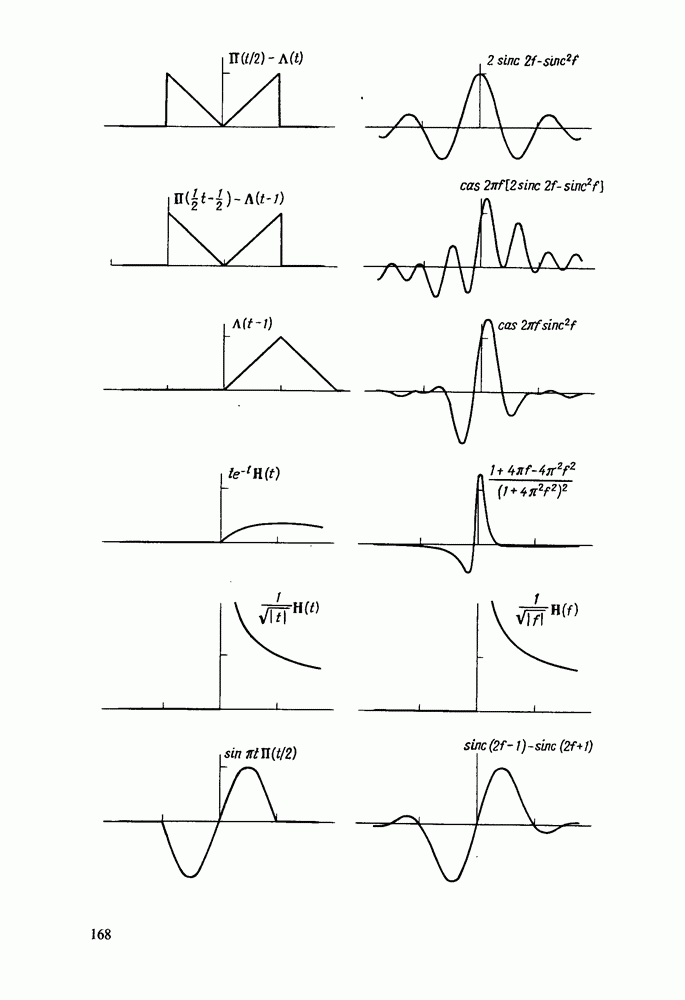
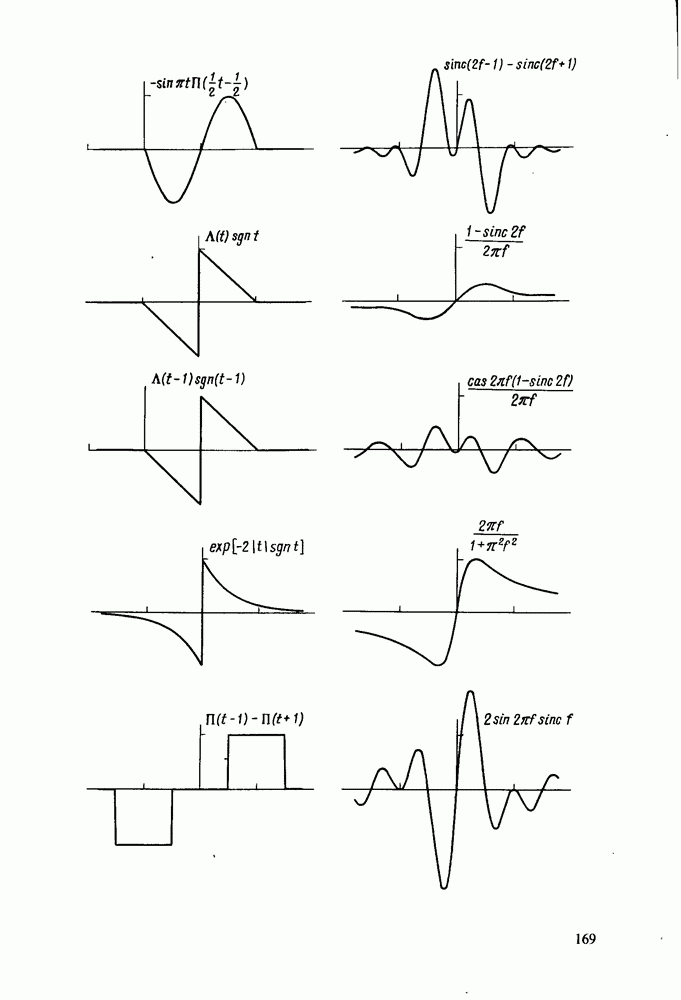
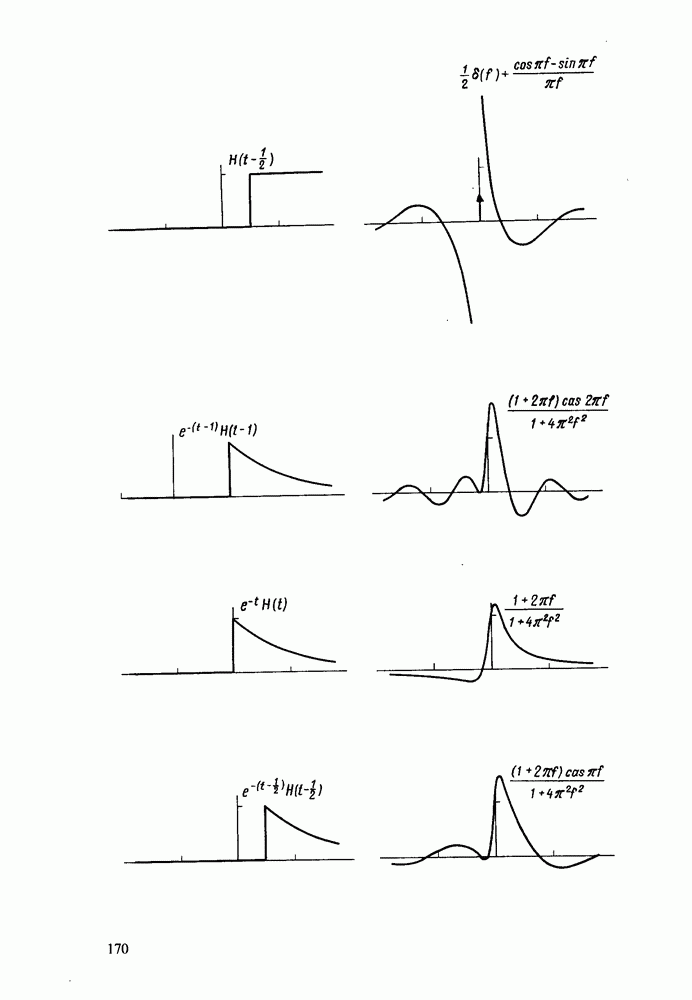
- Приложение 2. АТЛАС ПРЕОБРАЗОВАНИЙ ХАРТЛИ