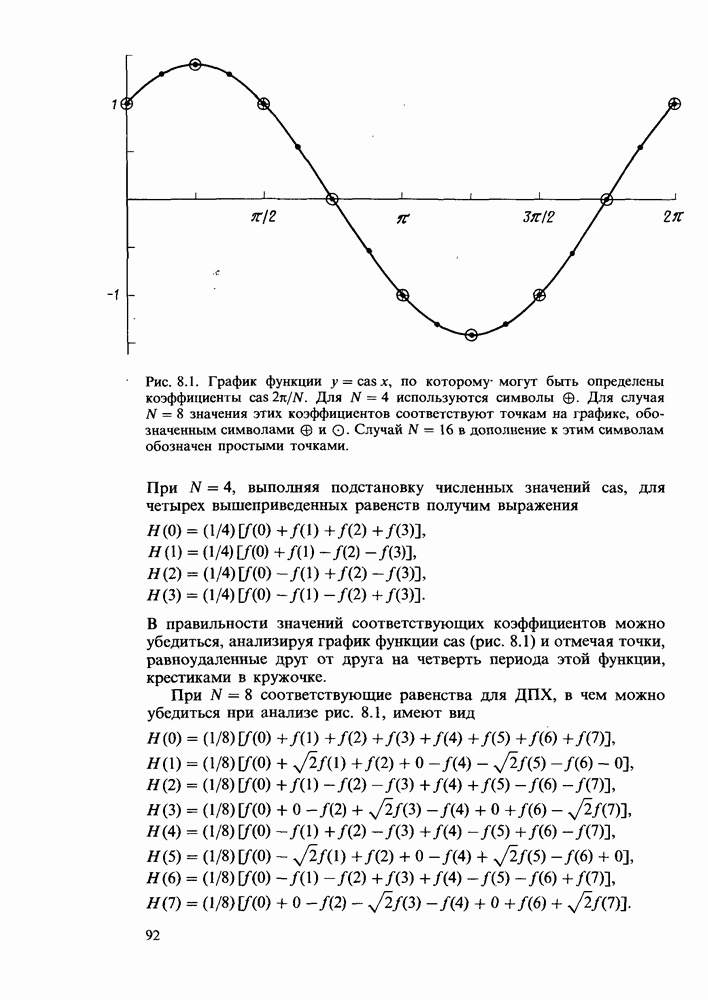
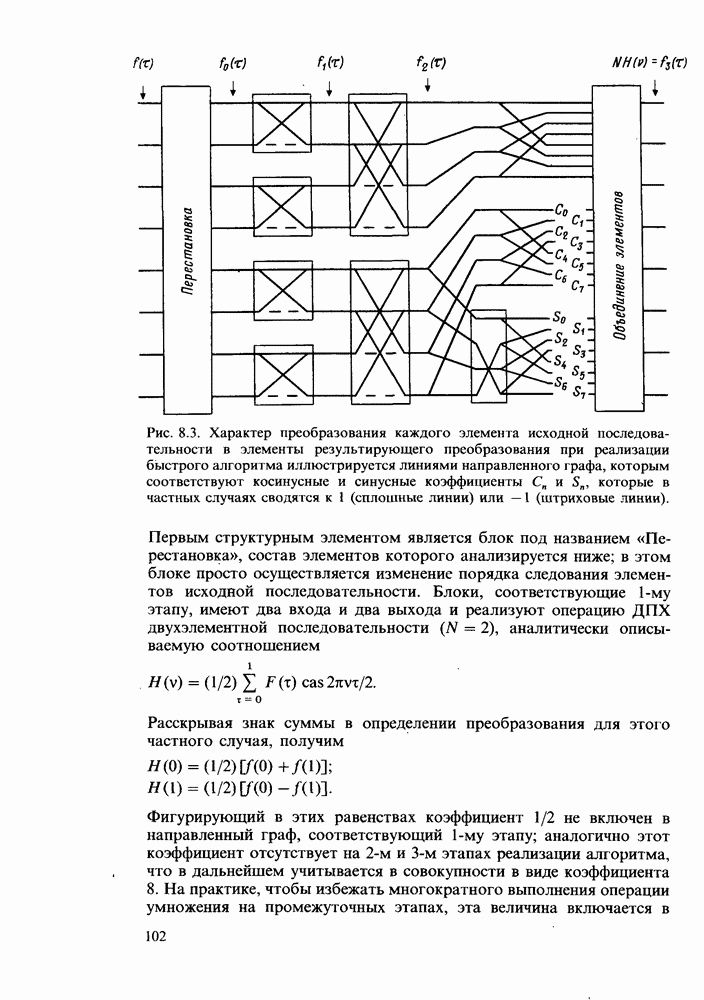
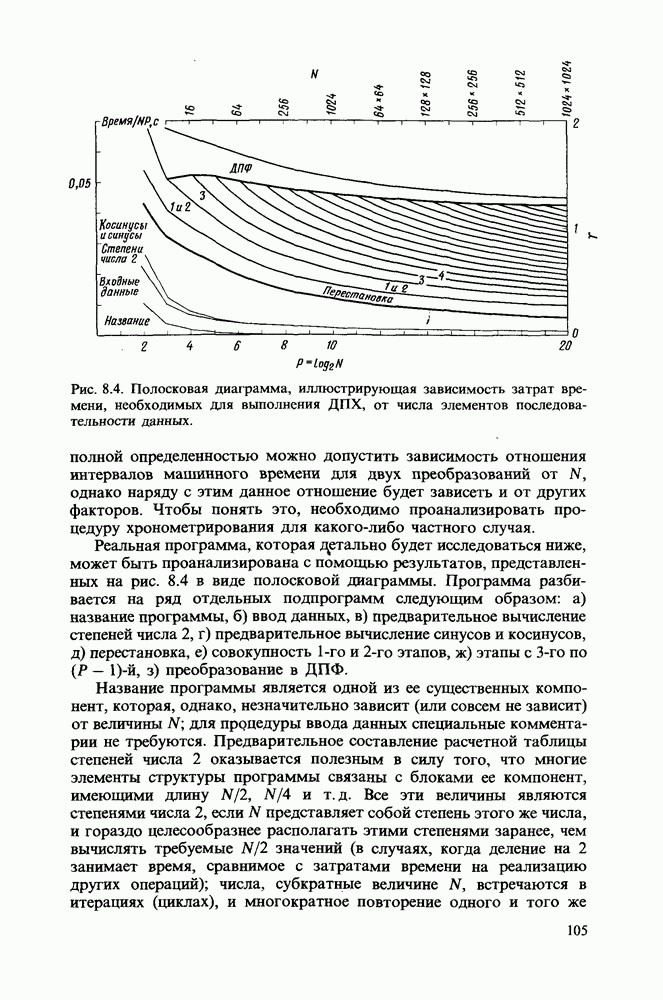
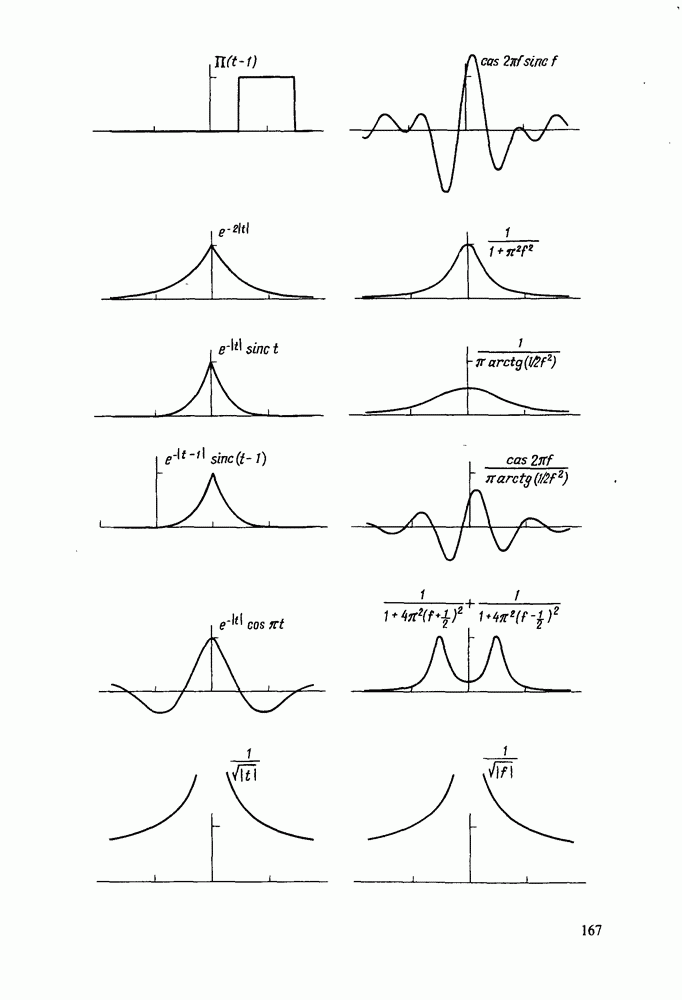
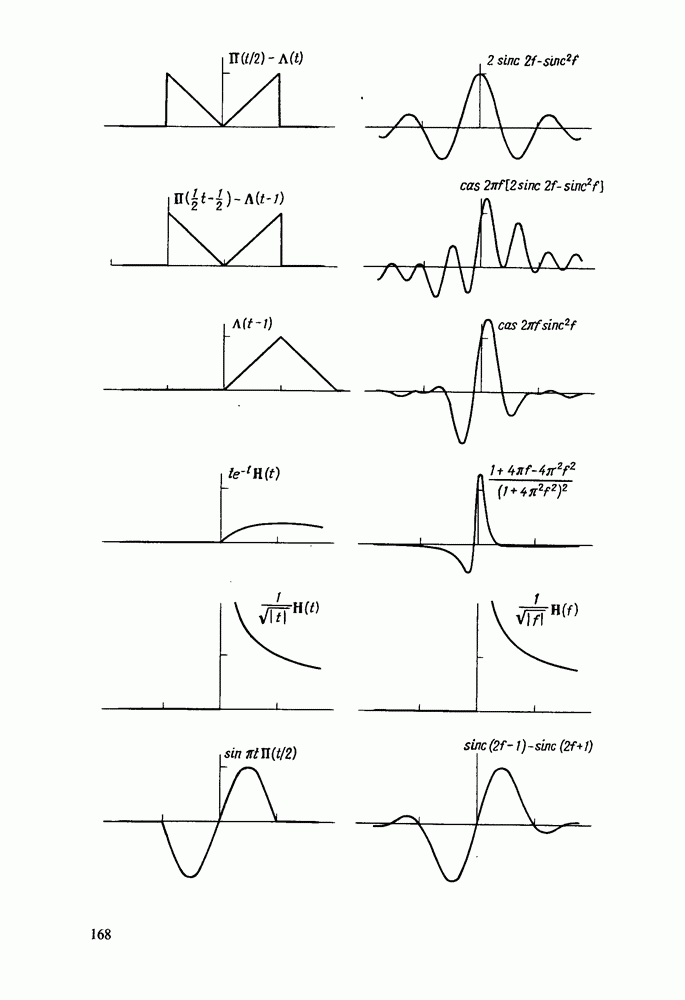
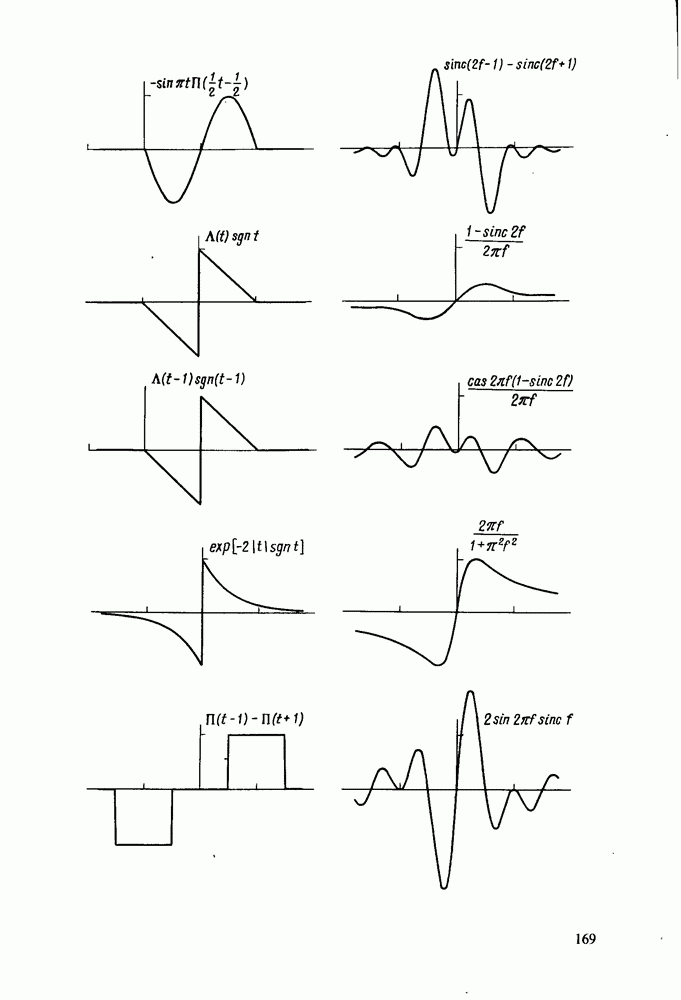
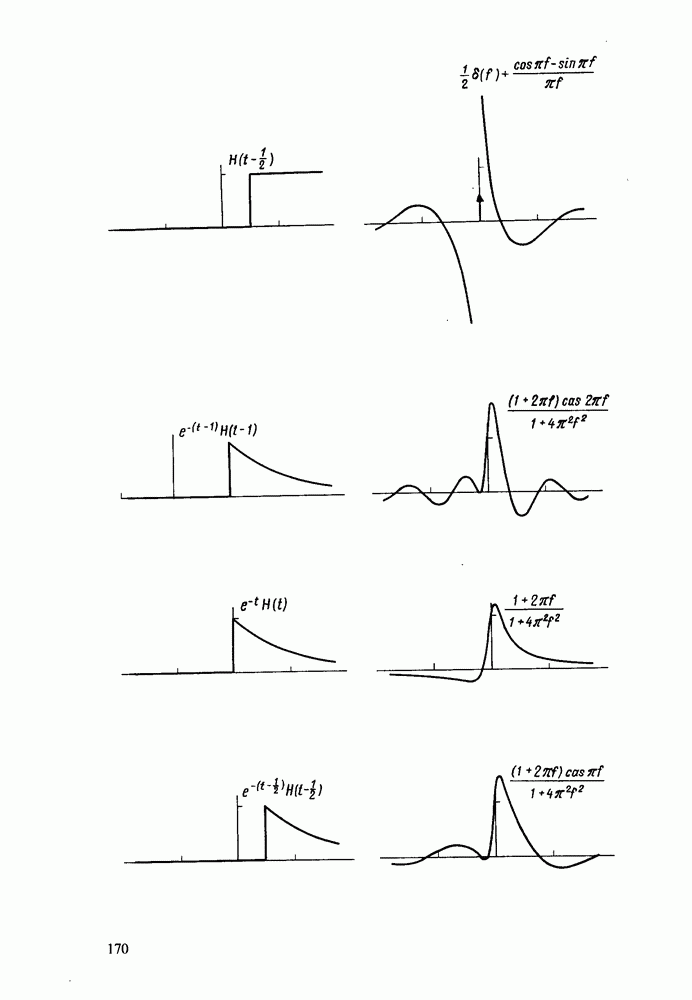
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
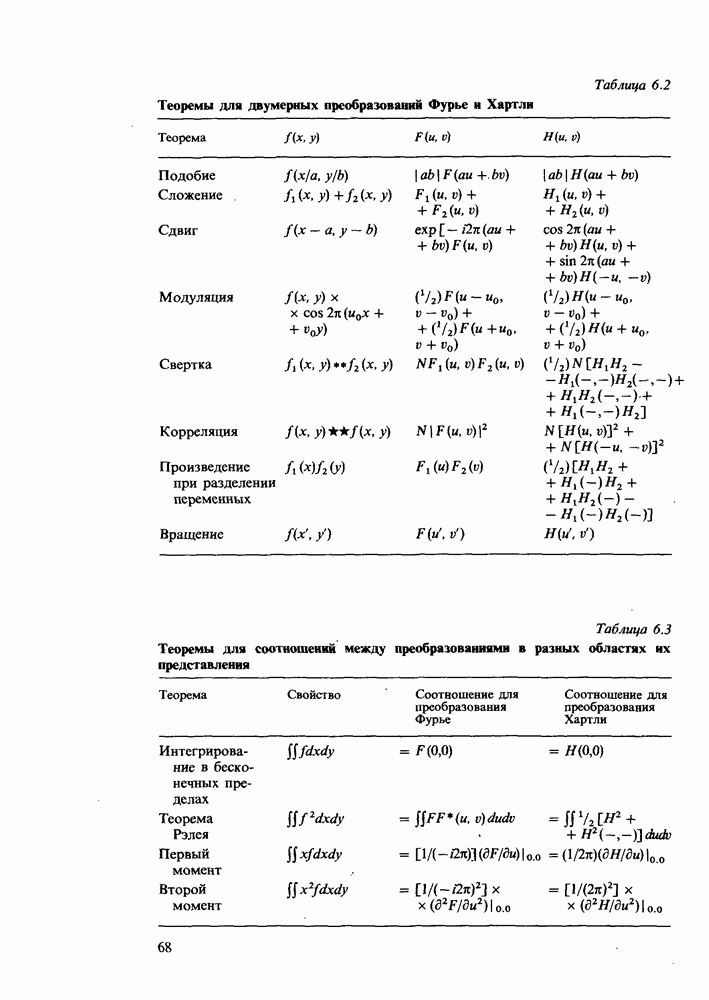
Свойство N log N
Пусть количество элементов N в последовательности равно числу 2, возведенному в степень Р. Тогда  Построение графиков логарифмов по основанию 2 является непростой задачей, однако желательно иметь некоторое представление о величине
Построение графиков логарифмов по основанию 2 является непростой задачей, однако желательно иметь некоторое представление о величине  просто равной степени Р в равенстве
просто равной степени Р в равенстве

В табл. 8.1 иллюстрируется взаимосвязь величин N и Р в пределах их изменения, имеющих практический интерес.
Полезно запомнить некоторые компоненты этой таблицы, особенно выделенные жирным шрифтом; тогда соседние компоненты будут восприниматься как таблица умножения. Если вы не знаете, что 210 приблизительно равно 1000, то вы окажетесь в затруднительном положении при беседах на технические темы. Другим полезным соотношением является следующее:  мегабайт.
мегабайт.
Таблица 8.1 Значения величин 
(см. скан)

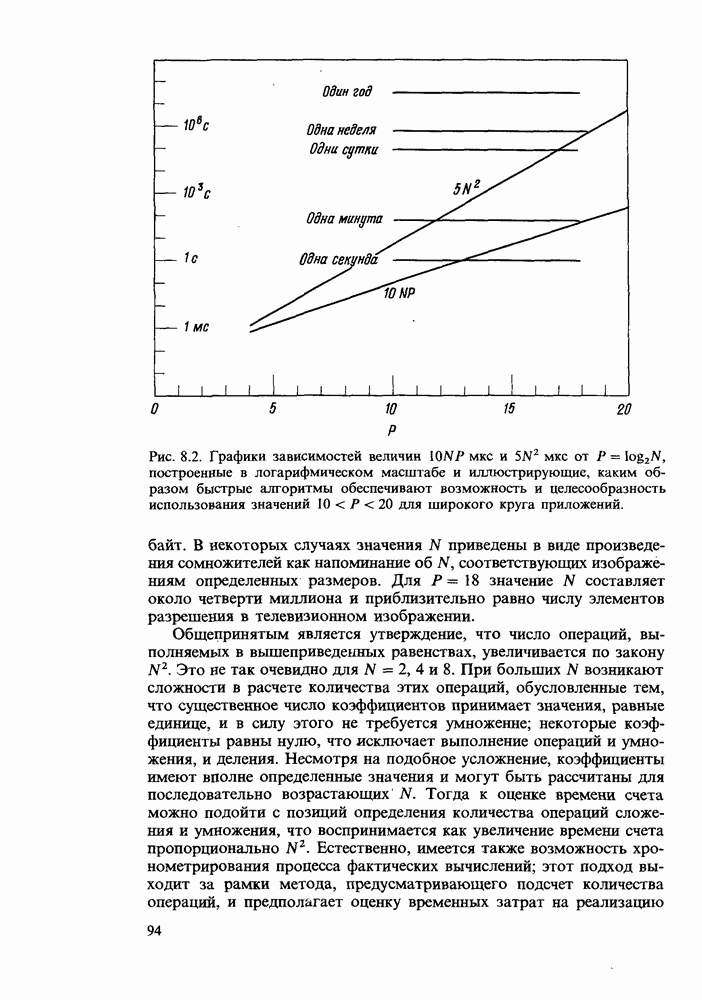
Рис. 8.2. Графики зависимостей величин  от
от  построенные в логарифмическом масштабе и иллюстрирующие, каким образом быстрые алгоритмы обеспечивают возможность и целесообразность использования значений
построенные в логарифмическом масштабе и иллюстрирующие, каким образом быстрые алгоритмы обеспечивают возможность и целесообразность использования значений  для широкого круга приложений.
для широкого круга приложений.
В некоторых случаях значения N приведены в виде произведения сомножителей как напоминание об N, соответствующих изображениям определенных размеров. Для  значение N составляет около четверти миллиона и приблизительно равно числу элементов разрешения в телевизионном изображении.
значение N составляет около четверти миллиона и приблизительно равно числу элементов разрешения в телевизионном изображении.
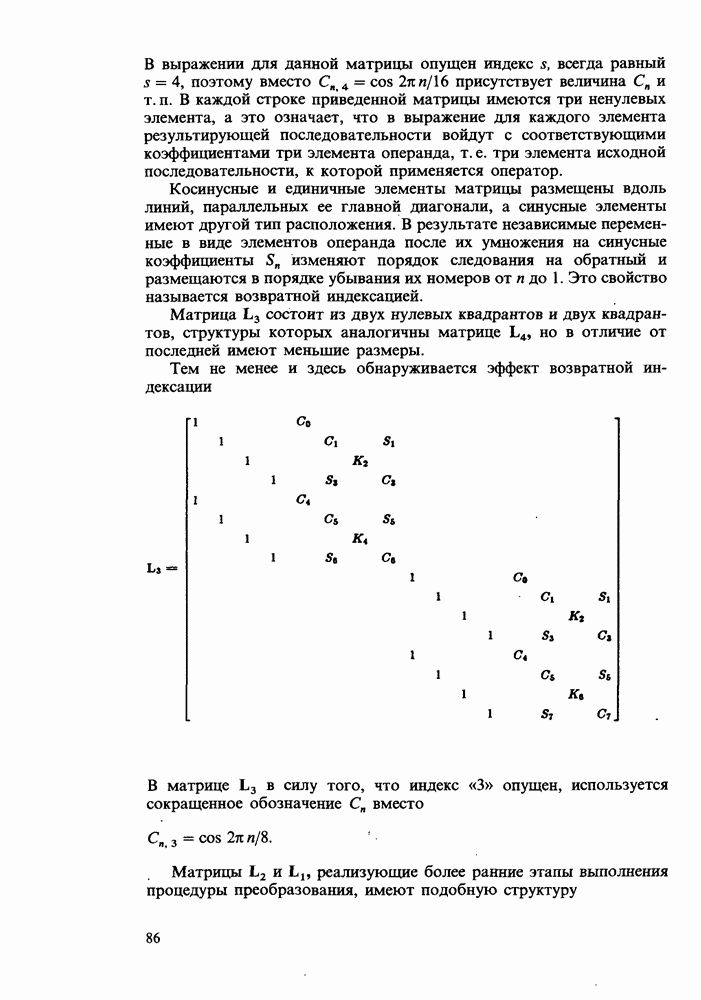
Общепринятым является утверждение, что число операций, выполняемых в вышеприведенных равенствах, увеличивается по закону  . Это не так очевидно для N = 2, 4 и 8. При больших N возникают сложности в расчете количества этих операций, обусловленные тем, что существенное число коэффициентов принимает значения, равные единице, и в силу этого не требуется умножение; некоторые коэффициенты равны нулю, что исключает выполнение операций и умножения, и деления. Несмотря на подобное усложнение, коэффициенты имеют вполне определенные значения и могут быть рассчитаны для последовательно возрастающих N. Тогда к оценке времени счета можно подойти с позиций определения количества операций сложения и умножения, что воспринимается как увеличение времени счета пропорционально
. Это не так очевидно для N = 2, 4 и 8. При больших N возникают сложности в расчете количества этих операций, обусловленные тем, что существенное число коэффициентов принимает значения, равные единице, и в силу этого не требуется умножение; некоторые коэффициенты равны нулю, что исключает выполнение операций и умножения, и деления. Несмотря на подобное усложнение, коэффициенты имеют вполне определенные значения и могут быть рассчитаны для последовательно возрастающих N. Тогда к оценке времени счета можно подойти с позиций определения количества операций сложения и умножения, что воспринимается как увеличение времени счета пропорционально  Естественно, имеется также возможность хронометрирования процесса фактических вычислений; этот подход выходит за рамки метода, предусматривающего подсчет количества операций, и предполагает оценку временных затрат на реализацию
Естественно, имеется также возможность хронометрирования процесса фактических вычислений; этот подход выходит за рамки метода, предусматривающего подсчет количества операций, и предполагает оценку временных затрат на реализацию
соответствующих прецедур, что не учитывается в вышеописанном методе подсчета.
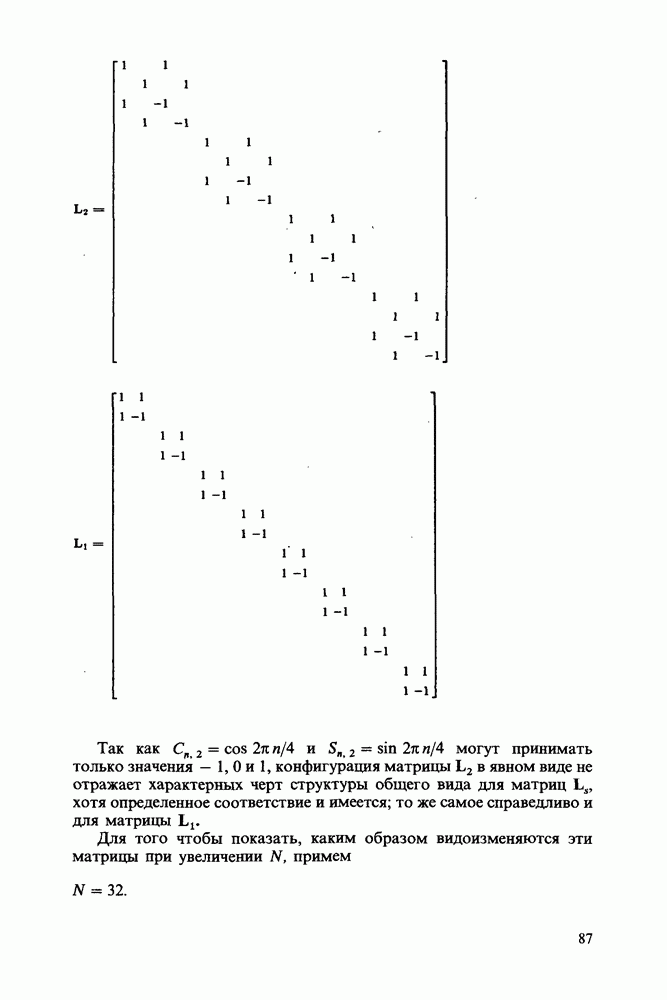
Когда величина N становится большой, зависимость вида  означает; что мы столкнемся с практическими пределами для временных затрат или стоимости. Быстрый алгоритм - это алгоритм, не реализующий в чистом виде все операции, предусмотренные в соответствии с определением преобразования, вследствие чего требуемое количество операций пропорционально
означает; что мы столкнемся с практическими пределами для временных затрат или стоимости. Быстрый алгоритм - это алгоритм, не реализующий в чистом виде все операции, предусмотренные в соответствии с определением преобразования, вследствие чего требуемое количество операций пропорционально  или
или  , а не
, а не  . В качестве примера, иллюстрирующего практическое значение этих рассуждений, рассмотрим быстрый алгоритм, для реализации которого требуется
. В качестве примера, иллюстрирующего практическое значение этих рассуждений, рассмотрим быстрый алгоритм, для реализации которого требуется  по сравнению с
по сравнению с  для обычного алгоритма дискретного преобразования. На рис. 8.2 построены соответствующие графики зависимости временных затрат от величины Р, изменяющейся от 0 до
для обычного алгоритма дискретного преобразования. На рис. 8.2 построены соответствующие графики зависимости временных затрат от величины Р, изменяющейся от 0 до  . Хотя
. Хотя  не является наибольшим значением Р, которое может встретиться на практике, оно фигурировало бы при анализе изображений, имеющих структуру вида
не является наибольшим значением Р, которое может встретиться на практике, оно фигурировало бы при анализе изображений, имеющих структуру вида  элементов разрешения, для которых разрешающая способность выше реализуемой при использовании телевизионного экрана. Подавляющее большинство преобразований, осуществляемых в повседневной практике, без сомнения оперирует величинами Р, не превышающими
элементов разрешения, для которых разрешающая способность выше реализуемой при использовании телевизионного экрана. Подавляющее большинство преобразований, осуществляемых в повседневной практике, без сомнения оперирует величинами Р, не превышающими  Графики наглядно иллюстрируют, что при цифровой обработке изображений больших размеров крайне важным становится вопрос о скорости реализации алгоритма. Ясно, что введение быстрого преобразования Фурье (БПФ) сильно расширяет наши возможности. Необходимость обработки изображений в реальном времени требует на сегодняшний день еще более высокого быстродействия, и обратно, по мере увеличения быстродействия будут открываться новые приложения.
Графики наглядно иллюстрируют, что при цифровой обработке изображений больших размеров крайне важным становится вопрос о скорости реализации алгоритма. Ясно, что введение быстрого преобразования Фурье (БПФ) сильно расширяет наши возможности. Необходимость обработки изображений в реальном времени требует на сегодняшний день еще более высокого быстродействия, и обратно, по мере увеличения быстродействия будут открываться новые приложения.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
- Глава 2. ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Преобразование Хартли
- Четная и нечетная составляющие
- Формулы связи
- Примеры
- Энергетический и фазовый спектры
- Глава 3. ТЕОРЕМЫ
- Свертка
- Соотношения между преобразованиями во временной и частотой областях
- Глава 4. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Физический смысл величин «тау» и v
- Четная и нечетная составляющие
- Примеры дискретных преобразований Хартли
- Степени свободы
- Другие вещественные ядра
- Теоремы
- Выводы
- Глава 5. ЦИФРОВАЯ ФИЛЬТРАЦИЯ ПОСРЕДСТВОМ СВЕРТКИ
- Циклическая свертка
- Дополнение нулями
- Обращение свертки
- Теорема о свертке
- Теорема о свертке в частотной области (спектральное сглаживание)
- Числовой пример свертки
- Коэффициент
- Числовой пример корреляционной функции
- Низкочастотная фильтрация
- Подчеркивание границ
- Свертка с использованием быстрого преобразования Хартли
- Способ без использования перестановок
- Свертка как умножение матриц
- Глава 6. Двумерные преобразования
- Двумерное преобразование Хартли
- Симметрия и антисимметрия
- Примеры
- Теоремы для двумерных преобразований
- Круговая симметрия
- Двумерная фильтрация
- Цикличность для двумерного случая
- Трехмерный случай
- Глава 7. ФАКТОРИЗАЦИЯ МАТРИЦЫ ПРЕОБРАЗОВАНИЯ
- Перестановка
- Перестановочные диаграммы
- Перестановочная матрица
- Ячеистая структура перестановочной диаграммы
- Каскадные матрицы
- Переход к дискретному преобразованию Фурье
- Глава 8. АЛГОРИТМ БЫСТРОГО ПРЕОБРАЗОВАНИЯ
- Свойство N log N
- Повторное разбиение последовательностей
- Преобразование с использованием разложения на подпоследовательности
- Общая формула разложения.
- Направленный сигнальный граф
- Вычисление с замещением
- Анализ временных затрат на вычисление с помощью полосковой диаграммы
- Степепи числа 2
- Тригонометрические функции
- Быстрое вычисление синусов
- Операция быстрого поворота
- Быстрая перестановка
- Преобразование для последовательностей с основанием 4 и другие модификации
- Ранее применявшиеся подходы к преобразованию вещественных данных
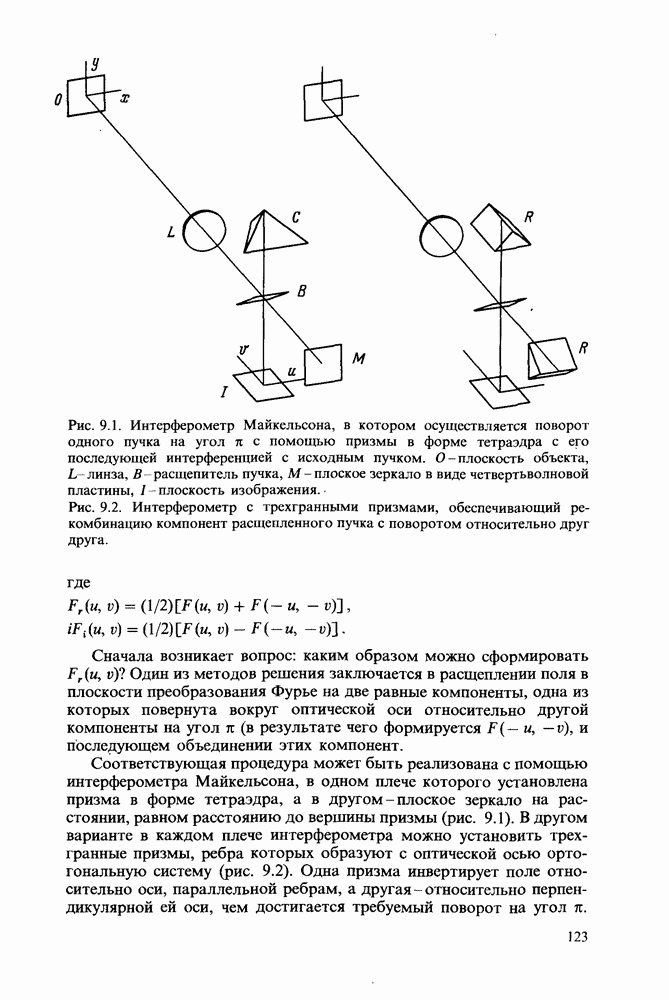
- Глава 9. ПРЕОБРАЗОВАНИЕ ХАРТЛИ В ОПТИКЕ
- Свойства симметрии
- Осуществление преобразования Хартли, использующее поляризацию
- Практическое осуществление
- Источник некогерентного излучения
- Пример
- Голография в плоскости Хартли
- Приложение 1. ПРОГРАММЫ ВЫЧИСЛЕНИЙ НА ЭВМ
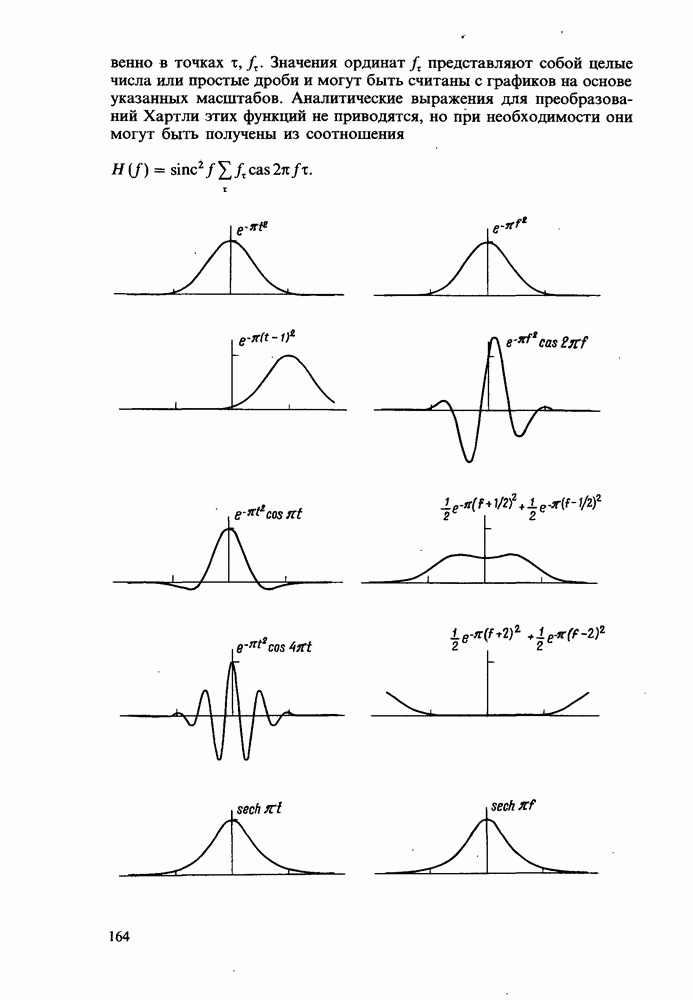
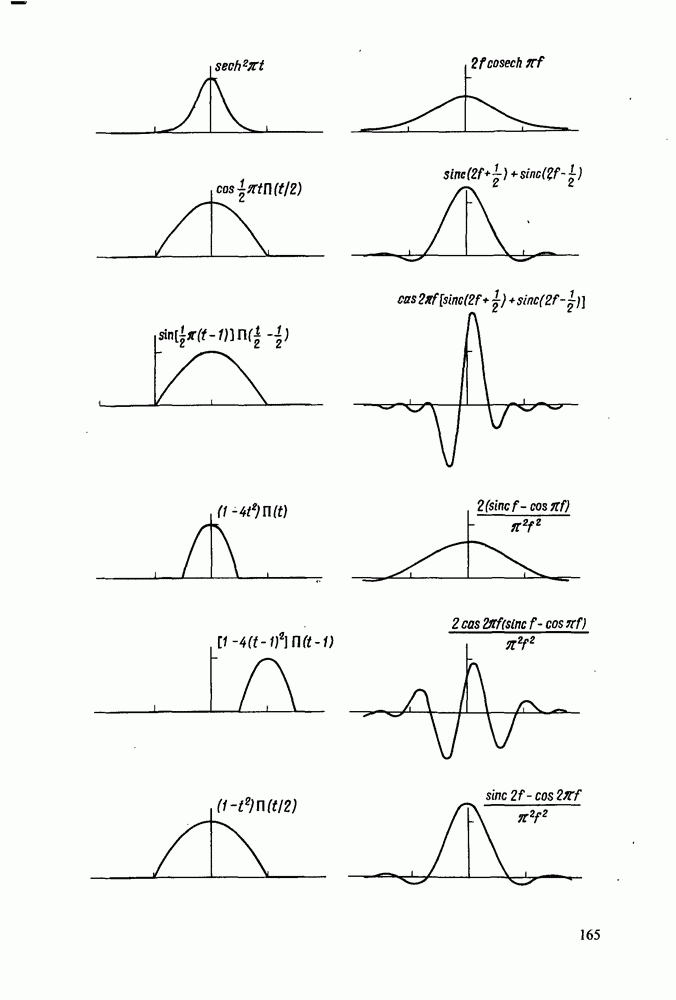
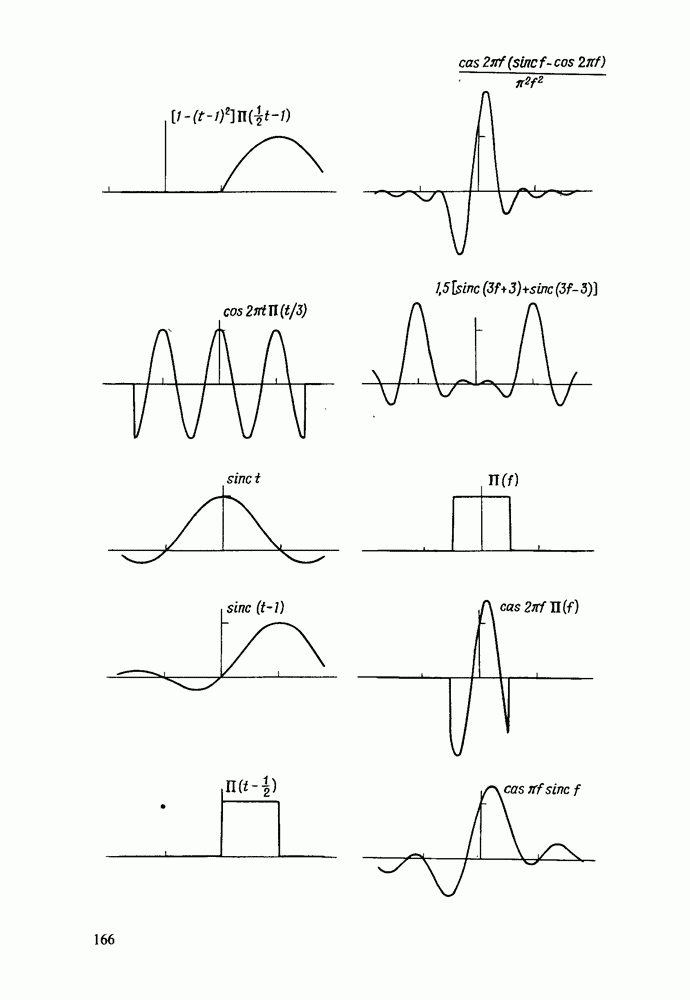
- Приложение 2. АТЛАС ПРЕОБРАЗОВАНИЙ ХАРТЛИ