| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
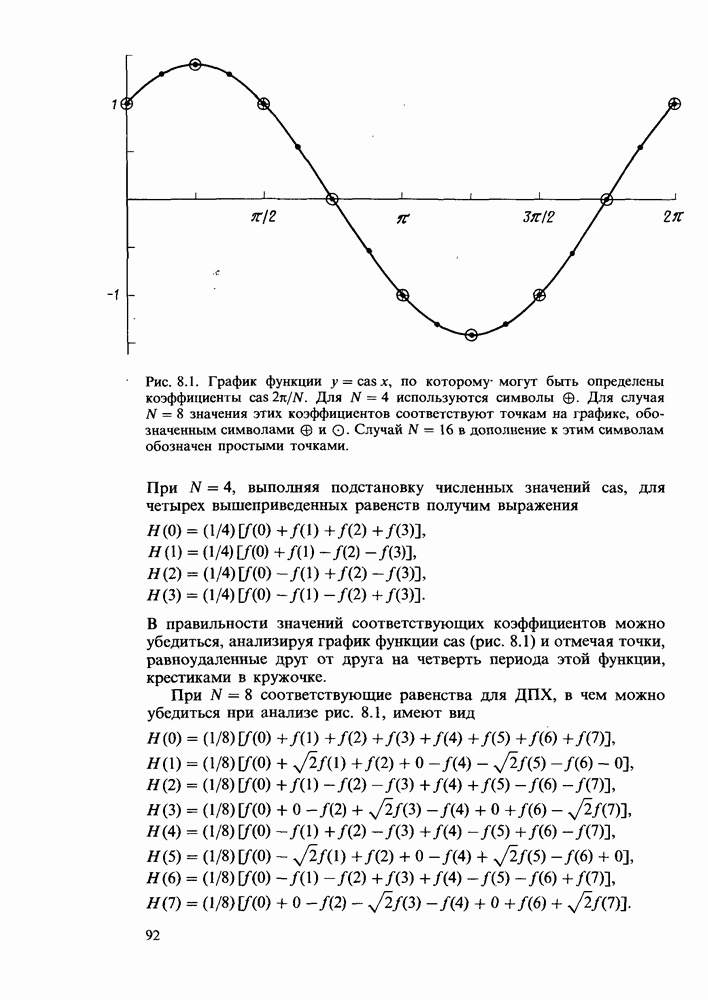
Циклическая свертка
Обычная дискретная свертка двух последовательностей  определяется следующим соотношением:
определяется следующим соотношением:

в котором диапазон значений  заключен в пределах области ненулевых значений произведений для каждого данного
заключен в пределах области ненулевых значений произведений для каждого данного  причем само
причем само  может принимать значения вплоть до бесконечности. Обе последовательности могут иметь любое число элементов от единицы до бесконечности, причем они не обязательно должны быть одинаковыми. Если число элементов последовательностей соответственно равно
может принимать значения вплоть до бесконечности. Обе последовательности могут иметь любое число элементов от единицы до бесконечности, причем они не обязательно должны быть одинаковыми. Если число элементов последовательностей соответственно равно  то число элементов свертки
то число элементов свертки  есть
есть  Число значений, принимаемых переменной
Число значений, принимаемых переменной  применительно к упорядоченным произведениям последовательностей, зависит от текущего выбора
применительно к упорядоченным произведениям последовательностей, зависит от текущего выбора  это число изменяется от единицы до наименьшего из
это число изменяется от единицы до наименьшего из  и
и  Программа вычислений для процедуры обычной свертки приведена в приложении 1 под названием
Программа вычислений для процедуры обычной свертки приведена в приложении 1 под названием 
В циклической свертке обе последовательности определены на окружности периметра N. Таким образом, можно считать, что переменная  пробегает по окружности, принимая только N различных значений. Имеется ровно N произведений, входящих в выражение для
пробегает по окружности, принимая только N различных значений. Имеется ровно N произведений, входящих в выражение для

Рис. 5.1. Последовательности  и их циклическая свертка
и их циклическая свертка 
каждого из N значений свертки. Циклическая свертка  определяется выражением
определяется выражением

В этом выражении  изменяется от 0 до
изменяется от 0 до  однако результат свертки не изменится в предположении, что
однако результат свертки не изменится в предположении, что  будет изменяться от 1 до N; необходимо только, чтобы были просуммированы все N произведений. При представлении операции свертки многие принимают в качестве начального элемента последовательности данных первый, а не нулевой, и это не должно вызывать путаницу.
будет изменяться от 1 до N; необходимо только, чтобы были просуммированы все N произведений. При представлении операции свертки многие принимают в качестве начального элемента последовательности данных первый, а не нулевой, и это не должно вызывать путаницу.
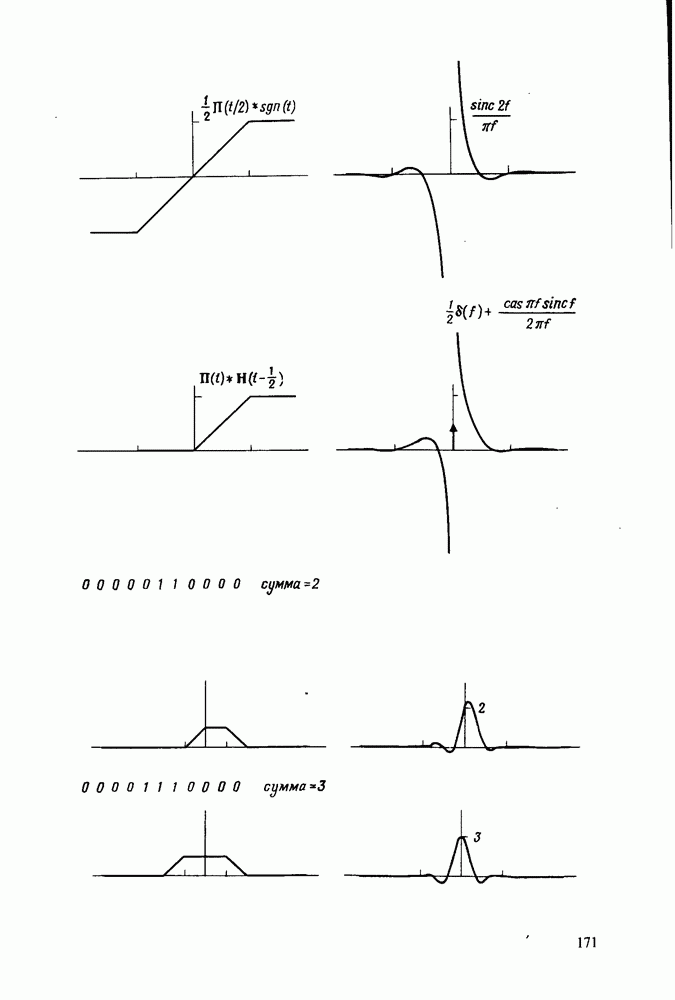
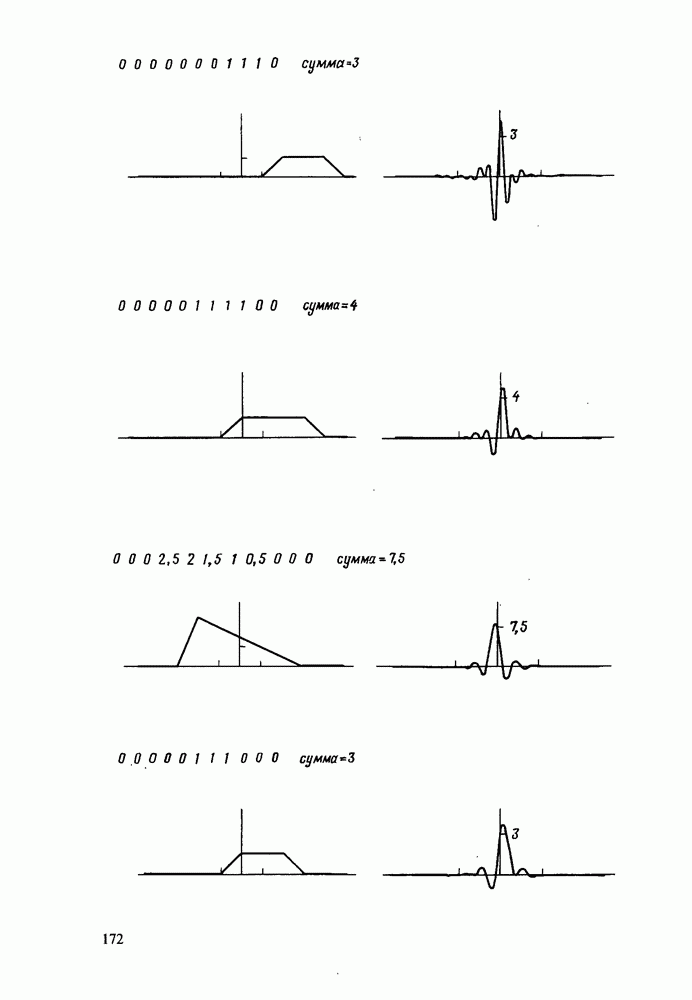
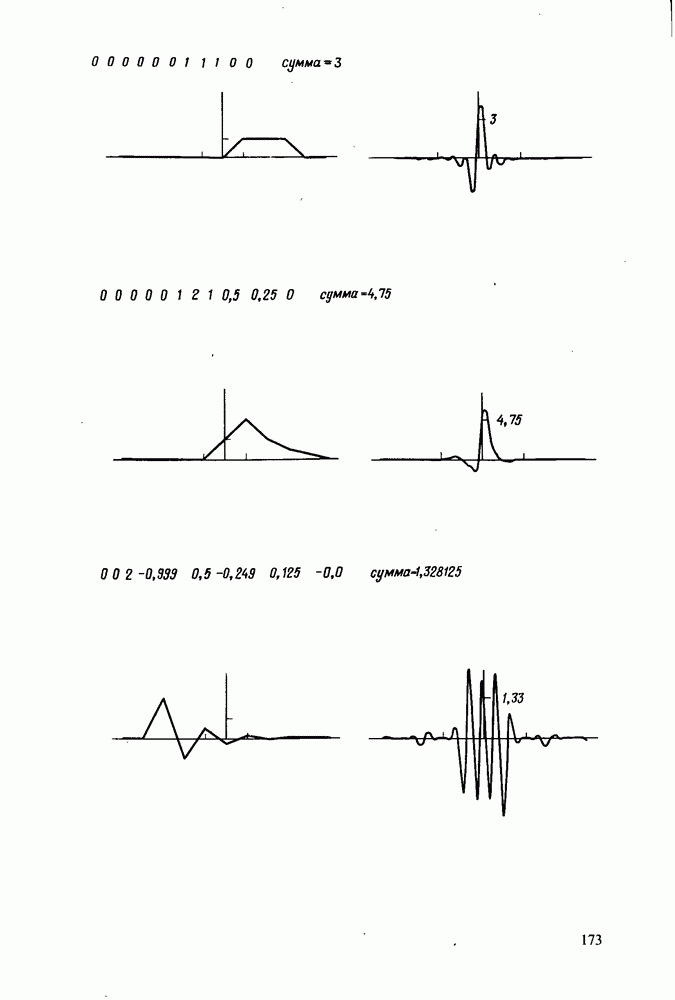
В качестве примера циклической свертки рассмотрим рис. 5.1, где представлен случай, для которого

В данном примере мы могли бы восстановить обычную свертку, разрезав окружность между  и распрямив ее. Это обусловлено тем, что свертка
и распрямив ее. Это обусловлено тем, что свертка  отлична от нуля только в интервале от
отлична от нуля только в интервале от  до
до  Одпако если рассмотреть последовательность с большим числом ненулевых элементов
Одпако если рассмотреть последовательность с большим числом ненулевых элементов

то обычная свертка будет существовать на интервале от  до
до  тогда как циклическая свертка заполняет один полный цикл, соответствующий окружности периметра N, причем имеет место наложение для
тогда как циклическая свертка заполняет один полный цикл, соответствующий окружности периметра N, причем имеет место наложение для  Следовательно, циклическая свертка начинается не с цифр
Следовательно, циклическая свертка начинается не с цифр  как это имеет место для обычной свертки, а с цифр
как это имеет место для обычной свертки, а с цифр  так как элементы «хвоста» последовательности
так как элементы «хвоста» последовательности  перекрываются с начальными элементами
перекрываются с начальными элементами 
Программа вычислений для циклической свертки дается в приложении 1 под названием  Обе программы
Обе программы  и
и  реализуют процедуры, определяющие обычную и циклическую свертки. однако в ряде ситуаций целесообразнее использовать методы
реализуют процедуры, определяющие обычную и циклическую свертки. однако в ряде ситуаций целесообразнее использовать методы
преобразования, рассматриваемые ниже в данной главе. Так, программа  реализует циклическую свертку двух последовательностей с числом элементов
реализует циклическую свертку двух последовательностей с числом элементов  с применением теоремы о свертке. Существует также метод, использующий умножение матриц, что оказывается удобным; скорость выполнения процедуры умножения матриц, реализуемой на ЭВМ, должна проверяться для каждой ЭВМ.
с применением теоремы о свертке. Существует также метод, использующий умножение матриц, что оказывается удобным; скорость выполнения процедуры умножения матриц, реализуемой на ЭВМ, должна проверяться для каждой ЭВМ.
Значительная часть последующего материала посвящена именно циклической свертке, и едва ли есть необходимость введения специального символа для этой операции. Напомним, что в данной главе будет использоваться символ  . Таким образом,
. Таким образом, 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
- Глава 2. ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Преобразование Хартли
- Четная и нечетная составляющие
- Формулы связи
- Примеры
- Энергетический и фазовый спектры
- Глава 3. ТЕОРЕМЫ
- Свертка
- Соотношения между преобразованиями во временной и частотой областях
- Глава 4. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Физический смысл величин «тау» и v
- Четная и нечетная составляющие
- Примеры дискретных преобразований Хартли
- Степени свободы
- Другие вещественные ядра
- Теоремы
- Выводы
- Глава 5. ЦИФРОВАЯ ФИЛЬТРАЦИЯ ПОСРЕДСТВОМ СВЕРТКИ
- Циклическая свертка
- Дополнение нулями
- Обращение свертки
- Теорема о свертке
- Теорема о свертке в частотной области (спектральное сглаживание)
- Числовой пример свертки
- Коэффициент
- Числовой пример корреляционной функции
- Низкочастотная фильтрация
- Подчеркивание границ
- Свертка с использованием быстрого преобразования Хартли
- Способ без использования перестановок
- Свертка как умножение матриц
- Глава 6. Двумерные преобразования
- Двумерное преобразование Хартли
- Симметрия и антисимметрия
- Примеры
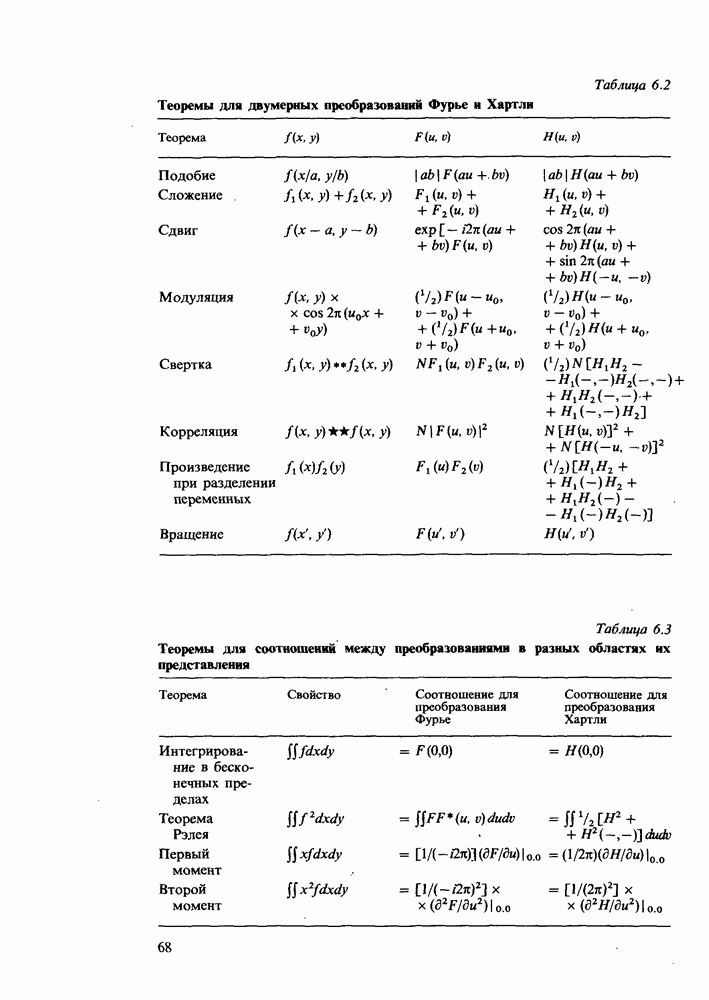
- Теоремы для двумерных преобразований
- Круговая симметрия
- Двумерная фильтрация
- Цикличность для двумерного случая
- Трехмерный случай
- Глава 7. ФАКТОРИЗАЦИЯ МАТРИЦЫ ПРЕОБРАЗОВАНИЯ
- Перестановка
- Перестановочные диаграммы
- Перестановочная матрица
- Ячеистая структура перестановочной диаграммы
- Каскадные матрицы
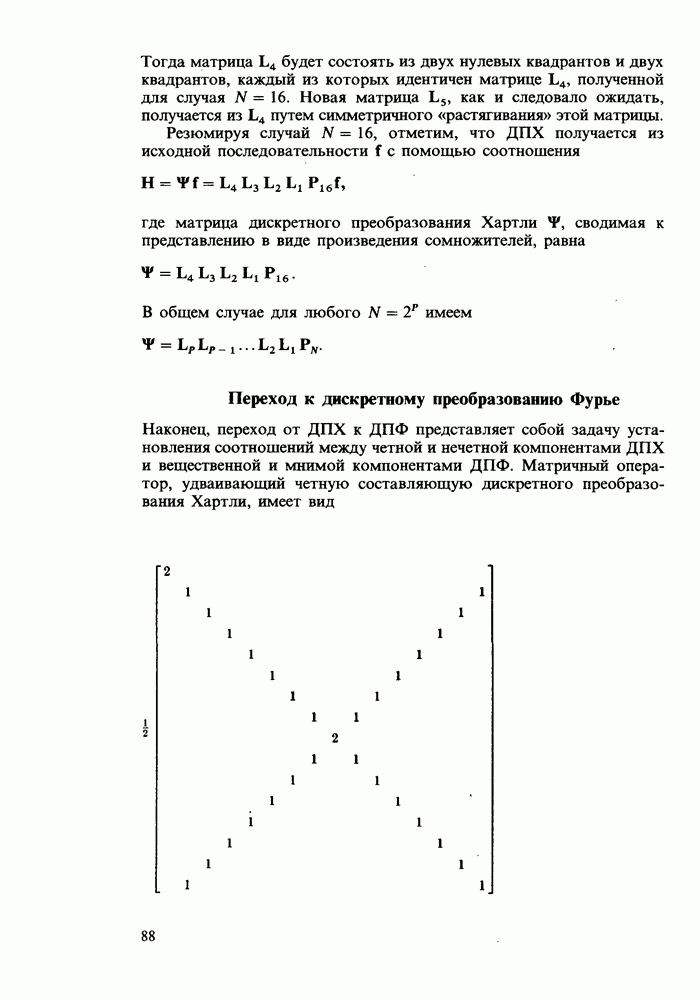
- Переход к дискретному преобразованию Фурье
- Глава 8. АЛГОРИТМ БЫСТРОГО ПРЕОБРАЗОВАНИЯ
- Свойство N log N
- Повторное разбиение последовательностей
- Преобразование с использованием разложения на подпоследовательности
- Общая формула разложения.
- Направленный сигнальный граф
- Вычисление с замещением
- Анализ временных затрат на вычисление с помощью полосковой диаграммы
- Степепи числа 2
- Тригонометрические функции
- Быстрое вычисление синусов
- Операция быстрого поворота
- Быстрая перестановка
- Преобразование для последовательностей с основанием 4 и другие модификации
- Ранее применявшиеся подходы к преобразованию вещественных данных
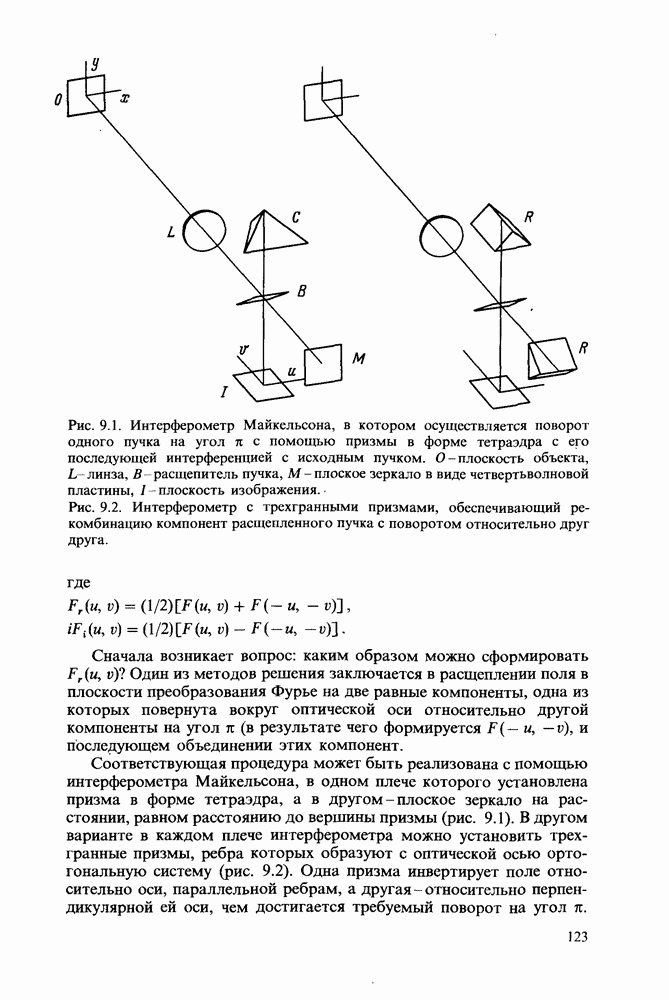
- Глава 9. ПРЕОБРАЗОВАНИЕ ХАРТЛИ В ОПТИКЕ
- Свойства симметрии
- Осуществление преобразования Хартли, использующее поляризацию
- Практическое осуществление
- Источник некогерентного излучения
- Пример
- Голография в плоскости Хартли
- Приложение 1. ПРОГРАММЫ ВЫЧИСЛЕНИЙ НА ЭВМ
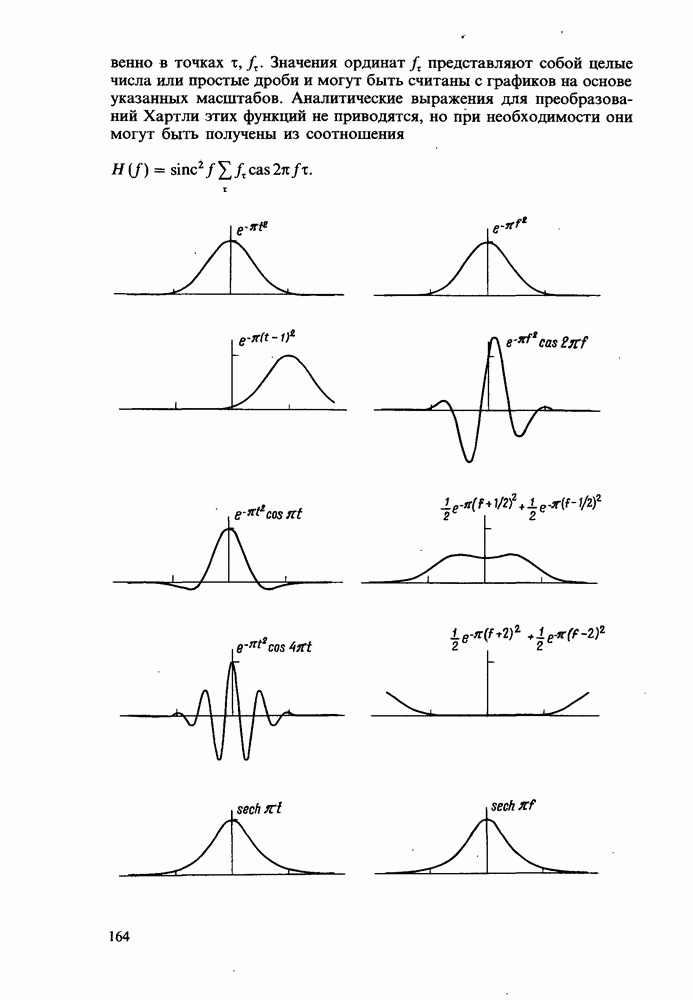
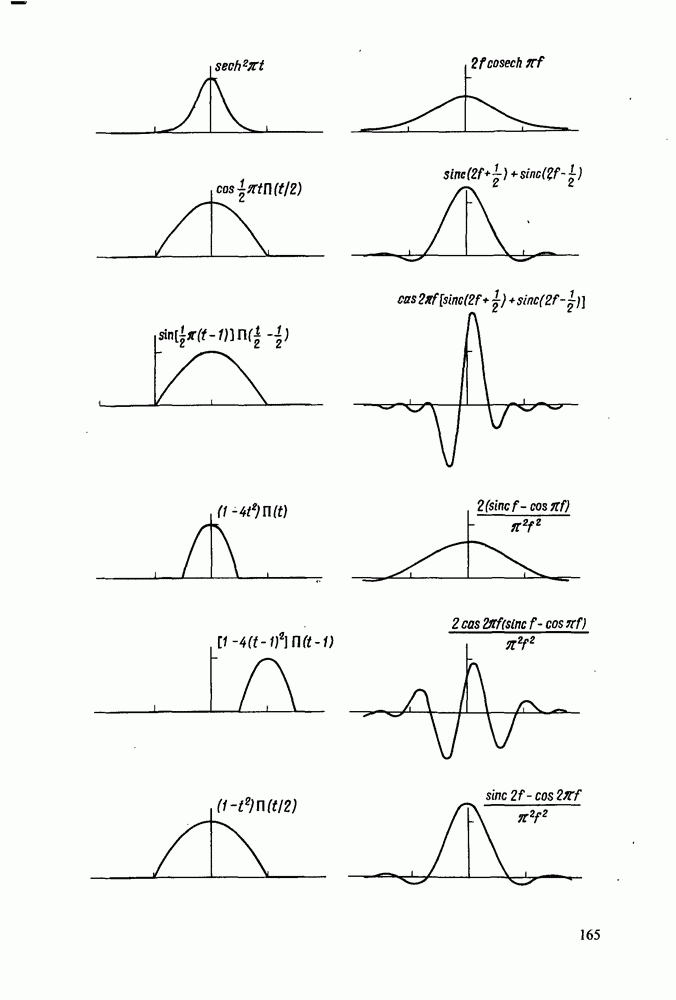
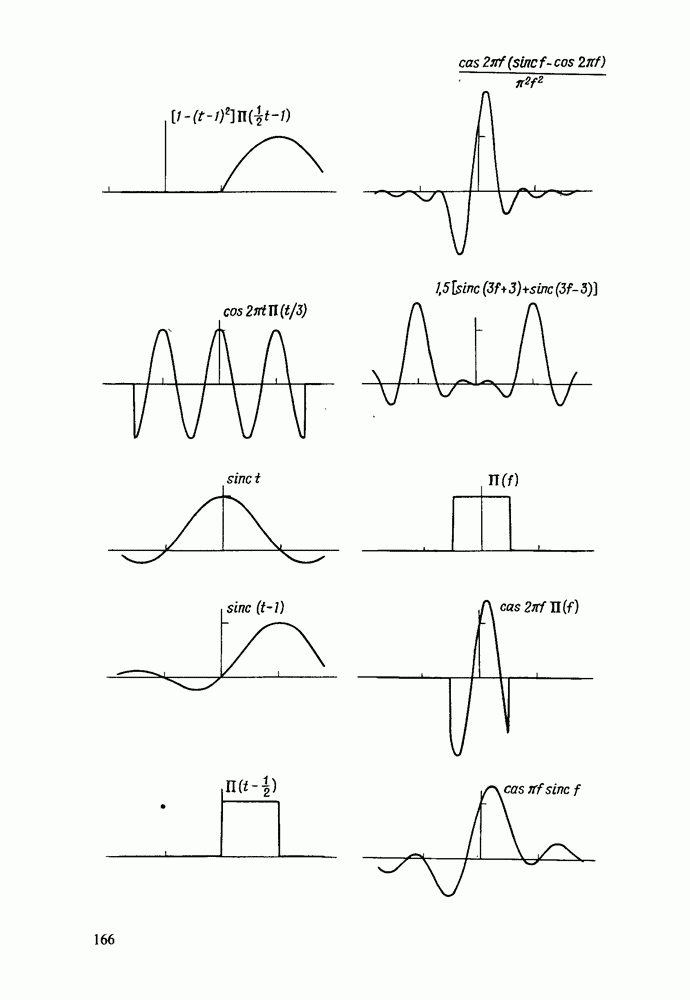
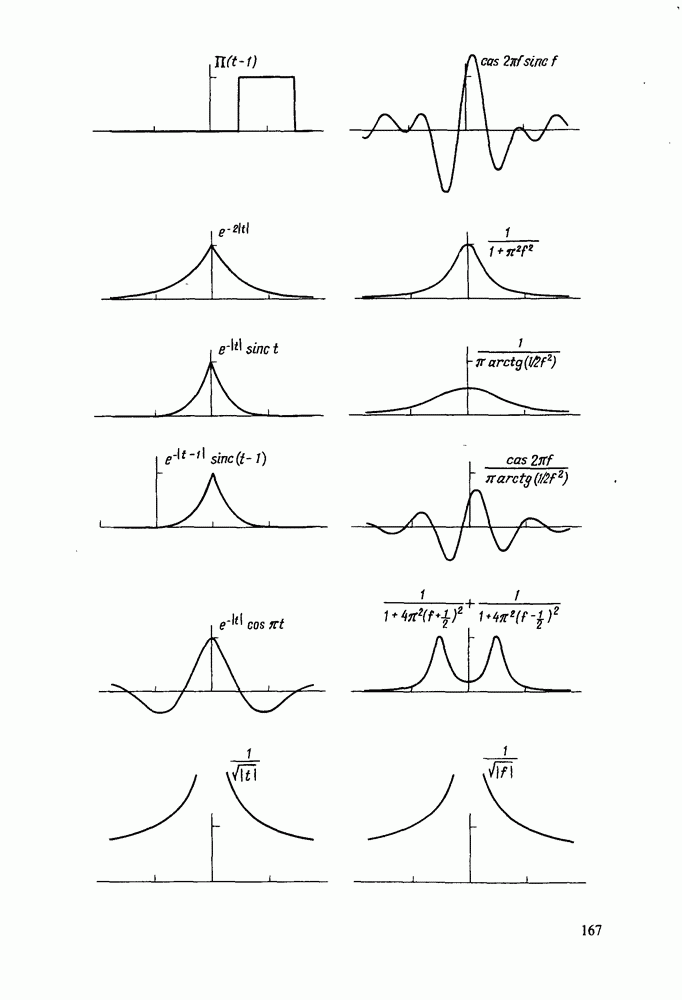
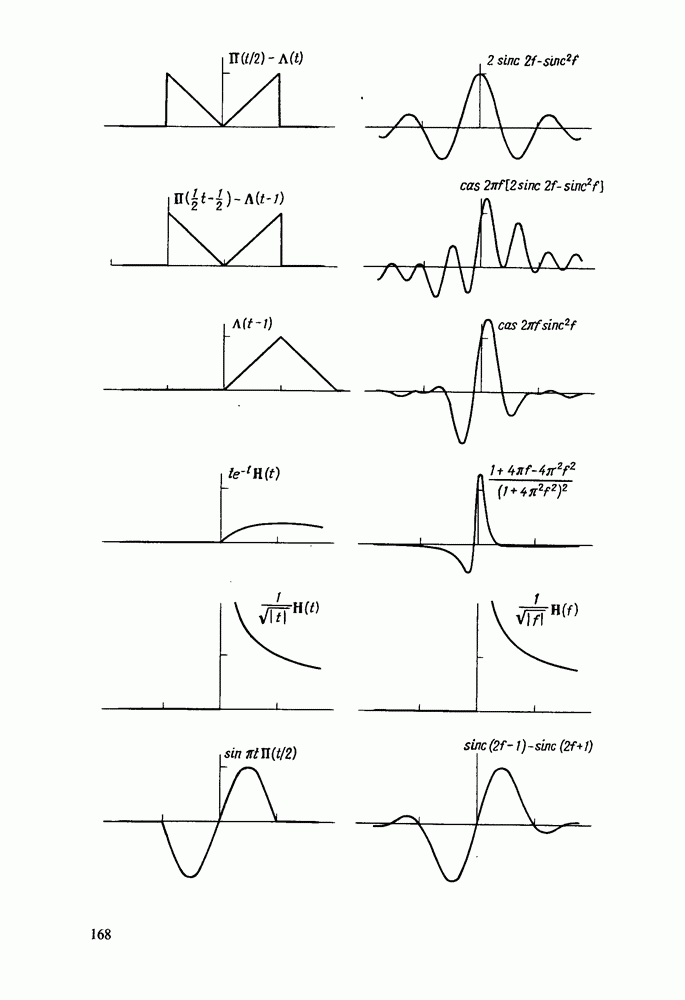
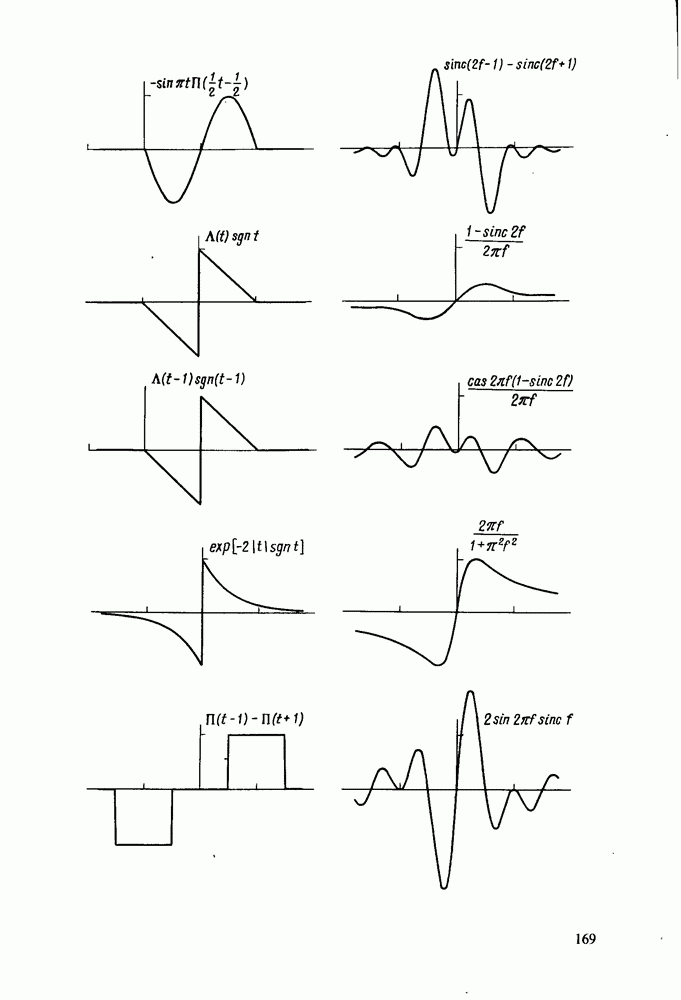
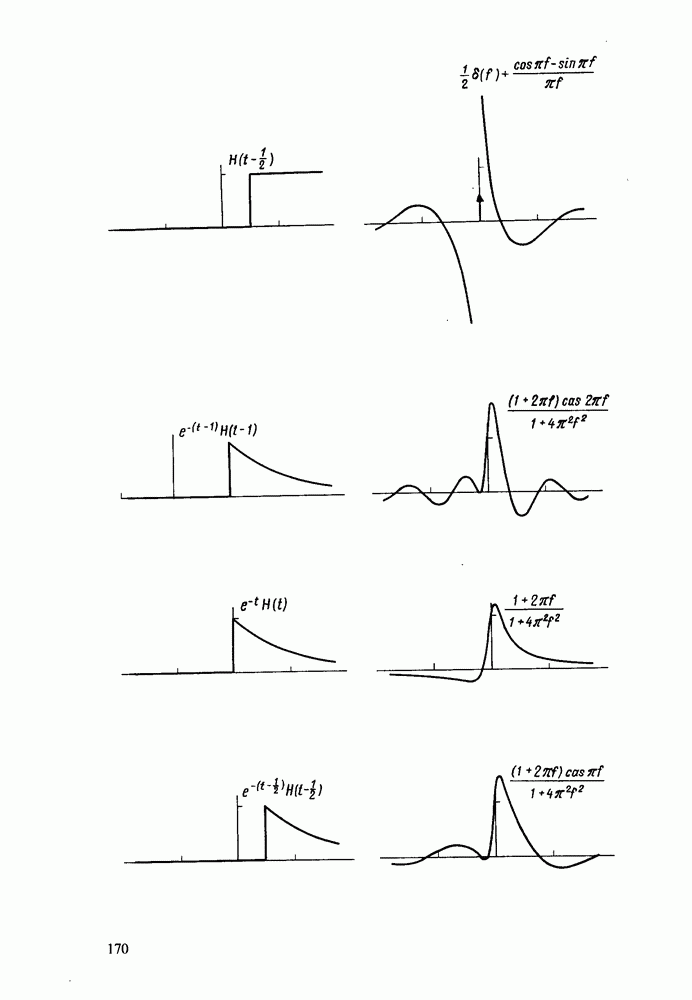
- Приложение 2. АТЛАС ПРЕОБРАЗОВАНИЙ ХАРТЛИ