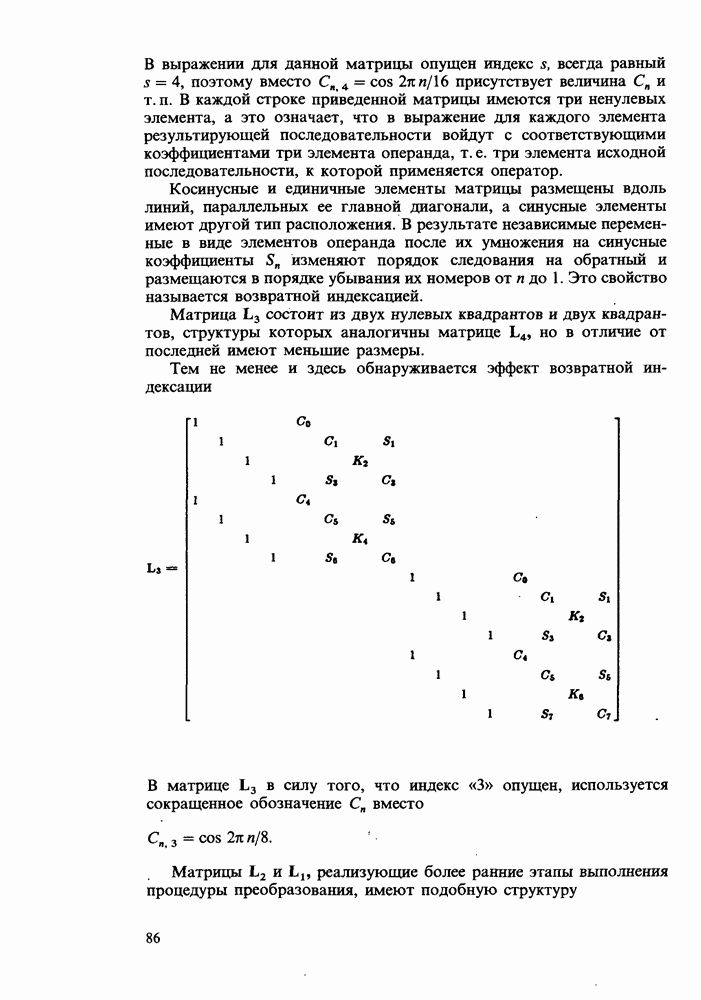
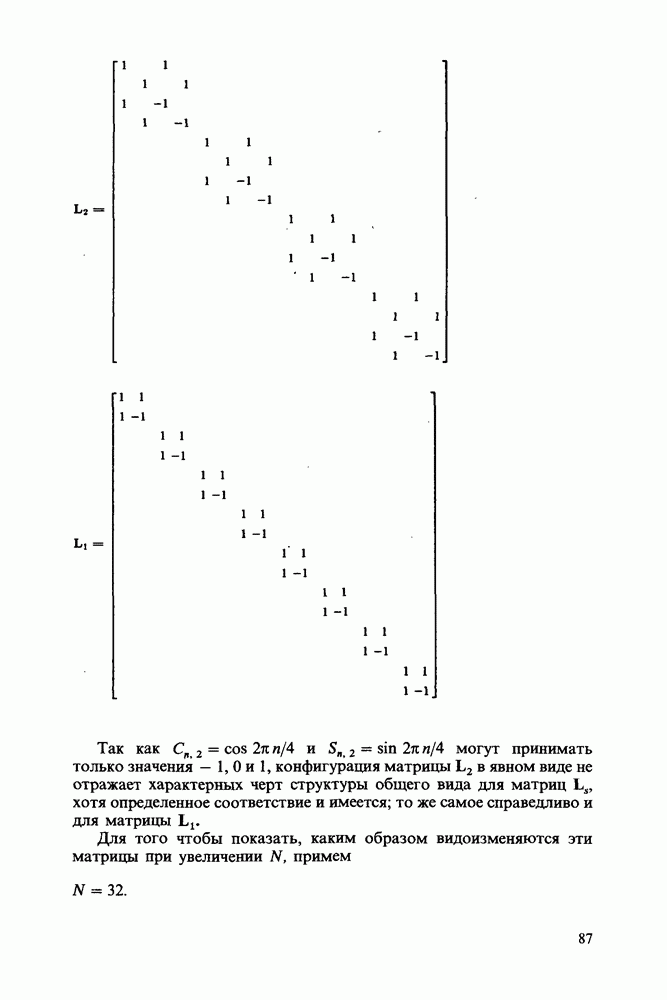
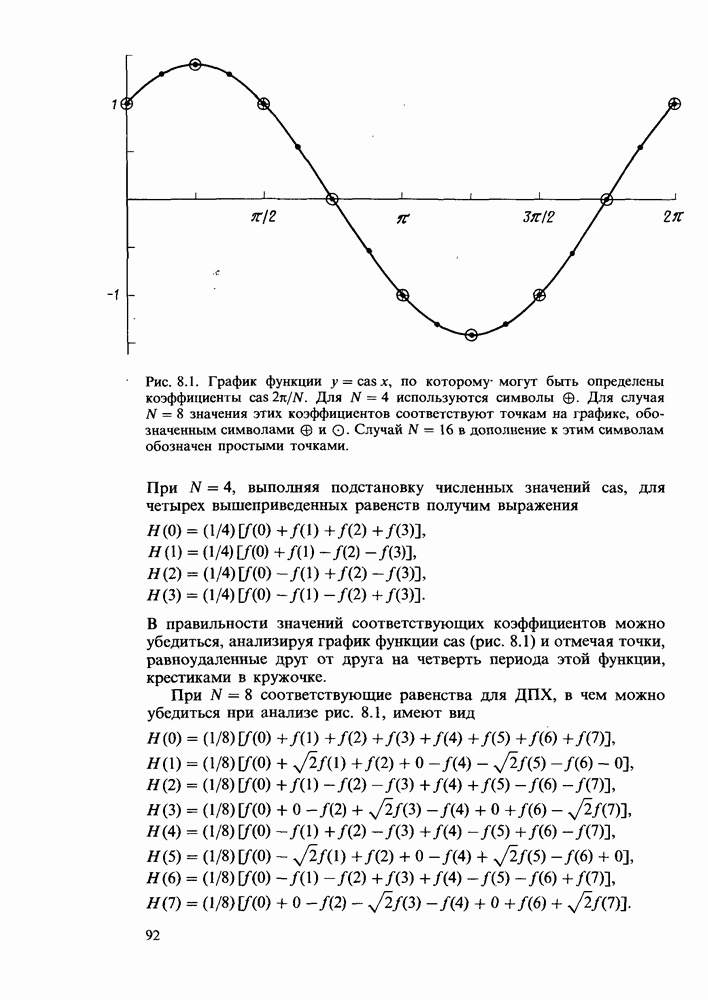
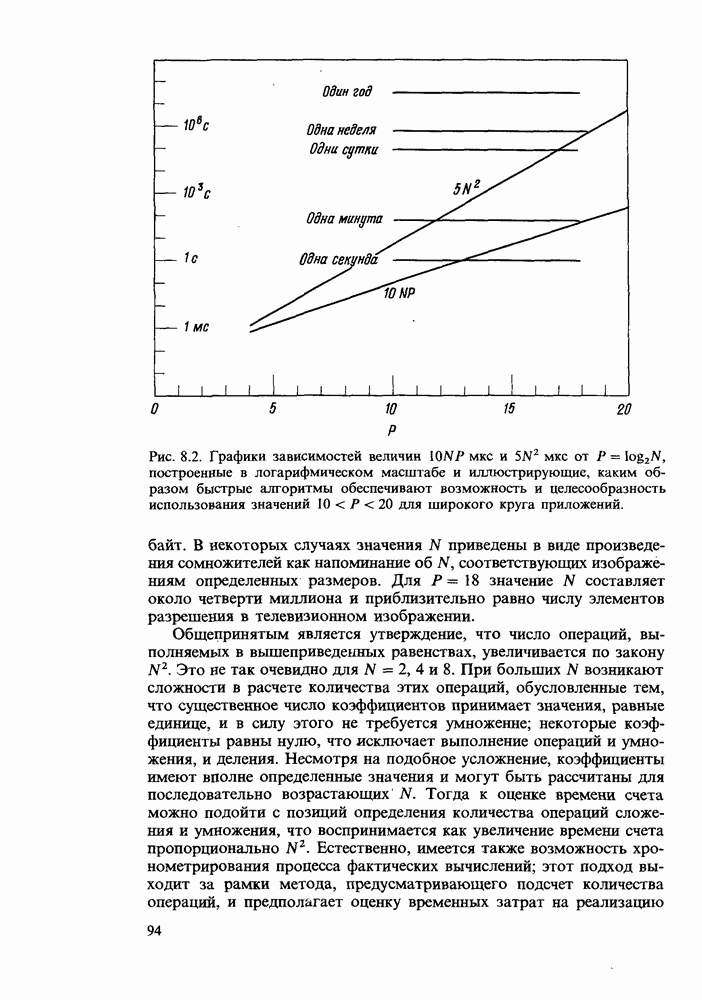
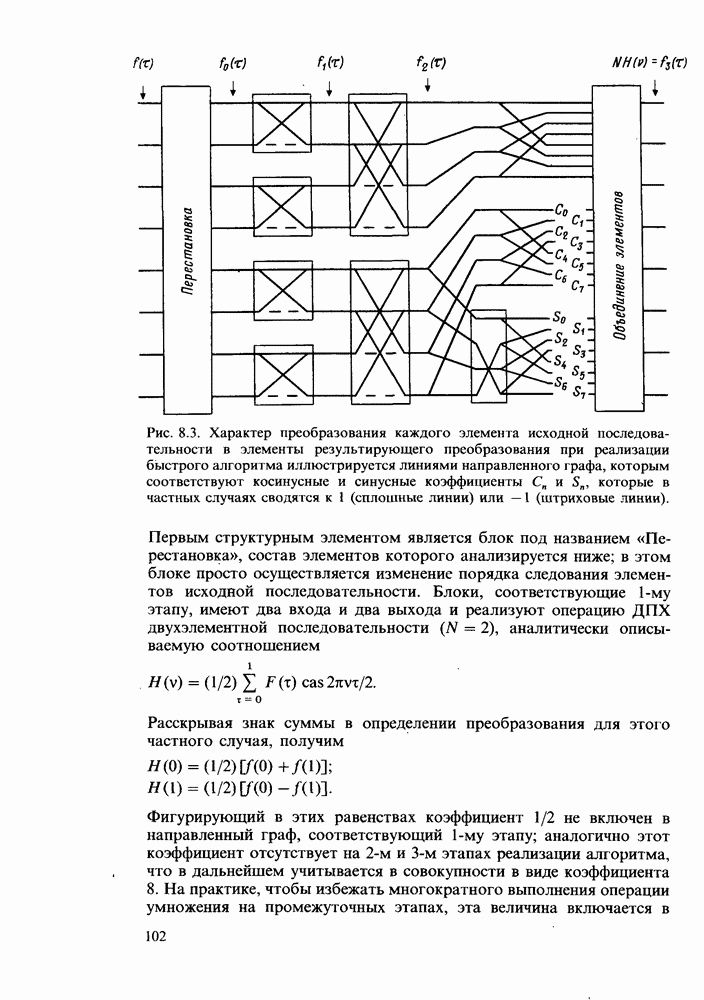
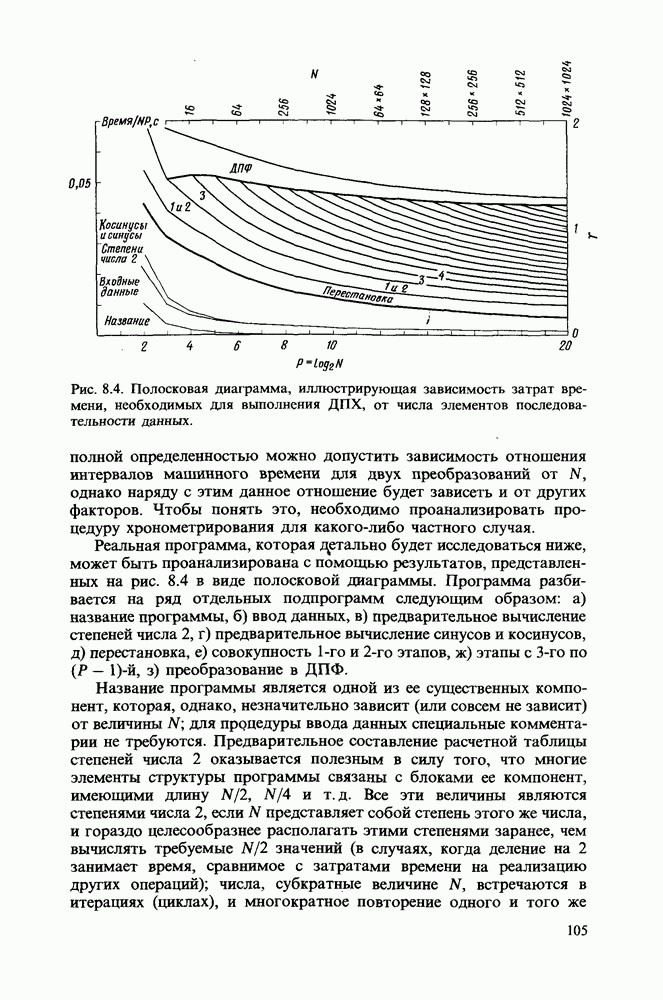
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
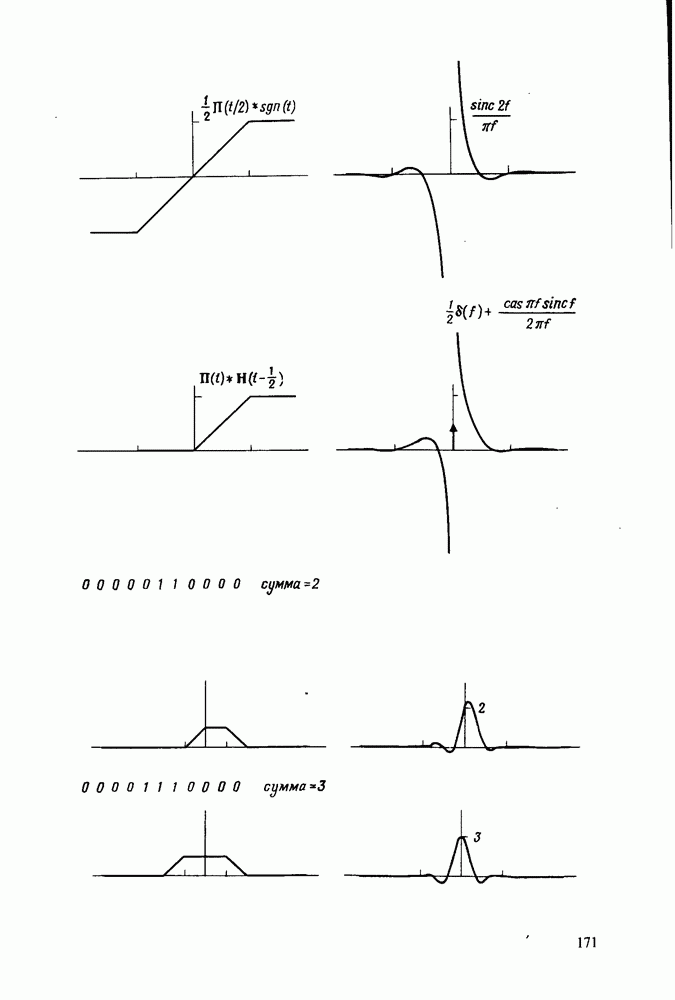
Числовой пример свертки
Вышеприведенный пример теперь можно использовать для иллюстрации метода преобразования для осуществления свертки.
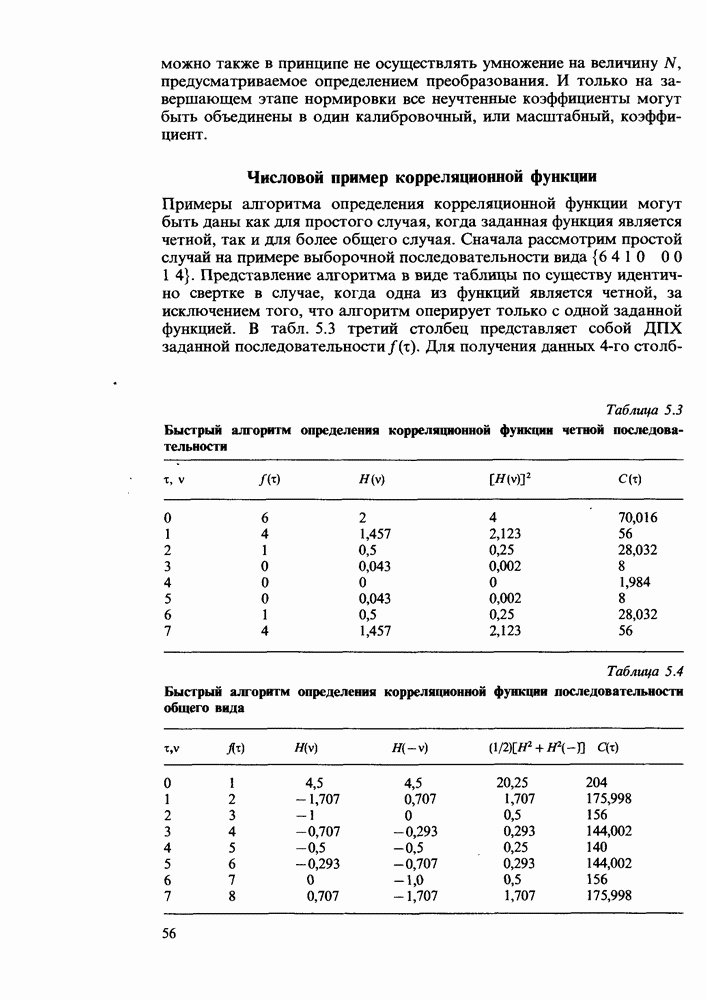
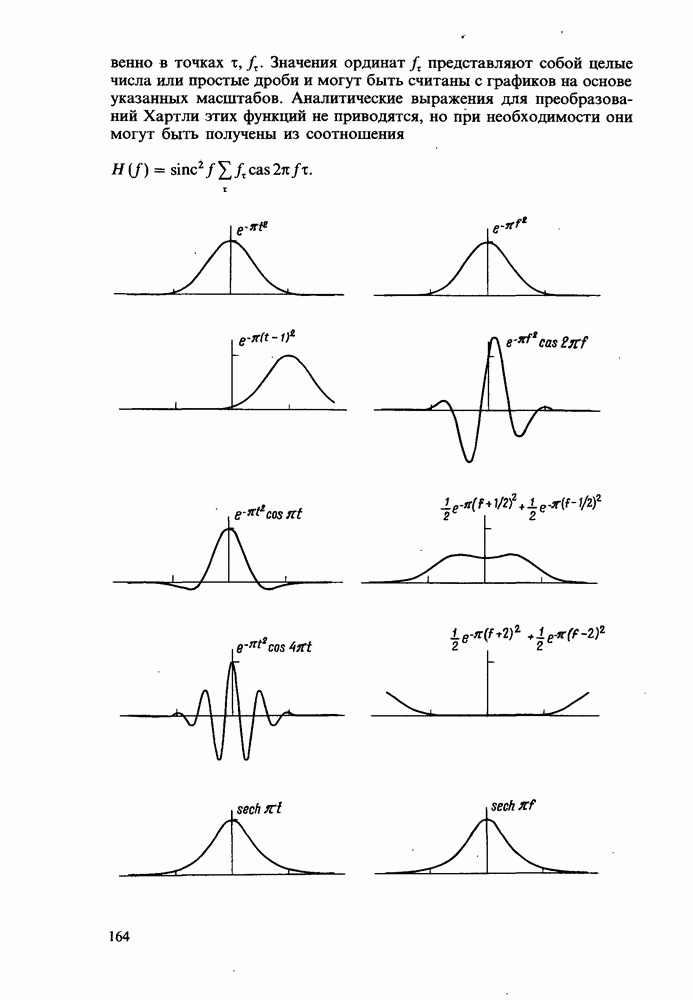
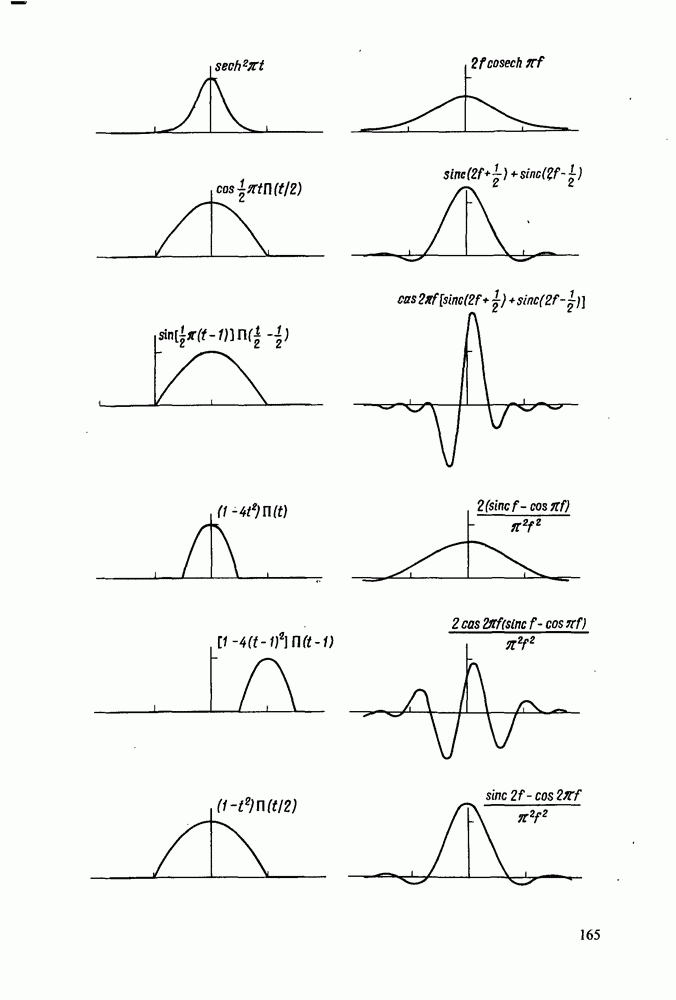
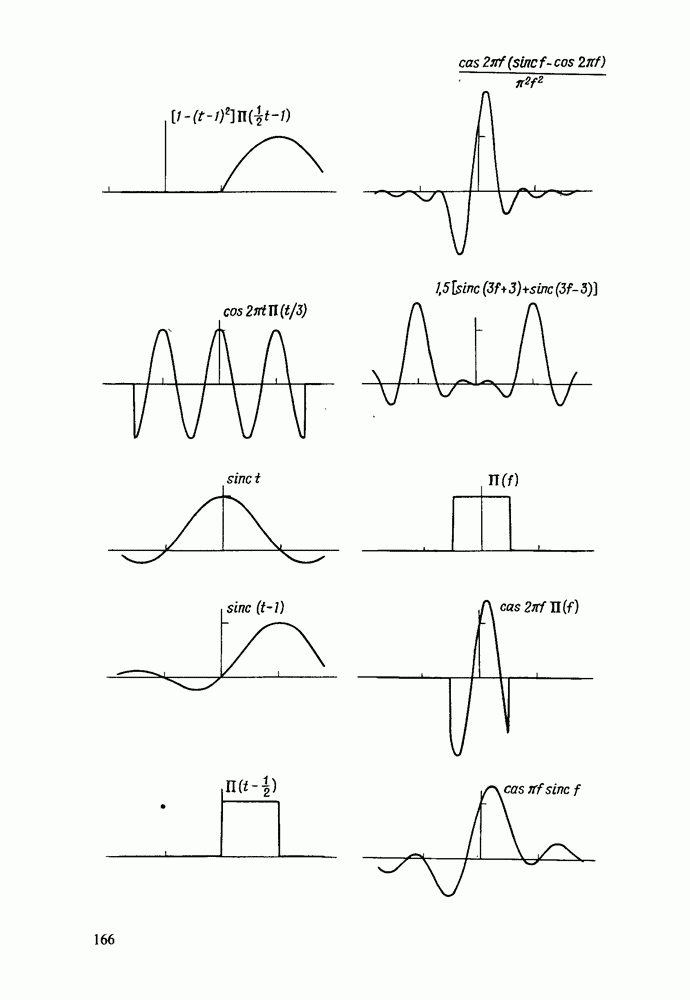
В табл. 5.1 в первых двух столбцах помещены две последовательности данных  подлежащие свертке. В следующих двух столбцах приводятся дискретные преобразования Хартли
подлежащие свертке. В следующих двух столбцах приводятся дискретные преобразования Хартли  Пятый столбец содержит произведение
Пятый столбец содержит произведение  , а последний - последовательность
, а последний - последовательность  которая представляет собой свертку, равную дискретному преобразованию Хартли столбца произведений
которая представляет собой свертку, равную дискретному преобразованию Хартли столбца произведений  умноженному на N. Появление коэффициента N обусловлено тем, что в определении ДПХ фигурирует коэффициент
умноженному на N. Появление коэффициента N обусловлено тем, что в определении ДПХ фигурирует коэффициент  Может оказаться более целесообразным умножение на
Может оказаться более целесообразным умножение на  на завершающем этапе вычислений в рамках нормировки, калибровки и других процедур.
на завершающем этапе вычислений в рамках нормировки, калибровки и других процедур.
Примечательно, что значения  приведенные в последнем столбце, отличаются от точных значений. Максимальное расхождение
приведенные в последнем столбце, отличаются от точных значений. Максимальное расхождение
Таблица 5.1. Процедура свертки

достигает в данном примере 0,0004. Однако приближенный характер результата в принципе свойствен методу с использованием преобразования, вычисляемого с конечной точностью.
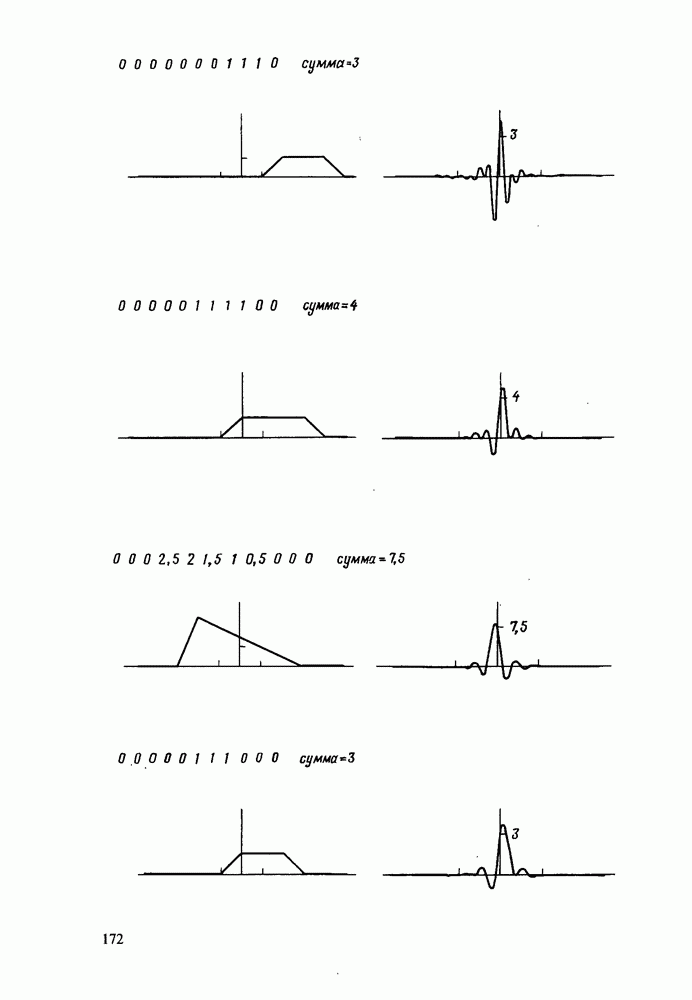
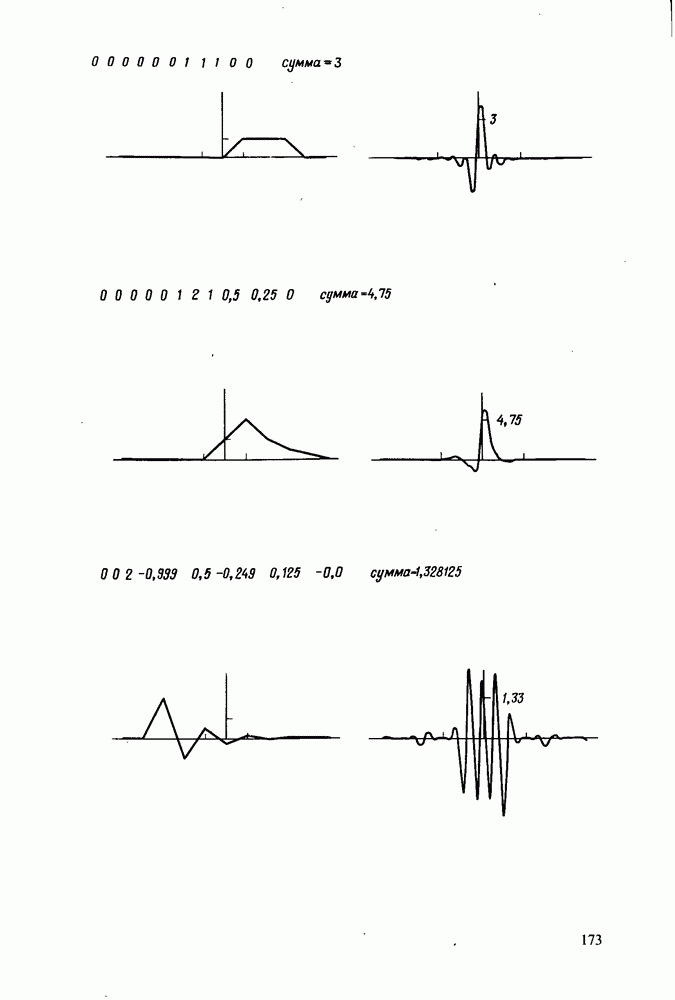
В табл. 5.2 представлен пример довольно общего характера. Все четыре произведения, фигурирующие в теореме о свертке, табулированы с использованием обозначения  . Предпоследний столбец содержит полусуммы элементов предыдущих четырех столбцов, а значения в последнем столбце представляют собой ДПХ столбца для суммы, умноженное на 8. При анализе столбцов, элементами которых являются произведения четырех видов, становится ясно, что 6-й столбец является зеркальным изображением 5-го столбца со знаком минус, а 8-й столбец - зеркальным изображением 7-го. Отсюда ясно, что нет необходимости выполнять четыре умножения, а достаточно двух. Один способ вычислений состоит в представлении требуемой суммы в виде
. Предпоследний столбец содержит полусуммы элементов предыдущих четырех столбцов, а значения в последнем столбце представляют собой ДПХ столбца для суммы, умноженное на 8. При анализе столбцов, элементами которых являются произведения четырех видов, становится ясно, что 6-й столбец является зеркальным изображением 5-го столбца со знаком минус, а 8-й столбец - зеркальным изображением 7-го. Отсюда ясно, что нет необходимости выполнять четыре умножения, а достаточно двух. Один способ вычислений состоит в представлении требуемой суммы в виде

что является другой формой записи тождественного выражения, приведенного в данной главе выше.
Подавляющее большинство сверток, реализуемых в численной форме в повседневной практике, требует только упрощенной процедуры, иллюстрируемой с помощью табл. 5.1. В приложении 1 приводится программа  реализующая эту свертку с использованием преобразования Хартли. Целесообразнее всего рассматривать эту программу как реализацию циклической свертки, однако она может быть использована и для выполнения обычной свертки путем дополнения данных достаточным количеством нулей для предотвращения наложения. Почти всегда необходимо дополнять одну из двух последовательностей нулями, но при большом количестве дополнительных нулей снижаются преимущества этого метода преобразования. Возможно, что непосредственное суммирование, реализуемое в программах
реализующая эту свертку с использованием преобразования Хартли. Целесообразнее всего рассматривать эту программу как реализацию циклической свертки, однако она может быть использована и для выполнения обычной свертки путем дополнения данных достаточным количеством нулей для предотвращения наложения. Почти всегда необходимо дополнять одну из двух последовательностей нулями, но при большом количестве дополнительных нулей снижаются преимущества этого метода преобразования. Возможно, что непосредственное суммирование, реализуемое в программах  и
и  окажется более быстрой процедурой; проверку достоверности этой возможности следует осуществлять путем сравнения времени машинного счета, когда число элементов более короткой последовательности меньше или сравнимо с логарифмом
окажется более быстрой процедурой; проверку достоверности этой возможности следует осуществлять путем сравнения времени машинного счета, когда число элементов более короткой последовательности меньше или сравнимо с логарифмом
Таблица 5.2. Свертка несимметричных последовательностей

(по основанию 2) числа элементов более длинной последовательности.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
- Глава 2. ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Преобразование Хартли
- Четная и нечетная составляющие
- Формулы связи
- Примеры
- Энергетический и фазовый спектры
- Глава 3. ТЕОРЕМЫ
- Свертка
- Соотношения между преобразованиями во временной и частотой областях
- Глава 4. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Физический смысл величин «тау» и v
- Четная и нечетная составляющие
- Примеры дискретных преобразований Хартли
- Степени свободы
- Другие вещественные ядра
- Теоремы
- Выводы
- Глава 5. ЦИФРОВАЯ ФИЛЬТРАЦИЯ ПОСРЕДСТВОМ СВЕРТКИ
- Циклическая свертка
- Дополнение нулями
- Обращение свертки
- Теорема о свертке
- Теорема о свертке в частотной области (спектральное сглаживание)
- Числовой пример свертки
- Коэффициент
- Числовой пример корреляционной функции
- Низкочастотная фильтрация
- Подчеркивание границ
- Свертка с использованием быстрого преобразования Хартли
- Способ без использования перестановок
- Свертка как умножение матриц
- Глава 6. Двумерные преобразования
- Двумерное преобразование Хартли
- Симметрия и антисимметрия
- Примеры
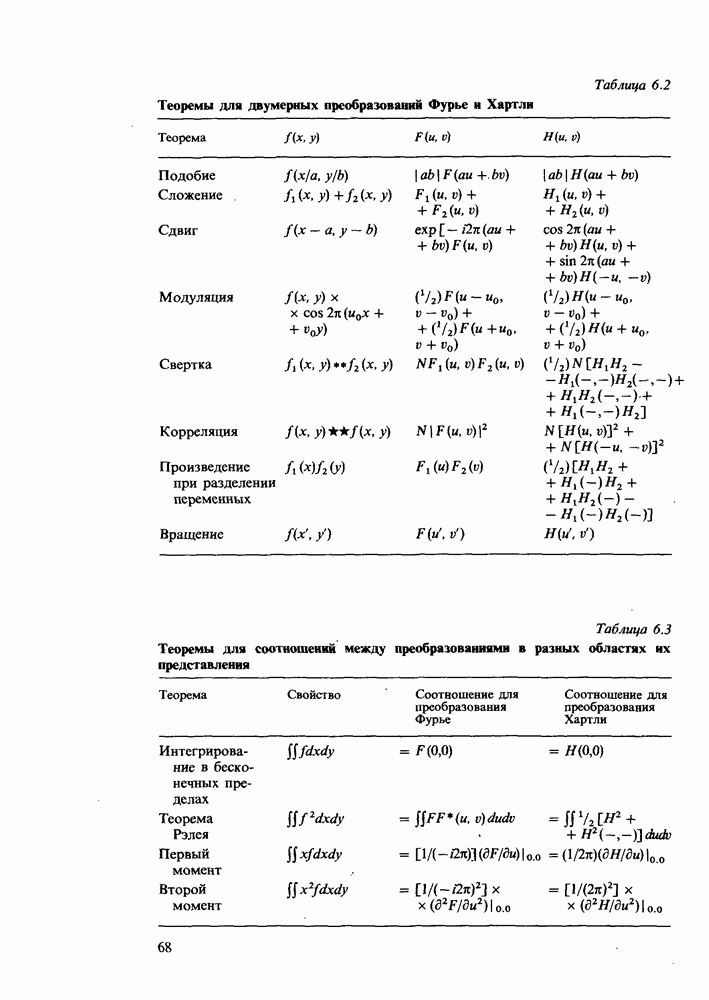
- Теоремы для двумерных преобразований
- Круговая симметрия
- Двумерная фильтрация
- Цикличность для двумерного случая
- Трехмерный случай
- Глава 7. ФАКТОРИЗАЦИЯ МАТРИЦЫ ПРЕОБРАЗОВАНИЯ
- Перестановка
- Перестановочные диаграммы
- Перестановочная матрица
- Ячеистая структура перестановочной диаграммы
- Каскадные матрицы
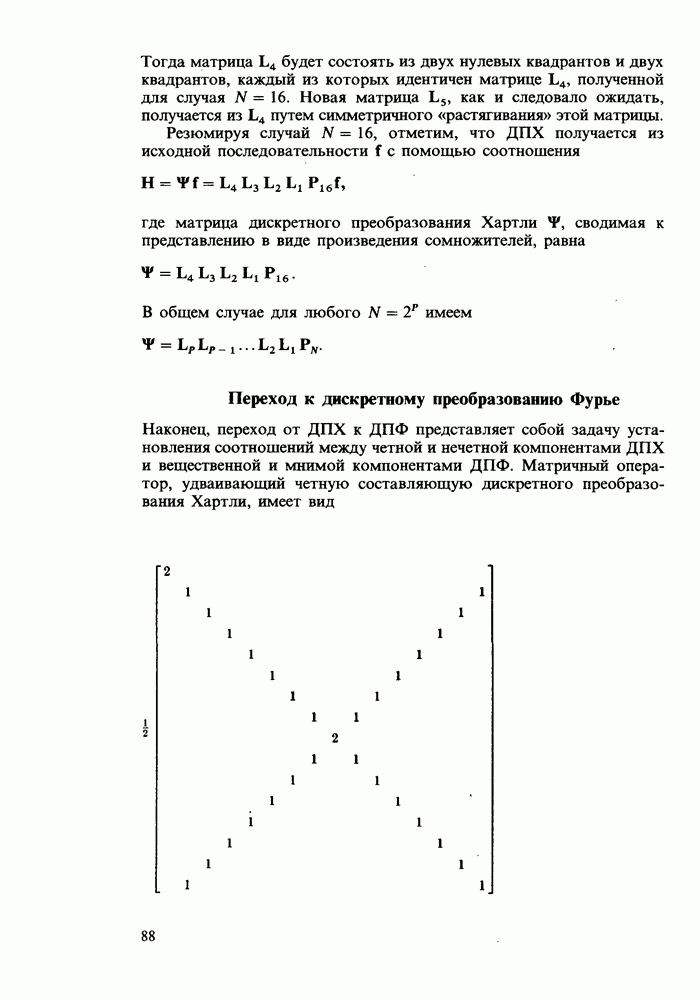
- Переход к дискретному преобразованию Фурье
- Глава 8. АЛГОРИТМ БЫСТРОГО ПРЕОБРАЗОВАНИЯ
- Свойство N log N
- Повторное разбиение последовательностей
- Преобразование с использованием разложения на подпоследовательности
- Общая формула разложения.
- Направленный сигнальный граф
- Вычисление с замещением
- Анализ временных затрат на вычисление с помощью полосковой диаграммы
- Степепи числа 2
- Тригонометрические функции
- Быстрое вычисление синусов
- Операция быстрого поворота
- Быстрая перестановка
- Преобразование для последовательностей с основанием 4 и другие модификации
- Ранее применявшиеся подходы к преобразованию вещественных данных
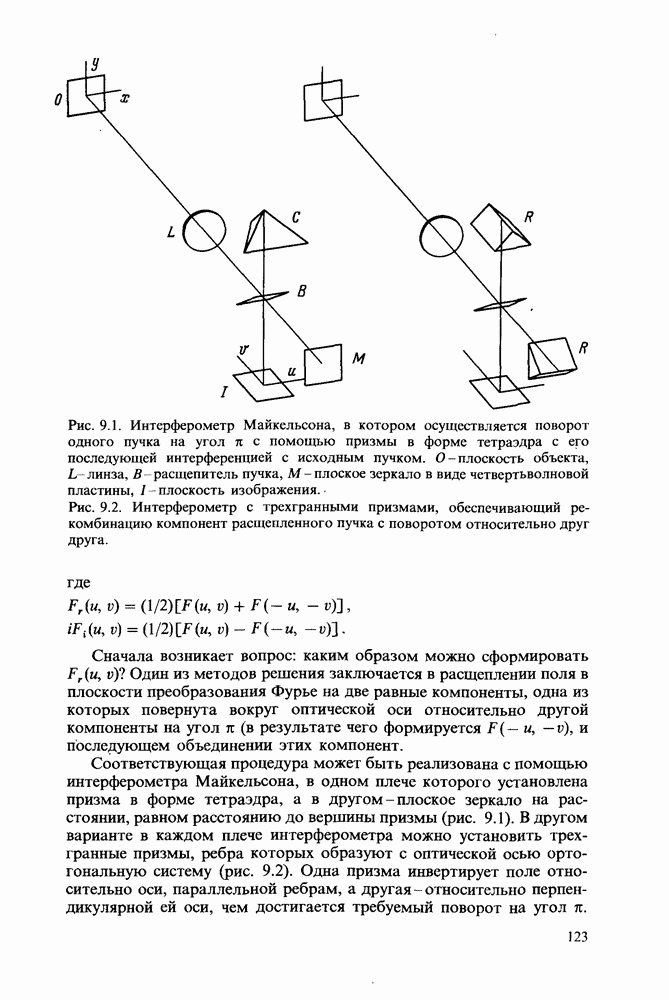
- Глава 9. ПРЕОБРАЗОВАНИЕ ХАРТЛИ В ОПТИКЕ
- Свойства симметрии
- Осуществление преобразования Хартли, использующее поляризацию
- Практическое осуществление
- Источник некогерентного излучения
- Пример
- Голография в плоскости Хартли
- Приложение 1. ПРОГРАММЫ ВЫЧИСЛЕНИЙ НА ЭВМ
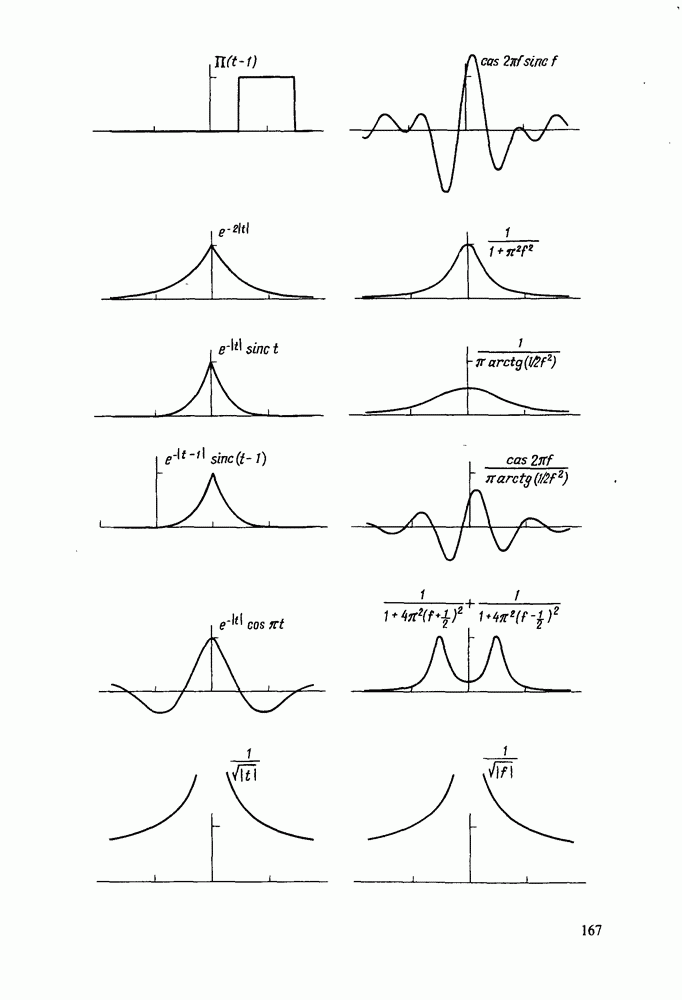
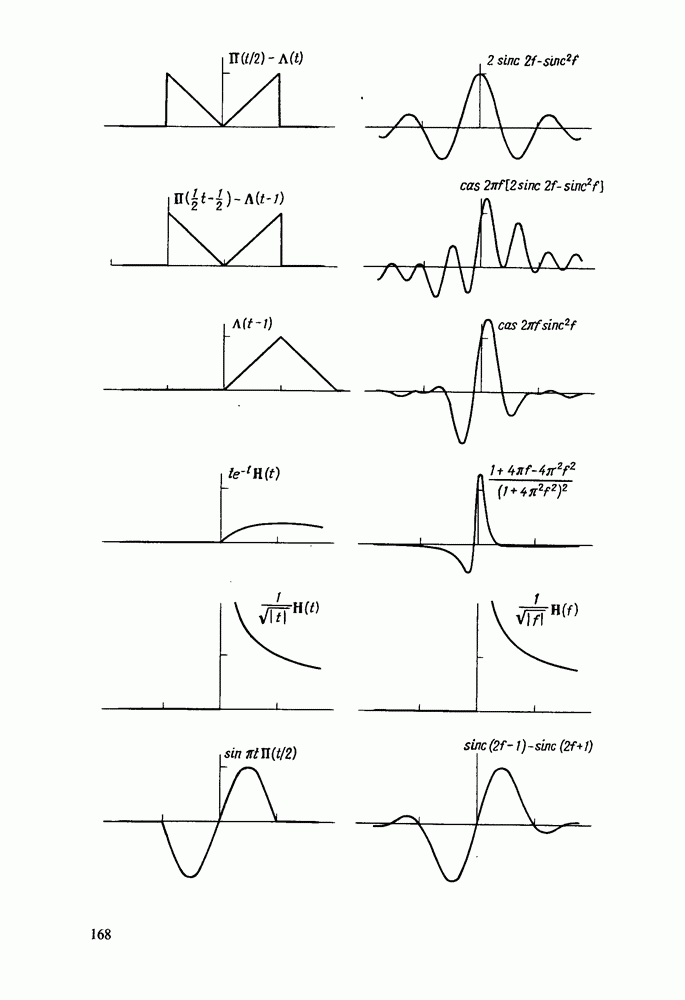
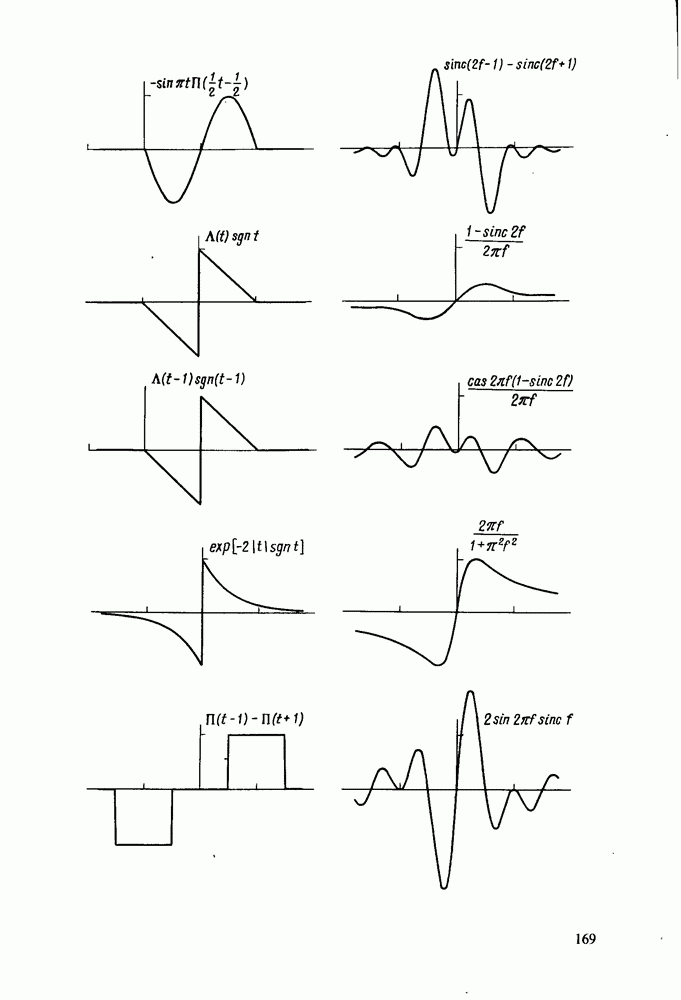
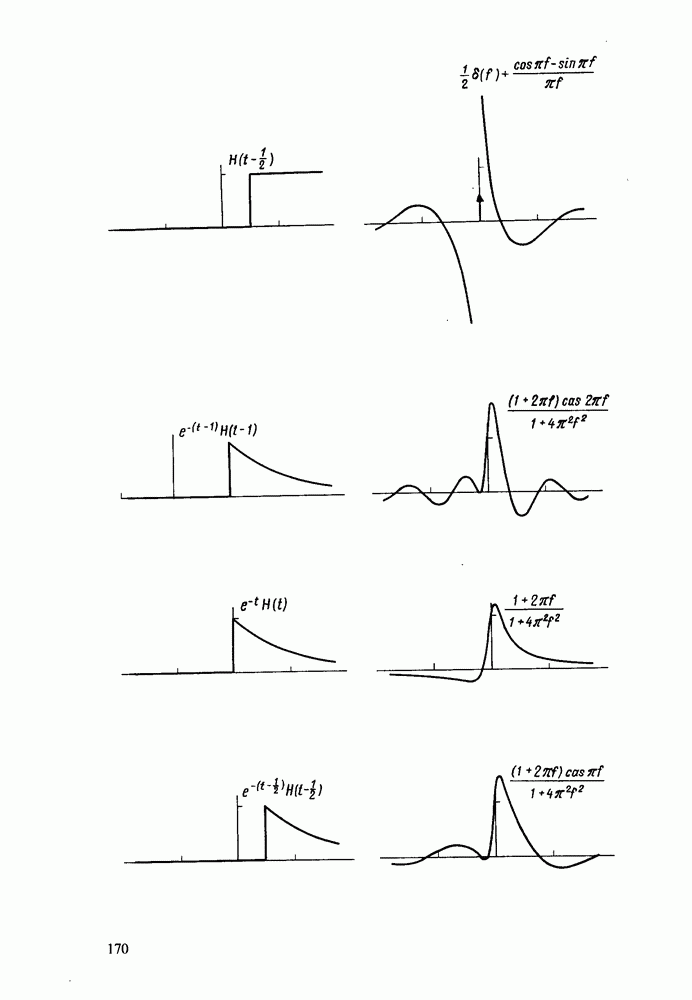
- Приложение 2. АТЛАС ПРЕОБРАЗОВАНИЙ ХАРТЛИ