| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Примеры
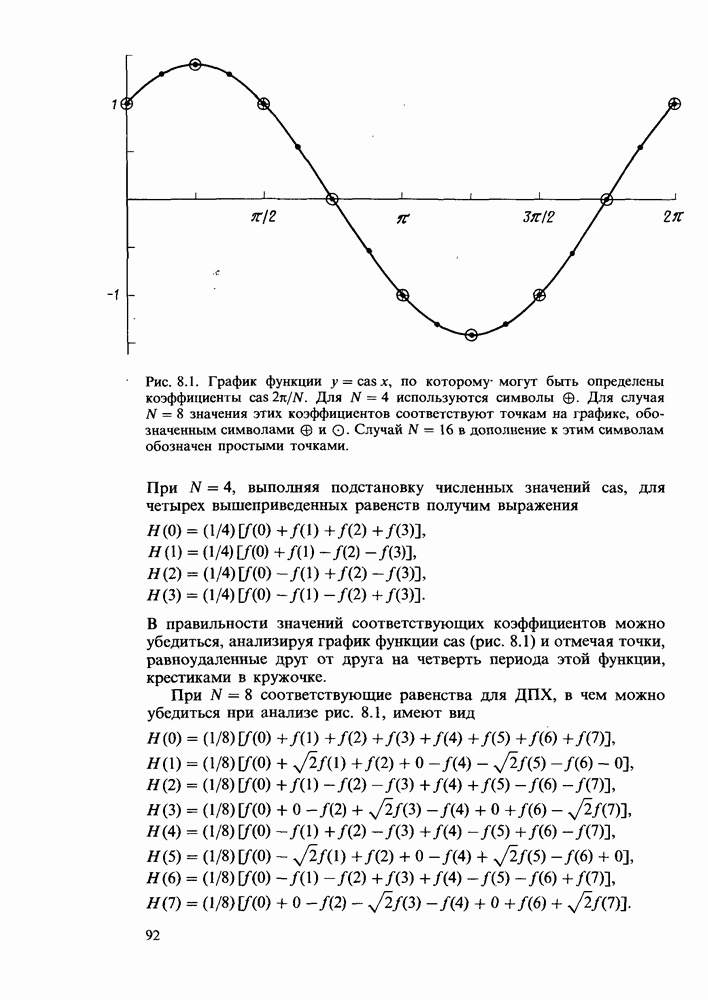
С целью иллюстрации может быть получен ряд частных преобразований.
Усеченная экспонента. В качестве первого примера рассмотрим функцию вида  которая в момент времени
которая в момент времени  имеет единичный скачок, а затем монотонно убывает по экспоненциальному закону. В данном выражении фигурирует единичная ступенчатая функция Хевисайда
имеет единичный скачок, а затем монотонно убывает по экспоненциальному закону. В данном выражении фигурирует единичная ступенчатая функция Хевисайда  которая определяется следующим образом:
которая определяется следующим образом:

Заметим, что значение функции  при
при  не определено. Причина этого заключается в следующем. Рассмотрим две функции
не определено. Причина этого заключается в следующем. Рассмотрим две функции  которые совпадают с
которые совпадают с  при
при  но в отличие от
но в отличие от  определены при
определены при  . Пусть
. Пусть  . Тогда разность
. Тогда разность  представляет собой нулевую функцию. Поскольку рассматриваются интегралы, на их величину не влияет выбор какого-либо определенного конечного значения
представляет собой нулевую функцию. Поскольку рассматриваются интегралы, на их величину не влияет выбор какого-либо определенного конечного значения  . Имея это в виду, представляется более благоразумным недоопределить
. Имея это в виду, представляется более благоразумным недоопределить

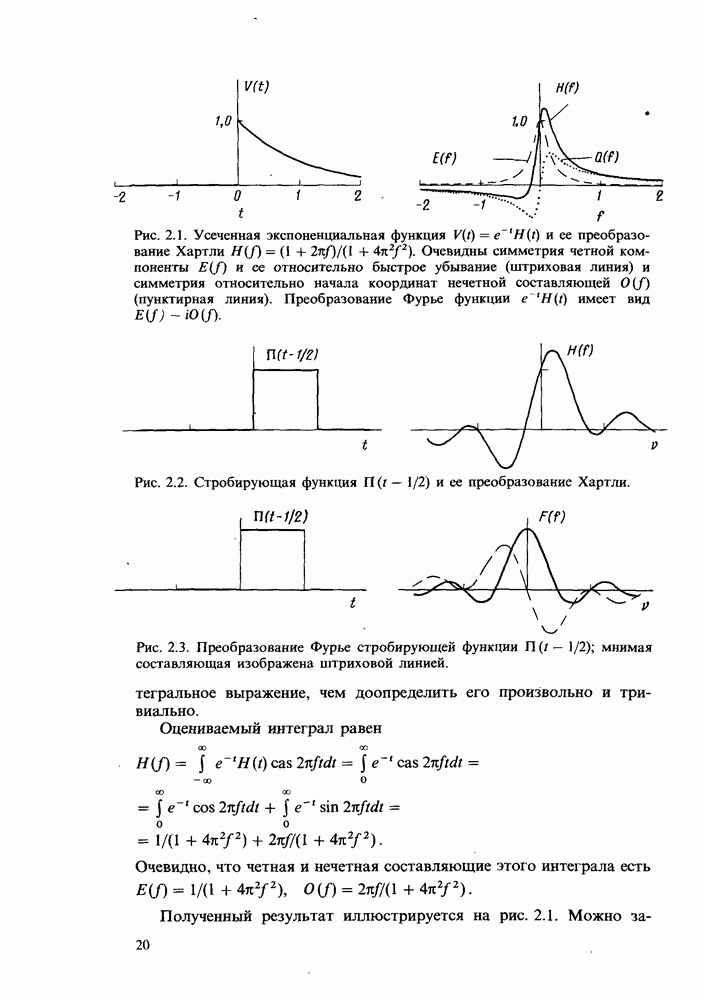
Рис. 2.1. Усеченная экспоненциальная функция  и ее преобразование Хартли
и ее преобразование Хартли  Очевидны симметрия четной компоненты
Очевидны симметрия четной компоненты  и ее относительно быстрое убывание (штриховая линия) и симметрия относительно начала координат нечетной составляющей
и ее относительно быстрое убывание (штриховая линия) и симметрия относительно начала координат нечетной составляющей  (пунктирная линия). Преобразование Фурье функции
(пунктирная линия). Преобразование Фурье функции  имеет вид
имеет вид  .
.

Рис. 2.2. Стробирующая функция  и ее преобразование Хартли.
и ее преобразование Хартли.

Рис. 2.3. Преобразование Фурье стробирующей функции  ; мнимая составляющая изображена штриховой линией.
; мнимая составляющая изображена штриховой линией.
подынтегральное выражение, чем доопределить его произвольно и тривиально.
Оцениваемый интеграл равен

Очевидно, что четная и нечетная составляющие этого интеграла есть

Полученный результат иллюстрируется на рис. 2.1. Можно
заметить, что  не является ни четной, ни нечетной функцией. Минимум функции
не является ни четной, ни нечетной функцией. Минимум функции  имеет место при
имеет место при  максимум - при
максимум - при  и она обращается в нуль при
и она обращается в нуль при  При
При  функция убывает как
функция убывает как 
Для сравнения с преобразованием Фурье необходим анализ четной и нечетной составляющих преобразования Хартли: четная составляющая  показана штриховой линией, а нечетная О (
показана штриховой линией, а нечетная О ( -пунктирной. Для преобразования Фурье имеем
-пунктирной. Для преобразования Фурье имеем

это известный результат, который может быть подтвержден при отдельном рассмотрении. Одна из этих составляющих является четной, а другая - нечетной.  вещественная составляющая быстро убывает как
вещественная составляющая быстро убывает как  тогда как мнимая компонента убывает по абсолютной величине относительно медленно. В результате
тогда как мнимая компонента убывает по абсолютной величине относительно медленно. В результате  мнимая компонента доминирует в спектре. Например, при
мнимая компонента доминирует в спектре. Например, при  отношение мнимой составляющей к вещественной равно 12,6.
отношение мнимой составляющей к вещественной равно 12,6.
Прямоугольный импульс. В качестве следующего примера рассмотрим сигнал  изображенный на рис. 2.2 слева, где
изображенный на рис. 2.2 слева, где  -смещенная единичная прямоугольная функция, имеющая свое начало при
-смещенная единичная прямоугольная функция, имеющая свое начало при  Стандартная единичная прямоугольная функция, которая часто необходима для стробирования сегментов колебаний, определяется как
Стандартная единичная прямоугольная функция, которая часто необходима для стробирования сегментов колебаний, определяется как

Для данного примера имеем преобразование Хартли

которое иллюстрируется на рис. 2.2. Здесь вновь наблюдается отсутствие симметрии. Для сравнения на рис. 2.3 приводится график преобразования Фурье, определяемого выражением

Как обычно, вещественная часть является четной, а мнимая - нечетной функцией.
Единичный импульс. В качестве примера другого рода рассмотрим единичный импульс для момента времени  так что
так что 
 Тогда
Тогда

Этот результат обусловлен использованием фильтрующего свойства  -функции, а именно:
-функции, а именно:

Другими словами, интегрирование произведения единичного импульса ( -функции) и данной функции аннулирует («стирает») значения этой исходной функции при всех значениях аргумента, исключая то из них, при котором существует
-функции) и данной функции аннулирует («стирает») значения этой исходной функции при всех значениях аргумента, исключая то из них, при котором существует  -функция, и восстанавливается исходная функция в точке, где локализована
-функция, и восстанавливается исходная функция в точке, где локализована  -функция.
-функция.
Теорема о фильтрующем свойстве  -функции может рассматриваться как отправная точка в теории обобщенных функций, что и делается в математическом труде Шварца [L. Schwartz. La Theorie des Distributions, Herman, 1950 (Л. Шварц. Теория распределений)]; при другом подходе теория может быть разработана как следствие предельных операций, позаимствованных из физики. Существуют три математических правила, резюмирующие подход с позиций физических задач, в которых возникают импульсы.
-функции может рассматриваться как отправная точка в теории обобщенных функций, что и делается в математическом труде Шварца [L. Schwartz. La Theorie des Distributions, Herman, 1950 (Л. Шварц. Теория распределений)]; при другом подходе теория может быть разработана как следствие предельных операций, позаимствованных из физики. Существуют три математических правила, резюмирующие подход с позиций физических задач, в которых возникают импульсы.
1. Заменить  на
на  [Точки в скобках означают наличие совокупности символов. Это дает возможность рассматривать
[Точки в скобках означают наличие совокупности символов. Это дает возможность рассматривать  и в общем случае
и в общем случае 
2. Выполнить интегрирование или другую указанную операцию, что не должно представлять труда, так как  может принимать только два значения: 0 и 1.
может принимать только два значения: 0 и 1.
3. Осуществить в выражении, полученном в результате выполнения  предельный переход при
предельный переход при 
Полученное в результате предельного перехода значение интеграла или другое выражение, содержит  Применим эти правила к интегралу, который выше был определен с использованием теоремы
Применим эти правила к интегралу, который выше был определен с использованием теоремы
0 фильтрующем свойстве  -функции:
-функции:

Применив правило 1, получим

Пределы интегрирования могут быть изменены, как показано, потому что функция  центрирована относительно точки
центрирована относительно точки  и имеет длительность
и имеет длительность  , таким образом, не равна нулю только в интервале
, таким образом, не равна нулю только в интервале  Теперь перейдем к правилу 2:
Теперь перейдем к правилу 2:

Рис. 2.4. Преобразование Хартли импульса с критическим затуханием вида 

Наконец, используя правило 3, перейдем к пределу при  в результате чего, как и выше, получим:
в результате чего, как и выше, получим:  Очевидно, применение теоремы о фильтрующем свойстве является менее трудоемким, однако общий подход с использованием приведенных выше трех правил всегда оказывается работоспособным и легким в практическом применении.
Очевидно, применение теоремы о фильтрующем свойстве является менее трудоемким, однако общий подход с использованием приведенных выше трех правил всегда оказывается работоспособным и легким в практическом применении.
Импульс с критическим затуханием. Колебание  известно как импульсная характеристика резонатора с критическим затуханием, т. е. резонатора, затухание которого не столь мало, чтобы импульсная характеристика превосходила определенный уровень, и не столь велико, чтобы было невозможно оценить инерционные характеристики системы. В данном случае (рис. 2.4) имеем
известно как импульсная характеристика резонатора с критическим затуханием, т. е. резонатора, затухание которого не столь мало, чтобы импульсная характеристика превосходила определенный уровень, и не столь велико, чтобы было невозможно оценить инерционные характеристики системы. В данном случае (рис. 2.4) имеем

При выполнении интегрирования целесообразно использовать таблицы интегралов. Другой подход заключается в применении известных теорем. Например, при известном преобразовании колебания  можно непосредственно получить преобразование функции
можно непосредственно получить преобразование функции  . В следующей главе для справки приводится ряд основных теорем.
. В следующей главе для справки приводится ряд основных теорем.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
- Глава 2. ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Преобразование Хартли
- Четная и нечетная составляющие
- Формулы связи
- Примеры
- Энергетический и фазовый спектры
- Глава 3. ТЕОРЕМЫ
- Свертка
- Соотношения между преобразованиями во временной и частотой областях
- Глава 4. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Физический смысл величин «тау» и v
- Четная и нечетная составляющие
- Примеры дискретных преобразований Хартли
- Степени свободы
- Другие вещественные ядра
- Теоремы
- Выводы
- Глава 5. ЦИФРОВАЯ ФИЛЬТРАЦИЯ ПОСРЕДСТВОМ СВЕРТКИ
- Циклическая свертка
- Дополнение нулями
- Обращение свертки
- Теорема о свертке
- Теорема о свертке в частотной области (спектральное сглаживание)
- Числовой пример свертки
- Коэффициент
- Числовой пример корреляционной функции
- Низкочастотная фильтрация
- Подчеркивание границ
- Свертка с использованием быстрого преобразования Хартли
- Способ без использования перестановок
- Свертка как умножение матриц
- Глава 6. Двумерные преобразования
- Двумерное преобразование Хартли
- Симметрия и антисимметрия
- Примеры
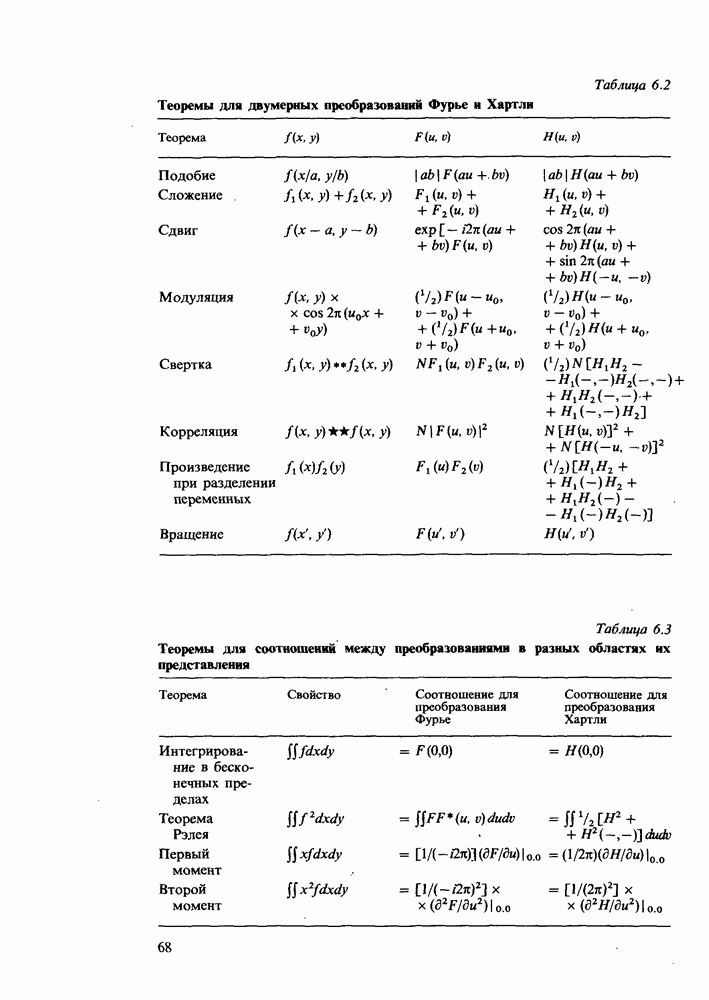
- Теоремы для двумерных преобразований
- Круговая симметрия
- Двумерная фильтрация
- Цикличность для двумерного случая
- Трехмерный случай
- Глава 7. ФАКТОРИЗАЦИЯ МАТРИЦЫ ПРЕОБРАЗОВАНИЯ
- Перестановка
- Перестановочные диаграммы
- Перестановочная матрица
- Ячеистая структура перестановочной диаграммы
- Каскадные матрицы
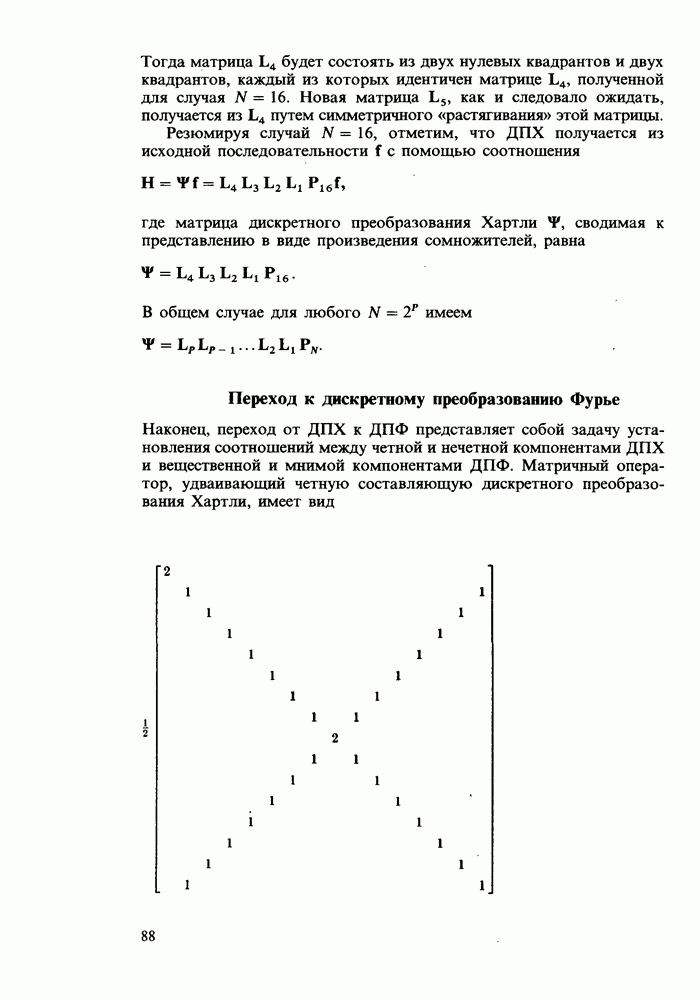
- Переход к дискретному преобразованию Фурье
- Глава 8. АЛГОРИТМ БЫСТРОГО ПРЕОБРАЗОВАНИЯ
- Свойство N log N
- Повторное разбиение последовательностей
- Преобразование с использованием разложения на подпоследовательности
- Общая формула разложения.
- Направленный сигнальный граф
- Вычисление с замещением
- Анализ временных затрат на вычисление с помощью полосковой диаграммы
- Степепи числа 2
- Тригонометрические функции
- Быстрое вычисление синусов
- Операция быстрого поворота
- Быстрая перестановка
- Преобразование для последовательностей с основанием 4 и другие модификации
- Ранее применявшиеся подходы к преобразованию вещественных данных
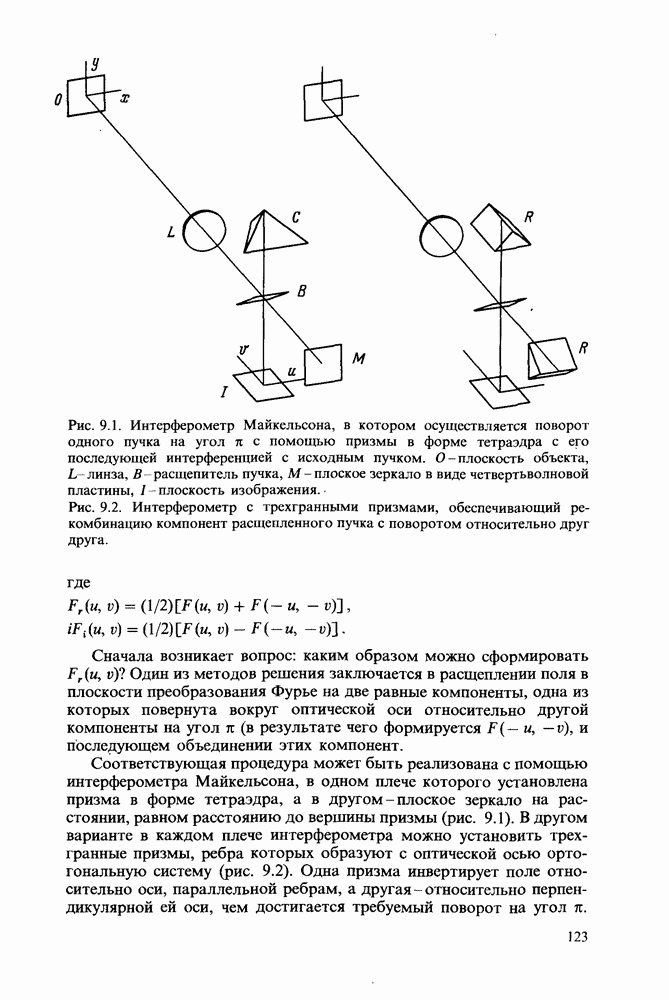
- Глава 9. ПРЕОБРАЗОВАНИЕ ХАРТЛИ В ОПТИКЕ
- Свойства симметрии
- Осуществление преобразования Хартли, использующее поляризацию
- Практическое осуществление
- Источник некогерентного излучения
- Пример
- Голография в плоскости Хартли
- Приложение 1. ПРОГРАММЫ ВЫЧИСЛЕНИЙ НА ЭВМ
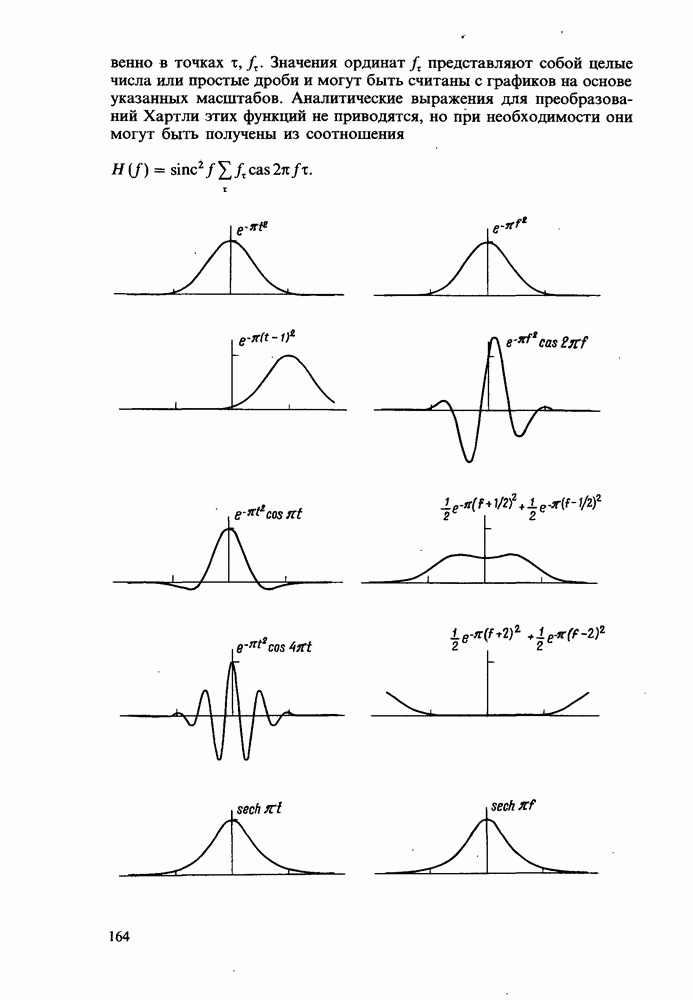
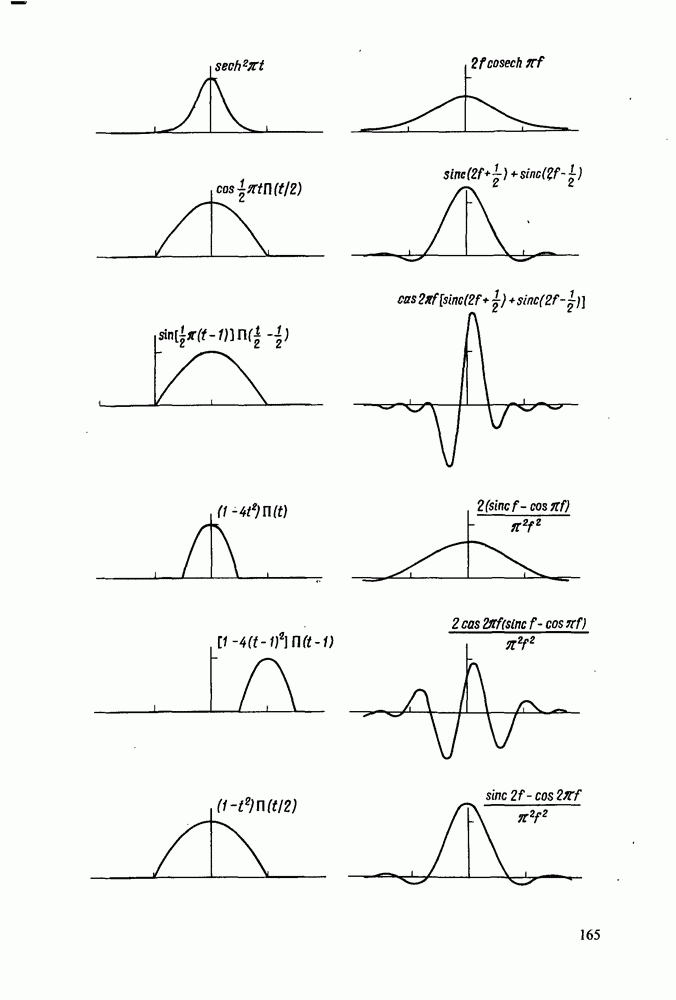
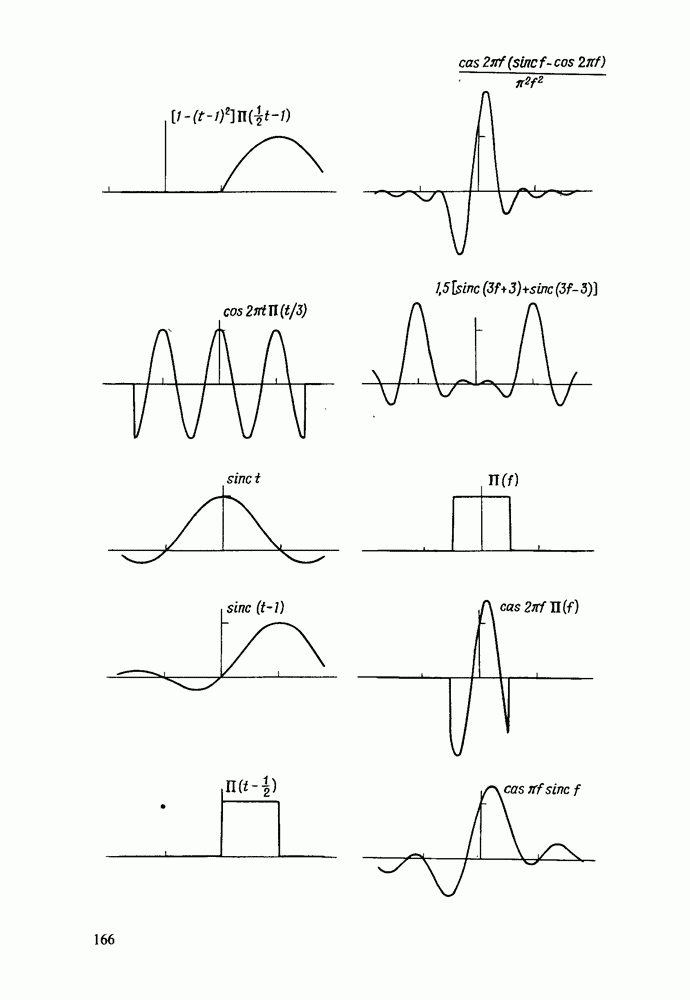
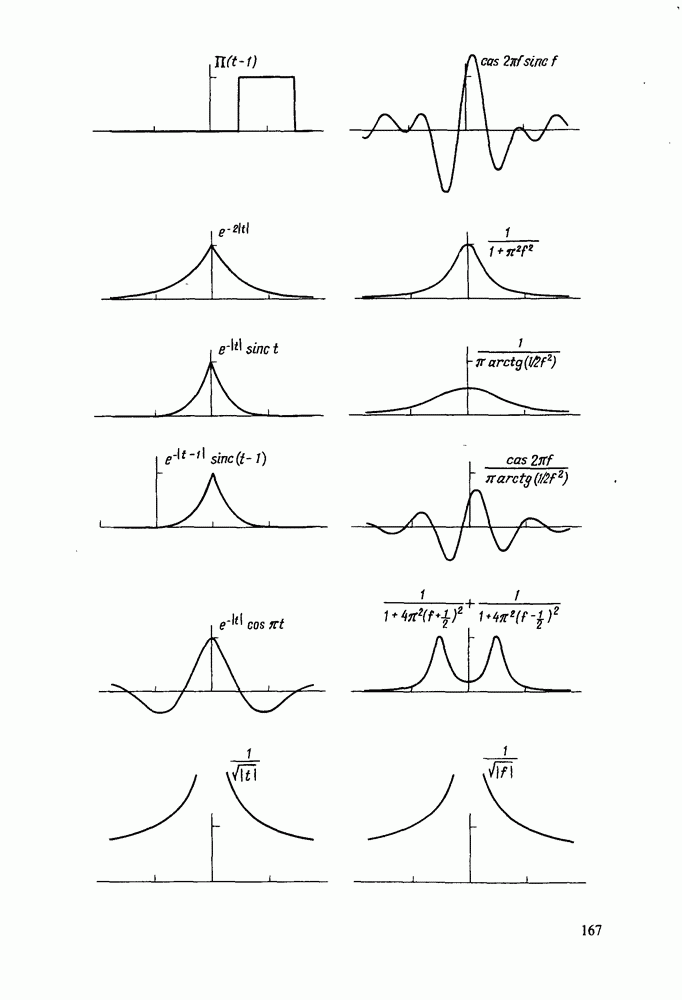
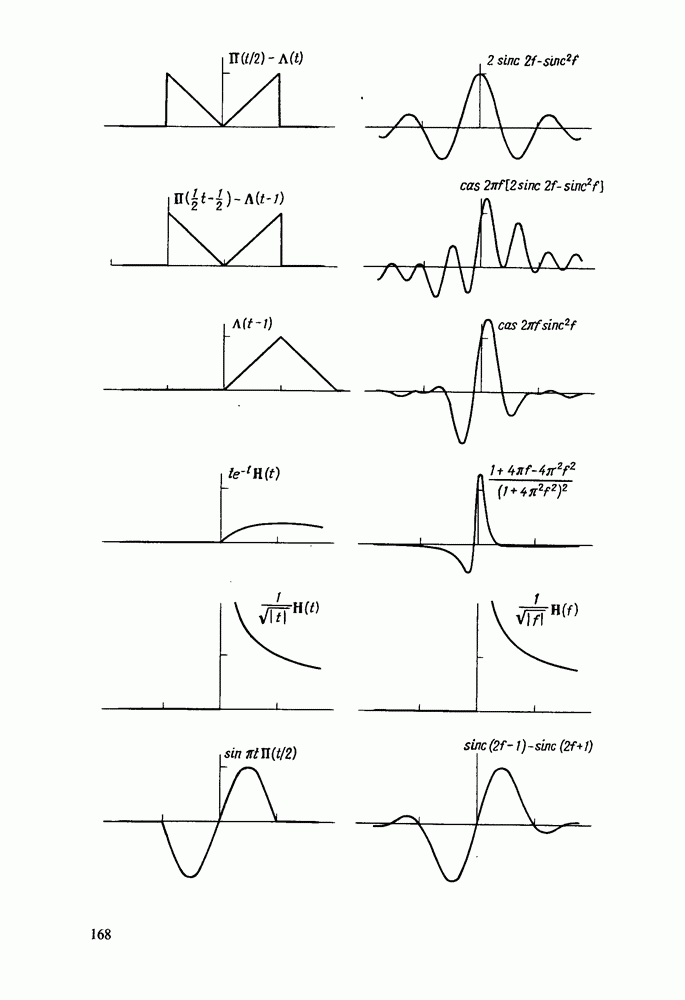
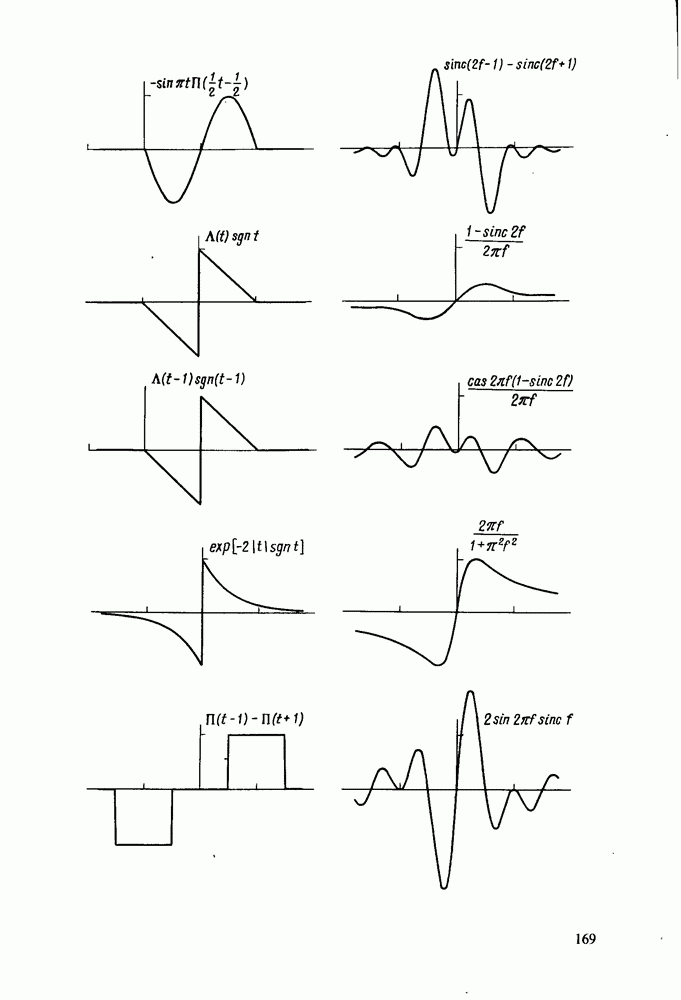
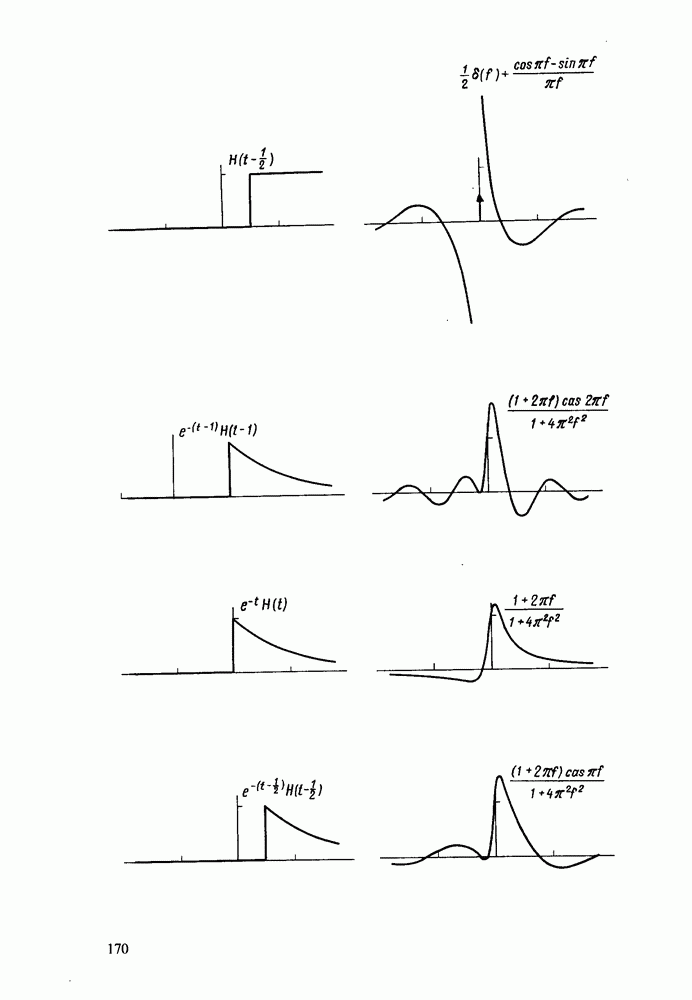
- Приложение 2. АТЛАС ПРЕОБРАЗОВАНИЙ ХАРТЛИ