| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Энергетический и фазовый спектры
Не всегда легко понять характер изменения комплексной функции, имея графики ее вещественной и мнимой частей, однако в оптике и других областях физики более привычным является использование понятия квадрата модуля преобразования, или энергетического спектра:


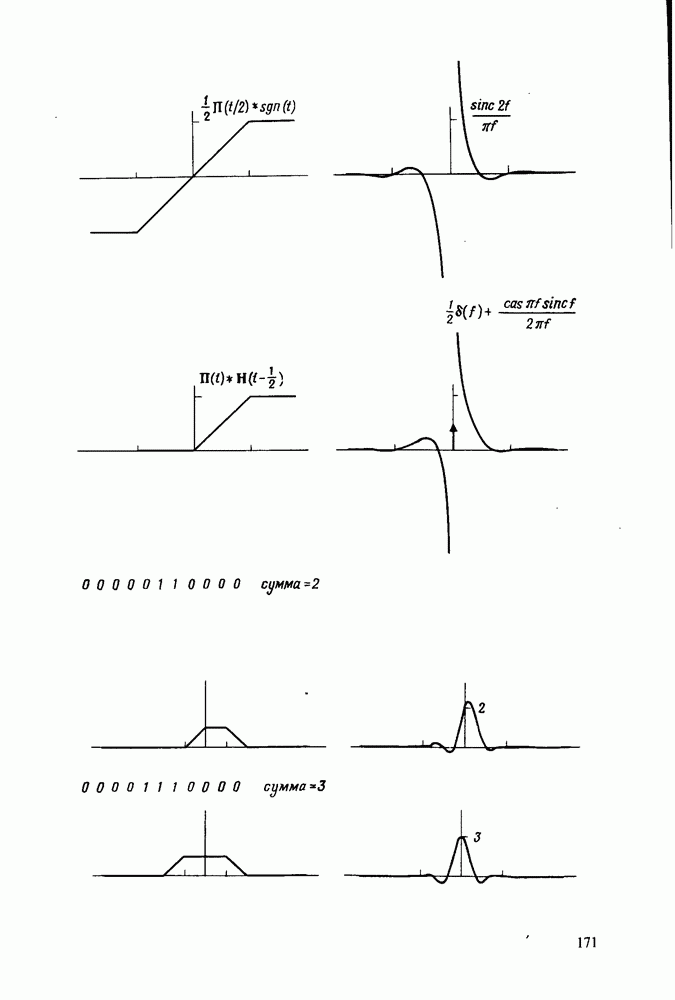
Рис. 2.5. Энергетический спектр (слева) и фазовый спектр (справа) стробирующей функции 
Энергетический спектр является четной функцией частоты и поэтому более прост для понимания. С другой стороны, энергетический спектр содержит в себе по крайней мере половину информации об исходном колебании, так как теряется информация о фазе. Тем не менее для ряда приложений энергетический спектр может оказаться инструментом исследования, который необходим.
Энергетический спектр можно получить непосредственно из преобразования Хартли. Имеем

Таким образом, вместо возведения в квадрат вещественной и мнимой частей и их суммирования при данном значении  мы возводим в квадрат и суммируем два значения преобразования Хартли для частот
мы возводим в квадрат и суммируем два значения преобразования Хартли для частот  При этом результат суммирования должен быть разделен на два, так как каждая из функций вида
При этом результат суммирования должен быть разделен на два, так как каждая из функций вида  возведенная в квадрат, равна полному энергетическому спектру, тогда как вещественная и мнимая части содержат по половине этой величины.
возведенная в квадрат, равна полному энергетическому спектру, тогда как вещественная и мнимая части содержат по половине этой величины.
В оптике представляет затруднение измерение фазы преобразования Фурье, однако в анализе сигналов рассмотрение фазовых функций (фазочастотных характеристик) является привычной процедурой, хотя их понимание и толкование требуют определенной подготовки и опыта. Примеры энергетического спектра и фазовой функции иллюстрируются на рис. 2.5. Фазовая функция может быть непосредственно вычислена из выражения

Фаза преобразования Фурье может быть также непосредственно
получена из преобразования Хартли

В объяснении характера изменения фазы при изменении частоты оказывается полезным опыт. При интерпретации фазы следует учитывать, что поведение фазы непосредственно связано с амплитудой, причем большие фазовые изменения происходят вблизи нуля амплитуды, и наоборот - незначительные изменения фазы при больших амплитудах.
Имеем следующую формулу для определения фазы преобразования Фурье через преобразование Хартли:

Полезной альтернативой одновременному представлению вещественной и мнимой частей является построение траектории на комплексной плоскости путем изображения  как функции
как функции  с обозначением на этой траектории значений частоты как параметра. Тогда для любой данной частоты амплитуда
с обозначением на этой траектории значений частоты как параметра. Тогда для любой данной частоты амплитуда  определяет расстояние от начала координат до соответствующей точки параметрически заданной кривой, а фаза преобразования определяет угловую координату. Такая диаграмма для функции
определяет расстояние от начала координат до соответствующей точки параметрически заданной кривой, а фаза преобразования определяет угловую координату. Такая диаграмма для функции  изображена на рис. 2.6. Комплексная плоскость для данной диаграммы - это не плоскость из теории функции комплексной переменной, где независимая переменная оказывается комплексной величиной. Здесь независимая переменная
изображена на рис. 2.6. Комплексная плоскость для данной диаграммы - это не плоскость из теории функции комплексной переменной, где независимая переменная оказывается комплексной величиной. Здесь независимая переменная  вещественна, однако зависимая переменная
вещественна, однако зависимая переменная  является
является

Рис. 2.6. Параметрически заданная кривая  на комплексной плоскости, где
на комплексной плоскости, где  рассматриваются как полярные координаты. Значения параметра
рассматриваются как полярные координаты. Значения параметра  фиксируются через интервалы, равные 0,2.
фиксируются через интервалы, равные 0,2.

Рис. 2.7. Представление комплексного преобразования в виде скрученной кривой, параметр которой обозначен через интервалы, равные 0,2. Вещественная и мнимая части заштрихованы.
комплексной, и можно рассматривать ее вещественную и мнимую части как декартовы координаты.
Заслуживает внимания тот факт, что при движении по траектории к началу координат скорость «вычерчивания» траектории, измеряемая отношением длины дуги к частотному интервалу, уменьшается таким образом, что угловая скорость «бегущей» точки на траектории остается постоянной. Это свойство отражает линейную природу графа  разрывы фазовой функции обусловлены прохождением траектории через начало координат.
разрывы фазовой функции обусловлены прохождением траектории через начало координат.
Можно также рассматривать это преобразование в виде трехмерной винтовой траектории, для которой в данном случае можем представить только перспективную проекцию, но может быть сделана проволочная модель этой кривой. На рис. 2.7 показана эта винтовая кривая, дополняющая наше представление еще одним измерением. Траекторию в полярных координатах можно представить в виде проекции винтовой кривой на плоскость  , а вещественную и мнимую части как проекции на горизонтальную и вертикальную плоскости прямоугольной системы координат соответственно.
, а вещественную и мнимую части как проекции на горизонтальную и вертикальную плоскости прямоугольной системы координат соответственно.
В определенном смысле преобразование Хартли может рассматриваться как гладкая форма представления вещественного колебания. Будучи чисто вещественным, преобразование Хартли не требует других способов представления, тогда как другие способы могут быть непосредственно получены из него.
Задачи
(см. скан)
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
- Глава 2. ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Преобразование Хартли
- Четная и нечетная составляющие
- Формулы связи
- Примеры
- Энергетический и фазовый спектры
- Глава 3. ТЕОРЕМЫ
- Свертка
- Соотношения между преобразованиями во временной и частотой областях
- Глава 4. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Физический смысл величин «тау» и v
- Четная и нечетная составляющие
- Примеры дискретных преобразований Хартли
- Степени свободы
- Другие вещественные ядра
- Теоремы
- Выводы
- Глава 5. ЦИФРОВАЯ ФИЛЬТРАЦИЯ ПОСРЕДСТВОМ СВЕРТКИ
- Циклическая свертка
- Дополнение нулями
- Обращение свертки
- Теорема о свертке
- Теорема о свертке в частотной области (спектральное сглаживание)
- Числовой пример свертки
- Коэффициент
- Числовой пример корреляционной функции
- Низкочастотная фильтрация
- Подчеркивание границ
- Свертка с использованием быстрого преобразования Хартли
- Способ без использования перестановок
- Свертка как умножение матриц
- Глава 6. Двумерные преобразования
- Двумерное преобразование Хартли
- Симметрия и антисимметрия
- Примеры
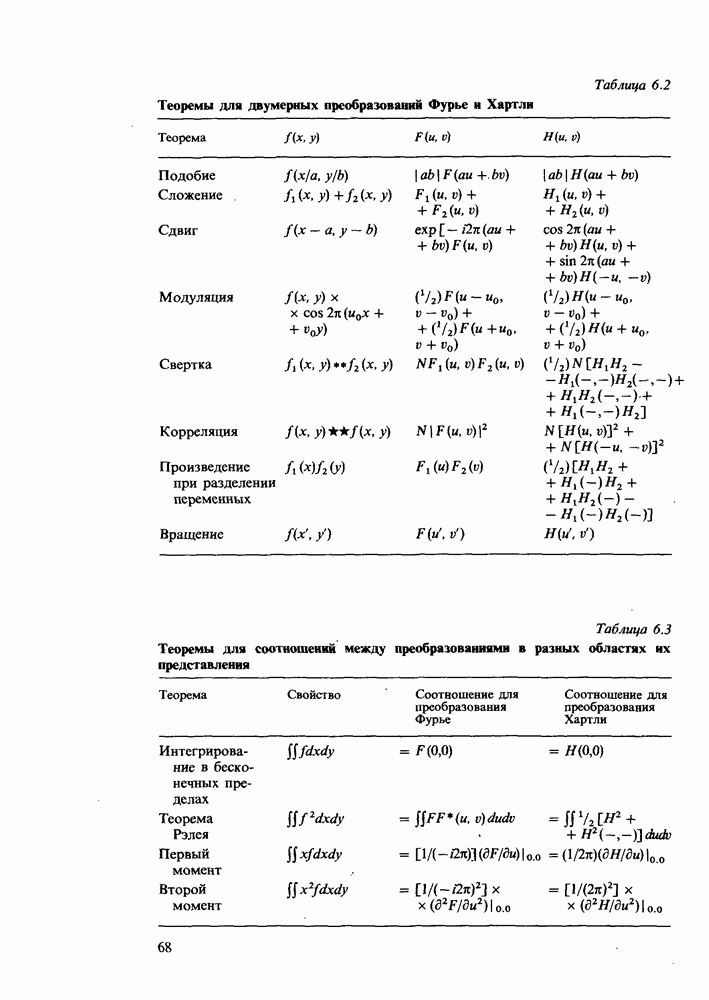
- Теоремы для двумерных преобразований
- Круговая симметрия
- Двумерная фильтрация
- Цикличность для двумерного случая
- Трехмерный случай
- Глава 7. ФАКТОРИЗАЦИЯ МАТРИЦЫ ПРЕОБРАЗОВАНИЯ
- Перестановка
- Перестановочные диаграммы
- Перестановочная матрица
- Ячеистая структура перестановочной диаграммы
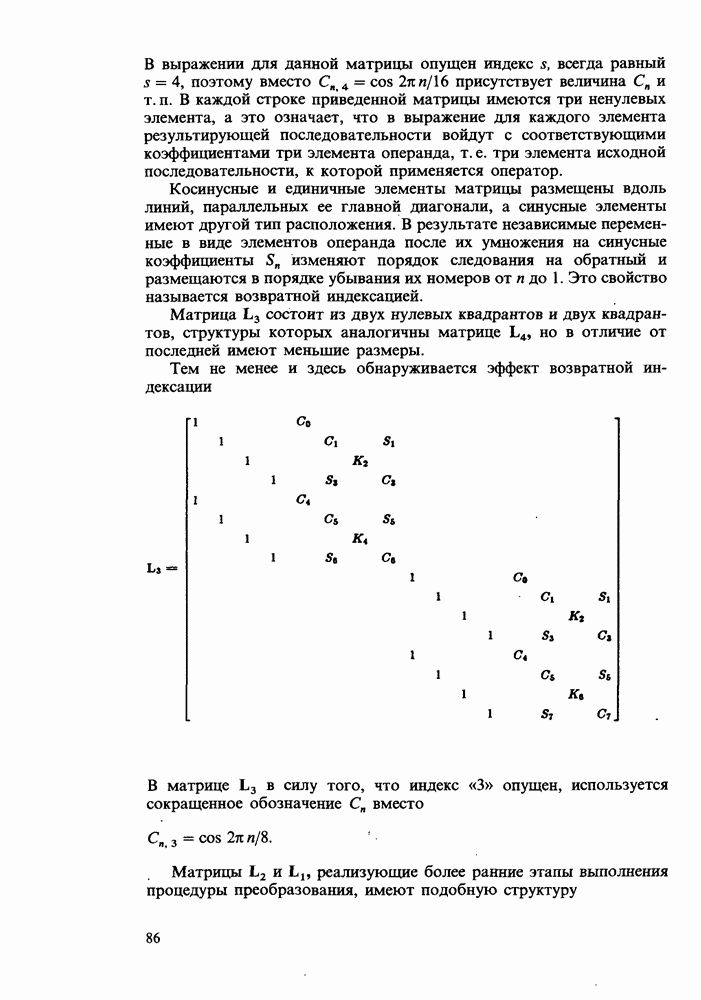
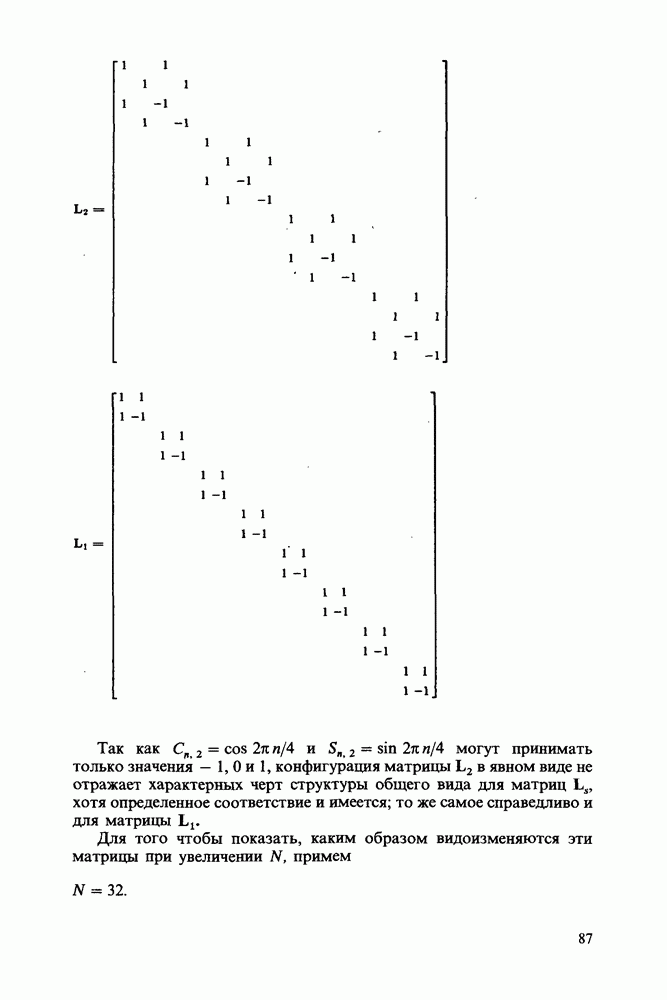
- Каскадные матрицы
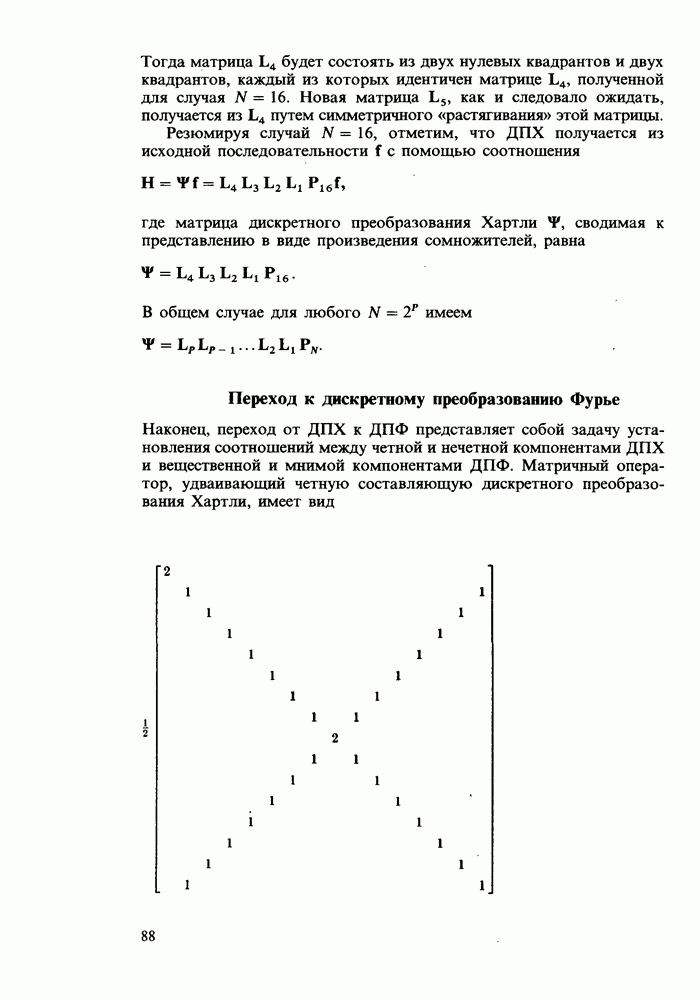
- Переход к дискретному преобразованию Фурье
- Глава 8. АЛГОРИТМ БЫСТРОГО ПРЕОБРАЗОВАНИЯ
- Свойство N log N
- Повторное разбиение последовательностей
- Преобразование с использованием разложения на подпоследовательности
- Общая формула разложения.
- Направленный сигнальный граф
- Вычисление с замещением
- Анализ временных затрат на вычисление с помощью полосковой диаграммы
- Степепи числа 2
- Тригонометрические функции
- Быстрое вычисление синусов
- Операция быстрого поворота
- Быстрая перестановка
- Преобразование для последовательностей с основанием 4 и другие модификации
- Ранее применявшиеся подходы к преобразованию вещественных данных
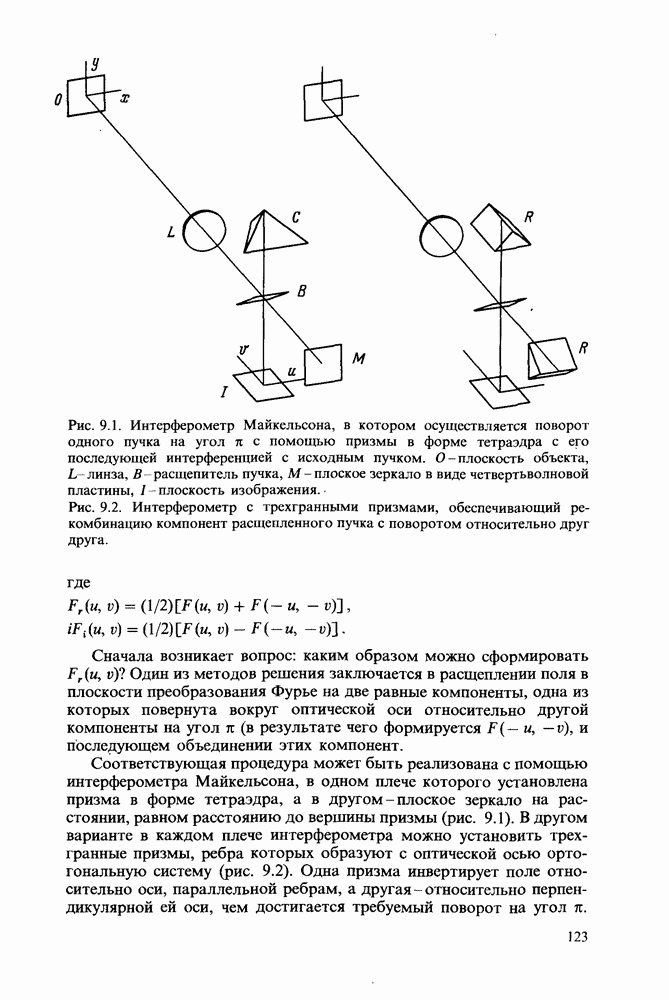
- Глава 9. ПРЕОБРАЗОВАНИЕ ХАРТЛИ В ОПТИКЕ
- Свойства симметрии
- Осуществление преобразования Хартли, использующее поляризацию
- Практическое осуществление
- Источник некогерентного излучения
- Пример
- Голография в плоскости Хартли
- Приложение 1. ПРОГРАММЫ ВЫЧИСЛЕНИЙ НА ЭВМ
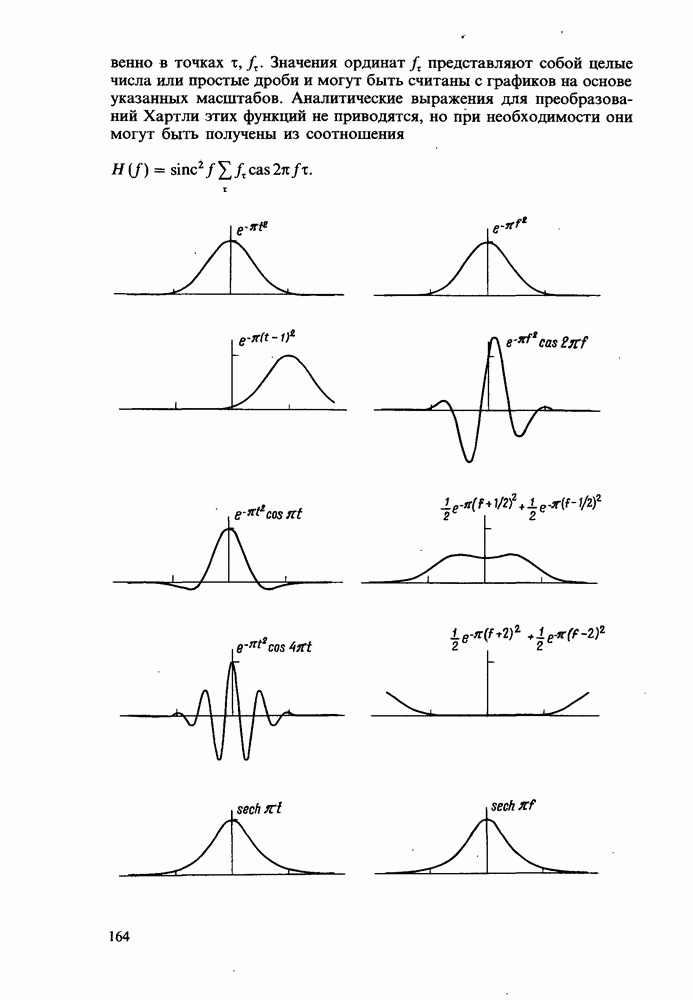
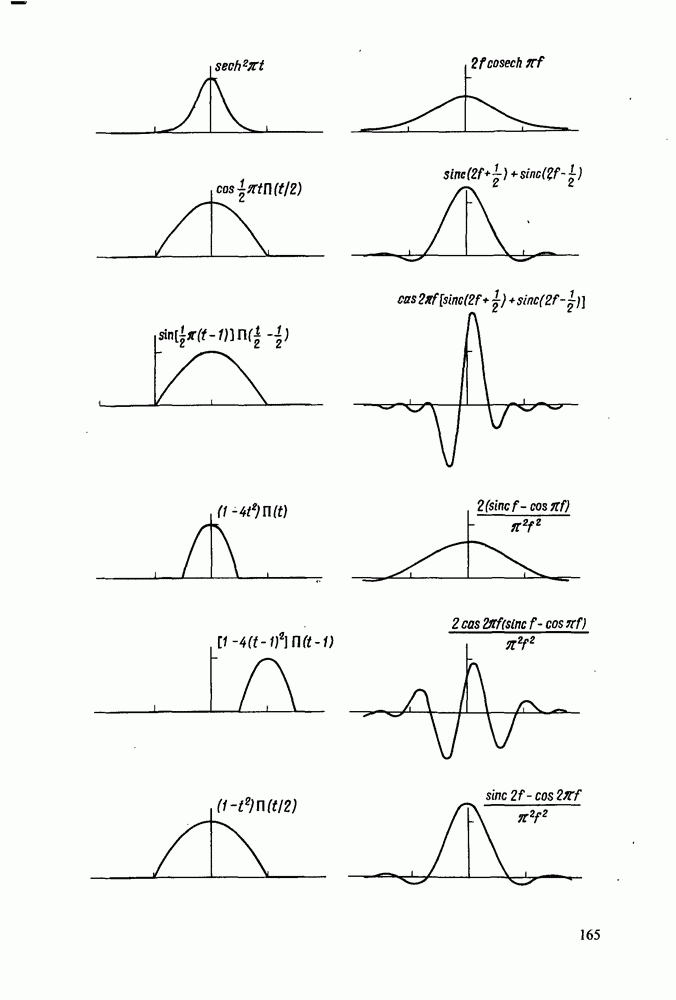
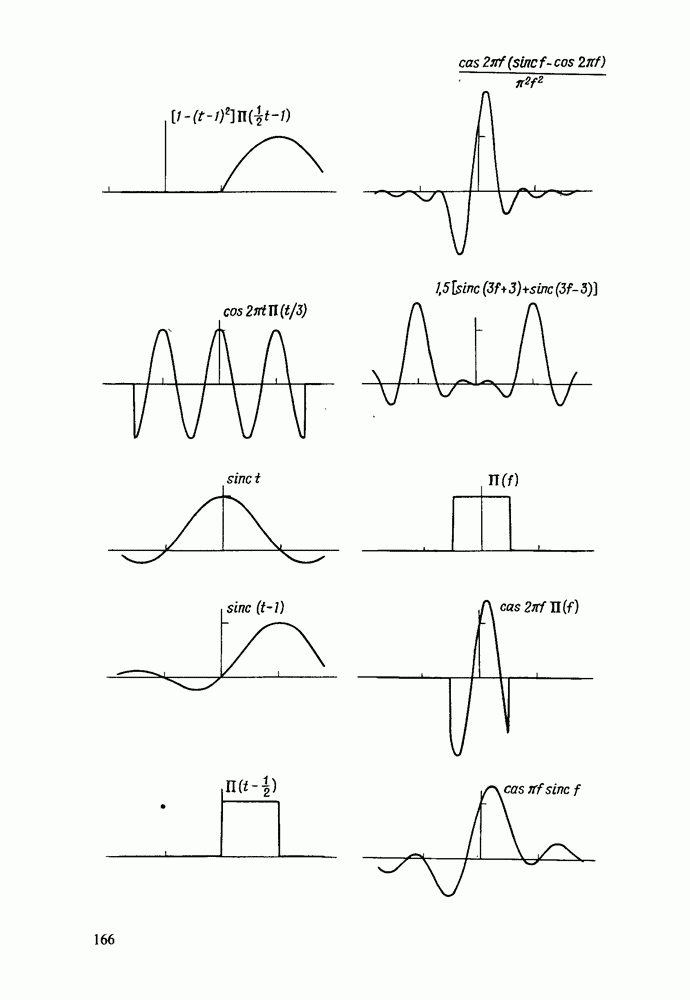
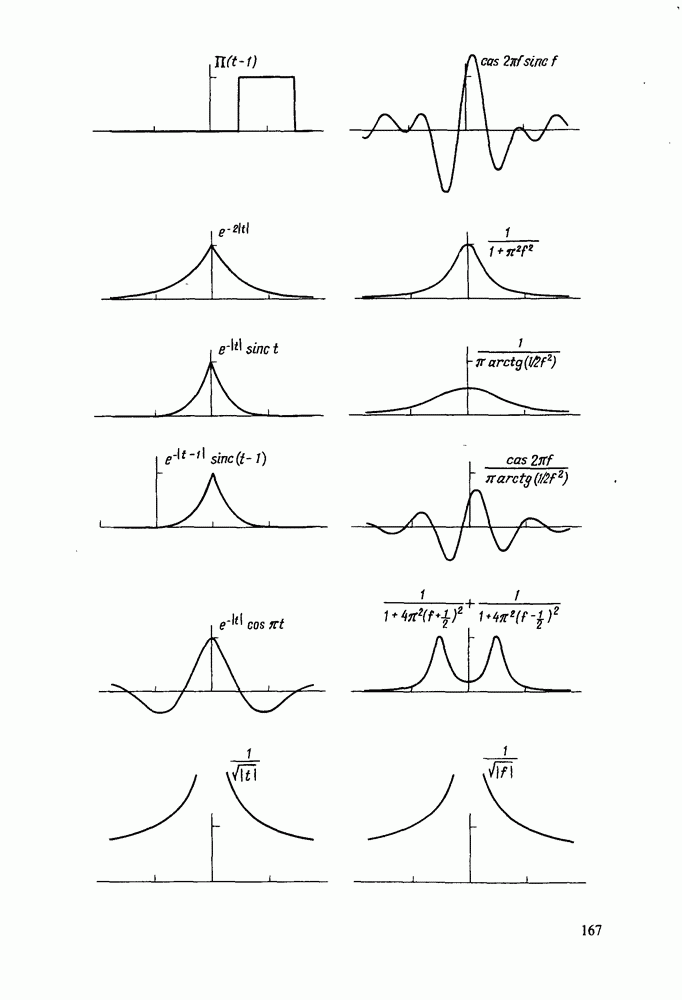
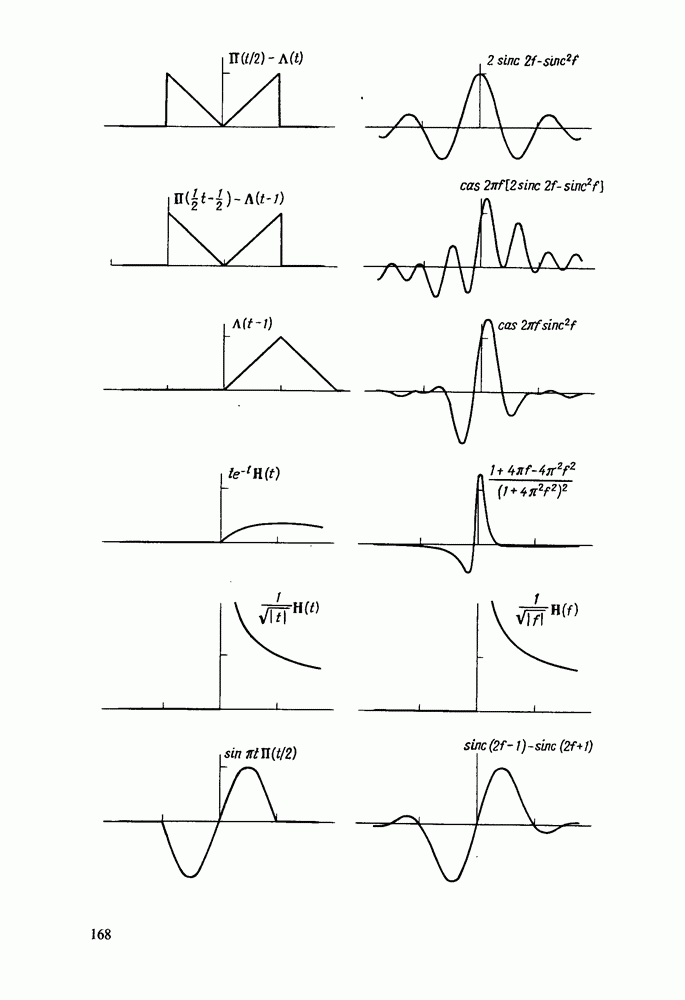
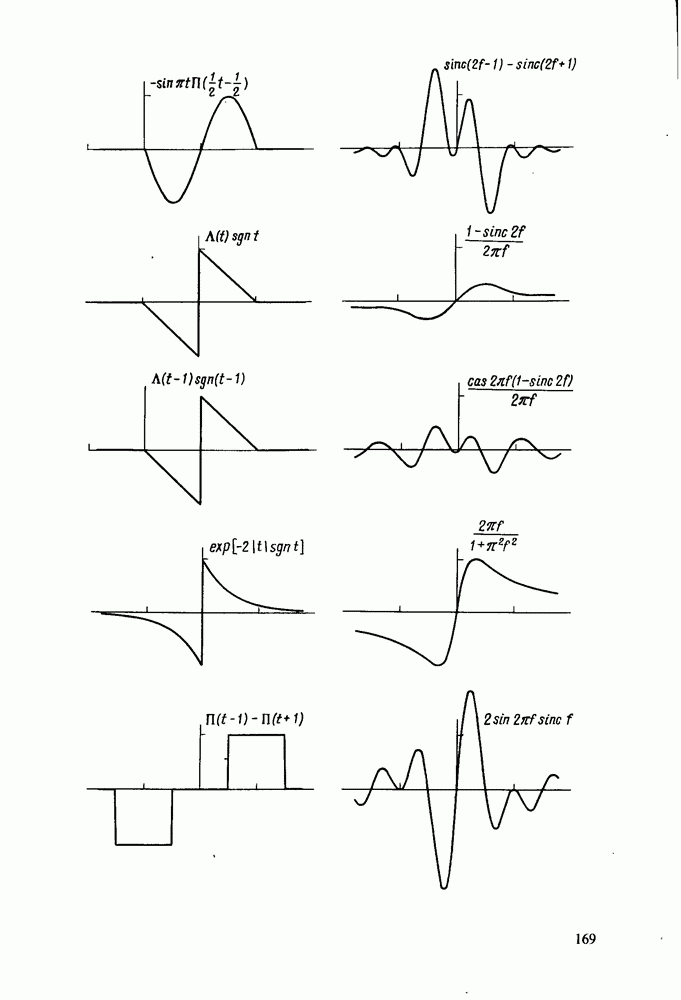
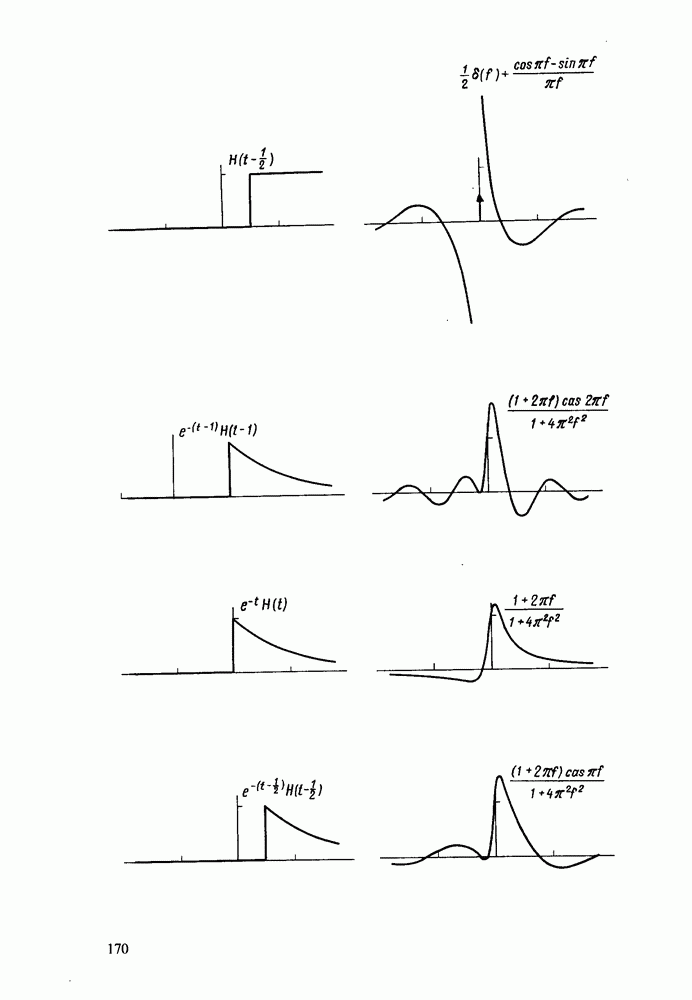
- Приложение 2. АТЛАС ПРЕОБРАЗОВАНИЙ ХАРТЛИ