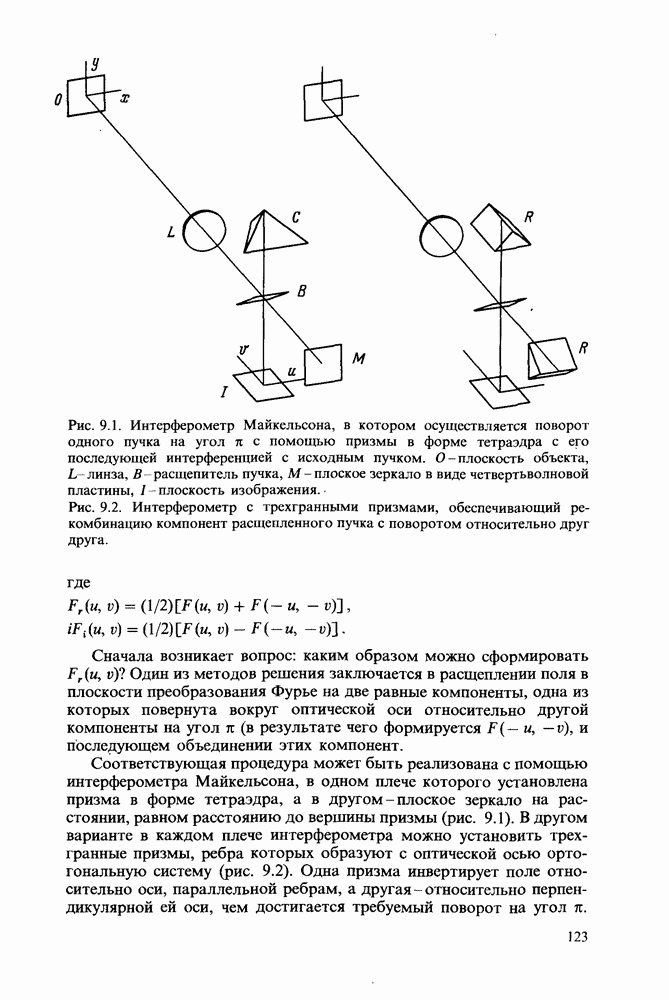
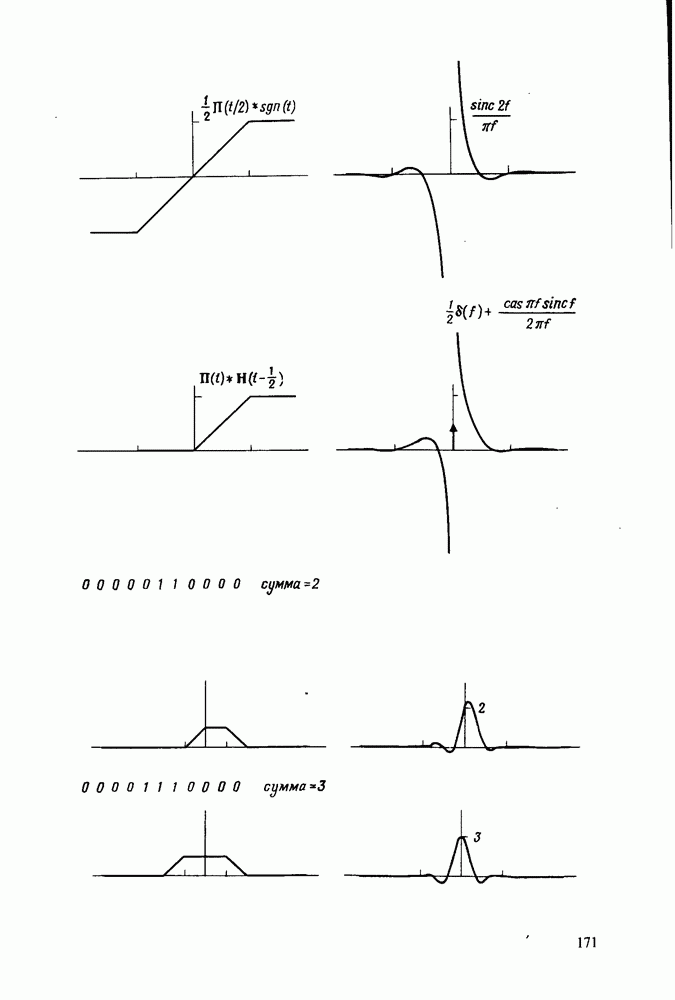
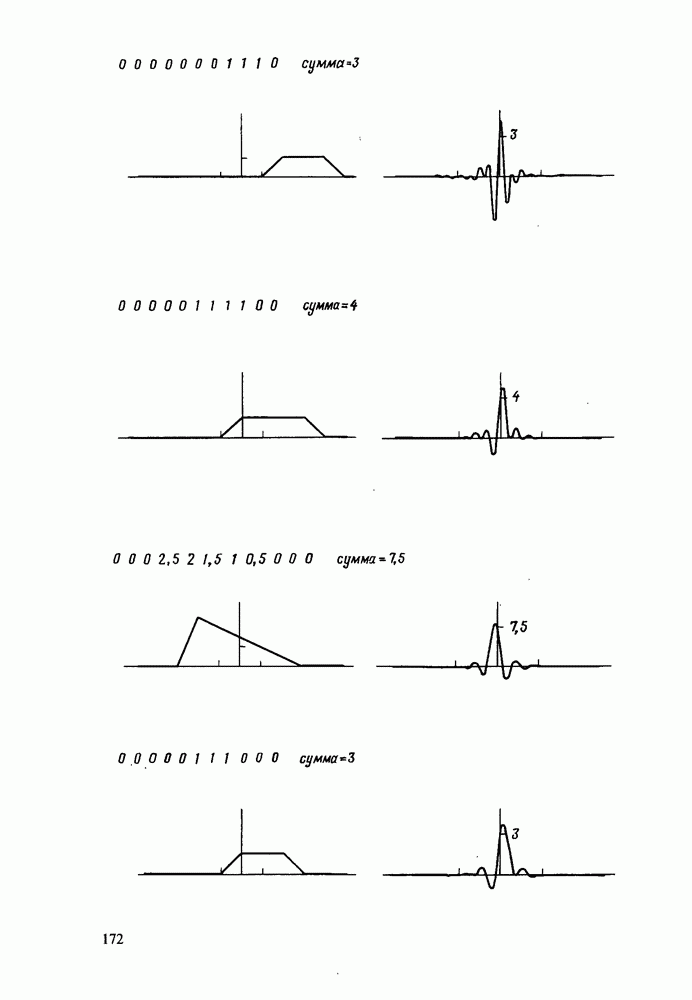
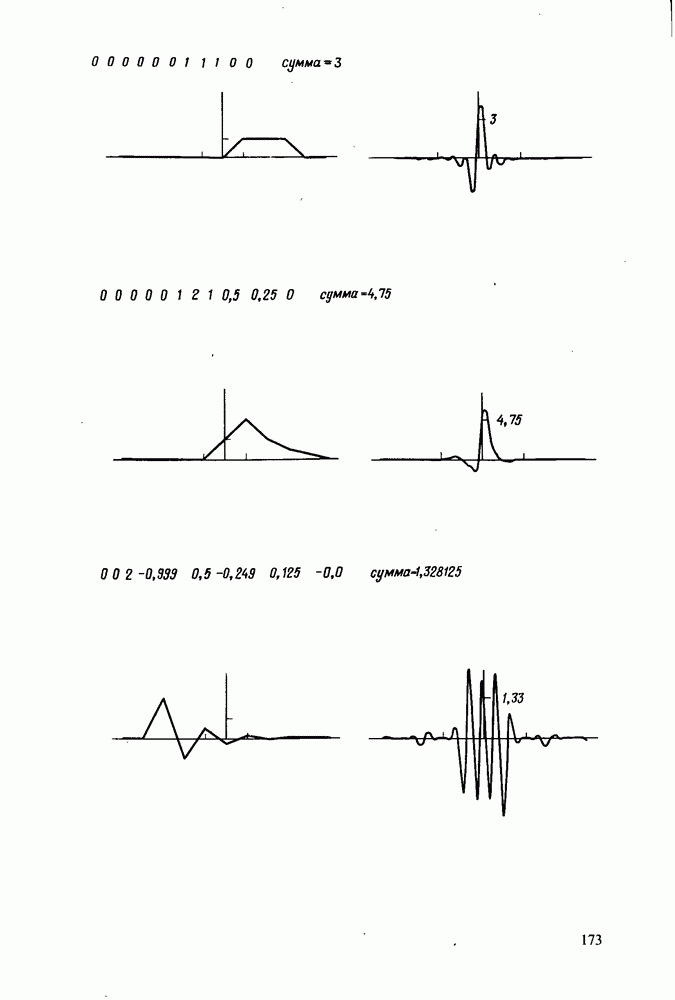
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 8. АЛГОРИТМ БЫСТРОГО ПРЕОБРАЗОВАНИЯ
Минуя древа молодые,
По грубой треснувшей земле Скакал он на коне галопом К подножию холма.
И лишь внизу коню дал отдых И сам был цел и невредим.
А. Б. (Банджо) Патерсон. Человек со снежной реки
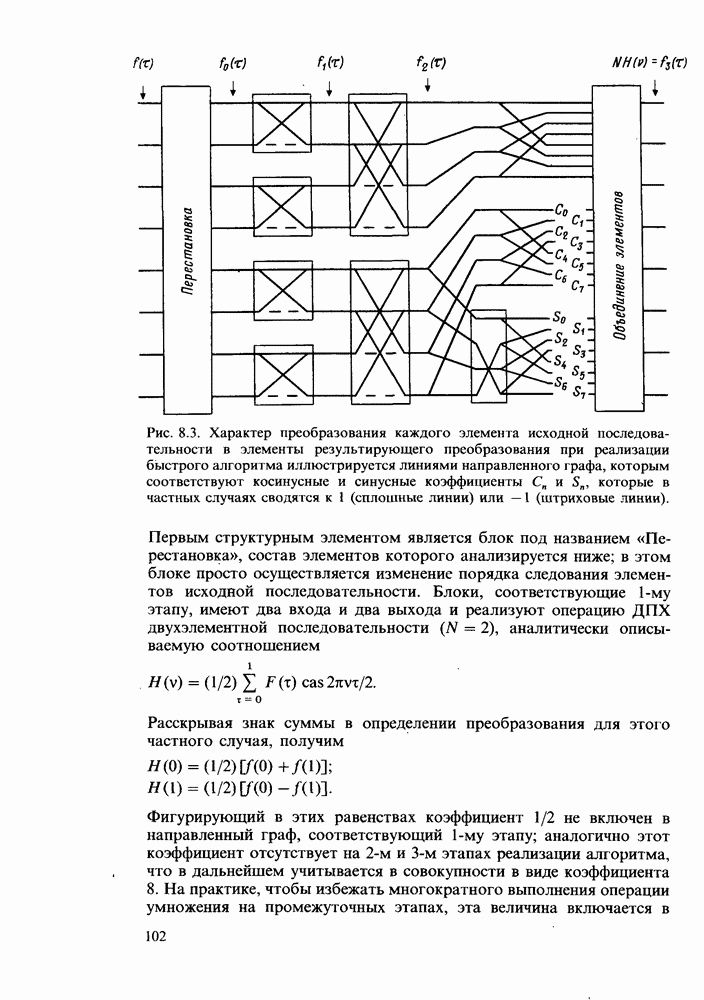
Мы убедились в том, что может быть определено вещественное дискретное преобразование по аналогии с дискретным преобразованием Фурье; теперь мы покажем, что имеется быстрый метод вычислений, аналогичный быстрому преобразованию Фурье. Как было показано выше при рассмотрении факторизации матриц, данная процедура представляет собой простой способ перехода от дискретного преобразования Хартли к дискретному преобразованию Фурье. Следовательно, анализируемая ниже процедура быстрого преобразования также создает основу быстрого метода получения дискретного преобразования Фурье. Действительно, метод, предусматривающий переход от преобразования Хартли, оказывается предпочтительным, в основном в силу упрощения, обусловленного тем, что при обработке вещественных данных не требуются операции с комплексными величинами.
Определяющие соотношения
Когда раскрывается знак суммирования, фигурирующий в определении дискретного преобразования Хартли, мы получаем N равенств, в правой части каждого из которых имеется N слагаемых. Четыре равенства, приведенные в предыдущей главе с целью иллюстрации сказанного, применительно к дискретному преобразованию Хартли

можно переписать в виде

Для N = 2 имеем только два равенства


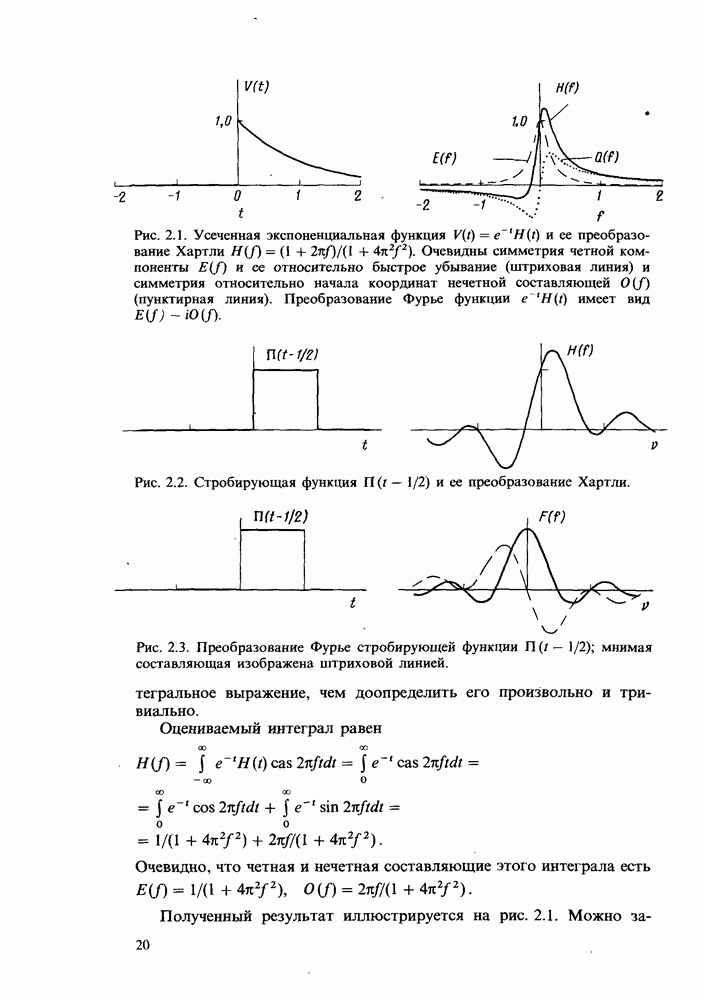
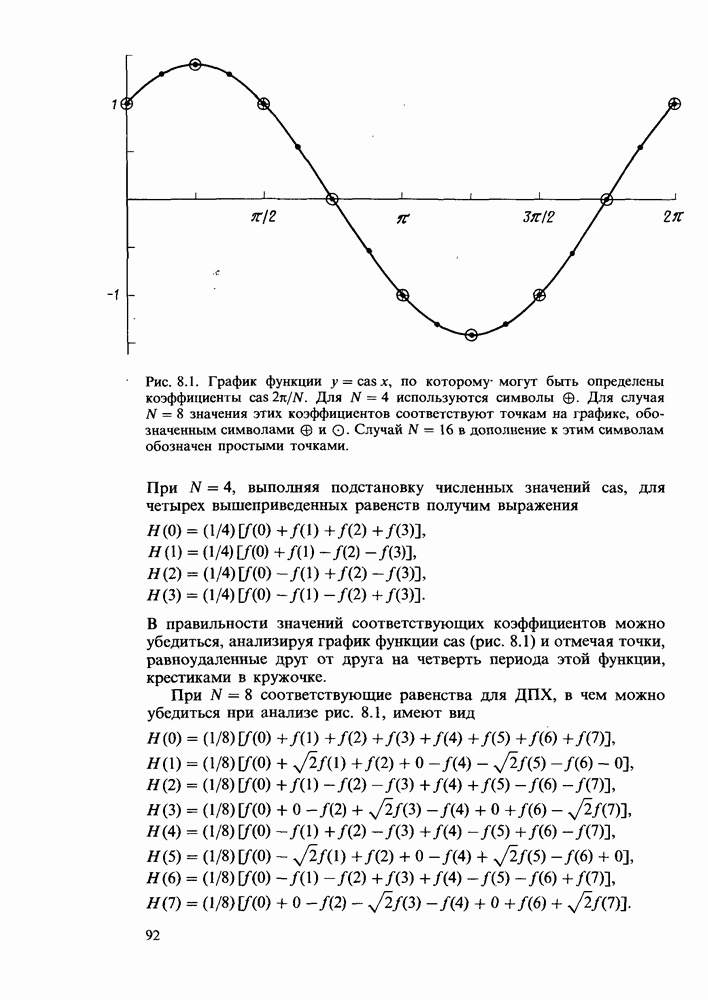
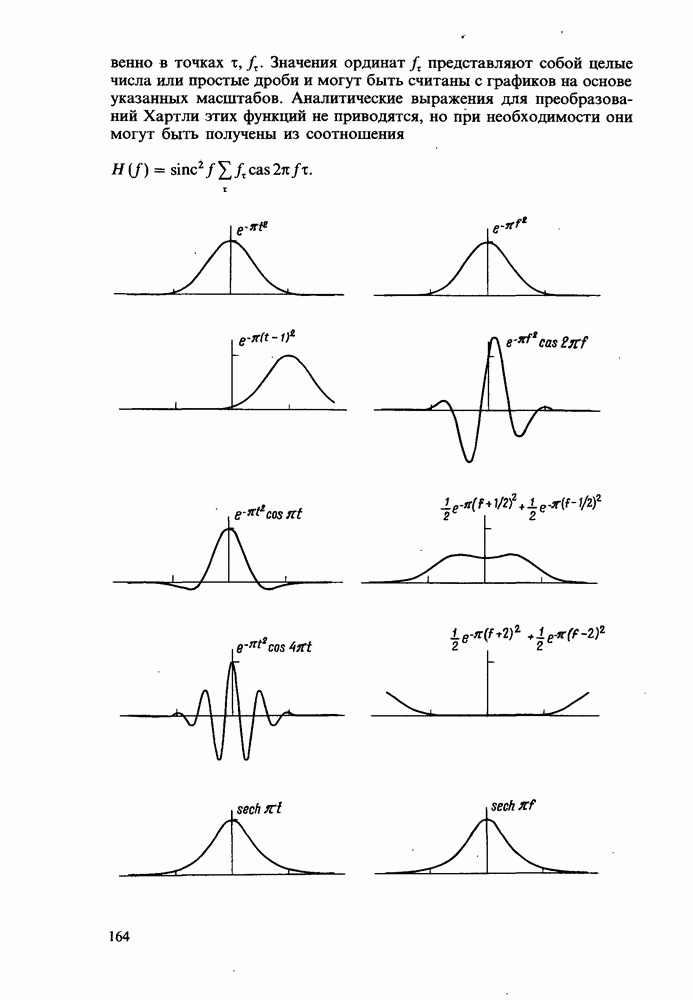
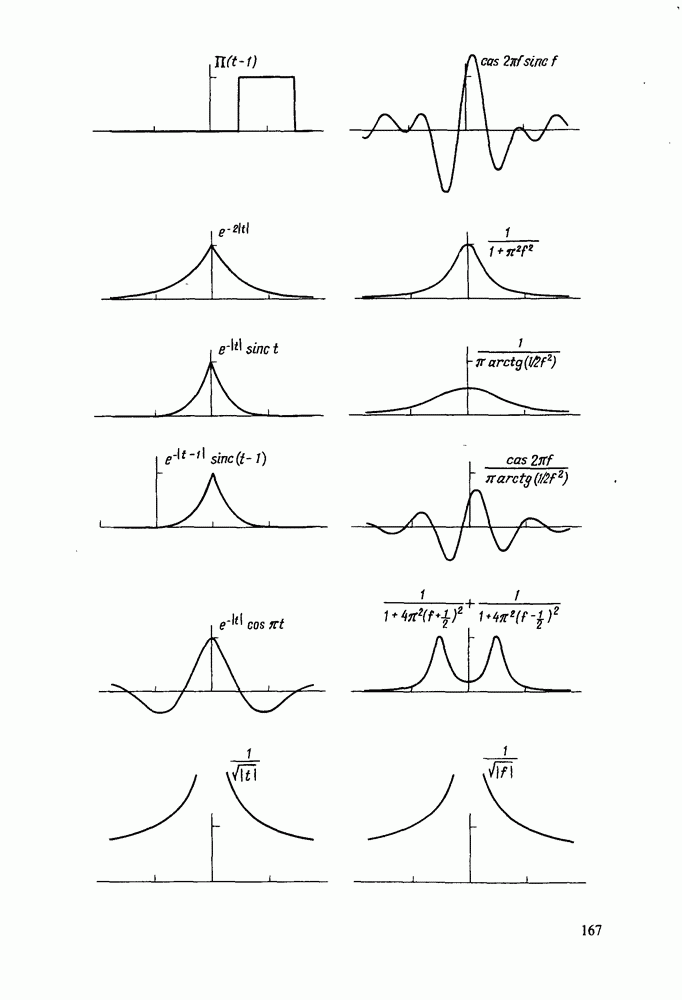
Рис. 8.1. График функции  по которому могут быть определены коэффициенты
по которому могут быть определены коэффициенты  Для
Для  используются символы
используются символы  Для случая
Для случая  значения этих коэффициентов соответствуют точкам на графике, обозначенным символами
значения этих коэффициентов соответствуют точкам на графике, обозначенным символами  Случай
Случай  в дополнение к этим символам обозначен простыми точками.
в дополнение к этим символам обозначен простыми точками.
При  выполняя подстановку численных значений
выполняя подстановку численных значений  для четырех вышеприведенных равенств получим выражения
для четырех вышеприведенных равенств получим выражения

В правильности значений соответствующих коэффициентов можно убедиться, анализируя график функции  (рис. 8.1) и отмечая точки, равноудаленные друг от друга на четверть периода этой функции, крестиками в кружочке.
(рис. 8.1) и отмечая точки, равноудаленные друг от друга на четверть периода этой функции, крестиками в кружочке.
При  соответствующие равенства для ДПХ, в чем можно убедиться при анализе рис. 8.1, имеют вид
соответствующие равенства для ДПХ, в чем можно убедиться при анализе рис. 8.1, имеют вид

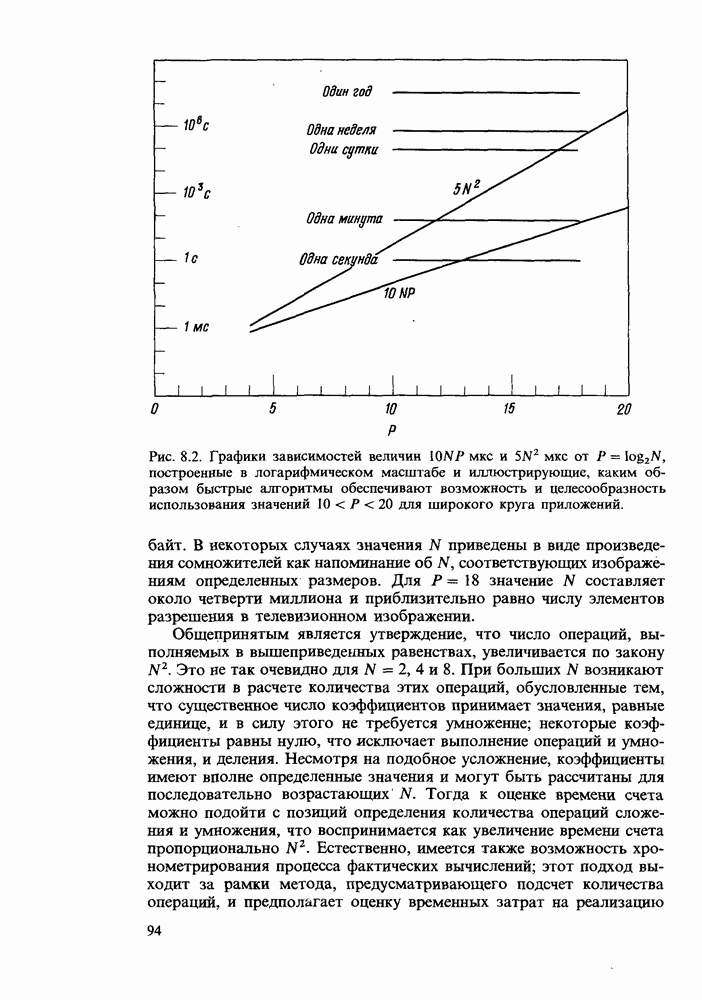
Можно рассчитать число онераций умножения и сложения и использовать результаты этого расчета для оценки временных затрат, необходимых для вычисления всех N значений преобразования.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
- Глава 2. ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Преобразование Хартли
- Четная и нечетная составляющие
- Формулы связи
- Примеры
- Энергетический и фазовый спектры
- Глава 3. ТЕОРЕМЫ
- Свертка
- Соотношения между преобразованиями во временной и частотой областях
- Глава 4. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Физический смысл величин «тау» и v
- Четная и нечетная составляющие
- Примеры дискретных преобразований Хартли
- Степени свободы
- Другие вещественные ядра
- Теоремы
- Выводы
- Глава 5. ЦИФРОВАЯ ФИЛЬТРАЦИЯ ПОСРЕДСТВОМ СВЕРТКИ
- Циклическая свертка
- Дополнение нулями
- Обращение свертки
- Теорема о свертке
- Теорема о свертке в частотной области (спектральное сглаживание)
- Числовой пример свертки
- Коэффициент
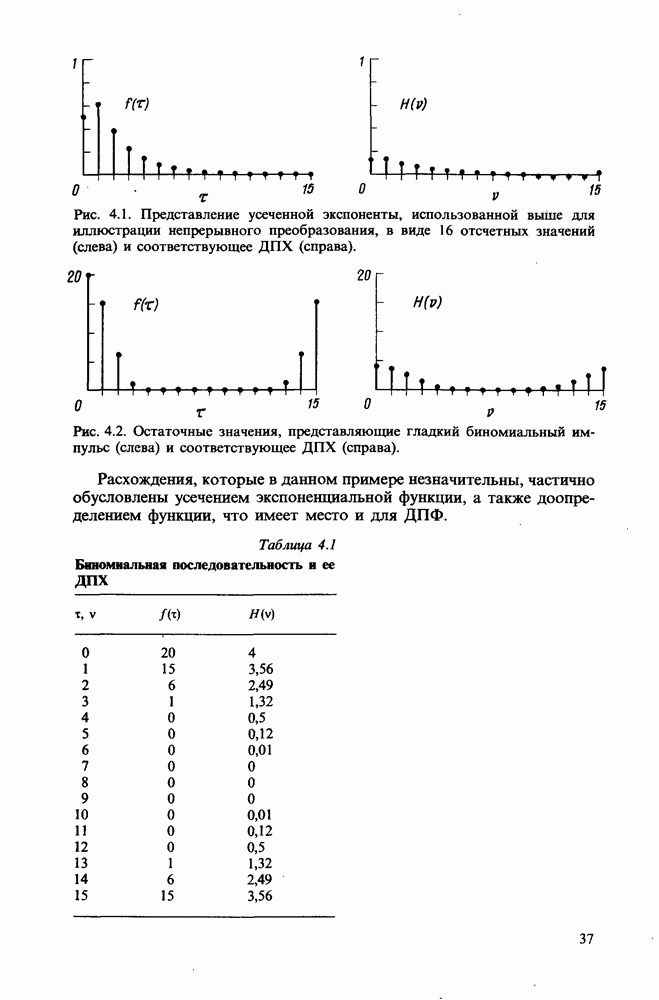
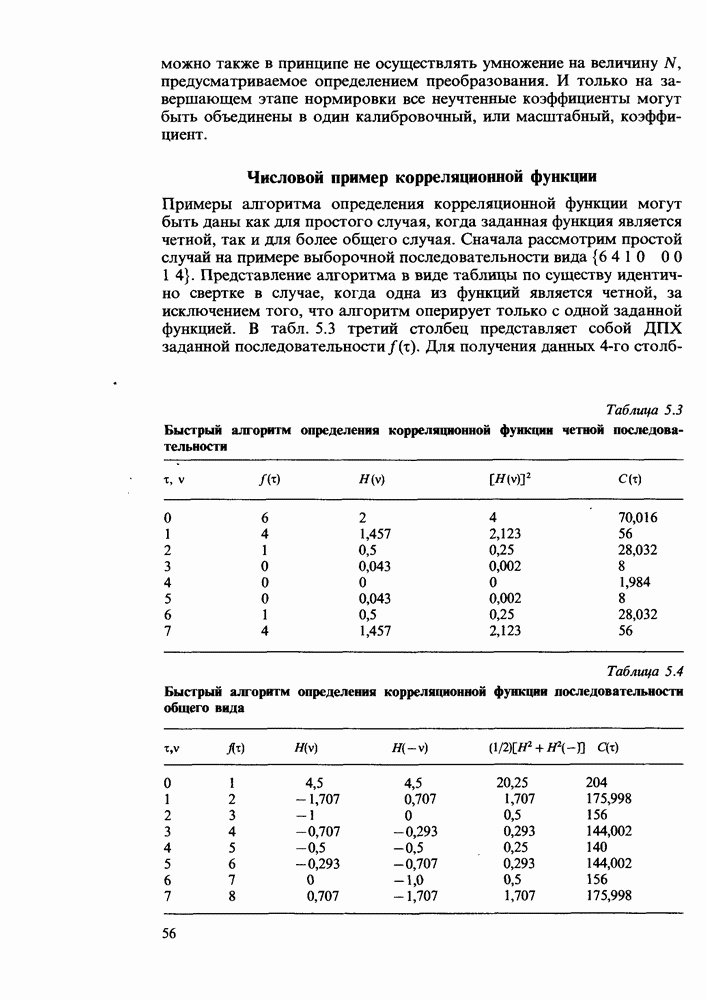
- Числовой пример корреляционной функции
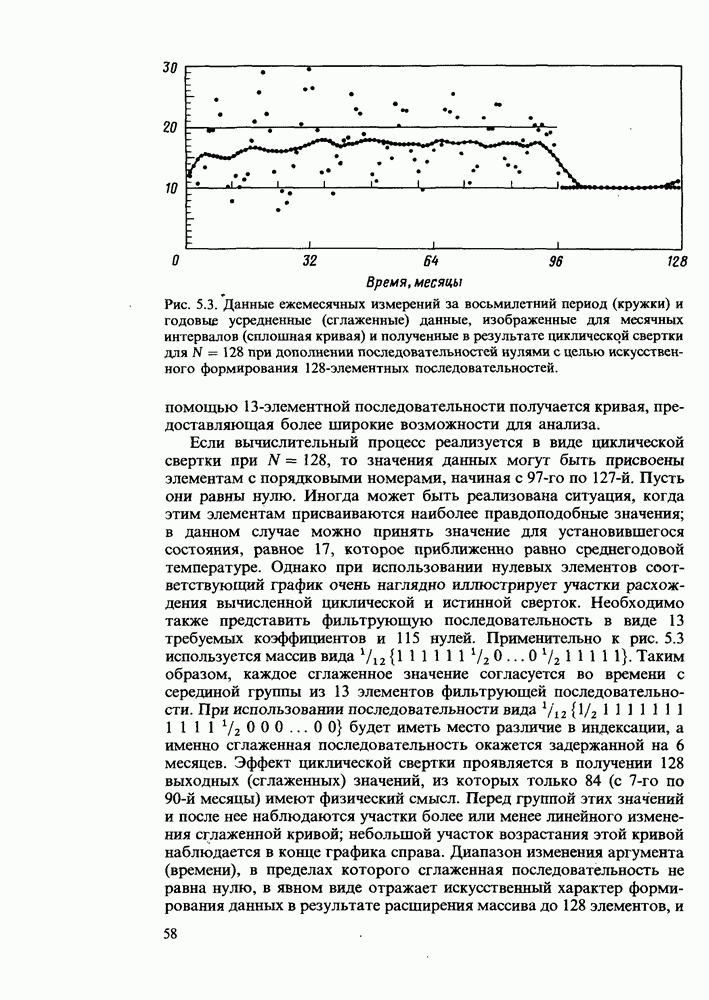
- Низкочастотная фильтрация
- Подчеркивание границ
- Свертка с использованием быстрого преобразования Хартли
- Способ без использования перестановок
- Свертка как умножение матриц
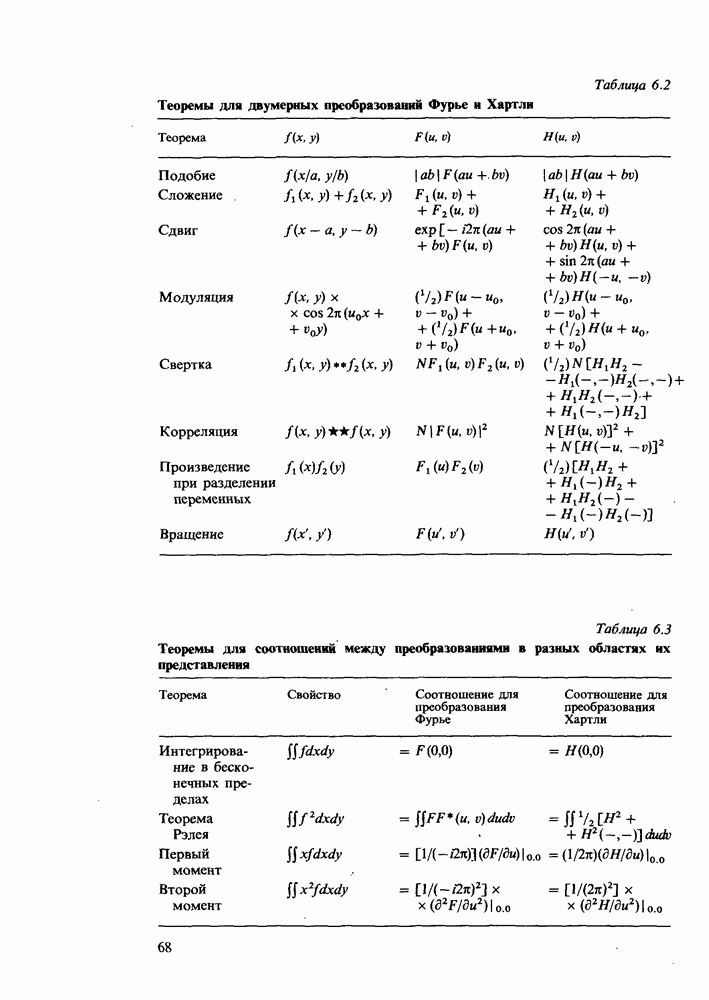
- Глава 6. Двумерные преобразования
- Двумерное преобразование Хартли
- Симметрия и антисимметрия
- Примеры
- Теоремы для двумерных преобразований
- Круговая симметрия
- Двумерная фильтрация
- Цикличность для двумерного случая
- Трехмерный случай
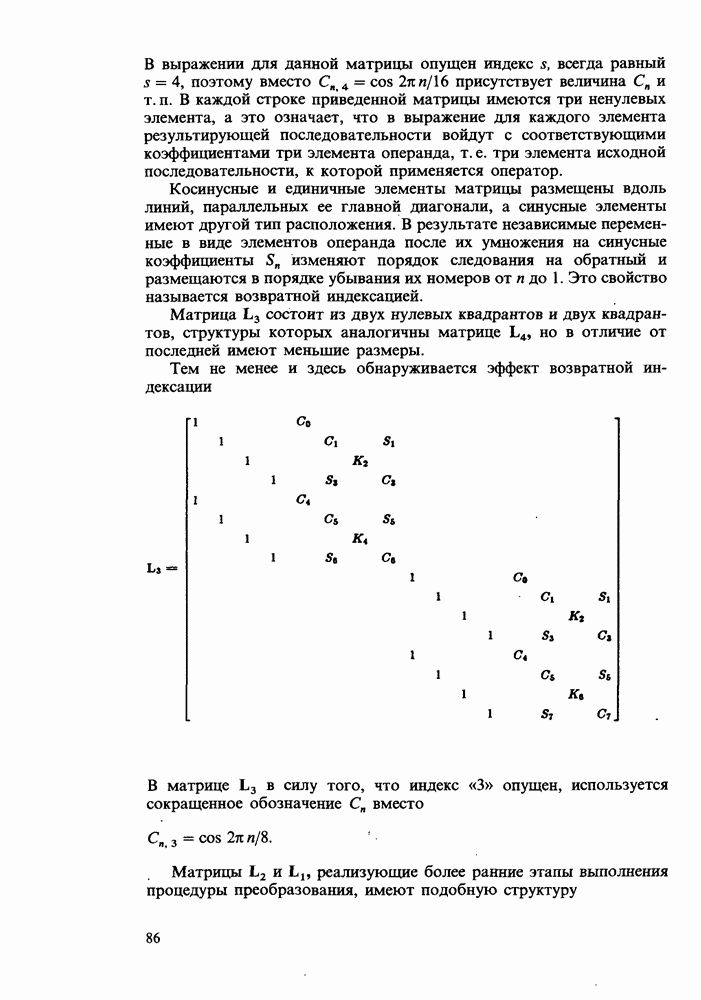
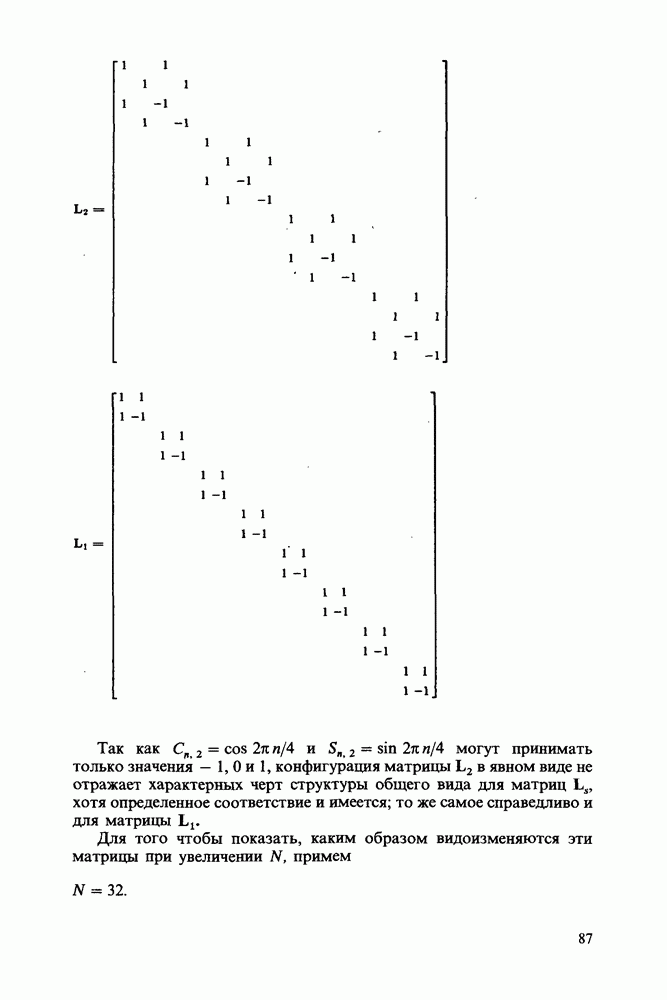
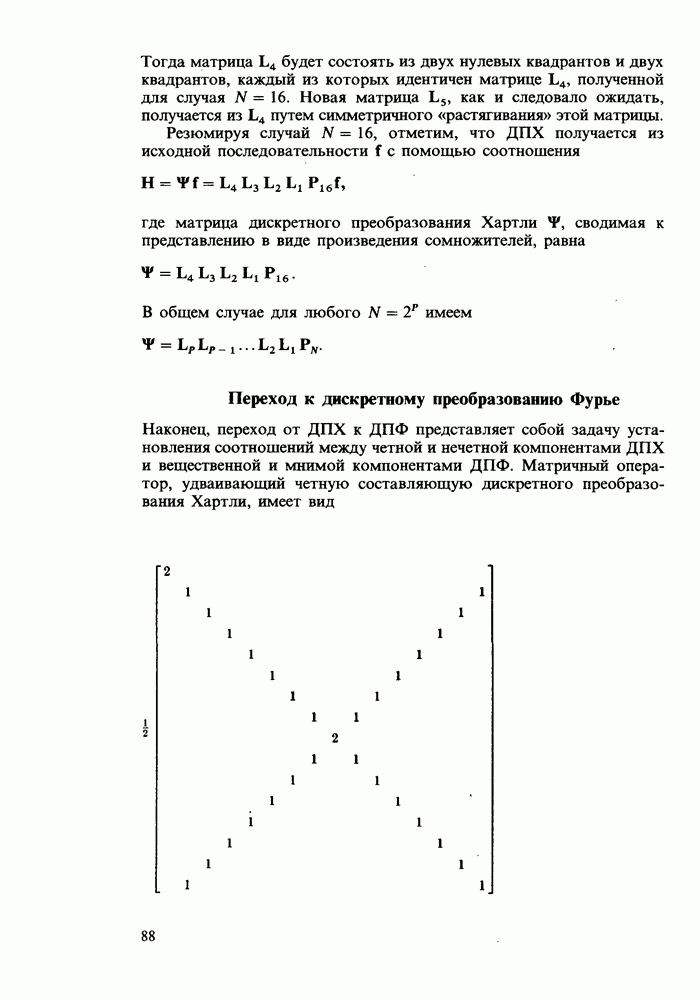
- Глава 7. ФАКТОРИЗАЦИЯ МАТРИЦЫ ПРЕОБРАЗОВАНИЯ
- Перестановка
- Перестановочные диаграммы
- Перестановочная матрица
- Ячеистая структура перестановочной диаграммы
- Каскадные матрицы
- Переход к дискретному преобразованию Фурье
- Глава 8. АЛГОРИТМ БЫСТРОГО ПРЕОБРАЗОВАНИЯ
- Свойство N log N
- Повторное разбиение последовательностей
- Преобразование с использованием разложения на подпоследовательности
- Общая формула разложения.
- Направленный сигнальный граф
- Вычисление с замещением
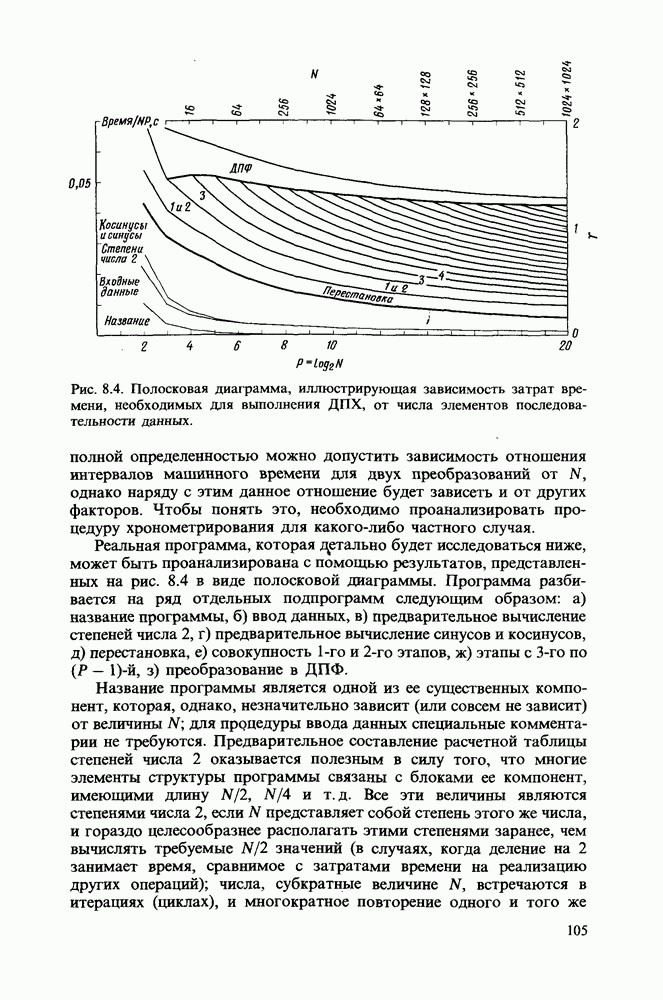
- Анализ временных затрат на вычисление с помощью полосковой диаграммы
- Степепи числа 2
- Тригонометрические функции
- Быстрое вычисление синусов
- Операция быстрого поворота
- Быстрая перестановка
- Преобразование для последовательностей с основанием 4 и другие модификации
- Ранее применявшиеся подходы к преобразованию вещественных данных
- Глава 9. ПРЕОБРАЗОВАНИЕ ХАРТЛИ В ОПТИКЕ
- Свойства симметрии
- Осуществление преобразования Хартли, использующее поляризацию
- Практическое осуществление
- Источник некогерентного излучения
- Пример
- Голография в плоскости Хартли
- Приложение 1. ПРОГРАММЫ ВЫЧИСЛЕНИЙ НА ЭВМ
- Приложение 2. АТЛАС ПРЕОБРАЗОВАНИЙ ХАРТЛИ