| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Преобразование с использованием разложения на подпоследовательности
Рассмотрим последовательность данных

которая представляется в виде суммы двух слагаемых. Две короткие последовательности  при их точном «прослаивании» по аналогии с идеальным «тасованием» воспроизводят исходную последовательность
при их точном «прослаивании» по аналогии с идеальным «тасованием» воспроизводят исходную последовательность 
Требуется найти преобразование Хартли  последовательности
последовательности  исходя из преобразований коротких последовательностей. Будем полагать, что последовательность
исходя из преобразований коротких последовательностей. Будем полагать, что последовательность

На основании теоремы о растяжении для ДПХ (см. гл. 4) непосредственно можем утверждать:

Однако применительно к последнему выражению следует отметить, что нам требуется ДПХ последовательности  . С целью получения преобразования этой последовательности применим теорему о сдвиге. При сдвиге на один элемент вправо эта теорема формулируется следующим образом:
. С целью получения преобразования этой последовательности применим теорему о сдвиге. При сдвиге на один элемент вправо эта теорема формулируется следующим образом:
Если последовательность  имеет
имеет  то
то  имеет ДПХ вида
имеет ДПХ вида

Используя обозначение  можем утверждать, что последовательность
можем утверждать, что последовательность  приобретает вид
приобретает вид

Следовательно, при условии что последовательность

имеет  . Для последовательности
. Для последовательности  равно
равно

Наконец, применяя теорему сложения, получим

Если в это равенство для  входят коэффициенты 0, 1 или — 1, то оно упрощается:
входят коэффициенты 0, 1 или — 1, то оно упрощается:

На этом завершается доказательство того, что  -элементное преобразование
-элементное преобразование  может быть сформировано из двух четырехэлементных преобразований
может быть сформировано из двух четырехэлементных преобразований 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
- Глава 2. ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Преобразование Хартли
- Четная и нечетная составляющие
- Формулы связи
- Примеры
- Энергетический и фазовый спектры
- Глава 3. ТЕОРЕМЫ
- Свертка
- Соотношения между преобразованиями во временной и частотой областях
- Глава 4. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Физический смысл величин «тау» и v
- Четная и нечетная составляющие
- Примеры дискретных преобразований Хартли
- Степени свободы
- Другие вещественные ядра
- Теоремы
- Выводы
- Глава 5. ЦИФРОВАЯ ФИЛЬТРАЦИЯ ПОСРЕДСТВОМ СВЕРТКИ
- Циклическая свертка
- Дополнение нулями
- Обращение свертки
- Теорема о свертке
- Теорема о свертке в частотной области (спектральное сглаживание)
- Числовой пример свертки
- Коэффициент
- Числовой пример корреляционной функции
- Низкочастотная фильтрация
- Подчеркивание границ
- Свертка с использованием быстрого преобразования Хартли
- Способ без использования перестановок
- Свертка как умножение матриц
- Глава 6. Двумерные преобразования
- Двумерное преобразование Хартли
- Симметрия и антисимметрия
- Примеры
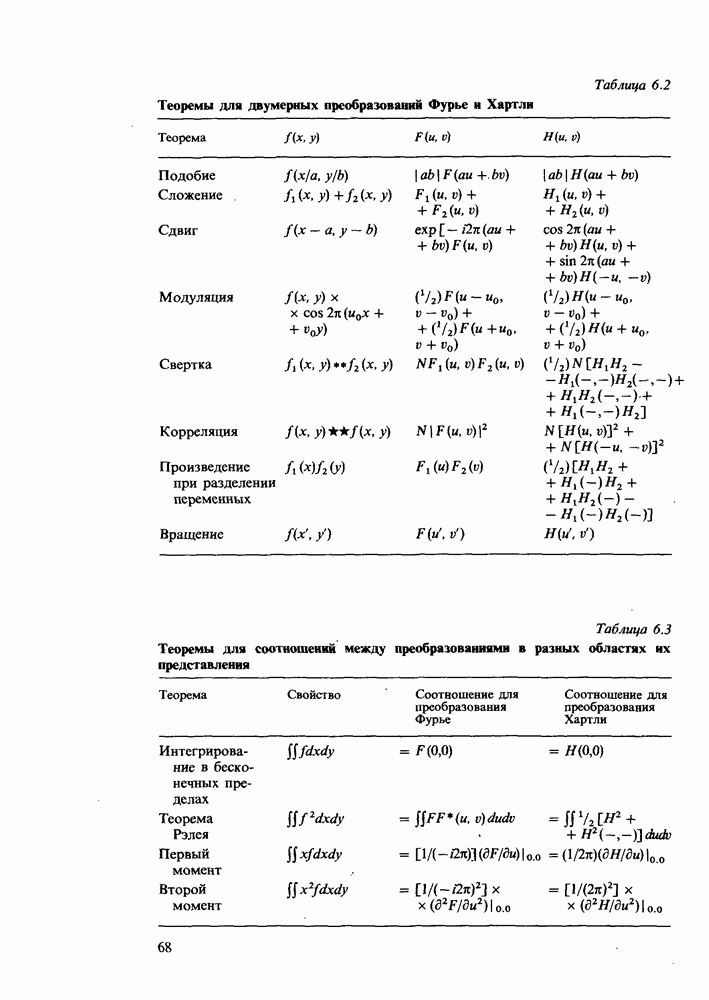
- Теоремы для двумерных преобразований
- Круговая симметрия
- Двумерная фильтрация
- Цикличность для двумерного случая
- Трехмерный случай
- Глава 7. ФАКТОРИЗАЦИЯ МАТРИЦЫ ПРЕОБРАЗОВАНИЯ
- Перестановка
- Перестановочные диаграммы
- Перестановочная матрица
- Ячеистая структура перестановочной диаграммы
- Каскадные матрицы
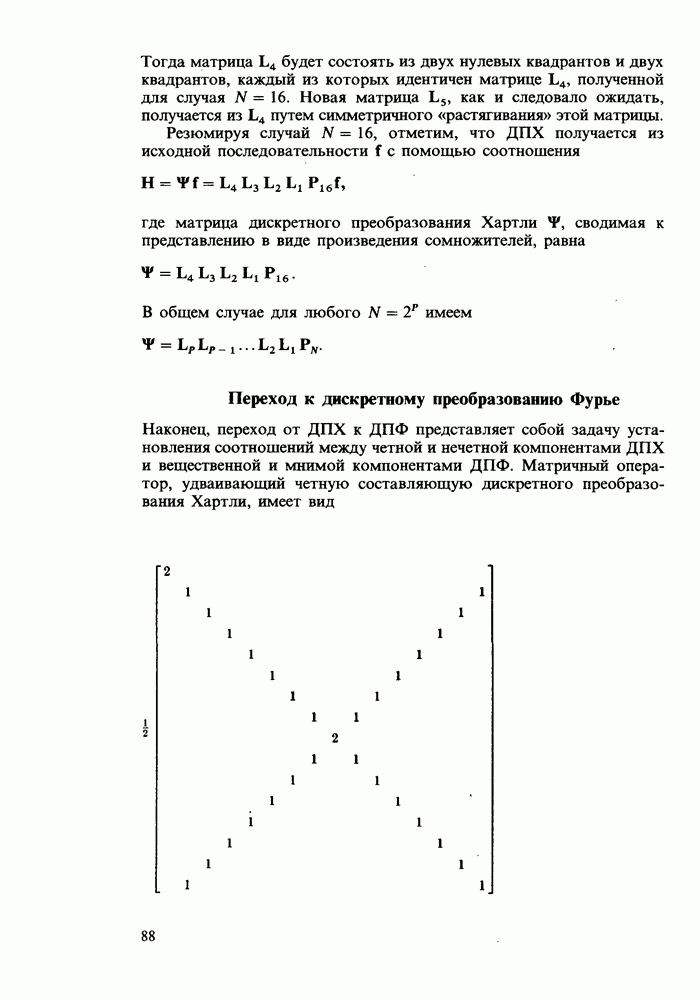
- Переход к дискретному преобразованию Фурье
- Глава 8. АЛГОРИТМ БЫСТРОГО ПРЕОБРАЗОВАНИЯ
- Свойство N log N
- Повторное разбиение последовательностей
- Преобразование с использованием разложения на подпоследовательности
- Общая формула разложения.
- Направленный сигнальный граф
- Вычисление с замещением
- Анализ временных затрат на вычисление с помощью полосковой диаграммы
- Степепи числа 2
- Тригонометрические функции
- Быстрое вычисление синусов
- Операция быстрого поворота
- Быстрая перестановка
- Преобразование для последовательностей с основанием 4 и другие модификации
- Ранее применявшиеся подходы к преобразованию вещественных данных
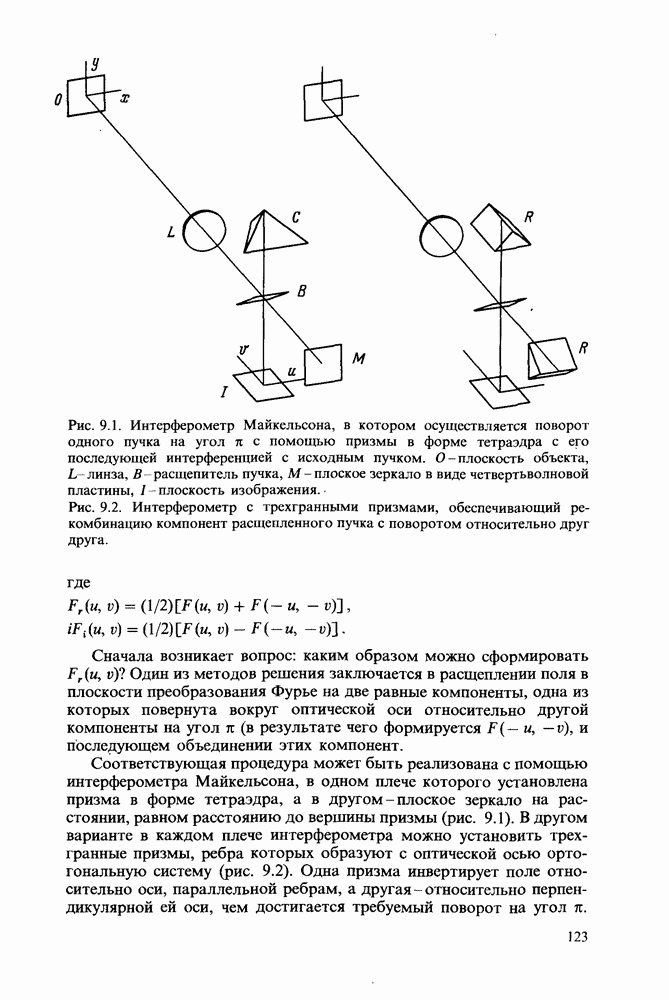
- Глава 9. ПРЕОБРАЗОВАНИЕ ХАРТЛИ В ОПТИКЕ
- Свойства симметрии
- Осуществление преобразования Хартли, использующее поляризацию
- Практическое осуществление
- Источник некогерентного излучения
- Пример
- Голография в плоскости Хартли
- Приложение 1. ПРОГРАММЫ ВЫЧИСЛЕНИЙ НА ЭВМ
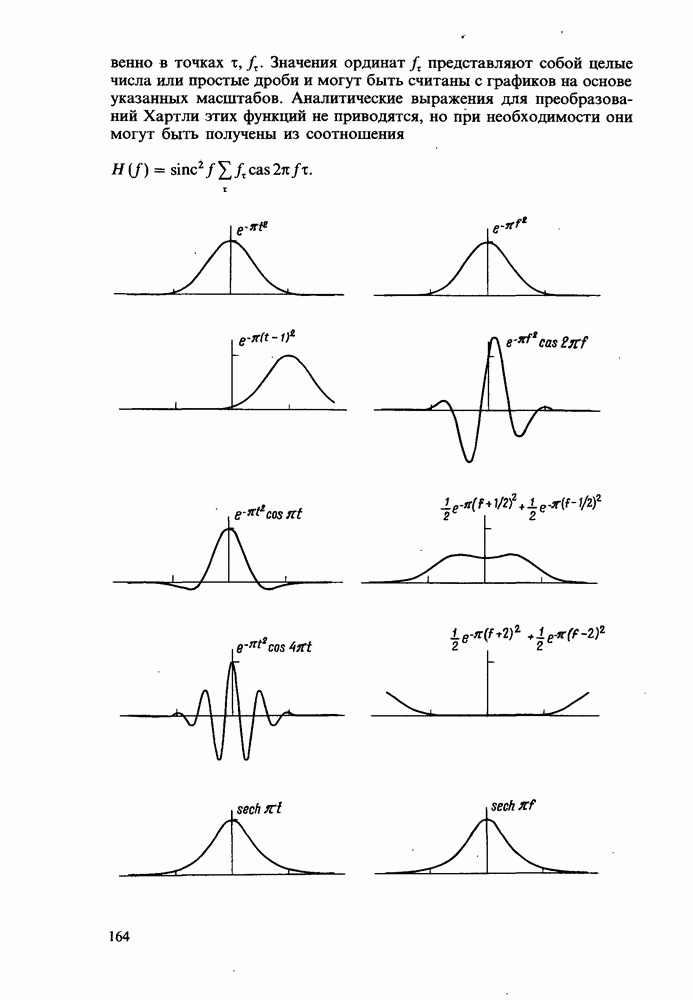
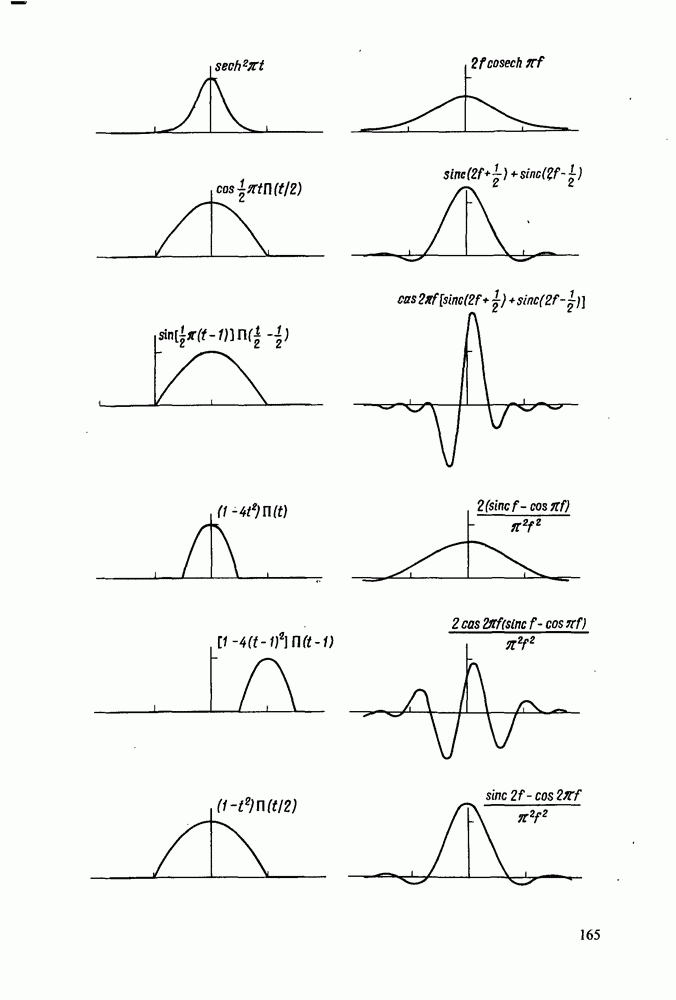
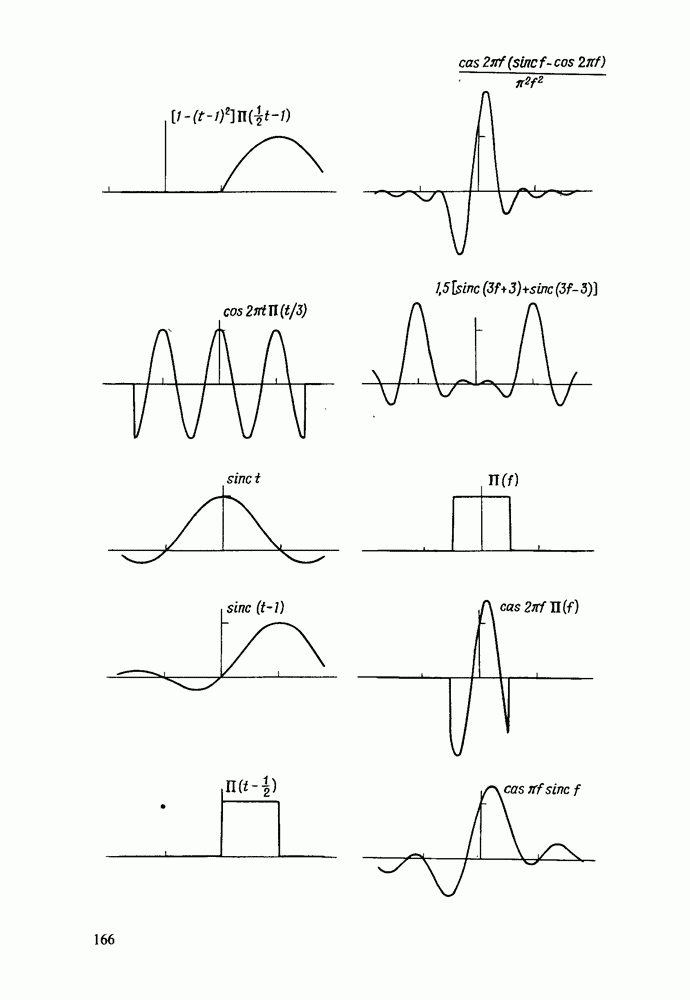
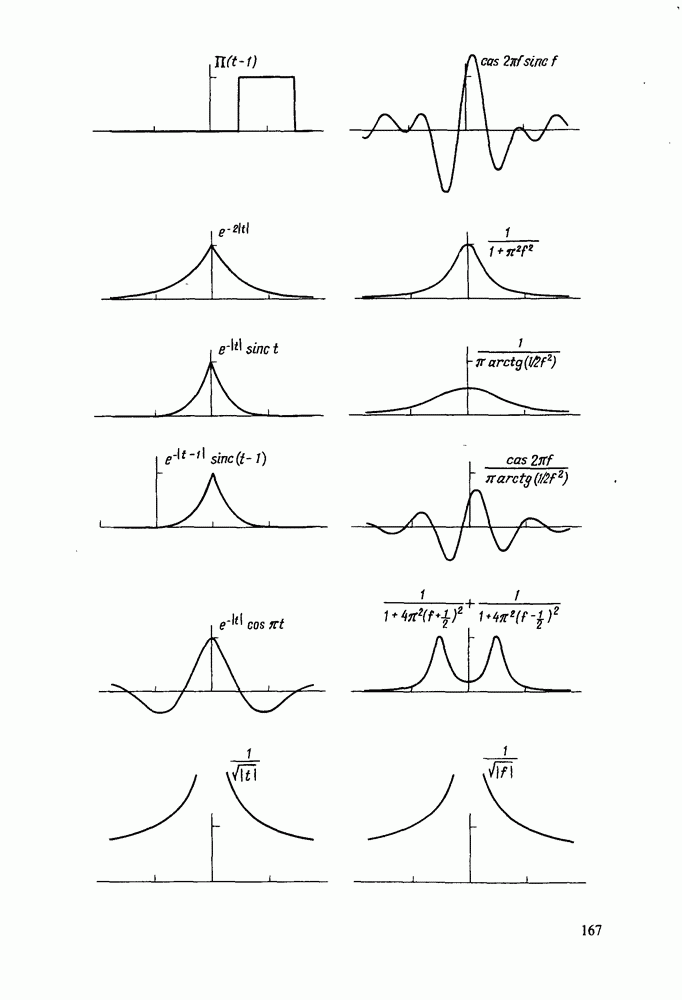
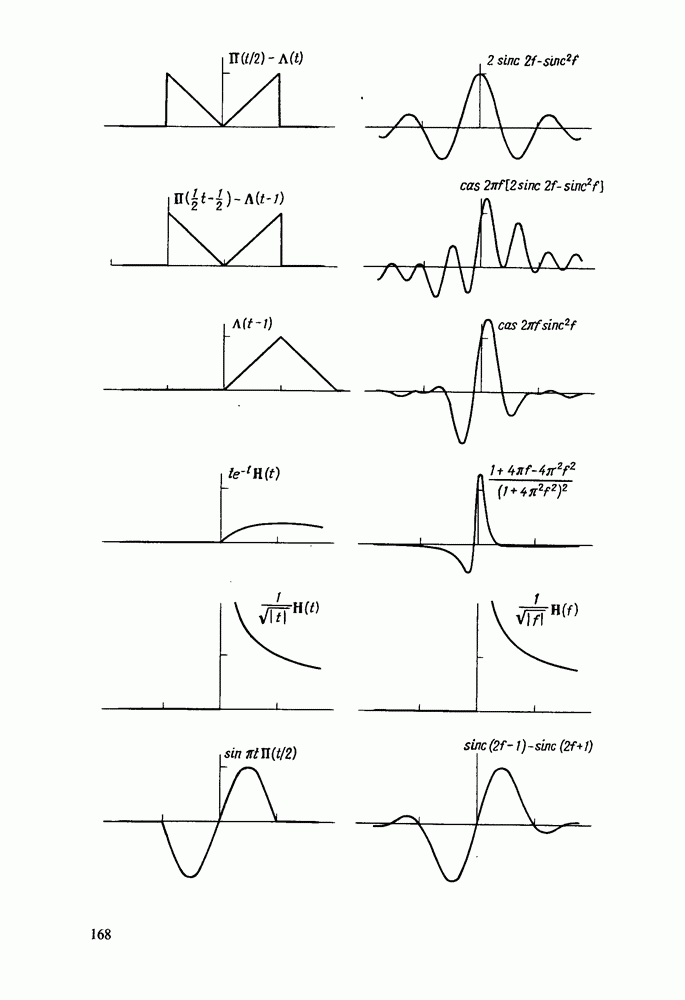
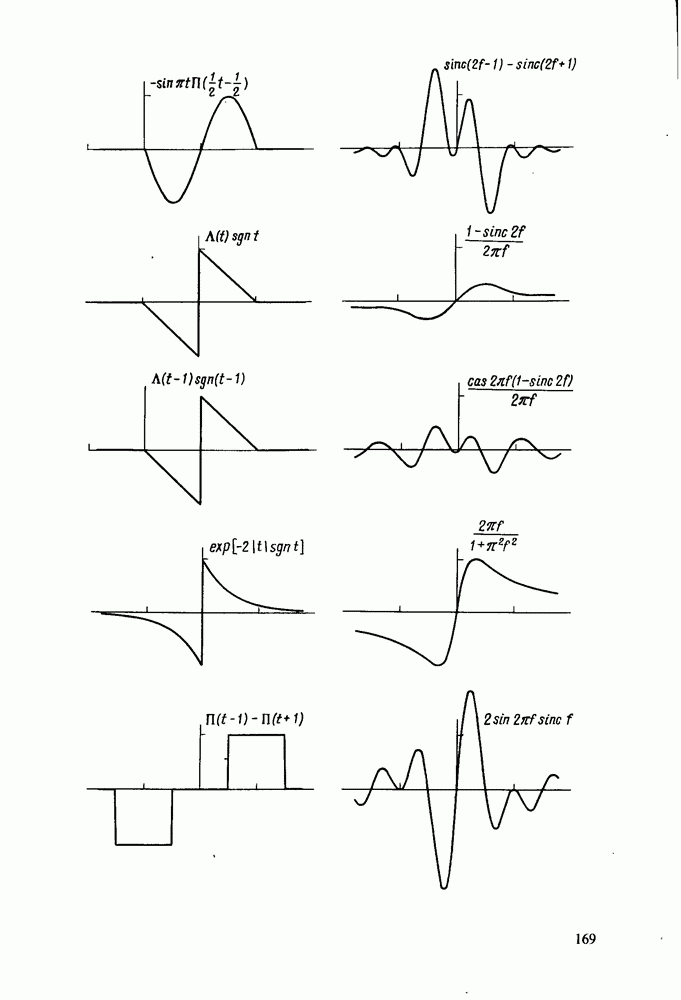
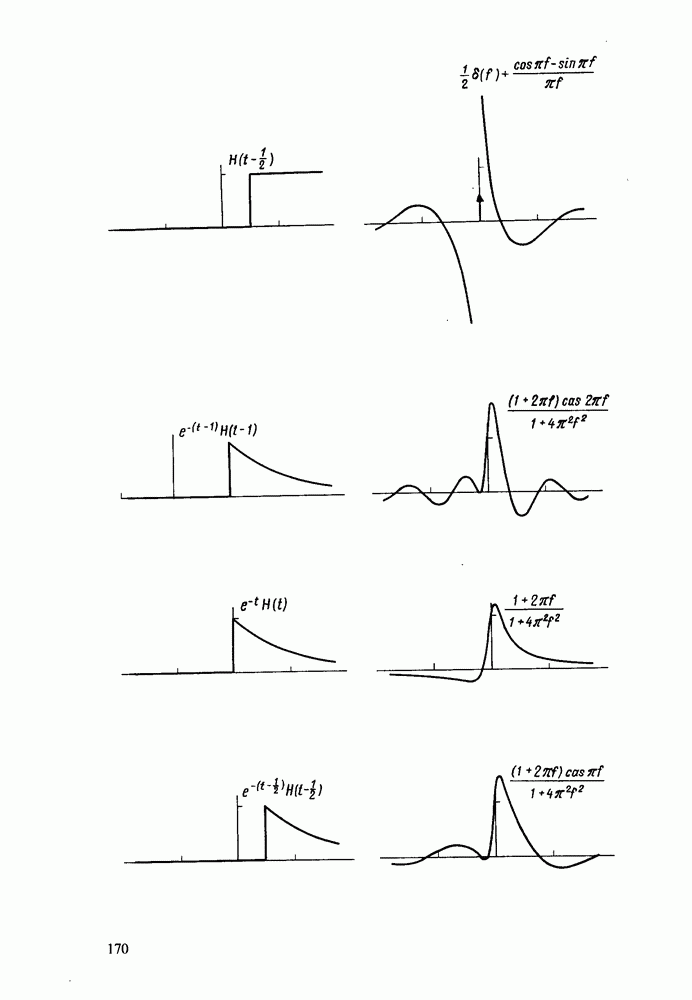
- Приложение 2. АТЛАС ПРЕОБРАЗОВАНИЙ ХАРТЛИ