| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Теорема о свертке
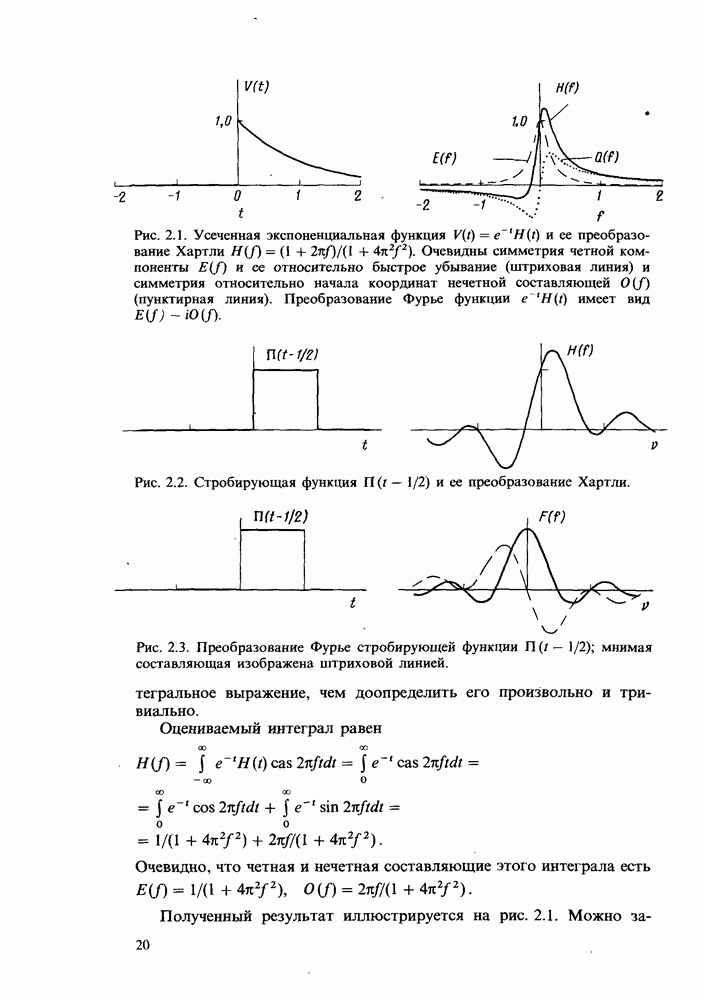
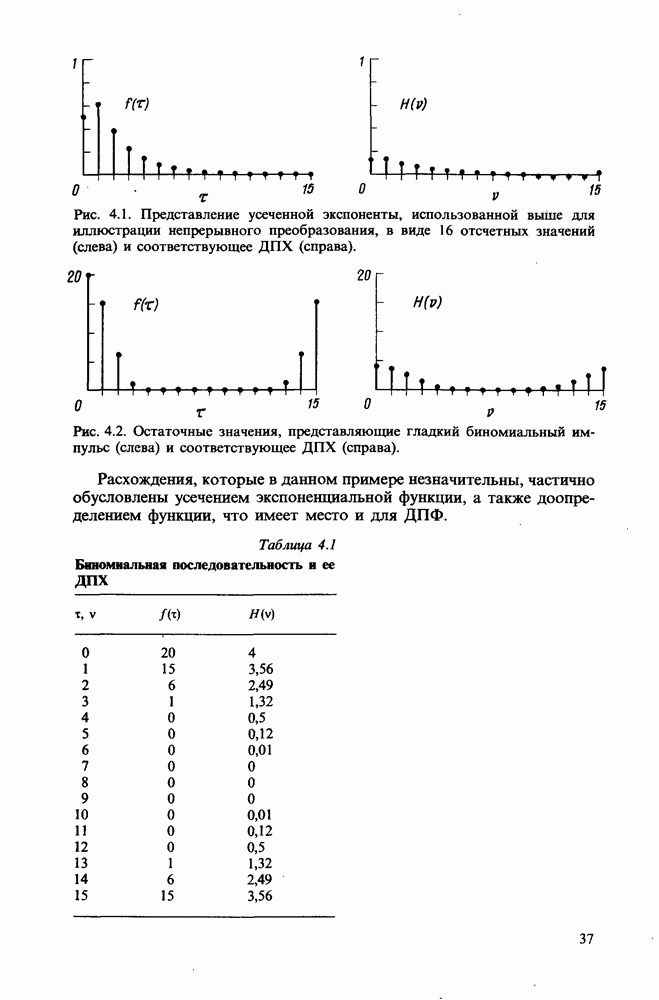
Теорема о свертке, удовлетворяющая дискретному преобразованию Хартли (ДПХ), формулируется следующим образом. Если  - циклическая
- циклическая
свертка последовательностей  т. е.
т. е.

то

где  - ДПХ последовательностей
- ДПХ последовательностей  соответственно. Этот результат может быть выражен другим способом в виде
соответственно. Этот результат может быть выражен другим способом в виде

где  - сумма четной и нечетной компонент.
- сумма четной и нечетной компонент.
Обычный путь численного выполнения свертки заключается в дискретном преобразовании Фурье каждой из двух заданных последовательностей и в последующем умножении их комплексных элементов в области преобразования Фурье, что равнозначно умножению четырех соответствующих вещественных величин в элементе ДПФ свертки. Далее следует выполнить обратное преобразование Фурье, не забывая при этом о необходимости изменения знака перед мнимой единицей  . Аналогичная процедура использования преобразования Хартли для выполнения свертки потребует только двух умножений вещественных величин в элементе ДПХ сверток.
. Аналогичная процедура использования преобразования Хартли для выполнения свертки потребует только двух умножений вещественных величин в элементе ДПХ сверток.
Однако очень часто возникают ситуации, особенно при обработке изображений, а также в общем случае при цифровой фильтрации, когда одна из свертываемых функций, например  является четной. Поэтому в данных ситуациях теорема о свертке упрощается и приводится к виду
является четной. Поэтому в данных ситуациях теорема о свертке упрощается и приводится к виду

Благодаря этому упрощению необходимо только определить ДПХ обеих последовательностей данных, затем поэлементно перемножить получившиеся вещественные последовательности и к полученному результату применить операцию ДПХ. Таким образом, предлагаемая процедура имеет вид

Этот изящный и простой результат имеет сходство с результатом для ДПФ, а различие состоит лишь в том, что применительно к преобразованию Фурье определяются два прямых ДПФ, выполняется ряд умножений комплексных величин, а затем получившаяся комплексная последовательность подвергается процедуре обратного ДПФ. Вопрос выбора коэффициента  будет рассмотрен ниже.
будет рассмотрен ниже.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ВВЕДЕНИЕ
- Глава 2. ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Преобразование Хартли
- Четная и нечетная составляющие
- Формулы связи
- Примеры
- Энергетический и фазовый спектры
- Глава 3. ТЕОРЕМЫ
- Свертка
- Соотношения между преобразованиями во временной и частотой областях
- Глава 4. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ХАРТЛИ
- Физический смысл величин «тау» и v
- Четная и нечетная составляющие
- Примеры дискретных преобразований Хартли
- Степени свободы
- Другие вещественные ядра
- Теоремы
- Выводы
- Глава 5. ЦИФРОВАЯ ФИЛЬТРАЦИЯ ПОСРЕДСТВОМ СВЕРТКИ
- Циклическая свертка
- Дополнение нулями
- Обращение свертки
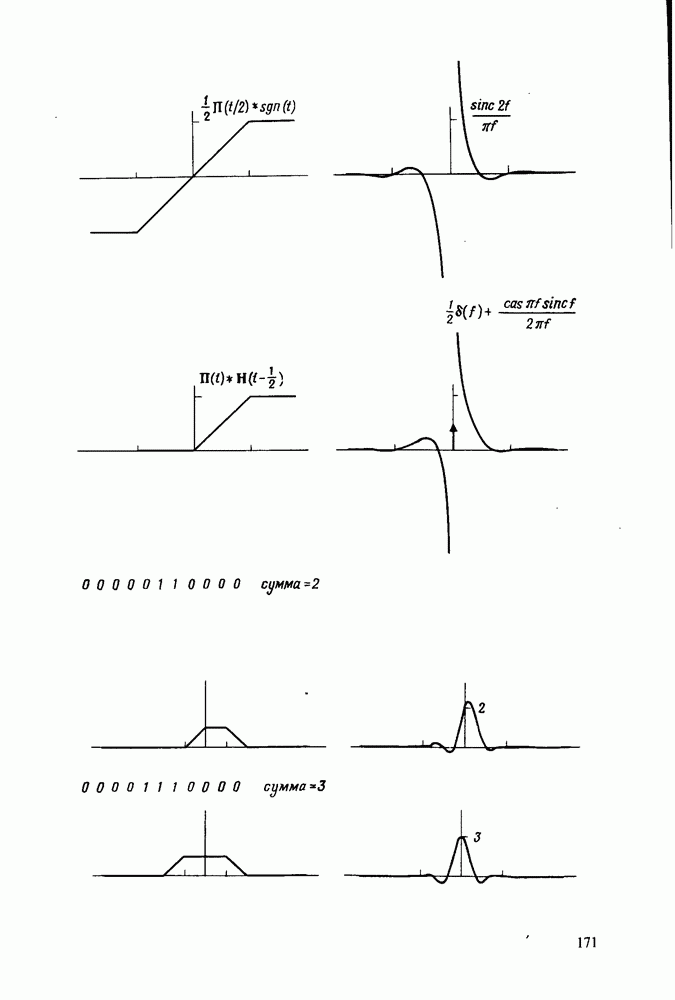
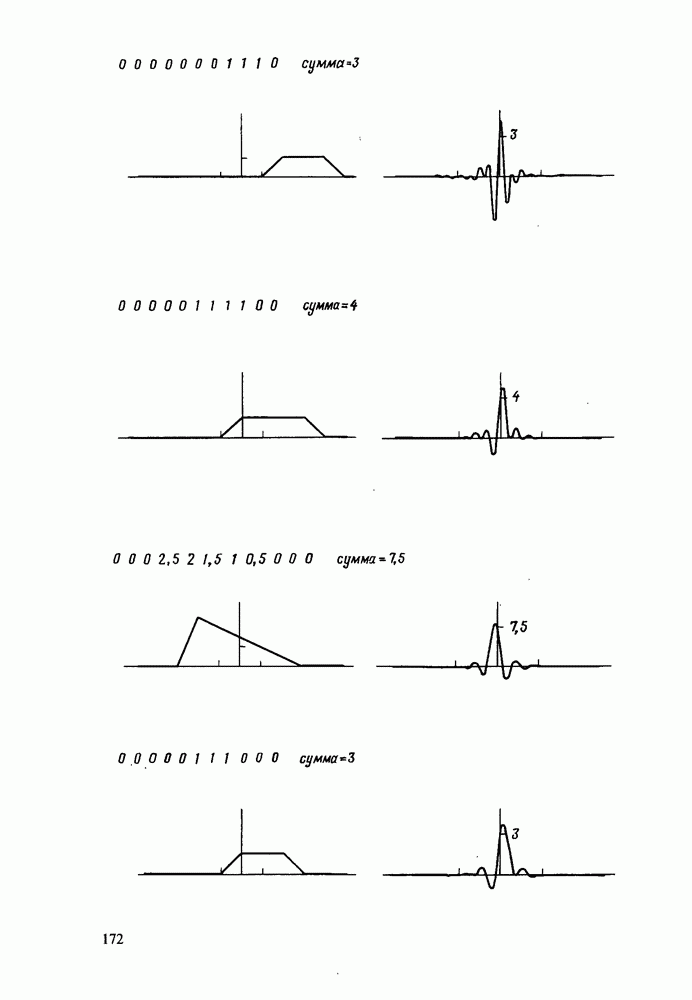
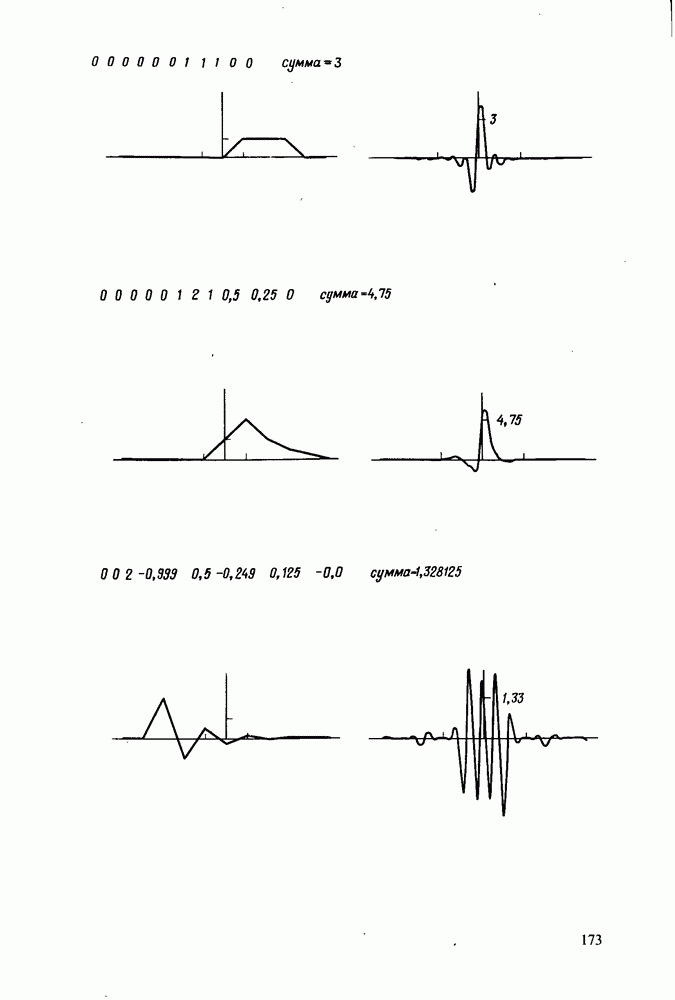
- Теорема о свертке
- Теорема о свертке в частотной области (спектральное сглаживание)
- Числовой пример свертки
- Коэффициент
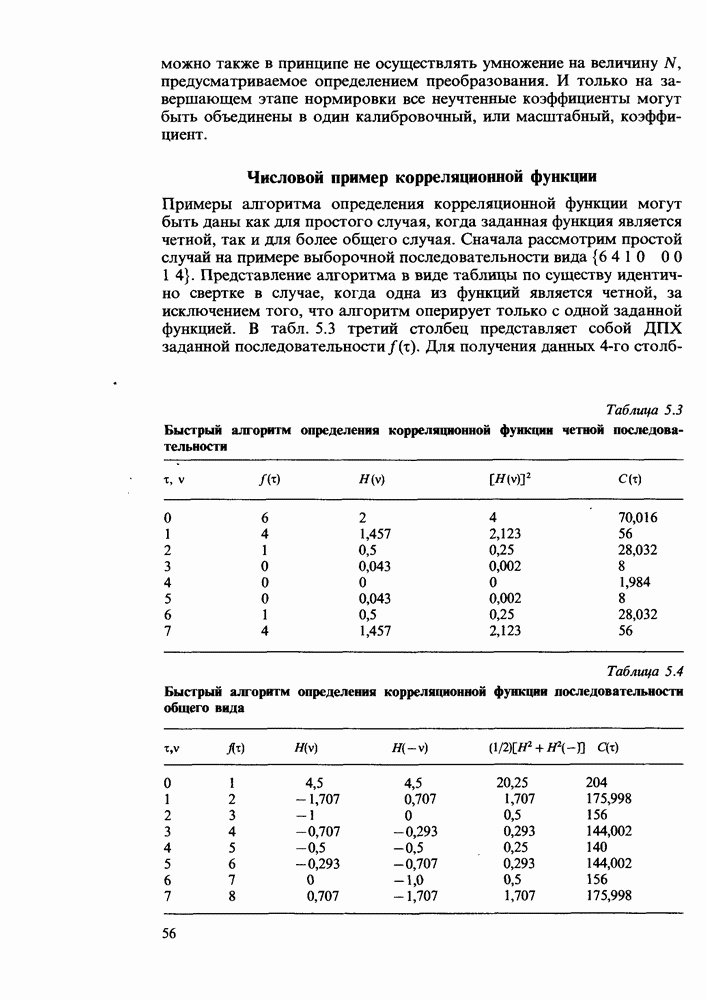
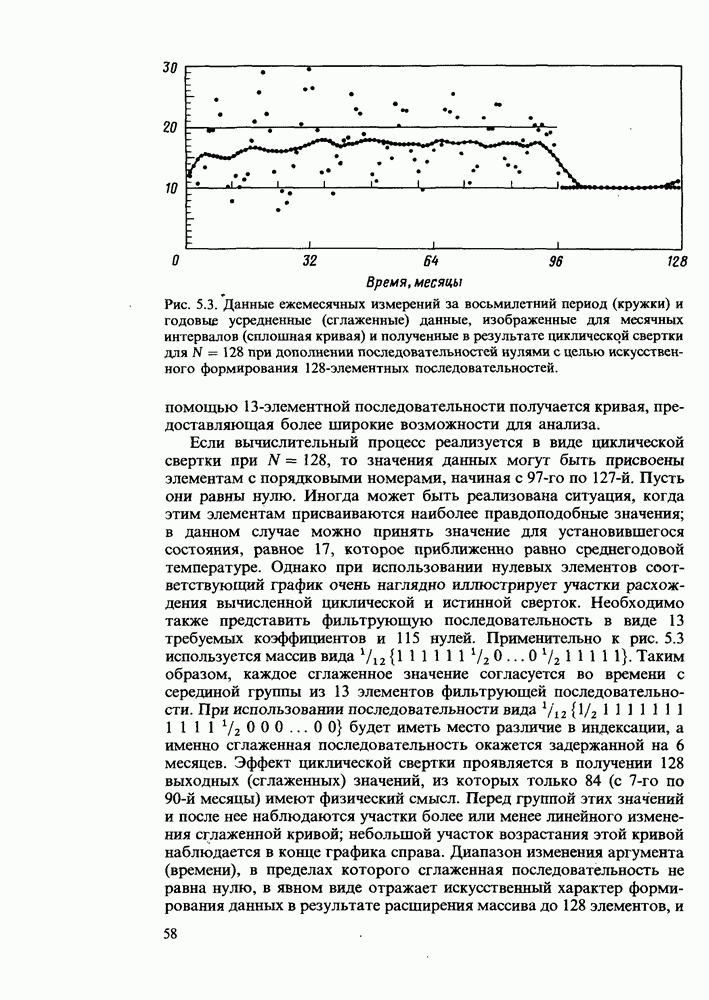
- Числовой пример корреляционной функции
- Низкочастотная фильтрация
- Подчеркивание границ
- Свертка с использованием быстрого преобразования Хартли
- Способ без использования перестановок
- Свертка как умножение матриц
- Глава 6. Двумерные преобразования
- Двумерное преобразование Хартли
- Симметрия и антисимметрия
- Примеры
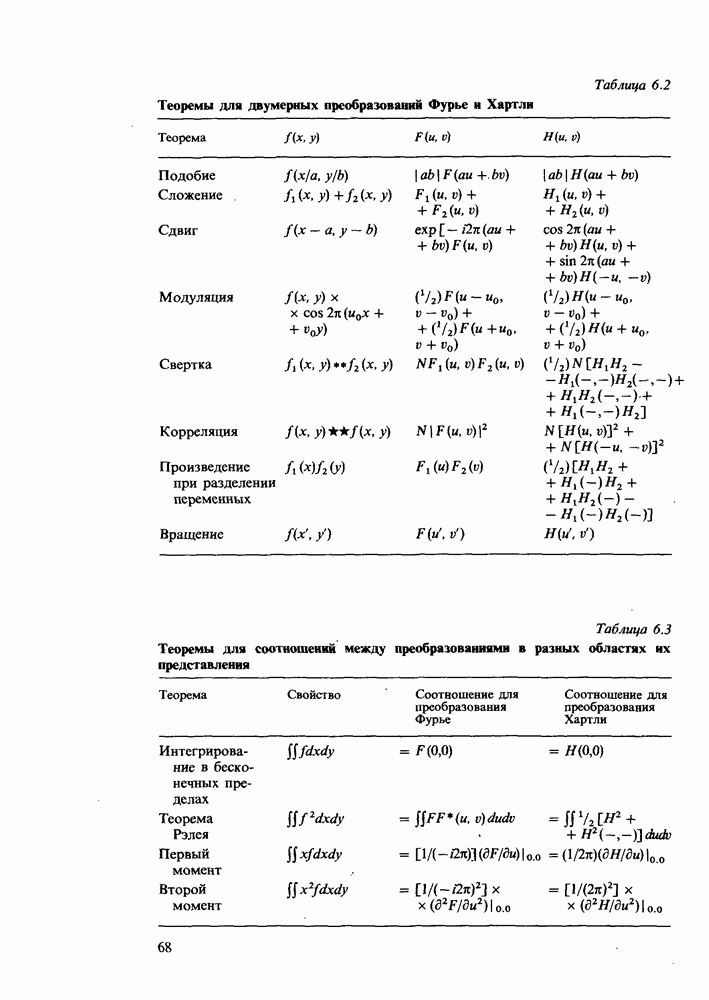
- Теоремы для двумерных преобразований
- Круговая симметрия
- Двумерная фильтрация
- Цикличность для двумерного случая
- Трехмерный случай
- Глава 7. ФАКТОРИЗАЦИЯ МАТРИЦЫ ПРЕОБРАЗОВАНИЯ
- Перестановка
- Перестановочные диаграммы
- Перестановочная матрица
- Ячеистая структура перестановочной диаграммы
- Каскадные матрицы
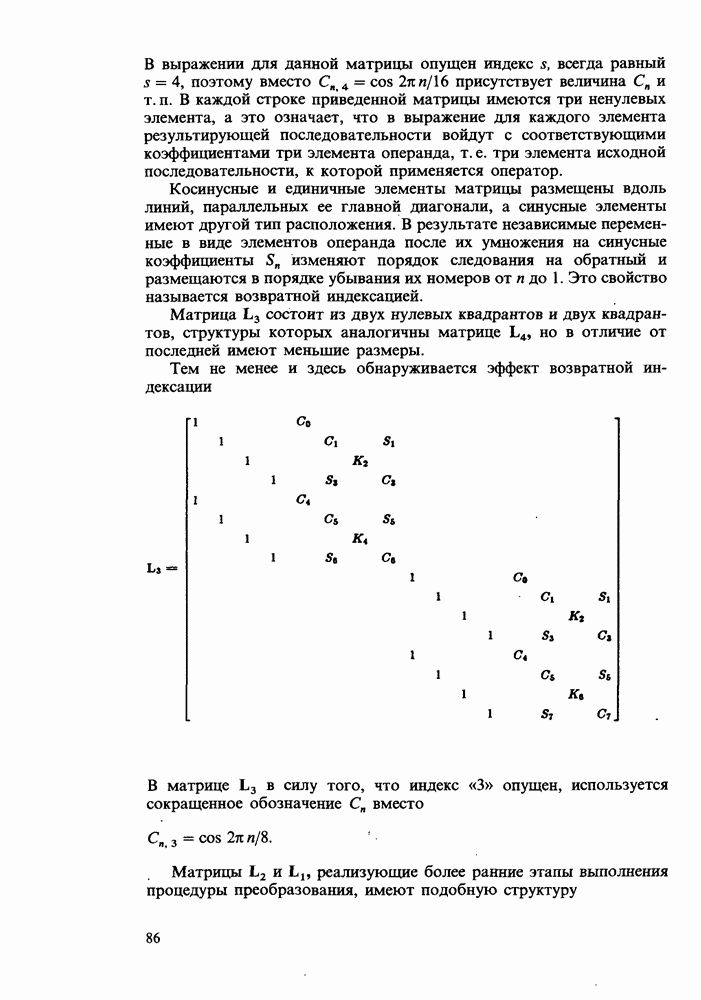
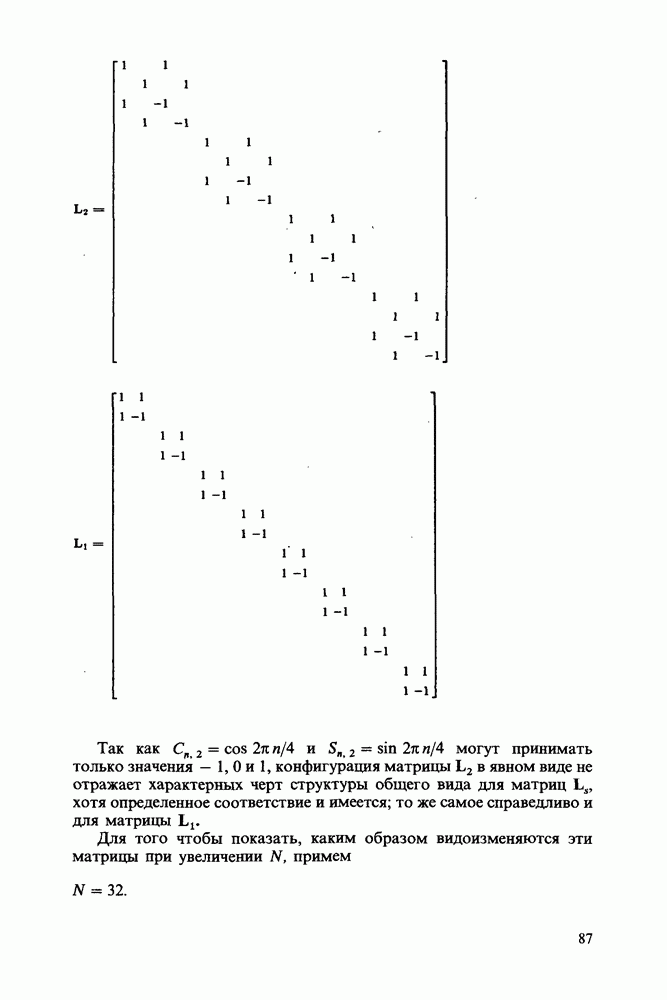
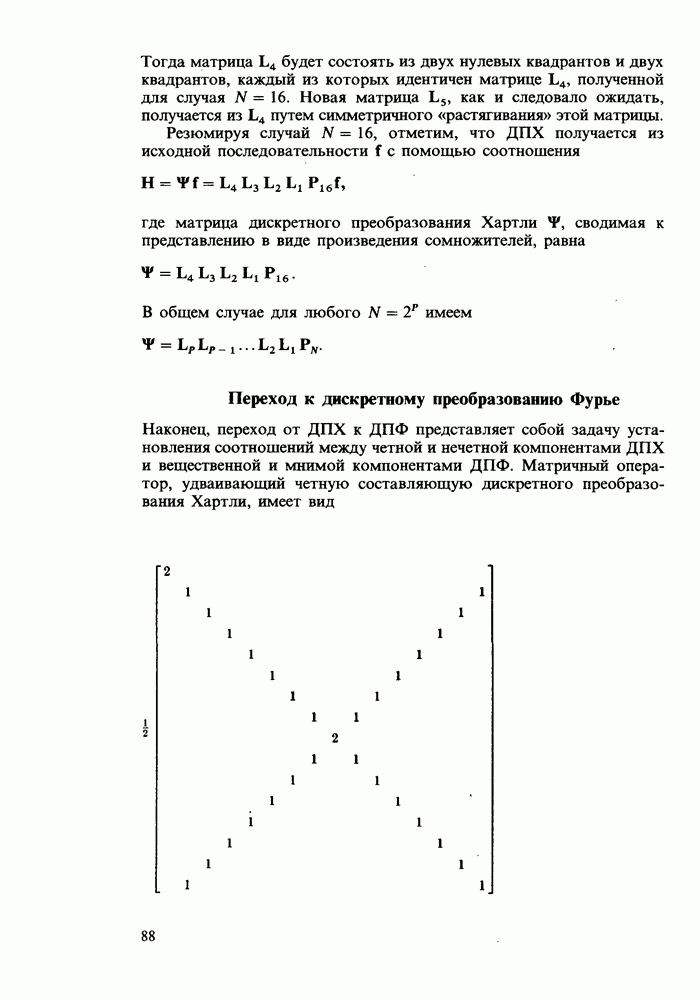
- Переход к дискретному преобразованию Фурье
- Глава 8. АЛГОРИТМ БЫСТРОГО ПРЕОБРАЗОВАНИЯ
- Свойство N log N
- Повторное разбиение последовательностей
- Преобразование с использованием разложения на подпоследовательности
- Общая формула разложения.
- Направленный сигнальный граф
- Вычисление с замещением
- Анализ временных затрат на вычисление с помощью полосковой диаграммы
- Степепи числа 2
- Тригонометрические функции
- Быстрое вычисление синусов
- Операция быстрого поворота
- Быстрая перестановка
- Преобразование для последовательностей с основанием 4 и другие модификации
- Ранее применявшиеся подходы к преобразованию вещественных данных
- Глава 9. ПРЕОБРАЗОВАНИЕ ХАРТЛИ В ОПТИКЕ
- Свойства симметрии
- Осуществление преобразования Хартли, использующее поляризацию
- Практическое осуществление
- Источник некогерентного излучения
- Пример
- Голография в плоскости Хартли
- Приложение 1. ПРОГРАММЫ ВЫЧИСЛЕНИЙ НА ЭВМ
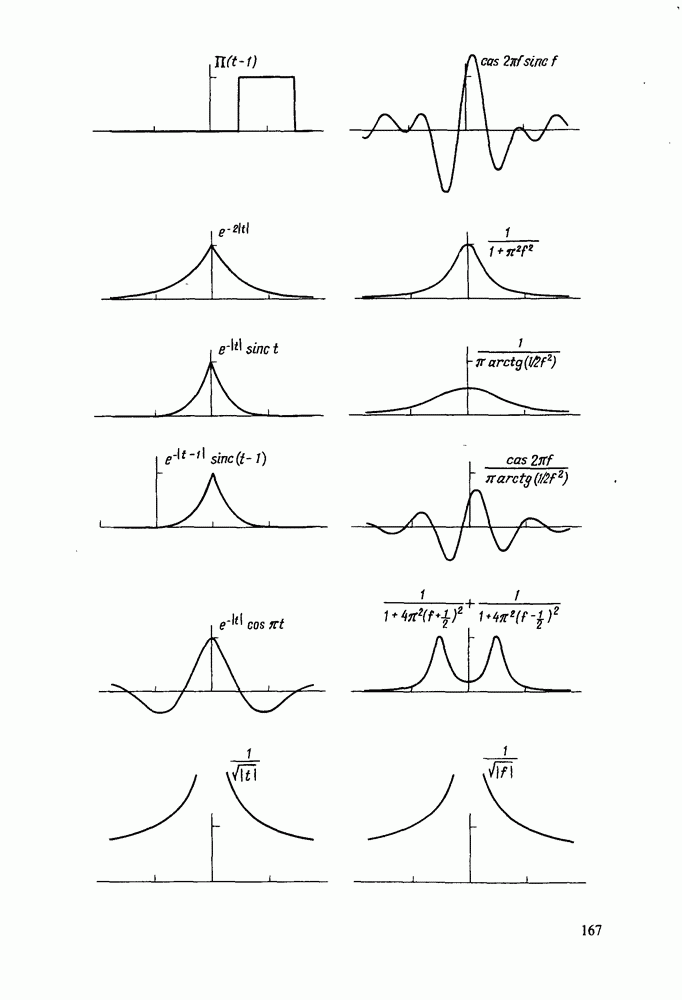
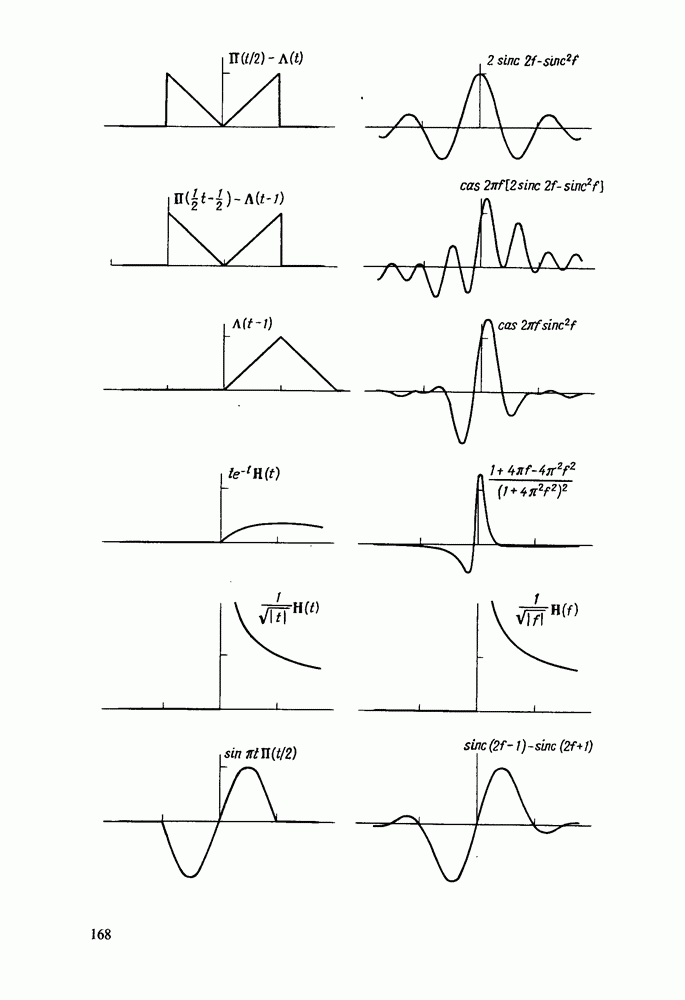
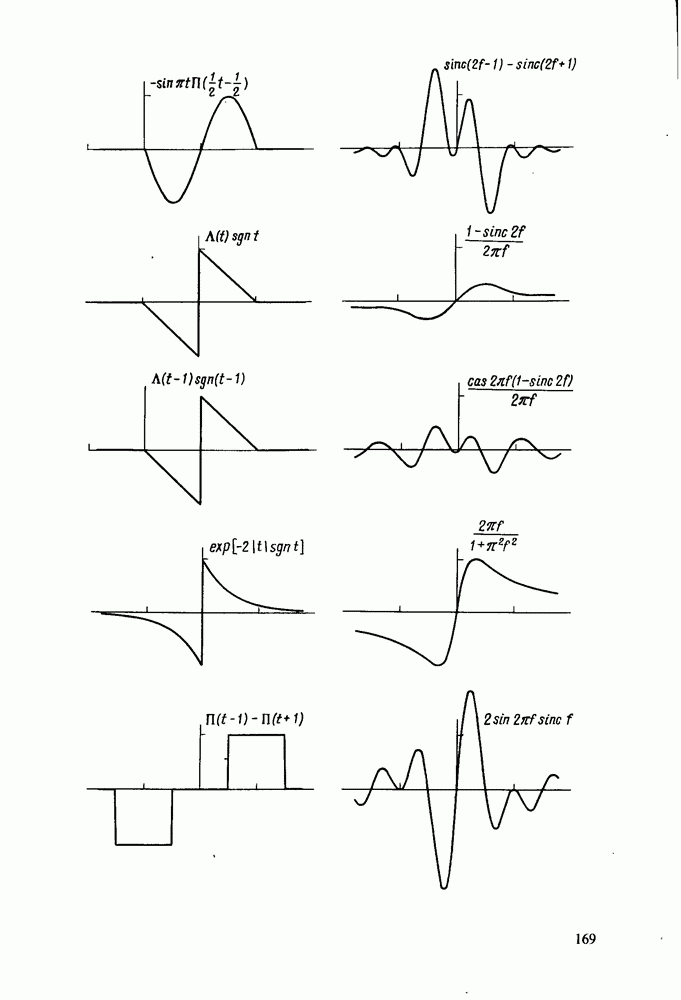
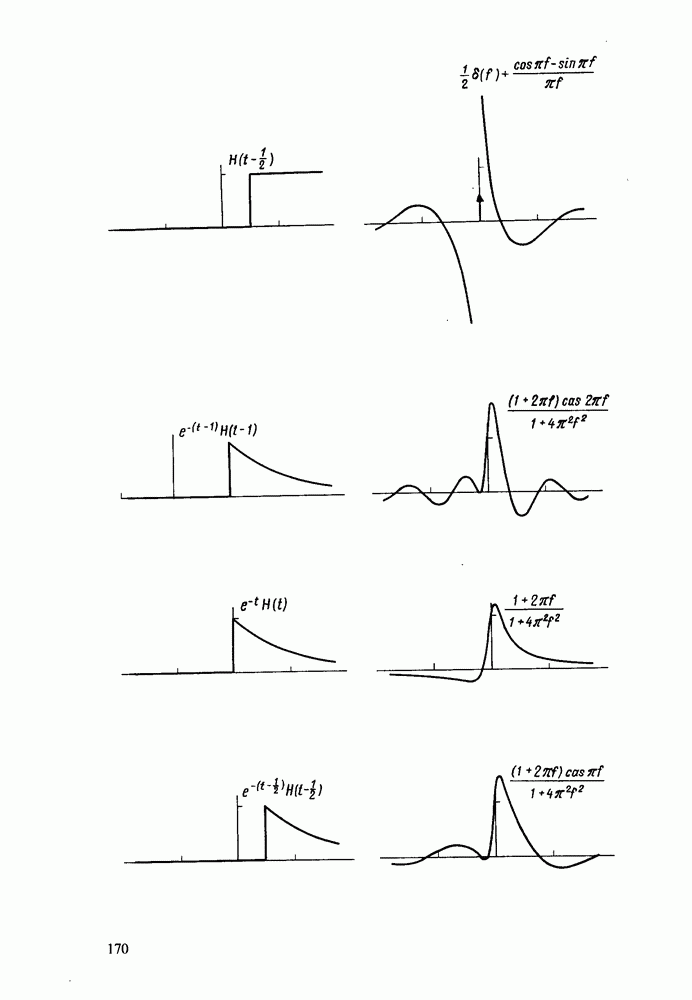
- Приложение 2. АТЛАС ПРЕОБРАЗОВАНИЙ ХАРТЛИ