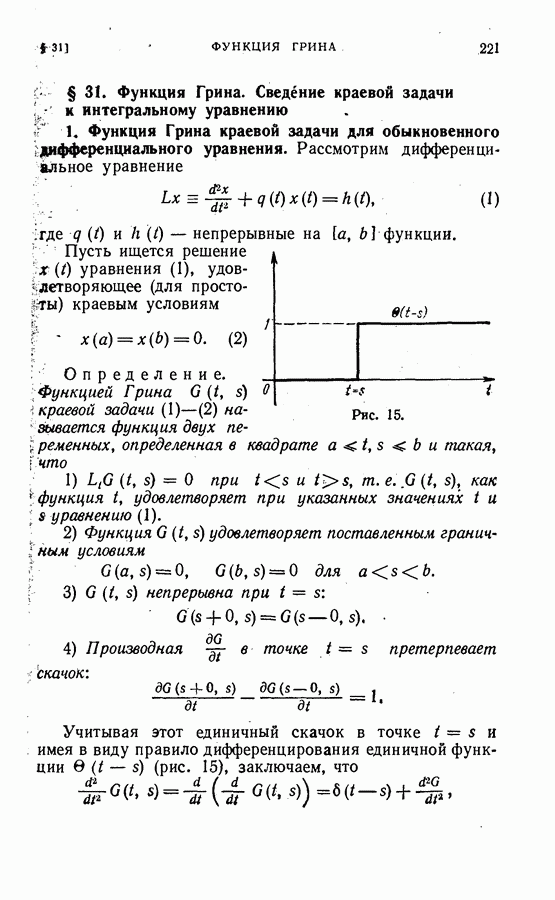
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 8. Применение принципа сжатых отображений к интегральным уравнениям
1°. Применим принцип сжатых отображений для доказательства существования и единственности решения неоднородного линейного интегрального уравнения Фредгольма 2-го рода

Предположим, что ядро  непрерывно в замкнутом квадрате
непрерывно в замкнутом квадрате  , следовательно, ограничено
, следовательно, ограничено
в нем:  Предположим также, что
Предположим также, что  Будем искать решение уравнения (1) в классе
Будем искать решение уравнения (1) в классе  функций, непрерывных на
функций, непрерывных на  .
.
При этом решением интегрального уравнения (1) будем называть всякую функцию  которая, будучи подстазлена в уравнение (1), обращает его в тождество по
которая, будучи подстазлена в уравнение (1), обращает его в тождество по  на
на 

Очевидно, что при  уравнение (1) имеет единственное непрерывное решение
уравнение (1) имеет единственное непрерывное решение 
Покажем, что уравнение (1) однозначно разрешимо и при всех Я, достаточно малых по абсолютной величине. Будем рассматривать правую часть уравнения (1) как оператор  определенный в пространстве
определенный в пространстве 

Всякую функцию  оператор А переводит в некоторую, вообще другую, функцию
оператор А переводит в некоторую, вообще другую, функцию  определенную на том же отрезке
определенную на том же отрезке  . И вопрос о существовании решения
. И вопрос о существовании решения  интегрального уравнения (1) тем самым сводится к вопросу о наличии неподвижной точки у оператора А, т. е. такой функции
интегрального уравнения (1) тем самым сводится к вопросу о наличии неподвижной точки у оператора А, т. е. такой функции  которая оператором А переводится в себя:
которая оператором А переводится в себя: 
Рассмотрим, например, уравнение

Оператор, отвечающий этому уравнению,

Полагая  имеем
имеем

т. е.

Положим теперь  Тогда
Тогда

т. е.

Таким образом, «точка»  есть неподвижная точка оператора А — решение интегрального уравнения
есть неподвижная точка оператора А — решение интегрального уравнения 
Покажем, что оператор А, определенный формулой (3), действует из полного пространства  опять в
опять в  , т. е. что если
, т. е. что если  где
где  , то и
, то и  .
.
Действительно, пусть  — произвольная точка отрезка
— произвольная точка отрезка  и пусть
и пусть  - любое, лишь бы
- любое, лишь бы  Имеем
Имеем

Возьмем любое  По условию
По условию  , и потому
, и потому  такое, что
такое, что

Пусть, далее,

Ядро  непрерывно в замкнутом квадрате
непрерывно в замкнутом квадрате  , значит, равномерно непрерывно в
, значит, равномерно непрерывно в  Поэтому для выбран ного
Поэтому для выбран ного  найдется
найдется  такое, что
такое, что 

при  и любом
и любом 
Возьмем  Тогда при
Тогда при  таких, что
таких, что  будут одновременно выполняться неравенства (5) и (6) и в силу неравенства (4) получим, что
будут одновременно выполняться неравенства (5) и (6) и в силу неравенства (4) получим, что

что и доказывает непрерывность функции  в любой; точке
в любой; точке  отрезка
отрезка 
Итак,

Выясним теперь, при каких условиях оператор А будет сжимающим. Имеем

 Вспоминая, что
Вспоминая, что  неравенству (7) придадим следующий вид:
неравенству (7) придадим следующий вид:

откуда видно, что при  оператор А будеч оператором сжатия.
оператор А будеч оператором сжатия.
Из принципа сжатых отображений заключаем, что для всякого  такого, что
такого, что

уравнение Фредгольма (1) с непрерывным ядром  и непррывным свободным членом
и непррывным свободным членом  имеет единственное непрерывное решение.
имеет единственное непрерывное решение.
Последовательные приближения  к этому решению определяются из соотношений
к этому решению определяются из соотношений

где в качестве  можно взять любую непрерывную на
можно взять любую непрерывную на  функцию.
функцию.
Пример. Решить интегральное уравнение

Решение. Ядро  непрерывно в квадрате
непрерывно в квадрате  причем
причем

Далее,  так что
так что  , и условие
, и условие  , обеспечивающее сжатость отображения, здесь выполнено. Поэтому интегральное уравнение (9) может быть решено мзтодом последовательных приближений. Доложим
, обеспечивающее сжатость отображения, здесь выполнено. Поэтому интегральное уравнение (9) может быть решено мзтодом последовательных приближений. Доложим  Тогда, согласно (8),
Тогда, согласно (8),

Отсюда

Если взять  то будем иметь
то будем иметь 
Таким образом, мы сразу получаем решение. Это как раз подчеркивает, что удачный выбор начальной функции  может значительно сократить процесс нахождения решения интегрального уравнения.
может значительно сократить процесс нахождения решения интегрального уравнения.
Вернемся снова к интегральному уравнению (1):

Будем по-прежнему предполагать, что ядро  непрерывны. Исходя из метрики пространства
непрерывны. Исходя из метрики пространства  мы показали, что уравнение 1) имеет единственное непрерывное, решение
мы показали, что уравнение 1) имеет единственное непрерывное, решение  если
если  , где
, где

Покажем теперь, пользуясь метрикой пространства 

что этот результат справедлив в более широком интервале значений Параметра 
Лемма. При любом  т. е. таком, что
т. е. таком, что

функция

непрерывна на 
Доказательство. Возьмем любую точку  По условию ядро К.
По условию ядро К.  непрерывно в замкнутом
непрерывно в замкнутом
том квадрате  , значит, равномерно непрерывно в нем. Поэтому для всякого
, значит, равномерно непрерывно в нем. Поэтому для всякого  существует такое
существует такое  что для всех
что для всех  таких, что
таких, что  справедливо неравенство
справедливо неравенство

Поэтому

В силу произвольности  отсюда и вытекает непрерывность функции
отсюда и вытекает непрерывность функции  в любой точке
в любой точке  Лемма доказана.
Лемма доказана.
Из леммы следует, что правая часть (1) есть непрерывная функция при любой  Следовательно, должна быть непрерывной и левая часть.
Следовательно, должна быть непрерывной и левая часть.
Таким образом, среди всех функций, входящих в  решениями уравнения (1) могут быть только непрерывные функции.
решениями уравнения (1) могут быть только непрерывные функции.
Будем рассматривать правую часть (1) как оператор  заданный в пространстве
заданный в пространстве 
В силу леммы

Положим

и покажем, что при  оператор А — сжимающий. Имеем
оператор А — сжимающий. Имеем

Используя неравенство Коши—Буняковского, отсюда получаем

Интегрируя обе части последнего неравенства по  от о до
от о до  найдем
найдем 

или

откуда

Следовательно, при  т. е. при
т. е. при  оператор А — сжимающий. И значит, при
оператор А — сжимающий. И значит, при  интегральное уравнение (1) имеет единственное непрерывное решение
интегральное уравнение (1) имеет единственное непрерывное решение 
Очевидно, что  (равенство возможно лишь при
(равенство возможно лишь при  и интервал
и интервал  вообще, шире, чем интервал
вообще, шире, чем интервал  .
.
Так, в рассмотренном выше примере имеем

и для  получаем следующую оценку:
получаем следующую оценку: 
Однако если  то для последовательных приближений
то для последовательных приближений  можно гарантировать лишь сходимость в среднем, а не равномерную сходимость, имеющую место при
можно гарантировать лишь сходимость в среднем, а не равномерную сходимость, имеющую место при  .
.
Замечание. Можно отказаться от непрерывности  «Штрабовать лишь, чтобы
«Штрабовать лишь, чтобы 

В этом случае естественно искать решение среди функций из  Можно показать, что и в этом случае при
Можно показать, что и в этом случае при  уравнение (1) имеет единственное решение. Но это решение уже не обязано быть непрерывной функцией, а его единственность означает единственность с точностью до функций, почти всюду равных нулю.
уравнение (1) имеет единственное решение. Но это решение уже не обязано быть непрерывной функцией, а его единственность означает единственность с точностью до функций, почти всюду равных нулю.
2°. Рассмотрим интегральное уравнение Вольтерра второго рода

Выше отмечалось, что это уравнение можно рассматривать как частный случай уравнения Фредгольма, доопределив ядро  равенством
равенством

Однако, в отличие от уравнений Фредгольма, к уравнениям Вольтерра принцип сжатых отображений (точнее, одно его обобщение) применим при всех значениях К. Введем предварительно следующее понятие.
Пусть X и  — метрические пространства. Оператор А, отображающий множество
— метрические пространства. Оператор А, отображающий множество  в пространство
в пространство  называется непрерывным в точке
называется непрерывным в точке  если для любого
если для любого  существует такое
существует такое  что для всех
что для всех  удовлетворяющих условию
удовлетворяющих условию

имеет место неравенство

(Здесь  — расстояния между элементами пространств X и
— расстояния между элементами пространств X и  соответственно.)
соответственно.)
Оператор А называется просто непрерывным, если он непрерывен в каждой точке того множества, на котором он задан.
Пусть оператор А действует из X в X. Возьмем любой элемент  (Тогда
(Тогда  будет опять принадлежать пространству X и к нему снова можно применить оператор А:
будет опять принадлежать пространству X и к нему снова можно применить оператор А:

Оператор, состоящий в последовательном применении дважды оператора А, будем обозначать символом  и называть квадратом оператора А.
и называть квадратом оператора А. 
Аналогично определяются операторы  и вообще любая целая положительная степень
и вообще любая целая положительная степень  оператора А.
оператора А.
Теорема 2.2. Пусть А — такое непрерывное отображение полного метрического пространства X в себя, что отображение Аппри некотором  является сжатым Тогда уравнение
является сжатым Тогда уравнение  имеет, и притом единственное, решение.
имеет, и притом единственное, решение.
Обратимся к интегральному уравнению (11)

Будем предполагать, что  и что ядро
и что ядро  непрерывно в замкнутом треугольнике
непрерывно в замкнутом треугольнике 
Введем оператор  определив его формулой
определив его формулой

Нетрудно установить, что

Покажем, что Л — непрерывный оператор.
Пусть  — любые две функции из
— любые две функции из  Тогда
Тогда

Здесь

Из оценки (13) получаем, что 

так что

Возьмем любое  Тогда при
Тогда при  из условия
из условия  будем иметь
будем иметь

Согласно определению, это и означает, что оператор А, определенный формулой (12), есть непрерывный оператор из 
Далее, используя оценку (16), находим

и, вообще,

Неравенство (14) верно для любого  , значит,
, значит,

При любом значении X число  можно выбрать настолько большим, что
можно выбрать настолько большим, что

Следовательно, оператор  будет сжимающим при достаточно большом
будет сжимающим при достаточно большом 
В силу теоремы 2.2 отсюда заключаем, что сам оператор А имеет единственную неподвижную точку и, значит, уравнение Вольтерра (11) при любом X имеет, и притом единственное, решение.
Это решение может быть найдено методом последовательных приближений, которые строятся по схеме

где в качестве  можно взять любую функцию из
можно взять любую функцию из 
Пример. Методом последовательных приближений решить интегральное уравнение

Решение. В данном случае  непрерывны и, значит, уравнение имеет единственное непрерывное решение.
непрерывны и, значит, уравнение имеет единственное непрерывное решение.
Будем его искать методом последовательных приближений. По ложим  . Тогда получим
. Тогда получим

Далее,

Ясно, чио

Непосредственной проверкой убеждаемся, что функция  есть решение данного интегрального уравнения.
есть решение данного интегрального уравнения.
3°. Принцип сжатых отображений применим к решению некоторых видов нелинейных интегральных уравнений. Пусть имеем уравнение

где  непрерывные функции своих аргументов для а
непрерывные функции своих аргументов для а 
Пусть, кроме того,  удовлетворяет условию Липшица по своему «функциональному» аргументу
удовлетворяет условию Липшица по своему «функциональному» аргументу  т. е.
т. е.

где  — некоторая постоянная, независящая от выбора
— некоторая постоянная, независящая от выбора 
Рассмотрим отображение  полного пространства
полного пространства  в себя, где
в себя, где

Пусть  — любые две функции из
— любые две функции из  . Тогда
. Тогда

Оценка (18) справедлива для любого  Значит, и
Значит, и

Следовательно, при  оператор А будет сжимающим и, в силу теоремы 2.1, интегральное уравнение (16) будет иметь при таких Я единственное непрерывное решение.
оператор А будет сжимающим и, в силу теоремы 2.1, интегральное уравнение (16) будет иметь при таких Я единственное непрерывное решение.
Это решение может быть найдено методом последовательных приближений по схеме

где в качестве  можно взять любую функцию из
можно взять любую функцию из 

Замечание. Если функция  имеет ограниченную частную производную по
имеет ограниченную частную производную по 

то такая функция удовлетворяет условию Липшица по  с константой
с константой  . В самом деле, воспользовавшись теоремой Лагранжа, будем иметь
. В самом деле, воспользовавшись теоремой Лагранжа, будем иметь

где  заключено между
заключено между  Из (19) получаем
Из (19) получаем  что и доказывает наше утверждение.
что и доказывает наше утверждение.
Пример. Решить интегральное уравнение

Решение. Функция  непрерывная функция своих аргументов; она имеет ограниченную производную по а
непрерывная функция своих аргументов; она имеет ограниченную производную по а

и, следовательно, удовлетворяет условию Липшица по  причем в качестве постоянной Липшица мы можем взять
причем в качестве постоянной Липшица мы можем взять  Далее,
Далее,  так что условие
так что условие

обеспечивающее сжатость отображения, здесь выполнено. Применим метод последовательных приближений, взяв за нулевое приближение  . Тогда
. Тогда

Ясно, что  откуда
откуда

Непосредственной проверкой убеждаемся, что функция  есть решение данного интегрального уравнения (кстати, при любом значении
есть решение данного интегрального уравнения (кстати, при любом значении  ).
).
4°. Системы интегральных уравнений. Система интегральных уравнений Фредгольма второго рода с одной независимой переменной имеет вид

Пусть ядра  интегрируемы. с квадратом в
интегрируемы. с квадратом в  а свободные члены
а свободные члены  Будем искать решение
Будем искать решение  системы (20) также в классе
системы (20) также в классе  Поступйм следующим образом.
Поступйм следующим образом.
Сведем систему (20) к одному интегральному уравнению типа Фредгольма, но только на интервале, в  раз большем исходного. Делается это так. Определим функции
раз большем исходного. Делается это так. Определим функции  и
и  на отрезке
на отрезке  положив
положив

если

Точно так же зададим ядро  в квадрате
в квадрате

положив

если

Тогда система (20) запишется в виде одного уравнения Фредгольма:

Нетрудно видеть, что построенное нами ядро  интегрируемо с квадратом
интегрируемо с квадратом

а свободный член  Действительно,
Действительно,

Точно так же

Итак, мы свели систему уравнений (1) к одному интегральному уравнению Фредгольма с ядром  и свободным членом
и свободным членом 
Применяя к нему рассуждения  , получаем, что если
, получаем, что если  то уравнение (21) имеет единственное решение в классе
то уравнение (21) имеет единственное решение в классе  Это последнее может быть найдено методом последовательных приближений.
Это последнее может быть найдено методом последовательных приближений.
Следовательно, и для системы (20) последовательные приближения сходятся в среднем к решению системы, коль скоро  где
где

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Основные классы интегральных уравнений
- 2. Уравнение Вольтерра.
- II. Нелинейные уравнения
- Задача Абеля.
- ГЛАВА I. ТЕОРИЯ ФРЕДГОЛЬМА
- § 3. Формулы Фредгольма
- § 4. Интегральные уравнения с вырожденным ядром. Теоремы Фредгольма
- ГЛАВА II. ПРИНЦИП СЖАТЫХ ОТОБРАЖЕНИЙ
- § 6. Полные пространства
- § 7. Принцип сжатых отображений
- § 8. Применение принципа сжатых отображений к интегральным уравнениям
- ГЛАВА III. ЛИНЕЙНЫЕ ОПЕРАТОРЫ. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
- § 9. Линейные нормированные пространства
- II. Линейное нормированное пространство
- § 10. Линейные операторы. Норма оператора
- § 11. Пространство операторов
- § 12. Обратные операторы
- § 13. Приложение к линейным интегральным уравнениям
- 2. Уравнение Вольтерра.
- § 14. Теоремы Фредгольма для общего случая уравнения Фредгольма
- § 15. Интегральные уравнения с ядром, имеющим слабую особенность
- § 16. Характер решения интегрального уравнения
- ГЛАВА IV. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
- § 18. Преобразование Лапласа
- § 19. Преобразование Меллина
- § 20. Метод Винера—Хопфа
- ГЛАВА V. ВПОЛНЕ НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ
- § 21. Компактность множества. Критерий компактности
- § 22. Вполне непрерывные операторы
- § 23. Уравнения Рисса—Шаудера
- ГЛАВА VI. СИММЕТРИЧНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
- § 24. Симметричные операторы. Теорема Гильберта—Шмидта
- § 25. Решение операторных уравнений
- § 26. Интегральные уравнения с симметричным ядром
- Билинейное разложение симметричных ядер
- § 27. Теорема Гильберта — Шмидта для интегральных операторов
- § 28. Экстремальные свойства характеристических чисел и собственных функций
- § 29. Интегральные уравнения, приводящиеся к симметричным
- § 30. Классификация симметричных ядер
- § 31. Функция Грина. Сведение краевой задачи к интегральному уравнению
- 2. Сведение краевой задачи к интегральному уравнению.
- ГЛАВА VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 1-го РОДА
- § 32. Уравнение Вольтерра 1-го рода
- § 33. Уравнение Фредгольма 1-го рода
- § 34. Операторные уравнения 1-го рода
- ГЛАВА VIII. НЕФРЕДГОЛЬМОВЫ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ. СИНГУЛЯРНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
- § 35. Нефредгольмовы интегральные уравнения
- § 36. Сингулярные интегральные уравнения. Преобразования Гильберта
- Преобразования Гильберта
- ГЛАВА IX. НЕЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
- § 37. Уравнения Гаммерштейна
- § 38. Интегральные уравнения с параметром. Дифференциал Фреше. Теорема существования абстрактной неявной функции
- § 39. Разветвление решений
- § 40. Точки бифуркации
- § 41. Метод Ньютона
- § 42. Принцип неподвижной точки Ю. Шаудера
- ЛИТЕРАТУРА