| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 20. Метод Винера—Хопфа
Этот метод был разработан приблизительно в  для решения интегральных уравнений специального вида
для решения интегральных уравнений специального вида

называемых уравнениями типа Винера — Хопфа.
Отличительная особенность этих уравнений — ядро зависит от разности аргументов, а интервал интегрирования полубесконечный. Такие уравнения возникают всякий раз, когда мы имеем дело с граничными задачами, где границы являются полубесконечными (например, задача о дифракции волн на полуплоскости).
В методе Винера—Хопфа производится аналитическое продолжение преобразований Фурье по переменной преобразования с вещественной оси в комплексную плоскость.
Рассмотрим преобразование Фурье функции 

для комплексных 
Тогда

Важным является следующее свойство преобразования Фурье.
Пусть абсолютно интегрируемо произведение  где
где  — фиксированная постоянная. В этом случае преобразование Фурье
— фиксированная постоянная. В этом случае преобразование Фурье  функции
функции  является аналитической функцией в полосе
является аналитической функцией в полосе  комплексной
комплексной  -плоскости. Действительно,
-плоскости. Действительно,

и интеграл (3), определяющий  сходится при
сходится при  равномерно относительно
равномерно относительно  Следовательно,
Следовательно,  аналитична во всякой внутренней точке
аналитична во всякой внутренней точке  полосы —
полосы — 
Можно утверждать, что функция  при
при  стремится к нулю равномерно
стремится к нулю равномерно  с
с 
Аналогично показывается, что если  при
при  функция
функция

аналитична в полуплоскости  если
если  при
при  то функция
то функция

аналитична в полуплоскости  (Здесь
(Здесь  — действительные постоянные.)
— действительные постоянные.)
Характерной особенностью любого решения по методу Винера — Хопфа является разложение функции комплексной переменной на сумму двух функций. Справедлива
Теорема 4.3. Пусть  — аналитическая функция
— аналитическая функция  в полосе
в полосе  и такая, что
и такая, что  при
при  причем это неравенство выполняется равномерно для всех
причем это неравенство выполняется равномерно для всех  в полосе
в полосе  Тогда при
Тогда при 

где функция  аналитична в полуплоскости
аналитична в полуплоскости  а функция
а функция  аналитична в полуплоскости
аналитична в полуплоскости 
При

В основе этого представления лежит теорема об интегральном представлении функции, аналитической в некотором кольце. Функция  аналитическая в кольце
аналитическая в кольце  представляется с помощью интегральной формулы Коши в виде суммы двух интегралов, причем контуром интегрирования служит граница кольца аналитичности
представляется с помощью интегральной формулы Коши в виде суммы двух интегралов, причем контуром интегрирования служит граница кольца аналитичности  Один из интегралов берется по внешней окружности, другой — по внутренней (для полосы им отвечают интегралы по прямым
Один из интегралов берется по внешней окружности, другой — по внутренней (для полосы им отвечают интегралы по прямым  (рис. 13, а, б).
(рис. 13, а, б).
Функция, представленная интегралом вдоль внешней окружности, аналитична внутри этой окружности, а функция,
представленная интегралом по внутренней окружности, аналитична вне этой окружности. Переходя к случаю полосы и помещая центр «кольца» в точку  получаем требуемое представление.
получаем требуемое представление.
Рассмотрим теперь факторизацию произвольной функции  т. е. представление этой функции в виде произведения
т. е. представление этой функции в виде произведения

где  аналитичны и не имеют нулей в верхней и нижней полуплоскостях
аналитичны и не имеют нулей в верхней и нижней полуплоскостях  соответственно.
соответственно.

Рис. 13.
Ясно, что такое представление эквивалентно разложению функции

на сумму двух функций, каждая из которых аналитична в соответствующей области.
Иногда такое представление удается угадать; например, если

и на плоскости  сделаны соответствующие разрезы, то можно взять
сделаны соответствующие разрезы, то можно взять

(аналитична и не имеет нулей при  ),
),

(аналитична и не имеет нулей при  ).
).
Такое представление, очевидно, не единственно, так как можно одновременно умножить  и разделить
и разделить  на любую целую функцию, не имеющую нулей.
на любую целую функцию, не имеющую нулей.
Приведем теорему, устанавливающую возможность факторизации для весьма широкого класса функций.
Теорема 4.4. Если функция  удовлетворяет условиям, теоремы 4.3 (это означает, в частности, что функция
удовлетворяет условиям, теоремы 4.3 (это означает, в частности, что функция  аналитична и не имеет нулей в полосе
аналитична и не имеет нулей в полосе  при
при  в полосе
в полосе  то существует представление
то существует представление  где
где  аналитичные, ограниченные и не имеющие нулей функции при
аналитичные, ограниченные и не имеющие нулей функции при  соответственно.
соответственно.
Для доказательства теоремы 4.4 применим теорему 4.3 к функции  Имеем
Имеем

Здесь  — любые числа, удовлетворяющие условиям
— любые числа, удовлетворяющие условиям  Интеграл для
Интеграл для  сходится для всех
сходится для всех  в полуплоскости
в полуплоскости  Так как с можно выбрать сколь угодно близким к
Так как с можно выбрать сколь угодно близким к  то
то  ограничена и аналитична при
ограничена и аналитична при  Аналогично, функция
Аналогично, функция  аналитична и ограничена при
аналитична и ограничена при  Полагая
Полагая

будем иметь

или

Из свойств  следует, что функция
следует, что функция  аналитична, ограничена и не имеет нулей при
аналитична, ограничена и не имеет нулей при  Аналогично, функция
Аналогично, функция  аналитична, ограничена и не имеет нулей при
аналитична, ограничена и не имеет нулей при 
Таким образом, построив функции  обладающие требуемыми свойствами, мы доказали теорему 4.4.
обладающие требуемыми свойствами, мы доказали теорему 4.4.
Отметим, что требования, накладываемые на функцию  можно существенно ослабить.
можно существенно ослабить.
Рассмотрим сначала однородное интегральное уравнение типа Винера — Хопфа

(Полагаем для простоты  поскольку это здесь несущественно: параметр
поскольку это здесь несущественно: параметр  можно считать входящим как множитель в ядро
можно считать входящим как множитель в ядро 
Введем функции  положив
положив

Тогда уравнение (6) запишется так:

Теперь можно  выразить через
выразить через 

Пусть функция  являющаяся преобразованием Фурье ядра
являющаяся преобразованием Фурье ядра  аналитична в полосе
аналитична в полосе

Это соответствует асимптотическому поведению  при
при 

Мы рассматриваем решения уравнения (6), которые ведут себя, как  при
при  Условие Это необходимо для сходимости интеграла, входящего в интегральное уравнение. Асимптотическое поведение
Условие Это необходимо для сходимости интеграла, входящего в интегральное уравнение. Асимптотическое поведение  можно установить непосредственно из уравнения (8);
можно установить непосредственно из уравнения (8);

Отсюда видно, что необходимо  должна рести себя при
должна рести себя при  как
как  Обозначая через
Обозначая через  преобразования Фурье функций
преобразования Фурье функций  соответственно, заключаем, что
соответственно, заключаем, что  аналитична в полуплоскости
аналитична в полуплоскости  будет аиалитична в полуплоскости
будет аиалитична в полуплоскости 

Рис. 14.
Значит, существует полоса  (рис. 14), в которой аналитичны все преобразования
(рис. 14), в которой аналитичны все преобразования  Этот результат является основным в методе Винера — Хопфа.
Этот результат является основным в методе Винера — Хопфа.
Применяя преобразование Фурье к обеим частям уравнения (7) и используя теорему о свертке, получим

или

Функция  аналитична в полосе
аналитична в полосе

Попытаемся разложить ее на множители  так, чтобы
так, чтобы

Эти множители должны быть аналитичны и отличны от нуля в полуплоскостях  соответственно.
соответственно.
Обычно дополнительно требуют, чтобы  имели алгебраический рост, а не экспоненциальный. Возможность такого разложения была показана Винером и Хопфом.
имели алгебраический рост, а не экспоненциальный. Возможность такого разложения была показана Винером и Хопфом.
В каждой данной задаче это разложение на множители должно быть фактически осуществлено.
Пусть такое разложение выполнено. Тогда уравнение (9) можно переписать так:

Левая часть этого соотношения анадитична в полуплоскости  в то время как правая часть аналитична в полуплоскости
в то время как правая часть аналитична в полуплоскости  Поскольку они имеют общую область аналитичности
Поскольку они имеют общую область аналитичности  в которой они равны, то можно утверждать, что
в которой они равны, то можно утверждать, что  является аналитическим продолжением
является аналитическим продолжением  в нижнюю полуплоскость. Следовательно, функция
в нижнюю полуплоскость. Следовательно, функция  аналитична во всей плоскости комплексной переменной
аналитична во всей плоскости комплексной переменной  и потому является целой функцией
и потому является целой функцией 

откуда

Чтобы найти вид  надо еще учесть поведение этой
надо еще учесть поведение этой
- функции при больших  Условие интегрируемости
Условие интегрируемости  в начале координат приводит к асимптотике
в начале координат приводит к асимптотике

Пусть  уже выбрана так, что имеет алгебраический рост, т. е. при больших
уже выбрана так, что имеет алгебраический рост, т. е. при больших  ведет себя, как полином. Тогда
ведет себя, как полином. Тогда  будет представлять собой полином степени меньшей, чем порядок роста
будет представлять собой полином степени меньшей, чем порядок роста  (так как должно стремиться к нулю при
(так как должно стремиться к нулю при  ). Этим определяется вид
). Этим определяется вид 
Таким образом, учитывая (11), находим

откуда по формулам обращения получаем

Этим завершается решение интегрального уравнения Винера — Хопфа (6). Заметим, что  определяются с точностью до некоторых постоянных. Последние можно определить из физического смысла задачи или подстановкой решения в исходное интегральное уравнение (6).
определяются с точностью до некоторых постоянных. Последние можно определить из физического смысла задачи или подстановкой решения в исходное интегральное уравнение (6).
Пример. Рассмотрим интегральное уравнение

Здесь ядро  Его преобразование Фурье
Его преобразование Фурье

так что  аналитично в полосе
аналитично в полосе

Выражение  в данном случае равно
в данном случае равно

Представим функцию в виде

Следовательно,

Функция  аналитична при
аналитична при  Функция
Функция  аналитична и не обращается в нуль при
аналитична и не обращается в нуль при  . Существует полоса
. Существует полоса  в которой обе функции,
в которой обе функции,  и
и  аналитичны и отличны от нуля. Имеем
аналитичны и отличны от нуля. Имеем

Функция  должна быть аналитичной во всей конечной плоскости комплексной переменной к, а
должна быть аналитичной во всей конечной плоскости комплексной переменной к, а  при
при  Из этого
Из этого  условия следует, что в данном примере
условия следует, что в данном примере  должна равняться постоянной С. Она не может расти так быстро, как
должна равняться постоянной С. Она не может расти так быстро, как  , иботогда
, иботогда  при
при  Она не может и убывать, так как отсюда вытекало бы существование особенности у функции
Она не может и убывать, так как отсюда вытекало бы существование особенности у функции  (полюса или точки разветвления) в конечной частя комплексной плоскости. Итак,
(полюса или точки разветвления) в конечной частя комплексной плоскости. Итак,  и
и

Отсюда 

Так как в этом выражении  , то, замыкая контур интегрирования полуокружностью, лежащей в нижней полуплоскости, и используя теорему Коши о вычетах, находим
, то, замыкая контур интегрирования полуокружностью, лежащей в нижней полуплоскости, и используя теорему Коши о вычетах, находим

Таким же способом находим

Исходя непосредственно из интегрального уравнения, легко установить, что при  функция
функция  удовлетворяет дифференциальному уравнению
удовлетворяет дифференциальному уравнению

для которого (13) является решением.
Рассмотрим теперь неоднородное уравнение Винера — Хопфа

Применяя преобразование Фурье, приходим к соотношению

Представляя  в виде
в виде  перепишем равенство (14) так:
перепишем равенство (14) так:

Первые два слагаемых имеют нужный вид. Третье слагаемое такого вида не имеет. Пусть существует полоса, в которой аналитичны и  Тогда мы можем применить разложение (4):
Тогда мы можем применить разложение (4):

Соотношение (15) перепишется после этого так:

Левая часть аналитична в некоторой полуплоскости  правая — в полуплоскости
правая — в полуплоскости  Существует полоса аналитичности, общая для них, так что правая часть (17) является аналитическим продолжением левой части в нижнюю полуплоскость. Функция
Существует полоса аналитичности, общая для них, так что правая часть (17) является аналитическим продолжением левой части в нижнюю полуплоскость. Функция  выбирается как целая функция; характер ее определяется асимптотическим поведением при
выбирается как целая функция; характер ее определяется асимптотическим поведением при  одного из определяющих ее выражений. Определив
одного из определяющих ее выражений. Определив  находим
находим

и по формуле обращения получаем 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Основные классы интегральных уравнений
- 2. Уравнение Вольтерра.
- II. Нелинейные уравнения
- Задача Абеля.
- ГЛАВА I. ТЕОРИЯ ФРЕДГОЛЬМА
- § 3. Формулы Фредгольма
- § 4. Интегральные уравнения с вырожденным ядром. Теоремы Фредгольма
- ГЛАВА II. ПРИНЦИП СЖАТЫХ ОТОБРАЖЕНИЙ
- § 6. Полные пространства
- § 7. Принцип сжатых отображений
- § 8. Применение принципа сжатых отображений к интегральным уравнениям
- ГЛАВА III. ЛИНЕЙНЫЕ ОПЕРАТОРЫ. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
- § 9. Линейные нормированные пространства
- II. Линейное нормированное пространство
- § 10. Линейные операторы. Норма оператора
- § 11. Пространство операторов
- § 12. Обратные операторы
- § 13. Приложение к линейным интегральным уравнениям
- 2. Уравнение Вольтерра.
- § 14. Теоремы Фредгольма для общего случая уравнения Фредгольма
- § 15. Интегральные уравнения с ядром, имеющим слабую особенность
- § 16. Характер решения интегрального уравнения
- ГЛАВА IV. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
- § 18. Преобразование Лапласа
- § 19. Преобразование Меллина
- § 20. Метод Винера—Хопфа
- ГЛАВА V. ВПОЛНЕ НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ
- § 21. Компактность множества. Критерий компактности
- § 22. Вполне непрерывные операторы
- § 23. Уравнения Рисса—Шаудера
- ГЛАВА VI. СИММЕТРИЧНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
- § 24. Симметричные операторы. Теорема Гильберта—Шмидта
- § 25. Решение операторных уравнений
- § 26. Интегральные уравнения с симметричным ядром
- Билинейное разложение симметричных ядер
- § 27. Теорема Гильберта — Шмидта для интегральных операторов
- § 28. Экстремальные свойства характеристических чисел и собственных функций
- § 29. Интегральные уравнения, приводящиеся к симметричным
- § 30. Классификация симметричных ядер
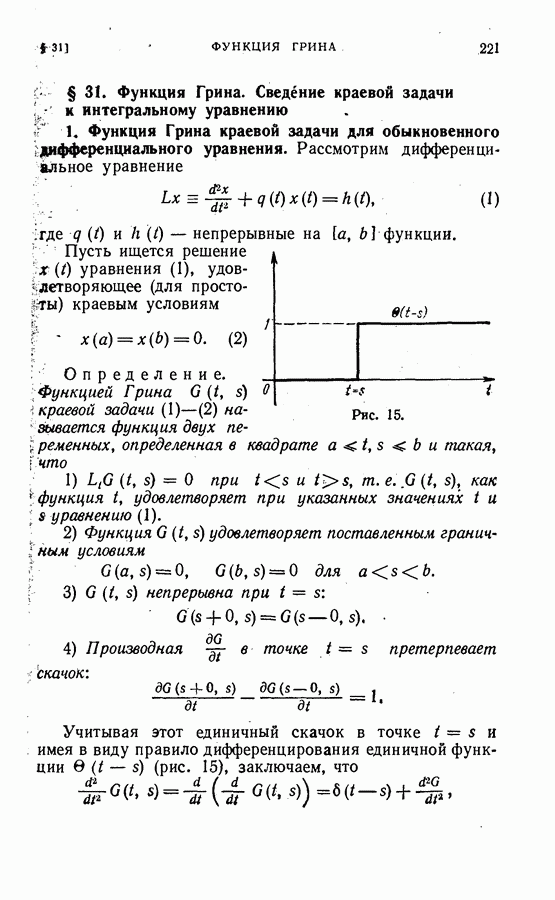
- § 31. Функция Грина. Сведение краевой задачи к интегральному уравнению
- 2. Сведение краевой задачи к интегральному уравнению.
- ГЛАВА VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 1-го РОДА
- § 32. Уравнение Вольтерра 1-го рода
- § 33. Уравнение Фредгольма 1-го рода
- § 34. Операторные уравнения 1-го рода
- ГЛАВА VIII. НЕФРЕДГОЛЬМОВЫ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ. СИНГУЛЯРНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
- § 35. Нефредгольмовы интегральные уравнения
- § 36. Сингулярные интегральные уравнения. Преобразования Гильберта
- Преобразования Гильберта
- ГЛАВА IX. НЕЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
- § 37. Уравнения Гаммерштейна
- § 38. Интегральные уравнения с параметром. Дифференциал Фреше. Теорема существования абстрактной неявной функции
- § 39. Разветвление решений
- § 40. Точки бифуркации
- § 41. Метод Ньютона
- § 42. Принцип неподвижной точки Ю. Шаудера
- ЛИТЕРАТУРА