| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 18. Преобразование Лапласа
Функцией-оригиналом называется любая комплекснозначная функция  действительного аргумента
действительного аргумента  удовлетворяющая условиям:
удовлетворяющая условиям:
1)  интегрируема на любом конечном интервале оси
интегрируема на любом конечном интервале оси  (локально интегрируема).
(локально интегрируема).
2) Для всех отрицательных  .
.
3)  с ростом
с ростом  возрастает (по модулю) не быстрее показательной функции, т. е. существуют такие постоянные
возрастает (по модулю) не быстрее показательной функции, т. е. существуют такие постоянные  и
и  что для всех
что для всех 

Если существует число  для которого выполняется неравенство (1), то оно будет выполняться и для
для которого выполняется неравенство (1), то оно будет выполняться и для
всех больших чисел  Нижняя грань всех чисел
Нижняя грань всех чисел  для которых выполняется неравенство (1),
для которых выполняется неравенство (1),

называется показателем роста функции 
В дальнейшей мы, как правило, будем рассматривать непрерывные функции-оригиналы.
Изображением функции  по Лапласу называется функция
по Лапласу называется функция  комплексной переменной
комплексной переменной  определяемая равенством
определяемая равенством

То, что  есть изображение функции
есть изображение функции  будем обозначать так:
будем обозначать так:

Функция  определена в полуплоскости
определена в полуплоскости  комплексной переменной
комплексной переменной  и является в этой полуплоскости аналитической функцией от
и является в этой полуплоскости аналитической функцией от 
В приложениях преобразования Лапласа к интегральным уравнениям большую роль играет теорема о свертке (теорема умножения).
Аналогично § 17, если функции  определены для всех
определены для всех  то сверткой этих функций называется новая функция от
то сверткой этих функций называется новая функция от  обозначаемая символом
обозначаемая символом  и определяемая равенством
и определяемая равенством

если интеграл (3) существует.
Основные свойства свертки
1. Операция свертки коммутативна:

2. Для функций-оригиналов  операция свертки всегда выполнима и
операция свертки всегда выполнима и

Действительно, произведение функций-оригиналов  как функция от
как функция от  является финитной функцией, т. е. обращается в нуль вне некоторого конечного интервала (в данном случае вне интервала
является финитной функцией, т. е. обращается в нуль вне некоторого конечного интервала (в данном случае вне интервала  Для финитных функций операция свертки выполнима, и мы получаем формулу (4).
Для финитных функций операция свертки выполнима, и мы получаем формулу (4).
3. Свертка функций-оригиналов есть снова функция-оригинал.
Теорема о свертке (теорема умножения). Если  и
и  то свертка
то свертка  имеет изображение
имеет изображение 

т. е. перемножение изображений равносильно свертыванию оригиналов.
В самом деле, свертка двух функций-оригиналов есть снова функция-оригинал.
Рассмотрим изображение интеграла 

Справа стоит двукратный интеграл, распространенный на сектор  плоскости
плоскости  (рис. 12). Меняя порядок интегрирования и полагая
(рис. 12). Меняя порядок интегрирования и полагая  получим
получим

что и требовалось доказать.
Рассмотрим интегральное уравнение Вольтерра 2-го рода типа свертки:

Предположим, что функции  непрерывны при
непрерывны при  и являются функциями-оригиналами. Пусть
и являются функциями-оригиналами. Пусть

Как было доказано ранее, интегральное уравнение (7) имеет единственно непрерывное решение при любом значении X.

Рис. 12.
Для решения  уравнения (7) при
уравнения (7) при  нетрудко получить оценку:
нетрудко получить оценку:

Таким образом, решение  уравнения (7) есть также функция-оригинал.
уравнения (7) есть также функция-оригинал.

Применяя к обеим частям (7) преобразование Лапласа и пользуясь теоремой умножения, будем иметь

откуда

Функция  будет аналитической в полуплоскости
будет аналитической в полуплоскости  так что знаменатель в (9) не может иметь корней в указанной полуплоскости. Используя формулу обращения преобразования Лапласа ([16]), находим решение
так что знаменатель в (9) не может иметь корней в указанной полуплоскости. Используя формулу обращения преобразования Лапласа ([16]), находим решение  интегрального уравнения (7):
интегрального уравнения (7):

(интеграл берется вдоль любой прямой  и понимается в смысле главного значения).
и понимается в смысле главного значения).
На практике для отыскания оригинала  по его изображению
по его изображению  не всегда целесообразно использовать формулу обращения (10). Часто бывает легче найти оригинал, используя другие теоремы операционного исчисления.
не всегда целесообразно использовать формулу обращения (10). Часто бывает легче найти оригинал, используя другие теоремы операционного исчисления.
Пример. Решить интегральное уравнение

Решение. Пусть  Как известно,
Как известно,

Применяя к обеим частям (11) преобразование Лапласа, перейдем от уравнения (11) к уравнению в пространстве изображений

Решая это последнее, найдем

Оригинал  для
для  будет решением уравнения (11):
будет решением уравнения (11):

Замечание. Выражению (9) для функции  можно придать вид
можно придать вид

или

где

Решение (12) легко перевести назад в пространство оригиналов, после чего будем иметь

или

где  — резольвента уравнения (7).
— резольвента уравнения (7).
Указанный метод решения уравнения (7) приложим к системам интегральных уравнений Вольтерра вида

где  — известные непрерывные функции-оригиналы.
— известные непрерывные функции-оригиналы.
Применяя к обеим частям (14) преобразование Лапласа, получим систему

Это система линейных алгебраических уравнений относительно 
Пусть  есть решение системы (15), Тогда система функций
есть решение системы (15), Тогда система функций  где
где  будет решением системы интегральных уравнений (14).
будет решением системы интегральных уравнений (14).
Преобразование Лапласа может быть применено к решению нелинейных интегральных уравнений вида 

Пусть  Применяя к обеим частям (16) преобразование Лапласа и используя теорему умножения, получим
Применяя к обеим частям (16) преобразование Лапласа и используя теорему умножения, получим

откуда

- операторные решения уравнения (16).
Пример. Решить уравнение

Переходя в пространство изображений, придем к уравнению

Отсюда

Из условия  при
при  выбираем
выбираем

Решением интегрального уравнения будет  — бесселева функция 1-го порядка.
— бесселева функция 1-го порядка.
При решении некоторых видов интегральных уравнений оказывается полезной обобщенная теорема умножения (теорема Эфроса).
Теорема 4.2. Пусть дано изображение  и аналитическиефункции
и аналитическиефункции  такие, что
такие, что

тогда

Действительно, изображение правой части (18)

(предполагаем, что можно изменить порядок интегрирования). Внутренний интеграл в правой части (19) есть изображение  Следовательно, используя соотношение (17), можно написать
Следовательно, используя соотношение (17), можно написать

что и требовалось показать.
Если, в частности, принять  то будем иметь
то будем иметь

и по теореме запаздывания  Формула (18) принимает вид
Формула (18) принимает вид

(так как при  в силу свойства функций-оригиналов), т. е. совпадает с обычной теоремой умножения.
в силу свойства функций-оригиналов), т. е. совпадает с обычной теоремой умножения.
Если  как можно показать ([161),
как можно показать ([161),

Поэтому, если известно, что  то по теореме Эфроса находим оригинал для
то по теореме Эфроса находим оригинал для 

Если 

где  — бесселева функция нулевого порядка. Поэтому, если
— бесселева функция нулевого порядка. Поэтому, если  то по теореме Эфроса
то по теореме Эфроса

Примеры. 1. Решить интегральное уравнение

Решение. Пусть  Применяя преобразование Лапласа к обеим частям (25), получим, используя формулу (22):
Применяя преобразование Лапласа к обеим частям (25), получим, используя формулу (22):

так что

откуда

Функция  есть решение уравнения (25).
есть решение уравнения (25).
2. Решить интегральное уравнение

Решение. Пусть  Применяя к обеим частям (26) преобразование Лапласа и учитывая теорему Эфроса, найдем
Применяя к обеим частям (26) преобразование Лапласа и учитывая теорему Эфроса, найдем

Заменяя  на
на  получим
получим 

Из (27) и (28) находим

Отсюда

Замечание. Пользуясь тем, что

и применяя теорему Эфроса, можно решать интегральные уравнения, ядро которых содержит бесселевы функции  рода порядка выше нулевого.
рода порядка выше нулевого.
Решение интегро-дифференциальных уравнений
Линейным интегро-дифференциальным уравнением называется уравнение вида

Здесь  известные функции,
известные функции,  — искомая функция.
— искомая функция.
При решении интегро-дифференциальных уравнений (29) для искомой функции  ставятся начальные условия:
ставятся начальные условия:

Пусть в (29) коэффициенты  — постоянные
— постоянные  и пусть
и пусть  т. е. все
т. е. все  зависят лишь от разности аргументов
зависят лишь от разности аргументов 
Не нарушая общности, можно считать  Тогда уравнение (29) будет иметь вид
Тогда уравнение (29) будет иметь вид

Пусть, далее, функции  суть непрерывные функции-оригиналы, и пусть
суть непрерывные функции-оригиналы, и пусть

Тогда, как можно показать, функция  будет также функцией-оригиналом. Пусть
будет также функцией-оригиналом. Пусть

Применим к обеим частям (31) преобразование Лапласа. Как известно (1161),

По теореме умножения

Поэтому уравнение (31) перейдет в следующее:

где  — некоторая известная функция от
— некоторая известная функция от  Решая (32), находим
Решая (32), находим  операторное решение задачи
операторное решение задачи  Находя оригинал для
Находя оригинал для  получим решение
получим решение  интегро-дифференциального уравнения (31), удовлетворяющее начальным условиям (30).
интегро-дифференциального уравнения (31), удовлетворяющее начальным условиям (30).
Пример. Решить интегро-дифференциальное уравнение 

Решение. Пусть  Тогда, учитывая начальные условия (34), будем иметь
Тогда, учитывая начальные условия (34), будем иметь

Применяя к обеим частям (33) преобразование Лапласа, получим

откуда

Оригиналом для этой функции будет функция

Эта последняя является решением интегро-дифференциального уравнения (33), удовлетворяющим начальным условиям (34).
Замечание. Если функции  достаточно гладкие, то можно понизить порядок производных искомой функции, входящих под знаком интеграла, путем интегрирования по частям.
достаточно гладкие, то можно понизить порядок производных искомой функции, входящих под знаком интеграла, путем интегрирования по частям.
Интегральные уравнения вида

возникающие в ряде задач физики, также можно решать с помощью преобразования Лапласа. Установим предварительно теорему о свертке для выражений

Для преобразования Фурье

где  — преобразования Фурье функций
— преобразования Фурье функций  соответственно.
соответственно.
Положим  т. е.
т. е.

Тогда (37) перепишется так:

Чтобы перейти от преобразования Фурье к преобразованию Лапласа, заметим, что

Здесь и в дальнейшем индексы  и
и  означают, что берется изображение функции соответственно по Фурье или по Лапласу.
означают, что берется изображение функции соответственно по Фурье или по Лапласу.
Следовательно, соотношение (38) дает

Выразим теперь  через преобразование Лапласа:
через преобразование Лапласа:

Итак,

где

Применяя теперь преобразование Лапласа к обеим частям (35), получим

(индекс  опущен) или
опущен) или

Функция

будет частным решением уравнения (35),
Чтобы решение (42) или (44) имело смысл, необходимо, чтобы области аналитичности  перекрывались.
перекрывались.
Пример. Решить уравнение

Здесь  . Поэтому
. Поэтому

Операторное уравнение (42) принимает в этом случае вид

откуда

Следовательно,

Применяя теорему Коши о вычетах, находим 

Нетрудно проверить, что решением уравнения (35) является функция

где  решение соответствующего однородного уравнения
решение соответствующего однородного уравнения

Заметим, что уравнение (35) сводится к дифференциальному уравнению

откуда сразу получаем

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. Основные классы интегральных уравнений
- 2. Уравнение Вольтерра.
- II. Нелинейные уравнения
- Задача Абеля.
- ГЛАВА I. ТЕОРИЯ ФРЕДГОЛЬМА
- § 3. Формулы Фредгольма
- § 4. Интегральные уравнения с вырожденным ядром. Теоремы Фредгольма
- ГЛАВА II. ПРИНЦИП СЖАТЫХ ОТОБРАЖЕНИЙ
- § 6. Полные пространства
- § 7. Принцип сжатых отображений
- § 8. Применение принципа сжатых отображений к интегральным уравнениям
- ГЛАВА III. ЛИНЕЙНЫЕ ОПЕРАТОРЫ. ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
- § 9. Линейные нормированные пространства
- II. Линейное нормированное пространство
- § 10. Линейные операторы. Норма оператора
- § 11. Пространство операторов
- § 12. Обратные операторы
- § 13. Приложение к линейным интегральным уравнениям
- 2. Уравнение Вольтерра.
- § 14. Теоремы Фредгольма для общего случая уравнения Фредгольма
- § 15. Интегральные уравнения с ядром, имеющим слабую особенность
- § 16. Характер решения интегрального уравнения
- ГЛАВА IV. ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
- § 18. Преобразование Лапласа
- § 19. Преобразование Меллина
- § 20. Метод Винера—Хопфа
- ГЛАВА V. ВПОЛНЕ НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ
- § 21. Компактность множества. Критерий компактности
- § 22. Вполне непрерывные операторы
- § 23. Уравнения Рисса—Шаудера
- ГЛАВА VI. СИММЕТРИЧНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
- § 24. Симметричные операторы. Теорема Гильберта—Шмидта
- § 25. Решение операторных уравнений
- § 26. Интегральные уравнения с симметричным ядром
- Билинейное разложение симметричных ядер
- § 27. Теорема Гильберта — Шмидта для интегральных операторов
- § 28. Экстремальные свойства характеристических чисел и собственных функций
- § 29. Интегральные уравнения, приводящиеся к симметричным
- § 30. Классификация симметричных ядер
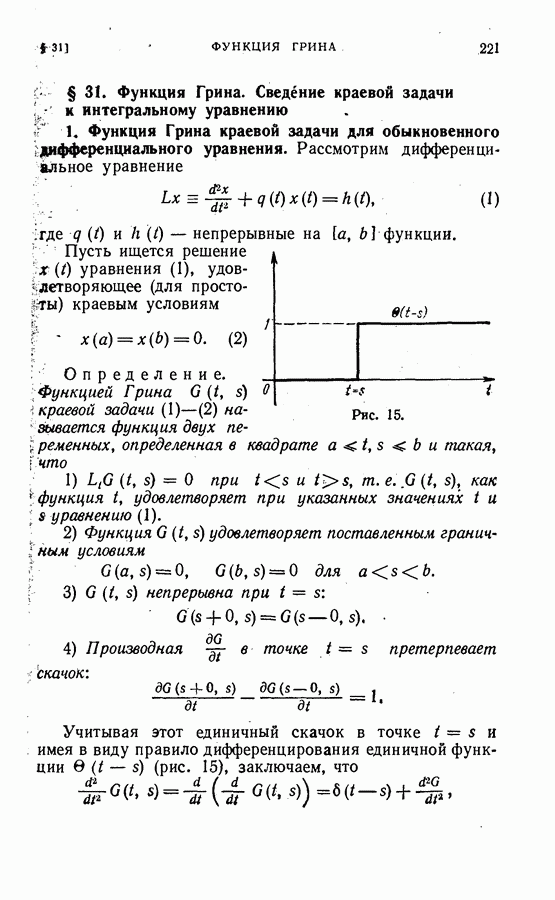
- § 31. Функция Грина. Сведение краевой задачи к интегральному уравнению
- 2. Сведение краевой задачи к интегральному уравнению.
- ГЛАВА VII. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 1-го РОДА
- § 32. Уравнение Вольтерра 1-го рода
- § 33. Уравнение Фредгольма 1-го рода
- § 34. Операторные уравнения 1-го рода
- ГЛАВА VIII. НЕФРЕДГОЛЬМОВЫ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ. СИНГУЛЯРНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
- § 35. Нефредгольмовы интегральные уравнения
- § 36. Сингулярные интегральные уравнения. Преобразования Гильберта
- Преобразования Гильберта
- ГЛАВА IX. НЕЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
- § 37. Уравнения Гаммерштейна
- § 38. Интегральные уравнения с параметром. Дифференциал Фреше. Теорема существования абстрактной неявной функции
- § 39. Разветвление решений
- § 40. Точки бифуркации
- § 41. Метод Ньютона
- § 42. Принцип неподвижной точки Ю. Шаудера
- ЛИТЕРАТУРА