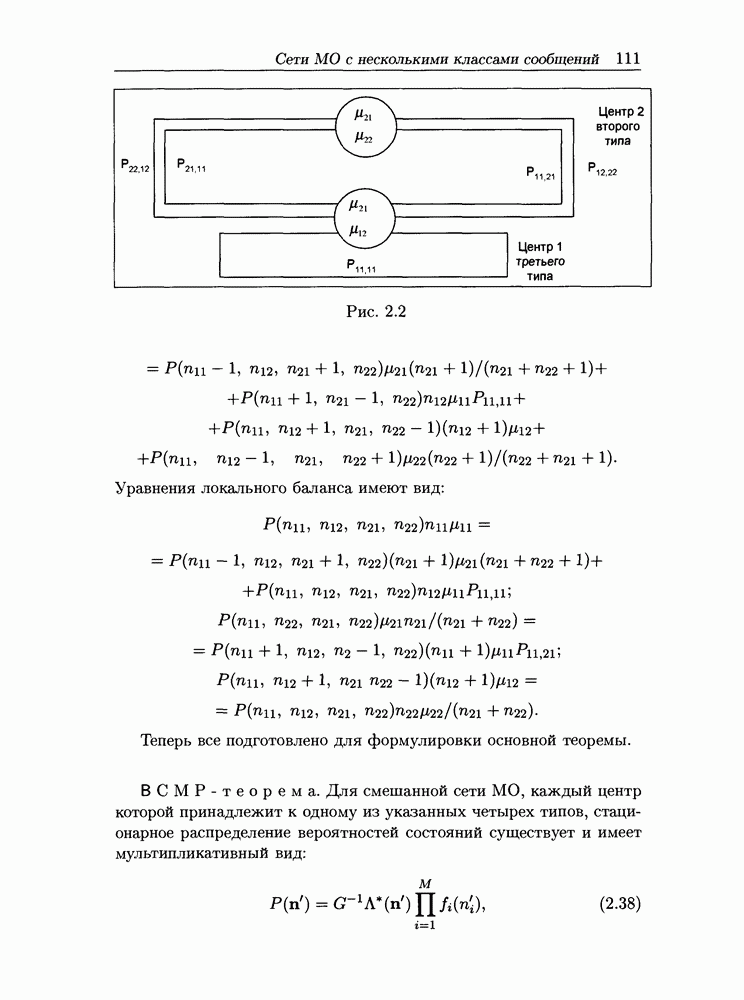
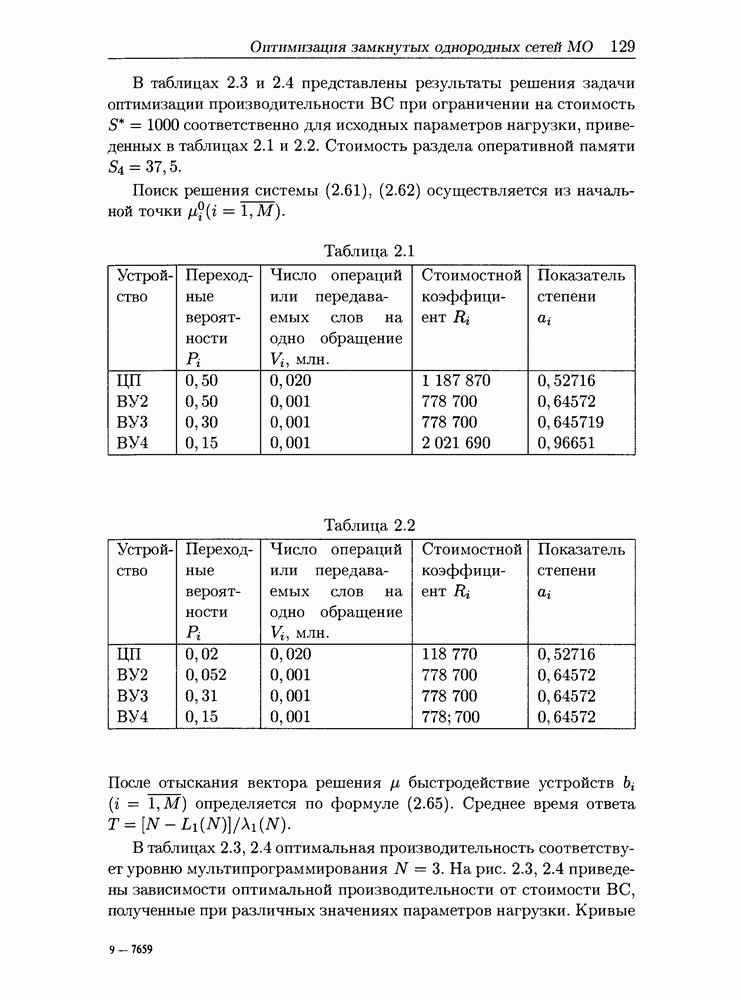
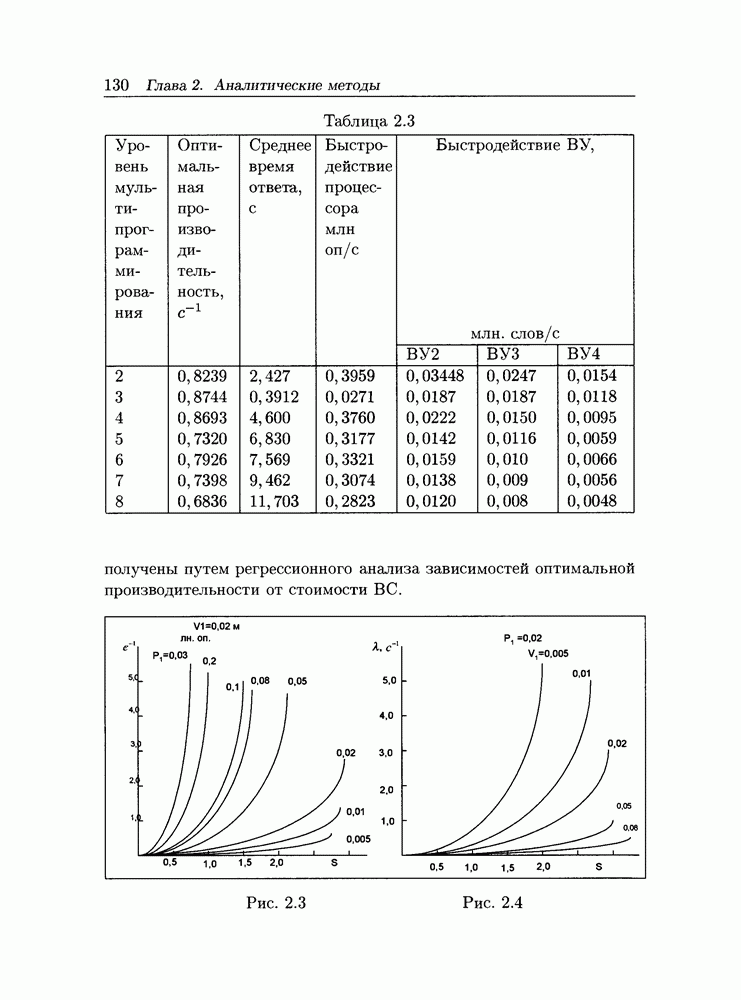
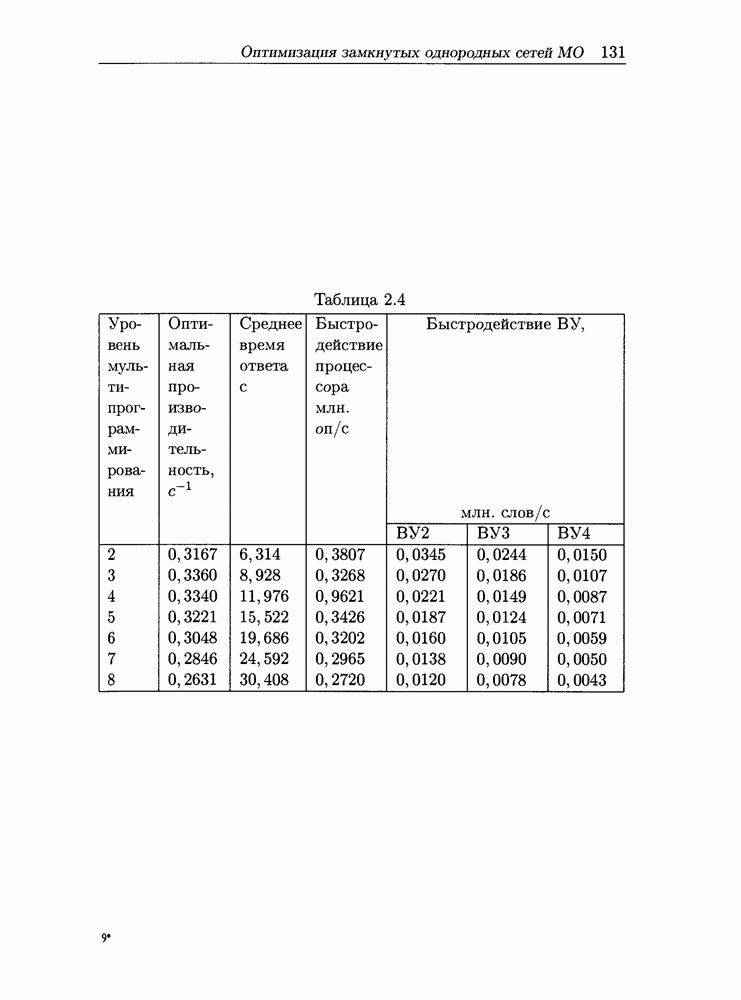
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
1.4 Преобразования Лапласа и Лапласа - Стилтьеса. Производящая функция
В теории массового обслуживания интенсивно используется аппарат преобразований Лапласа и Лапласа - Стилтьеса и производящих функций. В частности, выше мы уже упомянули о возможности использования преобразований Лапласа для сведения задачи решения системы линейных дифференциальных уравнений к решению системы линейных алгебраических уравнений. Приведем основные сведения об этих функциях и преобразованиях.
Определение 13. Преобразованием Лапласа - Стилтьеса распределения  будем называть функцию
будем называть функцию  определяемую следующим образом:
определяемую следующим образом:

а преобразованием Лапласа - функцию  определяемую как:
определяемую как:

Если s есть чисто мнимая переменная, преобразование Лапласа - Стилтьеса совпадает с характеристической функцией распределения  Областью определения функций
Областью определения функций  обычно считается правая полуплоскость комплексной плоскости. Однако, без существенного ограничения общности, в рамках данной главы и книги можно рассматривать s как действительное положительное число.
обычно считается правая полуплоскость комплексной плоскости. Однако, без существенного ограничения общности, в рамках данной главы и книги можно рассматривать s как действительное положительное число.
Отметим некоторые из свойств преобразования Лапласа - Стилтьеса.
Свойство 1. Если оба преобразования  существуют (то есть, соответствующие несобственные интегралы сходятся), то они связаны между собой следующим образом:
существуют (то есть, соответствующие несобственные интегралы сходятся), то они связаны между собой следующим образом: 
Свойство 2. Если две независимые случайные величины имеют преобразования Лапласа - Стилтьеса  их функций распределения, то преобразованием Лапласа - Стилтьеса функции распределения суммы этих величин является
их функций распределения, то преобразованием Лапласа - Стилтьеса функции распределения суммы этих величин является 
Свойство 3. Преобразованием Лапласа - Стилтьеса производной  функции
функции  является
является  .
.
Свойство 4.

Свойство 5. Пусть есть  начальный момент распределения:
начальный момент распределения:  Он вычисляется через преобразование Лапласа - Стилтьеса следующим образом:
Он вычисляется через преобразование Лапласа - Стилтьеса следующим образом:

Свойство 6. Преобразованию Лапласа - Стилтьеса  может быть придан вероятностный смысл следующим образом. Считаем, что
может быть придан вероятностный смысл следующим образом. Считаем, что  есть функция распределения длины некоторого интервала времени и в этом интервале времени поступает простейший поток «катастроф» с параметром
есть функция распределения длины некоторого интервала времени и в этом интервале времени поступает простейший поток «катастроф» с параметром  . Тогда легко видеть, что
. Тогда легко видеть, что  есть вероятность того, что за интервал не наступит ни одна «катастрофа».
есть вероятность того, что за интервал не наступит ни одна «катастрофа».
Свойство 7. Преобразование Лапласа - Стилтьеса  рассматриваемое как функция действительной переменной
рассматриваемое как функция действительной переменной  является вполне монотонной функцией, то есть оно имеет производные
является вполне монотонной функцией, то есть оно имеет производные  всех порядков и
всех порядков и 
Определение  Производящей функцией распределения вероятностей
Производящей функцией распределения вероятностей  дискретной случайной величины
дискретной случайной величины  называется функция
называется функция

Перечислим основные свойства этой функции.
Свойство 1.

Свойство 2. Для того, чтобы случайная величина  имела
имела  начальный момент
начальный момент  необходимо и достаточно, чтобы существовала конечная левосторонняя производная
необходимо и достаточно, чтобы существовала конечная левосторонняя производная  производящей функции
производящей функции  в точке
в точке  и начальные моменты легко подсчитываются через факториальные моменты
и начальные моменты легко подсчитываются через факториальные моменты

В частности, 
Свойство 3. В принципе производящая функция  позволяет вычислить (произвести) вероятности
позволяет вычислить (произвести) вероятности  по следующей формуле:
по следующей формуле:

Свойство 4. Производящей функции  можно придать вероятностный смысл следующим образом. Интерпретируем случайную величину
можно придать вероятностный смысл следующим образом. Интерпретируем случайную величину  как число запросов, пришедших за некоторый промежуток времени. Каждый приходящий запрос с вероятностью
как число запросов, пришедших за некоторый промежуток времени. Каждый приходящий запрос с вероятностью  окрашиваем в красный цвет, а с дополнительной вероятностью - в синий. Тогда из формулы полной вероятности следует, что
окрашиваем в красный цвет, а с дополнительной вероятностью - в синий. Тогда из формулы полной вероятности следует, что  есть вероятность того, за этот промежуток времени пришли только запросы красного цвета.
есть вероятность того, за этот промежуток времени пришли только запросы красного цвета.
Таким образом, зная производящую функцию  распределения вероятностей
распределения вероятностей  мы легко можем вычислить моменты этого распределения и в принципе можем вычислить сами вероятности
мы легко можем вычислить моменты этого распределения и в принципе можем вычислить сами вероятности  Если непосредственный подсчет по формуле (1.19) затруднителен, можно воспользоваться методом обращения производящей функции путем разложения ее на простые дроби или численными методами (см., например, [176], [261]). При решении практических задач можно пытаться аппроксимировать это распределение путем сглаживания по заданному числу совпадающих моментов распределения.
Если непосредственный подсчет по формуле (1.19) затруднителен, можно воспользоваться методом обращения производящей функции путем разложения ее на простые дроби или численными методами (см., например, [176], [261]). При решении практических задач можно пытаться аппроксимировать это распределение путем сглаживания по заданному числу совпадающих моментов распределения.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- ГЛАВА 1. Математические методы теории очередей
- 1.2 Входящий поток, время обслуживания
- 1.3 Марковские случайные процессы
- 1.3.1 Процессы гибели и размножения
- 1.3.2 Метод диаграмм интенсивностей переходов
- 1.3.3 Цепи Маркова с дискретным временем
- 1.4 Преобразования Лапласа и Лапласа — Стилтьеса. Производящая функция
- 1.5 Однолинейные марковские системы массового обслуживания
- 1.5.2 Система типа М\М\1\n
- 1.5.3 Система с конечным числом источников
- 1.6 Полумарковские однолинейные системы и методы их анализа
- 1.6.1 Метод вложенных цепей Маркова в приложении для системы M\G\1
- 1.6.2 Метод вложенных цепей Маркова в приложении для системы GI\M\1
- 1.6.3 Метод введения дополнительной переменной
- 1.6.4 Метод введения дополнительного события
- 1.7 Многолинейные системы массового обслуживания
- 1.7.2 Многоканальные системы без буфера для ожидания
- 1.7.3 Система М\М\оо
- 1.7.4 Система M\G\1 с дисциплиной равномерного распределения процессора и дисциплиной LIFO с прерыванием обслуживания
- 1.8 Приоритетные системы массового обслуживания
- 1.9 Многофазные системы
- 1.10 Перспективные направления исследований в теории очередей
- ГЛАВА 2. Аналитические методы теории сетей очередей
- 2.1.1 Маршрутная матрица и потоки в сетях
- 2.1.2 Другие определения
- 2.2 Однородные экспоненциальные сети
- 2.2.1 Уравнения глобального баланса для замкнутых цепей
- 2.2.2 Вид решения в мультипликативной форме
- 2.2.3 Сети, зависящие от нагрузки
- 2.2.4 Показатели качества функционирования однородных сетей
- 2.3 Сети массового обслуживания с несколькими классами сообщений
- 2.3.2 Теорема ВСМР
- 2.3.3 Открытые сети МО с несколькими классами
- 2.4 Итерационный метод анализа средних значений
- 2.4.1 Общее описание метода
- 2.4.2 Однородная замкнутая сеть МО, зависящая от нагрузки
- 2.5 Оптимизация замкнутых однородных сетей массового обслуживания
- 2.5.1 Некоторые свойства характеристик замкнутых однородных сетей МО
- 2.5.2 Постановка и решение задачи оптимизации
- 2.5.3 Пример расчета
- ГЛАВА 3. Вычислительные алгоритмы (методы вычислений характеристик сетей очередей)
- 3.1 Алгоритмы вычисления характеристик однородных замкнутых экспоненциальных сетей массового обслуживания
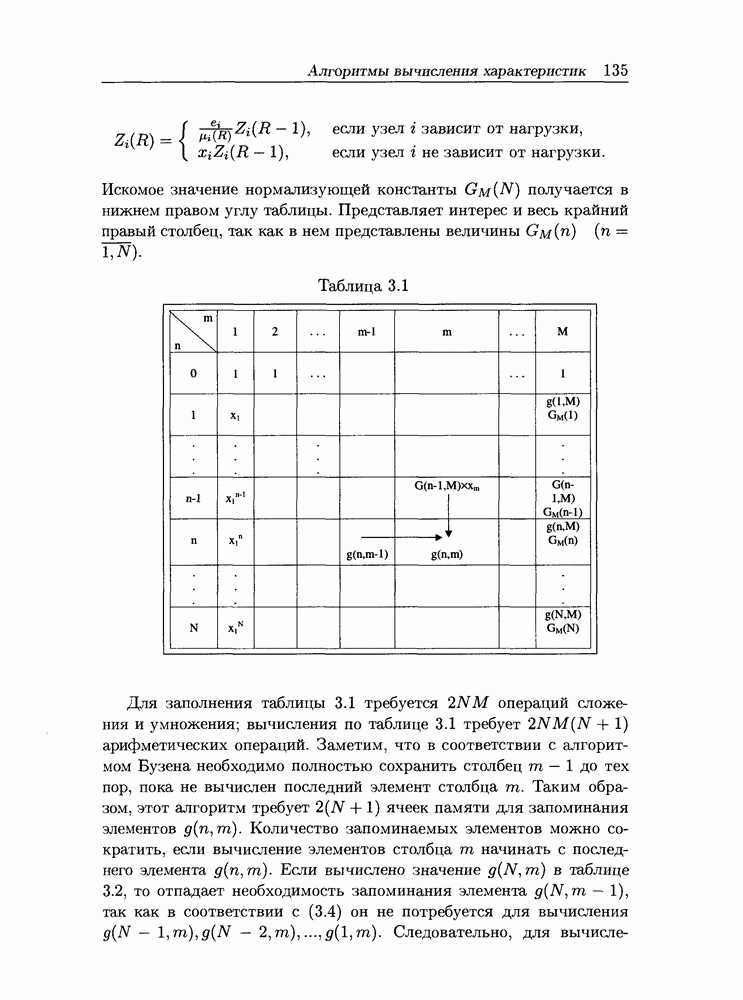
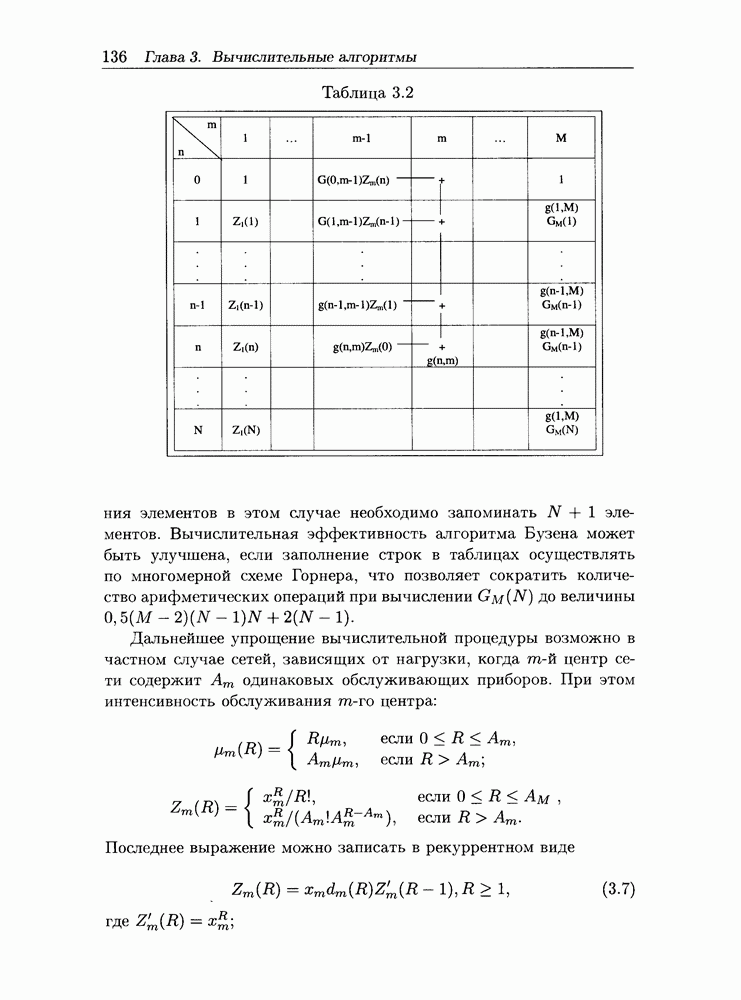
- 3.1.2 Вычисление характеристик сети
- 3.1.3 Аналитическое представление нормализующей константы
- 3.1.4 Пример расчета
- 3.2 Расчет сетей с несколькими классами сообщений
- 3.2.2 Маргинальное распределение длины очереди и пропускная способность
- 3.2.3 Расчет среднего времени ожидания и средней длины очереди
- 3.2.4 Алгоритм расчета замкнутой сети МО, допускающей изменение класса сообщений
- 3.3 Вычислительные аспекты метода анализа средних значений
- 3.3.1 Основные соотношения
- 3.3.2 Оценка эффективности вычислительного алгоритма
- 3.3.3 Расширение метода
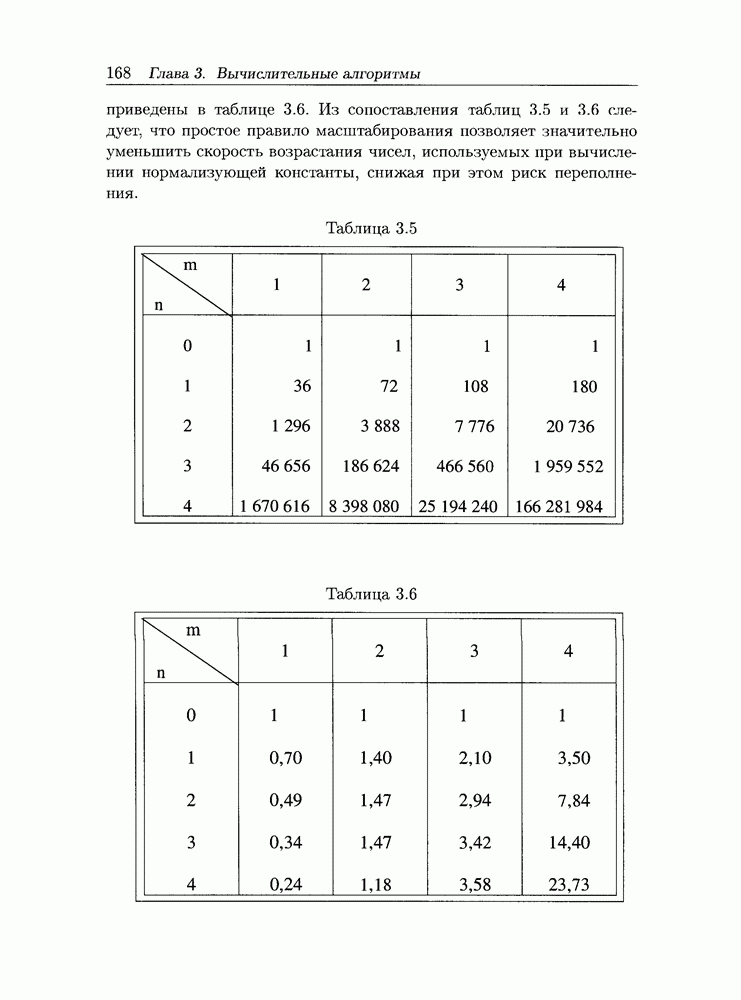
- 3.4 Практические аспекты реализации алгоритмов расчета сетей массового обслуживания большой размерности
- 3.4.2 Реконфигурация сети МО
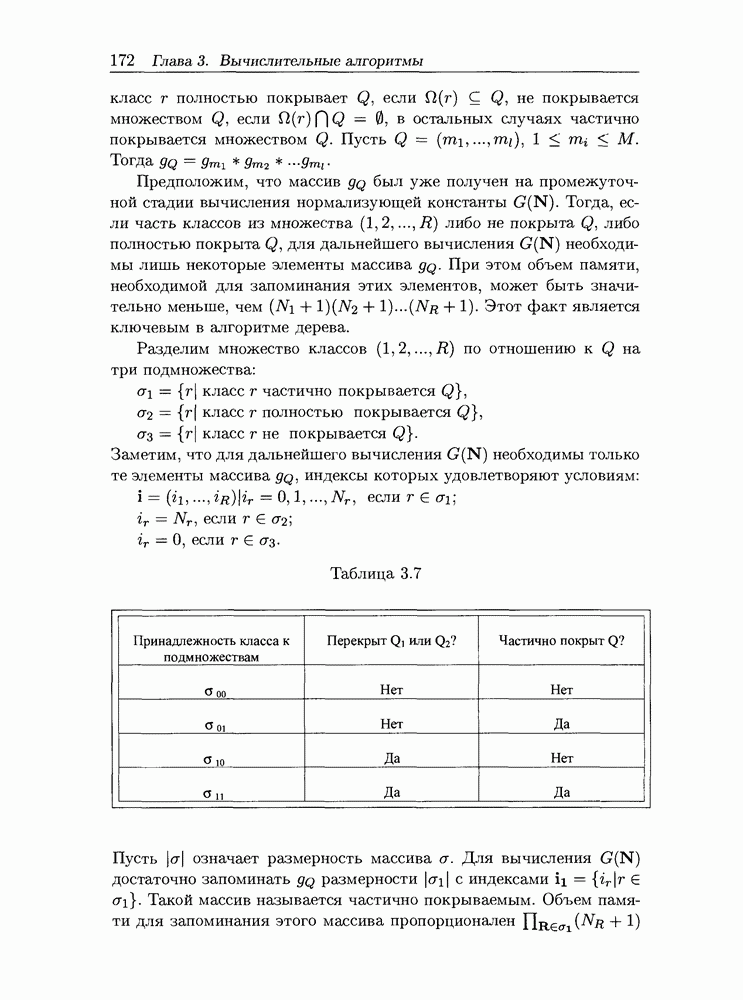
- 3.4.3 Обобщенный алгоритм свертки в виде дерева для расчета сетей МО
- ГЛАВА 4. Приближенные методы исследования сетей очередей
- 4.1 Область применения и краткий анализ приближенных методов
- 4.1.1 Аппроксимация функций распределения
- 4.1.2 Диффузионная и декомпозиционная аппроксимации
- 4.2 Декомпозиционные методы на основе теоремы Нортона
- 4.2.2 Приближенный декомпозиционный алгоритм
- 4.2.3 Пример расчета
- 4.3 Декомпозиция разомкнутых сетей массового обслуживания на уровне первых моментов
- 4.3.2 Диффузионная аппроксимация системы МО GI/G/1
- 4.4 Полиномиальная аппроксимация
- 4.4.2 Оценка вычислительной сложности метода
- 4.4.3 Пример расчета
- ГЛАВА 5. Развитие теории мультипликативных сетей очередей
- 5.1 Основные направления развития теории мультипликативных сетей
- 5.2 Сети массового обслуживания с зависимым обслуживанием
- 5.2.2 Частные случаи
- 5.2.3 Марковский процесс, описывающий функционирование сети
- 5.2.4 Основная теорема о мультипликативности сети
- 5.2.5 Частные случаи
- 5.3 G-сеть с отрицательными заявками
- 5.3.1 G-сеть с отрицательными заявками и групповыми удалениями положительных заявок
- 5.3.2 G-сеть с отрицательными заявками и триггерами
- 5.4 Решение уравнений баланса для интенсивности потоков и устойчивости G-сетей
- 5.5 G-сеть со случайным временем активизации сигналов
- 5.5.1 Однолинейные узлы
- 5.5.2 Симметричная G-сеть
- 5.5.3 Обсуждение результатов
- 5.6 G-сети с несколькими классами положительных заявок и сигналов
- 5.7 Другие модели и методы анализа G-сетей
- ГЛАВА 6. Стохастические модели компьютерных сетей
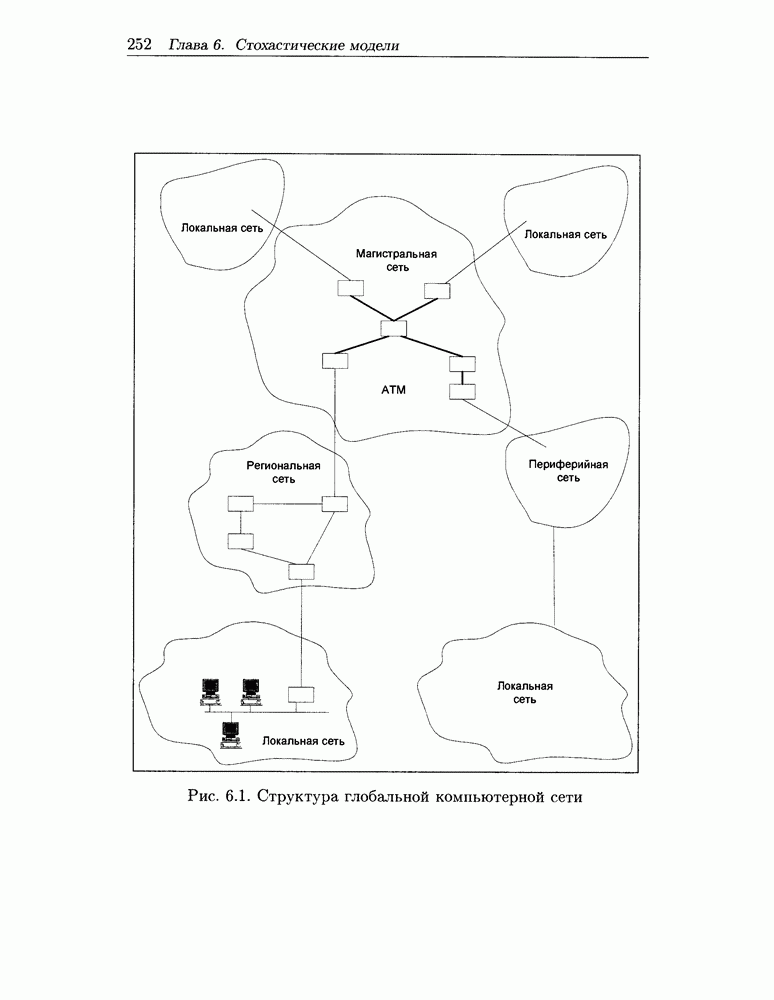
- 6.1.1 Структура компьютерных сетей
- 6.1.2 Сетевые протоколы
- 6.1.3 Использование теории сетей МО для исследования компьютерных сетей
- 6.2 Методы расчета характеристик сети пакетной коммутации
- 6.2.1 Анализ межконцевых задержек
- 6.2.2 Оптимизация пропускной способности и выбор маршрутов
- 6.2.3 Модель сети с ограниченной буферной памятью в узлах коммутации пакетов
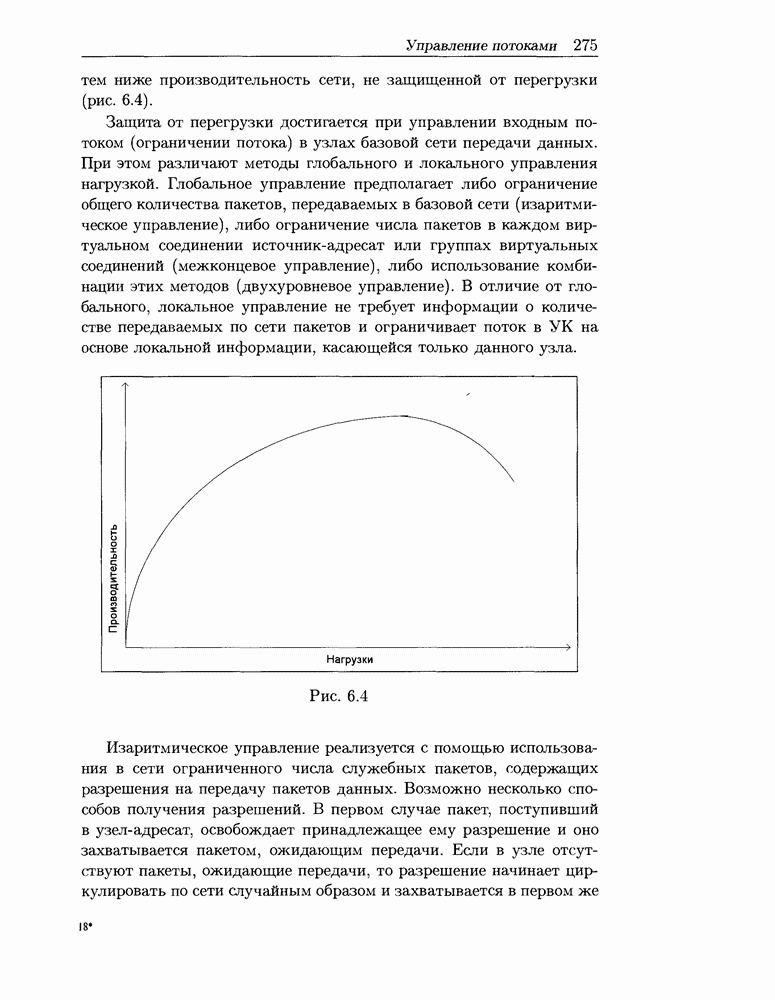
- 6.3 Управление потоками в сети пакетной коммутации
- 6.3.1 Методы управления потоками
- 6.3.2 Сетевая модель глобального управления
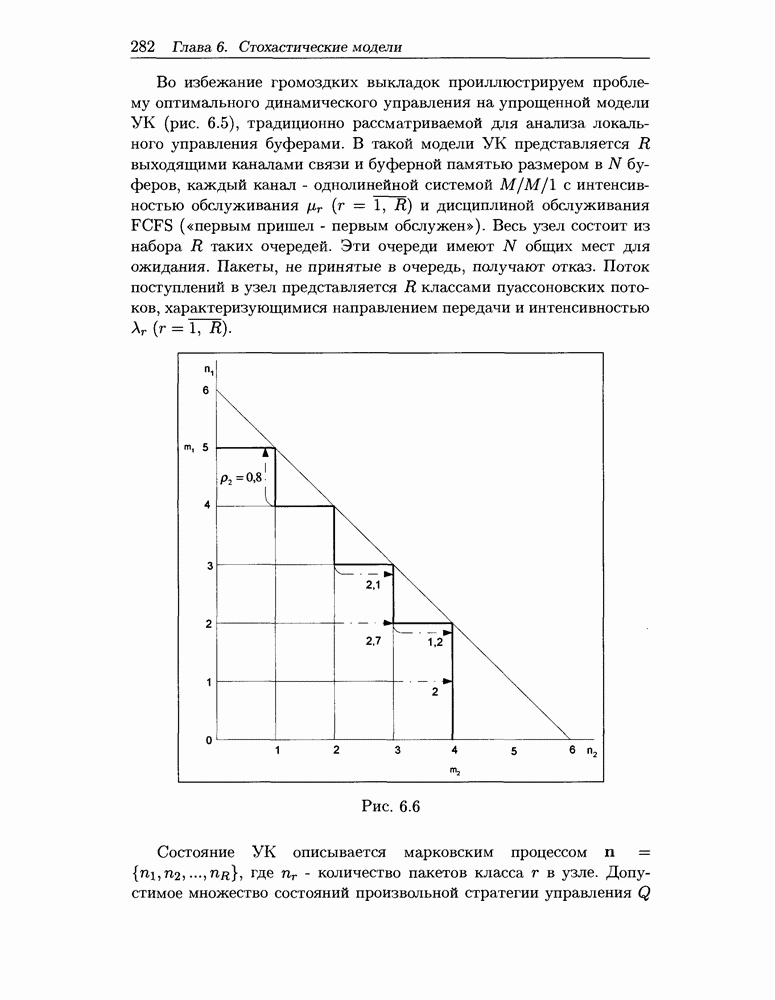
- 6.3.3 Локальное управление буферами
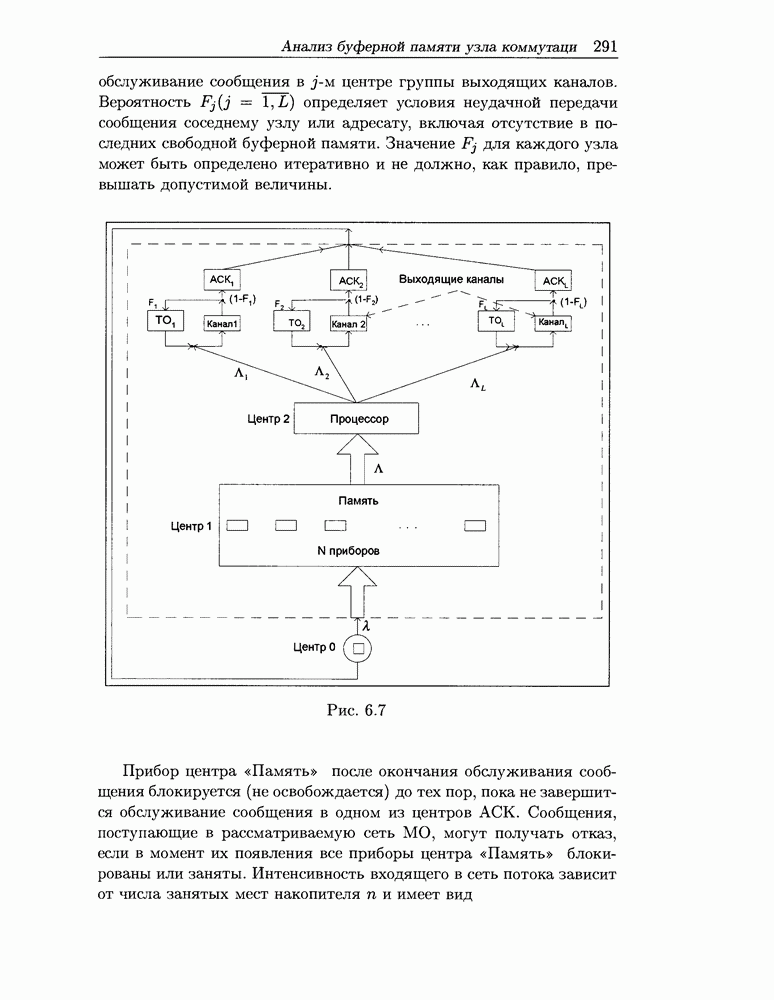
- 6.4 Анализ буферной памяти узла коммутаци
- 6.4.1 Процесс буферизации в узле коммутации и схемы организации буферной памяти
- 6.4.2 Анализ однородного пула равнодоступных буферов
- 6.4.3 Сетевая модель памяти секционной структуры
- 6.4.4 Анализ динамической памяти с цепочкой буферов
- ГЛАВА 7. Математические модели исследования алгоритмов маршрутизации
- 7.2 Постановка задачи
- 7.3 Алгоритмы решения задачи выбора оптимальных потоков в сети
- 7.3.1 Альтернативная маршрутизация
- 7.3.2 Фиксированная (однопутевая) маршрутизация
- 7.3.3 К-путевая маршрутизация
- 7.4 Примеры анализа алгоритмов маршрутизации в сетях передачи данных
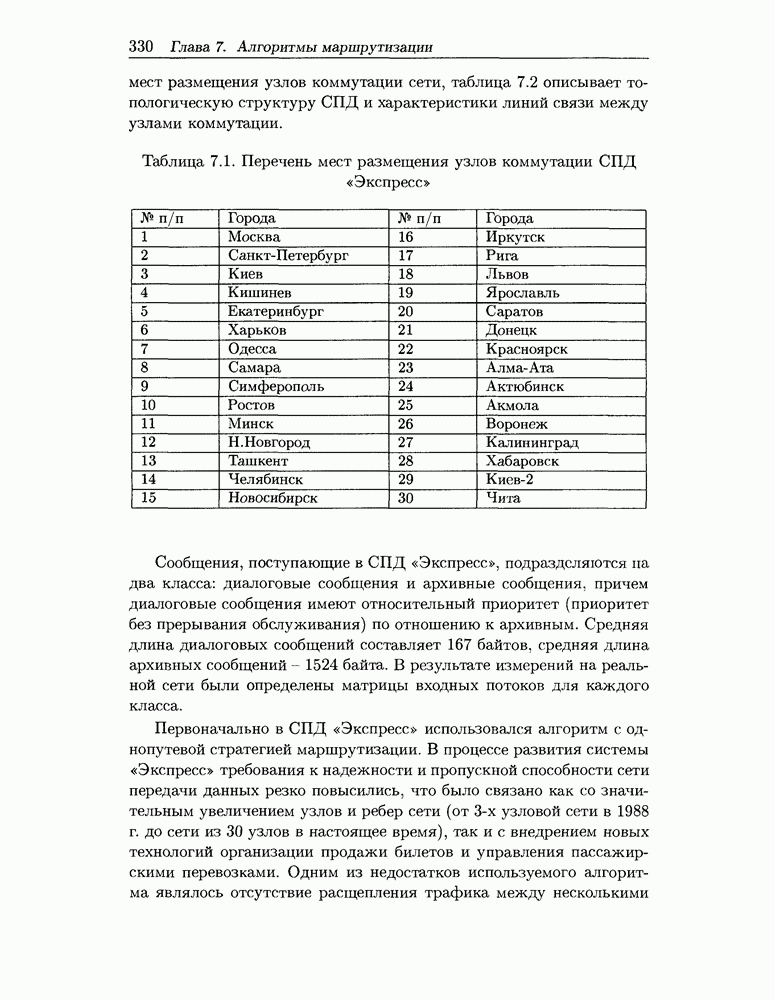
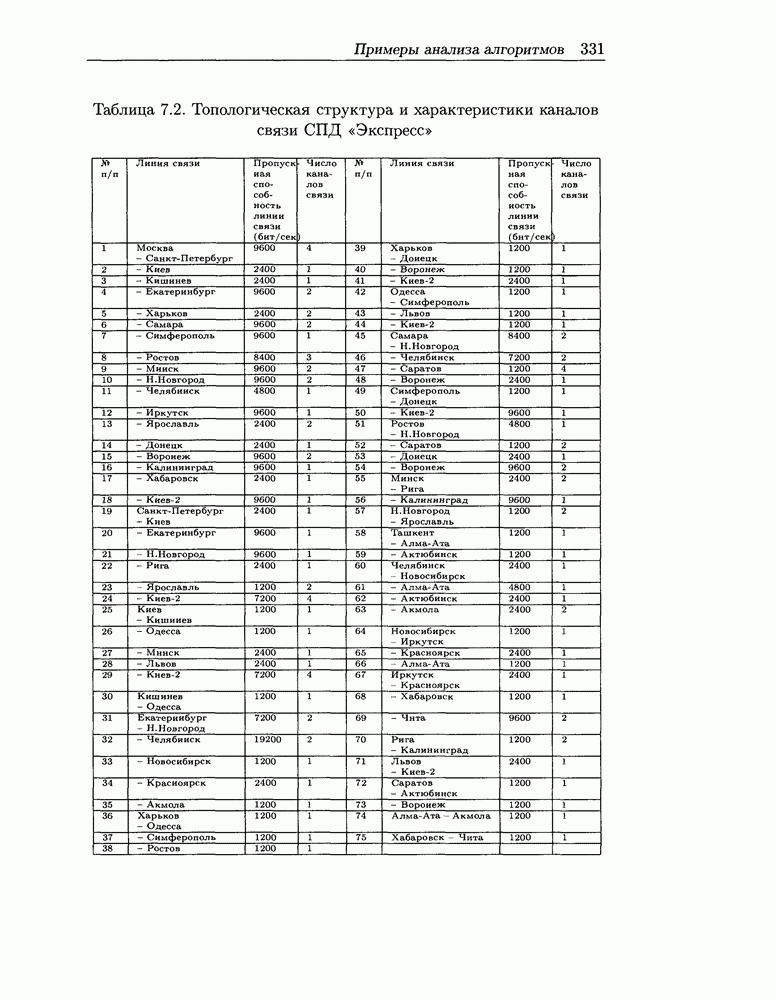
- 7.4.1 Анализ различных вариантов алгоритмов маршрутизации для СПД «Экспресс»
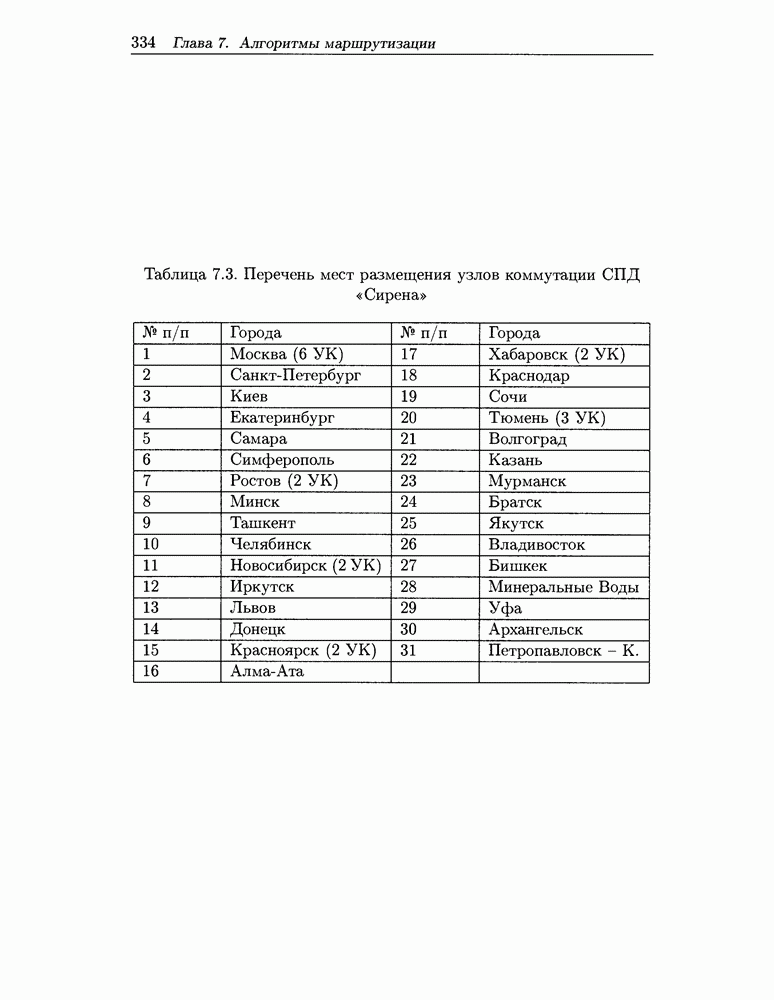
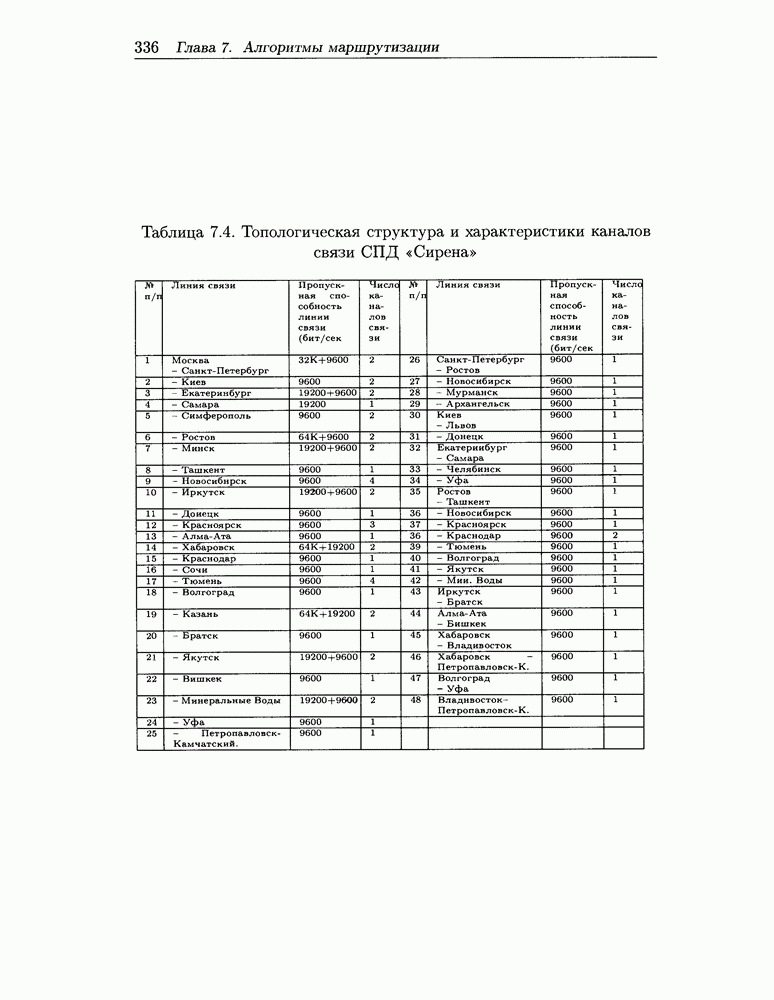
- 7.4.2 Анализ развития СПД «Сирена»
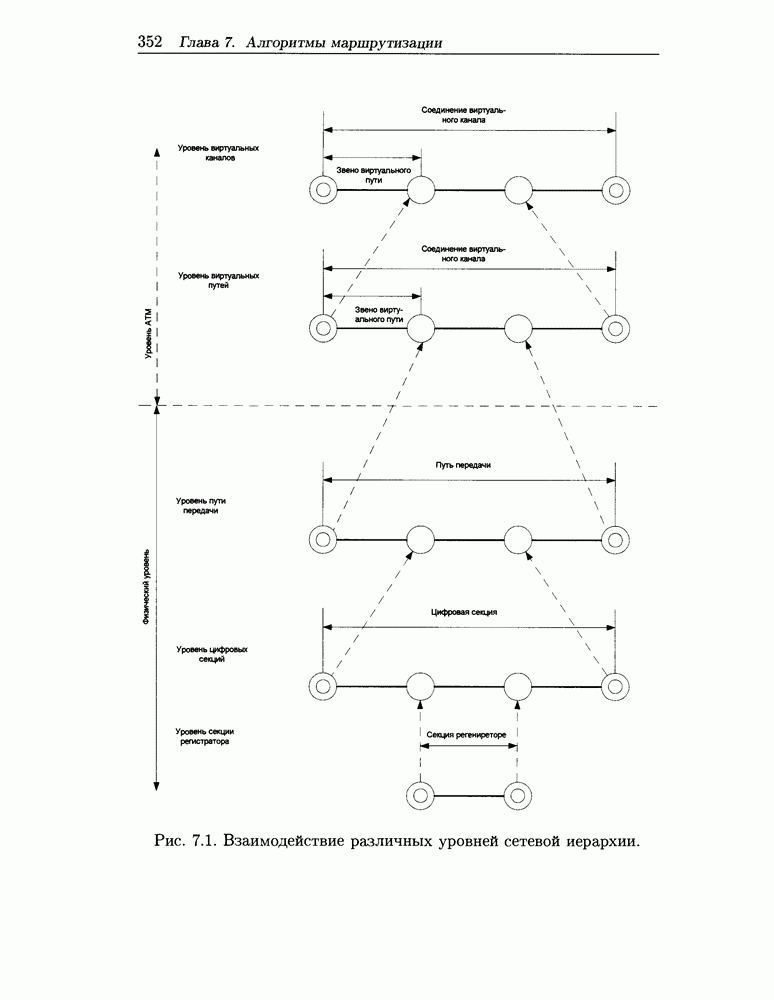
- 7.5 Динамическая маршрутизация в ATM сетях
- 7.5.1 Характерные особенности ATM сетей
- 7.5.2 Основные понятия маршрутизации для ATM сетей
- 7.5.3 Взаимосвязь с подсистемой установки соединения
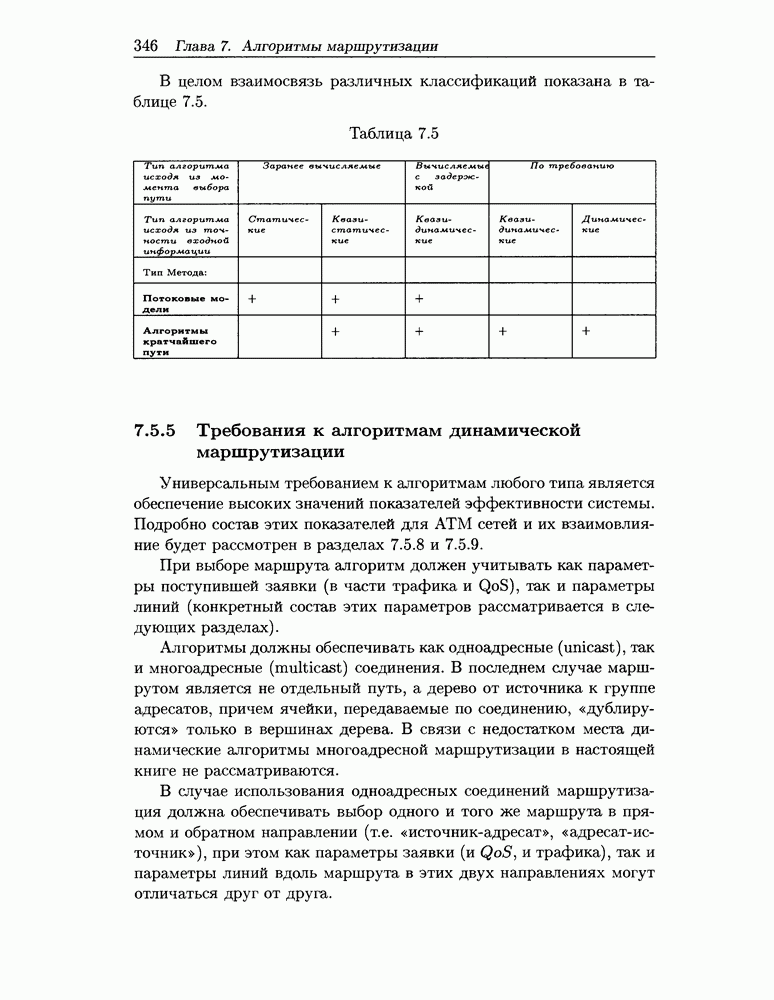
- 7.5.4 Классификация алгоритмов маршрутизации
- 7.5.5 Требования к алгоритмам динамической маршрутизации
- 7.5.6 Входные параметры заявки.
- 7.5.7 Параметры состояния сети
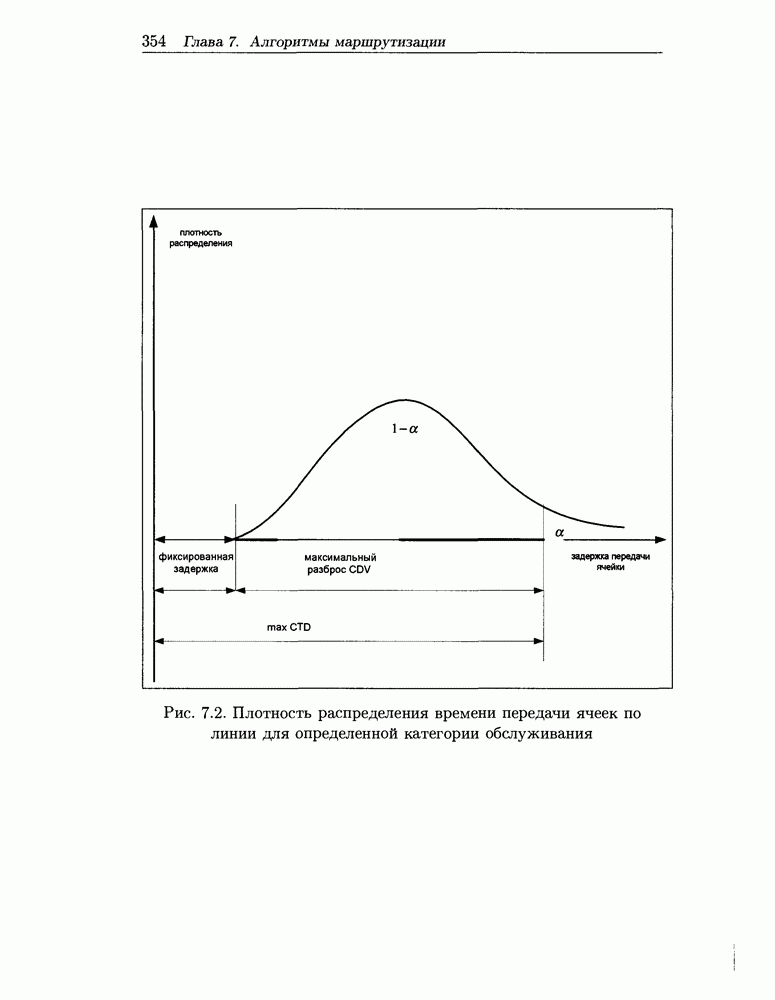
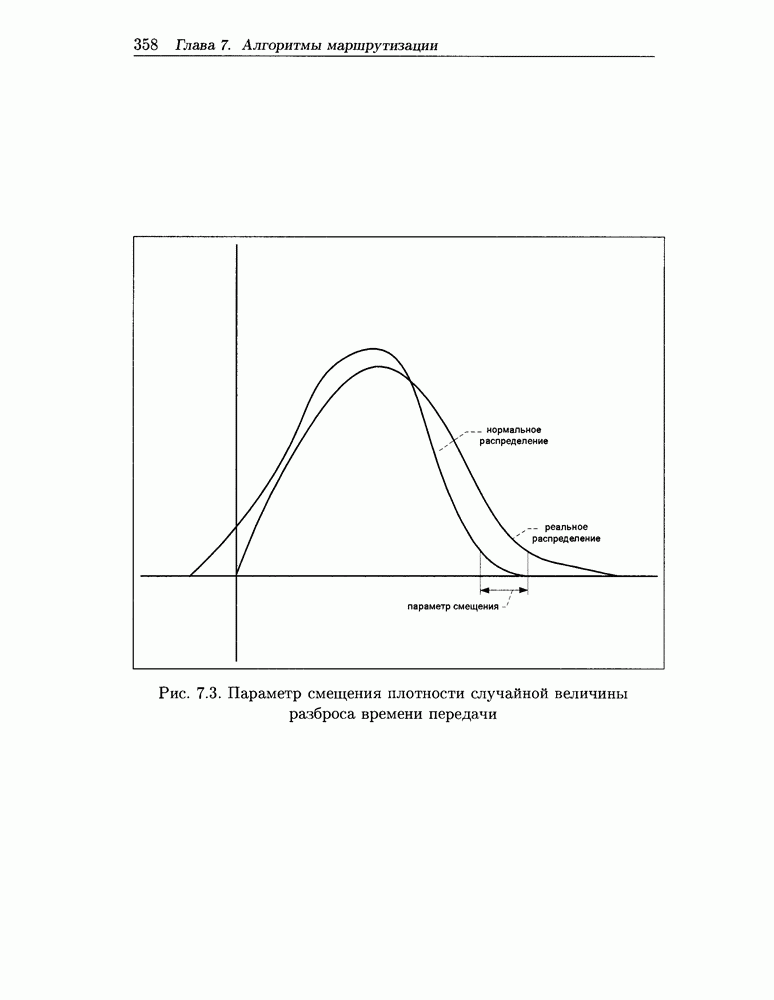
- 7.5.8 Показатели качества маршрутизации
- 7.5.9 Анализ подходов к реализации общих требований
- 7.5.10 Маршрутизация запасных соединений
- 7.5.11 Выбор оптимального алгоритма и значений его параметров
- ГЛАВА 8. Оптимизация топологической структуры компьютерной сети
- 8.1 Принципы топологического проектирования сетей передачи информации
- 8.2 Описание задачи синтеза топологии; исходные данные
- 8.3 Комбинаторный алгоритм топологической оптимизации сети передачи информации
- 8.4 Оптимизация топологической структуры по критериям стоимости и надежности
- 8.5 Алгоритм генерации остовных двухсвязных подграфов заданного графа
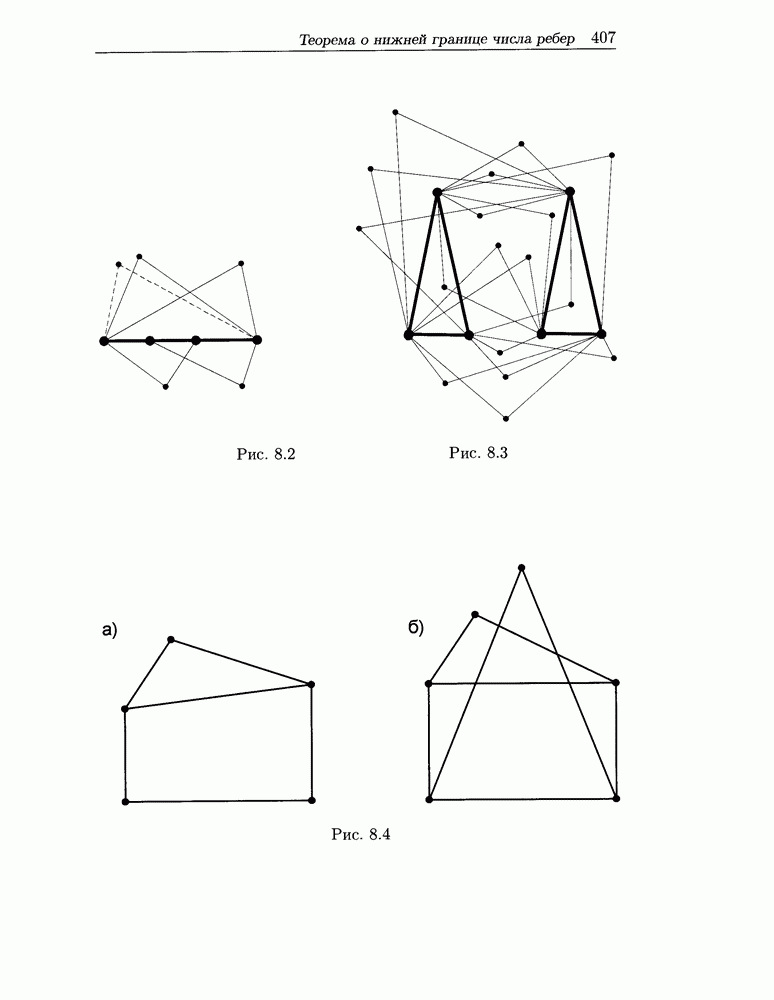
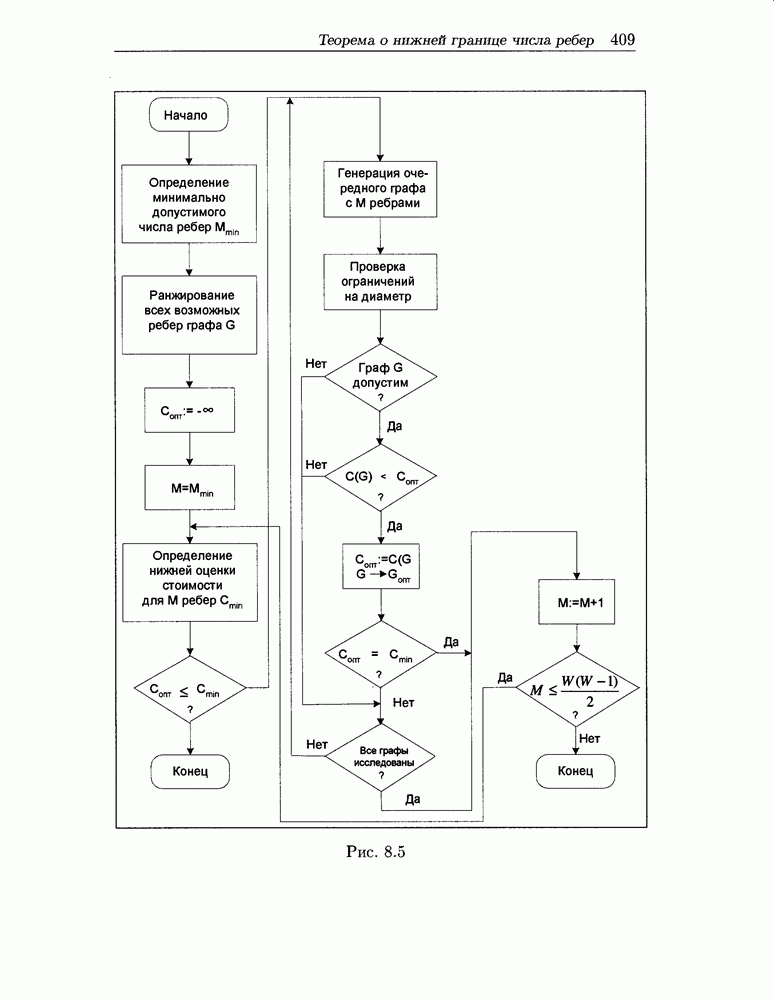
- 8.6 Характеристики некоторых экстремальных графов. Теорема о нижней границе числа ребер
- 8.7 Общая задача топологического синтеза компьютерной сети
- ГЛАВА 9. Методы анализа беспроводных компьютерных сетей
- 9.1 Состояние и перспективы развития беспроводных радиосетей
- 9.2 Схема распределенного управления
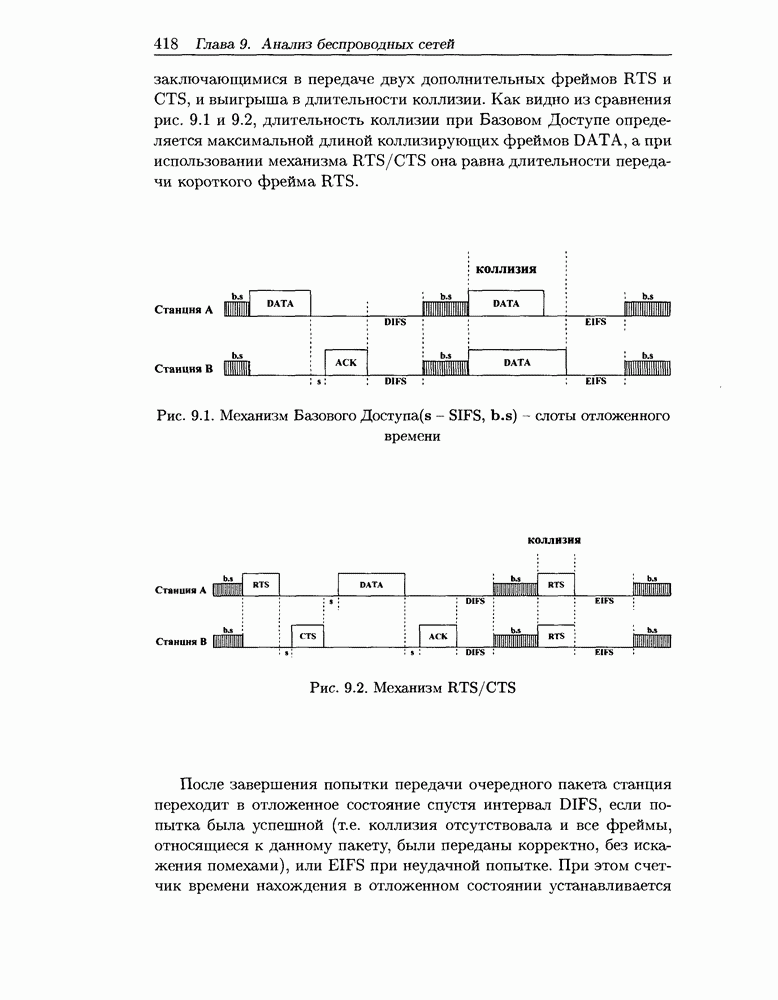
- 9.3 Моделирование беспроводной локальной сети в условиях высокой нагрузки
- 9.3.1 Оценка пропускной способности
- 9.3.2 Оценка вероятности передачи
- 9.3.3 Случай фрагментации пакетов
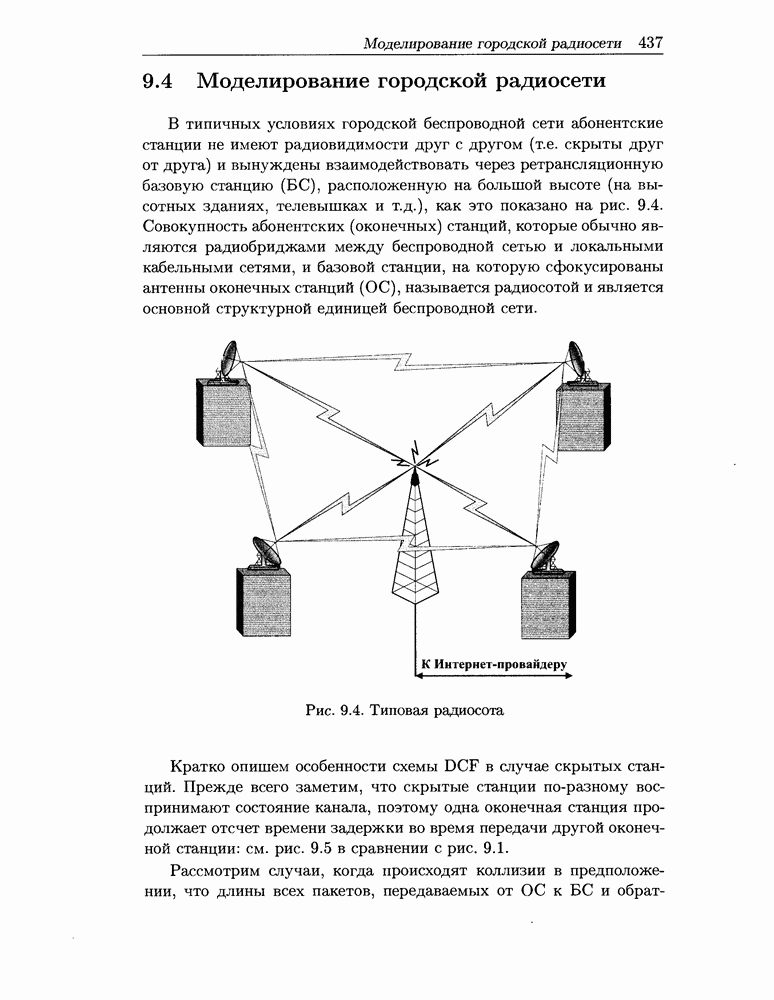
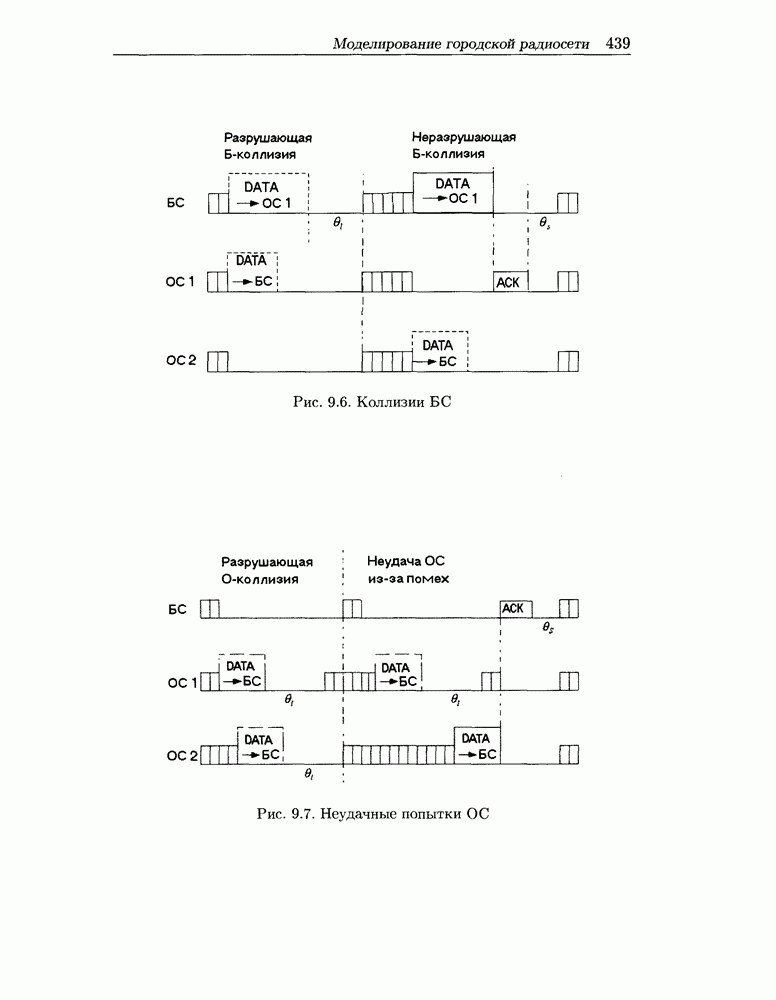
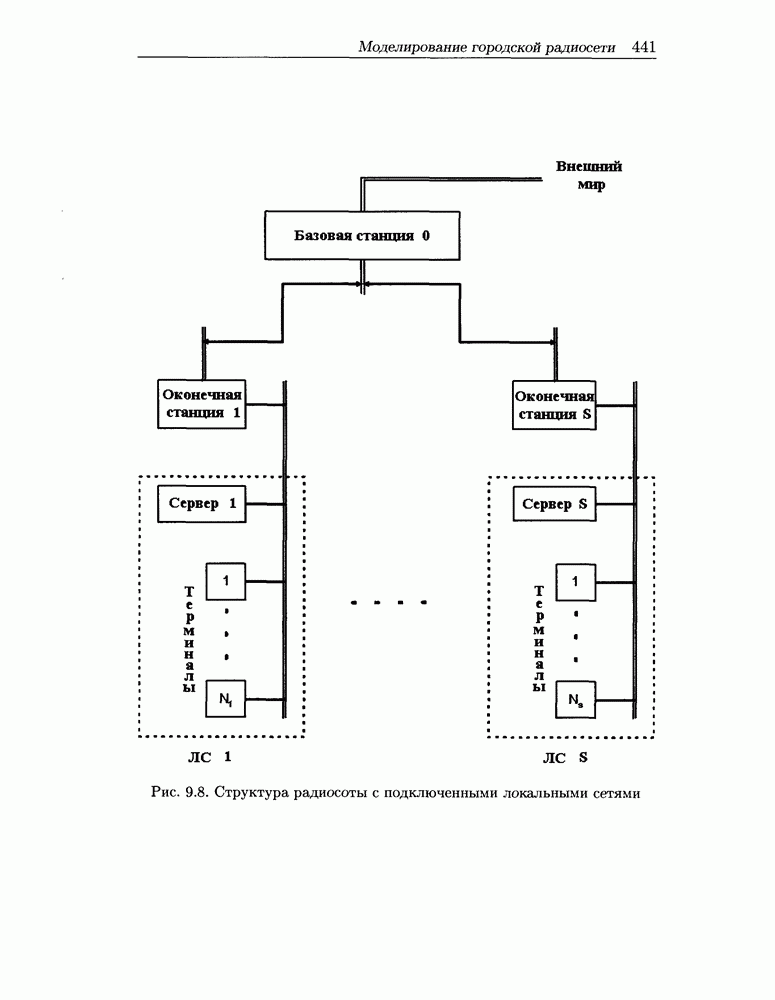
- 9.4 Моделирование городской радиосети
- 9.4.1 Имитационное моделирование радиосоты
- 9.4.2 Аналитический метод оценки пропускной способности
- 9.4.3 Метод оценки пропускной способности при технологии FHSS
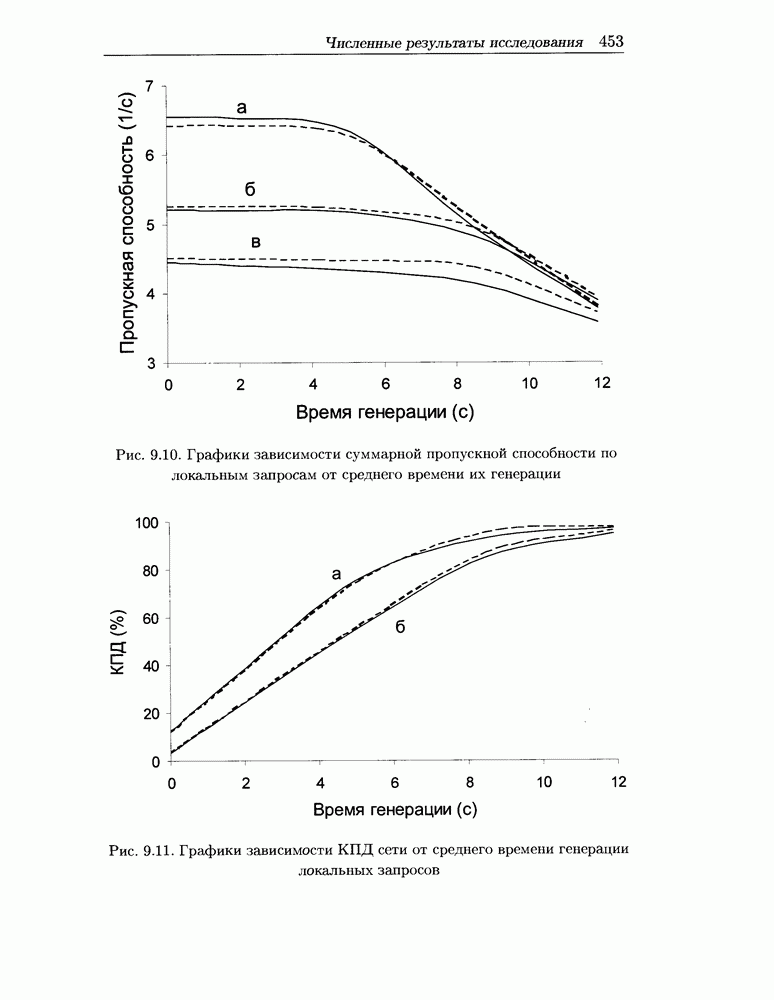
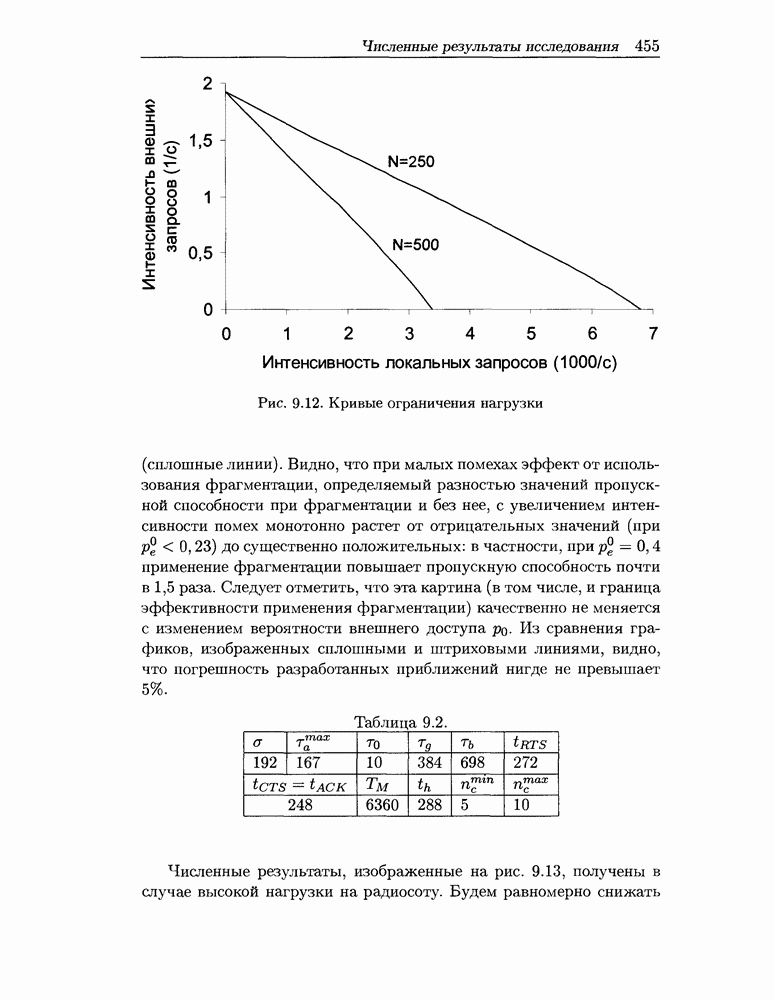
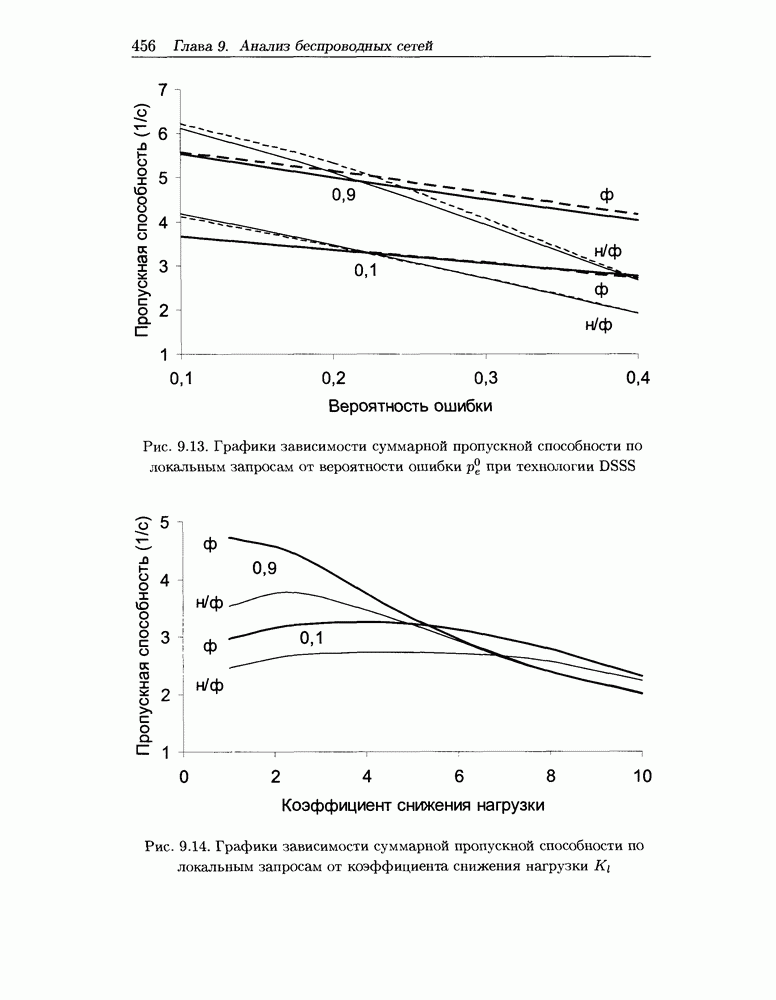
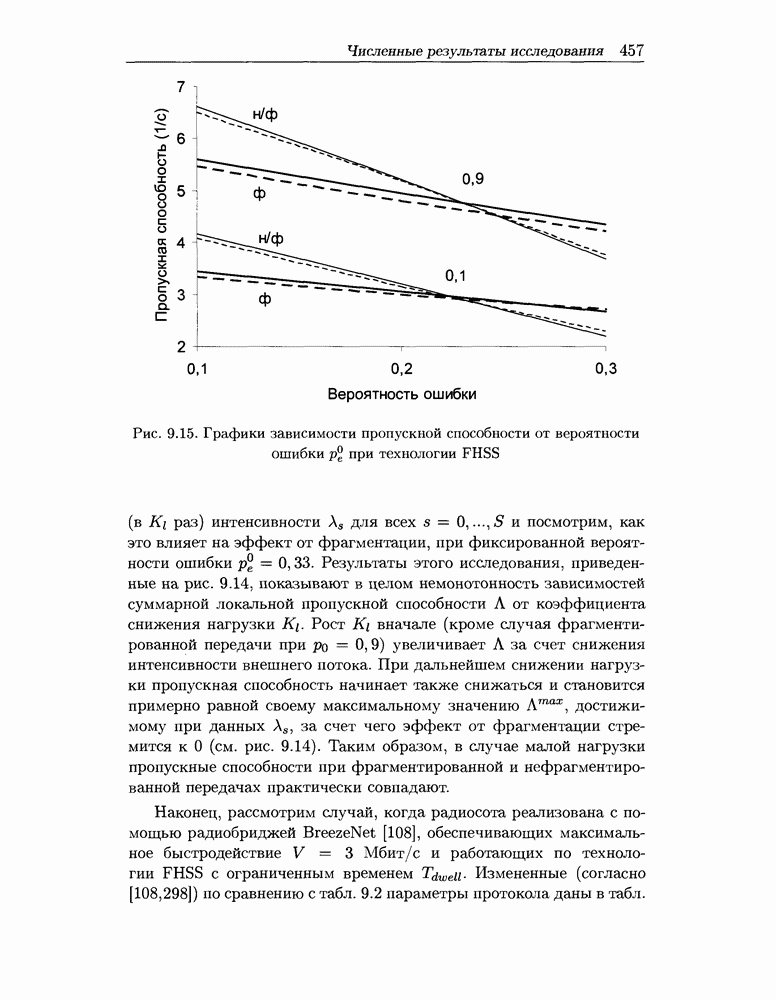
- 9.5 Численные результаты исследования городской радиосоты
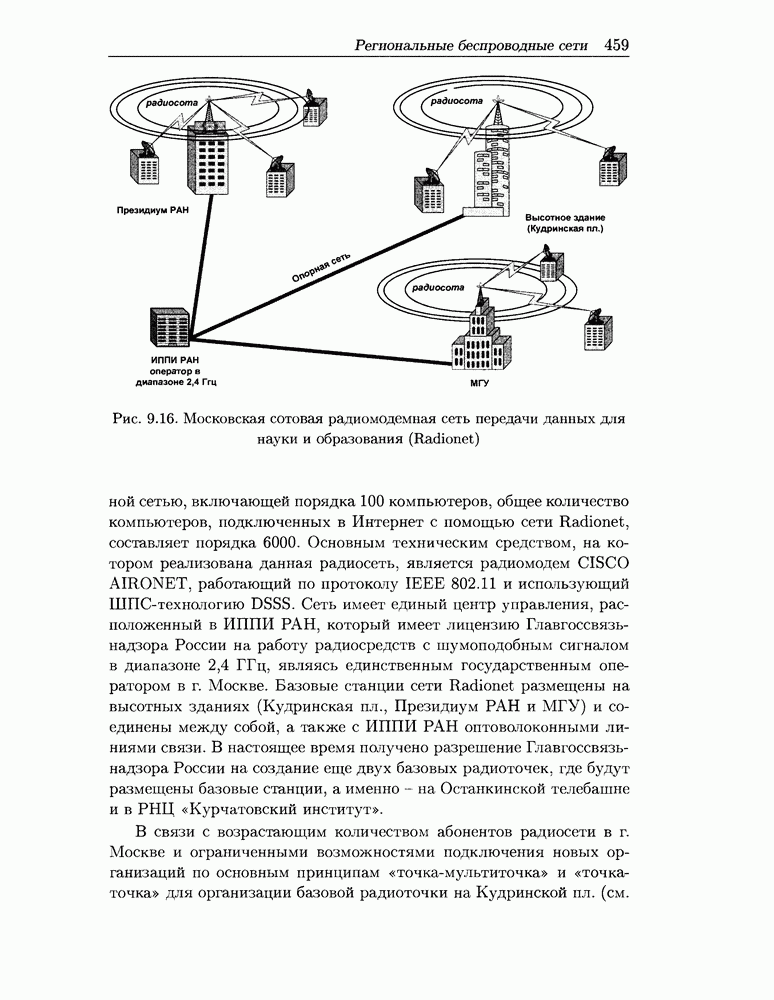
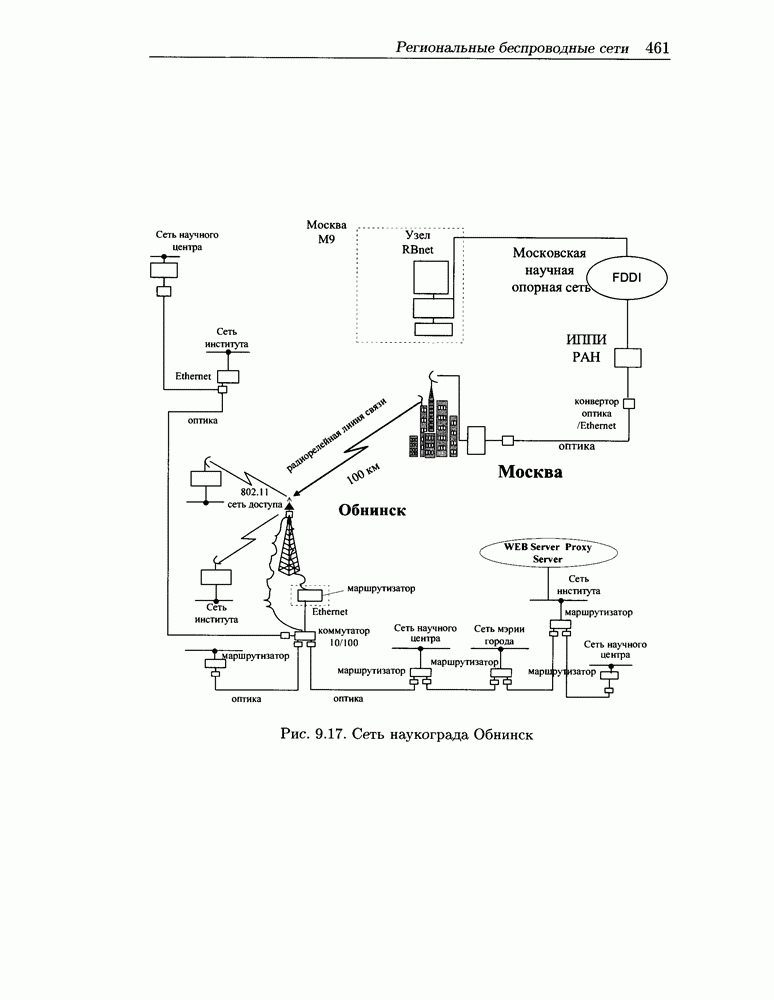
- 9.6 Региональные беспроводные сети на базе ШПС-радиомодемов
- 9.7 Аэростатная беспроводная сеть
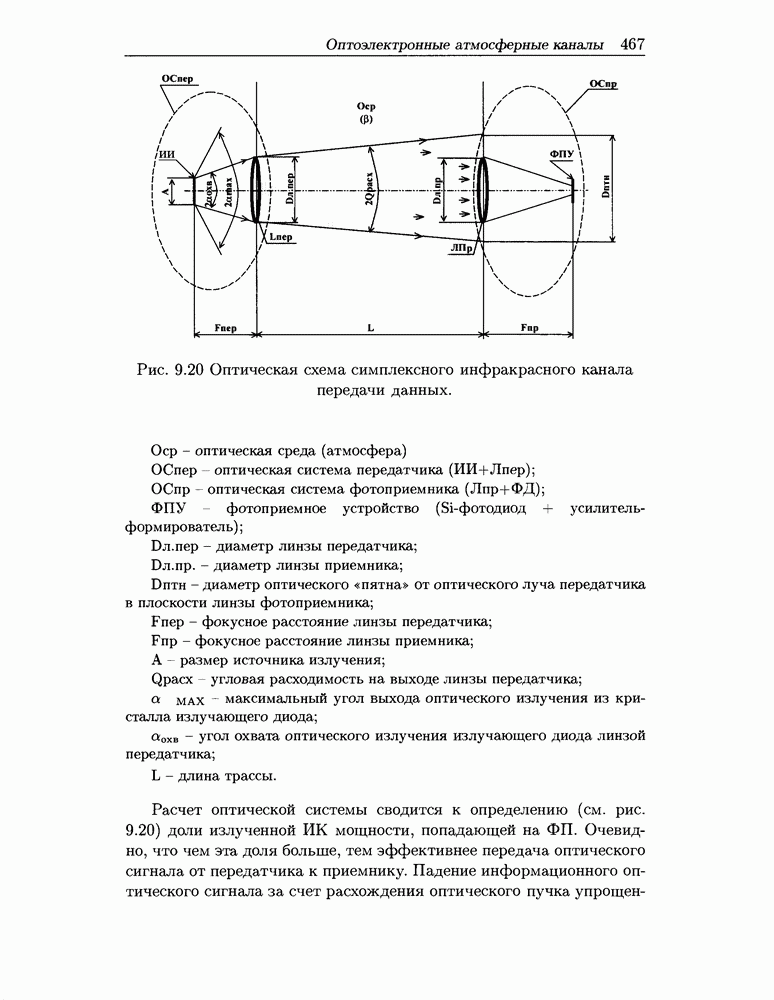
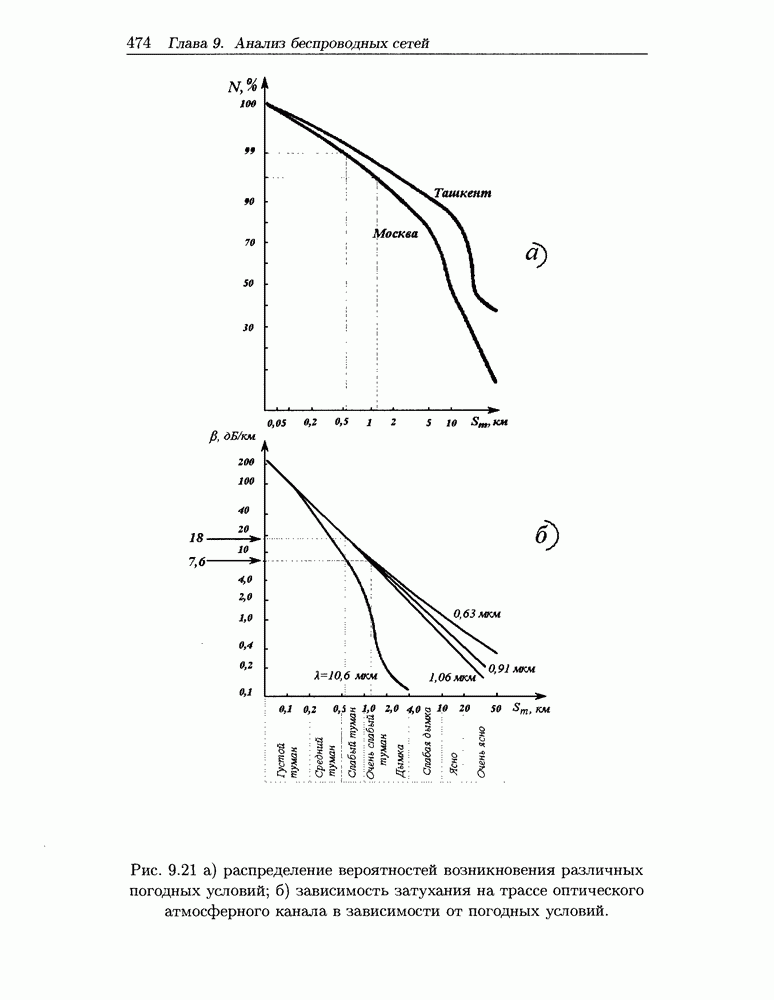
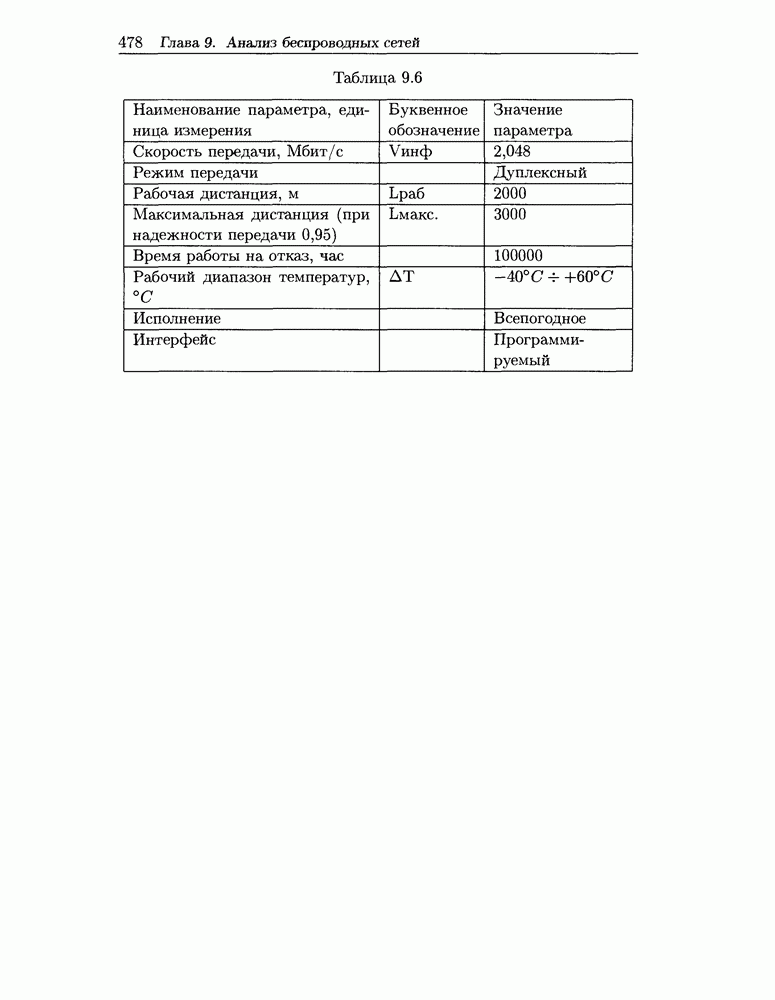
- 9.8 Оптоэлектронные атмосферные каналы передачи данных в компьютерных сетях
- Литература