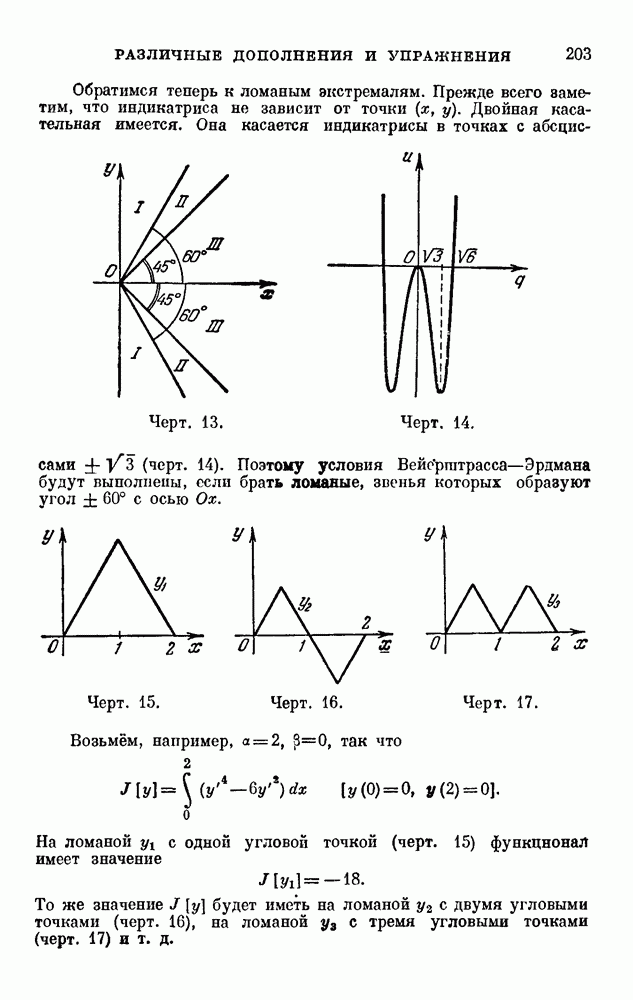
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
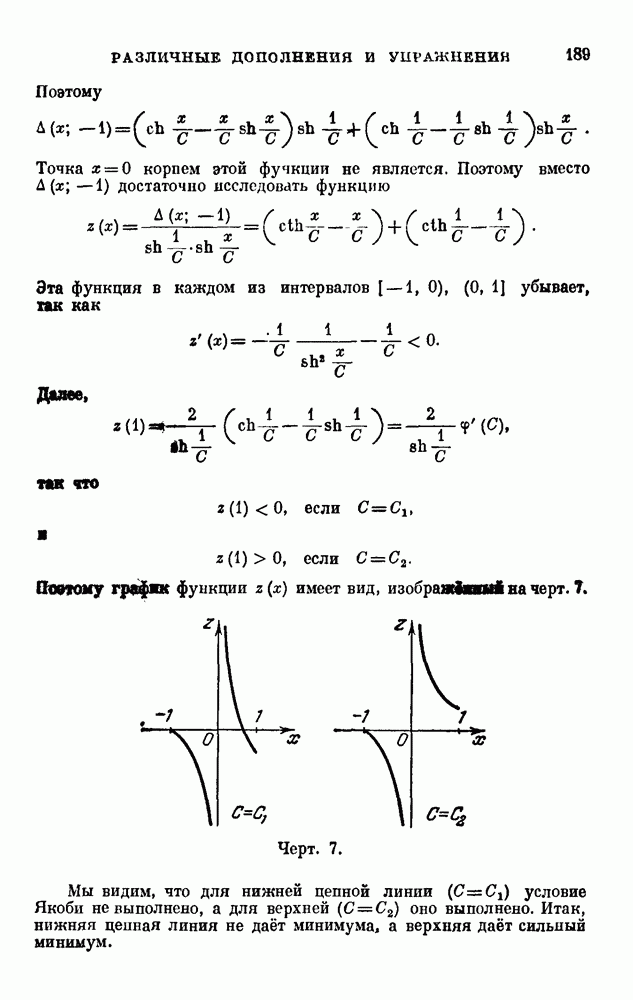
18. Условие Якоби.
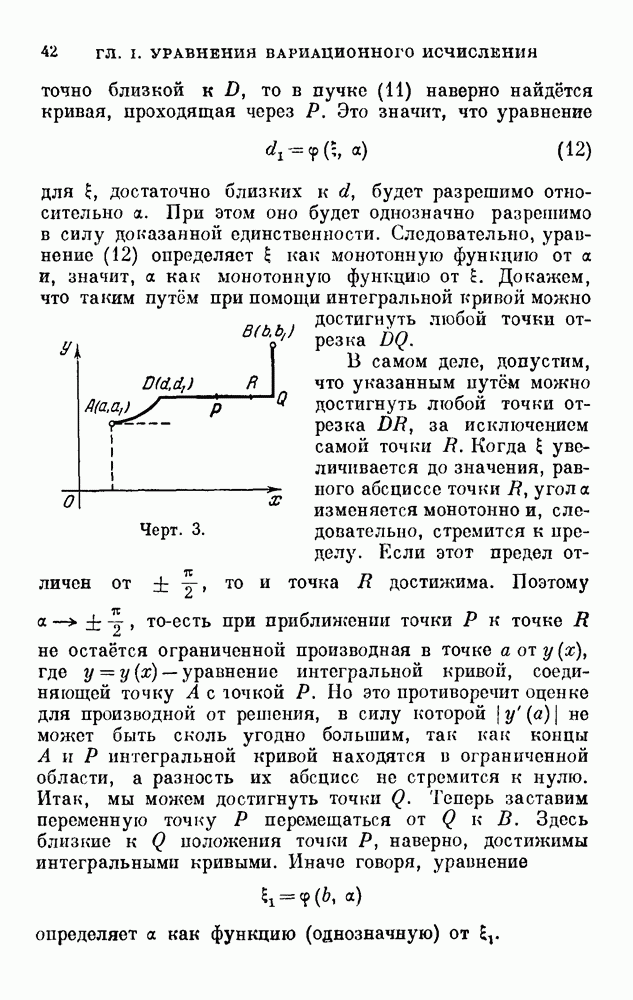
Переходим к вопросу о том, необходимо ли для экстремума функционала, чтобы экстремаль можно было окружить полем. Мы рассмотрим этот вопрос только для  хотя теория н переносится на любые
хотя теория н переносится на любые 
Итак, пусть дан функционал

при условиях

Пусть экстремаль

доставляет этому функционалу хотя бы слабый минимум. Как и при выводе основного необходимого условия для экстремума, положим

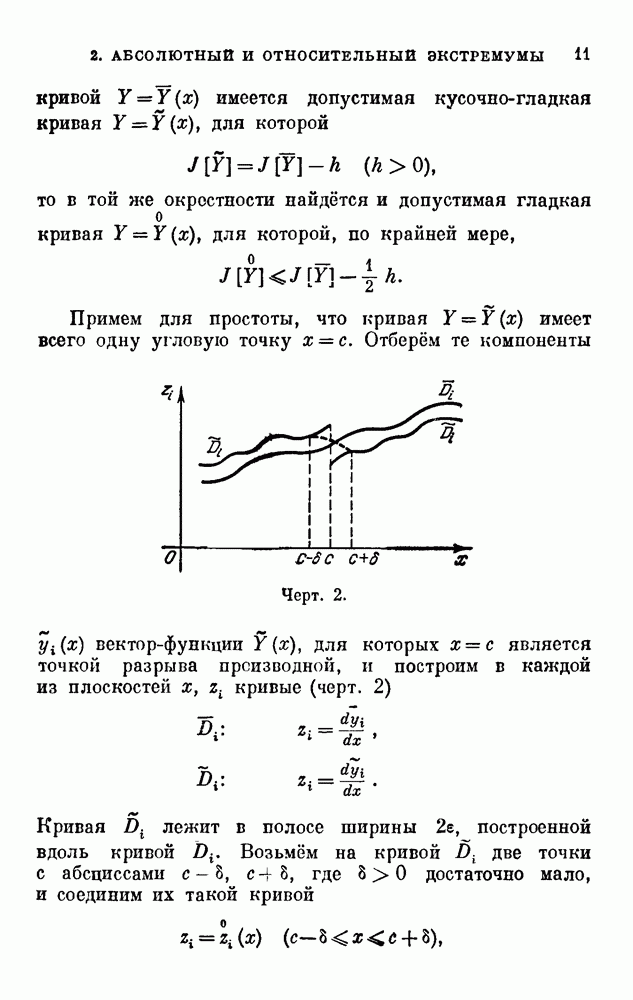
где  — кусочно-гладкая функция, равная нулю на концах интервала
— кусочно-гладкая функция, равная нулю на концах интервала  Функция
Функция

имеет по условию минимум при  . Отсюда следует, что
. Отсюда следует, что  Равенство
Равенство  уже было использовано нами ранее
уже было использовано нами ранее  привело к уравнению Эйлера — Лагранжа. Неравенство
привело к уравнению Эйлера — Лагранжа. Неравенство  мы используем теперь. Прежде всего заметим, что
мы используем теперь. Прежде всего заметим, что

есть некоторый квадратичный функционал от  . Его называют присоединённым функционалом и часто обозначают
. Его называют присоединённым функционалом и часто обозначают  . Коэффициенты подннтегрального трёхчлена в этом функционале являются некоторыми функциями лишь от
. Коэффициенты подннтегрального трёхчлена в этом функционале являются некоторыми функциями лишь от  Для них приняты обозначения
Для них приняты обозначения

Таким образом,

Первым из учением присоединённого функционала наука обязана Лежандру (1786), который путём преобразования этого функционала и пришёл к условию, носящему его имя.
Для преобразования присоединённого функционала Лежандр берёт вначале произвольную непрерывно дифференцируемую функцию  Так как
Так как  обращается в нуль на концах интервала, то
обращается в нуль на концах интервала, то

или

Поэтому

Далее Лежандр определённым образом выбирает функцию  При этом присоединённый функционал принимает упомянутую выше форму, из которой Лежандр получает следующие два предложения:
При этом присоединённый функционал принимает упомянутую выше форму, из которой Лежандр получает следующие два предложения:
1) чтобы экстремаль  давала минимум (хотя бы слабый), необходимо выполнение неравенства
давала минимум (хотя бы слабый), необходимо выполнение неравенства 
2) если выполнено усиленное неравенство  то экстремаль
то экстремаль  даёт минимум (слабый).
даёт минимум (слабый).
Первое предложение верно и является частным случаем теоремы, уже доказанной нами в п° 17. Что же касается второго предложения, то оно неверно. Несостоятельность доказательства Лежандра была обнаружена в 1797 году Лагранжем.
Однако некоторая модификация рассуждений Лежандра приводит к верному предложению, которое является, так сказать, локальным вариантом предложения 2) и состоит в следующем:
2*) если  , то можно указать такой достаточно малый подинтервал
, то можно указать такой достаточно малый подинтервал  содержащий точку
содержащий точку  что
что  доставит слабый минимум функционалу
доставит слабый минимум функционалу

при условиях

Так как переход от минимума к максимуму соответствует переходу от неравенства  (соответственно
(соответственно  ) к неравенству
) к неравенству  (соответственно
(соответственно  ), то из предложения 2), которое мы сейчас докажем, предложение 1) вытекает почти непосредственно). Предложение же 2), таким образом, будет доказано лишь для достаточно малых интервалов.
), то из предложения 2), которое мы сейчас докажем, предложение 1) вытекает почти непосредственно). Предложение же 2), таким образом, будет доказано лишь для достаточно малых интервалов.
Итак, пусть  . Возьмём дифференциальное уравнение
. Возьмём дифференциальное уравнение

где  — положительная константа. Так как в силу непрерывности функция
— положительная константа. Так как в силу непрерывности функция  положительна в некоторой окрестности точки
положительна в некоторой окрестности точки  то дифференциальное уравнение (2) обладает решением
то дифференциальное уравнение (2) обладает решением  в некотором интервале
в некотором интервале  , содержащем точку
, содержащем точку  и принадлежащем интервалу
и принадлежащем интервалу  . Это решение
. Это решение  имеет непрерывную производную, и его мы подставим в выражение (1) присоединённого функционала
имеет непрерывную производную, и его мы подставим в выражение (1) присоединённого функционала  после замены пределов
после замены пределов  на
на  .
.
Мы получим тогда, что

Сравним теперь значение функционала  на экстремали
на экстремали  с его значением на произвольной функции
с его значением на произвольной функции  принадлежащей некоторой слабой окрестности экстремали и удовлетворяющей условиям
принадлежащей некоторой слабой окрестности экстремали и удовлетворяющей условиям

Полагая

будем иметь по формуле Тейлора

где

Введём обозначение

тогда

и если принять, что

то величины А, В, С, D не будут превосходить по модулю некоторой константы Г, которую легко оценить наперёд.
Принимая во внимание полученное выше выражение для и равенство

можем, следовательно, написать соотношение

Теперь возьмём положительное число  столь малым, чтобы при
столь малым, чтобы при  имели место неравенства
имели место неравенства

Мы и получим тогда, что

всякий раз, когда функция  принадлежит слабой
принадлежит слабой  -окрестности экстремали
-окрестности экстремали  .
.
Тем самым предложение 2) доказано. Этим методом предложение 2) доказать нельзя, так как уравнение (2), несмотря на положительность во всём замкнутом интервале  непрерывной функции
непрерывной функции  может не иметь непрерывного решения
может не иметь непрерывного решения  во всём этом интервале.
во всём этом интервале.
Бот простой пример, иллюстрирующий это: пусть  , так что уравнение (2) имеет вид
, так что уравнение (2) имеет вид

где р — положительная константа. Интегрирование этого уравнения даёт

где С — произвольная постоянная. Мы видим, что во всяком интервале, длина которого  , полученная функция обязательно обращается в бесконечность.
, полученная функция обязательно обращается в бесконечность.
Но если, кроме положительности  в интервале
в интервале  ещё потребовать существование у уравнения
ещё потребовать существование у уравнения

непрерывного решения во всём интервале  то легко доказать, что экстремаль
то легко доказать, что экстремаль  в целом доставляет функционалу слабый минимум.
в целом доставляет функционалу слабый минимум.
Действительно, если уравнение (3) имеет непрерывное решение во всём интервале  то по теореме о непрерывной зависимости решения от параметра уравнение (2) будет иметь непрерывное во всём интервале
то по теореме о непрерывной зависимости решения от параметра уравнение (2) будет иметь непрерывное во всём интервале  решение для всех достаточно малых по модулю значений о, и приведённое доказательство годится для экстремали в целом.
решение для всех достаточно малых по модулю значений о, и приведённое доказательство годится для экстремали в целом.
Раньше (см. п° 15) мы видели, что при положительности  в интервале
в интервале  слабый минимум обеспечен, если экстремаль можно окружить полем. Теперь мы видим, что последнее требование можно заменить другим — наличием у уравнения (3) решения, непрерывного во всём интервале
слабый минимум обеспечен, если экстремаль можно окружить полем. Теперь мы видим, что последнее требование можно заменить другим — наличием у уравнения (3) решения, непрерывного во всём интервале  . Естественно возникает вопрос о том, не эквивалентны ли при
. Естественно возникает вопрос о том, не эквивалентны ли при  эти два условия. Мы покажем, что это действительно так, а затем рассмотрим вопрос о необходимости этих условий.
эти два условия. Мы покажем, что это действительно так, а затем рассмотрим вопрос о необходимости этих условий.
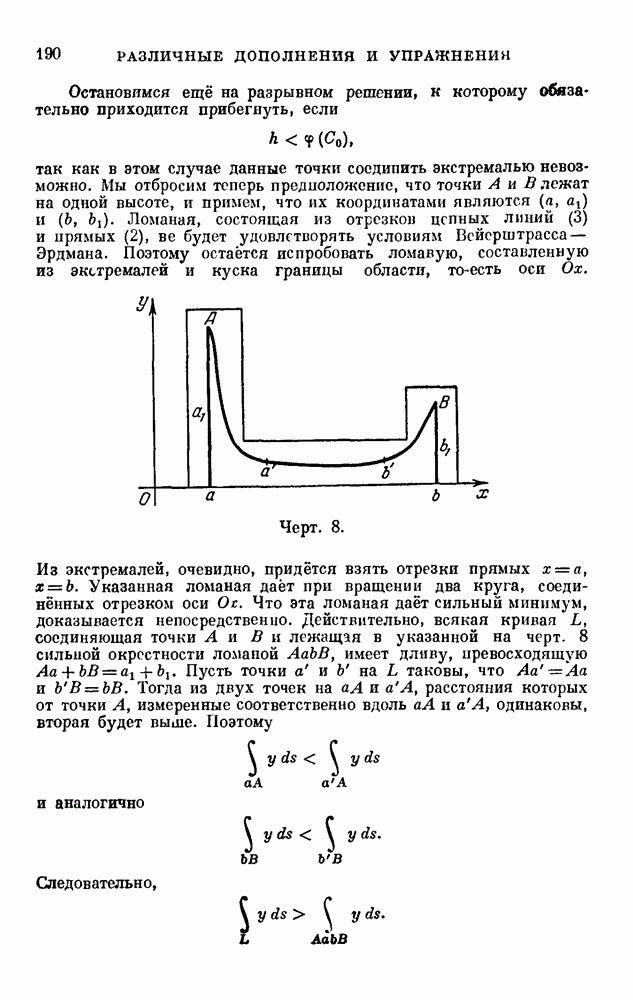
Предварительно приведём пример, из которого видно, что при обращении функции  в нуль хотя бы водной точке интервала
в нуль хотя бы водной точке интервала  упомянутая эквивалентность может не иметь места.
упомянутая эквивалентность может не иметь места.
Пусть

Общий интеграл уравнения Эйлера — Лагранжа имеет вид

Рассматриваемым краевым условиям удовлетворяет экстремаль

Полем её окружить нельзя, так как единственное однопараметрическое семейство экстремалей, содержащее экстремаль  имеет вид
имеет вид

а этим семейством нельзя покрыть область, внутри которой лежит точка с абсциссой  .
.
Вместе с тем в рассматриваемом случае

и уравнение Лежандра (3) имеет решение

непрерывное во всём интервале  .
.
Обращаясь к поставленным выше вопросам, начнём с того, что уравневие Лежандра (3) есть уравнение типа Риккати. С помощью известной подстановки мы можем перейти от него к некоторому линейному дифференциальному уравнению второго порядка. Для этого полагаем

Определяя из этого соотношения w, затем дифференцируя и подставляя w и w' в уравнение (3), получим для и уравнение

Это уравнение носит название уравнения Якоби.
По отношению к уравнению Лежандра (3) основной вопрос состоял в том, имеет ли оно решение, непрерывное в замкнутом интервале  .
.
Этот вопрос сводится к вопросу о том, имеет ли уравнение Якоби (4) решение, не обращающееся в нуль в замкнутом интервале  .
.
Заметим, что уравнение Якоби является уравнением Эйлера — Лагранжа для присоединённого функционала.
Кроме того, уравнение Якоби находится в тесной связи с уравнением Эйлера—Лагранжа

для исходного функционала

А именно уравнение Якоби является по отношению к уравнению Эйлера—Лагранжа уравнением в вариациях. Это означает следующее: пусть

есть какое-нибудь однопараметрическое семейство решений уравнения (5), причём не только  но и
но и  — непрерывно дифференцируемые функции от а, и пусть
— непрерывно дифференцируемые функции от а, и пусть

Тогда функция

является решением уравнения Якоби (4), построенного для экстремали  . К этому нужно добавить, что если
. К этому нужно добавить, что если

есть двухпараметрическое семейство решений уравнения (5), причём не только  , но и
, но и  — непрерывно дифференцируемые функции от
— непрерывно дифференцируемые функции от 

и если

то функции

представляют пару линейно независимых решений уравнения Якоби.
Линейная независимость следует из (6), если остальные утверждения уже доказаны. Последнее достигается подстановкой в уравнение (5) вместо у функции  или
или  с последующим дифференцированием полученного тождества по параметру
с последующим дифференцированием полученного тождества по параметру  или
или  .
.
Условимся обозначать через  нетривиальное решение уравнения Якоби, равное нулю при
нетривиальное решение уравнения Якоби, равное нулю при  . Ближайший справа к
. Ближайший справа к  корень функции
корень функции  , если таковой корень вообще существует, обозначим через с и назовём точкой, сопряжённой с точкой с. Мы будем также называть сопряжёнными две точки экстремали
, если таковой корень вообще существует, обозначим через с и назовём точкой, сопряжённой с точкой с. Мы будем также называть сопряжёнными две точки экстремали  , имеющие абсциссы с и с*.
, имеющие абсциссы с и с*.
Теперь мы можем перейти к теоремам, дающим ответ на поставленные нами вопросы.
Теорема 1. Если во всех точках интервала  имеет место неравенство R{x) > 0 и если сопряженная с а точка а* лежит внутри интервала
имеет место неравенство R{x) > 0 и если сопряженная с а точка а* лежит внутри интервала  то экстремаль
то экстремаль  не даёт минимума (даже слабого).
не даёт минимума (даже слабого).
Доказательство. Допустим, что экстремаль  даёт хотя бы слабый минимум функционалу
даёт хотя бы слабый минимум функционалу  .
.
Тогда присоединённый функционал положителен или равен нулю на всякой допустимой функции  . И поэтому всякая кусочно-гладкая функция, равная нулю при
. И поэтому всякая кусочно-гладкая функция, равная нулю при  и обращающая в нуль функционал
и обращающая в нуль функционал  должна состоять из кусков экстремалей этого функционала, а в точках разрыва должна удовлетворять условиям Вейерштрасса—Эрдмана для функционала
должна состоять из кусков экстремалей этого функционала, а в точках разрыва должна удовлетворять условиям Вейерштрасса—Эрдмана для функционала  . Но возьмём функцию
. Но возьмём функцию

Для нее

Поэтому функция  должна удовлетворять условиям Вейерштрасса—Эрдмана и, значит, должно иметь место равенство
должна удовлетворять условиям Вейерштрасса—Эрдмана и, значит, должно иметь место равенство

или

Но  и
и  . Поэтому из написанного соотношения следует, что
. Поэтому из написанного соотношения следует, что  . Однако это абсурдно, так как
. Однако это абсурдно, так как

а обращение в нуль производной  в точке
в точке  где сама функция
где сама функция  также обращается в нуль, невозможно на основании теоремы единственности теории дифференциальных уравнений, поскольку
также обращается в нуль, невозможно на основании теоремы единственности теории дифференциальных уравнений, поскольку  .
.
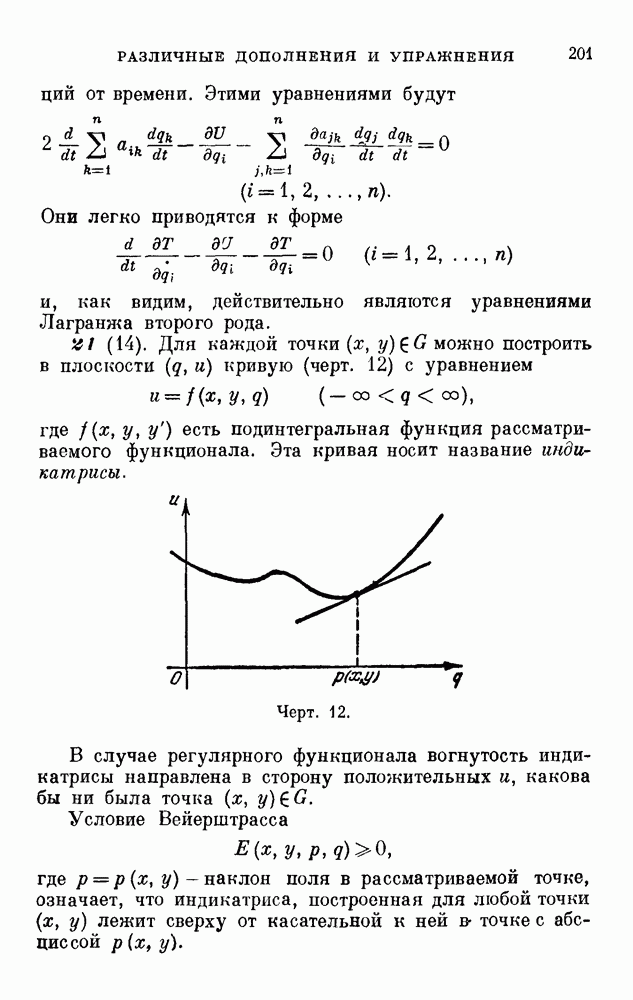
Требование, чтобы сопряжённая с левым концом интервала  точка не лежала внутри интервала, называют условием Якоби.
точка не лежала внутри интервала, называют условием Якоби.
Доказанная теорема утверждает, что если вдоль экстремали выполнено усиленное условие Лежандра, то для минимума (хотя бы слабого) необходимо, чтобы экстремаль удовлетворяла условию Якоби.
Теорема 2. Если во всех точках интервала  имеет место неравенство
имеет место неравенство  и если в замкнутом интервале
и если в замкнутом интервале  нет точки, сопряжённой с
нет точки, сопряжённой с  , то экстремаль
, то экстремаль  можно окружить полем и поэтому она даёт функционалу слабый минимум. При этом предполагается, что кривая
можно окружить полем и поэтому она даёт функционалу слабый минимум. При этом предполагается, что кривая  лежит целиком внутри области
лежит целиком внутри области  .
.
Заметим, что здесь условие Якоби фигурирует в усиленной форме.
Заметим также, что если оставить в стороне особые случаи, когда  или
или  обращается в нуль (но не меняет знака), то из сопоставления теорем 1 и 2 следует, что для экстремума необходимо, чтобы экстремаль можно было окружить полем.
обращается в нуль (но не меняет знака), то из сопоставления теорем 1 и 2 следует, что для экстремума необходимо, чтобы экстремаль можно было окружить полем.
Доказательство. Так как кривая  лежит целиком внутри области G, то она может быть несколько продолжена как влево, так и вправо с сохранением своего свойства быть экстремалью. Для нас важно, что найдётся такая достаточно близкая к х = а точка с < а, что замкнутый интервал [с, b] не будет содержать точки, сопряжённой с точкою с.
лежит целиком внутри области G, то она может быть несколько продолжена как влево, так и вправо с сохранением своего свойства быть экстремалью. Для нас важно, что найдётся такая достаточно близкая к х = а точка с < а, что замкнутый интервал [с, b] не будет содержать точки, сопряжённой с точкою с.
Для доказательства этого факта нам придётся воспользоваться теоремой Штурма, в силу которой между каждыми двумя корнями одного решения уравнения

лежит корень всякого другого решения этого уравнения
Построим решение уравнения Якоби  равное нулю на правом конце интервала. Эта функция будет отлична от нуля в полузамкнутом интервале
равное нулю на правом конце интервала. Эта функция будет отлична от нуля в полузамкнутом интервале  .
.
Действительно, если бы она обращалась в нуль при  то она совпадала бы с точностью до постоянного множителя с
то она совпадала бы с точностью до постоянного множителя с  , а функция
, а функция  по условию при
по условию при  отлична от нуля. Равным образом невозможно, чтобы
отлична от нуля. Равным образом невозможно, чтобы  обращалась в нуль в какой-нибудь точке
обращалась в нуль в какой-нибудь точке  между а и b
между а и b  ), так как тогда по теореме Штурма функция
), так как тогда по теореме Штурма функция  имела бы корень между точками
имела бы корень между точками  .
.
Функция  в силу непрерывности будет отлична от нуля в некотором большем интервале
в силу непрерывности будет отлична от нуля в некотором большем интервале  . Теперь возьмём какую-нибудь точку с, удовлетворяющую неравенству
. Теперь возьмём какую-нибудь точку с, удовлетворяющую неравенству  и докажем, что в замкнутом интервале
и докажем, что в замкнутом интервале  нет точки, сопряжённой с точкой с, то-есть что с и есть нужная нам точка. Равенство
нет точки, сопряжённой с точкой с, то-есть что с и есть нужная нам точка. Равенство  исключается немедленно, так как из него следовало бы, что
исключается немедленно, так как из него следовало бы, что  . С другой стороны, неравенство
. С другой стороны, неравенство  также невозможно, так как в силу теоремы Штурма из него следовало бы существование корня у функции
также невозможно, так как в силу теоремы Штурма из него следовало бы существование корня у функции  в интервале
в интервале  с и тем более в интервале
с и тем более в интервале  .
.
Теперь проведём через точку с координатами  пучок экстремалей нашего функционала, принимая за параметр а наклон экстремали в вершине пучка. Существование этого пучка вытекает из теоремы о погружении интегральной кривой в семейство (см. п° 8). Ураннение пучка пусть будет
пучок экстремалей нашего функционала, принимая за параметр а наклон экстремали в вершине пучка. Существование этого пучка вытекает из теоремы о погружении интегральной кривой в семейство (см. п° 8). Ураннение пучка пусть будет

Из теоремы о зависимости решения дифференциального уравнения от параметров (см. снова п° 8) следует, что как функция  , так и функция
, так и функция  непрерывно дифференцируемы по
непрерывно дифференцируемы по  .
.
Пусть наша экстремаль  получается при
получается при  . Так как по условию
. Так как по условию

то

и поэтому на основании непрерывности

Из этого неравенства следует, что никакие две экстремали семейства

не имеют общей точки (в полосе  ). Действительно, если бы при каком-нибудь
). Действительно, если бы при каком-нибудь  выполнялось равенство
выполнялось равенство

то по теореме Ролля функция  обращалась бы в нуль при некотором а из интервала
обращалась бы в нуль при некотором а из интервала  что противоречит (7). На основании общих рассмотрений п° 12 семейство (8) поэтому порождает поле, окружающее экстремаль
что противоречит (7). На основании общих рассмотрений п° 12 семейство (8) поэтому порождает поле, окружающее экстремаль 
Тем самым теорема доказана.
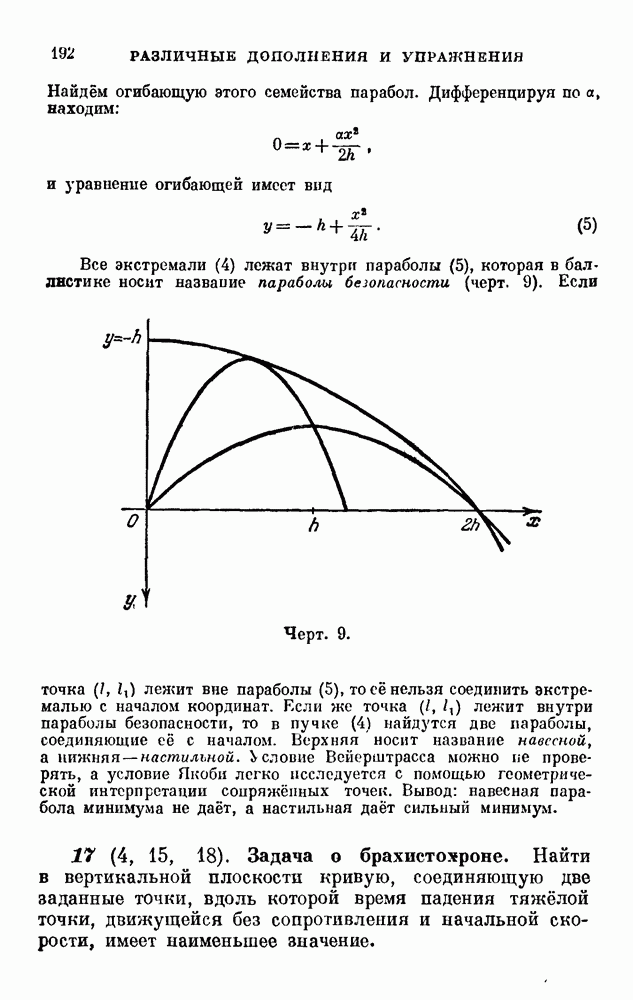
Закончим настоящий параграф геометрической интерпретацией сопряжённой точки. Чтобы использовать имеющиеся у нас формулы, возьмём на экстремали

точку  Точка экстремали, сопряжённая с этой точкой, имеет абсциссу с и ординату
Точка экстремали, сопряжённая с этой точкой, имеет абсциссу с и ординату  причём
причём

Но последнее равенство можно записать в виде

Таким образом, координаты сопряжённой точки определяются системой уравнений

Присоединяя уравнение

к уравнению

семейства криных, не имеющих особых точек, мы получаем систему уравнений для определения так называемых характеристических точек на кривых рассматриваемого семейства. Геометрическое же место характеристических точек есть, по определению, огибающая семейства.
Таким образом, сопряжённая с  точка на экстремали (9) есть ближайшая справа к точке
точка на экстремали (9) есть ближайшая справа к точке  характеристическая точка этой экстремали, если за семейство взять пучок экстремалей с вершиной
характеристическая точка этой экстремали, если за семейство взять пучок экстремалей с вершиной  Оставляя в стороне исключительные случаи (когда огибающая нырождается или имеет особые точки), мы можем сформулировать следующее правило: чтобы получить сопряженную с точкой
Оставляя в стороне исключительные случаи (когда огибающая нырождается или имеет особые точки), мы можем сформулировать следующее правило: чтобы получить сопряженную с точкой  точку, нужно построить огибающую пучка экстремалей с вершиной
точку, нужно построить огибающую пучка экстремалей с вершиной  и взять на рассматриваемой экстремали ближайшую справа к
и взять на рассматриваемой экстремали ближайшую справа к  точку касания этой экстремали с огибающей.
точку касания этой экстремали с огибающей.
На этой геометрической интерпретации основано интересное по идее доказательство теоремы 1, однако это доказательство довольно кропотливо в силу необходимости рассмотрения также и исключительных случаев.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. УРАВНЕНИЯ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
- 1. Основная задача вариационного исчисления
- 2. Абсолютный и относительный экстремумы.
- 3. Первое необходимое условие для экстремума.
- 5. Инвариантность уравнений Эйлера—Лагранжа.
- 6. Одна теорема Гильберта.
- 7. О существовании экстремалей.
- 8. Зависимость решений дифференциальных уравнений от параметров.
- 9. Одна теорема Бернштейна.
- 10. Задача вариационного исчисления в параметрической форме.
- ГЛАВА II. ТЕОРИЯ ПОЛЯ
- 11. Поле для функционала в обычной форме.
- 12. Построение поля.
- 13. Поле для функционала в параметрической форме.
- 14. Функция Вейерштрасса.
- 15. Достаточные условия для сильного и слабого минимума функционала в обычной форме.
- 16. Достаточные условия для сильного и слабого минимума функционала в параметрической форме.
- 17. Необходимые условия Вейерштрасса и Лежандра.
- 18. Условие Якоби.
- 19. Теория Гамильтона—Якоби.
- ГЛАВА III. РАЗЛИЧНЫЕ ОБОБЩЕНИЯ ОСНОВНОЙ ЗАДАЧИ
- 20. Понятие о вариациях функционала.
- 21. Скользящие концы.
- 22. Вариация двойных интегралов.
- 23. Вариация функционалов, зависящих от производных высших порядков.
- 24. Элементарное правило множителей.
- 25. Изопериметрическая задача
- 26. Задача Лагранжа.
- ГЛАВА IV. ПРЯМЫЕ МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
- 27. Понятие о прямых методах.
- 28. Задача об абсолютном минимуме функционала в обычной форме.
- 29. Некоторые вспомогательные рассмотрения.
- 30. Теорема об абсолютном минимуме.
- 31. Переход к уравнению Эйлера—Лагранжа.
- 32. Фактическое построение минимизирующих последовательностей.
- 33. Задача об абсолютном минимуме функционала в параметрической форме.
- 34. Доказательство теоремы Гильберта.
- 35. Одно вспомогательное предложение.
- 36. Доказательство теоремы Тонелли.
- РАЗЛИЧНЫЕ ДОПОЛНЕНИЯ И УПРАЖНЕНИЯ
- 6 (19). Доказать, что по уравнению Якоби — Гамильтона
- 15 (10, 15, 18). Задача о наименьшей поверхности вращения.
- 17 (4, 15, 18). Задача о брахистохроне.
- 20 (4, 10). Вариационные принципы механики.
- 25 (25). Задача Кельвина.
- 28 (26). Задача С. А. Чаплыгина.
- 30 (22). Необходимое условие для экстремума двойного интеграла (аналог условия Лежандра).
- 31 (22). Теорема Хаара о регулярных функционалах.
- 33 (31). Проблема Штурма—Лиувилля.
- 34. Множество собственных значений проблемы Штурма—Лиувилля
- 36. Максимально-минимальное свойство собственных значений.