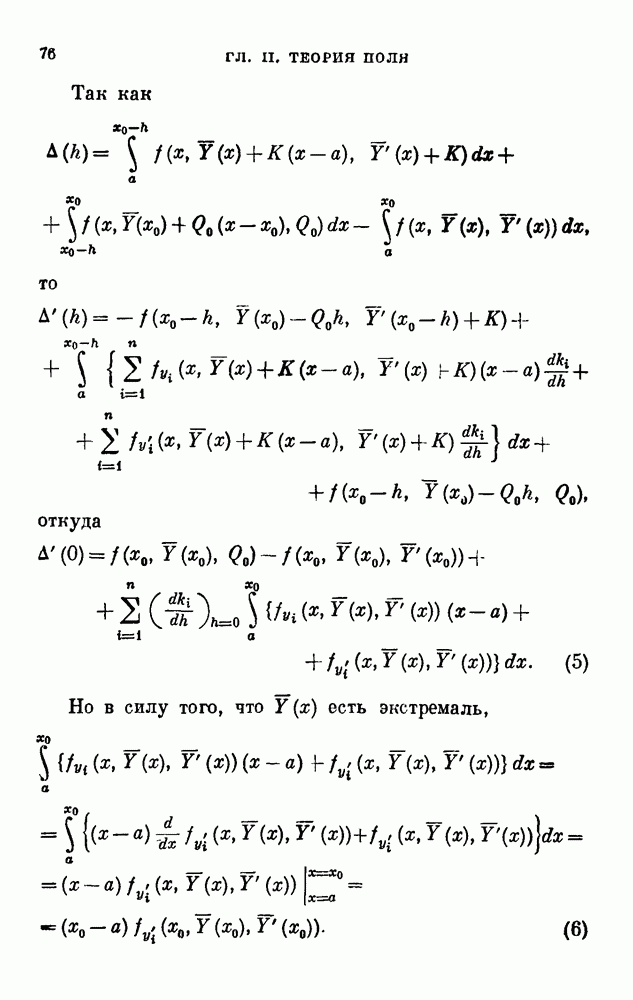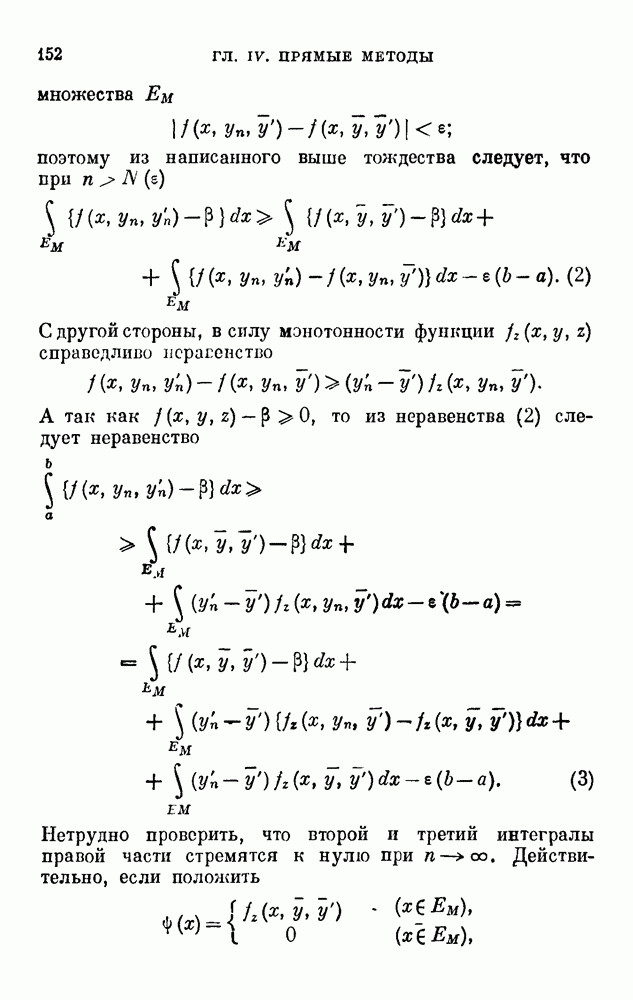| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
30. Теорема об абсолютном минимуме.
Возвратимся к нашей задаче. Пока доказано, что в совокупности  существует минимизирующая последовательность
существует минимизирующая последовательность  , равномерно сходящаяся к некоторой функции
, равномерно сходящаяся к некоторой функции  , а также доказано, что последовательность производных
, а также доказано, что последовательность производных  в разъяснённом выше смысле слабо сходится к
в разъяснённом выше смысле слабо сходится к  . При этом было использовано лишь условие (4) п° 28. Теперь сделаем ещё одно предположение о функции f(x,y,z). Оно может рассматриваться как некоторый ослабленный вариант предположения о квазирегулярности функционала и состоит в следующем: функция f(x,y,z) имеет непрерывную производную
. При этом было использовано лишь условие (4) п° 28. Теперь сделаем ещё одно предположение о функции f(x,y,z). Оно может рассматриваться как некоторый ослабленный вариант предположения о квазирегулярности функционала и состоит в следующем: функция f(x,y,z) имеет непрерывную производную  , и для любой точки
, и для любой точки  эта производная есть неубывающая функция от
эта производная есть неубывающая функция от  . Используя это свойство функции f{x,y,z), мы докажем неравенство
. Используя это свойство функции f{x,y,z), мы докажем неравенство

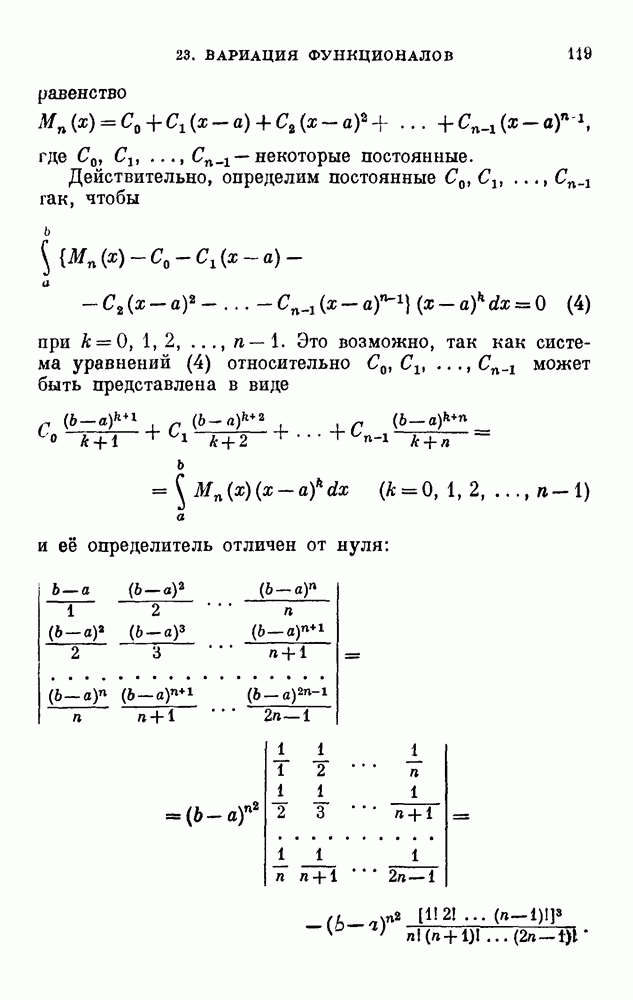
откуда и будет следовать, что

то-есть что функционал  при сделанных предположениях относительно функции f(x, у, z) имеет абсолютный минимум на совокупности ЭД всех абсолютно непрерывных функций, удовлетворяющих условию (2) и связям (3) п° 28. Эта важная теорема принадлежит Тонелли.
при сделанных предположениях относительно функции f(x, у, z) имеет абсолютный минимум на совокупности ЭД всех абсолютно непрерывных функций, удовлетворяющих условию (2) и связям (3) п° 28. Эта важная теорема принадлежит Тонелли.
Приступая к доказательству соотношения (1), обозначим через Ем множество точек интервала  , в которых
, в которых

Далее возьмём тождество

где  есть константа формулы (4) п° 28. Так как
есть константа формулы (4) п° 28. Так как  равномерно стремится к
равномерно стремится к  , то для любого
, то для любого  можно найти
можно найти  так, что при
так, что при  в каждой точке множества
в каждой точке множества 

поэтому из написанного выше тождества следует, что при 

С другой стороны, в силу монотонности функции  справедливо нсрагенство
справедливо нсрагенство

А так как  , то из неравенства (2) следует неравенство
, то из неравенства (2) следует неравенство

Нетрудно проверить, что второй и третий интегралы правой части стремятся к нулю при  . Действительно, если положить
. Действительно, если положить

то  , а потому
, а потому

в силу слабой сходимости последовательности  . С другой стороны, с помощью неравенства Гельдера и формулы (5) п° 29 находим:
. С другой стороны, с помощью неравенства Гельдера и формулы (5) п° 29 находим:

А так как на множестве  разность
разность

равномерно стремится к нулю при  , то
, то

После предельного перехода ( ) неравенство (3) принимает вид
) неравенство (3) принимает вид

или

Отсюда, увеличивая неограниченно M, находим:

или

Так как  произвольно, то неравенство (1) доказано, а вместе с ним доказана и теорема о минимуме.
произвольно, то неравенство (1) доказано, а вместе с ним доказана и теорема о минимуме.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
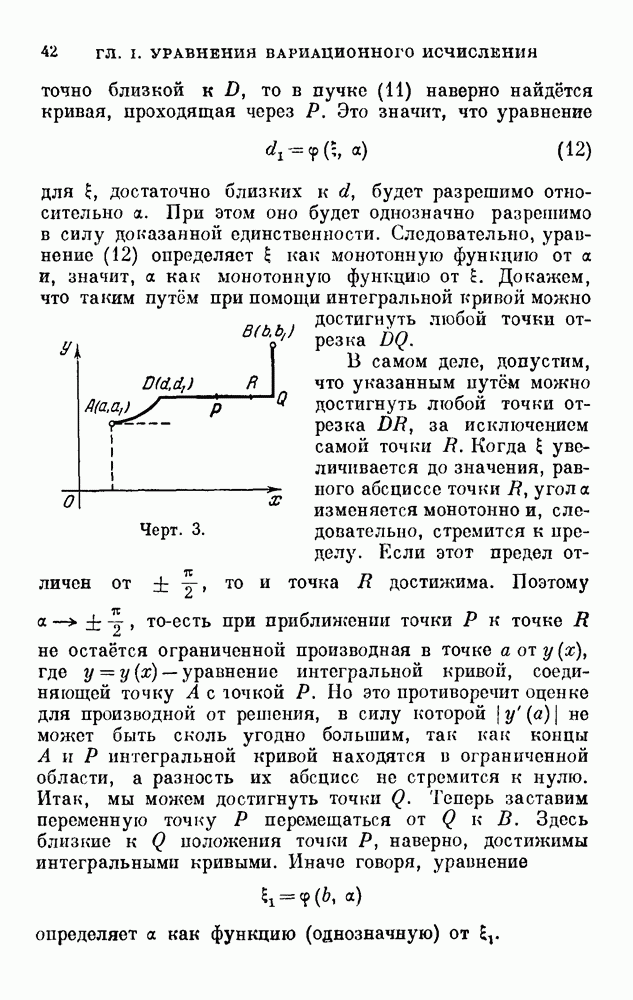
- ГЛАВА I. УРАВНЕНИЯ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
- 1. Основная задача вариационного исчисления
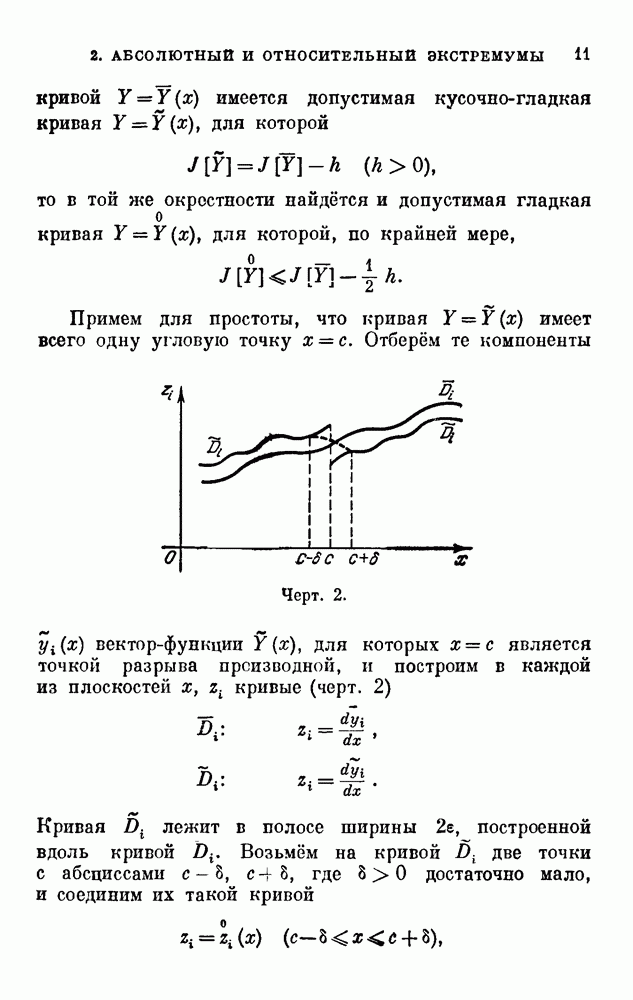
- 2. Абсолютный и относительный экстремумы.
- 3. Первое необходимое условие для экстремума.
- 5. Инвариантность уравнений Эйлера—Лагранжа.
- 6. Одна теорема Гильберта.
- 7. О существовании экстремалей.
- 8. Зависимость решений дифференциальных уравнений от параметров.
- 9. Одна теорема Бернштейна.
- 10. Задача вариационного исчисления в параметрической форме.
- ГЛАВА II. ТЕОРИЯ ПОЛЯ
- 11. Поле для функционала в обычной форме.
- 12. Построение поля.
- 13. Поле для функционала в параметрической форме.
- 14. Функция Вейерштрасса.
- 15. Достаточные условия для сильного и слабого минимума функционала в обычной форме.
- 16. Достаточные условия для сильного и слабого минимума функционала в параметрической форме.
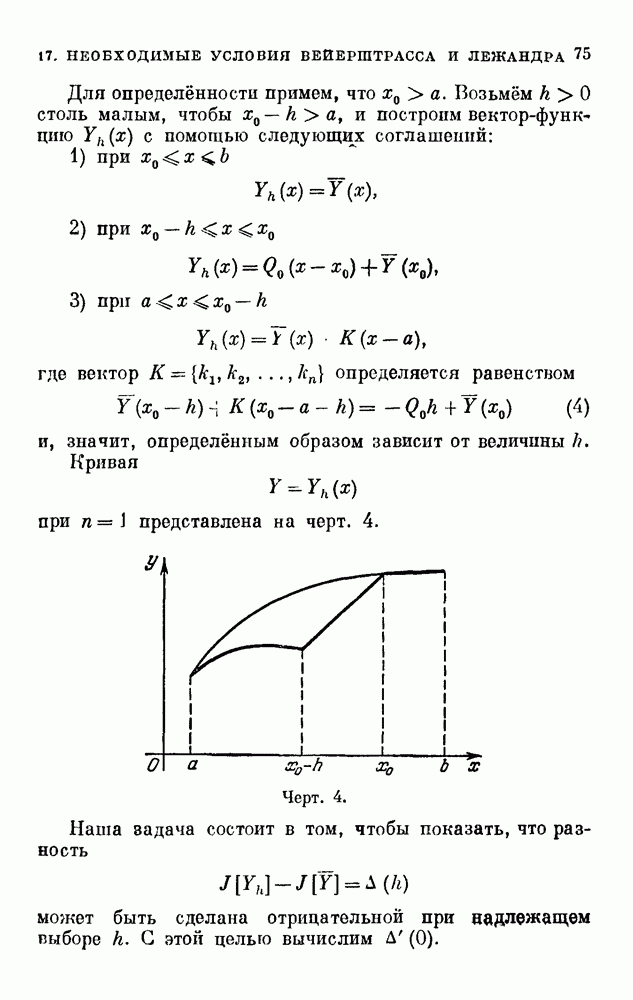
- 17. Необходимые условия Вейерштрасса и Лежандра.
- 18. Условие Якоби.
- 19. Теория Гамильтона—Якоби.
- ГЛАВА III. РАЗЛИЧНЫЕ ОБОБЩЕНИЯ ОСНОВНОЙ ЗАДАЧИ
- 20. Понятие о вариациях функционала.
- 21. Скользящие концы.
- 22. Вариация двойных интегралов.
- 23. Вариация функционалов, зависящих от производных высших порядков.
- 24. Элементарное правило множителей.
- 25. Изопериметрическая задача
- 26. Задача Лагранжа.
- ГЛАВА IV. ПРЯМЫЕ МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
- 27. Понятие о прямых методах.
- 28. Задача об абсолютном минимуме функционала в обычной форме.
- 29. Некоторые вспомогательные рассмотрения.
- 30. Теорема об абсолютном минимуме.
- 31. Переход к уравнению Эйлера—Лагранжа.
- 32. Фактическое построение минимизирующих последовательностей.
- 33. Задача об абсолютном минимуме функционала в параметрической форме.
- 34. Доказательство теоремы Гильберта.
- 35. Одно вспомогательное предложение.
- 36. Доказательство теоремы Тонелли.
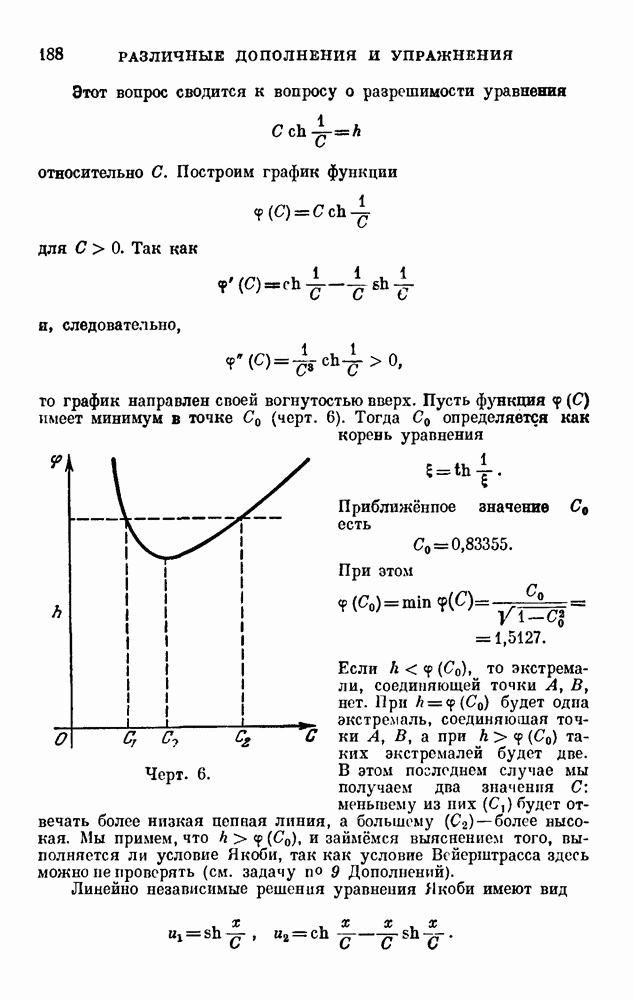
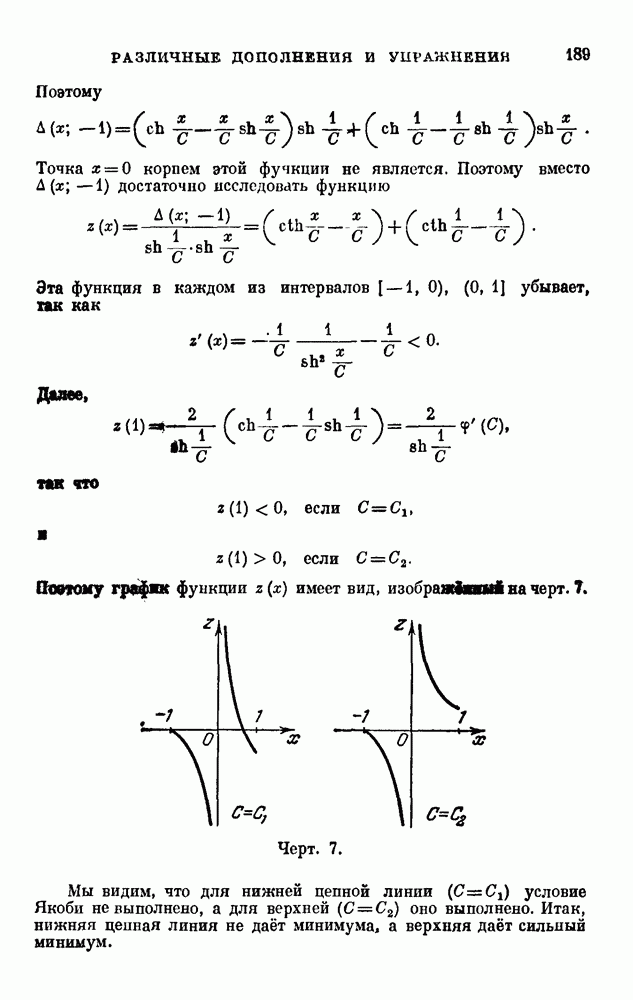
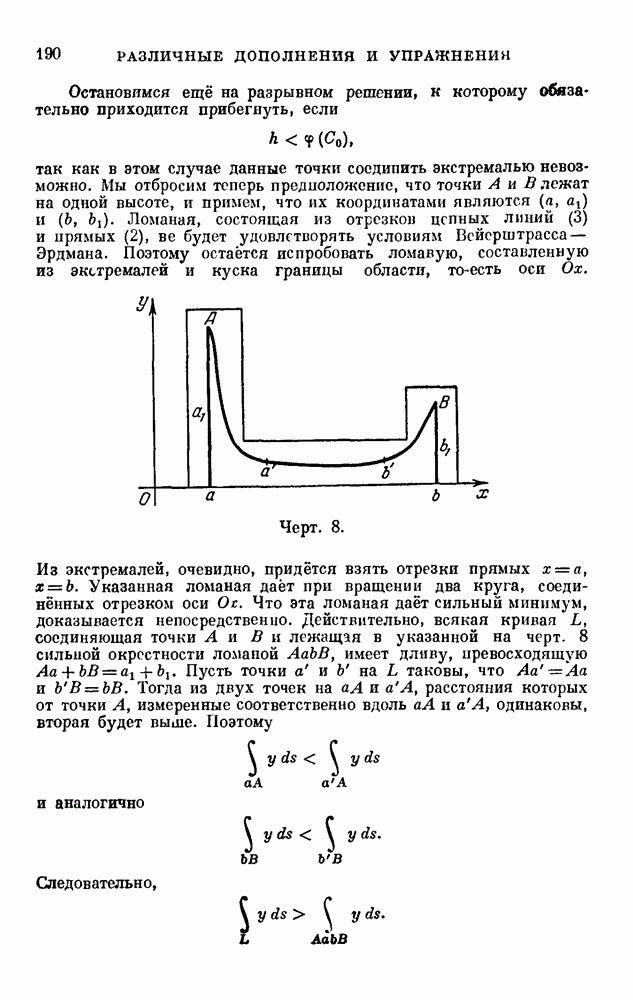
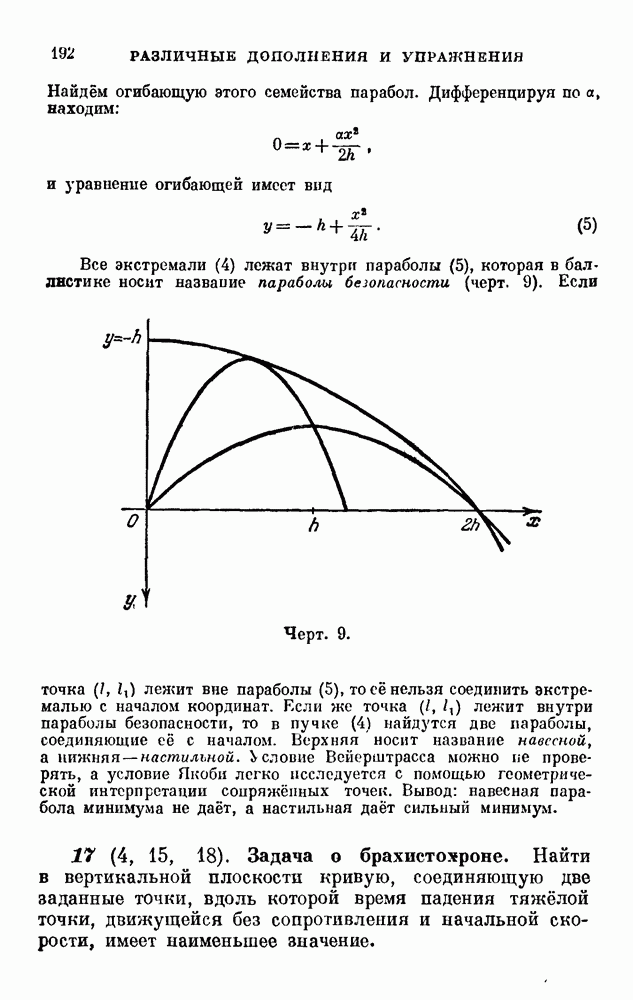
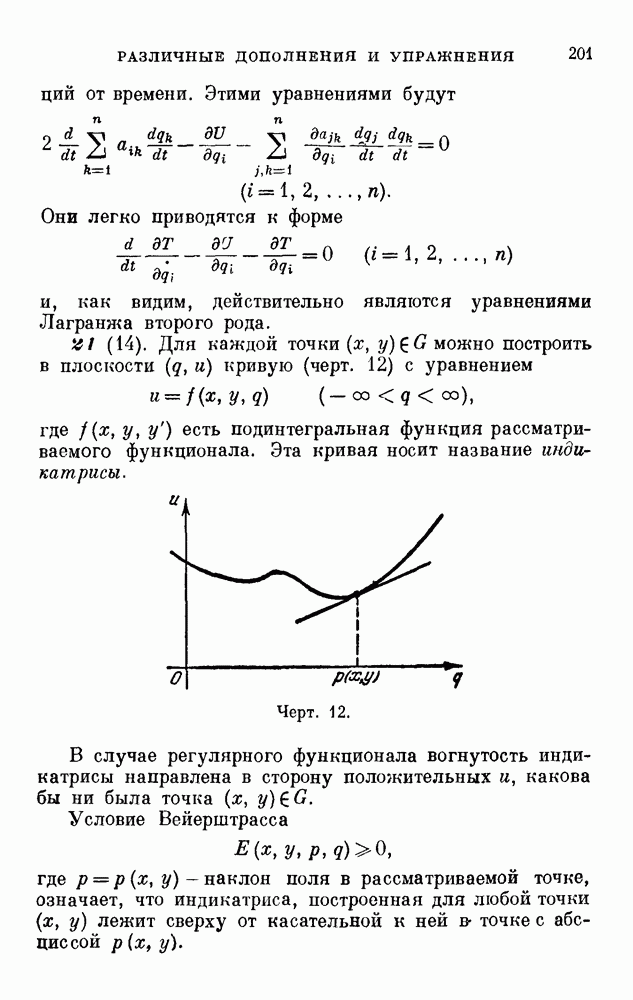
- РАЗЛИЧНЫЕ ДОПОЛНЕНИЯ И УПРАЖНЕНИЯ
- 6 (19). Доказать, что по уравнению Якоби — Гамильтона
- 15 (10, 15, 18). Задача о наименьшей поверхности вращения.
- 17 (4, 15, 18). Задача о брахистохроне.
- 20 (4, 10). Вариационные принципы механики.
- 25 (25). Задача Кельвина.
- 28 (26). Задача С. А. Чаплыгина.
- 30 (22). Необходимое условие для экстремума двойного интеграла (аналог условия Лежандра).
- 31 (22). Теорема Хаара о регулярных функционалах.
- 33 (31). Проблема Штурма—Лиувилля.
- 34. Множество собственных значений проблемы Штурма—Лиувилля
- 36. Максимально-минимальное свойство собственных значений.