20 (4, 10). Вариационные принципы механики.

Будем рассматривать механическую систему, всевозможные положения которой определяются значениями n независимых обобщённых координат . Пусть силы, действующие на систему, имеют силовую функцию U, которая может явно зависеть и от времени t. Живую силу системы обозначим через Т; это есть многочлен второй степени от обобщённых скоростей , коэффициенты которого являются функциями от обобщённых координат и, возможно, от времени.

В таком случае уравнения движения системы, как это известно из механики, можно представить в виде

где

есть так называемая функция Лагранжа рассматриваемой системы.

Но уравнения (1) являются уравнениями Эйлера — Лагранжа для функционала

Отсюда вытекает следующая теорема:

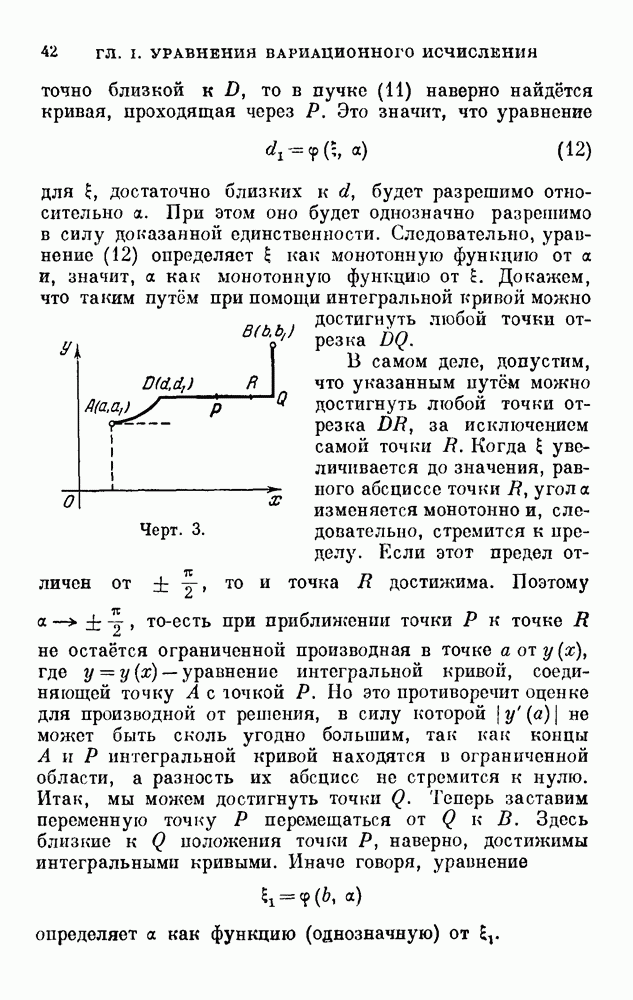
Если даны положения системы в начальный момент и конечный момент , то для определения движения системы служит уравнение

иначе говоря, функции

описывающие движение системы из данного начального ее положения в данное конечное положение, доставляют стационарное значение интегралу (2).

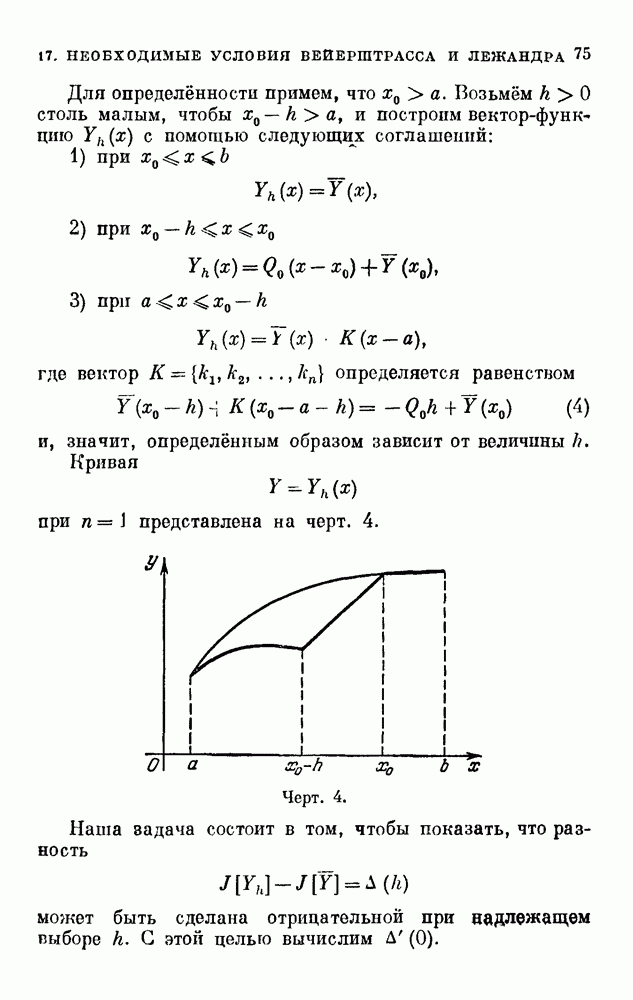
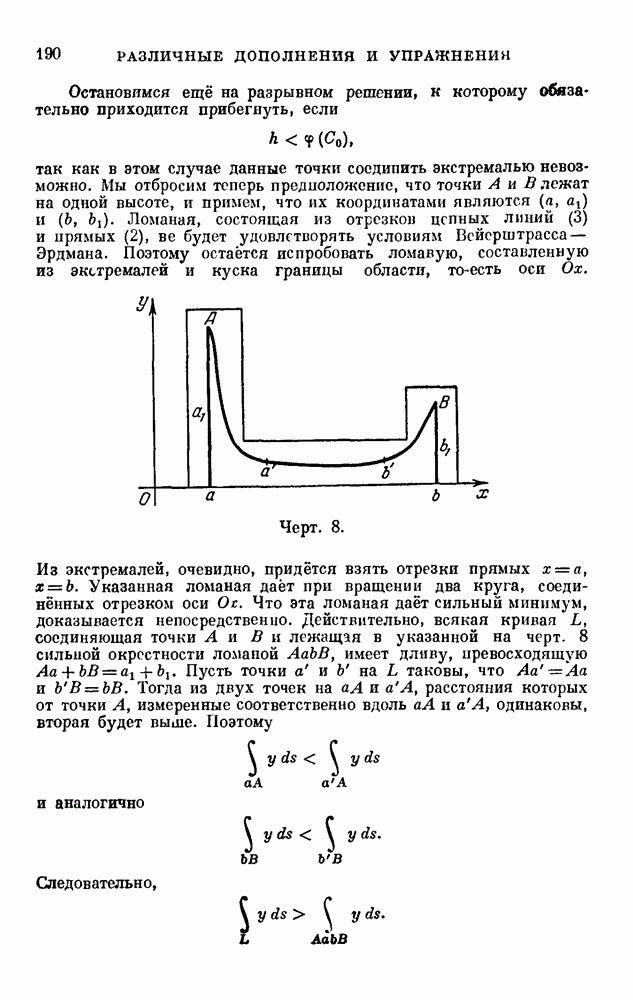
Это предложение носит название начала (или принципа) стационарного действия Гамильтона — Остроградского и может быть положено в основу динамики системы. Так как в формулировке этого начала участвуют лишь живая сила и силовая функция, то начало Гамильтона — Остроградского легко распространяется на механические системы с бесчисленным множеством степеней свободы, которые приходится рассматривать в механике сплошной среды. Это начало применяется также и в других разделах теоретической физики и притом не только классической, но и релятивистской.

Другим важным, но менее общим вариационным принципом динамики является принцип Мопертюи—Лагранжа.

Он применим только в том случае, когда силовая функция U явно времени не содержит, а живая сила Т является квадратичной формой от обощённых скоростей с коэффициентами, зависящими только от обобщённых координат:

Уравнения движения (1) в этом случае имеют первый интеграл

где h — постоянная. Нетрудно привести это равенство к виду

выражающему постоянство энергии системы и поэтому носящему название интеграла энергии.

На основании интеграла энергии имеет место соотношение

Если траектория движения системы известна в парамерической форме

то соотношение (4) позволяет связать параметр со временем и тем самым получить закон движения.

Принцип Мопертюи — Лагранжа состоит в том, что для движения рассматриваемой системы при заданном значении постоянной энергии h имеет стационарное значение следующий функционал:

В отличие от интеграла (2), который является функционалом в обычной форме, здесь мы имеем функционал в параметрической форме (5). Этот функционал можно, конечно, переписать в виде интеграла

который часто называют действием по Лагранжу. Однако здесь нужно помнить, что из подинтегрального выражения время должно быть исключено с помощью интеграла энергии (3). Это обстоятельство, не подчёркиваемое надлежащим образом, и приводило ранее к различным заблуждениям.

Чтобы доказать справедливость сформулированного принципа, нужно составить уравнения Эйлера — Лагранжа для функционала (5) и показать, что они в силу интеграла энергии (3) или, что то же, соотношения (4) совпадают с уравнениями динамики, то-есть уравнениями Лагранжа второго рода.

Уравнения Эйлера — Лагранжа для функционала (5) имеют вид

Они не независимы, а одно из них является следствием остальных. Но если ввести с помощью соотношения (4) время t вместо параметра , то получатся уже независимые уравнения для определения координат как функций от времени.

Этими уравнениями будут

Они легко приводятся к форме

и, как видим, действительно являются уравнениями Лагранжа второго рода.

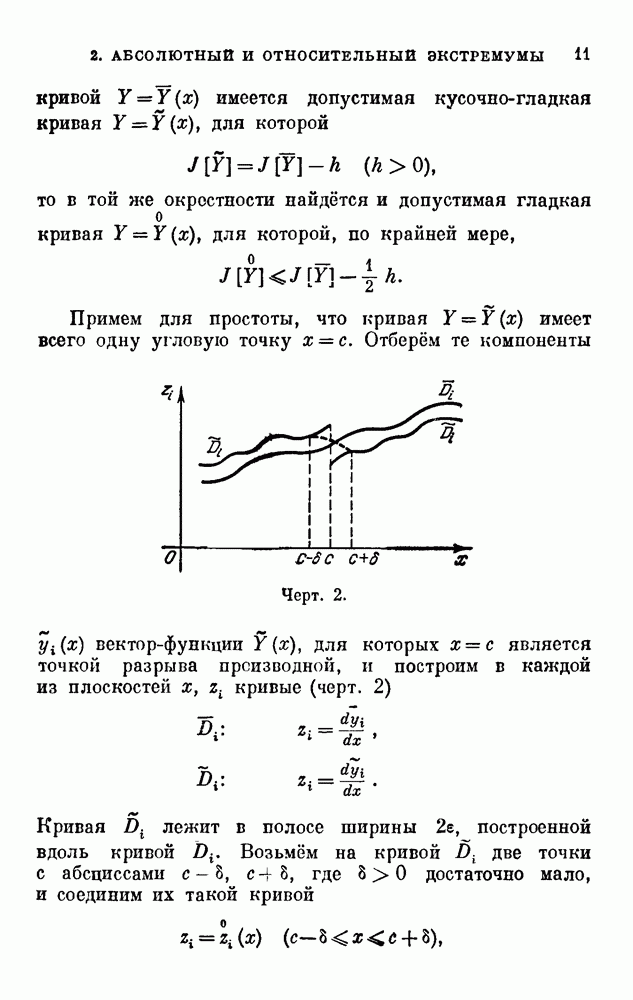
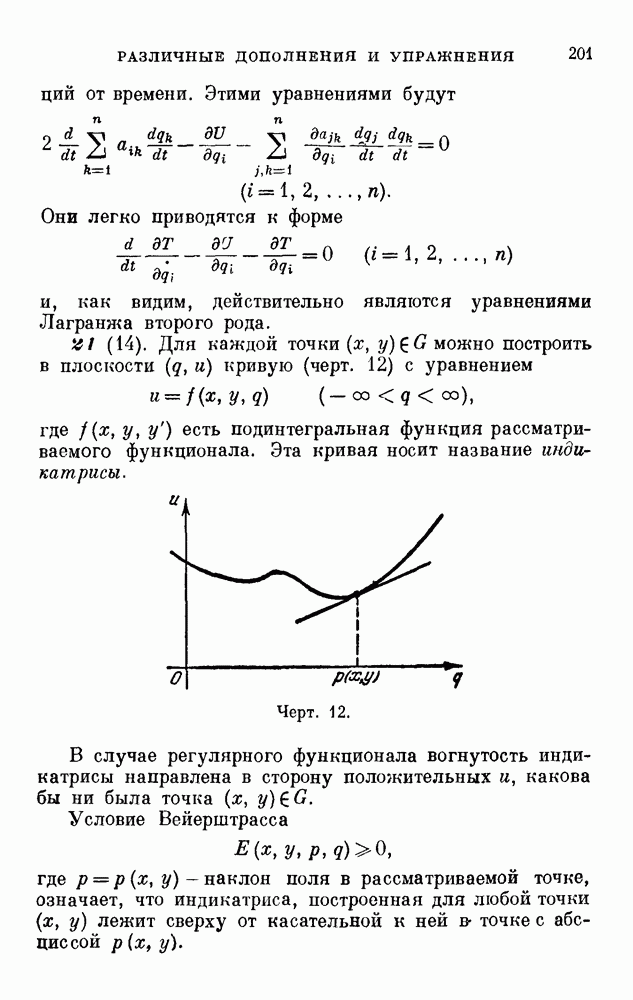
21 (14). Для каждой точки можно построить в плоскости кривую (черт. 12) с уравнением

где есть подинтегральная функция рассматриваемого функционала. Эта кривая носит название индикатрисы.

В случае регулярного функционала вогнутость индикатрисы направлена в сторону положительных и, какова бы ни была точка . Условие Вейерштрасса

где р = р(х, у) — наклон поля в рассматриваемой точке, означает, что индикатриса, построенная для любой точки (х, у) лежит сверху от касательной к ней в точке с абсциссой р(х, у).

Черт. 12.

Действительно, уравнение касательной к индикатрисе в её точке с абсциссой р(х, у) имеет вид

и чтобы точка лежала над этой касательной, необходимо и достаточно, чтобы имело место неравенство

Усиленное условие Лежандра

означает, что для каждой точки экстремали вогнутость индикатрисы, построенной для этой точки, направлена вверх в той точке индикатрисы, для которой .

Некоторая точка только тогда может быть угловой точкой экстремали, если индикатриса для этой точки обладает двойной касательной, то-есть если существует прямая, касающаяся индикатрисы в двух различных точках. При этом абсциссы этих точек касания дадут угловые коэффициенты экстремали в точке излома. 22 (4, 15). Найти минимум функционала

Решение. Экстремалями являются прямые. Пусть прямая, соединяющая точки (0, 0), , имеет угловой коэффициент . Поле имеется: его образуют прямые . Функция Вейерштрасса равна

Если , то получается сильный минимум, если же , то прямая не даёт сильного экстремума. Далее, так как

то при прямая даёт слабый минимум, а при — слабый максимум.

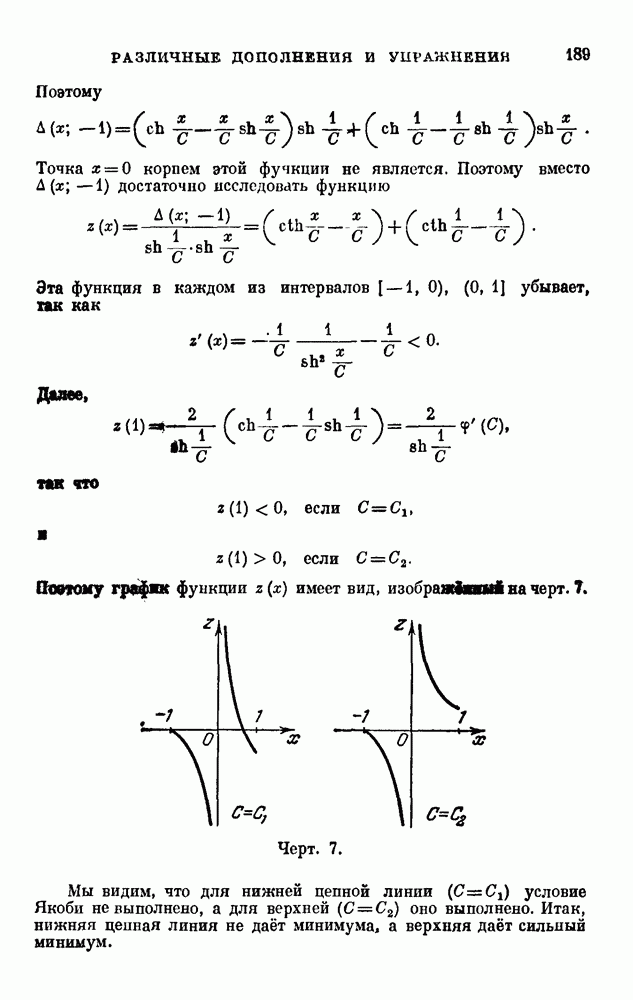
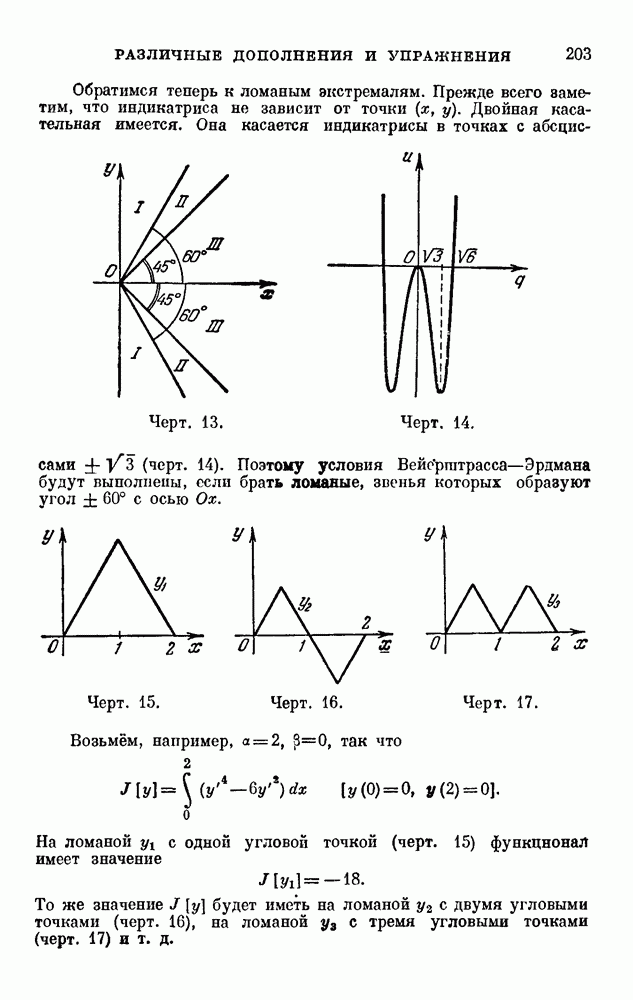
На черт. 13 представлены области для точки , которые отвечают различным возможностям: области соответствуют сильному минимуму, области II — слабому минимуму, а область III — слабому максимуму.

Обратимся теперь к ломаным экстремалям. Прежде всего заметим, что индикатриса не зависит от точки (х, у). Двойная касательная имеется. Она касается индикатрисы в точках с абсциссами (черт. 14). Поэтому условия Вейергатрасса—Эрдмана будут выполнены, если брать ломаные, звенья которых образуют угол ±60° с осью Ох.

Черт. 13.

Черт. 14.

Возьмём, например, , так что

На ломаной с одной угловой точкой (черт. 15) функционал имеет значение

То же значение будет иметь на ломаной с двумя угловыми точками (черт. 16), на ломаной с тремя угловыми точками (черт. 17) и т. д.

Черт. 15.

Черт. 16.

Черт. 17.

Каждая из этих ломаных даёт сильный минимум, в чём можно убедиться, рассматривая полное приращение. Например, полагая , находим:

Для простейшего функционала

всегда существуют допустимые функции (то-есть кусочно-гладкие функции, удовлетворяющие рассматриваемым краевым условиям), на которых он определён и имеет конечное значение. Иначе обстоит дело с функционалами

Здесь может не существовать ни одной допустимой функции и (х, у), доставляющей функционалу конечное значение. Первый пример этого рода принадлежит Адамару и относится к интегралу Дирихле

Уравнением Эйлера — Лагранжа для этого функционала является уравнение логарифмического потенциала и, следовательно, экстремалями для интеграла Дирихле являются гармонические функции.

Мы будем предполагать, что область D есть круг

и условимся этот круг обозначать , а интеграл Дирихле ПО этому кругу обозначим

Заметим, что в полярных координатах интеграл Дирихле имеет вид

Какова бы ни была непрерывная функция точки Р на окружности круга существует гармоническая в функция U (то-есть экстремаль), которая на окружности круга принимает значения . Для построения этой функции U лучше всего воспользоваться полярными координатами; тогда, если

то

Мы покажем теперь, что интеграл Дирихле на функции не всегда конечен. После этого мы покажем, что если интеграл Дирихле имеет бесконечное значение на этой функции , то он не будет конечным ни на одной допустимой функции.

Для доказательства первого утверждения возьмём, следуя Адамару, функцию

Соответствующая гармоническая функция равна

При любом положительном R < 1 будем иметь

Отсюда вытекает, что

Для доказательства второго утверждения примем, что на некоторой кусочно-гладкой функции интеграл Дирихле имеет конечное значение. Возьмём гармоническою функцию [она определяется формулой (1)], принимающую на окружности круга К те же значения , и заметим, что

Далее положим

и

Понимая под величину

очевидно, можем написать равенства

Теперь заметим, что при любом положительном

Последний член правой части стремится к нулю при Действительно,

так как — гармоническая функция и, следовательно,

Поэтому

откуда

и в силу (2) последний интеграл равен нулю. Таким образом,

и, значит,

В силу этого неравенства и подавно

каково бы ни было положительное R < 1. Переходя к пределу , находим отсюда, что

Второй предельный переход даёт

Это неравенство показывает, что . Таким образом, если , то , какова бы ни была допустимая функция V. Тем самым второе утверждение также доказано.

24 (3, 5, 22 — 24). Обобщённая лемма вариационного исчисления. В п° 23 при выводе уравнения Эйлера — Лагранжа получено и использовано следующее предложение: если есть кусочно-непрерывная функция и если для любой функции имеющей кусочно-непрерывную производную n-го порядка и равной нулю вместе с производными до порядка включительно на концах интервала , имеет место равенство

то есть многочлен степени :

где — константы.

Это предложение является частным случаем следующего более общего предложения:

Обобщённая лемма вариационного исчисления. Если

при единственном условии, что

где — заданные функции, то почти всюду

Доказательство. Равенство (1) выражает, что функция ортогональна функции , а равенства (2), что функция ортогональна функциям . Мы можем принять, что функции линейно независимы. В таком случае можно однозначно определить константы так, чтобы разность

была ортогональна ко всем функциям . Действительно, для этого нужно решить относительно систему

определителем которой является отличный от нуля определитель Грама функций . Итак, функция удовлетворяет условиям (2), и поэтому её можно взять в (1) в качестве . Тогда мы получим:

Из этсго равенства и следует, что почти всюду