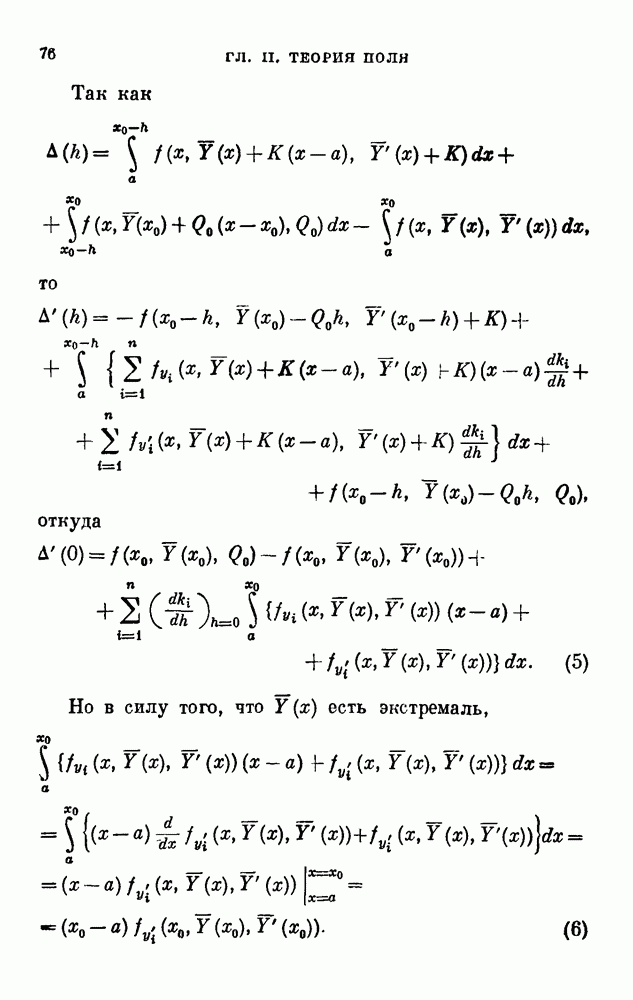| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
РАЗЛИЧНЫЕ ДОПОЛНЕНИЯ И УПРАЖНЕНИЯ
1 (4 — 7, 19). Найти экстремали функционала

Решение, а) Функционал регулярен во всякой части плоскости, не содержащей начала координат. Теорема Гильберта (п° 6) применима и позволяет ограничиться рассмотрением уравнения Эйлера—Лагранжа в дифференциальной форме.
Выгодно от декартовых координат перейти к полярным, воспользовавшись инвариантностью уравнения Эйлера—Лагранжа. В полярных координатах функционал примет вид

и немедленно пишется первый интеграл уравнения Эйлера—Лагранжа, а именно:

Дальнейшее интегрирование даёт

или, после перехода к первоначальным координатам,

где  и
и  — две произвольные постоянные.
— две произвольные постоянные.
б) Можно воспользоваться каноническими переменными. Полагая

получаем канонические уравнения

Первый интеграл этой системы имеет вид

Поэтому

и, значит,

откуда

и если положить

то снова получится (1).
в) Можно воспользоваться уравнением Якоби — Гамильтона:

или

Естественно искать решение в виде

Подстановка и сравнение коэффициентов дают

Таким образом, можно положить

Функция

есть решение уравнения Якоби — Гамильтона, удовлетворяющее условиям теоремы 2 п° 19. Общий интеграл уравнения Эйлера — Лагранжа поэтому имеет вид

что совпадает с (1).
2 (4, 9). Доказать, что через любые две точки плоскости с различными абсциссами проходит одна и только одна экстремаль каждого из функционалов

Решение. Это — примеры на применение георемы С. Н. Берн штейна (п° 9). Действительно, уравнение Эйлера — Лагранжа ДЛЯ обоих функционалов имеет вид

и теорема С. Н. Бернштейна применима.
3 (4, 9). Доказать, что не через всякие две точки плоскости с различными абсциссами можно провести экстремаль функционала

Решение. Уравнение Эйлера—Лагранжа имеет вид

и теорема С. Н. Бернштейна неприменима, но отсюда ещё не следует, что экстремаль можно провести не через всякие две точки с различными абсциссами.
Первый интеграл уравнения Эйлера—Лагранжа имеет вид

откуда

где С — вещественная постоянная. Однако ни при каком значении постоянной С это выражение не будет вещественным для всех значений у из интервала  , если, например,
, если, например,  .
.
4 (4, 18). Для функционала

общий интеграл уравнения Эйлера—Лагранжа имеет вид

где  — произвольные постоянные; таким образом, все экстремали получаются из одной, а именно из
— произвольные постоянные; таким образом, все экстремали получаются из одной, а именно из

с помощью преобразования подобия с центром в начале координат и последующего переноса параллельно оси Ох.
Если М и М* — две сопряжённые точки на экстремали, то касательные к ней в этих точках пересекаются на оси Ох.
5 (4, 27). Доказать, что всякое уравнение

является уравнением Эйлера — Лагранжа для некоторого функционала

Как определяется функция f(x, у, у') по функции F(x, у, у')?
Найти все функционалы, для которых экстремалями являются:
а) все прямые  ,
,
б) все параболы  . Решение. Будем искать функционал
. Решение. Будем искать функционал

для которого уравнение Эйлера — Лагранжа

или

совпадает с уравнением

Это значит, что должно иметь место тождество по 

Дифференцируя его по у', получим

Отсюда находим уравнение в частных производных для функции

а именно:

Таким образом, нахождение функционала сводится к интегрированию линейного уравнения в частных производных и квадратуре. В случае а) уравнение Эйлера — Лагранжа имеет вид

и для и получается уравнение

Его интегрирование даёт

где Ф — произвольная функция от своих аргументов. Отсюда

где  и
и  — произвольные функции от своих аргументов, удовлетворяющие соотношению
— произвольные функции от своих аргументов, удовлетворяющие соотношению

В случае б) уравнение Эйлера—Лагранжа имеет вид

и для и получается уравнение

Ищем решение в виде

Для v получается уравнение

Решаем систему

Первые интегралы имеют вид

Отсюда получаем следующее выражение для  :
:

где  — произвольная функция. Поэтому
— произвольная функция. Поэтому

где Ф — произвольная функция своих аргументов. Отсюда

где  и
и  — произвольные функции своих аргументов, удовлетворяющие соотношению
— произвольные функции своих аргументов, удовлетворяющие соотношению

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. УРАВНЕНИЯ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
- 1. Основная задача вариационного исчисления
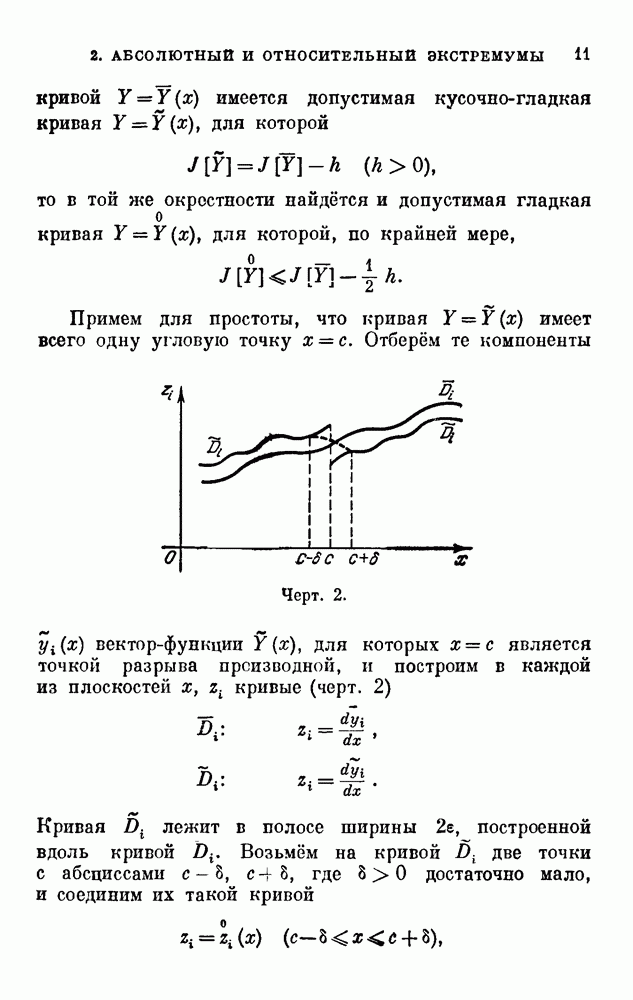
- 2. Абсолютный и относительный экстремумы.
- 3. Первое необходимое условие для экстремума.
- 5. Инвариантность уравнений Эйлера—Лагранжа.
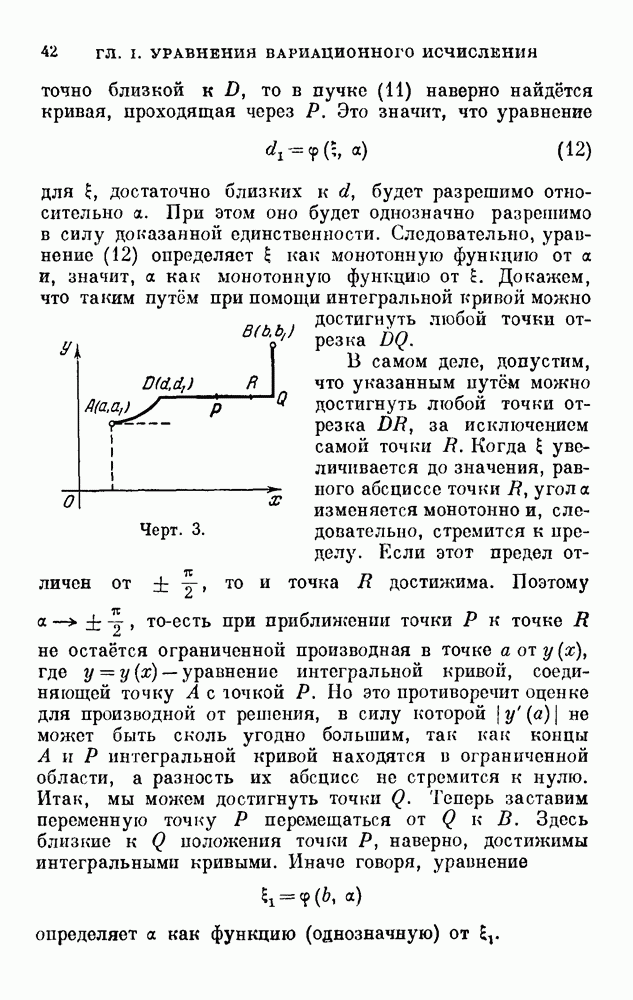
- 6. Одна теорема Гильберта.
- 7. О существовании экстремалей.
- 8. Зависимость решений дифференциальных уравнений от параметров.
- 9. Одна теорема Бернштейна.
- 10. Задача вариационного исчисления в параметрической форме.
- ГЛАВА II. ТЕОРИЯ ПОЛЯ
- 11. Поле для функционала в обычной форме.
- 12. Построение поля.
- 13. Поле для функционала в параметрической форме.
- 14. Функция Вейерштрасса.
- 15. Достаточные условия для сильного и слабого минимума функционала в обычной форме.
- 16. Достаточные условия для сильного и слабого минимума функционала в параметрической форме.
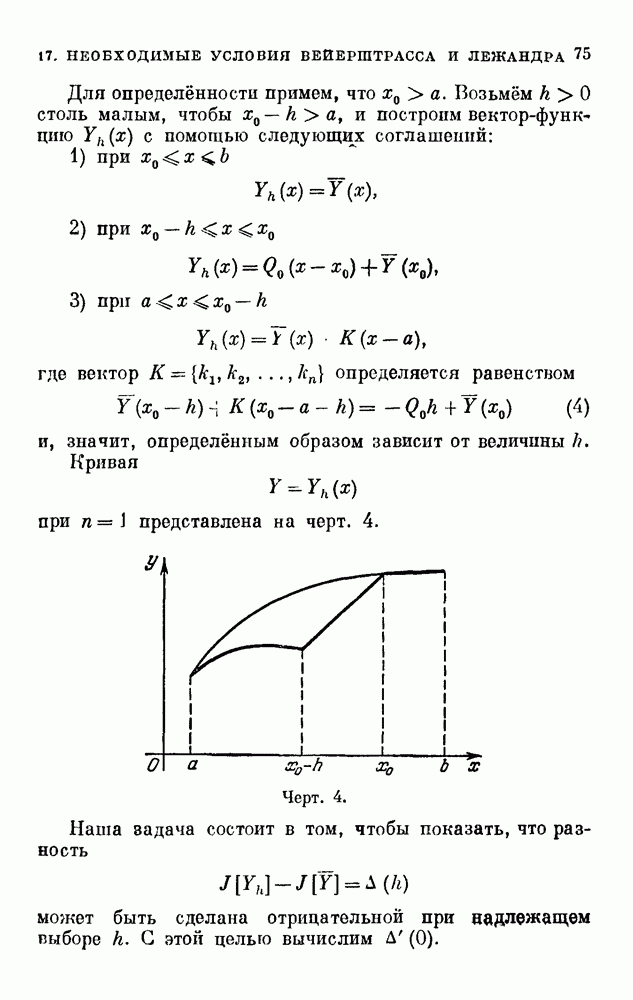
- 17. Необходимые условия Вейерштрасса и Лежандра.
- 18. Условие Якоби.
- 19. Теория Гамильтона—Якоби.
- ГЛАВА III. РАЗЛИЧНЫЕ ОБОБЩЕНИЯ ОСНОВНОЙ ЗАДАЧИ
- 20. Понятие о вариациях функционала.
- 21. Скользящие концы.
- 22. Вариация двойных интегралов.
- 23. Вариация функционалов, зависящих от производных высших порядков.
- 24. Элементарное правило множителей.
- 25. Изопериметрическая задача
- 26. Задача Лагранжа.
- ГЛАВА IV. ПРЯМЫЕ МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
- 27. Понятие о прямых методах.
- 28. Задача об абсолютном минимуме функционала в обычной форме.
- 29. Некоторые вспомогательные рассмотрения.
- 30. Теорема об абсолютном минимуме.
- 31. Переход к уравнению Эйлера—Лагранжа.
- 32. Фактическое построение минимизирующих последовательностей.
- 33. Задача об абсолютном минимуме функционала в параметрической форме.
- 34. Доказательство теоремы Гильберта.
- 35. Одно вспомогательное предложение.
- 36. Доказательство теоремы Тонелли.
- РАЗЛИЧНЫЕ ДОПОЛНЕНИЯ И УПРАЖНЕНИЯ
- 6 (19). Доказать, что по уравнению Якоби — Гамильтона
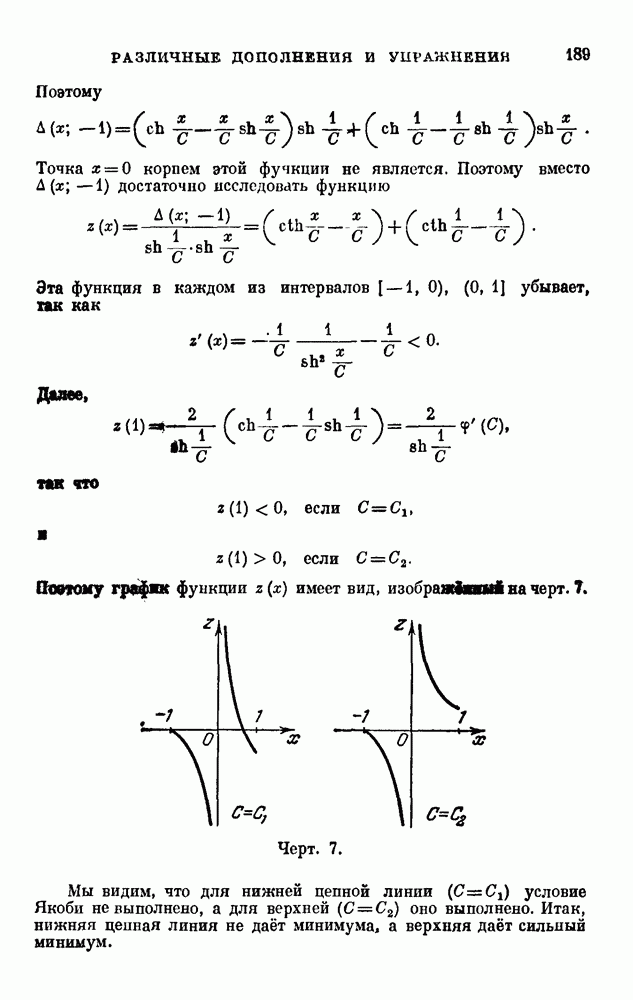
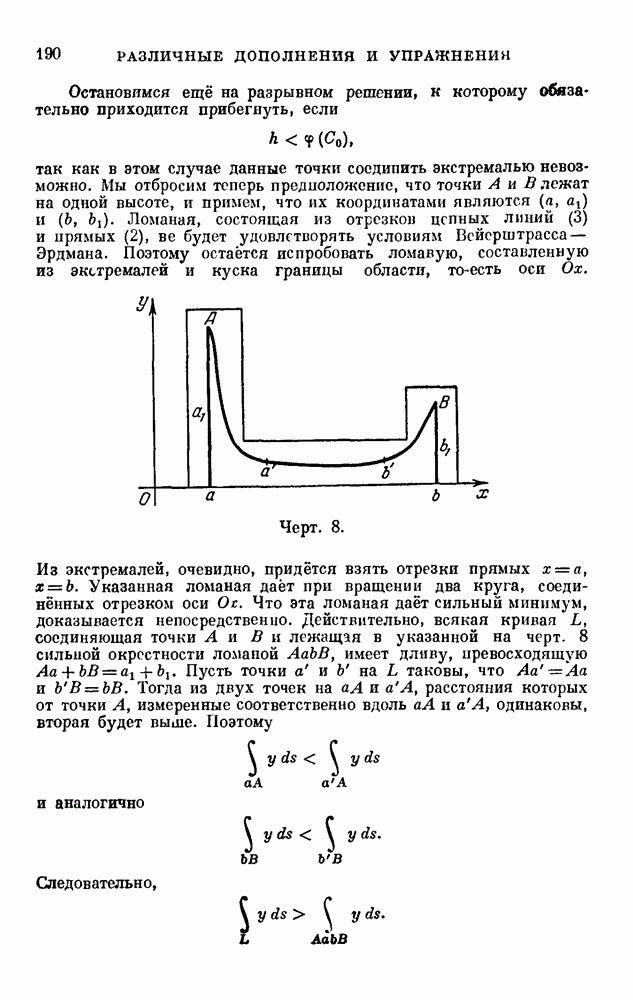
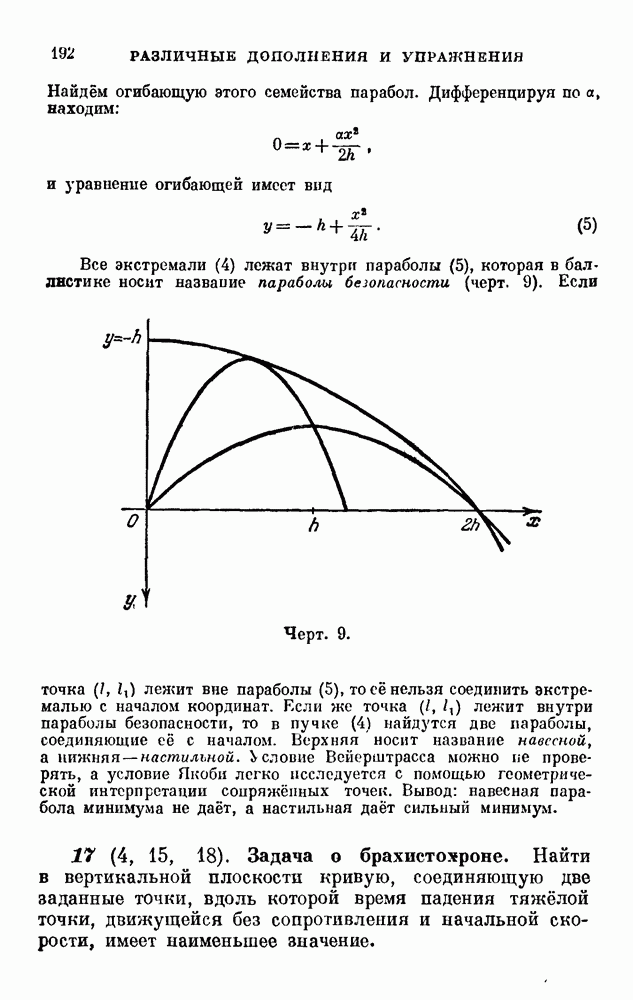
- 15 (10, 15, 18). Задача о наименьшей поверхности вращения.
- 17 (4, 15, 18). Задача о брахистохроне.
- 20 (4, 10). Вариационные принципы механики.
- 25 (25). Задача Кельвина.
- 28 (26). Задача С. А. Чаплыгина.
- 30 (22). Необходимое условие для экстремума двойного интеграла (аналог условия Лежандра).
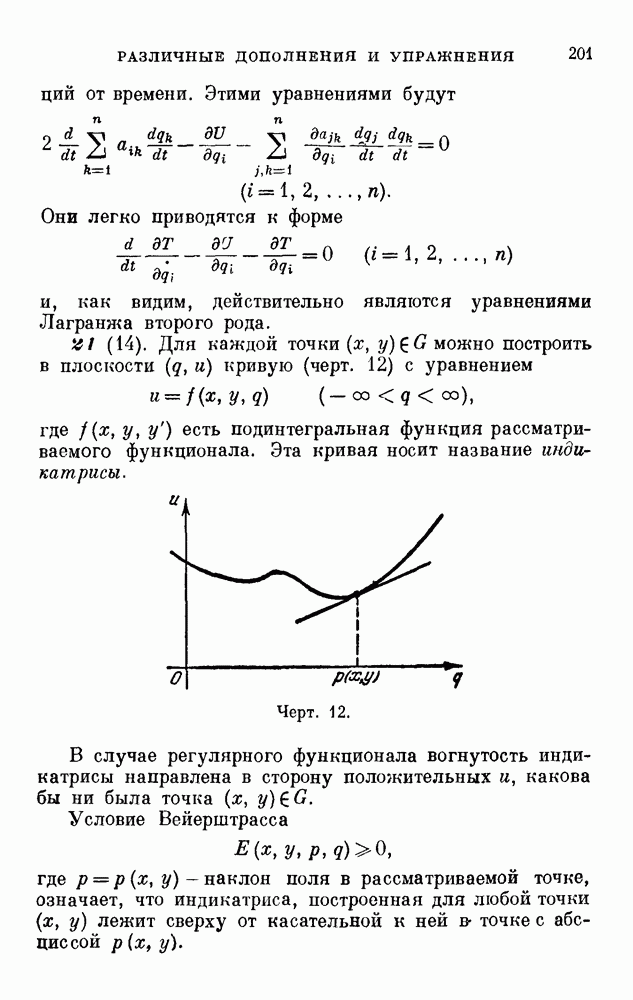
- 31 (22). Теорема Хаара о регулярных функционалах.
- 33 (31). Проблема Штурма—Лиувилля.
- 34. Множество собственных значений проблемы Штурма—Лиувилля
- 36. Максимально-минимальное свойство собственных значений.