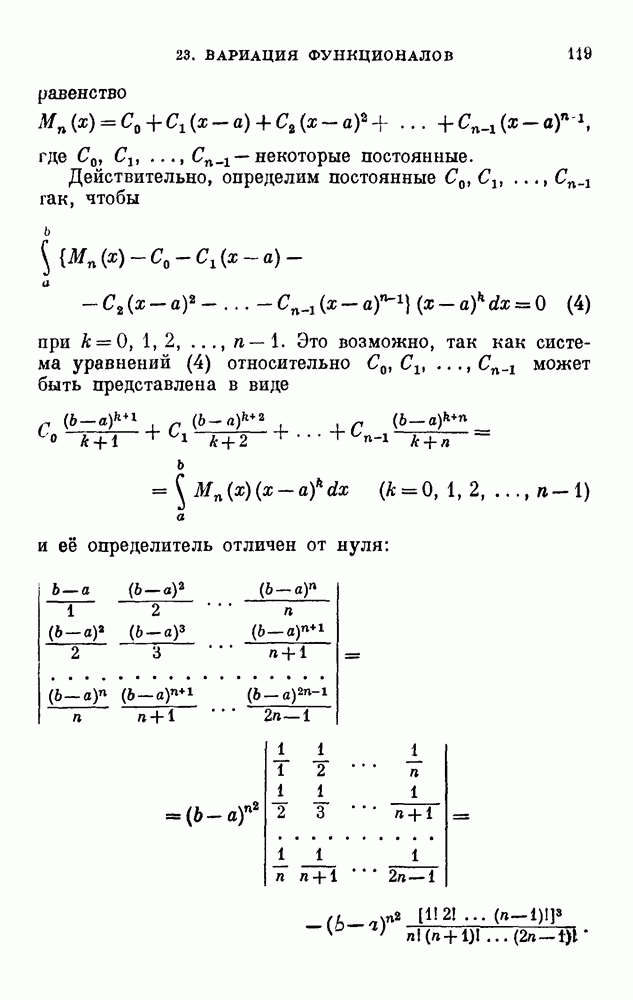
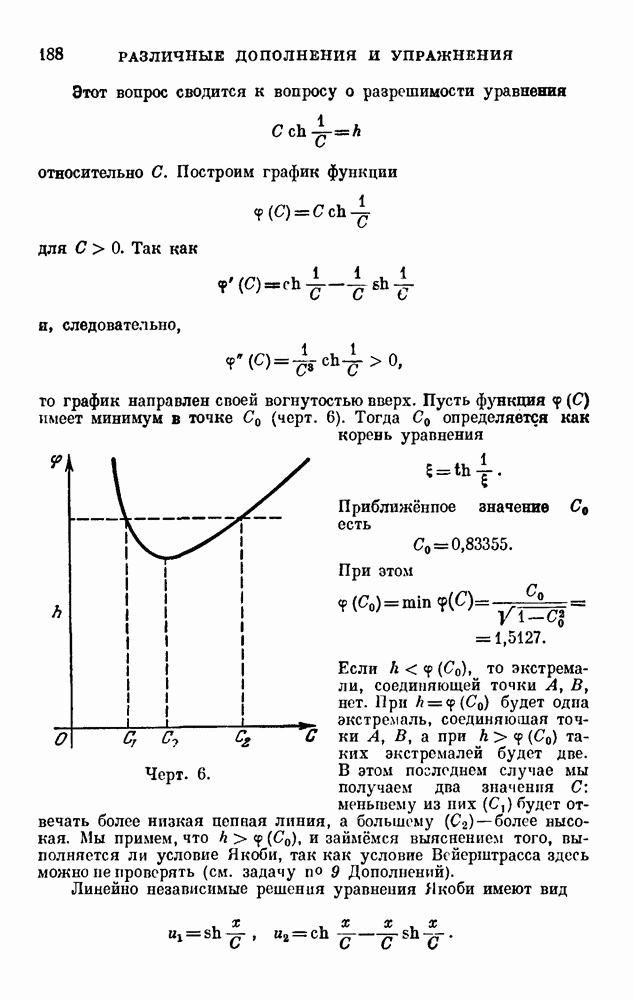
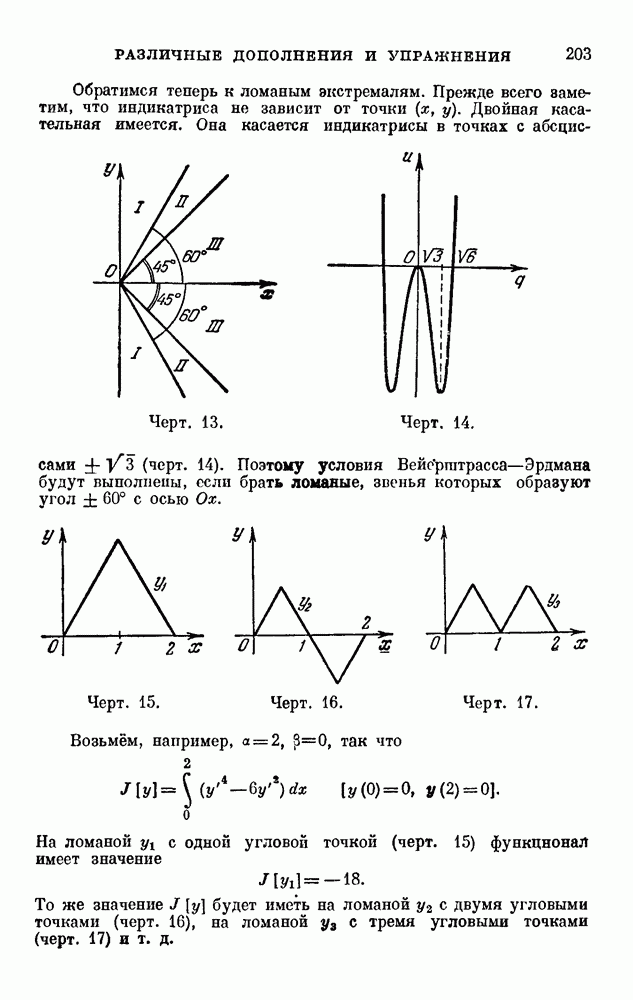
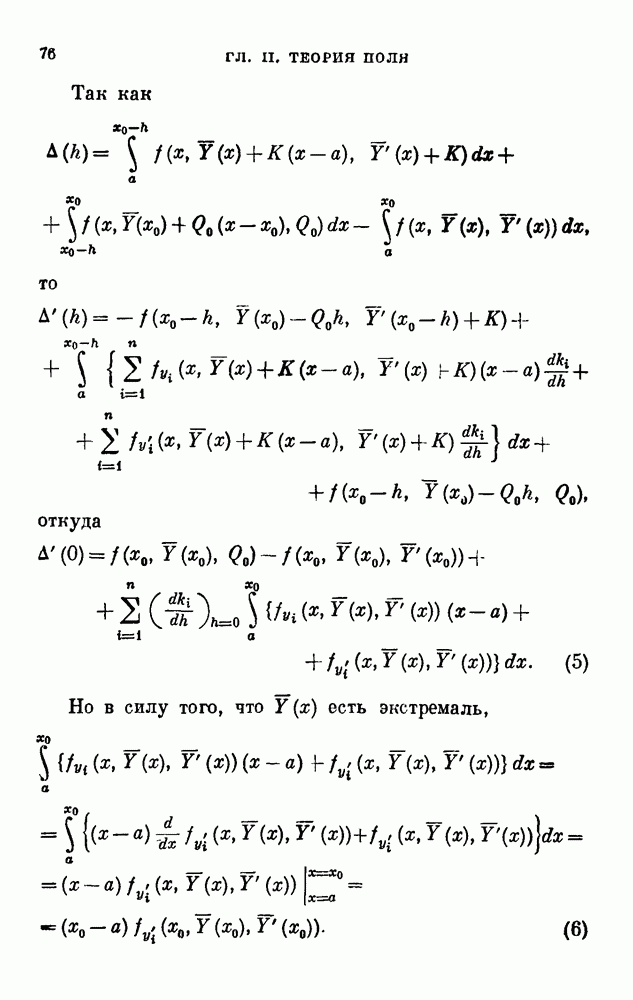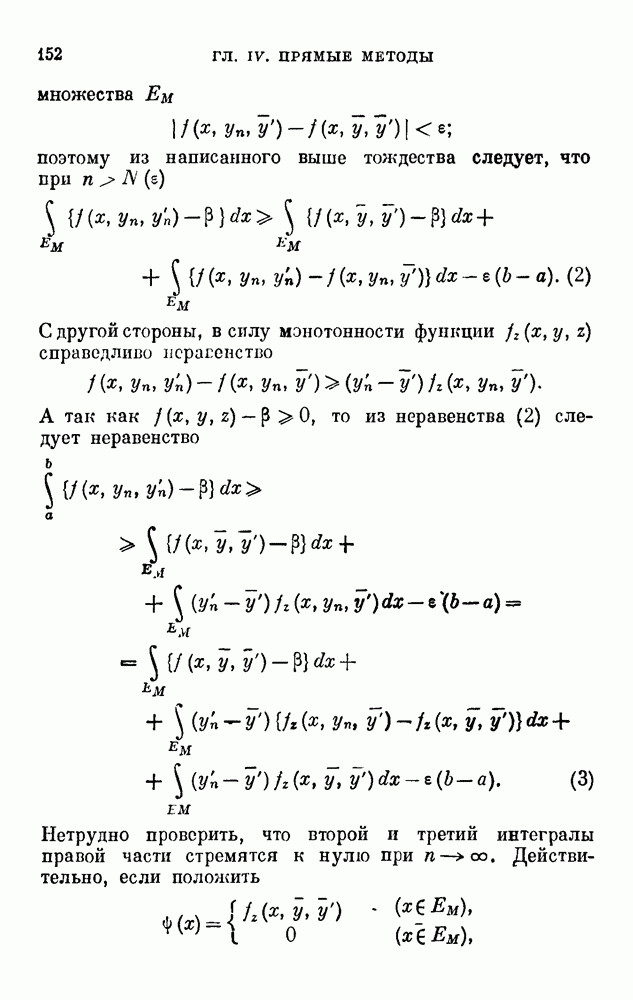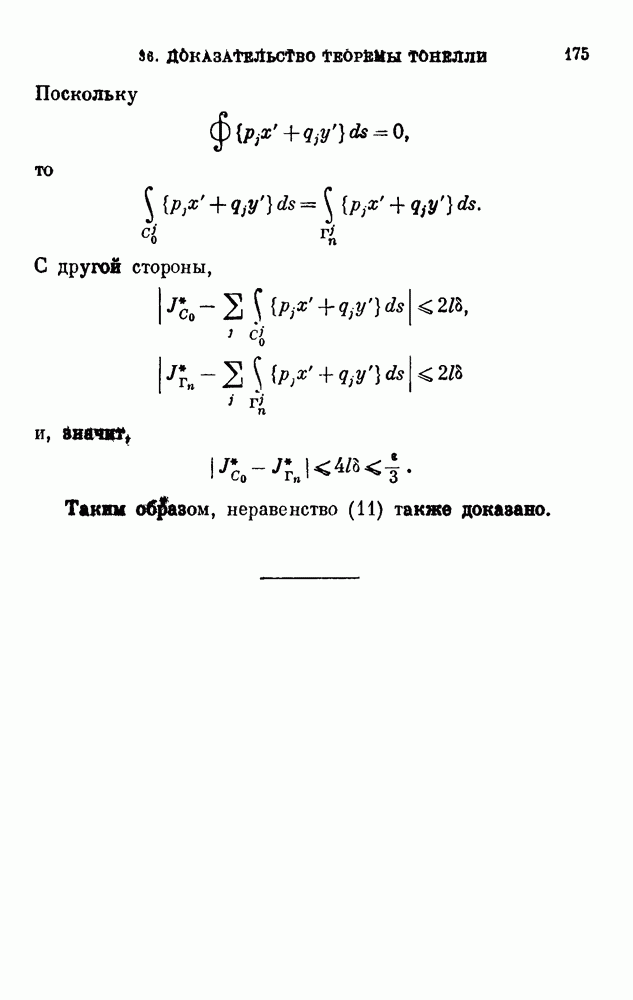| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
9. Одна теорема Бернштейна.
Предположим, что  и что функционал неособенный. В таком случае мы будем иметь всего одно уравнение Эйлера—Лагранжа и притом вида
и что функционал неособенный. В таком случае мы будем иметь всего одно уравнение Эйлера—Лагранжа и притом вида

Докажем для этого уравнения теорему С. Н. Бернштейна о существовании решения в целом. Эта теорема гласит:
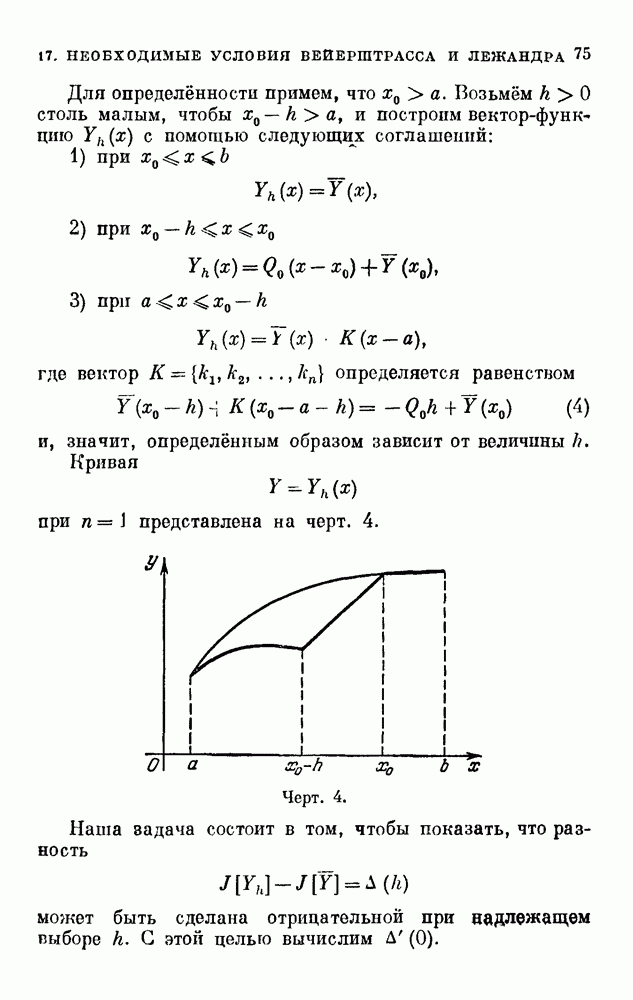
Если функции  непрерывны в каждой конечной точке
непрерывны в каждой конечной точке  для любого конечного
для любого конечного  и если существуют такая константа
и если существуют такая константа  и такие, ограниченные в каждой конечной части плоскости функции
и такие, ограниченные в каждой конечной части плоскости функции

что

то через любые две точки плоскости  имеющие различные абсциссы
имеющие различные абсциссы  , проходит одна и только одна интегральная кривая
, проходит одна и только одна интегральная кривая  уравнения (1).
уравнения (1).
Доказательство этой теоремы будет состоять из нескольких частей.
А. В первую очередь покажем, что через точки  проходит не более одной интегральной кривой. При этом мы используем лишь условие (2), а условие (3) не понадобится.
проходит не более одной интегральной кривой. При этом мы используем лишь условие (2), а условие (3) не понадобится.
Допустим, что имеются две интегральные кривые

Положим

Тогда

где

и  . Если
. Если  то разность
то разность  равная нулю на концах интервала
равная нулю на концах интервала  должна иметь внутри интервала
должна иметь внутри интервала  скажем в точке положительный максимум или отрицательный минимум. В первом случае в точке
скажем в точке положительный максимум или отрицательный минимум. В первом случае в точке 

что невозможно, так как  . Во втором случае в точке
. Во втором случае в точке 

что невозможно по той же причине. Итак, единственность доказана.
Б. Докажем теперь справедливость двух оценок, а именно: если в интервале  функция
функция  удовлетворяет уравнению (1) и
удовлетворяет уравнению (1) и

то во всём интервале

и

где постоянная М зависит от того прямоугольника с основанием  в котором в силу (4) находится кривая
в котором в силу (4) находится кривая  и верхних граней функций
и верхних граней функций  в этом прямоугольнике.
в этом прямоугольнике.
Для доказательства неравенства (4) возьмём вытекающее из (1) равенство

где

Функция

равна нулю в точках  Максимум её модуля достигается поэтому внутри интервала
Максимум её модуля достигается поэтому внутри интервала  , если она не есть тождественный нуль. В точке
, если она не есть тождественный нуль. В точке  где достигается максимум модуля, сама функция будет иметь либо положительный максимум, либо отрицательный минимум. Примем для определённости, что имеет место первое. Тогда
где достигается максимум модуля, сама функция будет иметь либо положительный максимум, либо отрицательный минимум. Примем для определённости, что имеет место первое. Тогда

и, значит,

откуда

Аналогичные рассмотрения проходят и во втором случае. Они показывают, что всюду в 

Таким образом, оценка (4) доказана.
Переходя к доказательству неравенства (5), обозначим через  правую часть неравенства (4), а через
правую часть неравенства (4), а через  и
и  — верхние грани функций
— верхние грани функций  в прямоугольнике
в прямоугольнике

Кроме того, мы можем принять, что  Затем введём функции
Затем введём функции  по формулам
по формулам

Так как левые части этих формул в интервале  неотрицательны, то в интервале
неотрицательны, то в интервале 

Дифференцируя, получаем:

Вторичное дифференцирование даёт

Заметим теперь, что в силу (3)

откуда

и

Из  и
и  следует поэтому, что
следует поэтому, что

откуда в силу неравенства  находим:
находим:

Аналогично из (62) и (72) вытекает, что

Обратим теперь внимание на те точки интервала  , в которых обращается в нуль величина
, в которых обращается в нуль величина

а значит, и  Эти точки существуют потому, что
Эти точки существуют потому, что  . С помощью указанных точек интервал
. С помощью указанных точек интервал  делится на иодхштервалы, в каждом из которых каждая из функций (9), и
делится на иодхштервалы, в каждом из которых каждая из функций (9), и  знаке не меняет и на одном из концов которого, по крайней мере, обращается в нуль. Пусть I - один из этих интервалов и пусть функции (9),
знаке не меняет и на одном из концов которого, по крайней мере, обращается в нуль. Пусть I - один из этих интервалов и пусть функции (9),  обращаются в нуль на его правом конце
обращаются в нуль на его правом конце  .
.
Могут представиться два случая в зависимости от того, положительна или отрицательна в I величина (9).
Рассмотрим вначале первый случай. Возьмём неравенство  и обе его части умножим на неотрицательную в силу
и обе его части умножим на неотрицательную в силу  величину
величину  . Получим неравенство
. Получим неравенство

Интегрируя его от  до
до  и учитывая, что
и учитывая, что  получаем:
получаем:

откуда

и, значит,

или

то-есть в интервале I

Во втором случае берём неравенство (82) и обе его части умножаем на неотрицательную в силу (62) величину  Поступая, как и выше, придём снова к неравенству (10), что и требовалось доказать.
Поступая, как и выше, придём снова к неравенству (10), что и требовалось доказать.
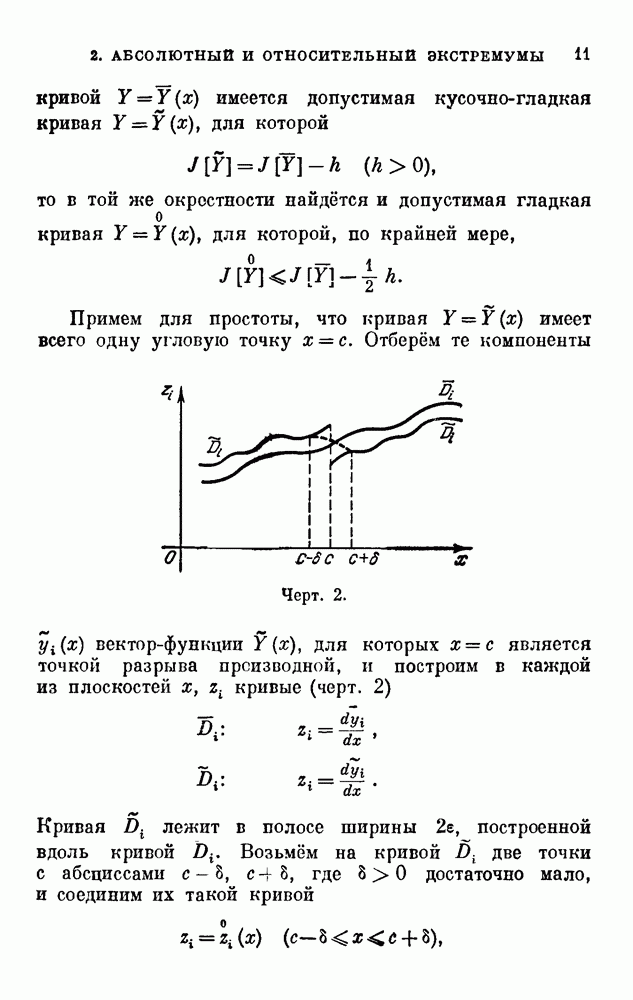
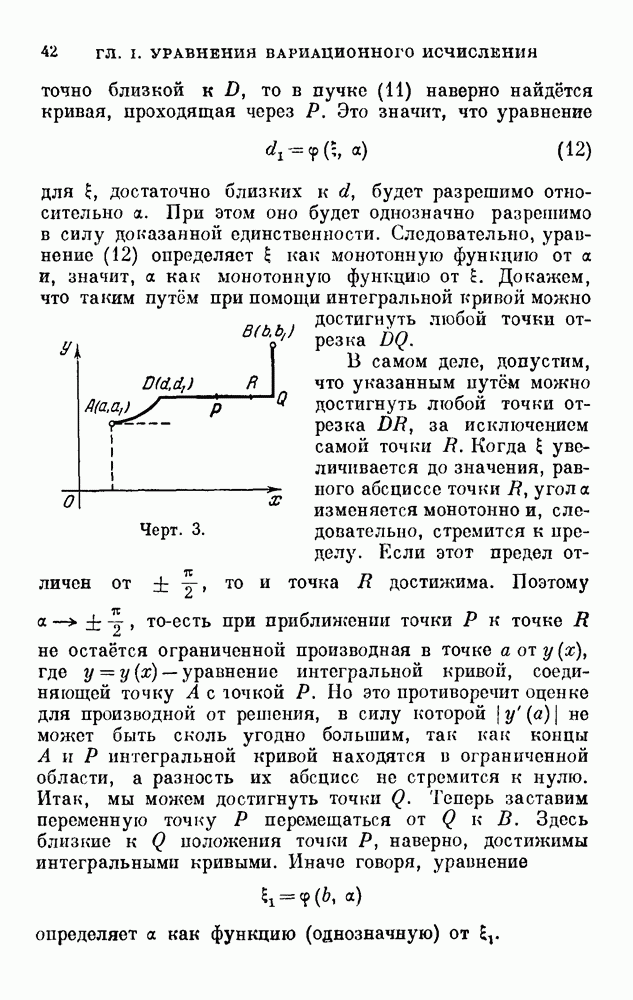
В. Переходим к доказательству теоремы. Проведём через точку  элемент интегральной кривой, для которого
элемент интегральной кривой, для которого  Возьмём на нём точку
Возьмём на нём точку  и соединим её с точкой
и соединим её с точкой  при помощи ломаной, состоящей из двух звеньев, параллельных осям координат (черт. 3). Переменную точку на ломаной DQB обозначим через
при помощи ломаной, состоящей из двух звеньев, параллельных осям координат (черт. 3). Переменную точку на ломаной DQB обозначим через 
Через точку А можно провести пучок интегральных кривых

где параметр а представляет  . При
. При  интегральная кривая совпадает
интегральная кривая совпадает  . Если точка Р будет достаточно близкой к D, то в пучке (11) наверно найдётся кривая, проходящая через Р.
. Если точка Р будет достаточно близкой к D, то в пучке (11) наверно найдётся кривая, проходящая через Р.
Это значит, что уравнение

для  , достаточно близких к d, будет разрешимо относительно
, достаточно близких к d, будет разрешимо относительно  . При этом оно будет однозначно разрешимо в силу доказанной единственности. Следовательно, уравнение (12) определяет Е как монотонную функцию от
. При этом оно будет однозначно разрешимо в силу доказанной единственности. Следовательно, уравнение (12) определяет Е как монотонную функцию от  и, значит,
и, значит,  как монотонную функцию от
как монотонную функцию от  . Докажем, что таким путём при помощи интегральной кривой можно достигнуть любой точки отрезка DQ.
. Докажем, что таким путём при помощи интегральной кривой можно достигнуть любой точки отрезка DQ.

Черт. 3.
В самом деле, допустим, что указанным путём можно достигнуть любой точки отрезка DR, за исключением самой точки R. Когда  увеличивается до значения, равного абсциссе точки В, угол а изменяется монотонно и, следовательно, стремится к пределу. Если этот предел отличен от
увеличивается до значения, равного абсциссе точки В, угол а изменяется монотонно и, следовательно, стремится к пределу. Если этот предел отличен от  , то и точка R достижима. Поэтому
, то и точка R достижима. Поэтому  то-есть при приближении точки Р к точке
то-есть при приближении точки Р к точке  не остаётся ограниченной производная в точке
не остаётся ограниченной производная в точке  от
от  где
где  — уравнение интегральной кривой, соединяющей точку А с точкой Р. Но это противоречит оценке для производной от решения, в силу которой
— уравнение интегральной кривой, соединяющей точку А с точкой Р. Но это противоречит оценке для производной от решения, в силу которой  не может быть сколь угодно большим, так как концы А и Р интегральной кривой находятся в ограниченной области, а разность их абсцисс не стремится к нулю. Итак, мы можем достигнуть точки Q. Теперь заставим переменную точку Р перемещаться от Q к В. Здесь близкие к Q положения точки Р, наверно, достижимы интегральными кривыми. Иначе говоря, уравнение
не может быть сколь угодно большим, так как концы А и Р интегральной кривой находятся в ограниченной области, а разность их абсцисс не стремится к нулю. Итак, мы можем достигнуть точки Q. Теперь заставим переменную точку Р перемещаться от Q к В. Здесь близкие к Q положения точки Р, наверно, достижимы интегральными кривыми. Иначе говоря, уравнение

определяет а как функцию (однозначную) от  .
.
Мы снова имеем монотонную зависимость, и для окончания доказательства остаётся ещё раз повторить применённое только что рассуждение.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. УРАВНЕНИЯ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
- 1. Основная задача вариационного исчисления
- 2. Абсолютный и относительный экстремумы.
- 3. Первое необходимое условие для экстремума.
- 5. Инвариантность уравнений Эйлера—Лагранжа.
- 6. Одна теорема Гильберта.
- 7. О существовании экстремалей.
- 8. Зависимость решений дифференциальных уравнений от параметров.
- 9. Одна теорема Бернштейна.
- 10. Задача вариационного исчисления в параметрической форме.
- ГЛАВА II. ТЕОРИЯ ПОЛЯ
- 11. Поле для функционала в обычной форме.
- 12. Построение поля.
- 13. Поле для функционала в параметрической форме.
- 14. Функция Вейерштрасса.
- 15. Достаточные условия для сильного и слабого минимума функционала в обычной форме.
- 16. Достаточные условия для сильного и слабого минимума функционала в параметрической форме.
- 17. Необходимые условия Вейерштрасса и Лежандра.
- 18. Условие Якоби.
- 19. Теория Гамильтона—Якоби.
- ГЛАВА III. РАЗЛИЧНЫЕ ОБОБЩЕНИЯ ОСНОВНОЙ ЗАДАЧИ
- 20. Понятие о вариациях функционала.
- 21. Скользящие концы.
- 22. Вариация двойных интегралов.
- 23. Вариация функционалов, зависящих от производных высших порядков.
- 24. Элементарное правило множителей.
- 25. Изопериметрическая задача
- 26. Задача Лагранжа.
- ГЛАВА IV. ПРЯМЫЕ МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
- 27. Понятие о прямых методах.
- 28. Задача об абсолютном минимуме функционала в обычной форме.
- 29. Некоторые вспомогательные рассмотрения.
- 30. Теорема об абсолютном минимуме.
- 31. Переход к уравнению Эйлера—Лагранжа.
- 32. Фактическое построение минимизирующих последовательностей.
- 33. Задача об абсолютном минимуме функционала в параметрической форме.
- 34. Доказательство теоремы Гильберта.
- 35. Одно вспомогательное предложение.
- 36. Доказательство теоремы Тонелли.
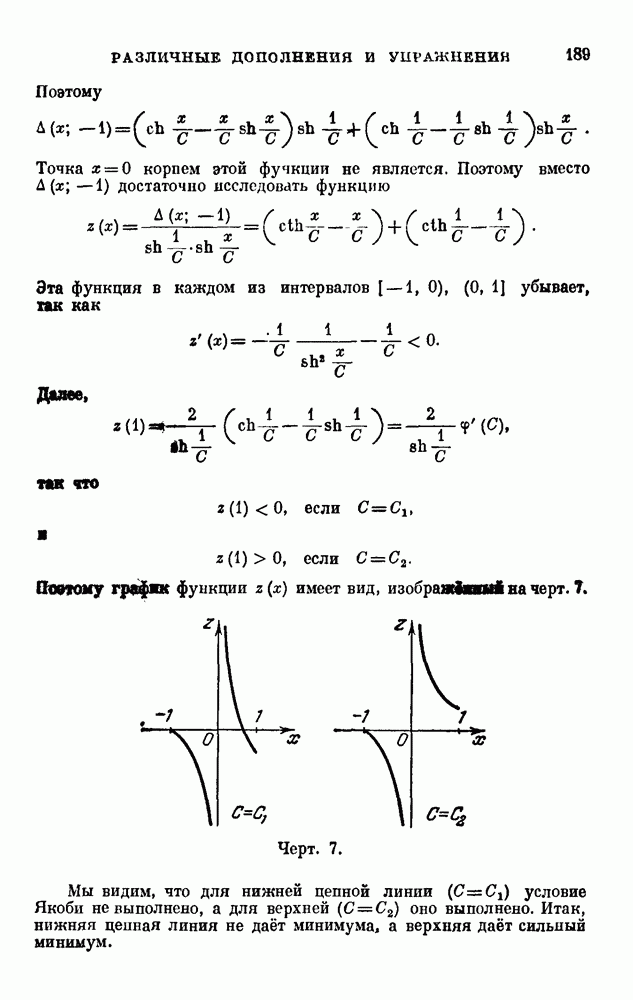
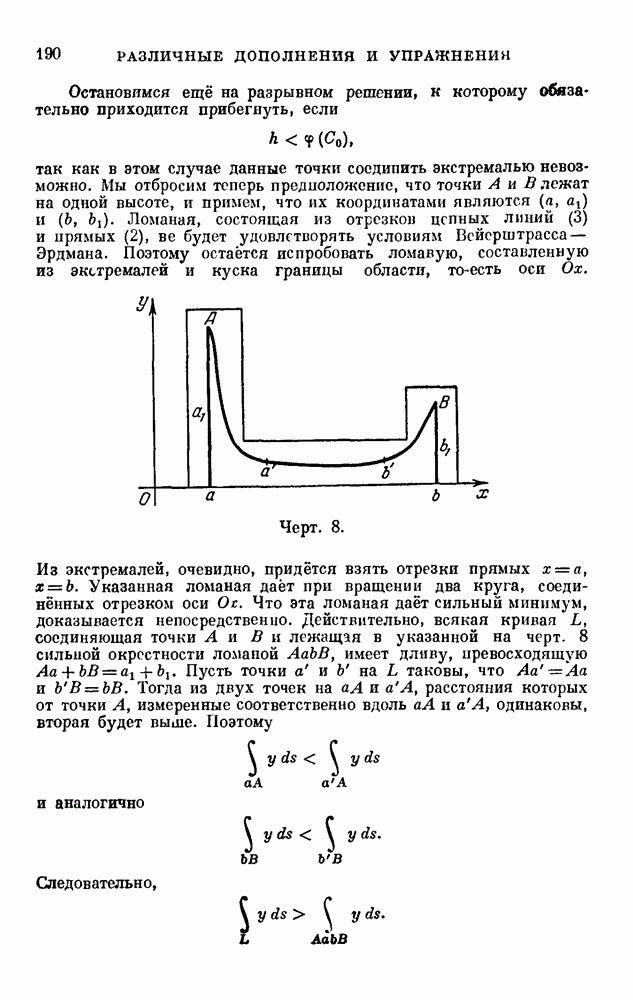
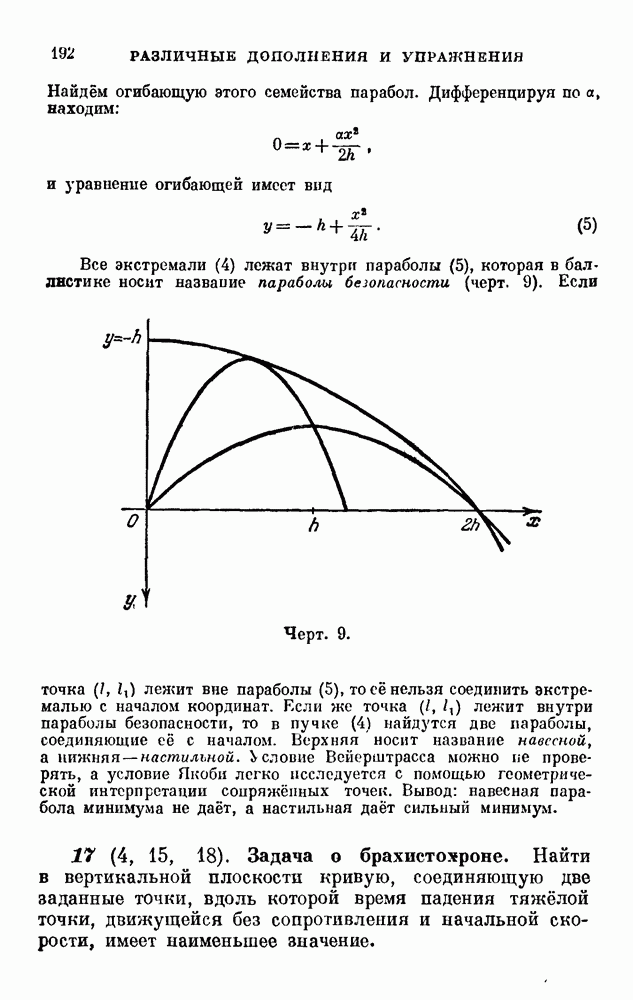
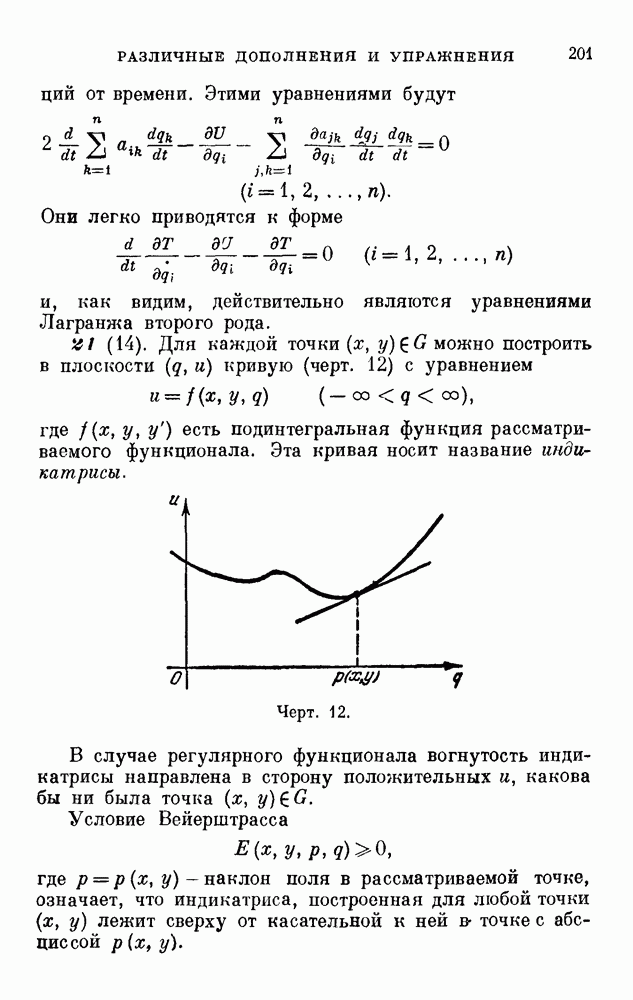
- РАЗЛИЧНЫЕ ДОПОЛНЕНИЯ И УПРАЖНЕНИЯ
- 6 (19). Доказать, что по уравнению Якоби — Гамильтона
- 15 (10, 15, 18). Задача о наименьшей поверхности вращения.
- 17 (4, 15, 18). Задача о брахистохроне.
- 20 (4, 10). Вариационные принципы механики.
- 25 (25). Задача Кельвина.
- 28 (26). Задача С. А. Чаплыгина.
- 30 (22). Необходимое условие для экстремума двойного интеграла (аналог условия Лежандра).
- 31 (22). Теорема Хаара о регулярных функционалах.
- 33 (31). Проблема Штурма—Лиувилля.
- 34. Множество собственных значений проблемы Штурма—Лиувилля
- 36. Максимально-минимальное свойство собственных значений.