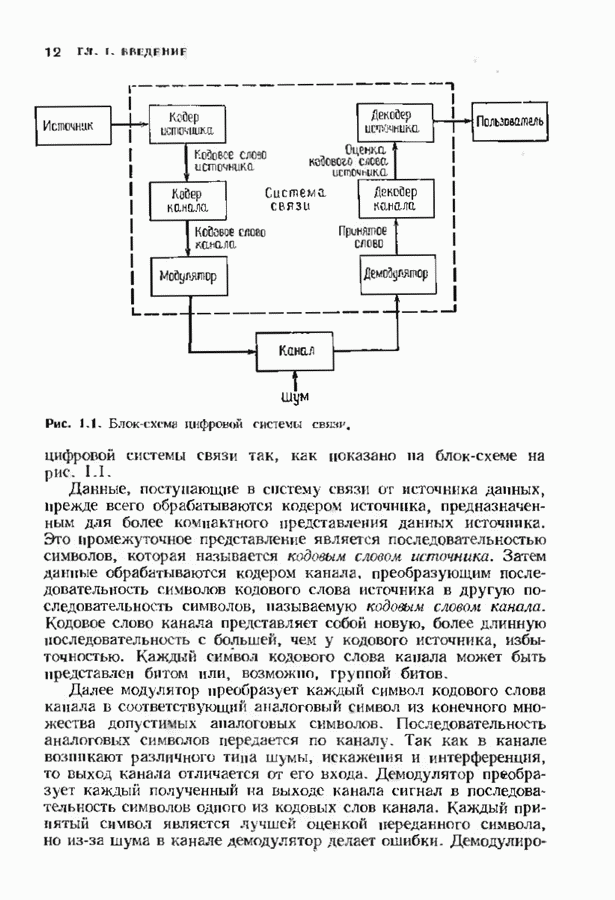
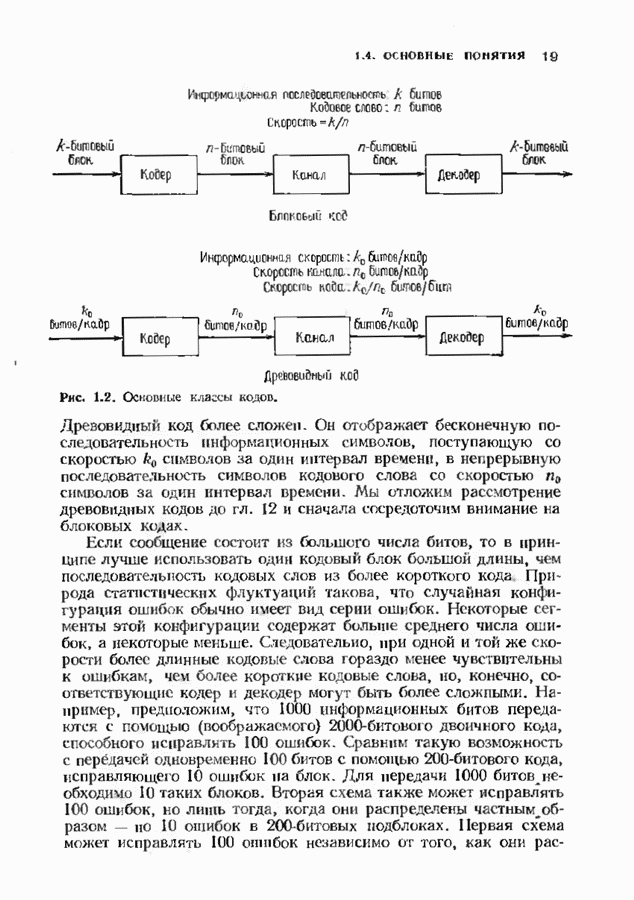
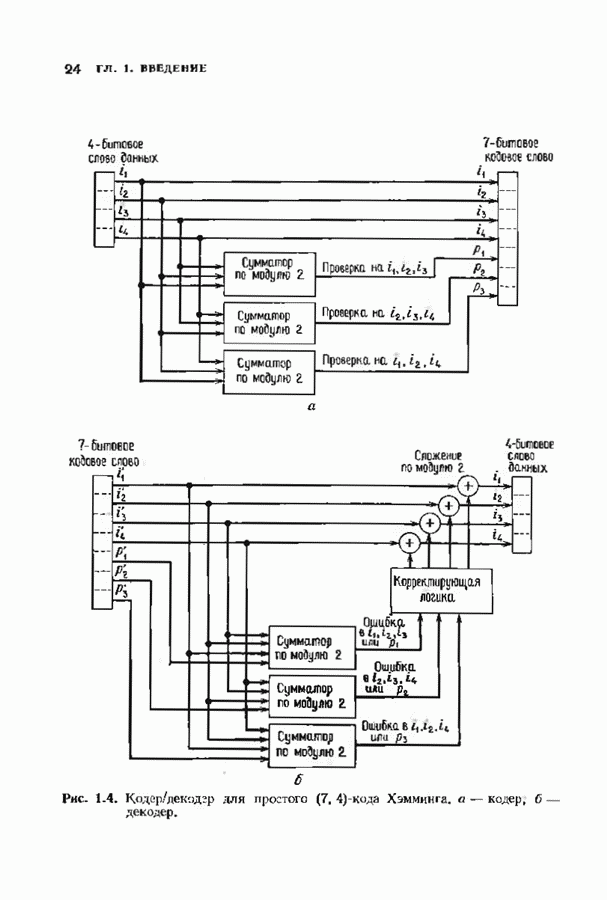
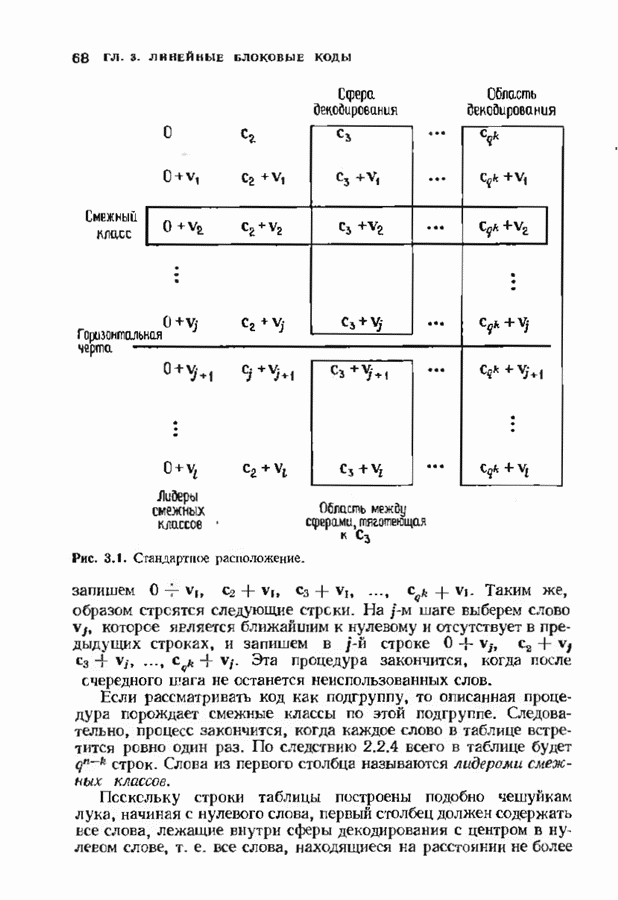
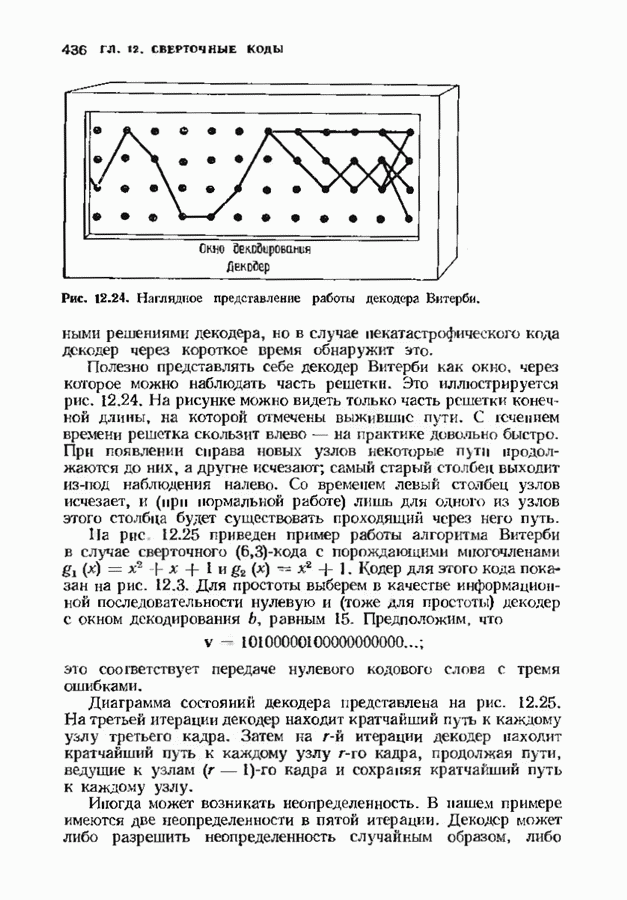
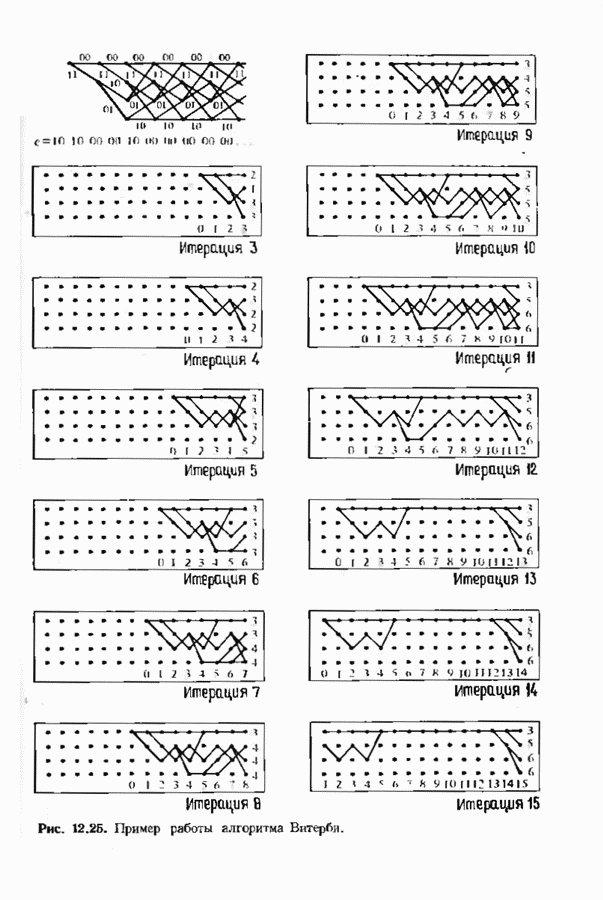
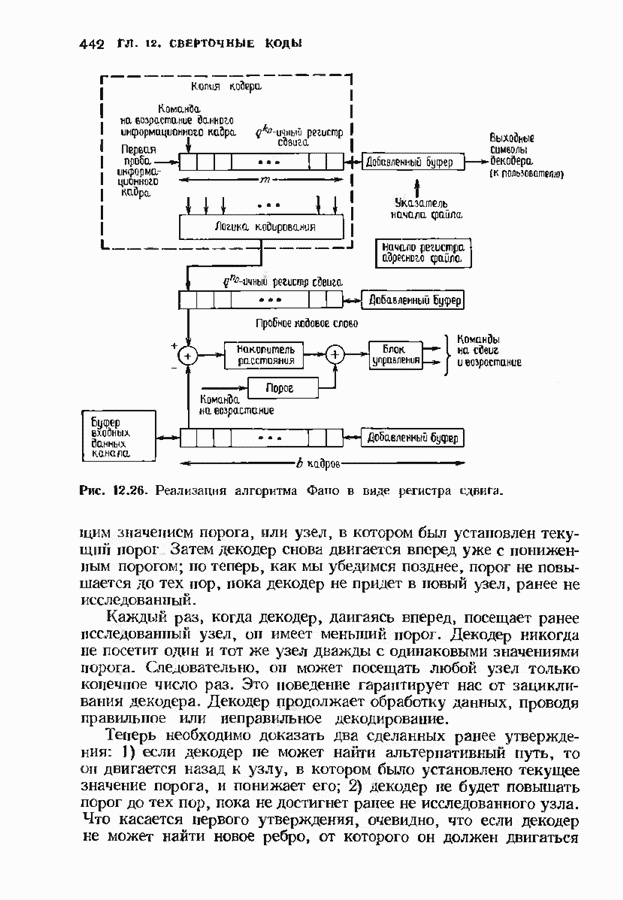
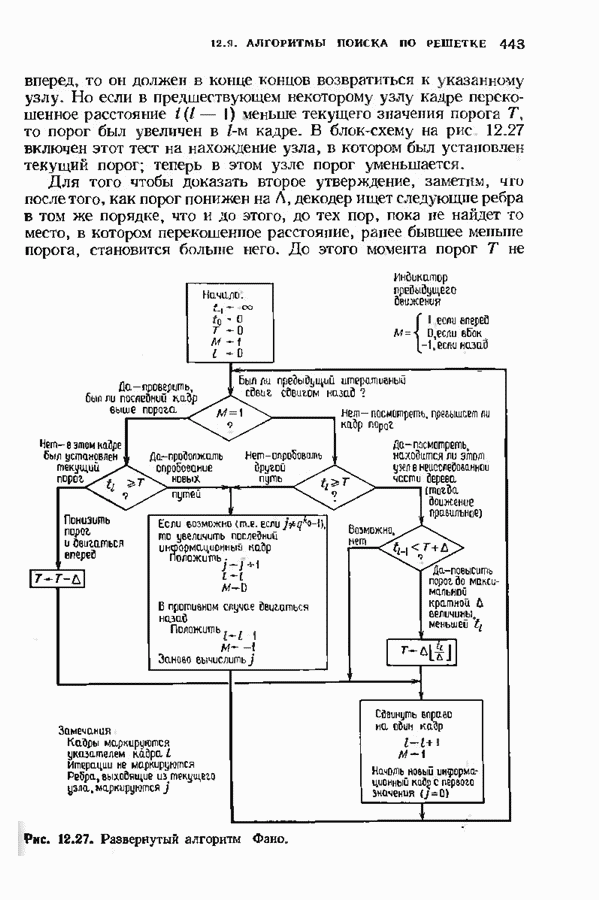
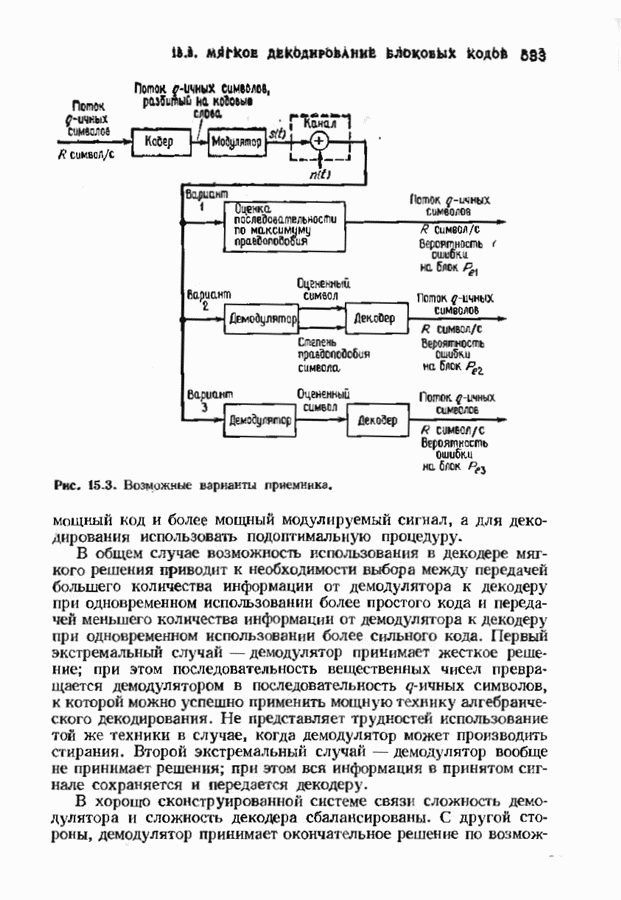
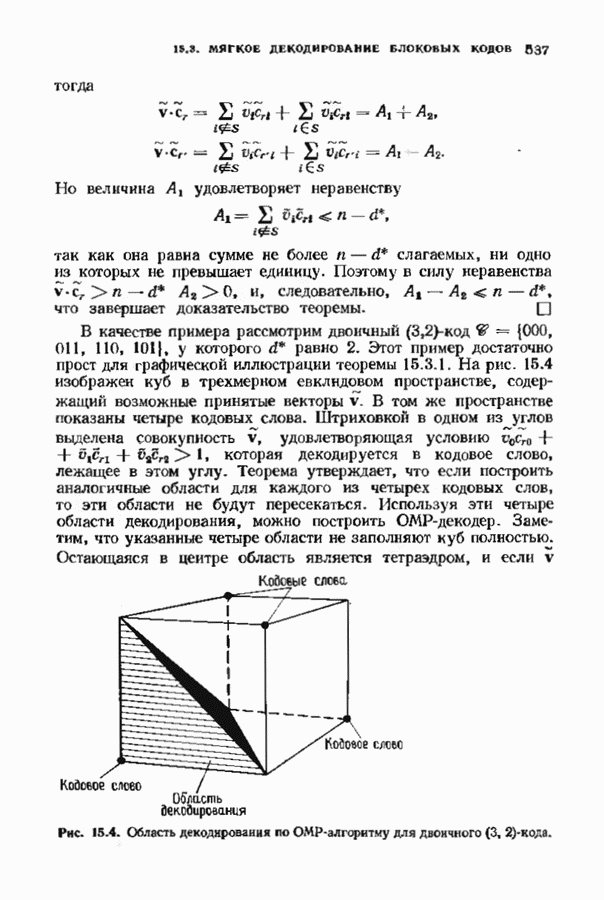
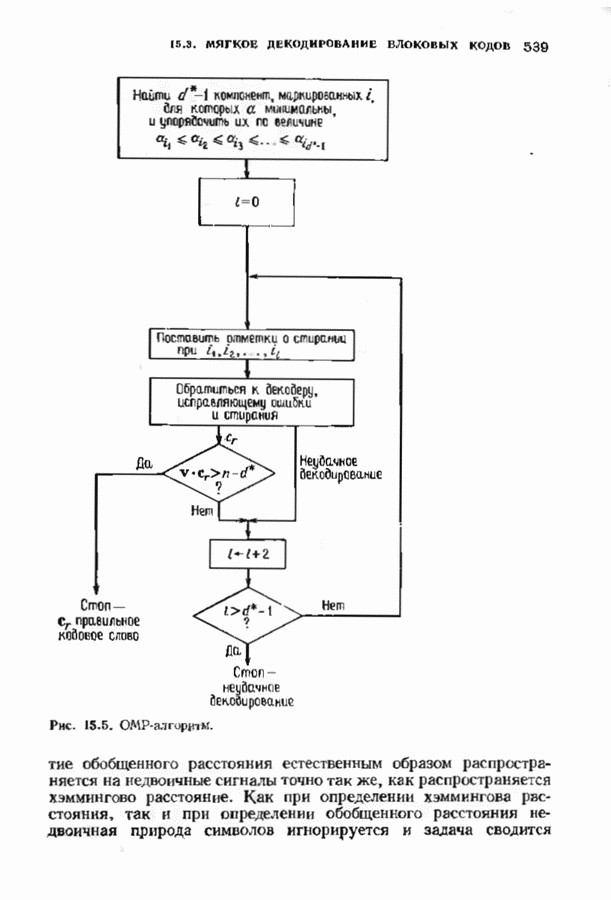
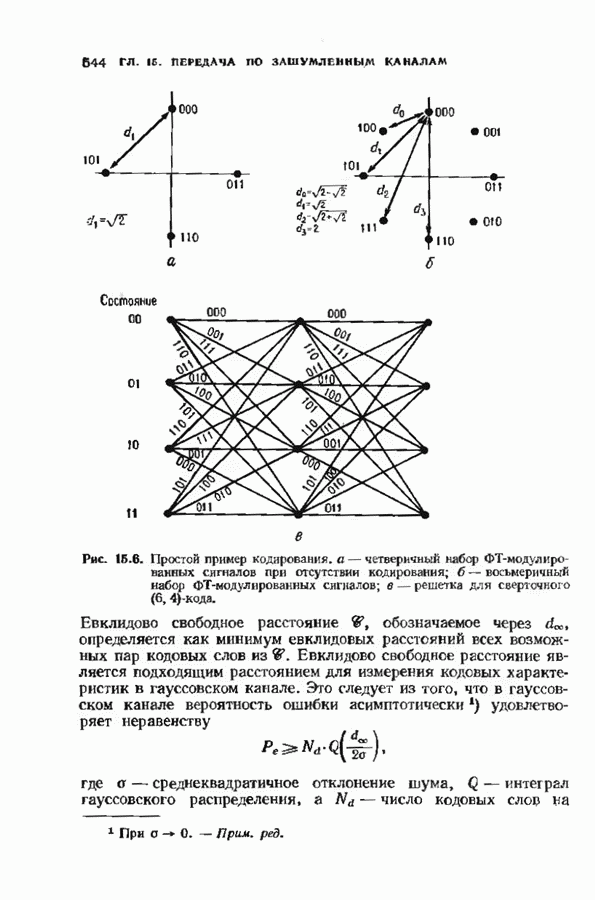
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
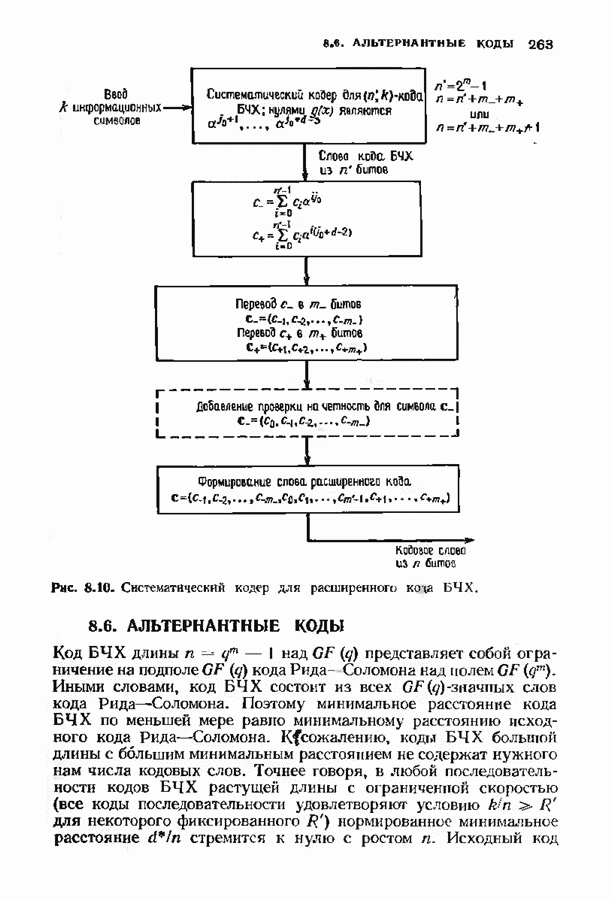
4.6. СТРУКТУРА КОНЕЧНОГО ПОЛЯ
Ранее в данной главе мы изучали, как строить поле. Предполагая, что можно найти простой многочлен степени  над нолем
над нолем  мы научились строить конечное поле с
мы научились строить конечное поле с  элементами.
элементами.
Теперь изменим точку зрения на противоположную. Вместо того чтобы строить ноле, предположим, что нам дано конечное поле, и докажем, что независимо от происхождения этого поля всегда можно предполагать, что оно построено соответственно идеям, изложенным в предыдущих параграфах. Никаких других полей так построить нельзя.
В процессе работы над материалом данного параграфа мы углубим «наше понимание структуры конечных нолей. Структурные свойства будут полезны во многих приложениях. Мы докажем также, что для всех нолей Галуа существуют простые многочлены всех степеней.
Определение 4.6.1. Число элементов наименьшего подполя поля  называется характеристикой поля
называется характеристикой поля 
Теорема 4.6.2. Каждое поле Галуа содрржит единственное наименьшее подполе, число элементов которого равно простому числу. Следовательно, характеристика каждого поля Галуа является простым числом.
Доказательство. Поле содержит элементы 0 и 1. Для задании подполя рассмотрим подмножество  обозначая его элементы через
обозначая его элементы через  Это подмножество является циклической группой по сложению, которая должна содержать конечное число
Это подмножество является циклической группой по сложению, которая должна содержать конечное число  элементов. Мы покажем, что
элементов. Мы покажем, что  простое число и что
простое число и что  Сложение в
Сложение в 
является сложением по модулю  так как С образует циклическую группу по сложению. В силу закона дистрибутивности умножение также должно быть умножением по модулю
так как С образует циклическую группу по сложению. В силу закона дистрибутивности умножение также должно быть умножением по модулю  ибо
ибо

где элемент  суммируется а раз и суммирование ведется но модулю
суммируется а раз и суммирование ведется но модулю  Следовательно, умножение также является умножением по модулю
Следовательно, умножение также является умножением по модулю  По умножению каждый элемент обратим, так как последовательность
По умножению каждый элемент обратим, так как последовательность  образует циклическую подгруппу в С.
образует циклическую подгруппу в С.
Таким образом, подмножество С содержит единичный элемент, замкнуто относительно операций сложения и умножения и содержит элементы, обратные его элементам и по сложению, в по умножению. Следовательно, оно является подполем, и арифметика в этом подполе есть арифметика по модулю  Но это в точности поле, описываемое теоремой 4.2.3, и, следовательно,
Но это в точности поле, описываемое теоремой 4.2.3, и, следовательно,  должно быть простым.
должно быть простым. 
В поле Галуа  мы построили подполе
мы построили подполе  где
где  простое число. В частности, если
простое число. В частности, если  с которого мы начинаем, само является простым числом, то, как мы видим, поле
с которого мы начинаем, само является простым числом, то, как мы видим, поле  можно., интерпретиропать как поле чисел по модулю
можно., интерпретиропать как поле чисел по модулю  Следовательно, для заданною простого числа действительно существует только одно поле с данным числом элементов, хотя, конечно, оно может быть представлено мпогими разными способами. Два поля, различающиеся только представлениями, называются изоморфными.
Следовательно, для заданною простого числа действительно существует только одно поле с данным числом элементов, хотя, конечно, оно может быть представлено мпогими разными способами. Два поля, различающиеся только представлениями, называются изоморфными.
Мы увидели, что исходное поле  является расширением подполя
является расширением подполя  Теперь мы рассмотрим многочлены над
Теперь мы рассмотрим многочлены над  корнями которых являются некоторые выбранные элементы поля
корнями которых являются некоторые выбранные элементы поля  Для большей точности введем следующее определение.
Для большей точности введем следующее определение.
Определение 4.6.3. Пусть  некоторое ноле, пусть
некоторое ноле, пусть  расширение поля
расширение поля  и пусть
и пусть  элемент
элемент  Простой многочлен
Простой многочлен  наименьшей степени над
наименьшей степени над  для которого
для которого  называется минимальным многочленом элемента
называется минимальным многочленом элемента  над
над 
Мы должны доказать, что минимальный многочлен всегда существует и является единственным.
Теорема 4.6.4. Каждый элемент  из
из  имеет единственный минимальный многочлен над
имеет единственный минимальный многочлен над  Если минимальный многочлен элемента
Если минимальный многочлен элемента  равен
равен  является корнем многочлена
является корнем многочлена  то
то  делит
делит 
Доказательство. Прежде всего  всегда является корнем многочлена
всегда является корнем многочлена  представляющего собой многочлен над
представляющего собой многочлен над  Воспользуемся теоремой об однозначном разложении:
Воспользуемся теоремой об однозначном разложении:

где множители в правой части — все простые многочлены над полем  Если
Если  корень левой части, то в правой части должен найтись некоторый член, корнем которого является
корень левой части, то в правой части должен найтись некоторый член, корнем которого является  Это может быть только один из членов правой части, так как над расширением
Это может быть только один из членов правой части, так как над расширением  простые многочлены дальше разлагаются в произведение линейных членов и констант, и
простые многочлены дальше разлагаются в произведение линейных членов и констант, и  может быть корнем только одного из линейных членов.
может быть корнем только одного из линейных членов.
Чтобы доказать вторую часть теоремы, положим

где степень многочлена  меньше степени
меньше степени  так что
так что  не может быть его корнем. Но
не может быть его корнем. Но

следовательно,  должен равняться нулю, и теорема доказана.
должен равняться нулю, и теорема доказана.  Следствие 4.6.5. Если
Следствие 4.6.5. Если  — все различные многочлены над
— все различные многочлены над  являющиеся минимальными для одного или нескольких элементов из
являющиеся минимальными для одного или нескольких элементов из  то
то

Доказательство следует из теоремы, так как каждый такой элемент  является корнем многочлена
является корнем многочлена 
При  разложение сводится к равенству
разложение сводится к равенству

которое мы уже встречали в теореме 4.5.2. Минимальный многочлен над  элемента
элемента  принадлежащего
принадлежащего  является многочленом первой степени
является многочленом первой степени 
Теорема 4.6.6. Пусть  произвольный многочлен над
произвольный многочлен над  Тогда существует расширение
Тогда существует расширение  в котором
в котором  распадается на произведение линейных множителей.
распадается на произведение линейных множителей.
Доказательство. Без потери общности можно предположить, что  приведен. Построим последовательность расширений
приведен. Построим последовательность расширений

по следующему правилу. На каждом шаге запишем  в виде произведения простых многочленов над
в виде произведения простых многочленов над  Если еще имеются нелинейные множители, то выберем один из них, скажем
Если еще имеются нелинейные множители, то выберем один из них, скажем  и построим расширение поля
и построим расширение поля  используя
используя  в качестве простого модуля. В этом расширении
в качестве простого модуля. В этом расширении  можно разложить далее, поскольку новый элемент
можно разложить далее, поскольку новый элемент  у является корнем многочлена
у является корнем многочлена  Таким образом (в случае необходимости унифицируя обозначения) будем действовать до тех пор, пока все множители не станут линейными. Поскольку степень
Таким образом (в случае необходимости унифицируя обозначения) будем действовать до тех пор, пока все множители не станут линейными. Поскольку степень  конечна, этот процесс закончится после конечного числа шагов. С
конечна, этот процесс закончится после конечного числа шагов. С
Определение 4.6.7. Любое расширение поля  в котором многочлен
в котором многочлен  над
над  распадается в произведение линейных множителей и констант, называется полем, разложения многочлена
распадается в произведение линейных множителей и констант, называется полем, разложения многочлена 
Теперь у нас есть все необходимое для описания структуры произвольного поля Галуа.
Теорема 4.6.8. Пусть  — примитивный элемент поля Галуа
— примитивный элемент поля Галуа  являющегося расширением поля
являющегося расширением поля  и пусть
и пусть  степень минимального многочлена
степень минимального многочлена  элемента
элемента  Тогда число элементов в поле равно
Тогда число элементов в поле равно  и каждый элемент
и каждый элемент  может быть представлен в виде
может быть представлен в виде

где  — элементы поля
— элементы поля 
Доказательство. Очевидно, что каждый элемент  вида
вида

принадлежит нолю  Такое разложение единственно, так как если
Такое разложение единственно, так как если

— другое представление элемента  то
то

и следовательно, а является корнем многочлена степени  что противоречит выбору числа
что противоречит выбору числа  Всего имеется
Всего имеется  таких элементов
таких элементов  следовательно, число элементов поля
следовательно, число элементов поля  не меньше
не меньше 
С другой стороны, каждый ненулевой элемент поля может быть представлен в виде некоторой степени элемента а. Но если  минимальный многочлен элемента а, то
минимальный многочлен элемента а, то  Следовательно,
Следовательно,

Полученное равенство можпо использовать для того, чтобы выразить элемент  через сумму меньших степеней элемента а:
через сумму меньших степеней элемента а:

Полученное соотношение можно повторно применять для редукции любой степени элемента а к линейной комбинации степеней  что дает
что дает

и т. д. Следовательно, каждый элемент поля  может быть представлен в виде линейной комбинации элементов
может быть представлен в виде линейной комбинации элементов  так что
так что  не может быть больше
не может быть больше  и теорема доказана.
и теорема доказана.  Следствие
Следствие  Каждое поле Галуа содержит
Каждое поле Галуа содержит  элементов, где
элементов, где  некоторое простое,
некоторое простое,  положительное целое число.
положительное целое число.
Доказательство. Каждое поле Галуа содержит подполе с  элементами, к которому надо применить теорему
элементами, к которому надо применить теорему 
Заметим, что теорему 4.6.8 можно использовать для того, чтобы связать с каждым элементом поля некоторый многочлен степени не выше  путем простой замены элемента а на неопре» деленную переменную х. Эти многочлены можно рассматривать как элементы поля. Складываться и умножаться они будут по модулю минимального многочлена
путем простой замены элемента а на неопре» деленную переменную х. Эти многочлены можно рассматривать как элементы поля. Складываться и умножаться они будут по модулю минимального многочлена  элемента а. Это в точности то же самое поле, которое получается в теореме 4.4.3, если в качестве простого многочлена выбрать
элемента а. Это в точности то же самое поле, которое получается в теореме 4.4.3, если в качестве простого многочлена выбрать  Следовательно, число элементов в каждом поле Галуа равно степени простого числа, и каждое поле Галуа может быть построено с помощью арифметики по модулю простого многочлена.
Следовательно, число элементов в каждом поле Галуа равно степени простого числа, и каждое поле Галуа может быть построено с помощью арифметики по модулю простого многочлена.
Наконец, мы должны доказать и обратное: такое поле существует для каждого простого  и целого положительного числа
и целого положительного числа  Прежде всего установим некоторые предварительные результаты.
Прежде всего установим некоторые предварительные результаты.
Теорема 4.6.10. Пусть характеристика поля  равна
равна  Тогда для любых элементов
Тогда для любых элементов  из
из  и любого положительного целого
и любого положительного целого 

Доказательство. Предположим, что теорема верна для  Тогда
Тогда

Возведем это равенство в  степень:
степень:

и снова используем теорему для 

Повторяя эту процедуру  раз, получаем
раз, получаем

Следовательно, теорему надо доказать только для  Воспользовавшись биномиальным разложением
Воспользовавшись биномиальным разложением

видим, что достаточно доказать, что в поле  выполняется равенство
выполняется равенство

Но для каждого 

 является целым числом, а
является целым числом, а  простое. Следовательно, знаменатель делит
простое. Следовательно, знаменатель делит  а число кратно
а число кратно  Таким образом,
Таким образом,  и поскольку арифметикой целых чисел в поле
и поскольку арифметикой целых чисел в поле  является арифметика по модулю
является арифметика по модулю  то в
то в  биномиальный коэффициент
биномиальный коэффициент  . Наконец, если
. Наконец, если  то
то  , а если
, а если  нечетно, то
нечетно, то  Это завершает доказательство теоремы.
Это завершает доказательство теоремы. 
Теорема 4.6.11. Пусть  простое,
простое,  положительное целое число. Тогда наименьшее поле разложения многочлена
положительное целое число. Тогда наименьшее поле разложения многочлена  рассматриваемого над полем
рассматриваемого над полем  содержит
содержит  элементов.
элементов.
Доказательство. Каждый многочлен над  имеет наименьшее поле разложения. Пусть
имеет наименьшее поле разложения. Пусть  наименьшее поле разложения многочлена
наименьшее поле разложения многочлена  Тогда в поле
Тогда в поле  многочлен
многочлен  имеет
имеет  корней (возможно, кратных). Мы покажем, что все
корней (возможно, кратных). Мы покажем, что все  корней различны и образуют поле. Из этого будет следовать, что
корней различны и образуют поле. Из этого будет следовать, что  содержит
содержит  элементов.
элементов.
Для того чтобы доказать, что множество корней образует поле, достаточно показать, что оно замкнуто относительно операций сложения и умножения и содержит обратные для всех ненулевых элементов. Пусть  корни многочлена
корни многочлена  Согласно теореме
Согласно теореме 

так что  также корень многочлена, и, следовательно, множество замкнуто относительно операции сложения. Далее,
также корень многочлена, и, следовательно, множество замкнуто относительно операции сложения. Далее,

и, таким образом,  тоже является корнем, и множество корней замкнуто относительно оиерации умножения. Далее, —а является аддитивпым обратным элементу а, так что каждый элемент имеет аддитивный обратный. Аналогично легко проверить, что если а — корень многочлена, то
тоже является корнем, и множество корней замкнуто относительно оиерации умножения. Далее, —а является аддитивпым обратным элементу а, так что каждый элемент имеет аддитивный обратный. Аналогично легко проверить, что если а — корень многочлена, то  также его корень.
также его корень.
Наконец, проверим, что все  корней многочлена
корней многочлена  различны. Это вытекает из вида формальной производной:
различны. Это вытекает из вида формальной производной:

так как  в поле
в поле  Следовательно, многочлен
Следовательно, многочлен  не имеет кратных корней.
не имеет кратных корней. 
Теперь мы получили обращение теоремы 4.6.9. Следствие Следствие 4.6.12. Для каждого простого  и положительного целого числа
и положительного целого числа  существует поле Галуа с
существует поле Галуа с  элементами.
элементами.
Покажем, наконец, что если  является не простым числом, а степенью простого числа, то
является не простым числом, а степенью простого числа, то  можно построить как расширение поля
можно построить как расширение поля  Для этого достаточпо доказать существование над
Для этого достаточпо доказать существование над  простых многочленов степени
простых многочленов степени 
Теорема 4.6.13. Для каждого целого положительного  над каждым конечным полем
над каждым конечным полем  существует хотя бы адин простой многочлен степени
существует хотя бы адин простой многочлен степени 
Доказательство. Так как  — степень простого числа, то
— степень простого числа, то  также яаляется степенью простого числа. Согласно следствию 4.6.12, существует поле с
также яаляется степенью простого числа. Согласно следствию 4.6.12, существует поле с  элементами. Это поле содержит примитивный элемент а, и, по теореме 4.6.8, минимальный многочлен этого элемента а над
элементами. Это поле содержит примитивный элемент а, и, по теореме 4.6.8, минимальный многочлен этого элемента а над  является простым многочленом степени
является простым многочленом степени  Следствие 4.6.14. Для каждого целого положительного
Следствие 4.6.14. Для каждого целого положительного  над каждым конечным полем
над каждым конечным полем  цеапвует хотя бы один примитивный многочлен степени
цеапвует хотя бы один примитивный многочлен степени 
Доказательство. Пусть а — примитивный элемент ноля  и пусть
и пусть  минимальный многочлен элемента а над
минимальный многочлен элемента а над  Тогда в поле многочленов по модулю
Тогда в поле многочленов по модулю  примитивный элемент
примитивный элемент  является корнем многочлена
является корнем многочлена  так что многочлен х представляет собой примитивный элемент поля.
так что многочлен х представляет собой примитивный элемент поля.  В заключение главы рассмотрим вопрос о существовании квадратного корня в поле Галуа.
В заключение главы рассмотрим вопрос о существовании квадратного корня в поле Галуа.
Теорема 4.6.15. Каждый элемент поля  имеет в этом поле квадратный корень. Для нечетных простых
имеет в этом поле квадратный корень. Для нечетных простых  половина ненулевых элементов поля
половина ненулевых элементов поля  имеет квадратный корень в
имеет квадратный корень в  Половина ненулевых элементов поля
Половина ненулевых элементов поля  имеет квадратный корень в расишрении
имеет квадратный корень в расишрении  а не в
а не в 
Доказательство. Так как нулевой элемент имеет квадратный корень в любом поле, то рассматривать надо только ненулевые элементы поля. Сначала рассмотрим поле  характеристики 2 с примитивным элементом а. Тогда порядок элемента а является
характеристики 2 с примитивным элементом а. Тогда порядок элемента а является
нечетным числом. Каждый элемент поля  может быть записан в виде
может быть записан в виде  для некоторого
для некоторого  и поэтому
и поэтому  если
если  четно, и
четно, и  если
если  нечетно. В любом случае
нечетно. В любом случае  является элементом поля
является элементом поля 
Рассмотрим теперь поле  характеристика которого равна простому нечетному числу
характеристика которого равна простому нечетному числу  а примитивным элементом является
а примитивным элементом является  где у — примитивный элемент расширения
где у — примитивный элемент расширения  (порядка
(порядка  четно, так как
четно, так как  равно степени нечетного простого числа. Любой элемент
равно степени нечетного простого числа. Любой элемент  может быть записан в виде а или в виде
может быть записан в виде а или в виде  для некоторого
для некоторого  Тогда если
Тогда если  четно, то
четно, то  и принадлежит нолю
и принадлежит нолю  а если
а если  нечетно, то
нечетно, то  и принадлежит полю
и принадлежит полю  но не полю
но не полю  так как
так как  в этом случае не кратно
в этом случае не кратно 
ЗАДАЧИ
(см. скан)
(см. скан)
ЗАМЕЧАНИЯ
Материал данной главы обычен для математической литературы. Свойства полей Галуа описываются во многих книгах по абстрактной алгебре, например в книгах Биркгофа и Маклейна [1953], а также Ван дер Вардсна [1950, 1953] Однако стандартное изложение является формальным, уделяет основное внимание абстрактным свойствам и содержит мало примеров и приложений. В книге Берлекэмпа [1968] подробпо рассматриваются те свойства полей Галуа, которые используются в теории кодирования
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ВВЕДЕНИЕ
- 1.1. ДИСКРЕТНЫЙ КАНАЛ, СВЯЗИ
- 1.2. ИСТОРИЯ КОДИРОВАНИЯ, КОНТРОЛИРУЮЩЕГО ОШИБКИ
- 1.3. ПРИЛОЖЕНИЯ
- 1.4. ОСНОВНЫЕ ПОНЯТИЯ
- 1.5. ПРОСТЕЙШИЕ КОДЫ
- ГЛАВА 2. ВВЕДЕНИЕ В АЛГЕБРУ
- 2.1. 2-ПОЛЕ И 6-10-ПОЛЕ
- 2.2. ГРУППЫ
- 2.3. КОЛЬЦА
- 2.4. ПОЛЯ
- 2.5. ВЕКТОРНЫЕ ПРОСТРАНСТВА
- 2.6. ЛИНЕЙНАЯ АЛГЕБРА
- ГЛАВА 3. ЛИНЕЙНЫЕ БЛОКОВЫЕ КОДЫ
- 3.1. СТРУКТУРА ЛИНЕЙНЫХ БЛОКОВЫХ КОДОВ
- 3.2. МАТРИЧНОЕ ОПИСАНИЕ ЛИНЕЙНЫХ БЛОКОВЫХ КОДОВ
- 3.3. СТАНДАРТНОЕ РАСПОЛОЖЕНИЕ
- 3.4. КОДЫ ХЭММИНГА
- 3.5. СОВЕРШЕННЫЕ И КВАЗИСОВЕРШЕННЫЕ КОДЫ
- 3.6. ПРОСТЫЕ ПРЕОБРАЗОВАНИЯ ЛИНЕЙНОГО КОДА
- 3.7. КОДЫ РИДА—МАЛЛЕРА
- ГЛАВА 4. АРИФМЕТИКА ПОЛЕЙ ГАЛУА
- 4.2. КОНЕЧНЫЕ ПОЛЯ, ОСНОВАННЫЕ НА КОЛЬЦЕ ЦЕЛЫХ ЧИСЕЛ
- 4.3. КОЛЬЦА МНОГОЧЛЕНОВ
- 4.4. КОНЕЧНЫЕ ПОЛЯ, ОСНОВАННЫЕ НА КОЛЬЦАХ МНОГОЧЛЕНОВ
- 4.5. ПРИМИТИВНЫЕ ЭЛЕМЕНТЫ
- 4.6. СТРУКТУРА КОНЕЧНОГО ПОЛЯ
- ГЛАВА 5. ЦИКЛИЧЕСКИЕ КОДЫ
- 5.2. ПОЛИНОМИАЛЬНОЕ ОПИСАНИЕ ЦИКЛИЧЕСКИХ КОДОВ
- 5.3. МИНИМАЛЬНЫЕ МНОГОЧЛЕНЫ И СОПРЯЖЕНИЯ
- 5.4. МАТРИЧНОЕ ОПИСАНИЕ ЦИКЛИЧЕСКИХ КОДОВ
- 5.5. КОДЫ ХЭММИНГА КАК ЦИКЛИЧЕСКИЕ КОДЫ
- 5.6. ЦИКЛИЧЕСКИЕ КОДЫ, ИСПРАВЛЯЮЩИЕ ДВЕ ОШИБКИ
- 5.7. ЦИКЛИЧЕСКИЕ КОДЫ, ИСПРАВЛЯЮЩИЕ ПАКЕТЫ ОШИБОК
- 5.8. ДВОИЧНЫЙ КОД ГОЛЕЯ
- 5.9. КВАДРАТИЧНО-ВЫЧЕТНЫЕ КОДЫ
- ГЛАВА 6. СХЕМНАЯ РЕАЛИЗАЦИЯ ЦИКЛИЧЕСКОГО КОДИРОВАНИЯ
- 6.1. ЛОГИЧЕСКИЕ ЦЕПИ ДЛЯ АРИФМЕТИКИ КОНЕЧНОГО ПОЛЯ
- 6.2. ЦИФРОВЫЕ ФИЛЬТРЫ
- 6.3. КОДЕРЫ И ДЕКОДЕРЫ НА РЕГИСТРАХ СДВИГА
- 6.4. ДЕКОДЕР МЕГГИТТА
- 6.5. ВЫЛАВЛИВАНИЕ ОШИБОК
- 6.6. УКОРОЧЕННЫЕ ЦИКЛИЧЕСКИЕ КОДЫ
- 6.7. ДЕКОДЕР МЕГГИТТА ДЛЯ. КОДА ГОЛЕЯ
- ГЛАВА 7. КОДЫ БОУЗА-ЧОУДХУРИ-ХОКВИНГЕМА
- 7.2. ДЕКОДЕР ПИТЕРСОНА ГОРЕНСТЕЙНА—ЦИРЛЕРА
- 7.3. КОДЫ РИДА СОЛОМОНА
- 7.4. СИНТЕЗ АВТОРЕГРЕССИОННЫХ ФИЛЬТРОВ
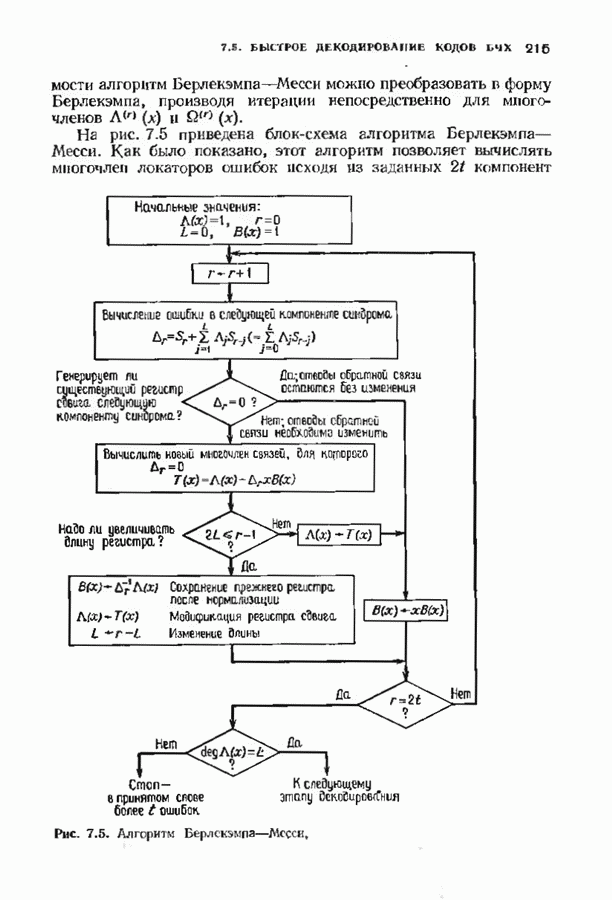
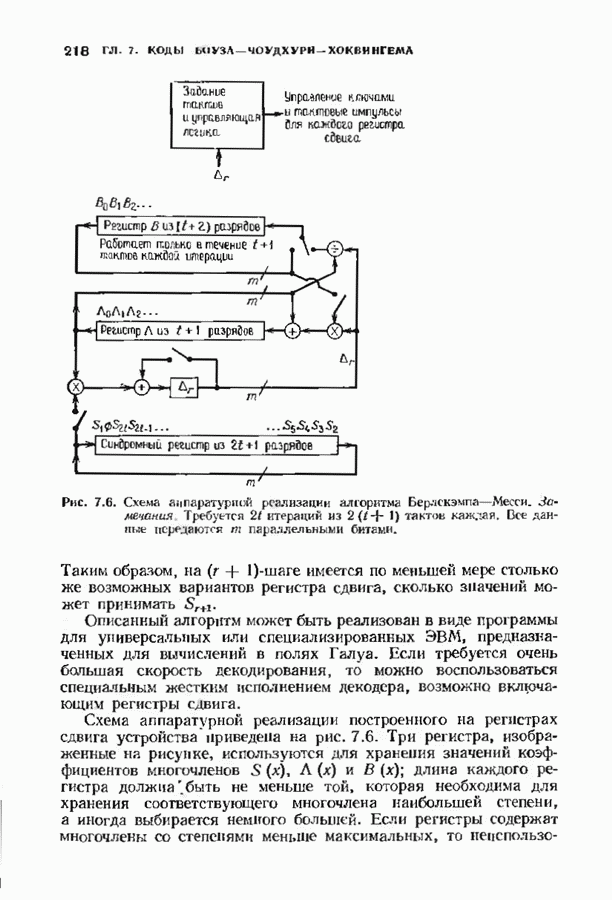
- 7.5. БЫСТРОЕ ДЕКОДИРОВАНИЕ КОДОВ БЧХ
- 7.6. ДЕКОДИРОВАНИЕ ДВОИЧНЫХ КОДОВ БЧХ
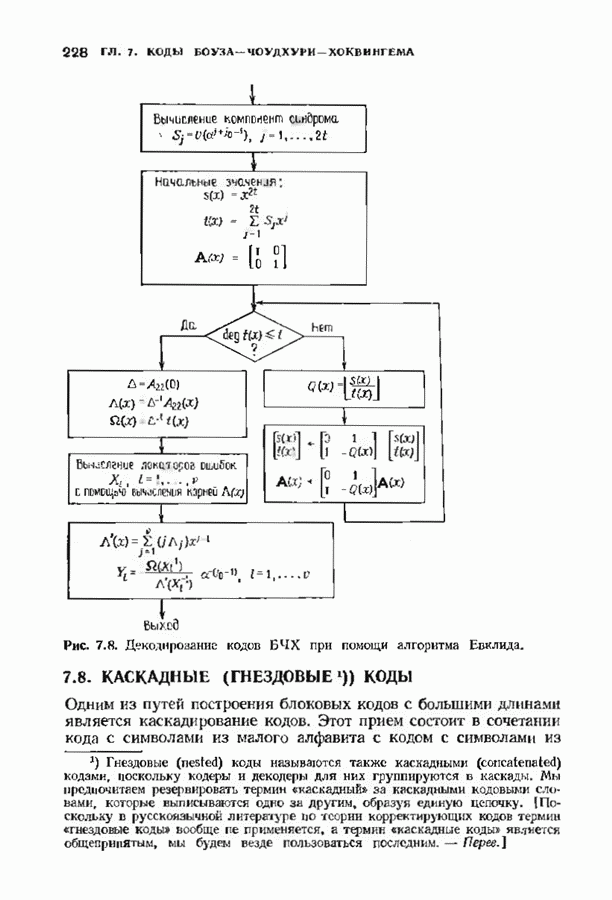
- 7.7. ДЕКОДИРОВАНИЕ С ПОМОЩЬЮ АЛГОРИТМА ЕВКЛИДА
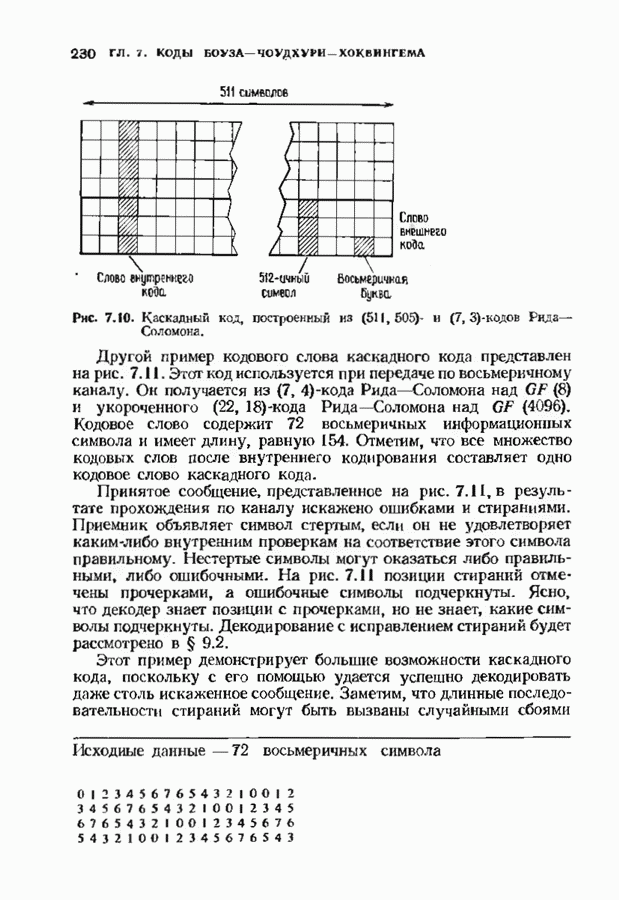
- 7.8. КАСКАДНЫЕ (ГНЕЗДОВЫЕ) КОДЫ
- 7.9. КОДЫ ЮСТЕСЕНА
- ГЛАВА 8. КОДЫ, ОСНОВАННЫЕ НА СПЕКТРАЛЬНЫХ МЕТОДАХ
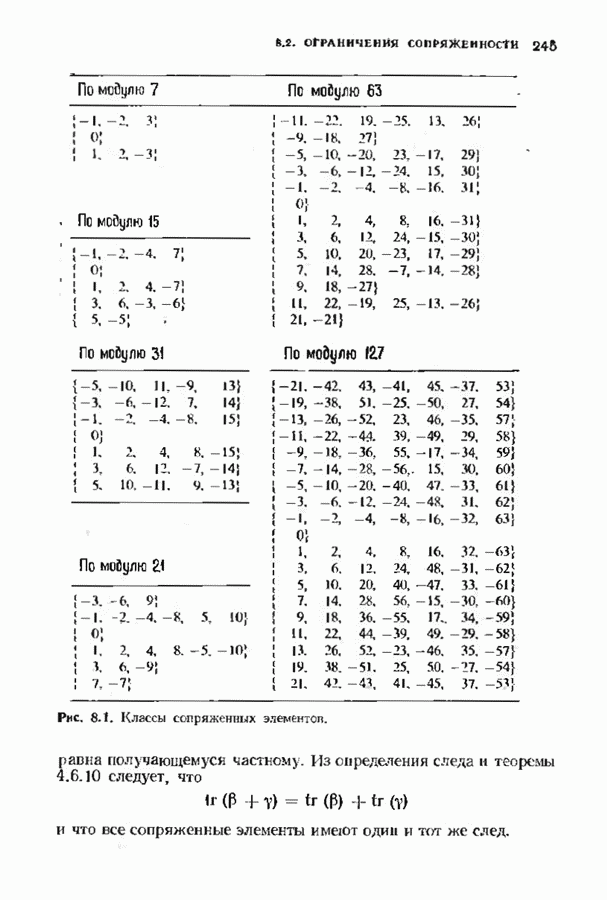
- 8.2. ОГРАНИЧЕНИЯ СОПРЯЖЕННОСТИ И ИДЕМПОТЕНТЫ
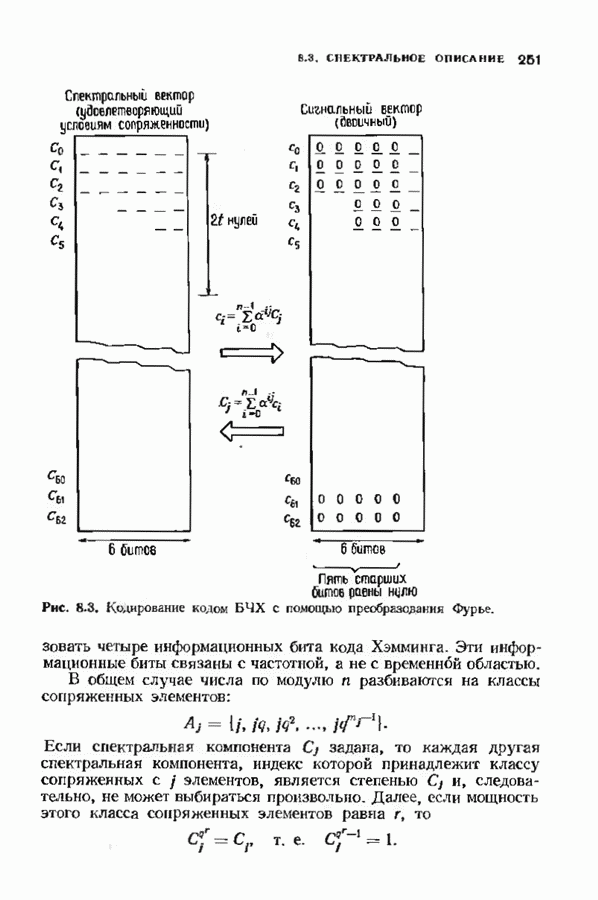
- 8.3. СПЕКТРАЛЬНОЕ ОПИСАНИЕ ЦИКЛИЧЕСКИХ КОДОВ
- 8.4. РАСШИРЕННЫЕ КОДЫ РИДА-СОЛОМОНА
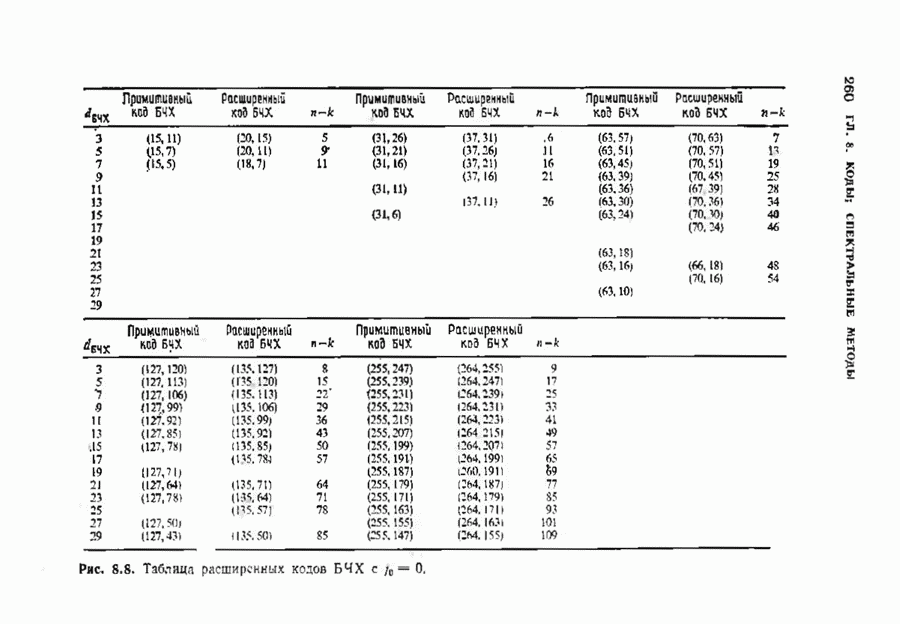
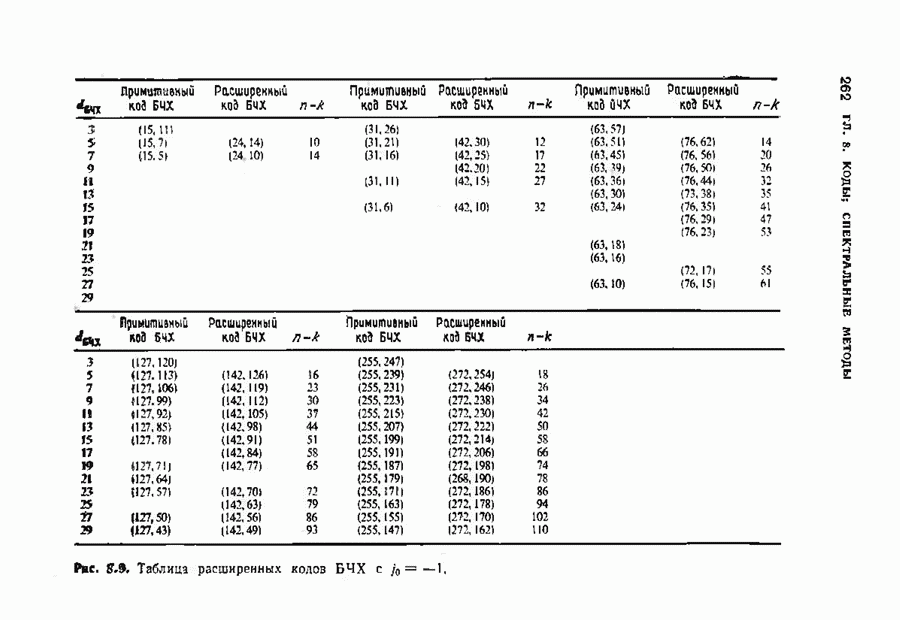
- 8.5. РАСШИРЕННЫЕ КОДЫ БЧХ
- 8.6. АЛЬТЕРНАНТНЫЕ КОДЫ
- 8.7. ХАРАКТЕРИСТИКИ АЛЬТЕРНАНТНЫХ КОДОВ
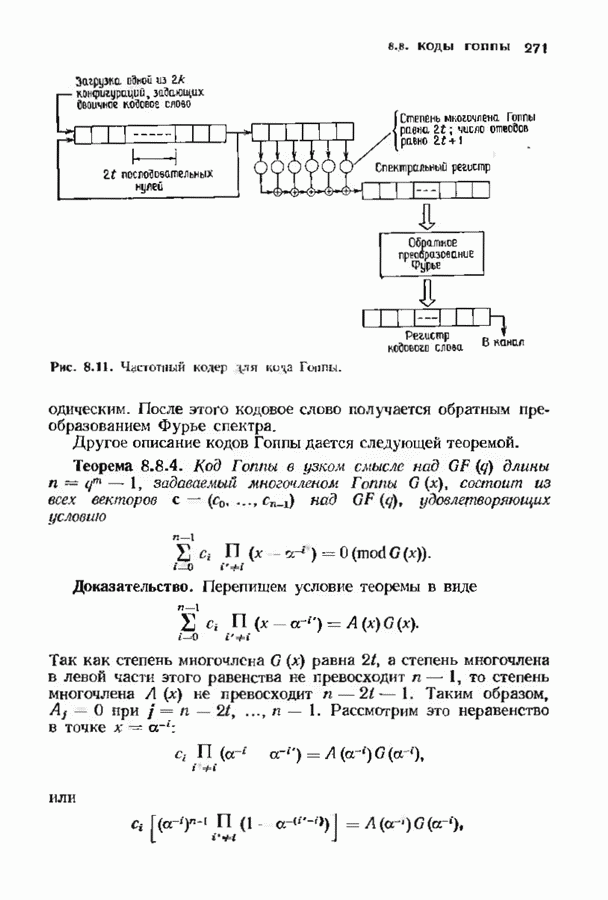
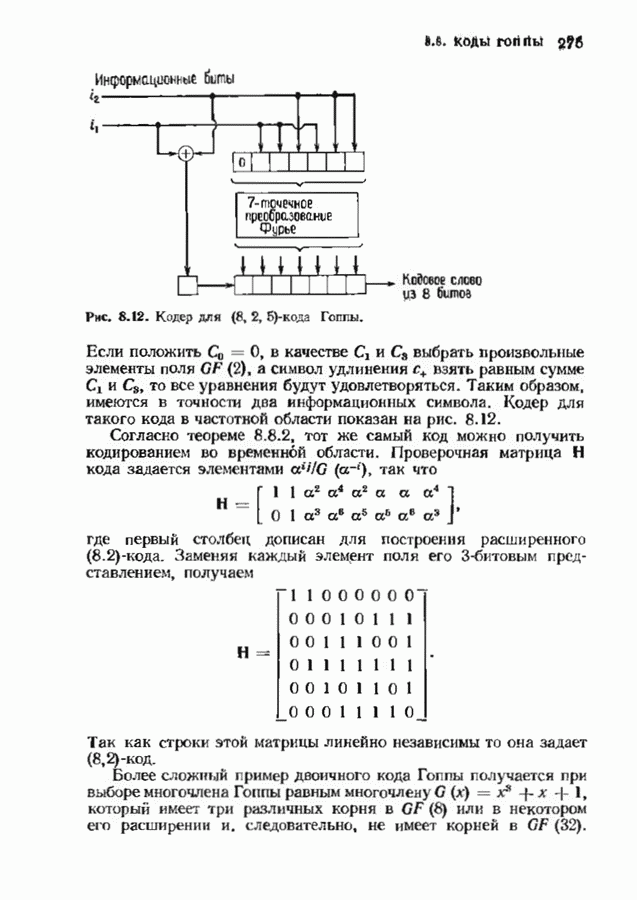
- 8.8. КОДЫ ГОППЫ
- 8.9. КОДЫ ПРЕПАРАТЫ
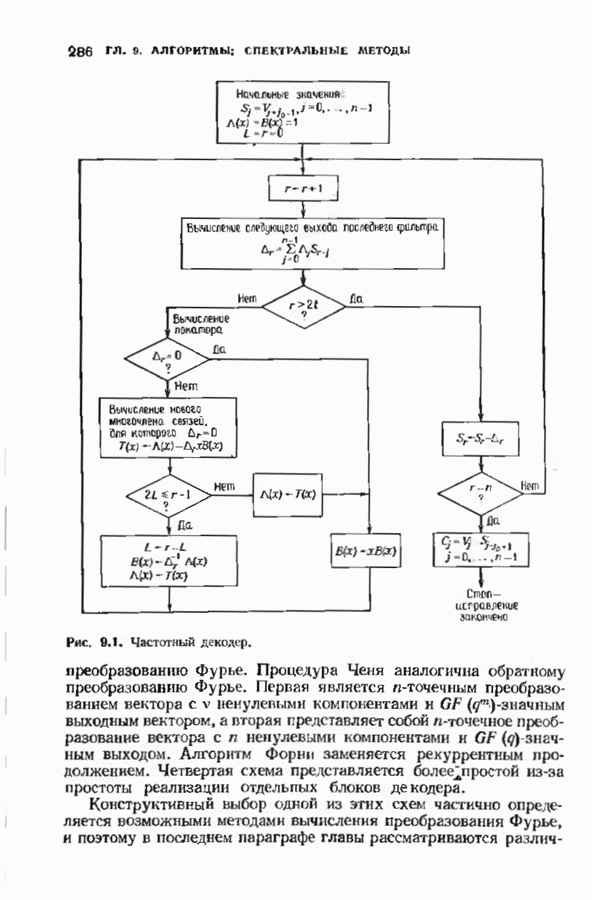
- ГЛАВА 9. АЛГОРИТМЫ, ОСНОВАННЫЕ НА СПЕКТРАЛЬНЫХ МЕТОДАХ
- 9.2. ИСПРАВЛЕНИЕ СТИРАНИЙ И ОШИБОК
- 9.3. ДЕКОДИРОВАНИЕ РАСШИРЕННЫХ КОДОВ РИДА—СОЛОМОНА
- 9.4. ДЕКОДИРОВАНИЕ РАСШИРЕННЫХ КОДОВ БЧХ
- 9.5. ДЕКОДИРОВАНИЕ ВО ВРЕМЕННОЙ ОБЛАСТИ
- 9.6. ДЕКОДИРОВАНИЕ ЗА ГРАНИЦЕЙ БЧХ
- 9.7. ДЕКОДИРОВАНИЕ АЛЬТЕРНАНТНЫХ КОДОВ
- 9.8. ВЫЧИСЛЕНИЕ ПРЕОБРАЗОВАНИЙ В КОНЕЧНЫХ ПОЛЯХ
- ГЛАВА 10. МНОГОМЕРНЫЕ СПЕКТРАЛЬНЫЕ МЕТОДЫ
- 10.1. КОДЫ-ПРОИЗВЕДЕНИЯ
- 10.2. КИТАЙСКИЕ ТЕОРЕМЫ ОБ ОСТАТКАХ
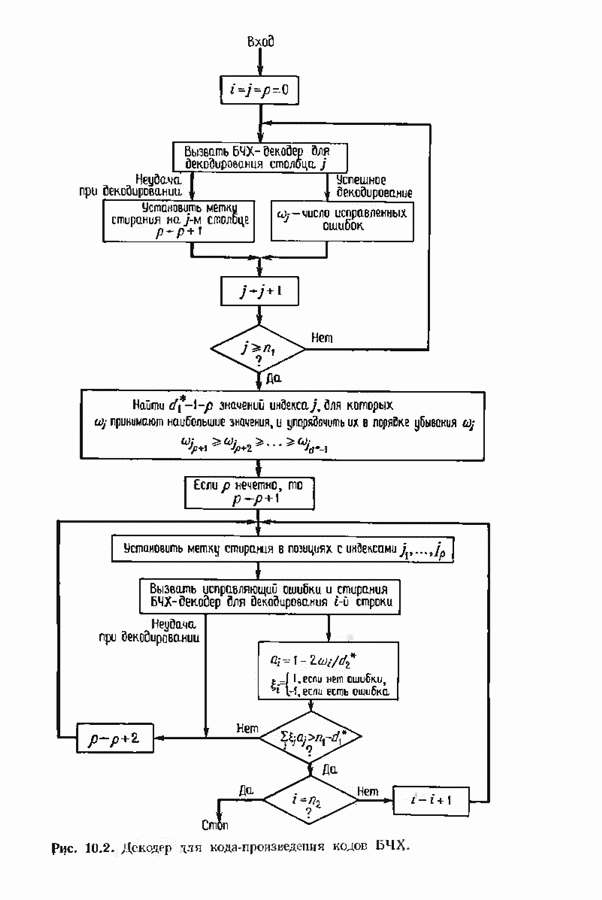
- 10.3. ДЕКОДИРОВАНИЕ КОДА-ПРОИЗВЕДЕНИЯ
- 10.4. МНОГОМЕРНЫЕ СПЕКТРЫ
- 10.5. БЫСТРЫЕ КОДЫ БЧХ
- 10.6. ДЕКОДИРОВАНИЕ МНОГОМЕРНЫХ КОДОВ
- 10.7. ДЛИННЫЕ КОДЫ НАД МАЛЫМИ ПОЛЯМИ
- ГЛАВА 11. БЫСТРЫЕ АЛГОРИТМЫ
- 11.1. ЛИНЕЙНАЯ СВЕРТКА И ЦИКЛИЧЕСКАЯ СВЕРТКА
- 11.2. БЫСТРЫЕ АЛГОРИТМЫ СВЕРТКИ
- 11.3. БЫСТРЫЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 11.4. АЛГОРИТМЫ АГАРВАЛА—КУЛИ ВЫЧИСЛЕНИЯ СВЕРТОК
- 11.5. АЛГОРИТМ ВИНОГРАДА БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ
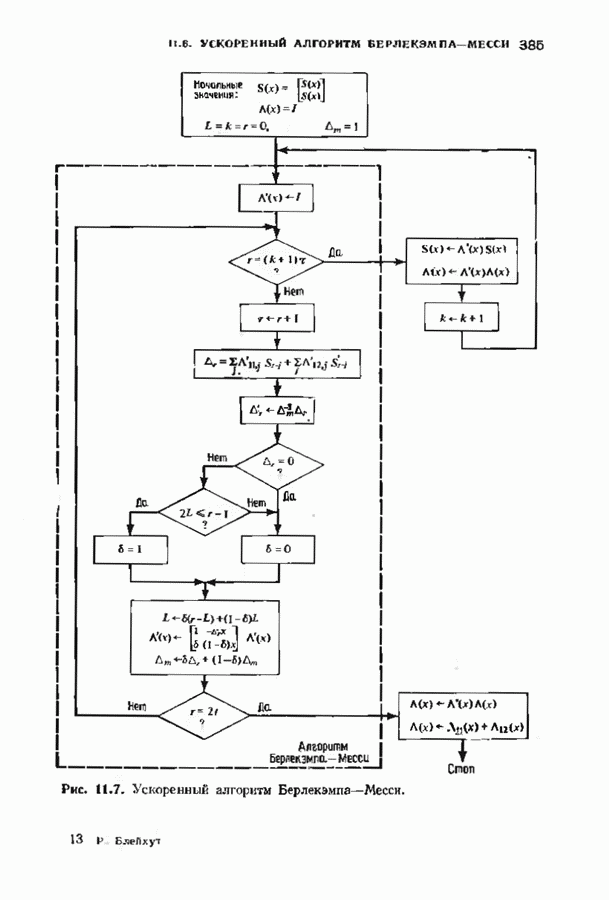
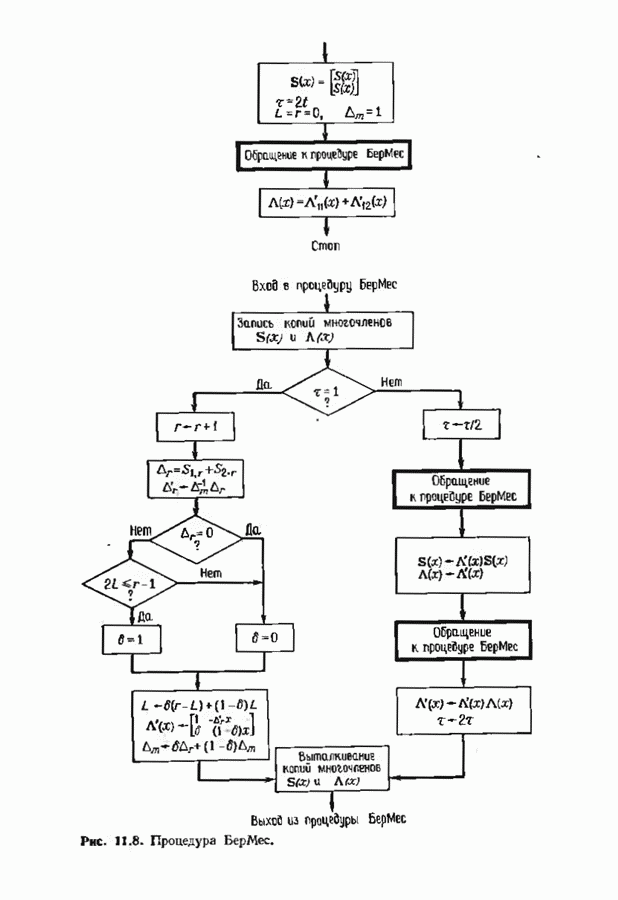
- 11.6. УСКОРЕННЫЙ АЛГОРИТМ БЕРЛЕКЭМПА—МЕССИ
- 11.7. РЕКУРРЕНТНЫЙ АЛГОРИТМ БЕРЛЕКЭМПА—МЕССИ
- 11.8. УСКОРЕННОЕ ДЕКОДИРОВАНИЕ КОДОВ БЧХ
- 11.9. СВЕРТКА В СУРРОГАТНЫХ ПОЛЯХ
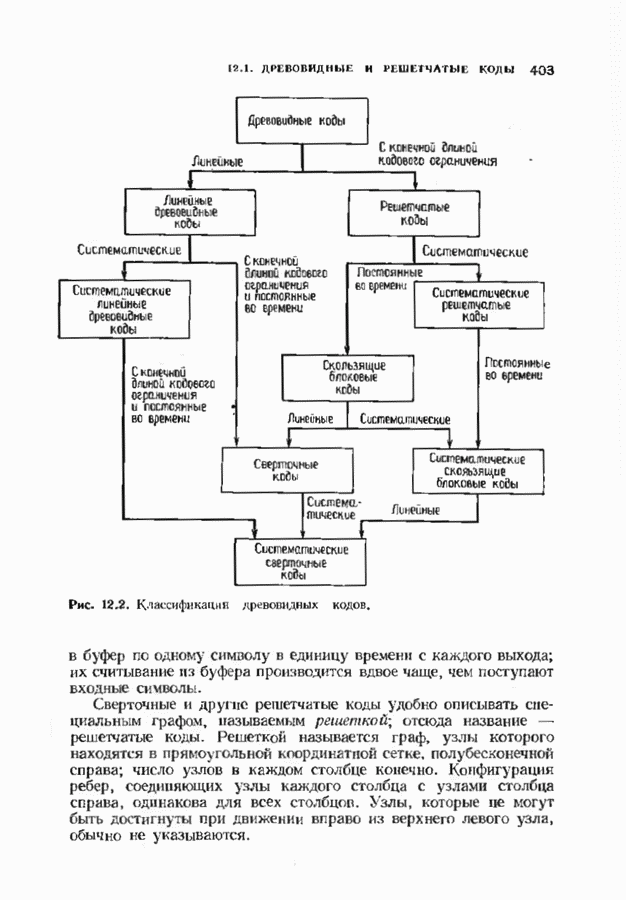
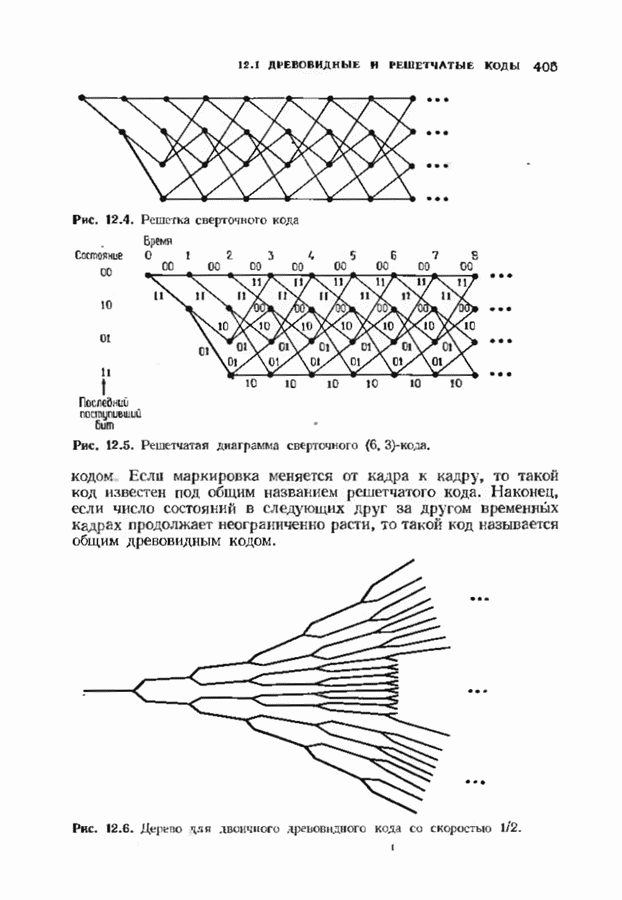
- ГЛАВА 12. СВЕРТОЧНЫЕ КОДЫ
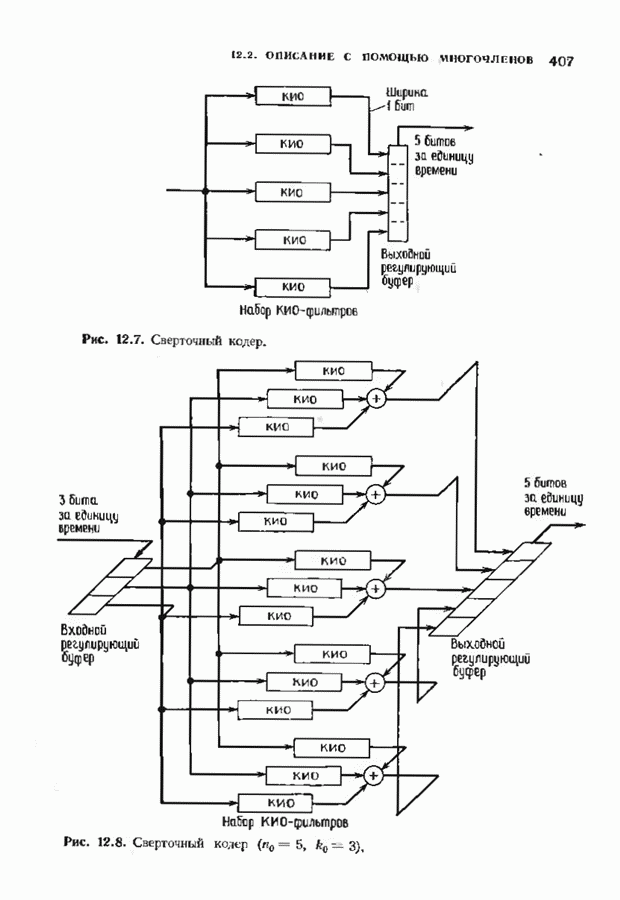
- 12.2. ОПИСАНИЕ СВЕРТОЧНЫХ КОДОВ С ПОМОЩЬЮ МНОГОЧЛЕНОВ
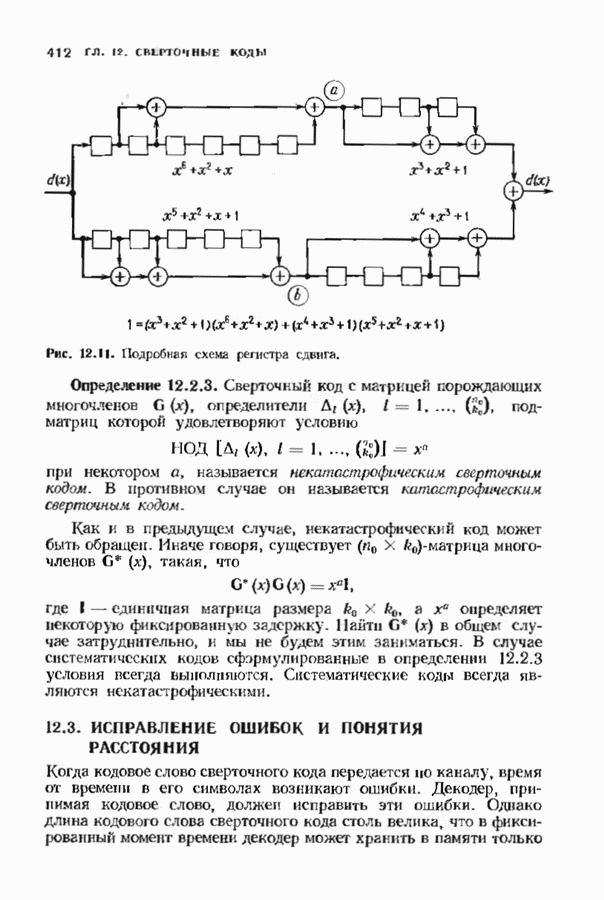
- 12.3. ИСПРАВЛЕНИЕ ОШИБОК И ПОНЯТИЯ РАССТОЯНИЯ
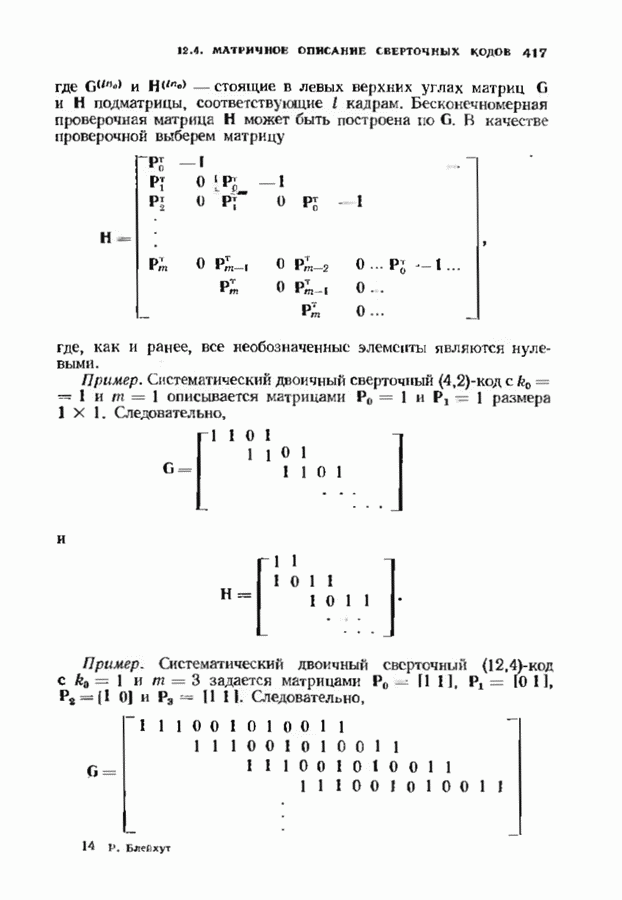
- 12.4. МАТРИЧНОЕ ОПИСАНИЕ СВЕРТОЧНЫХ КОДОВ
- 12.5. НЕКОТОРЫЕ ПРОСТЫЕ СВЕРТОЧНЫЕ КОДЫ
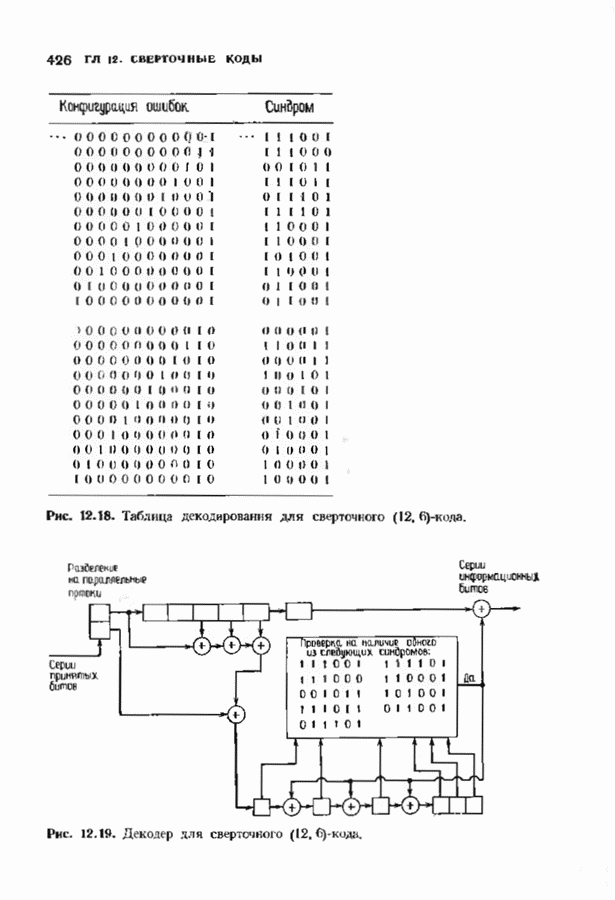
- 12.6. АЛГОРИТМЫ СИНДРОМНОГО ДЕКОДИРОВАНИЯ
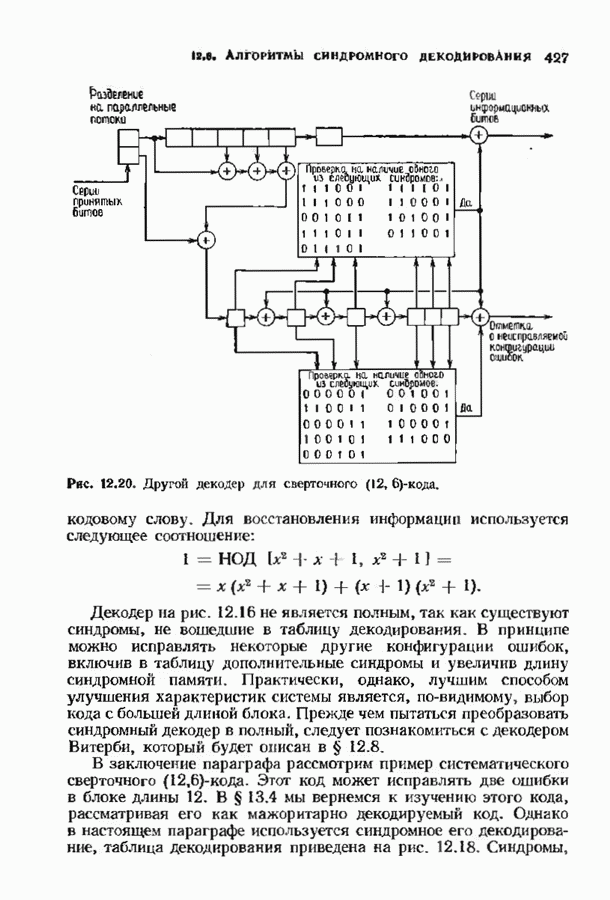
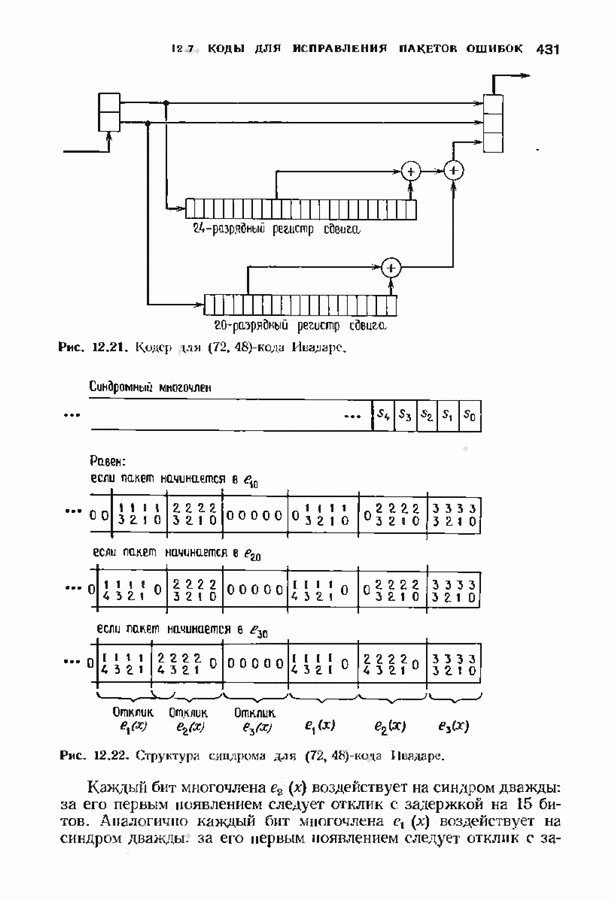
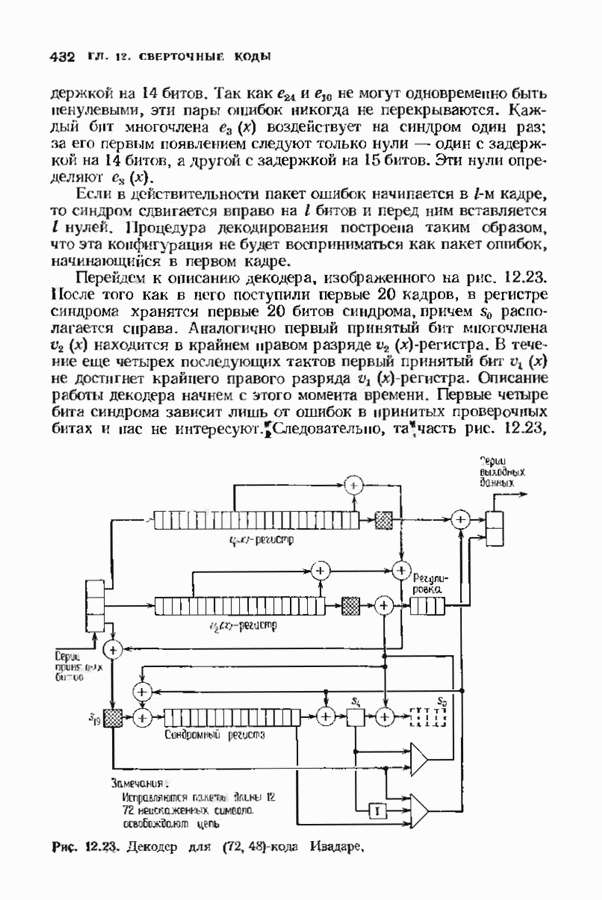
- 12.7. ОБЕРТОЧНЫЕ КОДЫ ДЛЯ ИСПРАВЛЕНИЯ ПАКЕТОВ ОШИБОК
- 12.8. АЛГОРИТМ ДЕКОДИРОВАНИЯ ВИТЕРБИ
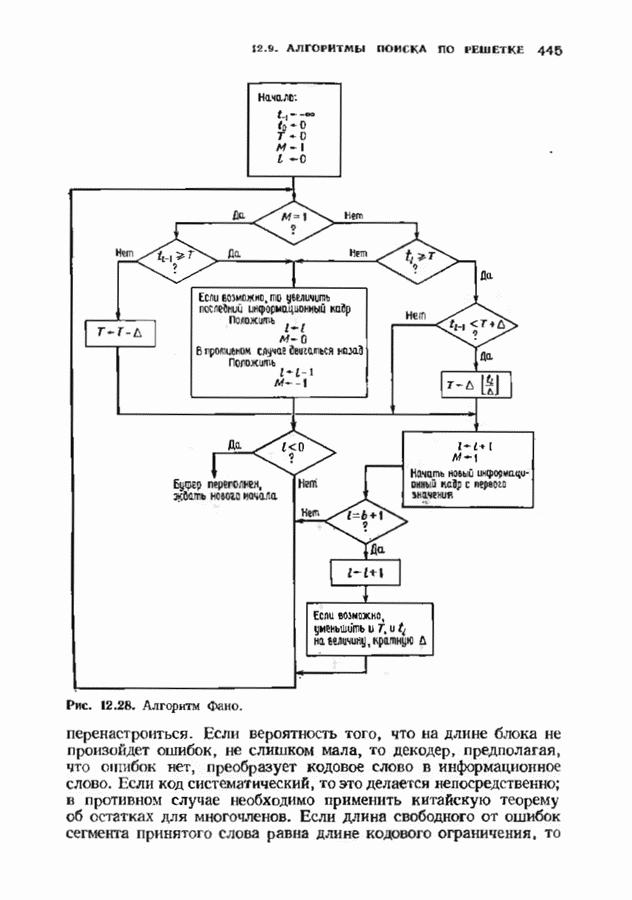
- 12.9. АЛГОРИТМЫ ПОИСКА ПО РЕШЕТКЕ
- ГЛАВА 13. КОДЫ И АЛГОРИТМЫ ДЛЯ ДЕКОДИРОВАНИЯ МАЖОРИТАРНЫМ МЕТОДОМ
- 13.1. ДЕКОДИРОВАНИЕ МАЖОРИТАРНЫМ МЕТОДОМ
- 13.2. СХЕМЫ МАЖОРИТАРНОГО ДЕКОДИРОВАНИЯ
- 13.3. АФФИННЫЕ ПЕРЕСТАНОВКИ ДЛЯ ЦИКЛИЧЕСКИХ КОДОВ
- 13.4. ЦИКЛИЧЕСКИЕ КОДЫ, ОСНОВАННЫЕ НА ПЕРЕСТАНОВКАХ
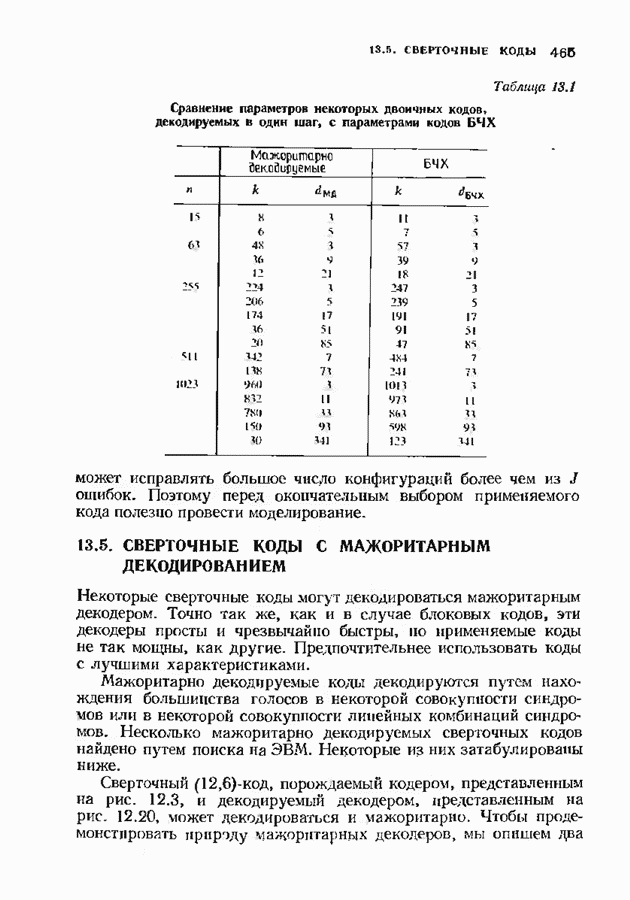
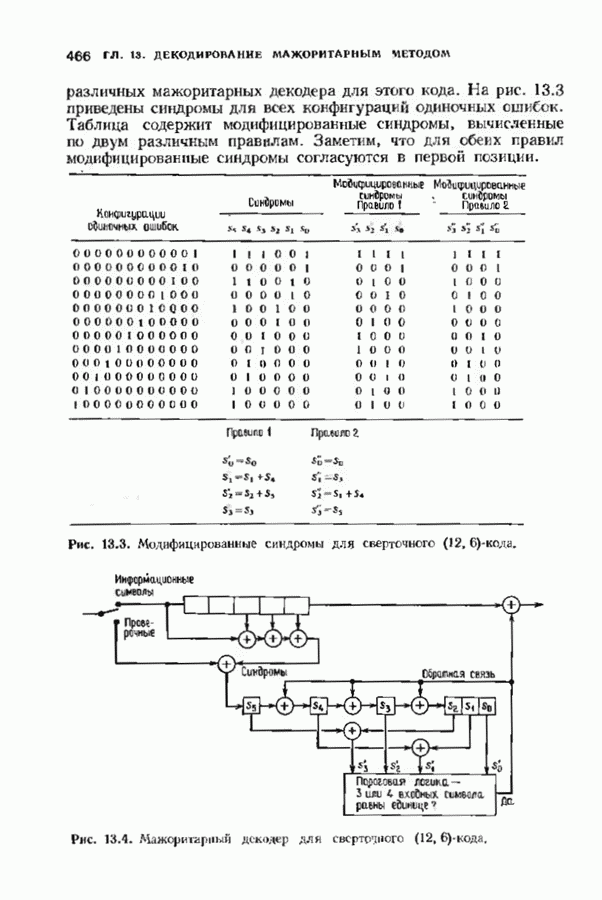
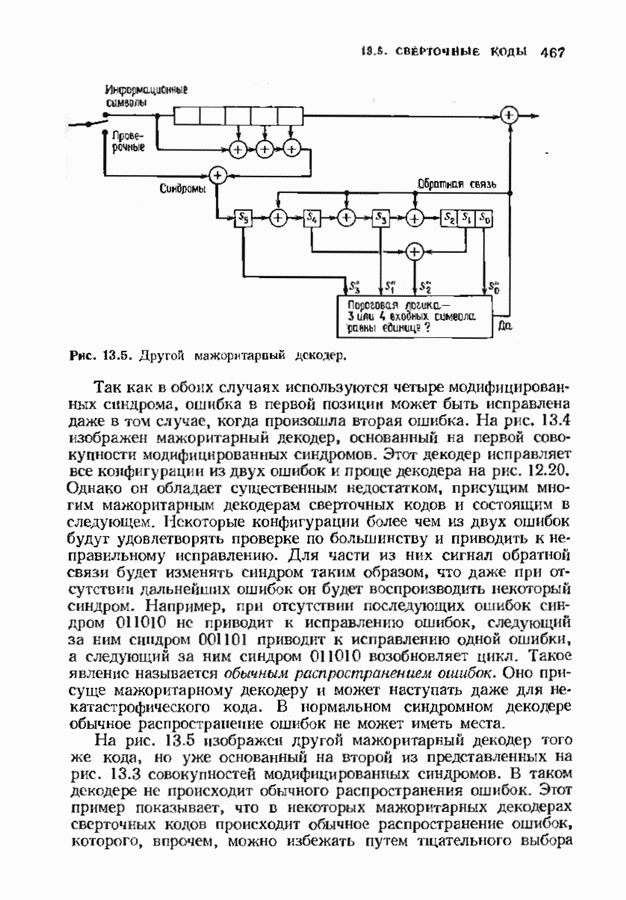
- 13.5. СВЕРТОЧНЫЕ КОДЫ С МАЖОРИТАРНЫМ ДЕКОДИРОВАНИЕМ
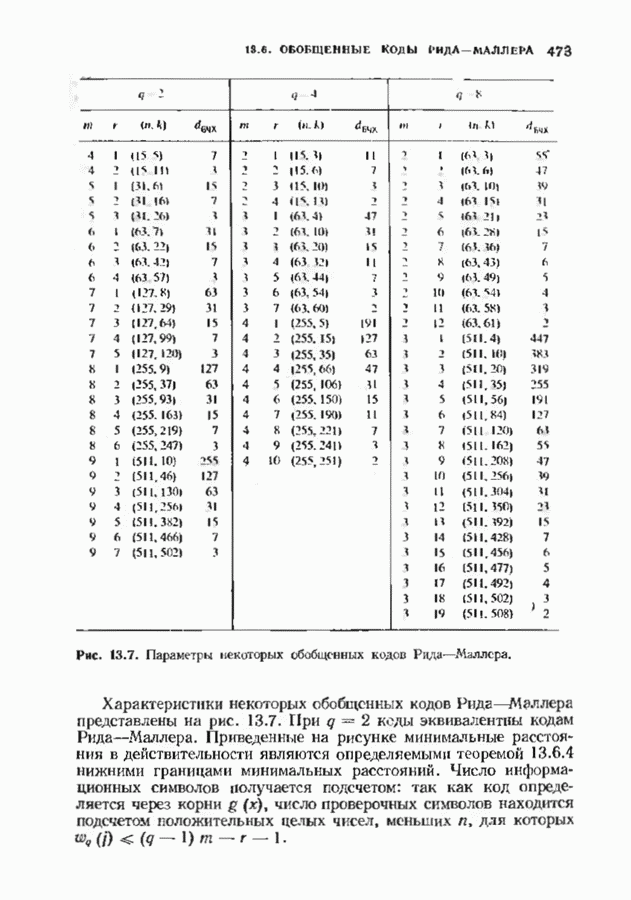
- 13.6. ОБОБЩЕННЫЕ КОДЫ РИДА—МАЛЛЕРА
- 13.7. ЕВКЛИДОВО-ГЕОМЕТРИЧЕСКИЕ КОДЫ
- 13.8. ПРОЕКТИВНО-ГЕОМЕТРИЧЕСКИЕ КОДЫ
- ГЛАВА 14. КОМПОЗИЦИЯ И ХАРАКТЕРИСТИКИ КОНТРОЛИРУЮЩИХ ОШИБКИ КОДОВ
- 14.2. ВЕРОЯТНОСТИ ОШИБОЧНОГО ДЕКОДИРОВАНИЯ И НЕУДАЧНОГО ДЕКОДИРОВАНИЯ
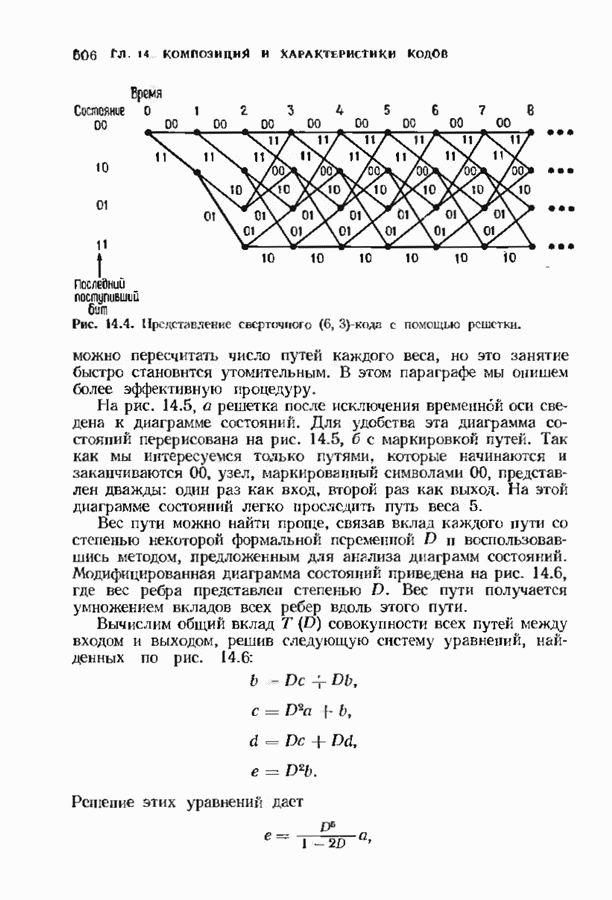
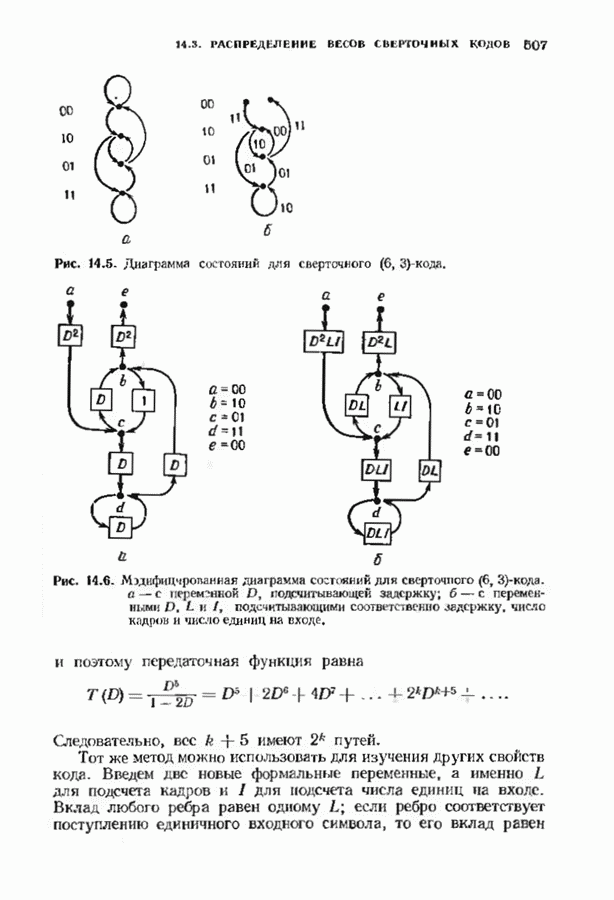
- 14.3. РАСПРЕДЕЛЕНИЕ ВЕСОВ СВЕРТОЧНЫХ КОДОВ
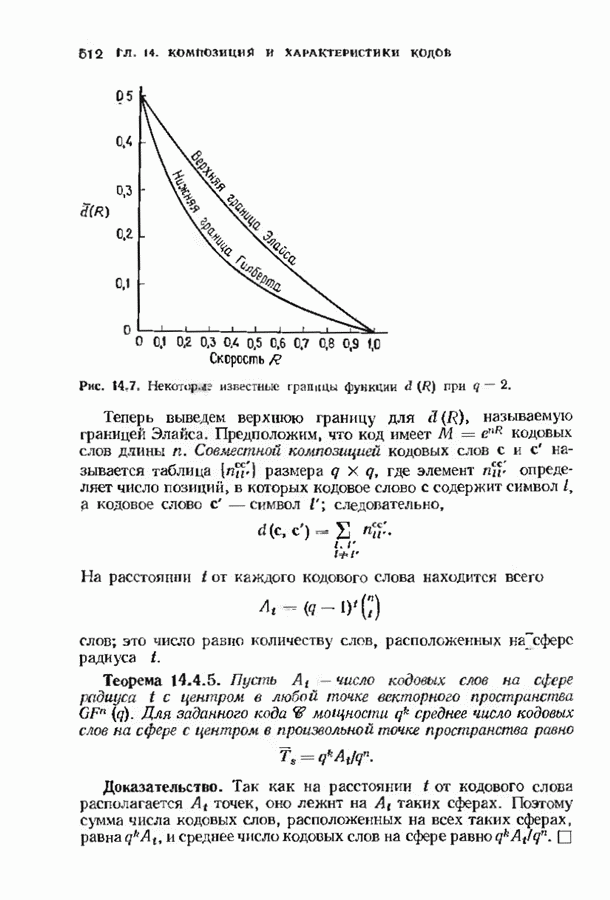
- 14.4. ГРАНИЦЫ МИНИМАЛЬНОГО РАССТОЯНИЯ ДЛЯ БЛОКОВЫХ КОДОВ
- 14.5. ГРАНИЦЫ МИНИМАЛЬНОГО РАССТОЯНИЯ ДЛЯ СВЕРТОЧНЫХ КОДОВ
- ГЛАВА 15. ЭФФЕКТИВНАЯ ПЕРЕДАЧА СИГНАЛОВ ПО ЗАШУМЛЕННЫМ КАНАЛАМ
- 15.1. ОГРАНИЧЕННЫЙ ПО ПОЛОСЕ ГАУССОВСКИЙ КАНАЛ
- 15.2. ЭНЕРГИЯ НА БИТ И ЧАСТОТА ОШИБОК НА БИТ
- 15.3. МЯГКОЕ ДЕКОДИРОВАНИЕ БЛОКОВЫХ КОДОВ
- 15.4. МЯГКОЕ ДЕКОДИРОВАНИЕ СВЕРТОЧНЫХ КОДОВ
- 15.5. ПОСЛЕДОВАТЕЛЬНОЕ ДЕКОДИРОВАНИЕ
- ЛИТЕРАТУРА