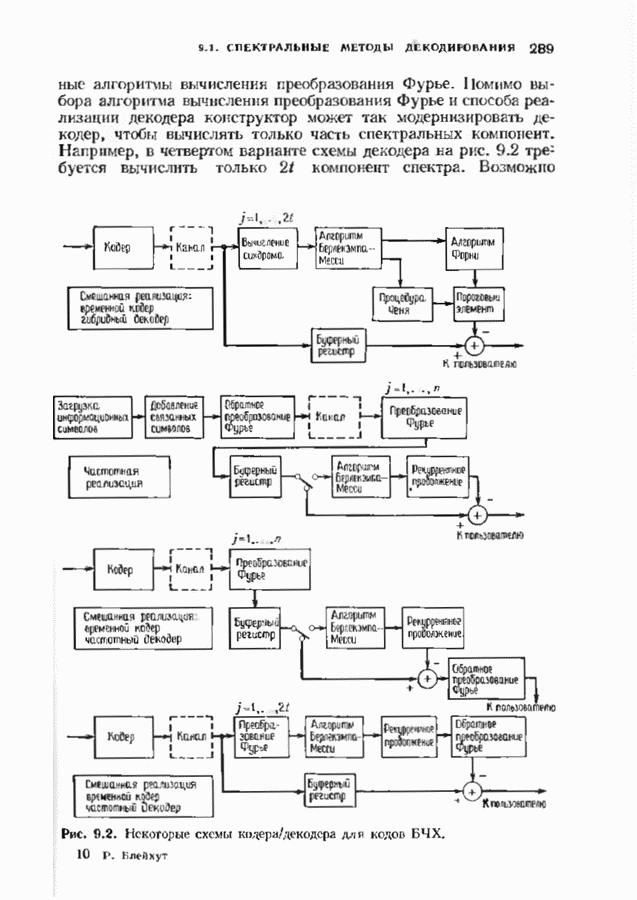
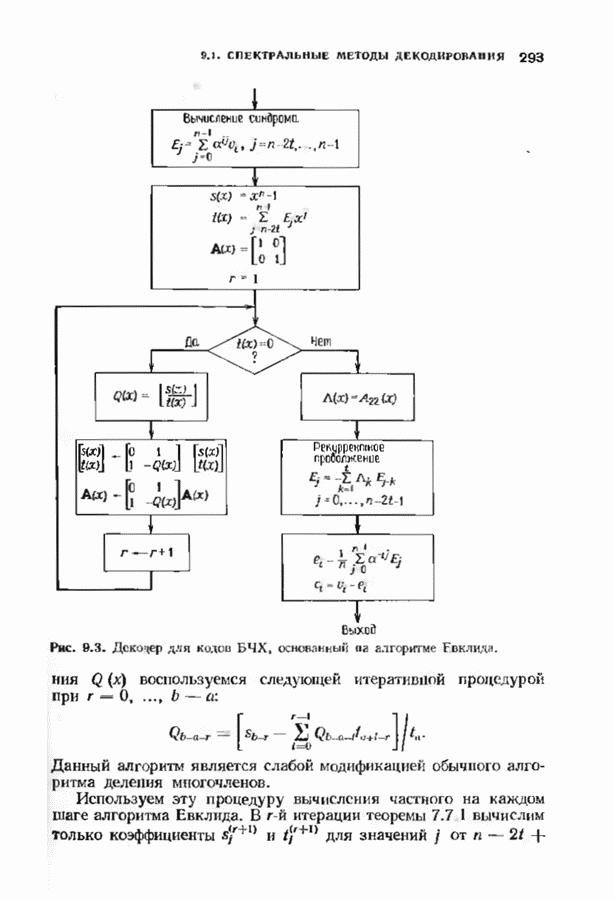
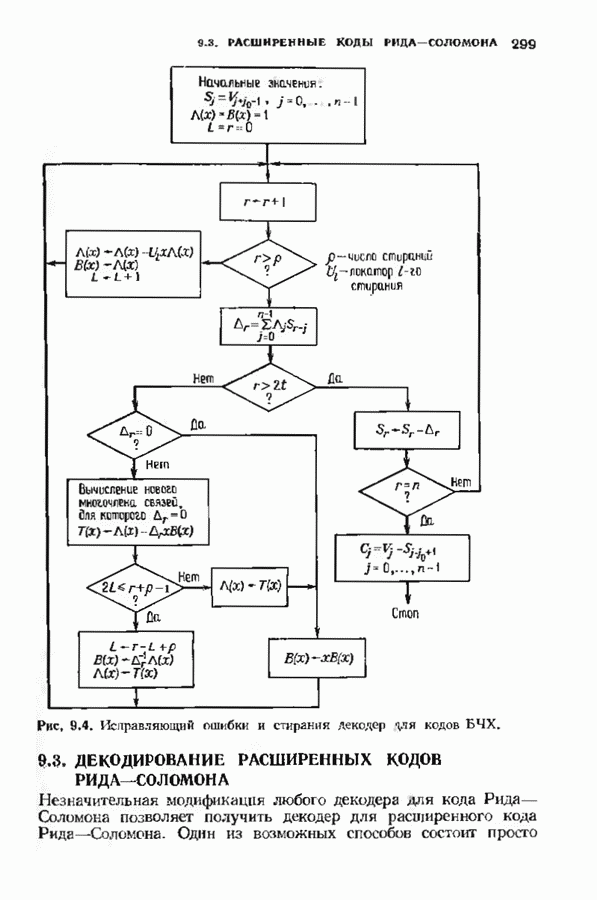
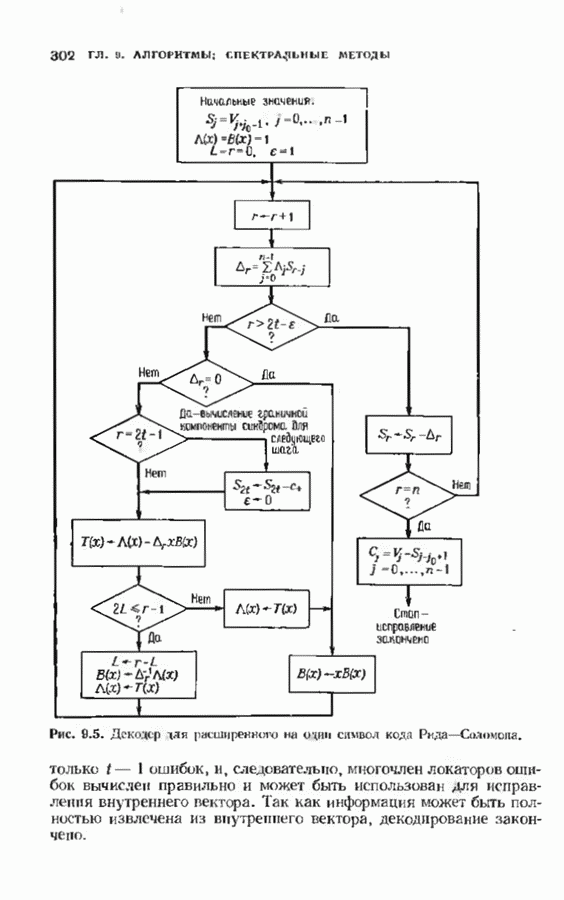
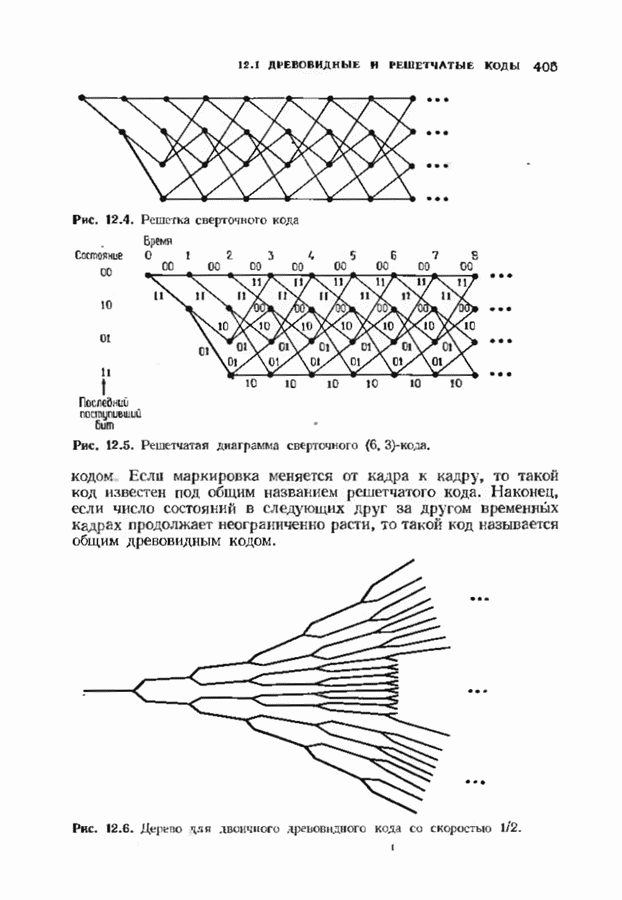
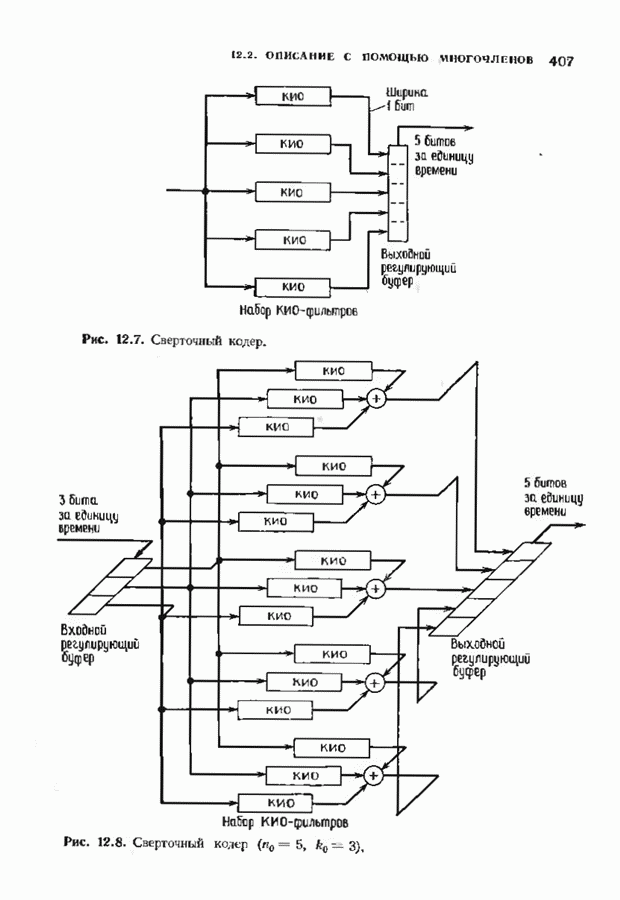
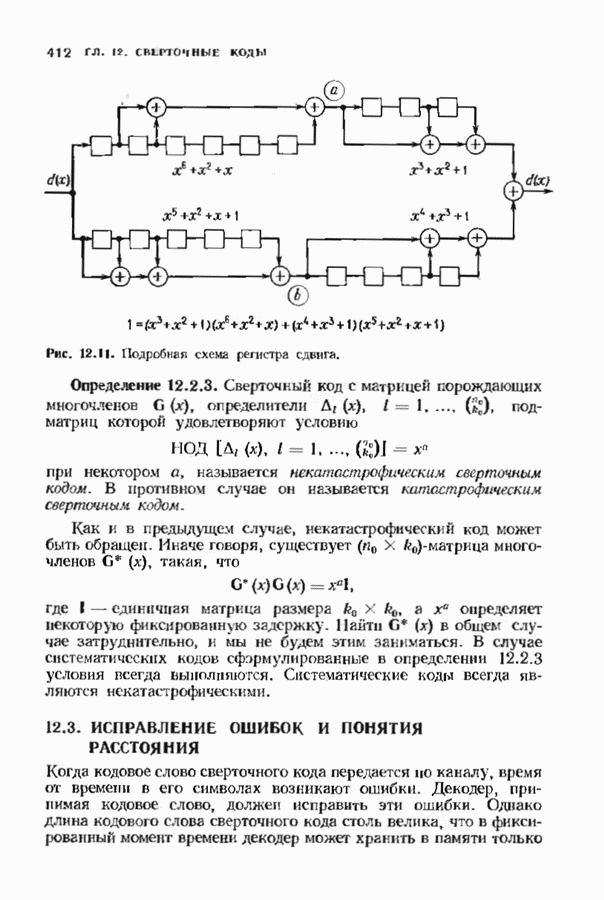
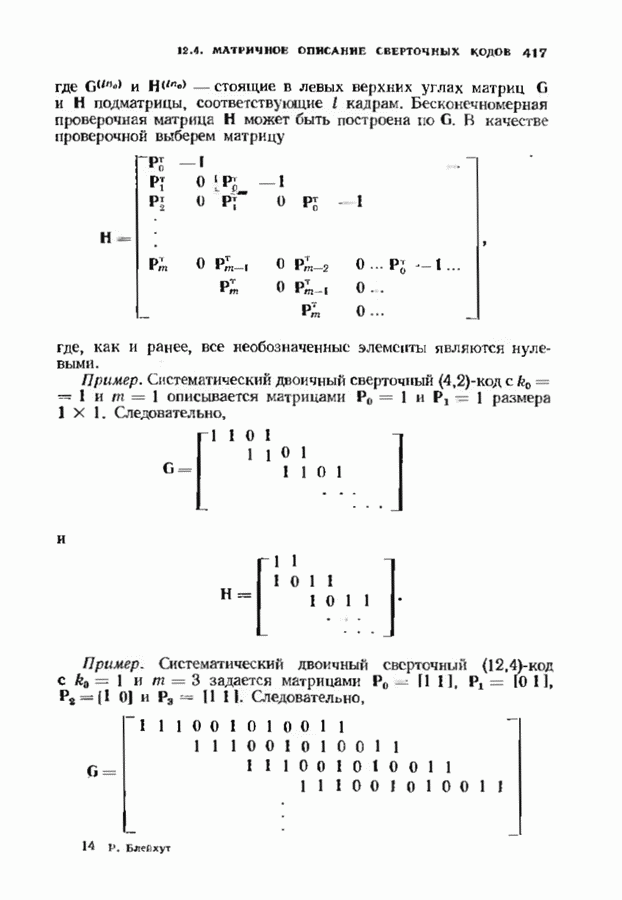
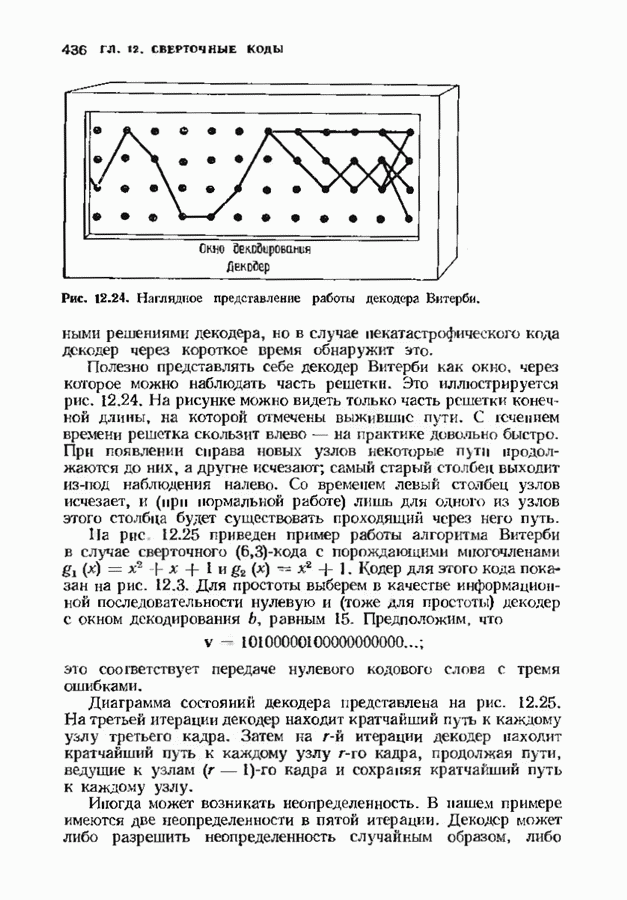
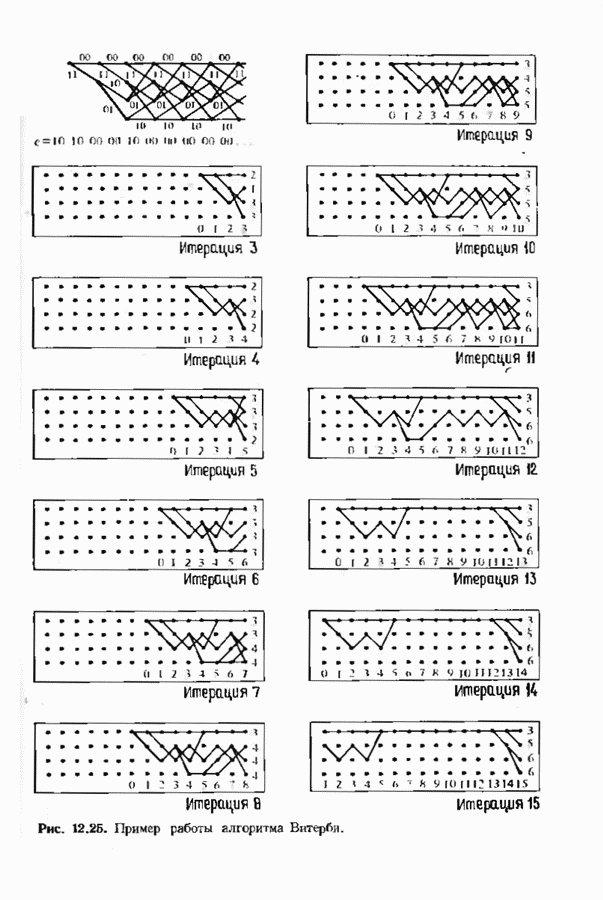
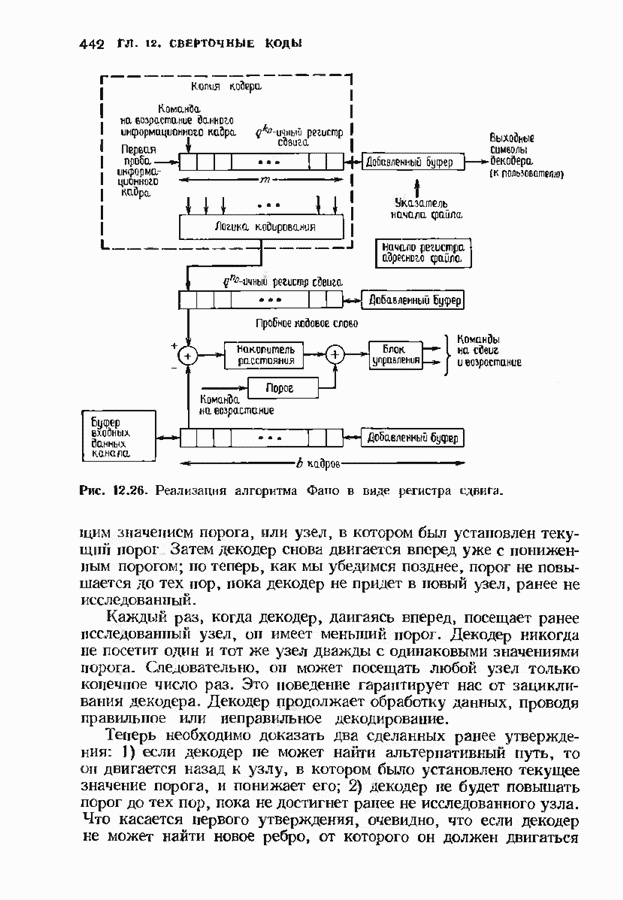
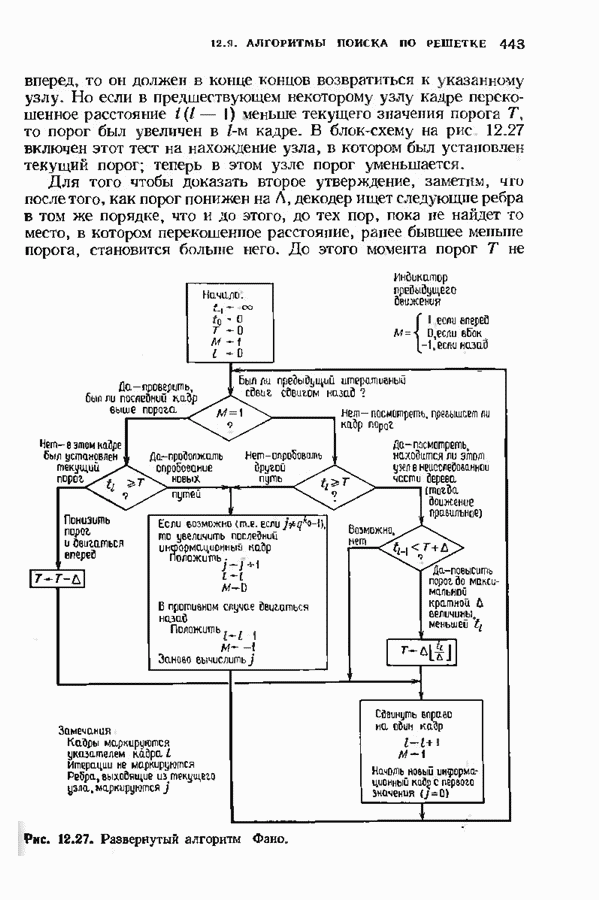
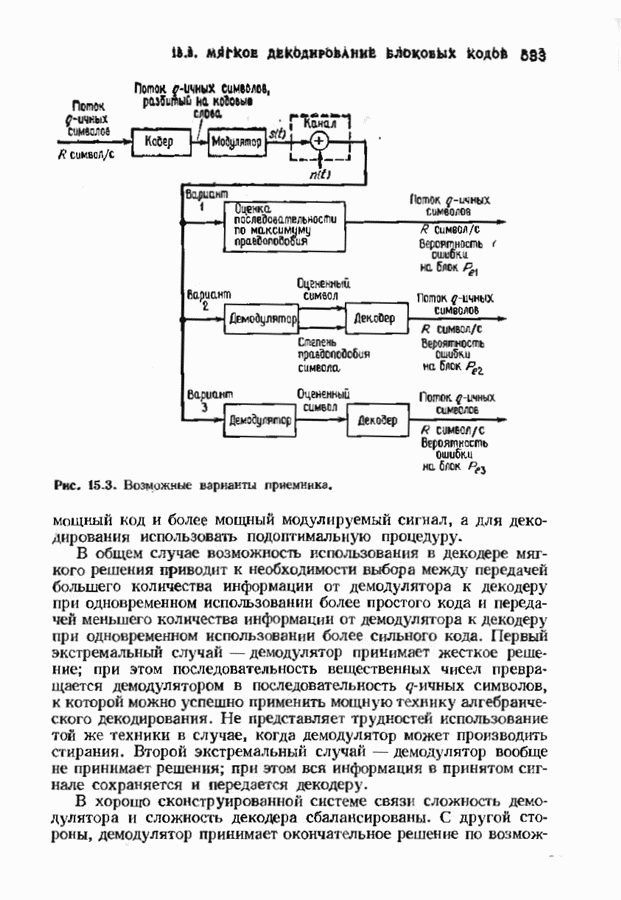
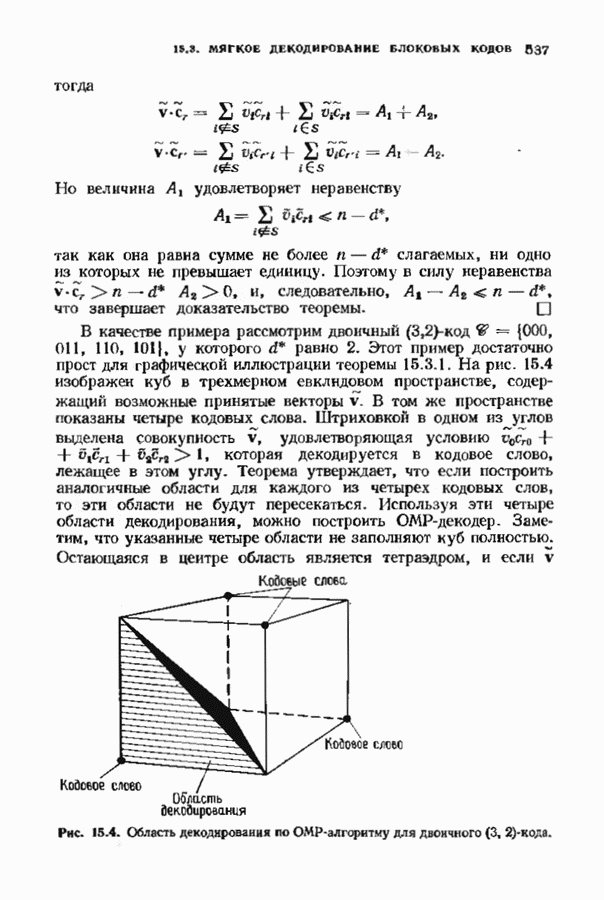
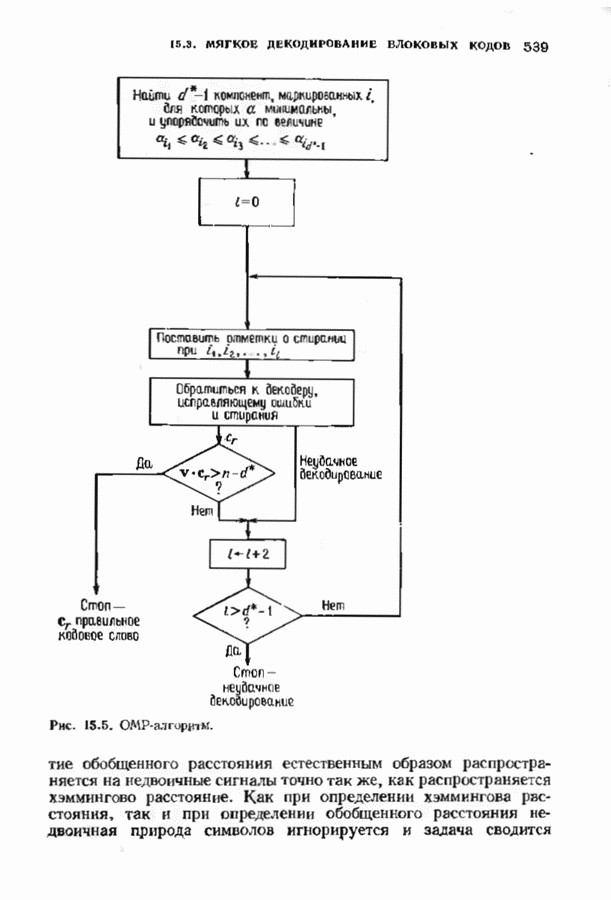
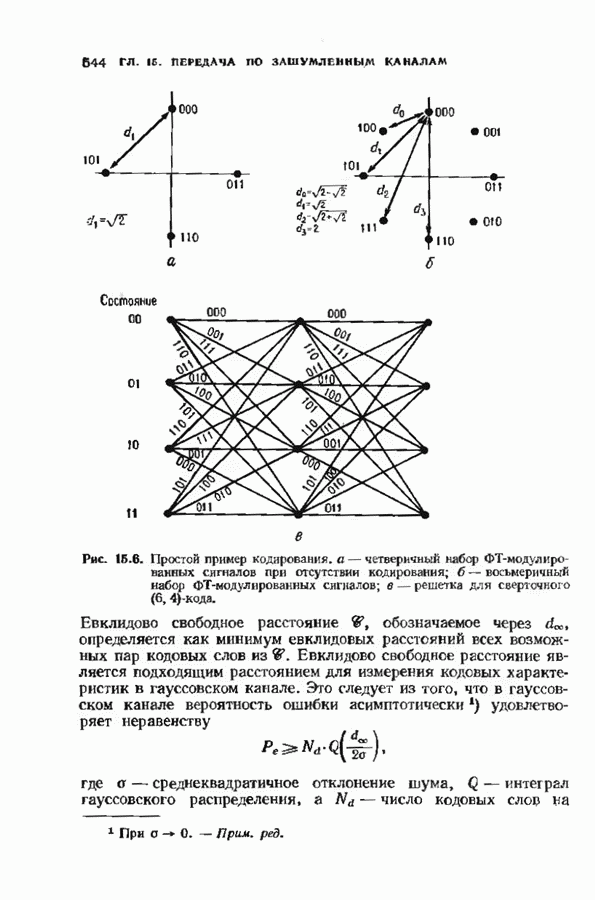
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
11.5. АЛГОРИТМ ВИНОГРАДА БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ
Отличный от рассмотренного ранее мегод вычисления быстрого преобразования Фурье дается БПФ-алгоритмом Винограда. Этот алгоритм основывается на четырех отдельных идеях: алгоритме Рейдера, описанном в § 11.2 алгоритме Винограда вычисления коротких сверток, схеме индексации алгоритма Гуда-Томаса для простых множителей, гнездовом алгоритме Винограда (см.
ниже). БПФ-алгоритм Винограда лучше БПФ-алгоритмов Кули— Тьюки и Гуда-Томаса по числу умножений, но сложнее по структуре. За уменьшение числа умножений приходится платить усложнением индексации и использованием операций отображения.
БПФ-алгоритм Винограда подразделяется на малый БПФ-алгоритм Винограда и большой БПФ-алгоритм Винограда. К малому алгоритму относятся преобразования, длина которых равна малому простому числу или степени малого простого числа. Большой БПФ-алгоритм Винограда объединяет малые БПФ-алгоритмы Винограда, чтобы получить преобразование на большой длине 
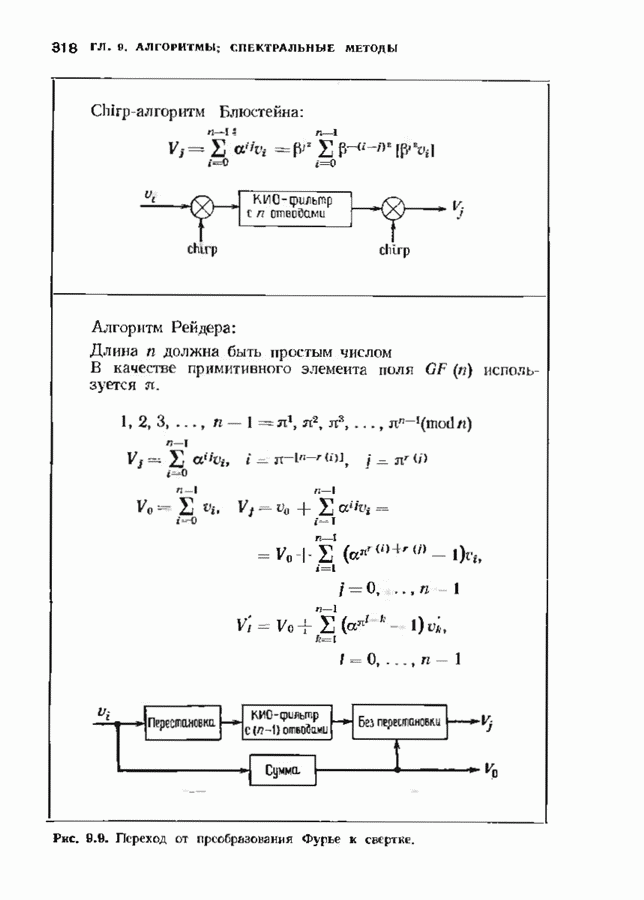
Первым шагом является построение малого БПФ-алгоритма Винограда. Если  малое простое число, то воспользуемся алгоритмом Рейдера, сводя вычисление преобразования Фурье к вычислению циклической свертки, которую в свою очередь вычислим с помощью алгоритма Винограда вычисления коротких сверток. В общем случае уравнения выписываются непосредственно, так что выбирать слишком большие и непрактично. В алгоритме Рейдера сведения дискретного преобразования Фурье к свертке используется только переиндексация; на этом шаге не требуется никаких сложений и умножений. Структура алгоритма вычисления свертки включает сначала сложения, потом умножения и затем опять сложения. Если
малое простое число, то воспользуемся алгоритмом Рейдера, сводя вычисление преобразования Фурье к вычислению циклической свертки, которую в свою очередь вычислим с помощью алгоритма Винограда вычисления коротких сверток. В общем случае уравнения выписываются непосредственно, так что выбирать слишком большие и непрактично. В алгоритме Рейдера сведения дискретного преобразования Фурье к свертке используется только переиндексация; на этом шаге не требуется никаких сложений и умножений. Структура алгоритма вычисления свертки включает сначала сложения, потом умножения и затем опять сложения. Если  представляет собой степень малого простого числа, то можно использовать ту же самую процедуру, заменив алгоритм Рейдера некоторым более общим алгоритмом, который мы рассматривать не будем.
представляет собой степень малого простого числа, то можно использовать ту же самую процедуру, заменив алгоритм Рейдера некоторым более общим алгоритмом, который мы рассматривать не будем.
Построим алгоритм Винограда вычисления пятиточечного БПФ в поле  находящий величины
находящий величины 

Воспользуемся рассмотренным ранее (см. § 9.8) алгоритмом Рейдера, сводящим пятиточечное преобразование Фурье к свертке

где

Здесь многочлен  фиксирован, многочлен
фиксирован, многочлен  получается из многочлена
получается из многочлена  перестановкой коэффициентов с отбрасыванием, а мпогочлеи
перестановкой коэффициентов с отбрасыванием, а мпогочлеи  получается из многочлена
получается из многочлена  без отбрасывания коэффициента.
без отбрасывания коэффициента.
Малый иятиточечпый алгоритм Винограда вычисления БПФ получится, если для вычисления произведения  воспользоваться алгоритмом Винограда вычисления короткой свертки. Обращаясь к таблице на рис. 11.2, находим алгоритм Винограда вычисления четырехточечной циклической свертки, содержащий девять умножений. Воспользуемся этим алгоритмом для построения алгоритма преобразования Фурье. Соединим операции переиндексации алгоритма Рейдера с матричными операциями алгоритма свертки, выполняя соответствующие перестановки строк и столбцов. Далее, так как коэффициенты многочлена
воспользоваться алгоритмом Винограда вычисления короткой свертки. Обращаясь к таблице на рис. 11.2, находим алгоритм Винограда вычисления четырехточечной циклической свертки, содержащий девять умножений. Воспользуемся этим алгоритмом для построения алгоритма преобразования Фурье. Соединим операции переиндексации алгоритма Рейдера с матричными операциями алгоритма свертки, выполняя соответствующие перестановки строк и столбцов. Далее, так как коэффициенты многочлена  являются фиксированными константами поля
являются фиксированными константами поля  то произведение
то произведение  на соответствующую матрицу можно вычислить заранее. Внеся все эти изменения в алгоритм чешрехточечной свертки и присоединяя к нему компоненты
на соответствующую матрицу можно вычислить заранее. Внеся все эти изменения в алгоритм чешрехточечной свертки и присоединяя к нему компоненты  и
и  получаем малый пятиточечный алгоритм Винограда БПФ. На рис. 11.6 приведена запись этого алгоритма в матричном виде:
получаем малый пятиточечный алгоритм Винограда БПФ. На рис. 11.6 приведена запись этого алгоритма в матричном виде:

Отметим, что матрица А предварительных сложений и матрица В последующих сложений не являются квадратными. Пятиточечный входной вектор перед выполнением покомпонентного умножения вытягивается в десятиточечный, задаваемый матрицей  Первая строка матричного равенства связана с вычислением компоненты
Первая строка матричного равенства связана с вычислением компоненты  и не содержит умножений. Остальные девять строк определяются алгоритмом чешрехточечной циклической свертки. Одна из констант, на которую происходит умножение, равна
и не содержит умножений. Остальные девять строк определяются алгоритмом чешрехточечной циклической свертки. Одна из констант, на которую происходит умножение, равна

Рис. 11.6. Чалый питмточечпыи алгоритм Винограда вычисление БПФ.
единице, так что на самом деле приходится выполнять только восемь умножений.
Рассмотренный способ реализации малого БПФ-алгоритма Винограда можно использовать в случае, когда  является простым числом. Можно также построить малый БПФ-алгоритм Винограда, когда
является простым числом. Можно также построить малый БПФ-алгоритм Винограда, когда  является степенью малого простого числа. Вообще говоря, пользоваться малыми БПФ-алгоритмами
является степенью малого простого числа. Вообще говоря, пользоваться малыми БПФ-алгоритмами
Винограда можно только при малых длинах. При больших длинах преобразований предпочтительнее алгоритмы с менее четкой структурой, хотя бы и за счет некоторого увеличения числа умножений. Этим требованиям удовлетворяет большой  -алгоритм Винограда.
-алгоритм Винограда.
В общем случае БПф-алгоритм Винограда строится для длины  равной произведению простых чисел или степеней простых чисел. Рассмотрим случай двух множителей, когда
равной произведению простых чисел или степеней простых чисел. Рассмотрим случай двух множителей, когда  Воспользуемся алгоритмом Гуда-Томаса для преобразования
Воспользуемся алгоритмом Гуда-Томаса для преобразования  -точечного преобразования Фурье в двумерное
-точечного преобразования Фурье в двумерное  -точечное преобразование Фурье. Отдельные компоненты этого двумерного преобразования Фурье могут быть вычислены с помощью соответственно
-точечное преобразование Фурье. Отдельные компоненты этого двумерного преобразования Фурье могут быть вычислены с помощью соответственно  -точечного и
-точечного и  -точечного алгоритмов Винограда. Сначала выполняется
-точечного алгоритмов Винограда. Сначала выполняется  -точечное преобразование Фурье каждой строки, а затем
-точечное преобразование Фурье каждой строки, а затем  -точечное преобразование Фурье каждого столбца.
-точечное преобразование Фурье каждого столбца.
Перед БПФ-алгоритмом Винограда выполняется, однако, еще один шаг. Так как не существенно, применяется ли преобразование Фурье сначала к строкам или сначала к столбцам двумерного блока, то представляется возможным как-то их совместить. Именно это и делает БПФ-алгоритм Винограда. Он совмещает вычисления преобразований строк и столбцов, уменьшая при этом число умножений. Этот метод использует кронскеровское произведение матриц. Сделаем перерыв в изложении, чтобы ввести определение кронекеровского произведения матриц и доказать одну важную теорему. После этого мы сможем завершить построение БПФ-алгоритма Винограда.
Определение 11.5.1. Пусть  — матрицы соответственно размеров
— матрицы соответственно размеров  и
и  Тогда кронекеровским произведением матриц
Тогда кронекеровским произведением матриц  обозначаемым
обозначаемым  называется матрица, содержащая
называется матрица, содержащая  строк и
строк и  столбцов, у которой на пересечении строки с номером
столбцов, у которой на пересечении строки с номером  и столбца с номером
и столбца с номером  стоит элемент
стоит элемент

Чтобы проще попять структуру кронекеровского произведения матриц, следует представить матрицу  в виде
в виде  -таблицы, состоящей из
-таблицы, состоящей из  -блоков,
-блоков,  из которых равен
из которых равен  Непосредственно из определения вытекает, что кронекеровское произведение матриц некоммутативно, но ассоциативно:
Непосредственно из определения вытекает, что кронекеровское произведение матриц некоммутативно, но ассоциативно:

Элементы матриц  одни и те же, но упорядочены по-разному. Очевидно также, что кронекеровское произведение дистрибутивно относительно обычного сложения матриц.
одни и те же, но упорядочены по-разному. Очевидно также, что кронекеровское произведение дистрибутивно относительно обычного сложения матриц.
Следующая теорема утверждает, что кронекеровское произведение двух произведений матриц равно матричному произведению кронекеровских произведений соответствующих матриц.
Теорема 11.5.2. Если все матричные произведения определены, то кронекеровское произведение удовлетворяет равенству

Доказательство. Пусть матрицы  имеют соответственно размеры
имеют соответственно размеры  Так как матрица
Так как матрица  содержит
содержит  столбцов, а матрица
столбцов, а матрица  содержит
содержит  строк, то матричное произведение
строк, то матричное произведение  определено. Оно содержит
определено. Оно содержит  строк, которые мы занумеруем парами
строк, которые мы занумеруем парами  и
и  столбцов, которые мы занумеруем парами
столбцов, которые мы занумеруем парами  Элемент, стоящий на пересечении строки
Элемент, стоящий на пересечении строки  и столбца
и столбца  равен
равен  Так как матрица
Так как матрица  содержит I строк и
содержит I строк и  столбцов, а матрица
столбцов, а матрица  содержит
содержит  строк и
строк и  столбцов, то матрица
столбцов, то матрица  также является
также является  -матри-цей. Стоящий на пересечении
-матри-цей. Стоящий на пересечении  -строкн и
-строкн и  -столбца элемент этой матрицы равен
-столбца элемент этой матрицы равен

что и завершает доказательство.
Кронекеровское произведение матриц применяется в теории преобразования Фурье. Пусть  матрицы преобразования Фурье соответственно длин
матрицы преобразования Фурье соответственно длин  Тогда
Тогда

являются соответственно матричными записями преобразований Фурье

Двумерное  -преобразование Фурье двумерного сигнала
-преобразование Фурье двумерного сигнала  получается применением преобразования
получается применением преобразования  к каждой строке с последующим применением преобразования
к каждой строке с последующим применением преобразования  к каждому столбцу. Считывая двумерный
к каждому столбцу. Считывая двумерный  -сигнал по строкам, можно преобразовать его в одномерный. (Возможно, что двумерный сигнал был предварительно сформирован из одномерного с помощью китайской теоремы об остатках. Считывание такого сигнала по строкам дает новое одномерное представление этого сигнала, которое получается из исходного одномерного сигнала перестановкой его компонент.)
-сигнал по строкам, можно преобразовать его в одномерный. (Возможно, что двумерный сигнал был предварительно сформирован из одномерного с помощью китайской теоремы об остатках. Считывание такого сигнала по строкам дает новое одномерное представление этого сигнала, которое получается из исходного одномерного сигнала перестановкой его компонент.)
Если предполагать, что одномерные  -точечные векторы
-точечные векторы  упорядочены описанным выше способом, то
упорядочены описанным выше способом, то
двумерное преобразование записывается через кронекеровское произведение в виде

Для алгоритма Винограда преобразований длин  имеет место матричное разложение
имеет место матричное разложение

где  - матрицы целых чисел рассматриваемого поля,
- матрицы целых чисел рассматриваемого поля,  диагональные матрицы над
диагональные матрицы над  Умножения на
Умножения на  описывают все умножения, которые приходится выполнять в алгоритме Винограда. Положим
описывают все умножения, которые приходится выполнять в алгоритме Винограда. Положим  и дважды применим теорему 11.7.2:
и дважды применим теорему 11.7.2:

где кронекеровскис произведения  содержат только элементы из поля
содержат только элементы из поля  а кронекеровское произведение
а кронекеровское произведение  опять яаляется диагональной матрицей над
опять яаляется диагональной матрицей над  Следовательно, мы опять получили
Следовательно, мы опять получили  -точечное преобразование Фурье в форме алгоритма Винограда БПФ. Это дает способ построения большого алгоритма Винограда БПФ из малых.
-точечное преобразование Фурье в форме алгоритма Винограда БПФ. Это дает способ построения большого алгоритма Винограда БПФ из малых.
Из приведенного описания матрицы  видно, что такое преобразование предполагает предварительную запись (с помощью алгоритма Гуда-Томаса для взаимно простых множителей)
видно, что такое преобразование предполагает предварительную запись (с помощью алгоритма Гуда-Томаса для взаимно простых множителей)  -точечного одномерного преобразования в виде двумерного преобразования с последующим считыванием преобразуемого двумерного вектора по строкам в виде одномерного
-точечного одномерного преобразования в виде двумерного преобразования с последующим считыванием преобразуемого двумерного вектора по строкам в виде одномерного  -точечного вектора
-точечного вектора  Следовательно, описанный способ вычисления
Следовательно, описанный способ вычисления  -точечного преобразования
-точечного преобразования  предполагает предварительную перестановку компонент вектора
предполагает предварительную перестановку компонент вектора  и вычисление компонент вектора V также в переставленном порядке. Но поскольку вид матриц
и вычисление компонент вектора V также в переставленном порядке. Но поскольку вид матриц  известен, то тривиальная перестановка столбцов матрицы А и строк матрицы В позполяет выписывать компоненты векторов
известен, то тривиальная перестановка столбцов матрицы А и строк матрицы В позполяет выписывать компоненты векторов  и V в их естественном порядке.
и V в их естественном порядке.
Пусть  и
и  означают соответственное число умножений, необходимых для выполнения
означают соответственное число умножений, необходимых для выполнения  и
и  -точечного БПФ по алгоритму Винограда. Тогда число
-точечного БПФ по алгоритму Винограда. Тогда число  умножений, необходимых для вычисления
умножений, необходимых для вычисления  -точечного преобразования по алгоритму Винограда, равно примерно
-точечного преобразования по алгоритму Винограда, равно примерно  Более точно,
Более точно,

и величины  и
и  не превосходят размеров матриц
не превосходят размеров матриц  соответственно, так как один или более элементов диагональных матриц могут оказаться равными единице. Если учитывать все умножения диагональных матриц, включая и умножения на единицу, то получаем простую формулу
соответственно, так как один или более элементов диагональных матриц могут оказаться равными единице. Если учитывать все умножения диагональных матриц, включая и умножения на единицу, то получаем простую формулу

| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ВВЕДЕНИЕ
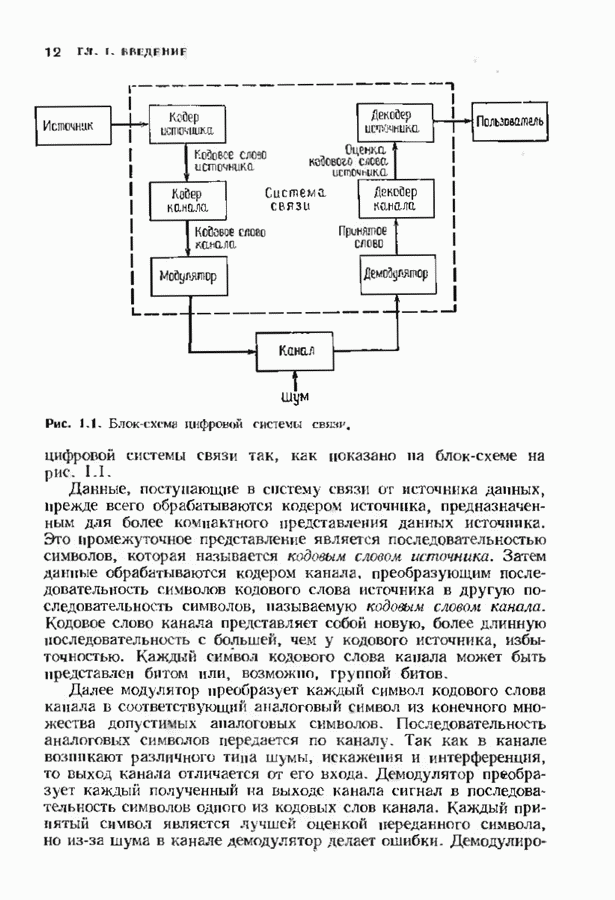
- 1.1. ДИСКРЕТНЫЙ КАНАЛ, СВЯЗИ
- 1.2. ИСТОРИЯ КОДИРОВАНИЯ, КОНТРОЛИРУЮЩЕГО ОШИБКИ
- 1.3. ПРИЛОЖЕНИЯ
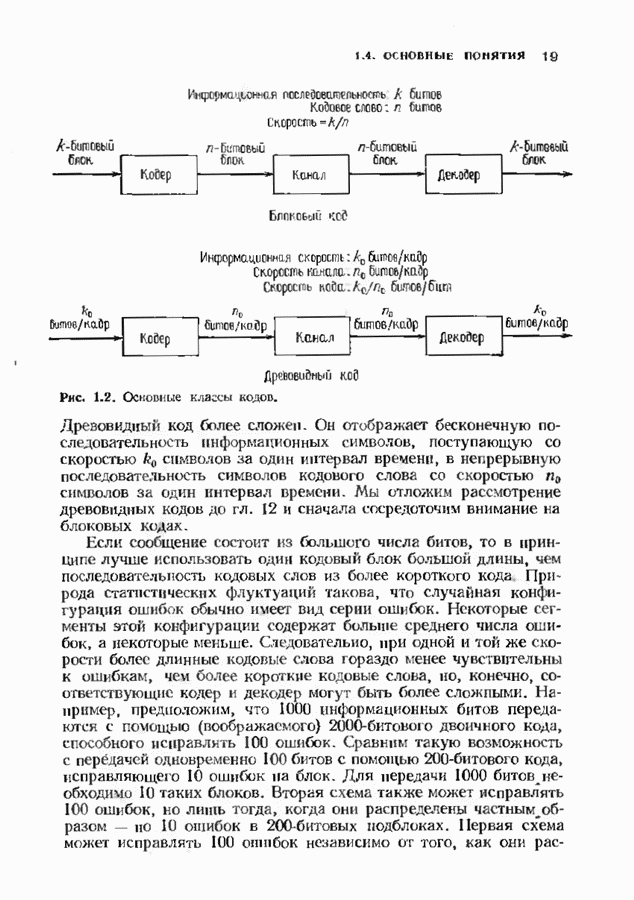
- 1.4. ОСНОВНЫЕ ПОНЯТИЯ
- 1.5. ПРОСТЕЙШИЕ КОДЫ
- ГЛАВА 2. ВВЕДЕНИЕ В АЛГЕБРУ
- 2.1. 2-ПОЛЕ И 6-10-ПОЛЕ
- 2.2. ГРУППЫ
- 2.3. КОЛЬЦА
- 2.4. ПОЛЯ
- 2.5. ВЕКТОРНЫЕ ПРОСТРАНСТВА
- 2.6. ЛИНЕЙНАЯ АЛГЕБРА
- ГЛАВА 3. ЛИНЕЙНЫЕ БЛОКОВЫЕ КОДЫ
- 3.1. СТРУКТУРА ЛИНЕЙНЫХ БЛОКОВЫХ КОДОВ
- 3.2. МАТРИЧНОЕ ОПИСАНИЕ ЛИНЕЙНЫХ БЛОКОВЫХ КОДОВ
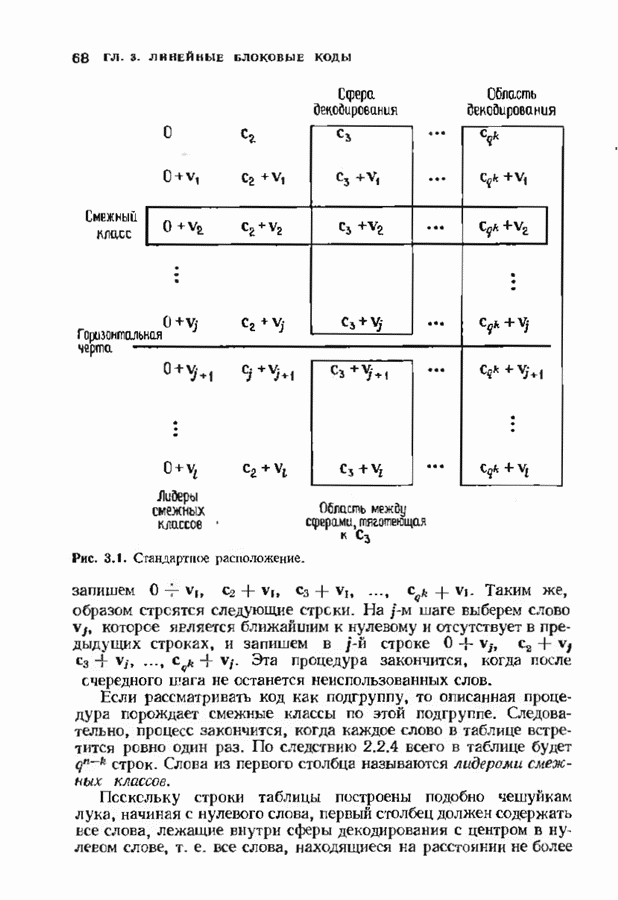
- 3.3. СТАНДАРТНОЕ РАСПОЛОЖЕНИЕ
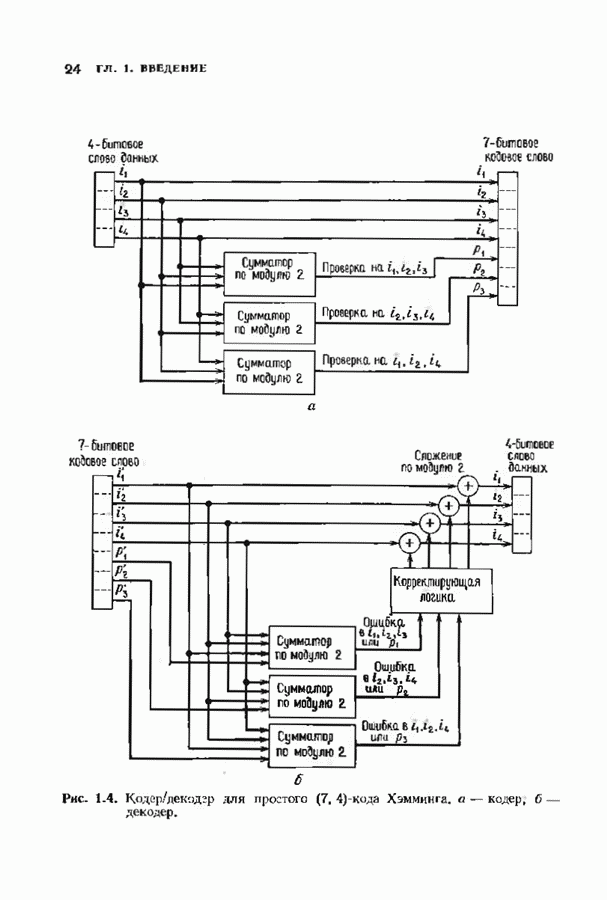
- 3.4. КОДЫ ХЭММИНГА
- 3.5. СОВЕРШЕННЫЕ И КВАЗИСОВЕРШЕННЫЕ КОДЫ
- 3.6. ПРОСТЫЕ ПРЕОБРАЗОВАНИЯ ЛИНЕЙНОГО КОДА
- 3.7. КОДЫ РИДА—МАЛЛЕРА
- ГЛАВА 4. АРИФМЕТИКА ПОЛЕЙ ГАЛУА
- 4.2. КОНЕЧНЫЕ ПОЛЯ, ОСНОВАННЫЕ НА КОЛЬЦЕ ЦЕЛЫХ ЧИСЕЛ
- 4.3. КОЛЬЦА МНОГОЧЛЕНОВ
- 4.4. КОНЕЧНЫЕ ПОЛЯ, ОСНОВАННЫЕ НА КОЛЬЦАХ МНОГОЧЛЕНОВ
- 4.5. ПРИМИТИВНЫЕ ЭЛЕМЕНТЫ
- 4.6. СТРУКТУРА КОНЕЧНОГО ПОЛЯ
- ГЛАВА 5. ЦИКЛИЧЕСКИЕ КОДЫ
- 5.2. ПОЛИНОМИАЛЬНОЕ ОПИСАНИЕ ЦИКЛИЧЕСКИХ КОДОВ
- 5.3. МИНИМАЛЬНЫЕ МНОГОЧЛЕНЫ И СОПРЯЖЕНИЯ
- 5.4. МАТРИЧНОЕ ОПИСАНИЕ ЦИКЛИЧЕСКИХ КОДОВ
- 5.5. КОДЫ ХЭММИНГА КАК ЦИКЛИЧЕСКИЕ КОДЫ
- 5.6. ЦИКЛИЧЕСКИЕ КОДЫ, ИСПРАВЛЯЮЩИЕ ДВЕ ОШИБКИ
- 5.7. ЦИКЛИЧЕСКИЕ КОДЫ, ИСПРАВЛЯЮЩИЕ ПАКЕТЫ ОШИБОК
- 5.8. ДВОИЧНЫЙ КОД ГОЛЕЯ
- 5.9. КВАДРАТИЧНО-ВЫЧЕТНЫЕ КОДЫ
- ГЛАВА 6. СХЕМНАЯ РЕАЛИЗАЦИЯ ЦИКЛИЧЕСКОГО КОДИРОВАНИЯ
- 6.1. ЛОГИЧЕСКИЕ ЦЕПИ ДЛЯ АРИФМЕТИКИ КОНЕЧНОГО ПОЛЯ
- 6.2. ЦИФРОВЫЕ ФИЛЬТРЫ
- 6.3. КОДЕРЫ И ДЕКОДЕРЫ НА РЕГИСТРАХ СДВИГА
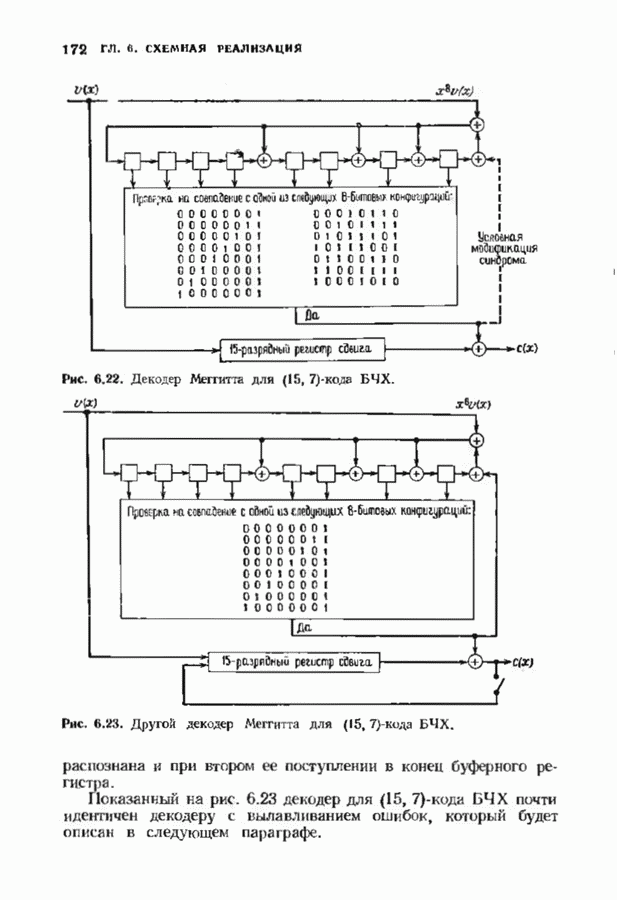
- 6.4. ДЕКОДЕР МЕГГИТТА
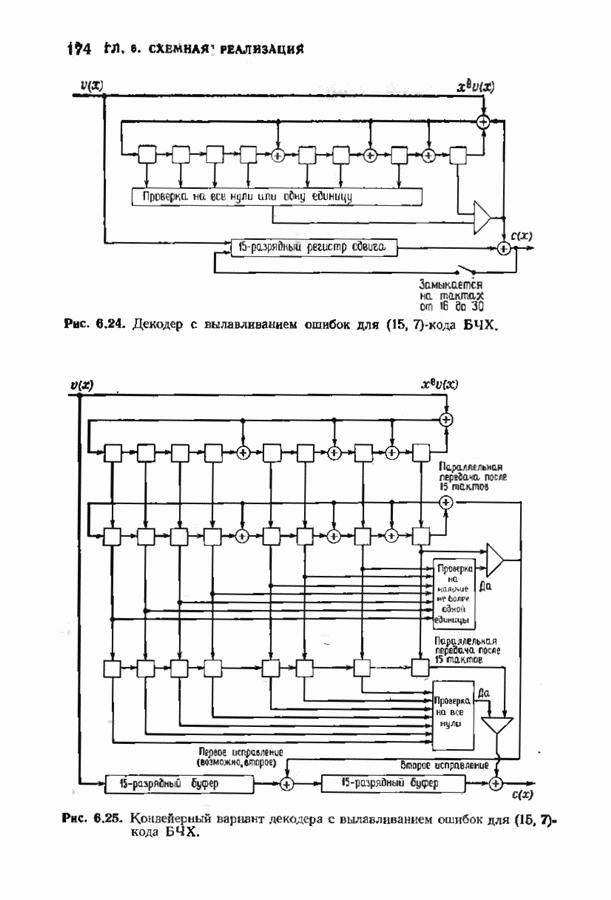
- 6.5. ВЫЛАВЛИВАНИЕ ОШИБОК
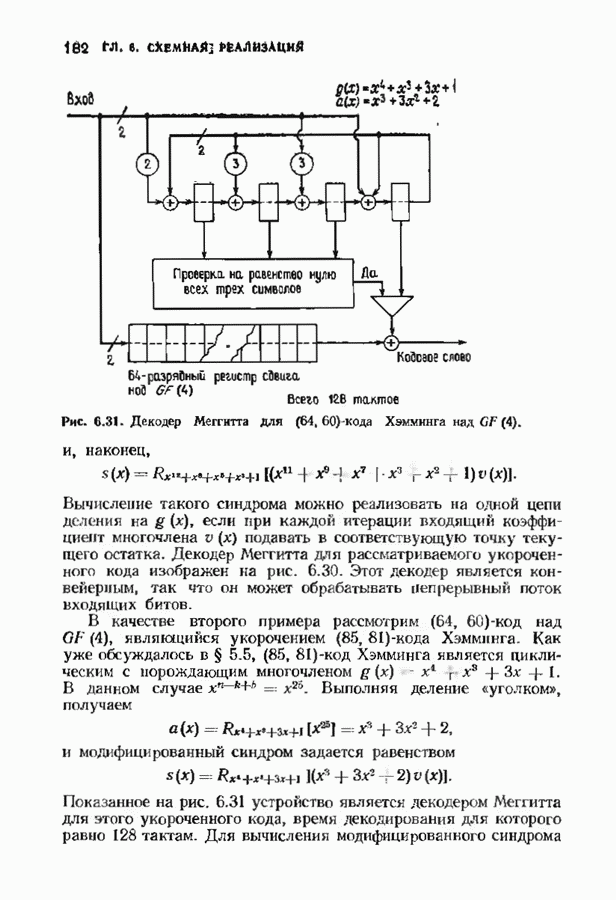
- 6.6. УКОРОЧЕННЫЕ ЦИКЛИЧЕСКИЕ КОДЫ
- 6.7. ДЕКОДЕР МЕГГИТТА ДЛЯ. КОДА ГОЛЕЯ
- ГЛАВА 7. КОДЫ БОУЗА-ЧОУДХУРИ-ХОКВИНГЕМА
- 7.2. ДЕКОДЕР ПИТЕРСОНА ГОРЕНСТЕЙНА—ЦИРЛЕРА
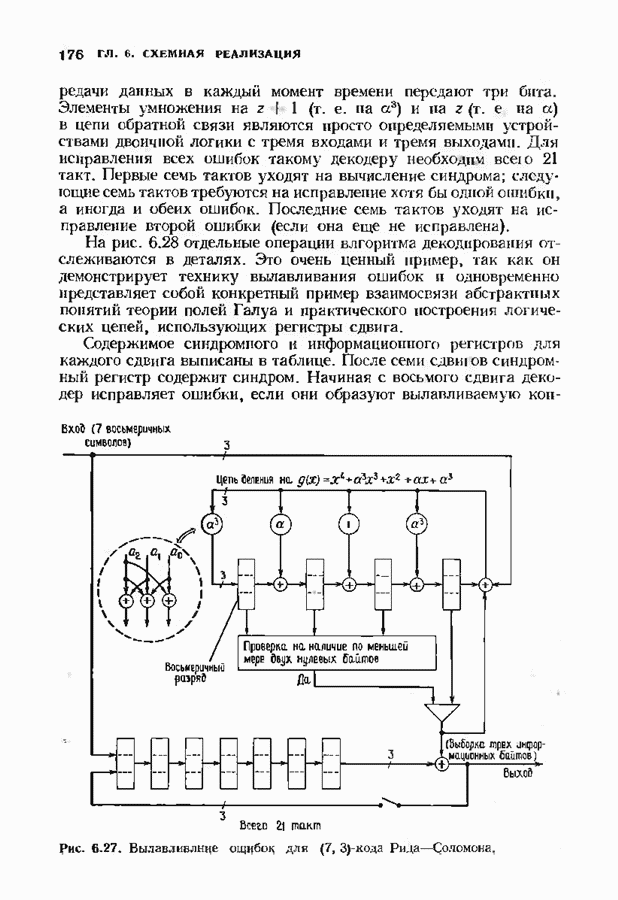
- 7.3. КОДЫ РИДА СОЛОМОНА
- 7.4. СИНТЕЗ АВТОРЕГРЕССИОННЫХ ФИЛЬТРОВ
- 7.5. БЫСТРОЕ ДЕКОДИРОВАНИЕ КОДОВ БЧХ
- 7.6. ДЕКОДИРОВАНИЕ ДВОИЧНЫХ КОДОВ БЧХ
- 7.7. ДЕКОДИРОВАНИЕ С ПОМОЩЬЮ АЛГОРИТМА ЕВКЛИДА
- 7.8. КАСКАДНЫЕ (ГНЕЗДОВЫЕ) КОДЫ
- 7.9. КОДЫ ЮСТЕСЕНА
- ГЛАВА 8. КОДЫ, ОСНОВАННЫЕ НА СПЕКТРАЛЬНЫХ МЕТОДАХ
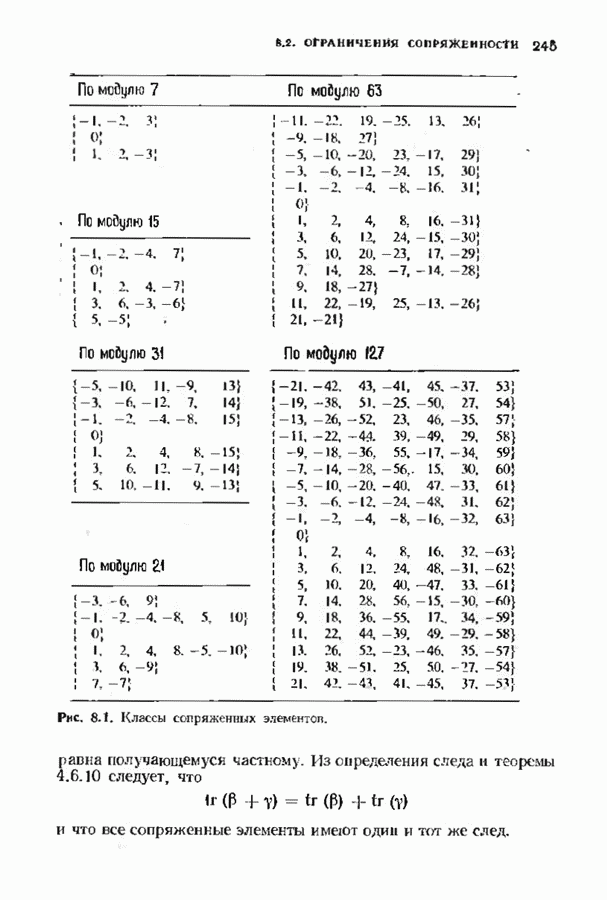
- 8.2. ОГРАНИЧЕНИЯ СОПРЯЖЕННОСТИ И ИДЕМПОТЕНТЫ
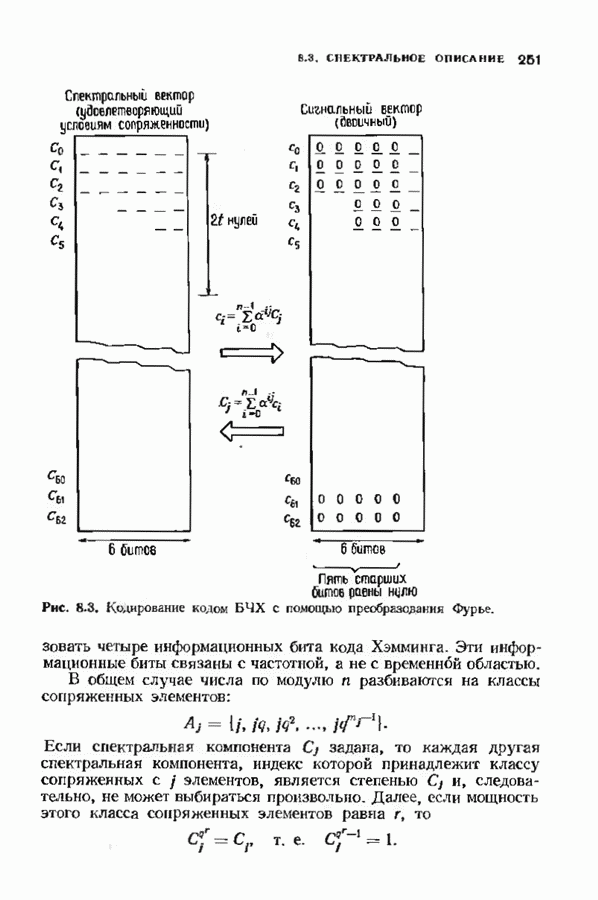
- 8.3. СПЕКТРАЛЬНОЕ ОПИСАНИЕ ЦИКЛИЧЕСКИХ КОДОВ
- 8.4. РАСШИРЕННЫЕ КОДЫ РИДА-СОЛОМОНА
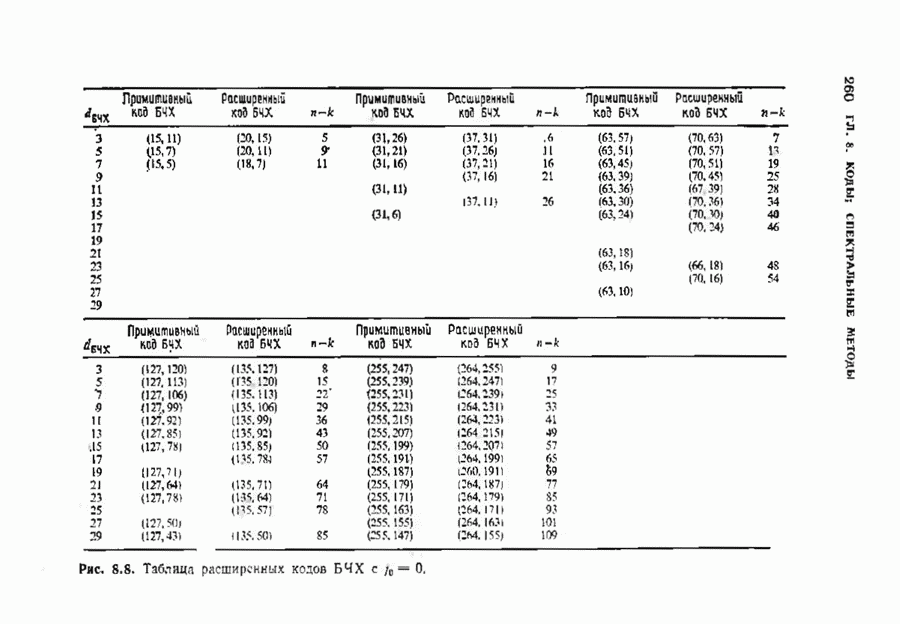
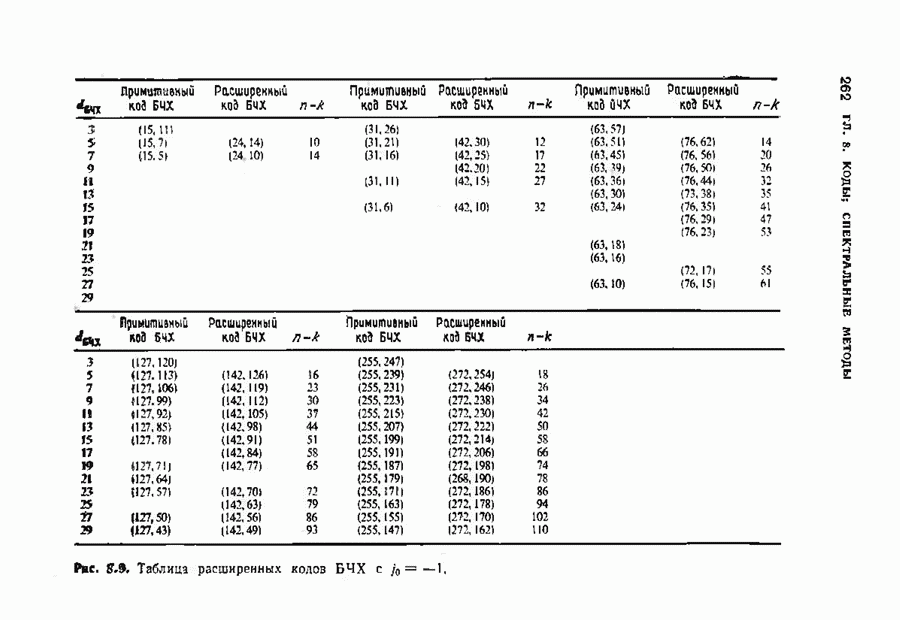
- 8.5. РАСШИРЕННЫЕ КОДЫ БЧХ
- 8.6. АЛЬТЕРНАНТНЫЕ КОДЫ
- 8.7. ХАРАКТЕРИСТИКИ АЛЬТЕРНАНТНЫХ КОДОВ
- 8.8. КОДЫ ГОППЫ
- 8.9. КОДЫ ПРЕПАРАТЫ
- ГЛАВА 9. АЛГОРИТМЫ, ОСНОВАННЫЕ НА СПЕКТРАЛЬНЫХ МЕТОДАХ
- 9.2. ИСПРАВЛЕНИЕ СТИРАНИЙ И ОШИБОК
- 9.3. ДЕКОДИРОВАНИЕ РАСШИРЕННЫХ КОДОВ РИДА—СОЛОМОНА
- 9.4. ДЕКОДИРОВАНИЕ РАСШИРЕННЫХ КОДОВ БЧХ
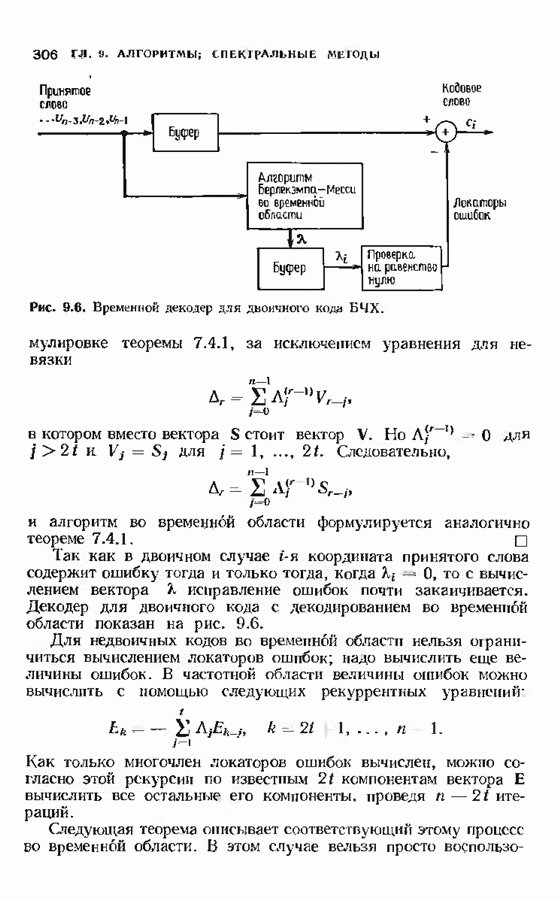
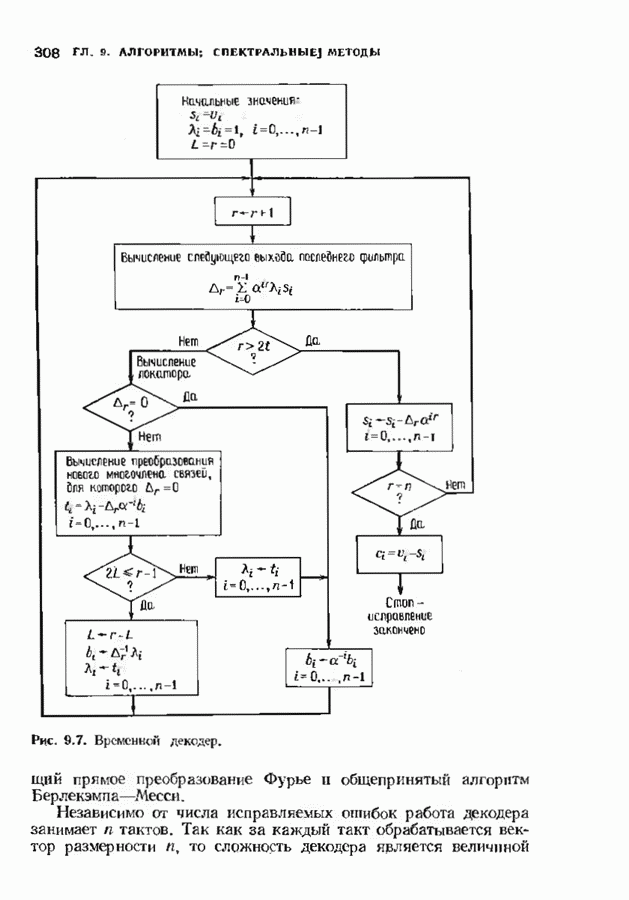
- 9.5. ДЕКОДИРОВАНИЕ ВО ВРЕМЕННОЙ ОБЛАСТИ
- 9.6. ДЕКОДИРОВАНИЕ ЗА ГРАНИЦЕЙ БЧХ
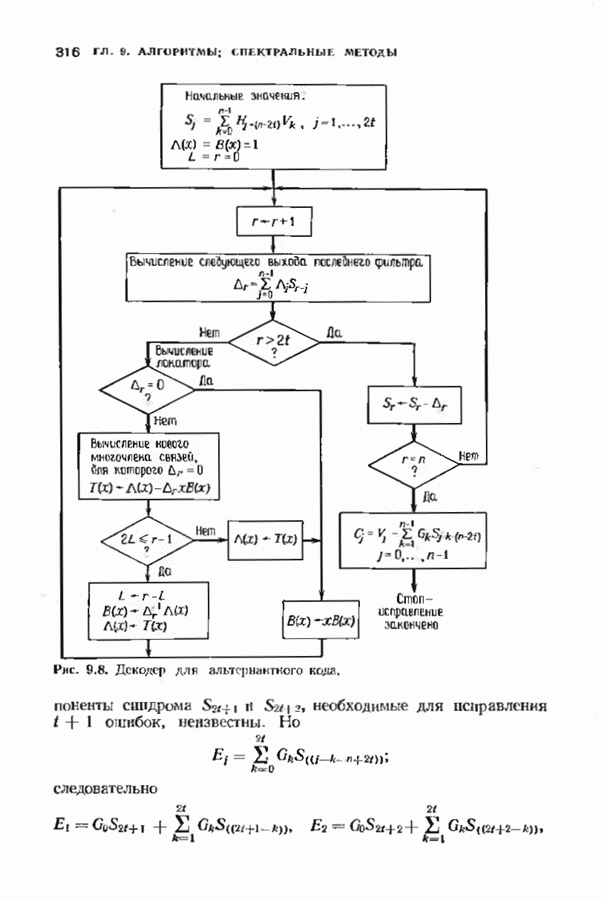
- 9.7. ДЕКОДИРОВАНИЕ АЛЬТЕРНАНТНЫХ КОДОВ
- 9.8. ВЫЧИСЛЕНИЕ ПРЕОБРАЗОВАНИЙ В КОНЕЧНЫХ ПОЛЯХ
- ГЛАВА 10. МНОГОМЕРНЫЕ СПЕКТРАЛЬНЫЕ МЕТОДЫ
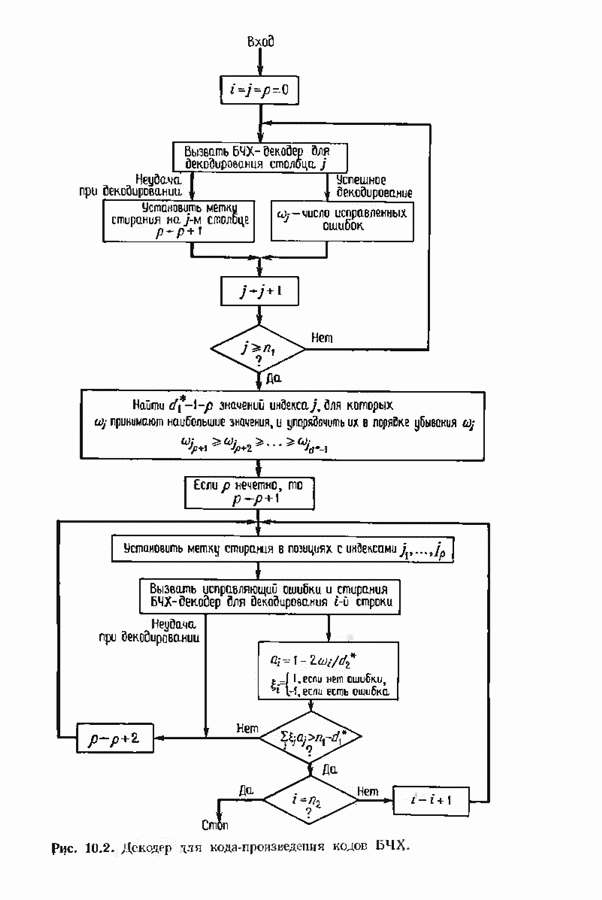
- 10.1. КОДЫ-ПРОИЗВЕДЕНИЯ
- 10.2. КИТАЙСКИЕ ТЕОРЕМЫ ОБ ОСТАТКАХ
- 10.3. ДЕКОДИРОВАНИЕ КОДА-ПРОИЗВЕДЕНИЯ
- 10.4. МНОГОМЕРНЫЕ СПЕКТРЫ
- 10.5. БЫСТРЫЕ КОДЫ БЧХ
- 10.6. ДЕКОДИРОВАНИЕ МНОГОМЕРНЫХ КОДОВ
- 10.7. ДЛИННЫЕ КОДЫ НАД МАЛЫМИ ПОЛЯМИ
- ГЛАВА 11. БЫСТРЫЕ АЛГОРИТМЫ
- 11.1. ЛИНЕЙНАЯ СВЕРТКА И ЦИКЛИЧЕСКАЯ СВЕРТКА
- 11.2. БЫСТРЫЕ АЛГОРИТМЫ СВЕРТКИ
- 11.3. БЫСТРЫЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 11.4. АЛГОРИТМЫ АГАРВАЛА—КУЛИ ВЫЧИСЛЕНИЯ СВЕРТОК
- 11.5. АЛГОРИТМ ВИНОГРАДА БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ
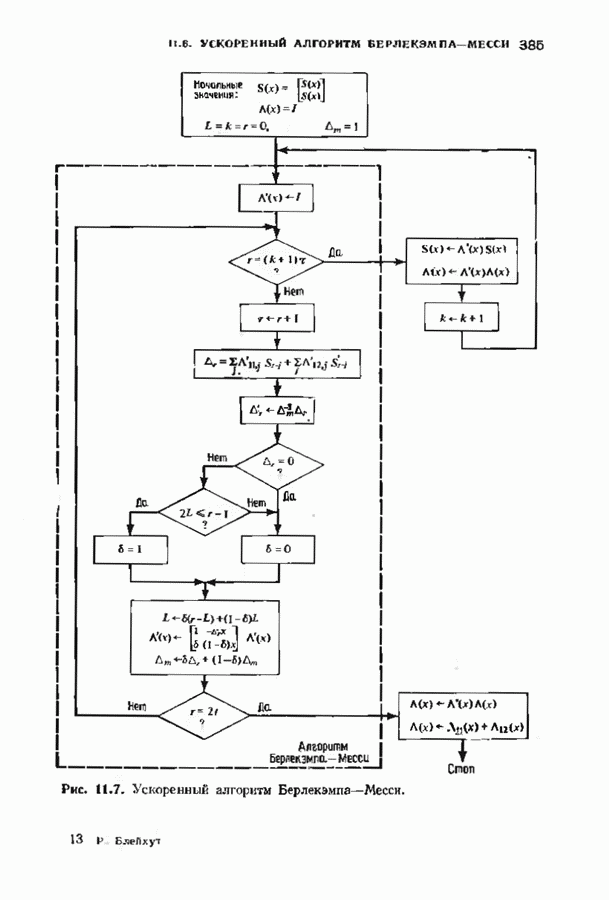
- 11.6. УСКОРЕННЫЙ АЛГОРИТМ БЕРЛЕКЭМПА—МЕССИ
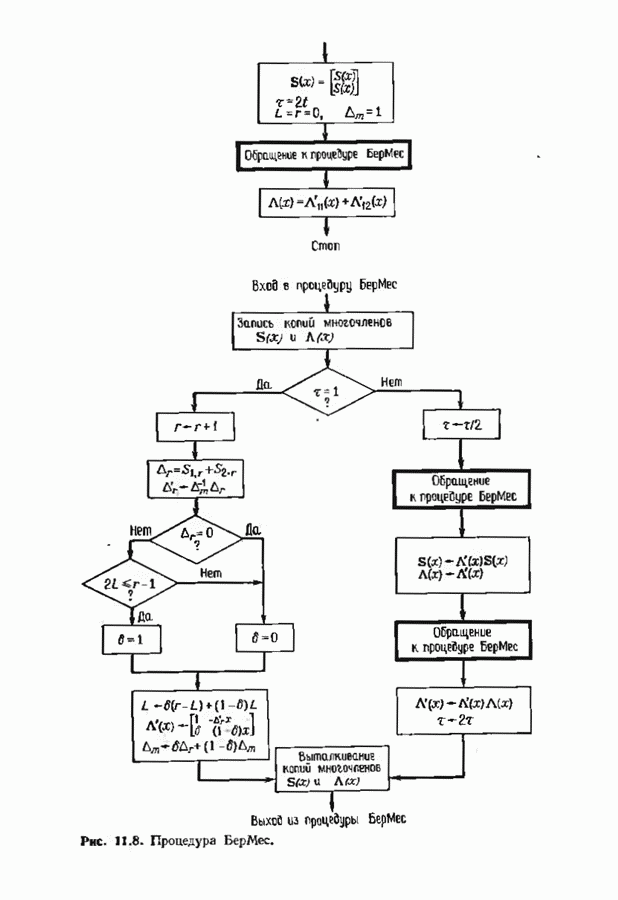
- 11.7. РЕКУРРЕНТНЫЙ АЛГОРИТМ БЕРЛЕКЭМПА—МЕССИ
- 11.8. УСКОРЕННОЕ ДЕКОДИРОВАНИЕ КОДОВ БЧХ
- 11.9. СВЕРТКА В СУРРОГАТНЫХ ПОЛЯХ
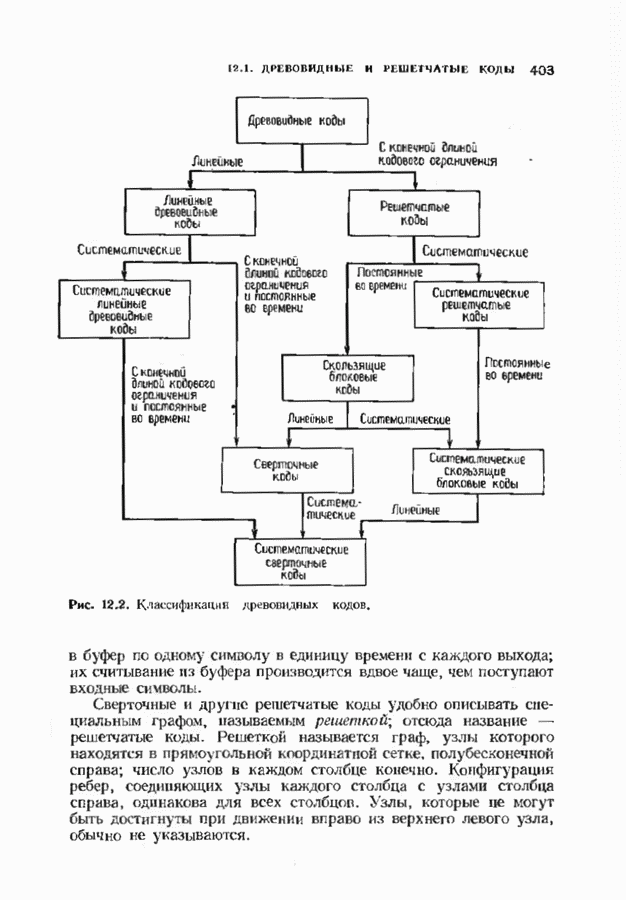
- ГЛАВА 12. СВЕРТОЧНЫЕ КОДЫ
- 12.2. ОПИСАНИЕ СВЕРТОЧНЫХ КОДОВ С ПОМОЩЬЮ МНОГОЧЛЕНОВ
- 12.3. ИСПРАВЛЕНИЕ ОШИБОК И ПОНЯТИЯ РАССТОЯНИЯ
- 12.4. МАТРИЧНОЕ ОПИСАНИЕ СВЕРТОЧНЫХ КОДОВ
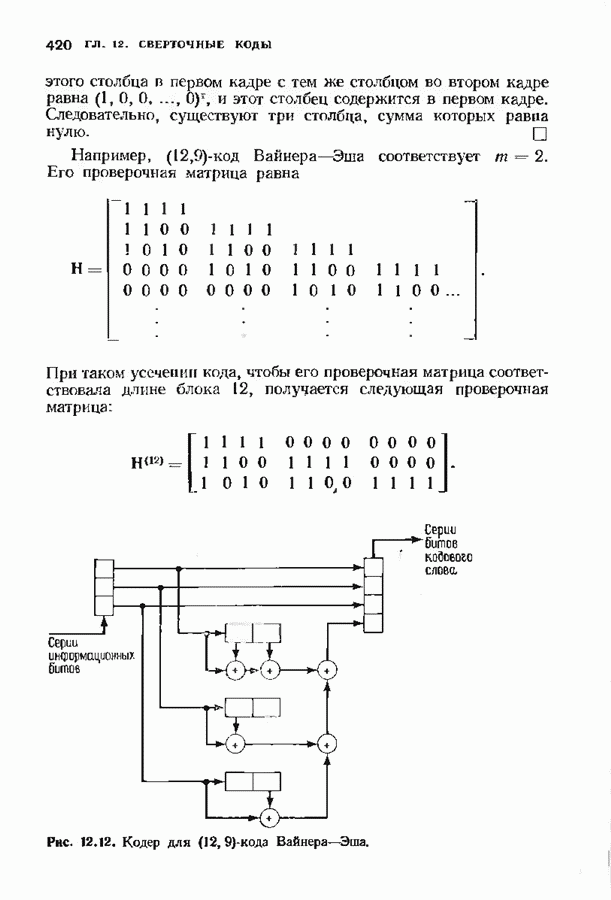
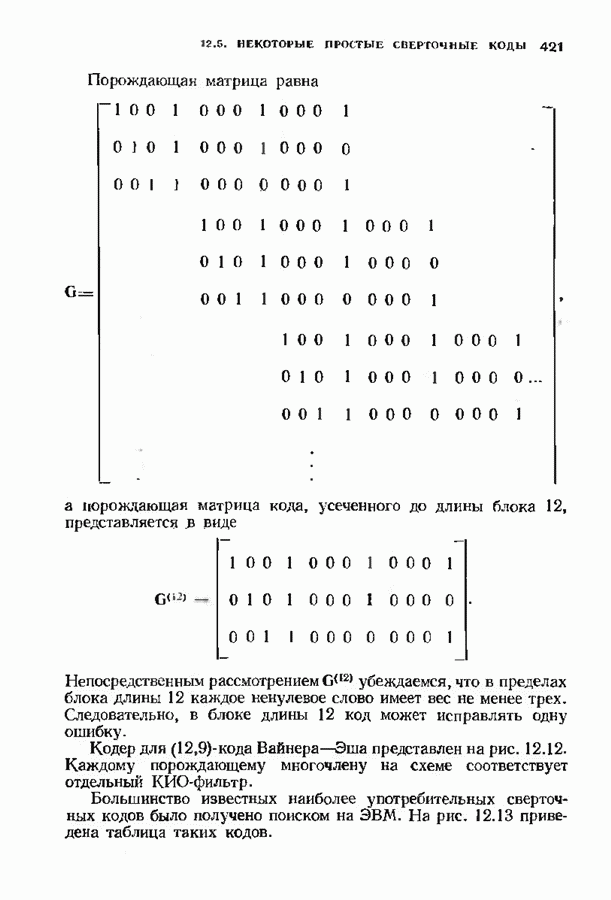
- 12.5. НЕКОТОРЫЕ ПРОСТЫЕ СВЕРТОЧНЫЕ КОДЫ
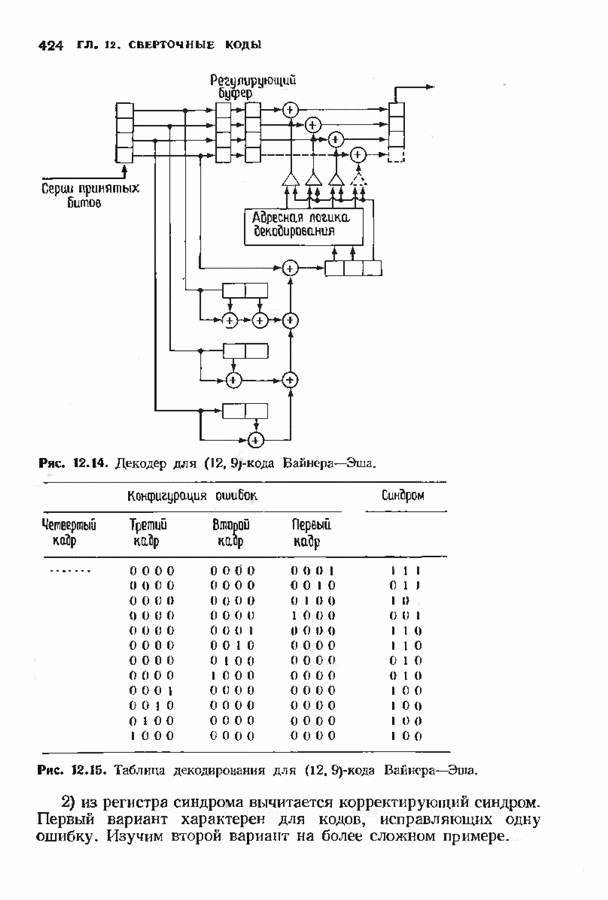
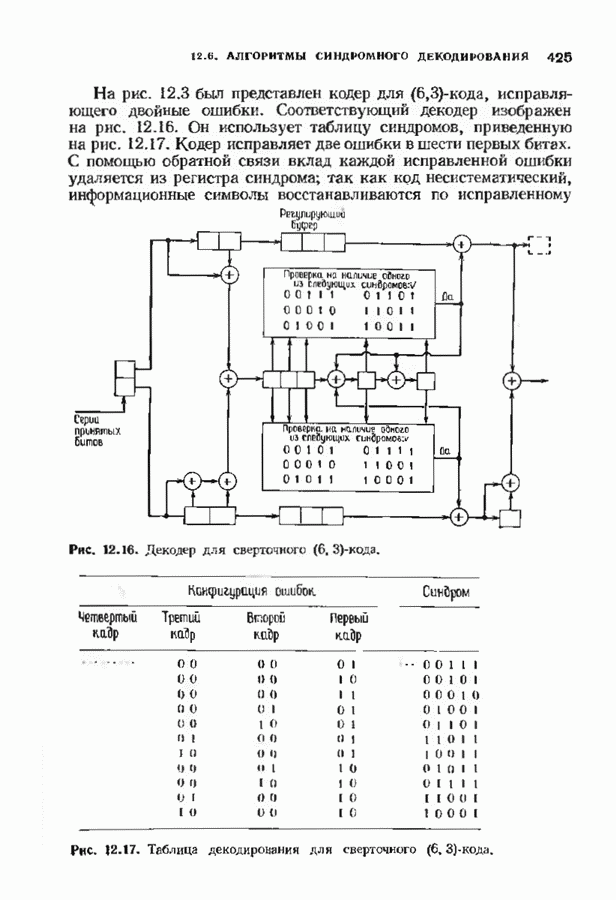
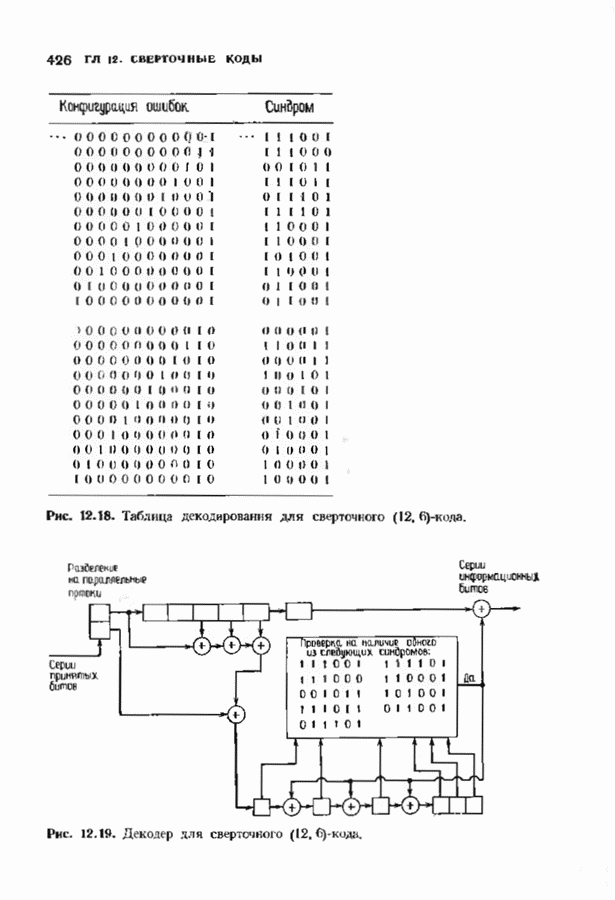
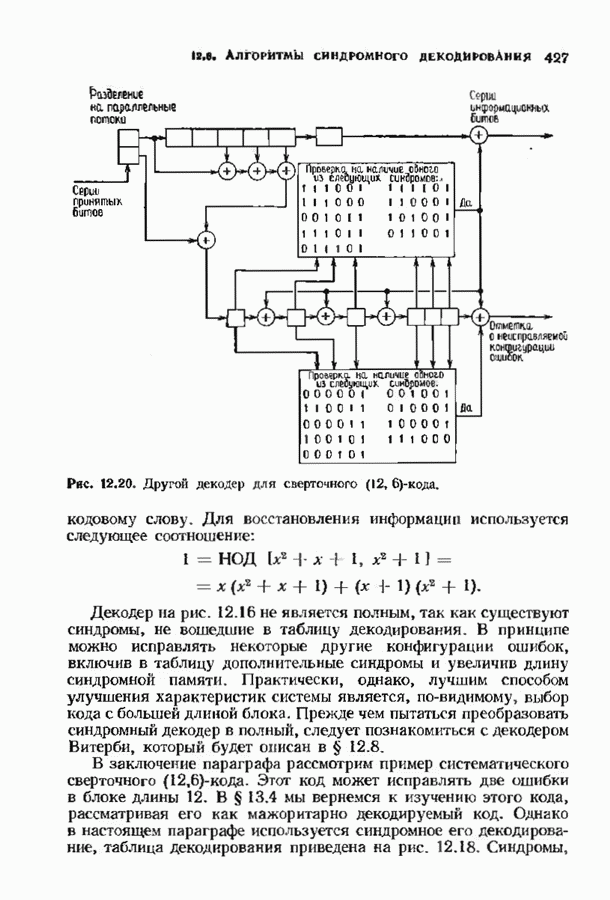
- 12.6. АЛГОРИТМЫ СИНДРОМНОГО ДЕКОДИРОВАНИЯ
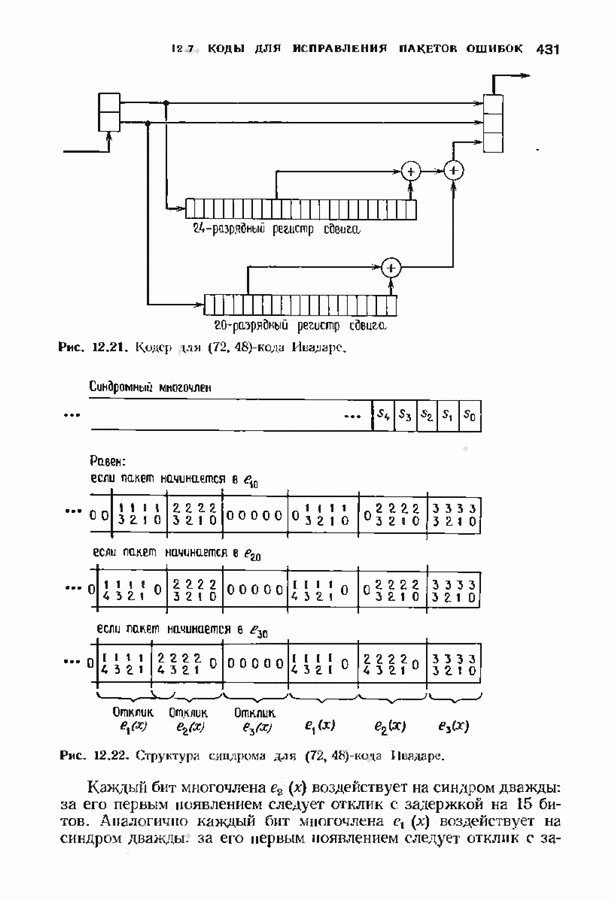
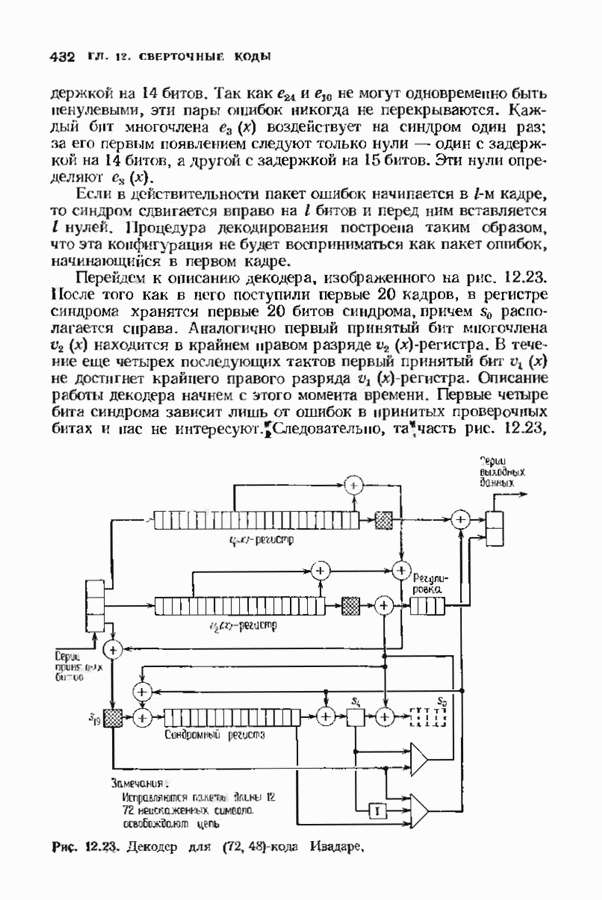
- 12.7. ОБЕРТОЧНЫЕ КОДЫ ДЛЯ ИСПРАВЛЕНИЯ ПАКЕТОВ ОШИБОК
- 12.8. АЛГОРИТМ ДЕКОДИРОВАНИЯ ВИТЕРБИ
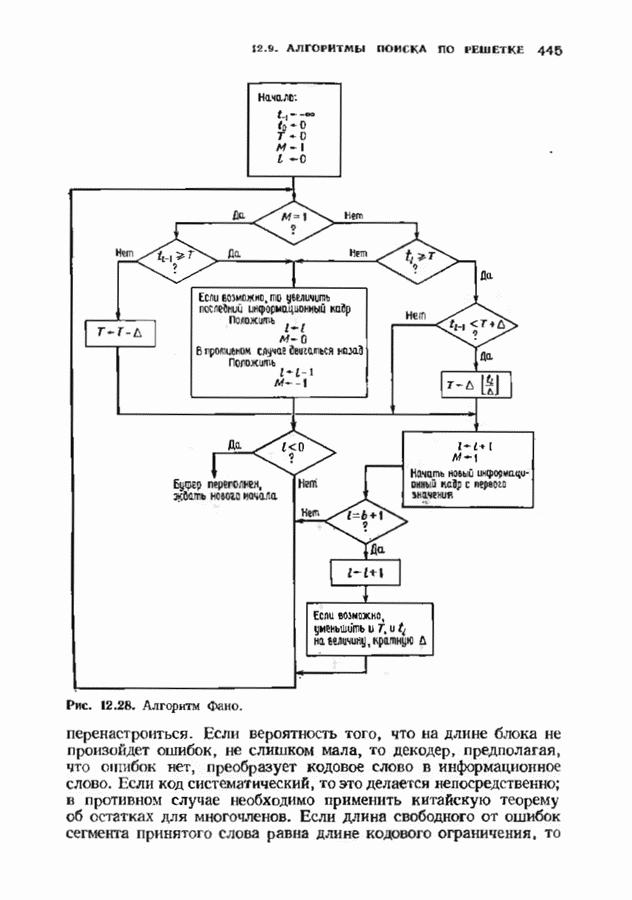
- 12.9. АЛГОРИТМЫ ПОИСКА ПО РЕШЕТКЕ
- ГЛАВА 13. КОДЫ И АЛГОРИТМЫ ДЛЯ ДЕКОДИРОВАНИЯ МАЖОРИТАРНЫМ МЕТОДОМ
- 13.1. ДЕКОДИРОВАНИЕ МАЖОРИТАРНЫМ МЕТОДОМ
- 13.2. СХЕМЫ МАЖОРИТАРНОГО ДЕКОДИРОВАНИЯ
- 13.3. АФФИННЫЕ ПЕРЕСТАНОВКИ ДЛЯ ЦИКЛИЧЕСКИХ КОДОВ
- 13.4. ЦИКЛИЧЕСКИЕ КОДЫ, ОСНОВАННЫЕ НА ПЕРЕСТАНОВКАХ
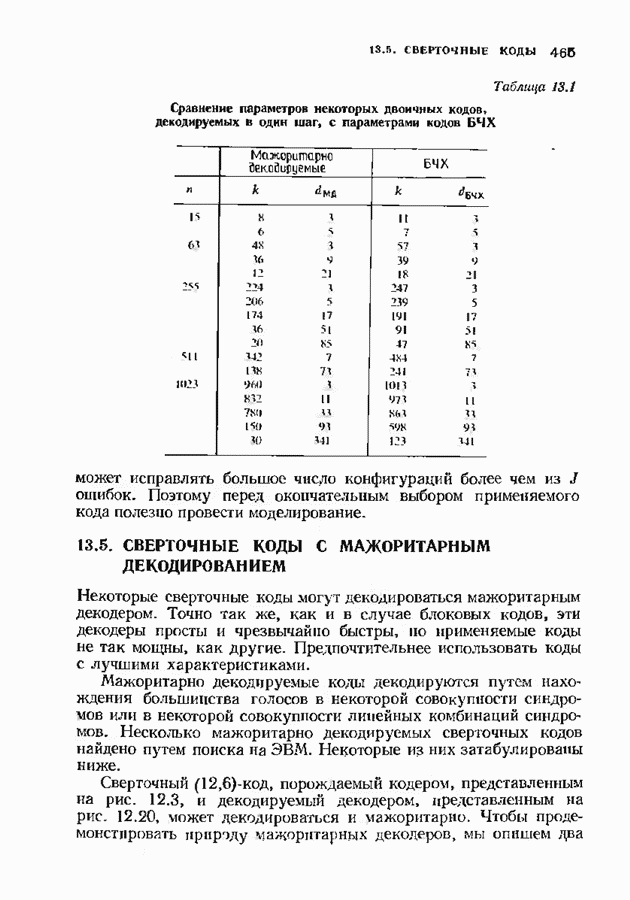
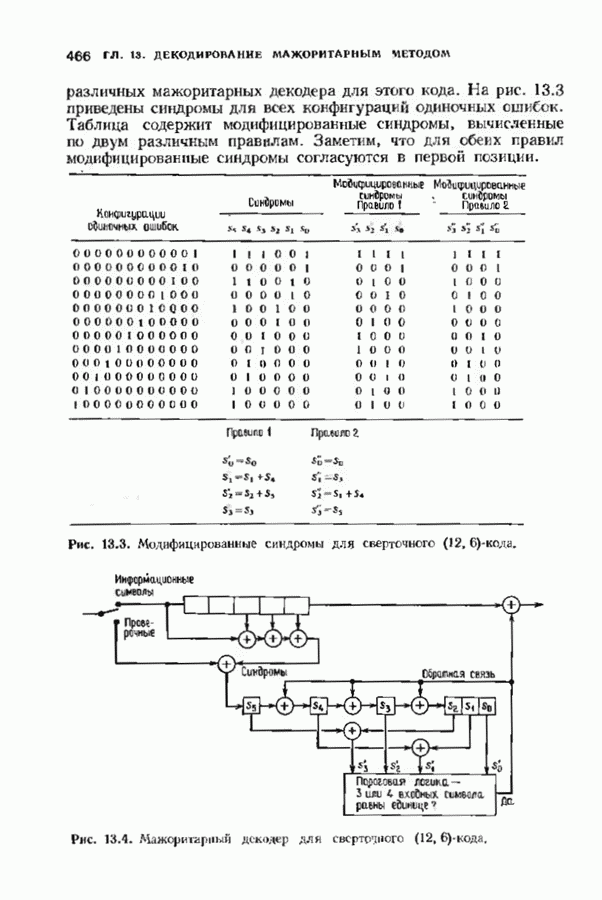
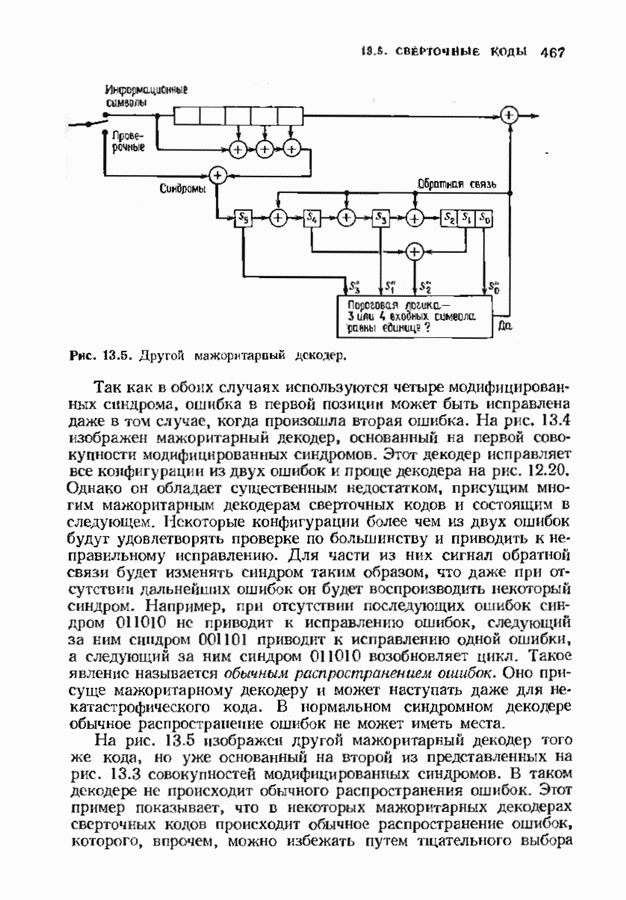
- 13.5. СВЕРТОЧНЫЕ КОДЫ С МАЖОРИТАРНЫМ ДЕКОДИРОВАНИЕМ
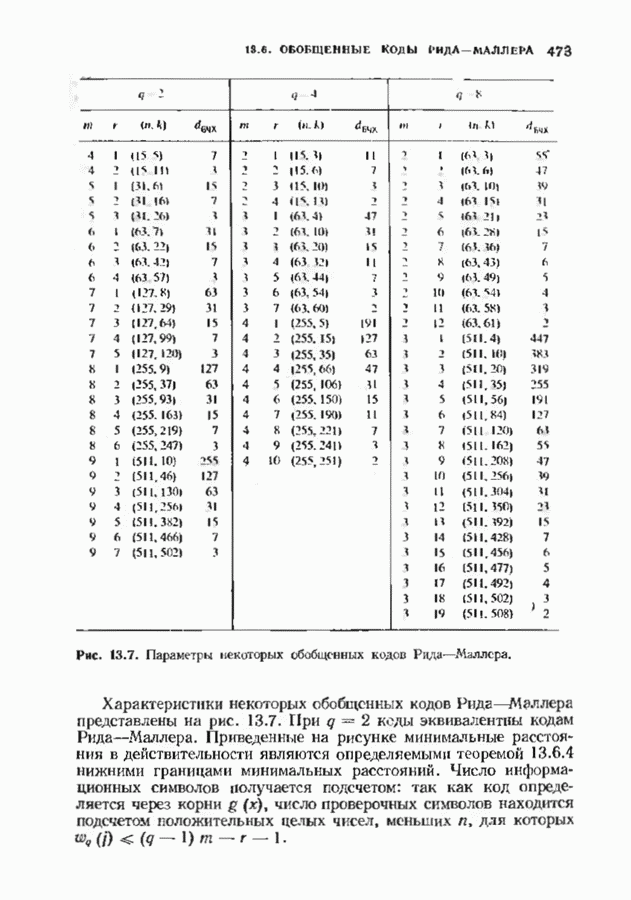
- 13.6. ОБОБЩЕННЫЕ КОДЫ РИДА—МАЛЛЕРА
- 13.7. ЕВКЛИДОВО-ГЕОМЕТРИЧЕСКИЕ КОДЫ
- 13.8. ПРОЕКТИВНО-ГЕОМЕТРИЧЕСКИЕ КОДЫ
- ГЛАВА 14. КОМПОЗИЦИЯ И ХАРАКТЕРИСТИКИ КОНТРОЛИРУЮЩИХ ОШИБКИ КОДОВ
- 14.2. ВЕРОЯТНОСТИ ОШИБОЧНОГО ДЕКОДИРОВАНИЯ И НЕУДАЧНОГО ДЕКОДИРОВАНИЯ
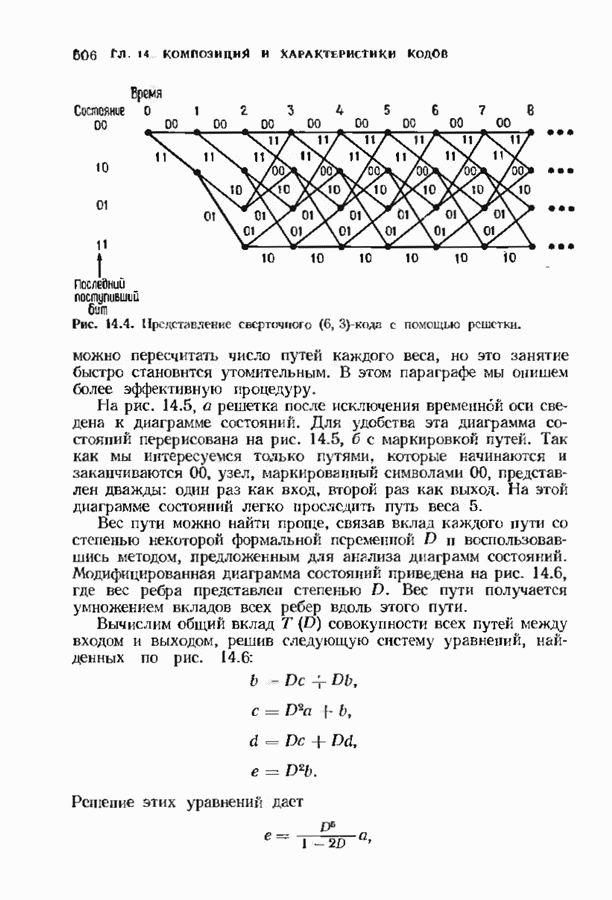
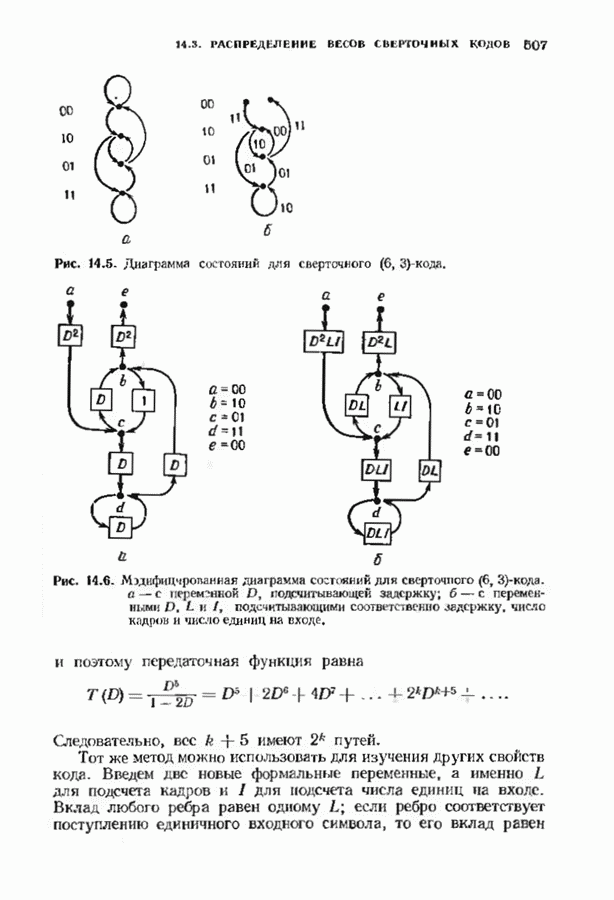
- 14.3. РАСПРЕДЕЛЕНИЕ ВЕСОВ СВЕРТОЧНЫХ КОДОВ
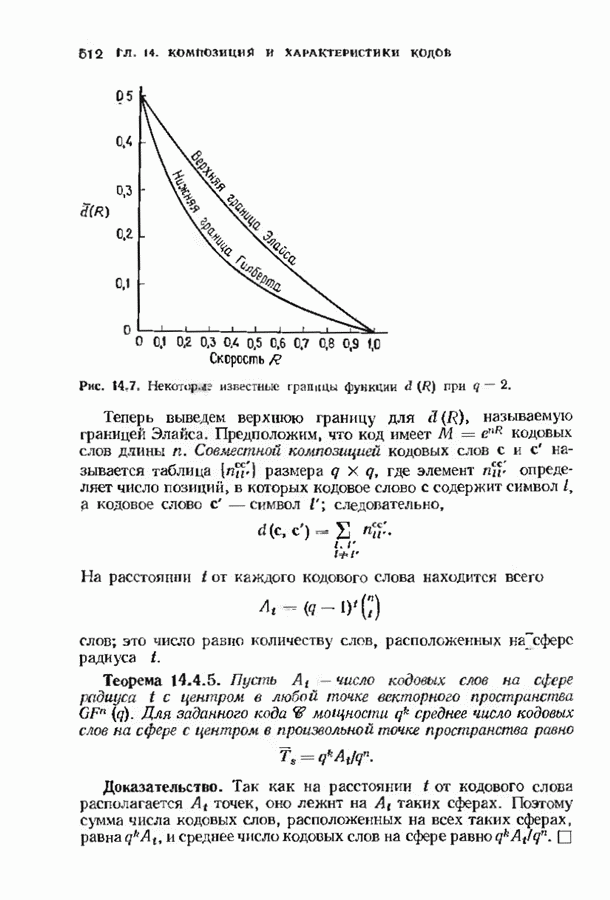
- 14.4. ГРАНИЦЫ МИНИМАЛЬНОГО РАССТОЯНИЯ ДЛЯ БЛОКОВЫХ КОДОВ
- 14.5. ГРАНИЦЫ МИНИМАЛЬНОГО РАССТОЯНИЯ ДЛЯ СВЕРТОЧНЫХ КОДОВ
- ГЛАВА 15. ЭФФЕКТИВНАЯ ПЕРЕДАЧА СИГНАЛОВ ПО ЗАШУМЛЕННЫМ КАНАЛАМ
- 15.1. ОГРАНИЧЕННЫЙ ПО ПОЛОСЕ ГАУССОВСКИЙ КАНАЛ
- 15.2. ЭНЕРГИЯ НА БИТ И ЧАСТОТА ОШИБОК НА БИТ
- 15.3. МЯГКОЕ ДЕКОДИРОВАНИЕ БЛОКОВЫХ КОДОВ
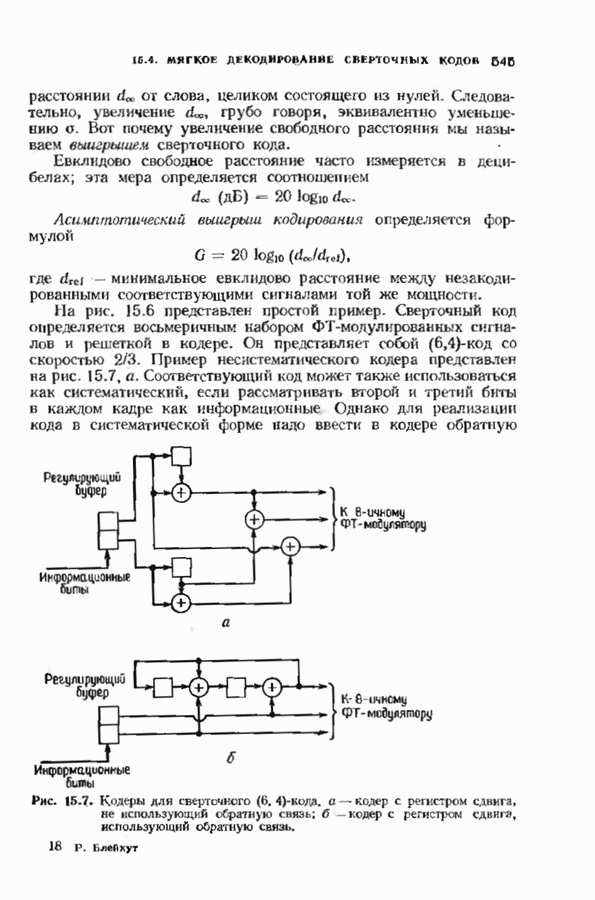
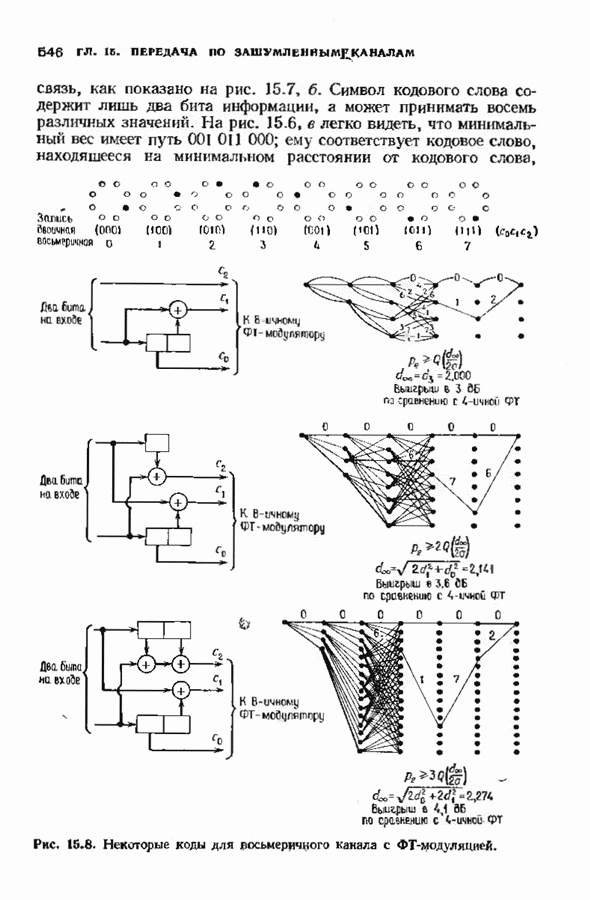
- 15.4. МЯГКОЕ ДЕКОДИРОВАНИЕ СВЕРТОЧНЫХ КОДОВ
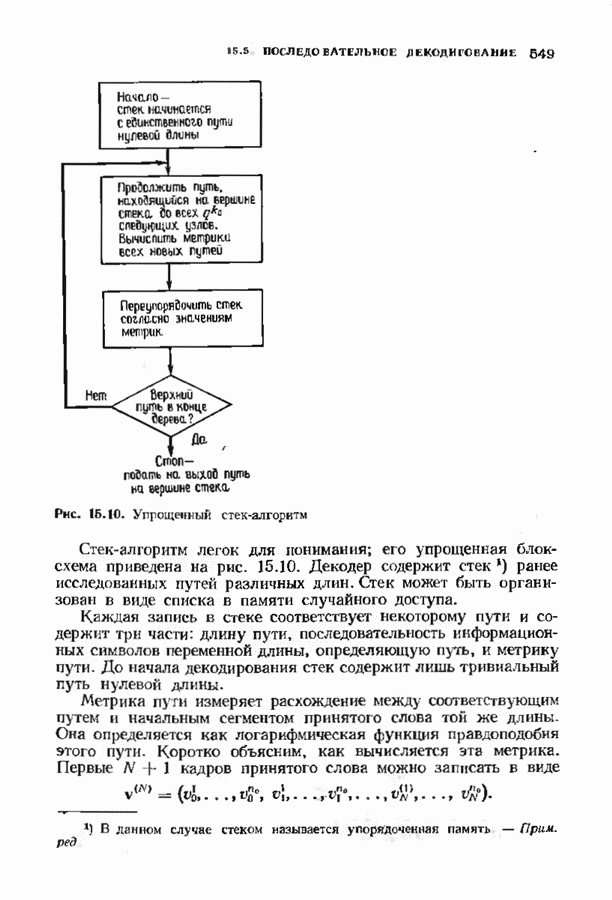
- 15.5. ПОСЛЕДОВАТЕЛЬНОЕ ДЕКОДИРОВАНИЕ
- ЛИТЕРАТУРА