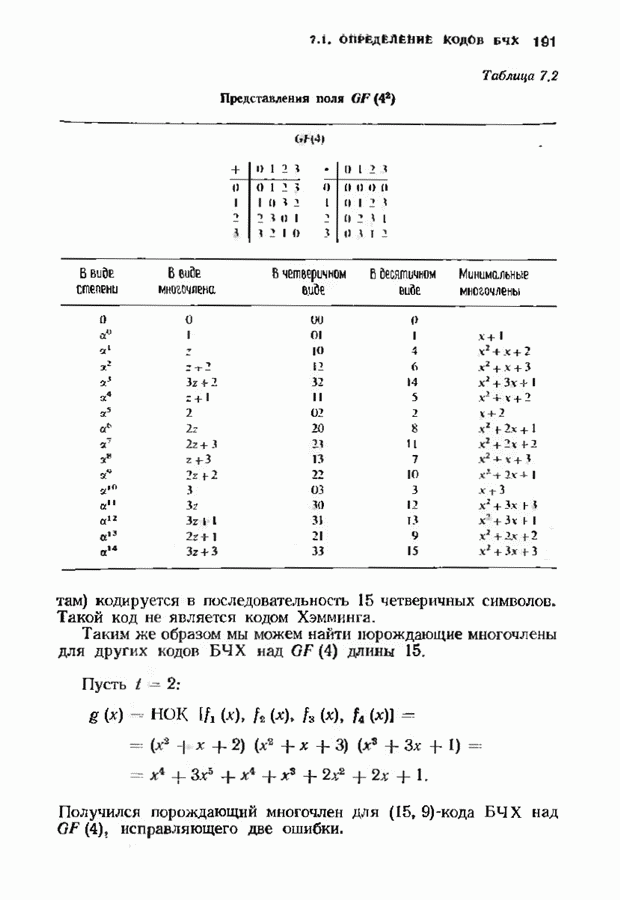
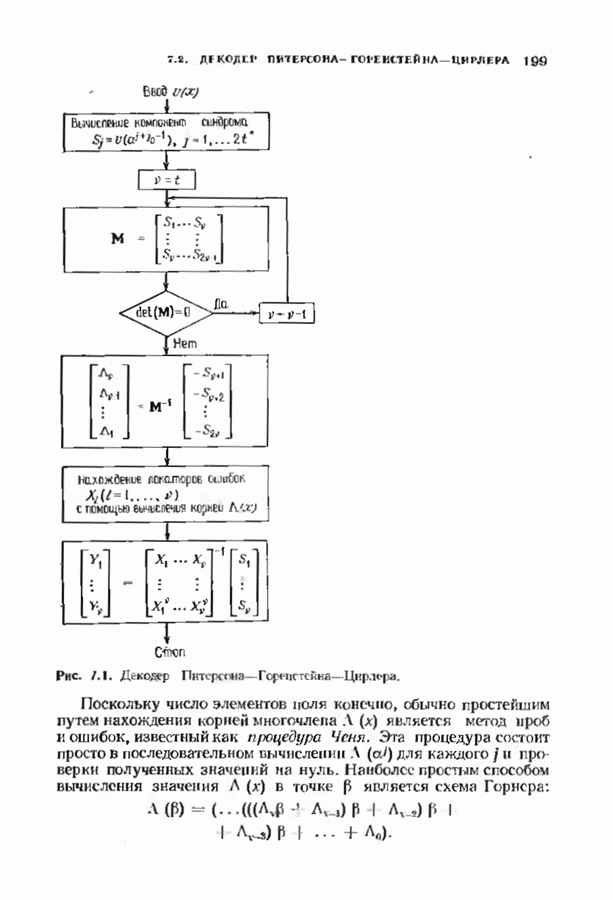
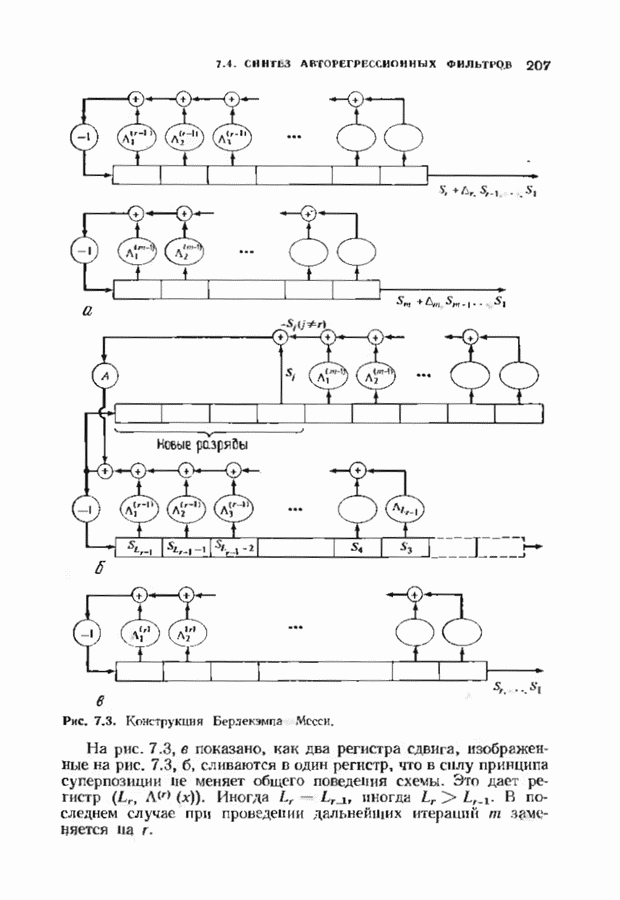
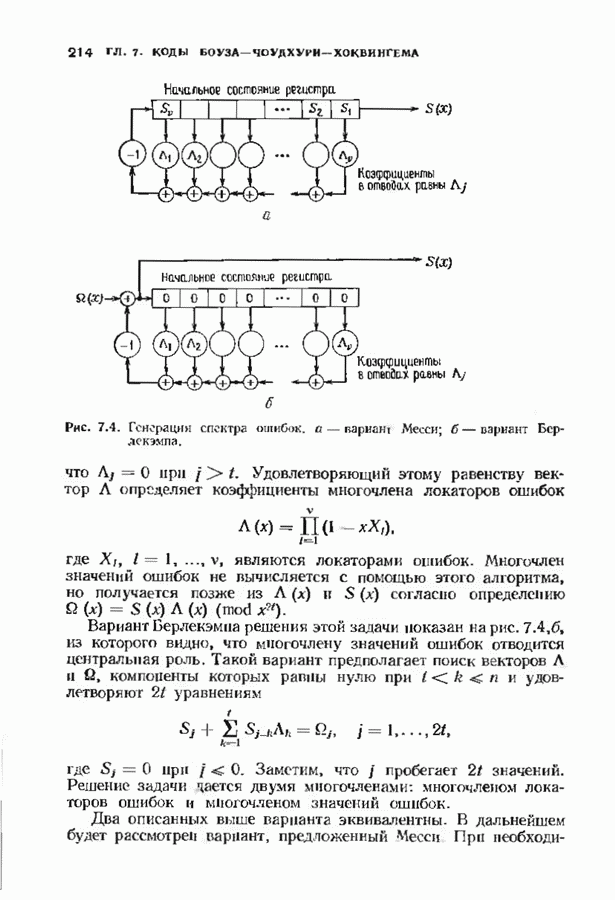
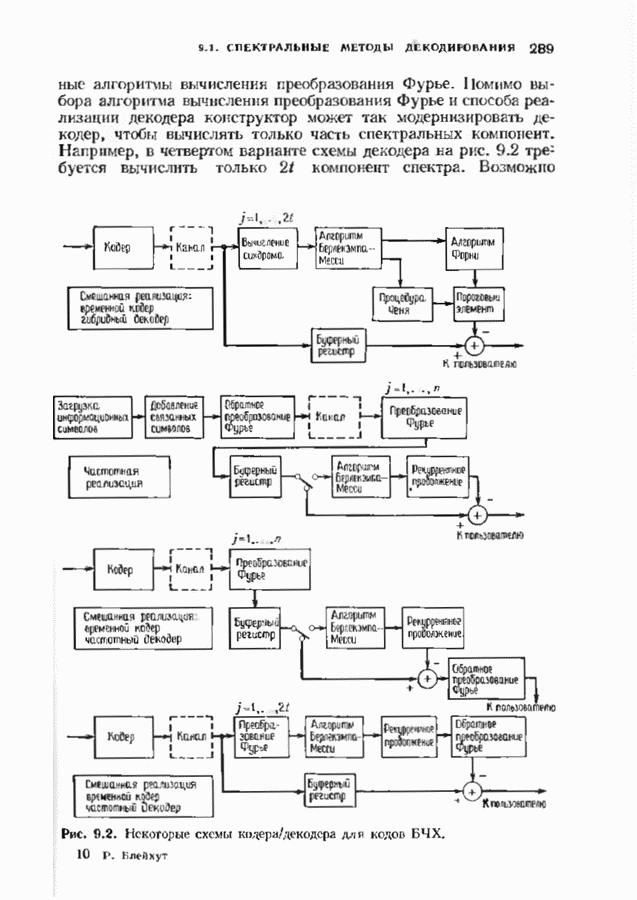
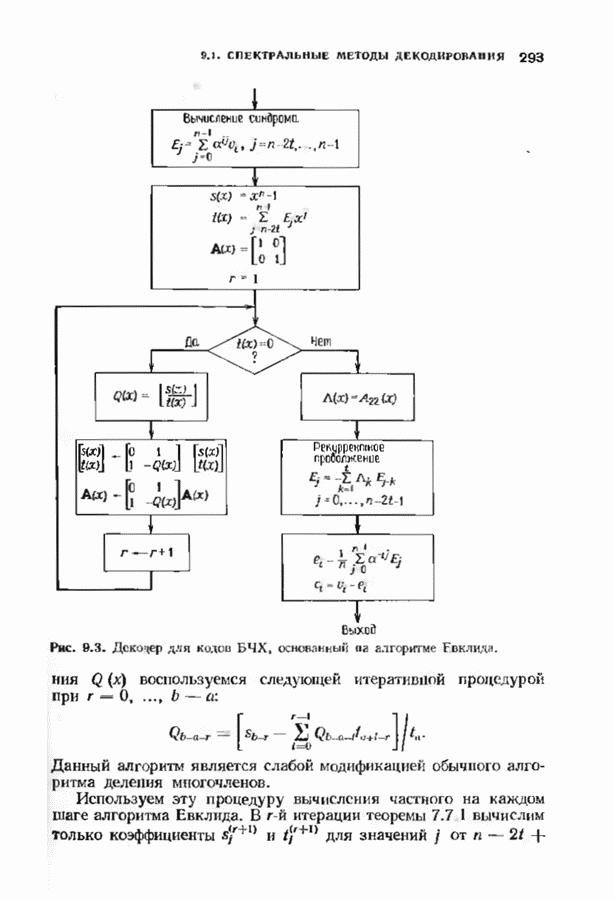
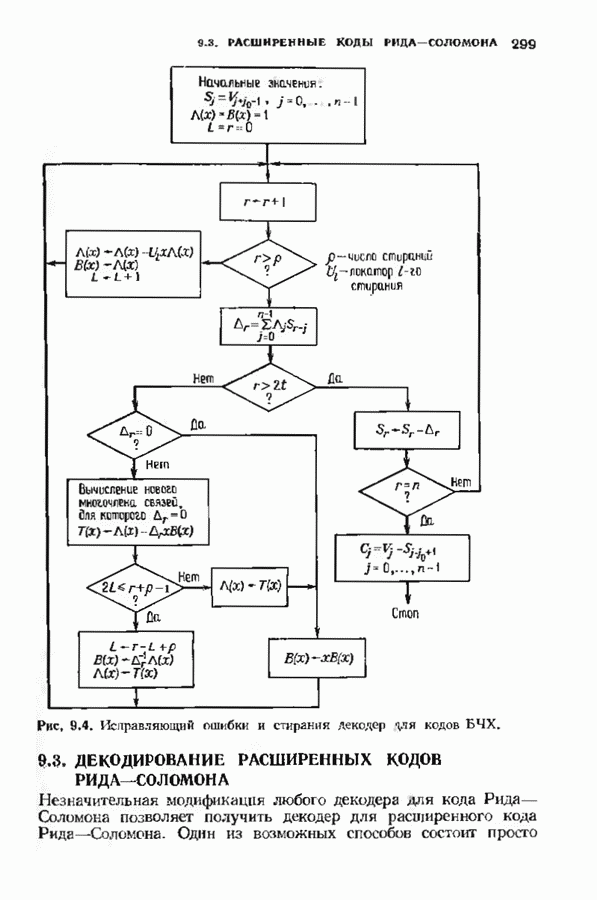
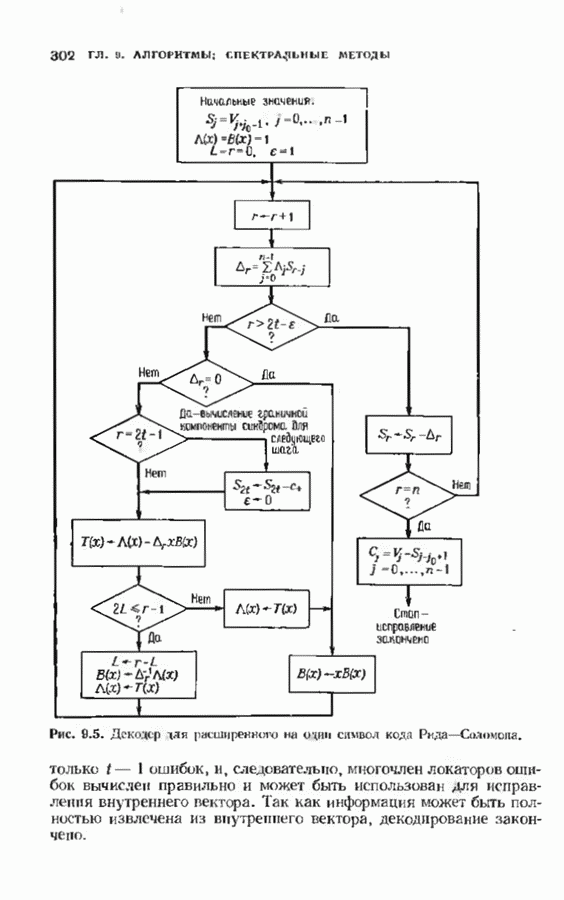
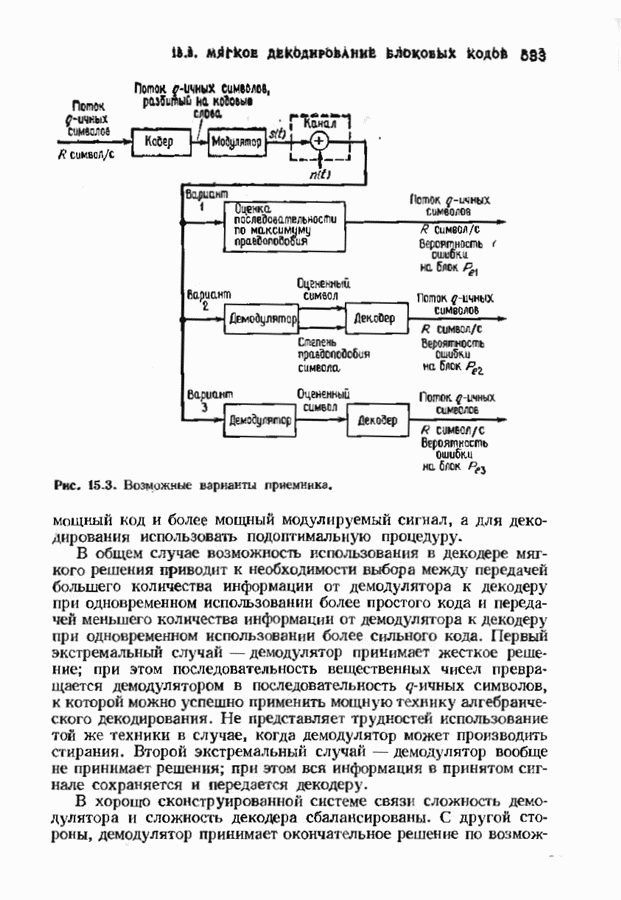
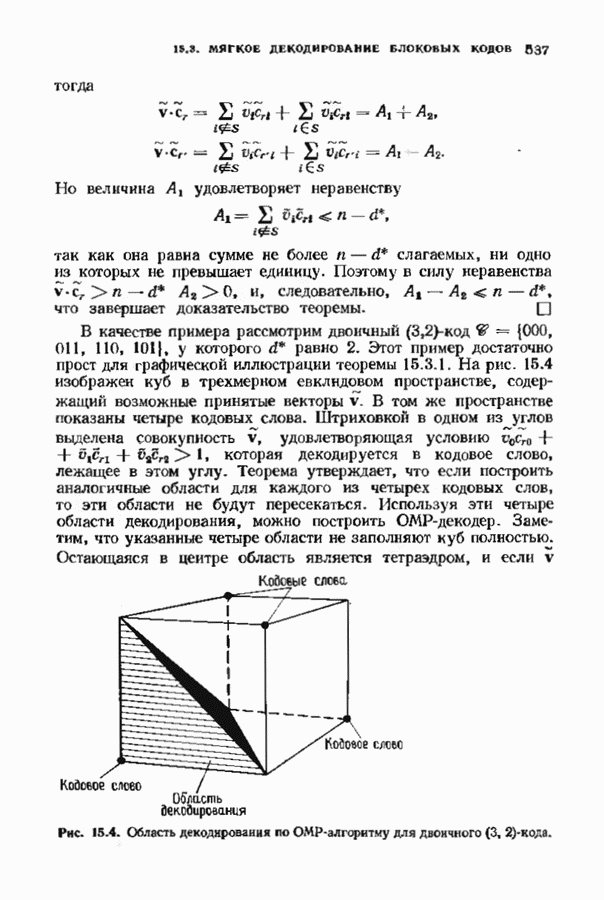
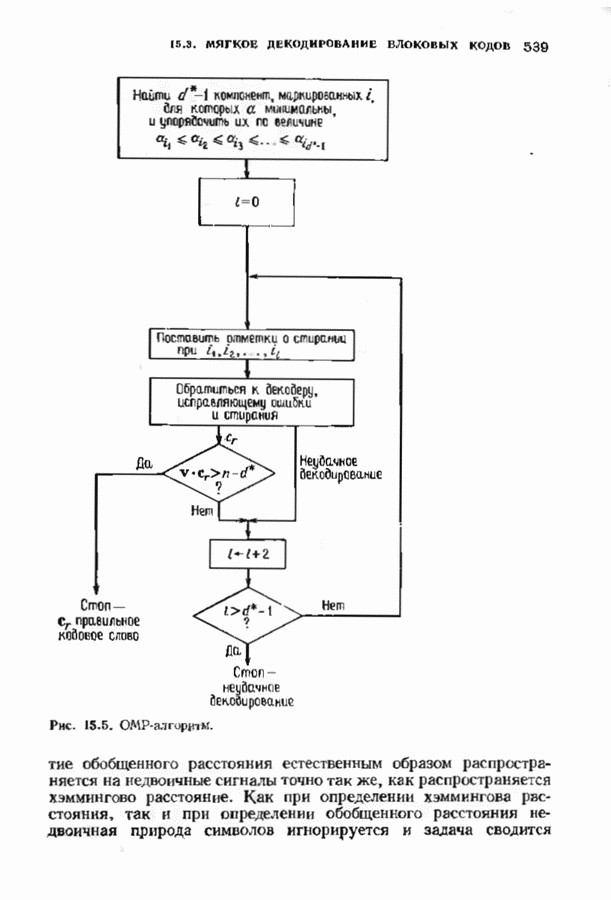
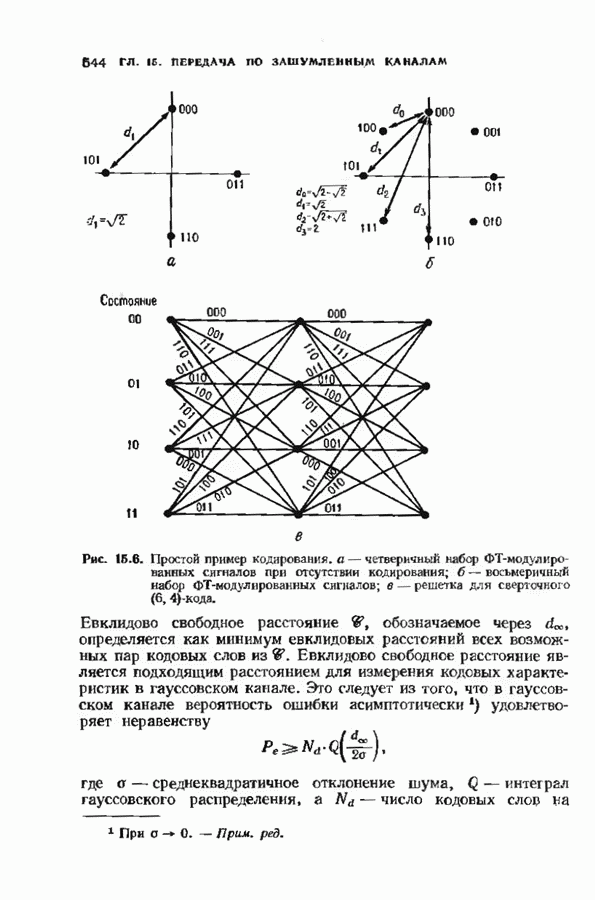
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
8.2. ОГРАНИЧЕНИЯ СОПРЯЖЕННОСТИ И ИДЕМПОТЕНТЫ
Преобразование Фурье длины  над
над  принимает значения в расширении поля
принимает значения в расширении поля  Если мы начнем с произвольного
Если мы начнем с произвольного  -мерного вектора над
-мерного вектора над  и вычислим обратное преобразование Фурье, то в общем случае не получим временного вектора над
и вычислим обратное преобразование Фурье, то в общем случае не получим временного вектора над  возможны компоненты из большего поля. Нам надо найти ограничения на спектр, которые бы гарантировали попадание компонент времен нбго вектора в
возможны компоненты из большего поля. Нам надо найти ограничения на спектр, которые бы гарантировали попадание компонент времен нбго вектора в 
Ограничения такого рода знакомы по полю комплексных чисел. Напомним, что в ноле комплексных чисел спектр  имеет вещественное обратное преобразование Фурье тогда и только
имеет вещественное обратное преобразование Фурье тогда и только  когда
когда  Следующая теорема описывает множество ограничении, которые называются ограничениями (или условиями) сопряженности и устанавливают аналогичное условие для конечного поля.
Следующая теорема описывает множество ограничении, которые называются ограничениями (или условиями) сопряженности и устанавливают аналогичное условие для конечного поля.
Теорема 8.2.1. Пусть V есть  -мерный вектор с компонентами из
-мерный вектор с компонентами из  где
где  делит
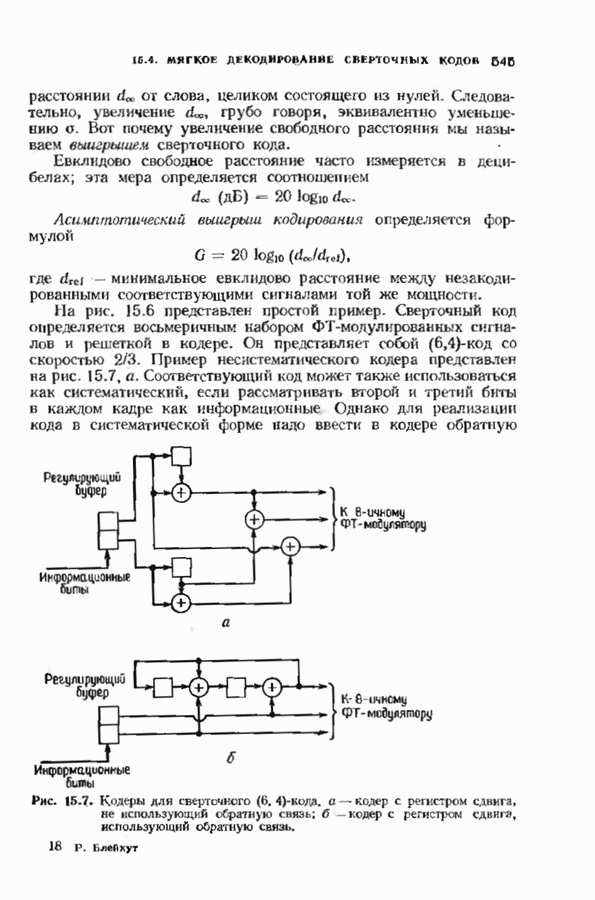
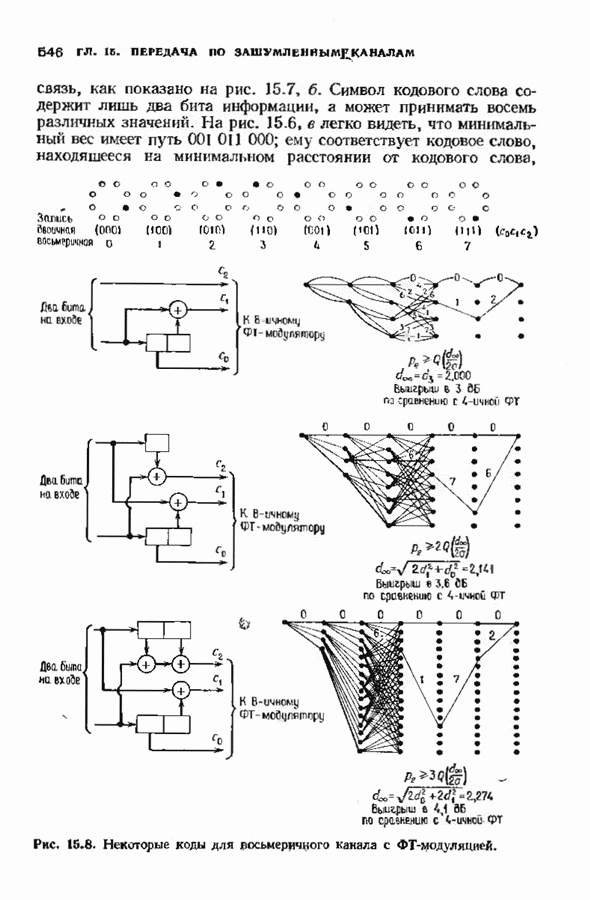
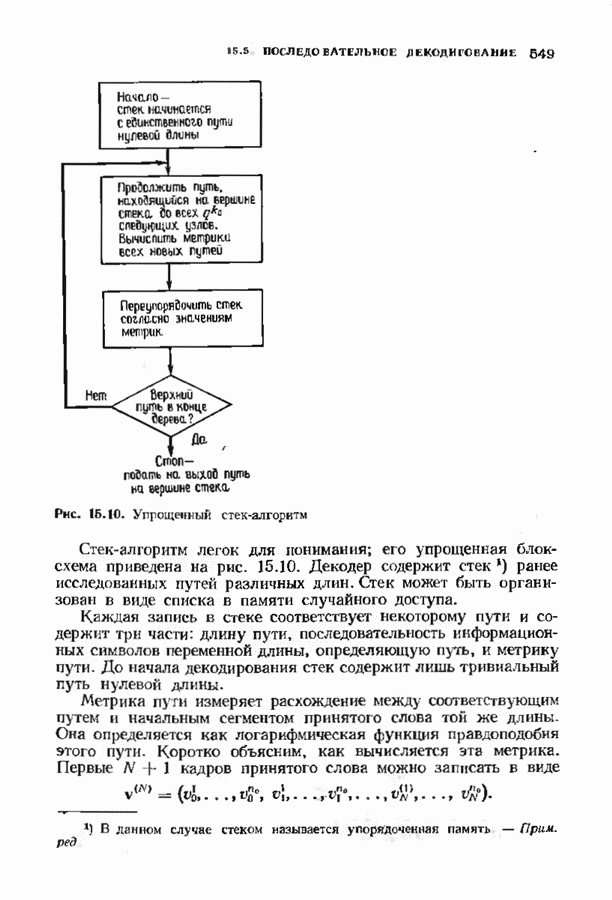
делит  Тогда обратное преобразование Фурье
Тогда обратное преобразование Фурье  является вектором с компонентами из
является вектором с компонентами из  тогда и только тогда, когда выполняются следующие равенства:
тогда и только тогда, когда выполняются следующие равенства:

Доказательство. По определению

В ноле характеристики  для любого целого
для любого целого  справедливо равенство
справедливо равенство  Далее, если
Далее, если  элемент поля
элемент поля  то
то  при всех
при всех  Следовательно,
Следовательно,

Обратно, предположим, что  для всех
для всех  Тогда
Тогда

Пусть  Так как
Так как  взаимно просто с
взаимно просто с  то, когда
то, когда  принимает все значения от 0 до
принимает все значения от 0 до  число
число  также принимает все значения от 0 до
также принимает все значения от 0 до  Следовательно,
Следовательно,

и в силу однозначности преобразования Фурье  для всех
для всех  Таким образом,
Таким образом,  являются корнями многочлена
являются корнями многочлена  при всех
при всех  и этими корнями исчерпывается все поле
и этими корнями исчерпывается все поле 
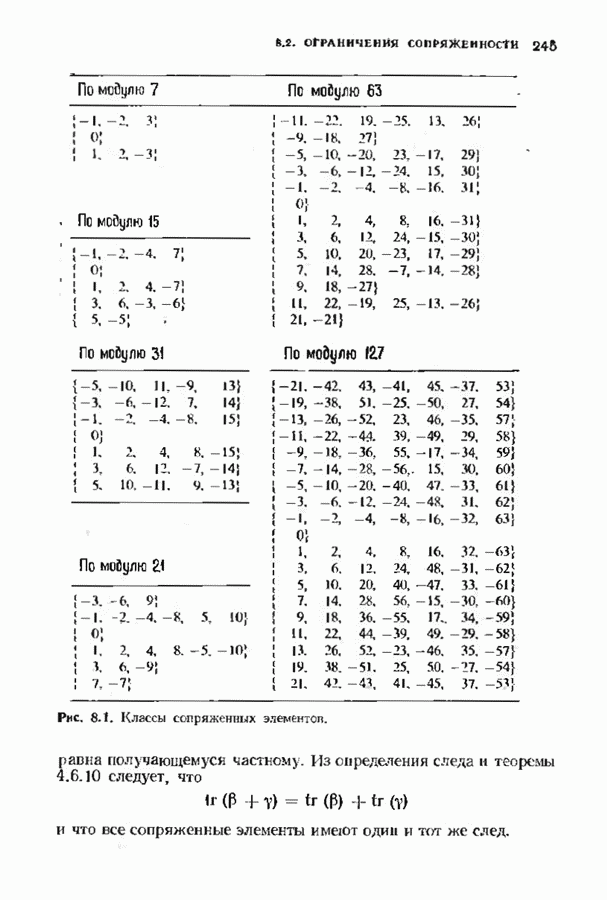
Чтобы применить данную теорему, следующим образом разобьем числа по  на подмножества, известные под названием классов сопряженных элементов:
на подмножества, известные под названием классов сопряженных элементов:

где  наименьшее целое положительное число, удовлетворяющее равенству
наименьшее целое положительное число, удовлетворяющее равенству  В силу конечности поля такое
В силу конечности поля такое  всегда существует. Например, если
всегда существует. Например, если  то классы сопряженных элементов имеют вид
то классы сопряженных элементов имеют вид

Класс сопряженных элементов  выделяет в спектре множество частот. Назовем это множество частот хордой.Теорема 8.2.1 утверждает, что если временной сигнал принимает значения в поле
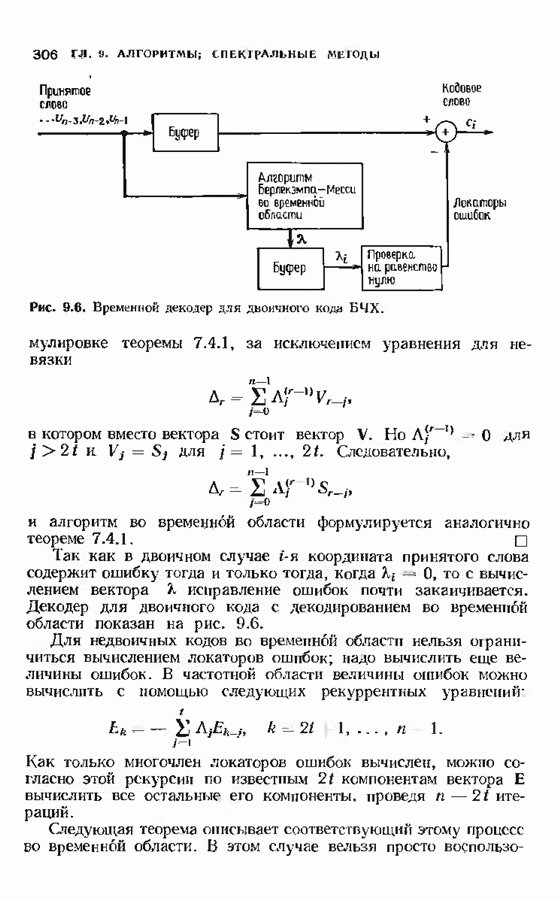
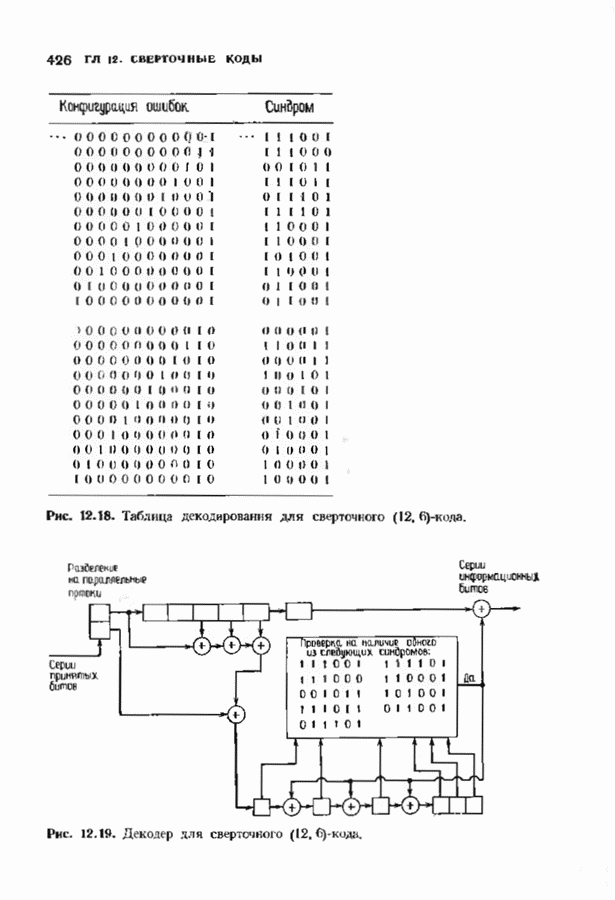
выделяет в спектре множество частот. Назовем это множество частот хордой.Теорема 8.2.1 утверждает, что если временной сигнал принимает значения в поле  то значение спектра в одной из частот хорды определяет значення спектра при всех частотах этой хорды. В следующем параграфе мы воспользуемся этим, чтобы дать спектральное описание кодов.
то значение спектра в одной из частот хорды определяет значення спектра при всех частотах этой хорды. В следующем параграфе мы воспользуемся этим, чтобы дать спектральное описание кодов.
На рис. 8.1 приведены классы сопряженных элементов для некоторых малых полей в несколько измененных обозначениях. Для того чтобы подчеркнуть получающиеся симметрии, классы сопряженных элементов выписаны с использованием отрицатель  целых чисел. При желании на рис. 8.1 отрицательное целое число
целых чисел. При желании на рис. 8.1 отрицательное целое число  можно заменить положительным целым
можно заменить положительным целым  Классы сопряженных элементов по модулю 21 включены в таблицу для напоминания того, что в качестве модуля можно выбирать любое целое число. Заметим, что если члены классов сопряженных элементов по модулю 21 умножить на 3, то эти классы становятся классами сопряженных элементов по модулю 63.
Классы сопряженных элементов по модулю 21 включены в таблицу для напоминания того, что в качестве модуля можно выбирать любое целое число. Заметим, что если члены классов сопряженных элементов по модулю 21 умножить на 3, то эти классы становятся классами сопряженных элементов по модулю 63.
Определение  -ичным следом элемента
-ичным следом элемента  поля
поля  называется сумма
называется сумма

Согласно теореме  степень
степень  -ичного следа элемента
-ичного следа элемента  равна
равна  ичному следу элемента
ичному следу элемента  следовательно,
следовательно,  -ичный след является элементом поля
-ичный след является элементом поля  Если класс сопряженных элементов, которому принадлежит
Если класс сопряженных элементов, которому принадлежит  содержит
содержит  элементов, то
элементов, то  равен сумме всех элементов этого класса сопряженных элементов. В противном случае число элементов в классе сопряженных делит
равен сумме всех элементов этого класса сопряженных элементов. В противном случае число элементов в классе сопряженных делит  и кратность, с которой каждый элемент входит в след.
и кратность, с которой каждый элемент входит в след.
Рис. 8.1. (см. скан) Классы сопряженных элементов.
равна получающемуся частному. Из определения следа и теоремы 4.6.10 следует, что

и что все сопряженные элементы имеют один и тот же след.
Теорема 8.2.3. Над  q-ичный след принимает в каче стве своего значения каждое из чисел поля
q-ичный след принимает в каче стве своего значения каждое из чисел поля  одинаково часто, а именно
одинаково часто, а именно  раз.
раз.
Доказательство. Пусть у — элемент поля  элемент из
элемент из  след которого равен -у. Тогда
след которого равен -у. Тогда  является корнем многочлена
является корнем многочлена

Степень этого многочлена равна  следовательно, он имеет не более
следовательно, он имеет не более  корней. Но всего существует только
корней. Но всего существует только  таких многочленов, и каждый из элементов поля
таких многочленов, и каждый из элементов поля  является корнем одного из них. Это доказывает теорему.
является корнем одного из них. Это доказывает теорему. 
Одно из полезных свойств следа устанавливает следующая теорема.
Теорема 8.2.4. Квадратное уравнение

где а — элемент поля  имеет корни в поле
имеет корни в поле  тогда и только тогда, когда двоичный след элемента а равен нулю.
тогда и только тогда, когда двоичный след элемента а равен нулю.
Доказательство. Пусть  корень этого квадратного уравнения. Вычисленный в точке
корень этого квадратного уравнения. Вычисленный в точке  двоичный след соответствующего квадратичного трехчлена равен
двоичный след соответствующего квадратичного трехчлена равен

По отношению к сложению след дистрибутивен, а следы элементов  являются одним и тем же элементом поля GF (2). Следовательно,
являются одним и тем же элементом поля GF (2). Следовательно,

Обратно, каждое  является корнем многочлена
является корнем многочлена  а для некоторого с, а именно для а, равного
а для некоторого с, а именно для а, равного  Всего имеется
Всего имеется  таких с, для которых след равен нулю, и этого в точности хватает, чтобы составить
таких с, для которых след равен нулю, и этого в точности хватает, чтобы составить  уравнений с двумя корнями каждое. Доказательство закончено.
уравнений с двумя корнями каждое. Доказательство закончено. 
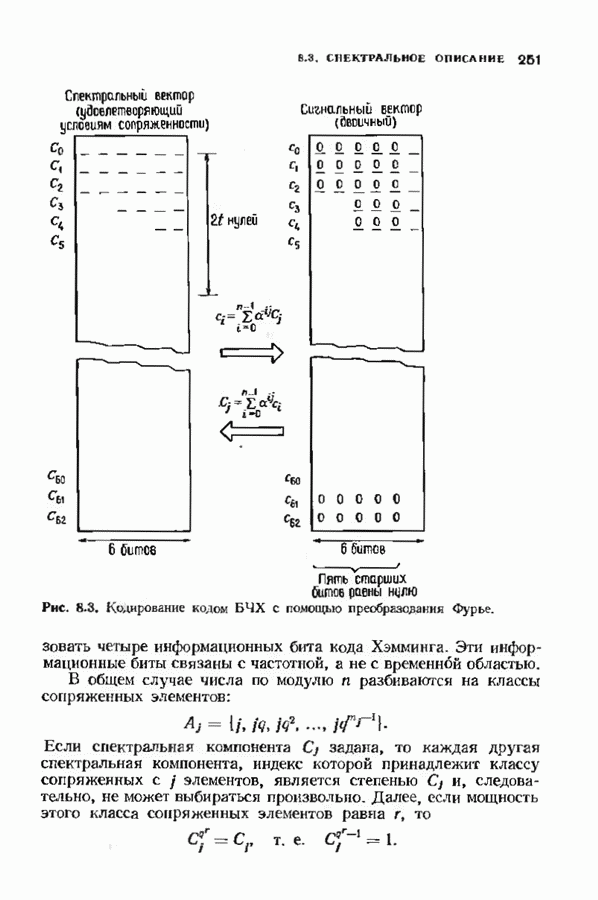
Предположим теперь, что мы выбрали хорду  и определили спектр
и определили спектр

Согласно теореме 8.2.1, обратное преобразование Фурье для этого спектра является вектором над  который можно представить многочленом
который можно представить многочленом  Так как в частотной области свертка
Так как в частотной области свертка  преобразуется в произведение
преобразуется в произведение  то
то 
и, следовательно, многочлен  обладает следующим специальным свойством:
обладает следующим специальным свойством:

Произвольный многочлен  удовлетворяющий условию
удовлетворяющий условию  называется идемпотентом.
называется идемпотентом.
Каждый идемиотент может быть получен следующим образом. Выберем несколько хорд и положим  если
если  принадлежит одной из них, и
принадлежит одной из них, и  в противном случае. Обратное преобразование Фурье дает во временной области многочлен, который является идемпотентом, и каждый идемпотент можно построить таким способом.
в противном случае. Обратное преобразование Фурье дает во временной области многочлен, который является идемпотентом, и каждый идемпотент можно построить таким способом.
Завершим этот параграф применением полученных результатов к циклическим кодам.
Теорема 8.2.5. Каждый циклический код содержит в качестве кодового слова единственный многочлен  такой, что многочлен с
такой, что многочлен с  является кодовым словом тогда и только тогда, когда
является кодовым словом тогда и только тогда, когда

Многочлен  является идемпотентом.
является идемпотентом.
Доказательство. Пусть  порождающий многочлен, и пусть
порождающий многочлен, и пусть

Тогда  является идемпонентом. Его корни совпадают с корнями
является идемпонентом. Его корни совпадают с корнями  следовательно, он является кодовым словом. Кроме того,
следовательно, он является кодовым словом. Кроме того,  для всех
для всех  и поэтому
и поэтому  Далее, многочлен с
Далее, многочлен с  является кодовым словом тогда и только тогда, когда для некоторого
является кодовым словом тогда и только тогда, когда для некоторого  выполняется равенство с
выполняется равенство с  откуда следует, что
откуда следует, что

это и доказывает теорему.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ВВЕДЕНИЕ
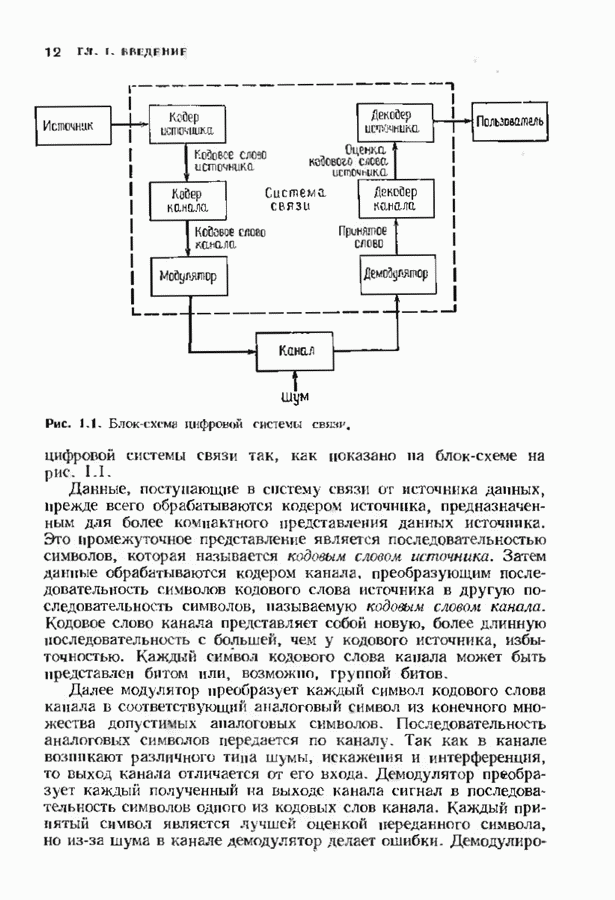
- 1.1. ДИСКРЕТНЫЙ КАНАЛ, СВЯЗИ
- 1.2. ИСТОРИЯ КОДИРОВАНИЯ, КОНТРОЛИРУЮЩЕГО ОШИБКИ
- 1.3. ПРИЛОЖЕНИЯ
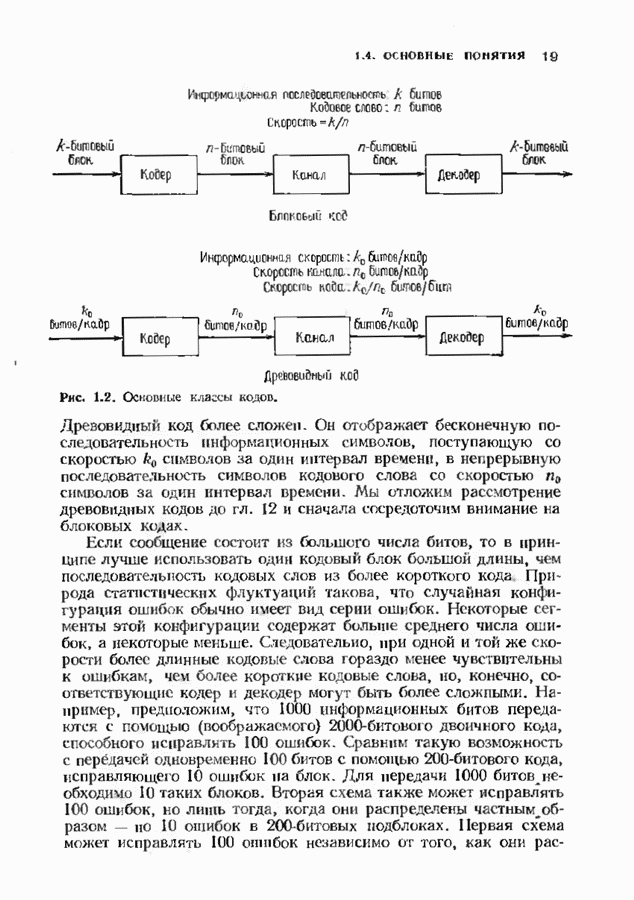
- 1.4. ОСНОВНЫЕ ПОНЯТИЯ
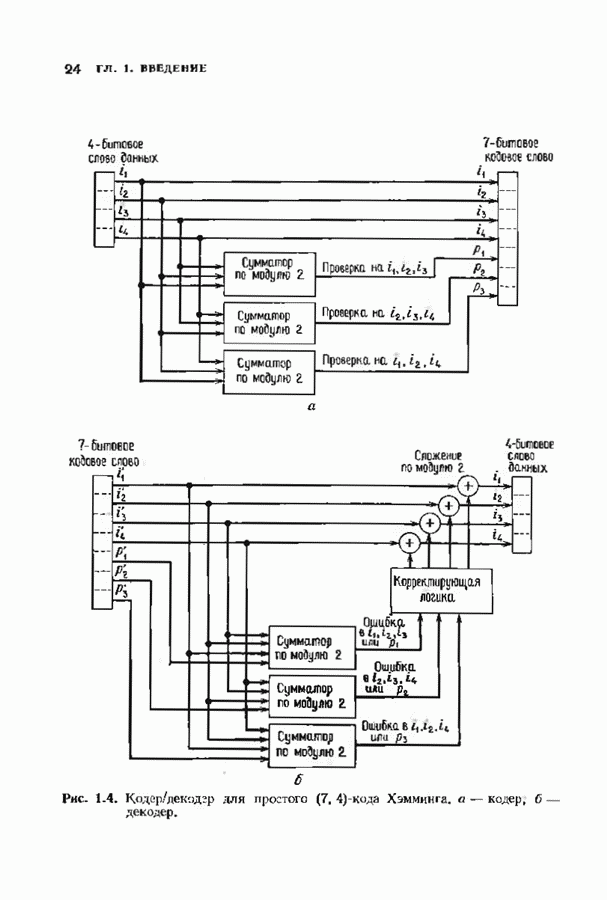
- 1.5. ПРОСТЕЙШИЕ КОДЫ
- ГЛАВА 2. ВВЕДЕНИЕ В АЛГЕБРУ
- 2.1. 2-ПОЛЕ И 6-10-ПОЛЕ
- 2.2. ГРУППЫ
- 2.3. КОЛЬЦА
- 2.4. ПОЛЯ
- 2.5. ВЕКТОРНЫЕ ПРОСТРАНСТВА
- 2.6. ЛИНЕЙНАЯ АЛГЕБРА
- ГЛАВА 3. ЛИНЕЙНЫЕ БЛОКОВЫЕ КОДЫ
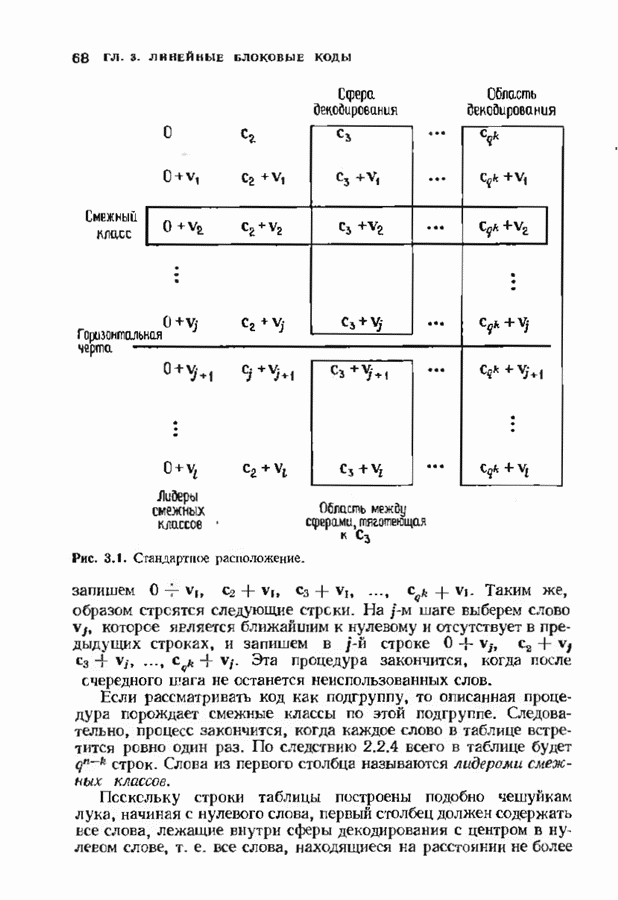
- 3.1. СТРУКТУРА ЛИНЕЙНЫХ БЛОКОВЫХ КОДОВ
- 3.2. МАТРИЧНОЕ ОПИСАНИЕ ЛИНЕЙНЫХ БЛОКОВЫХ КОДОВ
- 3.3. СТАНДАРТНОЕ РАСПОЛОЖЕНИЕ
- 3.4. КОДЫ ХЭММИНГА
- 3.5. СОВЕРШЕННЫЕ И КВАЗИСОВЕРШЕННЫЕ КОДЫ
- 3.6. ПРОСТЫЕ ПРЕОБРАЗОВАНИЯ ЛИНЕЙНОГО КОДА
- 3.7. КОДЫ РИДА—МАЛЛЕРА
- ГЛАВА 4. АРИФМЕТИКА ПОЛЕЙ ГАЛУА
- 4.2. КОНЕЧНЫЕ ПОЛЯ, ОСНОВАННЫЕ НА КОЛЬЦЕ ЦЕЛЫХ ЧИСЕЛ
- 4.3. КОЛЬЦА МНОГОЧЛЕНОВ
- 4.4. КОНЕЧНЫЕ ПОЛЯ, ОСНОВАННЫЕ НА КОЛЬЦАХ МНОГОЧЛЕНОВ
- 4.5. ПРИМИТИВНЫЕ ЭЛЕМЕНТЫ
- 4.6. СТРУКТУРА КОНЕЧНОГО ПОЛЯ
- ГЛАВА 5. ЦИКЛИЧЕСКИЕ КОДЫ
- 5.2. ПОЛИНОМИАЛЬНОЕ ОПИСАНИЕ ЦИКЛИЧЕСКИХ КОДОВ
- 5.3. МИНИМАЛЬНЫЕ МНОГОЧЛЕНЫ И СОПРЯЖЕНИЯ
- 5.4. МАТРИЧНОЕ ОПИСАНИЕ ЦИКЛИЧЕСКИХ КОДОВ
- 5.5. КОДЫ ХЭММИНГА КАК ЦИКЛИЧЕСКИЕ КОДЫ
- 5.6. ЦИКЛИЧЕСКИЕ КОДЫ, ИСПРАВЛЯЮЩИЕ ДВЕ ОШИБКИ
- 5.7. ЦИКЛИЧЕСКИЕ КОДЫ, ИСПРАВЛЯЮЩИЕ ПАКЕТЫ ОШИБОК
- 5.8. ДВОИЧНЫЙ КОД ГОЛЕЯ
- 5.9. КВАДРАТИЧНО-ВЫЧЕТНЫЕ КОДЫ
- ГЛАВА 6. СХЕМНАЯ РЕАЛИЗАЦИЯ ЦИКЛИЧЕСКОГО КОДИРОВАНИЯ
- 6.1. ЛОГИЧЕСКИЕ ЦЕПИ ДЛЯ АРИФМЕТИКИ КОНЕЧНОГО ПОЛЯ
- 6.2. ЦИФРОВЫЕ ФИЛЬТРЫ
- 6.3. КОДЕРЫ И ДЕКОДЕРЫ НА РЕГИСТРАХ СДВИГА
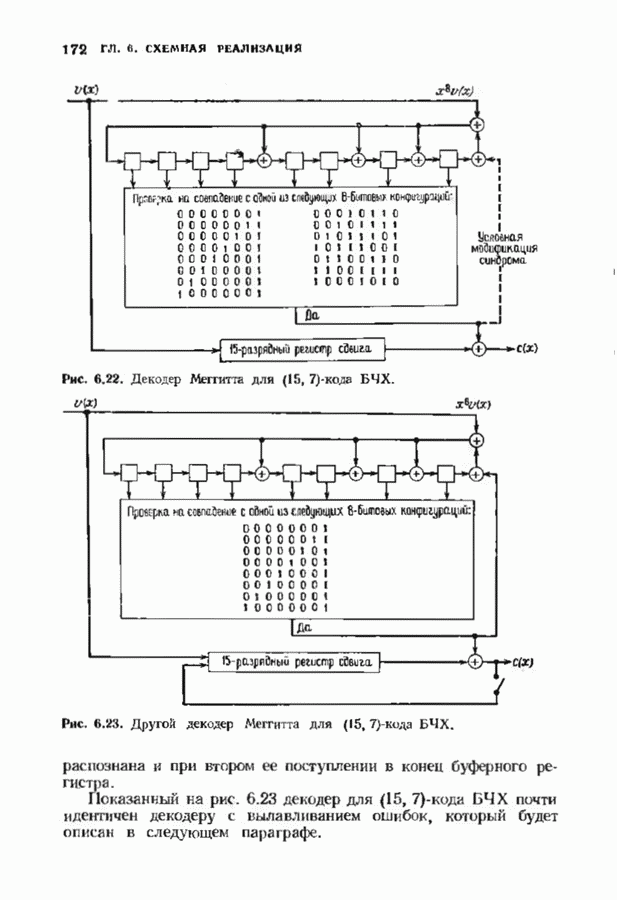
- 6.4. ДЕКОДЕР МЕГГИТТА
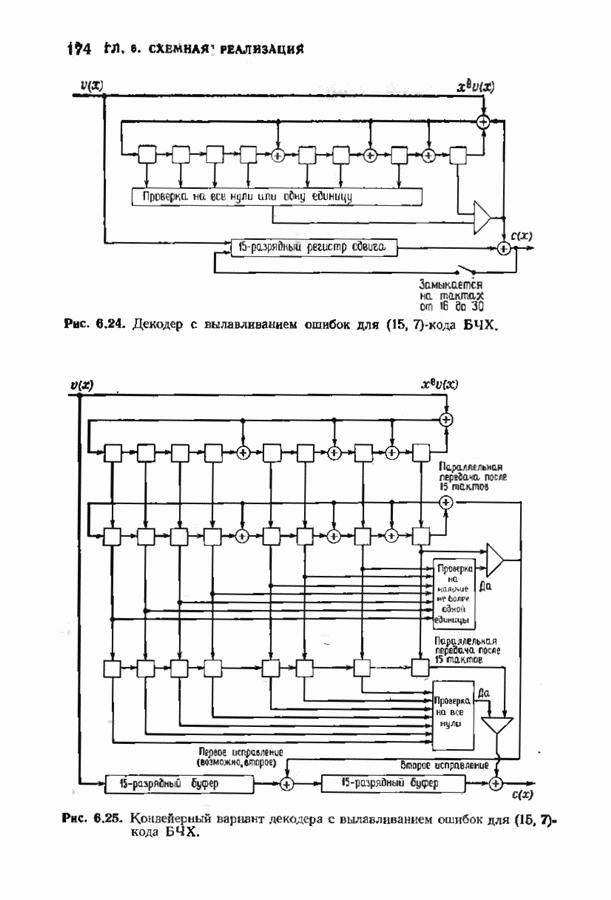
- 6.5. ВЫЛАВЛИВАНИЕ ОШИБОК
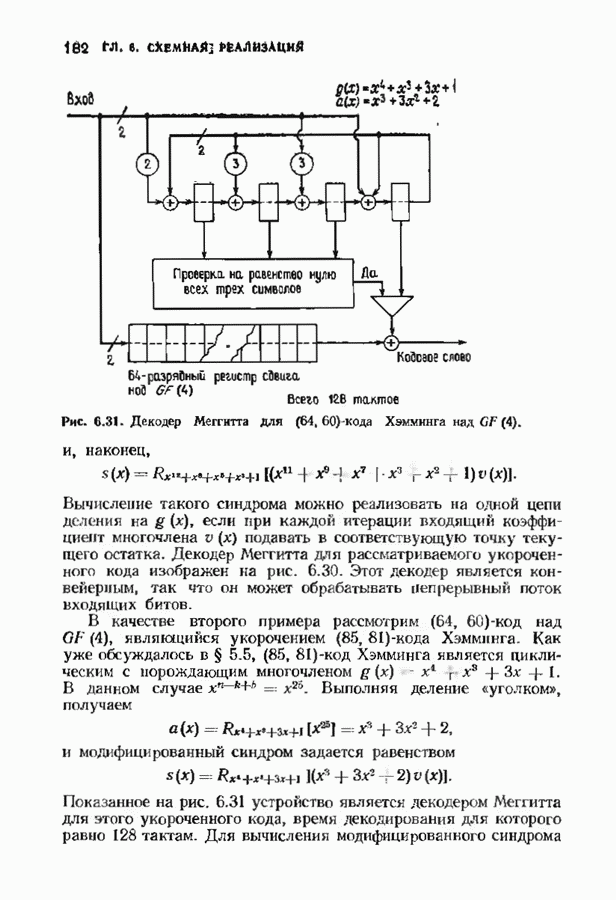
- 6.6. УКОРОЧЕННЫЕ ЦИКЛИЧЕСКИЕ КОДЫ
- 6.7. ДЕКОДЕР МЕГГИТТА ДЛЯ. КОДА ГОЛЕЯ
- ГЛАВА 7. КОДЫ БОУЗА-ЧОУДХУРИ-ХОКВИНГЕМА
- 7.2. ДЕКОДЕР ПИТЕРСОНА ГОРЕНСТЕЙНА—ЦИРЛЕРА
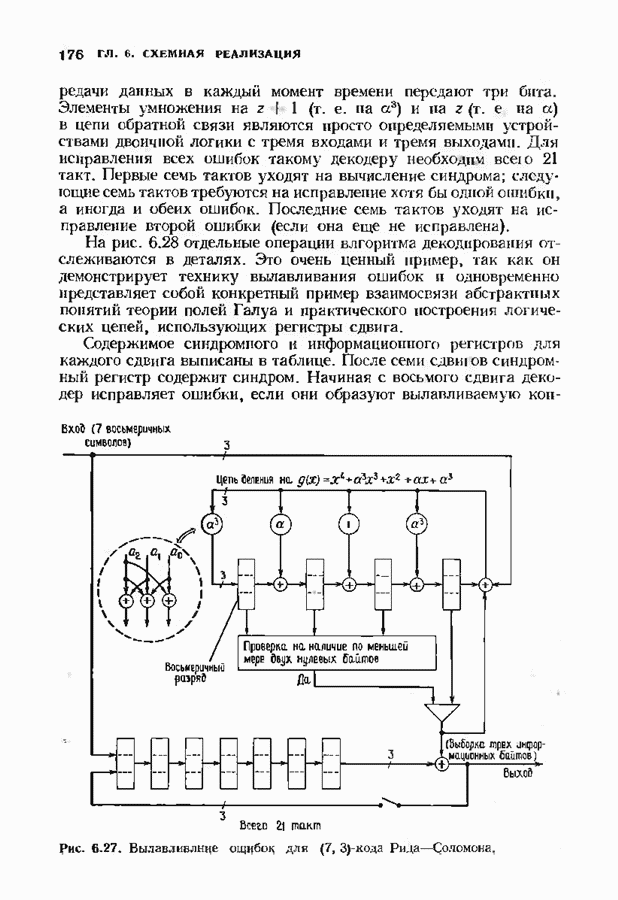
- 7.3. КОДЫ РИДА СОЛОМОНА
- 7.4. СИНТЕЗ АВТОРЕГРЕССИОННЫХ ФИЛЬТРОВ
- 7.5. БЫСТРОЕ ДЕКОДИРОВАНИЕ КОДОВ БЧХ
- 7.6. ДЕКОДИРОВАНИЕ ДВОИЧНЫХ КОДОВ БЧХ
- 7.7. ДЕКОДИРОВАНИЕ С ПОМОЩЬЮ АЛГОРИТМА ЕВКЛИДА
- 7.8. КАСКАДНЫЕ (ГНЕЗДОВЫЕ) КОДЫ
- 7.9. КОДЫ ЮСТЕСЕНА
- ГЛАВА 8. КОДЫ, ОСНОВАННЫЕ НА СПЕКТРАЛЬНЫХ МЕТОДАХ
- 8.2. ОГРАНИЧЕНИЯ СОПРЯЖЕННОСТИ И ИДЕМПОТЕНТЫ
- 8.3. СПЕКТРАЛЬНОЕ ОПИСАНИЕ ЦИКЛИЧЕСКИХ КОДОВ
- 8.4. РАСШИРЕННЫЕ КОДЫ РИДА-СОЛОМОНА
- 8.5. РАСШИРЕННЫЕ КОДЫ БЧХ
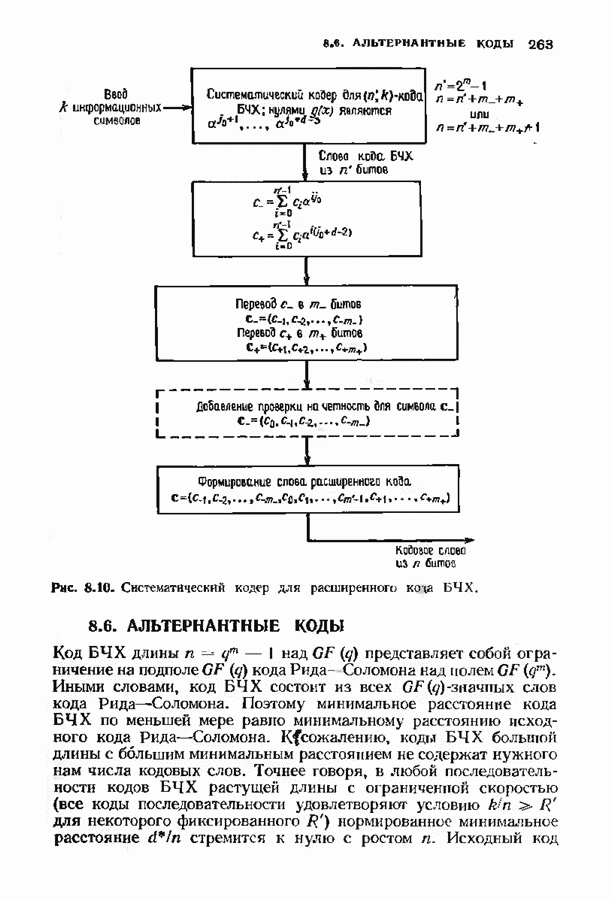
- 8.6. АЛЬТЕРНАНТНЫЕ КОДЫ
- 8.7. ХАРАКТЕРИСТИКИ АЛЬТЕРНАНТНЫХ КОДОВ
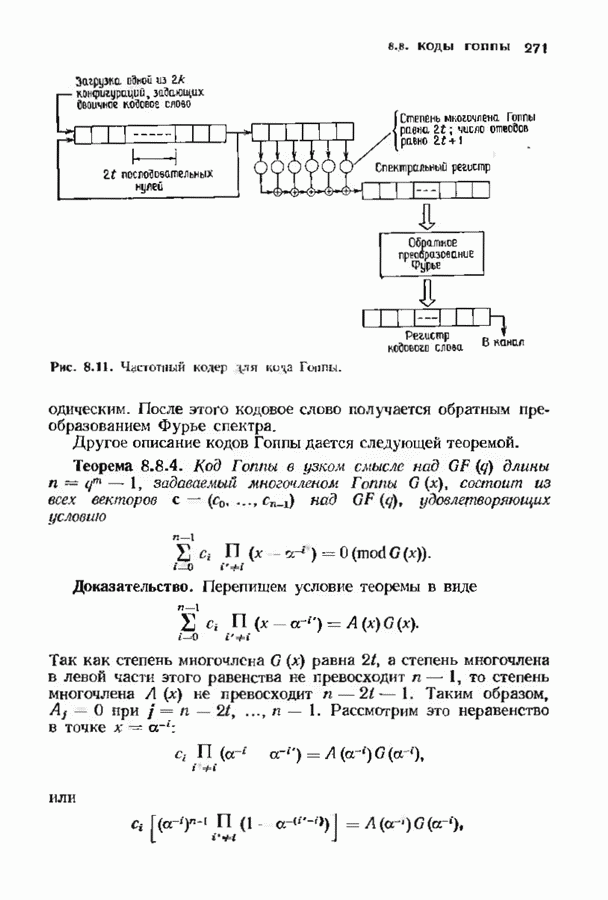
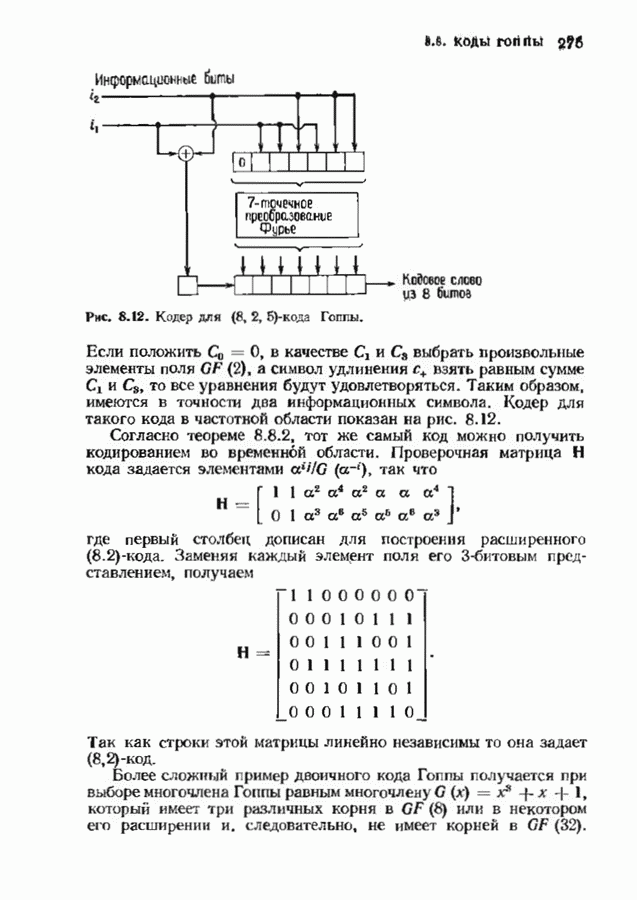
- 8.8. КОДЫ ГОППЫ
- 8.9. КОДЫ ПРЕПАРАТЫ
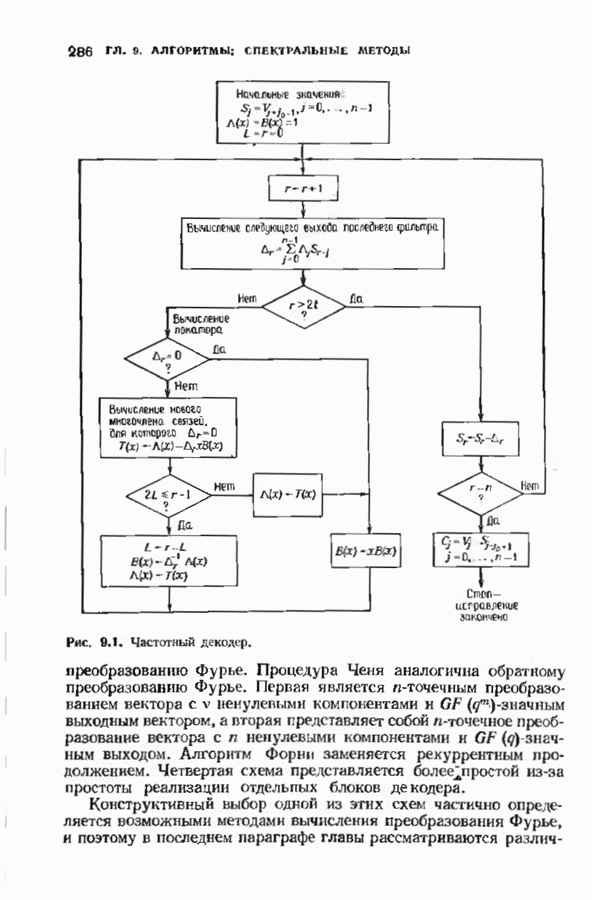
- ГЛАВА 9. АЛГОРИТМЫ, ОСНОВАННЫЕ НА СПЕКТРАЛЬНЫХ МЕТОДАХ
- 9.2. ИСПРАВЛЕНИЕ СТИРАНИЙ И ОШИБОК
- 9.3. ДЕКОДИРОВАНИЕ РАСШИРЕННЫХ КОДОВ РИДА—СОЛОМОНА
- 9.4. ДЕКОДИРОВАНИЕ РАСШИРЕННЫХ КОДОВ БЧХ
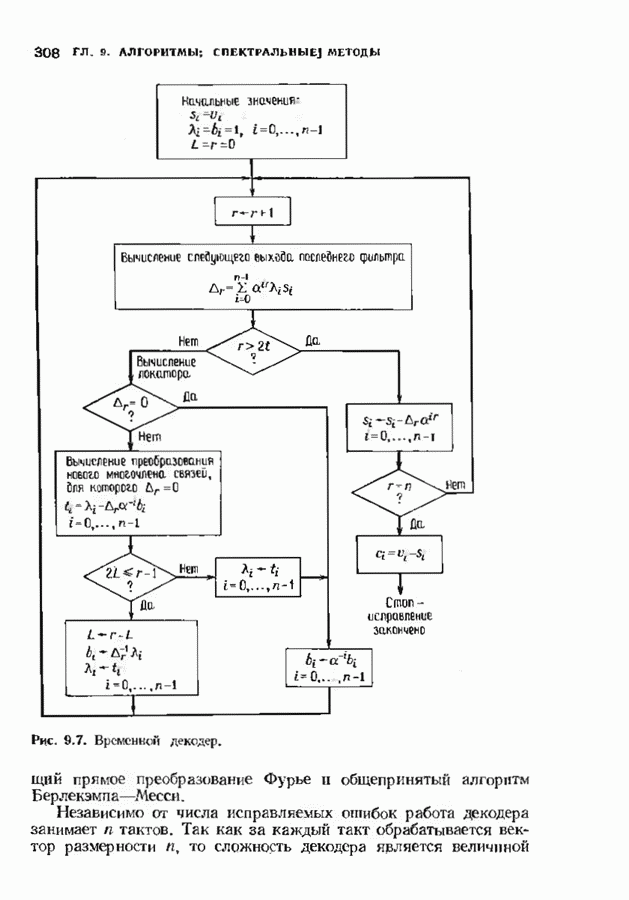
- 9.5. ДЕКОДИРОВАНИЕ ВО ВРЕМЕННОЙ ОБЛАСТИ
- 9.6. ДЕКОДИРОВАНИЕ ЗА ГРАНИЦЕЙ БЧХ
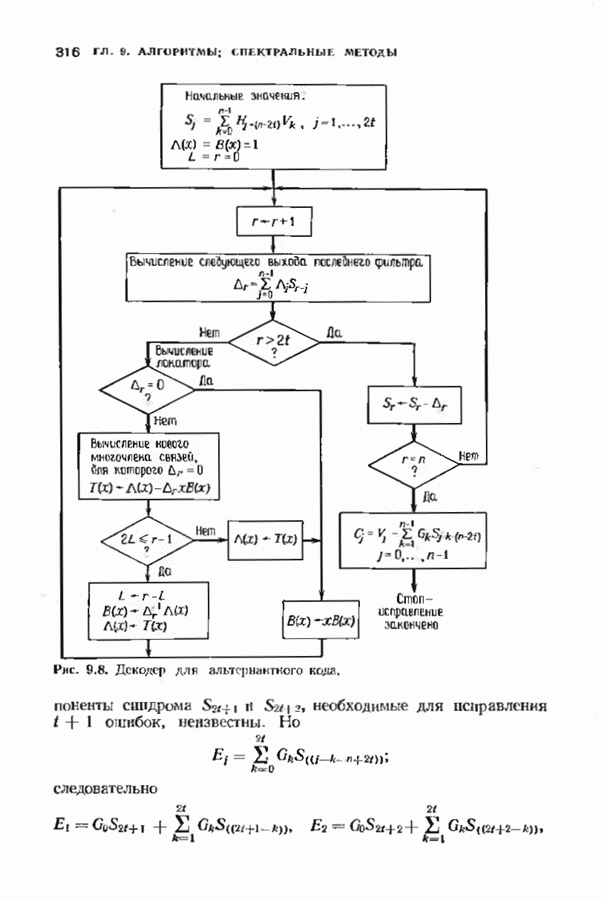
- 9.7. ДЕКОДИРОВАНИЕ АЛЬТЕРНАНТНЫХ КОДОВ
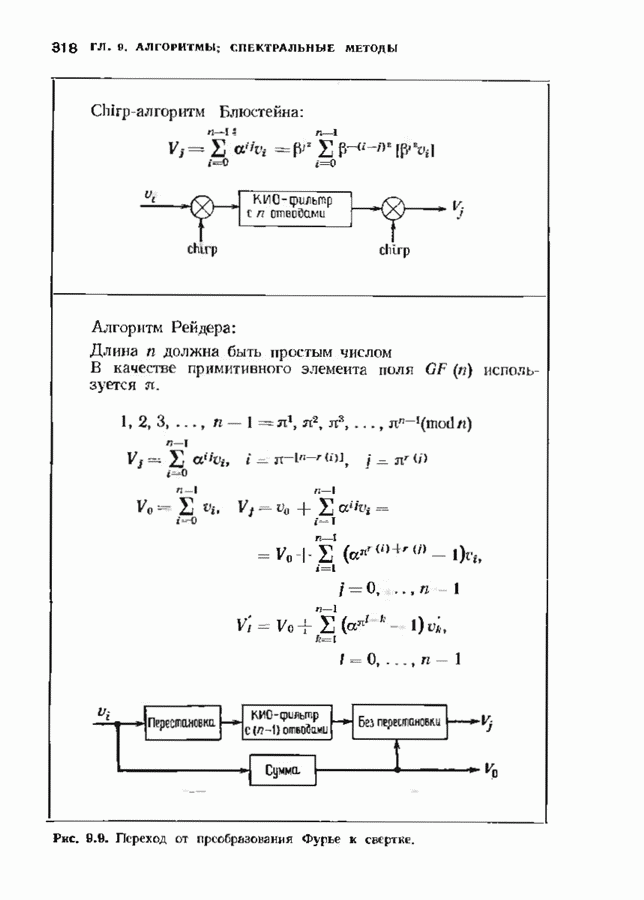
- 9.8. ВЫЧИСЛЕНИЕ ПРЕОБРАЗОВАНИЙ В КОНЕЧНЫХ ПОЛЯХ
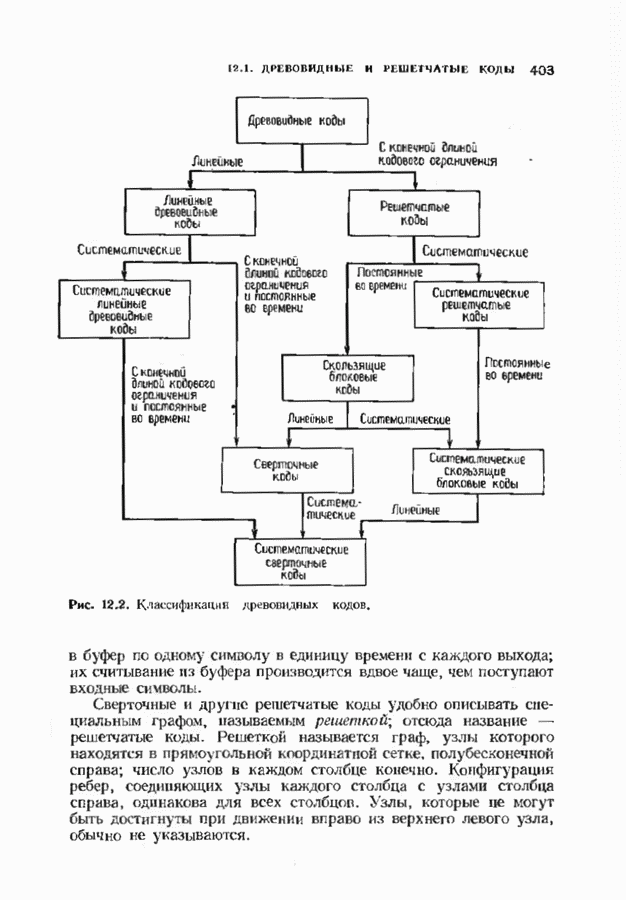
- ГЛАВА 10. МНОГОМЕРНЫЕ СПЕКТРАЛЬНЫЕ МЕТОДЫ
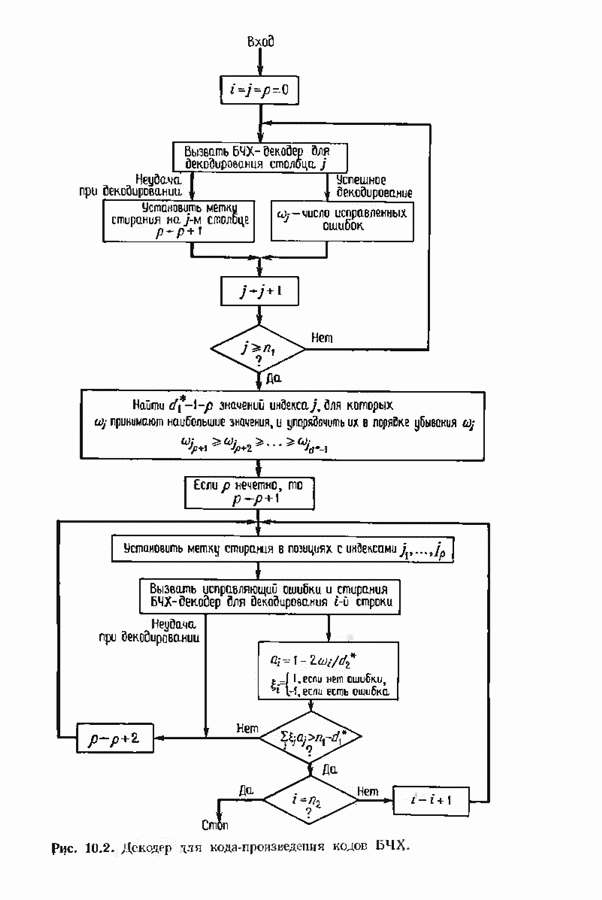
- 10.1. КОДЫ-ПРОИЗВЕДЕНИЯ
- 10.2. КИТАЙСКИЕ ТЕОРЕМЫ ОБ ОСТАТКАХ
- 10.3. ДЕКОДИРОВАНИЕ КОДА-ПРОИЗВЕДЕНИЯ
- 10.4. МНОГОМЕРНЫЕ СПЕКТРЫ
- 10.5. БЫСТРЫЕ КОДЫ БЧХ
- 10.6. ДЕКОДИРОВАНИЕ МНОГОМЕРНЫХ КОДОВ
- 10.7. ДЛИННЫЕ КОДЫ НАД МАЛЫМИ ПОЛЯМИ
- ГЛАВА 11. БЫСТРЫЕ АЛГОРИТМЫ
- 11.1. ЛИНЕЙНАЯ СВЕРТКА И ЦИКЛИЧЕСКАЯ СВЕРТКА
- 11.2. БЫСТРЫЕ АЛГОРИТМЫ СВЕРТКИ
- 11.3. БЫСТРЫЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 11.4. АЛГОРИТМЫ АГАРВАЛА—КУЛИ ВЫЧИСЛЕНИЯ СВЕРТОК
- 11.5. АЛГОРИТМ ВИНОГРАДА БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ
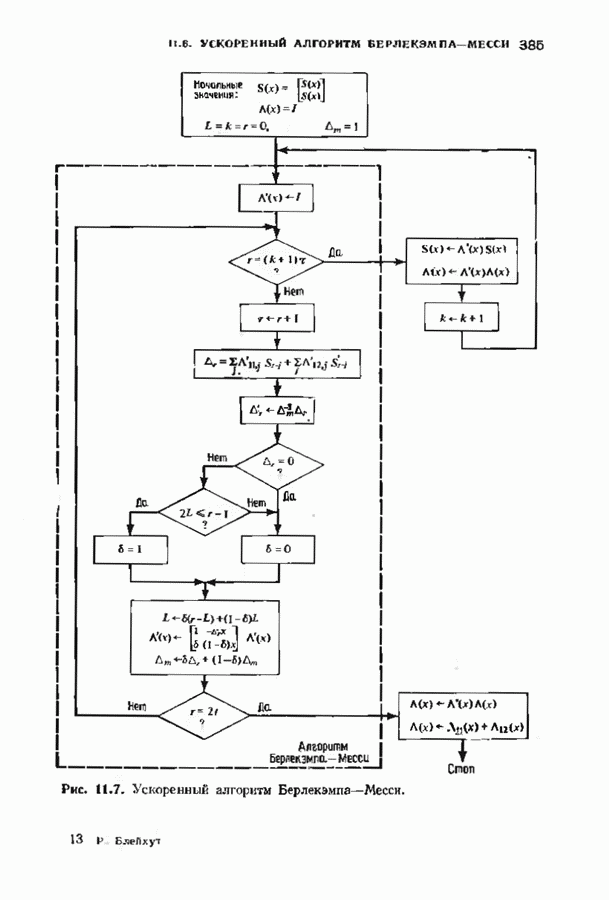
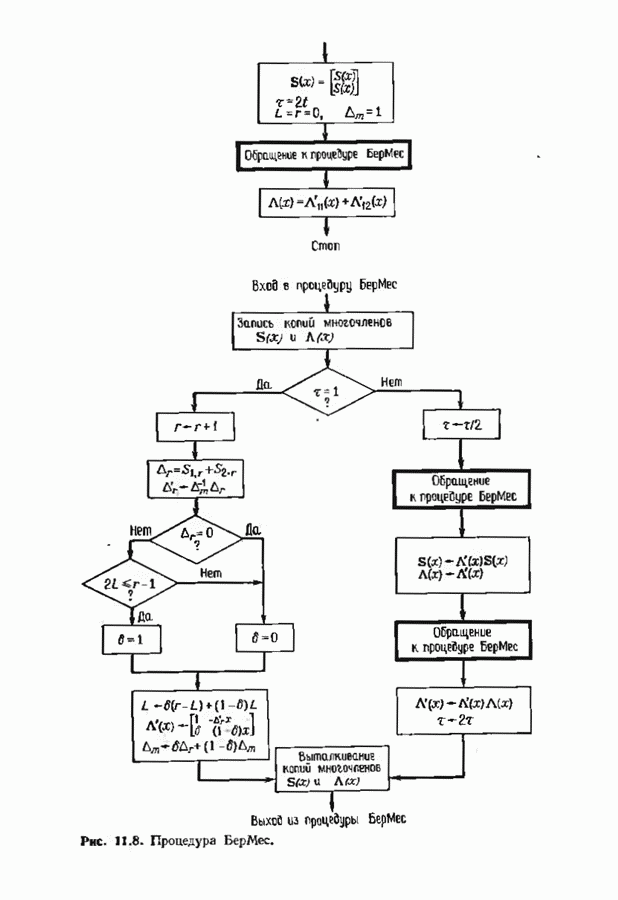
- 11.6. УСКОРЕННЫЙ АЛГОРИТМ БЕРЛЕКЭМПА—МЕССИ
- 11.7. РЕКУРРЕНТНЫЙ АЛГОРИТМ БЕРЛЕКЭМПА—МЕССИ
- 11.8. УСКОРЕННОЕ ДЕКОДИРОВАНИЕ КОДОВ БЧХ
- 11.9. СВЕРТКА В СУРРОГАТНЫХ ПОЛЯХ
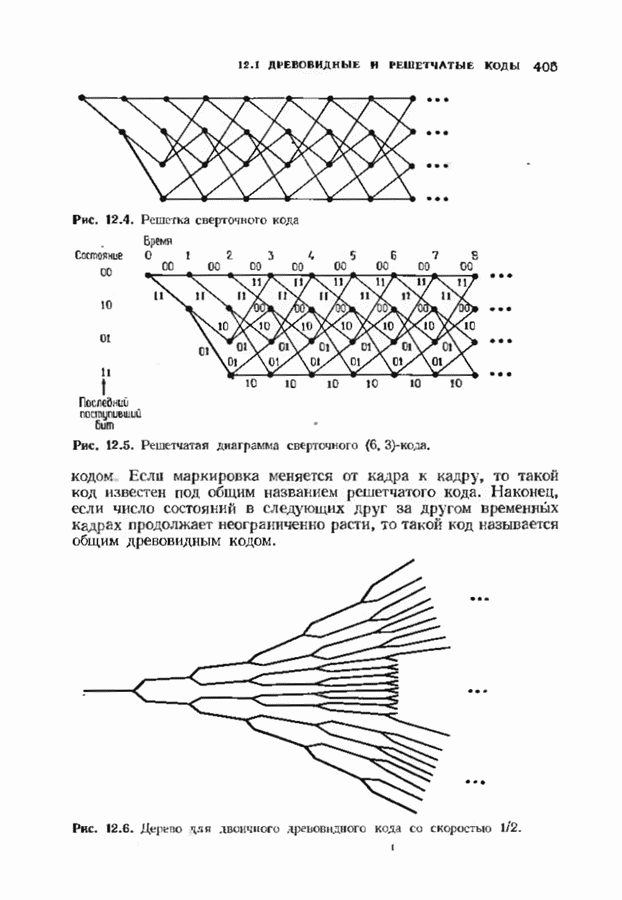
- ГЛАВА 12. СВЕРТОЧНЫЕ КОДЫ
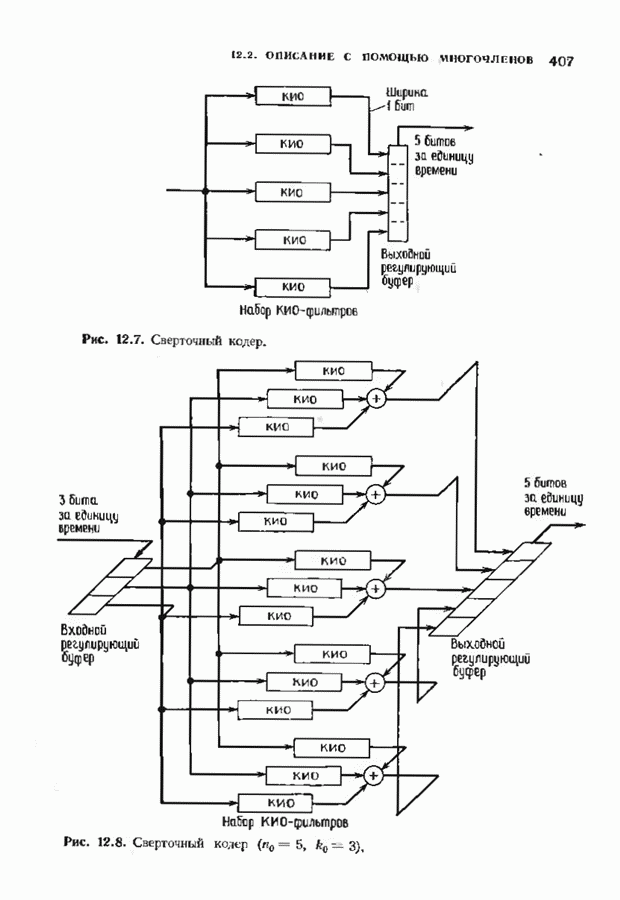
- 12.2. ОПИСАНИЕ СВЕРТОЧНЫХ КОДОВ С ПОМОЩЬЮ МНОГОЧЛЕНОВ
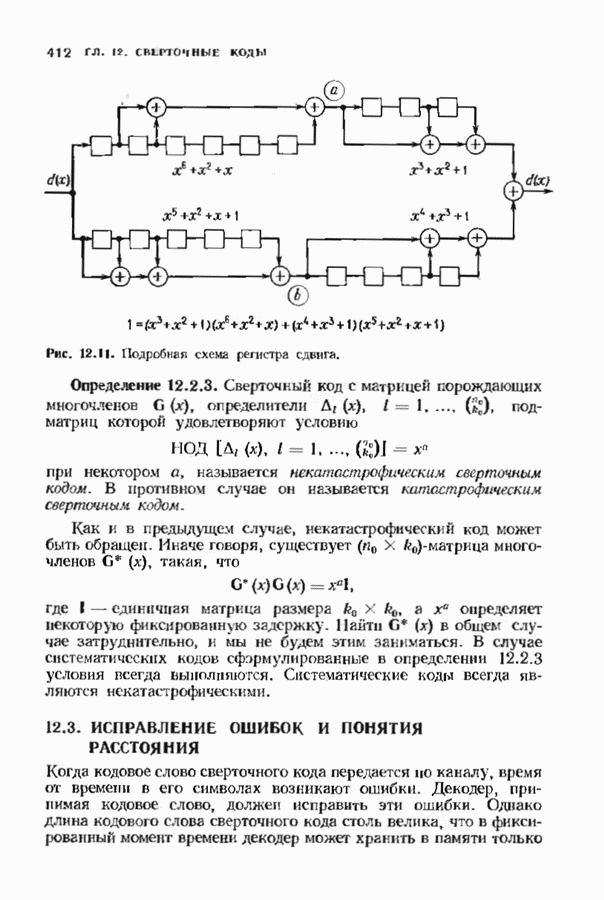
- 12.3. ИСПРАВЛЕНИЕ ОШИБОК И ПОНЯТИЯ РАССТОЯНИЯ
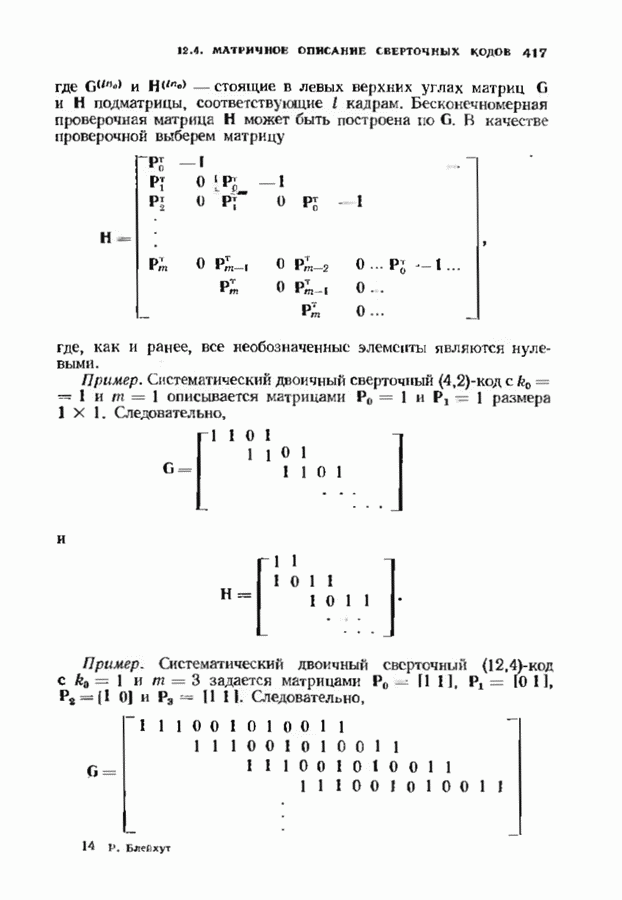
- 12.4. МАТРИЧНОЕ ОПИСАНИЕ СВЕРТОЧНЫХ КОДОВ
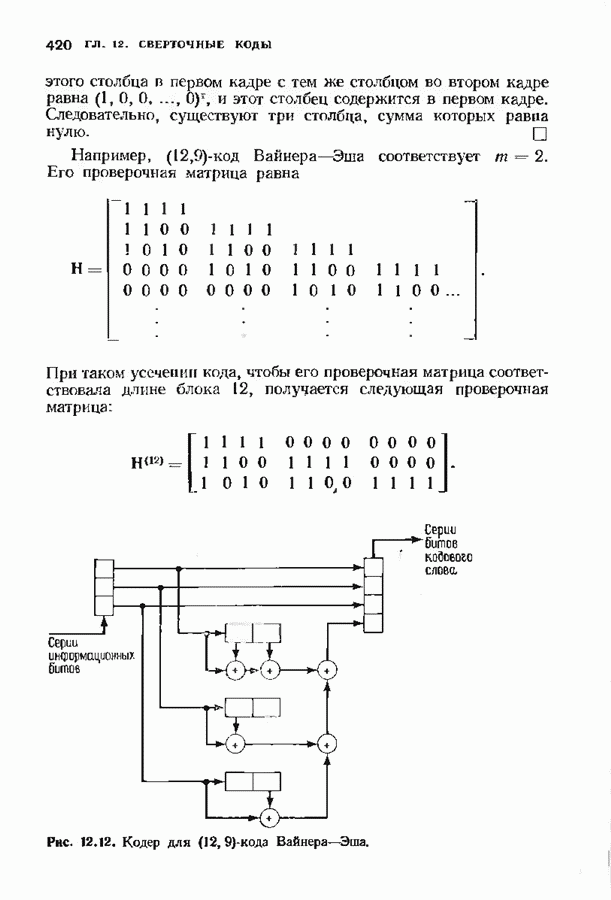
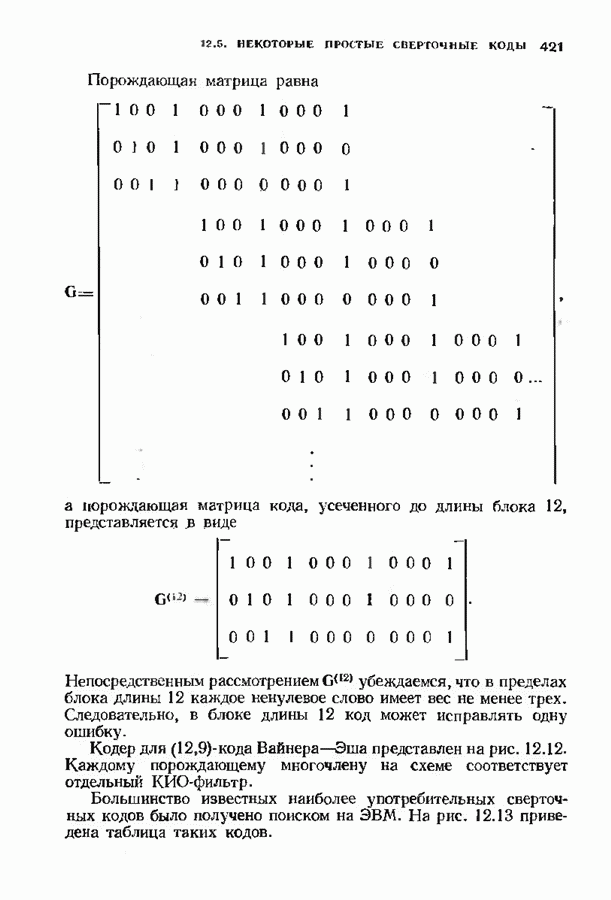
- 12.5. НЕКОТОРЫЕ ПРОСТЫЕ СВЕРТОЧНЫЕ КОДЫ
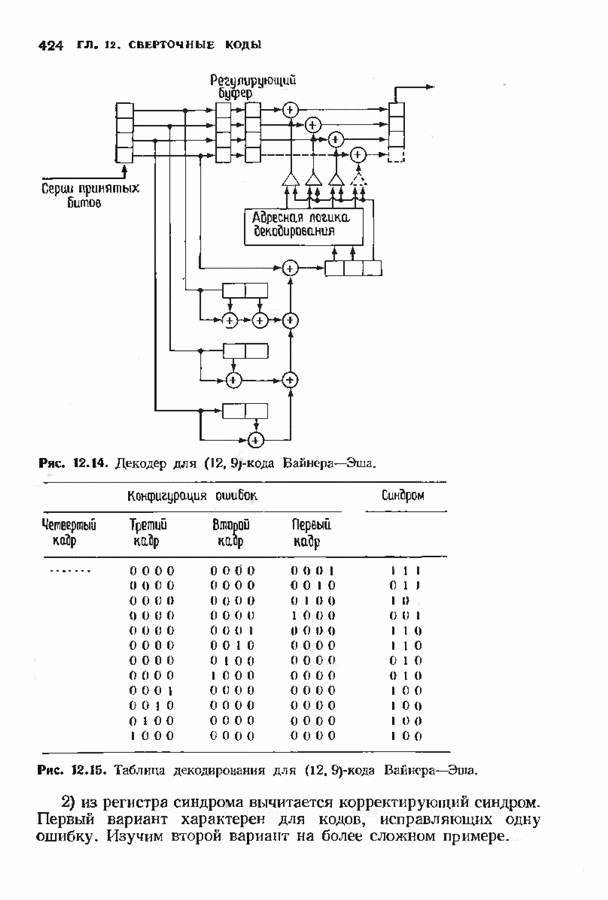
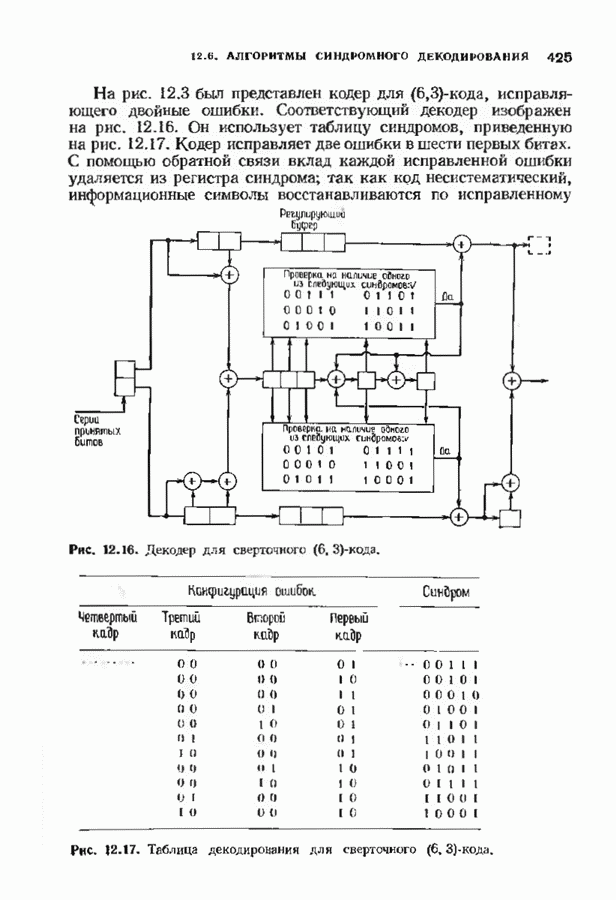
- 12.6. АЛГОРИТМЫ СИНДРОМНОГО ДЕКОДИРОВАНИЯ
- 12.7. ОБЕРТОЧНЫЕ КОДЫ ДЛЯ ИСПРАВЛЕНИЯ ПАКЕТОВ ОШИБОК
- 12.8. АЛГОРИТМ ДЕКОДИРОВАНИЯ ВИТЕРБИ
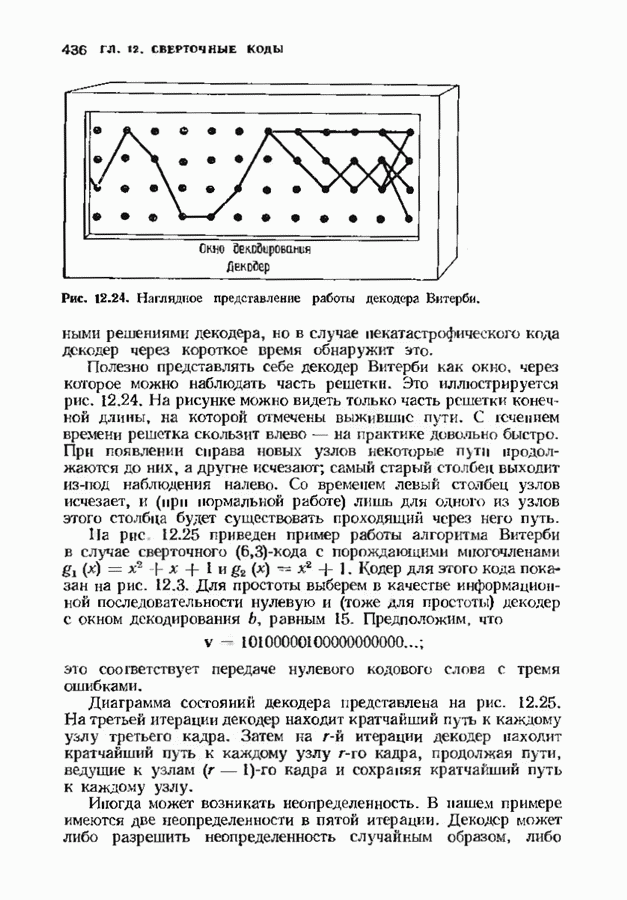
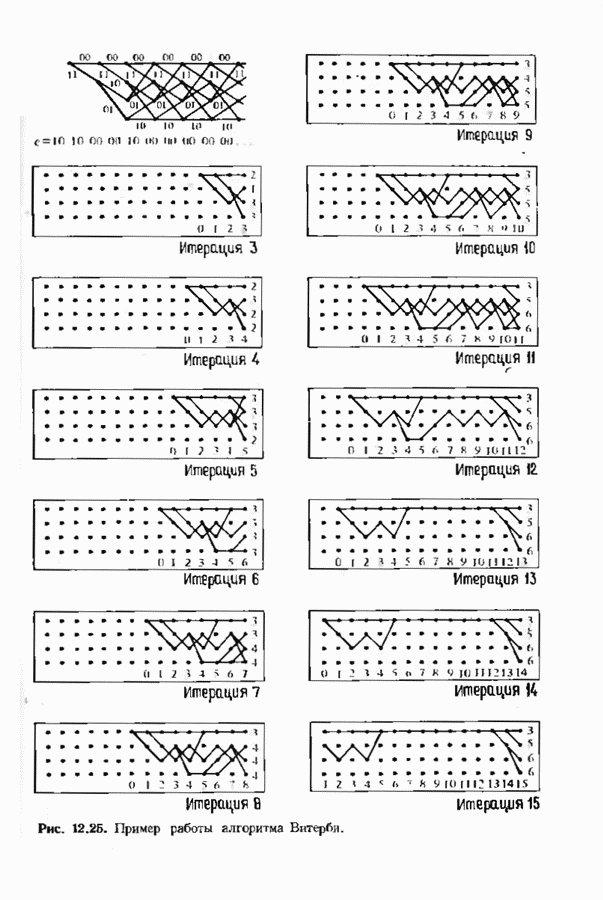
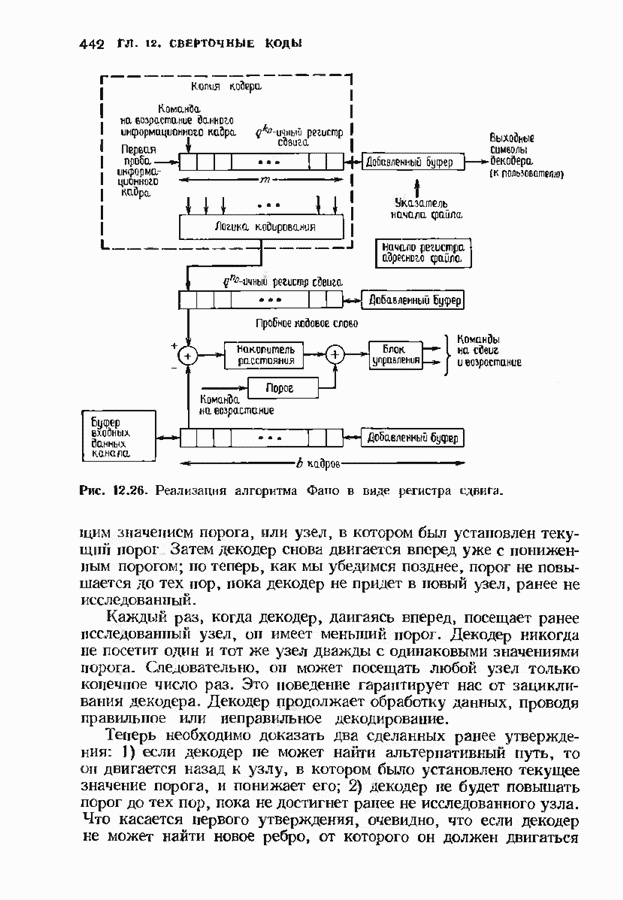
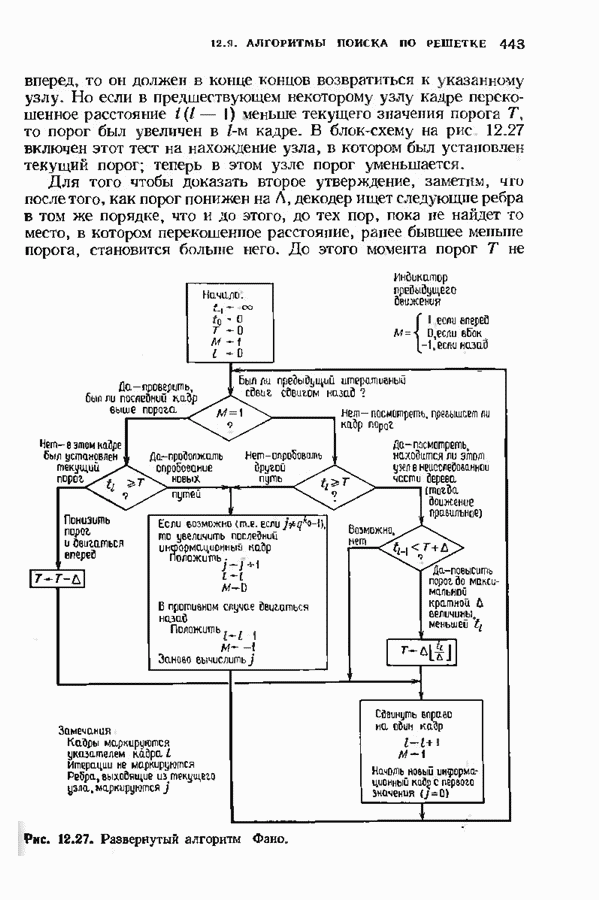
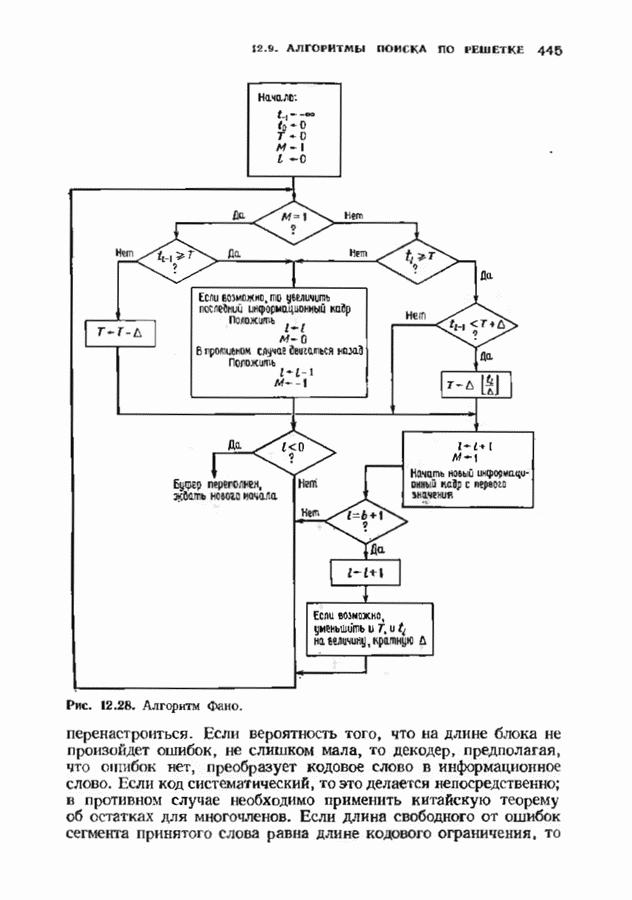
- 12.9. АЛГОРИТМЫ ПОИСКА ПО РЕШЕТКЕ
- ГЛАВА 13. КОДЫ И АЛГОРИТМЫ ДЛЯ ДЕКОДИРОВАНИЯ МАЖОРИТАРНЫМ МЕТОДОМ
- 13.1. ДЕКОДИРОВАНИЕ МАЖОРИТАРНЫМ МЕТОДОМ
- 13.2. СХЕМЫ МАЖОРИТАРНОГО ДЕКОДИРОВАНИЯ
- 13.3. АФФИННЫЕ ПЕРЕСТАНОВКИ ДЛЯ ЦИКЛИЧЕСКИХ КОДОВ
- 13.4. ЦИКЛИЧЕСКИЕ КОДЫ, ОСНОВАННЫЕ НА ПЕРЕСТАНОВКАХ
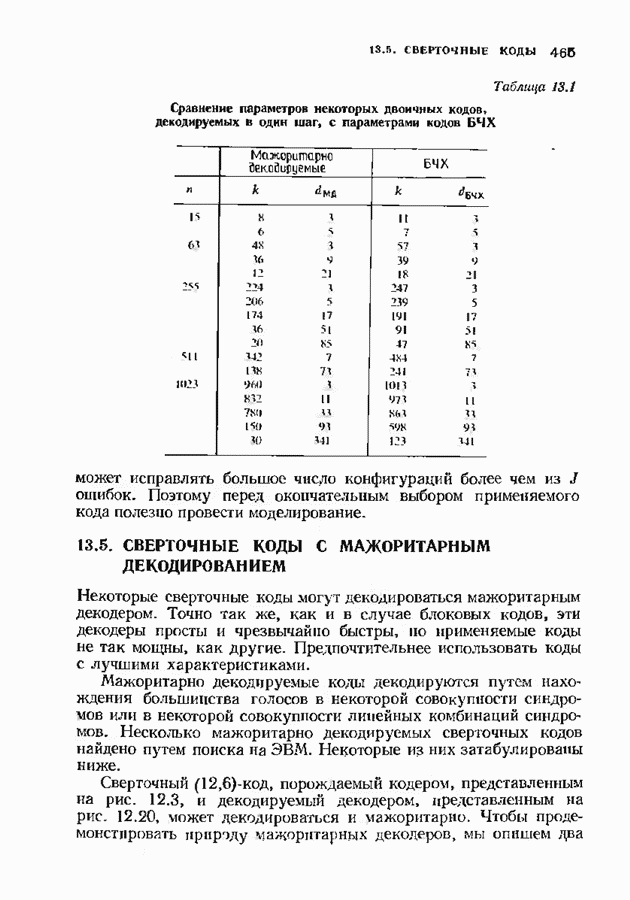
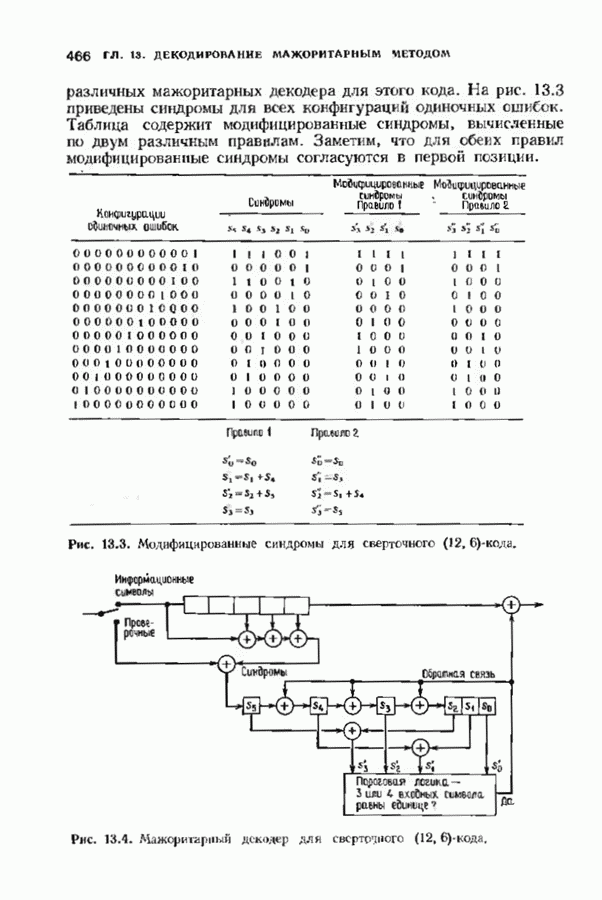
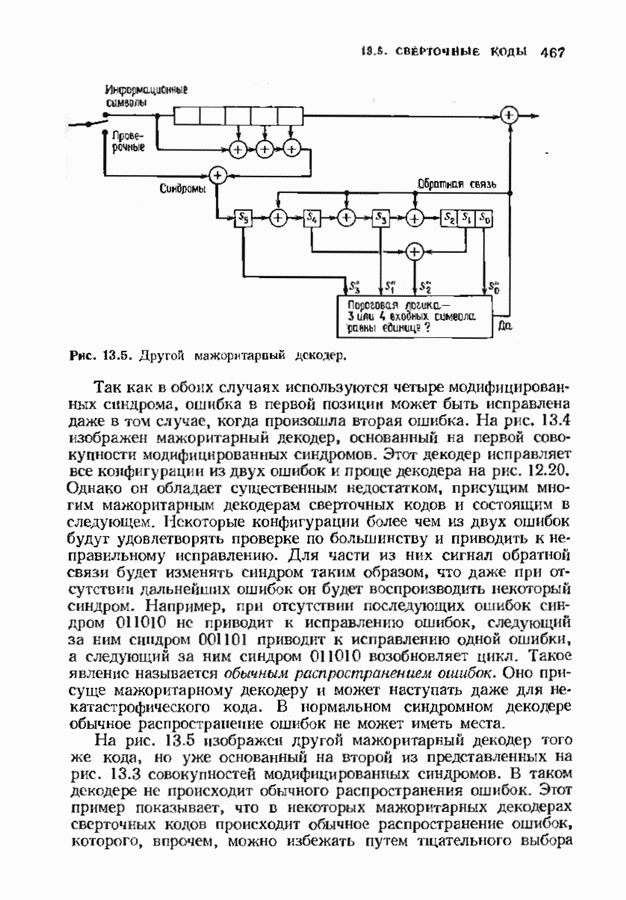
- 13.5. СВЕРТОЧНЫЕ КОДЫ С МАЖОРИТАРНЫМ ДЕКОДИРОВАНИЕМ
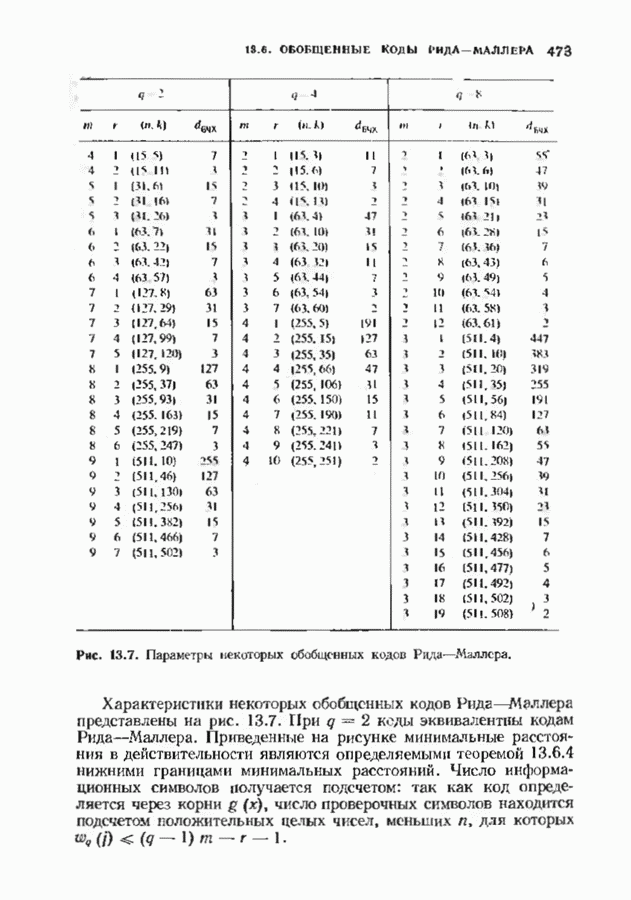
- 13.6. ОБОБЩЕННЫЕ КОДЫ РИДА—МАЛЛЕРА
- 13.7. ЕВКЛИДОВО-ГЕОМЕТРИЧЕСКИЕ КОДЫ
- 13.8. ПРОЕКТИВНО-ГЕОМЕТРИЧЕСКИЕ КОДЫ
- ГЛАВА 14. КОМПОЗИЦИЯ И ХАРАКТЕРИСТИКИ КОНТРОЛИРУЮЩИХ ОШИБКИ КОДОВ
- 14.2. ВЕРОЯТНОСТИ ОШИБОЧНОГО ДЕКОДИРОВАНИЯ И НЕУДАЧНОГО ДЕКОДИРОВАНИЯ
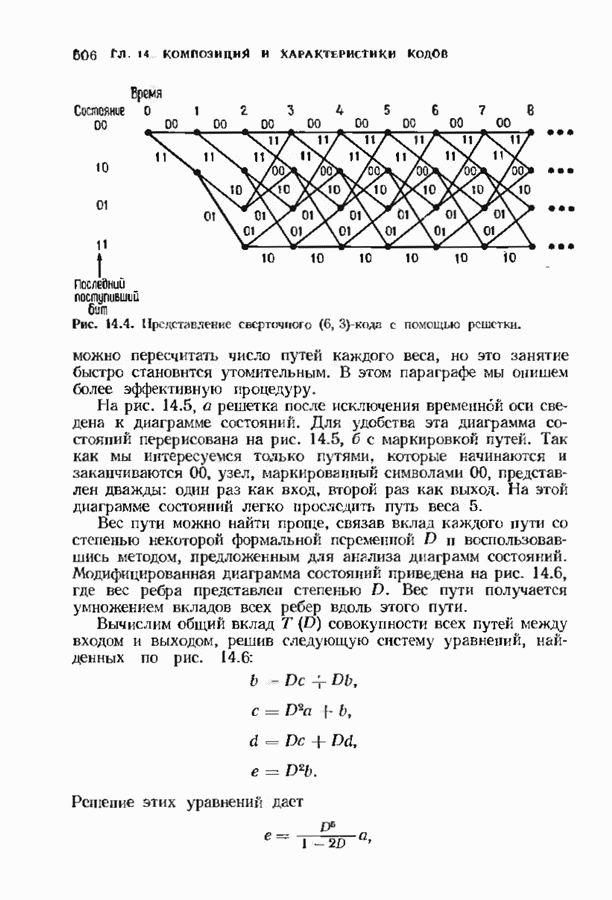
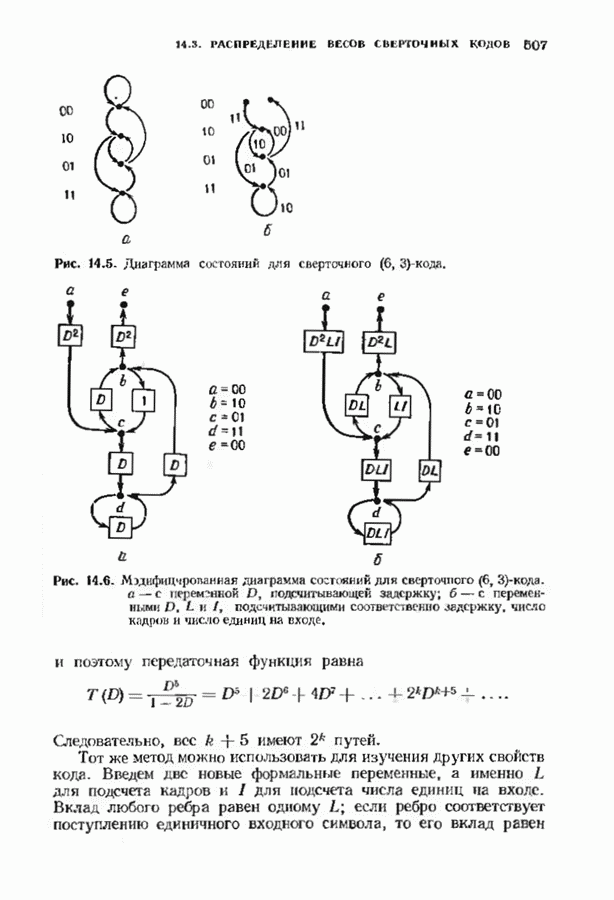
- 14.3. РАСПРЕДЕЛЕНИЕ ВЕСОВ СВЕРТОЧНЫХ КОДОВ
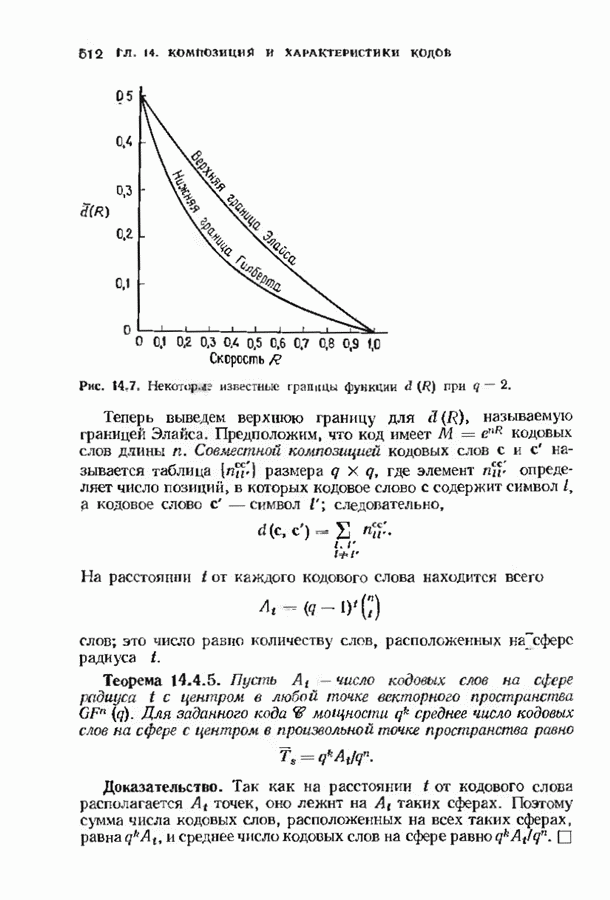
- 14.4. ГРАНИЦЫ МИНИМАЛЬНОГО РАССТОЯНИЯ ДЛЯ БЛОКОВЫХ КОДОВ
- 14.5. ГРАНИЦЫ МИНИМАЛЬНОГО РАССТОЯНИЯ ДЛЯ СВЕРТОЧНЫХ КОДОВ
- ГЛАВА 15. ЭФФЕКТИВНАЯ ПЕРЕДАЧА СИГНАЛОВ ПО ЗАШУМЛЕННЫМ КАНАЛАМ
- 15.1. ОГРАНИЧЕННЫЙ ПО ПОЛОСЕ ГАУССОВСКИЙ КАНАЛ
- 15.2. ЭНЕРГИЯ НА БИТ И ЧАСТОТА ОШИБОК НА БИТ
- 15.3. МЯГКОЕ ДЕКОДИРОВАНИЕ БЛОКОВЫХ КОДОВ
- 15.4. МЯГКОЕ ДЕКОДИРОВАНИЕ СВЕРТОЧНЫХ КОДОВ
- 15.5. ПОСЛЕДОВАТЕЛЬНОЕ ДЕКОДИРОВАНИЕ
- ЛИТЕРАТУРА