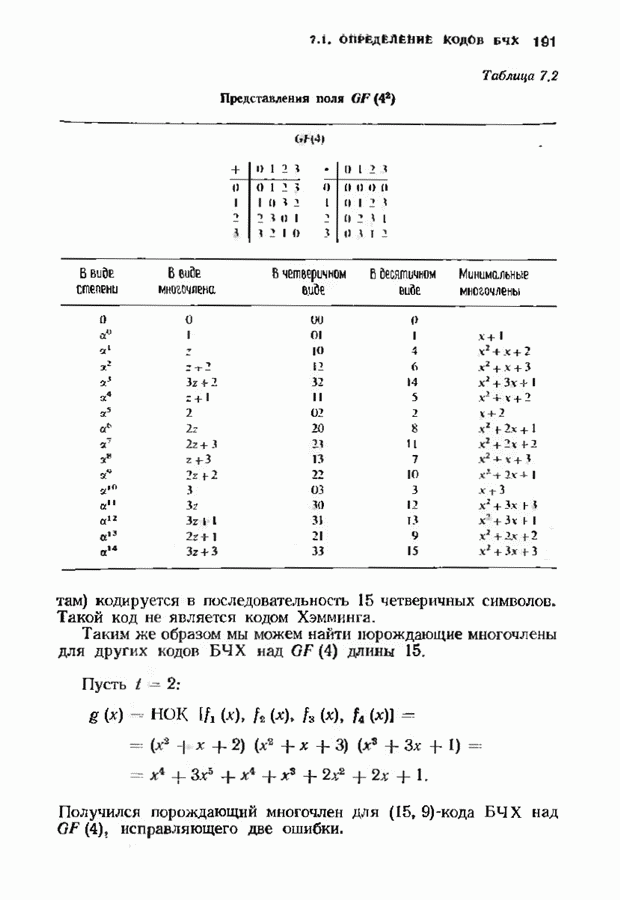
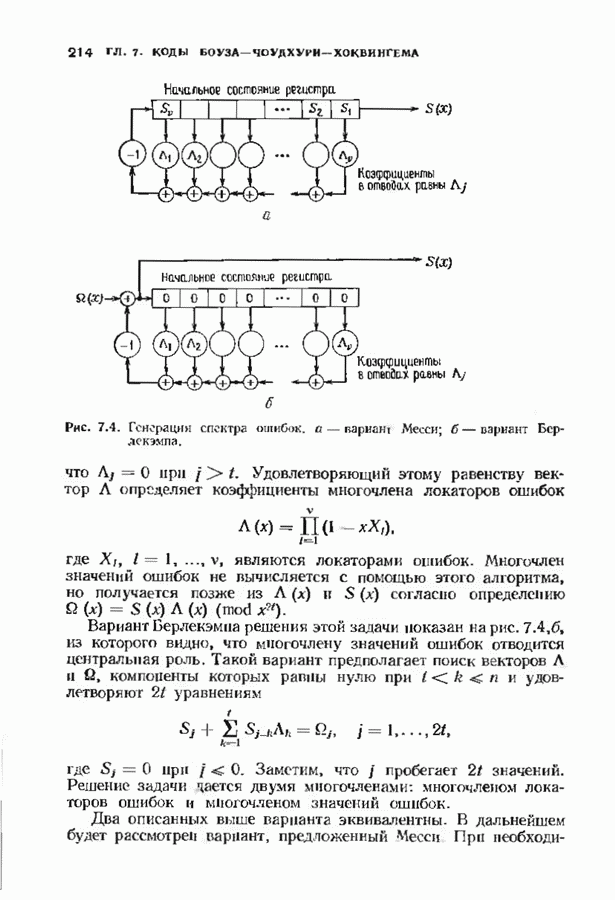
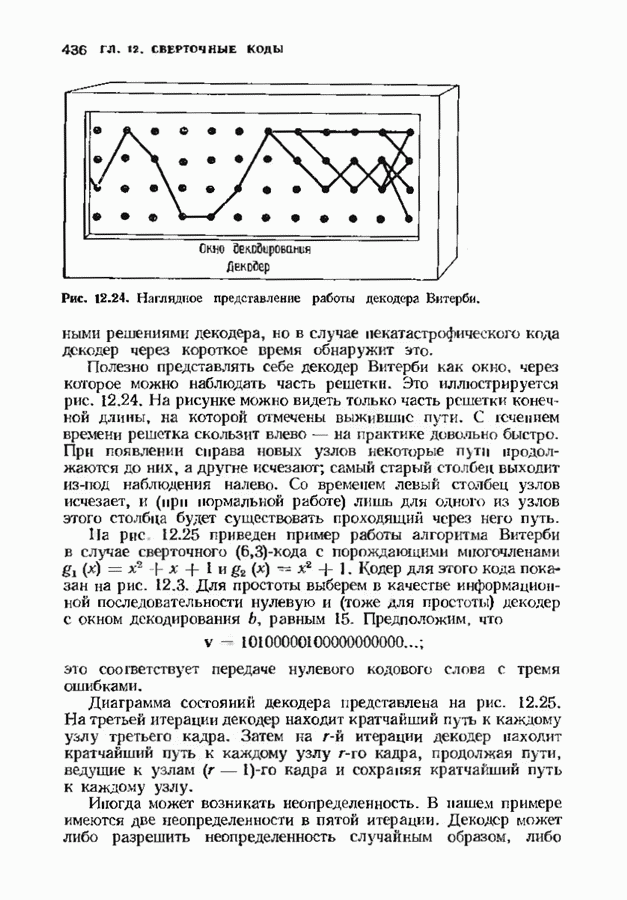
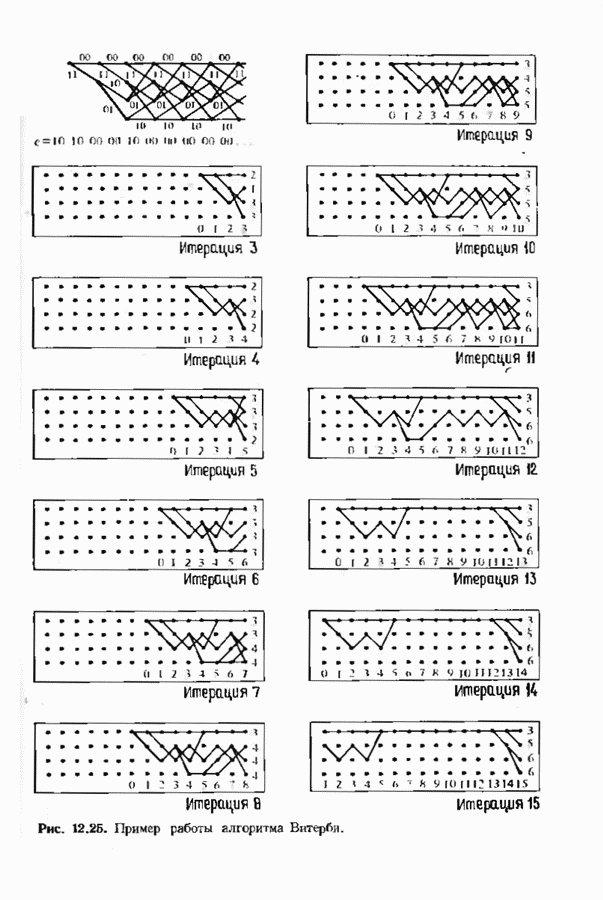
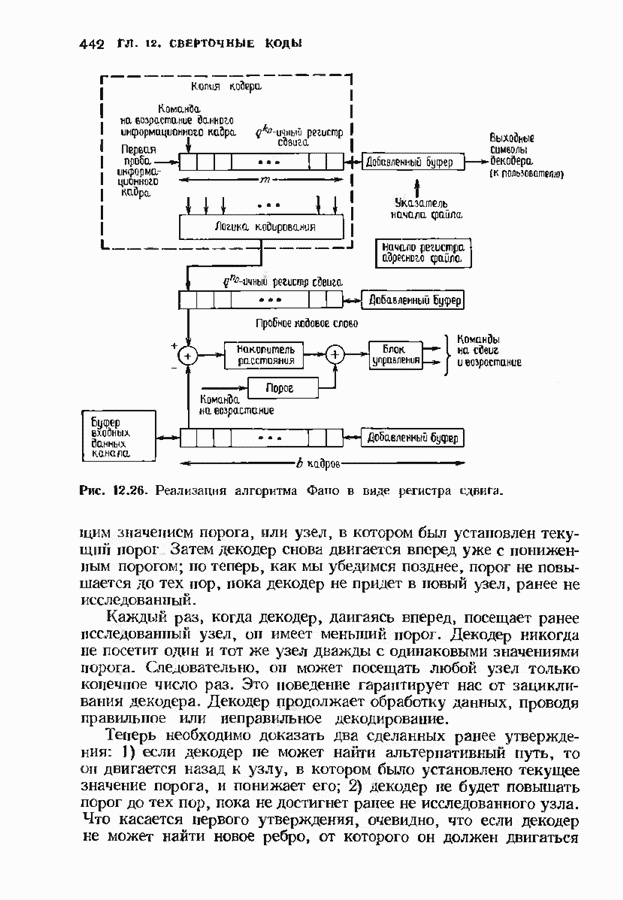
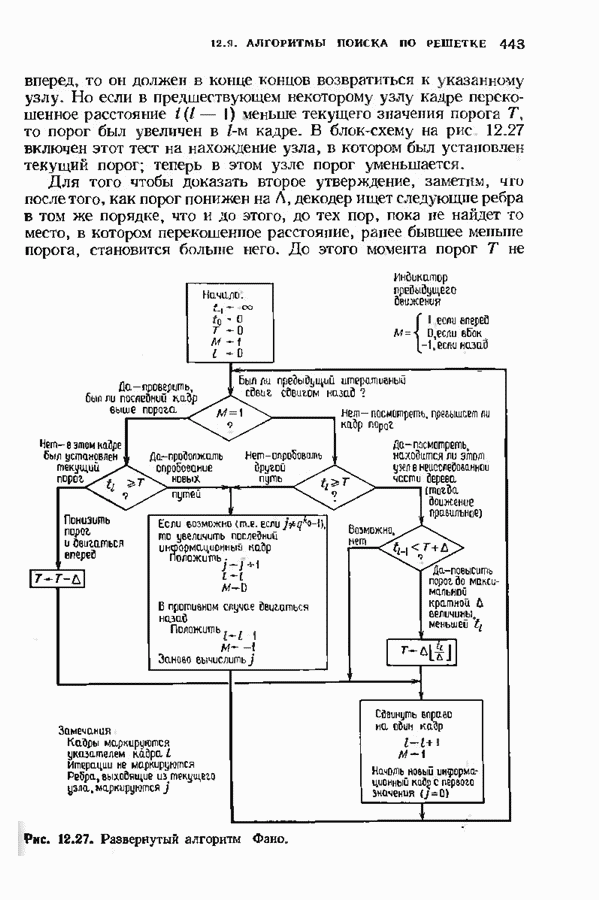
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.8. ДВОИЧНЫЙ КОД ГОЛЕЯ
Любой, кто займется исследованием таблицы биномиальных коэффициентов, может заметить, что

Это равенство представляет собой необходимое (но не достаточное) условие существования совершенного исправляющего тройные ошибки  -кода над
-кода над  так как: 1) число точек внутри сферы декодирования задается записанным в квадратных скобках выражением, 2) всего имеется 212 таких сфер и 3) все пространство содержит
так как: 1) число точек внутри сферы декодирования задается записанным в квадратных скобках выражением, 2) всего имеется 212 таких сфер и 3) все пространство содержит  точек. Следовательно, можно ожидать существования
точек. Следовательно, можно ожидать существования  -кода. Такой код, названный кодом Голея, действительно существует. Он удовлетворяет границе Хэмминга из задачи 1.5 со знаком равенства.
-кода. Такой код, названный кодом Голея, действительно существует. Он удовлетворяет границе Хэмминга из задачи 1.5 со знаком равенства.
Код Голея занимает уннкальное и важное место в теории кодирования. В силу такой хорошей упаковки сфер не удивительно, что код Голея тесно связан со многими математическими объектами, и поэтому его можно использовать для перехода от изучения теории кодирования к глубоким задачам теории групп и других областей математики. Однако встав на практическую точку зрения, вероятно, справедливо было бы заметить, что из-за малой длины код Голея, по-видимому, не найдет дальнейших конкретных приложений.
Определим код Голея как двоичный циклический код через ею порождающий многочлен.
Пусть  следующие взаимные многочлены:
следующие взаимные многочлены:

Простым вычислением проверяется, что

так что в качестве порождающего многочлена циклического  -кода можно использовать как
-кода можно использовать как  так и
так и  Мы воспользуемся многочленом
Мы воспользуемся многочленом  Проведенное в начале параграфа комбинаторное рассуждение показывает, что минимальное расстояние этого кода не может быть больше 7. Мы сейчас докажем, что оно равно по меньшей мере 7, однако это доказательство не будет одновременно столь элементарным и кратким, как предыдущее. Можно было бы выписать матрицу
Проведенное в начале параграфа комбинаторное рассуждение показывает, что минимальное расстояние этого кода не может быть больше 7. Мы сейчас докажем, что оно равно по меньшей мере 7, однако это доказательство не будет одновременно столь элементарным и кратким, как предыдущее. Можно было бы выписать матрицу  и проверить, что никакие шесть ее столбцов не являются линейно зависимыми, но из-за больших размеров матрицы это неудобно. Поэтому мы проведем доказательство непосредственно, хотя оно и окажется длинным (длина этого доказательства показывает, насколько трудным может быть вычисление минимального веса в коде).
и проверить, что никакие шесть ее столбцов не являются линейно зависимыми, но из-за больших размеров матрицы это неудобно. Поэтому мы проведем доказательство непосредственно, хотя оно и окажется длинным (длина этого доказательства показывает, насколько трудным может быть вычисление минимального веса в коде).
Доказательство будет состоять из трех шагов, которые совместно покажут, что минимальный вес не меньше 7- Этими тремя шагами являются доказательства следующих утверждений:
1) в коде нет слов веса 4 или меньше;
2) в коде нет слов веса 2, 6, 10, 14, 18 и 22;
3) в коде нет слов веса 1, 5, 9, 13, 17 и 21.
Совместно эти три утверждения означают, что минимвльный вес кода равен по меньшей мере 7. Так как мы уже видели, что он не может быть больше 7, то заключаем, что он в точности равен 7.
Начнем с рассмотрения корней многочленов  в соответствующем расширении поля GF (2). Сделаем это не впрямую, а построив минимальные многочлены некоторых элементов из
в соответствующем расширении поля GF (2). Сделаем это не впрямую, а построив минимальные многочлены некоторых элементов из  которые затем окажутся равными
которые затем окажутся равными  Если а — примитивный элемент поля, то в силу разложения
Если а — примитивный элемент поля, то в силу разложения  и элемент поля
и элемент поля  и обратный ему элемент
и обратный ему элемент  имеют порядок
имеют порядок  . Пусть
. Пусть  минимальные многочлены элементов
минимальные многочлены элементов  и соответственно.
и соответственно.
Согласно теореме 5.3.6, минимальный многочлен элемента  равен
равен

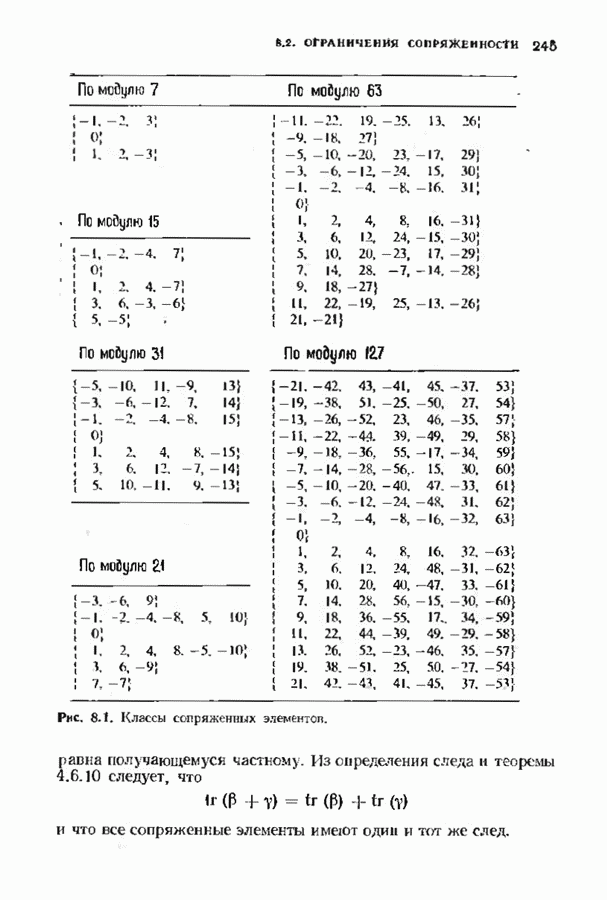
где все показатели степеней приводятся но модулю  Сопряженными являются элементы множества
Сопряженными являются элементы множества

которых всего 11, так что степень многочлена  равна 11. Аналогично минимальный многочлен элемента
равна 11. Аналогично минимальный многочлен элемента  равен
равен

а множество сопряженных элементов равно

Вместе множества В к В содержат 22 элемента ноля, порядок каждого из которых равен 23; следовательно,

причем, согласно теореме о единственности разложения, это разложение единственно. Но мы видели, что такое же разложение имеет место для порождающих многочленов  кода Голея. Следовательно, эти порождающие многочлены представляют собой минимальные многочлены элементов
кода Голея. Следовательно, эти порождающие многочлены представляют собой минимальные многочлены элементов  из поля
из поля 
Лемма 5.8.1. Код Голея не содержит ненулевых кодовых слов веса 4 и менее.
Доказательство. Так как элементы  принадлежат множеству В, то они являются корнями каждого кодового многочлена. Следовательно, каждое кодовое слово удовлетворяет равенству
принадлежат множеству В, то они являются корнями каждого кодового многочлена. Следовательно, каждое кодовое слово удовлетворяет равенству  где
где

и, таким образом, с является кодовым словом кода с проверочной матрицей  Но любые четыре столбца матрицы
Но любые четыре столбца матрицы  образуют ненулевую матрицу, кратную матрице Вандермонда, определитель которой, как известно, отличен от нуля, если все элементы ее первой строки различны (это будет доказано в § 7.2). Следовательно, согласно следствию
образуют ненулевую матрицу, кратную матрице Вандермонда, определитель которой, как известно, отличен от нуля, если все элементы ее первой строки различны (это будет доказано в § 7.2). Следовательно, согласно следствию  является проверочной матрицей кода, минимальный вес в котором равен по меньшей мере 5.
является проверочной матрицей кода, минимальный вес в котором равен по меньшей мере 5.
Следующая лемма утверждает, что код Голея не содержит слов веса 2, 6, 10, 14. 18 и 22.
Лемма 5.8.2. Если вес слова Голея четен, то он кратен 4.
Доказательство. Пусть с  кодовое слово, вес которого четен:
кодовое слово, вес которого четен:

где число коэффициентов  равных единице, четно. Тогда с
равных единице, четно. Тогда с  и поэтому к — 1 делит с
и поэтому к — 1 делит с  Но
Но  не делит
не делит  следовательно,
следовательно,

для некоторого  Определим взаимный многочлен:
Определим взаимный многочлен:

Поскольку с  для некоторого
для некоторого  имеем
имеем

Таким образом,

Ниже мы используем это равенство, а сейчас вычислим с  отметив, что произведение многочленов может быть записано в виде свертки:
отметив, что произведение многочленов может быть записано в виде свертки:

Если считать, что коэффициенты с индексами, меньшими нуля и большими 22, равны нулю, то сумму по  можно заменить суммой от
можно заменить суммой от  до
до  (это позволит избежать двльнейших хлопот с пределами суммирования). Сумму можно разбить на части следующим образом:
(это позволит избежать двльнейших хлопот с пределами суммирования). Сумму можно разбить на части следующим образом:

Второе слагаемое равно нулю, так как  , в поле
, в поле  и по предположению число коэффициентов
и по предположению число коэффициентов  равных единице, четно. В последнем слагаемом сделаем подстановку
равных единице, четно. В последнем слагаемом сделаем подстановку  и в обоих слагаемых заменим
и в обоих слагаемых заменим  на
на  Тогда
Тогда

Далее заменим  на I во втором слагаемом и положим
на I во втором слагаемом и положим  в первом слагаемом и
в первом слагаемом и  во втором. Это дает
во втором. Это дает

Но с  кратно многочлену
кратно многочлену  и следовательно,
и следовательно,

Это равенство должно выполняться при сложении по модулю 2. Следовательно, при целочисленном сложении при каждом  в левой части должно получаться четное число:
в левой части должно получаться четное число:

для некоторых чисел  Левая часть не меняется при замене
Левая часть не меняется при замене  на
на  Следовательно,
Следовательно,  Таким образом, суммирование по
Таким образом, суммирование по  дает
дает

для некоторого  . Наконец, левую часть можно переупорядочить. Положим
. Наконец, левую часть можно переупорядочить. Положим  в первом слагаемом и
в первом слагаемом и  во втором; тогда
во втором; тогда

что вырождается в

Так как двоичные компоненты  отличны от нуля в
отличны от нуля в  позициях, отсюда следует, что
позициях, отсюда следует, что

В силу четности  это означает, что
это означает, что  кратно 4, что и доказывает лемму.
кратно 4, что и доказывает лемму.
Теперь можно перейти к доказательству следующей теоремы.
Теорема 5.8.3. Код Голея является совершенным кодом, исправляющим три ошибки.
Доказательство. Как уже было указано в начале этого параграфа, необходимо только доказать, что минимальное расстояние равно по меньшей мере 7. В силу леммы 5.8.1 оно равно по меньшей мере 5, а в силу леммы 5.8.2 оно не может быть равно 6. Таким образом, необходимо только доказать, что код не содержит слов веса 5.
Рассмотрим кодовое слово  в действительности
в действительности  так как
так как  Таким образом, коду принадлежит слово, все компоненты которого равны 1. Прибавление этого кодового слова к любому кодовому слову веса
Таким образом, коду принадлежит слово, все компоненты которого равны 1. Прибавление этого кодового слова к любому кодовому слову веса  дает кодовое слово веса
дает кодовое слово веса  Тогда, согласно лемме 5.8.2, в коде не содержится слов с весами, равными 21, 17, 13, 9, 5 и 1; в частности, не содержится слов веса 5. Теорема доказана.
Тогда, согласно лемме 5.8.2, в коде не содержится слов с весами, равными 21, 17, 13, 9, 5 и 1; в частности, не содержится слов веса 5. Теорема доказана. 
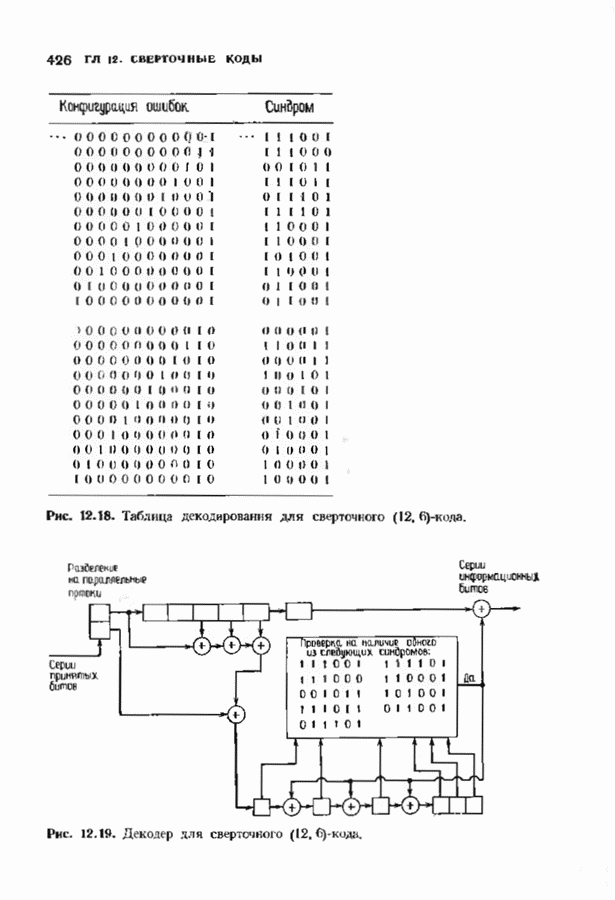
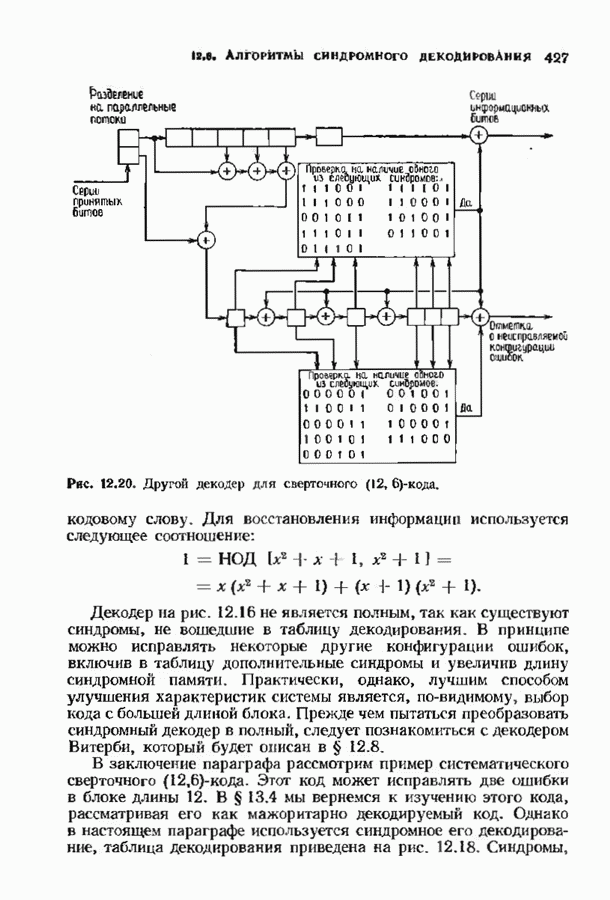
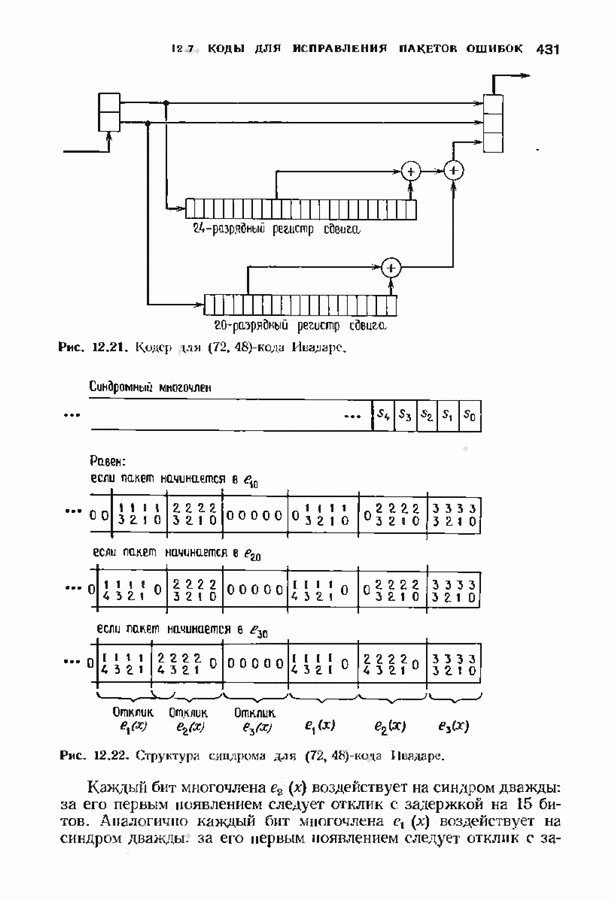
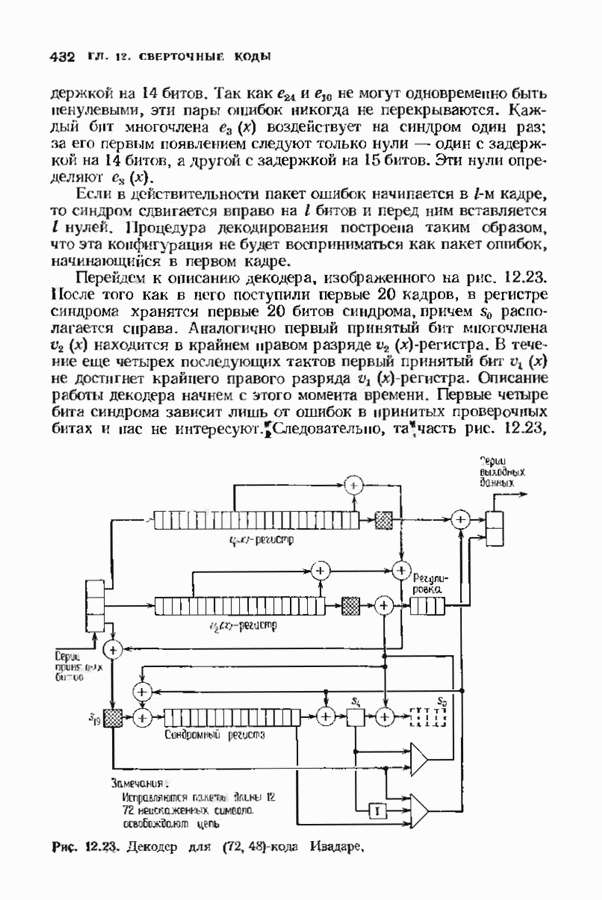
Отметим, что из доказательства теоремы следует также, что все веса слов в коде Голея исчерпываются числами 0, 7, 8, 11, 12, 15, 16 и 23. Просчитанное на ЭВМ число слов каждого веса приведено в табл. 5.3.
Кроме двоичного кода Голея существует также совершенный троичный  -код Голея. Этими двумя кодами исчерпываются все нетривиальные примеры совершенных кодов, исправляющих более одной ошибки.
-код Голея. Этими двумя кодами исчерпываются все нетривиальные примеры совершенных кодов, исправляющих более одной ошибки.
Таблица 5.3 (см. скан) Веса слов кода Голея
| << Предыдущий параграф | Следующий параграф >> |
- ОТ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ВВЕДЕНИЕ
- 1.1. ДИСКРЕТНЫЙ КАНАЛ, СВЯЗИ
- 1.2. ИСТОРИЯ КОДИРОВАНИЯ, КОНТРОЛИРУЮЩЕГО ОШИБКИ
- 1.3. ПРИЛОЖЕНИЯ
- 1.4. ОСНОВНЫЕ ПОНЯТИЯ
- 1.5. ПРОСТЕЙШИЕ КОДЫ
- ГЛАВА 2. ВВЕДЕНИЕ В АЛГЕБРУ
- 2.1. 2-ПОЛЕ И 6-10-ПОЛЕ
- 2.2. ГРУППЫ
- 2.3. КОЛЬЦА
- 2.4. ПОЛЯ
- 2.5. ВЕКТОРНЫЕ ПРОСТРАНСТВА
- 2.6. ЛИНЕЙНАЯ АЛГЕБРА
- ГЛАВА 3. ЛИНЕЙНЫЕ БЛОКОВЫЕ КОДЫ
- 3.1. СТРУКТУРА ЛИНЕЙНЫХ БЛОКОВЫХ КОДОВ
- 3.2. МАТРИЧНОЕ ОПИСАНИЕ ЛИНЕЙНЫХ БЛОКОВЫХ КОДОВ
- 3.3. СТАНДАРТНОЕ РАСПОЛОЖЕНИЕ
- 3.4. КОДЫ ХЭММИНГА
- 3.5. СОВЕРШЕННЫЕ И КВАЗИСОВЕРШЕННЫЕ КОДЫ
- 3.6. ПРОСТЫЕ ПРЕОБРАЗОВАНИЯ ЛИНЕЙНОГО КОДА
- 3.7. КОДЫ РИДА—МАЛЛЕРА
- ГЛАВА 4. АРИФМЕТИКА ПОЛЕЙ ГАЛУА
- 4.2. КОНЕЧНЫЕ ПОЛЯ, ОСНОВАННЫЕ НА КОЛЬЦЕ ЦЕЛЫХ ЧИСЕЛ
- 4.3. КОЛЬЦА МНОГОЧЛЕНОВ
- 4.4. КОНЕЧНЫЕ ПОЛЯ, ОСНОВАННЫЕ НА КОЛЬЦАХ МНОГОЧЛЕНОВ
- 4.5. ПРИМИТИВНЫЕ ЭЛЕМЕНТЫ
- 4.6. СТРУКТУРА КОНЕЧНОГО ПОЛЯ
- ГЛАВА 5. ЦИКЛИЧЕСКИЕ КОДЫ
- 5.2. ПОЛИНОМИАЛЬНОЕ ОПИСАНИЕ ЦИКЛИЧЕСКИХ КОДОВ
- 5.3. МИНИМАЛЬНЫЕ МНОГОЧЛЕНЫ И СОПРЯЖЕНИЯ
- 5.4. МАТРИЧНОЕ ОПИСАНИЕ ЦИКЛИЧЕСКИХ КОДОВ
- 5.5. КОДЫ ХЭММИНГА КАК ЦИКЛИЧЕСКИЕ КОДЫ
- 5.6. ЦИКЛИЧЕСКИЕ КОДЫ, ИСПРАВЛЯЮЩИЕ ДВЕ ОШИБКИ
- 5.7. ЦИКЛИЧЕСКИЕ КОДЫ, ИСПРАВЛЯЮЩИЕ ПАКЕТЫ ОШИБОК
- 5.8. ДВОИЧНЫЙ КОД ГОЛЕЯ
- 5.9. КВАДРАТИЧНО-ВЫЧЕТНЫЕ КОДЫ
- ГЛАВА 6. СХЕМНАЯ РЕАЛИЗАЦИЯ ЦИКЛИЧЕСКОГО КОДИРОВАНИЯ
- 6.1. ЛОГИЧЕСКИЕ ЦЕПИ ДЛЯ АРИФМЕТИКИ КОНЕЧНОГО ПОЛЯ
- 6.2. ЦИФРОВЫЕ ФИЛЬТРЫ
- 6.3. КОДЕРЫ И ДЕКОДЕРЫ НА РЕГИСТРАХ СДВИГА
- 6.4. ДЕКОДЕР МЕГГИТТА
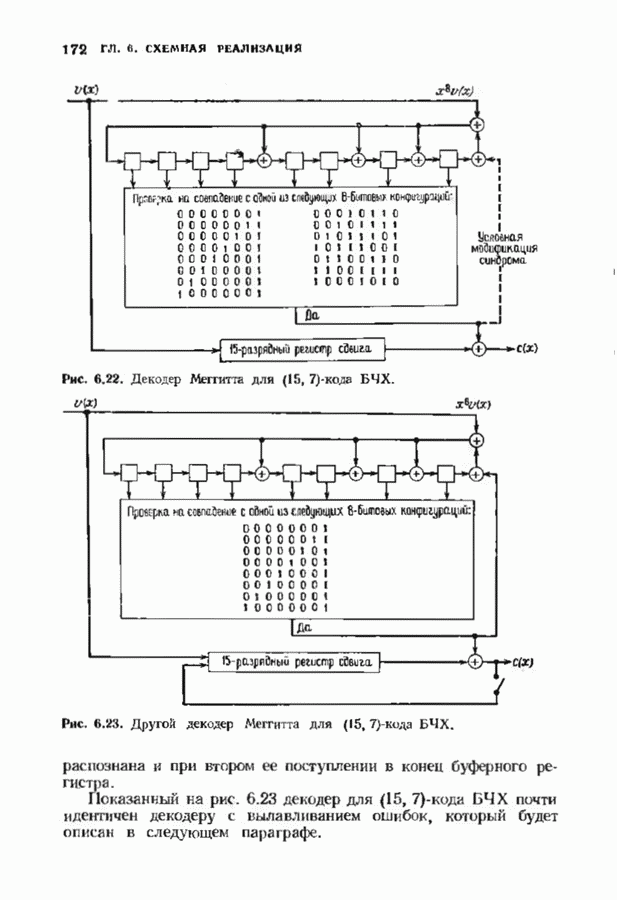
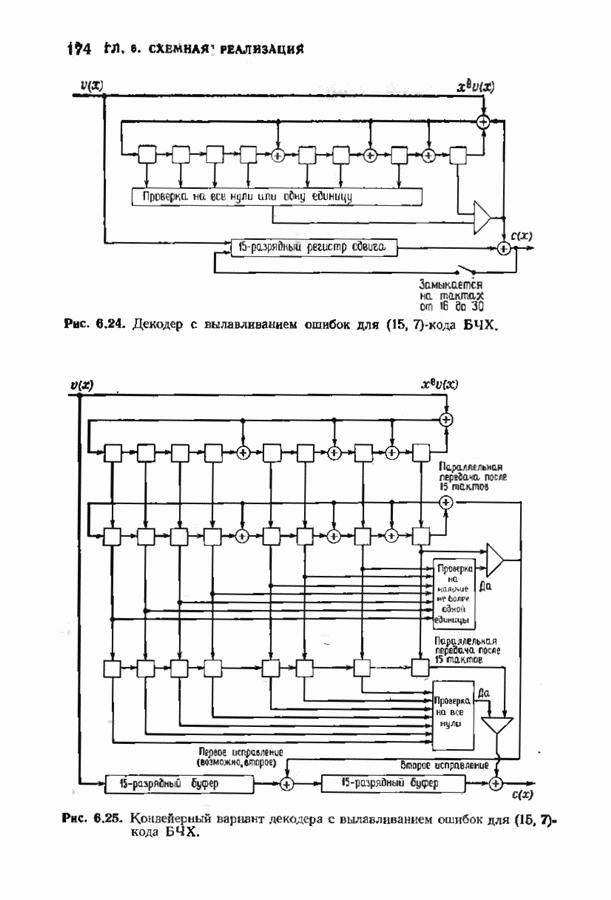
- 6.5. ВЫЛАВЛИВАНИЕ ОШИБОК
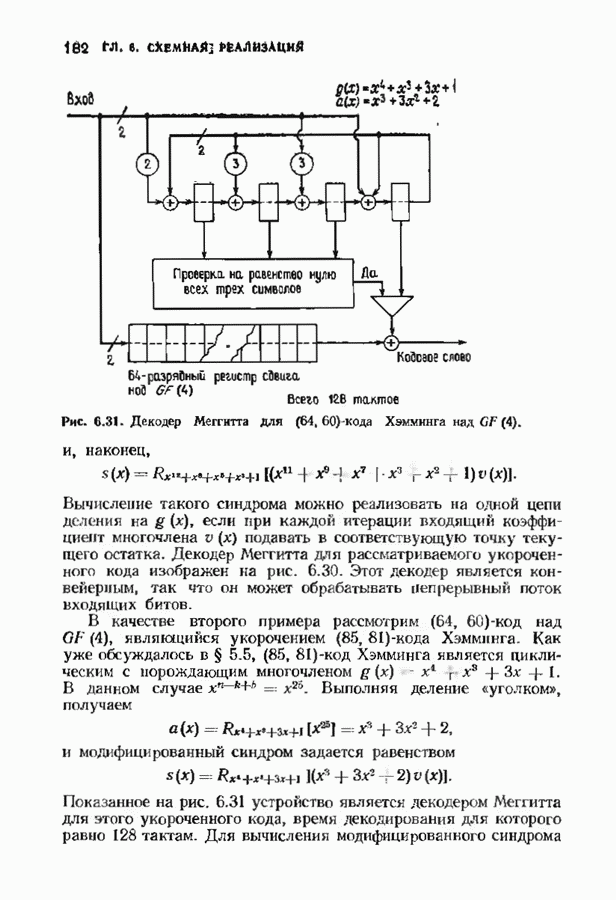
- 6.6. УКОРОЧЕННЫЕ ЦИКЛИЧЕСКИЕ КОДЫ
- 6.7. ДЕКОДЕР МЕГГИТТА ДЛЯ. КОДА ГОЛЕЯ
- ГЛАВА 7. КОДЫ БОУЗА-ЧОУДХУРИ-ХОКВИНГЕМА
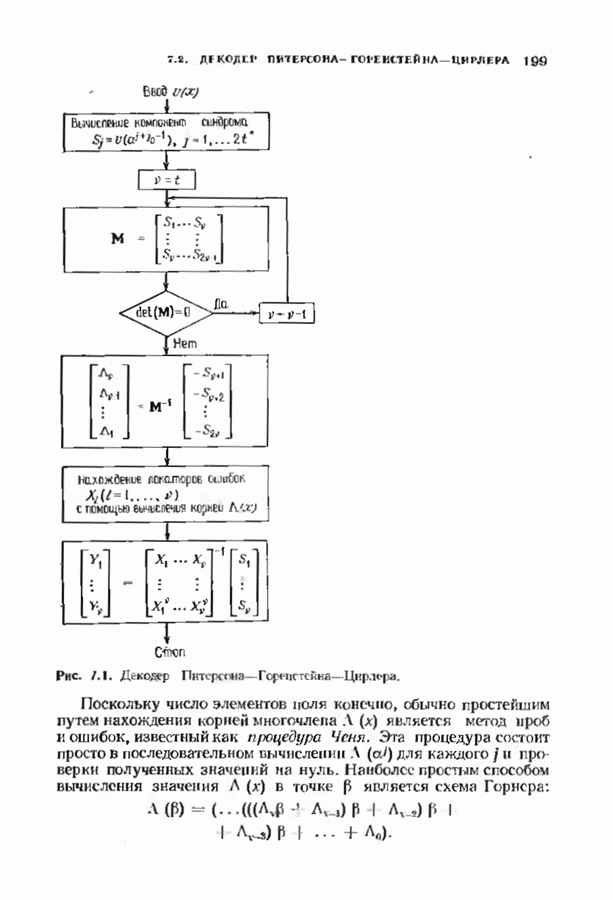
- 7.2. ДЕКОДЕР ПИТЕРСОНА ГОРЕНСТЕЙНА—ЦИРЛЕРА
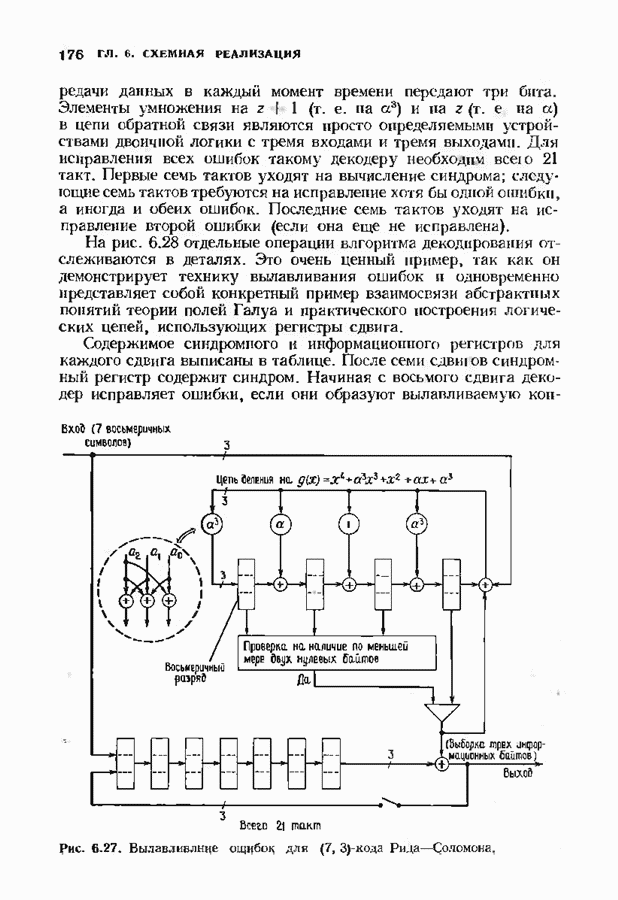
- 7.3. КОДЫ РИДА СОЛОМОНА
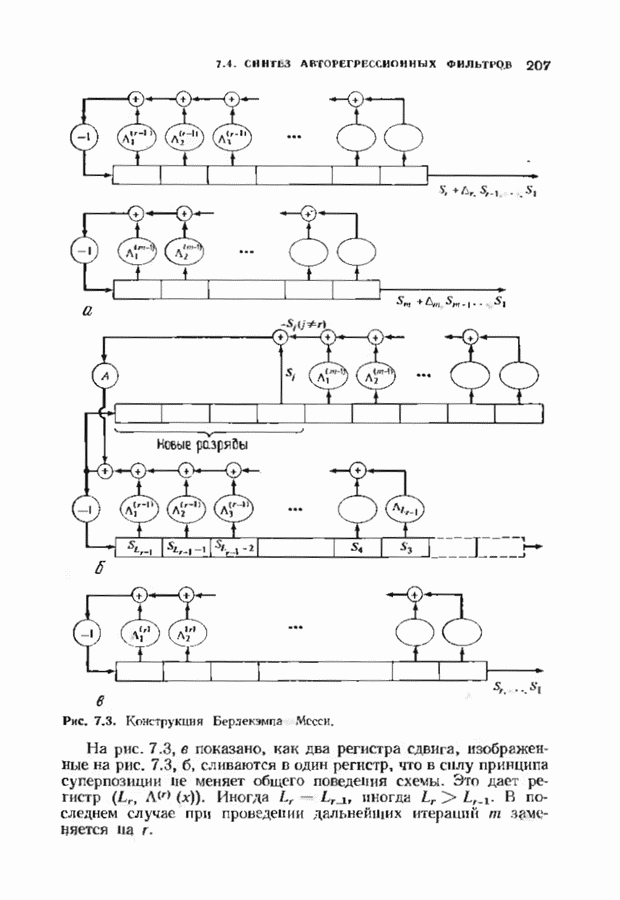
- 7.4. СИНТЕЗ АВТОРЕГРЕССИОННЫХ ФИЛЬТРОВ
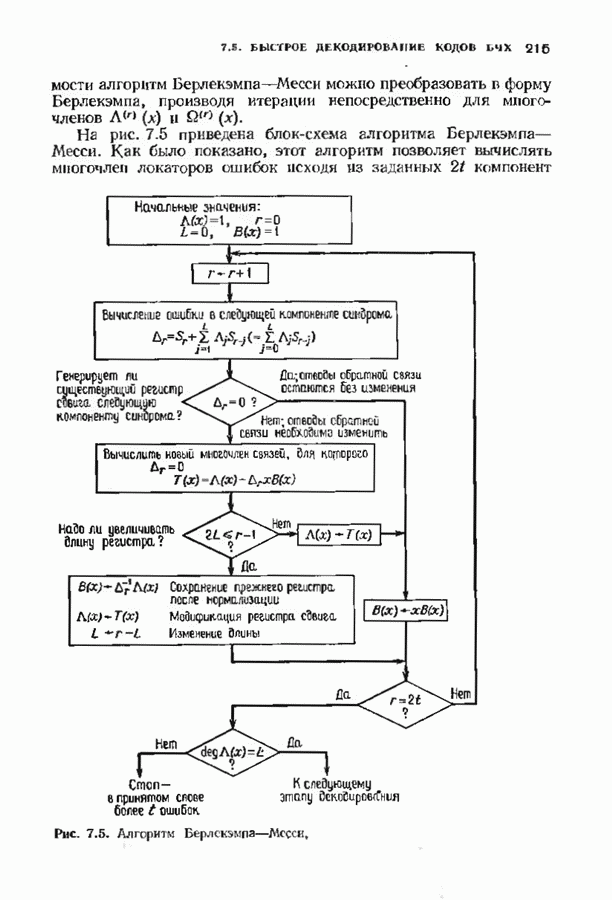
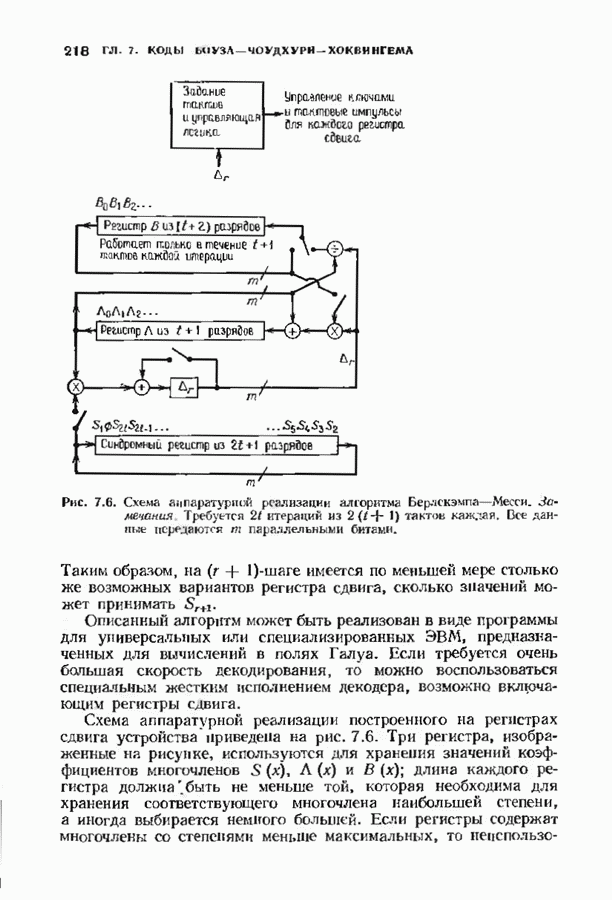
- 7.5. БЫСТРОЕ ДЕКОДИРОВАНИЕ КОДОВ БЧХ
- 7.6. ДЕКОДИРОВАНИЕ ДВОИЧНЫХ КОДОВ БЧХ
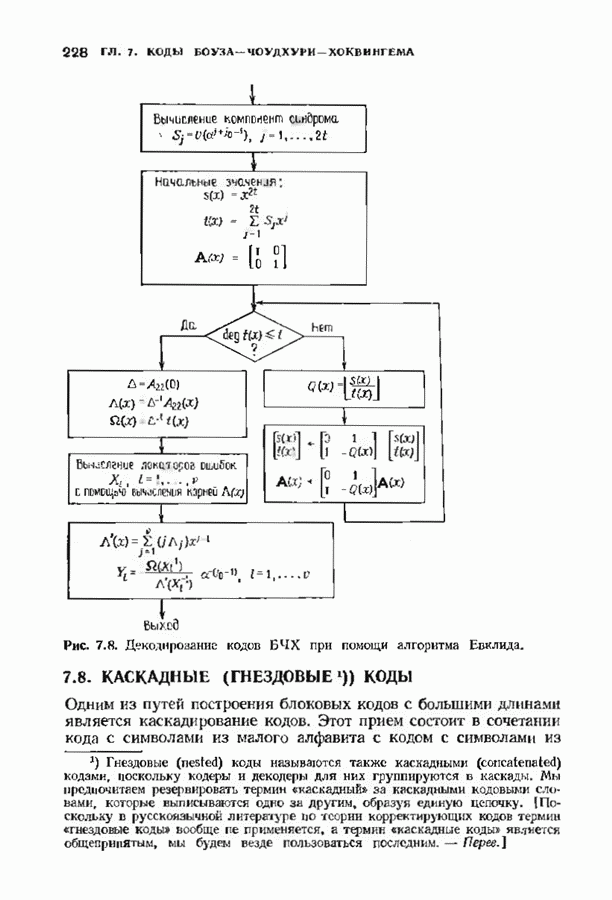
- 7.7. ДЕКОДИРОВАНИЕ С ПОМОЩЬЮ АЛГОРИТМА ЕВКЛИДА
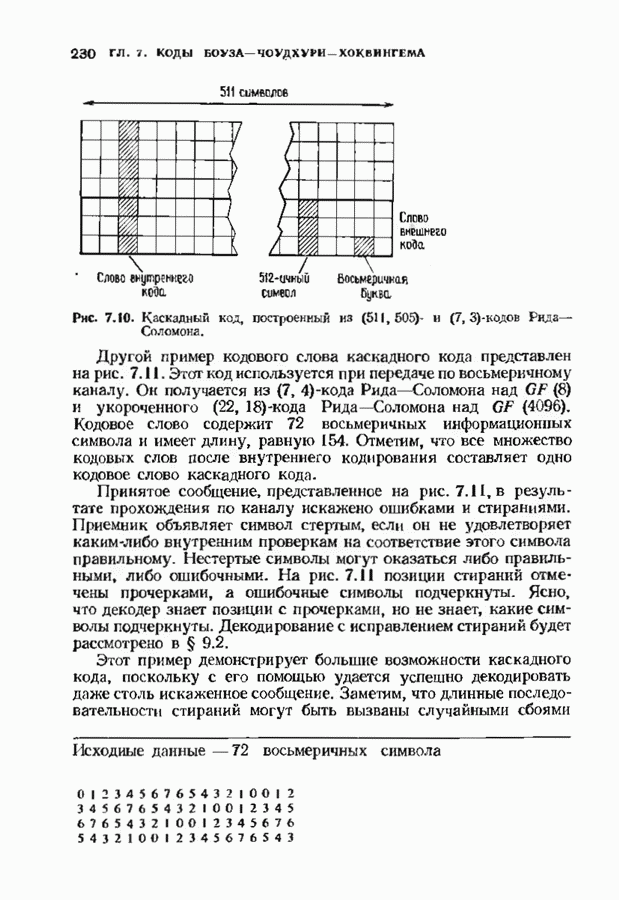
- 7.8. КАСКАДНЫЕ (ГНЕЗДОВЫЕ) КОДЫ
- 7.9. КОДЫ ЮСТЕСЕНА
- ГЛАВА 8. КОДЫ, ОСНОВАННЫЕ НА СПЕКТРАЛЬНЫХ МЕТОДАХ
- 8.2. ОГРАНИЧЕНИЯ СОПРЯЖЕННОСТИ И ИДЕМПОТЕНТЫ
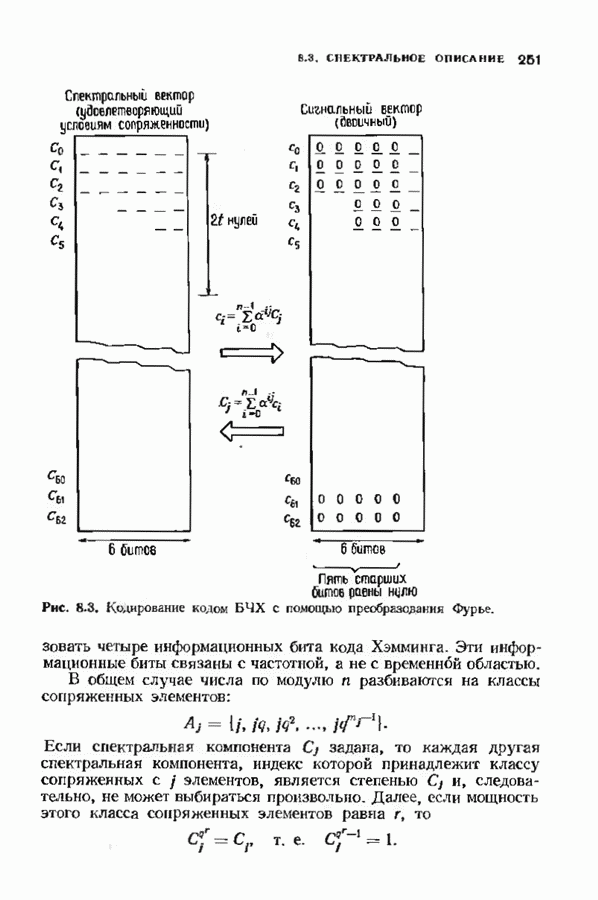
- 8.3. СПЕКТРАЛЬНОЕ ОПИСАНИЕ ЦИКЛИЧЕСКИХ КОДОВ
- 8.4. РАСШИРЕННЫЕ КОДЫ РИДА-СОЛОМОНА
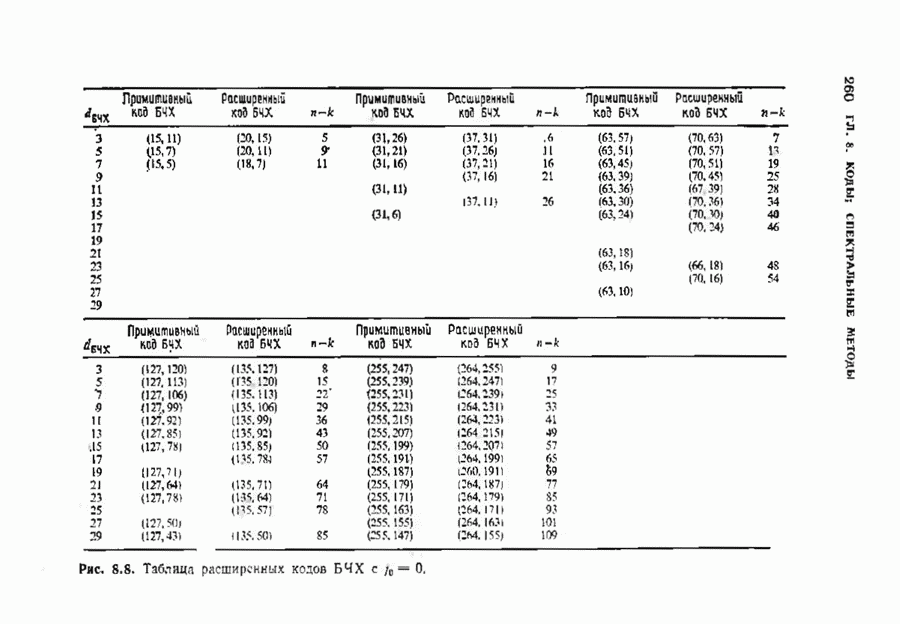
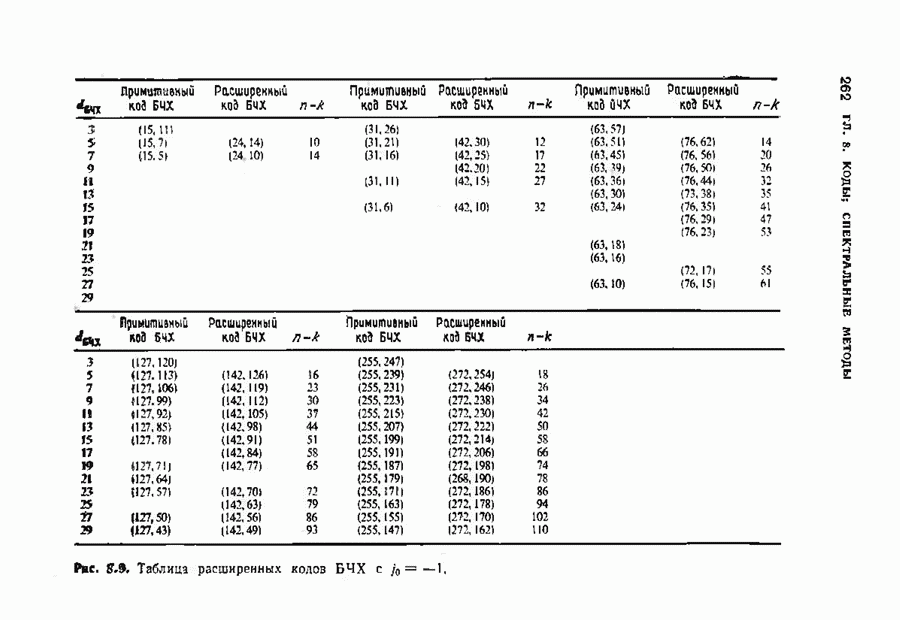
- 8.5. РАСШИРЕННЫЕ КОДЫ БЧХ
- 8.6. АЛЬТЕРНАНТНЫЕ КОДЫ
- 8.7. ХАРАКТЕРИСТИКИ АЛЬТЕРНАНТНЫХ КОДОВ
- 8.8. КОДЫ ГОППЫ
- 8.9. КОДЫ ПРЕПАРАТЫ
- ГЛАВА 9. АЛГОРИТМЫ, ОСНОВАННЫЕ НА СПЕКТРАЛЬНЫХ МЕТОДАХ
- 9.2. ИСПРАВЛЕНИЕ СТИРАНИЙ И ОШИБОК
- 9.3. ДЕКОДИРОВАНИЕ РАСШИРЕННЫХ КОДОВ РИДА—СОЛОМОНА
- 9.4. ДЕКОДИРОВАНИЕ РАСШИРЕННЫХ КОДОВ БЧХ
- 9.5. ДЕКОДИРОВАНИЕ ВО ВРЕМЕННОЙ ОБЛАСТИ
- 9.6. ДЕКОДИРОВАНИЕ ЗА ГРАНИЦЕЙ БЧХ
- 9.7. ДЕКОДИРОВАНИЕ АЛЬТЕРНАНТНЫХ КОДОВ
- 9.8. ВЫЧИСЛЕНИЕ ПРЕОБРАЗОВАНИЙ В КОНЕЧНЫХ ПОЛЯХ
- ГЛАВА 10. МНОГОМЕРНЫЕ СПЕКТРАЛЬНЫЕ МЕТОДЫ
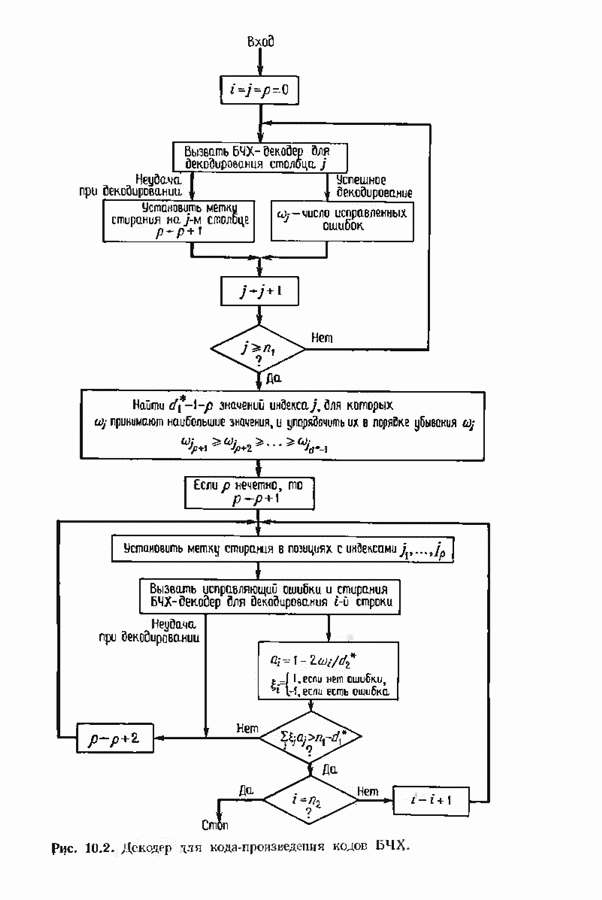
- 10.1. КОДЫ-ПРОИЗВЕДЕНИЯ
- 10.2. КИТАЙСКИЕ ТЕОРЕМЫ ОБ ОСТАТКАХ
- 10.3. ДЕКОДИРОВАНИЕ КОДА-ПРОИЗВЕДЕНИЯ
- 10.4. МНОГОМЕРНЫЕ СПЕКТРЫ
- 10.5. БЫСТРЫЕ КОДЫ БЧХ
- 10.6. ДЕКОДИРОВАНИЕ МНОГОМЕРНЫХ КОДОВ
- 10.7. ДЛИННЫЕ КОДЫ НАД МАЛЫМИ ПОЛЯМИ
- ГЛАВА 11. БЫСТРЫЕ АЛГОРИТМЫ
- 11.1. ЛИНЕЙНАЯ СВЕРТКА И ЦИКЛИЧЕСКАЯ СВЕРТКА
- 11.2. БЫСТРЫЕ АЛГОРИТМЫ СВЕРТКИ
- 11.3. БЫСТРЫЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 11.4. АЛГОРИТМЫ АГАРВАЛА—КУЛИ ВЫЧИСЛЕНИЯ СВЕРТОК
- 11.5. АЛГОРИТМ ВИНОГРАДА БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ
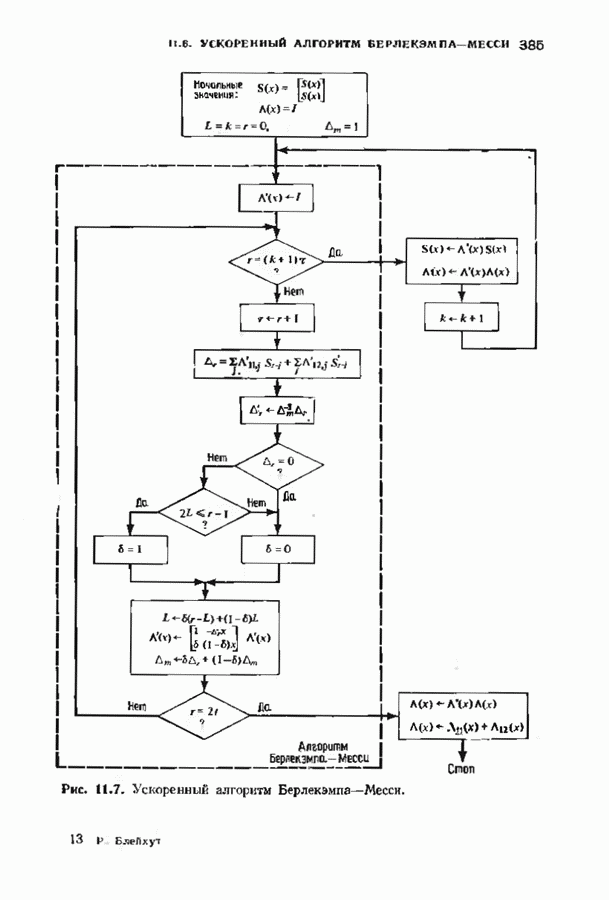
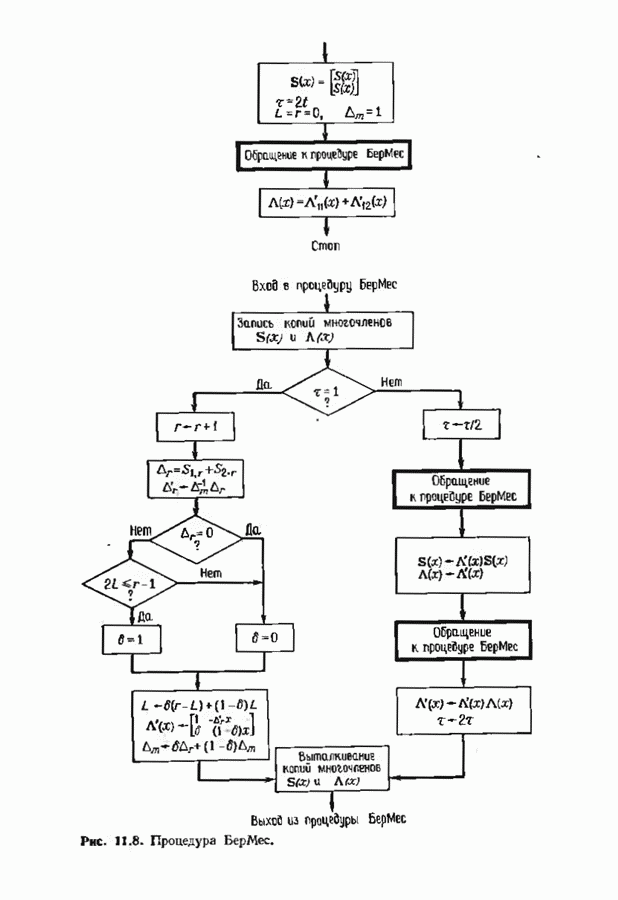
- 11.6. УСКОРЕННЫЙ АЛГОРИТМ БЕРЛЕКЭМПА—МЕССИ
- 11.7. РЕКУРРЕНТНЫЙ АЛГОРИТМ БЕРЛЕКЭМПА—МЕССИ
- 11.8. УСКОРЕННОЕ ДЕКОДИРОВАНИЕ КОДОВ БЧХ
- 11.9. СВЕРТКА В СУРРОГАТНЫХ ПОЛЯХ
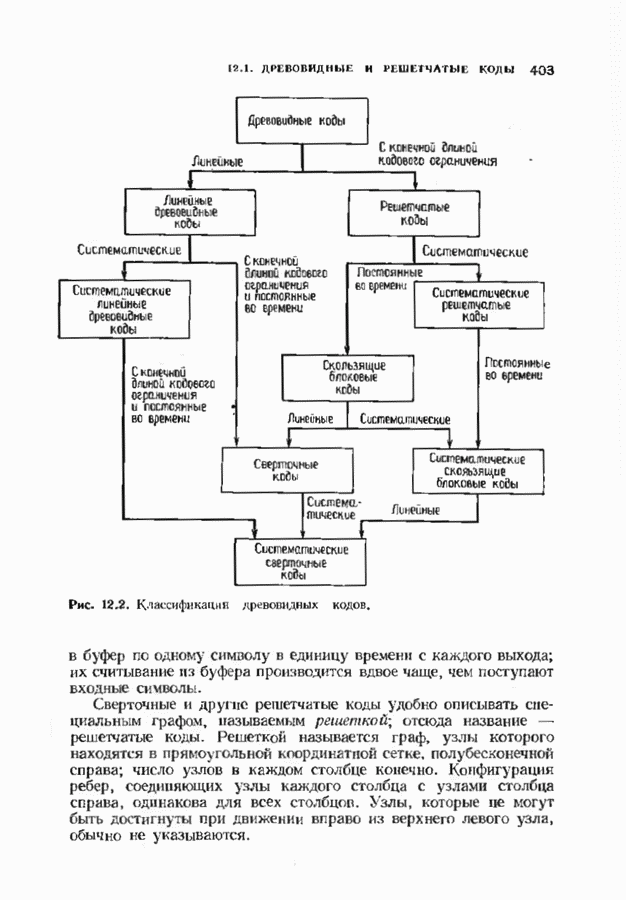
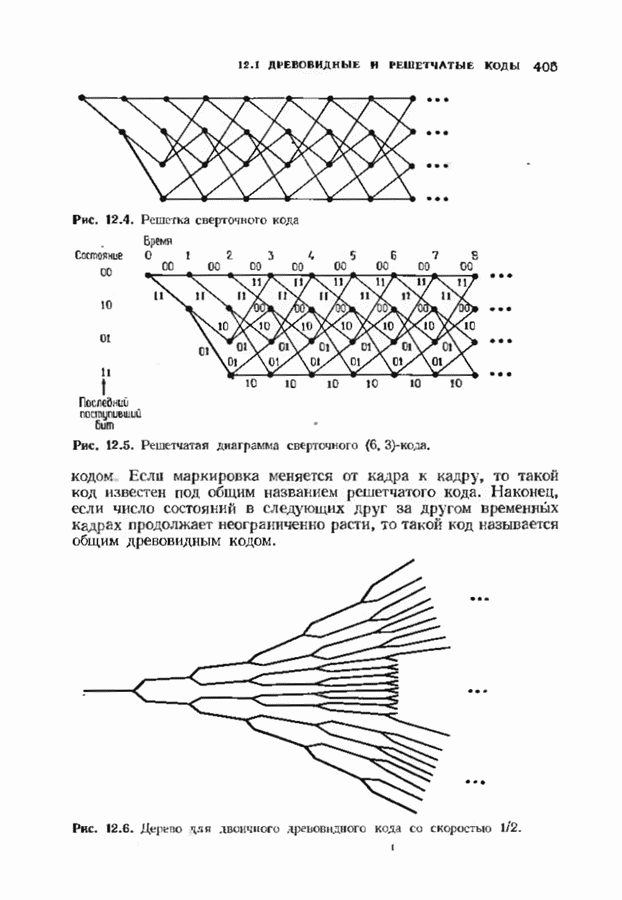
- ГЛАВА 12. СВЕРТОЧНЫЕ КОДЫ
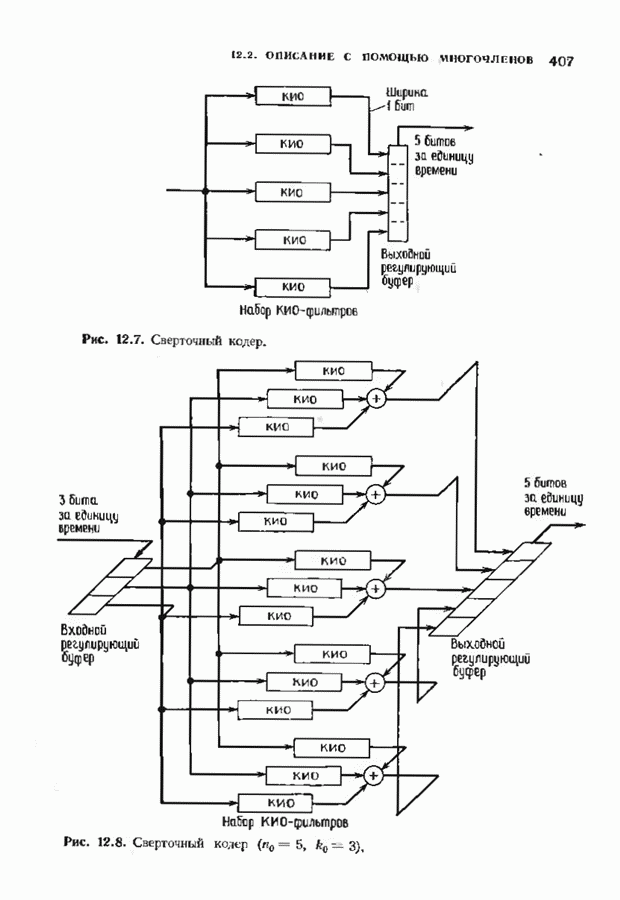
- 12.2. ОПИСАНИЕ СВЕРТОЧНЫХ КОДОВ С ПОМОЩЬЮ МНОГОЧЛЕНОВ
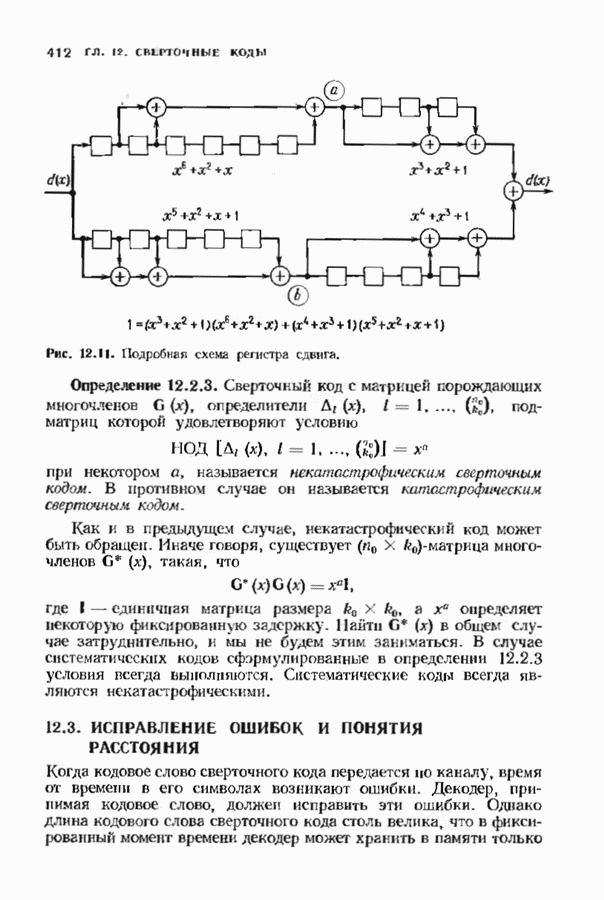
- 12.3. ИСПРАВЛЕНИЕ ОШИБОК И ПОНЯТИЯ РАССТОЯНИЯ
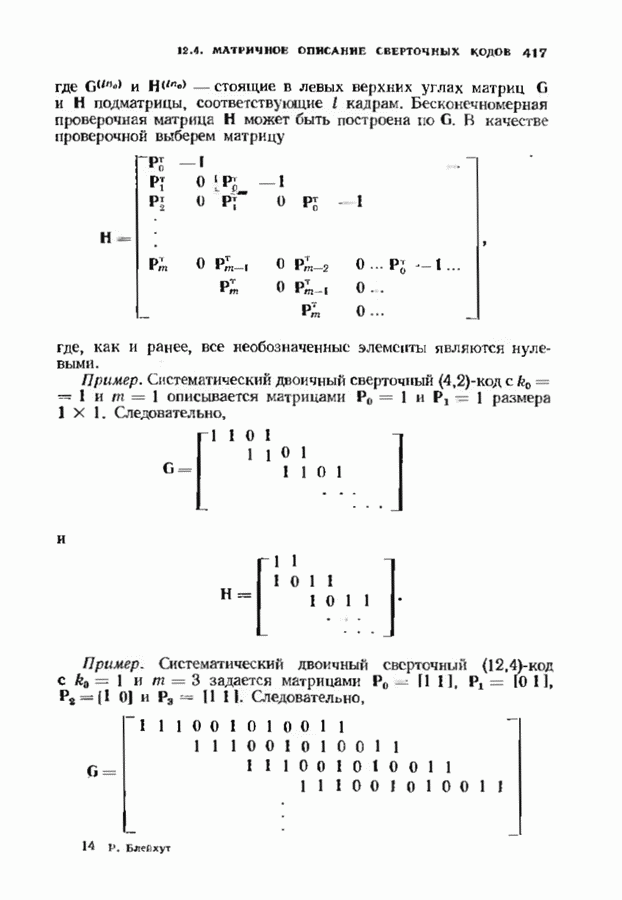
- 12.4. МАТРИЧНОЕ ОПИСАНИЕ СВЕРТОЧНЫХ КОДОВ
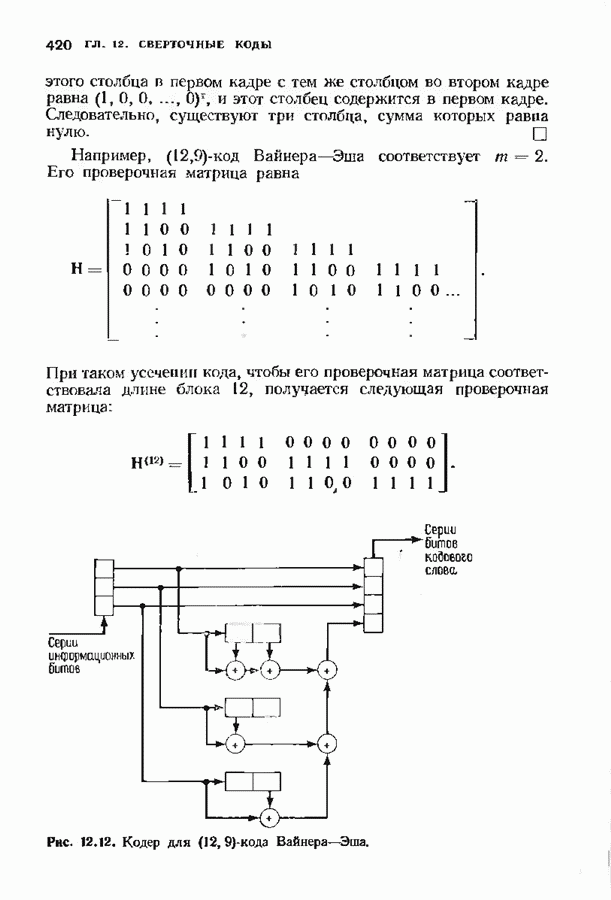
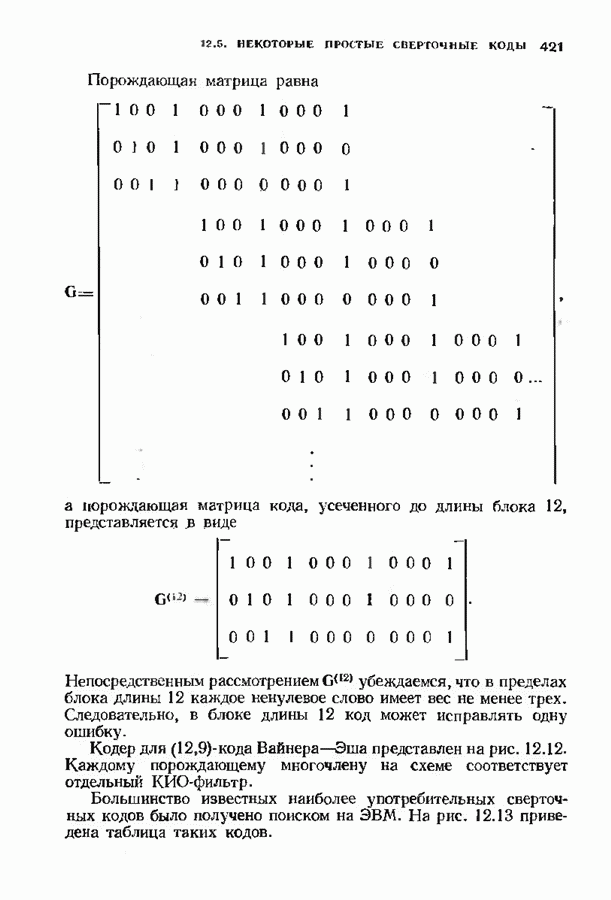
- 12.5. НЕКОТОРЫЕ ПРОСТЫЕ СВЕРТОЧНЫЕ КОДЫ
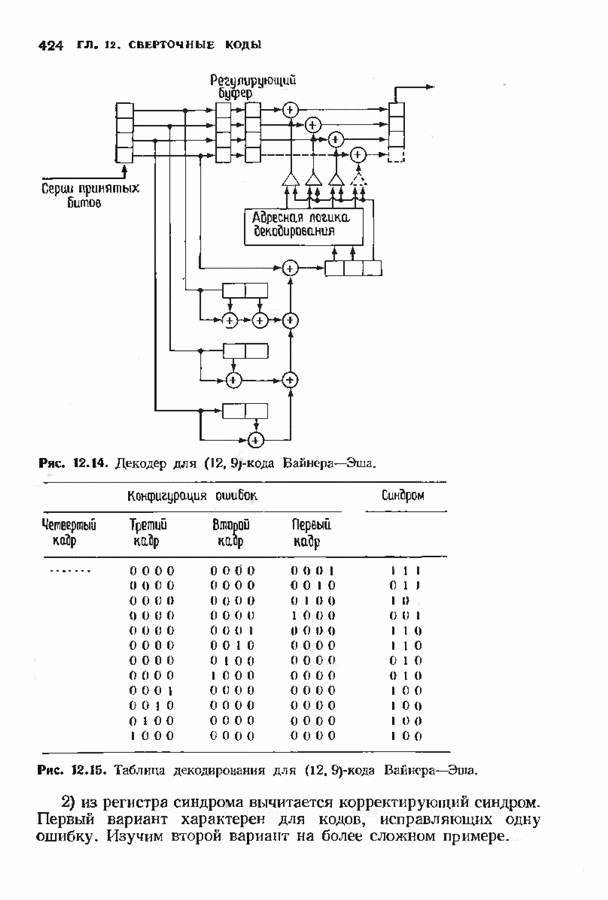
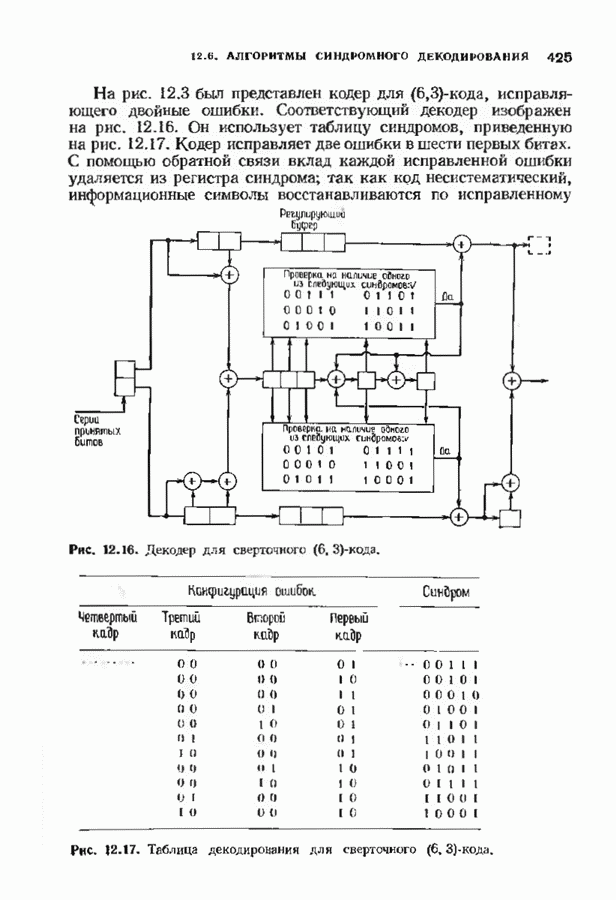
- 12.6. АЛГОРИТМЫ СИНДРОМНОГО ДЕКОДИРОВАНИЯ
- 12.7. ОБЕРТОЧНЫЕ КОДЫ ДЛЯ ИСПРАВЛЕНИЯ ПАКЕТОВ ОШИБОК
- 12.8. АЛГОРИТМ ДЕКОДИРОВАНИЯ ВИТЕРБИ
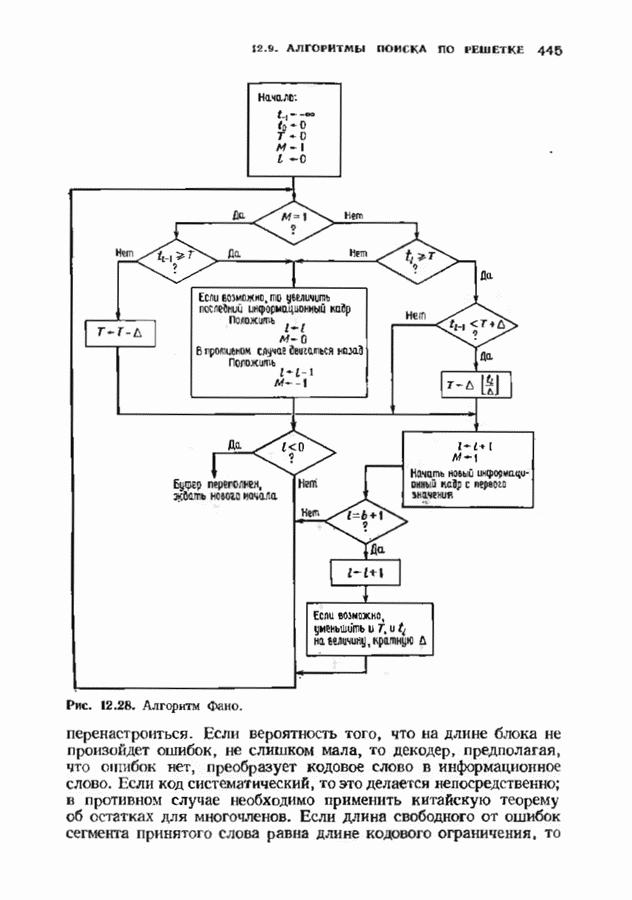
- 12.9. АЛГОРИТМЫ ПОИСКА ПО РЕШЕТКЕ
- ГЛАВА 13. КОДЫ И АЛГОРИТМЫ ДЛЯ ДЕКОДИРОВАНИЯ МАЖОРИТАРНЫМ МЕТОДОМ
- 13.1. ДЕКОДИРОВАНИЕ МАЖОРИТАРНЫМ МЕТОДОМ
- 13.2. СХЕМЫ МАЖОРИТАРНОГО ДЕКОДИРОВАНИЯ
- 13.3. АФФИННЫЕ ПЕРЕСТАНОВКИ ДЛЯ ЦИКЛИЧЕСКИХ КОДОВ
- 13.4. ЦИКЛИЧЕСКИЕ КОДЫ, ОСНОВАННЫЕ НА ПЕРЕСТАНОВКАХ
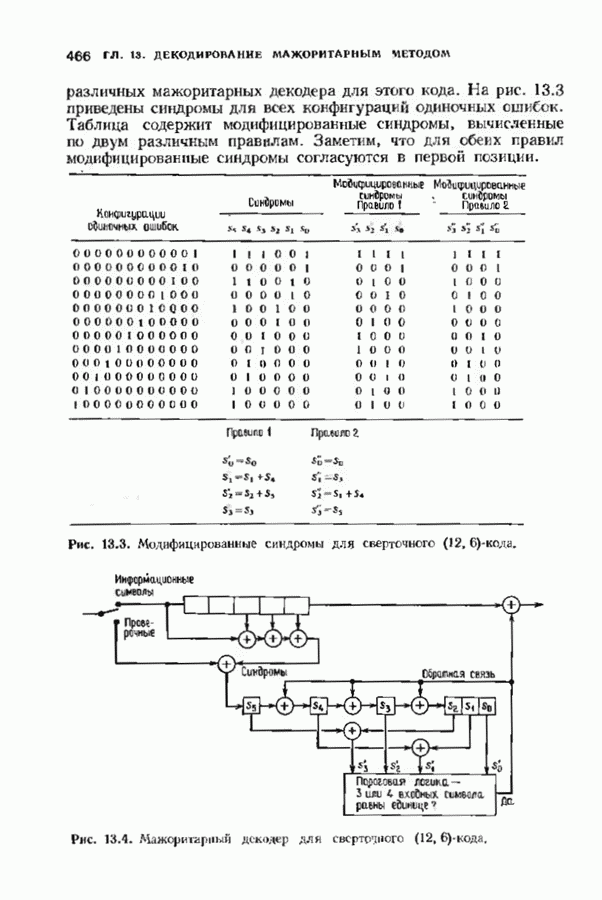
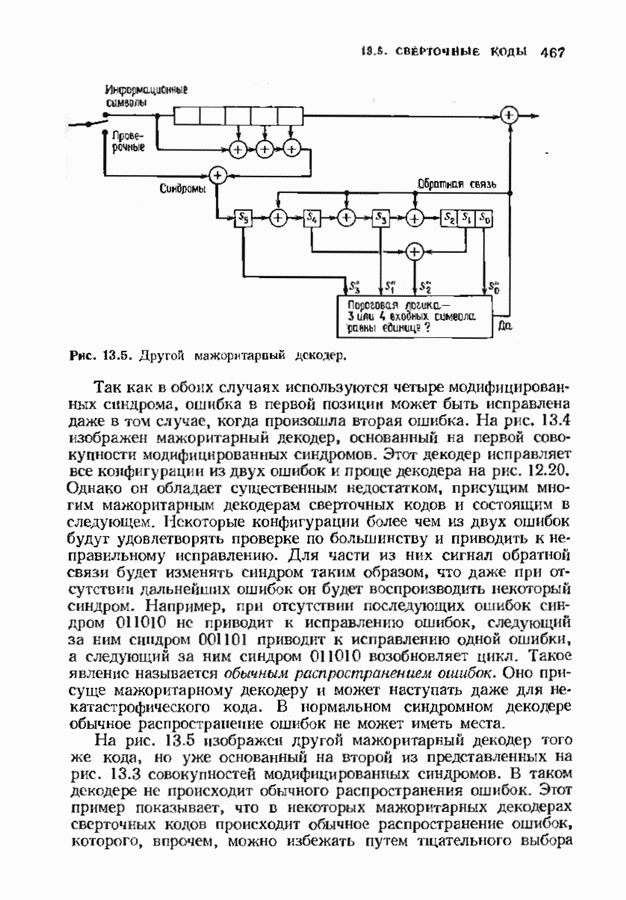
- 13.5. СВЕРТОЧНЫЕ КОДЫ С МАЖОРИТАРНЫМ ДЕКОДИРОВАНИЕМ
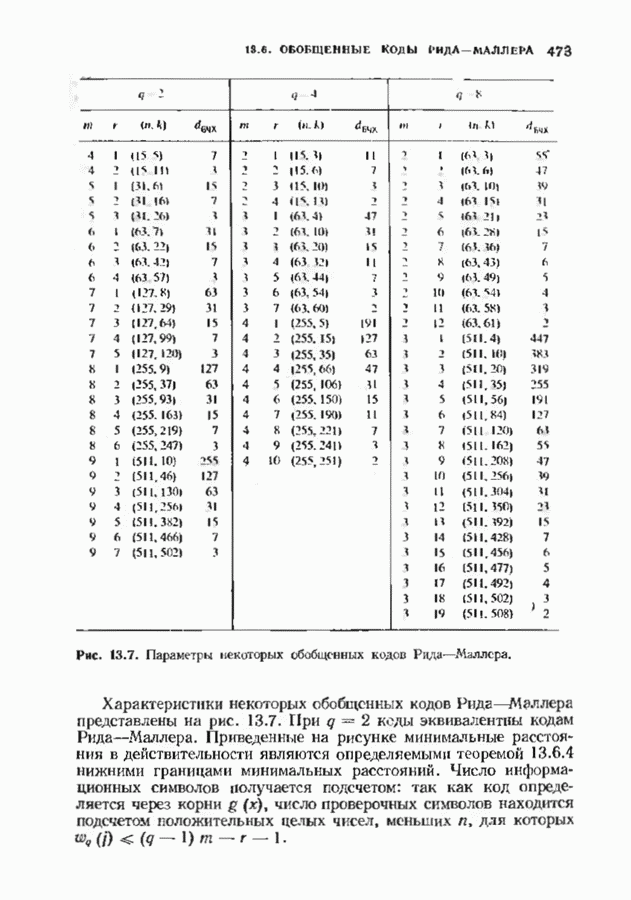
- 13.6. ОБОБЩЕННЫЕ КОДЫ РИДА—МАЛЛЕРА
- 13.7. ЕВКЛИДОВО-ГЕОМЕТРИЧЕСКИЕ КОДЫ
- 13.8. ПРОЕКТИВНО-ГЕОМЕТРИЧЕСКИЕ КОДЫ
- ГЛАВА 14. КОМПОЗИЦИЯ И ХАРАКТЕРИСТИКИ КОНТРОЛИРУЮЩИХ ОШИБКИ КОДОВ
- 14.2. ВЕРОЯТНОСТИ ОШИБОЧНОГО ДЕКОДИРОВАНИЯ И НЕУДАЧНОГО ДЕКОДИРОВАНИЯ
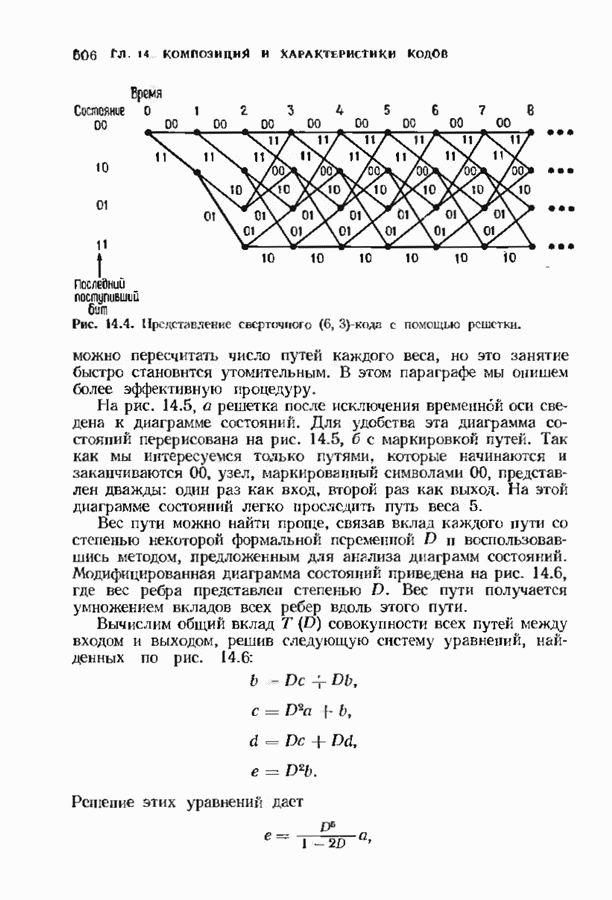
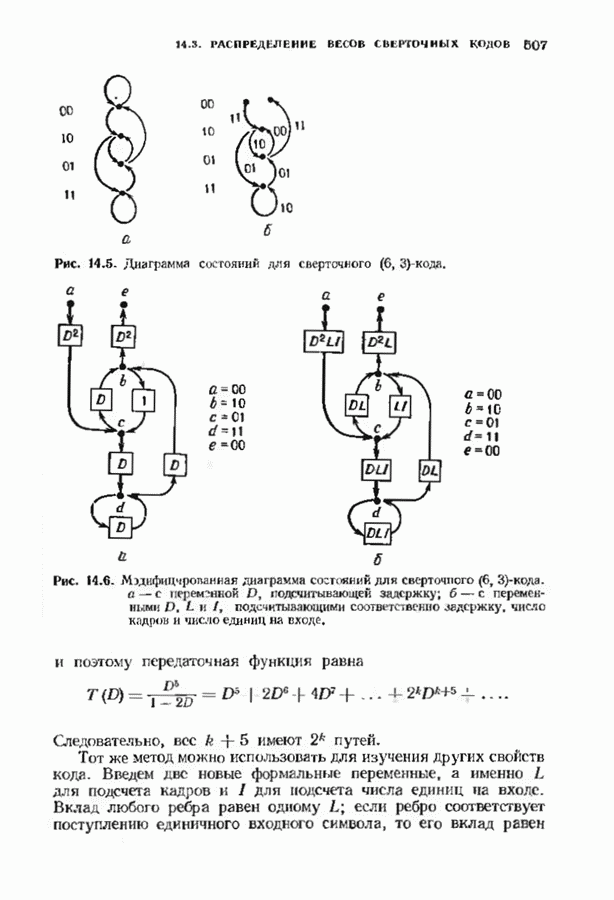
- 14.3. РАСПРЕДЕЛЕНИЕ ВЕСОВ СВЕРТОЧНЫХ КОДОВ
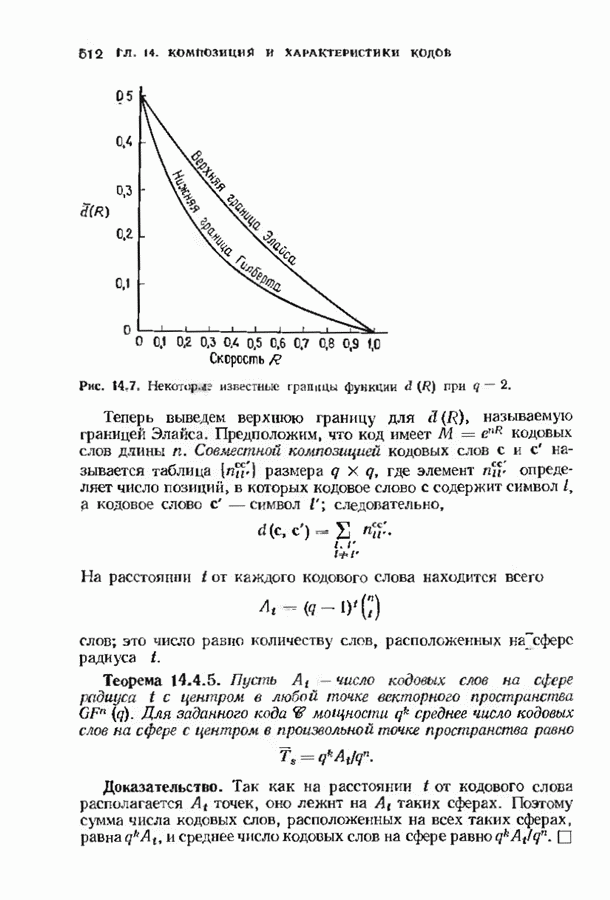
- 14.4. ГРАНИЦЫ МИНИМАЛЬНОГО РАССТОЯНИЯ ДЛЯ БЛОКОВЫХ КОДОВ
- 14.5. ГРАНИЦЫ МИНИМАЛЬНОГО РАССТОЯНИЯ ДЛЯ СВЕРТОЧНЫХ КОДОВ
- ГЛАВА 15. ЭФФЕКТИВНАЯ ПЕРЕДАЧА СИГНАЛОВ ПО ЗАШУМЛЕННЫМ КАНАЛАМ
- 15.1. ОГРАНИЧЕННЫЙ ПО ПОЛОСЕ ГАУССОВСКИЙ КАНАЛ
- 15.2. ЭНЕРГИЯ НА БИТ И ЧАСТОТА ОШИБОК НА БИТ
- 15.3. МЯГКОЕ ДЕКОДИРОВАНИЕ БЛОКОВЫХ КОДОВ
- 15.4. МЯГКОЕ ДЕКОДИРОВАНИЕ СВЕРТОЧНЫХ КОДОВ
- 15.5. ПОСЛЕДОВАТЕЛЬНОЕ ДЕКОДИРОВАНИЕ
- ЛИТЕРАТУРА