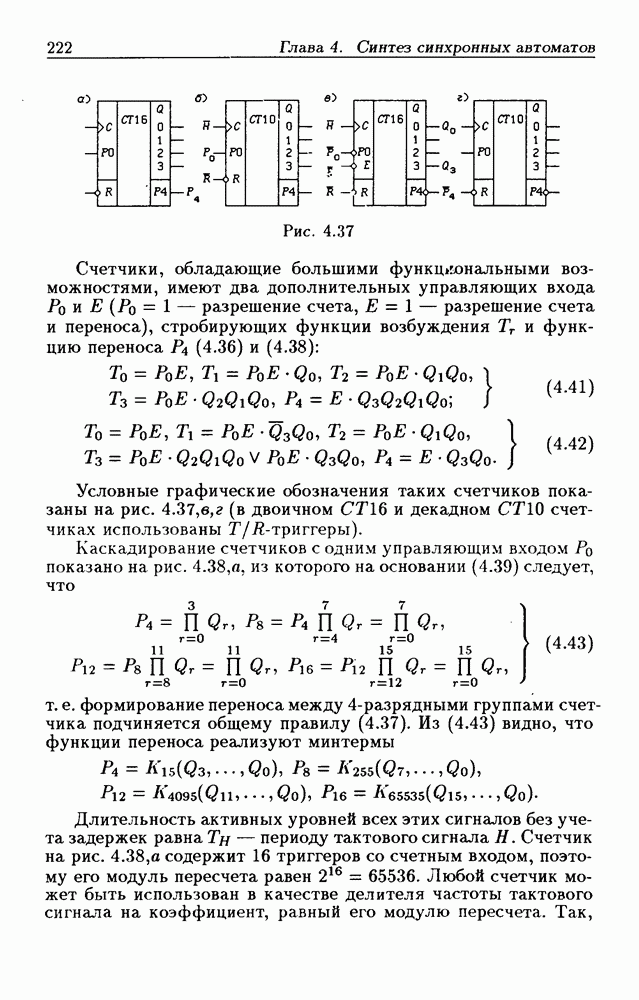| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.10. Минимизация переключательных функций
Физическое устройство, реализующее одну из основных операций алгебры логики или простейшую переключательную функцию, называется логическим элементом (ЛЭ). Схема, составленная из конечного числа ЛЭ по определенным правилам (см. § 2.3), называется логической схемой (ЛС). Если ЛС полностью описывается переключательными функциями (одной или несколькими), то она называется комбинационной схемой (КС).
Одной из основных задач, возникающих при синтезе КС, является минимизация переключательных функций, которые она реализует. Чем проще логические выражения, описывающие функции, тем проще и дешевле реализующая их КС.
В качестве критерия сложности логического выражения, описывающего функцию, целесообразно принять количество первичных термов  в него входящих. Очевидно, что любой метод минимизации может основываться только на тождественных преобразованиях логических выражений.
в него входящих. Очевидно, что любой метод минимизации может основываться только на тождественных преобразованиях логических выражений.
Общие правила минимизации можно установить только для случаев, когда в результате минимизации получаются так называемые минимальные нормальные формы функций (термин "нормальные формы" означает, что в логическом выражении, определяющем функцию  последовательно выполняется не более двух операций из совокупности операций И, ИЛИ, И-НЕ и ИЛИ-НЕ).
последовательно выполняется не более двух операций из совокупности операций И, ИЛИ, И-НЕ и ИЛИ-НЕ).
Два минтерма  будем называть соседними, если они различаются только одним первичным термом
будем называть соседними, если они различаются только одним первичным термом  т.е., если для одного из минтермов
т.е., если для одного из минтермов  а для другого
а для другого  (все же остальные первичные термы одинаковые). Так, например, если
(все же остальные первичные термы одинаковые). Так, например, если  то минтермы
то минтермы  являются соседними, так как они различаются только одним первичным термом
являются соседними, так как они различаются только одним первичным термом  Для минтерма
Для минтерма  соседними будут также минтермы
соседними будут также минтермы  Понятно, что каждый минтерм
Понятно, что каждый минтерм  переменных
переменных  имеет по
имеет по  соседних из общего числа
соседних из общего числа  минтермов.
минтермов.
Рассмотрим контерм  переменных
переменных  не зависящий от одной переменной
не зависящий от одной переменной  т. е. случай, когда контерм является конъюнкцией
т. е. случай, когда контерм является конъюнкцией  -го первичного терма. Данный контерм можно представить в СДНФ:
-го первичного терма. Данный контерм можно представить в СДНФ:

где  Очевидно, что полученные минтермы
Очевидно, что полученные минтермы  являются соседними, так как они различаются только одним первичным термом
являются соседними, так как они различаются только одним первичным термом 
Отсюда следует правило минимизации: дизъюнкцию двух соседних минтермов можно заменить одним контермом, не зависящим от одной переменной.
Пусть контерм  переменных не зависит от двух переменных
переменных не зависит от двух переменных  Выполним тождественные преобразования контерма для его представления в СДНФ:
Выполним тождественные преобразования контерма для его представления в СДНФ:

где  Из этих соотношений видно, что каждый из четырех полученных минтермов
Из этих соотношений видно, что каждый из четырех полученных минтермов
имеет среди остальных по два соседних.
Отсюда следует правило минимизации: дизъюнкцию четырех минтермов, каждый из которых имеет среди остальных по два соседних, можно заменить одним контермом, не зависящим от двух переменных, причем исключаются те переменные, которые входят в минтермы как с инверсией, так и без инверсии.
Рассмотрим пример. В § 1.9 было показано, что контерм трех переменных  т. е. данный контерм является вырожденной функцией, независящей от двух переменных
т. е. данный контерм является вырожденной функцией, независящей от двух переменных  и Тогда легко показать, что
и Тогда легко показать, что

где каждый минтерм имеет по два соседних.
Продолжив вышеприведенные рассуждения дальше, можно установить общее правило минимизации: одним контермом  переменных
переменных  не зависящим от
не зависящим от  переменных
переменных  можно заменить дизъюнкцию
можно заменить дизъюнкцию  минтермов, если каждый из них имеет по
минтермов, если каждый из них имеет по  соседних среди остальных
соседних среди остальных  минтермов.
минтермов.
Если контерм  не зависит от m переменных, то принято говорить, что он покрывает
не зависит от m переменных, то принято говорить, что он покрывает  минтермов. На этом свойстве контермов и основывается минимизация функций
минтермов. На этом свойстве контермов и основывается минимизация функций  заданных в СДНФ, которая в соответствии с выражением (1.72) представляет собой дизъюнкцию некоторого числа минтермов А:
заданных в СДНФ, которая в соответствии с выражением (1.72) представляет собой дизъюнкцию некоторого числа минтермов А:

и
Заменив в данном выражении дизъюнкцию  минтермов
минтермов  в случаях, когда какие-либо минтермы не имеют ни одного соседнего) соответствующими контермами
в случаях, когда какие-либо минтермы не имеют ни одного соседнего) соответствующими контермами  функцию можно представить в виде дизъюнкции некоторого числа контермов, покрывающих все минтермы
функцию можно представить в виде дизъюнкции некоторого числа контермов, покрывающих все минтермы  входящие в СДНФ функции:
входящие в СДНФ функции:

Такая форма представления функций называется дизъюнктивной нормальной формой (ДНФ). Если ДНФ содержит минимально возможное число первичных термов  то она называется минимальной дизъюнктивной нормальной формой (МДНФ). Следует отметить, что любые правила минимизации
то она называется минимальной дизъюнктивной нормальной формой (МДНФ). Следует отметить, что любые правила минимизации
сводятся к сформулированному выше общему правилу, в то время как алгоритмы (методы) минимизации могут сильно различаться между собой.
На основании идемпотентных законов один и тот же мин-терм  входящий в СДНФ, может использоваться несколько раз для образования различных контермов
входящий в СДНФ, может использоваться несколько раз для образования различных контермов  так как
так как

В общем случае для минимизации функций  переменных возникает необходимость использовать любой минтерм не более
переменных возникает необходимость использовать любой минтерм не более  раз, так как он может быть соседним не более чем с
раз, так как он может быть соседним не более чем с  другими минтермами.
другими минтермами.
Рассмотрим пример. Пусть задана СДНФ функции трех переменных

Здесь для получения МДНФ минтерм  необходимо использовать три раза:
необходимо использовать три раза:

Уже из этого элементарного примера видно, сколь сложно использовать аналитический метод минимизации ввиду трудоемкости работы по отысканию соседних минтермов (задача еще более усложняется при наличии в СДНФ группы, состоящей из  минтермов при
минтермов при  которые можно заменить одним контермом).
которые можно заменить одним контермом).
Рассмотрим теперь методику получения минимальных нормальных форм (МНФ) в других базисах. Для этой цели наиболее удобно использовать закон двойственности, который обладает замечательным свойством: при преобразовании любого логического выражения на основании закона двойственности ни число первичных термов  ни общее число операций дизъюнкции и конъюнкции, входящих в исходное логическое выражение, не изменяется.
ни общее число операций дизъюнкции и конъюнкции, входящих в исходное логическое выражение, не изменяется.
Пусть получена МДНФ некоторой функции  Тогда, используя закон двойного отрицания и закон двойственности, будем иметь:
Тогда, используя закон двойного отрицания и закон двойственности, будем иметь: 

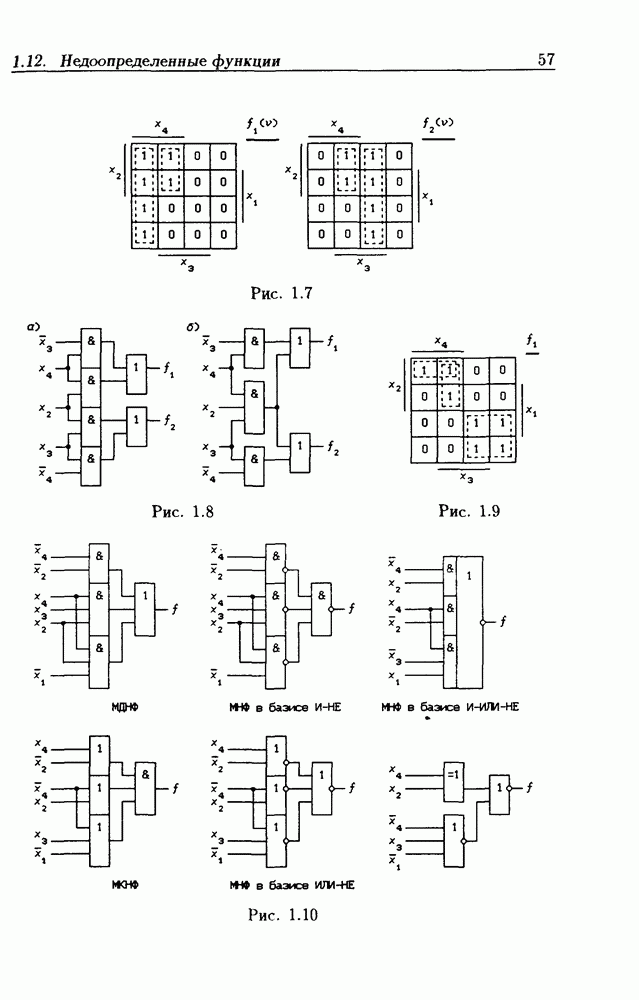
Это соотношение и дает минимальную нормальную форму в базисе И-НЕ функции  так как для ее реализации требуются только операции И-НЕ. В качестве примера запишем в
так как для ее реализации требуются только операции И-НЕ. В качестве примера запишем в
базисе И-НЕ МНФ функции трех переменных, МДНФ которой была найдена выше:

Конъюнкция любого числа дизтермов называется конъюнктивной нормальной формой. Получение минимальной конъюнктивной нормальной формы (МКНФ) функции  легко сводится к получению МДНФ инверсной функции
легко сводится к получению МДНФ инверсной функции  и преобразованию ее с помощью закона двойственности:
и преобразованию ее с помощью закона двойственности:

где  дизъюнктивные термы (1.78).
дизъюнктивные термы (1.78).
Рассмотрим пример. Пусть требуется найти МКНФ функции трех переменных значения которой равны 0 только в точках  и
и  . СДНФ инверсной функции
. СДНФ инверсной функции

Используя минтерм  дважды, легко показать, что МДНФ (1.81) инверсной функции
дважды, легко показать, что МДНФ (1.81) инверсной функции  Тогда МКНФ функции
Тогда МКНФ функции  получается с помощью закона двойственности:
получается с помощью закона двойственности: 

Минимальная нормальная форма в базисе ИЛИ-НЕ функции  может быть получена непосредственно из МКНФ (1.82) с помощью закона двойного отрицания и закона двойственности:
может быть получена непосредственно из МКНФ (1.82) с помощью закона двойного отрицания и закона двойственности:

Найдем МНФ в базисе ИЛИ-НЕ для функции  рассмотренной в предыдущем примере:
рассмотренной в предыдущем примере:

Таким образом, получение МКНФ и МНФ в базисах И-НЕ и ИЛИ-НЕ функции  всегда можно свести к получению МДНФ либо функции
всегда можно свести к получению МДНФ либо функции  либо ее инверсии
либо ее инверсии  Это позволяет использовать для всех нормальных минимальных форм представления переключательных функций только метод их минимизации, приводящий к получению МДНФ.
Это позволяет использовать для всех нормальных минимальных форм представления переключательных функций только метод их минимизации, приводящий к получению МДНФ.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Основы теории переключательных функций
- 1.2. Позиционные системы счисления
- 1.3. Переключательные функции
- 1.4. Принцип и закон двойственности
- 1.5. Теоремы разложения
- 1.6. Решение систем логических уравнений
- 1.7. Первичные термы, минтермы и макстермы
- 1.8. Совершенные нормальные формы представления функций
- 1.9. Конъюнктивные и дизъюнктивные термы
- 1.10. Минимизация переключательных функций
- 1.11. Диаграммы Вейча
- 1.12. Минимизация неполностью определенных функций, совместная минимизация нескольких функций
- 1.13. Скобочные формы функций
- 1.14. Закон двойственности для логических схем
- 1.15. Линейные функции
- Глава 2. Анализ и синтез логических схем
- 2.2. Модели логических элементов
- 2.3. Модели логических схем
- 2.4. Анализ логических схем
- 2.5. Синтез комбинационных схем, свободных от состязаний
- Глава 3. Синтез асинхронных потенциальных автоматов
- 3.2. Асинхронные потенциальные автоматы
- 3.3. Асинхронные потенциальные триггеры и элементы памяти
- Триггеры типа R-S
- Триггеры типа D-L
- Триггеры типа D-L-R с приоритетом входа R.
- Триггеры типа D-L-R с приоритетом входа L.
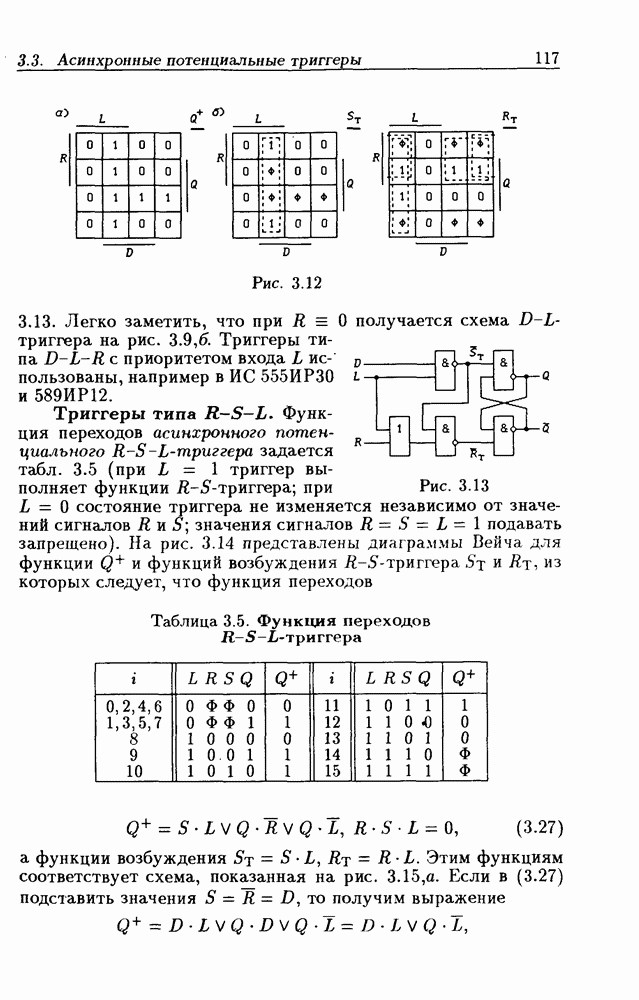
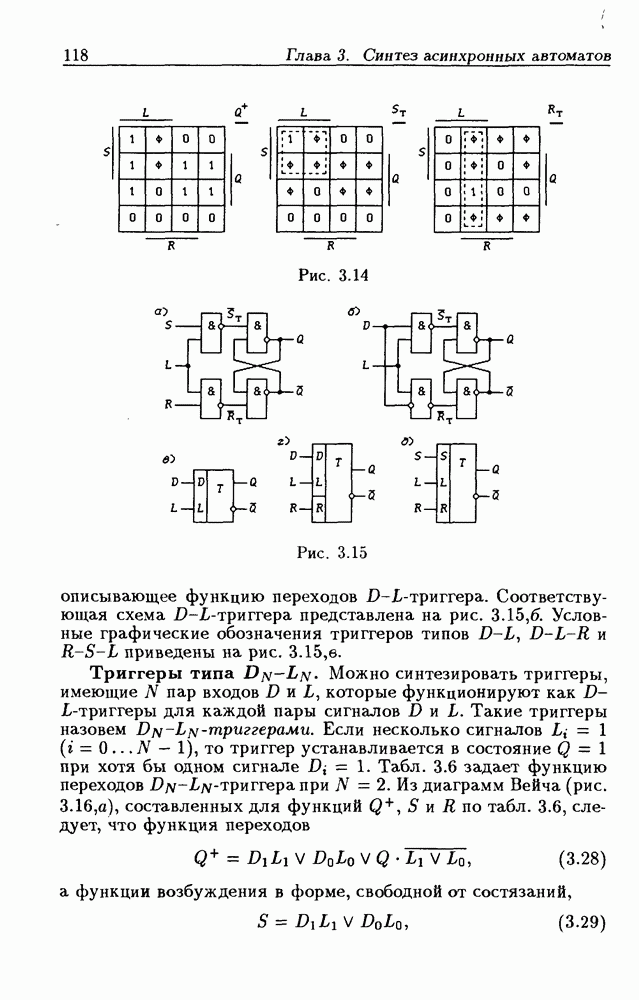
- Триггеры типа R-S-L.
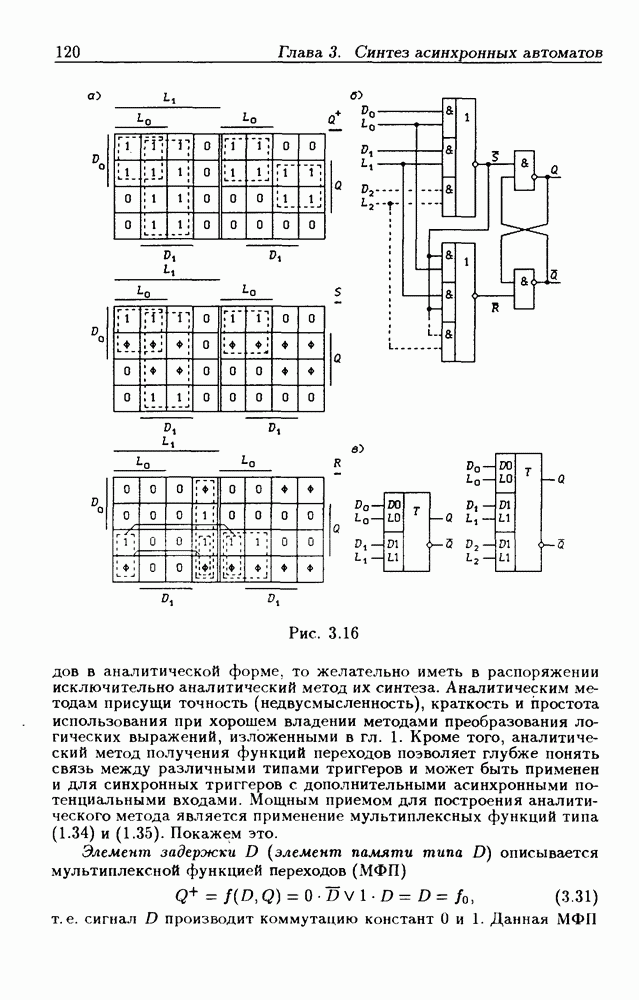
- Триггеры типа DN-LN
- Аналитический метод синтеза и анализа триггеров.
- 3.4. Задание асинхронных потенциальных автоматов таблицами и графами переходов
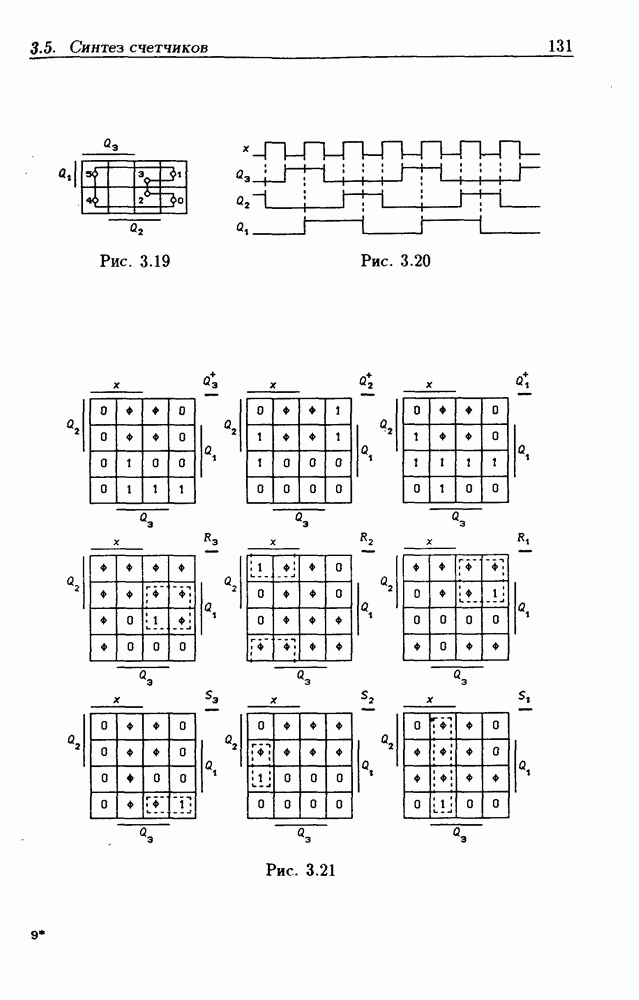
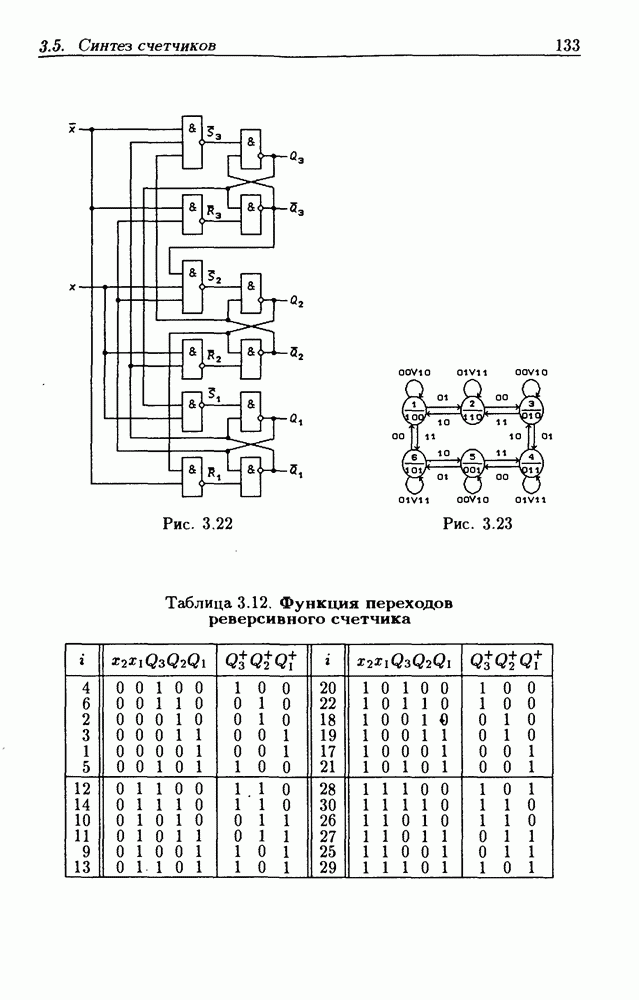
- 3.5. Синтез асинхронных потенциальных счетчиков
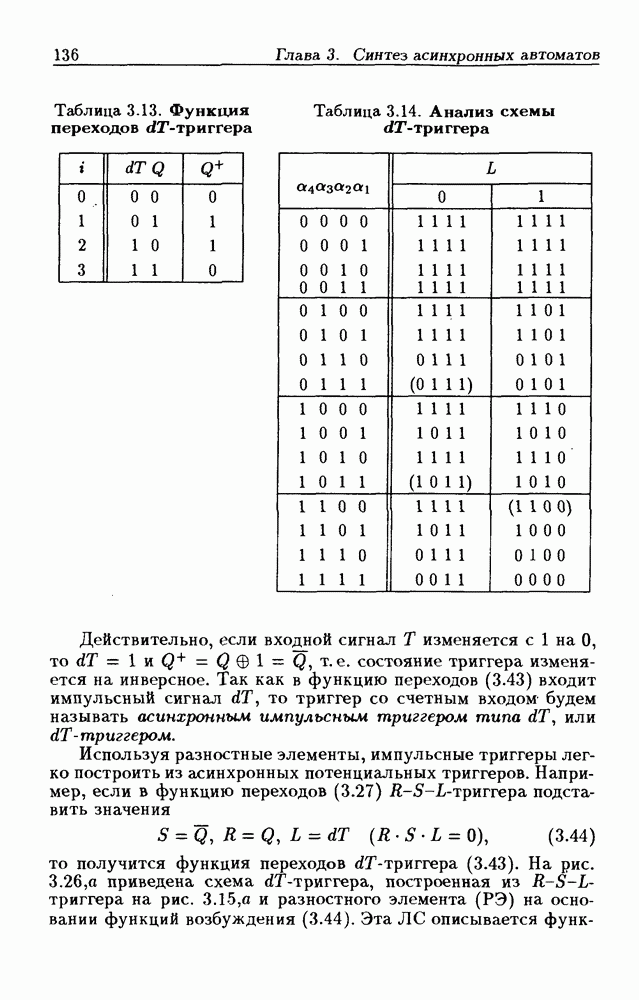
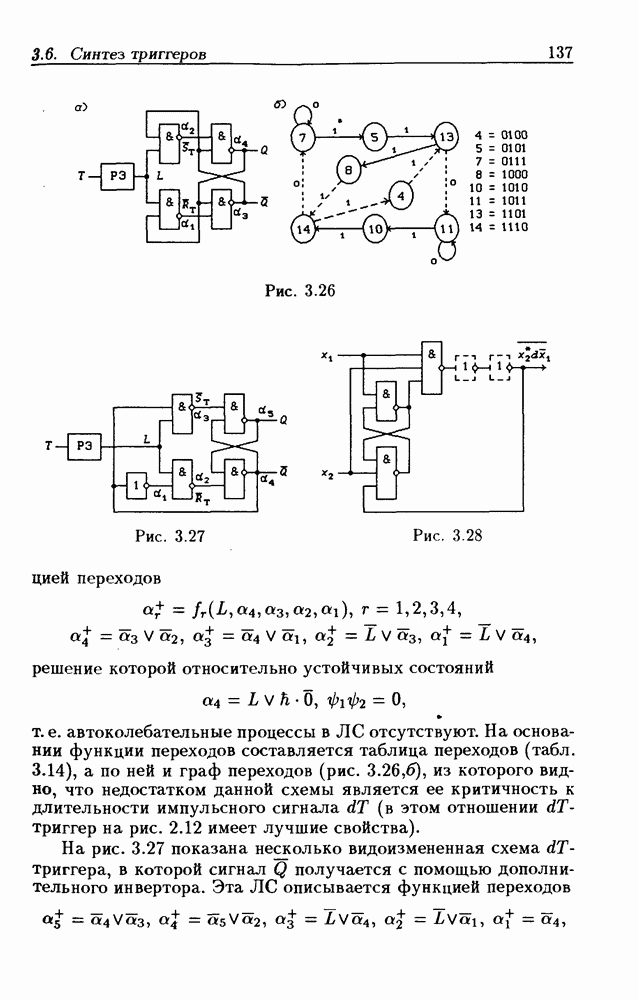
- 3.6. Синтез асинхронных импульсных триггеров
- Триггеры типа dJ-dK.
- Классификация триггеров.
- 3.7. Синтез синхронных триггеров
- Триггеры типа J-K
- Синхронно-асинхронные триггеры.
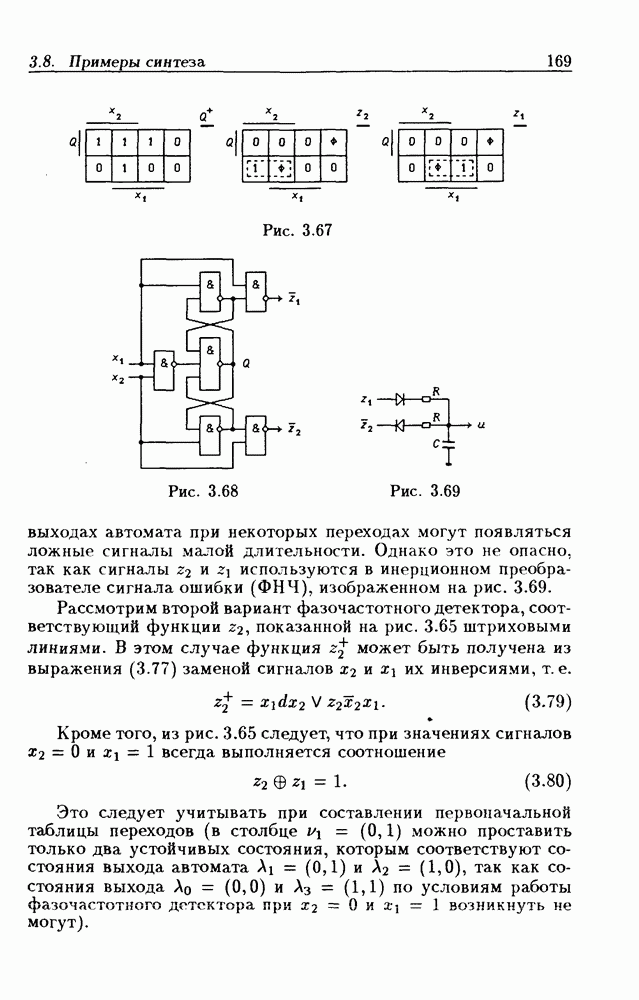
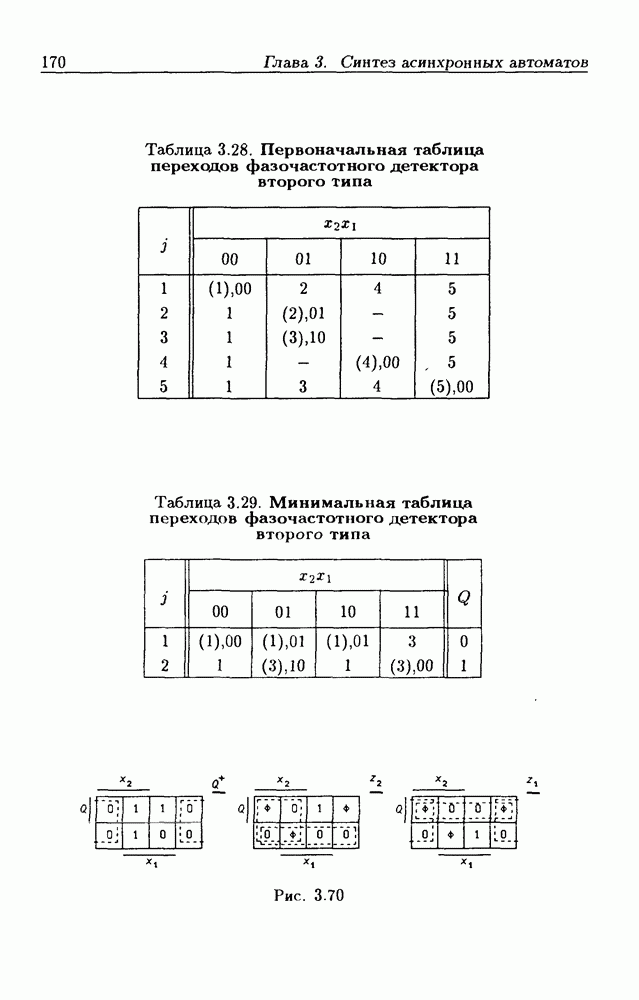
- 3.8. Примеры синтеза асинхронных потенциальных автоматов
- Цифровые фазочастотные детекторы.
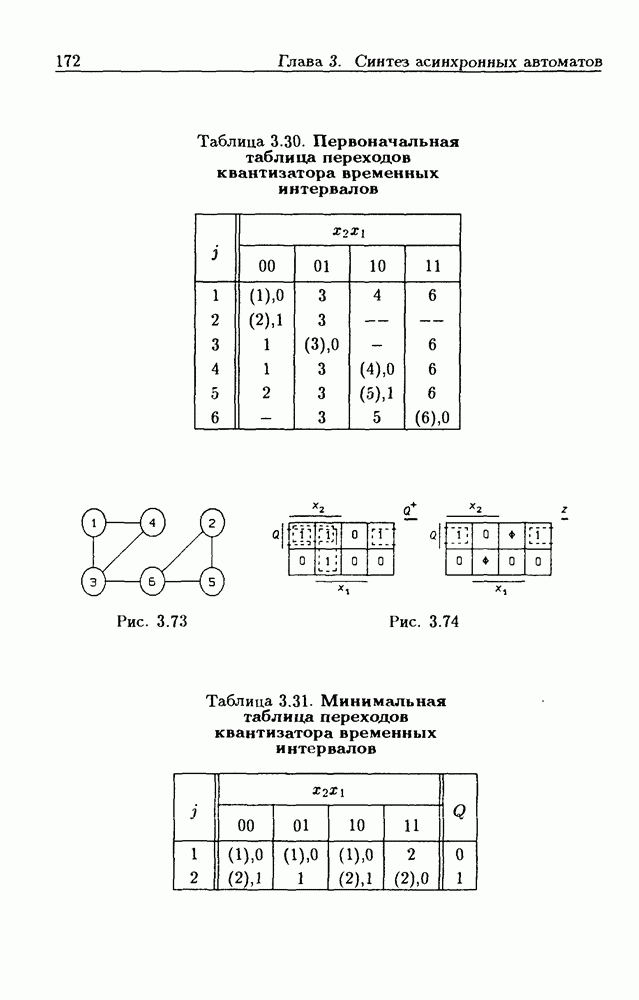
- Квантизатор временных интервалов.
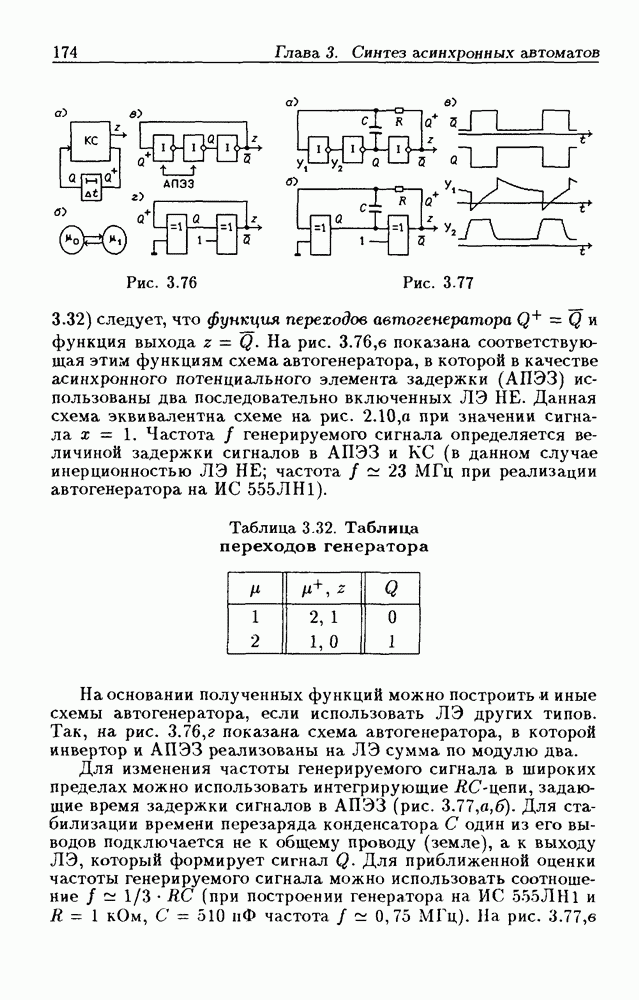
- 3.9. Генераторы сигналов
- Автогенераторы.
- Управляемые автогенераторы.
- Глава 4. Синтез синхронных автоматов
- 4.2. Синхронные триггеры
- Триггеры типов D и R-S с импульсным тактовым сигналом.
- Синхронные триггеры типов R-S и D-L
- Синхронно-асинхронные триггеры.
- Синхронные триггеры типа J-K
- Триггеры типа Т.
- Классификация синхронных триггеров.
- Преобразования типов синхронных триггеров.
- Триггеры типов D-T-L и D-T-L/R
- Функции переходов синхронно-асинхронных триггеров.
- 4.3. Примеры синтеза синхронных автоматов
- 4.4. Сдвигающие регистры
- Синтез счетчиков на сдвигающих регистрах.
- Сдвигающие регистры с загрузкой данных.
- Реверсивные сдвигающие регистры.
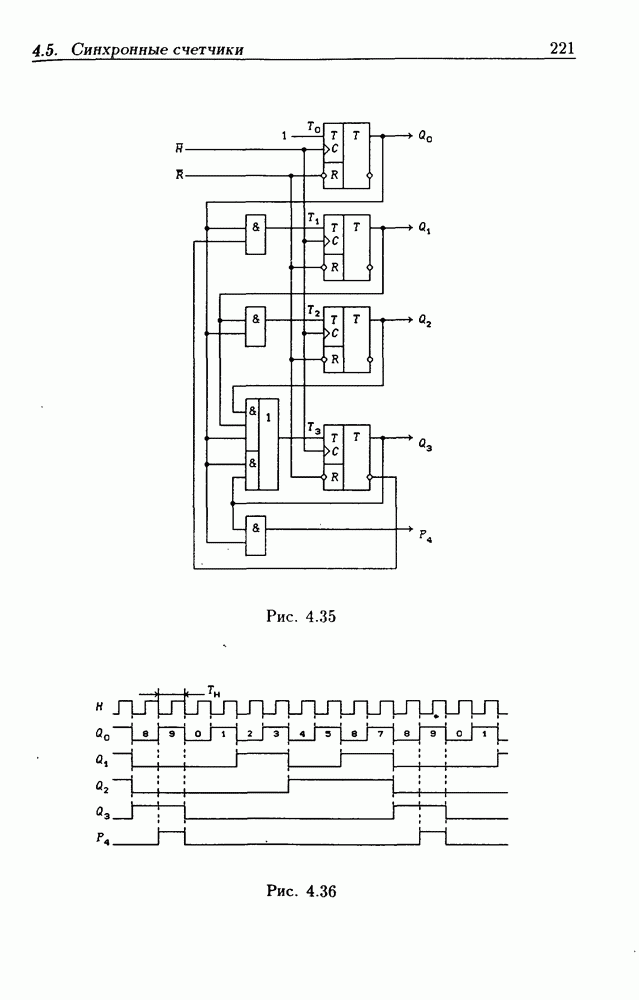
- 4.5. Синхронные счетчики
- Синхронные двоичные счетчики.
- Синхронные двоично-десятичные счетчики.
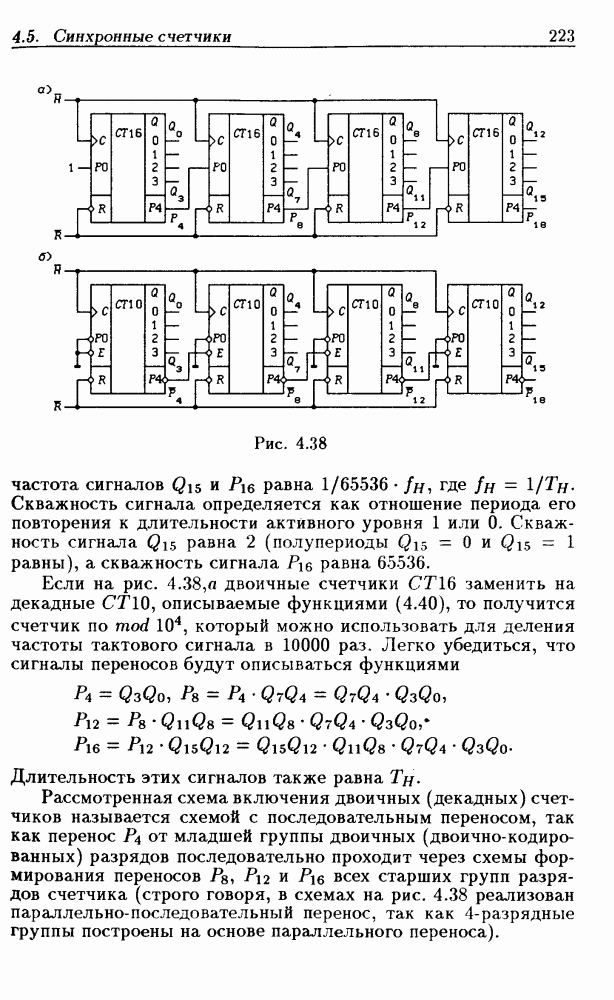
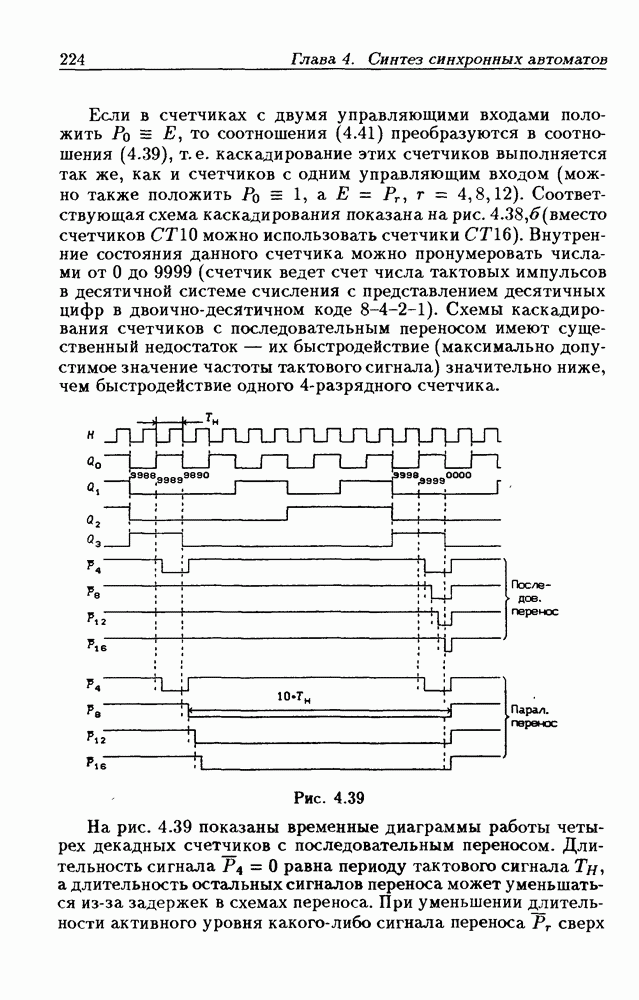
- Каскадирование двоичных и двоично-десятичных счетчиков.
- Синхронные двоичные реверсивные счетчики.
- Реверсивные двоично-десятичные счетчики.
- Каскадирование реверсивных счетчиков.
- Счетчики на сдвигающих регистрах.
- Кольцевые счетчики.
- Линейные счетчики.
- Программируемые счетчики.
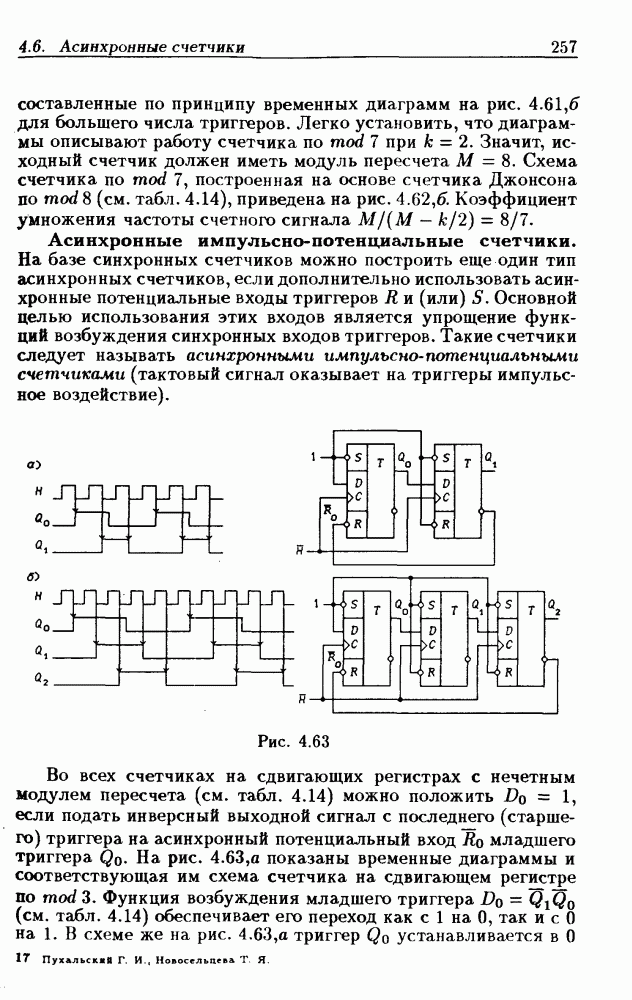
- 4.6. Асинхронные счетчики
- Асинхронные счетчики с умножением частоты счетного сигнала.
- Асинхронные импульсно-потенциальные счетчики.
- Асинхронное программирование модуля пересчета счетчиков.
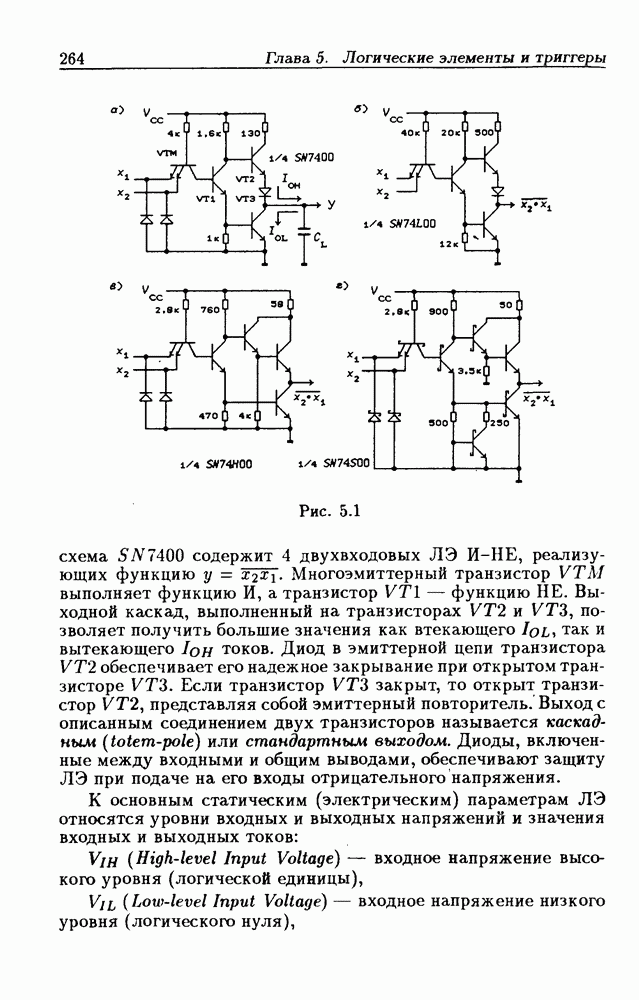
- Глава 5. Логические элементы и триггеры
- Логические элементы.
- Классификация ИС по степени интеграции.
- 5.2. Интегральные схемы КМОП серий
- 5.3. Триггеры Шмитта
- 5.4. Логические элементы с открытым коллекторным выходом
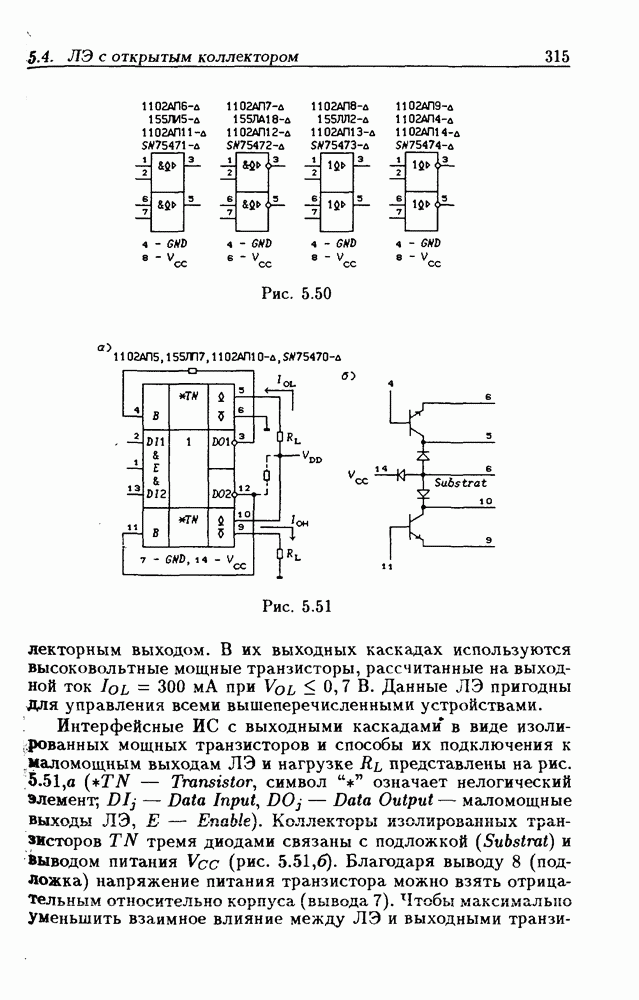
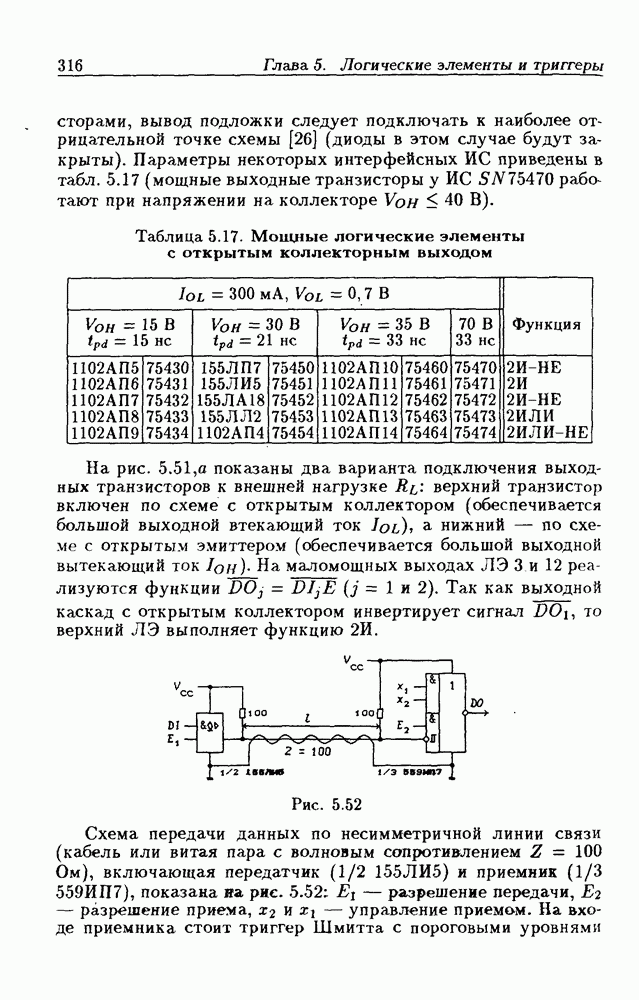
- Логические элементы с открытым коллекторным выходом.
- Применения ЛЭ с открытым коллекторным выходом.
- Интерфейсные ЛЭ с открытым коллекторным выходом.
- Логические элементы с открытым стоковым выходом.
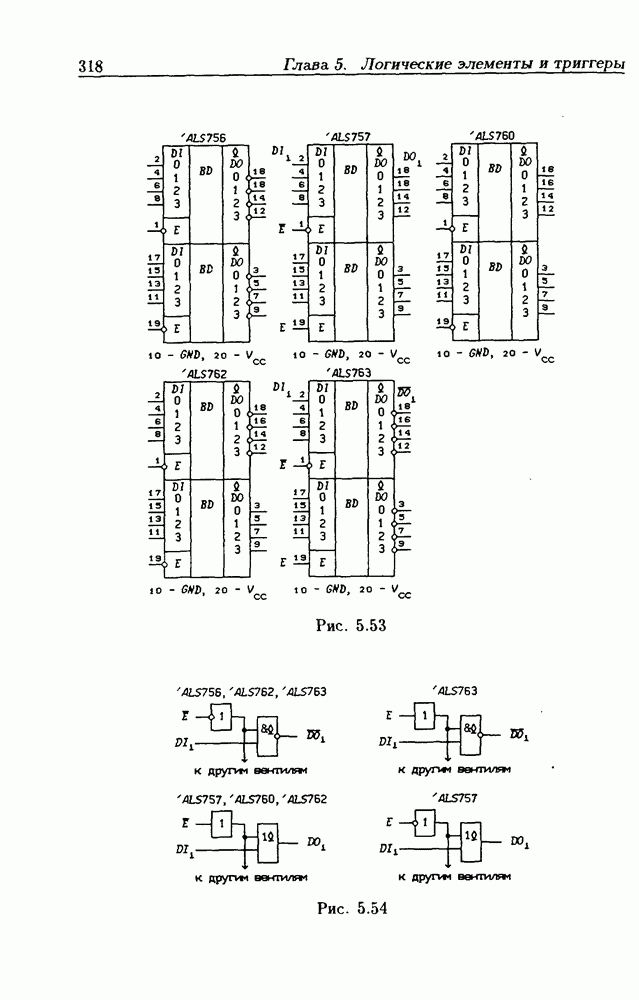
- Типовые цоколевки ИС.
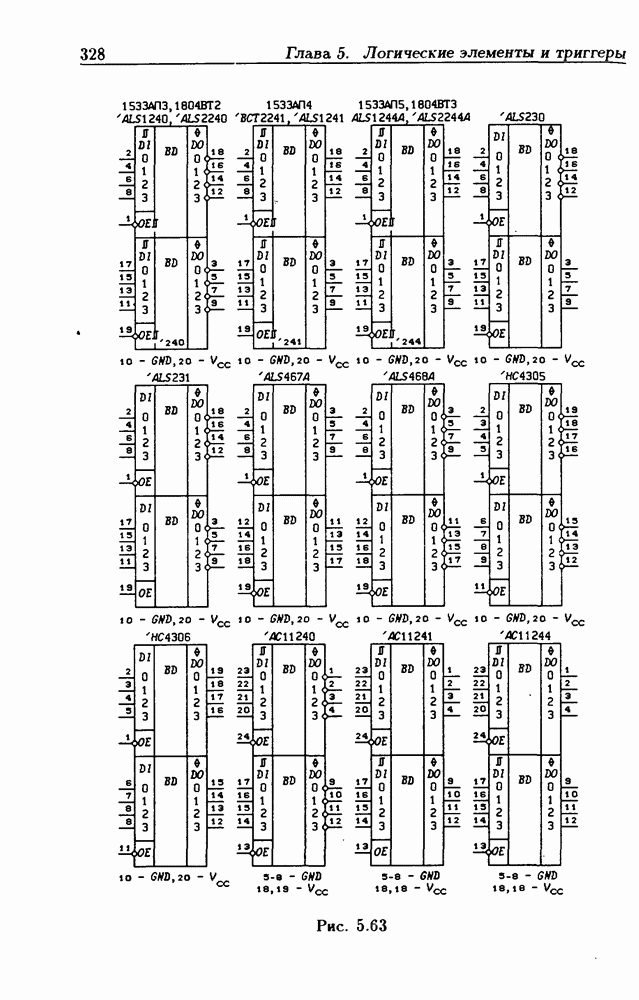
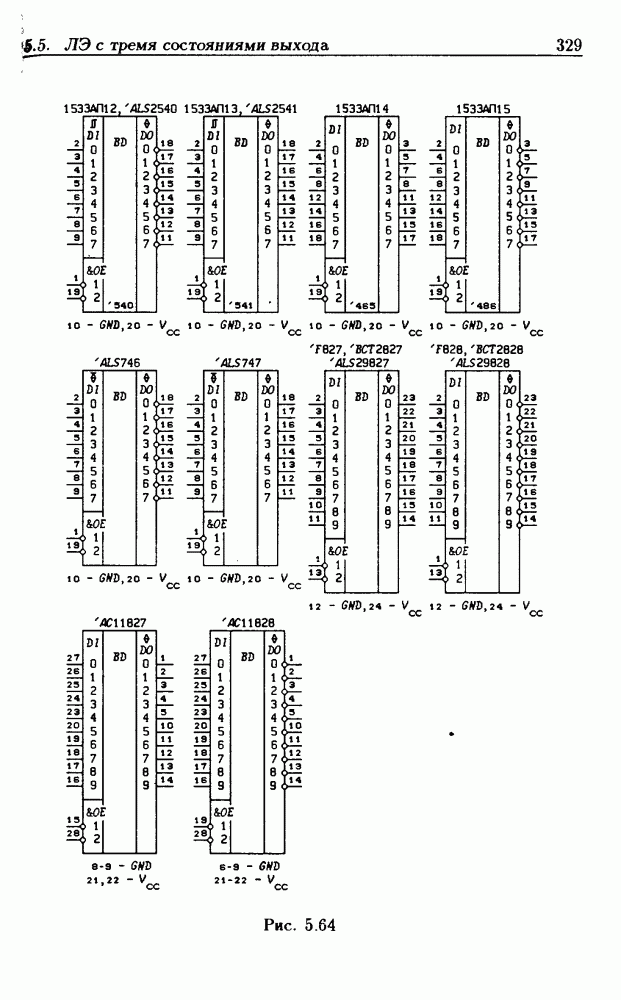
- 5.5. Логические элементы с тремя состояниями выхода
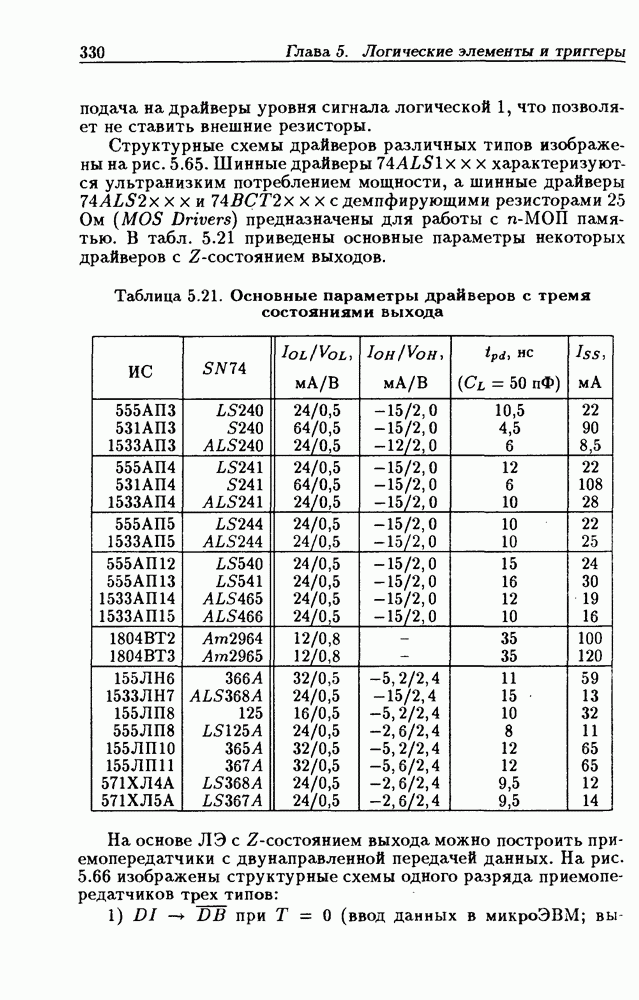
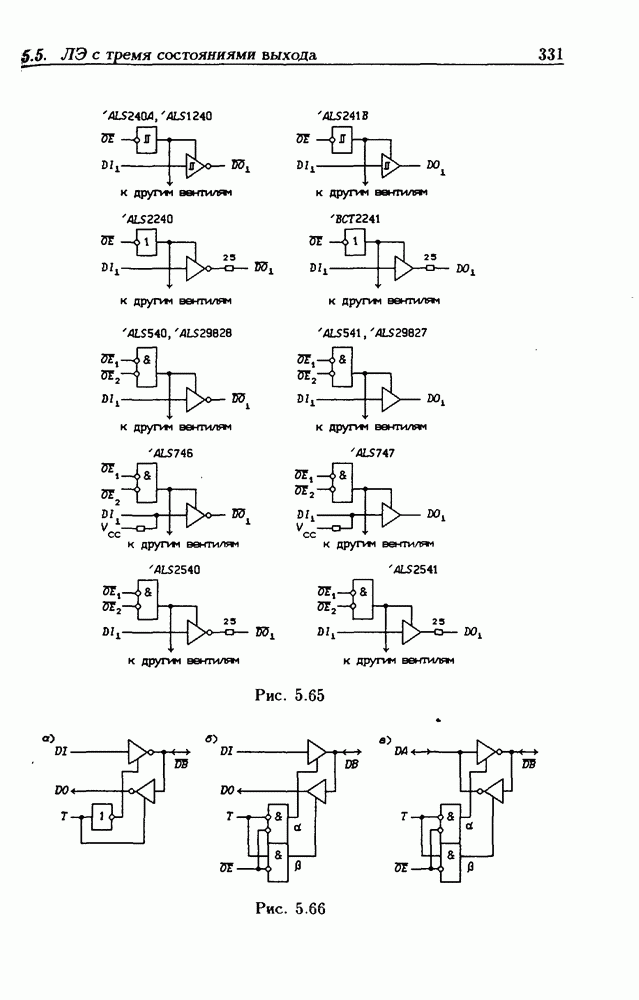
- Шинные драйверы с Z-состоянием выхода.
- Основные правила графического изображения ИС.
- 5.6. Преобразователи уровней напряжения и тока
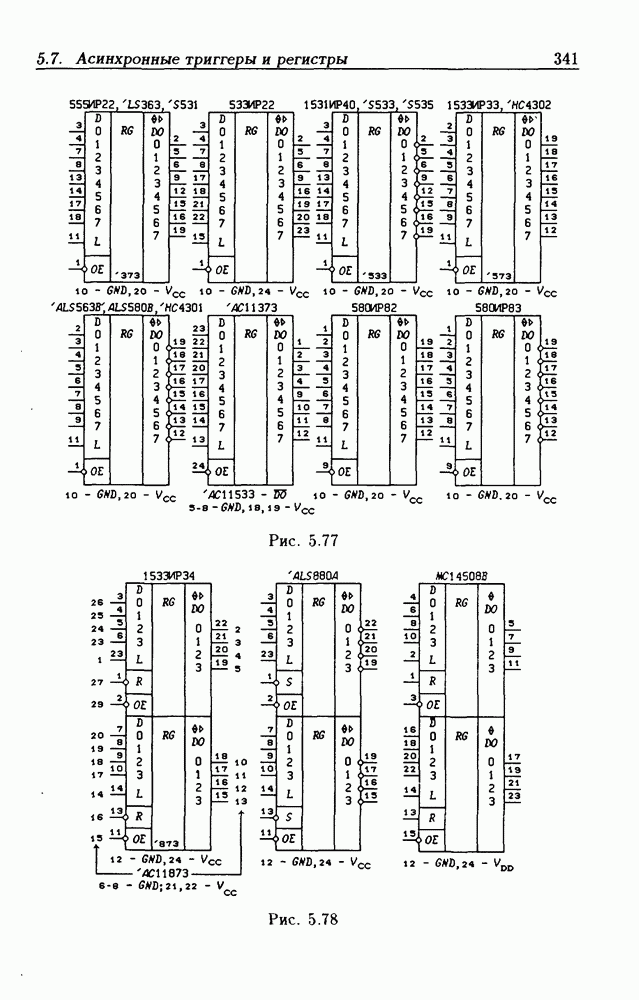
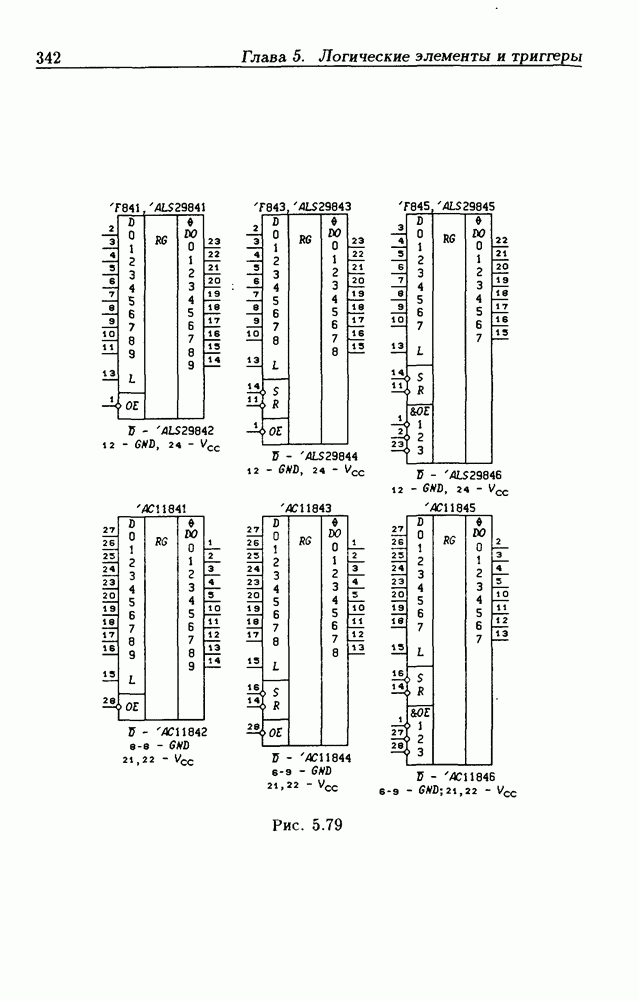
- 5.7. Асинхронные потенциальные триггеры и регистры памяти
- 5.8. Синхронные триггеры и регистры памяти
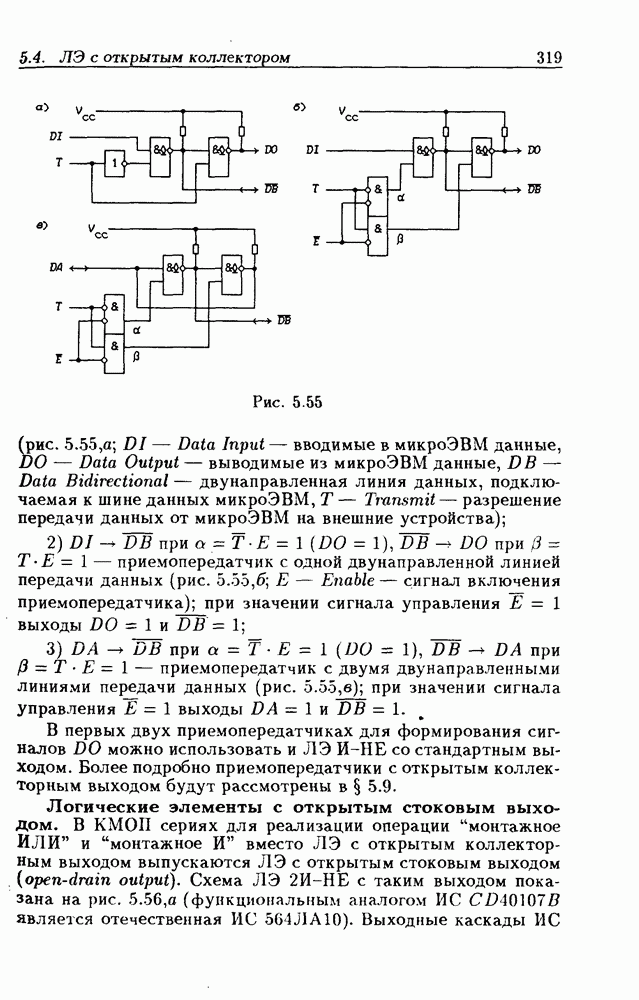
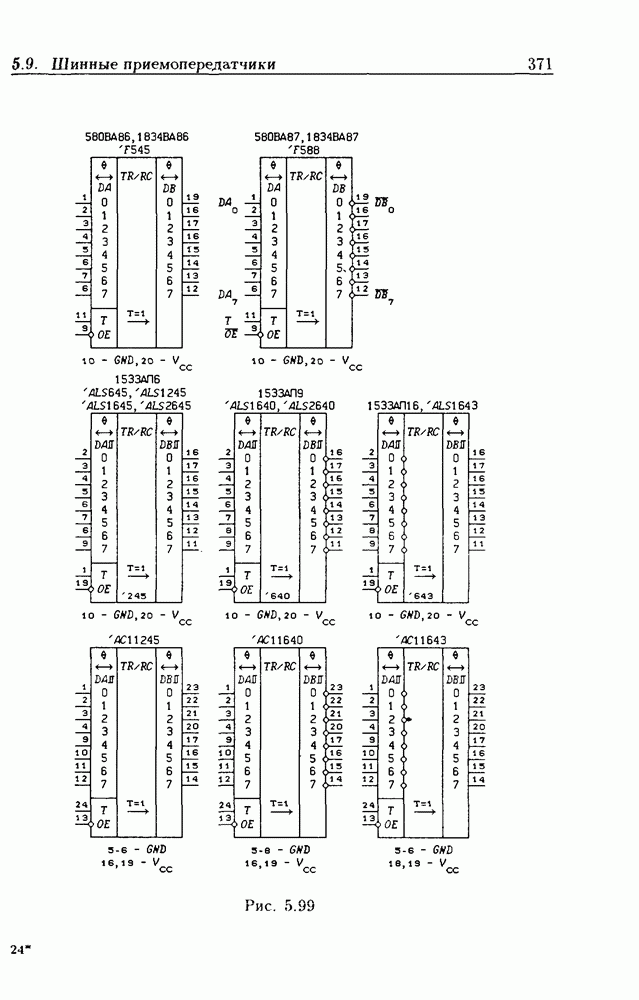
- 5.9. Шинные приемопередатчики
- Шинные приемопередатчики с Z-состоянием выхода.
- Шинные приемопередатчики с открытым коллекторным выходом.
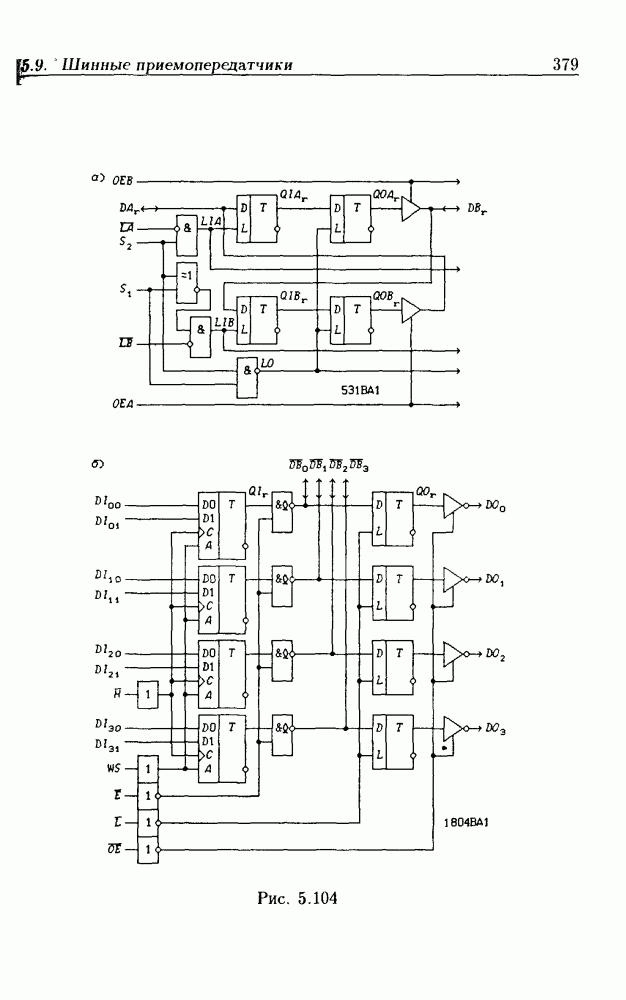
- Шинные приемопередатчики с регистрами памяти.
- Шинные приемопередатчики со сдвигающим регистром.
- Шинные трехнаправленные приемопередатчики.
- 5.10. Мультивибраторы
- 5.11. Генераторы
- Схемы устранения «дребезга» механических контактов.
- Автогенераторы периодических сигналов.
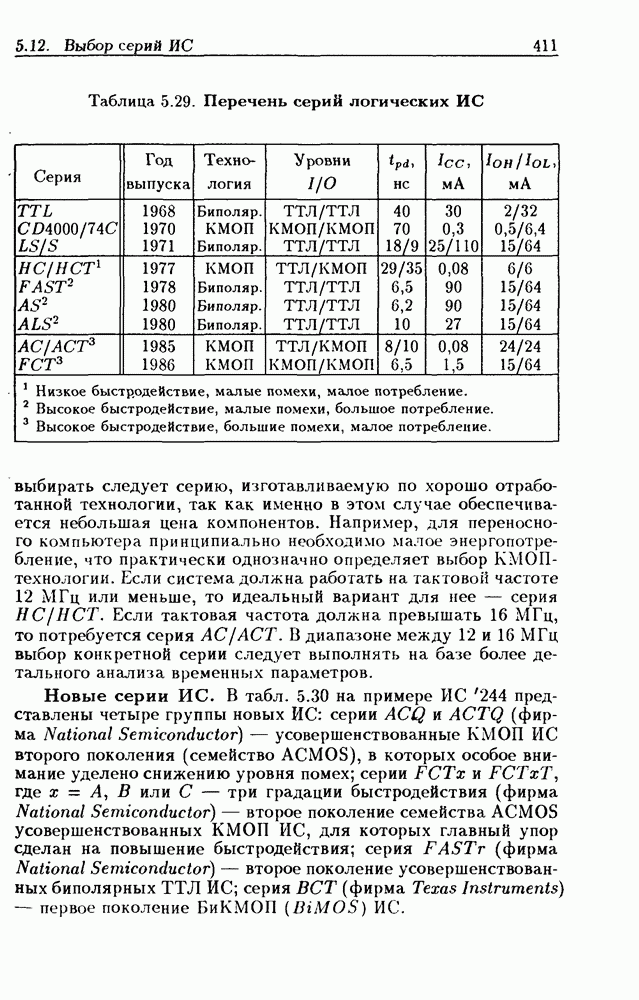
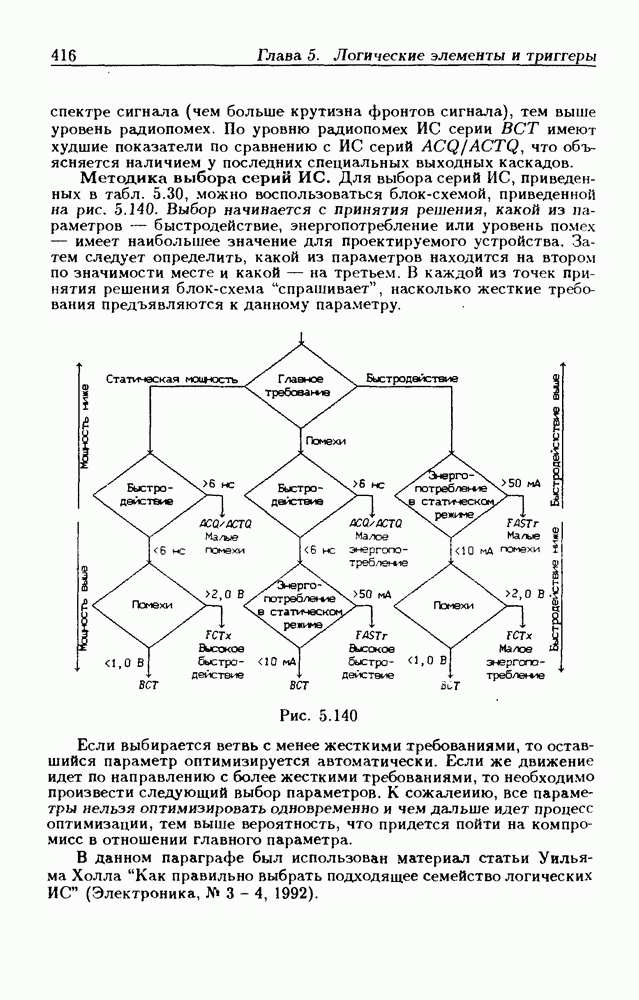
- 5.12. Рекомендации по выбору серий ИС
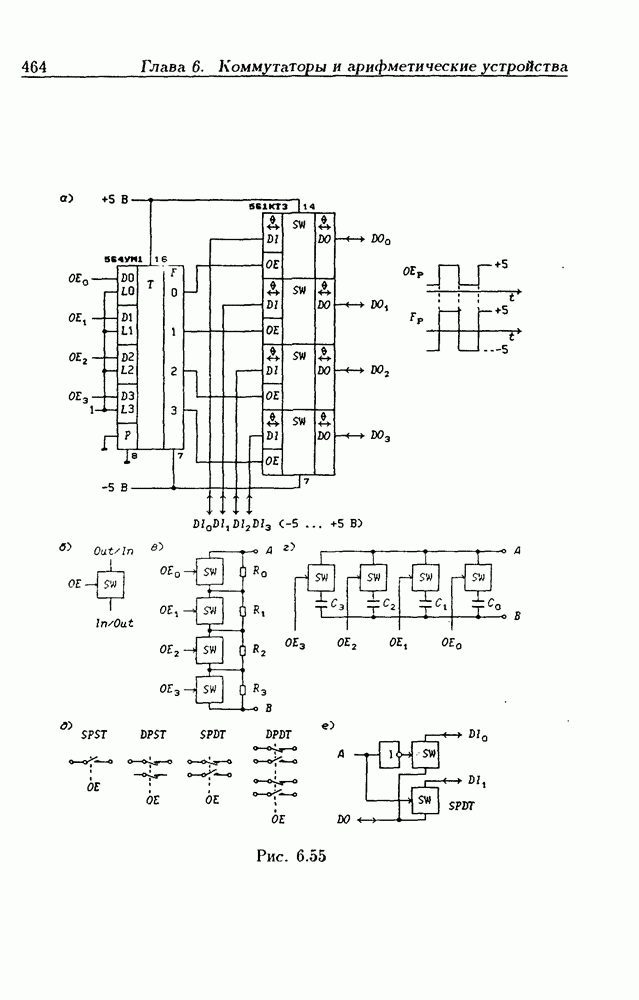
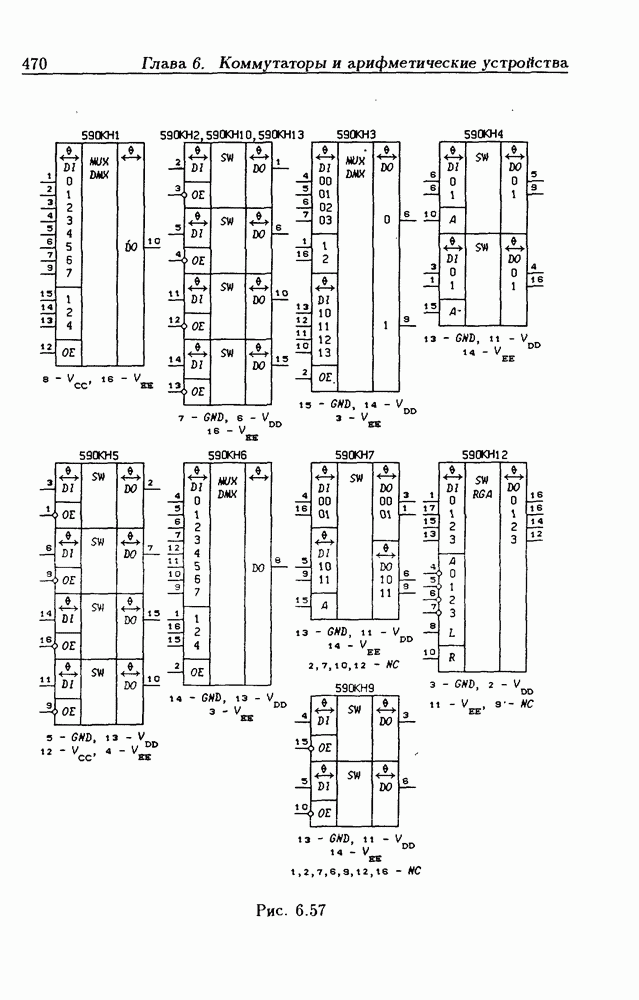
- Глава 6. Коммутаторы и арифметические устройства
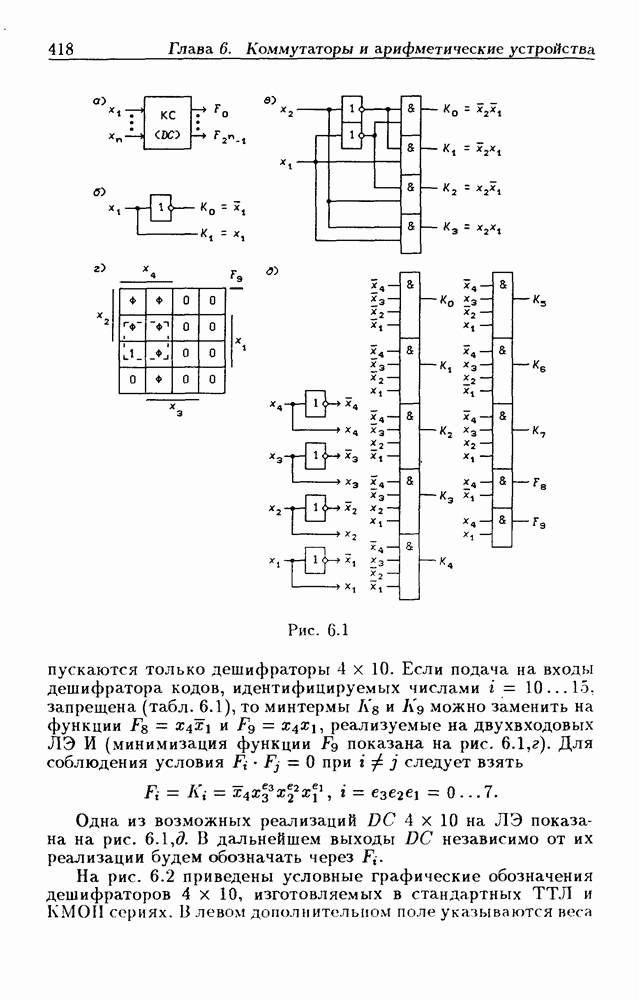
- 6.1. Дешифраторы
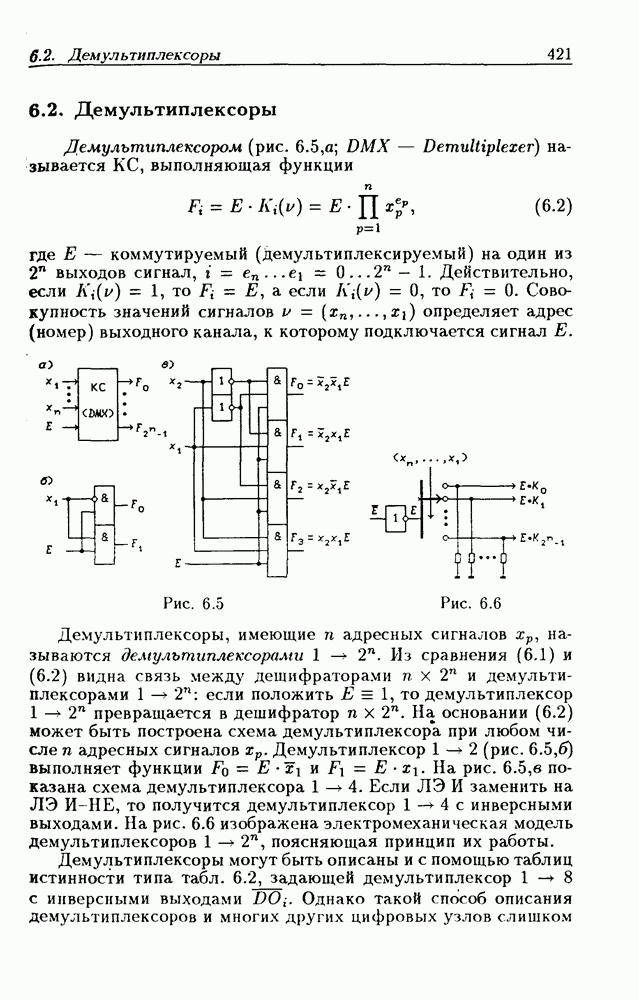
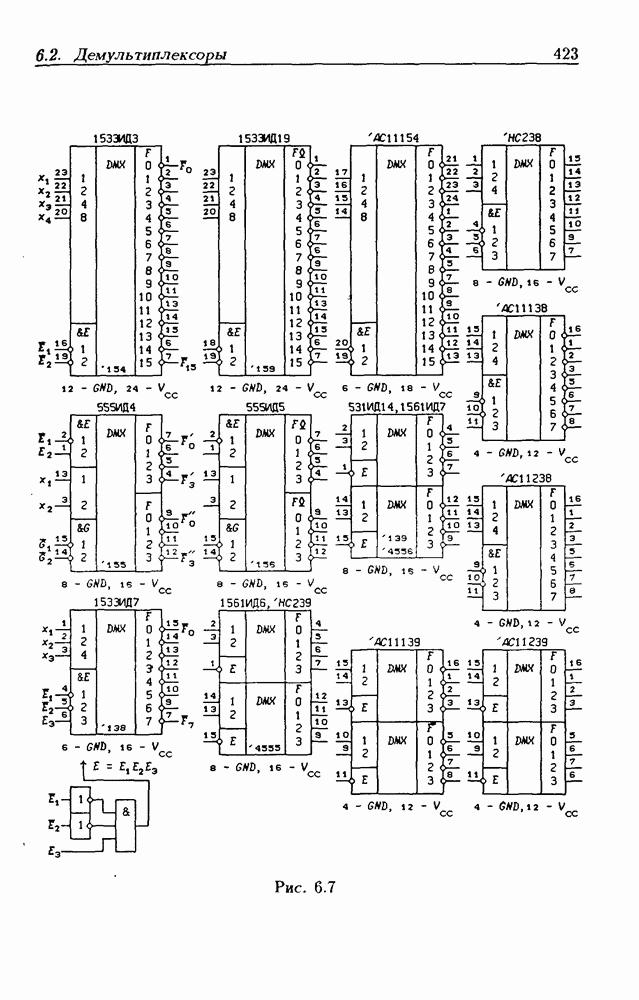
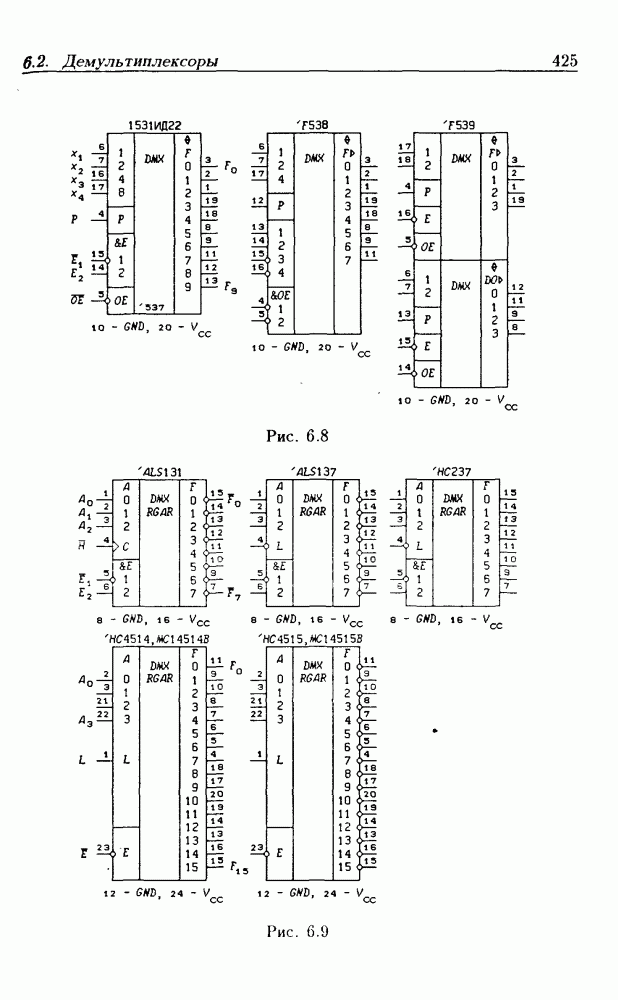
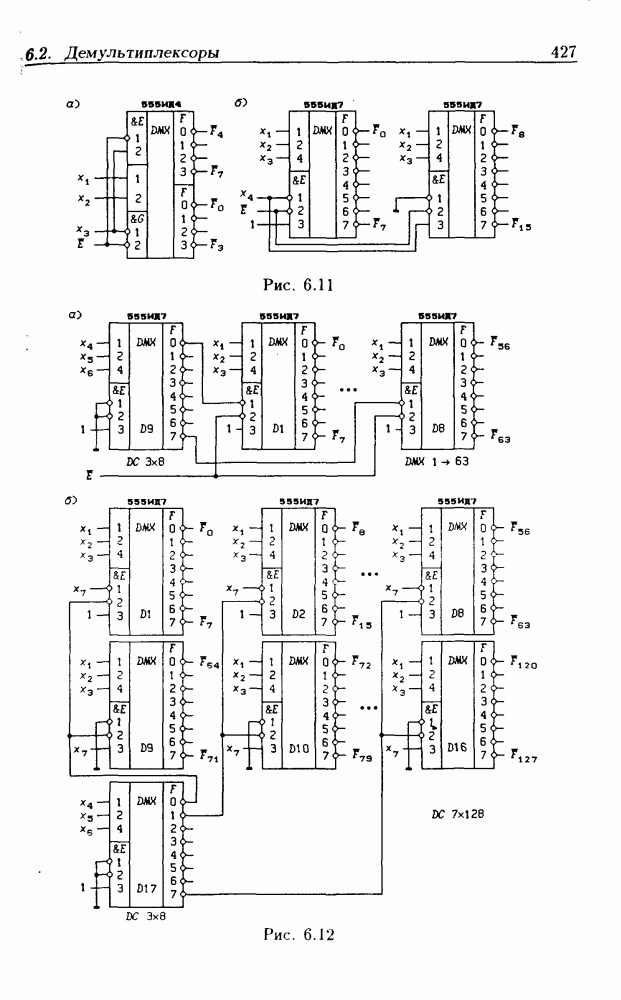
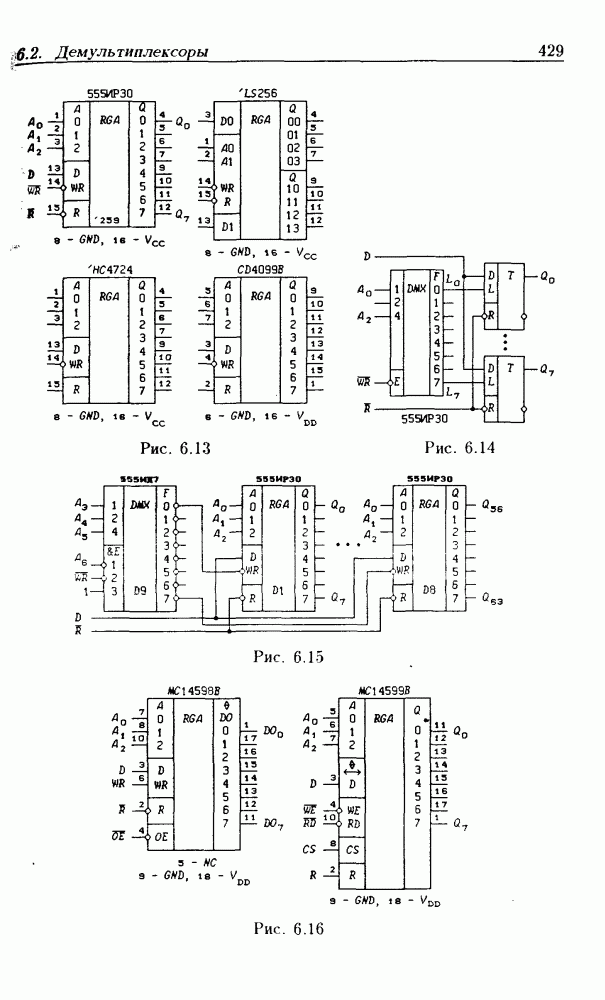
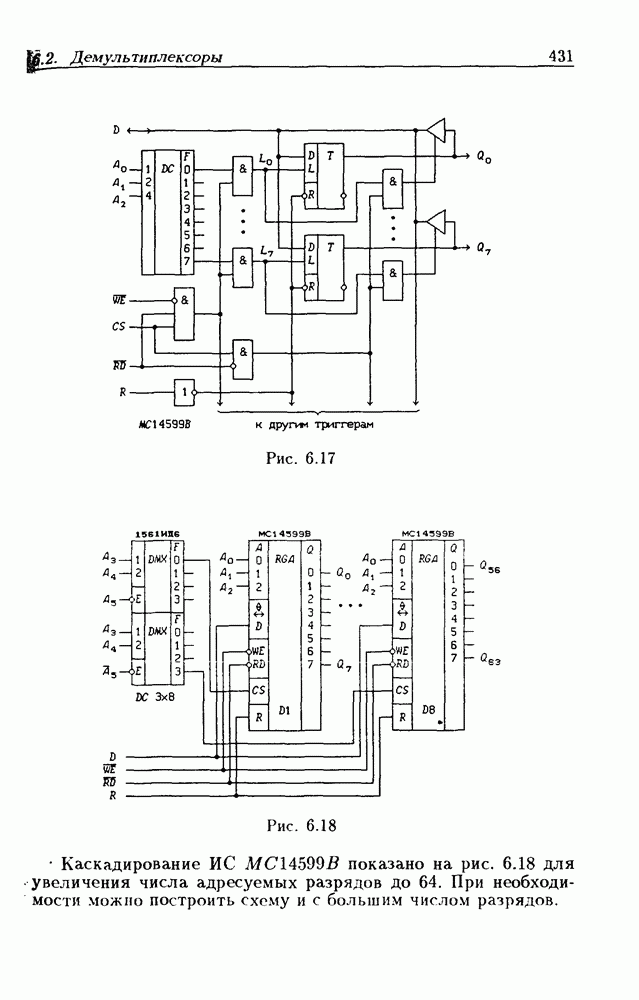
- 6.2. Демультиплексоры
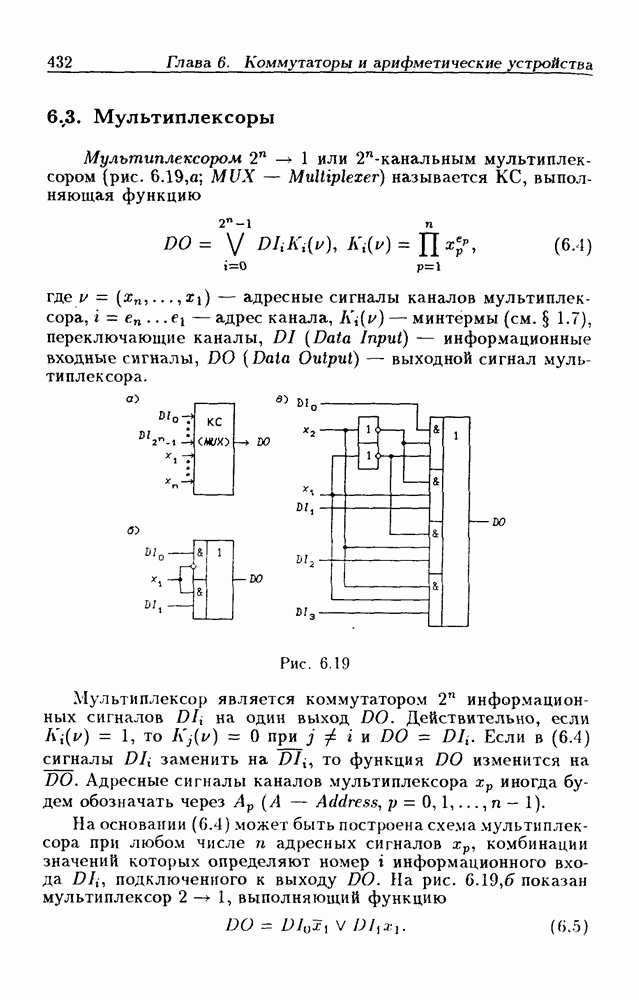
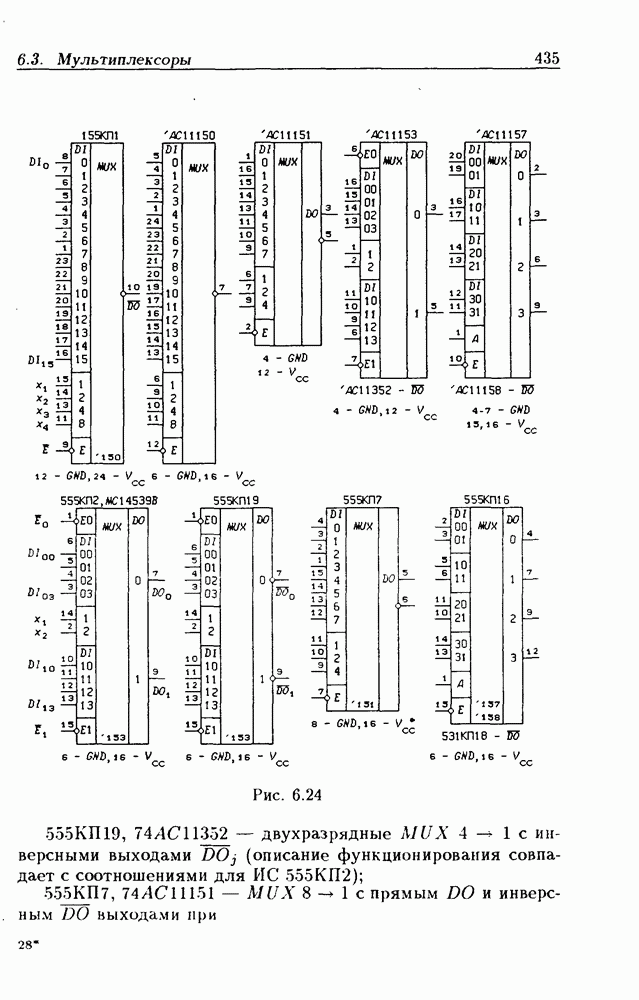
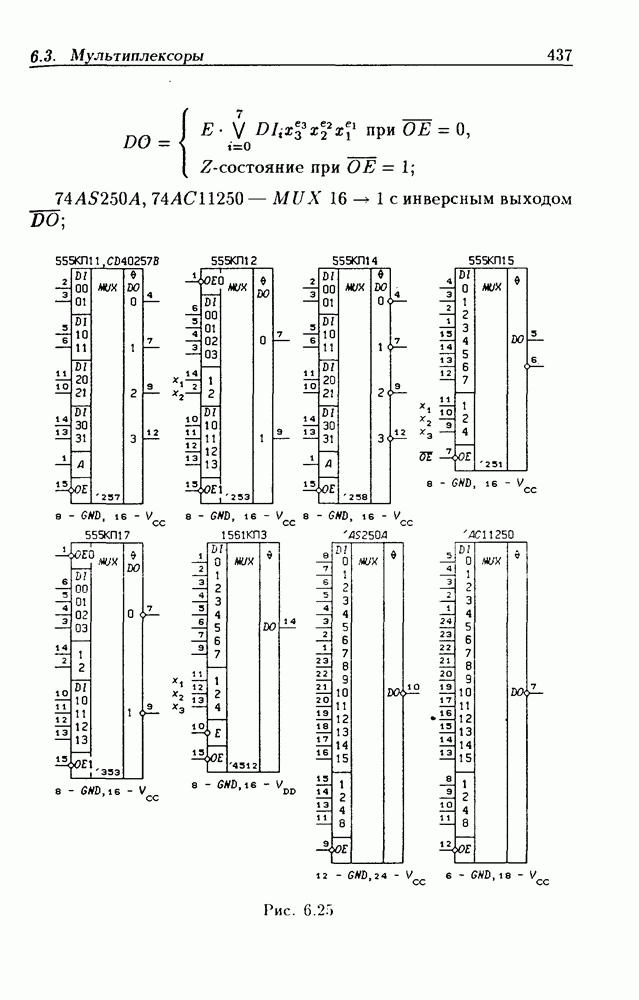
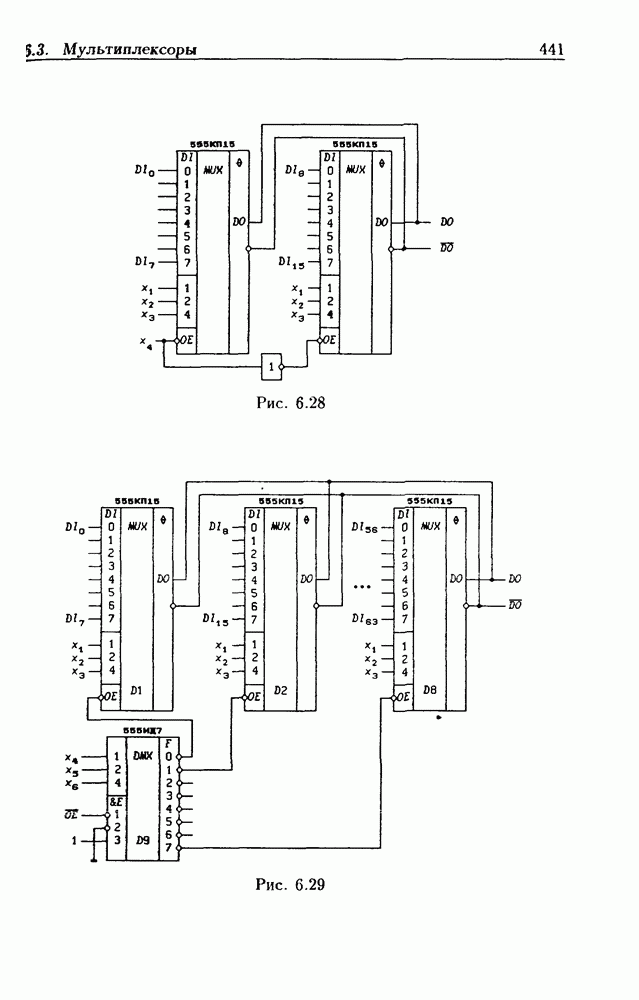
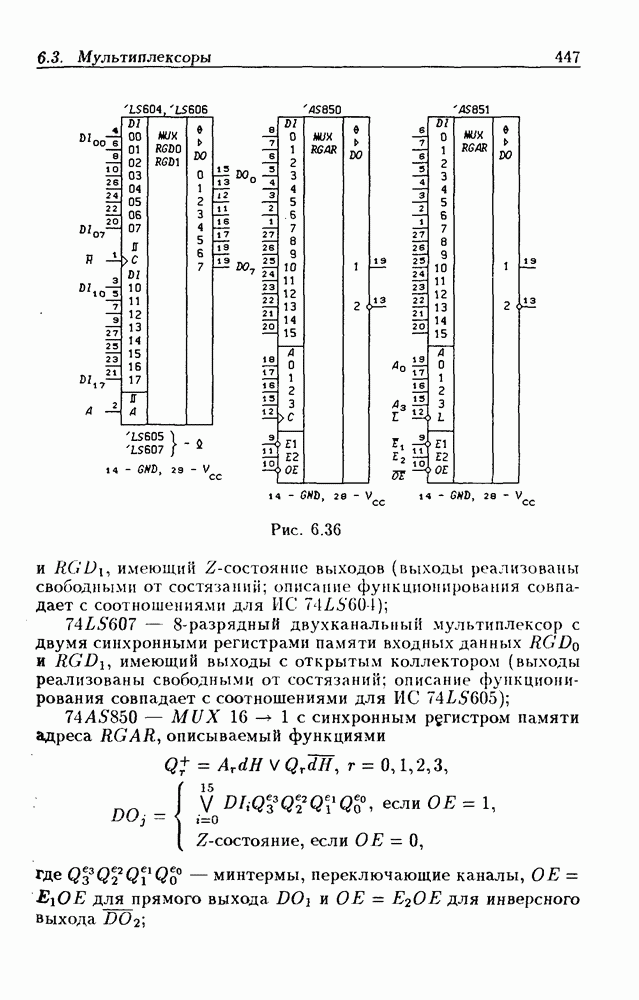
- 6.3. Мультиплексоры
- Мультиплексоры без стробирования.
- Мультиплексоры со стробированием.
- Мультиплексоры с Z-состоянием выхода.
- Каскадирование мультиплексоров.
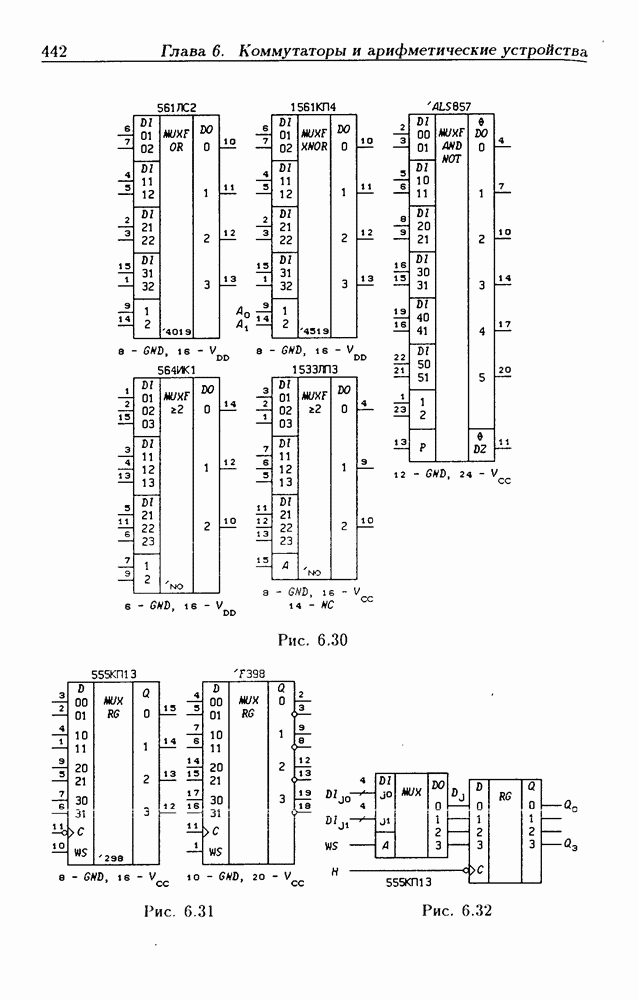
- Функциональные мультиплексоры.
- Регистры памяти с мультиплексными входами данных.
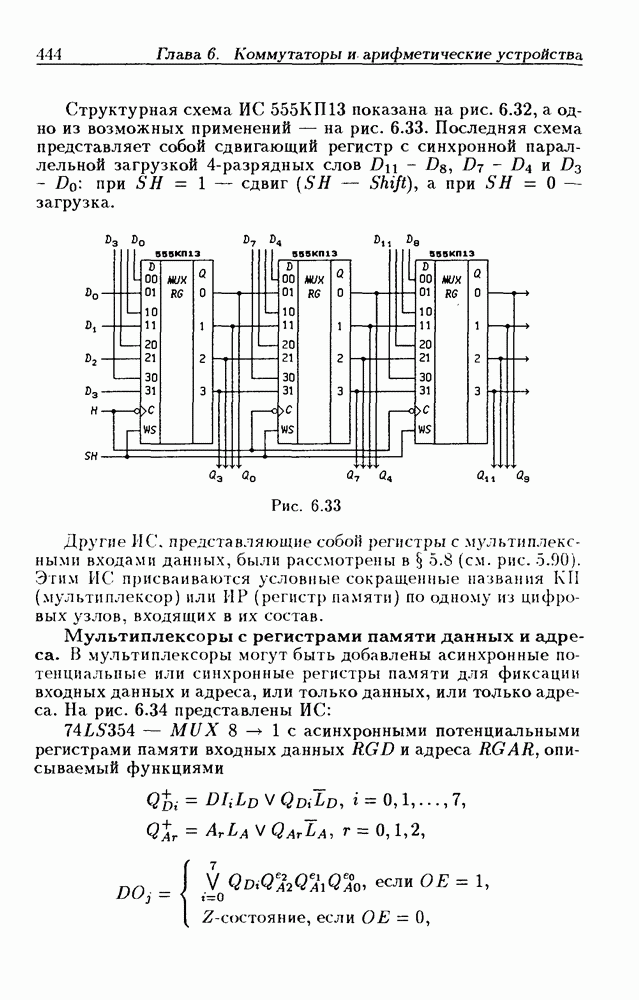
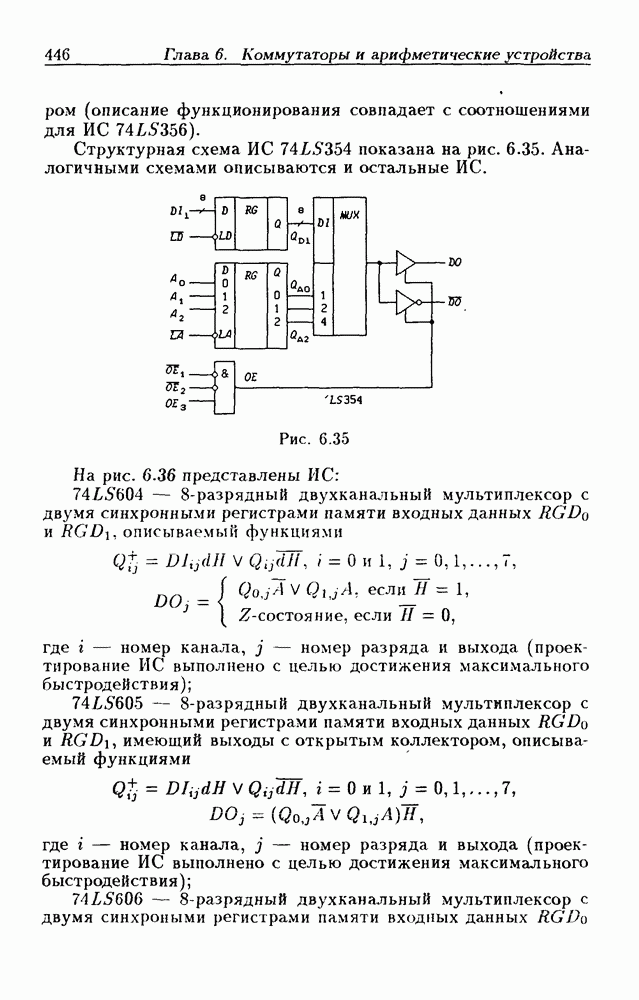
- Мультиплексоры с регистрами памяти данных и адреса.
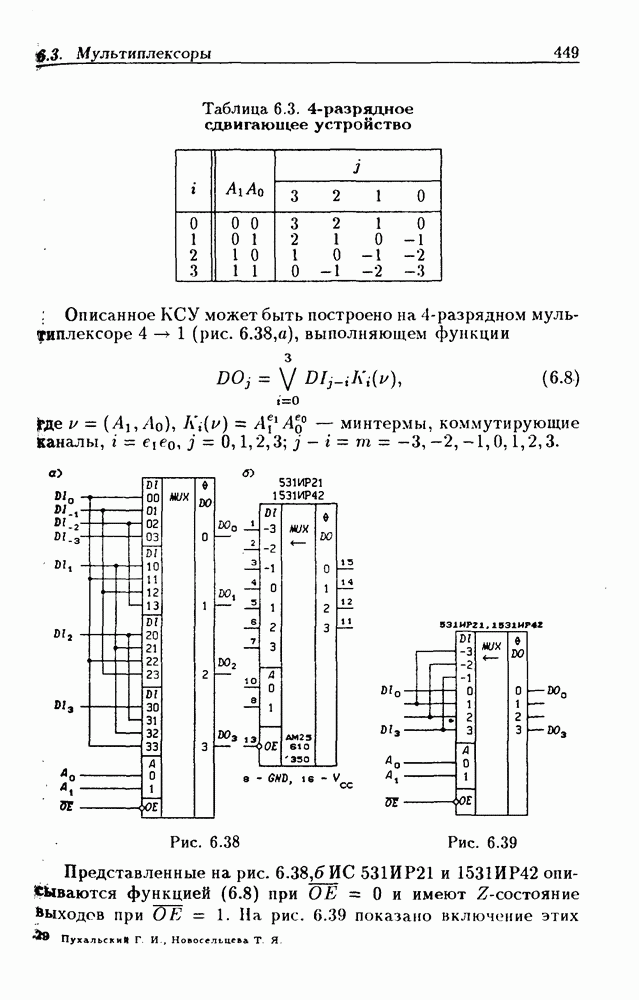
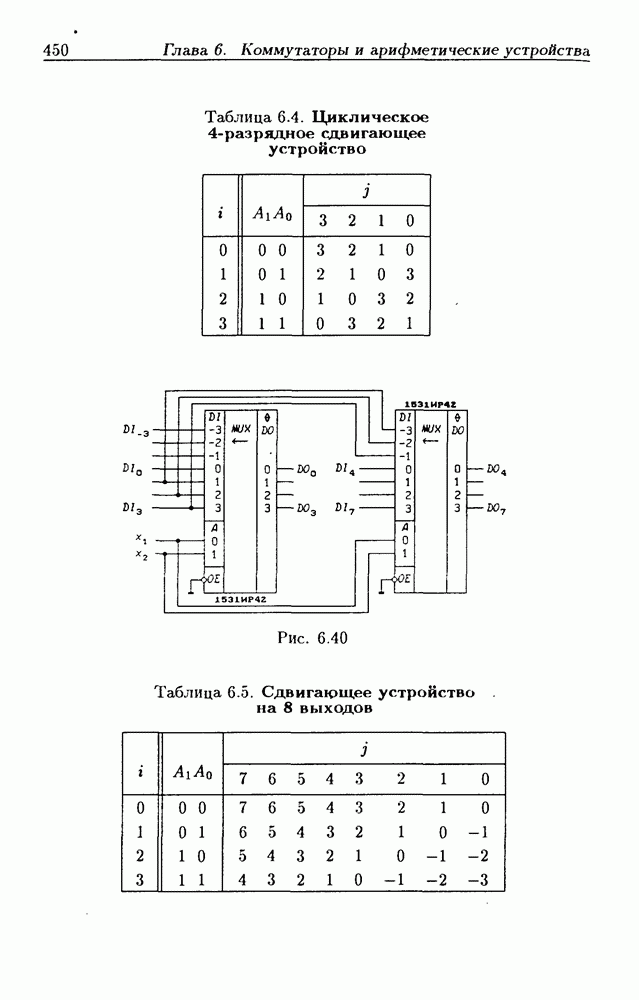
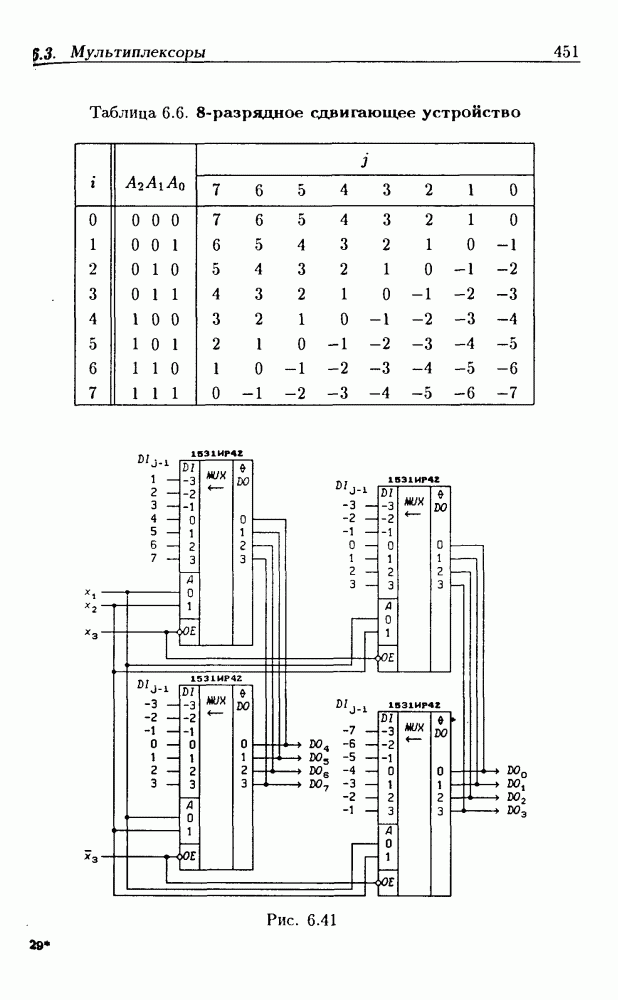
- Сдвигающие мультиплексоры.
- 6.4. Синтез комбинационных схем и цифровых автоматов на мультиплексорах
- Синтез схем на 8-канальных мультиплексорах.
- Синтез на двухразрядных 4-канальных мультиплексорах.
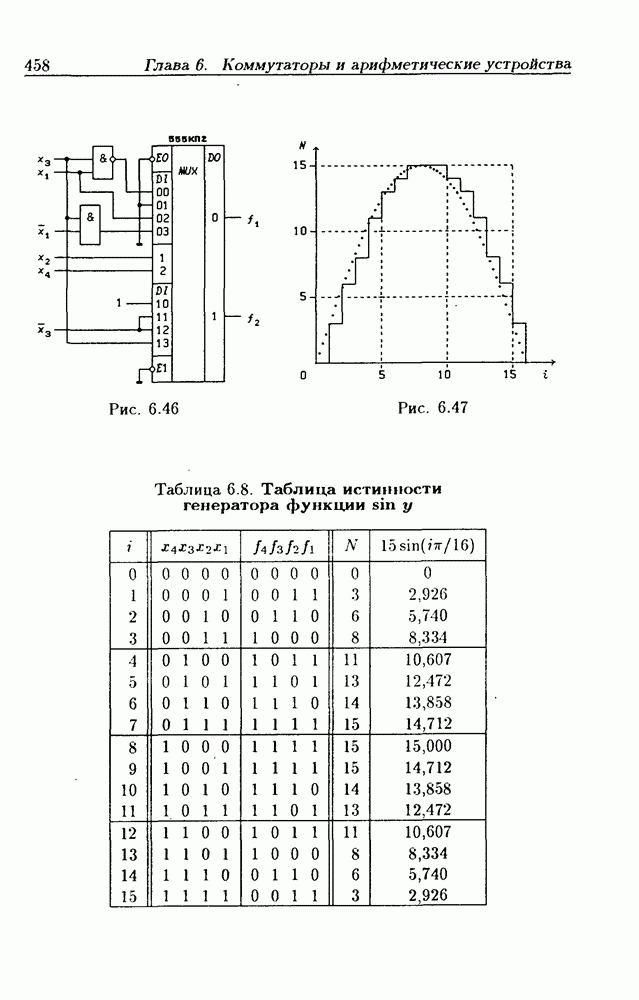
- Синтез генератора синусоидальной функции на мультиплексорах.
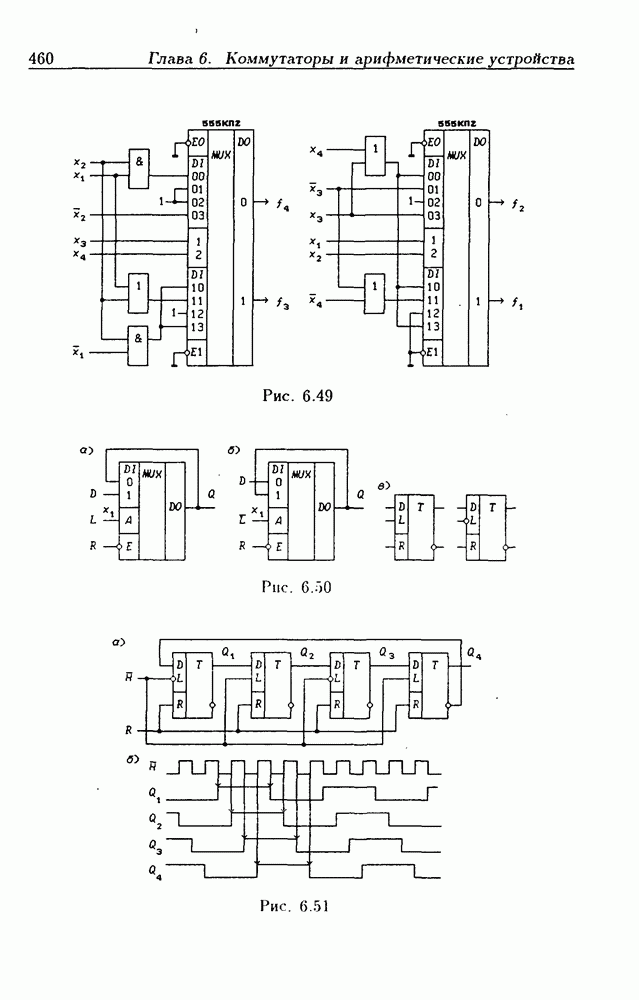
- Синтез триггеров на мультиплексорах.
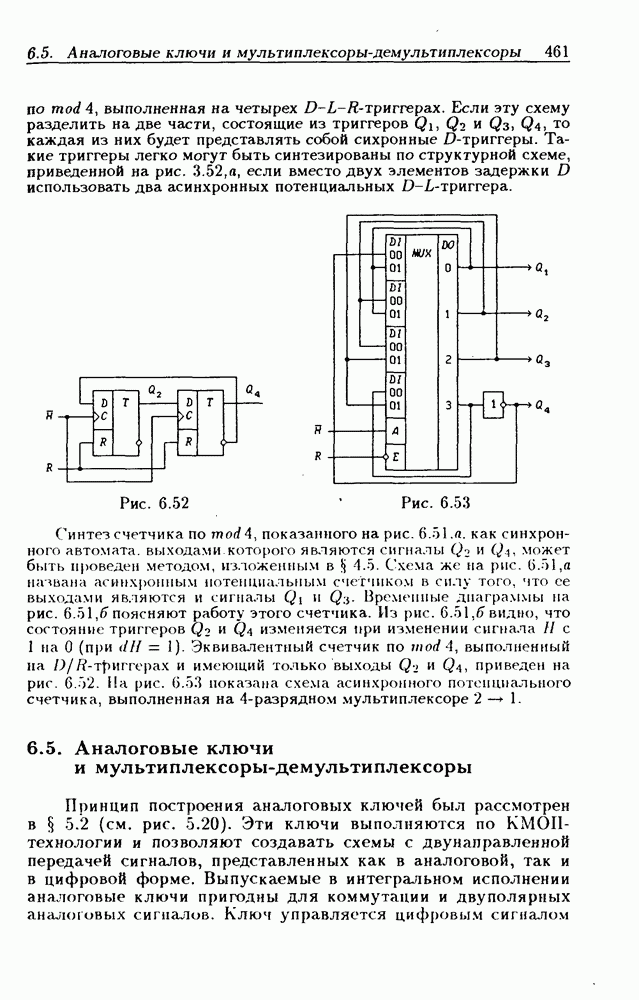
- Синтез счетчиков на мультиплексорах.
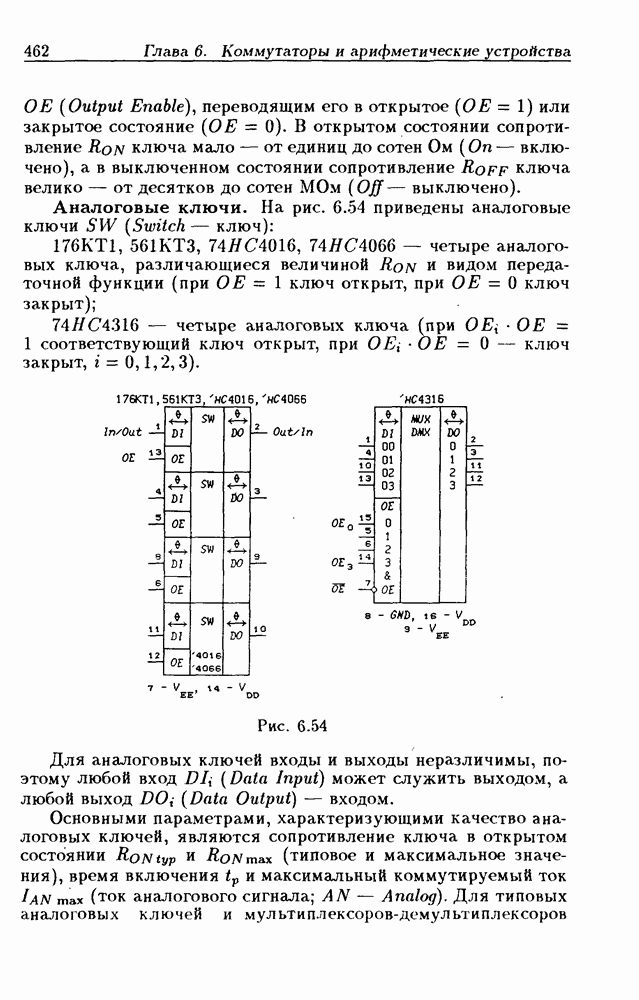
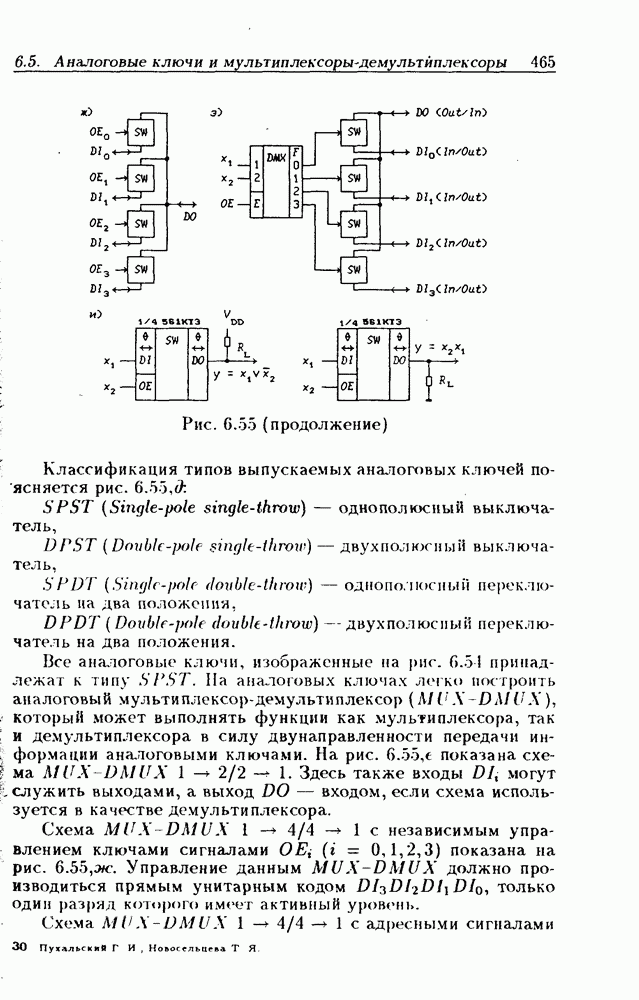
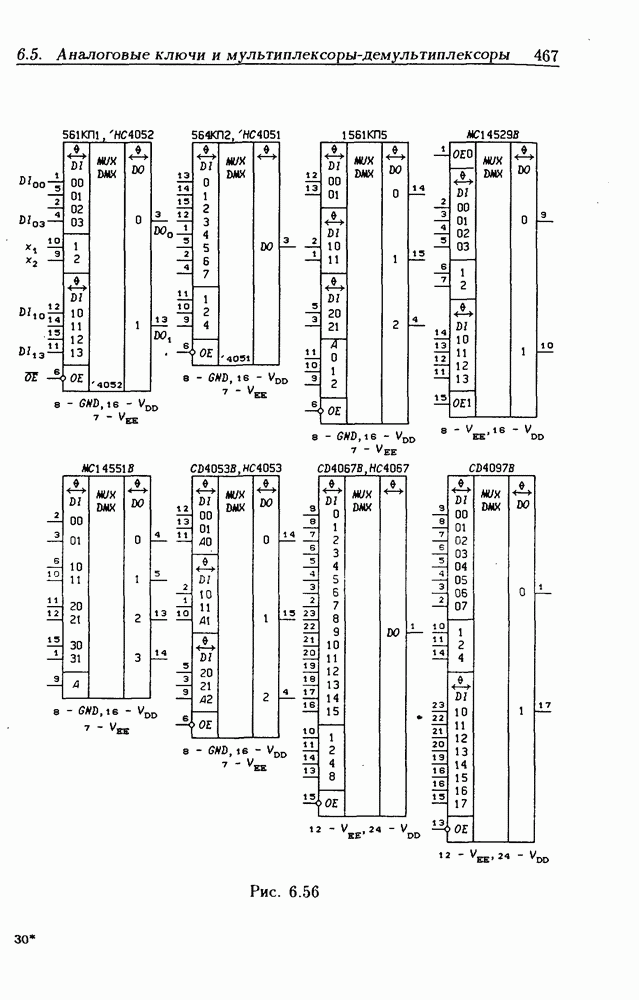
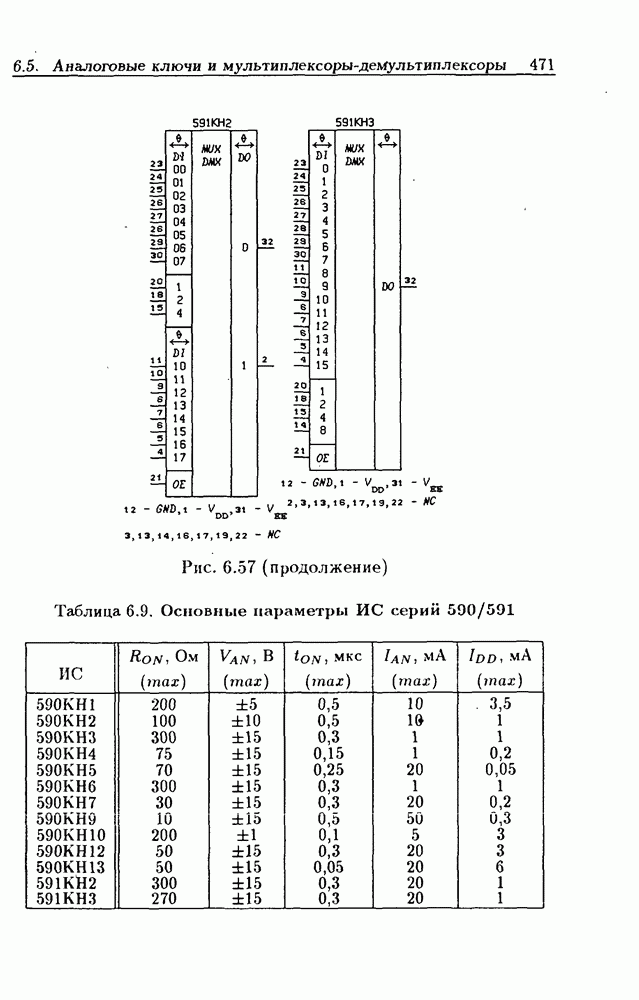
- 6.5. Аналоговые ключи и мультиплексоры-демультиплексоры
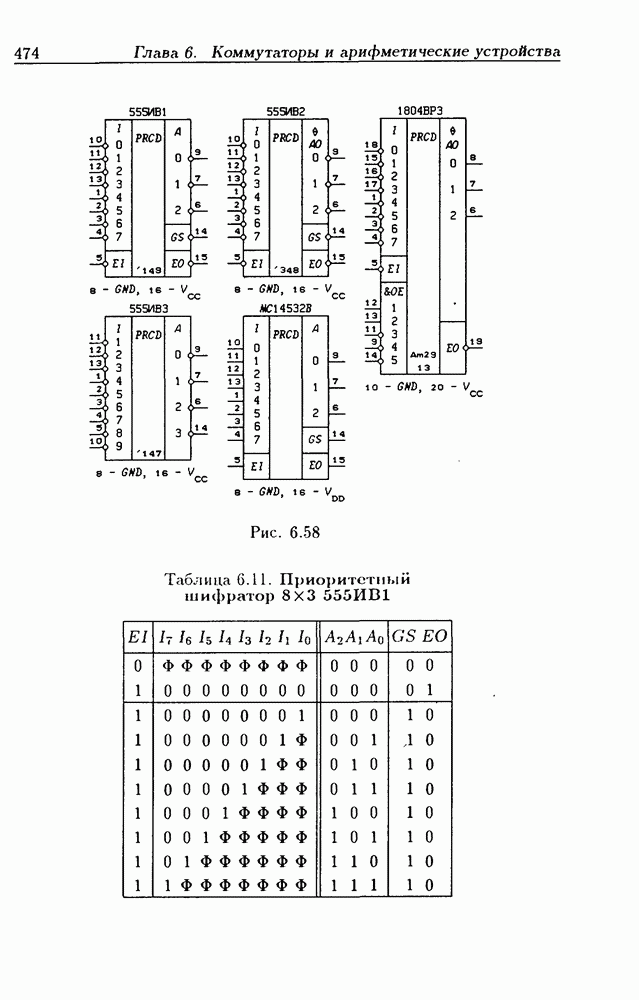
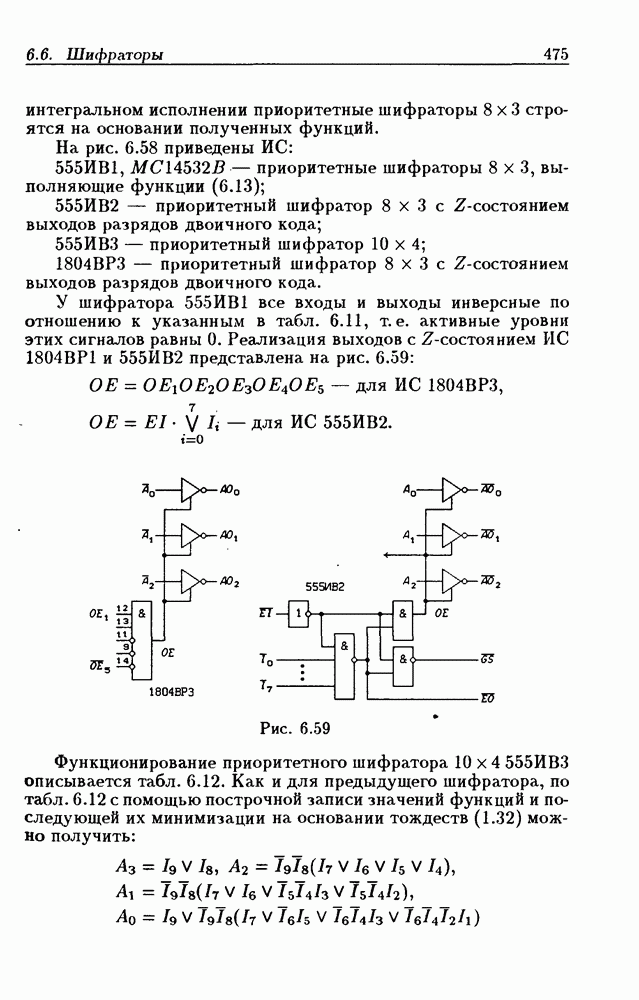
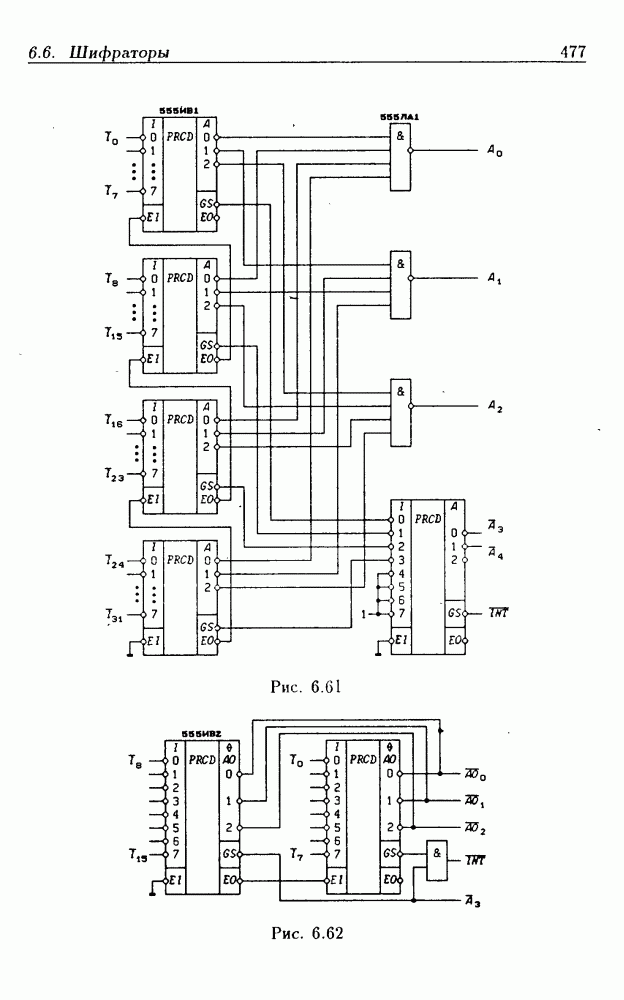
- 6.6. Шифраторы
- 6.7. Цифровые компараторы
- Программируемые цифровые компараторы.
- Адресные компараторы.
- Применения адресных компараторов.
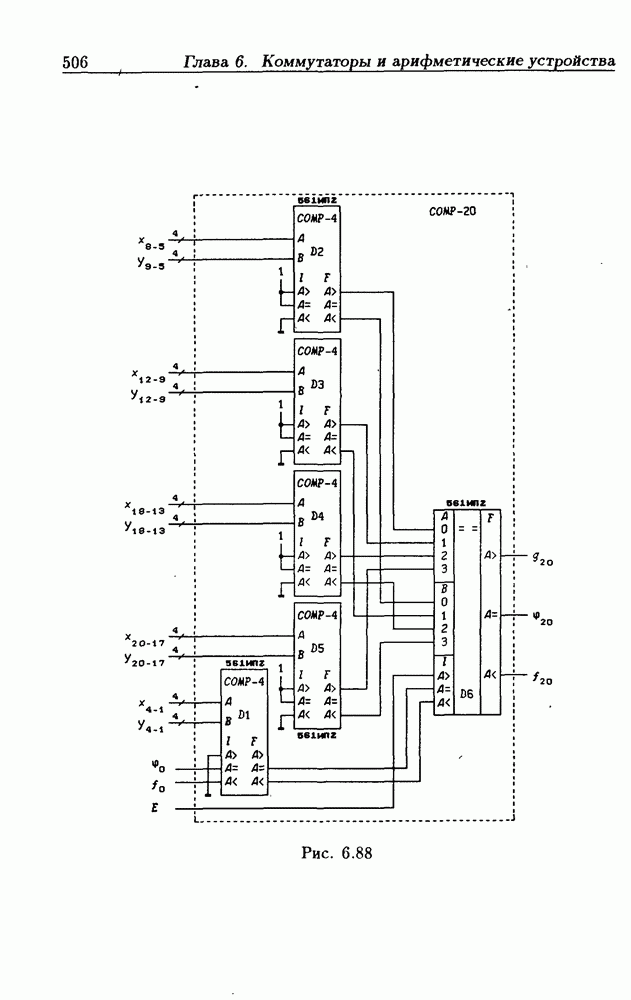
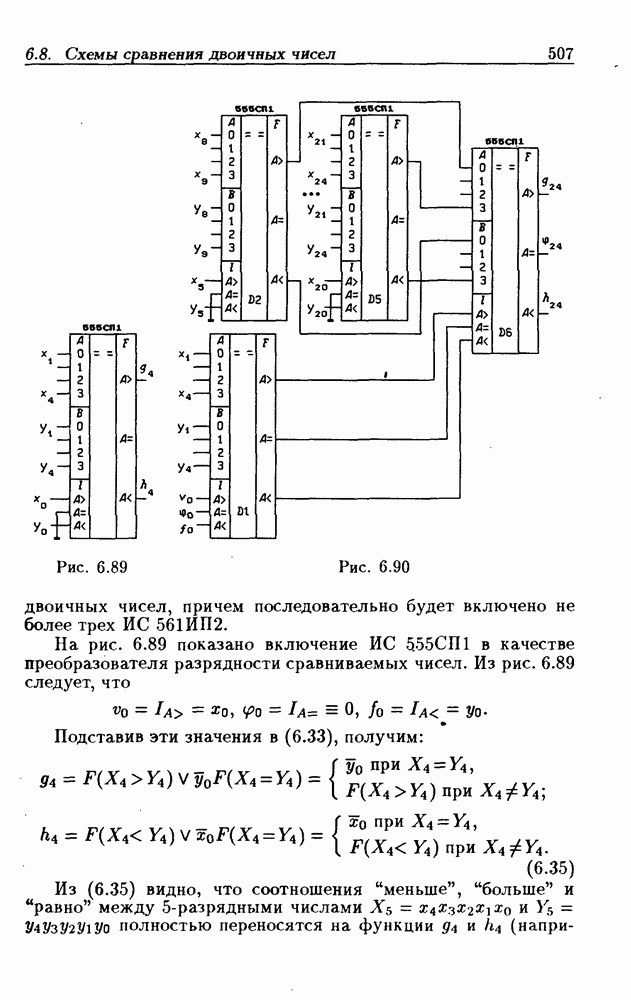
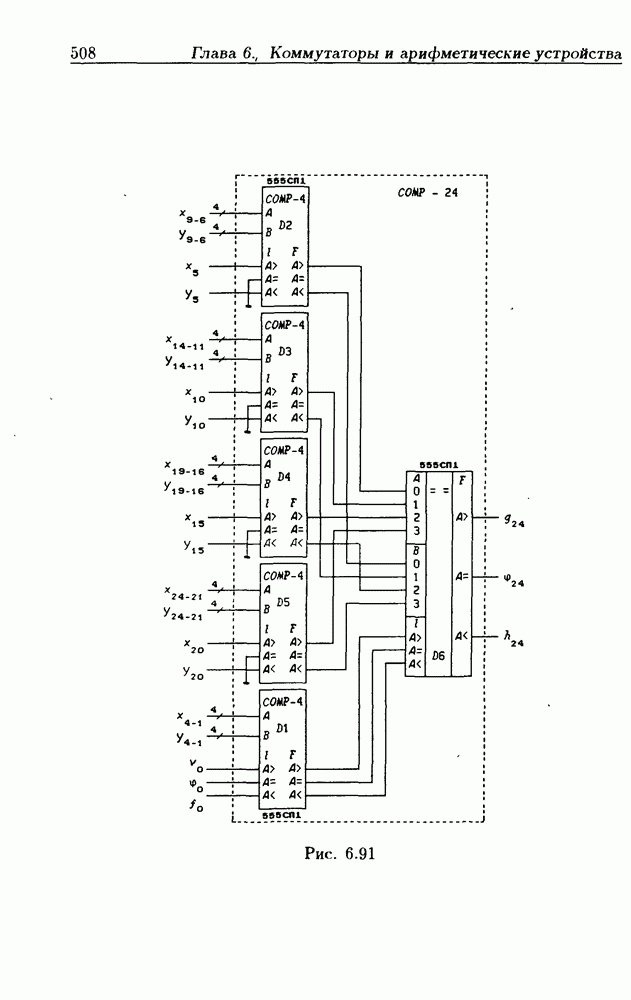
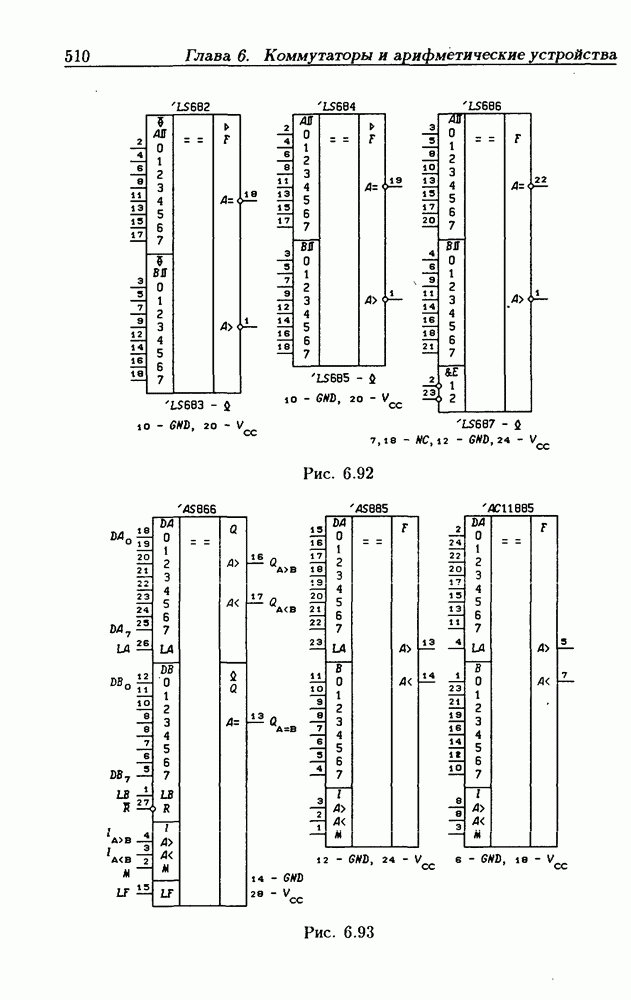
- 6.8. Схемы сравнения двоичных чисел
- 8-разрядные схемы сравнения двоичных чисел.
- 6.9. Прямой, обратный и дополнительный коды
- Дополнительный код.
- Сложение чисел в обратном коде.
- Код с избытком 3.
- 6.10. Сумматоры
- Двоичные параллельные сумматоры с последовательным переносом.
- Двоичные сумматоры с параллельным переносом.
- Применения сумматоров.
- Десятичные сумматоры.
- Последовательные двоичные сумматоры.
- 6.11. Арифметическо-логические устройства
- 6.12. Пороговые схемы и мажоритарные элементы
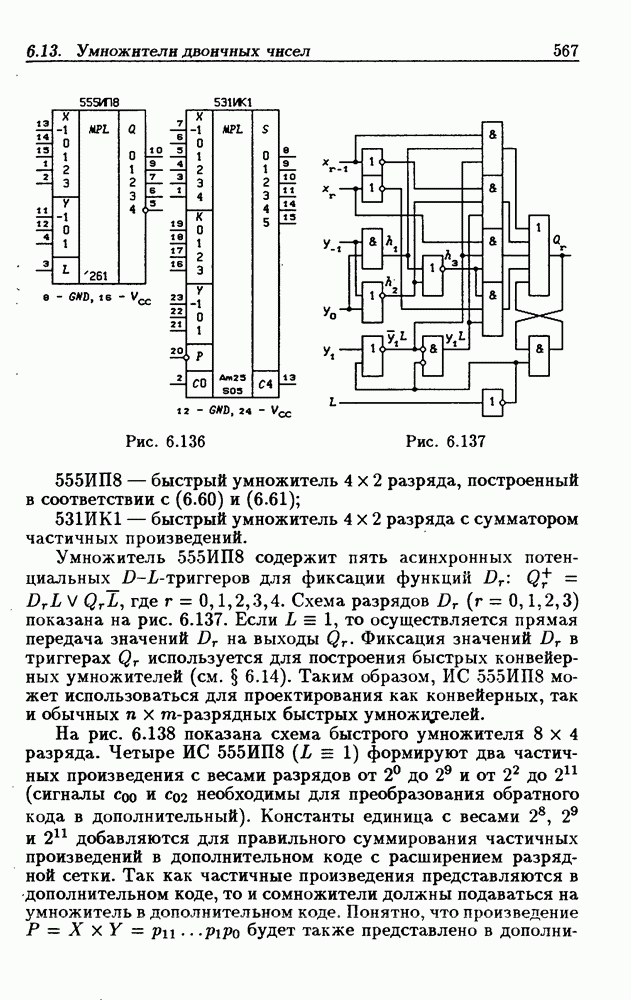
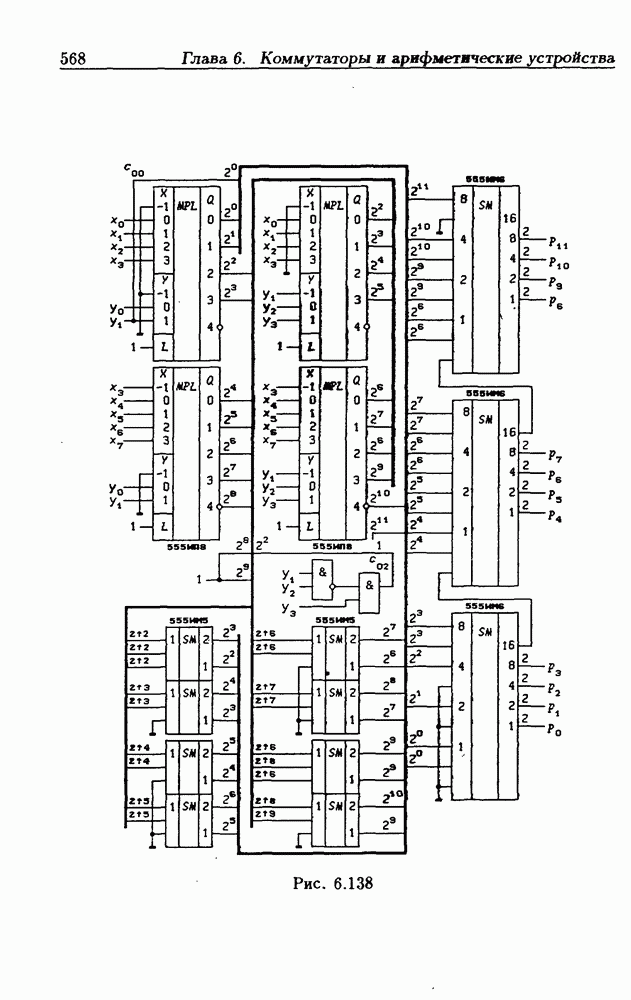
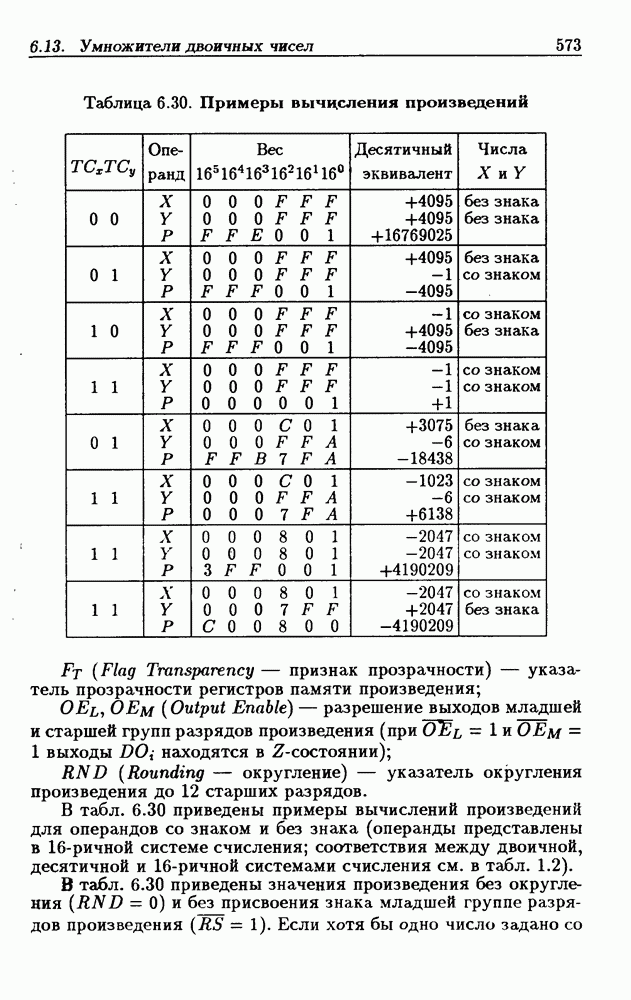
- 6.13. Умножители двоичных чисел
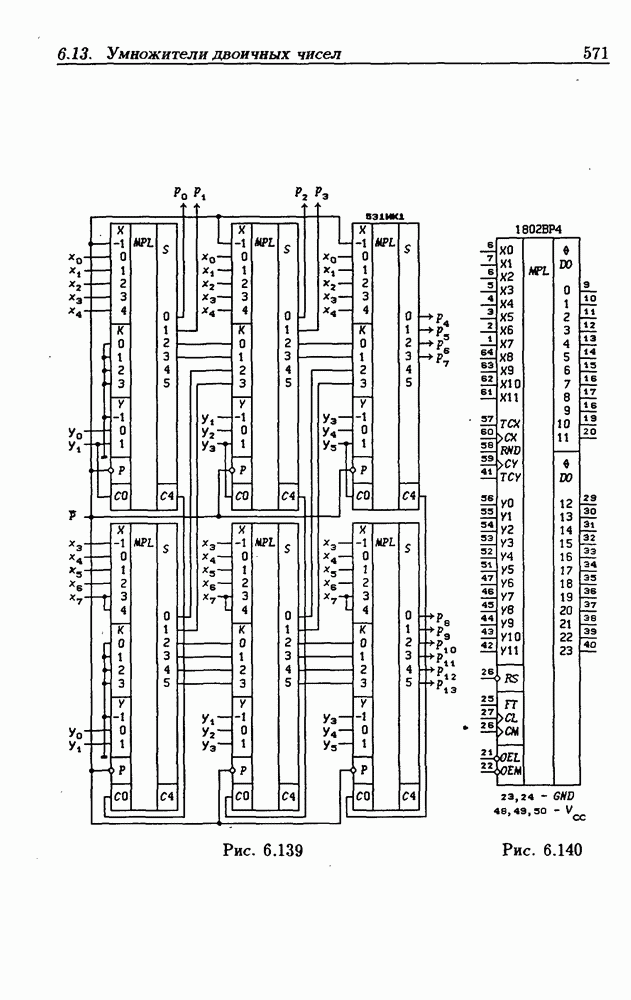
- Быстрые умножители.
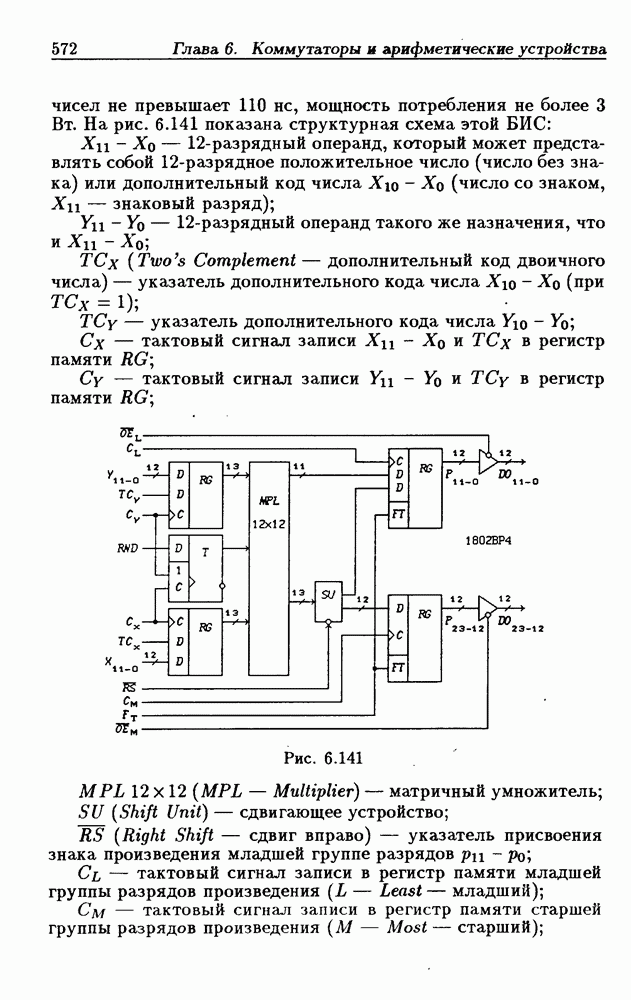
- БИС умножителя 12×12 разрядов 1802ВР4.
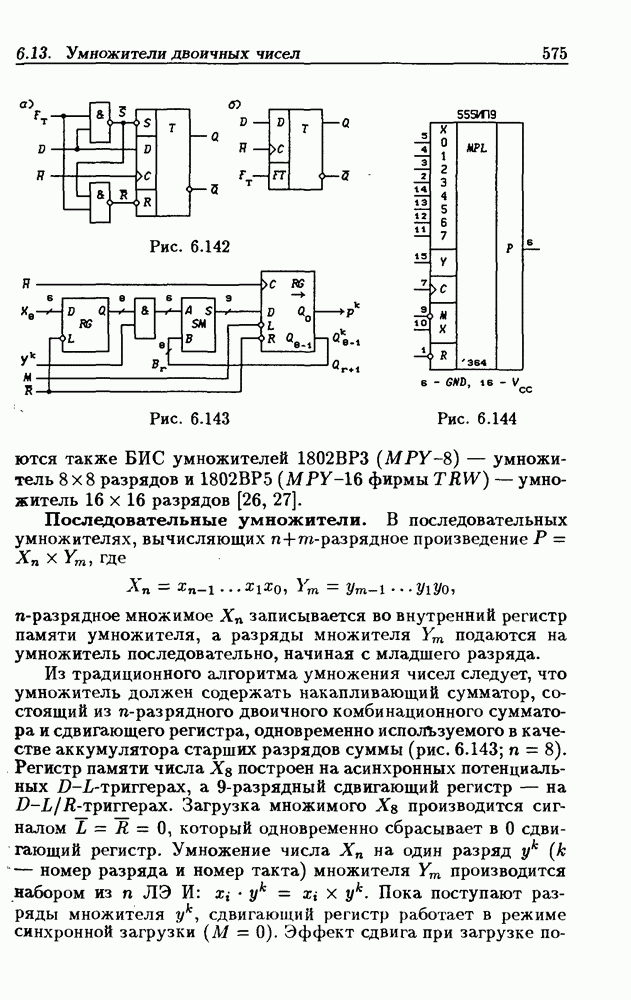
- Последовательные умножители.
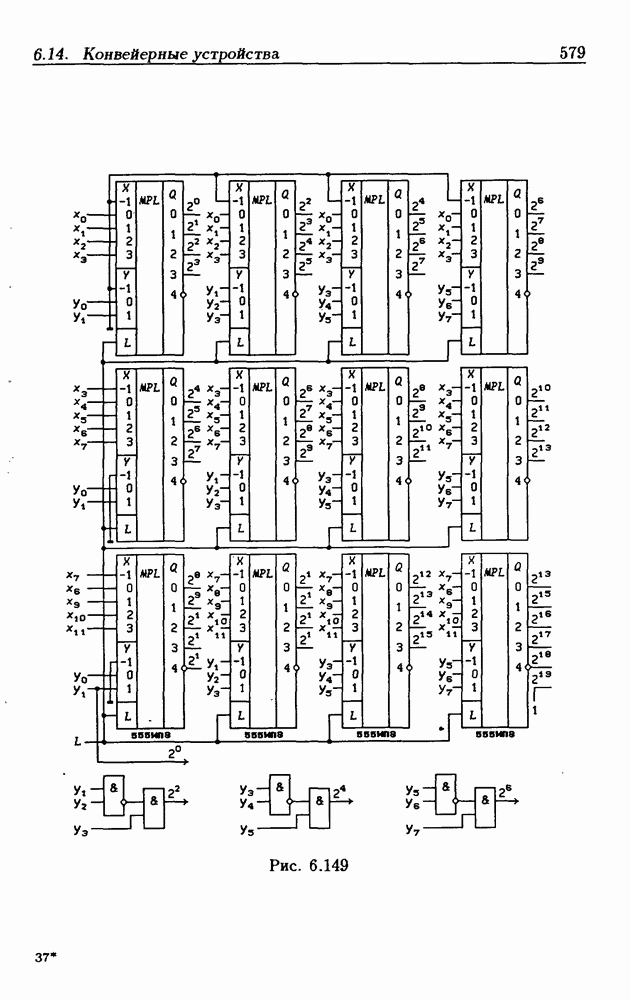
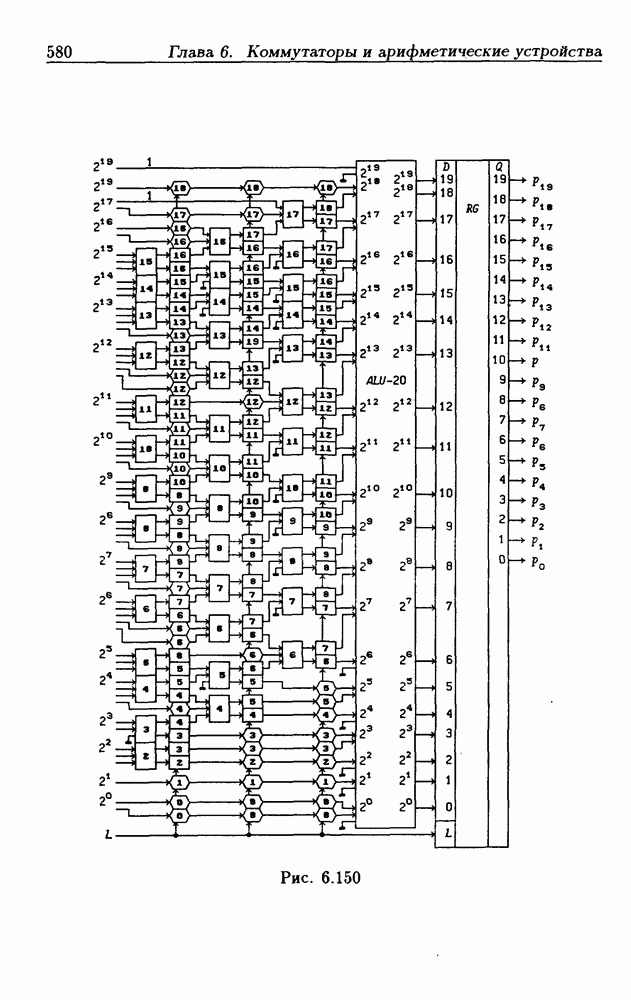
- 6.14. Конвейерные устройства
- Конвейерный быстрый умножитель.
- Конвейерные АЦП.
- 6.15. Синтез линейных комбинационных схем
- Сумматор по модулю q.
- Умножитель по модулю q.
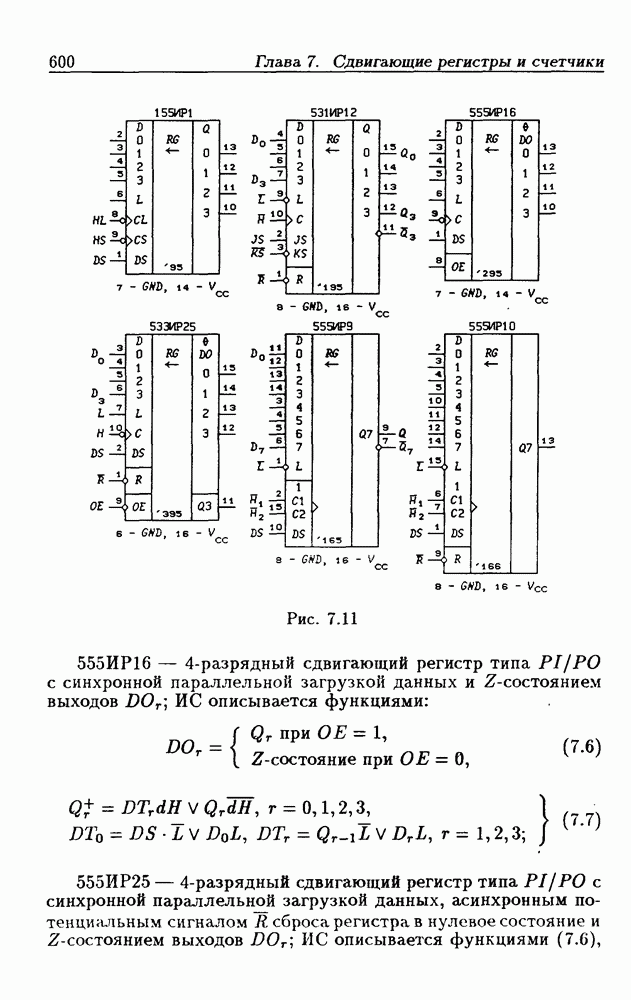
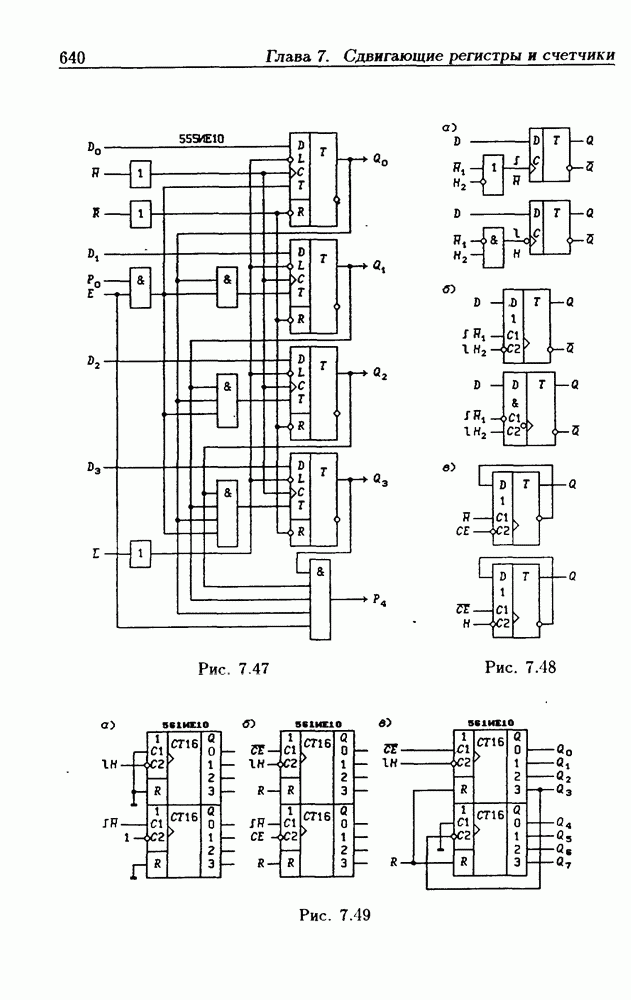
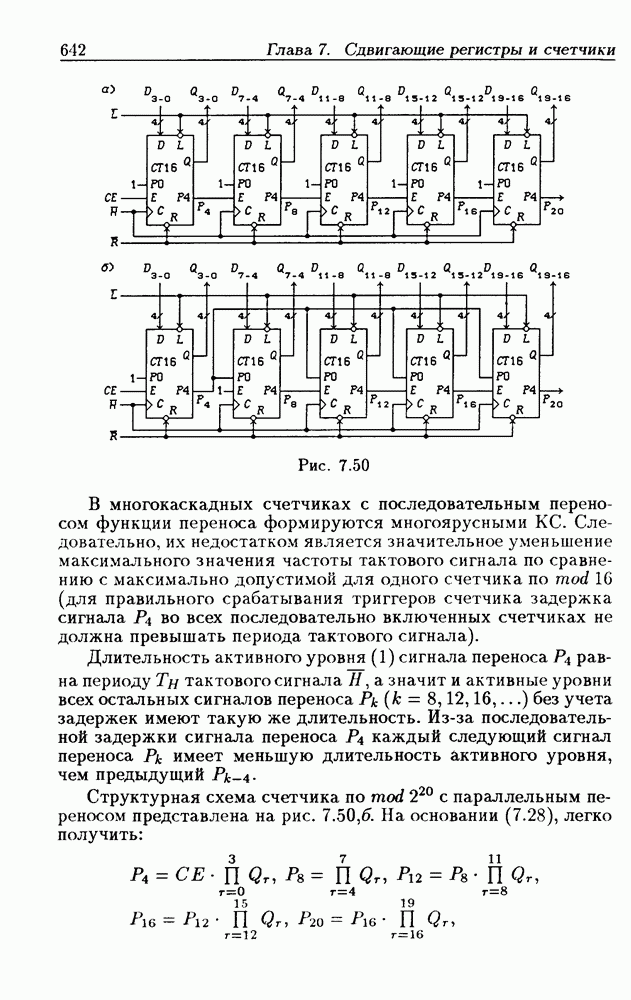
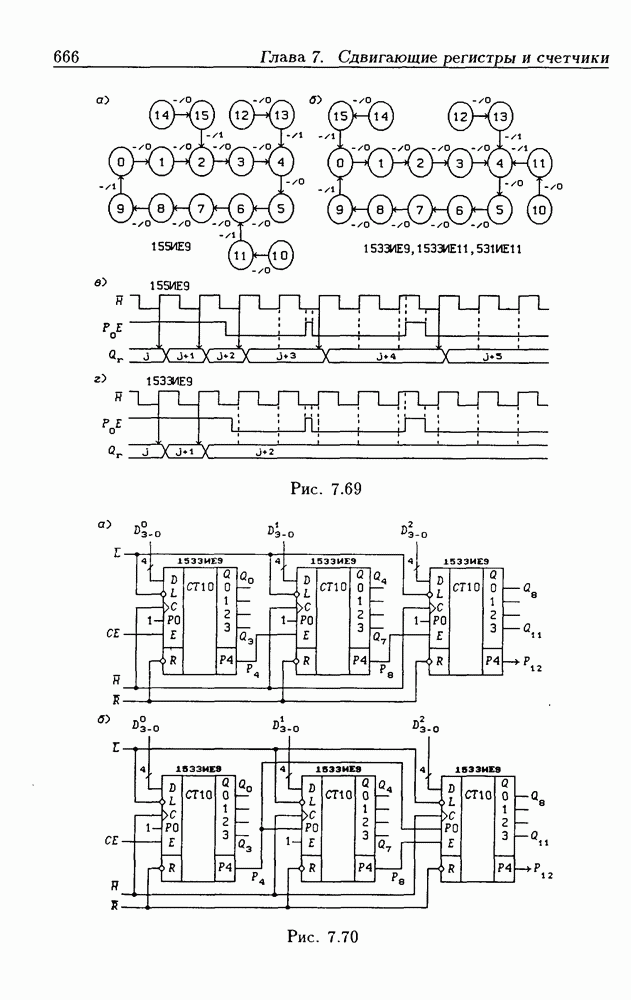
- Глава 7. Сдвигающие регистры и счетчики
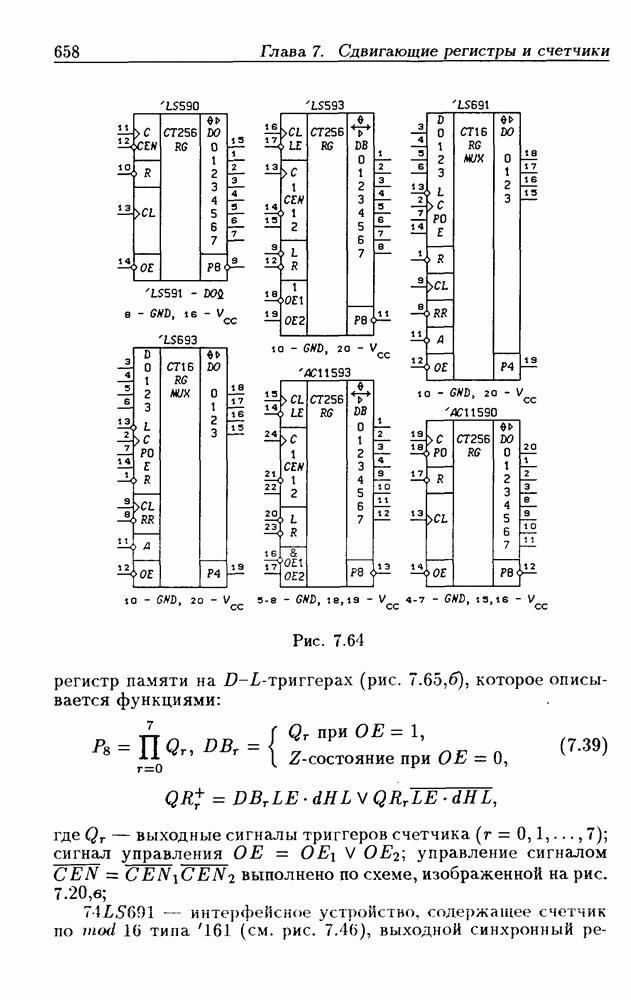
- 7.1. Сдвигающие регистры без параллельной записи данных
- Сдвигающие устройства с выходными регистрами памяти.
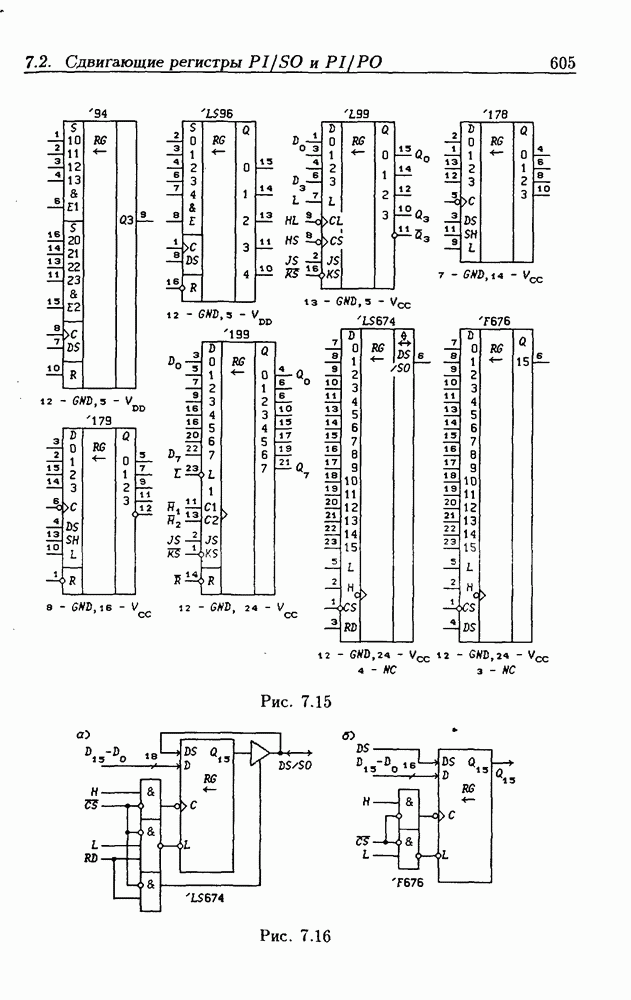
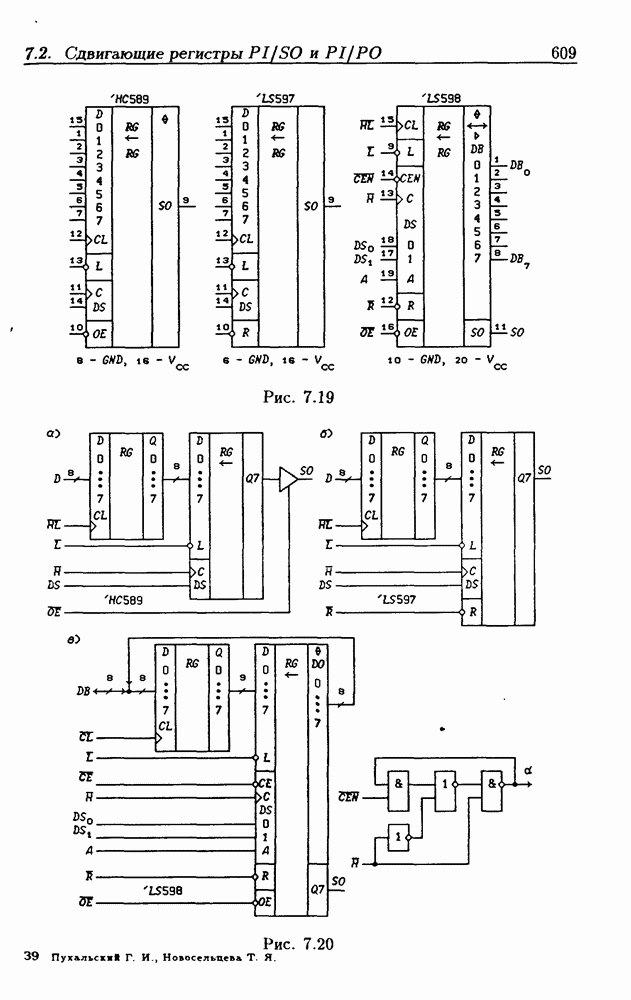
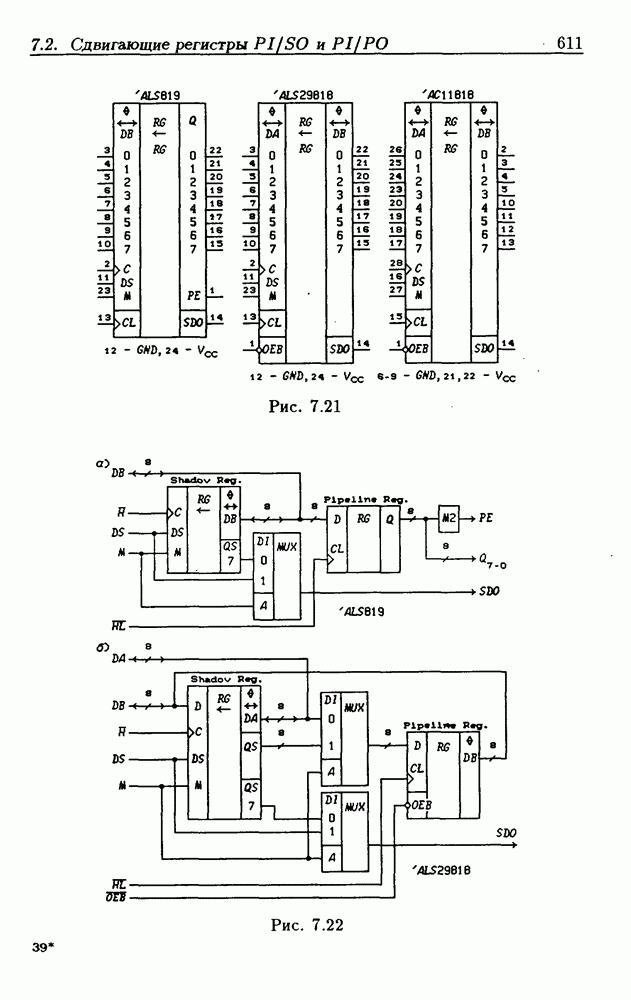
- 7.2. Сдвигающие регистры с параллельной записью данных
- Сдвигающие регистры с расширением знака.
- Сдвигающие регистры с входным регистром памяти.
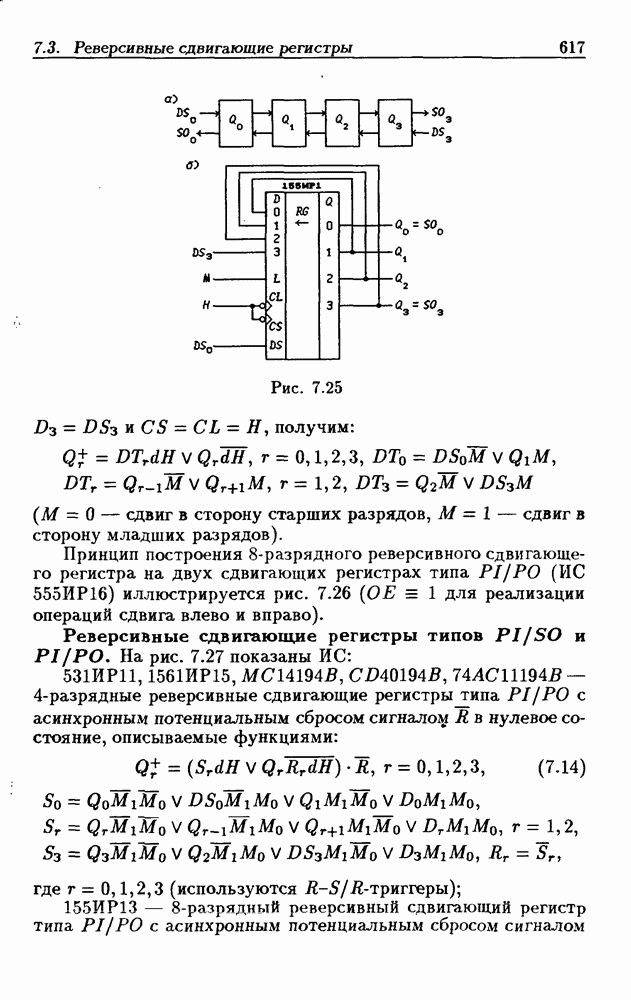
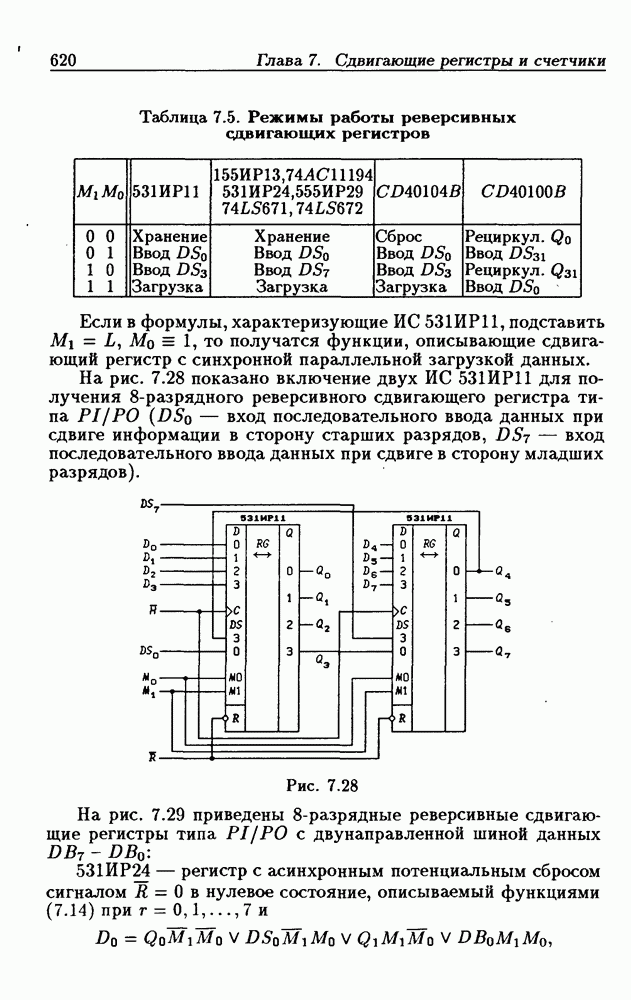
- 7.3. Реверсивные сдвигающие регистры
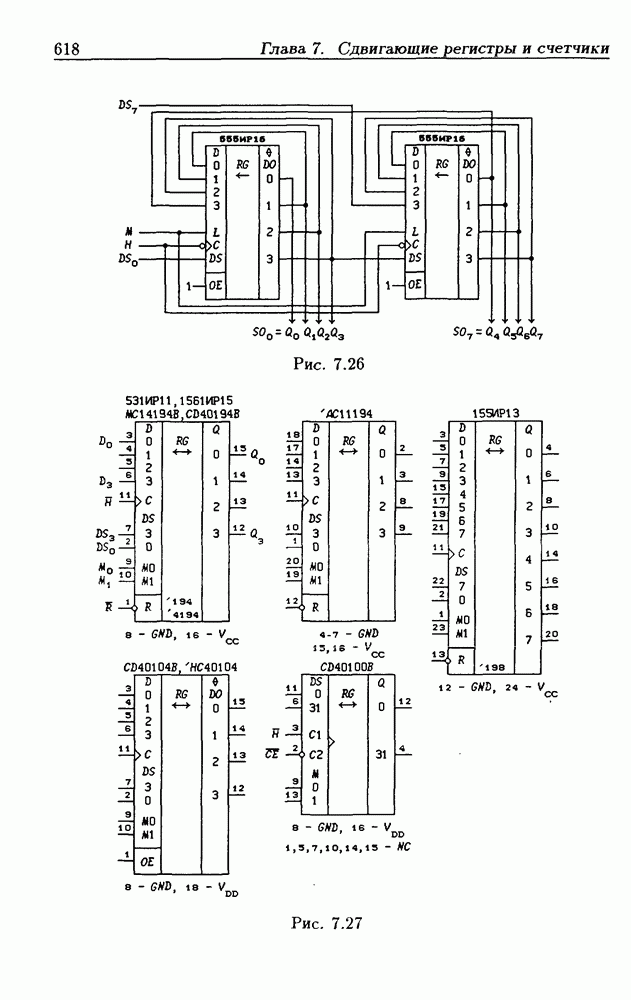
- Реверсивные сдвигающие регистры типов PI/SO и PI/PO.
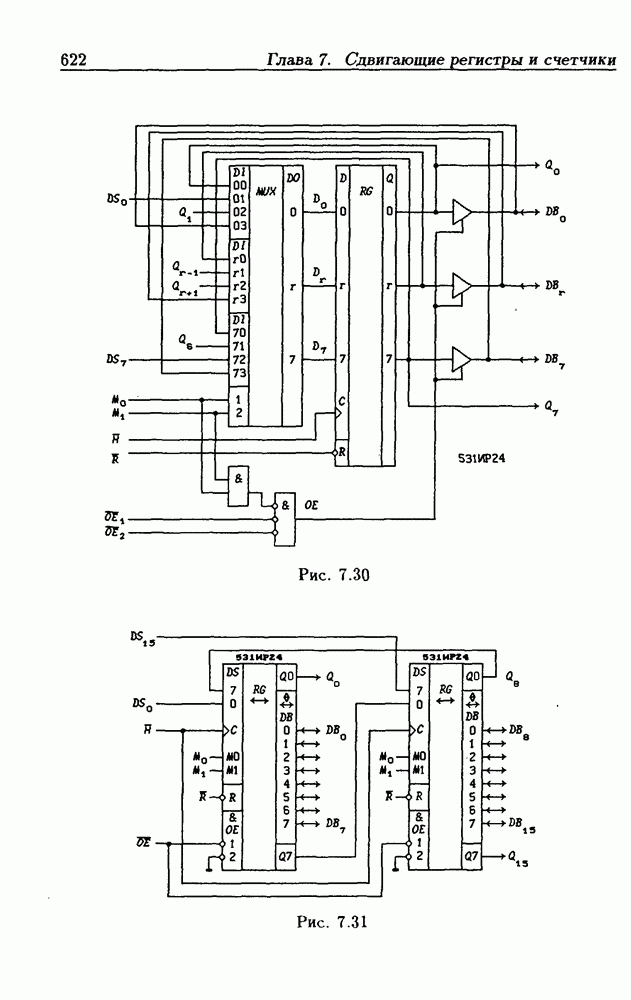
- Многофункциональные устройства на основе реверсивных сдвигающих регистров.
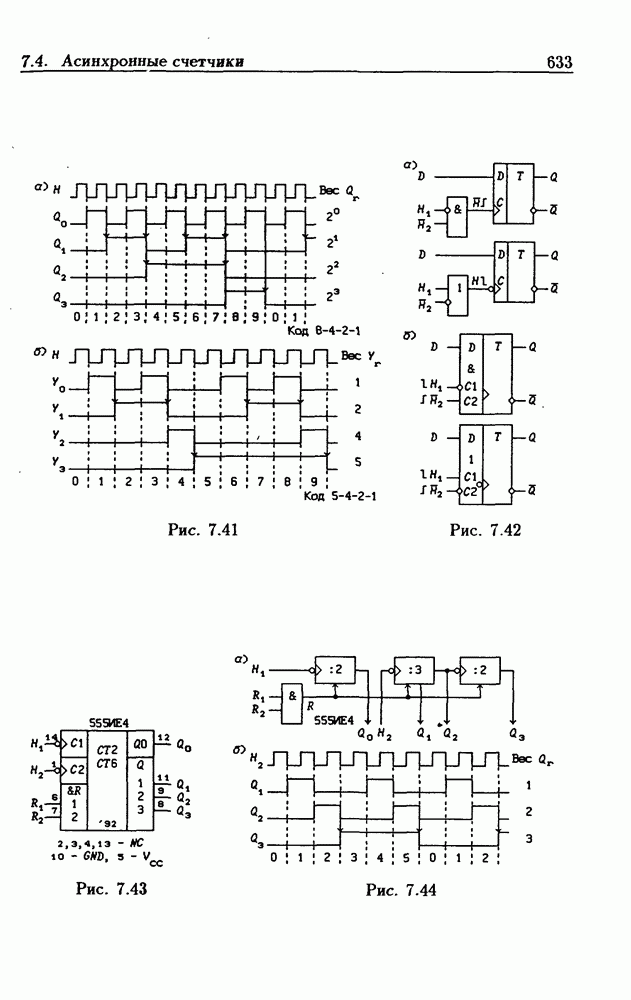
- 7.4. Асинхронные счетчики
- Двоично-десятичные асинхронные счетчики.
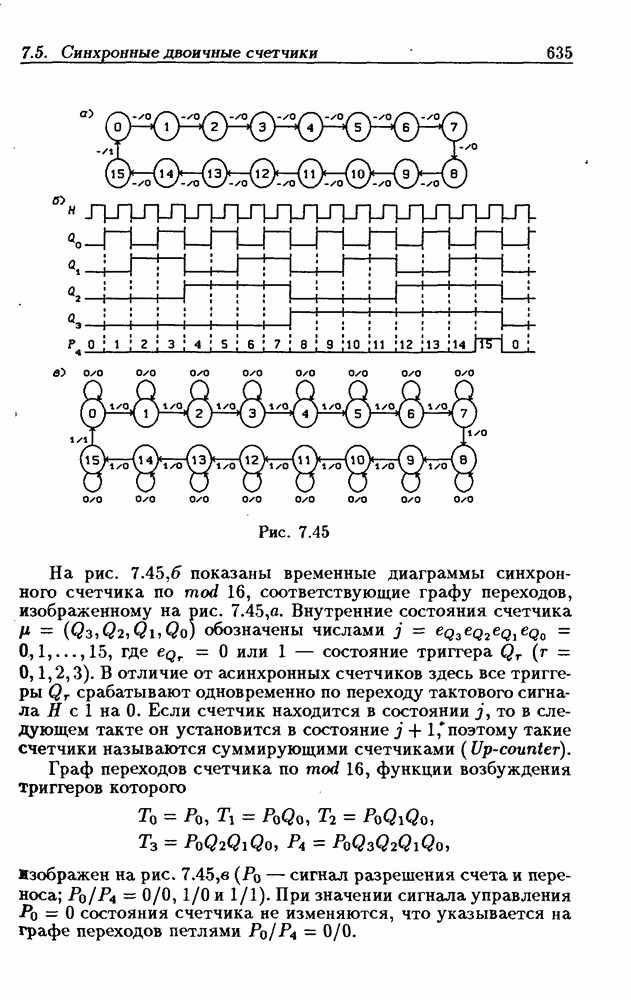
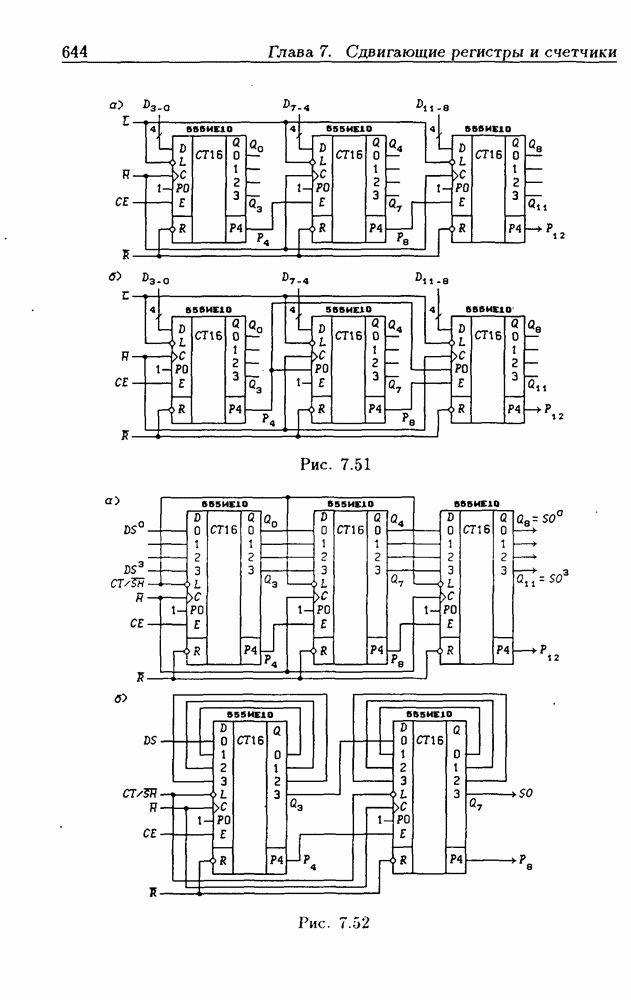
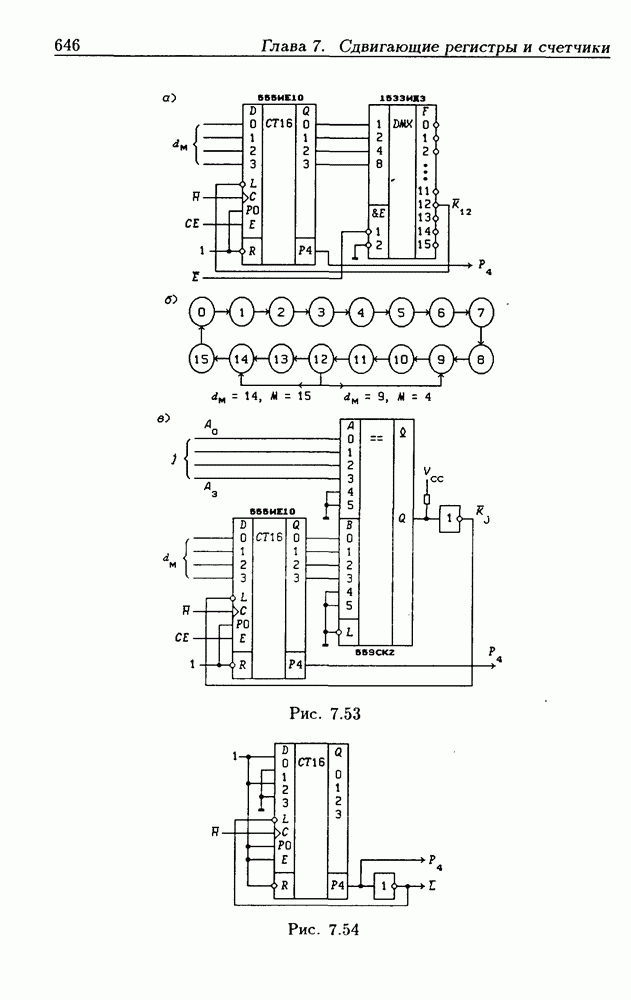
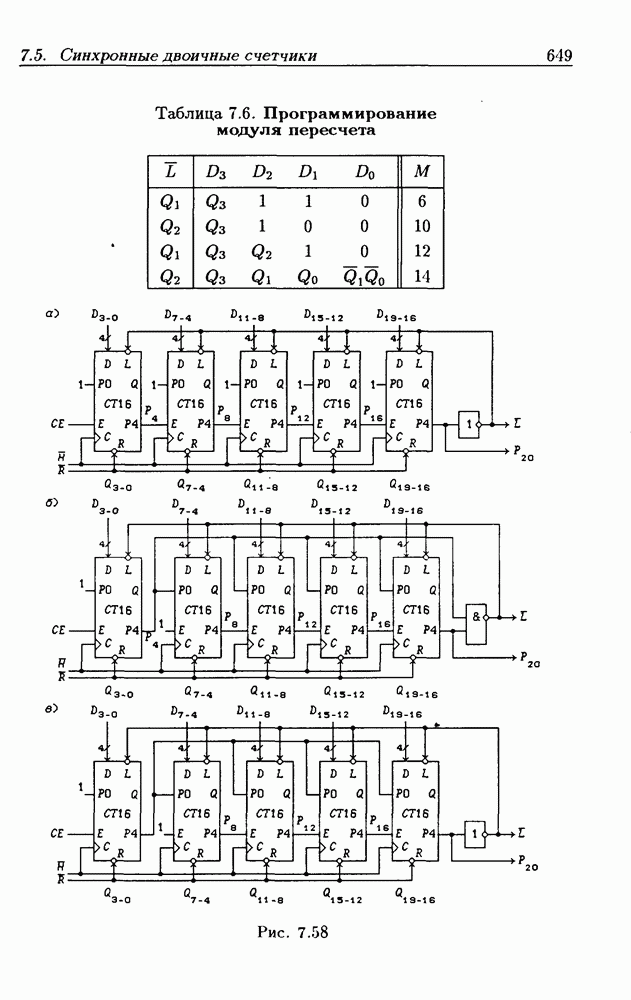
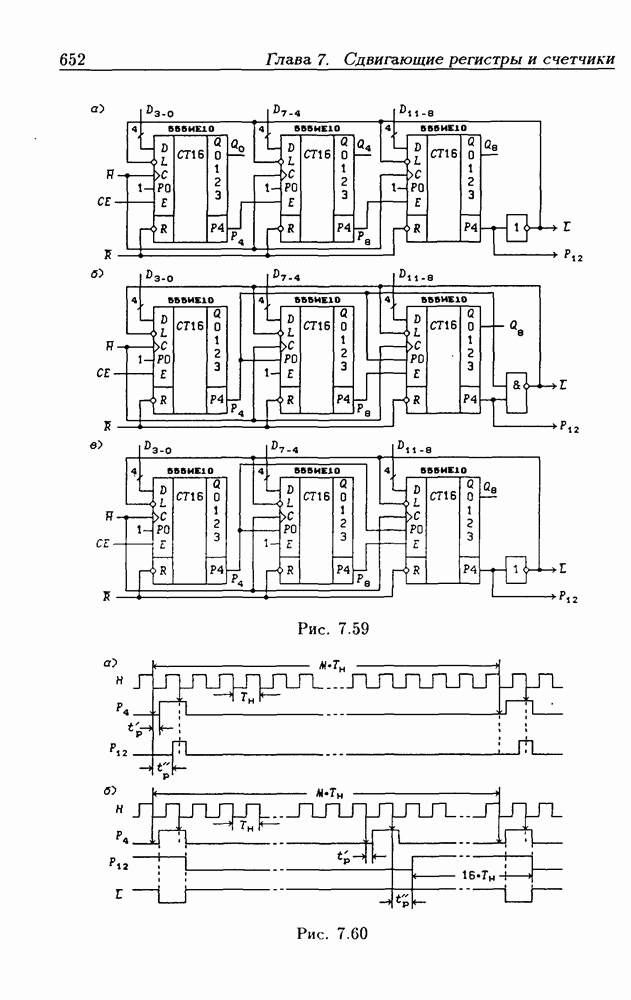
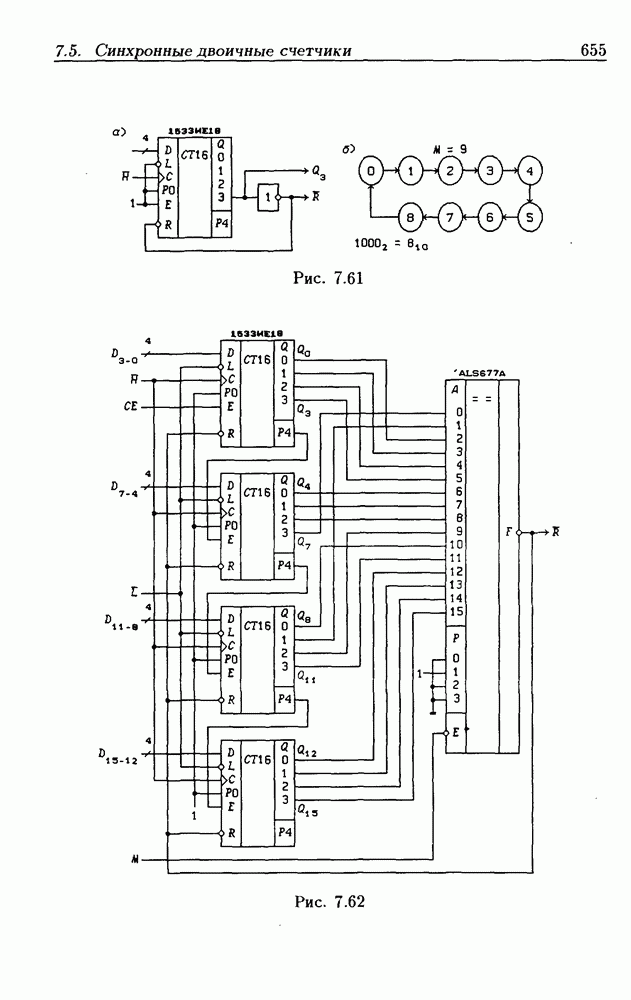
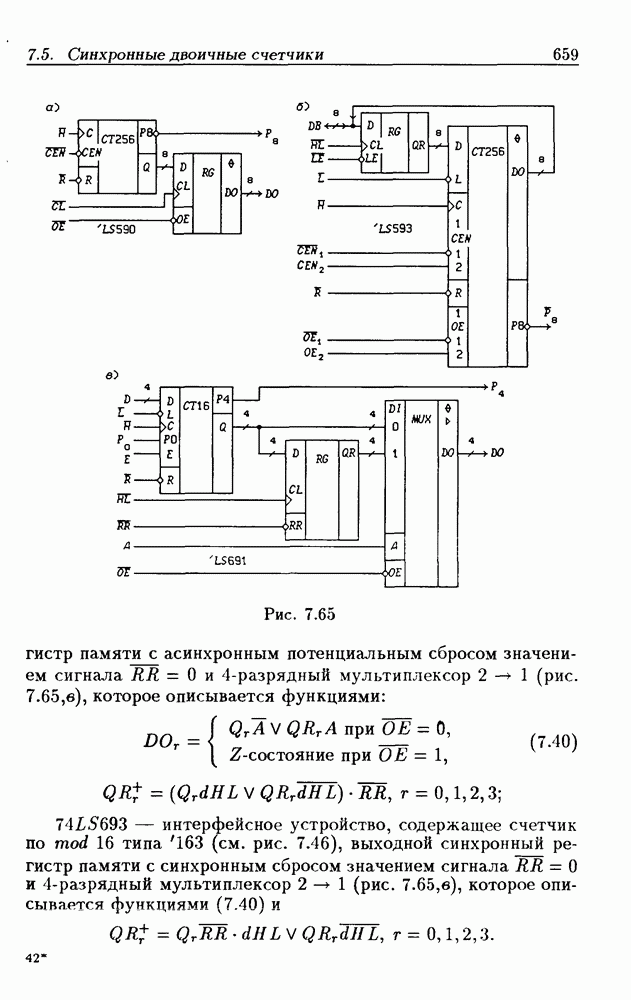
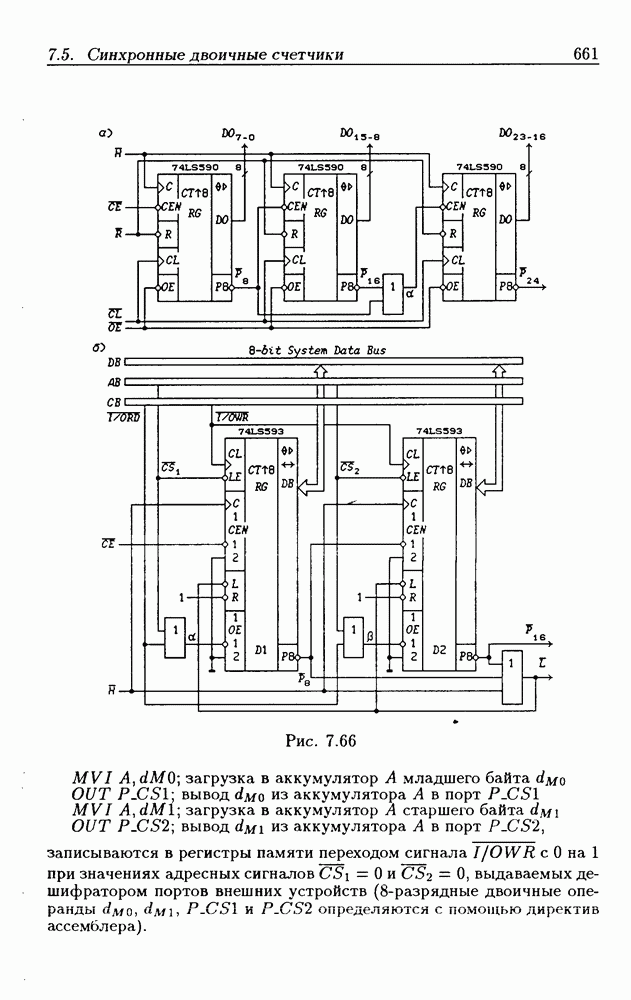
- 7.5. Синхронные двоичные счетчики
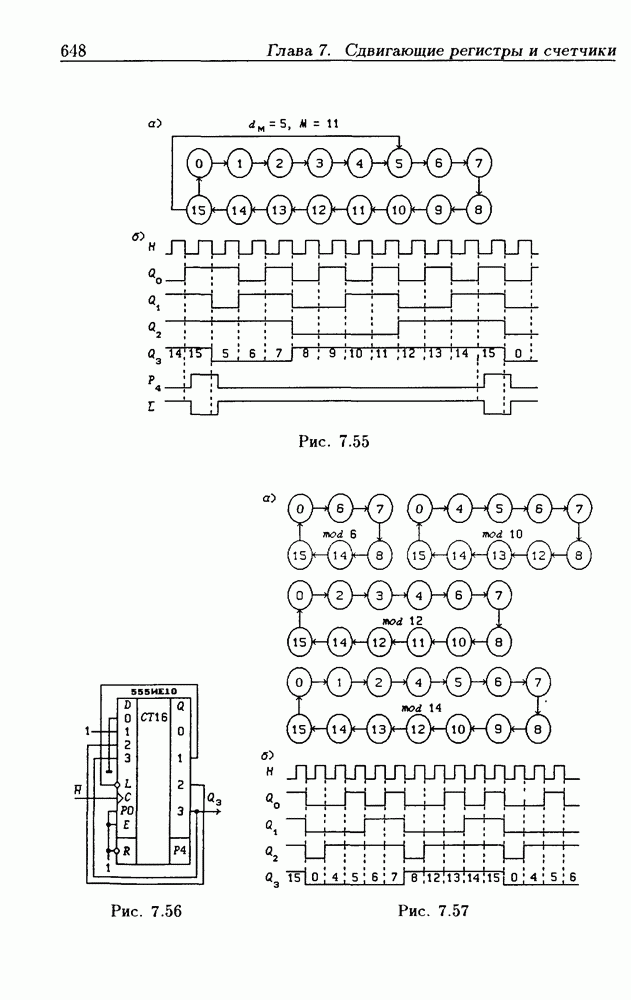
- Программирование модуля пересчета двоичных счетчиков.
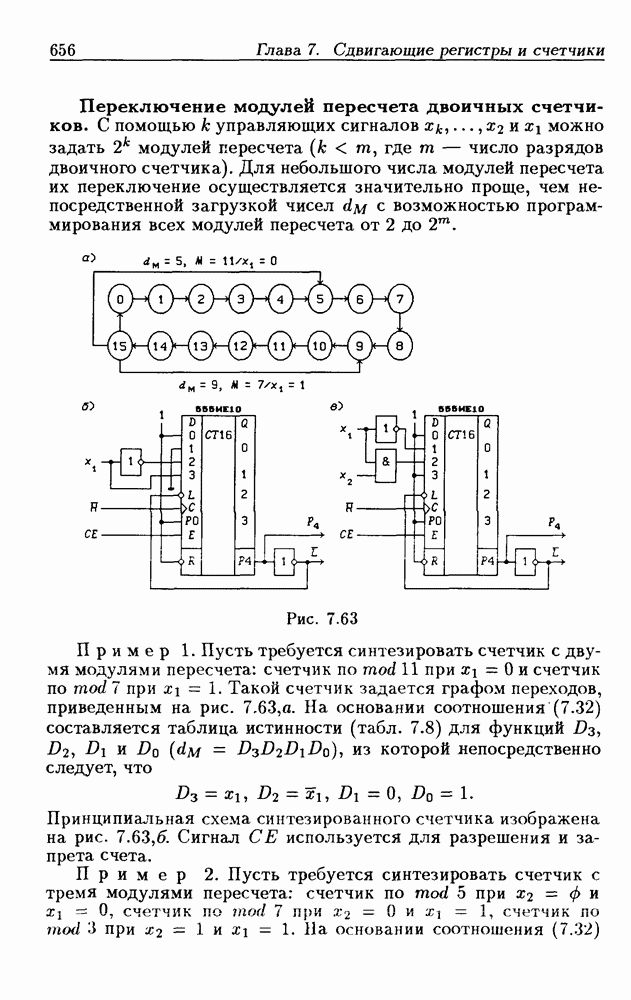
- Переключение модулей пересчета двоичных счетчиков.
- Функциональные устройства на основе двоичных счетчиков.
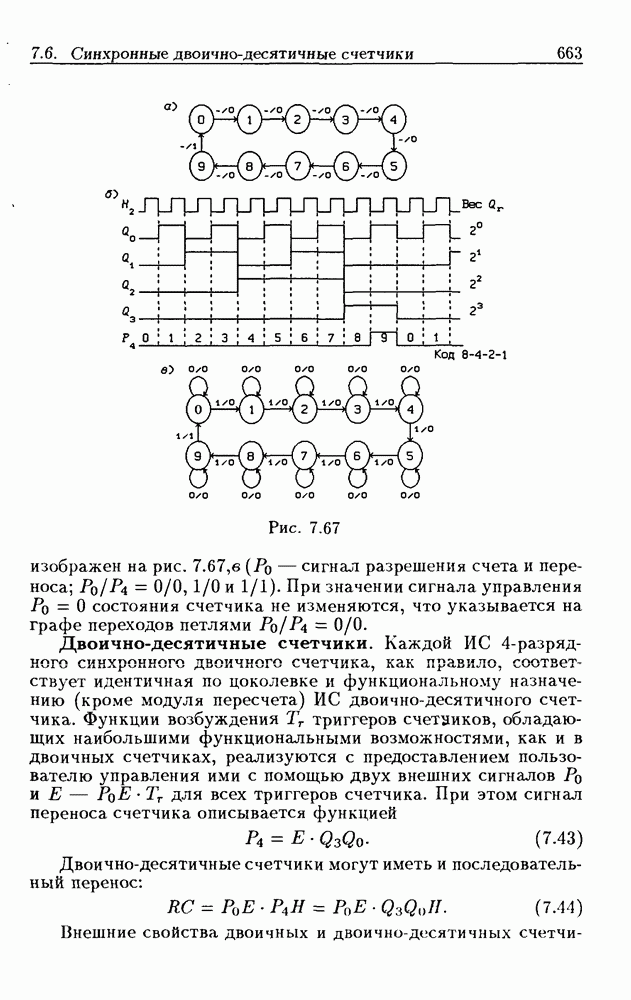
- 7.6. Синхронные двоично-десятичные счетчики
- 7.7. Синхронные реверсивные счетчики
- 7.8. Счетчики с расщепленным тактовым сигналом
- 7.9. Счетчики на сдвигающих регистрах
- 7.10. Кольцевые счетчики
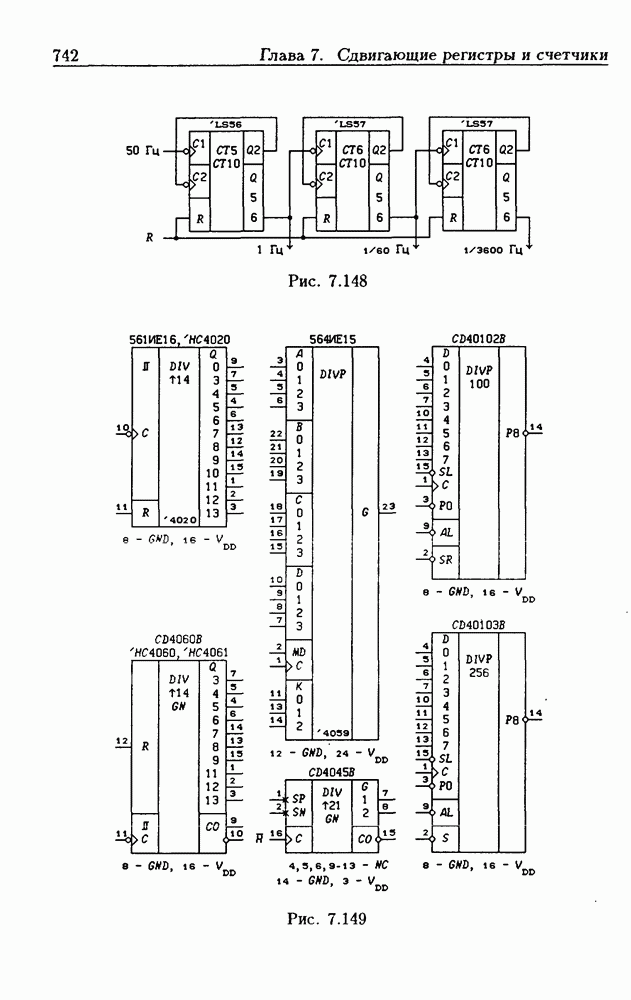
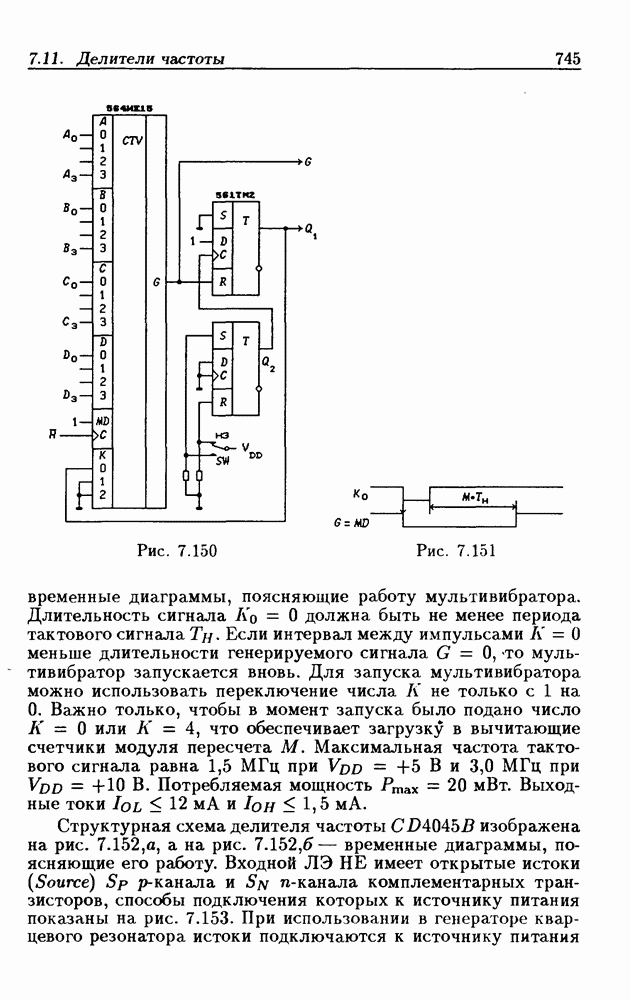
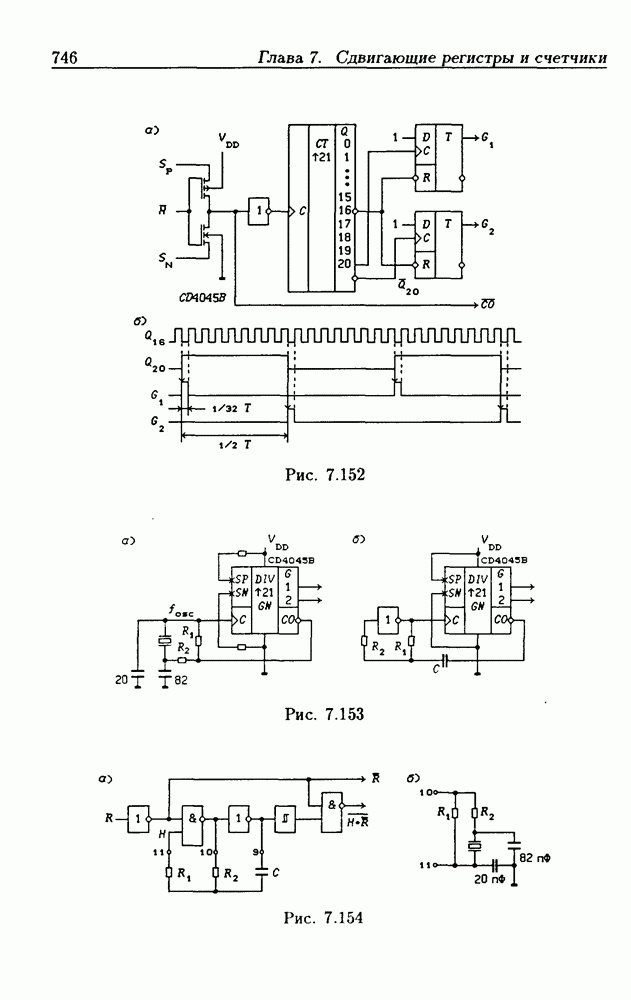
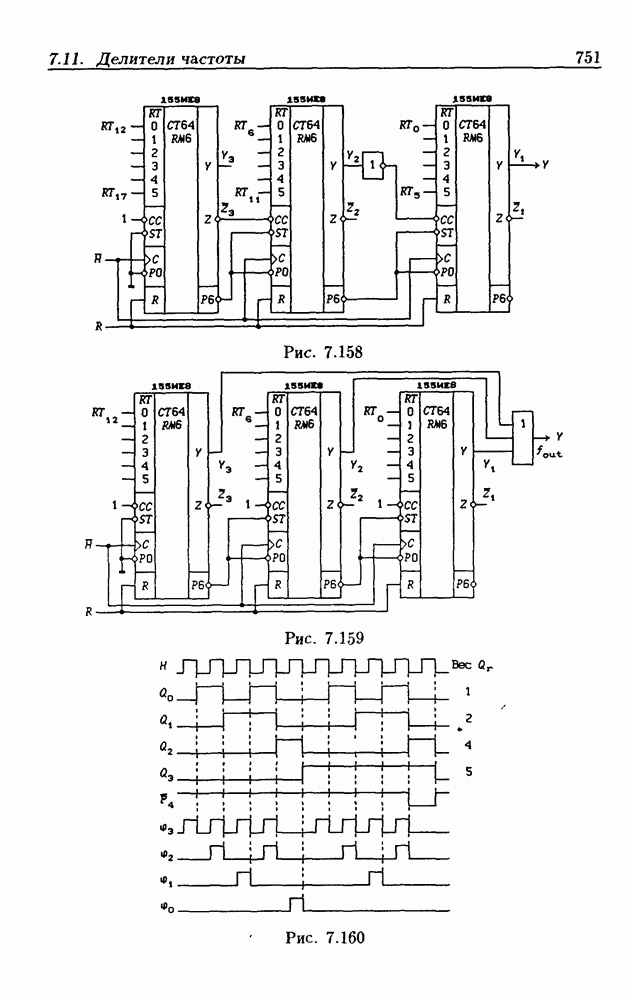
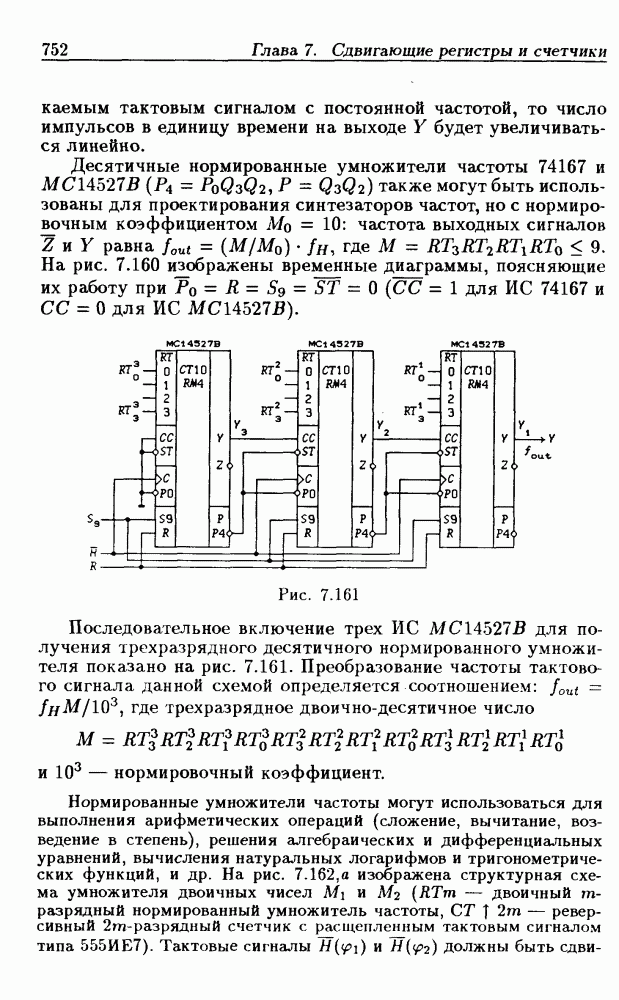
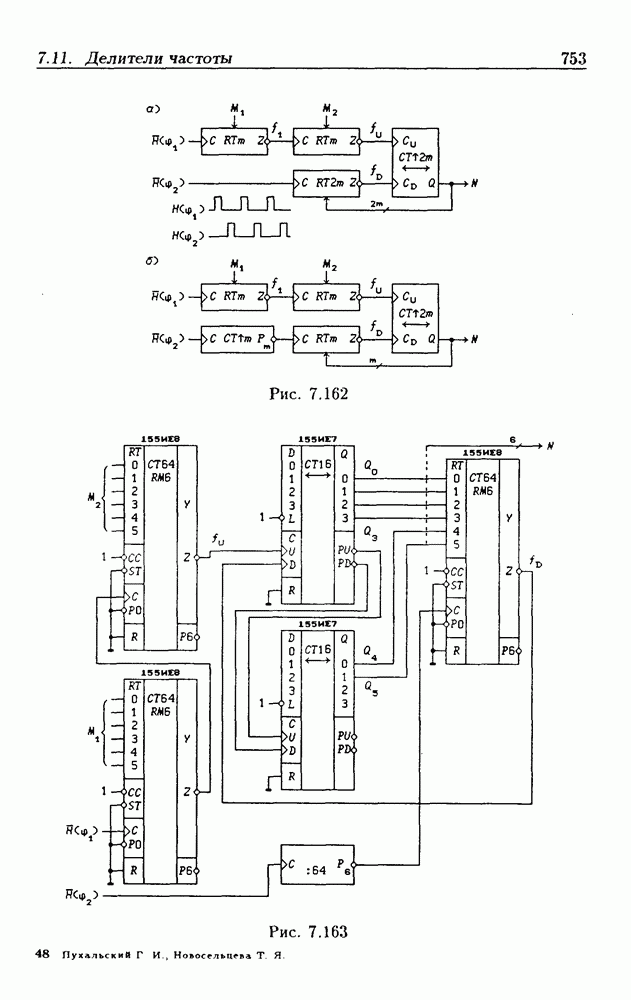
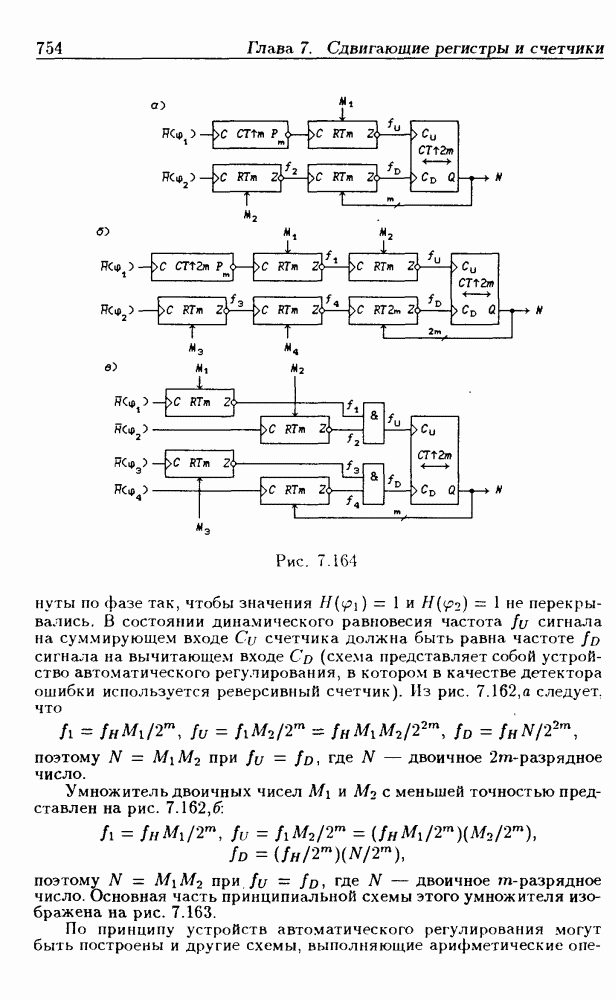
- 7.11. Делители частоты
- Нормированные умножители частоты.
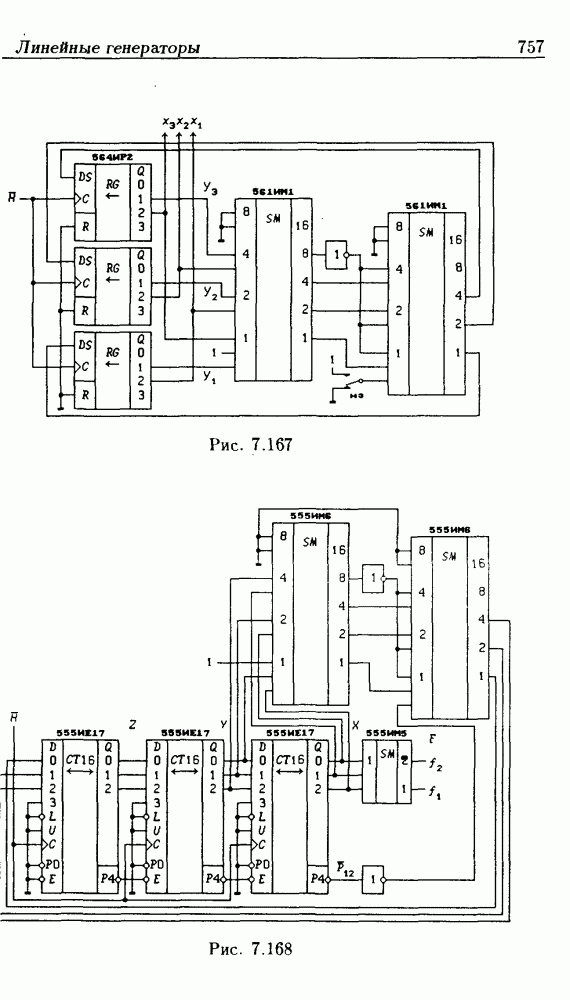
- 7.12. Линейные генераторы
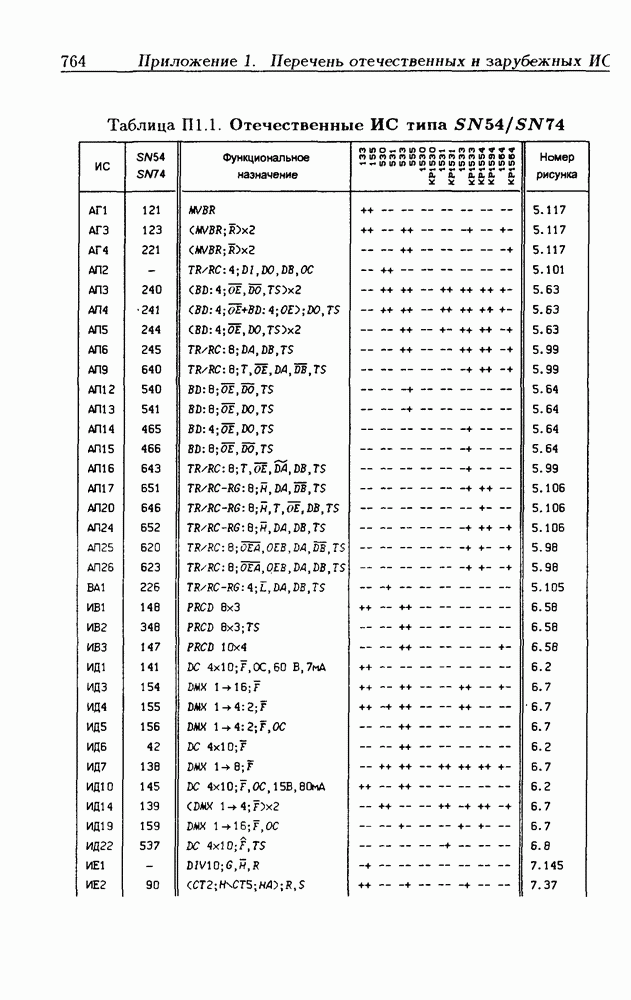
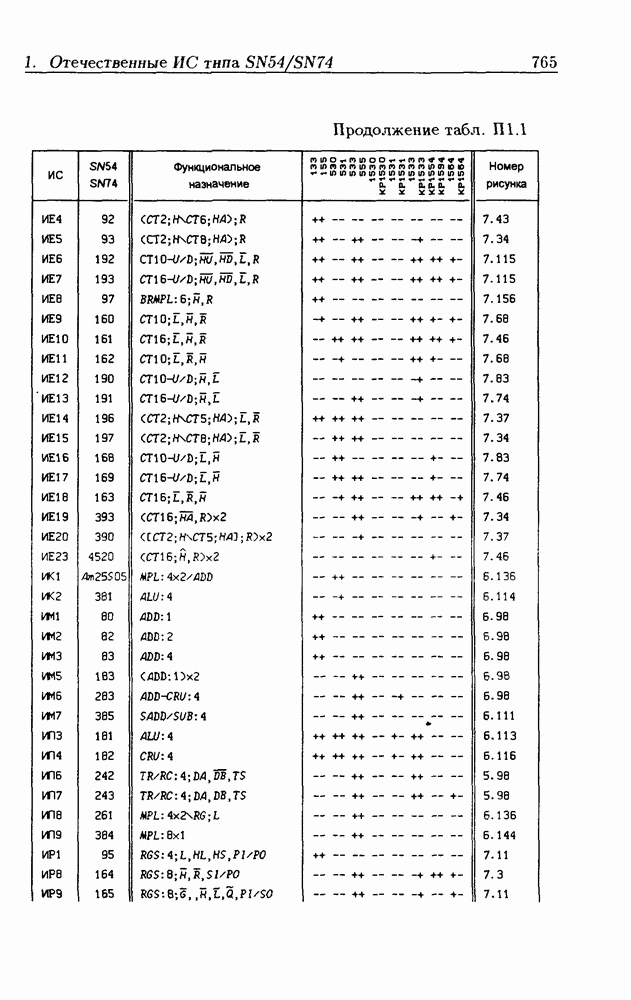
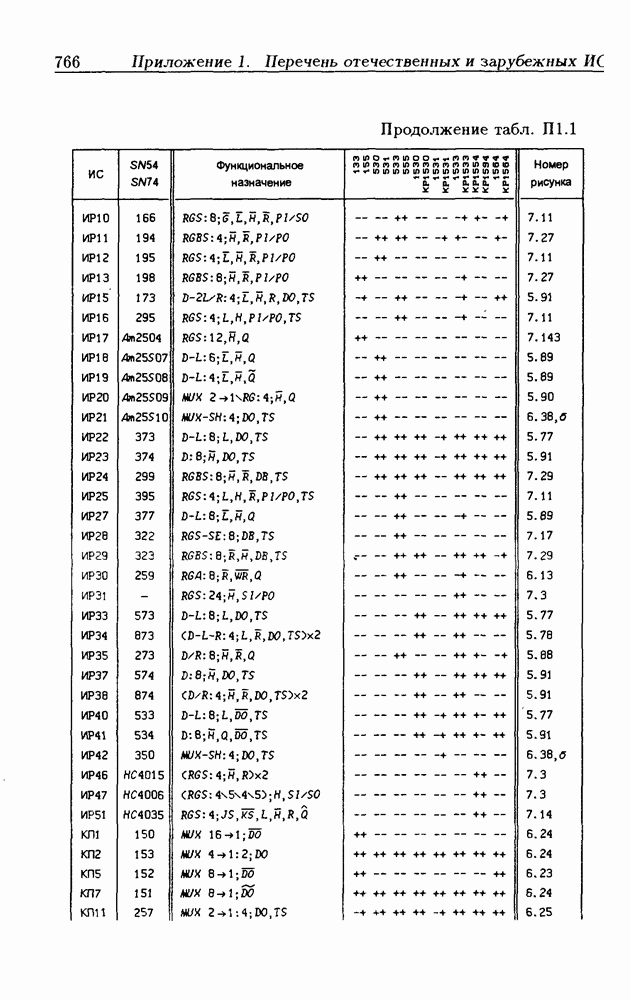
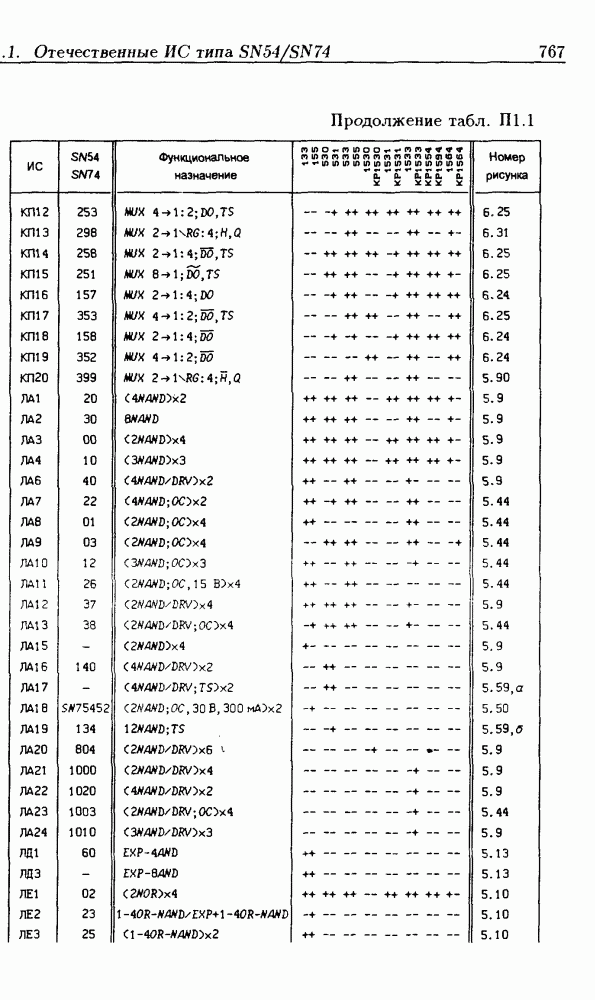
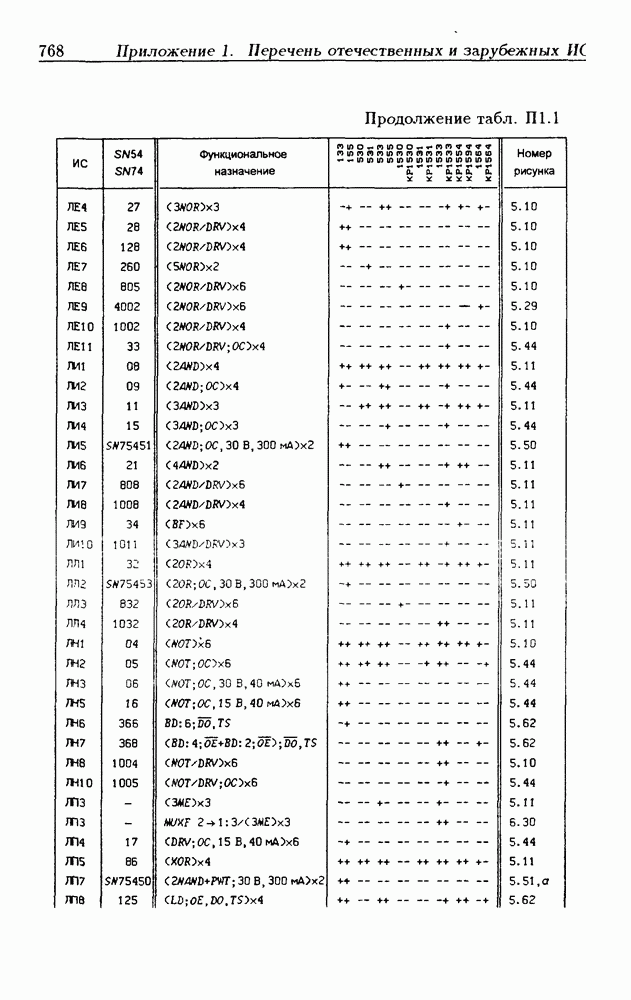
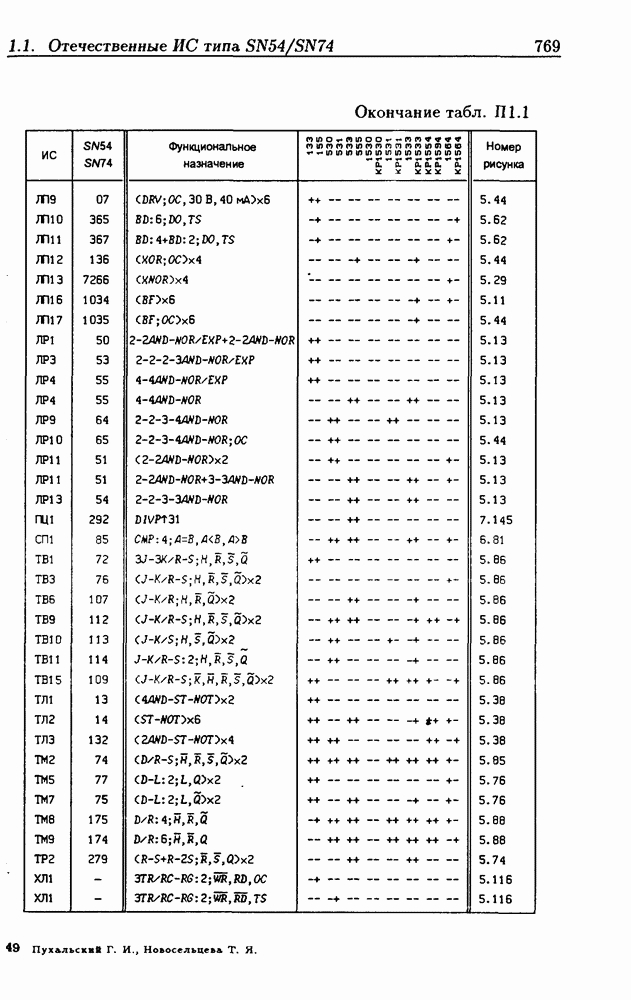
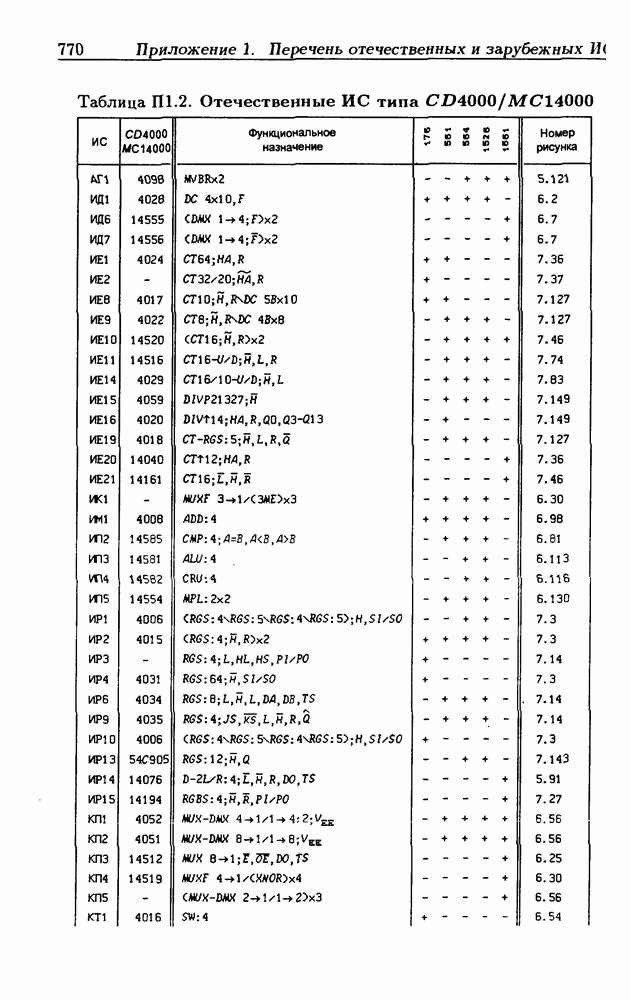
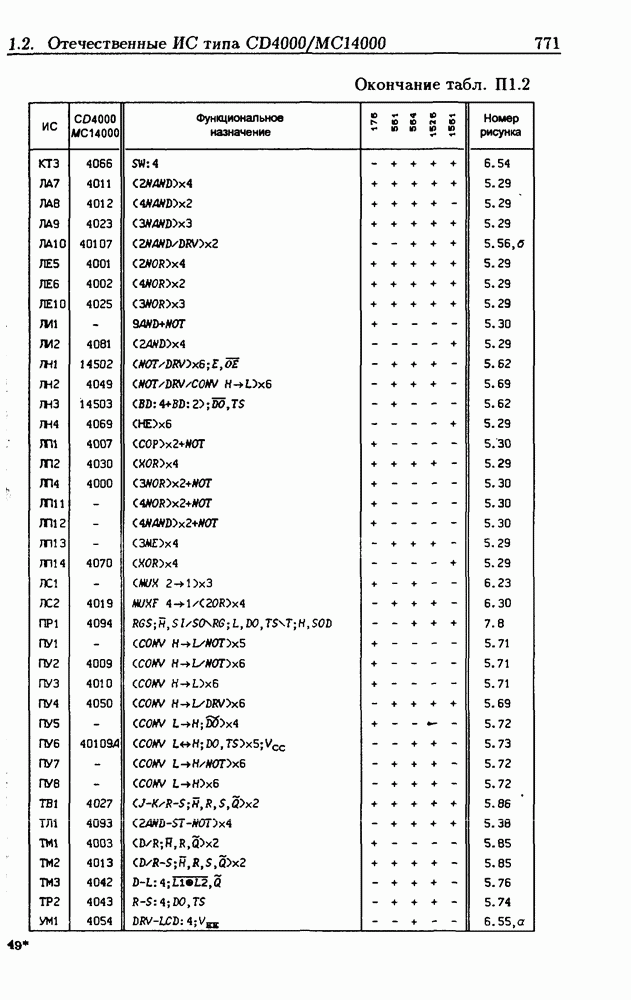
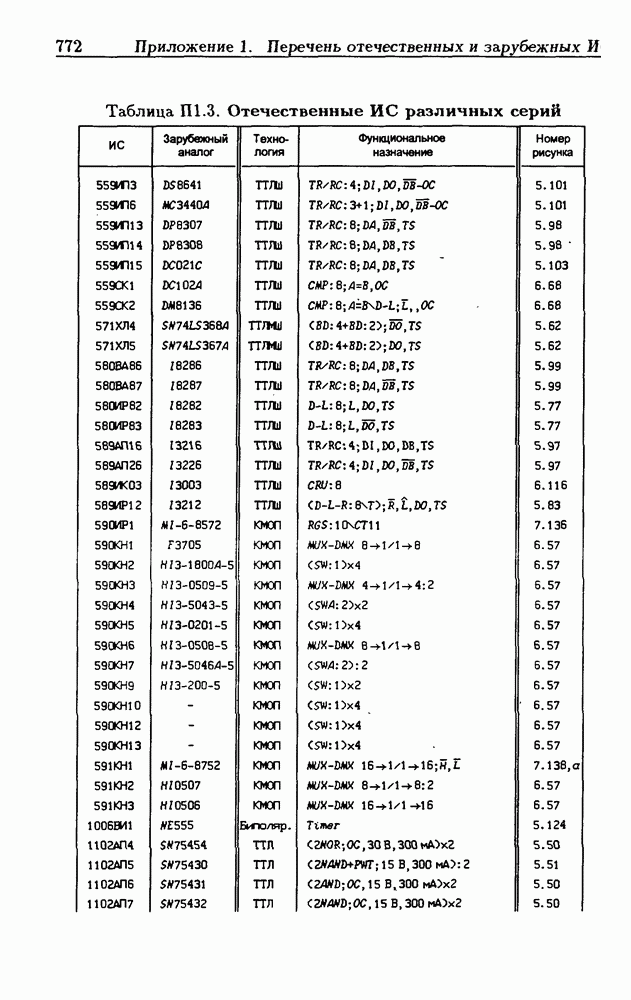
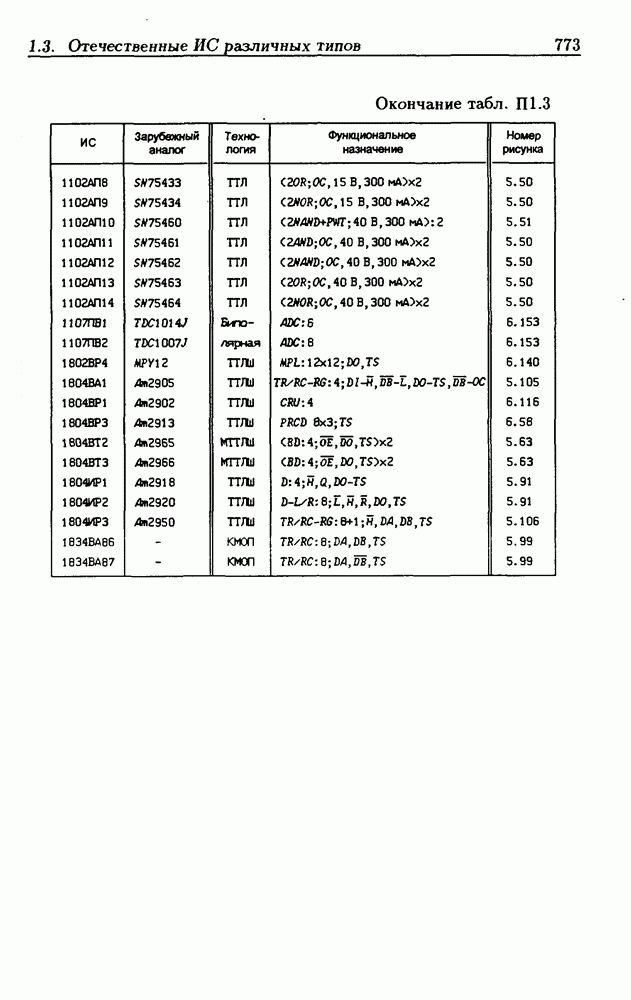
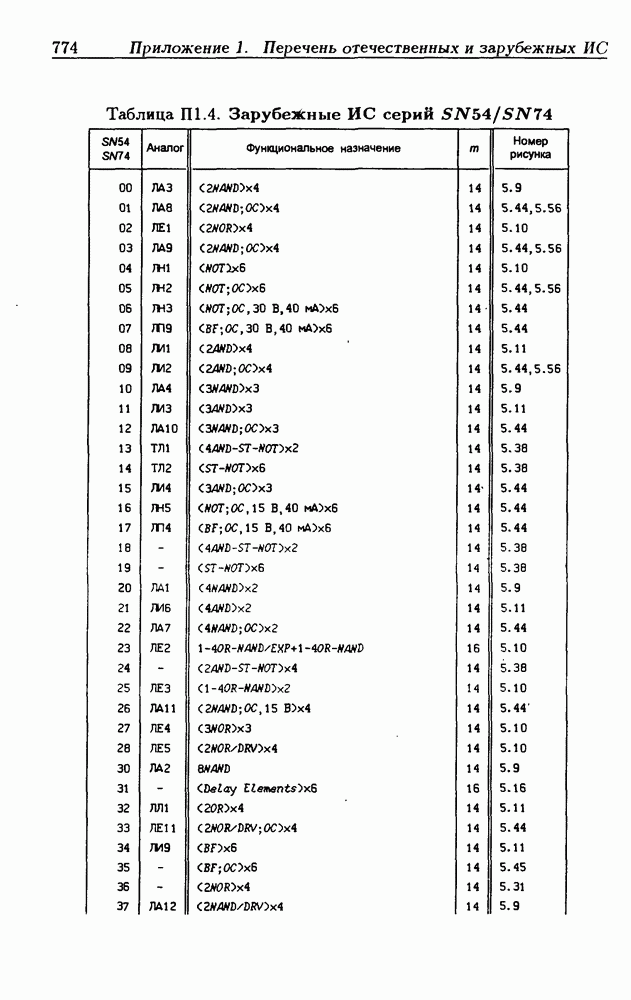
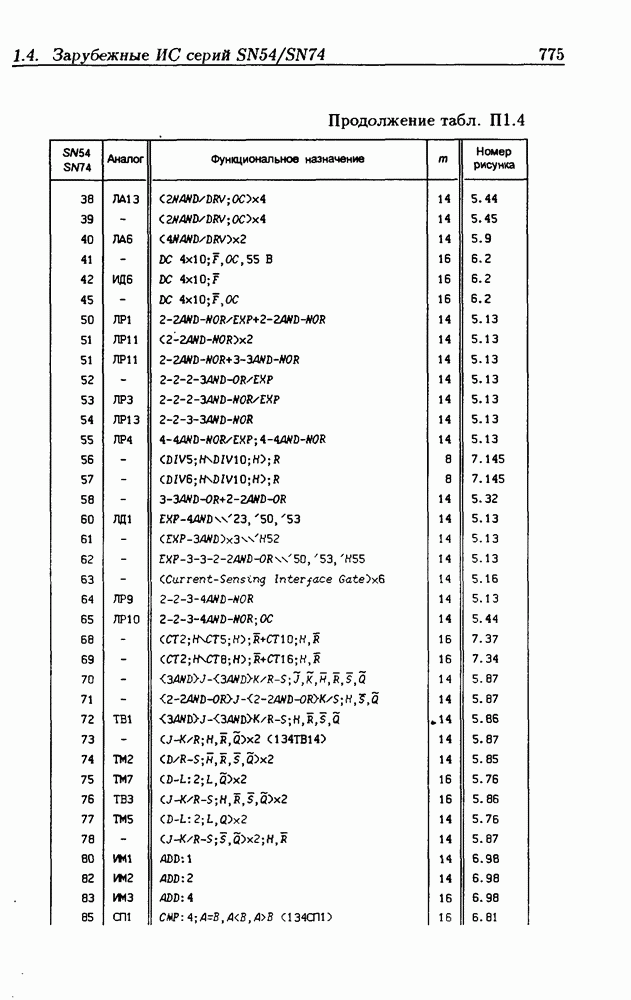
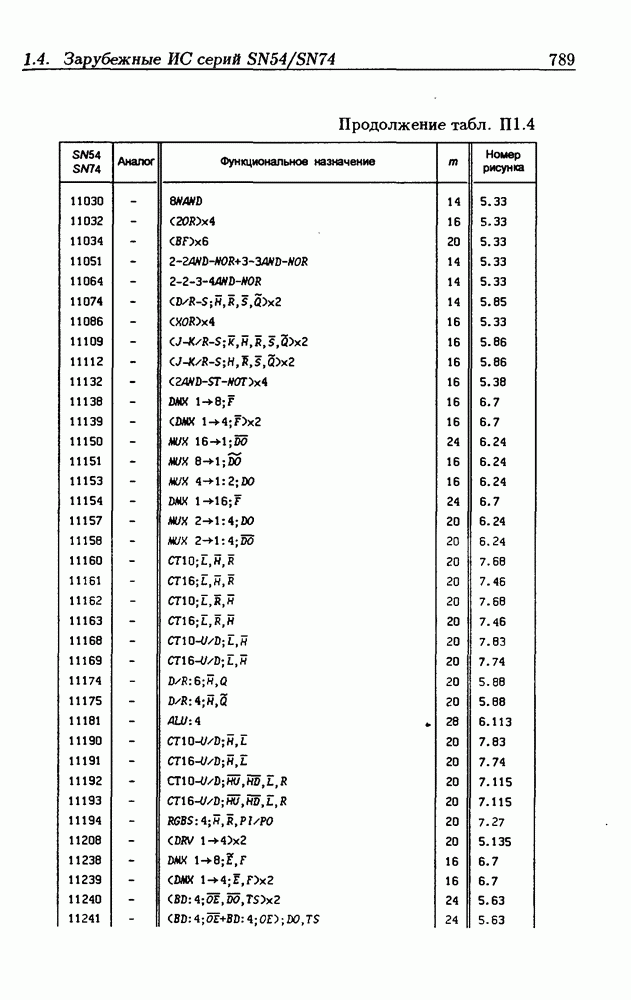
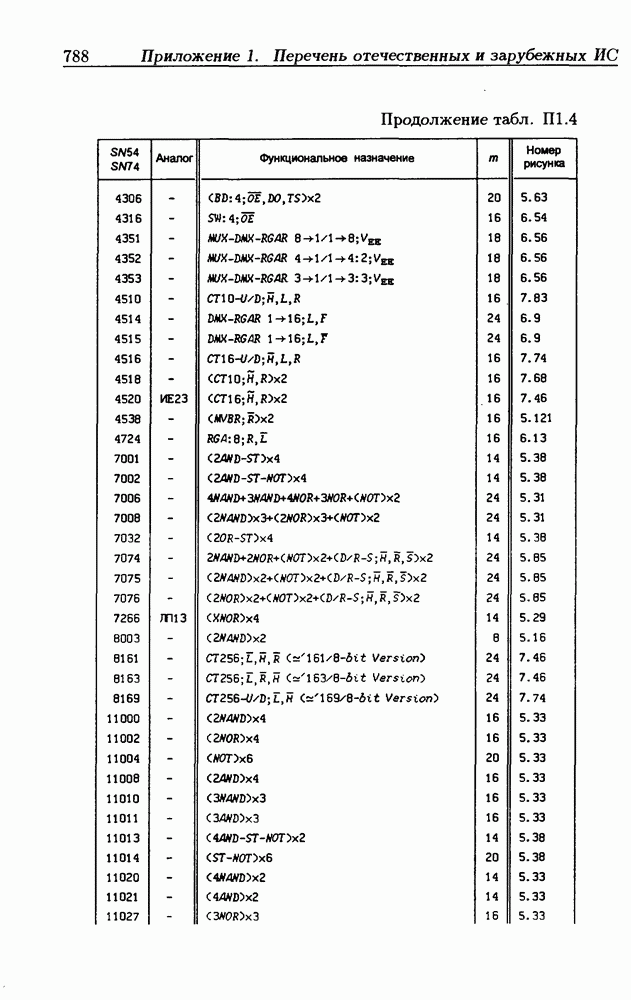
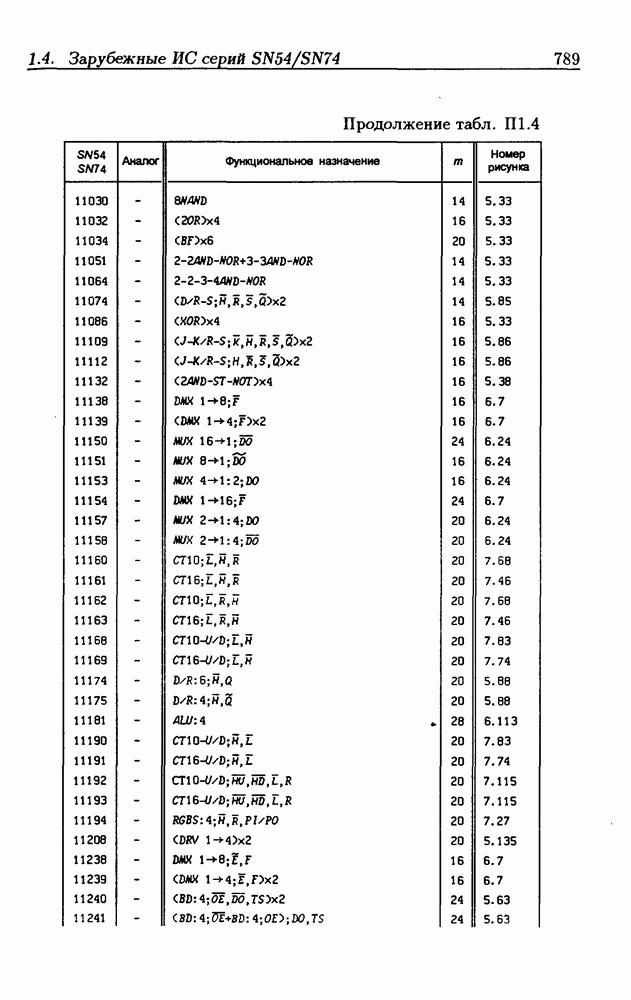
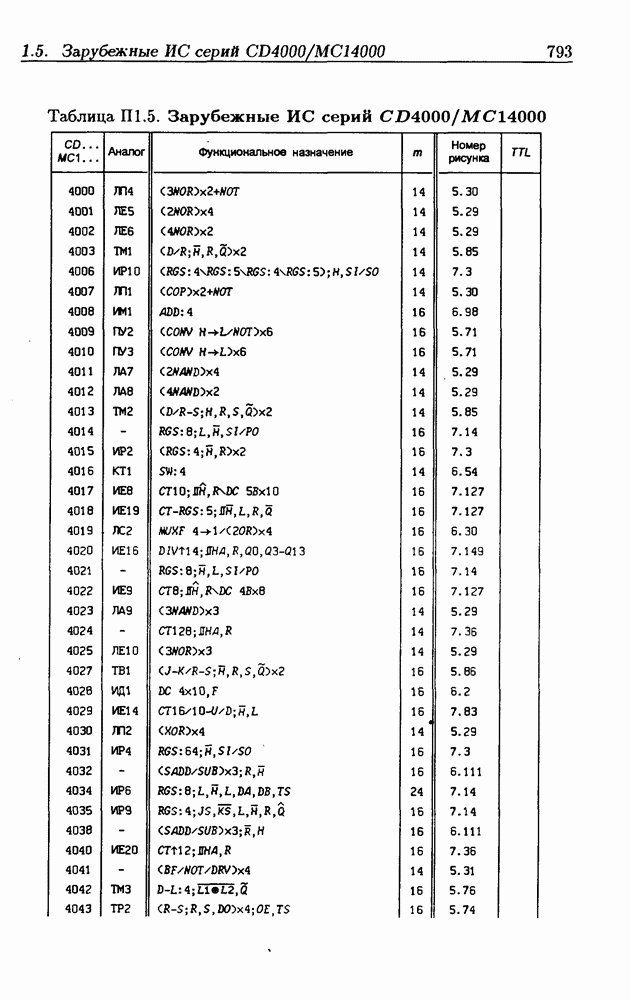
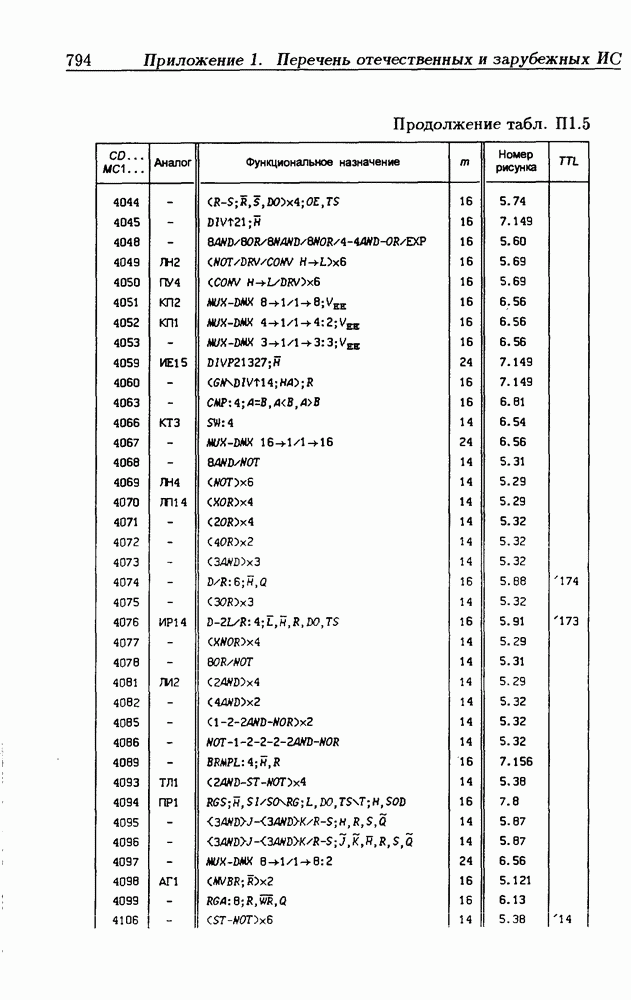
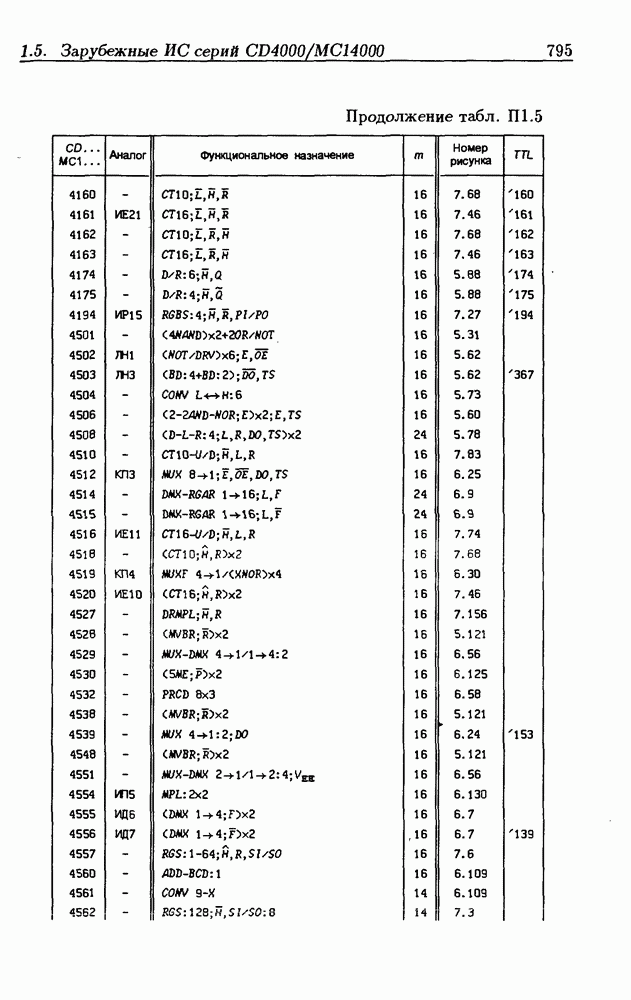
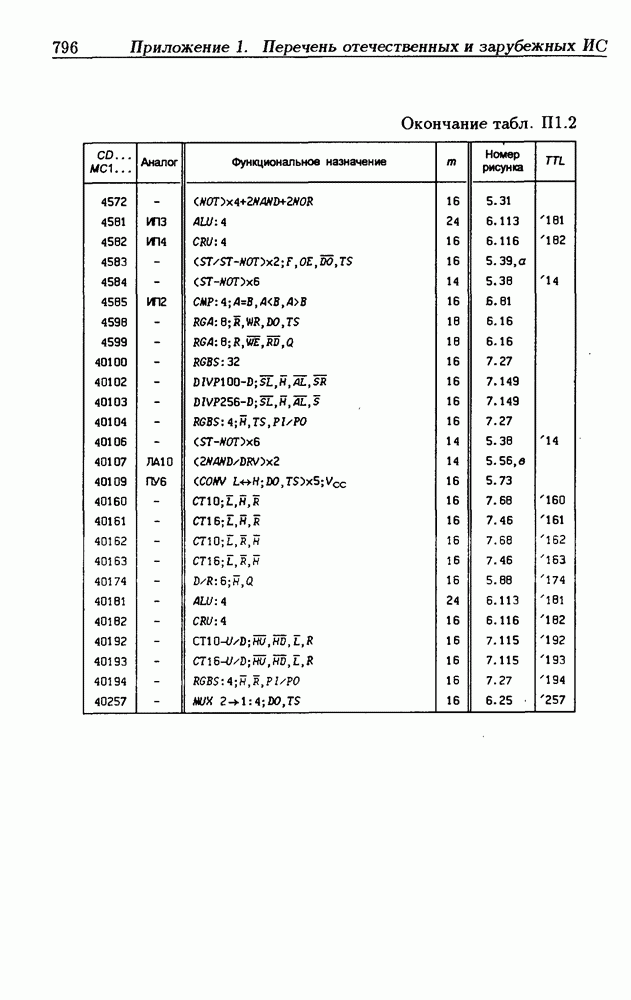
- Приложение 1. Перечень отечественных и зарубежных ИС
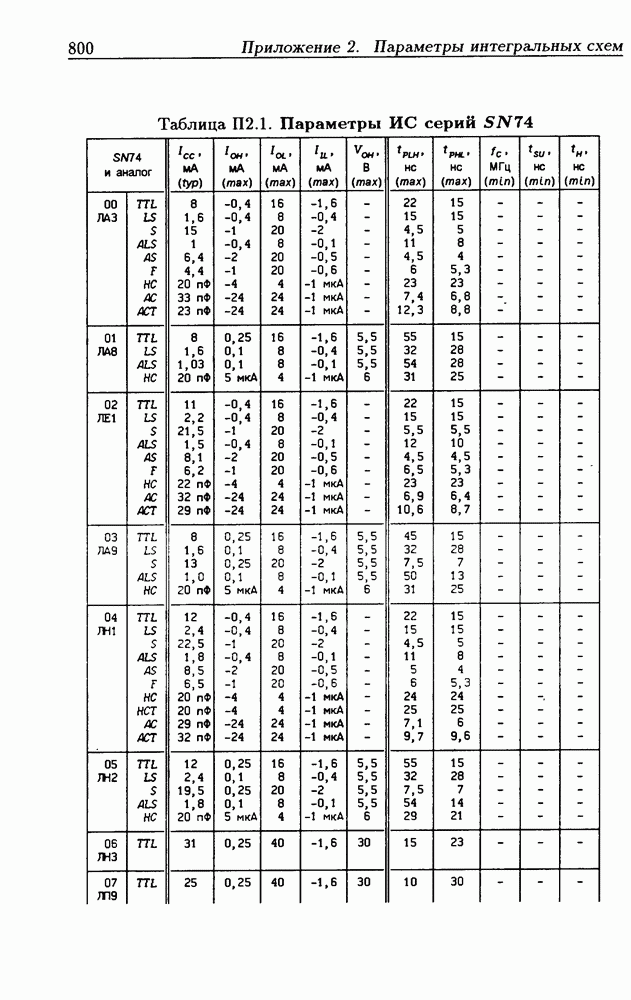
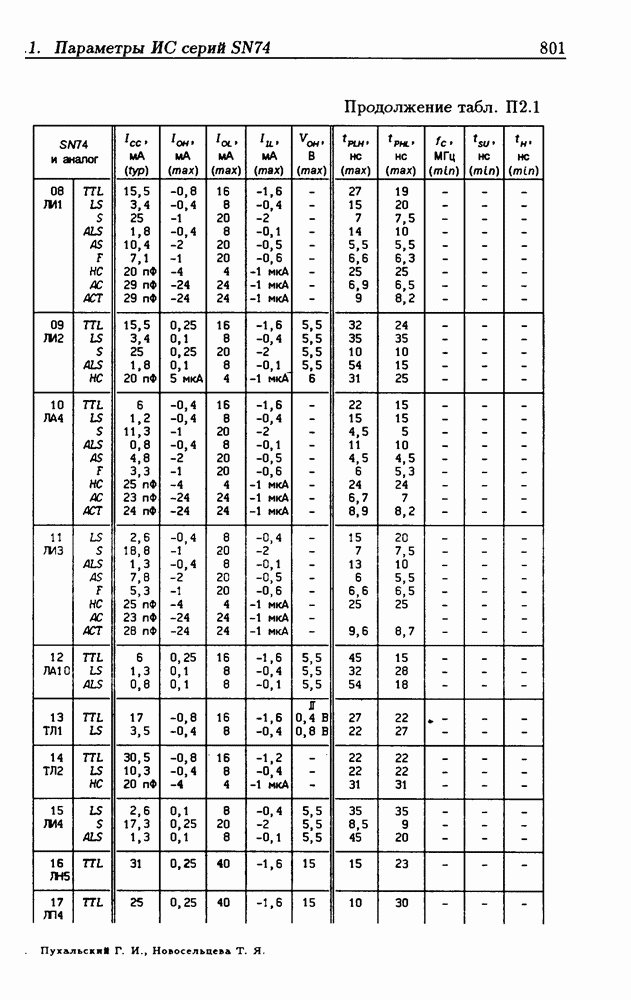
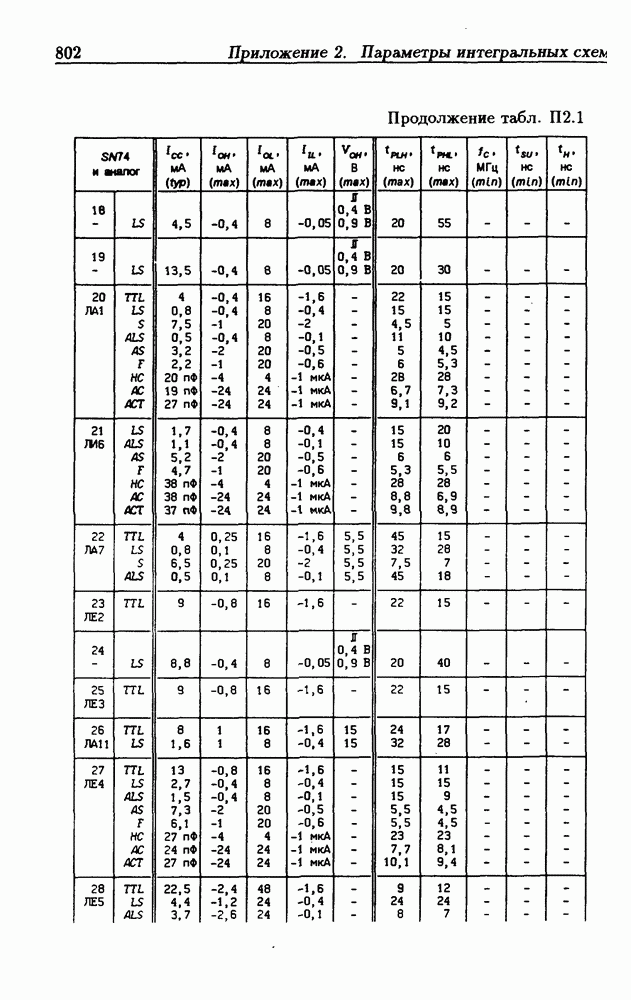
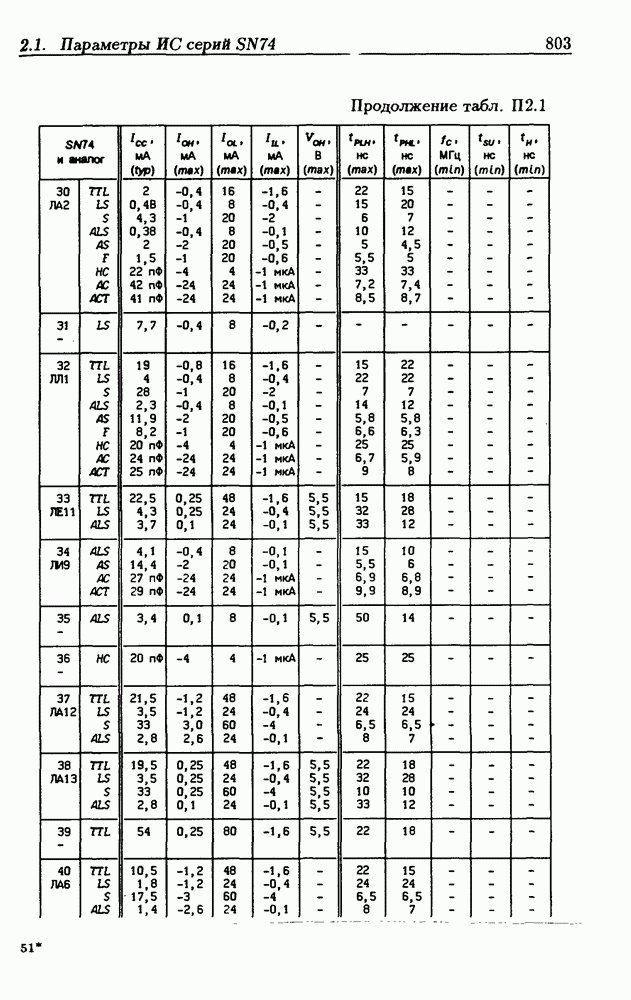
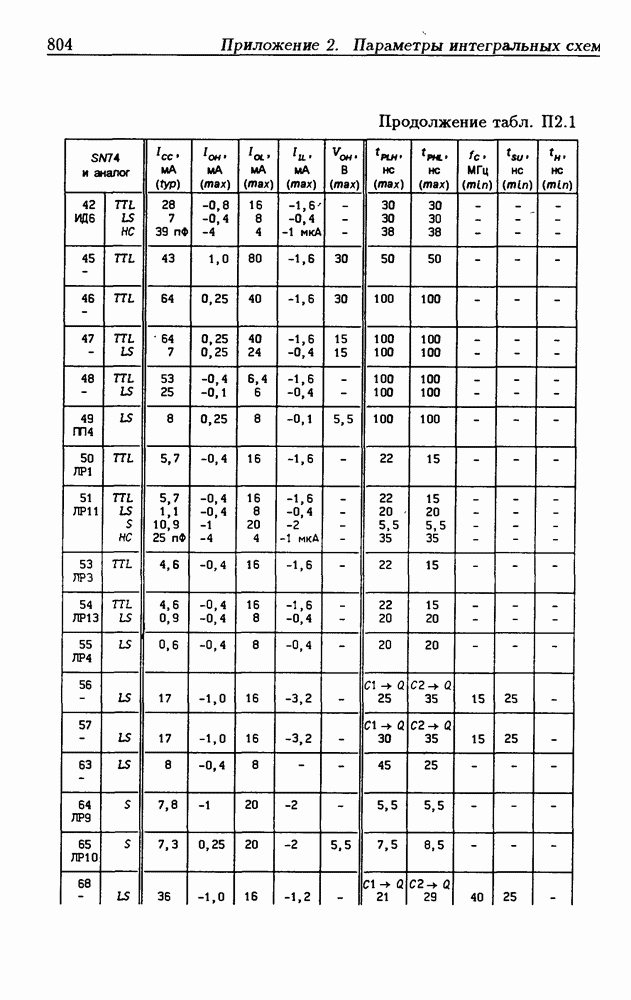
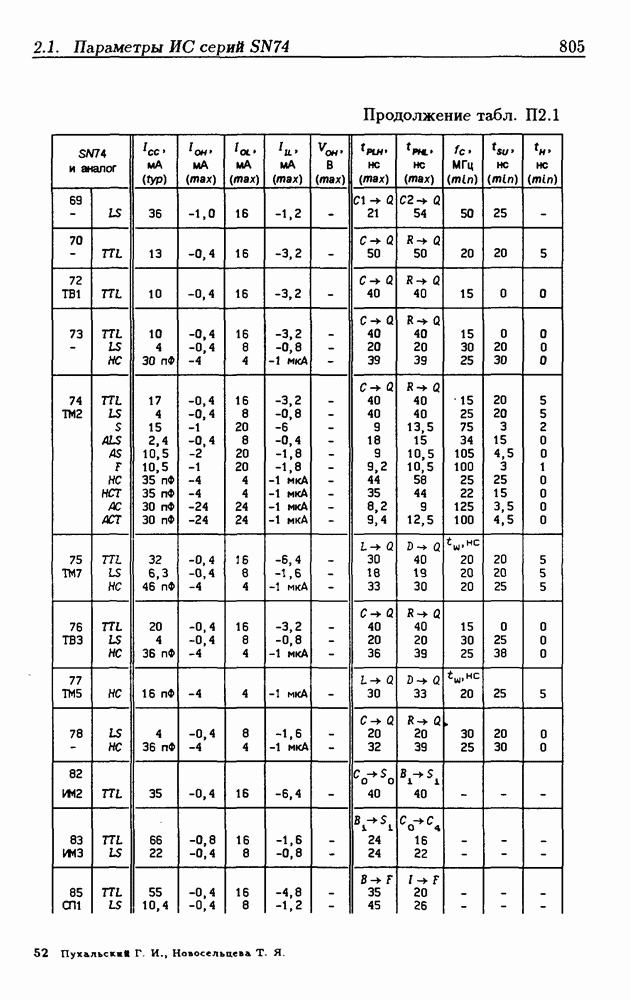
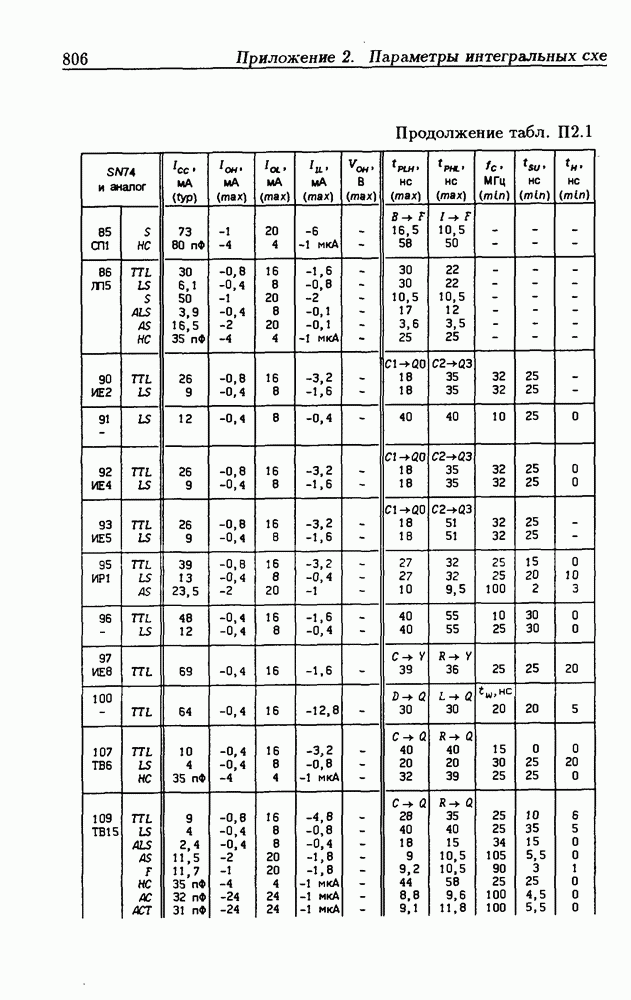
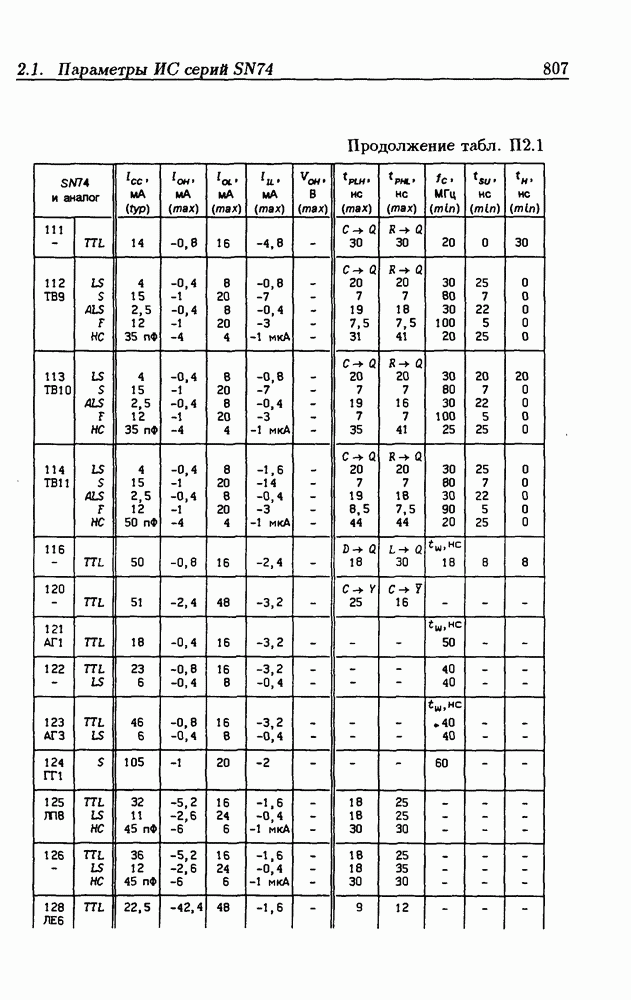
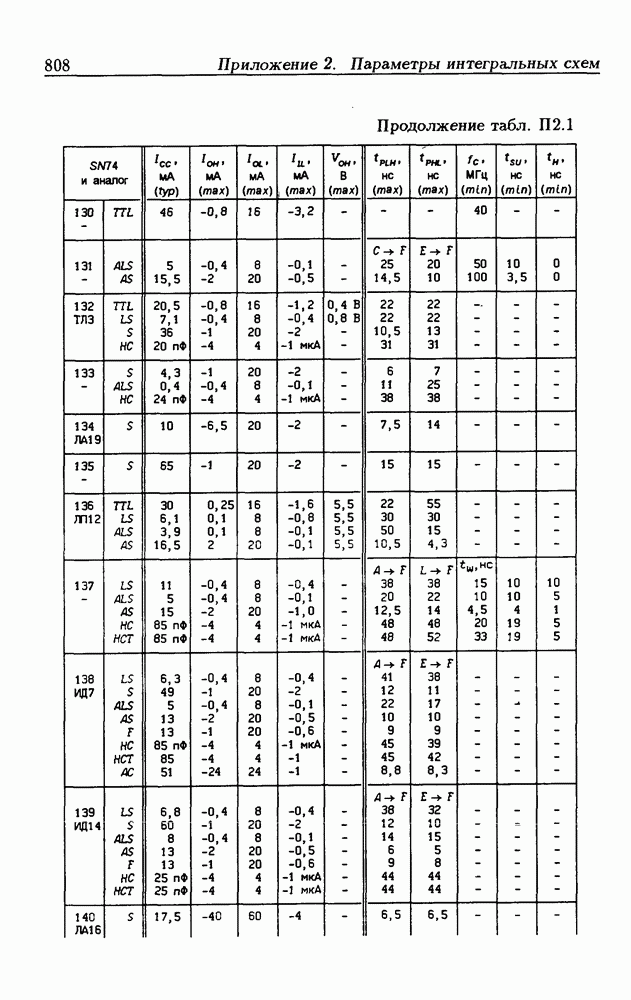
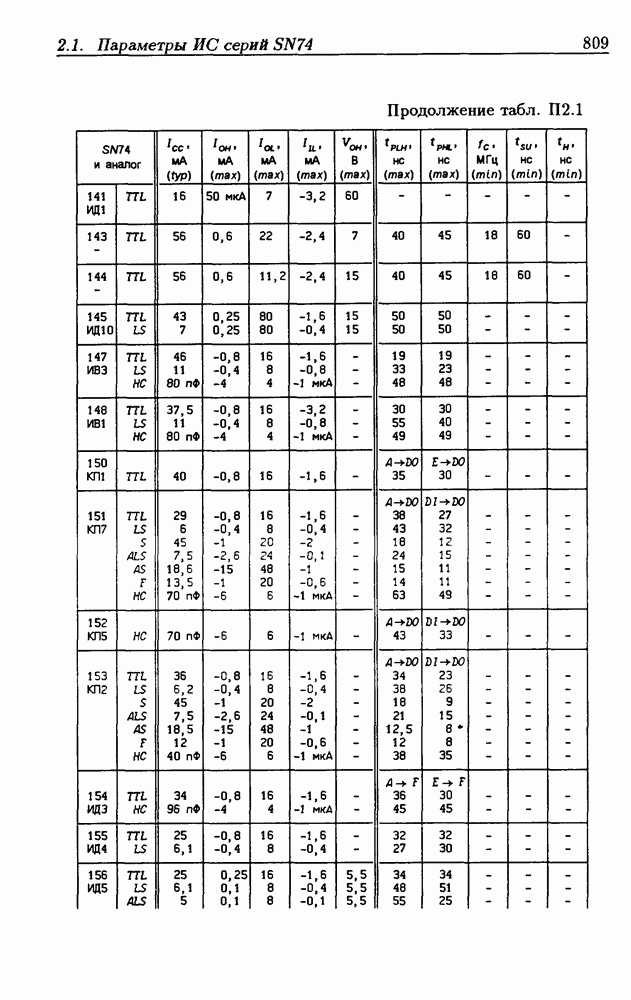
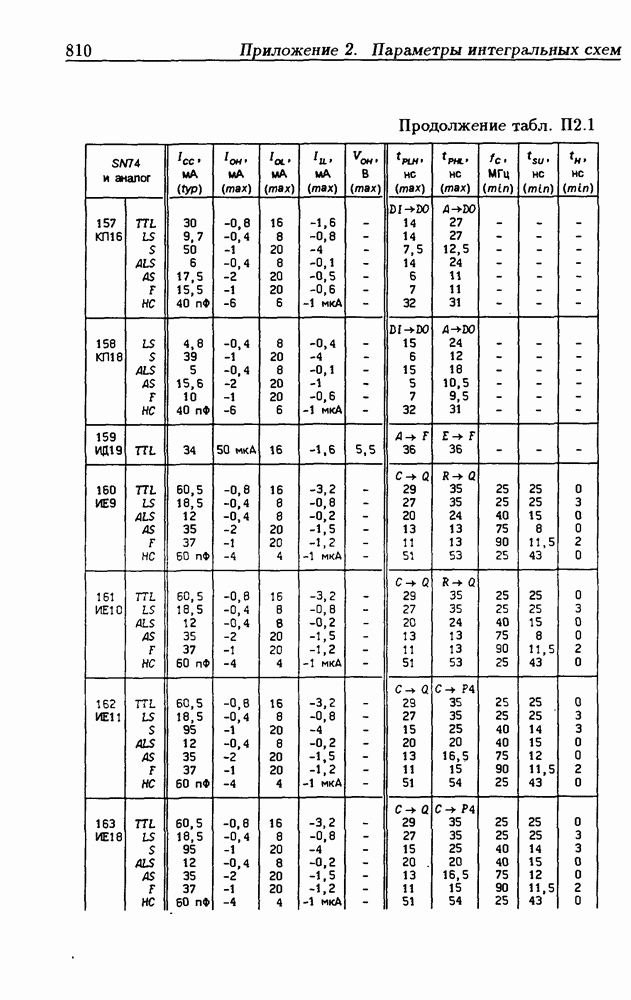
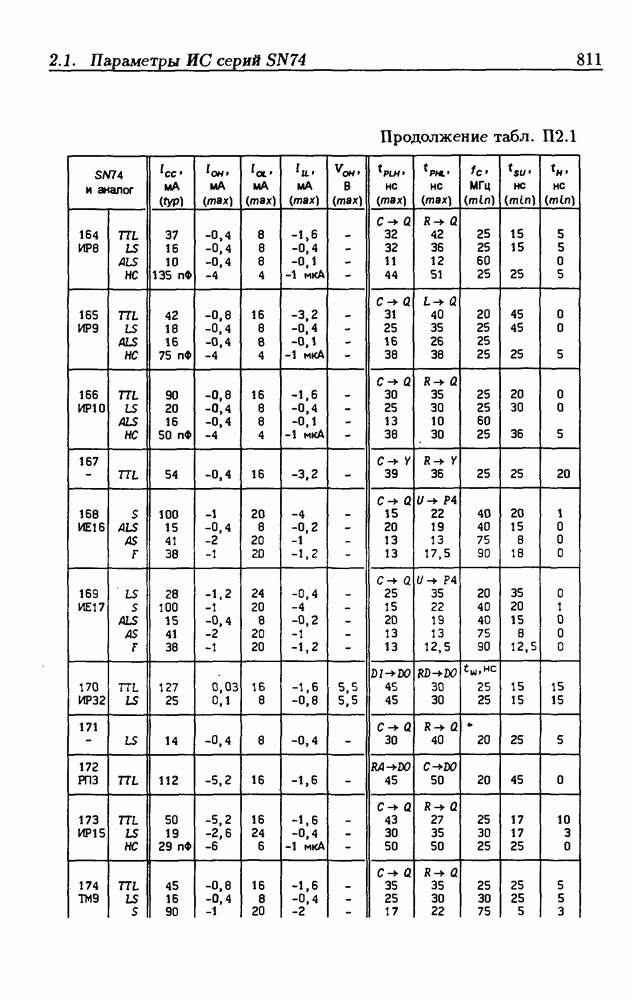
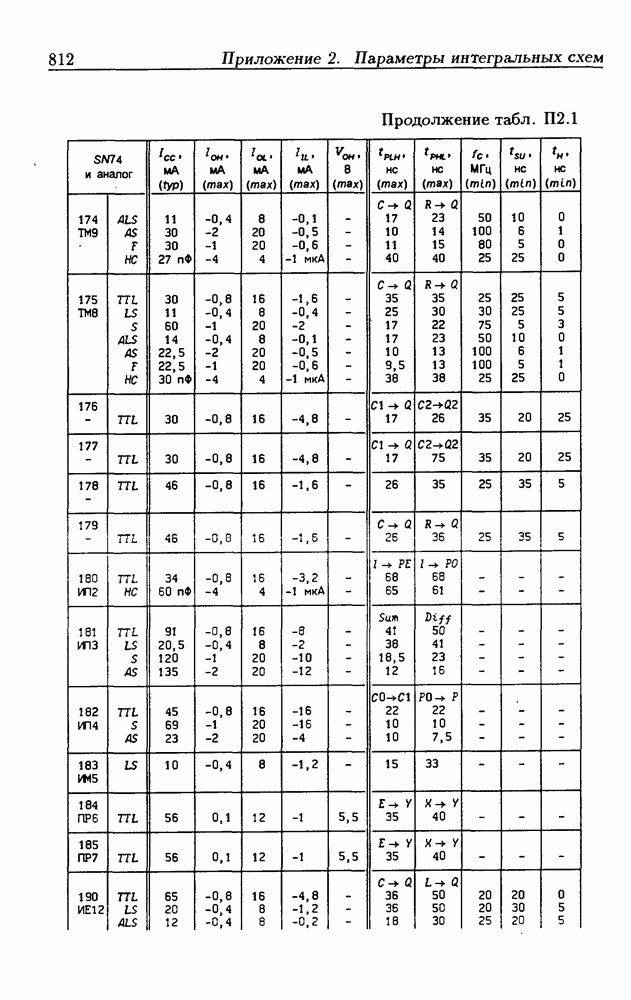
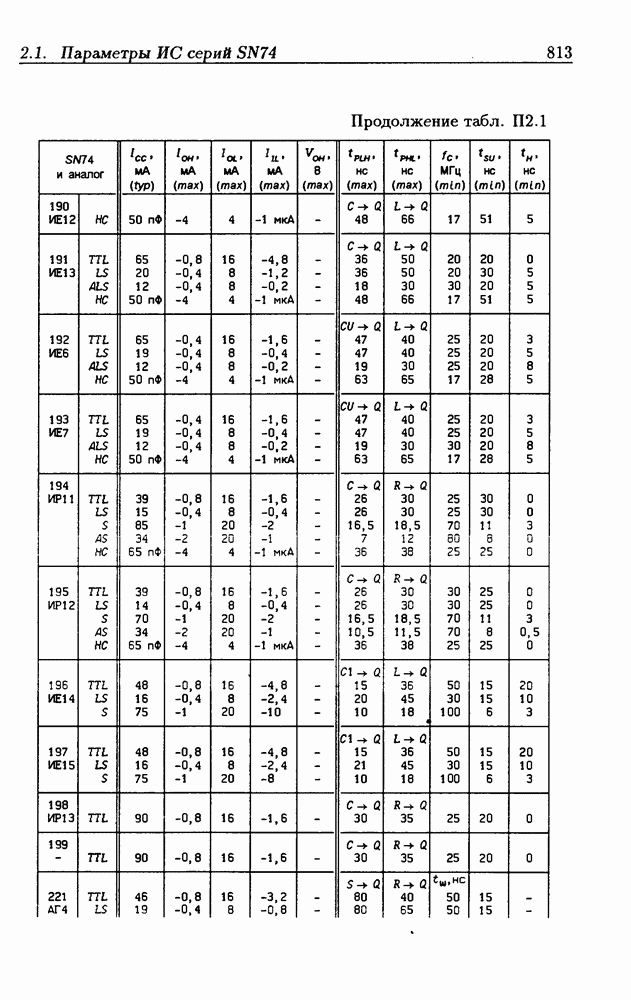
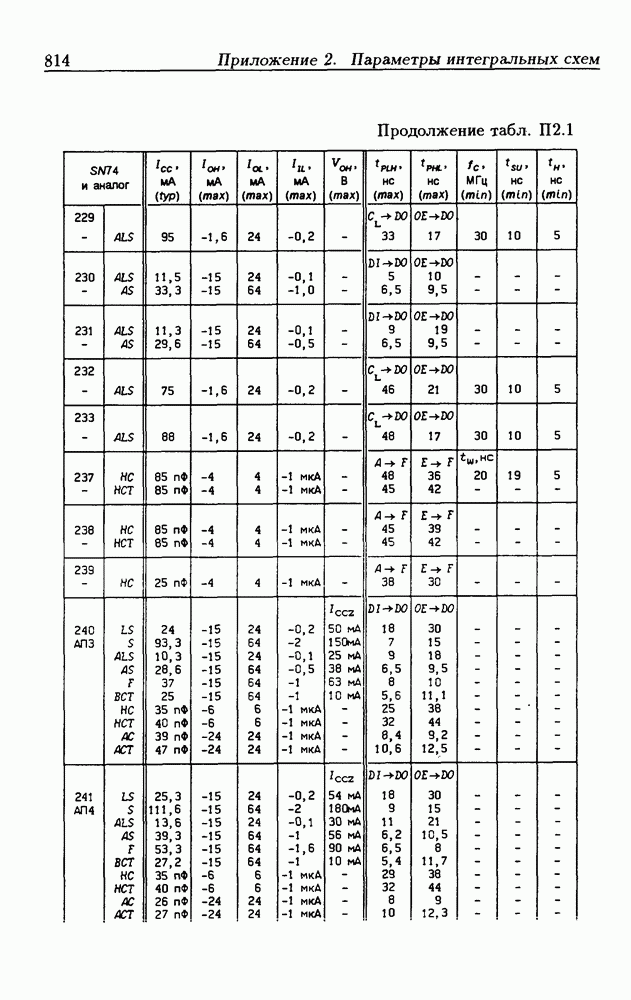
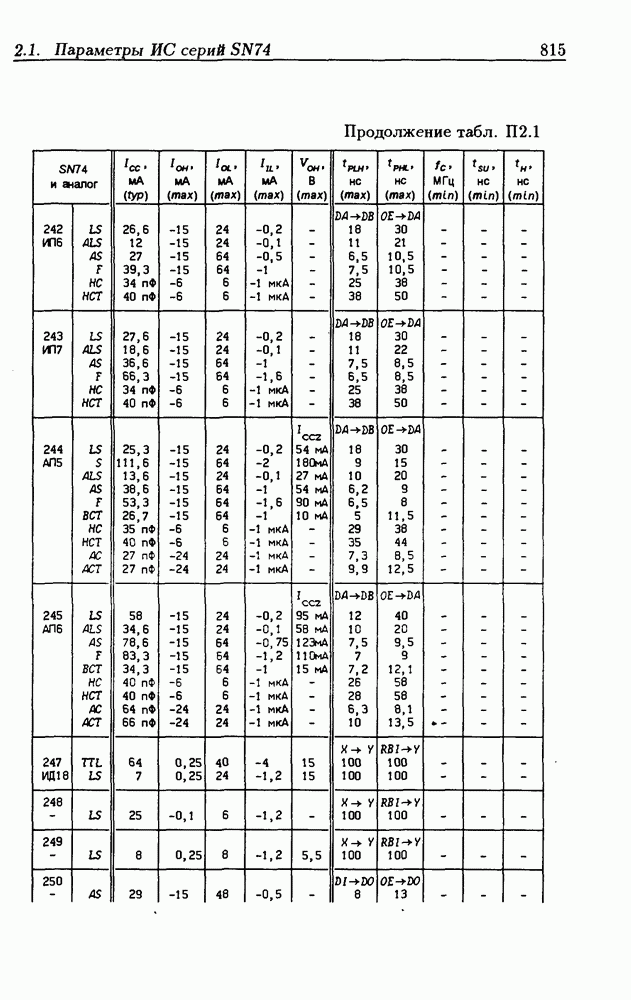
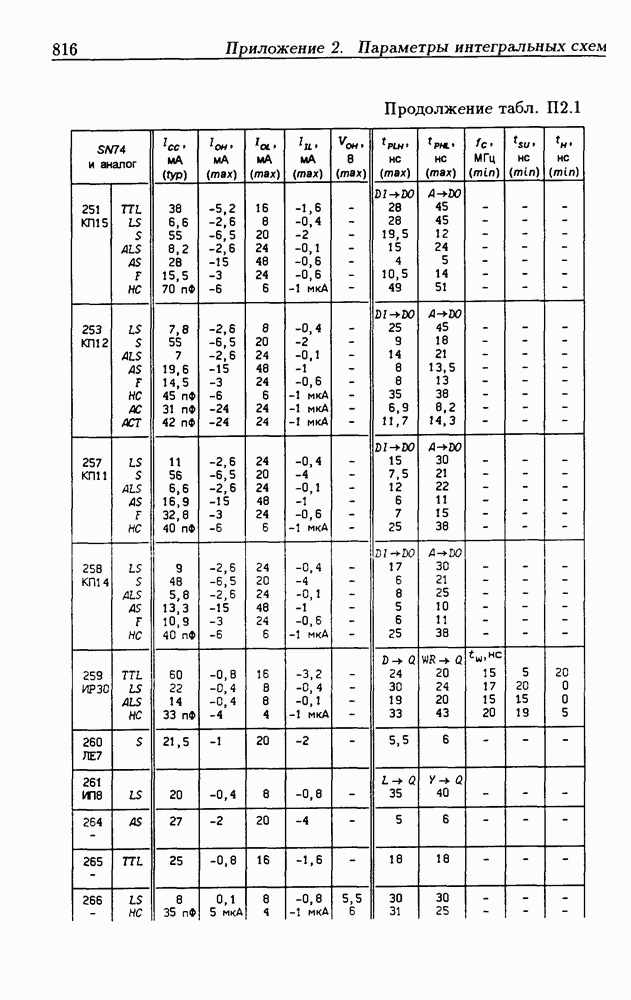
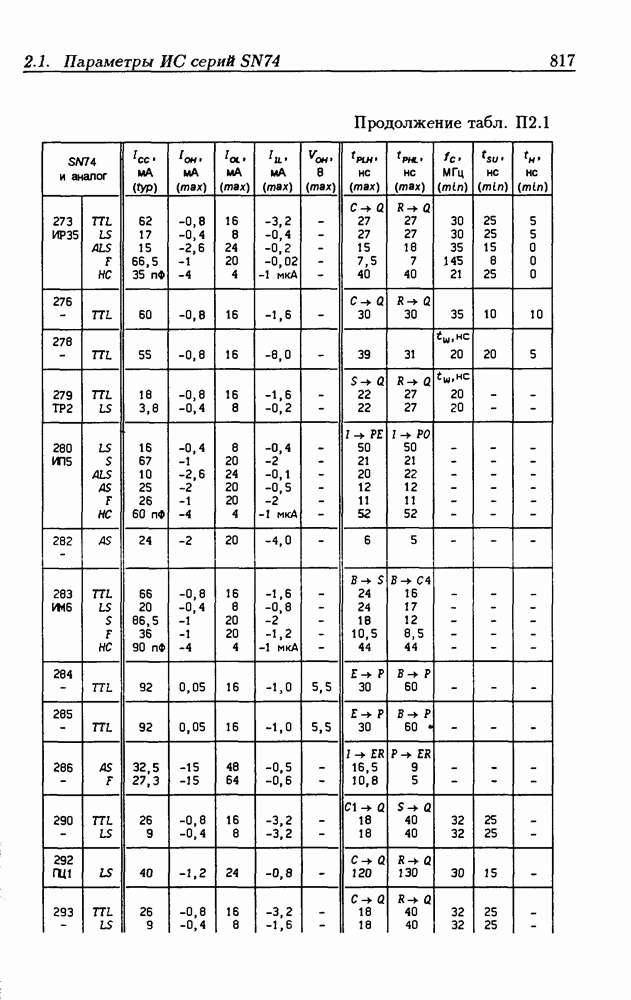
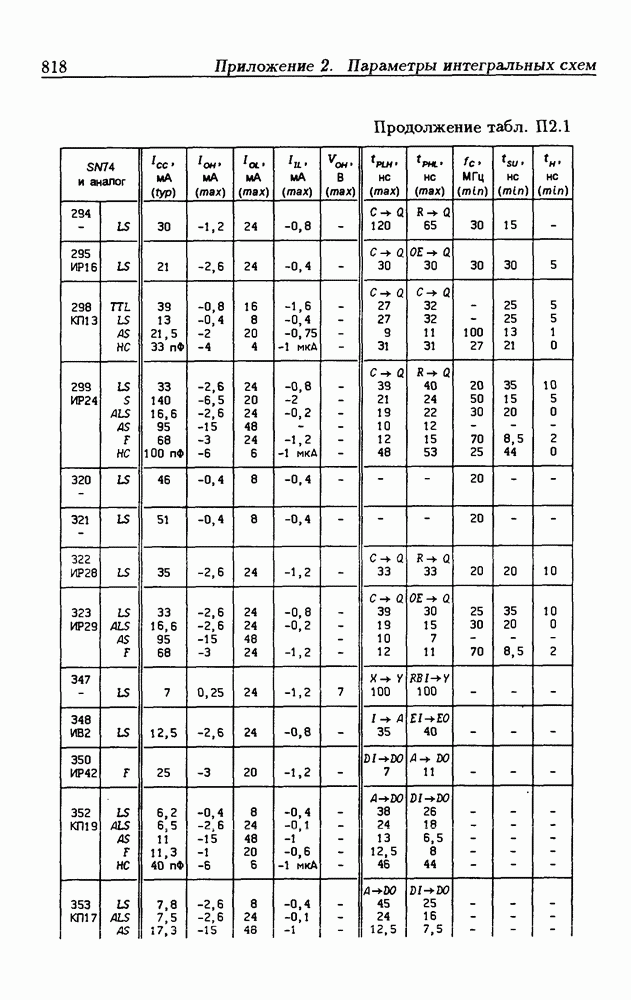
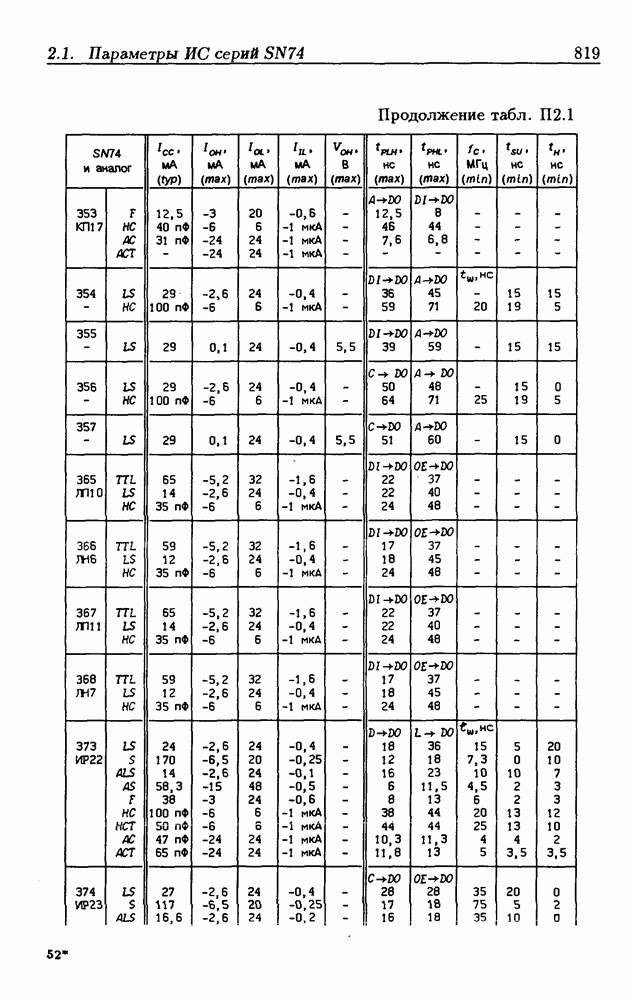
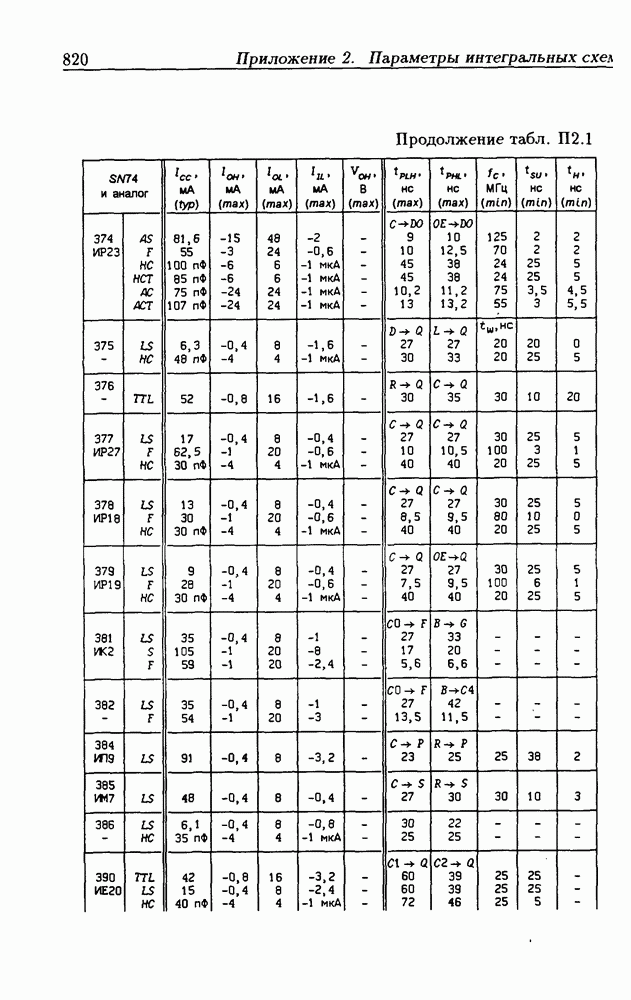
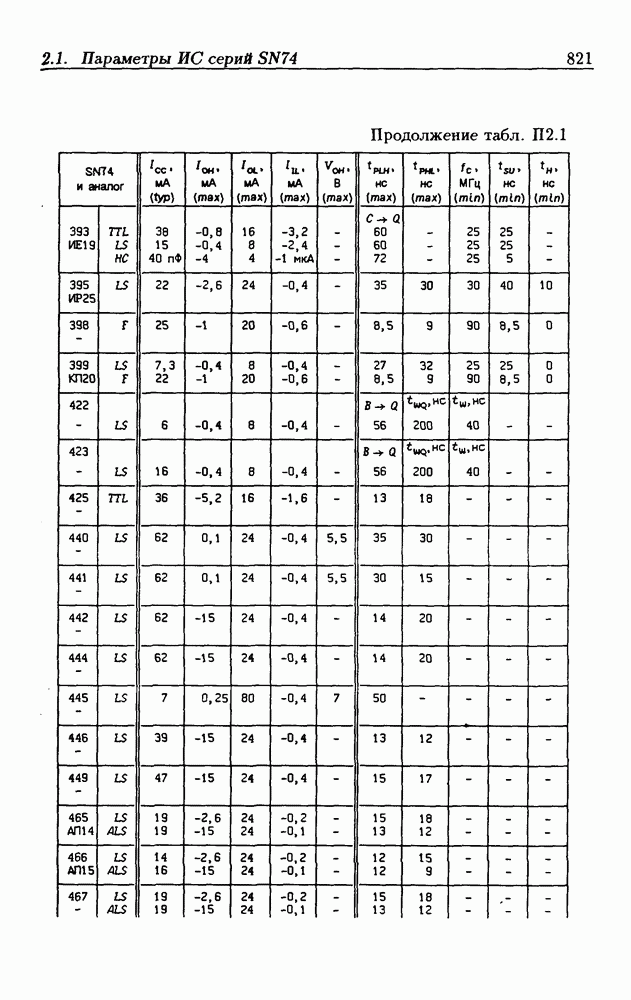
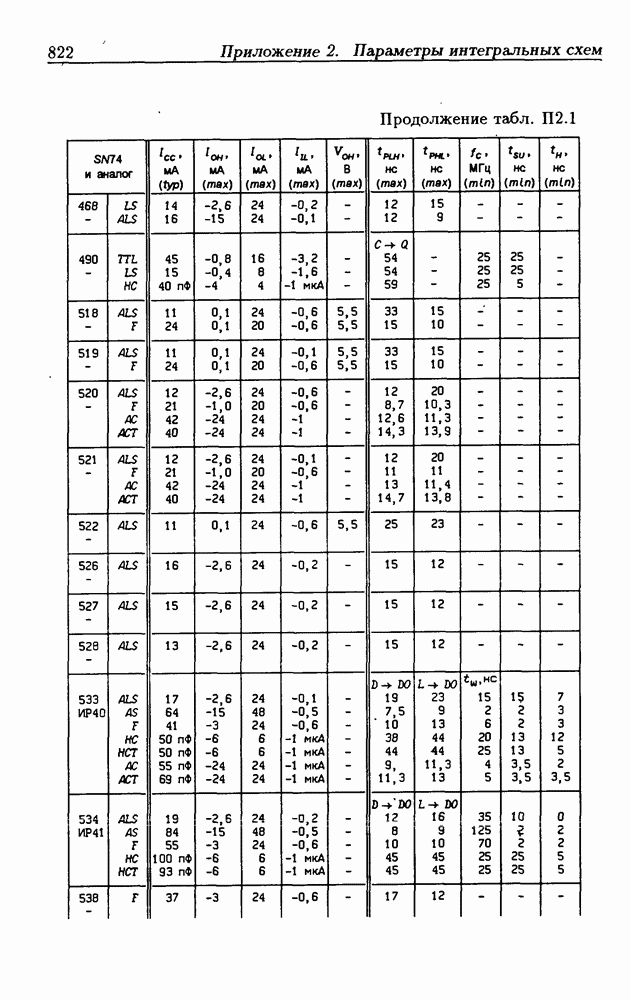
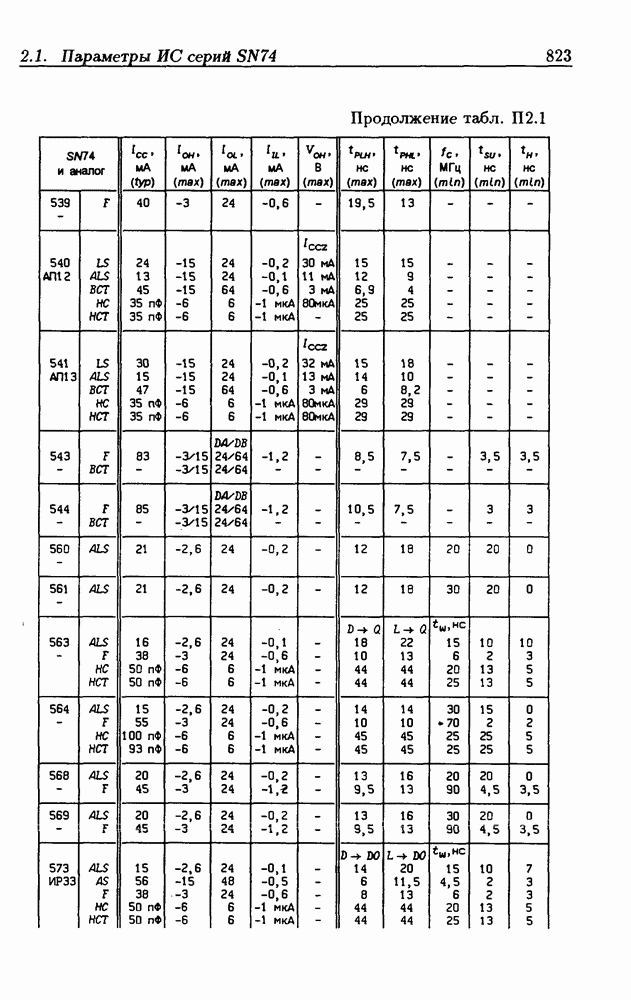
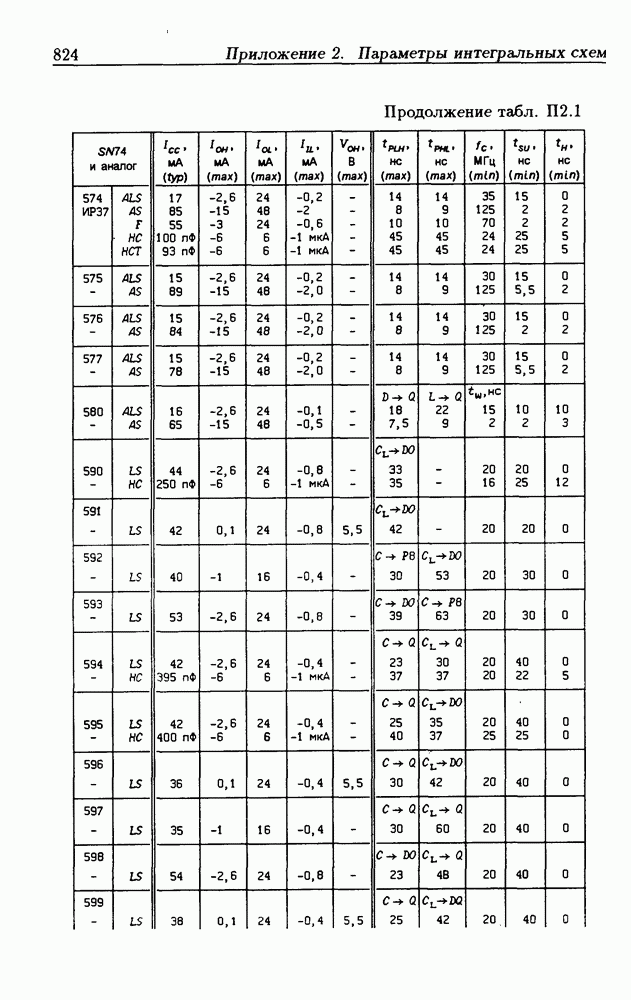
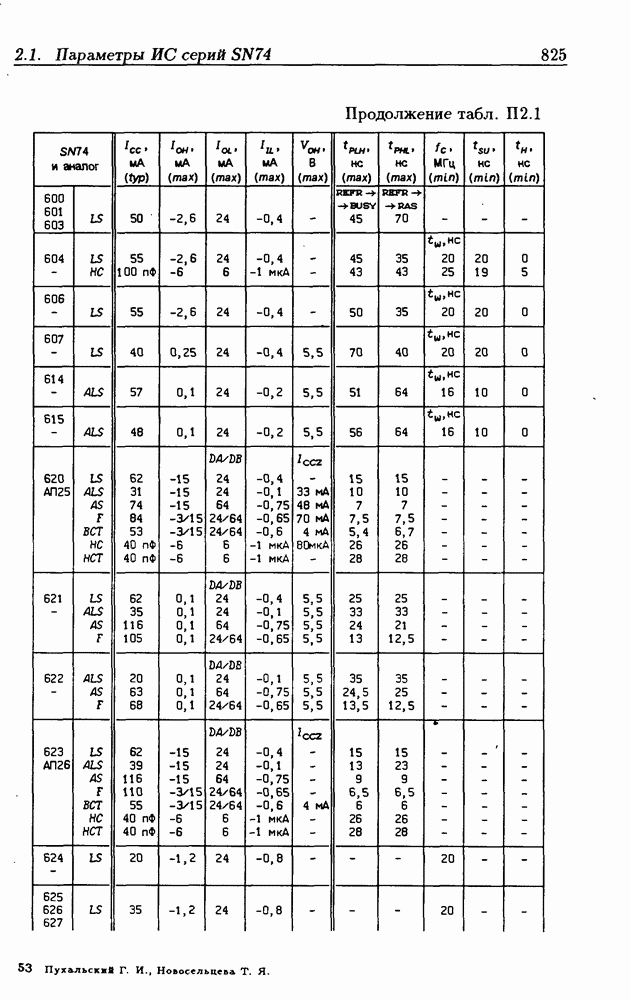
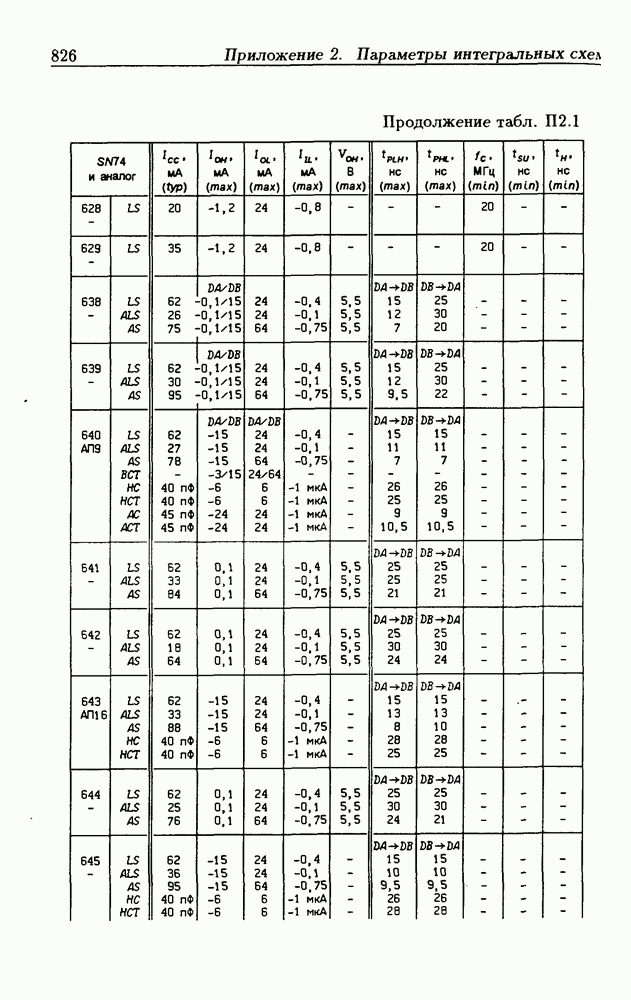
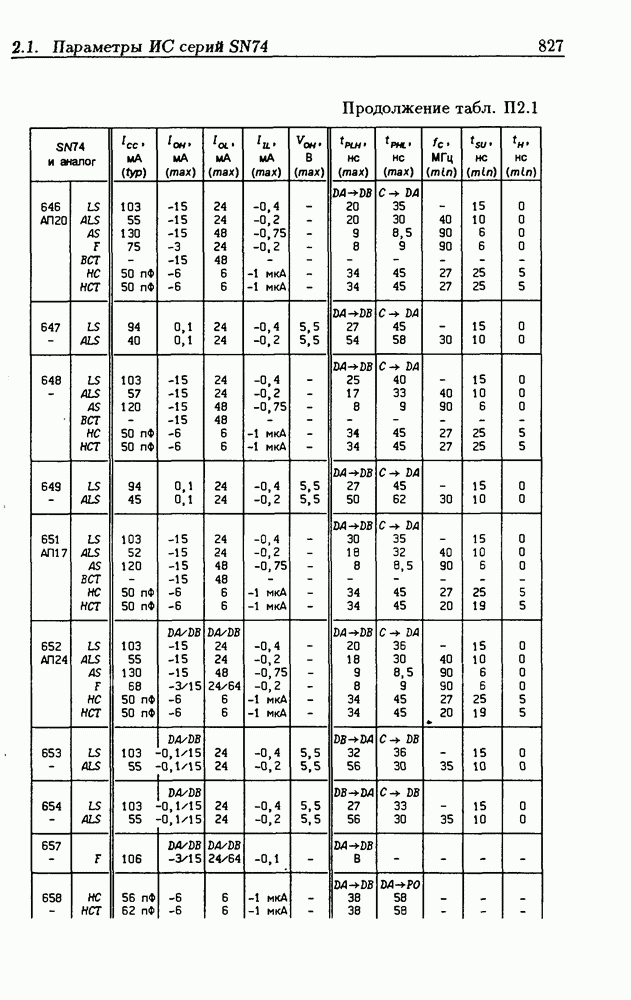
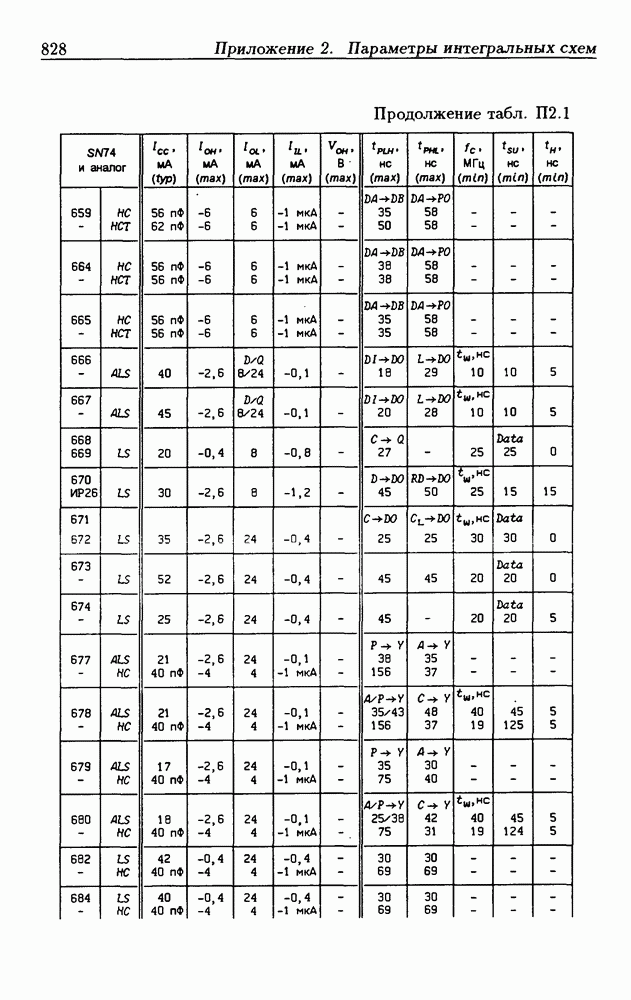
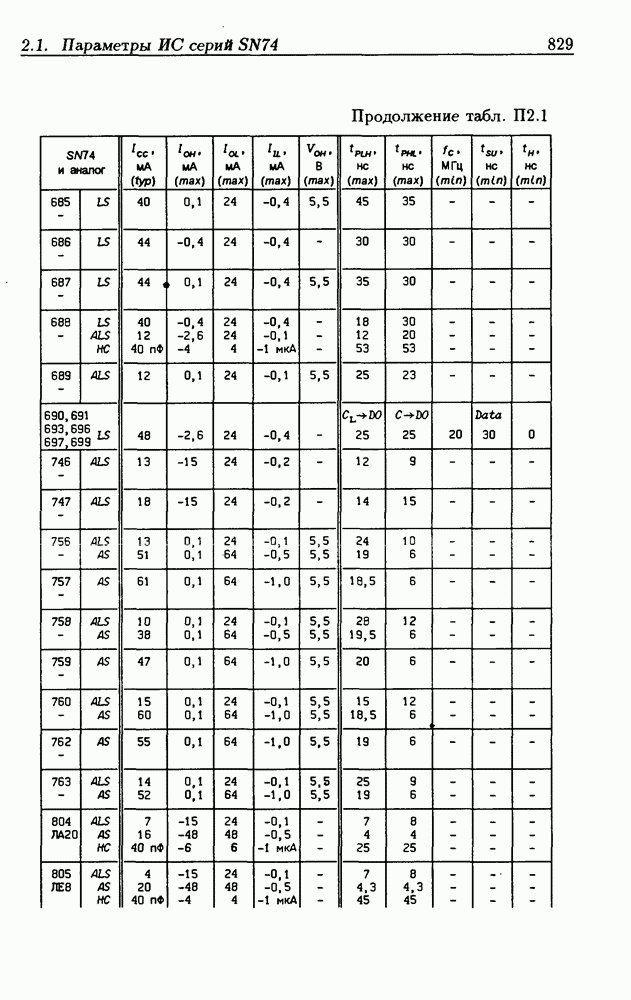
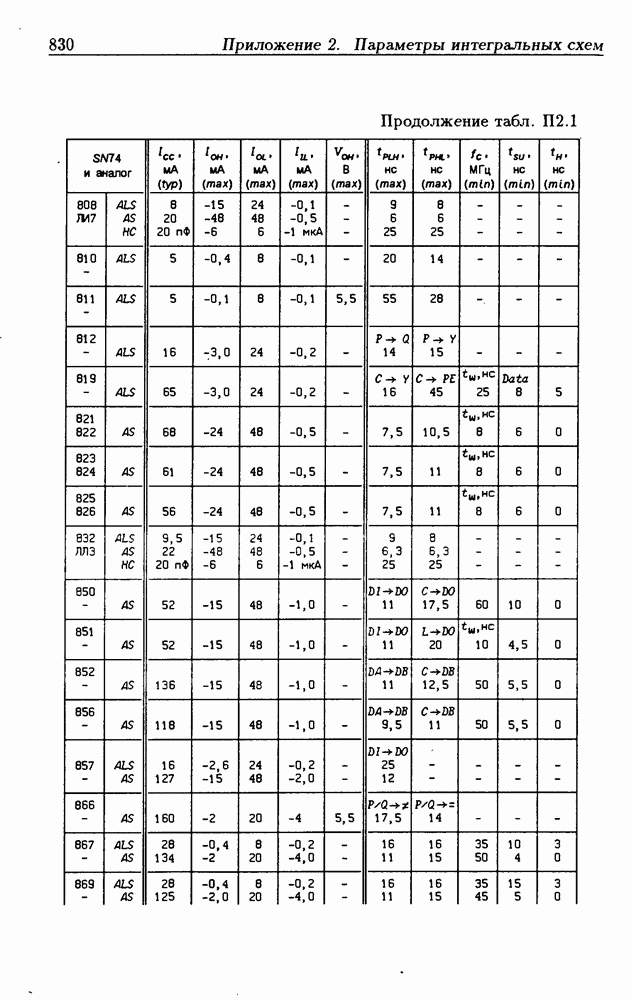
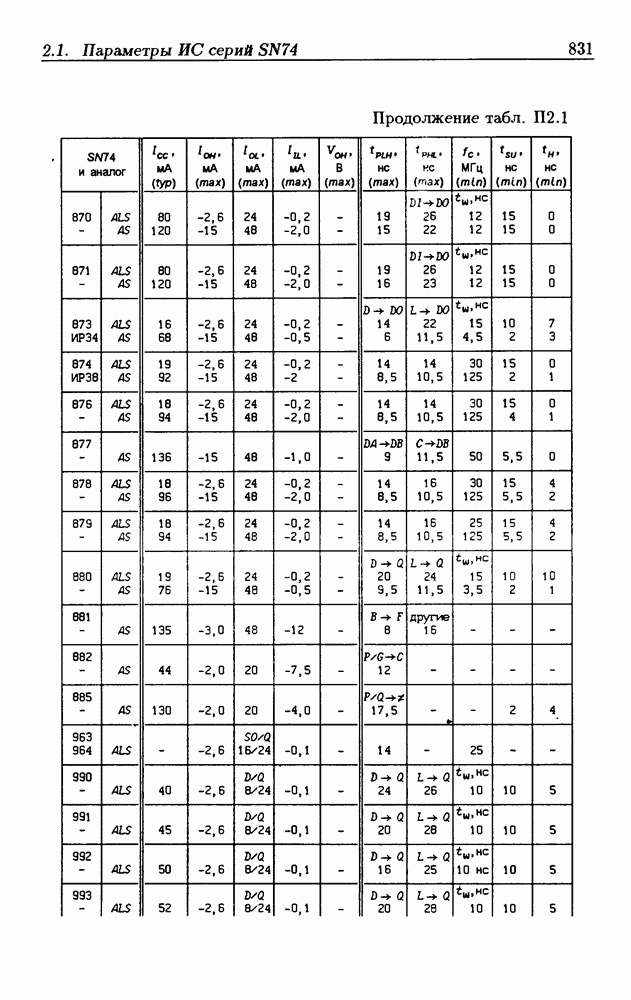
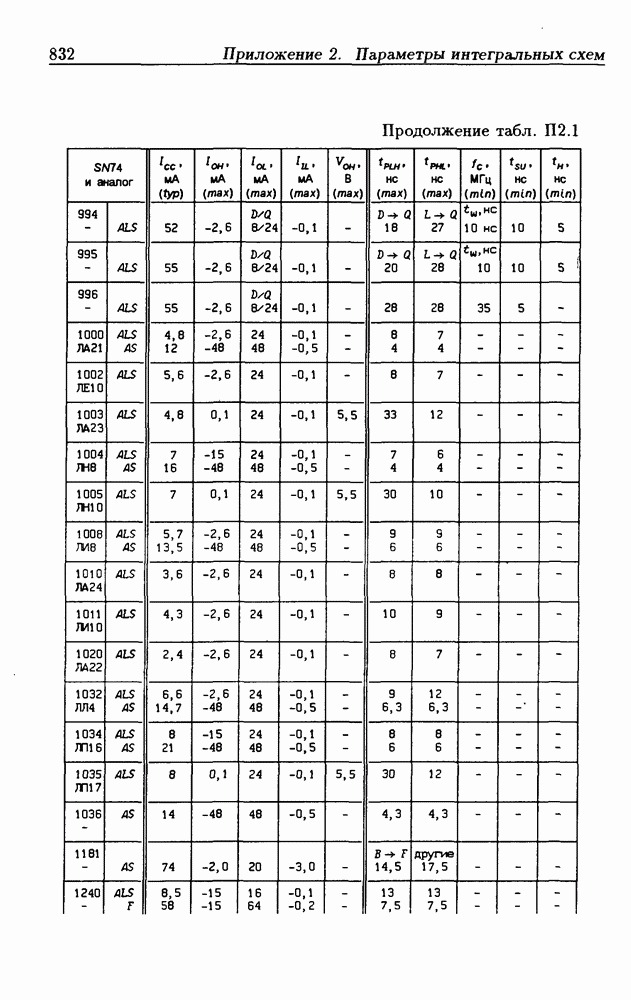
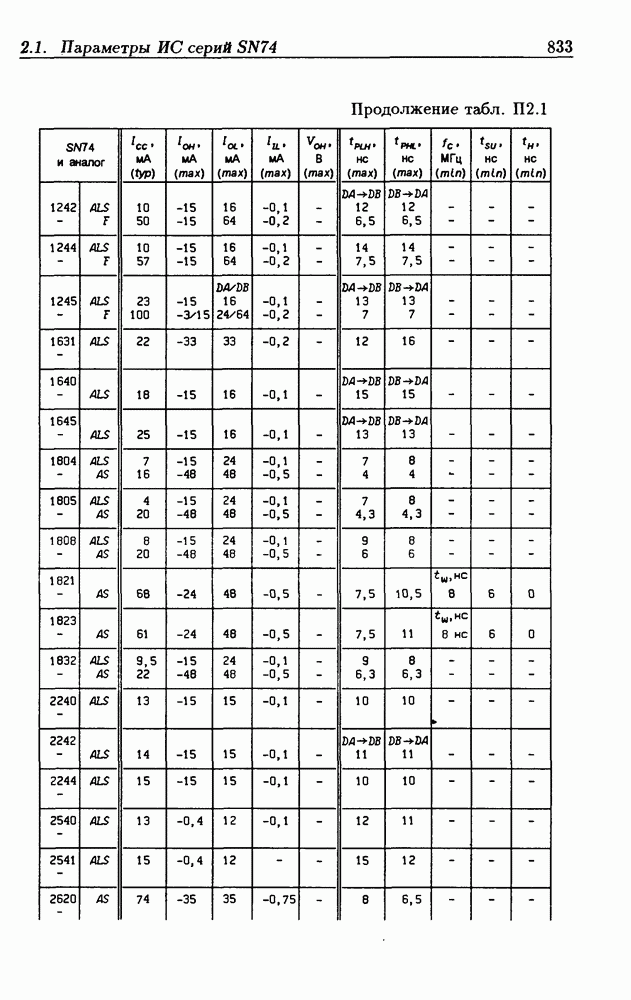
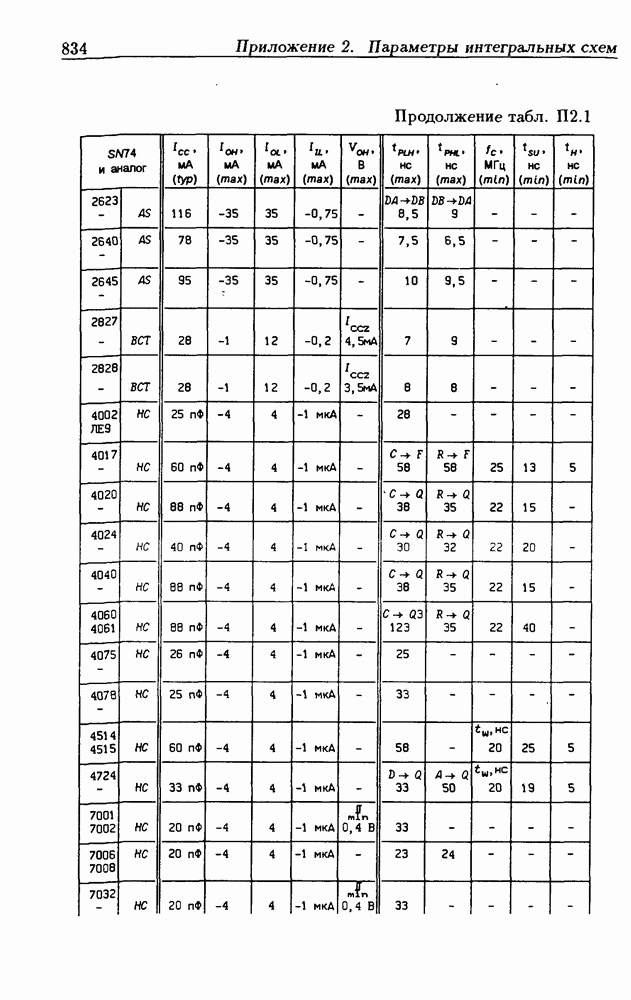
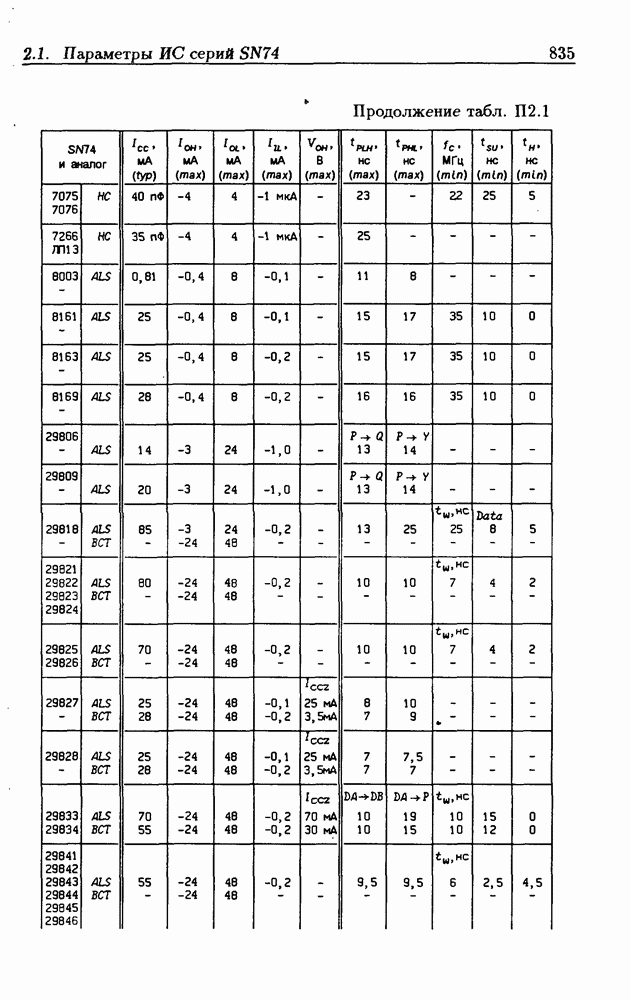
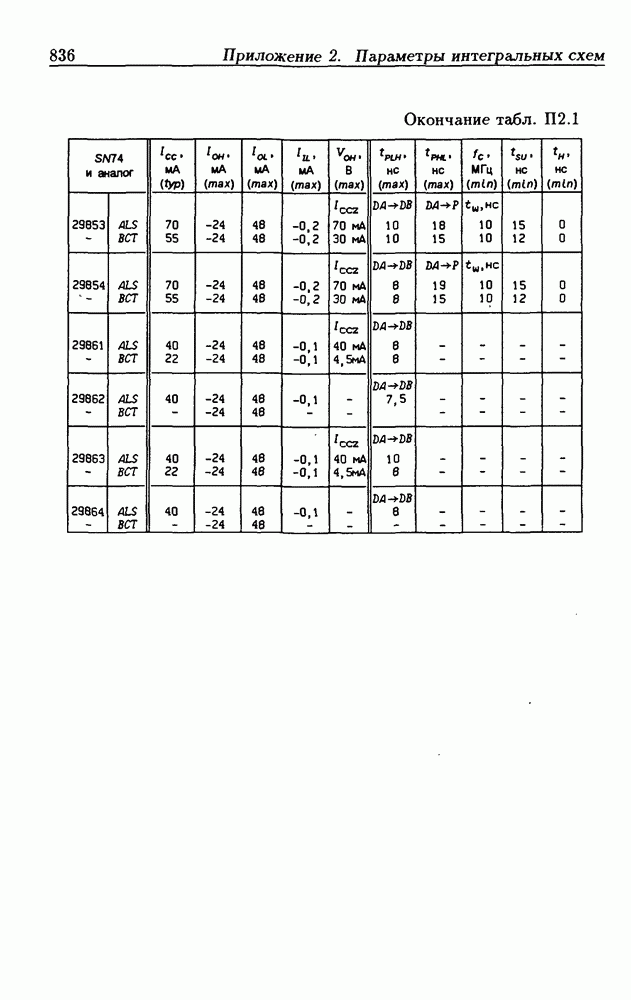
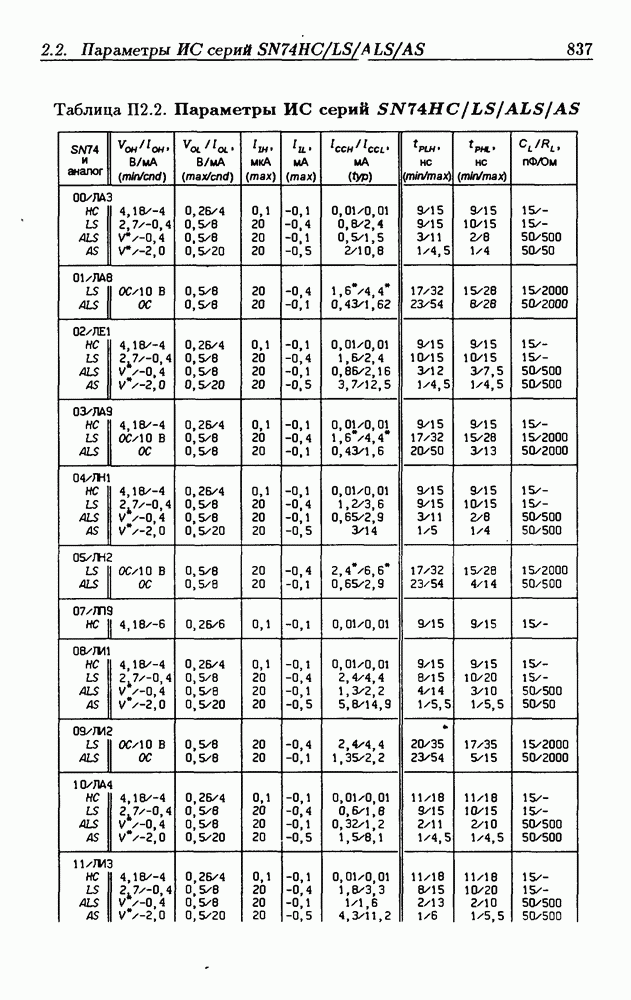
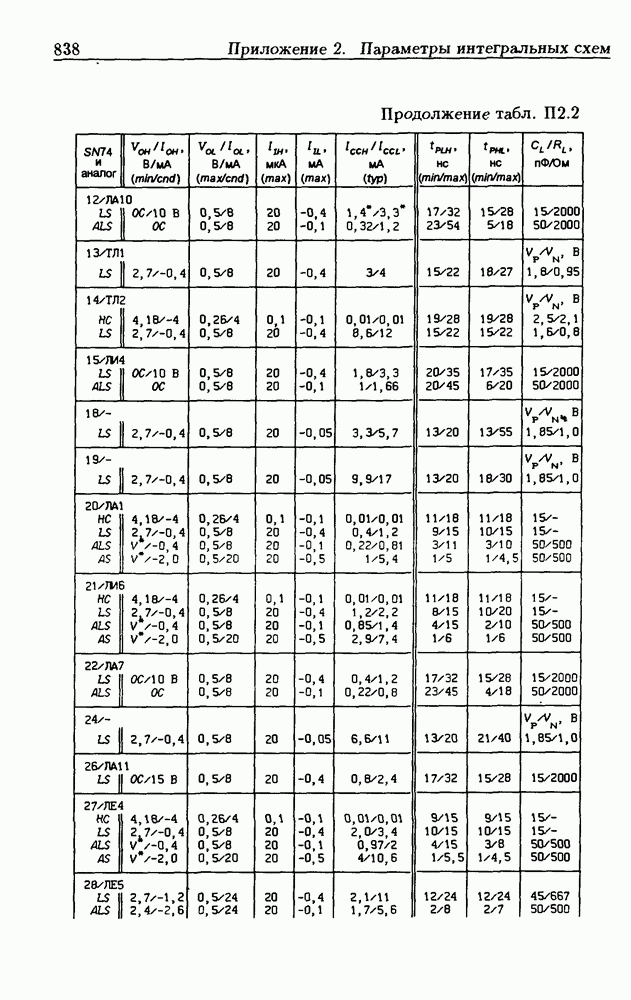
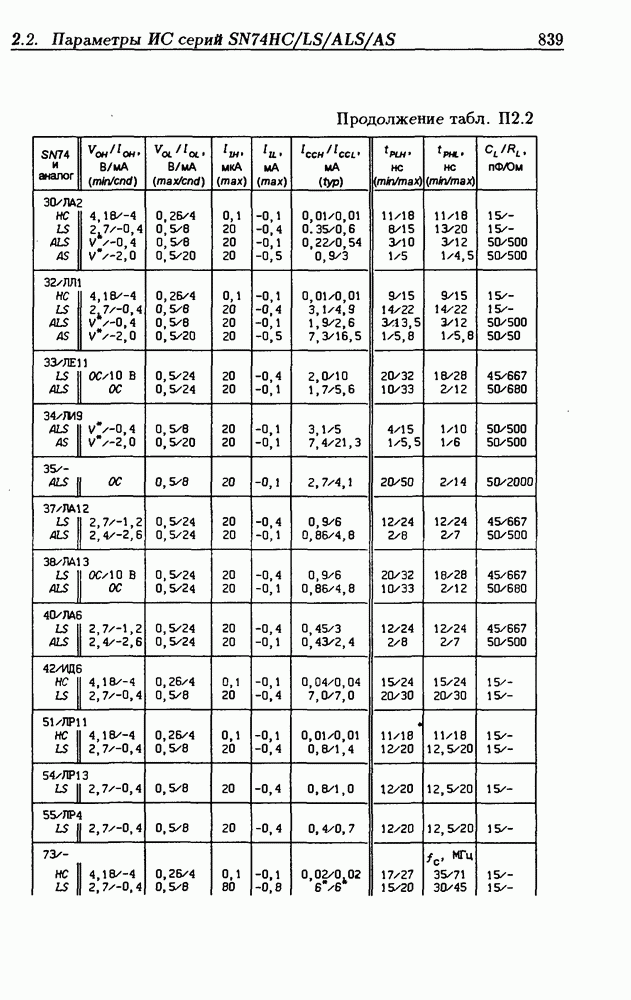
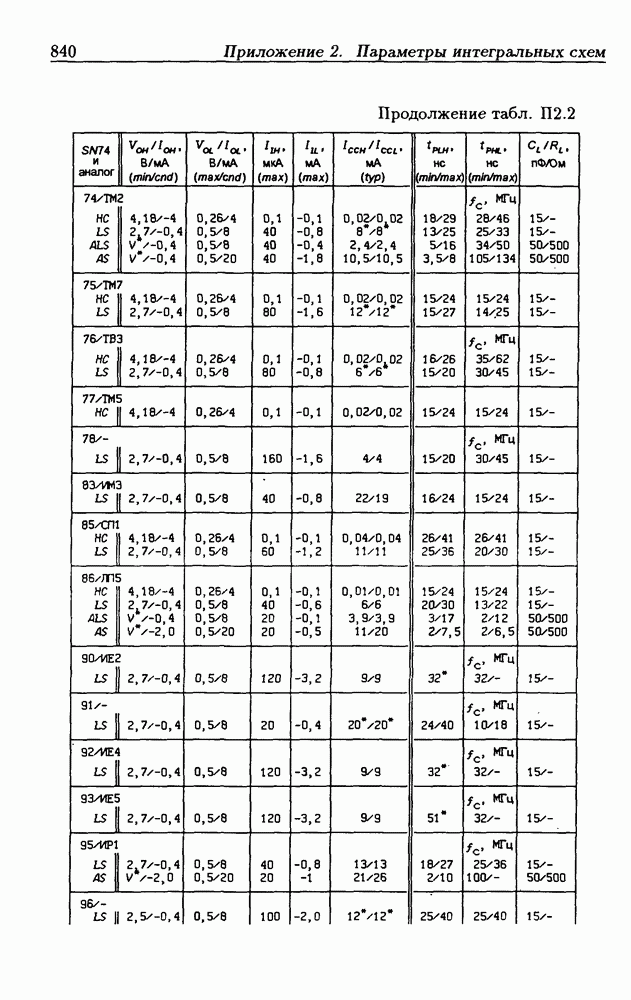
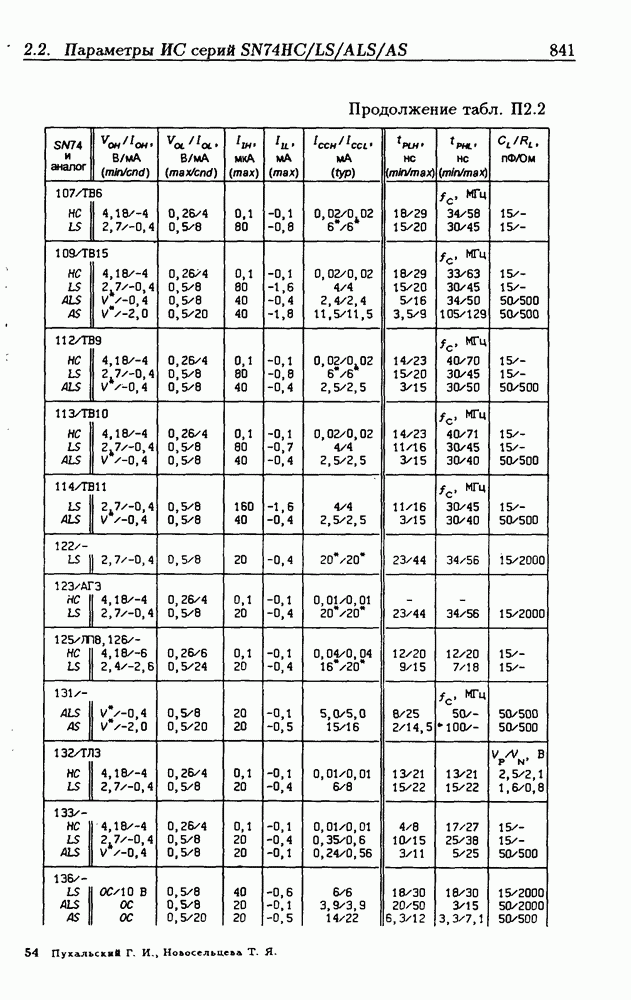
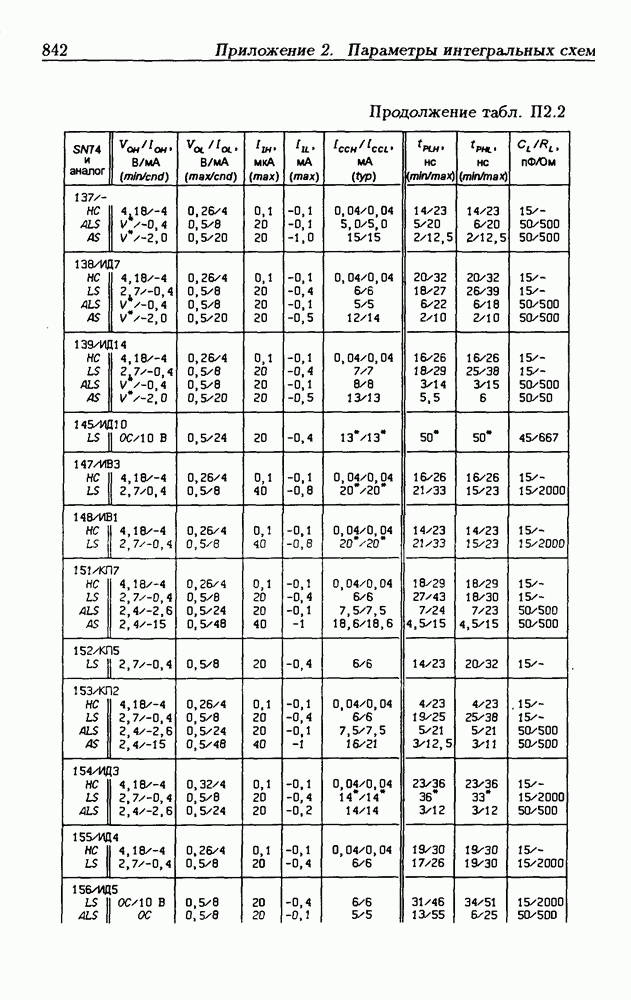
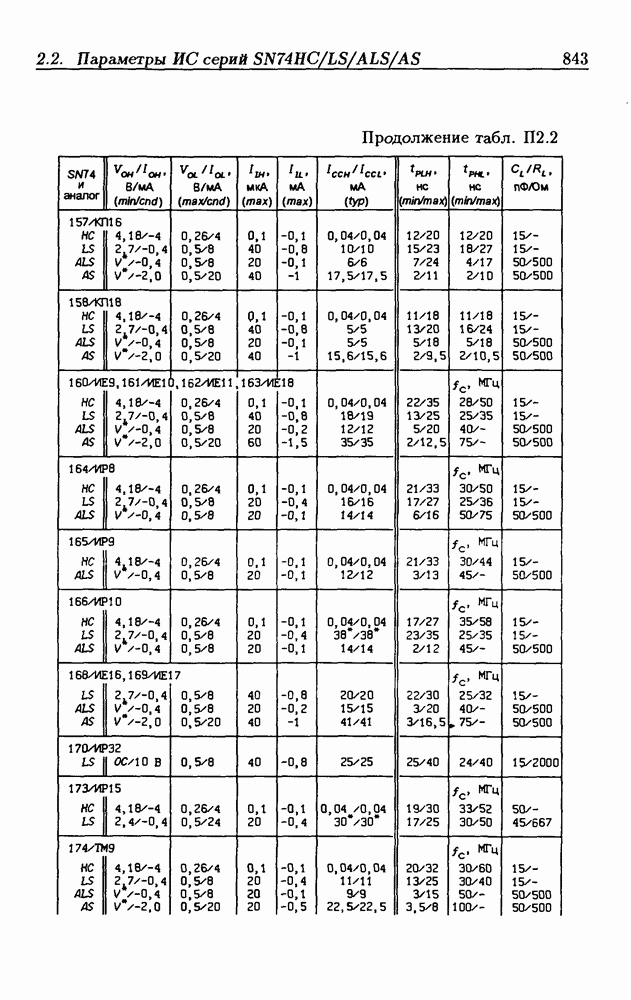
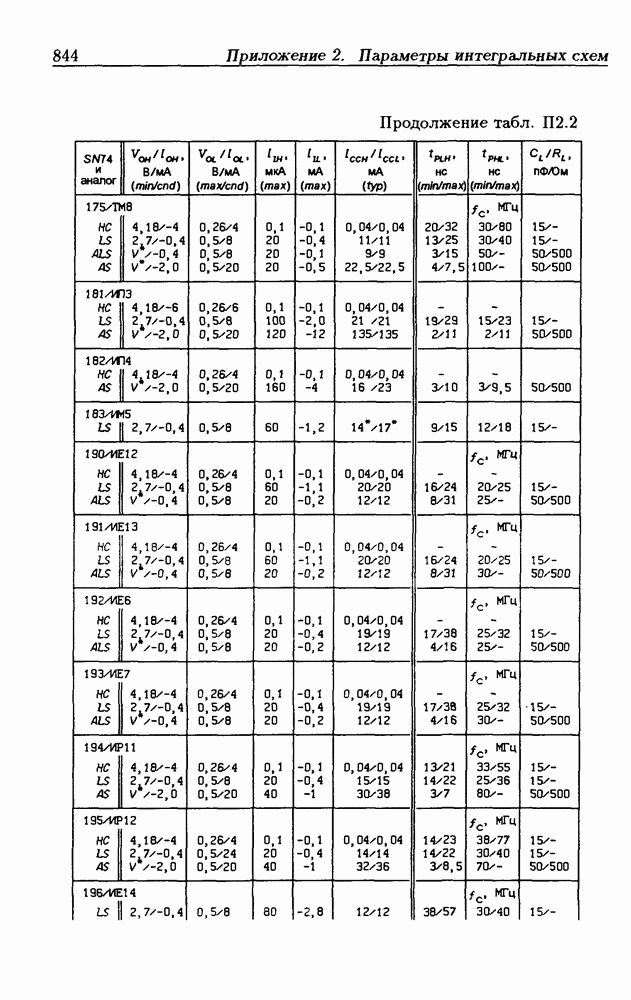
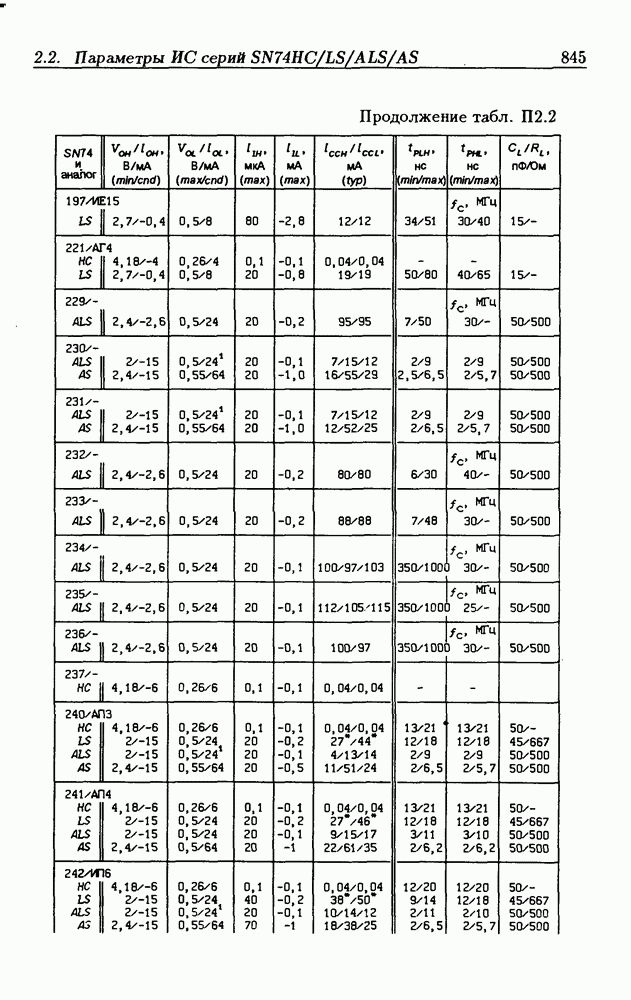
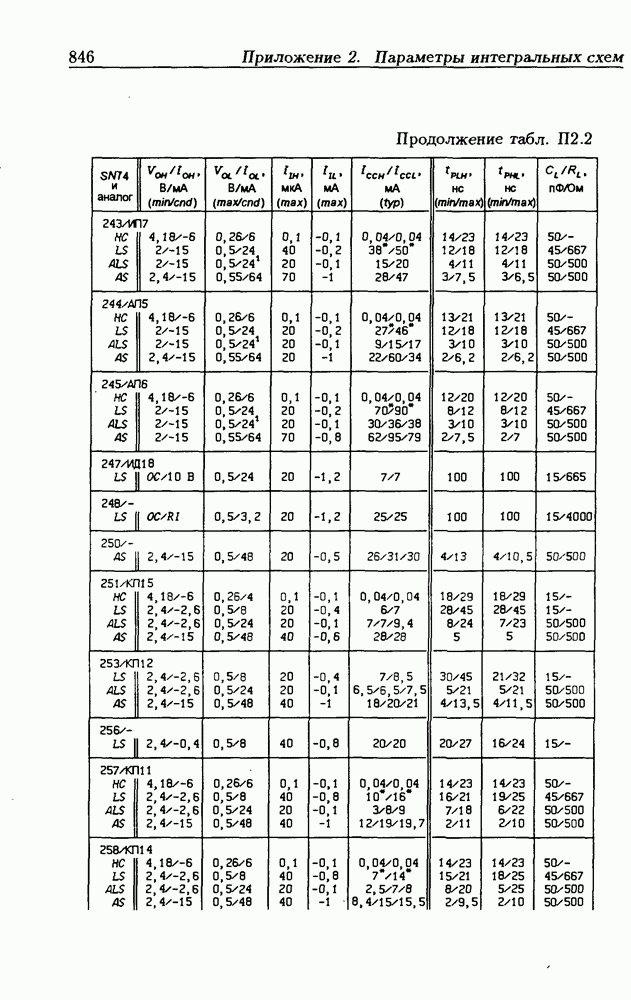
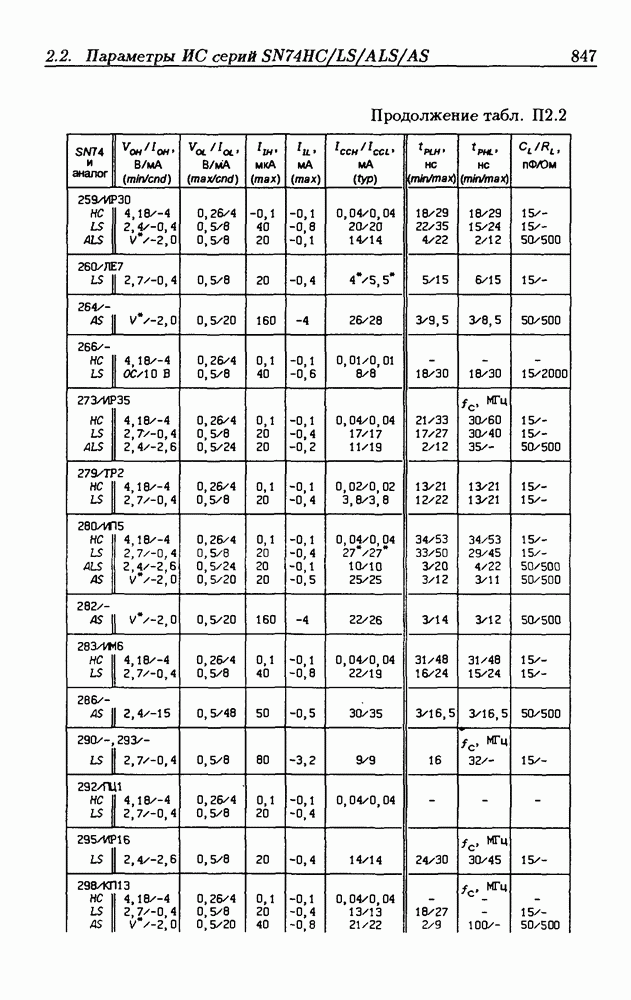
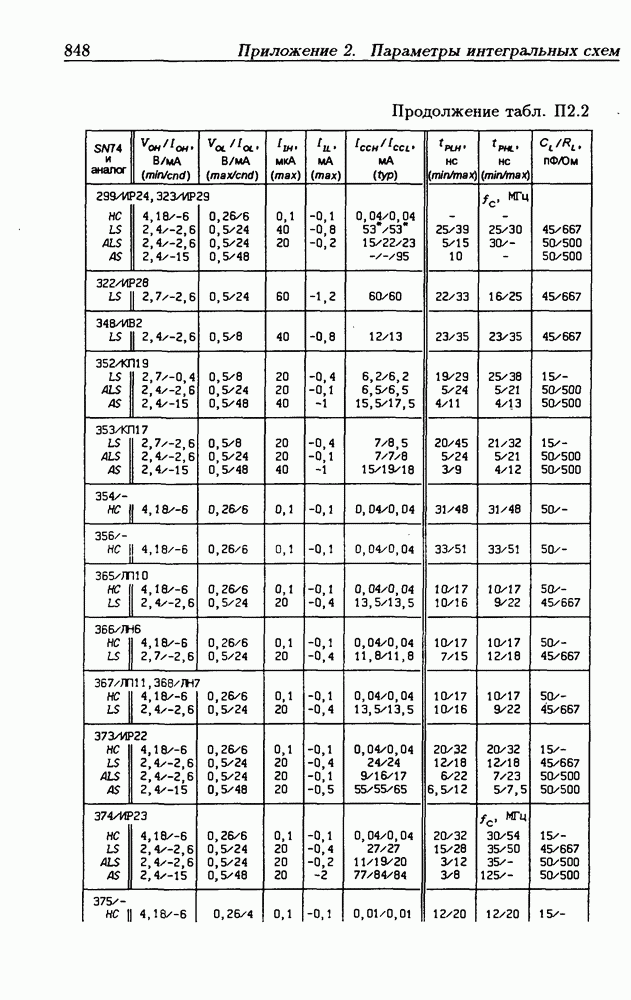
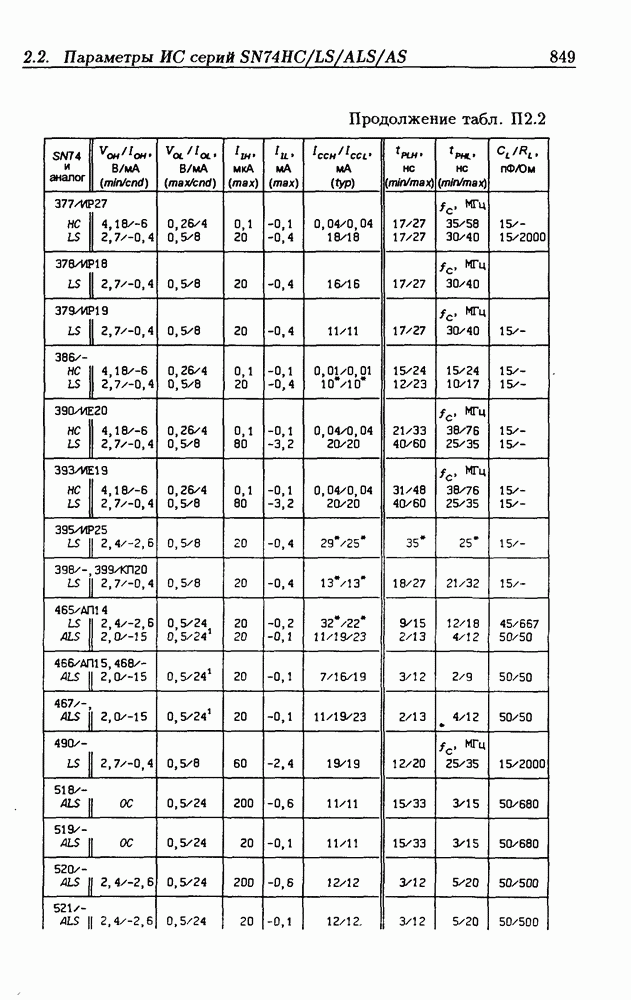
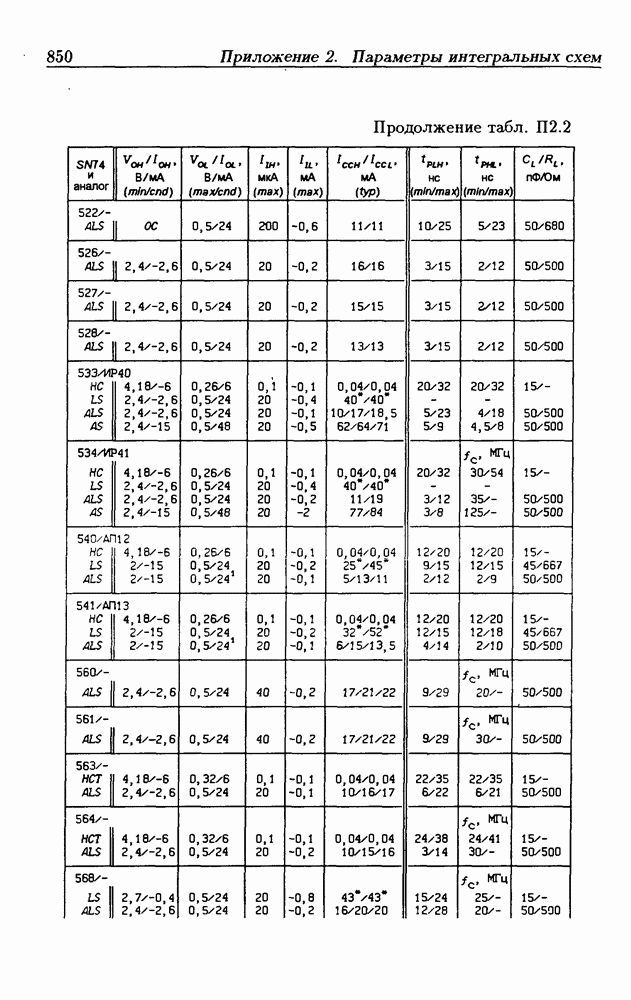
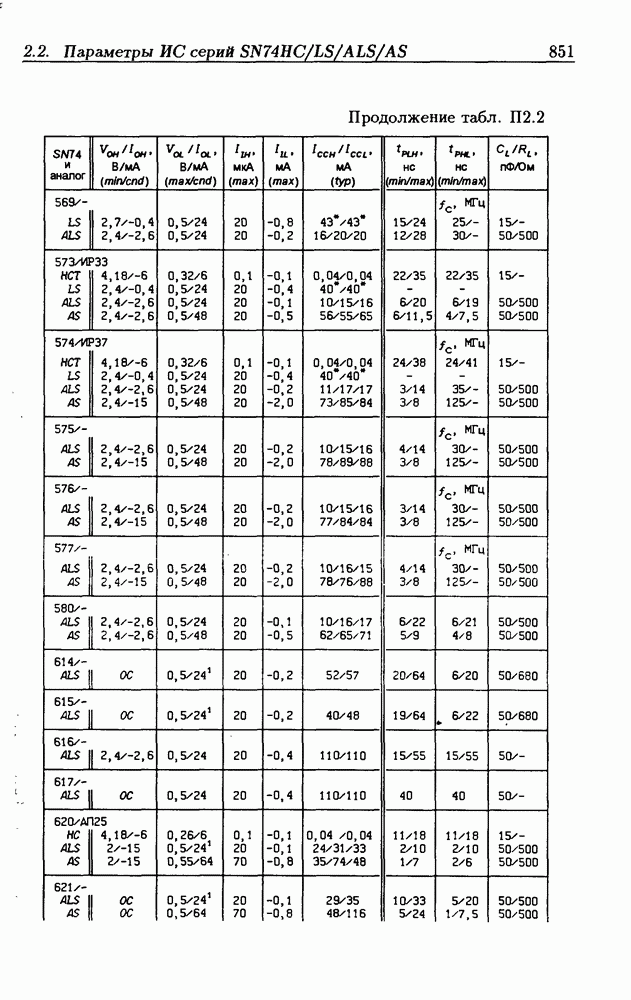
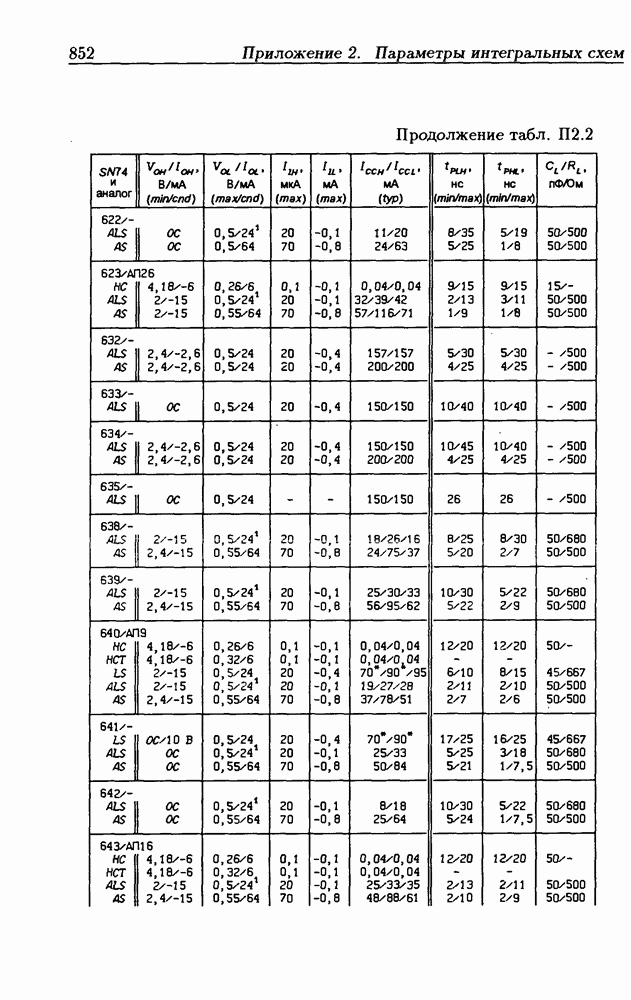
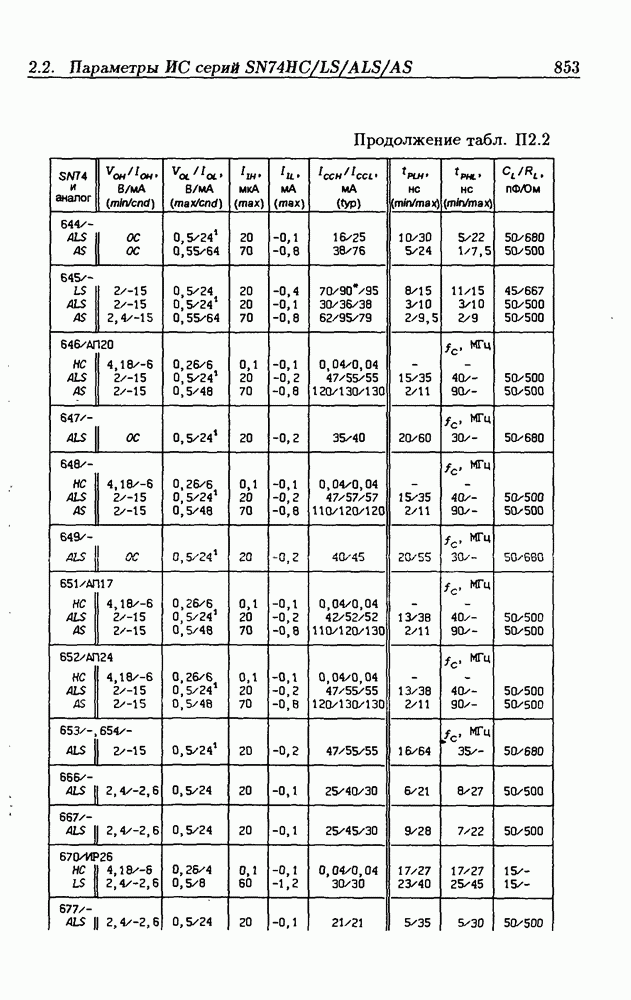
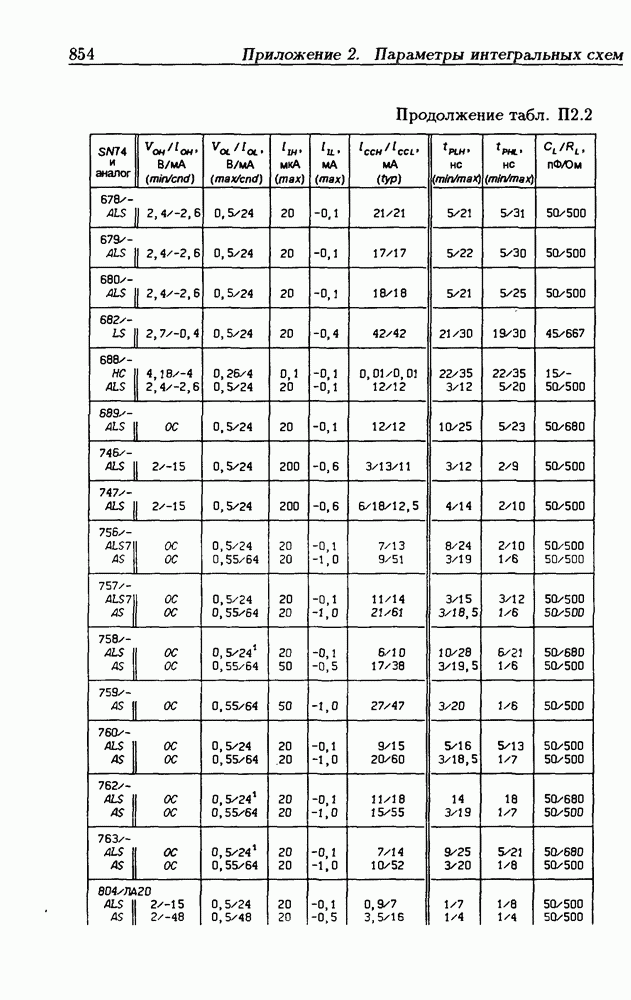
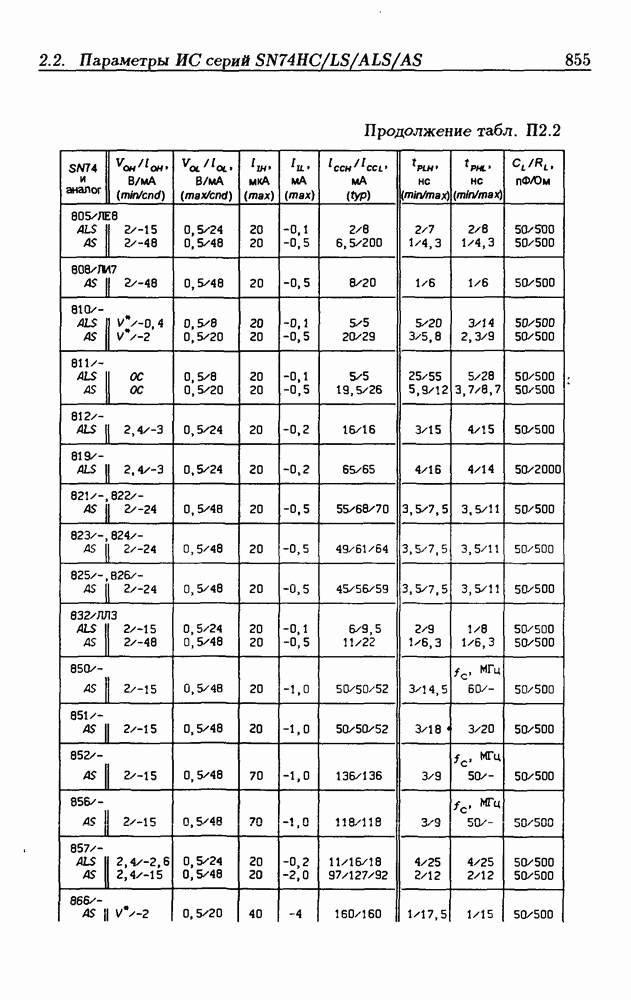
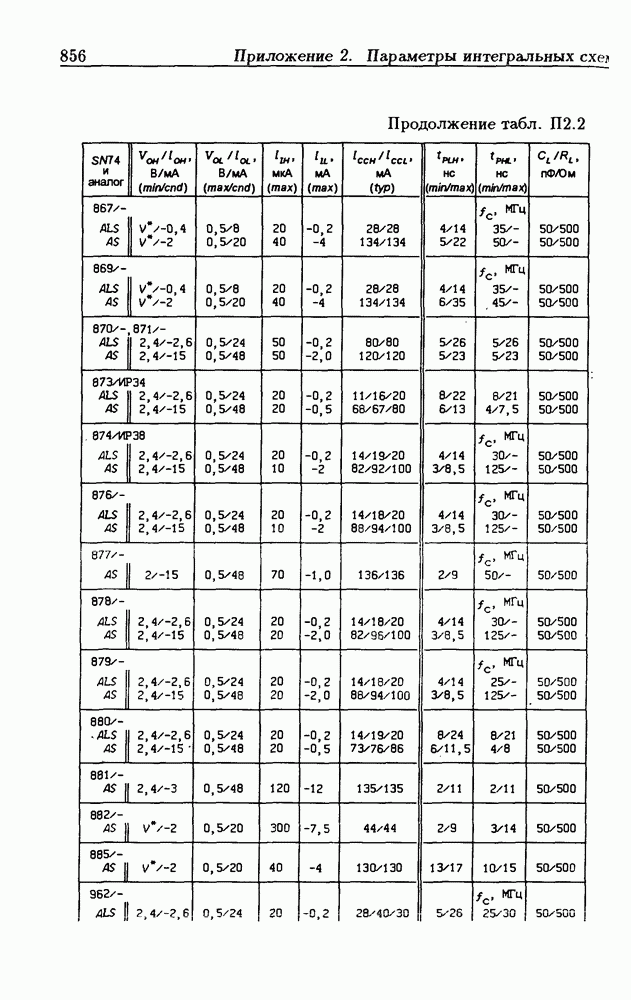
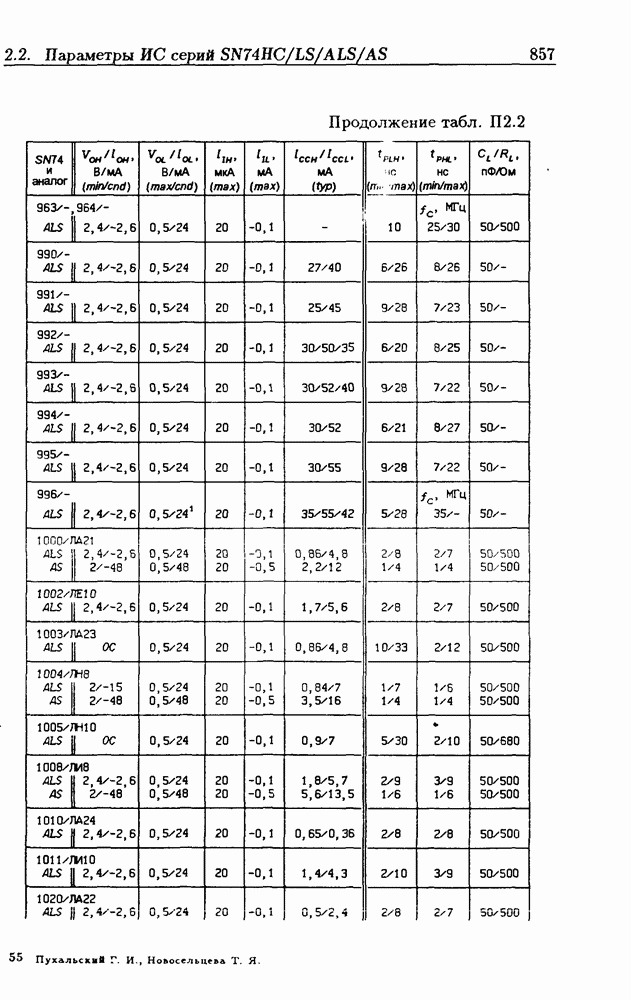
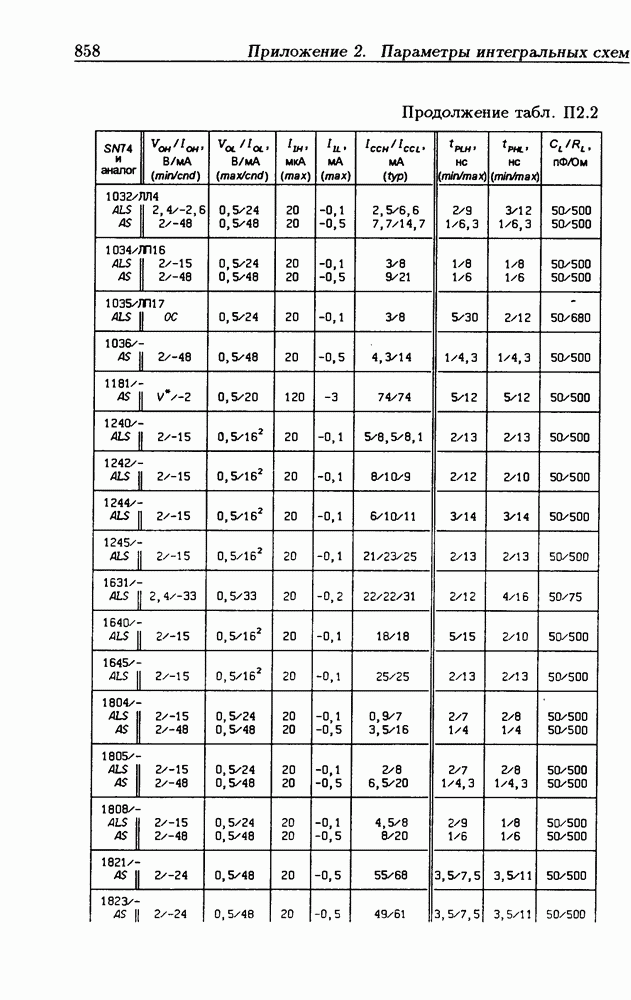
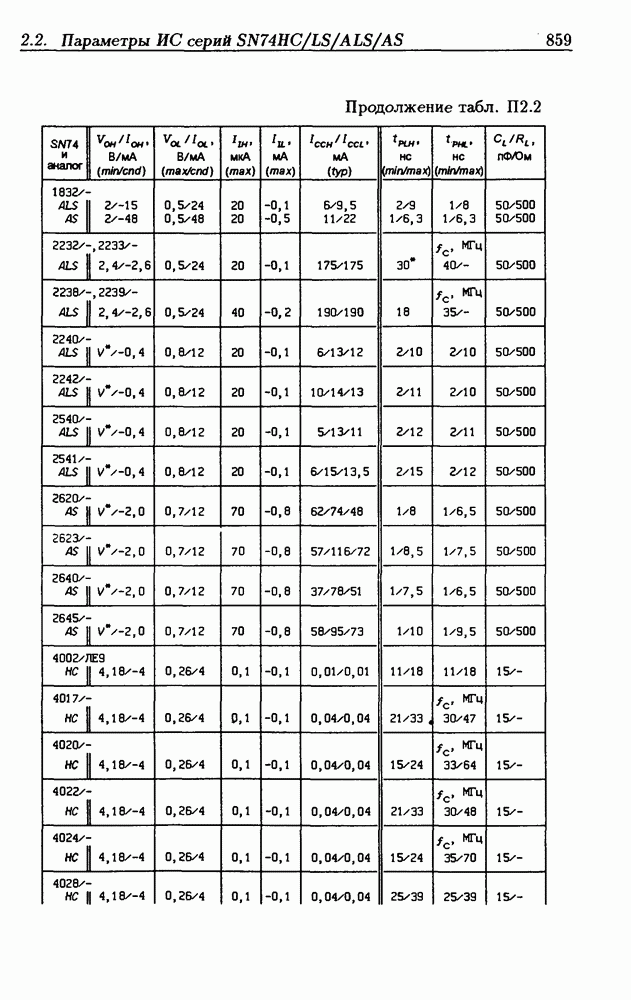
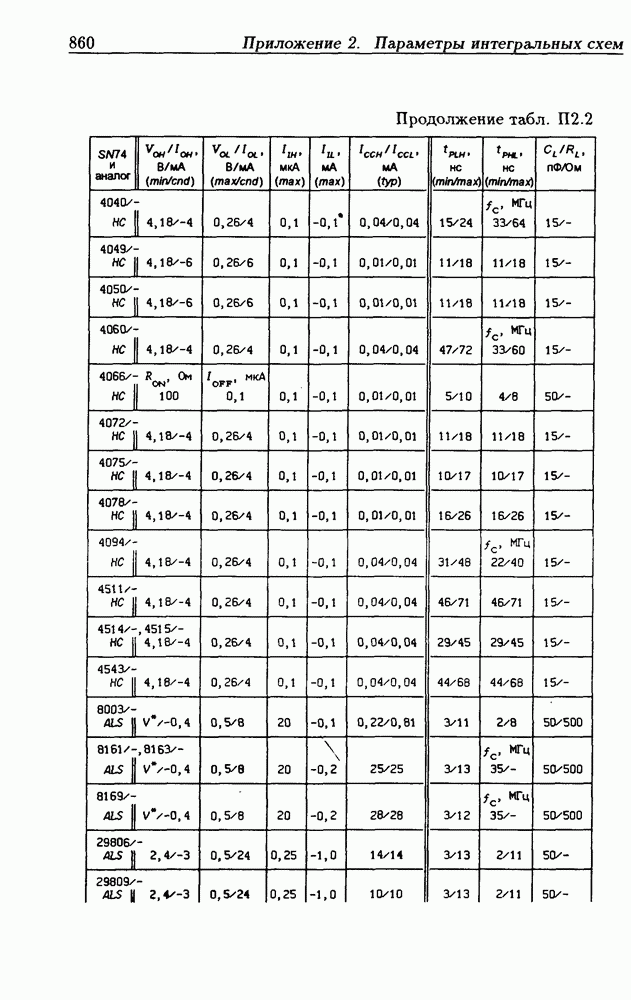
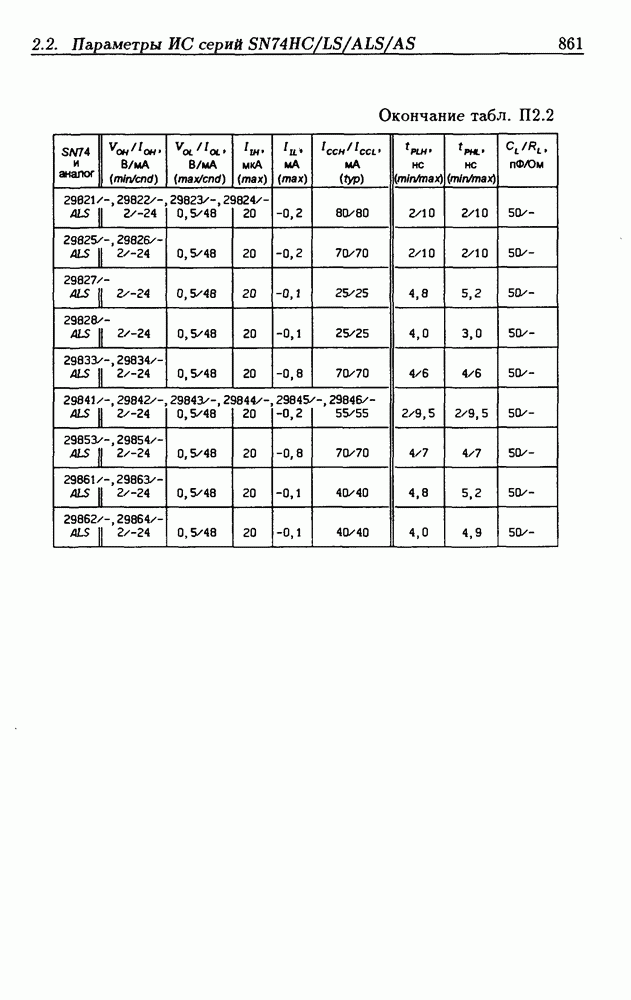
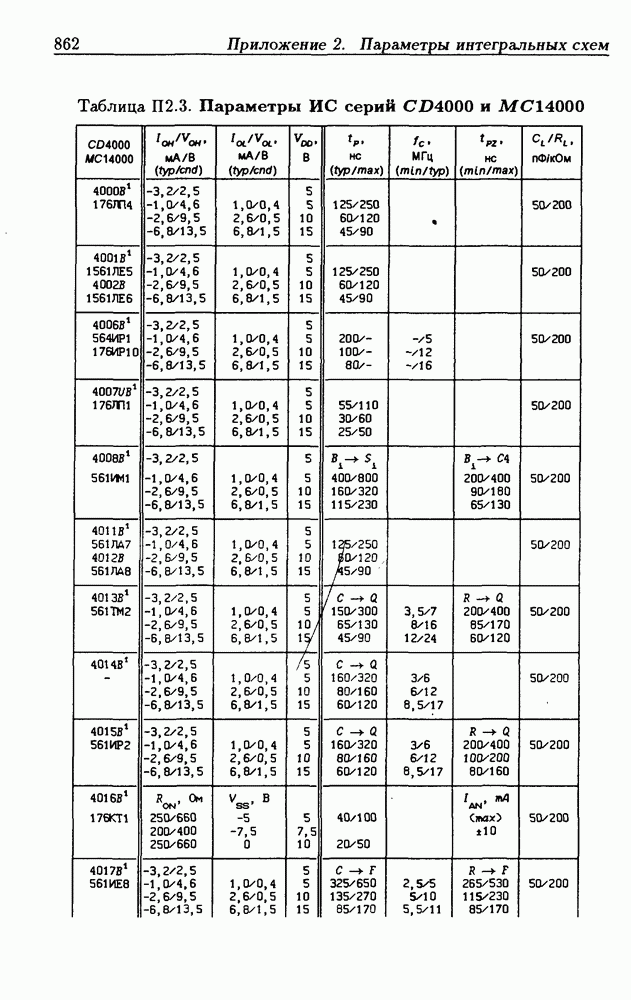
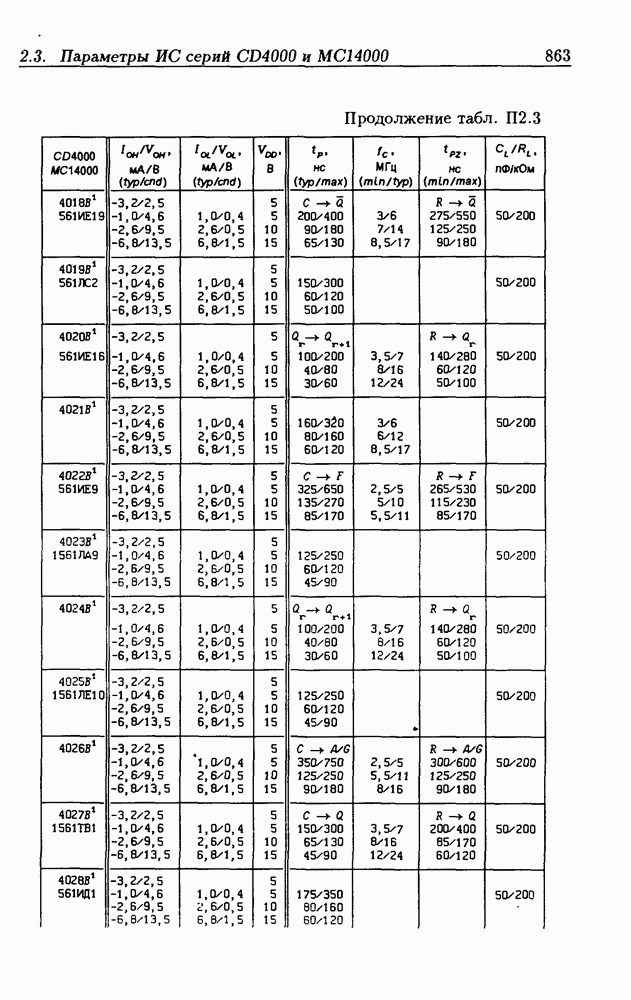
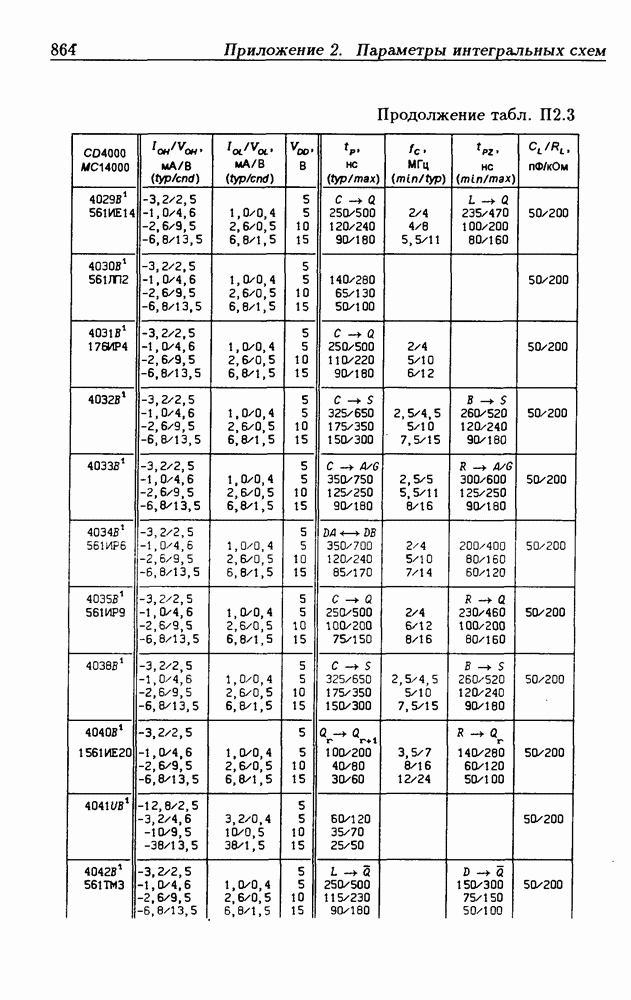
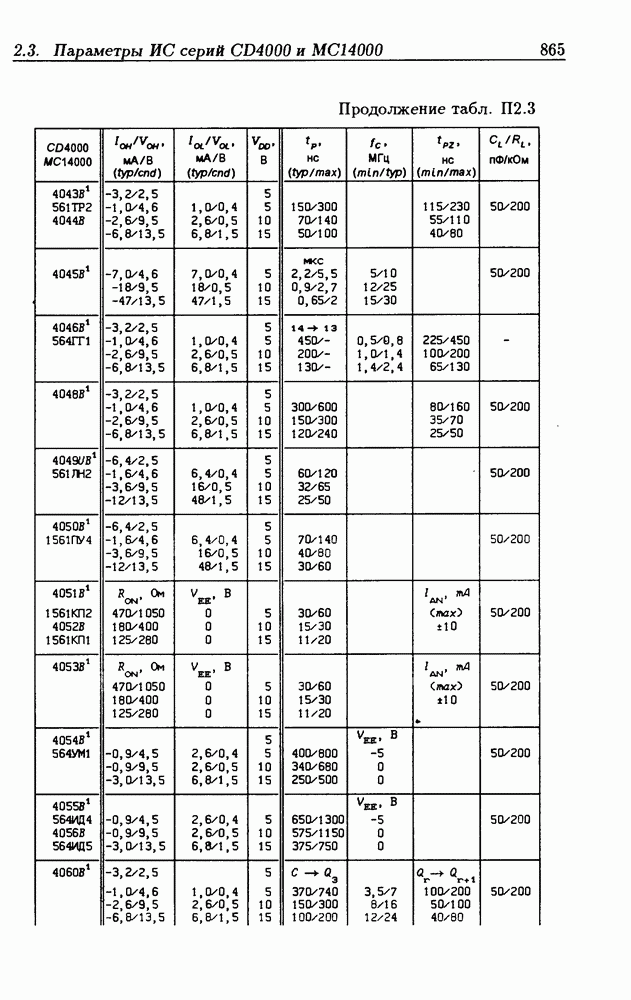
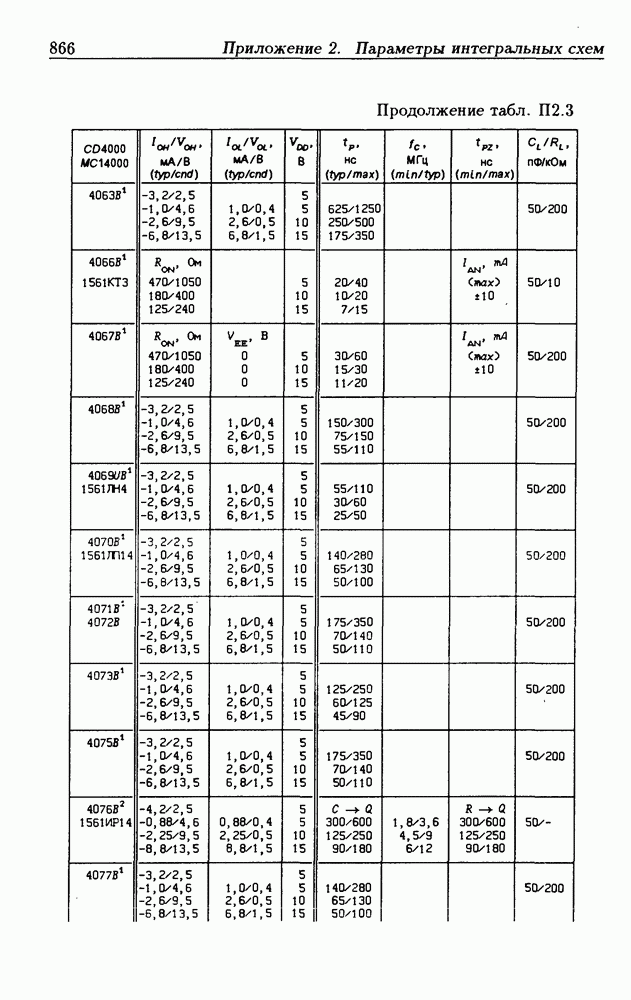
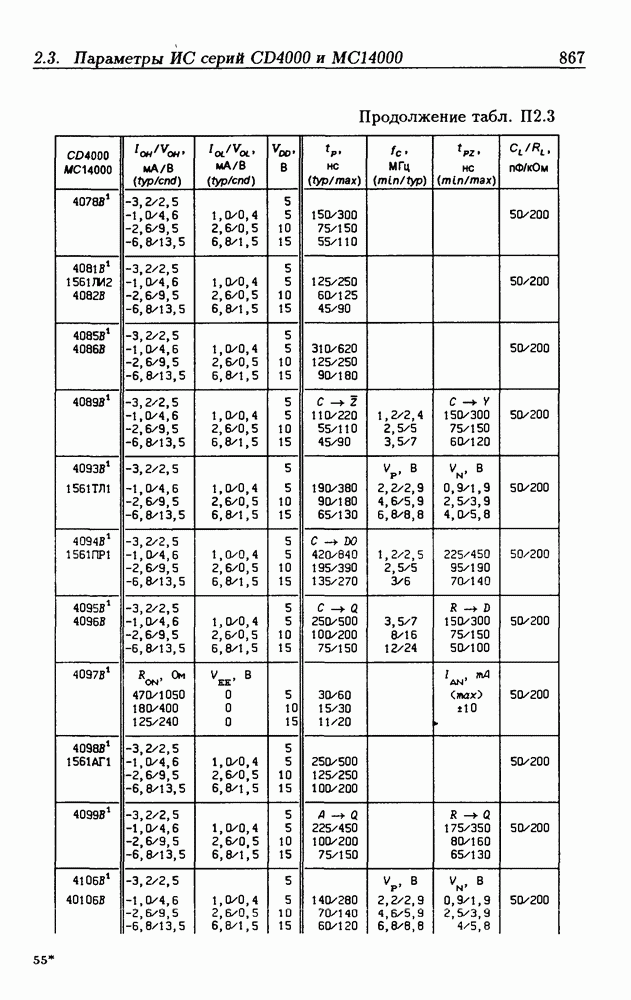
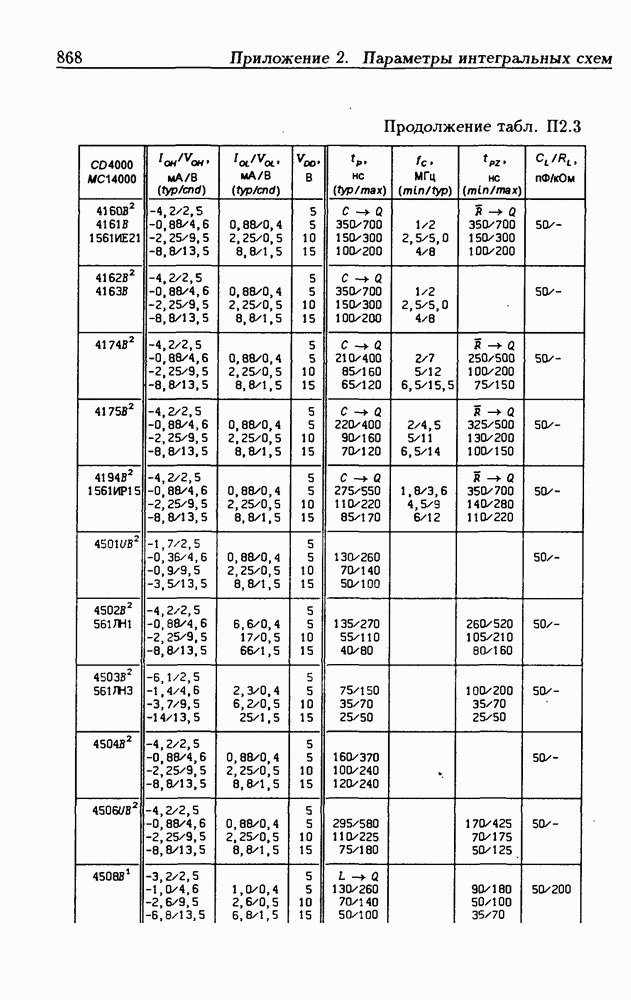
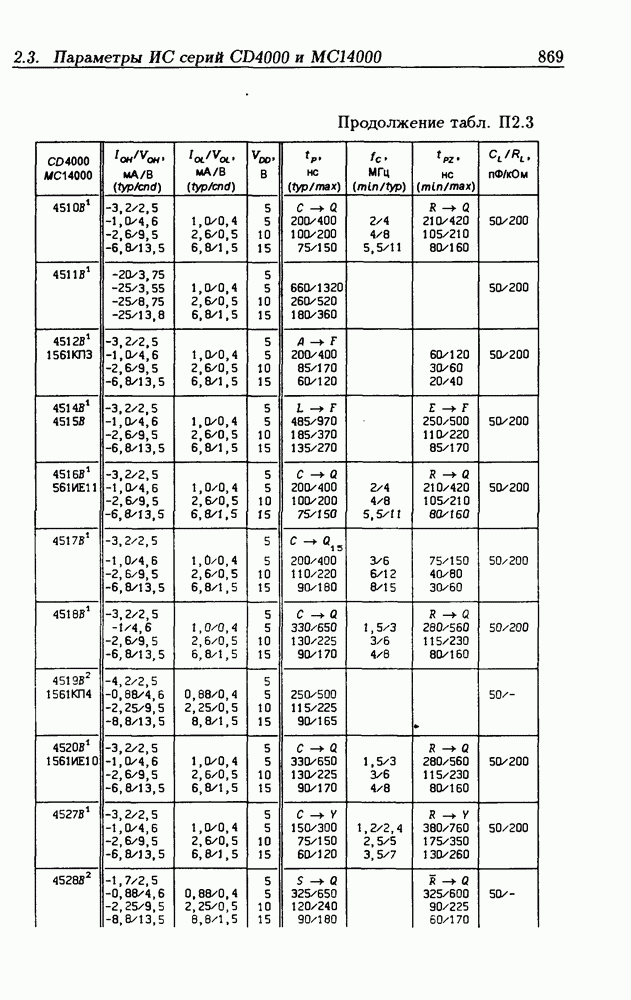
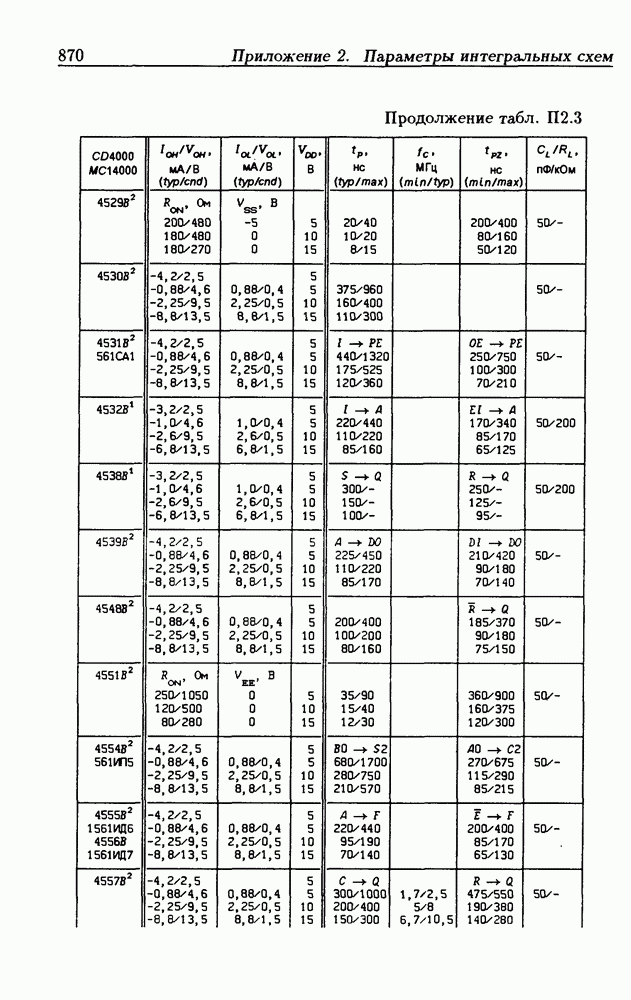
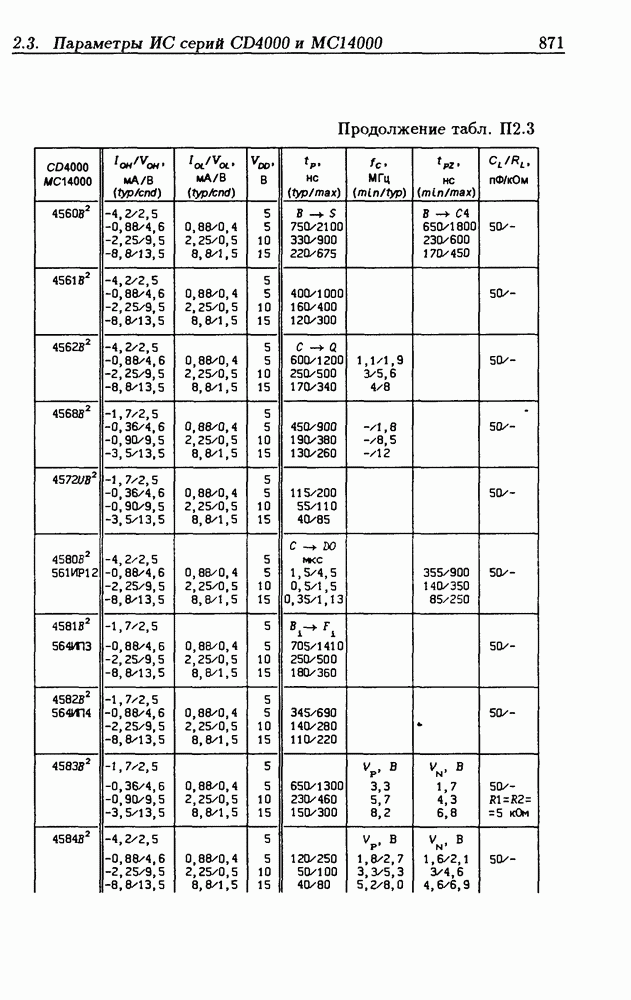
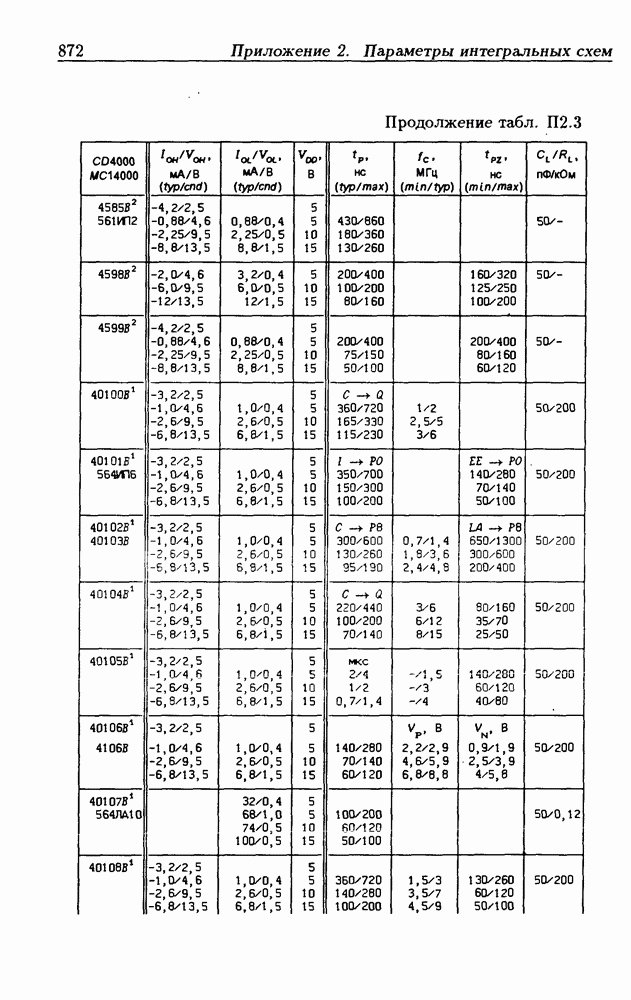
- Приложение 2. Параметры интегральных схем