| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.6. Решение систем логических уравнений
В общем случае равенство  где
где  может задавать не тождество, а логическое уравнение, которое обращается в тождество только при определенных значениях
может задавать не тождество, а логическое уравнение, которое обращается в тождество только при определенных значениях  т. е.
т. е.

Тогда исходное равенство можно рассматривать как уравнение с  неизвестными
неизвестными  Один из методов решения систем логических уравнений приведен в [9]. Рассмотрим универсальный метод решения, пригодный для систем с произвольным числом уравнений и любым числом переменных.
Один из методов решения систем логических уравнений приведен в [9]. Рассмотрим универсальный метод решения, пригодный для систем с произвольным числом уравнений и любым числом переменных.
Системы логических уравнений с одним неизвестным. Пусть задана система логических уравнений с одним неизвестным у

где  Необходимо решить ее относительно у, т. е. найти такие значения
Необходимо решить ее относительно у, т. е. найти такие значения  которые обращают в тождества все уравнения системы (1.40):
которые обращают в тождества все уравнения системы (1.40):

Для этого рассмотрим сначала, какие операции можно выполнять над равенствами без нарушения логических связей, которые они выражают. Если  то
то  , где
, где  — любая двухместная операция алгебры логики:
— любая двухместная операция алгебры логики:  и др. В этом легко убедиться, подставив в правую часть на основании принципа подстановки х вместо у. Однако в общем случае из равенства
и др. В этом легко убедиться, подставив в правую часть на основании принципа подстановки х вместо у. Однако в общем случае из равенства  вовсе не следует, что
вовсе не следует, что  например, из равенства
например, из равенства  не следует, что
не следует, что  а также из равенства
а также из равенства  не следует, что
не следует, что  Поэтому такие операции нельзя применять для преобразования уравнений (1.40).
Поэтому такие операции нельзя применять для преобразования уравнений (1.40).
Возьмем теперь в качестве операции операцию  Из равенства
Из равенства  следует, что
следует, что  Используем еще раз эту операцию:
Используем еще раз эту операцию:

т. е. из равенства  следует, что
следует, что  Итак,
Итак,

а значит, логические связи, выражаемые уравнениями, не нарушаются при преобразовании последних с помощью операции  (в качестве
(в качестве  можно взять и любую из переменных х или
можно взять и любую из переменных х или  На основании (1.42) уравнения (1.40) можно привести к виду
На основании (1.42) уравнения (1.40) можно привести к виду

где  Используя аксиомы (1.2) и (1.3), легко убедиться, что если
Используя аксиомы (1.2) и (1.3), легко убедиться, что если  то а:
то а:  и наоборот: если
и наоборот: если  то
то  т. е.
т. е.

а значит, операцию V можно использовать для преобразования уравнений, правая часть которых равна нулю. На основании (1.44) систему логических уравнений (1.43) можно представить в виде

т. е. любую систему логических уравнений можно свести к одному уравнению  решение которого относительно у и нужно найти.
решение которого относительно у и нужно найти.
Разложив левую часть уравнения (1.45) по у, будем иметь

где

 Решением данного уравнения может быть только некоторая функция
Решением данного уравнения может быть только некоторая функция  от переменных
от переменных  Подставив в уравнение все возможные комбинации значений этих переменных, получим:
Подставив в уравнение все возможные комбинации значений этих переменных, получим:
 произвольная (полностью неопределенная) функция;
произвольная (полностью неопределенная) функция;

 решение не существует или, другими словами, решение имеется только при выполнении условия
решение не существует или, другими словами, решение имеется только при выполнении условия  а значит, при отсутствии решения можно взять произвольное значение
а значит, при отсутствии решения можно взять произвольное значение  (0 или 1).
(0 или 1).
Из сказанного следует, что решение можно представить в виде мультиплексной функции (1.35):

Если положить  то
то

причем решение (1.47) существует лишь при выполнении условия

Подстановка решения (1.47) в уравнение (1.46) дает

т. е., действительно, при выполнении условия (1.48) левая часть уравнения (1.46) обращается в нуль, и решение  некоторая функция переменных
некоторая функция переменных 
Если функция  то решение
то решение  полностью определенная функция (существует единственное решение). Если
полностью определенная функция (существует единственное решение). Если  то
то  полностью неопределенная функция. Это означает, что решаемое уравнение является тождеством, так как оно выполняется при любых значениях переменных
полностью неопределенная функция. Это означает, что решаемое уравнение является тождеством, так как оно выполняется при любых значениях переменных 
В общем случае решение  где
где  — 0 или 1 в точках, в которых функция
— 0 или 1 в точках, в которых функция  а в остальных точках
а в остальных точках  т.е. решением является неполностью определенная функция, которой соответствут целый класс полностью определенных функций.
т.е. решением является неполностью определенная функция, которой соответствут целый класс полностью определенных функций.
Несмотря на кажущуюся сложность выражения (1.47), его достаточно просто применять при решении многих практических задач. Это связано с тем, что при решении вместо неизвестных в уравнения подставляются константы 0 и 1.
Пример 1. Доказать тождество  Решим уравнение относительно
Решим уравнение относительно 

(при выполнении этих вычислений упрощение функций  можно производить только по отдельности). Решение существует, так как
можно производить только по отдельности). Решение существует, так как  Дальнейшее упрощение полученного решения дает:
Дальнейшее упрощение полученного решения дает:  уравнение справедливо для произвольных значений х независимо от значений остальных переменных, а значит, является тождеством.
уравнение справедливо для произвольных значений х независимо от значений остальных переменных, а значит, является тождеством.
Из данного примера следует общий вывод: разработанный метод решения логических уравнений можно использовать в качестве универсального метода для доказательства любых теорем и тождеств алгебры логики, формулируемых в виде равенств логических выражений (решением логического уравнения должна быть полностью неопределенная функция 
Пример 2. Найдем решение уравнения 

следовательно, решение отсутствует.
Пример 3. Найдем решение уравнения 

т. е. имеется единственное решение 
Пример 4. Докажем высказанное в начале данного раздела утверждение, что из равенства  не следует, что
не следует, что  Для этого решим первое равенство относительно у:
Для этого решим первое равенство относительно у:

поэтому  т. е.
т. е. 
Пример 5. Докажем теорему, утверждающую, что если  Для этого решим систему двух логических уравнений относительно у:
Для этого решим систему двух логических уравнений относительно у:

так как  Действительно, получили, что
Действительно, получили, что 
Алгебраическое представление логических уравнений. Если символы 0 и 1 считать числами, то все логические операции можно заменить на арифметические операции или алгебраические формулы на основании очевидных соотношений

(в левой части используются логические переменные и операции, а в правой — алгебраические). Так, можно получить

(здесь знаки конъюнкции  и алгебраического умножения х заменены точками — какая из этих операций используется, устанавливается по другим имеющимся в выражении операциям).
и алгебраического умножения х заменены точками — какая из этих операций используется, устанавливается по другим имеющимся в выражении операциям).
На основании приведенных соотношений логическое уравнение (1.46) преобразуется в алгебраическое

решением которого будет  Легко заметить, что при
Легко заметить, что при  решения не существует и
решения не существует и  при
при 
Системы логических уравнений с более чем одним неизвестным. Решение систем логических уравнений с двумя неизвестными

где  неизвестные,
неизвестные,  сводится к их последовательному решению относительно неизвестных
сводится к их последовательному решению относительно неизвестных  При этом следует найти такие функции
При этом следует найти такие функции  что
что

Решив систему (1.49) относительно у в соответствии с (1-47) и (1.48), получим:

где

Если функция  это означает, что решение системы (1.49) относительно у существует независимо от значений
это означает, что решение системы (1.49) относительно у существует независимо от значений  Поэтому можно взять
Поэтому можно взять  Тогда, подставив это значение
Тогда, подставив это значение  в (1.50), получим:
в (1.50), получим:

Рассмотрим случай, когда функция  Так как условием существования решения системы логических уравнений (1.49) относительно у является уравнение
Так как условием существования решения системы логических уравнений (1.49) относительно у является уравнение  то, возможно, оно будет удовлетворено соответствующим выбором неизвестного
то, возможно, оно будет удовлетворено соответствующим выбором неизвестного  Поэтому нужно найти относительно него решение уравнения
Поэтому нужно найти относительно него решение уравнения 

которое существует только в том случае, если выполняется условие

где  и
и  независимая от
независимая от  полностью неопределенная функция. Если данное условие выполняется, то решение системы логических уравнений (1.49) относительно у находится подстановкой в функцию (1.50) найденного значения
полностью неопределенная функция. Если данное условие выполняется, то решение системы логических уравнений (1.49) относительно у находится подстановкой в функцию (1.50) найденного значения 

В результате получены функции  не зависящие от неизвестных
не зависящие от неизвестных 
Таким образом, решение системы логических уравнений с двумя неизвестными сводится к последовательному решению одного или двух уравнений с одним неизвестным. Точно так же решаются системы логических уравнений и с большим числом неизвестных.
В общем случае в зависимости от порядка решения систем логических уравнений относительно неизвестных получаются различные формы функций. Однако все эти формы являются эквивалентными, т.е. различным формам полученных неполностью определенных функций соответствует один и тот же класс полностью определенных функций.
Пример 1. Решим относительно неизвестных у и 2 уравнение

Найдем решение уравнения сначала относительно у:

поэтому решаем уравнение  относительно z:
относительно z:

Значит,  и
и

Легко убедиться, что при подстановке в исходное уравнение найденных значений  оно обращается в тождество.
оно обращается в тождество.
Пример 2. Найдем решение уравнения

относительно у.

Легко убедиться, что  поэтому решаем уравнение
поэтому решаем уравнение

относительно 

Так как  то решение исходного уравнения существует.
то решение исходного уравнения существует.
Подставив найденное значение  в выражение для у, получим:
в выражение для у, получим:

Если решить исходное уравнение относительно неизвестных в другом порядке, то функции  будут иметь вид:
будут иметь вид:

Сравнив решения (1.52) и (1.53), легко заметить, что полностью определенные части у них одинаковые. Решения для  зависимые, Так как полностью неопределенная функция
зависимые, Так как полностью неопределенная функция  входит в оба решения. Поэтому решением уравнения (1-51) будет зависимая пара функций
входит в оба решения. Поэтому решением уравнения (1-51) будет зависимая пара функций  По выражениям (1.52) или (1.53) (результат получается один и тот же) легко вычислить значения этой пары в точках
По выражениям (1.52) или (1.53) (результат получается один и тот же) легко вычислить значения этой пары в точках 

Из полученных значений можно составить класс из  полностью определенных пар функций
полностью определенных пар функций  В качестве конкретного решения можно взять любую из этих пар.
В качестве конкретного решения можно взять любую из этих пар.
Пример 3. Найдем решение уравнения  относительно у:
относительно у:

Далее решаем уравнение

относительно 

Так как  то логическое уравнение решений не имеет.
то логическое уравнение решений не имеет.
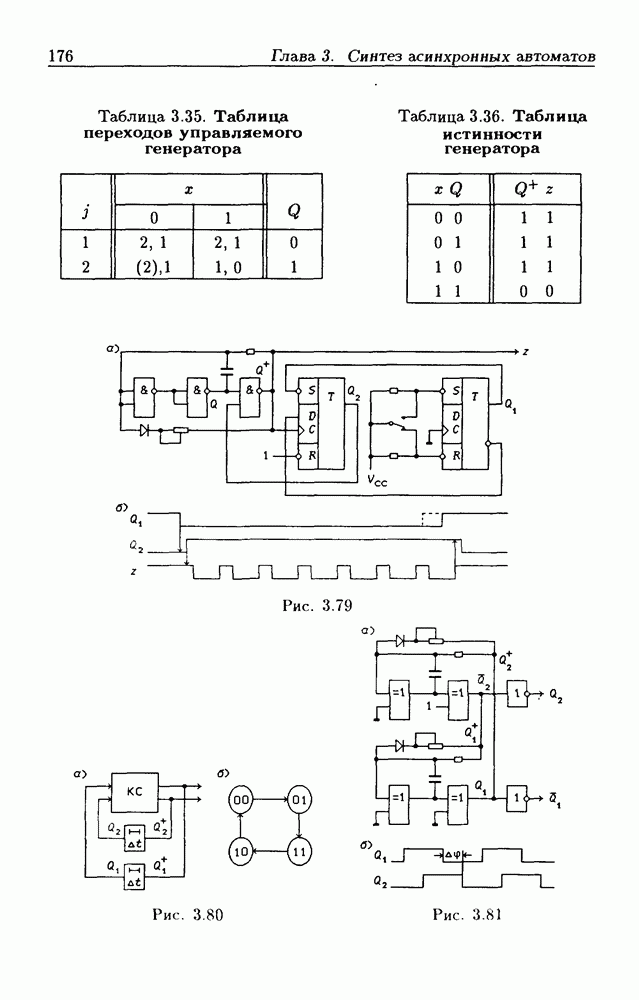
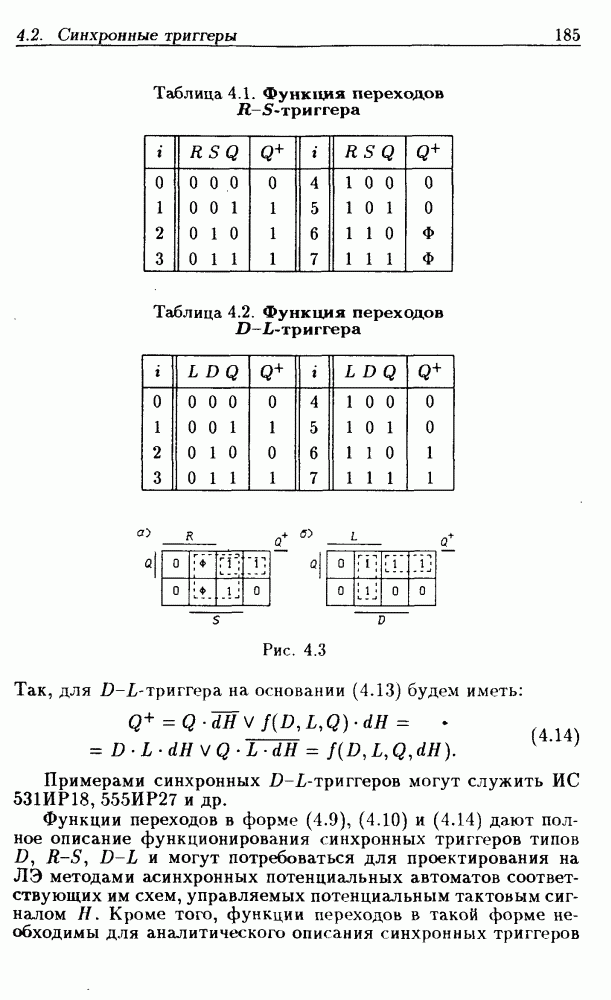
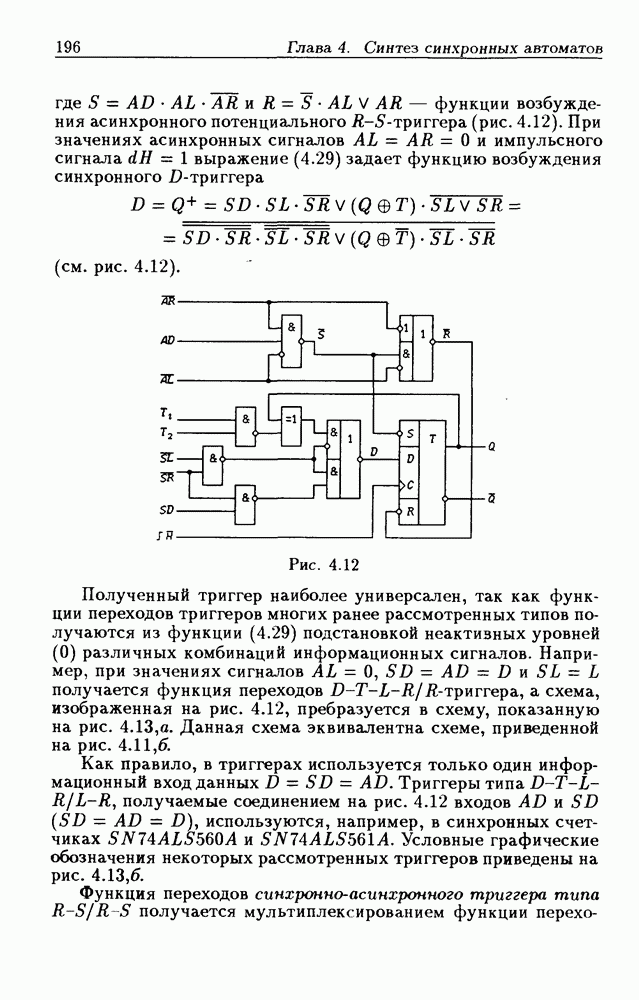
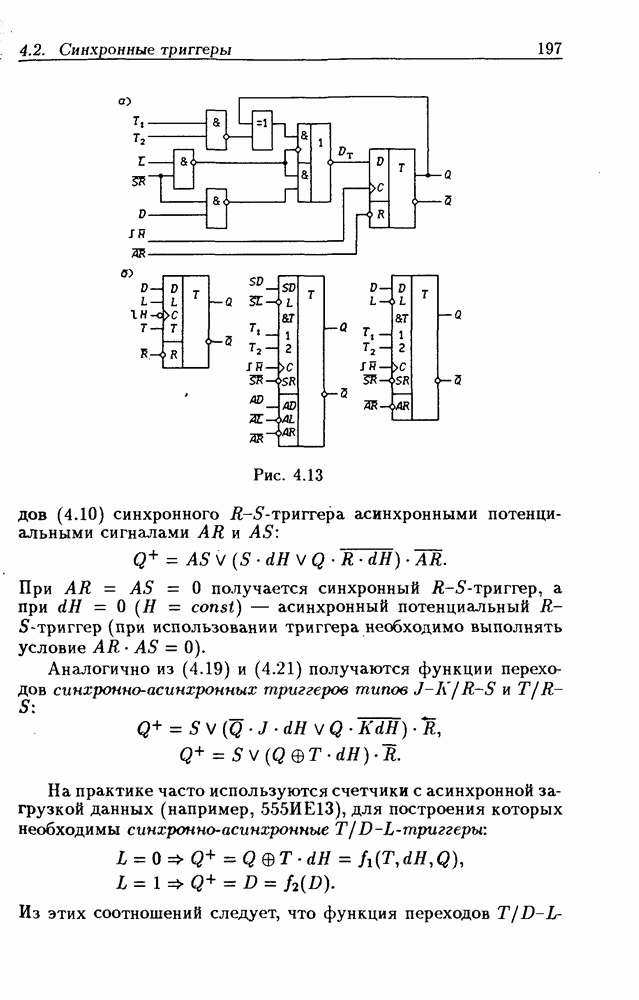
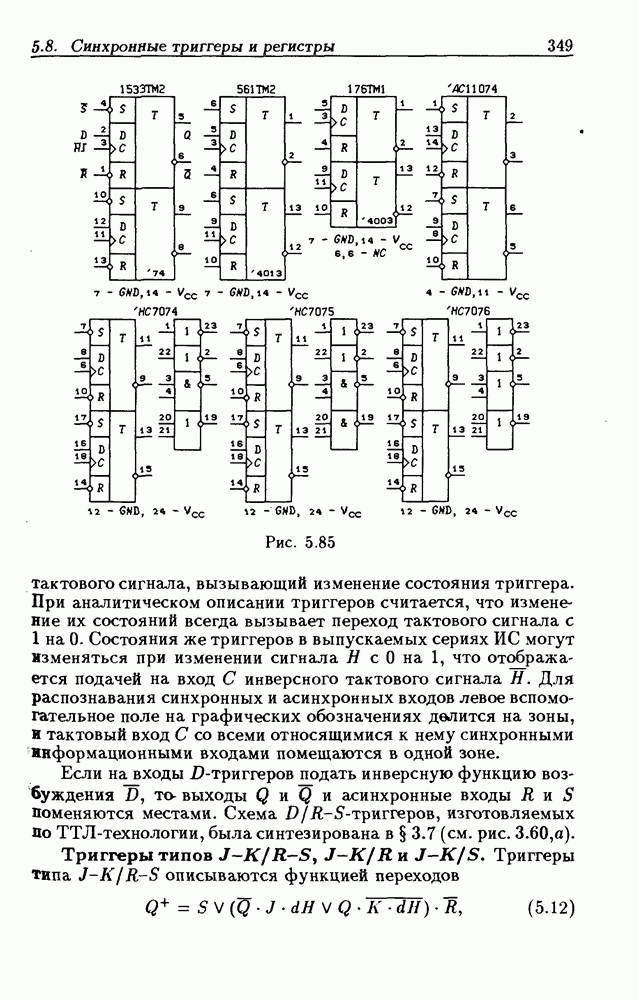
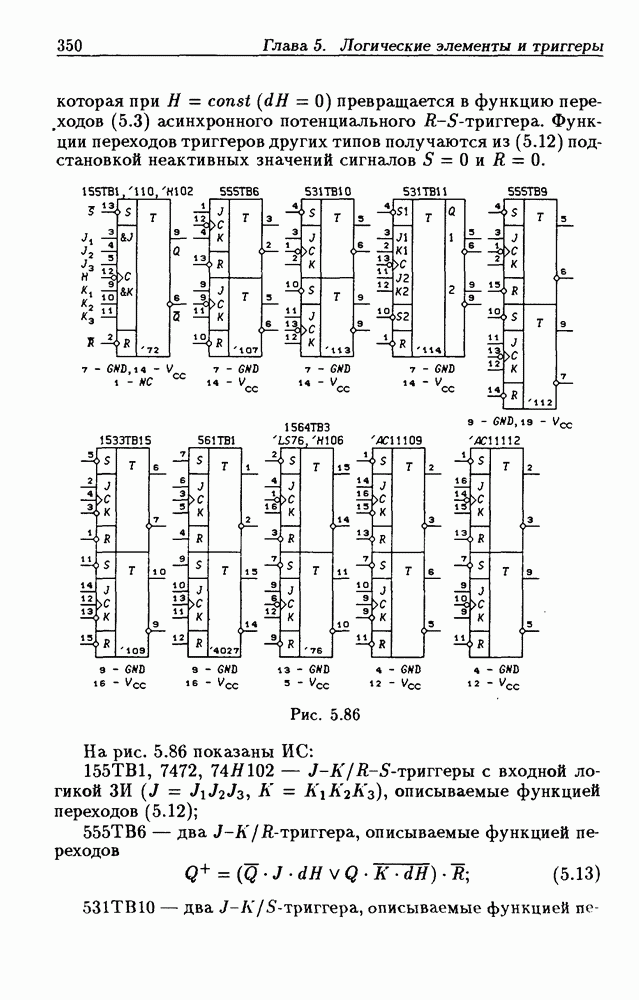
Приложения систем логических уравнений. Разработанный метод решения систем логических уравнений является мощным инструментом для анализа (см. гл. 2) и синтеза (см. гл. 3) логических схем, широко используемых на практике при проектировании цифровых устройств. Так, он был применен при разработке общего метода структурного синтеза цифровых автоматов на триггерах типов  и др. [10, 11]. Перечисленные триггеры описываются функциями переходов
и др. [10, 11]. Перечисленные триггеры описываются функциями переходов


где  и
и  входные сигналы триггеров,
входные сигналы триггеров,  исходное состояние триггера,
исходное состояние триггера,  следующее состояние триггера (после воздействия входных сигналов). Триггеры типов
следующее состояние триггера (после воздействия входных сигналов). Триггеры типов  могут быть только синхронными, а типов
могут быть только синхронными, а типов  и
и  как синхронными, так и асинхронными потенциальными.
как синхронными, так и асинхронными потенциальными.
При проектировании автоматов в виде таблицы задается функциональная связь между исходным состоянием триггера  и следующим его состоянием
и следующим его состоянием  (переменные в алгебре логики не зависят от времени, поэтому
(переменные в алгебре логики не зависят от времени, поэтому  разные переменные). Основная задача проектирования заключается в отыскании функций возбуждения триггеров
разные переменные). Основная задача проектирования заключается в отыскании функций возбуждения триггеров  и
и  реализующих эту функциональную связь. Для этого следует найти решения функций переходов (1.54) - (1-57) относительно неизвестных функций возбуждения, выразив их через переменные
реализующих эту функциональную связь. Для этого следует найти решения функций переходов (1.54) - (1-57) относительно неизвестных функций возбуждения, выразив их через переменные 
Триггер типа  Решение уравнения (1-54) относительно Т:
Решение уравнения (1-54) относительно Т:

Для отыскания данной функции возбуждения можно воспользоваться и более простым методом — применить операцию  к левой и правой частям уравнения относительно переменной
к левой и правой частям уравнения относительно переменной 

Триггер типа  Решение уравнения (1.55) относительно
Решение уравнения (1.55) относительно 

Приравняв последнее уравнение нулю, находим:

Подставив найденное значение К в функцию для  получим:
получим:

Триггер типа  Решение системы уравнений (1.56) относительно
Решение системы уравнений (1.56) относительно 

Приравняв последнее уравнение нулю, находим:

Подставив найденное значение  в функцию для
в функцию для  получим:
получим:

Триггер типа  Решение уравнения (1-57) сначала относительно
Решение уравнения (1-57) сначала относительно  а затем относительно
а затем относительно  дает:
дает:

Наиболее часто для проектирования цифровых автоматов формальными методами используются триггеры типов  и
и  функции возбуждения которых
функции возбуждения которых

Функции возбуждения  -триггера (1.58) использовать значительно сложнее, чем функции (1.59) - (1.61), так как они взаимозависимы (полностью неопределенная функция
-триггера (1.58) использовать значительно сложнее, чем функции (1.59) - (1.61), так как они взаимозависимы (полностью неопределенная функция  входит и в
входит и в  Методика синтеза автоматов на
Методика синтеза автоматов на  -триггерах изложена в [10].
-триггерах изложена в [10].
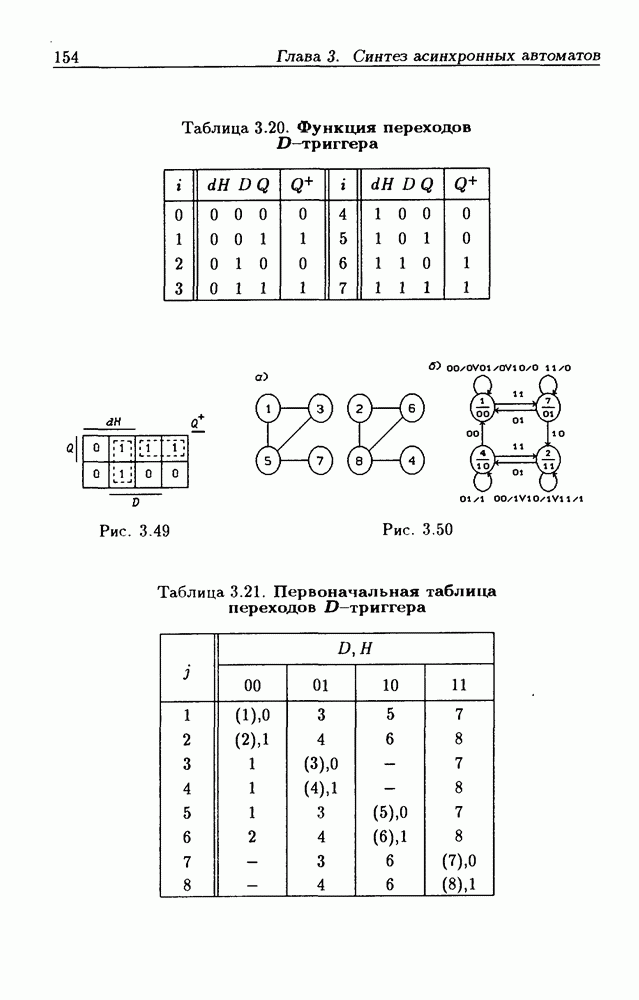
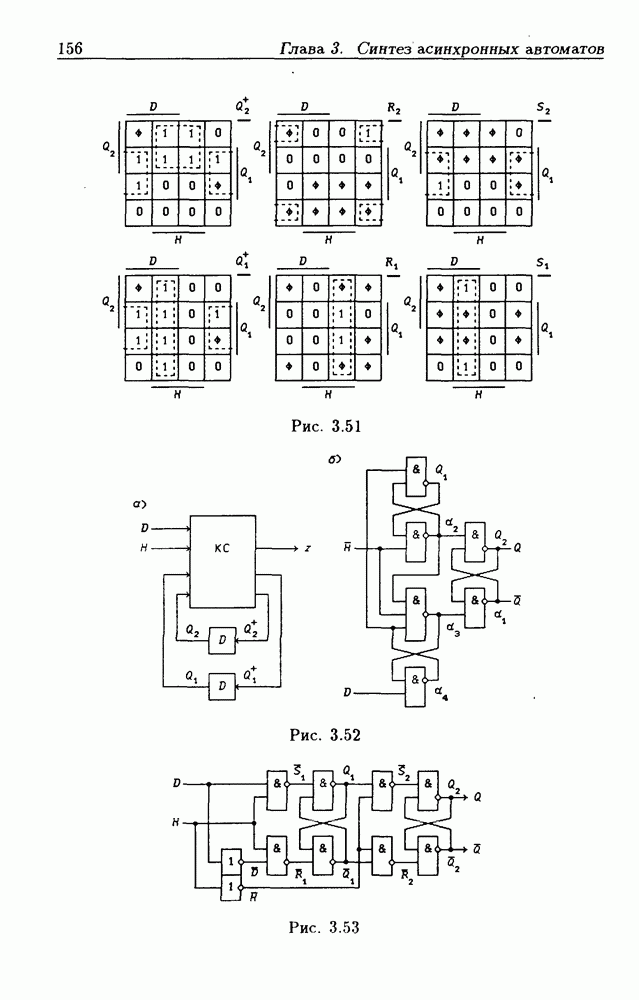
Триггер типа  Рассмотрим пример решения уравнения
Рассмотрим пример решения уравнения

с тремя неизвестными  и
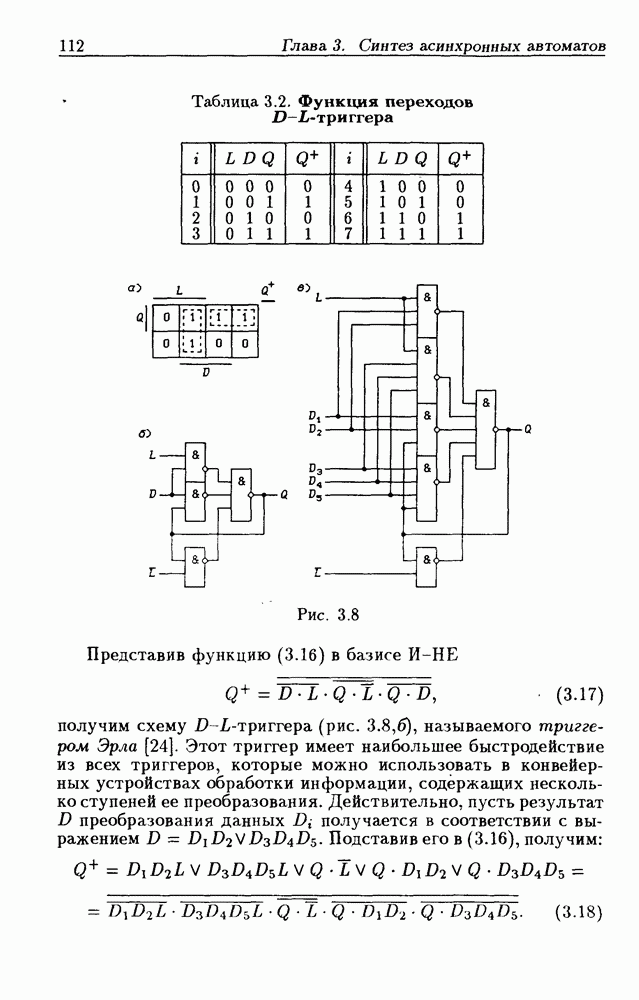
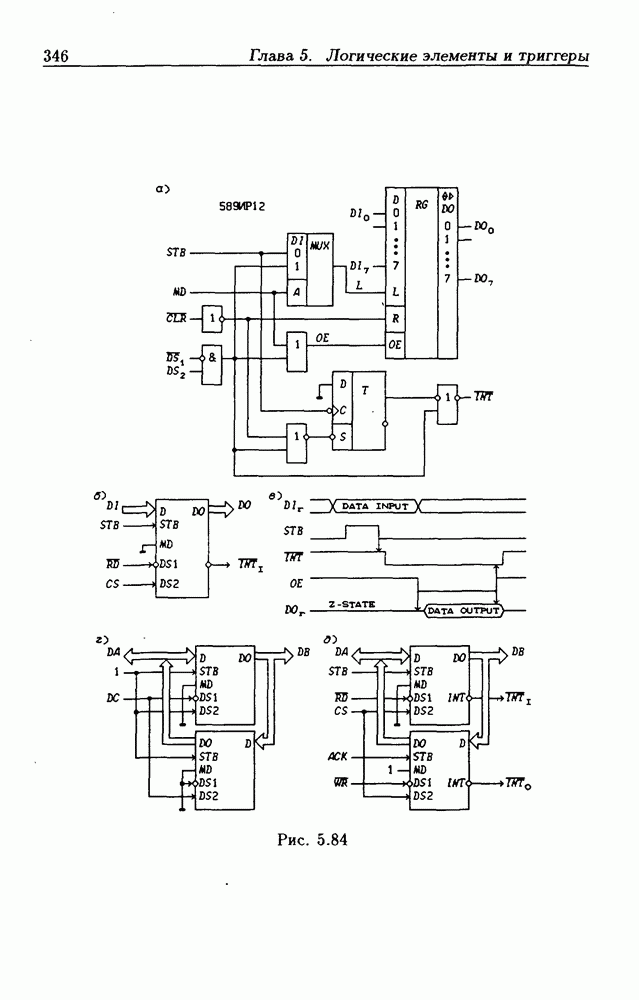
и  которое представляет собой функцию переходов D-L-триггера. Решение относительно
которое представляет собой функцию переходов D-L-триггера. Решение относительно  дает
дает

Решив уравнение

относительно  получим:
получим:

Из этого следует уравнение

решением которого является  Подставив найденное значение
Подставив найденное значение  в функцию
в функцию  а затем
а затем  в функцию
в функцию  окончательно получим:
окончательно получим:

Решение  означает, что триггер может быть использован для синтеза автоматов и при исключении входа
означает, что триггер может быть использован для синтеза автоматов и при исключении входа  подачей на него значений 0 или 1. При значении
подачей на него значений 0 или 1. При значении  функции возбуждения
функции возбуждения 
(вход D не используется) и  а при
а при  функции
функции  не используется), что полностью соответствует мультиплексной относительно сигнала
не используется), что полностью соответствует мультиплексной относительно сигнала  функции переходов
функции переходов  -триггера. Таким образом,
-триггера. Таким образом,  -триггер обладает избыточностью в числе информационных входов, а значит и большей универсальностью по отношению к триггерам других типов.
-триггер обладает избыточностью в числе информационных входов, а значит и большей универсальностью по отношению к триггерам других типов.
Приведенные методы решения систем логических уравнений можно применять и при решении задач теории множеств.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Основы теории переключательных функций
- 1.2. Позиционные системы счисления
- 1.3. Переключательные функции
- 1.4. Принцип и закон двойственности
- 1.5. Теоремы разложения
- 1.6. Решение систем логических уравнений
- 1.7. Первичные термы, минтермы и макстермы
- 1.8. Совершенные нормальные формы представления функций
- 1.9. Конъюнктивные и дизъюнктивные термы
- 1.10. Минимизация переключательных функций
- 1.11. Диаграммы Вейча
- 1.12. Минимизация неполностью определенных функций, совместная минимизация нескольких функций
- 1.13. Скобочные формы функций
- 1.14. Закон двойственности для логических схем
- 1.15. Линейные функции
- Глава 2. Анализ и синтез логических схем
- 2.2. Модели логических элементов
- 2.3. Модели логических схем
- 2.4. Анализ логических схем
- 2.5. Синтез комбинационных схем, свободных от состязаний
- Глава 3. Синтез асинхронных потенциальных автоматов
- 3.2. Асинхронные потенциальные автоматы
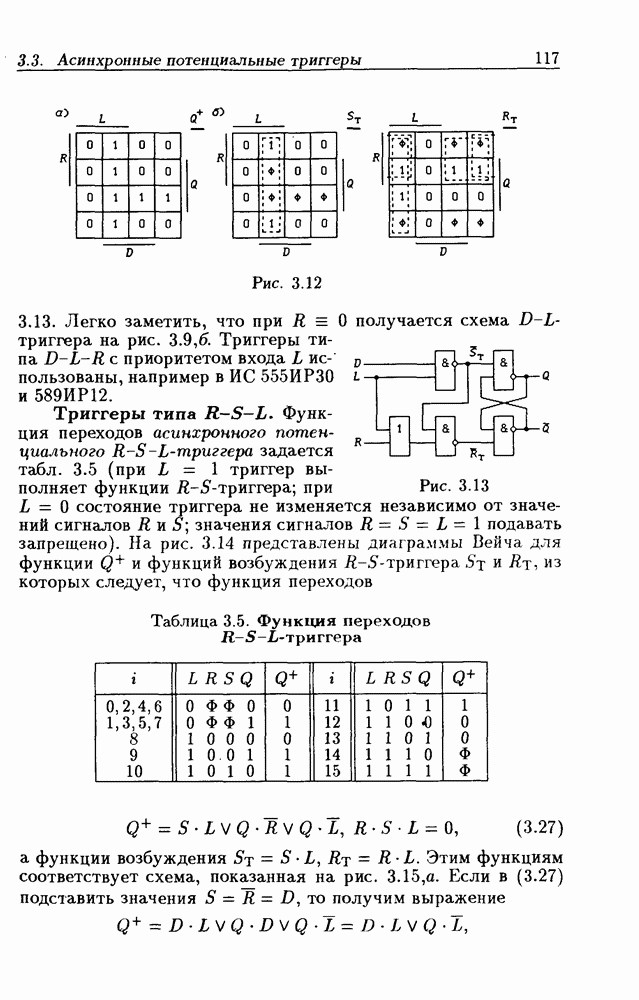
- 3.3. Асинхронные потенциальные триггеры и элементы памяти
- Триггеры типа R-S
- Триггеры типа D-L
- Триггеры типа D-L-R с приоритетом входа R.
- Триггеры типа D-L-R с приоритетом входа L.
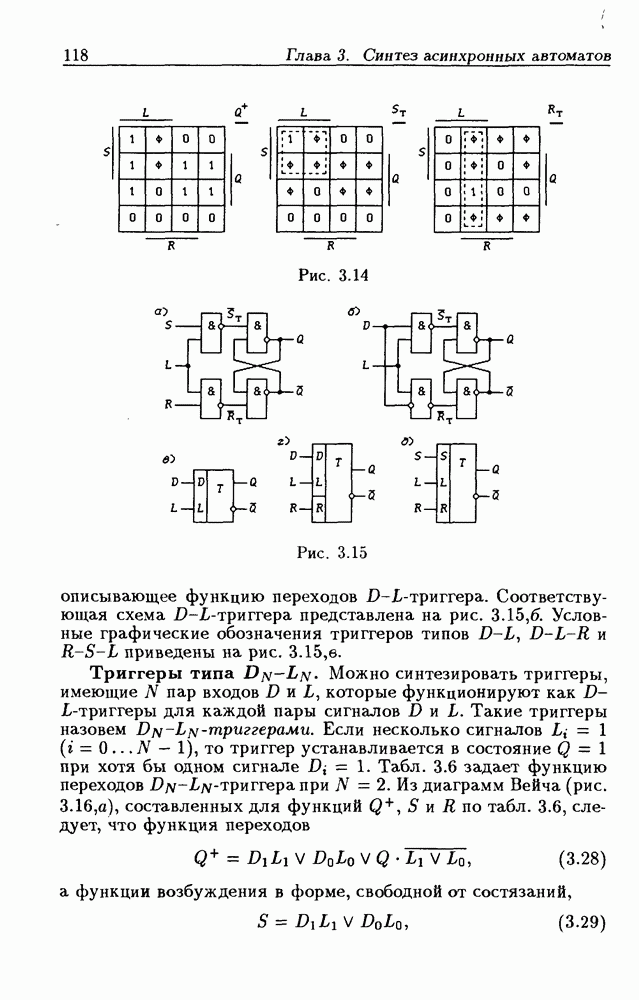
- Триггеры типа R-S-L.
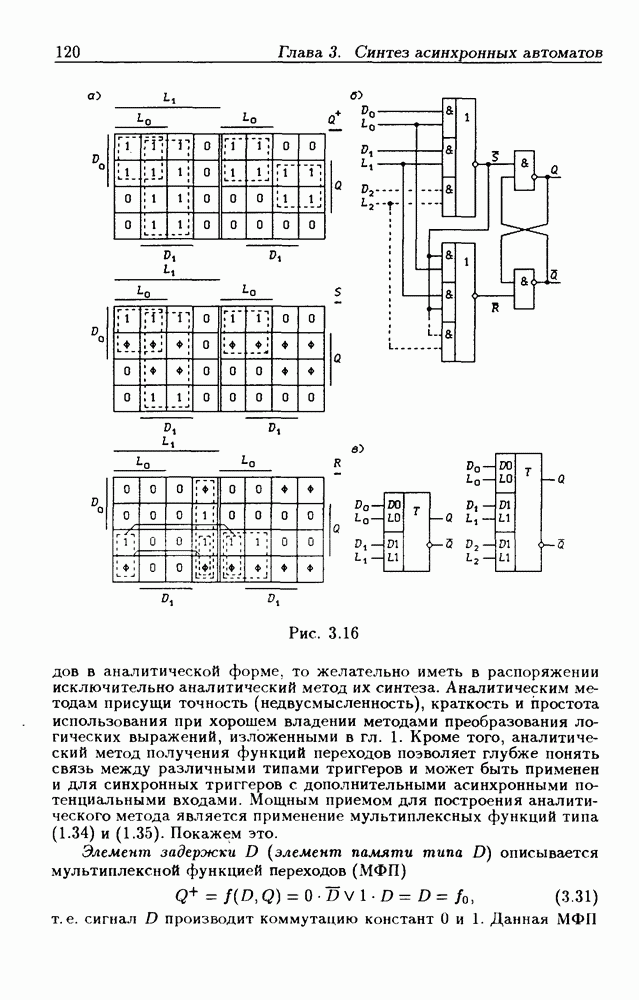
- Триггеры типа DN-LN
- Аналитический метод синтеза и анализа триггеров.
- 3.4. Задание асинхронных потенциальных автоматов таблицами и графами переходов
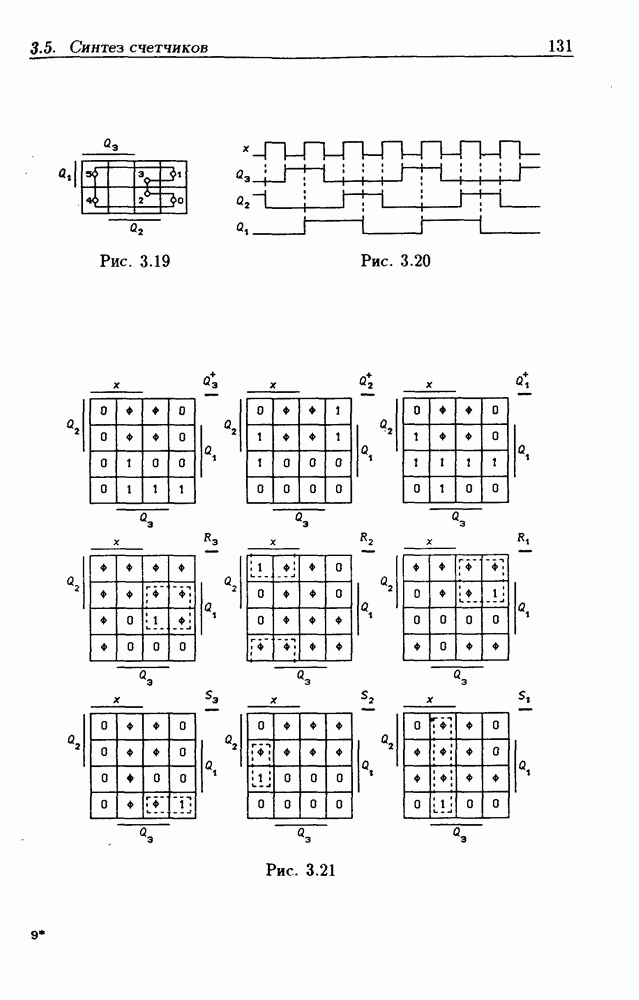
- 3.5. Синтез асинхронных потенциальных счетчиков
- 3.6. Синтез асинхронных импульсных триггеров
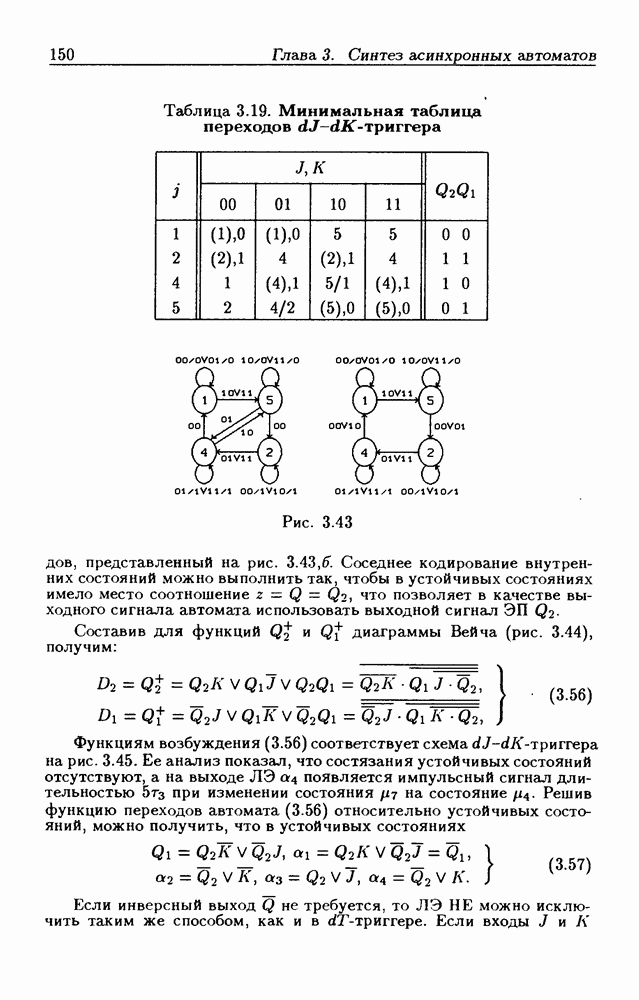
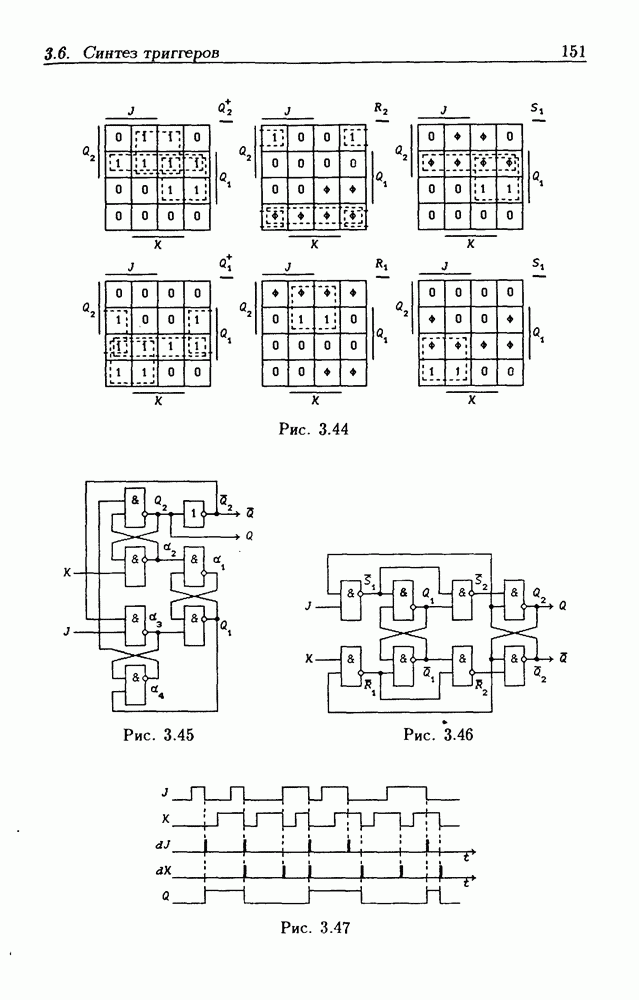
- Триггеры типа dJ-dK.
- Классификация триггеров.
- 3.7. Синтез синхронных триггеров
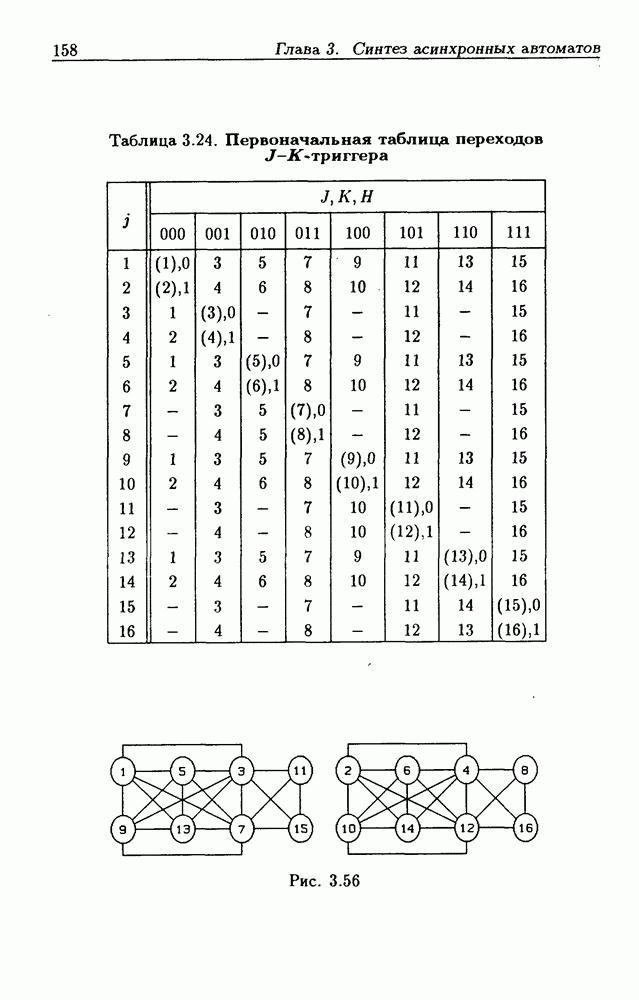
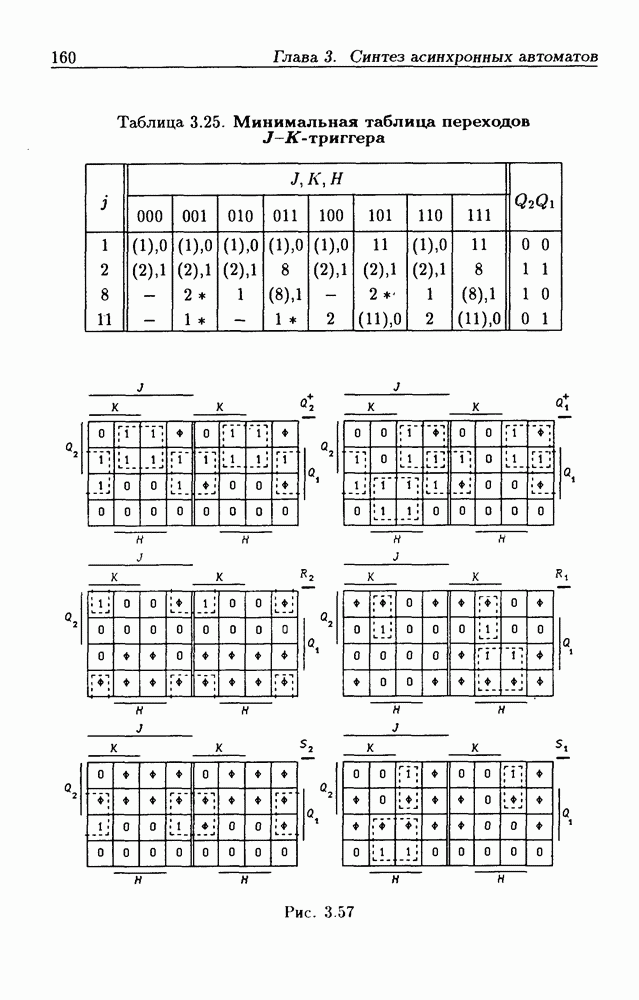
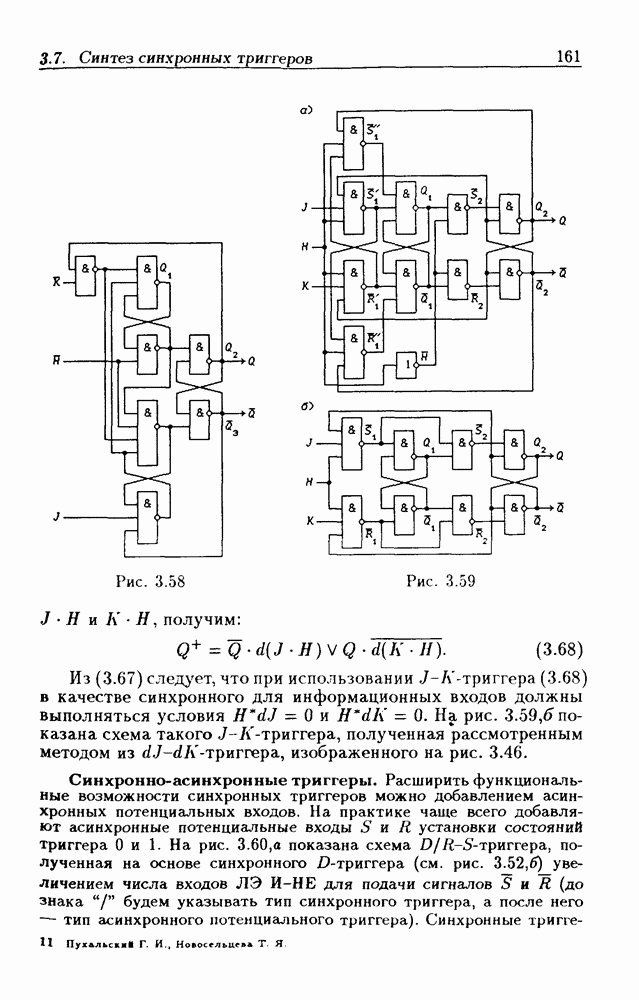
- Триггеры типа J-K
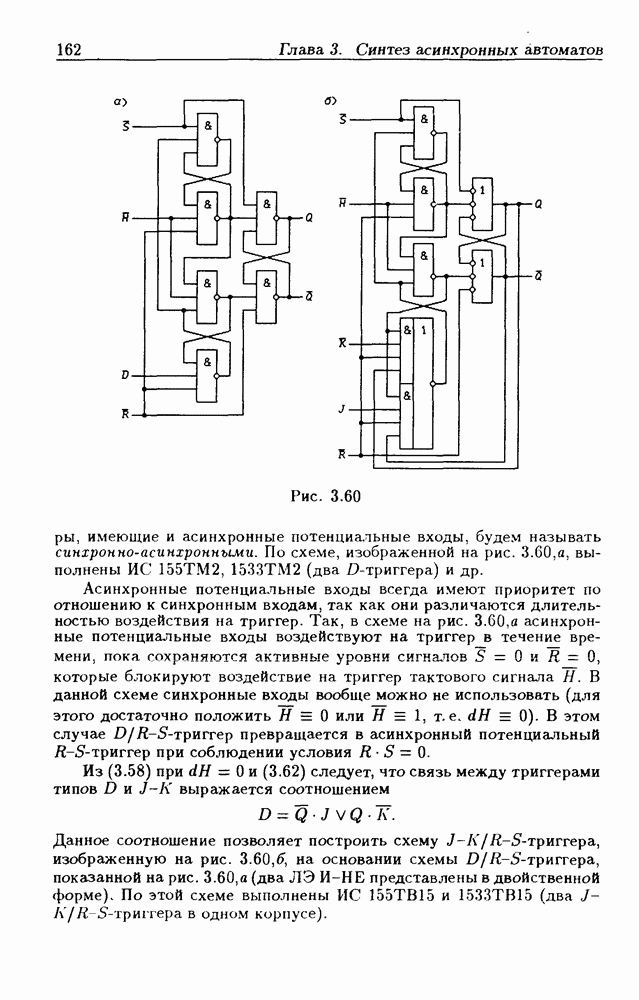
- Синхронно-асинхронные триггеры.
- 3.8. Примеры синтеза асинхронных потенциальных автоматов
- Цифровые фазочастотные детекторы.
- Квантизатор временных интервалов.
- 3.9. Генераторы сигналов
- Автогенераторы.
- Управляемые автогенераторы.
- Глава 4. Синтез синхронных автоматов
- 4.2. Синхронные триггеры
- Триггеры типов D и R-S с импульсным тактовым сигналом.
- Синхронные триггеры типов R-S и D-L
- Синхронно-асинхронные триггеры.
- Синхронные триггеры типа J-K
- Триггеры типа Т.
- Классификация синхронных триггеров.
- Преобразования типов синхронных триггеров.
- Триггеры типов D-T-L и D-T-L/R
- Функции переходов синхронно-асинхронных триггеров.
- 4.3. Примеры синтеза синхронных автоматов
- 4.4. Сдвигающие регистры
- Синтез счетчиков на сдвигающих регистрах.
- Сдвигающие регистры с загрузкой данных.
- Реверсивные сдвигающие регистры.
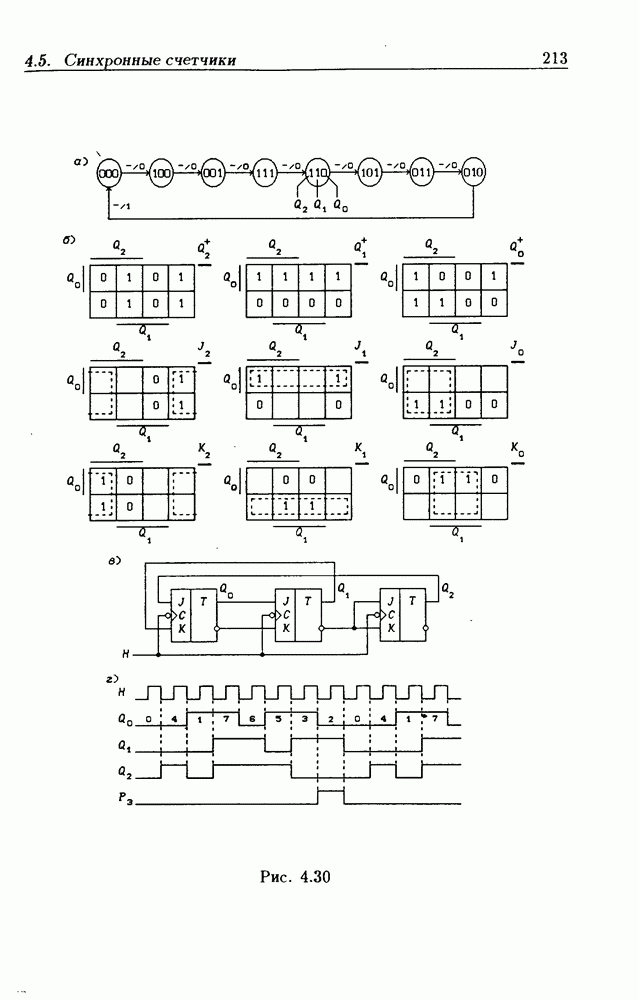
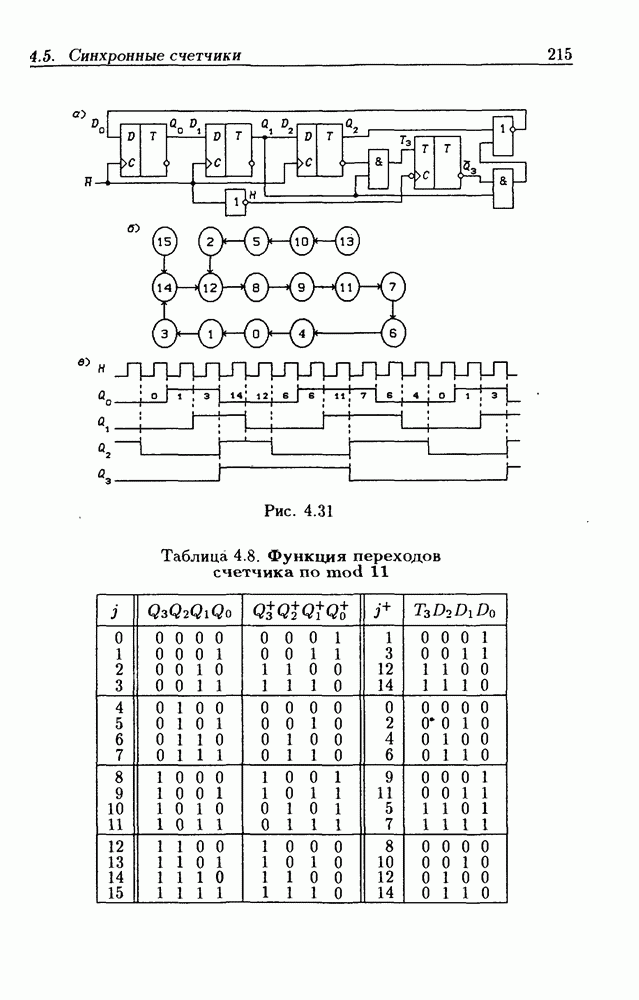
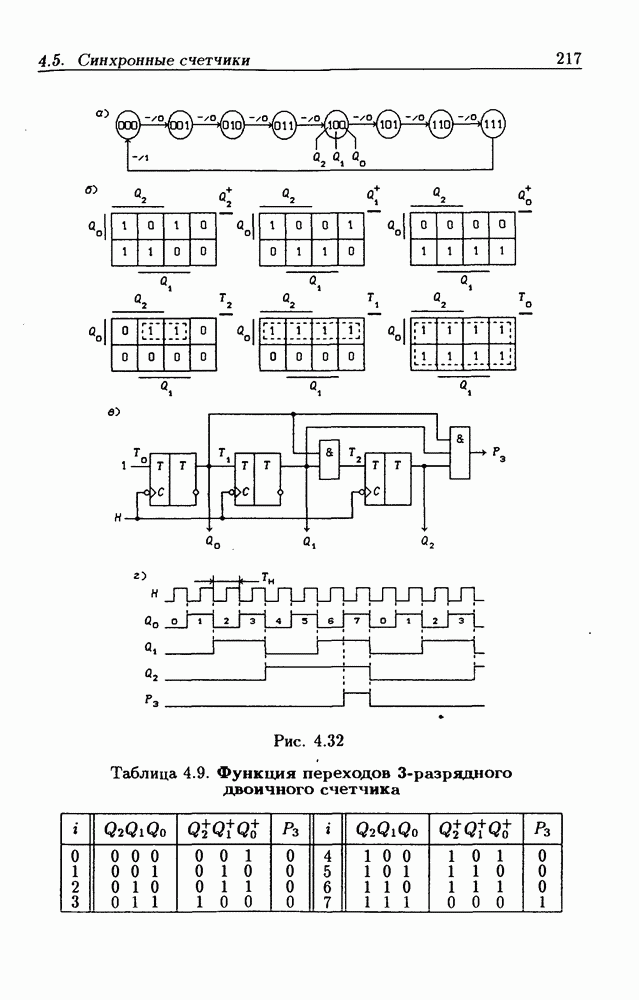
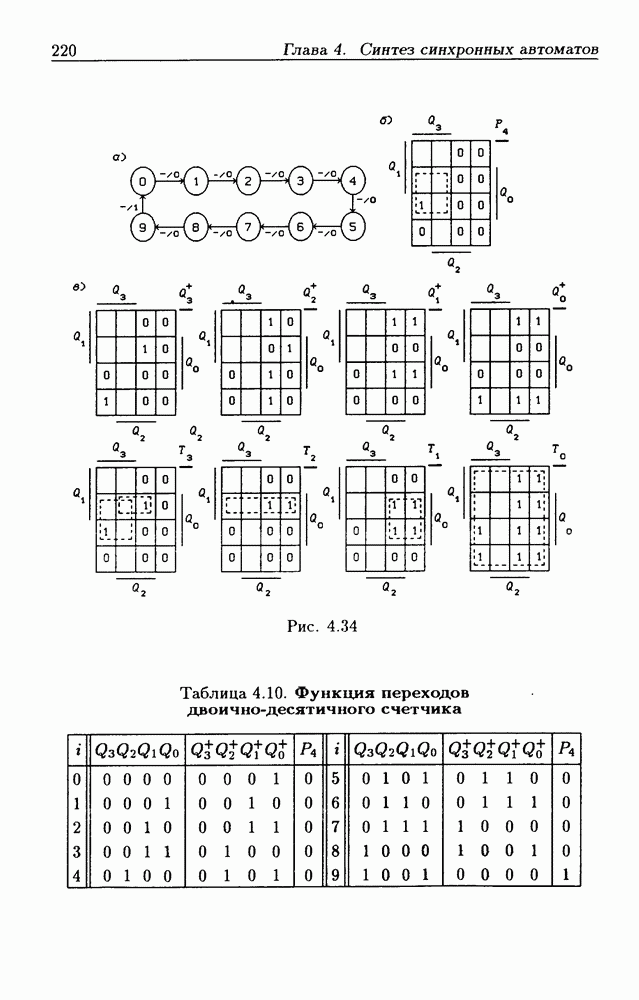
- 4.5. Синхронные счетчики
- Синхронные двоичные счетчики.
- Синхронные двоично-десятичные счетчики.
- Каскадирование двоичных и двоично-десятичных счетчиков.
- Синхронные двоичные реверсивные счетчики.
- Реверсивные двоично-десятичные счетчики.
- Каскадирование реверсивных счетчиков.
- Счетчики на сдвигающих регистрах.
- Кольцевые счетчики.
- Линейные счетчики.
- Программируемые счетчики.
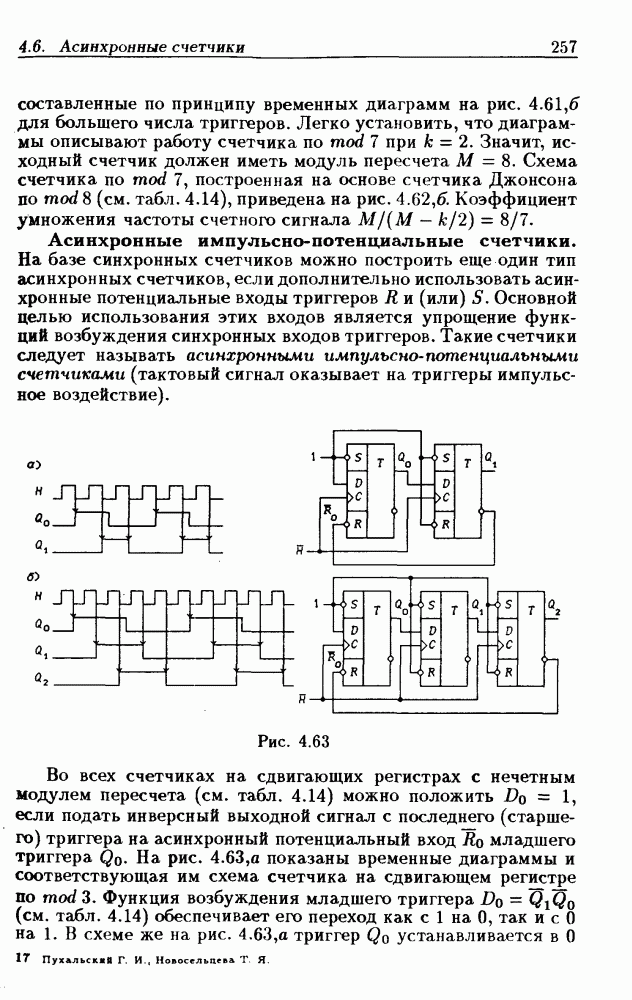
- 4.6. Асинхронные счетчики
- Асинхронные счетчики с умножением частоты счетного сигнала.
- Асинхронные импульсно-потенциальные счетчики.
- Асинхронное программирование модуля пересчета счетчиков.
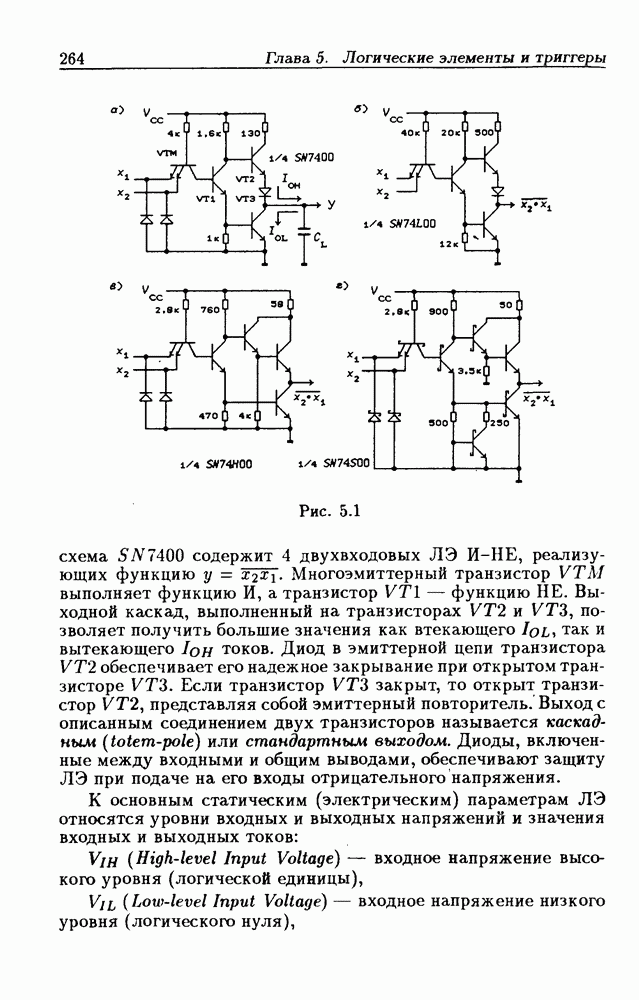
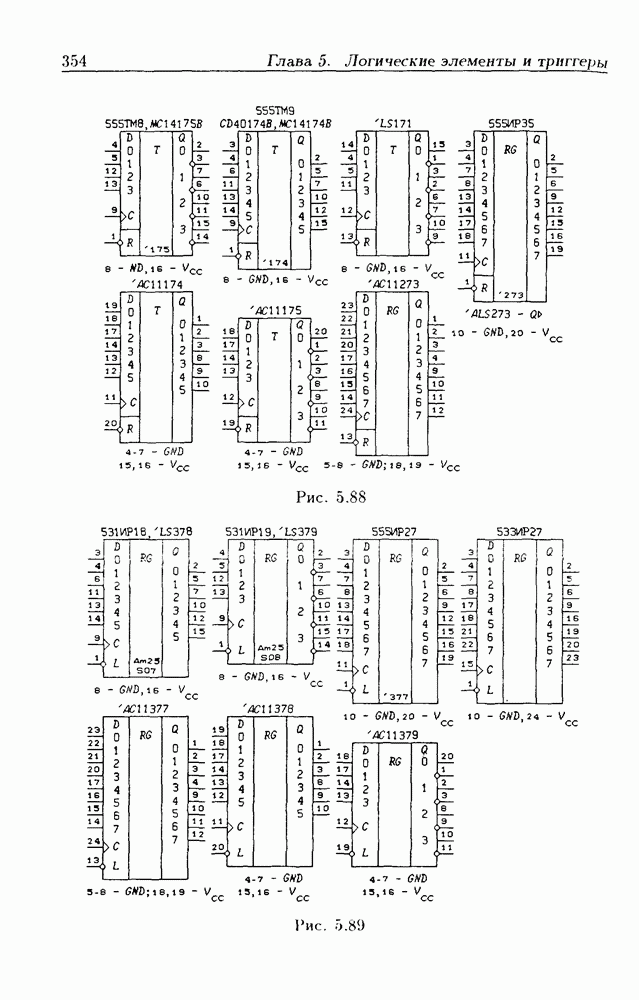
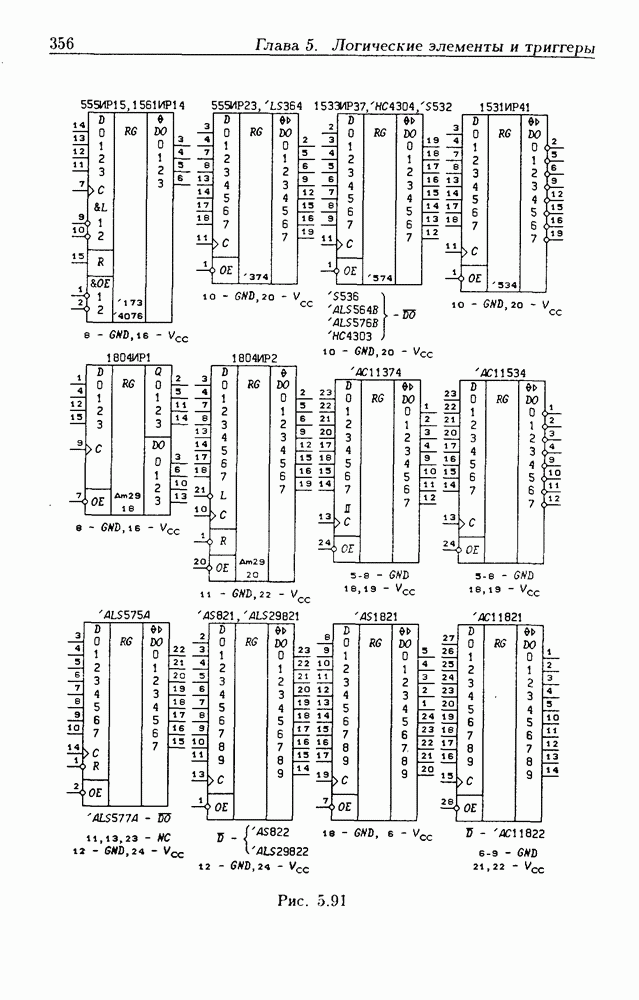
- Глава 5. Логические элементы и триггеры
- Логические элементы.
- Классификация ИС по степени интеграции.
- 5.2. Интегральные схемы КМОП серий
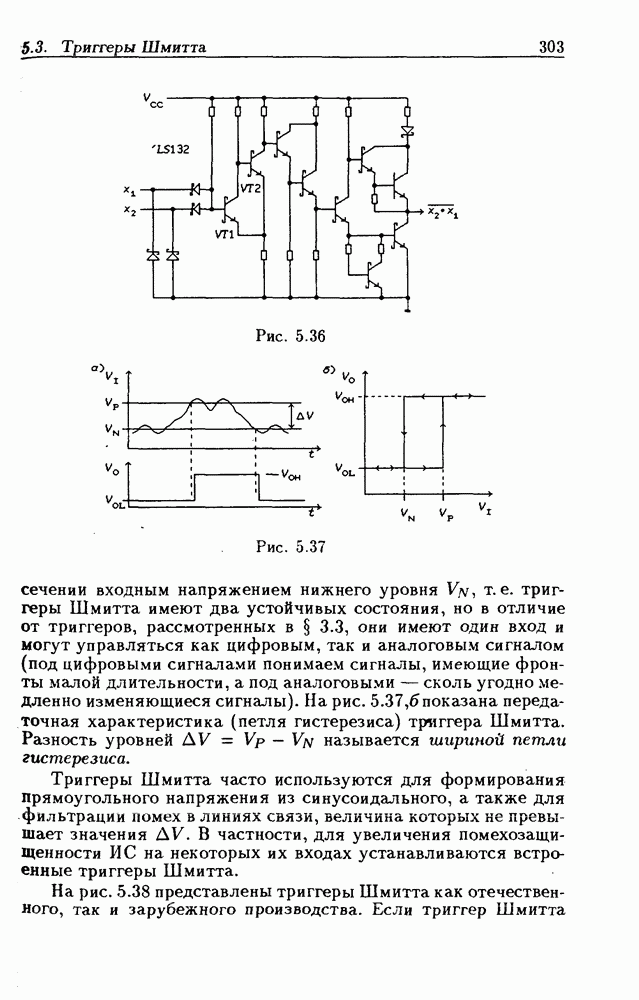
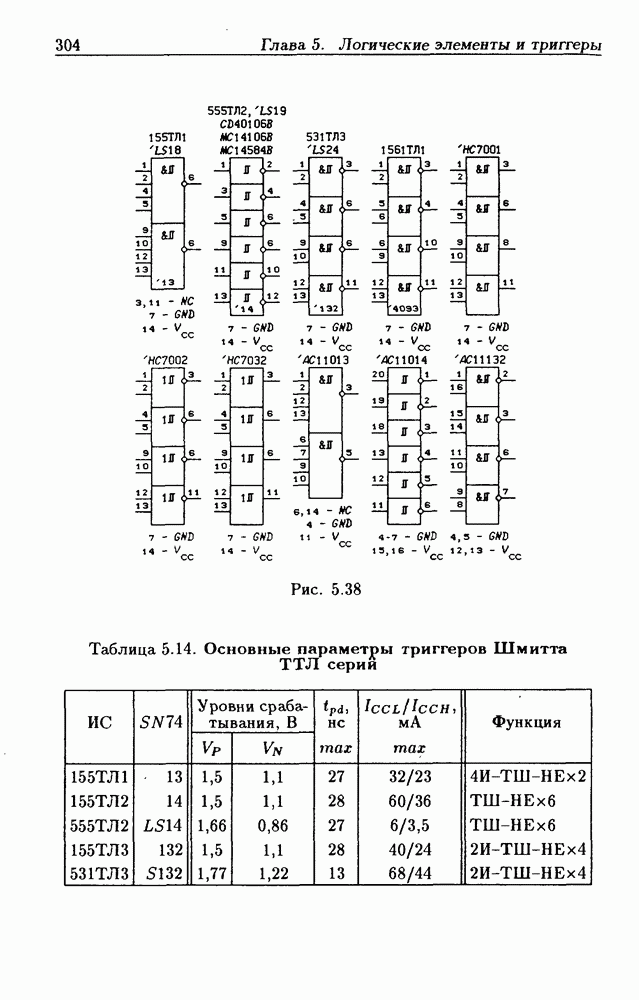
- 5.3. Триггеры Шмитта
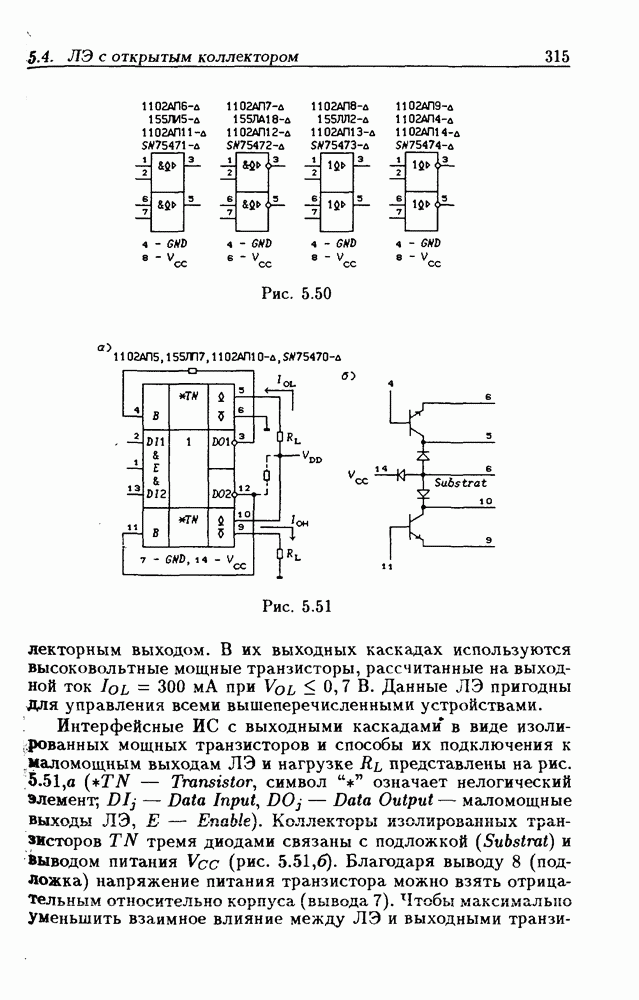
- 5.4. Логические элементы с открытым коллекторным выходом
- Логические элементы с открытым коллекторным выходом.
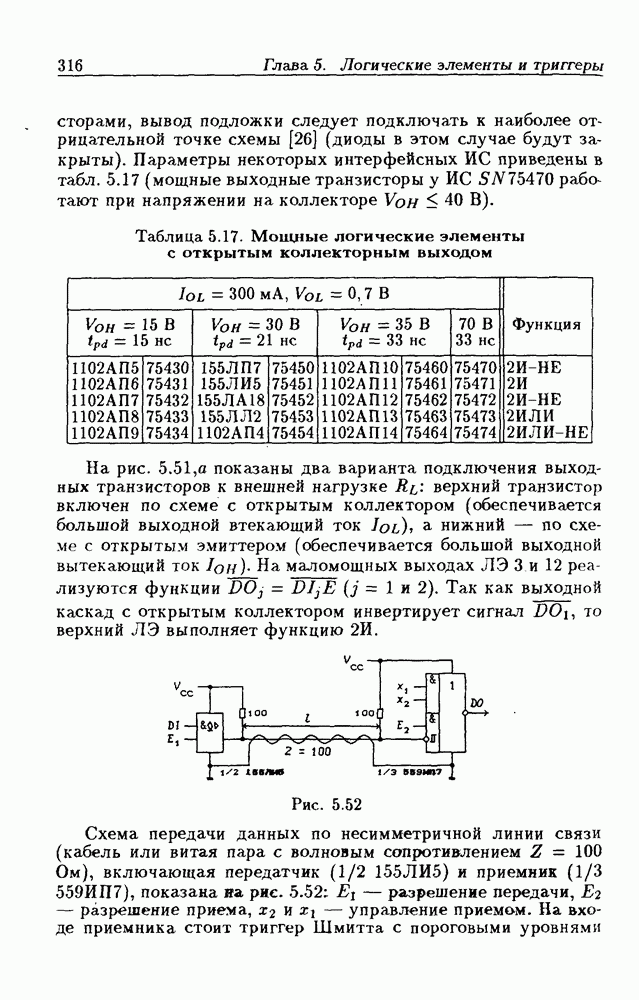
- Применения ЛЭ с открытым коллекторным выходом.
- Интерфейсные ЛЭ с открытым коллекторным выходом.
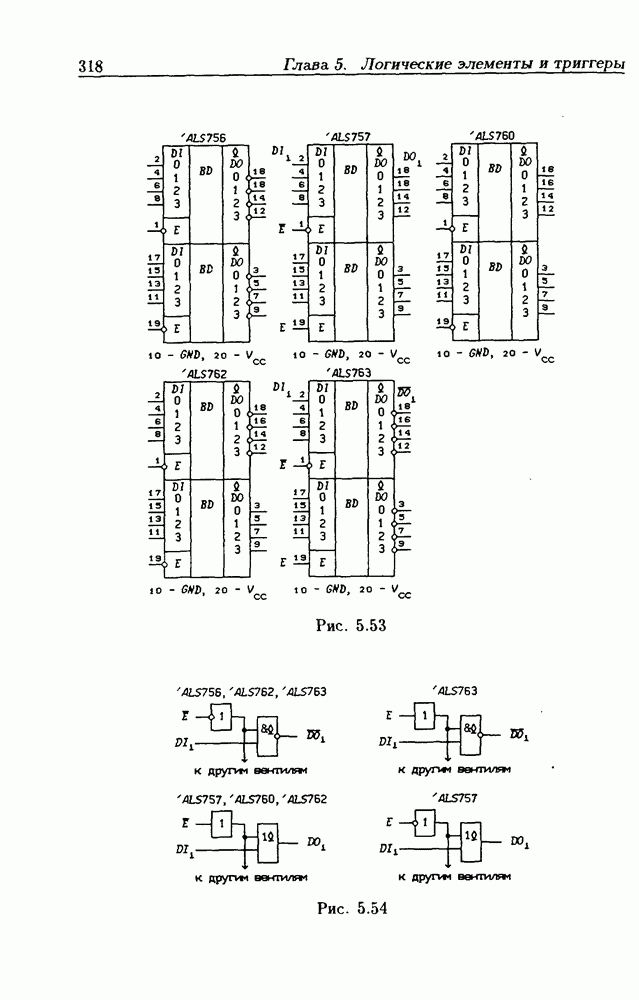
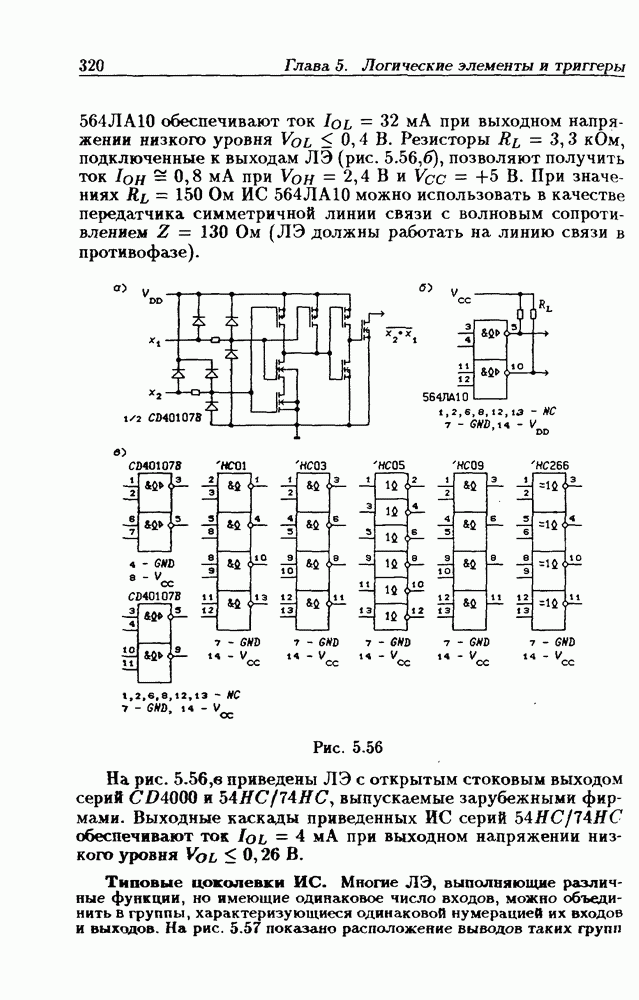
- Логические элементы с открытым стоковым выходом.
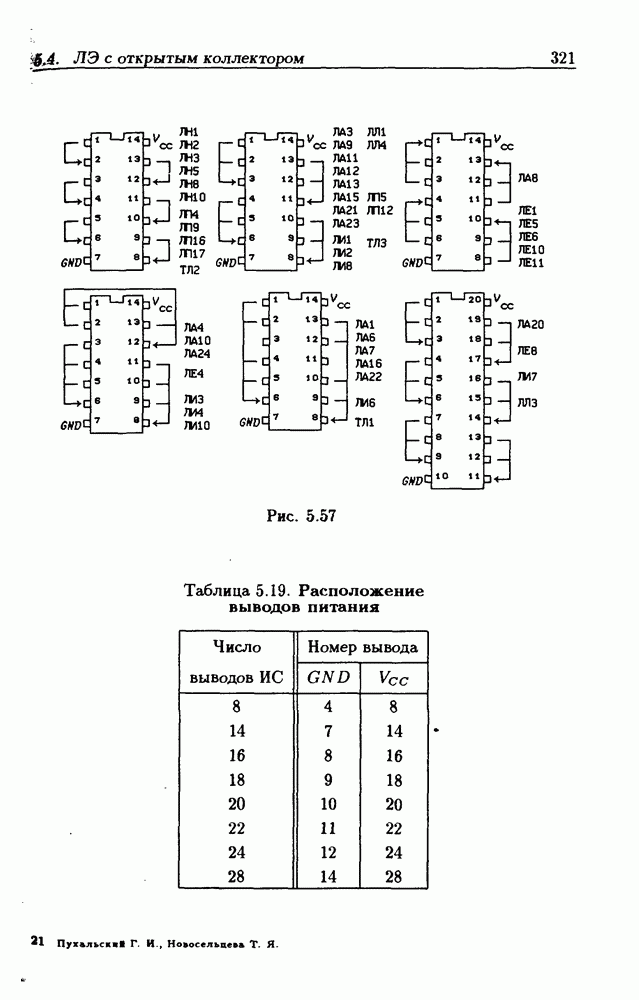
- Типовые цоколевки ИС.
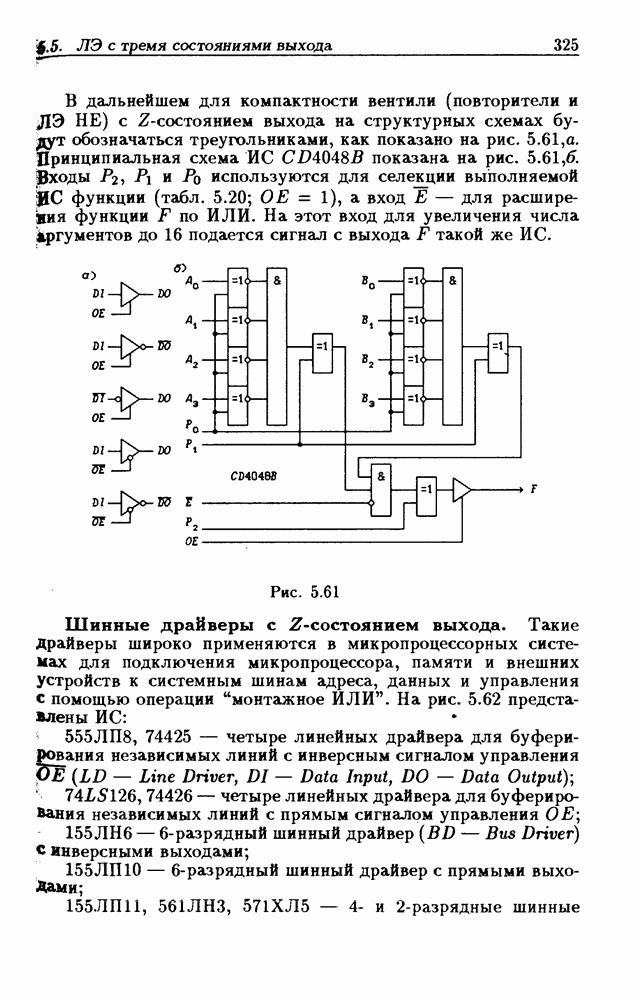
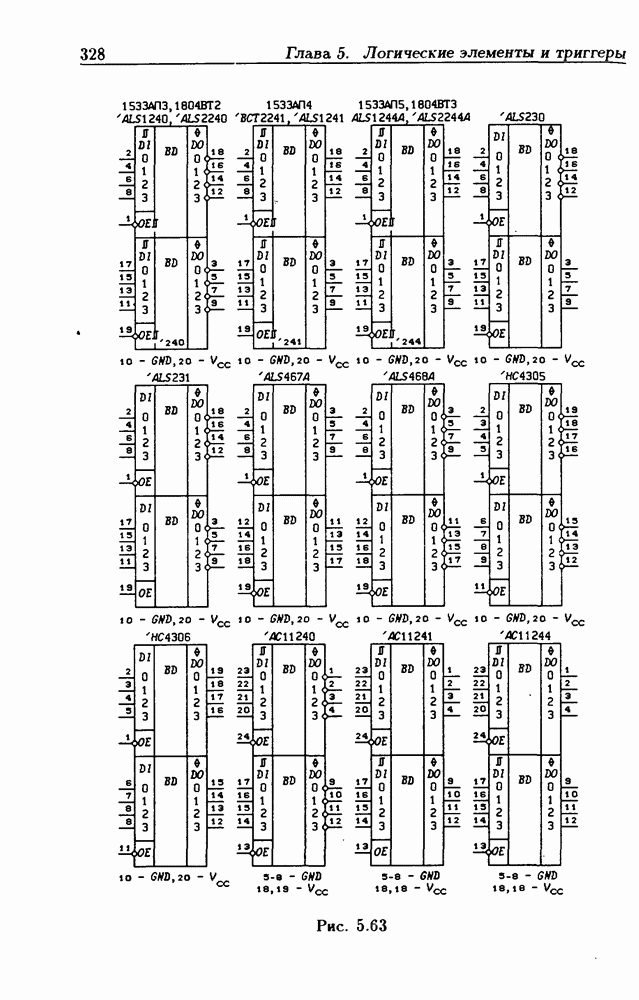
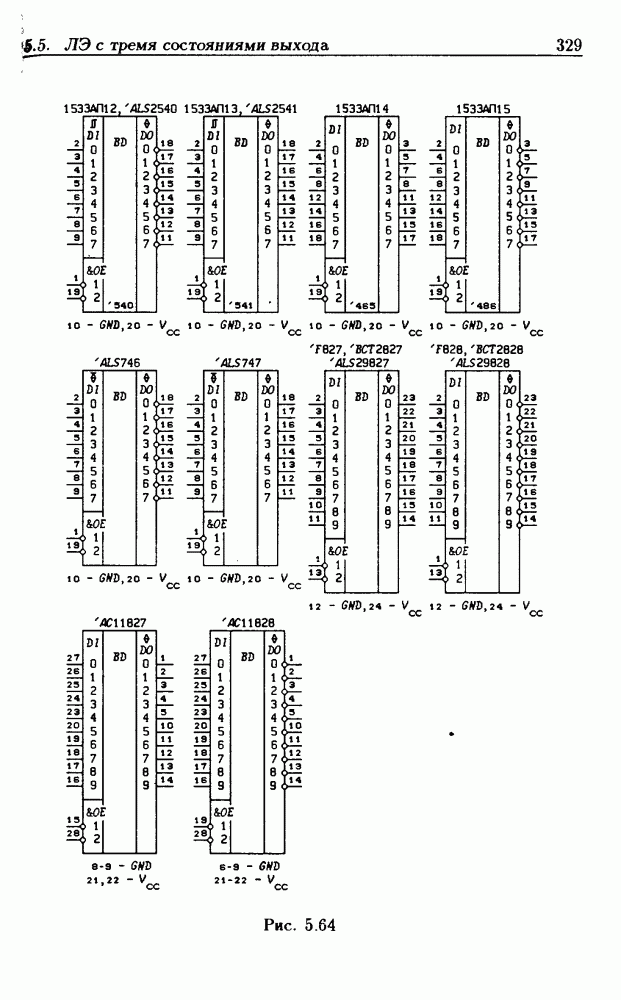
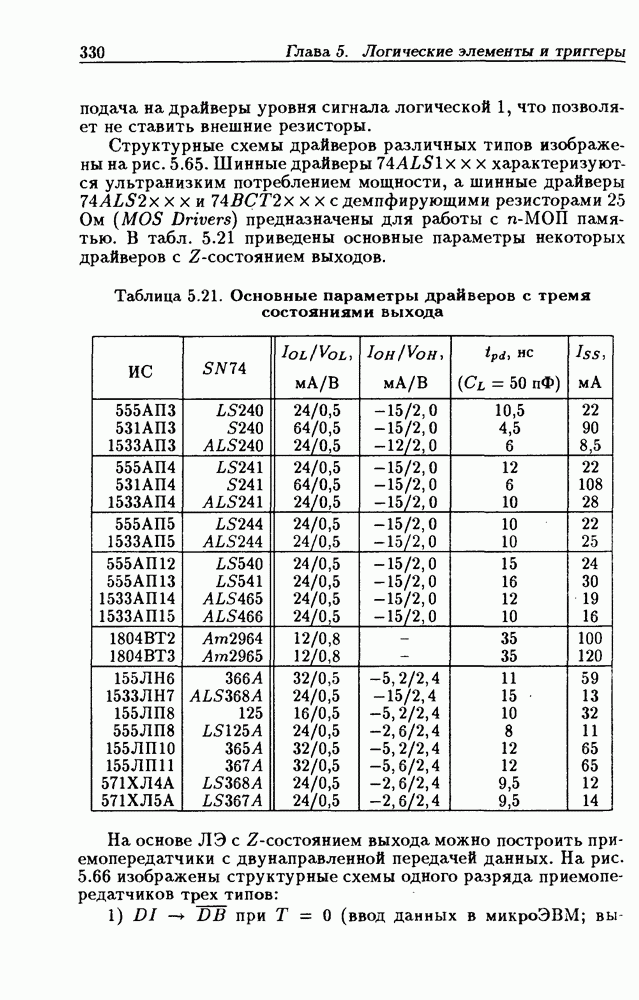
- 5.5. Логические элементы с тремя состояниями выхода
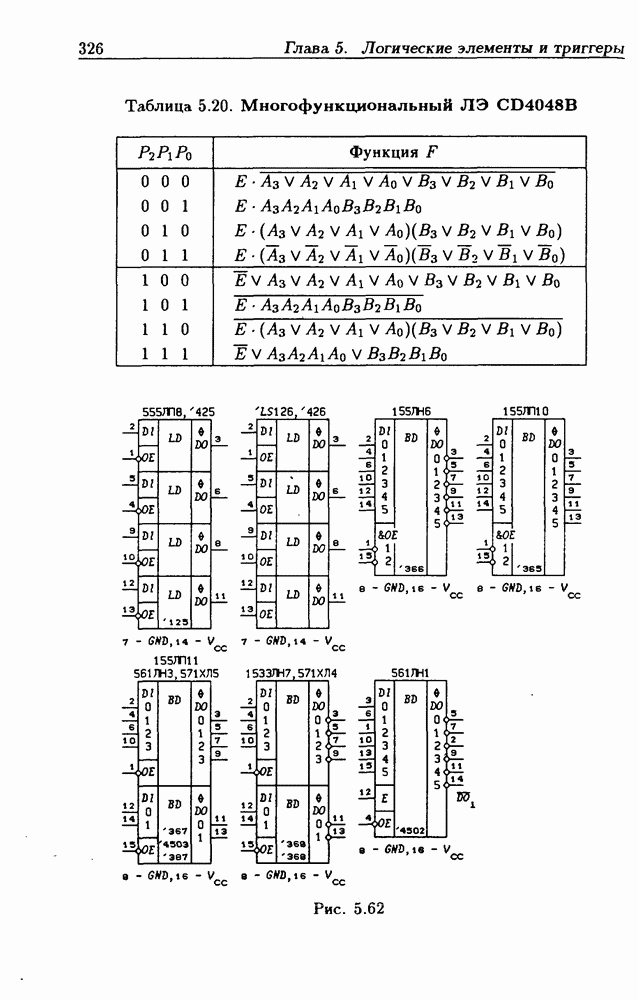
- Шинные драйверы с Z-состоянием выхода.
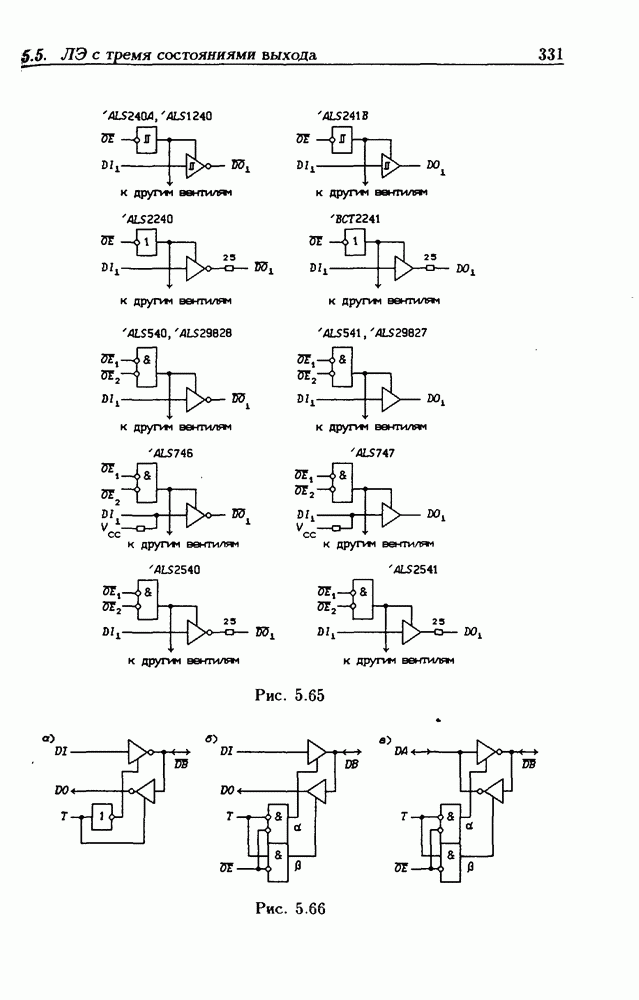
- Основные правила графического изображения ИС.
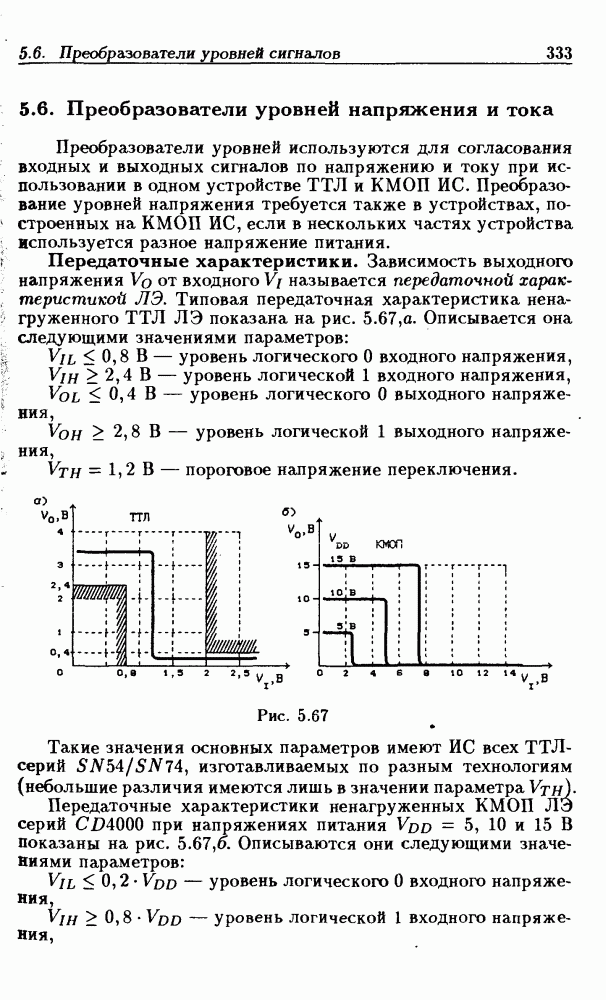
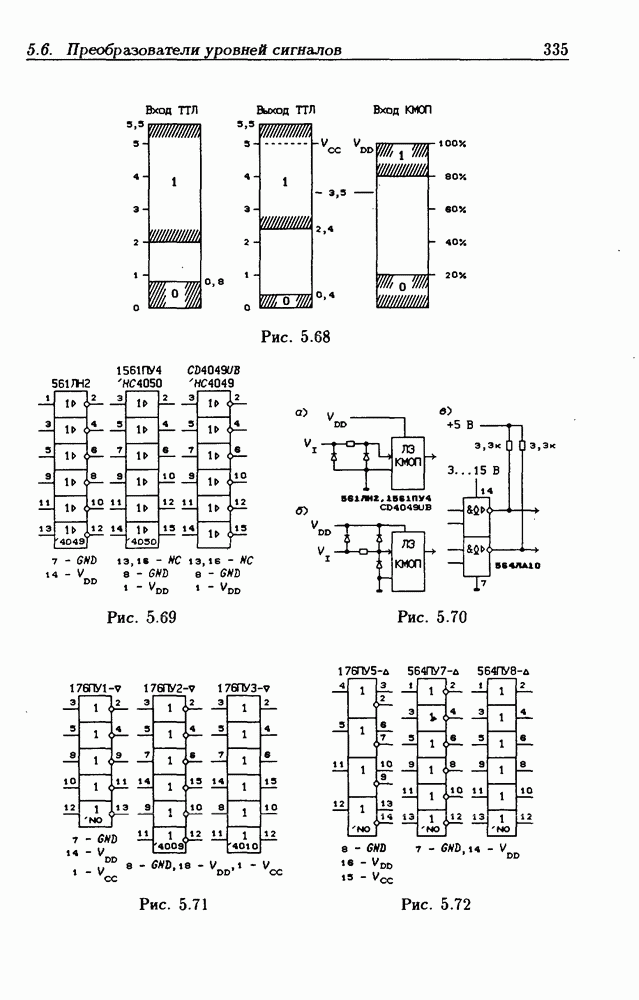
- 5.6. Преобразователи уровней напряжения и тока
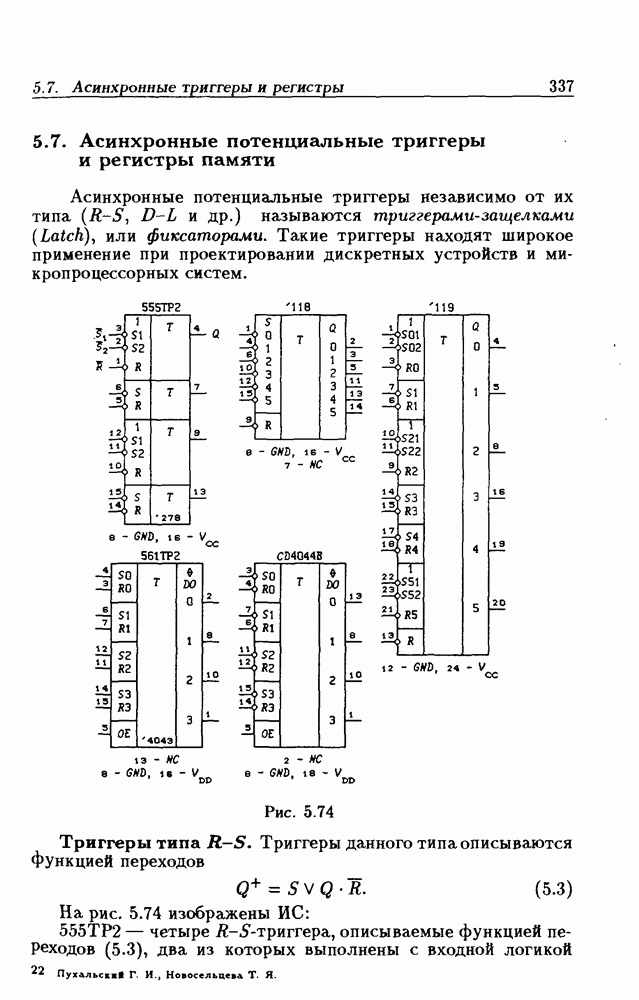
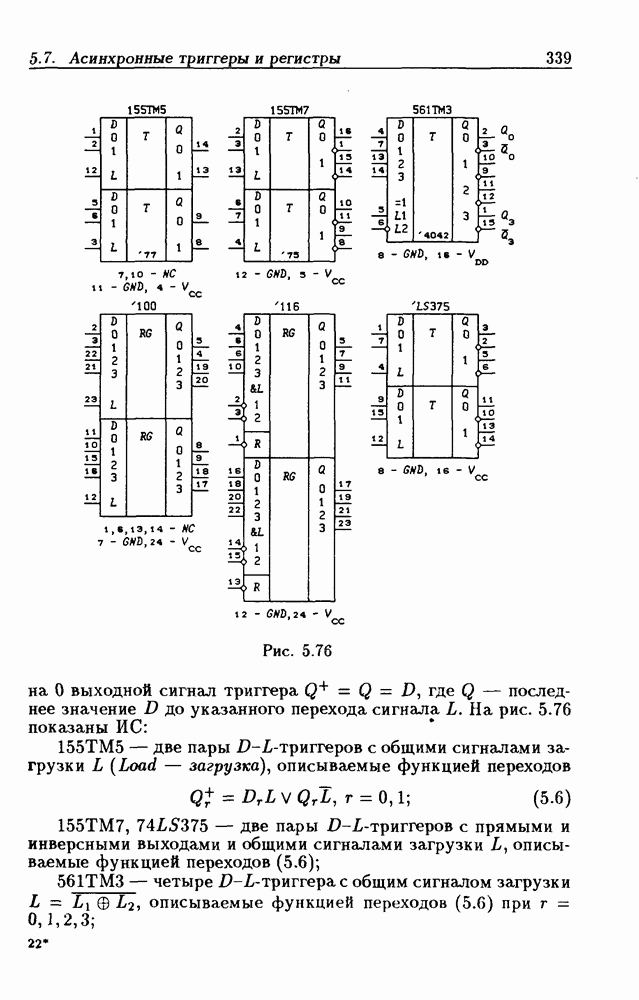
- 5.7. Асинхронные потенциальные триггеры и регистры памяти
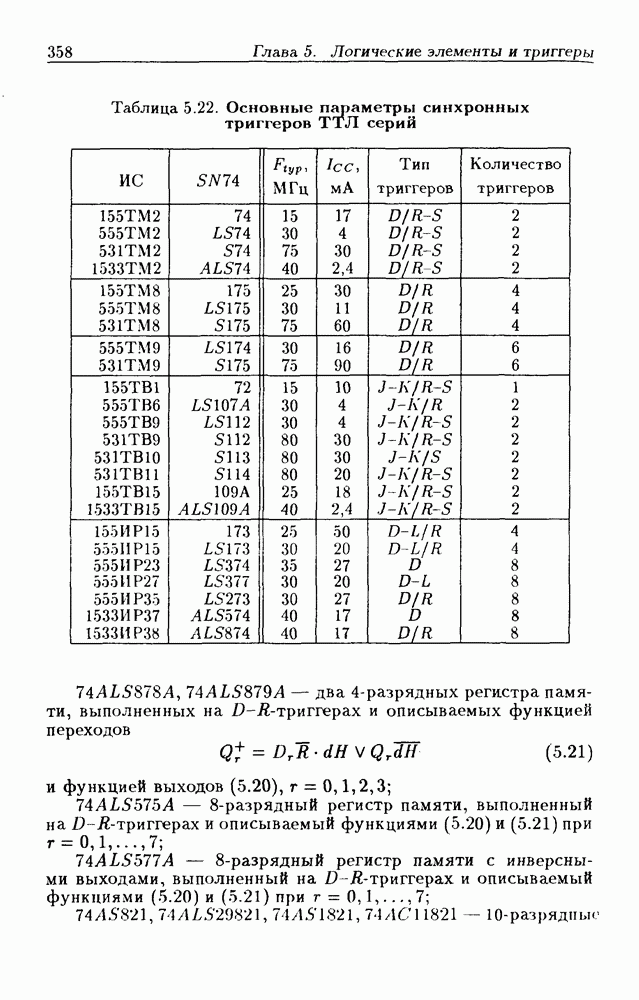
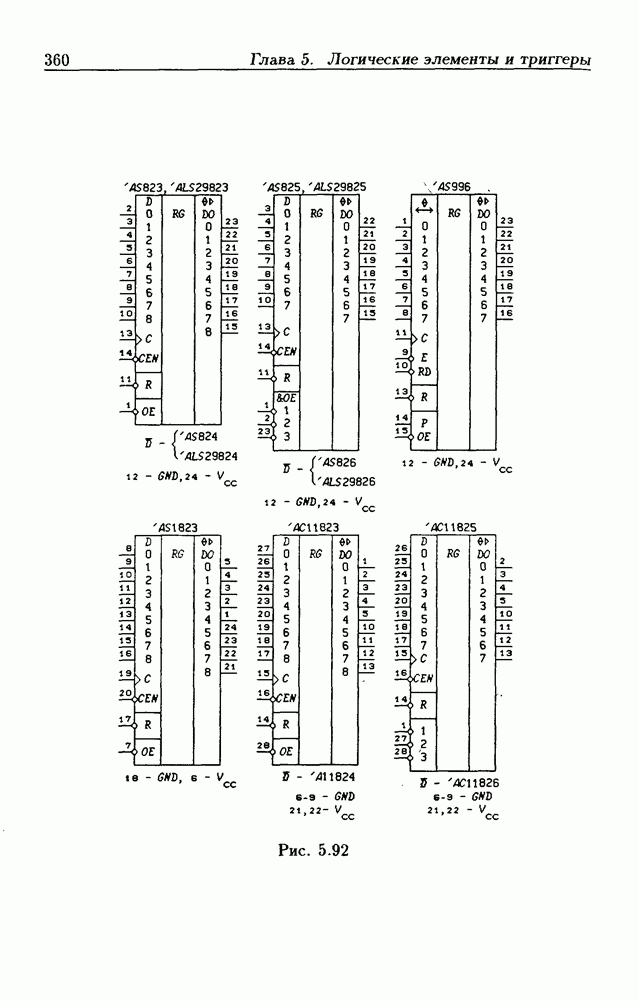
- 5.8. Синхронные триггеры и регистры памяти
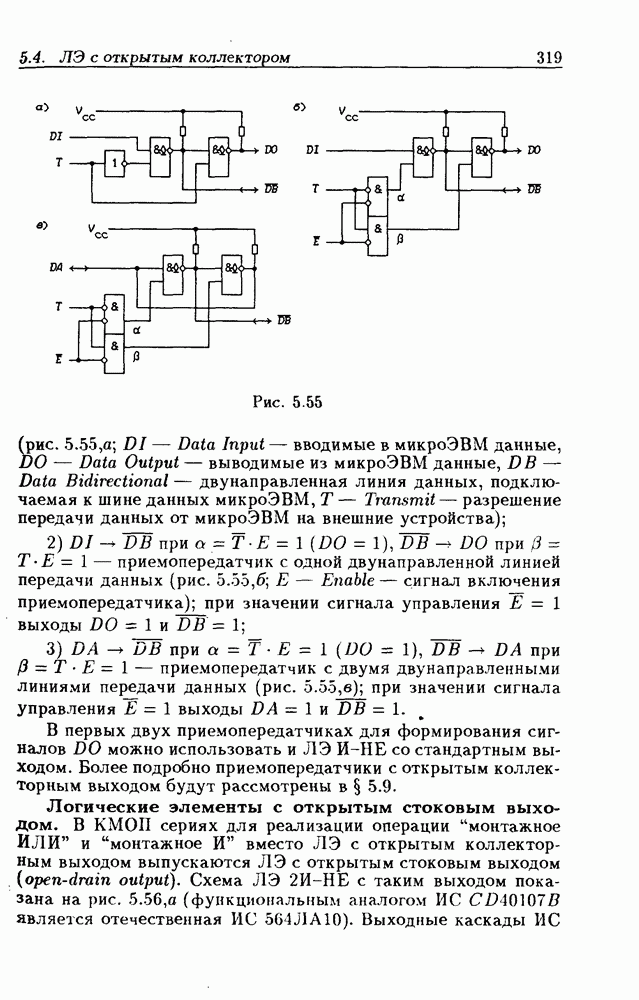
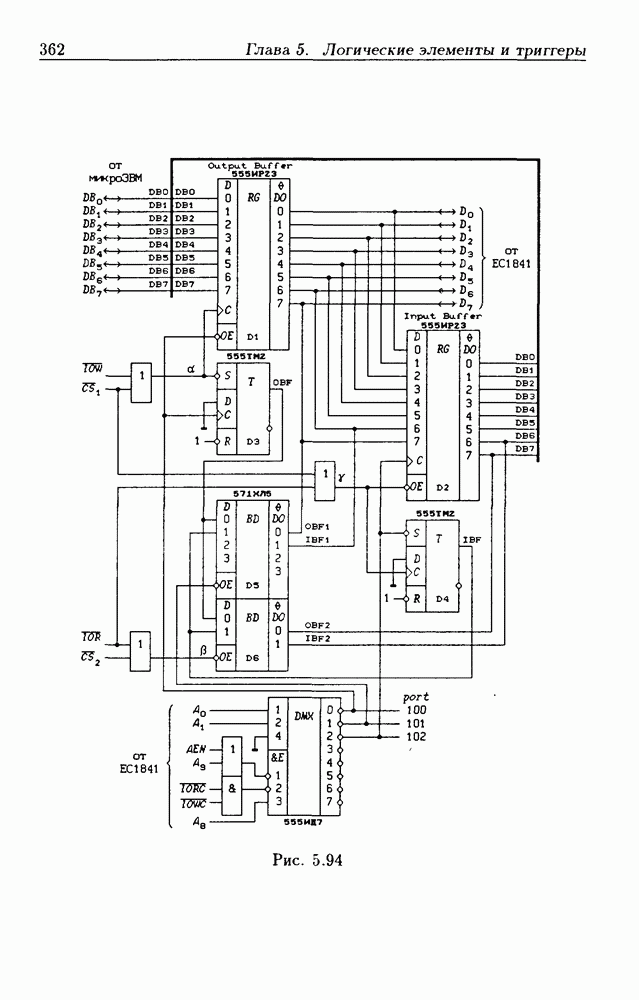
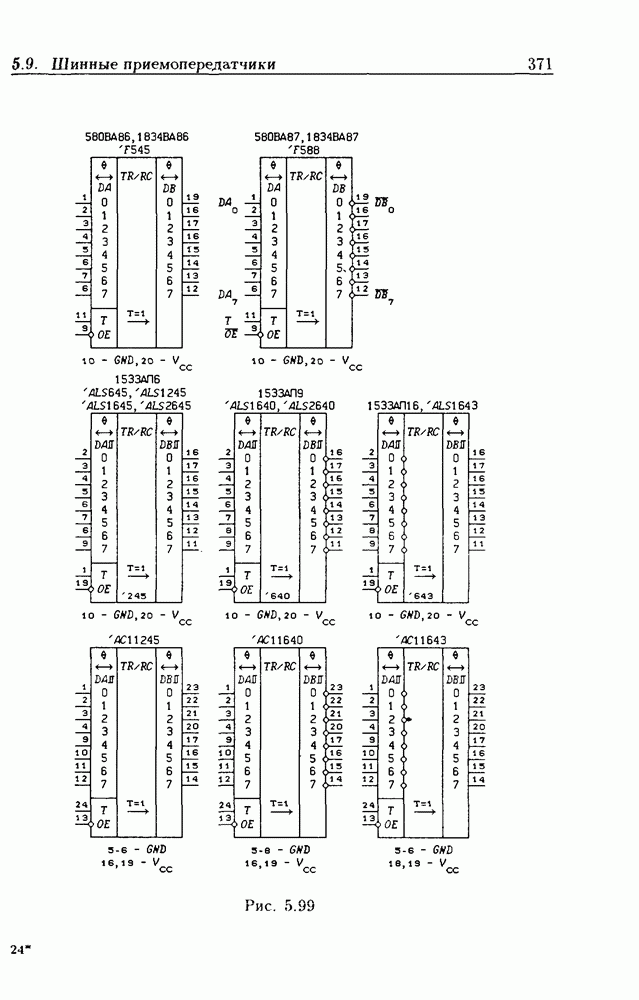
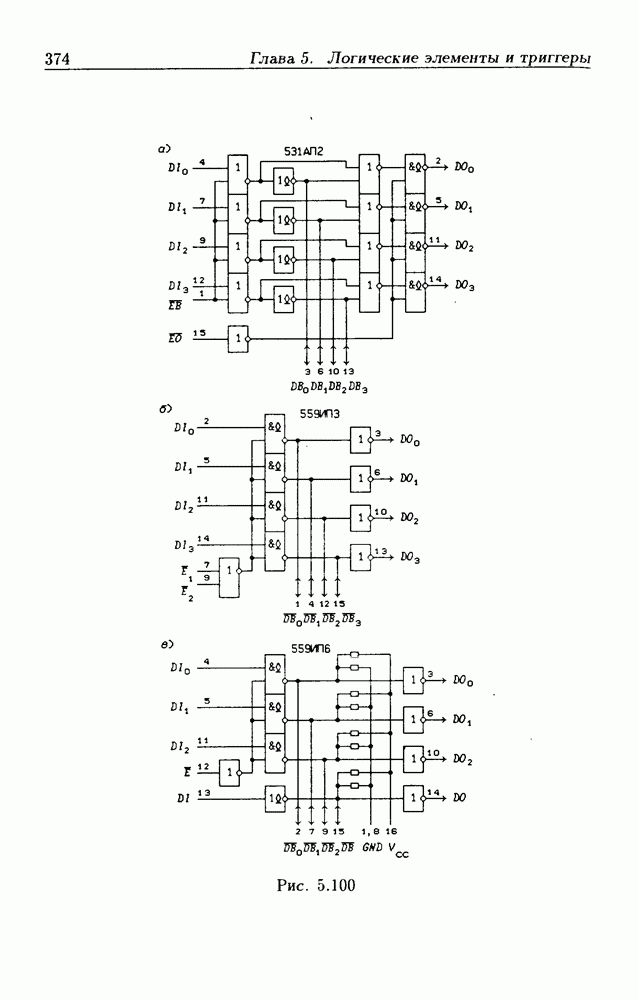
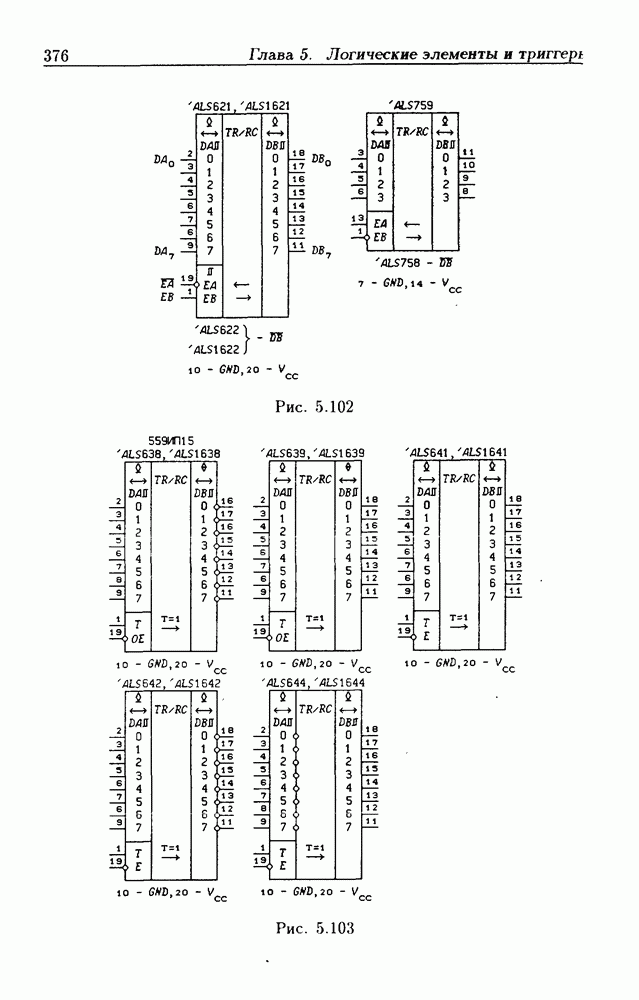
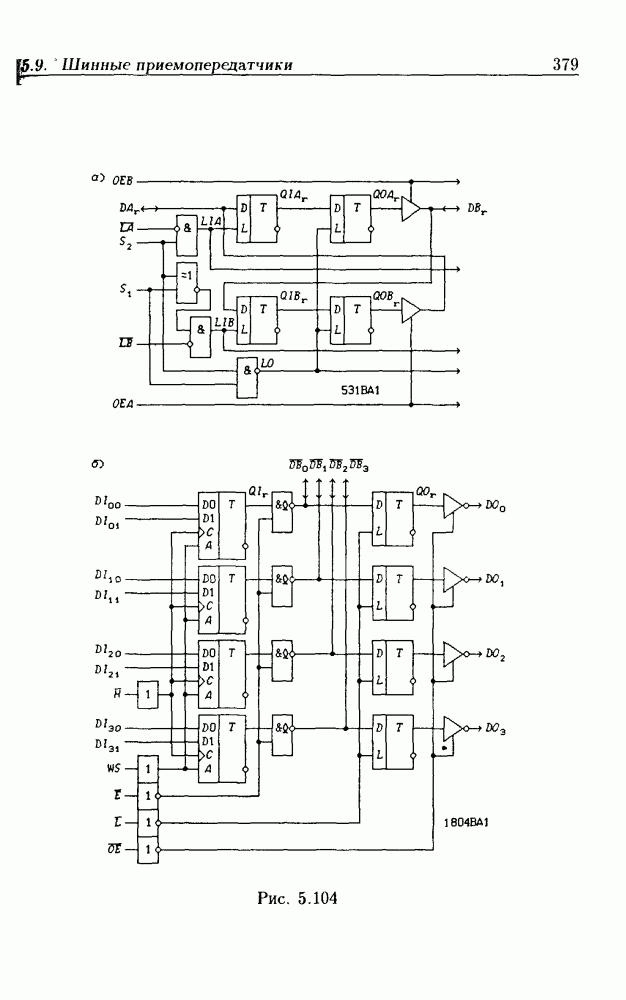
- 5.9. Шинные приемопередатчики
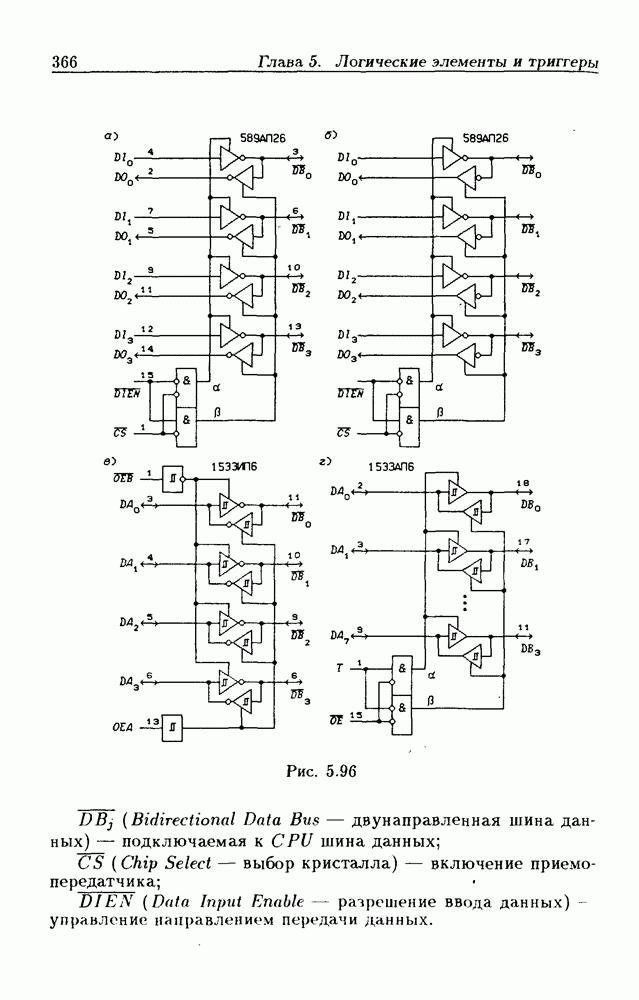
- Шинные приемопередатчики с Z-состоянием выхода.
- Шинные приемопередатчики с открытым коллекторным выходом.
- Шинные приемопередатчики с регистрами памяти.
- Шинные приемопередатчики со сдвигающим регистром.
- Шинные трехнаправленные приемопередатчики.
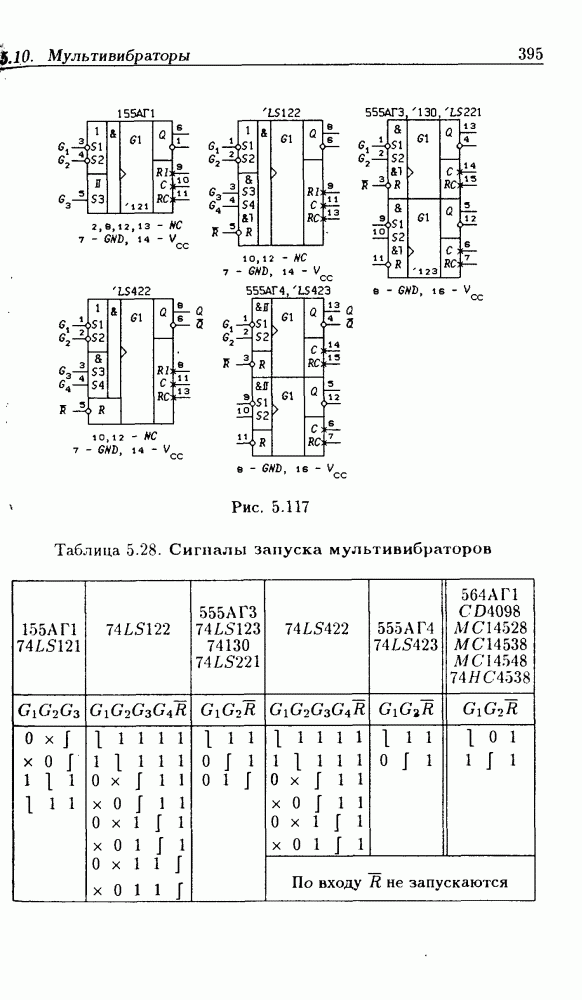
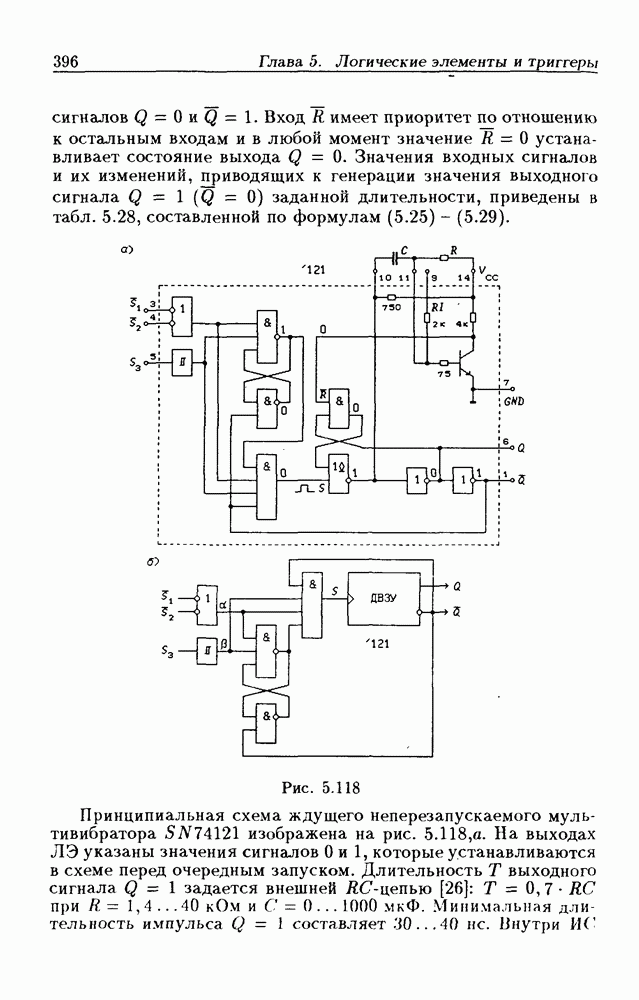
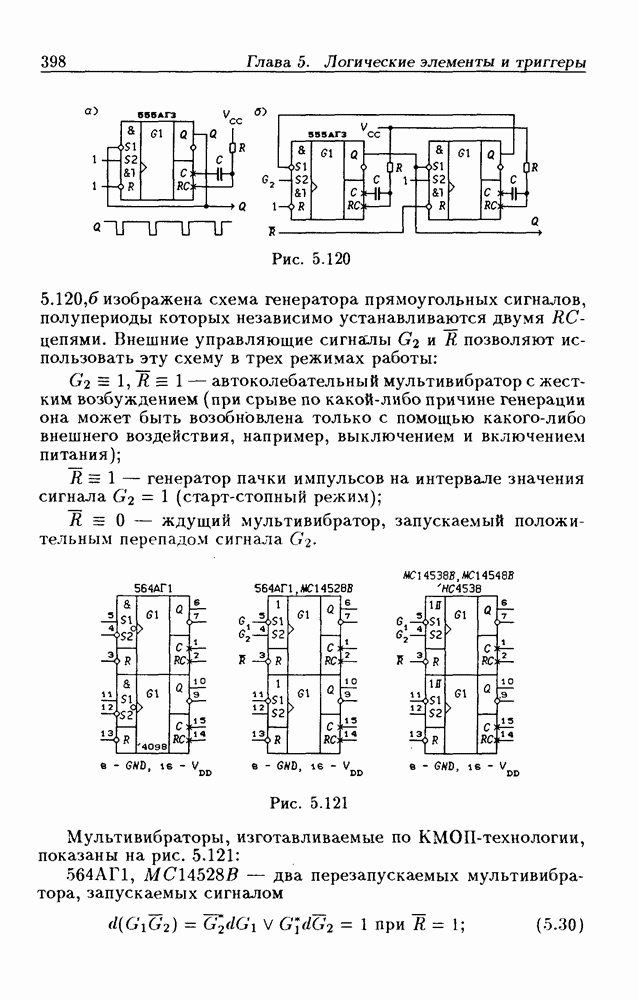
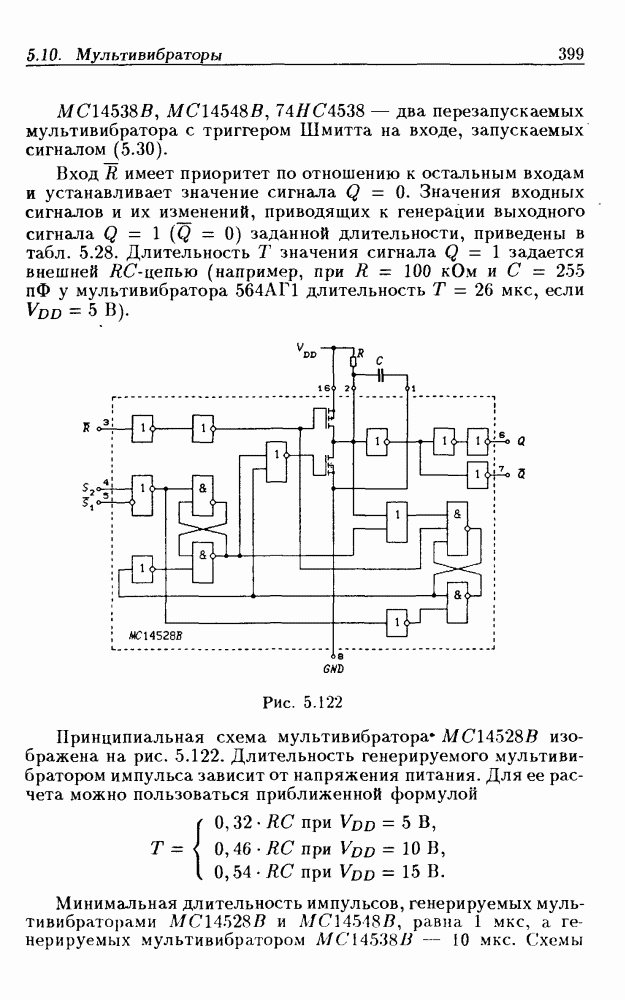
- 5.10. Мультивибраторы
- 5.11. Генераторы
- Схемы устранения «дребезга» механических контактов.
- Автогенераторы периодических сигналов.
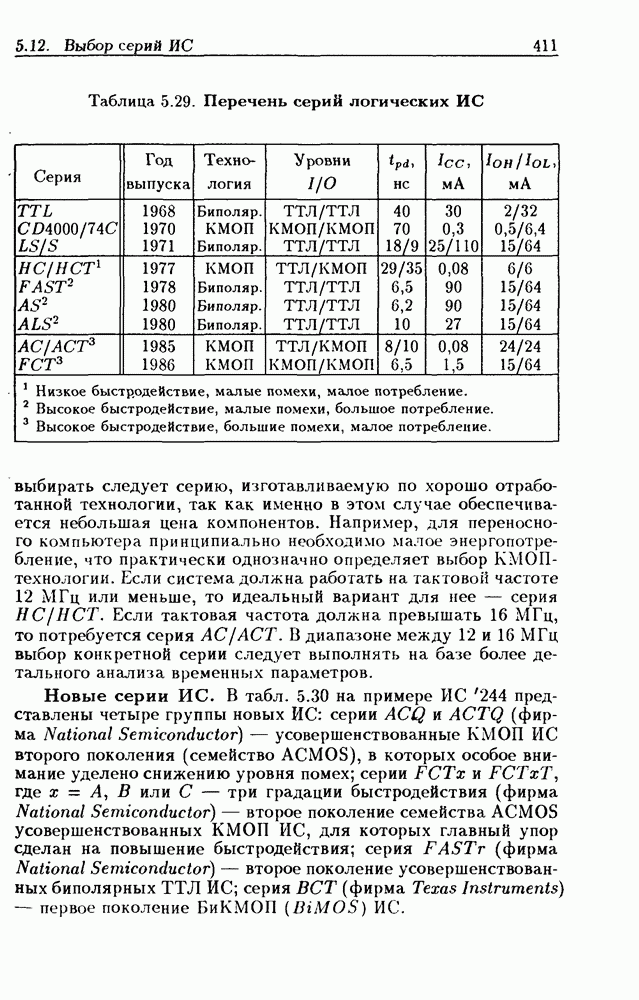
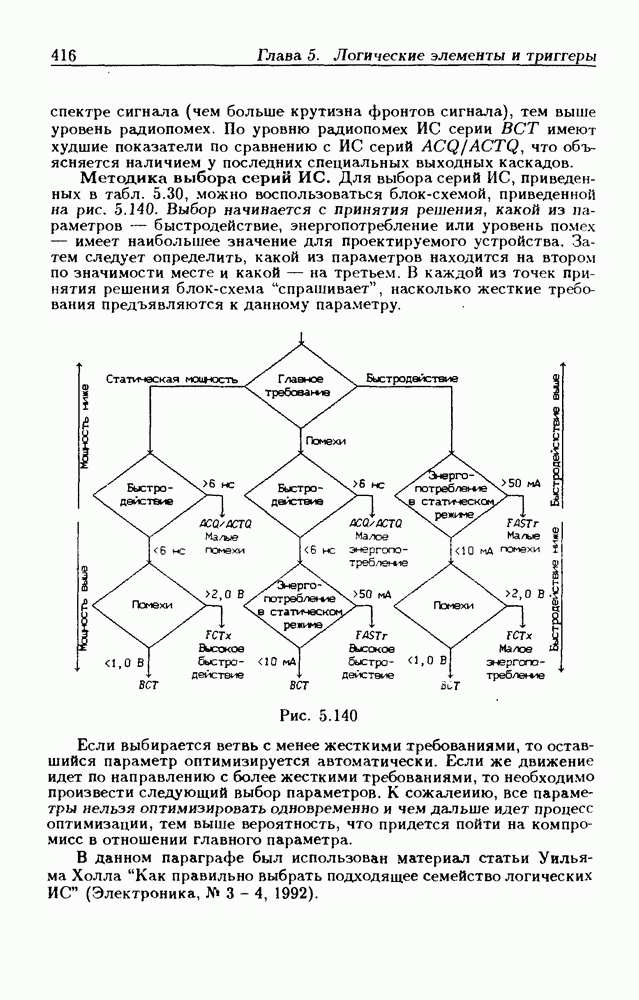
- 5.12. Рекомендации по выбору серий ИС
- Глава 6. Коммутаторы и арифметические устройства
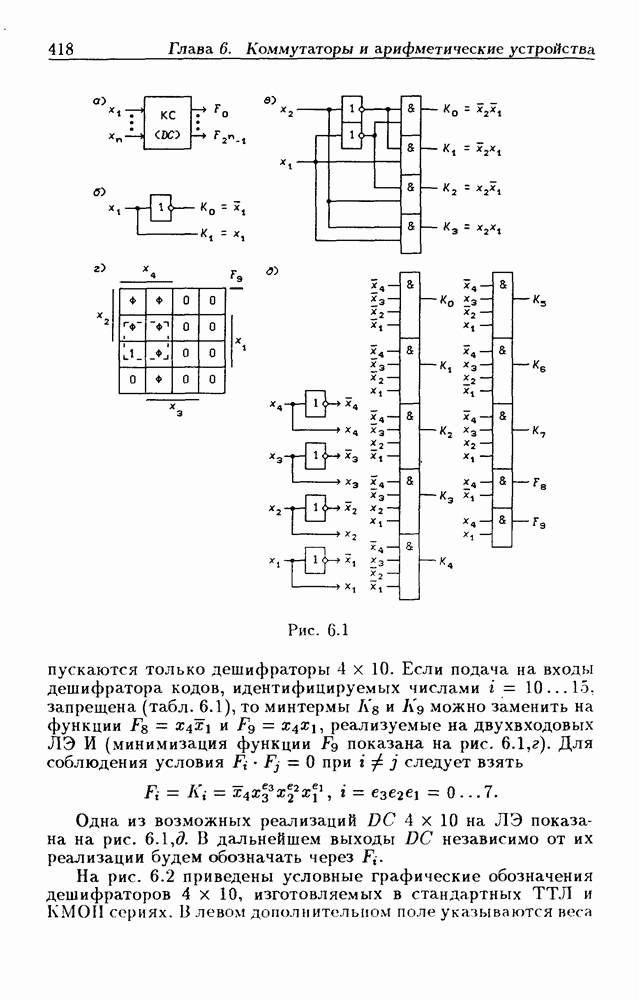
- 6.1. Дешифраторы
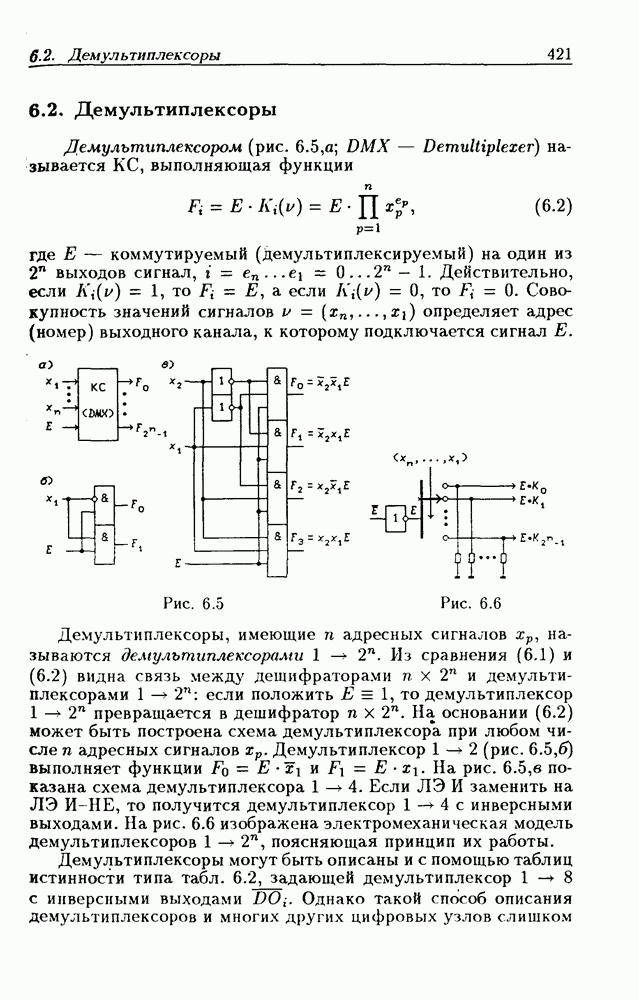
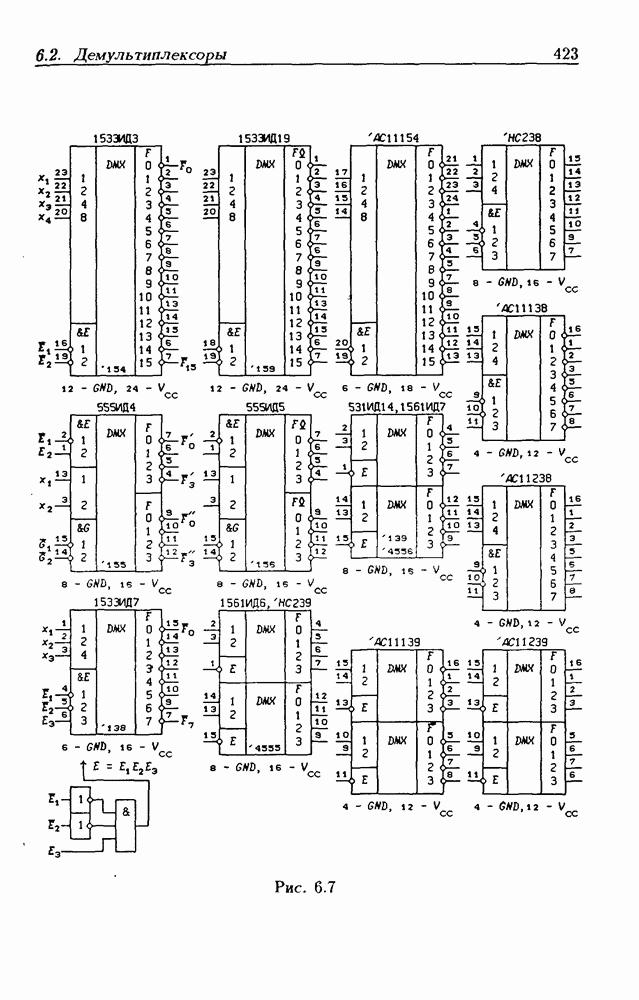
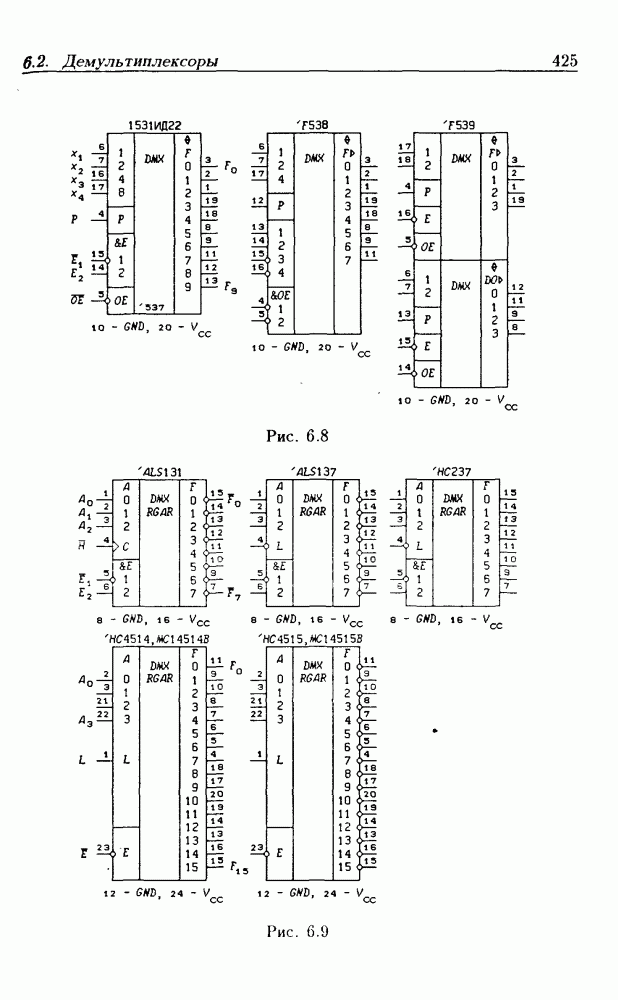
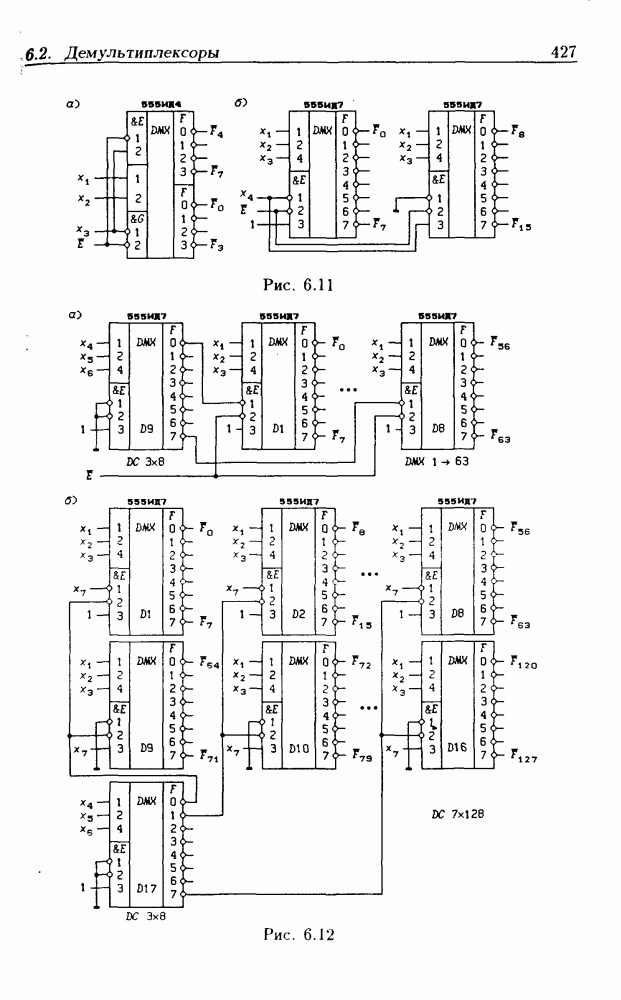
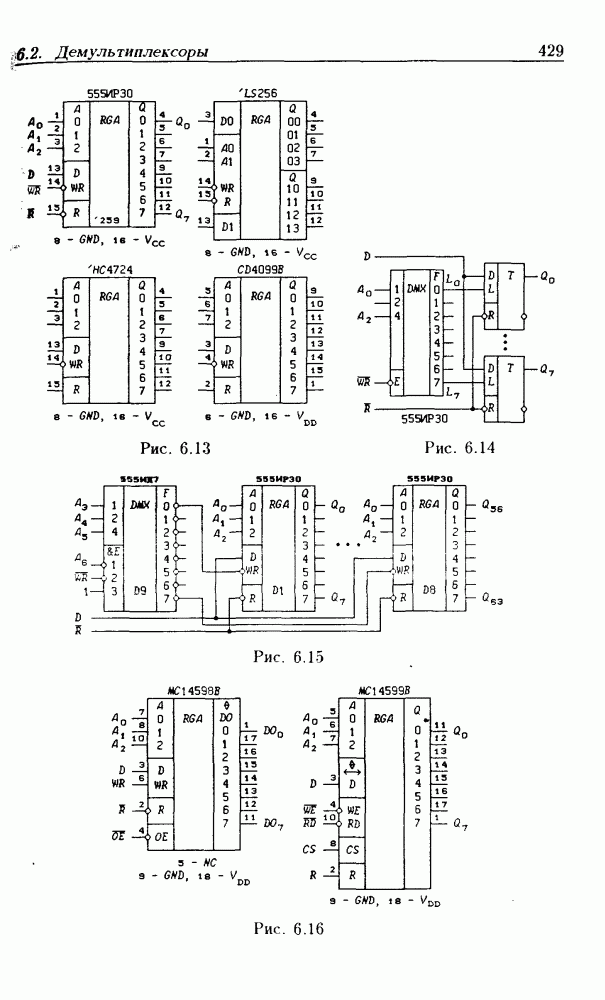
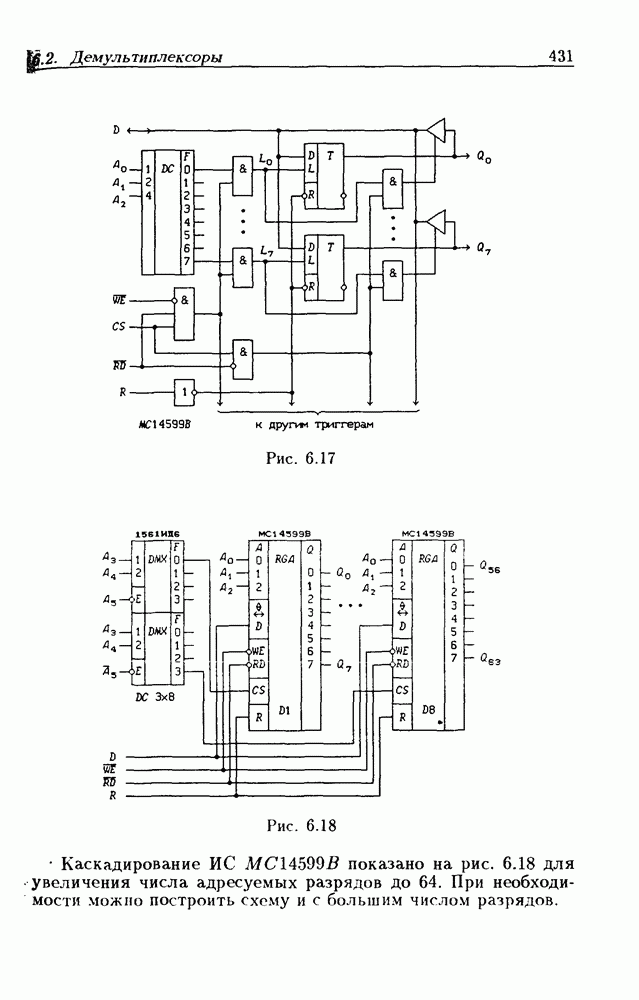
- 6.2. Демультиплексоры
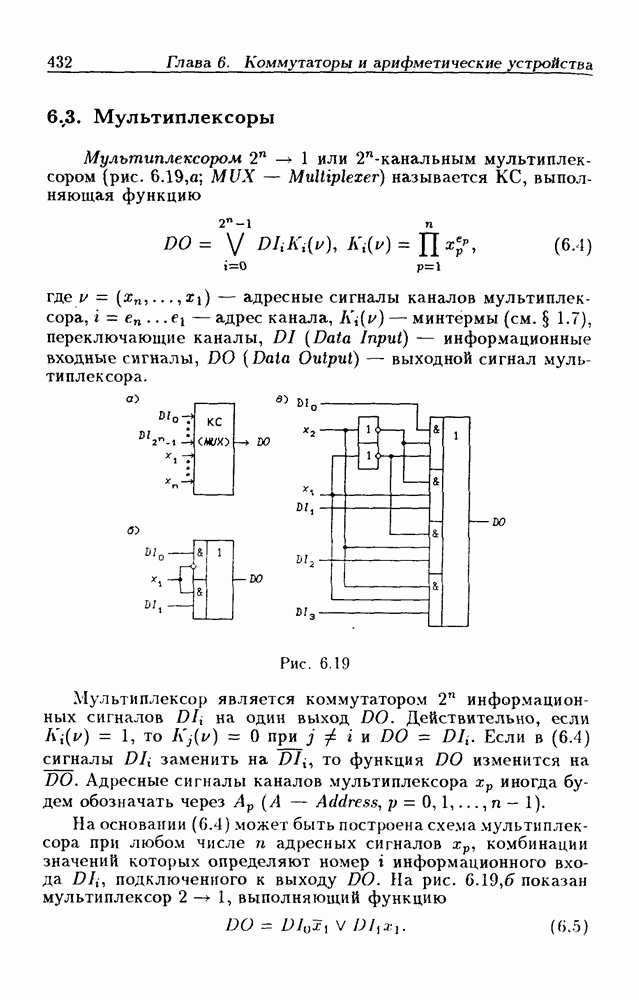
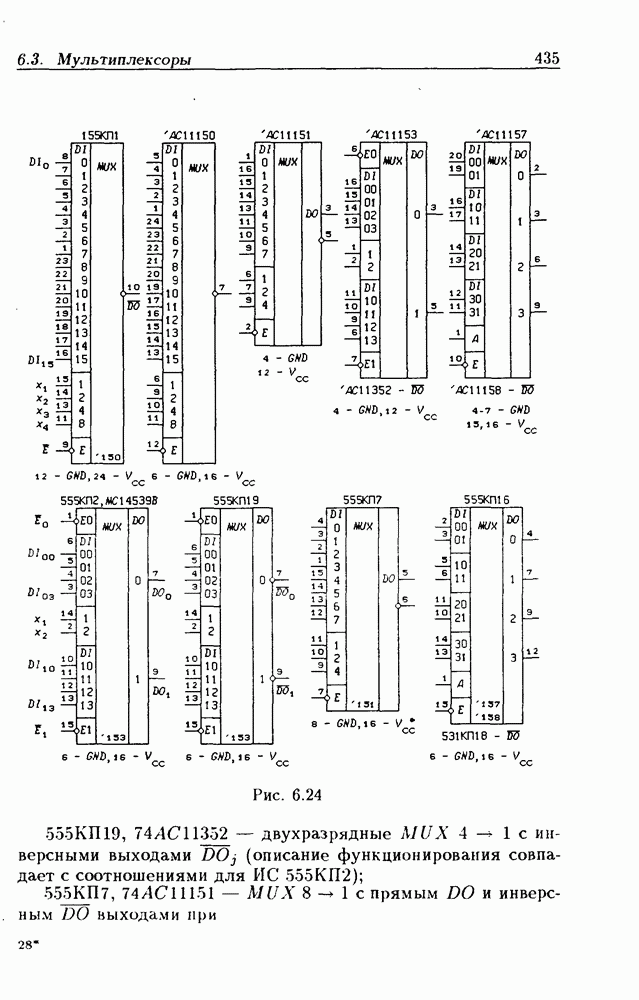
- 6.3. Мультиплексоры
- Мультиплексоры без стробирования.
- Мультиплексоры со стробированием.
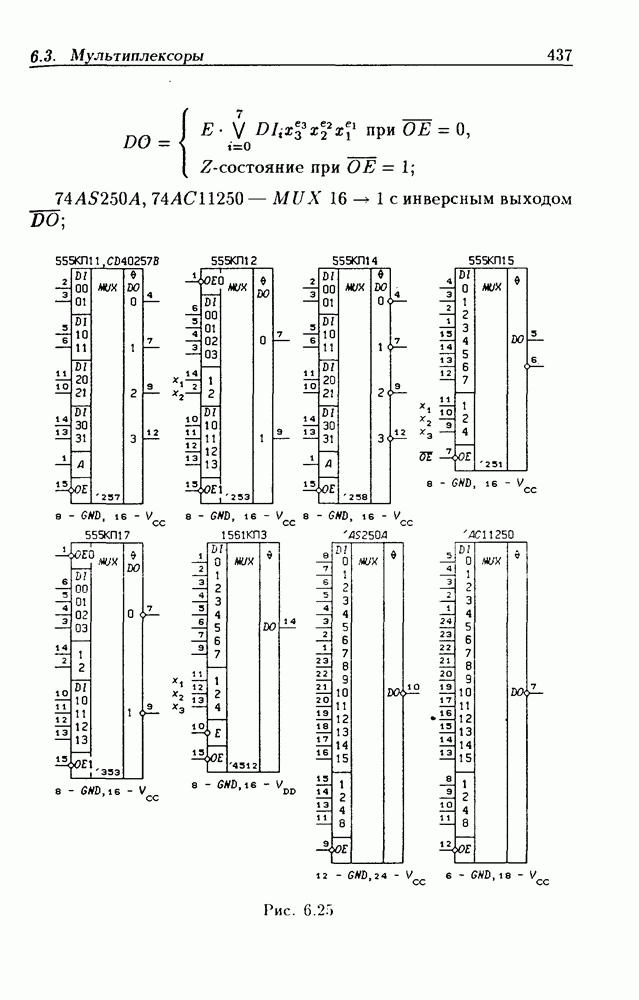
- Мультиплексоры с Z-состоянием выхода.
- Каскадирование мультиплексоров.
- Функциональные мультиплексоры.
- Регистры памяти с мультиплексными входами данных.
- Мультиплексоры с регистрами памяти данных и адреса.
- Сдвигающие мультиплексоры.
- 6.4. Синтез комбинационных схем и цифровых автоматов на мультиплексорах
- Синтез схем на 8-канальных мультиплексорах.
- Синтез на двухразрядных 4-канальных мультиплексорах.
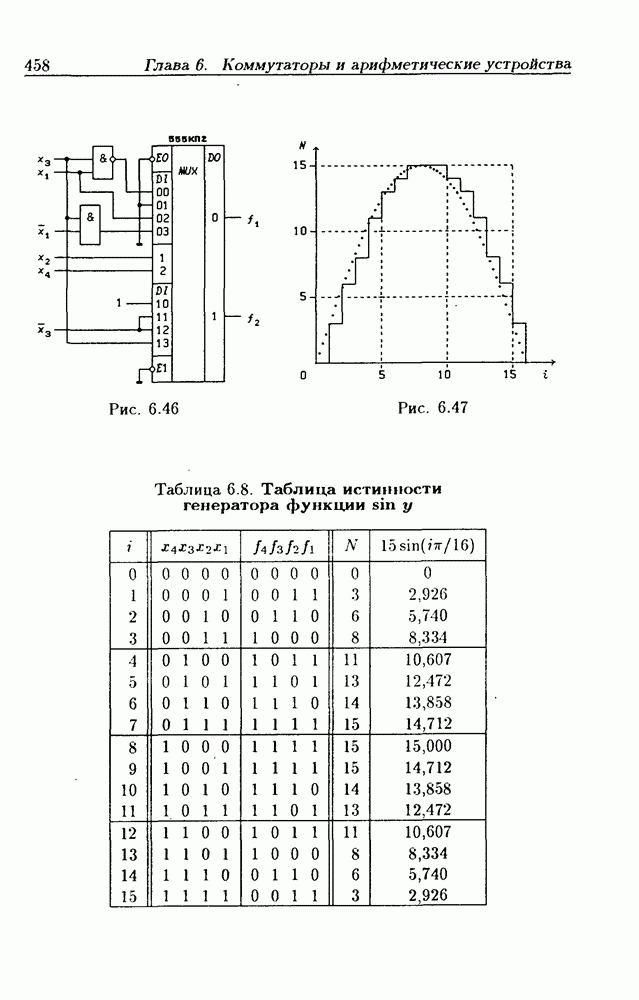
- Синтез генератора синусоидальной функции на мультиплексорах.
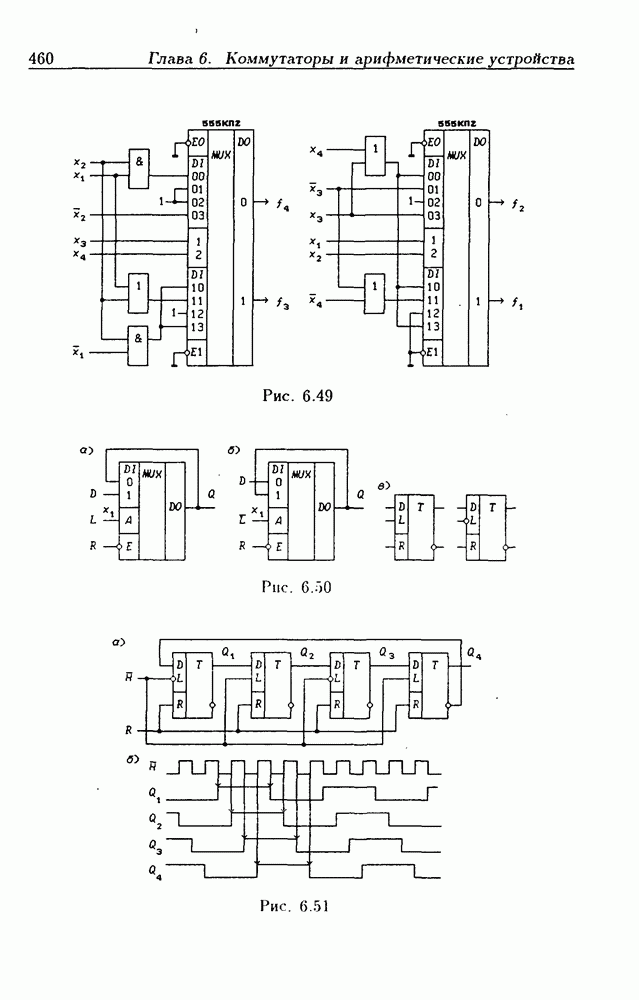
- Синтез триггеров на мультиплексорах.
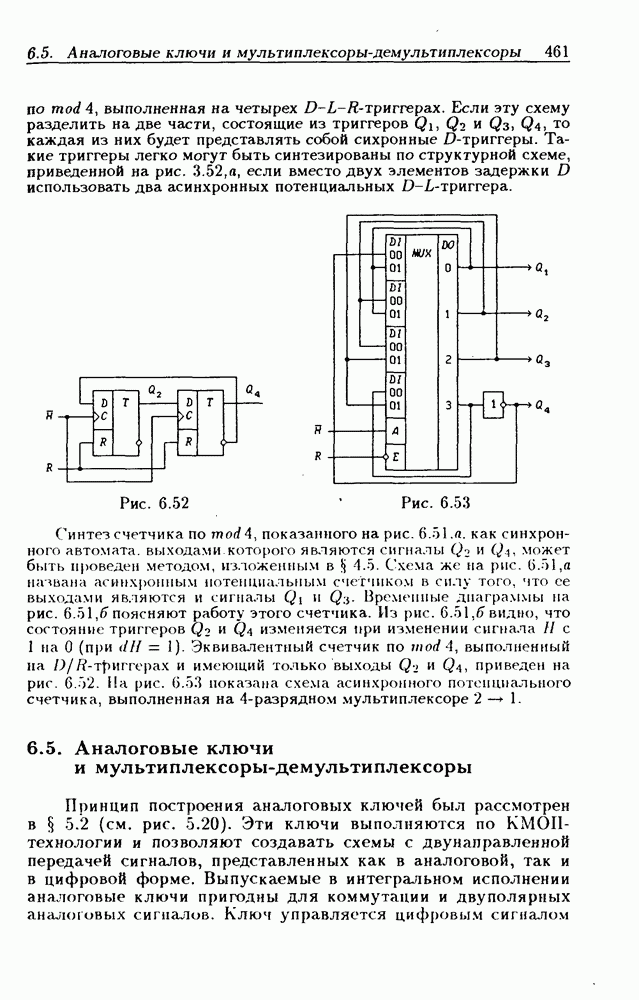
- Синтез счетчиков на мультиплексорах.
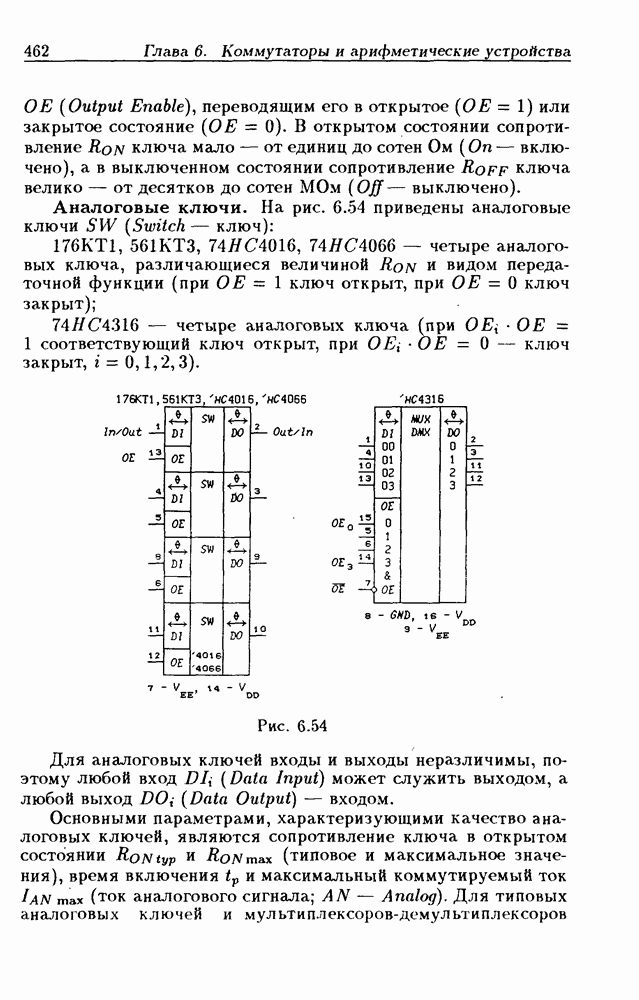
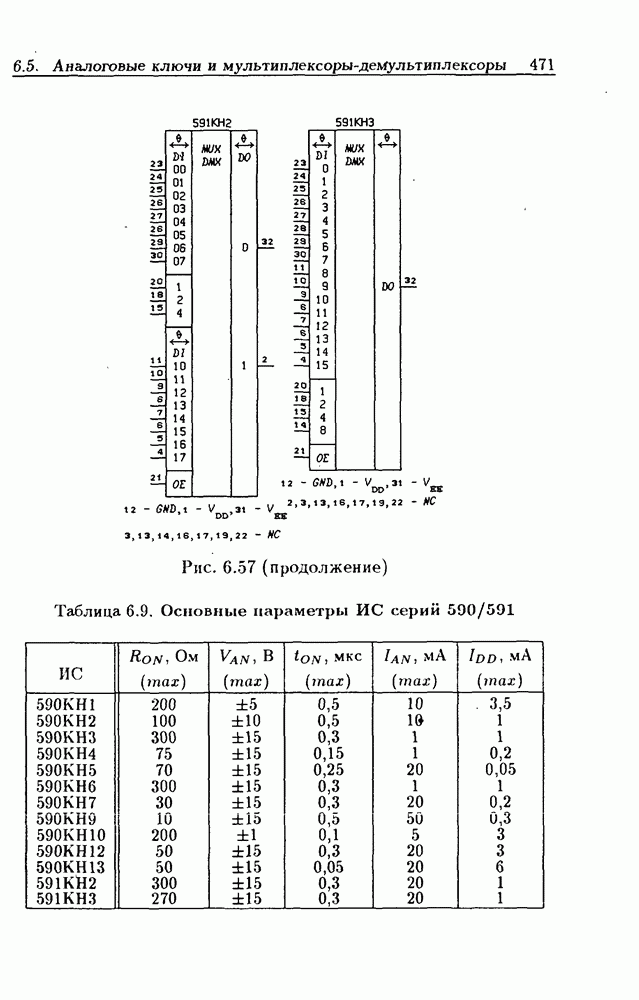
- 6.5. Аналоговые ключи и мультиплексоры-демультиплексоры
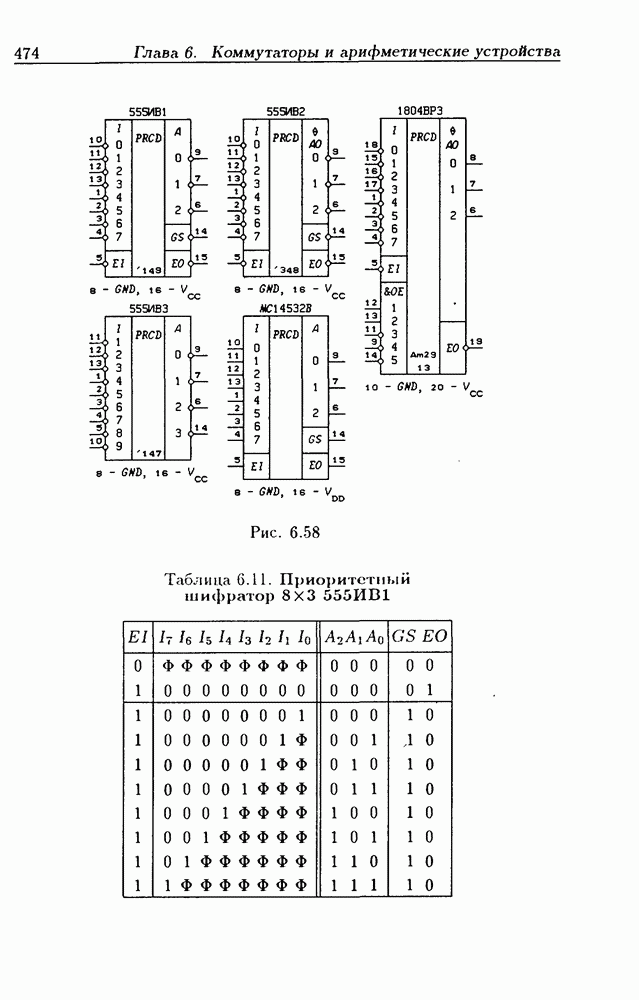
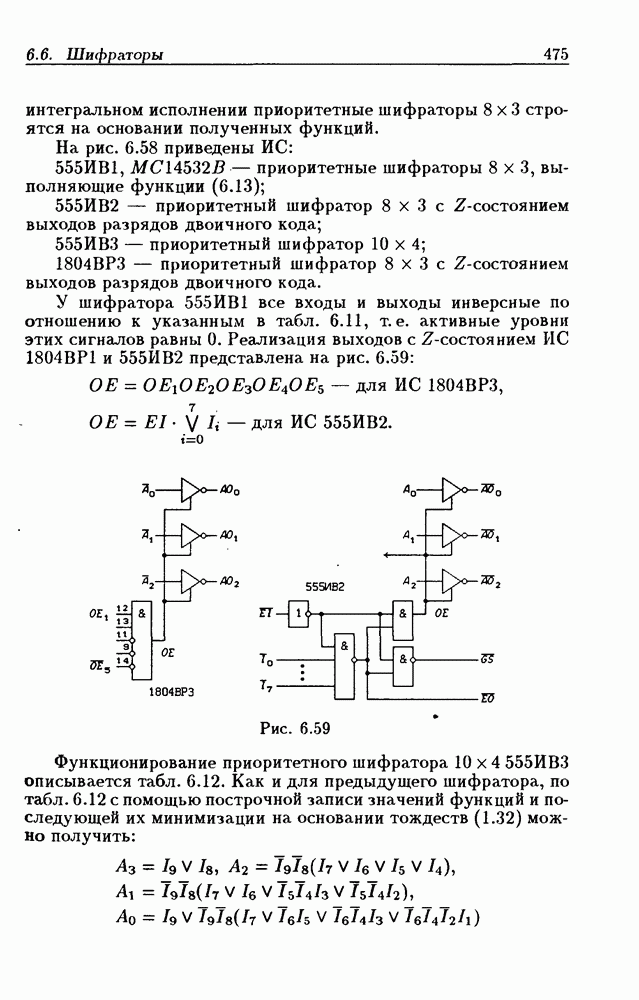
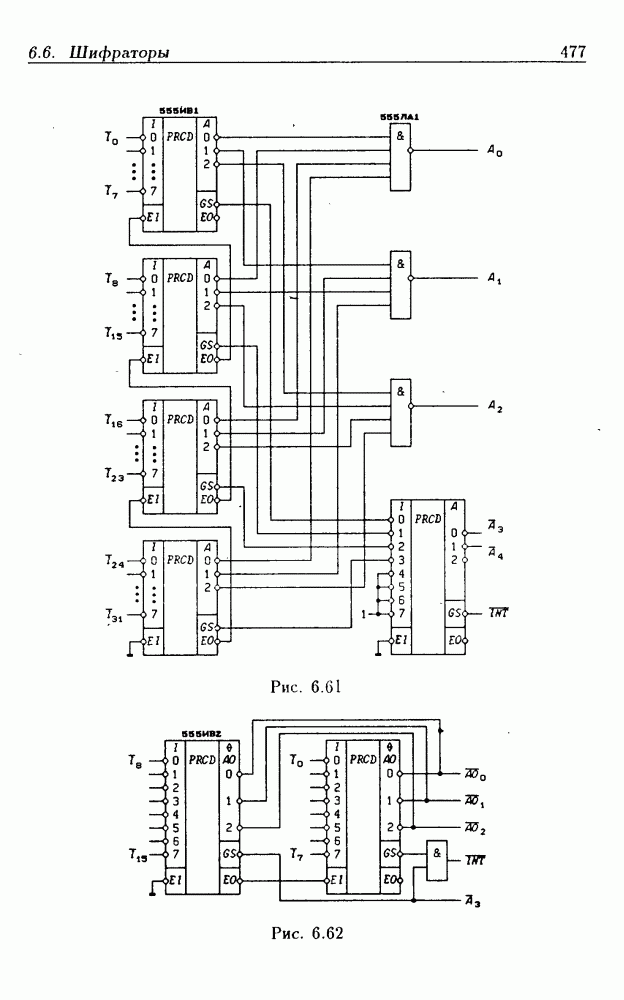
- 6.6. Шифраторы
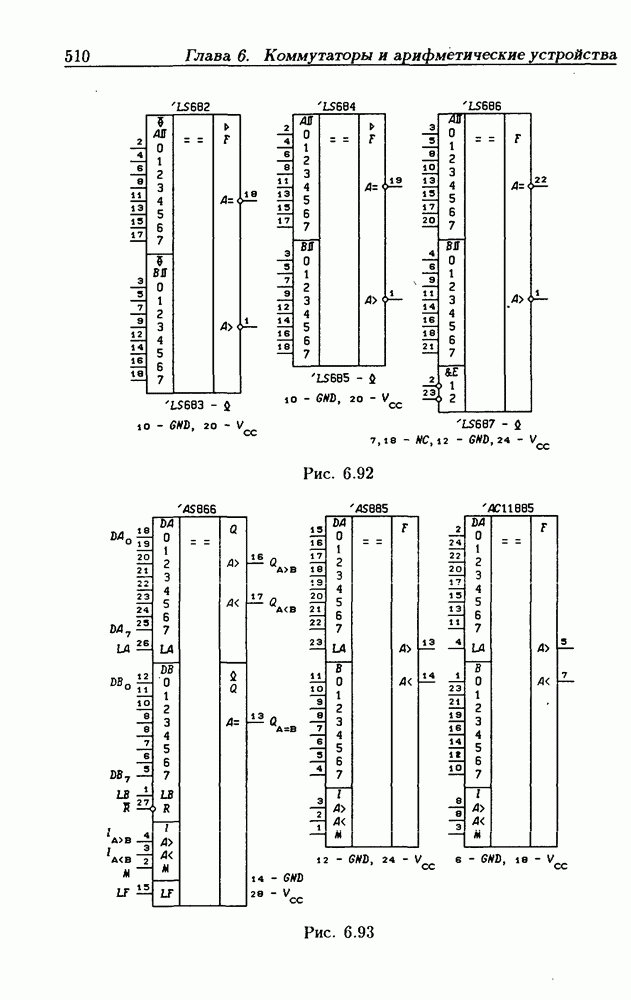
- 6.7. Цифровые компараторы
- Программируемые цифровые компараторы.
- Адресные компараторы.
- Применения адресных компараторов.
- 6.8. Схемы сравнения двоичных чисел
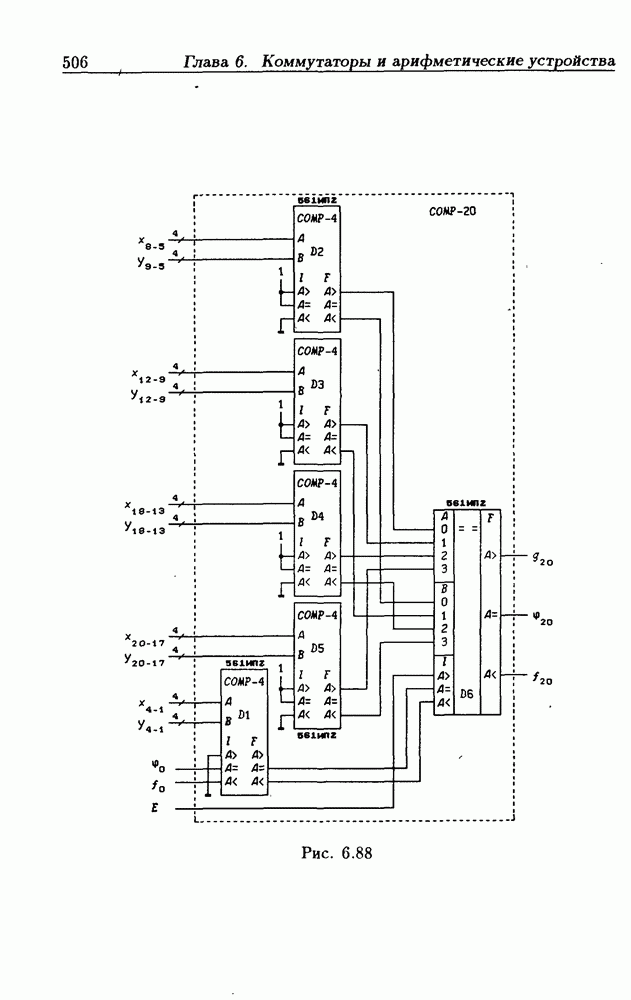
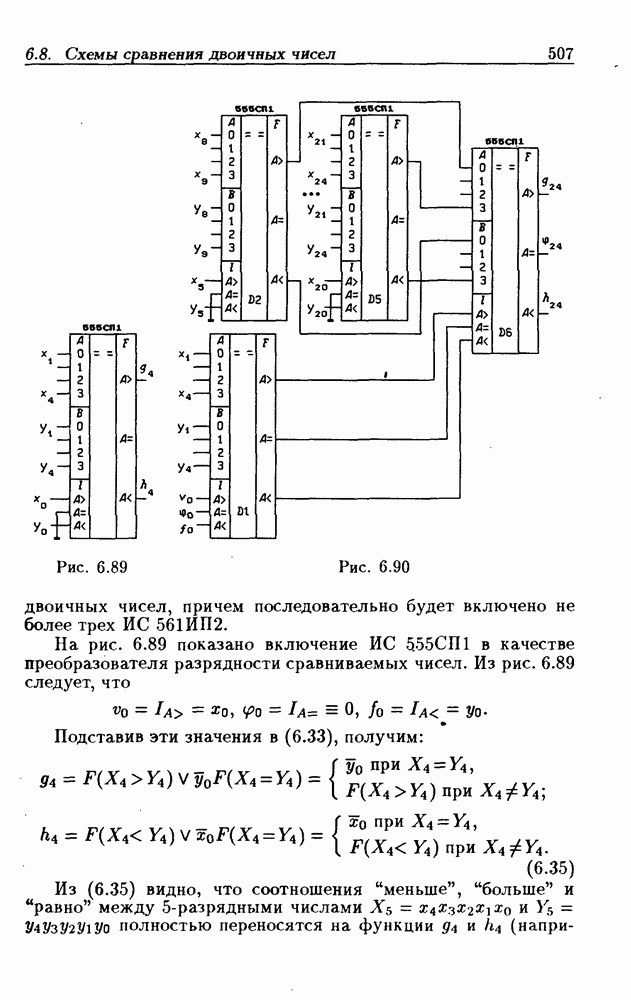
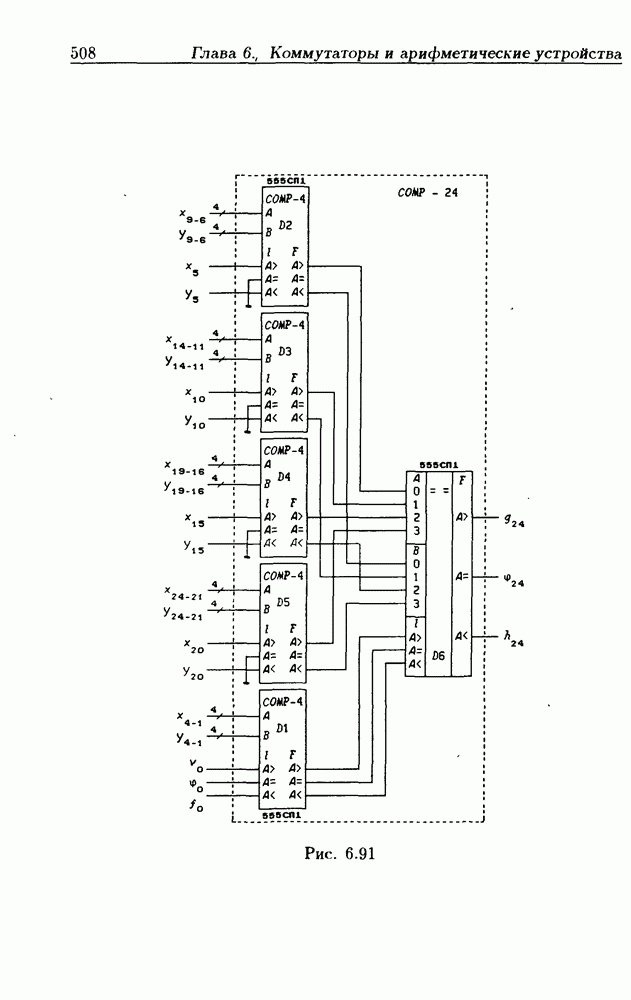
- 8-разрядные схемы сравнения двоичных чисел.
- 6.9. Прямой, обратный и дополнительный коды
- Дополнительный код.
- Сложение чисел в обратном коде.
- Код с избытком 3.
- 6.10. Сумматоры
- Двоичные параллельные сумматоры с последовательным переносом.
- Двоичные сумматоры с параллельным переносом.
- Применения сумматоров.
- Десятичные сумматоры.
- Последовательные двоичные сумматоры.
- 6.11. Арифметическо-логические устройства
- 6.12. Пороговые схемы и мажоритарные элементы
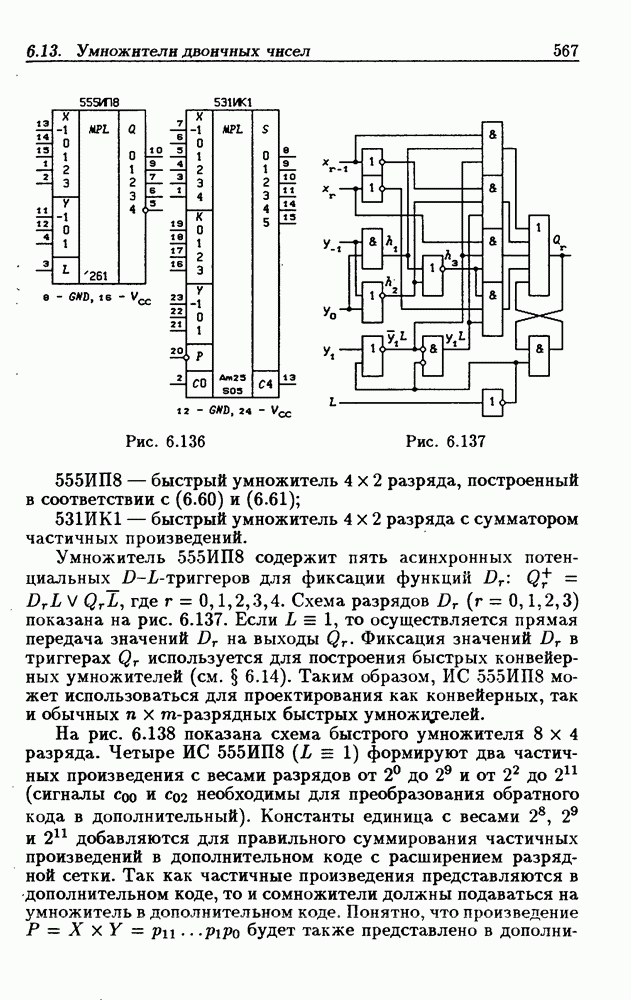
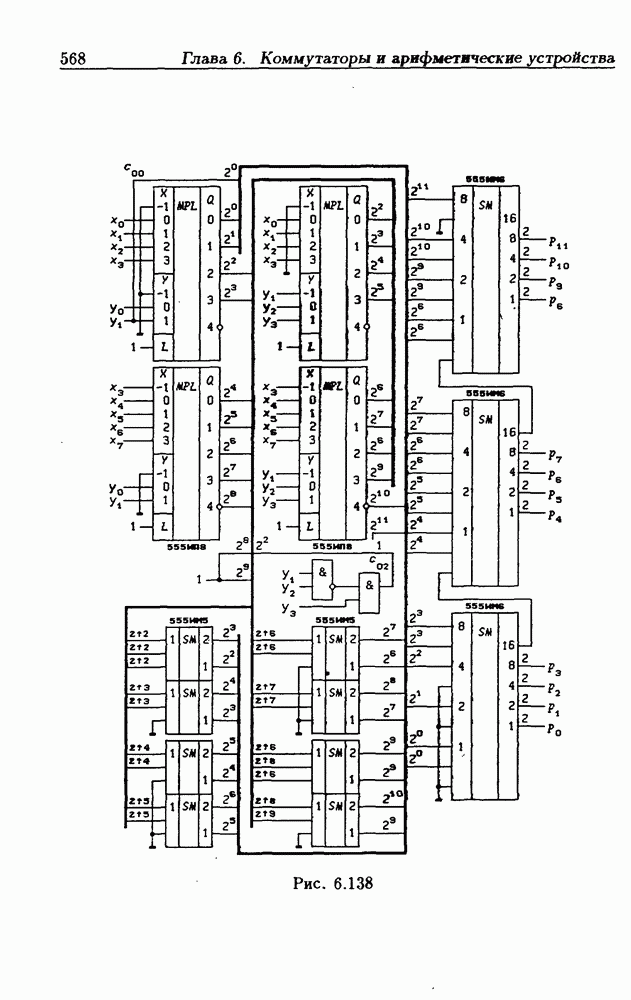
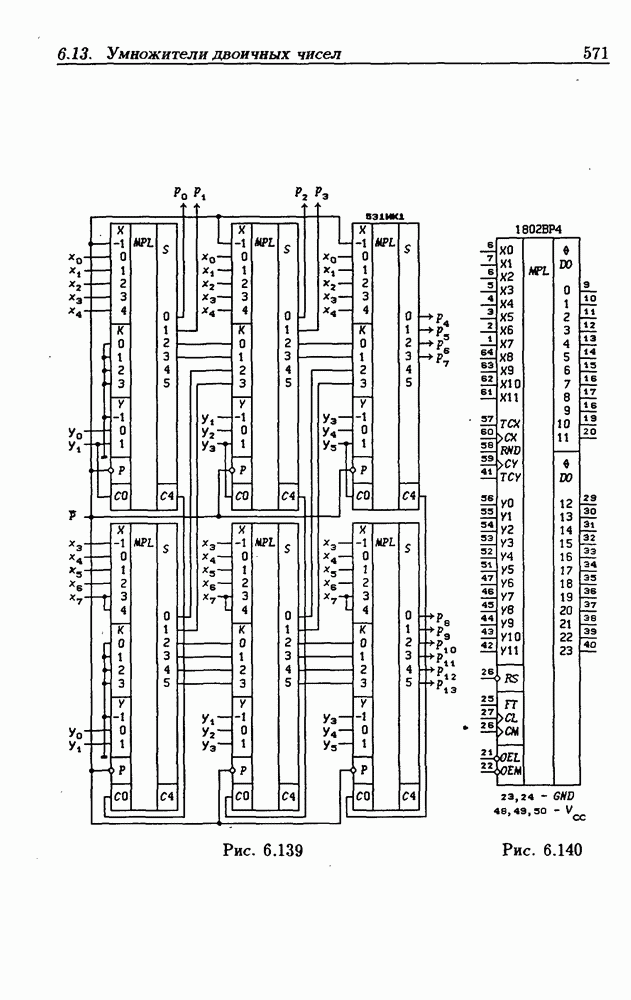
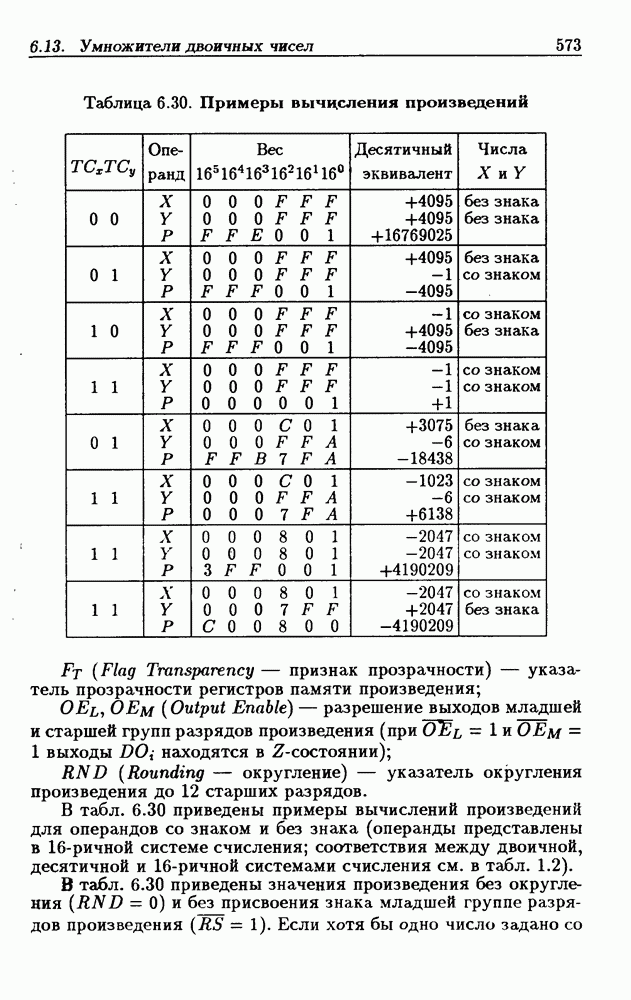
- 6.13. Умножители двоичных чисел
- Быстрые умножители.
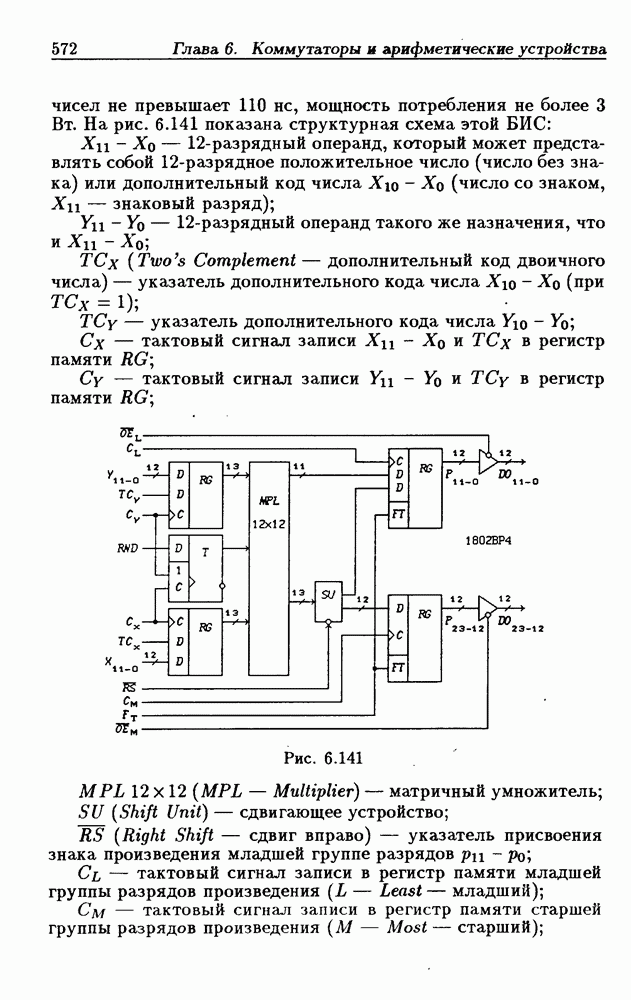
- БИС умножителя 12×12 разрядов 1802ВР4.
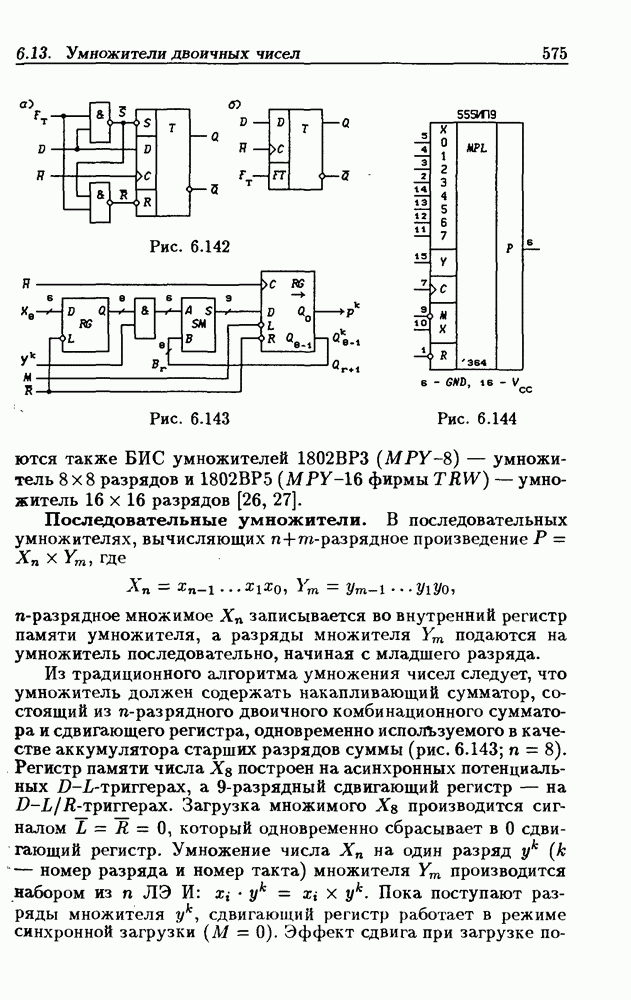
- Последовательные умножители.
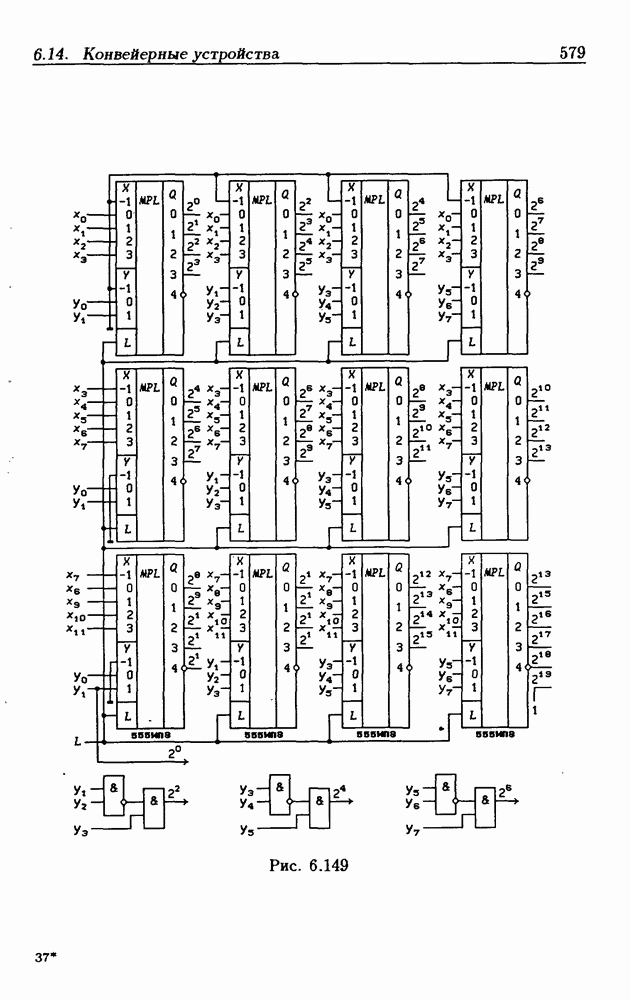
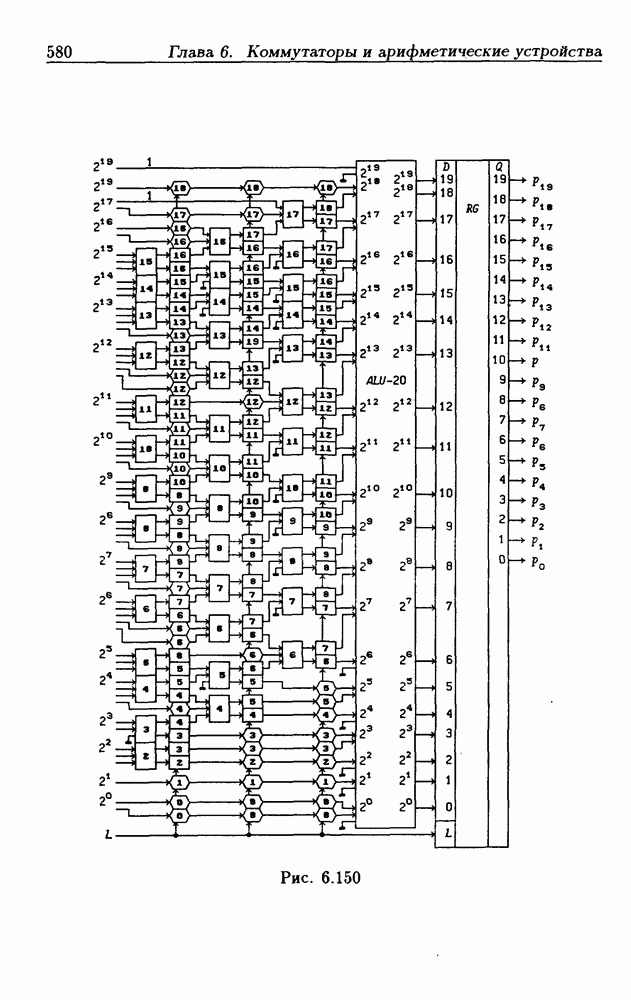
- 6.14. Конвейерные устройства
- Конвейерный быстрый умножитель.
- Конвейерные АЦП.
- 6.15. Синтез линейных комбинационных схем
- Сумматор по модулю q.
- Умножитель по модулю q.
- Глава 7. Сдвигающие регистры и счетчики
- 7.1. Сдвигающие регистры без параллельной записи данных
- Сдвигающие устройства с выходными регистрами памяти.
- 7.2. Сдвигающие регистры с параллельной записью данных
- Сдвигающие регистры с расширением знака.
- Сдвигающие регистры с входным регистром памяти.
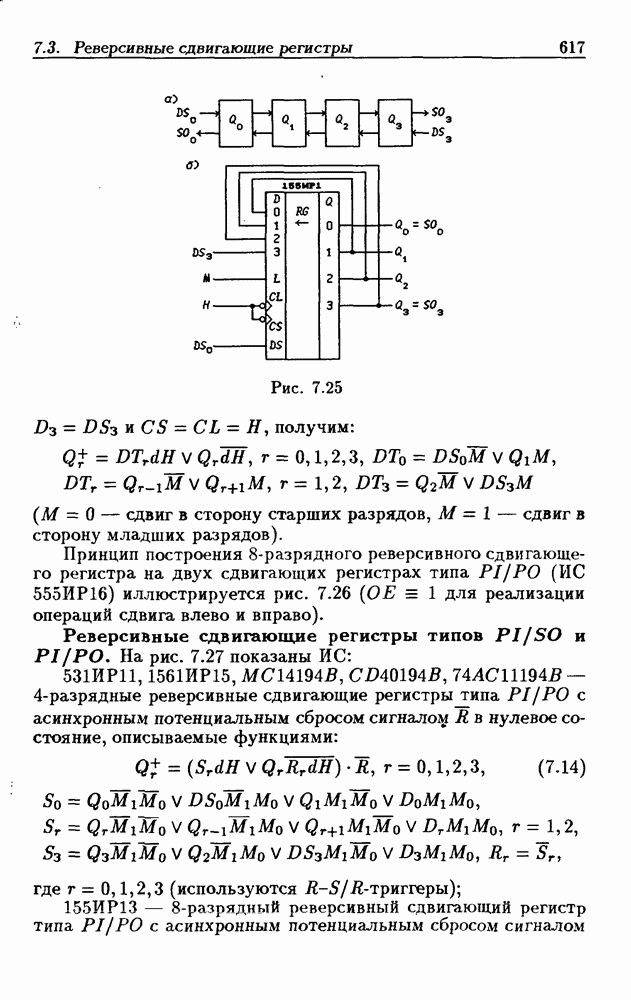
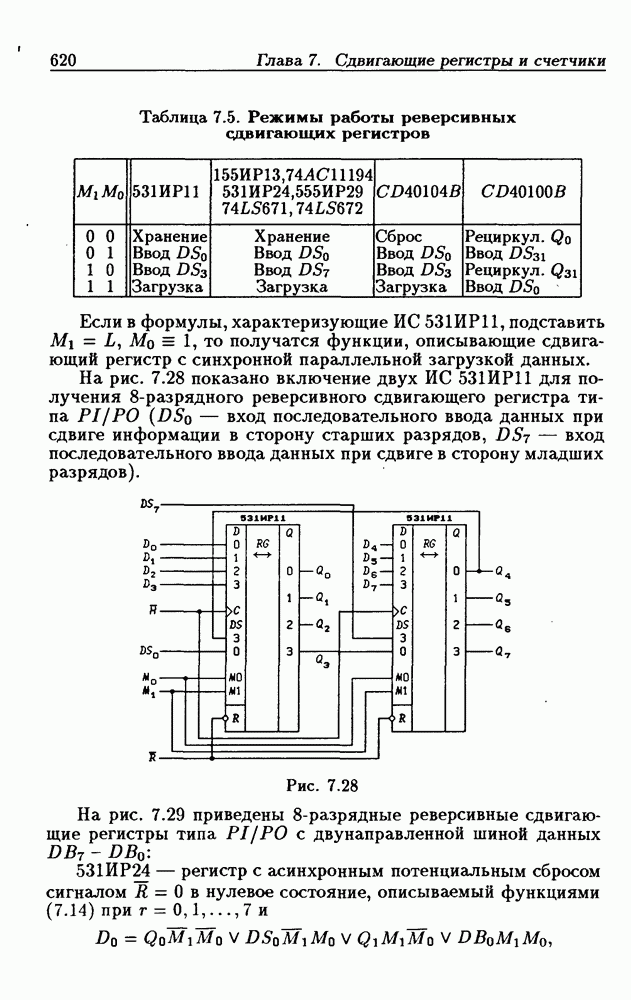
- 7.3. Реверсивные сдвигающие регистры
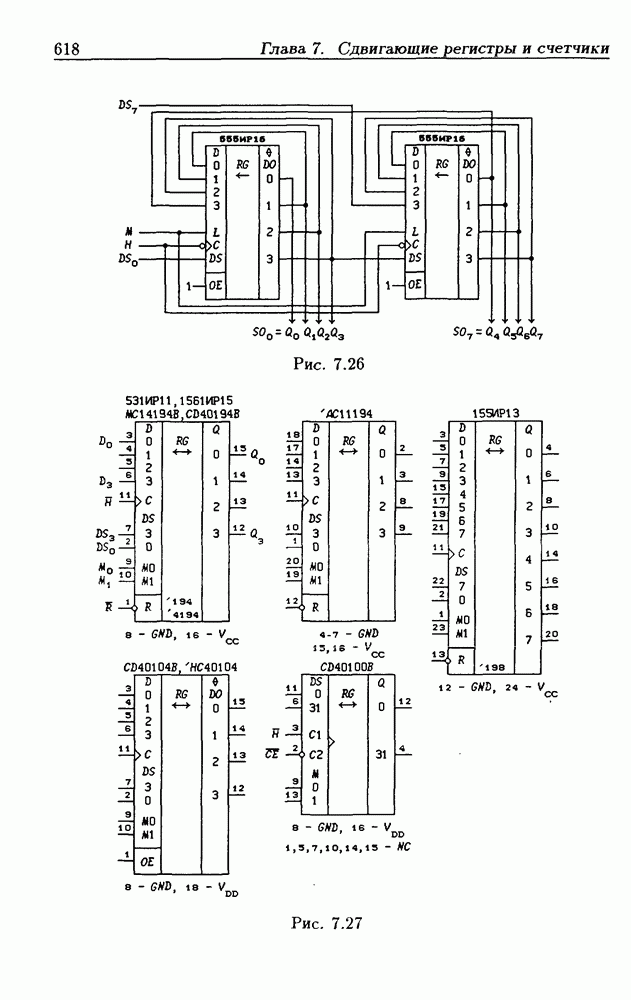
- Реверсивные сдвигающие регистры типов PI/SO и PI/PO.
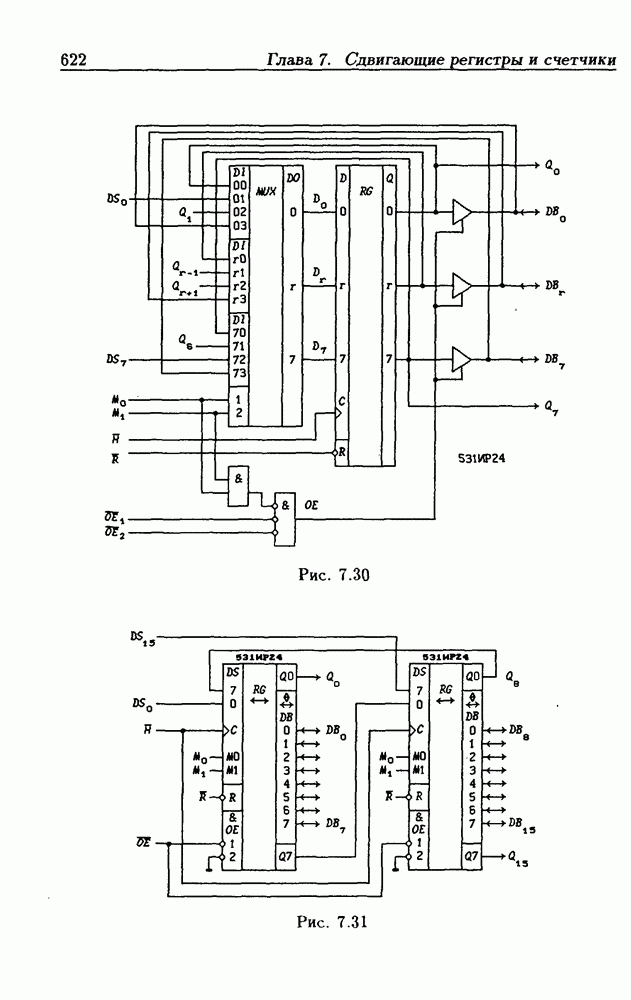
- Многофункциональные устройства на основе реверсивных сдвигающих регистров.
- 7.4. Асинхронные счетчики
- Двоично-десятичные асинхронные счетчики.
- 7.5. Синхронные двоичные счетчики
- Программирование модуля пересчета двоичных счетчиков.
- Переключение модулей пересчета двоичных счетчиков.
- Функциональные устройства на основе двоичных счетчиков.
- 7.6. Синхронные двоично-десятичные счетчики
- 7.7. Синхронные реверсивные счетчики
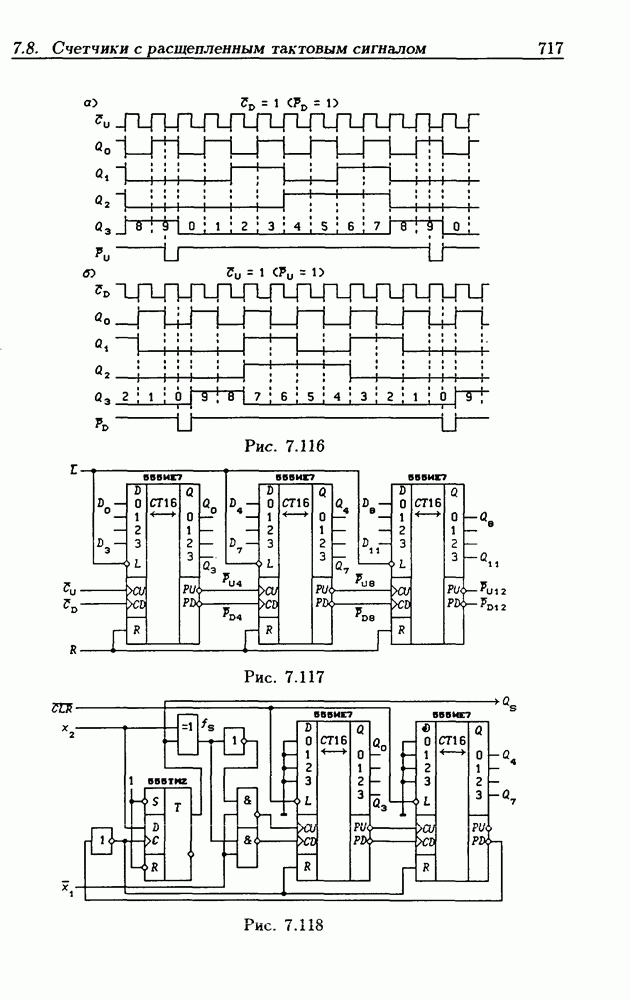
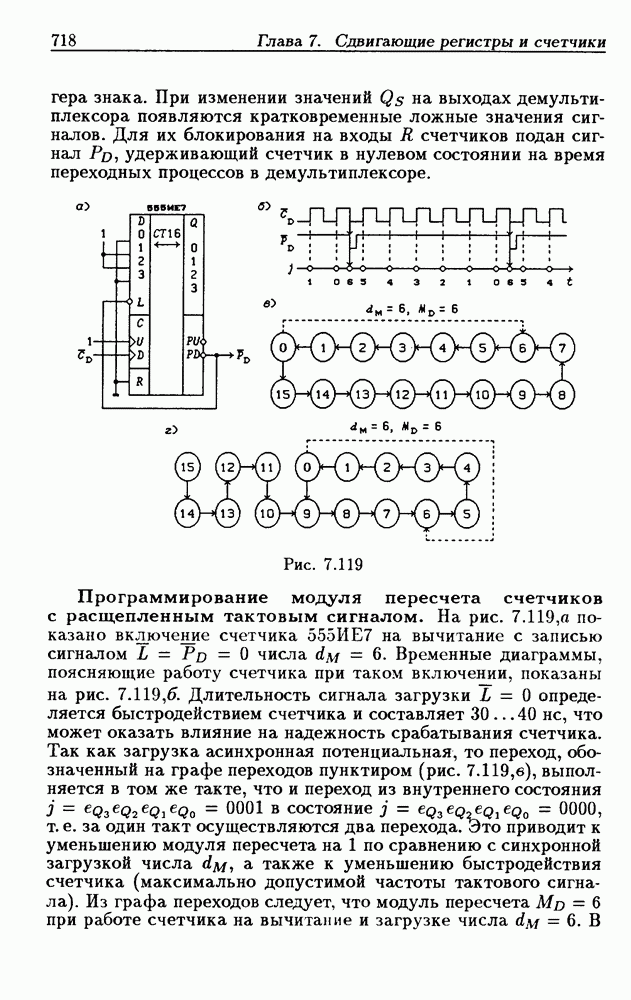
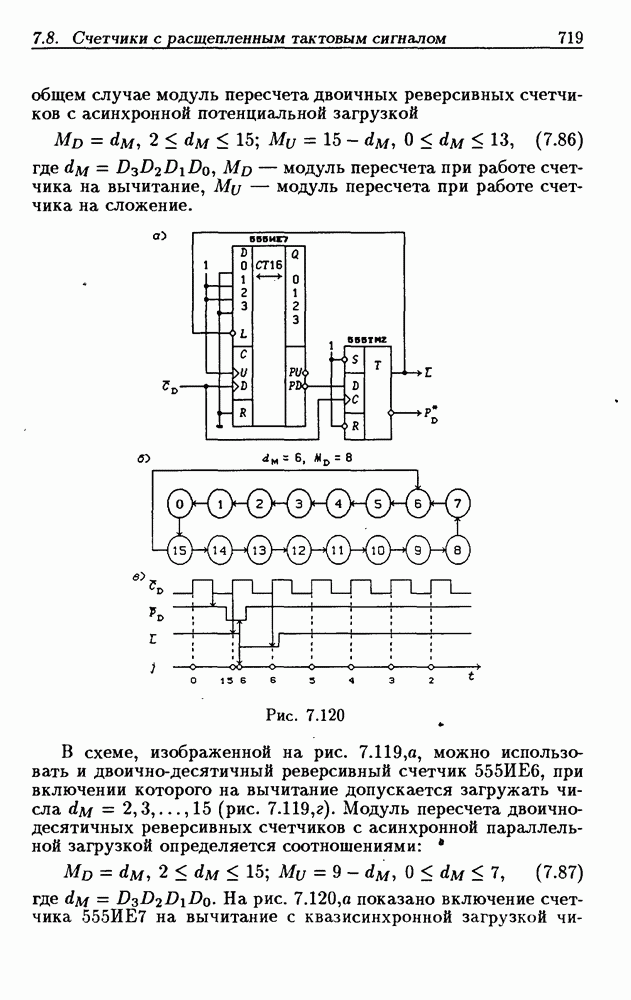
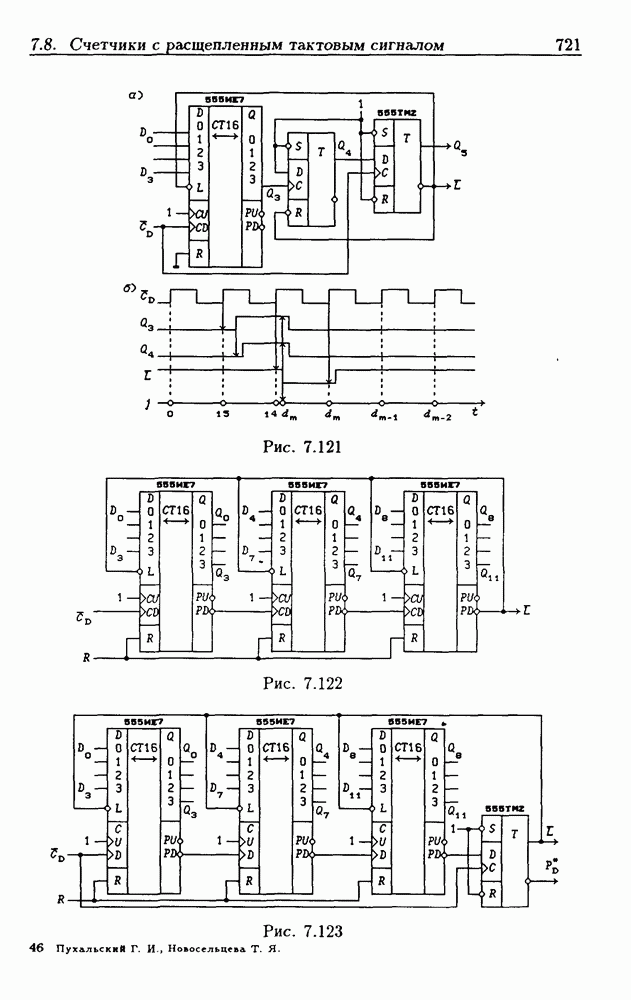
- 7.8. Счетчики с расщепленным тактовым сигналом
- 7.9. Счетчики на сдвигающих регистрах
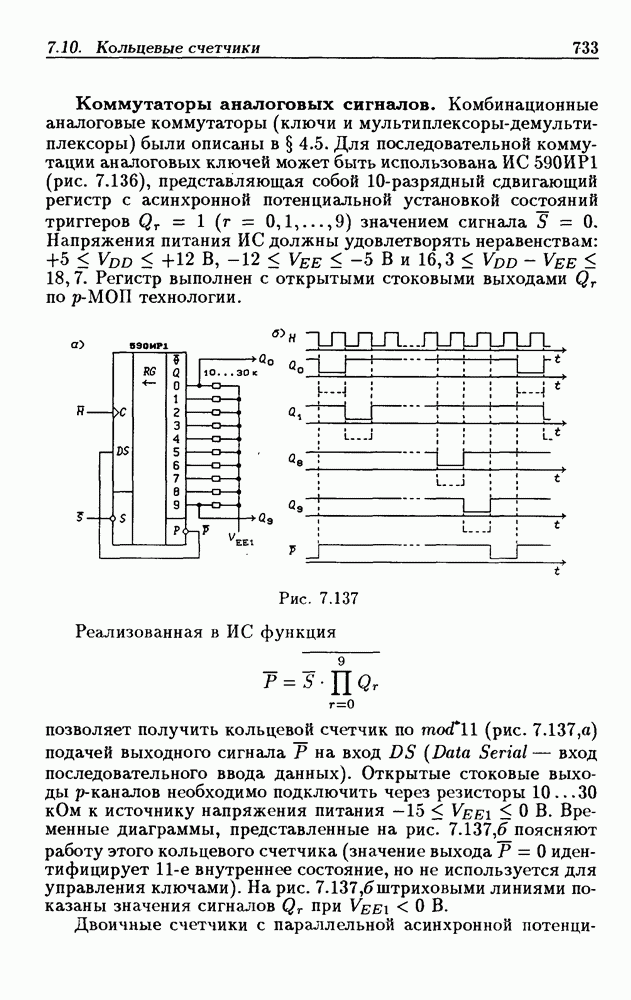
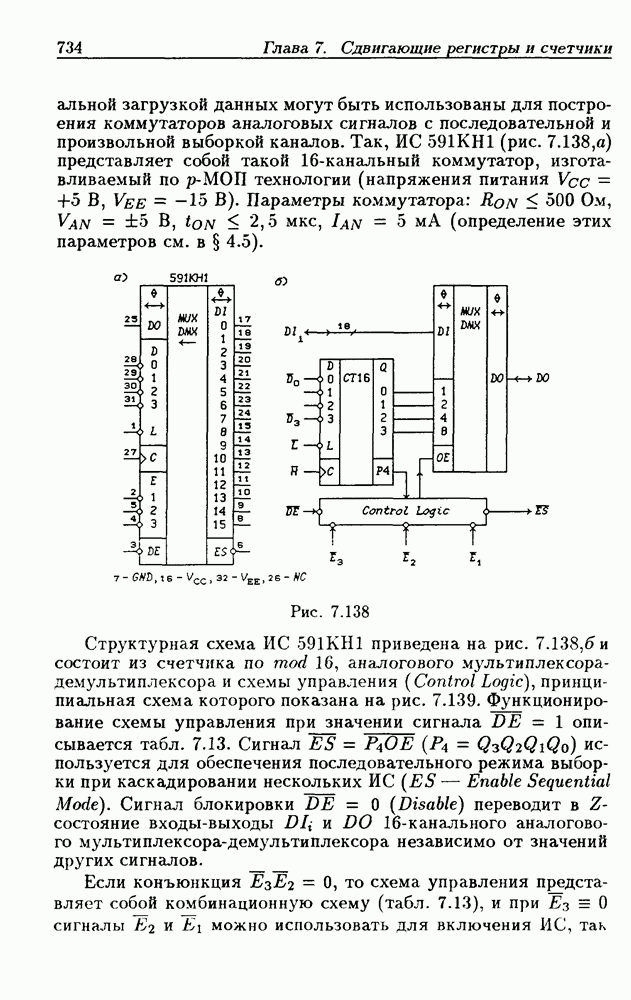
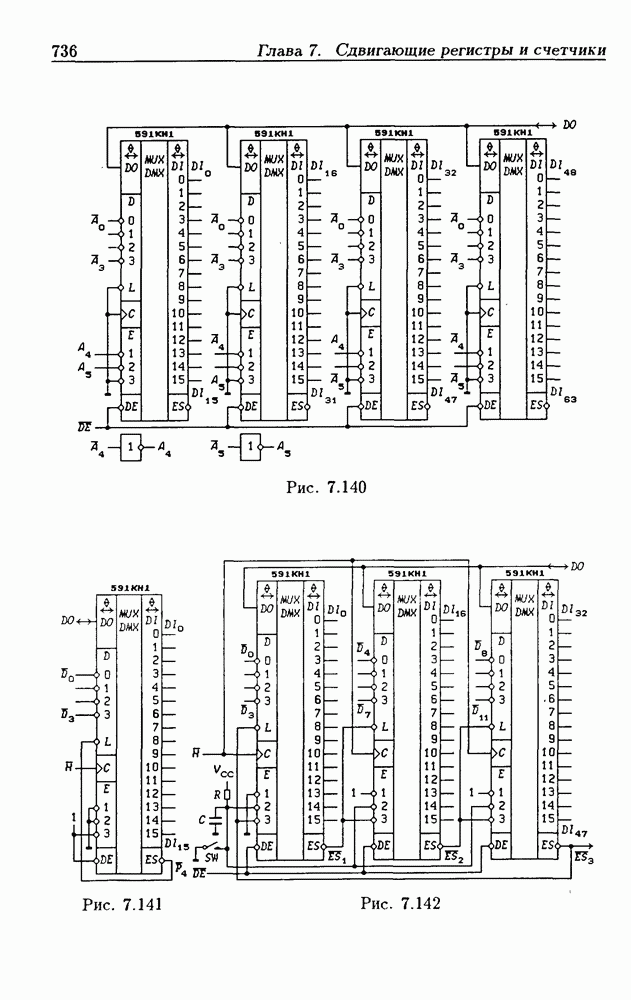
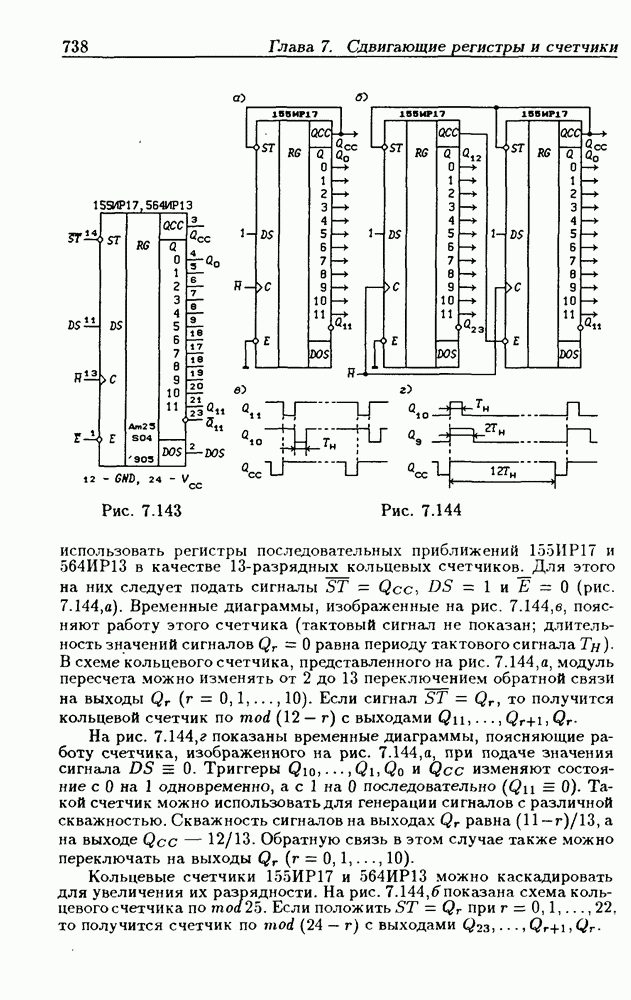
- 7.10. Кольцевые счетчики
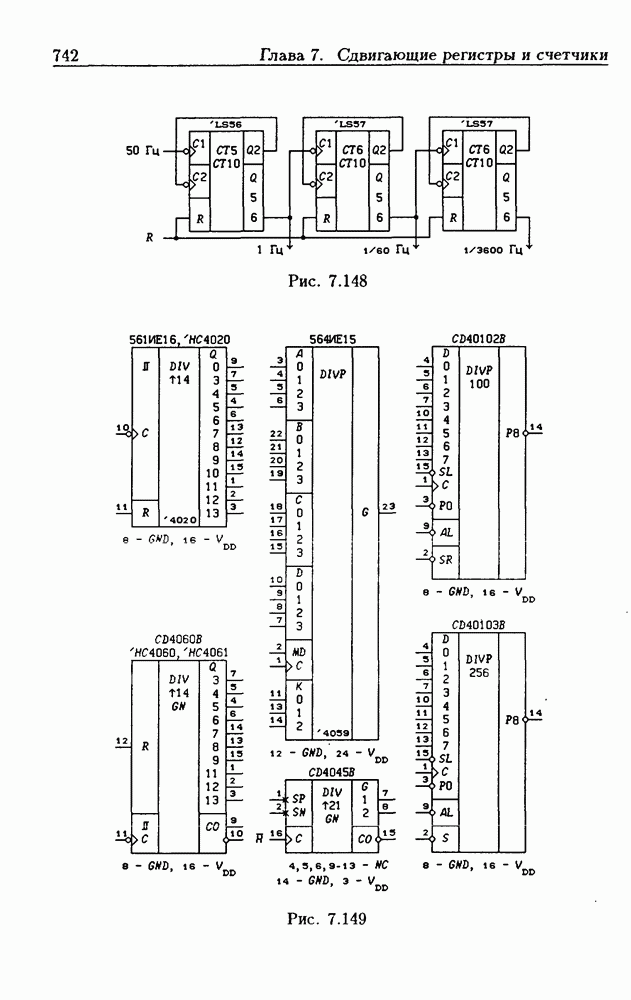
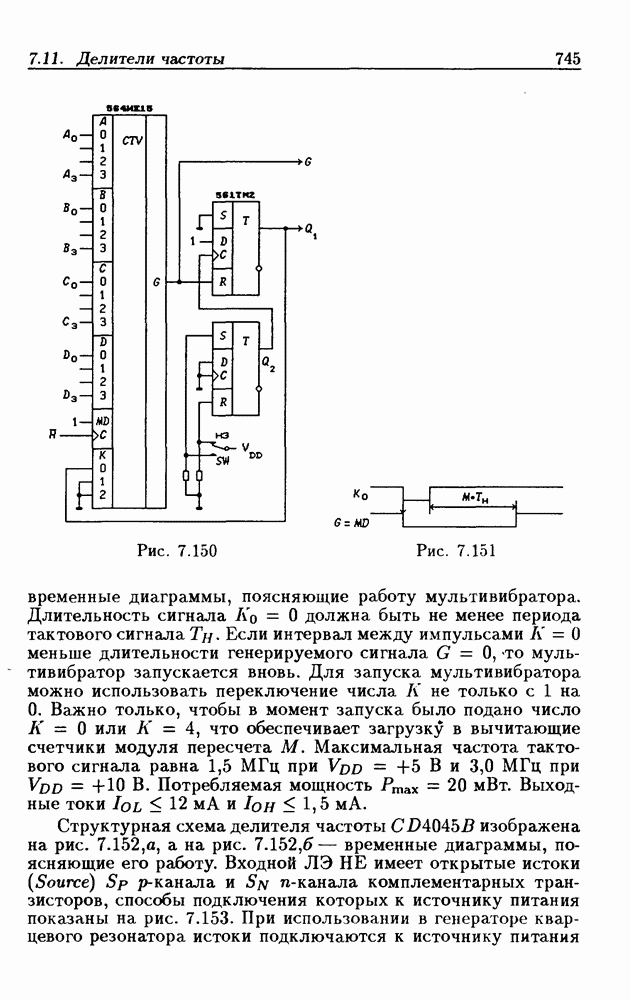
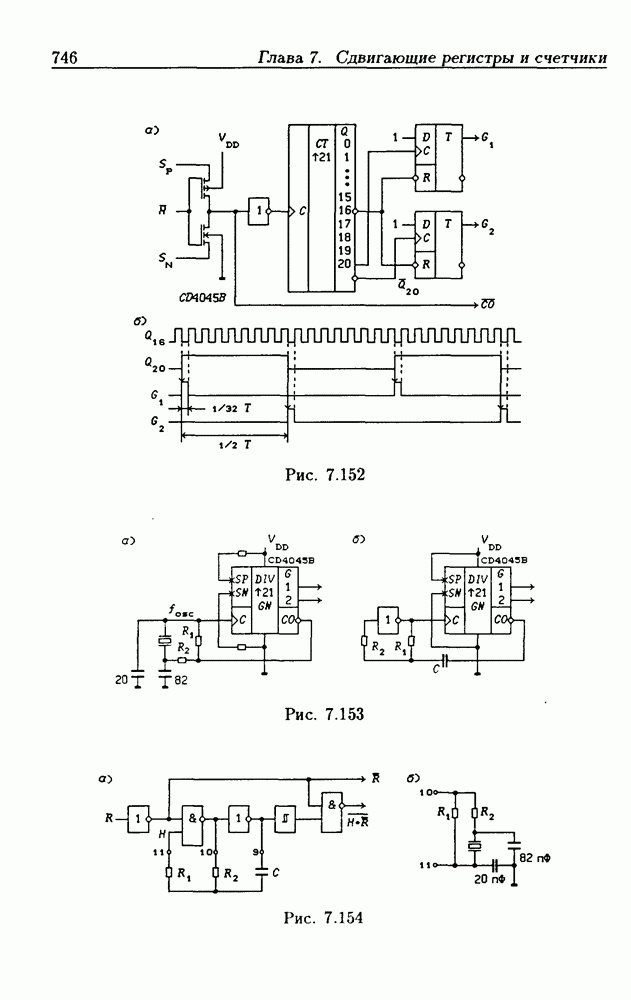
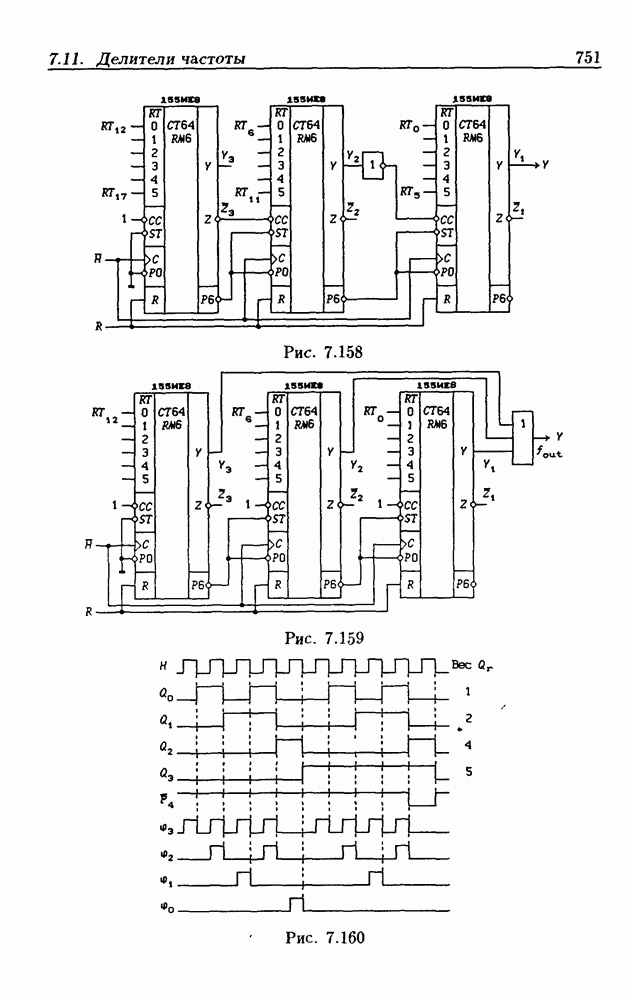
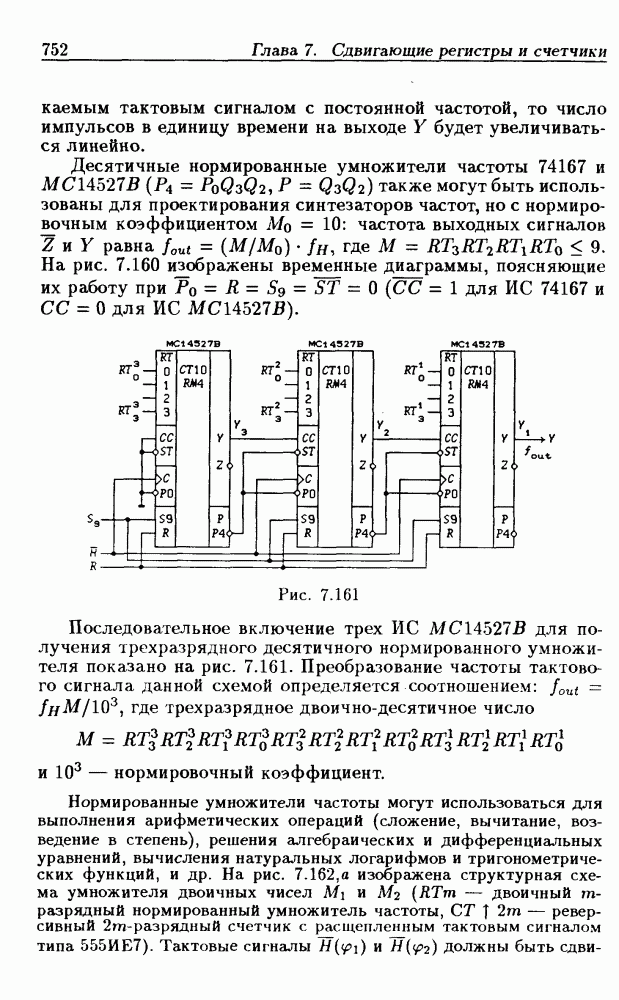
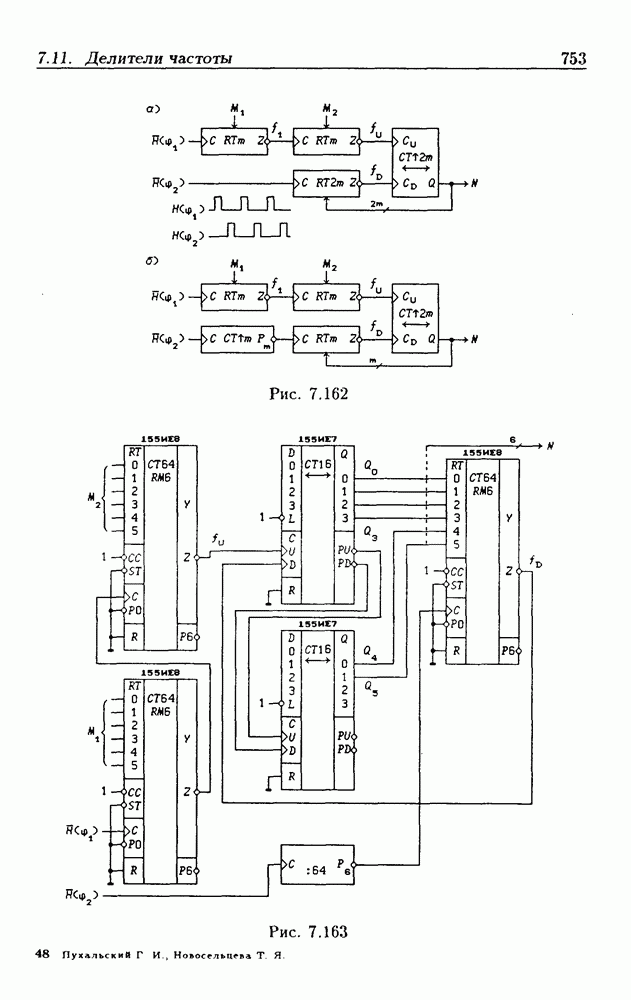
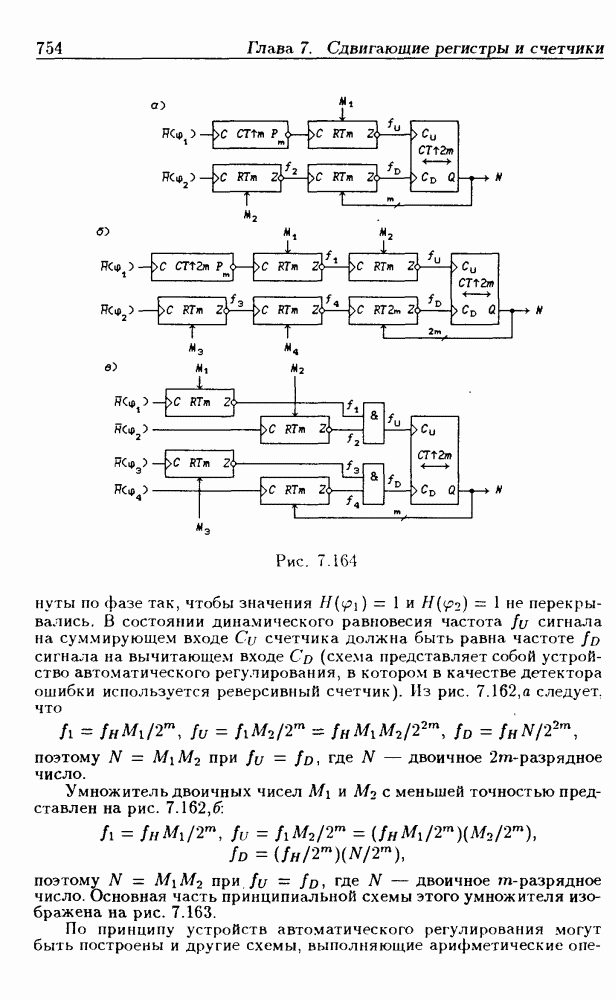
- 7.11. Делители частоты
- Нормированные умножители частоты.
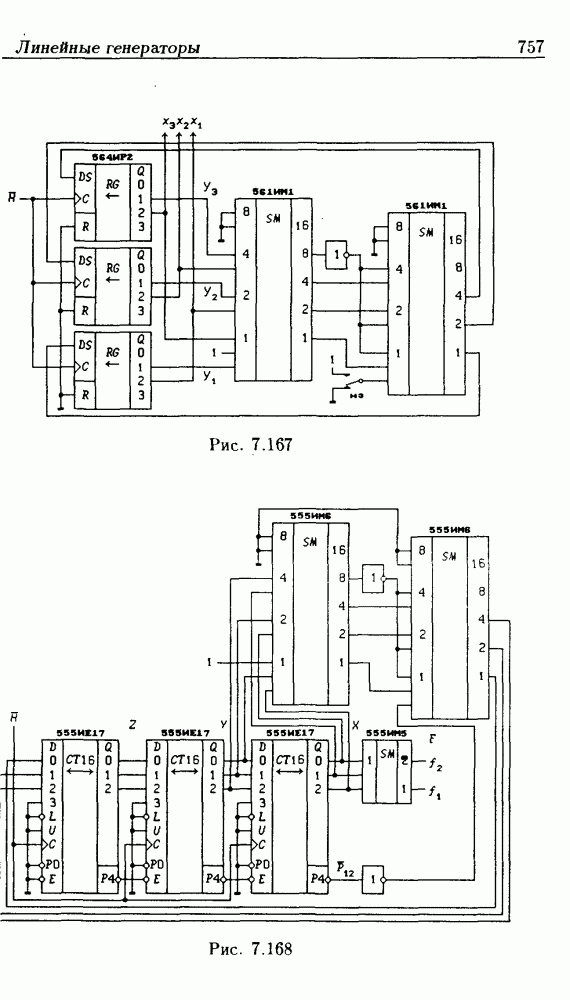
- 7.12. Линейные генераторы
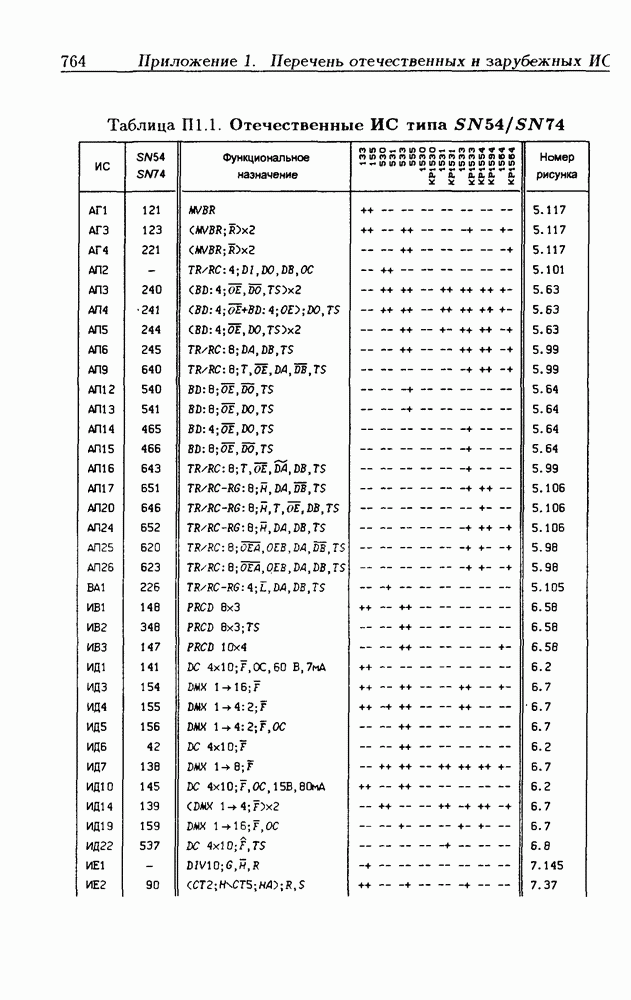
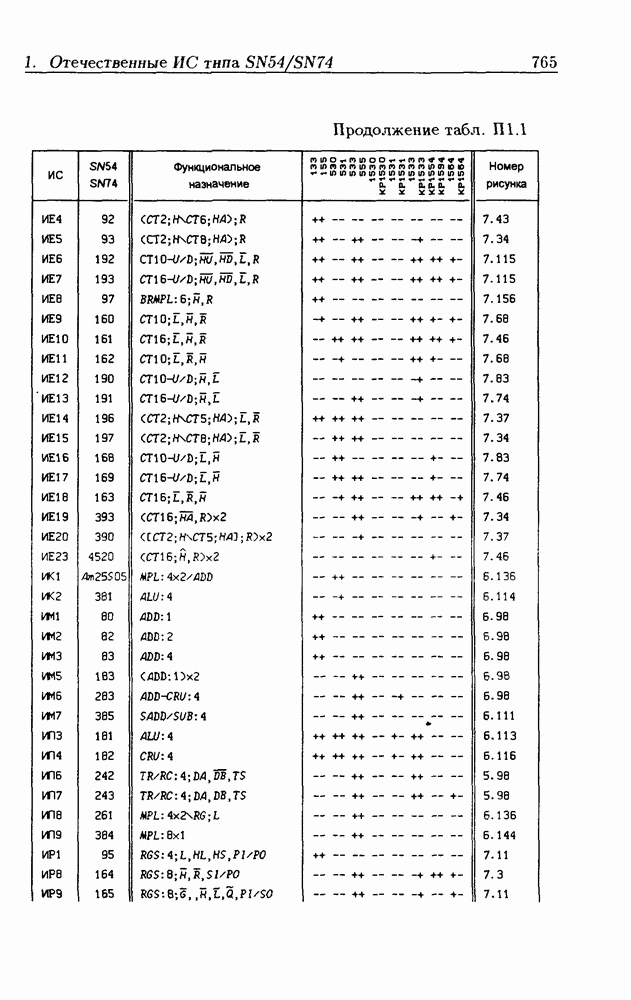
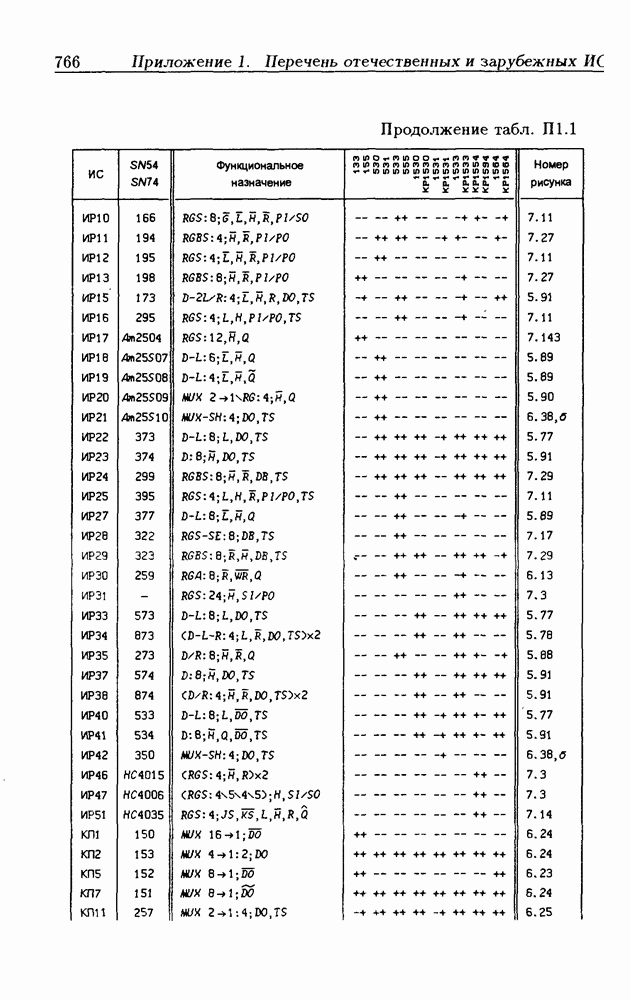
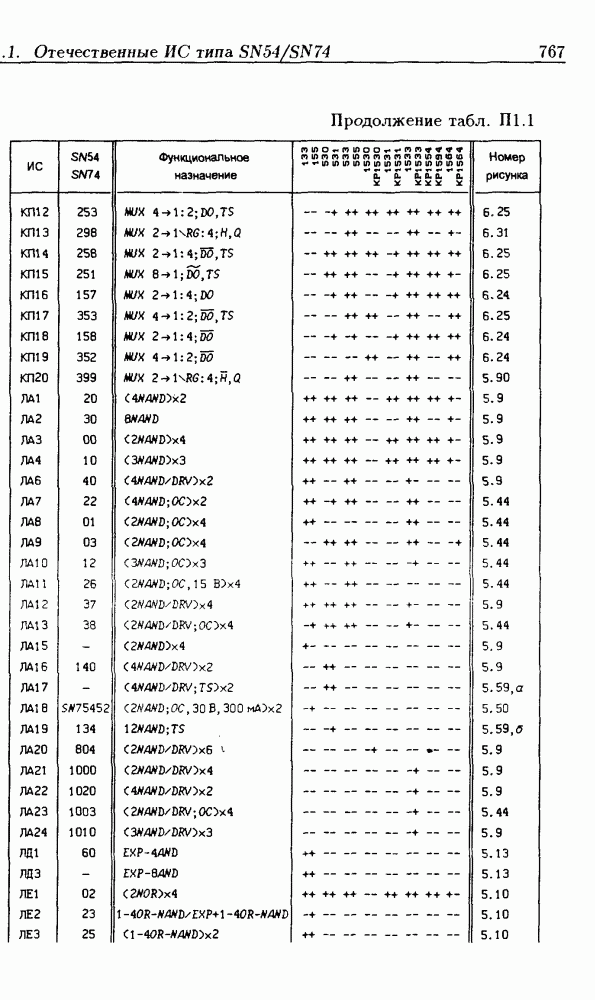
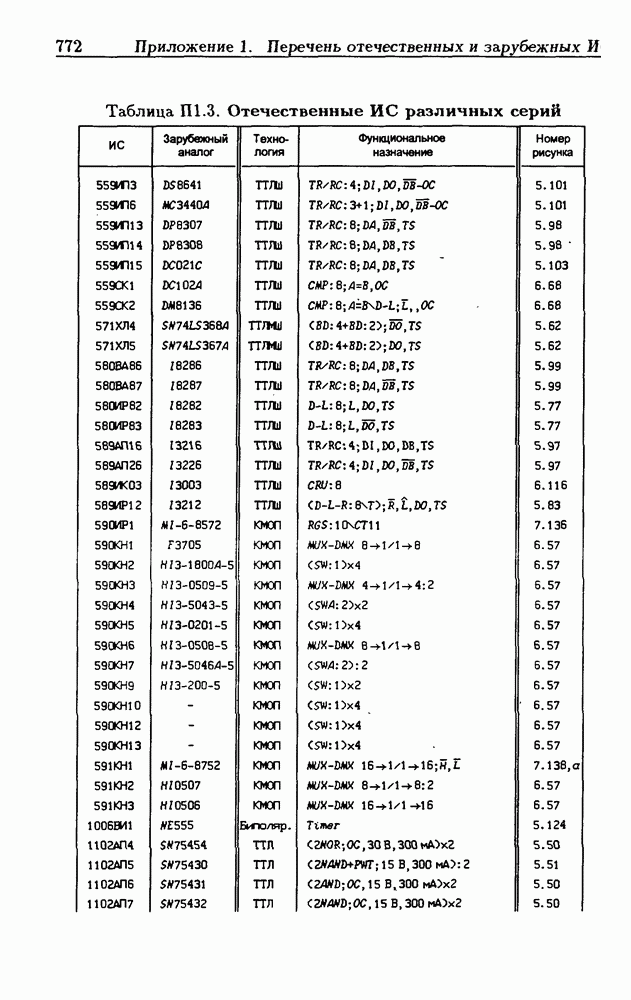
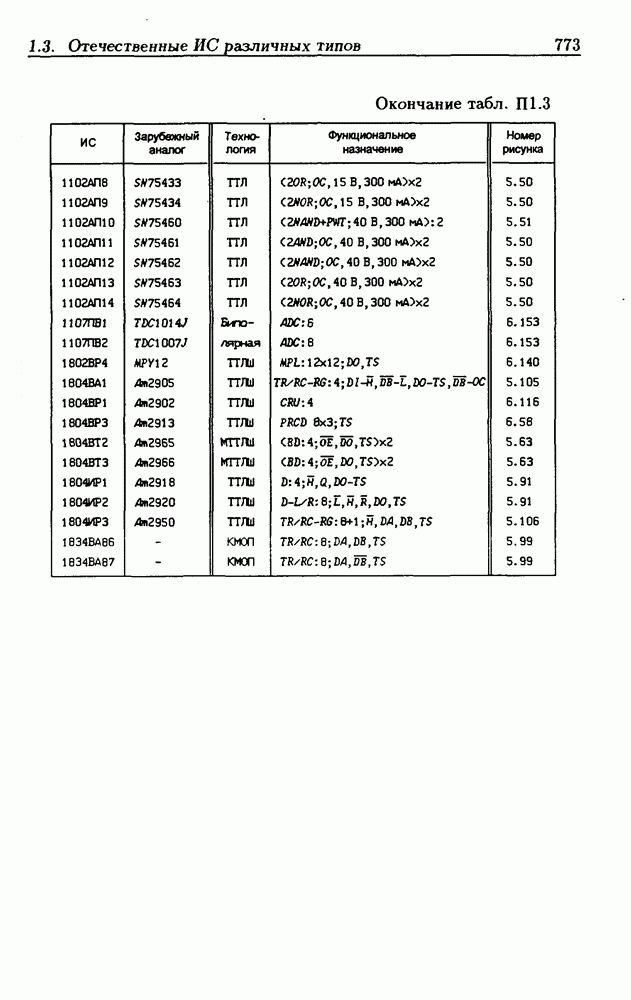
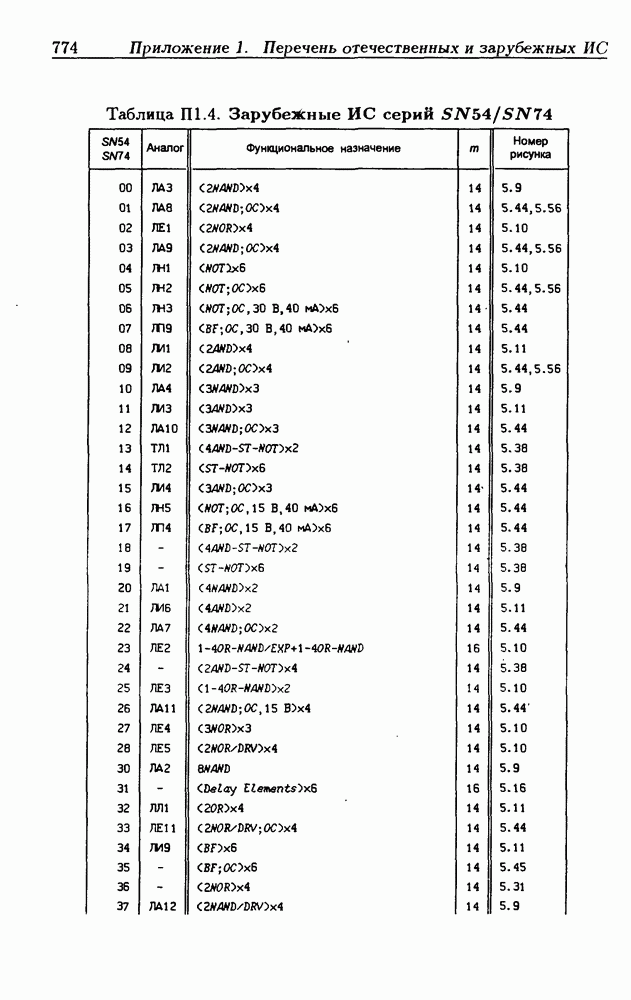
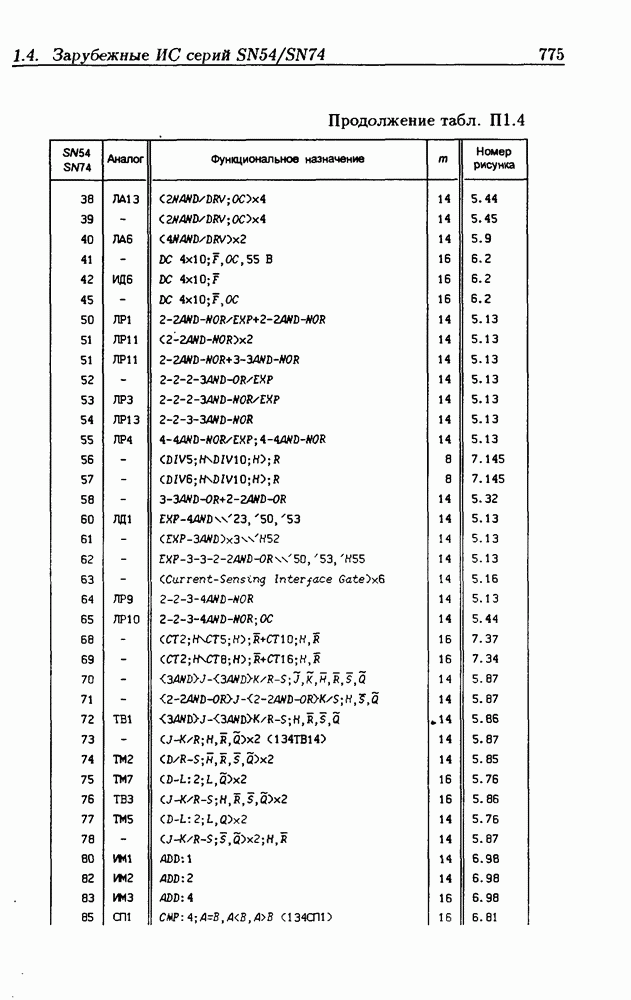
- Приложение 1. Перечень отечественных и зарубежных ИС
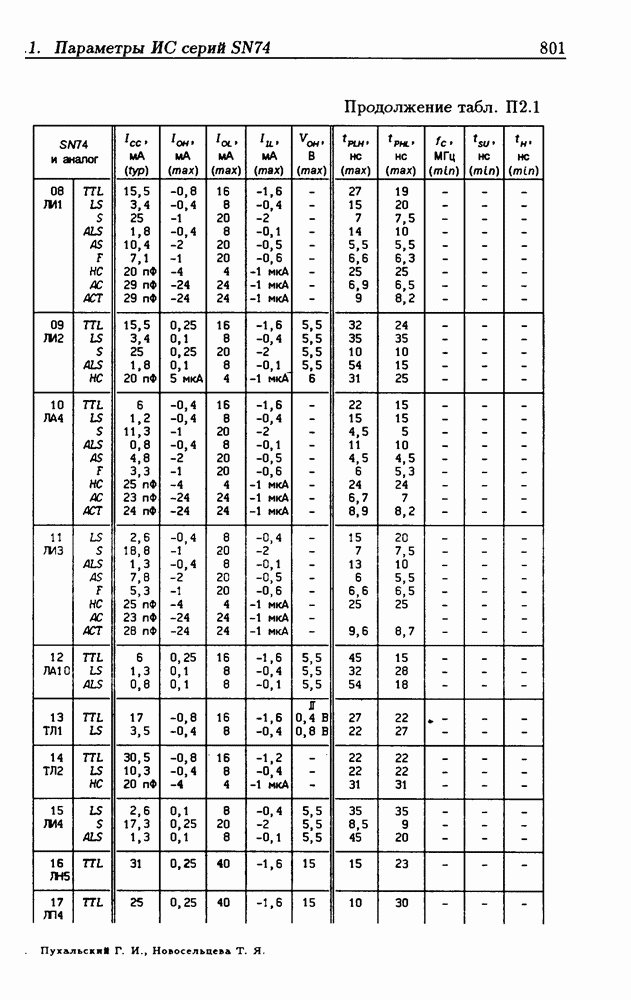
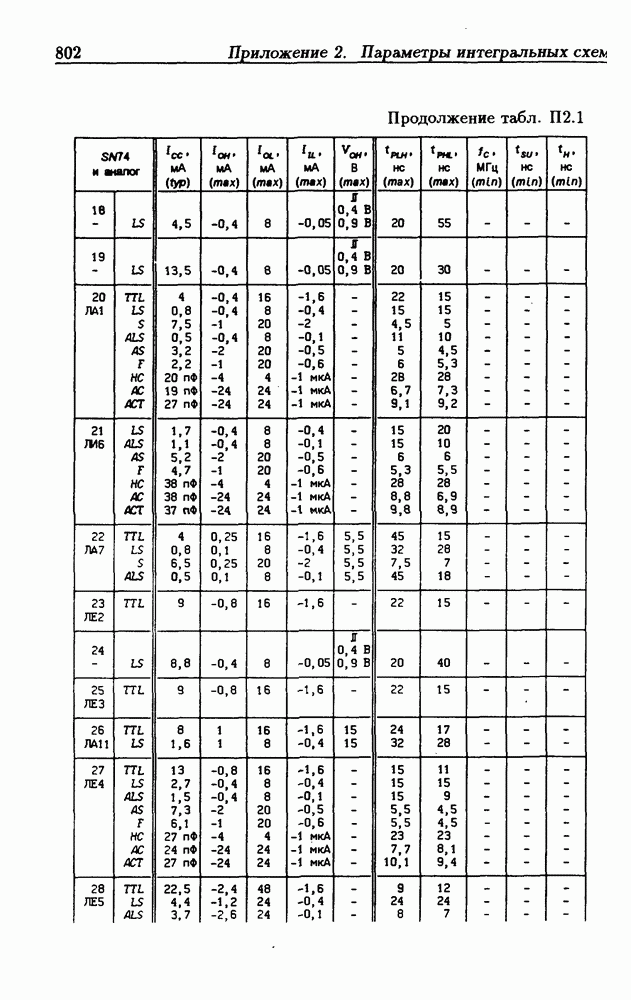
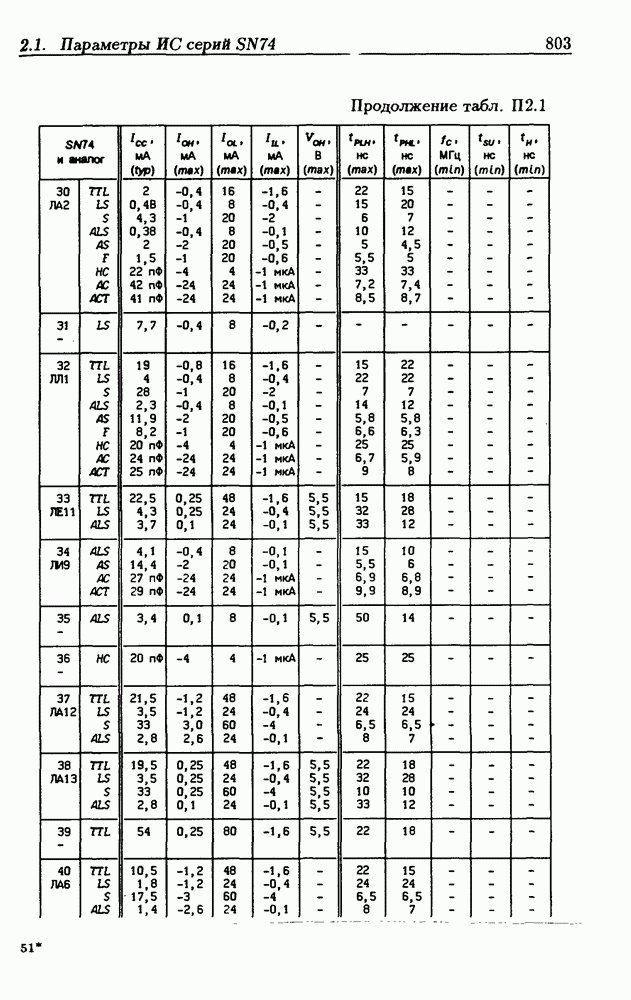
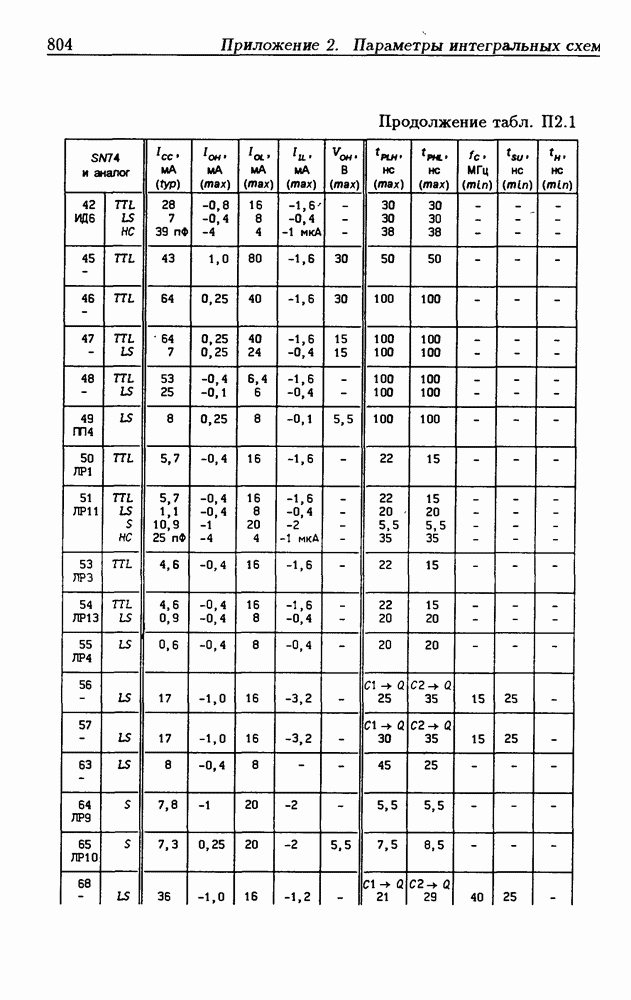
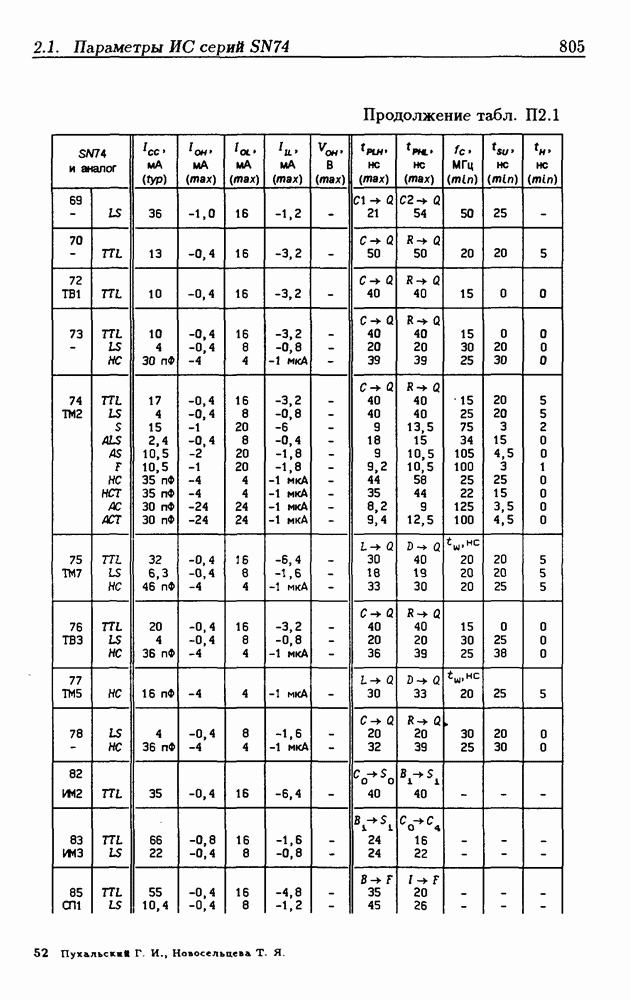
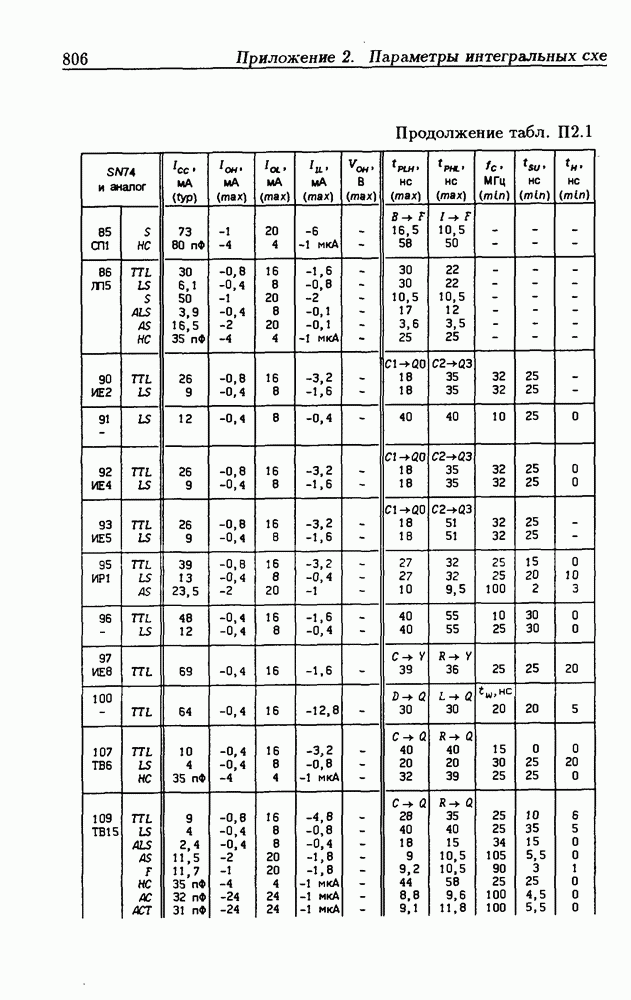
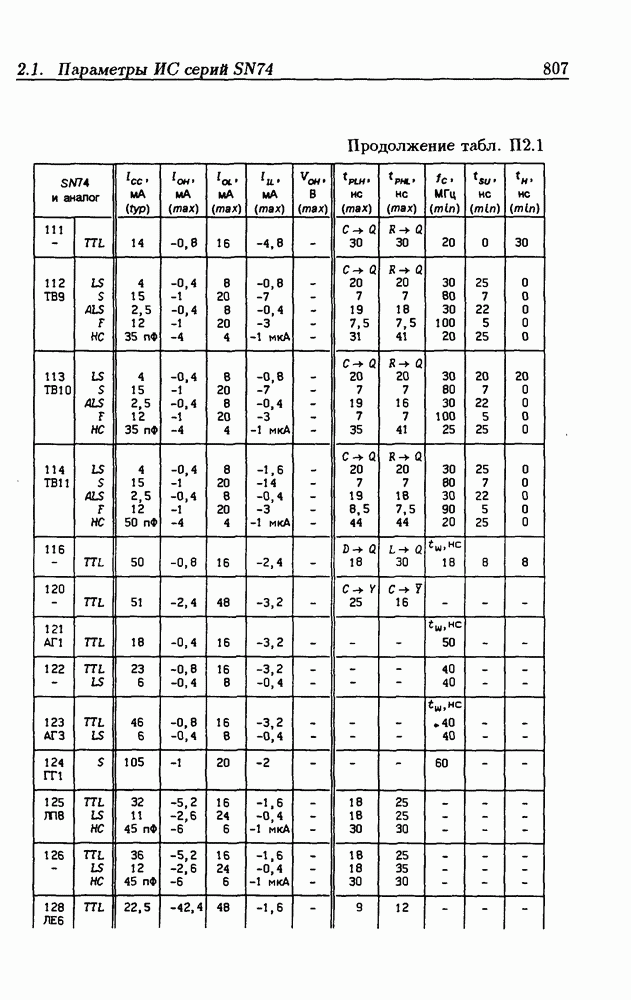
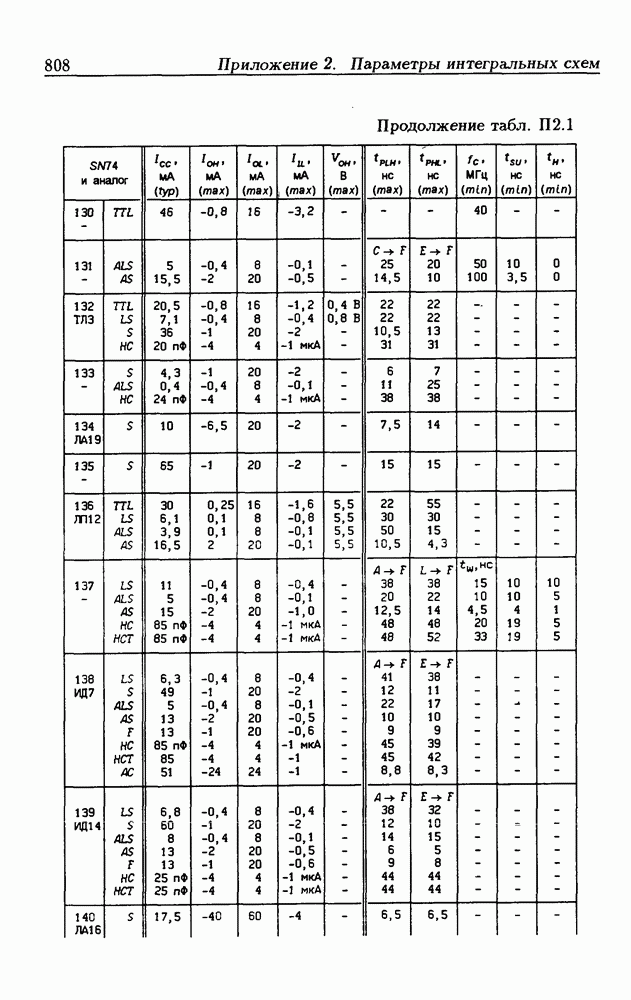
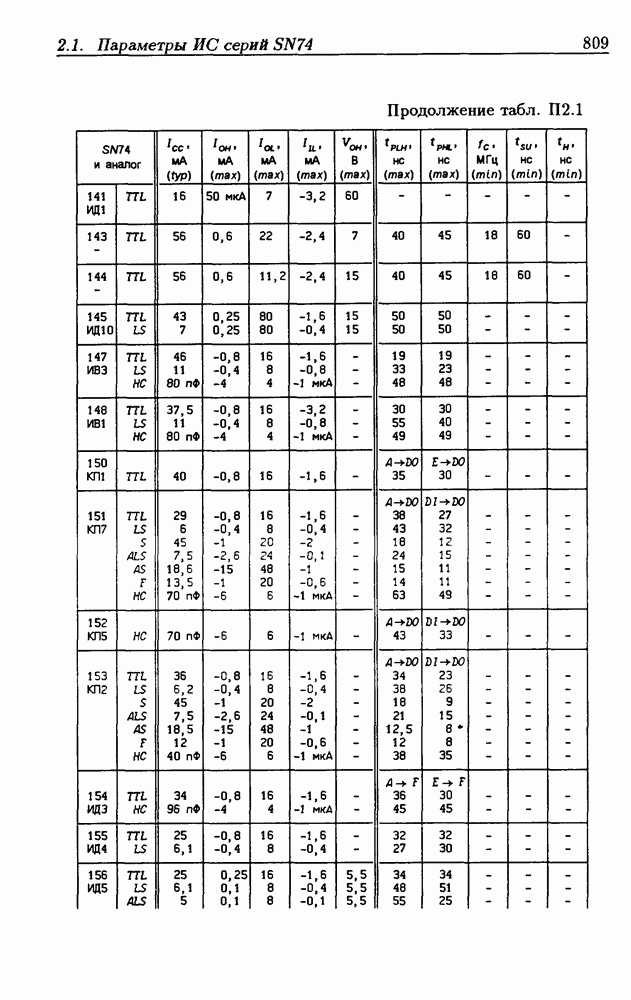
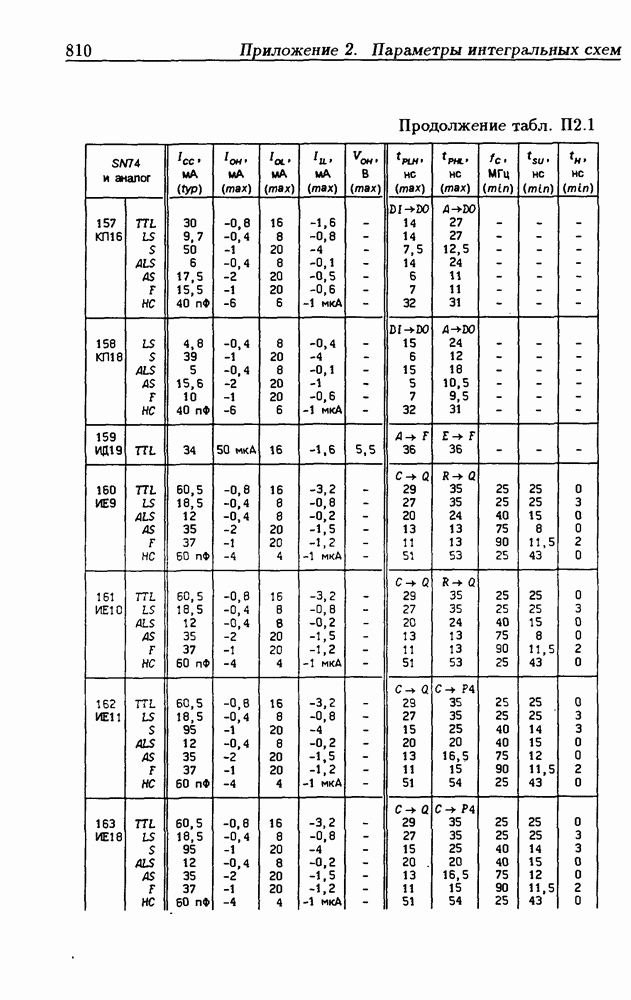
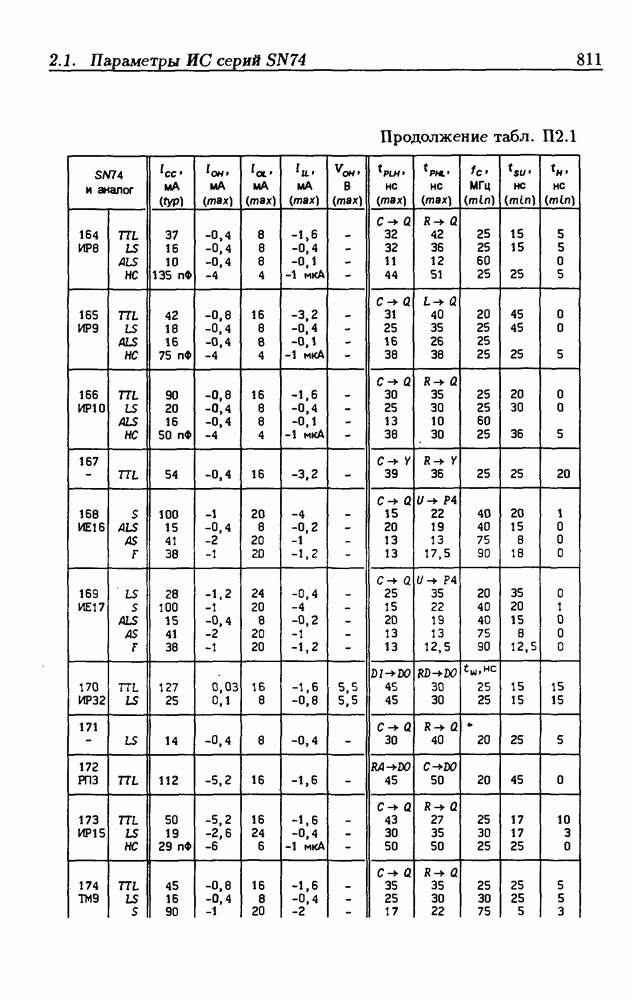
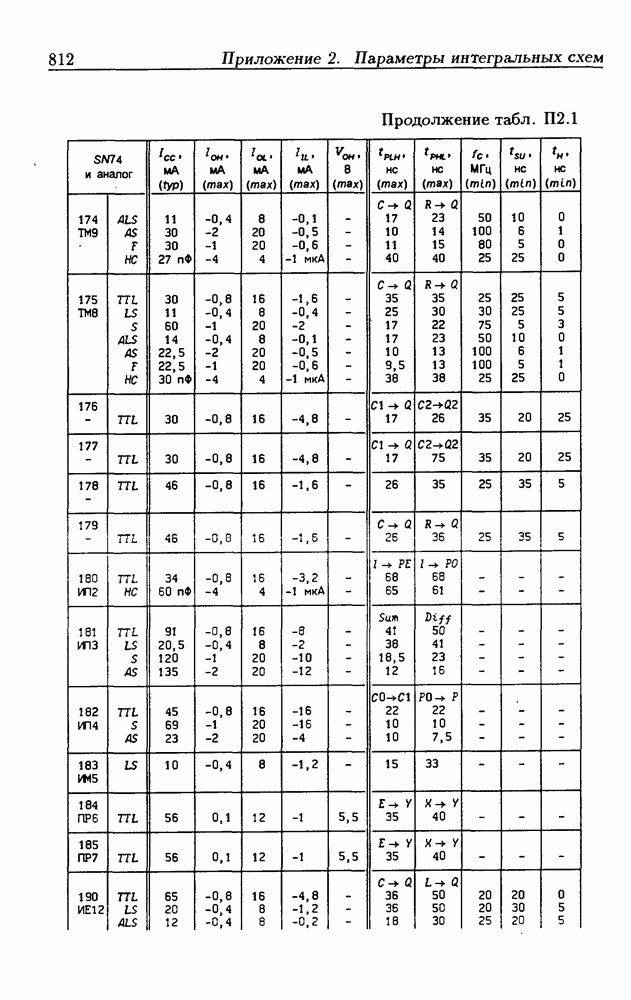
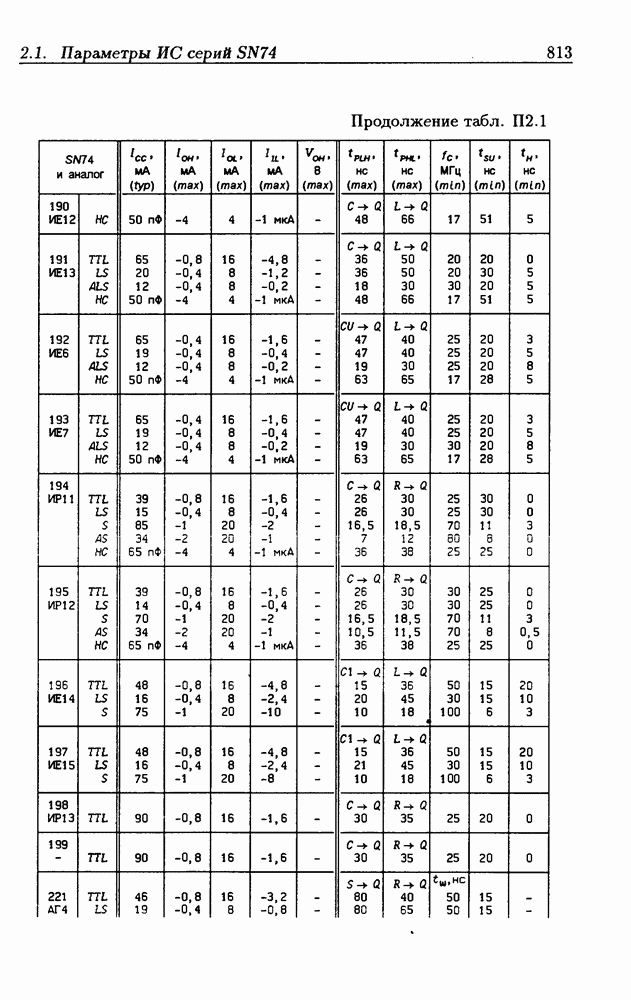
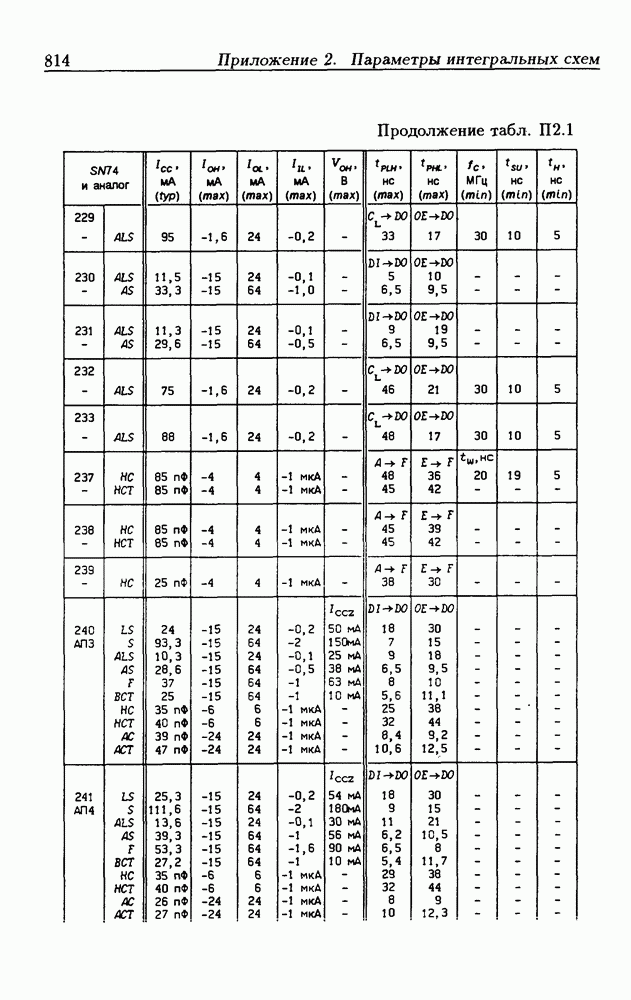
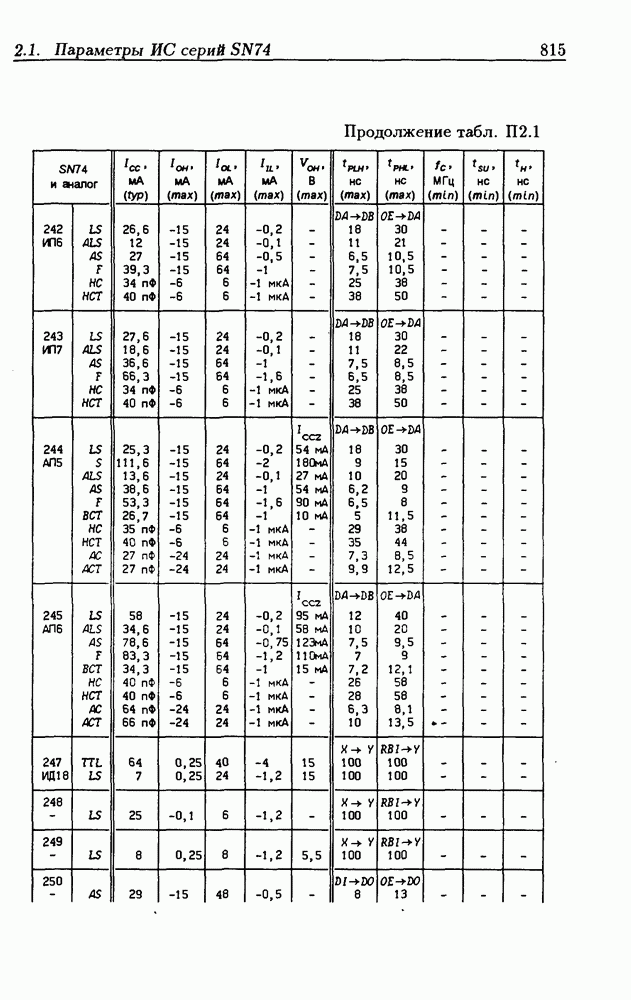
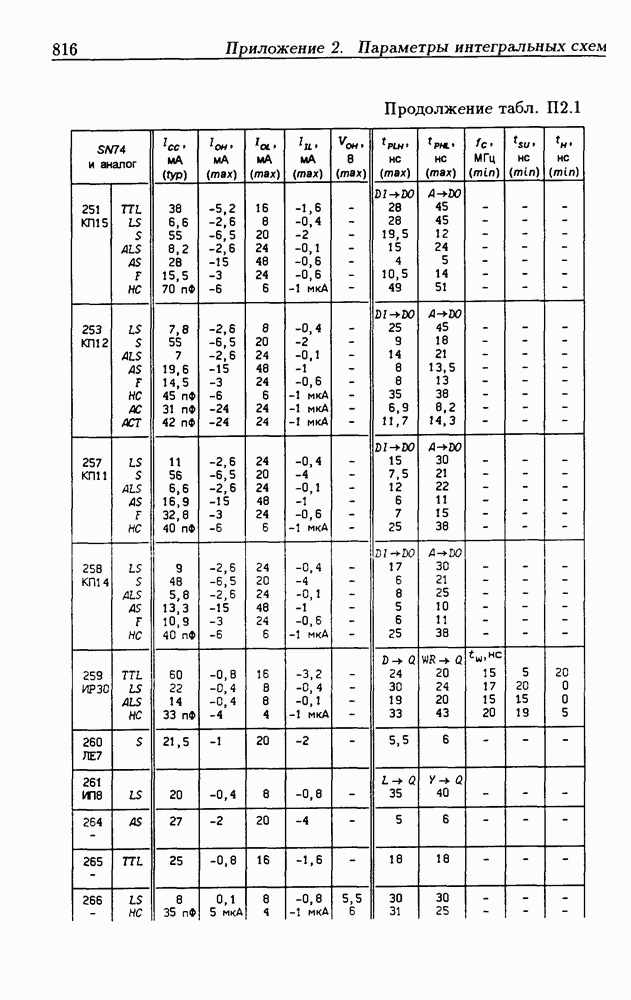
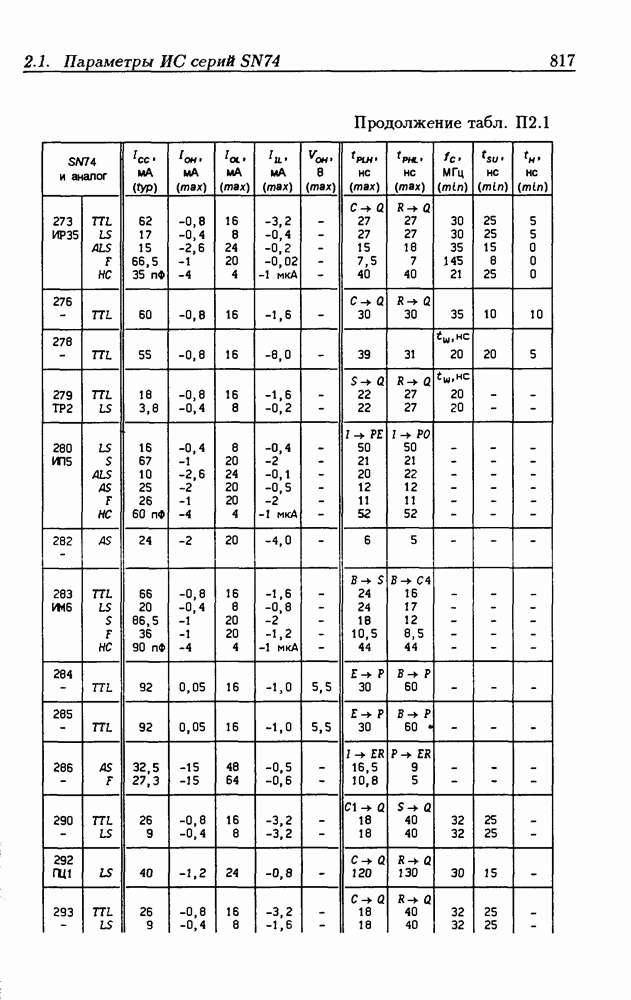
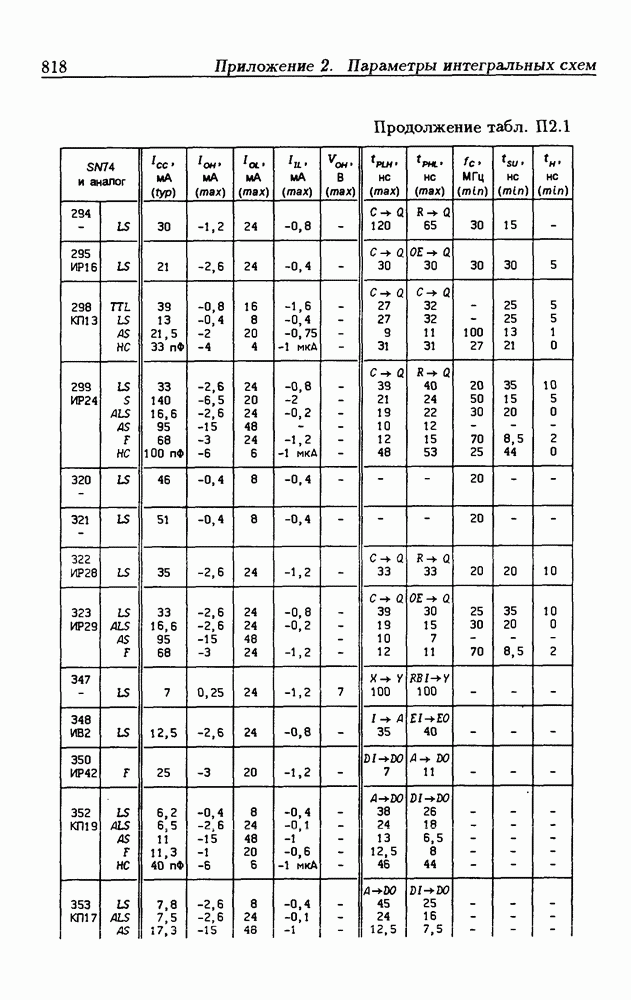
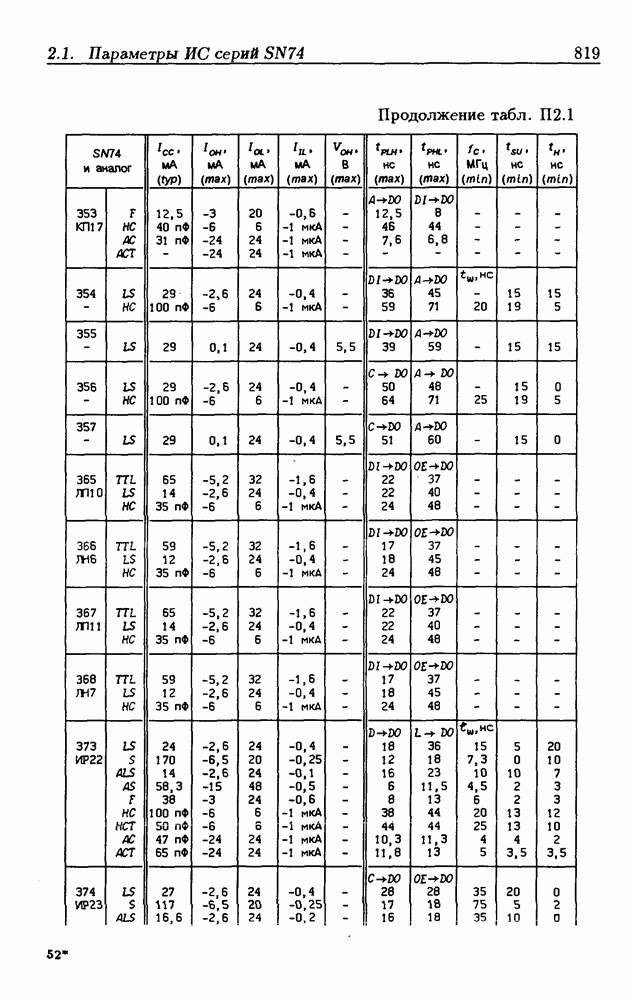
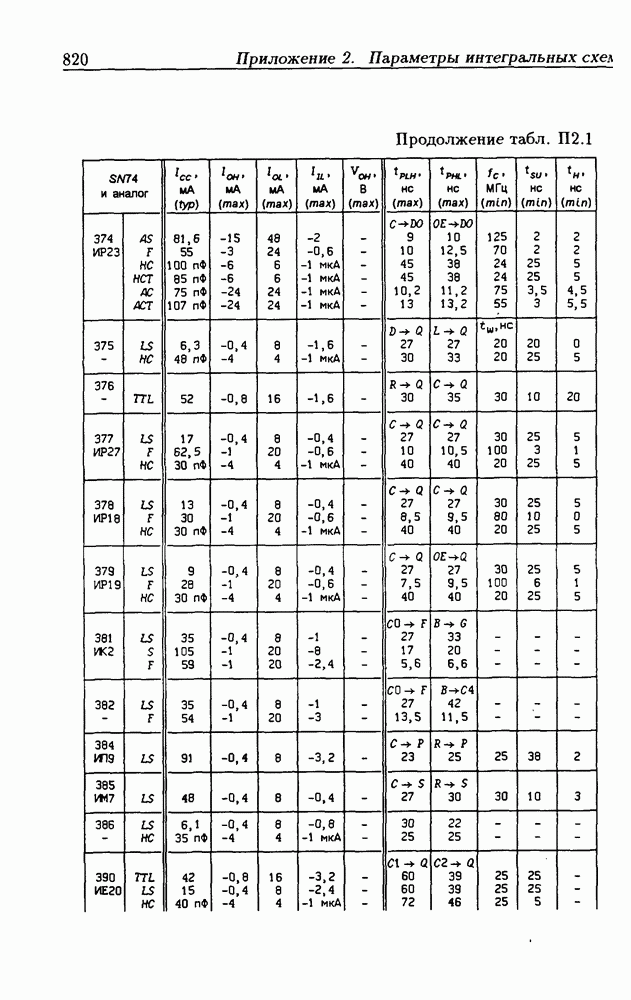
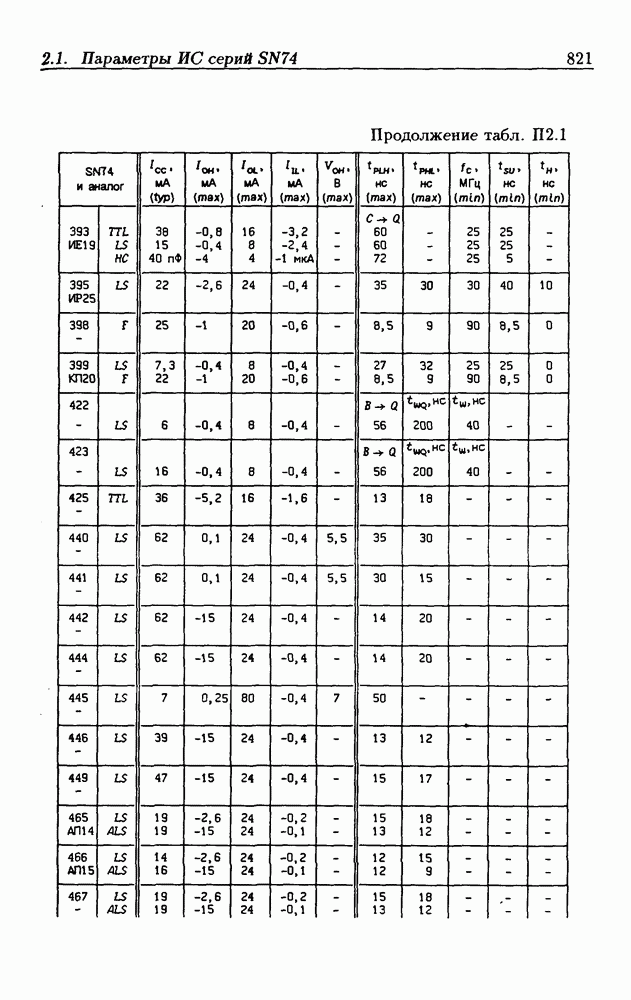
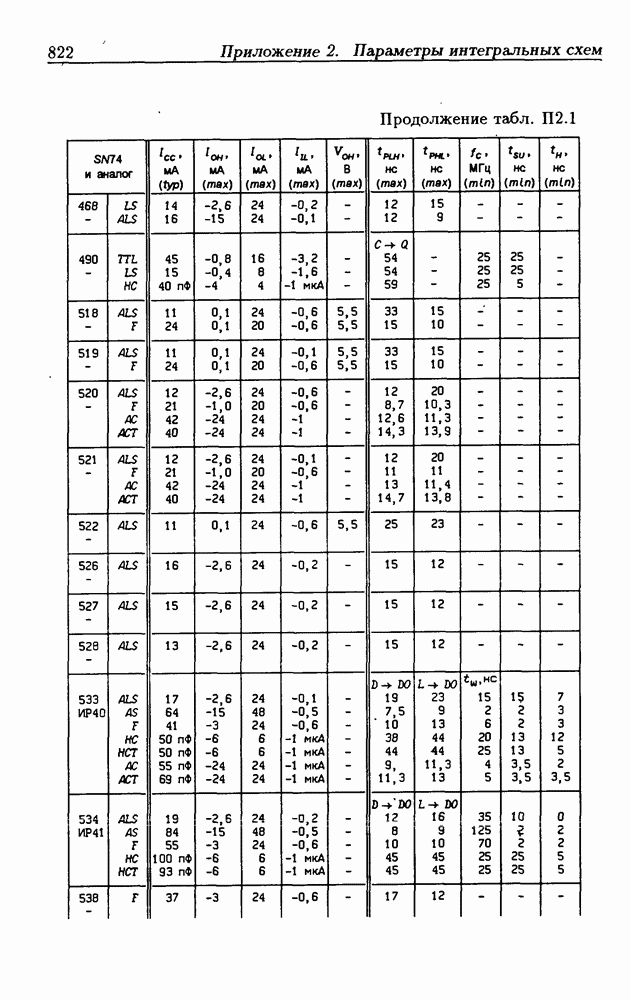
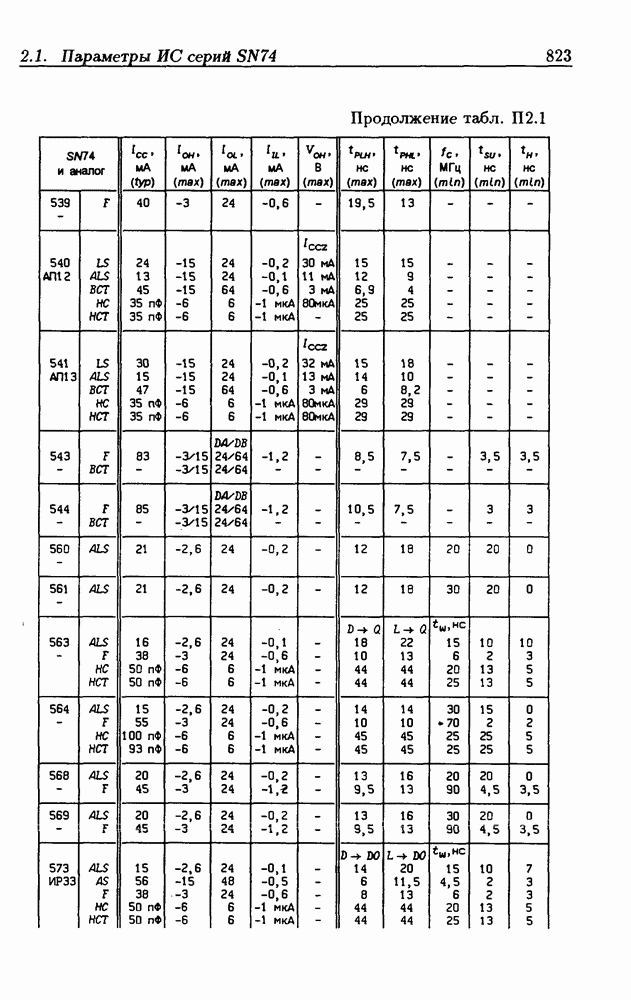
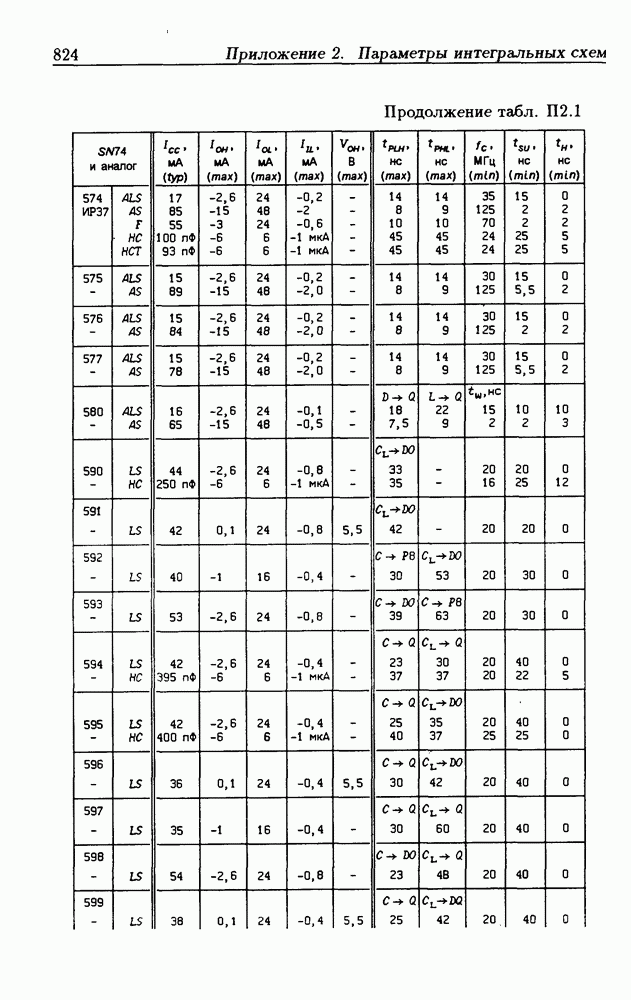
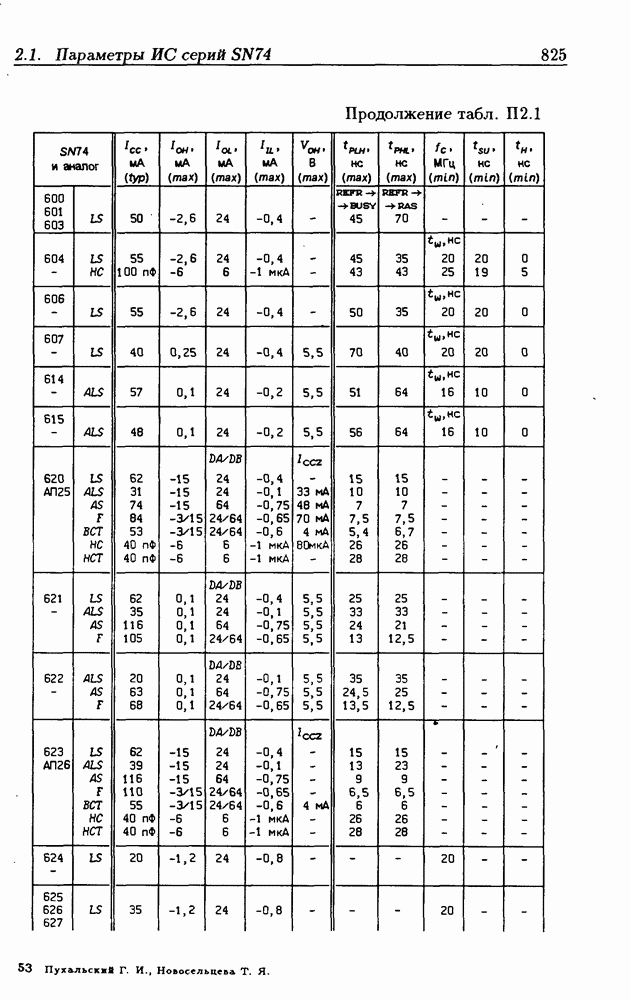
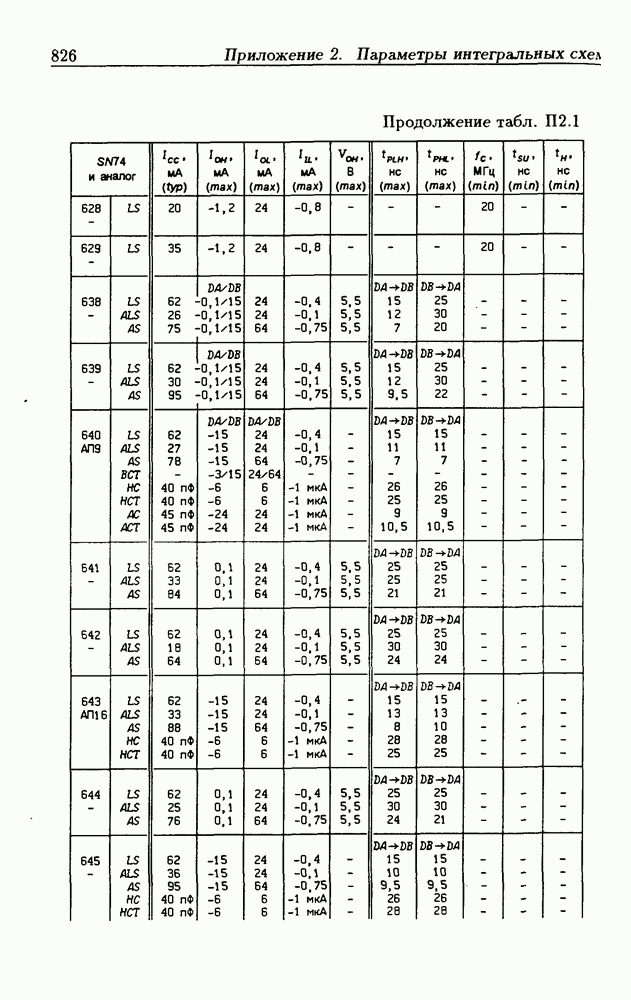
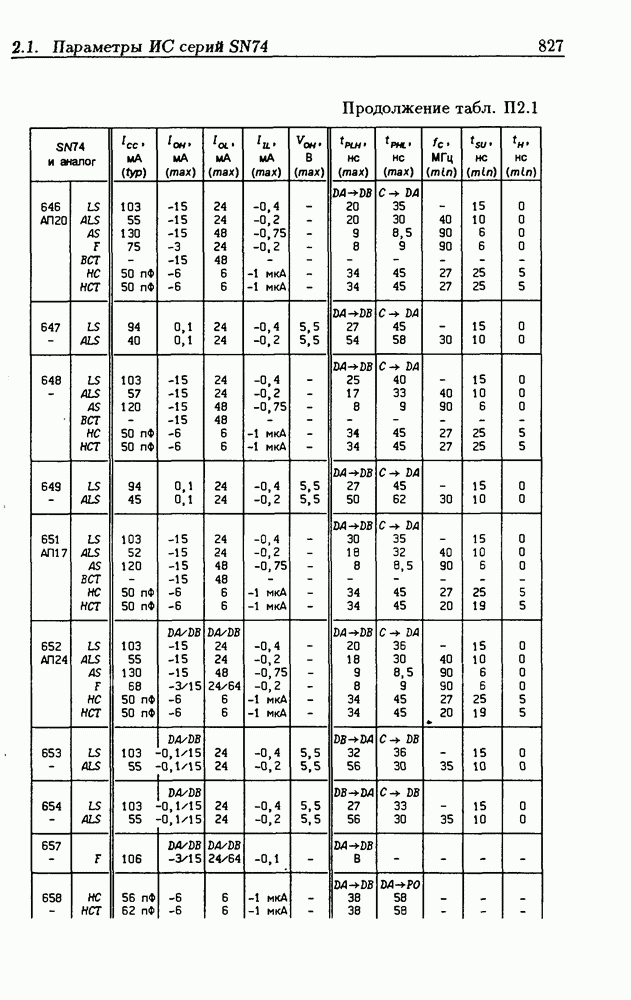
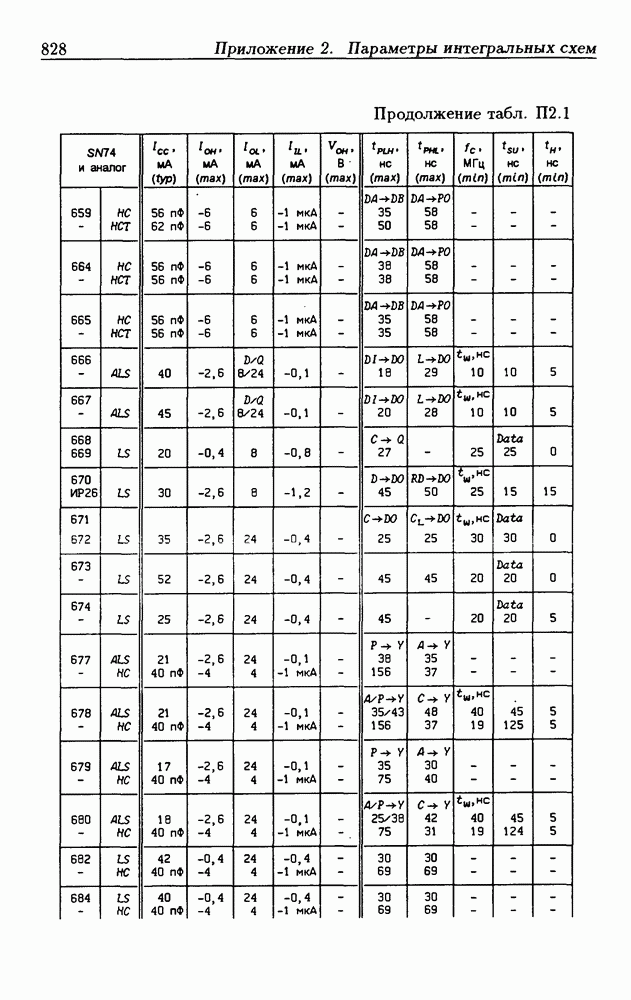
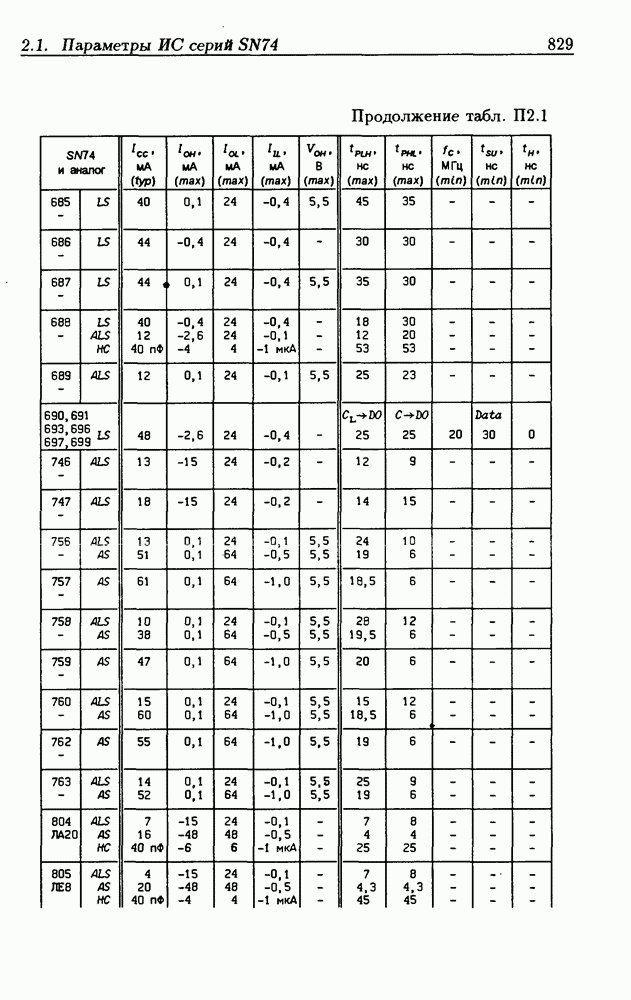
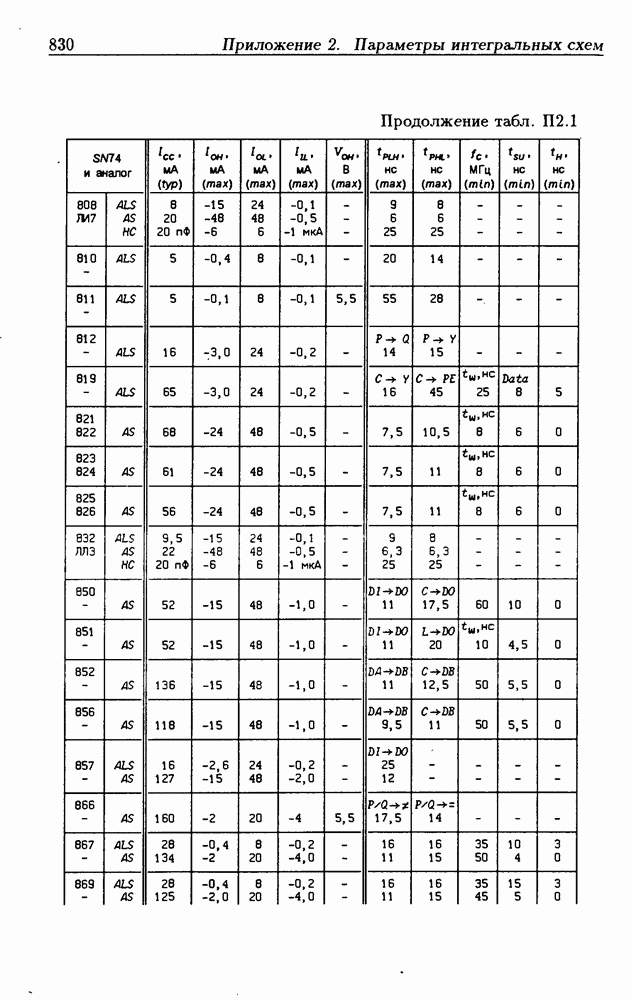
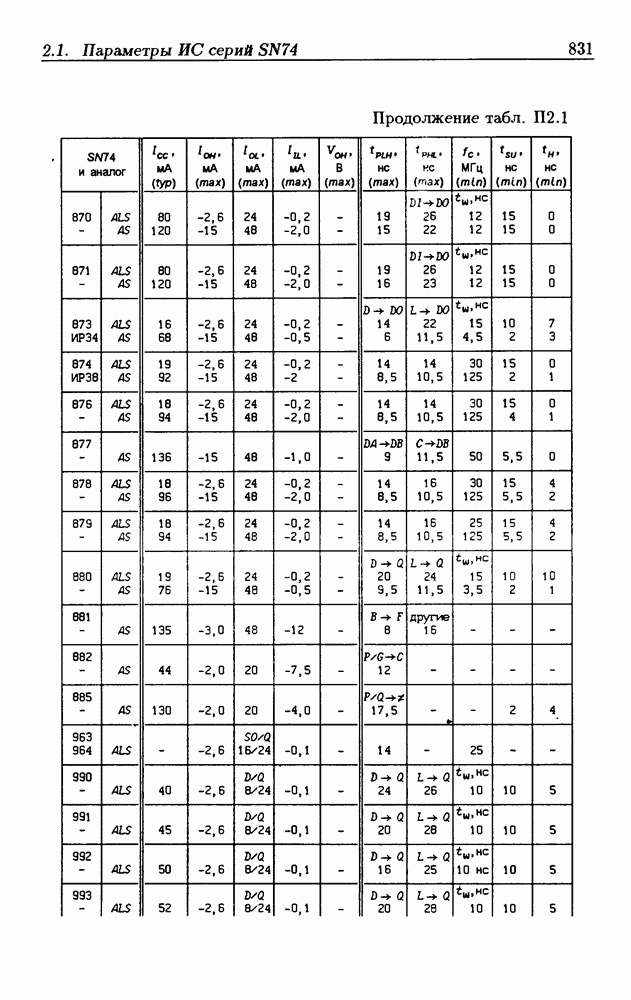
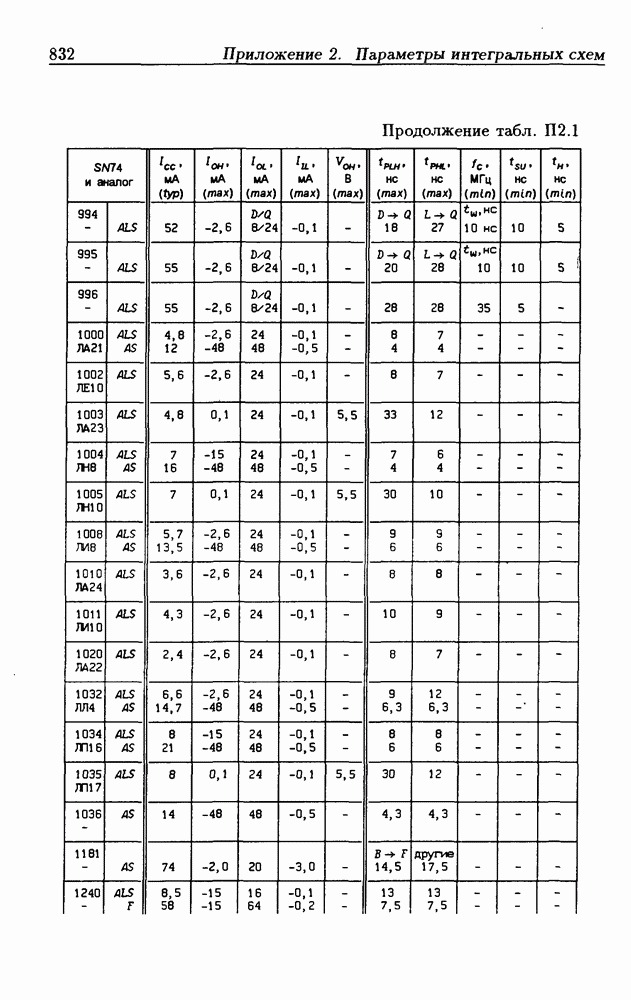
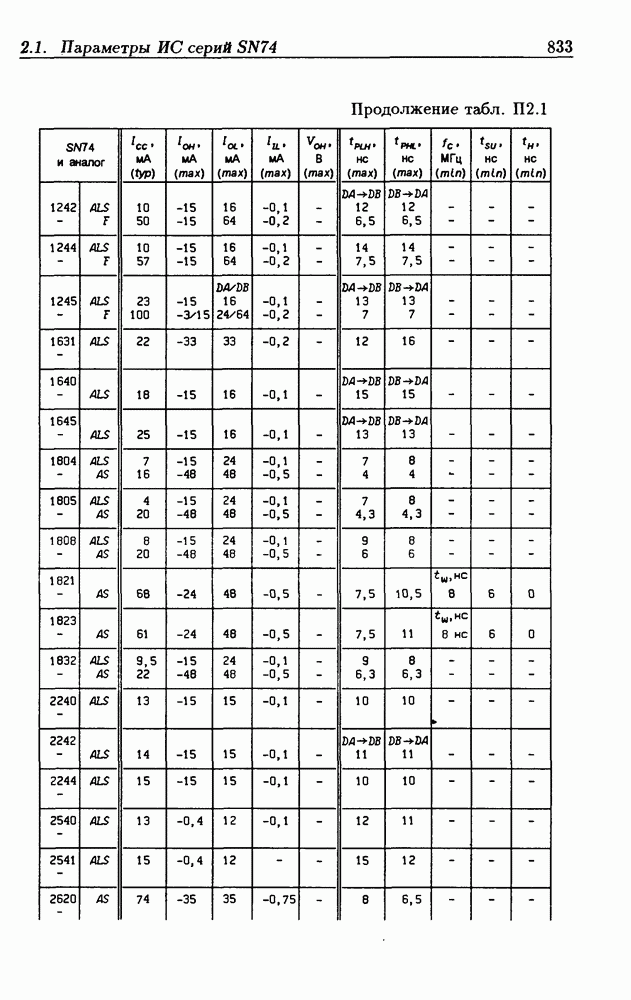
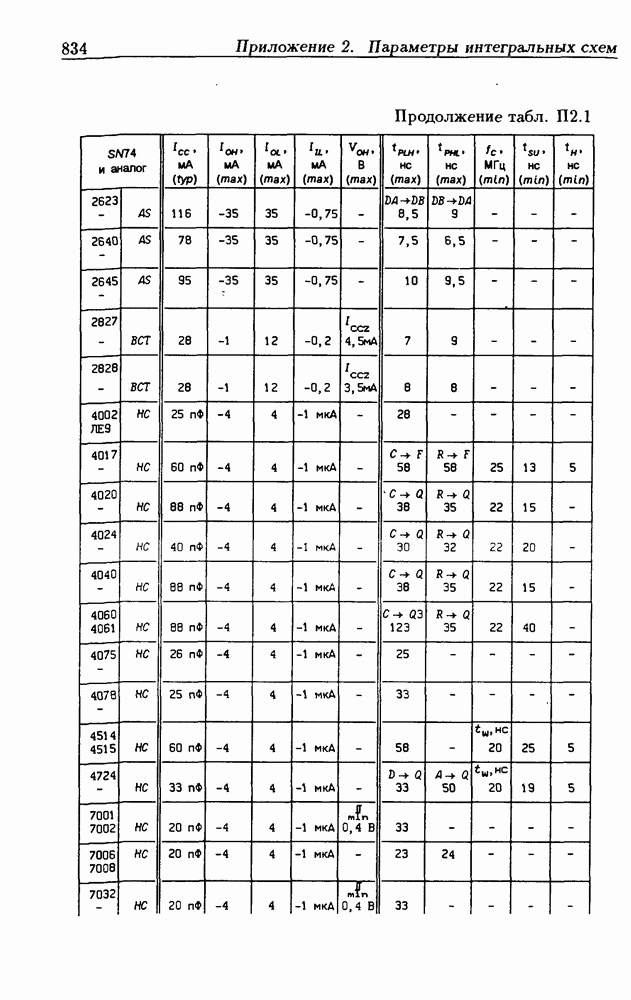
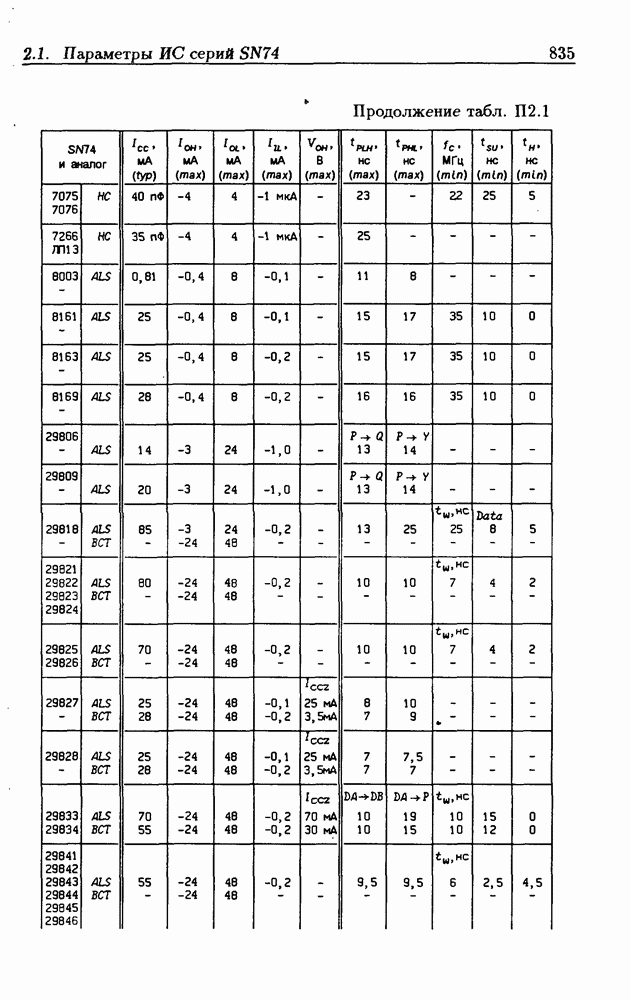
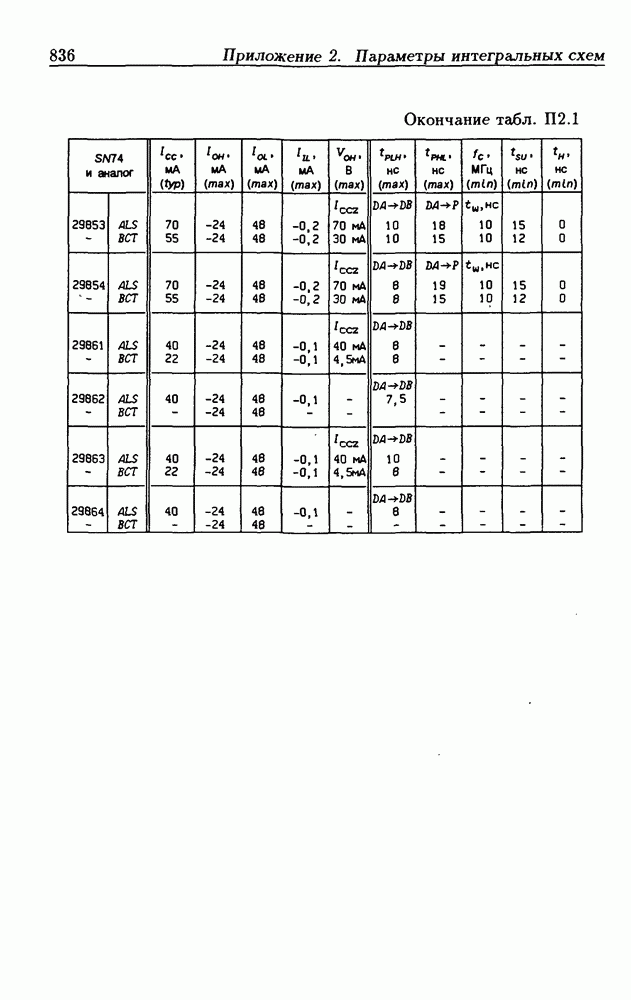
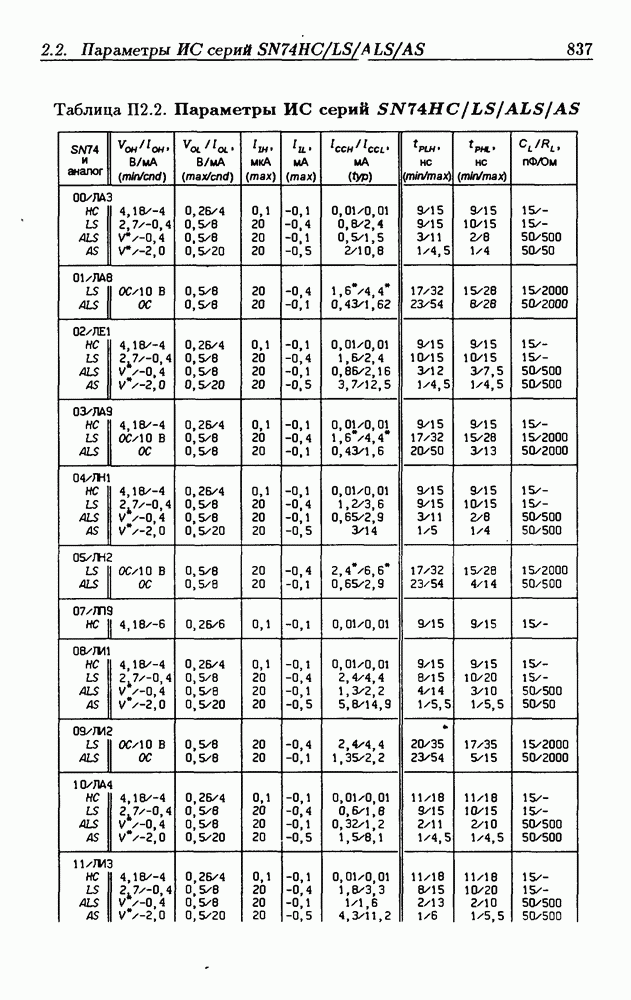
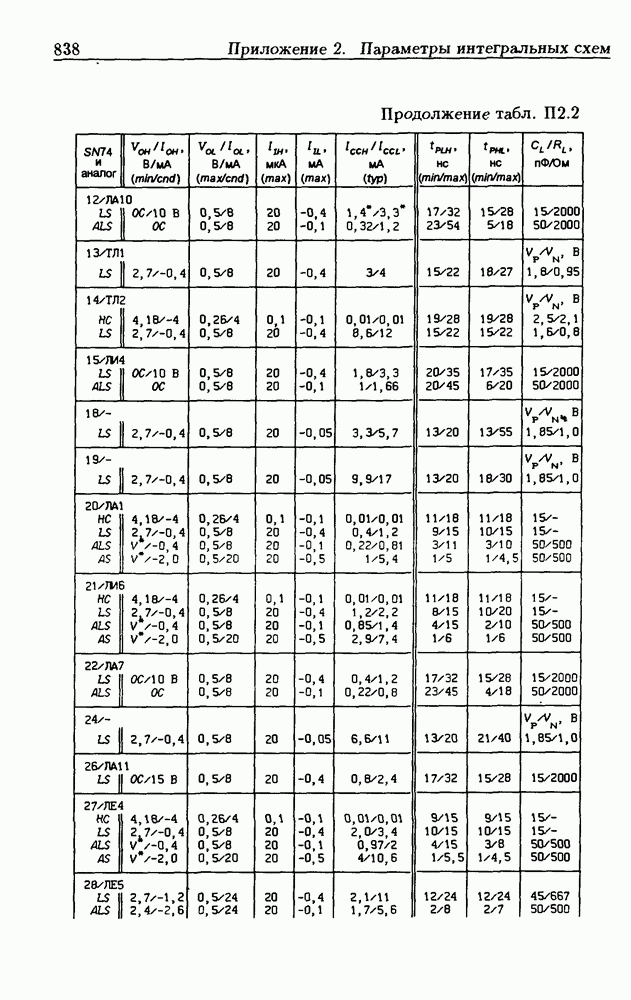
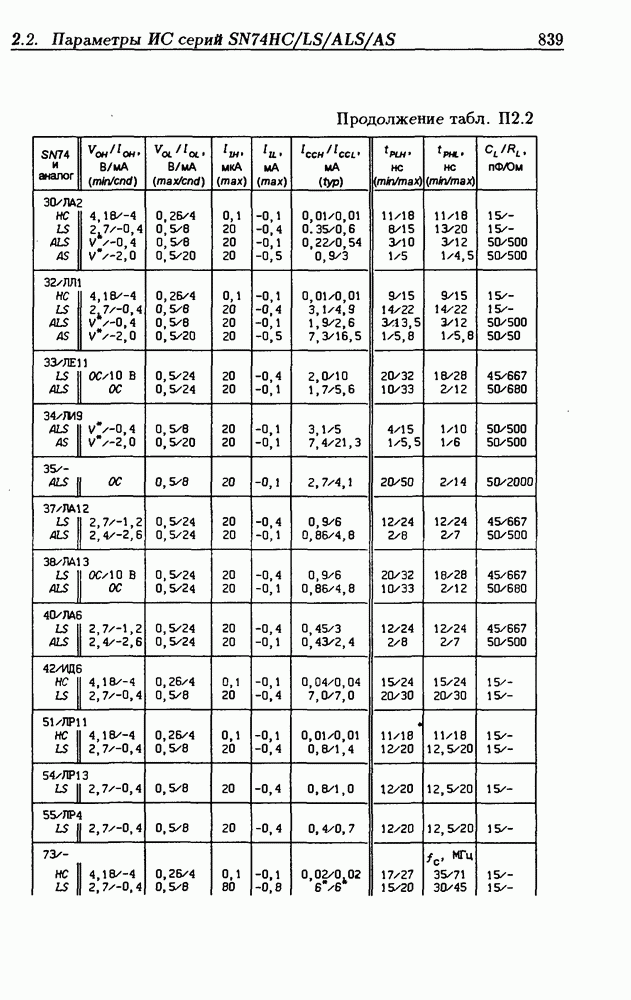
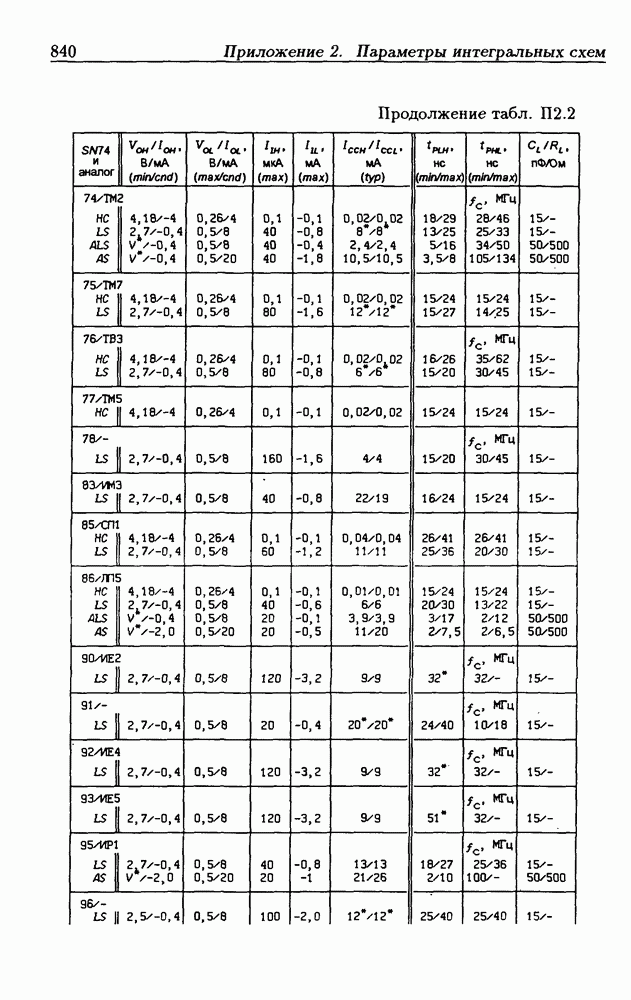
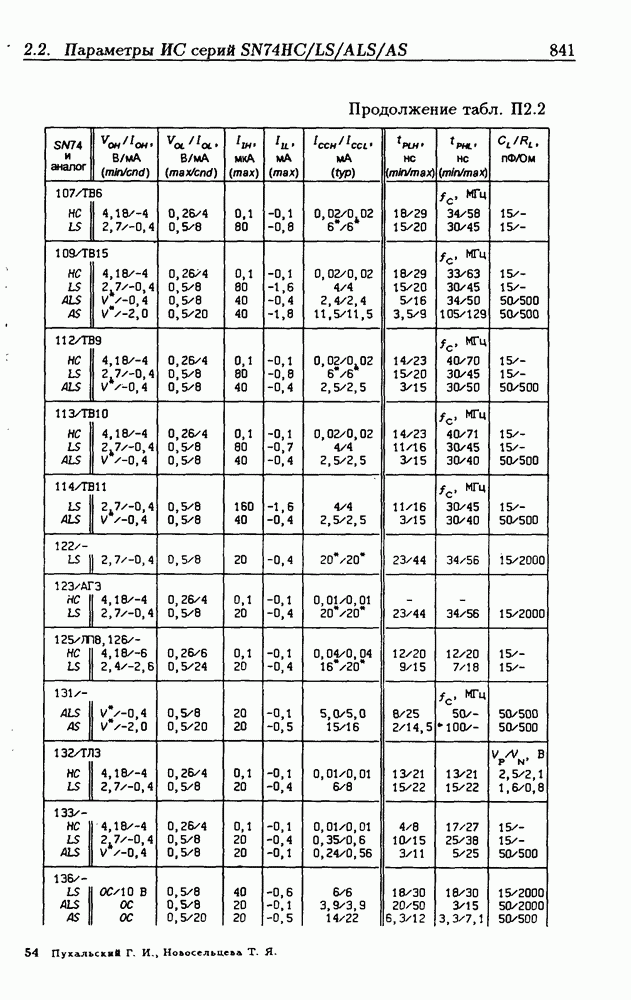
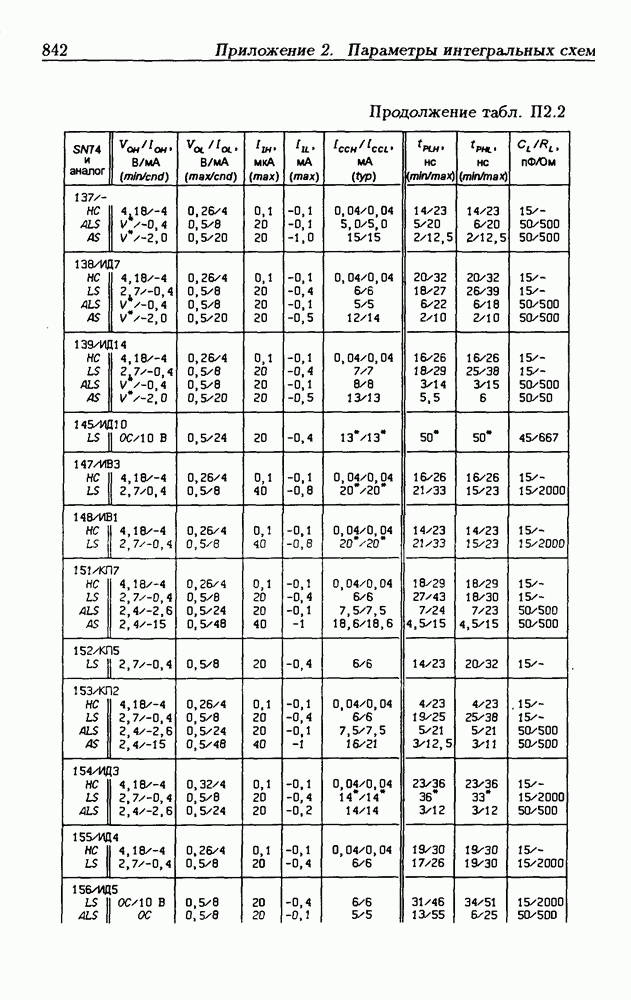
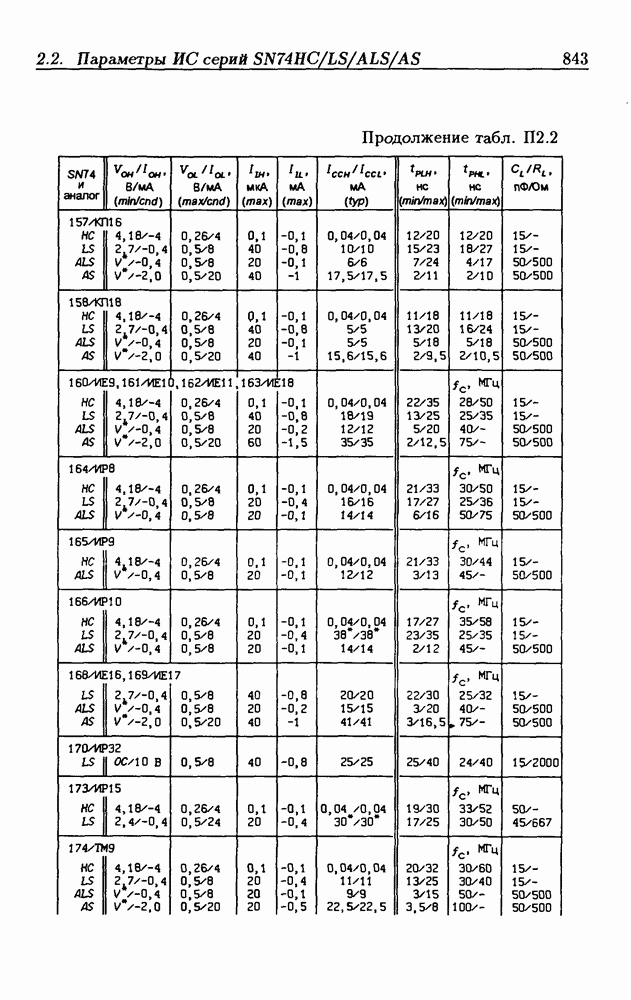
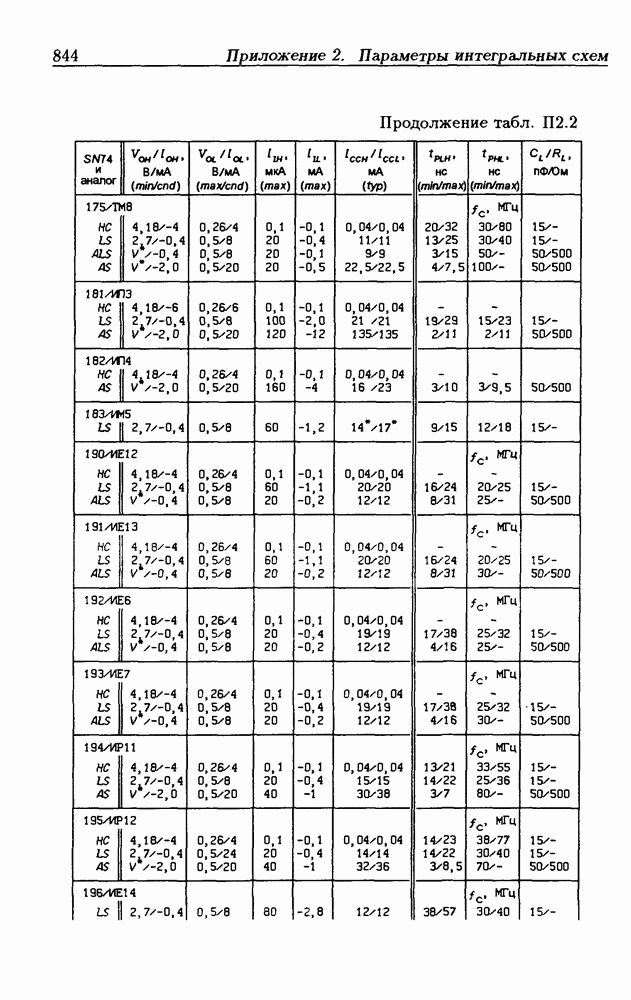
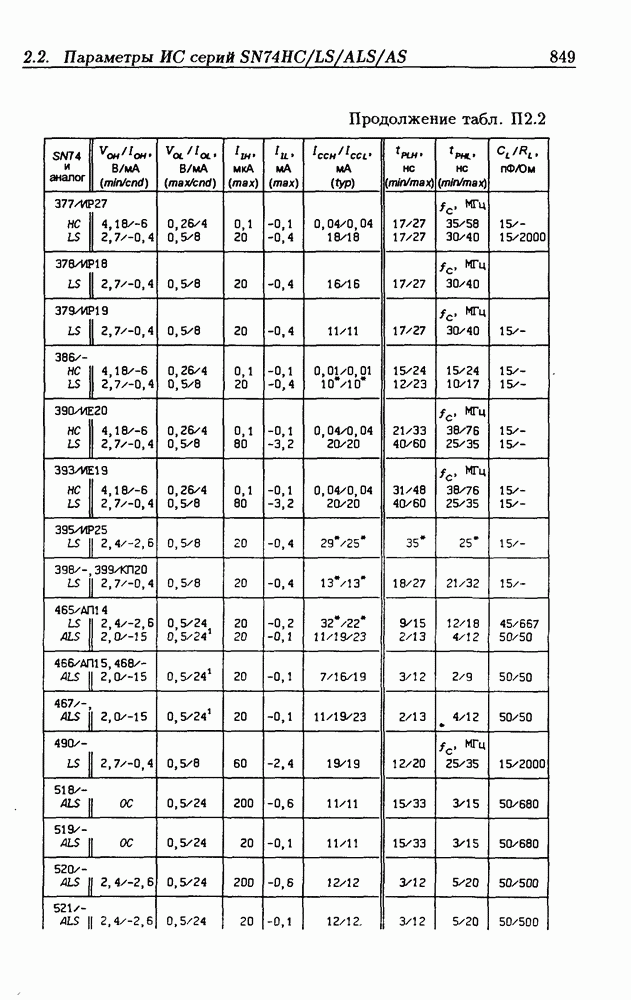
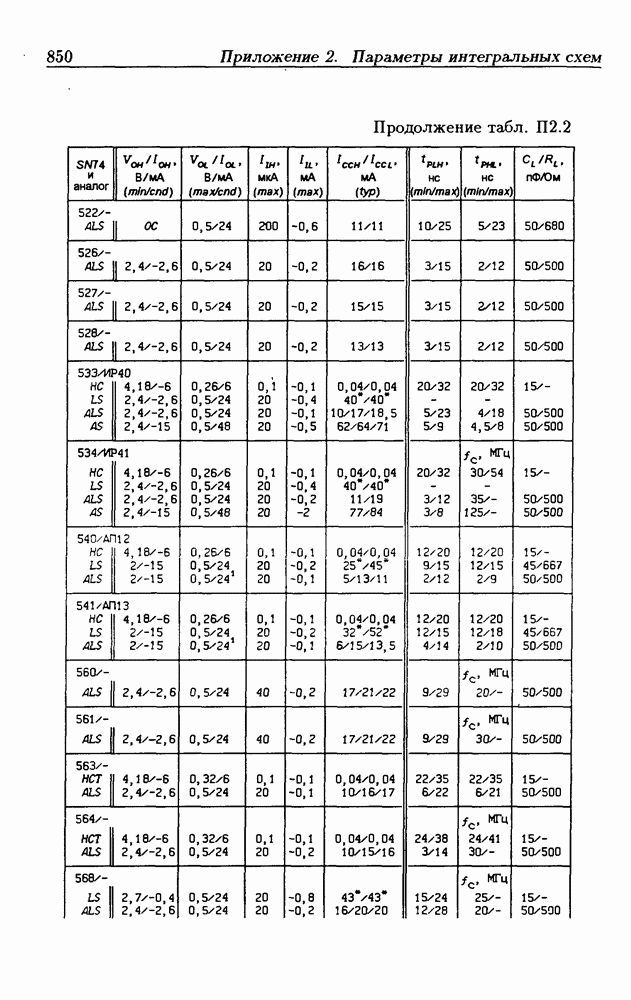
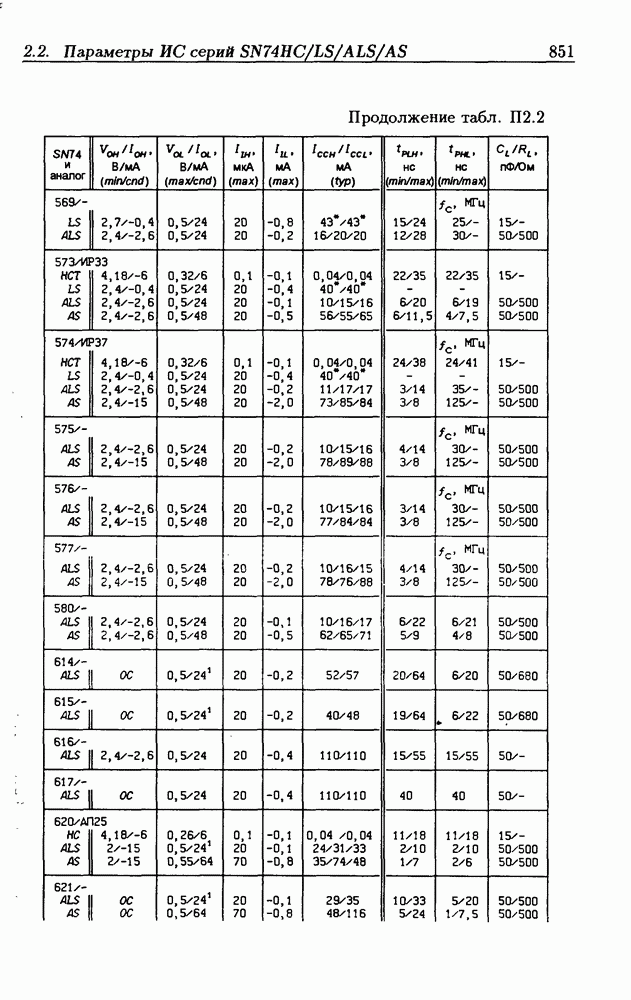
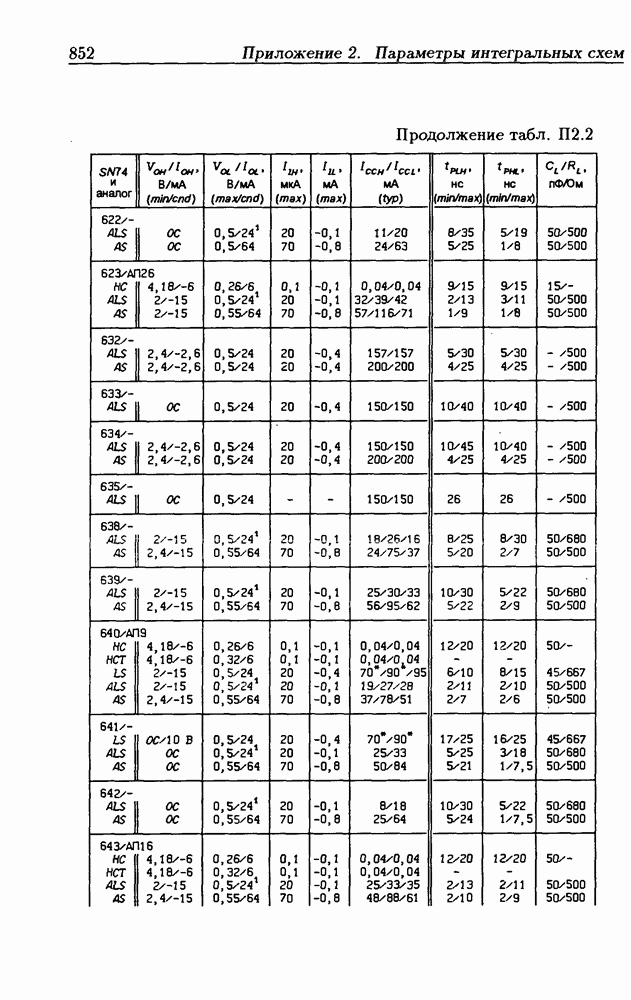
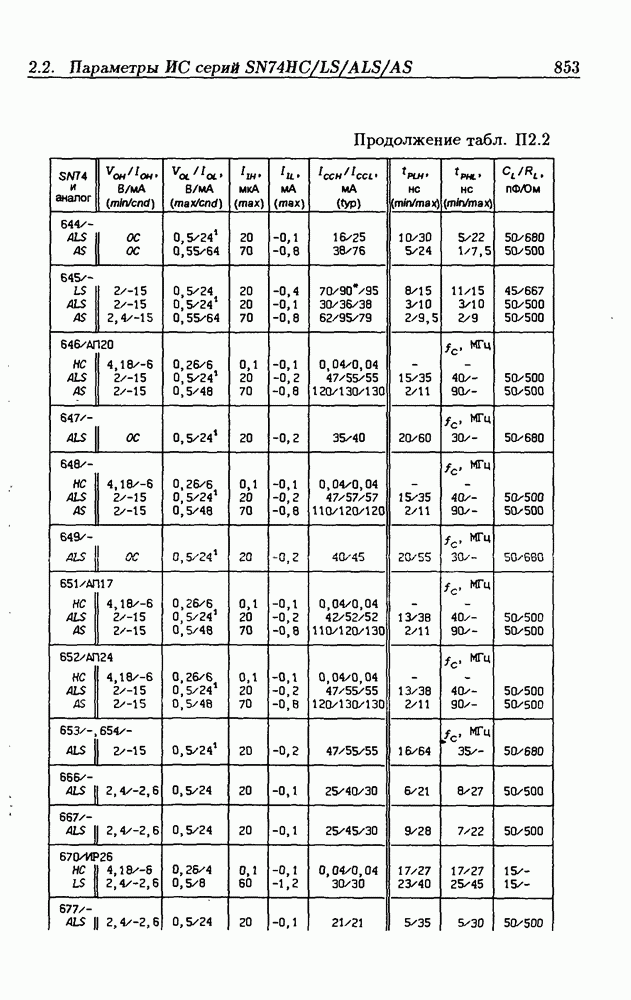
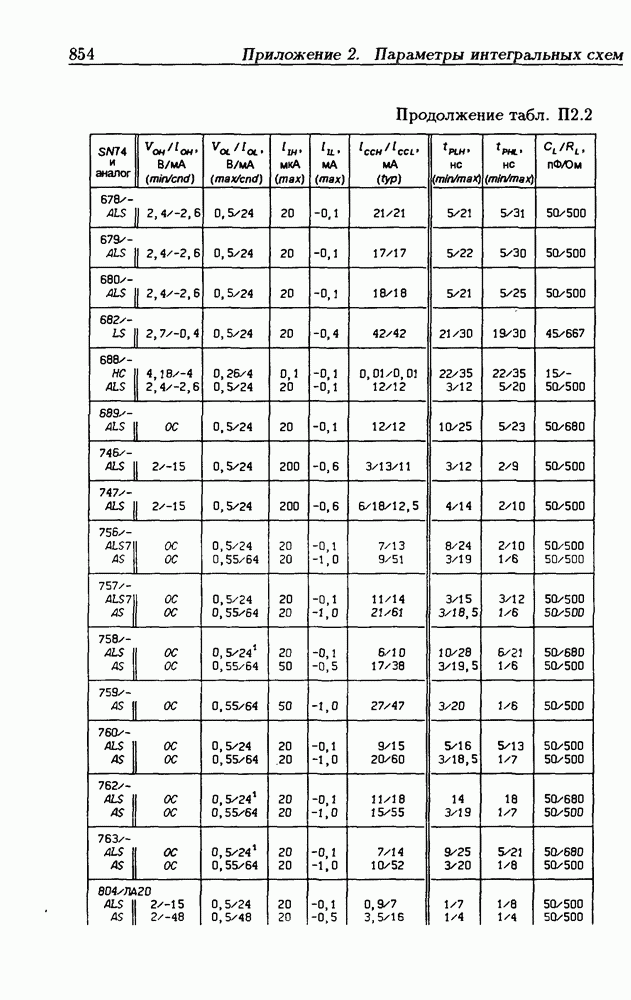
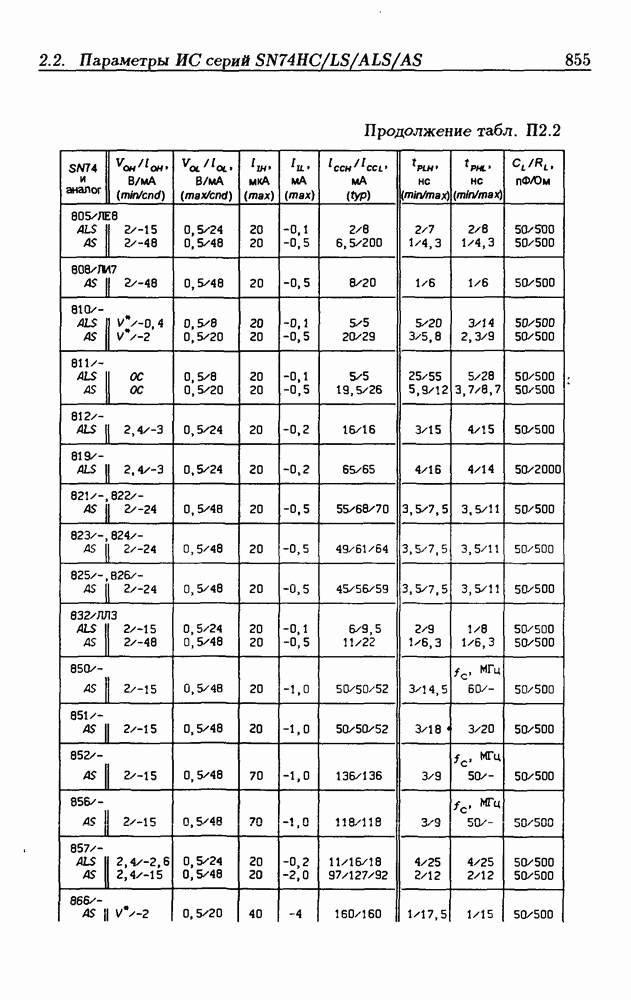
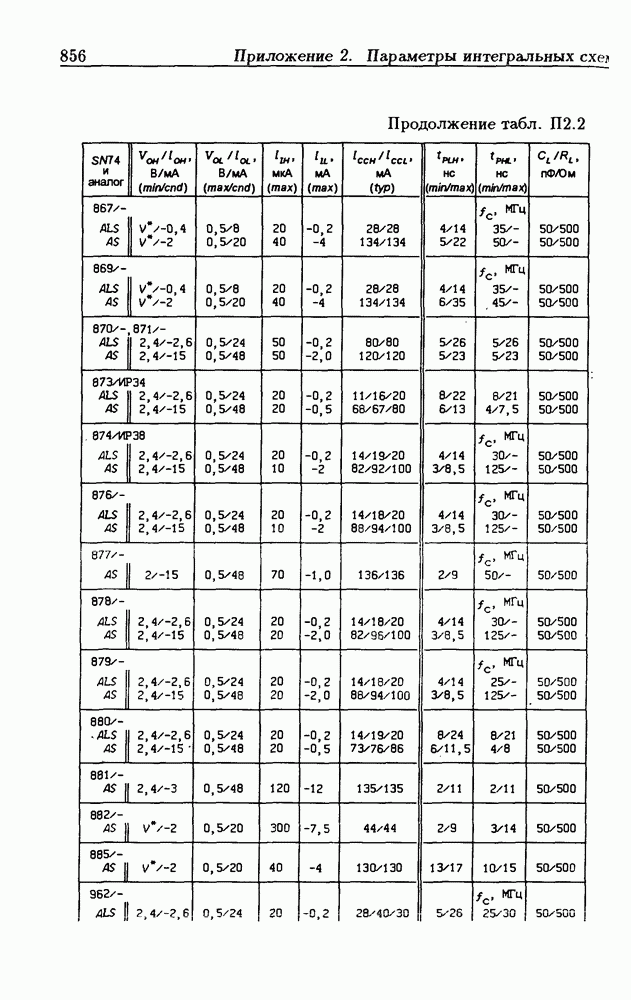
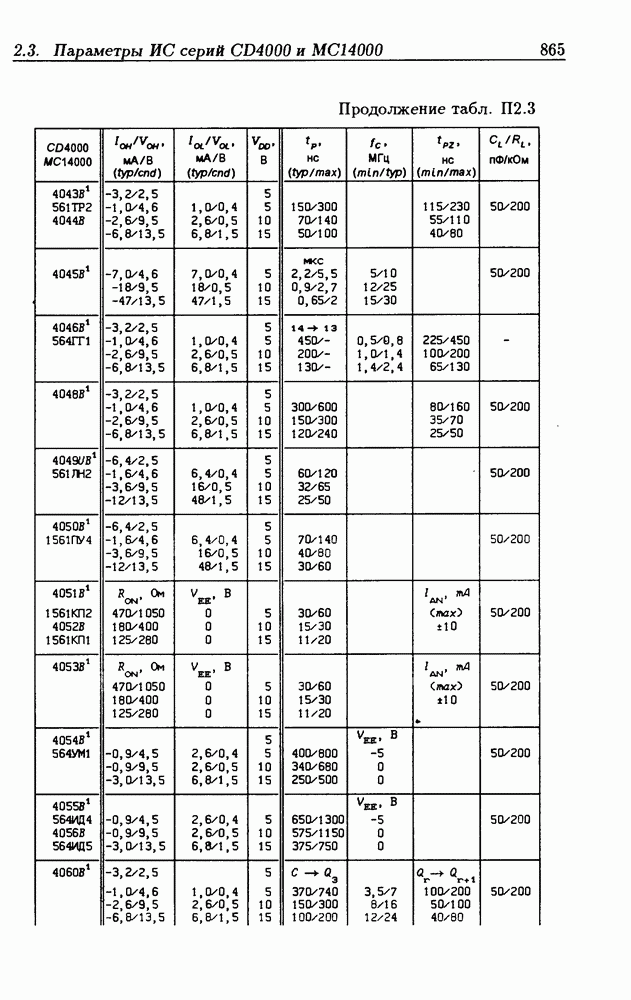
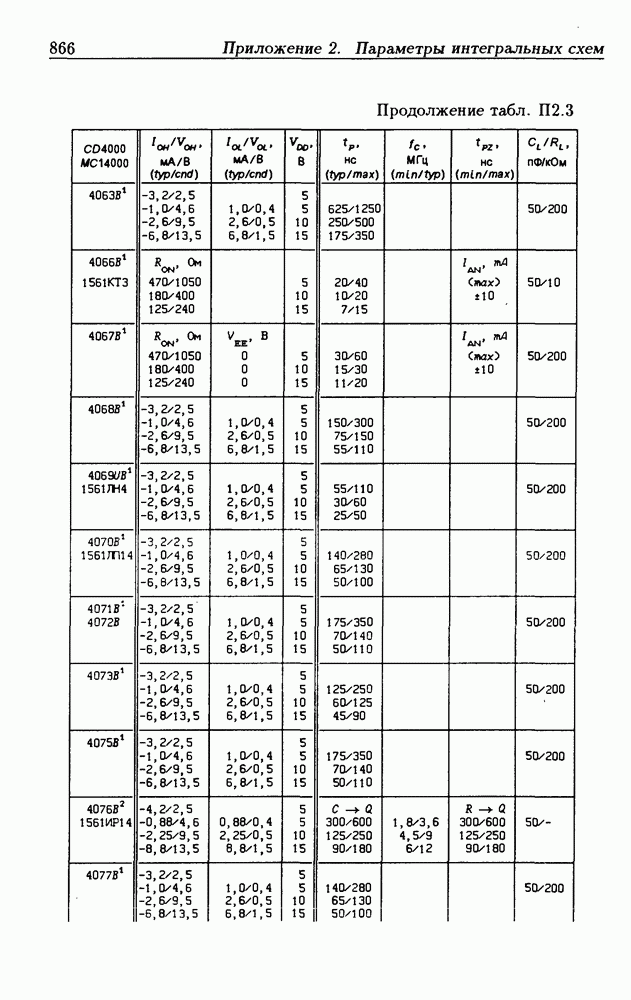
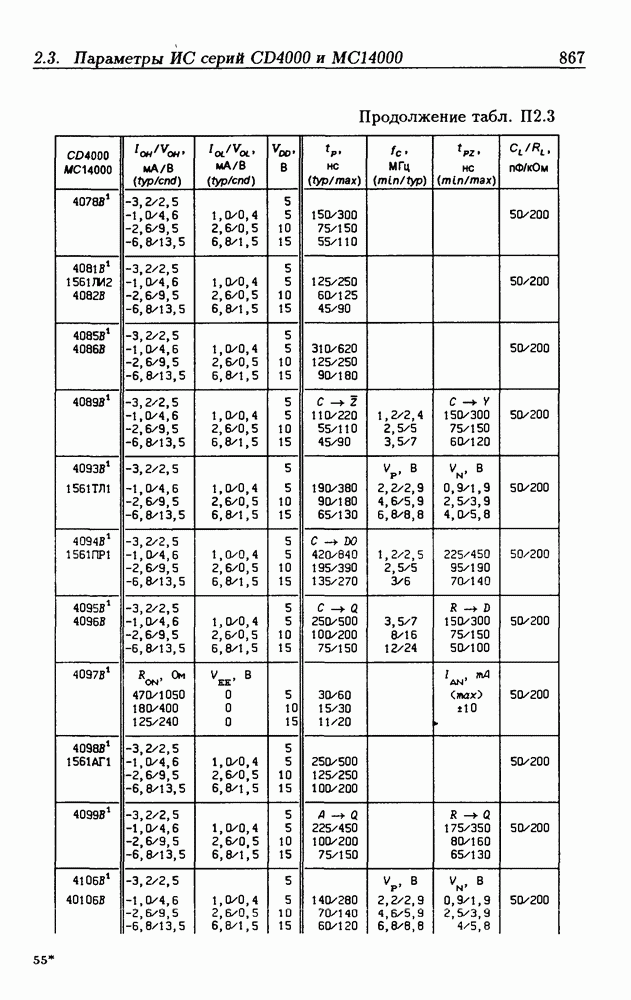
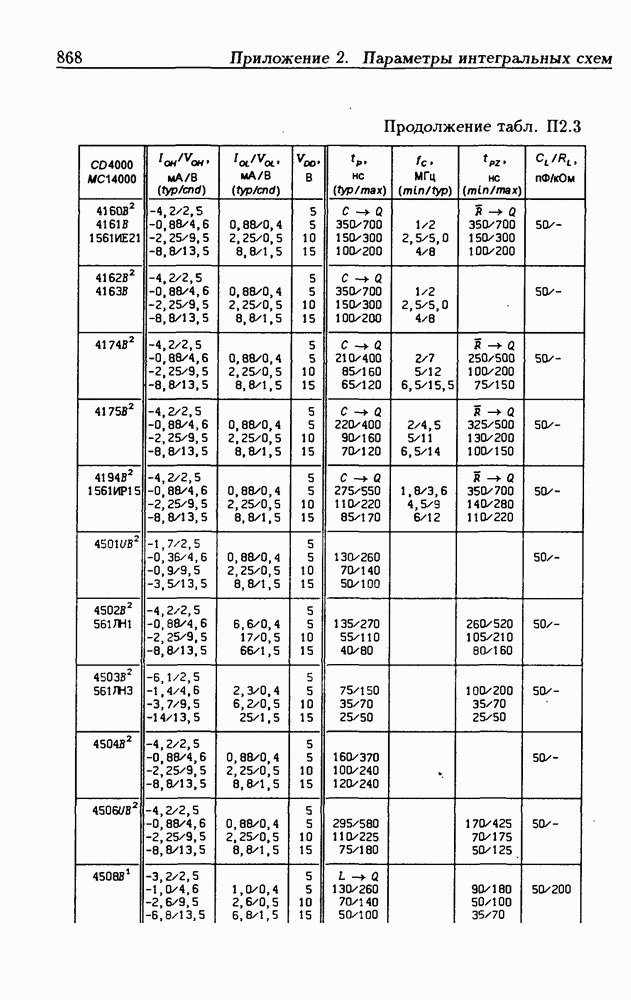
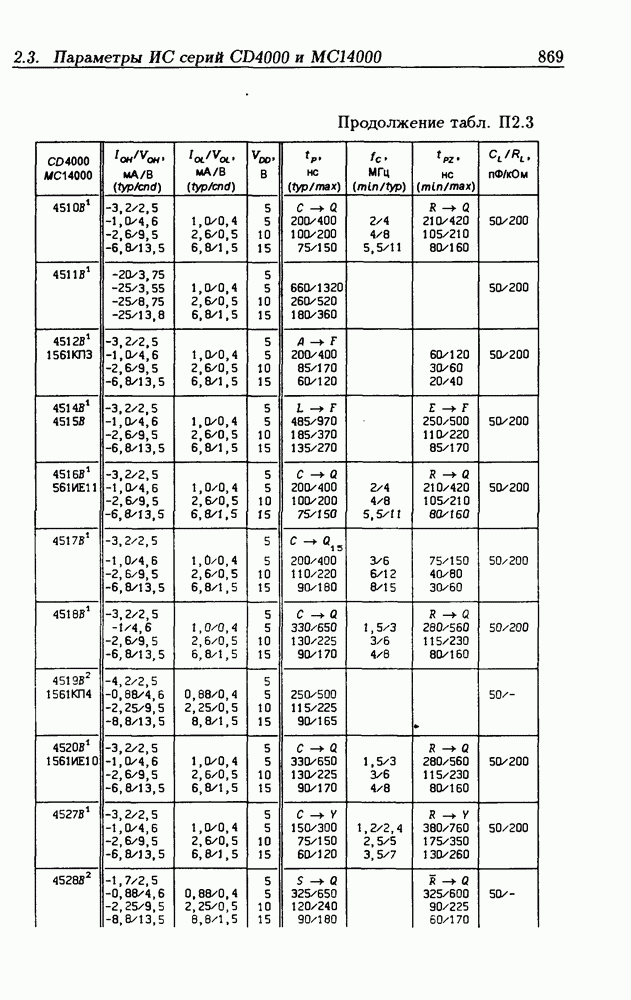
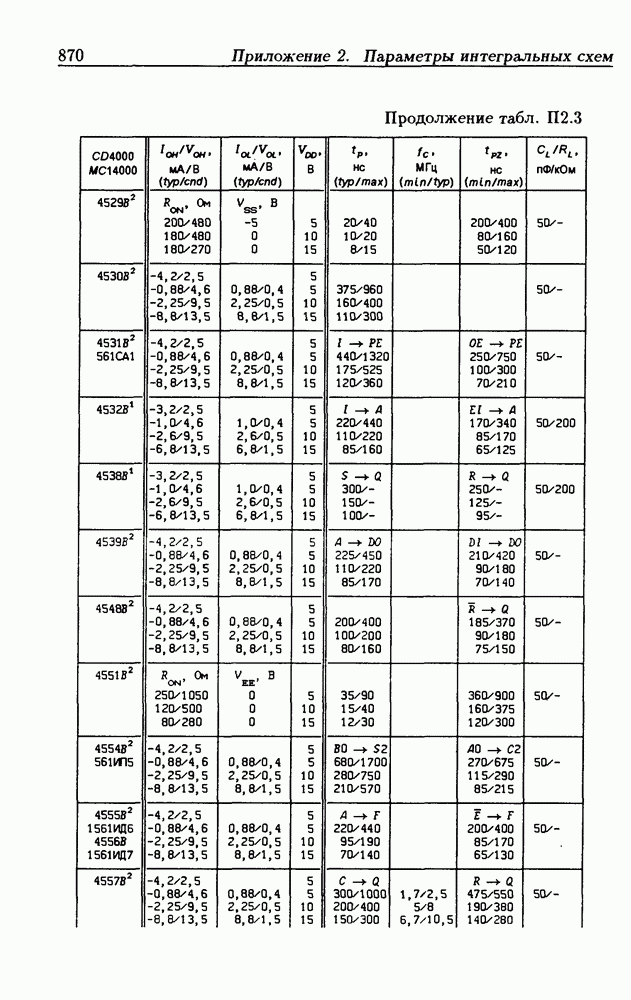
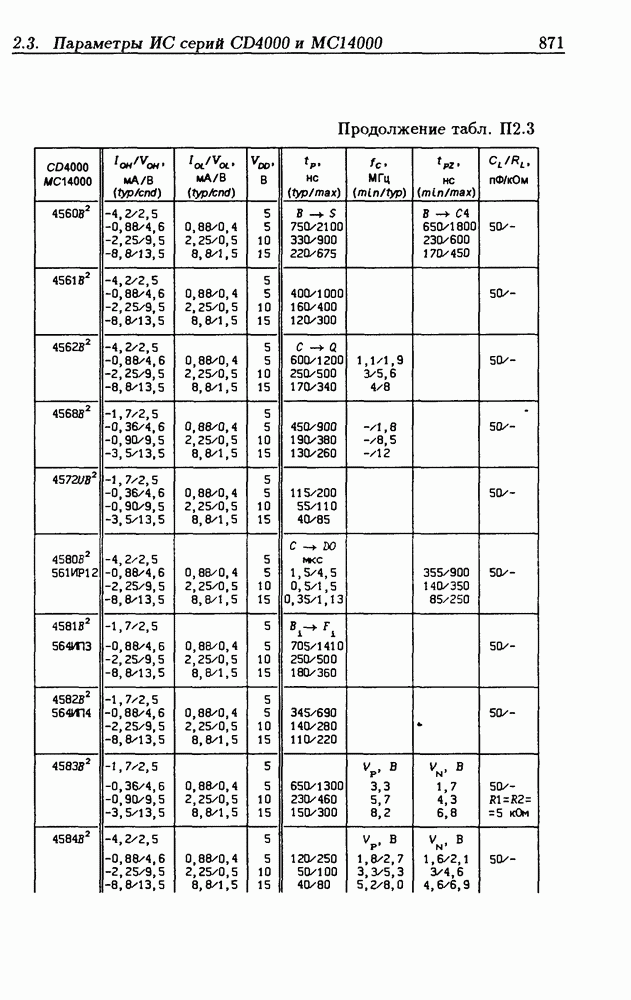
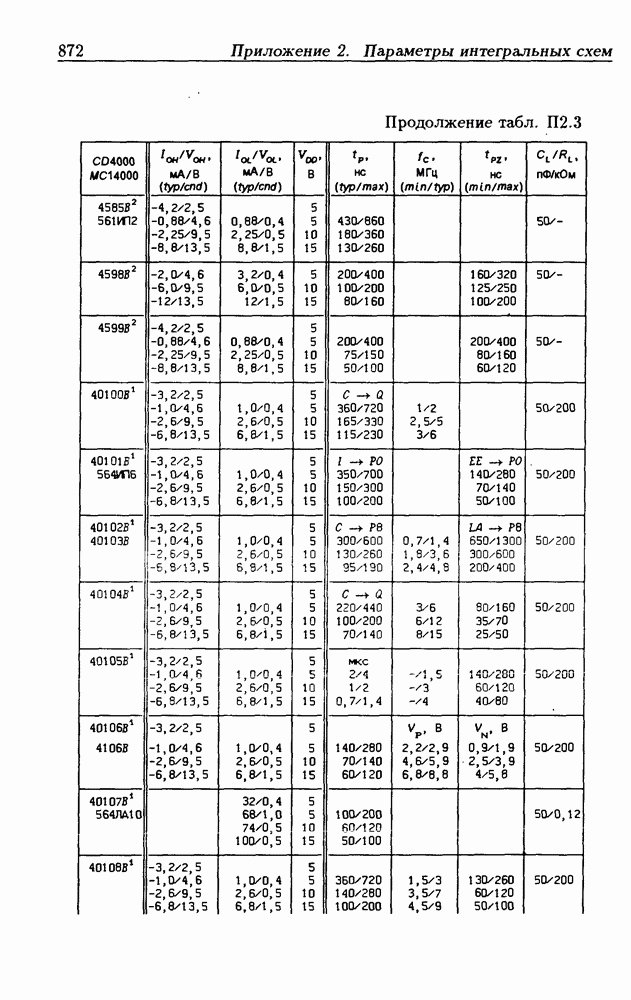
- Приложение 2. Параметры интегральных схем