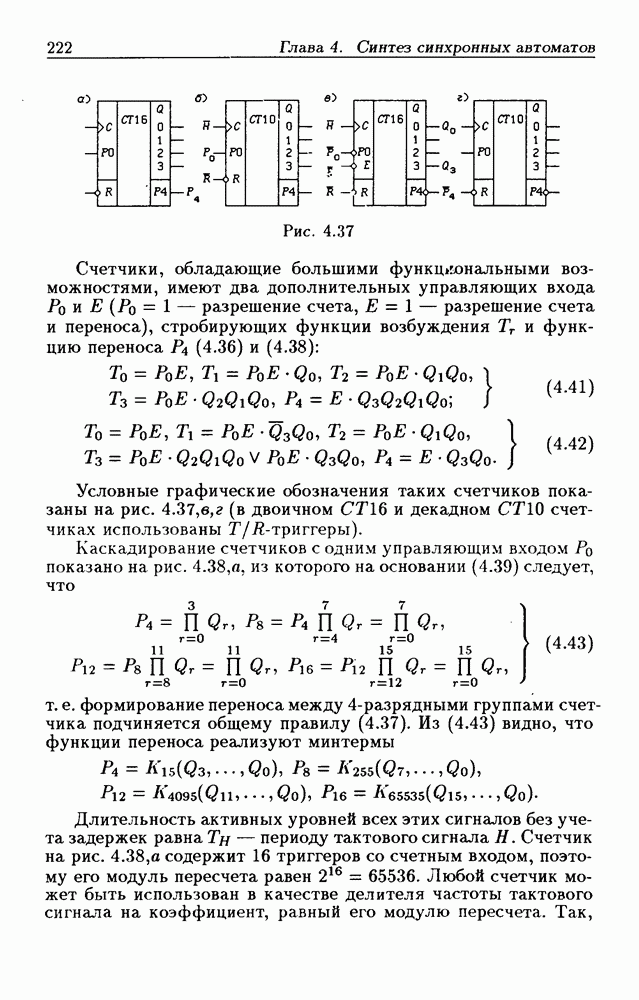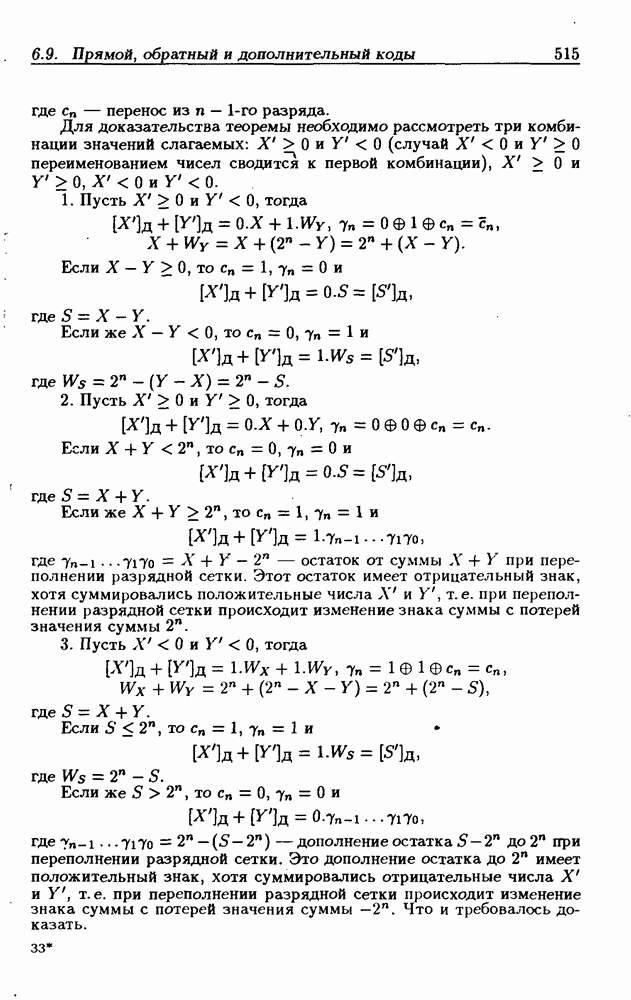| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.5. Синтез комбинационных схем, свободных от состязаний
В § 2.2 была показана возможность появления на выходах КС кратковременных ложных значений сигналов из-за состязаний ЛЭ. Эти ложные значения могут привести к неправильной работе других ЛС, в которых выходные сигналы КС используются в качестве входных. Воздействие кратковременных
ложных сигналов на ЛС с низким быстродействием не опасно, так как они не успевают на них отреагировать. Однако поступление ложных значений сигналов, хотя и кратковременных, на быстродействующие ЛС может вызвать ошибки в их работе. Покажем, что если допускаются только соседние изменения состояний входа, то можно синтезировать КС, на выходах которой ложные значения сигналов будут отсутствовать [5, 10].
Комбинационная схема называется свободной от состязаний, если в ней при соседних изменениях состояний входа отсутствуют критические состязания ЛЭ. Пусть функция  задана в некоторой нормальной форме в базисе И-НЕ:
задана в некоторой нормальной форме в базисе И-НЕ:

где 
Если в каждый момент времени может изменяться только один входной сигнал  то для ЛЭ, реализующих инверсии контермов, можно использовать модель с виртуальной задержкой (см. рис. 2.4,в). Использовав для ЛЭ И-НЕ второго яруса общую модель (см. рис. 2.4,а), получим схему на рис. 2.15 (паразитные задержки на входах ЛЭ второго яруса просуммированы с задержками ЛЭ первого яруса и перемещены на их входы).
то для ЛЭ, реализующих инверсии контермов, можно использовать модель с виртуальной задержкой (см. рис. 2.4,в). Использовав для ЛЭ И-НЕ второго яруса общую модель (см. рис. 2.4,а), получим схему на рис. 2.15 (паразитные задержки на входах ЛЭ второго яруса просуммированы с задержками ЛЭ первого яруса и перемещены на их входы).

Рис. 2.15
Итак, при соседних изменениях состояний входа динамическая модель КС состоит из статической (безынерционной) части и паразитных элементов задержки, включенных на входах и выходе КС. Для исследования статической части модели форма представления функции не имеет значения, так как в статических моделях изменения всех сигналов происходят мгновенно. Поэтому для анализа статической части модели можно производить любые тождественные преобразования функции  в соответствии с правилами алгебры логики.
в соответствии с правилами алгебры логики.
Поведение КС в переходных режимах определяется ее структурой, задаваемой выражением (2.22), и динамической моделью ЛЭ. Динамическая модель КС, представленная на рис. 2.15, позволяет довольно просто определить условия, при которых могут возникнуть критические состязания ЛЭ. Пусть изменяется только один входной сигнал  и в функцию (2.22) входит как
и в функцию (2.22) входит как
переменная  так и ее инверсия
так и ее инверсия  Поскольку в общем случае величины задержек
Поскольку в общем случае величины задержек  не равны между собой, то некоторое время на статическую часть модели КС могут поступать одинаковые значения сигналов
не равны между собой, то некоторое время на статическую часть модели КС могут поступать одинаковые значения сигналов  или 1) даже при одновременном изменении их в противоположных направлениях на входах динамической модели КС. Таким образом, в переходном режиме сигналы
или 1) даже при одновременном изменении их в противоположных направлениях на входах динамической модели КС. Таким образом, в переходном режиме сигналы  следует считать независимыми сигналами
следует считать независимыми сигналами  которые могут принимать также значения
которые могут принимать также значения 
На основании выражения (2.22) статическую модель КС можно представить в виде

где  функции, не зависящие от
функции, не зависящие от  и представляющие собой дизъюнкцию некоторого числа контермов;
и представляющие собой дизъюнкцию некоторого числа контермов;

Тогда поведение КС в переходных режимах можно описать функцией:

Если изменяется только один входной сигнал  то некоторое из состояний входа
то некоторое из состояний входа  или
или  изменяется на соседнее состояние 1) или
изменяется на соседнее состояние 1) или  соответственно, где
соответственно, где  так как остальные сигналы сохраняют свои значения. Пусть функция
так как остальные сигналы сохраняют свои значения. Пусть функция  при изменении сигнала
при изменении сигнала  сохраняет значение 0, т.е.
сохраняет значение 0, т.е.  Тогда из выражения (2.23) следует, что
Тогда из выражения (2.23) следует, что

Подставим эти значения функций  в выражение (2.24):
в выражение (2.24):  т.е. в данном случае в КС вообще отсутствуют изменения каких-либо сигналов.
т.е. в данном случае в КС вообще отсутствуют изменения каких-либо сигналов.
Рассмотрим второй случай, когда  а значит, как это следует из выражения (2.23), должны выполняться следующие соотношения:
а значит, как это следует из выражения (2.23), должны выполняться следующие соотношения:

Подставим эти значения функций  в выражение (2.24):
в выражение (2.24):

Из последних соотношений можно сделать вывод, что выходной сигнал  (рис. 2.15) изменяется с 1 на 0 (с 0 на 1), как только новое значение сигнала
(рис. 2.15) изменяется с 1 на 0 (с 0 на 1), как только новое значение сигнала  поступит на входы статической части всех тех ЛЭ (хотя бы одного
поступит на входы статической части всех тех ЛЭ (хотя бы одного  от которых зависит значение функции
от которых зависит значение функции  а значит, в данном случае состязания ЛЭ являются некритическими. Аналогично этому доказывается, что состязания ЛЭ являются некритическими и при
а значит, в данном случае состязания ЛЭ являются некритическими. Аналогично этому доказывается, что состязания ЛЭ являются некритическими и при 
Пусть теперь функция  при изменении сигнала
при изменении сигнала  сохраняет значение 1, т.е.
сохраняет значение 1, т.е.  Тогда из выражения (2.23) следует, что
Тогда из выражения (2.23) следует, что

Предположим, что  Тогда
Тогда  Подставив эти значения функций
Подставив эти значения функций  в выражение (2.24), получим
в выражение (2.24), получим  Если
Если  то
то  а если
а если  то
то  т.е. в данном случае значение функции
т.е. в данном случае значение функции  в переходном режиме в зависимости от соотношений задержек
в переходном режиме в зависимости от соотношений задержек  может измениться два раза (сначала с 1 на 0, а затем с 0 на 1). Это означает, что в КС имеют место критические состязания ЛЭ. если
может измениться два раза (сначала с 1 на 0, а затем с 0 на 1). Это означает, что в КС имеют место критические состязания ЛЭ. если  при
при 
Таким образом, критические состязания ЛЭ при соседних изменениях состояний входа могут возникнуть только в том случае, когда при этих состояниях входа функция сохраняет значение 1.
Из выражений (2.25) видно, что возможен также случай, когда  Подставив это значение функции
Подставив это значение функции  в выражение (2.24), получим
в выражение (2.24), получим  независимо от значений
независимо от значений  Из этого следует, что независимо от соотношений задержек
Из этого следует, что независимо от соотношений задержек  и способов получения сигналов
и способов получения сигналов  критические состязания ЛЭ будут отсутствовать, если
критические состязания ЛЭ будут отсутствовать, если  при
при  Если это условие соблюдается для всех сигналов
Если это условие соблюдается для всех сигналов  то КС будет свободна от состязаний.
то КС будет свободна от состязаний.
Из доказанного условия, при выполнении которого критические состязания ЛЭ отсутствуют, легко вывести правила синтеза КС, свободных от состязаний. Рассмотрим эти правила для синтеза КС с помощью диаграмм Вейча.
Если  то это означает, что в диаграмме Вейча имеются две соседние 1-клетки, для которых переменная
то это означает, что в диаграмме Вейча имеются две соседние 1-клетки, для которых переменная  имеет различные значения, а все остальные переменные не изменяются. Если покрыть эти 1-клетки 1-кубом, то получим контерм такой, что
имеет различные значения, а все остальные переменные не изменяются. Если покрыть эти 1-клетки 1-кубом, то получим контерм такой, что  а это и означает, что получена функция
а это и означает, что получена функция  Очевидно, что для покрытия 1-клеток можно использовать m-кубы и большего размера. Если покрыть все соседние 1-клетки m-кубами и взять дизъюнкцию соответствующих им контермов, то функция
Очевидно, что для покрытия 1-клеток можно использовать m-кубы и большего размера. Если покрыть все соседние 1-клетки m-кубами и взять дизъюнкцию соответствующих им контермов, то функция  будет представлена в форме (2.23), причем такой, что если
будет представлена в форме (2.23), причем такой, что если  то
то  для любых и
для любых и 
Таким образом, одной из основных задач синтеза КС, свободных от состязаний, является отыскание таких минимальных покрытий 1-клеток функции  -кубами, в которых любые соседние 1-клетки покрыты по меньшей мере одним m-кубом. Соответствующая этим покрытиям форма представления функции называется минимальной дизъюнктивной нормальной формой, свободной от состязаний (МДНФС). Используя закон двойного отрицания (1.14) и закон двойственности (1.25), из МДНФС можно получить минимальную нормальную форму в базисе И-НЕ, свободную от состязаний (МНФС в базисе И-НЕ).
-кубами, в которых любые соседние 1-клетки покрыты по меньшей мере одним m-кубом. Соответствующая этим покрытиям форма представления функции называется минимальной дизъюнктивной нормальной формой, свободной от состязаний (МДНФС). Используя закон двойного отрицания (1.14) и закон двойственности (1.25), из МДНФС можно получить минимальную нормальную форму в базисе И-НЕ, свободную от состязаний (МНФС в базисе И-НЕ).

Рис. 2.16
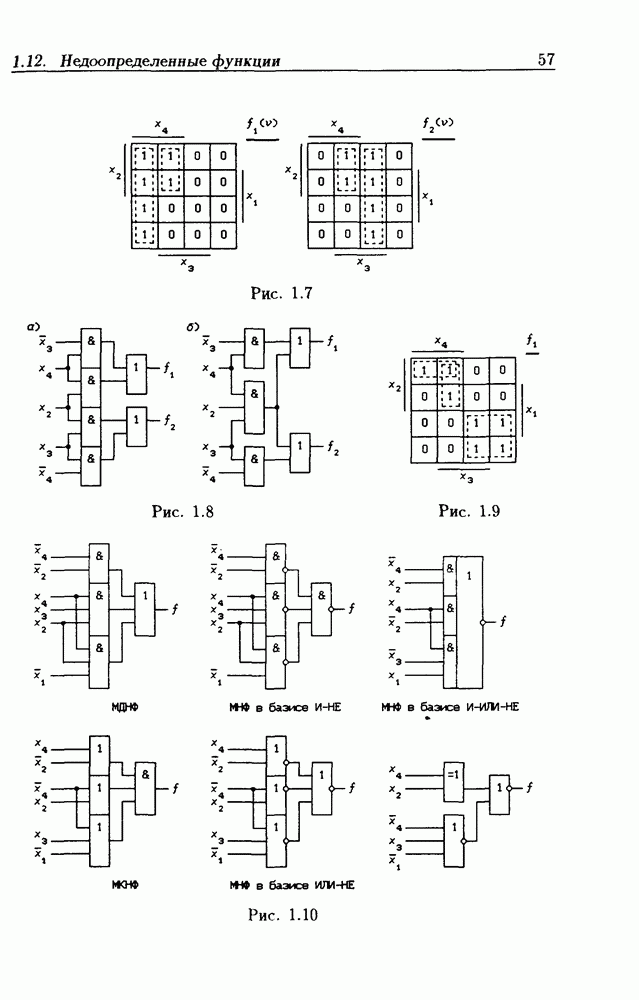
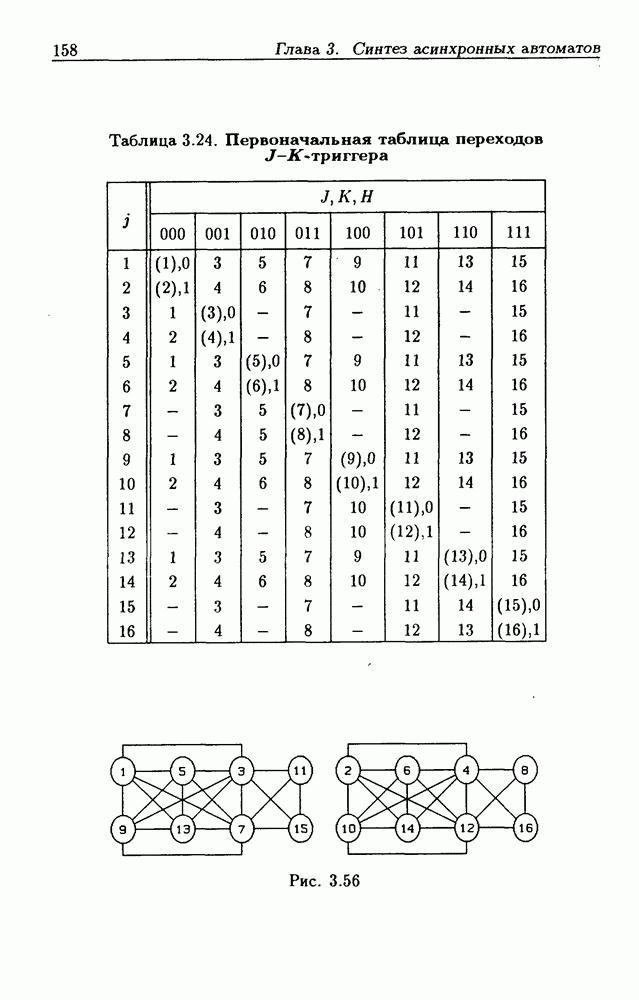
Рассмотрим несколько примеров. На рис. 2.16 приведены диаграммы Вейча, в которых m-кубы, необходимые для получения МДНФ, отмечены сплошными контурами. Для получения МДНФС функции, представленной на рис. 2.16,а, необходимо добавить два 1-куба и один  -куб (штриховые контуры), чтобы покрыть m-кубами соседние 1-клетки с номерами 1 и 9, 3 и 7, 13 и 15. Для функции, представленной на рис.
-куб (штриховые контуры), чтобы покрыть m-кубами соседние 1-клетки с номерами 1 и 9, 3 и 7, 13 и 15. Для функции, представленной на рис.  число 1-кубов для получения МДНФС удваивается по сравнению с МДНФ. Рис. 2.16,в поясняет отыскание МДНФС функции пяти переменных. В качестве примера запишем МДНФ и МДНФС
число 1-кубов для получения МДНФС удваивается по сравнению с МДНФ. Рис. 2.16,в поясняет отыскание МДНФС функции пяти переменных. В качестве примера запишем МДНФ и МДНФС
этой функции:

Аналогичным образом можно показать, что в КС, построенных в соответствии с КНФ или нормальными формами в базисе ИЛИ-НЕ, критические состязания ЛЭ могут возникнуть только в тех случах, когда функция выхода при двух соседних состояниях входа сохраняет значение 0, т.е., если  Из вывода выражения (1.74) следует, что минимальная конъюнктивная нормальная форма, свободная от состязаний (МКНФС), функции
Из вывода выражения (1.74) следует, что минимальная конъюнктивная нормальная форма, свободная от состязаний (МКНФС), функции  может быть получена из МДНФС инверсной функции
может быть получена из МДНФС инверсной функции  т.е. для получения МКНФС необходимо найти такое минимальное покрытие 0-клеток диаграммы Вейча для функции
т.е. для получения МКНФС необходимо найти такое минимальное покрытие 0-клеток диаграммы Вейча для функции  в котором любые две соседние 0-клетки покрыты по крайней мере хотя бы одним m-кубом. С помощью закона двойного отрицания (1.14) и закона двойственности (1.25), из МКНФС можно получить минимальную нормальную форму в базисе ИЛИ-НЕ, свободную от состязаний (МНФС в базисе ИЛИ-НЕ).
в котором любые две соседние 0-клетки покрыты по крайней мере хотя бы одним m-кубом. С помощью закона двойного отрицания (1.14) и закона двойственности (1.25), из МКНФС можно получить минимальную нормальную форму в базисе ИЛИ-НЕ, свободную от состязаний (МНФС в базисе ИЛИ-НЕ).
В заключение отметим, что из МДНФС можно получать скобочные формы функций, которым также соответствуют КС, свободные от состязаний. Если допускаются несоседние изменения состояний входа, то в общем случае невозможно синтезировать КС, свободные от состязаний.
Изложенный материал имеет первостепенное значение для разработки методов синтеза асинхронных потенциальных автоматов.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Основы теории переключательных функций
- 1.2. Позиционные системы счисления
- 1.3. Переключательные функции
- 1.4. Принцип и закон двойственности
- 1.5. Теоремы разложения
- 1.6. Решение систем логических уравнений
- 1.7. Первичные термы, минтермы и макстермы
- 1.8. Совершенные нормальные формы представления функций
- 1.9. Конъюнктивные и дизъюнктивные термы
- 1.10. Минимизация переключательных функций
- 1.11. Диаграммы Вейча
- 1.12. Минимизация неполностью определенных функций, совместная минимизация нескольких функций
- 1.13. Скобочные формы функций
- 1.14. Закон двойственности для логических схем
- 1.15. Линейные функции
- Глава 2. Анализ и синтез логических схем
- 2.2. Модели логических элементов
- 2.3. Модели логических схем
- 2.4. Анализ логических схем
- 2.5. Синтез комбинационных схем, свободных от состязаний
- Глава 3. Синтез асинхронных потенциальных автоматов
- 3.2. Асинхронные потенциальные автоматы
- 3.3. Асинхронные потенциальные триггеры и элементы памяти
- Триггеры типа R-S
- Триггеры типа D-L
- Триггеры типа D-L-R с приоритетом входа R.
- Триггеры типа D-L-R с приоритетом входа L.
- Триггеры типа R-S-L.
- Триггеры типа DN-LN
- Аналитический метод синтеза и анализа триггеров.
- 3.4. Задание асинхронных потенциальных автоматов таблицами и графами переходов
- 3.5. Синтез асинхронных потенциальных счетчиков
- 3.6. Синтез асинхронных импульсных триггеров
- Триггеры типа dJ-dK.
- Классификация триггеров.
- 3.7. Синтез синхронных триггеров
- Триггеры типа J-K
- Синхронно-асинхронные триггеры.
- 3.8. Примеры синтеза асинхронных потенциальных автоматов
- Цифровые фазочастотные детекторы.
- Квантизатор временных интервалов.
- 3.9. Генераторы сигналов
- Автогенераторы.
- Управляемые автогенераторы.
- Глава 4. Синтез синхронных автоматов
- 4.2. Синхронные триггеры
- Триггеры типов D и R-S с импульсным тактовым сигналом.
- Синхронные триггеры типов R-S и D-L
- Синхронно-асинхронные триггеры.
- Синхронные триггеры типа J-K
- Триггеры типа Т.
- Классификация синхронных триггеров.
- Преобразования типов синхронных триггеров.
- Триггеры типов D-T-L и D-T-L/R
- Функции переходов синхронно-асинхронных триггеров.
- 4.3. Примеры синтеза синхронных автоматов
- 4.4. Сдвигающие регистры
- Синтез счетчиков на сдвигающих регистрах.
- Сдвигающие регистры с загрузкой данных.
- Реверсивные сдвигающие регистры.
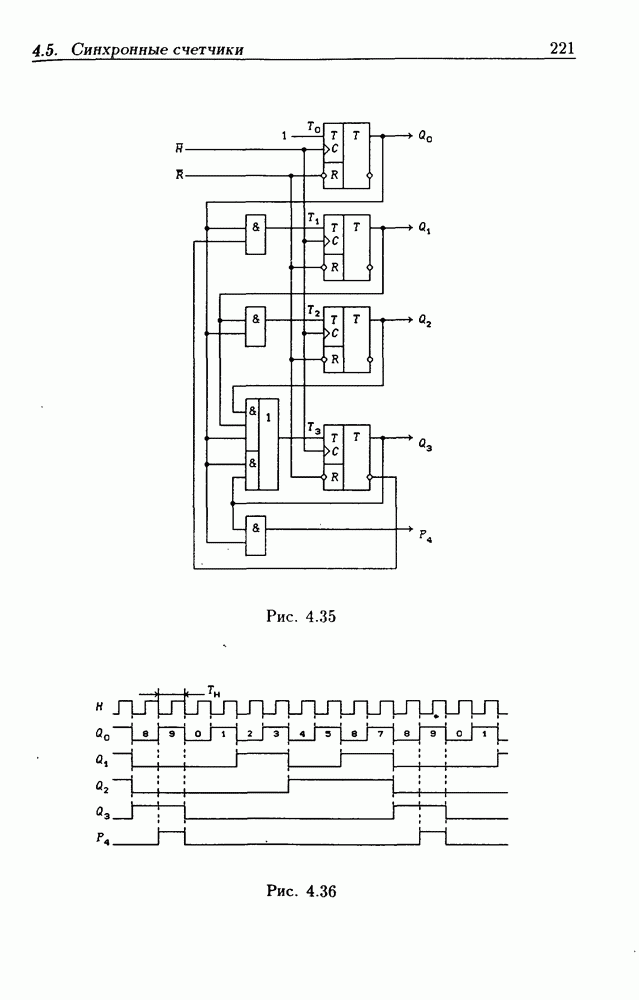
- 4.5. Синхронные счетчики
- Синхронные двоичные счетчики.
- Синхронные двоично-десятичные счетчики.
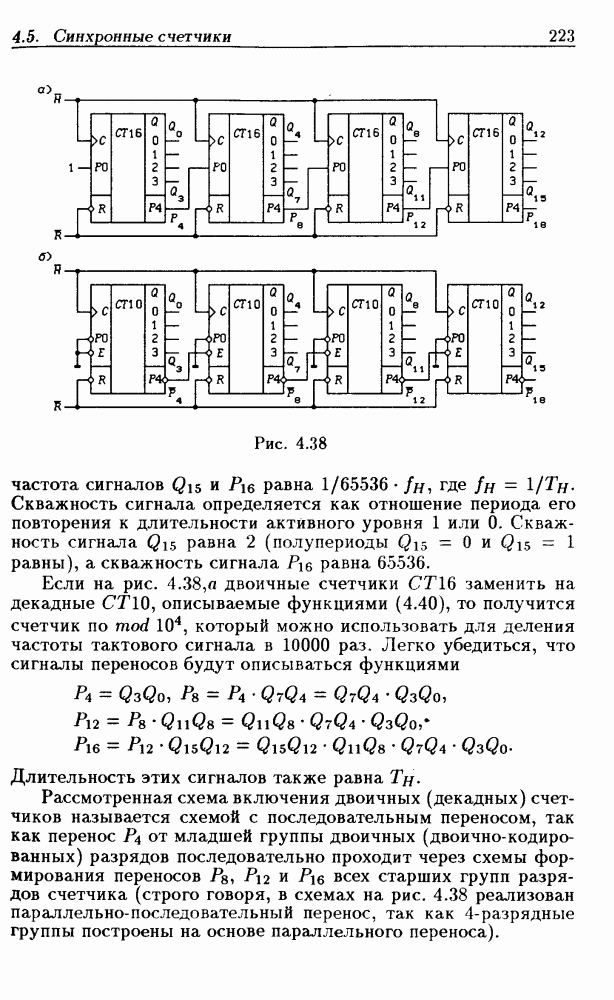
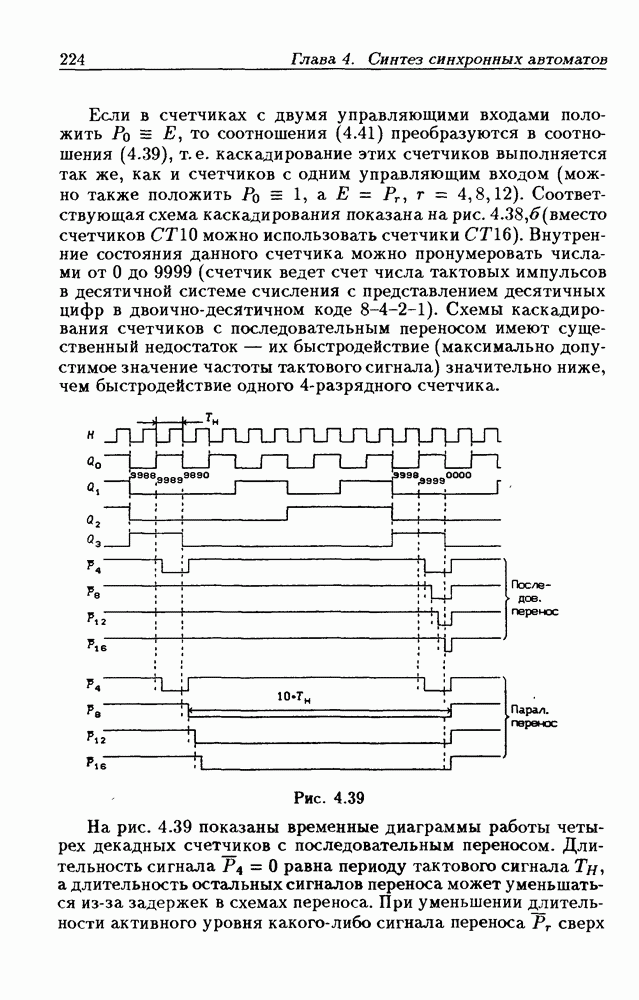
- Каскадирование двоичных и двоично-десятичных счетчиков.
- Синхронные двоичные реверсивные счетчики.
- Реверсивные двоично-десятичные счетчики.
- Каскадирование реверсивных счетчиков.
- Счетчики на сдвигающих регистрах.
- Кольцевые счетчики.
- Линейные счетчики.
- Программируемые счетчики.
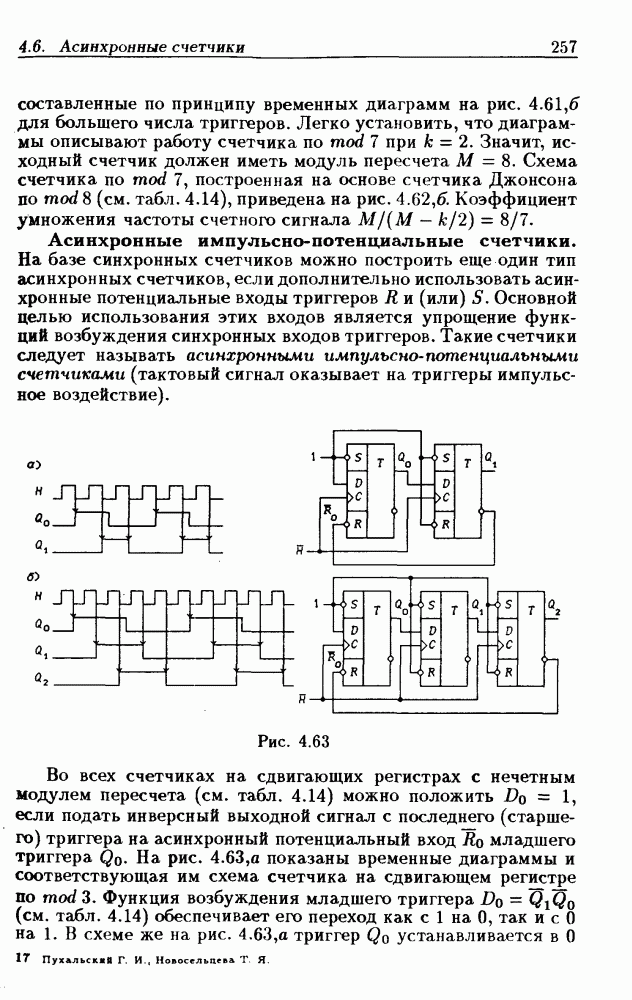
- 4.6. Асинхронные счетчики
- Асинхронные счетчики с умножением частоты счетного сигнала.
- Асинхронные импульсно-потенциальные счетчики.
- Асинхронное программирование модуля пересчета счетчиков.
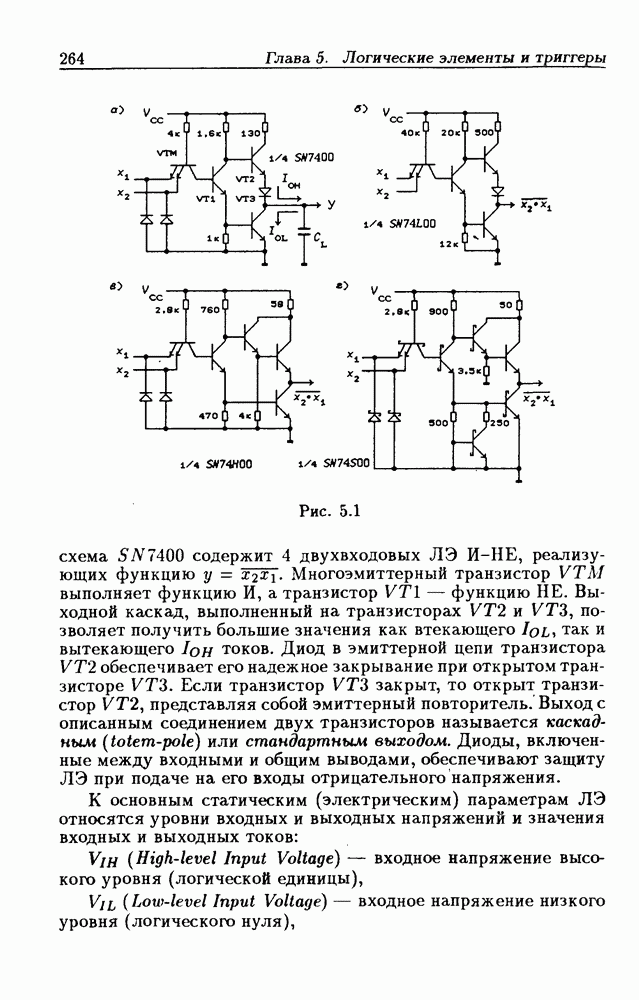
- Глава 5. Логические элементы и триггеры
- Логические элементы.
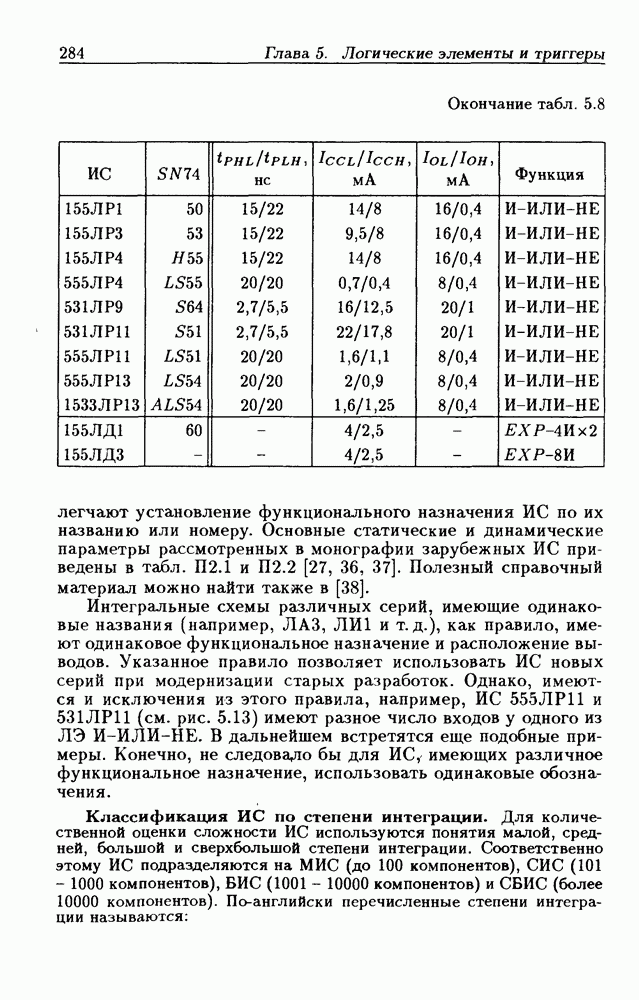
- Классификация ИС по степени интеграции.
- 5.2. Интегральные схемы КМОП серий
- 5.3. Триггеры Шмитта
- 5.4. Логические элементы с открытым коллекторным выходом
- Логические элементы с открытым коллекторным выходом.
- Применения ЛЭ с открытым коллекторным выходом.
- Интерфейсные ЛЭ с открытым коллекторным выходом.
- Логические элементы с открытым стоковым выходом.
- Типовые цоколевки ИС.
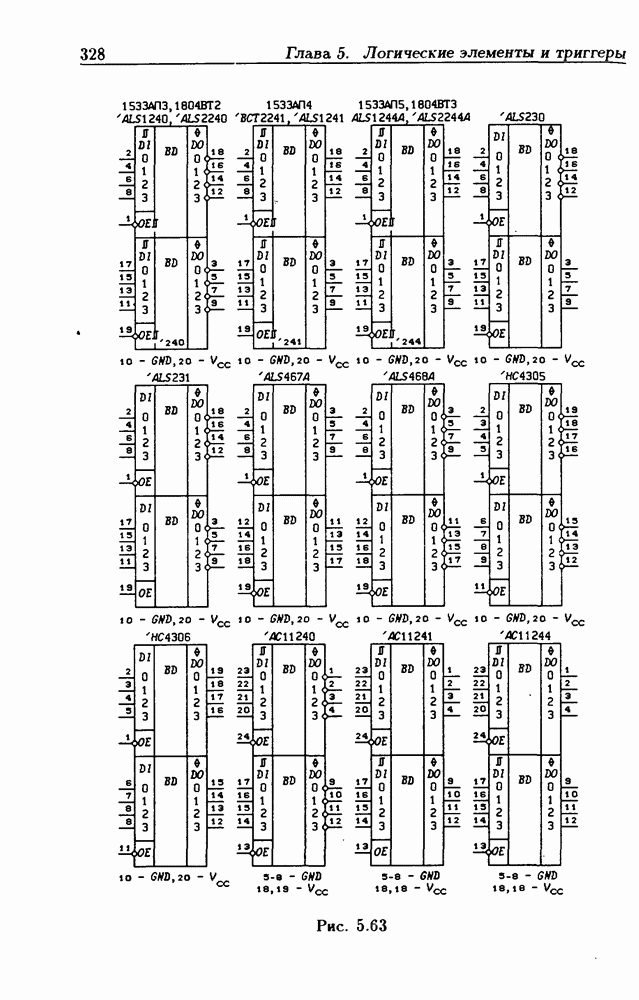
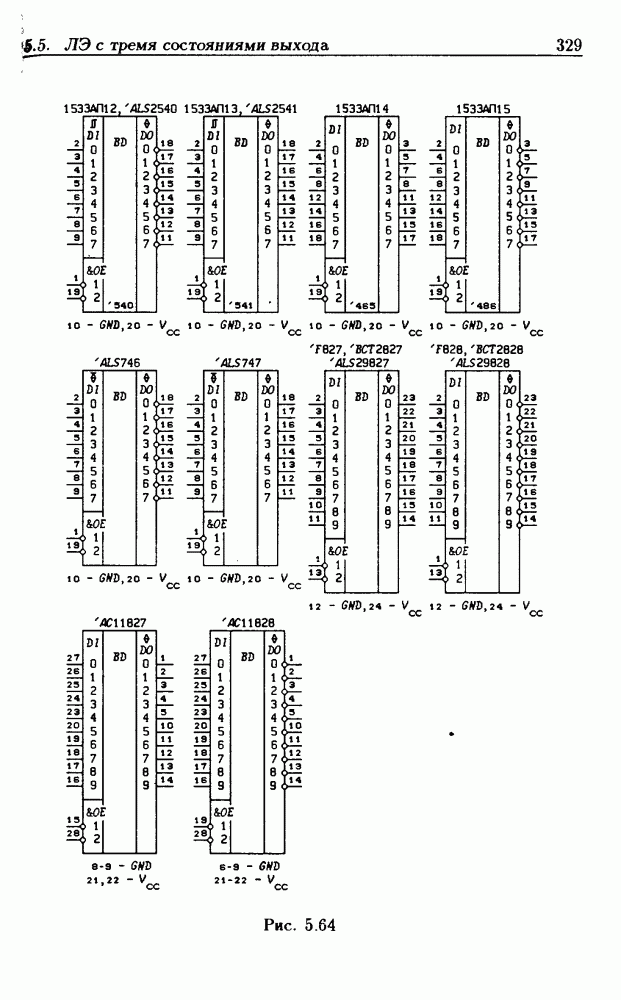
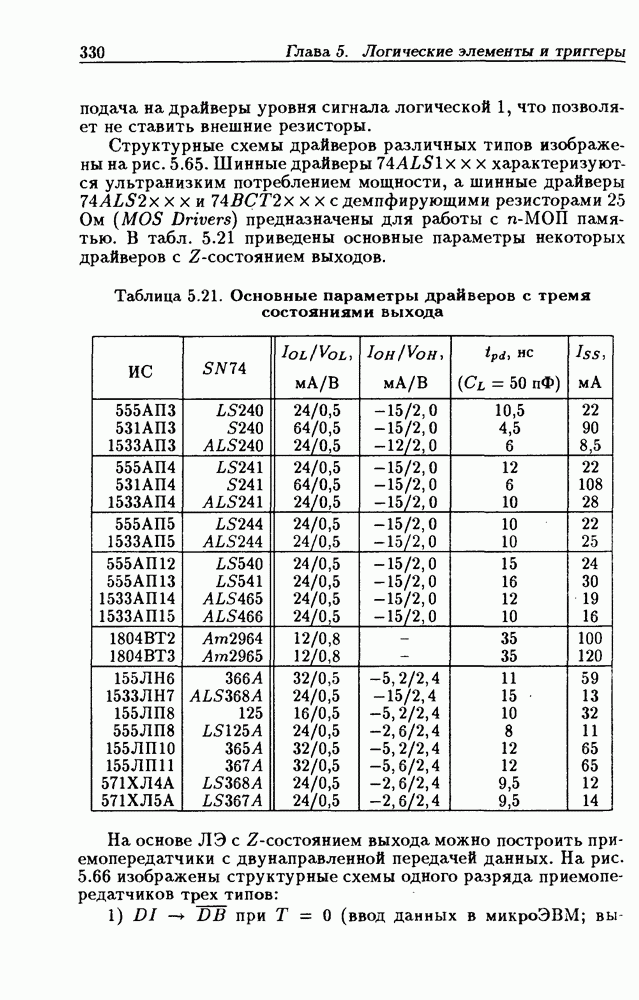
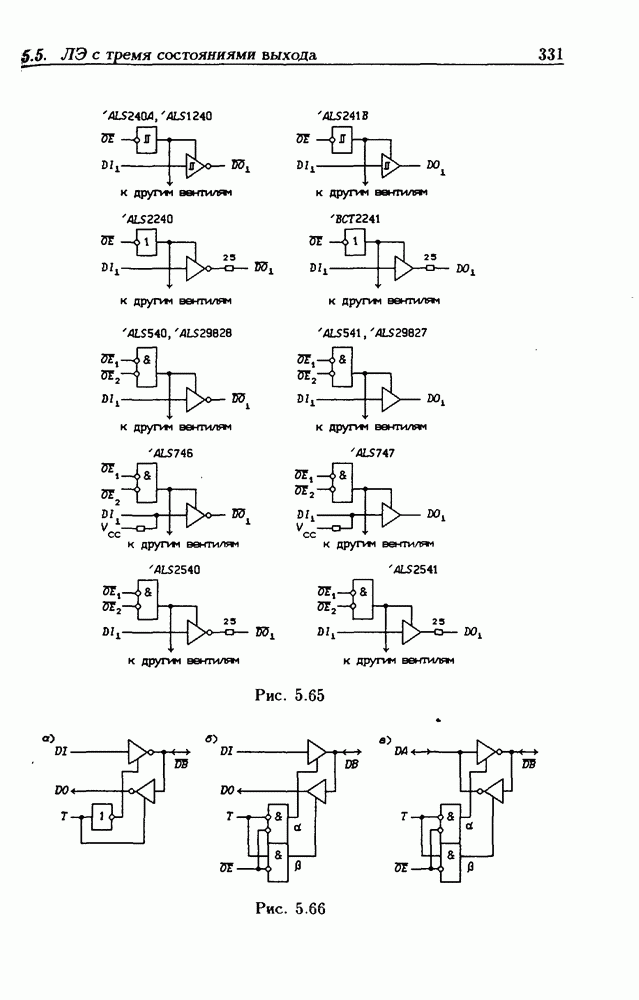
- 5.5. Логические элементы с тремя состояниями выхода
- Шинные драйверы с Z-состоянием выхода.
- Основные правила графического изображения ИС.
- 5.6. Преобразователи уровней напряжения и тока
- 5.7. Асинхронные потенциальные триггеры и регистры памяти
- 5.8. Синхронные триггеры и регистры памяти
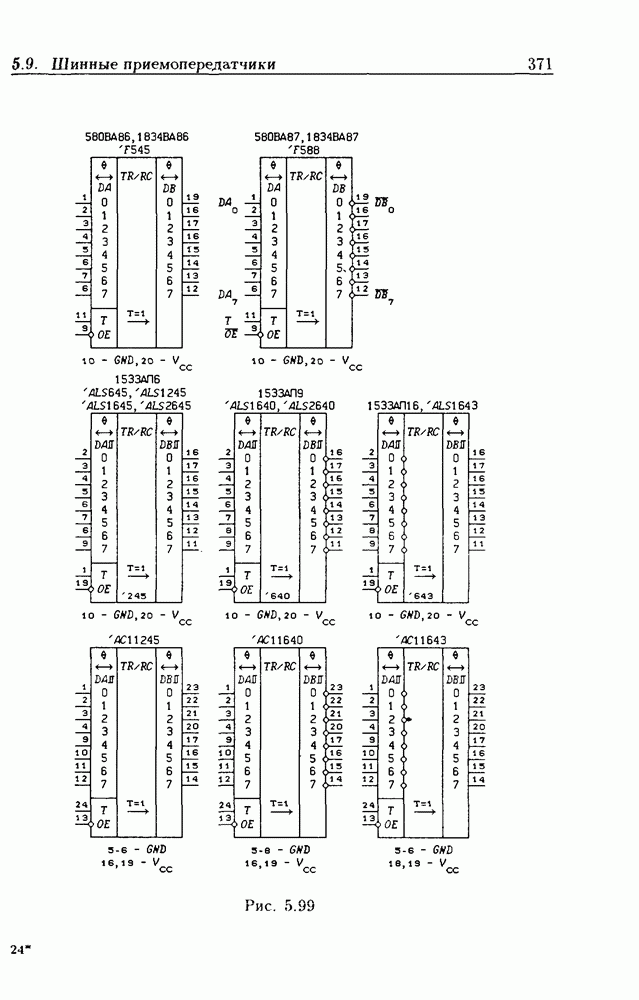
- 5.9. Шинные приемопередатчики
- Шинные приемопередатчики с Z-состоянием выхода.
- Шинные приемопередатчики с открытым коллекторным выходом.
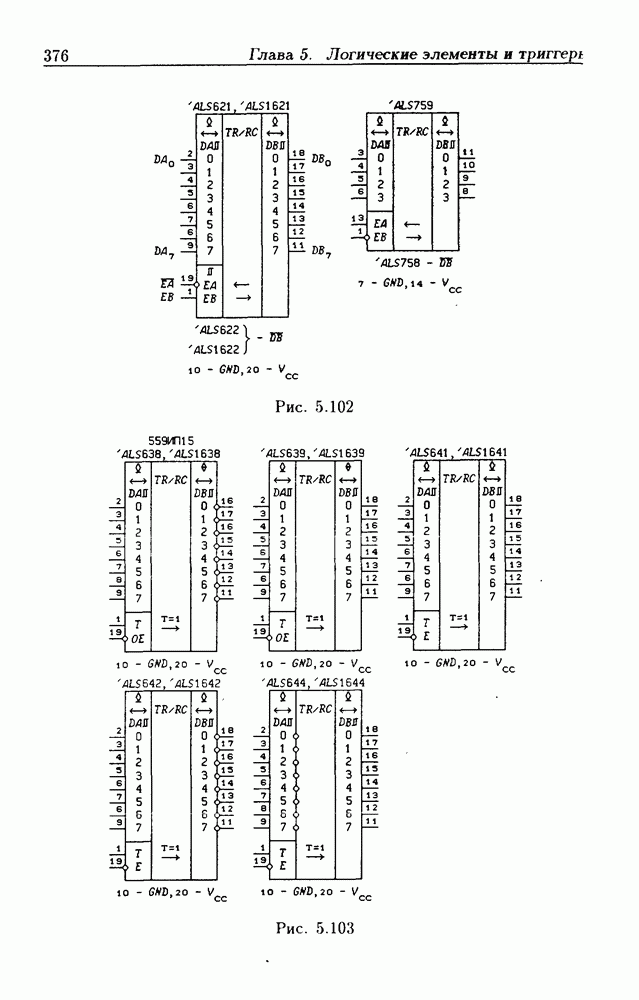
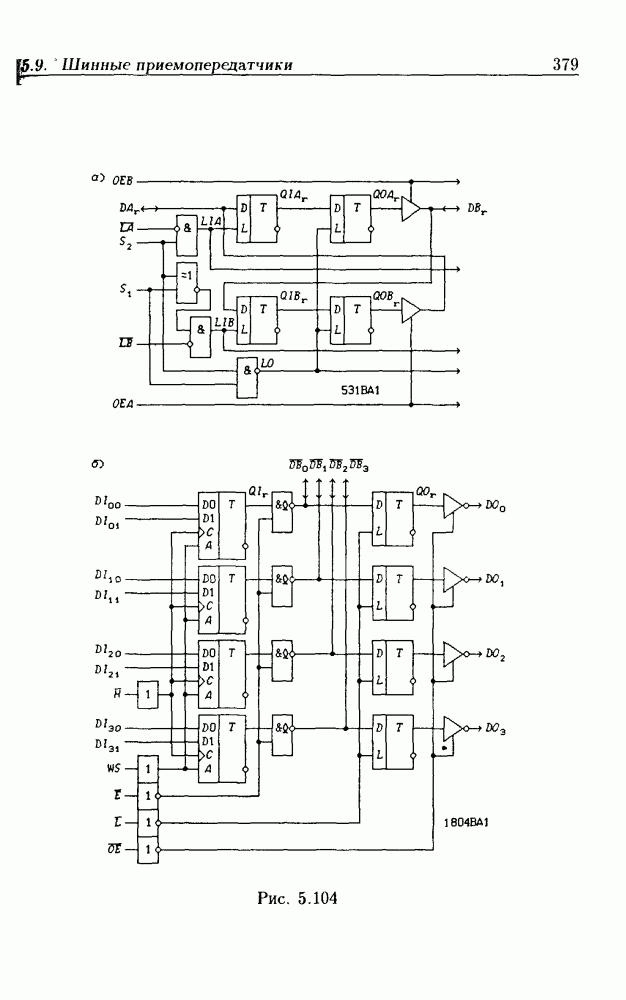
- Шинные приемопередатчики с регистрами памяти.
- Шинные приемопередатчики со сдвигающим регистром.
- Шинные трехнаправленные приемопередатчики.
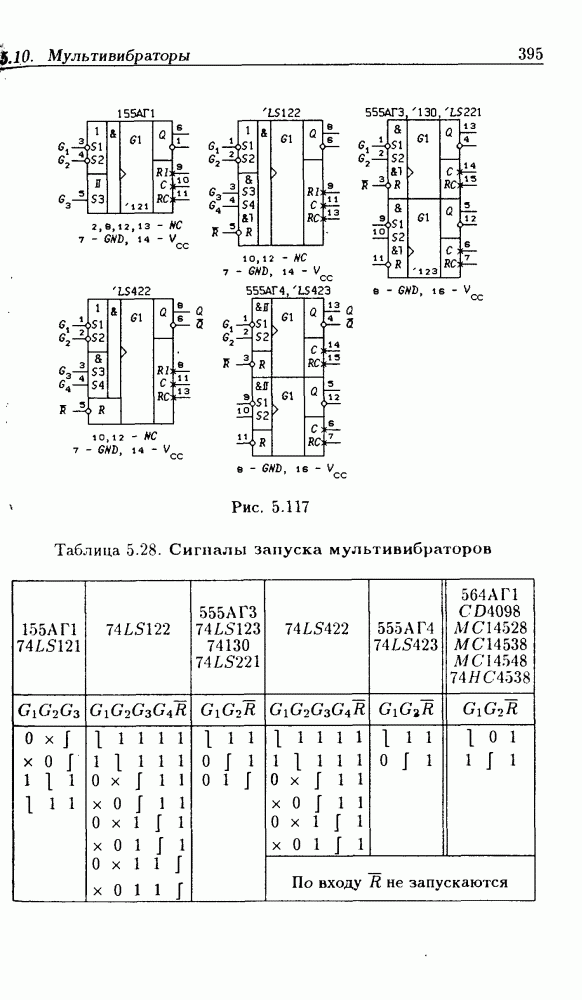
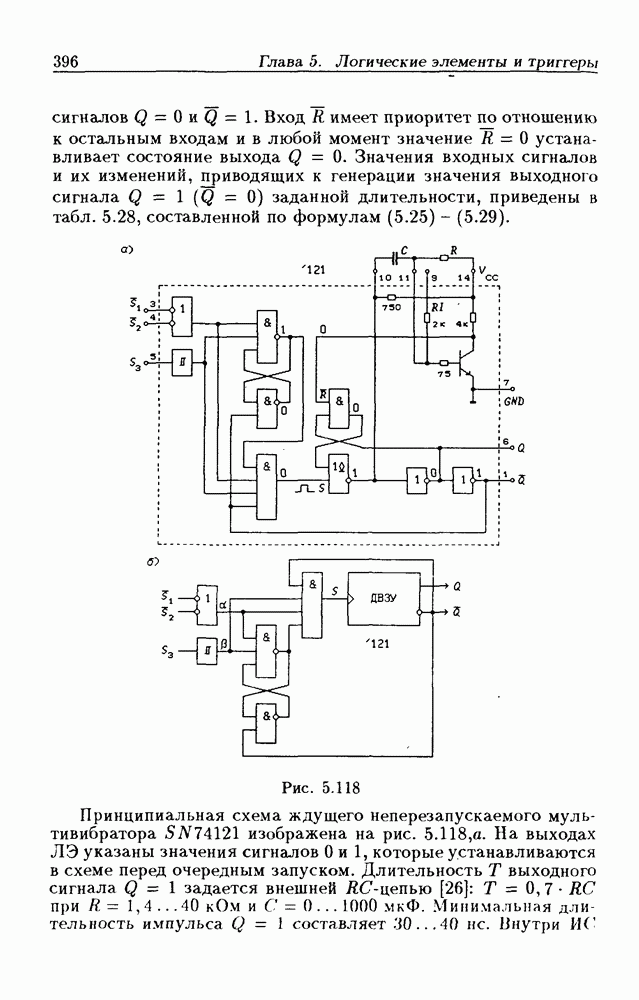
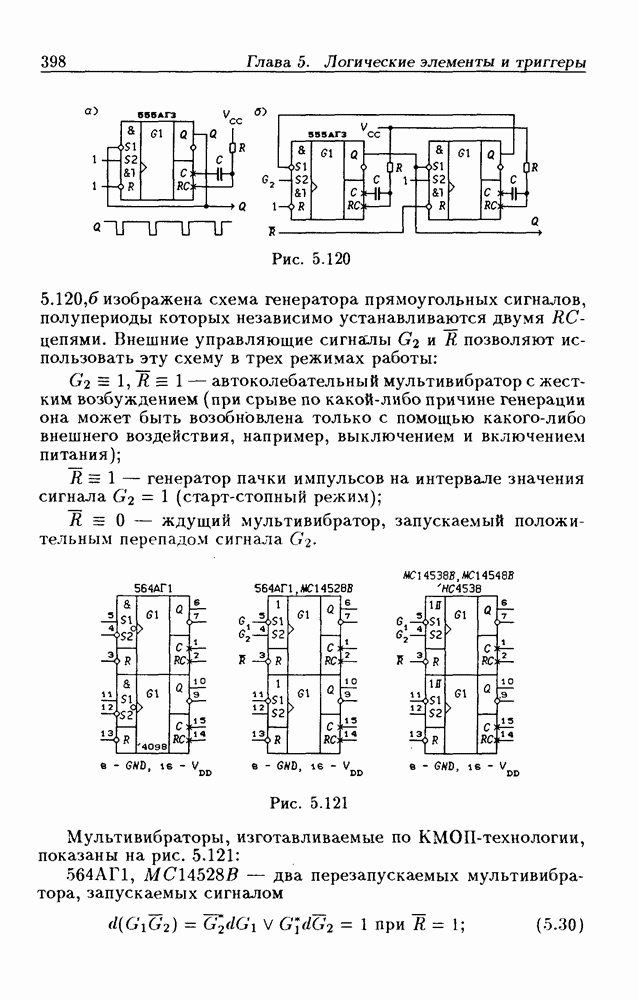
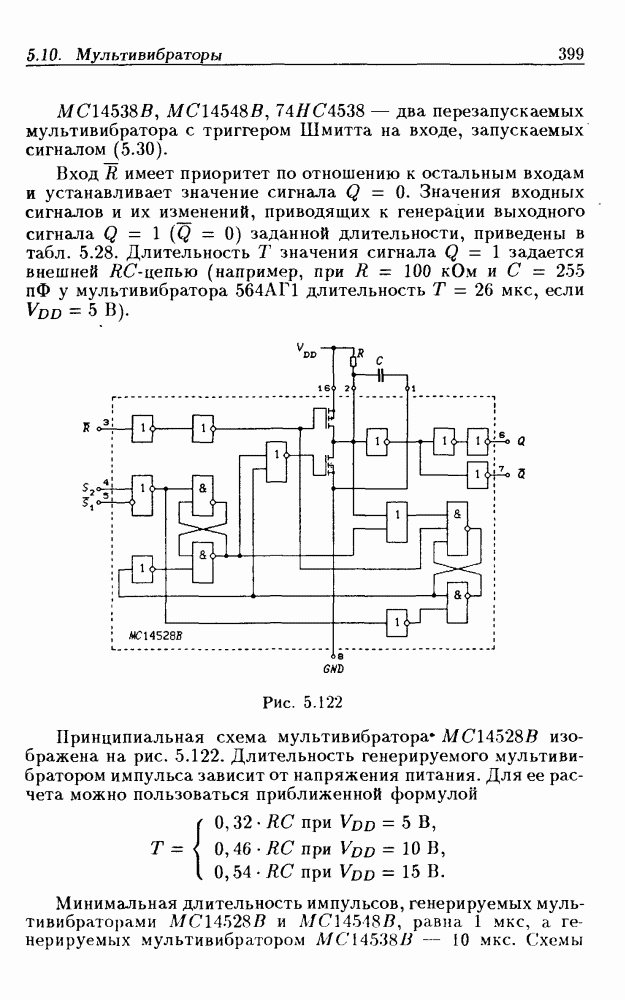
- 5.10. Мультивибраторы
- 5.11. Генераторы
- Схемы устранения «дребезга» механических контактов.
- Автогенераторы периодических сигналов.
- 5.12. Рекомендации по выбору серий ИС
- Глава 6. Коммутаторы и арифметические устройства
- 6.1. Дешифраторы
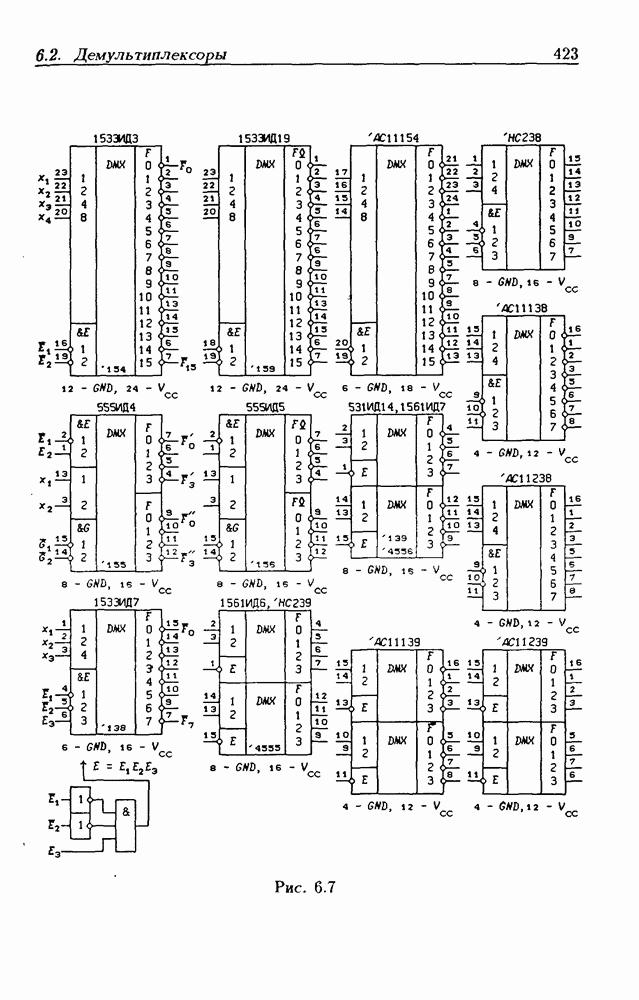
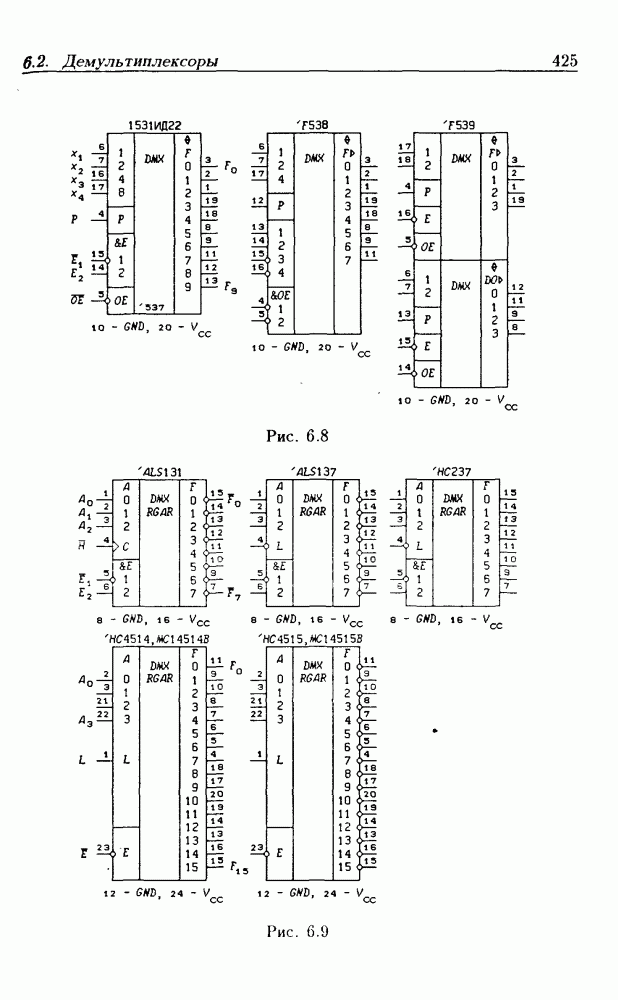
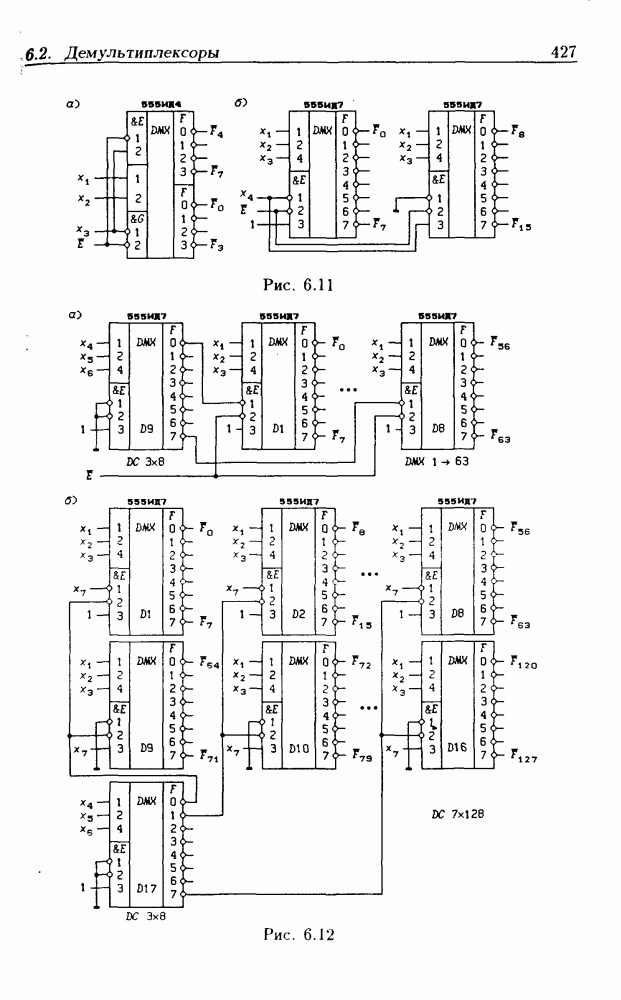
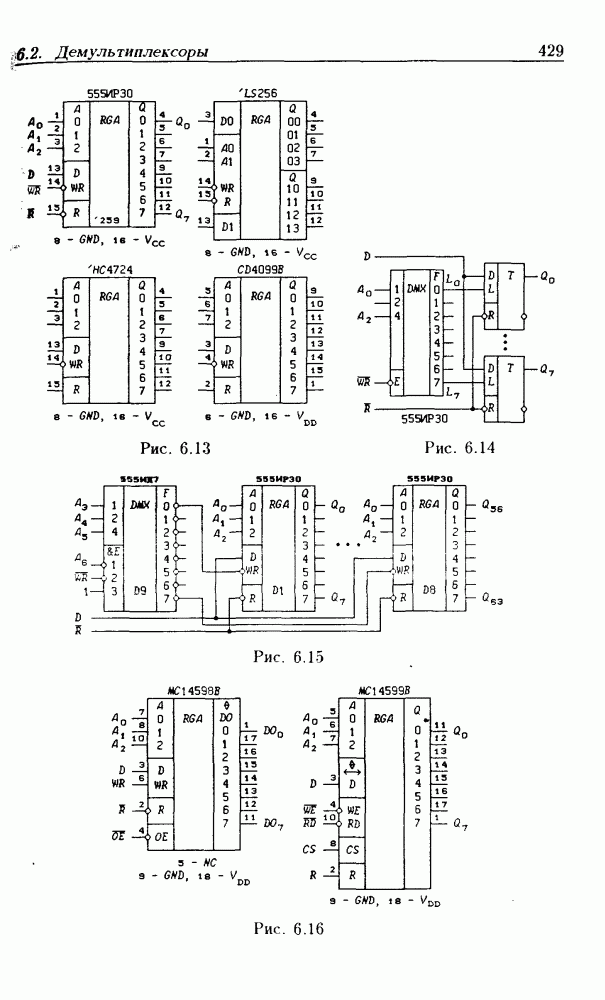
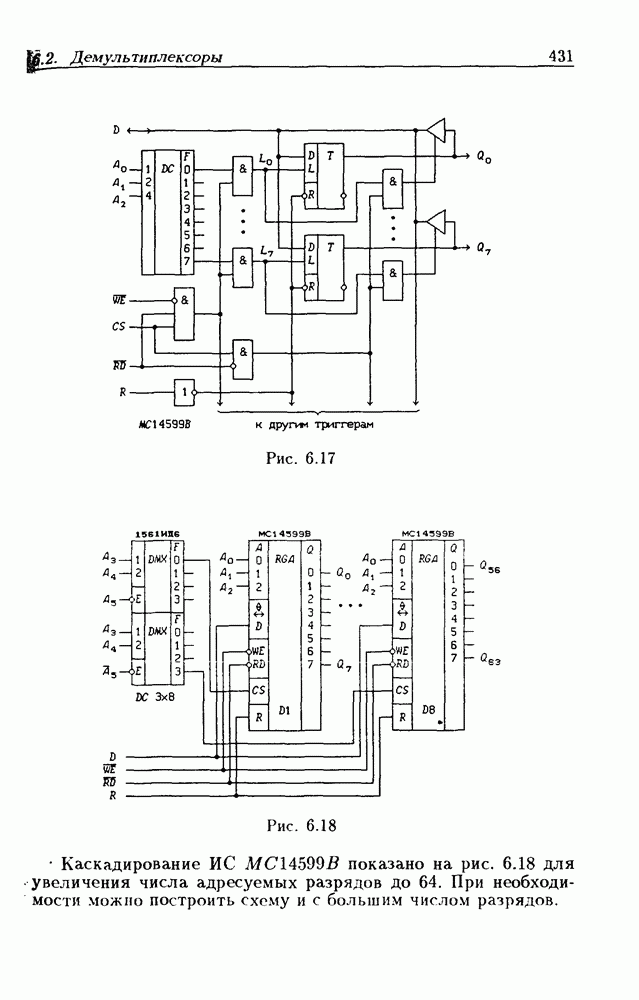
- 6.2. Демультиплексоры
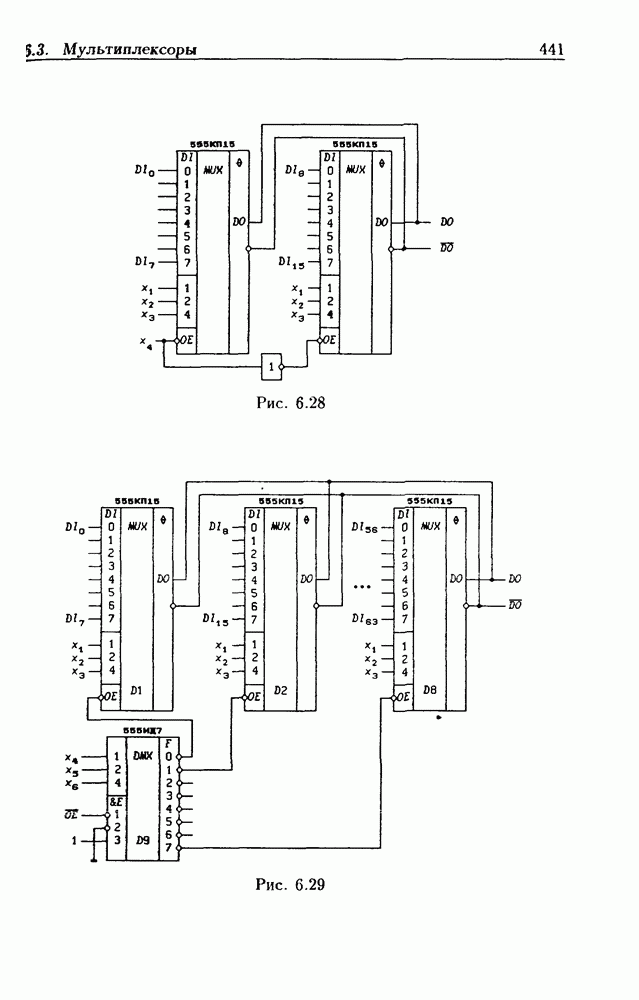
- 6.3. Мультиплексоры
- Мультиплексоры без стробирования.
- Мультиплексоры со стробированием.
- Мультиплексоры с Z-состоянием выхода.
- Каскадирование мультиплексоров.
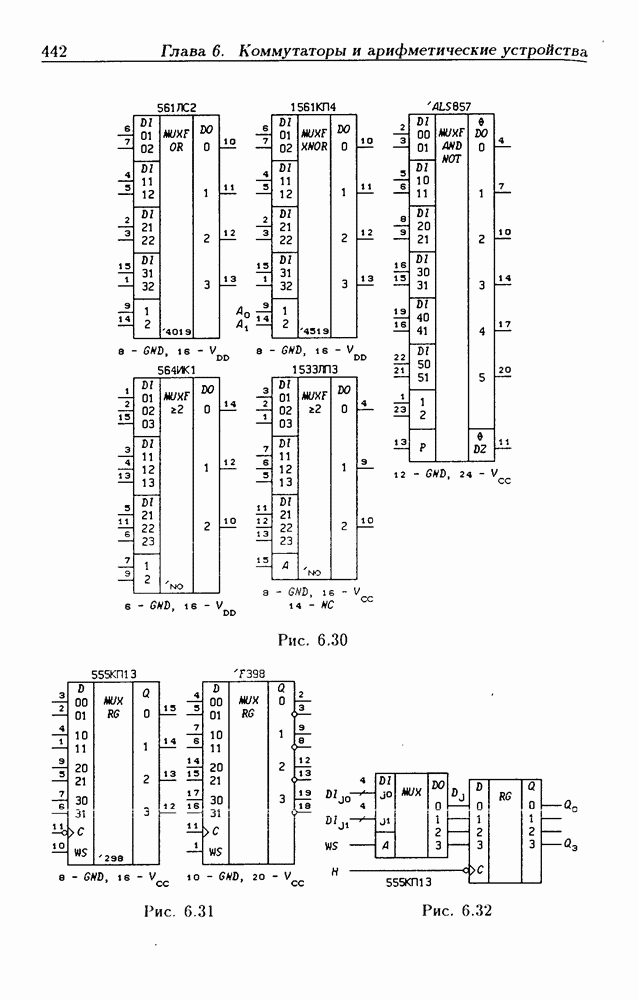
- Функциональные мультиплексоры.
- Регистры памяти с мультиплексными входами данных.
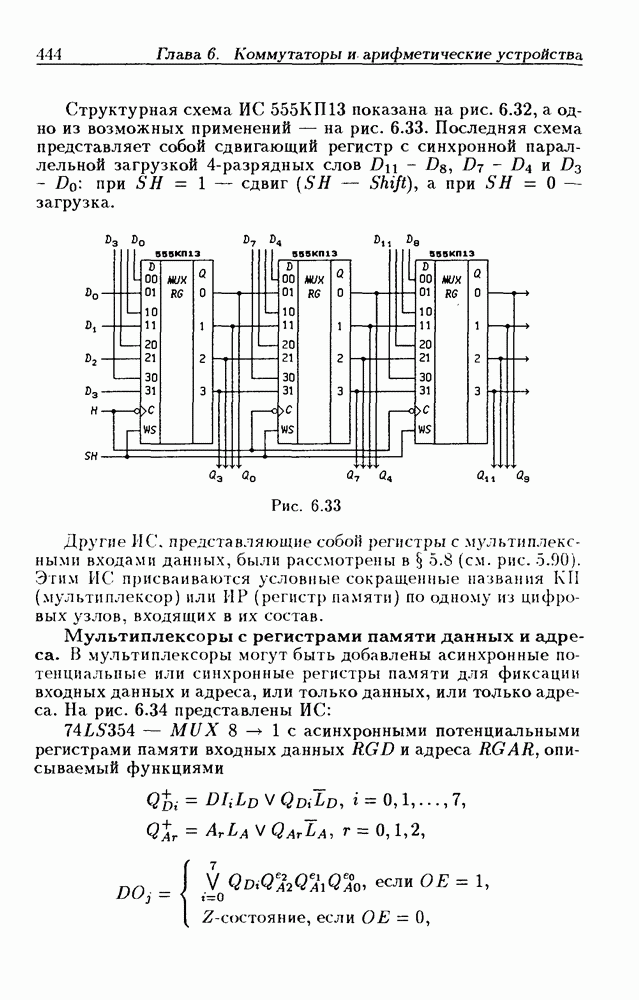
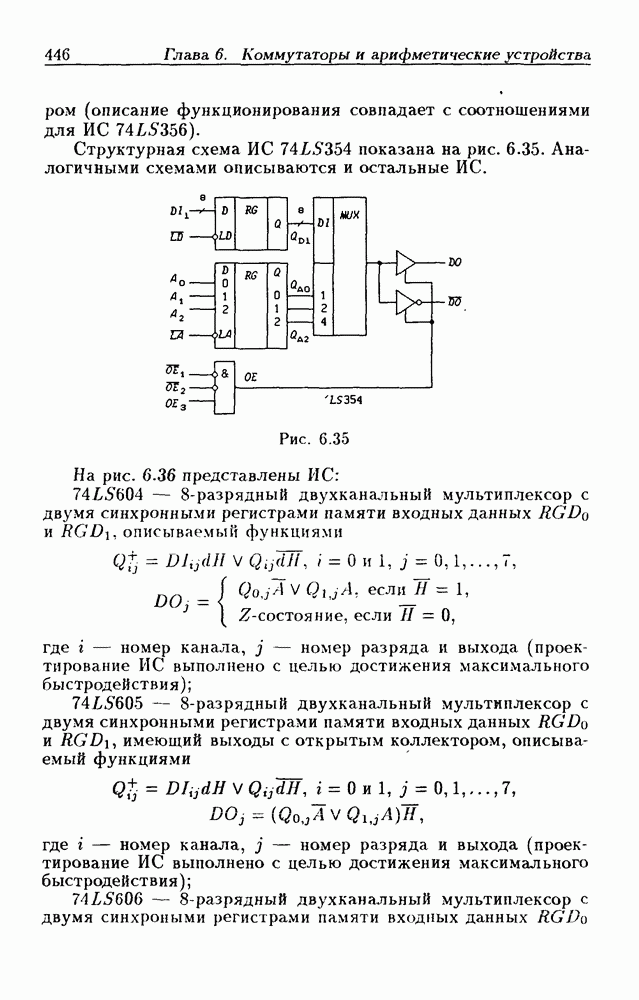
- Мультиплексоры с регистрами памяти данных и адреса.
- Сдвигающие мультиплексоры.
- 6.4. Синтез комбинационных схем и цифровых автоматов на мультиплексорах
- Синтез схем на 8-канальных мультиплексорах.
- Синтез на двухразрядных 4-канальных мультиплексорах.
- Синтез генератора синусоидальной функции на мультиплексорах.
- Синтез триггеров на мультиплексорах.
- Синтез счетчиков на мультиплексорах.
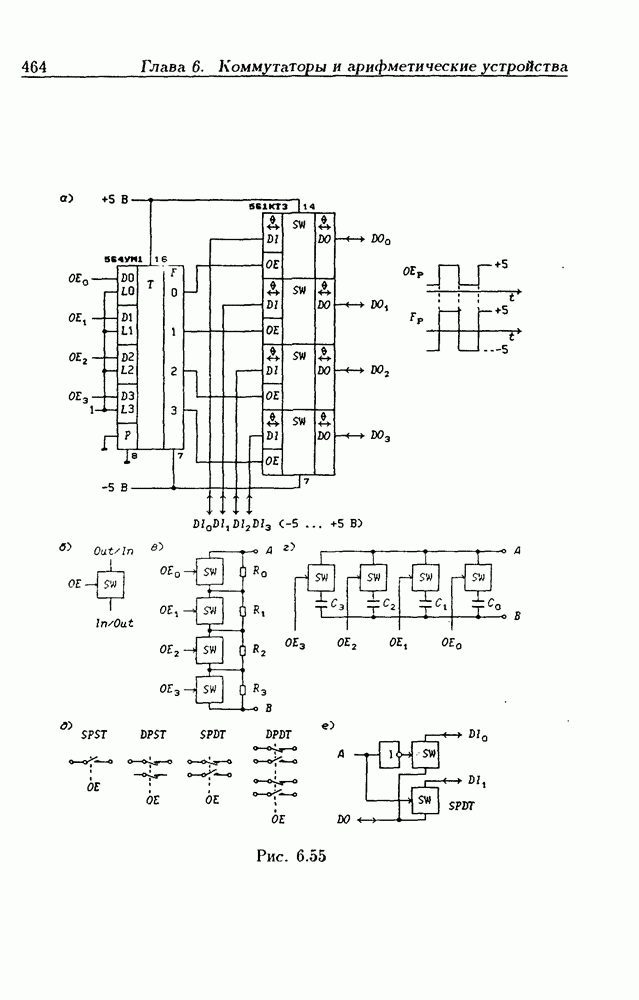
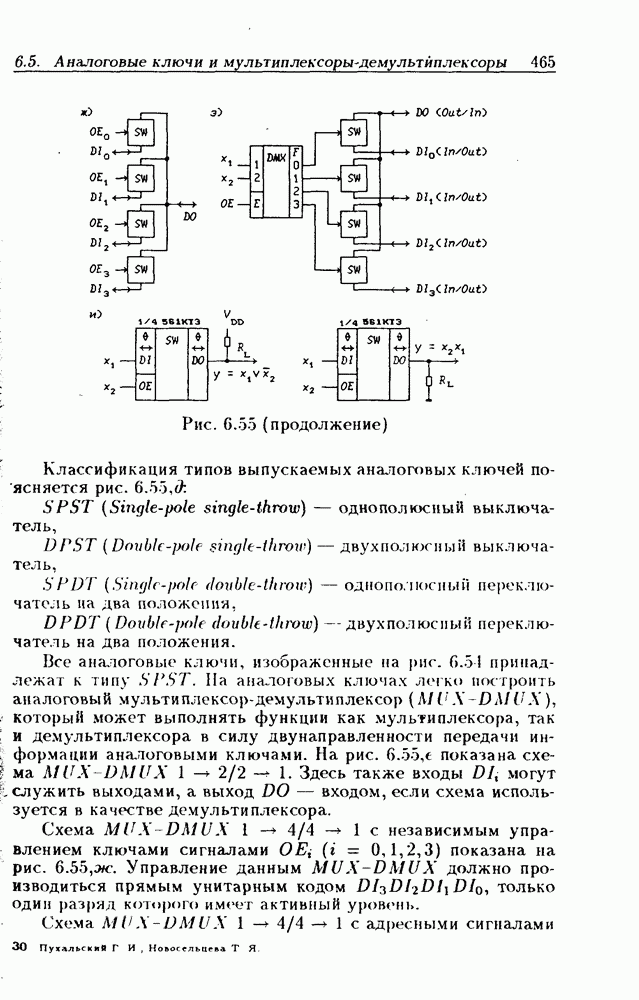
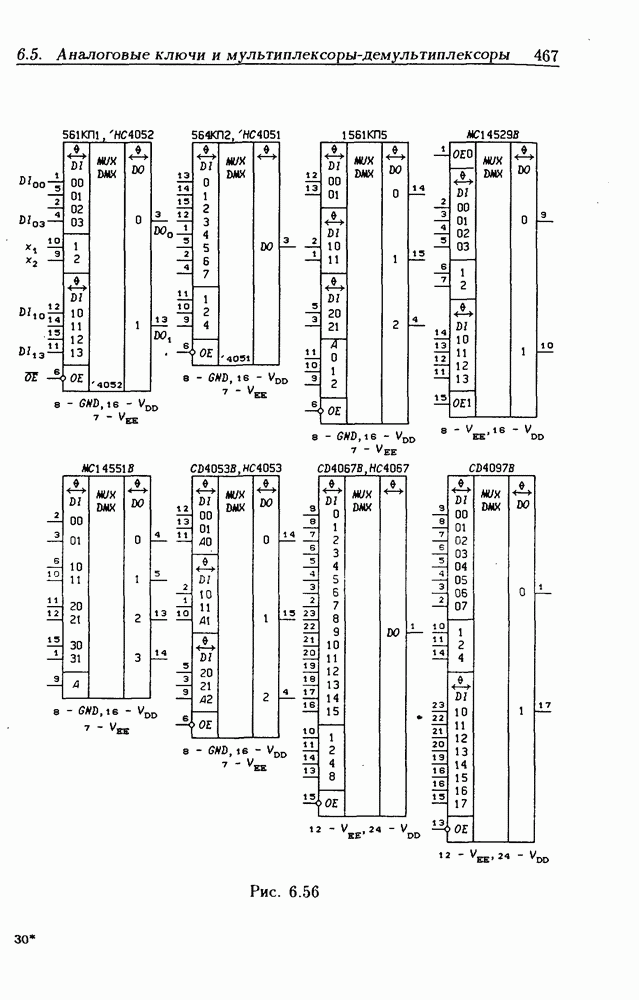
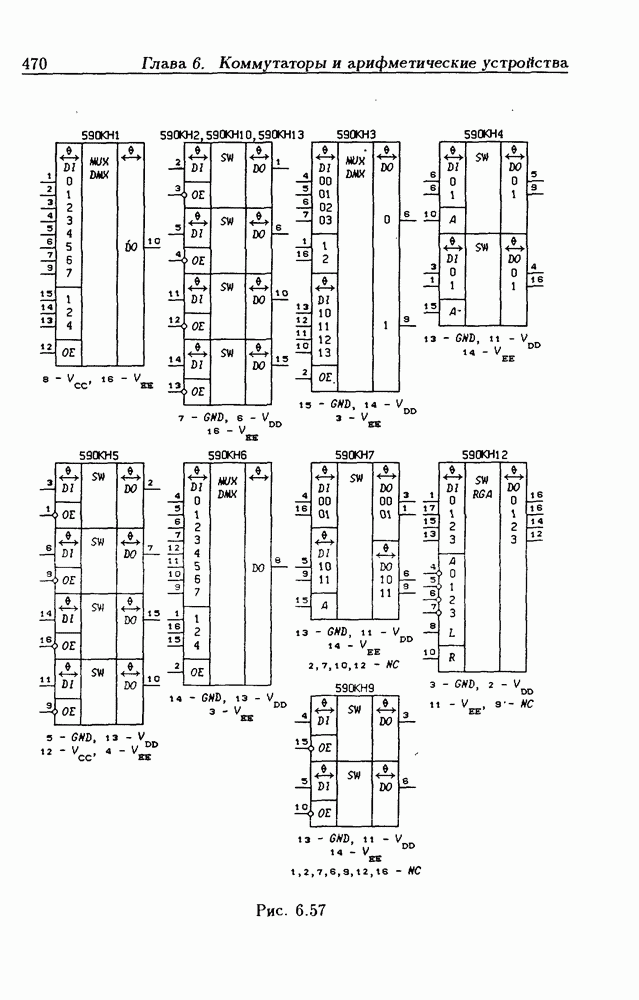
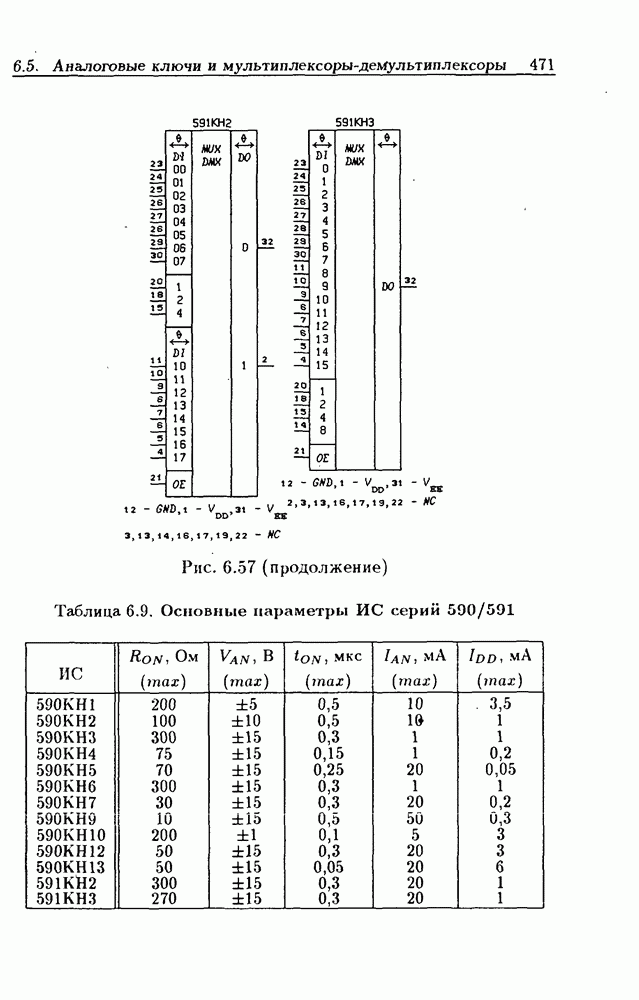
- 6.5. Аналоговые ключи и мультиплексоры-демультиплексоры
- 6.6. Шифраторы
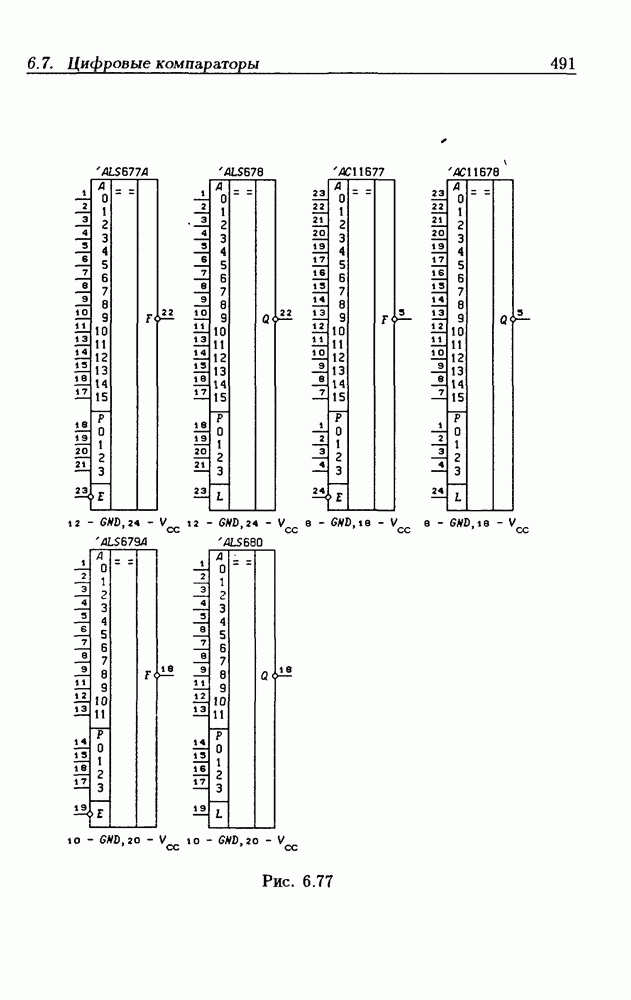
- 6.7. Цифровые компараторы
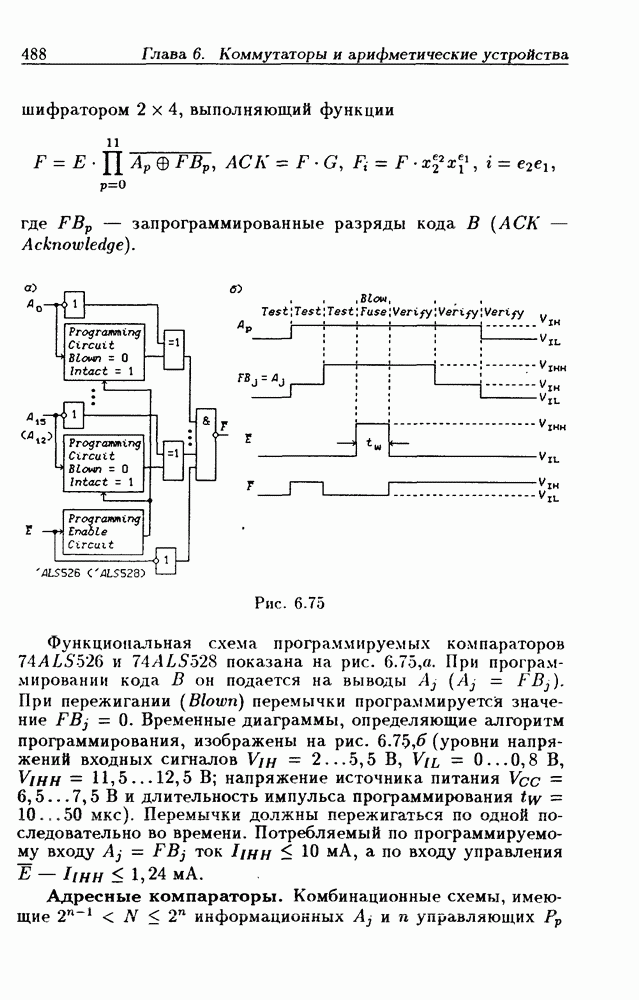
- Программируемые цифровые компараторы.
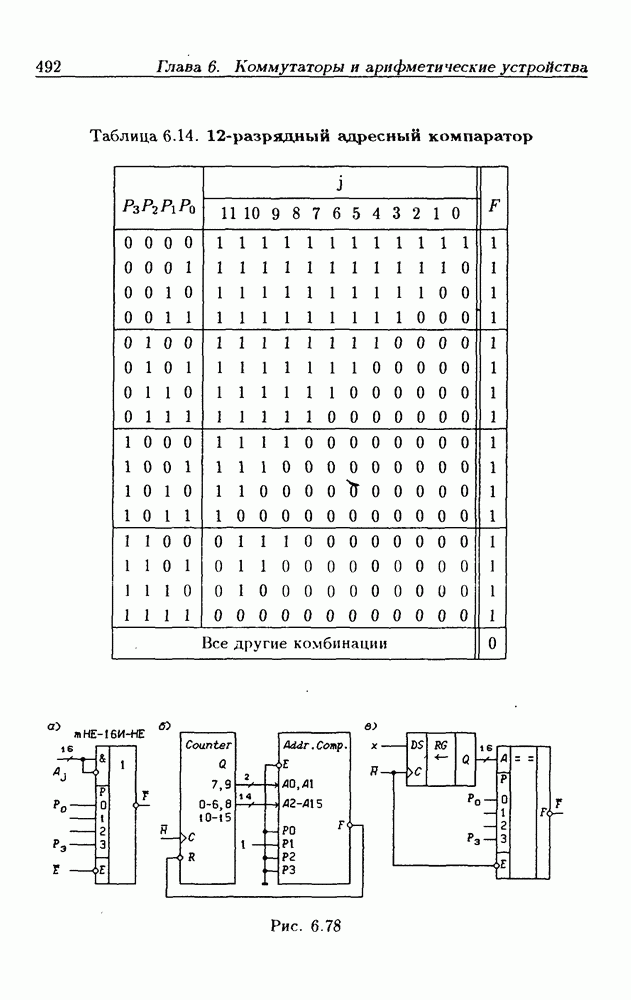
- Адресные компараторы.
- Применения адресных компараторов.
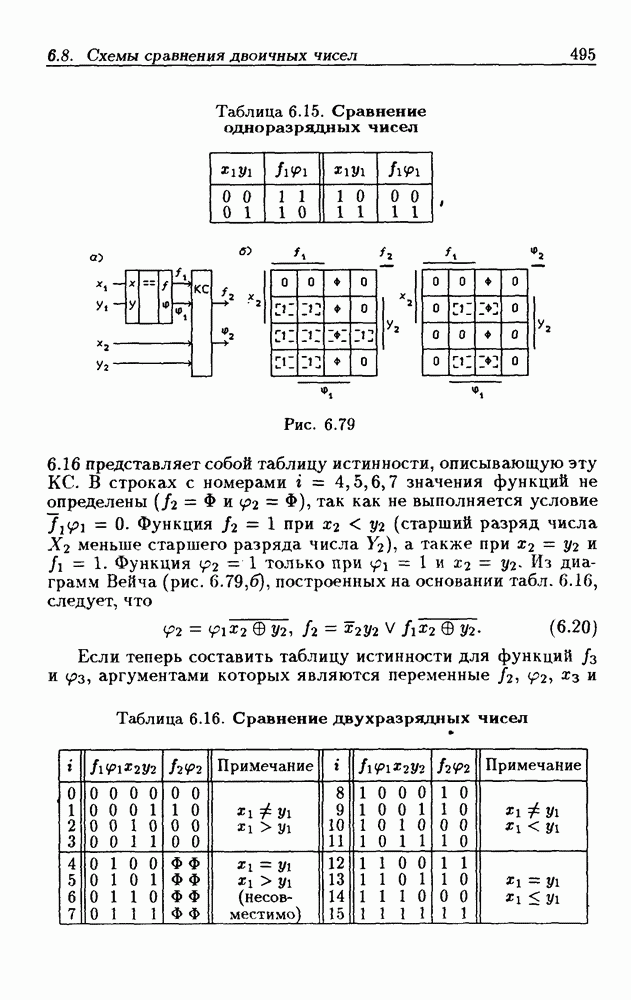
- 6.8. Схемы сравнения двоичных чисел
- 8-разрядные схемы сравнения двоичных чисел.
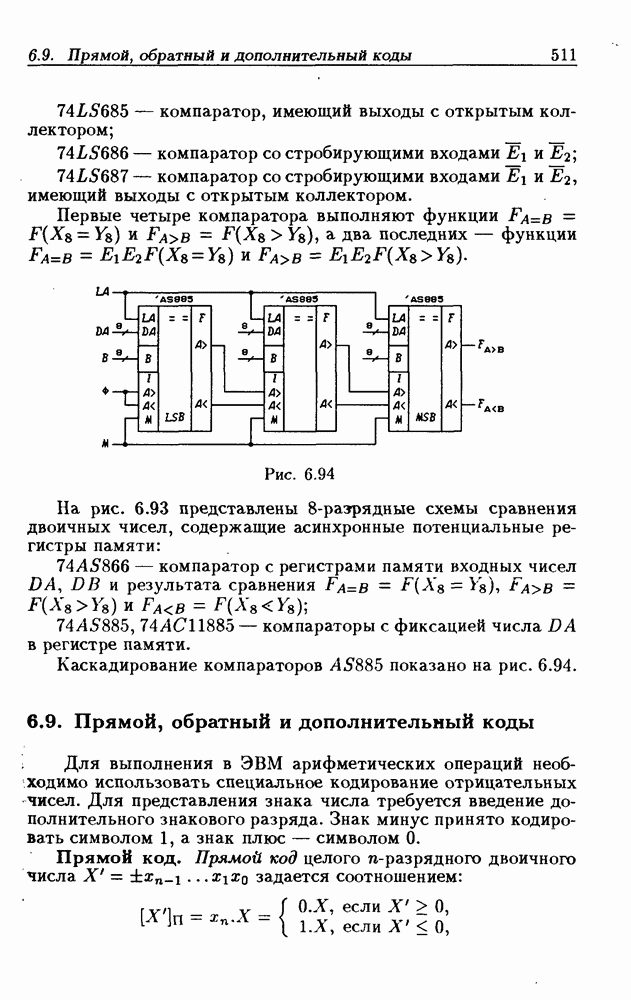
- 6.9. Прямой, обратный и дополнительный коды
- Дополнительный код.
- Сложение чисел в обратном коде.
- Код с избытком 3.
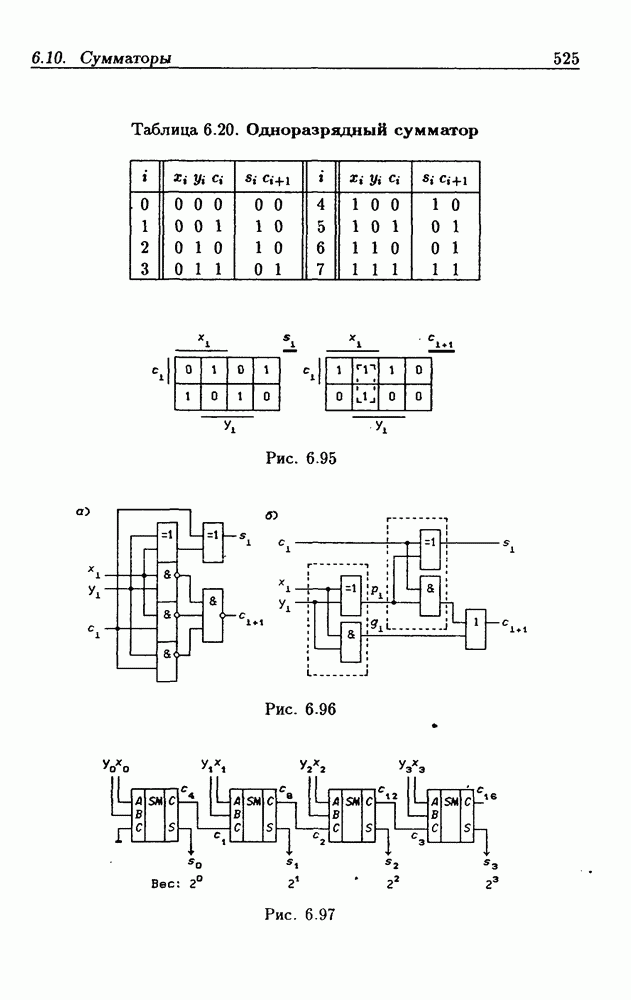
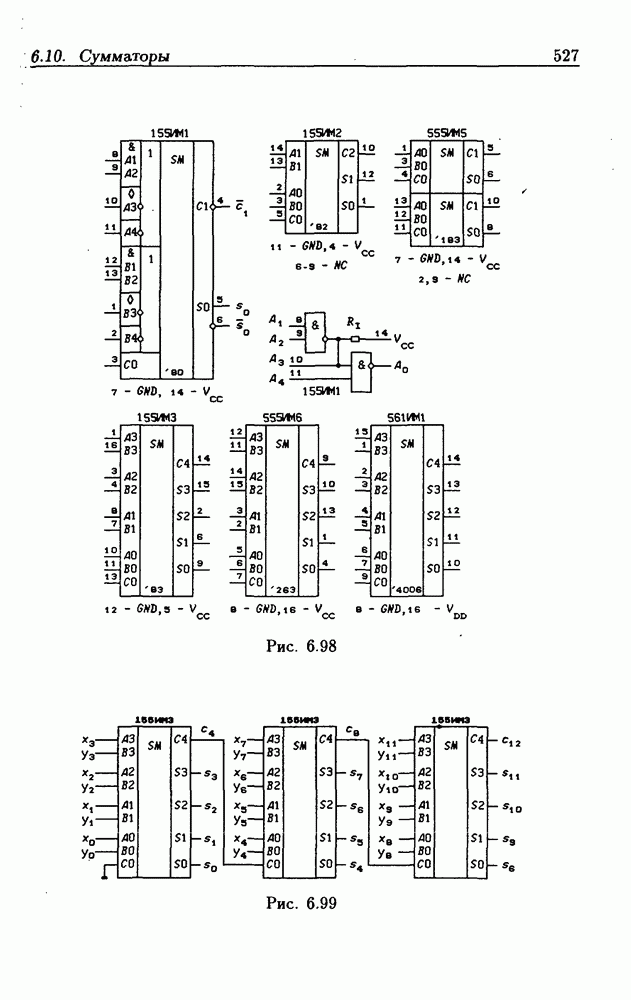
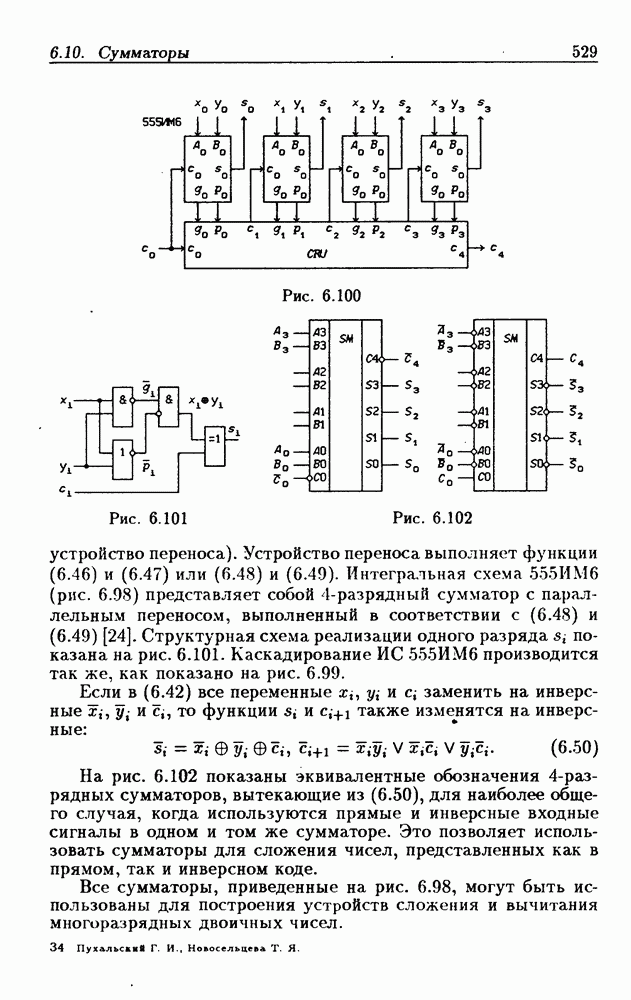
- 6.10. Сумматоры
- Двоичные параллельные сумматоры с последовательным переносом.
- Двоичные сумматоры с параллельным переносом.
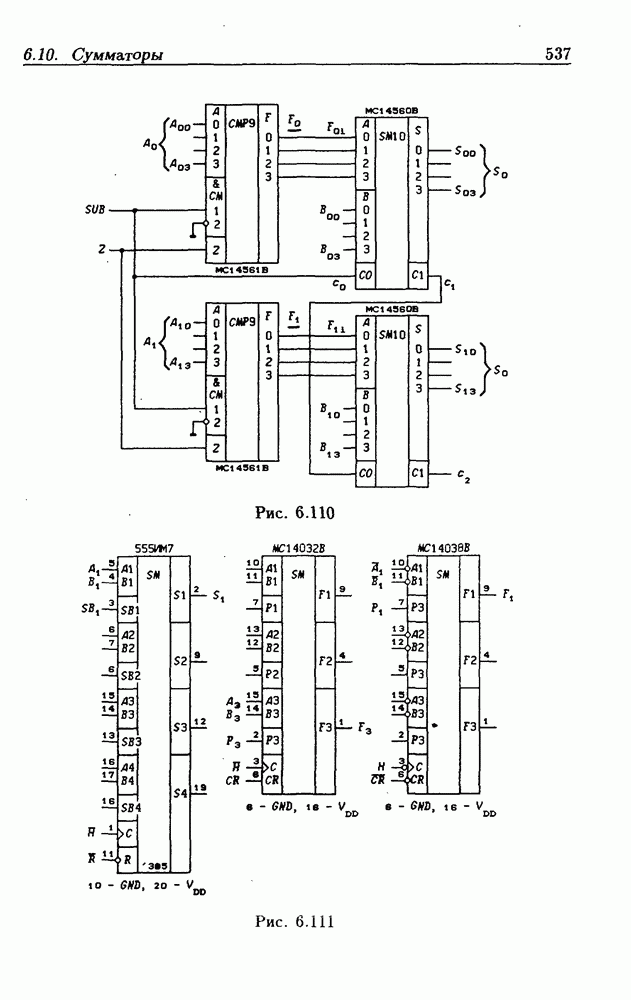
- Применения сумматоров.
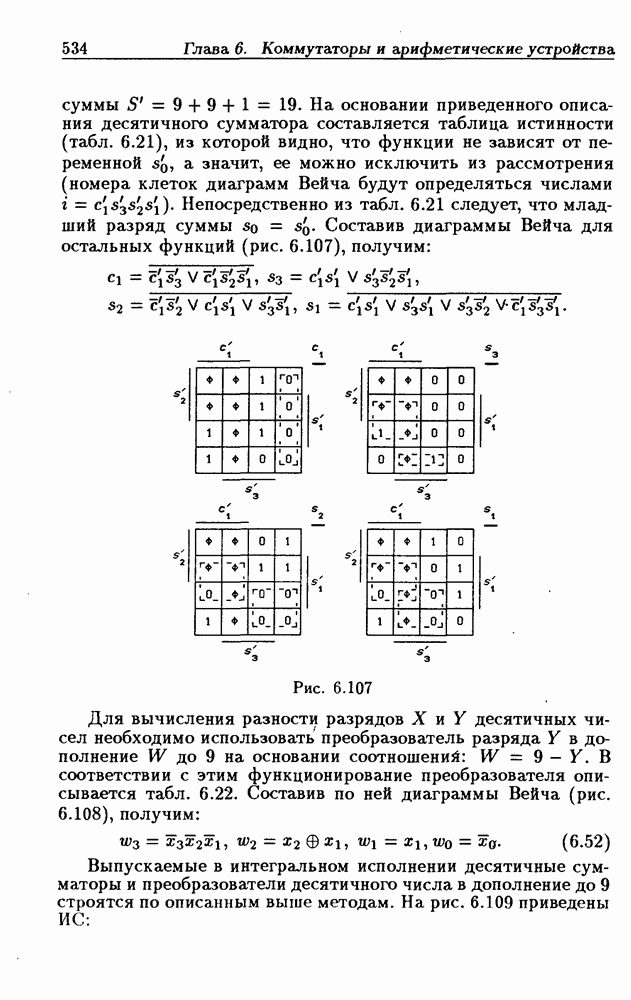
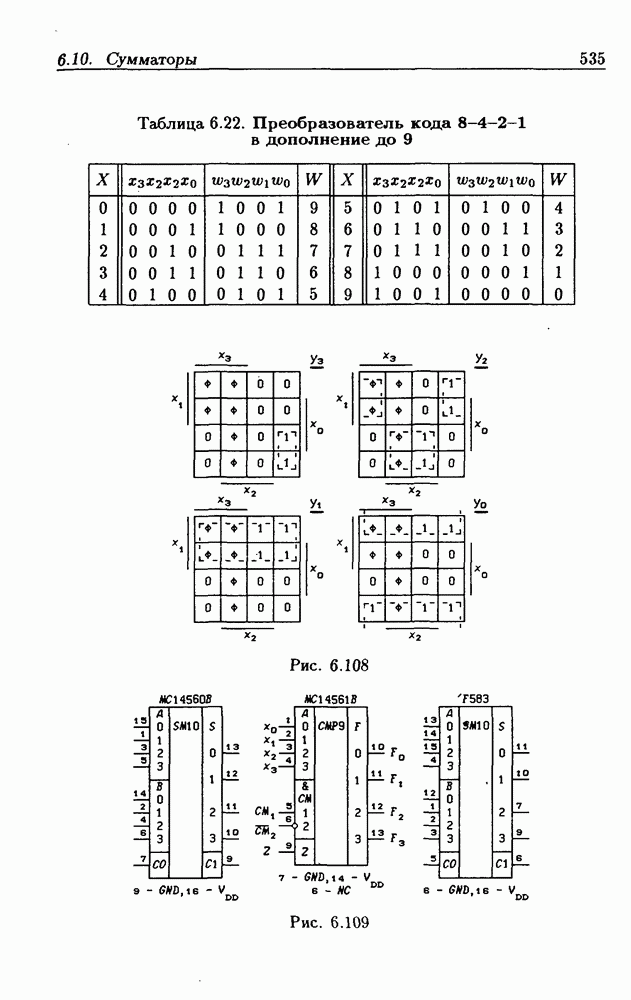
- Десятичные сумматоры.
- Последовательные двоичные сумматоры.
- 6.11. Арифметическо-логические устройства
- 6.12. Пороговые схемы и мажоритарные элементы
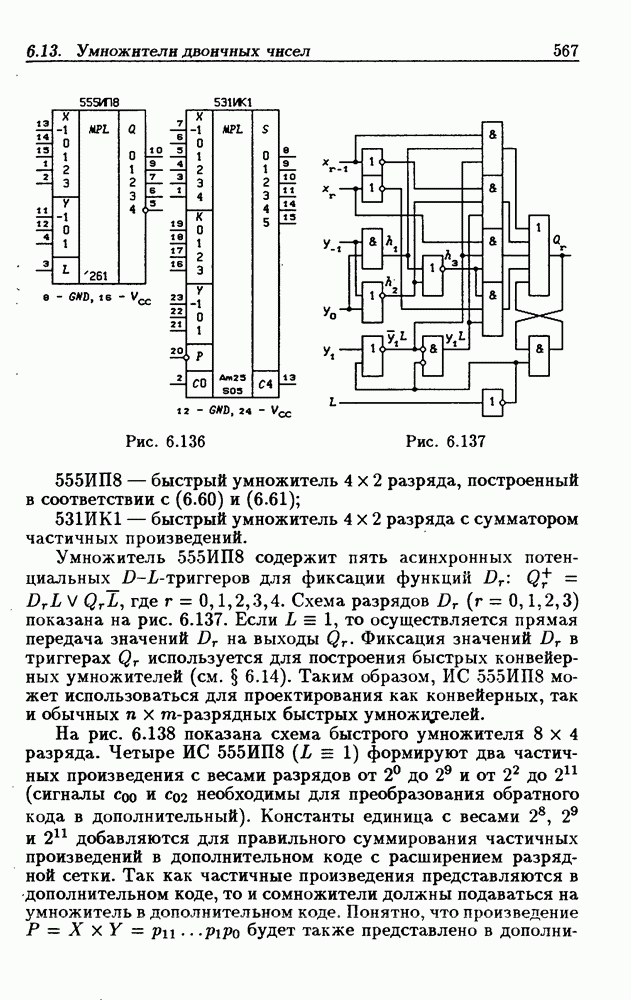
- 6.13. Умножители двоичных чисел
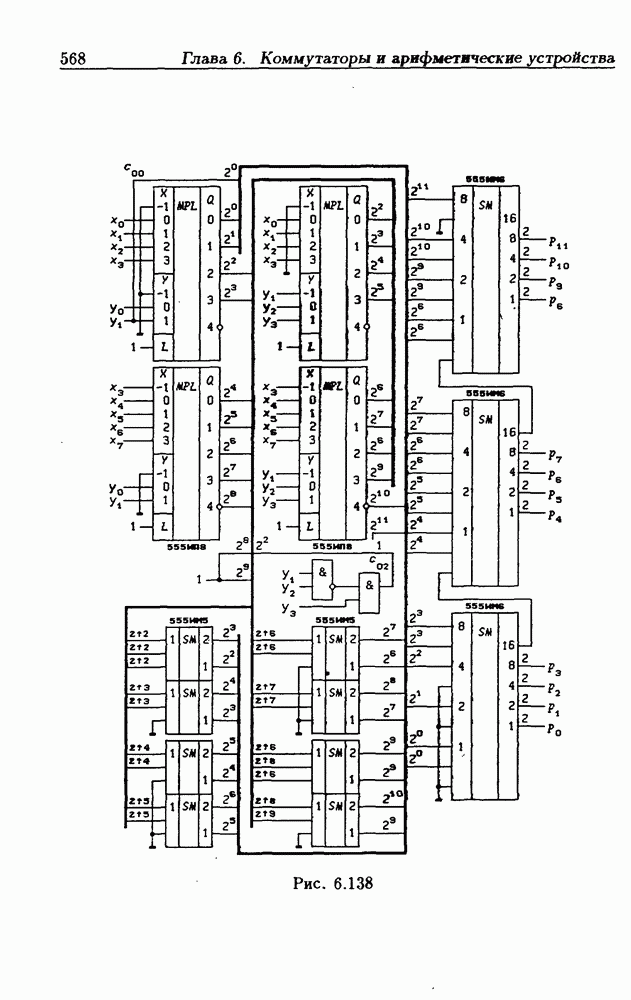
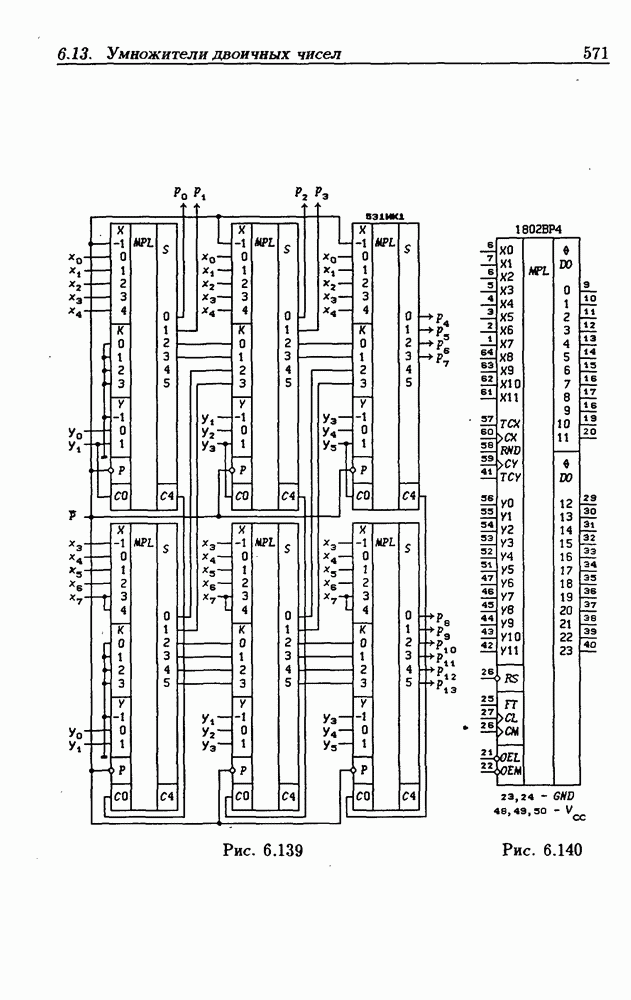
- Быстрые умножители.
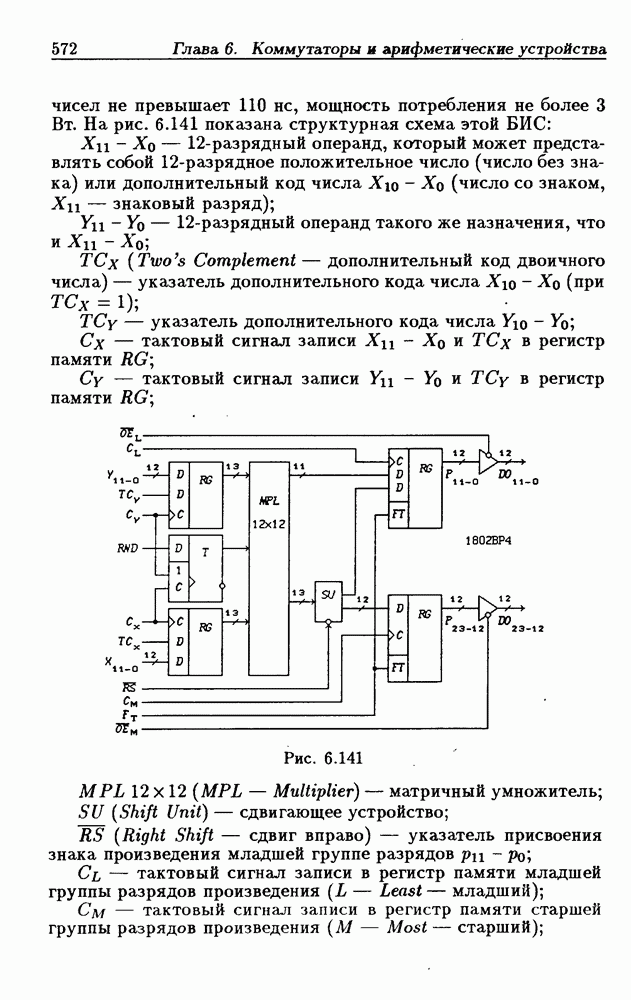
- БИС умножителя 12×12 разрядов 1802ВР4.
- Последовательные умножители.
- 6.14. Конвейерные устройства
- Конвейерный быстрый умножитель.
- Конвейерные АЦП.
- 6.15. Синтез линейных комбинационных схем
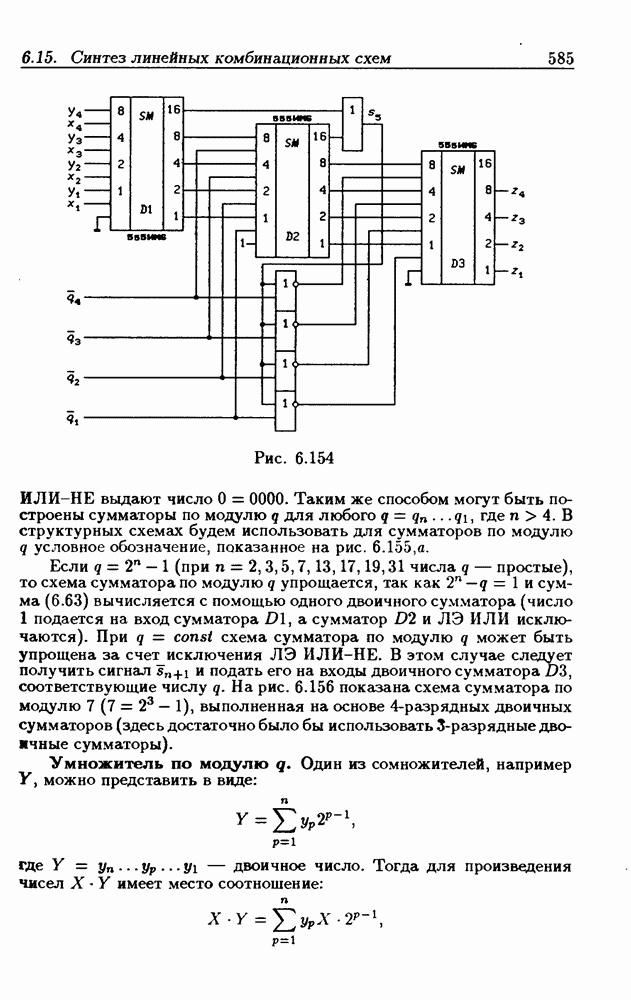
- Сумматор по модулю q.
- Умножитель по модулю q.
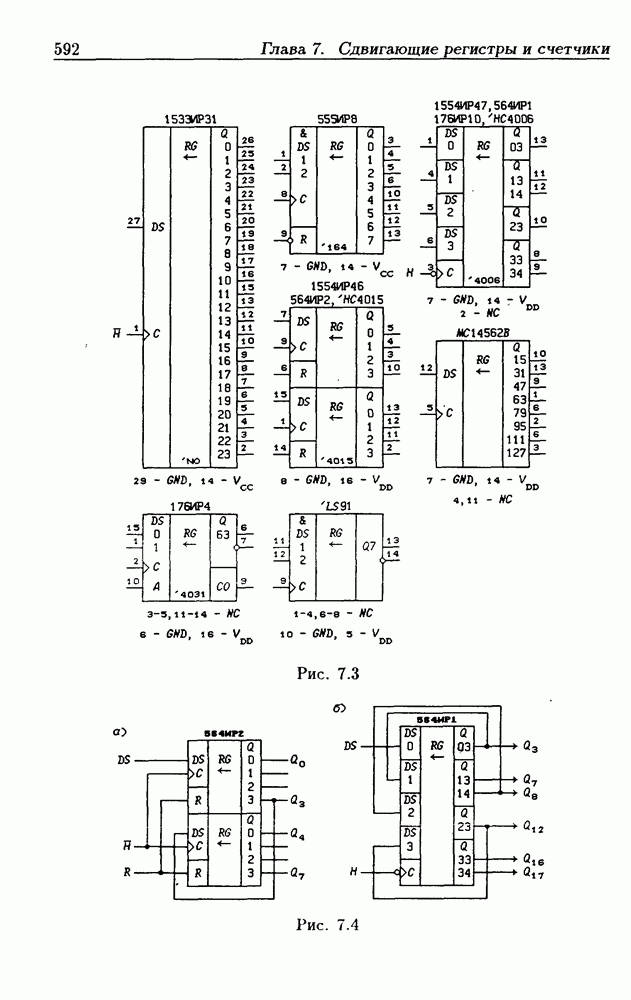
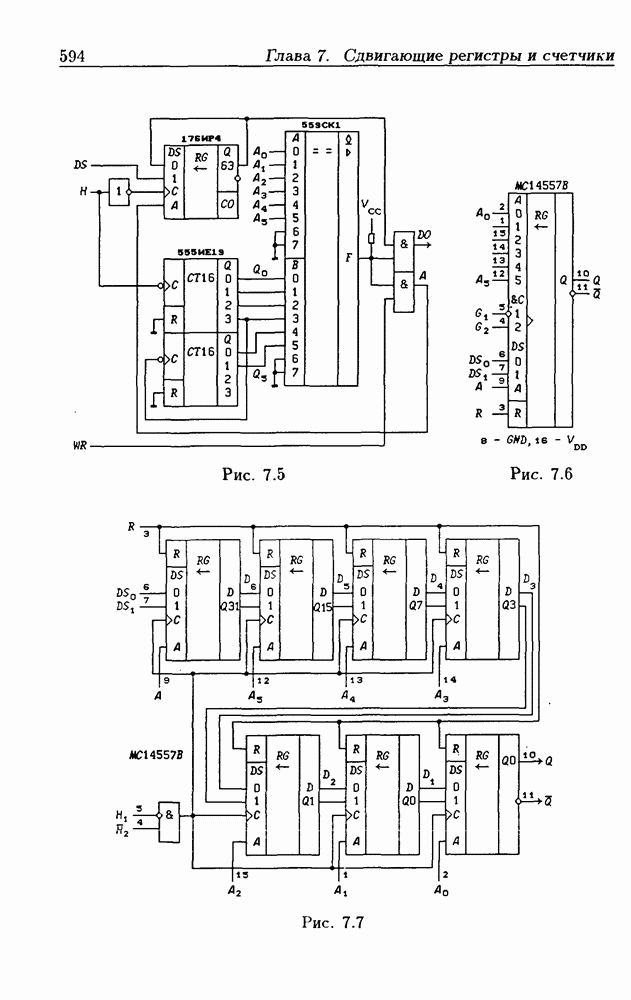
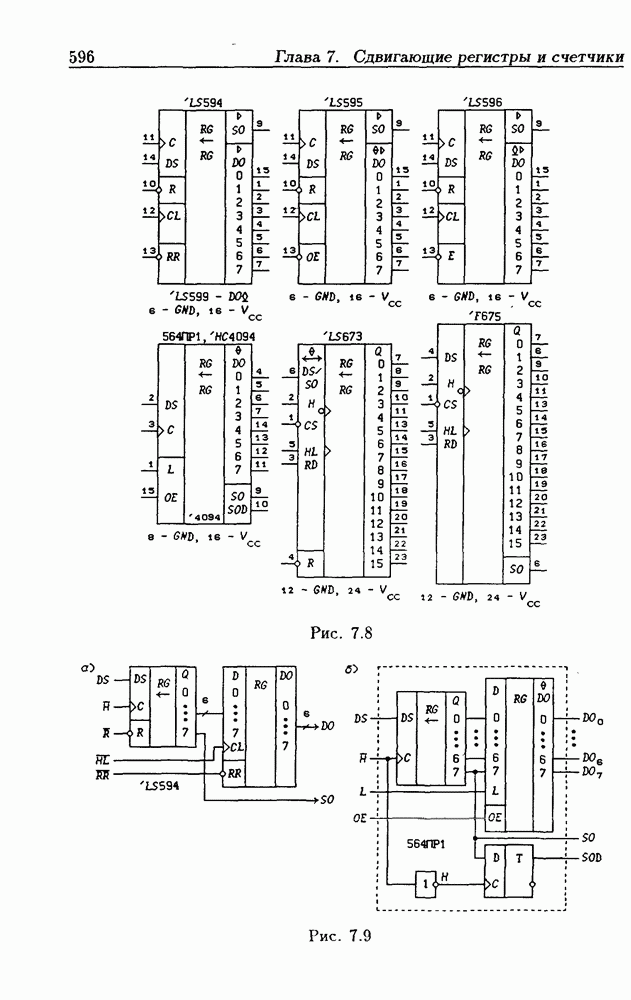
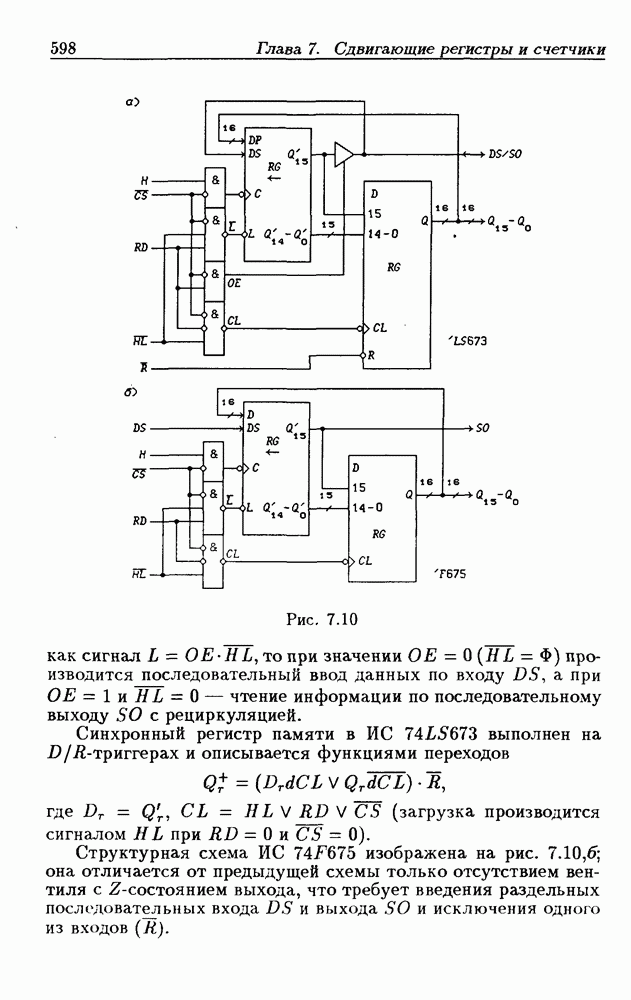
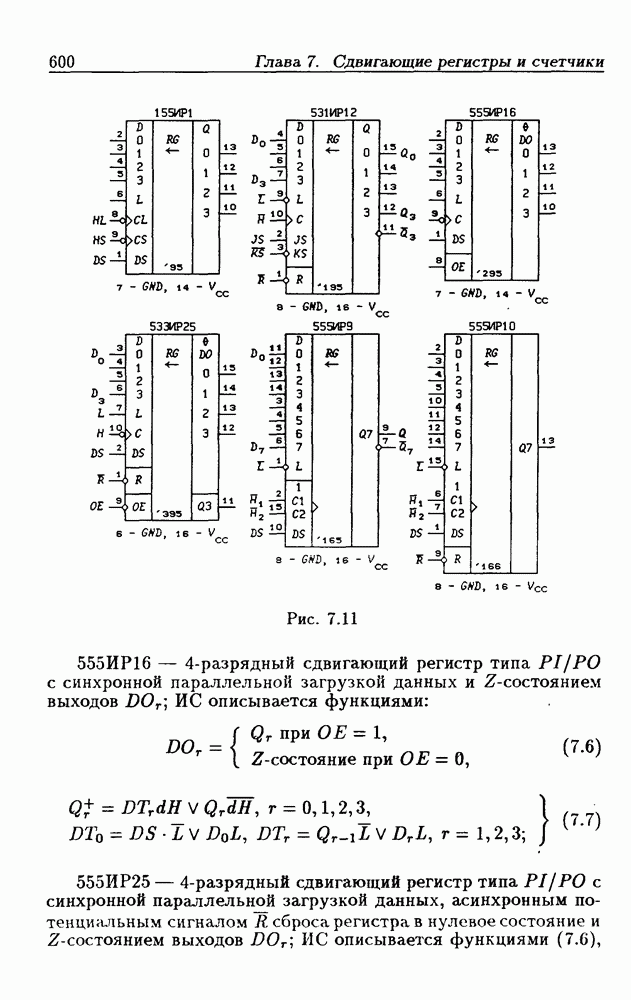
- Глава 7. Сдвигающие регистры и счетчики
- 7.1. Сдвигающие регистры без параллельной записи данных
- Сдвигающие устройства с выходными регистрами памяти.
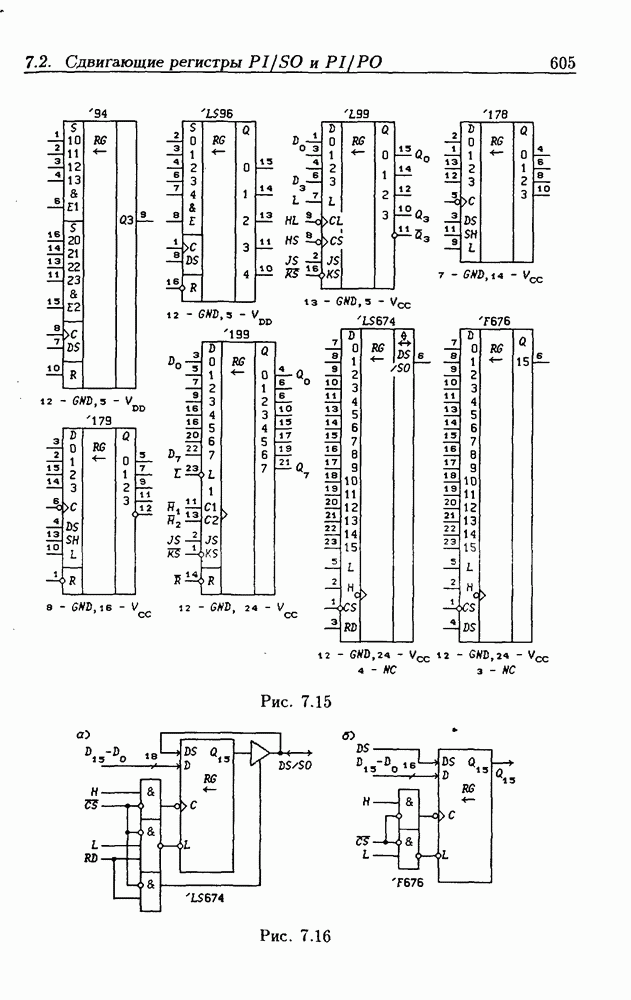
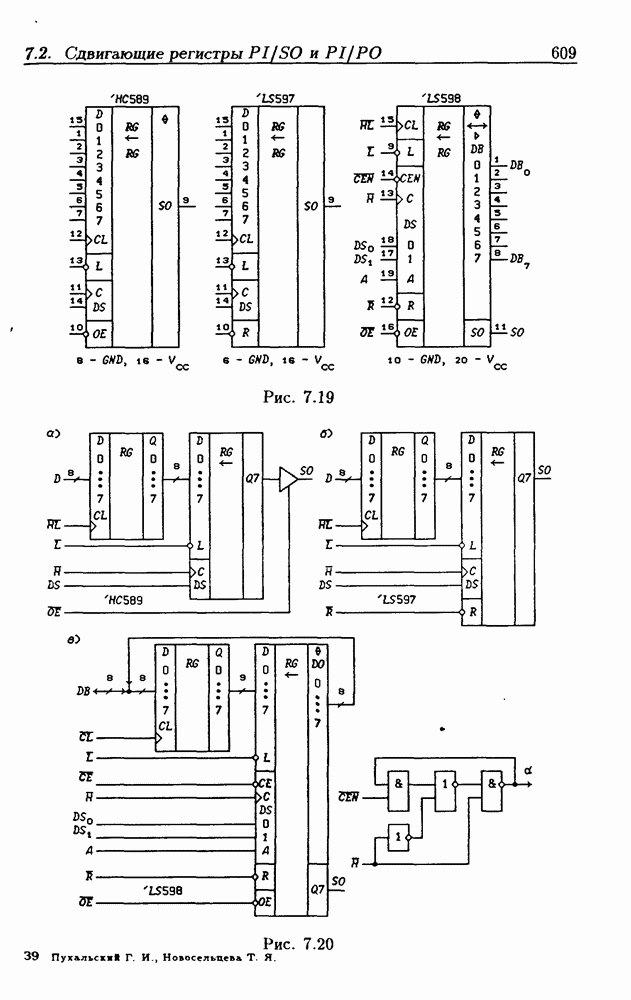
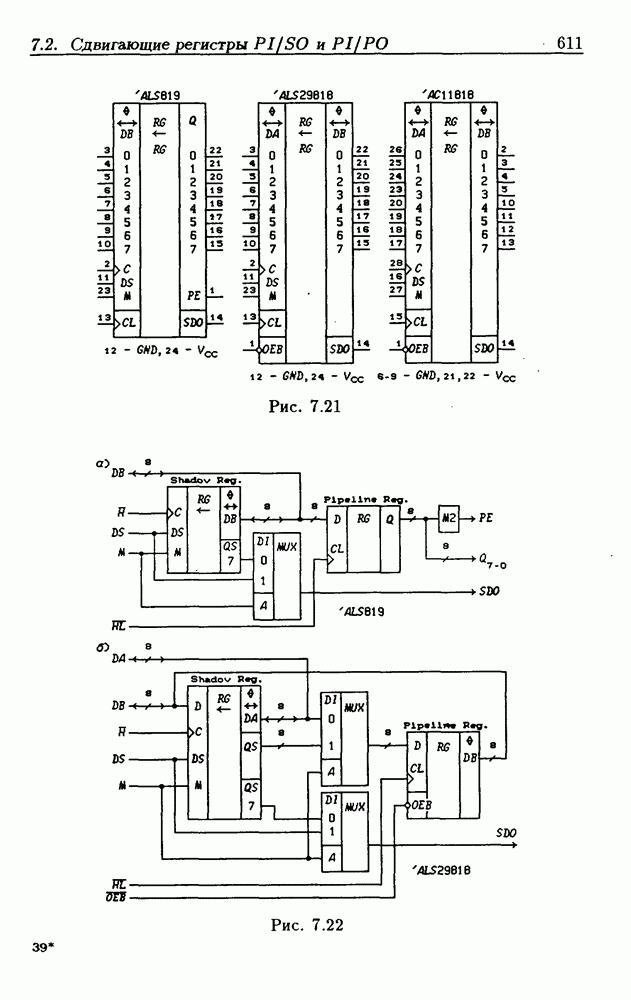
- 7.2. Сдвигающие регистры с параллельной записью данных
- Сдвигающие регистры с расширением знака.
- Сдвигающие регистры с входным регистром памяти.
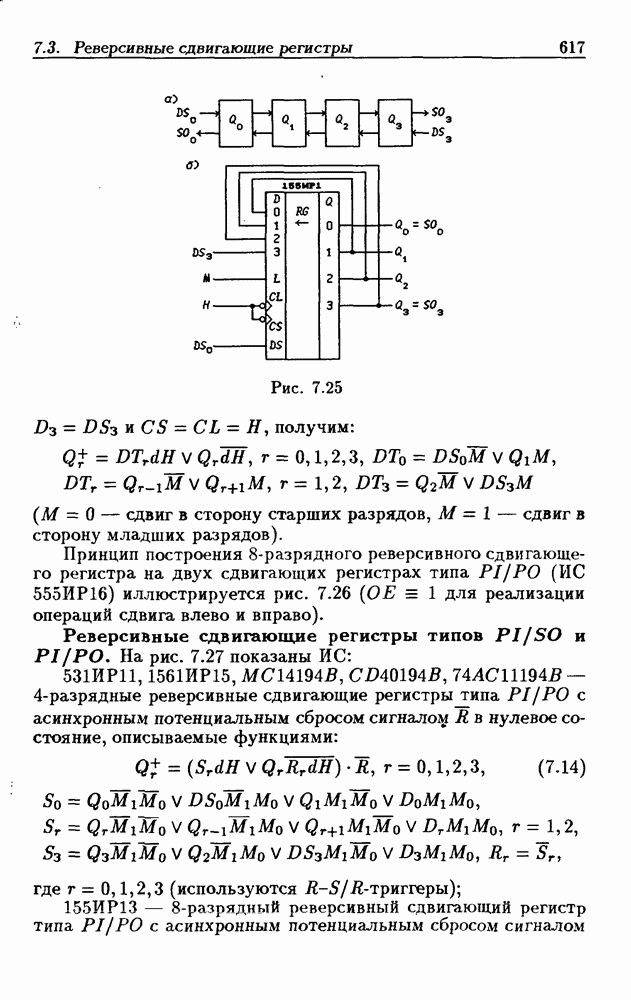
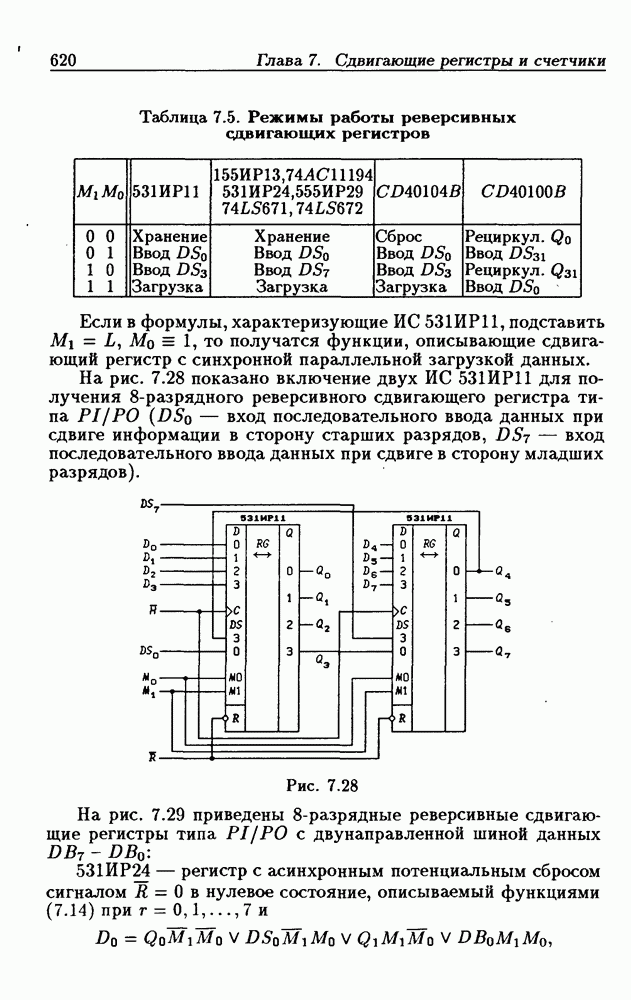
- 7.3. Реверсивные сдвигающие регистры
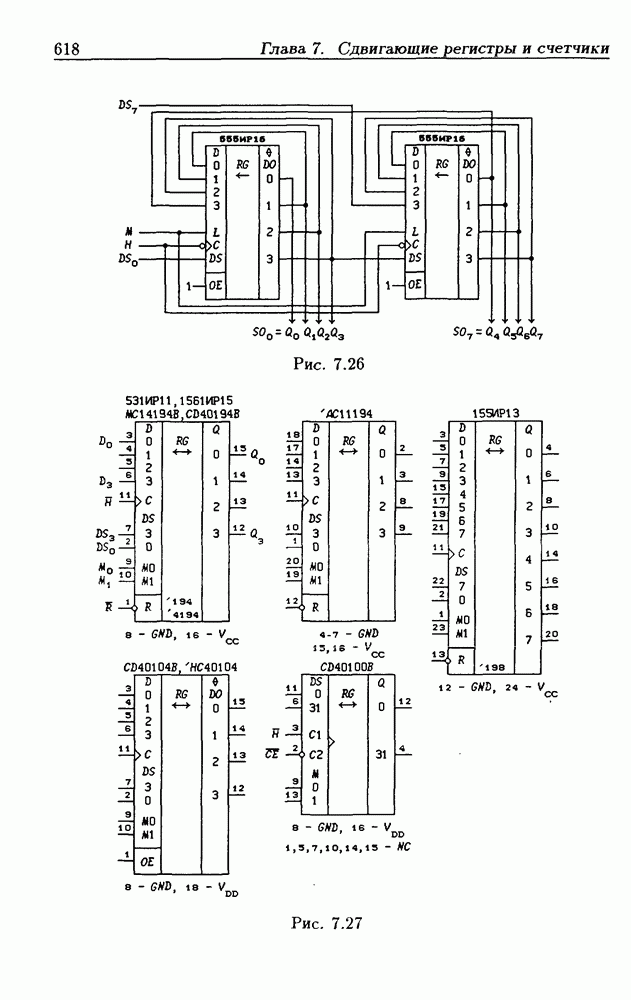
- Реверсивные сдвигающие регистры типов PI/SO и PI/PO.
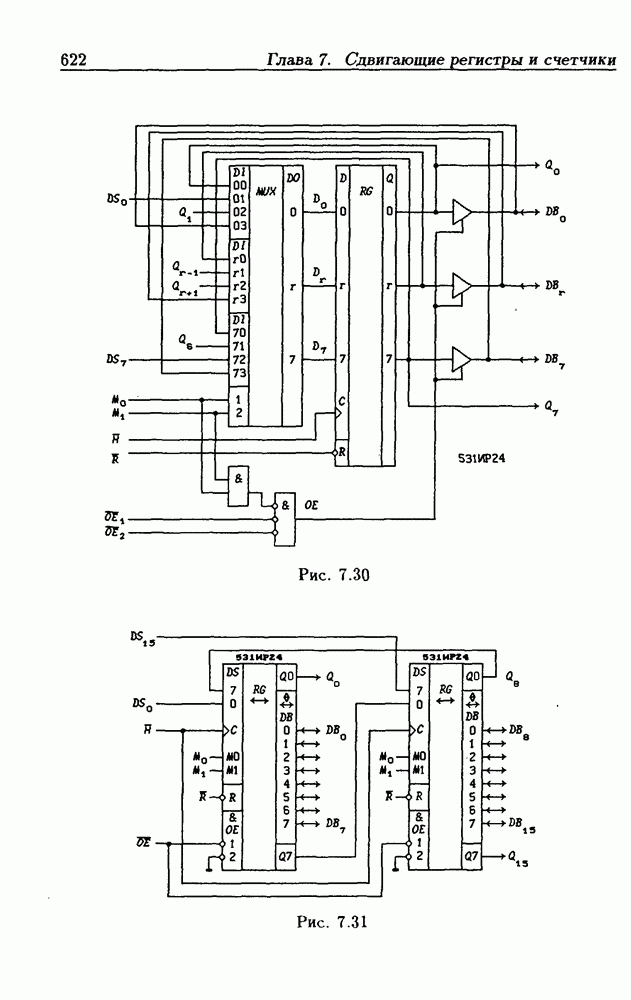
- Многофункциональные устройства на основе реверсивных сдвигающих регистров.
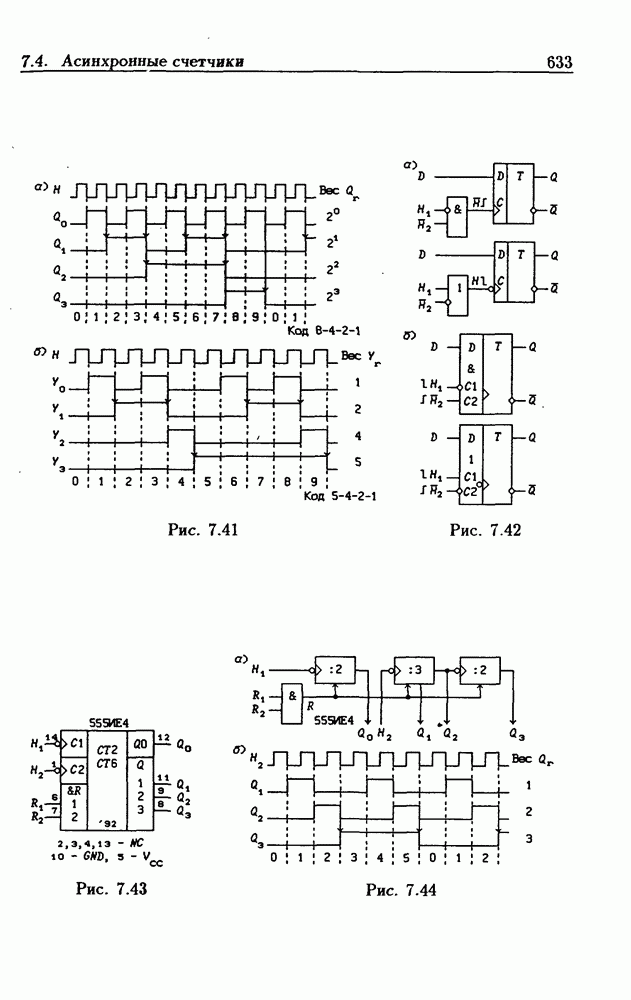
- 7.4. Асинхронные счетчики
- Двоично-десятичные асинхронные счетчики.
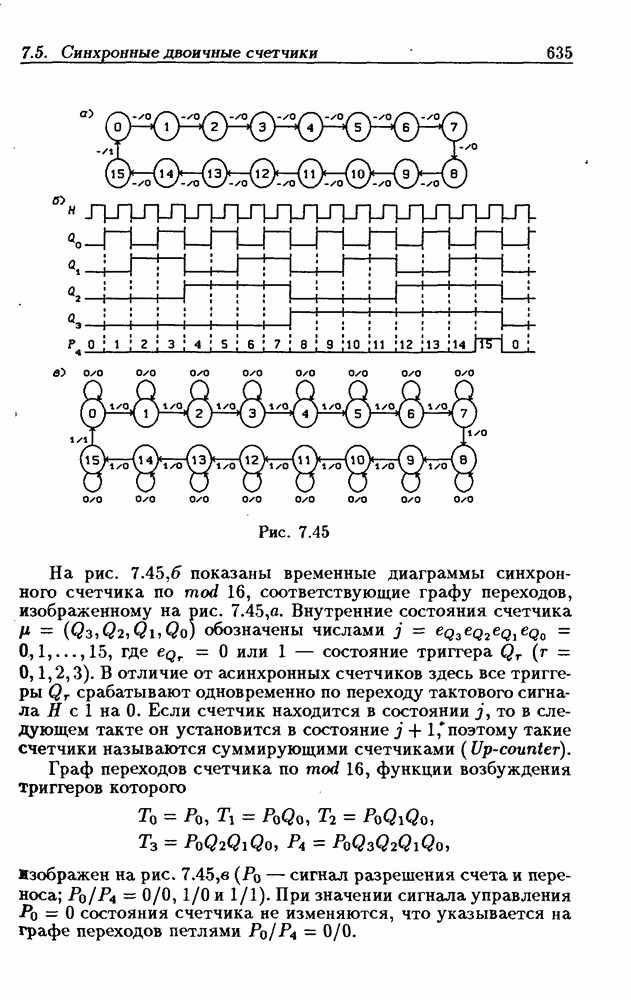
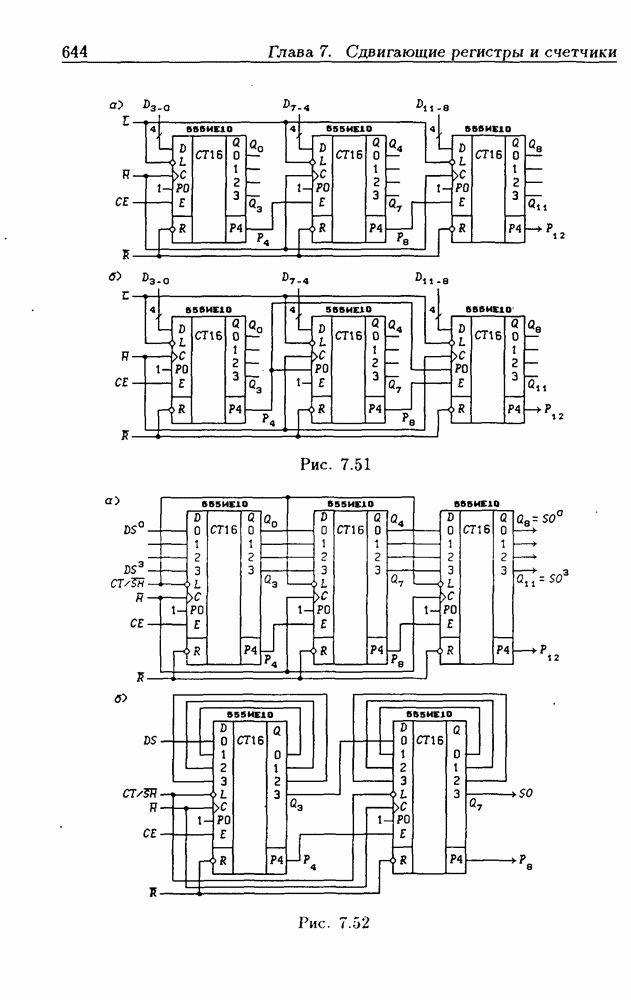
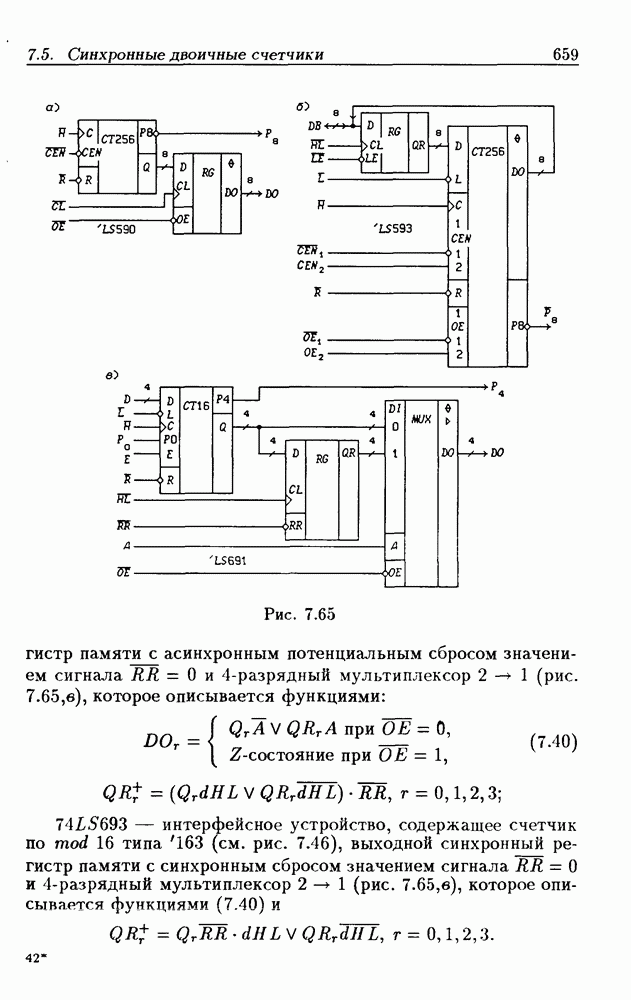
- 7.5. Синхронные двоичные счетчики
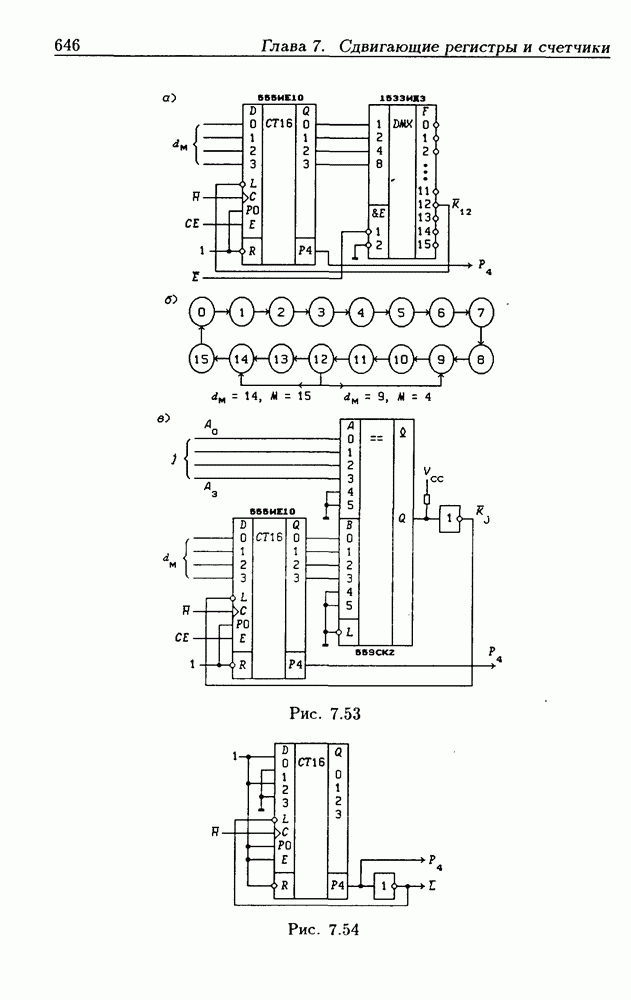
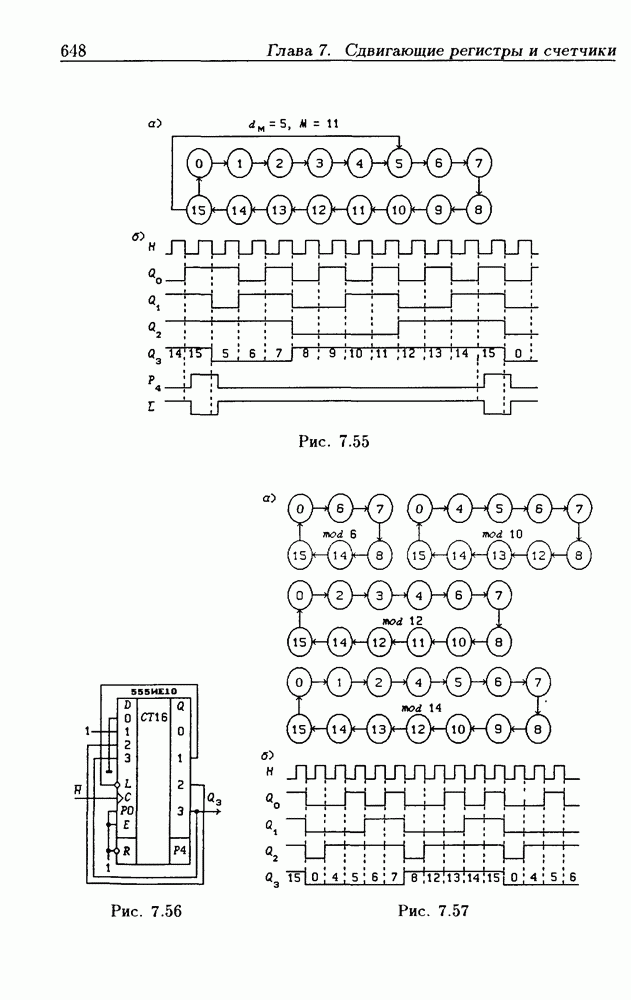
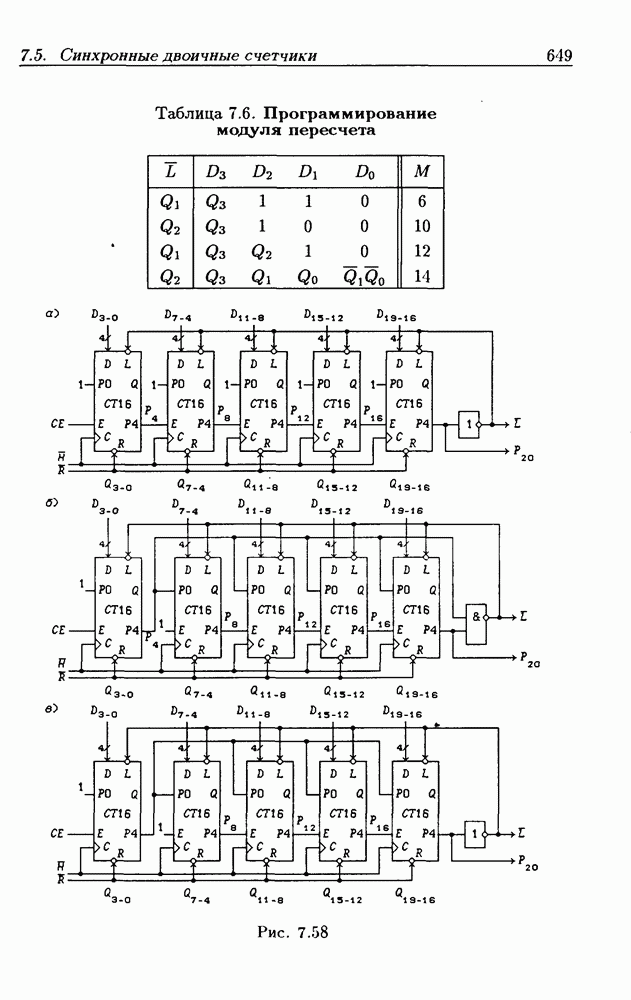
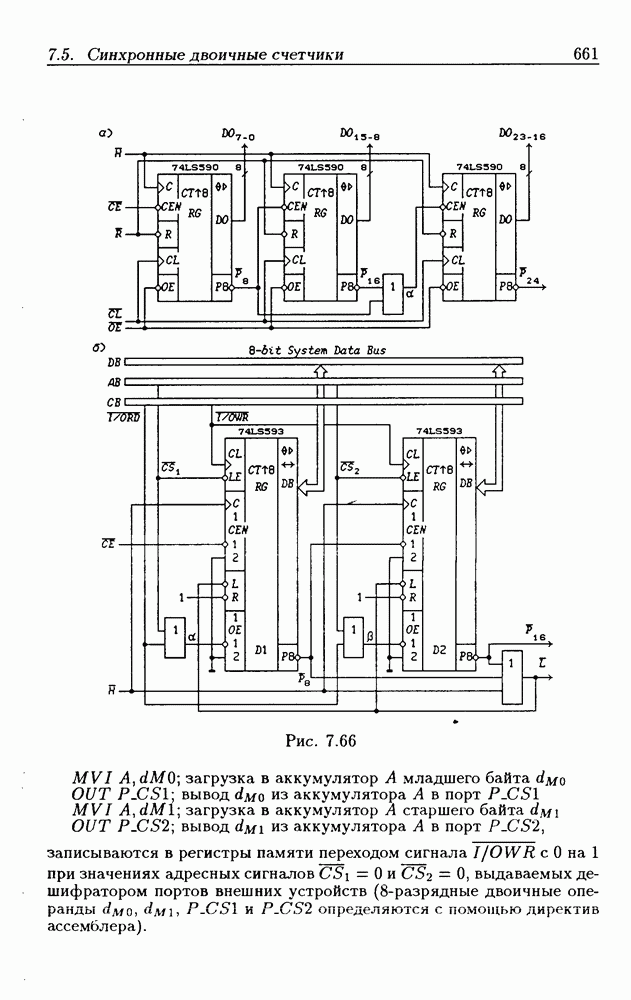
- Программирование модуля пересчета двоичных счетчиков.
- Переключение модулей пересчета двоичных счетчиков.
- Функциональные устройства на основе двоичных счетчиков.
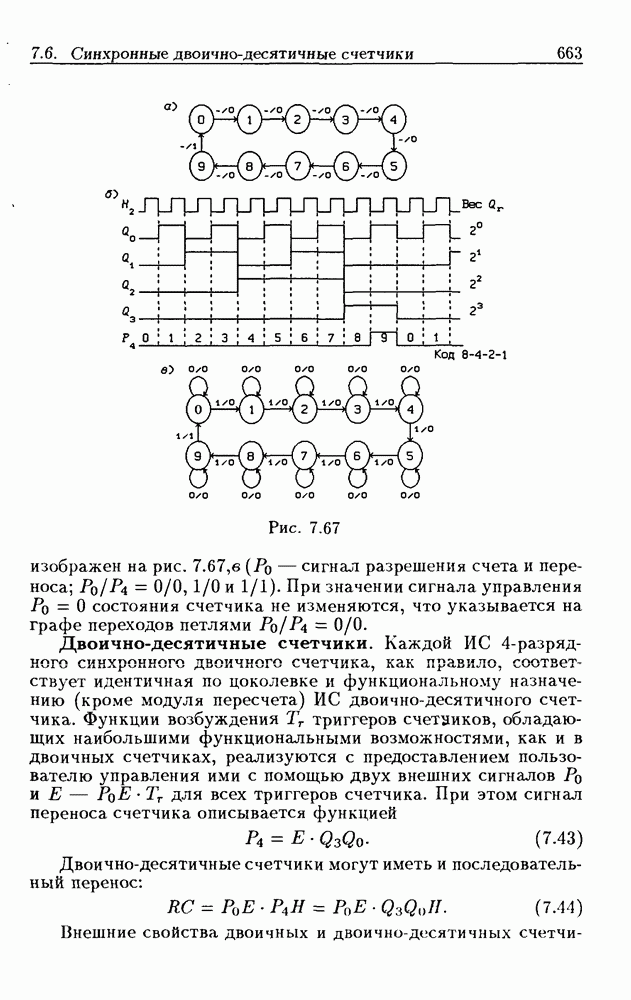
- 7.6. Синхронные двоично-десятичные счетчики
- 7.7. Синхронные реверсивные счетчики
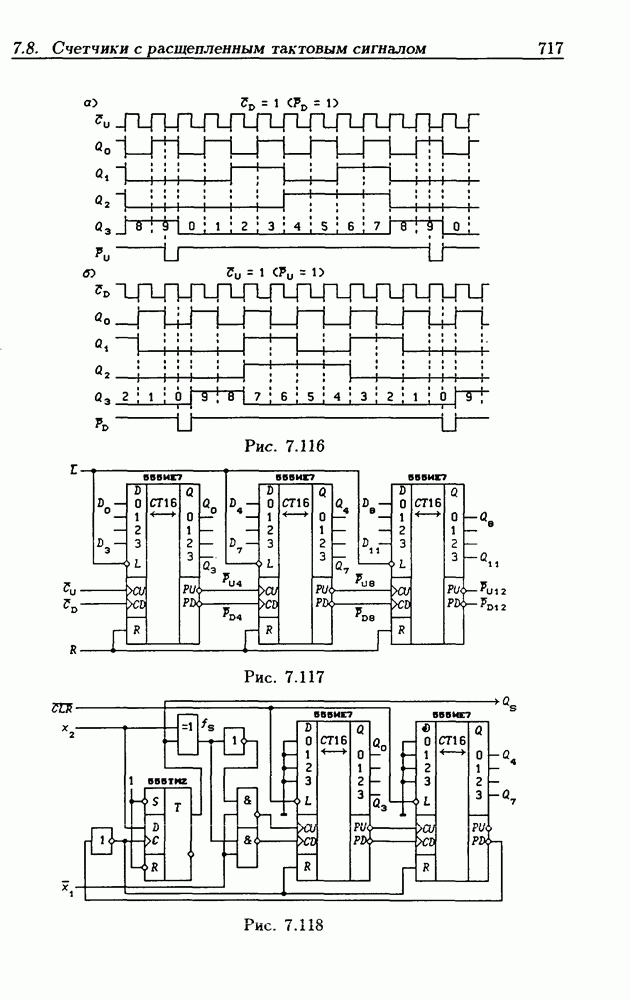
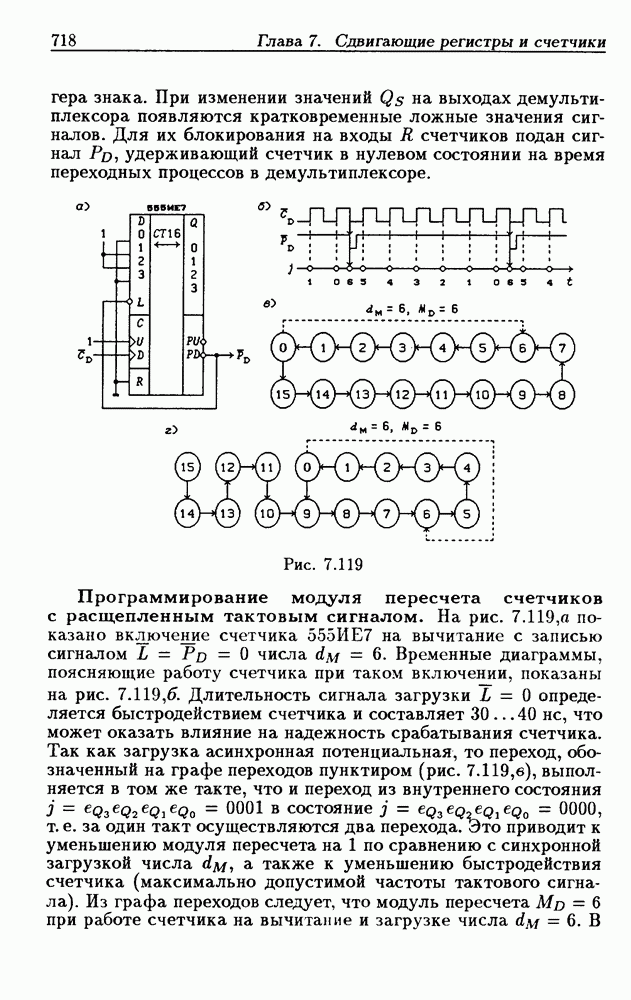
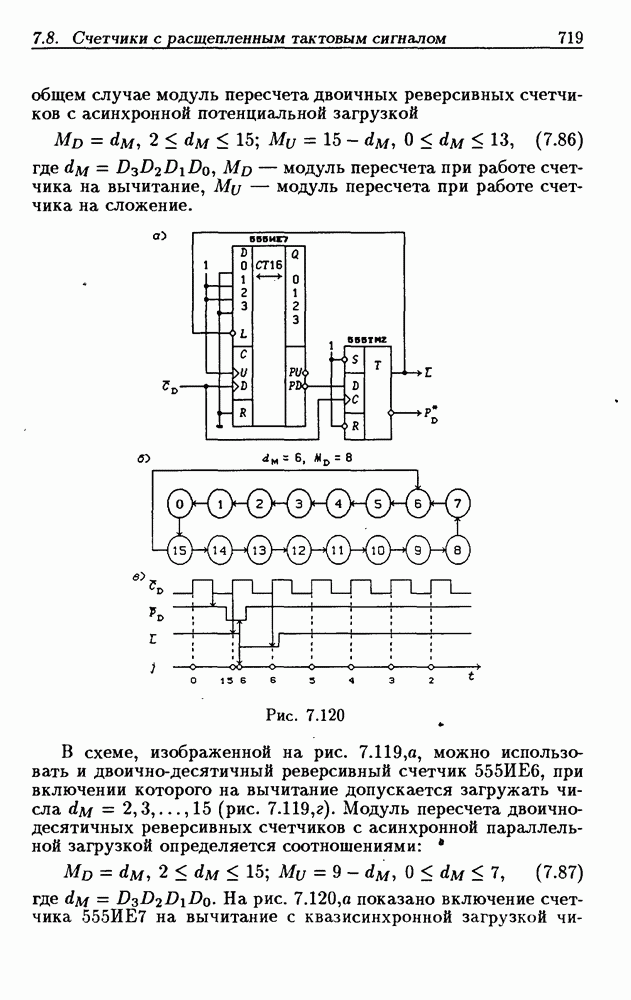
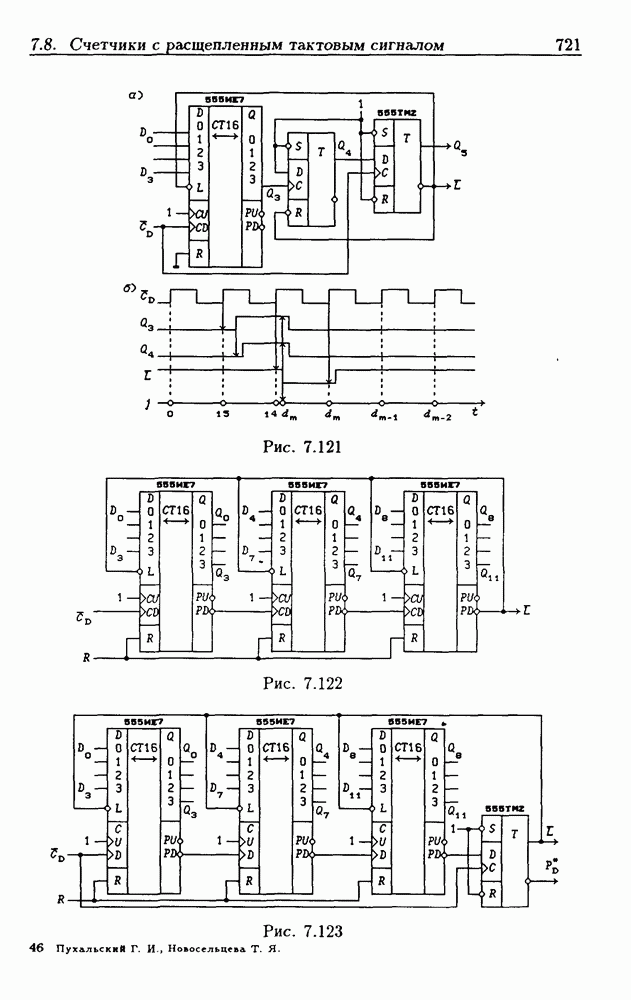
- 7.8. Счетчики с расщепленным тактовым сигналом
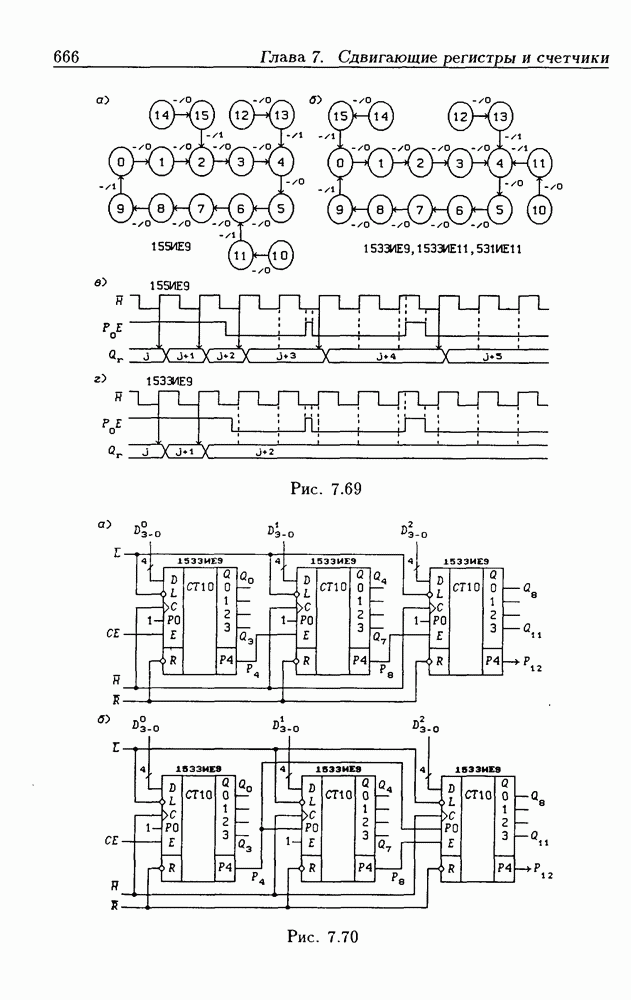
- 7.9. Счетчики на сдвигающих регистрах
- 7.10. Кольцевые счетчики
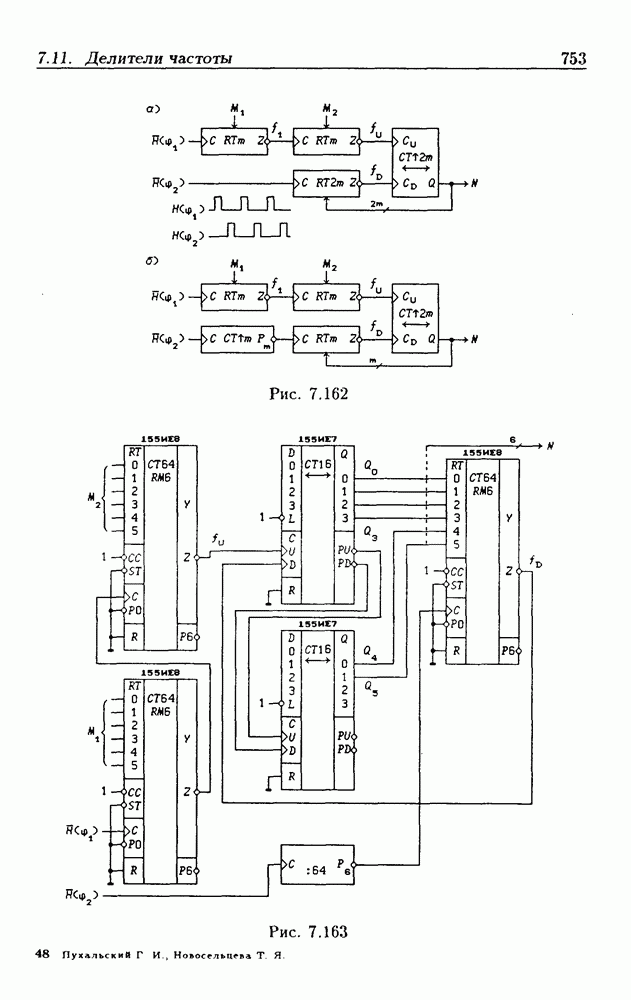
- 7.11. Делители частоты
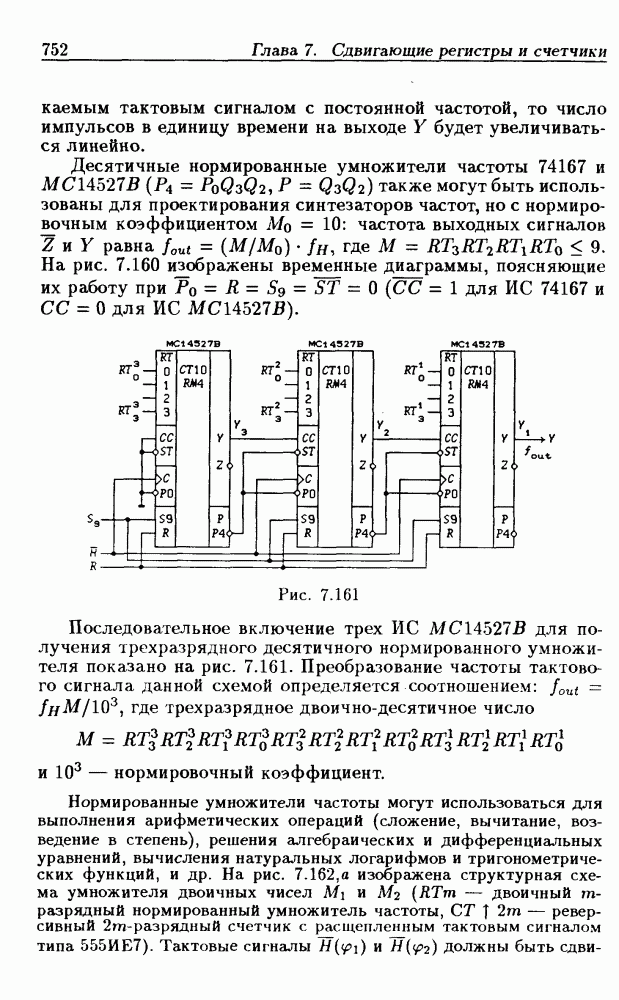
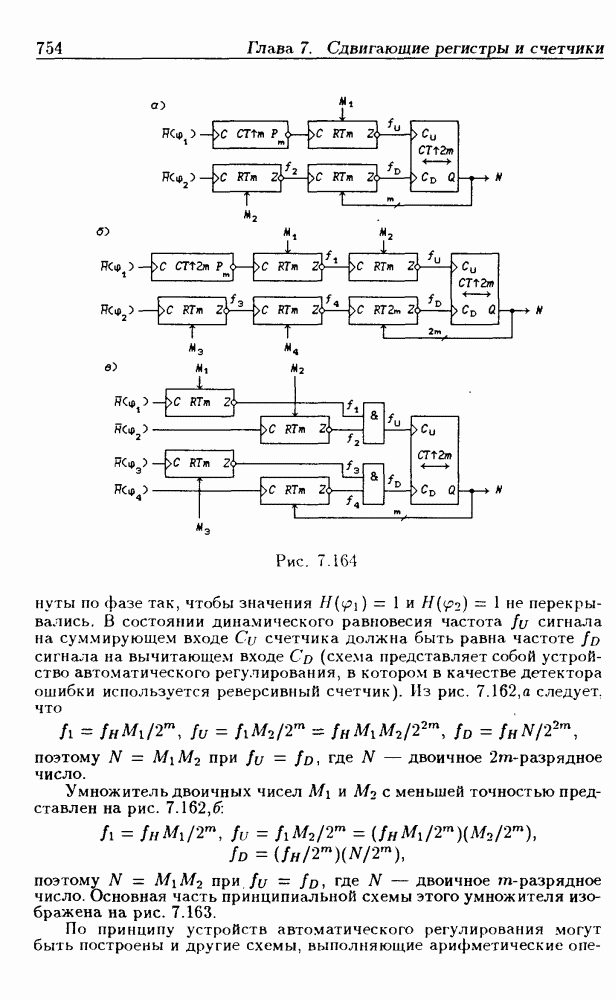
- Нормированные умножители частоты.
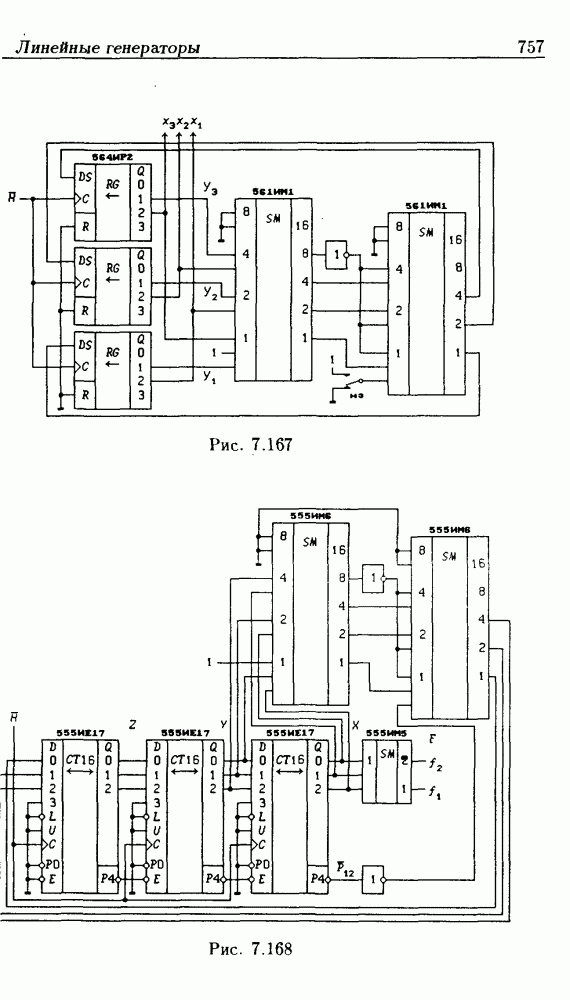
- 7.12. Линейные генераторы
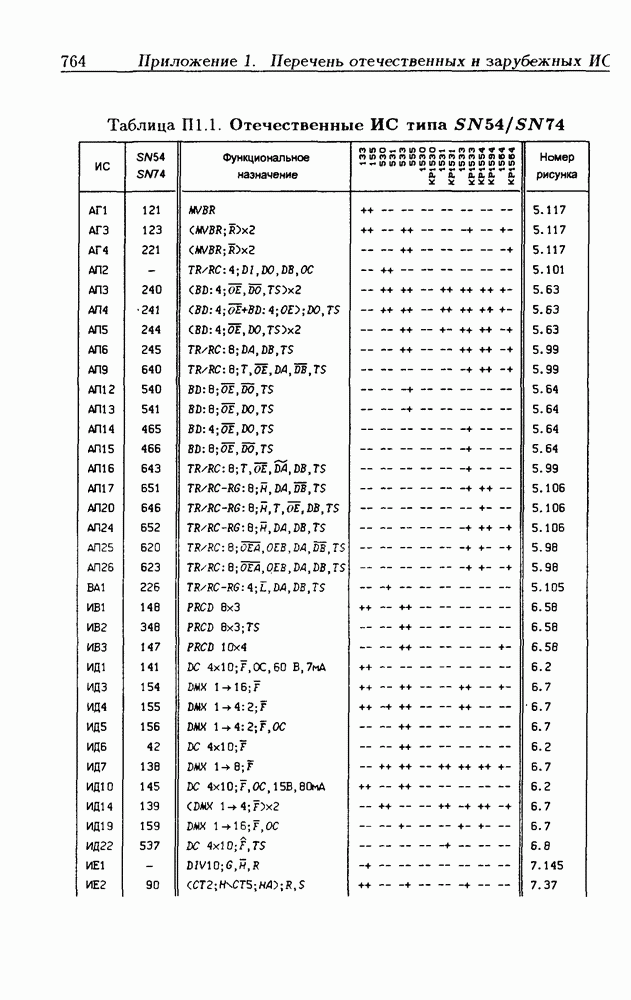
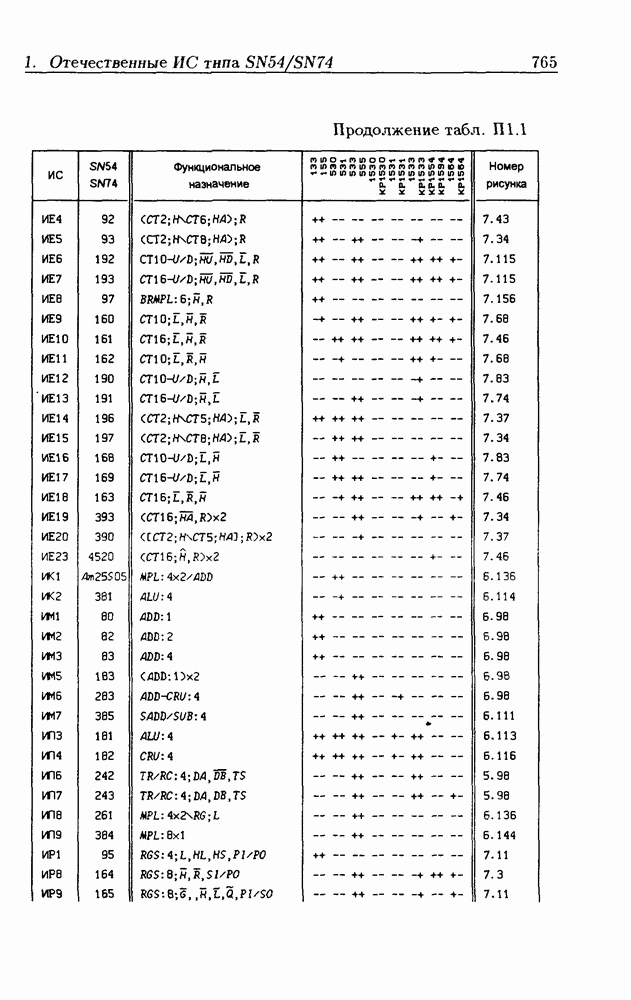
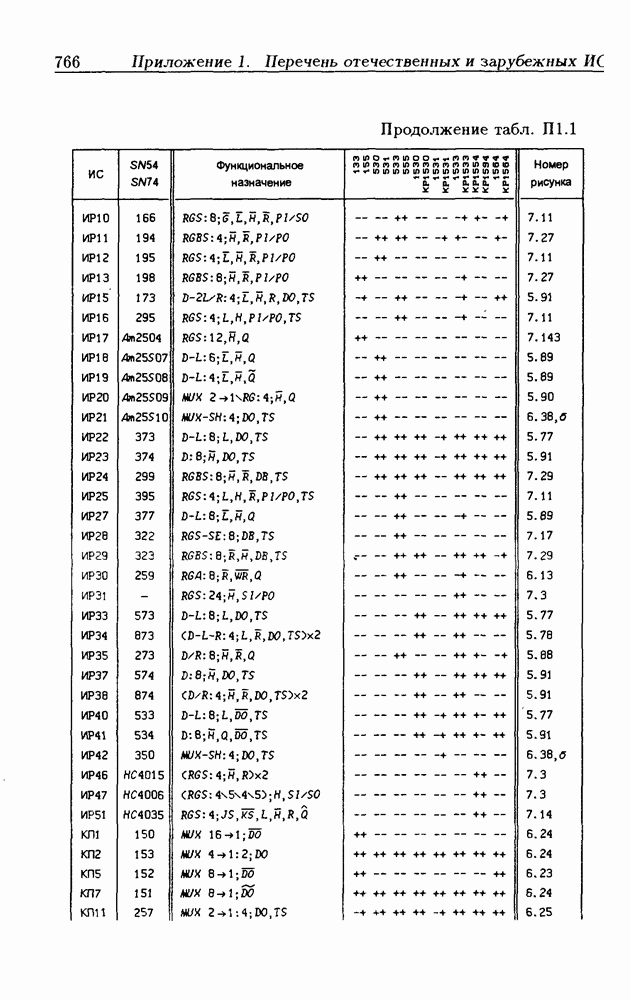
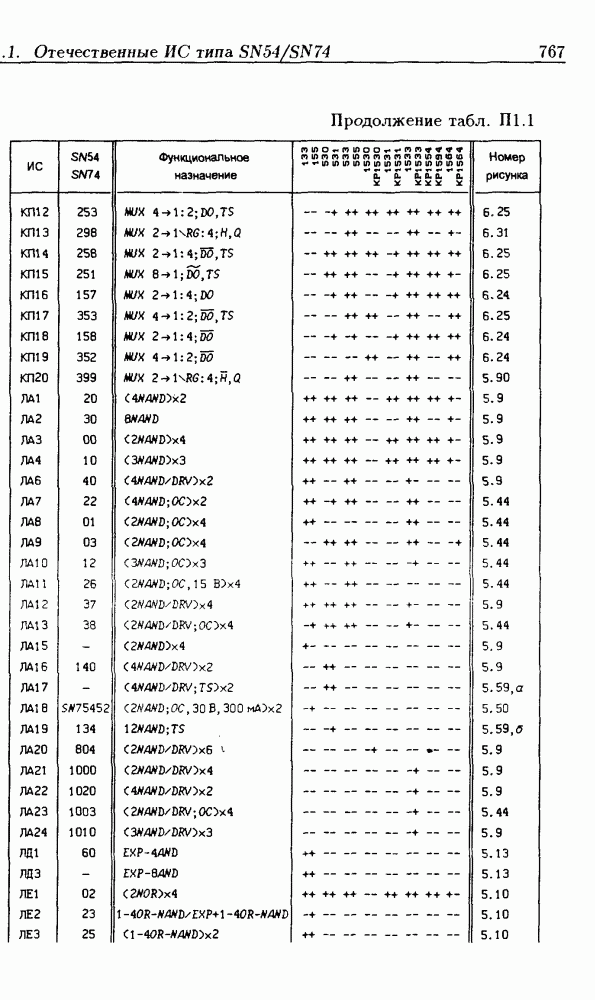
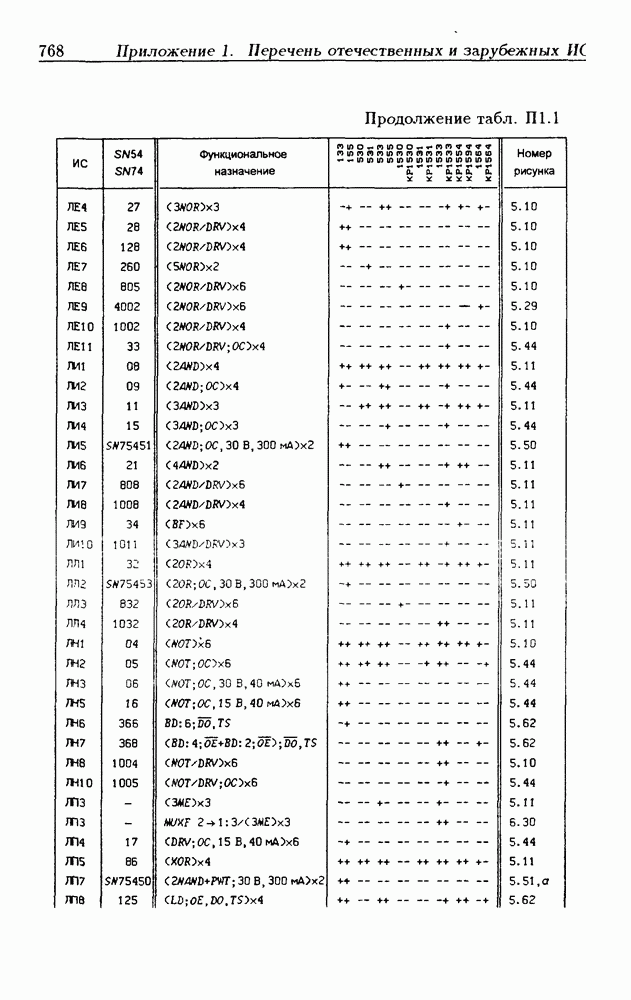
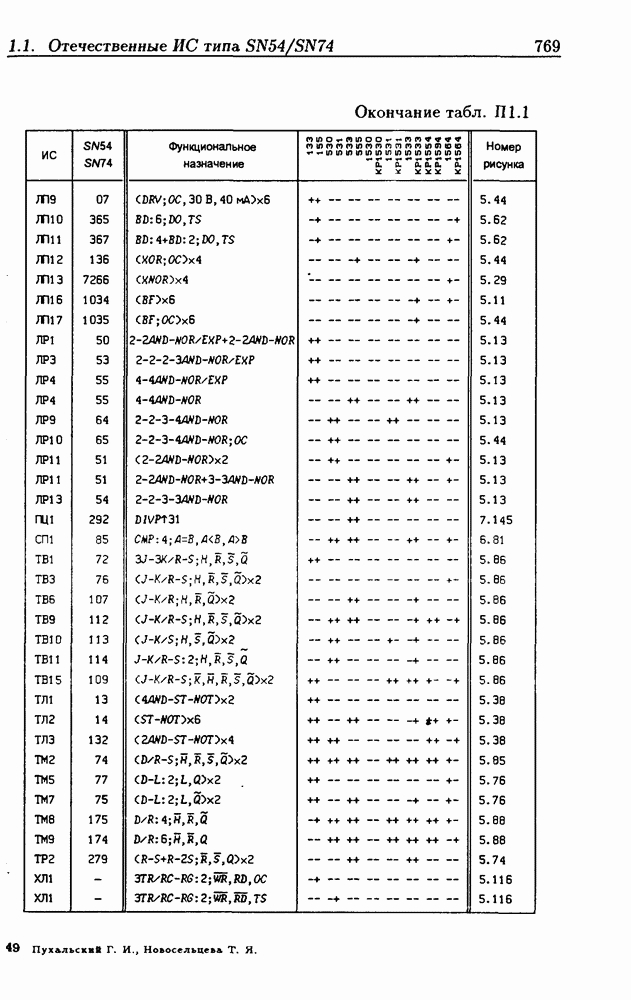
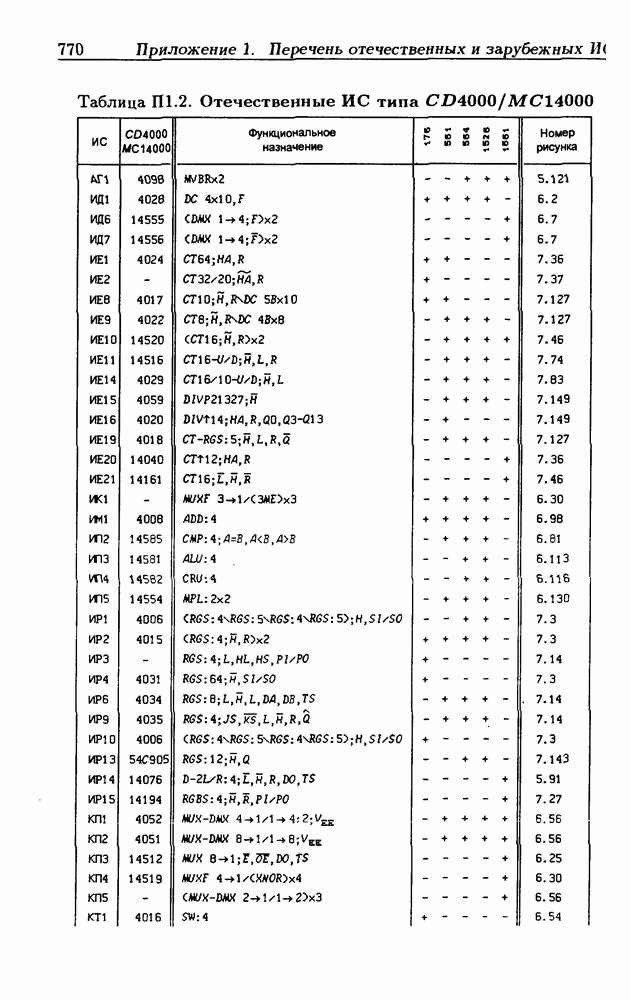
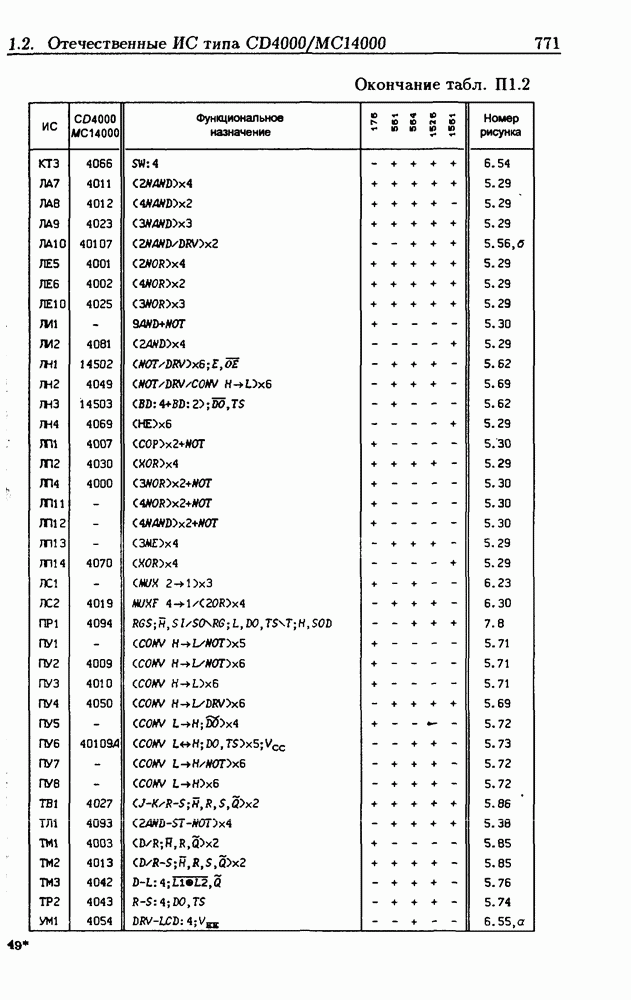
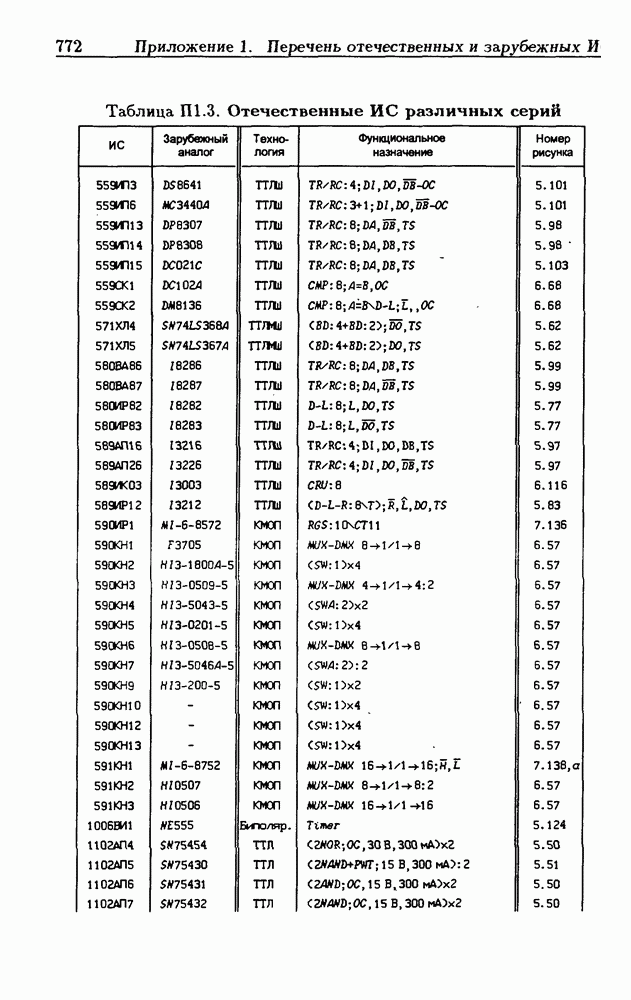
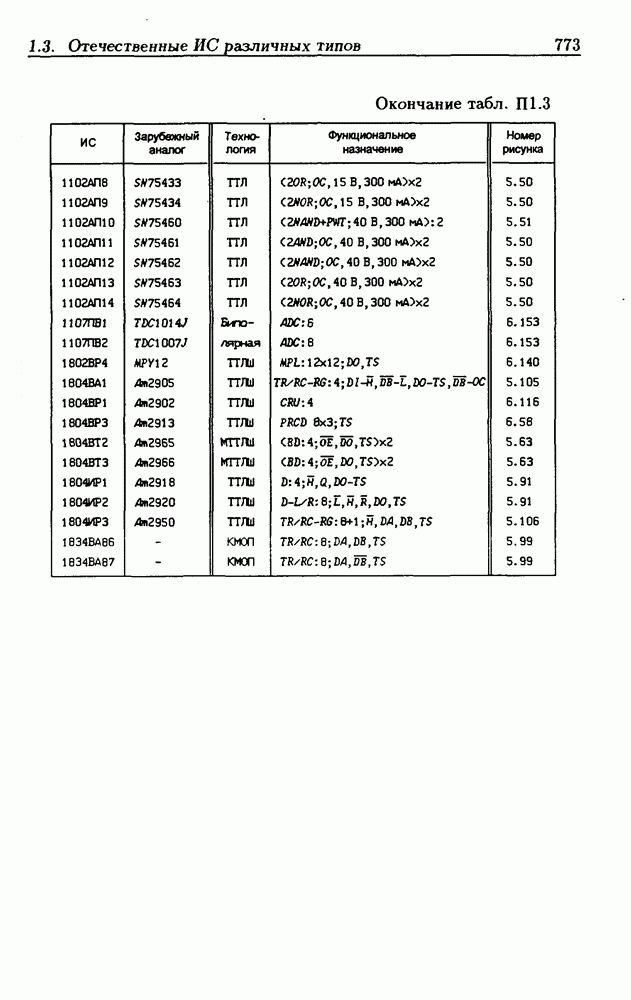
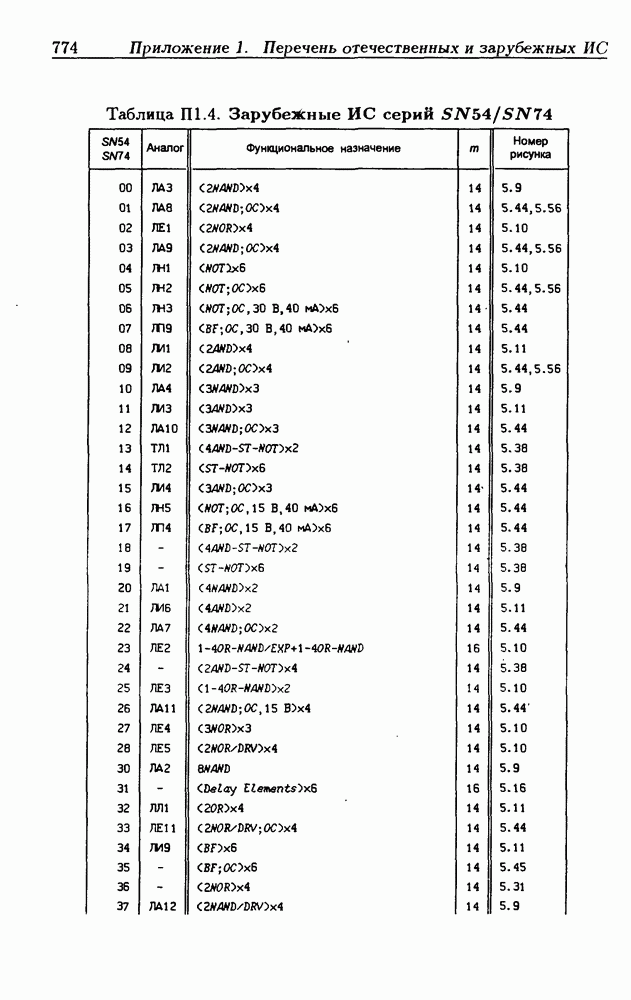
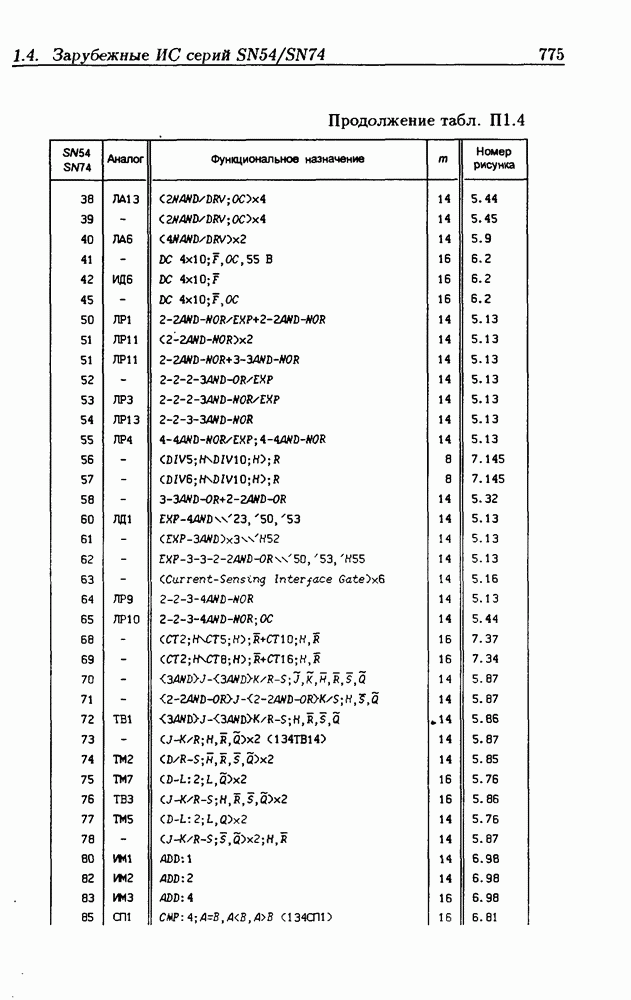
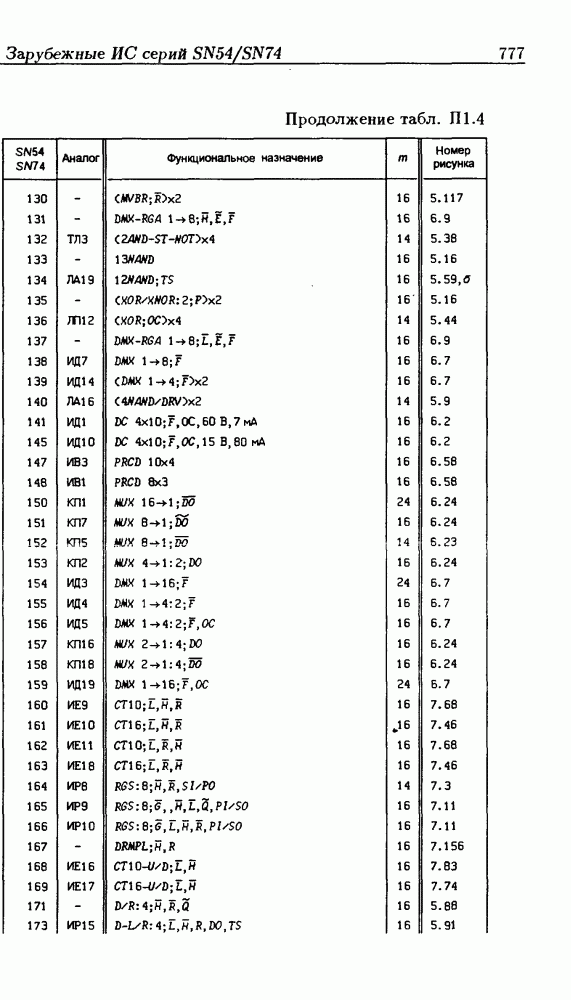
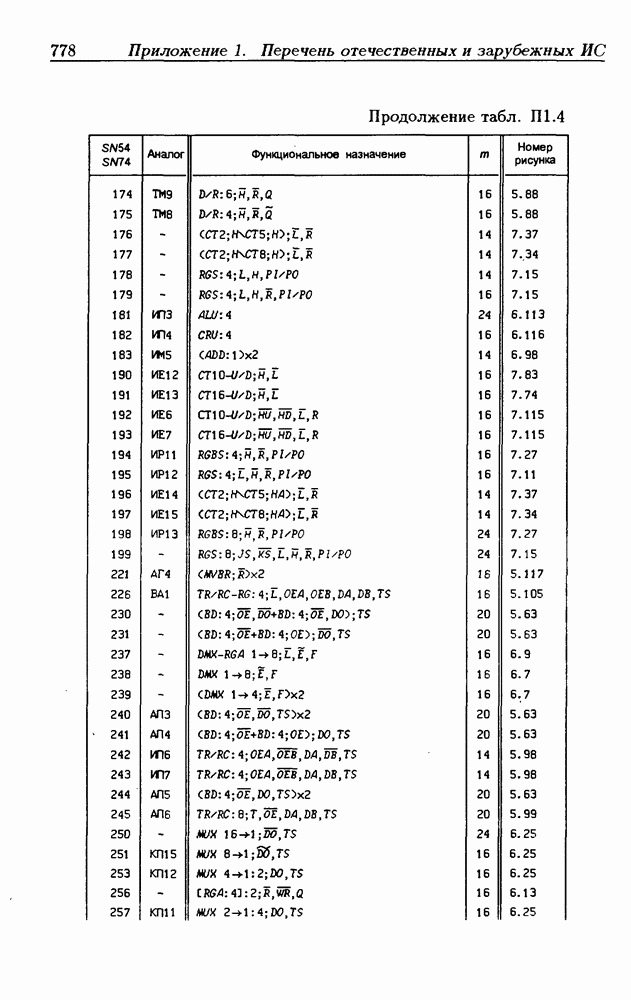
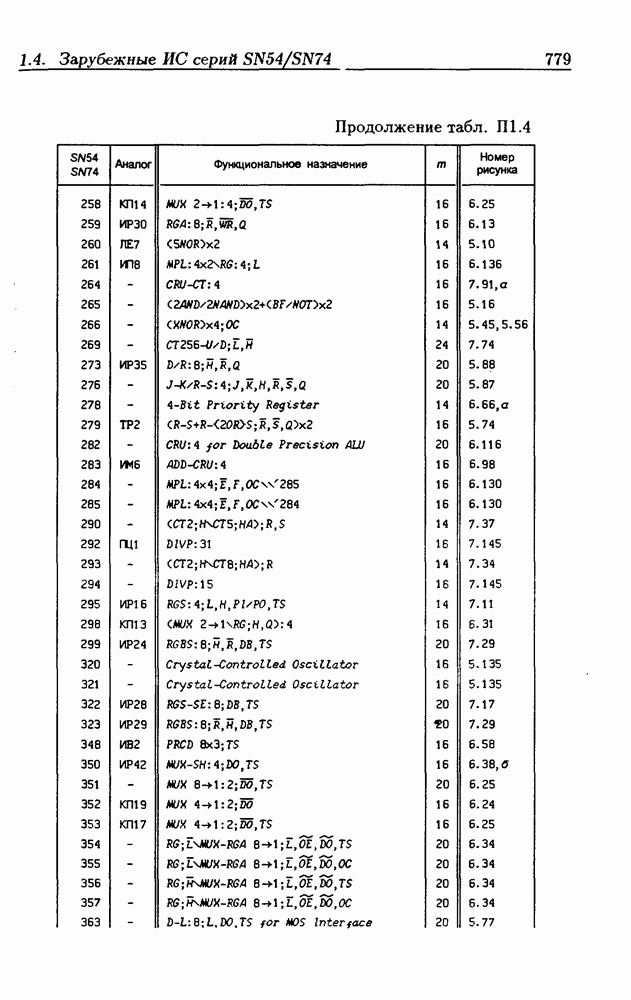
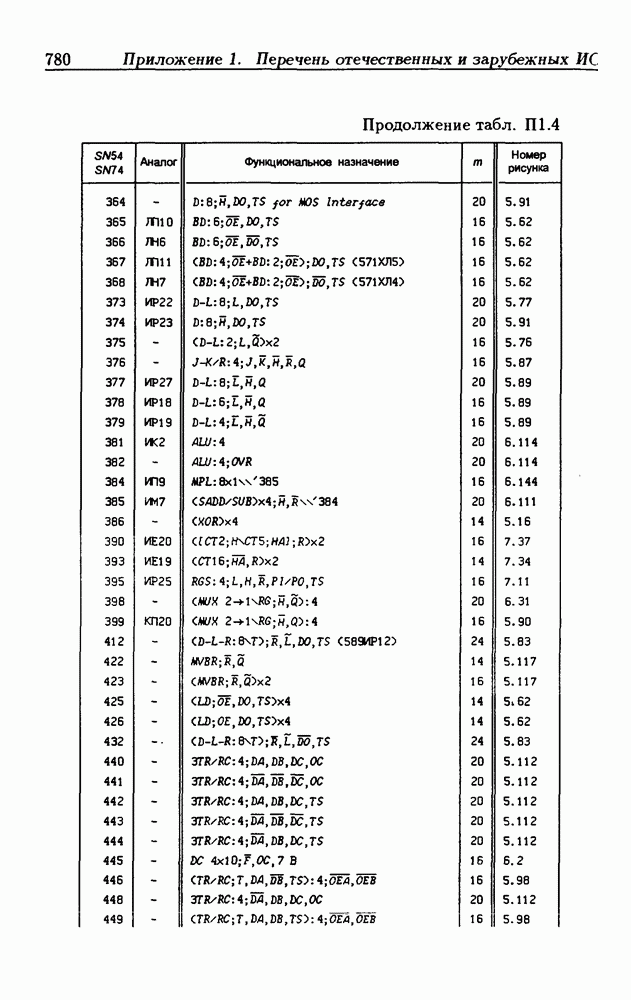
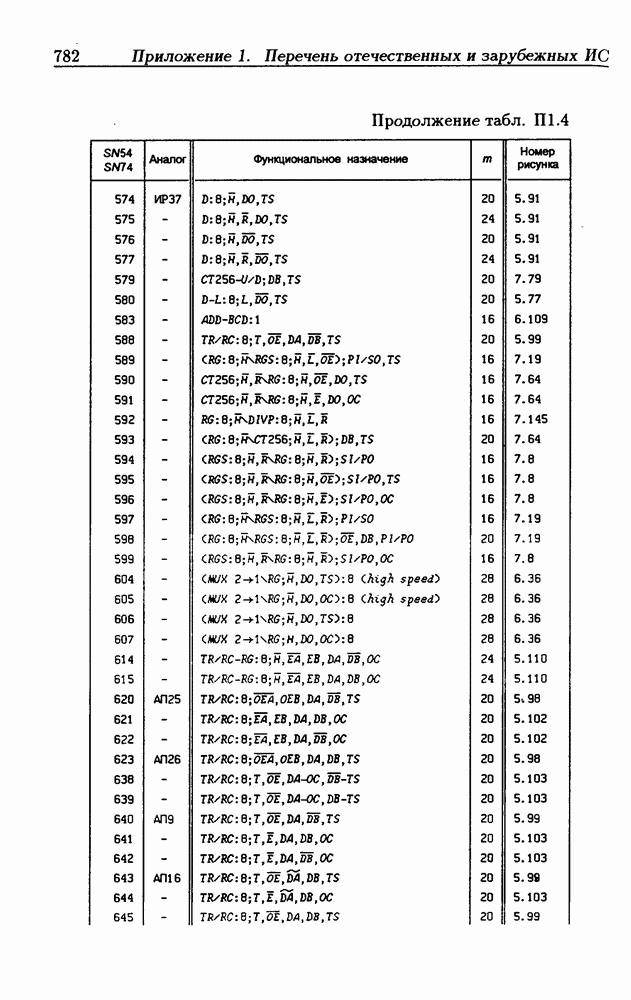
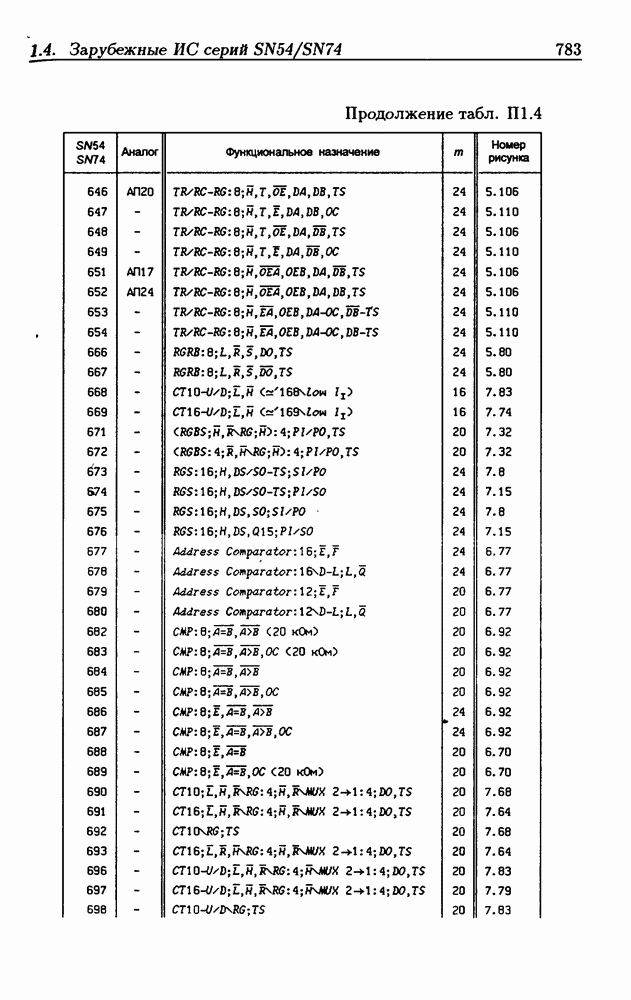
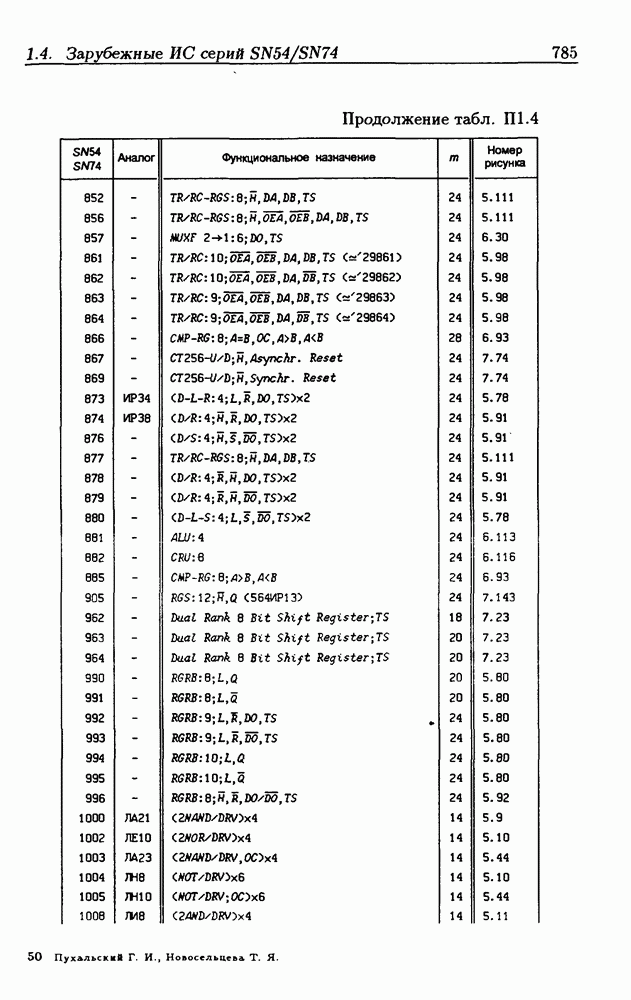
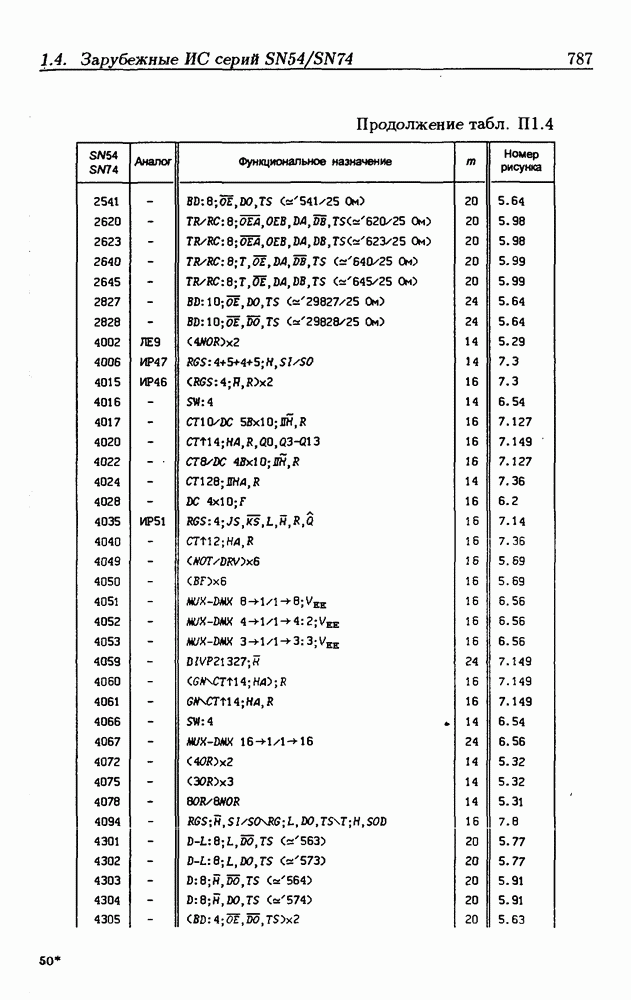
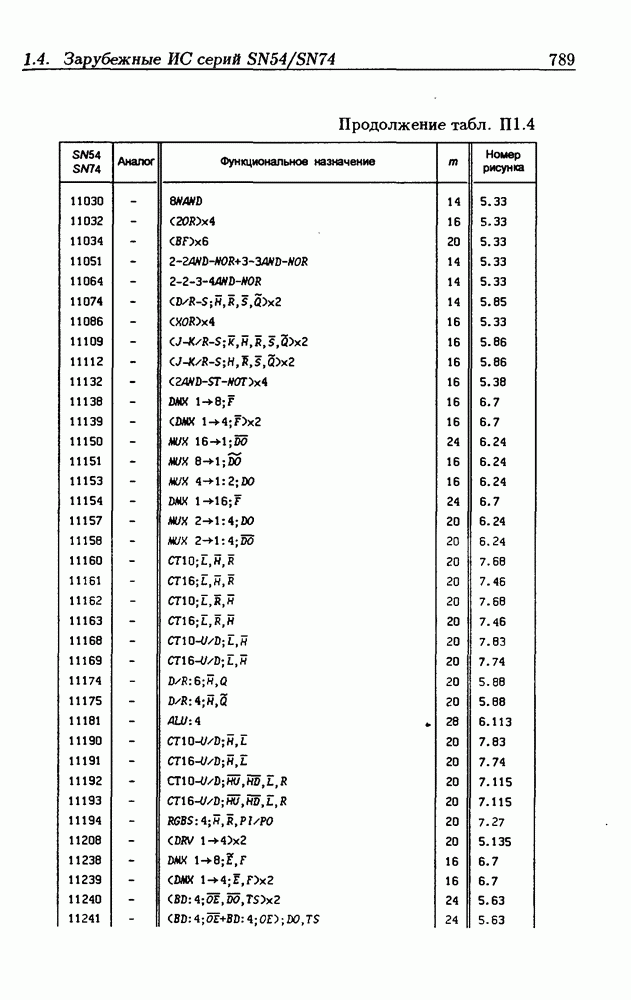
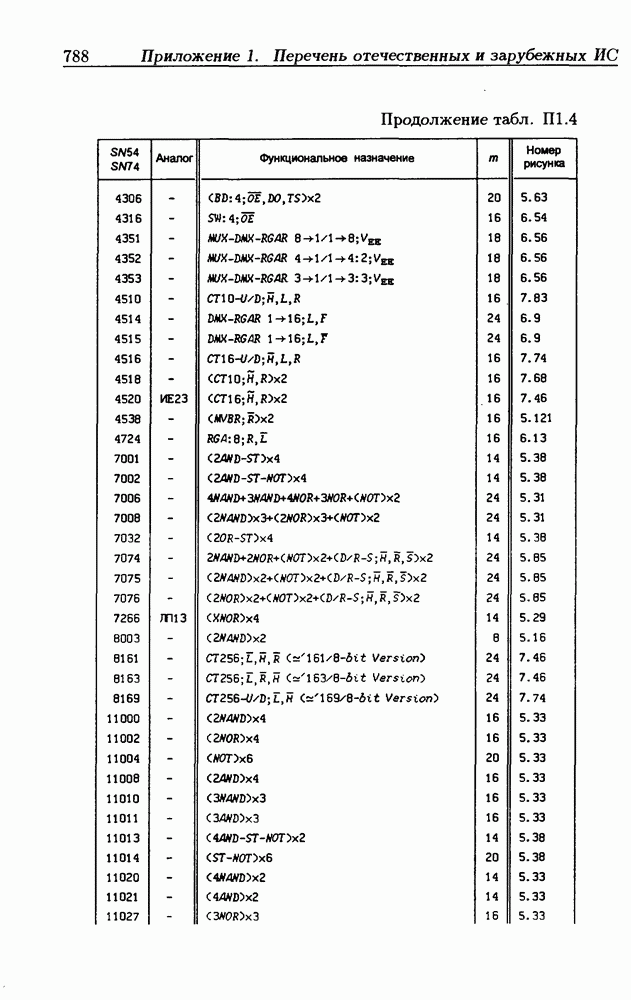
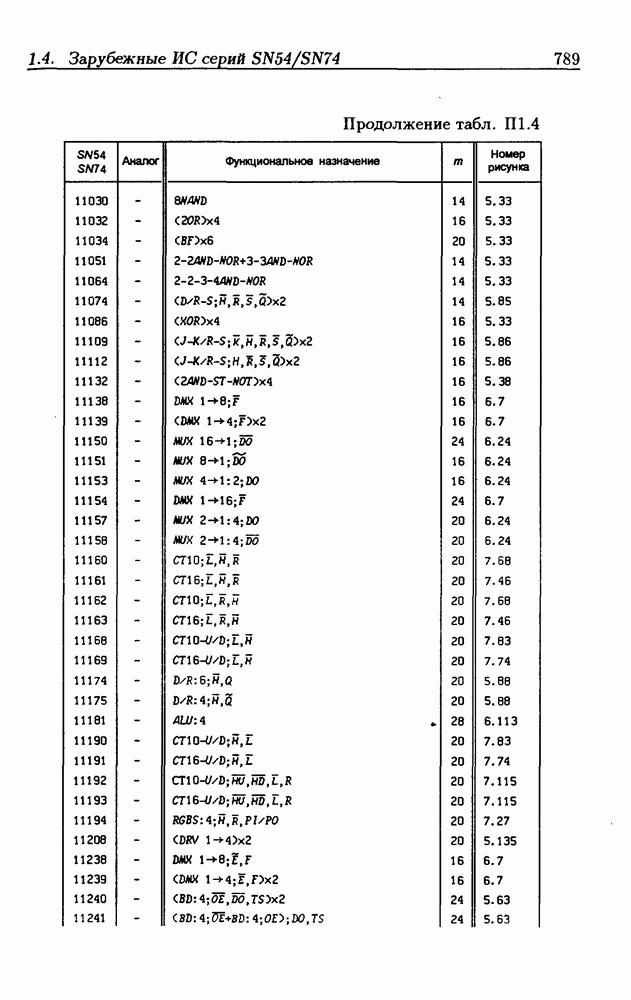
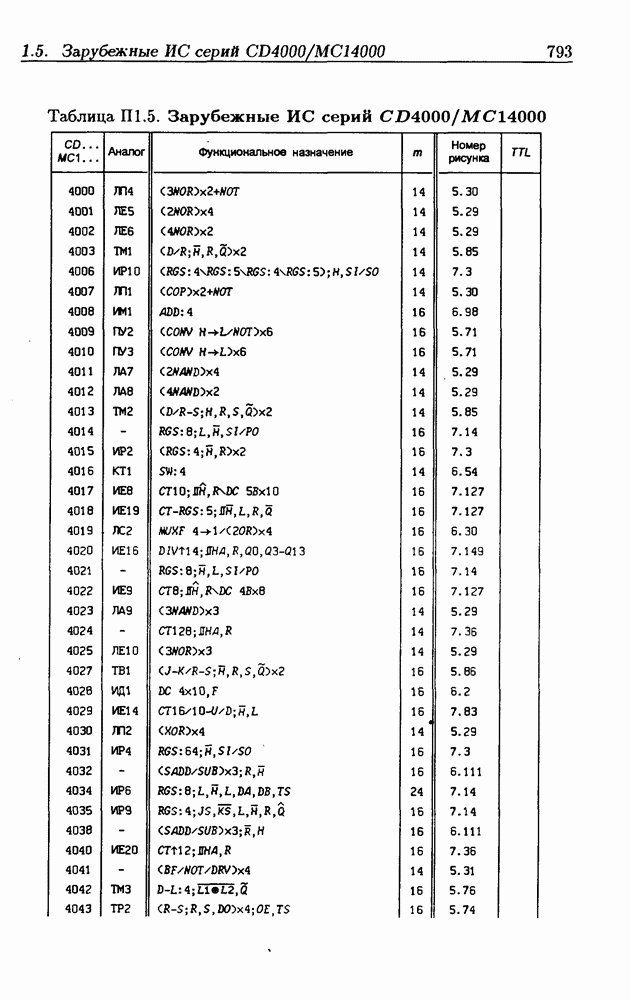
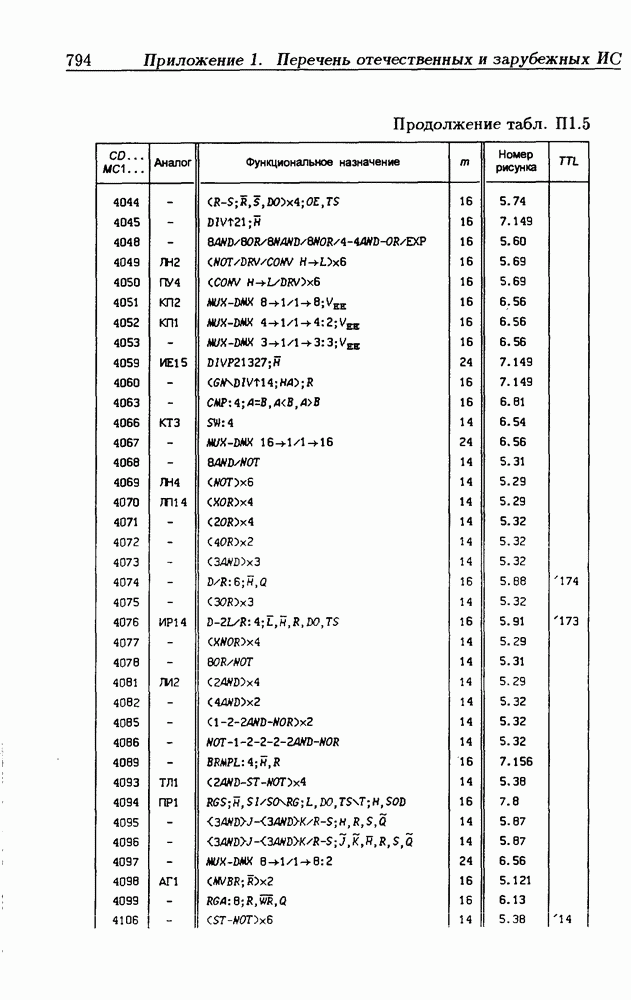
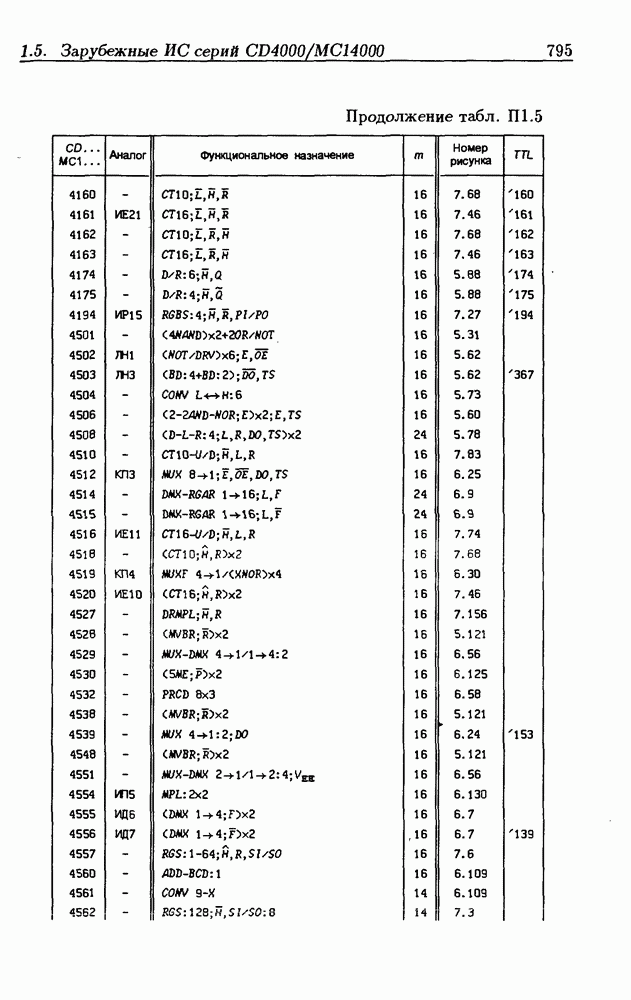
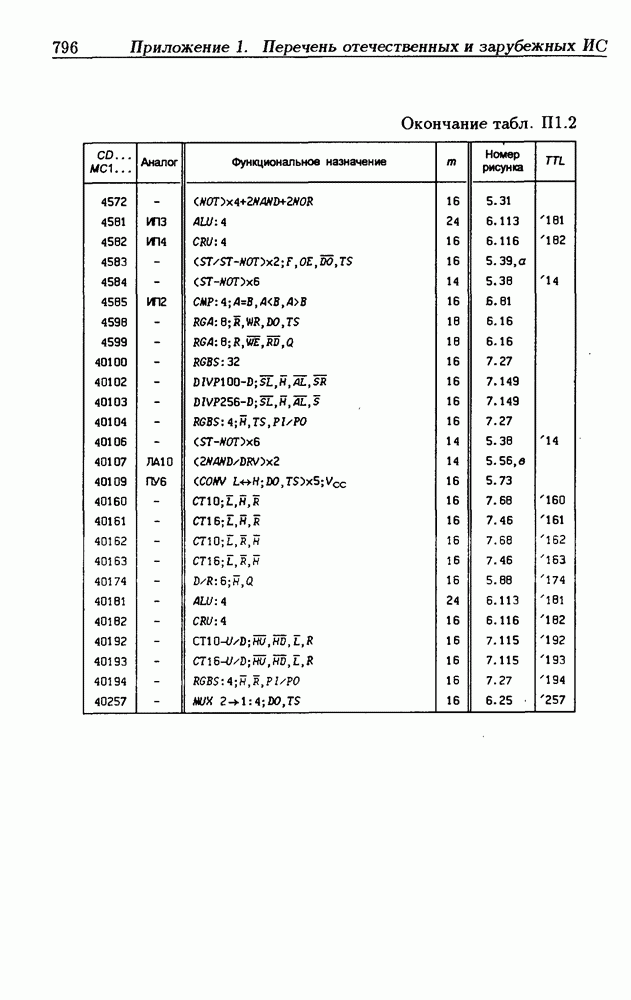
- Приложение 1. Перечень отечественных и зарубежных ИС
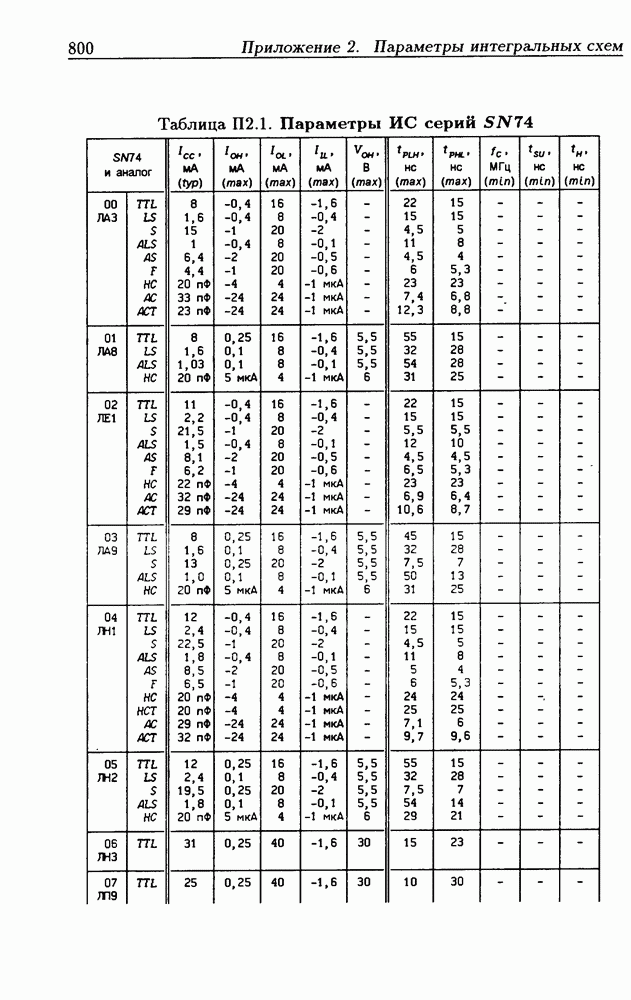
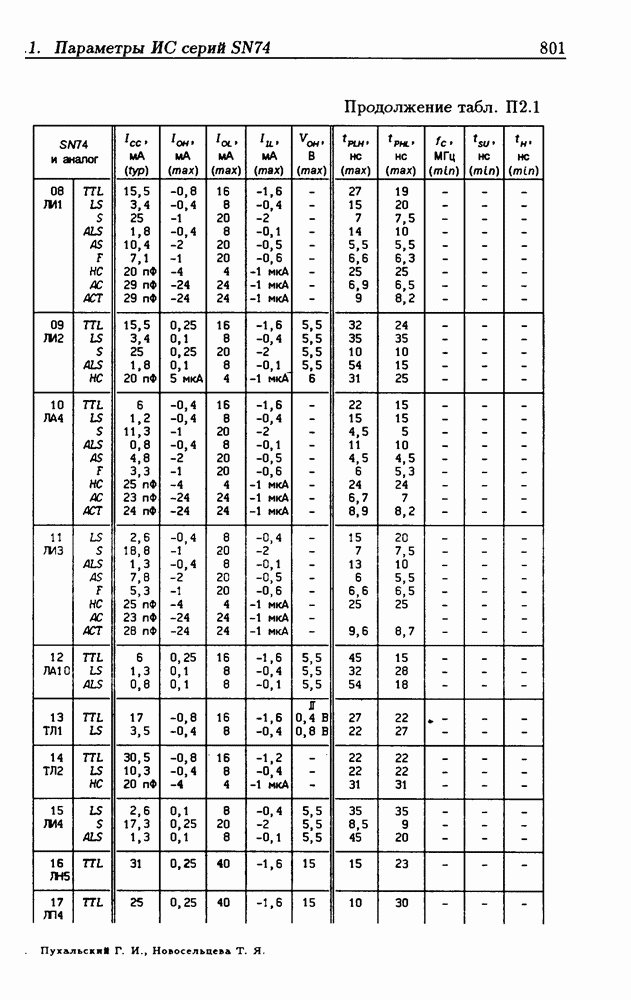
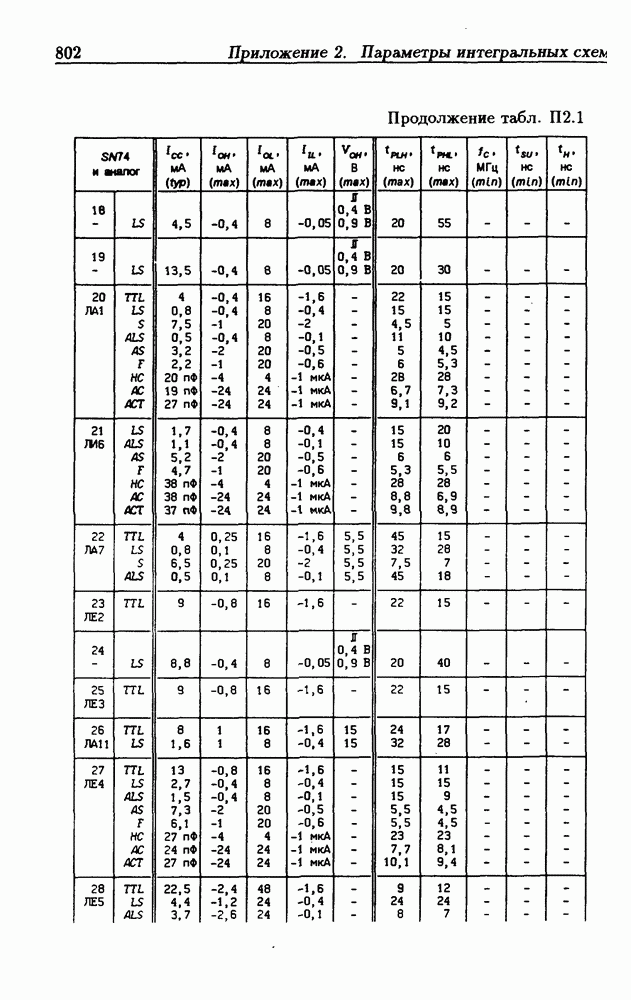
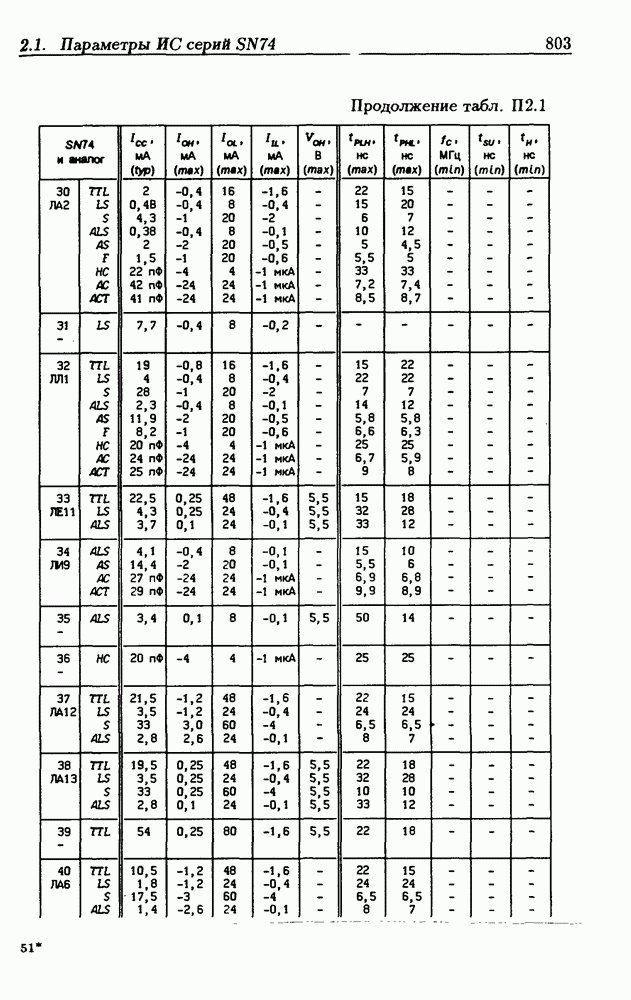
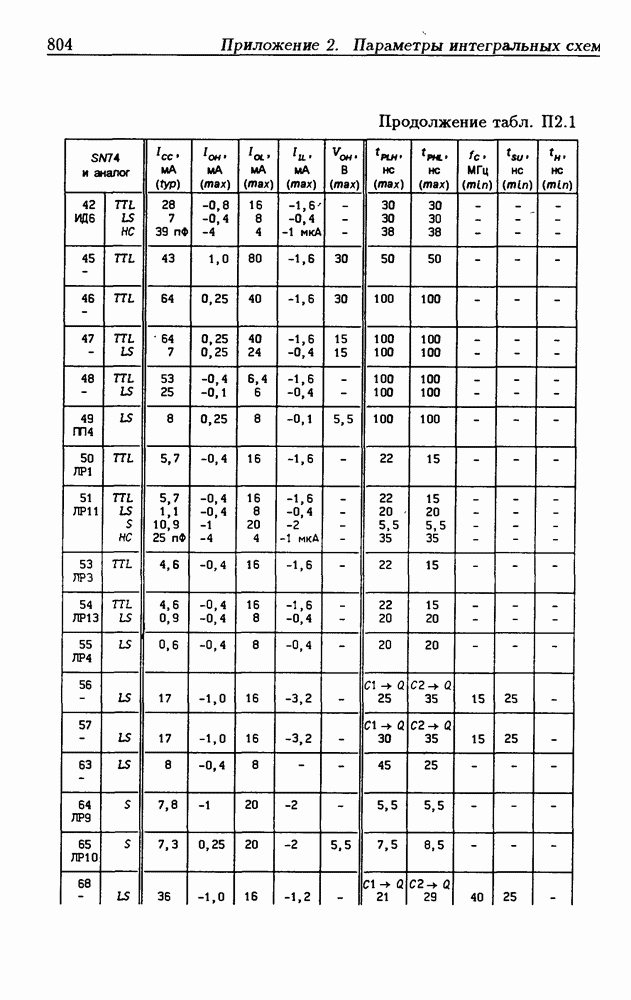
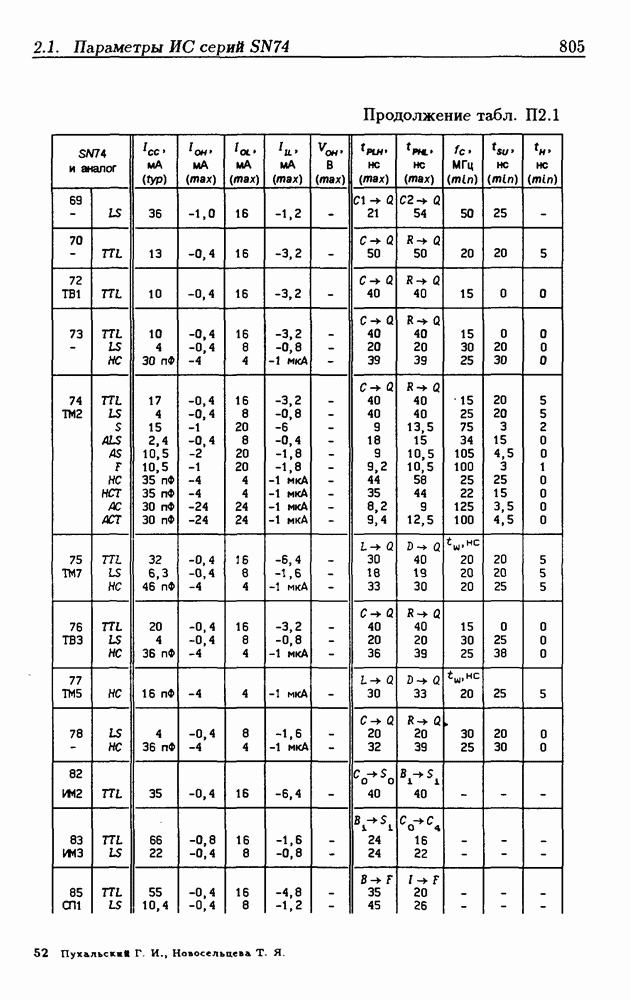
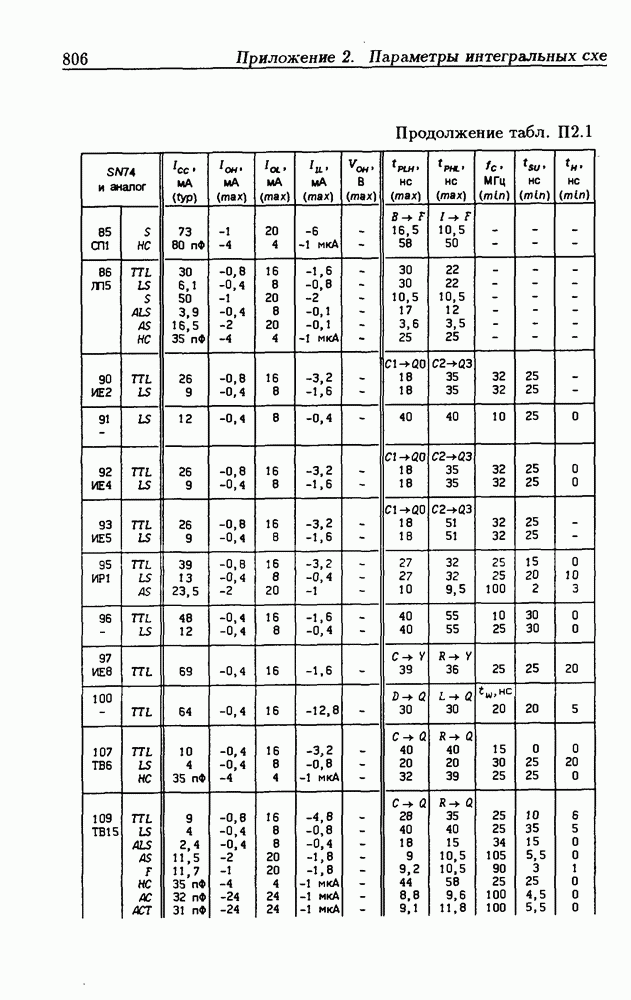
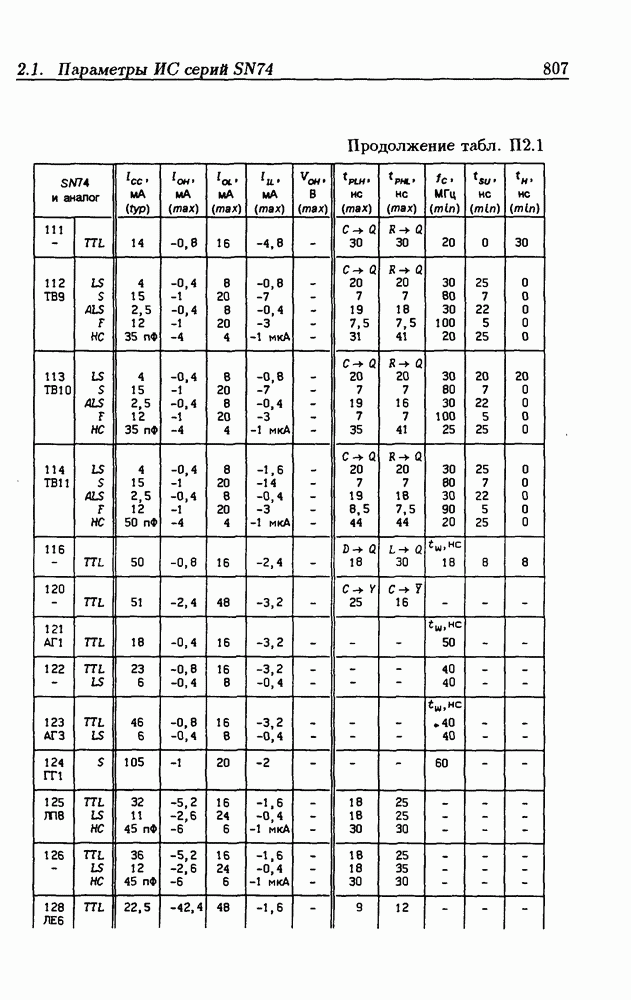
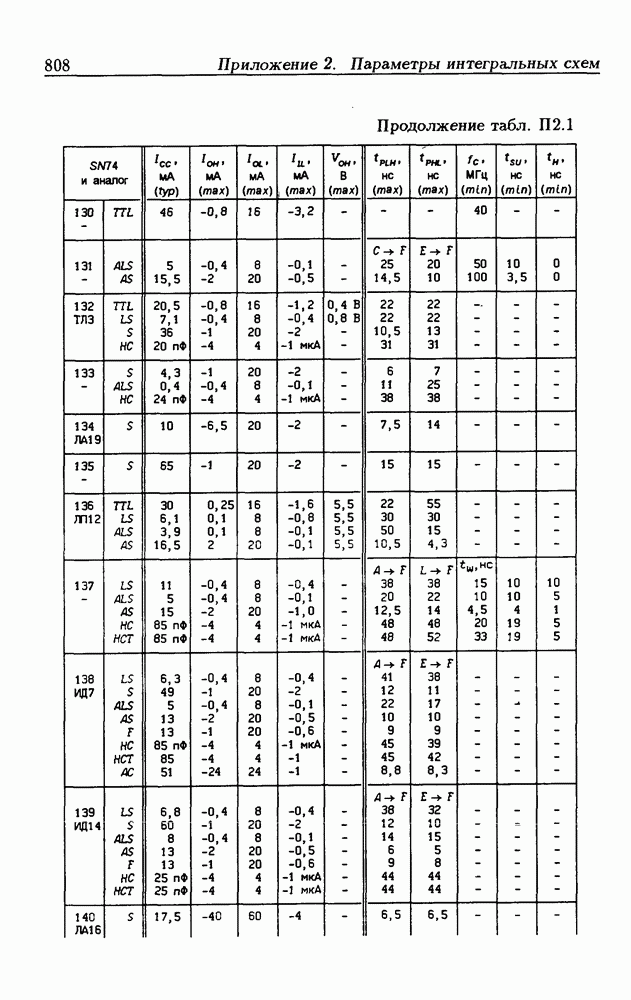
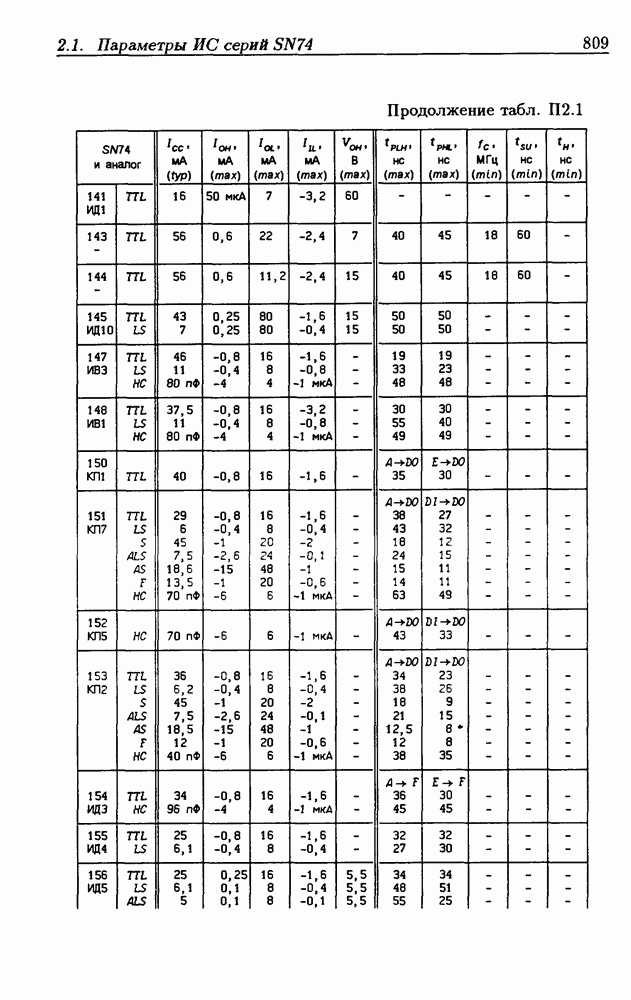
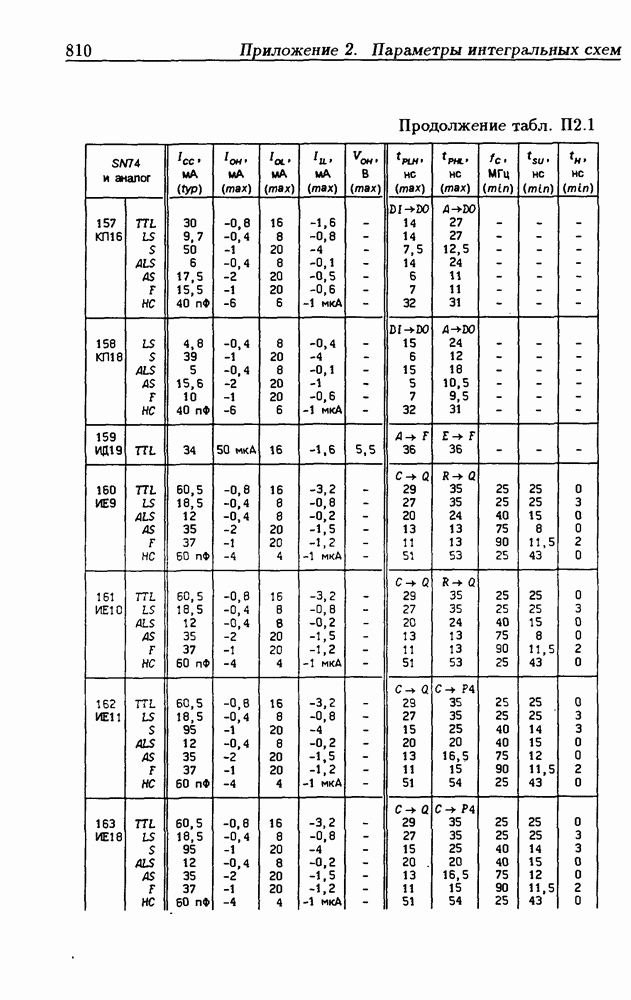
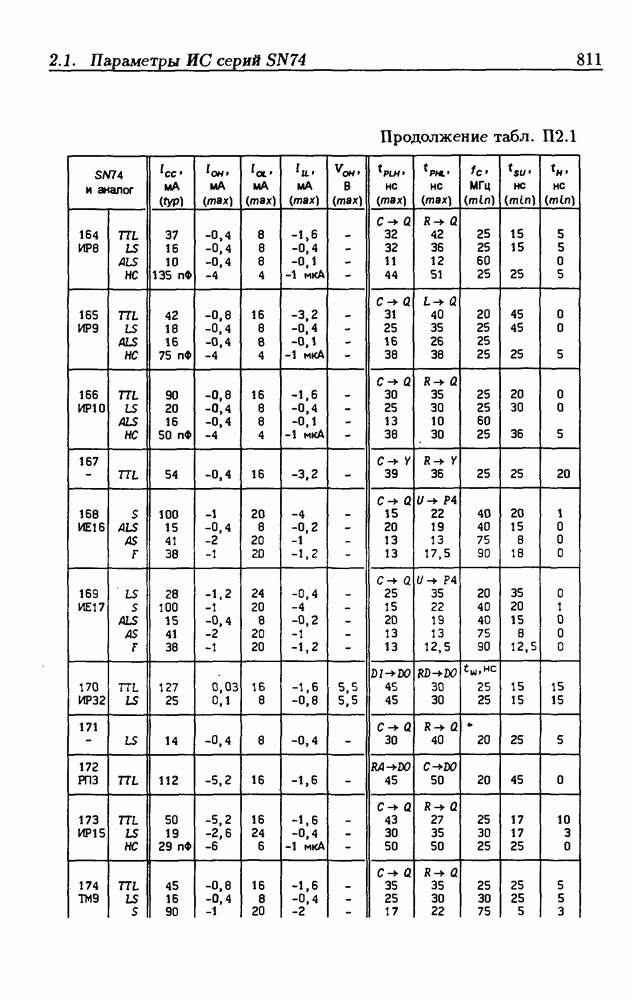
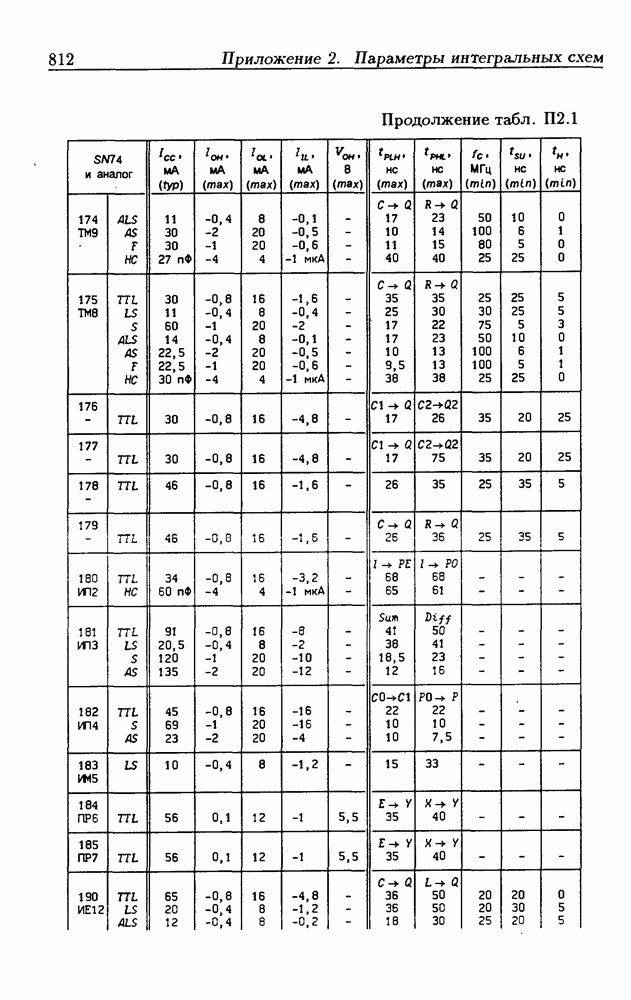
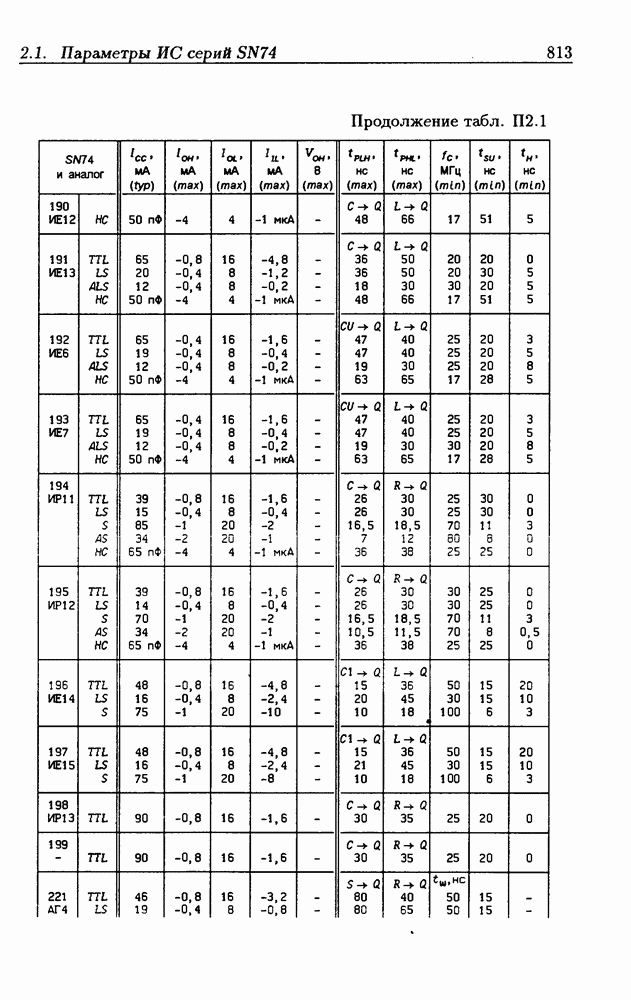
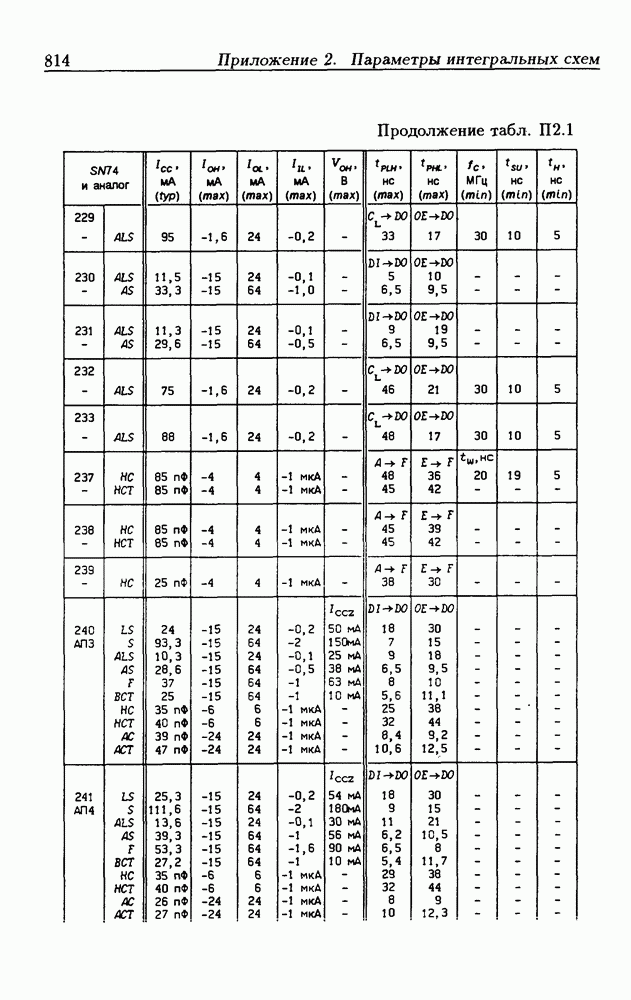
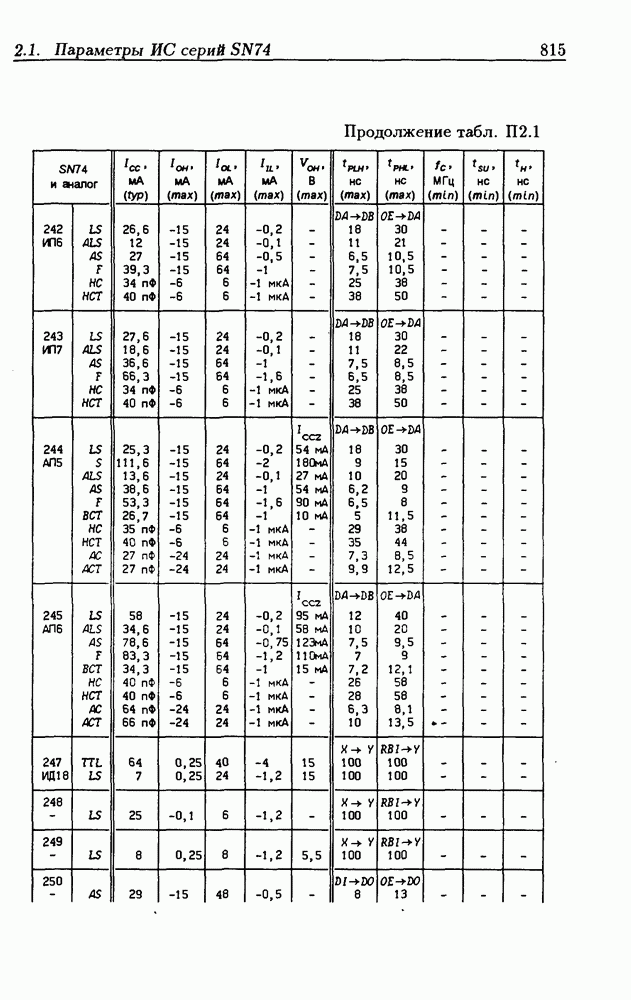
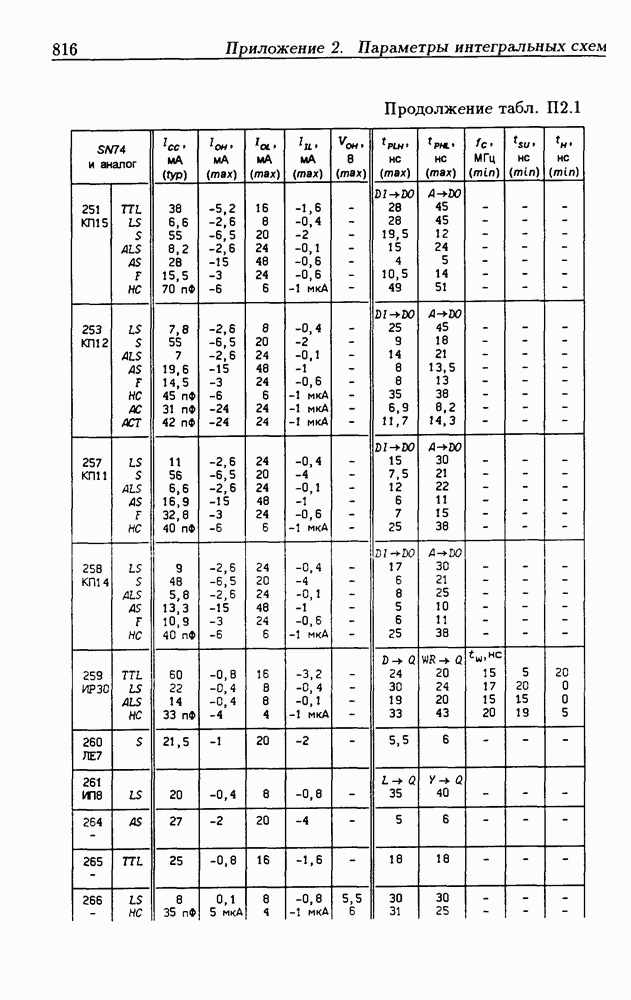
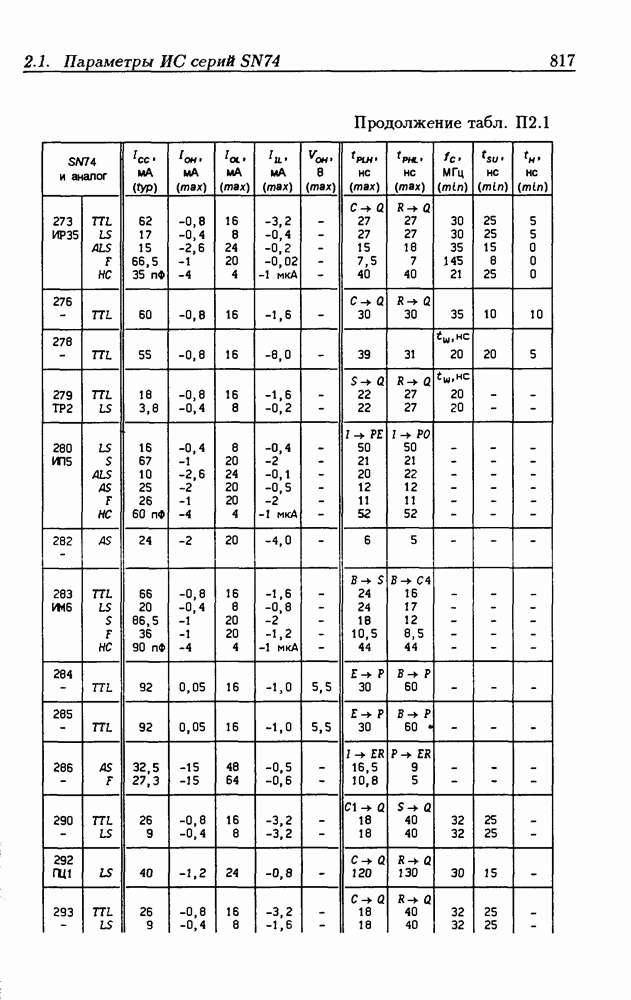
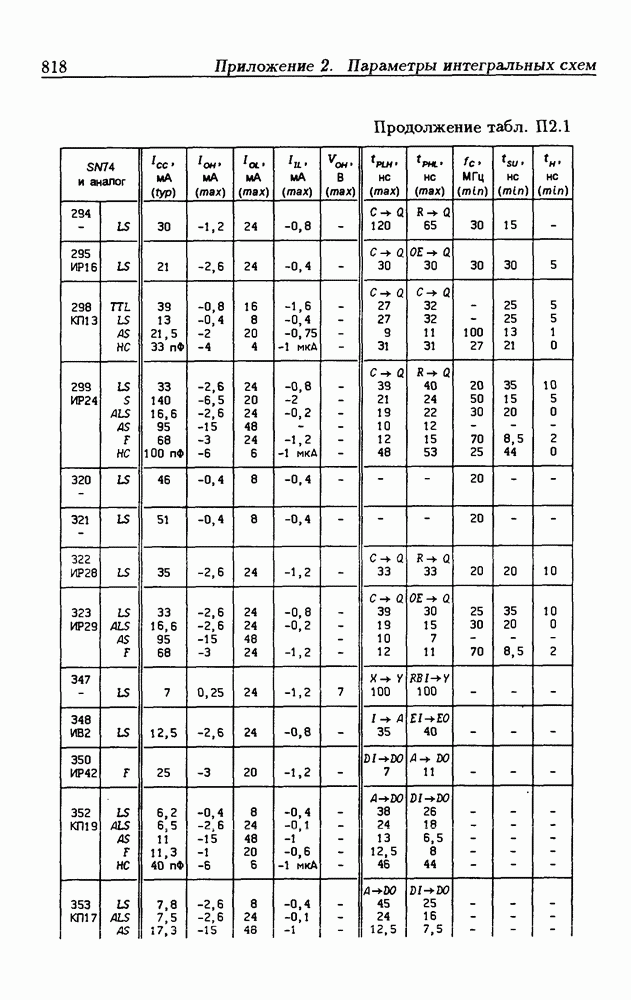
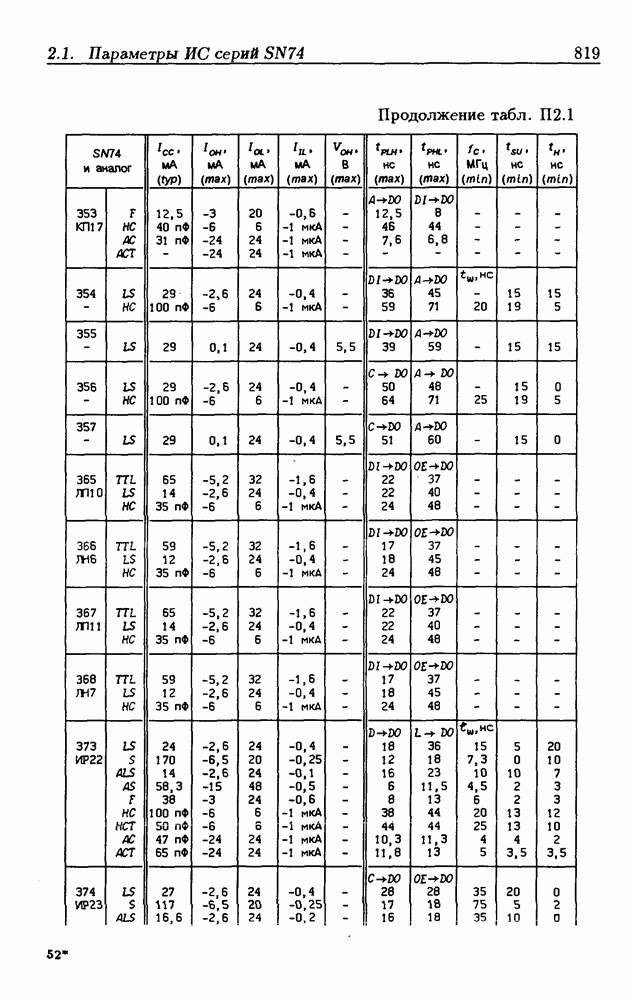
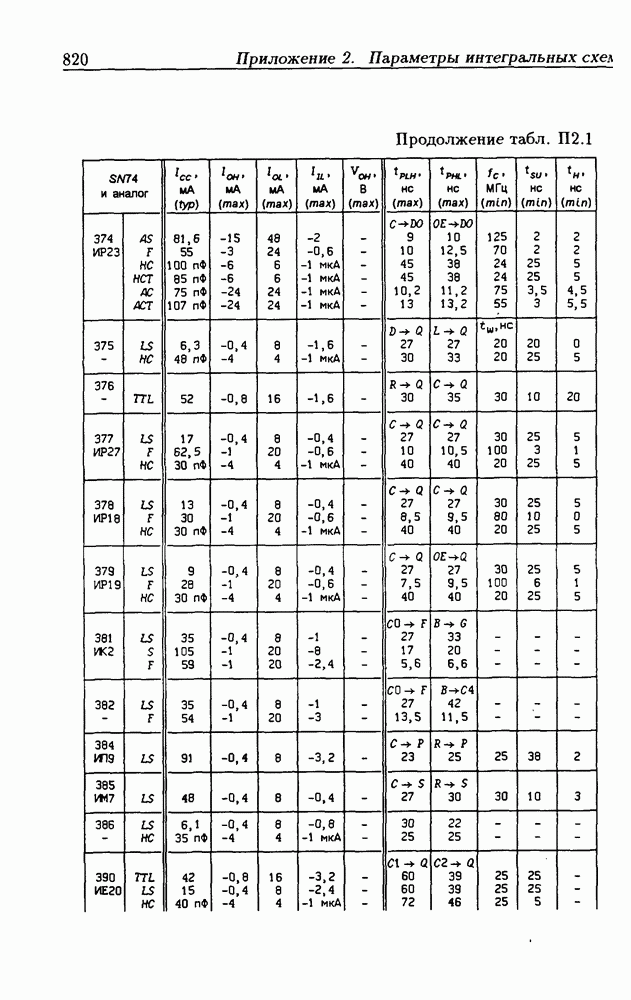
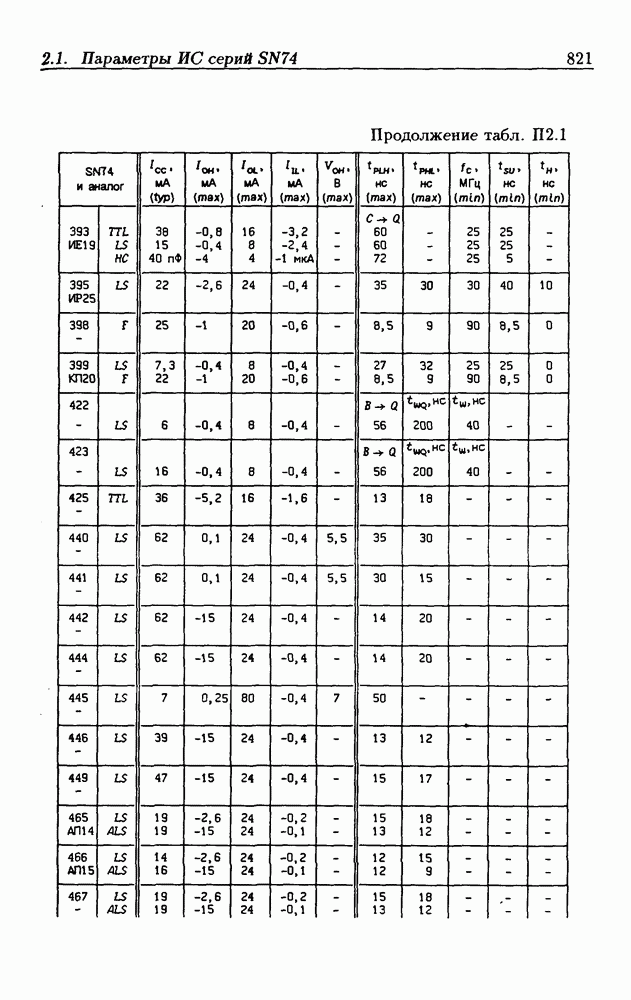
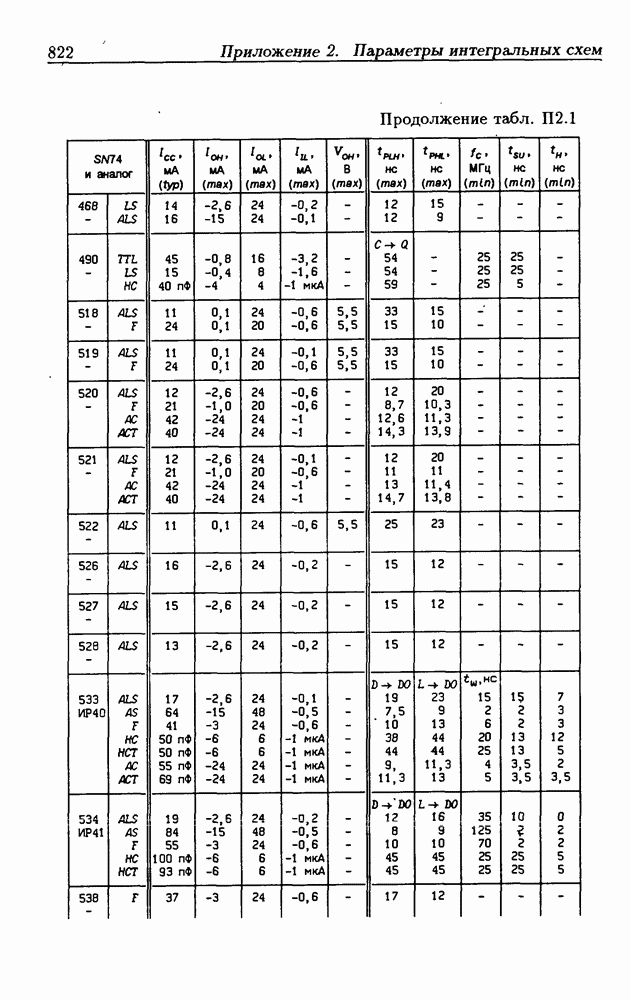
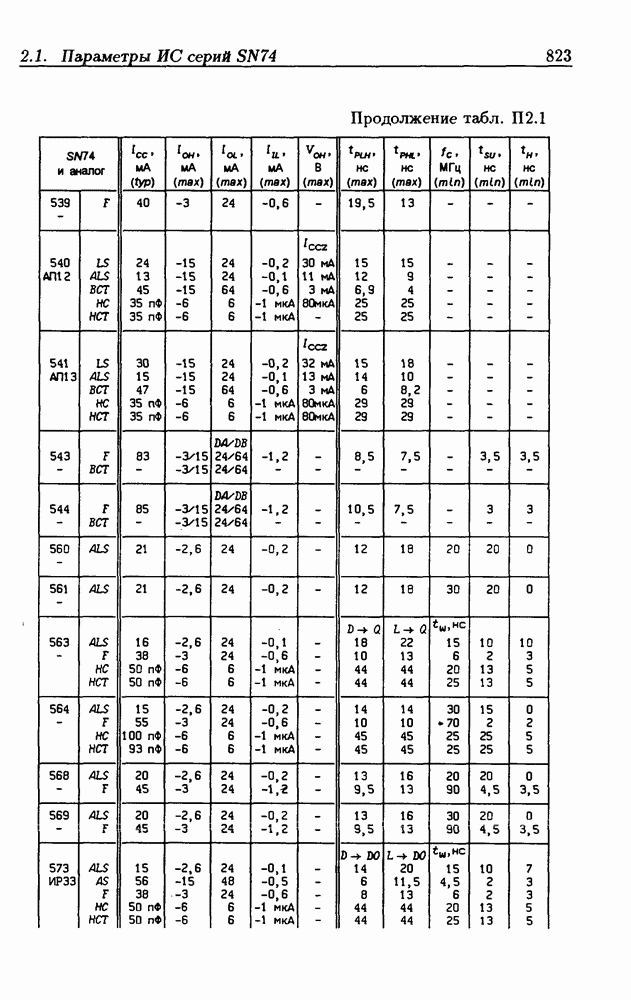
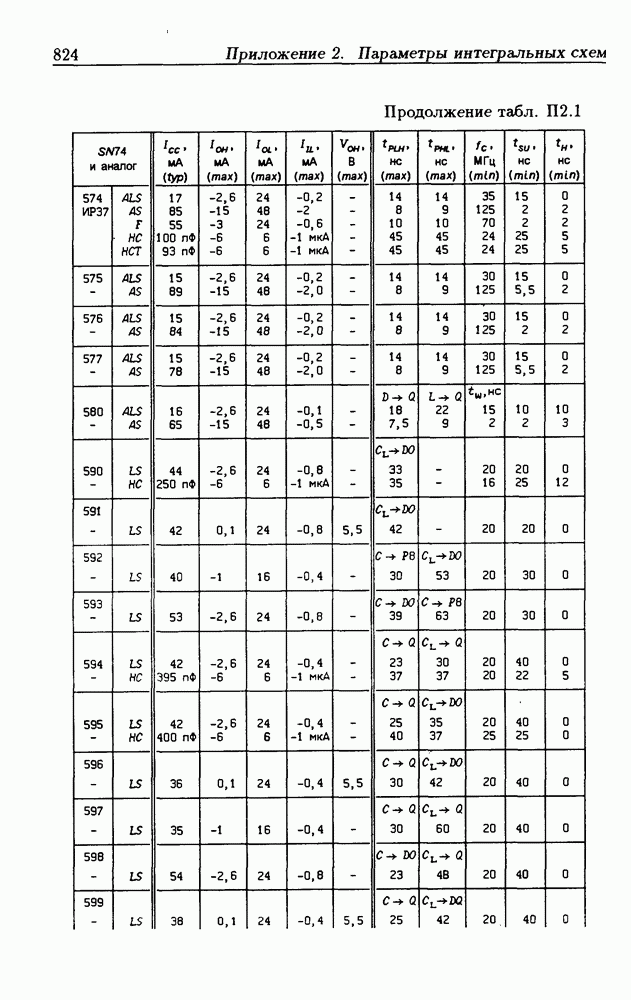
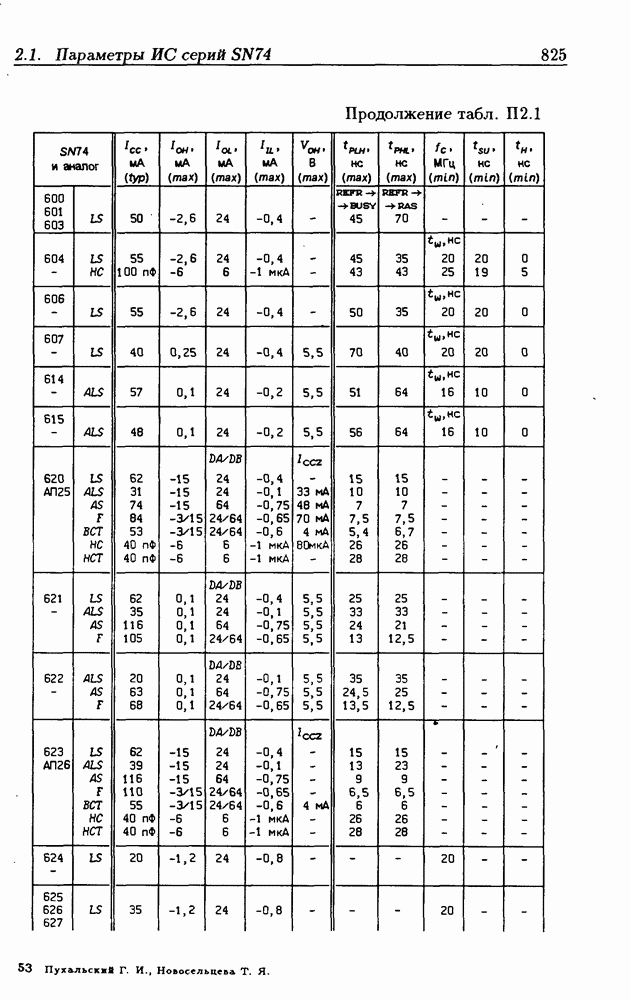
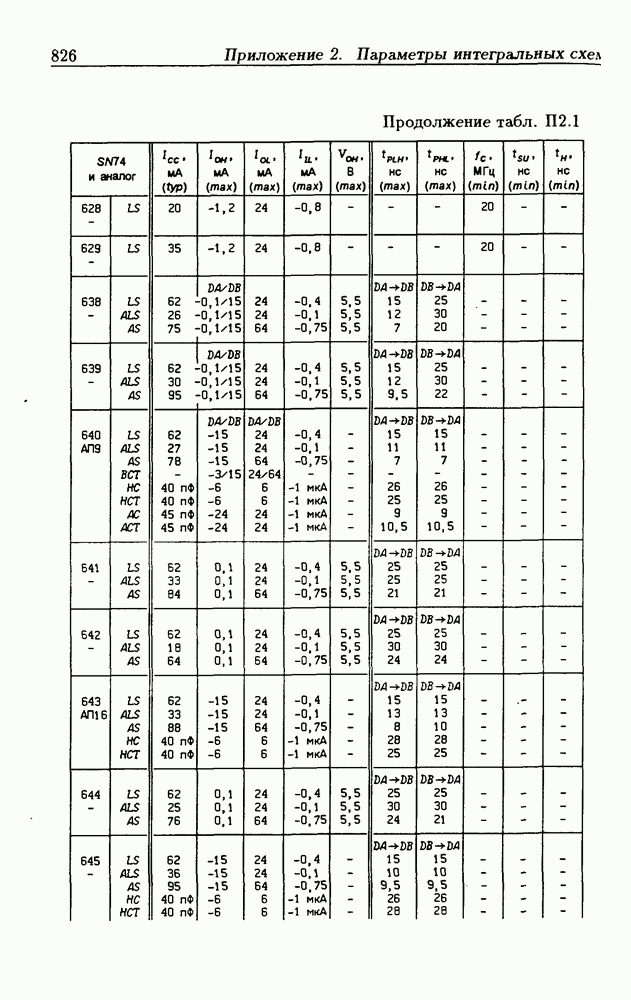
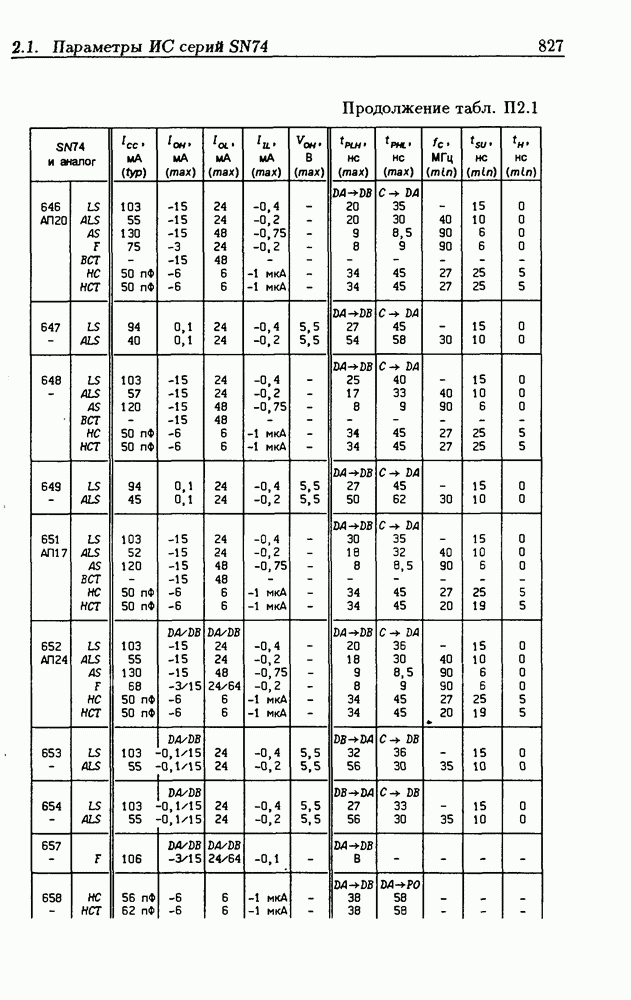
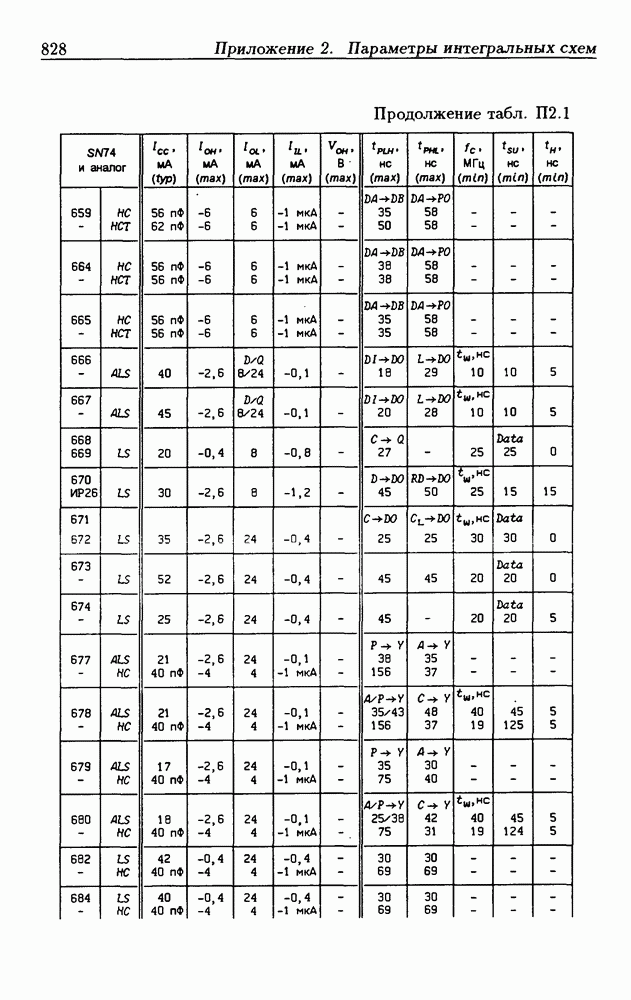
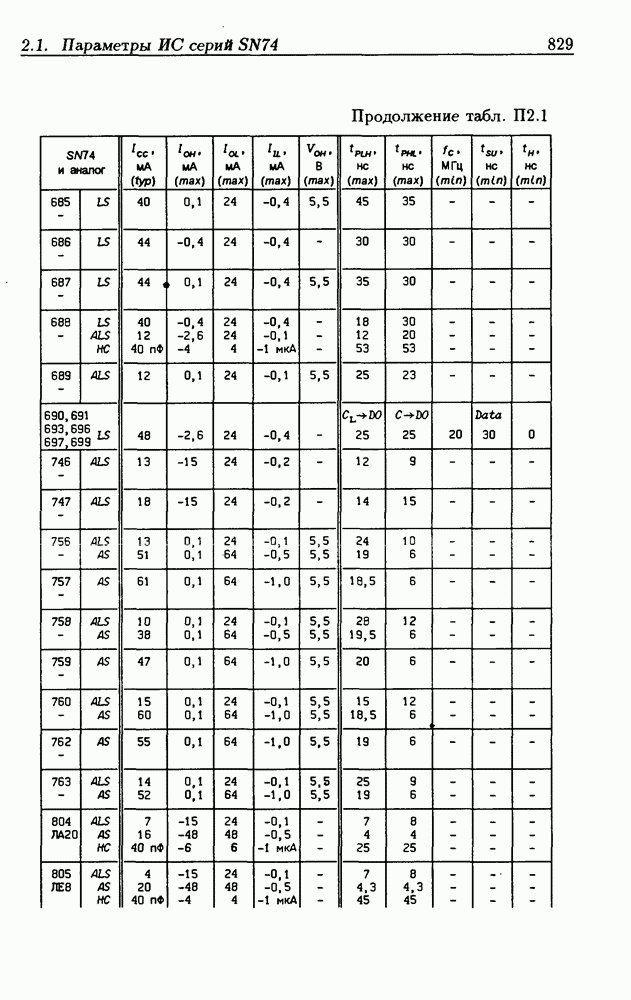
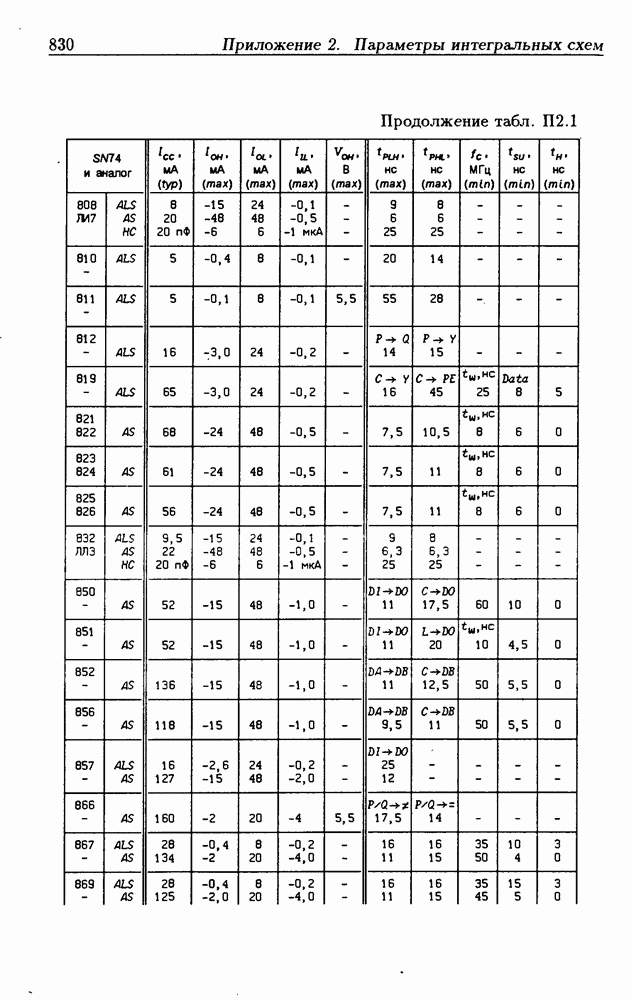
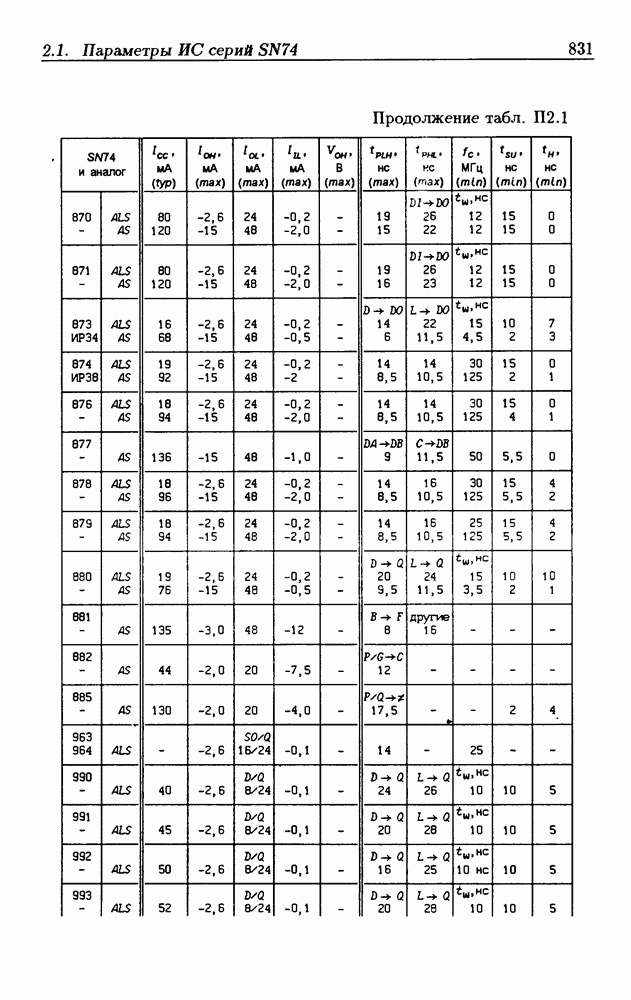
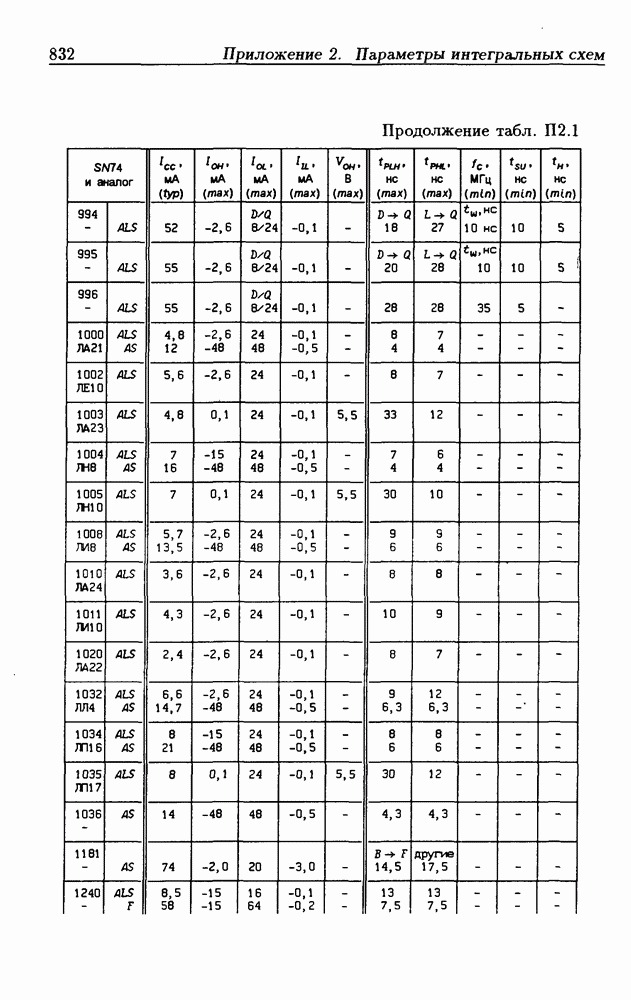
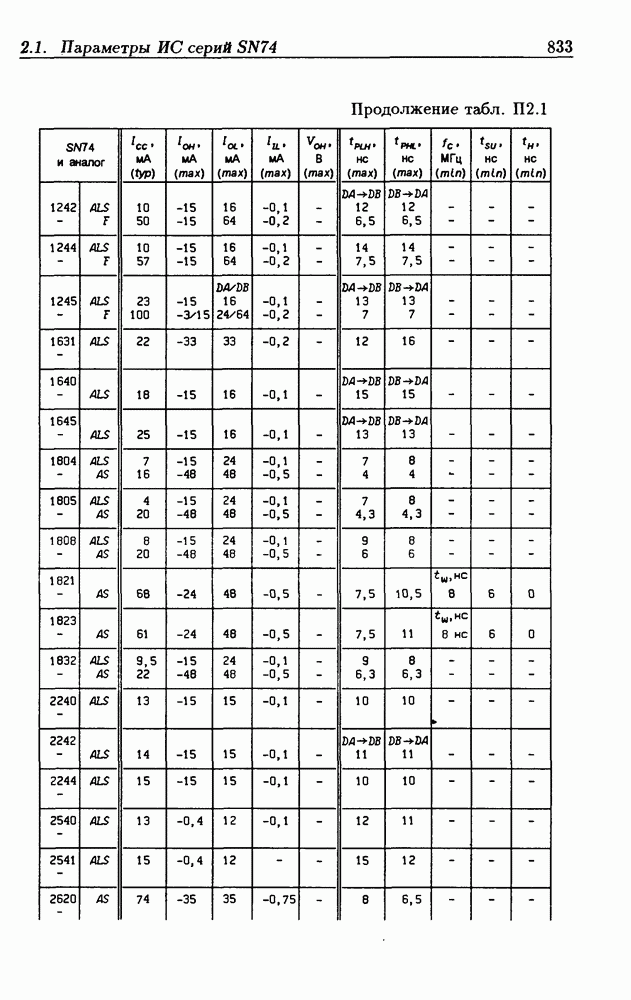
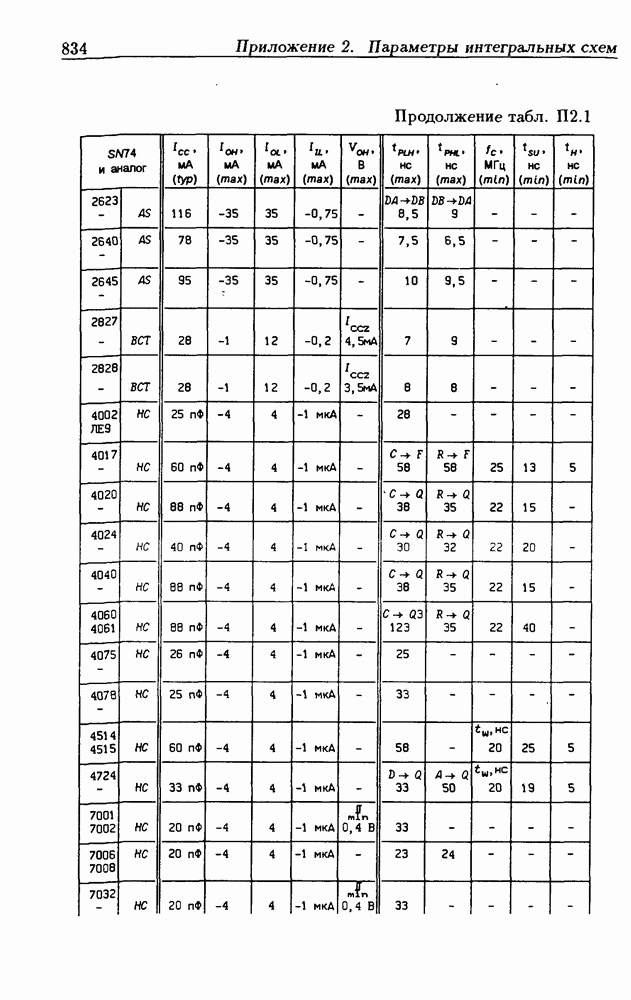
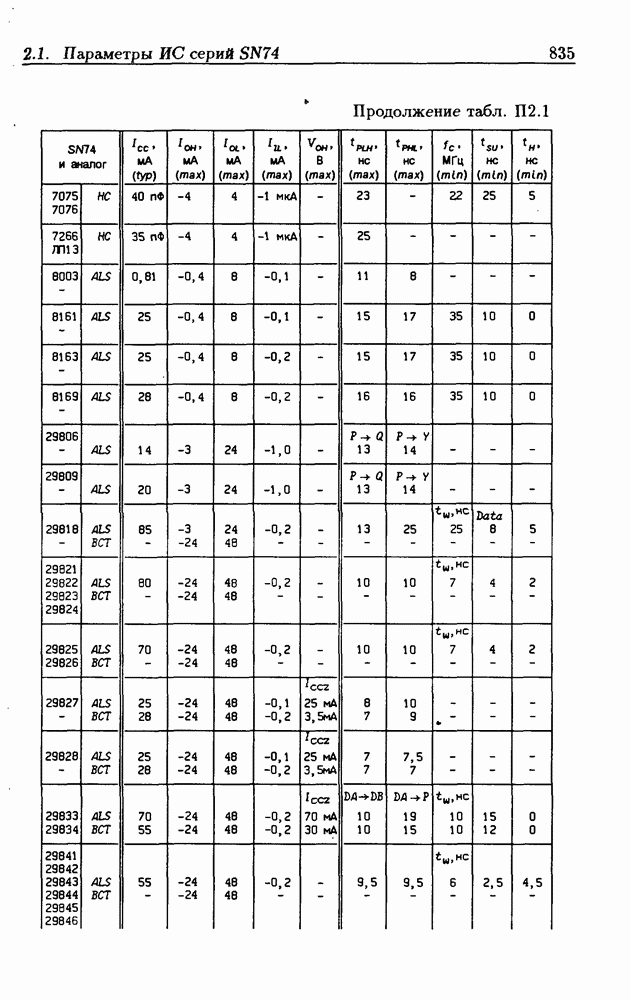
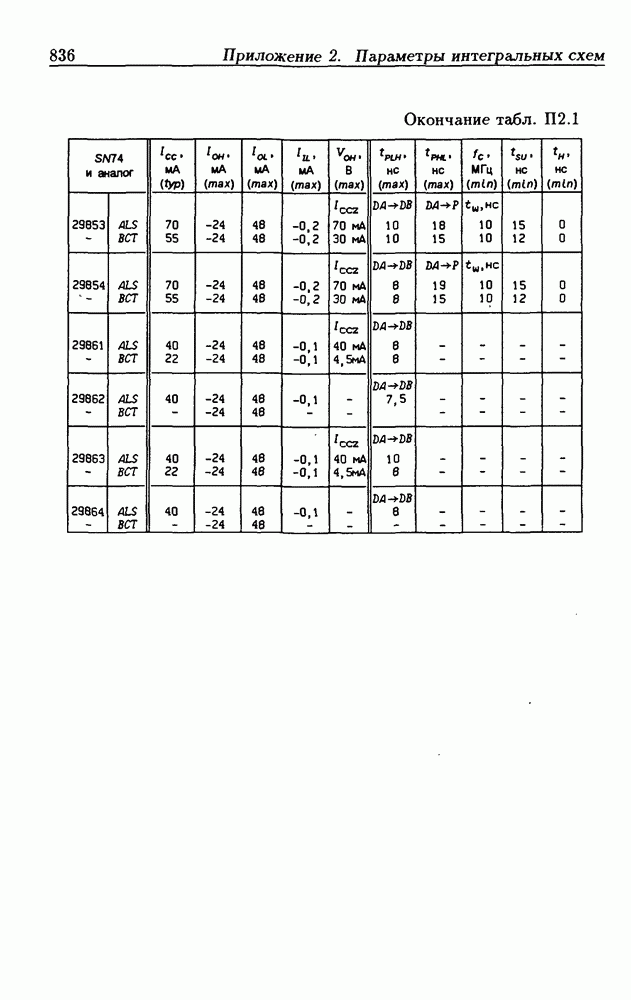
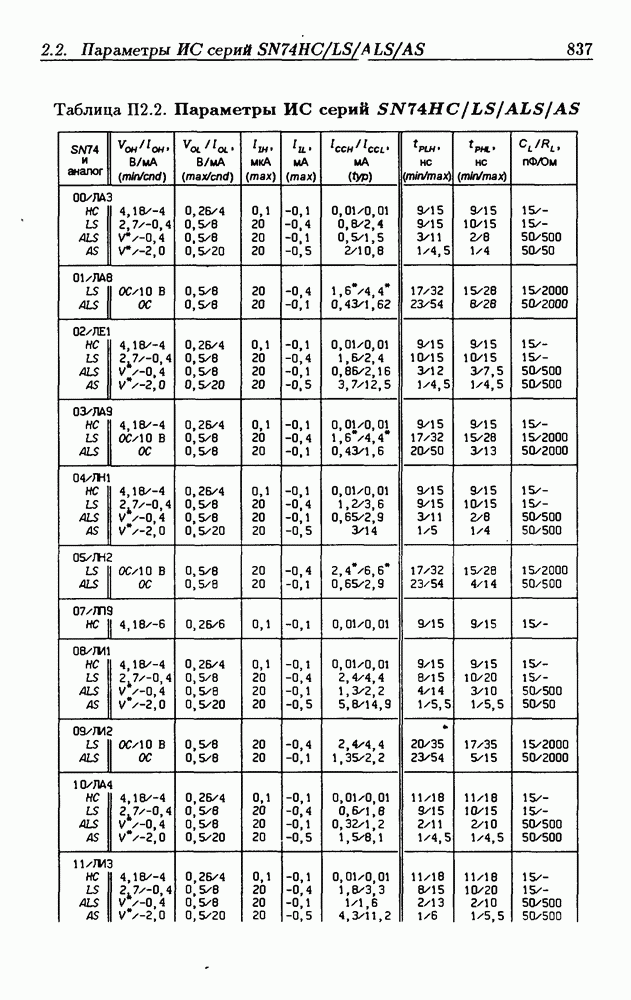
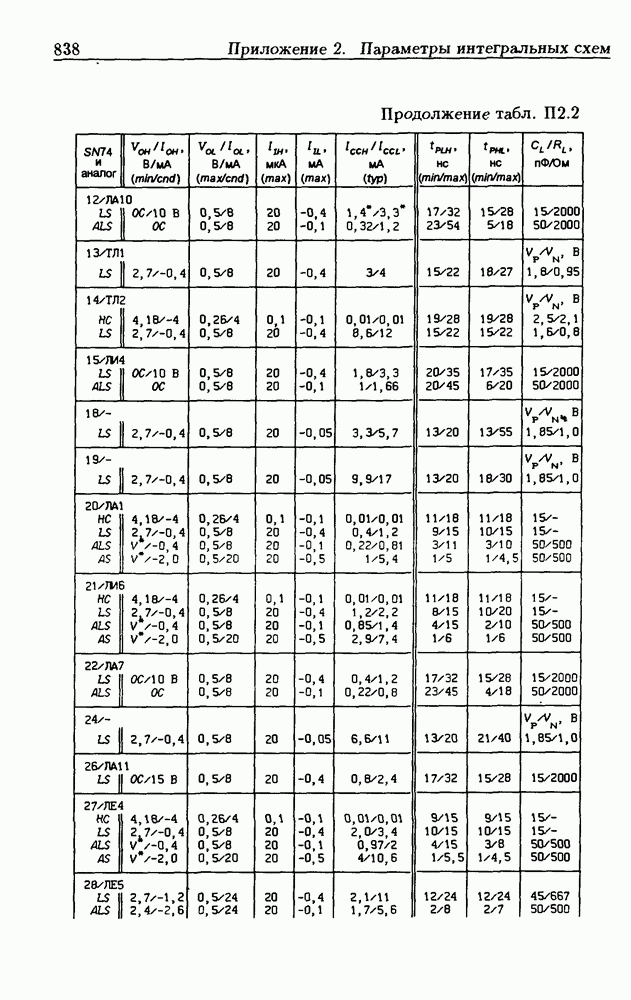
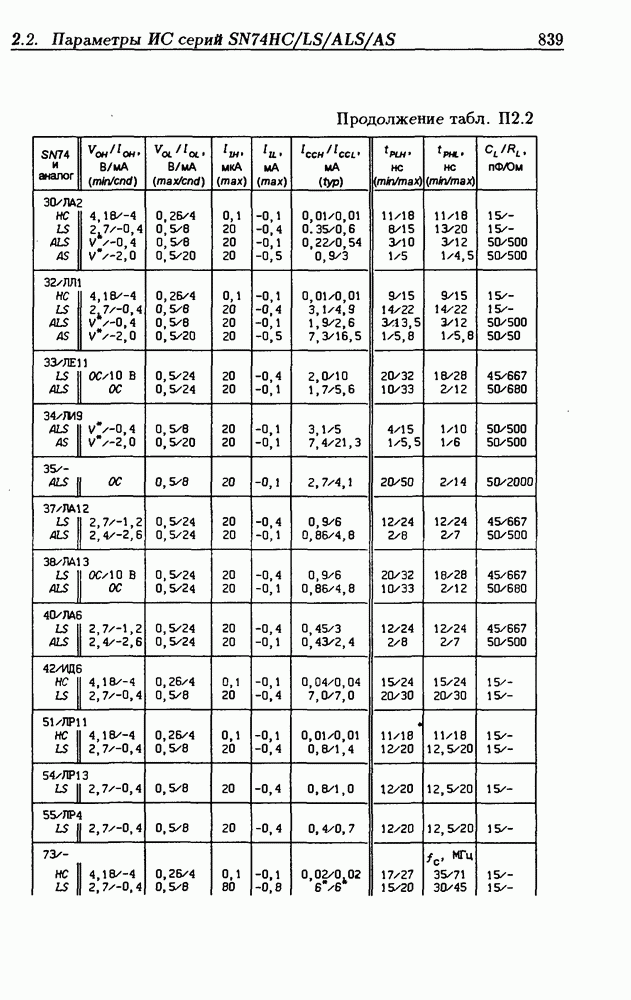
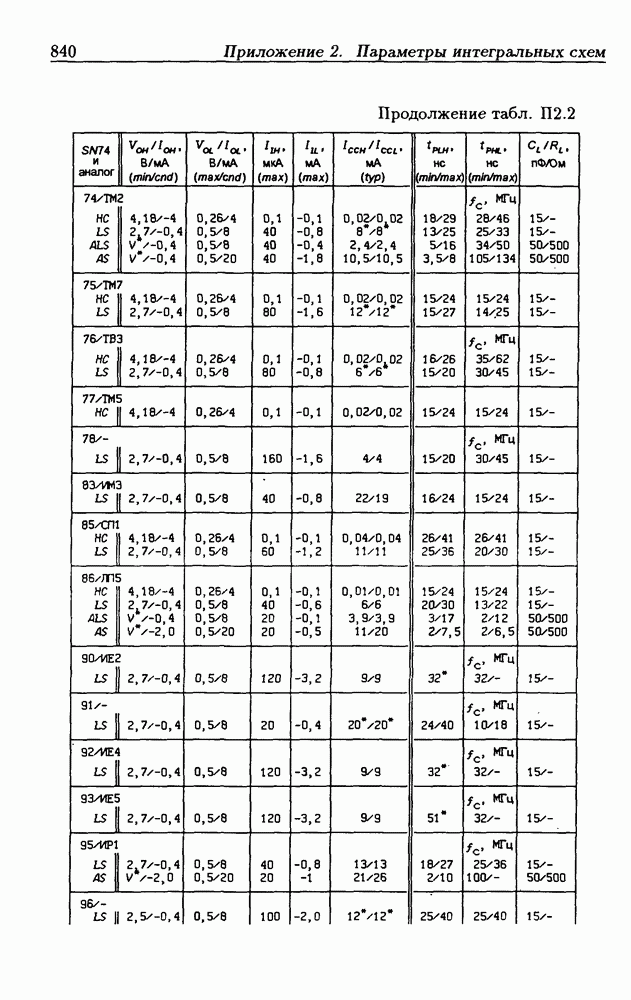
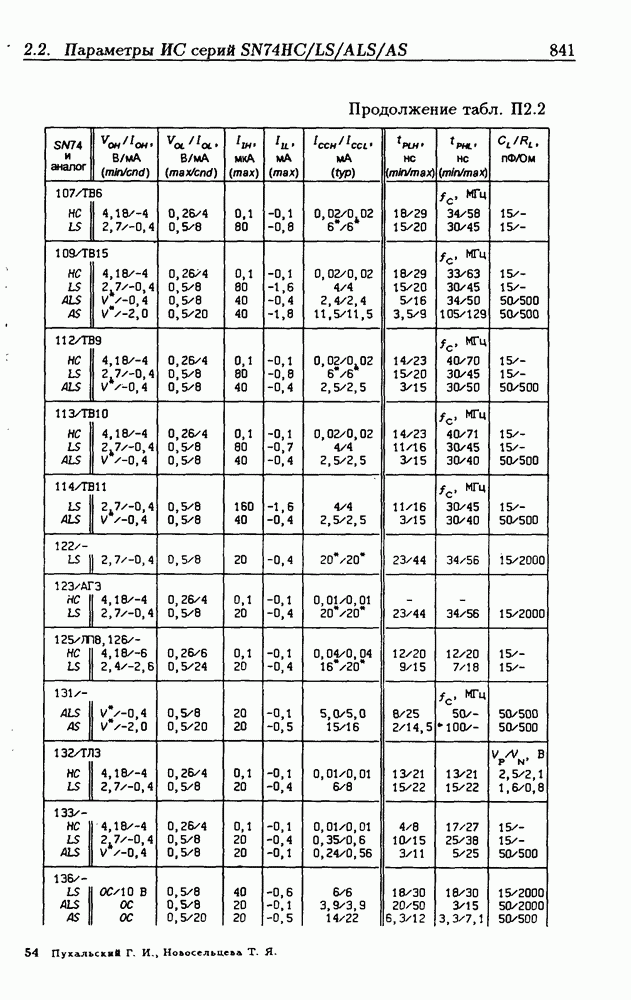
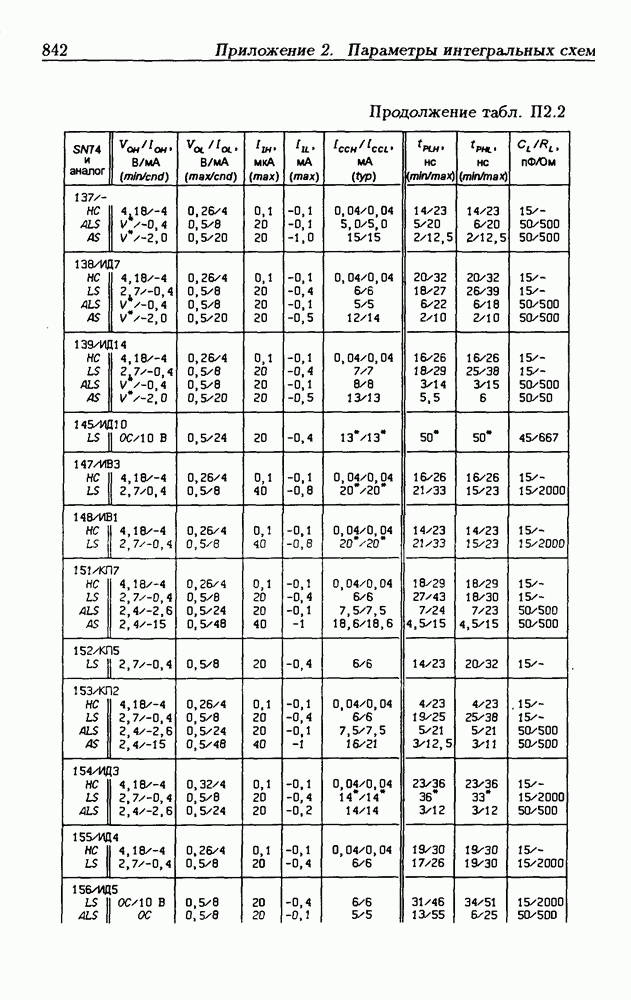
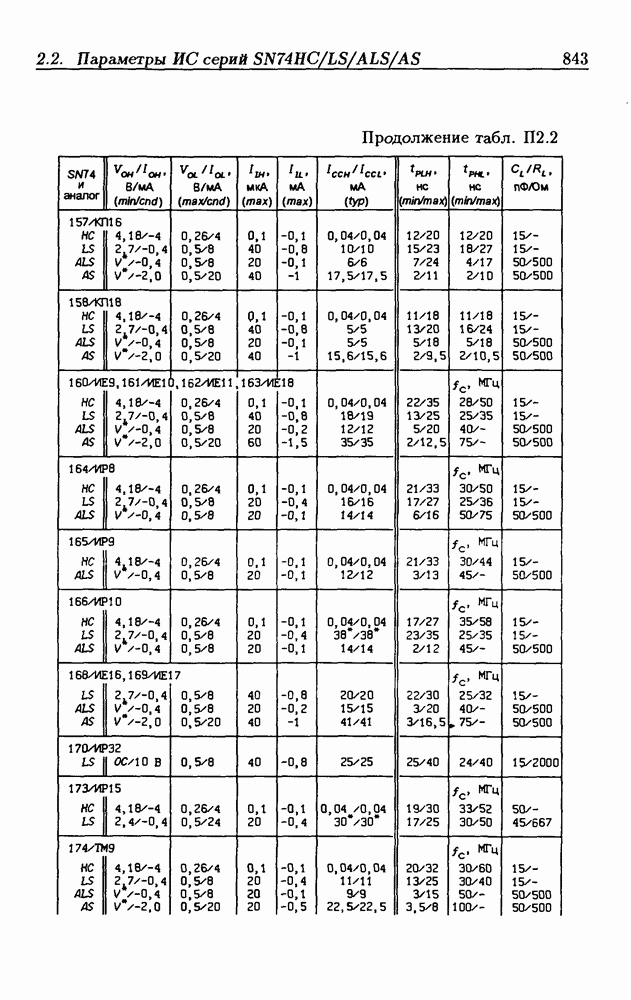
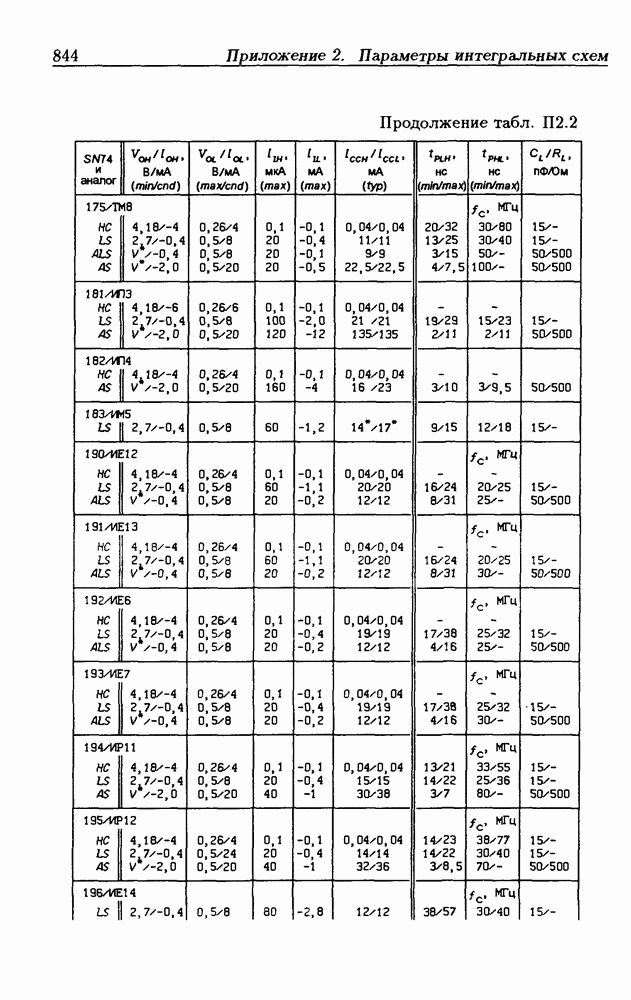
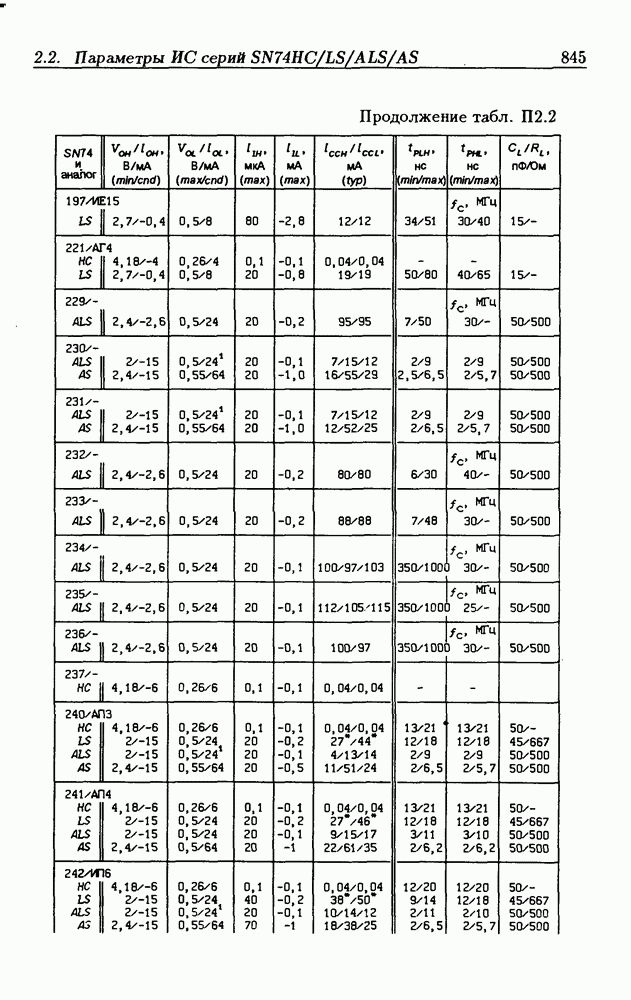
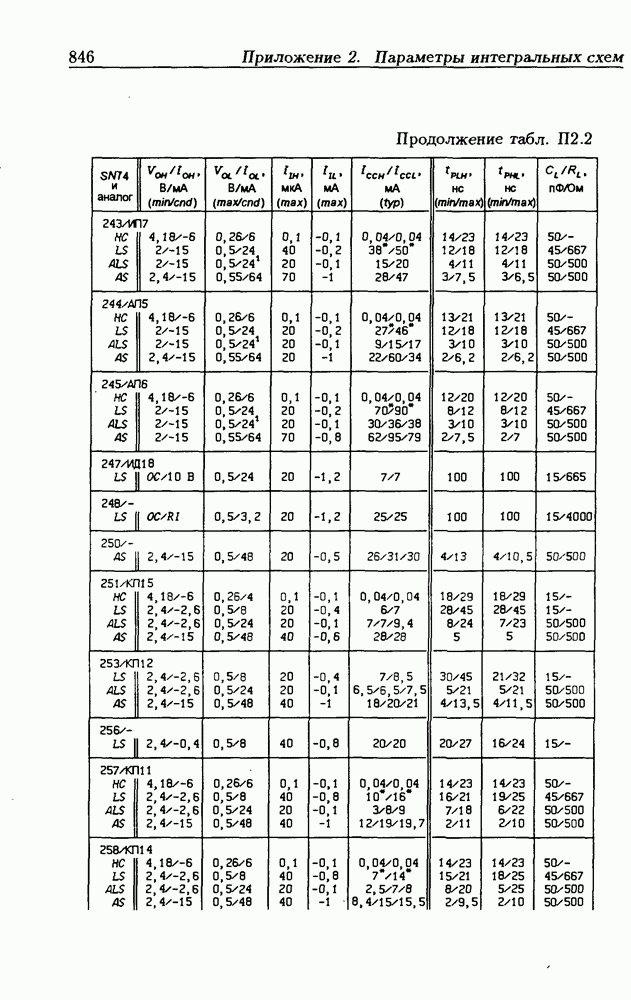
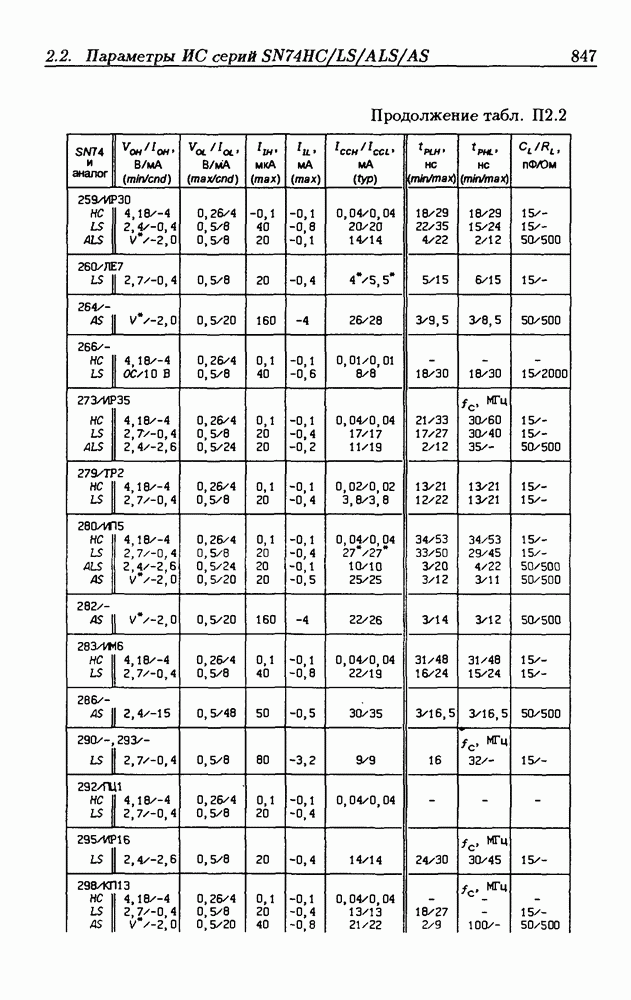
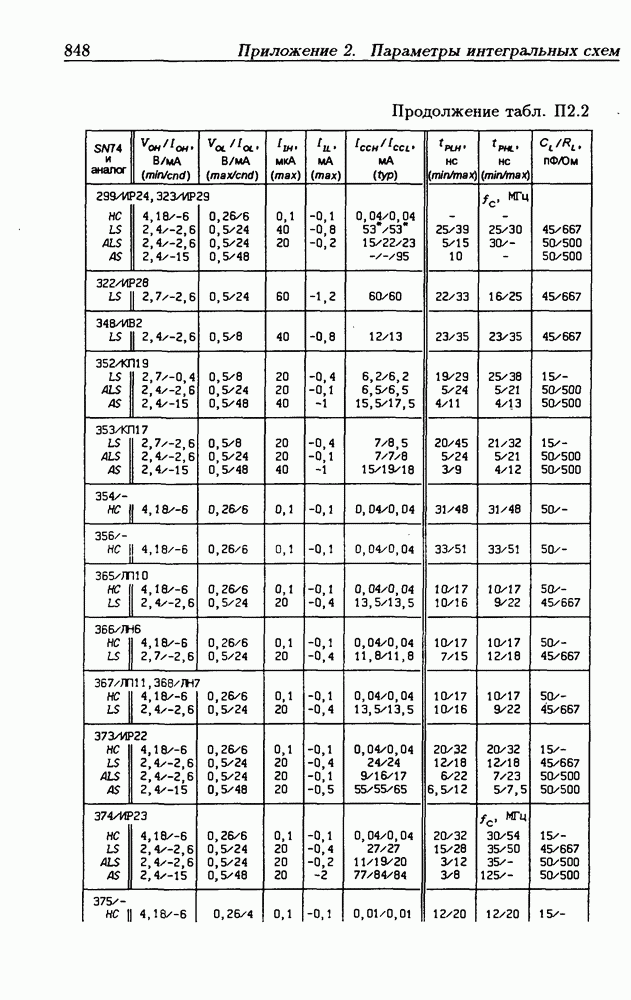
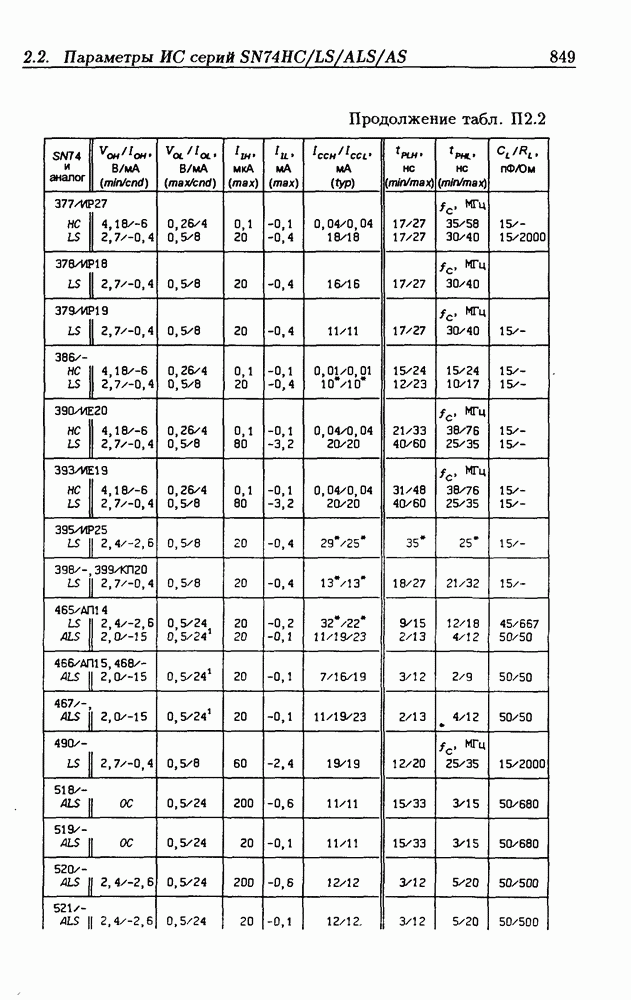
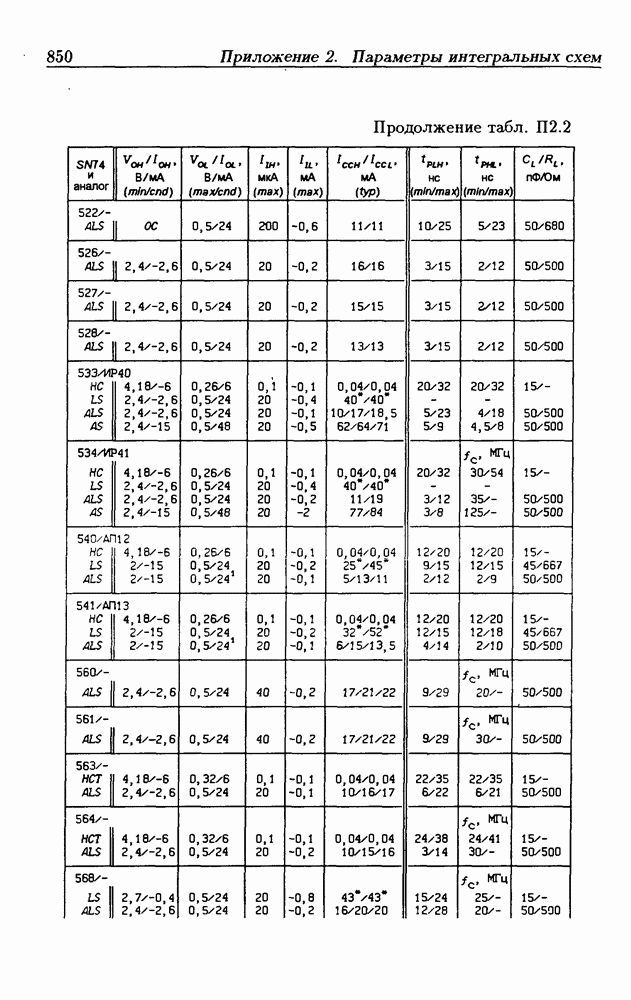
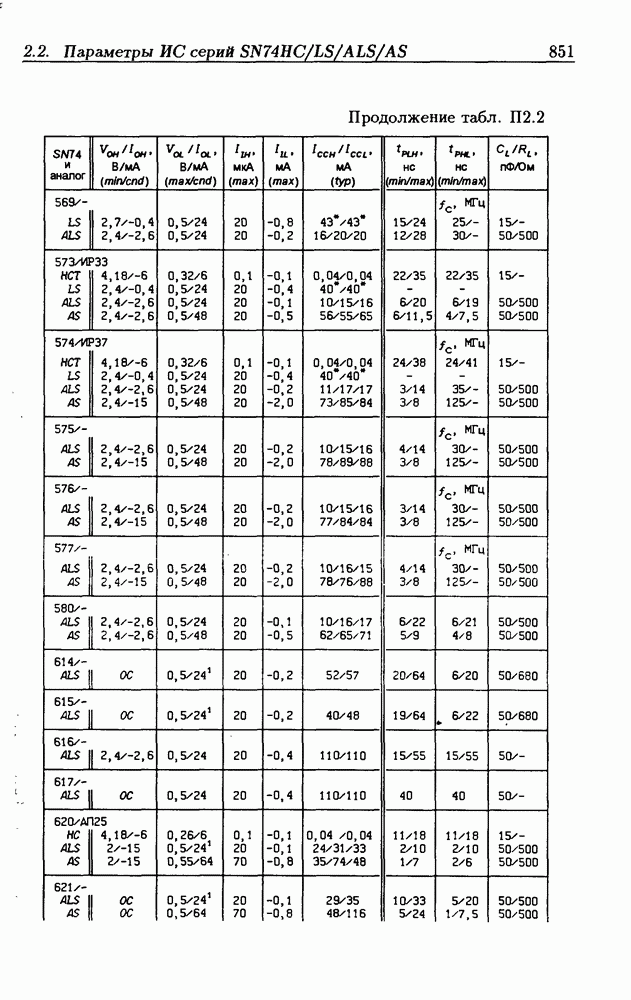
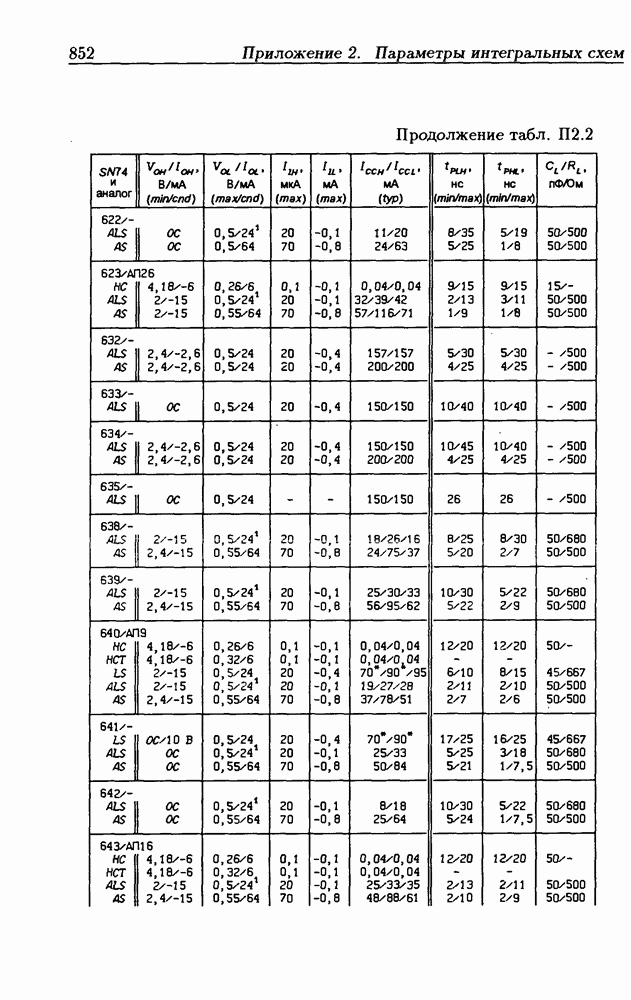
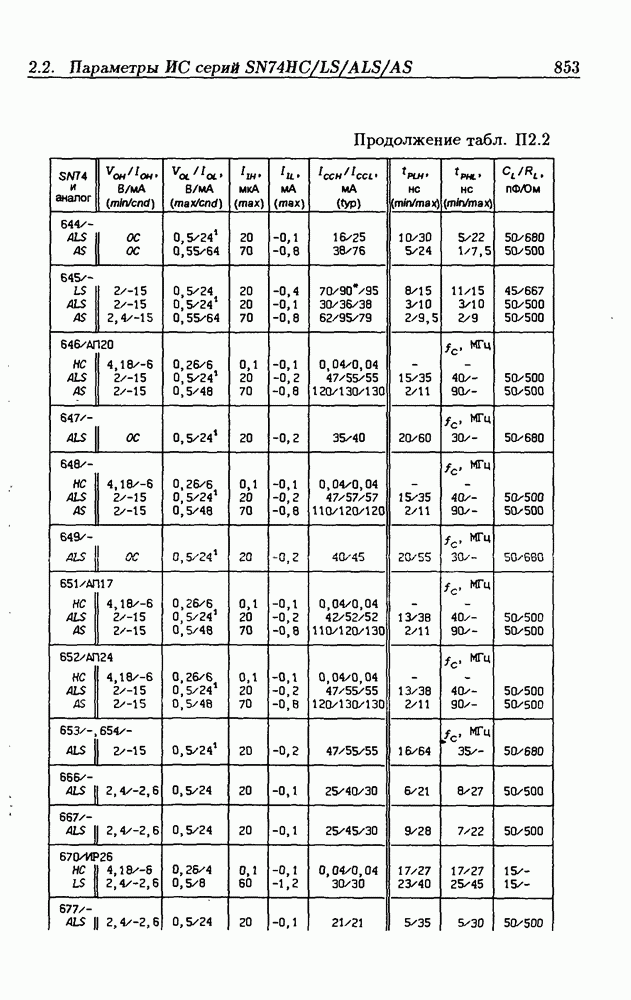
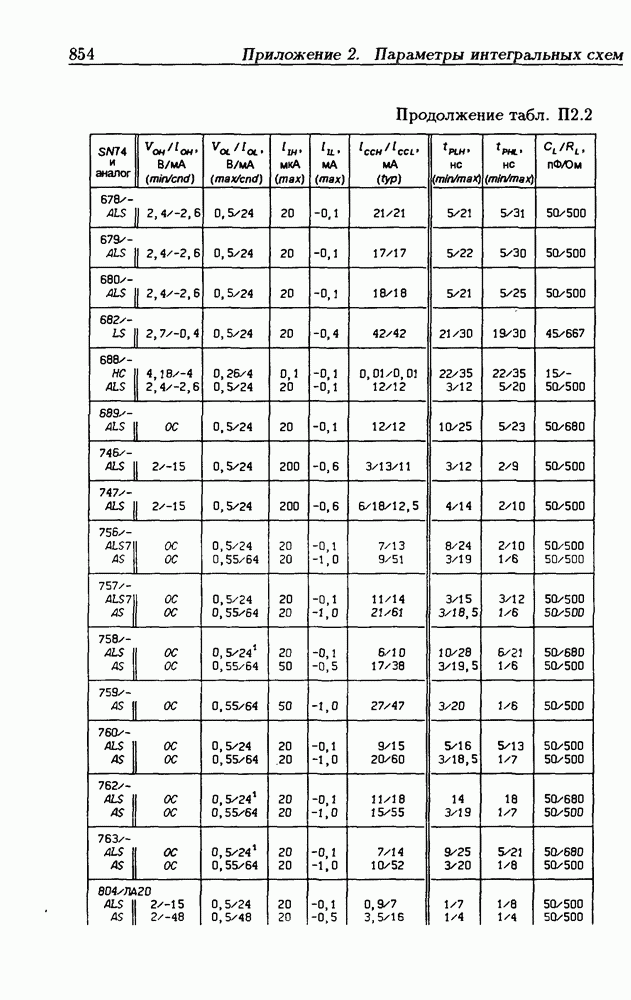
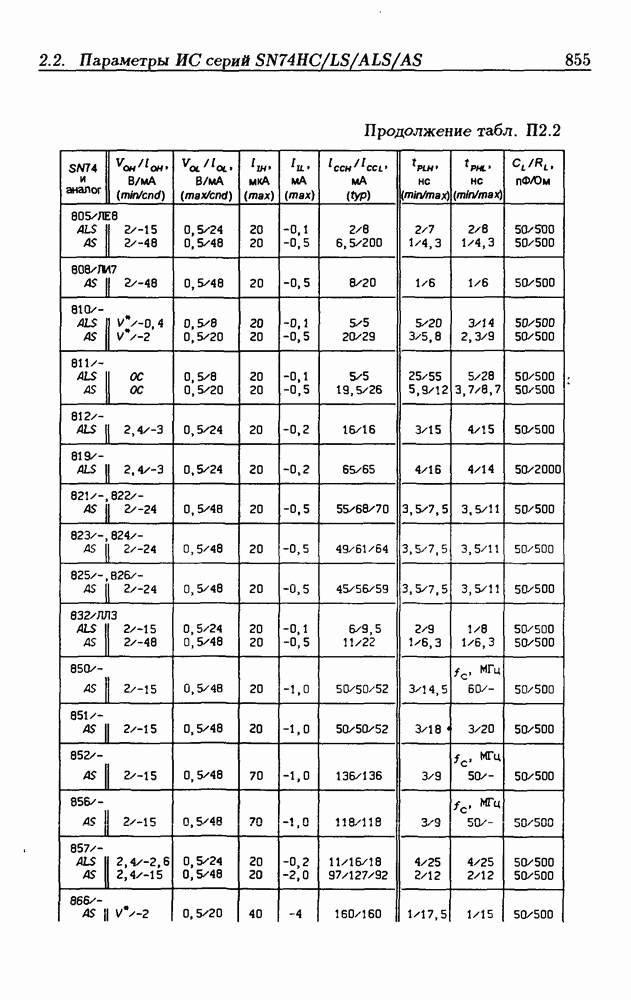
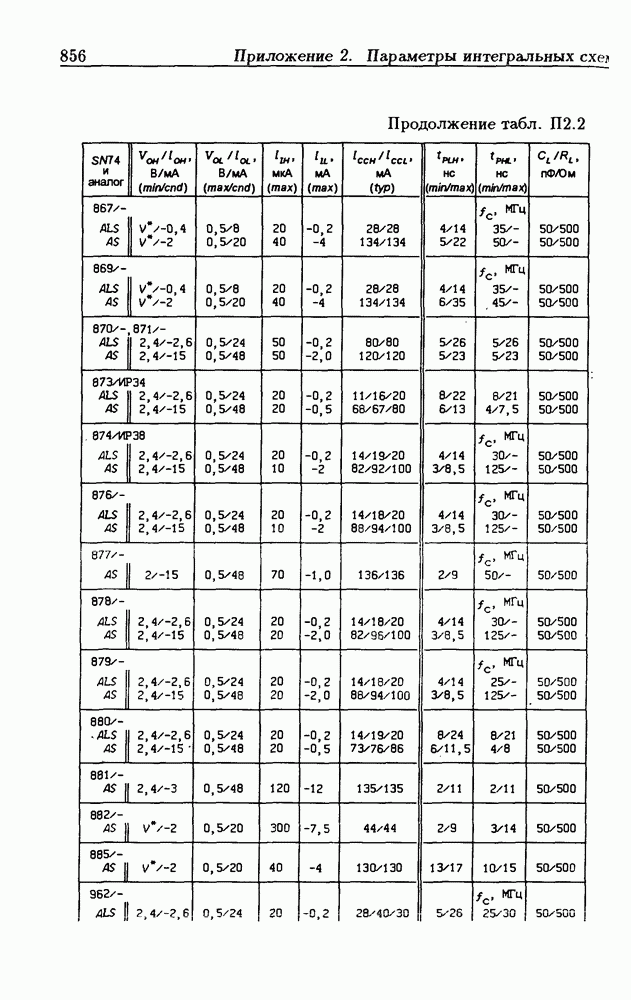
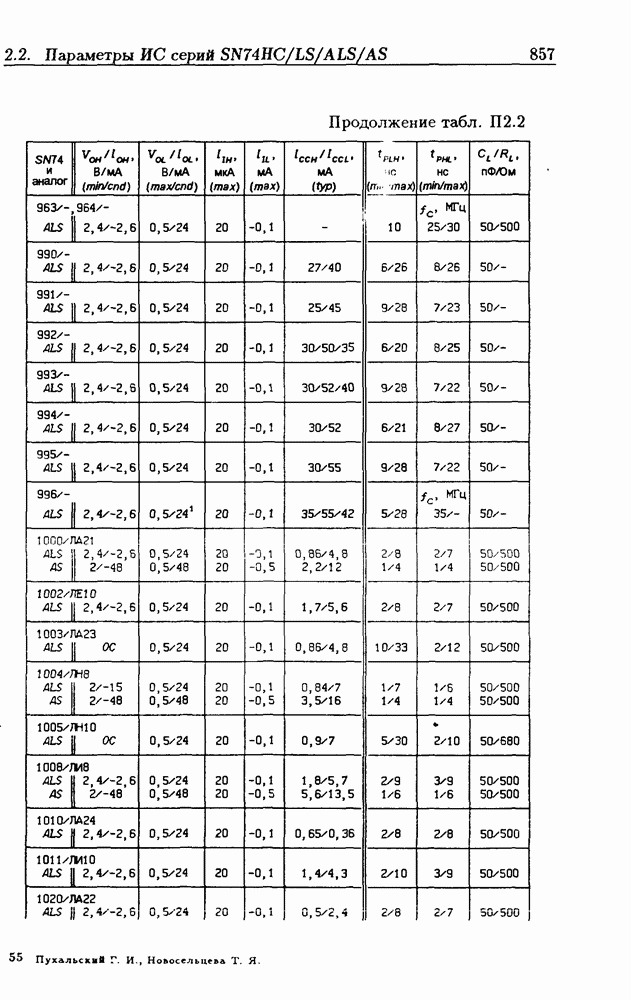
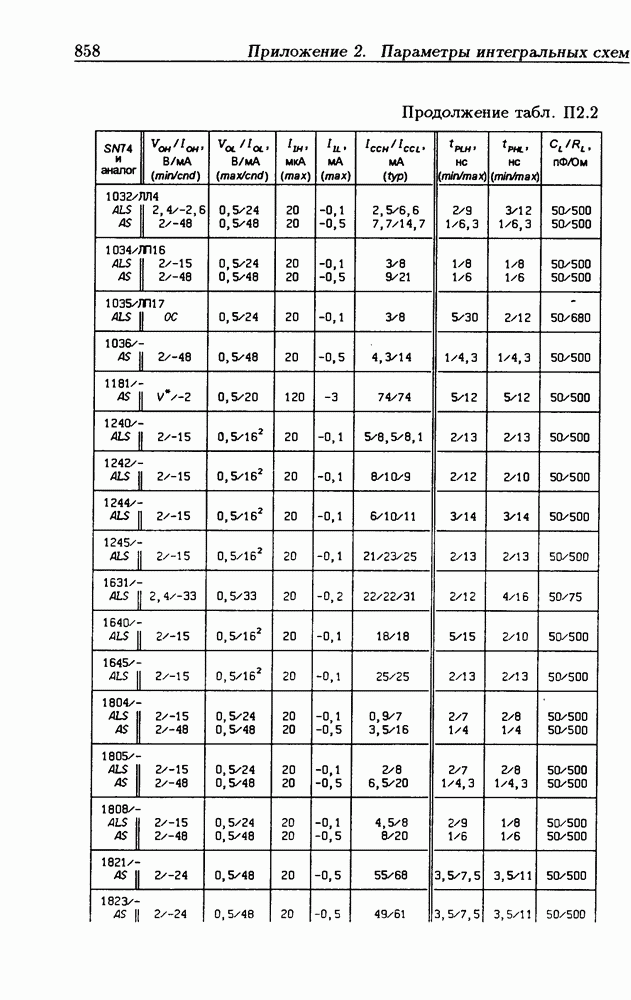
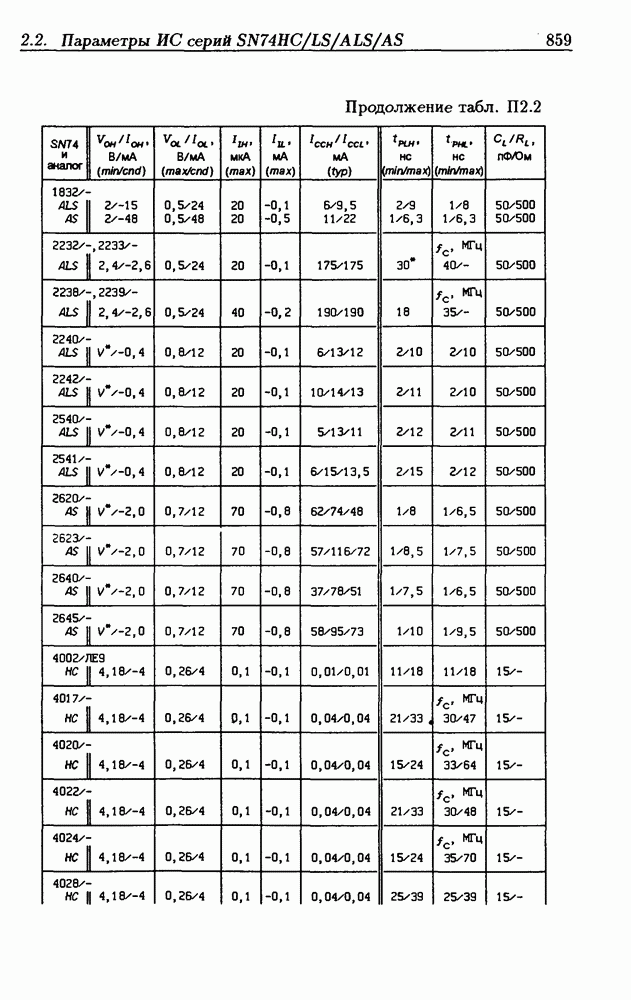
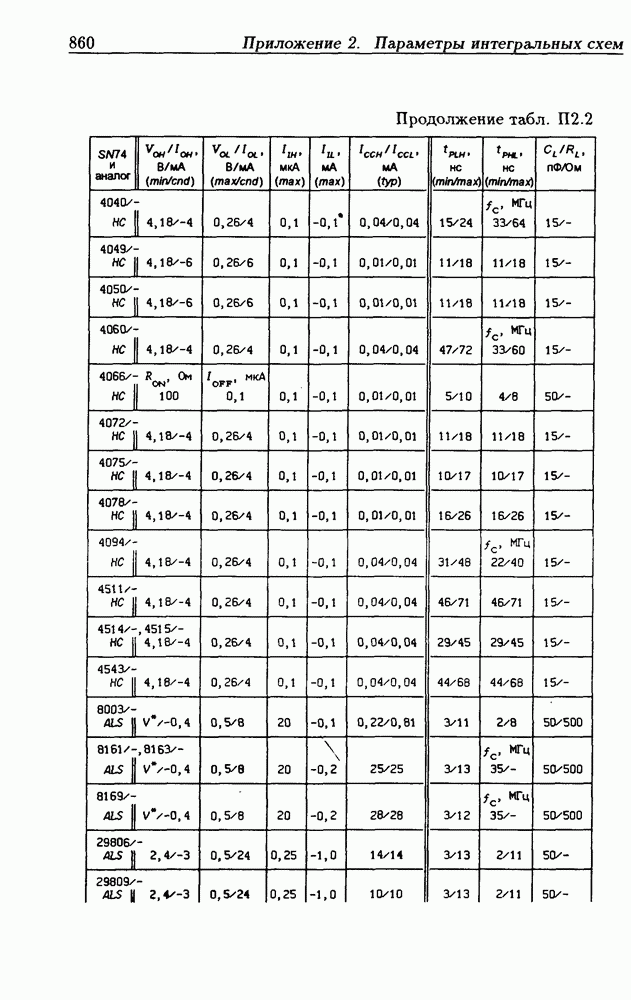
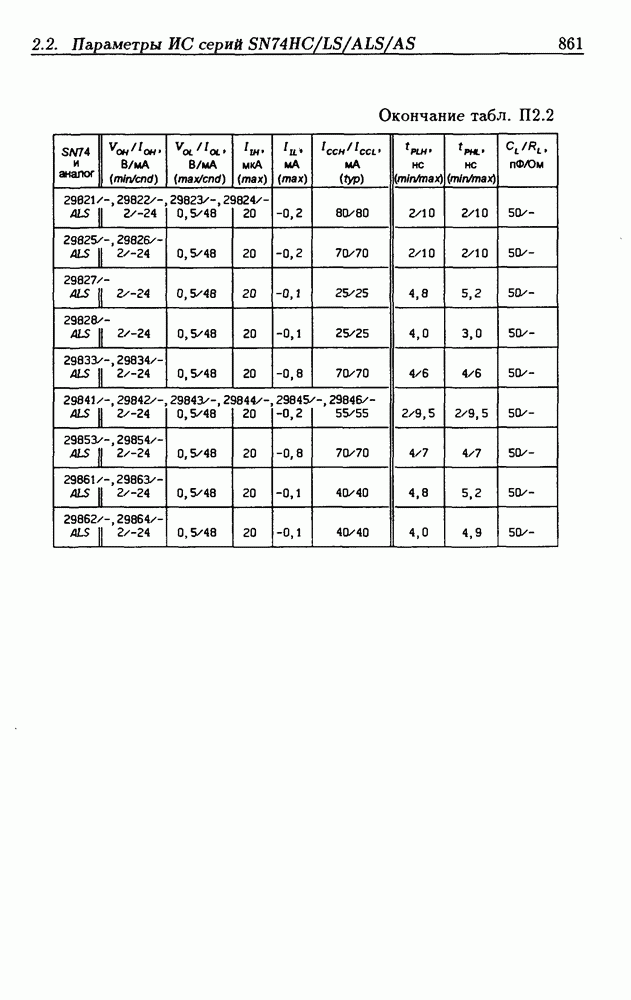
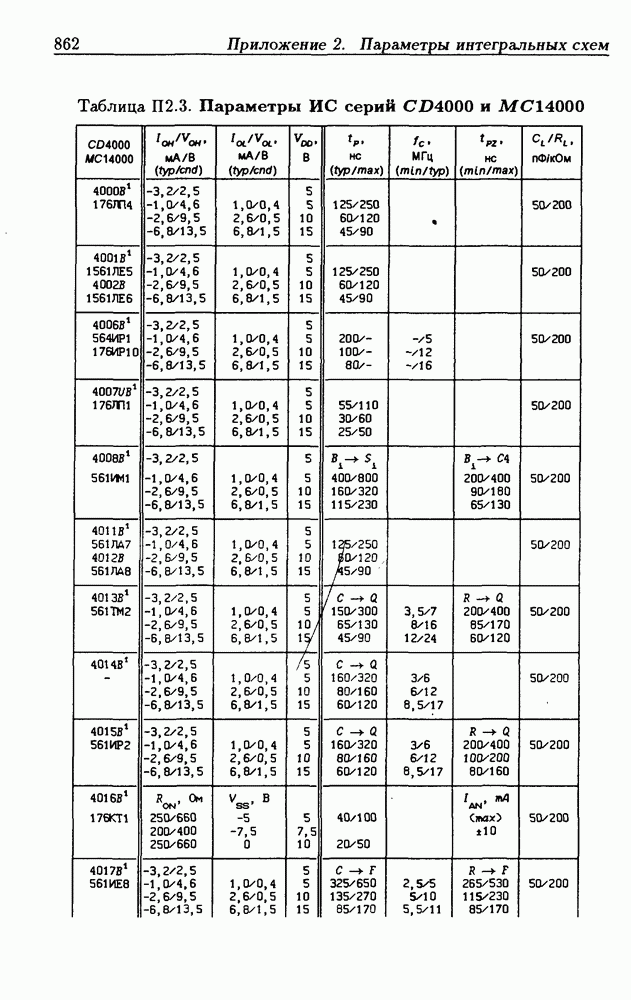
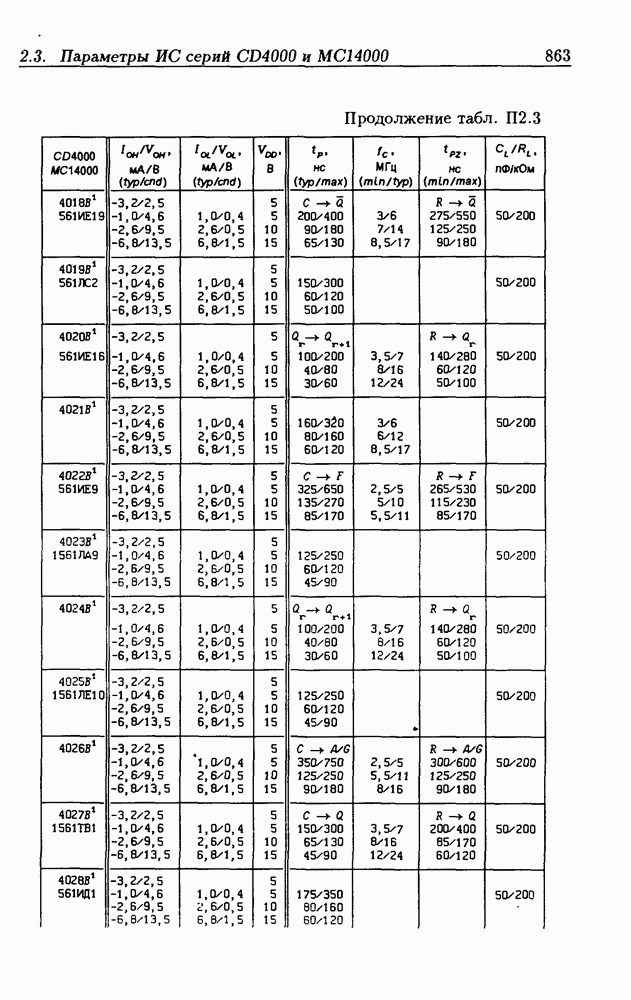
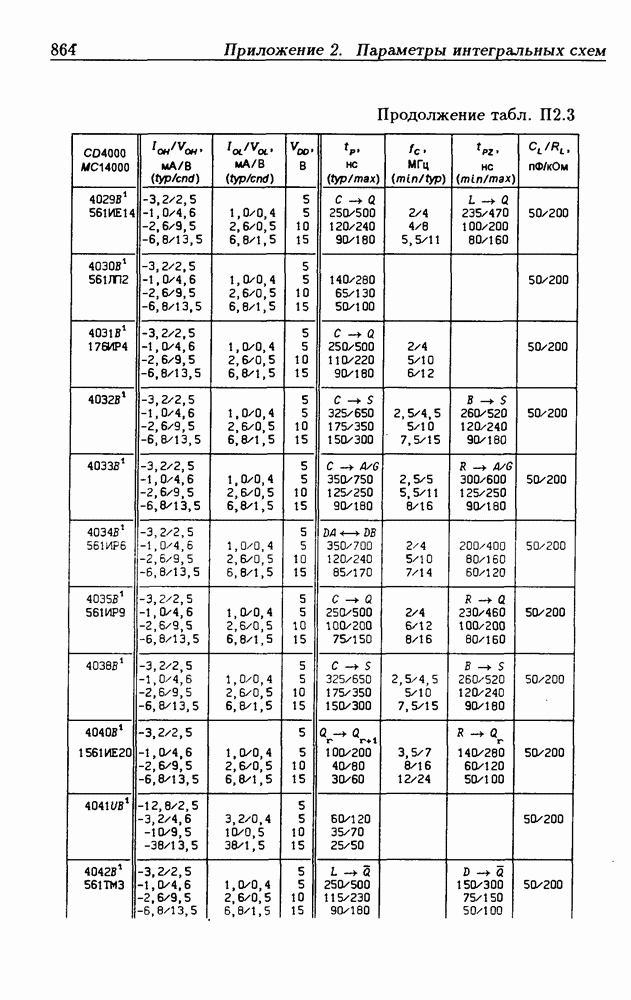
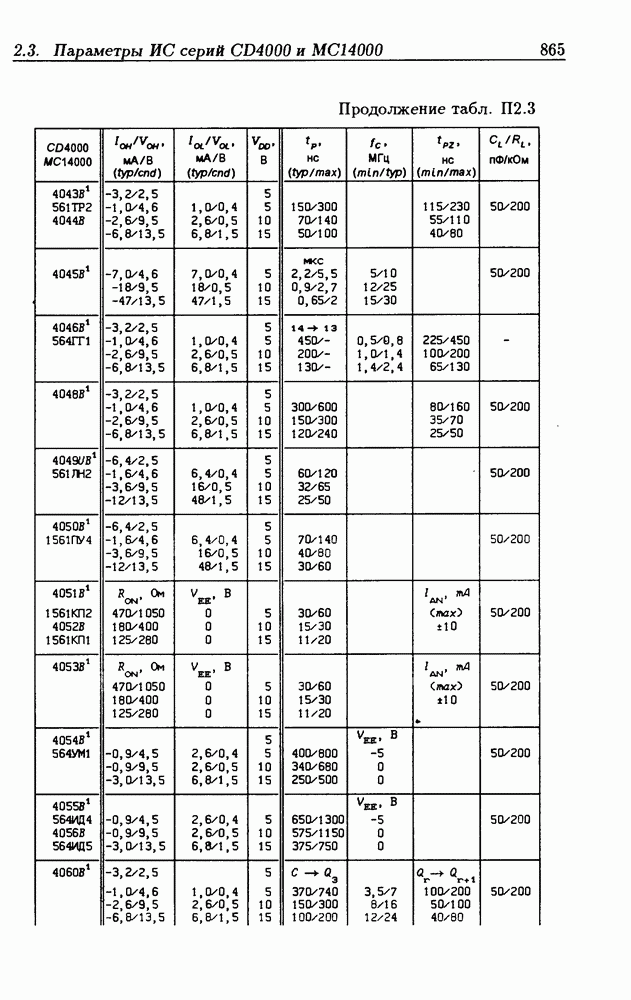
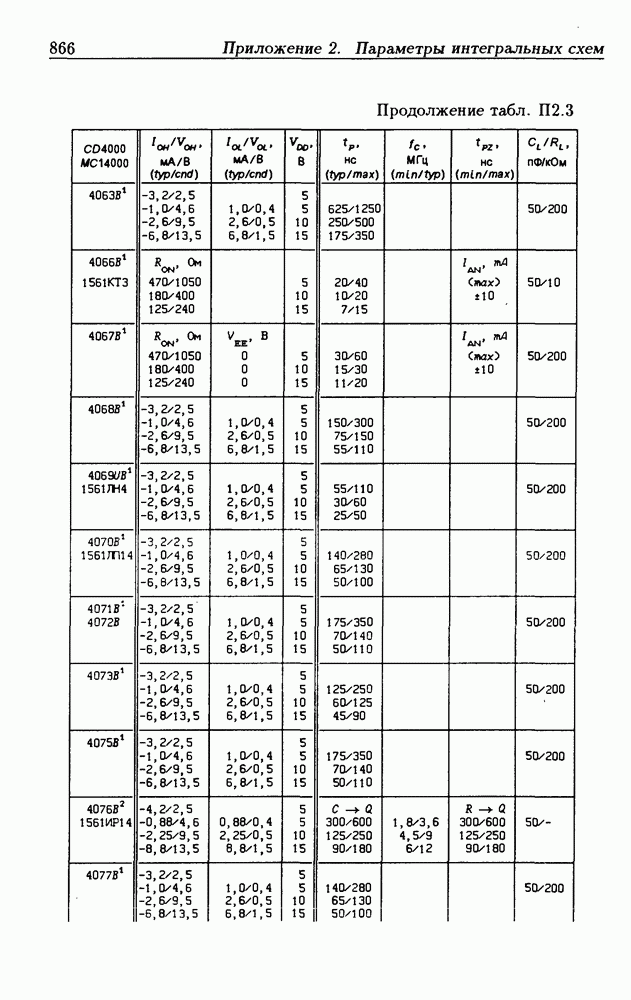
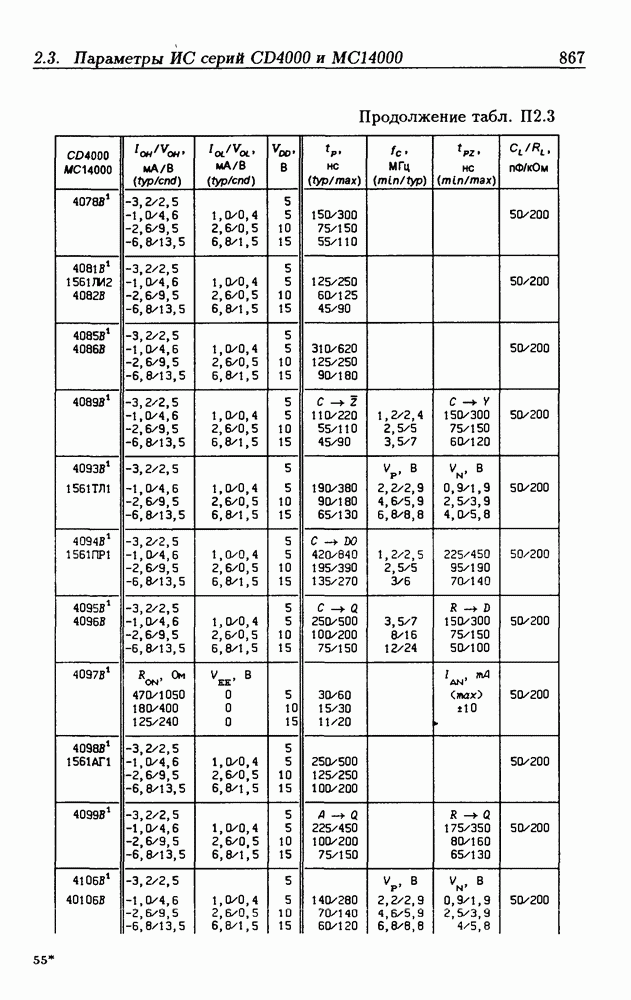
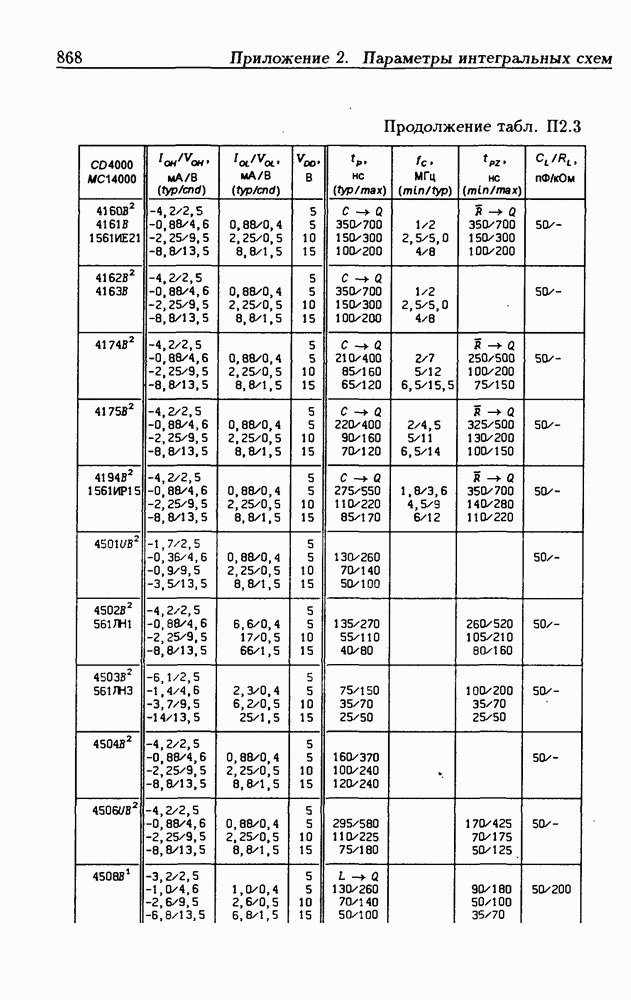
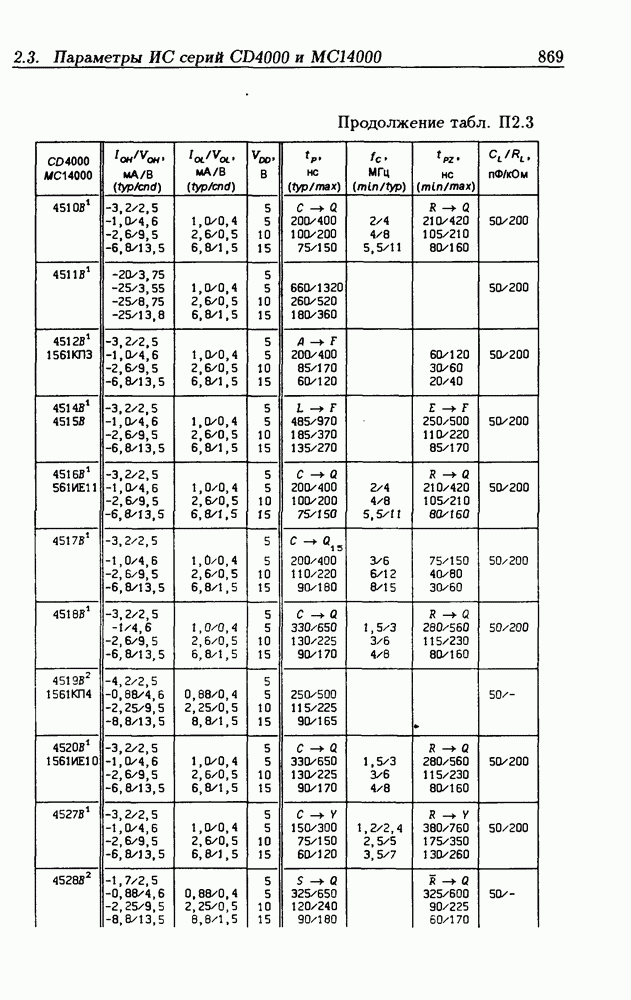
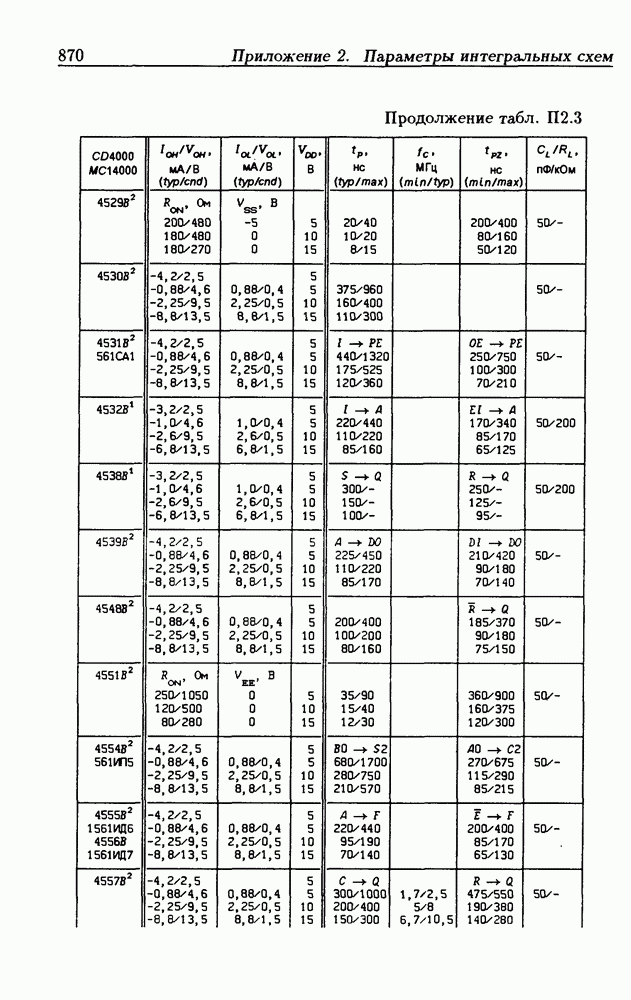
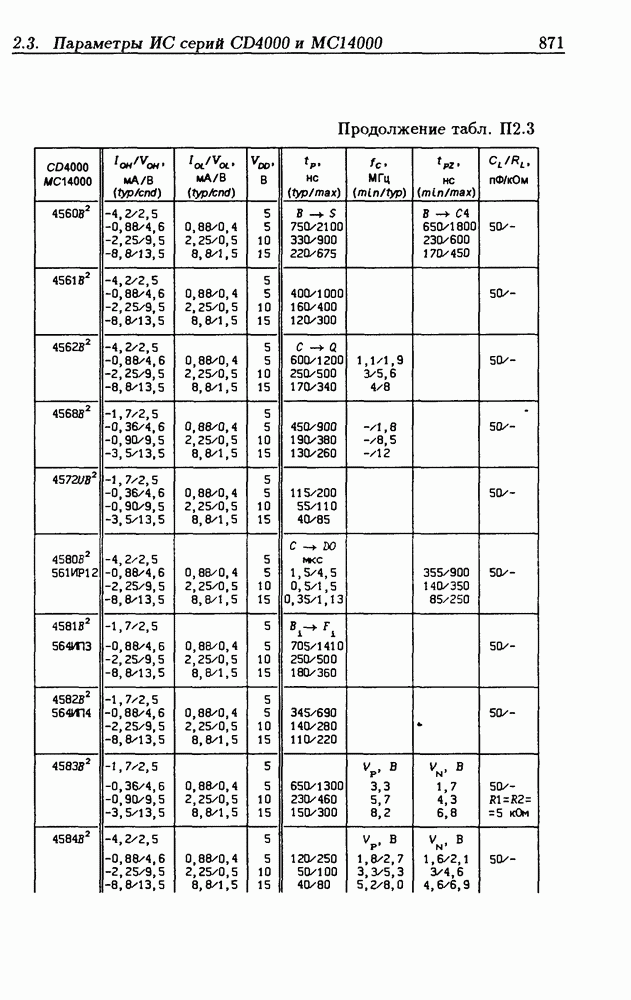
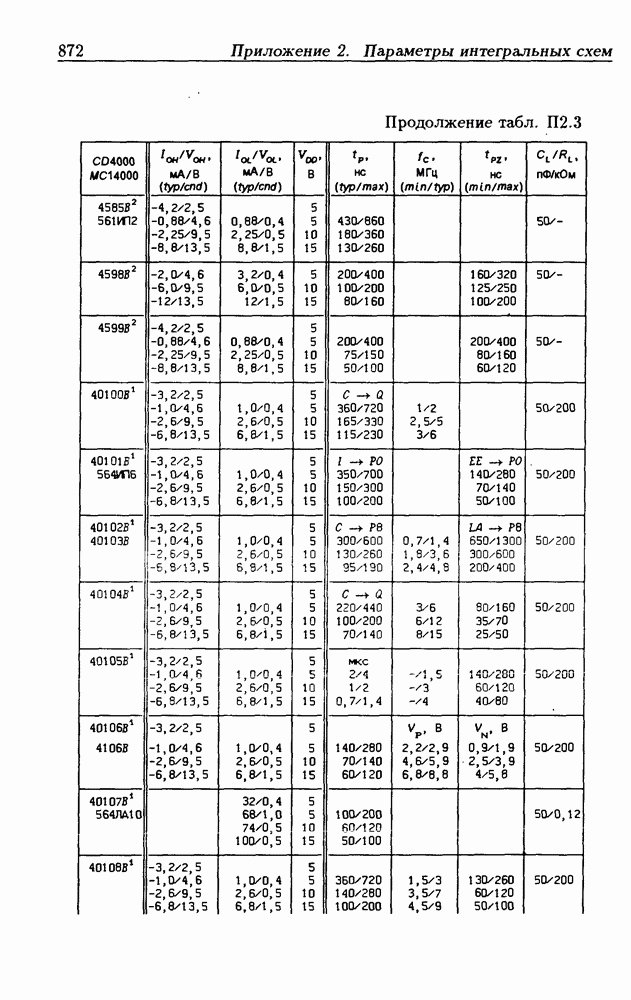
- Приложение 2. Параметры интегральных схем