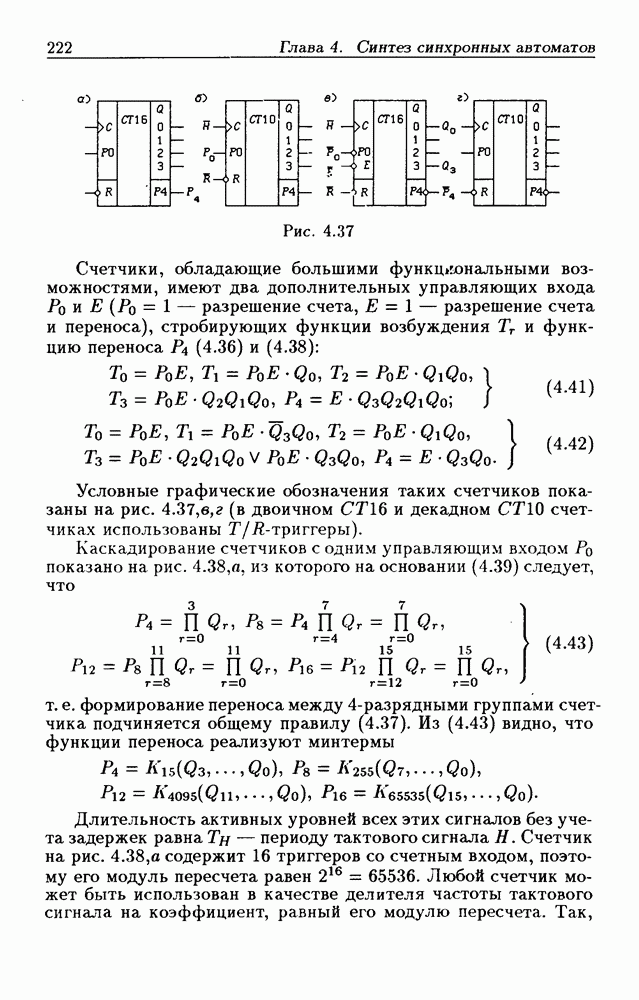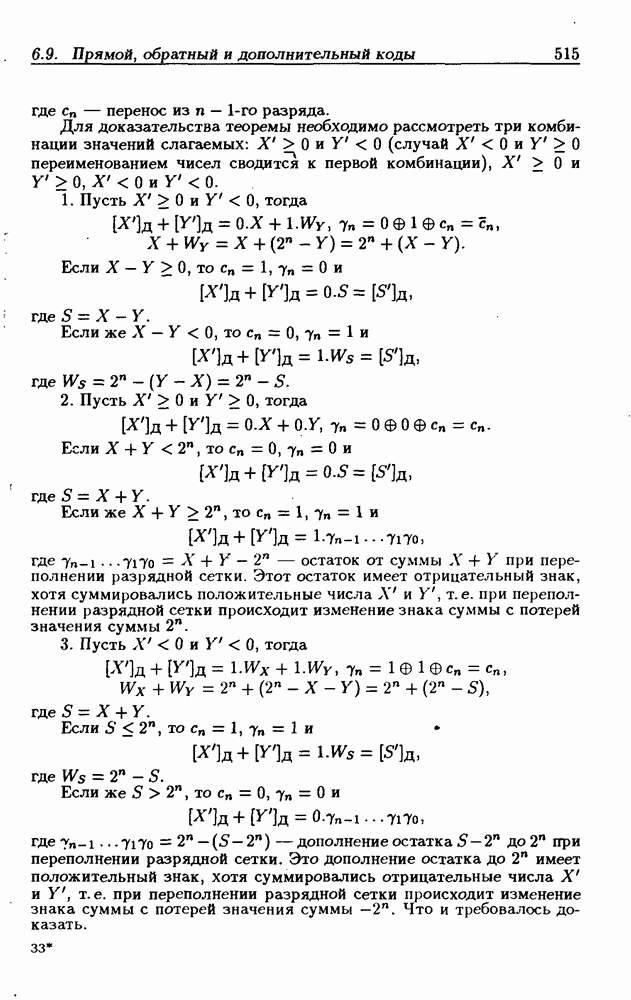| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Аналитический метод синтеза и анализа триггеров.
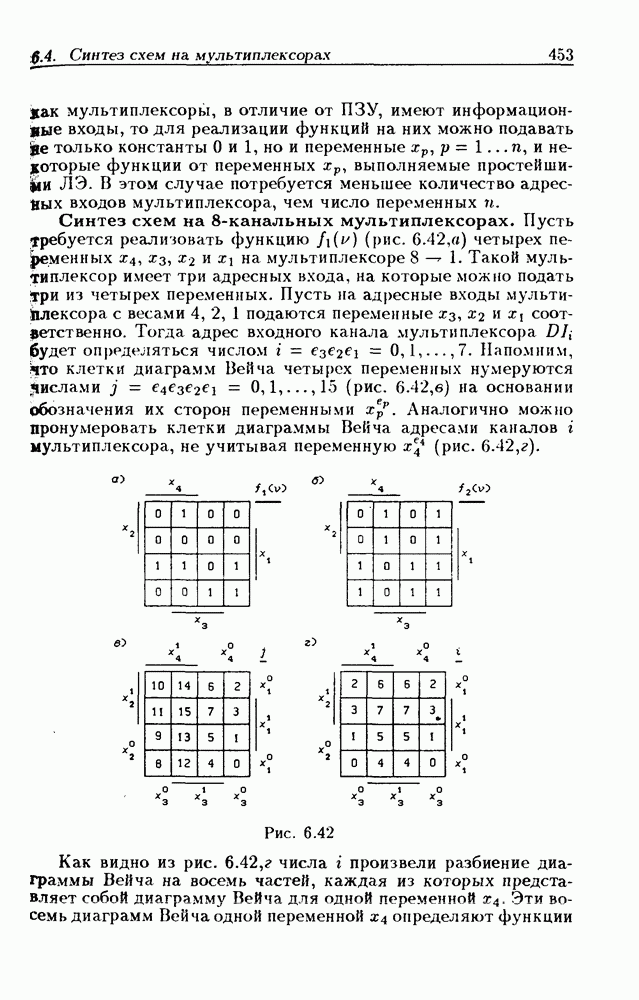
Выше изложен путь перехода от словесного описания закона функционирования триггера через таблицу истинности и диаграмму Вейча к аналитическому его заданию с помощью функции переходов. Однако такой путь представляет интерес только для первоначального знакомства с задачей описания триггеров, так как в нем отсутствуют регулярные правила, позволяющие получить функции переходов триггеров любого типа, в том числе и не описанных в литературе. Кроме того, словесное описание имеет недостаток, заключающийся в возможности неоднозначного его истолкования. Существенным же недостатком таблиц истинности является их громоздкость при большом числе информационных входов триггера.
Поскольку конечной целью является получение функции
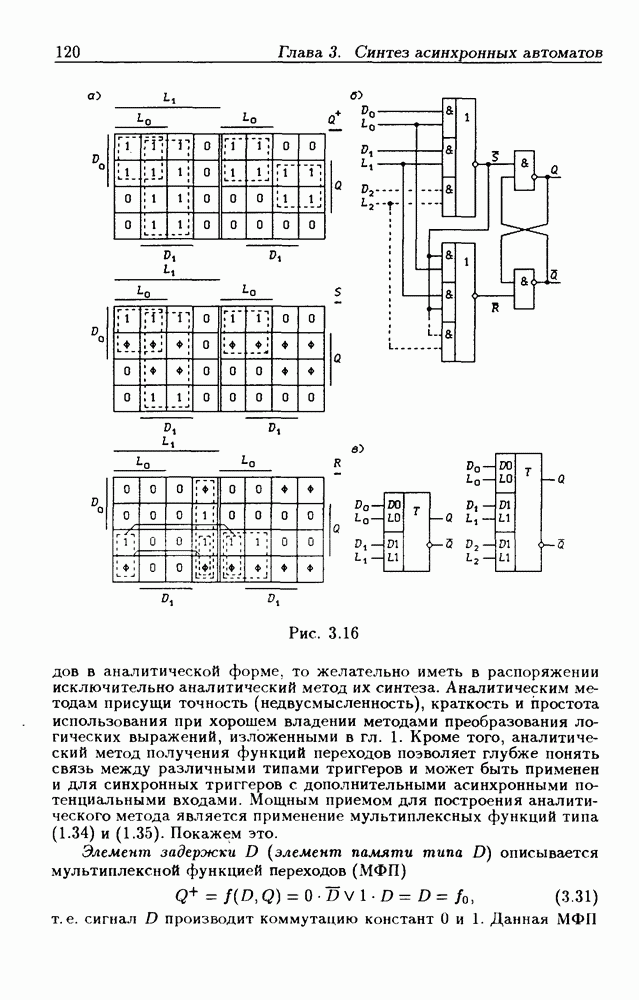
Рис. 3.16 (см. скан)
переходов в аналитической форме, то желательно иметь в распоряжении исключительно аналитический метод их синтеза. Аналитическим методам присущи точность (недвусмысленность), краткость и простота использования при хорошем владении методами преобразования логических выражений, изложенными в гл. 1. Кроме того, аналитический метод получения функций переходов позволяет глубже понять связь между различными типами триггеров и может быть применен и для синхронных триггеров с дополнительными асинхронными потенциальными входами. Мощным приемом для построения аналитического метода является применение мультиплексных функций типа (1.34) и (1.35). Покажем это.
Элемент задержки  (элемент памяти типа
(элемент памяти типа  описывается мультиплексной функцией переходов (МФП)
описывается мультиплексной функцией переходов (МФП)

т.е. сигнал  производит коммутацию констант 0 и 1. Данная МФП
производит коммутацию констант 0 и 1. Данная МФП
— вырожденная, так как не зависит от переменной  Элемент задержки является самым примитивным ЭП, поэтому он используется в основных моделях автоматов. Добавляя число входов у элемента задержки, можно получать ЭП и других типов.
Элемент задержки является самым примитивным ЭП, поэтому он используется в основных моделях автоматов. Добавляя число входов у элемента задержки, можно получать ЭП и других типов.
Добавим вход  производящий коммутацию функции
производящий коммутацию функции  и константы 0. Тогда МФП будет иметь вид
и константы 0. Тогда МФП будет иметь вид

Соответствующий этой функции ЭП будет представлять собой элемент задержки, на входе которого включен ЛЭ И. Такой ЭП следует назвать элементом памяти типа 
Добавим к полученному ЭП вход  производящий коммутацию функции
производящий коммутацию функции  и константы 1. Тогда МФП будет иметь вид:
и константы 1. Тогда МФП будет иметь вид:

Такой ЭП следует назвать элементом памяти типа  Функции переходов
Функции переходов  и (3.33) не зависят от сигнала
и (3.33) не зависят от сигнала  поэтому они не являются триггерами.
поэтому они не являются триггерами.
Для синтеза автоматов на этих ЭП следует найти их функции возбуждения. Так, например, решение уравнения (3.32) дает

При  функции возбуждения
функции возбуждения  т.е. получился элемент задержки со входом
т.е. получился элемент задержки со входом  и инверсным выходом
и инверсным выходом 
Функции переходов триггеров описываются выражениями типа (3.8), основной особенностью которых является вхождение в них состояния  в качестве аргумента, что обеспечивает длительное хранение информации (длительное запоминание входных воздействий). Поэтому для аналитического описания триггеров следует использовать мультиплексные функции с коммутацией сигнала
в качестве аргумента, что обеспечивает длительное хранение информации (длительное запоминание входных воздействий). Поэтому для аналитического описания триггеров следует использовать мультиплексные функции с коммутацией сигнала 
Пусть сигнал  производит коммутацию сигнала
производит коммутацию сигнала  и константы 0, тогда мультиплексная функция
и константы 0, тогда мультиплексная функция

Данная функция не является функцией переходов триггера, так как не обладает полной системой переходов. Действительно, если состояние  то сигнал
то сигнал  не может установить значение
не может установить значение  Поэтому для получения триггера следует добавить еще один сигнал 5, производящий коммутацию функции
Поэтому для получения триггера следует добавить еще один сигнал 5, производящий коммутацию функции  и константы 1:
и константы 1:

Данная функция обладает полной системой переходов, а значит задает триггер некоторого типа. Функция переходов (3.34) отличается от функции переходов (3.10), так как отсутствует ограничение, задаваемое уравнением  Поскольку при получении (3.34) последним мультиплексирование производил сигнал 5, то он имеет приоритет по отношению к сигналу
Поскольку при получении (3.34) последним мультиплексирование производил сигнал 5, то он имеет приоритет по отношению к сигналу  т. е. при подаче значений
т. е. при подаче значений  устанавливается состояние
устанавливается состояние  что следует из (3.34).
что следует из (3.34).
Триггер типа  с приоритетом входа
с приоритетом входа  можно синтезировать на основе
можно синтезировать на основе  -триггера, описываемого функцией переходов (3.10). В
-триггера, описываемого функцией переходов (3.10). В
результате будут получены функции возбуждения  По этим функциям можно построить схему на основе
По этим функциям можно построить схему на основе  -триггера, приведенного на рис. 3.4,в (для реализации функции
-триггера, приведенного на рис. 3.4,в (для реализации функции  следует добавить
следует добавить  Входные сигналы этого триггера будут иметь разные активные уровни:
Входные сигналы этого триггера будут иметь разные активные уровни: 
Функция переходов  -триггера с приоритетом входа
-триггера с приоритетом входа  получается мультиплексированием состояния
получается мультиплексированием состояния  и константы 1 сигналом
и константы 1 сигналом  с последующей коммутацией полученной функции и константы 0 сигналом
с последующей коммутацией полученной функции и константы 0 сигналом 

Этот же результат может быть получен коммутацией функции  и константы 0 сигналом
и константы 0 сигналом 

Схему  с приоритетом входа
с приоритетом входа  можно построить непосредственно по функции (3.35), переведя ее в базис И-НЕ:
можно построить непосредственно по функции (3.35), переведя ее в базис И-НЕ:

Если функцию (3.35) и константу 1 опять прокоммутировать сигналом  то заново будет получена функция переходов
то заново будет получена функция переходов  -триггера с приоритетом входа
-триггера с приоритетом входа  Такой результат является следствием свойства коммутаторов периодически повторять результат при неизменности коммутируемых функций.
Такой результат является следствием свойства коммутаторов периодически повторять результат при неизменности коммутируемых функций.
Сигнал  -триггере производит коммутацию сигнала
-триггере производит коммутацию сигнала  и функции
и функции  поэтому МФП имеет вид
поэтому МФП имеет вид

что совпадает с (3.15). Добавим вход  производящий коммутацию функции
производящий коммутацию функции  и константы 0. Тогда МФП будет иметь вид
и константы 0. Тогда МФП будет иметь вид

что совпадает с (3.21). Так как сигнал  последним производит коммутацию, то он имеет приоритет по отношению к сигналу
последним производит коммутацию, то он имеет приоритет по отношению к сигналу 
Пусть теперь тот же сигнал  производит коммутацию функций
производит коммутацию функций 

что совпадает с (3.25). Здесь вход  имеет приоритет по отношению ко входу
имеет приоритет по отношению ко входу  так как он последним производил коммутацию. Этот же результат может быть получен коммутацией сигналом
так как он последним производил коммутацию. Этот же результат может быть получен коммутацией сигналом  функций
функций 
Если функции  в выражении (3.38) поменять местами, то получится
в выражении (3.38) поменять местами, то получится  -триггер нового типа:
-триггер нового типа:

Здесь ни один из входов не имеет приоритета.
Коммутация сигналом ML (Master Load) функций  дает МФП
дает МФП

описывающую  -триггер с двумя входами загрузки
-триггер с двумя входами загрузки  и ML и приоритетами информационных входов:
и ML и приоритетами информационных входов:  наибольший приоритет,
наибольший приоритет,  средний приоритет,
средний приоритет,  наименьший приоритет.
наименьший приоритет.
Коммутация сигналом MR (Master Reset) функции  и константы 0 дает МФП
и константы 0 дает МФП

описывающую  -триггер с двумя входами сброса
-триггер с двумя входами сброса  и MR и приоритетами информационных входов:
и MR и приоритетами информационных входов:  наибольший приоритет,
наибольший приоритет,  средний приоритет,
средний приоритет,  наименьший приоритет.
наименьший приоритет.
По функциям переходов триггеров достаточно легко установить, какие значения входных сигналов изменяют их состояния. Для этого удобно использовать оператор переходов  Действительно, состояние триггера изменяется с 1 на 0, если
Действительно, состояние триггера изменяется с 1 на 0, если  и с 0 на 1, если
и с 0 на 1, если  где в соответствии с определением оператора переходов (2.1)
где в соответствии с определением оператора переходов (2.1)

На основании (3.39) и (3.40) будем иметь:

 -триггер без приоритетных входов изменяет состояние с 1 на 0 под воздействием значения функции
-триггер без приоритетных входов изменяет состояние с 1 на 0 под воздействием значения функции  а с 0 на 1 — под воздействием значения функции
а с 0 на 1 — под воздействием значения функции  Из последних соотношений наглядно видно, что приоритета не имеет ни один из входов (сигналы
Из последних соотношений наглядно видно, что приоритета не имеет ни один из входов (сигналы  во всех случаях связаны операцией
во всех случаях связаны операцией 
Для других типов триггеров в соответствии с (3.10), (3.34) - (3.38) и (3.40) будем иметь:

Уже из этих элементарных примеров видно, сколь эффективен аналитический метод синтеза и анализа последовательностных схем. Кроме того, он всегда точно и исчерпывающе дает ответ на все поставленные вопросы.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Основы теории переключательных функций
- 1.2. Позиционные системы счисления
- 1.3. Переключательные функции
- 1.4. Принцип и закон двойственности
- 1.5. Теоремы разложения
- 1.6. Решение систем логических уравнений
- 1.7. Первичные термы, минтермы и макстермы
- 1.8. Совершенные нормальные формы представления функций
- 1.9. Конъюнктивные и дизъюнктивные термы
- 1.10. Минимизация переключательных функций
- 1.11. Диаграммы Вейча
- 1.12. Минимизация неполностью определенных функций, совместная минимизация нескольких функций
- 1.13. Скобочные формы функций
- 1.14. Закон двойственности для логических схем
- 1.15. Линейные функции
- Глава 2. Анализ и синтез логических схем
- 2.2. Модели логических элементов
- 2.3. Модели логических схем
- 2.4. Анализ логических схем
- 2.5. Синтез комбинационных схем, свободных от состязаний
- Глава 3. Синтез асинхронных потенциальных автоматов
- 3.2. Асинхронные потенциальные автоматы
- 3.3. Асинхронные потенциальные триггеры и элементы памяти
- Триггеры типа R-S
- Триггеры типа D-L
- Триггеры типа D-L-R с приоритетом входа R.
- Триггеры типа D-L-R с приоритетом входа L.
- Триггеры типа R-S-L.
- Триггеры типа DN-LN
- Аналитический метод синтеза и анализа триггеров.
- 3.4. Задание асинхронных потенциальных автоматов таблицами и графами переходов
- 3.5. Синтез асинхронных потенциальных счетчиков
- 3.6. Синтез асинхронных импульсных триггеров
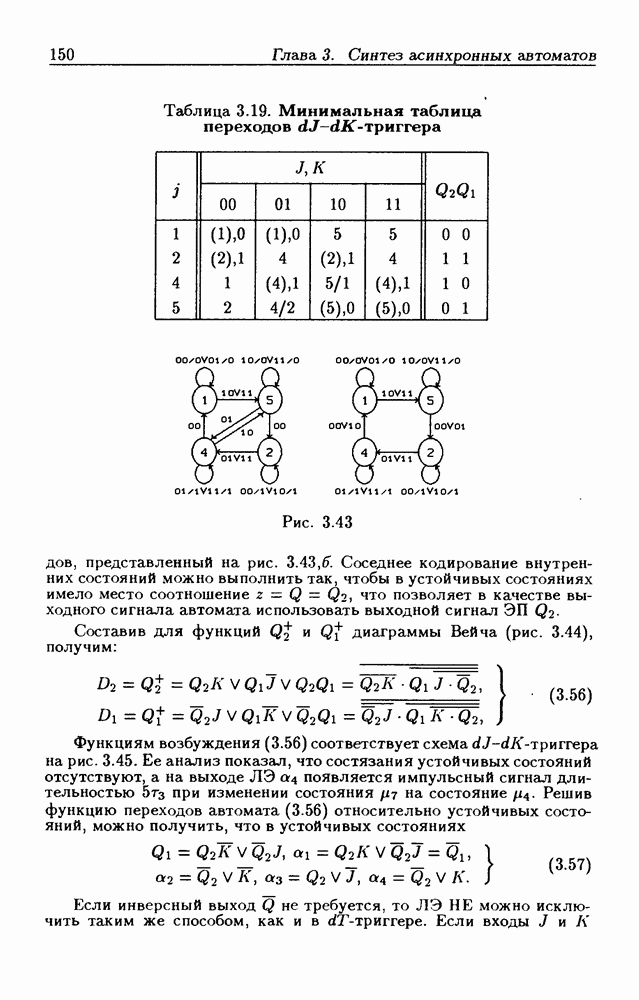
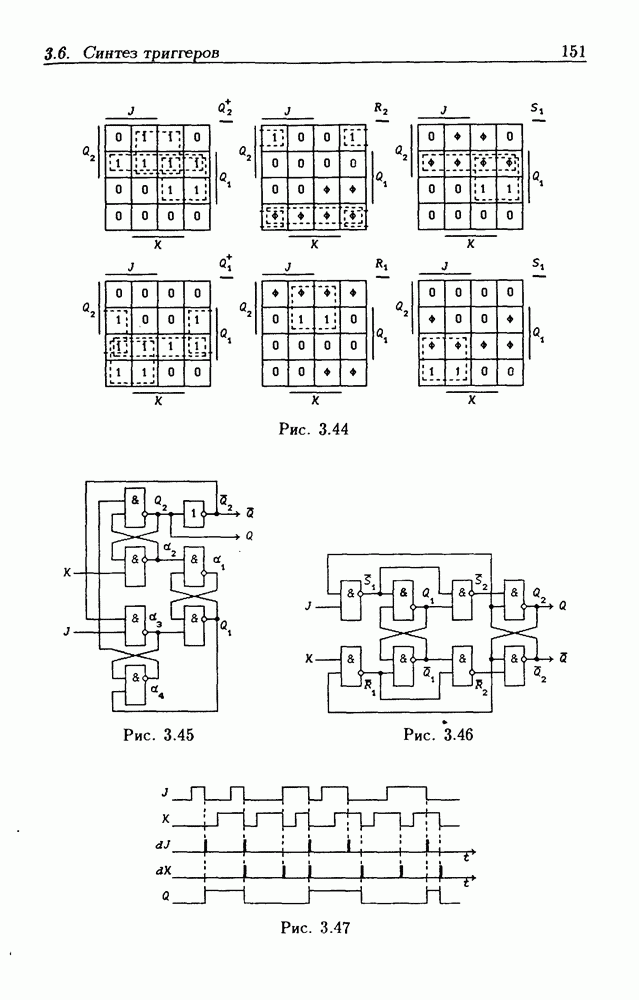
- Триггеры типа dJ-dK.
- Классификация триггеров.
- 3.7. Синтез синхронных триггеров
- Триггеры типа J-K
- Синхронно-асинхронные триггеры.
- 3.8. Примеры синтеза асинхронных потенциальных автоматов
- Цифровые фазочастотные детекторы.
- Квантизатор временных интервалов.
- 3.9. Генераторы сигналов
- Автогенераторы.
- Управляемые автогенераторы.
- Глава 4. Синтез синхронных автоматов
- 4.2. Синхронные триггеры
- Триггеры типов D и R-S с импульсным тактовым сигналом.
- Синхронные триггеры типов R-S и D-L
- Синхронно-асинхронные триггеры.
- Синхронные триггеры типа J-K
- Триггеры типа Т.
- Классификация синхронных триггеров.
- Преобразования типов синхронных триггеров.
- Триггеры типов D-T-L и D-T-L/R
- Функции переходов синхронно-асинхронных триггеров.
- 4.3. Примеры синтеза синхронных автоматов
- 4.4. Сдвигающие регистры
- Синтез счетчиков на сдвигающих регистрах.
- Сдвигающие регистры с загрузкой данных.
- Реверсивные сдвигающие регистры.
- 4.5. Синхронные счетчики
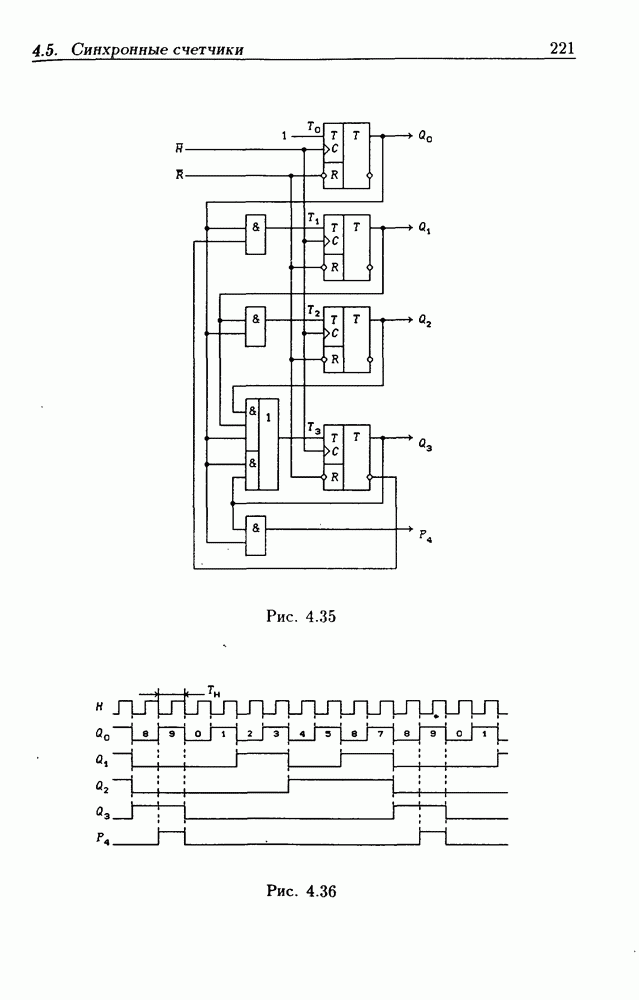
- Синхронные двоичные счетчики.
- Синхронные двоично-десятичные счетчики.
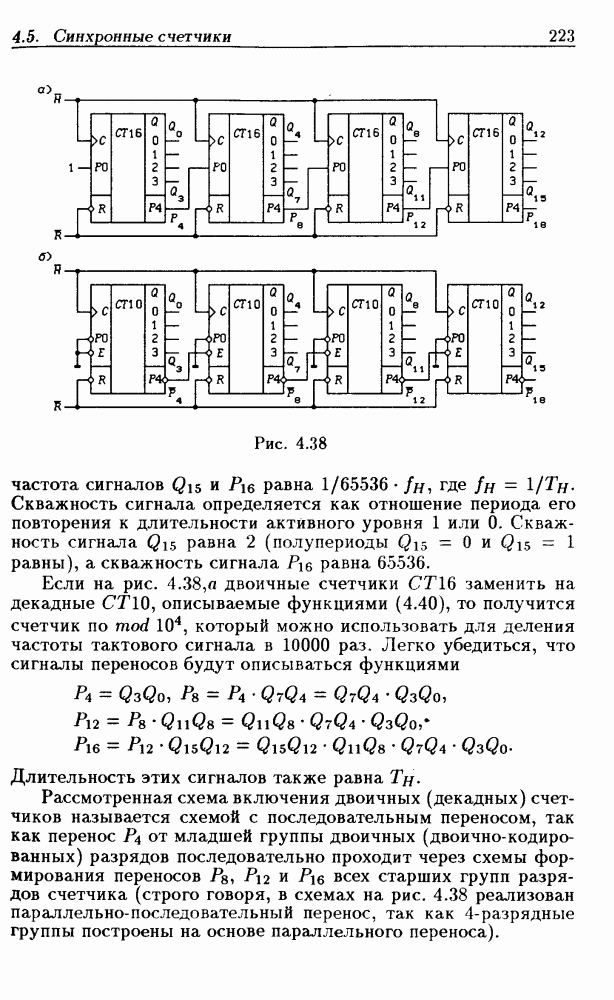
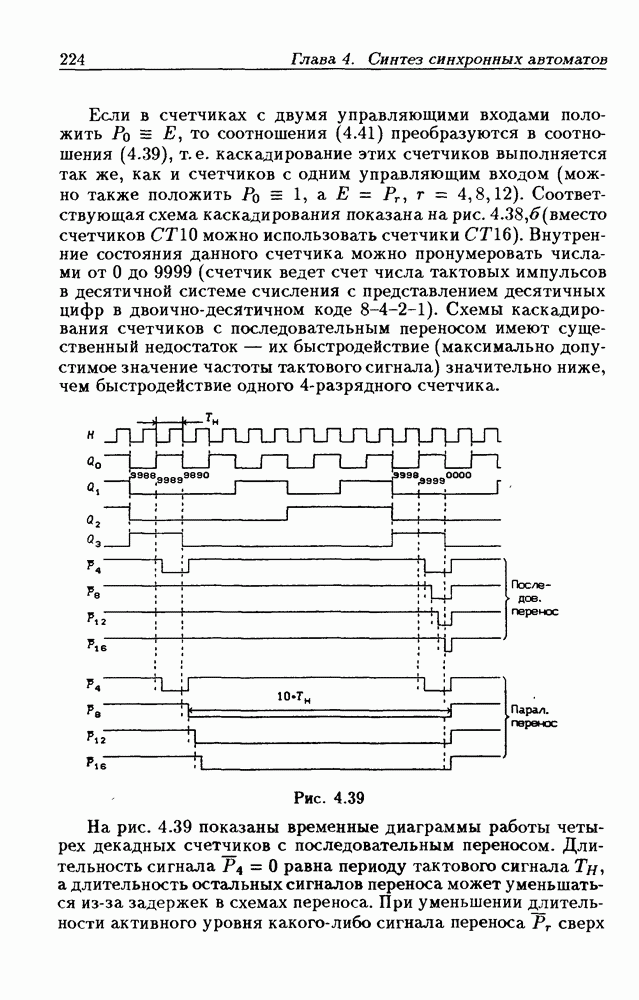
- Каскадирование двоичных и двоично-десятичных счетчиков.
- Синхронные двоичные реверсивные счетчики.
- Реверсивные двоично-десятичные счетчики.
- Каскадирование реверсивных счетчиков.
- Счетчики на сдвигающих регистрах.
- Кольцевые счетчики.
- Линейные счетчики.
- Программируемые счетчики.
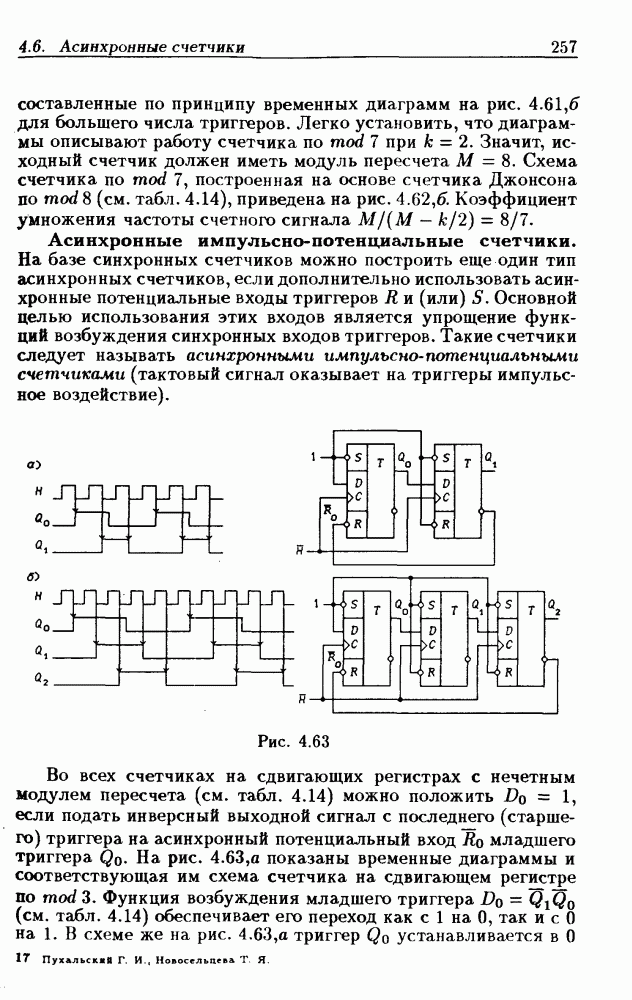
- 4.6. Асинхронные счетчики
- Асинхронные счетчики с умножением частоты счетного сигнала.
- Асинхронные импульсно-потенциальные счетчики.
- Асинхронное программирование модуля пересчета счетчиков.
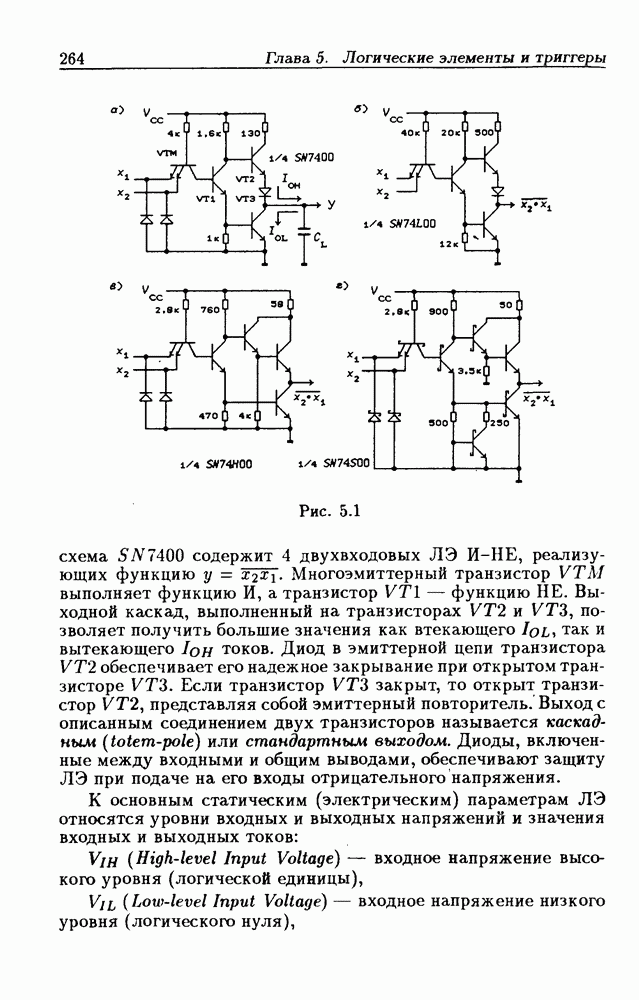
- Глава 5. Логические элементы и триггеры
- Логические элементы.
- Классификация ИС по степени интеграции.
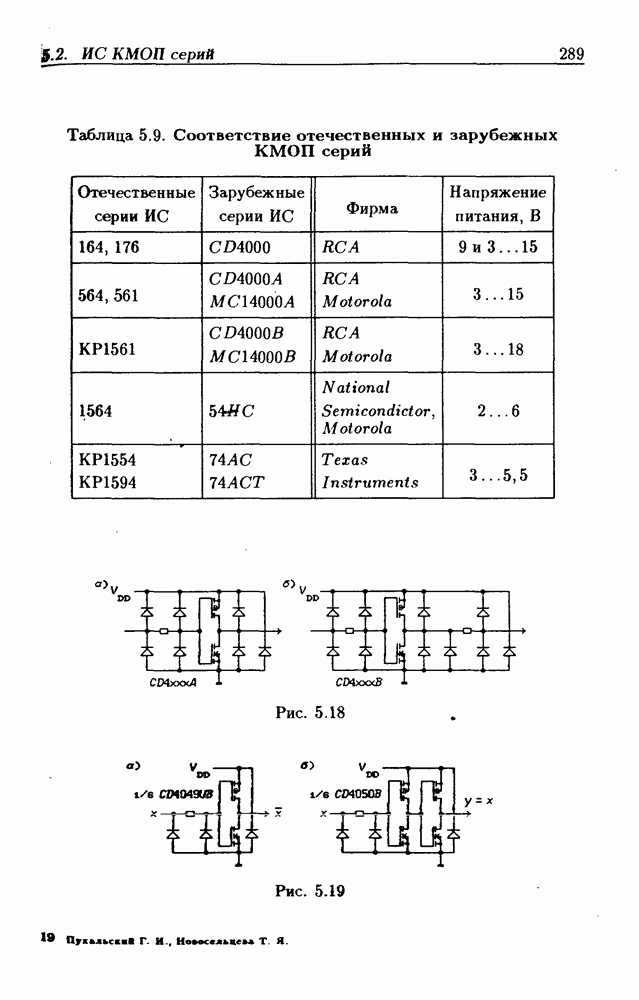
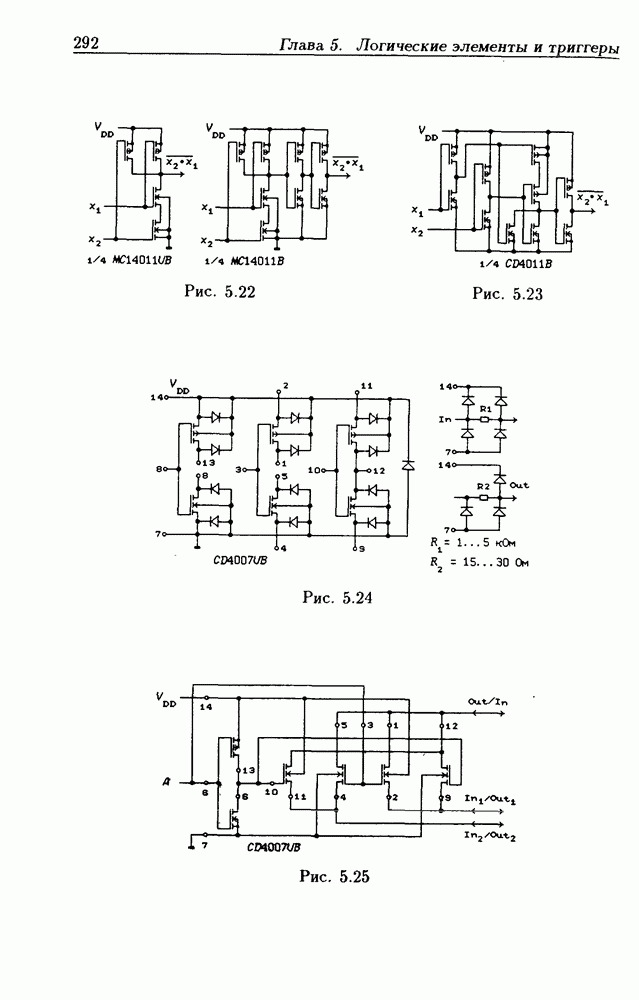
- 5.2. Интегральные схемы КМОП серий
- 5.3. Триггеры Шмитта
- 5.4. Логические элементы с открытым коллекторным выходом
- Логические элементы с открытым коллекторным выходом.
- Применения ЛЭ с открытым коллекторным выходом.
- Интерфейсные ЛЭ с открытым коллекторным выходом.
- Логические элементы с открытым стоковым выходом.
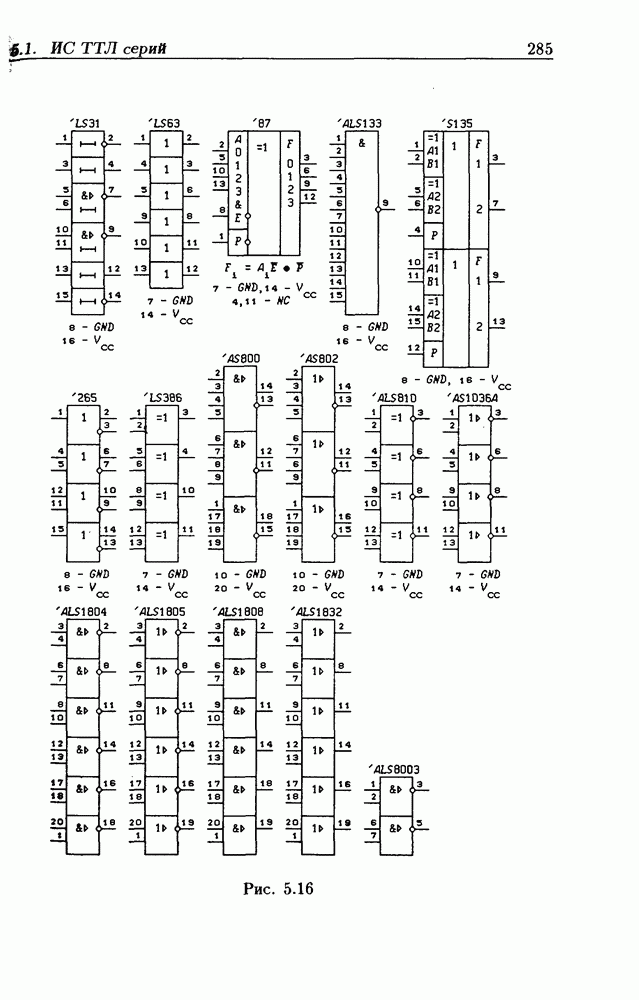
- Типовые цоколевки ИС.
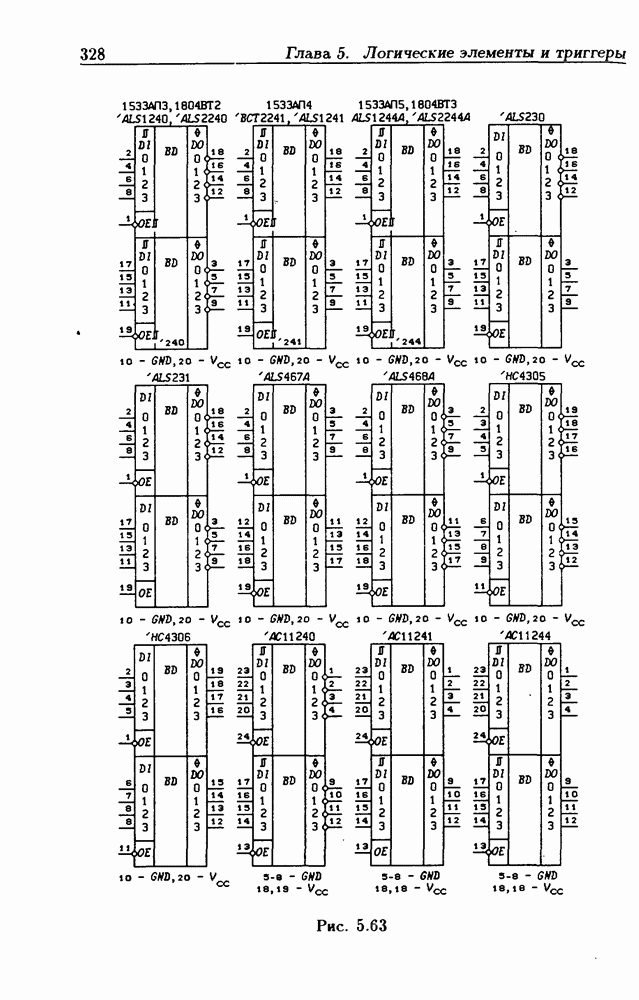
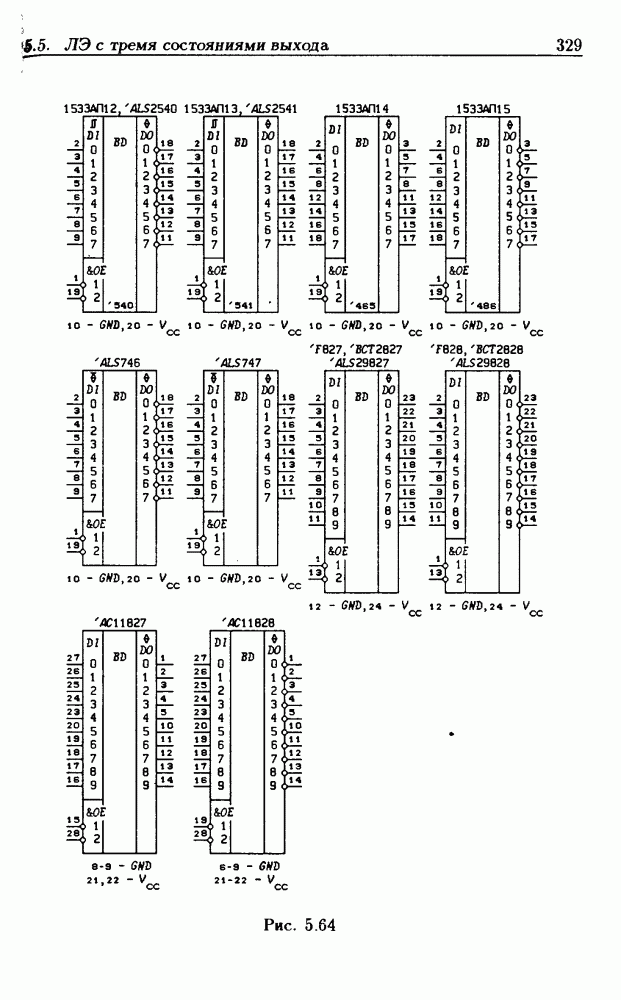
- 5.5. Логические элементы с тремя состояниями выхода
- Шинные драйверы с Z-состоянием выхода.
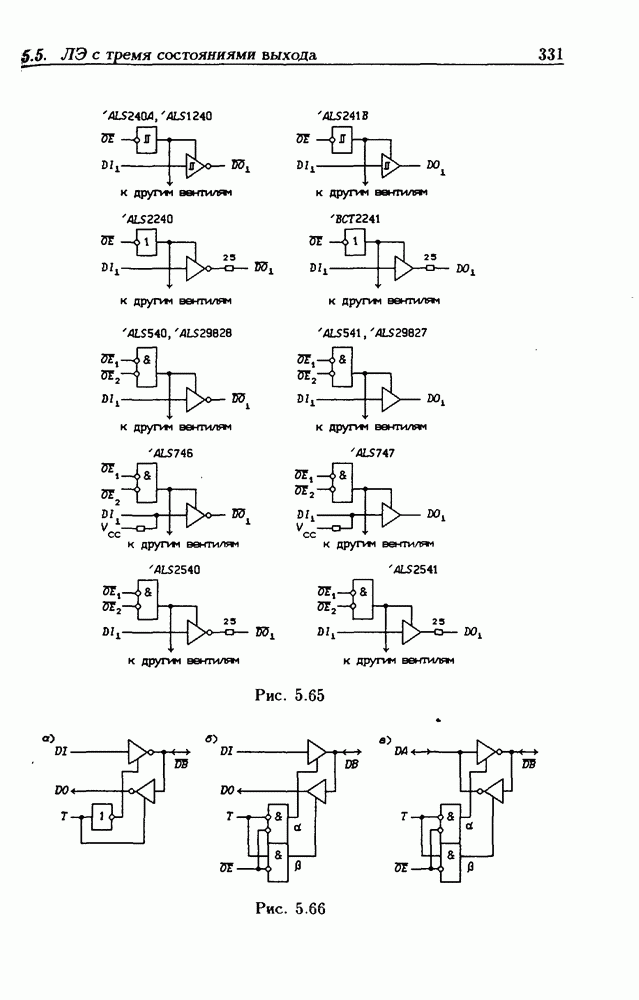
- Основные правила графического изображения ИС.
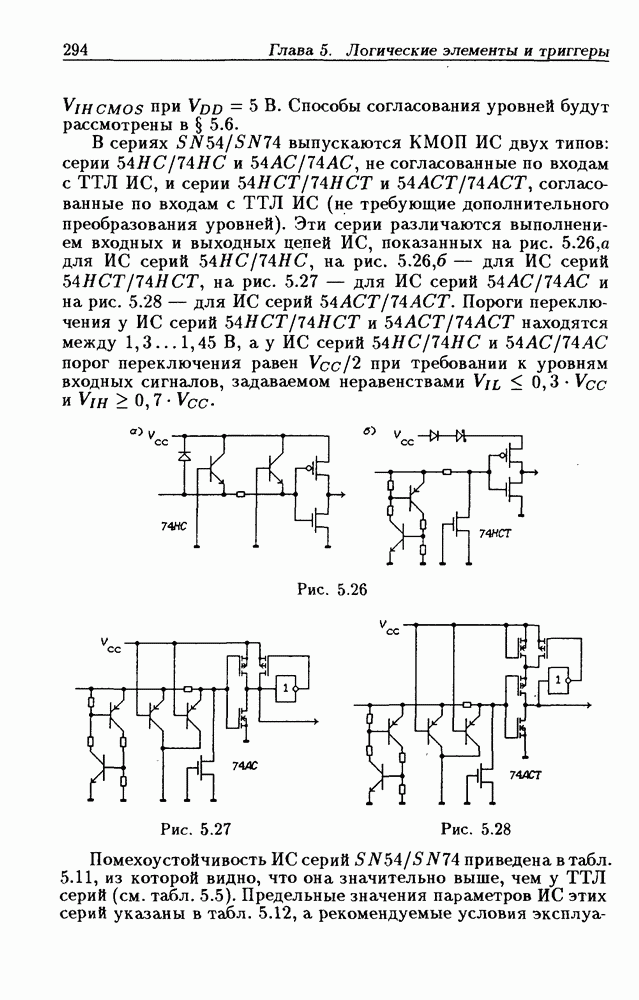
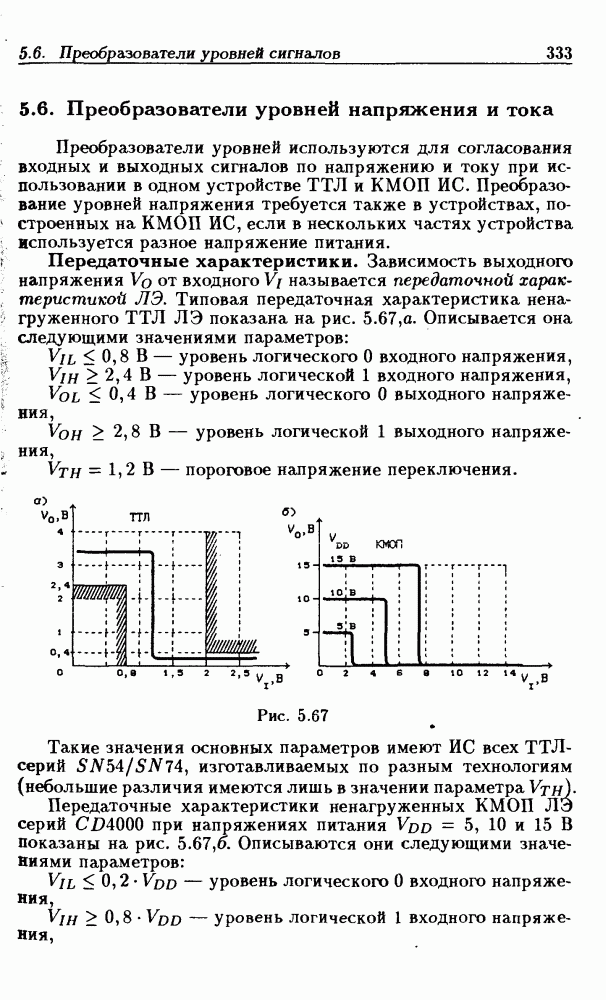
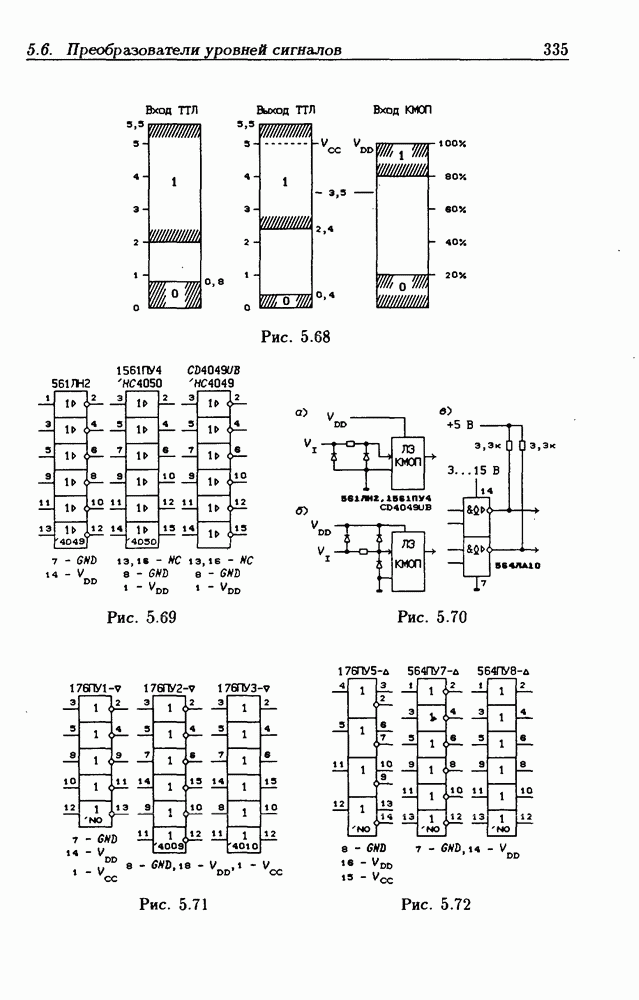
- 5.6. Преобразователи уровней напряжения и тока
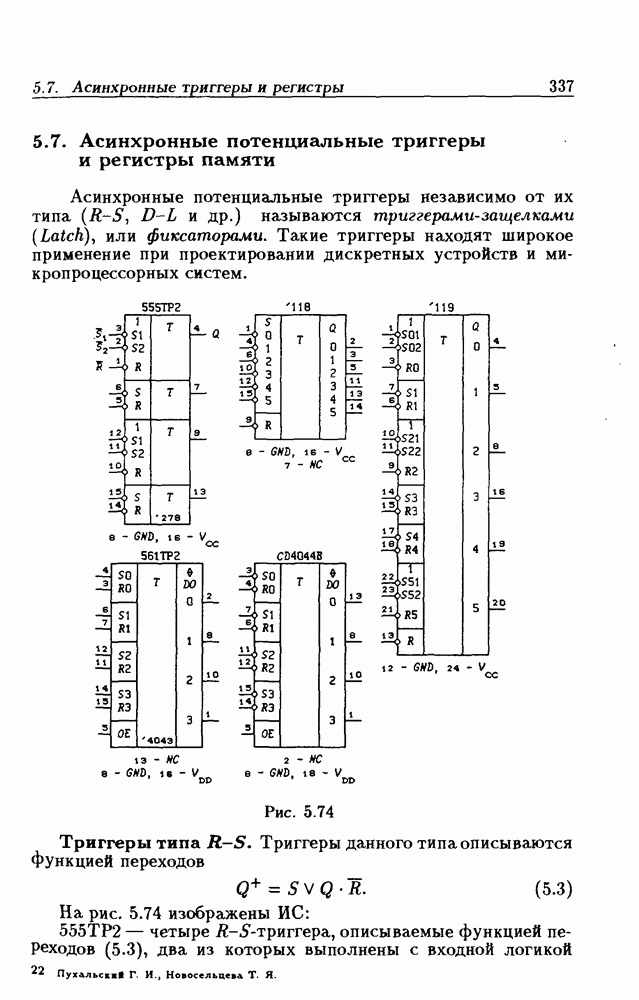
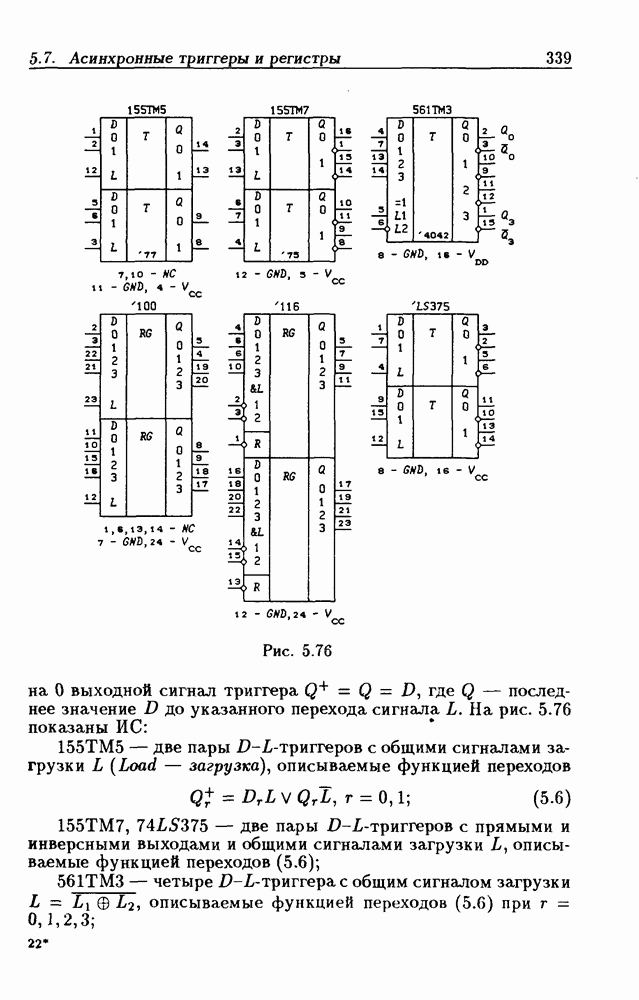
- 5.7. Асинхронные потенциальные триггеры и регистры памяти
- 5.8. Синхронные триггеры и регистры памяти
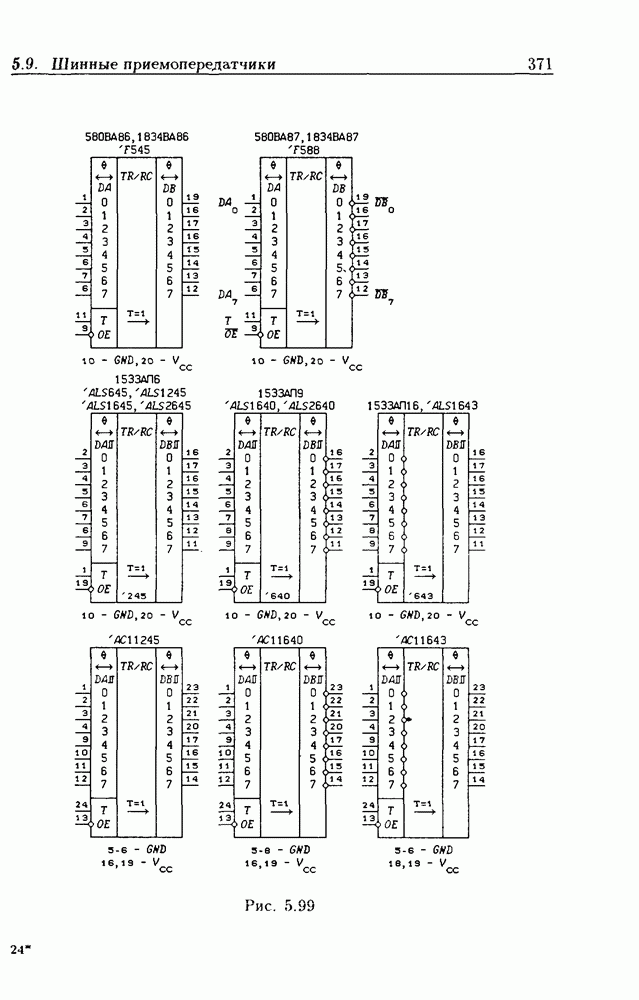
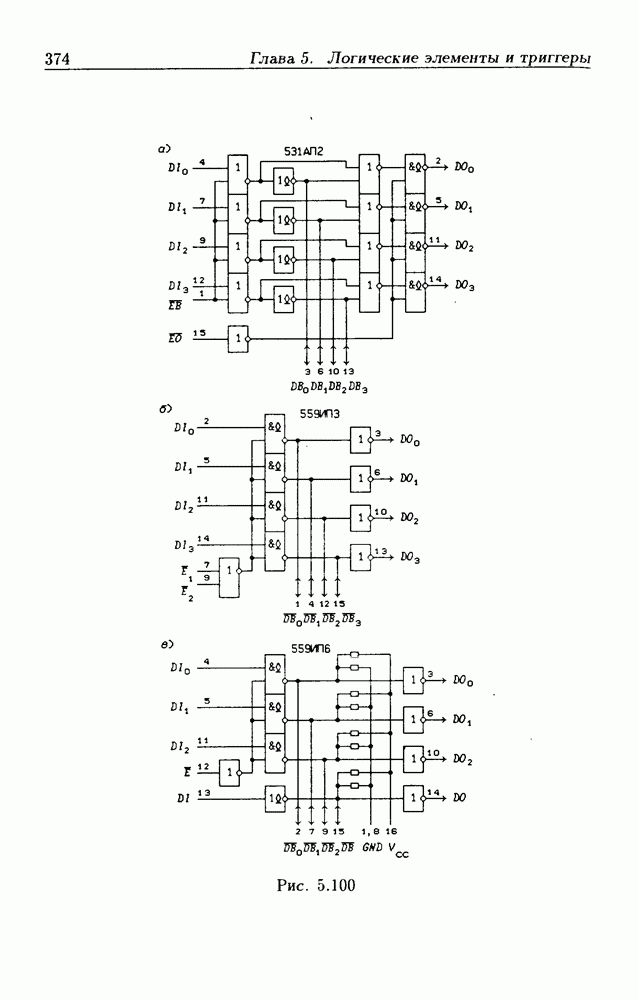
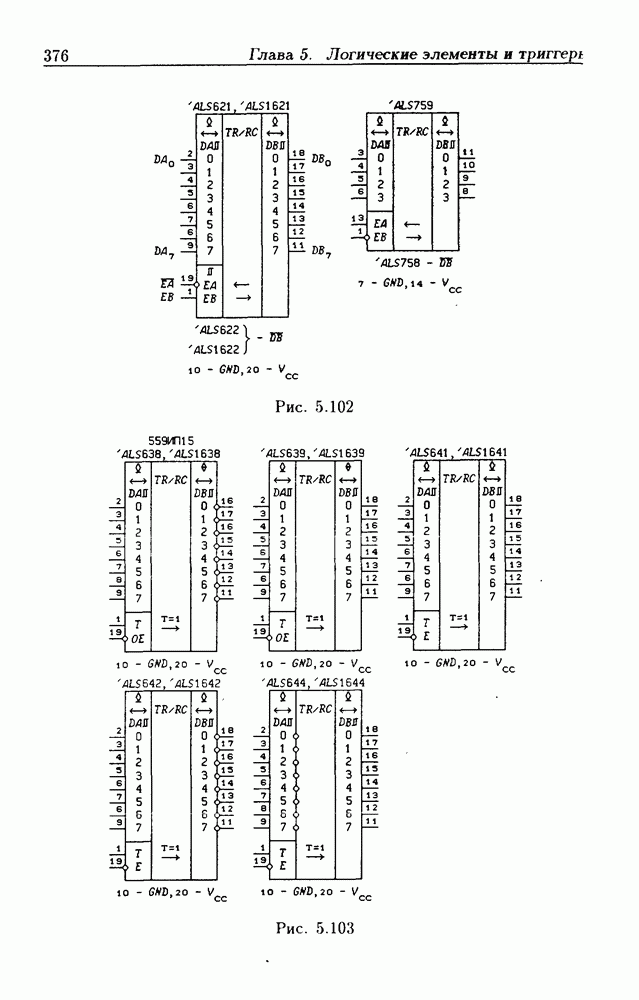
- 5.9. Шинные приемопередатчики
- Шинные приемопередатчики с Z-состоянием выхода.
- Шинные приемопередатчики с открытым коллекторным выходом.
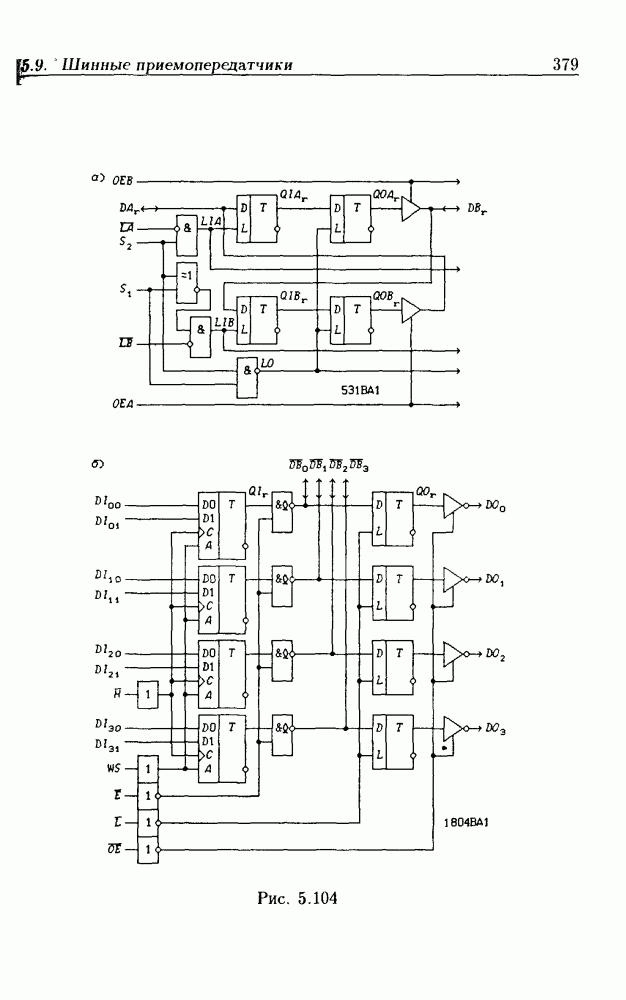
- Шинные приемопередатчики с регистрами памяти.
- Шинные приемопередатчики со сдвигающим регистром.
- Шинные трехнаправленные приемопередатчики.
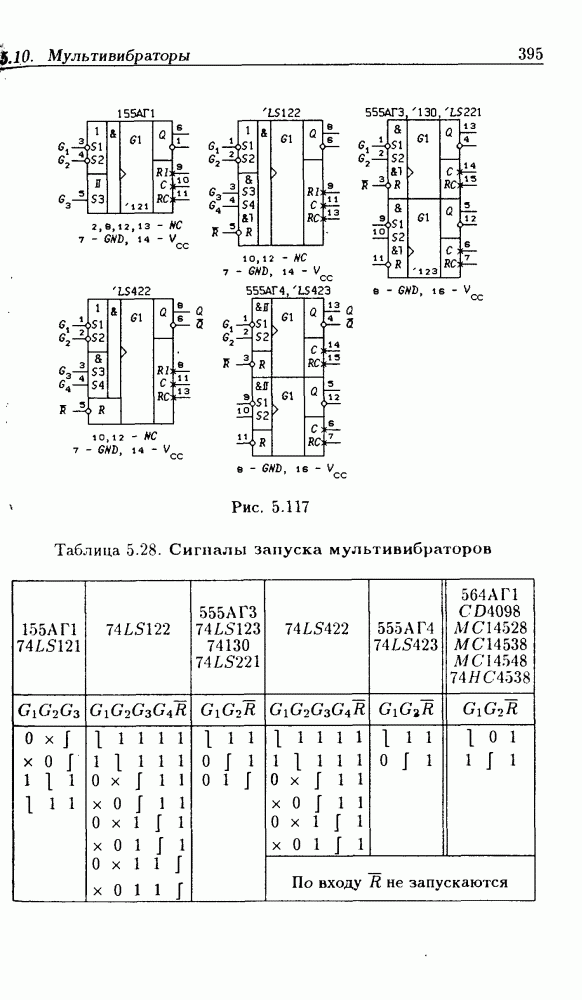
- 5.10. Мультивибраторы
- 5.11. Генераторы
- Схемы устранения «дребезга» механических контактов.
- Автогенераторы периодических сигналов.
- 5.12. Рекомендации по выбору серий ИС
- Глава 6. Коммутаторы и арифметические устройства
- 6.1. Дешифраторы
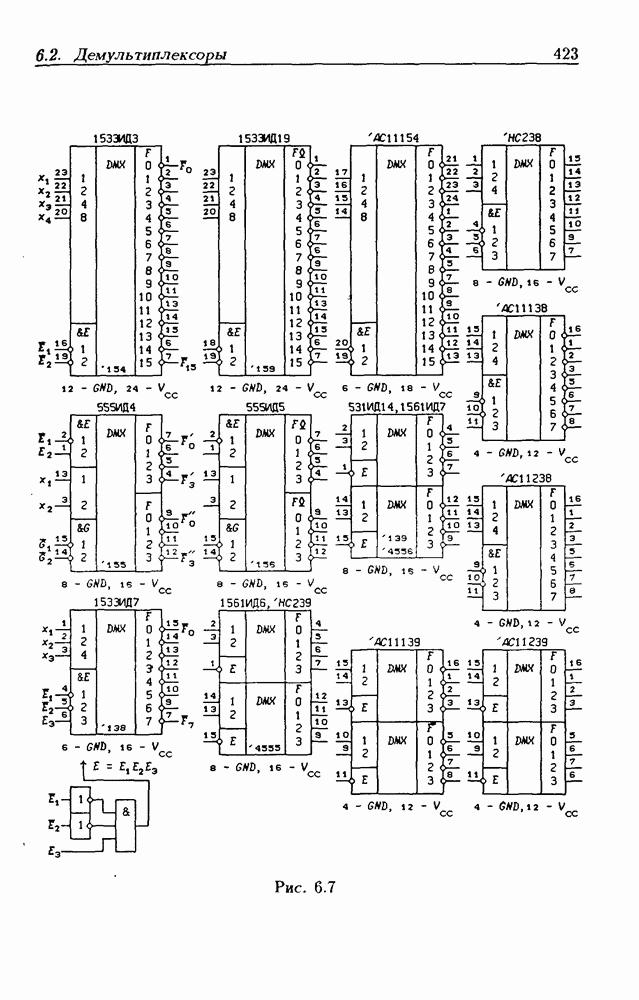
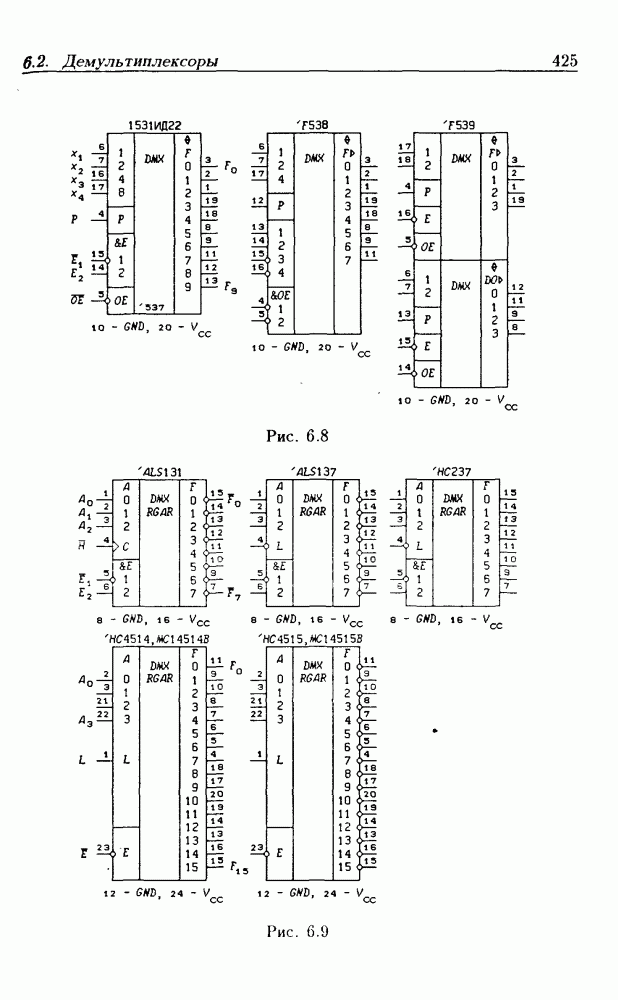
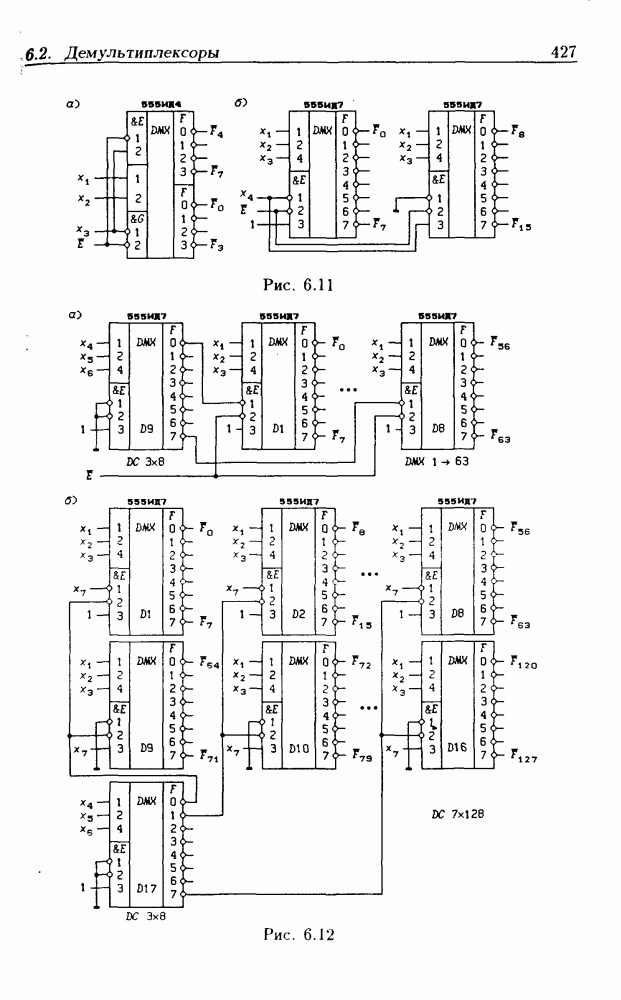
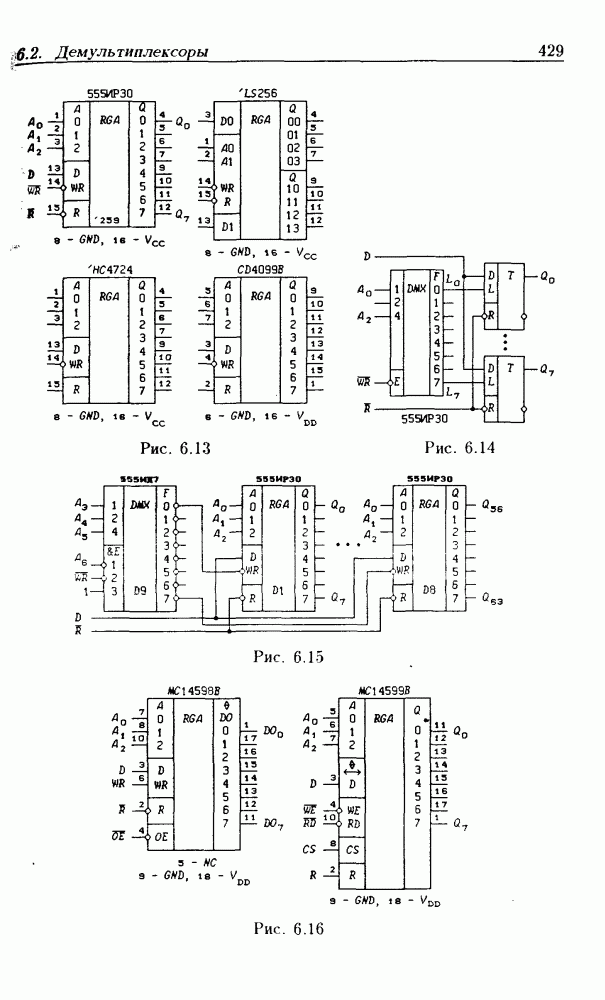
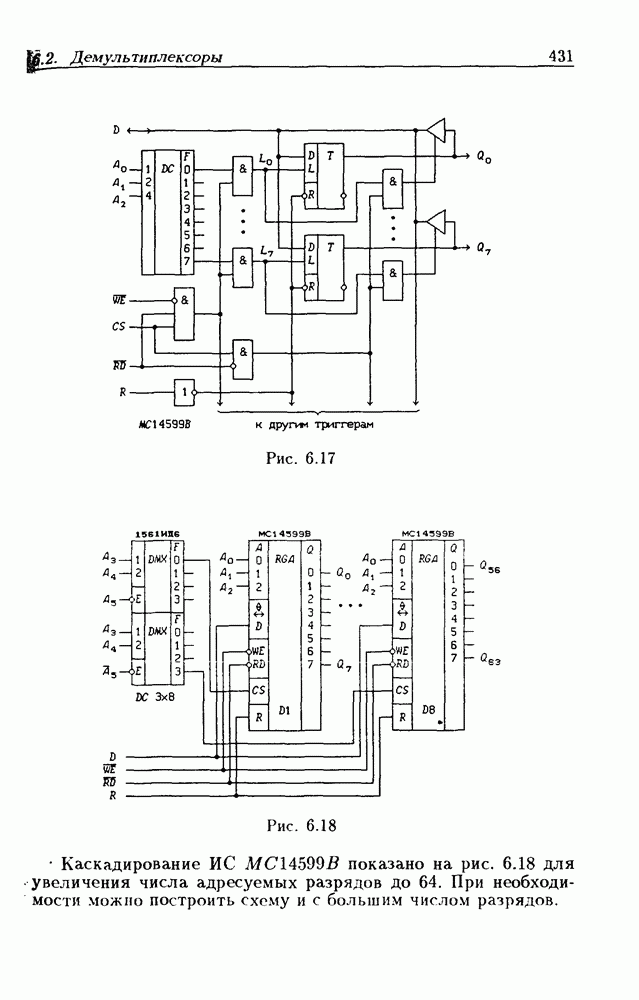
- 6.2. Демультиплексоры
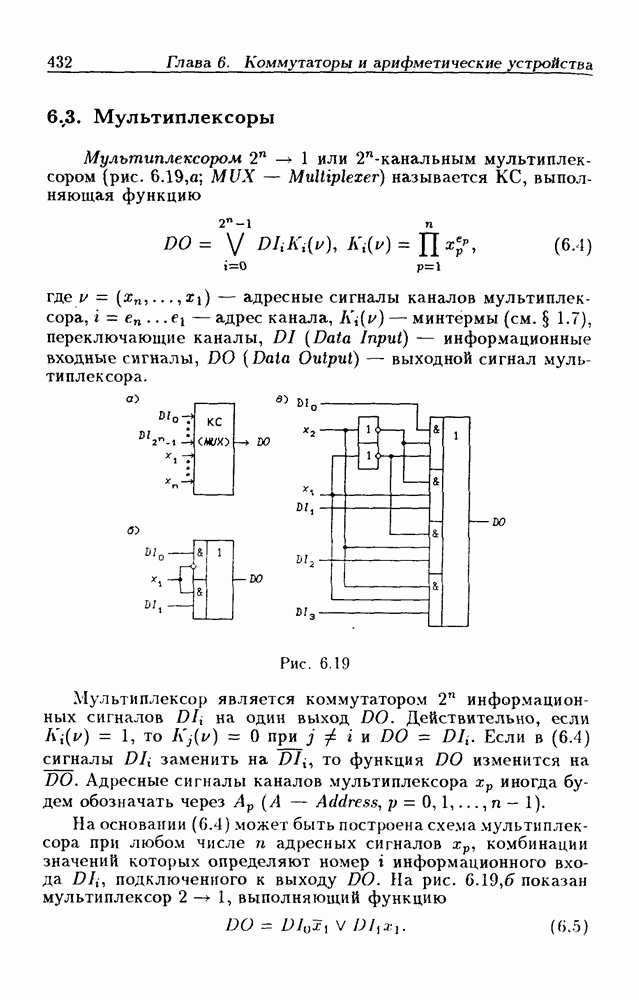
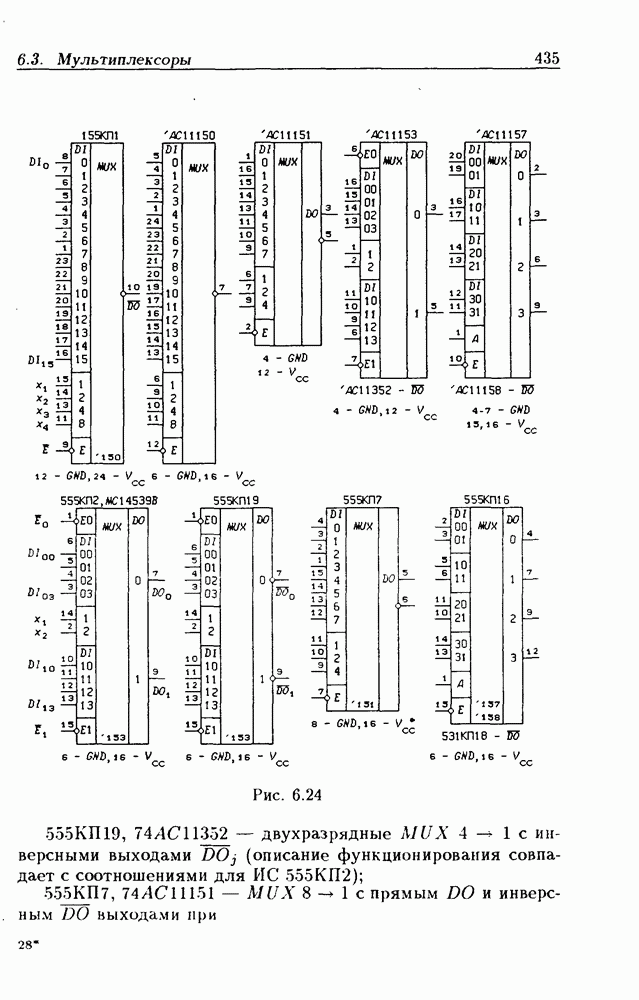
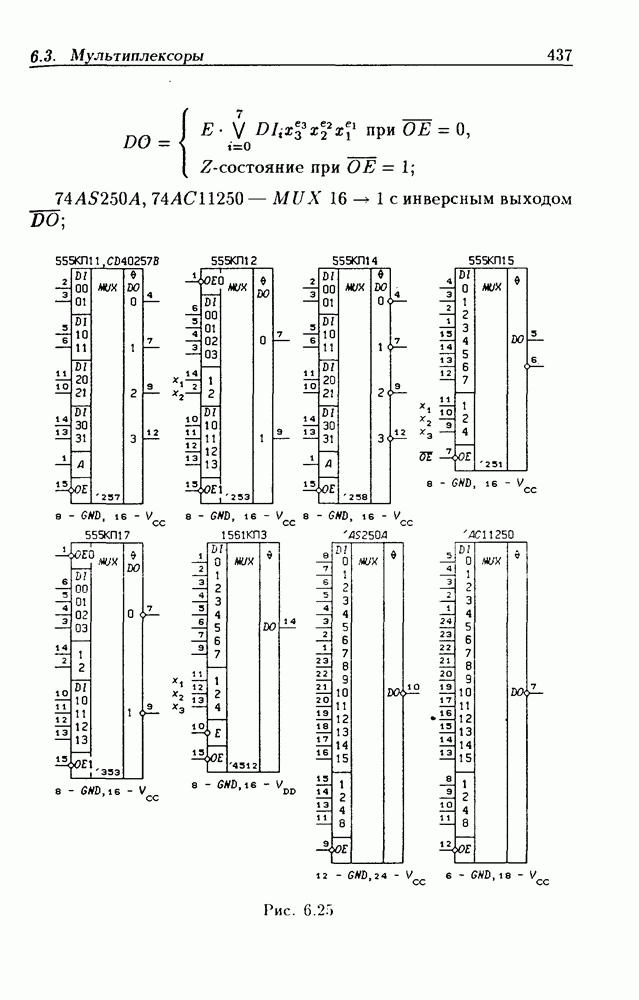
- 6.3. Мультиплексоры
- Мультиплексоры без стробирования.
- Мультиплексоры со стробированием.
- Мультиплексоры с Z-состоянием выхода.
- Каскадирование мультиплексоров.
- Функциональные мультиплексоры.
- Регистры памяти с мультиплексными входами данных.
- Мультиплексоры с регистрами памяти данных и адреса.
- Сдвигающие мультиплексоры.
- 6.4. Синтез комбинационных схем и цифровых автоматов на мультиплексорах
- Синтез схем на 8-канальных мультиплексорах.
- Синтез на двухразрядных 4-канальных мультиплексорах.
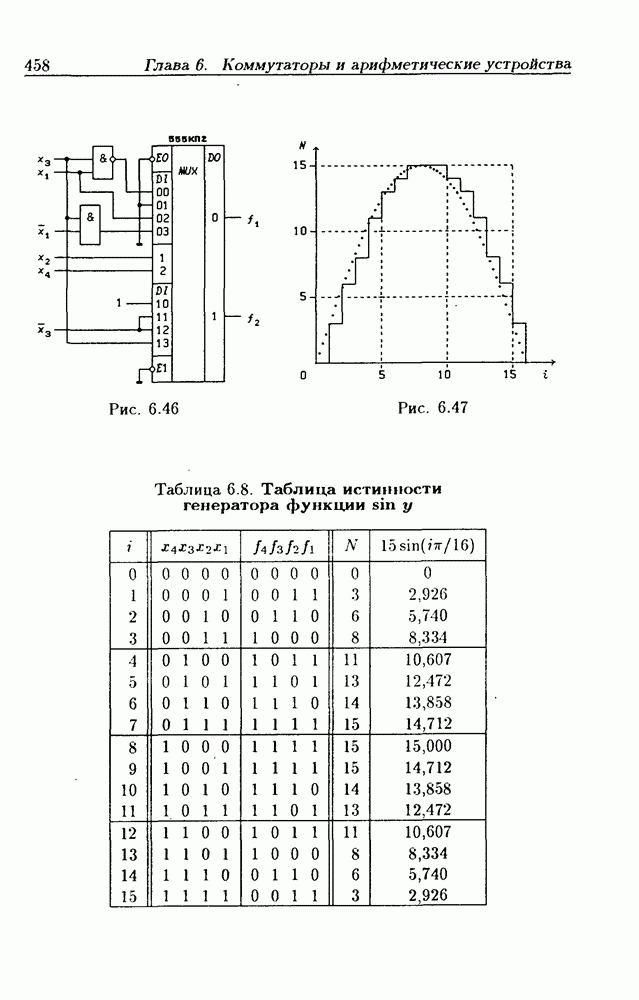
- Синтез генератора синусоидальной функции на мультиплексорах.
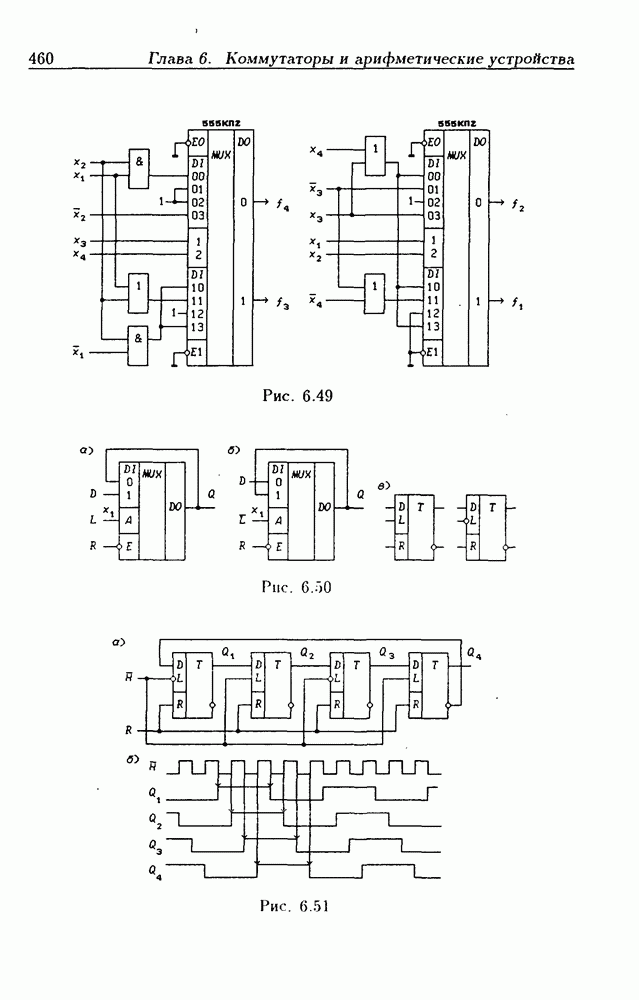
- Синтез триггеров на мультиплексорах.
- Синтез счетчиков на мультиплексорах.
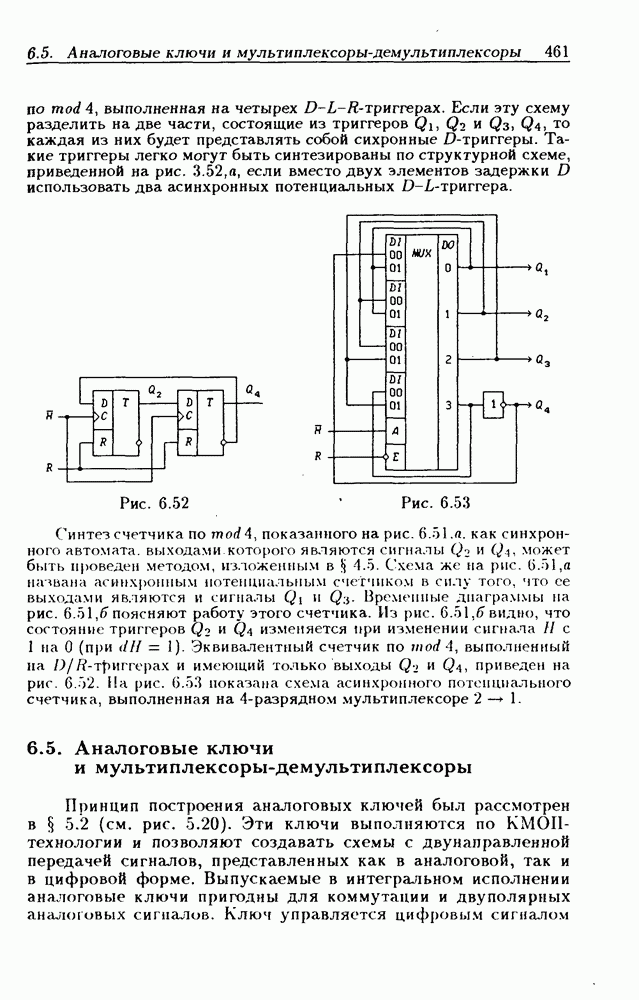
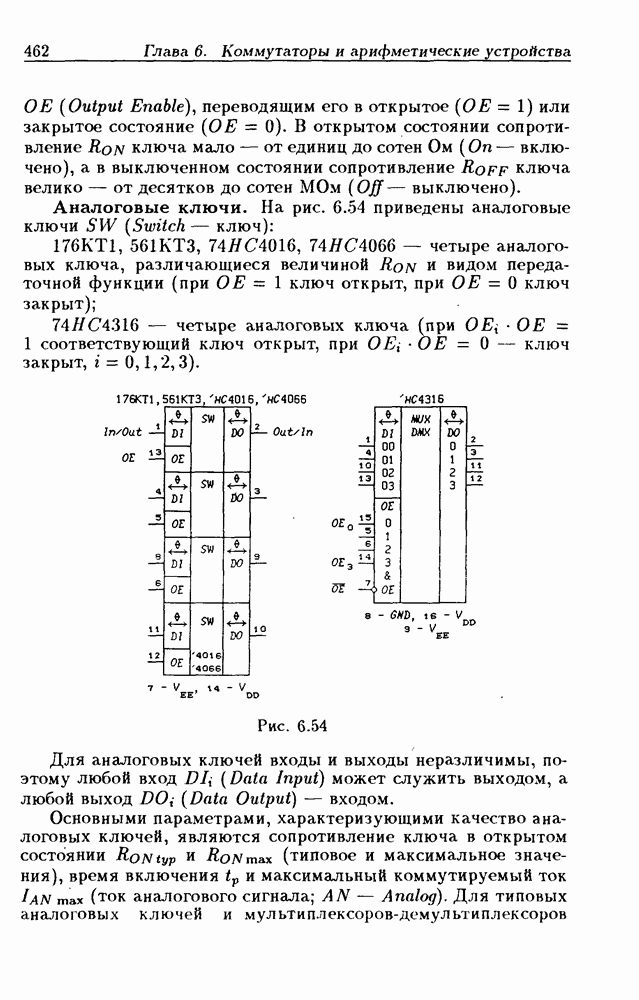
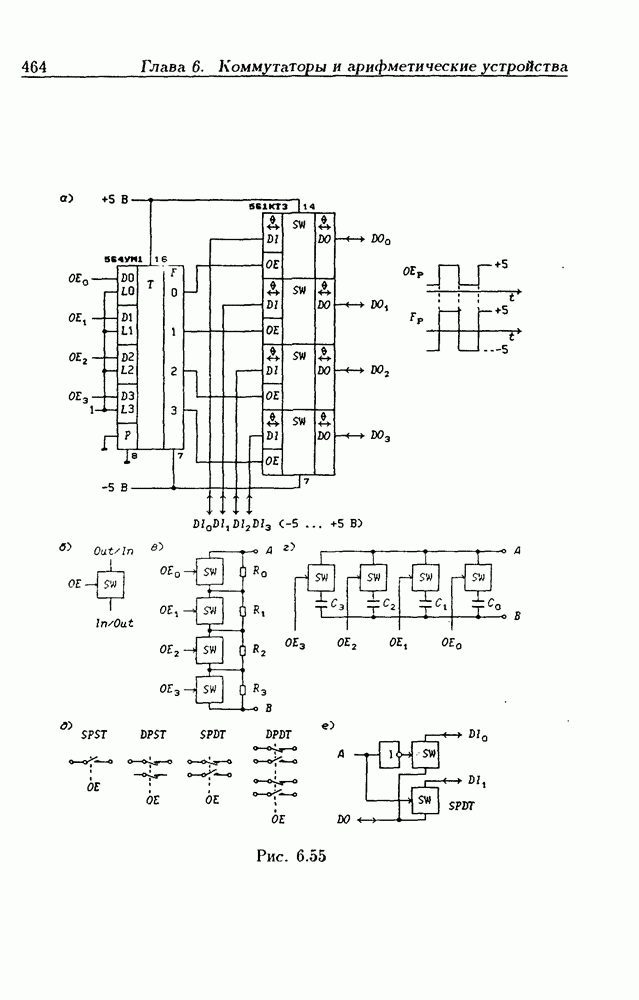
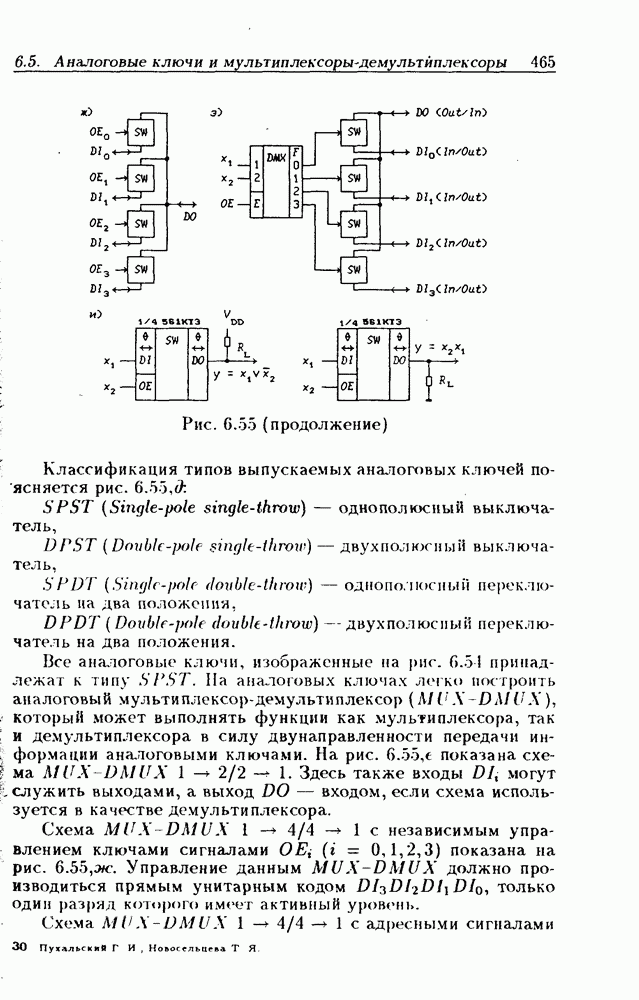
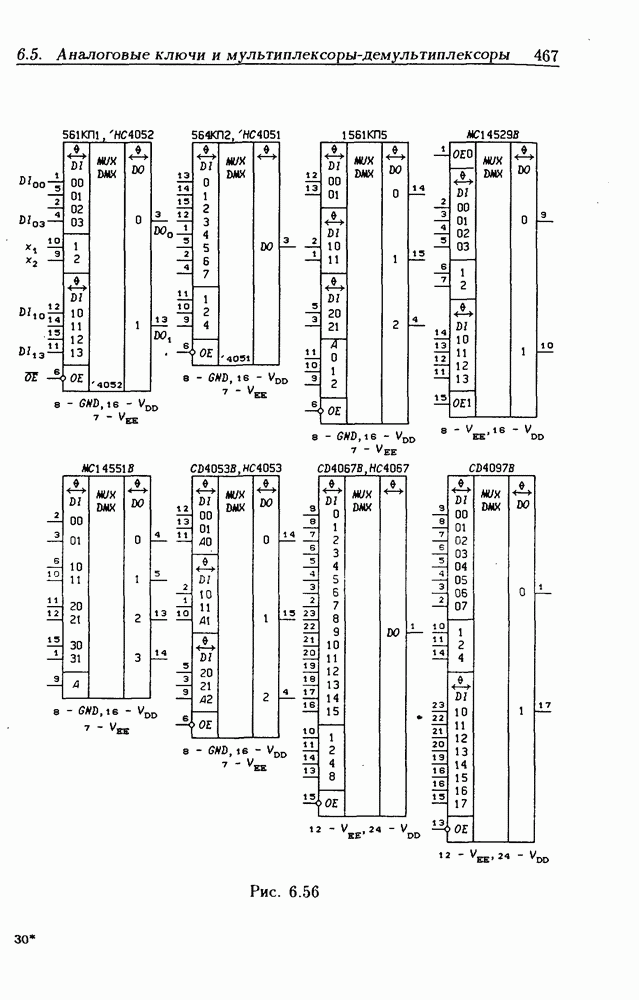
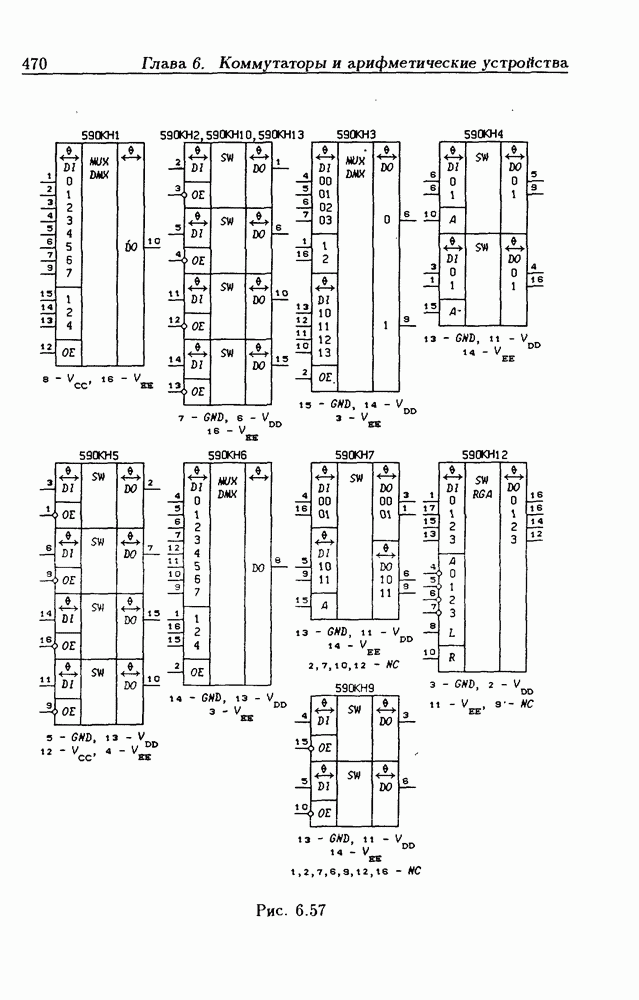
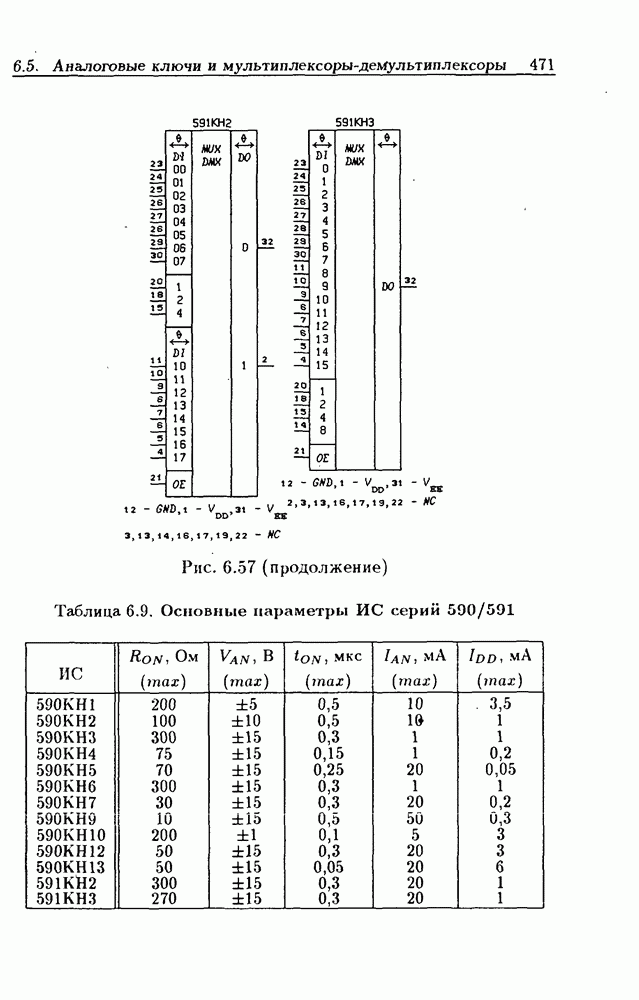
- 6.5. Аналоговые ключи и мультиплексоры-демультиплексоры
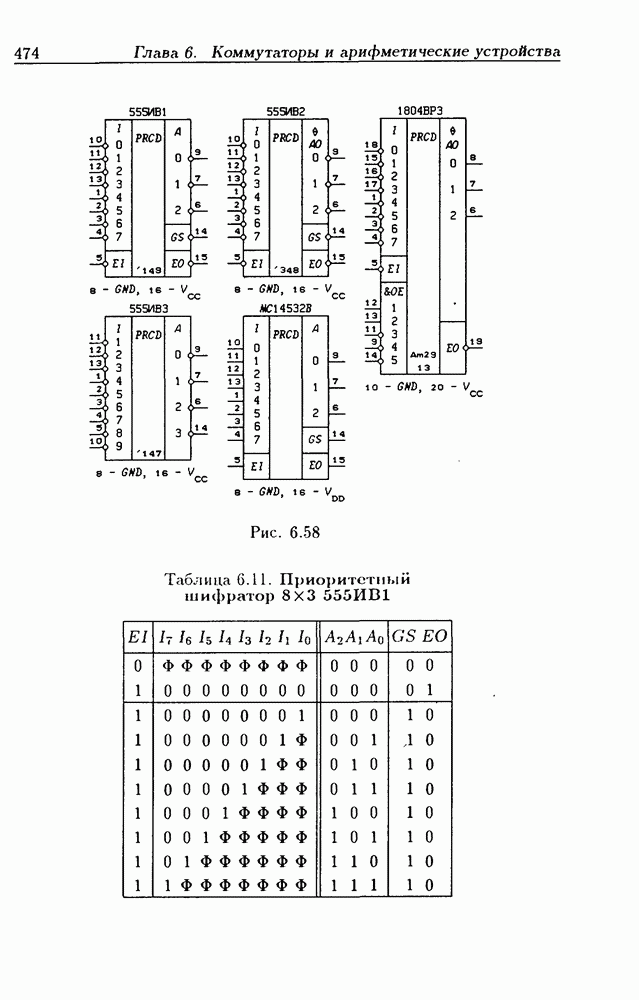
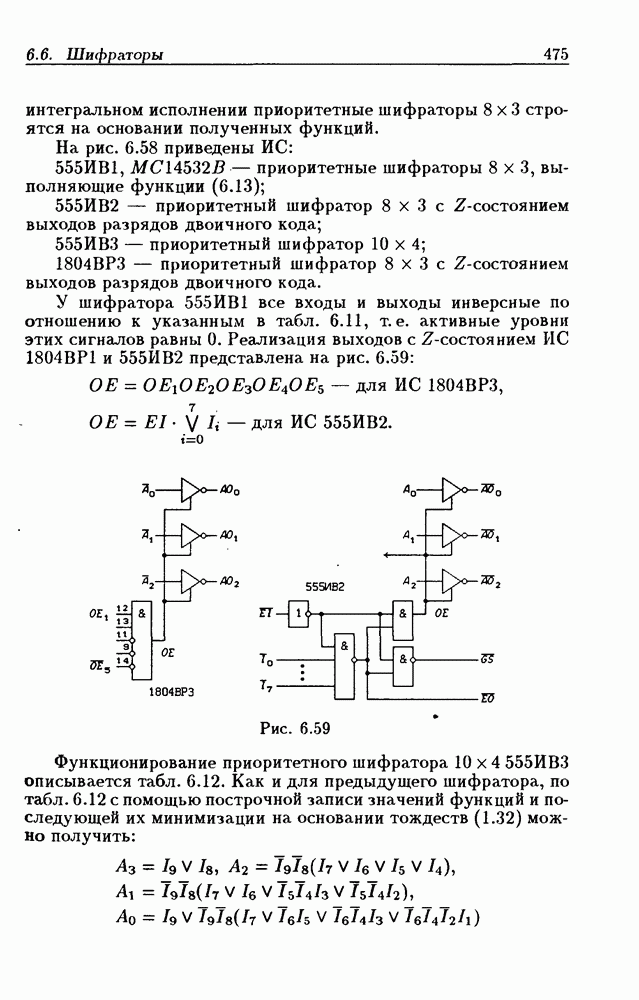
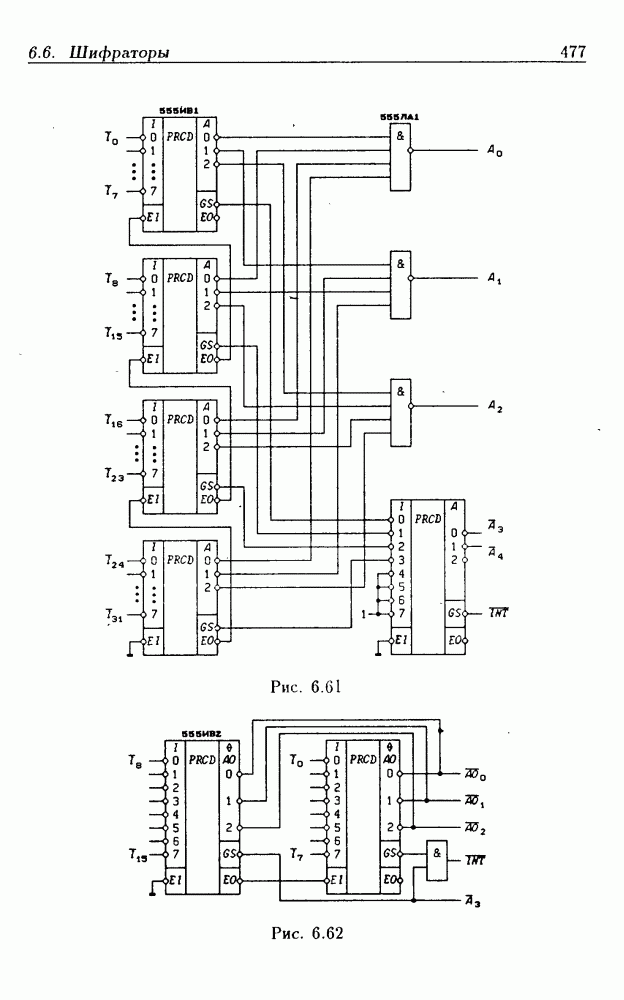
- 6.6. Шифраторы
- 6.7. Цифровые компараторы
- Программируемые цифровые компараторы.
- Адресные компараторы.
- Применения адресных компараторов.
- 6.8. Схемы сравнения двоичных чисел
- 8-разрядные схемы сравнения двоичных чисел.
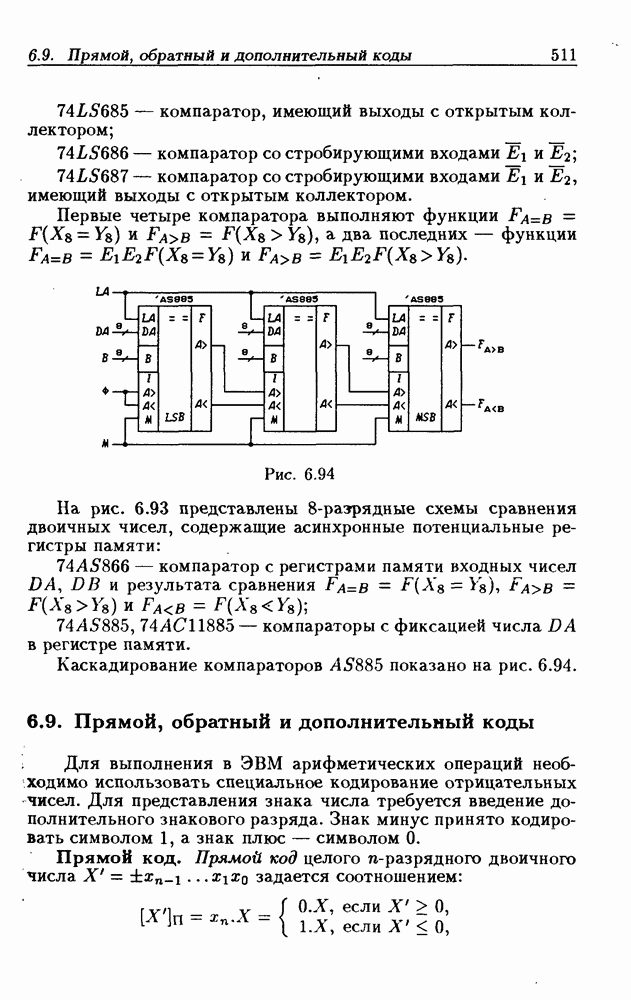
- 6.9. Прямой, обратный и дополнительный коды
- Дополнительный код.
- Сложение чисел в обратном коде.
- Код с избытком 3.
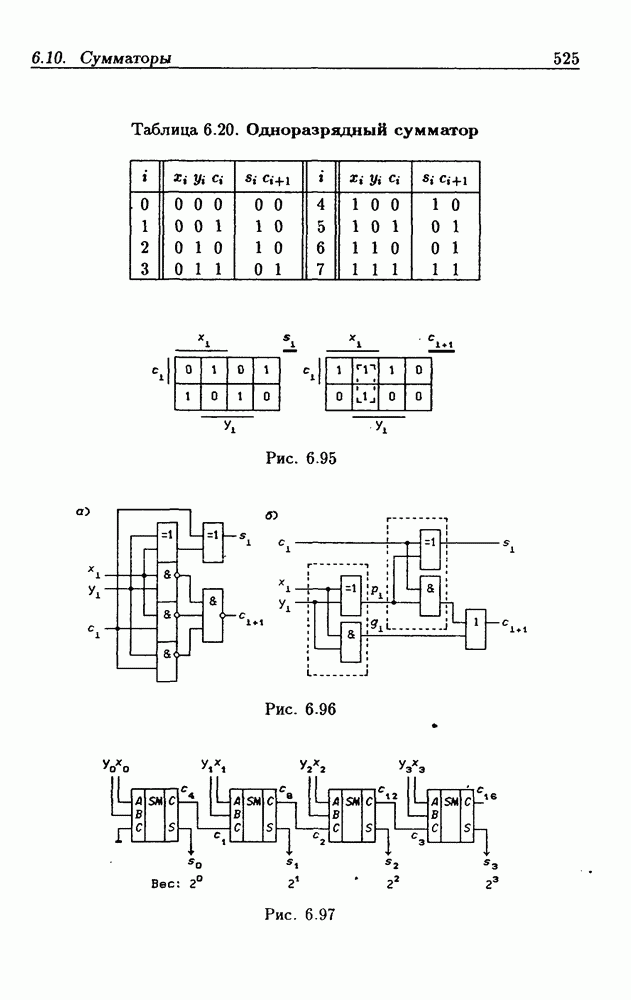
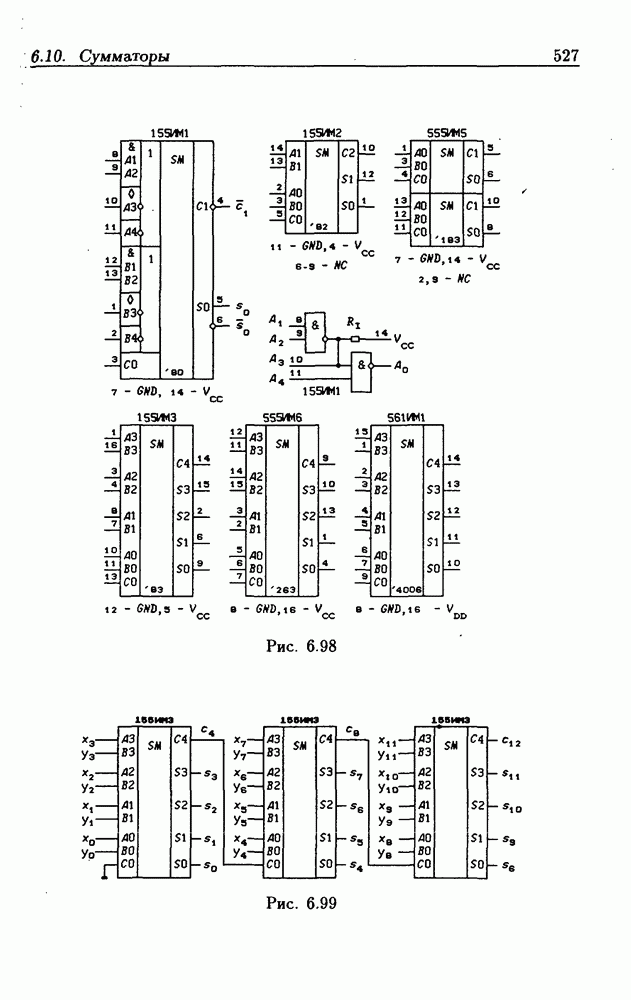
- 6.10. Сумматоры
- Двоичные параллельные сумматоры с последовательным переносом.
- Двоичные сумматоры с параллельным переносом.
- Применения сумматоров.
- Десятичные сумматоры.
- Последовательные двоичные сумматоры.
- 6.11. Арифметическо-логические устройства
- 6.12. Пороговые схемы и мажоритарные элементы
- 6.13. Умножители двоичных чисел
- Быстрые умножители.
- БИС умножителя 12×12 разрядов 1802ВР4.
- Последовательные умножители.
- 6.14. Конвейерные устройства
- Конвейерный быстрый умножитель.
- Конвейерные АЦП.
- 6.15. Синтез линейных комбинационных схем
- Сумматор по модулю q.
- Умножитель по модулю q.
- Глава 7. Сдвигающие регистры и счетчики
- 7.1. Сдвигающие регистры без параллельной записи данных
- Сдвигающие устройства с выходными регистрами памяти.
- 7.2. Сдвигающие регистры с параллельной записью данных
- Сдвигающие регистры с расширением знака.
- Сдвигающие регистры с входным регистром памяти.
- 7.3. Реверсивные сдвигающие регистры
- Реверсивные сдвигающие регистры типов PI/SO и PI/PO.
- Многофункциональные устройства на основе реверсивных сдвигающих регистров.
- 7.4. Асинхронные счетчики
- Двоично-десятичные асинхронные счетчики.
- 7.5. Синхронные двоичные счетчики
- Программирование модуля пересчета двоичных счетчиков.
- Переключение модулей пересчета двоичных счетчиков.
- Функциональные устройства на основе двоичных счетчиков.
- 7.6. Синхронные двоично-десятичные счетчики
- 7.7. Синхронные реверсивные счетчики
- 7.8. Счетчики с расщепленным тактовым сигналом
- 7.9. Счетчики на сдвигающих регистрах
- 7.10. Кольцевые счетчики
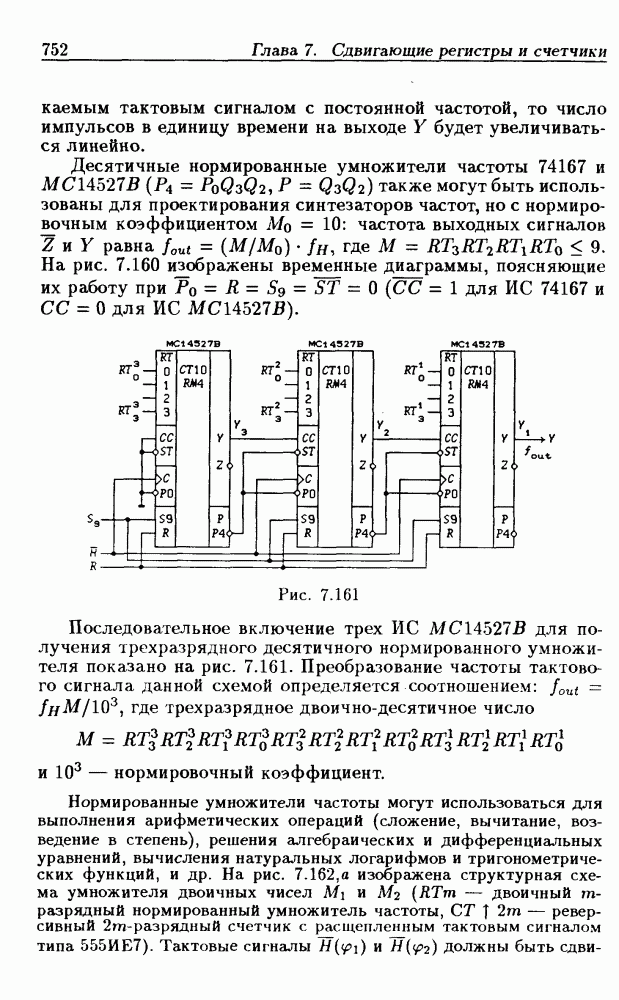
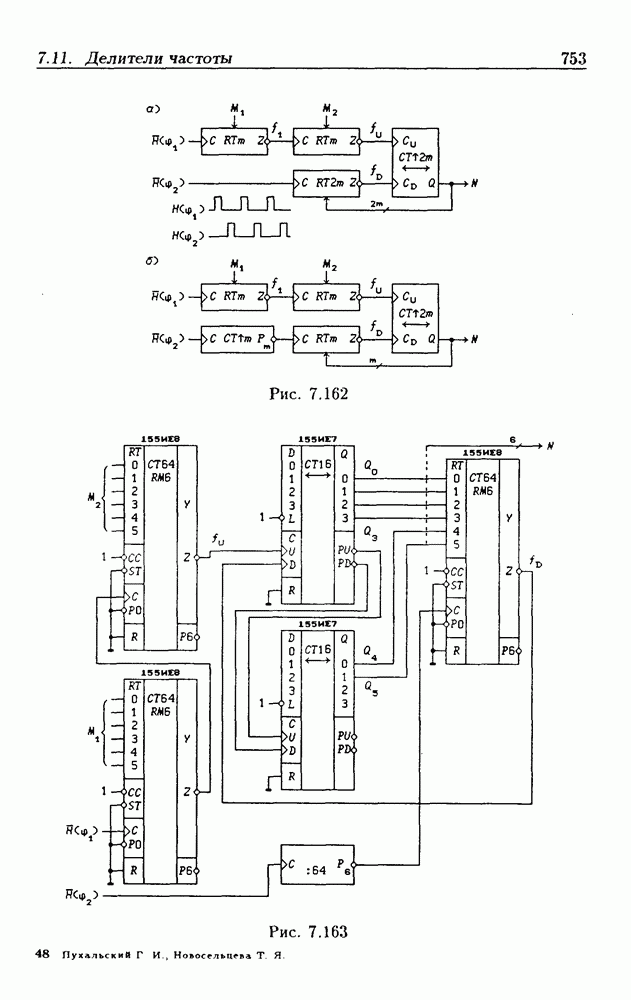
- 7.11. Делители частоты
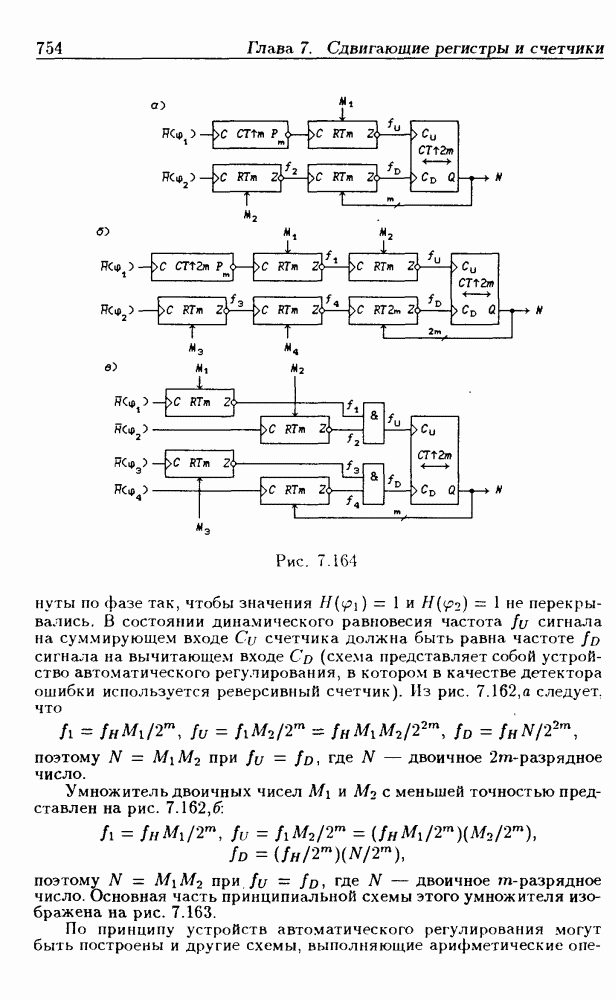
- Нормированные умножители частоты.
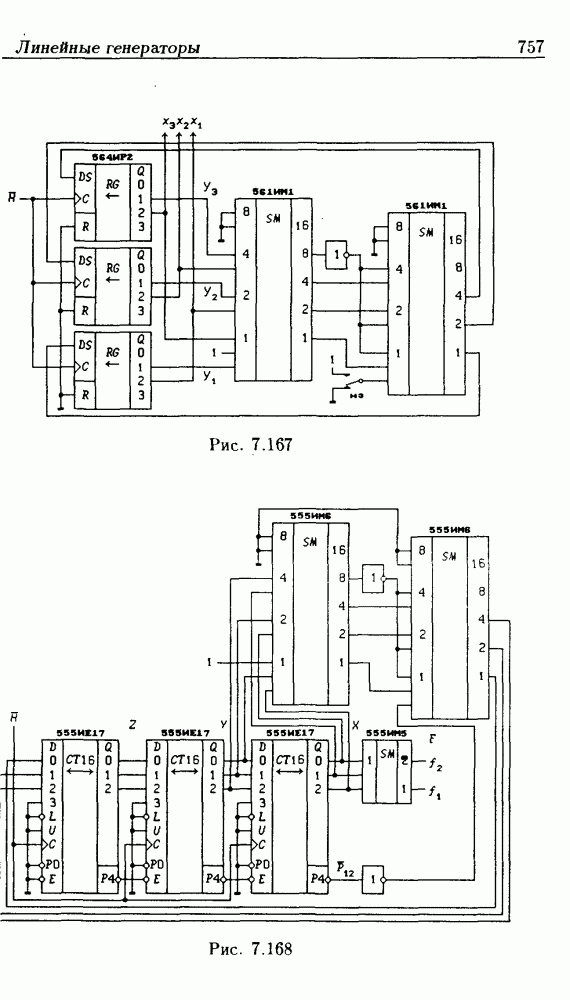
- 7.12. Линейные генераторы
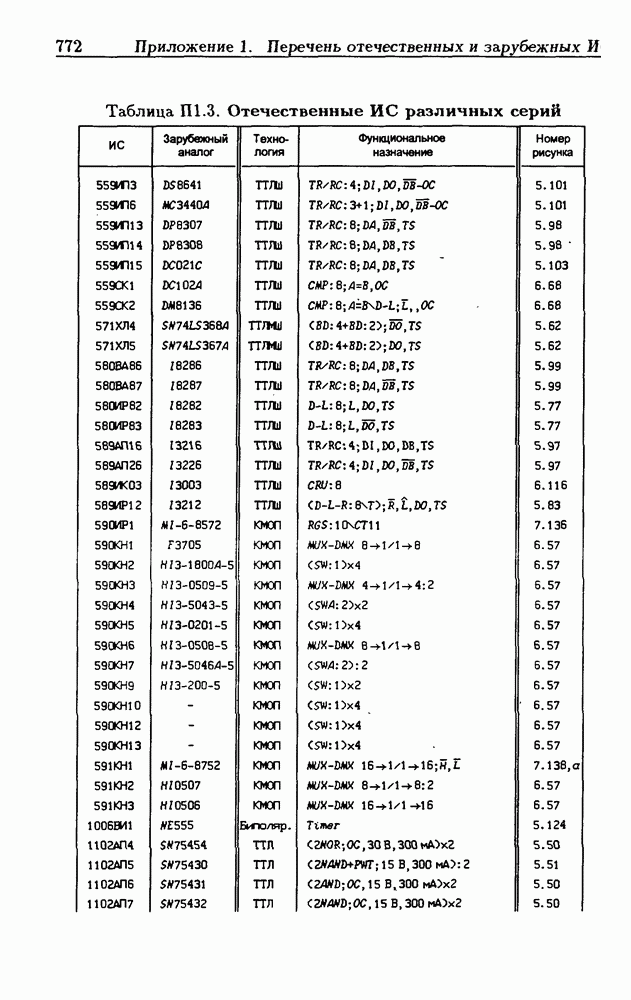
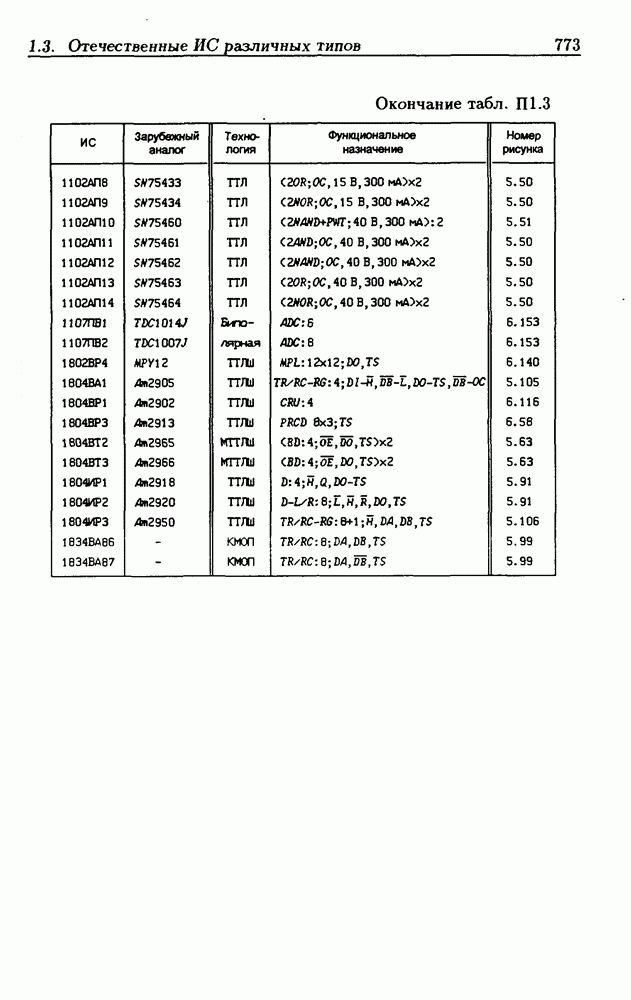
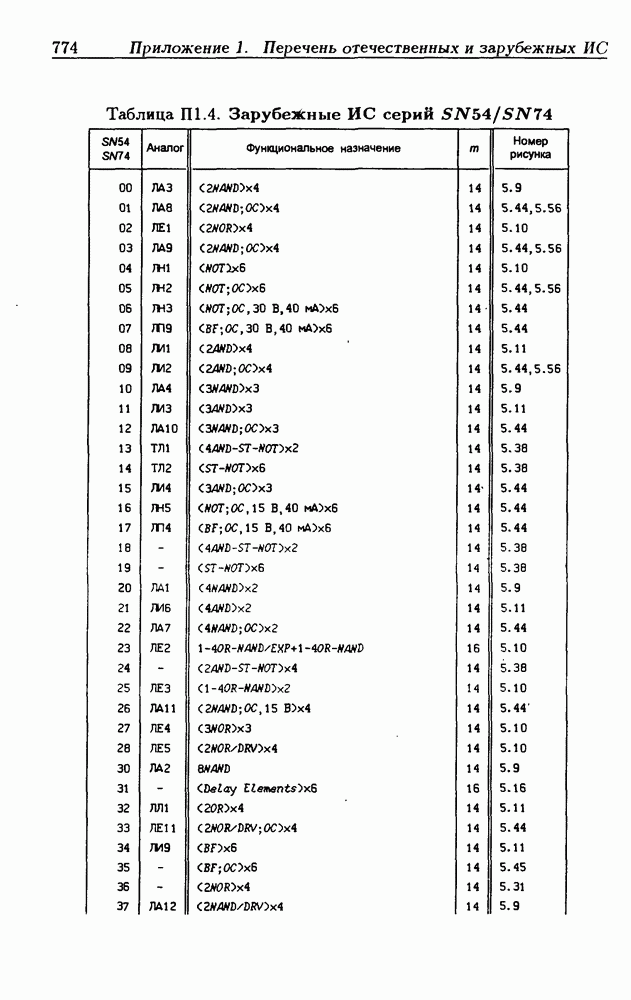
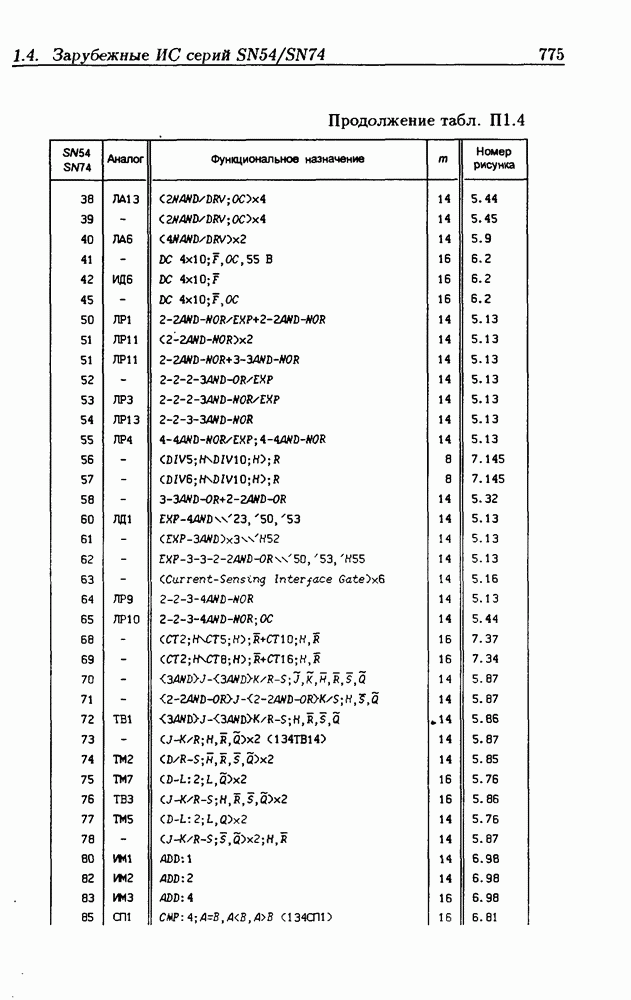
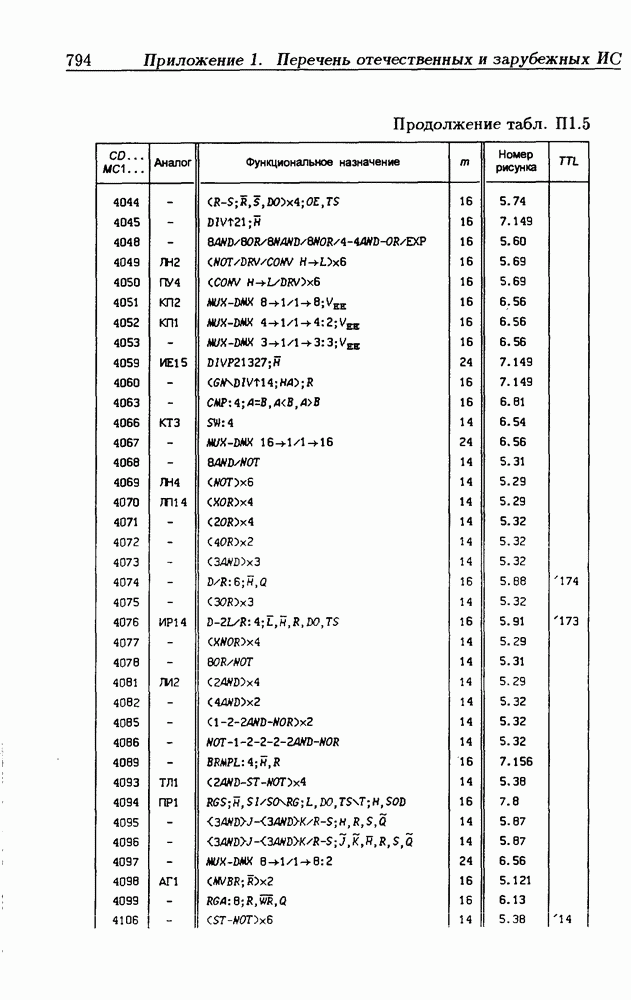
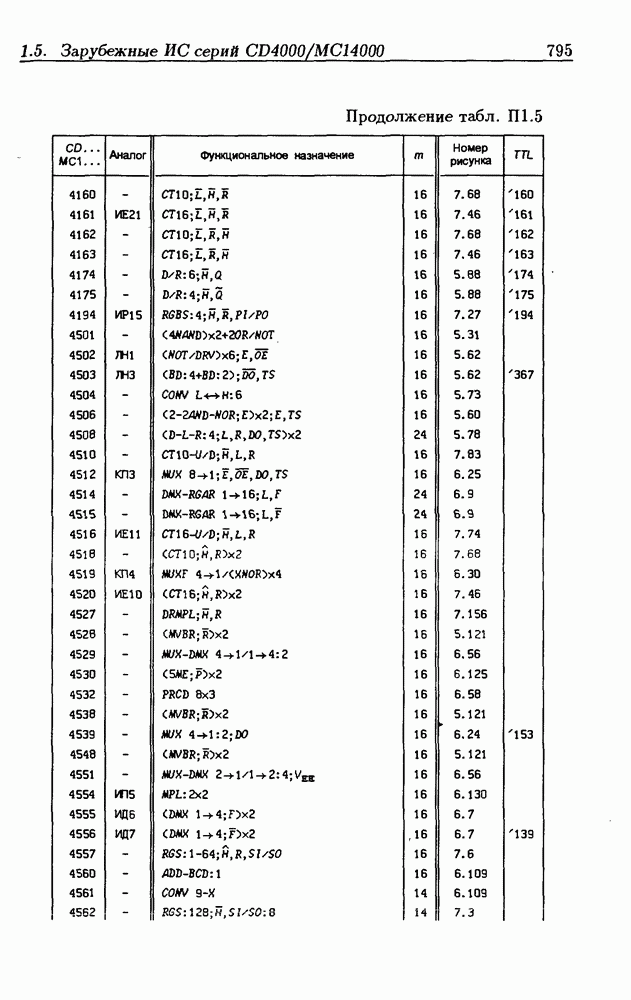
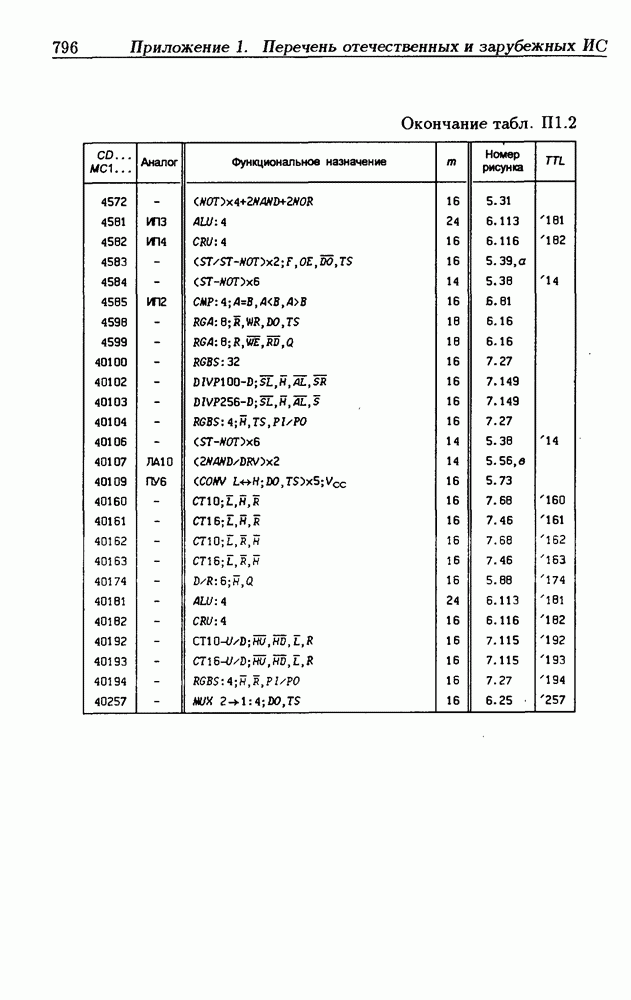
- Приложение 1. Перечень отечественных и зарубежных ИС
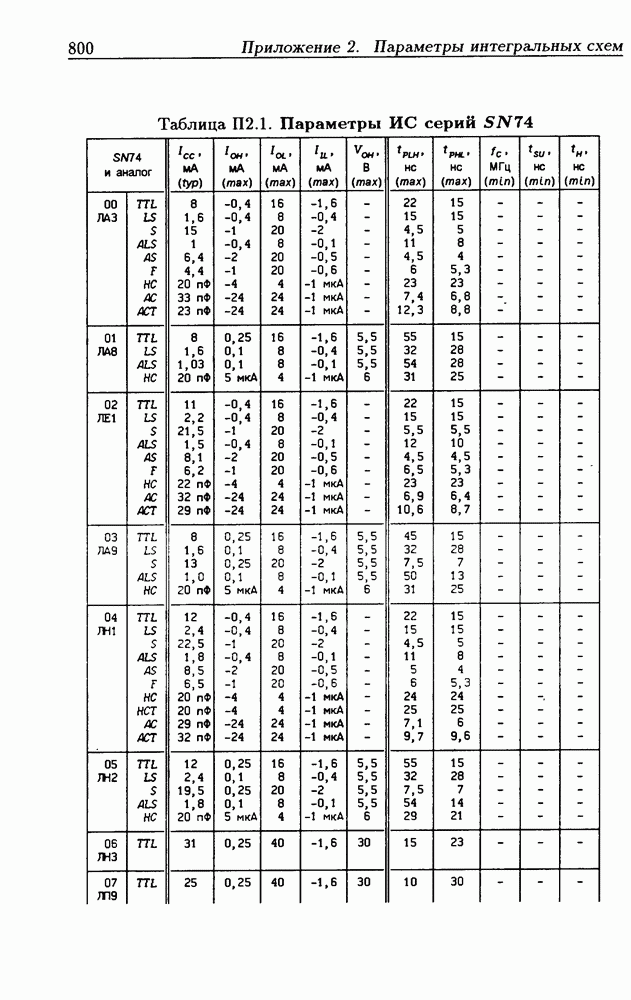
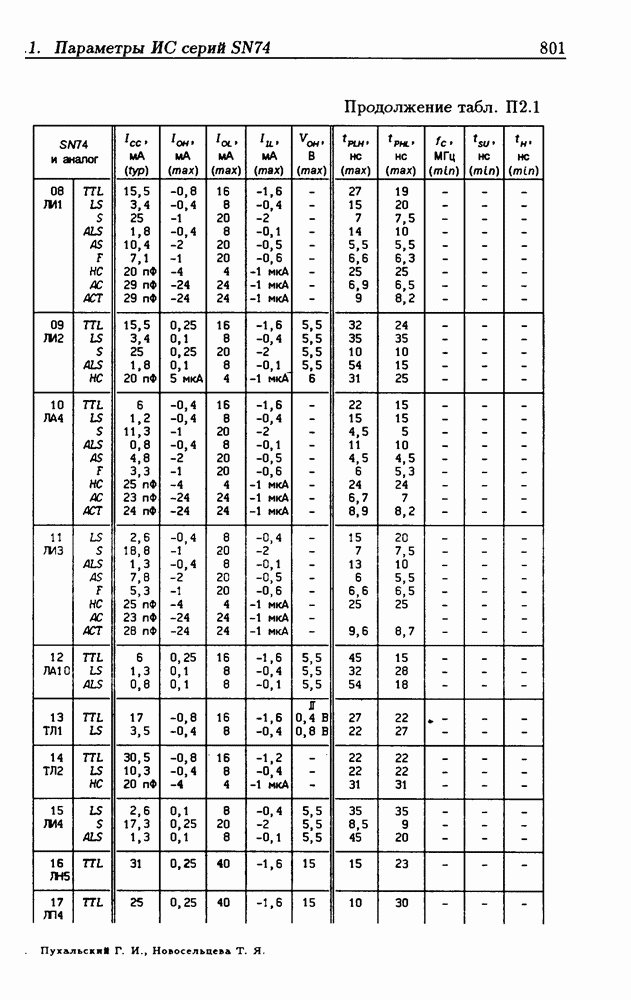
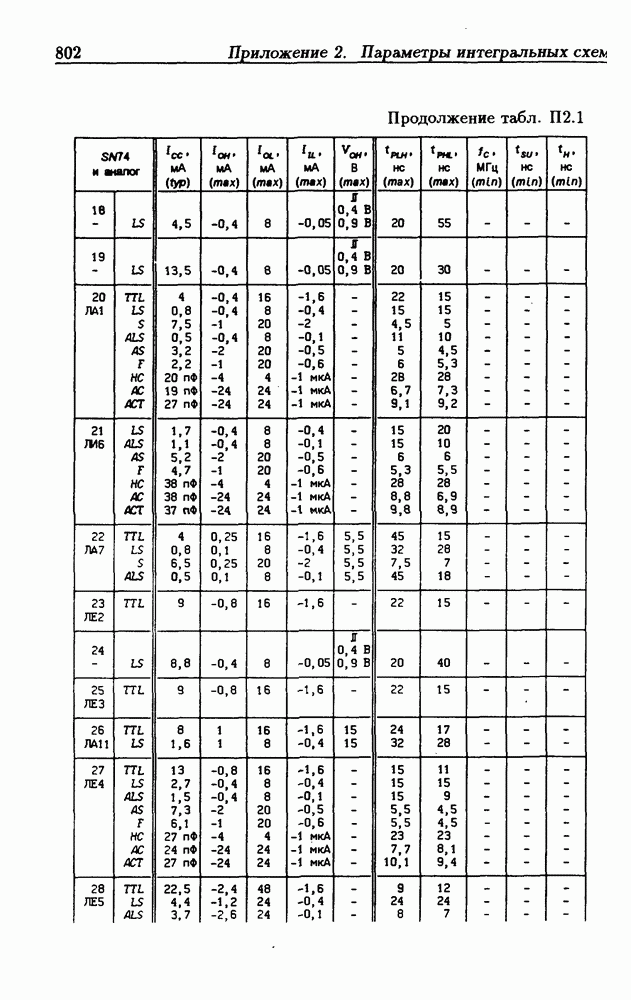
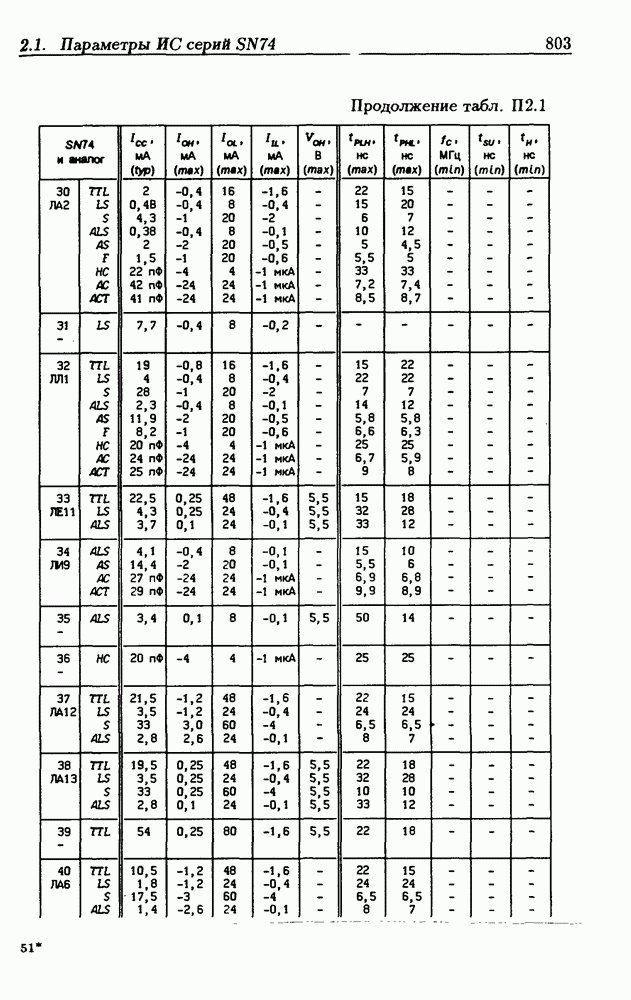
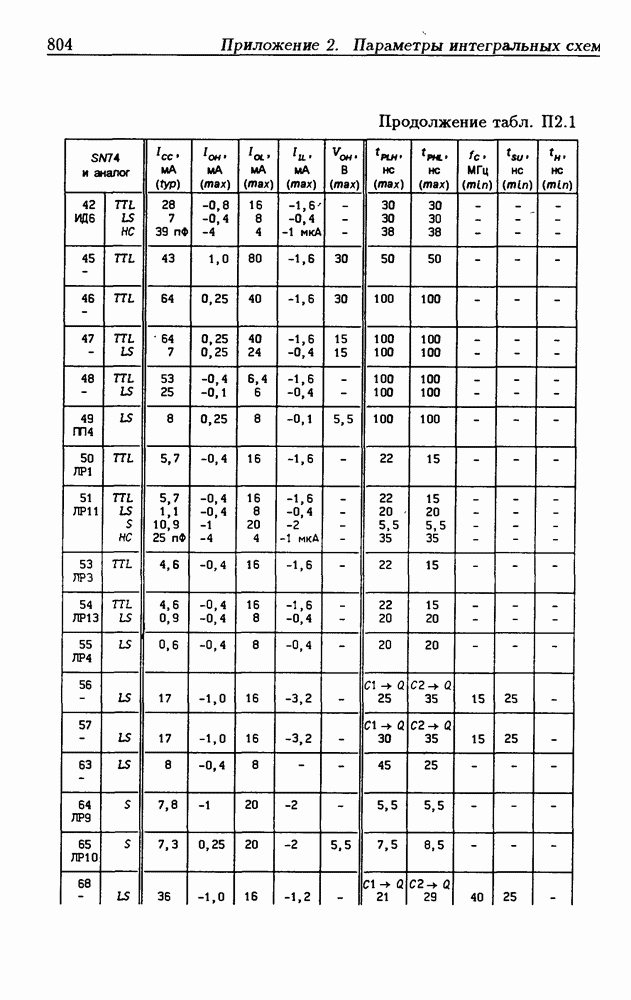
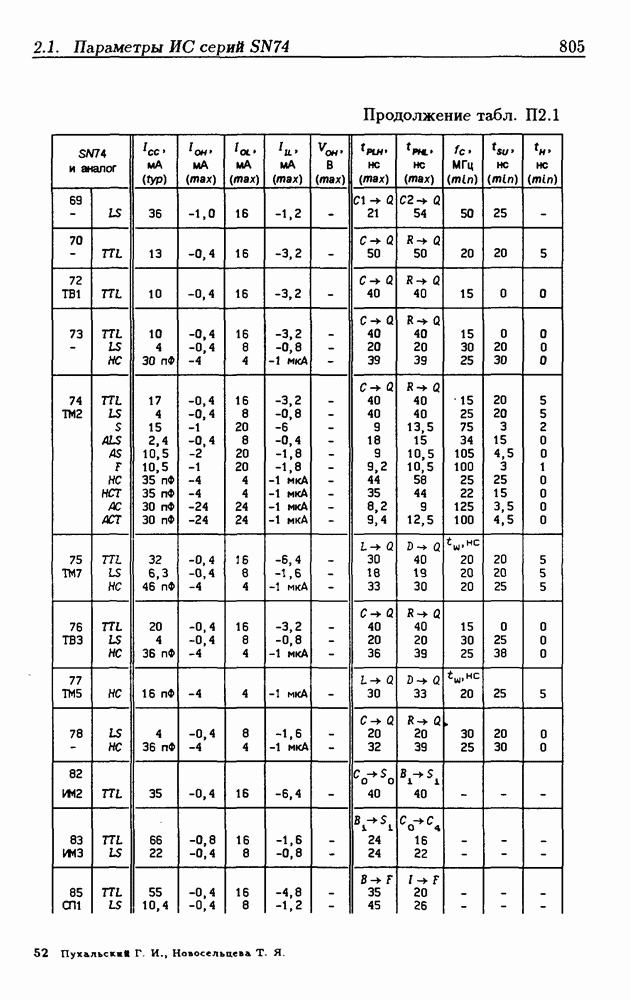
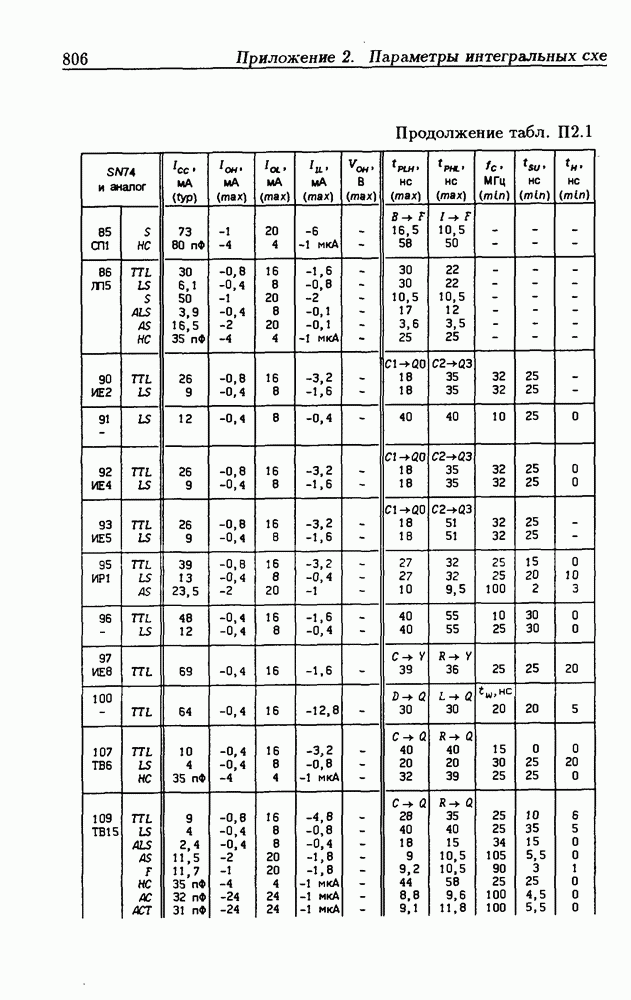
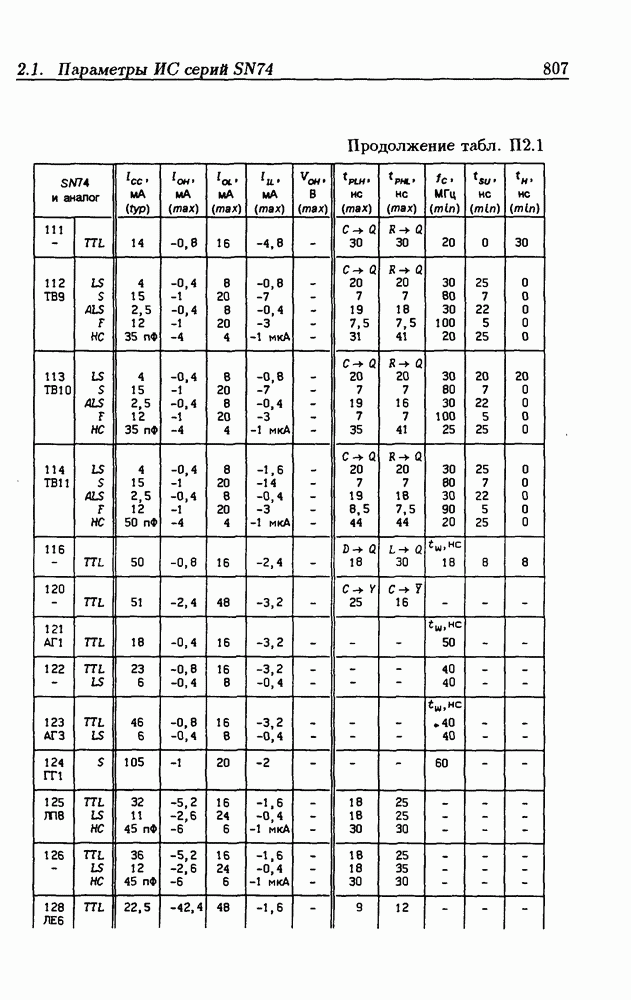
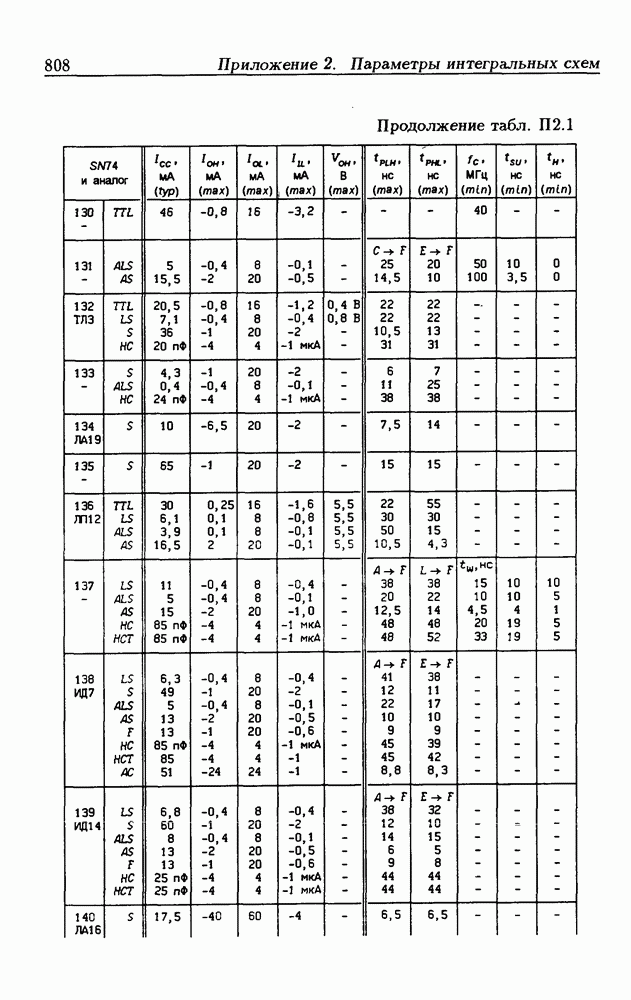
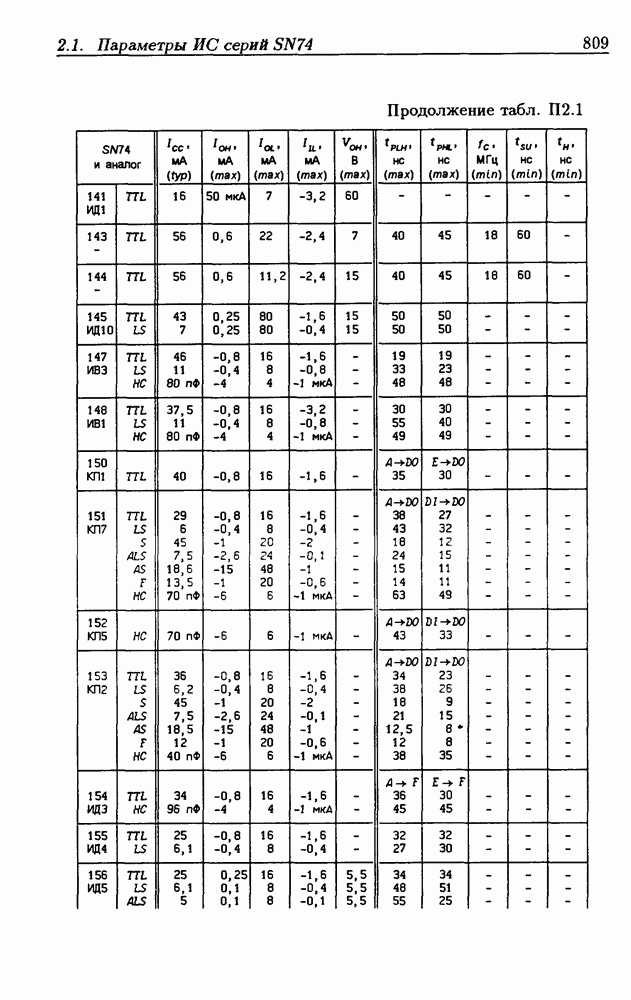
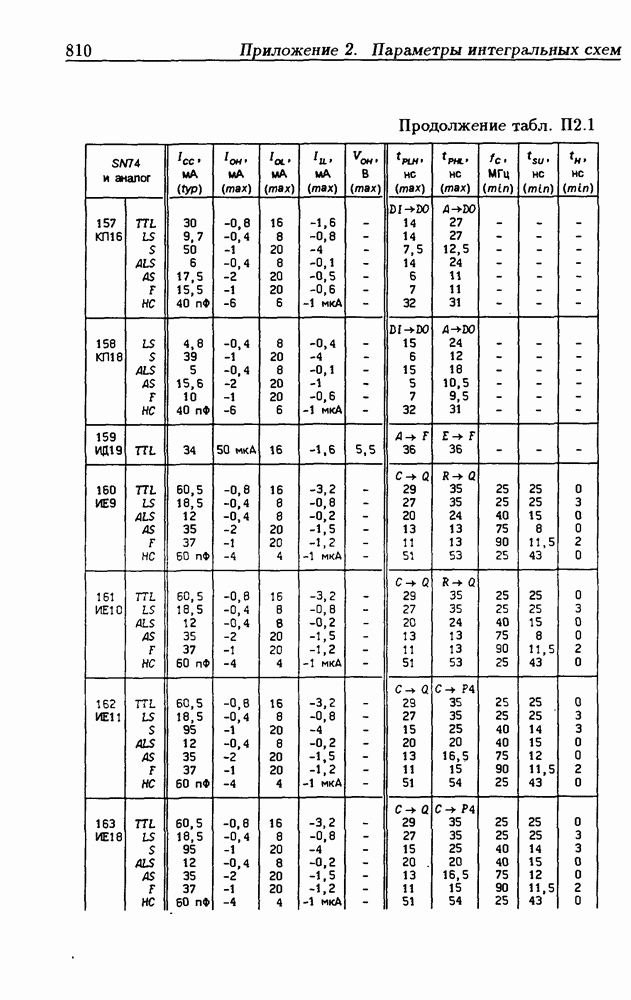
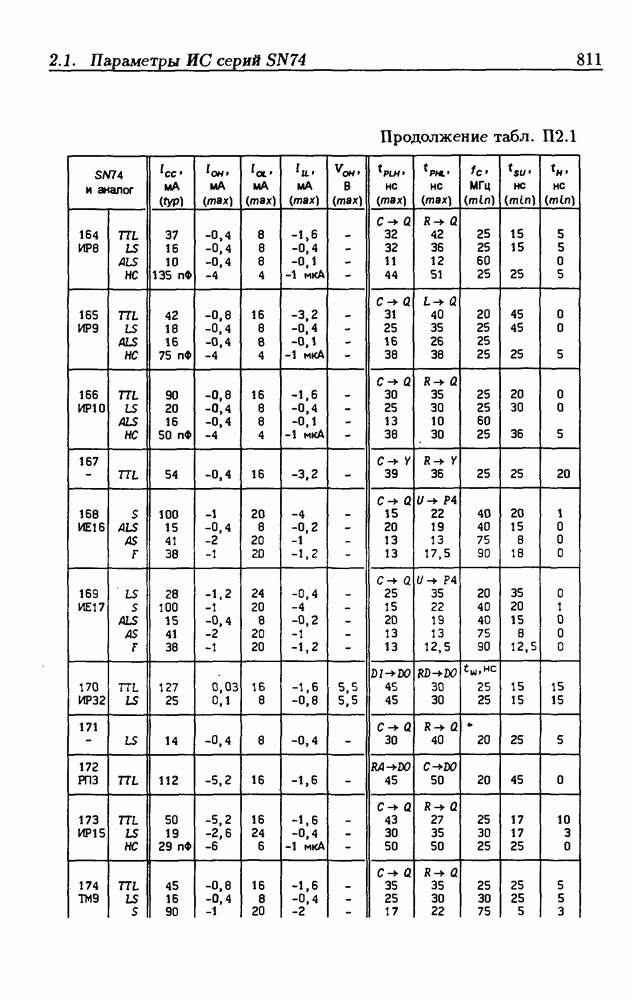
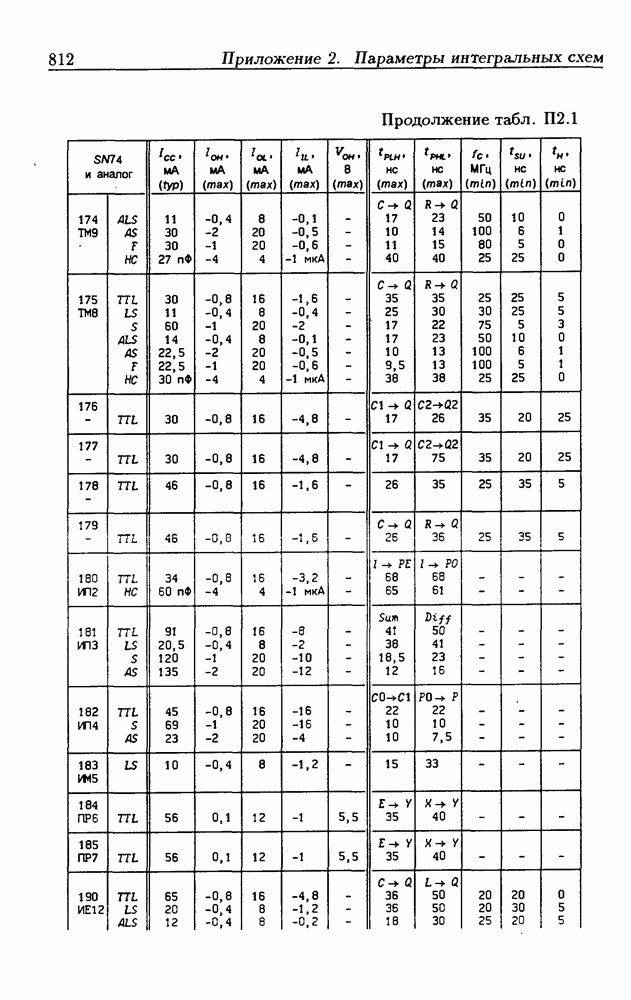
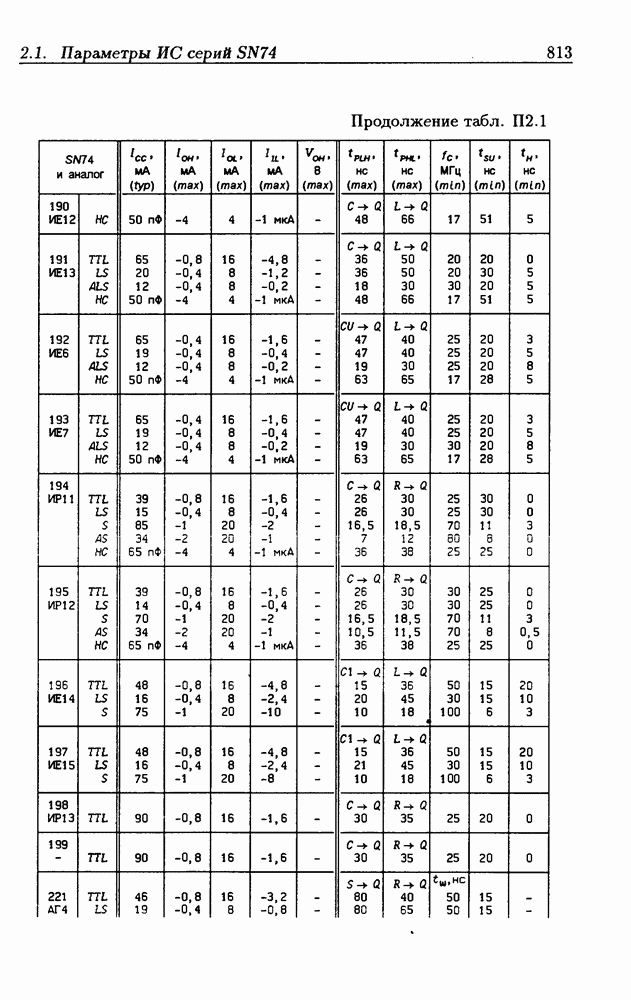
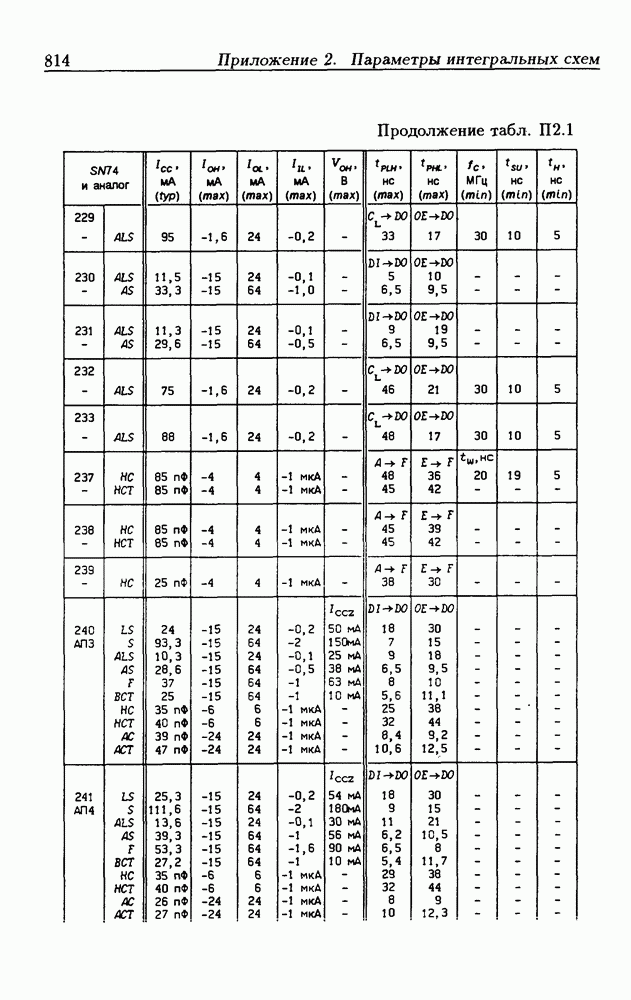
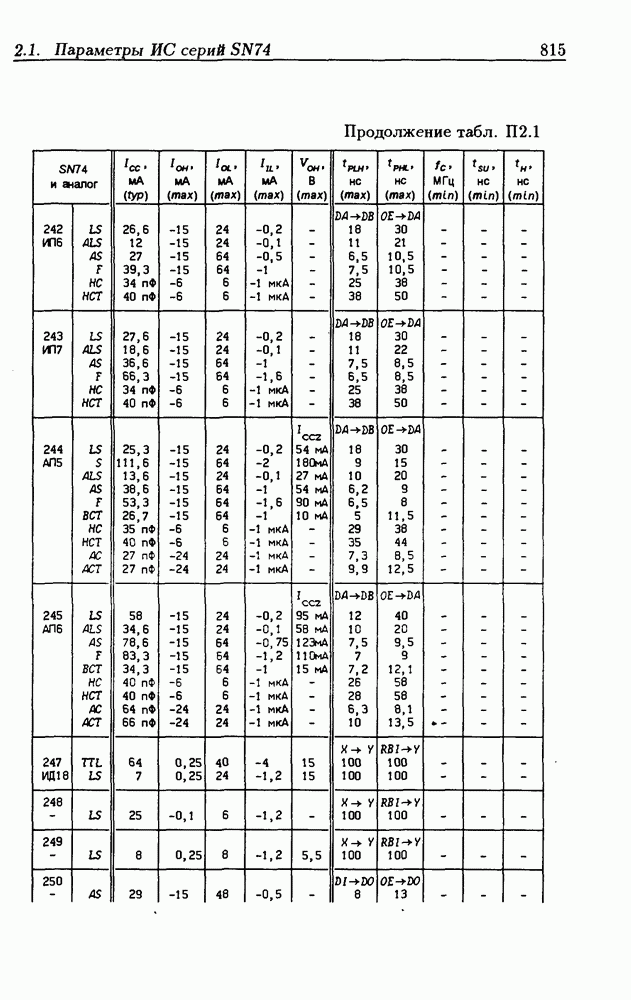
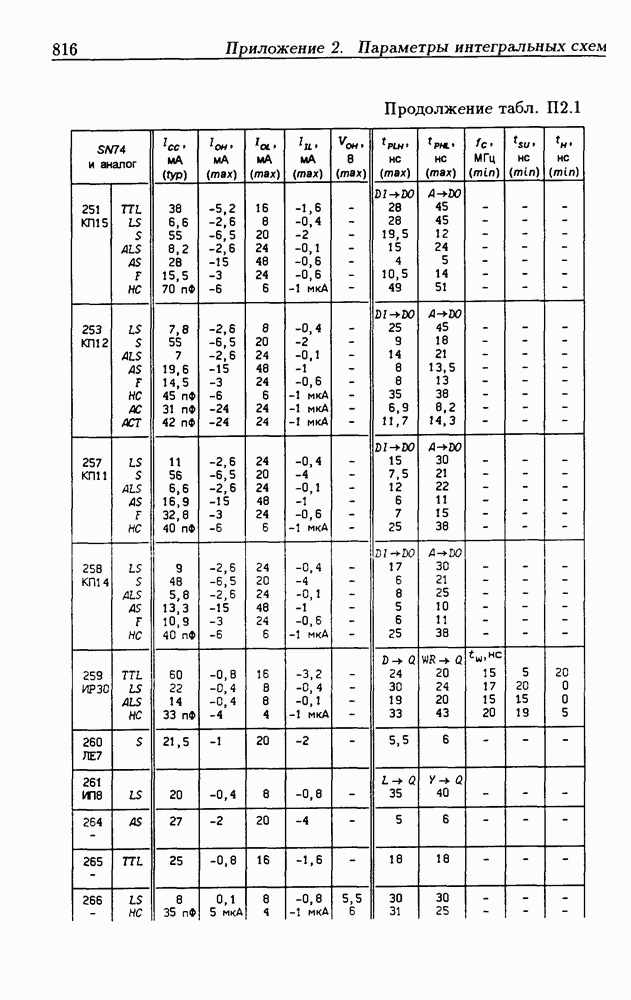
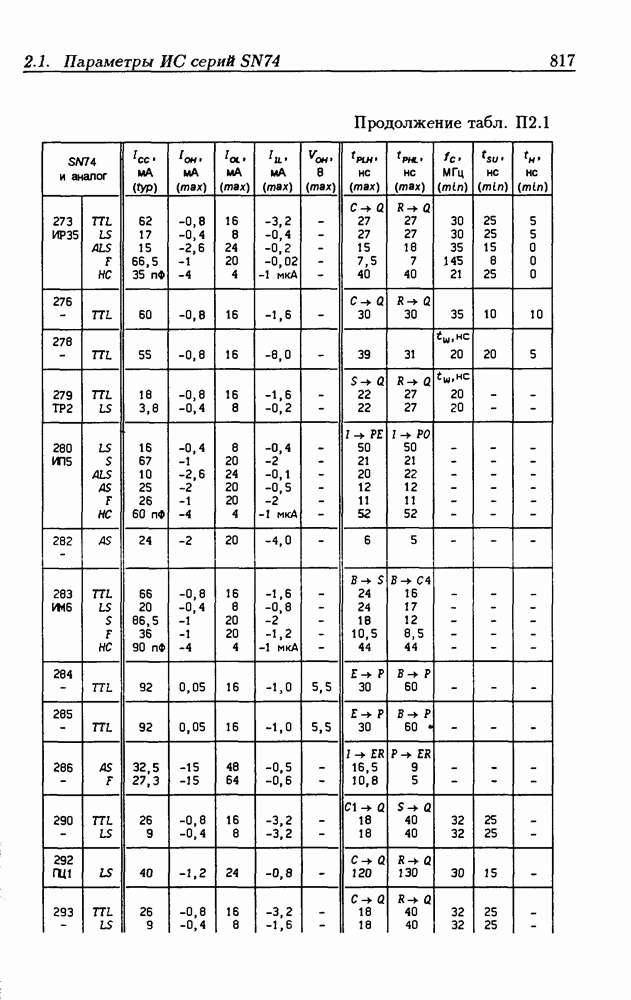
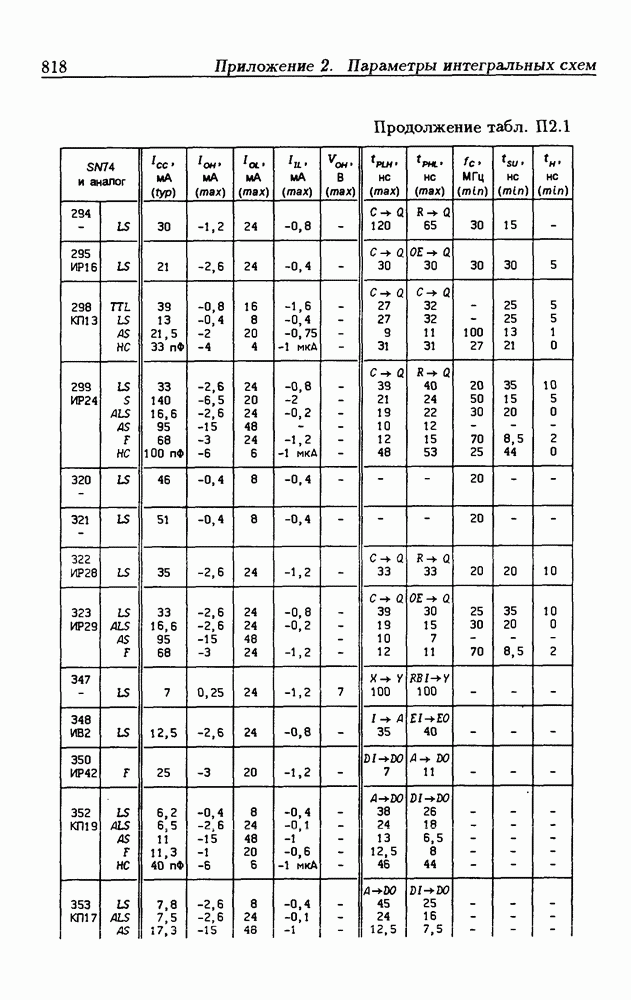
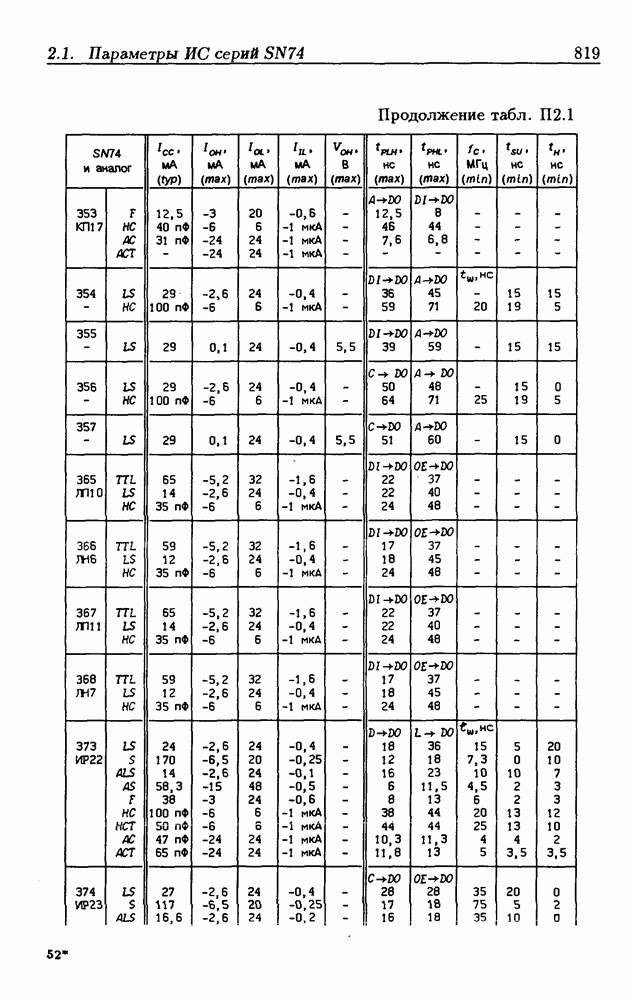
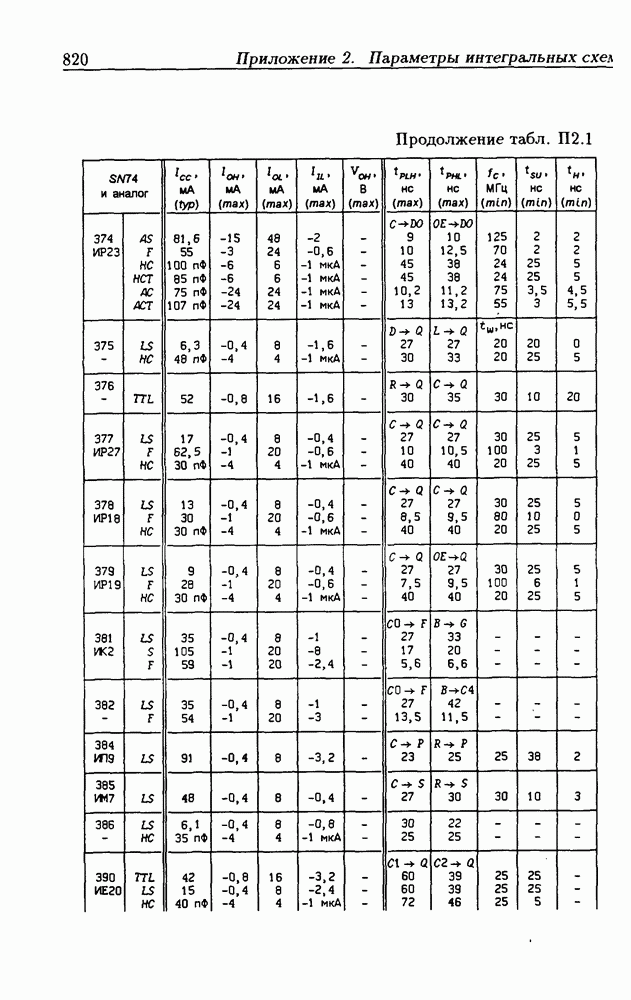
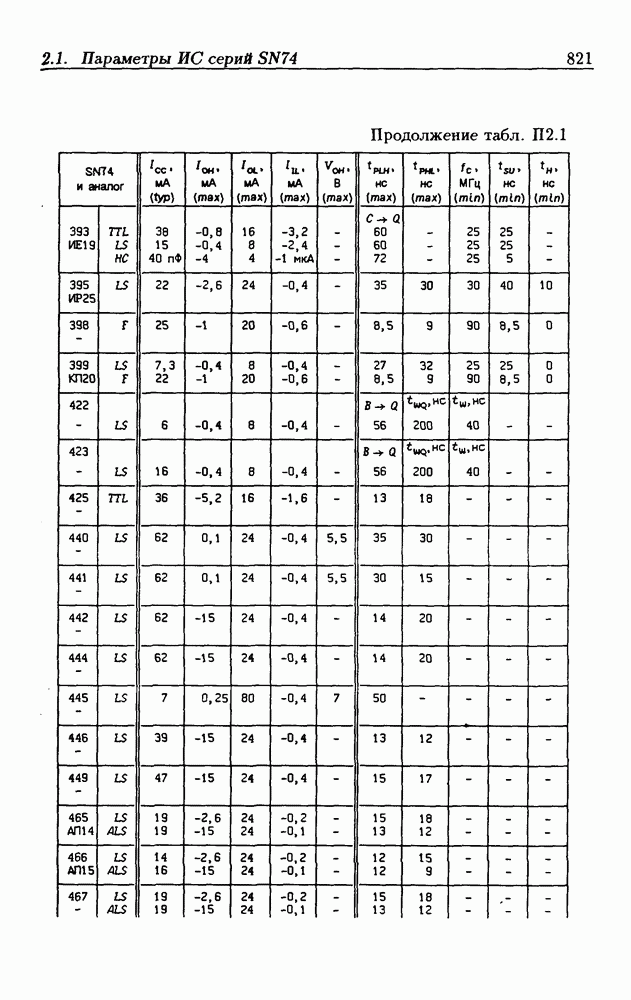
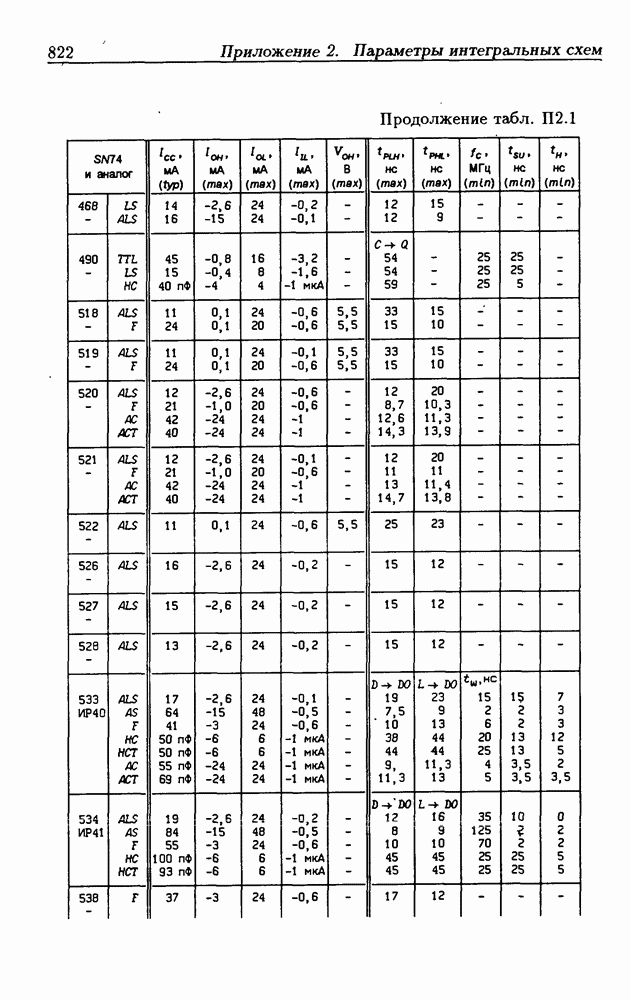
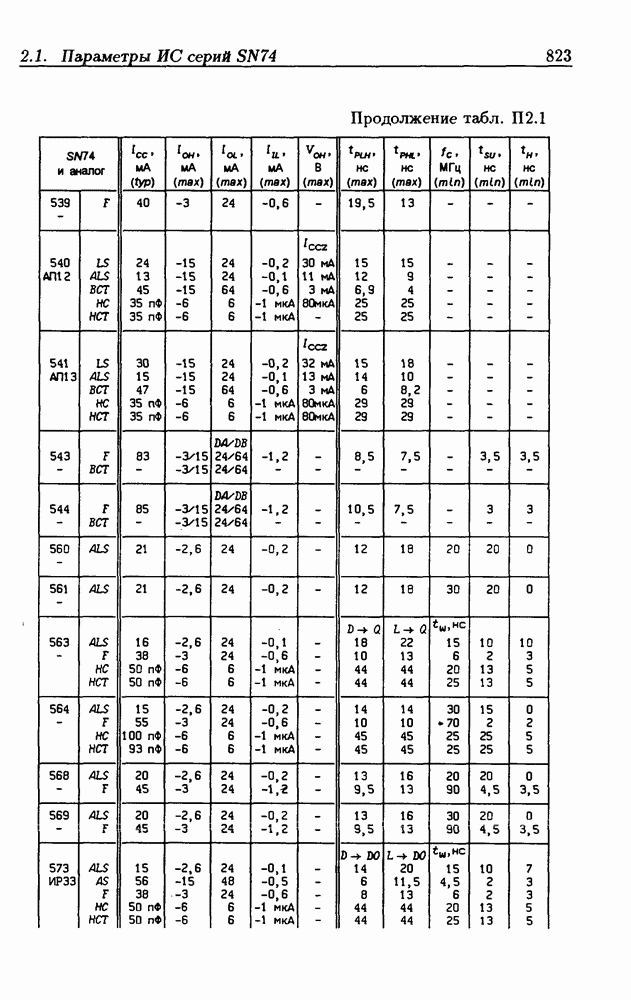
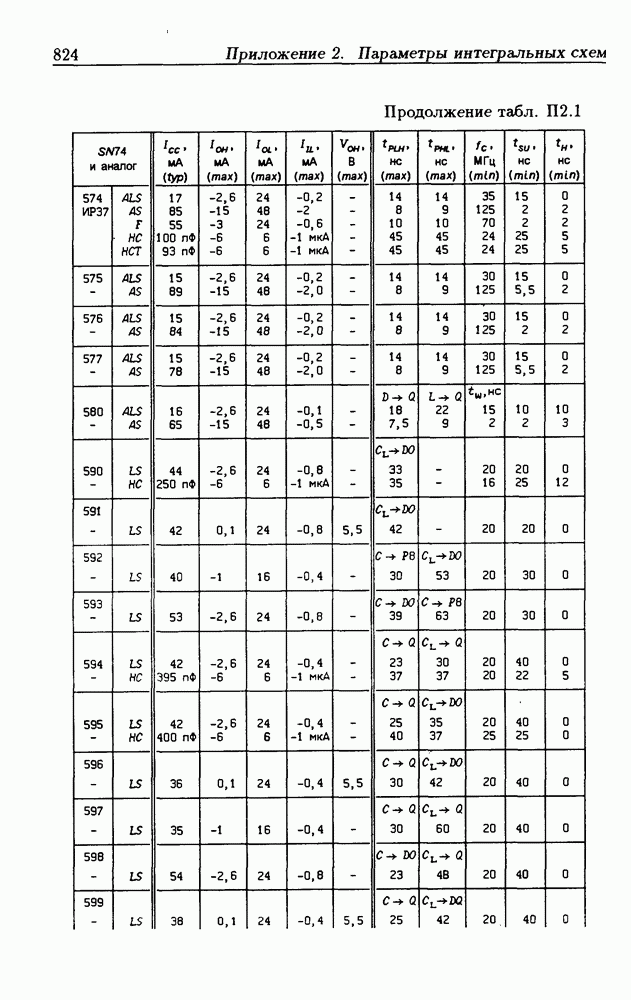
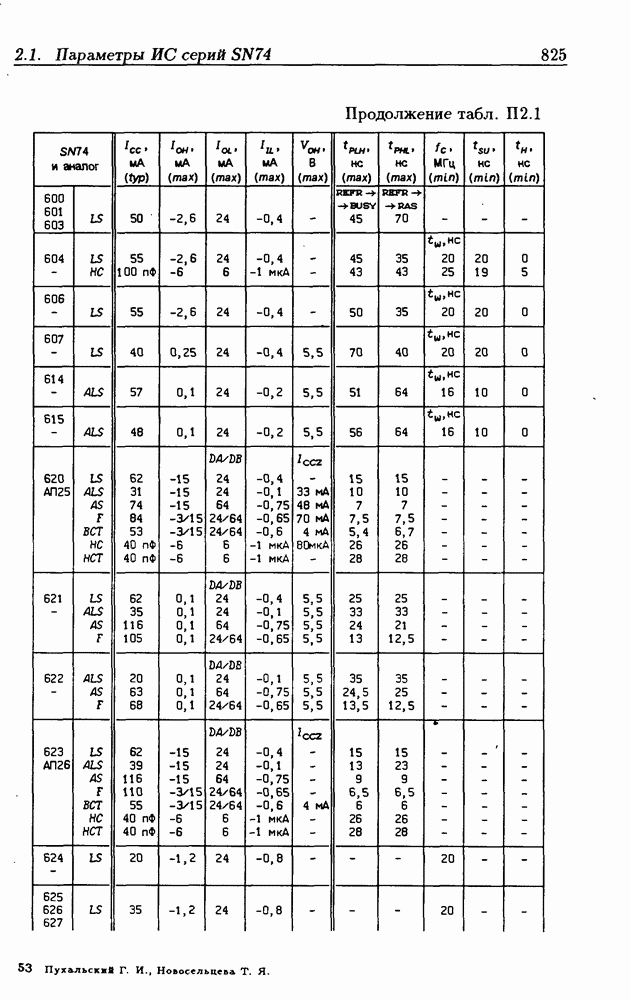
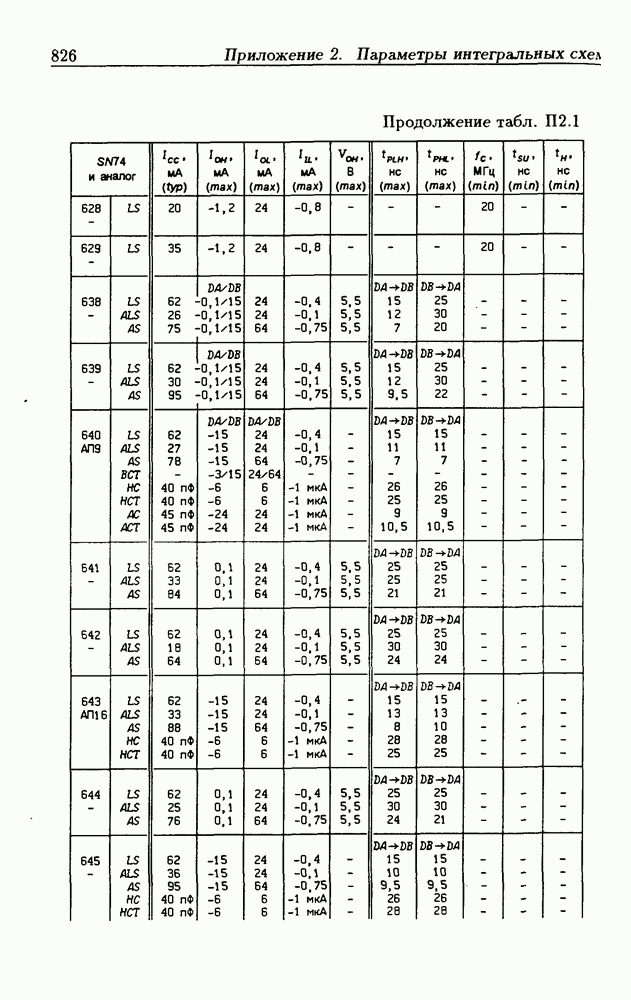
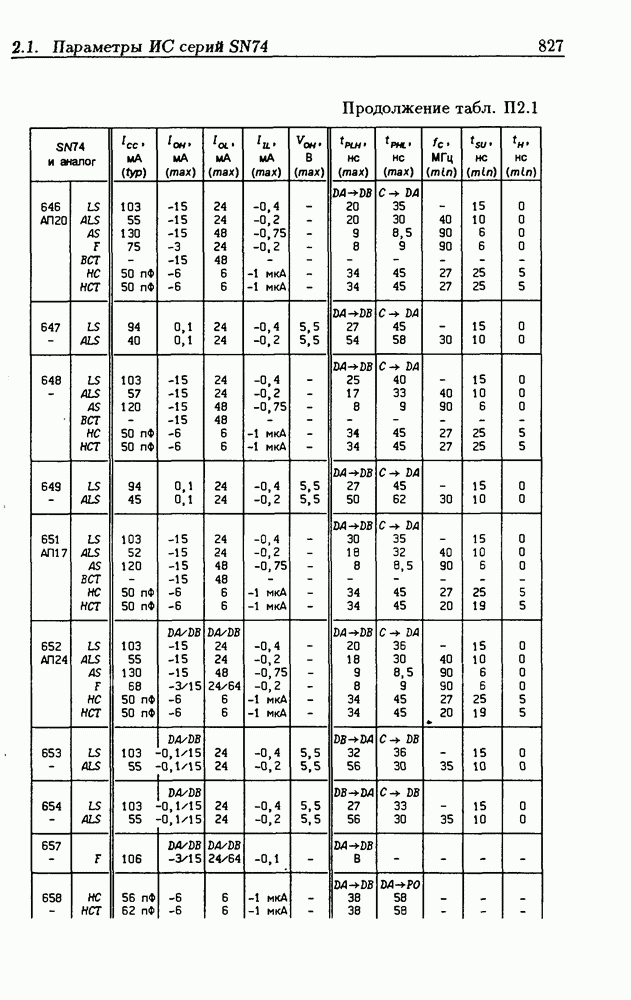
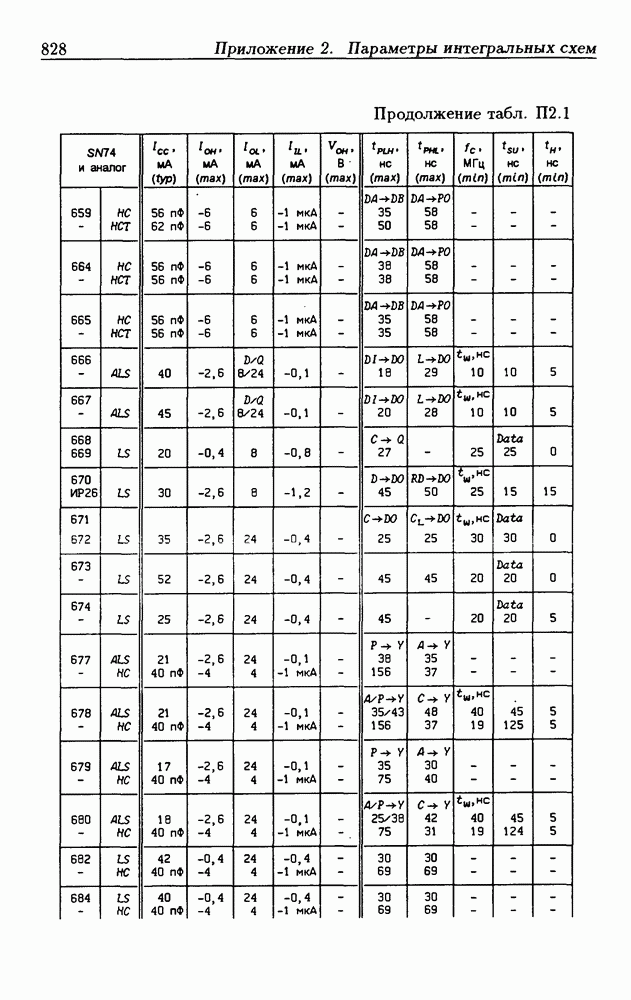
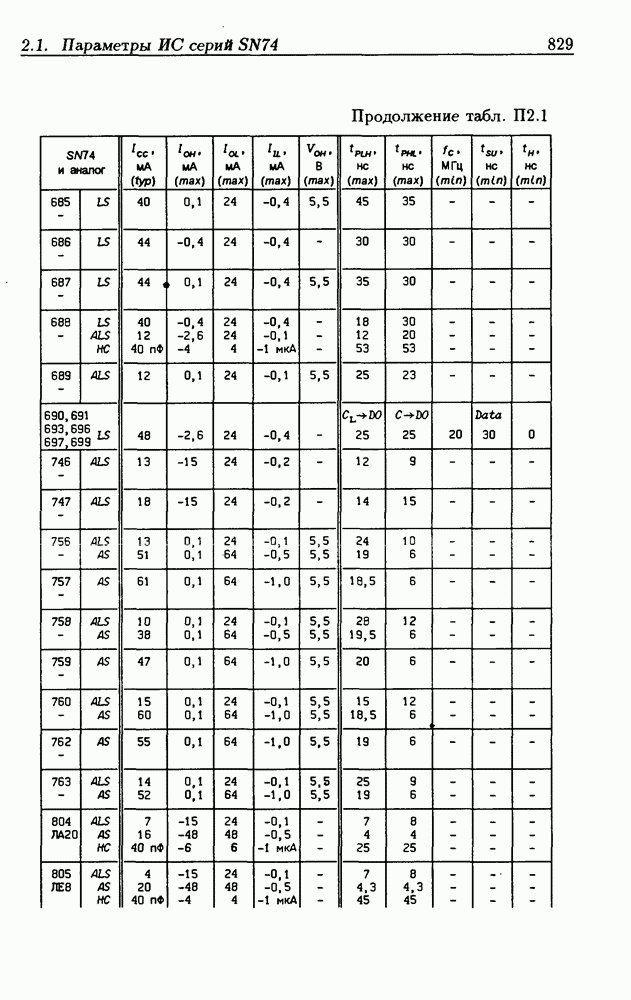
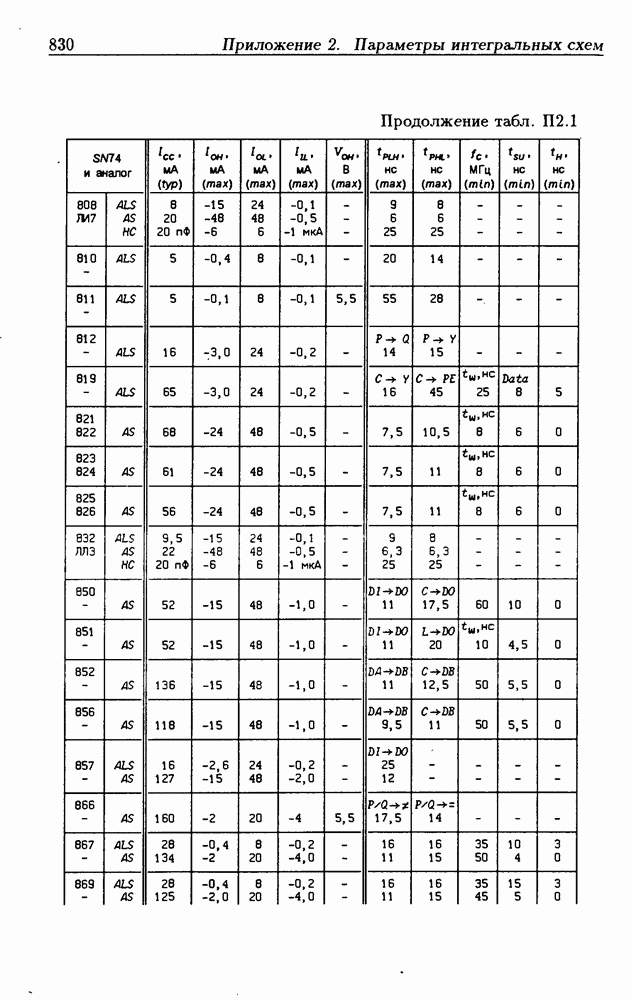
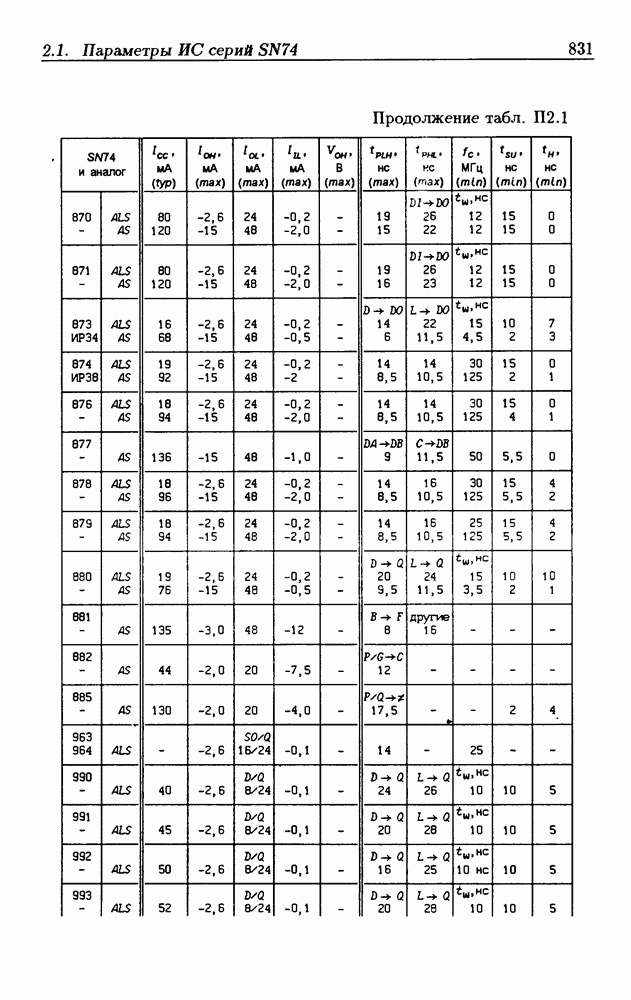
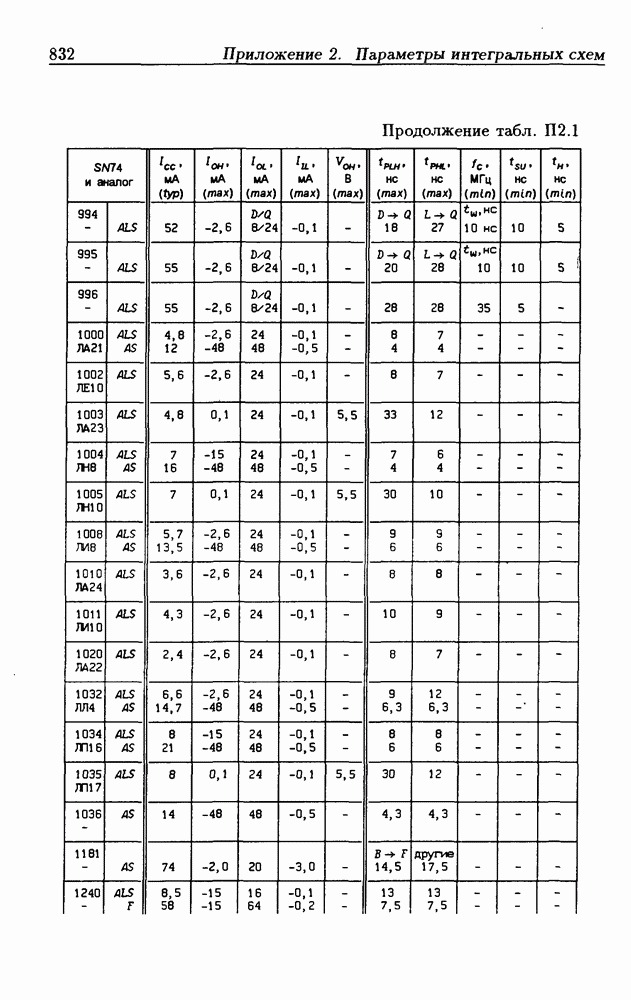
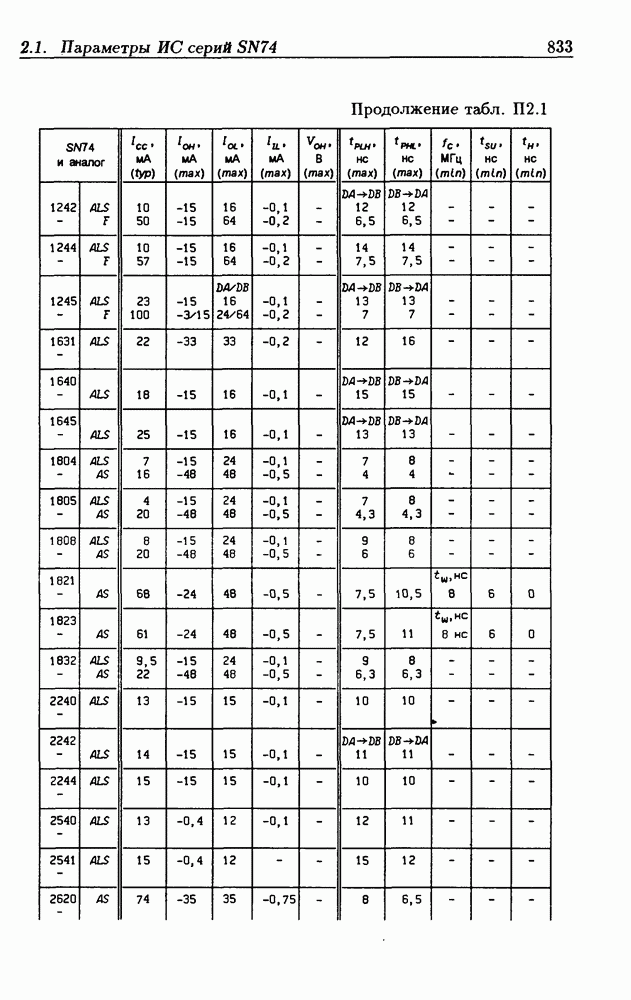
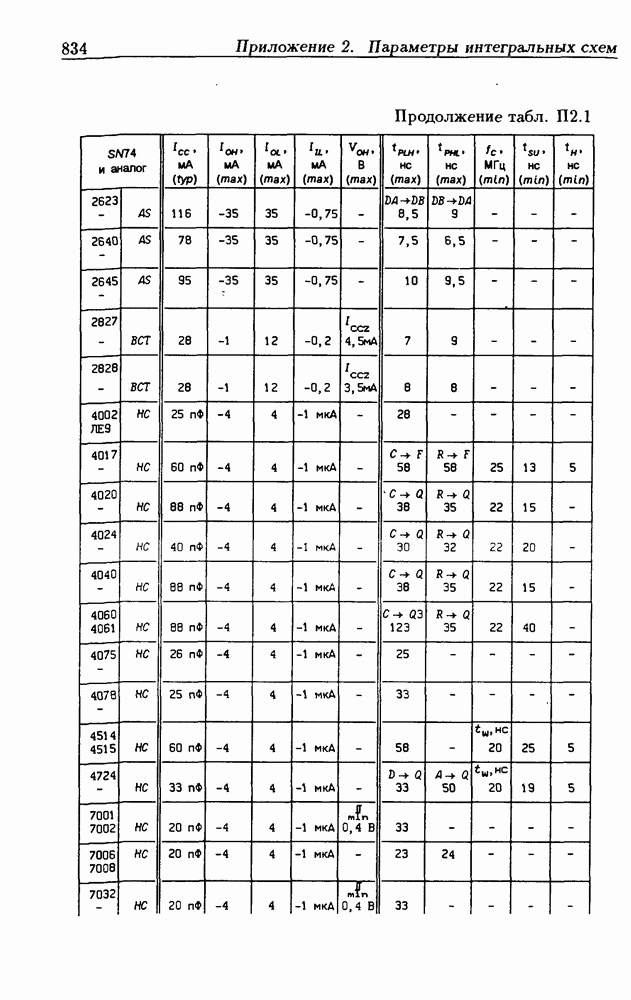
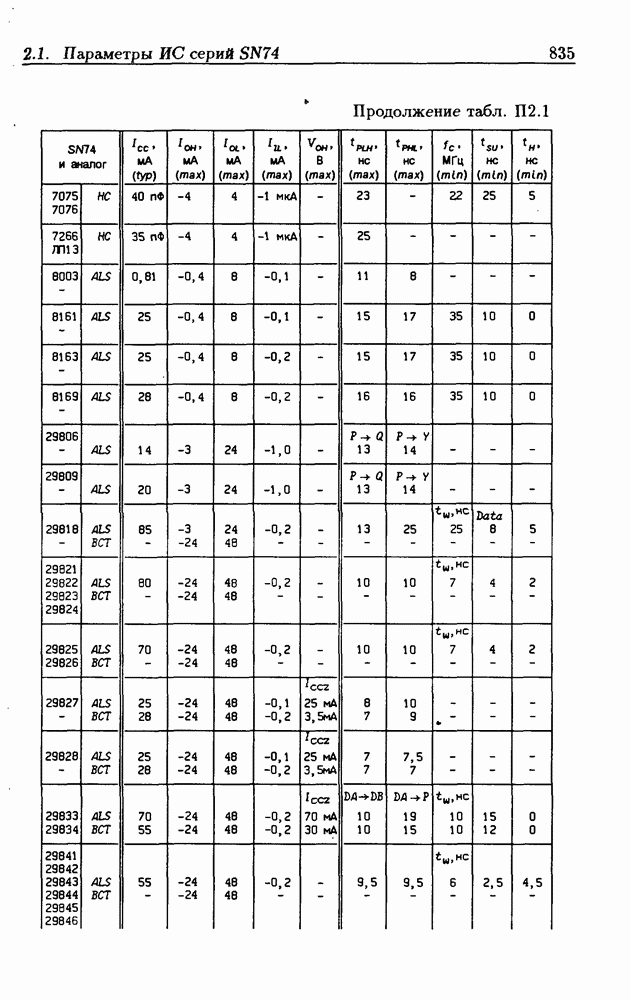
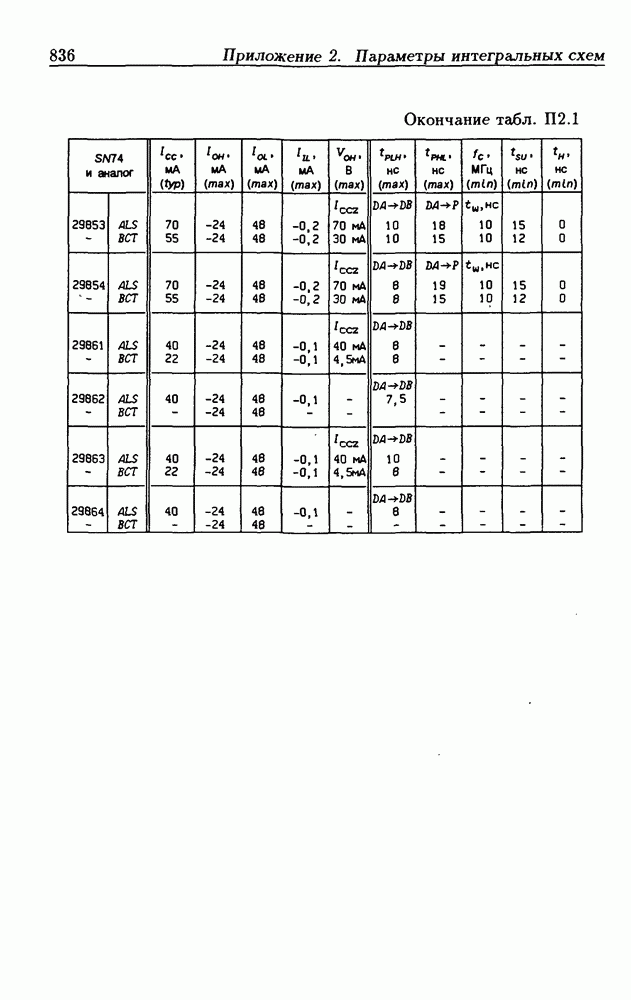
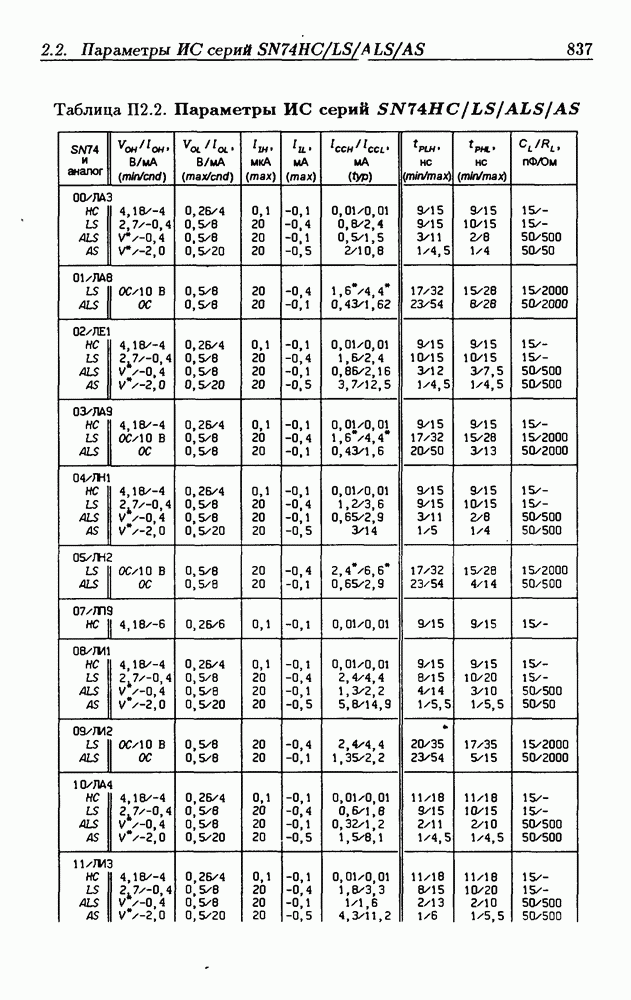
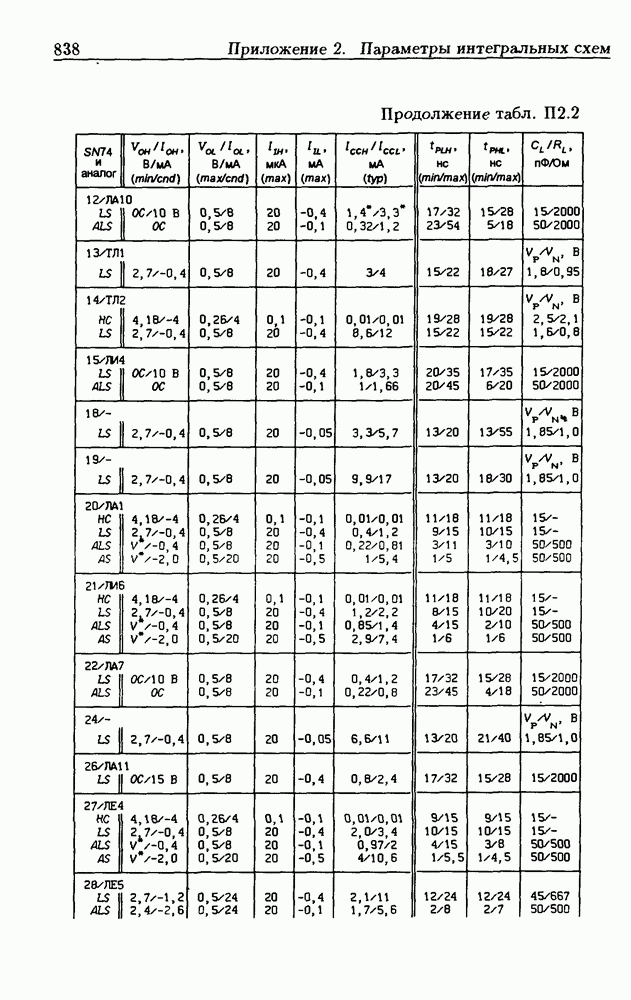
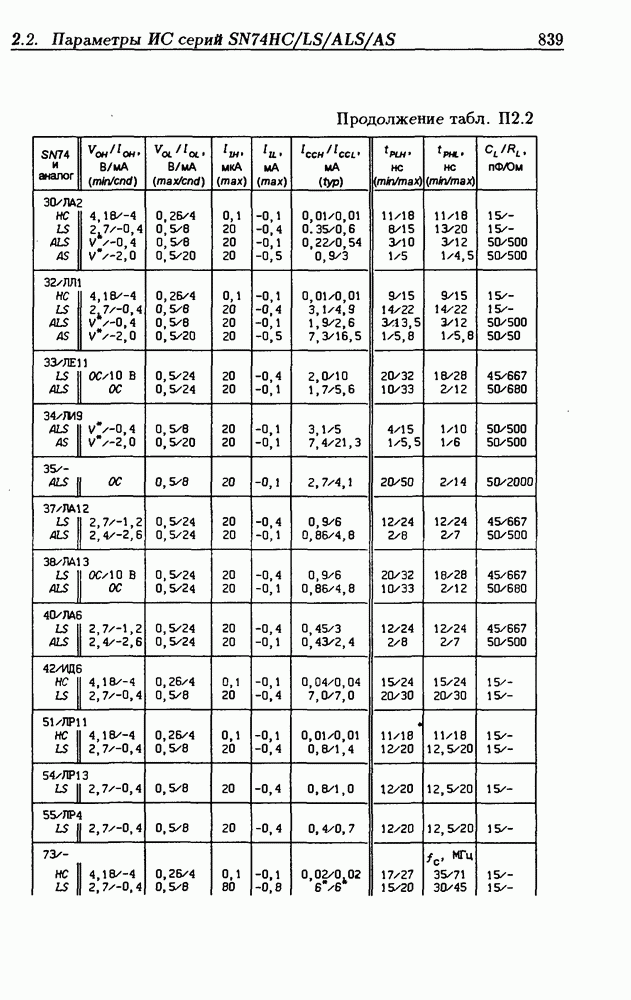
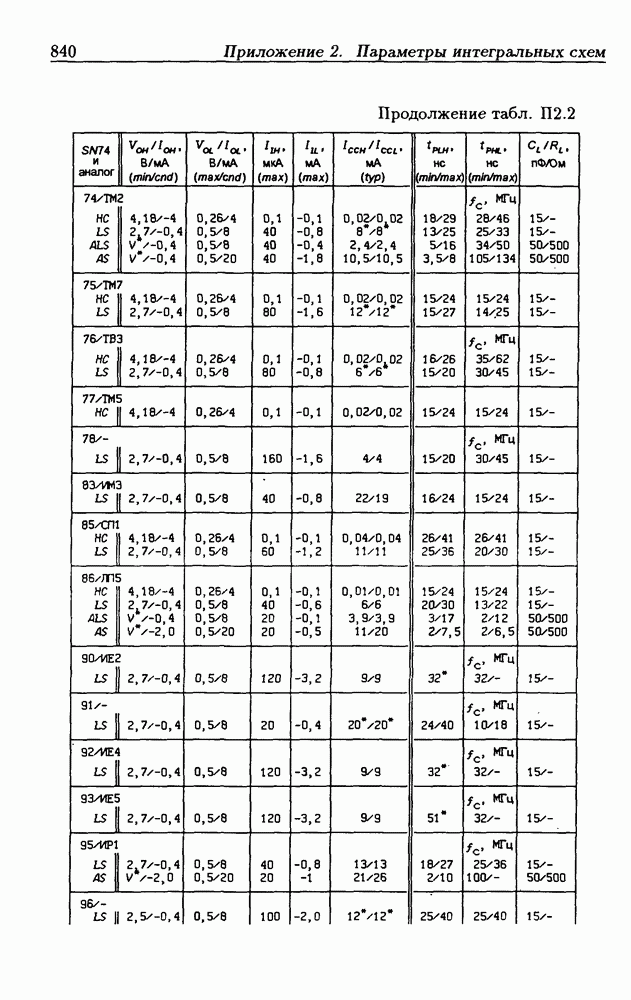
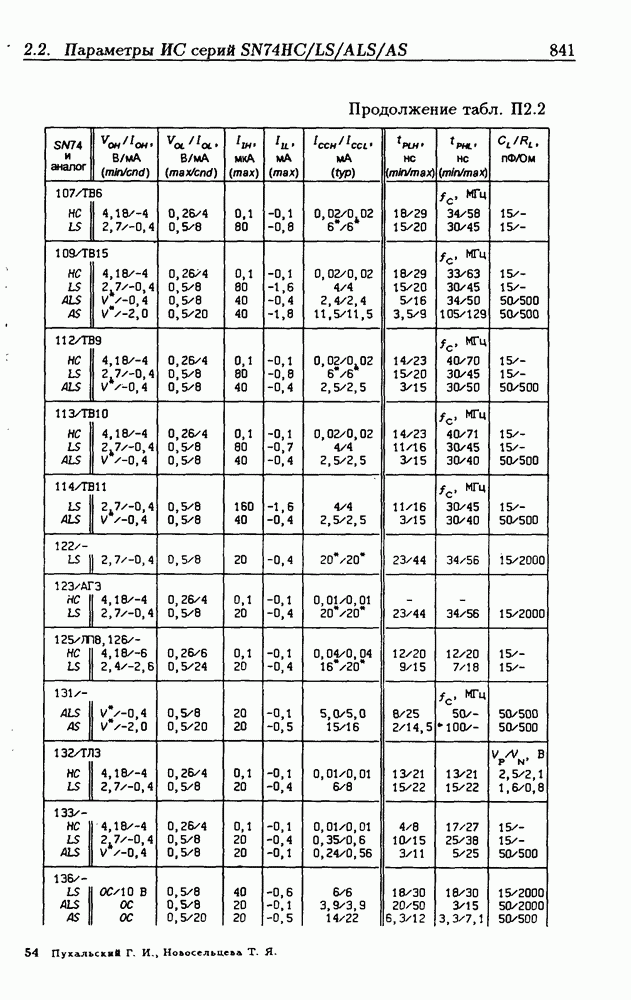
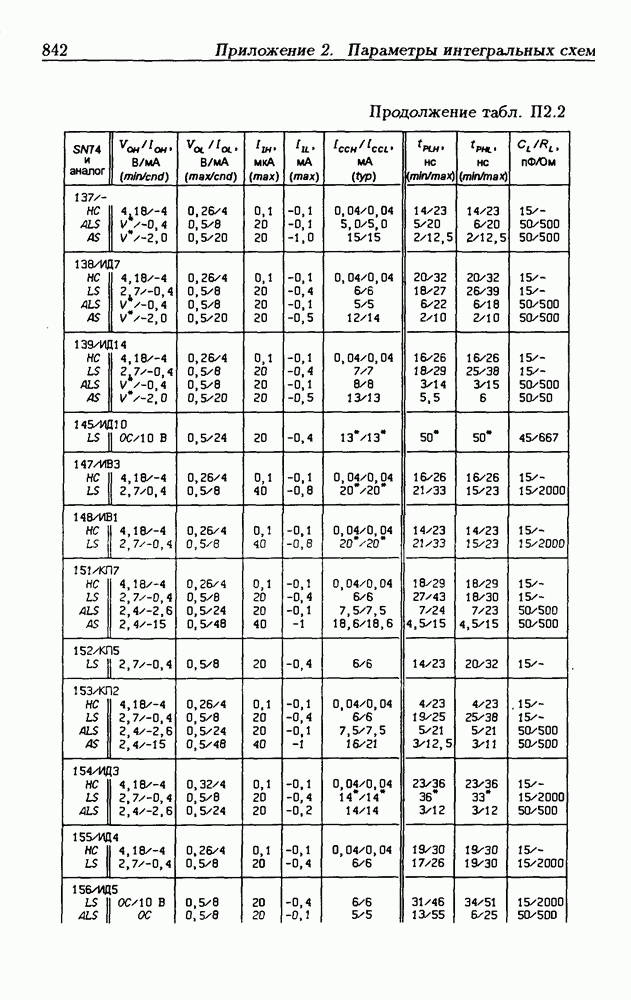
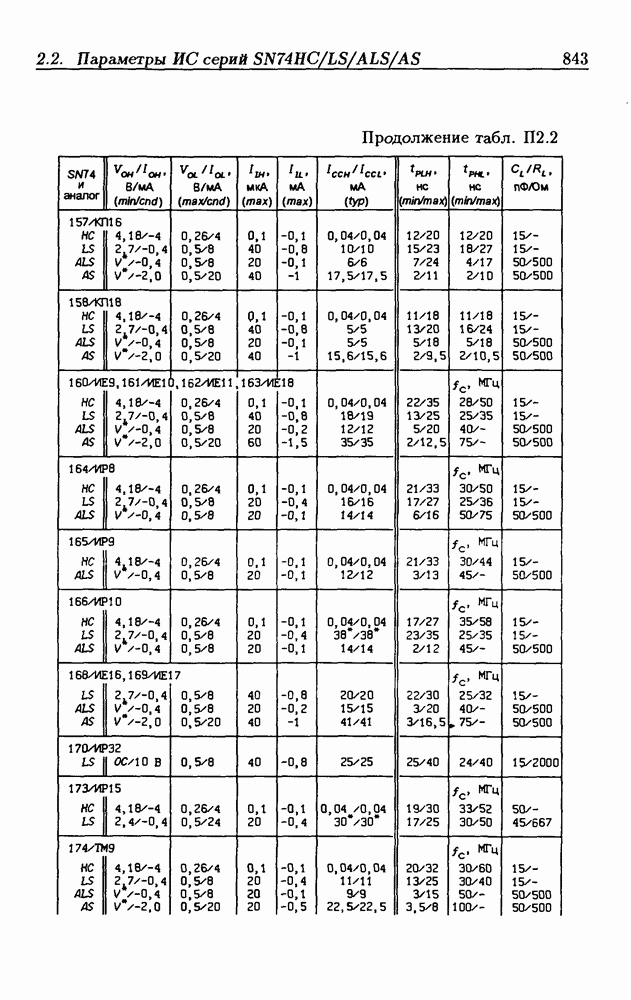
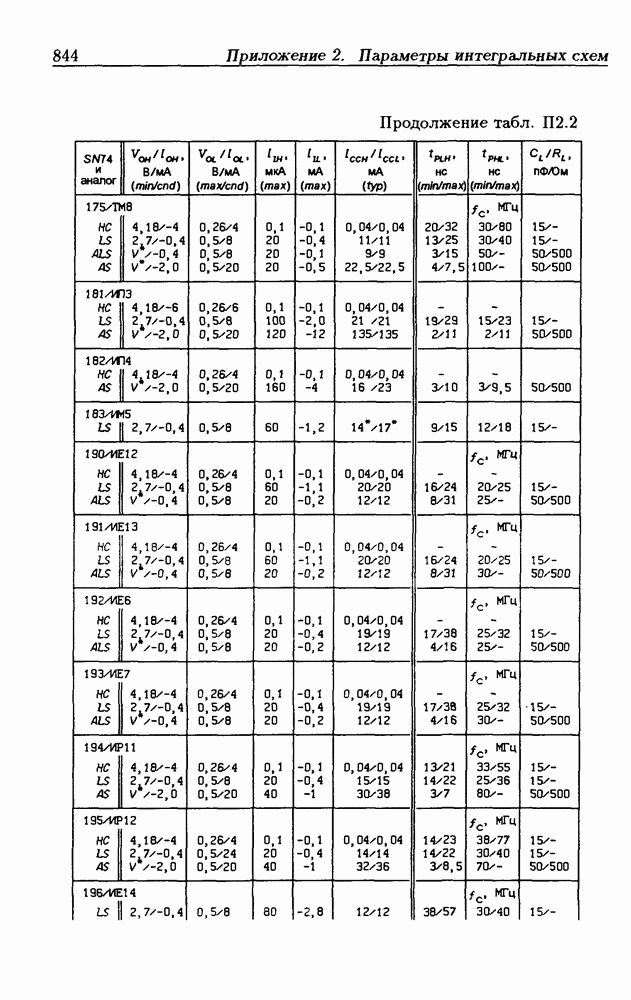
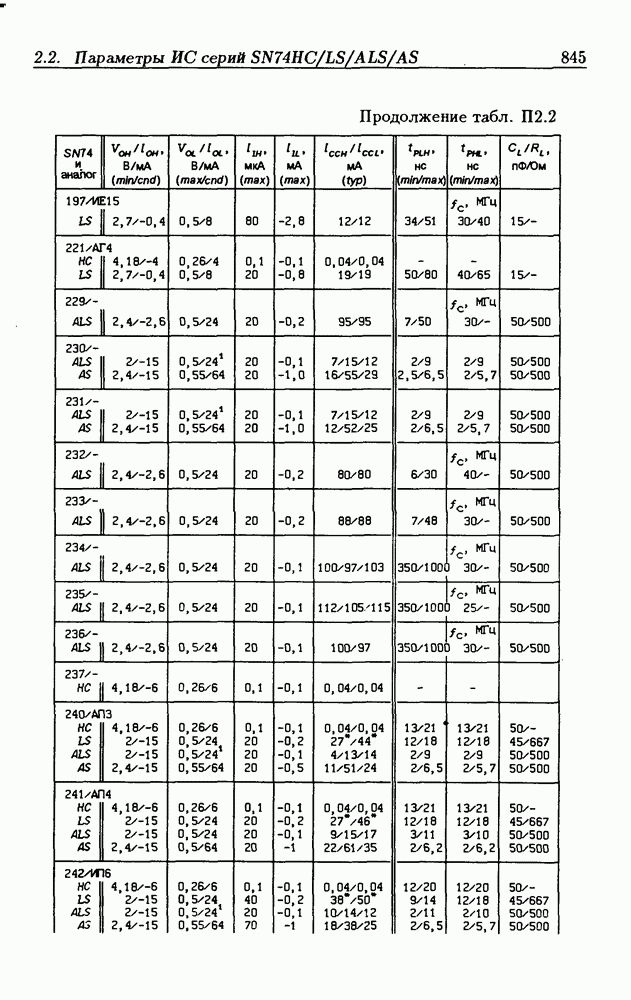
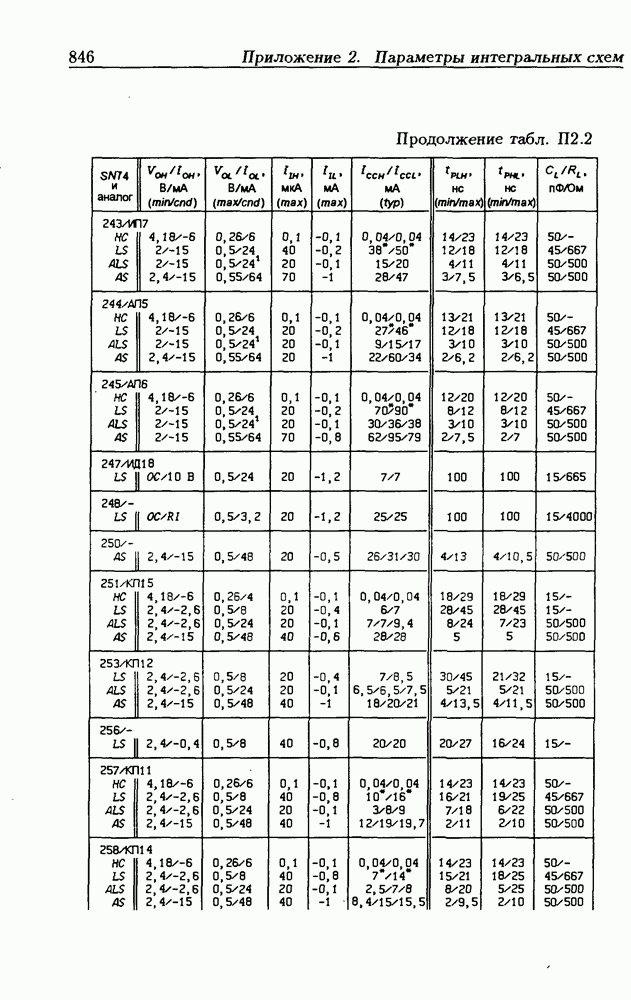
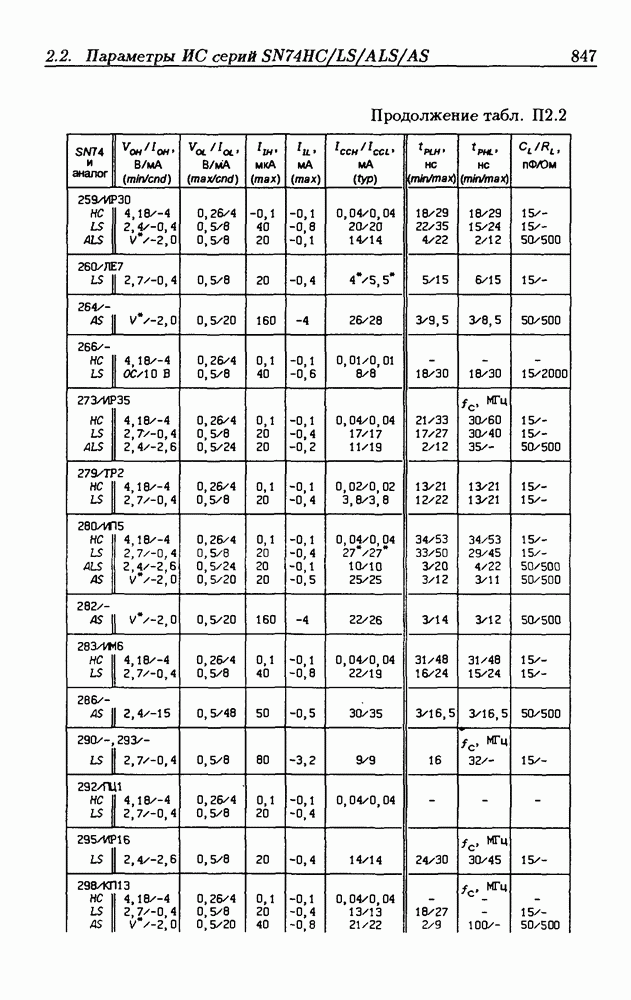
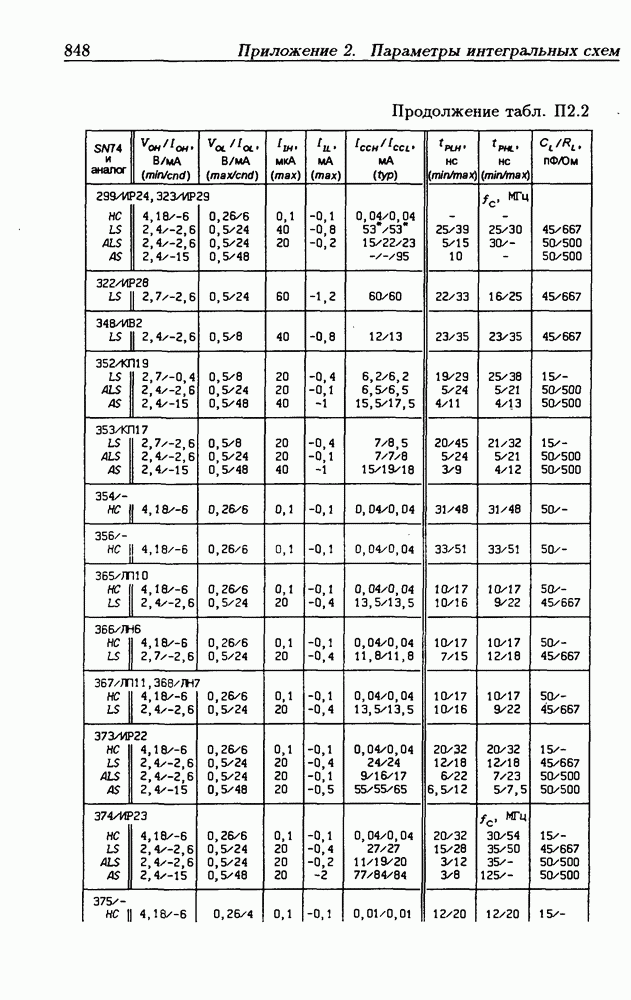
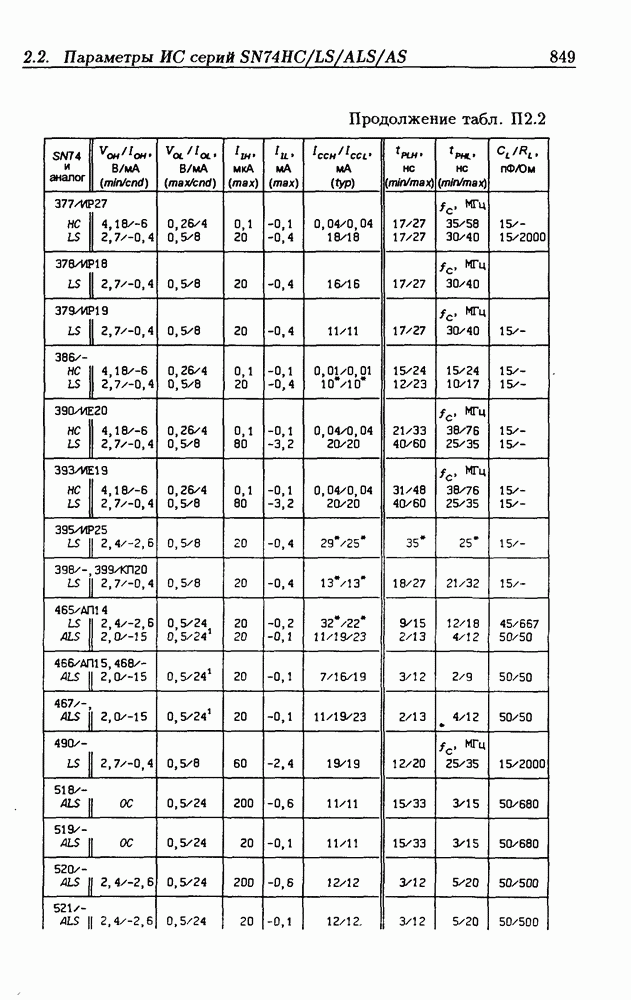
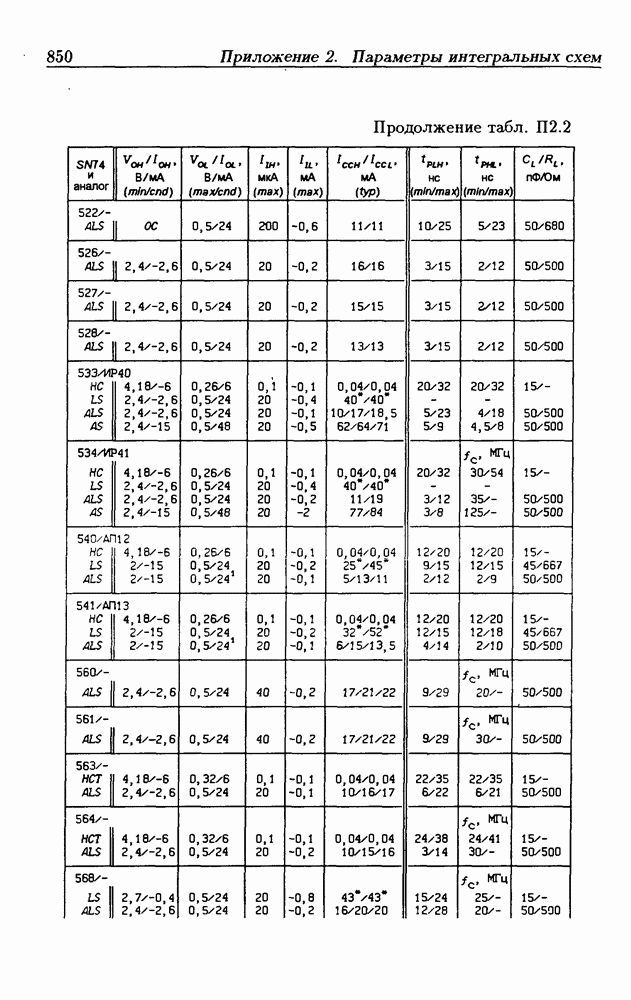
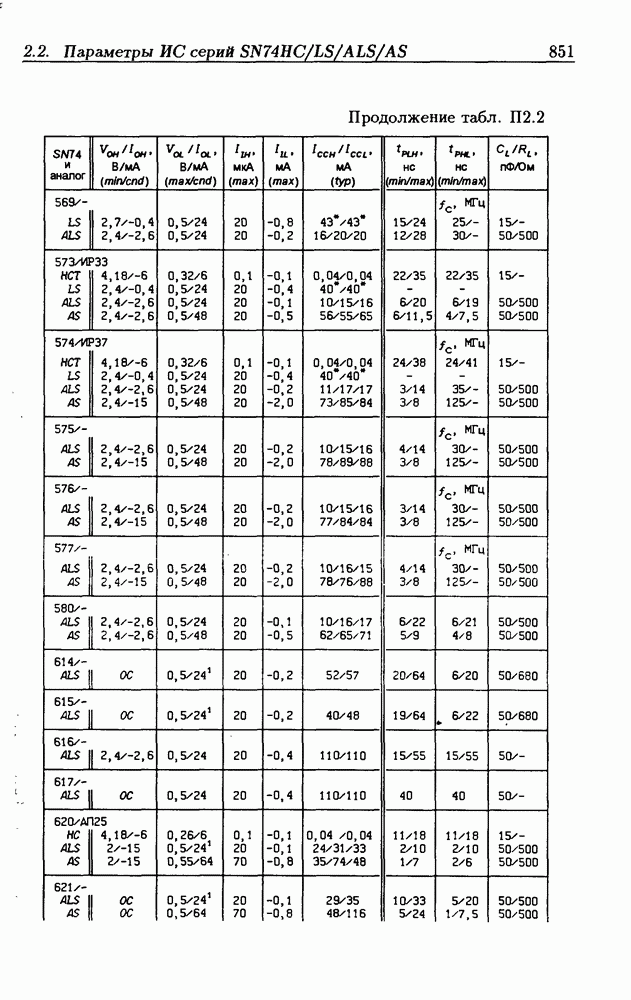
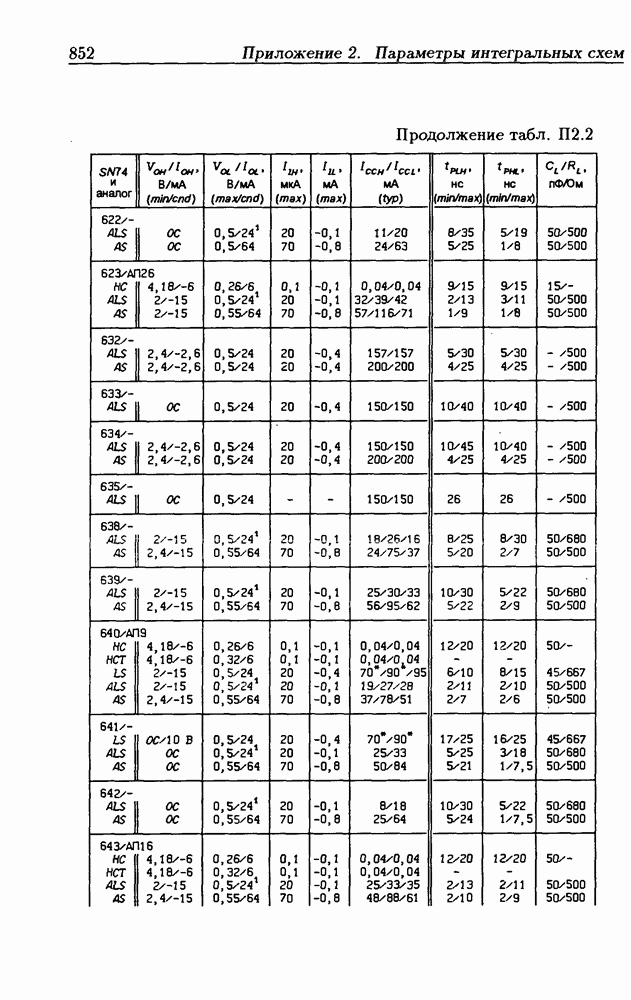
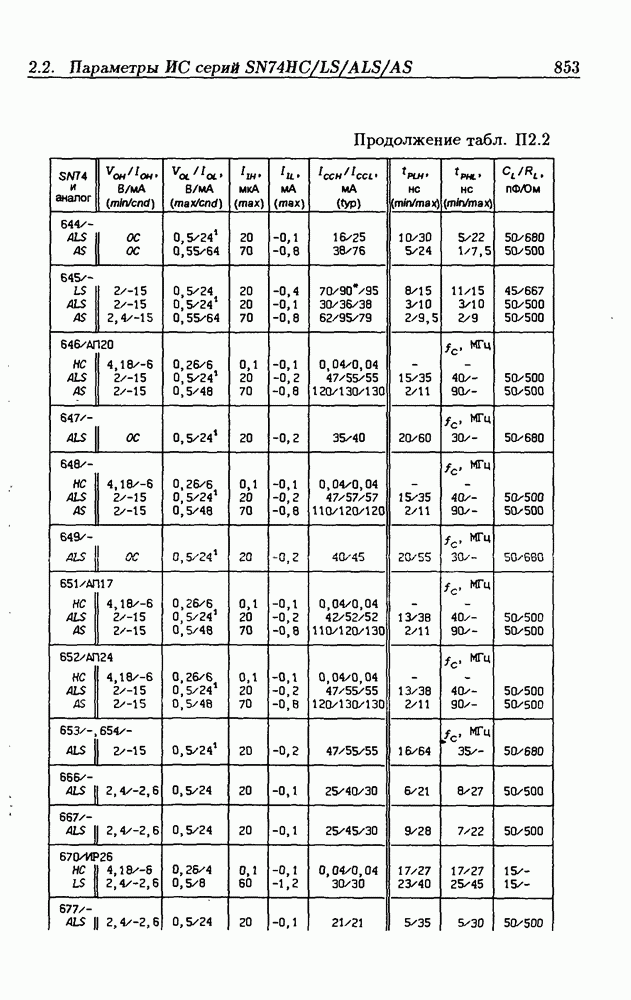
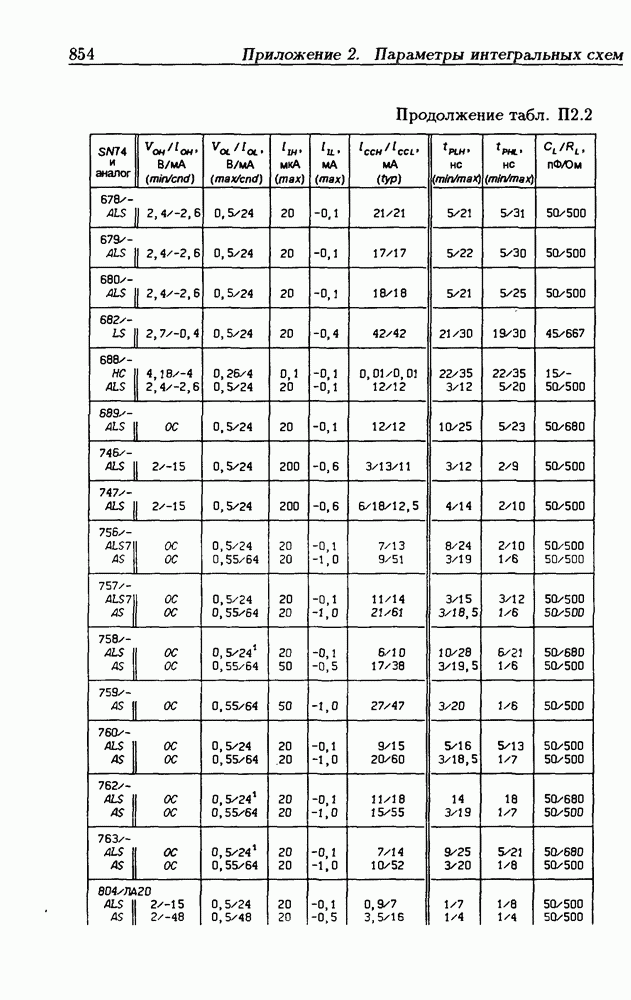
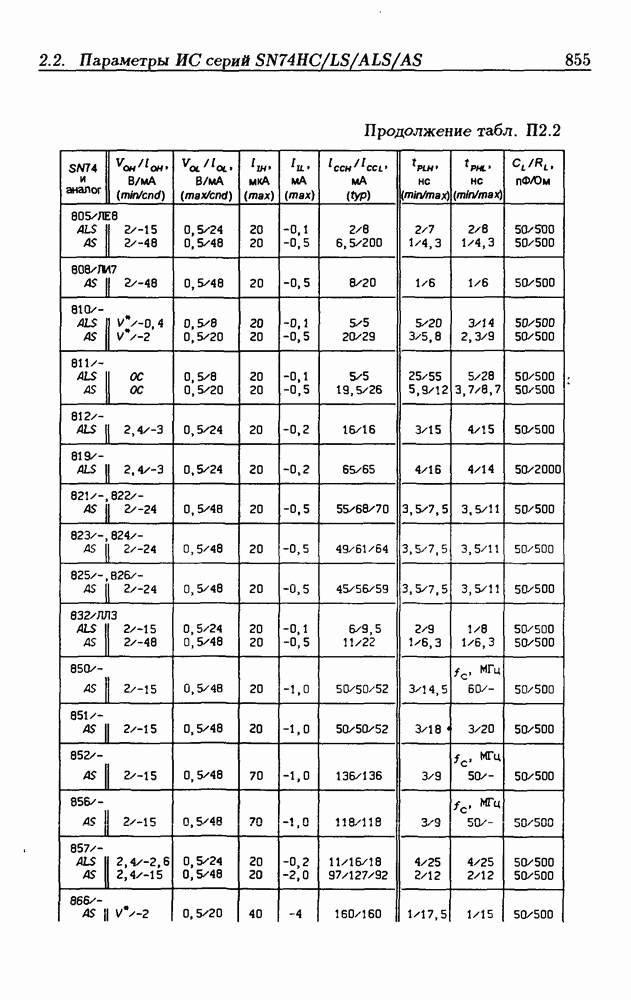
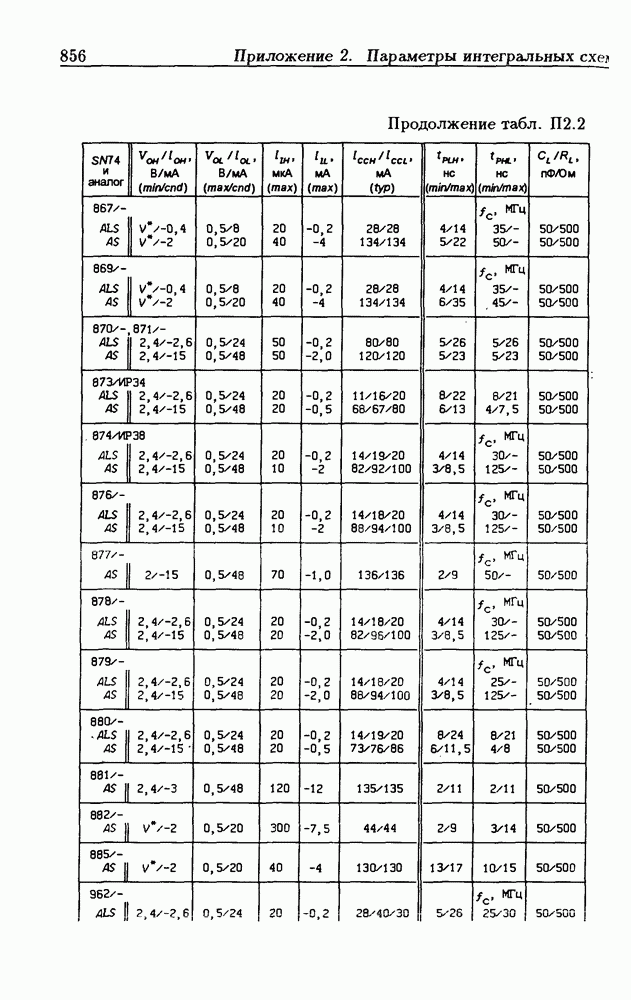
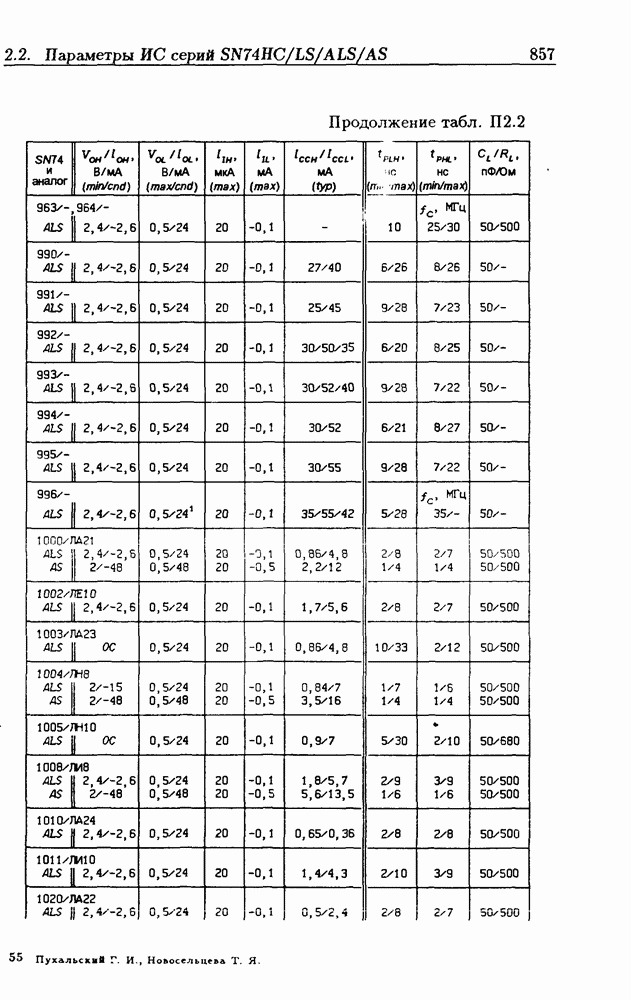
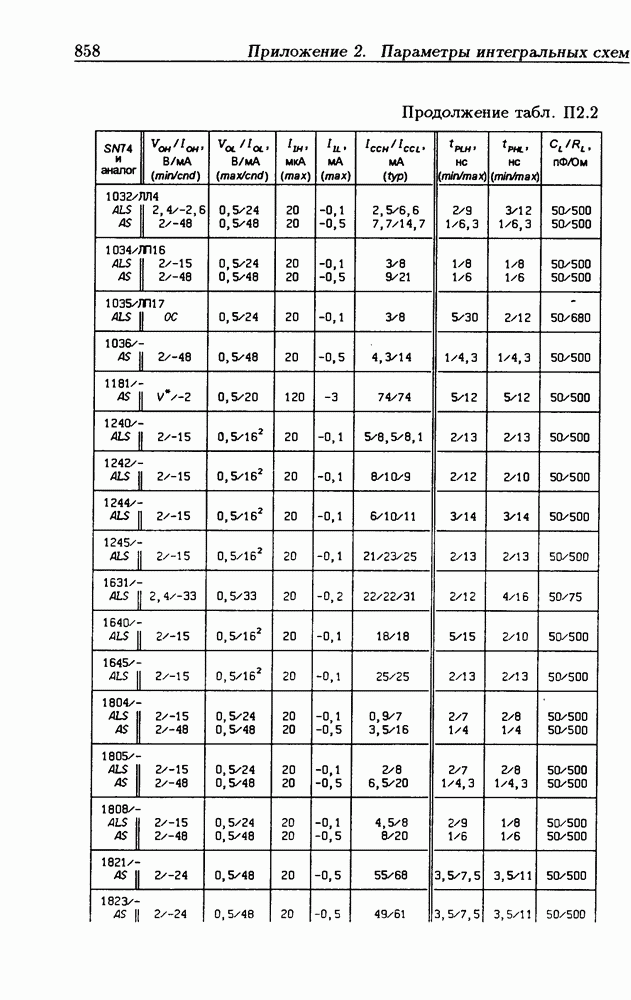
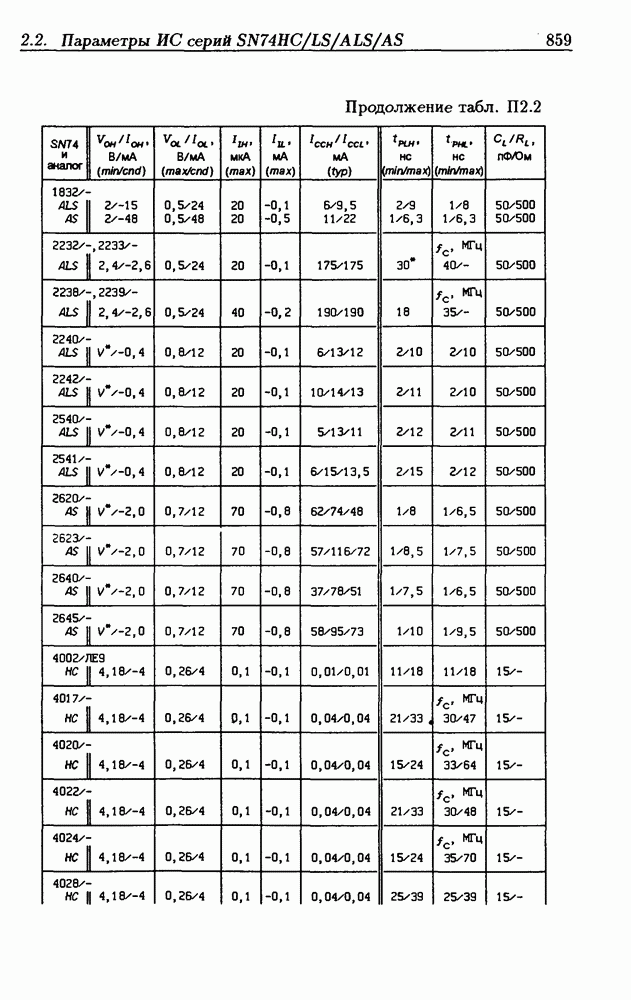
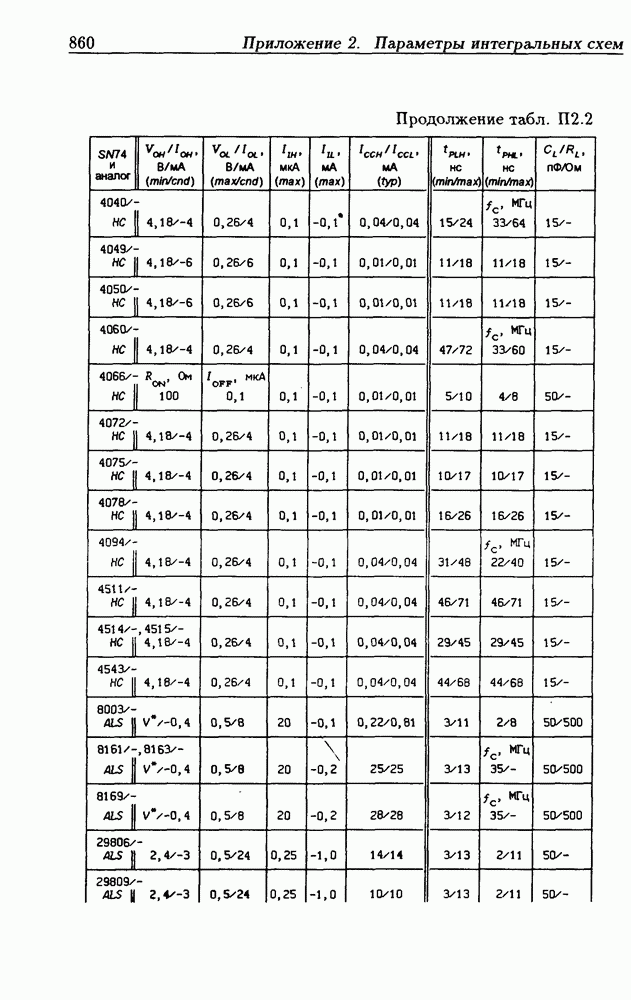
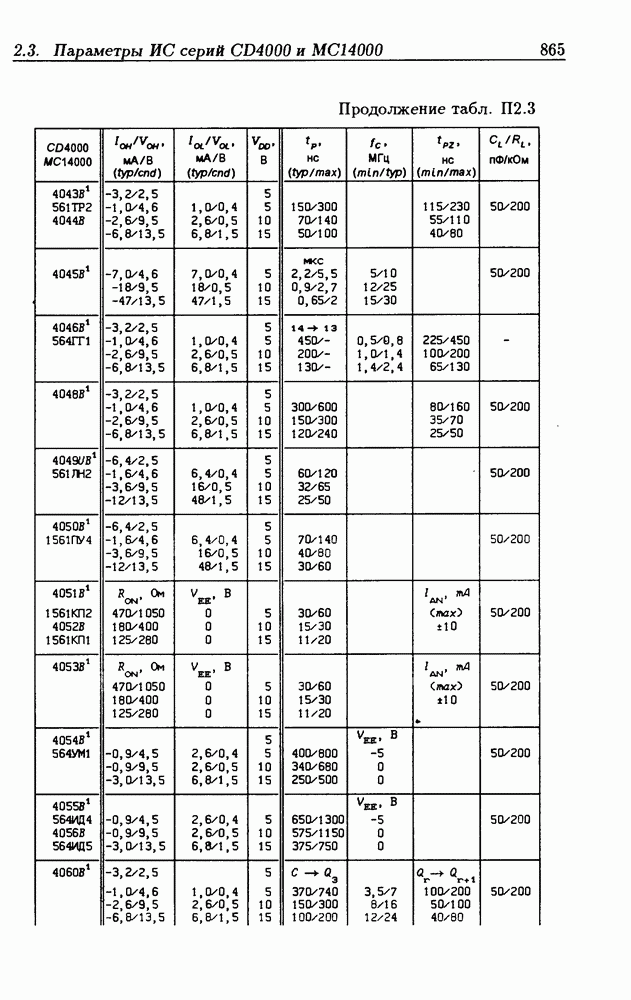
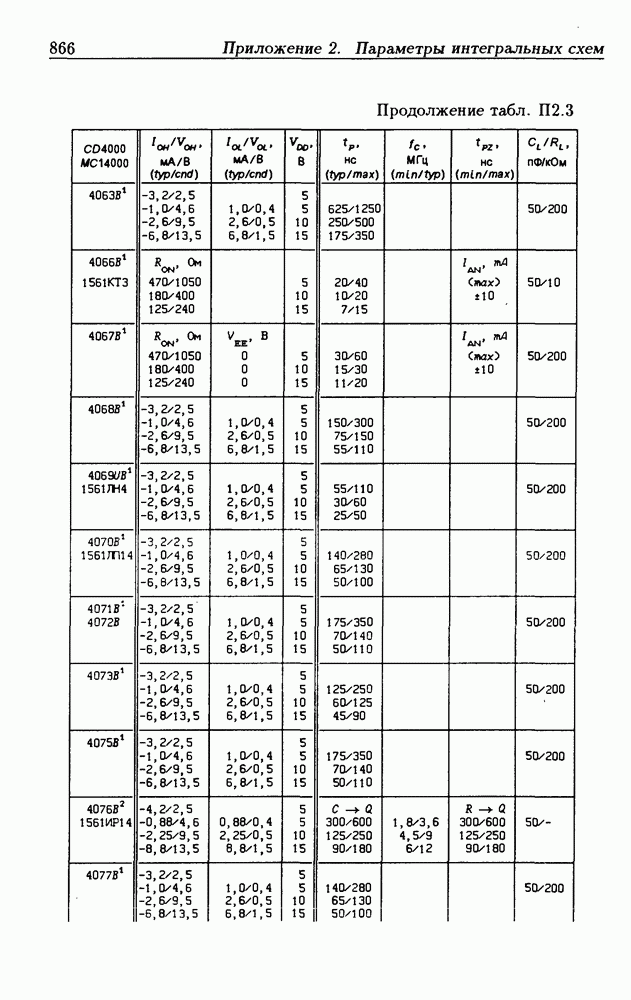
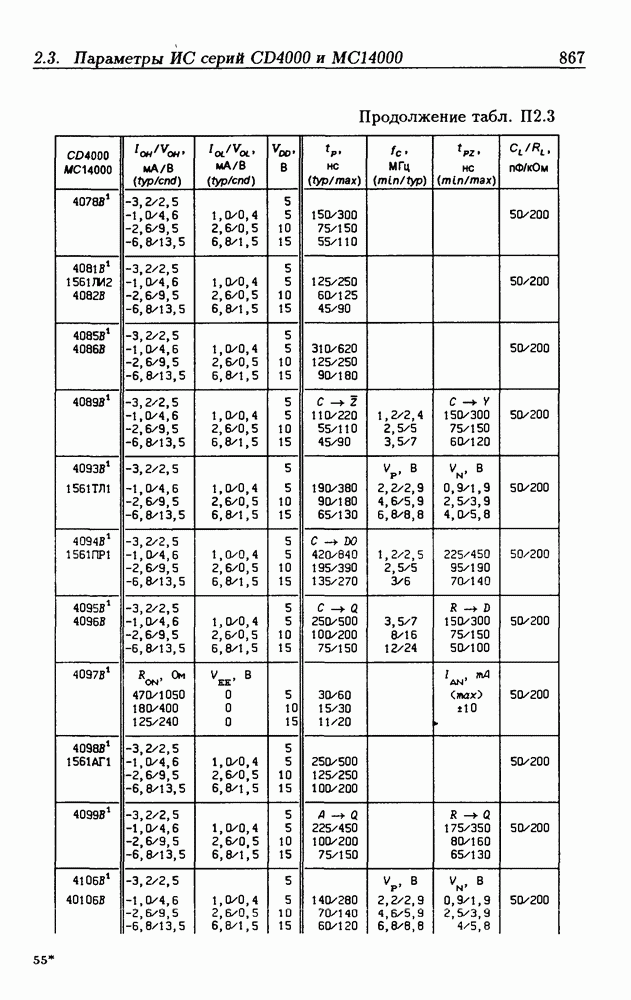
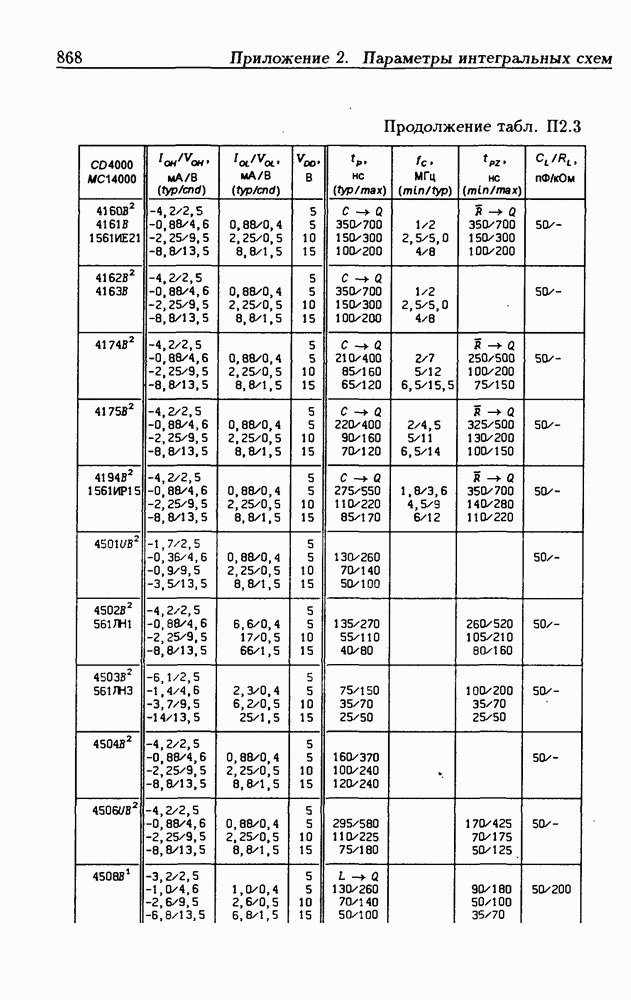
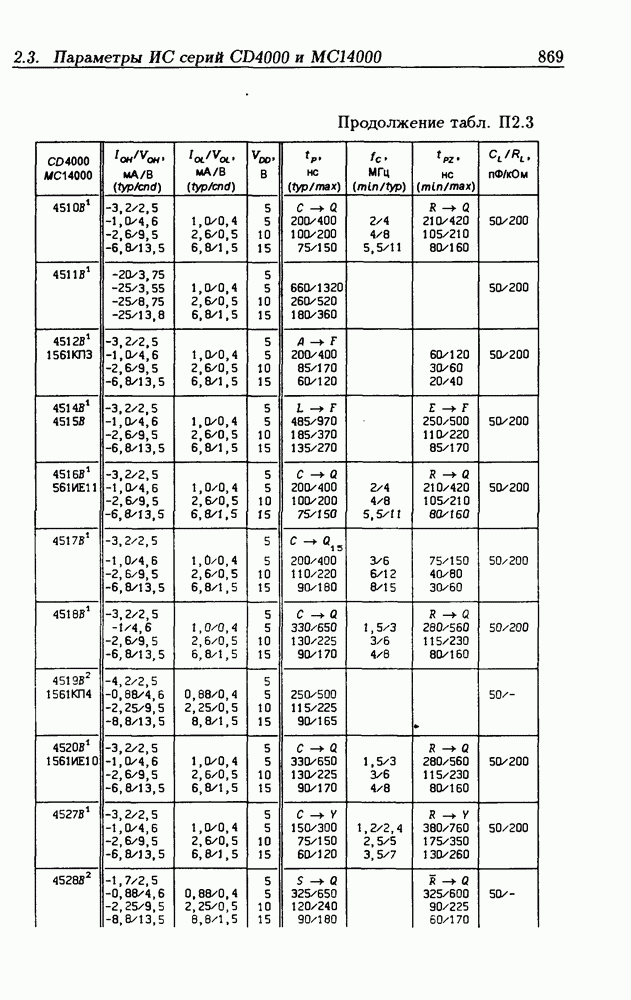
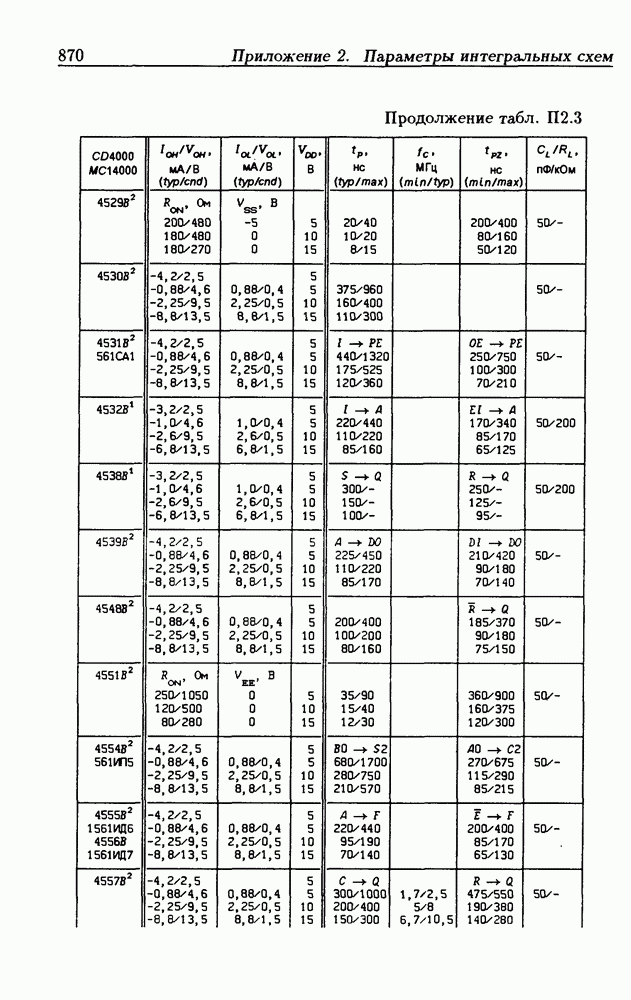
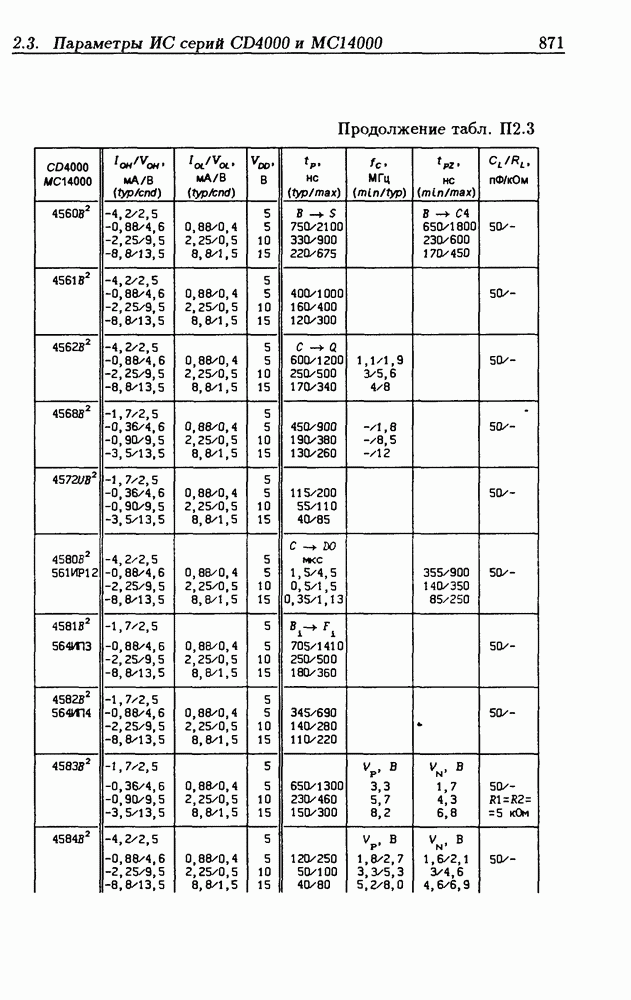
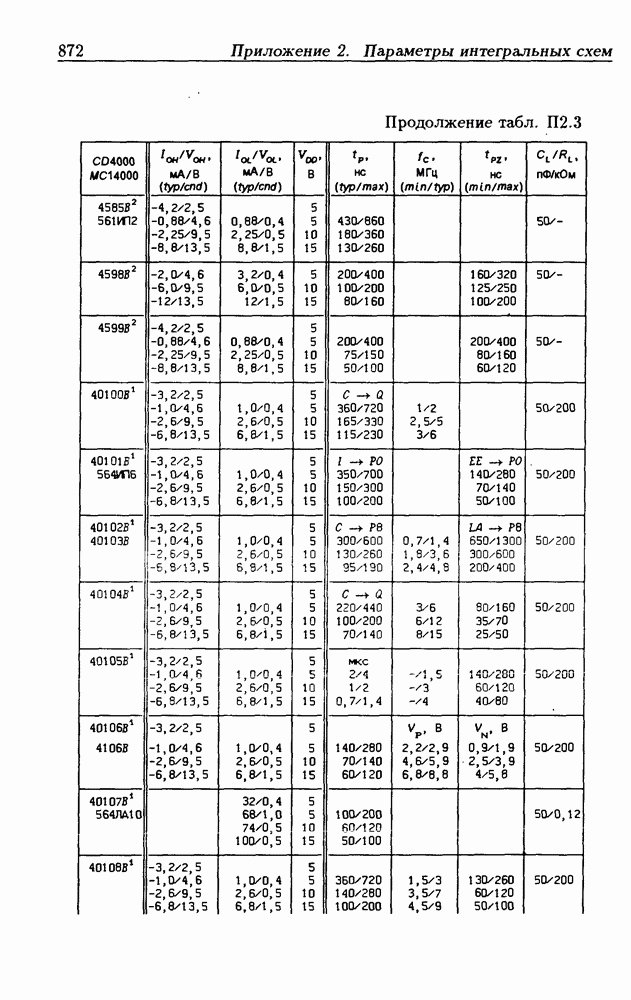
- Приложение 2. Параметры интегральных схем