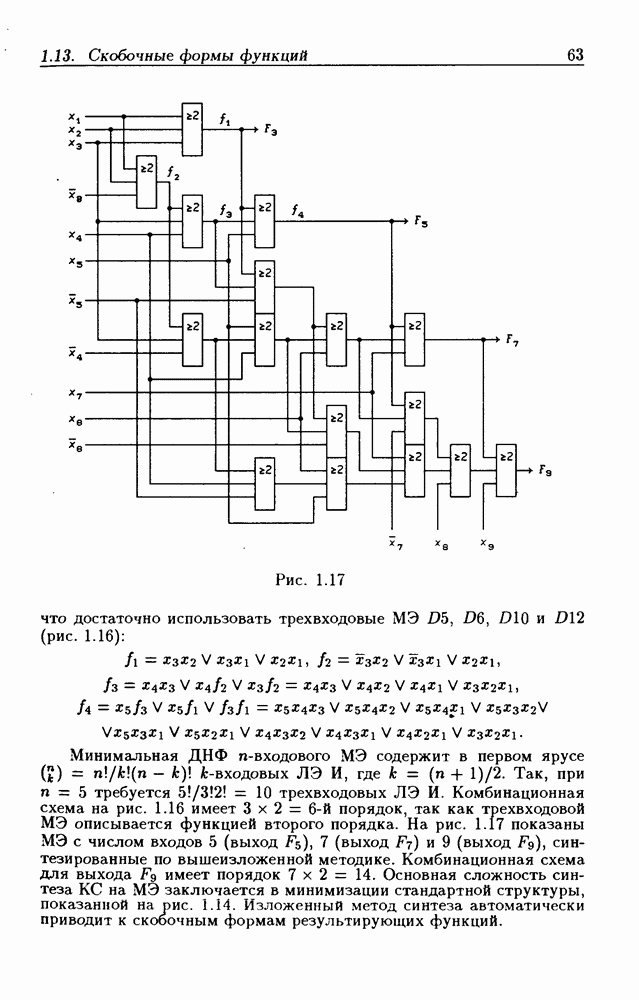
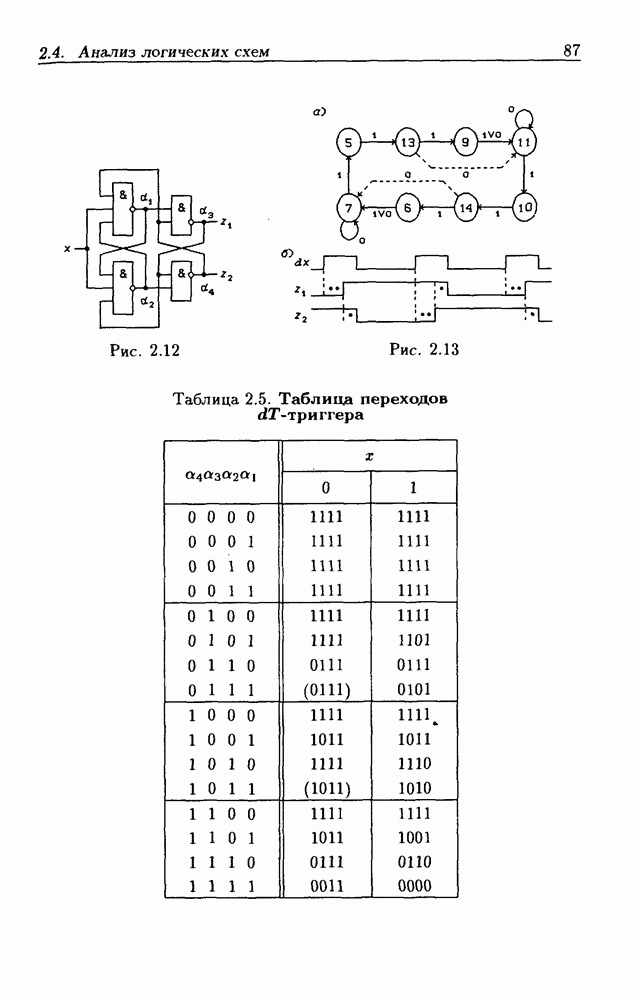
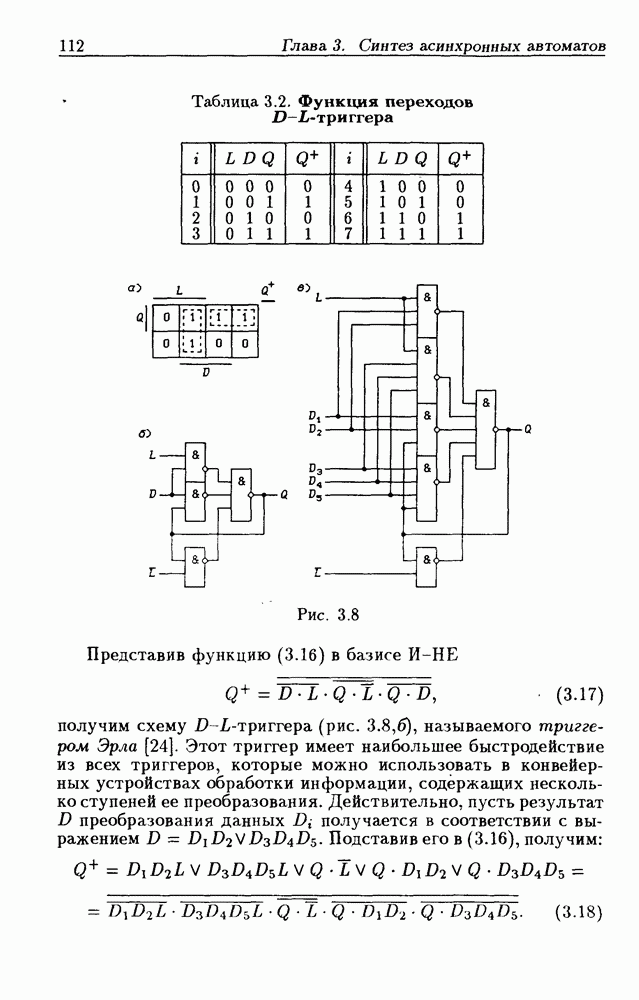
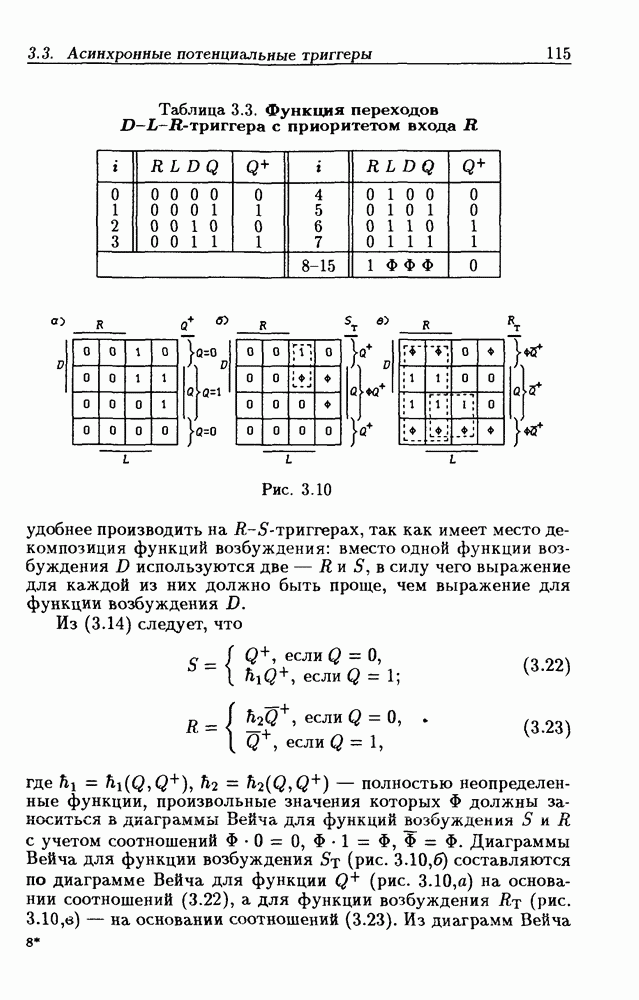
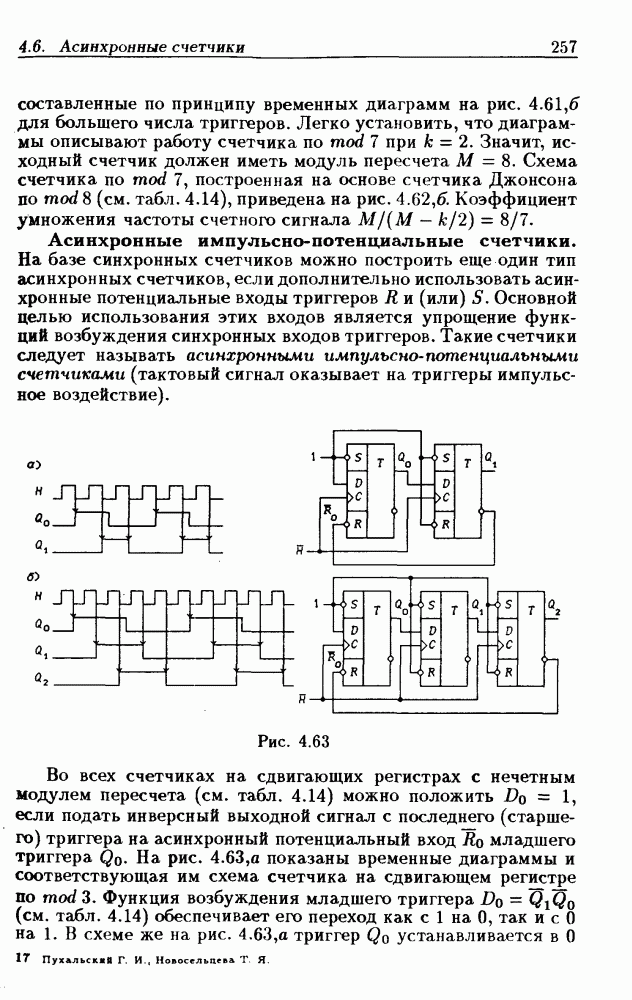
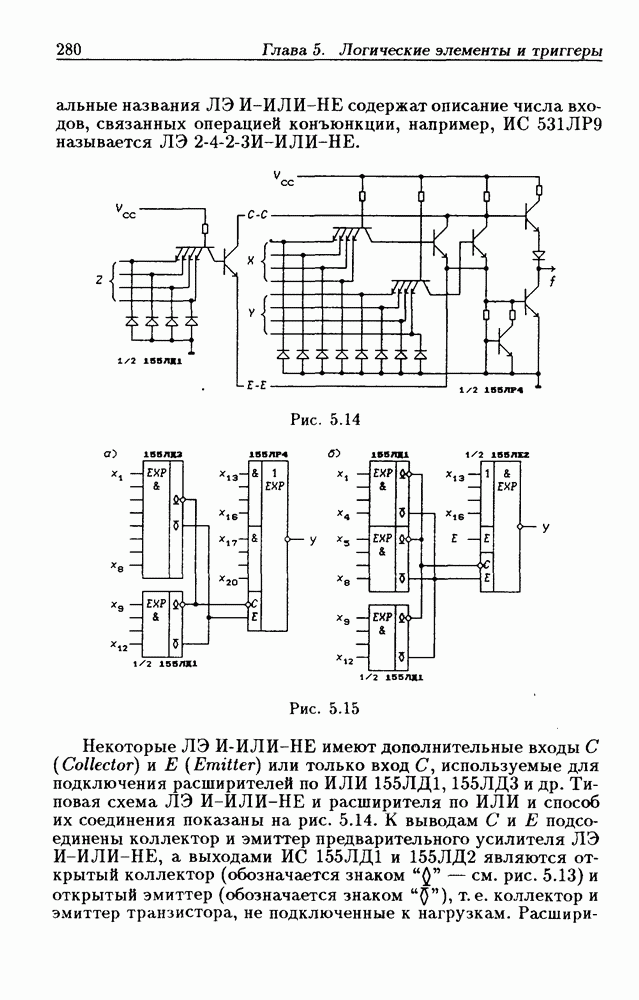
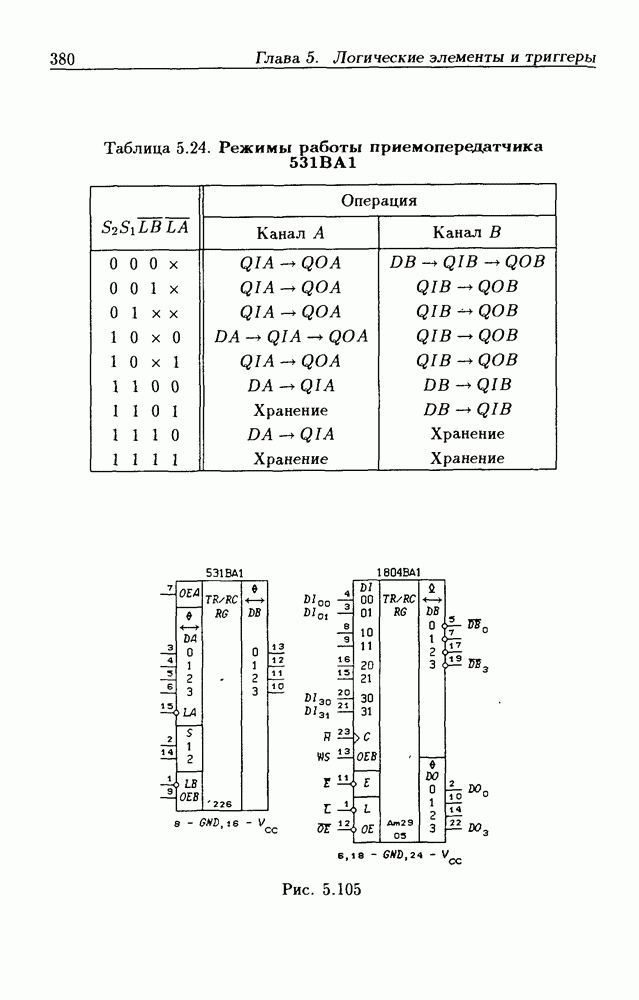
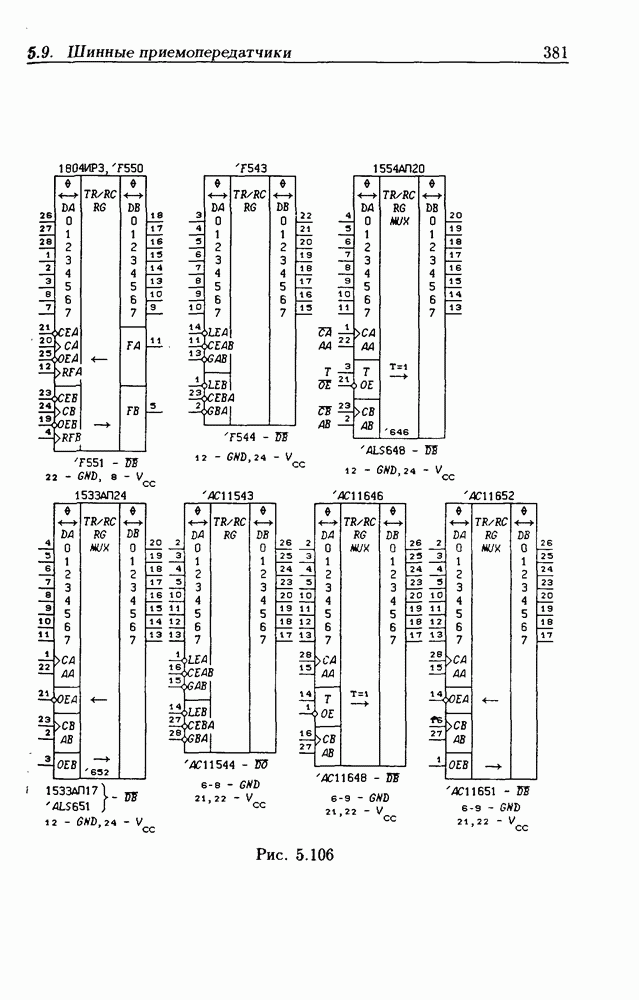
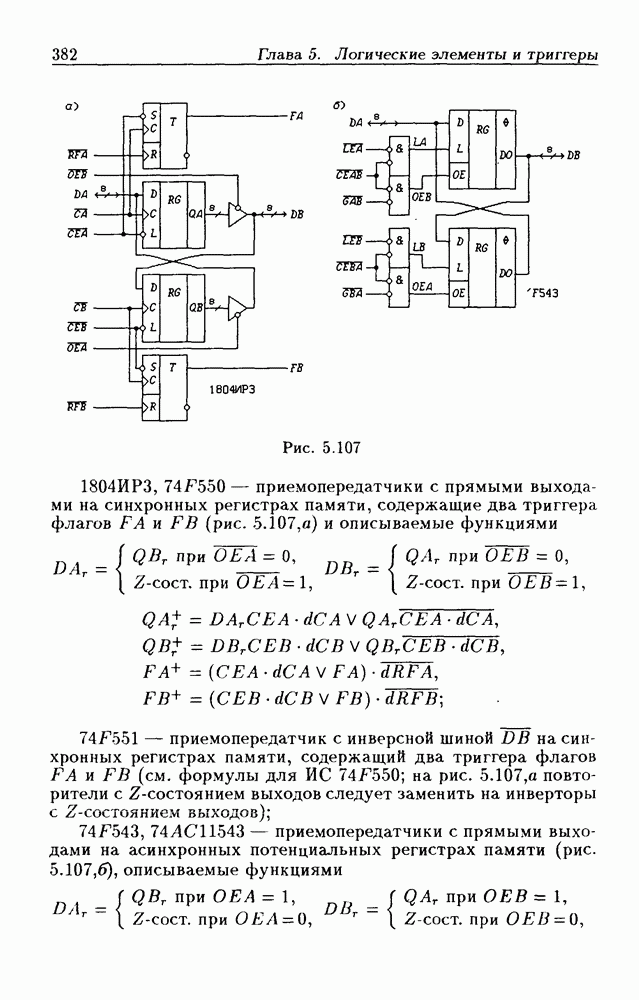
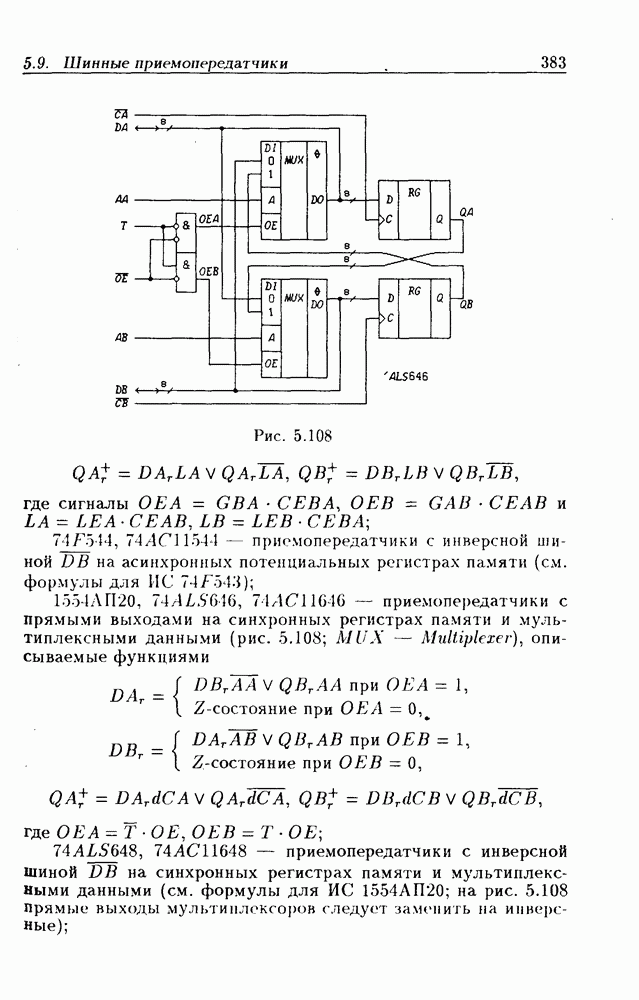
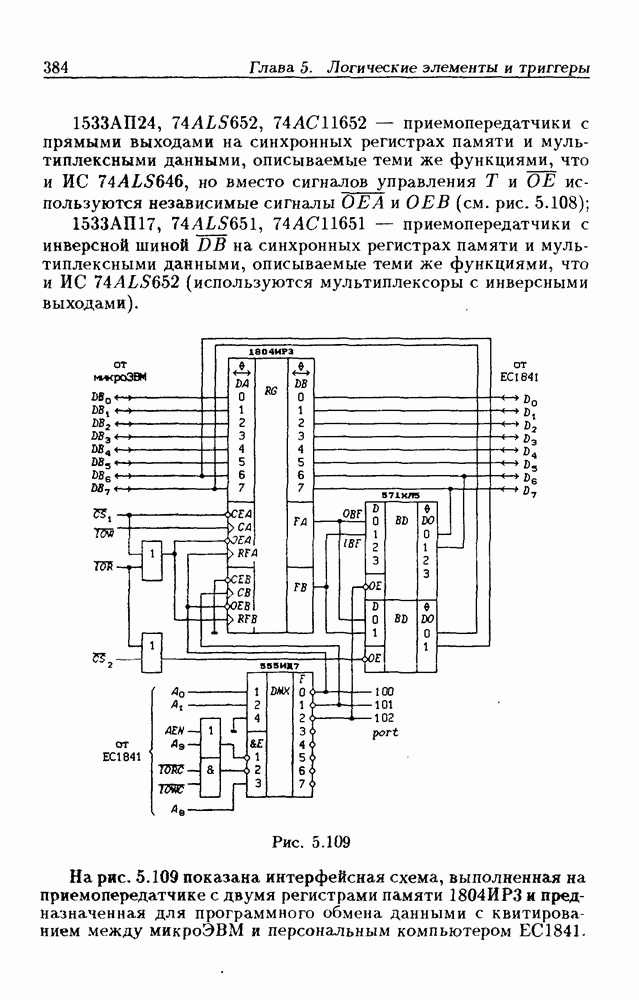
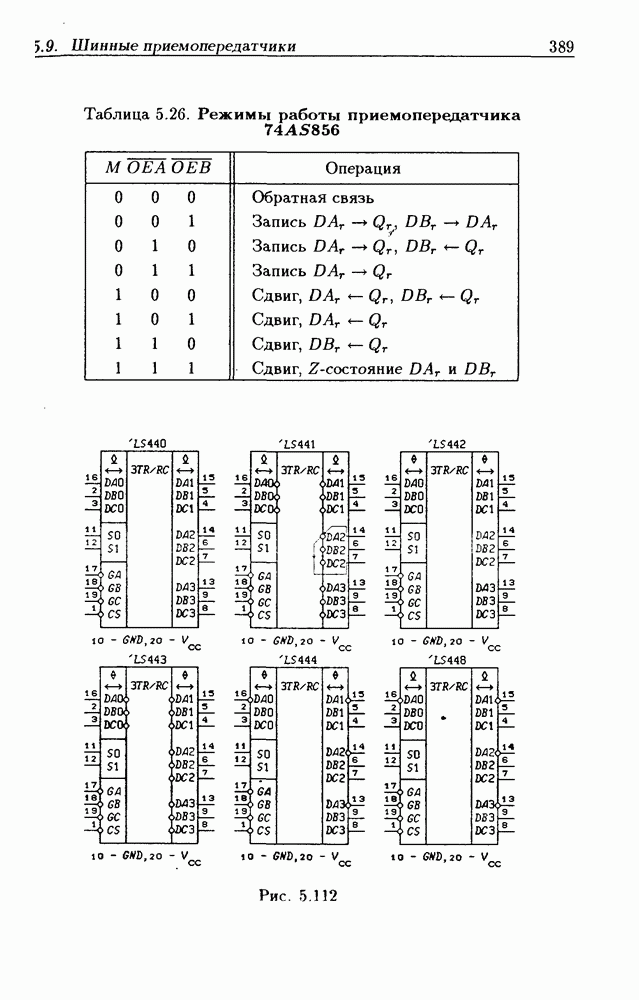
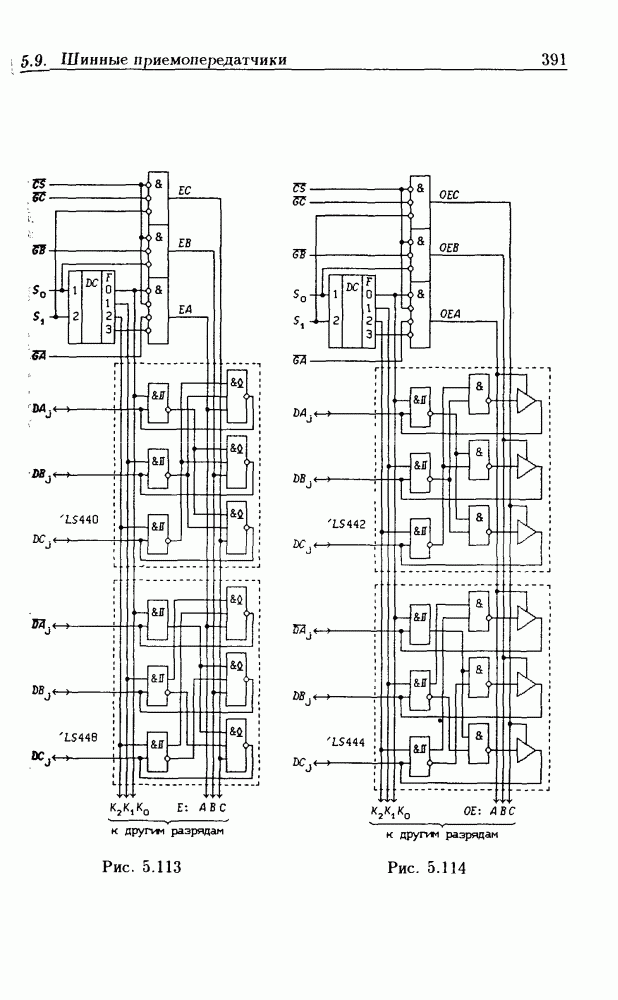
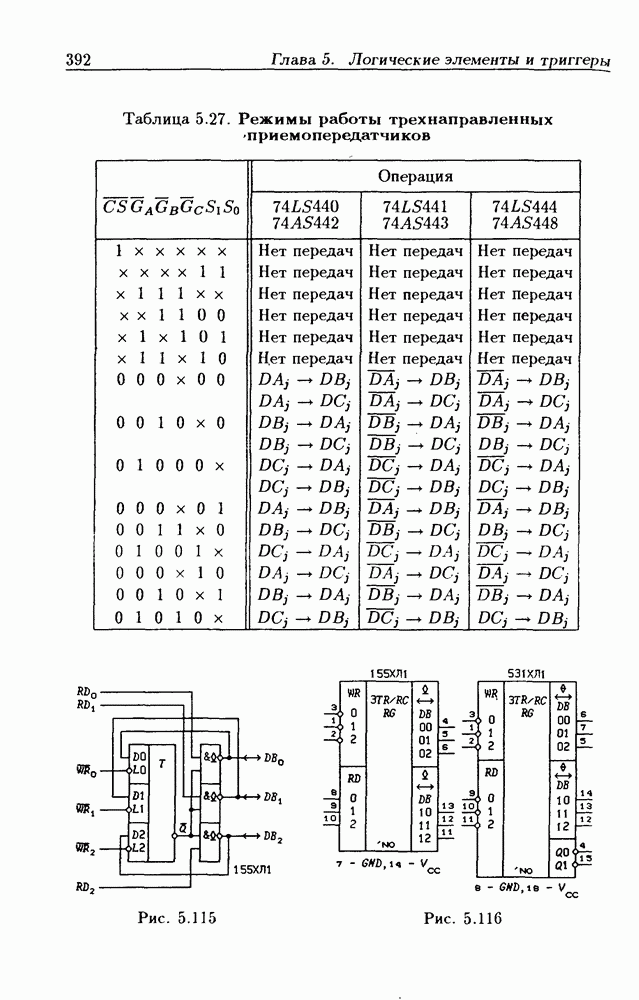
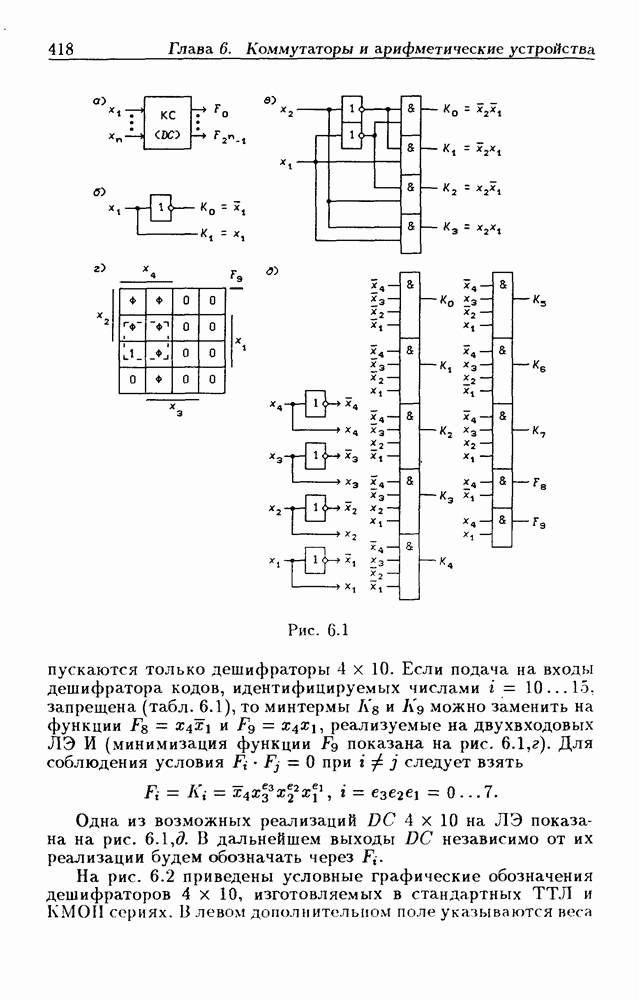
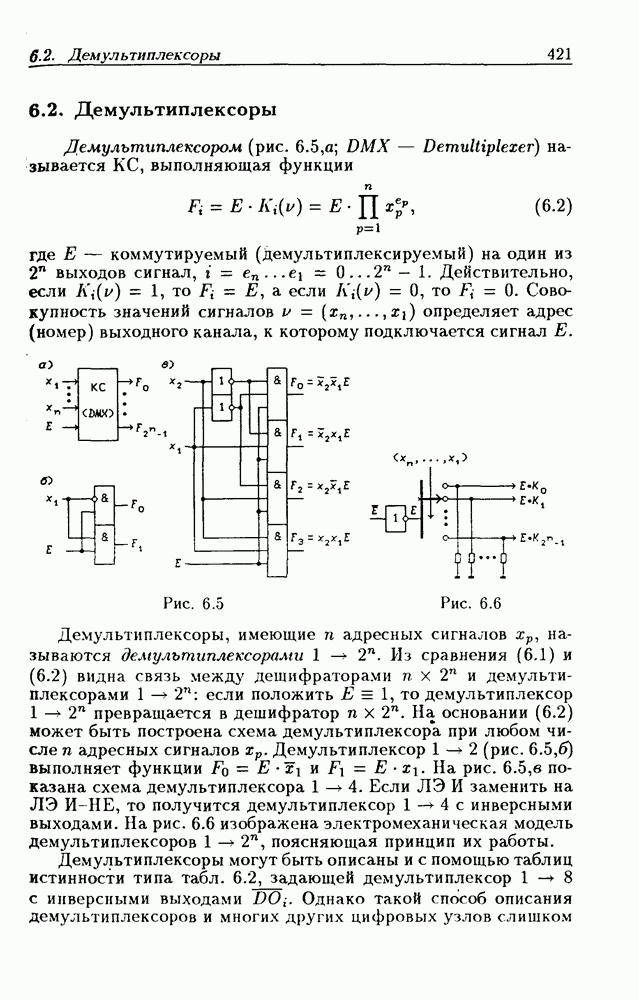
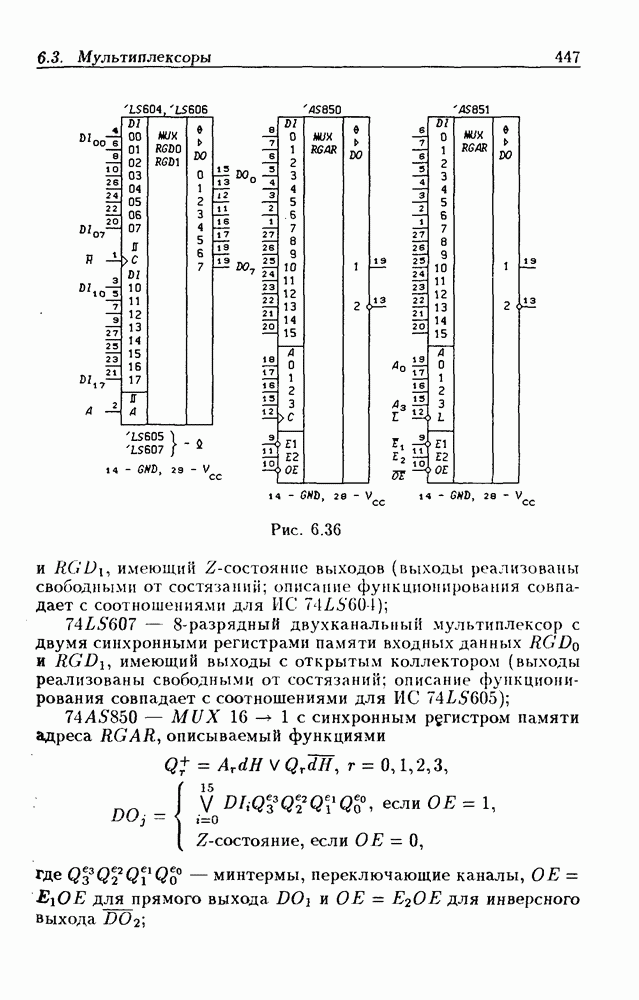
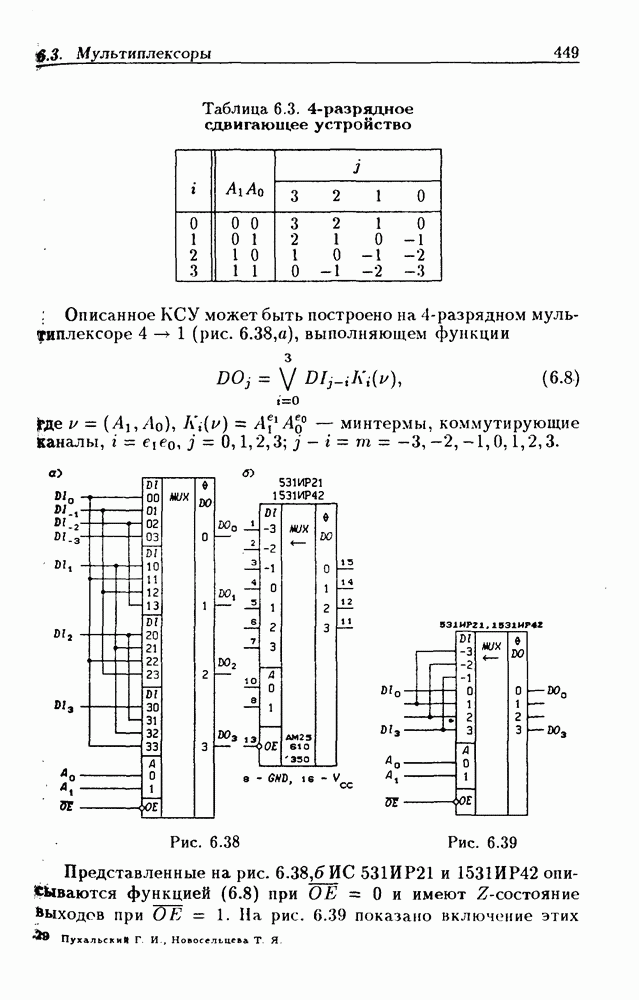
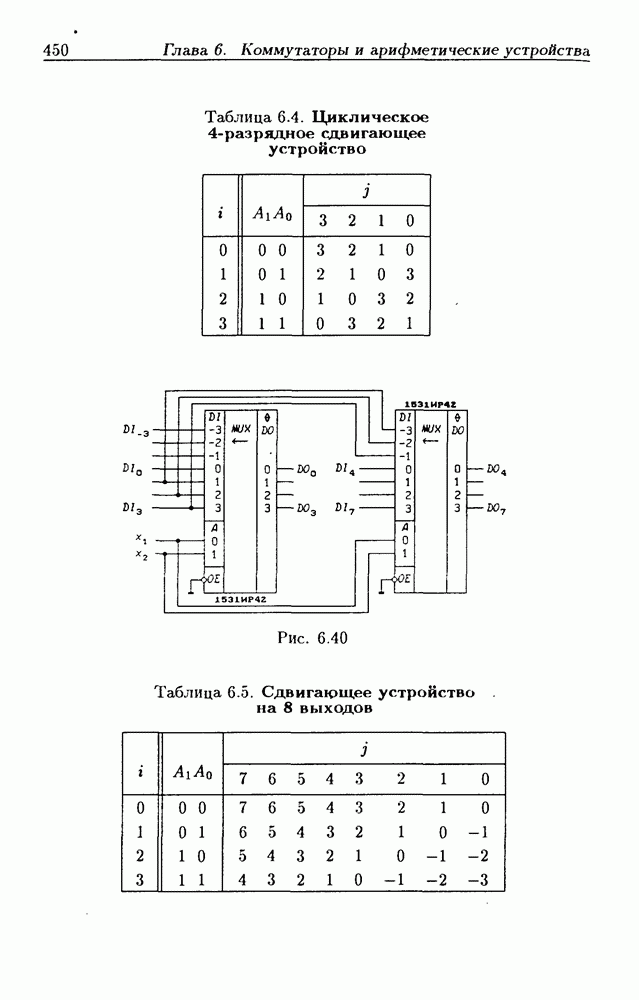
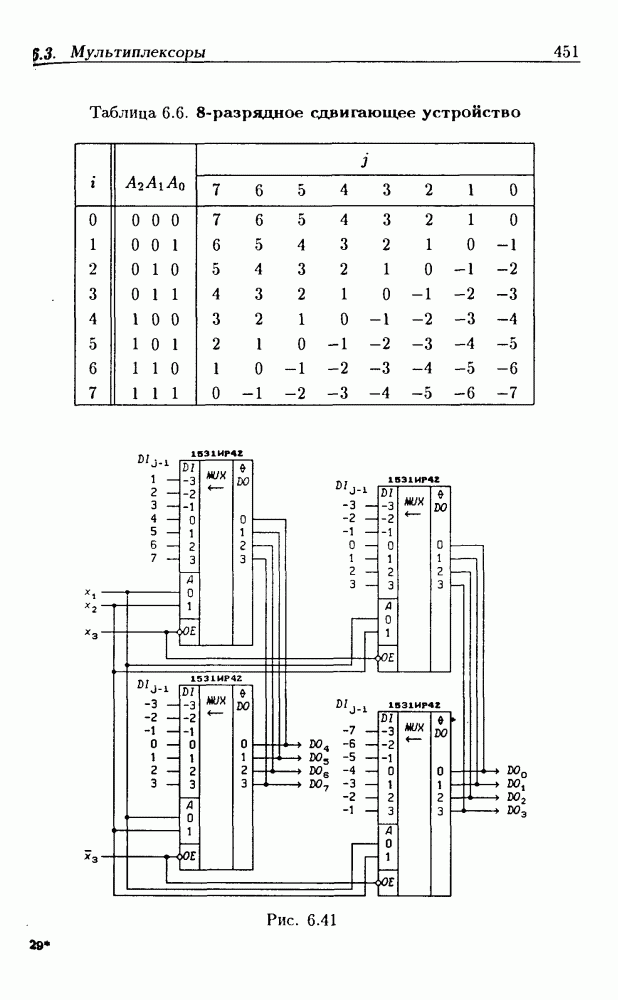
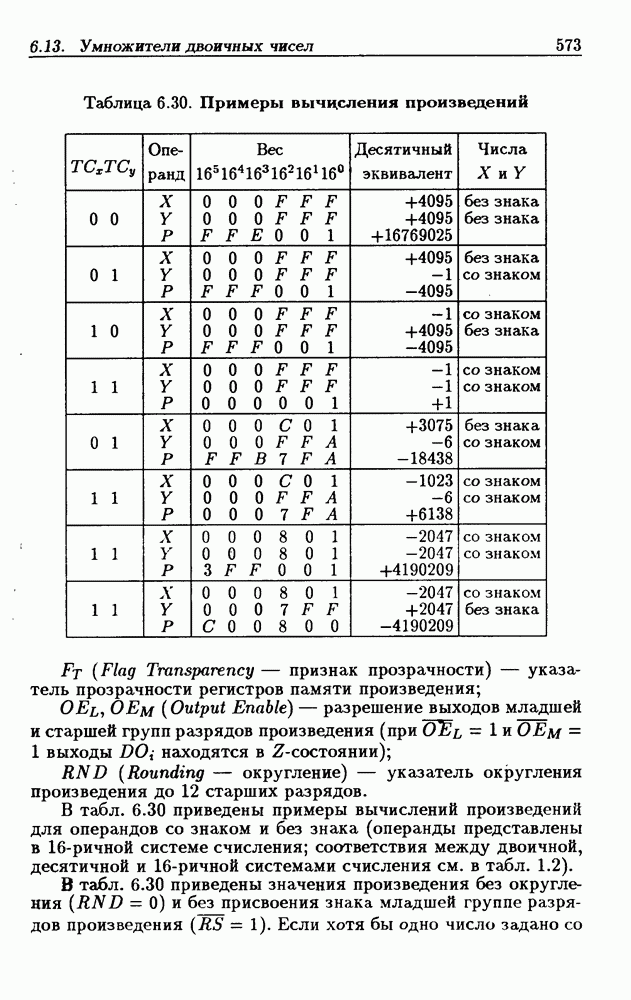
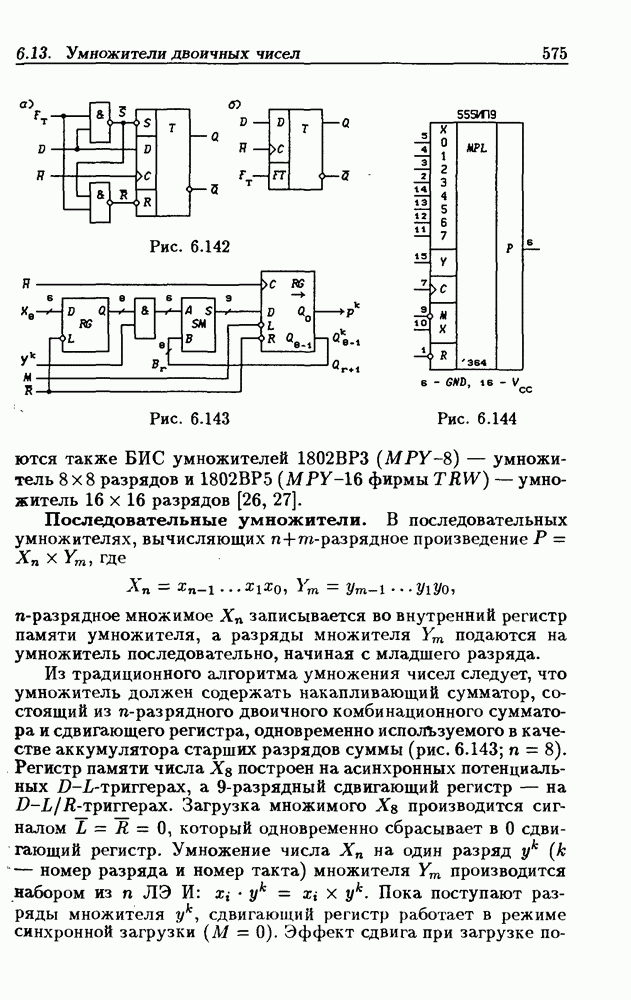
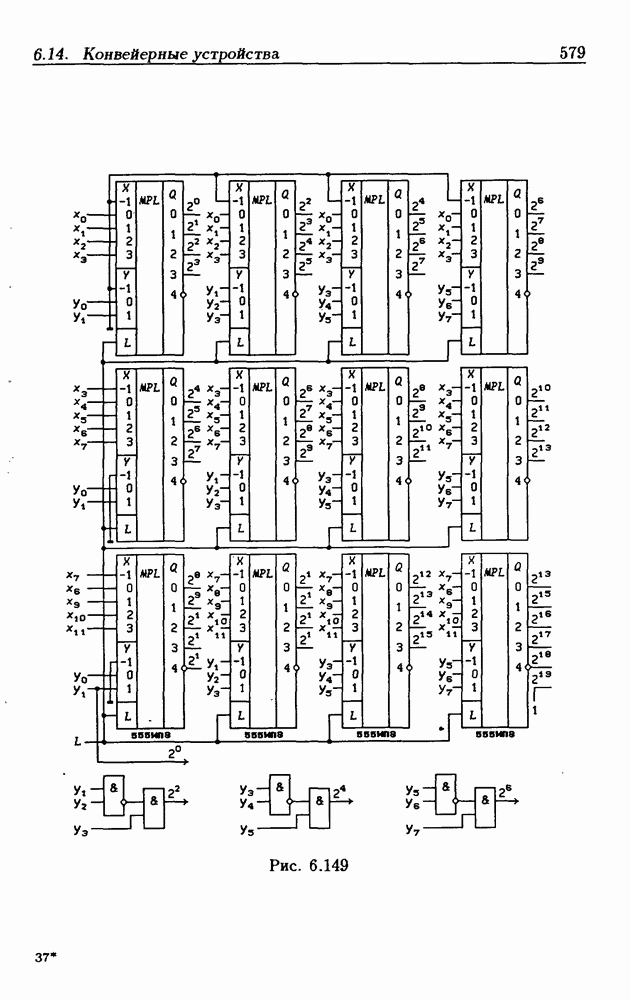
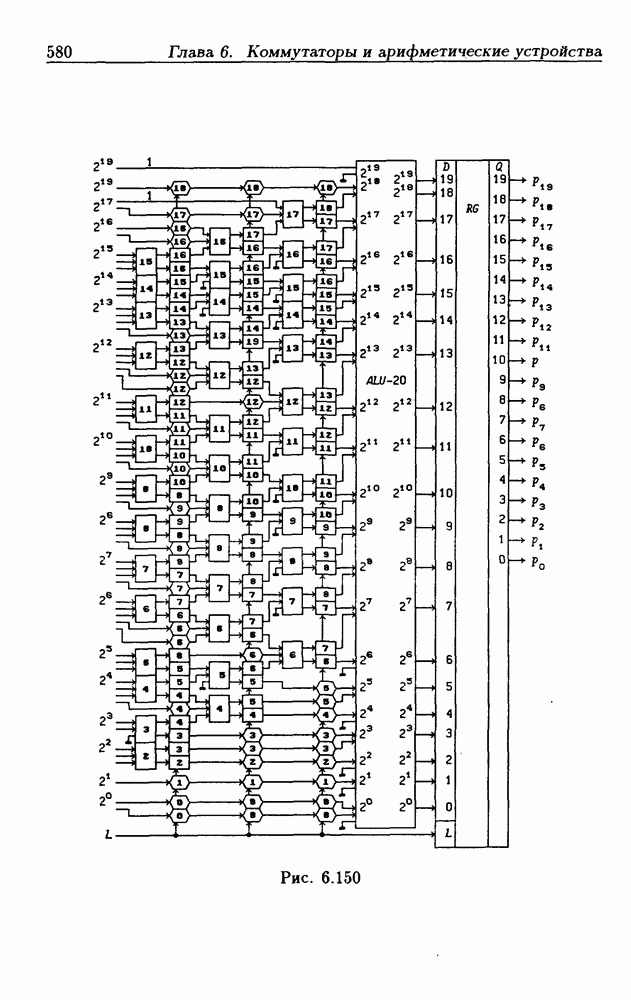
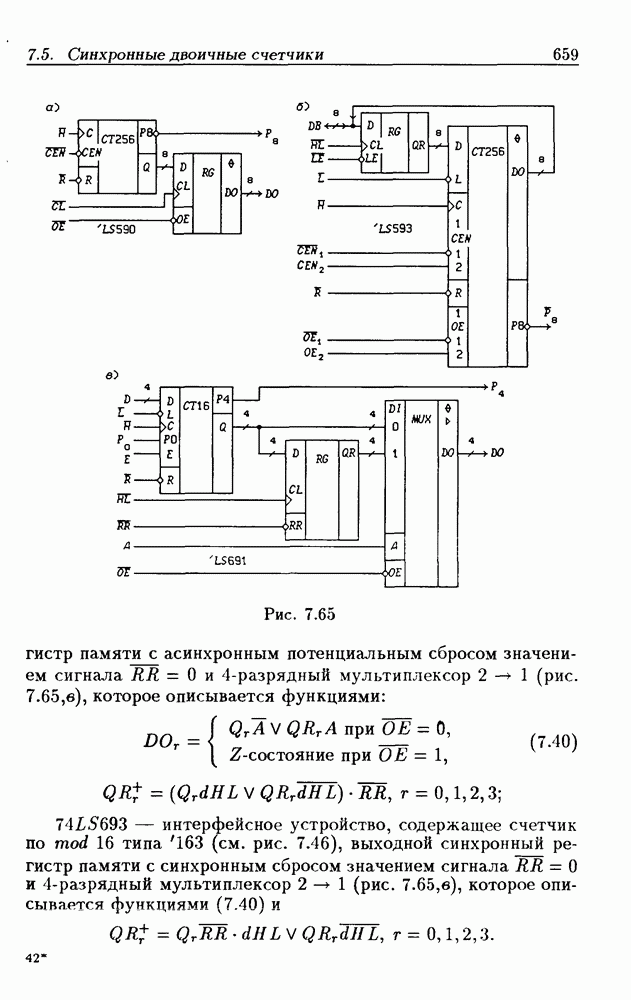
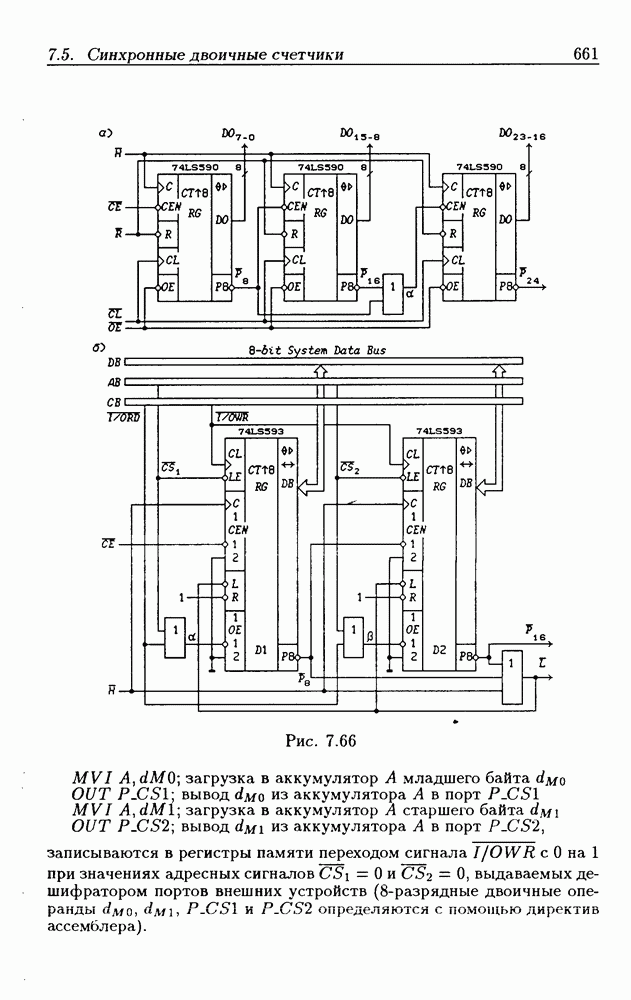
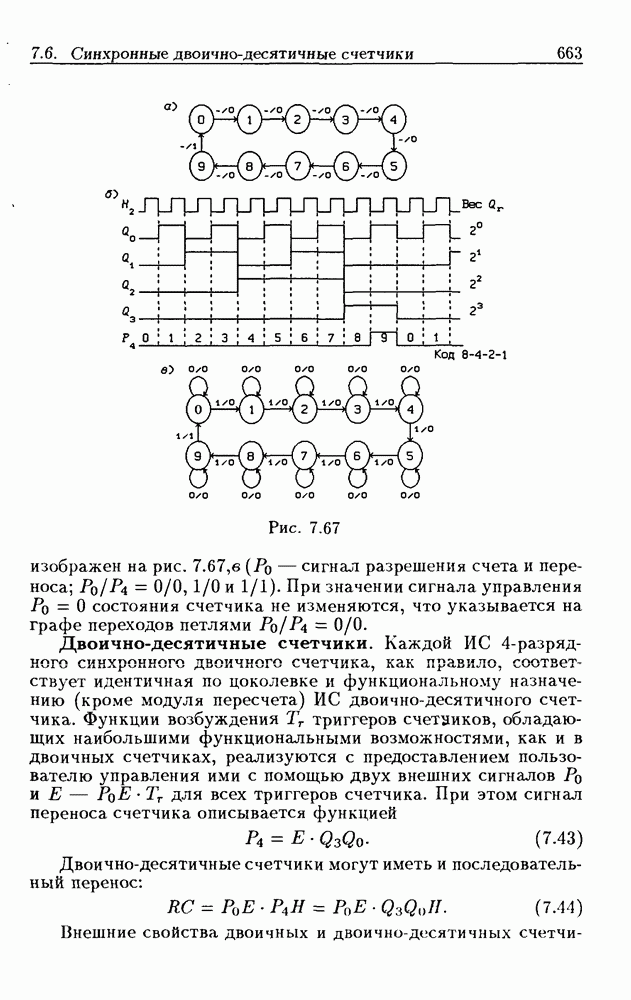
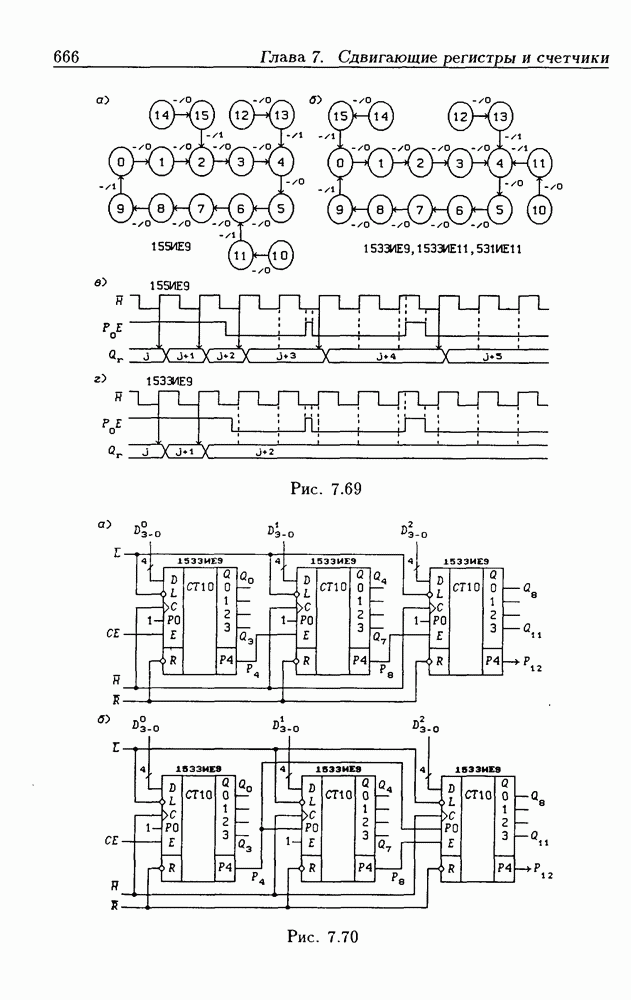
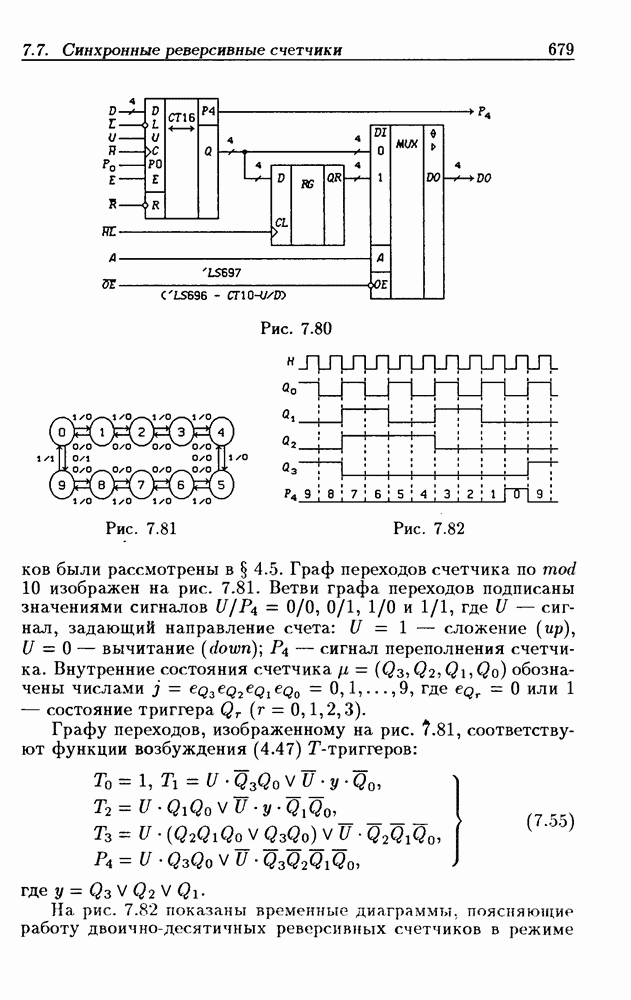
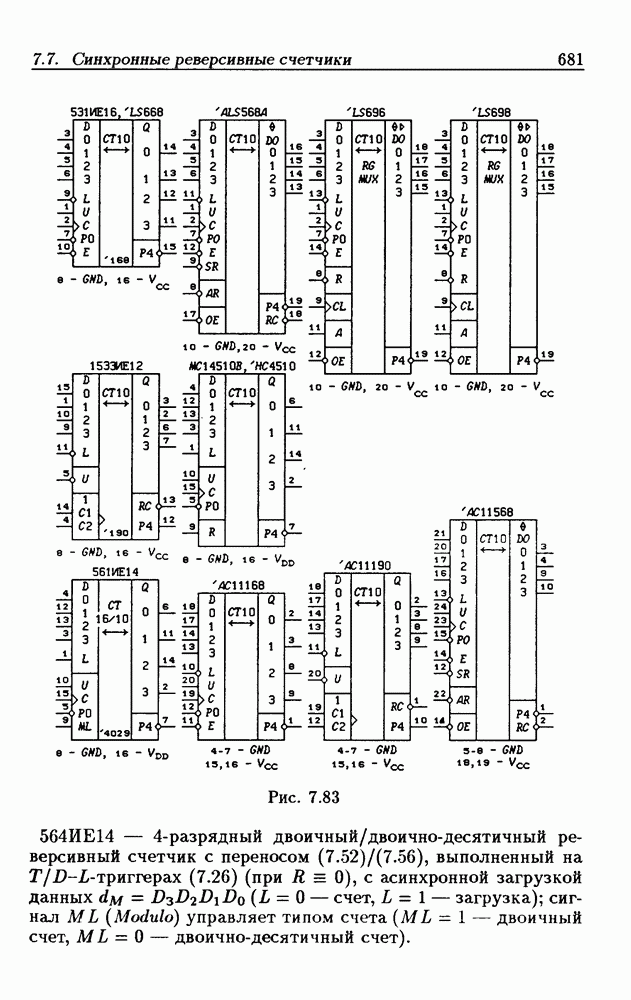
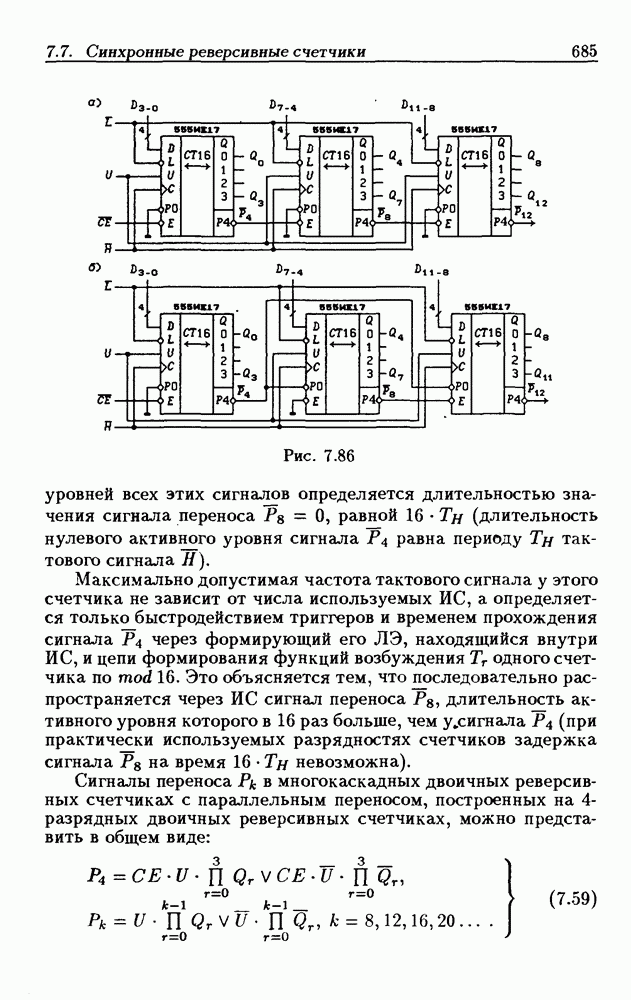
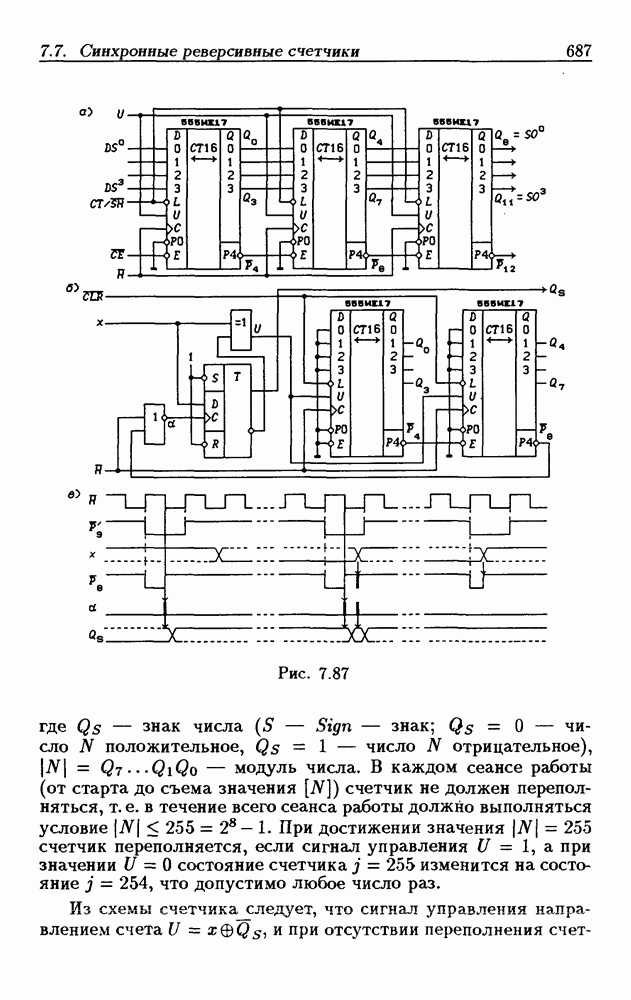
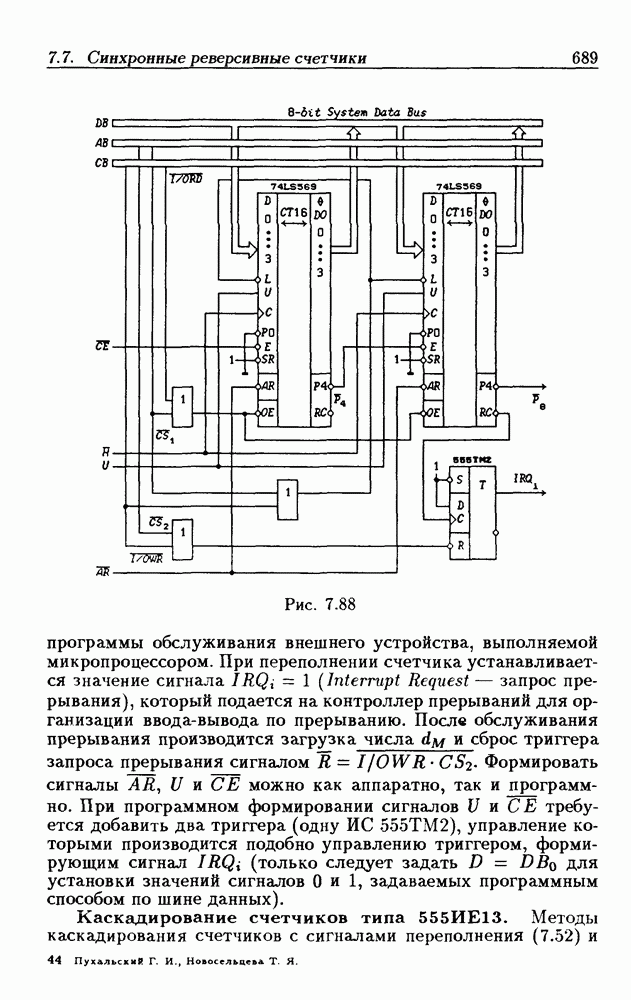
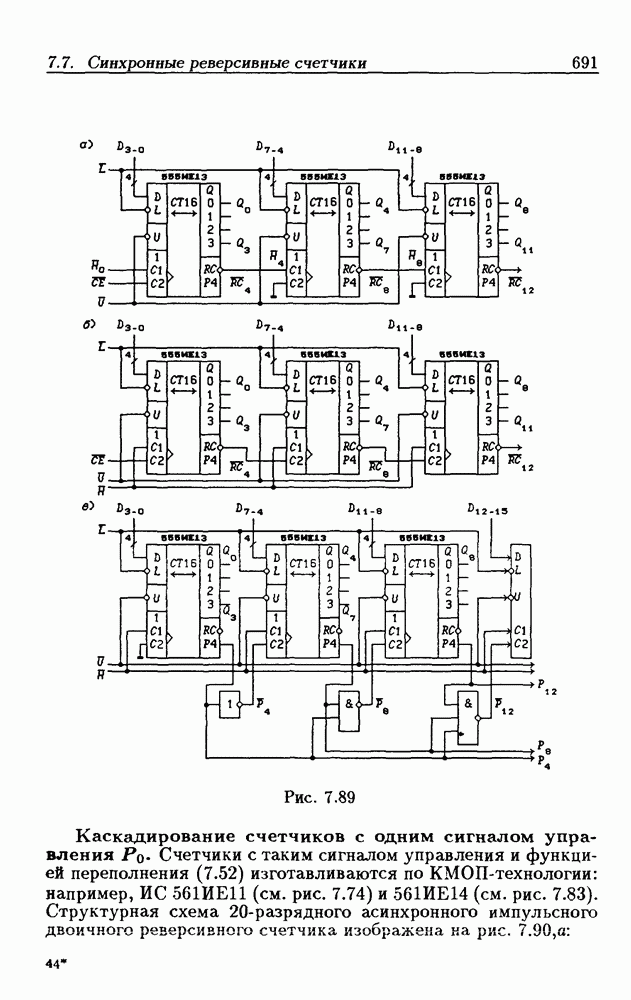
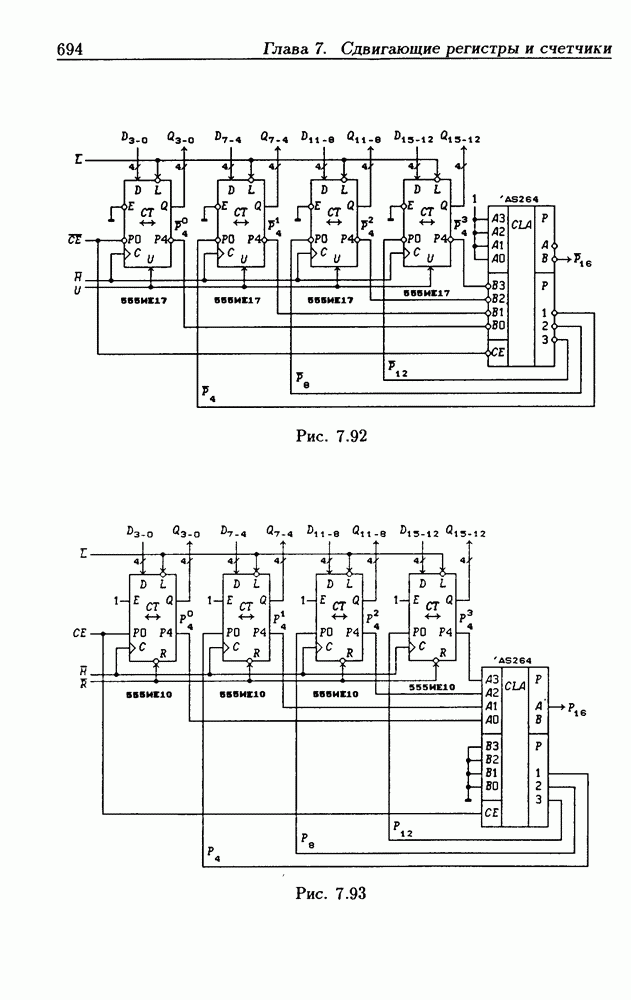
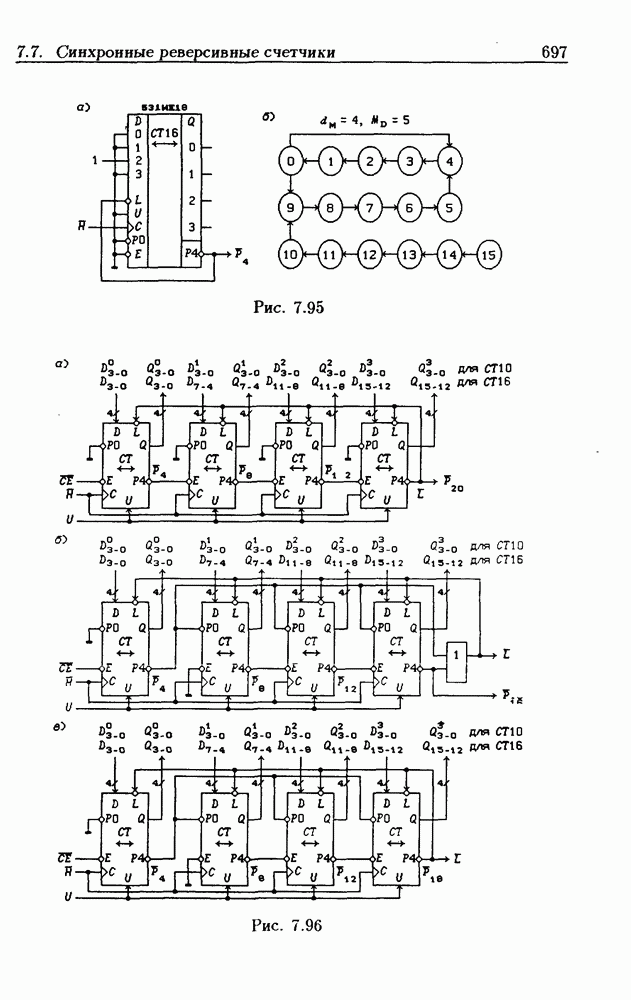
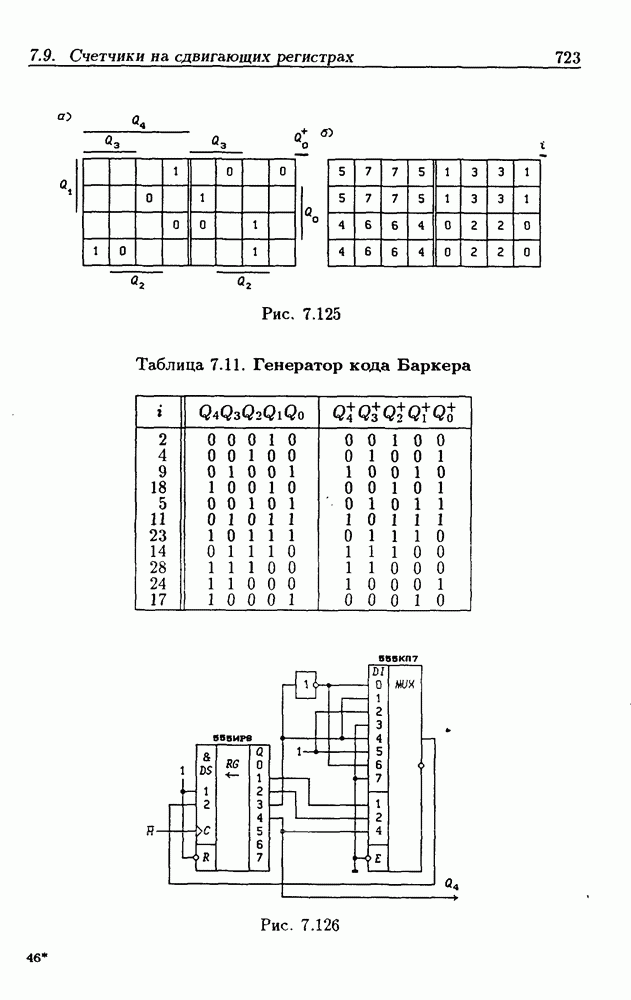
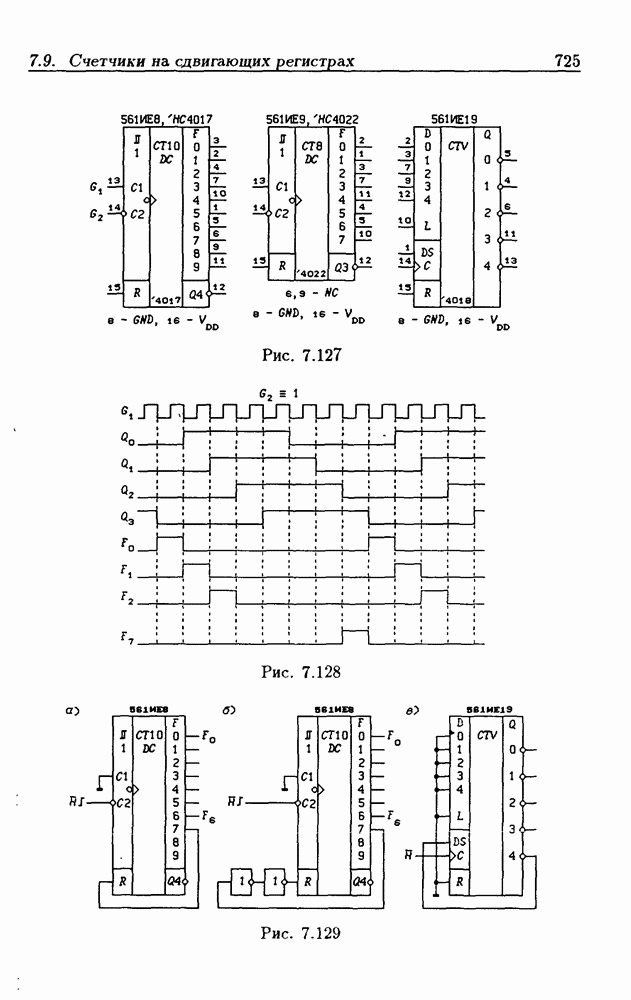
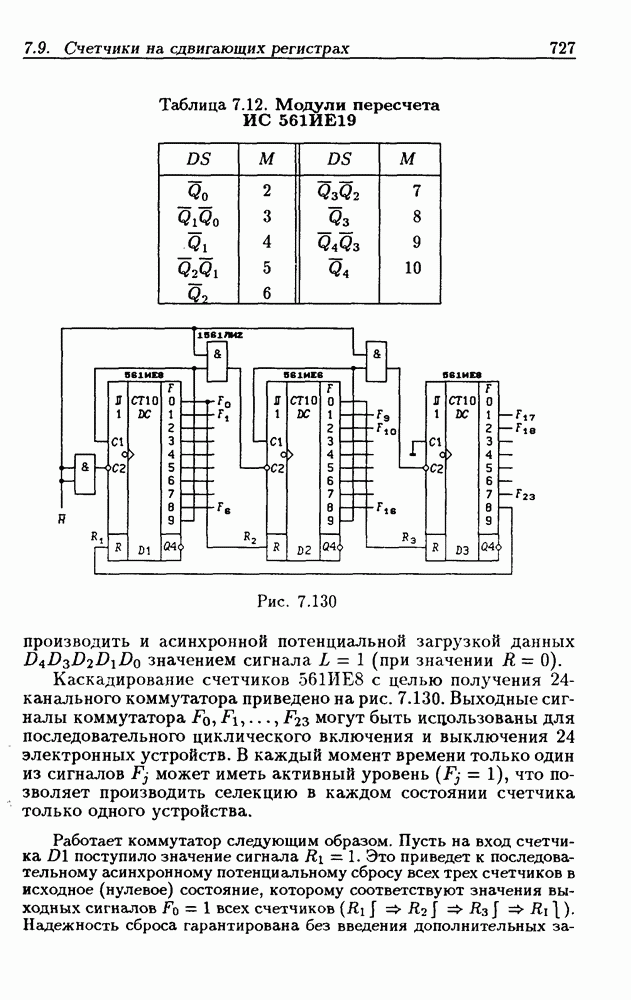
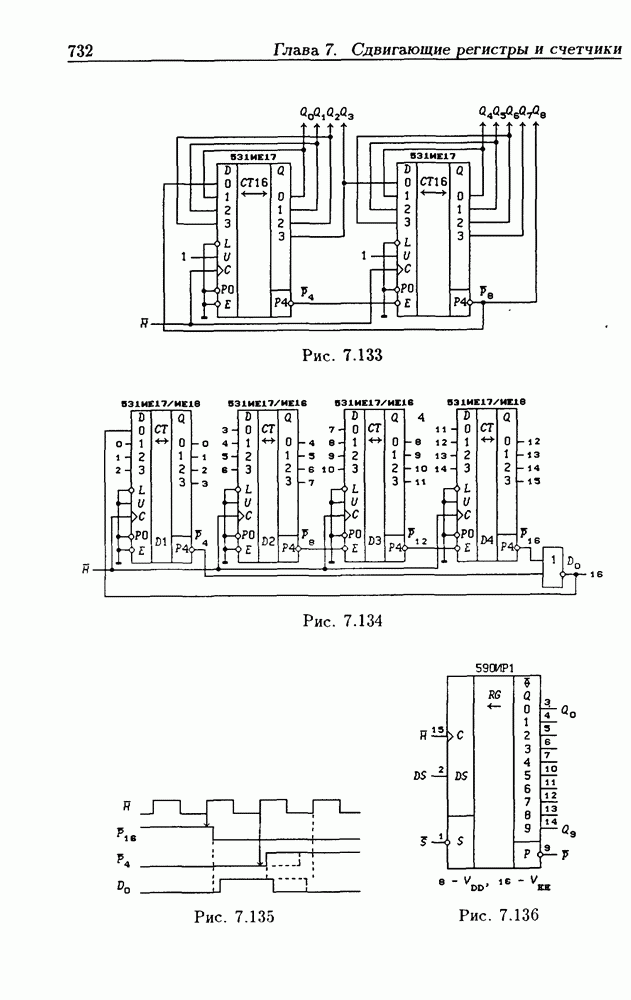
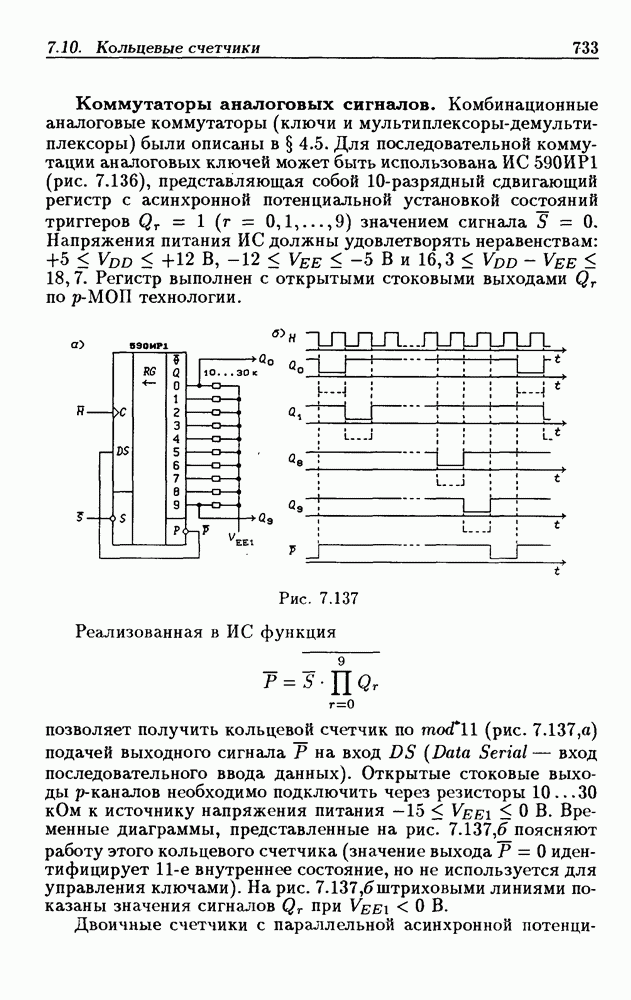
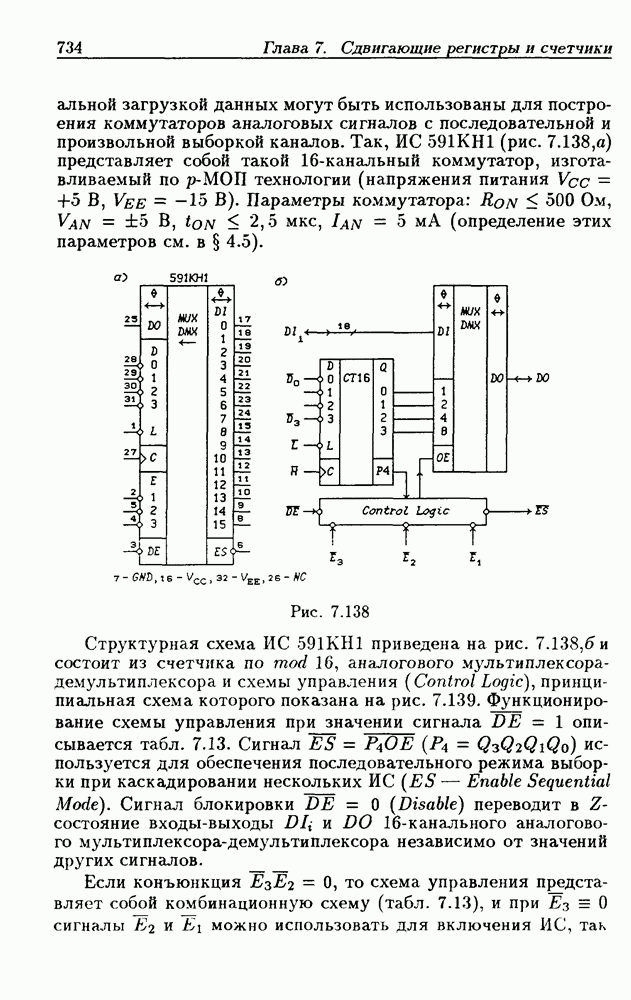
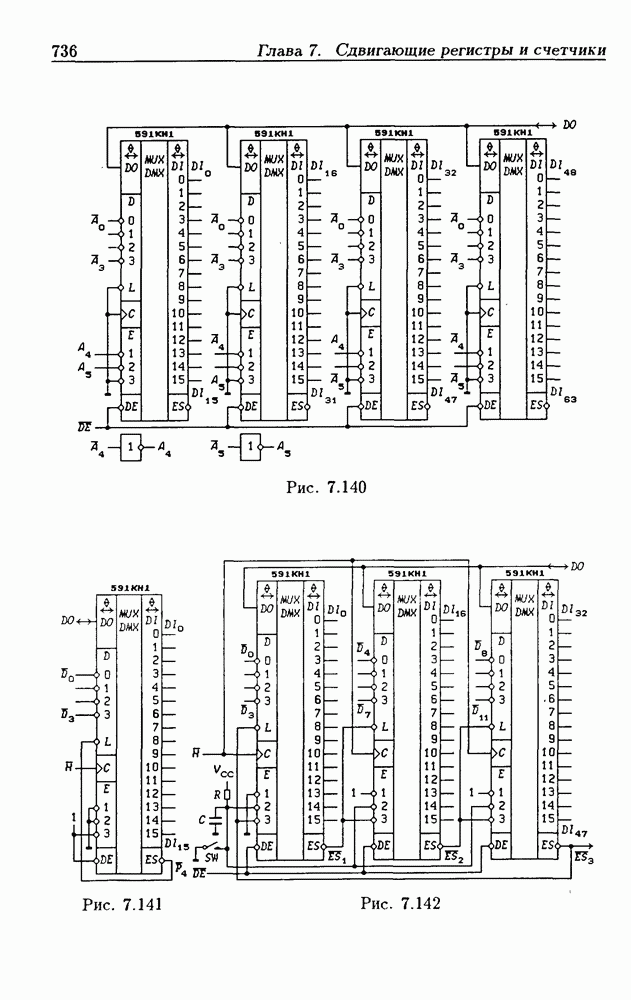
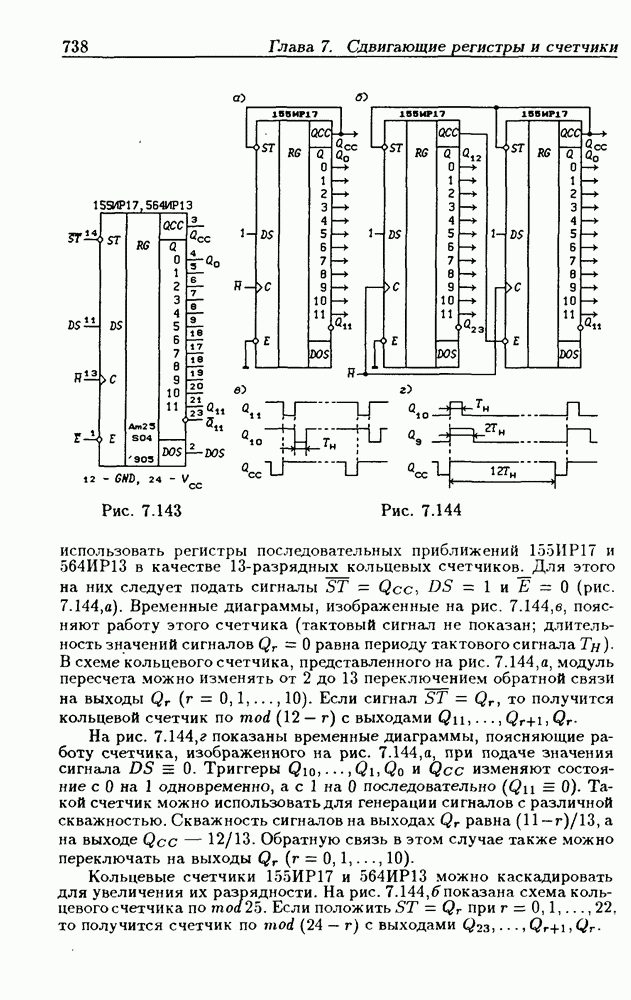
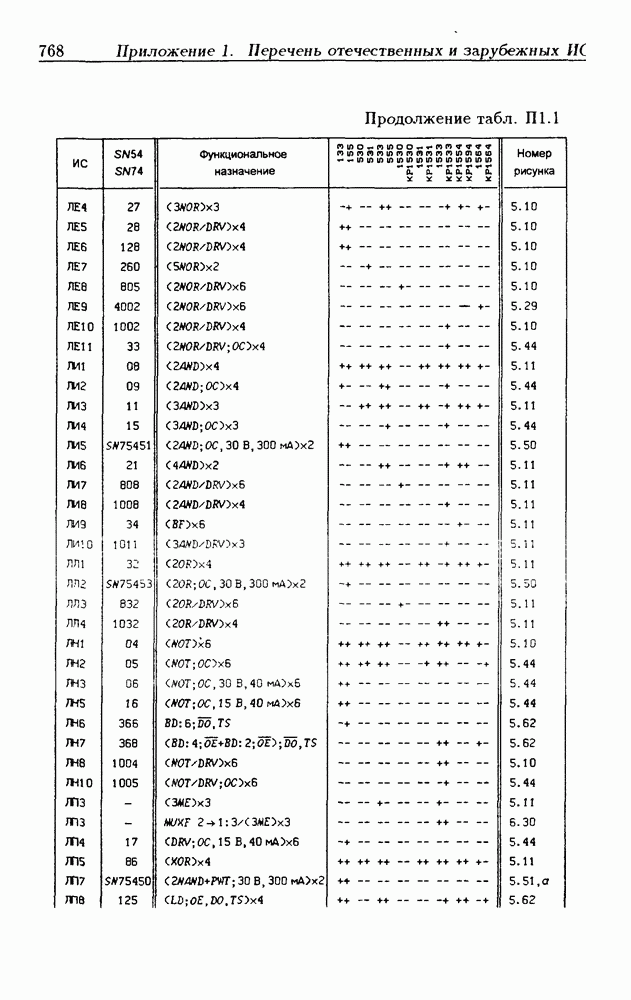
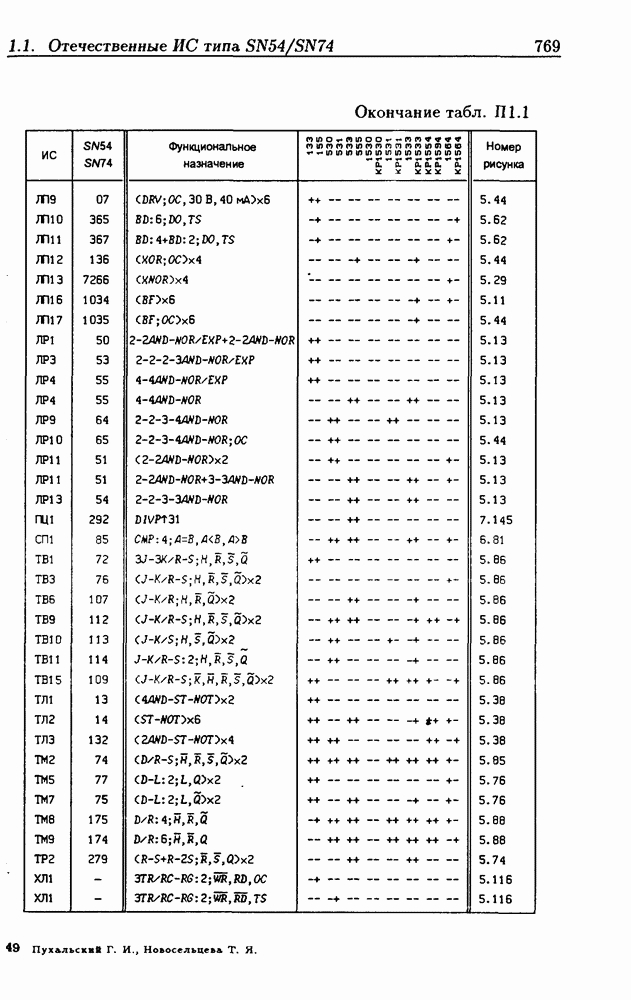
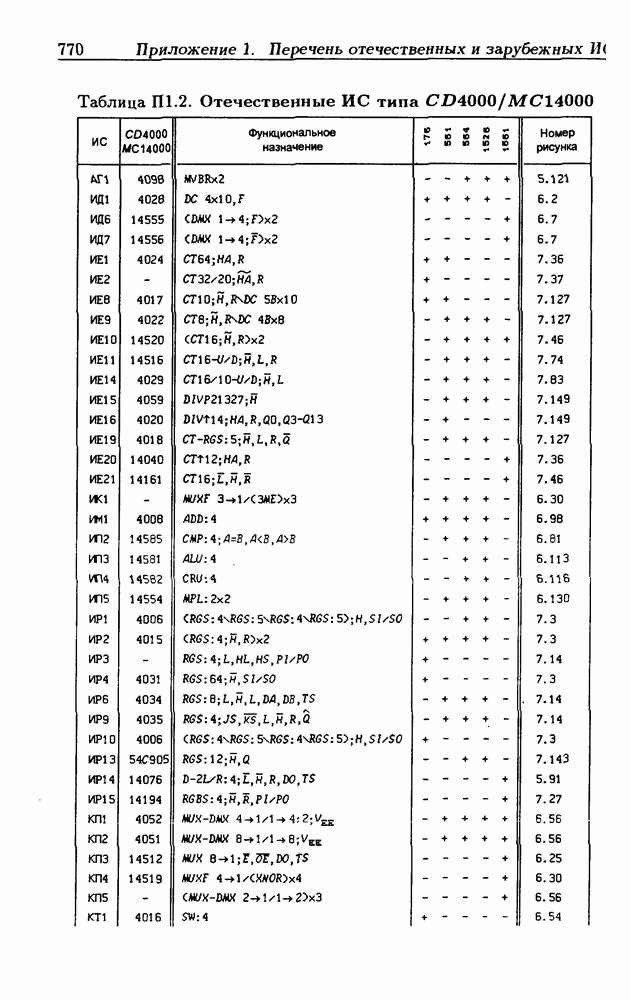
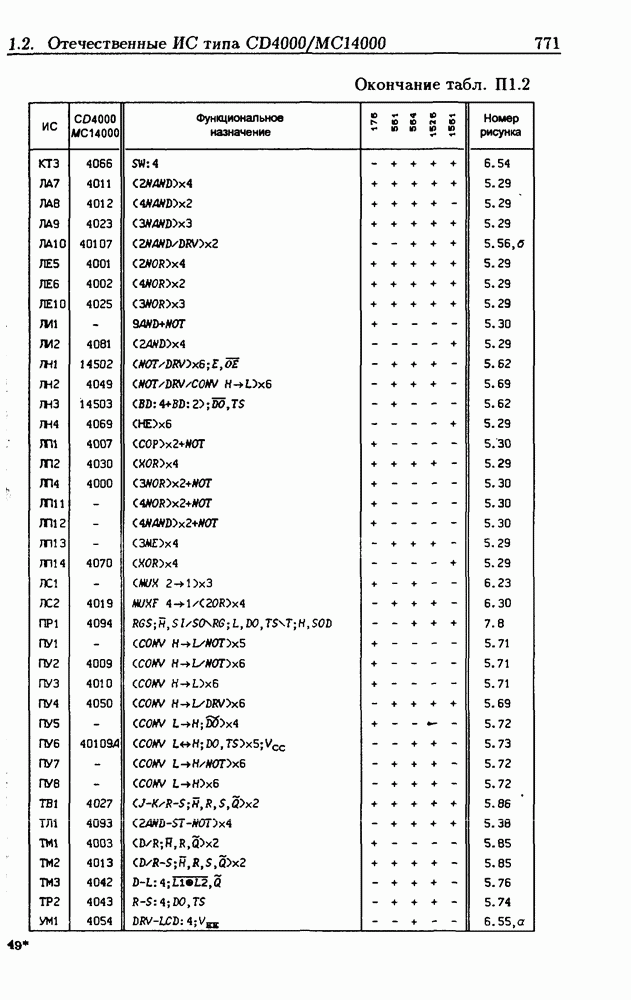
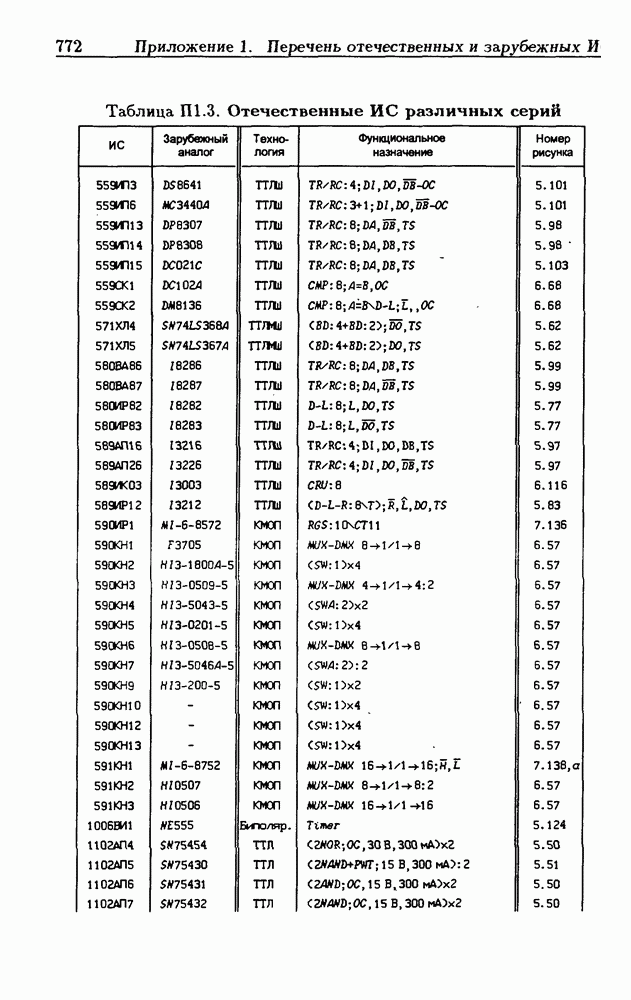
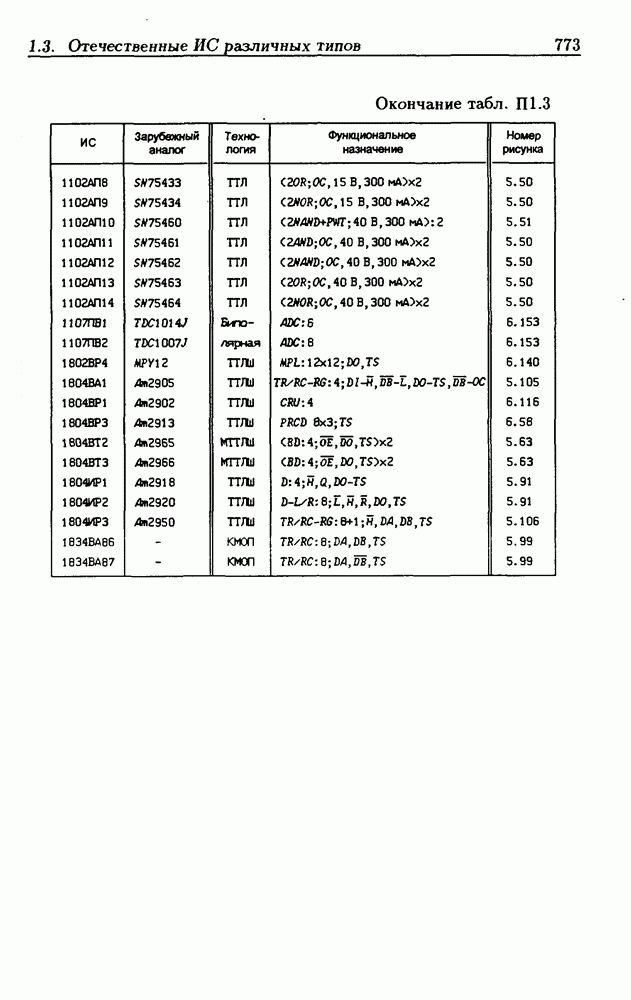
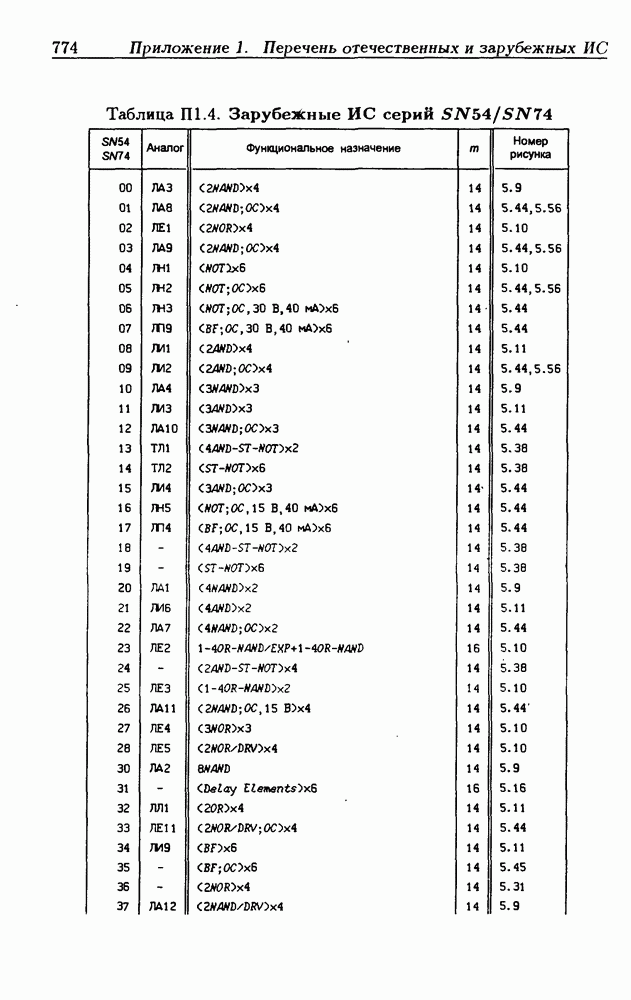
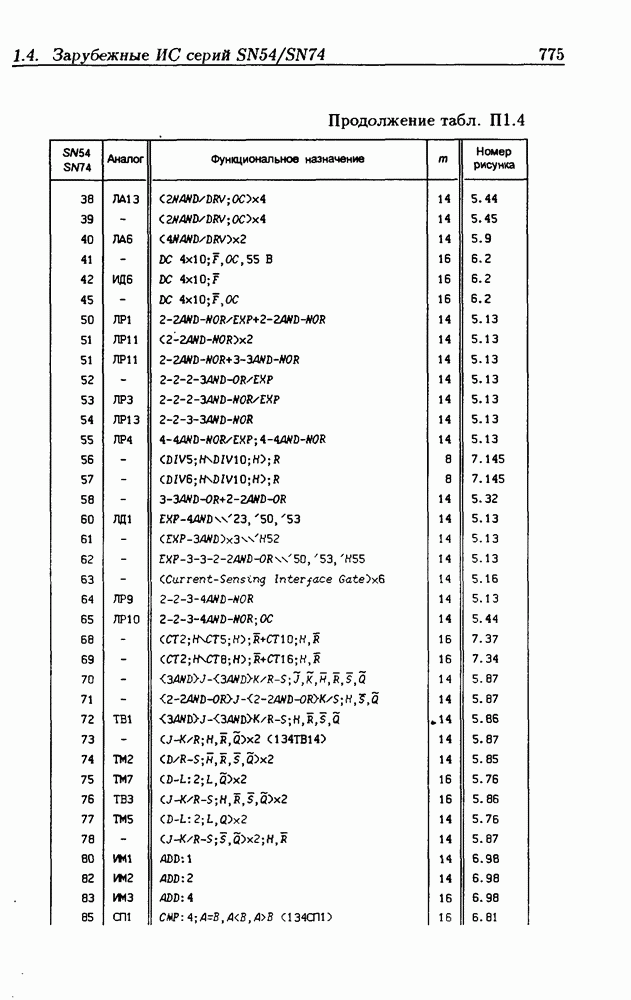
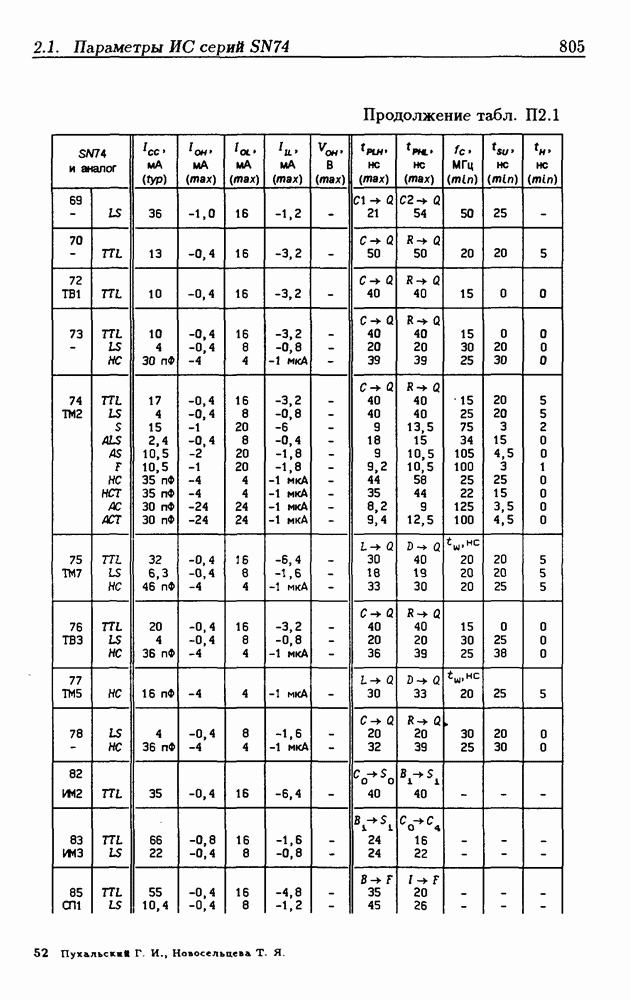
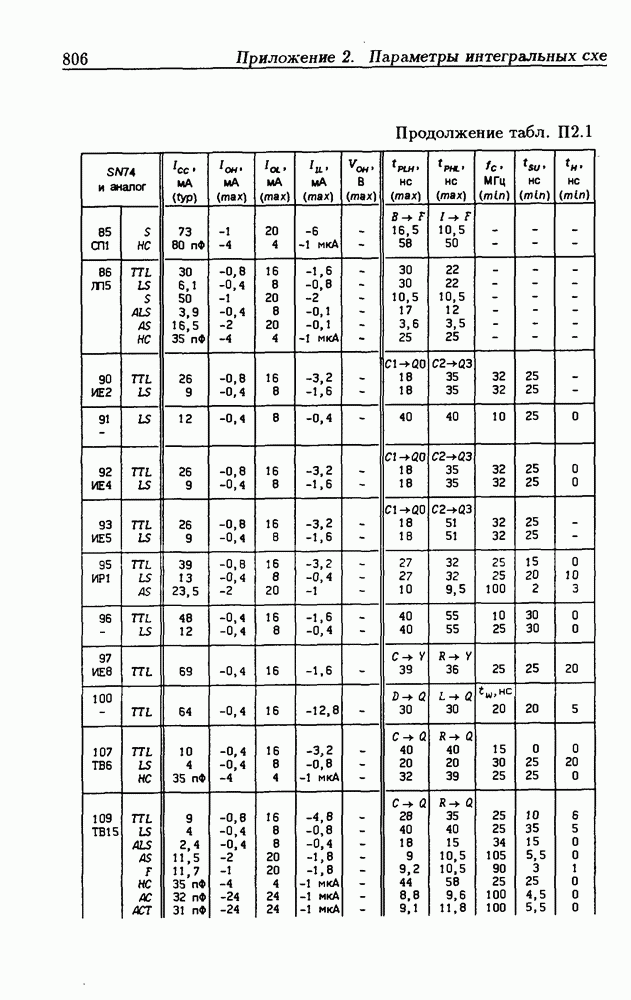
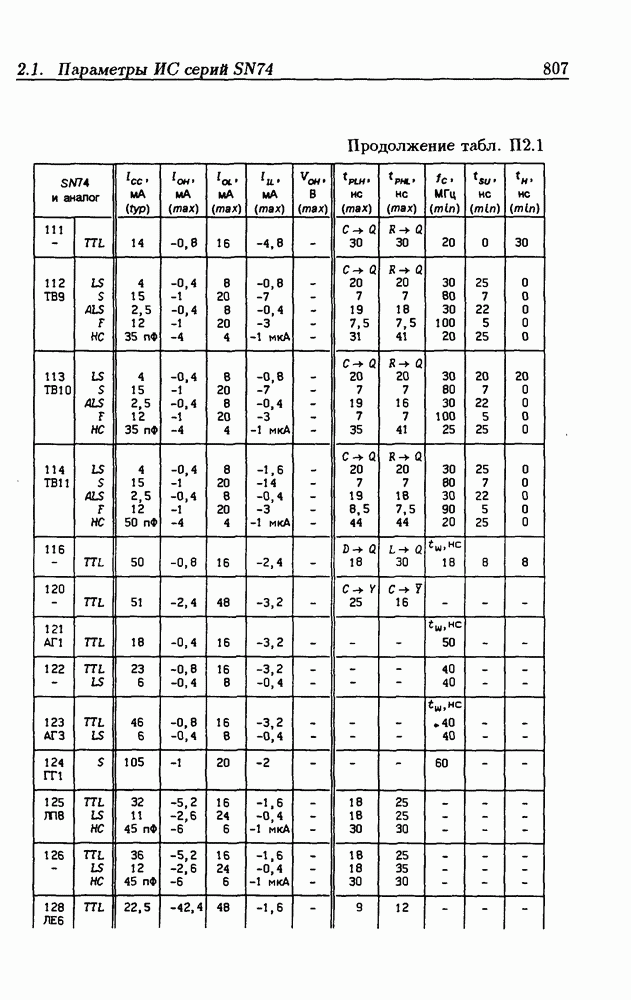
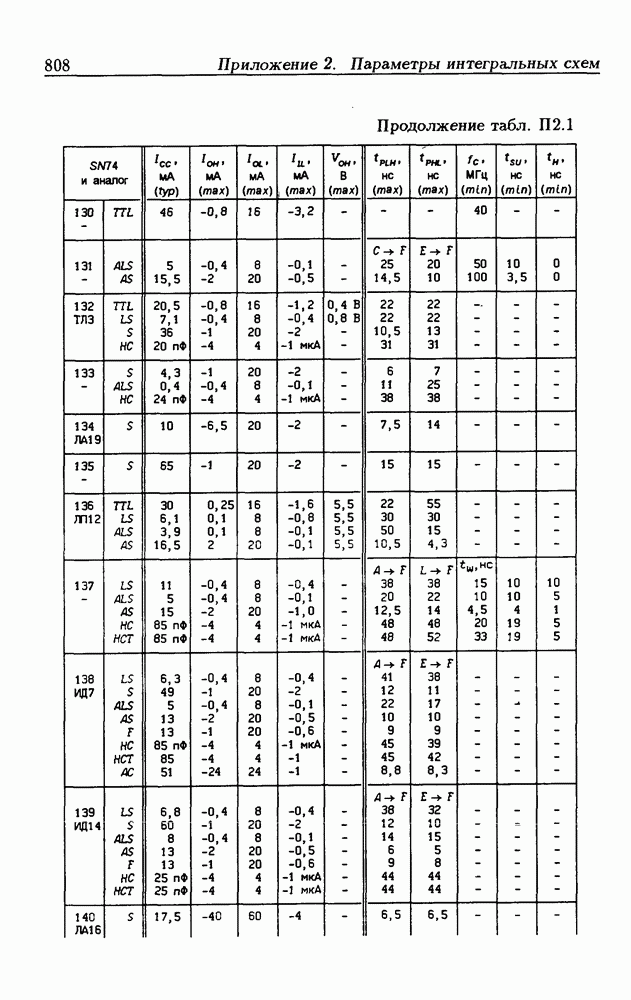
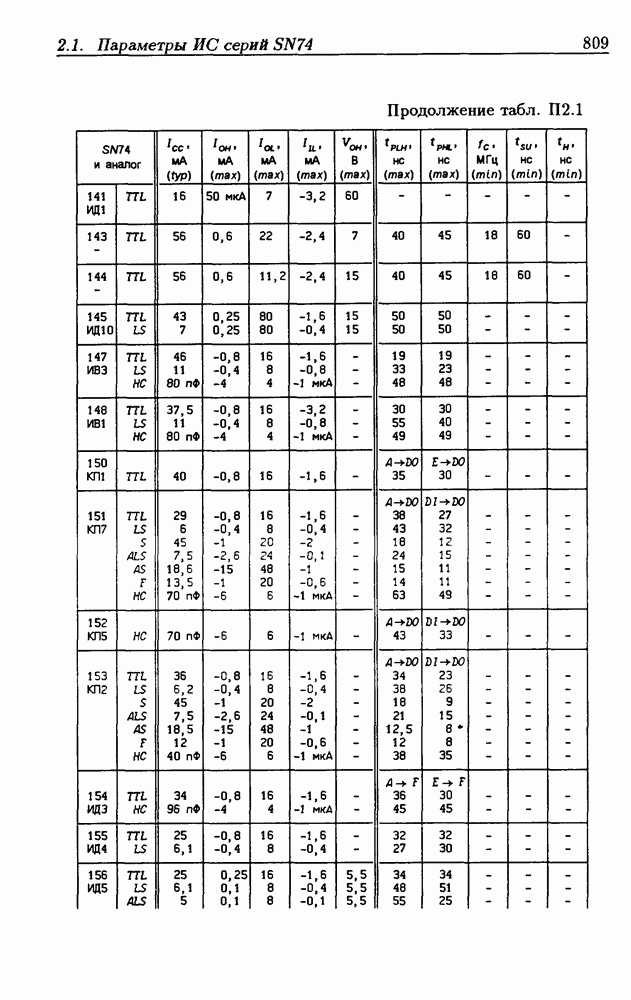
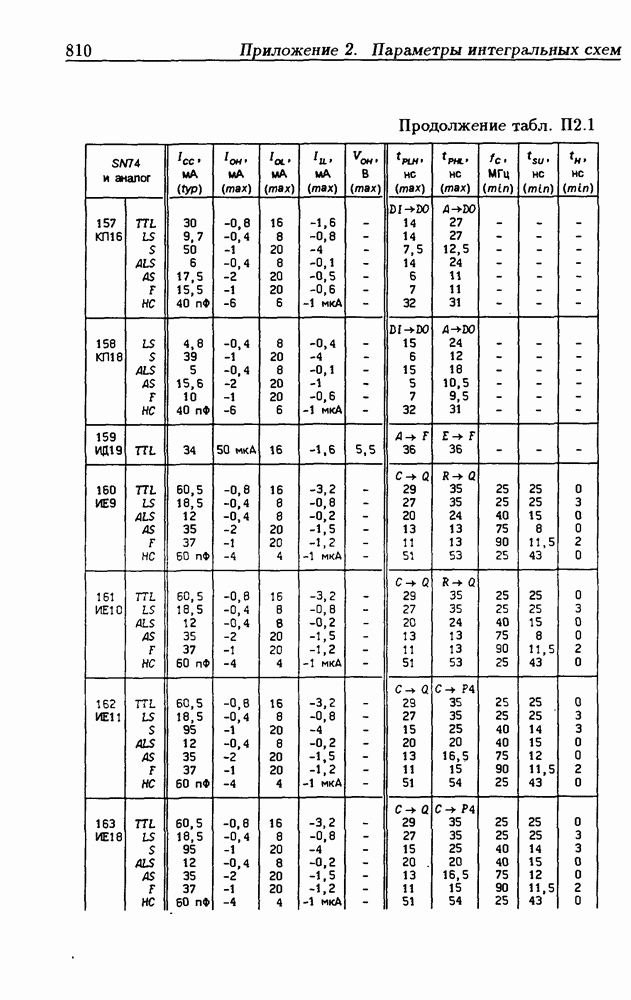
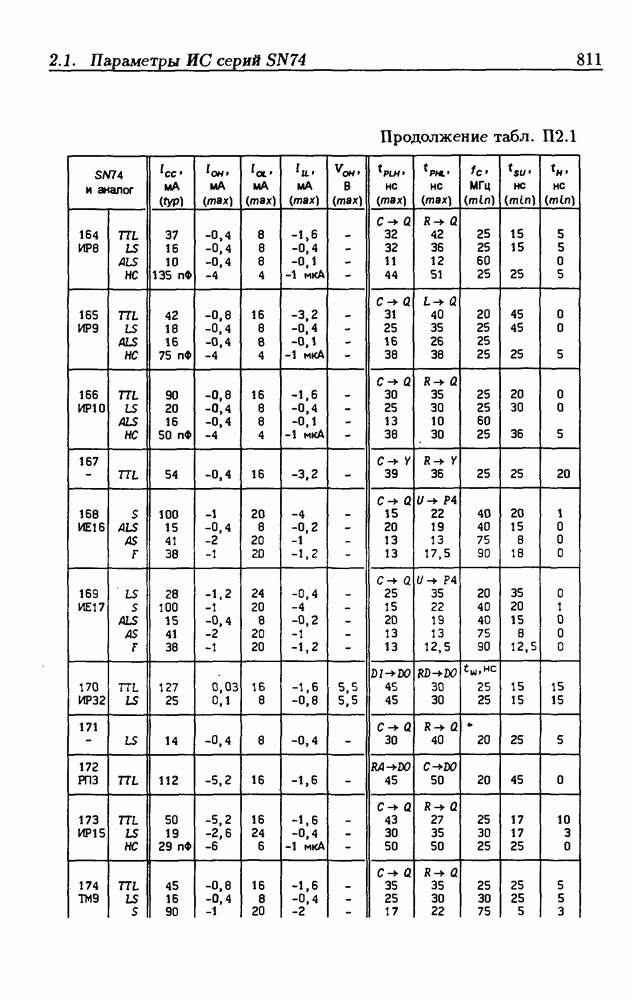
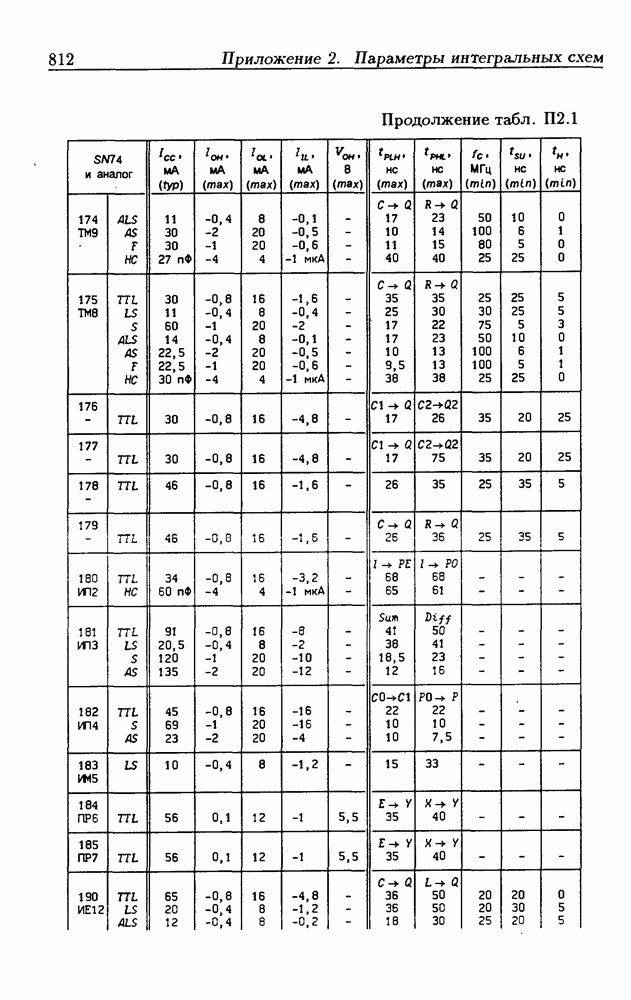
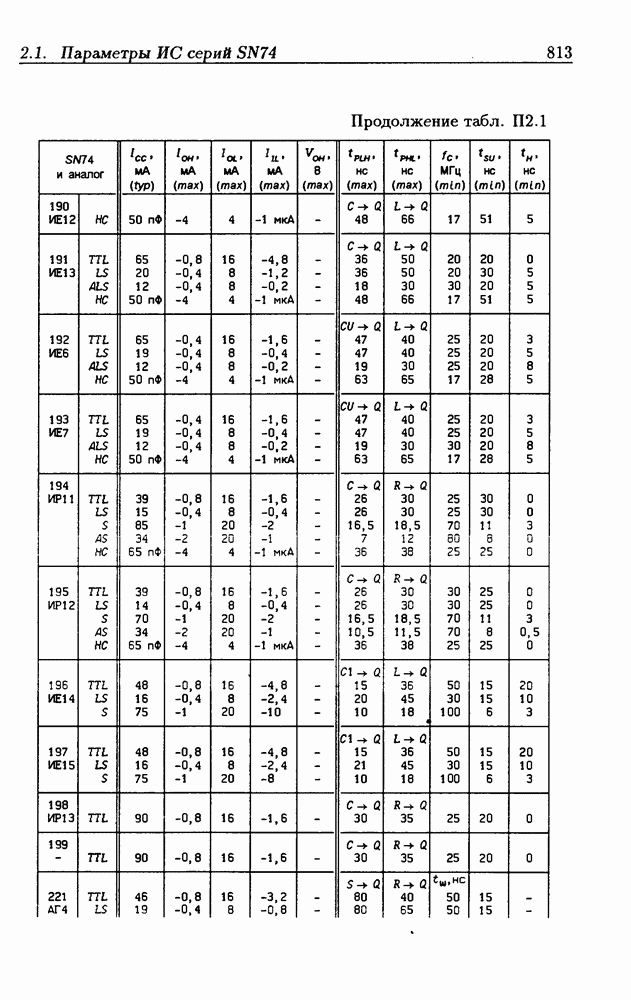
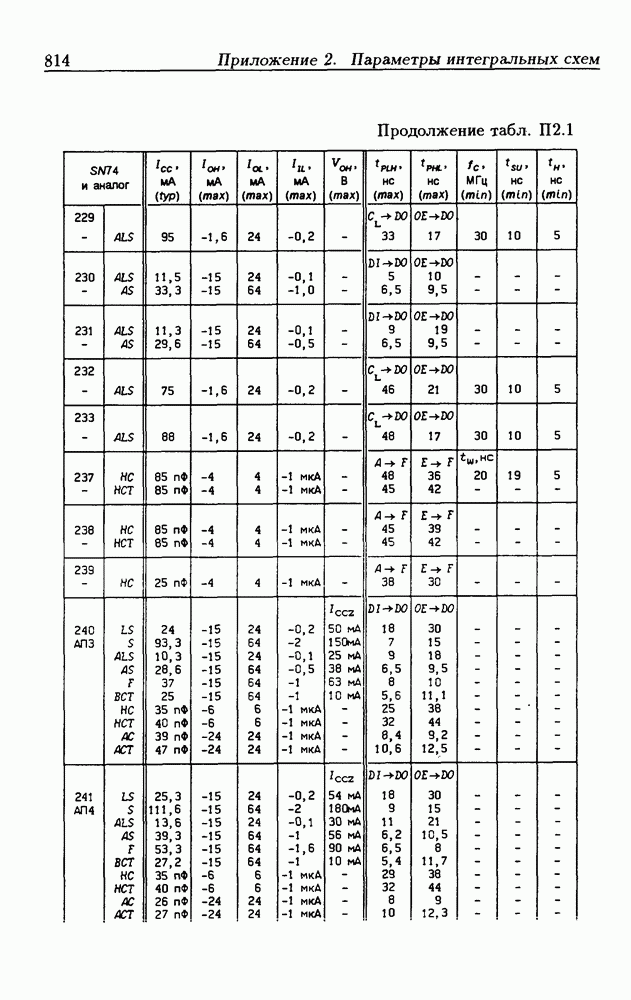
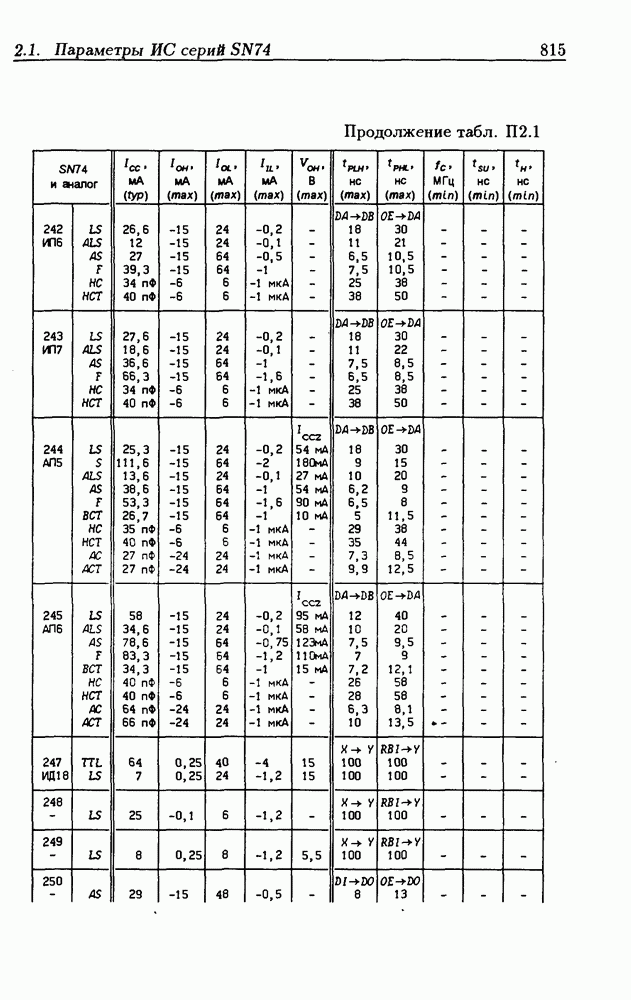
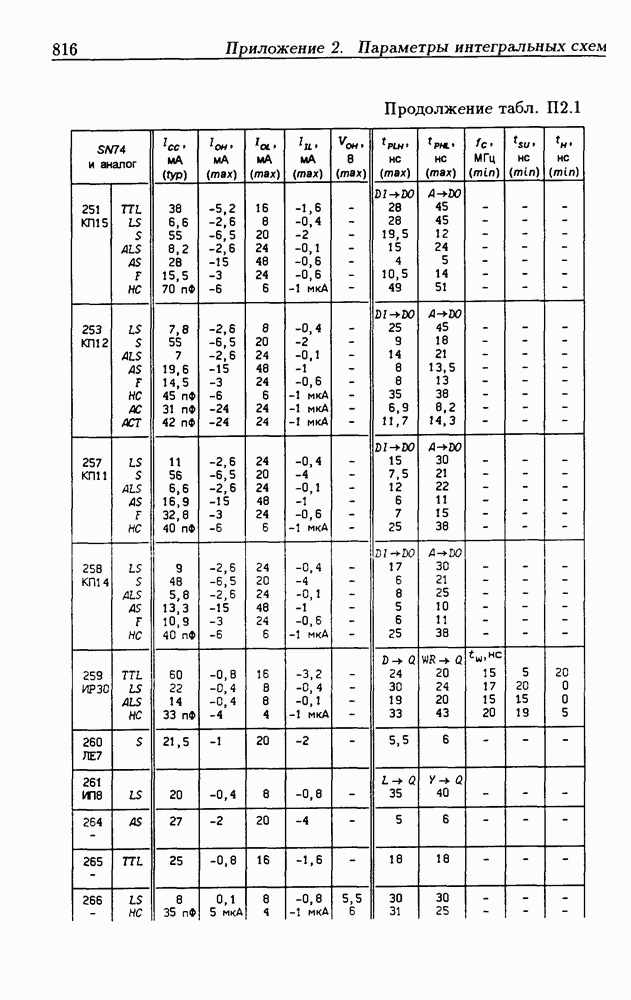
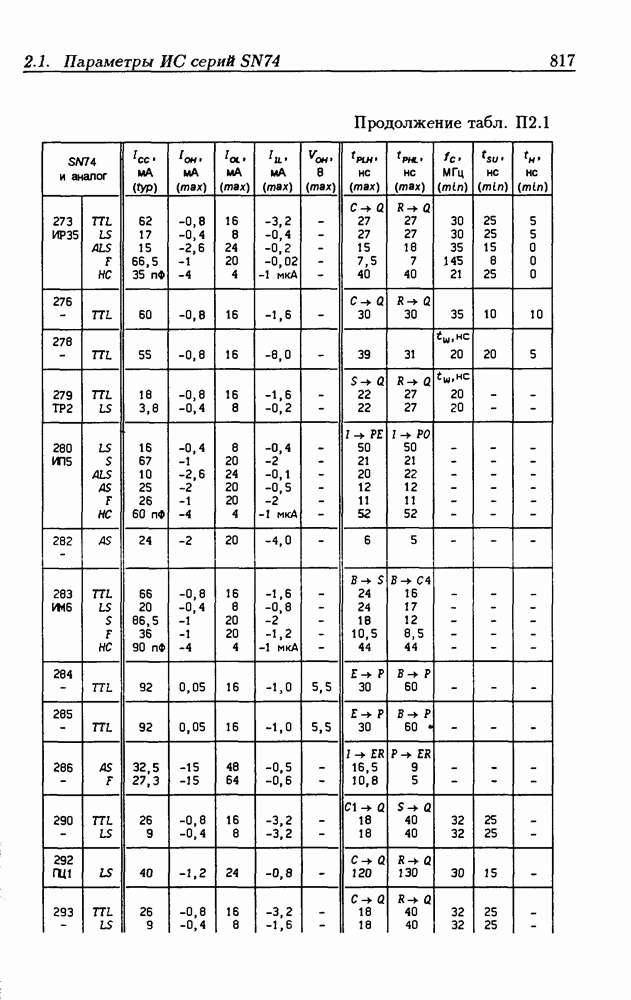
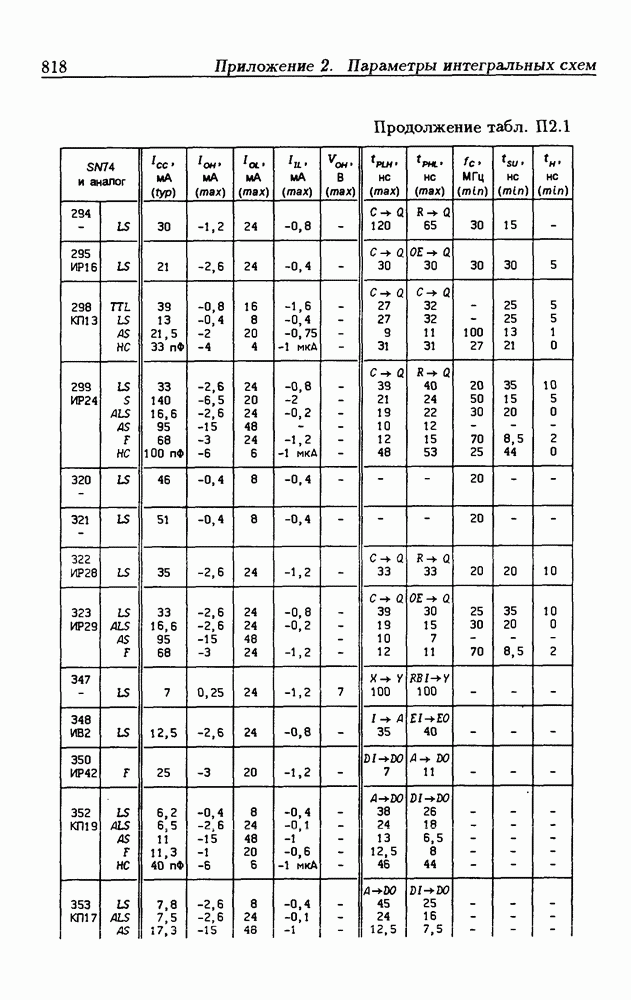
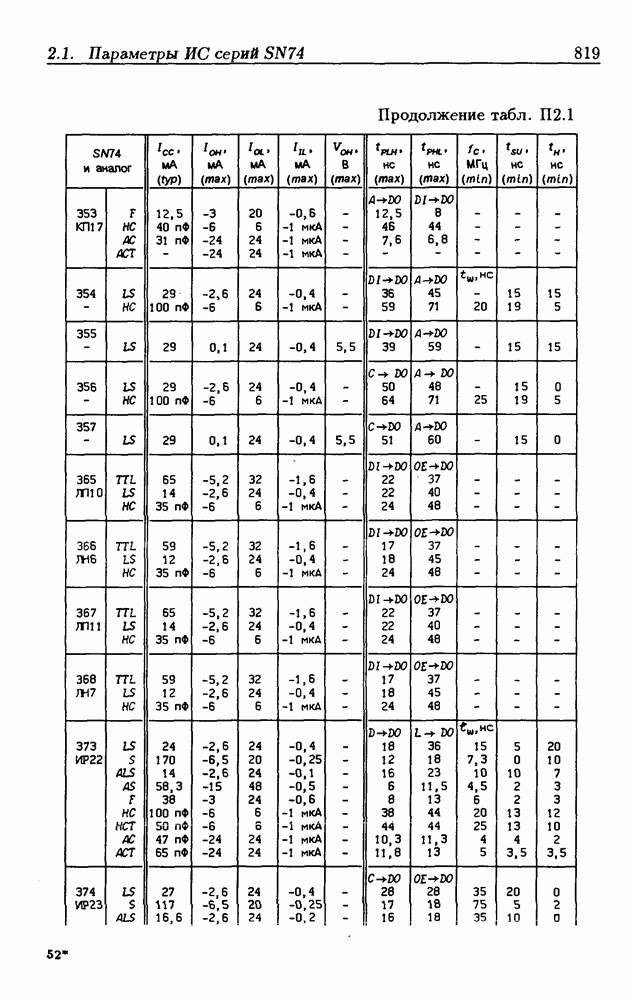
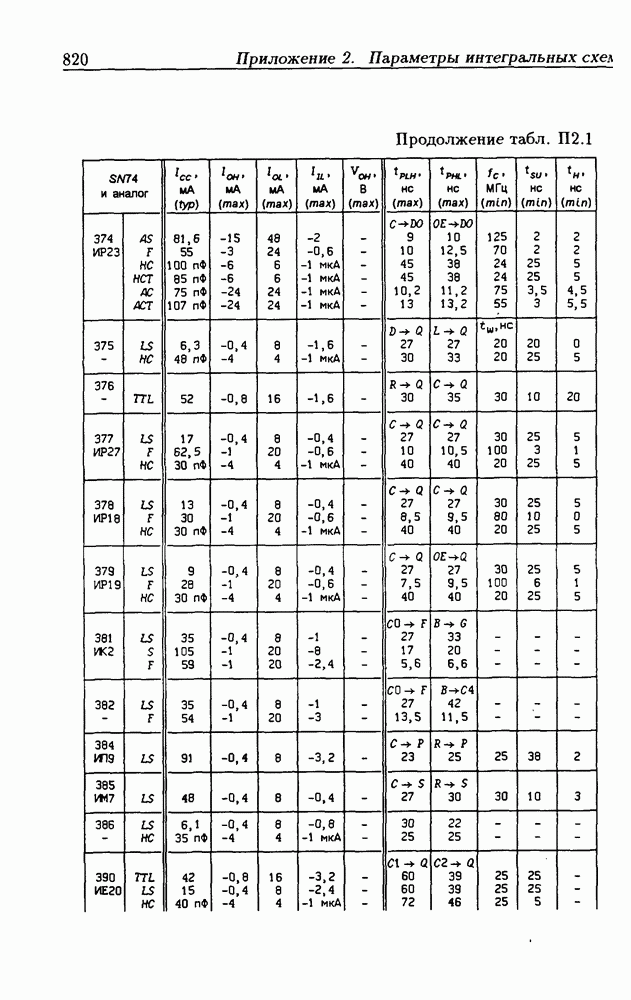
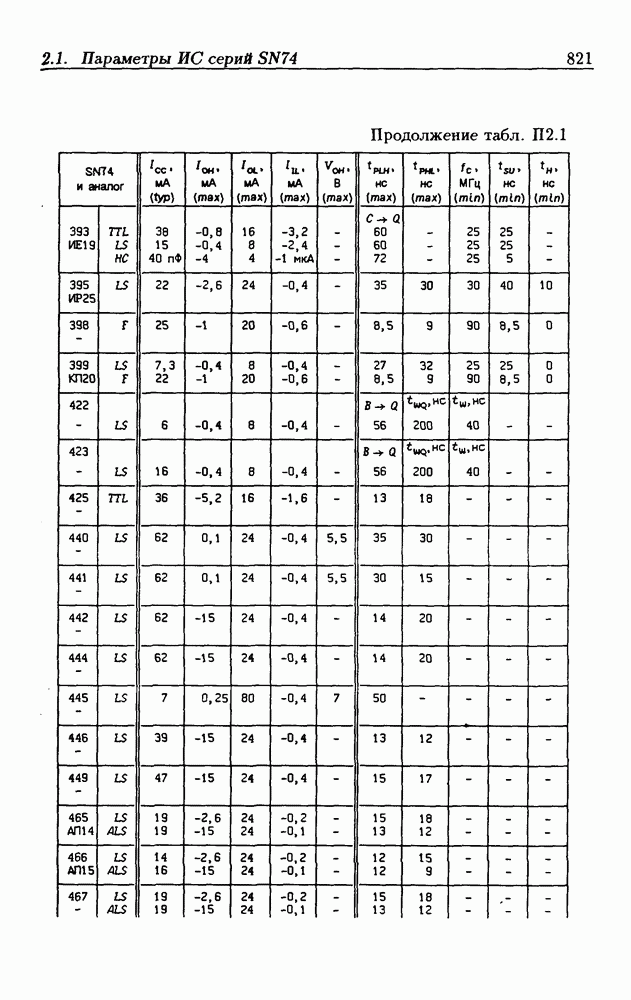
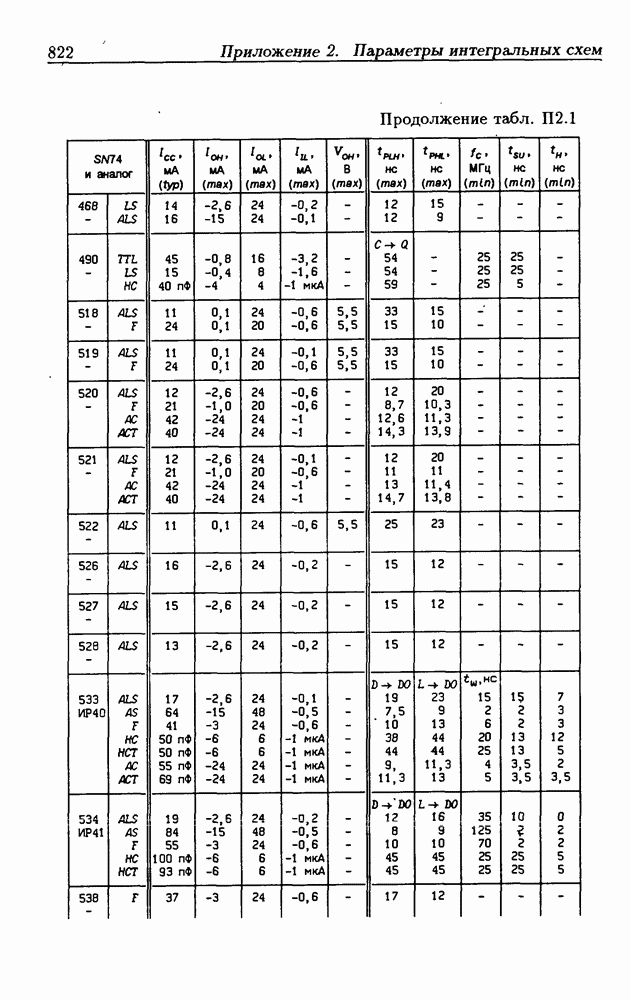
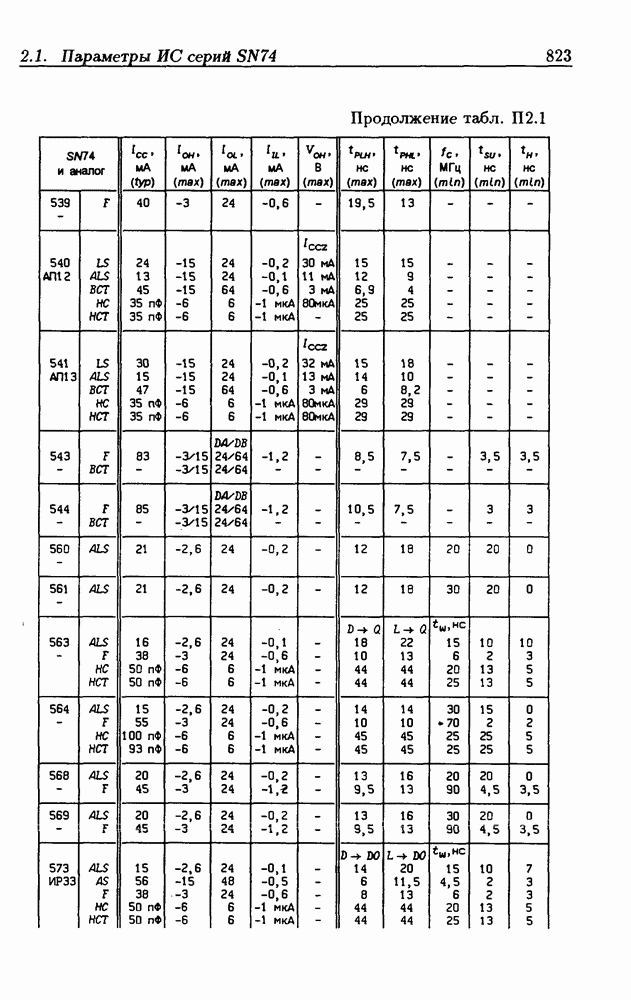
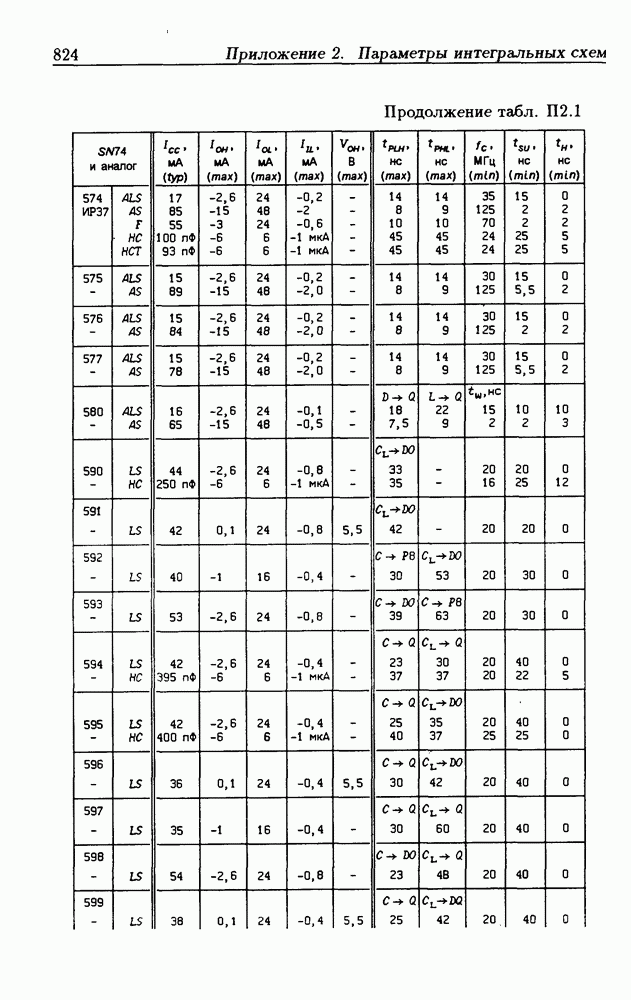
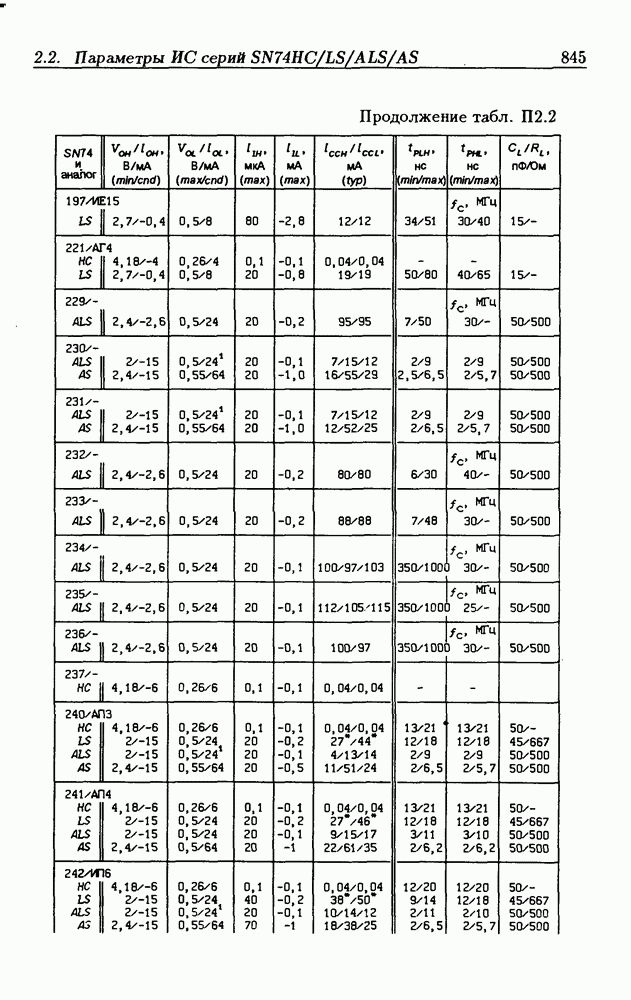
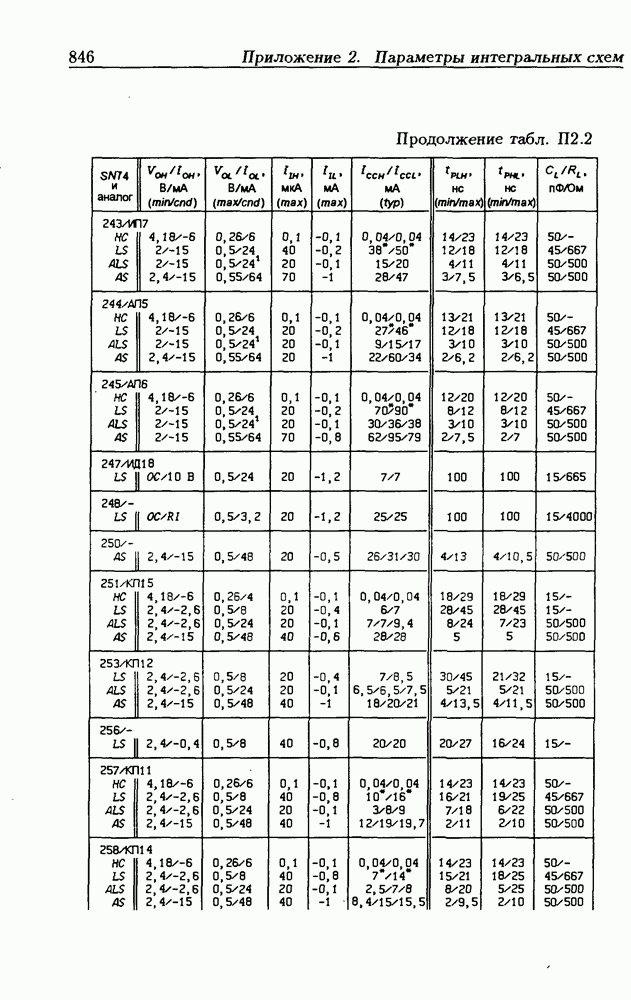
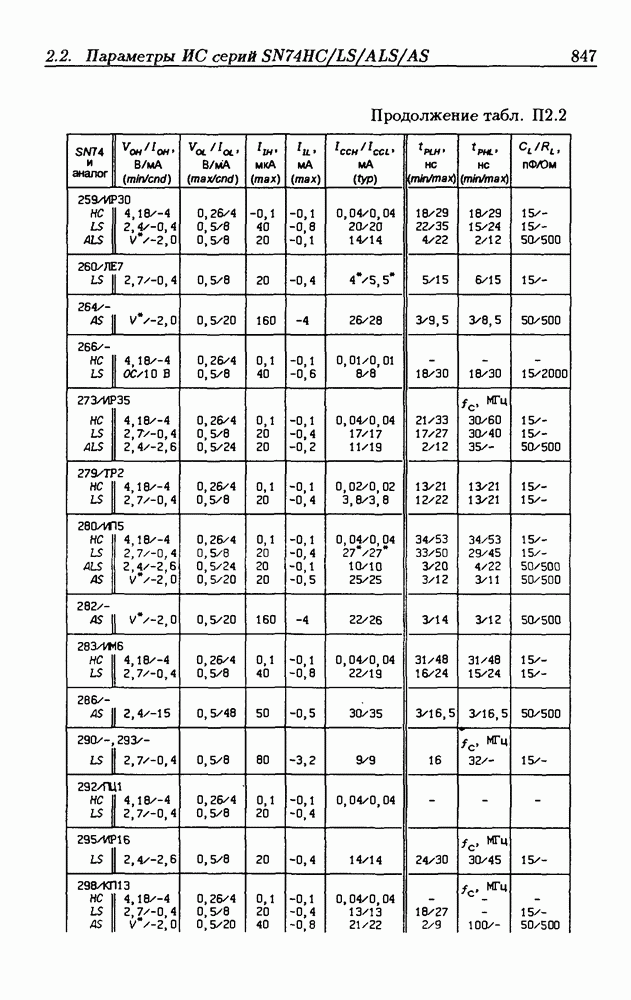
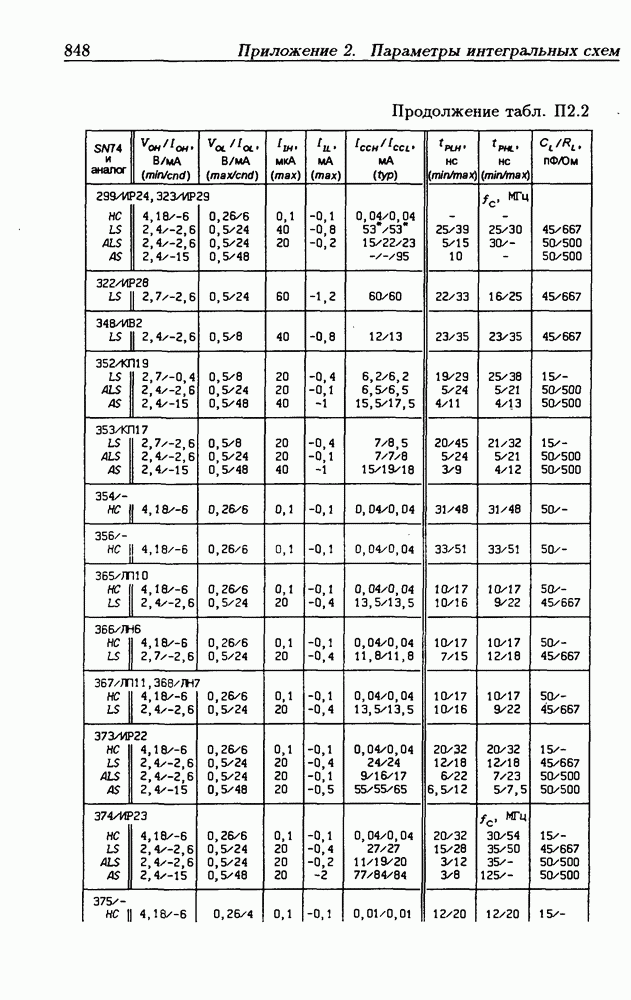
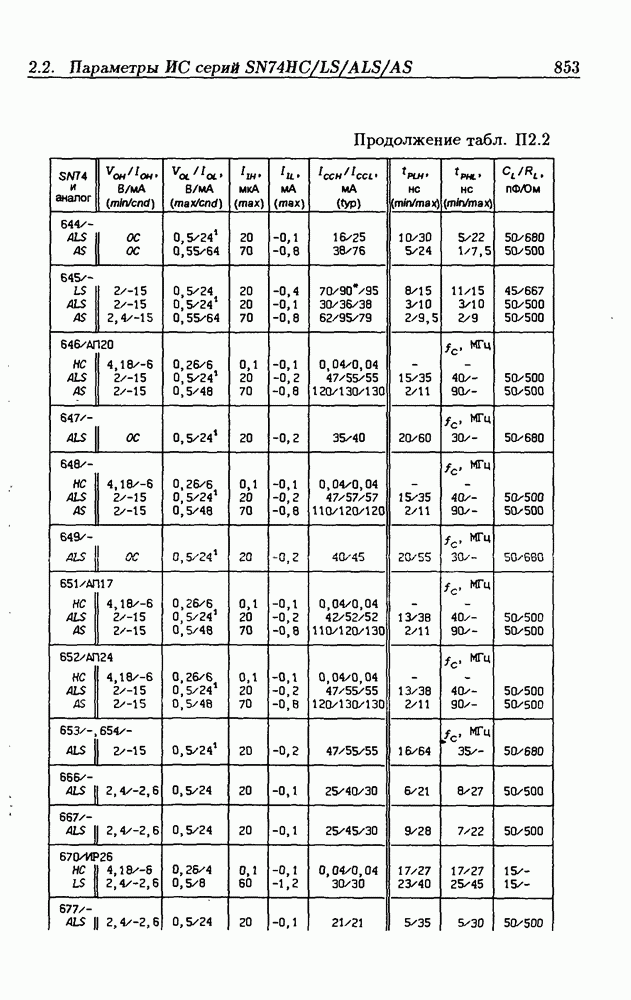
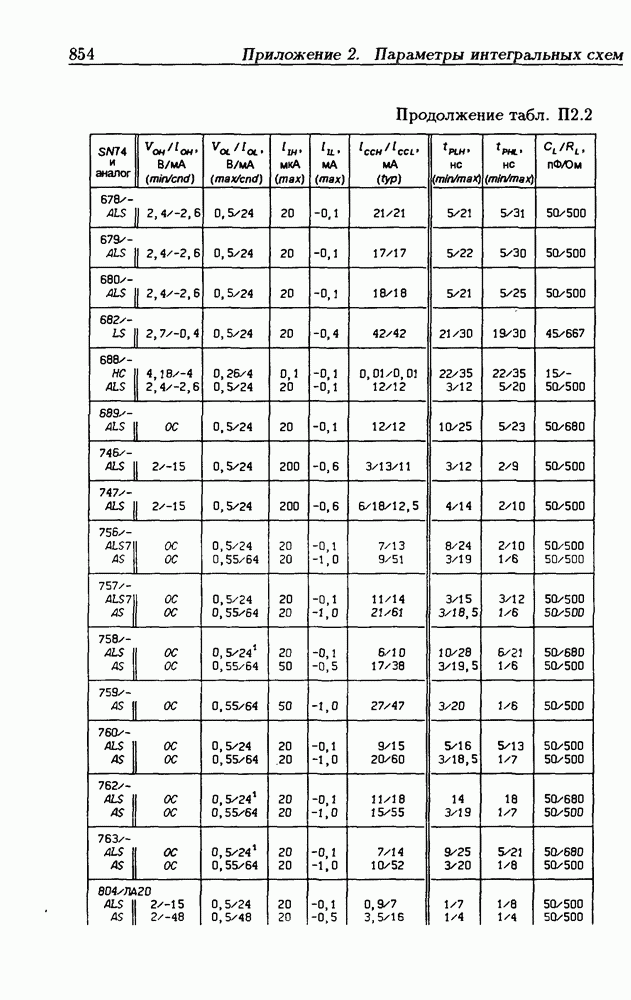
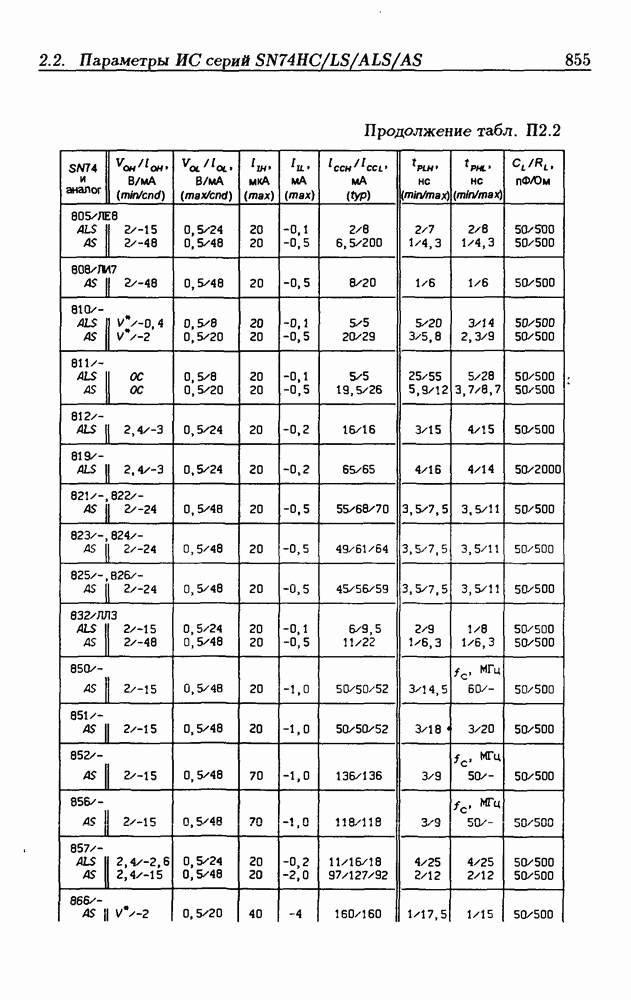
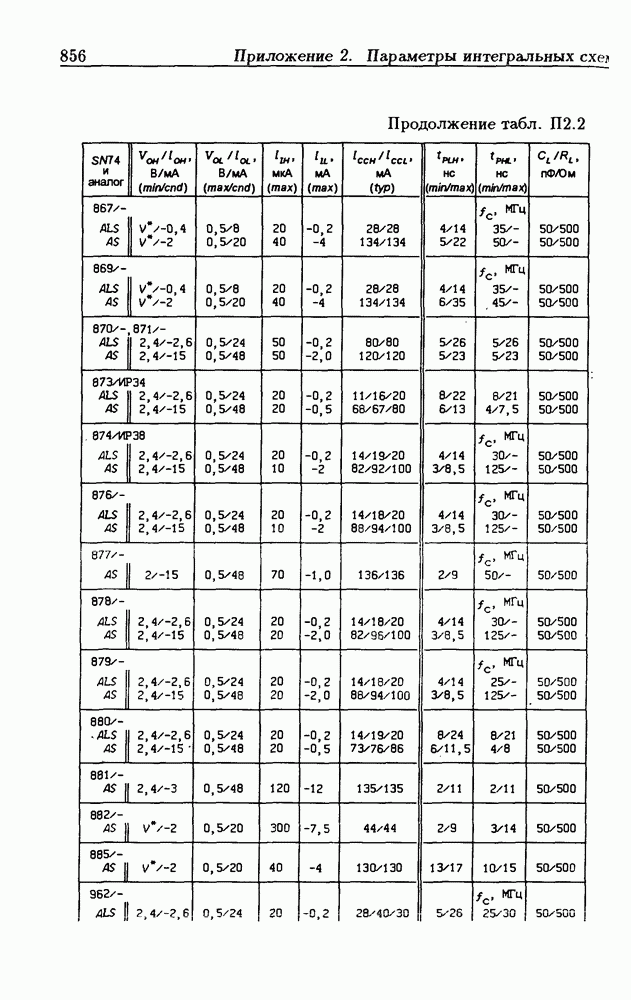
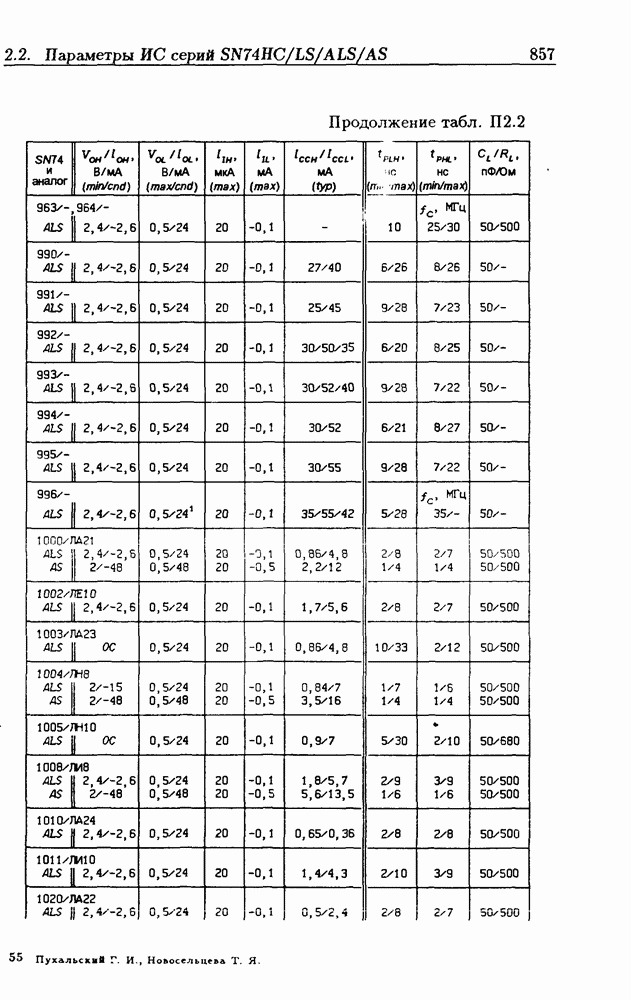
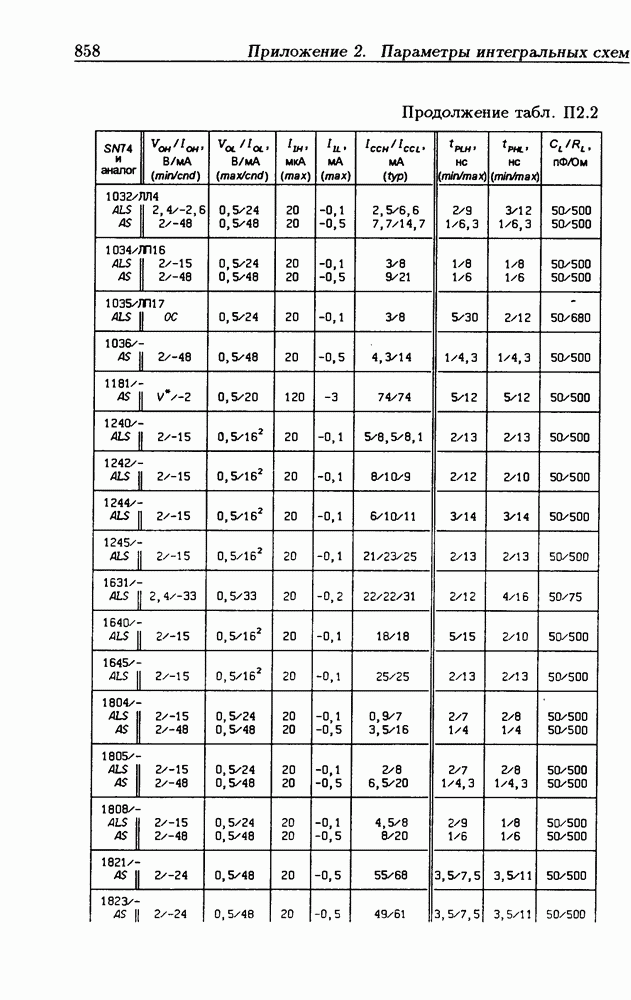
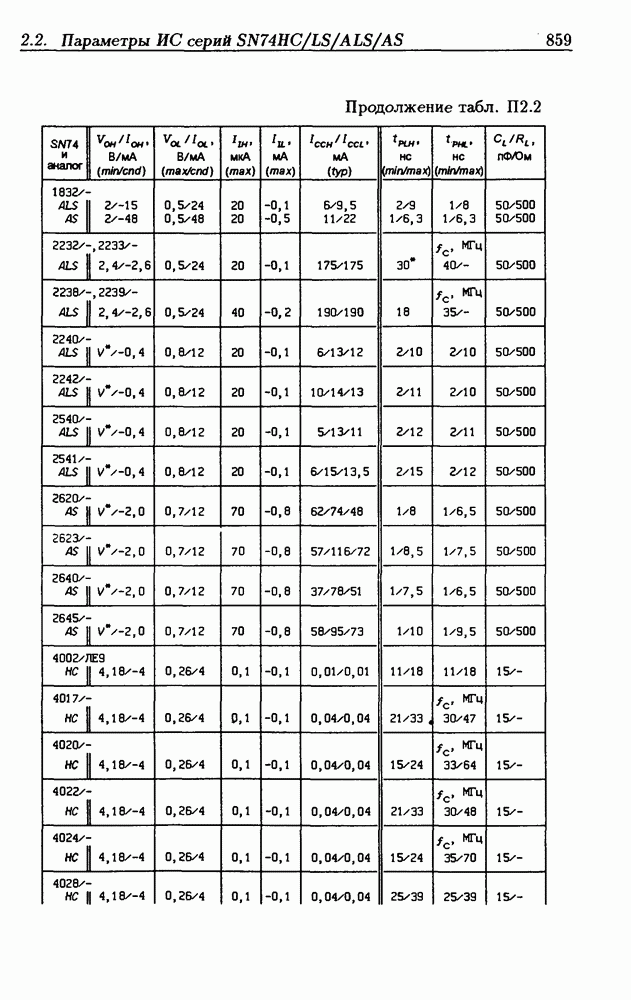
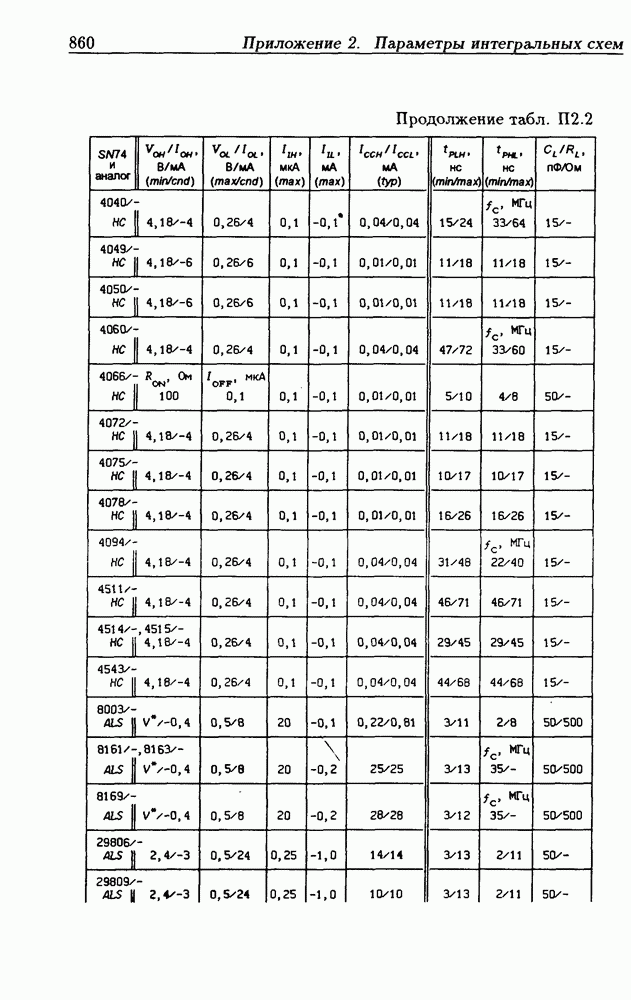
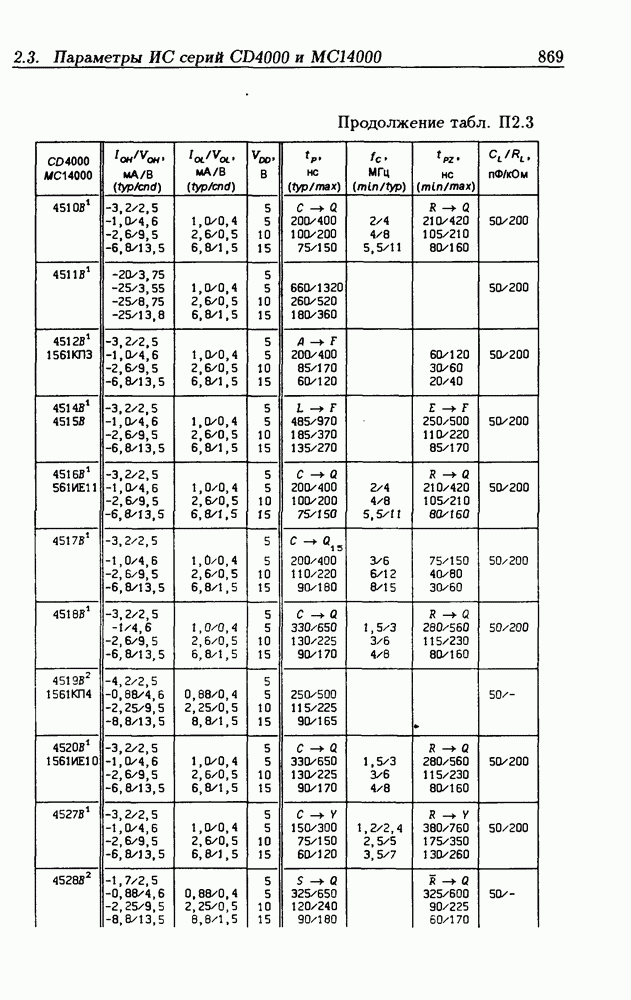
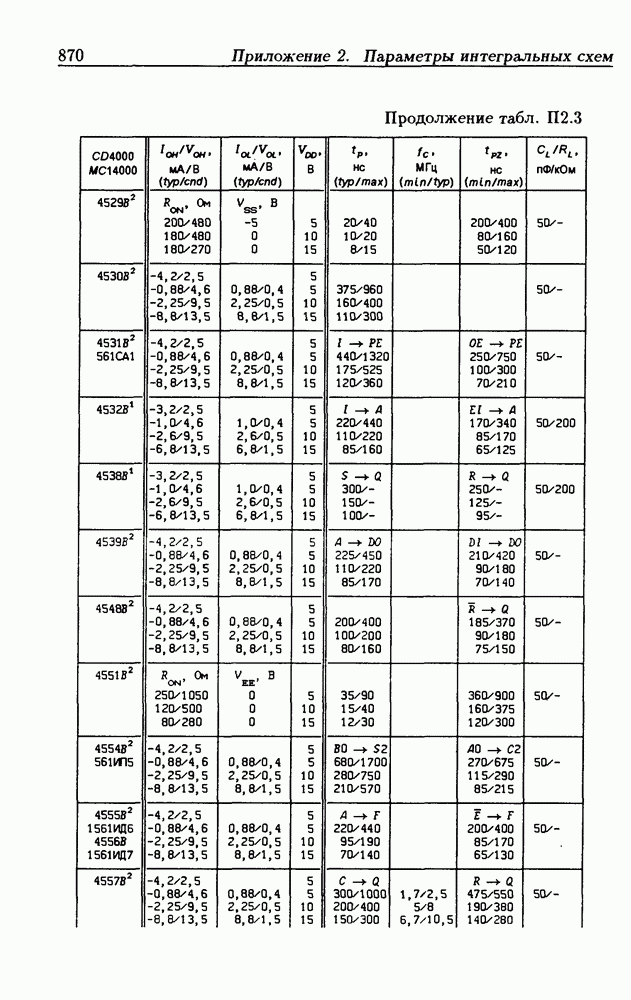
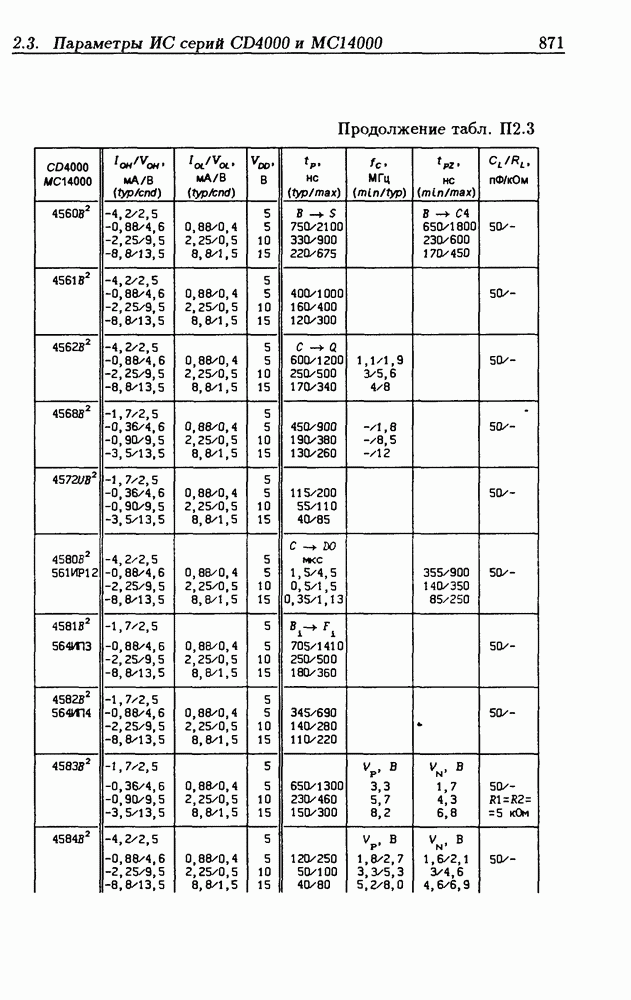
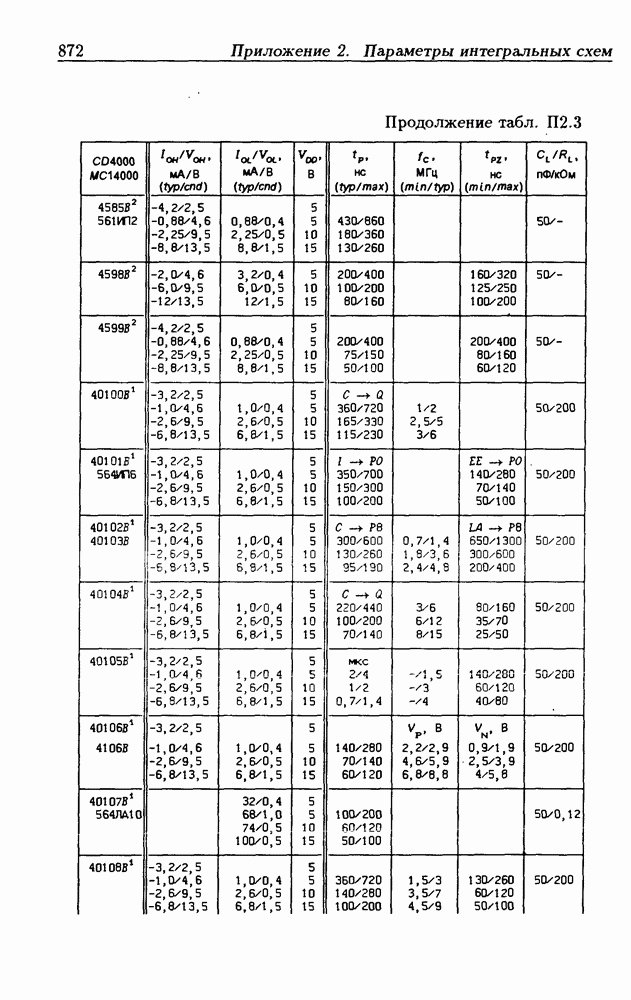
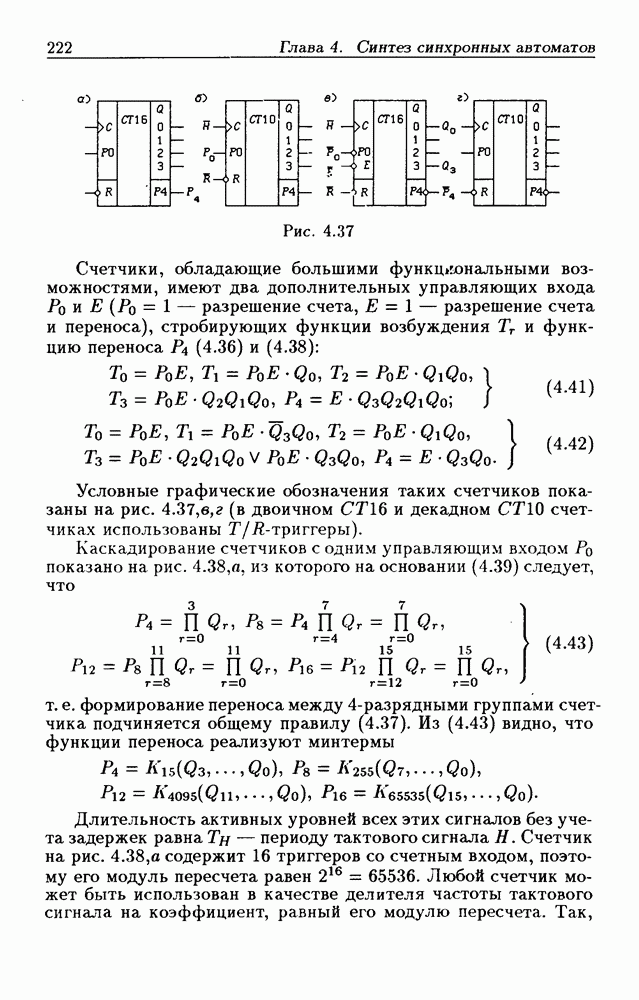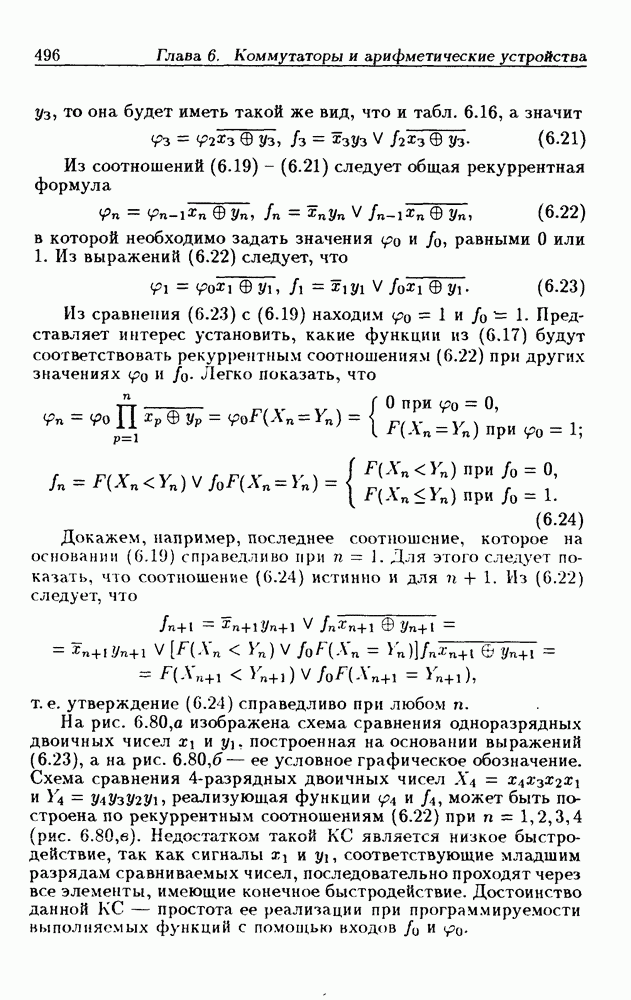| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.11. Диаграммы Вейча
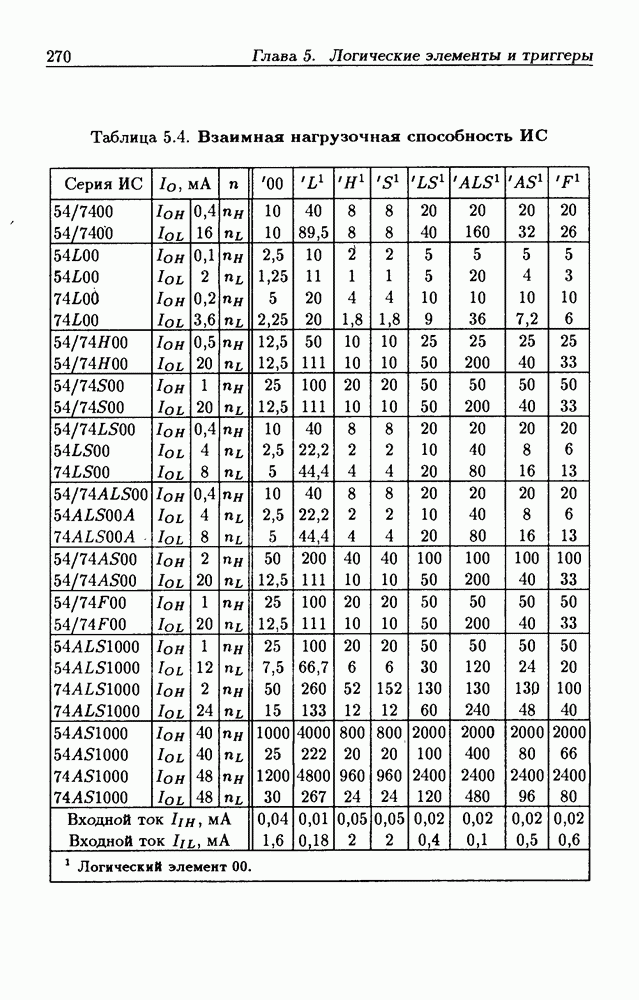
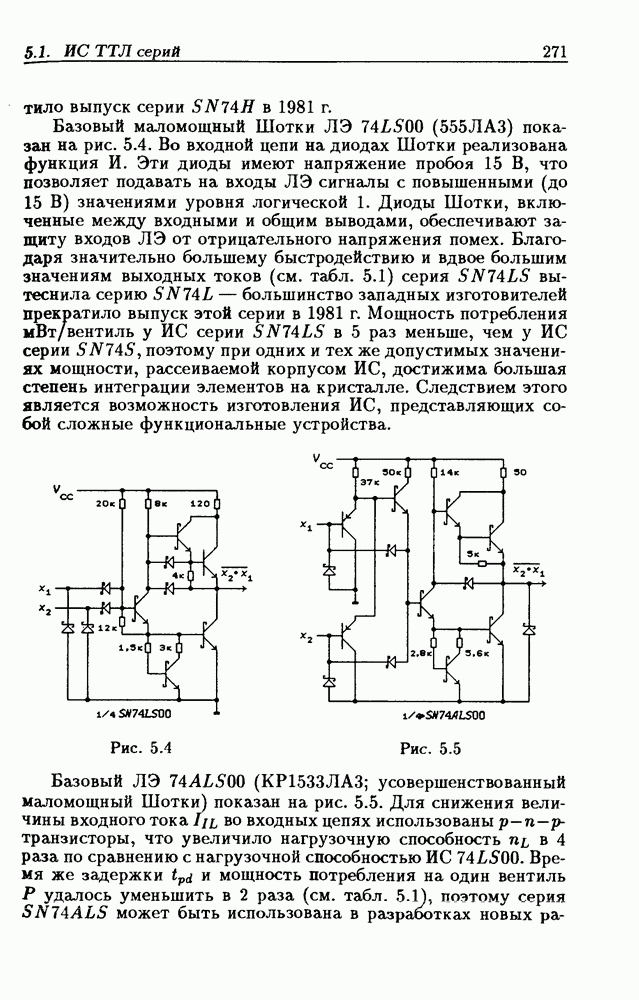
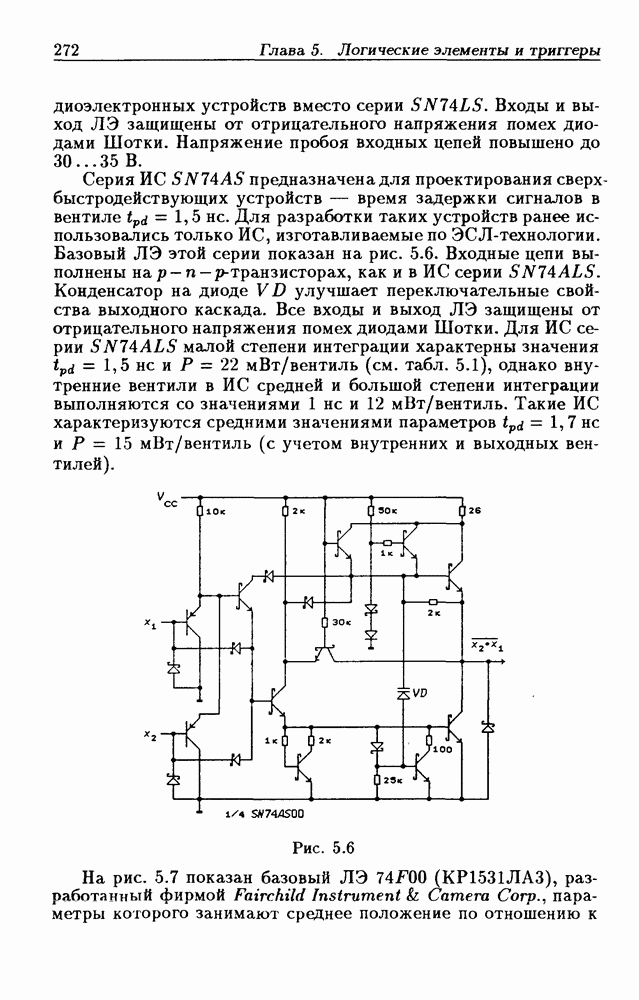
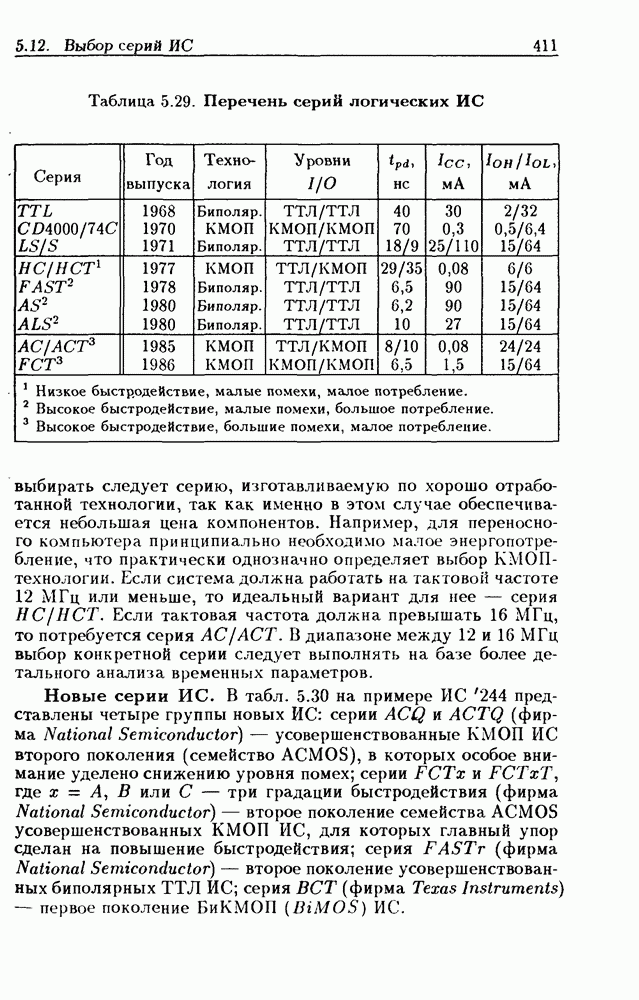
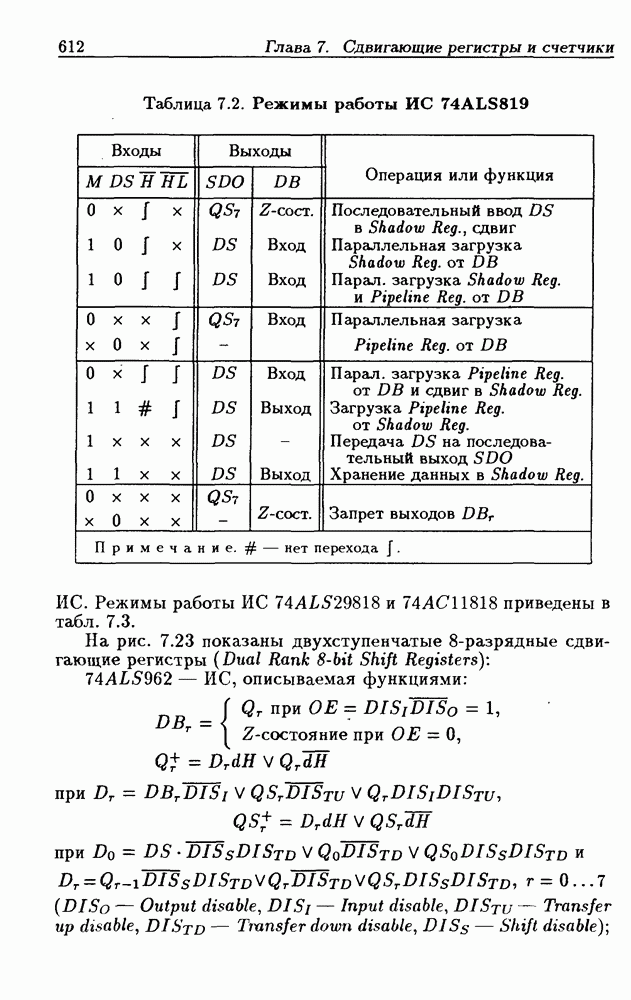
Из-за сложности использования аналитического метода минимизации, связанной с трудоемкой работой по отысканию соседних минтермов, наибольшее распространение получил графический метод минимизации с помощью диаграмм Вейча, несомненным достоинством которого является наглядность и простота использования при небольшом числе переменных 
Диаграммы Вейча (ДВ) представляют собой один из табличных способов задания функций и состоят из клеток, каждая из которых соответствует определенной точке  области определения функций, т. е. диаграммы Вейча для функции
области определения функций, т. е. диаграммы Вейча для функции  переменных состоят из
переменных состоят из  клеток, которые можно пронумеровать числами
клеток, которые можно пронумеровать числами  Таким образом, ДВ отображают
Таким образом, ДВ отображают  -мерное пространство на плоскость. Чтобы с помощью диаграммы Вейча задать функцию
-мерное пространство на плоскость. Чтобы с помощью диаграммы Вейча задать функцию  необходимо в каждую клетку с номером
необходимо в каждую клетку с номером  занести значение функции
занести значение функции  или 1, которое она принимает в точке
или 1, которое она принимает в точке 

Рис. 1.1
Для минимизации функций двух переменных использовать диаграммы Вейча нет смысла, так как эти функции легко упрощаются аналитическим методом или непосредственно по таблице истинности. Рассмотрим диаграммы Вейча для функций трех переменных  Так как
Так как  то ДВ-3 состоит из восьми клеток (рис. 1.1,а). Каждой стороне ДВ-3 соответствует своя переменная
то ДВ-3 состоит из восьми клеток (рис. 1.1,а). Каждой стороне ДВ-3 соответствует своя переменная  причем одной половине стороны соответствует первичный терм
причем одной половине стороны соответствует первичный терм  а другой — первичный терм
а другой — первичный терм  Поэтому каждой клетке будет соответствовать совокупность первичных термов
Поэтому каждой клетке будет соответствовать совокупность первичных термов  а
а
номер данной клетки будет Определяться числом 
Любой минтерм  представляет собой функцию, равную 1 только в одной точке
представляет собой функцию, равную 1 только в одной точке  области определения, поэтому на ДВ-3 он представляется единицей, стоящей Только в одной клетке с номером
области определения, поэтому на ДВ-3 он представляется единицей, стоящей Только в одной клетке с номером  Например, на рис. 1.1, показана ДВ-3 для минтерма
Например, на рис. 1.1, показана ДВ-3 для минтерма  На рис. 1.1,б,в,г использованы упрощенные обозначения сторон ДВ-3, полностью соответствующие обозначениям на рис. 1.1,а (одна половина сторон соответствует
На рис. 1.1,б,в,г использованы упрощенные обозначения сторон ДВ-3, полностью соответствующие обозначениям на рис. 1.1,а (одна половина сторон соответствует  а другая —
а другая —  Клетке с номером
Клетке с номером  соответствует на основании принятых обозначений совокупность первичных термов
соответствует на основании принятых обозначений совокупность первичных термов  конъюнкция которых и представляет собой минтерм
конъюнкция которых и представляет собой минтерм  Таким образом можно сказать, что каждой клетке с номером
Таким образом можно сказать, что каждой клетке с номером  соответствует минтерм
соответствует минтерм 
Две клетки диаграммы Вейча называются соседними, если им соответствуют соседние минтермы. Для удобства отыскания контермов, покрывающих  минтермов
минтермов  где
где  число переменных), стороны диаграмм Вейча обозначают с помощью первичных термов
число переменных), стороны диаграмм Вейча обозначают с помощью первичных термов  так, чтобы как можно больше соседних клеток имели общую грань. Этому требованию могут удовлетворять многие варианты обозначений. При изображении диаграмм Вейча для трехмерного пространства на плоскости не все клетки, которым соответствуют соседние минтермы, имеют общую грань. Легко убедиться (см.
так, чтобы как можно больше соседних клеток имели общую грань. Этому требованию могут удовлетворять многие варианты обозначений. При изображении диаграмм Вейча для трехмерного пространства на плоскости не все клетки, которым соответствуют соседние минтермы, имеют общую грань. Легко убедиться (см.  что клеткам с номерами О и 4, 1 и 5 соответствуют соседние минтермы. Поэтому ДВ-3 следует представлять себе в виде трехмерной фигуры — цилиндра, получаемого путем совмещения боковых сторон
что клеткам с номерами О и 4, 1 и 5 соответствуют соседние минтермы. Поэтому ДВ-3 следует представлять себе в виде трехмерной фигуры — цилиндра, получаемого путем совмещения боковых сторон  Тогда клетки с номерами 0 и 4, 1 и 5 будут иметь общую грань.
Тогда клетки с номерами 0 и 4, 1 и 5 будут иметь общую грань.
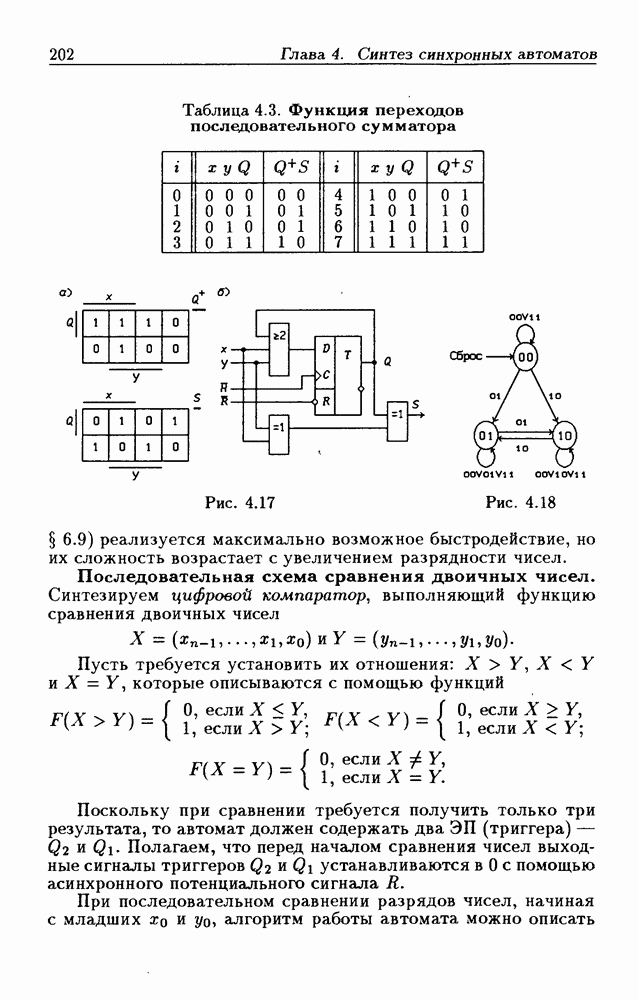
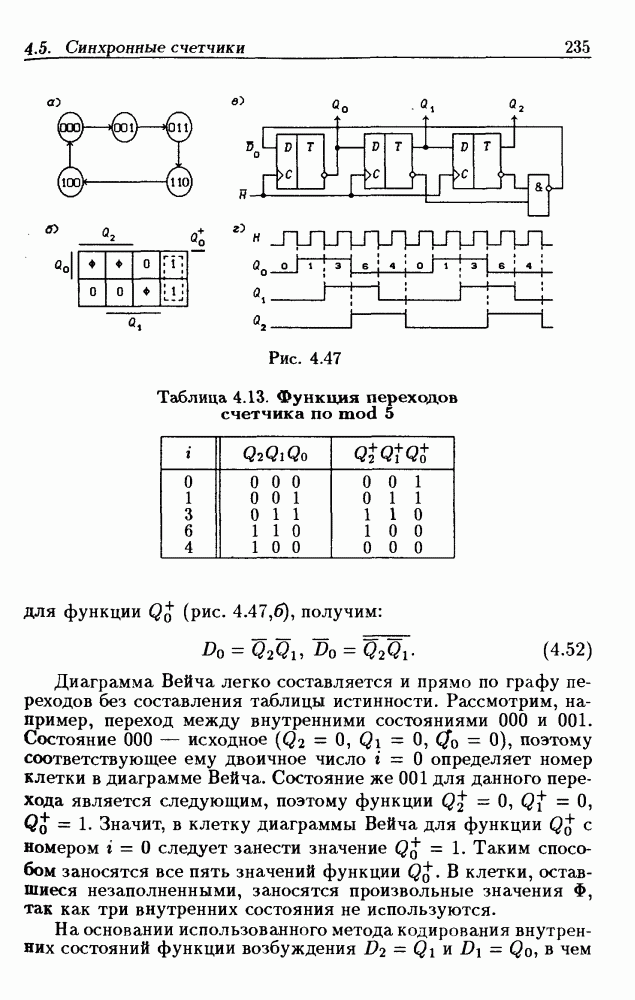
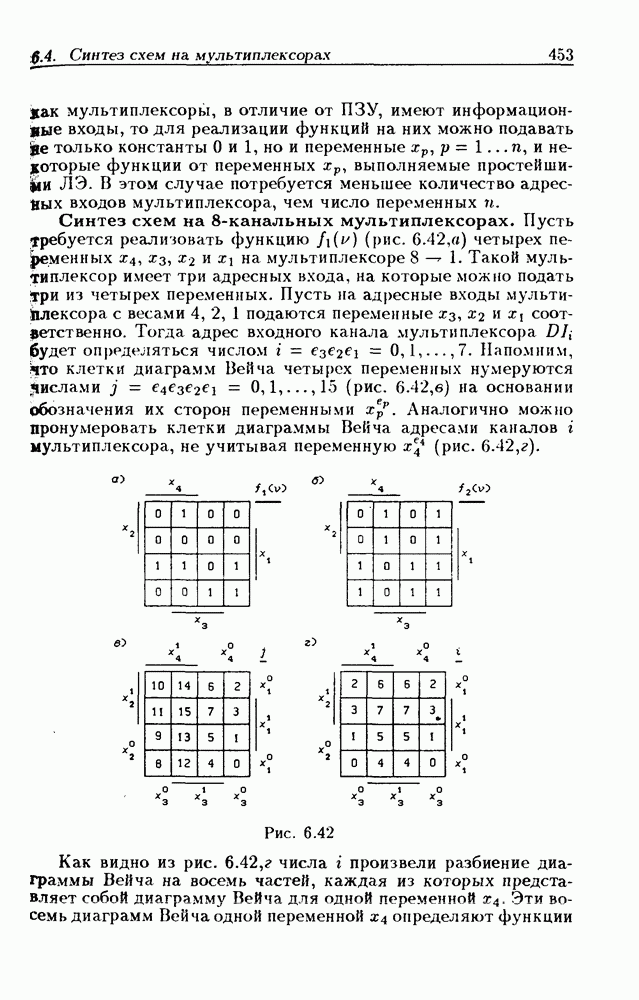
Рассмотрим пример. Пусть требуется составить ДВ-3 для функции  заданной табл. 1.5. Для этого в клетки с номерами
заданной табл. 1.5. Для этого в клетки с номерами  (см. рис. 1.1,а) следует занести значения функции
(см. рис. 1.1,а) следует занести значения функции  или 1, которые она принимает в точках
или 1, которые она принимает в точках  (см. рис. 1.1,е). В § 1.8 было показано, что СДНФ данной функции имеет вид
(см. рис. 1.1,е). В § 1.8 было показано, что СДНФ данной функции имеет вид

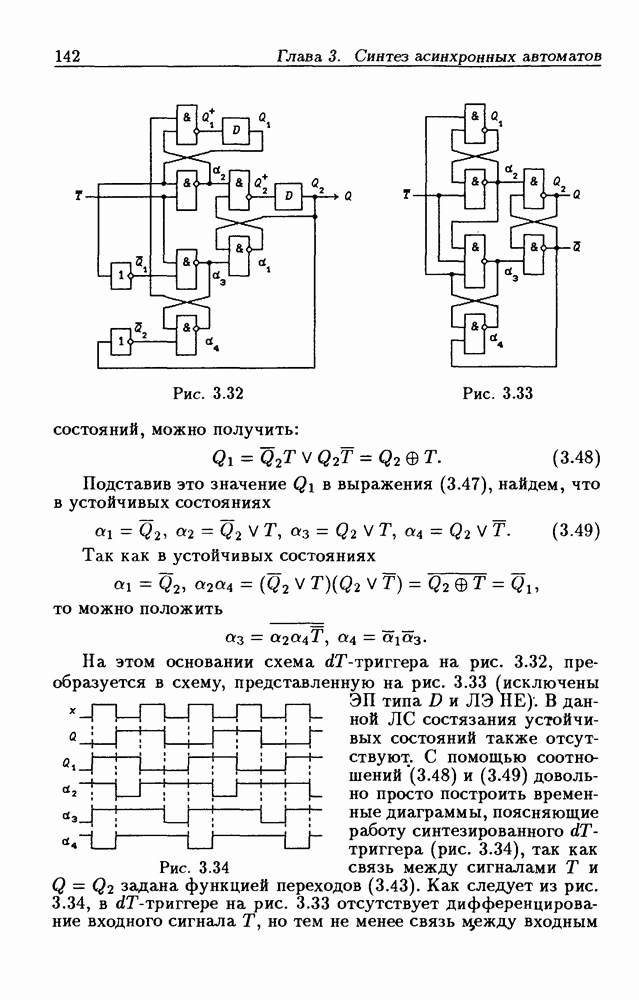
т.е. в ДВ-3 (см. рис. 1.1,в) единицами заполняются клетки, соответствующие этим минтермам. Таким образом, имеется жесткая связь между таблицей истинности (см. табл. 1.5), аналитическим выражением для функции и диаграммой Вейча (см. рис. 1.1,в).
Некоторые особенности взаимосвязи таблицы истинности и диаграммы Вейча требуют пояснений. В таблице истинности (табл. 1.5) значения аргументов указаны в явном виде в трех столбцах, обозначенных через  эти значения в явном виде отсутствуют. Однако, поскольку каждой клетке с номером
эти значения в явном виде отсутствуют. Однако, поскольку каждой клетке с номером  соответствует точка
соответствует точка  области определения функции, то данной клетке соответствует вполне определенная совокупность значений переменных
области определения функции, то данной клетке соответствует вполне определенная совокупность значений переменных  и
и
х (это соответствие указано в табл. 1.5). Легко заметить, что половине клеток ДВ-3, обозначенной через  соответствуют значения
соответствуют значения  другой половине клеток — значения
другой половине клеток — значения  Другая особенность взаимосвязи заключается в том, что минтермы, равные 1 в точке с номером
Другая особенность взаимосвязи заключается в том, что минтермы, равные 1 в точке с номером  в диаграмме Вейча указаны в явном виде, а в таблице истинности — в неявном (с помощью значений аргументов
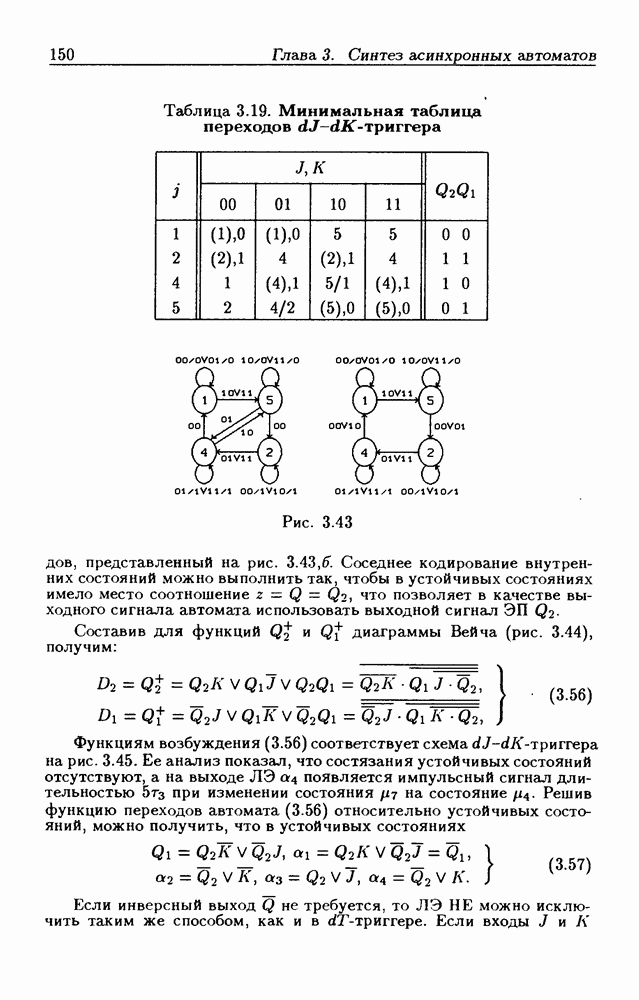
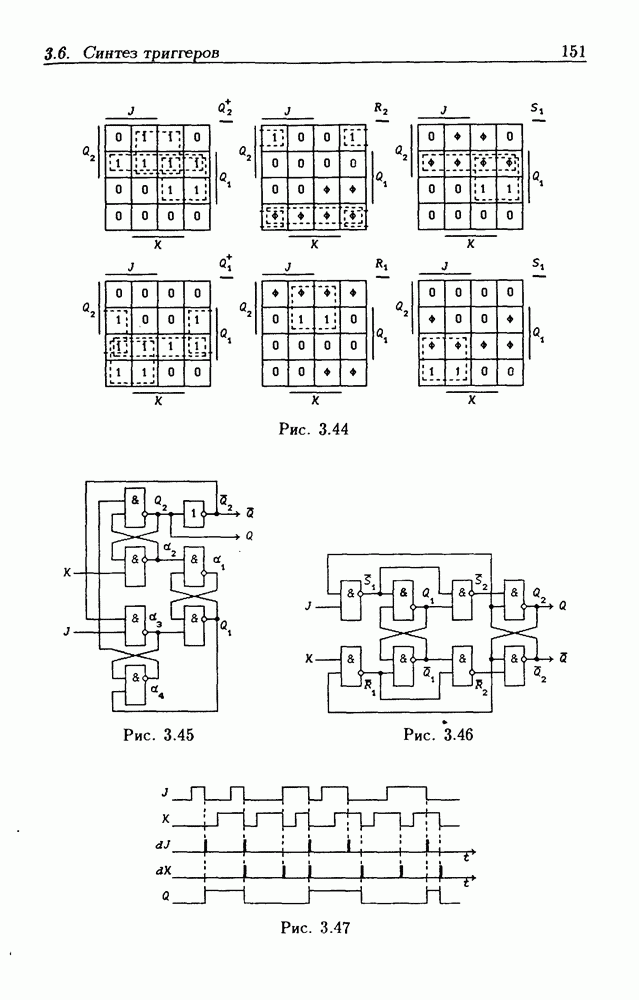
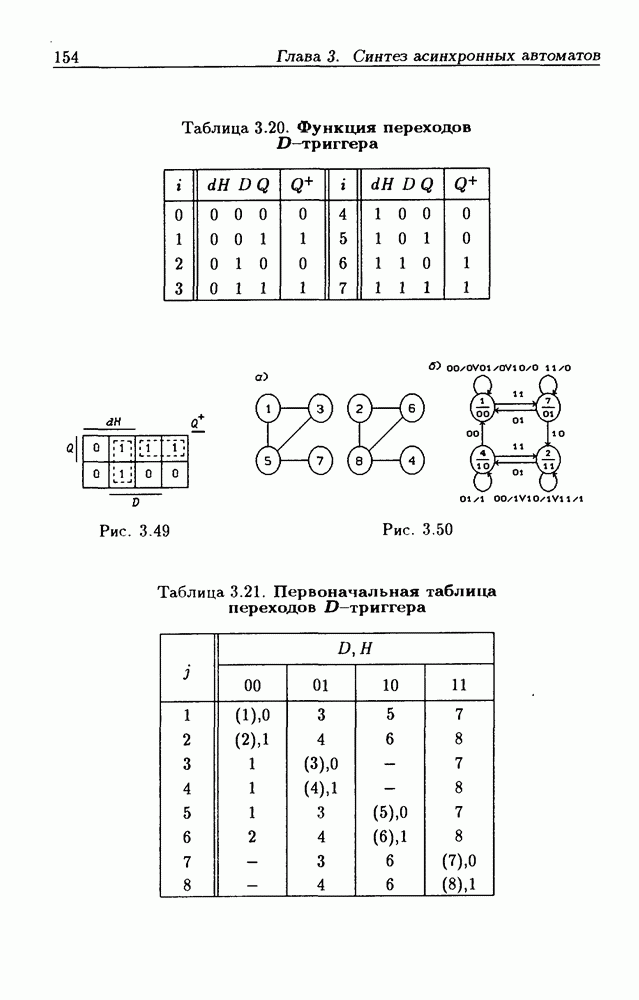
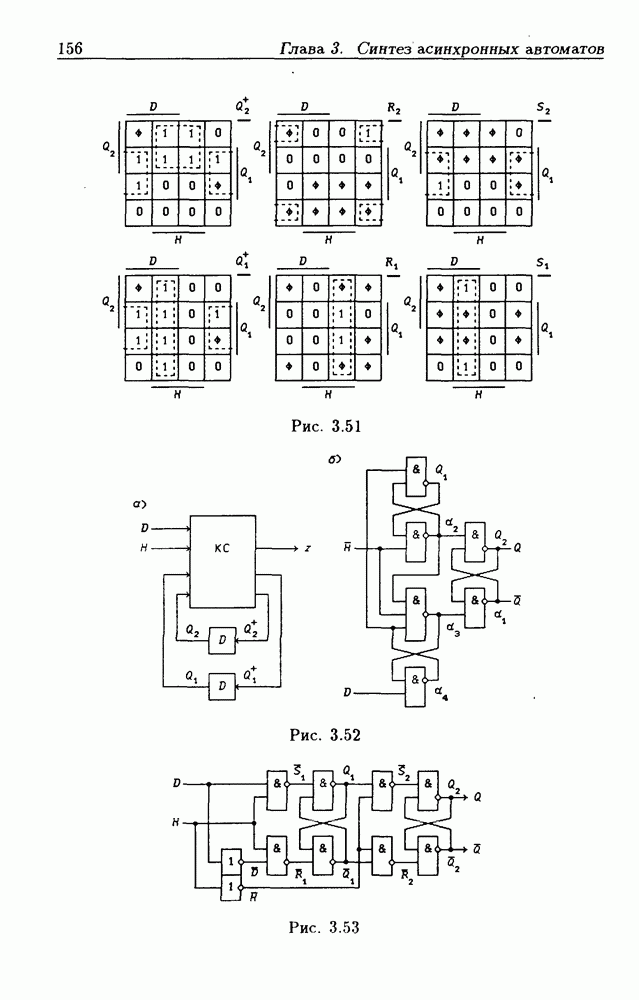
в диаграмме Вейча указаны в явном виде, а в таблице истинности — в неявном (с помощью значений аргументов  Например, строке с номером
Например, строке с номером  соответствуют значения
соответствуют значения  Поэтому
Поэтому  клетка с номером
клетка с номером  непосредственно обозначена через
непосредственно обозначена через  рис. 1.1,6).
рис. 1.1,6).
Указание в явном виде одних величин вместо других в таблицах истинности и диаграммах Вейча связано с различием в их назначении-, таблицы истинности наиболее удобны для первоначального описания переключательных функций, а диаграммы Вейча — для их минимизации.
Клетки, содержащие в диаграмме Вейча единицы, будем называть 1-клетками, а клетки, содержащие йули, —  -клетками. Выше было показано, что любой контерм
-клетками. Выше было показано, что любой контерм  не зависящий от
не зависящий от  переменных
переменных  где
где  число переменных), представляет собой дизъюнкцию
число переменных), представляет собой дизъюнкцию  минтермов, каждый из которых имеет среди остальных по
минтермов, каждый из которых имеет среди остальных по  соседних. Поэтому диаграмма Вейча для таких контермов содержит
соседних. Поэтому диаграмма Вейча для таких контермов содержит  -клеток.
-клеток.
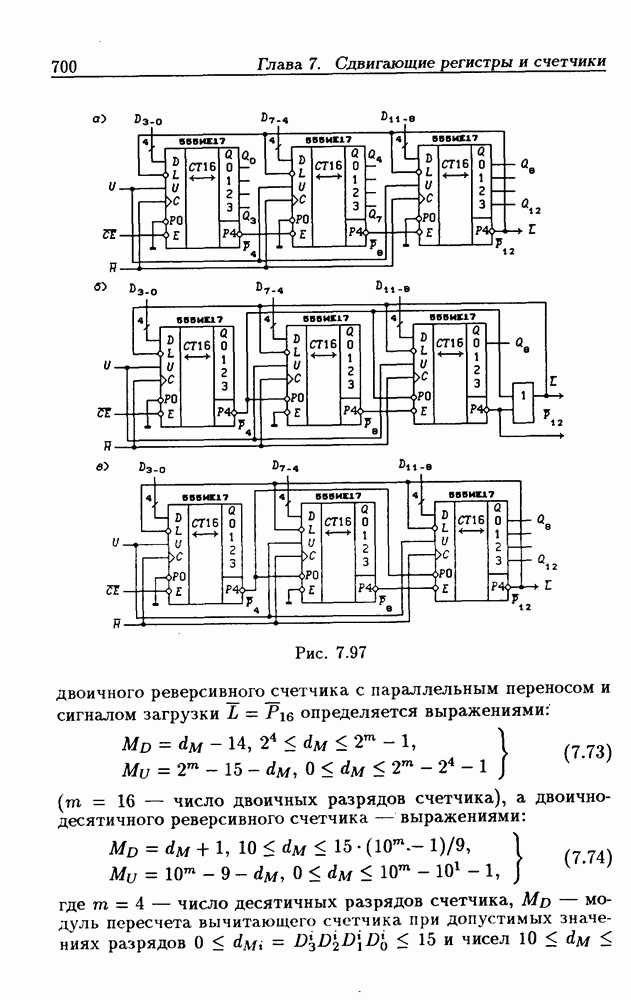
Основное свойство диаграммы Вейча заключается в том, что 1-клетки любого контерма  образуют на ней область, являющуюся прямоугольником и только прямоугольником (для трех переменных эта область представляет собой прямоугольник на цилиндре), причем переменные
образуют на ней область, являющуюся прямоугольником и только прямоугольником (для трех переменных эта область представляет собой прямоугольник на цилиндре), причем переменные  от которых контерм
от которых контерм  не зависит, имеют в этой области различные значения
не зависит, имеют в этой области различные значения  а остальные переменные — только одно значение
а остальные переменные — только одно значение  или
или  Такие области называются m-кубами
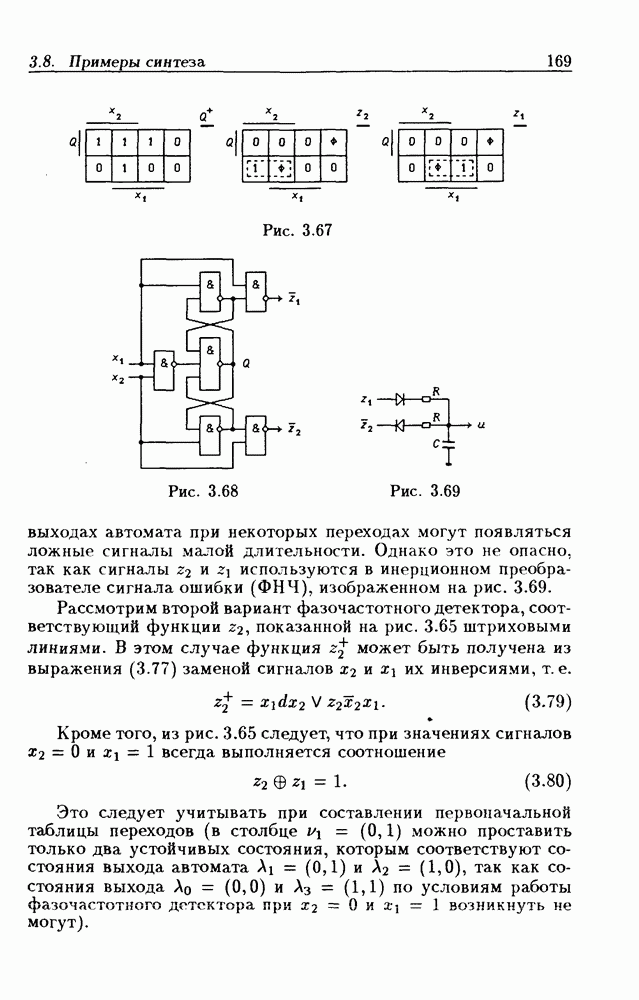
Такие области называются m-кубами  -кубу соответствует минтерм, а
-кубу соответствует минтерм, а  -кубу — константа единица). Так как m-куб представляет собой область, состоящую из
-кубу — константа единица). Так как m-куб представляет собой область, состоящую из  -клеток, то говорят, что m-куб покрывает
-клеток, то говорят, что m-куб покрывает  -клеток. Чтобы записать контерм
-клеток. Чтобы записать контерм  соответствующий некоторой прямоугольной области (некоторому
соответствующий некоторой прямоугольной области (некоторому  -кубу) в явном виде, необходимо просто составить конъюнкцию из первичных термов
-кубу) в явном виде, необходимо просто составить конъюнкцию из первичных термов  которые в этой области на диаграмме Вейча имеют постоянные значения (только
которые в этой области на диаграмме Вейча имеют постоянные значения (только  или только
или только 
Таким образом, в соответствии с общим правилом минимизации, получение МДНФ с помощью диаграмм Вейча сводится к отысканию минимального числа m-кубов максимального размера, состоящих из 1-клеток, т.е. к отысканию минимального покрытия m-кубами 1-клеток и составлению дизъюнкции контермов  соответствующих этим m-кубам (любая 1-клетка
соответствующих этим m-кубам (любая 1-клетка
должна войти хотя бы в один m-куб). Согласно идемпотентным законам любая 1-клетка может входить в несколько различных  -кубов.
-кубов.
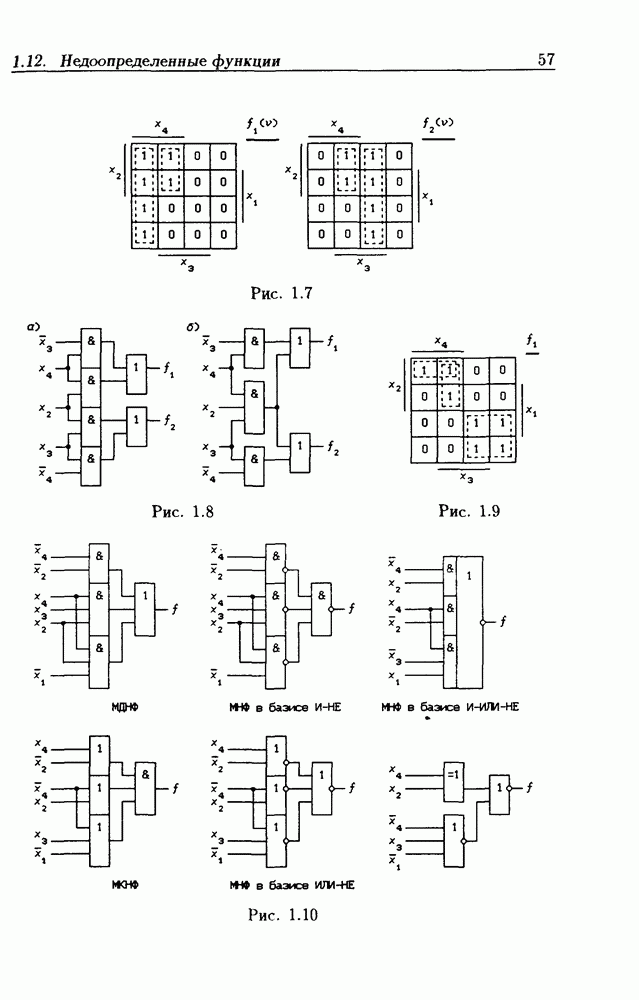
На рис. 1.1,в пунктиром обозначены два 1-куба, образованные 1-клетками с номерами 5 и 7, 1 и 5, которым соответствуют контермы  а 1-клетка с номером 2 не имеет ни одной соседней 1-клетки, поэтому ей соответствует 0-куб, представляемый минтермом
а 1-клетка с номером 2 не имеет ни одной соседней 1-клетки, поэтому ей соответствует 0-куб, представляемый минтермом  . МДНФ данной функции записывается в виде
. МДНФ данной функции записывается в виде

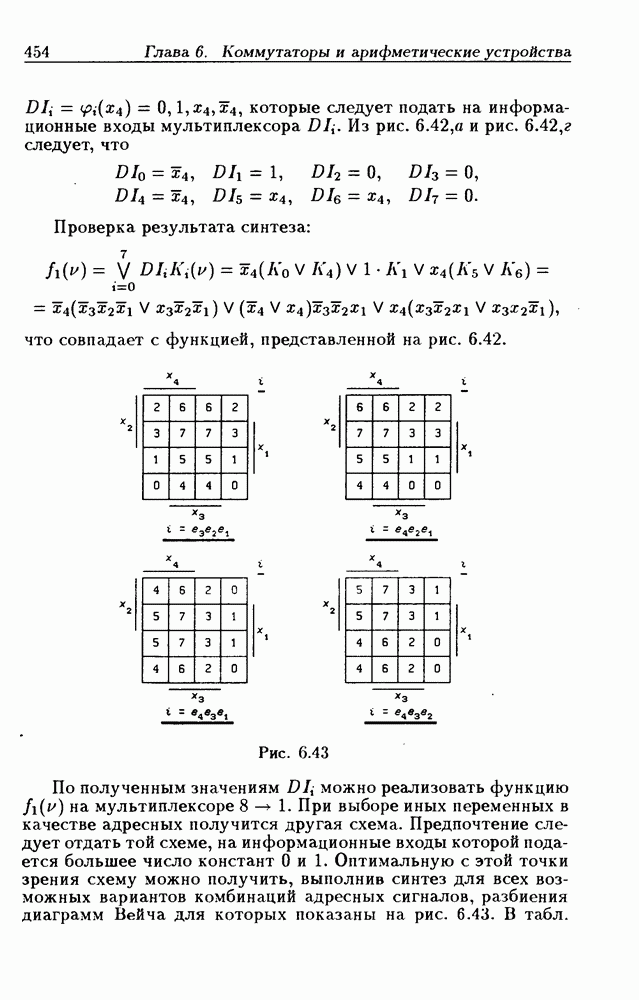
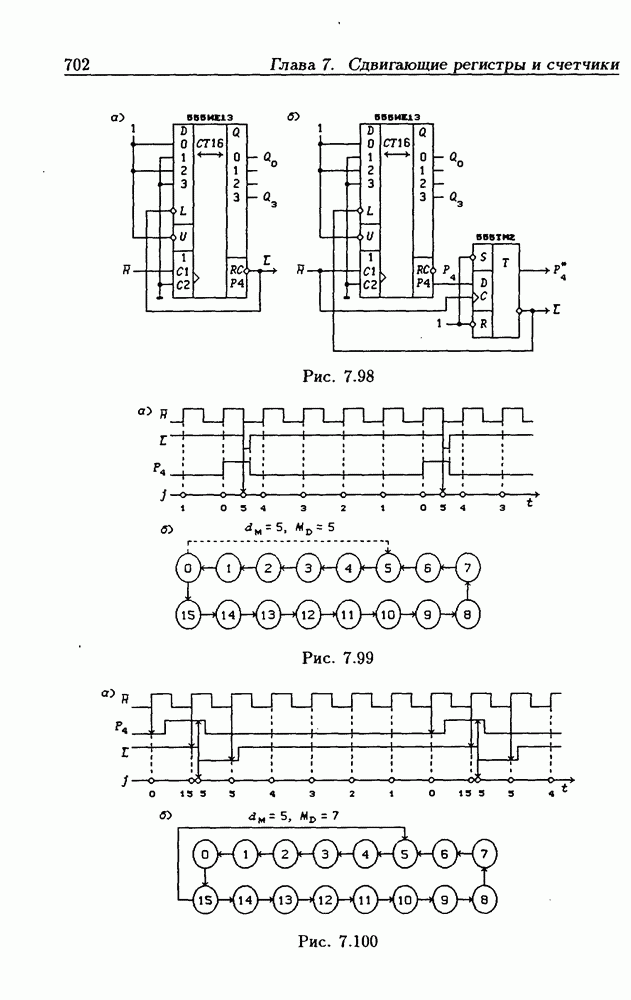
Минимальная нормальная форма в базисе И-НЕ этой функции получается из МДНФ в соответствии с (1.80):

Для получения МКНФ функции  следует найти МДНФ инверсной функции
следует найти МДНФ инверсной функции  т.е. найти минимальное покрытие всех 0-клеток функции
т.е. найти минимальное покрытие всех 0-клеток функции 

а МКНФ получается на основании закона двойственности:

Минимальная нормальная форма в базисе ИЛИ-НЕ данной функции получается из МКНФ в соответствии с (1.76):

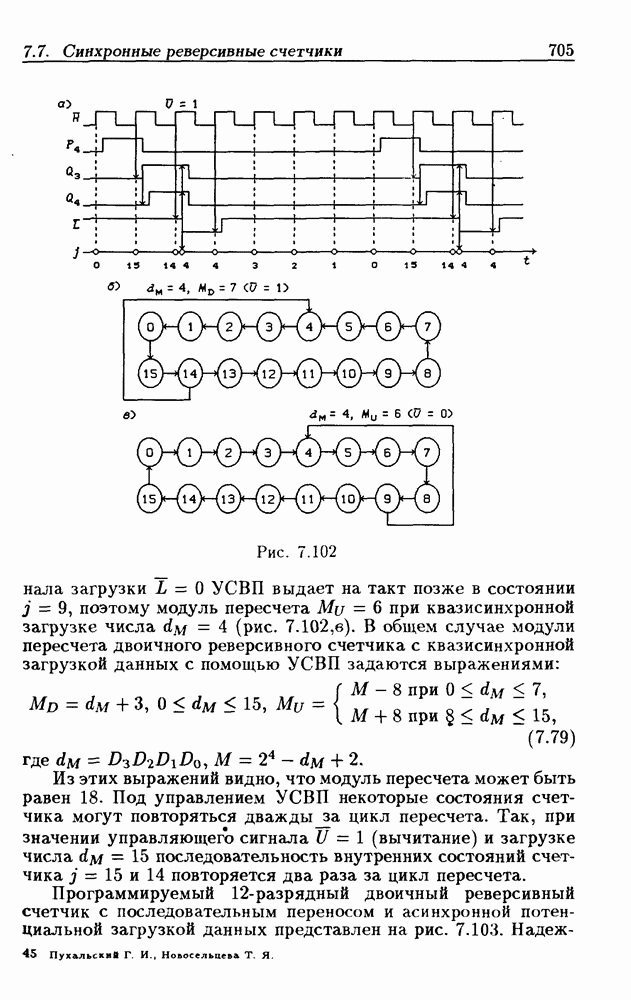
Из рис. 1.1, г следует, что минимальное покрытие 1-клеток функции  состоит из двух
состоит из двух  -кубов, которым соответствуют контермы
-кубов, которым соответствуют контермы  поэтому
поэтому  Минимальная КНФ в данном случае совпадает с МДНФ, а также можно получить формы:
Минимальная КНФ в данном случае совпадает с МДНФ, а также можно получить формы:

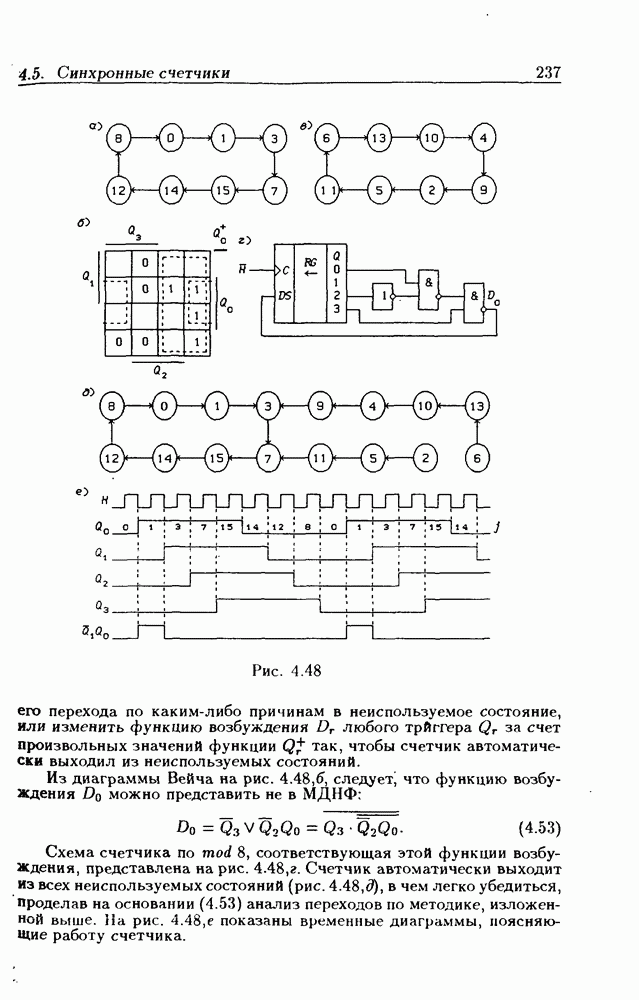
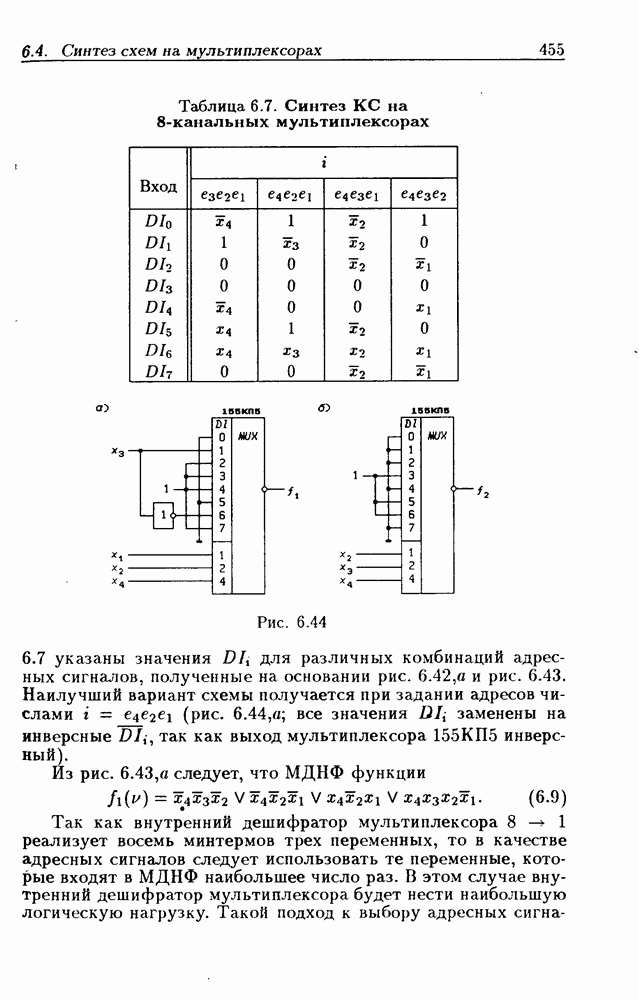
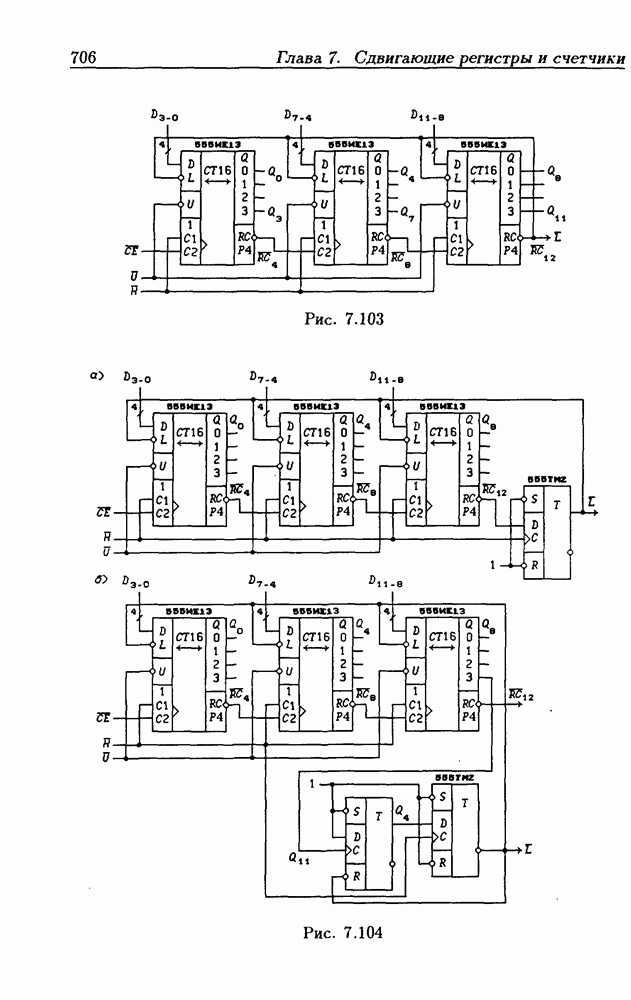
Диаграммы Вейча для четырех переменных (ДВ-4) показаны на рис. 1.2. Так как  где
где  то номера клеток
то номера клеток  для ДВ-4 вычисляются на основании первичных термов
для ДВ-4 вычисляются на основании первичных термов  , используемых для обозначения ее сторон (рис. 1.2,а). Легко убедиться, что клеткам с номерами 0 и
, используемых для обозначения ее сторон (рис. 1.2,а). Легко убедиться, что клеткам с номерами 0 и  и 8, 2 и 10, 8 и 10 соответствуют соседние минтермы. Чтобы эти клетки имели общую грань, ДВ-4 для четырехмерного пространства следует представлять себе свернутой в тор путем соединения боковых сторон (получается цилиндр) и совмещения оснований цилиндра. Тогда, например, область, состоящая из 1-клеток с номерами 0, 2, 8 и 10, будет представлять собой прямоугольник на торе, т.е.
и 8, 2 и 10, 8 и 10 соответствуют соседние минтермы. Чтобы эти клетки имели общую грань, ДВ-4 для четырехмерного пространства следует представлять себе свернутой в тор путем соединения боковых сторон (получается цилиндр) и совмещения оснований цилиндра. Тогда, например, область, состоящая из 1-клеток с номерами 0, 2, 8 и 10, будет представлять собой прямоугольник на торе, т.е.  -куб, который соответствует контерму
-куб, который соответствует контерму 
Диаграмма Вейча, показанная на рис.  задает некоторую функцию
задает некоторую функцию  Минимальное покрытие 1-клеток состоит из одного
Минимальное покрытие 1-клеток состоит из одного

Рис. 1.2
3-куба и двух 2-кубов, которым соответствуют контермы  поэтому МДНФ данной функции
поэтому МДНФ данной функции

Минимальное же покрытие 0-клеток состоит из двух 1-кубов, которым соответствуют контермы  поэтому МКНФ этой функции
поэтому МКНФ этой функции

Из МДНФ и МКНФ не составляет труда получить МНФ в базисах И-НЕ и ИЛИ-НЕ.
Выбор m-кубов, покрывающих 1-клетки диаграммы Вейча, не всегда столь очевиден, как это было в предыдущих примерах. На рис. 1.2.6 часть 1-клеток можно было бы покрыть  -кубом (ему соответствует контерм
-кубом (ему соответствует контерм  однако при покрытии 1-кубами остальных четырех 1-клеток становится понятным, что необходимость использования
однако при покрытии 1-кубами остальных четырех 1-клеток становится понятным, что необходимость использования  -куба отпадает. МДНФ этой функции
-куба отпадает. МДНФ этой функции

Таким образом, не всегда следует начинать покрытие 1-клеток с отыскания m-кубов максимального размера.
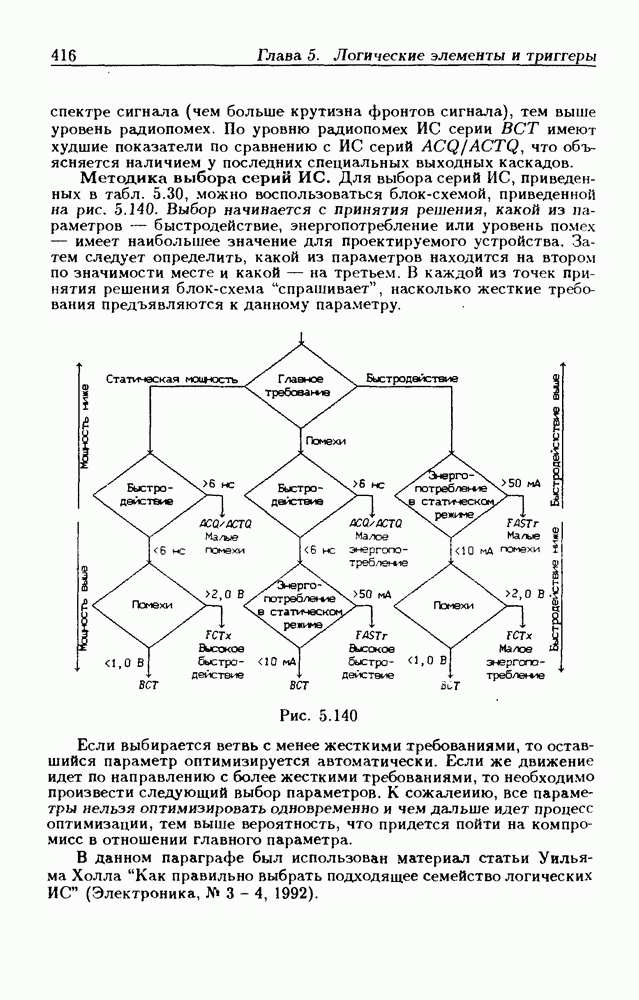
Сформулируем общие правила минимизации функций с помощью диаграмм Вейча, справедливые для любого числа переменных 
для получения МДНФ необходимо найти минимальное покрытие 1-клеток, которое состоит из минимального числа  -кубов максимального размера;
-кубов максимального размера;
m-кубу, покрывающему  -клеток, соответствует контерм, не зависящий от
-клеток, соответствует контерм, не зависящий от  переменных, причем исключаются те
переменных, причем исключаются те  переменные, которые в прямоугольной области на диаграмме Вейча, состоящей из 1-клеток, имеют различное значение
переменные, которые в прямоугольной области на диаграмме Вейча, состоящей из 1-клеток, имеют различное значение 
прямоугольные области на диаграммах Вейча, используемые при покрытии функции  могут состоять только из
могут состоять только из  -клеток, где
-клеток, где  т. е. из 1, 2, 4, 8, 16 и т. д. 1-клеток;
т. е. из 1, 2, 4, 8, 16 и т. д. 1-клеток;
покрытие следует начинать с выбора тех 1-клеток, которые могут войти в один и только один m-куб, а затем выбранные таким образом 1-клетки покрываются m-кубами максимального размера (это правило позволяет исключить возможность появления лишних m-кубов, как это могло иметь место в примере на рис. 1.2,в);
если 1-клеток, входящих только в один m-куб, нет, то следует рассмотреть несколько вариантов минимизации.

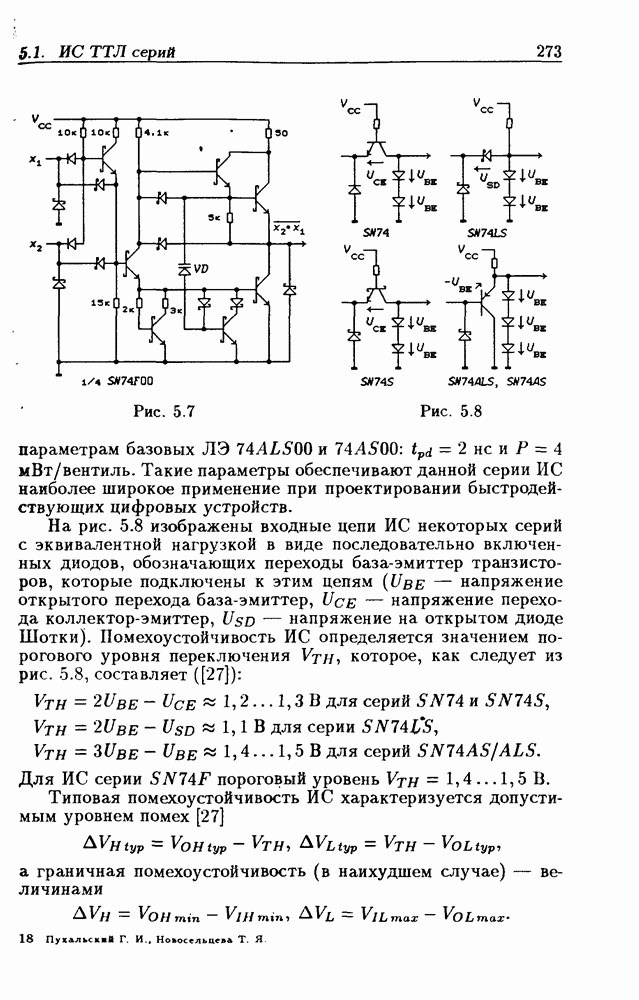
Рис. 1.3
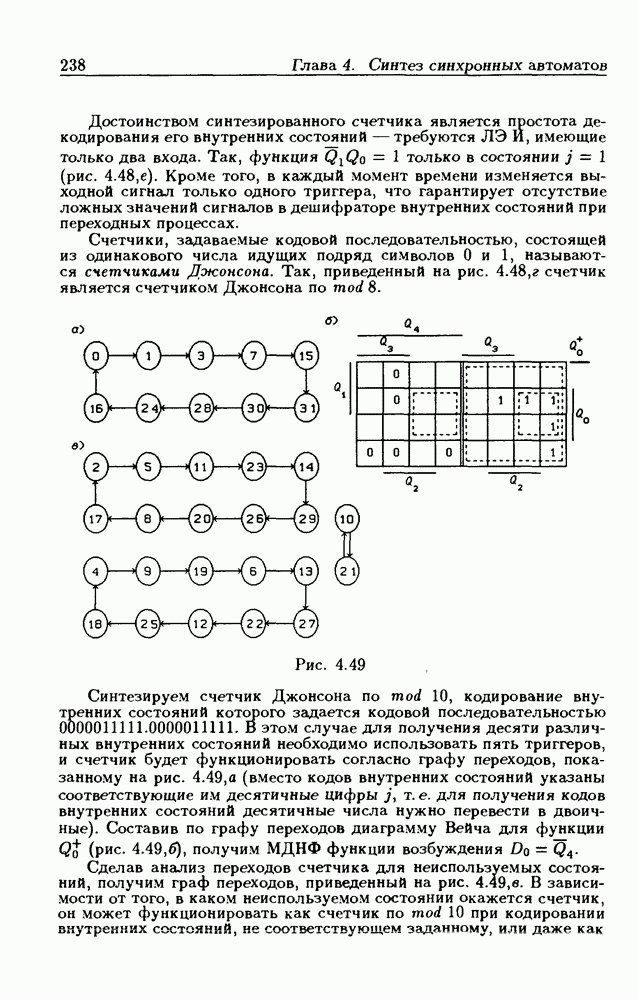
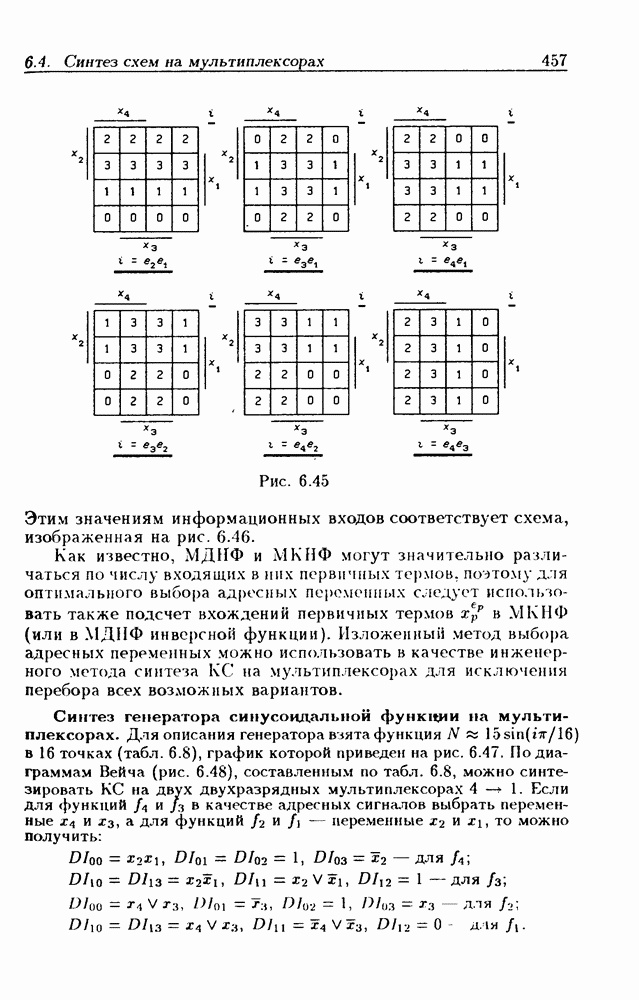
Диаграммы Вейча для числа переменных  составляются из идентичных ДВ-4 (в смысле обозначения сторон первичными термами
составляются из идентичных ДВ-4 (в смысле обозначения сторон первичными термами  Знак
Знак  означает, что имеется несколько одинаковых ДВ-4. На рис. 1.3 представлены диаграммы Вейча для
означает, что имеется несколько одинаковых ДВ-4. На рис. 1.3 представлены диаграммы Вейча для  Две ДВ-4 будем называть соседними, если они имеют общую грань. Клетки, расположенные в одинаковых местах соседних ДВ-4, являются соседними, так как им соответствуют соседние минтермы. Так, например, клетки с номерами 0 и 16, 5 и 21 и т. п. (рис. 1.3,а), 0 и 16,0 и 32, 5 и 21,5 и 37 и т. п. (рис. 1.3,в) являются соседними, но клетки 0 и
Две ДВ-4 будем называть соседними, если они имеют общую грань. Клетки, расположенные в одинаковых местах соседних ДВ-4, являются соседними, так как им соответствуют соседние минтермы. Так, например, клетки с номерами 0 и 16, 5 и 21 и т. п. (рис. 1.3,а), 0 и 16,0 и 32, 5 и 21,5 и 37 и т. п. (рис. 1.3,в) являются соседними, но клетки 0 и
48, 5 и 53, 16 и 32 и т. п. (см. рис. 1.3,в) не являются соседними, так как они расположены не в соседних ДВ-4.
Легко убедиться в том, что  -кубы, расположенные в одинаковых местах двух соседних ДВ-4, образуют
-кубы, расположенные в одинаковых местах двух соседних ДВ-4, образуют  -куб. С учетом этого МДНФ функции
-куб. С учетом этого МДНФ функции  представленной на рис.
представленной на рис.  имеет вид:
имеет вид:

В ДВ-6 ш-кубы, расположенные в одинаковых местах всех четырех ДВ-4, образуют  -куб. Поэтому МДНФ функции, показанной на рис. 1.3,г,
-куб. Поэтому МДНФ функции, показанной на рис. 1.3,г,

Основываясь на сформулированных выше правилах минимизации с помощью диаграмм Вейча, достаточно просто также отыскивать МДНФ функций семи и восьми переменных. Для этого нужно только подходящим образом выбрать способ расположения  на ДВ-7 и ДВ-8. Удобнее всего располагать эти ДВ-4 так, как и клетки на ДВ-3 и ДВ-4, т.е. на рис. 1.1 и 1.2 следует заменить
на ДВ-7 и ДВ-8. Удобнее всего располагать эти ДВ-4 так, как и клетки на ДВ-3 и ДВ-4, т.е. на рис. 1.1 и 1.2 следует заменить  на
на  а каждую клетку заменить на ДВ-4. Тогда соседними будут те же ДВ-4, что и клетки на рис. 1.1 и 1.2. Правила покрытия ш-кубами 1-клеток функций трех и четырех переменных полностью переносятся на покрытие одинаковых m-кубов (по размеру и местоположению на
а каждую клетку заменить на ДВ-4. Тогда соседними будут те же ДВ-4, что и клетки на рис. 1.1 и 1.2. Правила покрытия ш-кубами 1-клеток функций трех и четырех переменных полностью переносятся на покрытие одинаковых m-кубов (по размеру и местоположению на  на ДВ-7 и ДВ-8.
на ДВ-7 и ДВ-8.
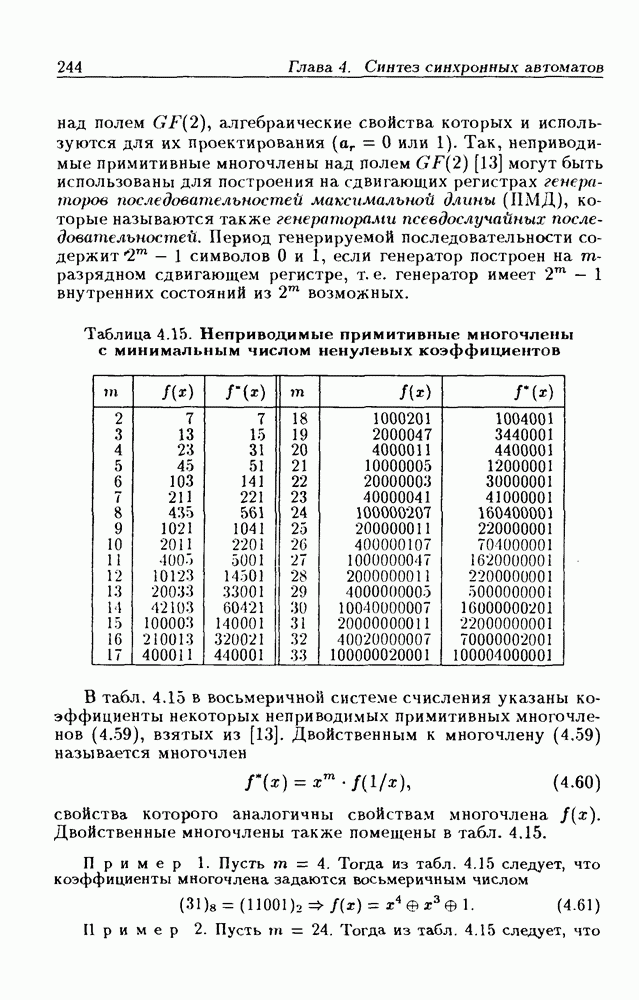
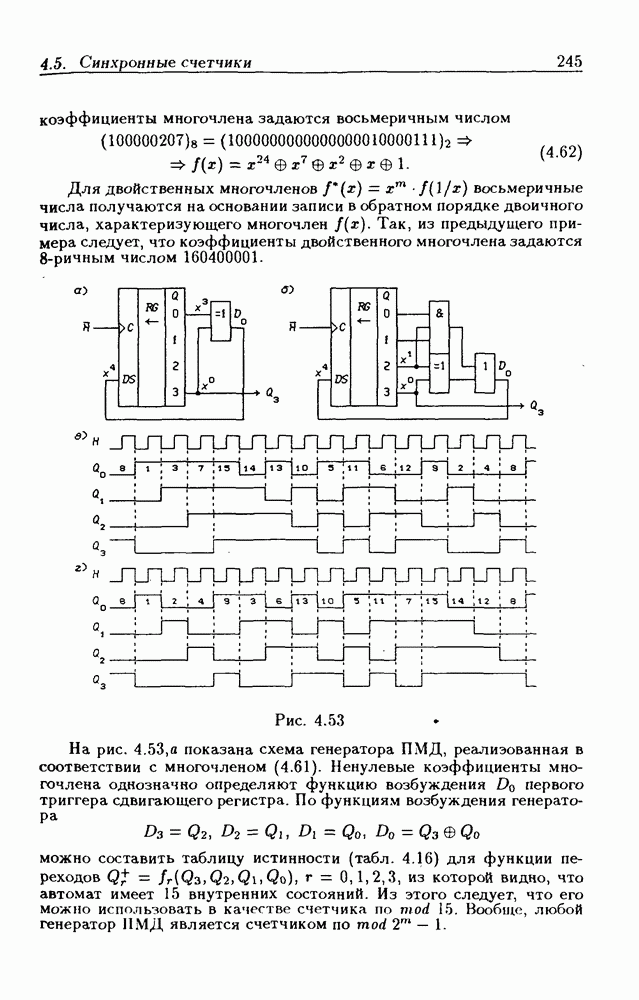
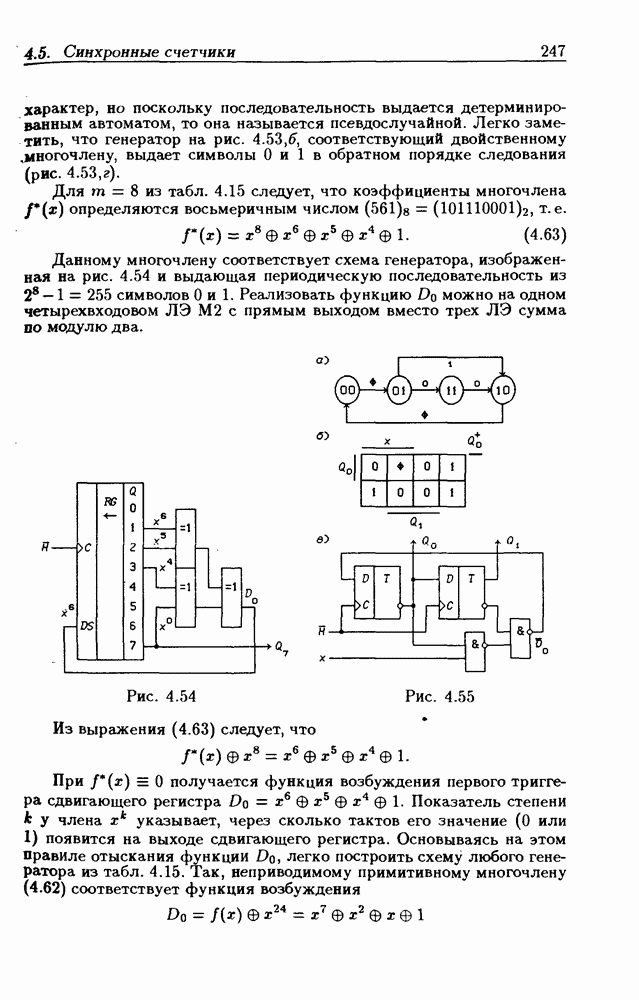
Модификация диаграмм (карт) Вейча, введенных в 1952 г., известна под названием карт Карно (1953 г.) [7, 9]. Известны также методы минимизации Квайна — Мак-Класки, Блейка и др. [7].
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Основы теории переключательных функций
- 1.2. Позиционные системы счисления
- 1.3. Переключательные функции
- 1.4. Принцип и закон двойственности
- 1.5. Теоремы разложения
- 1.6. Решение систем логических уравнений
- 1.7. Первичные термы, минтермы и макстермы
- 1.8. Совершенные нормальные формы представления функций
- 1.9. Конъюнктивные и дизъюнктивные термы
- 1.10. Минимизация переключательных функций
- 1.11. Диаграммы Вейча
- 1.12. Минимизация неполностью определенных функций, совместная минимизация нескольких функций
- 1.13. Скобочные формы функций
- 1.14. Закон двойственности для логических схем
- 1.15. Линейные функции
- Глава 2. Анализ и синтез логических схем
- 2.2. Модели логических элементов
- 2.3. Модели логических схем
- 2.4. Анализ логических схем
- 2.5. Синтез комбинационных схем, свободных от состязаний
- Глава 3. Синтез асинхронных потенциальных автоматов
- 3.2. Асинхронные потенциальные автоматы
- 3.3. Асинхронные потенциальные триггеры и элементы памяти
- Триггеры типа R-S
- Триггеры типа D-L
- Триггеры типа D-L-R с приоритетом входа R.
- Триггеры типа D-L-R с приоритетом входа L.
- Триггеры типа R-S-L.
- Триггеры типа DN-LN
- Аналитический метод синтеза и анализа триггеров.
- 3.4. Задание асинхронных потенциальных автоматов таблицами и графами переходов
- 3.5. Синтез асинхронных потенциальных счетчиков
- 3.6. Синтез асинхронных импульсных триггеров
- Триггеры типа dJ-dK.
- Классификация триггеров.
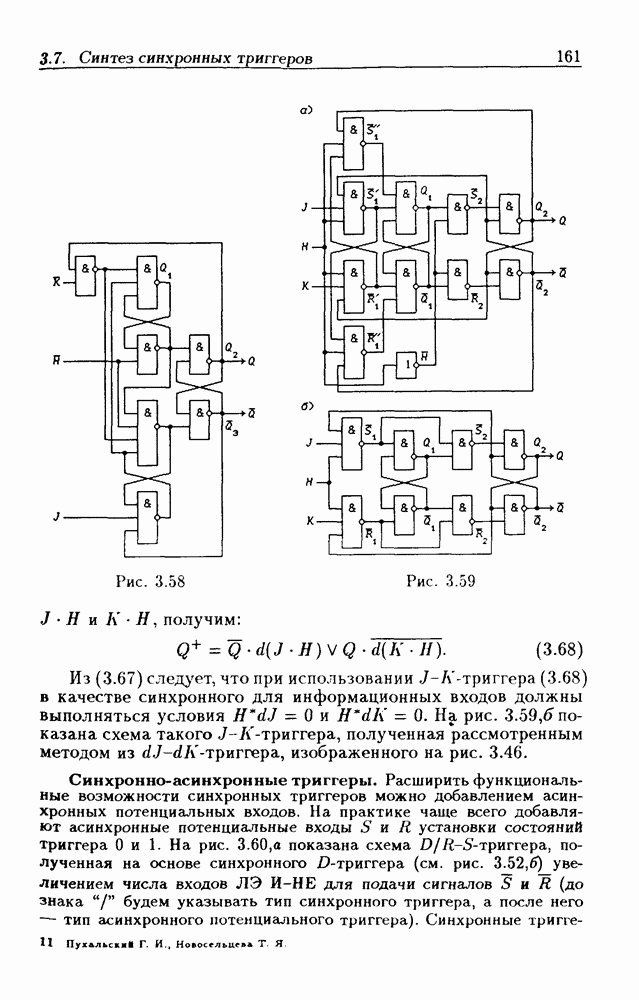
- 3.7. Синтез синхронных триггеров
- Триггеры типа J-K
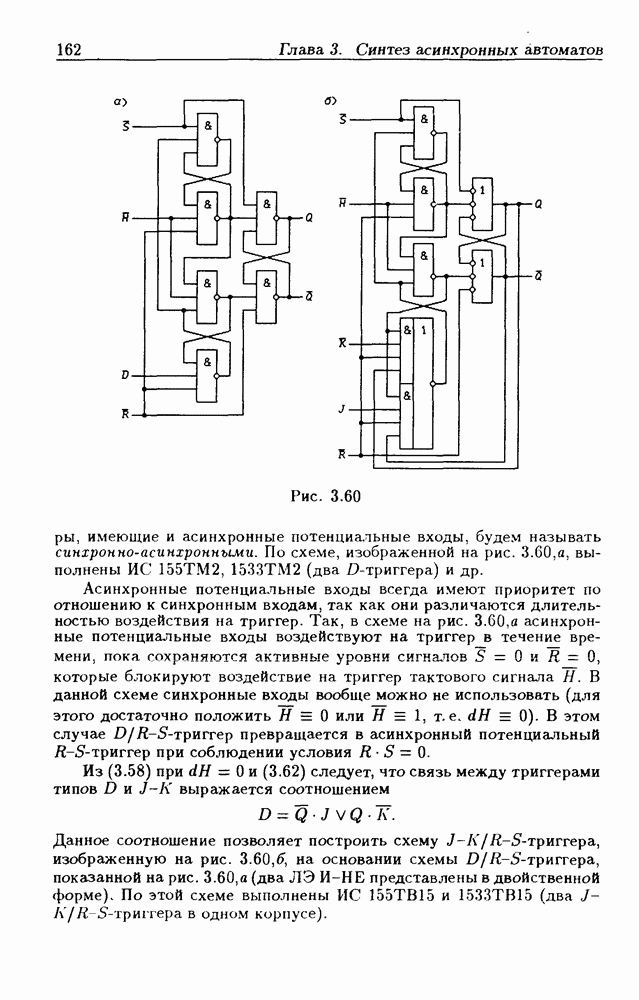
- Синхронно-асинхронные триггеры.
- 3.8. Примеры синтеза асинхронных потенциальных автоматов
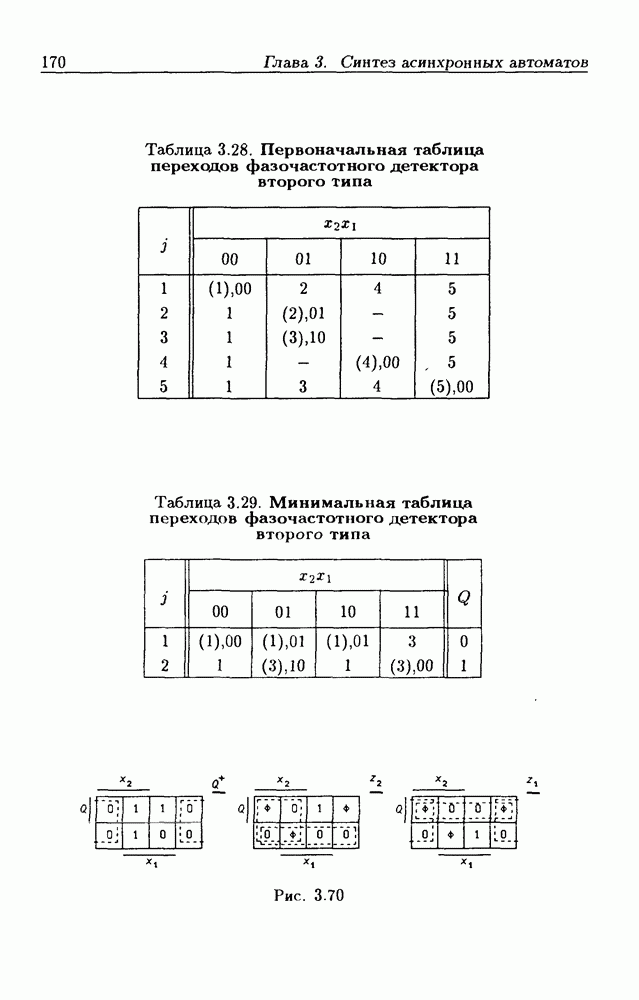
- Цифровые фазочастотные детекторы.
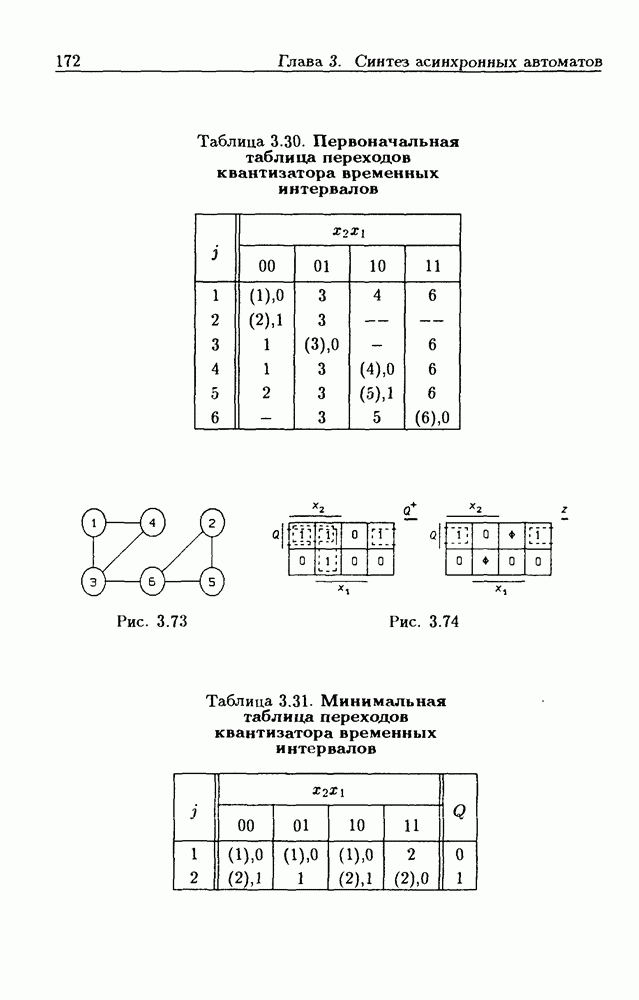
- Квантизатор временных интервалов.
- 3.9. Генераторы сигналов
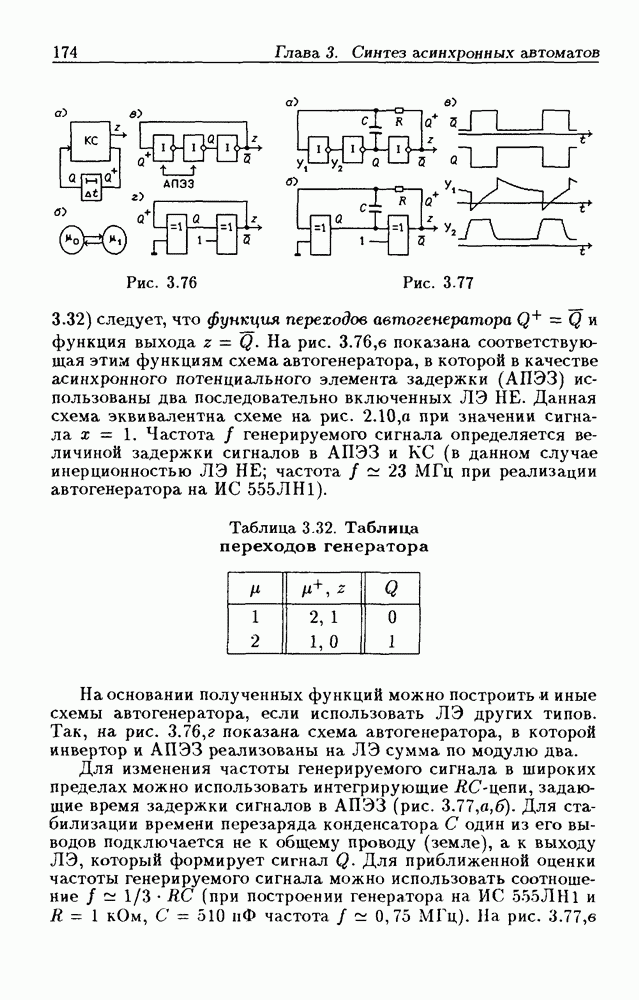
- Автогенераторы.
- Управляемые автогенераторы.
- Глава 4. Синтез синхронных автоматов
- 4.2. Синхронные триггеры
- Триггеры типов D и R-S с импульсным тактовым сигналом.
- Синхронные триггеры типов R-S и D-L
- Синхронно-асинхронные триггеры.
- Синхронные триггеры типа J-K
- Триггеры типа Т.
- Классификация синхронных триггеров.
- Преобразования типов синхронных триггеров.
- Триггеры типов D-T-L и D-T-L/R
- Функции переходов синхронно-асинхронных триггеров.
- 4.3. Примеры синтеза синхронных автоматов
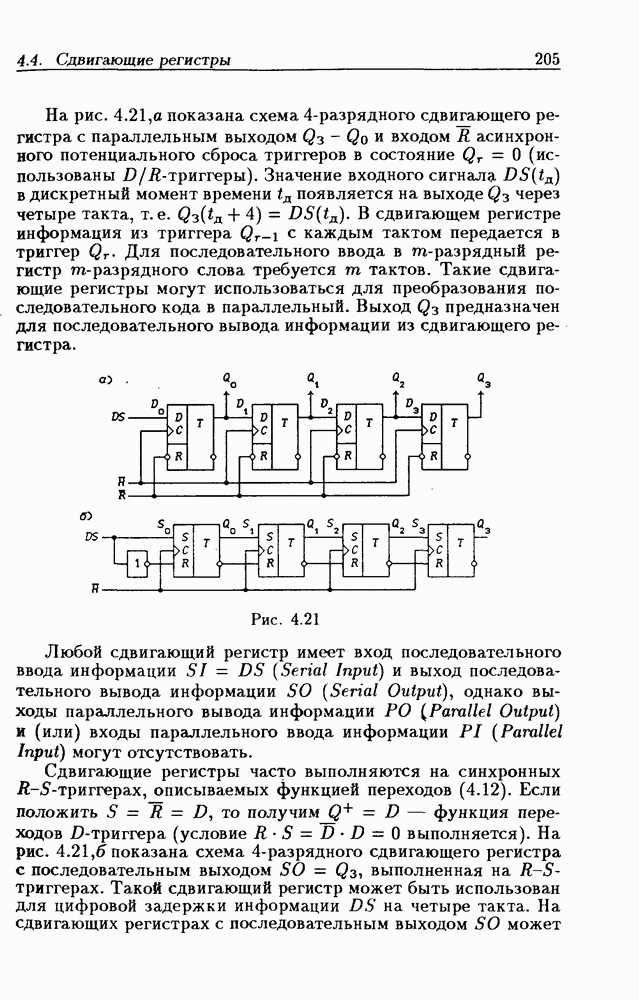
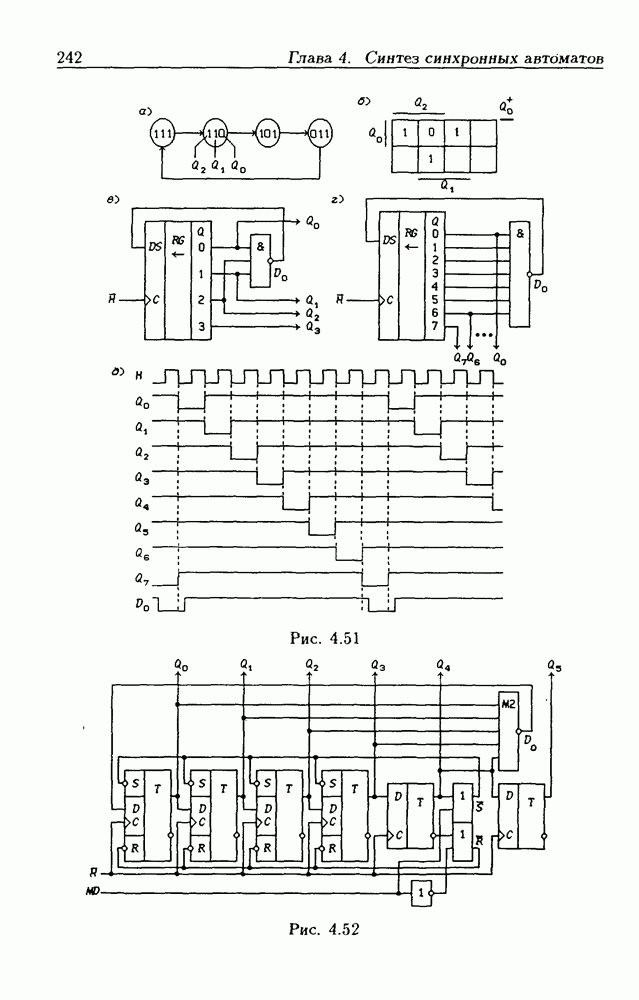
- 4.4. Сдвигающие регистры
- Синтез счетчиков на сдвигающих регистрах.
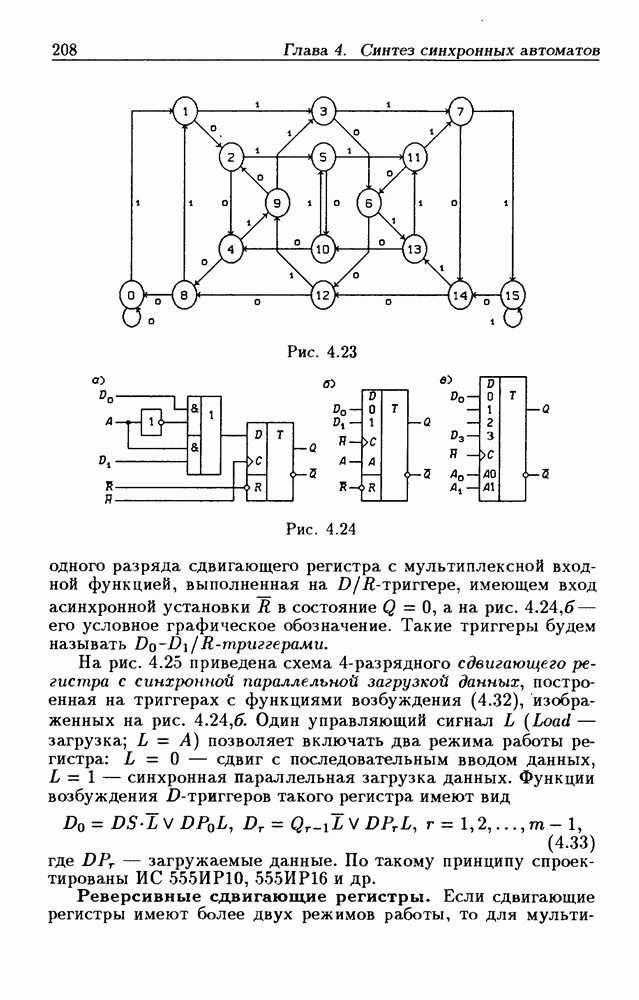
- Сдвигающие регистры с загрузкой данных.
- Реверсивные сдвигающие регистры.
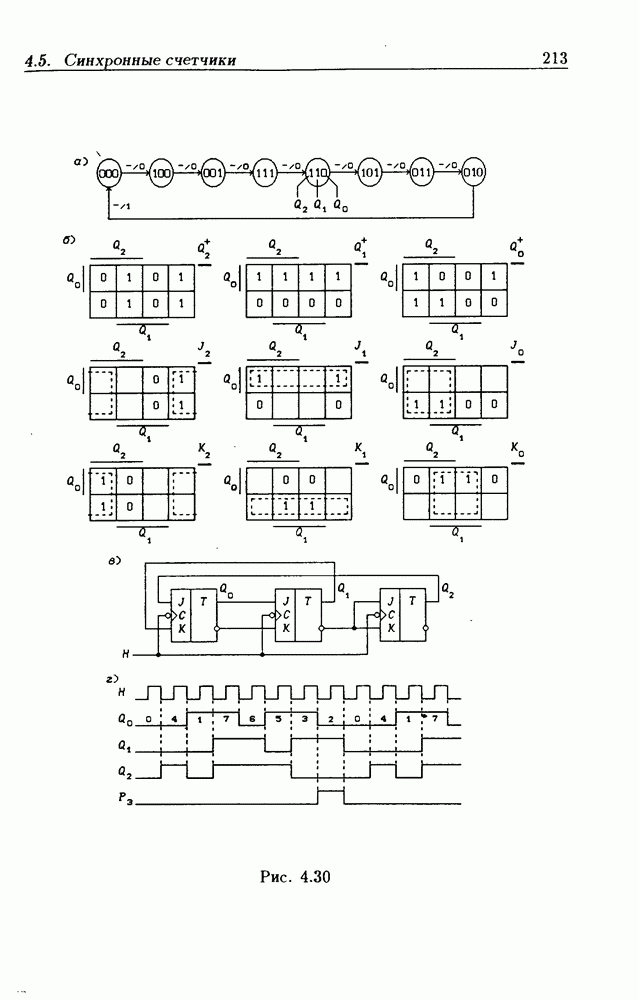
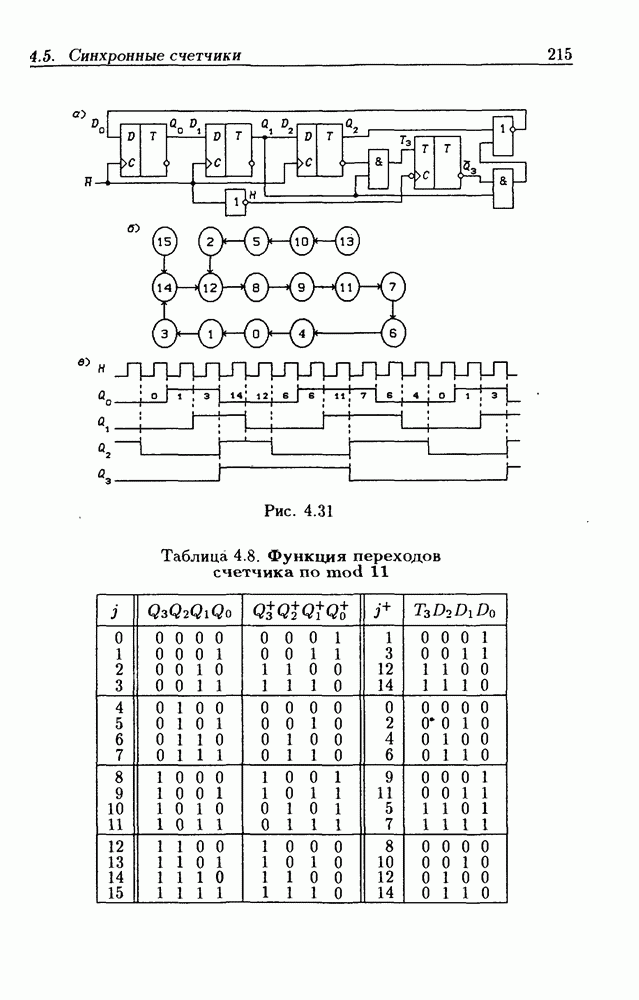
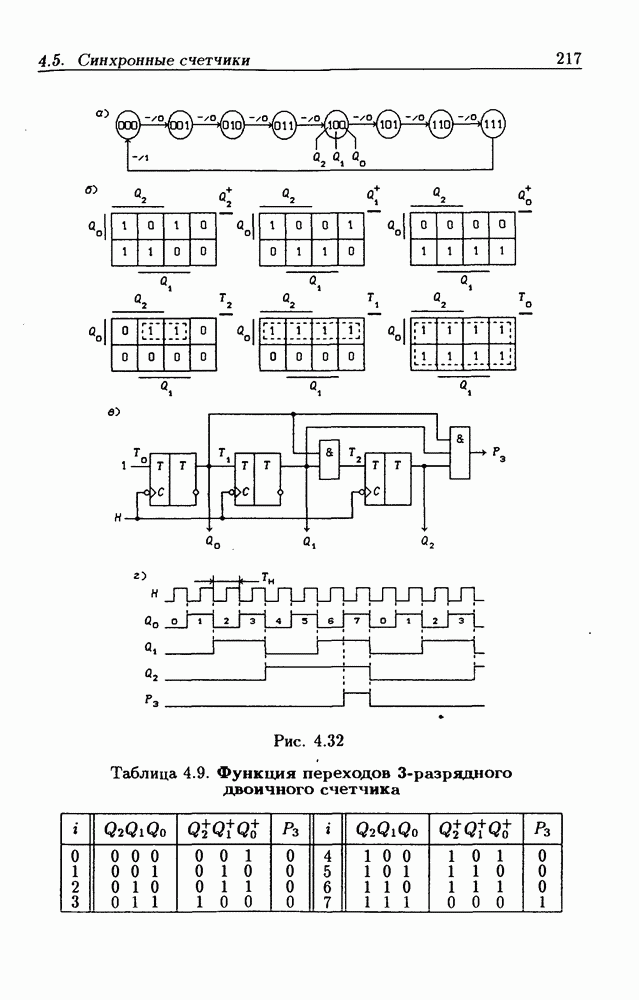
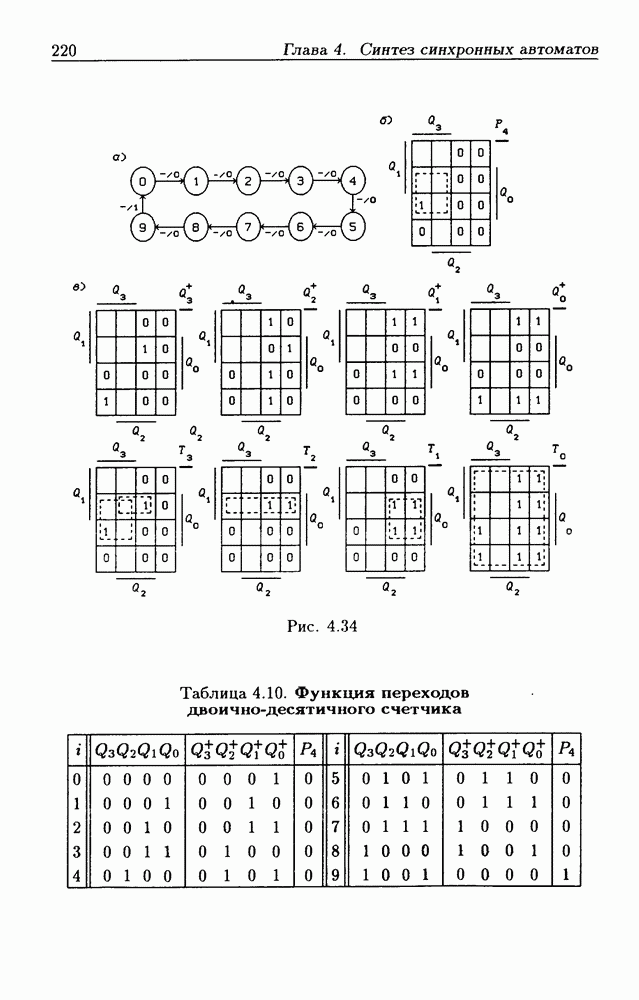
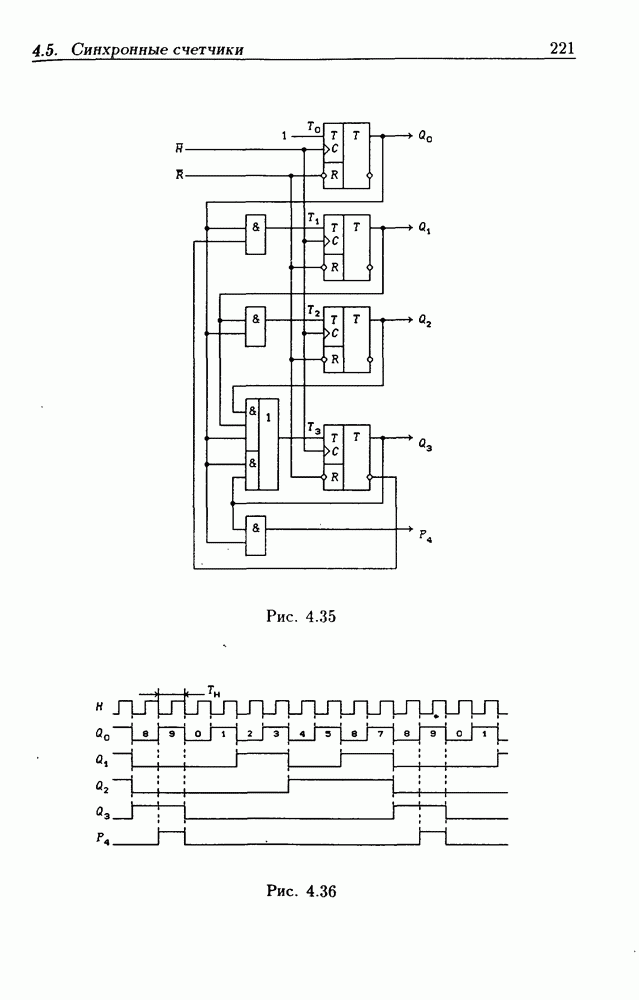
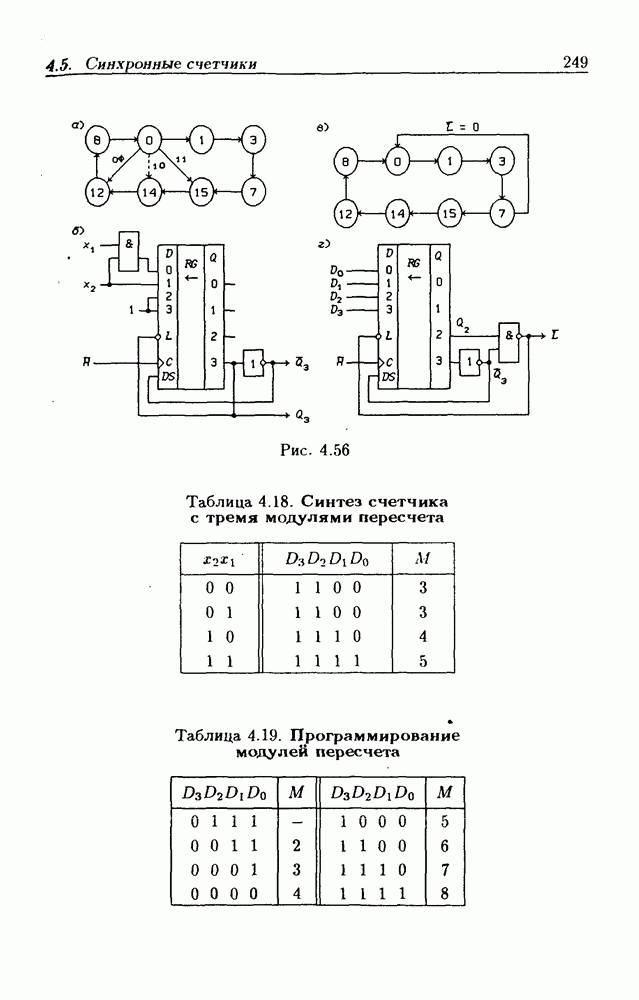
- 4.5. Синхронные счетчики
- Синхронные двоичные счетчики.
- Синхронные двоично-десятичные счетчики.
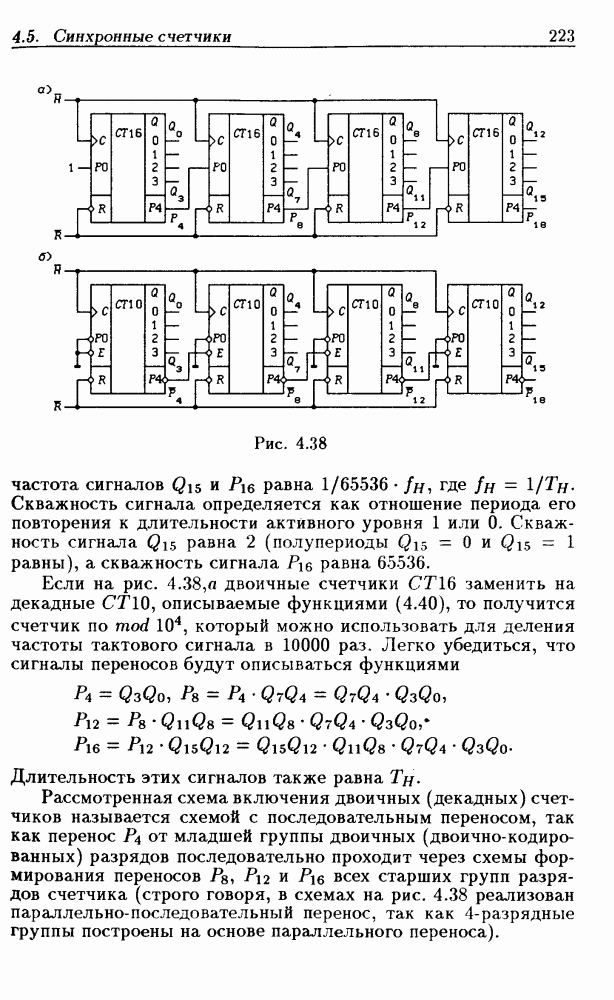
- Каскадирование двоичных и двоично-десятичных счетчиков.
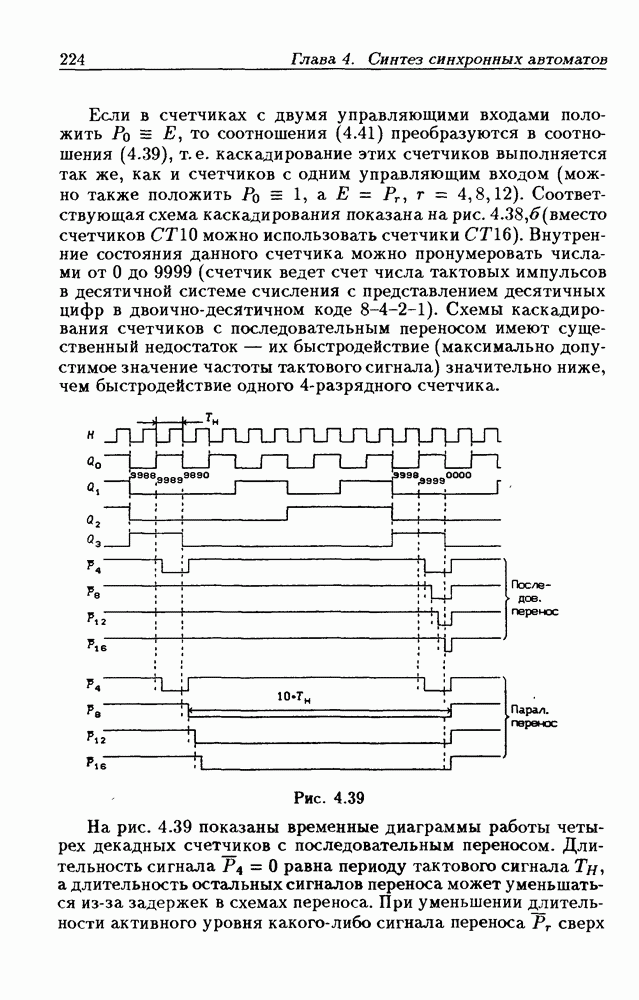
- Синхронные двоичные реверсивные счетчики.
- Реверсивные двоично-десятичные счетчики.
- Каскадирование реверсивных счетчиков.
- Счетчики на сдвигающих регистрах.
- Кольцевые счетчики.
- Линейные счетчики.
- Программируемые счетчики.
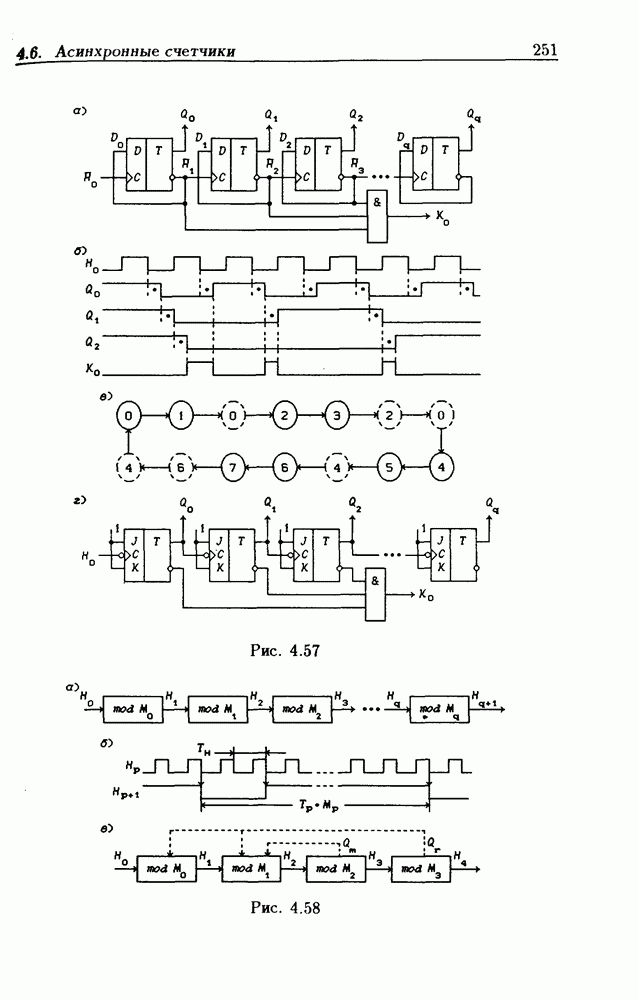
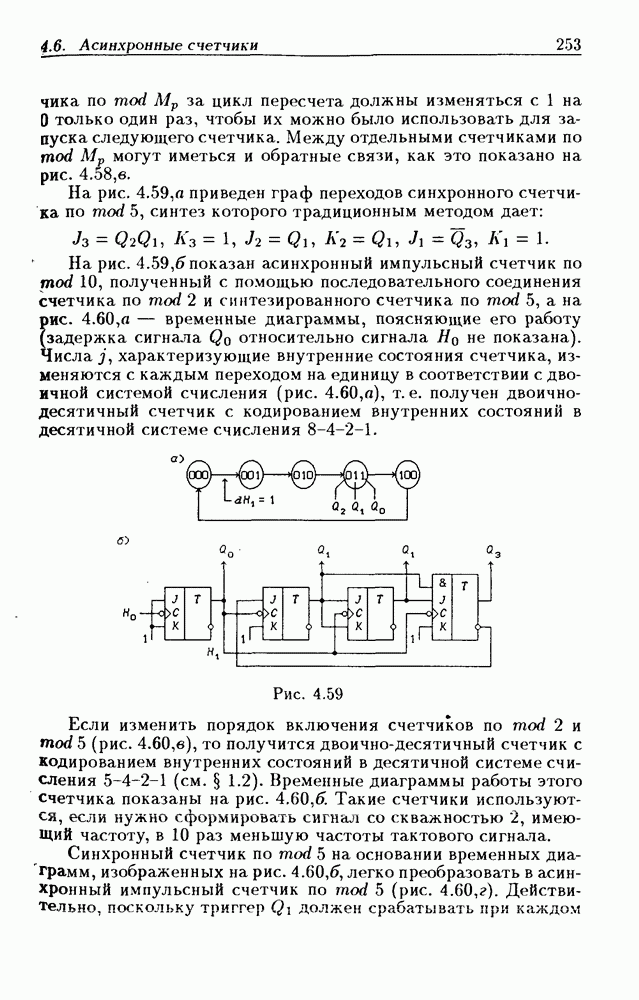
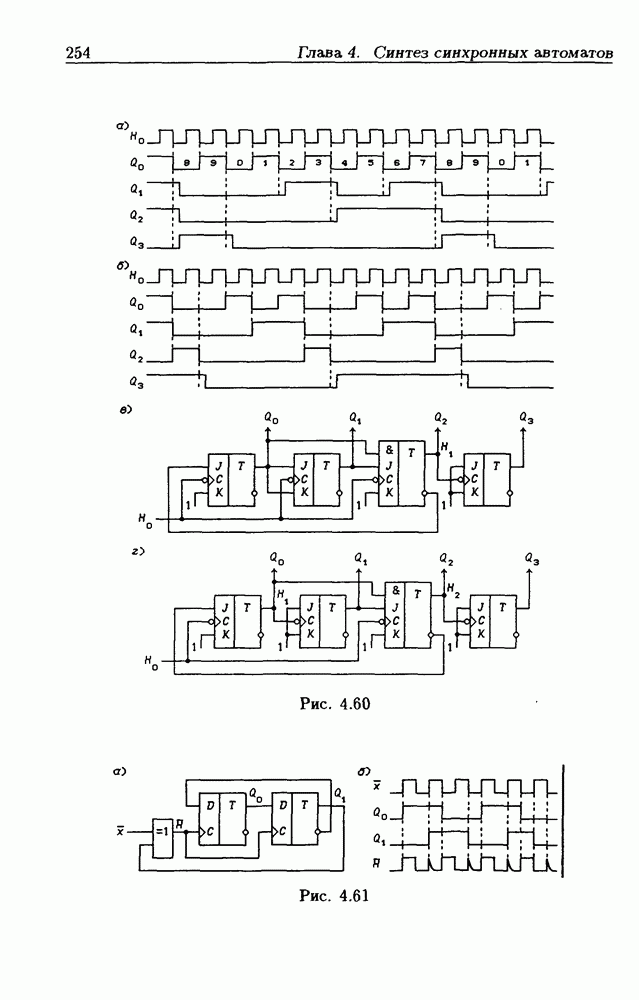
- 4.6. Асинхронные счетчики
- Асинхронные счетчики с умножением частоты счетного сигнала.
- Асинхронные импульсно-потенциальные счетчики.
- Асинхронное программирование модуля пересчета счетчиков.
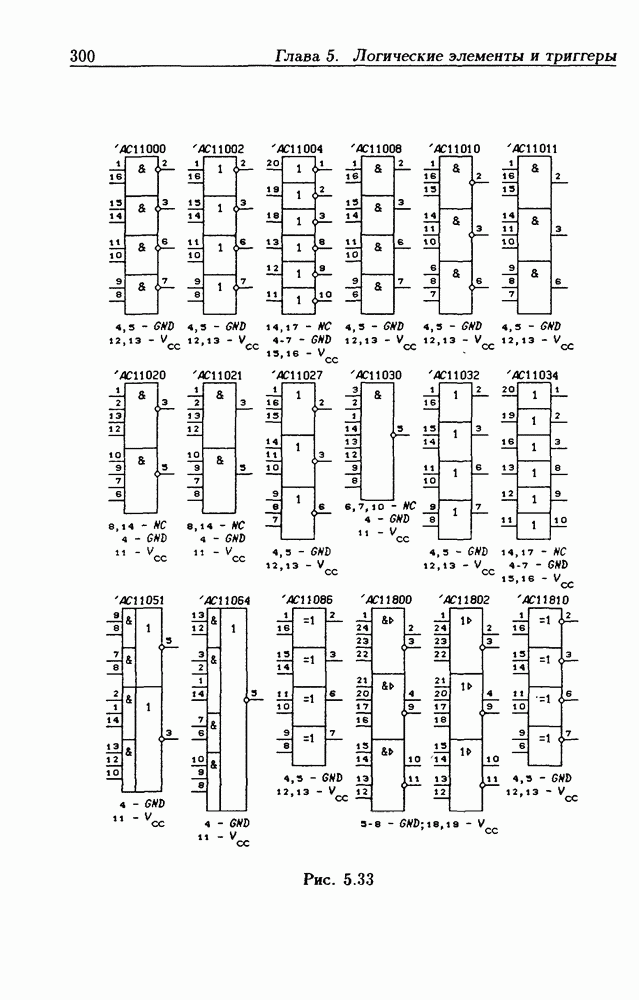
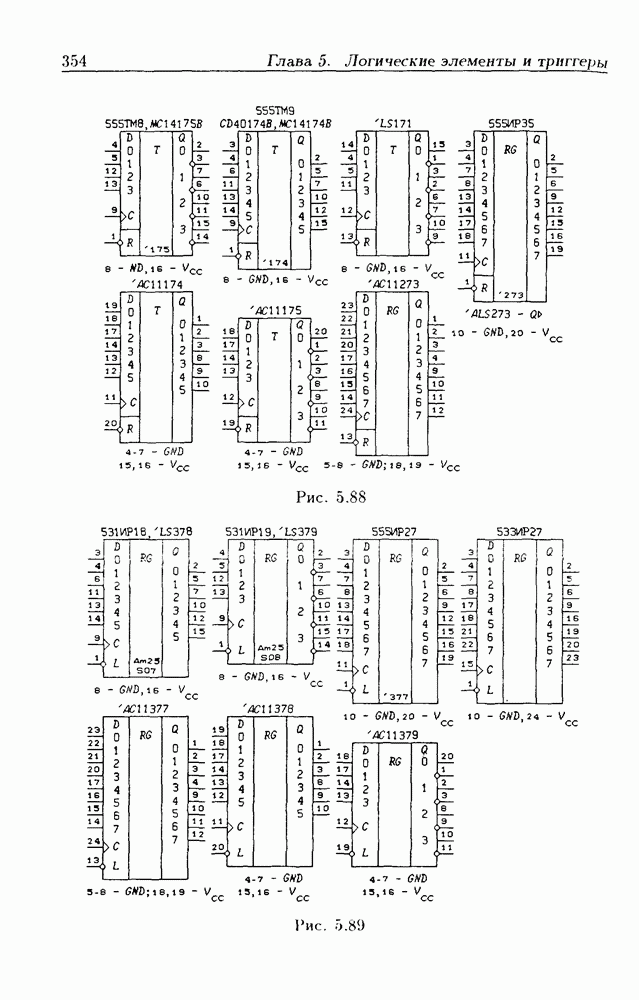
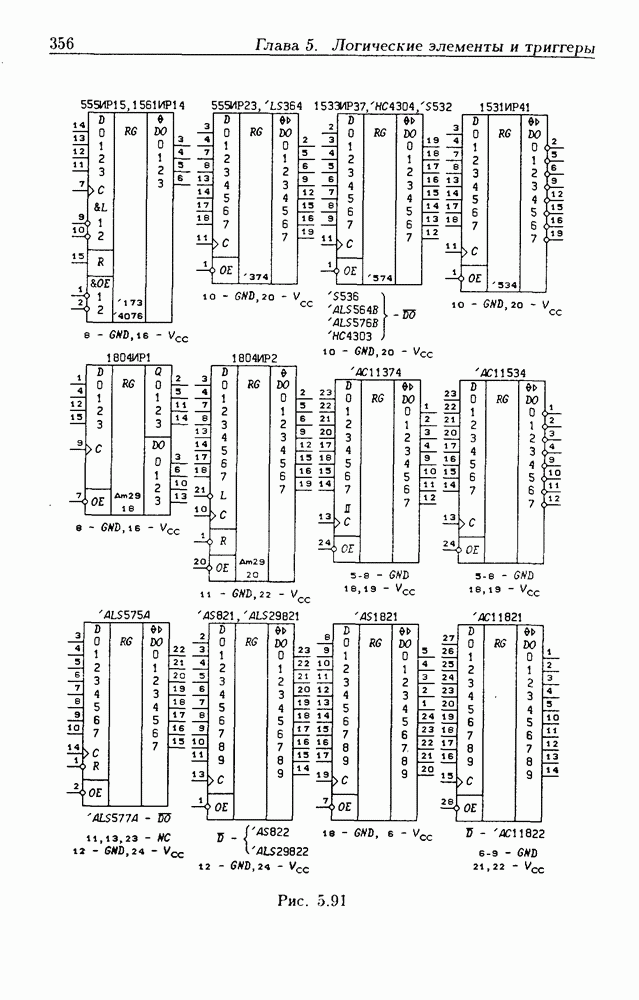
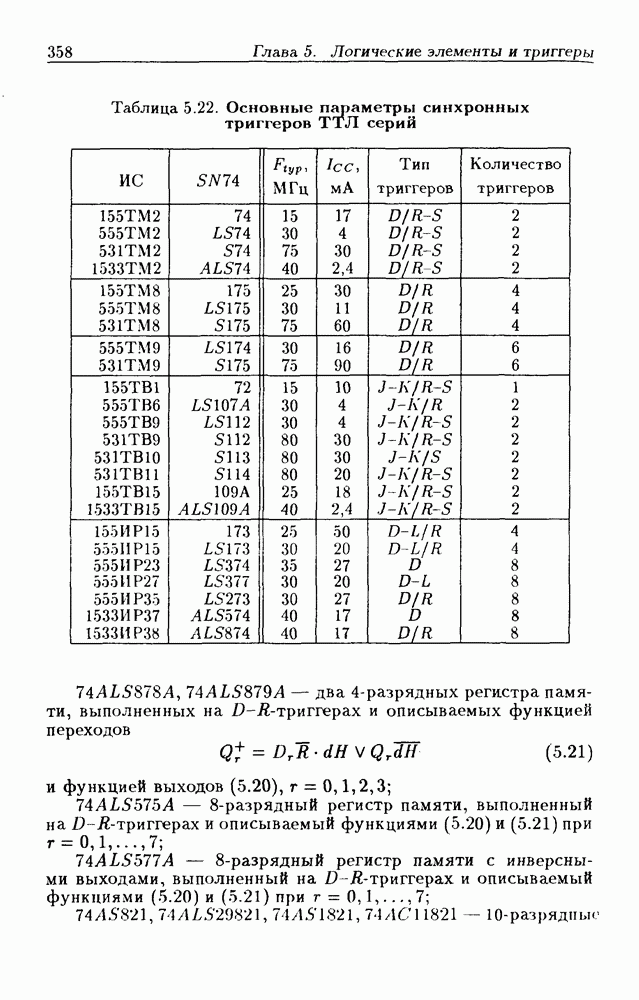
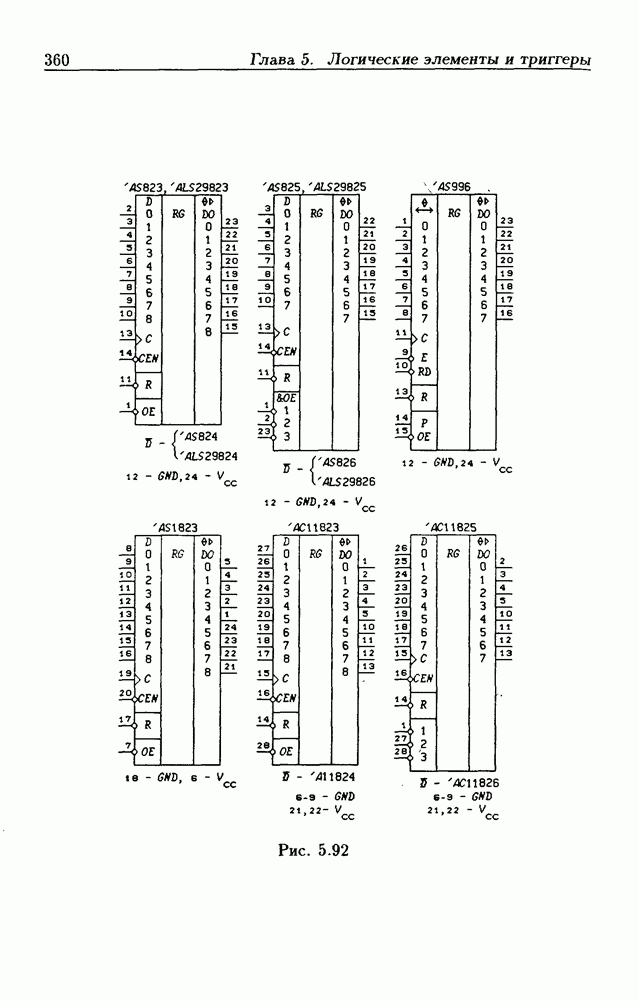
- Глава 5. Логические элементы и триггеры
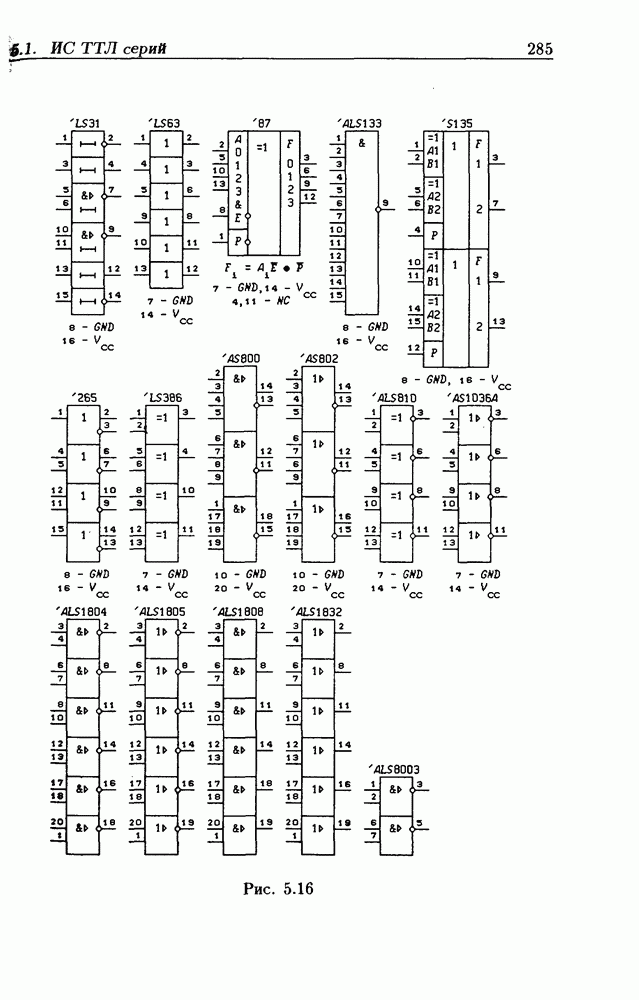
- Логические элементы.
- Классификация ИС по степени интеграции.
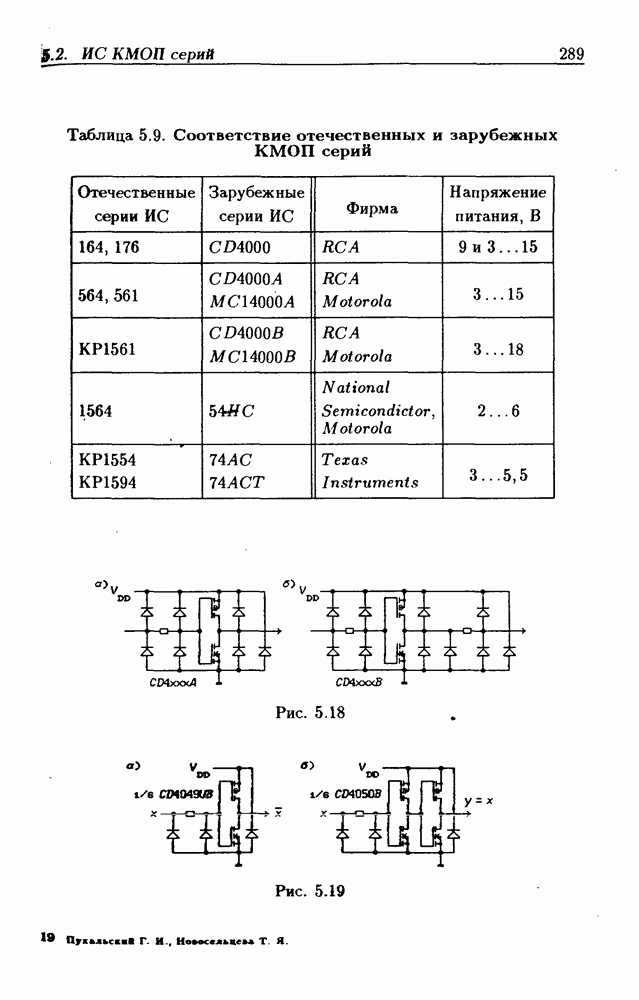
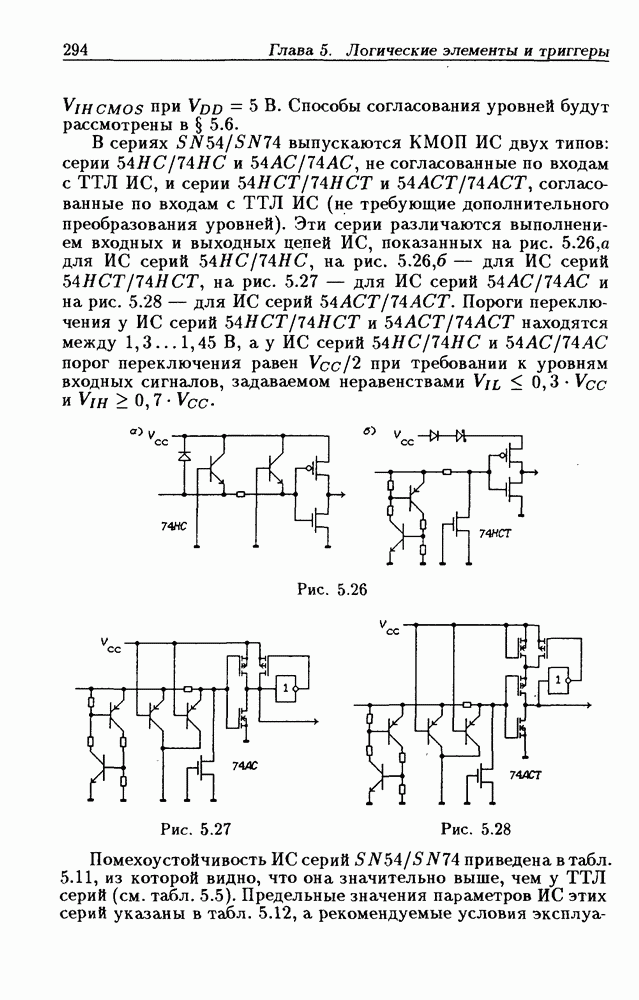
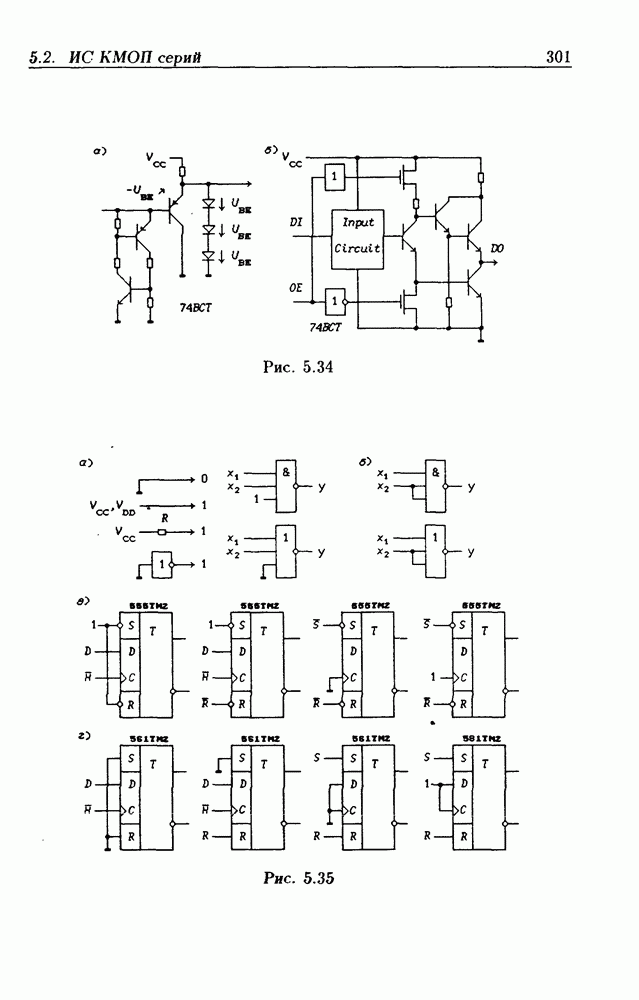
- 5.2. Интегральные схемы КМОП серий
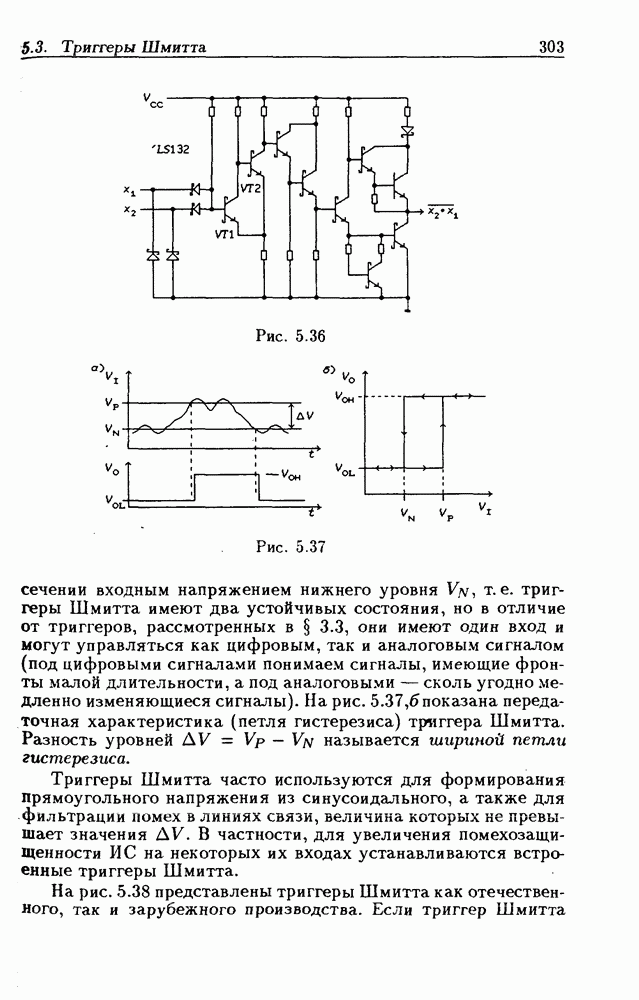
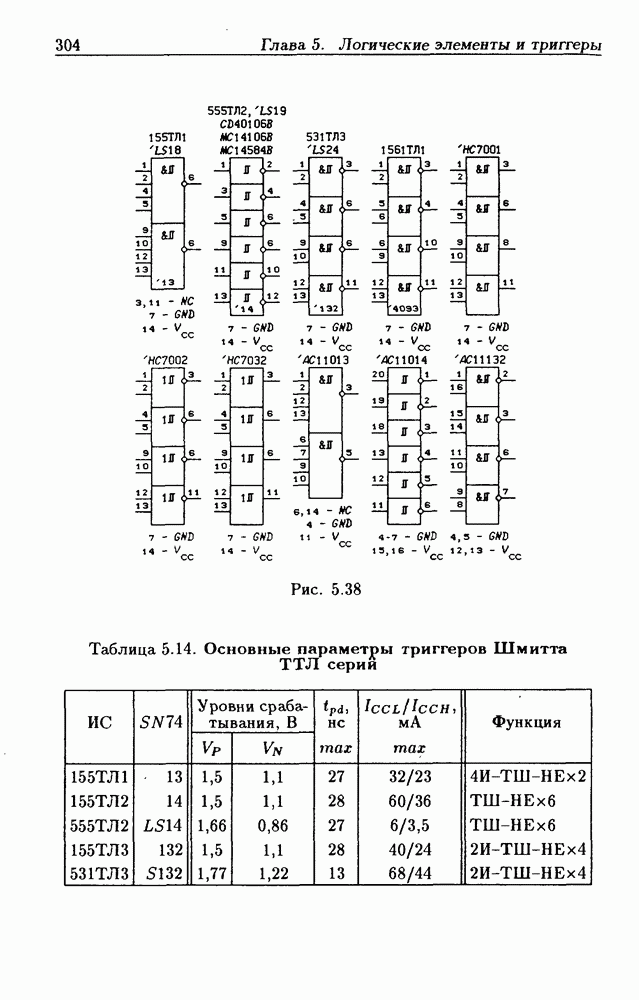
- 5.3. Триггеры Шмитта
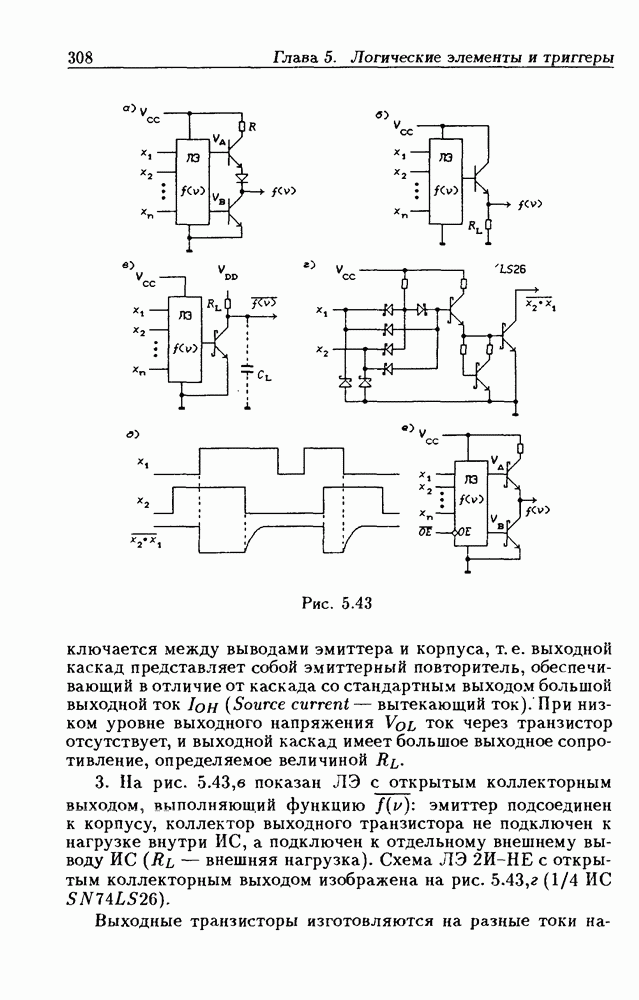
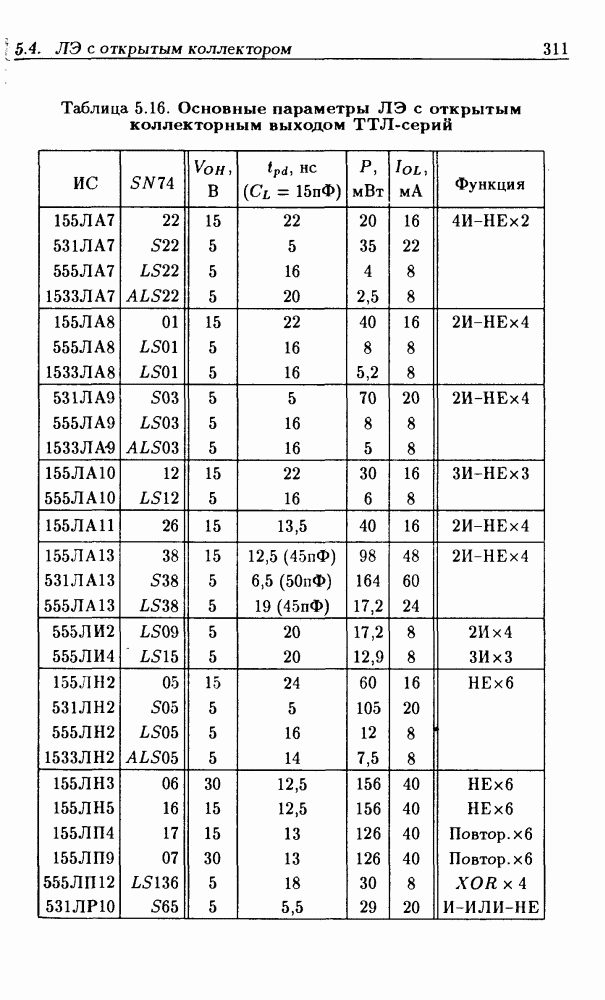
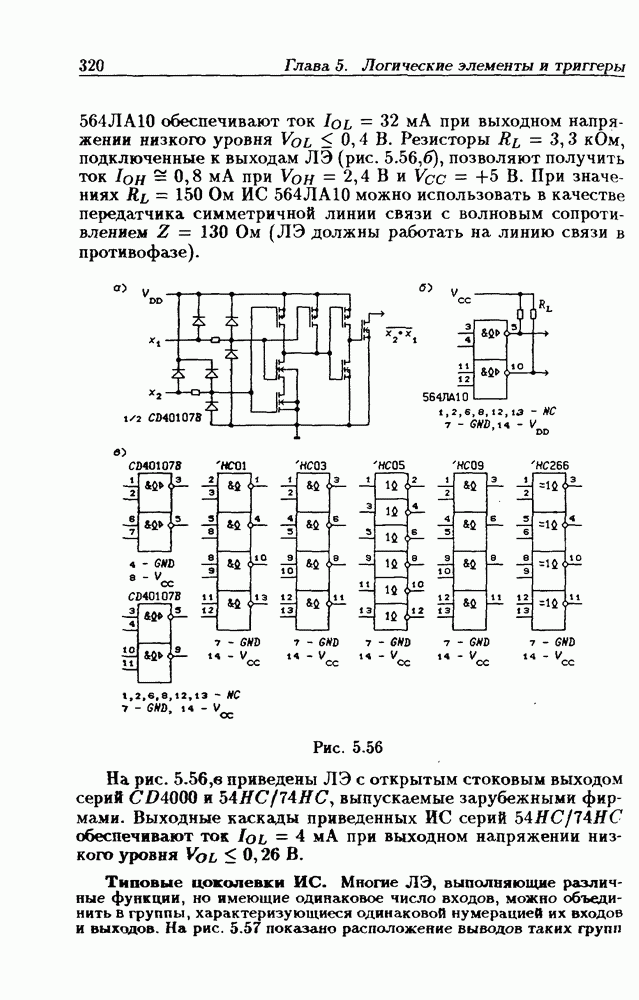
- 5.4. Логические элементы с открытым коллекторным выходом
- Логические элементы с открытым коллекторным выходом.
- Применения ЛЭ с открытым коллекторным выходом.
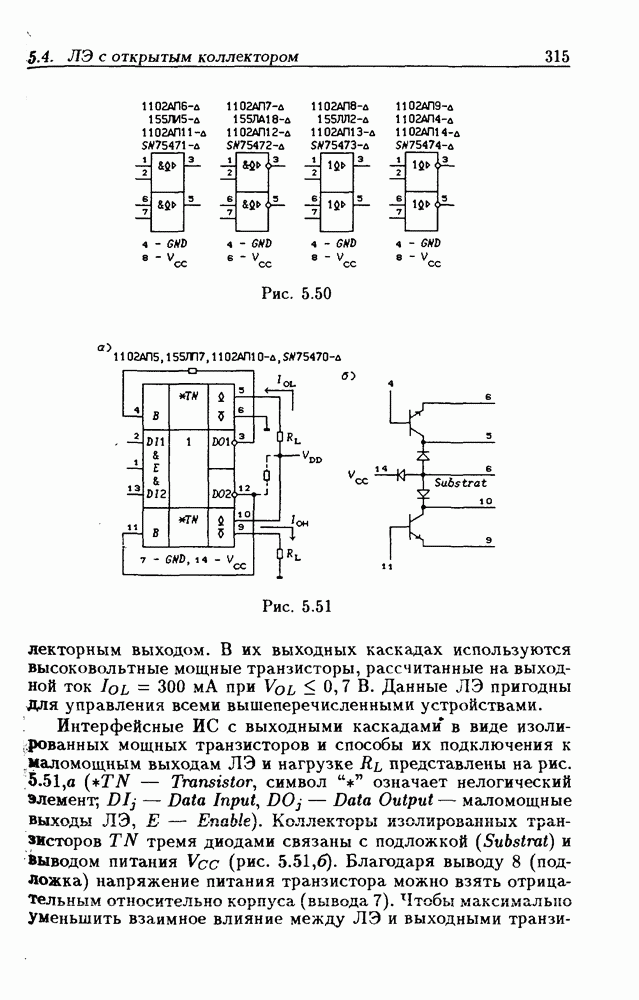
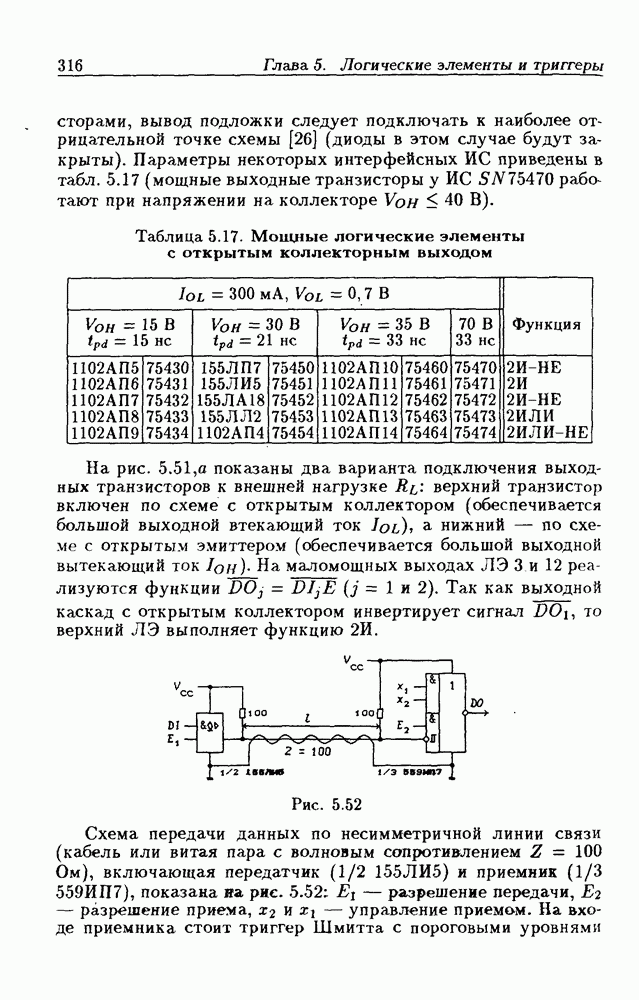
- Интерфейсные ЛЭ с открытым коллекторным выходом.
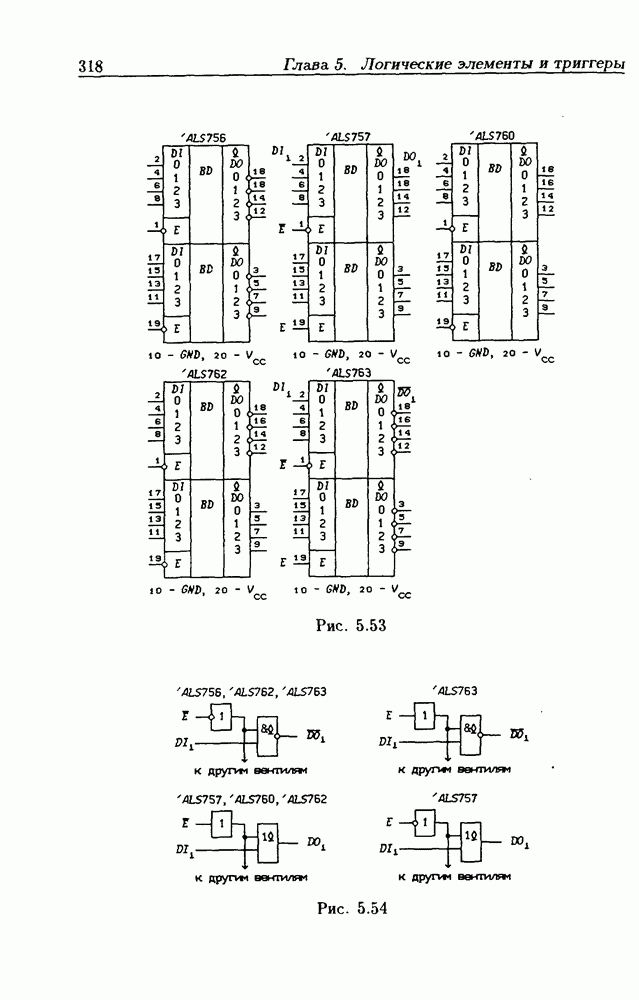
- Логические элементы с открытым стоковым выходом.
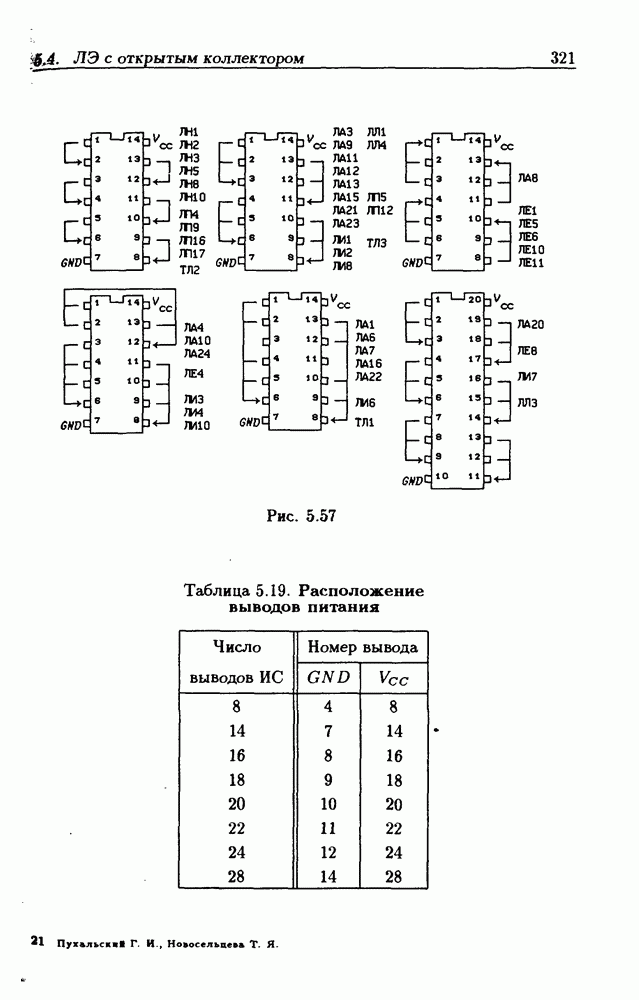
- Типовые цоколевки ИС.
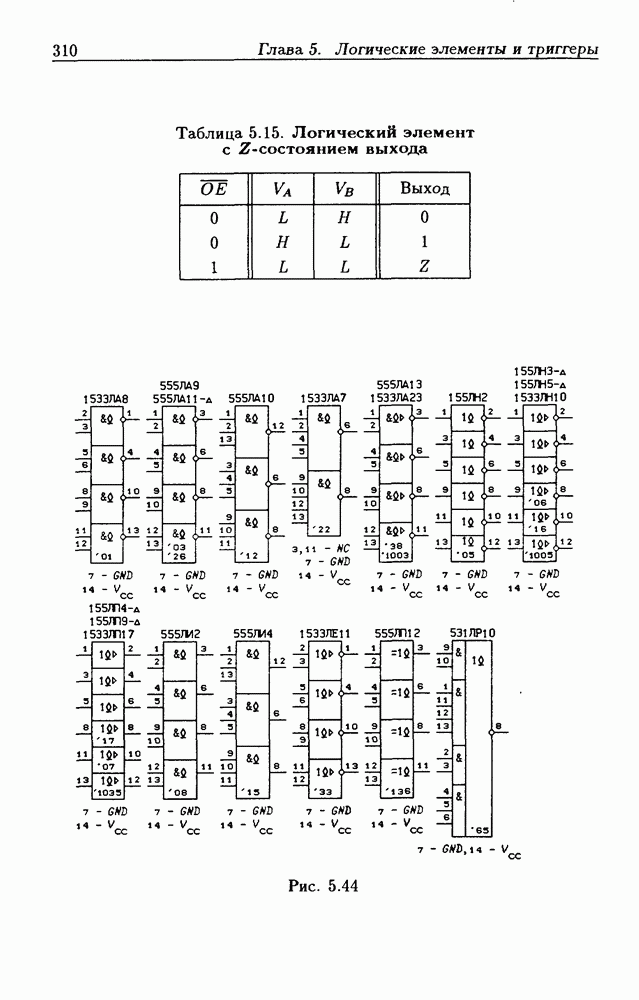
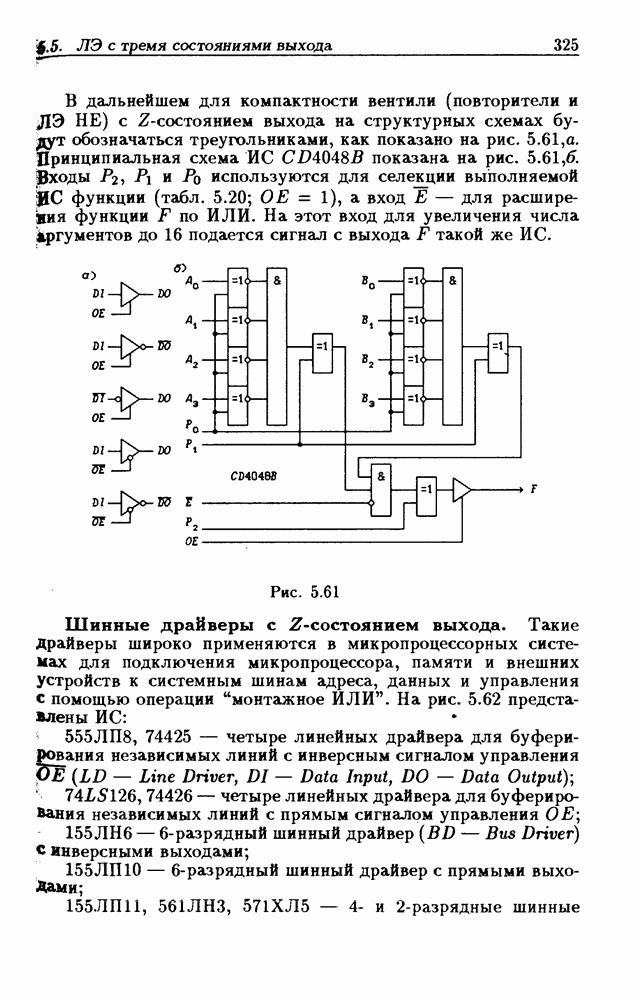
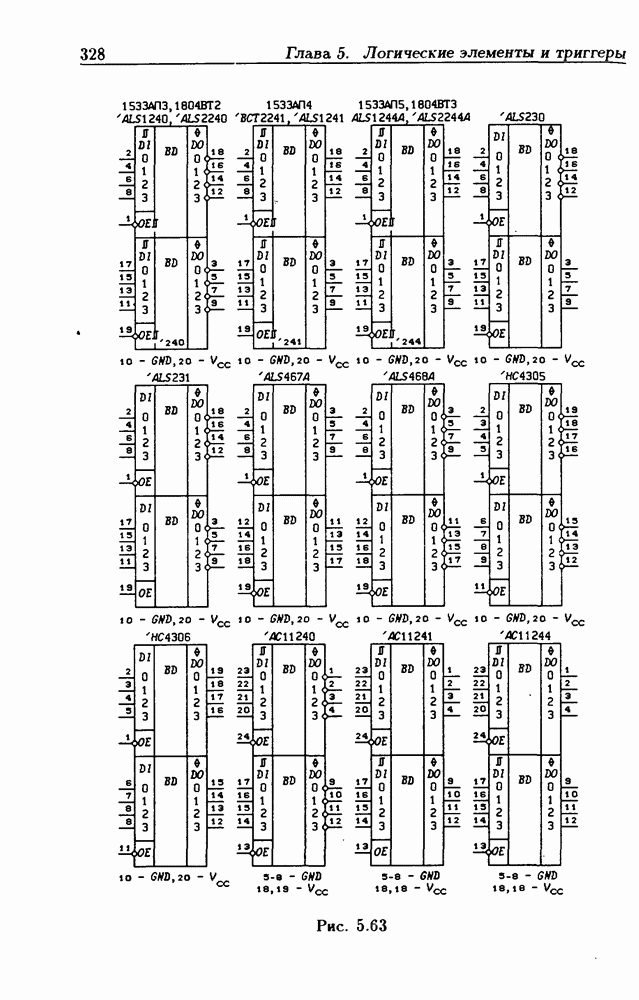
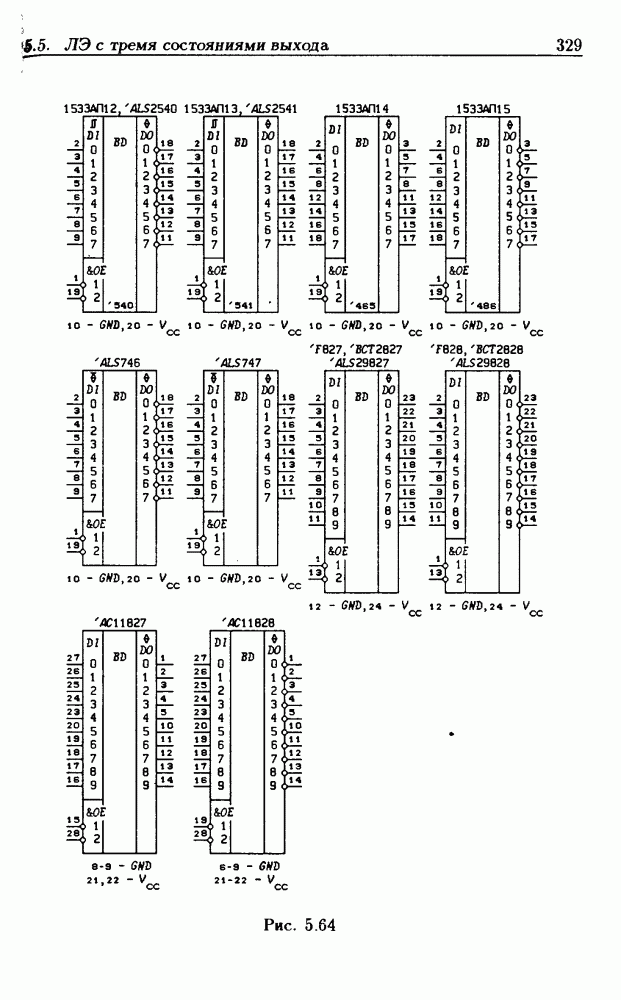
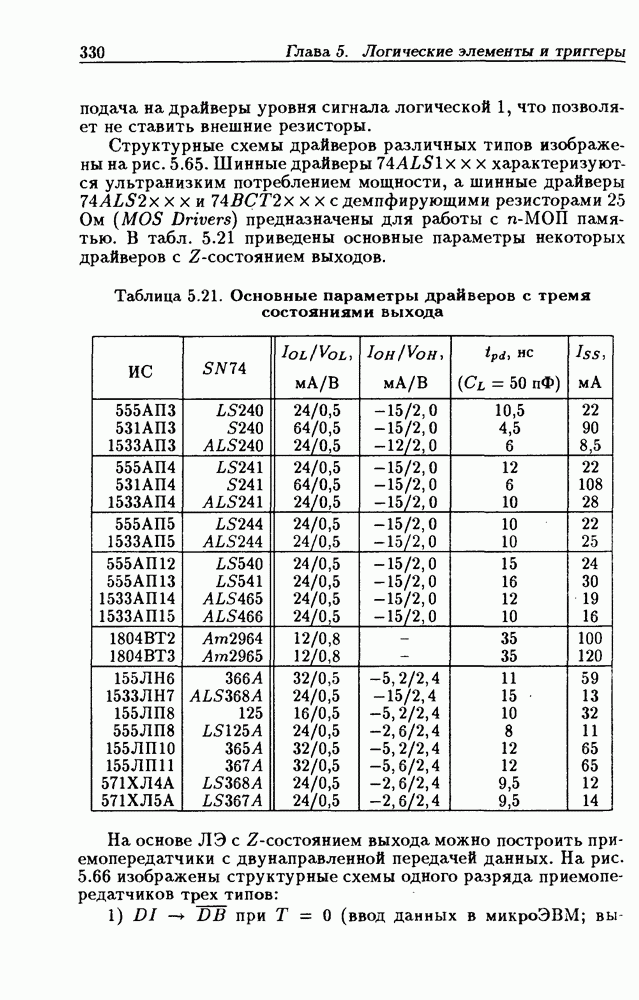
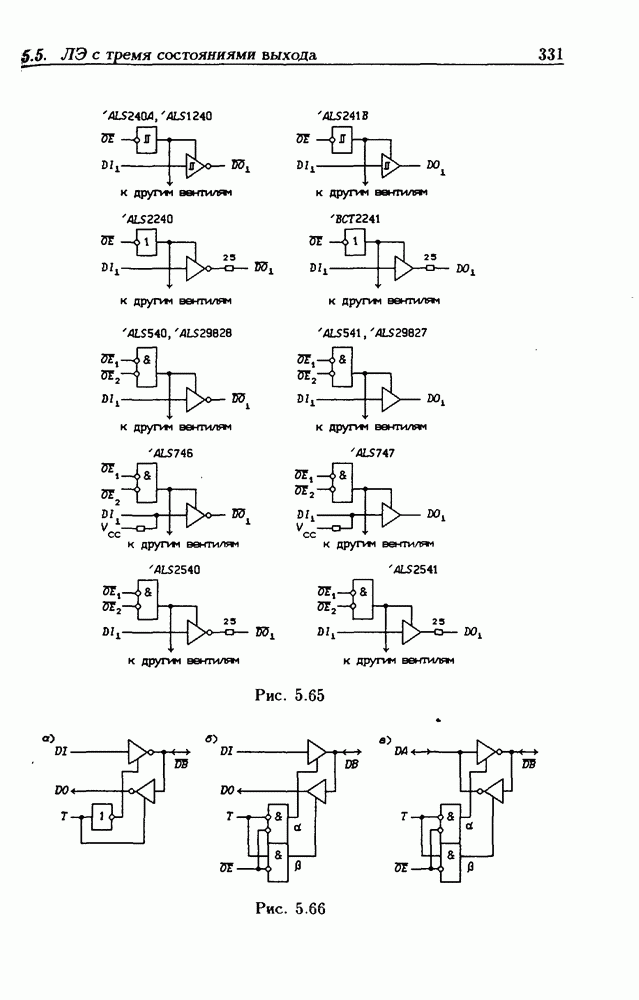
- 5.5. Логические элементы с тремя состояниями выхода
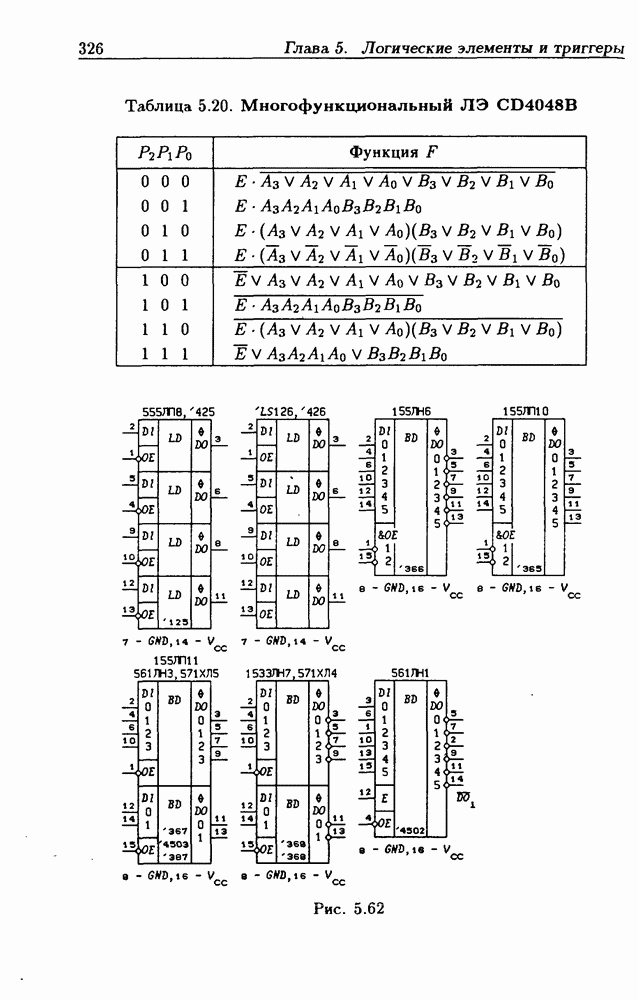
- Шинные драйверы с Z-состоянием выхода.
- Основные правила графического изображения ИС.
- 5.6. Преобразователи уровней напряжения и тока
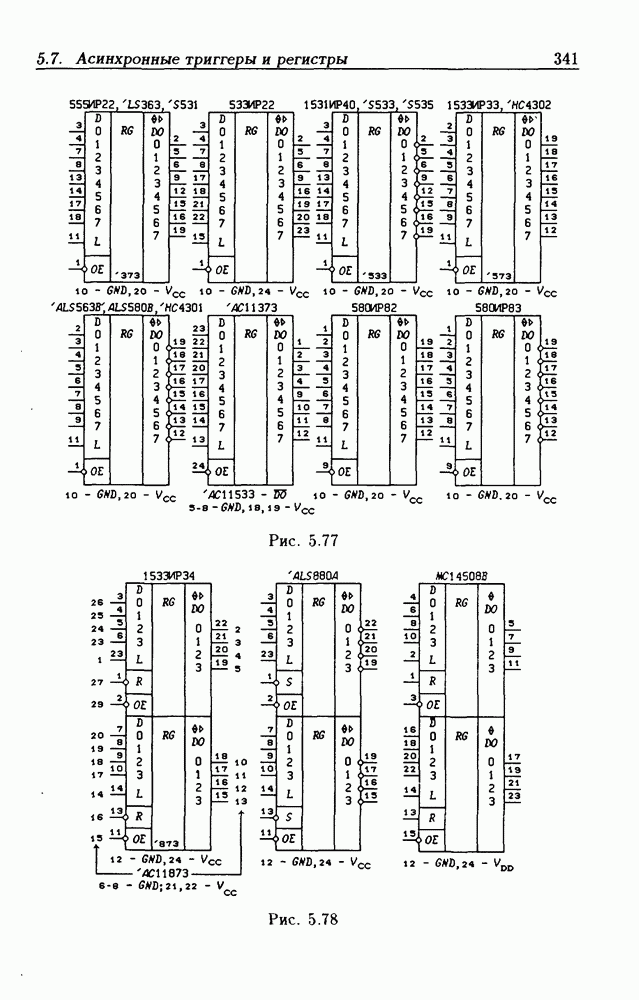
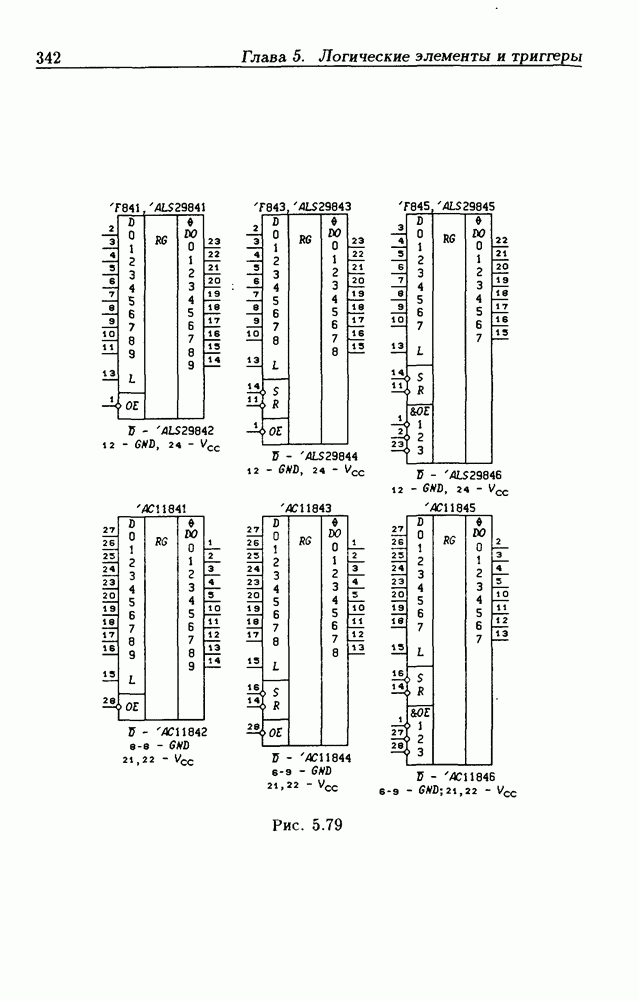
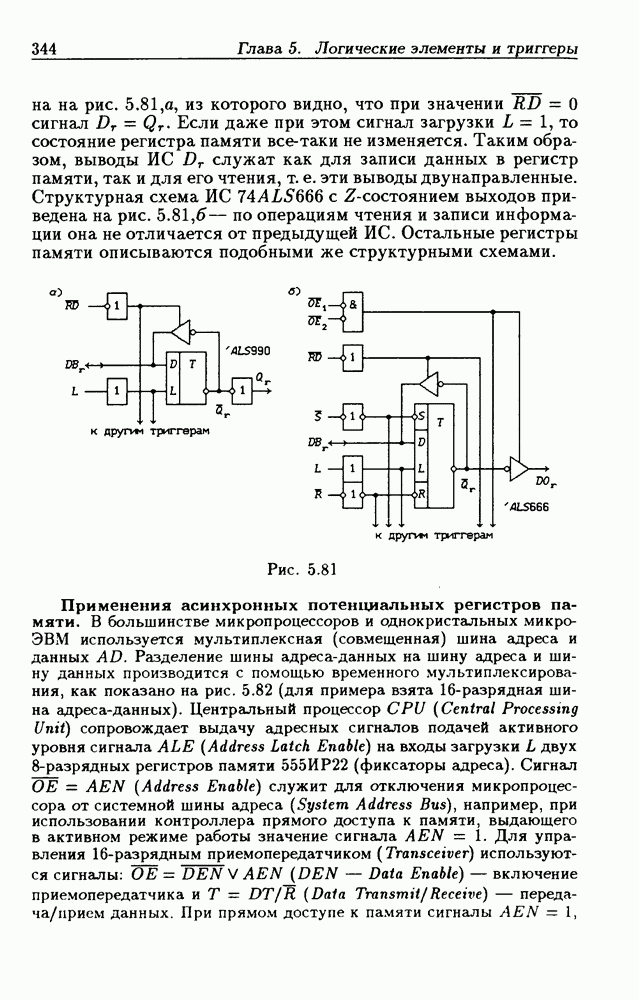
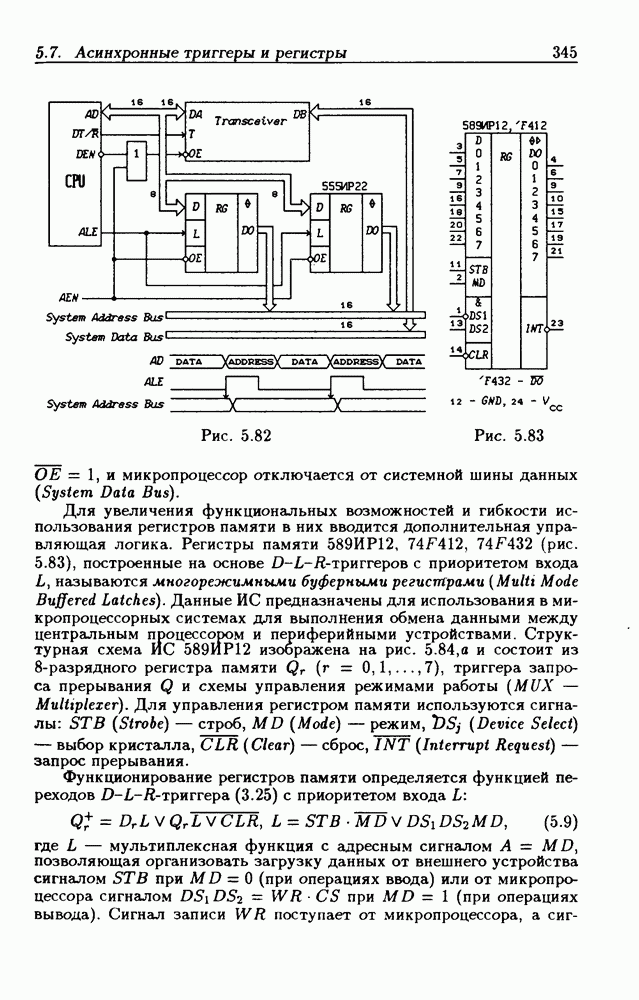
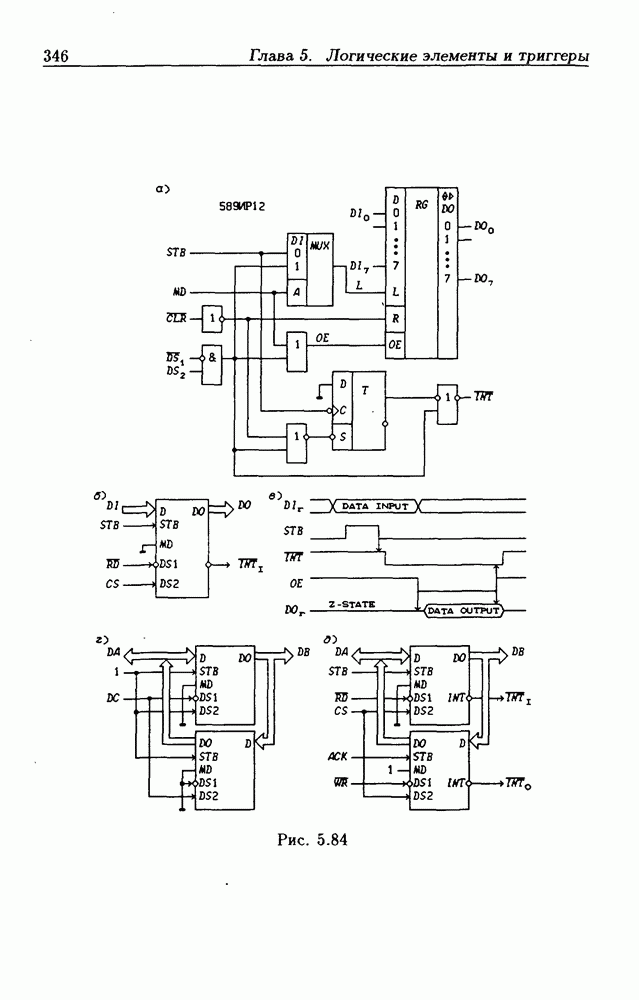
- 5.7. Асинхронные потенциальные триггеры и регистры памяти
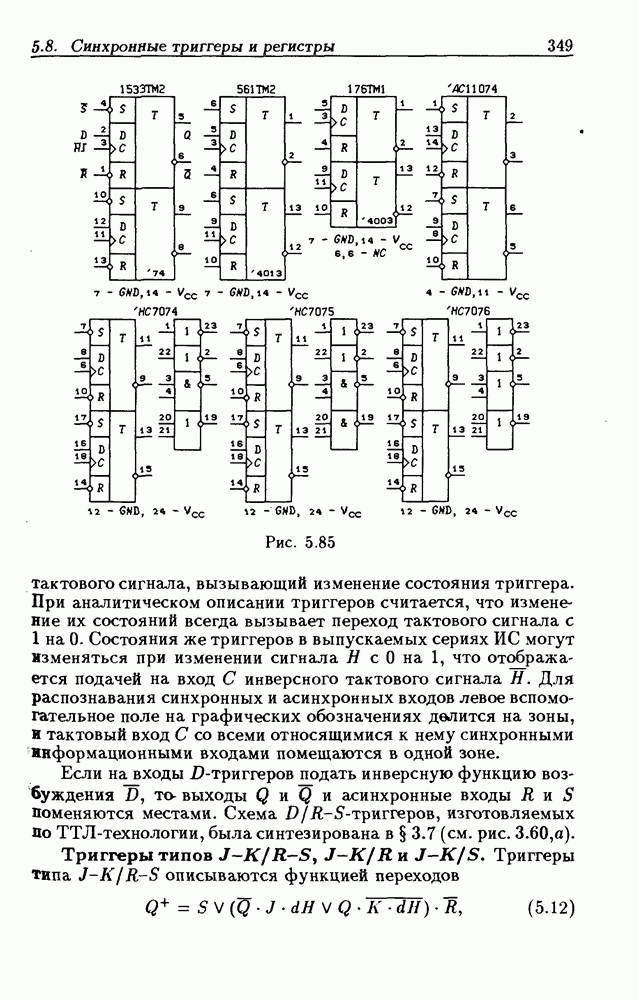
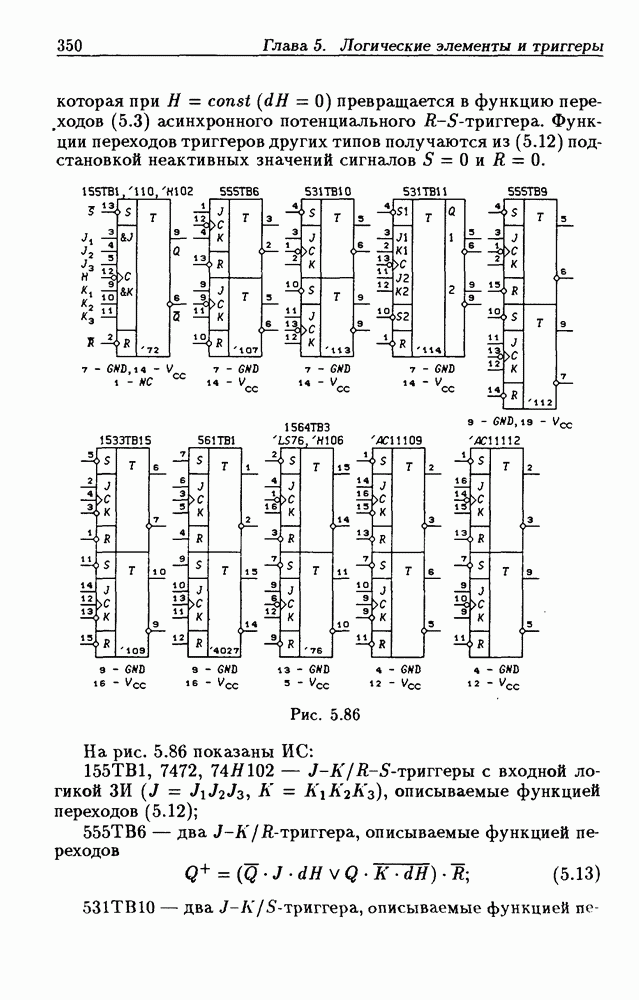
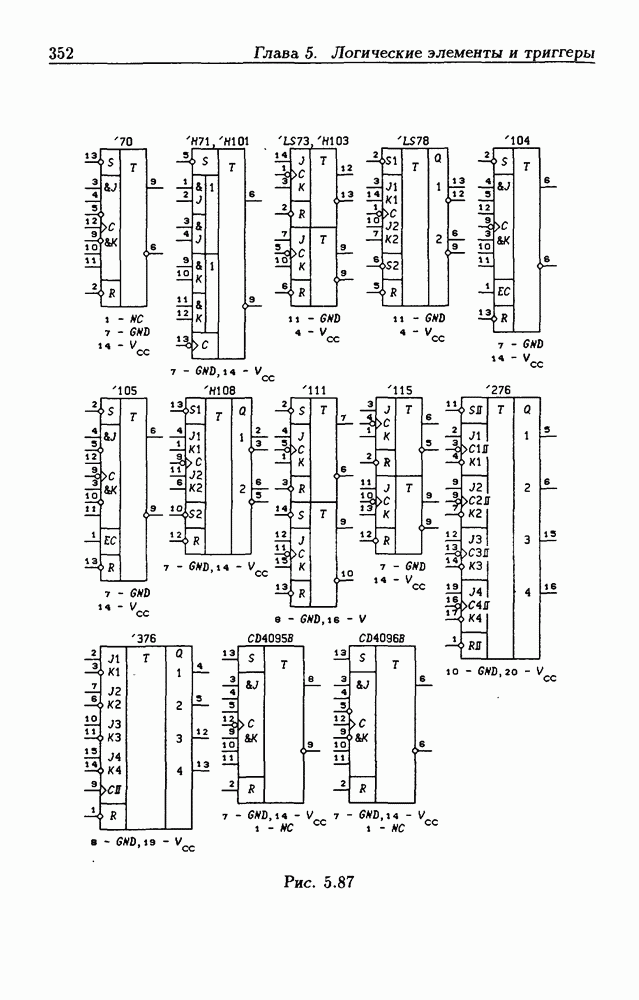
- 5.8. Синхронные триггеры и регистры памяти
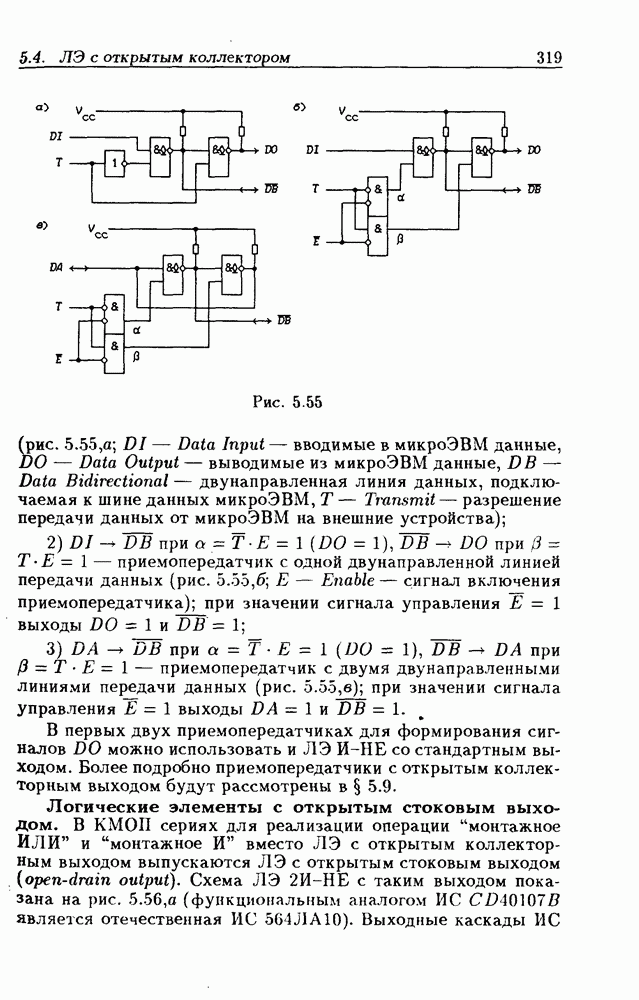
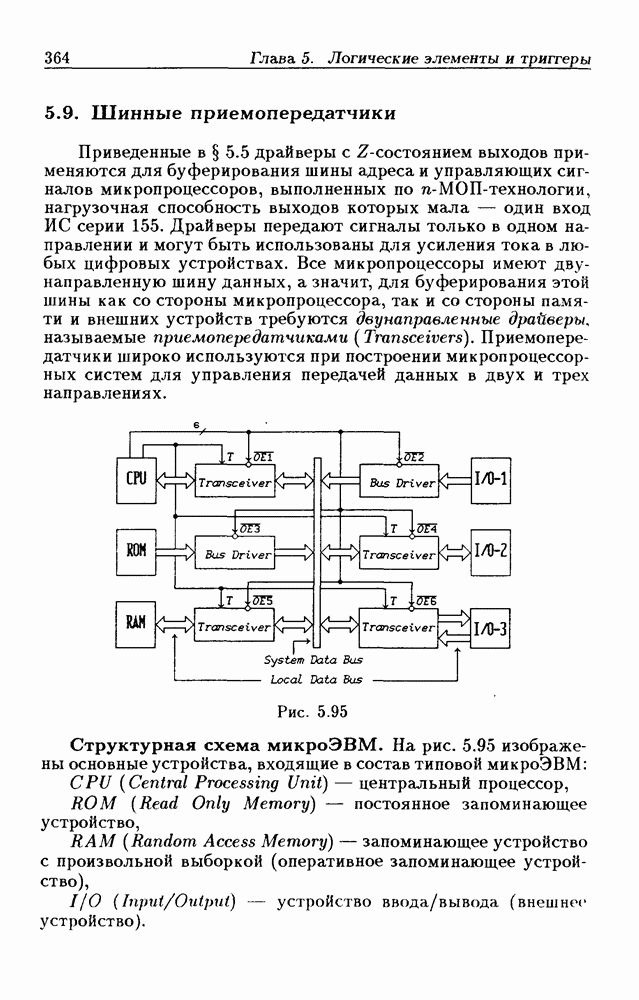
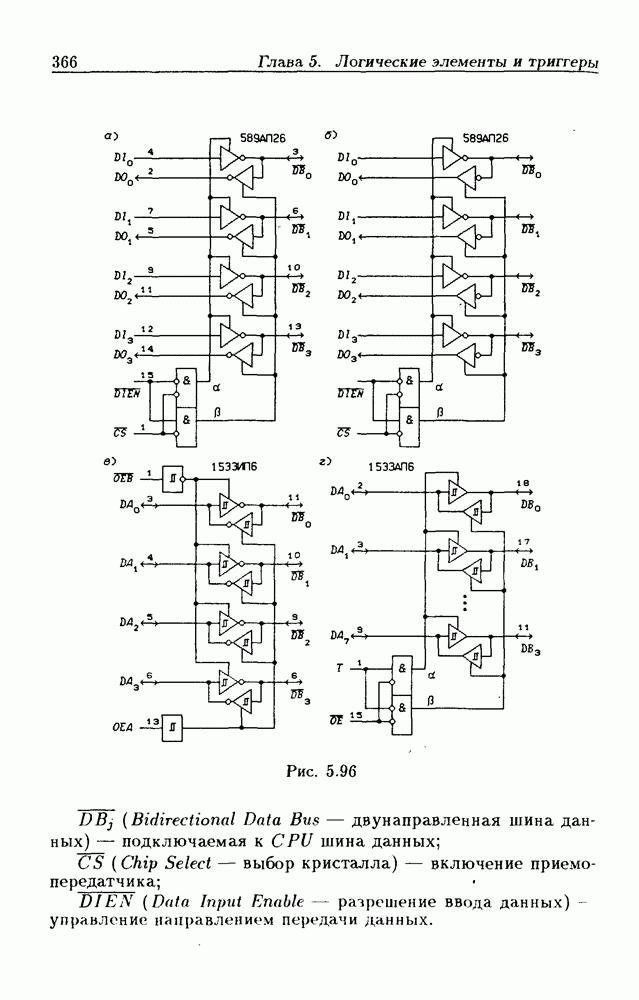
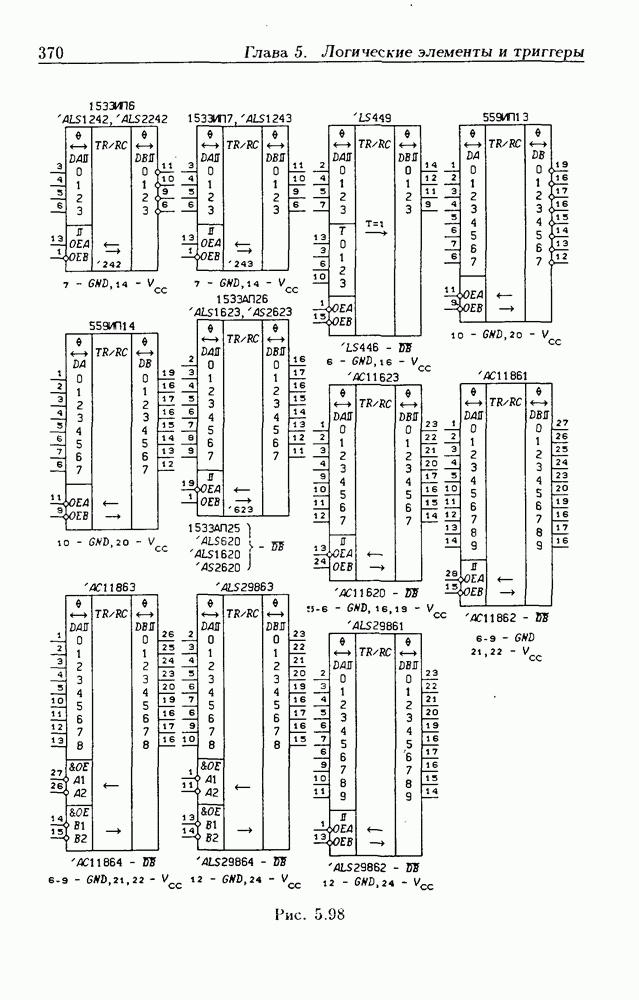
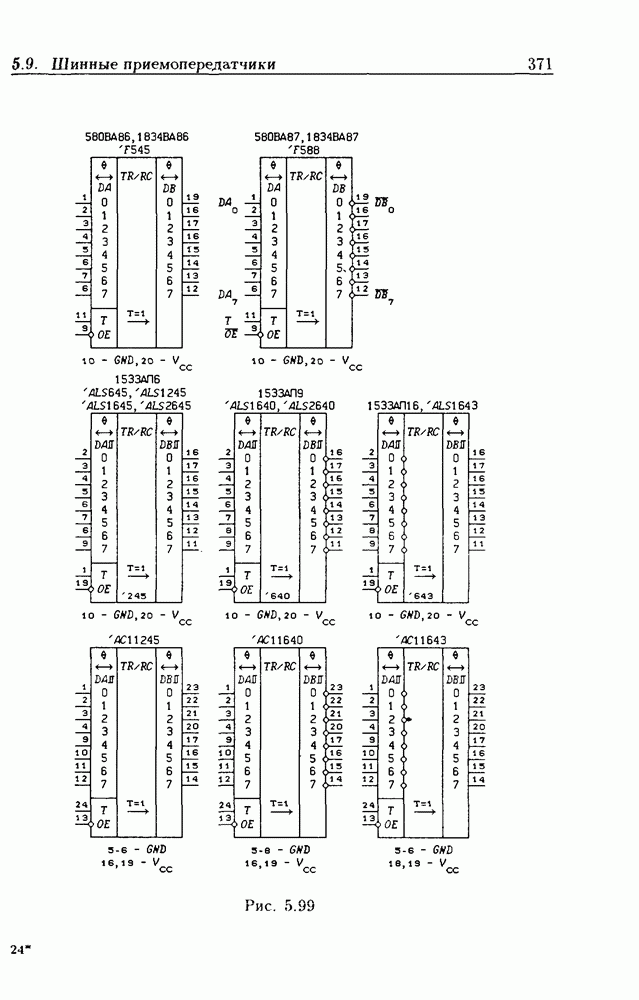
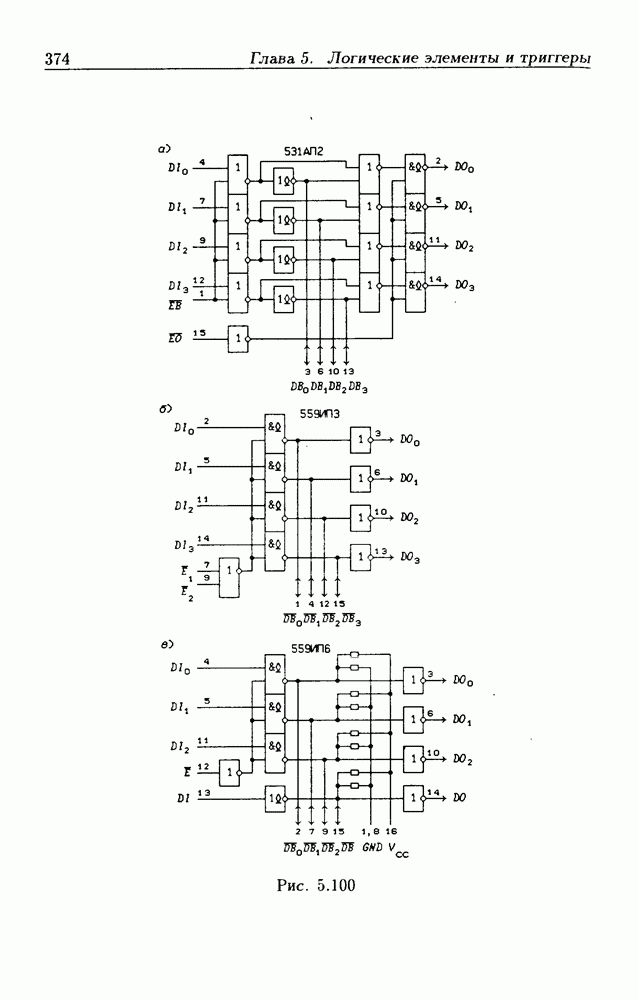
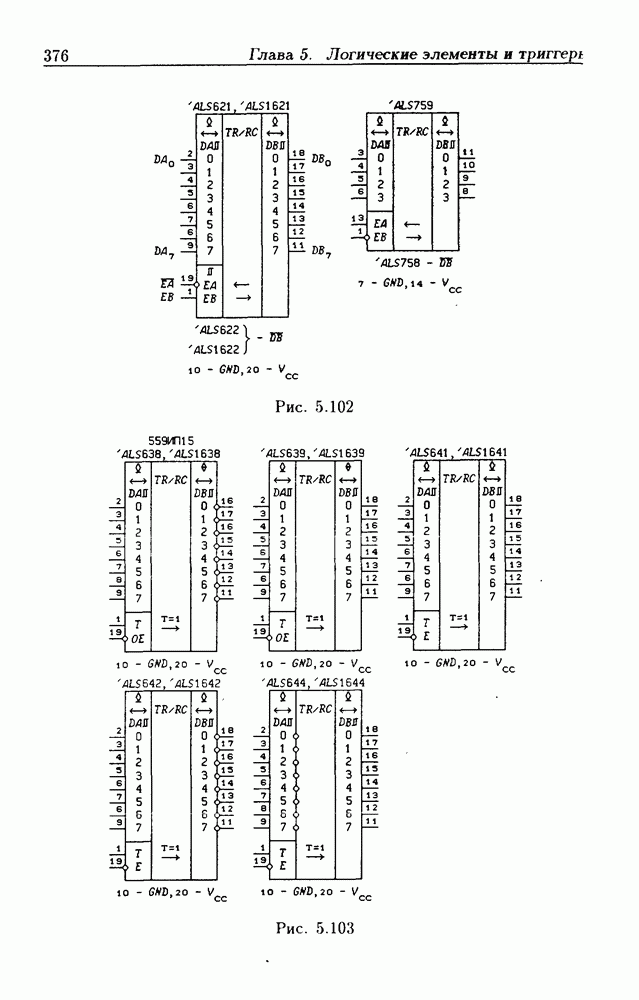
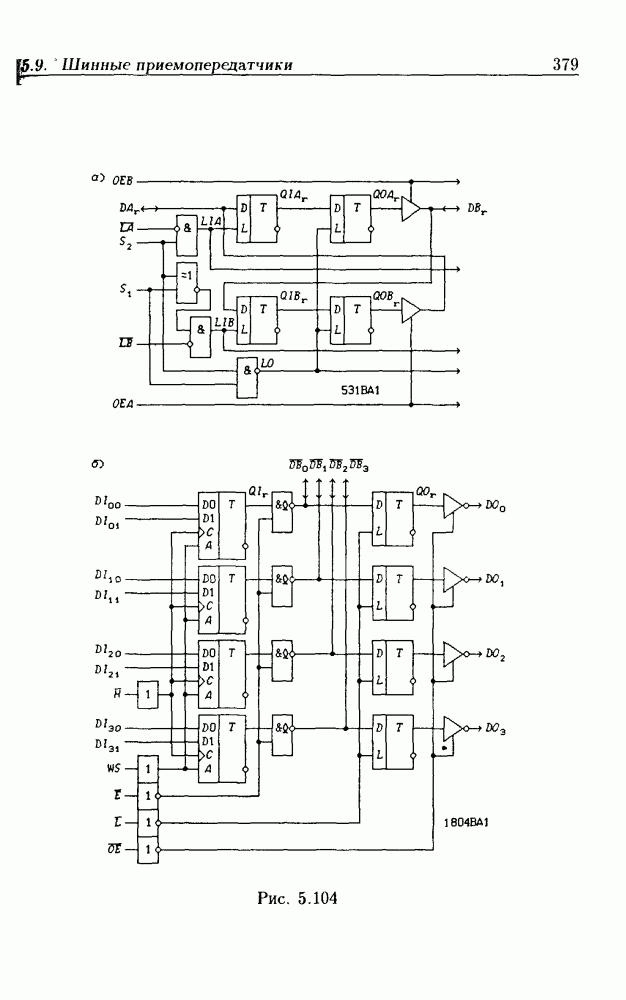
- 5.9. Шинные приемопередатчики
- Шинные приемопередатчики с Z-состоянием выхода.
- Шинные приемопередатчики с открытым коллекторным выходом.
- Шинные приемопередатчики с регистрами памяти.
- Шинные приемопередатчики со сдвигающим регистром.
- Шинные трехнаправленные приемопередатчики.
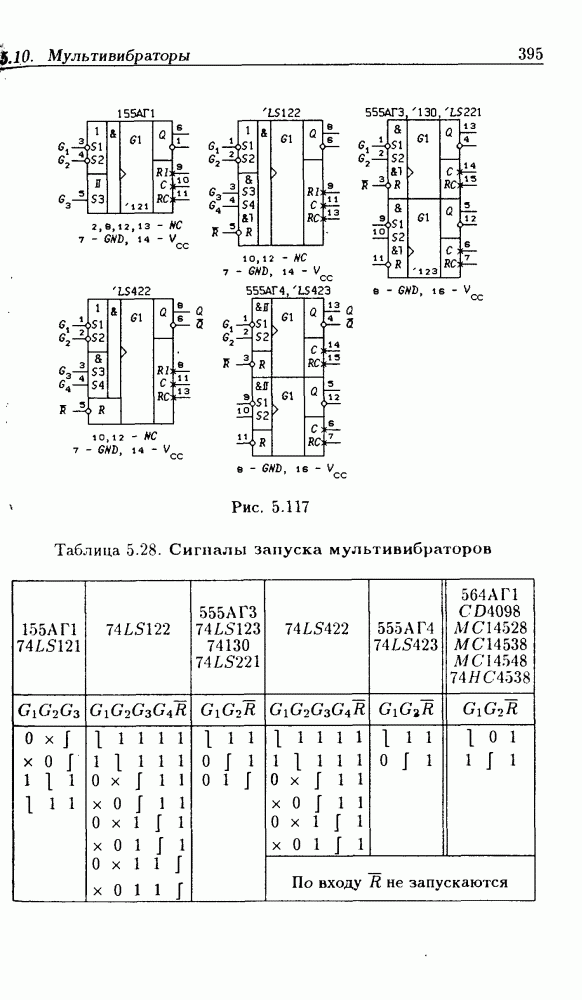
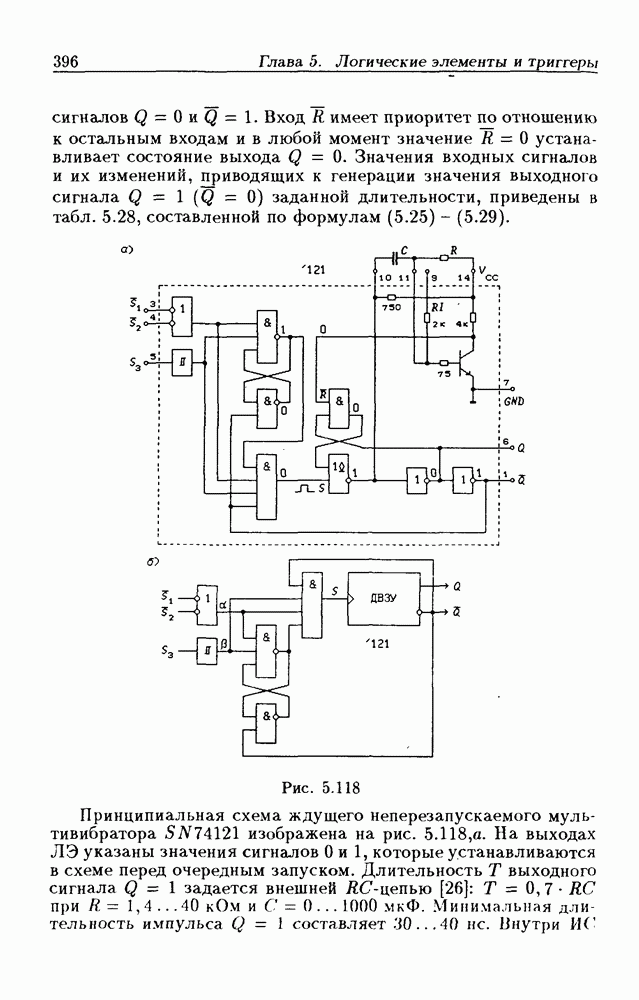
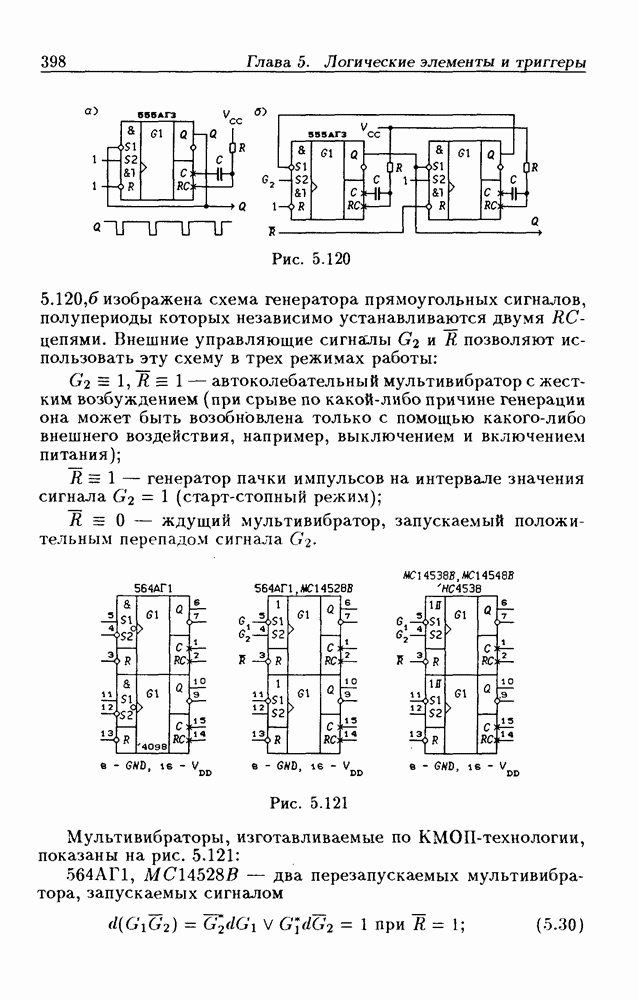
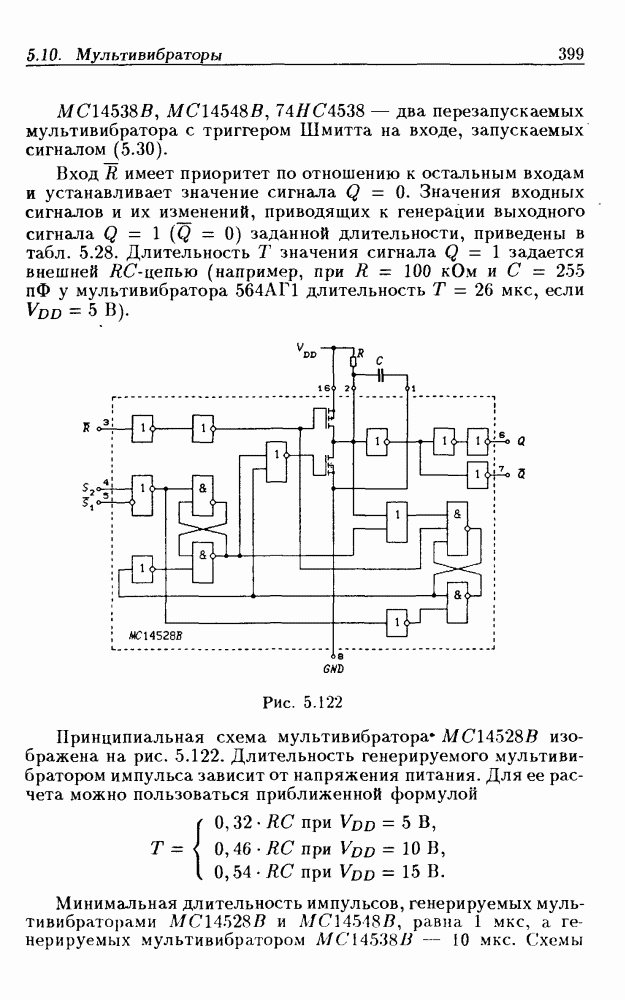
- 5.10. Мультивибраторы
- 5.11. Генераторы
- Схемы устранения «дребезга» механических контактов.
- Автогенераторы периодических сигналов.
- 5.12. Рекомендации по выбору серий ИС
- Глава 6. Коммутаторы и арифметические устройства
- 6.1. Дешифраторы
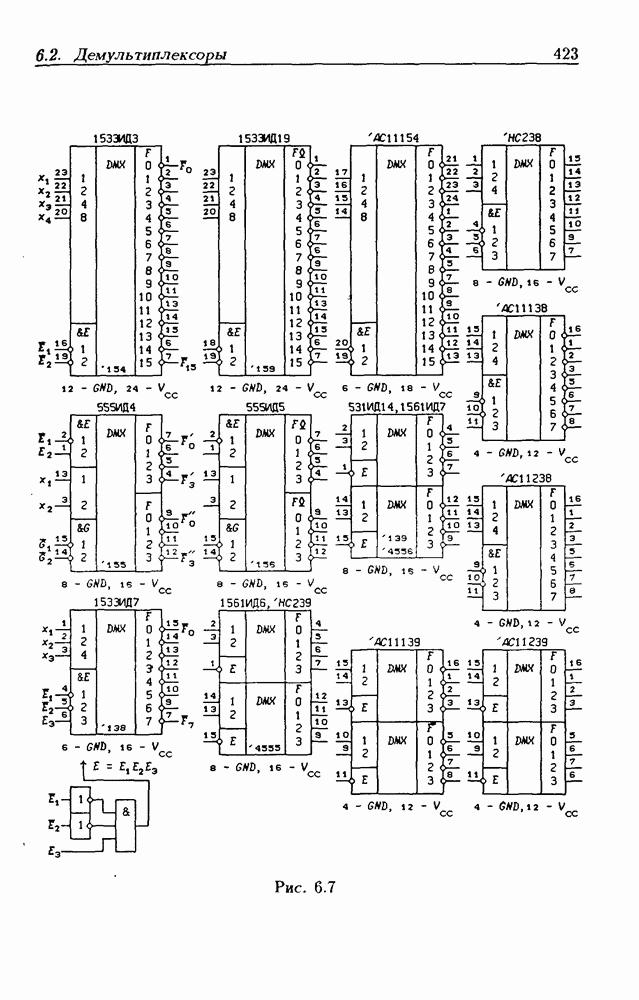
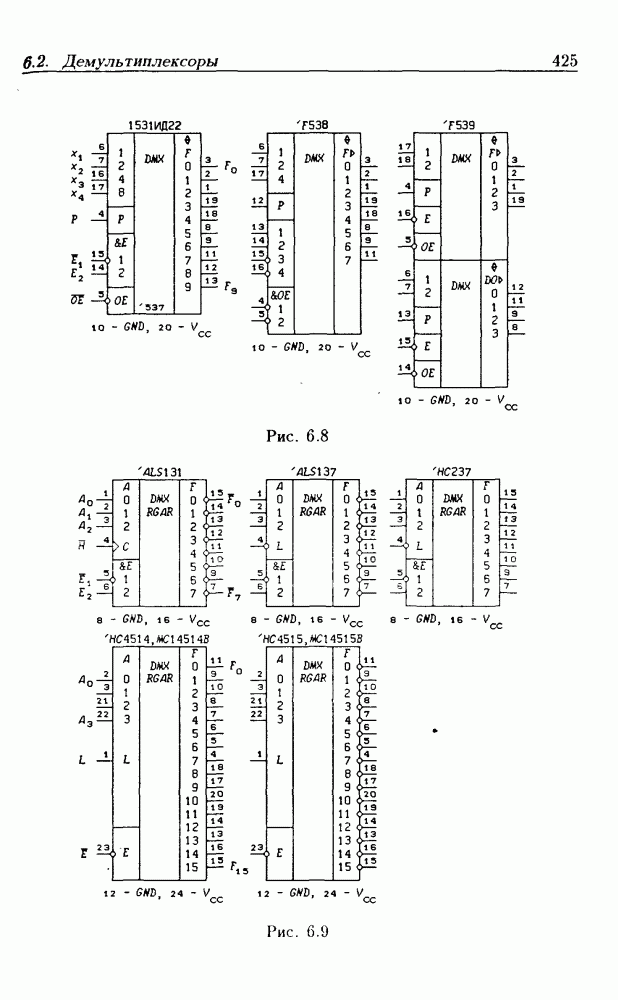
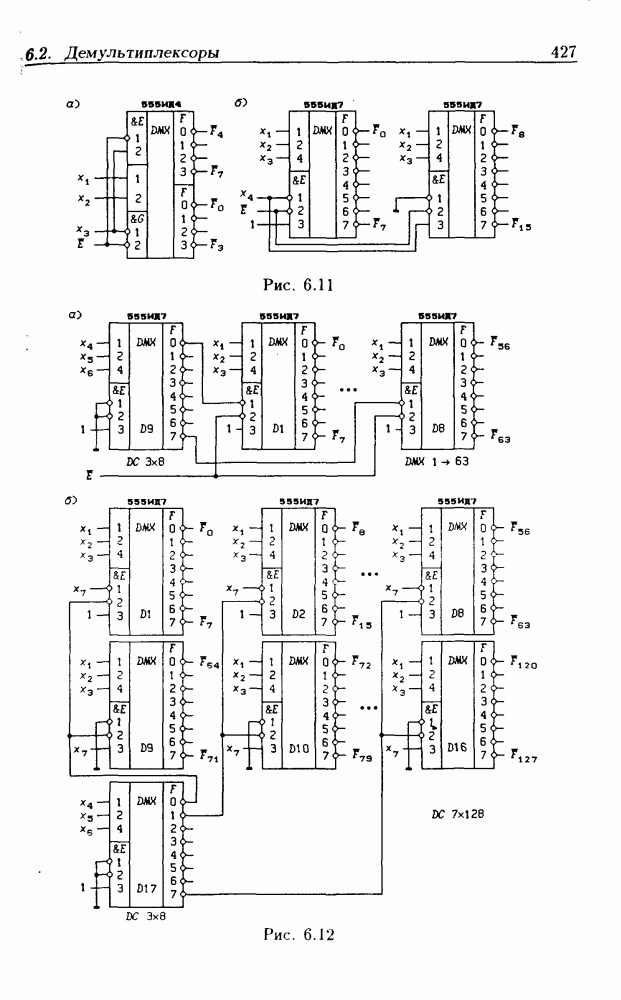
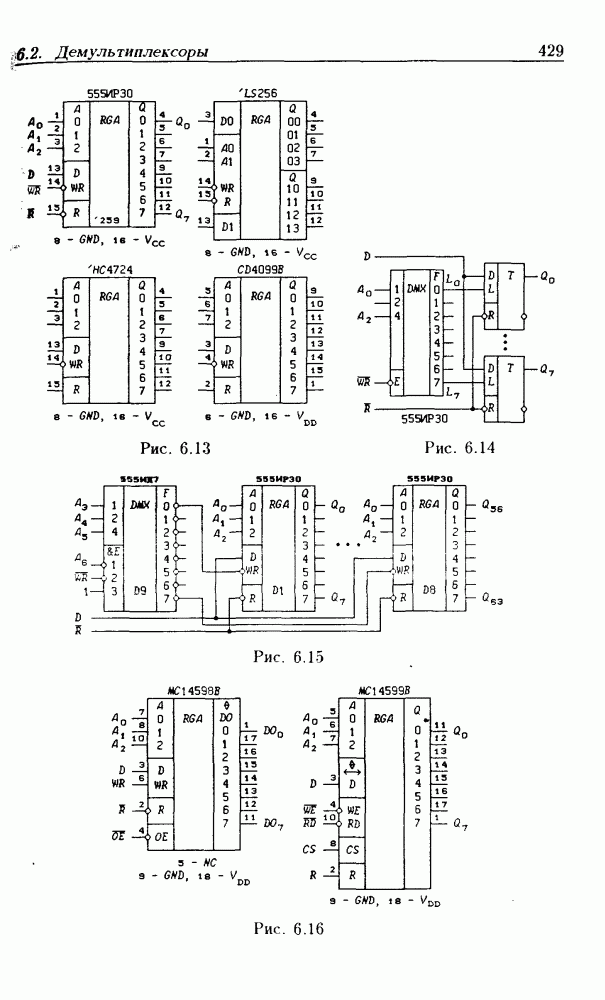
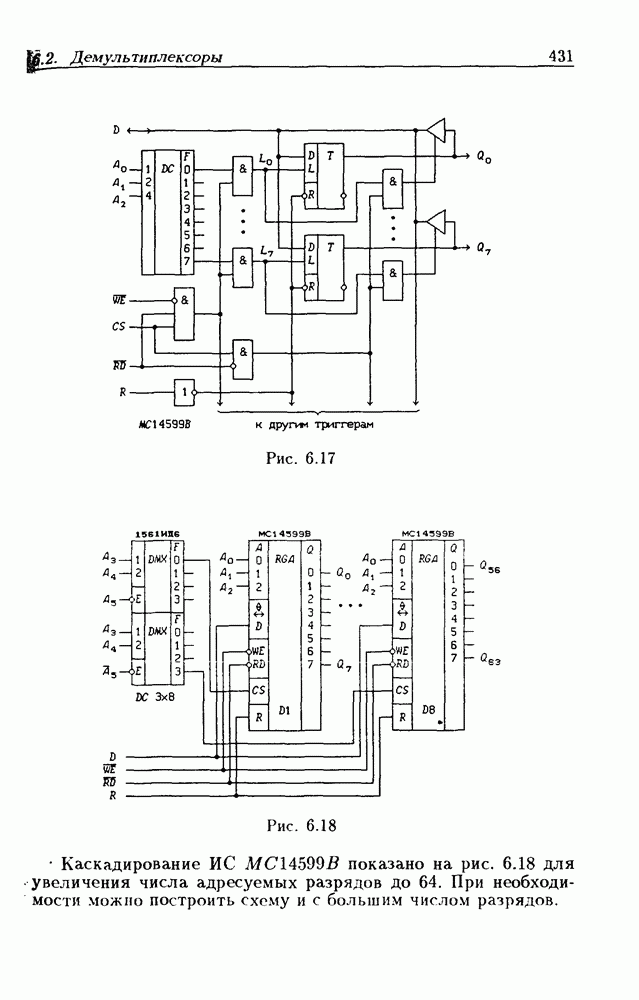
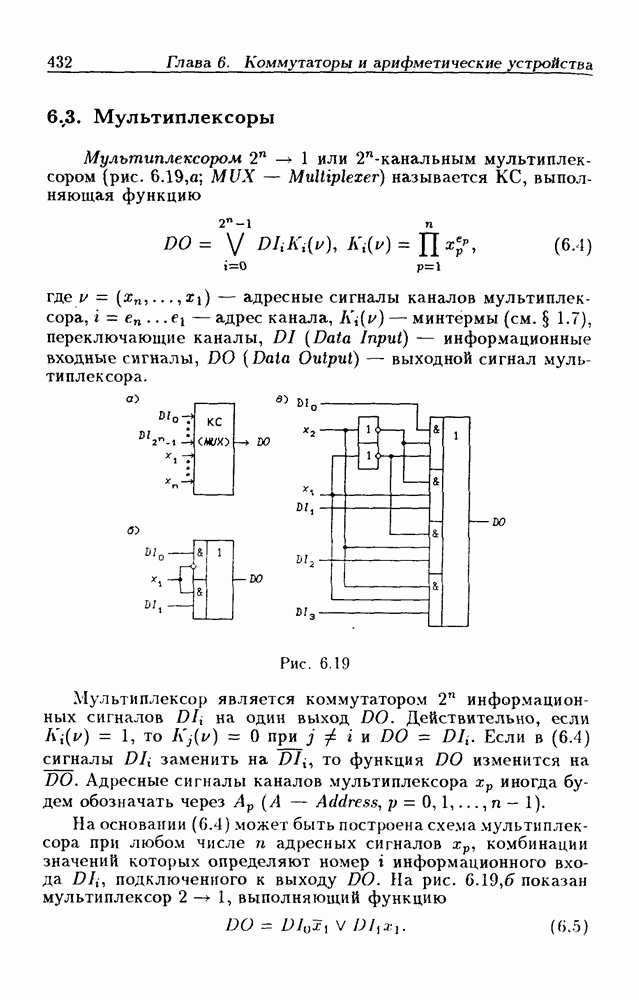
- 6.2. Демультиплексоры
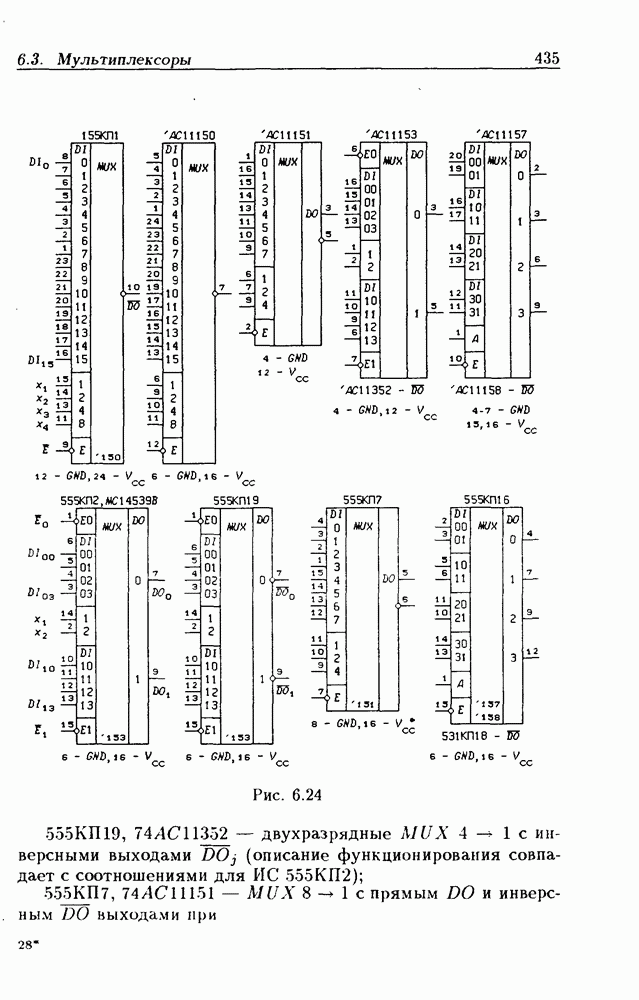
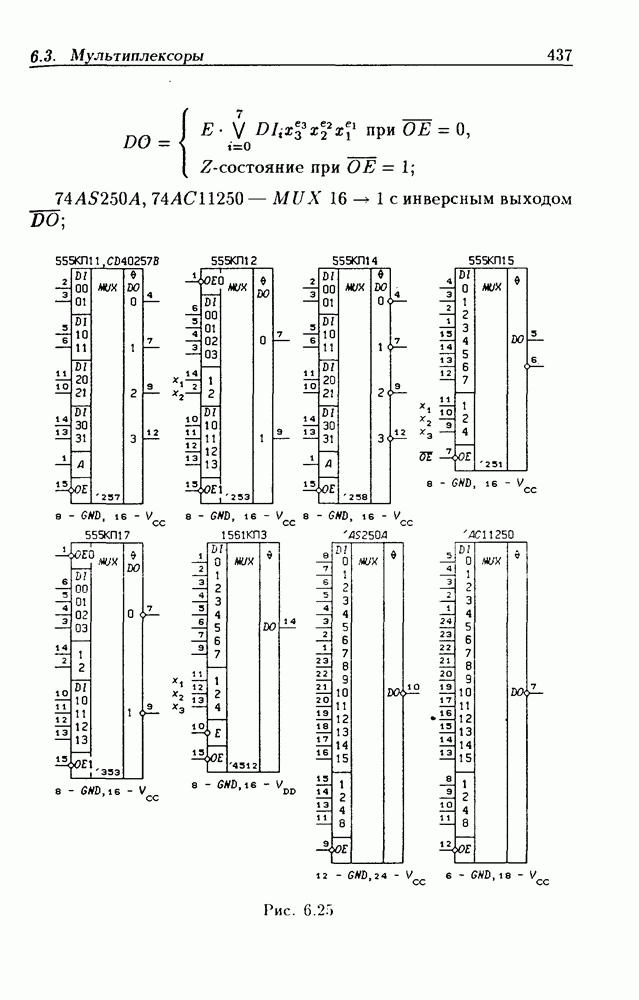
- 6.3. Мультиплексоры
- Мультиплексоры без стробирования.
- Мультиплексоры со стробированием.
- Мультиплексоры с Z-состоянием выхода.
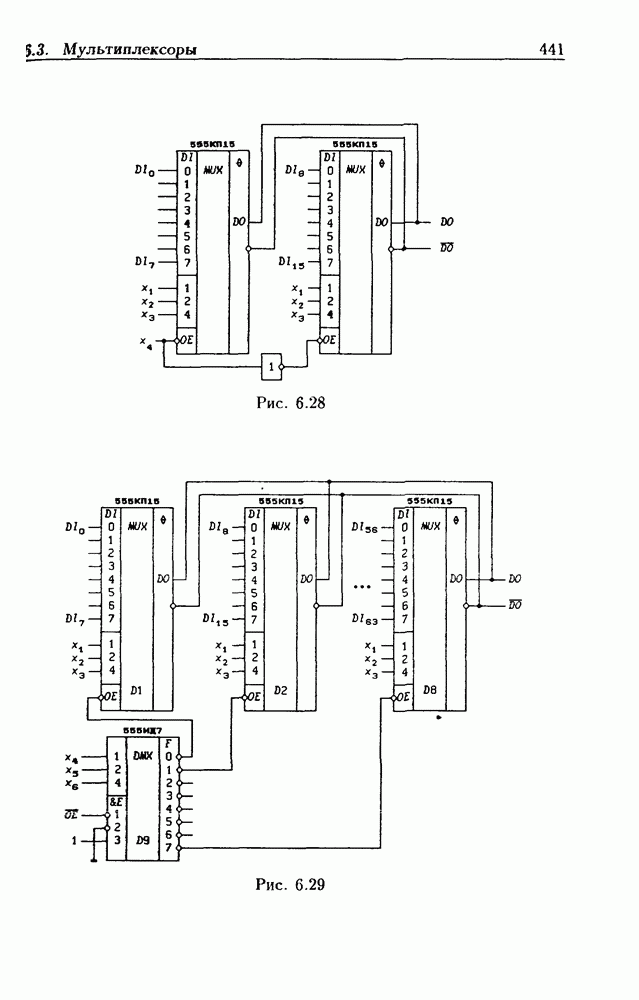
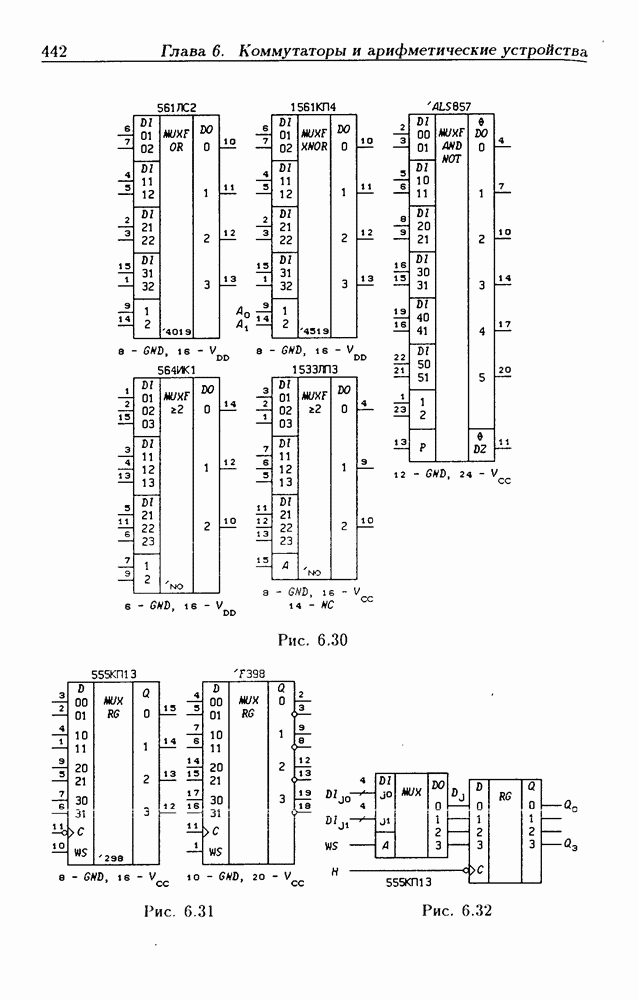
- Каскадирование мультиплексоров.
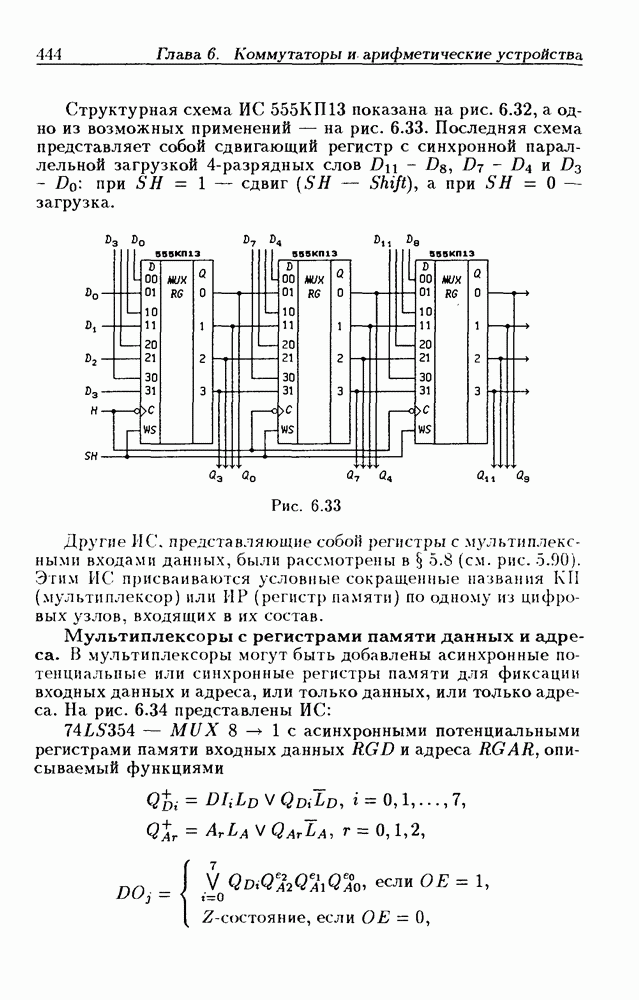
- Функциональные мультиплексоры.
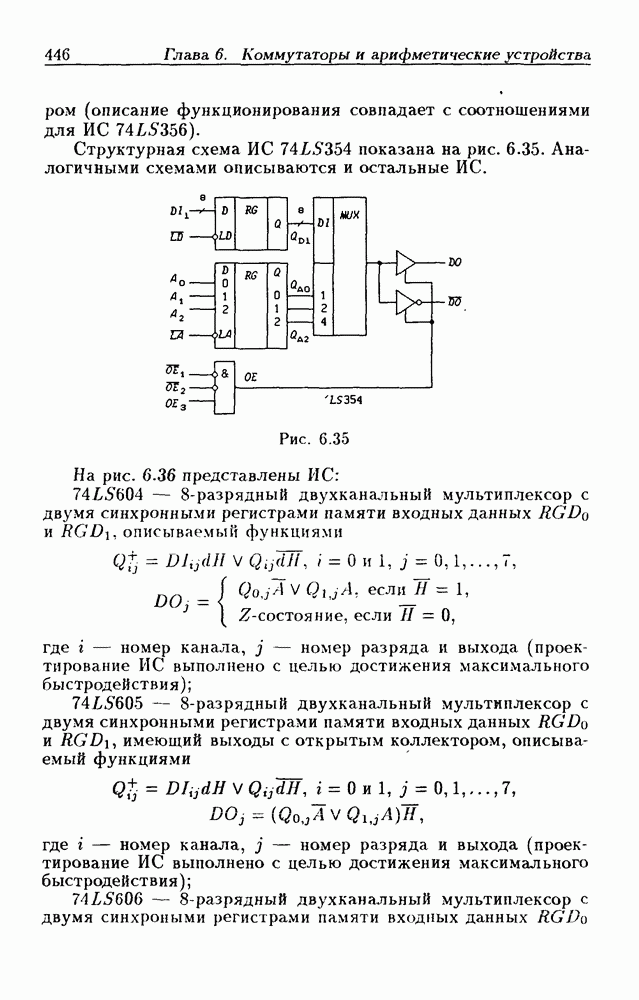
- Регистры памяти с мультиплексными входами данных.
- Мультиплексоры с регистрами памяти данных и адреса.
- Сдвигающие мультиплексоры.
- 6.4. Синтез комбинационных схем и цифровых автоматов на мультиплексорах
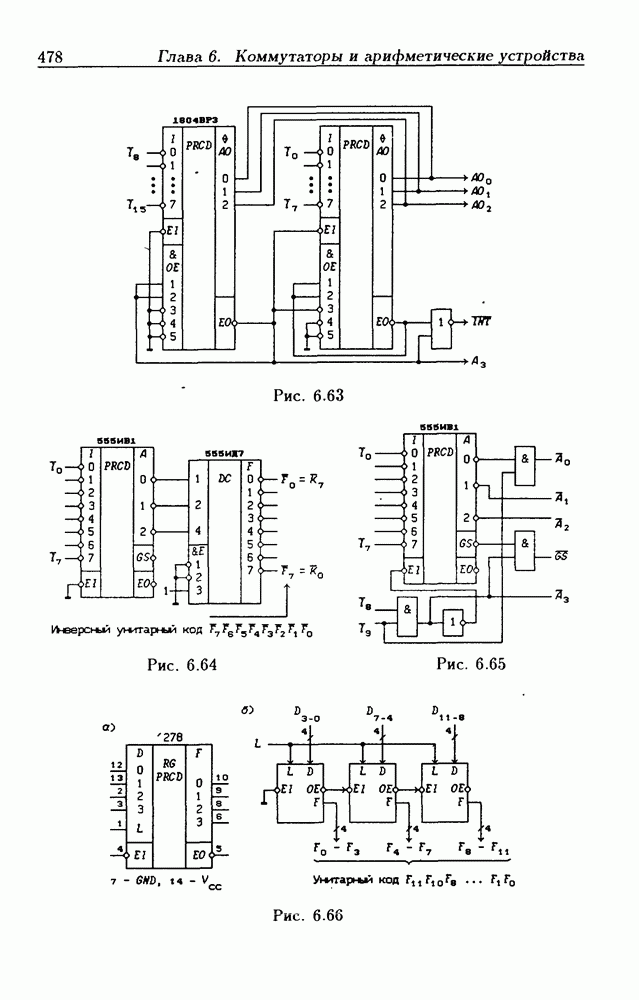
- Синтез схем на 8-канальных мультиплексорах.
- Синтез на двухразрядных 4-канальных мультиплексорах.
- Синтез генератора синусоидальной функции на мультиплексорах.
- Синтез триггеров на мультиплексорах.
- Синтез счетчиков на мультиплексорах.
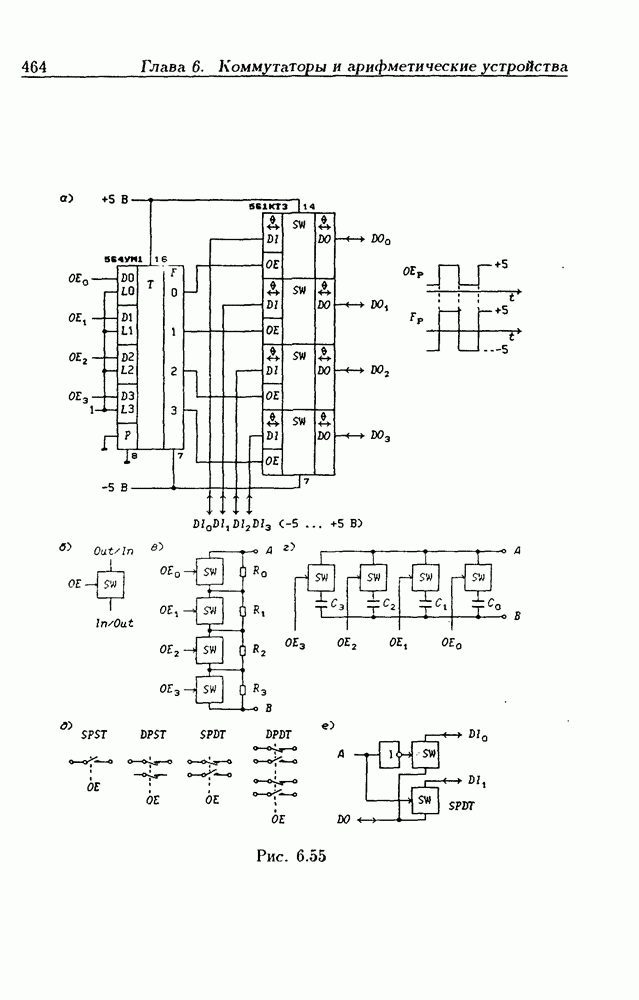
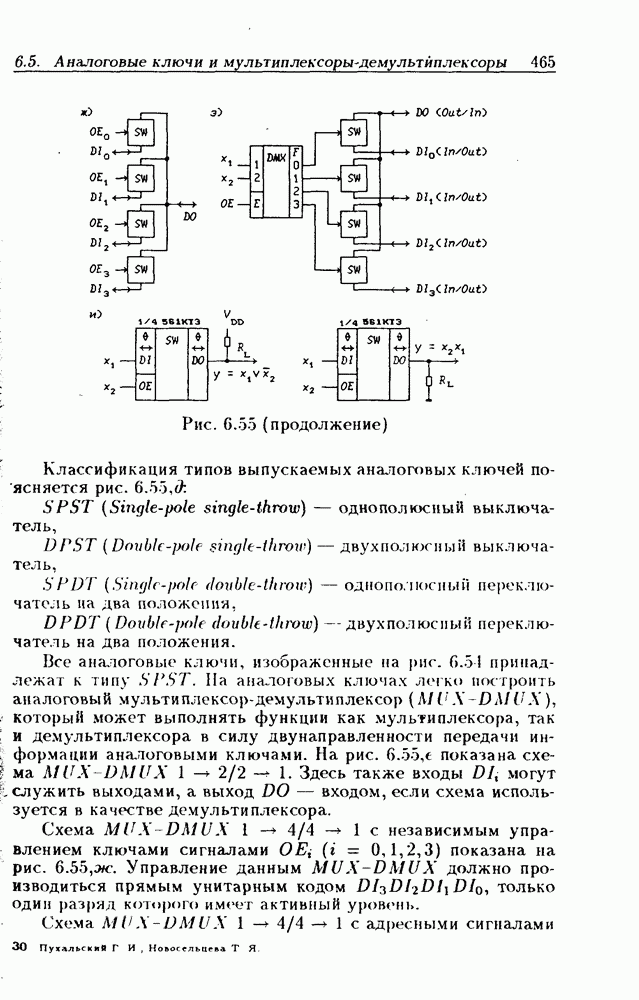
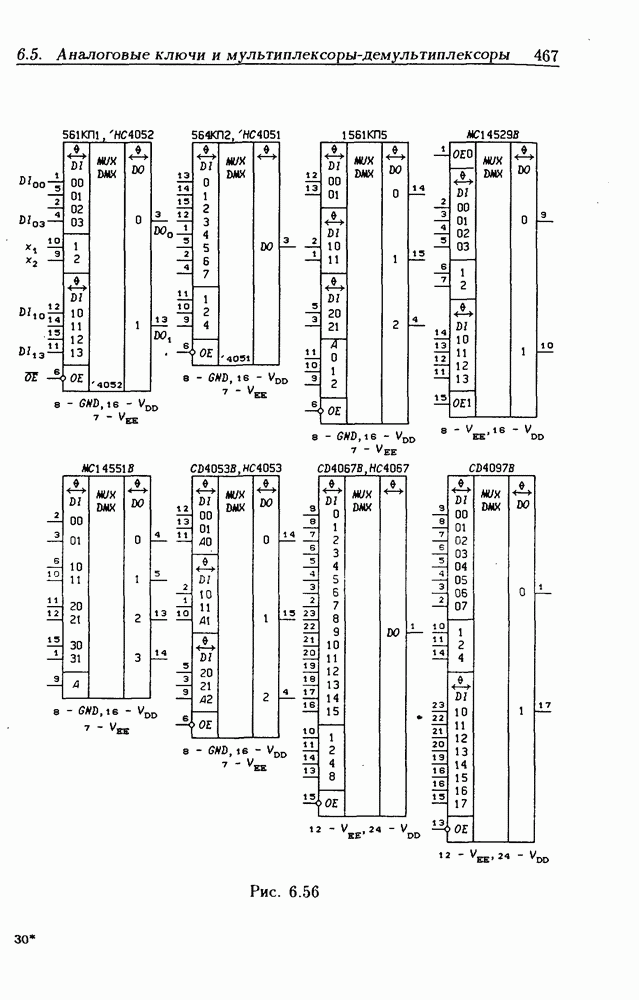
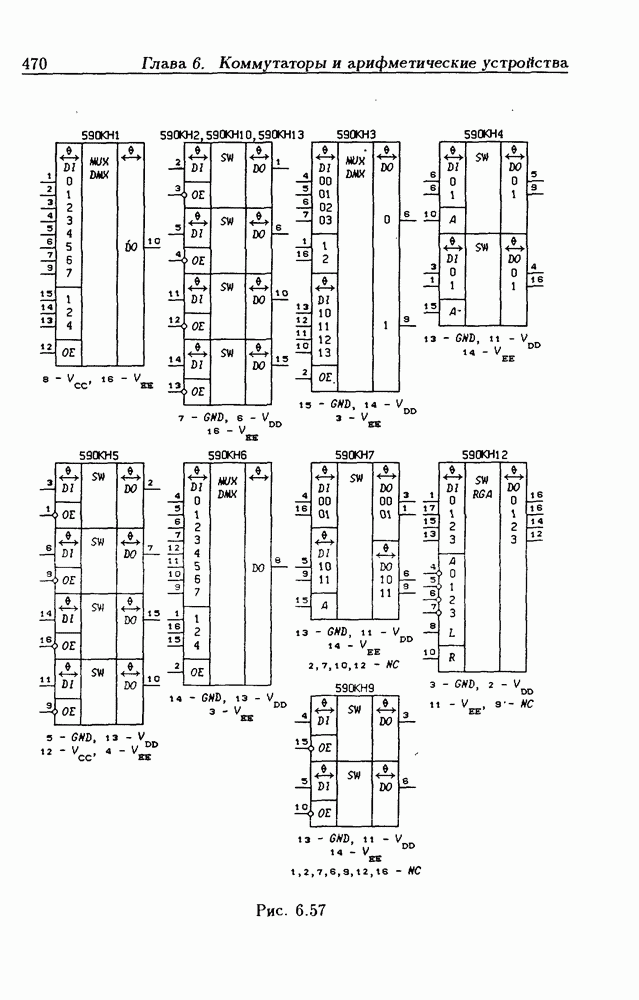
- 6.5. Аналоговые ключи и мультиплексоры-демультиплексоры
- 6.6. Шифраторы
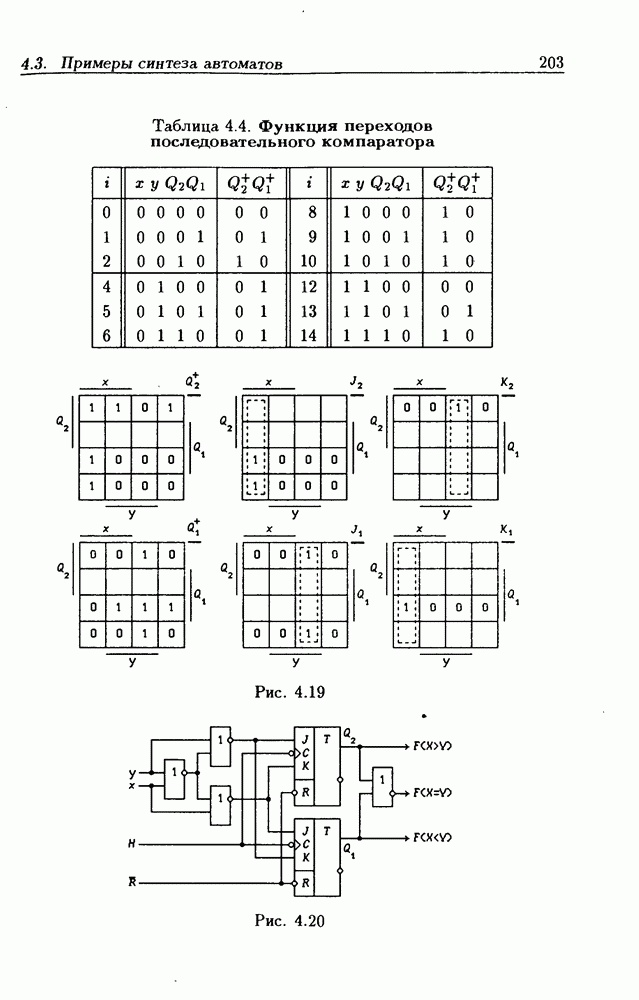
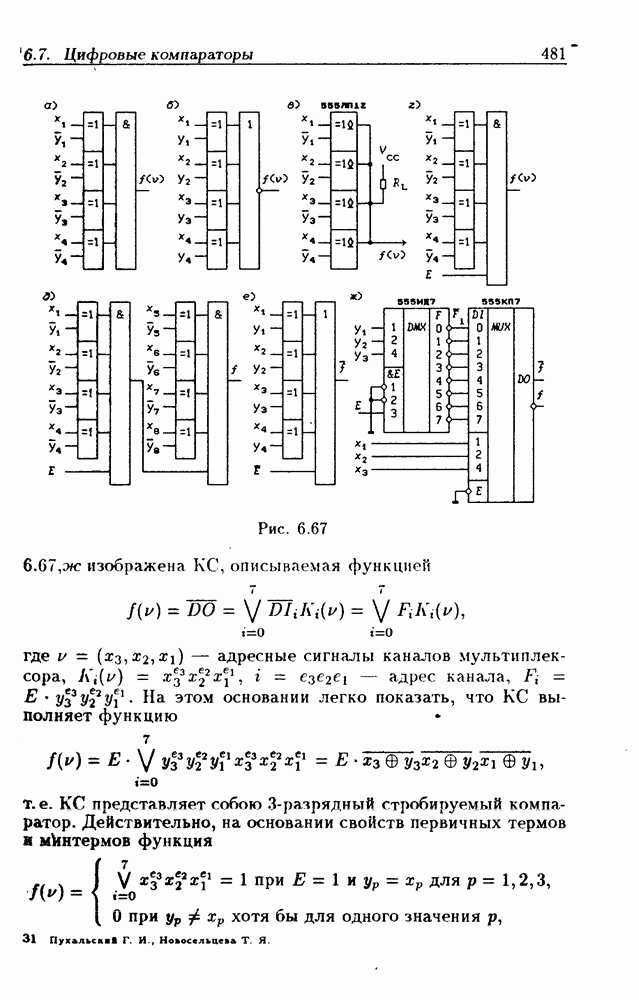
- 6.7. Цифровые компараторы
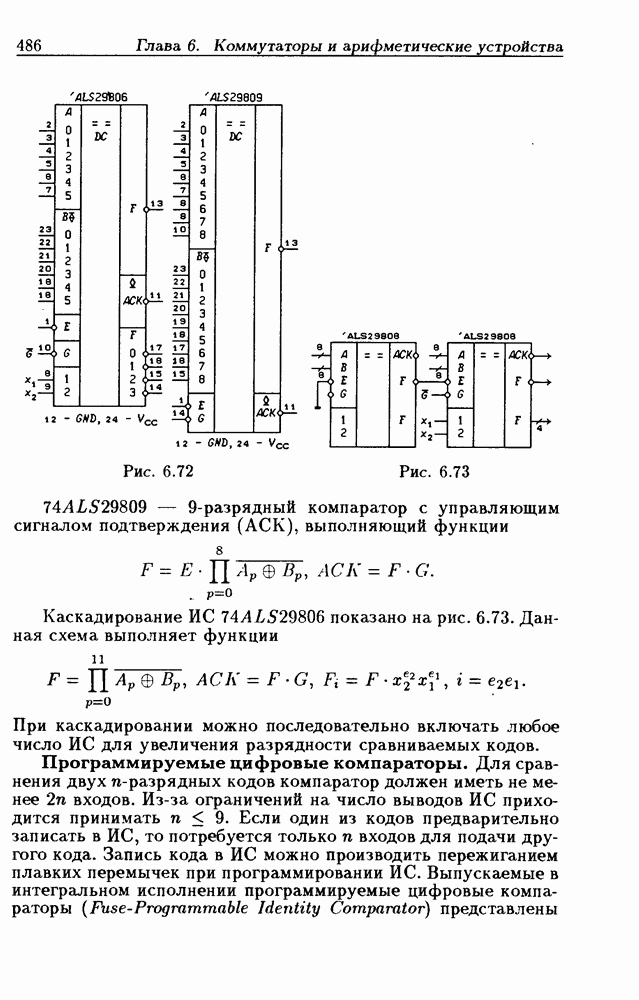
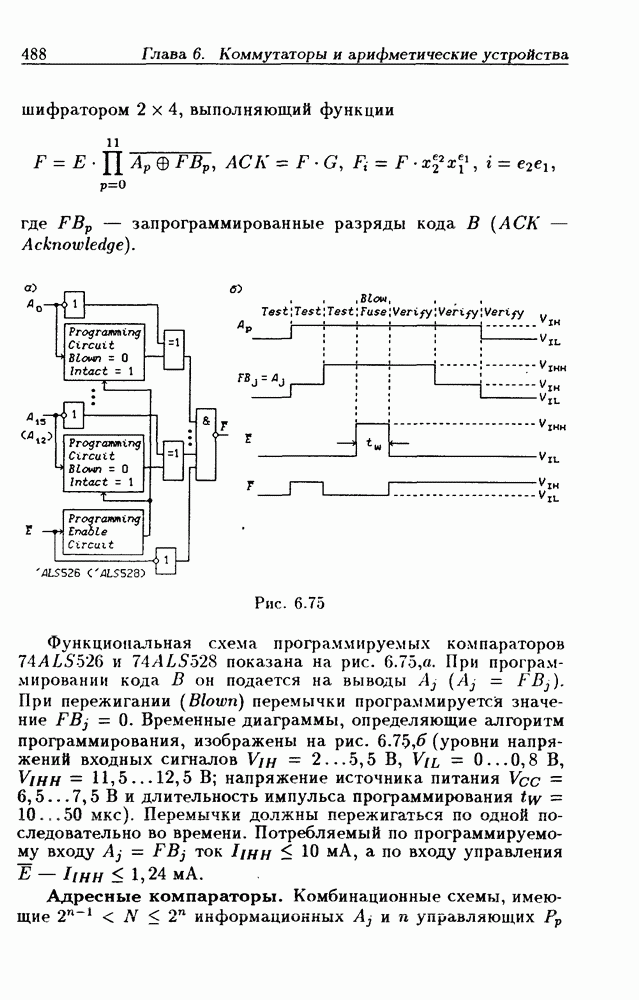
- Программируемые цифровые компараторы.
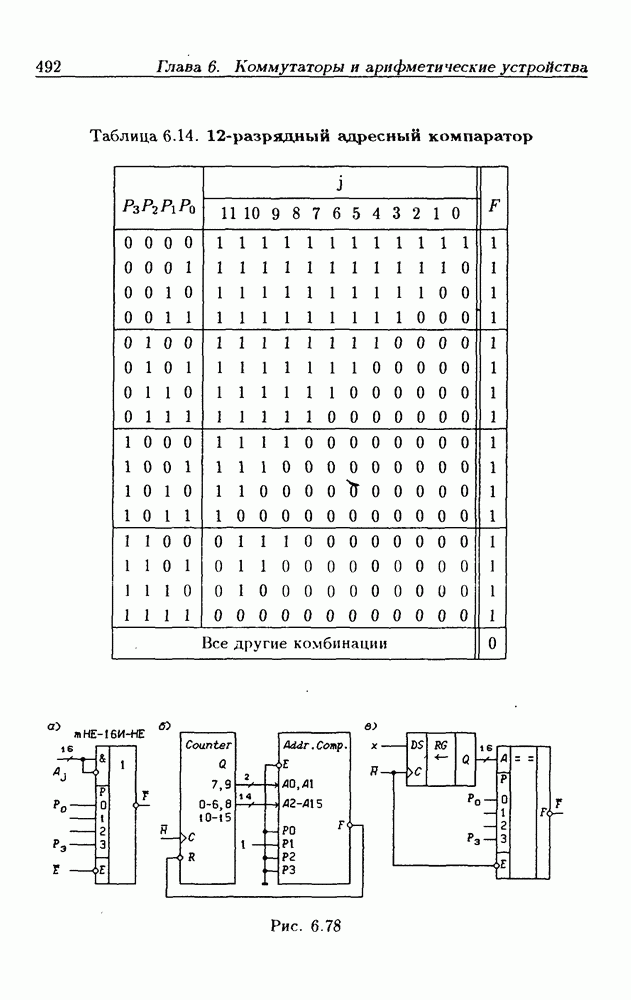
- Адресные компараторы.
- Применения адресных компараторов.
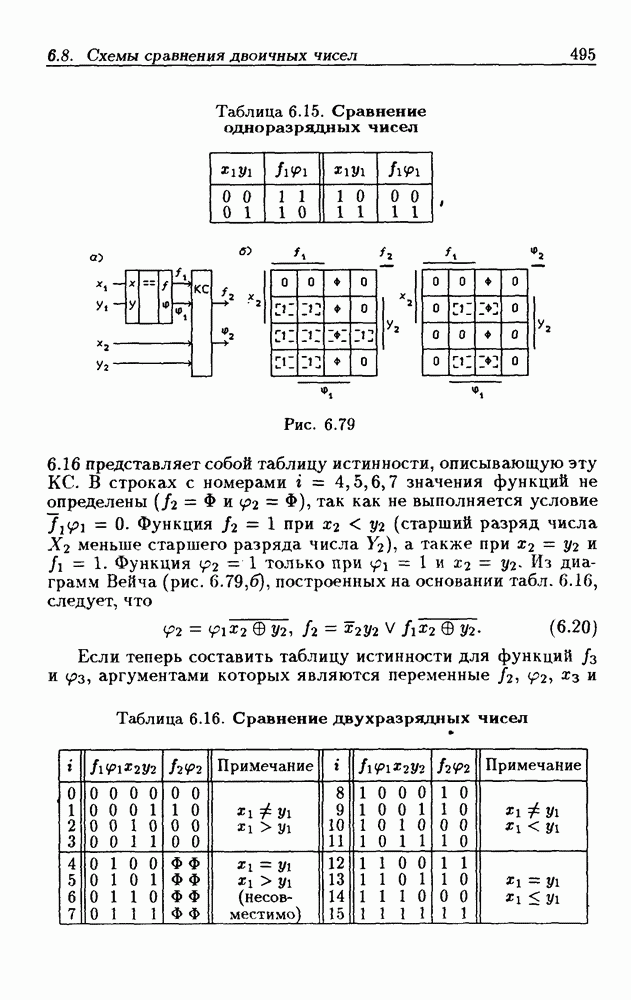
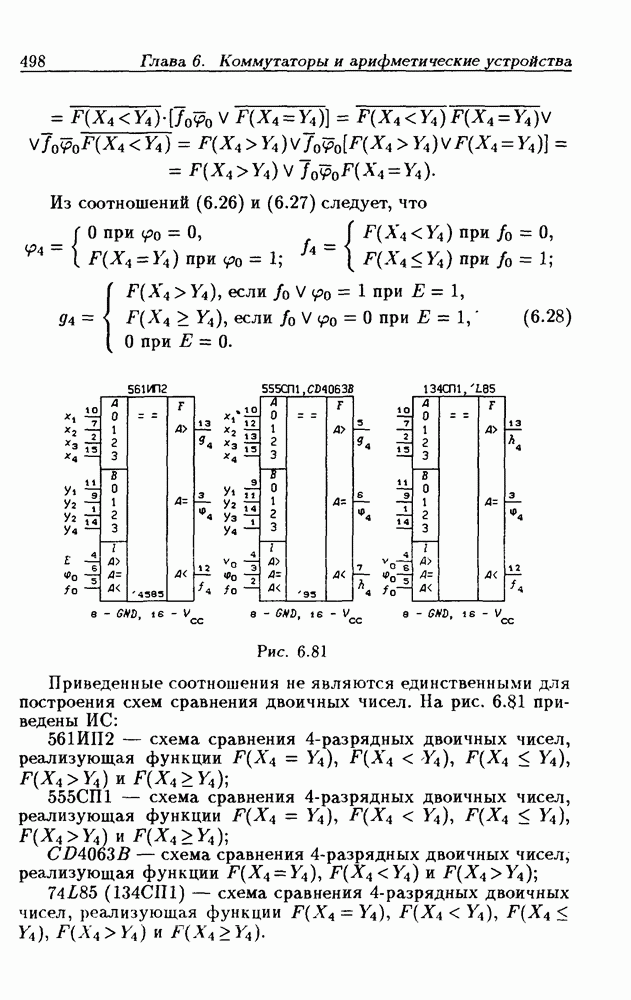
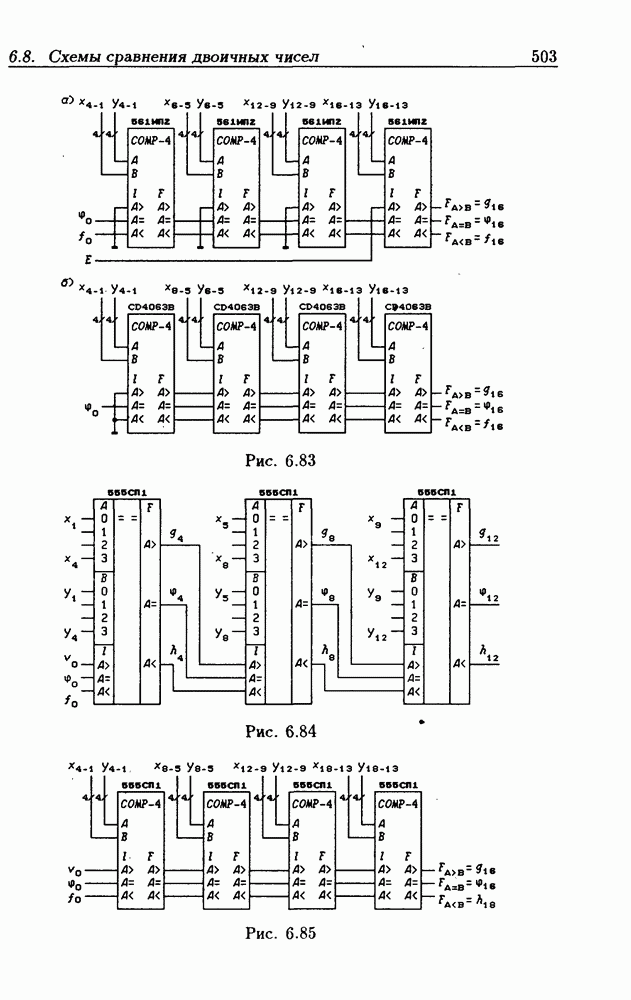
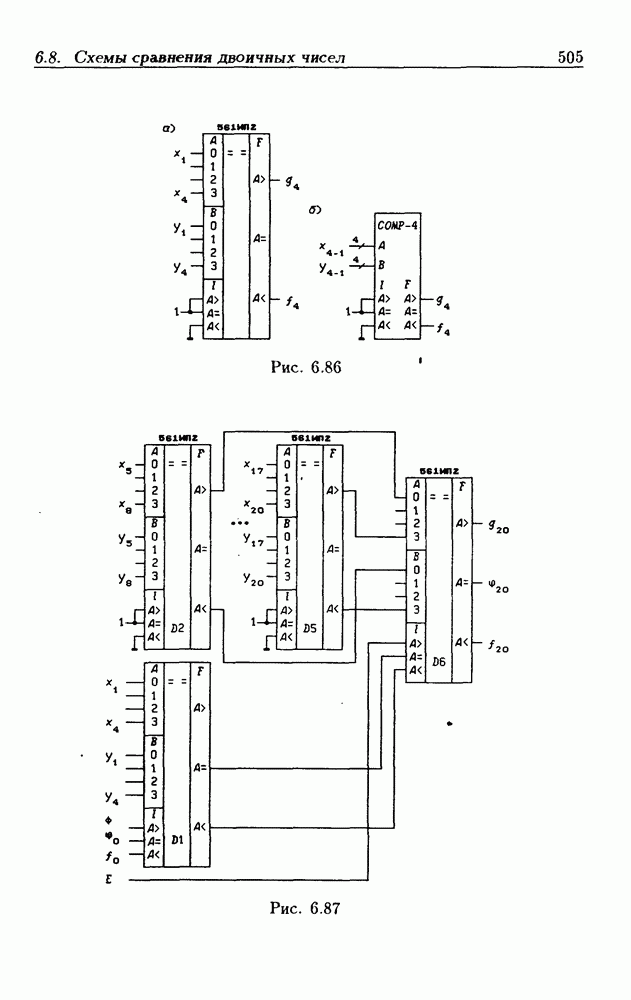
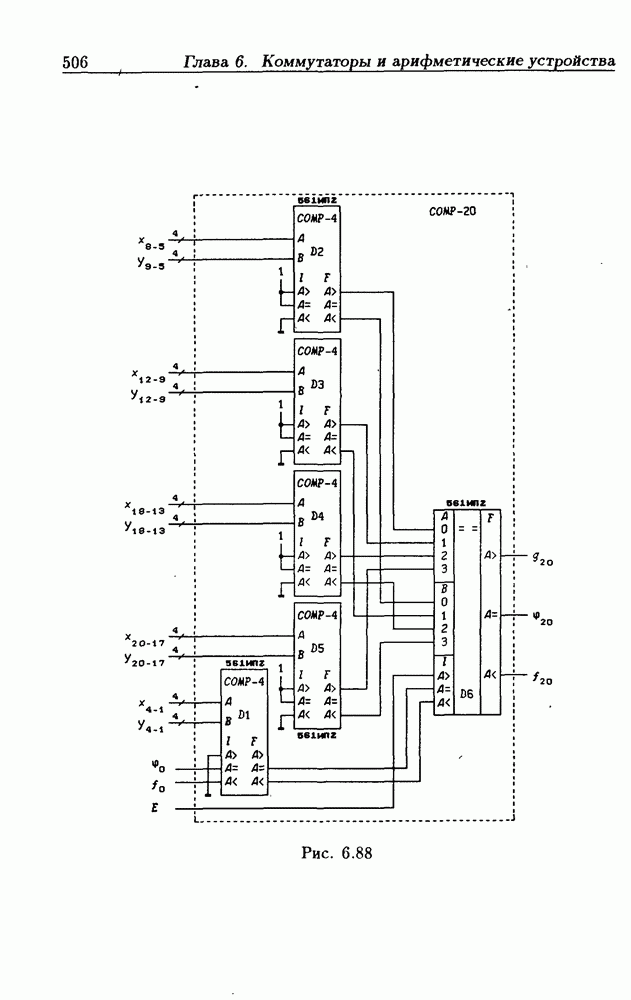
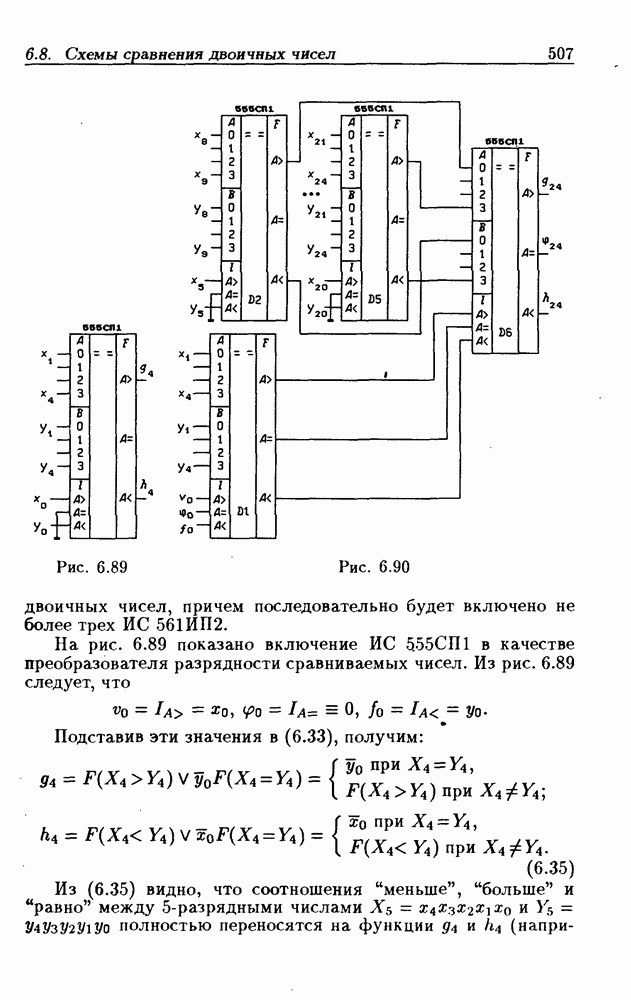
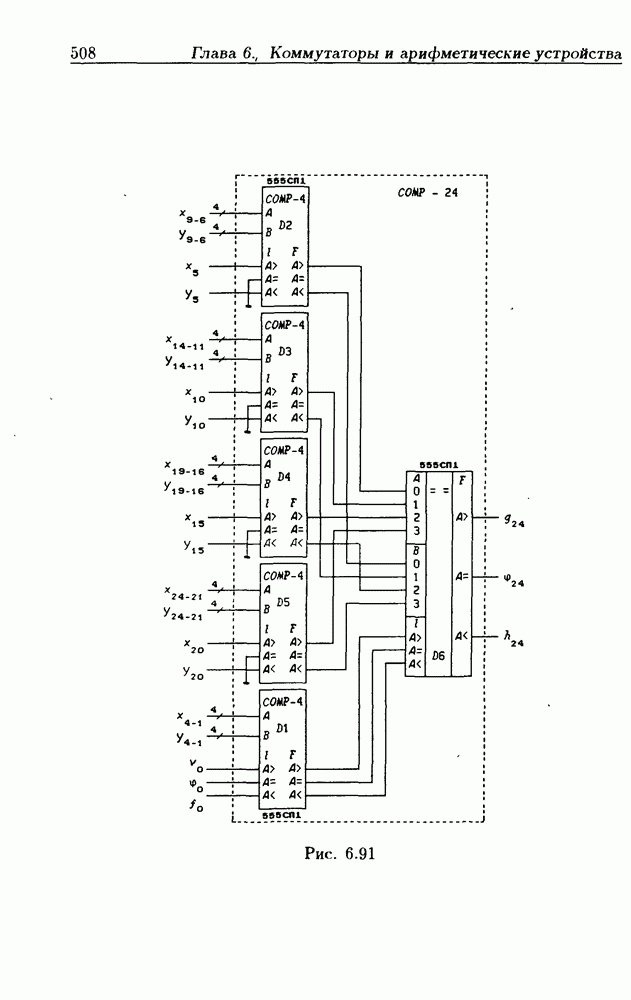
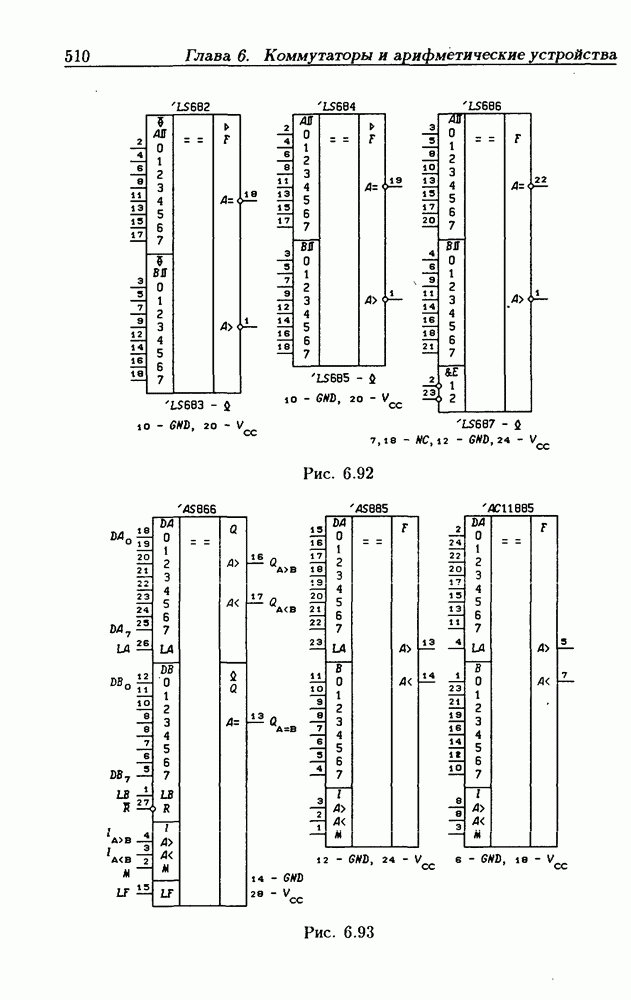
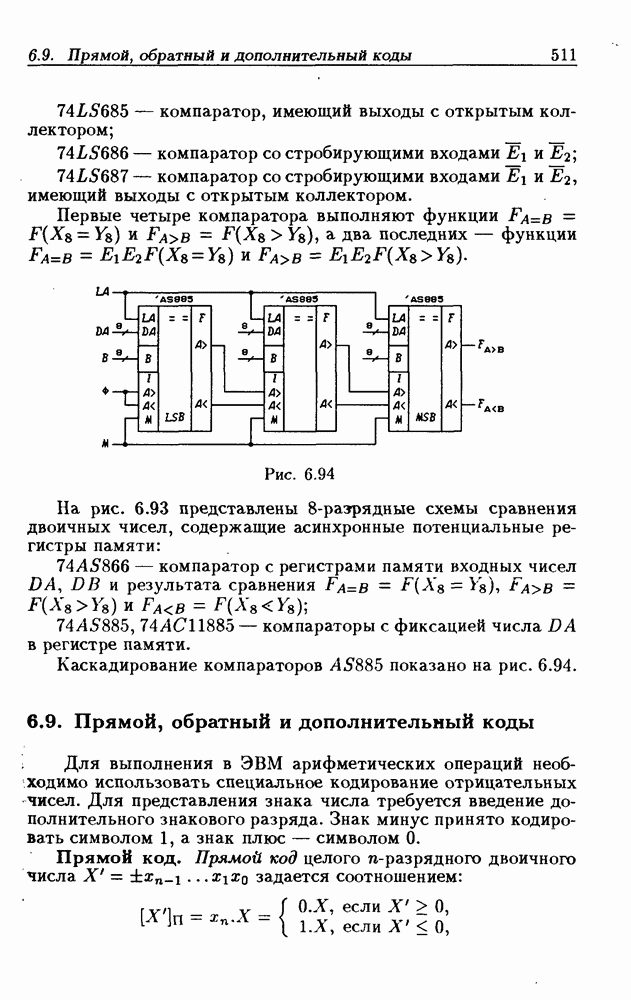
- 6.8. Схемы сравнения двоичных чисел
- 8-разрядные схемы сравнения двоичных чисел.
- 6.9. Прямой, обратный и дополнительный коды
- Дополнительный код.
- Сложение чисел в обратном коде.
- Код с избытком 3.
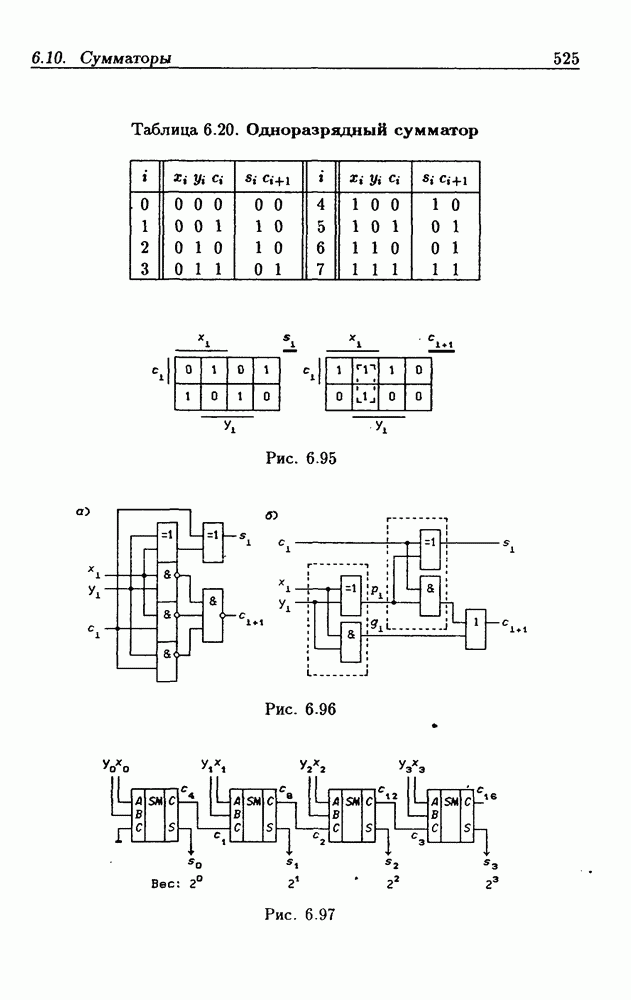
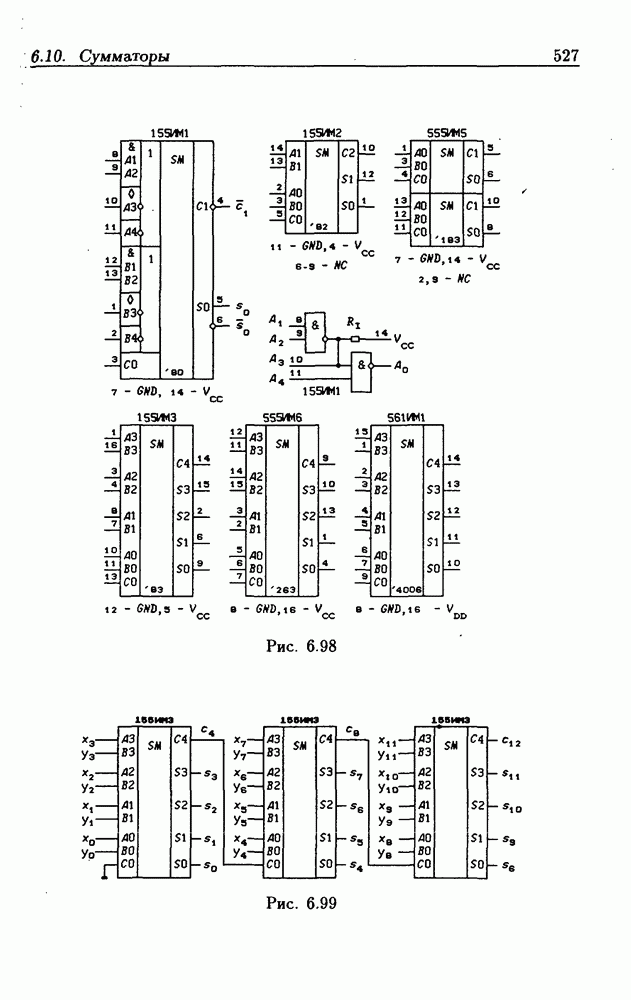
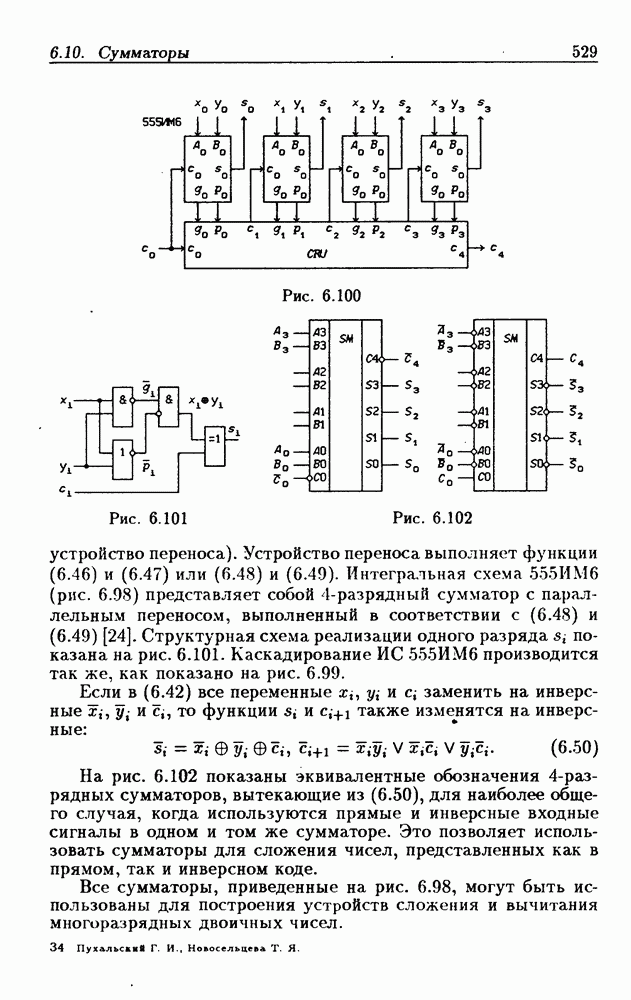
- 6.10. Сумматоры
- Двоичные параллельные сумматоры с последовательным переносом.
- Двоичные сумматоры с параллельным переносом.
- Применения сумматоров.
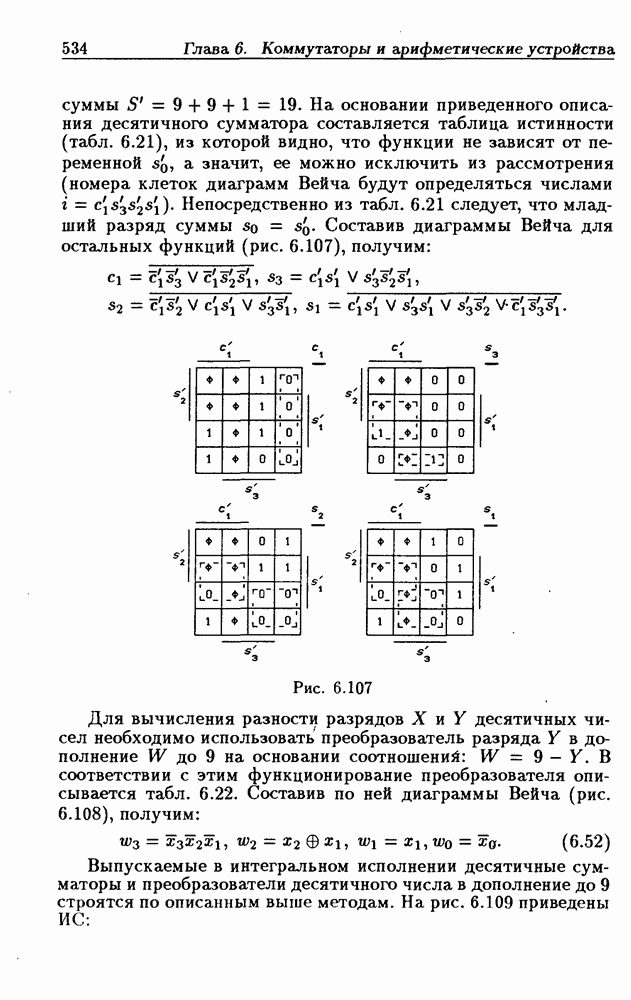
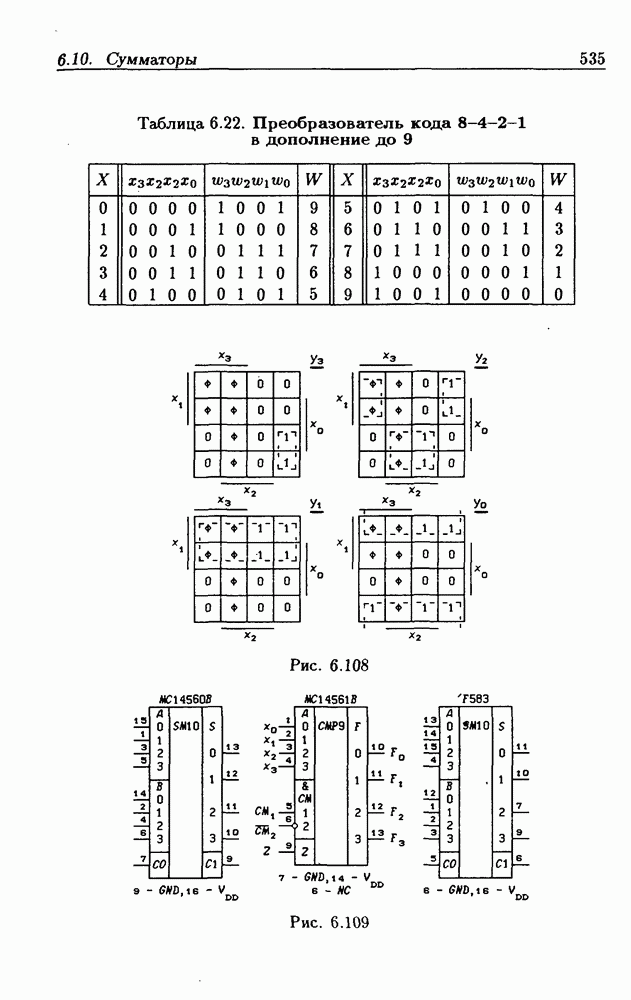
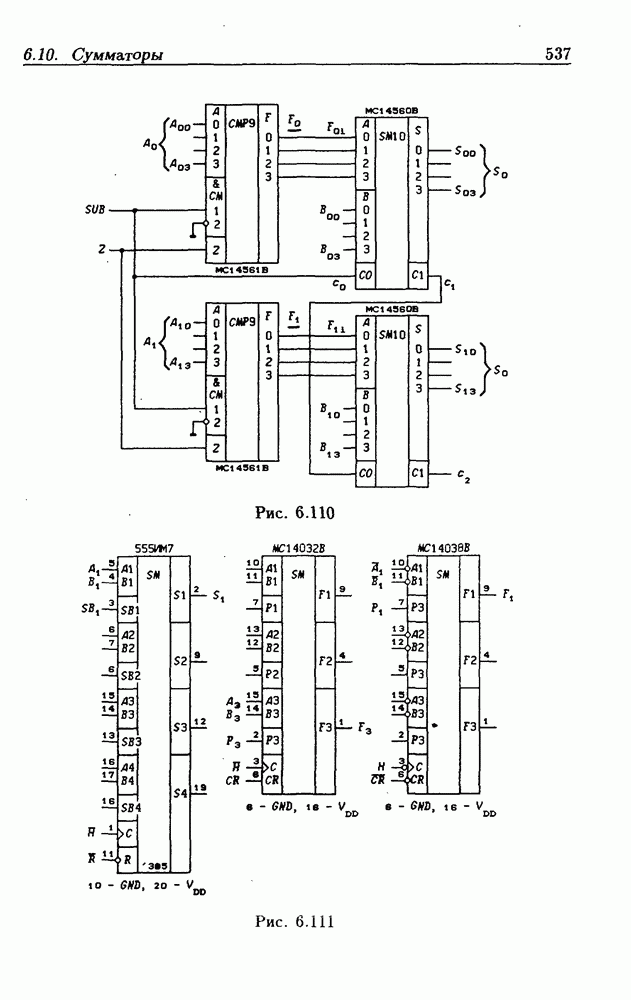
- Десятичные сумматоры.
- Последовательные двоичные сумматоры.
- 6.11. Арифметическо-логические устройства
- 6.12. Пороговые схемы и мажоритарные элементы
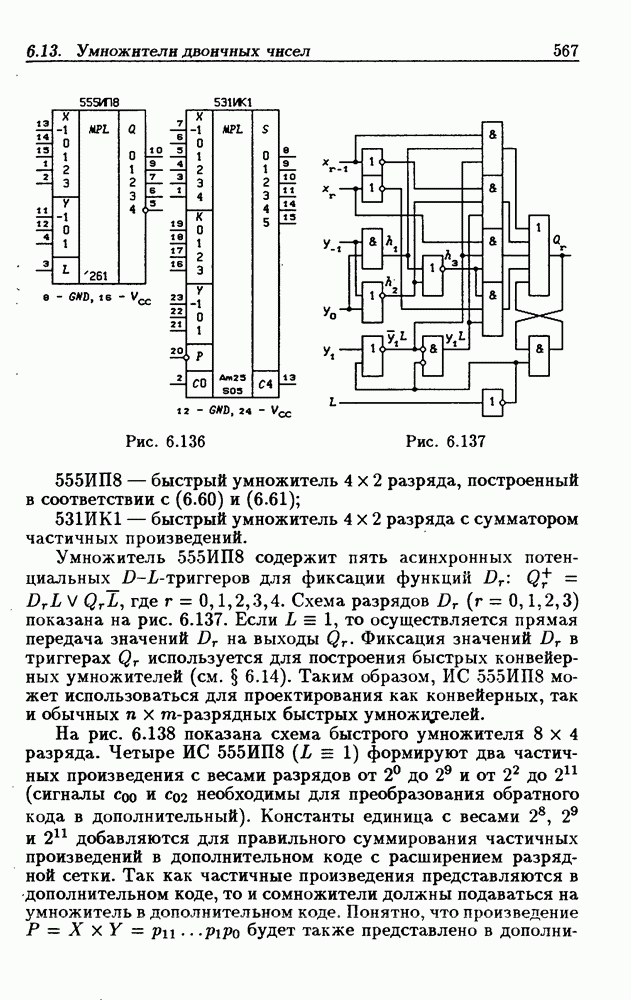
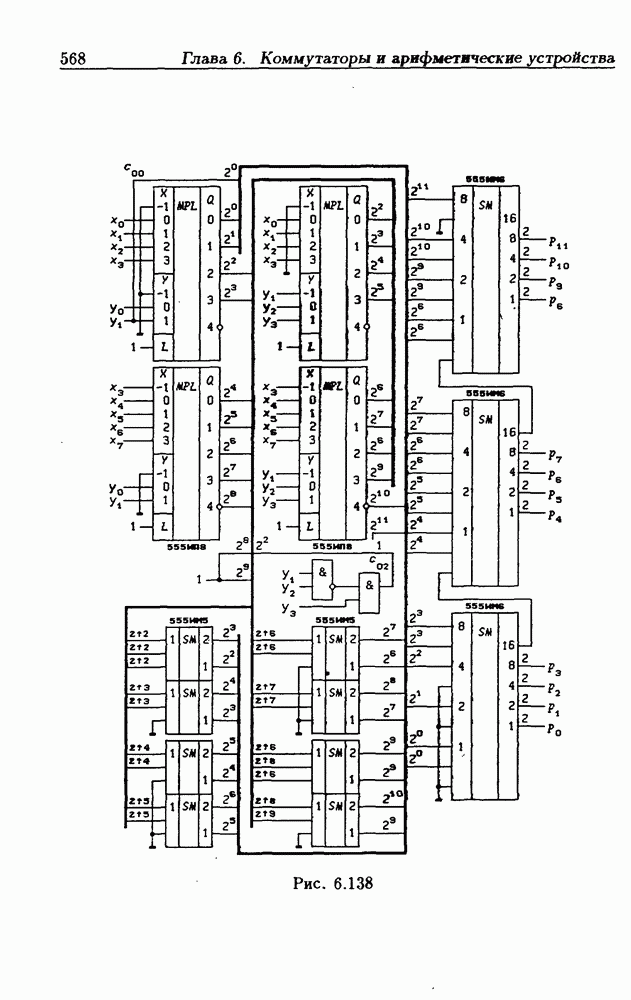
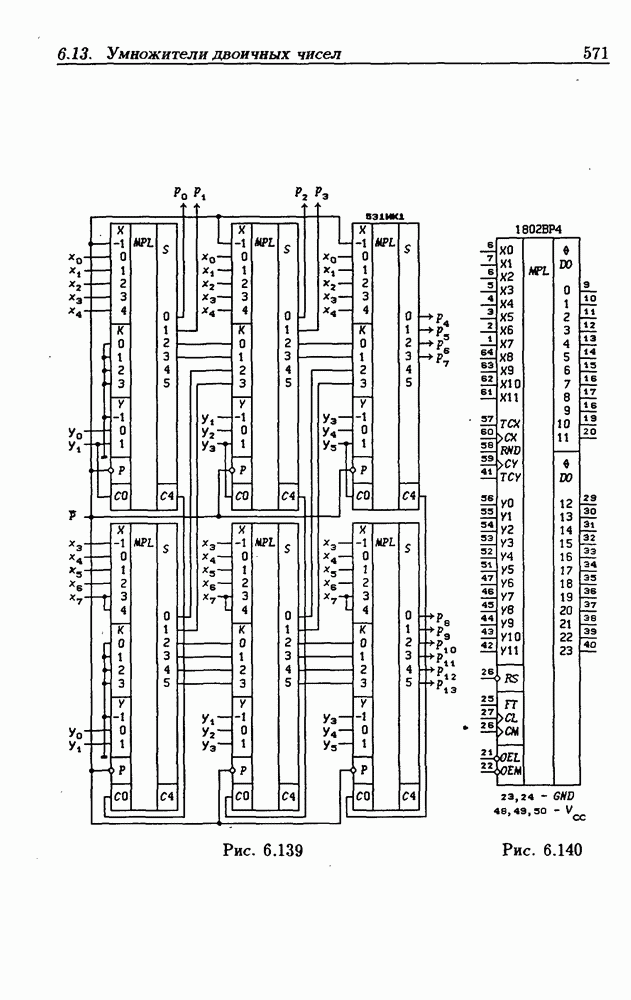
- 6.13. Умножители двоичных чисел
- Быстрые умножители.
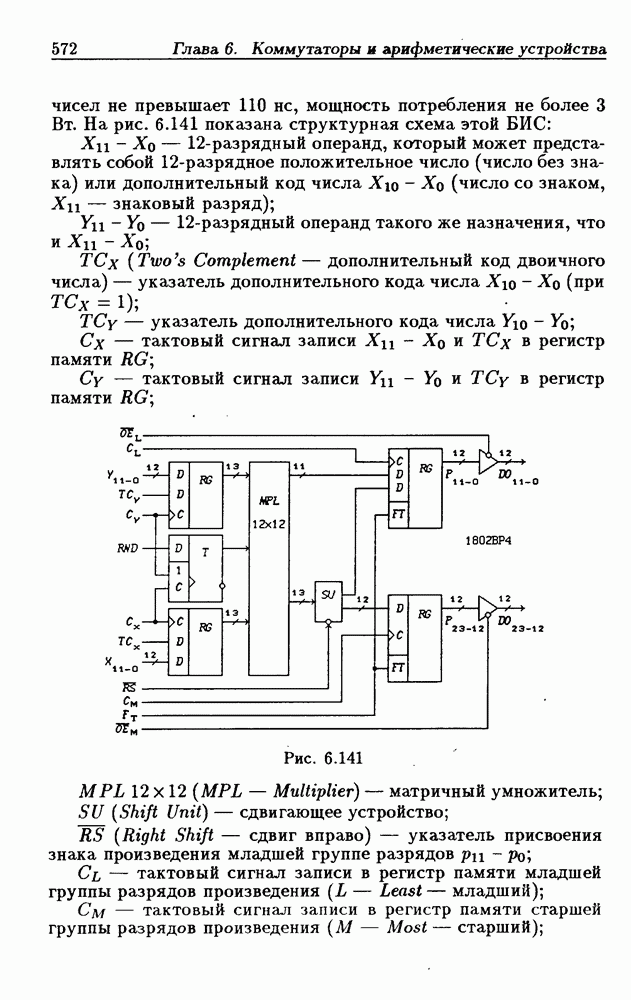
- БИС умножителя 12×12 разрядов 1802ВР4.
- Последовательные умножители.
- 6.14. Конвейерные устройства
- Конвейерный быстрый умножитель.
- Конвейерные АЦП.
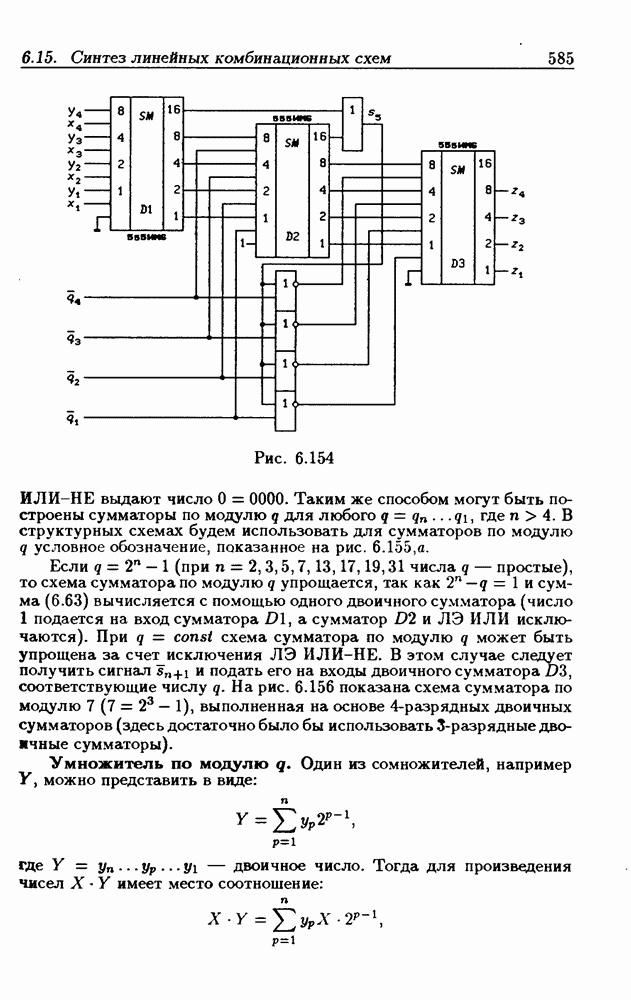
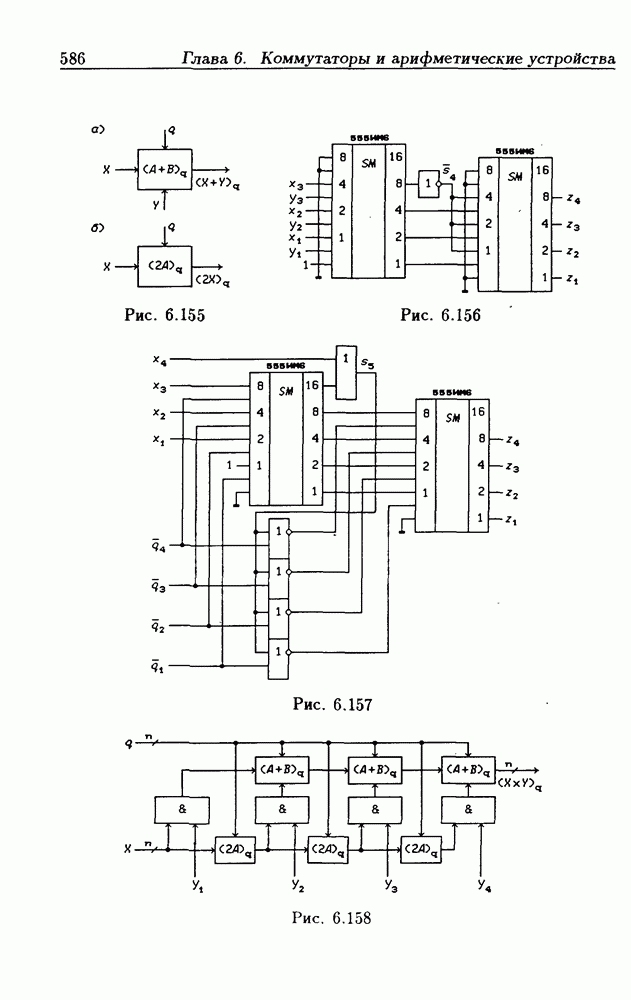
- 6.15. Синтез линейных комбинационных схем
- Сумматор по модулю q.
- Умножитель по модулю q.
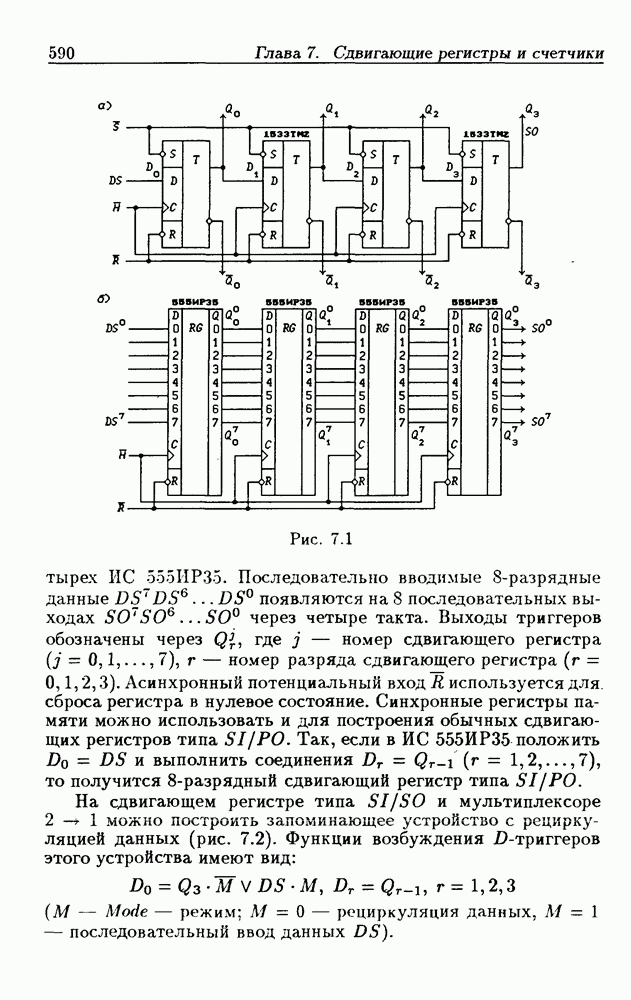
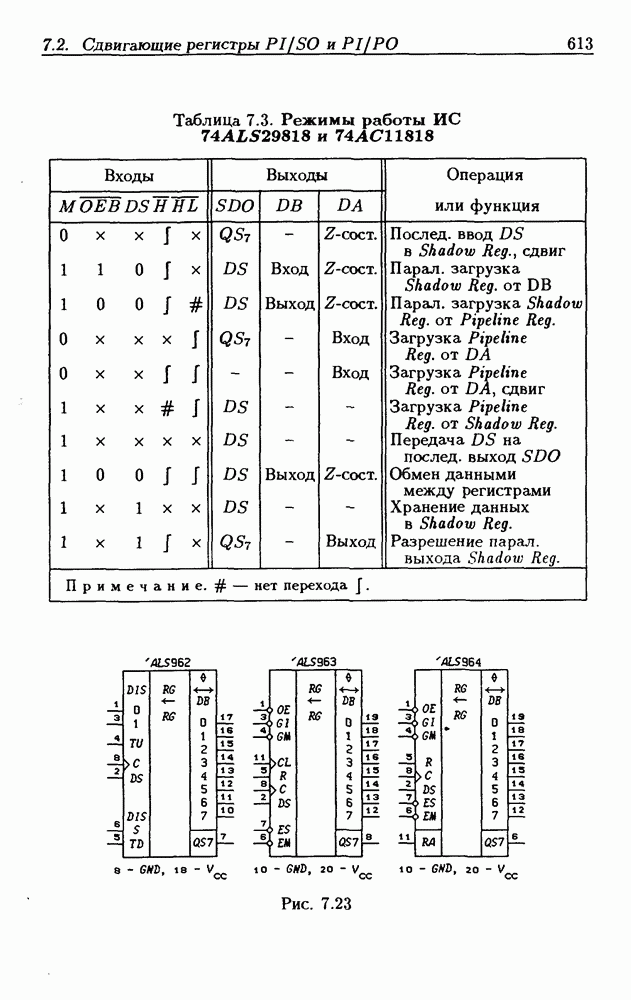
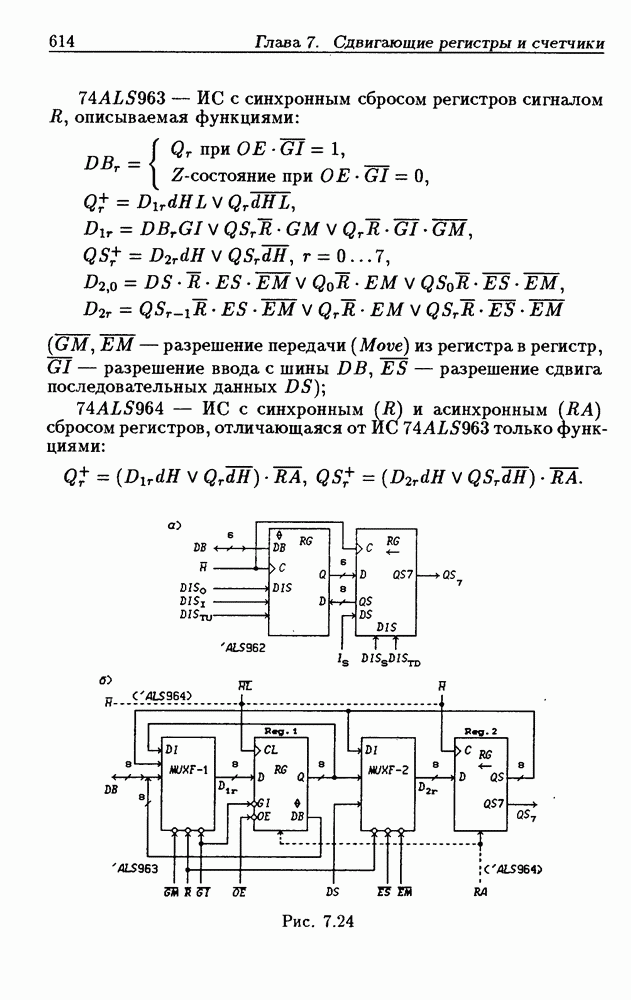
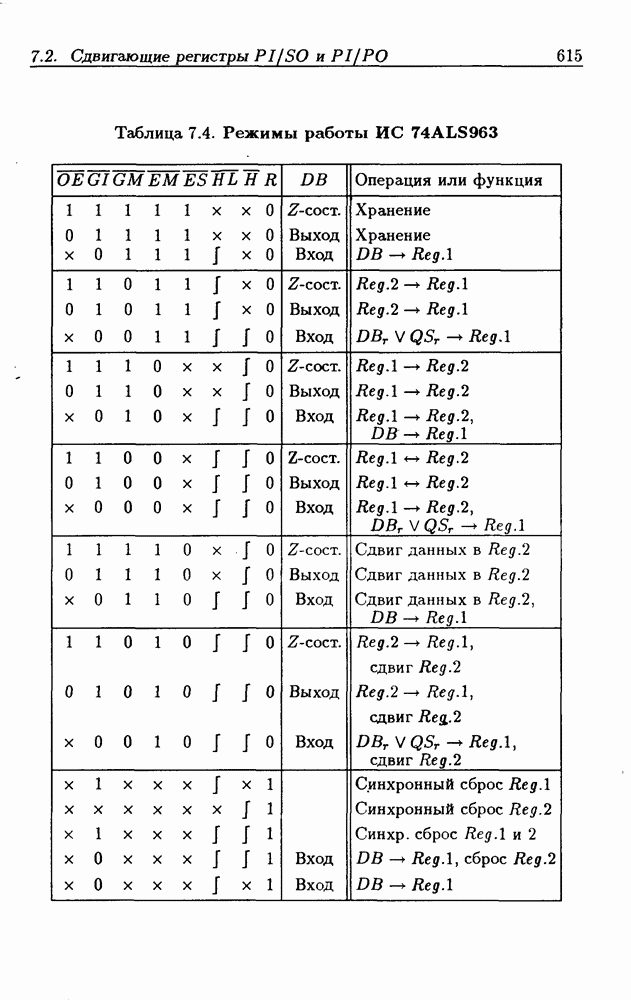
- Глава 7. Сдвигающие регистры и счетчики
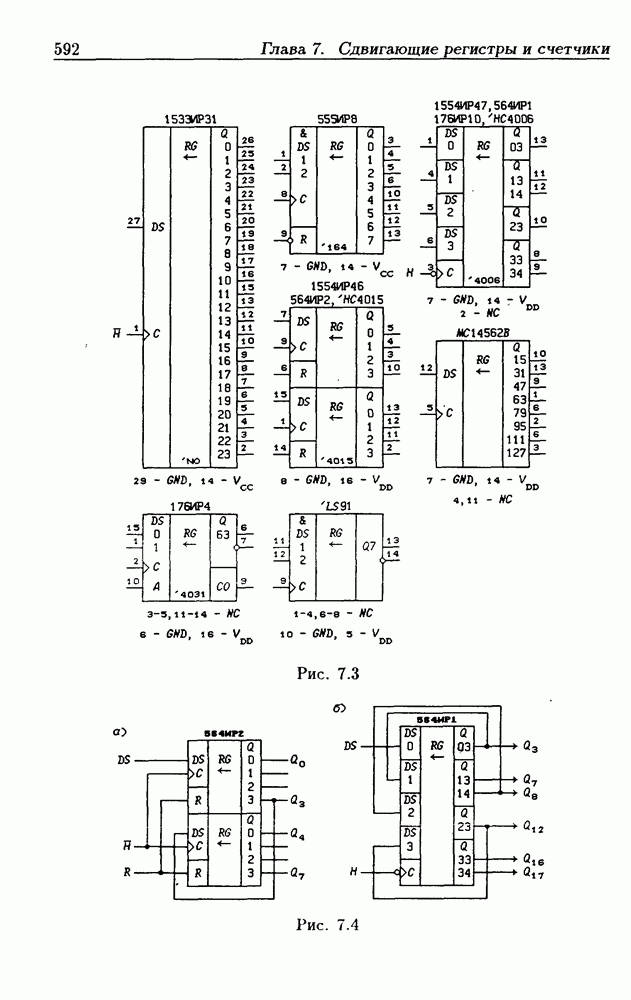
- 7.1. Сдвигающие регистры без параллельной записи данных
- Сдвигающие устройства с выходными регистрами памяти.
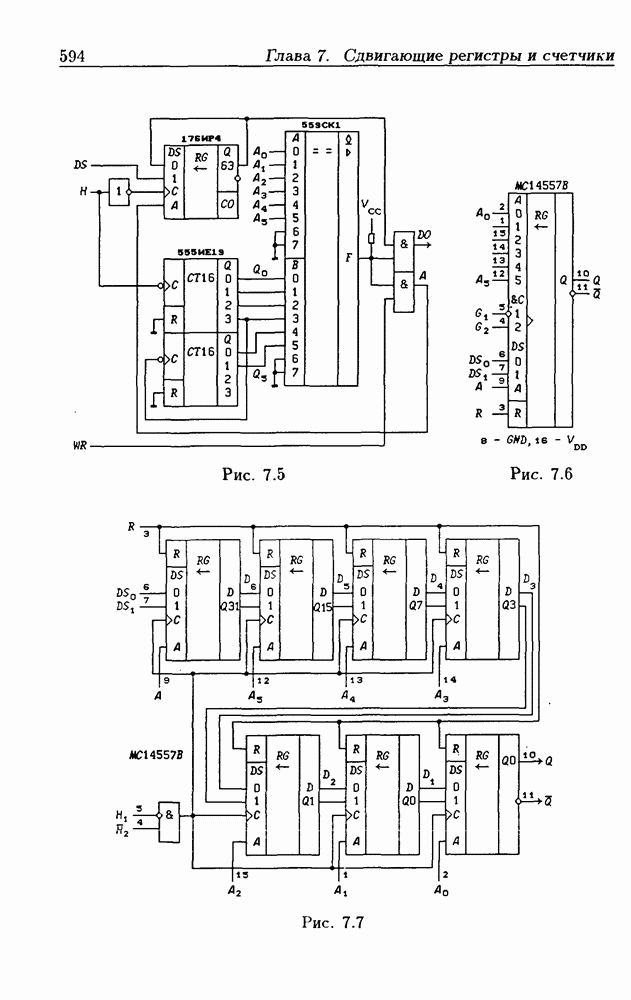
- 7.2. Сдвигающие регистры с параллельной записью данных
- Сдвигающие регистры с расширением знака.
- Сдвигающие регистры с входным регистром памяти.
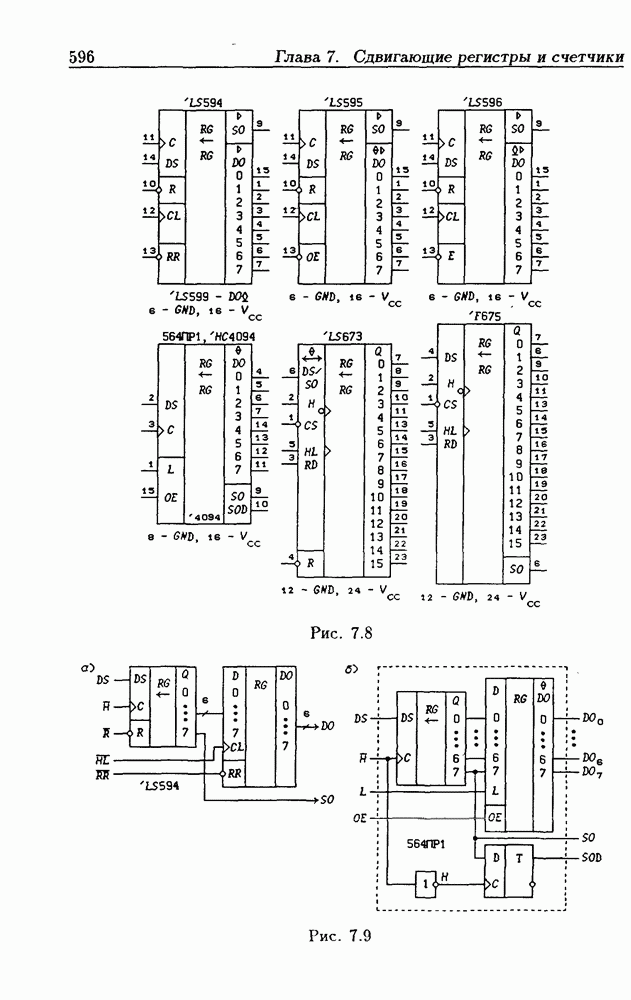
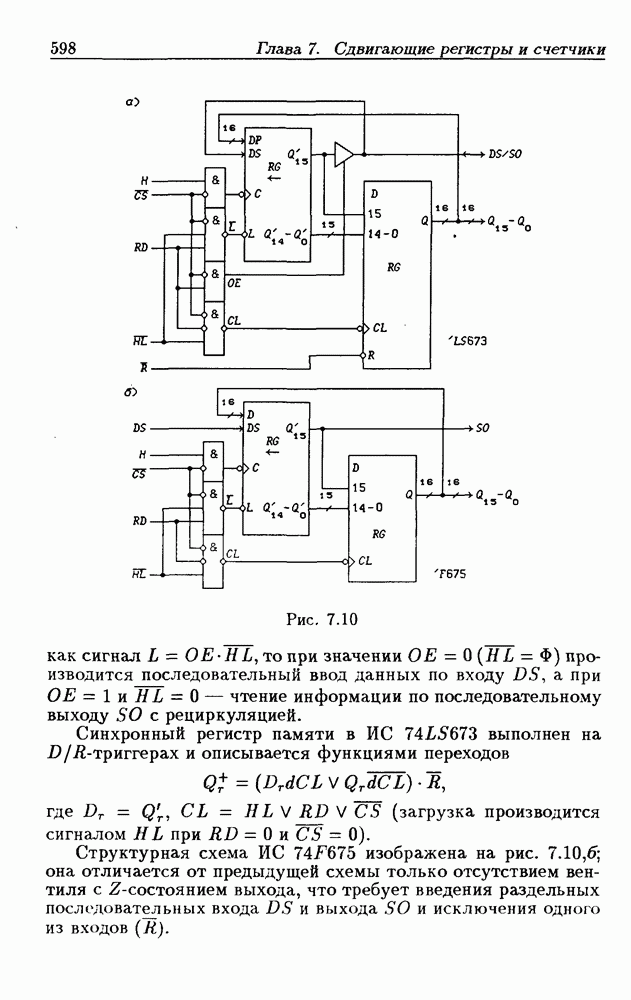
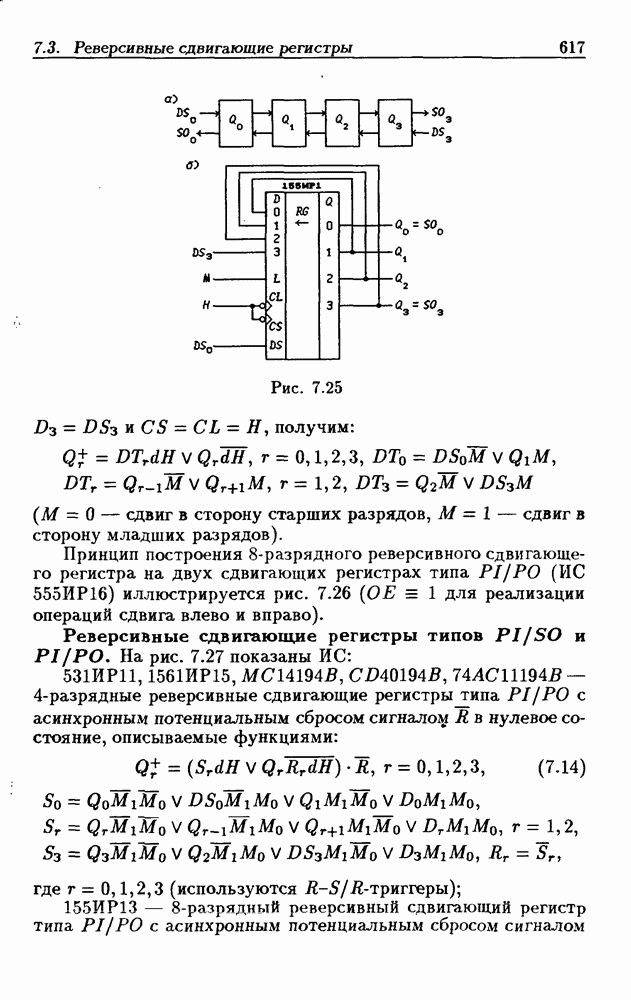
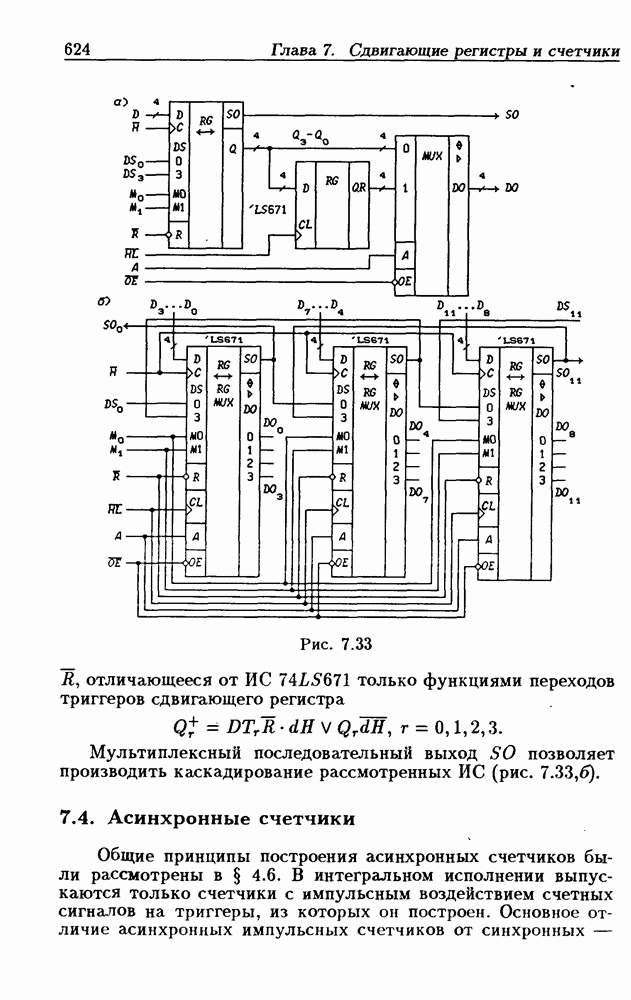
- 7.3. Реверсивные сдвигающие регистры
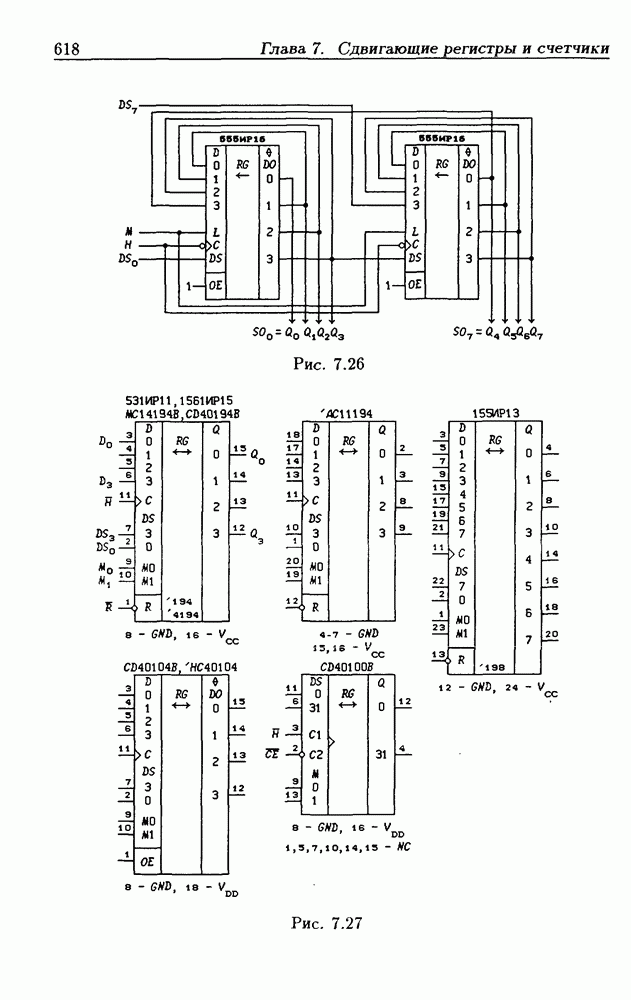
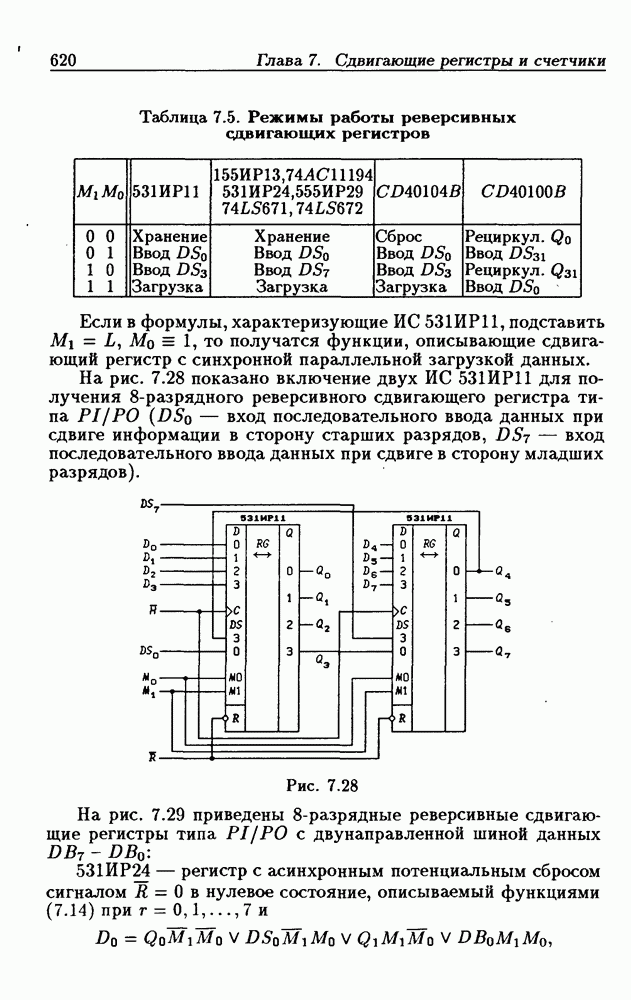
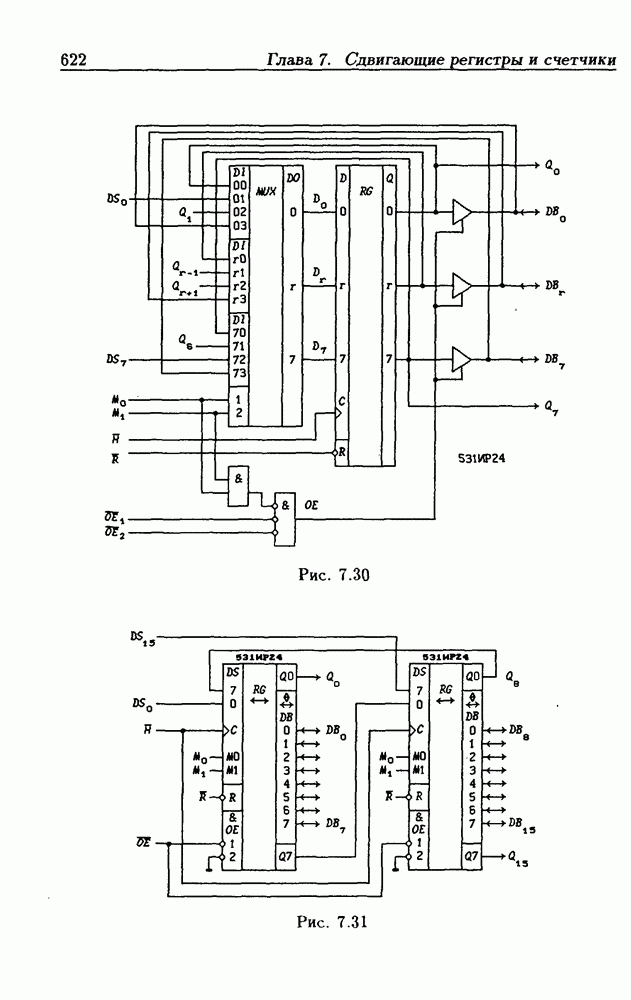
- Реверсивные сдвигающие регистры типов PI/SO и PI/PO.
- Многофункциональные устройства на основе реверсивных сдвигающих регистров.
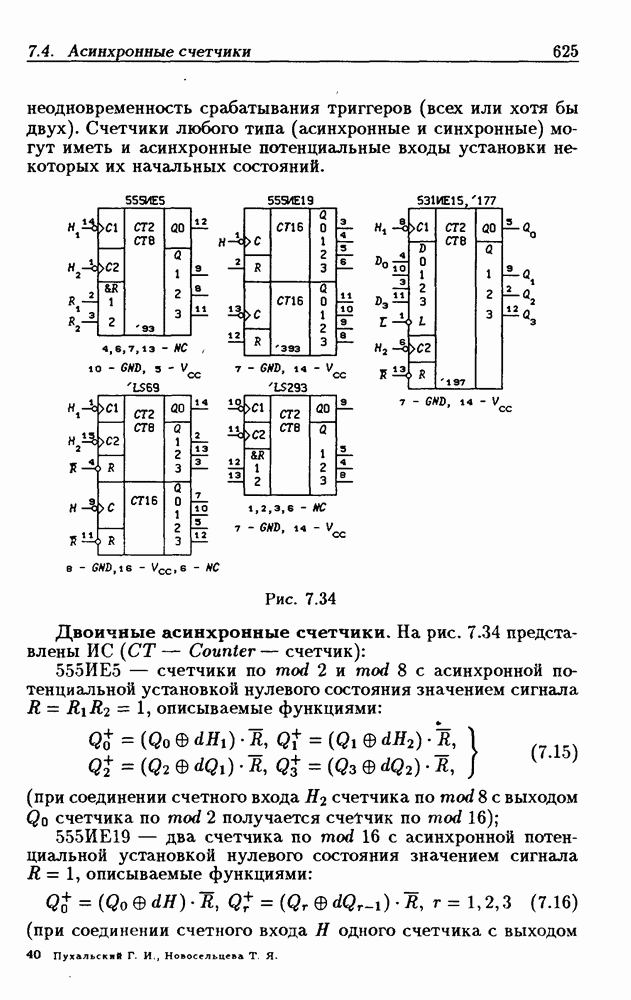
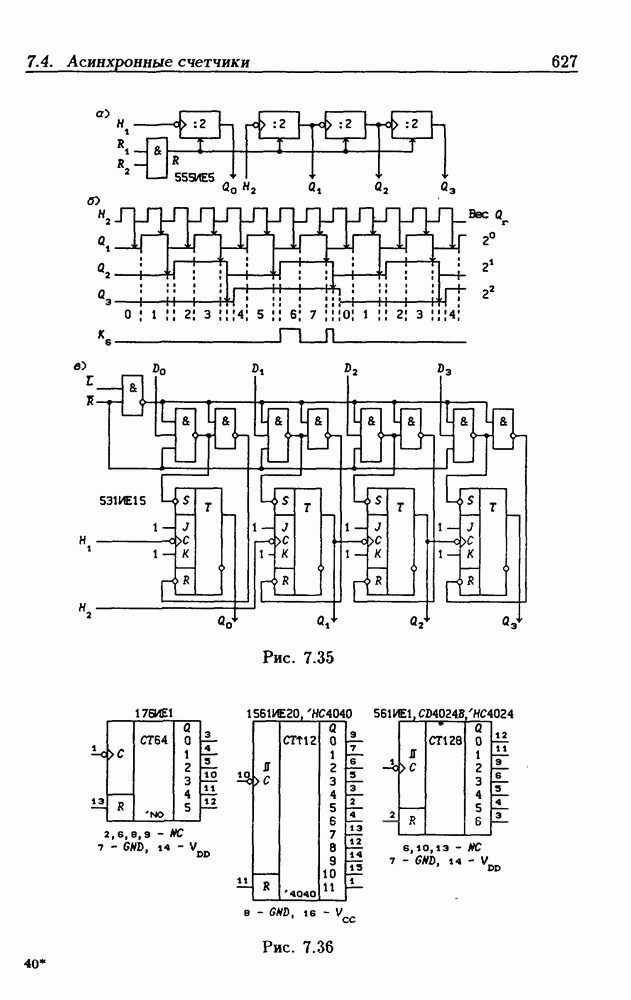
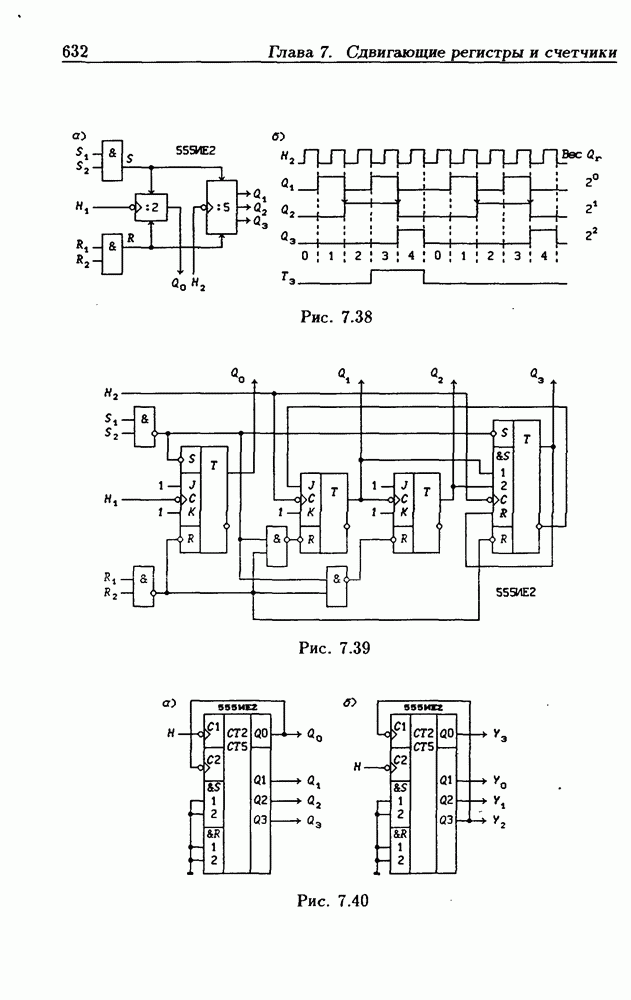
- 7.4. Асинхронные счетчики
- Двоично-десятичные асинхронные счетчики.
- 7.5. Синхронные двоичные счетчики
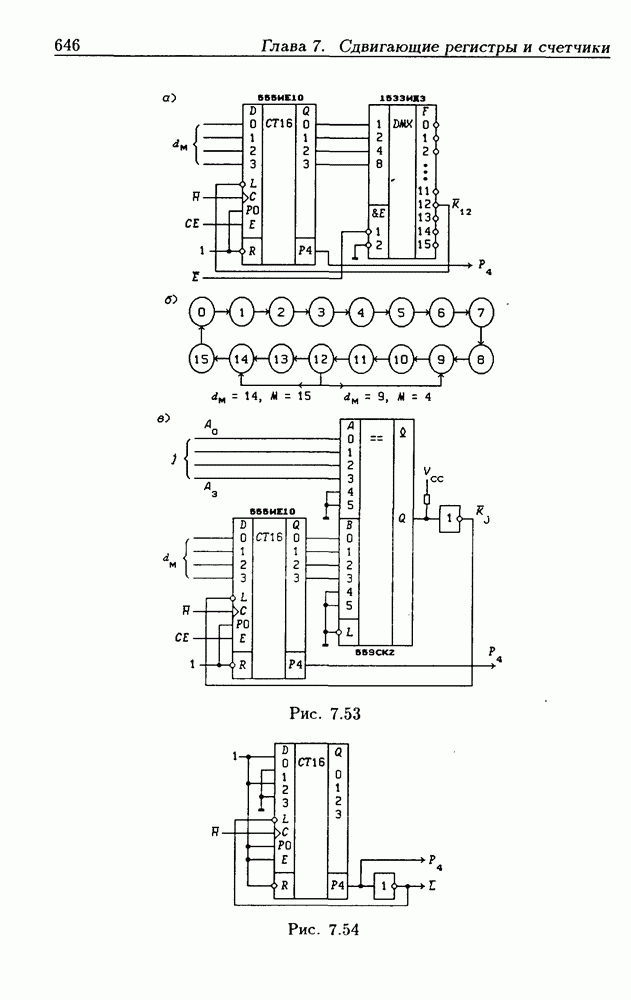
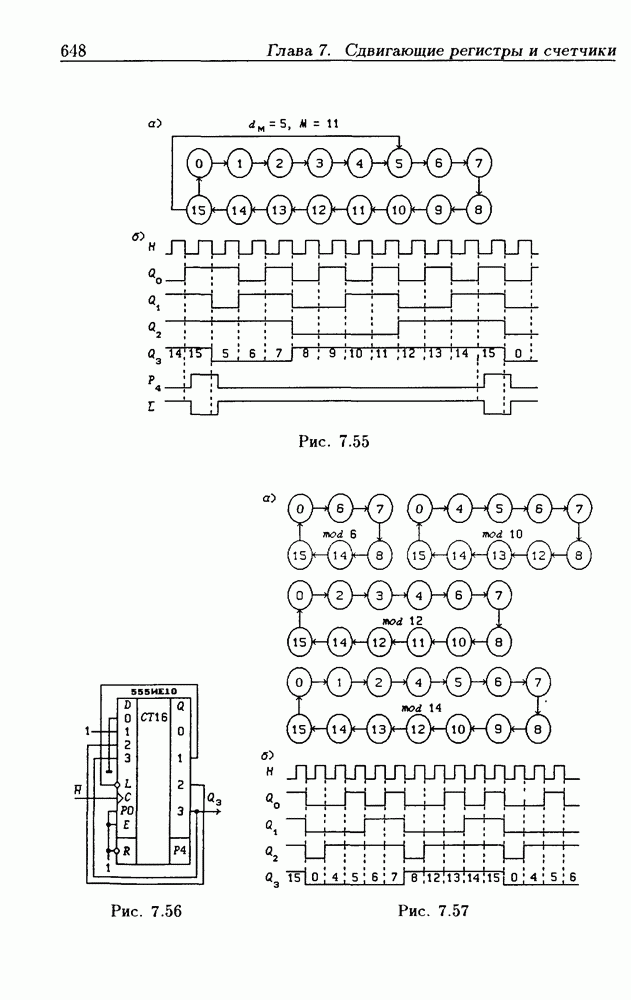
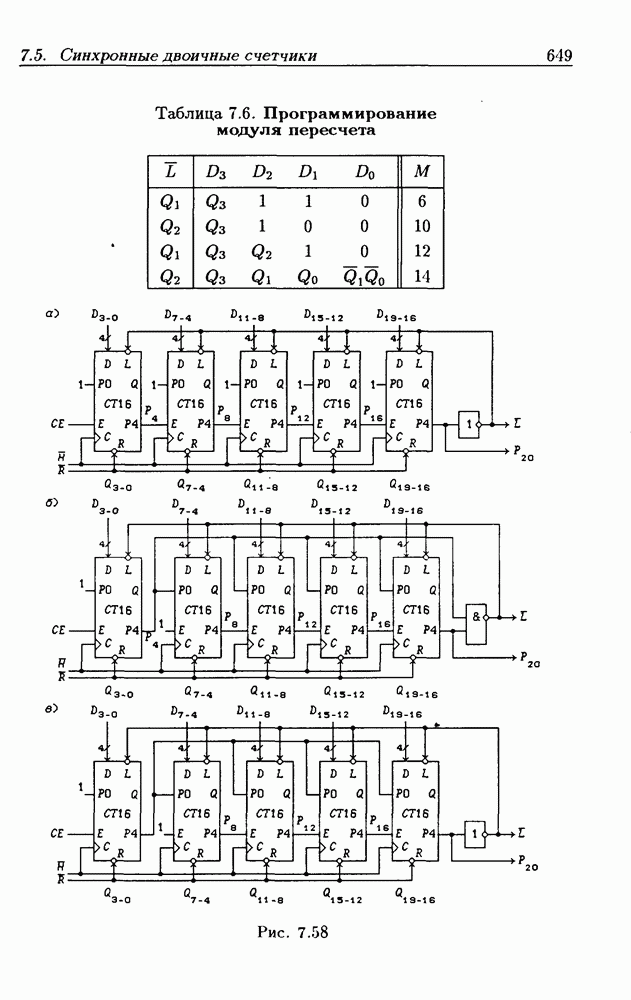
- Программирование модуля пересчета двоичных счетчиков.
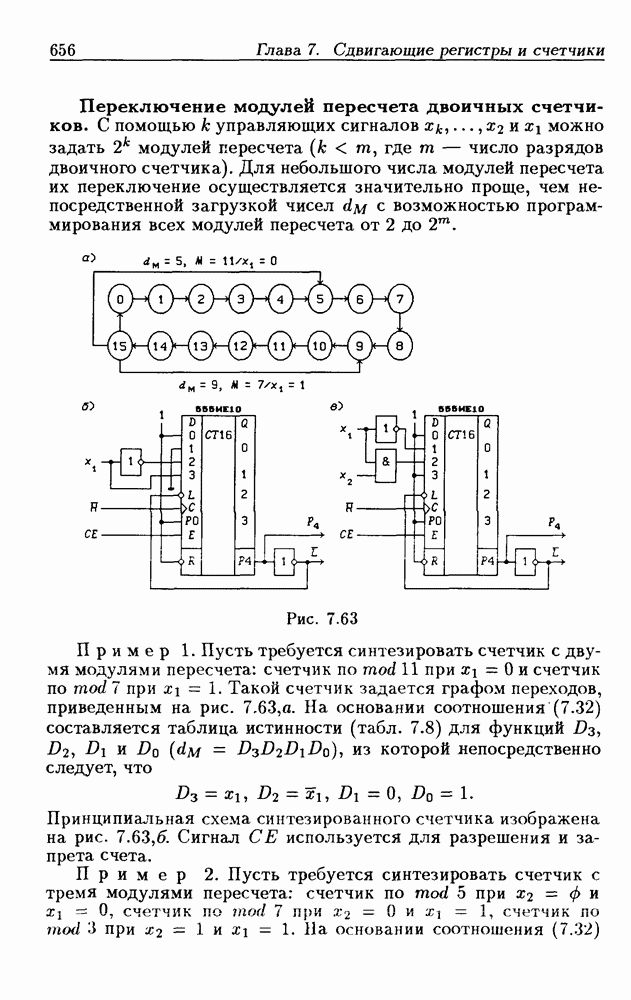
- Переключение модулей пересчета двоичных счетчиков.
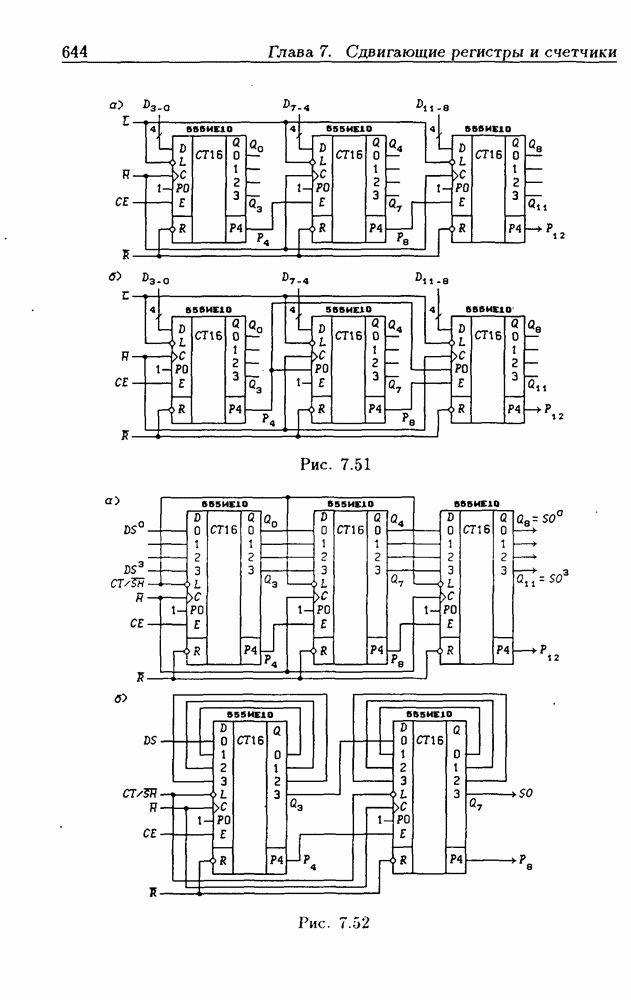
- Функциональные устройства на основе двоичных счетчиков.
- 7.6. Синхронные двоично-десятичные счетчики
- 7.7. Синхронные реверсивные счетчики
- 7.8. Счетчики с расщепленным тактовым сигналом
- 7.9. Счетчики на сдвигающих регистрах
- 7.10. Кольцевые счетчики
- 7.11. Делители частоты
- Нормированные умножители частоты.
- 7.12. Линейные генераторы
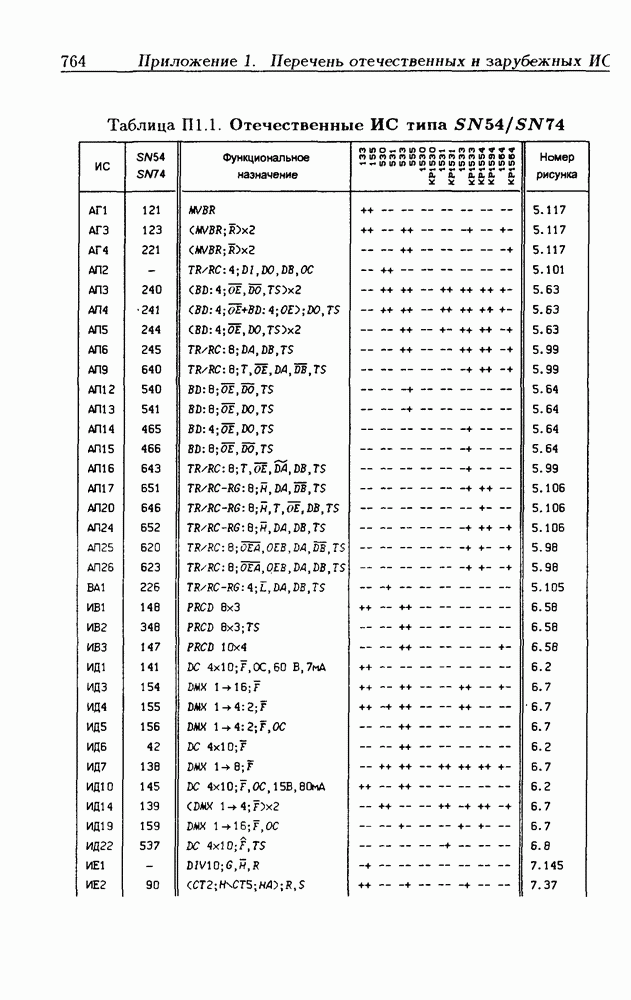
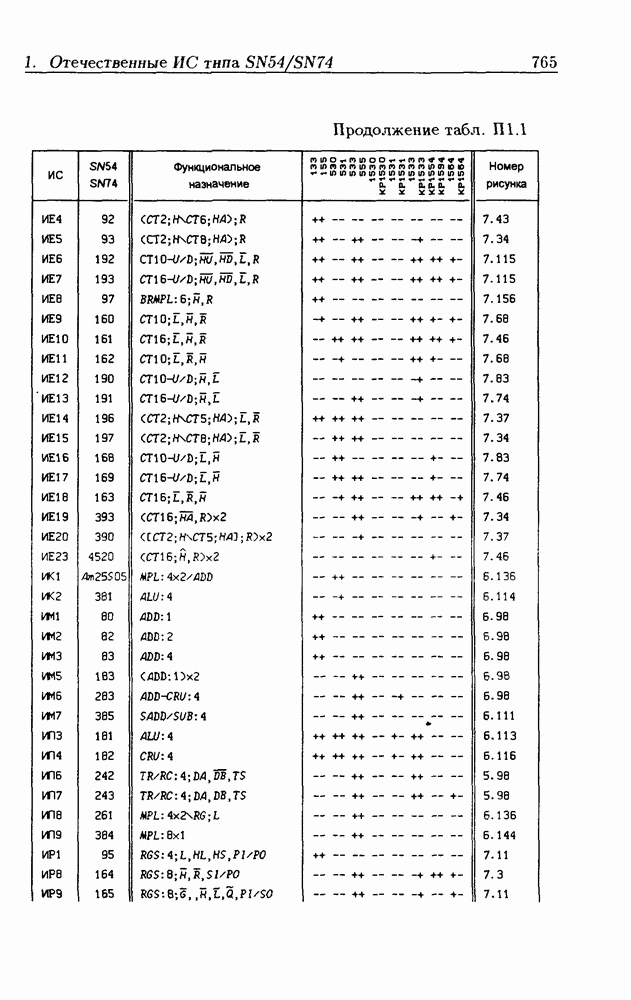
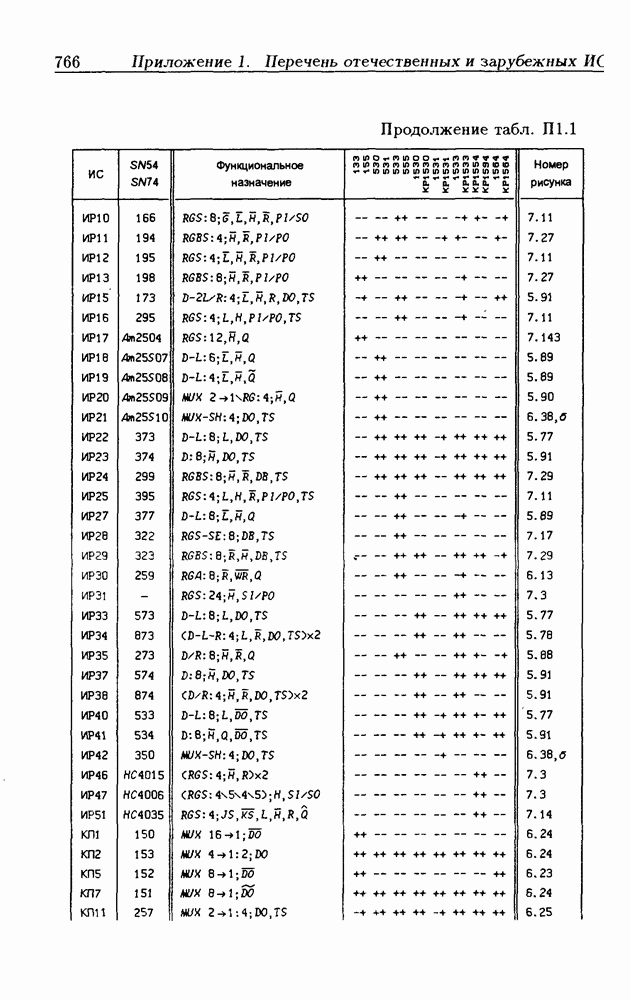
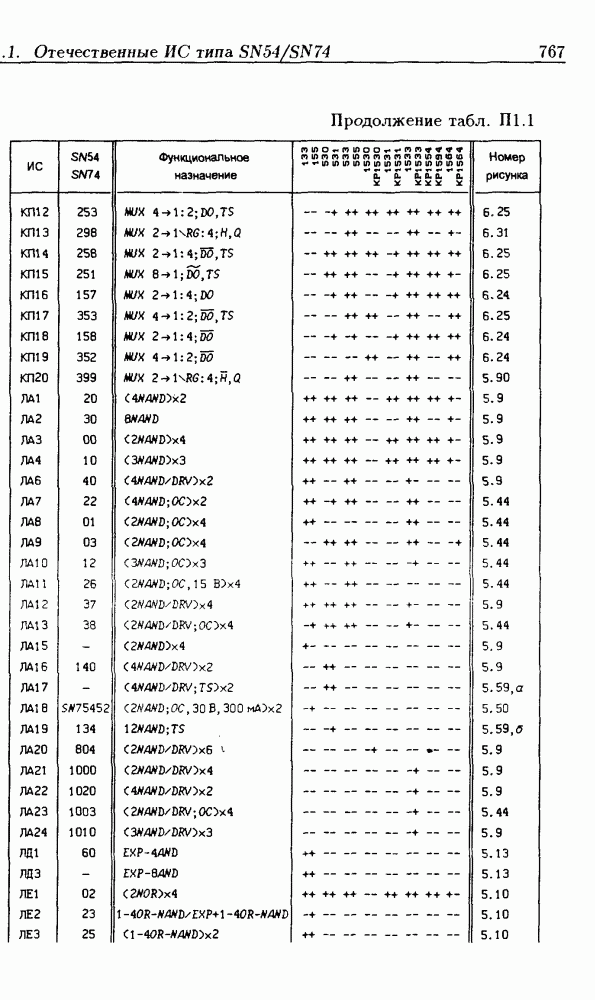
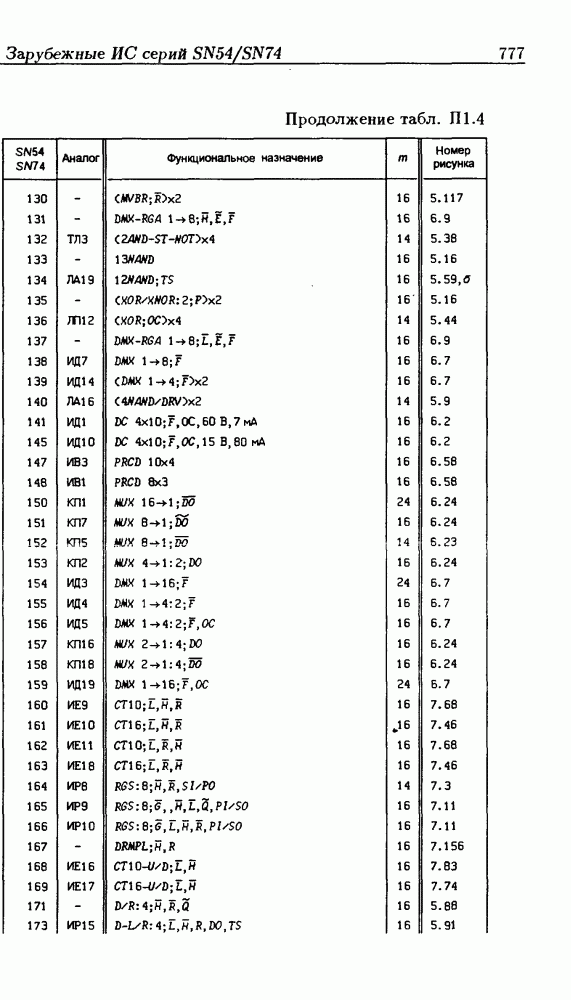
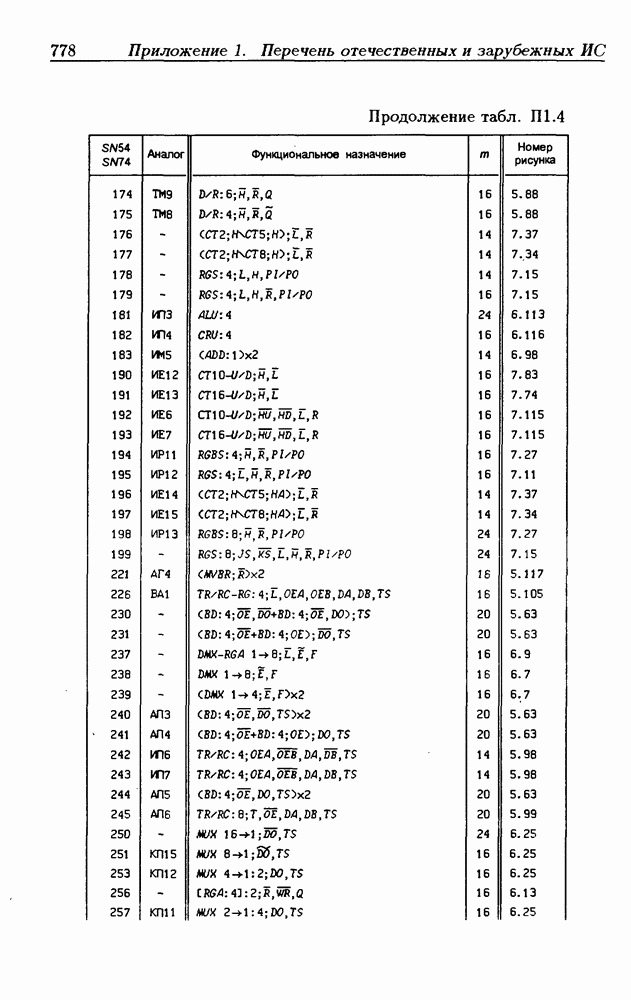
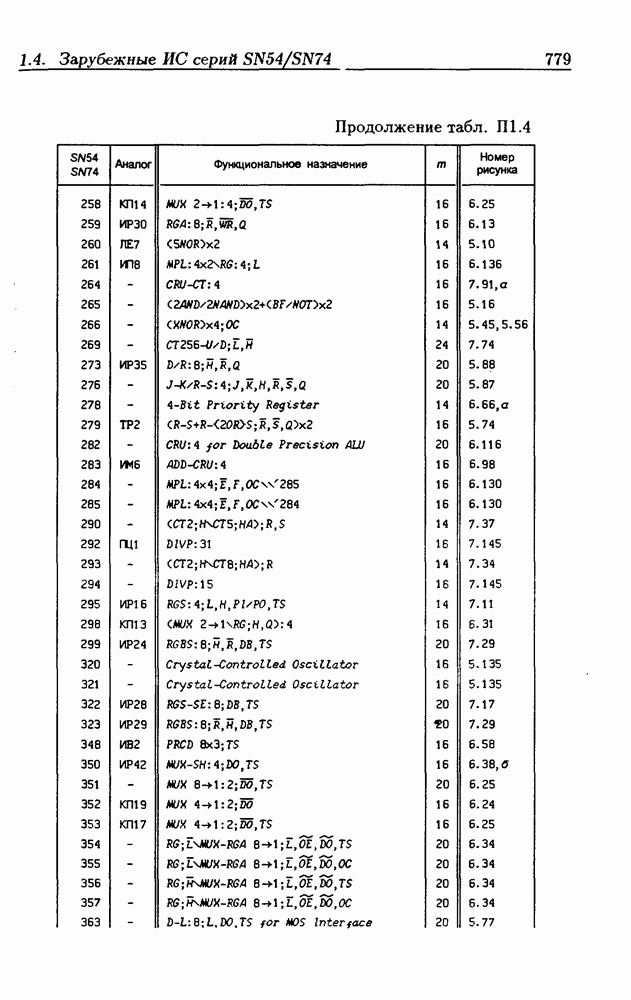
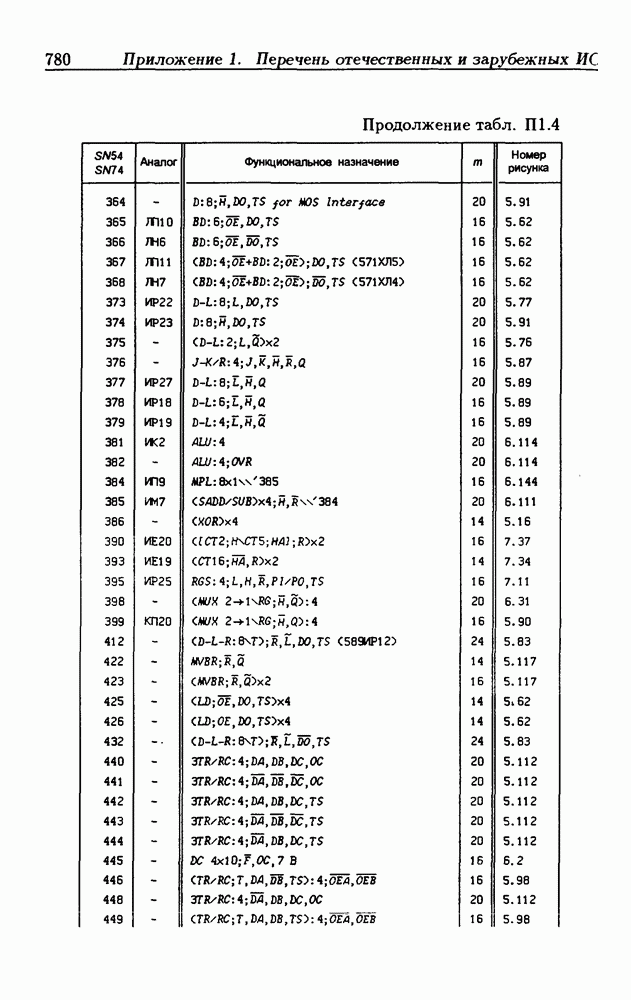
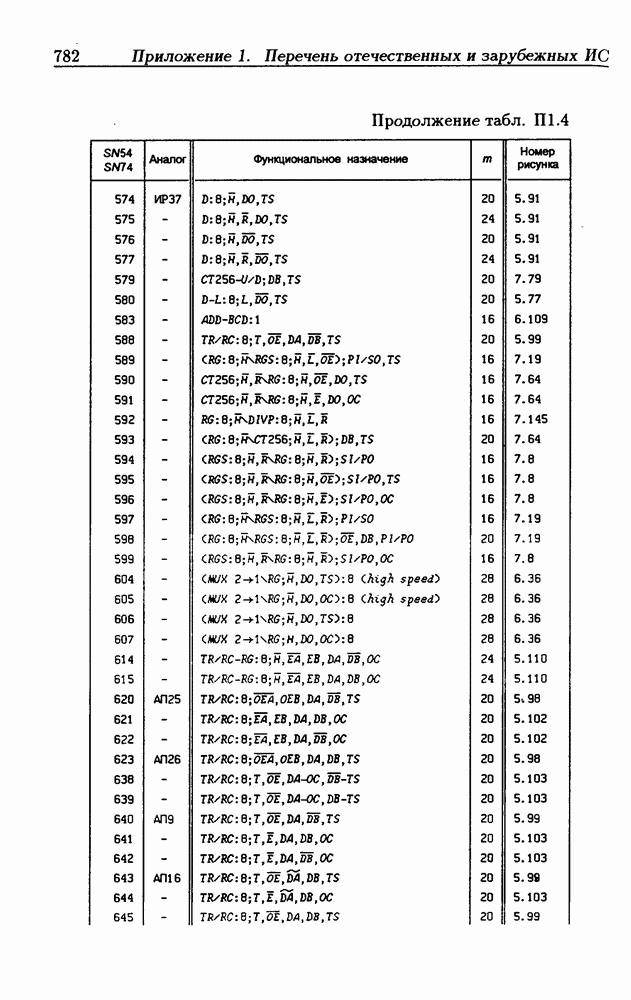
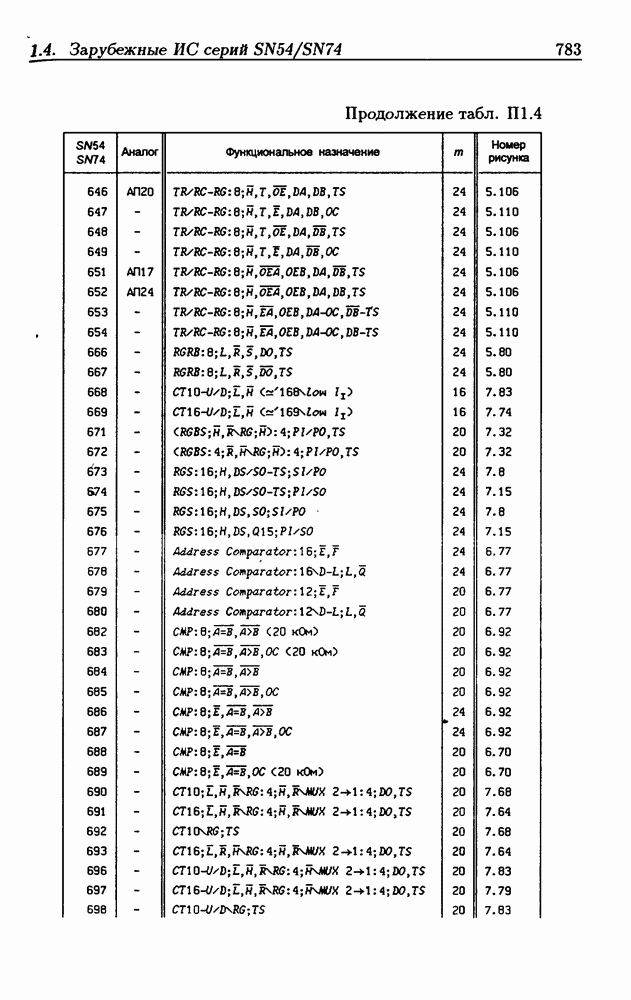
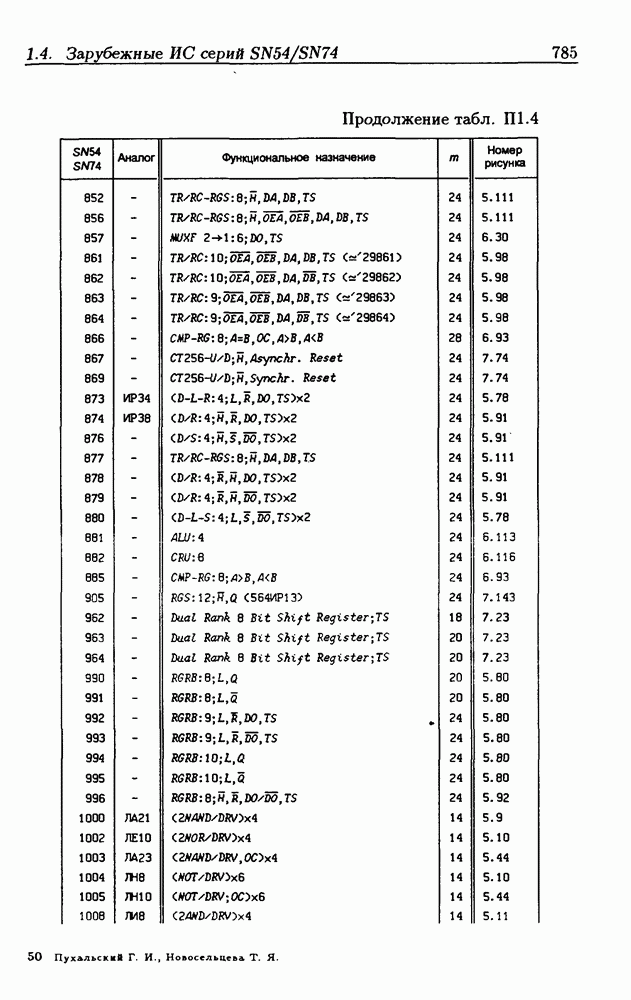
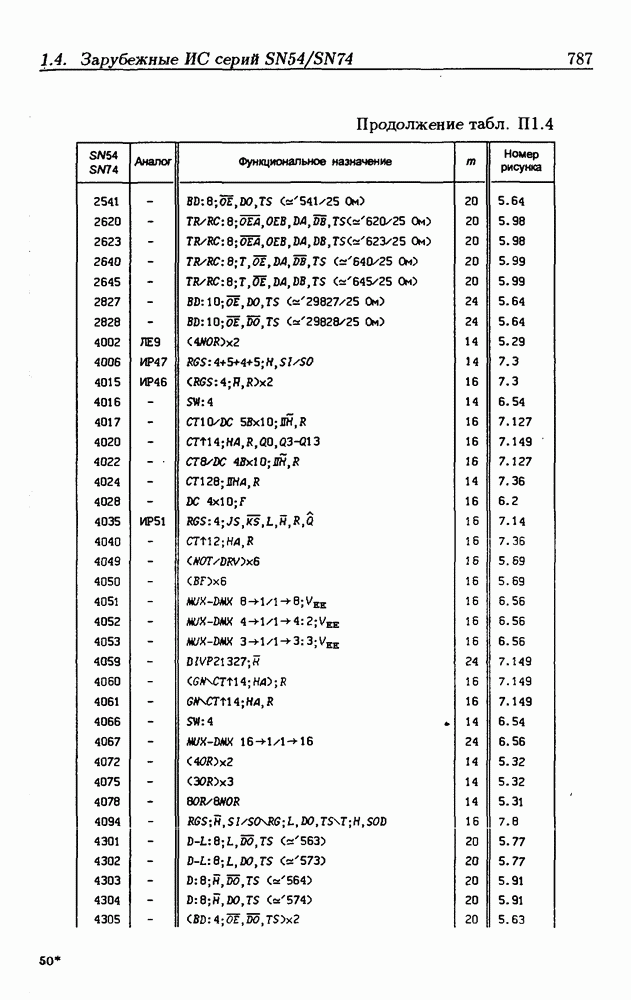
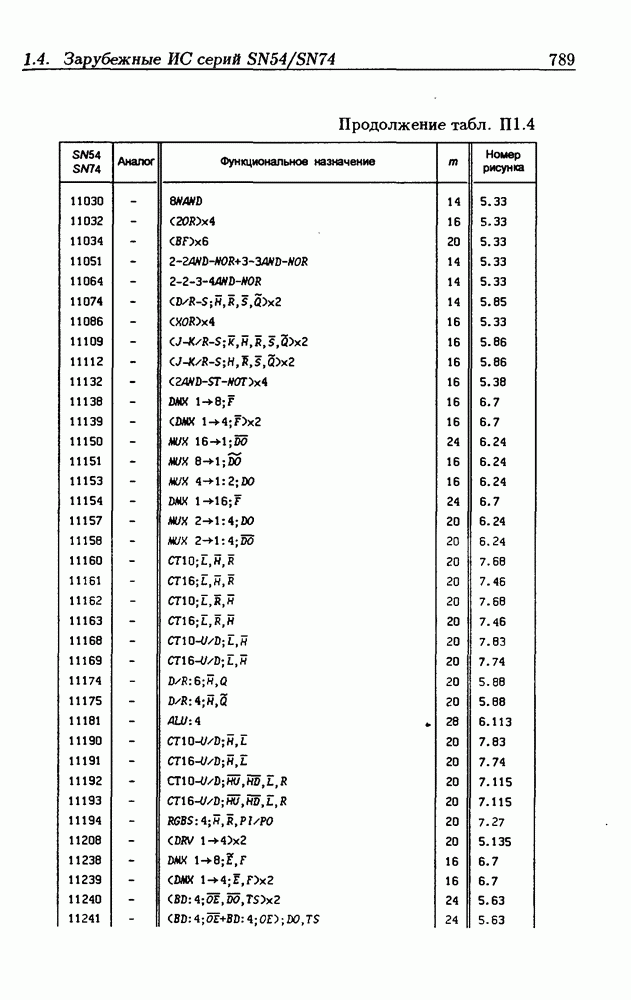
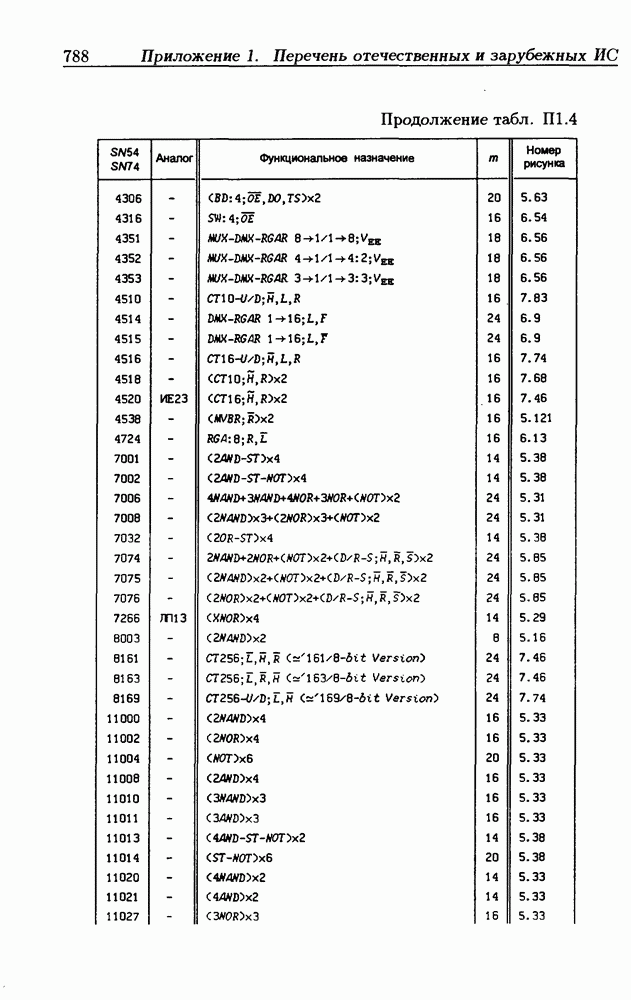
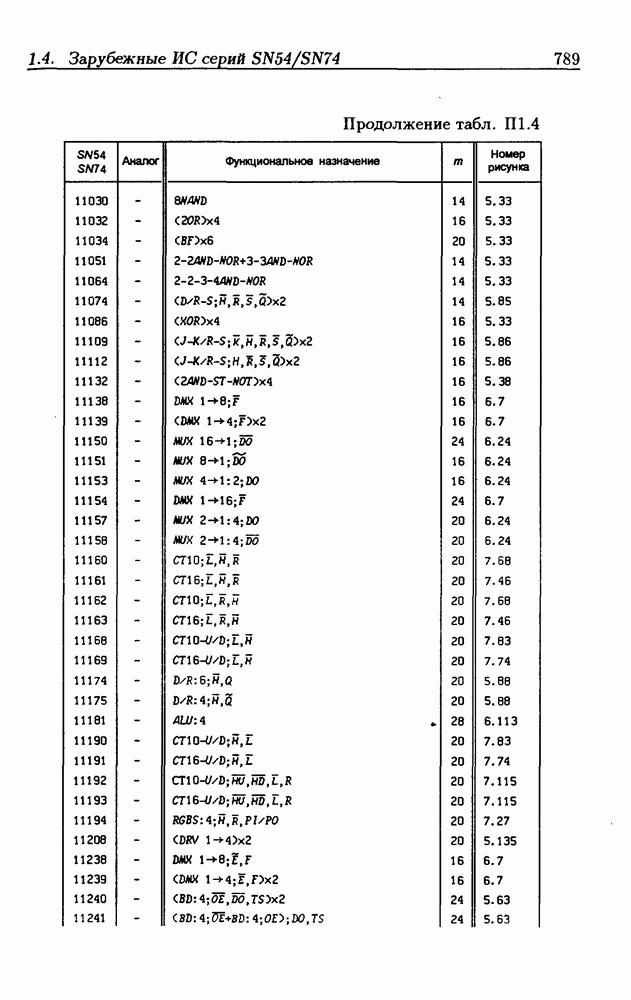
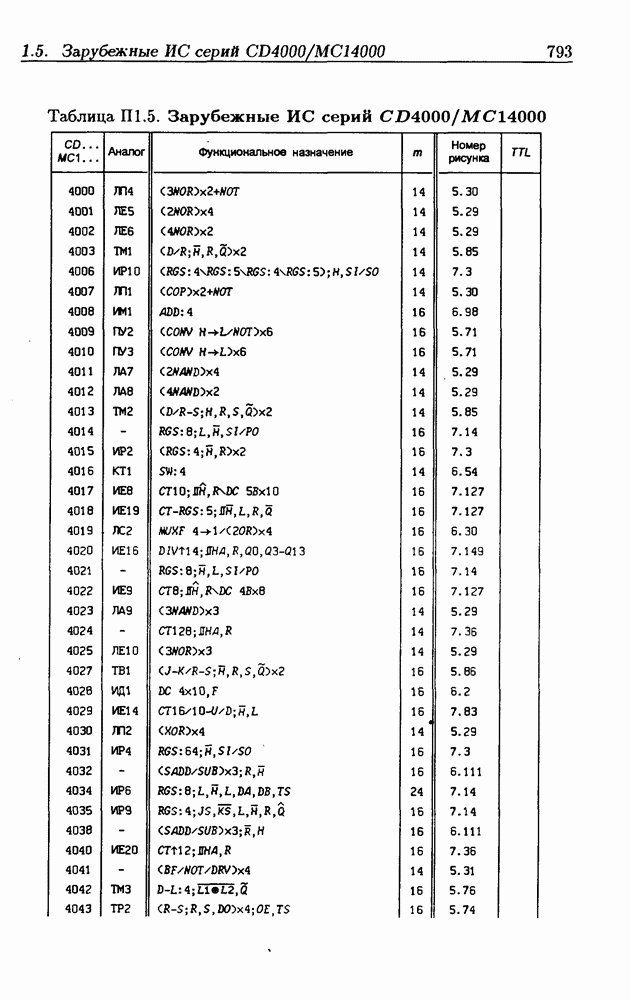
- Приложение 1. Перечень отечественных и зарубежных ИС
- Приложение 2. Параметры интегральных схем