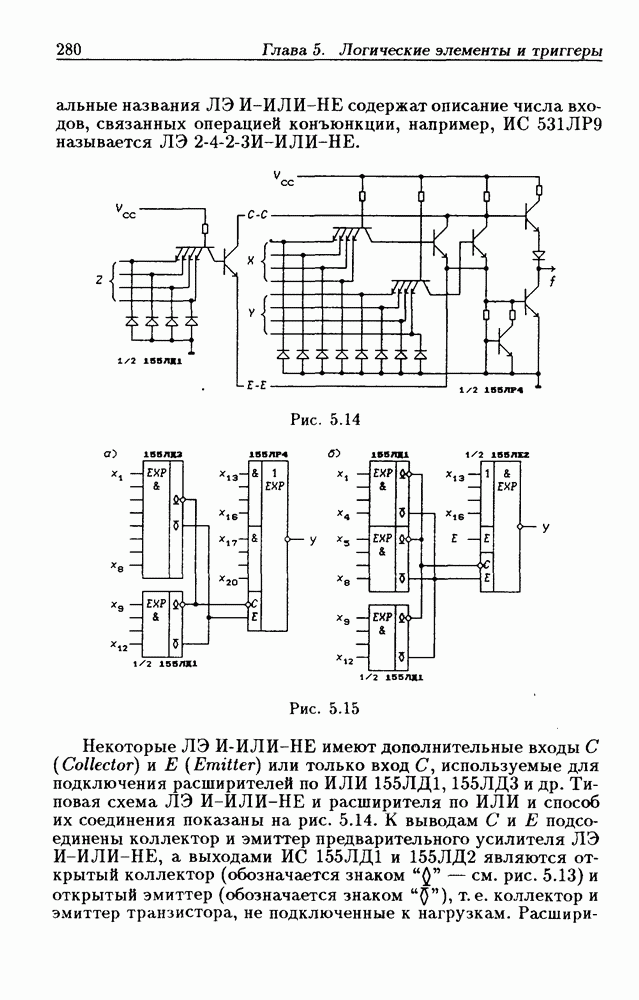
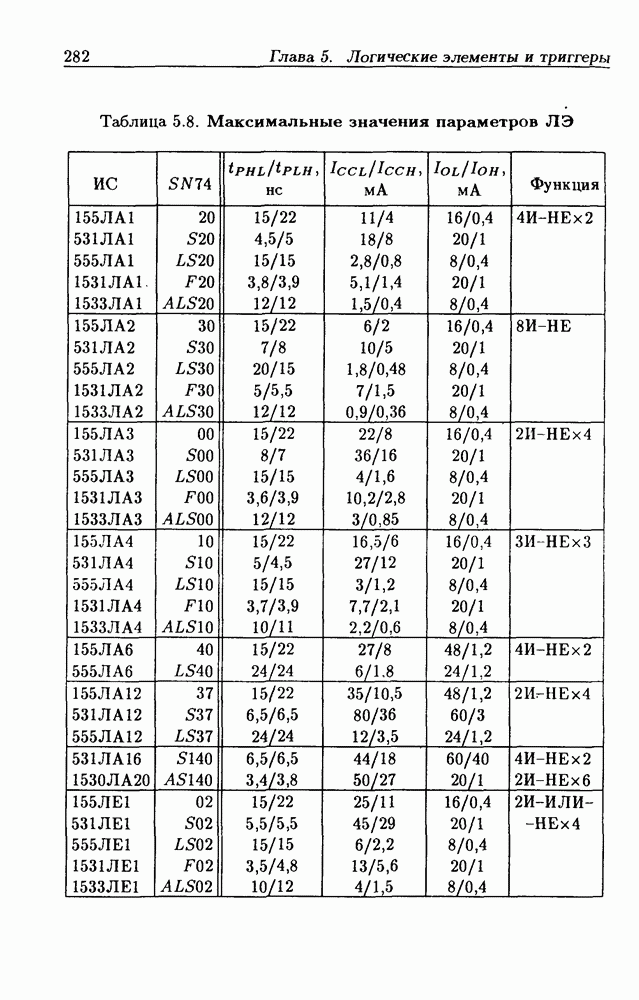
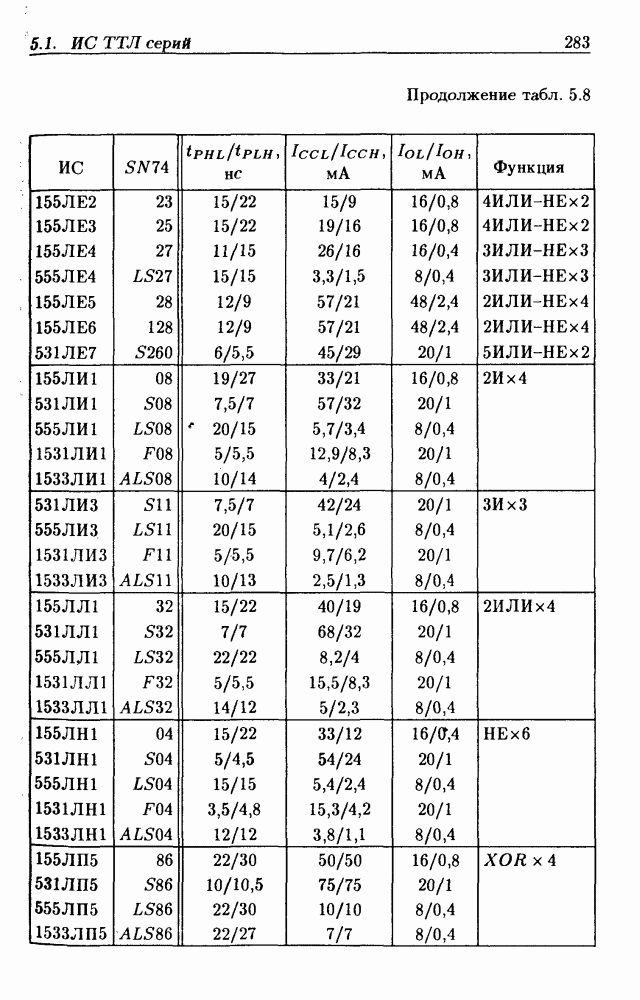
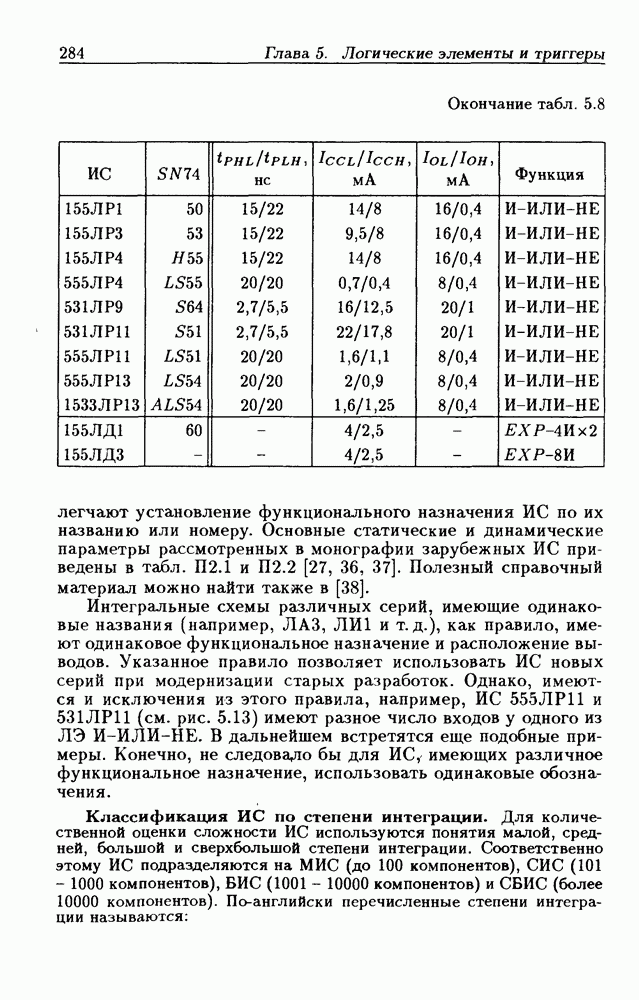
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
1.3. Переключательные функции
Любое логическое выражение, составленное из  переменных
переменных  с помощью конечного числа операций алгебры логики, можно рассматривать как некоторую функцию
с помощью конечного числа операций алгебры логики, можно рассматривать как некоторую функцию  переменных. В соответствии с аксиомами (1.1) - (1.5) функция может принимать в зависимости от значений переменных
переменных. В соответствии с аксиомами (1.1) - (1.5) функция может принимать в зависимости от значений переменных  или 1 только два значения: 0 и 1. Такие функции являются весьма удобным инструментом для описания, анализа и синтеза переключательных схем, выходные сигналы которых характеризуются лишь двумя уровнями напряжения: высоким (1) и низким (0). В связи с этим такие функции называются переключательными (термин "переключательная" обычно будем опускать, так как никакие другие функции рассматриваться не будут).
или 1 только два значения: 0 и 1. Такие функции являются весьма удобным инструментом для описания, анализа и синтеза переключательных схем, выходные сигналы которых характеризуются лишь двумя уровнями напряжения: высоким (1) и низким (0). В связи с этим такие функции называются переключательными (термин "переключательная" обычно будем опускать, так как никакие другие функции рассматриваться не будут).
Для функций  переменных
переменных  будем использовать общее обозначение
будем использовать общее обозначение  где
где  т. е. совокупность переменных
т. е. совокупность переменных  можно рассматривать как
можно рассматривать как  -мерный вектор. Каждая переменная
-мерный вектор. Каждая переменная  может принимать только два значения: 0 и 1. Поэтому число всех возможных комбинаций значений
может принимать только два значения: 0 и 1. Поэтому число всех возможных комбинаций значений  конечно. В общем виде конкретное значение переменной
конечно. В общем виде конкретное значение переменной  (0 или 1) будем обозначать через
(0 или 1) будем обозначать через 
Для обозначения произвольных десятичных чисел будем использовать символы  п., а двоичные числа будем записывать в виде
п., а двоичные числа будем записывать в виде  где
где  или 1. Равенства для десятичных и двоичных чисел будем записывать, опуская индекс, указывающий основание системы счисления:
или 1. Равенства для десятичных и двоичных чисел будем записывать, опуская индекс, указывающий основание системы счисления:  Значения
Значения  и 1 являются элементами алгебры логики (булевой алгебры), если они используются в качестве значений переменных
и 1 являются элементами алгебры логики (булевой алгебры), если они используются в качестве значений переменных  Для этих элементов не существует соотношений больше и меньше. В записи же двоичного числа
Для этих элементов не существует соотношений больше и меньше. В записи же двоичного числа  значения
значения  и 1 считаются элементами кольца целых чисел
и 1 считаются элементами кольца целых чисел  Какими элементами являются символы 0 и 1, всегда ясно из контекста или используемых в выражениях операций. На основании этого, например, можно записать, что
Какими элементами являются символы 0 и 1, всегда ясно из контекста или используемых в выражениях операций. На основании этого, например, можно записать, что  (в левой части используется логическая операция отрицания, а в правой — арифметическая операция вычитания).
(в левой части используется логическая операция отрицания, а в правой — арифметическая операция вычитания).
Областью определения функции  переменных
переменных  является совокупность точек n-мерного пространства, причем каждая из точек задается определенной комбинацией значений этих переменных:
является совокупность точек n-мерного пространства, причем каждая из точек задается определенной комбинацией значений этих переменных:

где  или
или  Точки, задающие область определения функции
Точки, задающие область определения функции  будем обозначать через
будем обозначать через

где  т. е. все точки области определения функции
т. е. все точки области определения функции  переменных можно пронумеровать с помощью двоичных n-разрядных чисел
переменных можно пронумеровать с помощью двоичных n-разрядных чисел  или десятичных чисел
или десятичных чисел  На основании (1.23) имеется
На основании (1.23) имеется  различных n-разрядных двоичных чисел, поэтому область определения функции
различных n-разрядных двоичных чисел, поэтому область определения функции  переменных состоит из
переменных состоит из  точек, т. е.
точек, т. е.

Для задания функции  следует указать ее значения во всех точках области определения, т.е. следует задать значения
следует указать ее значения во всех точках области определения, т.е. следует задать значения  или 1, где
или 1, где  Каждой конкретной функции
Каждой конкретной функции  переменных можно поставить в соответствие
переменных можно поставить в соответствие  -разрядное число, составленное из значений
-разрядное число, составленное из значений  или
или  которые она принимает в
которые она принимает в  точках области определения. Так как имеется всего 22 различных
точках области определения. Так как имеется всего 22 различных  -разрядных двоичных чисел, то и число различных функций
-разрядных двоичных чисел, то и число различных функций  переменных равно
переменных равно 
Функции  переменных могут зависеть не от всех переменных
переменных могут зависеть не от всех переменных  Такие функции называются вырожденными. В частности, функция
Такие функции называются вырожденными. В частности, функция  равная нулю во всех точках
равная нулю во всех точках  и функция
и функция  равная единице во всех точках
равная единице во всех точках  не зависят ни от одной переменной. Эти функции называются константой нуль и константой единица соответственно.
не зависят ни от одной переменной. Эти функции называются константой нуль и константой единица соответственно.
Значительный интерес представляют следующие невырожденные функции двух переменных  названия которым даны по используемым для их образования операциям алгебры логики:
названия которым даны по используемым для их образования операциям алгебры логики:
 дизъюнкция (ИЛИ),
дизъюнкция (ИЛИ),
 — конъюнкция И),
— конъюнкция И),
 - функция И-НЕ,
- функция И-НЕ,
 — функция ИЛИ-НЕ,
— функция ИЛИ-НЕ,
 - сумма по модулю два.
- сумма по модулю два.
Область определения этих функций состоит из четырех точек:

поскольку 
Так как область определения любой функции  переменных конечна
переменных конечна  точек), она может быть задана таблицей значений
точек), она может быть задана таблицей значений  или 1, которые она принимает в точках
или 1, которые она принимает в точках  где
где  Такие таблицы называются таблицами истинности. Табл. 1.3, которая составлена в соответствии с аксиомами (1.2) - (1.5) для указанных выше функций двух переменных, представляет собой таблицу истинности, задающую эти функции. В предпоследнем столбце помещена функция, заданная в общем виде коэффициентами
Такие таблицы называются таблицами истинности. Табл. 1.3, которая составлена в соответствии с аксиомами (1.2) - (1.5) для указанных выше функций двух переменных, представляет собой таблицу истинности, задающую эти функции. В предпоследнем столбце помещена функция, заданная в общем виде коэффициентами  где
где  а в последнем столбце — инверсная функция, заданная коэффициентами
а в последнем столбце — инверсная функция, заданная коэффициентами  Подставляя различные значения
Подставляя различные значения  или 1, можно задать все 16 функций двух переменных
или 1, можно задать все 16 функций двух переменных  В частности, можно получить вырожденные функции:
В частности, можно получить вырожденные функции:

называемые инверсиями переменных (в табл. 1.3 показаны вырожденные функции  константа нуль и
константа нуль и  константа единица).
константа единица).
Таблица 1.3. (см. скан) Функции двух переменных
Функции двух переменных исключительно важны в силу того, что любая функция  переменных может быть получена из них методом суперпозиции [7] — подстановкой этих функций вместо переменных в другие функции. Такая подстановка возможна на основании того, что области значений функций и переменных совпадают (0 и 1).
переменных может быть получена из них методом суперпозиции [7] — подстановкой этих функций вместо переменных в другие функции. Такая подстановка возможна на основании того, что области значений функций и переменных совпадают (0 и 1).
Функция  переменных
переменных  называется полностью определенной, если ее значения
называется полностью определенной, если ее значения  или 1 заданы во всех
или 1 заданы во всех  точках
точках  области определения. Если же значение функции не задано хотя бы в одной точке
области определения. Если же значение функции не задано хотя бы в одной точке  то она называется неполностью определенной. Не определенное в точке
то она называется неполностью определенной. Не определенное в точке  значение функции будем задавать произвольным коэффициентом
значение функции будем задавать произвольным коэффициентом  совмещенные символы 0 и 1, что указывает на неопределенность значения
совмещенные символы 0 и 1, что указывает на неопределенность значения  т.е., если в точке
т.е., если в точке  значение функции не
значение функции не
задано, то 
Неполностью определенные функции можно доопределять произвольным способом, полагая  или 1. Если значения функции не заданы в
или 1. Если значения функции не заданы в  точках, то функцию можно доопределить
точках, то функцию можно доопределить  способами, так как имеется
способами, так как имеется  различных
различных  -разрядных двоичных чисел, соответствующих различным способам доопределения функции в
-разрядных двоичных чисел, соответствующих различным способам доопределения функции в  точках. Таким образом, не определенной в
точках. Таким образом, не определенной в  точках функции соответствует класс из
точках функции соответствует класс из  полностью определенных функций. Если значения функции а, не заданы ни в одной точке
полностью определенных функций. Если значения функции а, не заданы ни в одной точке  то она называется полностью неопределенной и обозначается через h [10].
то она называется полностью неопределенной и обозначается через h [10].
Теории переключательных функций посвящено много работ, среди которых следует выделить [5, 7, 8] как наиболее фундаментальные.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Глава 1. Основы теории переключательных функций
- 1.2. Позиционные системы счисления
- 1.3. Переключательные функции
- 1.4. Принцип и закон двойственности
- 1.5. Теоремы разложения
- 1.6. Решение систем логических уравнений
- 1.7. Первичные термы, минтермы и макстермы
- 1.8. Совершенные нормальные формы представления функций
- 1.9. Конъюнктивные и дизъюнктивные термы
- 1.10. Минимизация переключательных функций
- 1.11. Диаграммы Вейча
- 1.12. Минимизация неполностью определенных функций, совместная минимизация нескольких функций
- 1.13. Скобочные формы функций
- 1.14. Закон двойственности для логических схем
- 1.15. Линейные функции
- Глава 2. Анализ и синтез логических схем
- 2.2. Модели логических элементов
- 2.3. Модели логических схем
- 2.4. Анализ логических схем
- 2.5. Синтез комбинационных схем, свободных от состязаний
- Глава 3. Синтез асинхронных потенциальных автоматов
- 3.2. Асинхронные потенциальные автоматы
- 3.3. Асинхронные потенциальные триггеры и элементы памяти
- Триггеры типа R-S
- Триггеры типа D-L
- Триггеры типа D-L-R с приоритетом входа R.
- Триггеры типа D-L-R с приоритетом входа L.
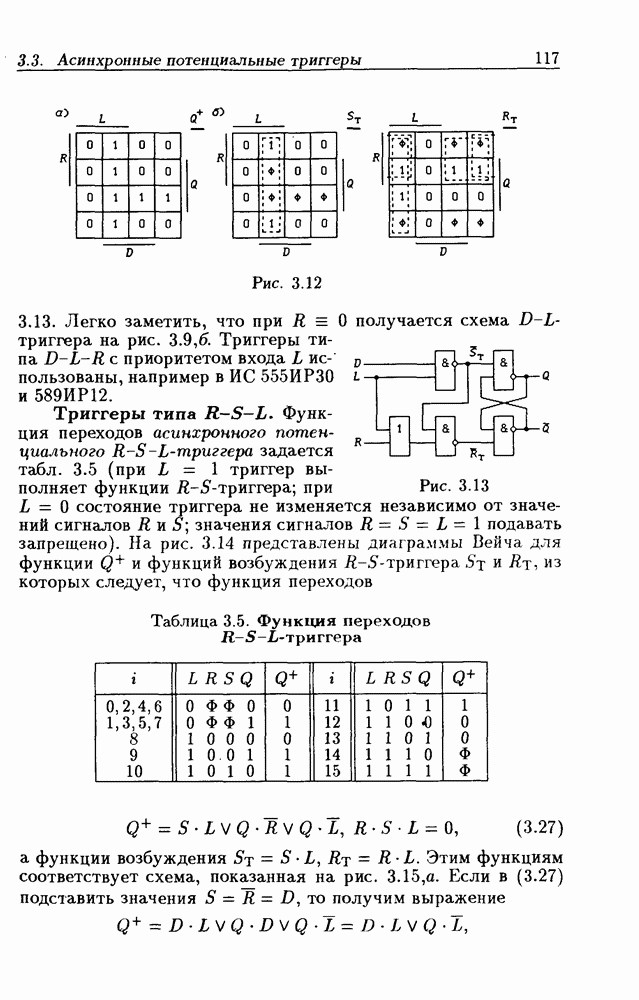
- Триггеры типа R-S-L.
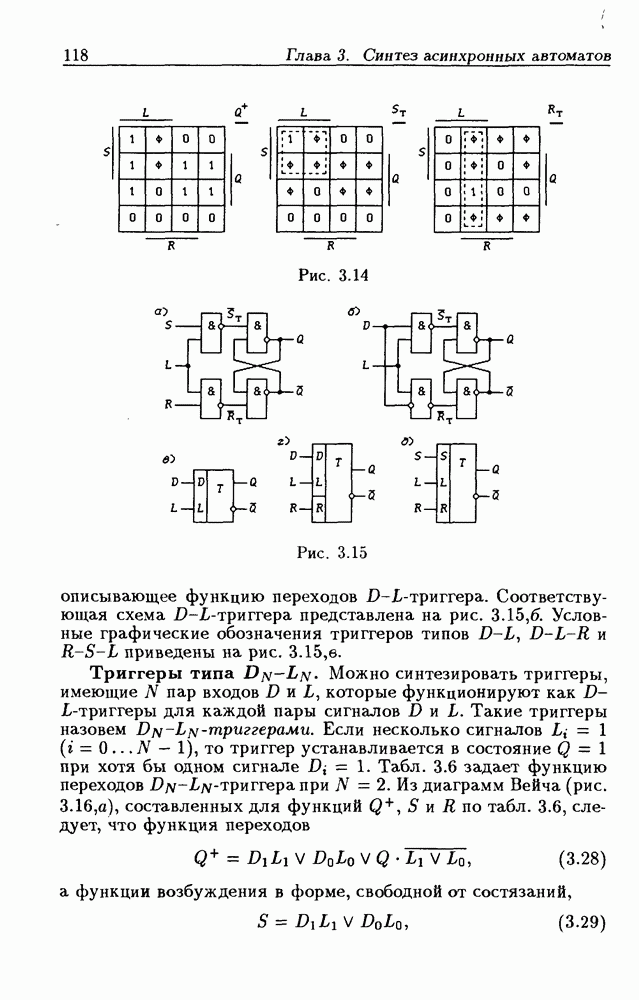
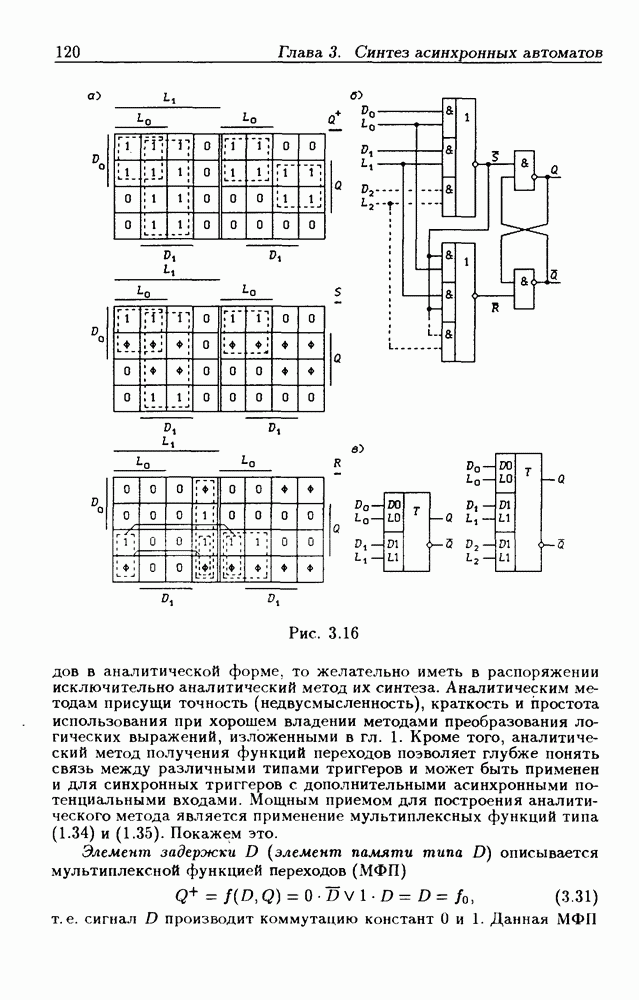
- Триггеры типа DN-LN
- Аналитический метод синтеза и анализа триггеров.
- 3.4. Задание асинхронных потенциальных автоматов таблицами и графами переходов
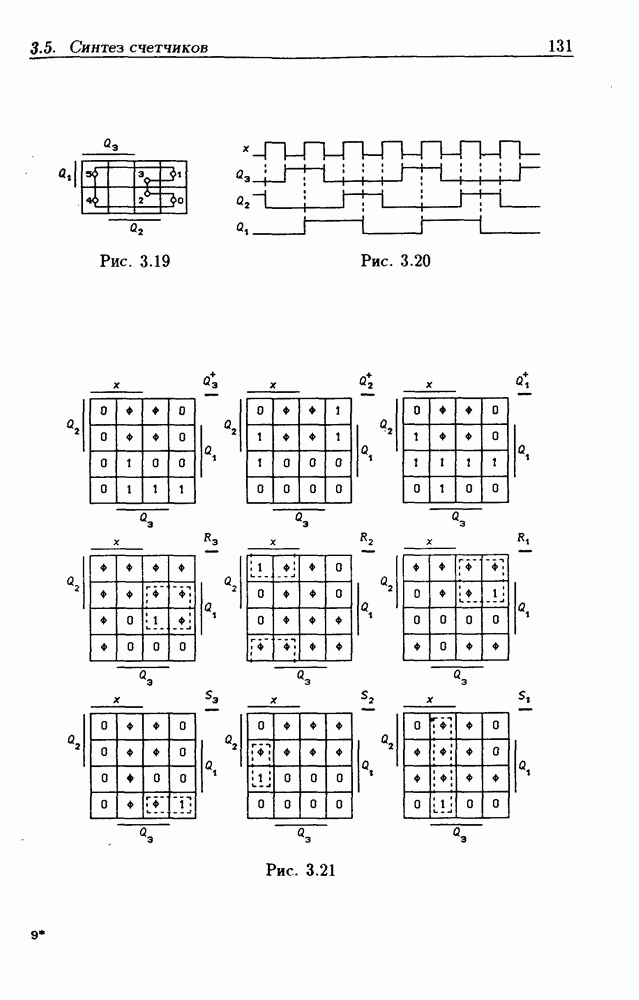
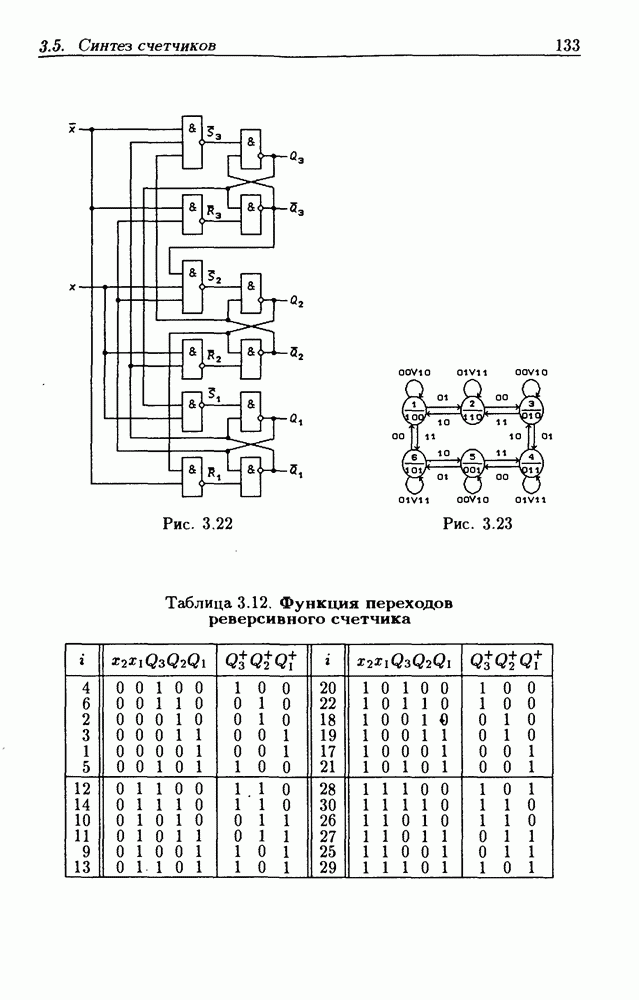
- 3.5. Синтез асинхронных потенциальных счетчиков
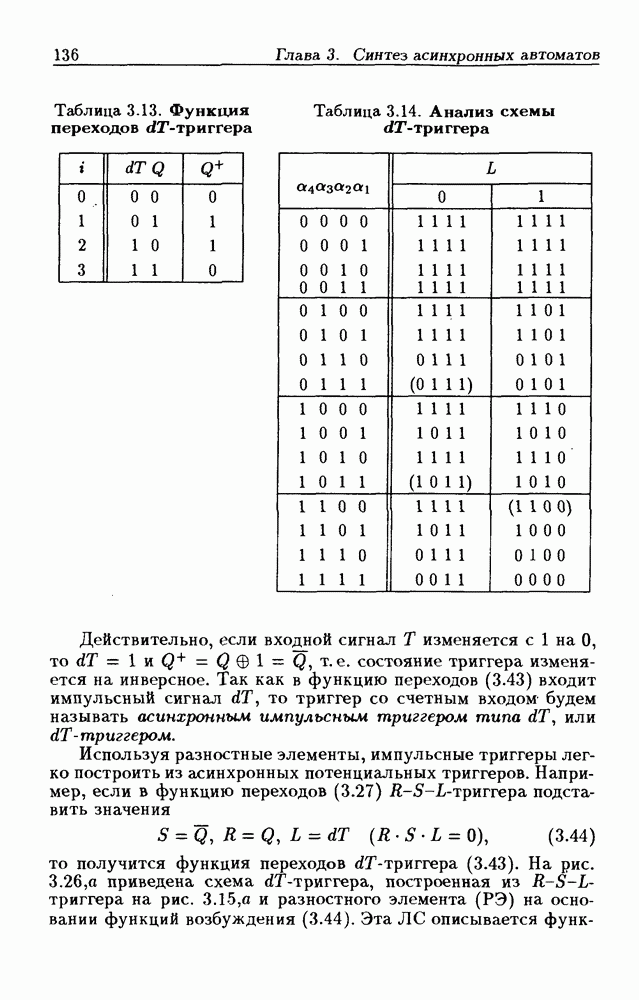
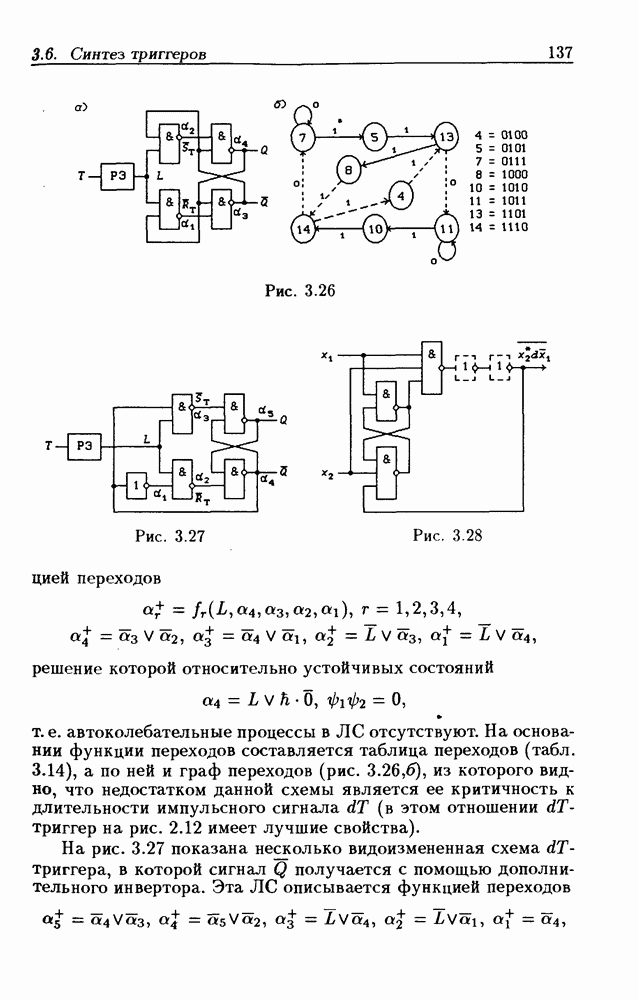
- 3.6. Синтез асинхронных импульсных триггеров
- Триггеры типа dJ-dK.
- Классификация триггеров.
- 3.7. Синтез синхронных триггеров
- Триггеры типа J-K
- Синхронно-асинхронные триггеры.
- 3.8. Примеры синтеза асинхронных потенциальных автоматов
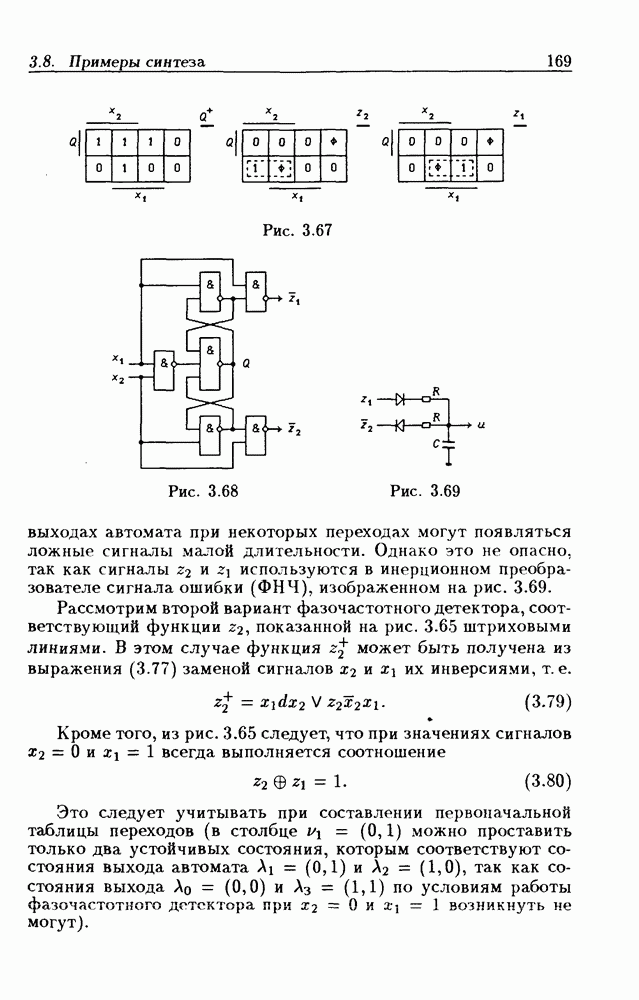
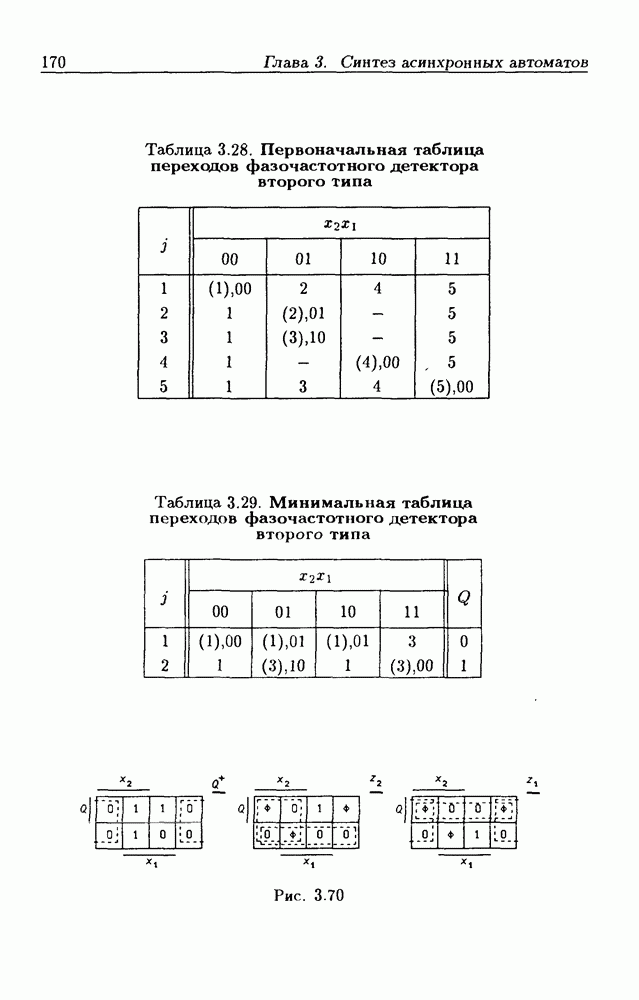
- Цифровые фазочастотные детекторы.
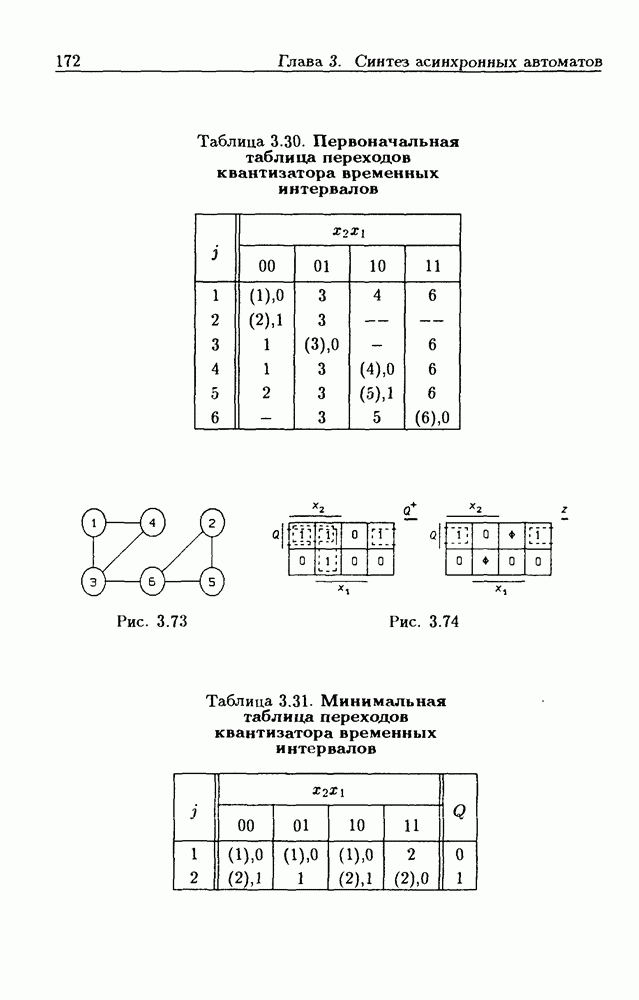
- Квантизатор временных интервалов.
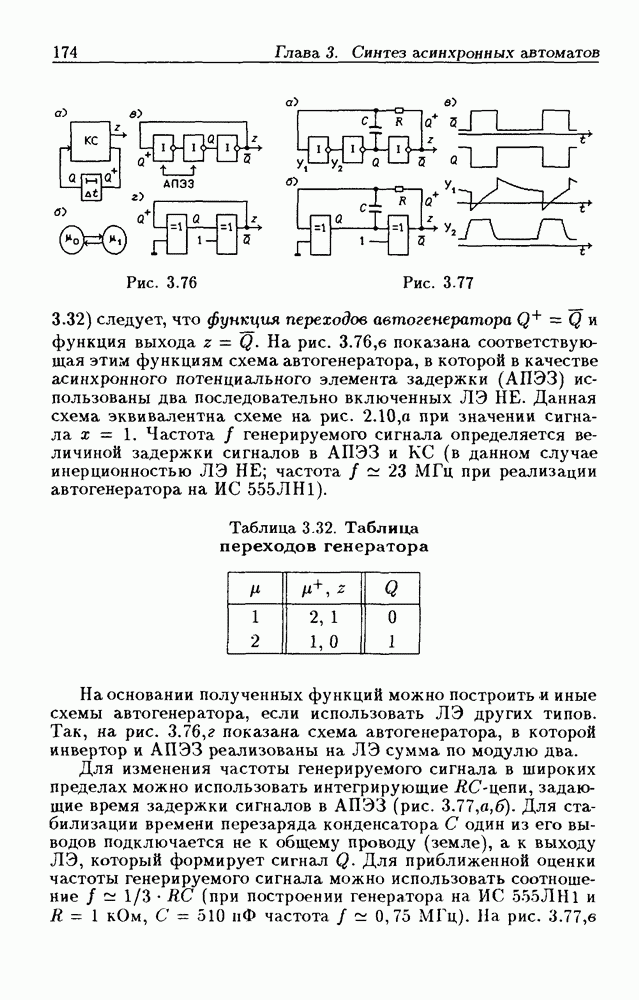
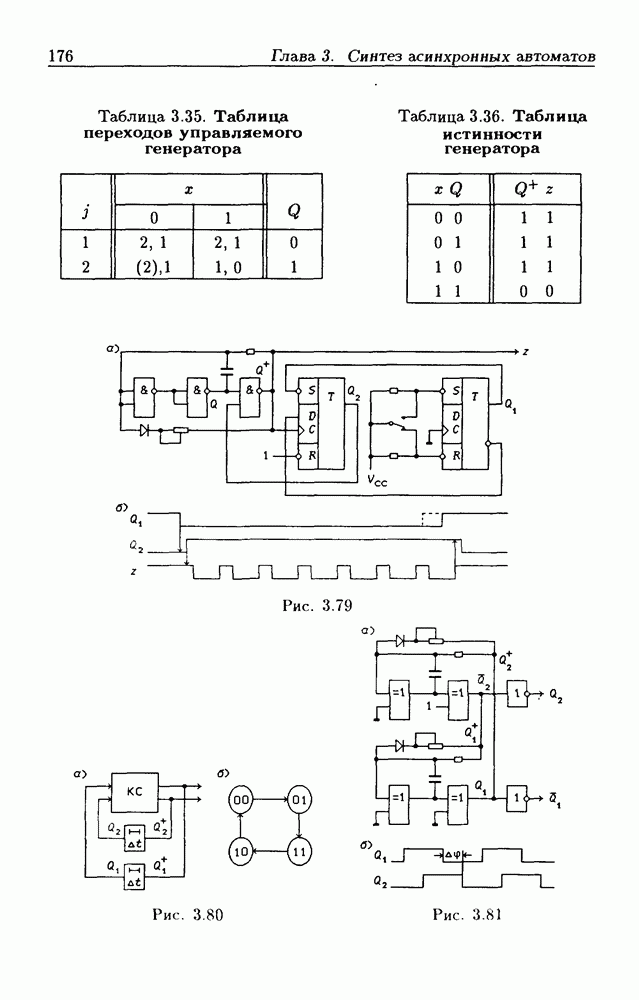
- 3.9. Генераторы сигналов
- Автогенераторы.
- Управляемые автогенераторы.
- Глава 4. Синтез синхронных автоматов
- 4.2. Синхронные триггеры
- Триггеры типов D и R-S с импульсным тактовым сигналом.
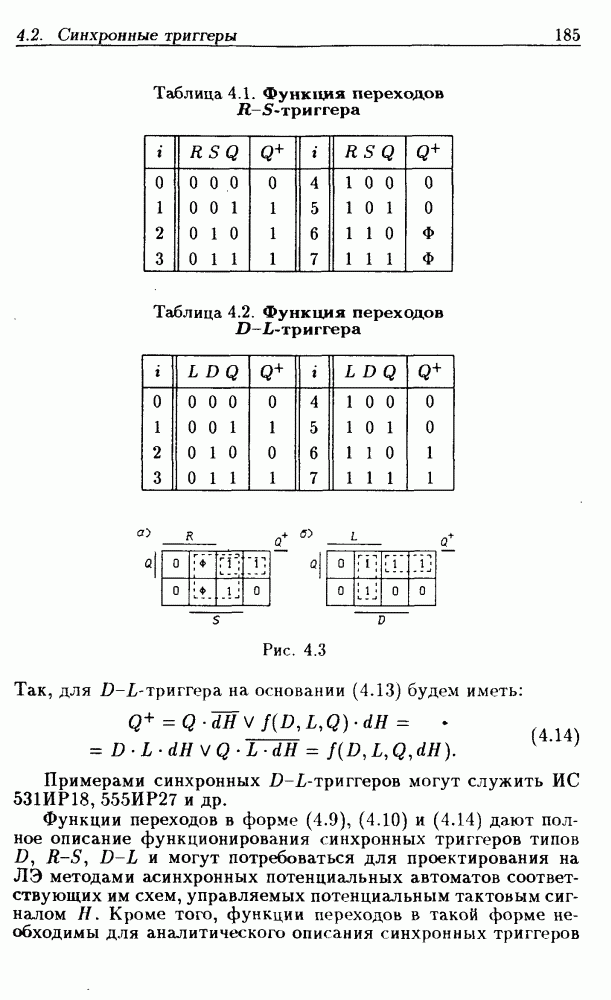
- Синхронные триггеры типов R-S и D-L
- Синхронно-асинхронные триггеры.
- Синхронные триггеры типа J-K
- Триггеры типа Т.
- Классификация синхронных триггеров.
- Преобразования типов синхронных триггеров.
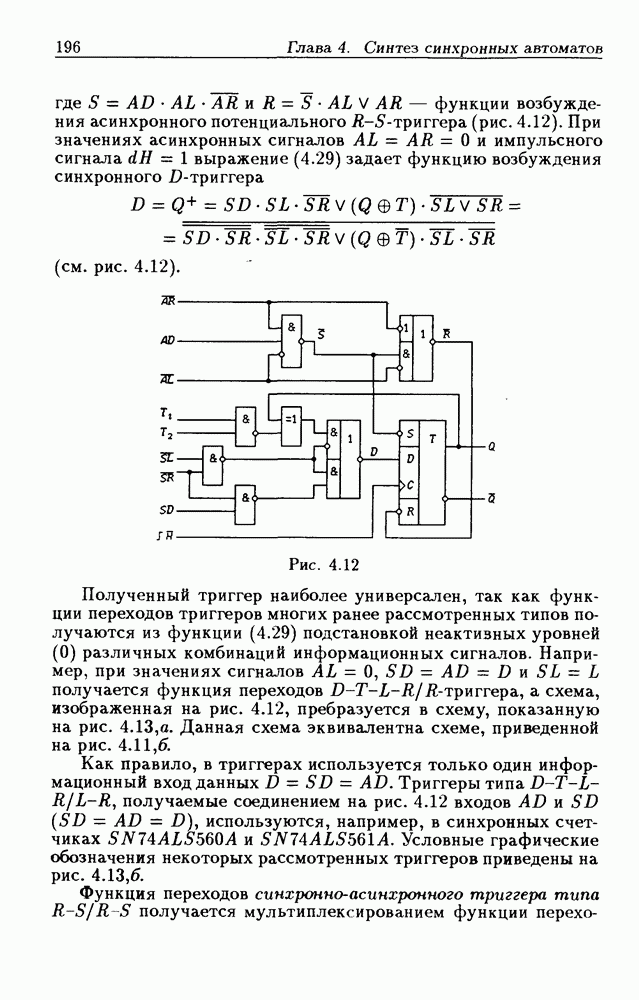
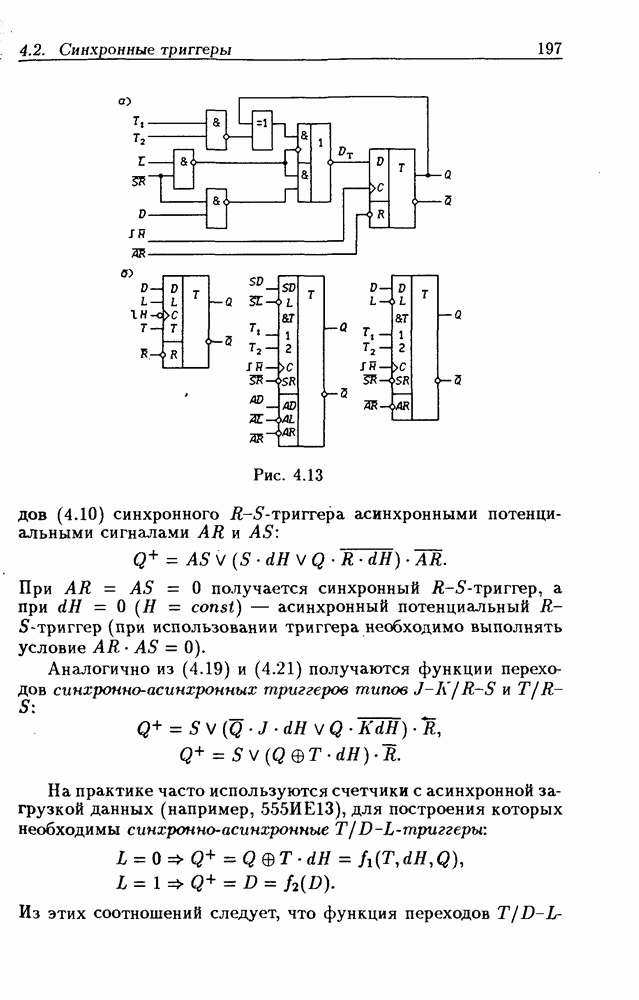
- Триггеры типов D-T-L и D-T-L/R
- Функции переходов синхронно-асинхронных триггеров.
- 4.3. Примеры синтеза синхронных автоматов
- 4.4. Сдвигающие регистры
- Синтез счетчиков на сдвигающих регистрах.
- Сдвигающие регистры с загрузкой данных.
- Реверсивные сдвигающие регистры.
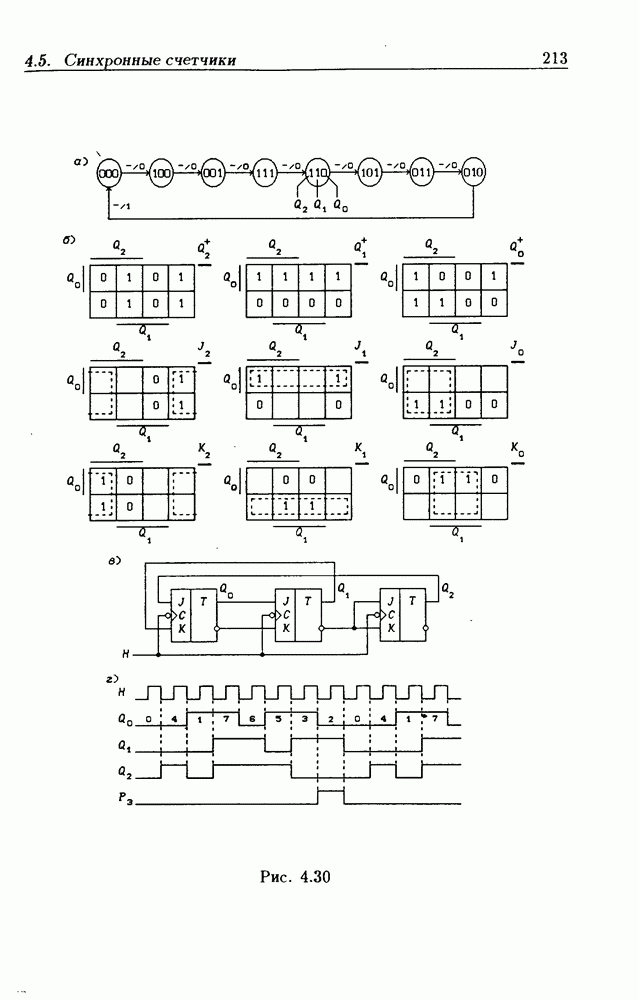
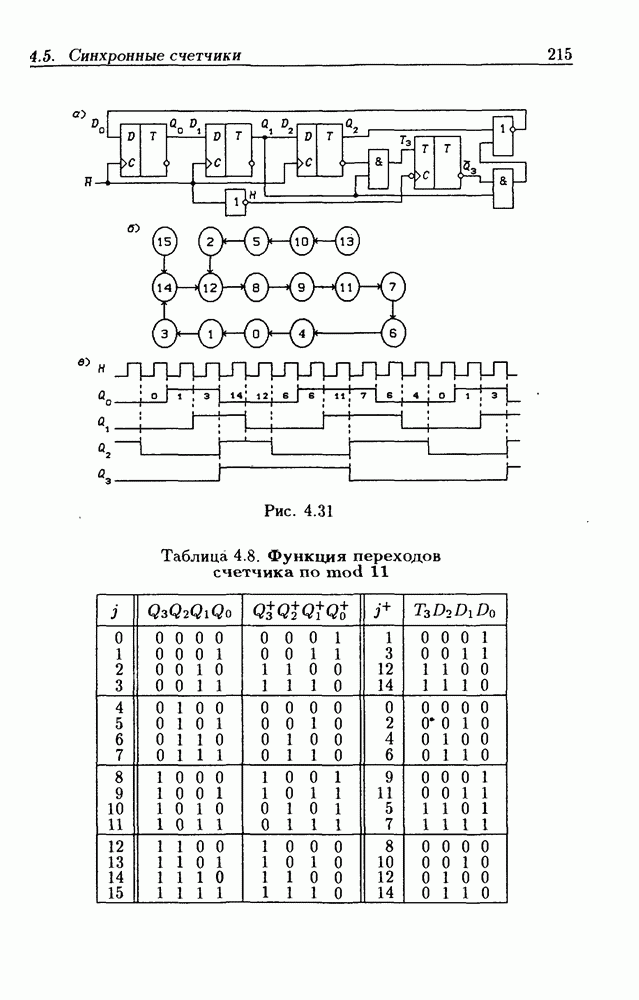
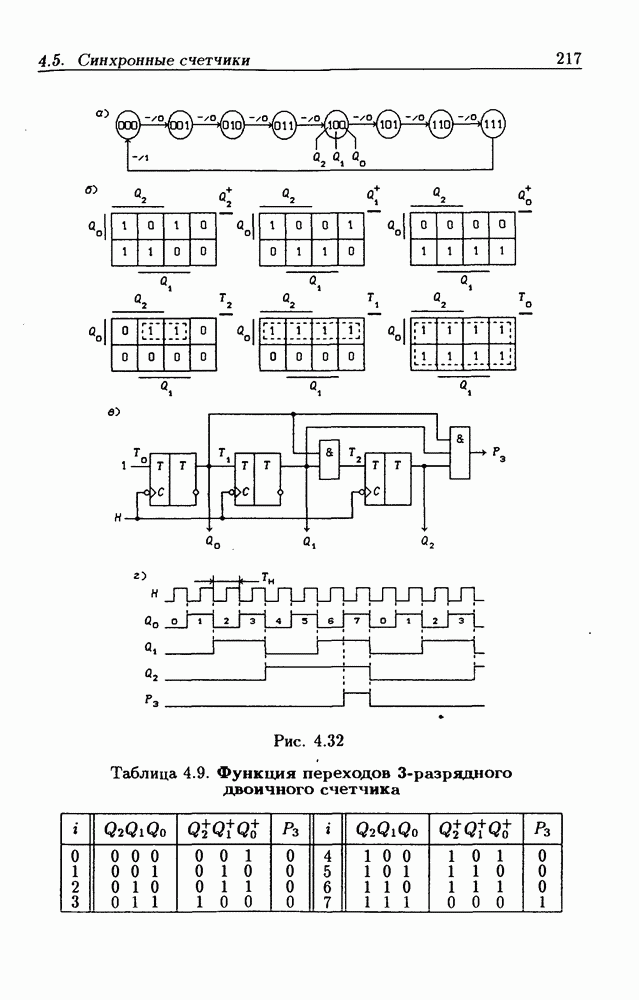
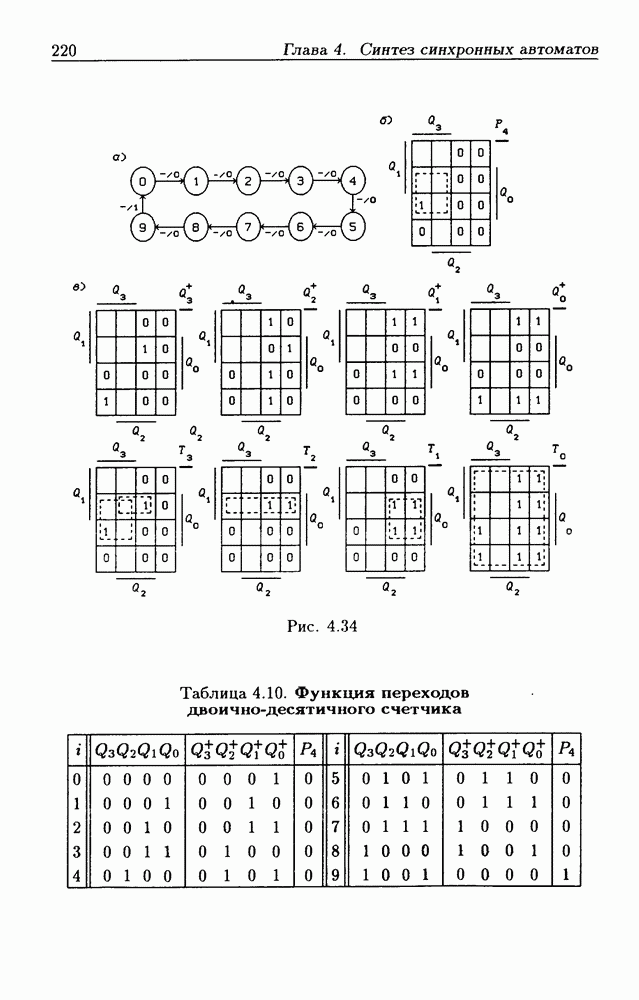
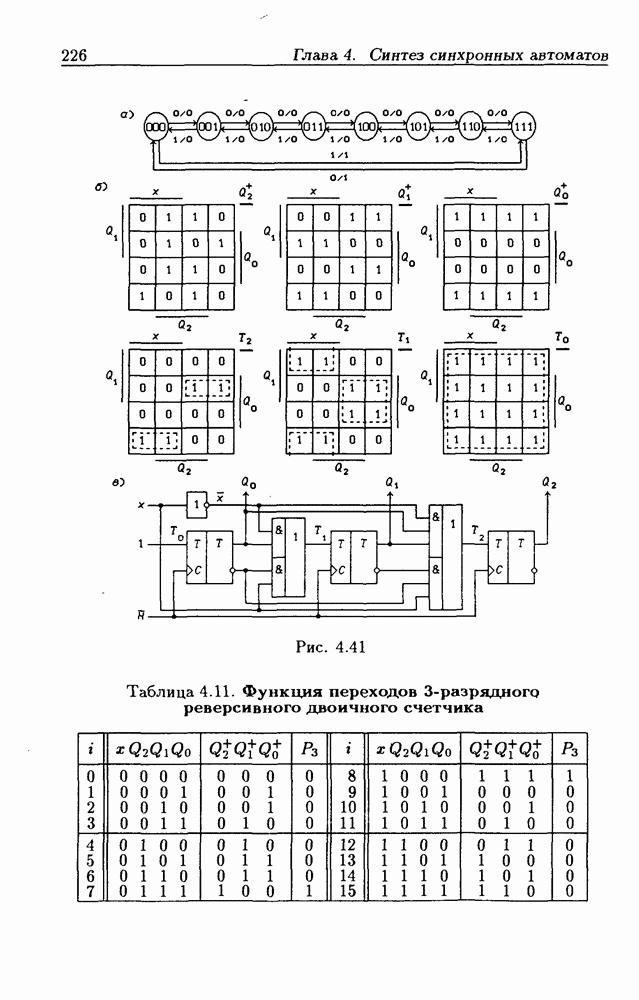
- 4.5. Синхронные счетчики
- Синхронные двоичные счетчики.
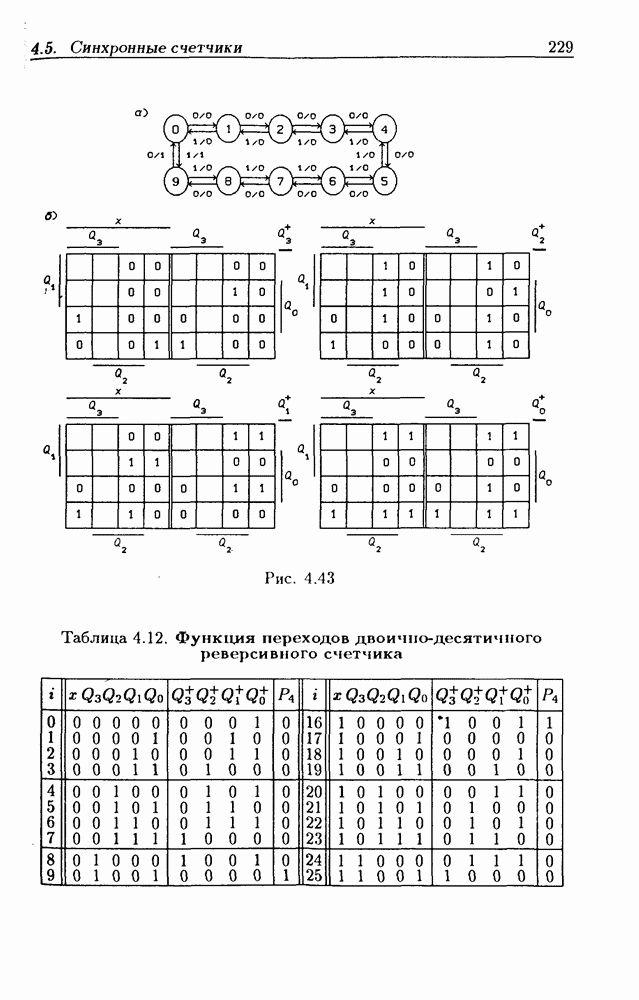
- Синхронные двоично-десятичные счетчики.
- Каскадирование двоичных и двоично-десятичных счетчиков.
- Синхронные двоичные реверсивные счетчики.
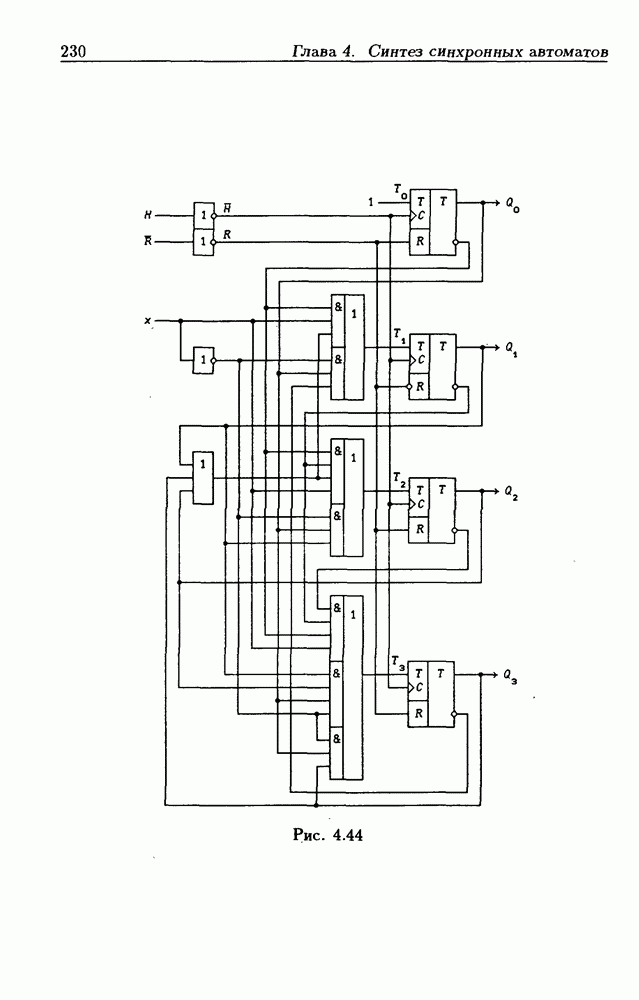
- Реверсивные двоично-десятичные счетчики.
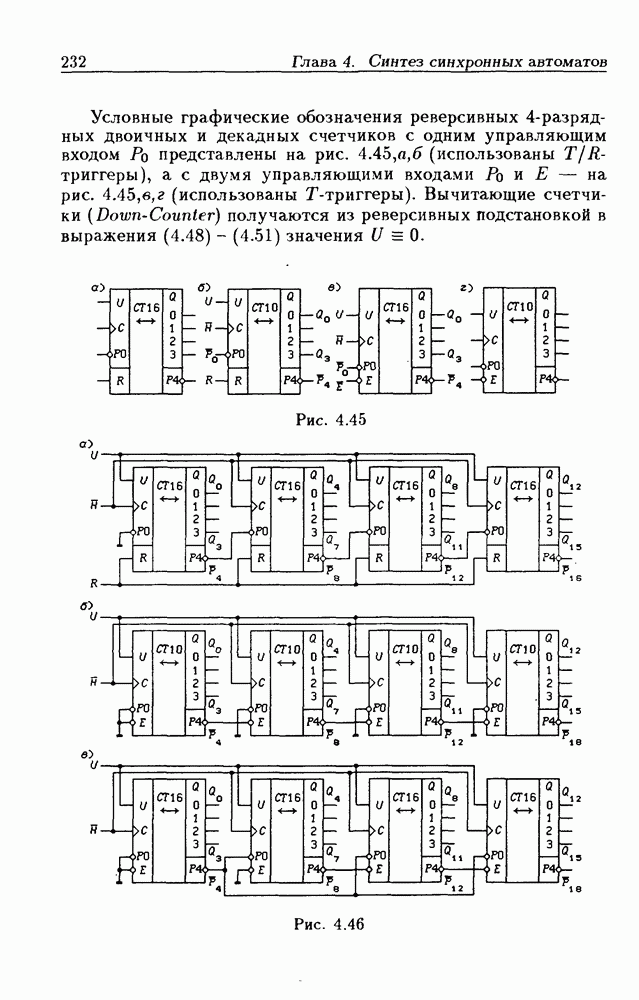
- Каскадирование реверсивных счетчиков.
- Счетчики на сдвигающих регистрах.
- Кольцевые счетчики.
- Линейные счетчики.
- Программируемые счетчики.
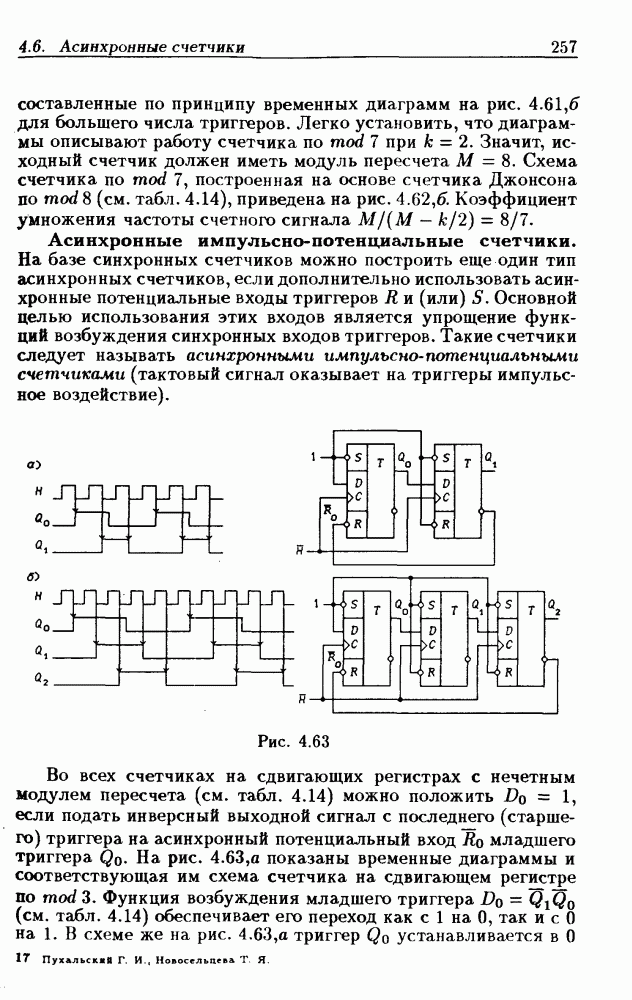
- 4.6. Асинхронные счетчики
- Асинхронные счетчики с умножением частоты счетного сигнала.
- Асинхронные импульсно-потенциальные счетчики.
- Асинхронное программирование модуля пересчета счетчиков.
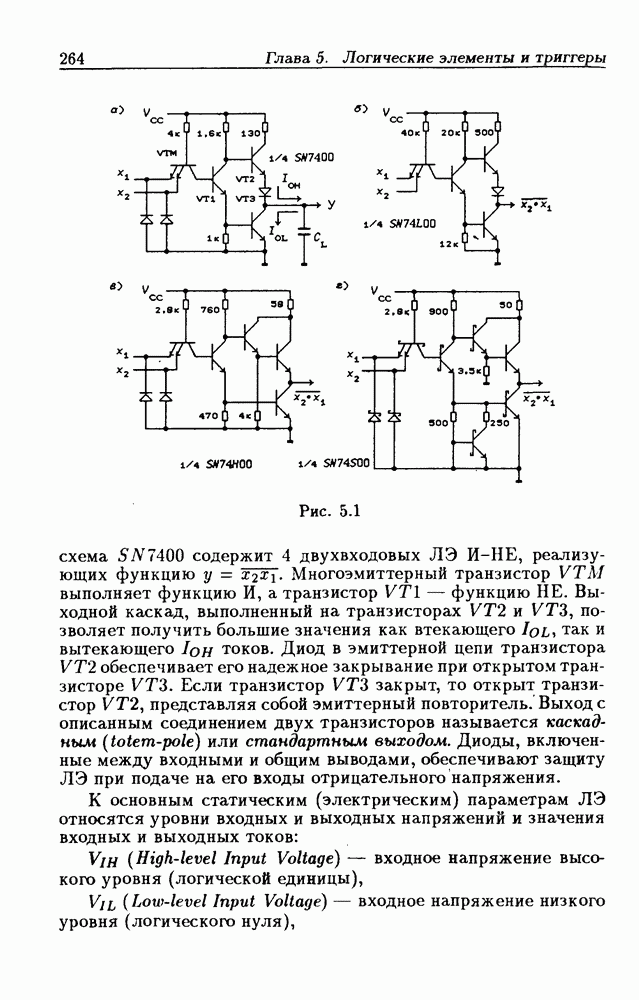
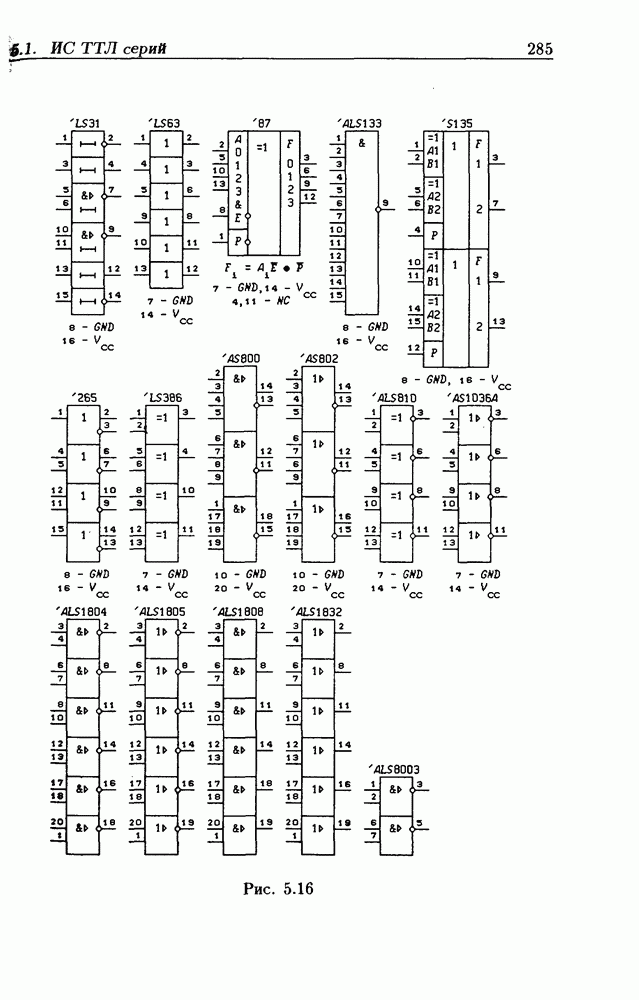
- Глава 5. Логические элементы и триггеры
- Логические элементы.
- Классификация ИС по степени интеграции.
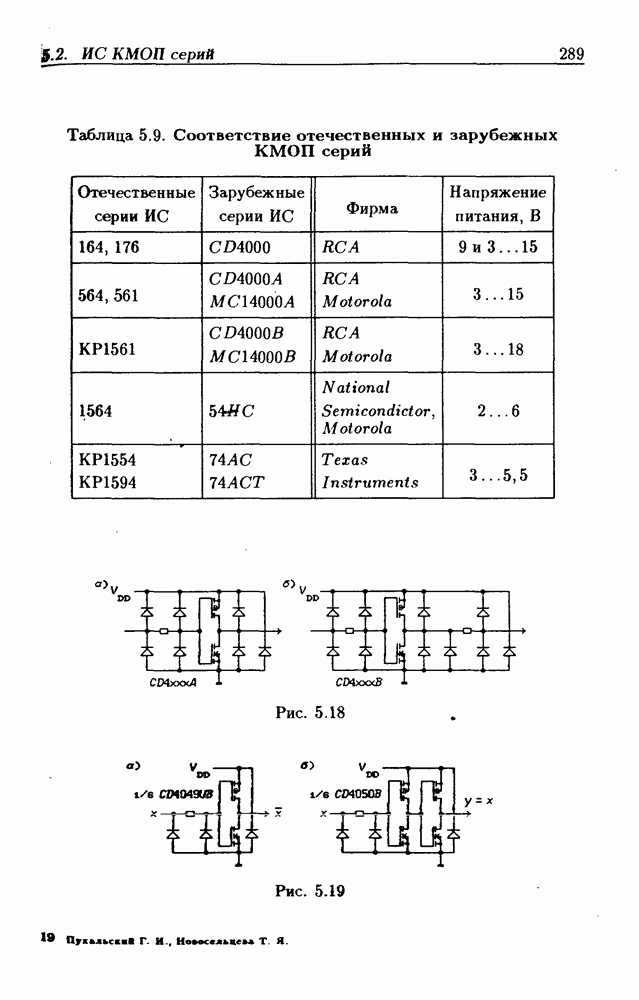
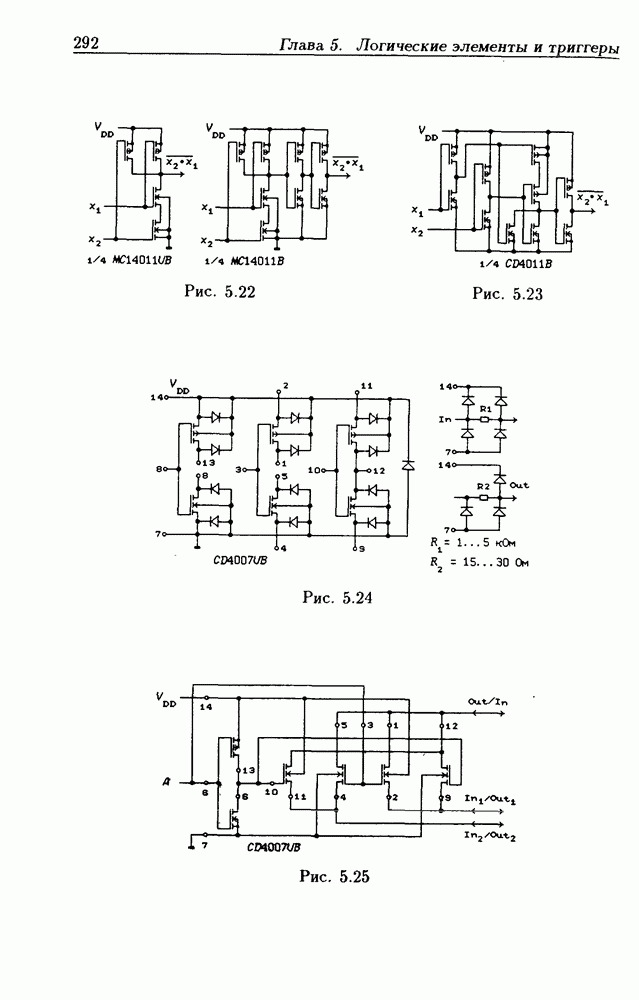
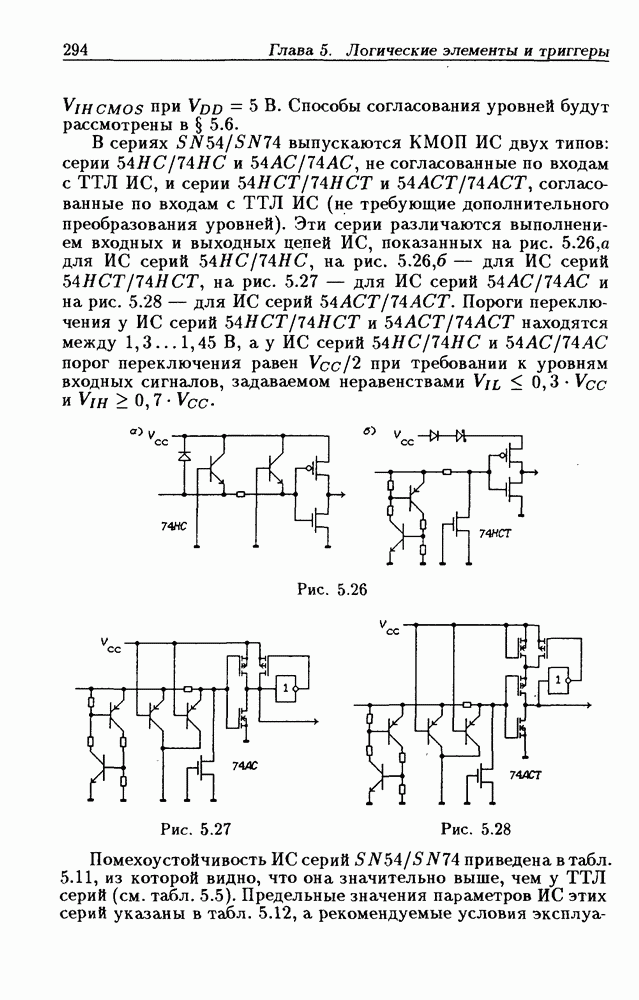
- 5.2. Интегральные схемы КМОП серий
- 5.3. Триггеры Шмитта
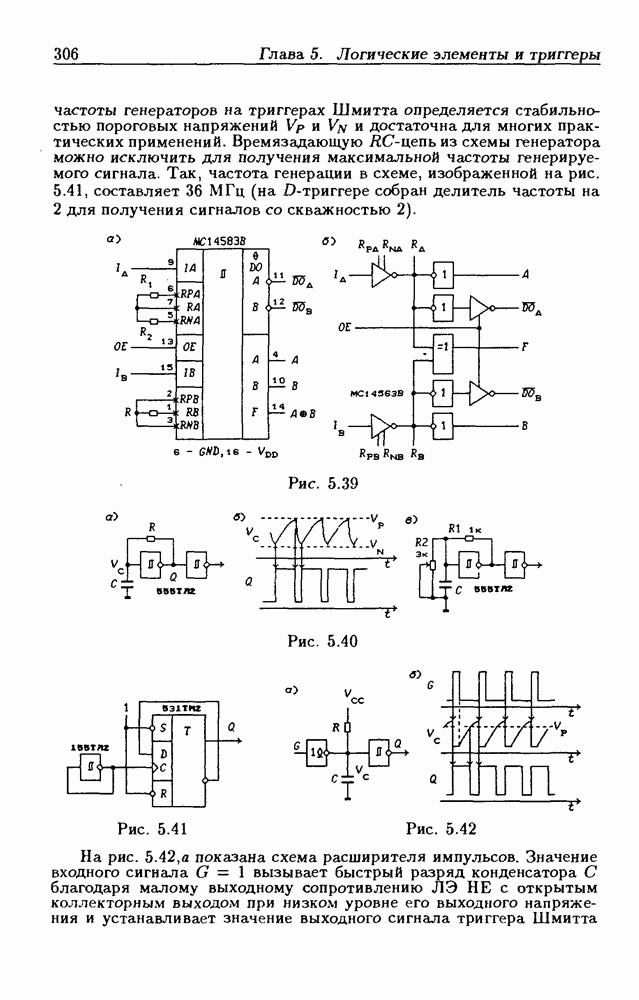
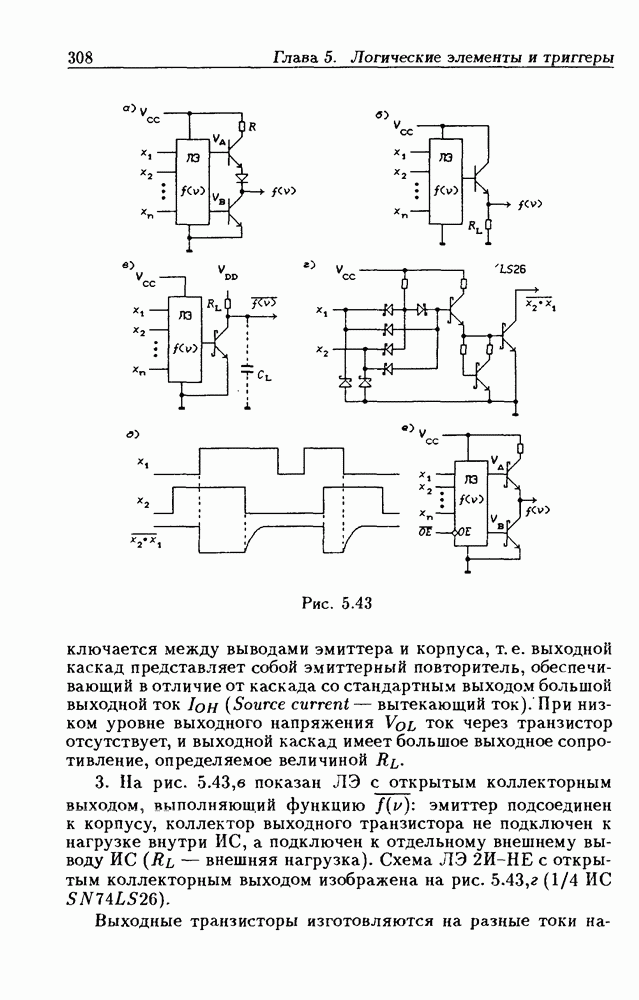
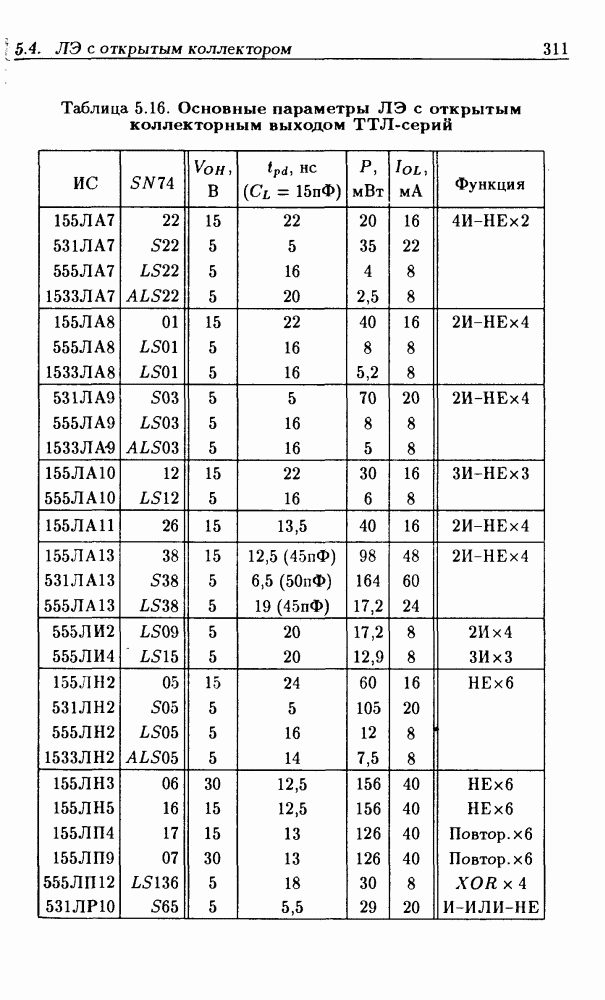
- 5.4. Логические элементы с открытым коллекторным выходом
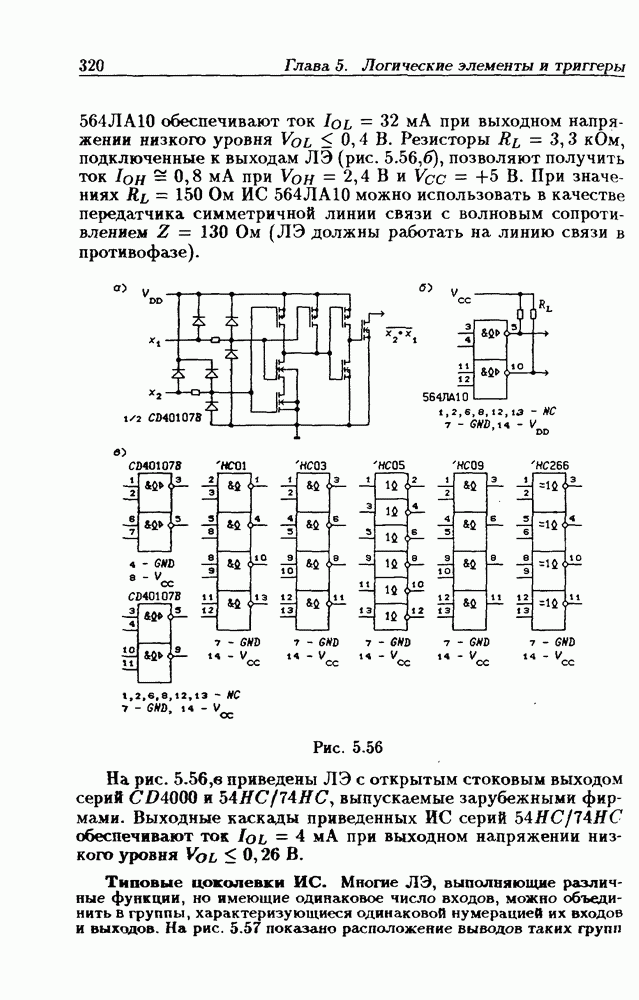
- Логические элементы с открытым коллекторным выходом.
- Применения ЛЭ с открытым коллекторным выходом.
- Интерфейсные ЛЭ с открытым коллекторным выходом.
- Логические элементы с открытым стоковым выходом.
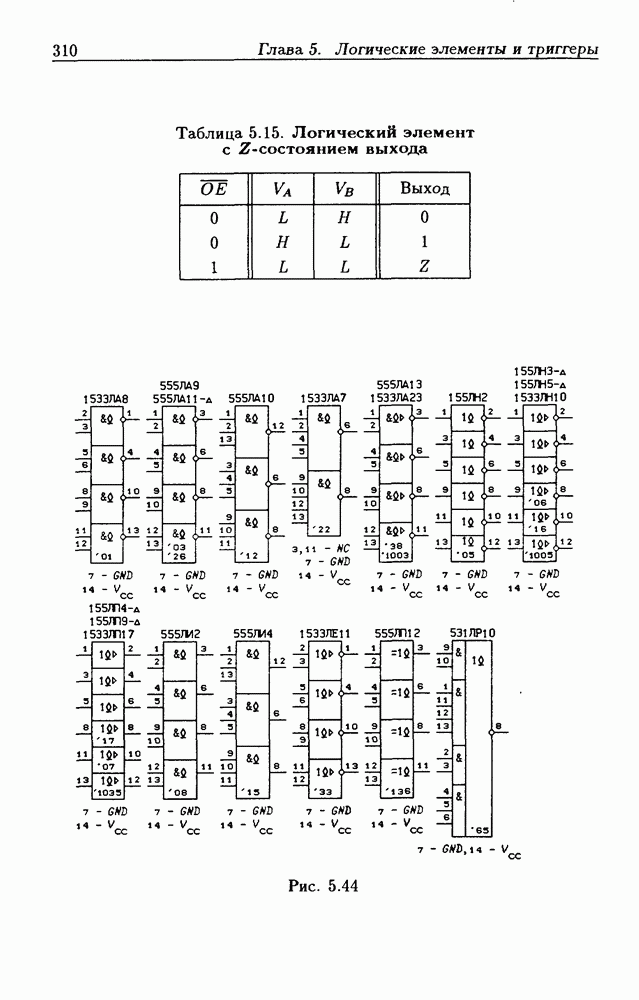
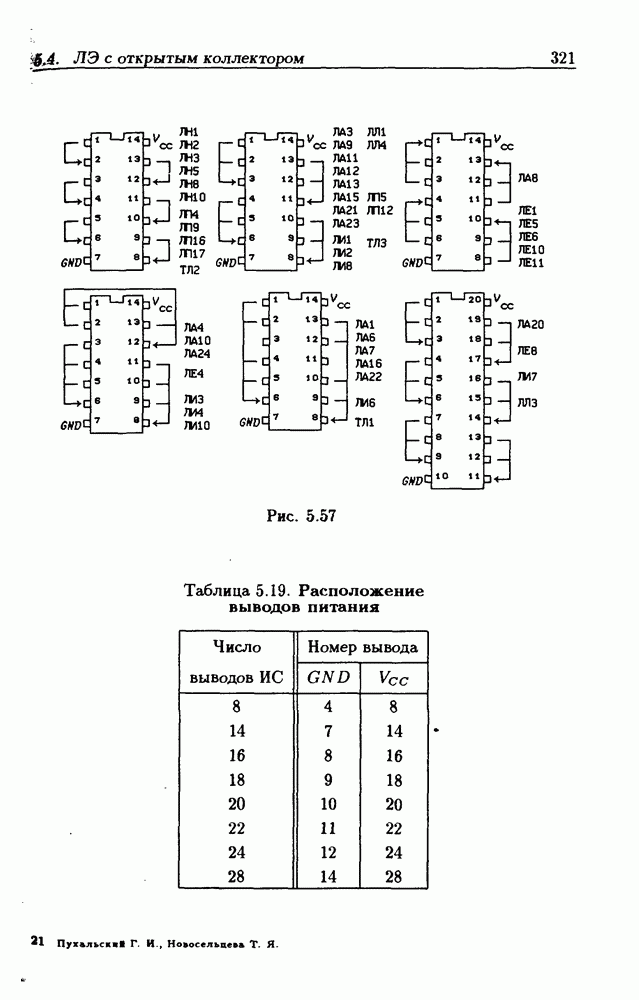
- Типовые цоколевки ИС.
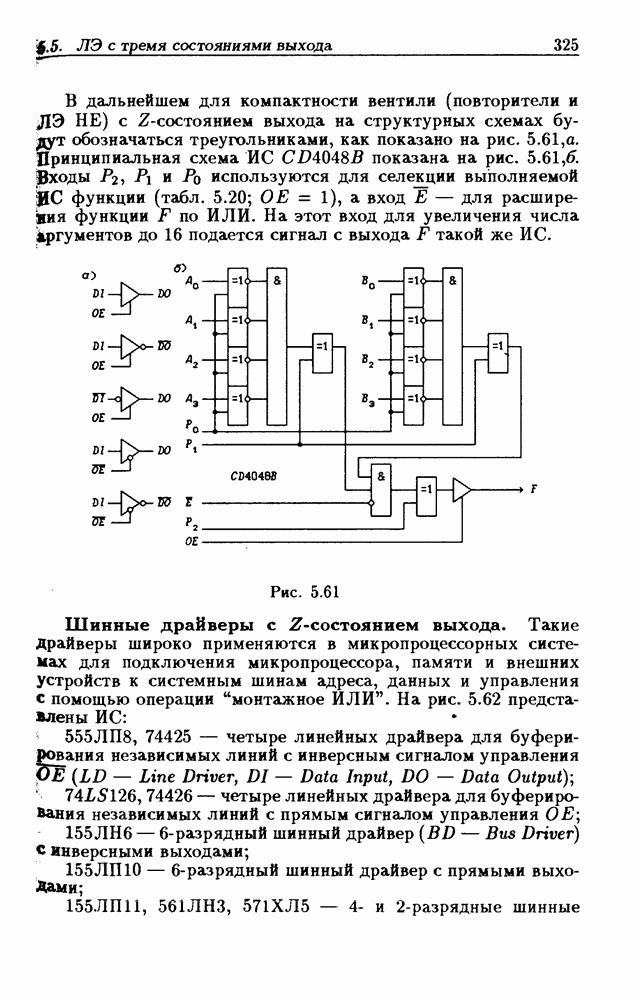
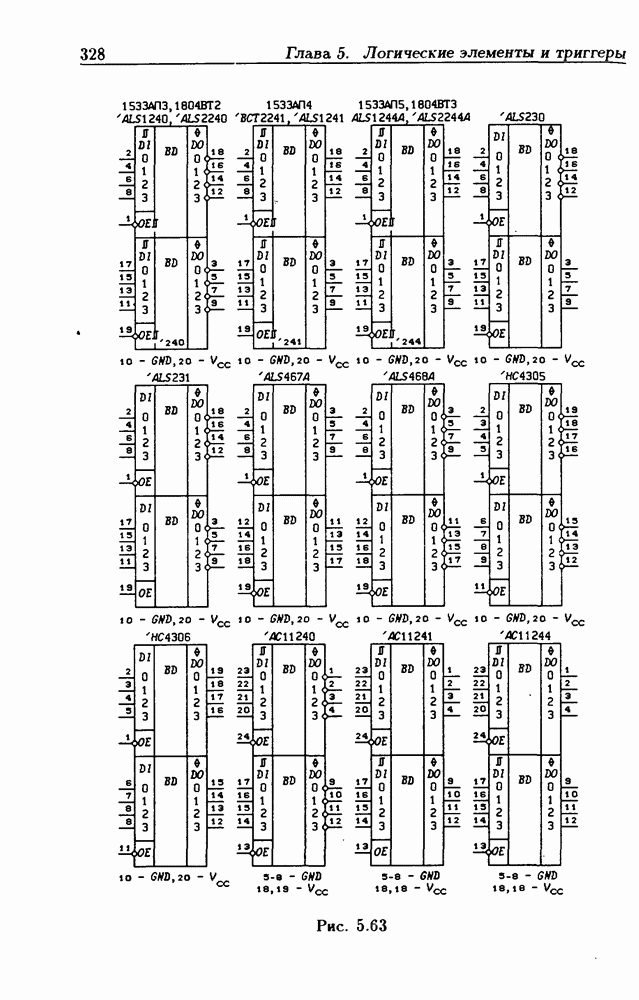
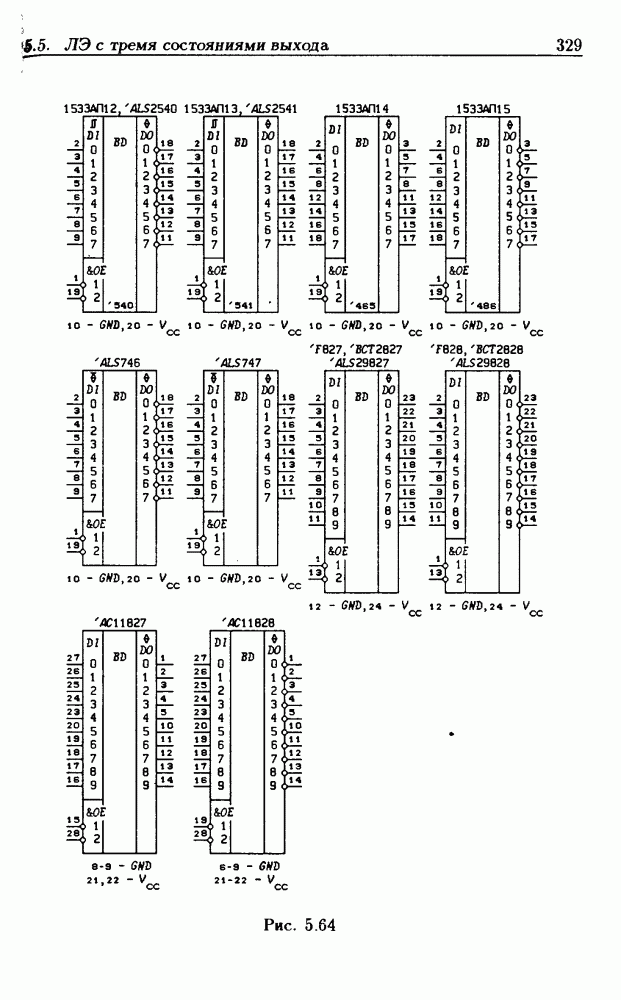
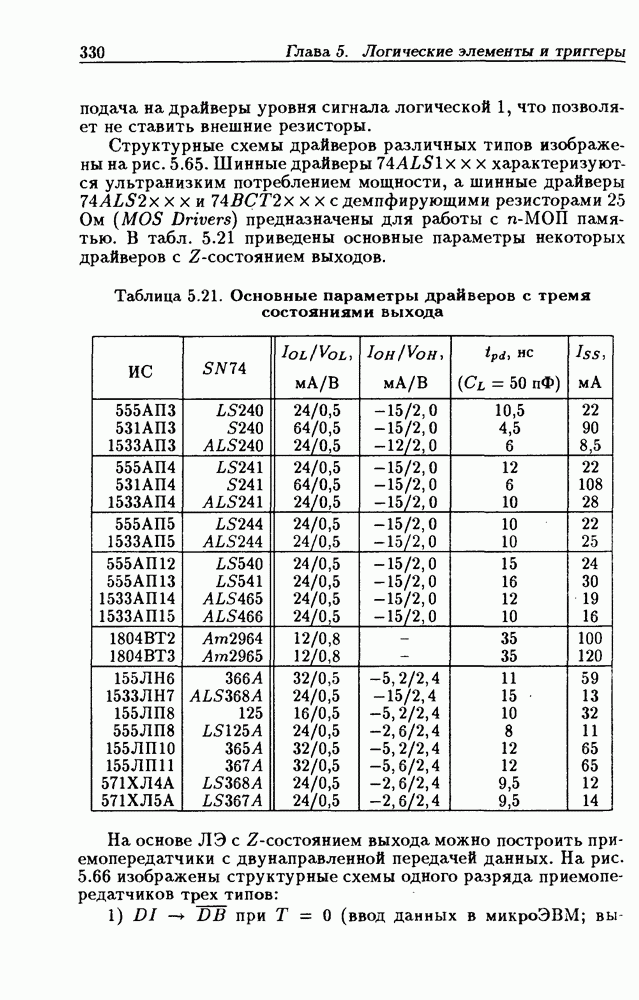
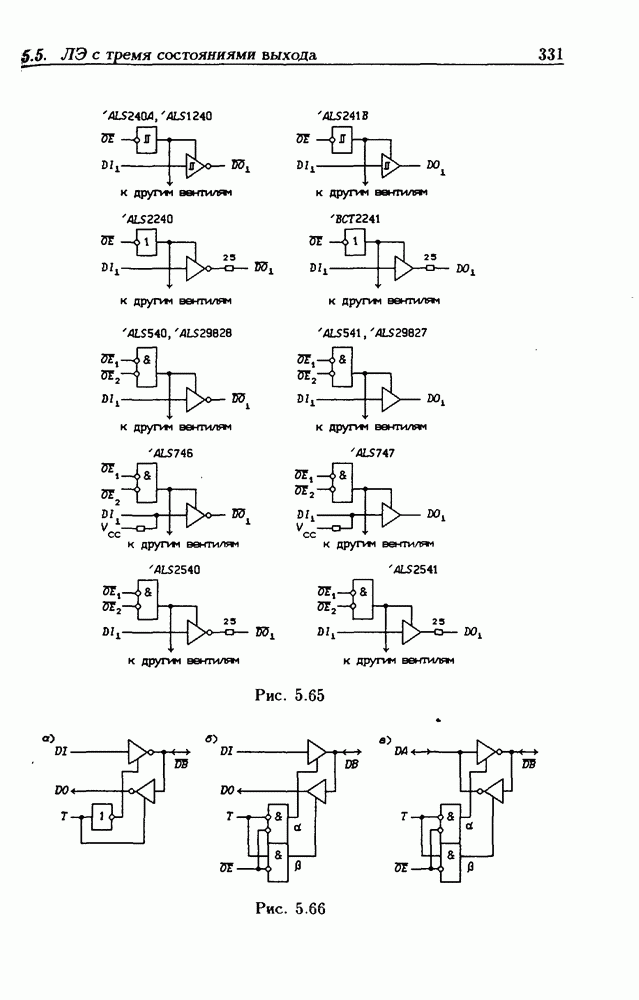
- 5.5. Логические элементы с тремя состояниями выхода
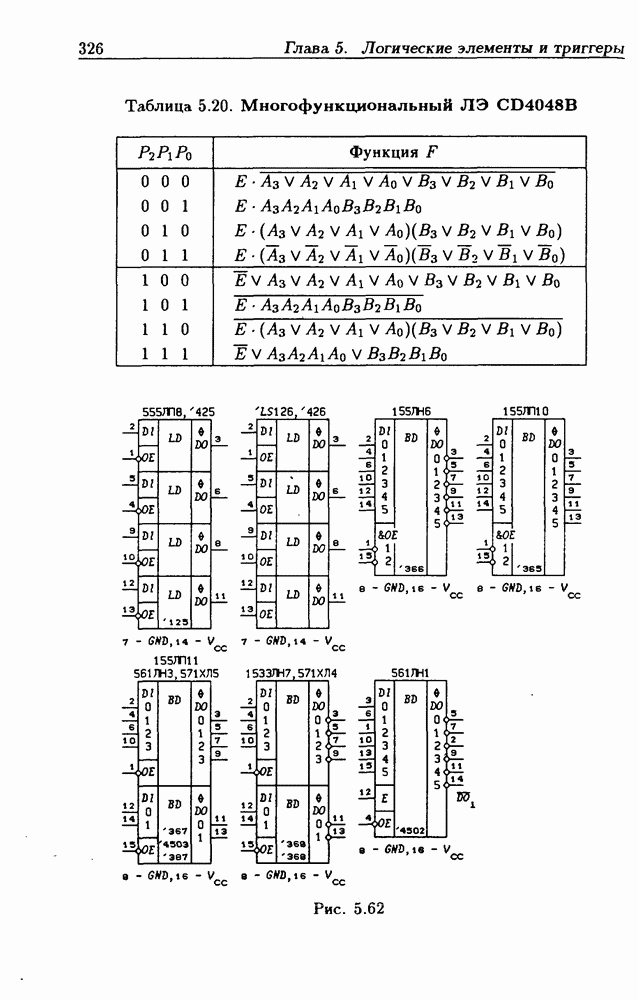
- Шинные драйверы с Z-состоянием выхода.
- Основные правила графического изображения ИС.
- 5.6. Преобразователи уровней напряжения и тока
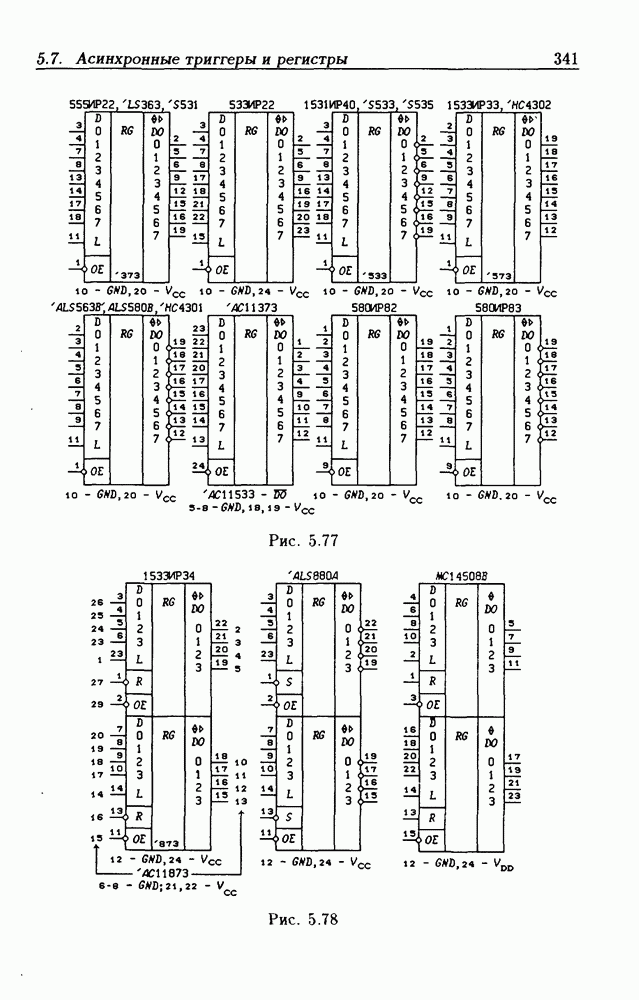
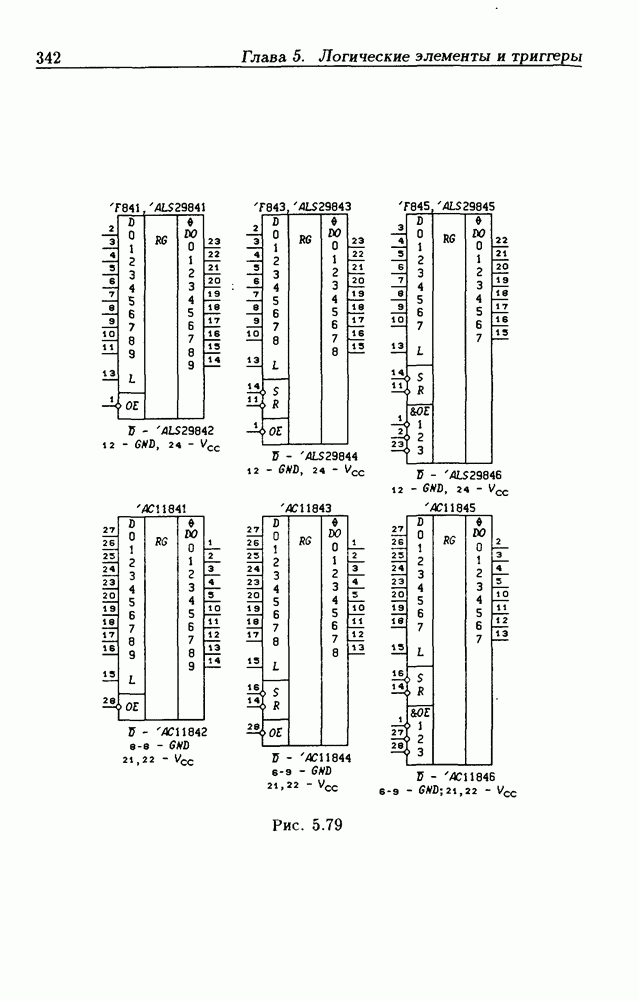
- 5.7. Асинхронные потенциальные триггеры и регистры памяти
- 5.8. Синхронные триггеры и регистры памяти
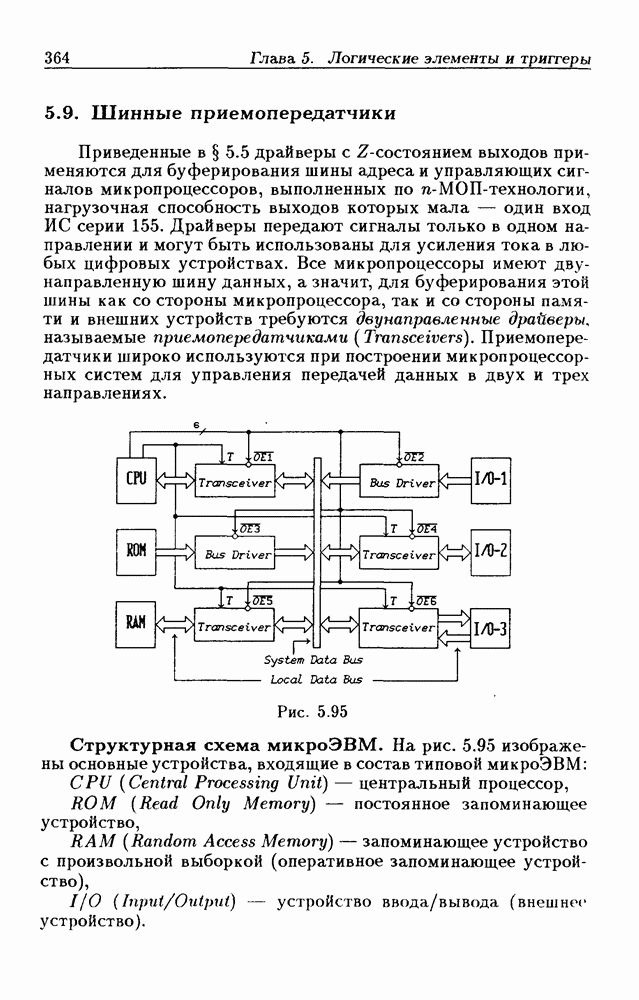
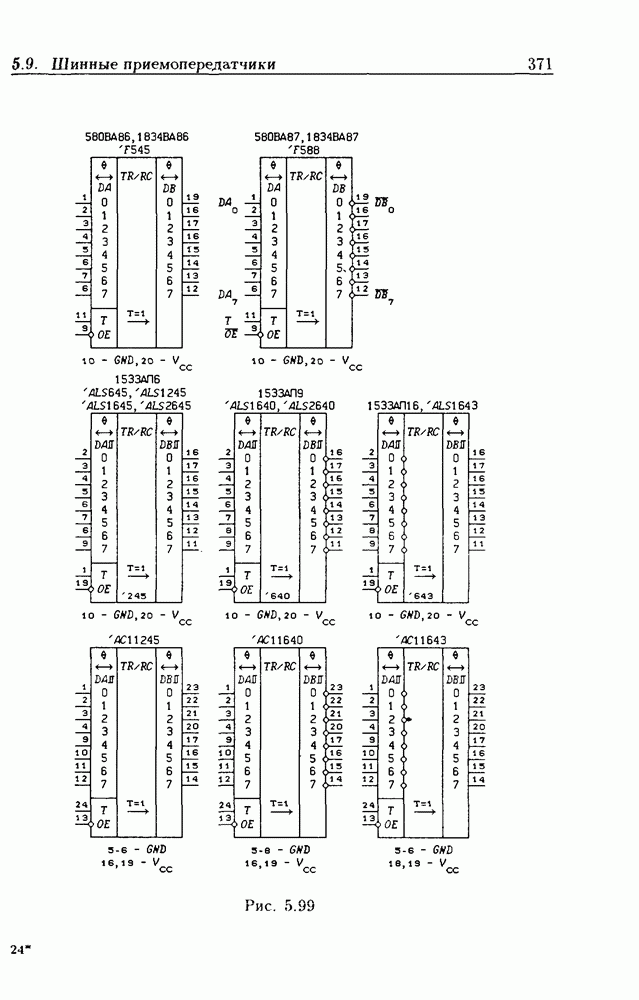
- 5.9. Шинные приемопередатчики
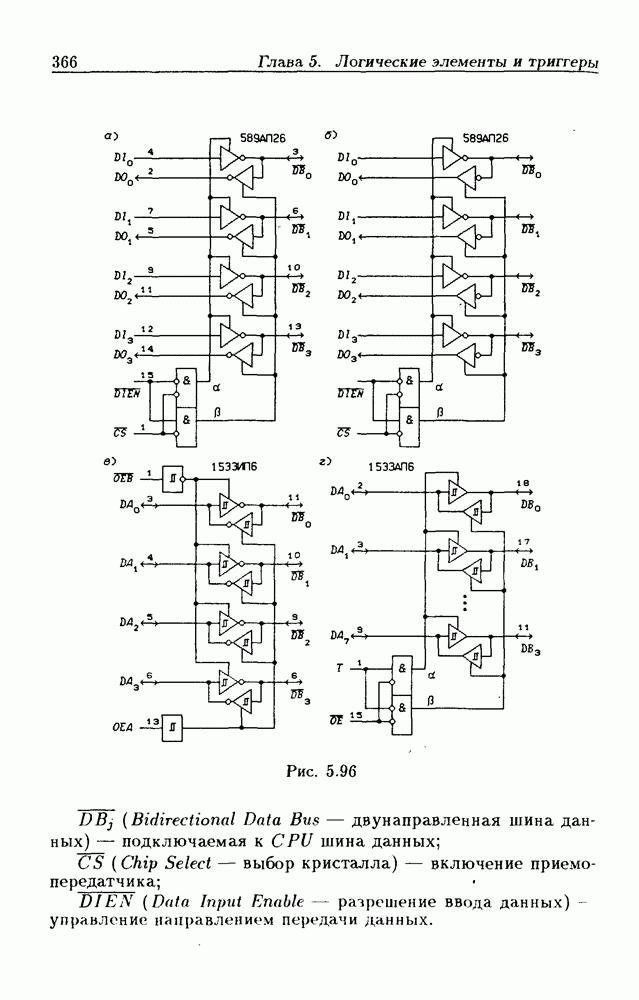
- Шинные приемопередатчики с Z-состоянием выхода.
- Шинные приемопередатчики с открытым коллекторным выходом.
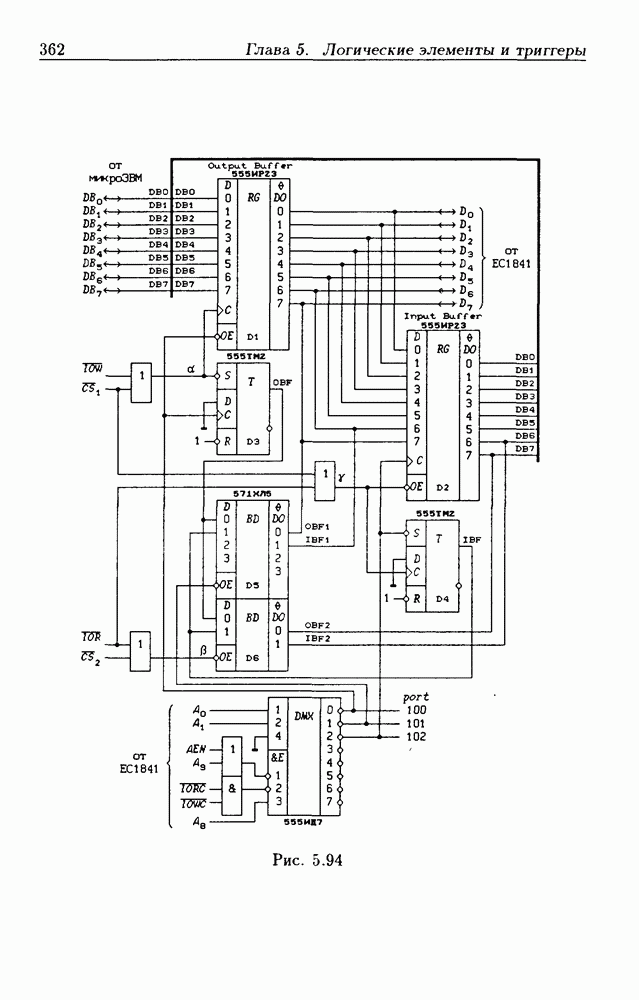
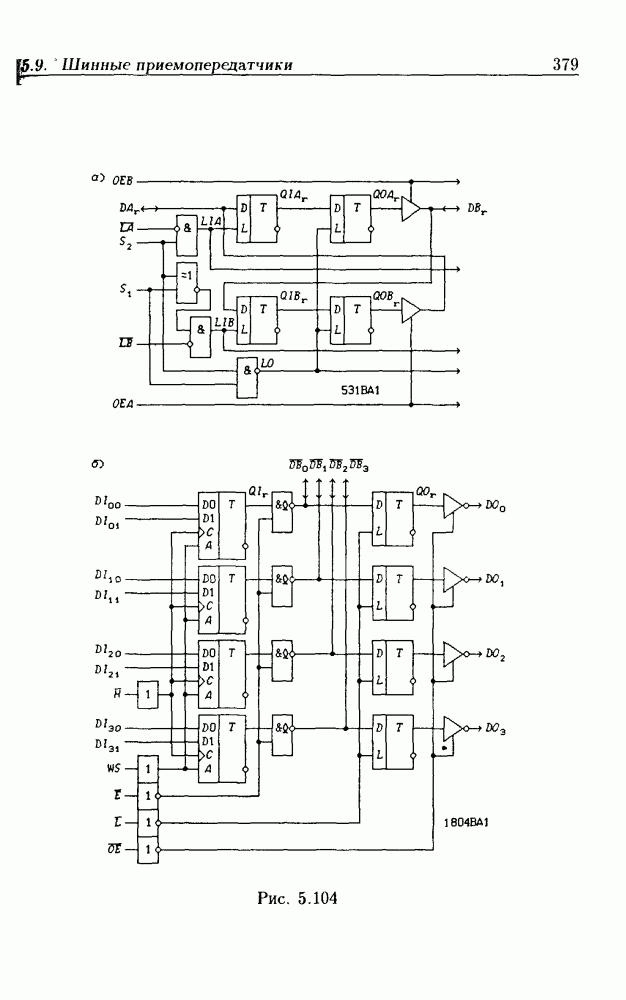
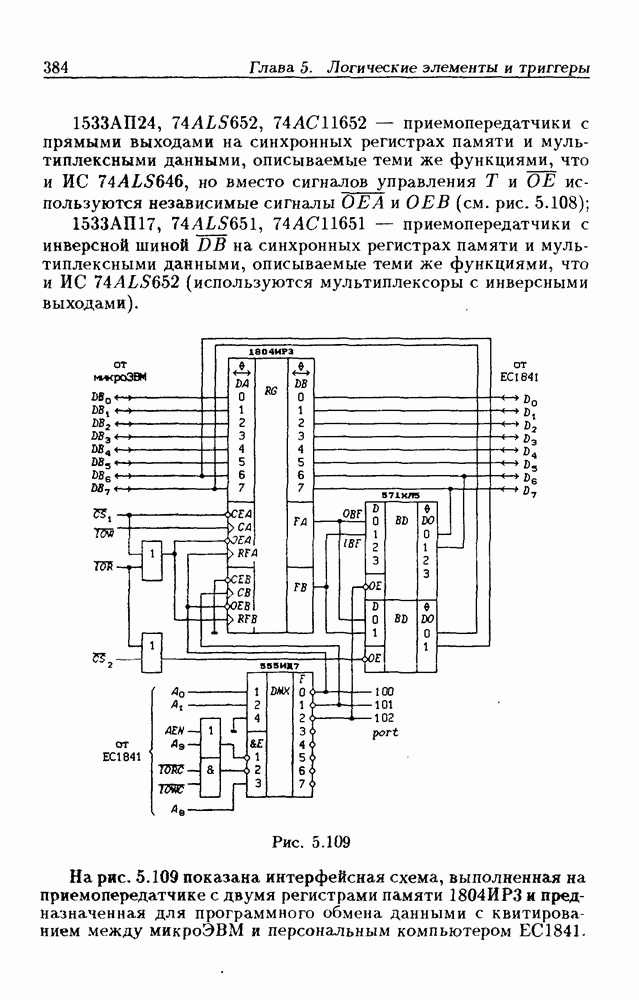
- Шинные приемопередатчики с регистрами памяти.
- Шинные приемопередатчики со сдвигающим регистром.
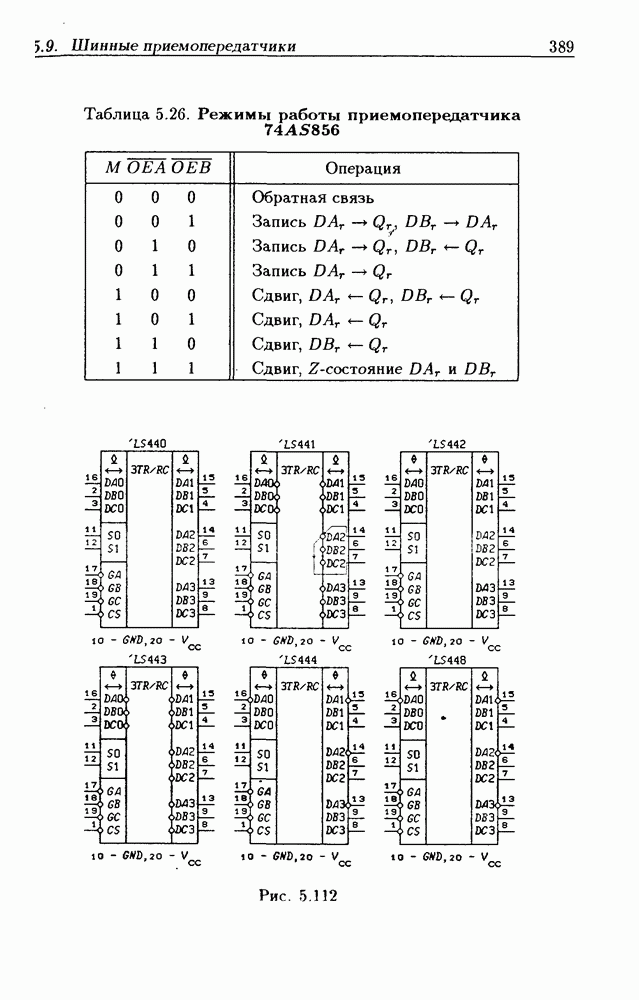
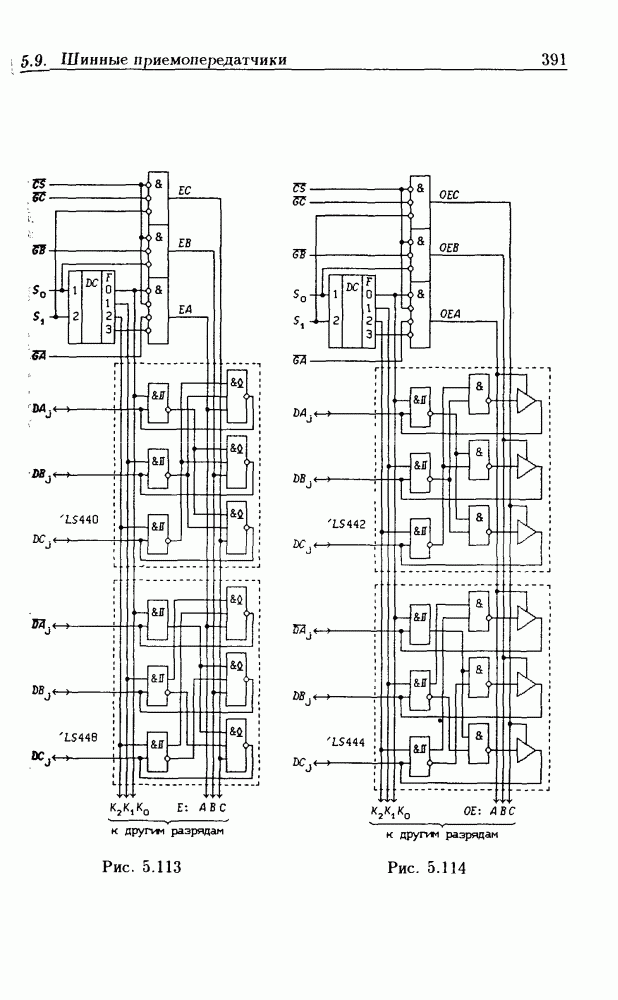
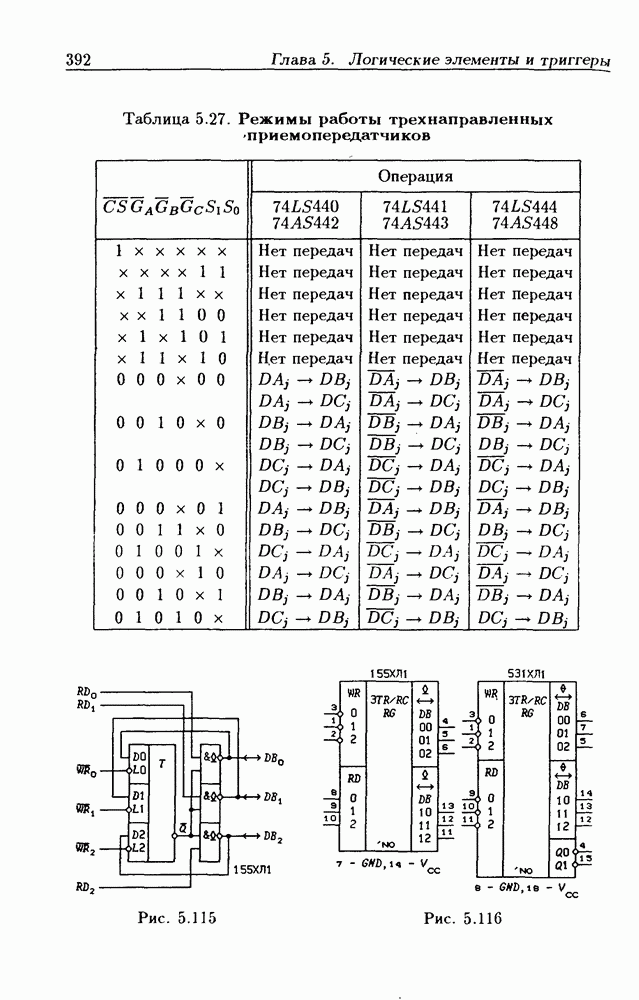
- Шинные трехнаправленные приемопередатчики.
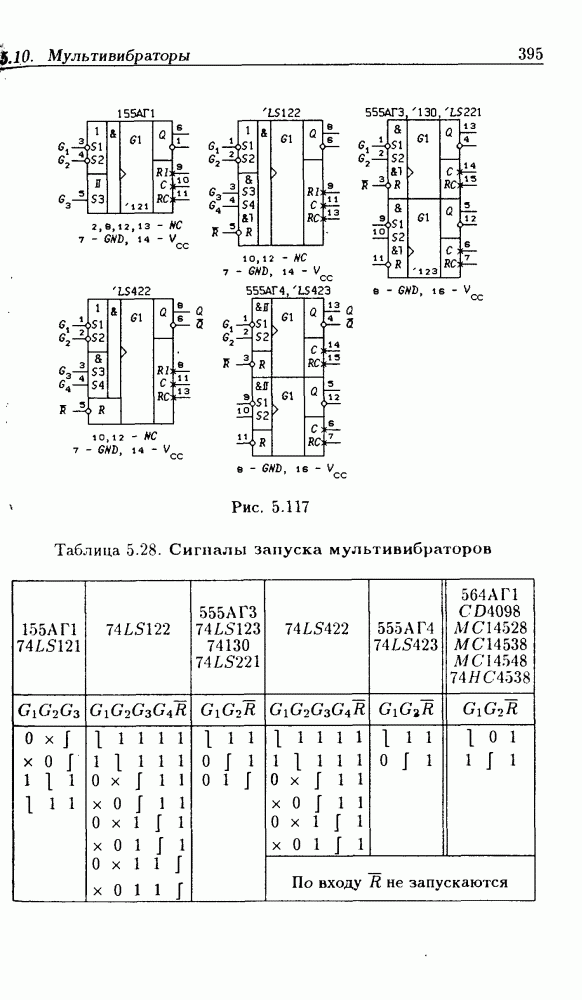
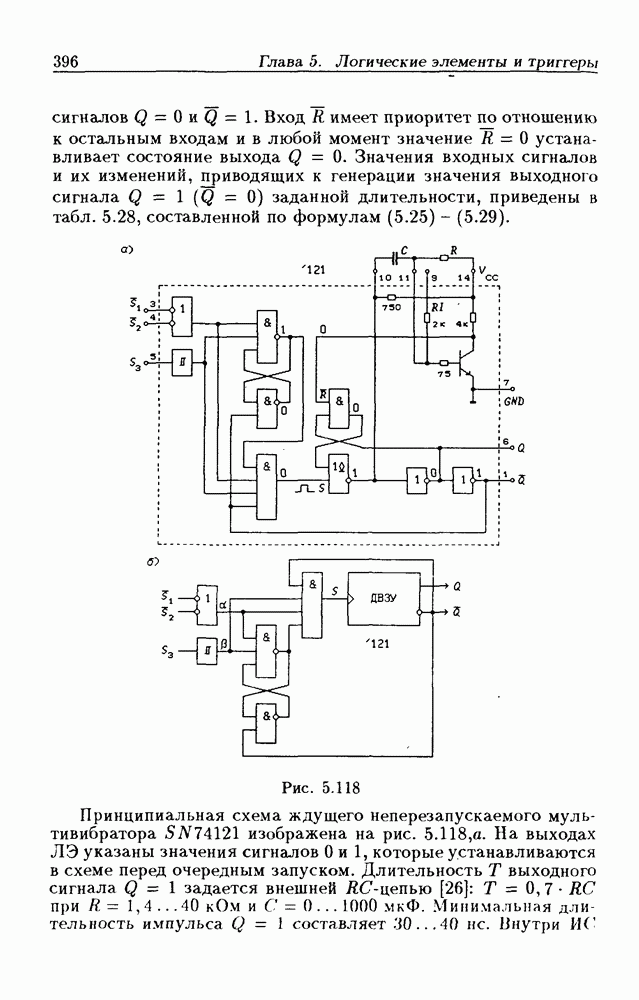
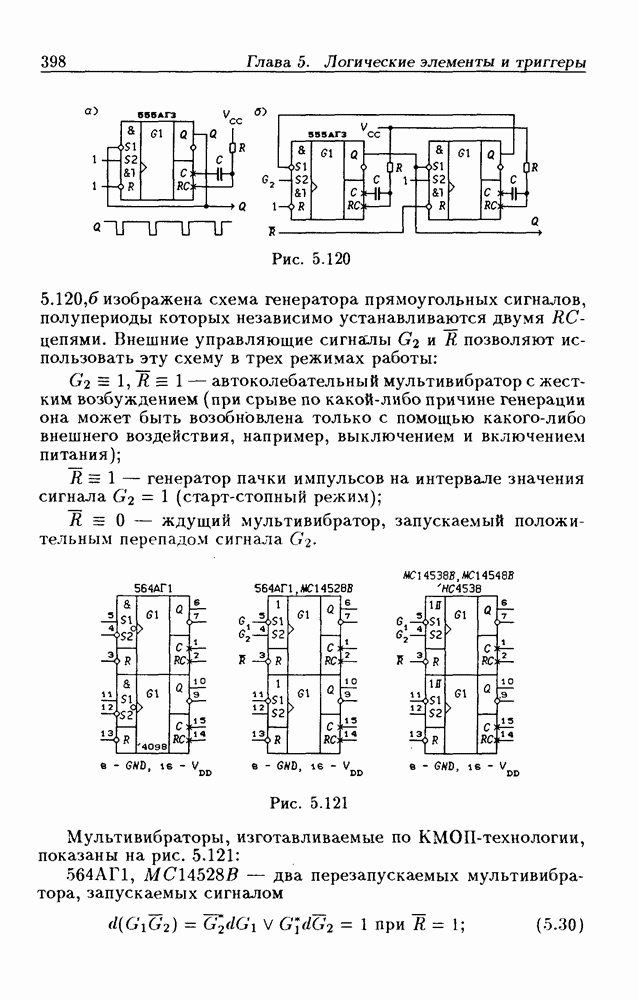
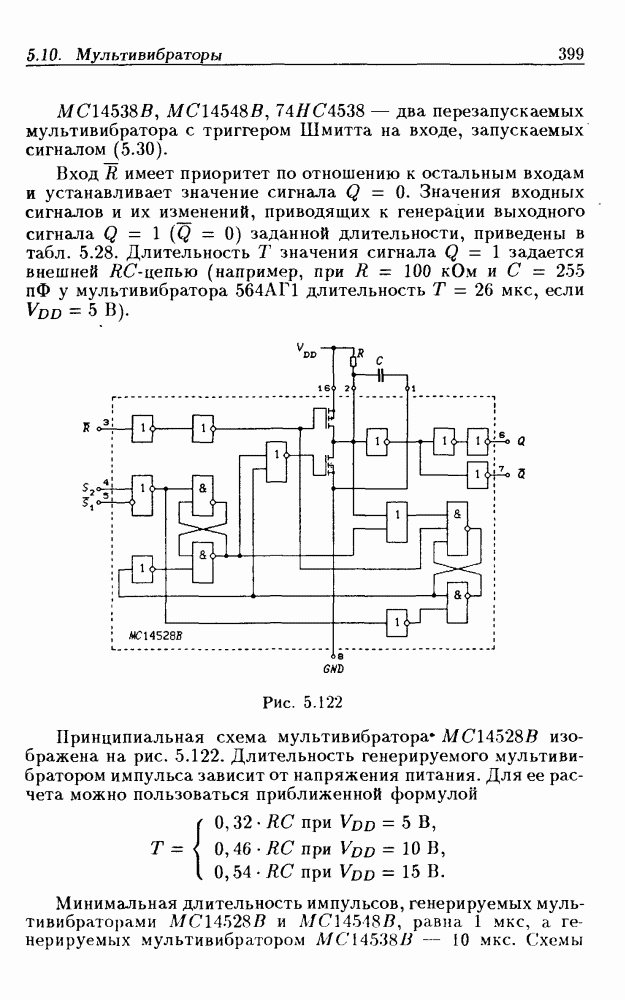
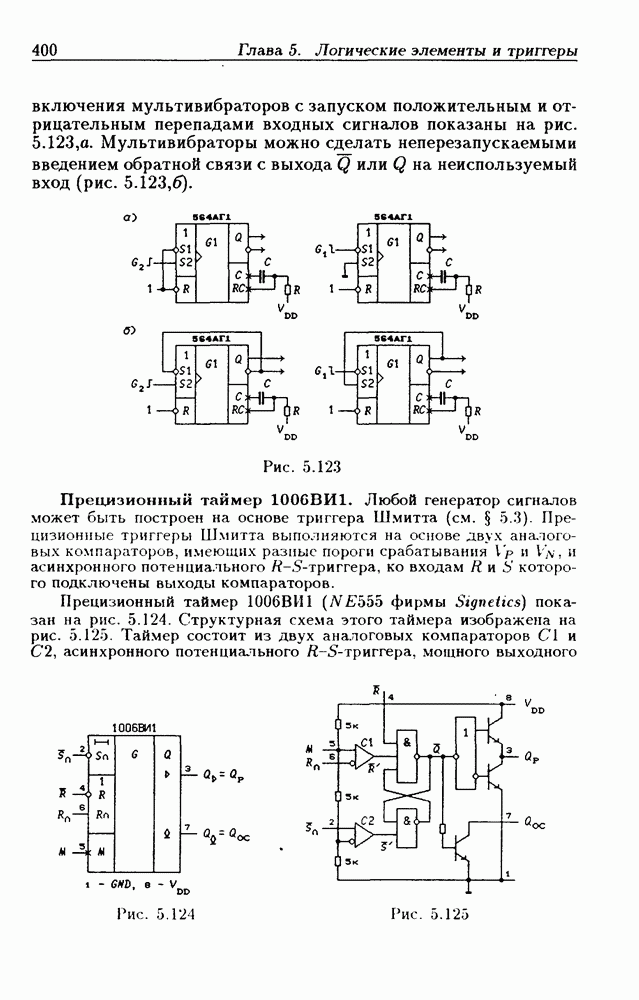
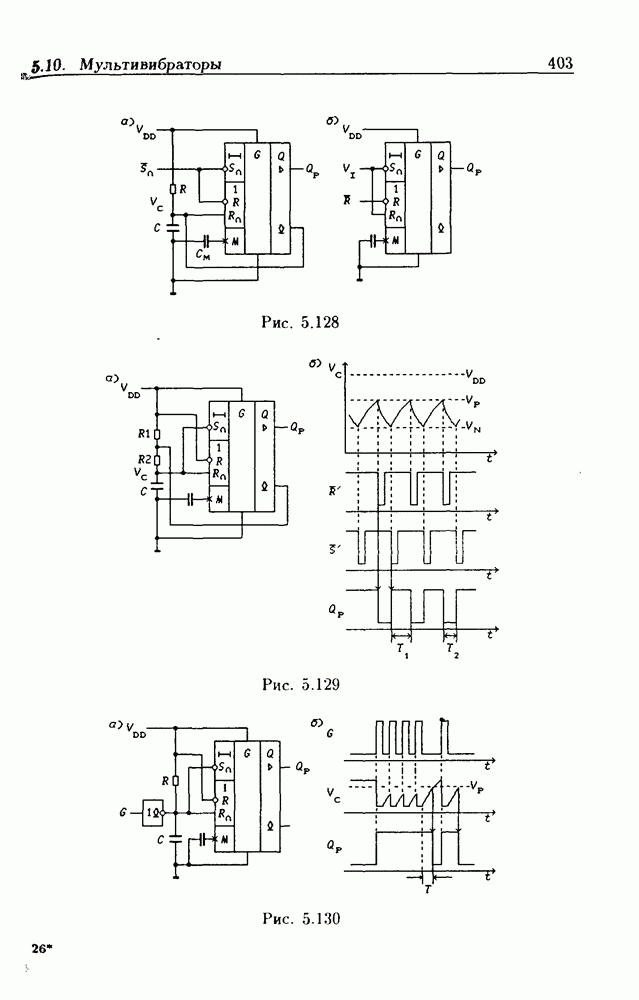
- 5.10. Мультивибраторы
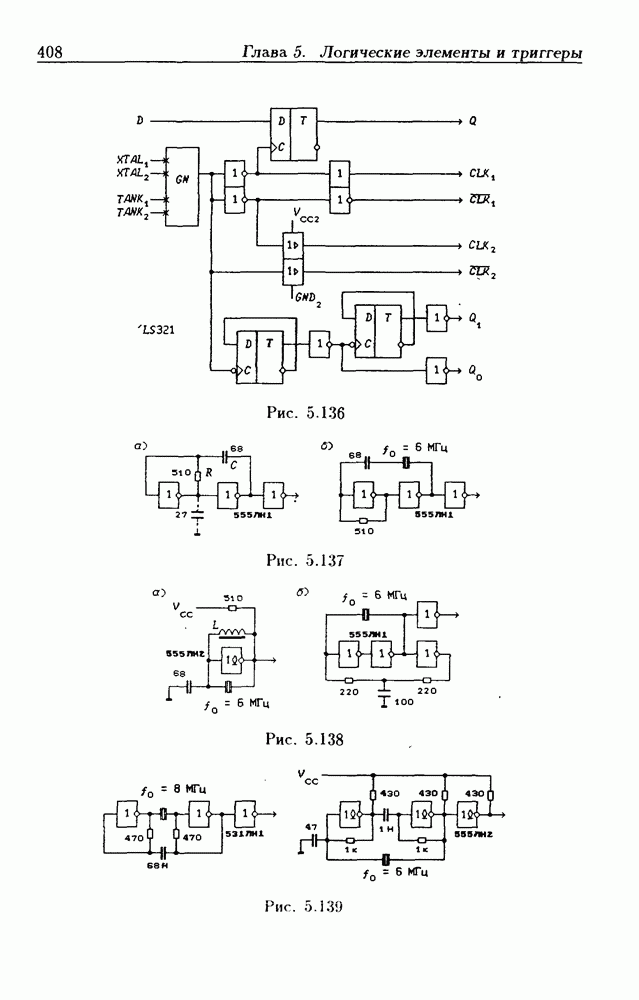
- 5.11. Генераторы
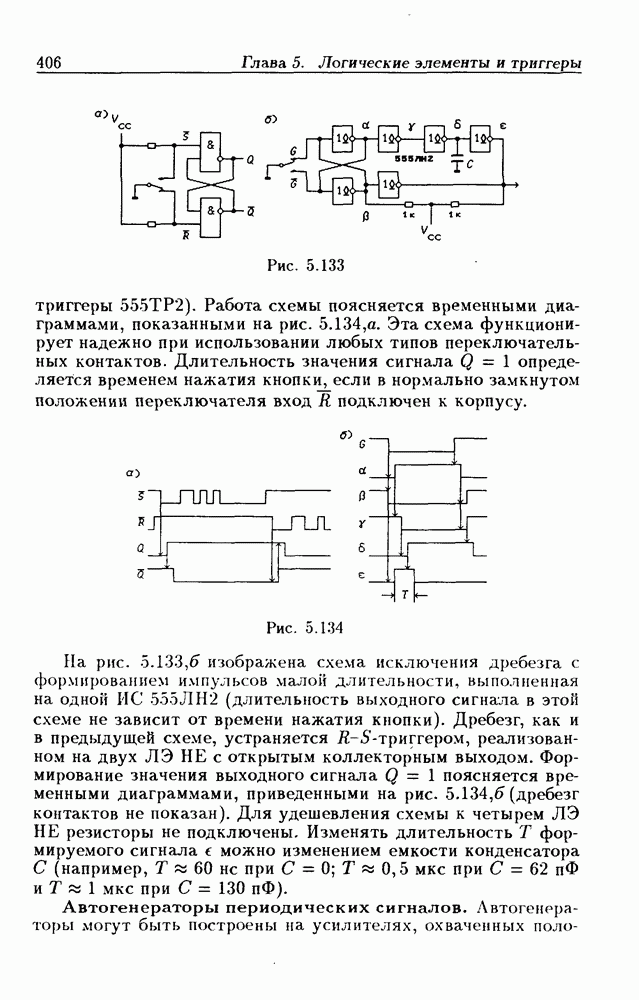
- Схемы устранения «дребезга» механических контактов.
- Автогенераторы периодических сигналов.
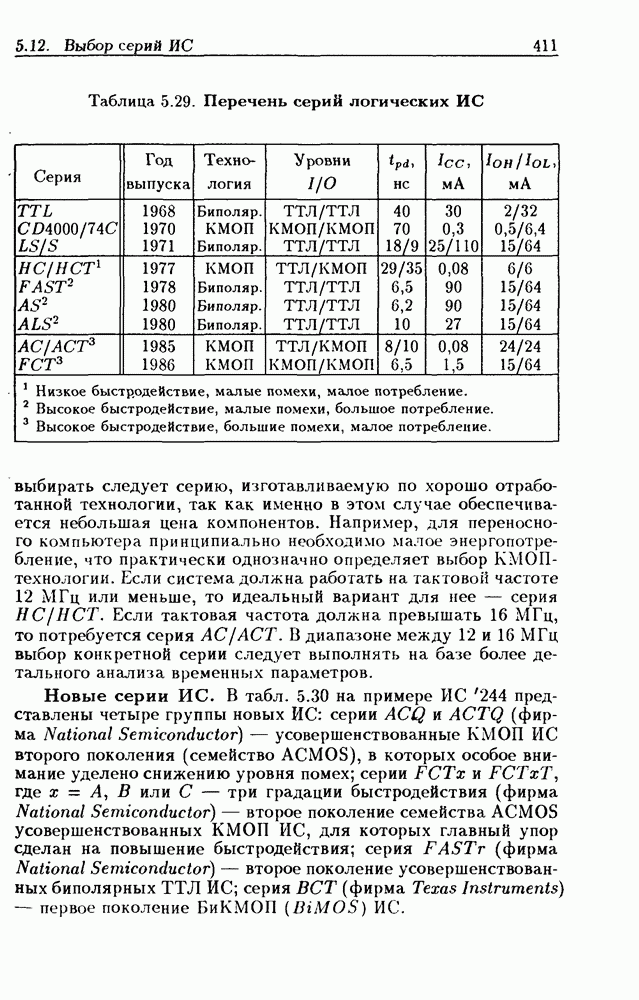
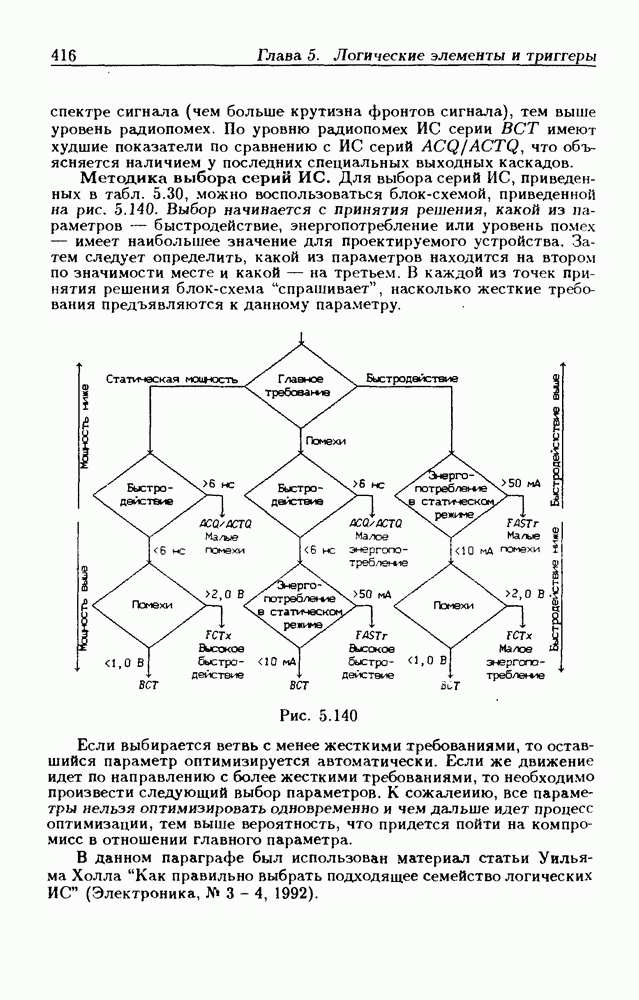
- 5.12. Рекомендации по выбору серий ИС
- Глава 6. Коммутаторы и арифметические устройства
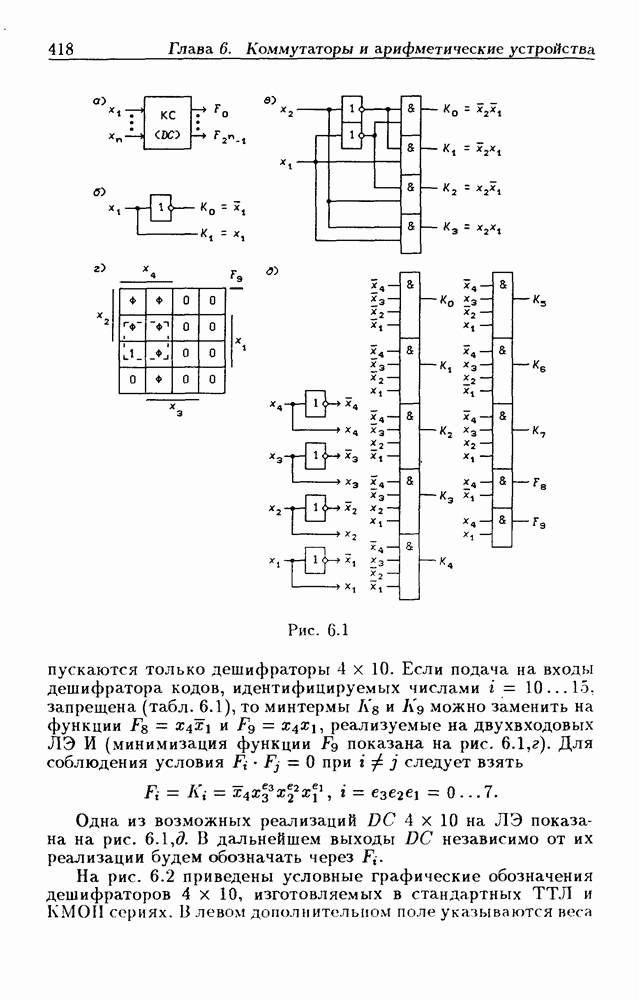
- 6.1. Дешифраторы
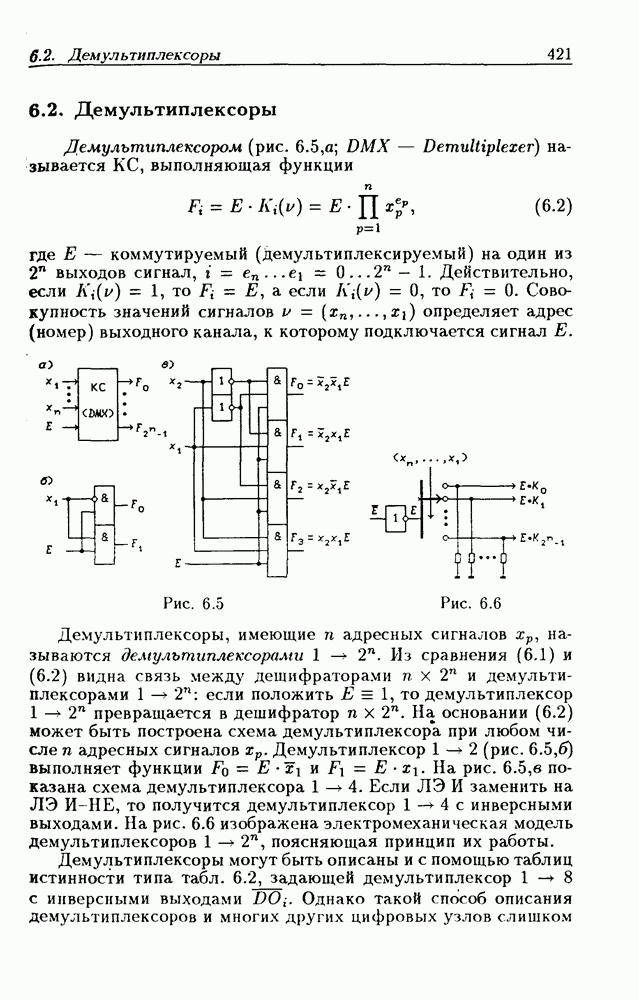
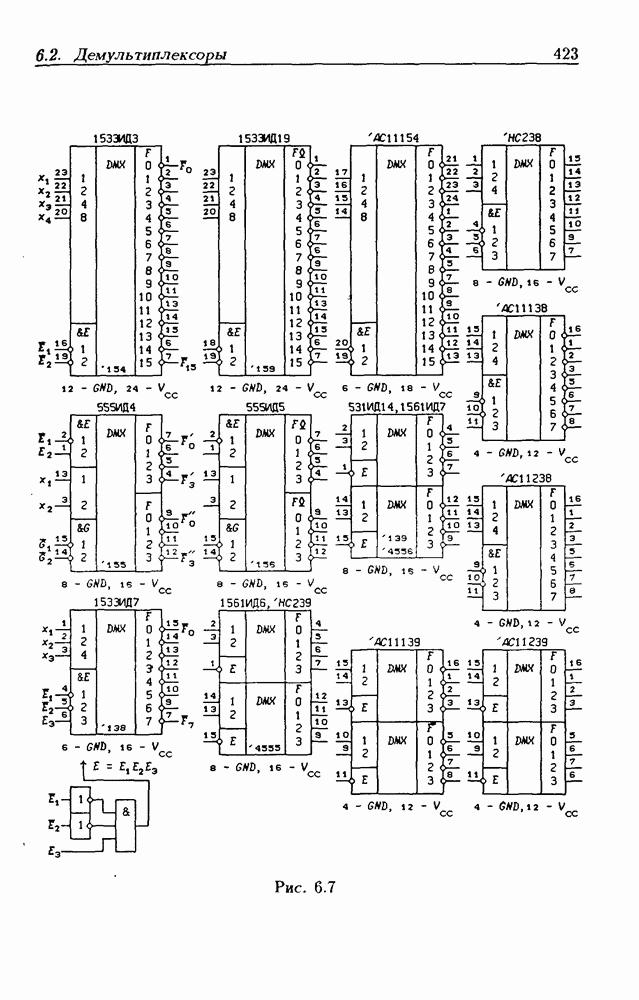
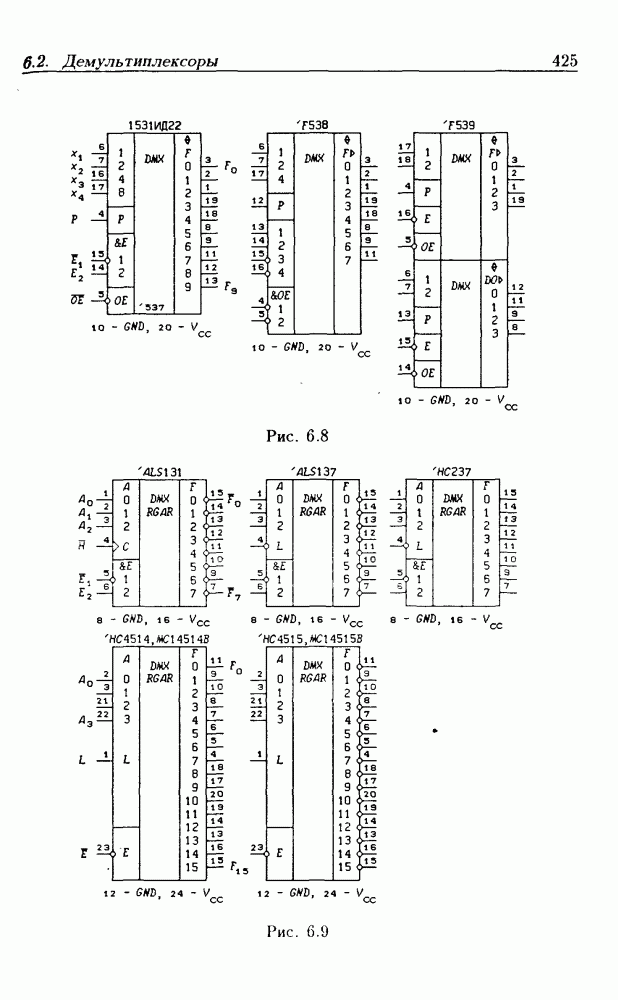
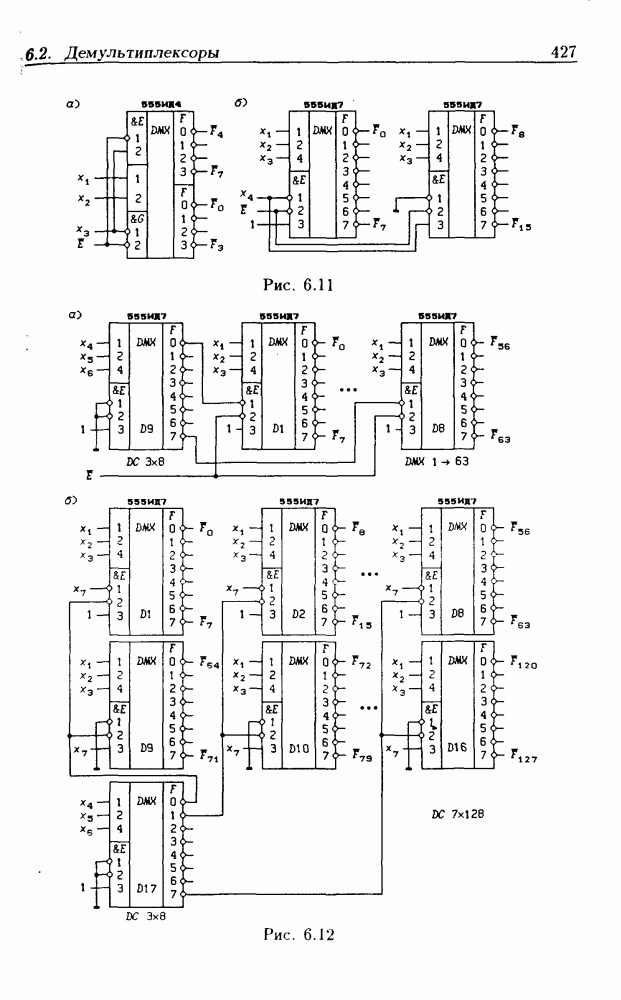
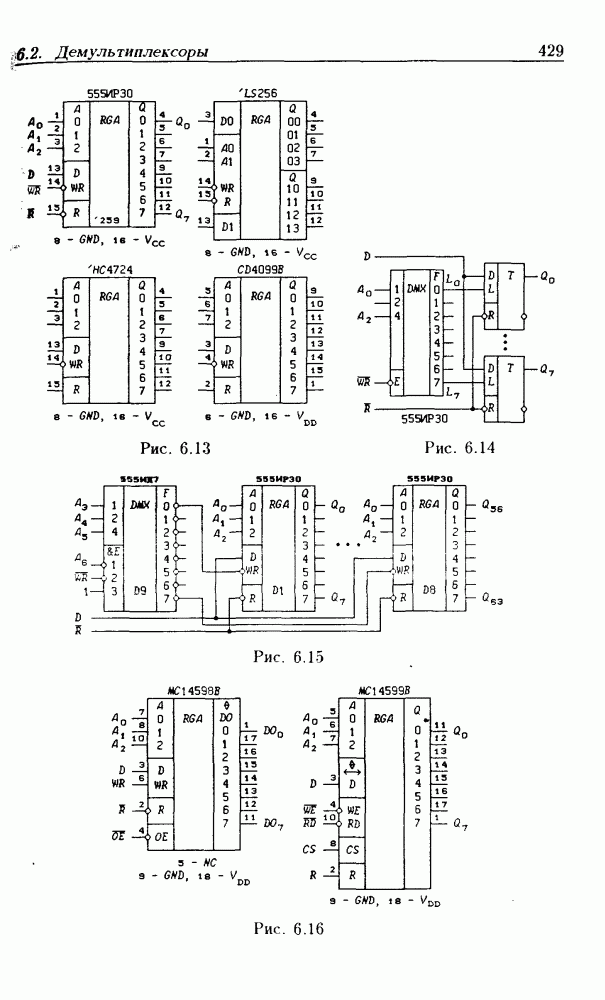
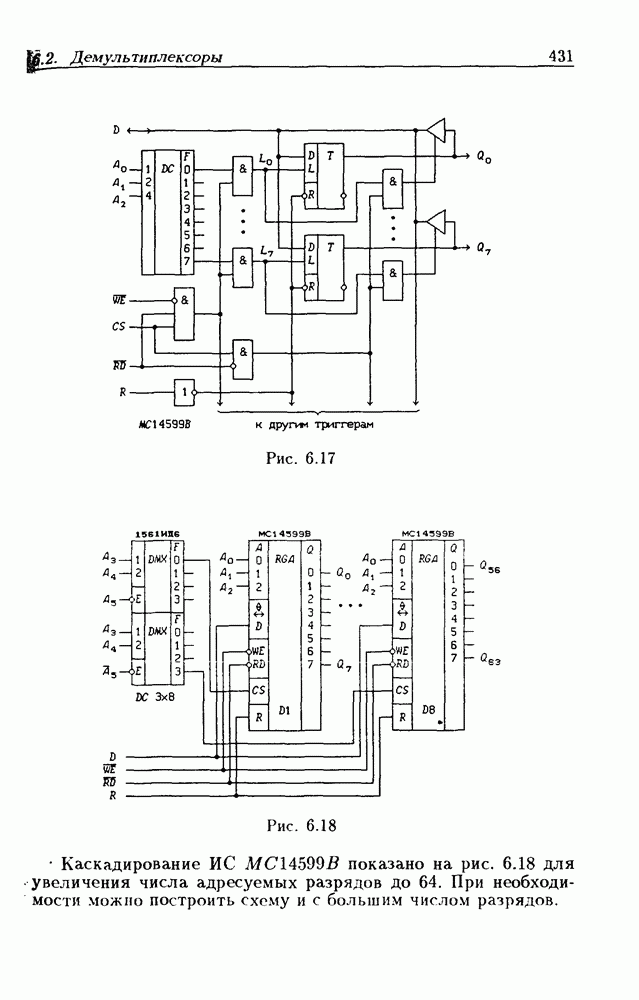
- 6.2. Демультиплексоры
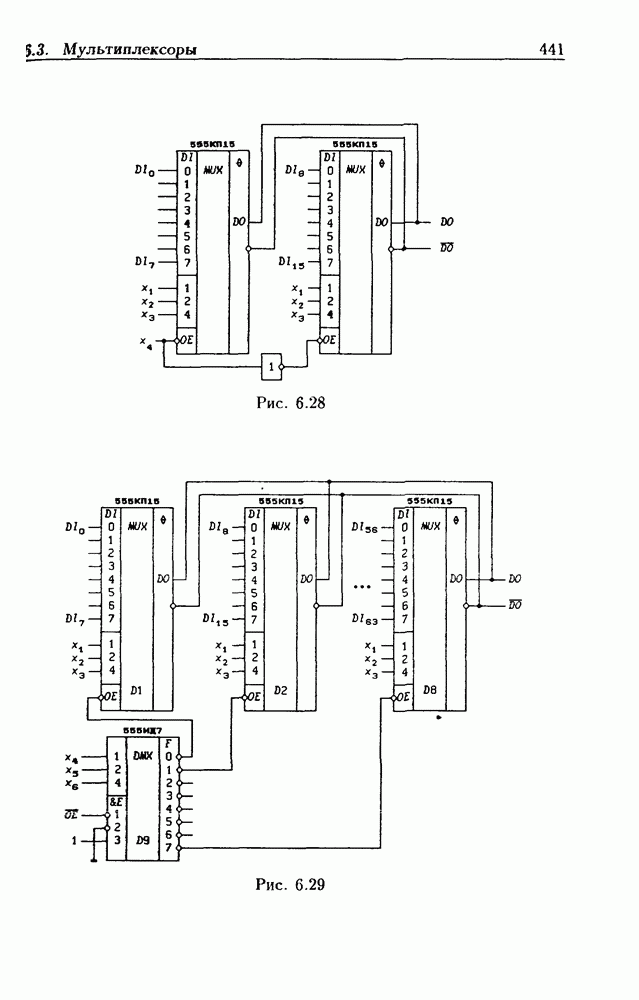
- 6.3. Мультиплексоры
- Мультиплексоры без стробирования.
- Мультиплексоры со стробированием.
- Мультиплексоры с Z-состоянием выхода.
- Каскадирование мультиплексоров.
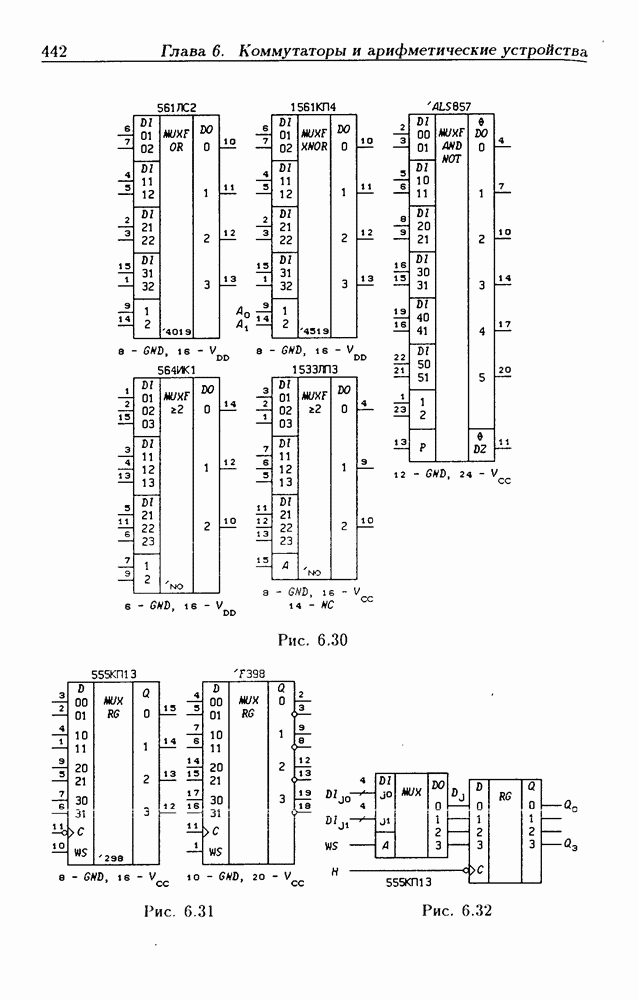
- Функциональные мультиплексоры.
- Регистры памяти с мультиплексными входами данных.
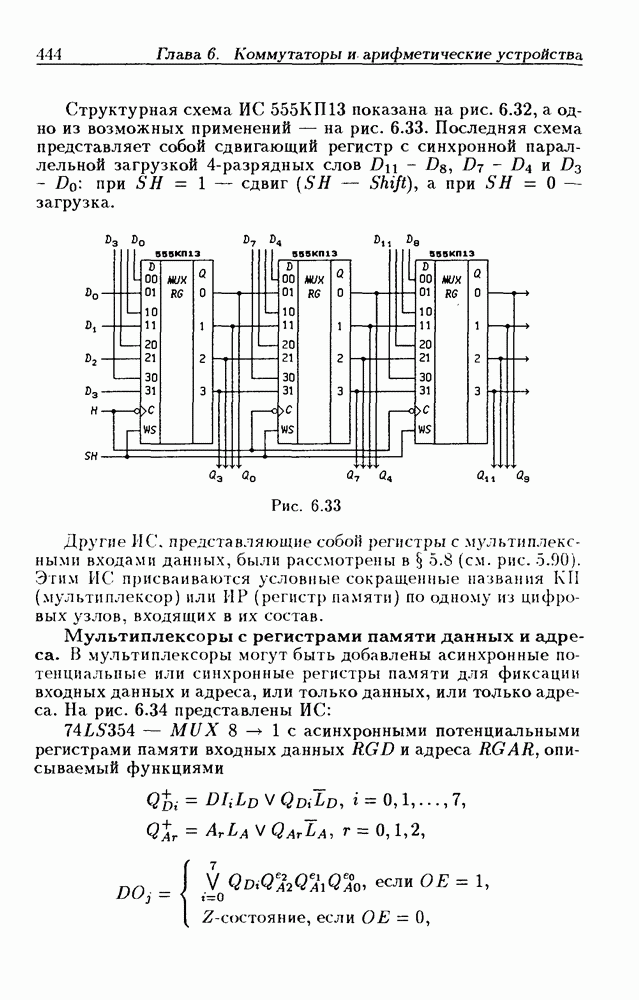
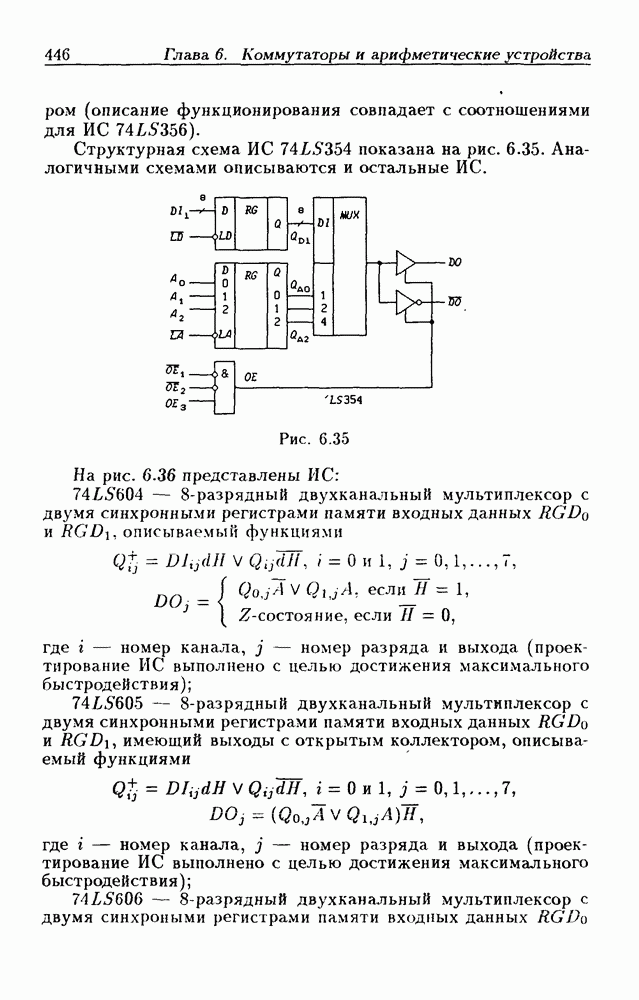
- Мультиплексоры с регистрами памяти данных и адреса.
- Сдвигающие мультиплексоры.
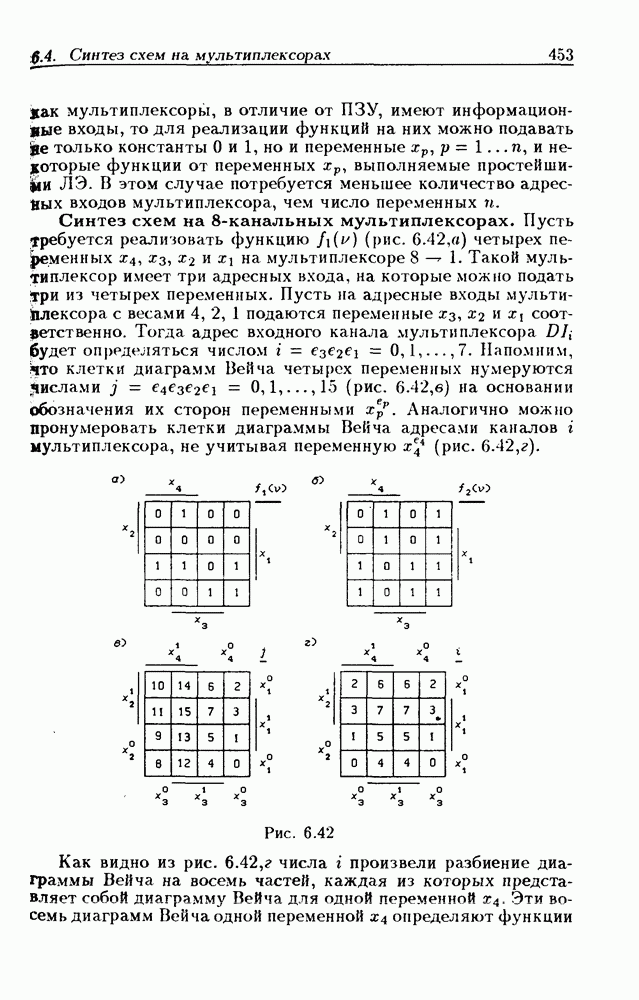
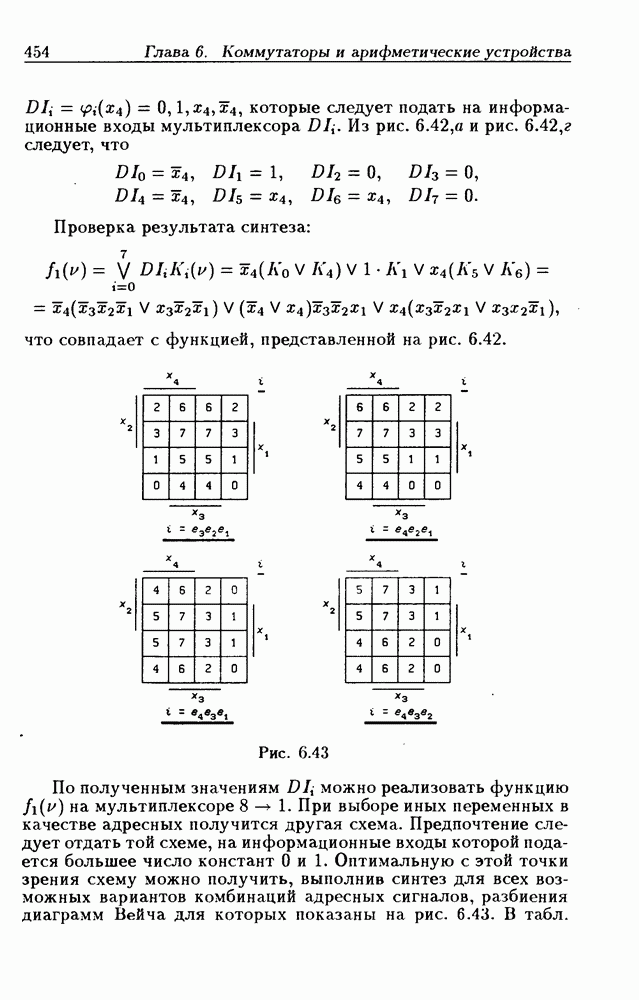
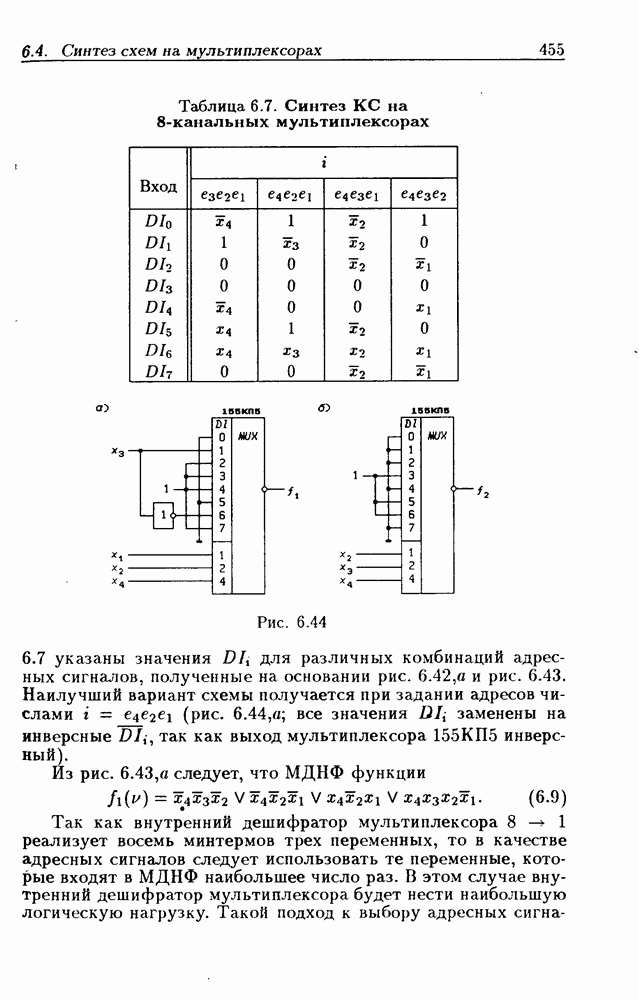
- 6.4. Синтез комбинационных схем и цифровых автоматов на мультиплексорах
- Синтез схем на 8-канальных мультиплексорах.
- Синтез на двухразрядных 4-канальных мультиплексорах.
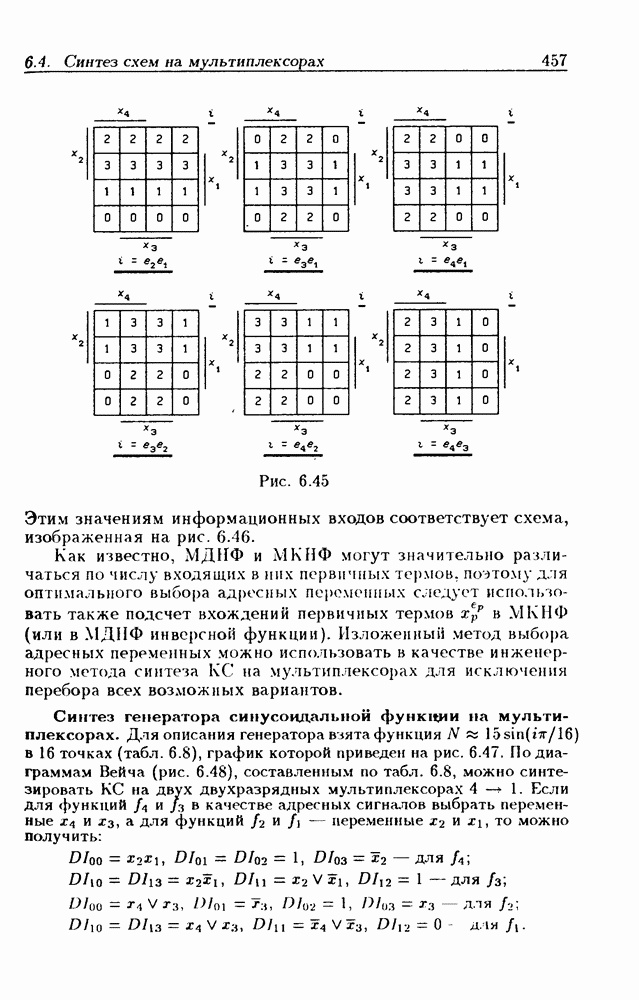
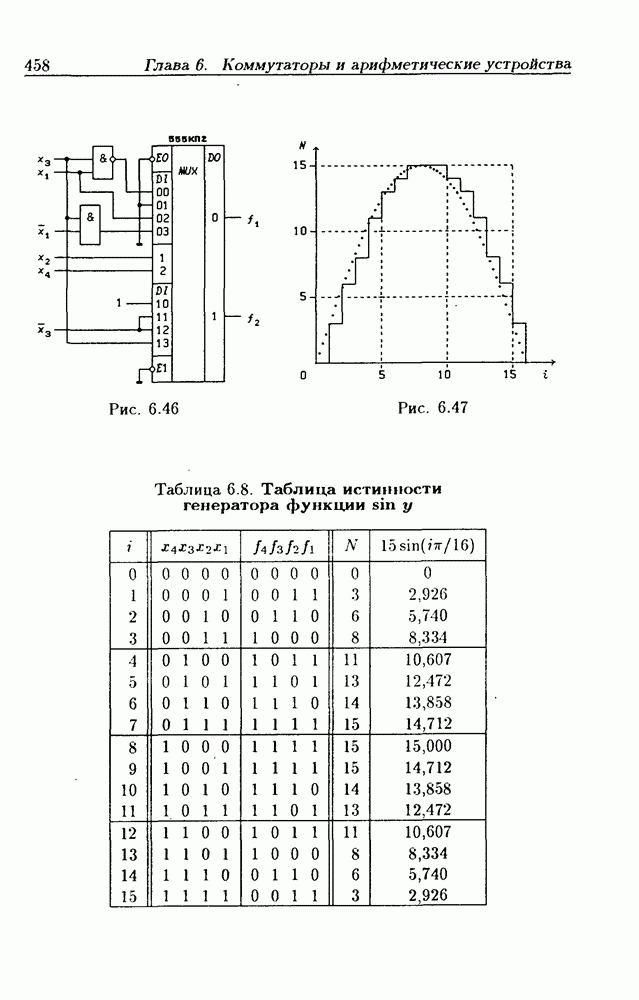
- Синтез генератора синусоидальной функции на мультиплексорах.
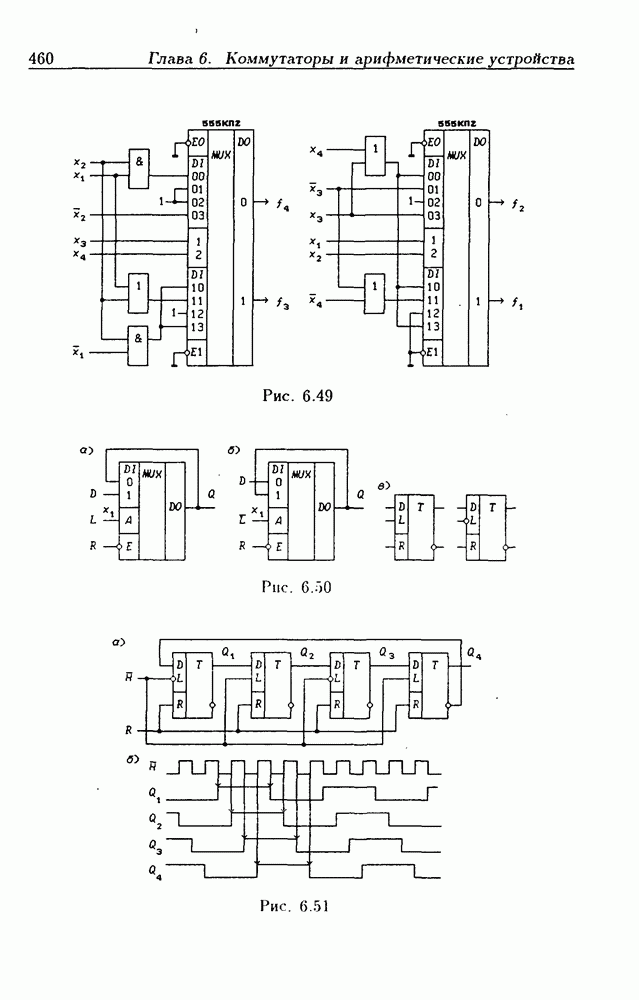
- Синтез триггеров на мультиплексорах.
- Синтез счетчиков на мультиплексорах.
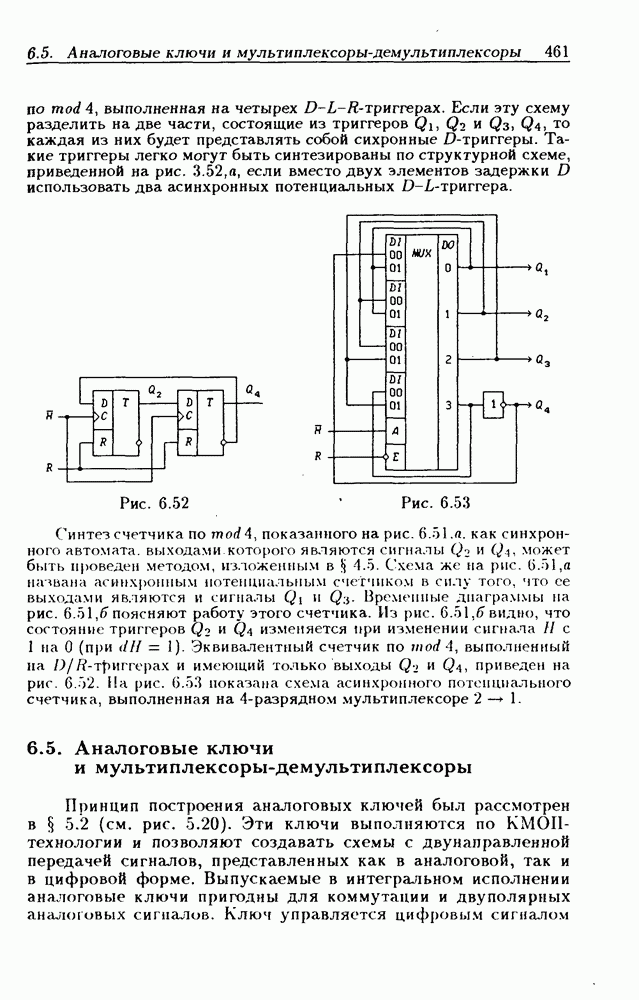
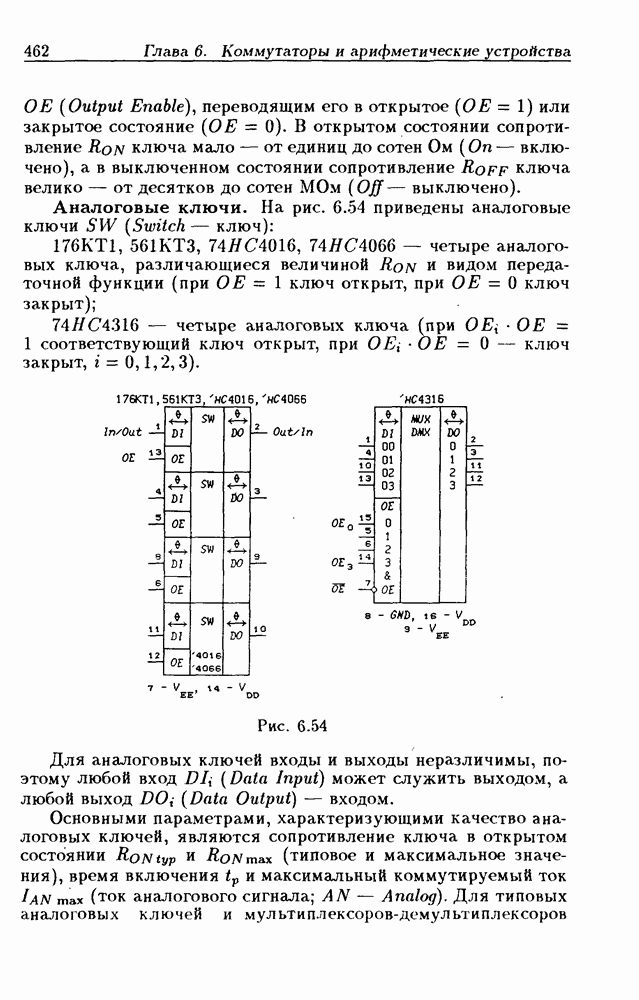
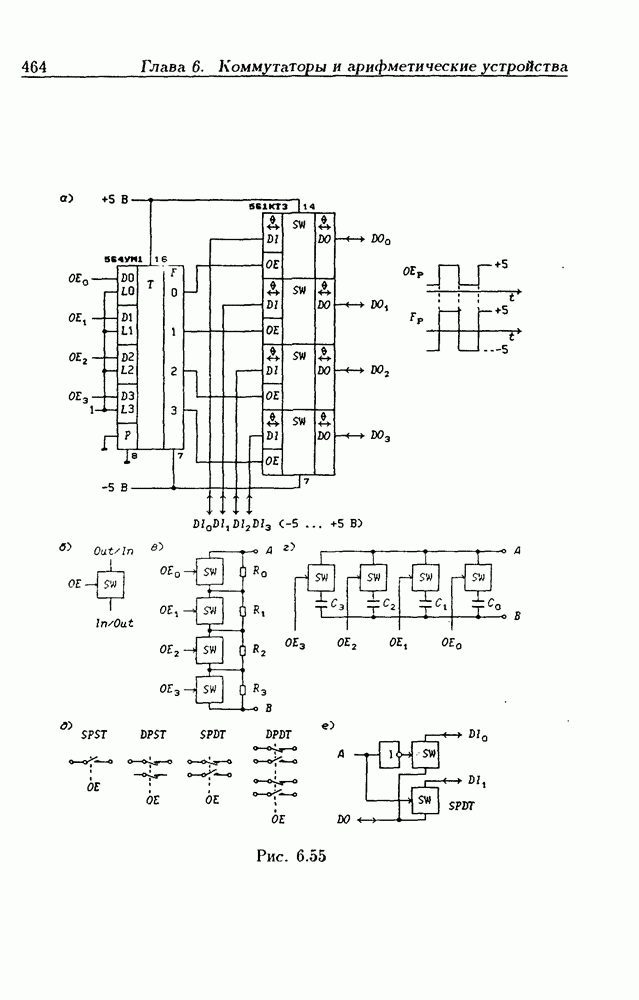
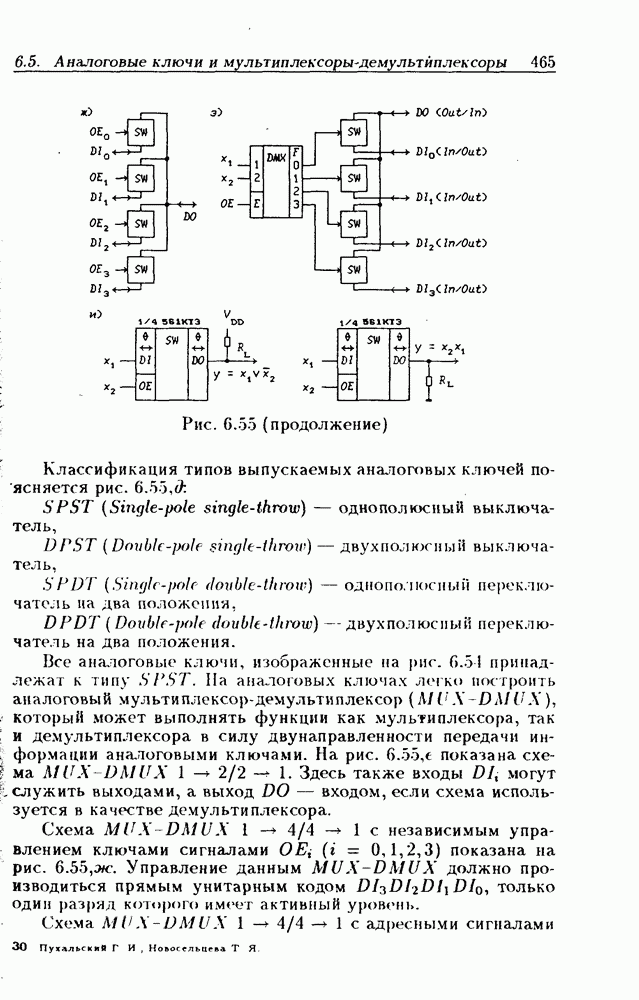
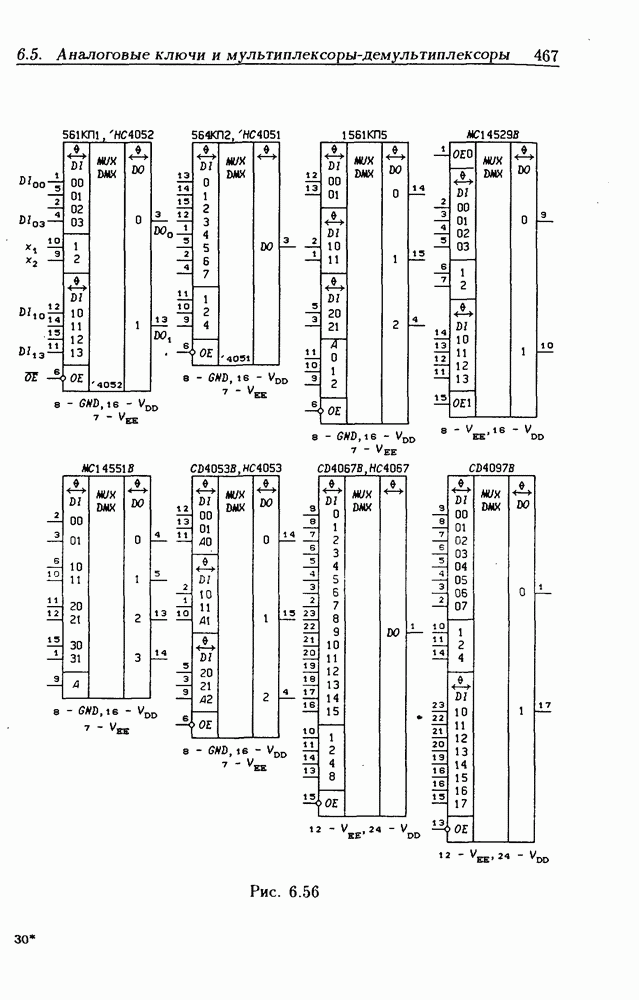
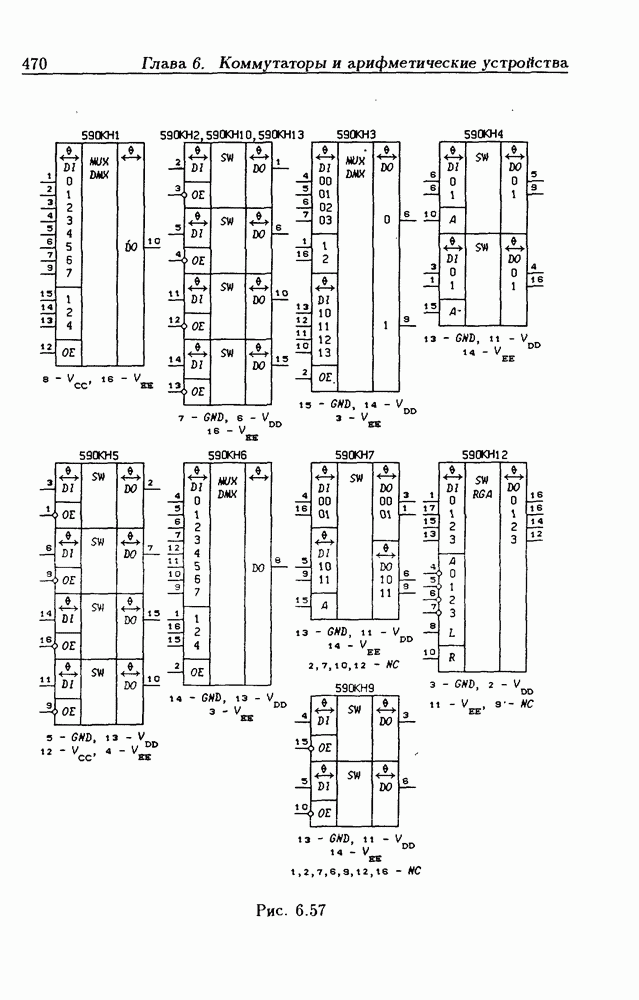
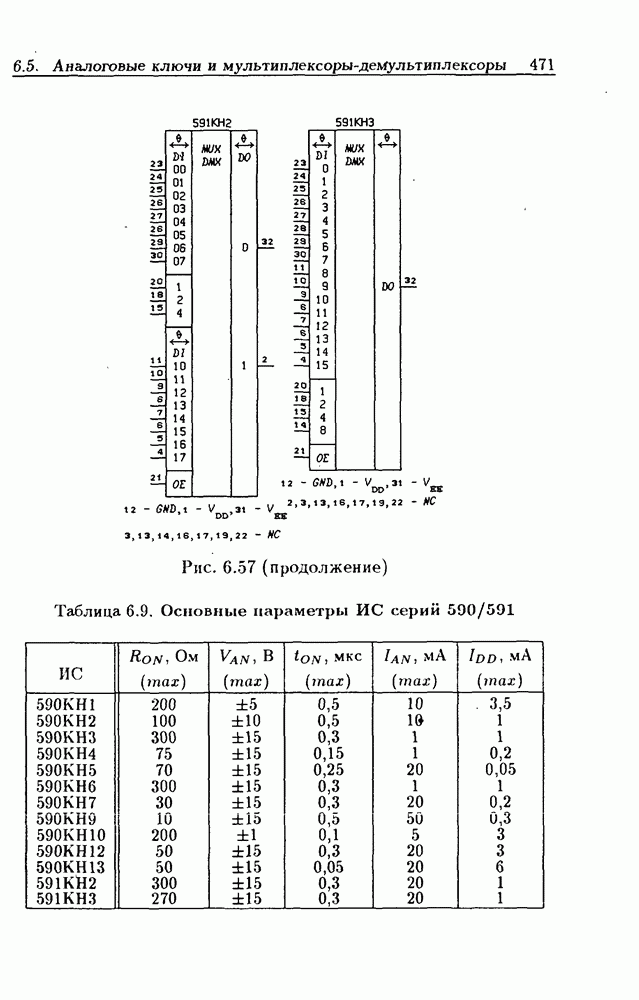
- 6.5. Аналоговые ключи и мультиплексоры-демультиплексоры
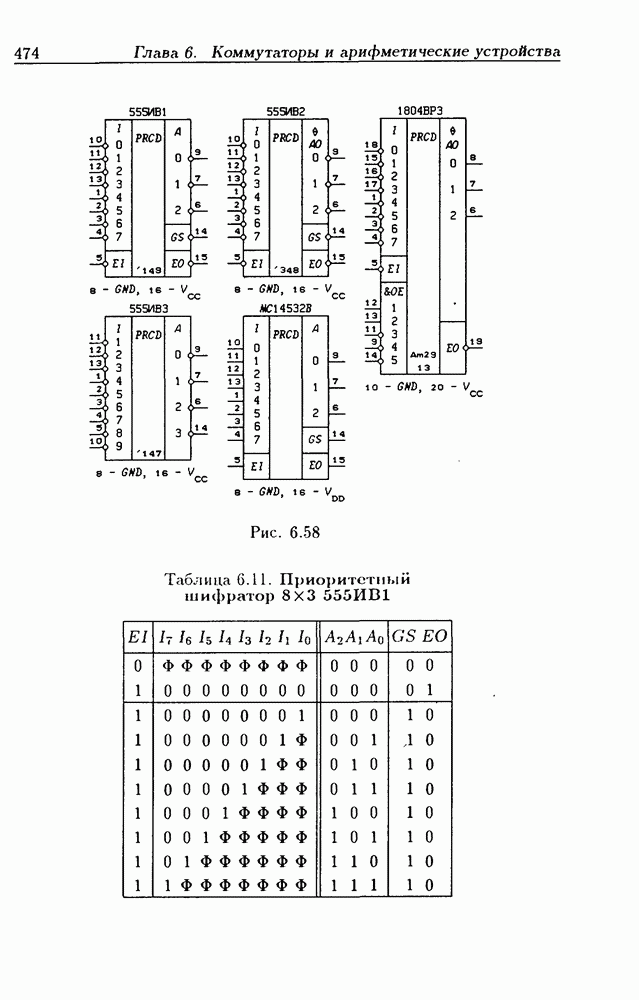
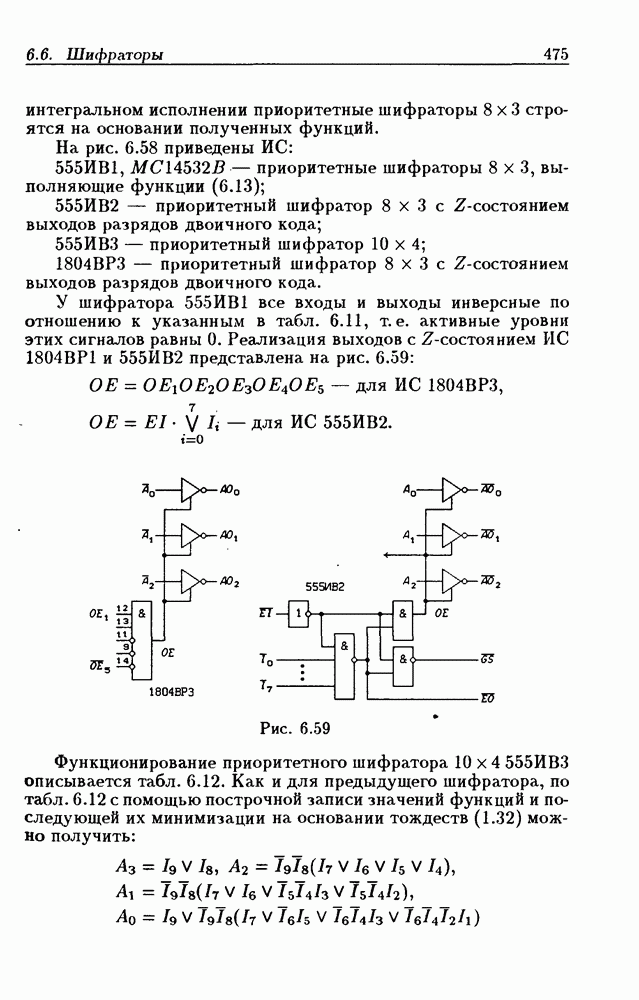
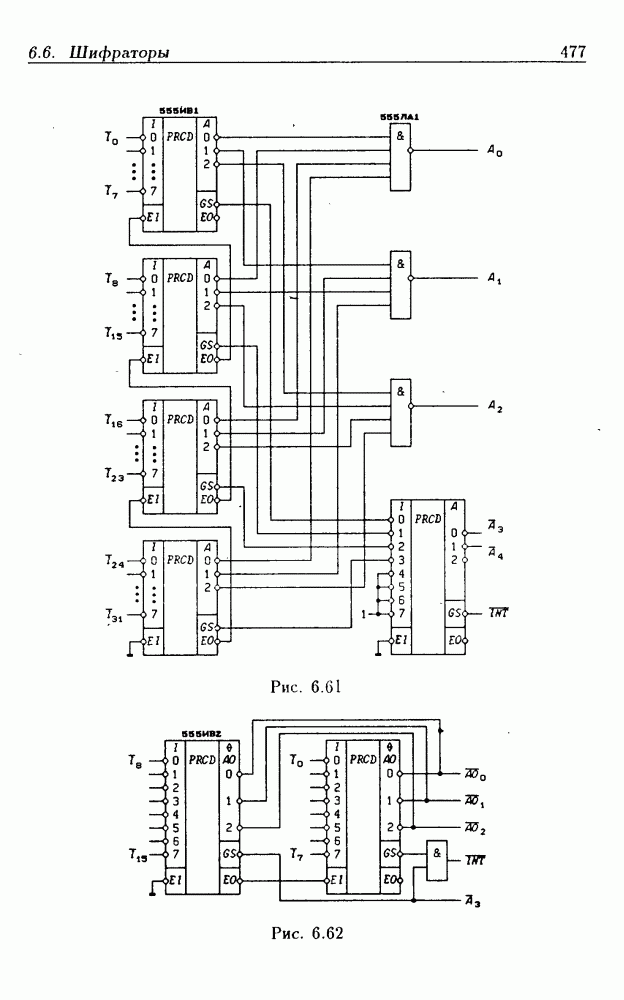
- 6.6. Шифраторы
- 6.7. Цифровые компараторы
- Программируемые цифровые компараторы.
- Адресные компараторы.
- Применения адресных компараторов.
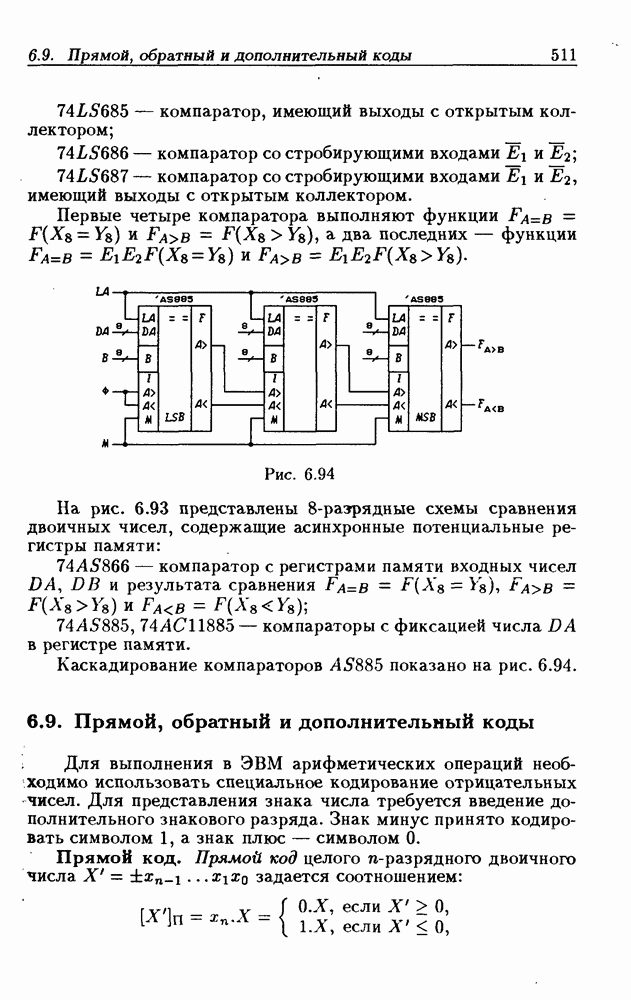
- 6.8. Схемы сравнения двоичных чисел
- 8-разрядные схемы сравнения двоичных чисел.
- 6.9. Прямой, обратный и дополнительный коды
- Дополнительный код.
- Сложение чисел в обратном коде.
- Код с избытком 3.
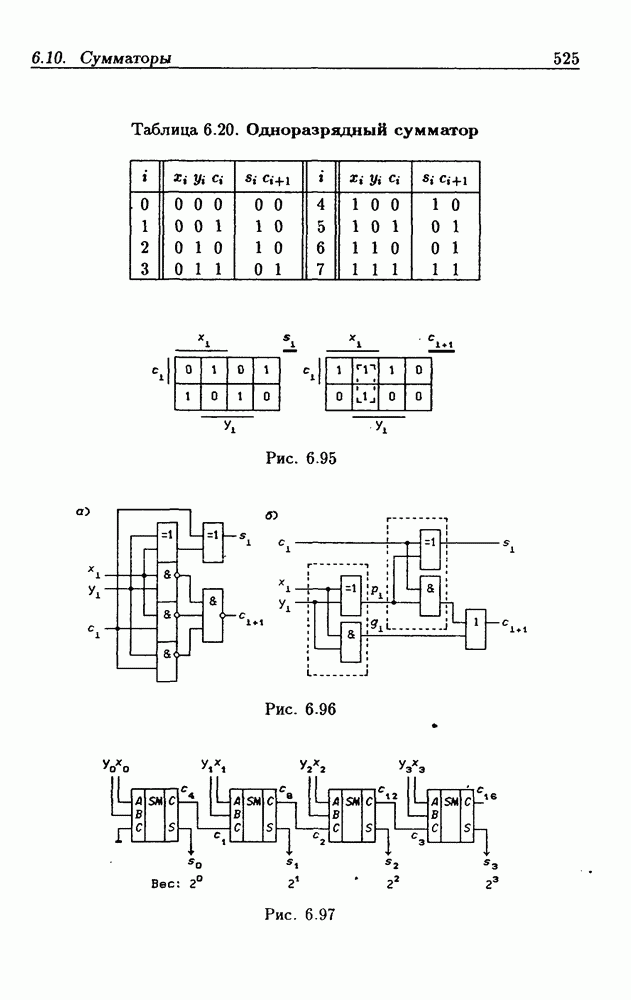
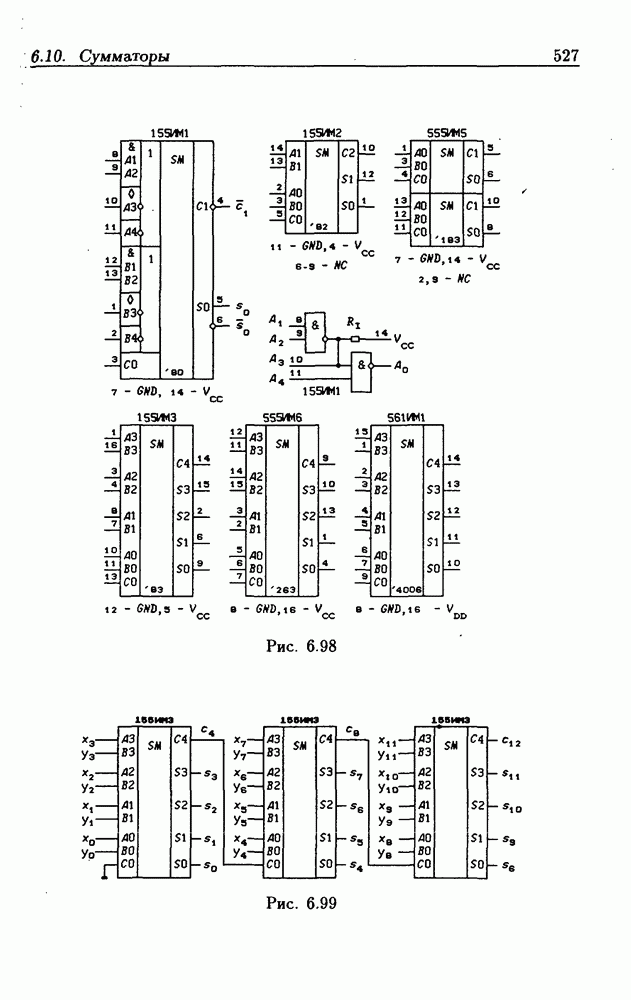
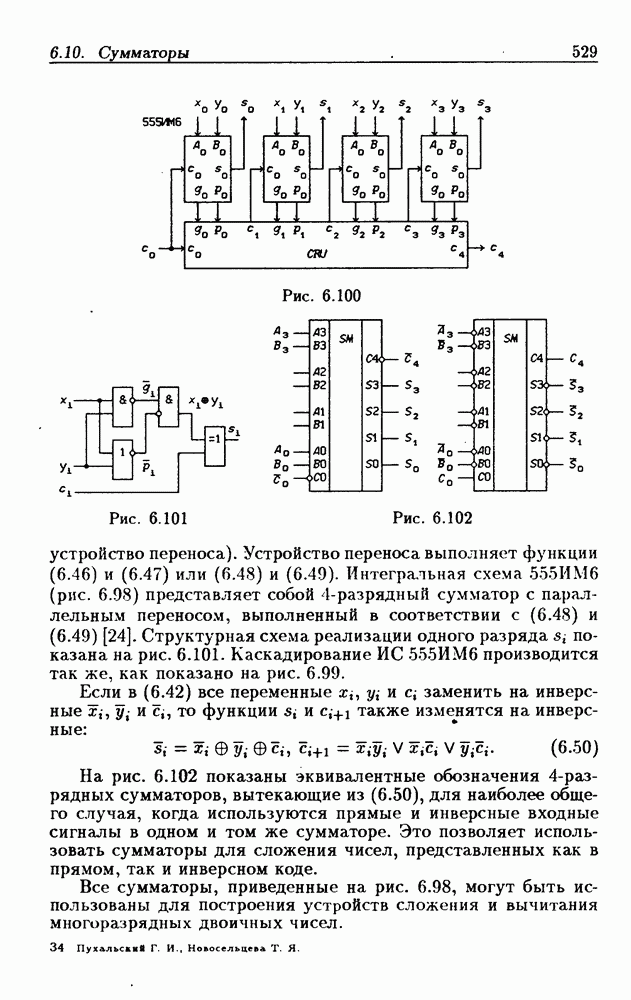
- 6.10. Сумматоры
- Двоичные параллельные сумматоры с последовательным переносом.
- Двоичные сумматоры с параллельным переносом.
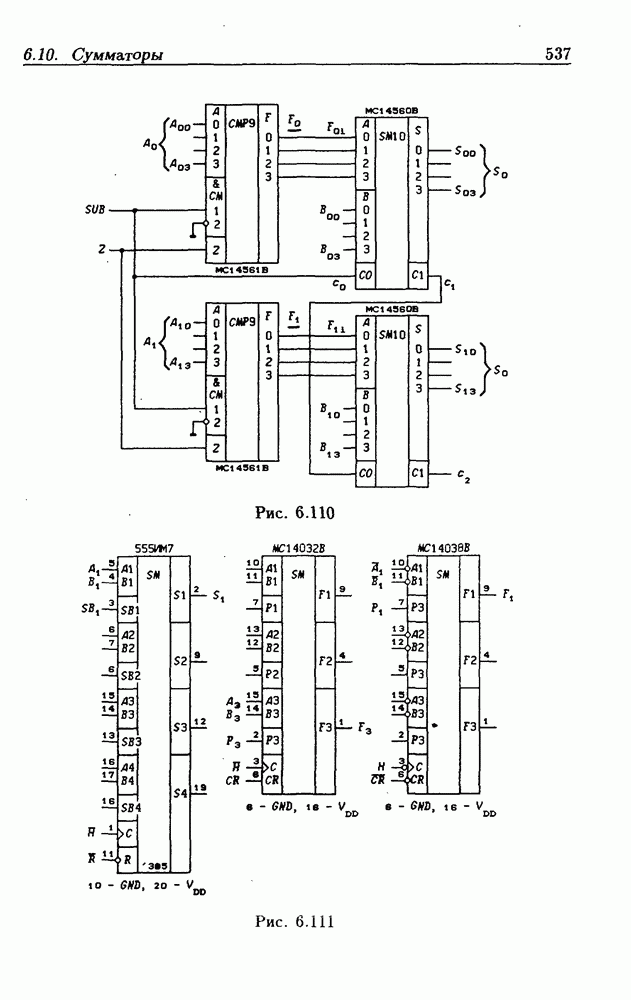
- Применения сумматоров.
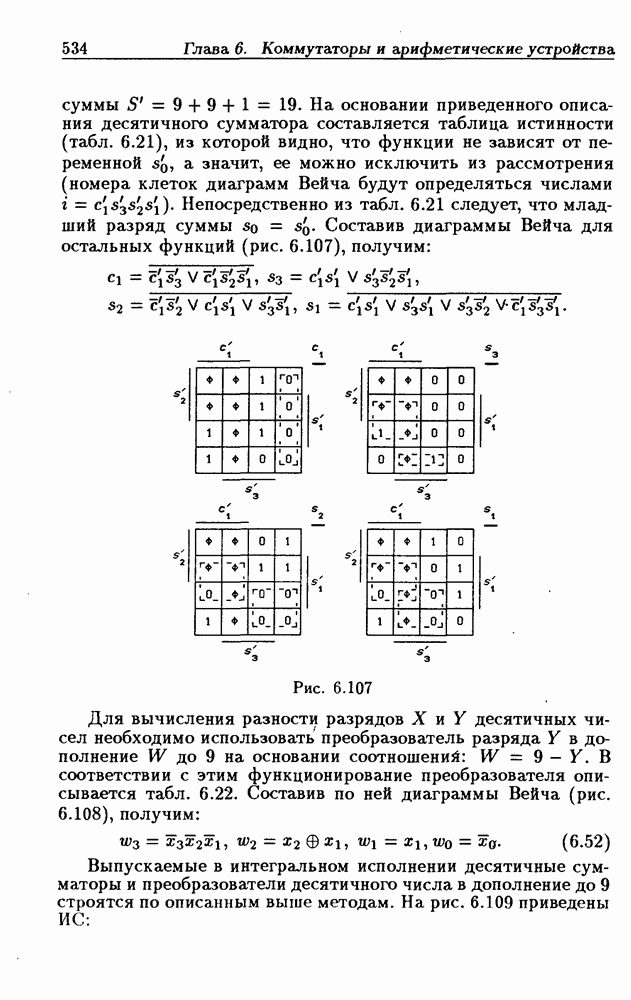
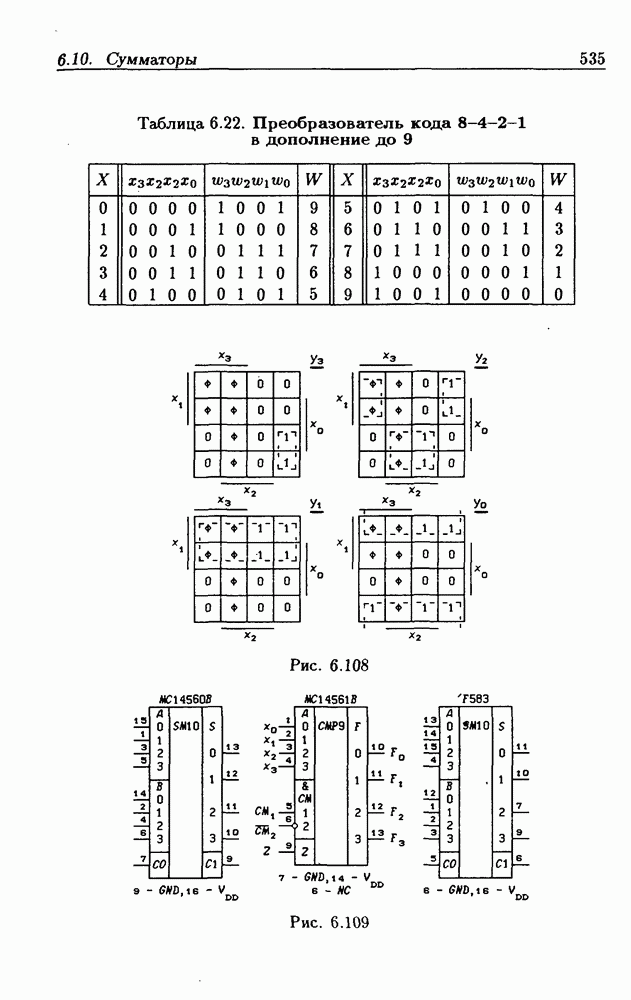
- Десятичные сумматоры.
- Последовательные двоичные сумматоры.
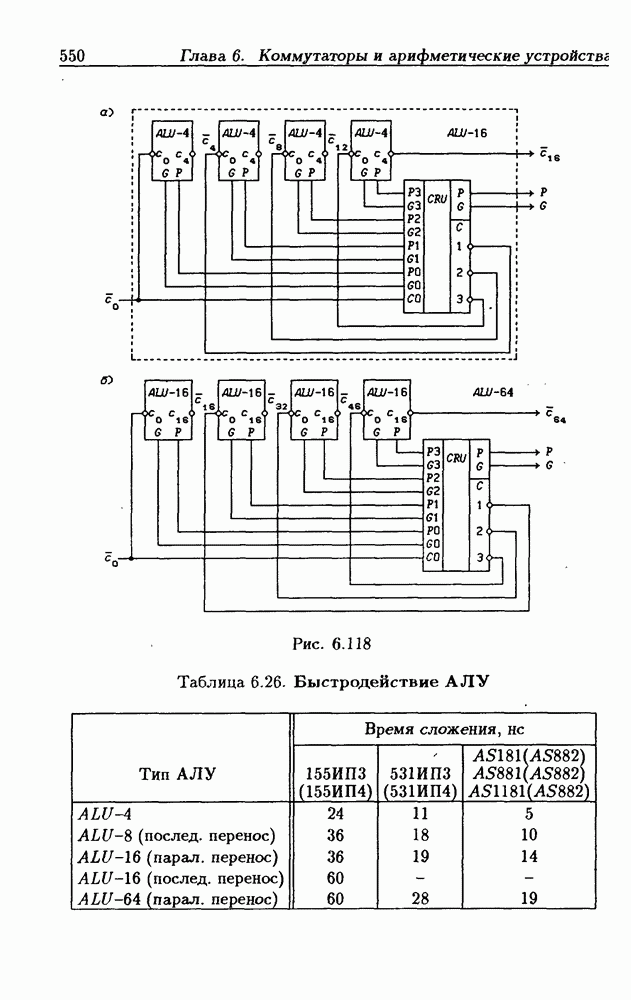
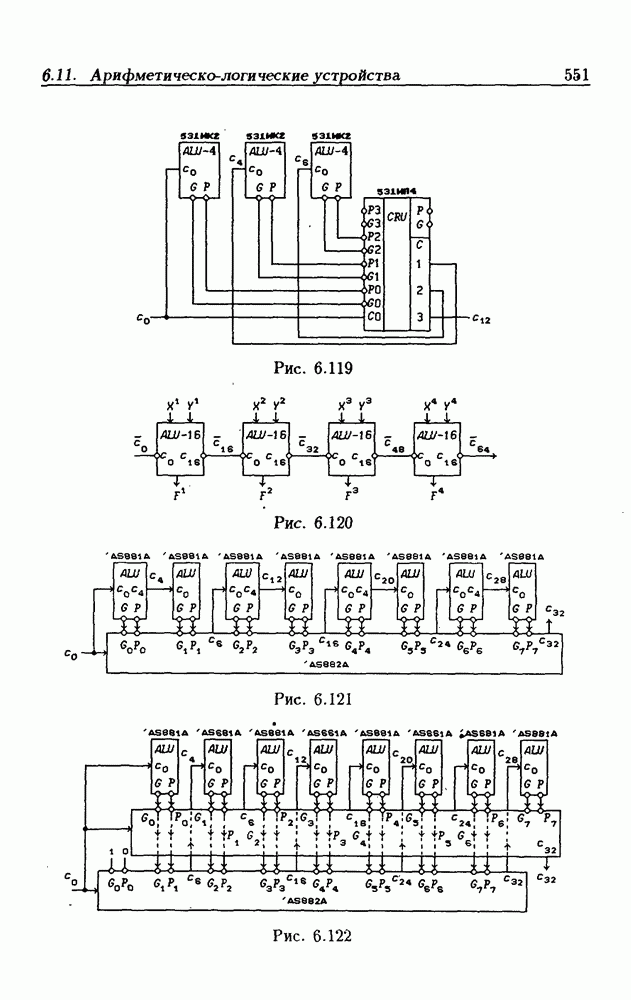
- 6.11. Арифметическо-логические устройства
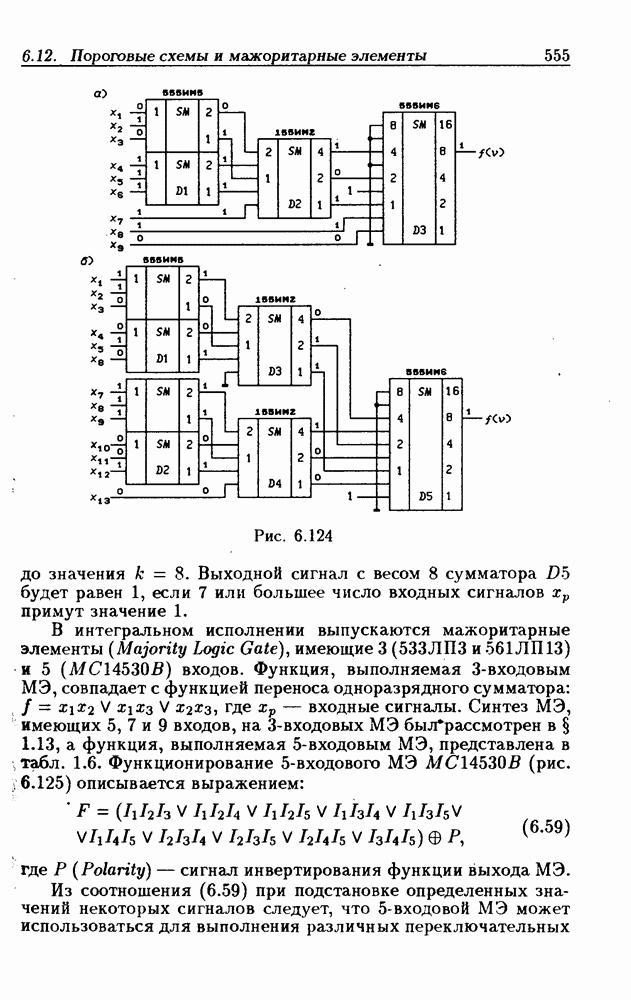
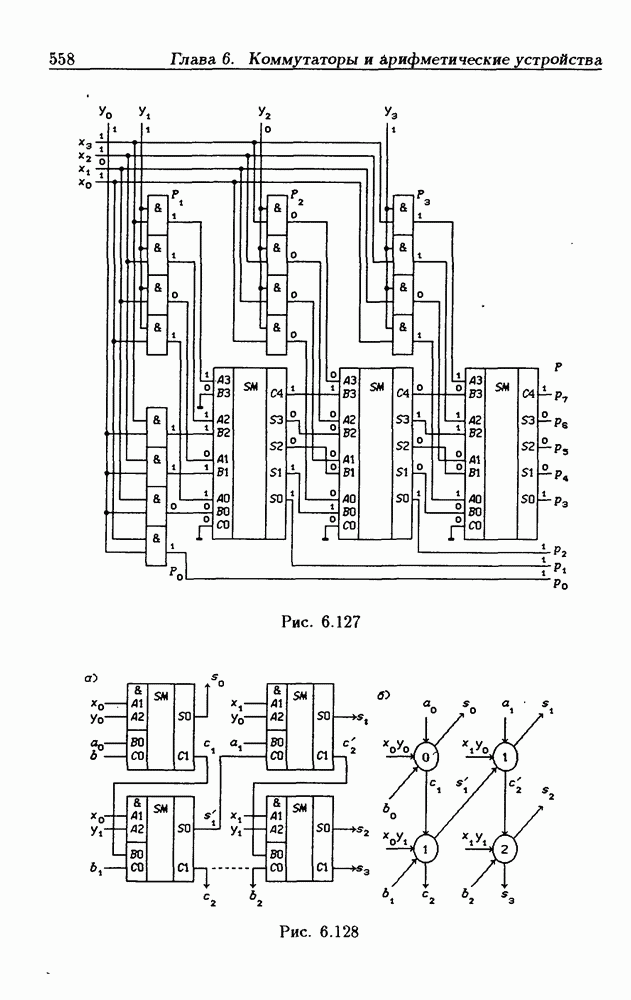
- 6.12. Пороговые схемы и мажоритарные элементы
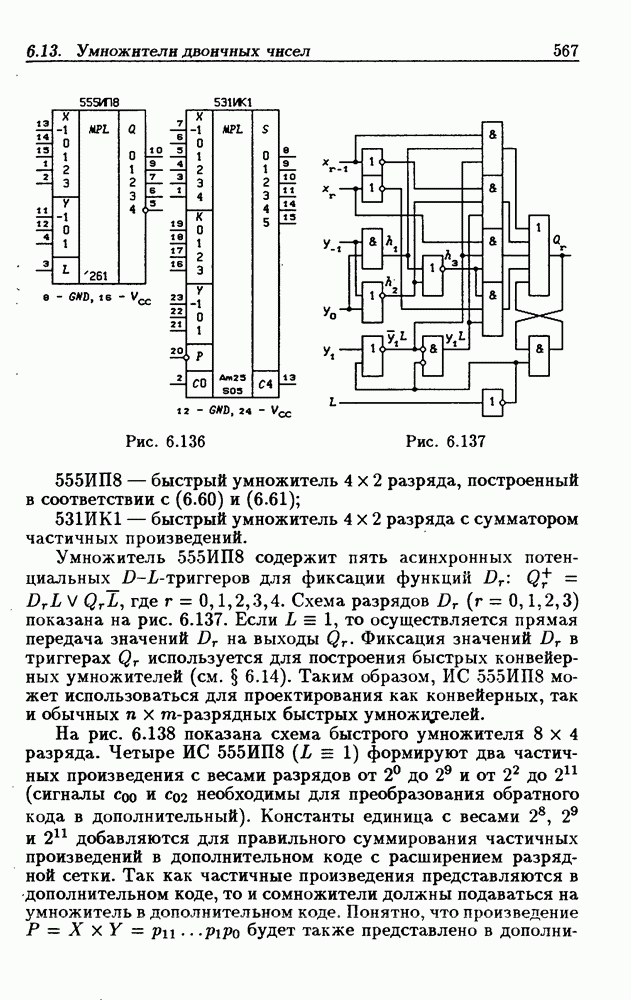
- 6.13. Умножители двоичных чисел
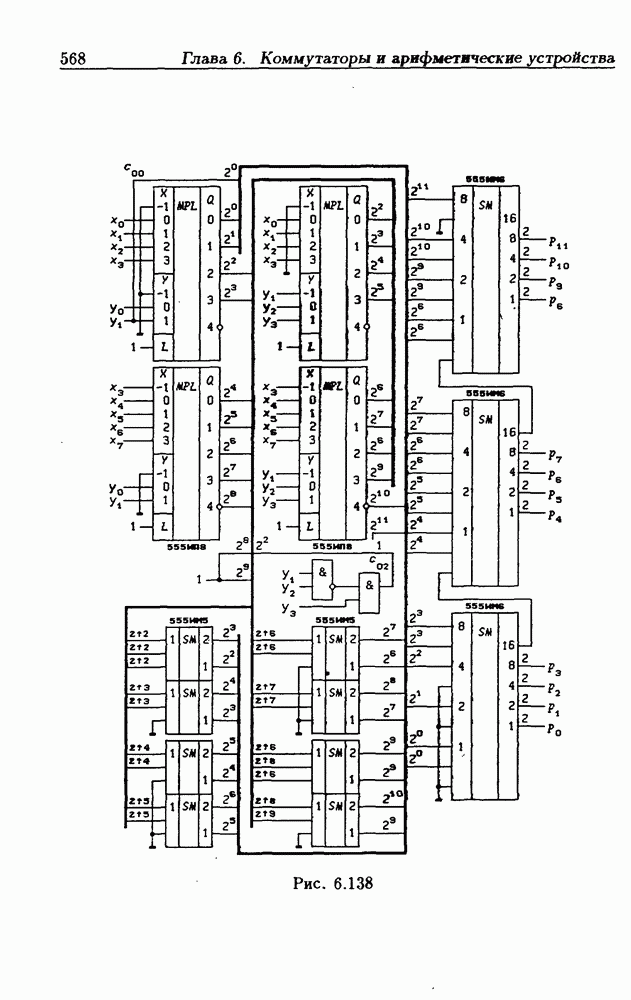
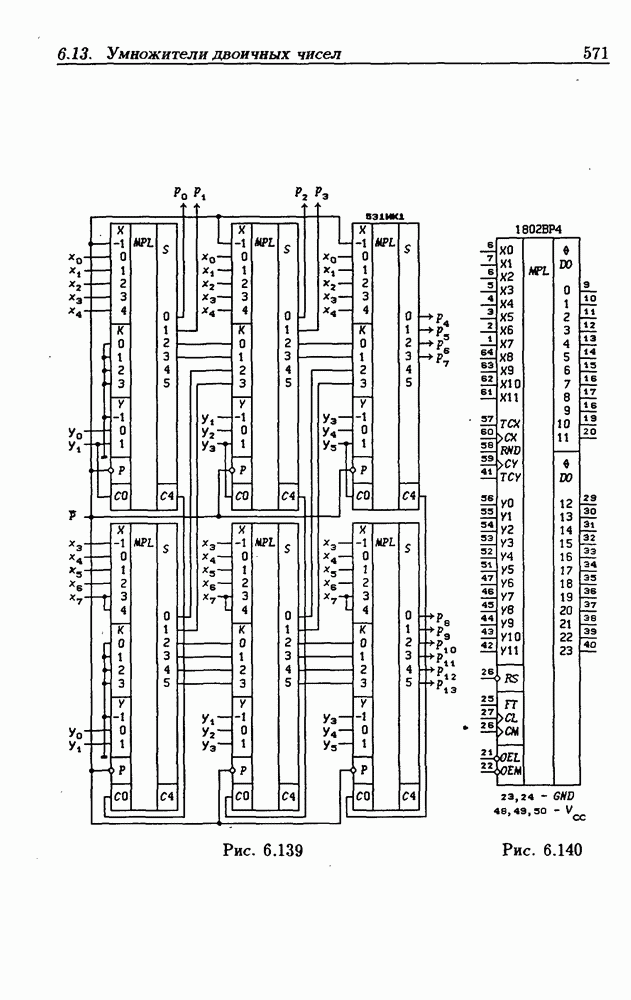
- Быстрые умножители.
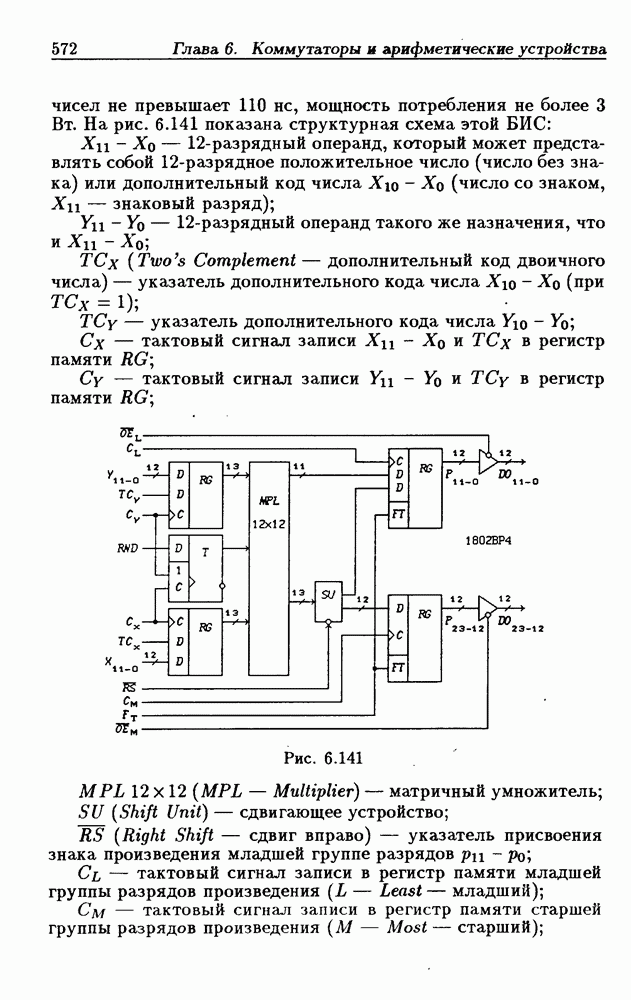
- БИС умножителя 12×12 разрядов 1802ВР4.
- Последовательные умножители.
- 6.14. Конвейерные устройства
- Конвейерный быстрый умножитель.
- Конвейерные АЦП.
- 6.15. Синтез линейных комбинационных схем
- Сумматор по модулю q.
- Умножитель по модулю q.
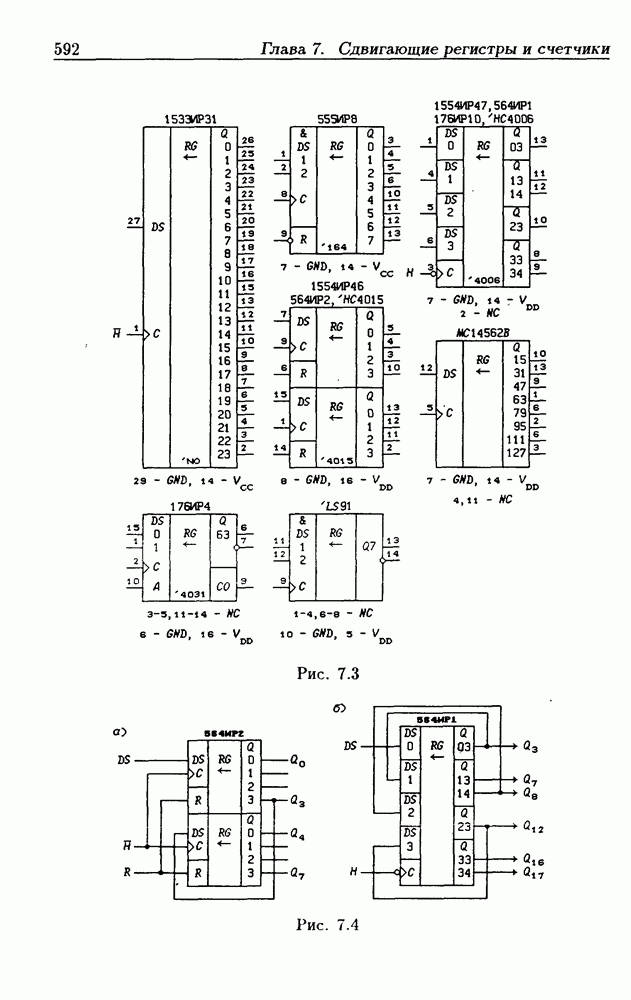
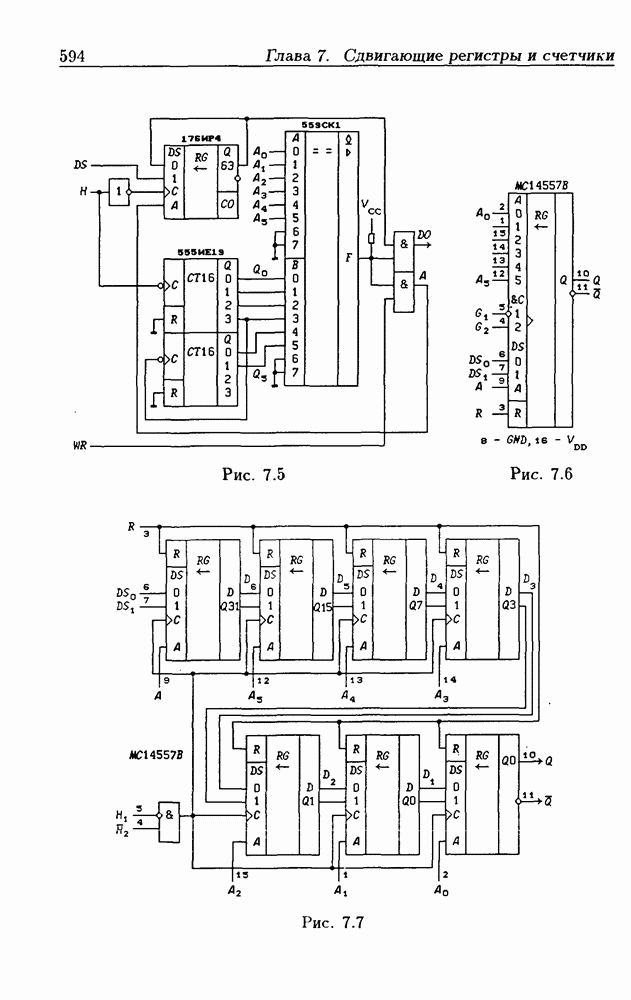
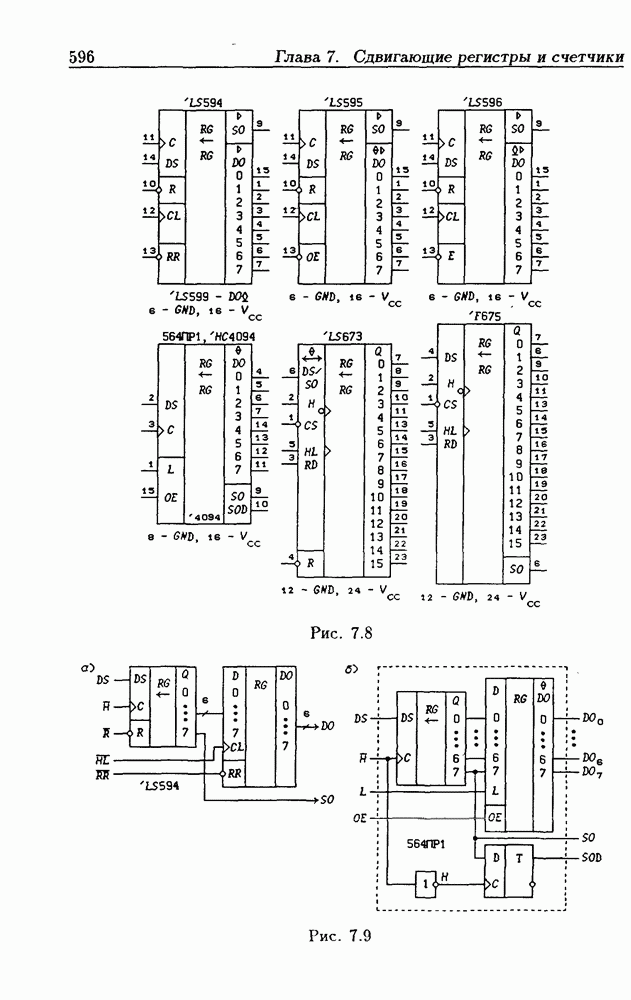
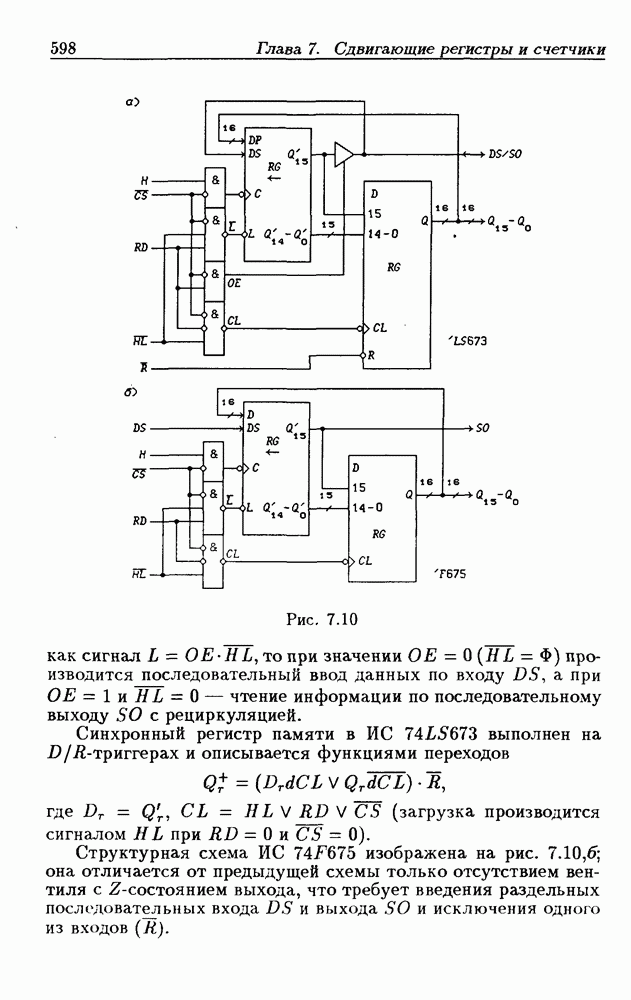
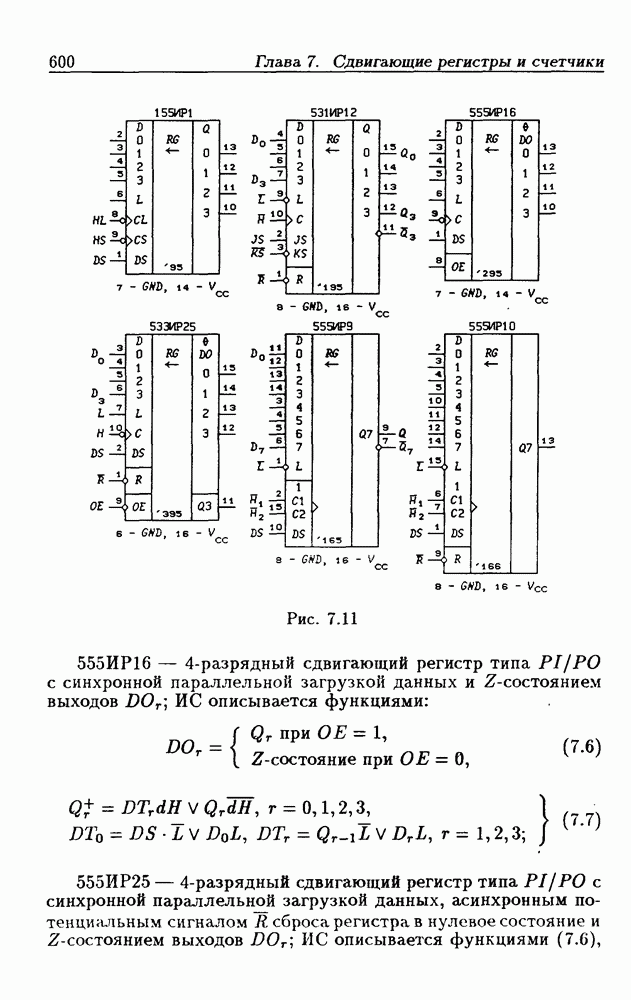
- Глава 7. Сдвигающие регистры и счетчики
- 7.1. Сдвигающие регистры без параллельной записи данных
- Сдвигающие устройства с выходными регистрами памяти.
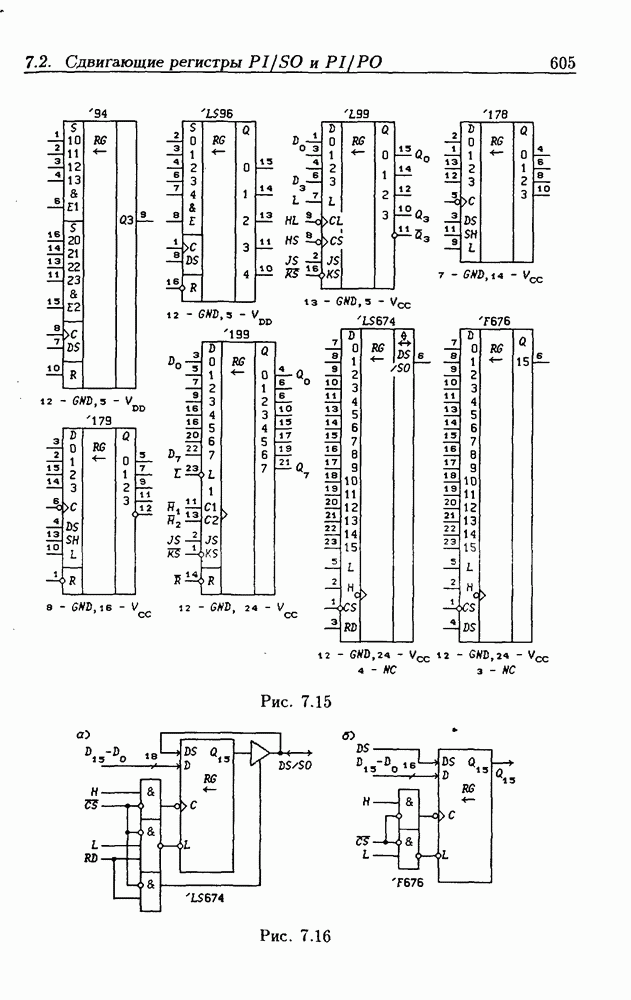
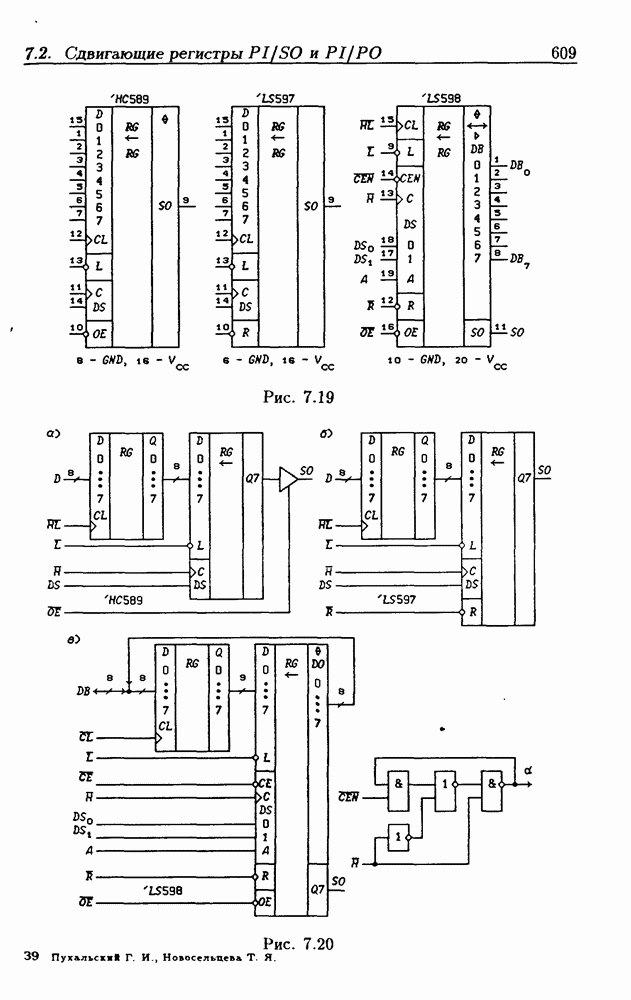
- 7.2. Сдвигающие регистры с параллельной записью данных
- Сдвигающие регистры с расширением знака.
- Сдвигающие регистры с входным регистром памяти.
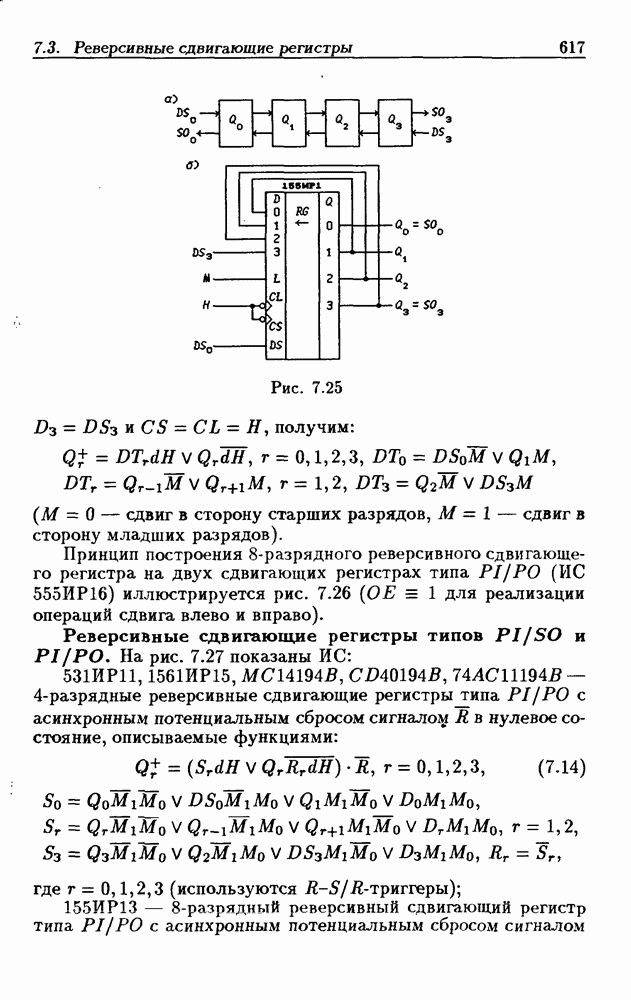
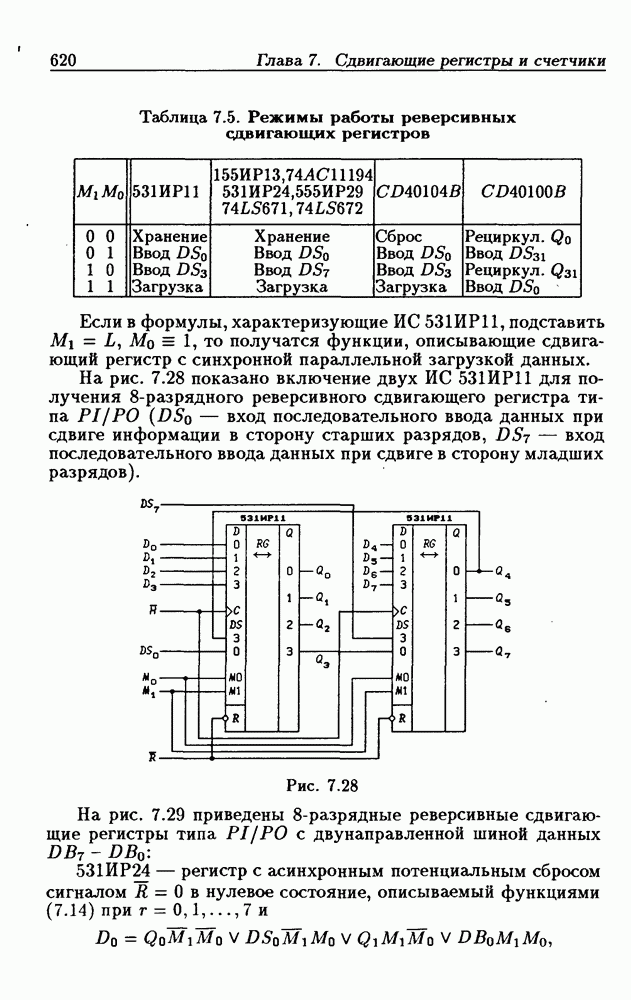
- 7.3. Реверсивные сдвигающие регистры
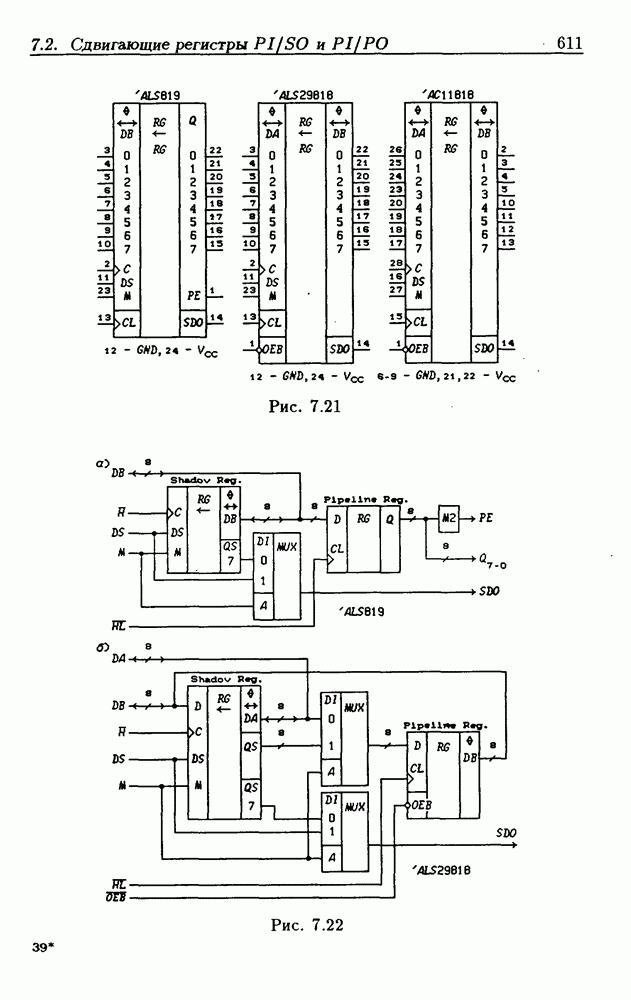
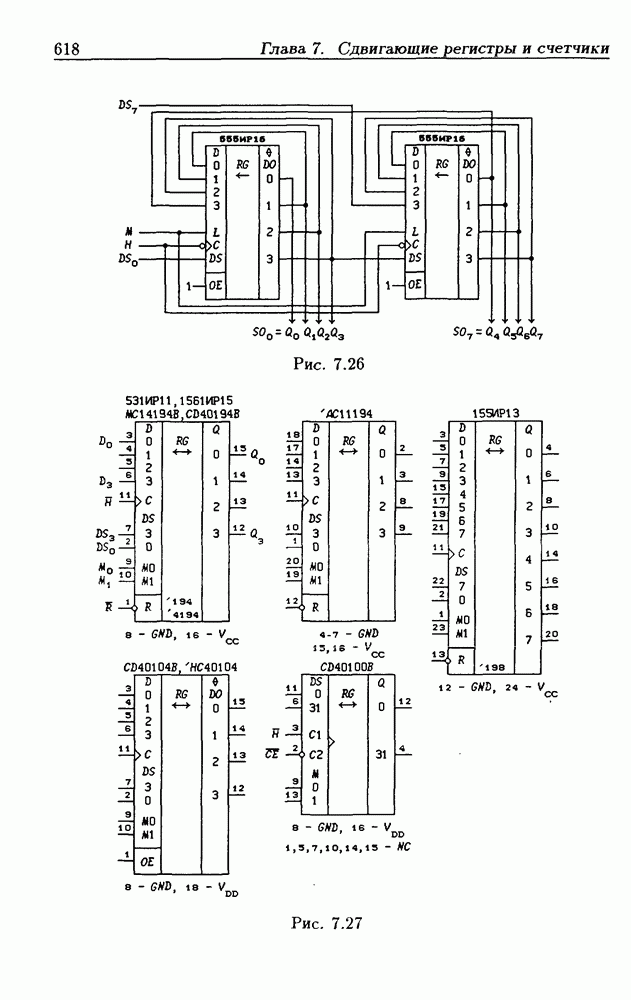
- Реверсивные сдвигающие регистры типов PI/SO и PI/PO.
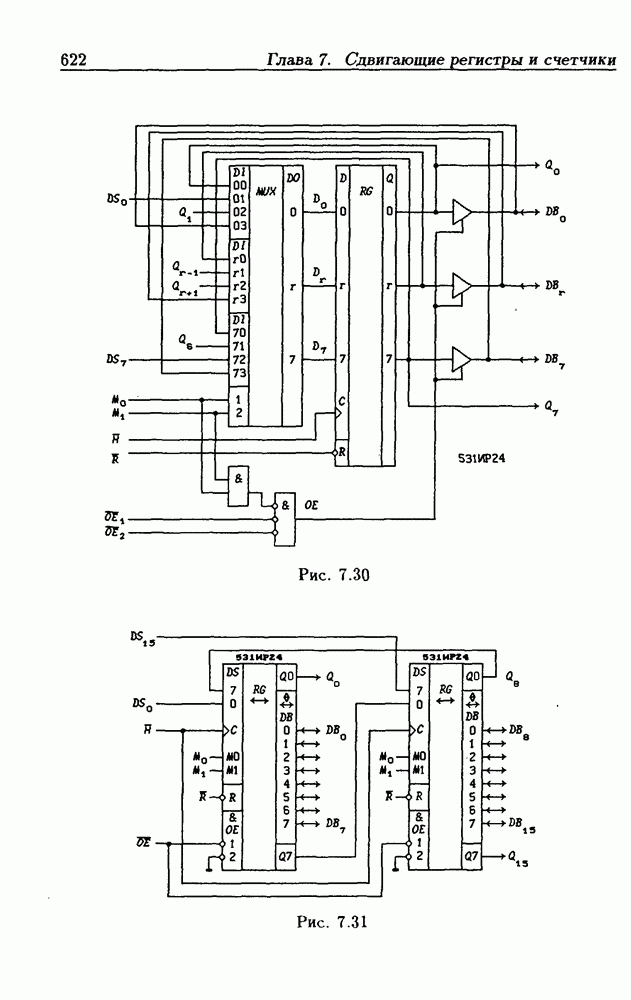
- Многофункциональные устройства на основе реверсивных сдвигающих регистров.
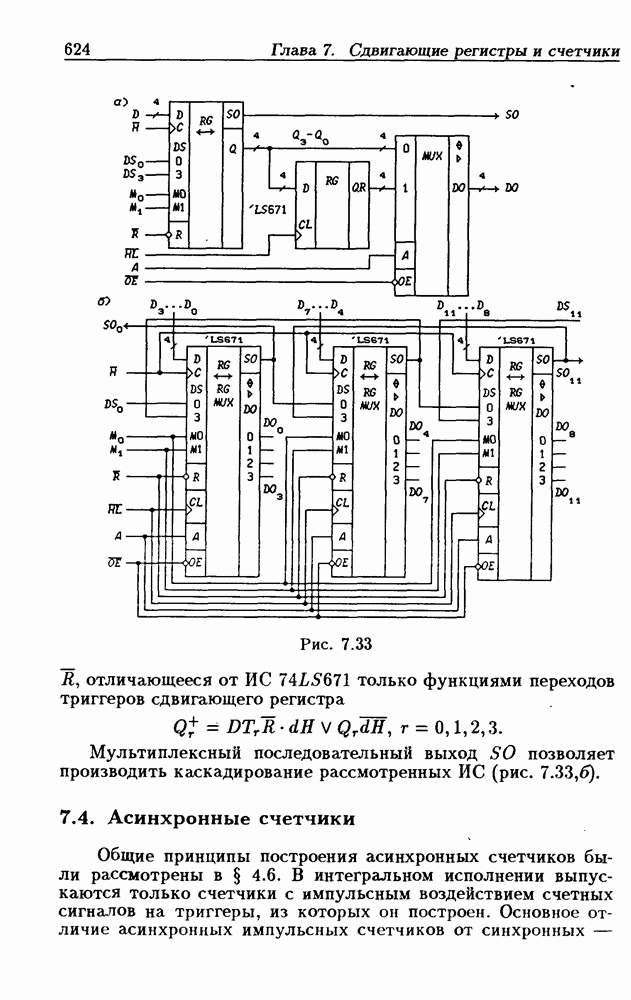
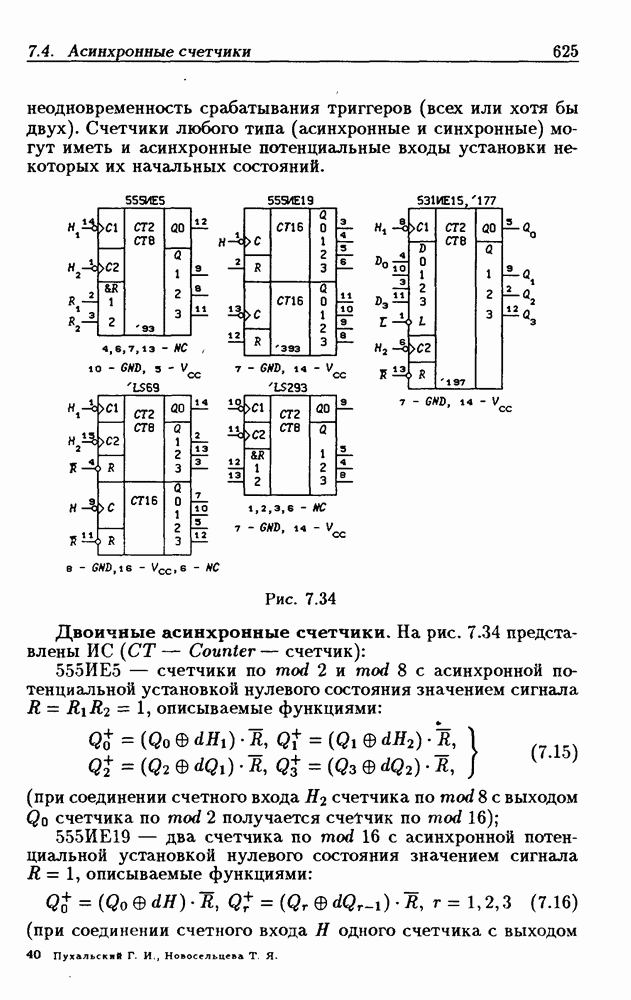
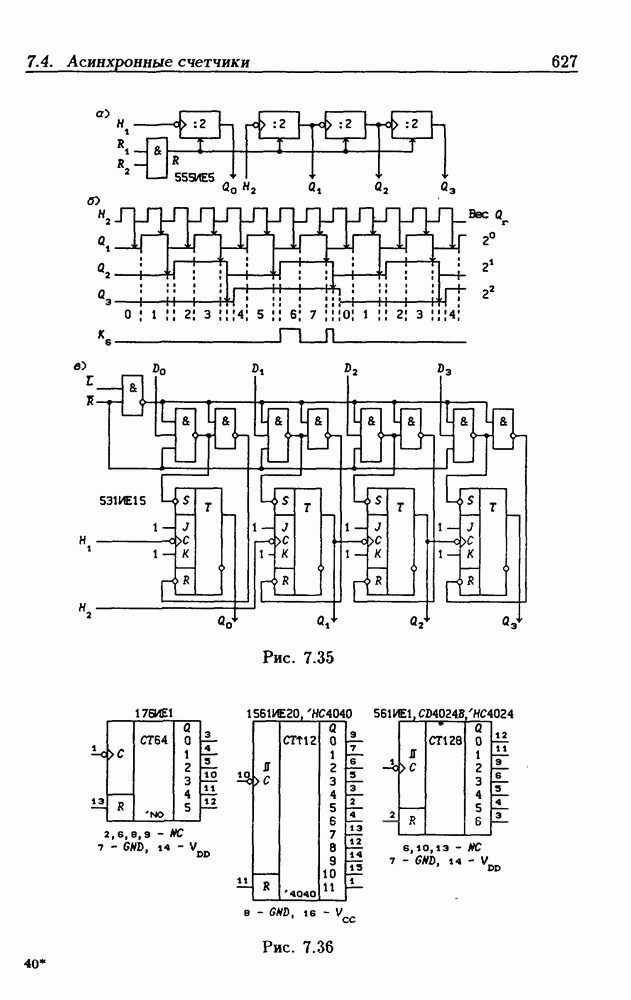
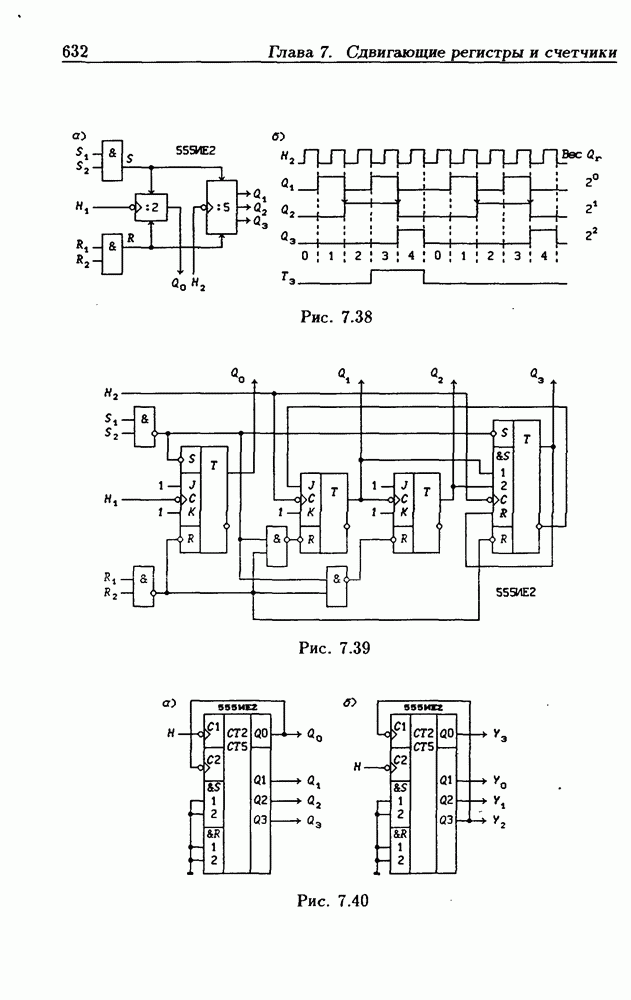
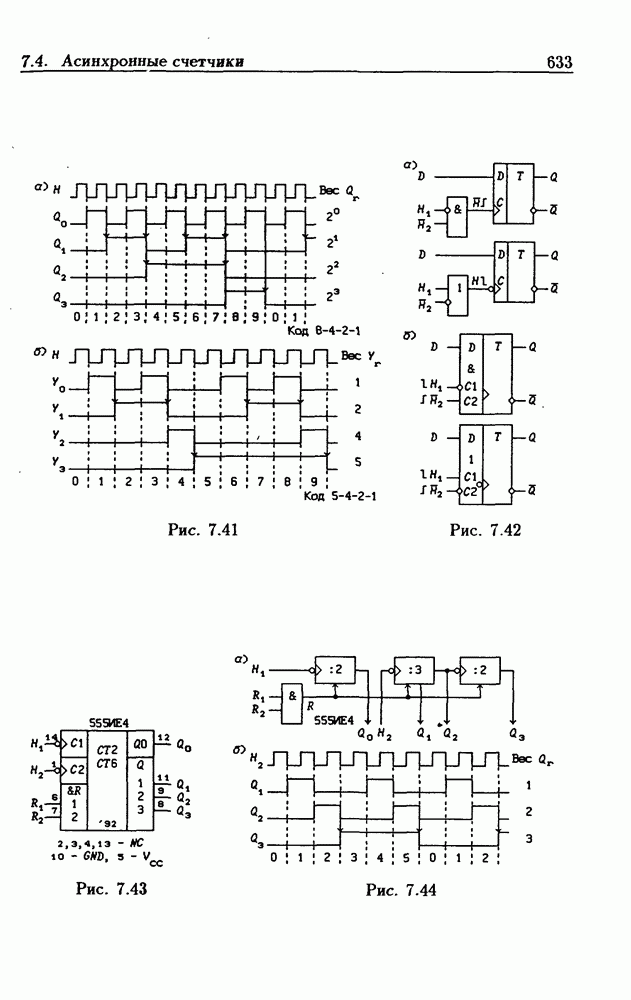
- 7.4. Асинхронные счетчики
- Двоично-десятичные асинхронные счетчики.
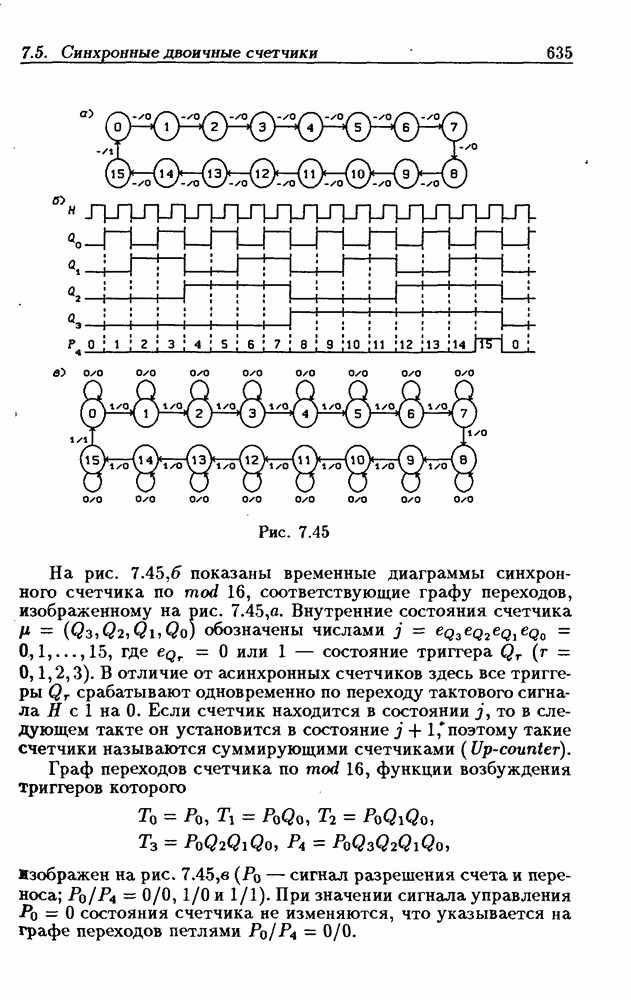
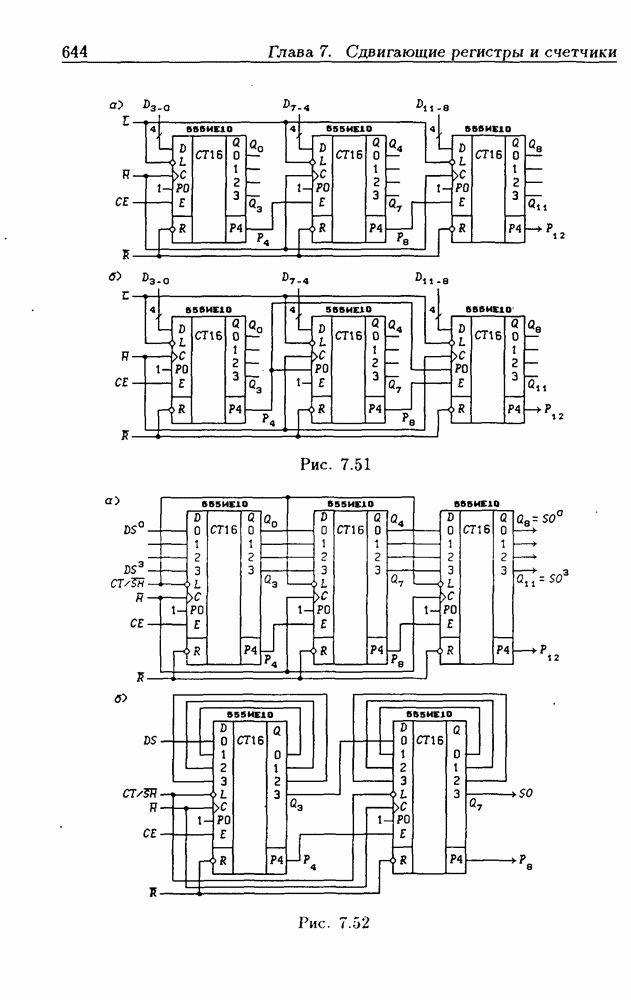
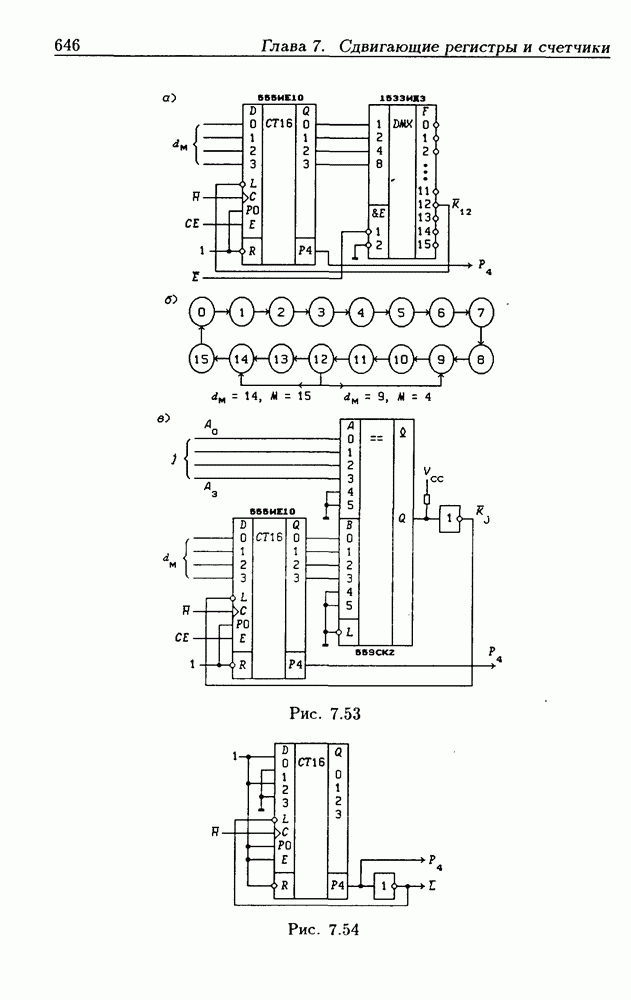
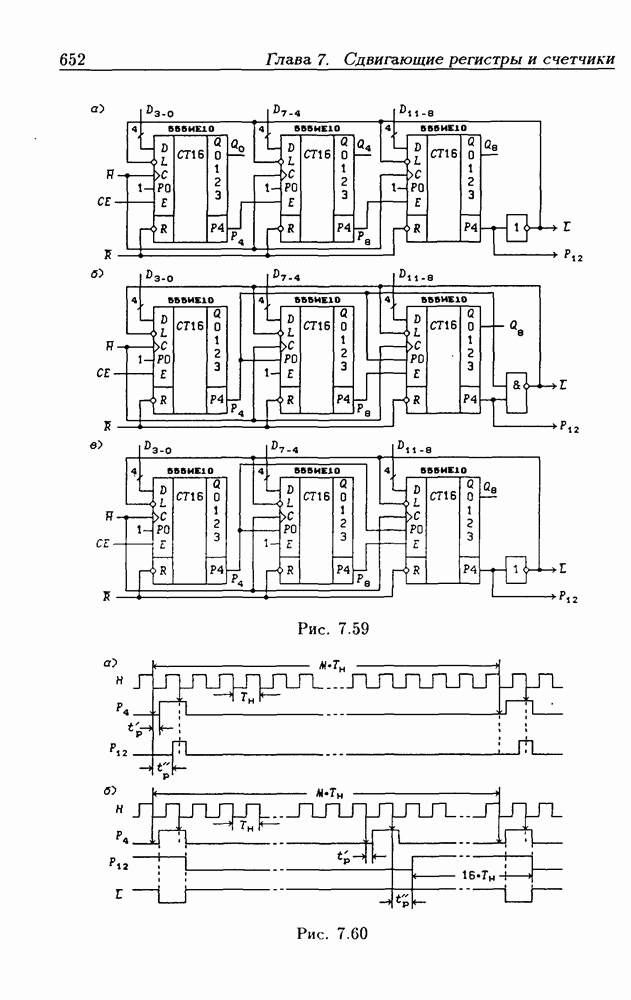
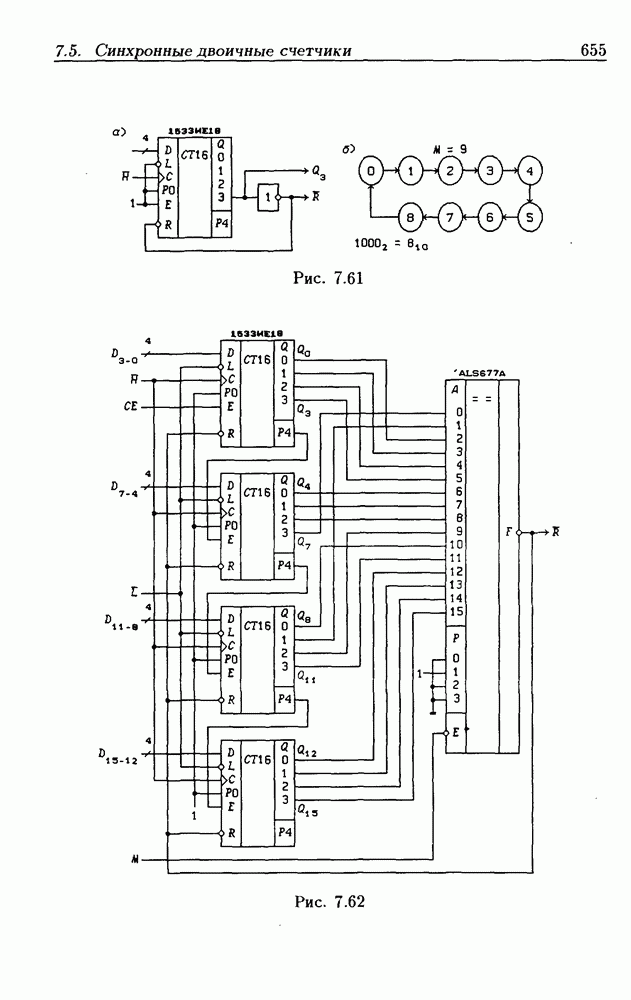
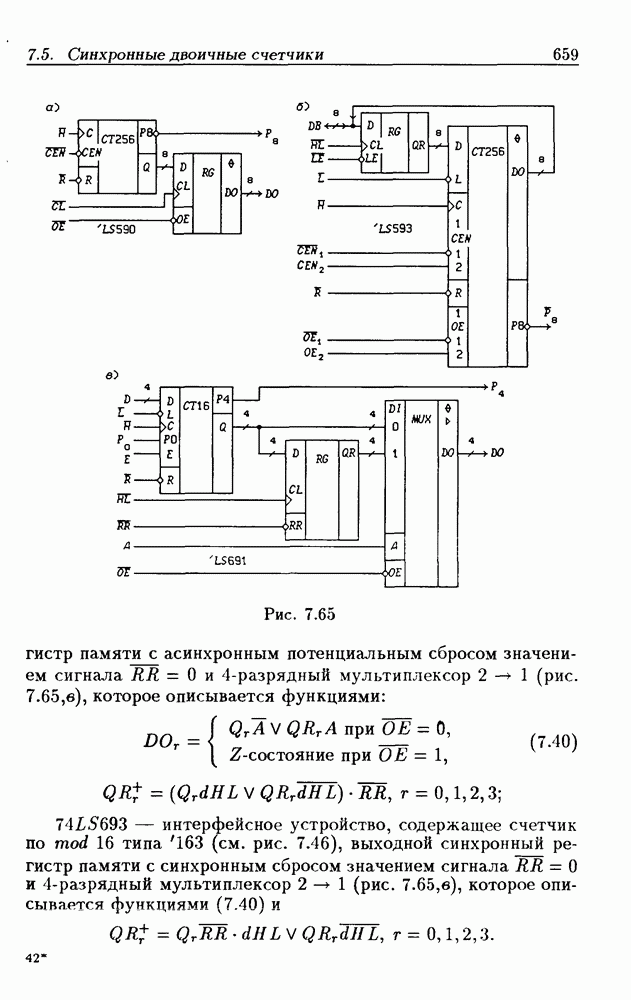
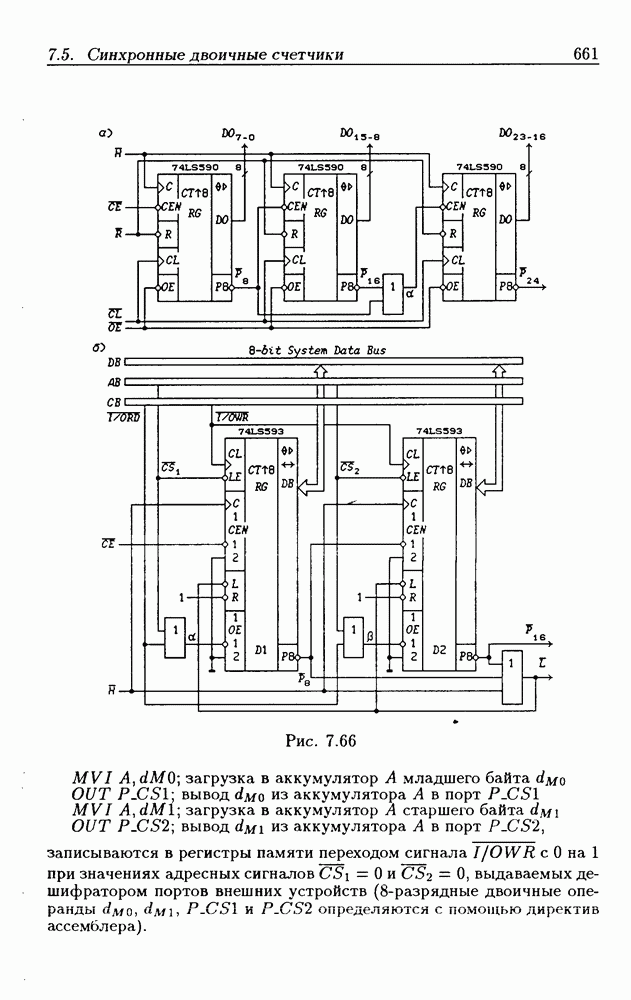
- 7.5. Синхронные двоичные счетчики
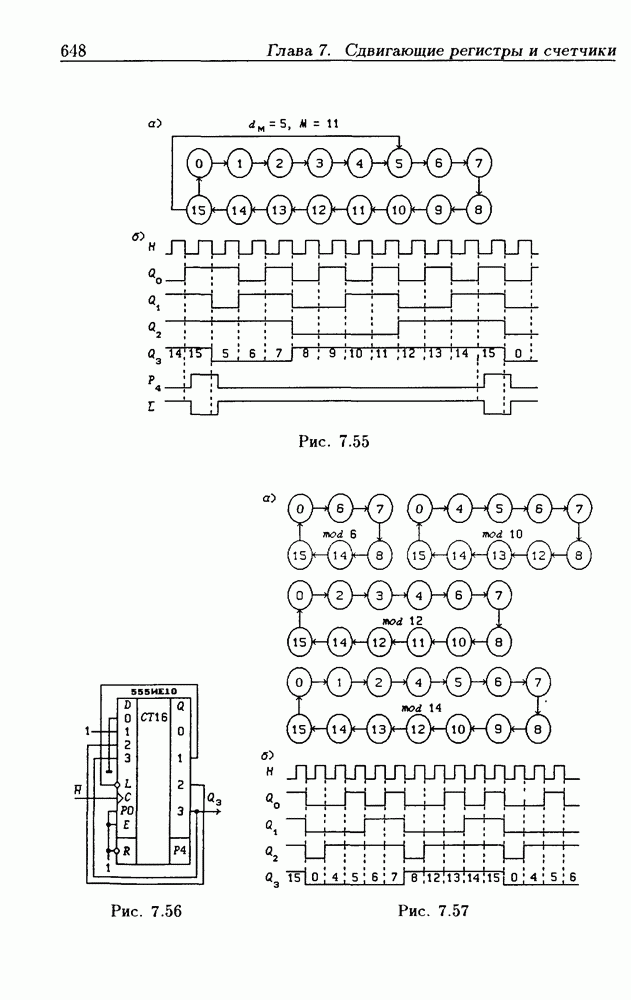
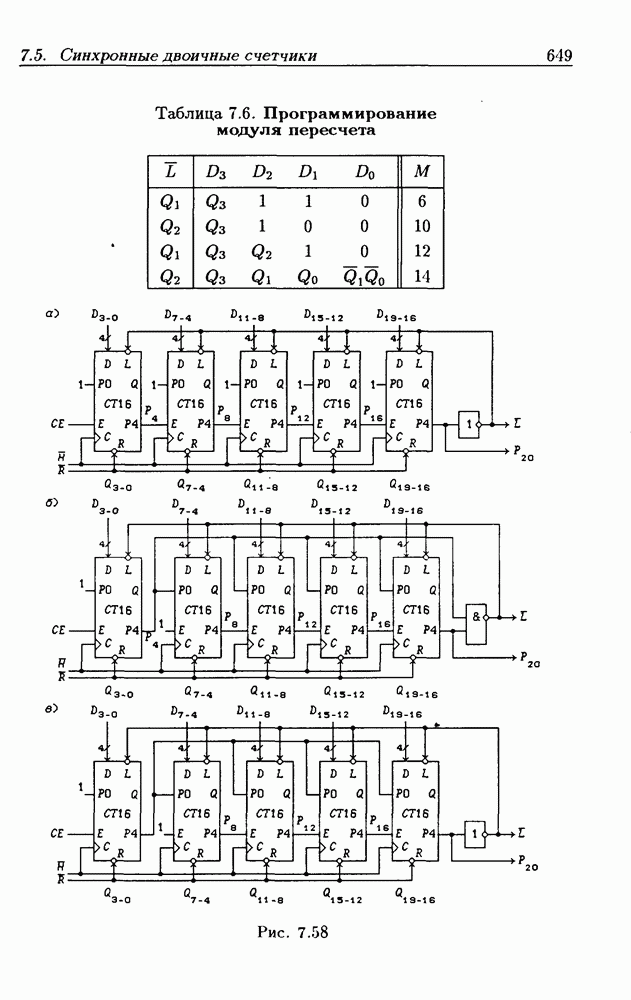
- Программирование модуля пересчета двоичных счетчиков.
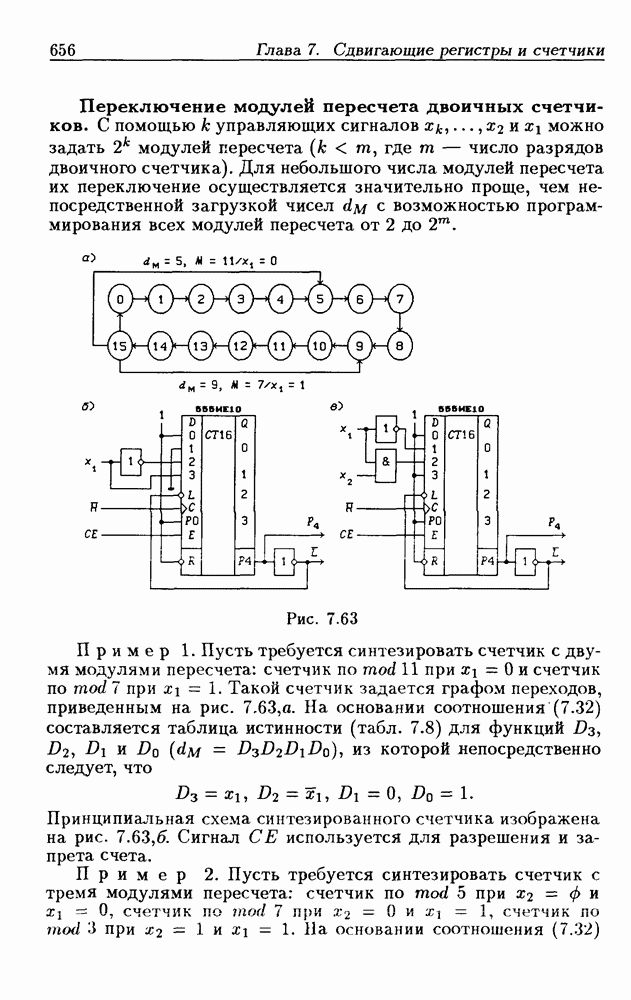
- Переключение модулей пересчета двоичных счетчиков.
- Функциональные устройства на основе двоичных счетчиков.
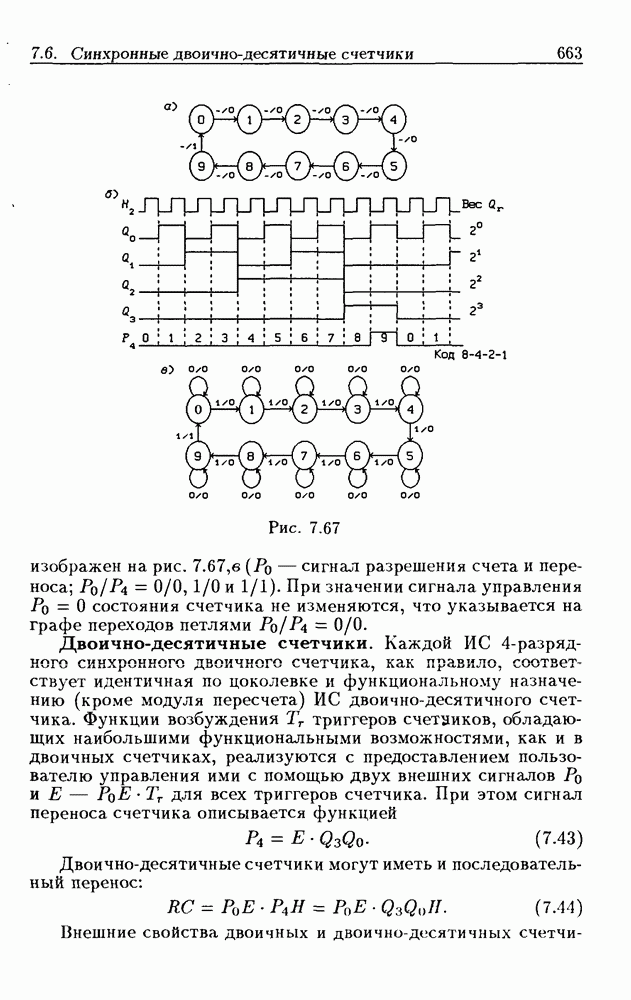
- 7.6. Синхронные двоично-десятичные счетчики
- 7.7. Синхронные реверсивные счетчики
- 7.8. Счетчики с расщепленным тактовым сигналом
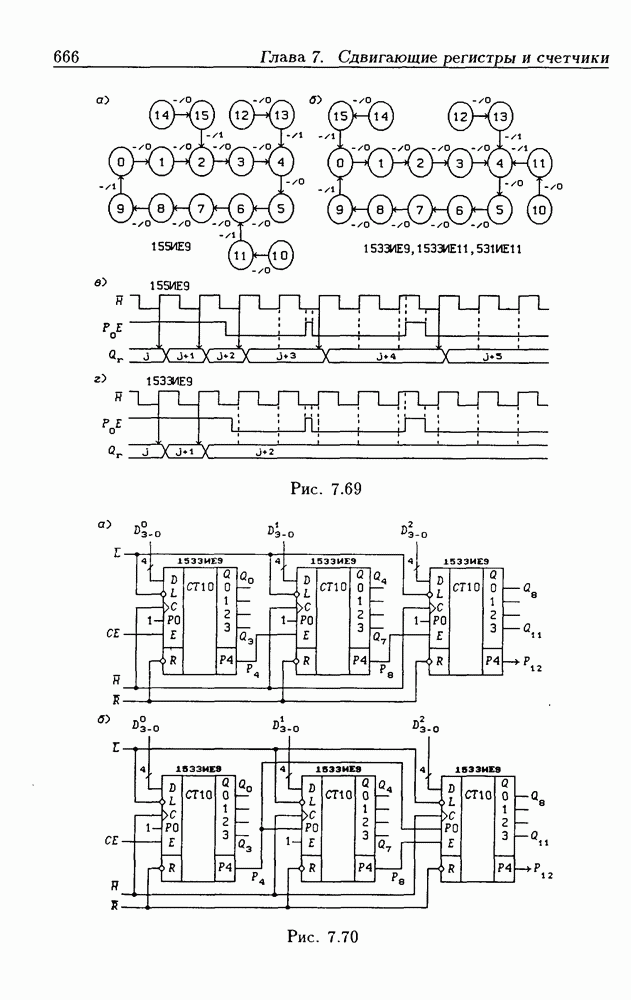
- 7.9. Счетчики на сдвигающих регистрах
- 7.10. Кольцевые счетчики
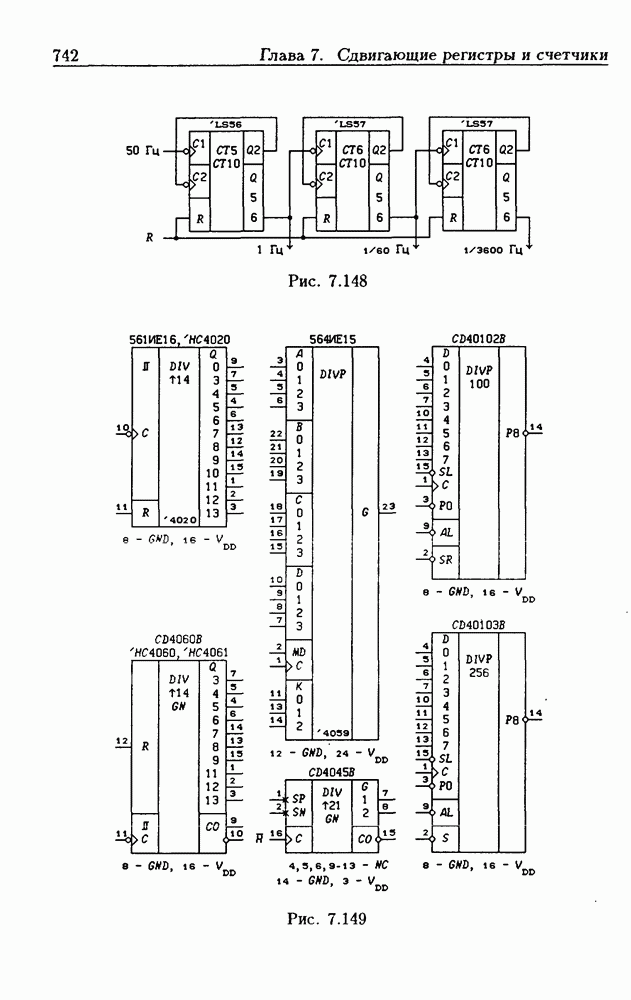
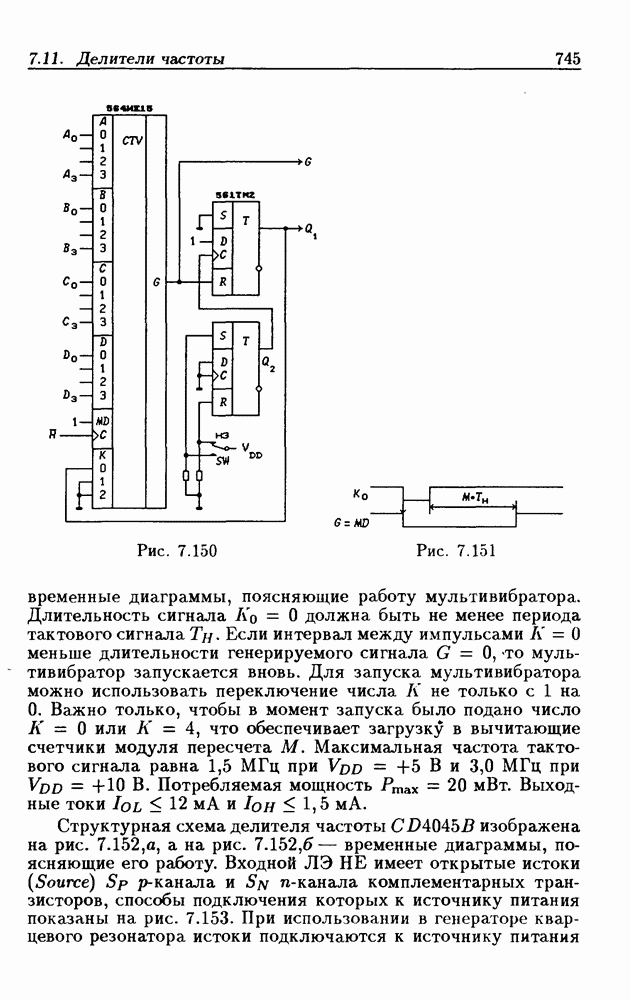
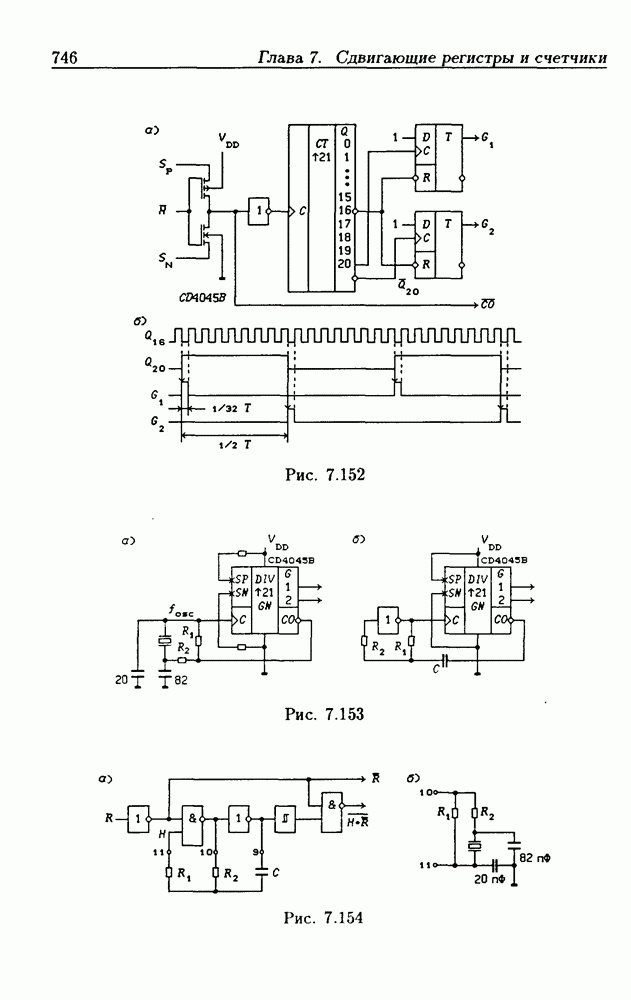
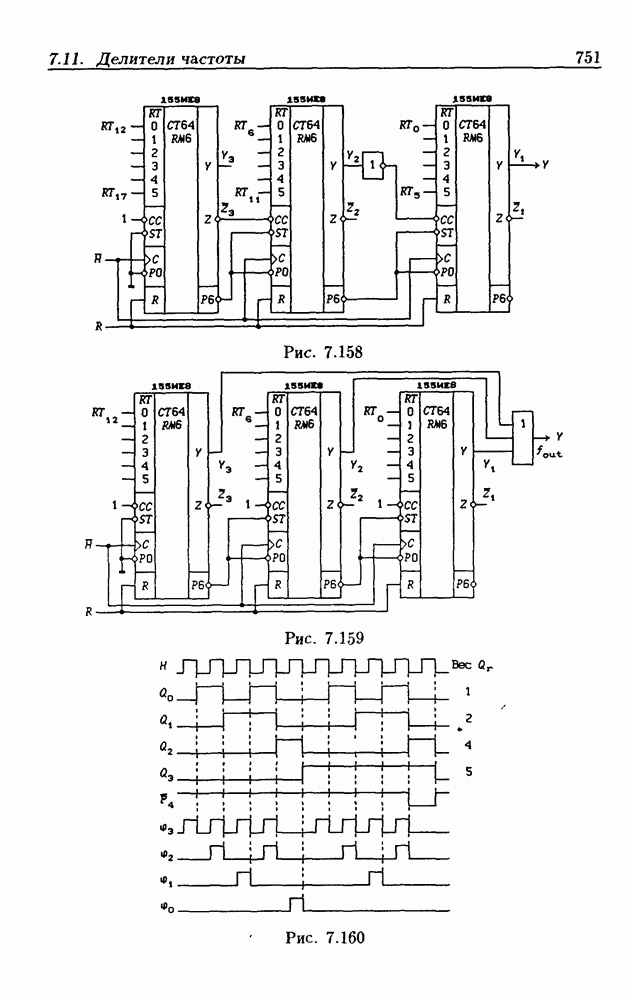
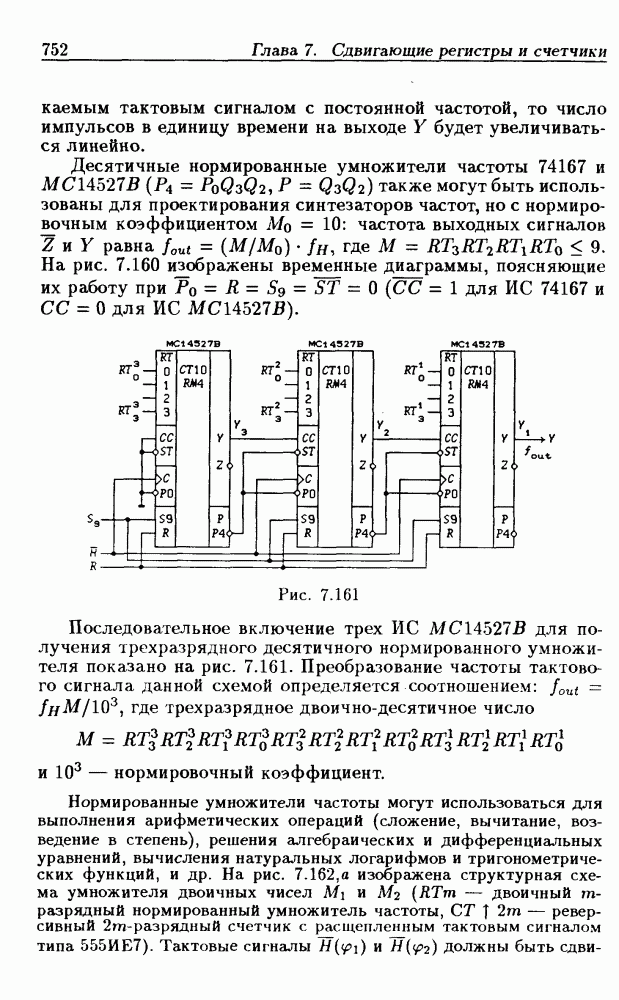
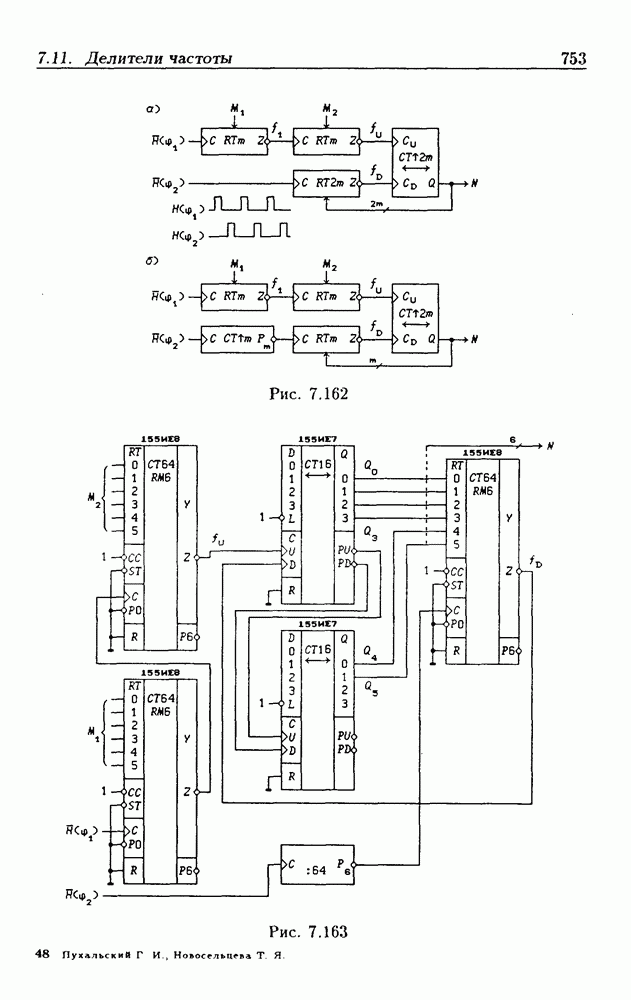
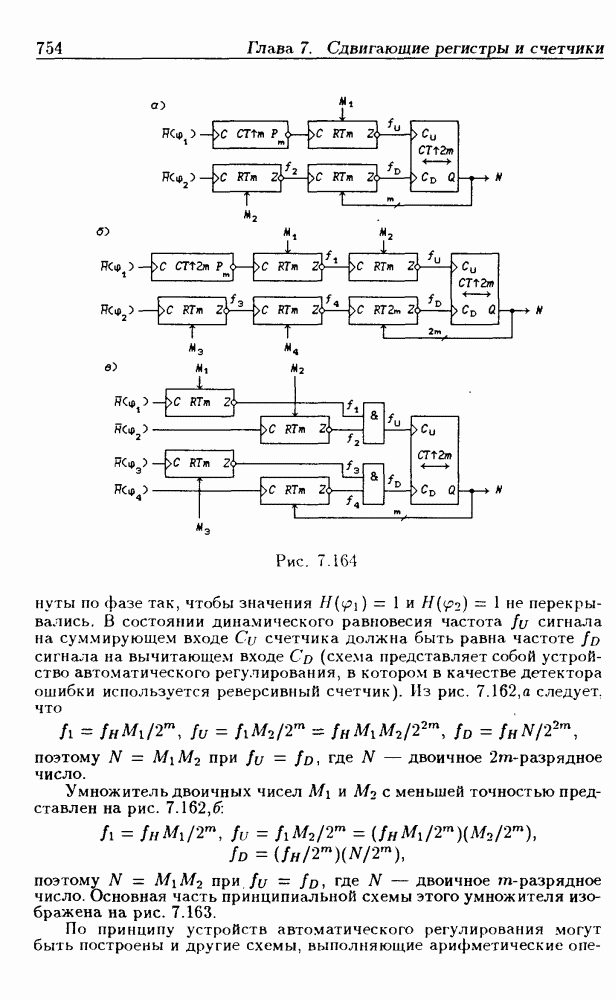
- 7.11. Делители частоты
- Нормированные умножители частоты.
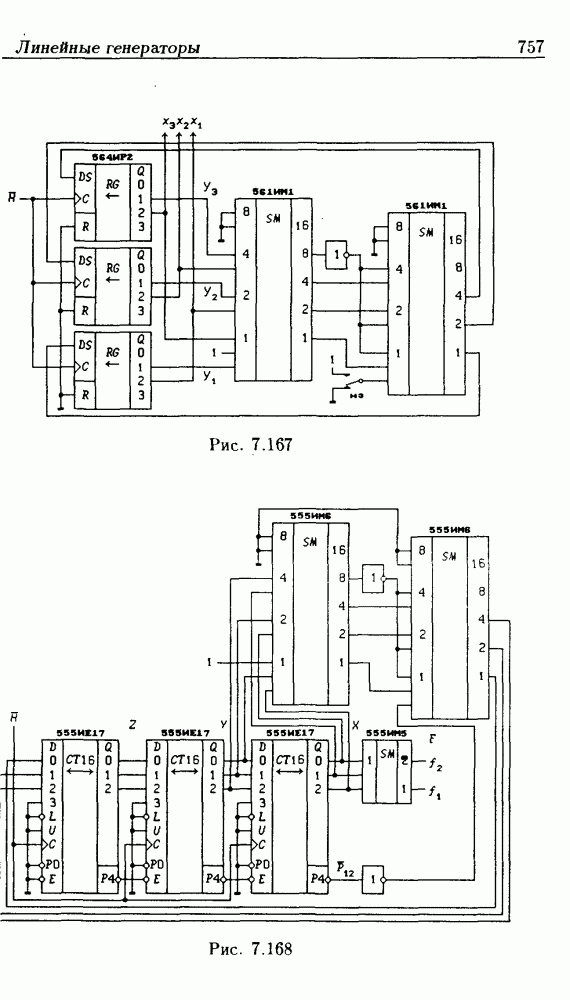
- 7.12. Линейные генераторы
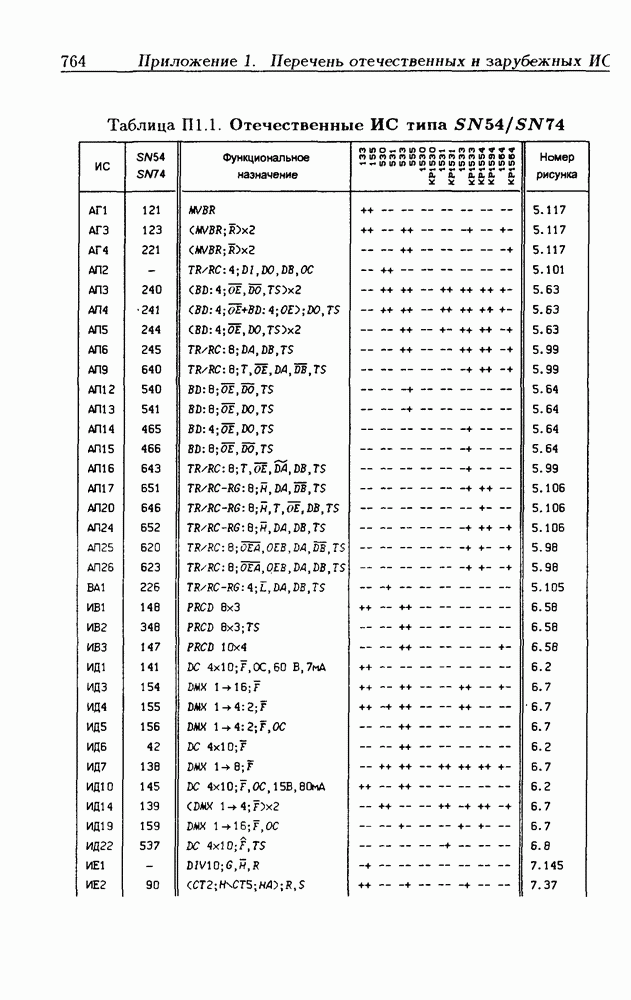
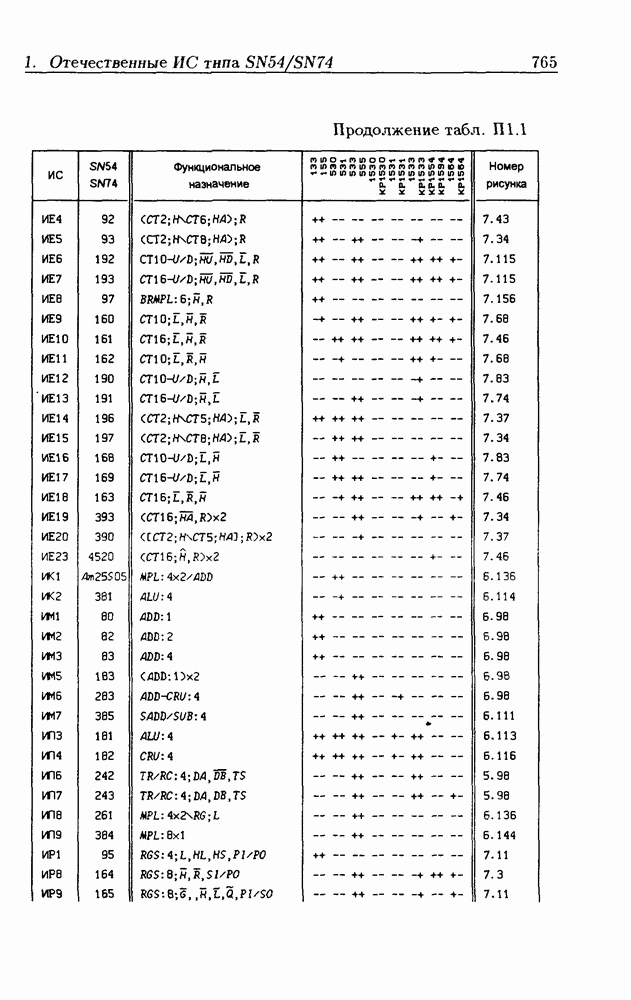
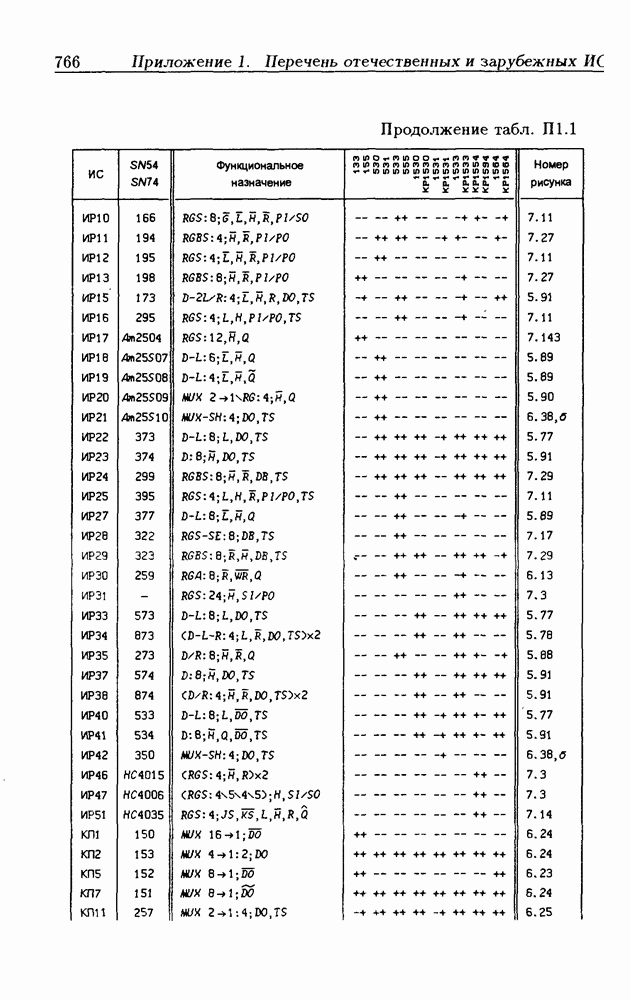
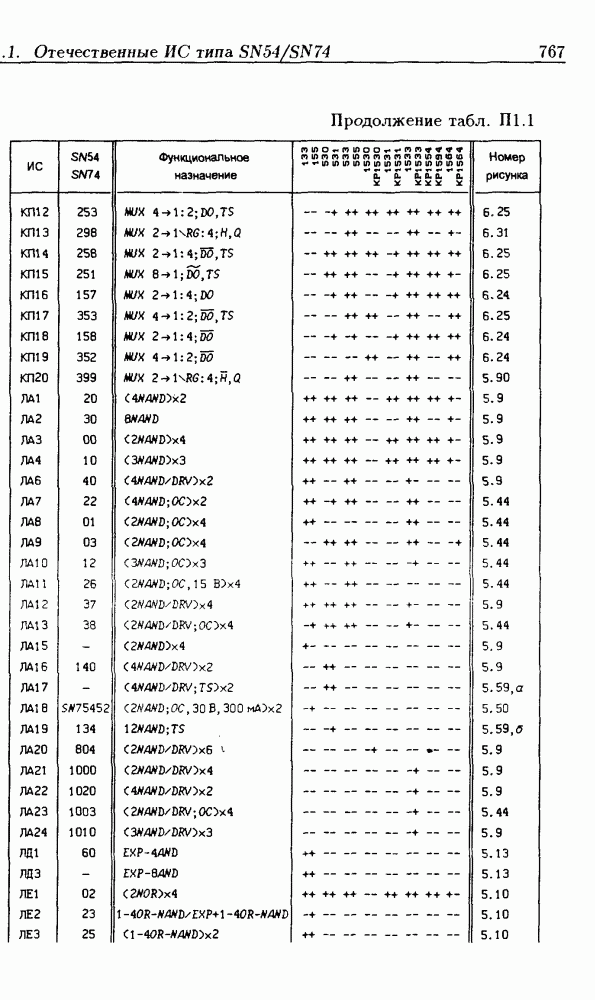
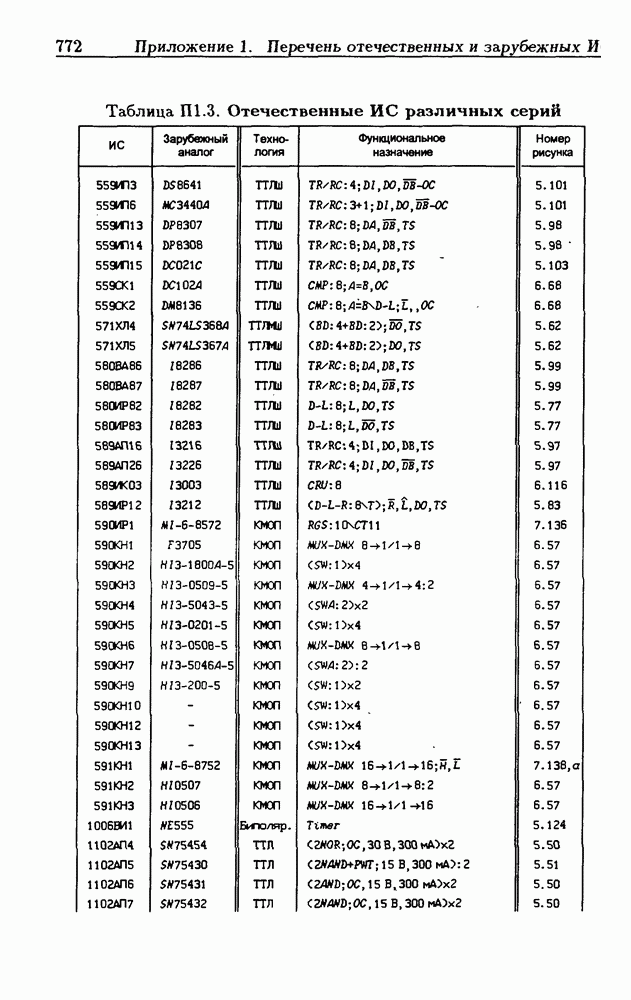
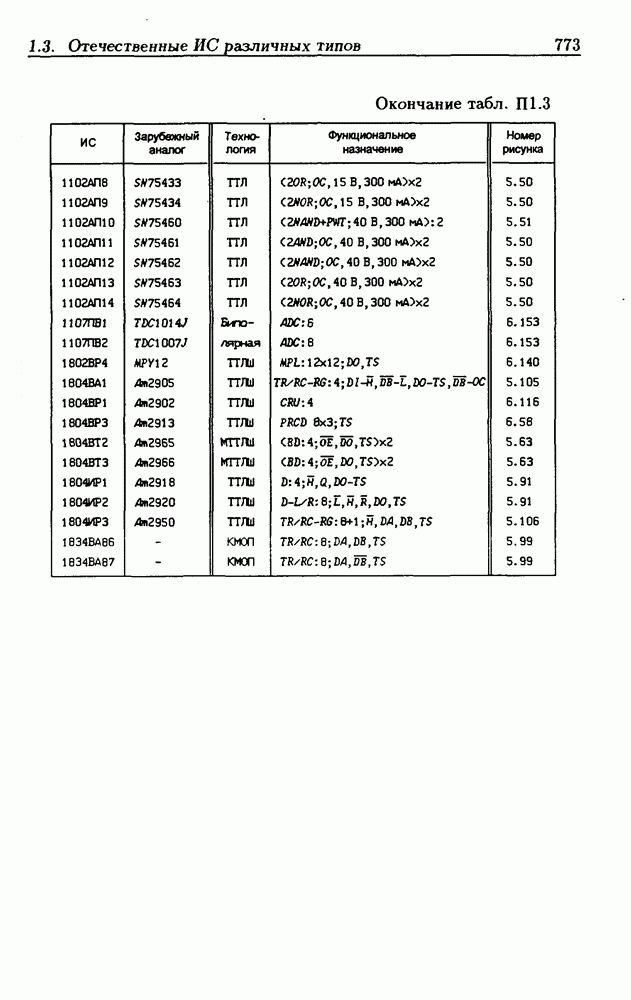
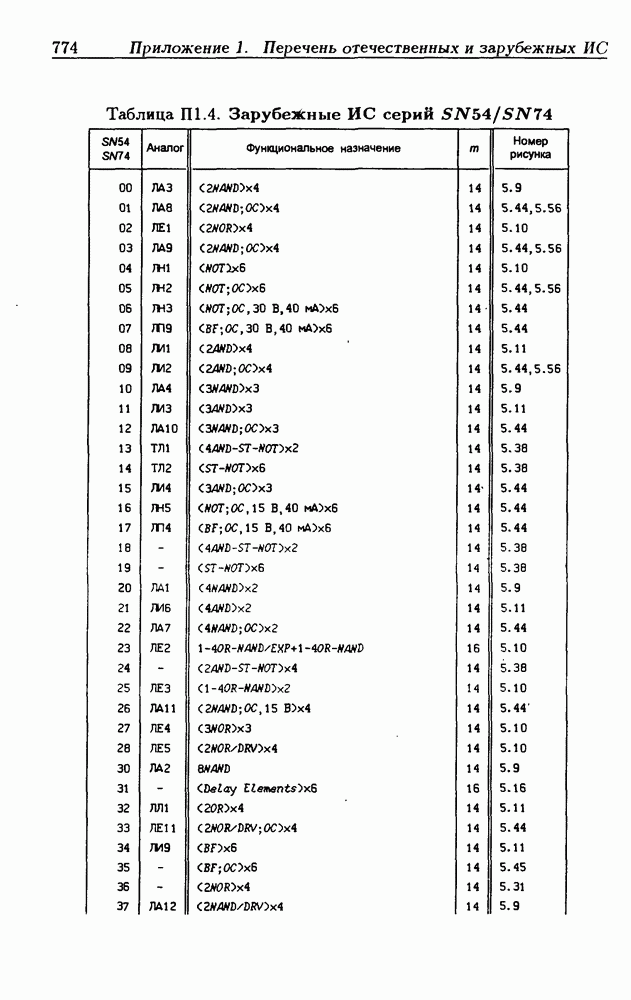
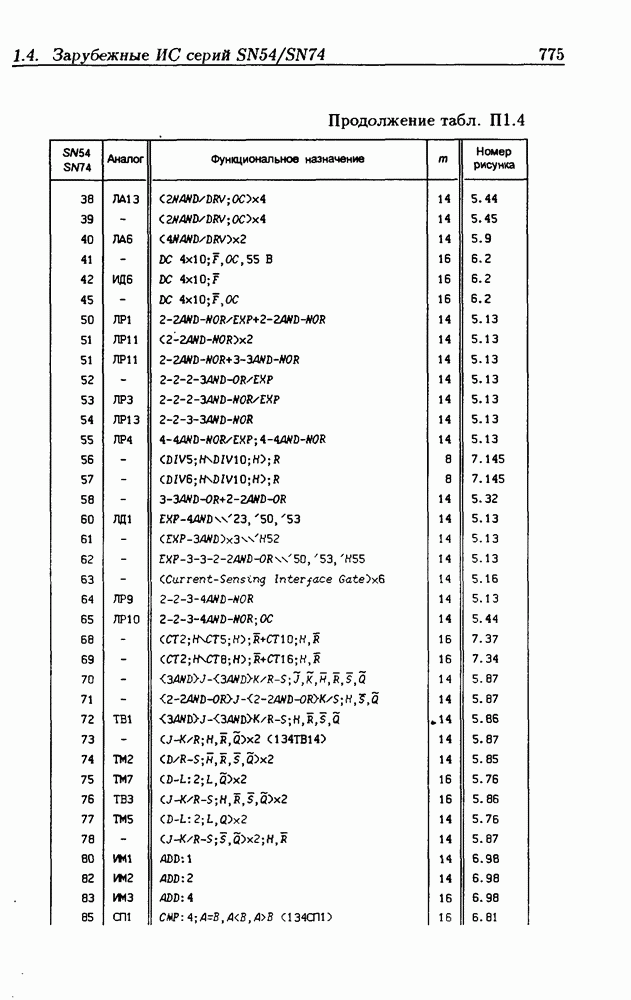
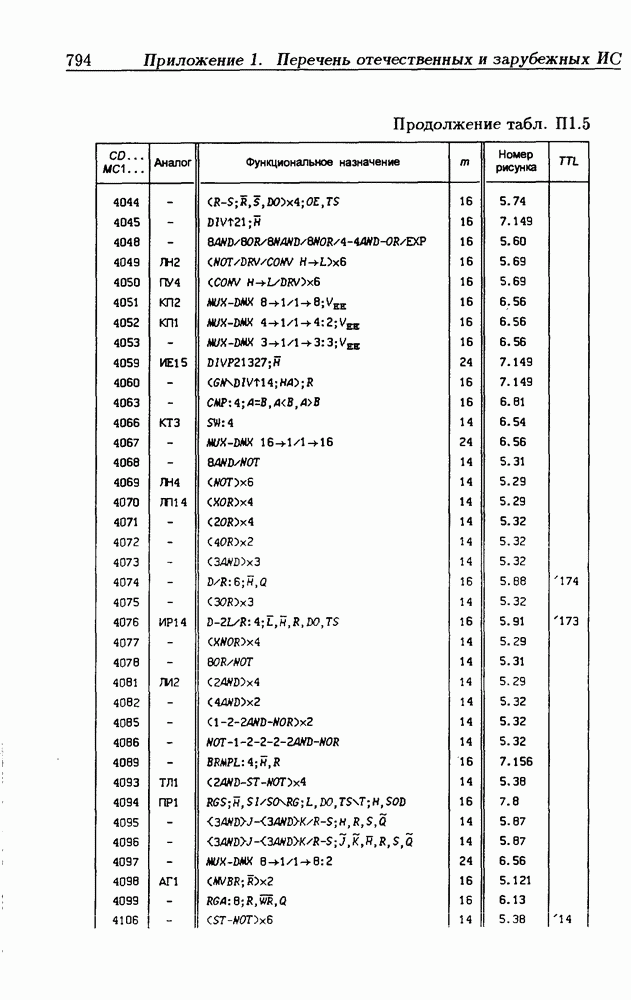
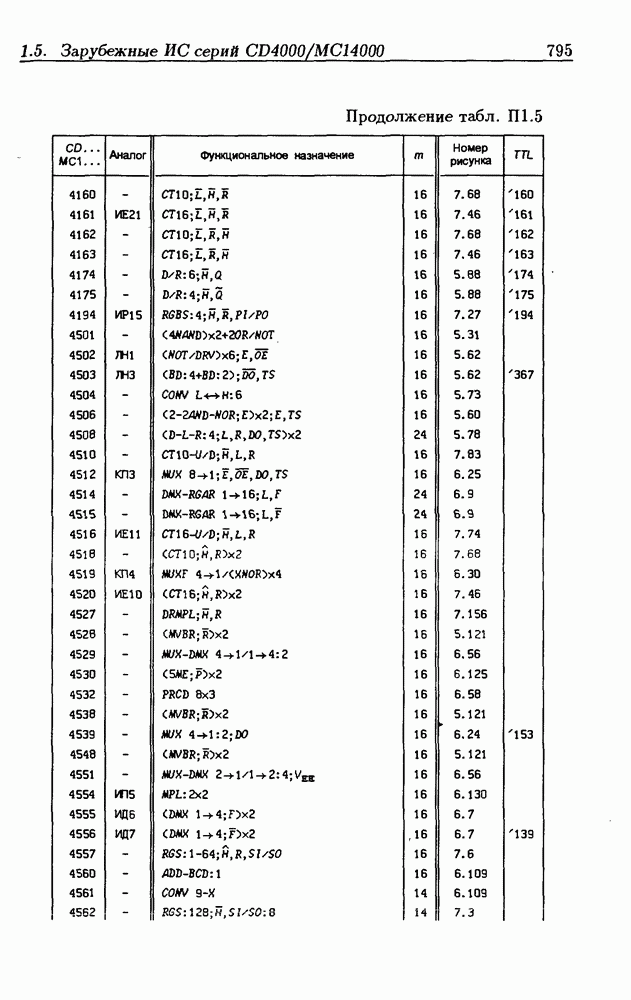
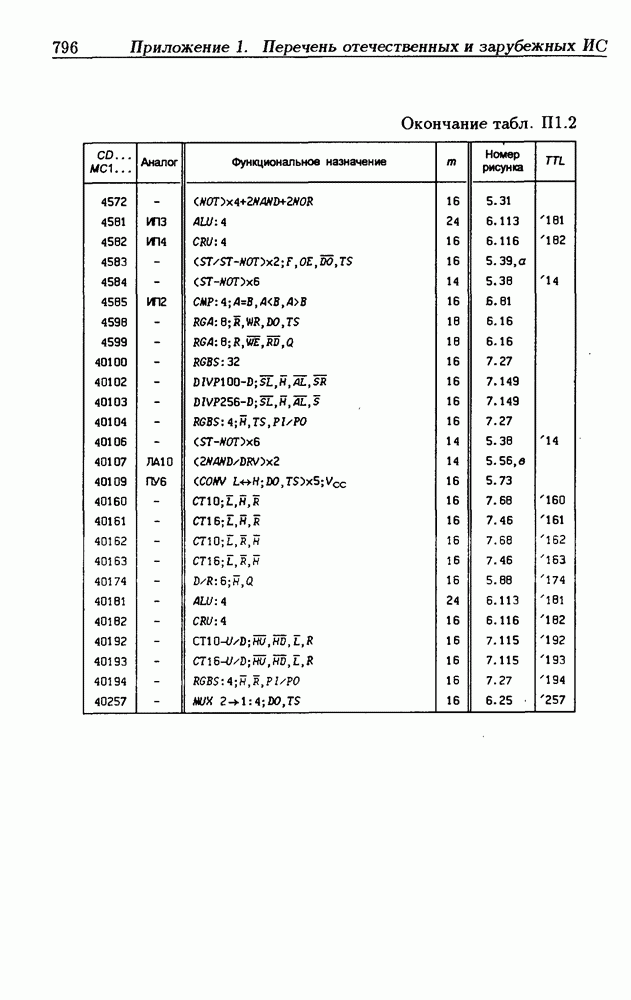
- Приложение 1. Перечень отечественных и зарубежных ИС
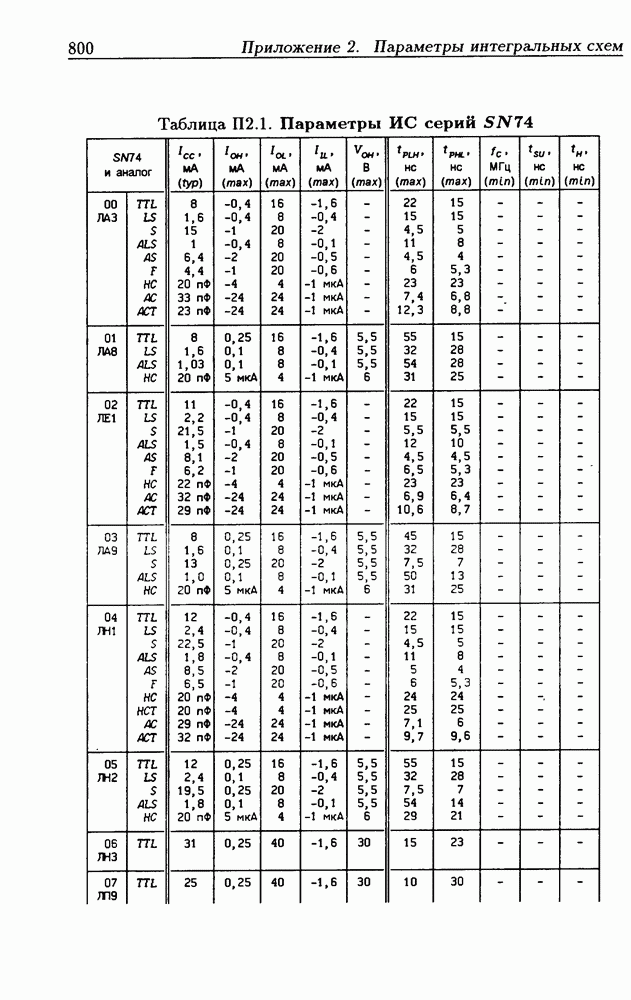
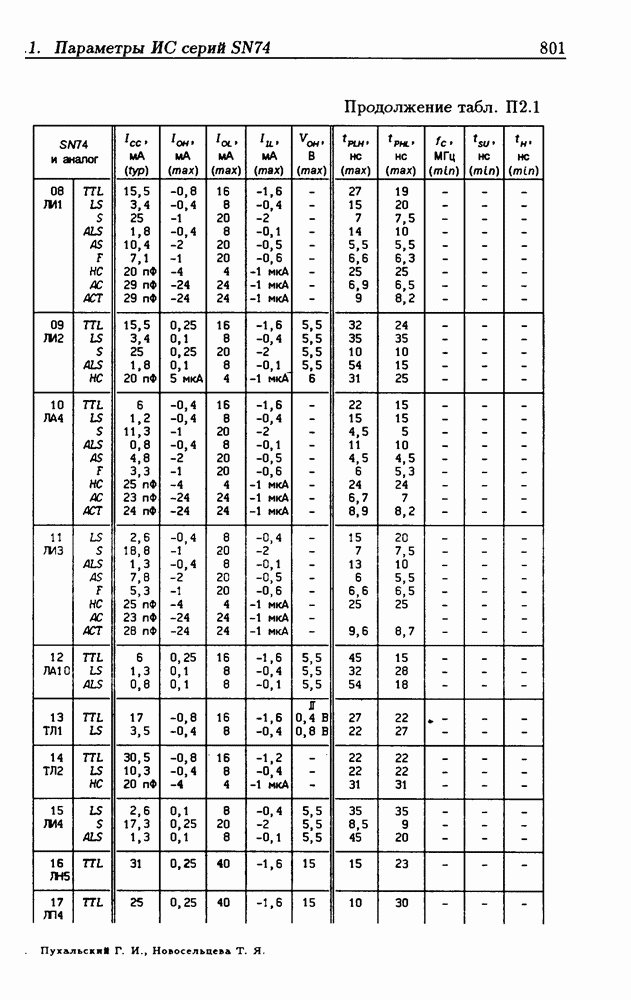
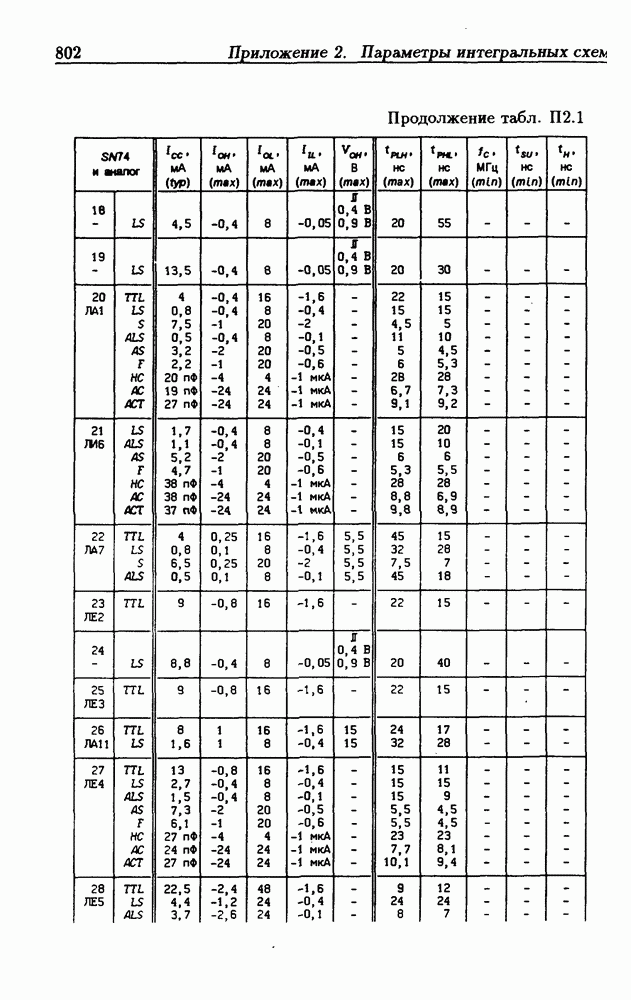
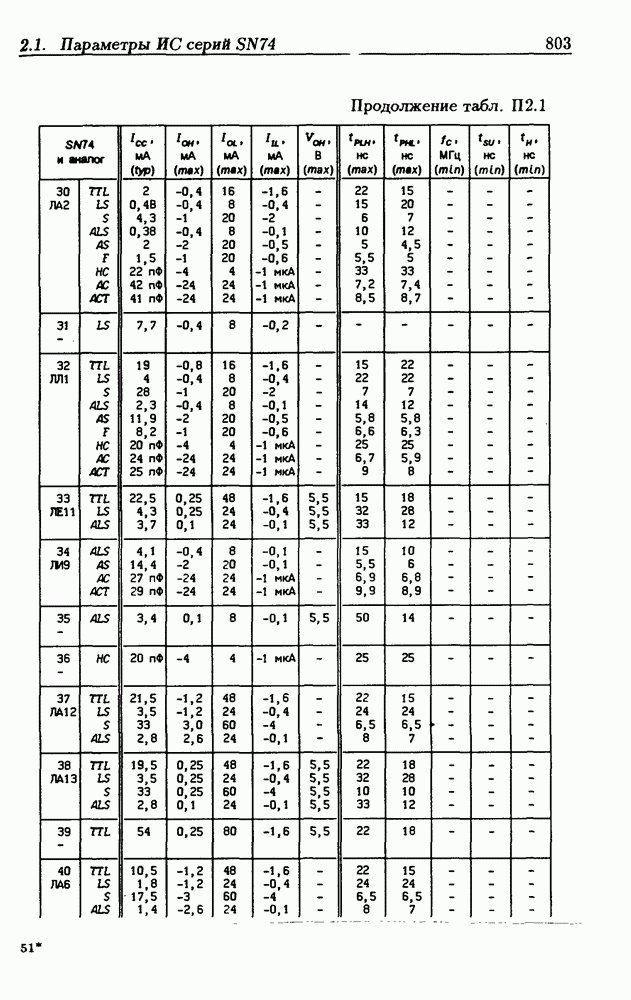
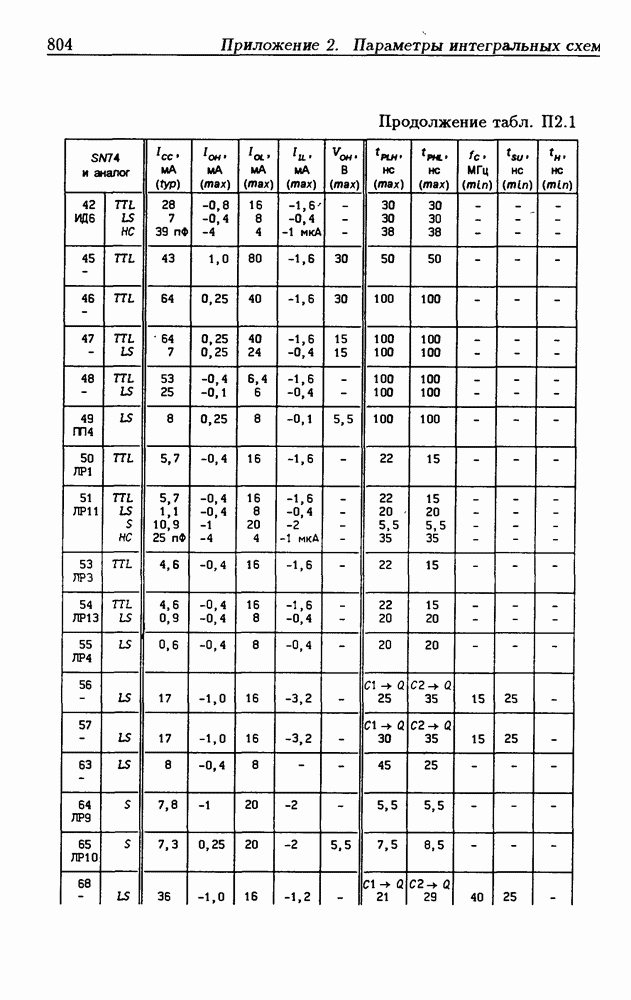
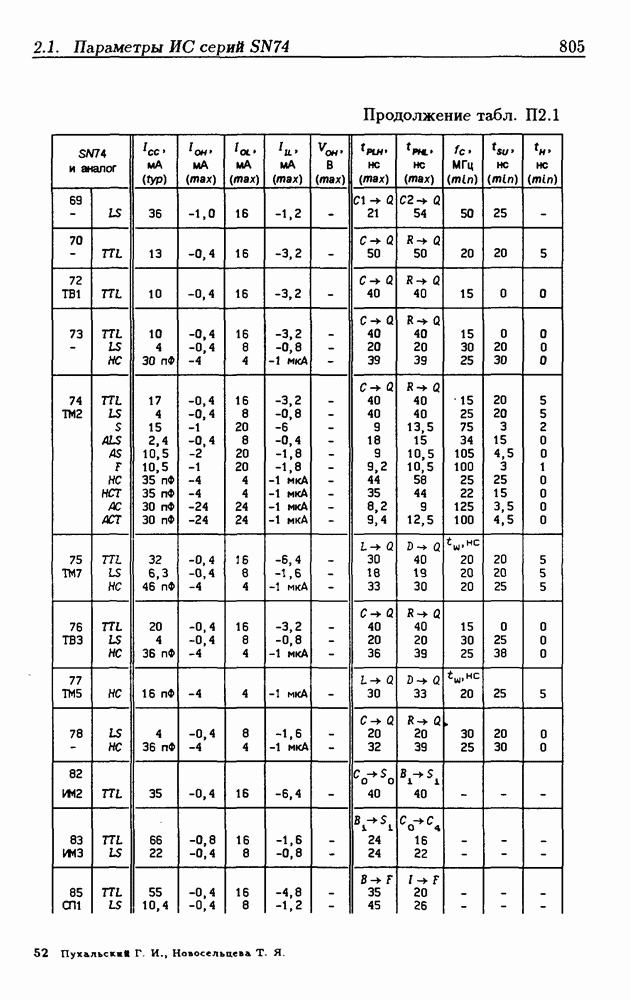
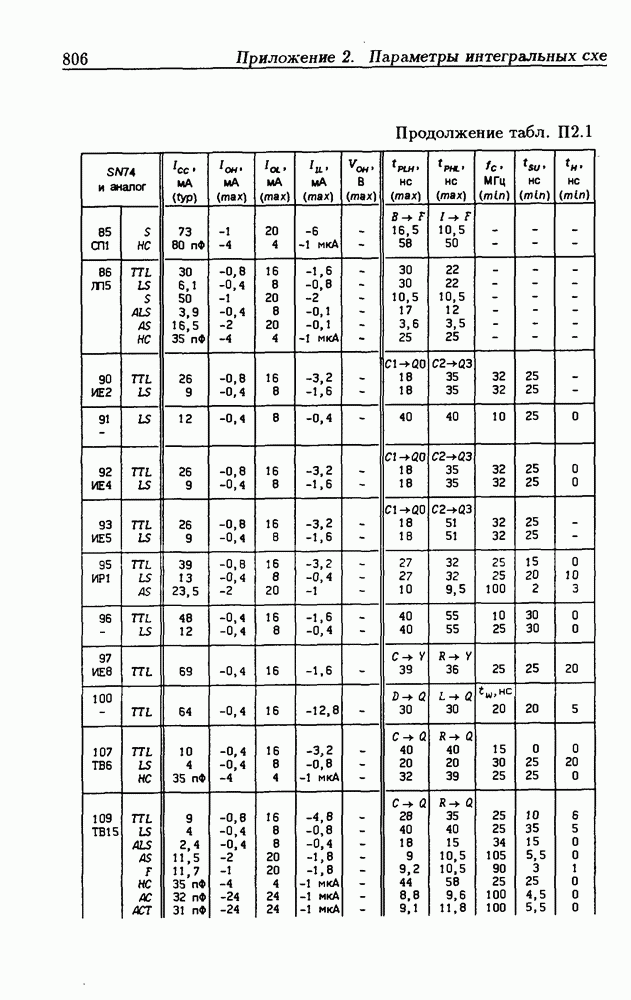
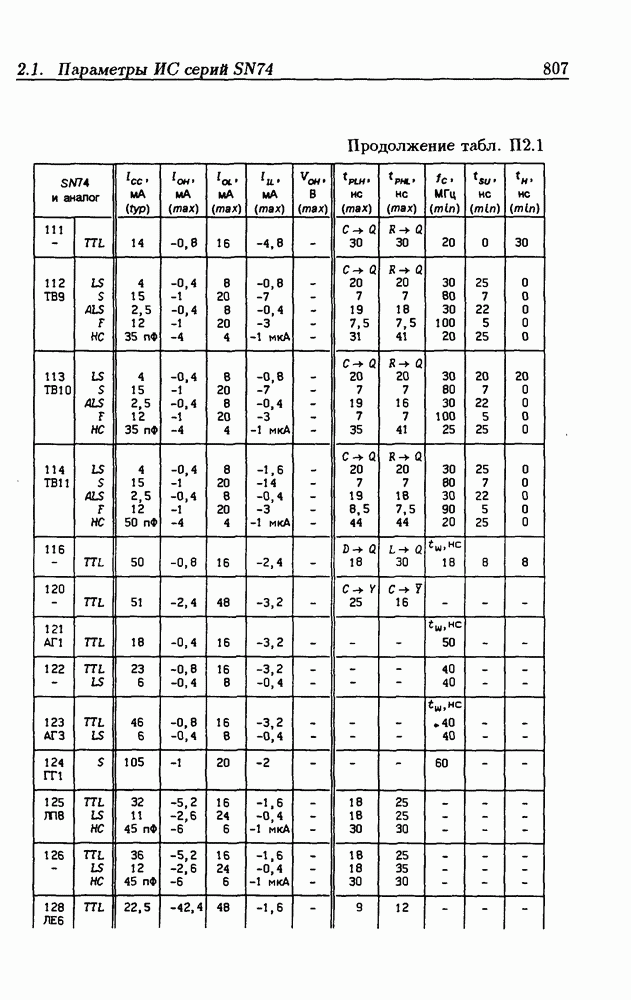
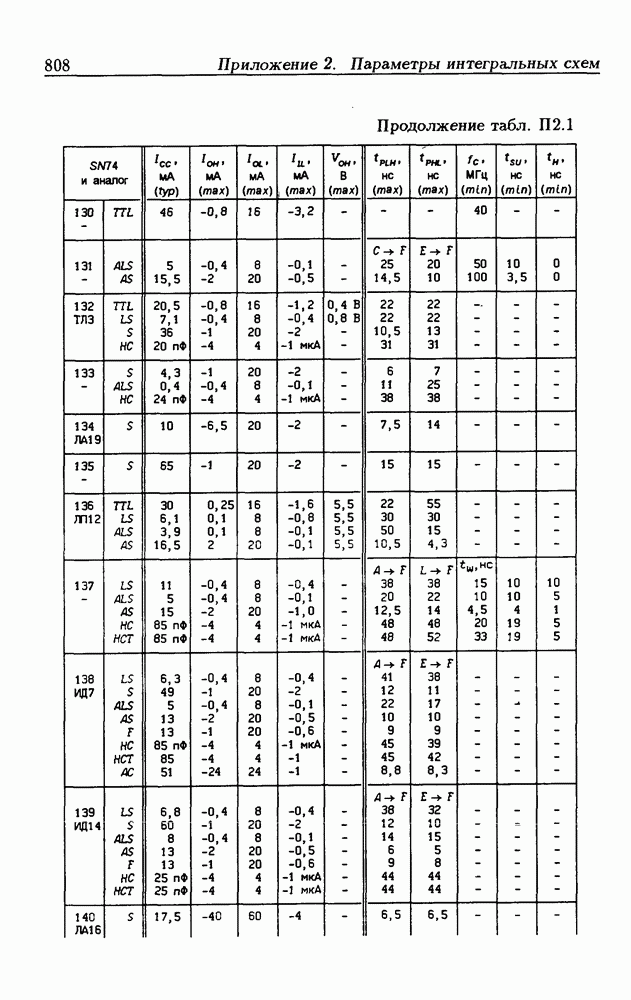
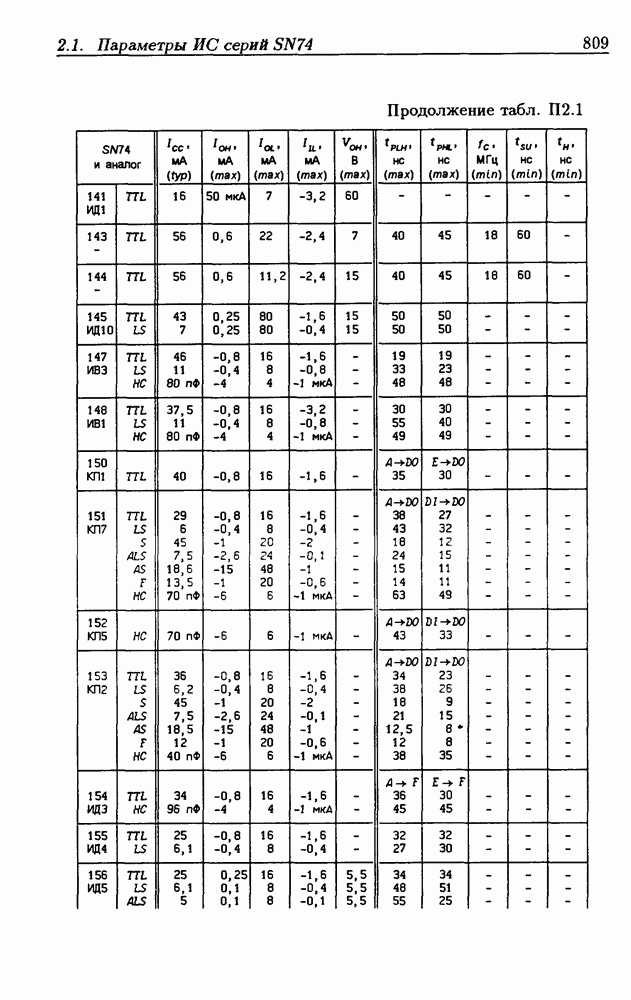
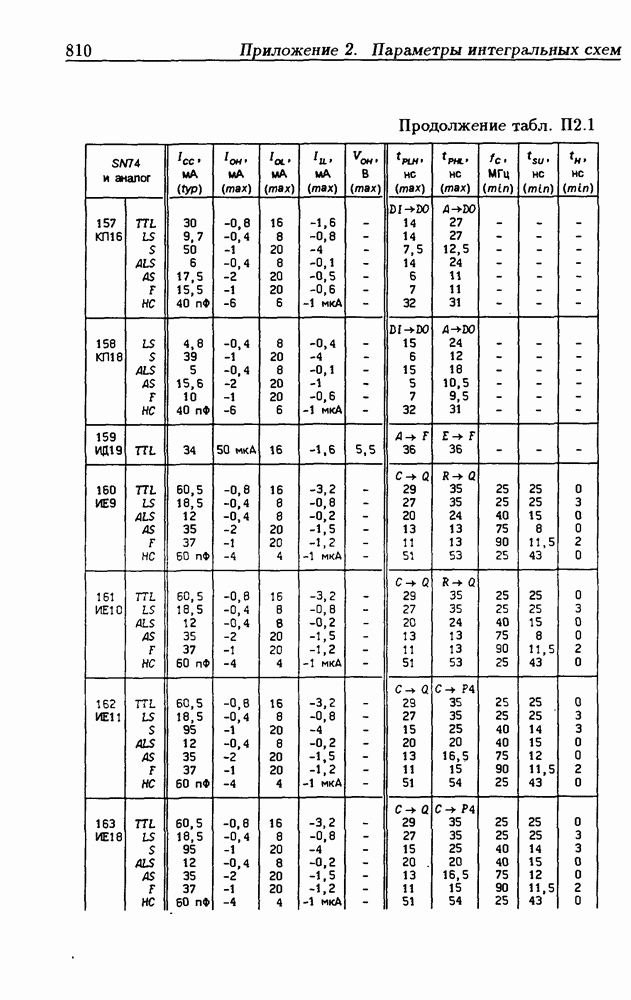
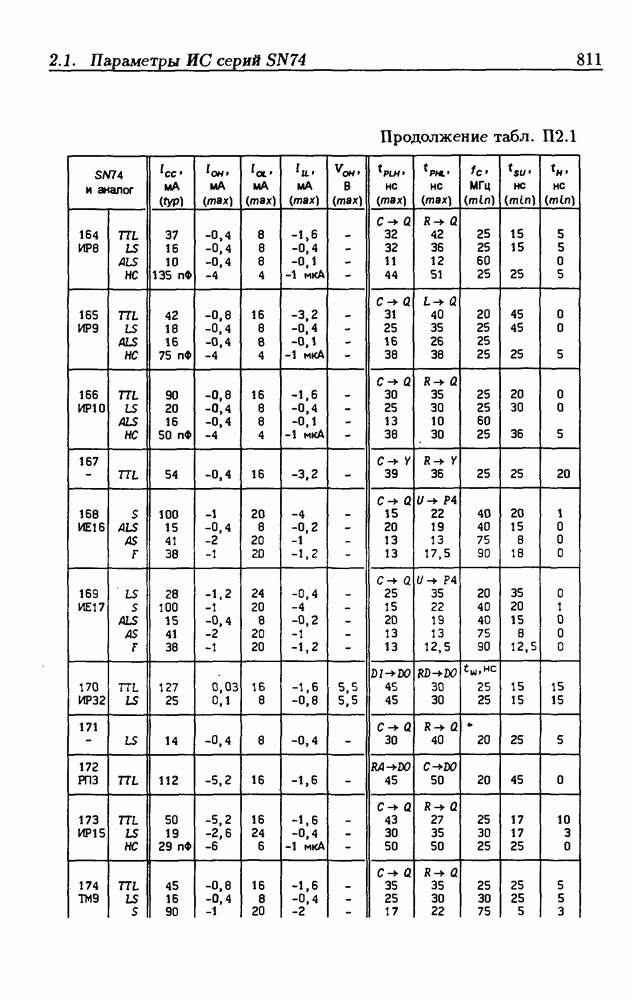
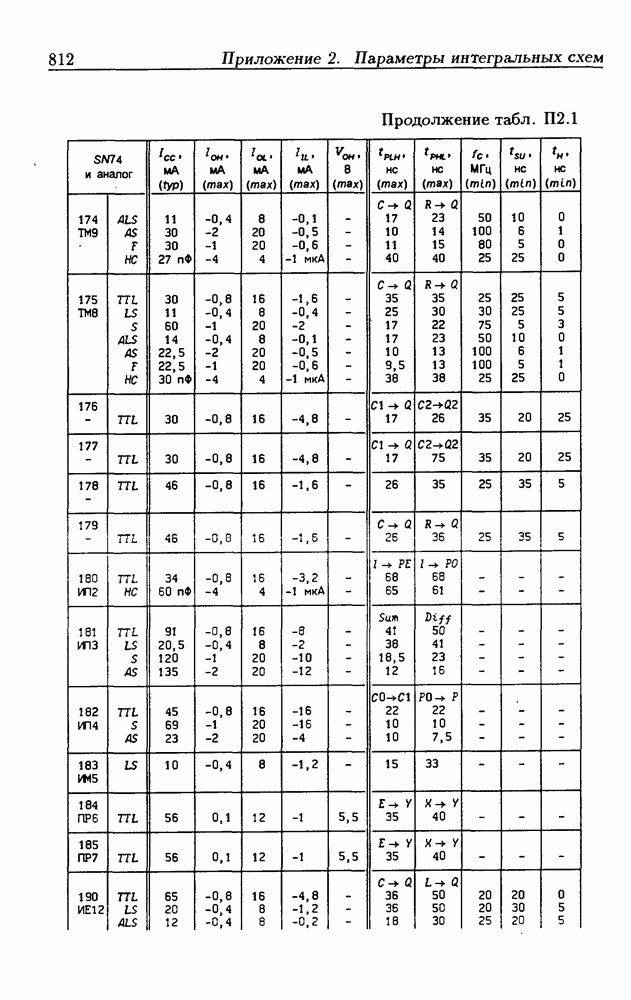
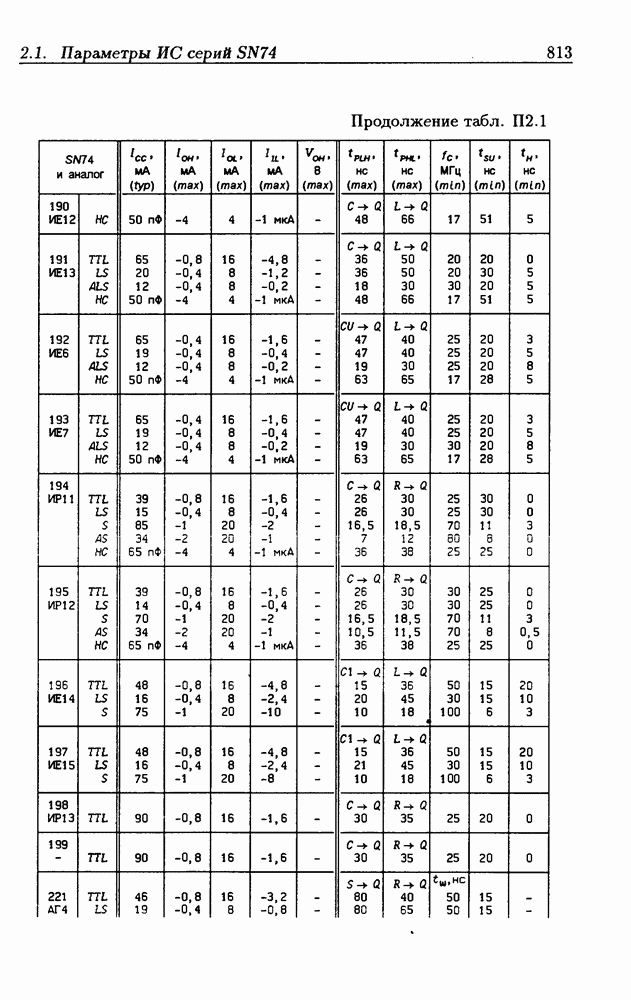
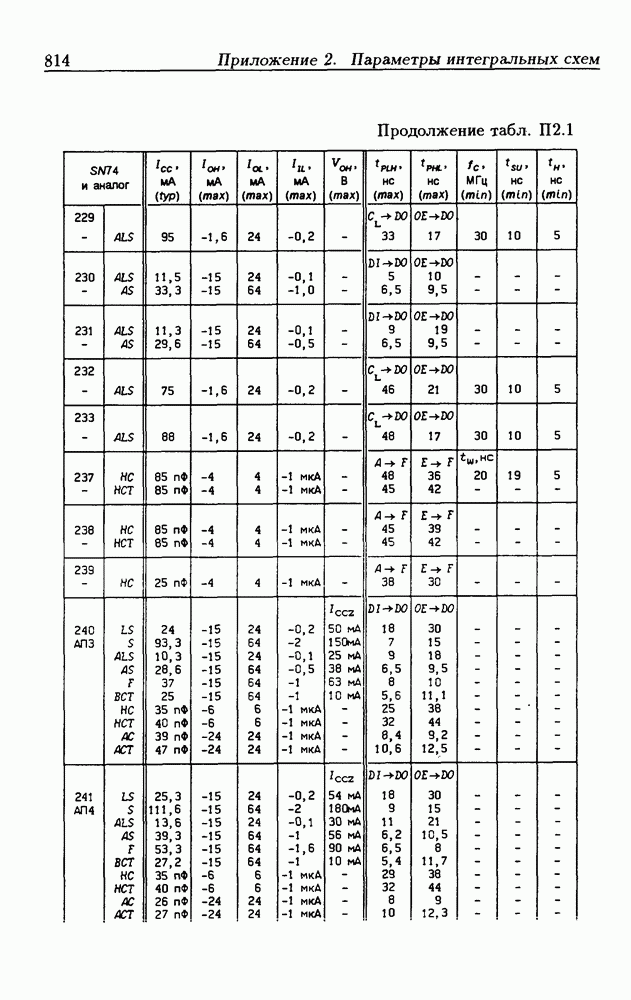
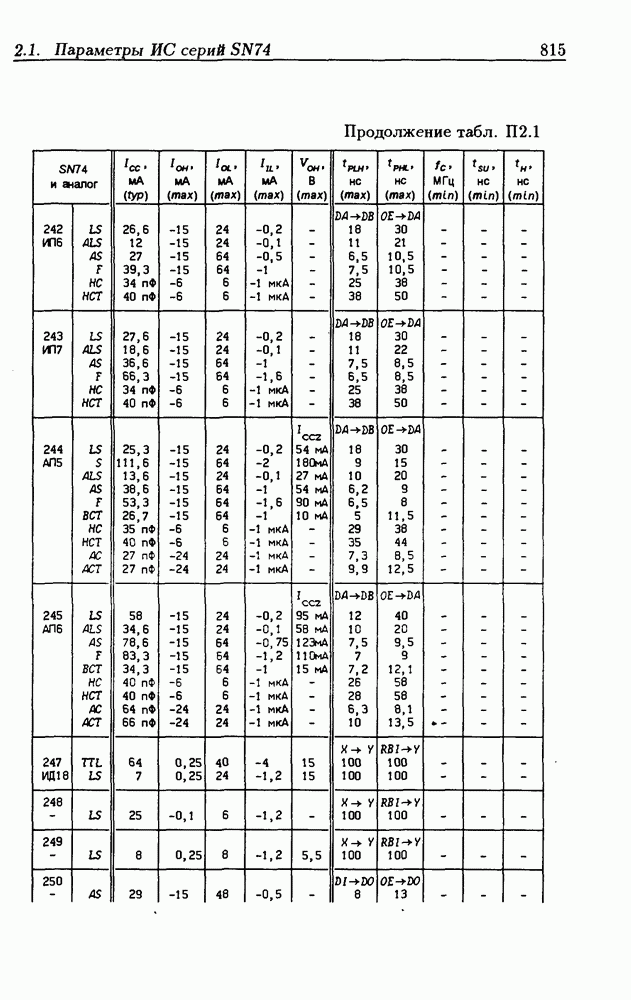
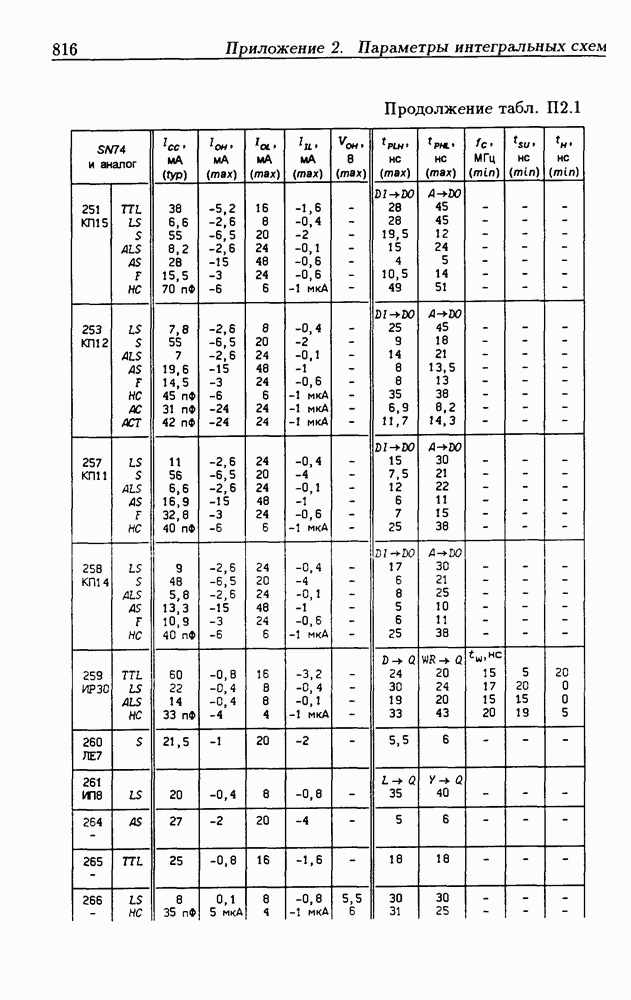
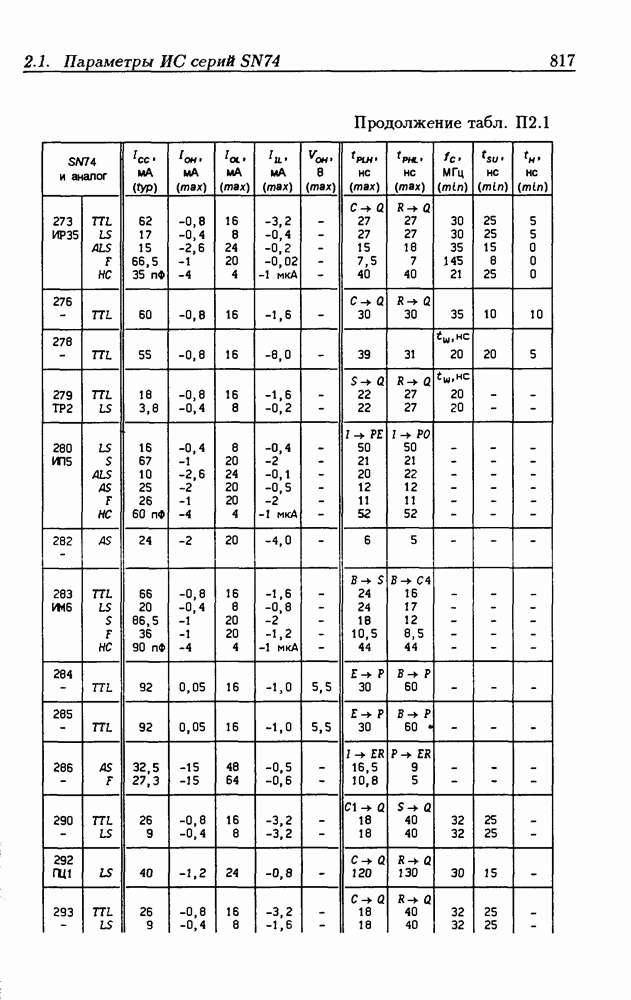
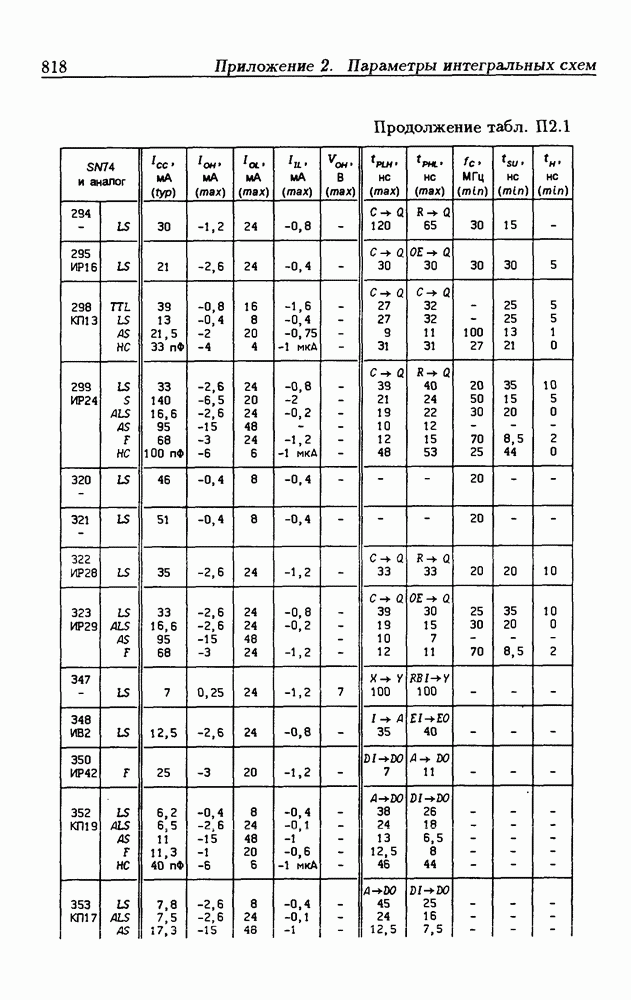
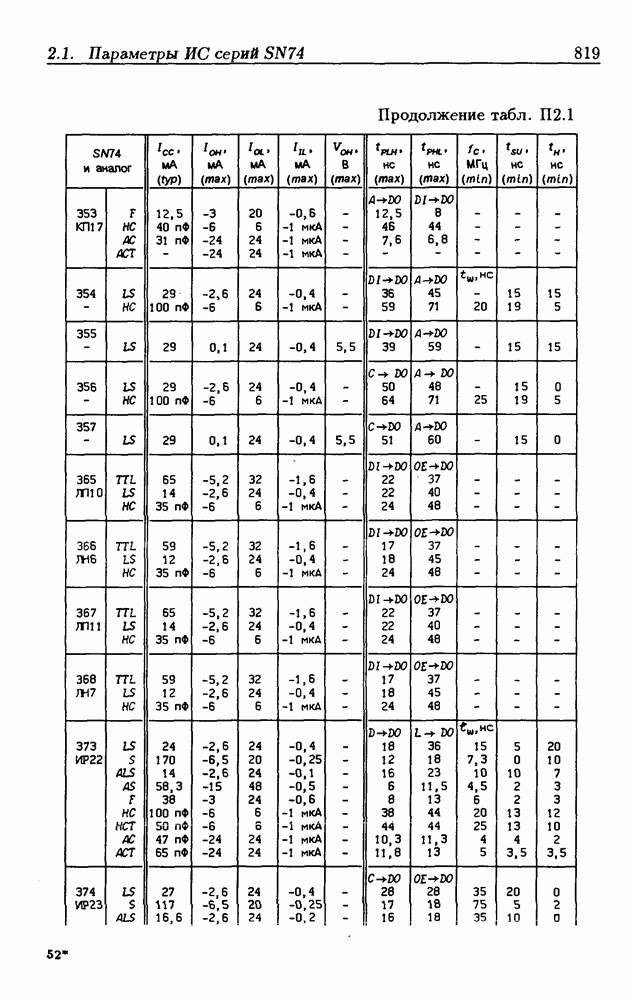
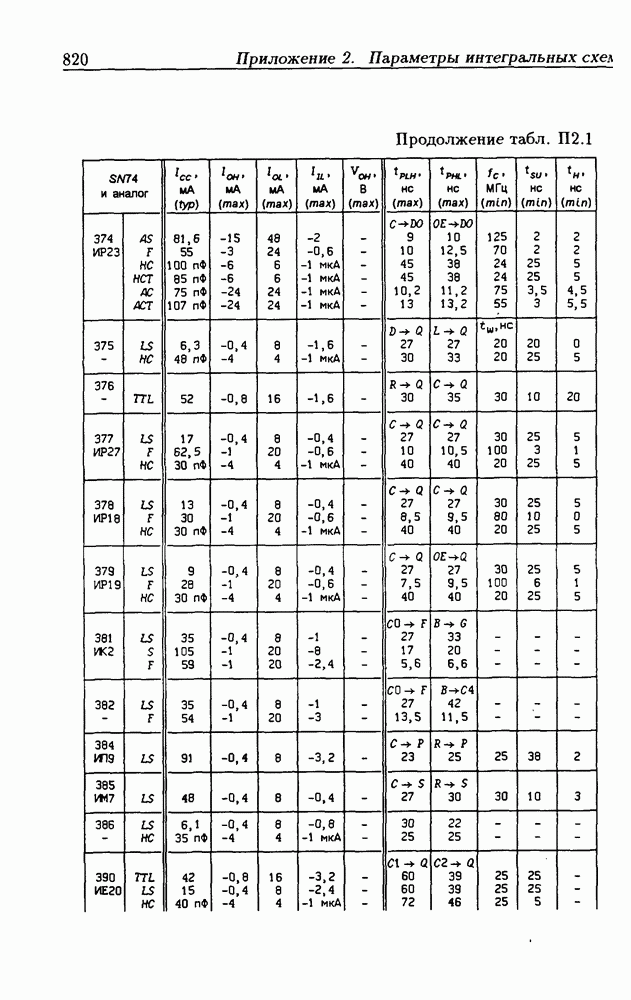
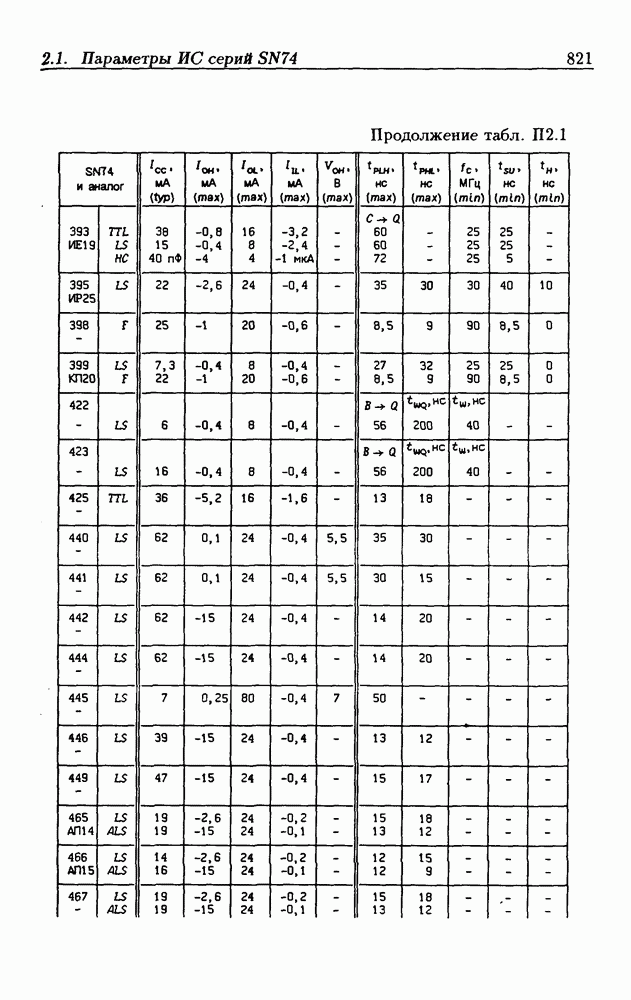
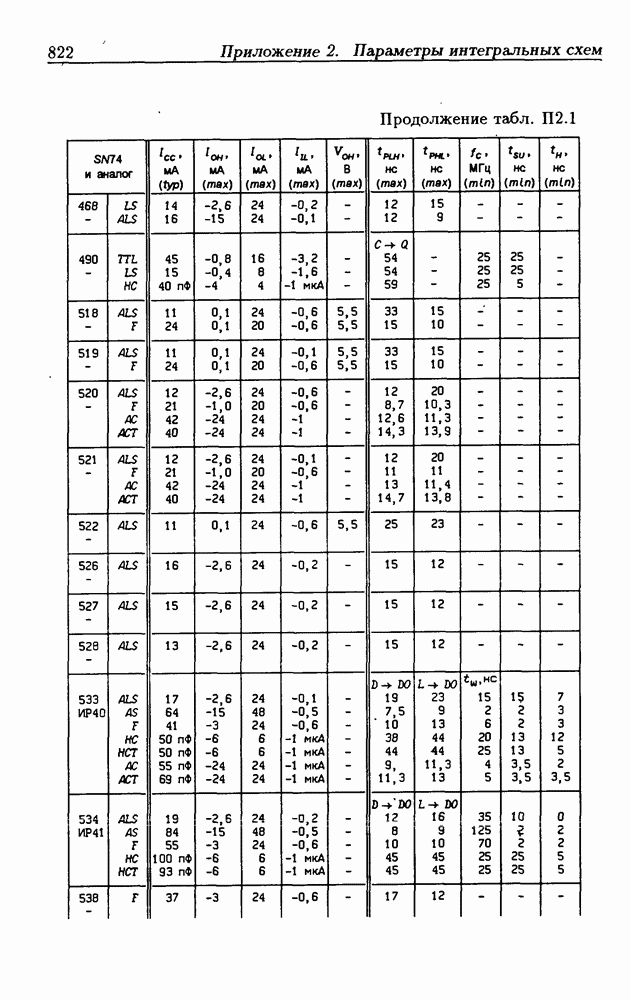
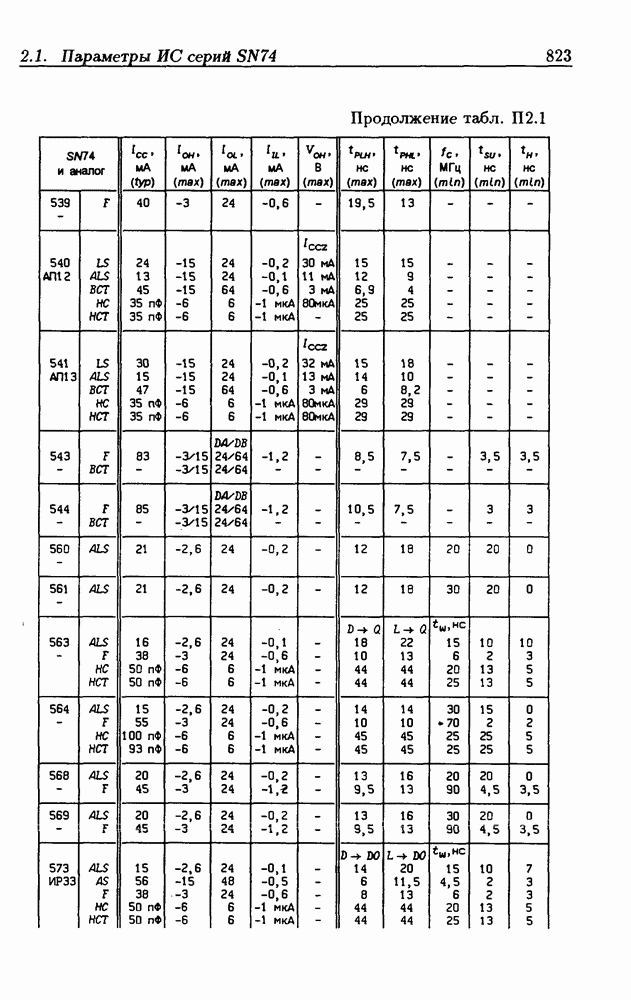
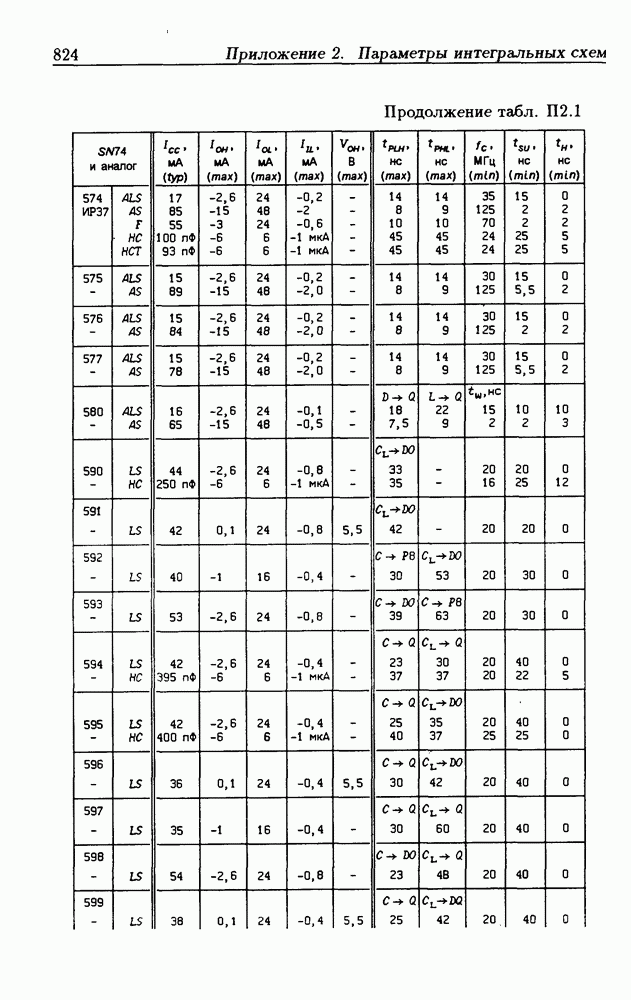
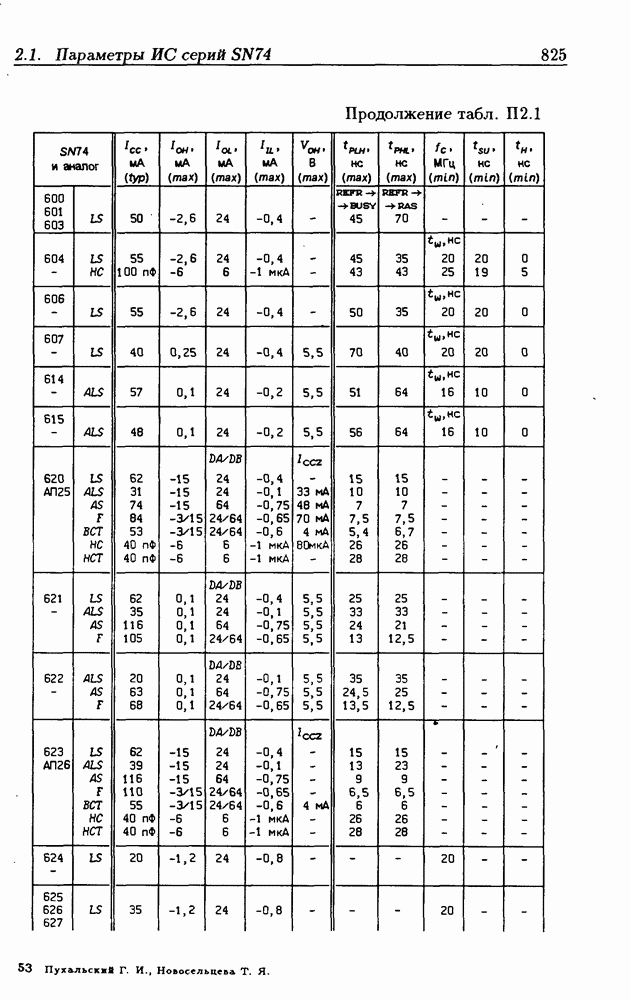
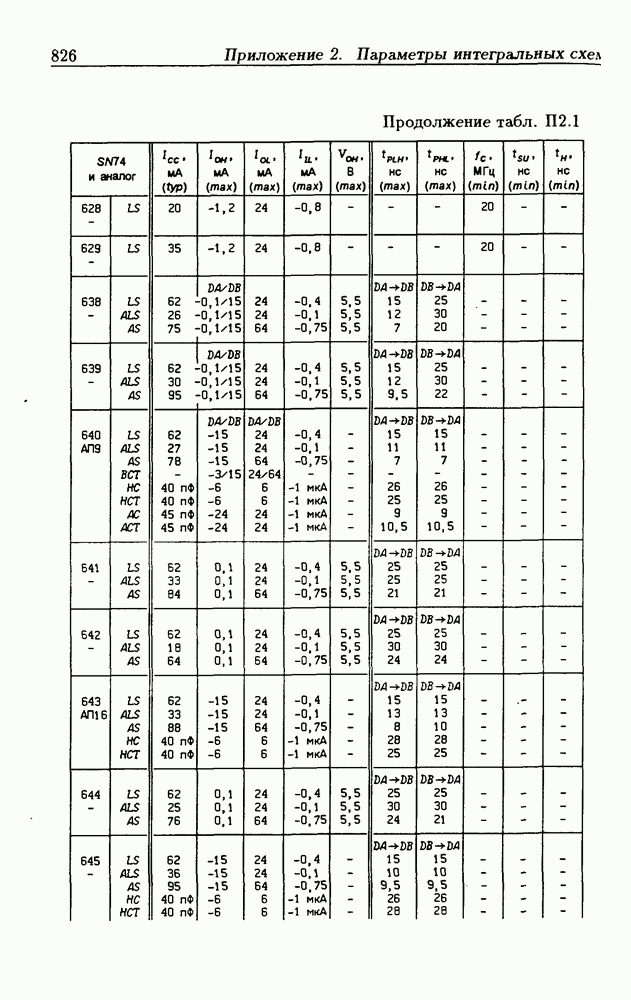
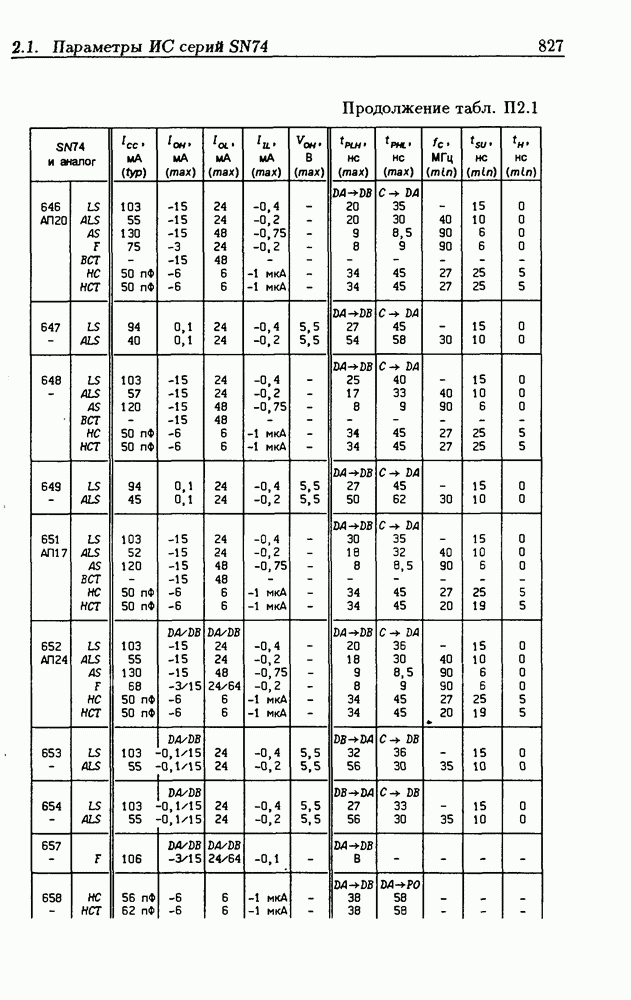
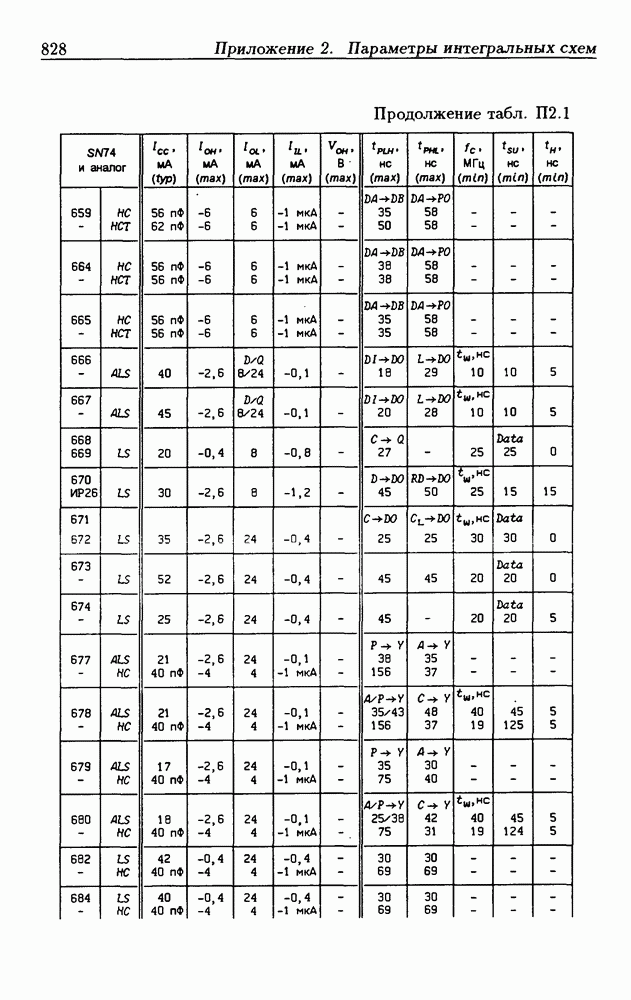
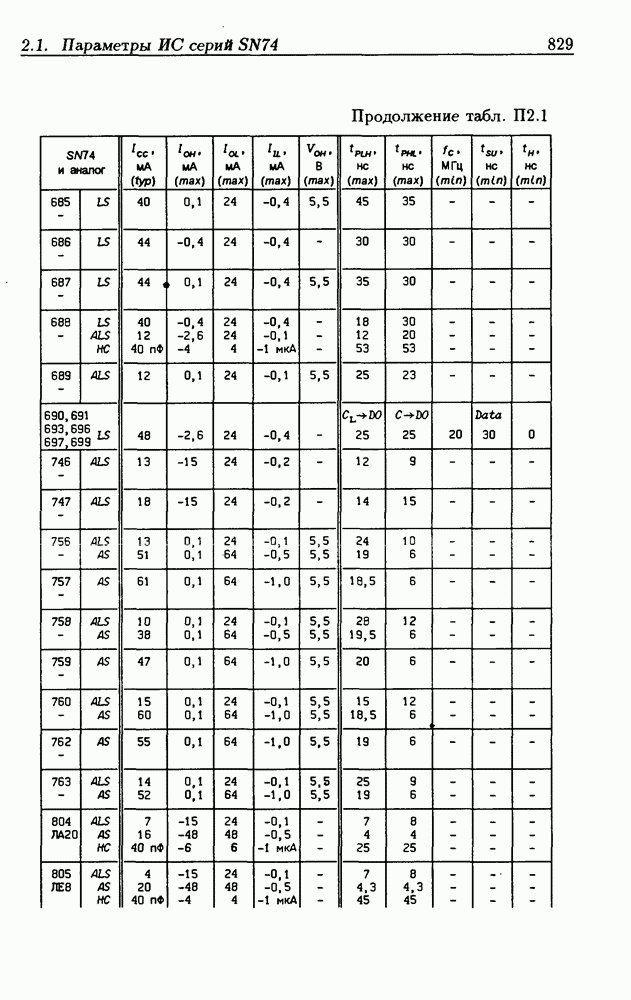
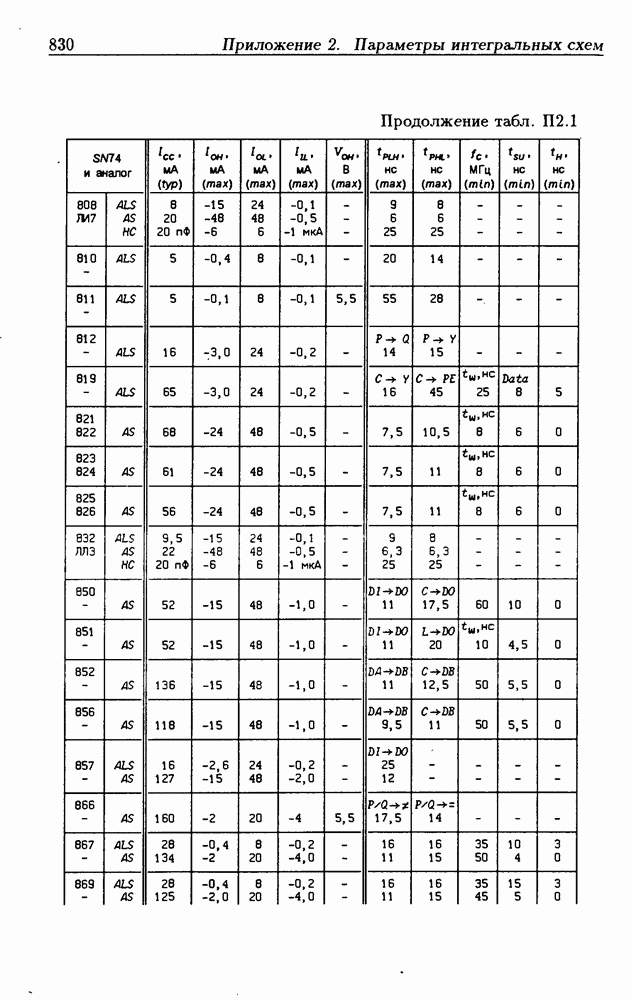
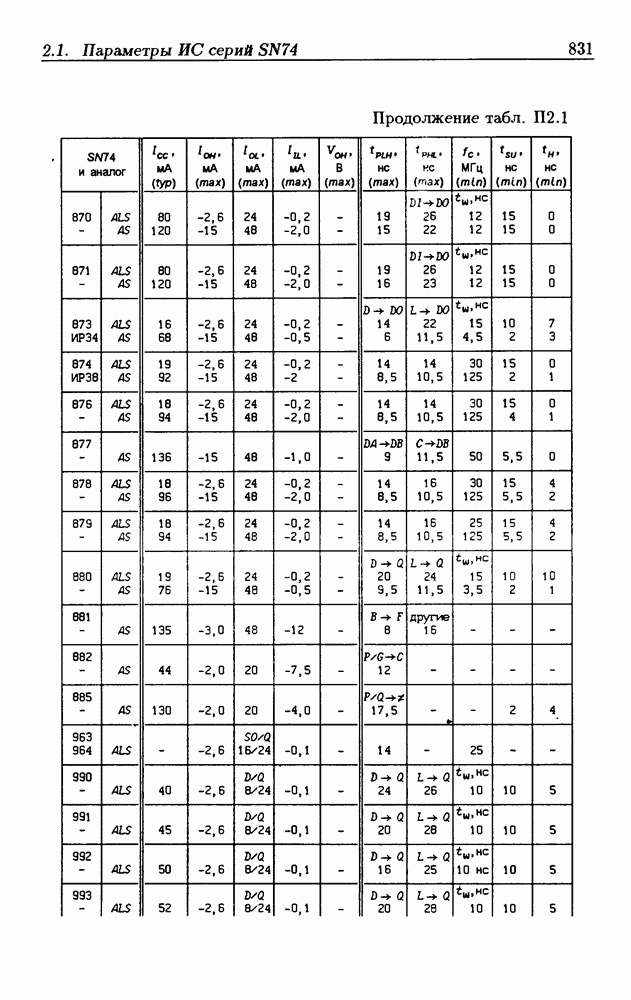
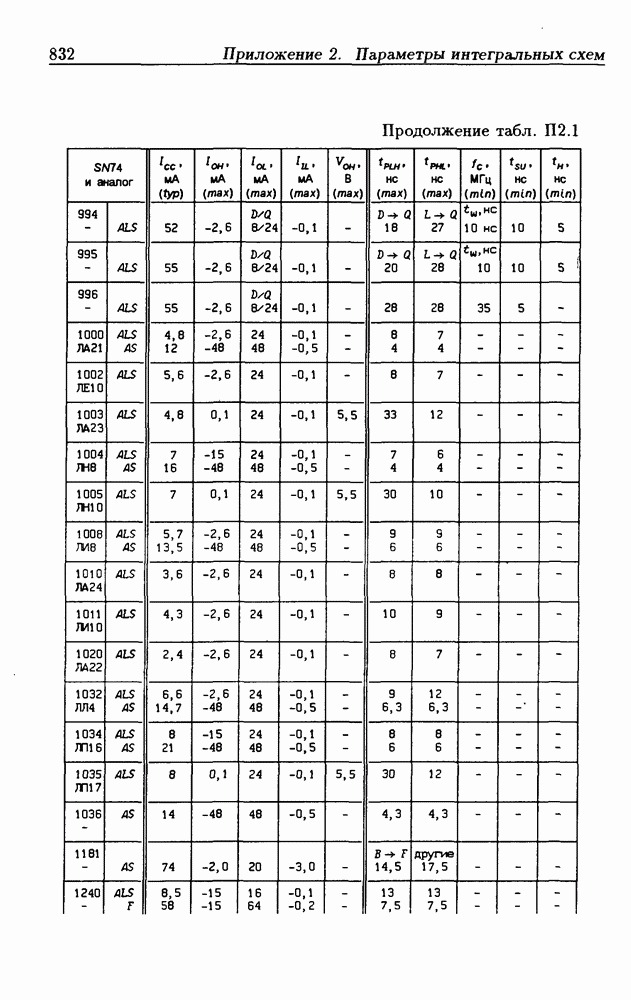
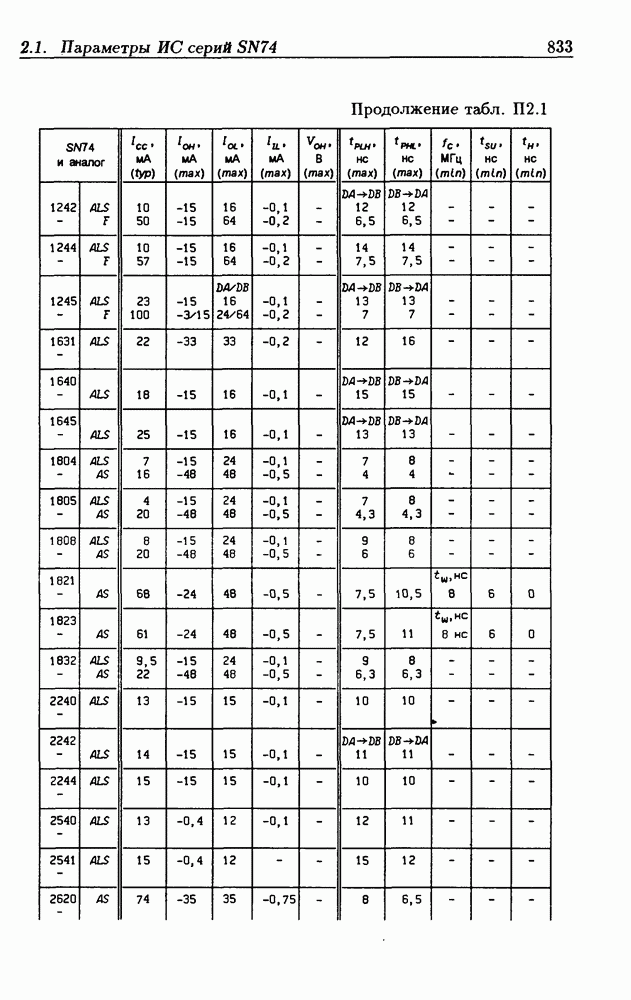
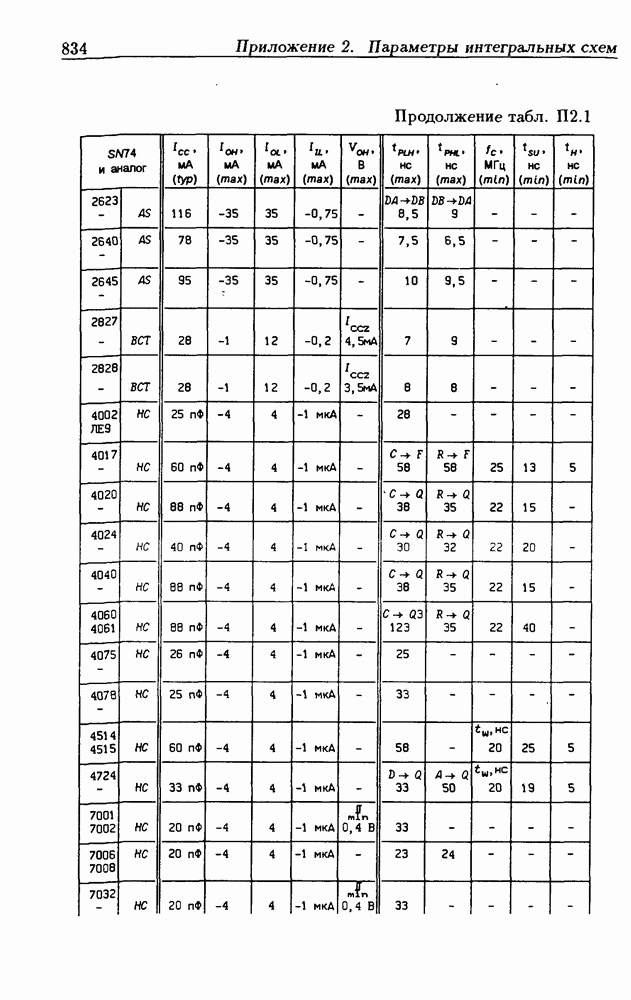
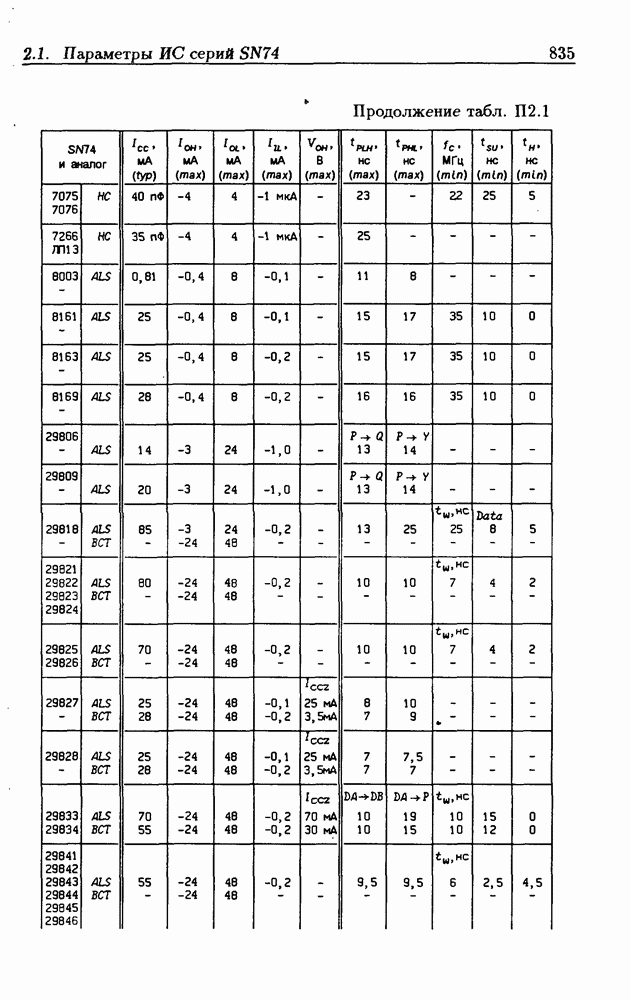
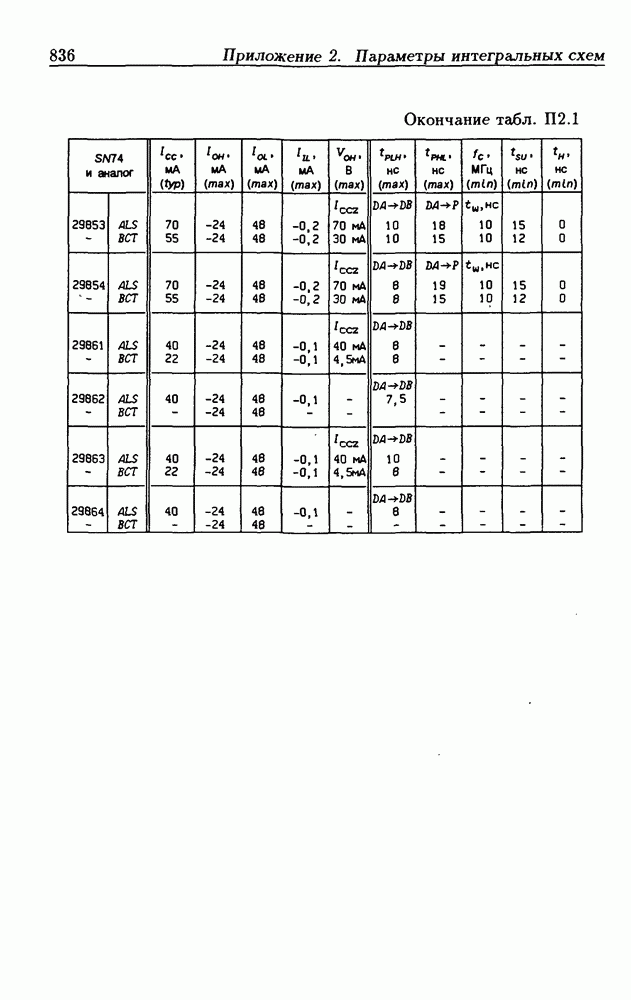
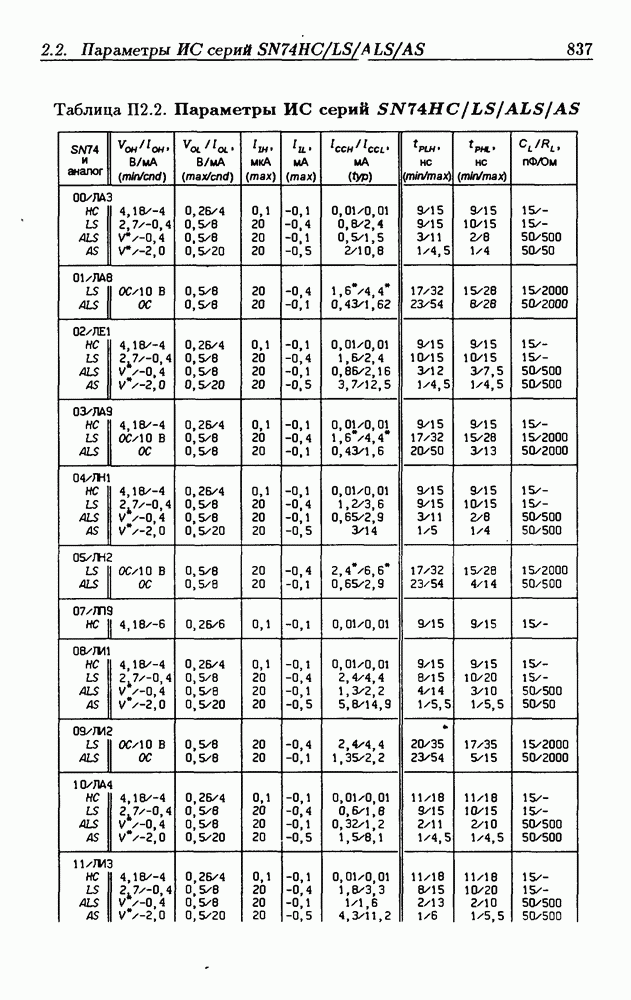
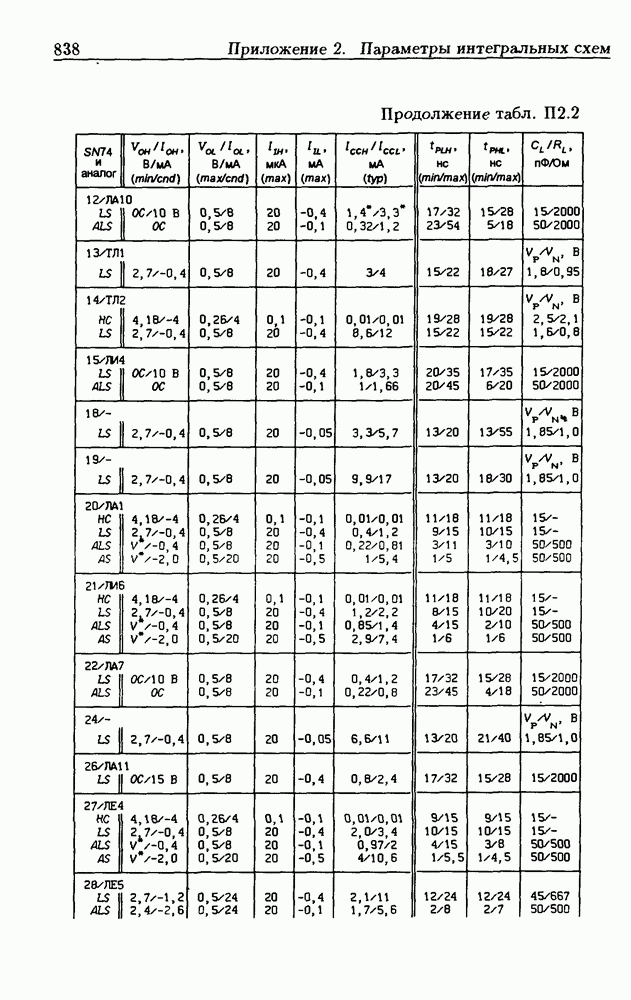
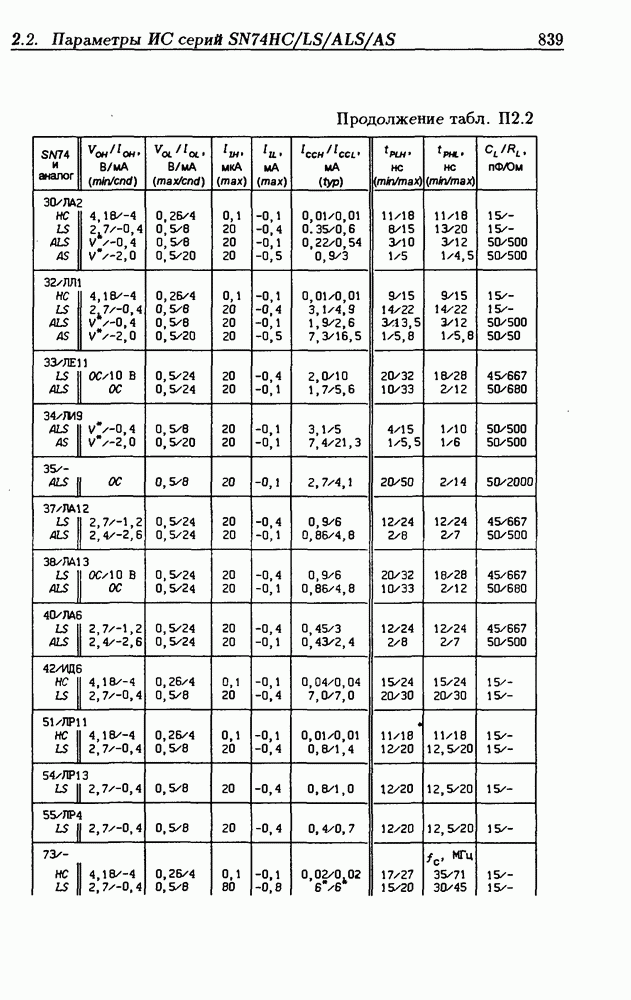
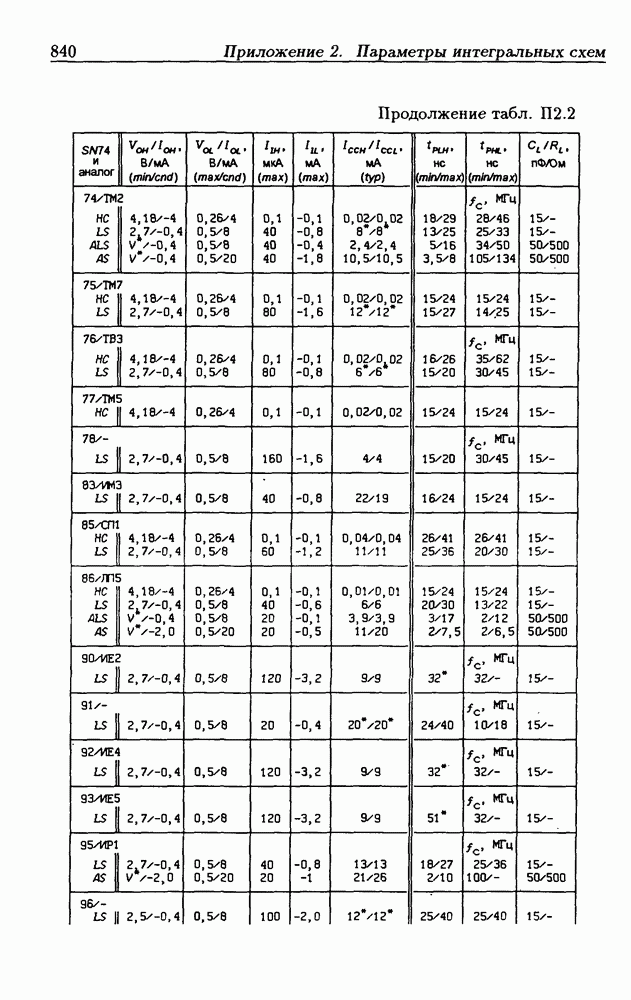
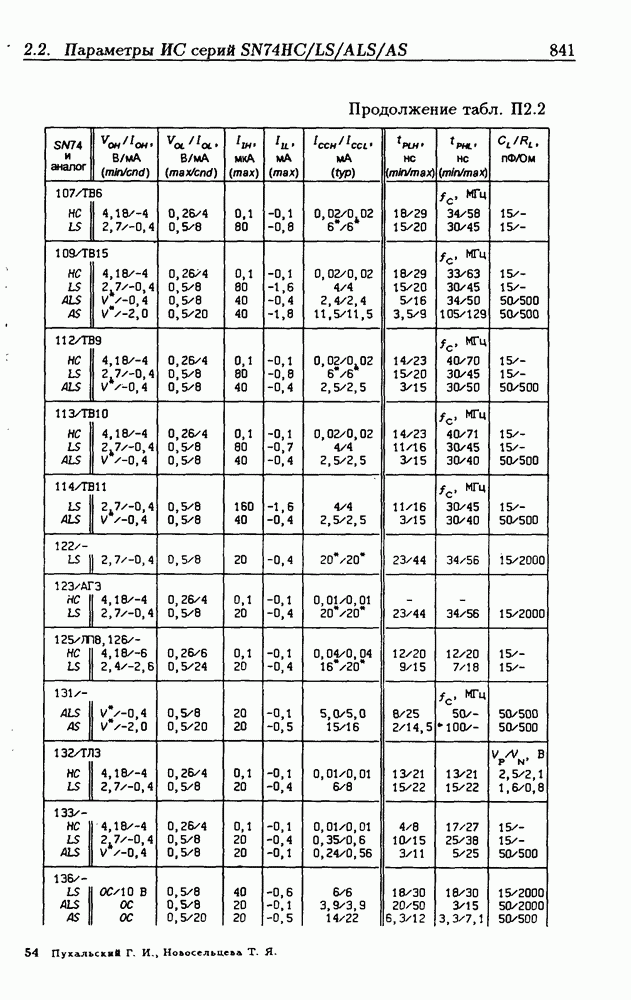
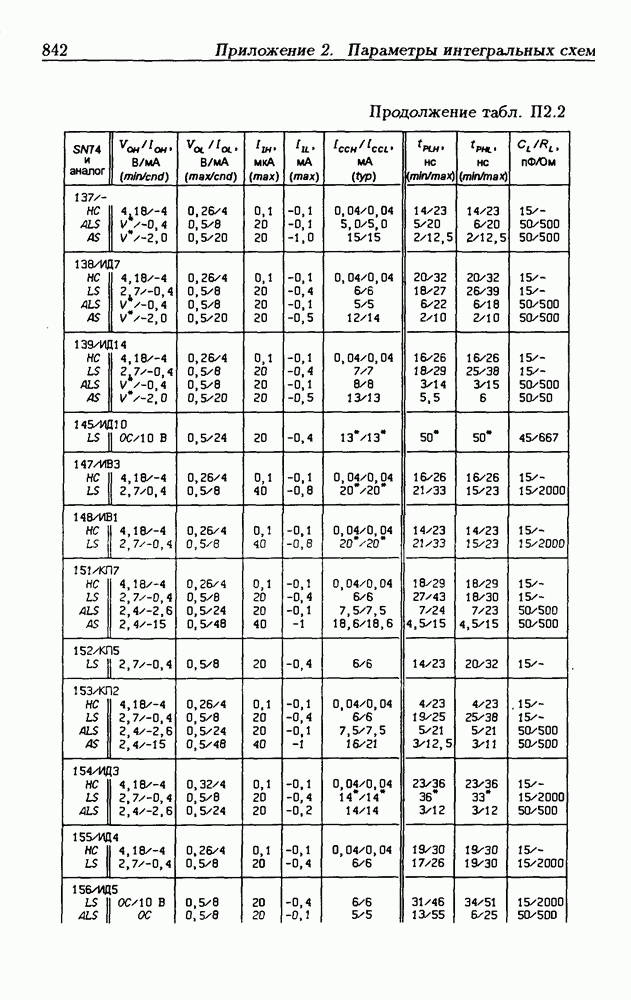
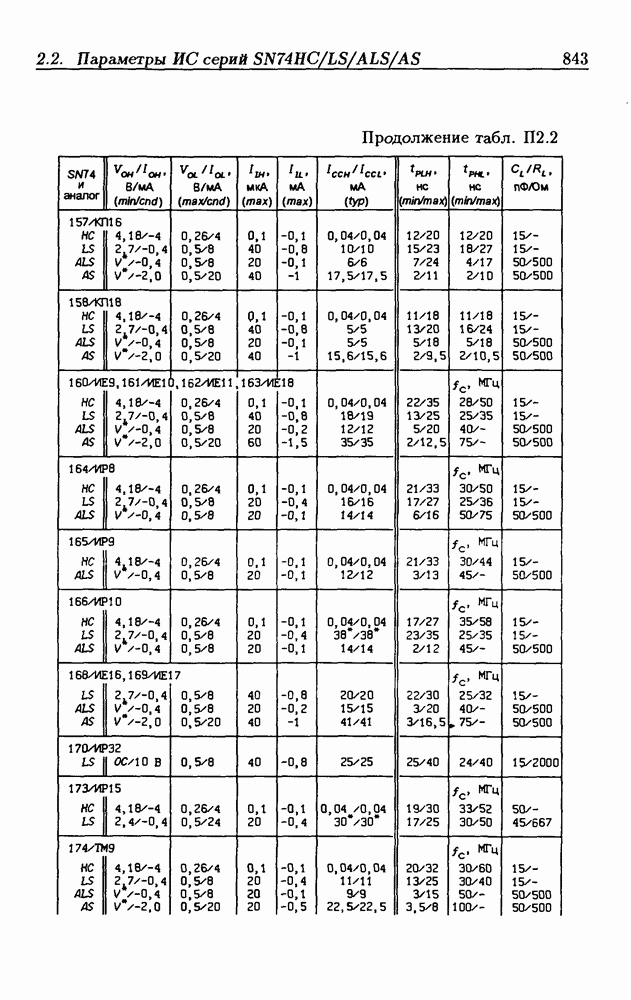
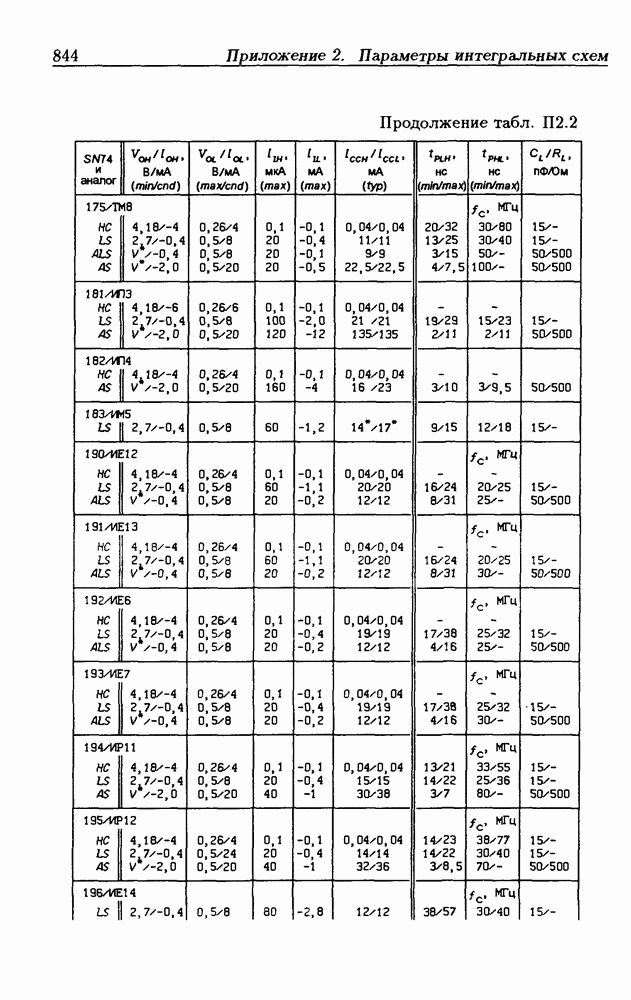
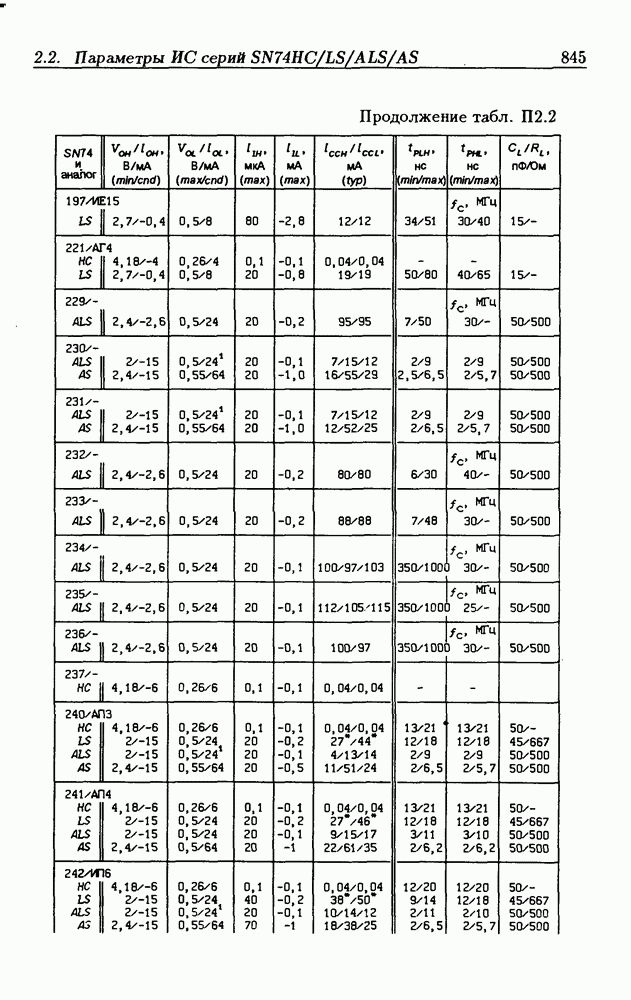
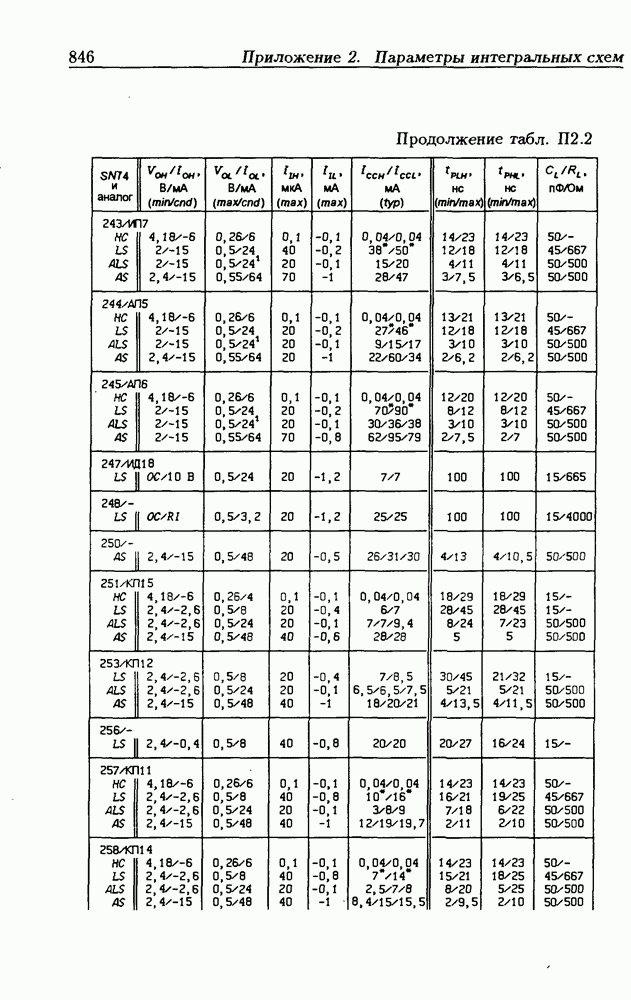
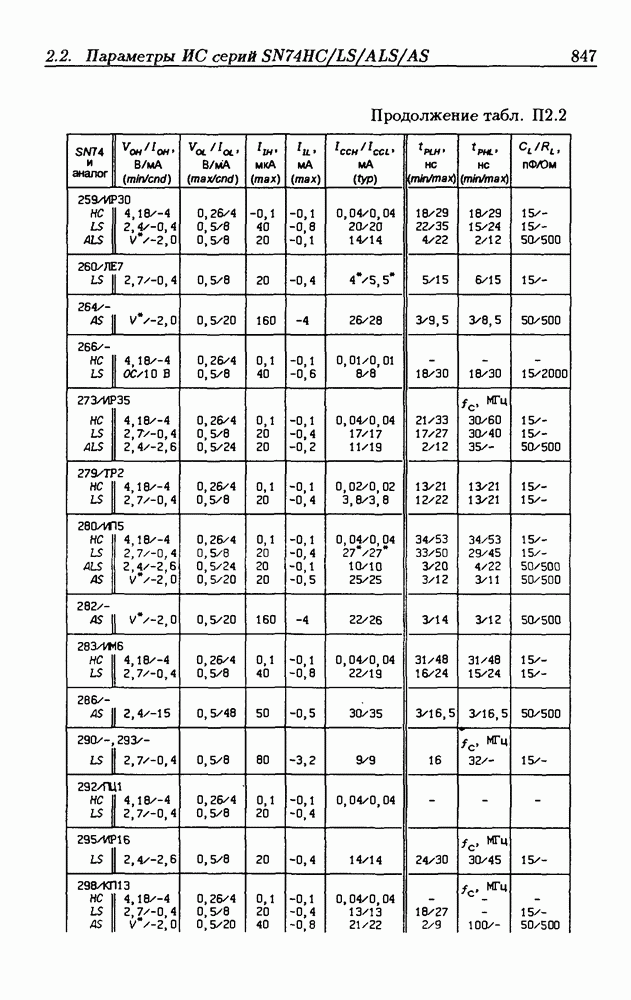
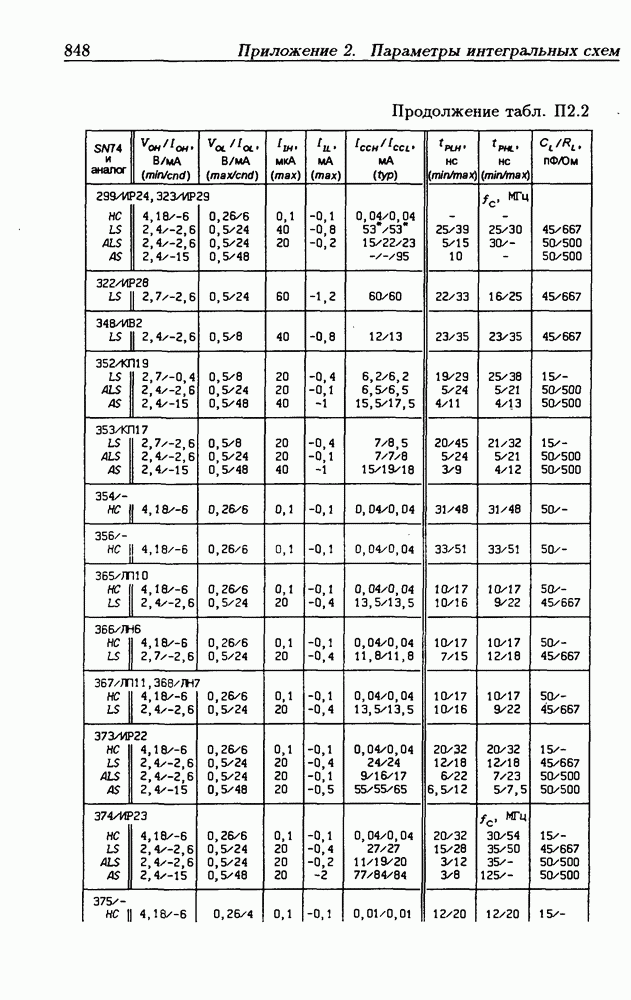
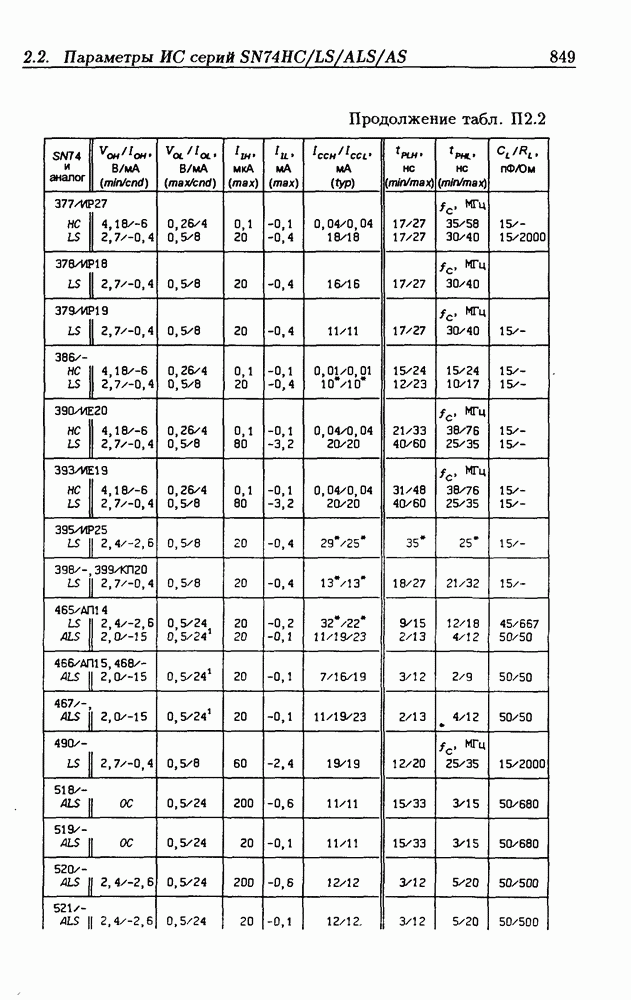
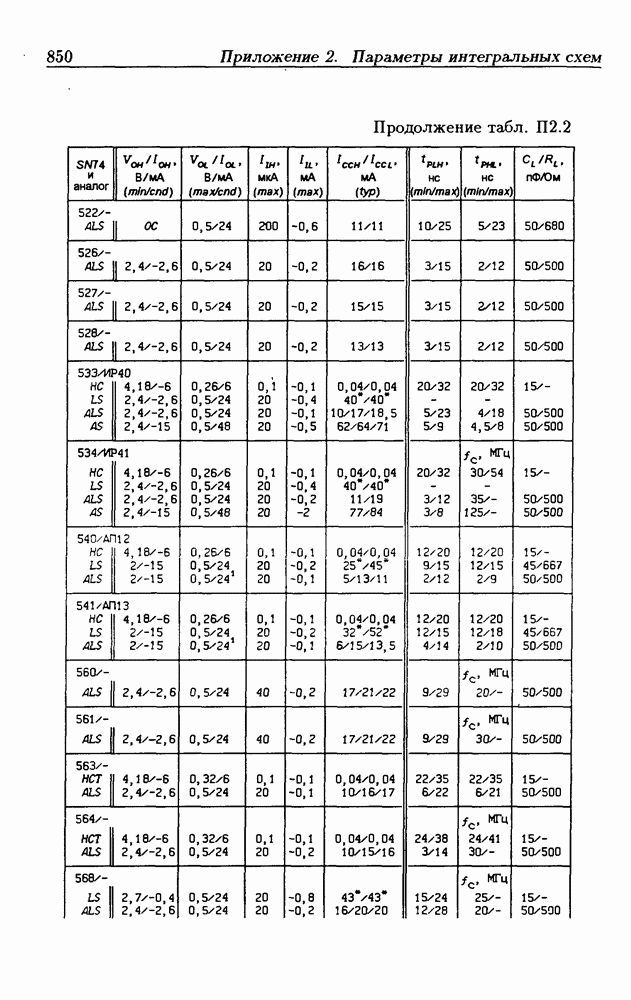
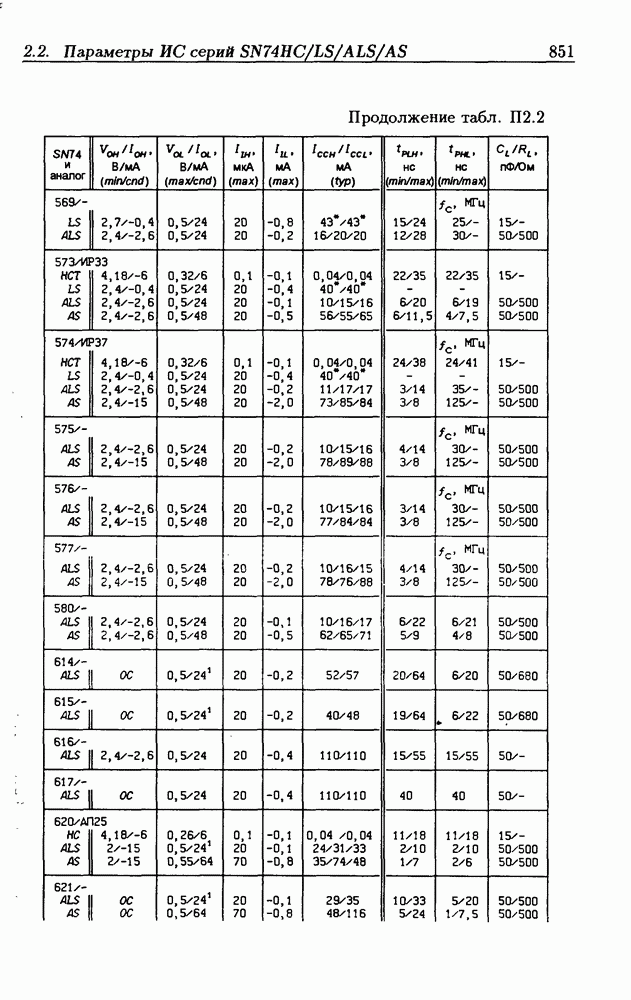
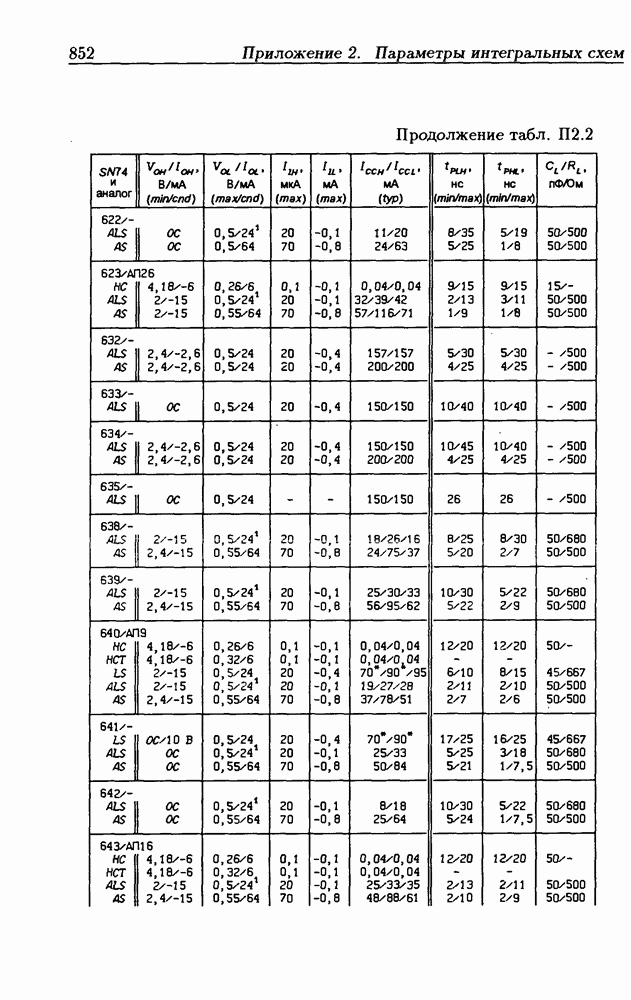
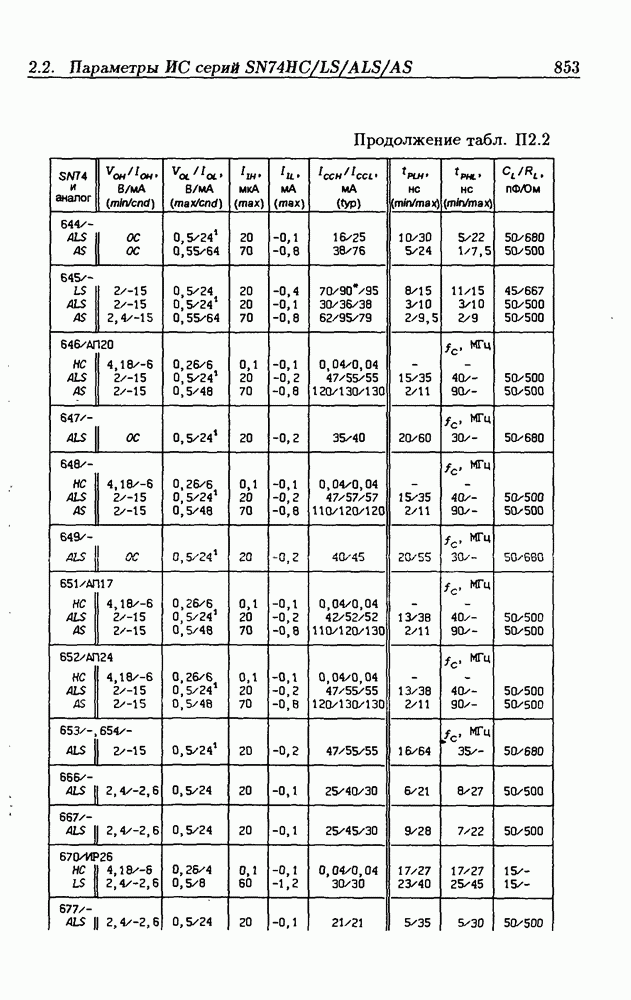
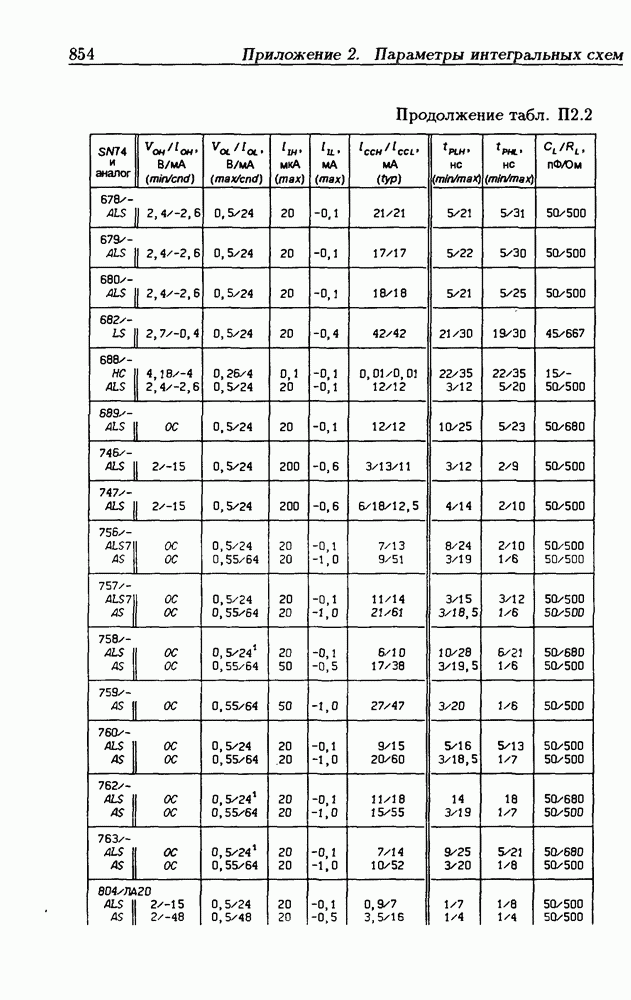
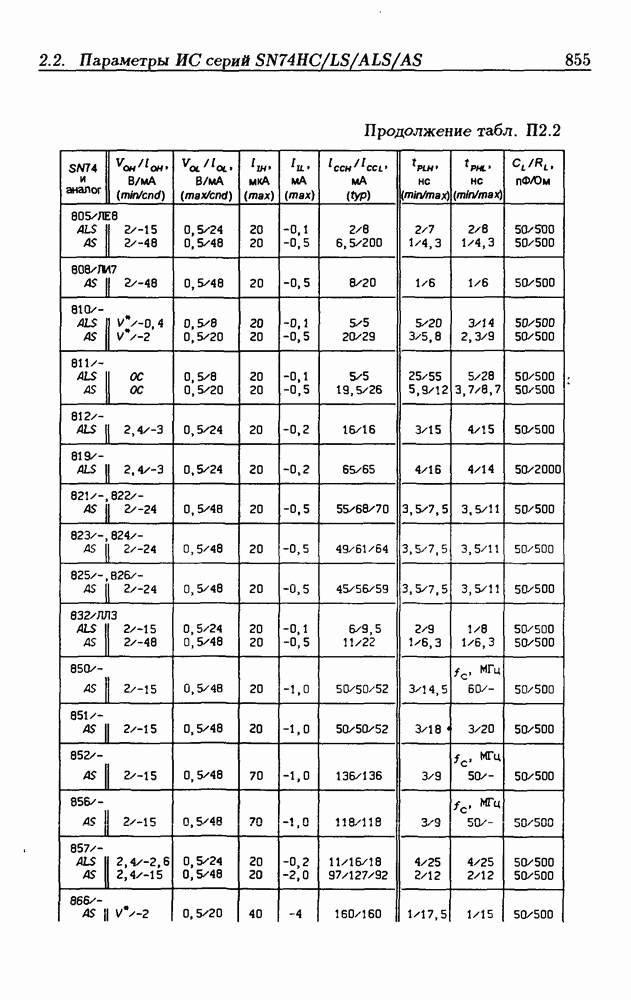
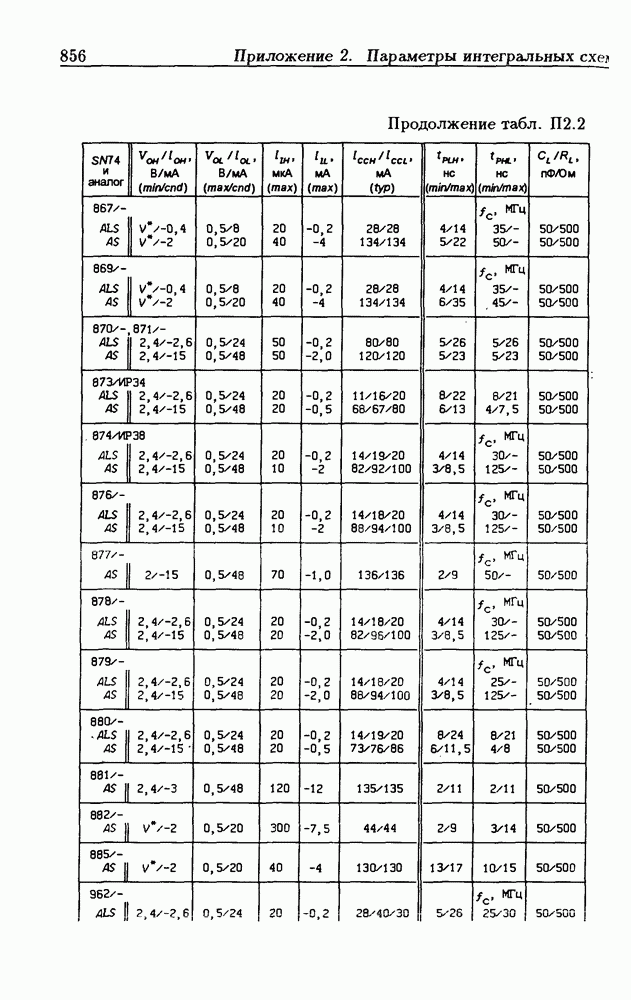
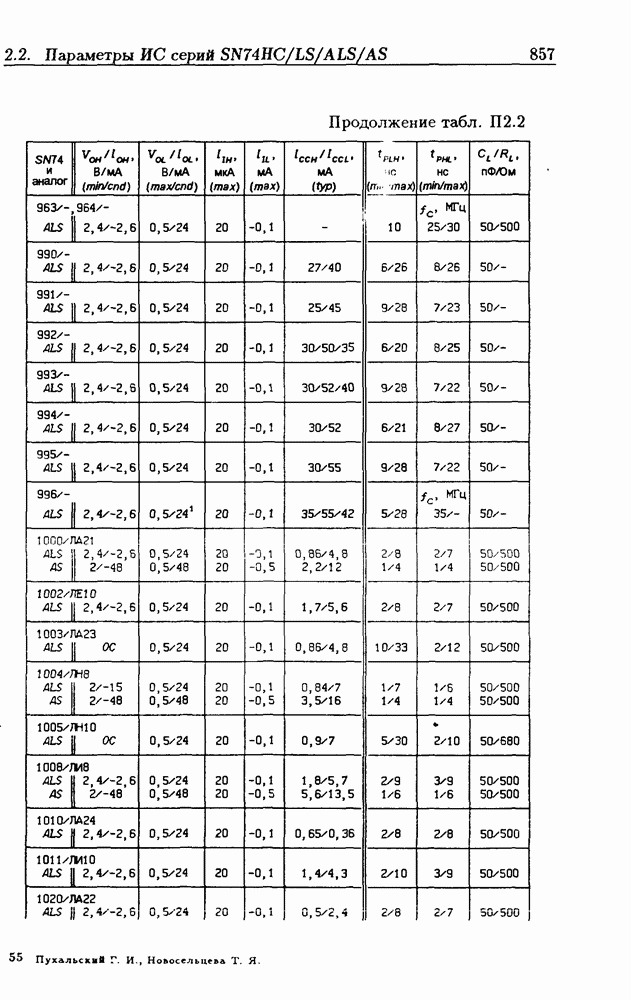
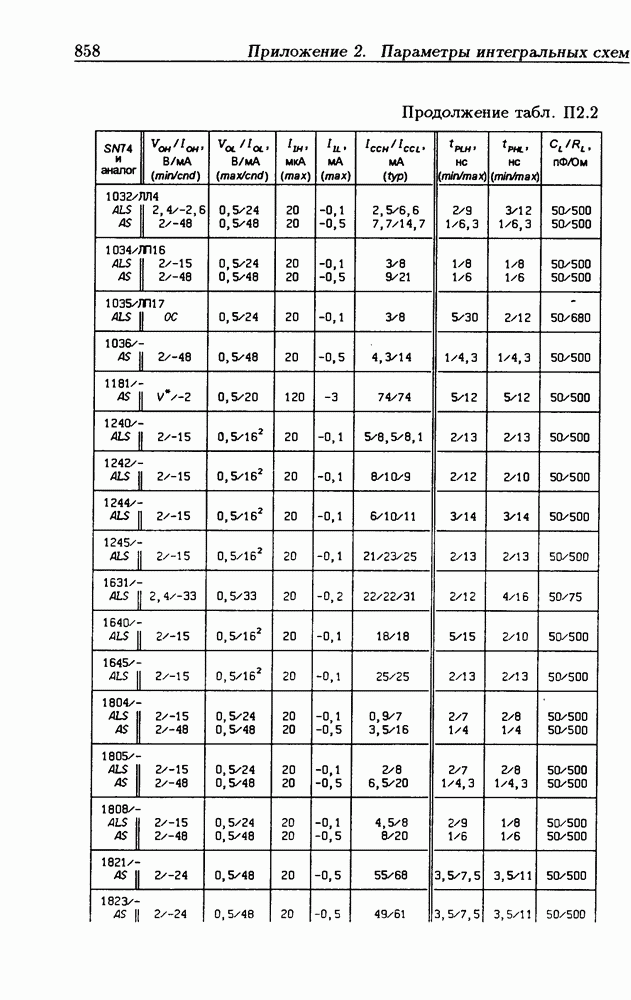
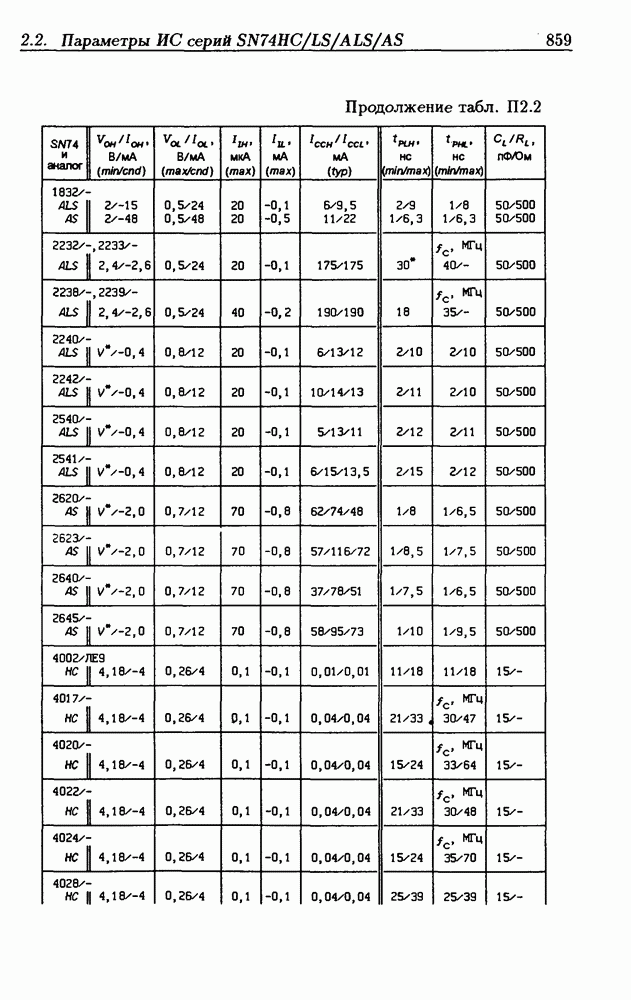
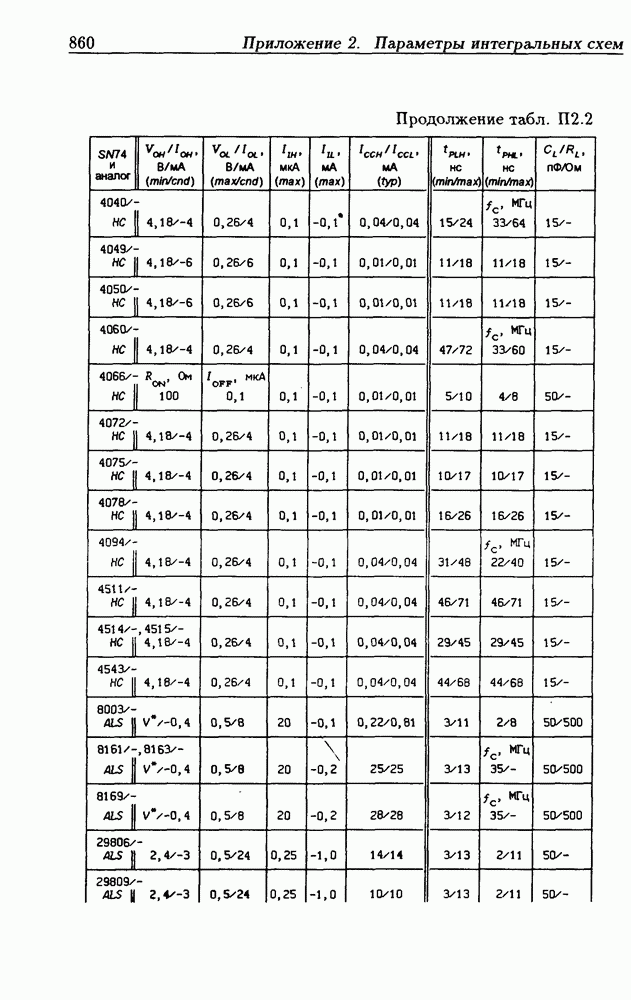
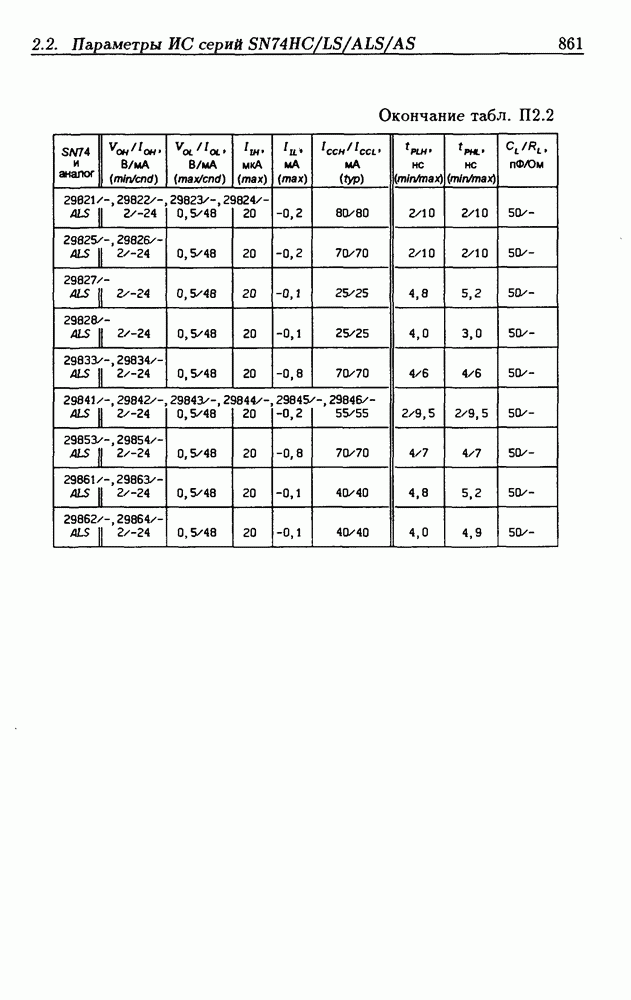
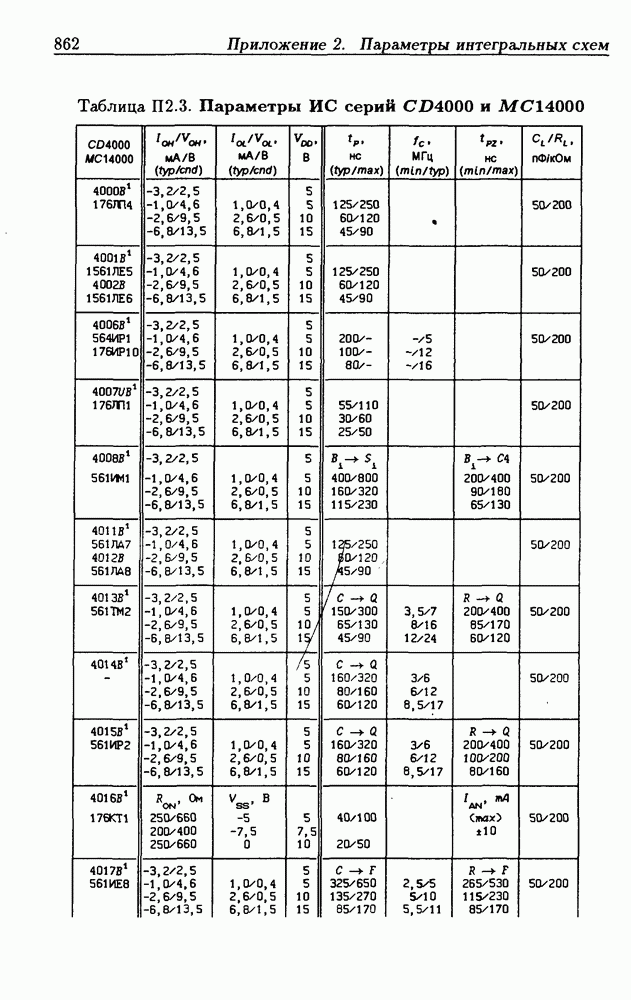
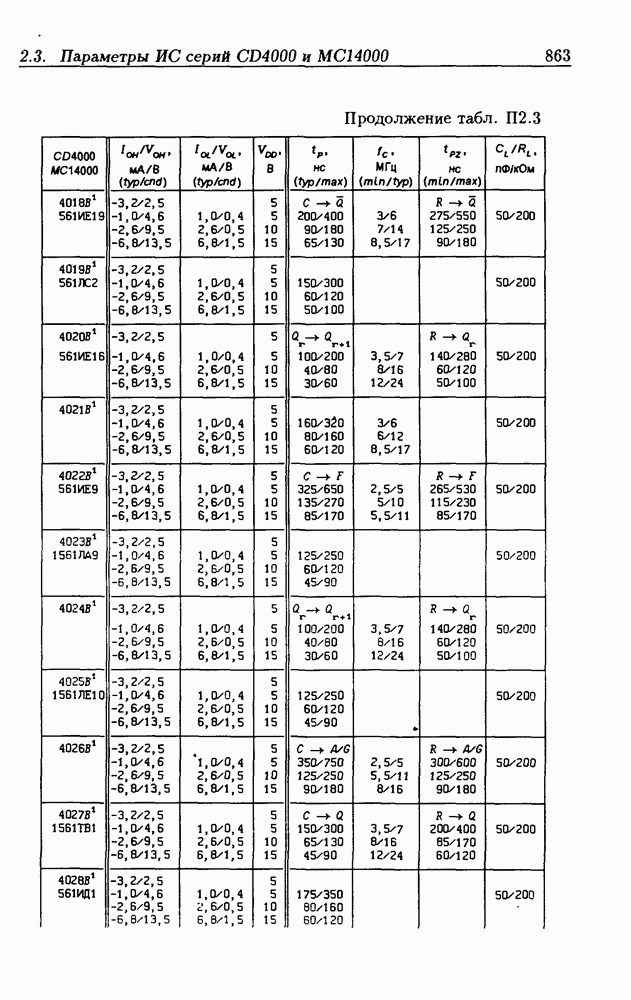
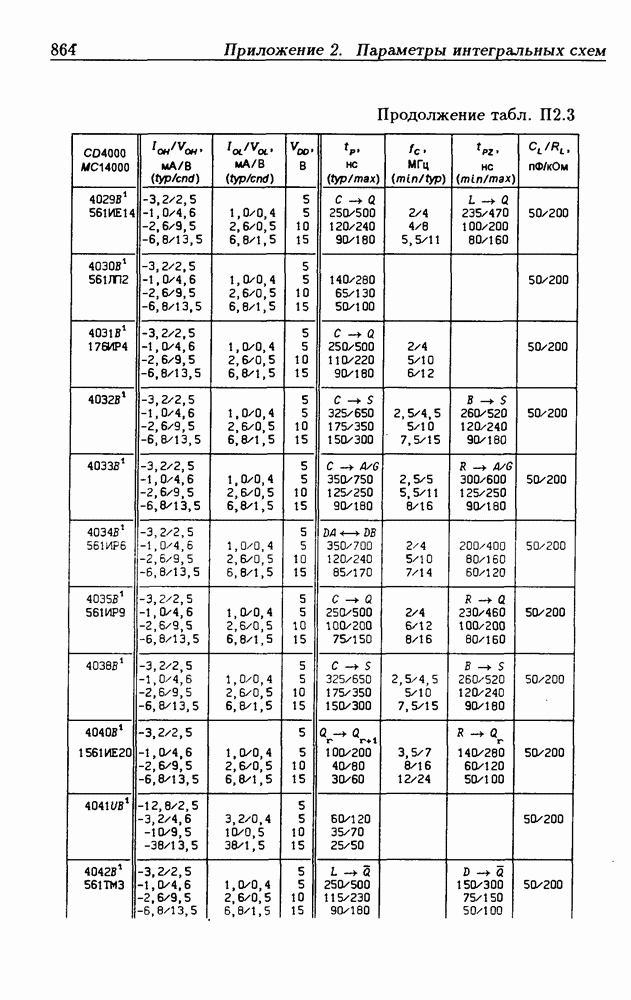
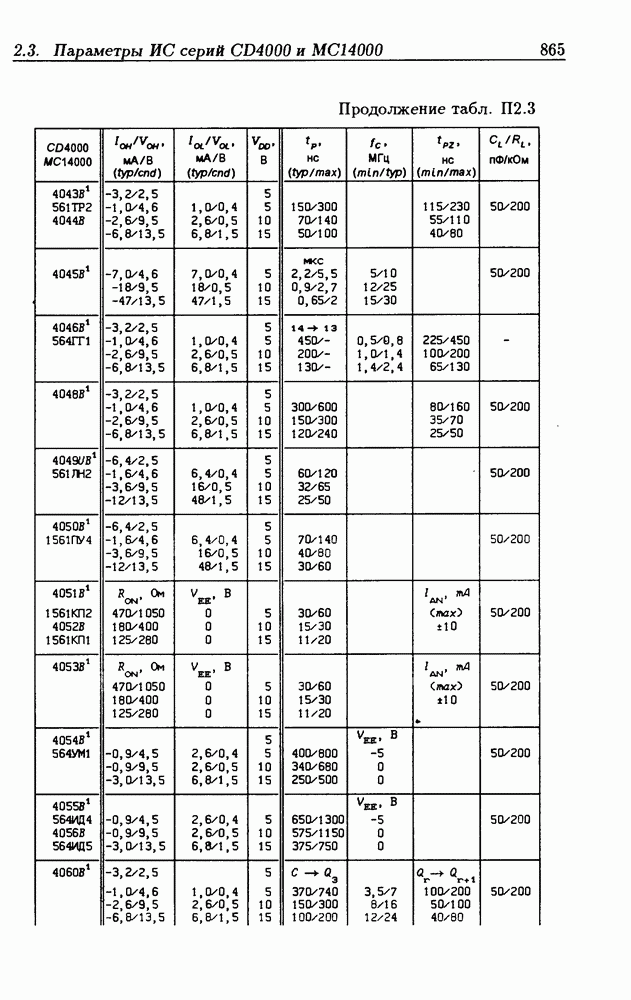
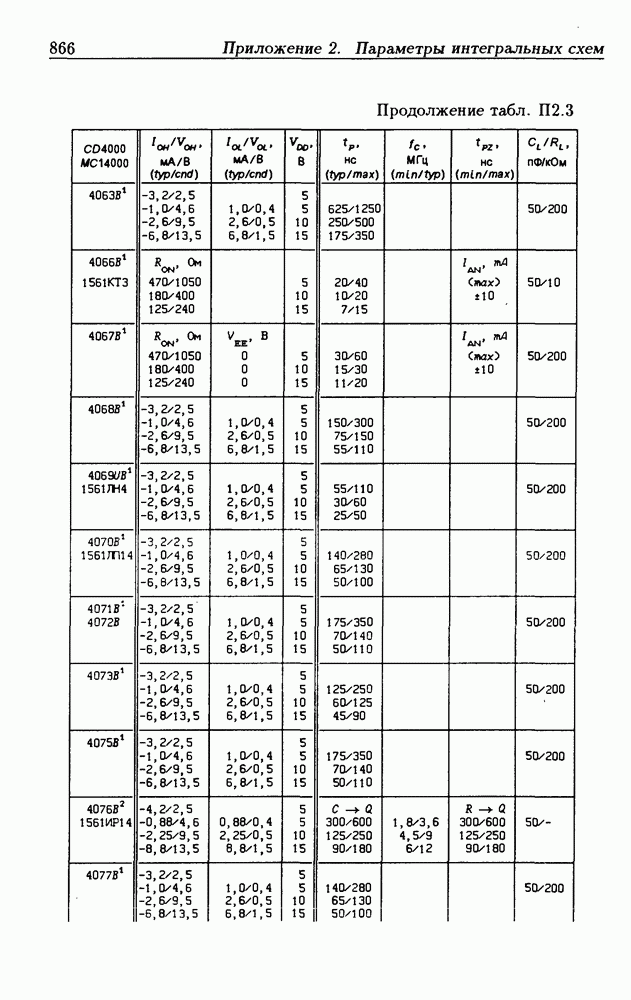
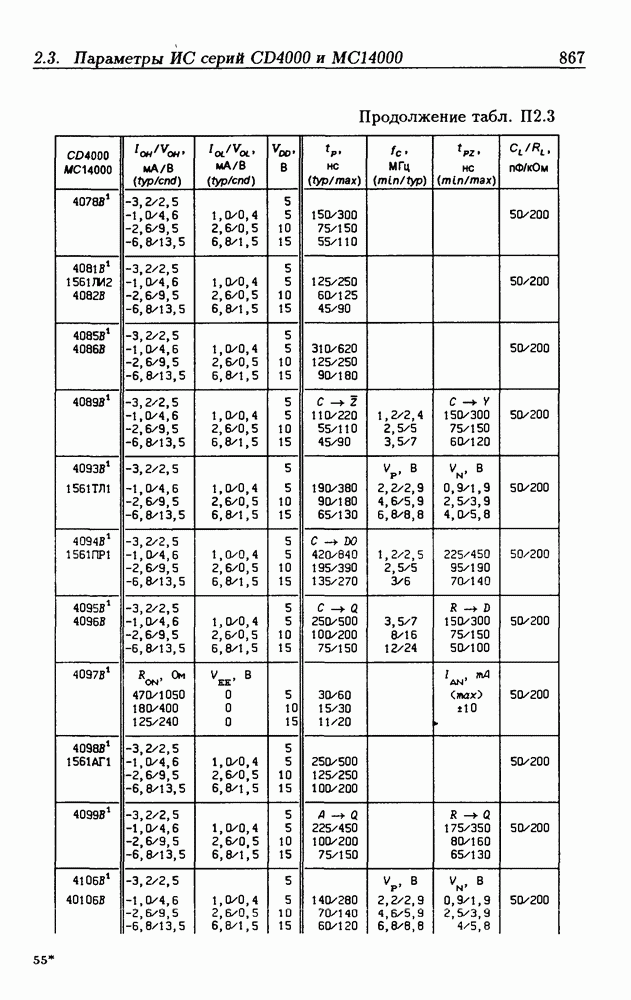
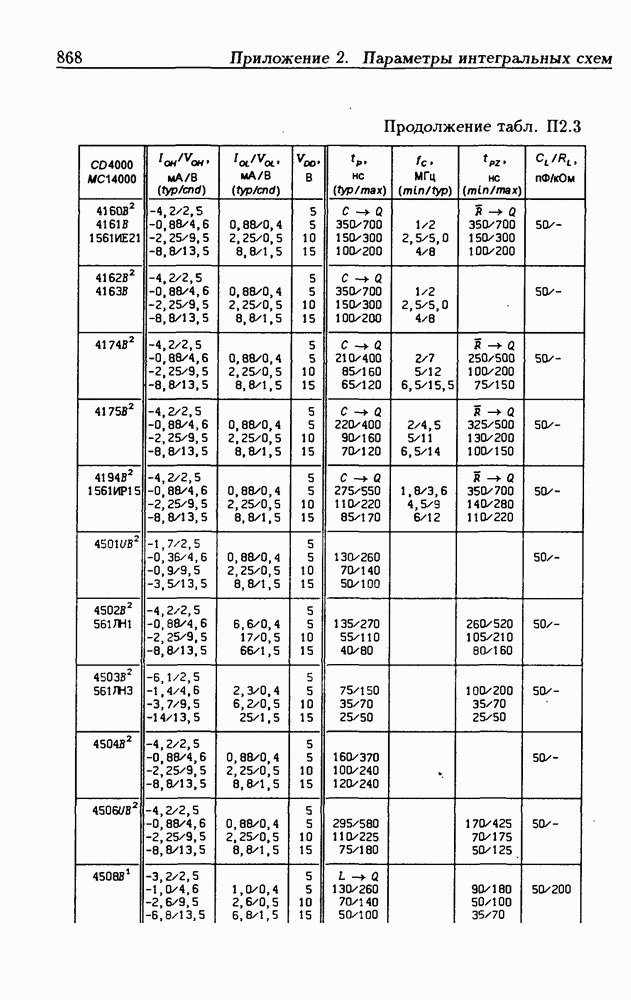
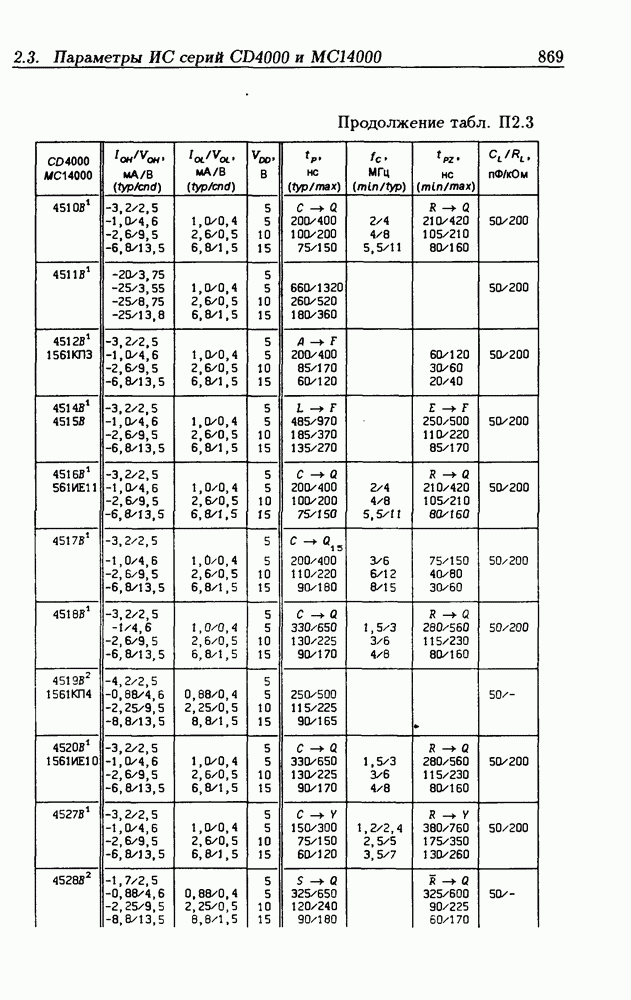
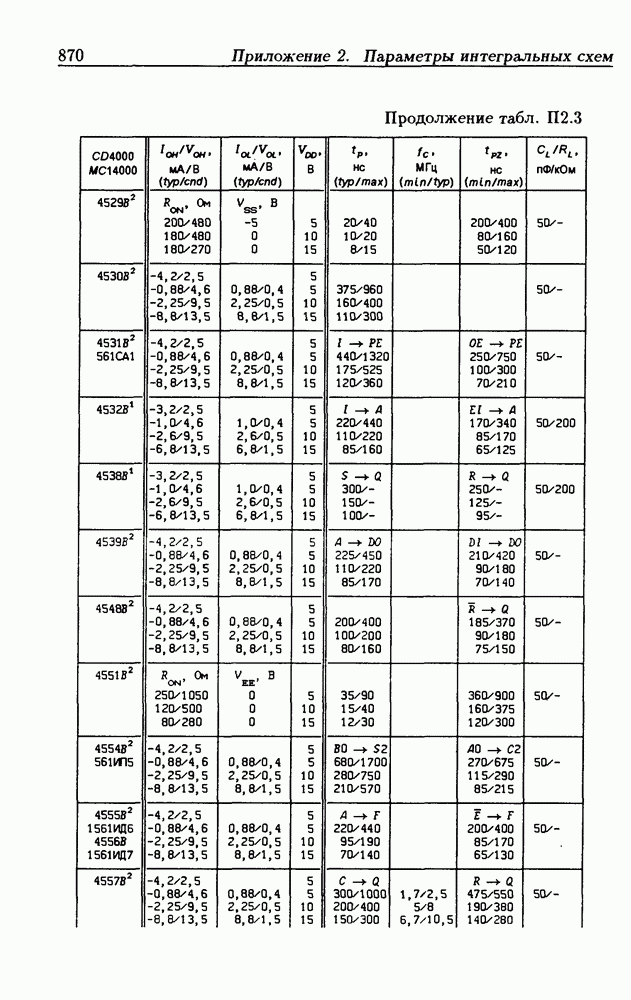
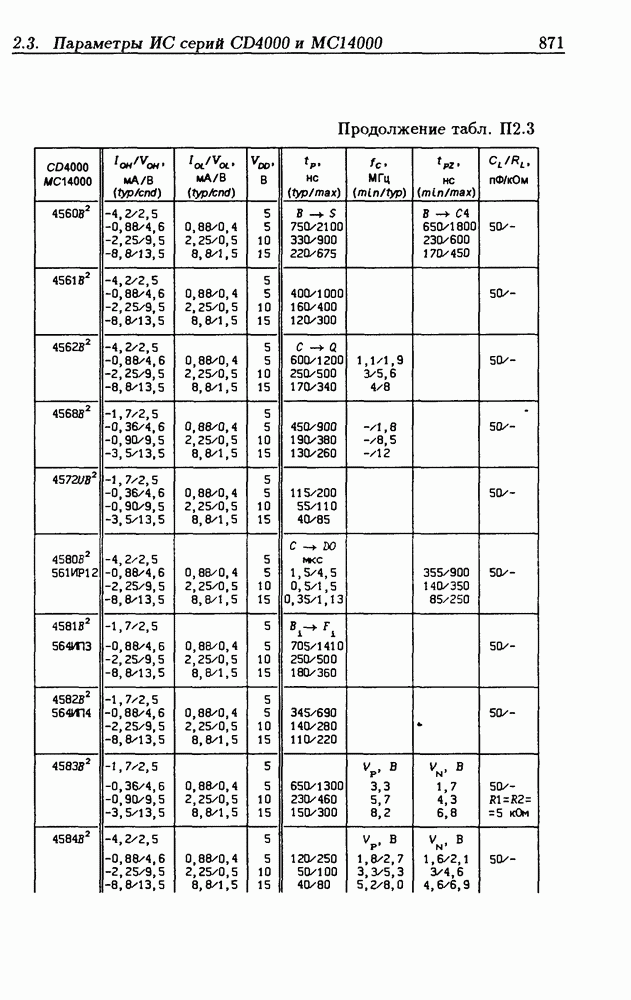
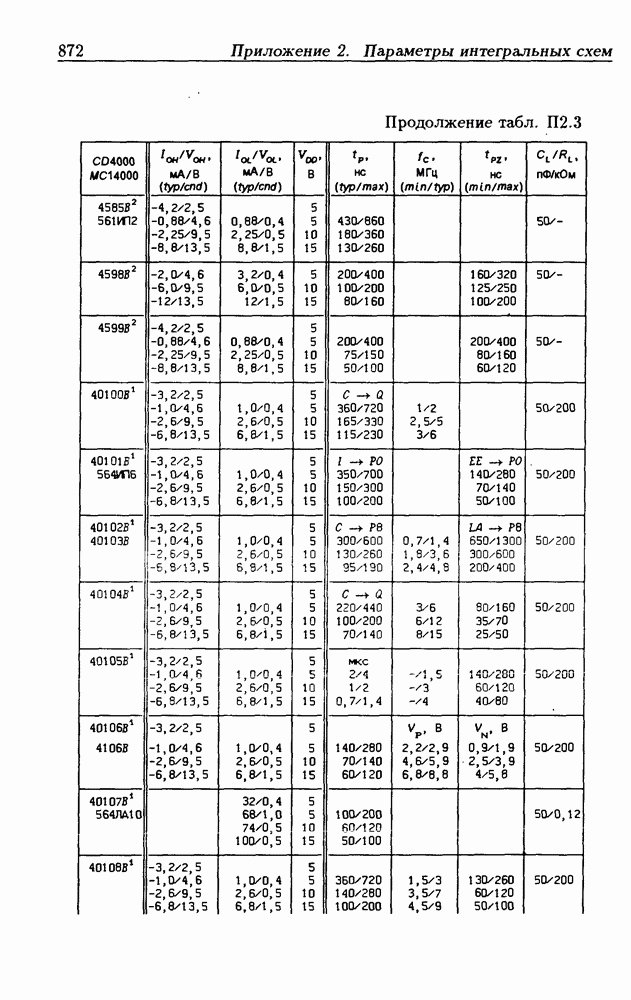
- Приложение 2. Параметры интегральных схем