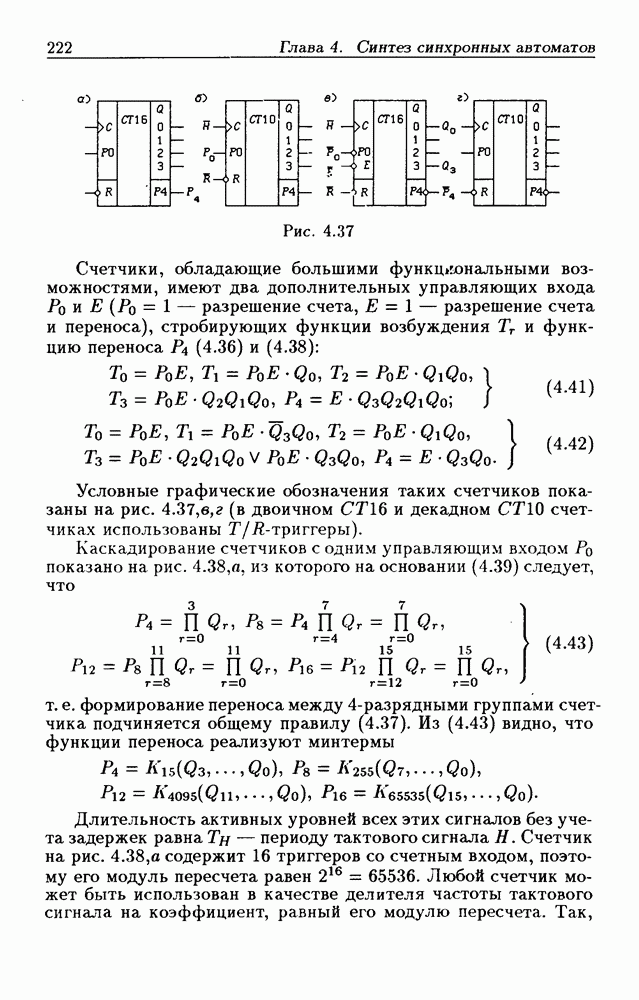| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Быстрые умножители.
Пусть требуется вычислить произведение двух целых положительных чисел

Тогда произведение  можно представить в виде
можно представить в виде

Величины  называются частичными произведениями. Число частичных произведений равно числу разрядов множителя
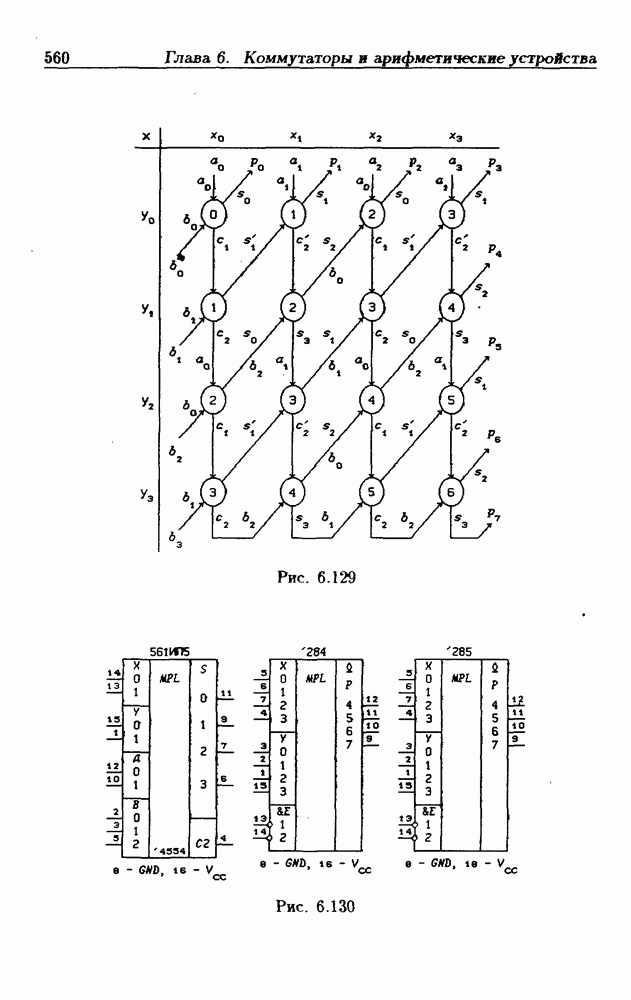
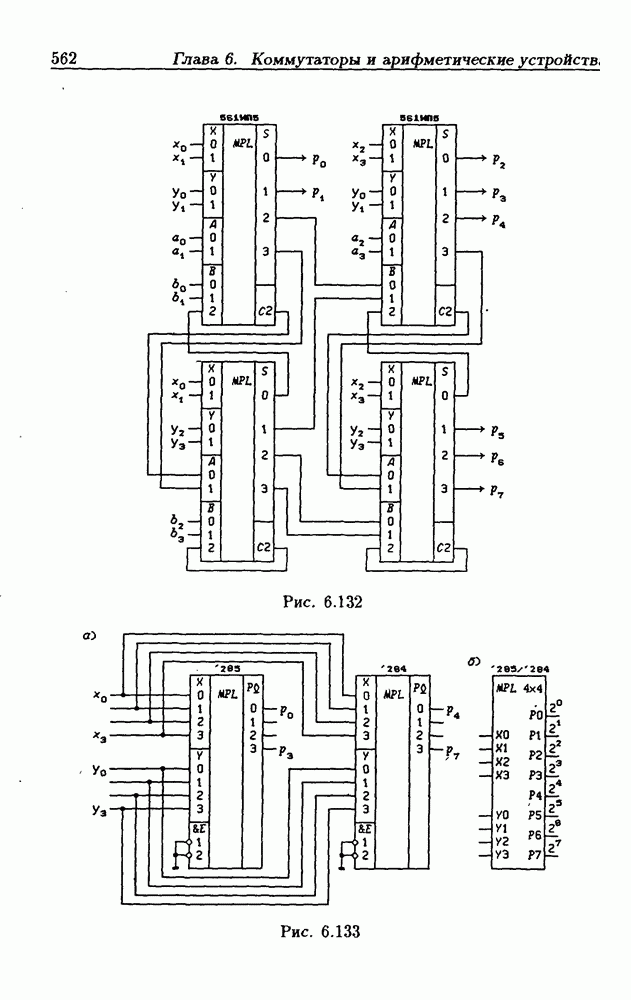
называются частичными произведениями. Число частичных произведений равно числу разрядов множителя  Рассмотренный выше матричный умножитель (рис. 6.132) и производит вычисление таких частичных произведений с совмещением операции их суммирования в каждой ступени вычисления
Рассмотренный выше матричный умножитель (рис. 6.132) и производит вычисление таких частичных произведений с совмещением операции их суммирования в каждой ступени вычисления 
Выражение для  можно преобразовать к виду:
можно преобразовать к виду:

на основании элементарного соотношения

используемого для нечетных значений  Все частичные произведения
Все частичные произведения


(кликните для просмотра скана)
имеют одинаковую структуру, а их число уменьшилось вдвое по сравнению с числом частичных произведений  при использовании рассмотренного преобразования в каждой ступени вычисления частичного произведения производится умножение сразу на два разряда множителя У. Такой метод вычисления произведения называется модифицированным алгоритмом Бута. Легко показать, что алгоритм Бута справедлив и для умножения двоичных чисел, представленных в дополнительном коде, причем произведение выдается также в дополнительном коде.
при использовании рассмотренного преобразования в каждой ступени вычисления частичного произведения производится умножение сразу на два разряда множителя У. Такой метод вычисления произведения называется модифицированным алгоритмом Бута. Легко показать, что алгоритм Бута справедлив и для умножения двоичных чисел, представленных в дополнительном коде, причем произведение выдается также в дополнительном коде.
Покажем, что частичные произведения  достаточно просто реализуются с помощью КС. Не теряя общности, можно положить
достаточно просто реализуются с помощью КС. Не теряя общности, можно положить  тогда функционирование КС будет описываться выражением:
тогда функционирование КС будет описываться выражением:

Так как  или 1, то величина в скобках может принимать значения от -2 до +2, т.е. число
или 1, то величина в скобках может принимать значения от -2 до +2, т.е. число  Пусть
Пусть  . Это означает, что множимое X следует сдвинуть на один разряд влево, а результат необходимо представить в дополнительном коде для выполнения суммирования частичных произведений. Дополнительный код частичного произведения в этом случае
. Это означает, что множимое X следует сдвинуть на один разряд влево, а результат необходимо представить в дополнительном коде для выполнения суммирования частичных произведений. Дополнительный код частичного произведения в этом случае  При этом возникает задача расширения разрядной сетки частичных произведений до разрядной сетки всего произведения
При этом возникает задача расширения разрядной сетки частичных произведений до разрядной сетки всего произведения  которое имеет большее число разрядов по сравнению с младшим частичным произведением.
которое имеет большее число разрядов по сравнению с младшим частичным произведением.
Пример 1: 

Пример 2: 

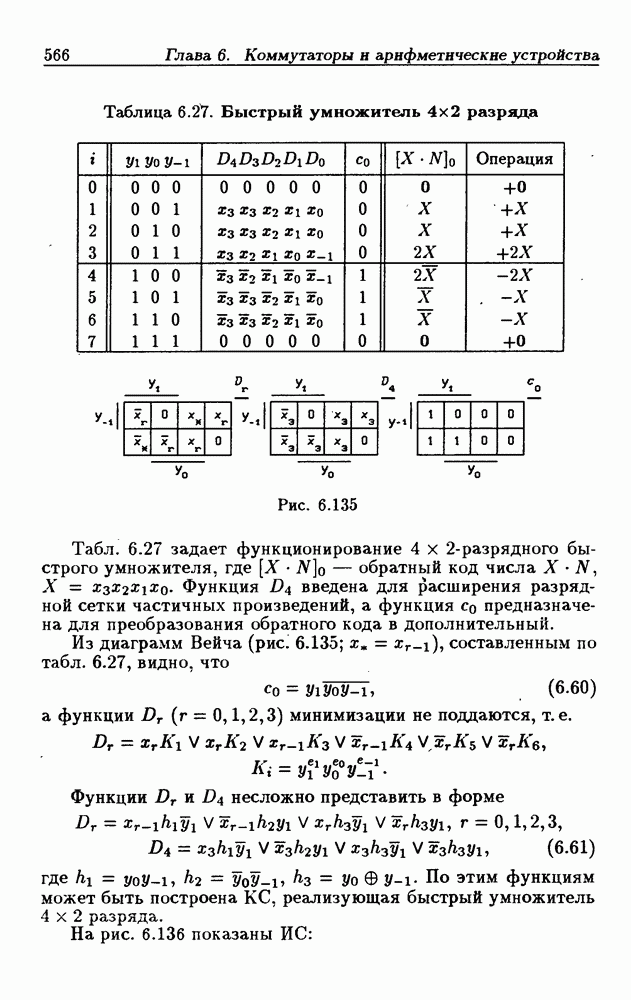
Таблица 6.27. (см. скан) Быстрый умножитель  разряда
разряда

Рис. 6.135
Табл. 6.27 задает функционирование  -разрядного быстрого умножителя, где
-разрядного быстрого умножителя, где  обратный код числа
обратный код числа  Функция
Функция  введена для расширения разрядной сетки частичных произведений, а функция со предназначена для преобразования обратного кода в дополнительный.
введена для расширения разрядной сетки частичных произведений, а функция со предназначена для преобразования обратного кода в дополнительный.
Из диаграмм Вейча (рис. 6.135;  составленным по табл. 6.27, видно, что
составленным по табл. 6.27, видно, что

а функции  минимизации не поддаются, т.е.
минимизации не поддаются, т.е.

Функции  несложно представить в форме
несложно представить в форме

где  По этим функциям может быть построена КС, реализующая быстрый умножитель
По этим функциям может быть построена КС, реализующая быстрый умножитель  разряда.
разряда.
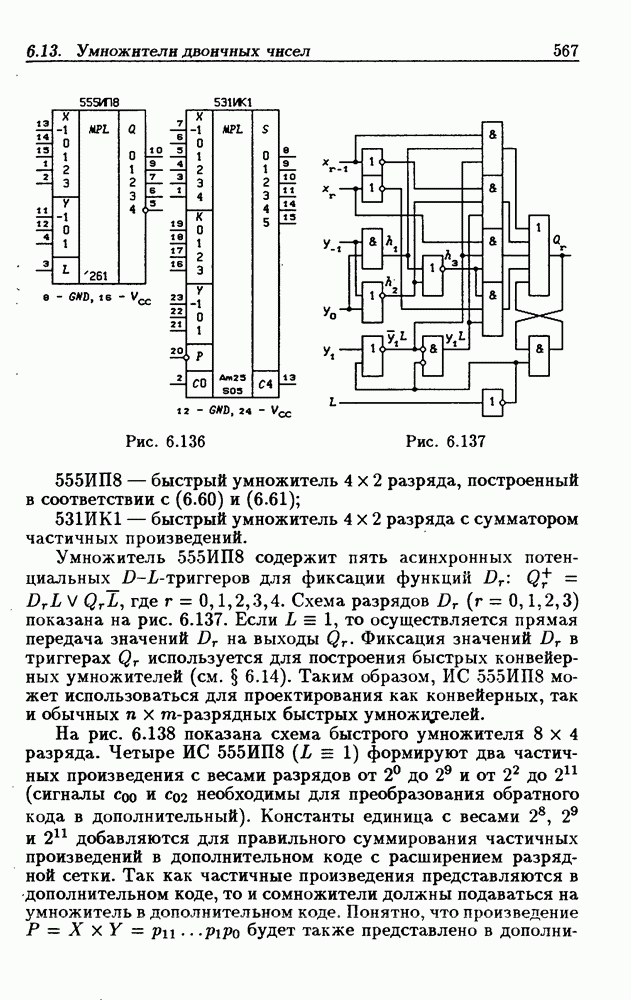
На рис. 6.136 показаны ИС:

Рис. 6.136

Рис. 6.137
555ИП8 - быстрый умножитель  разряда, построенный в соответствии с (6.60) и (6.61);
разряда, построенный в соответствии с (6.60) и (6.61);
531ИК1 - быстрый умножитель  разряда с сумматором частичных произведений.
разряда с сумматором частичных произведений.
Умножитель  содержит пять асинхронных потенциальных
содержит пять асинхронных потенциальных  -триггеров для фиксации функций
-триггеров для фиксации функций  где
где  Схема разрядов
Схема разрядов  показана на рис. 6.137. Если
показана на рис. 6.137. Если  то осуществляется прямая передача значений
то осуществляется прямая передача значений  на выходы
на выходы  Фиксация значений
Фиксация значений  в триггерах
в триггерах  используется для построения быстрых конвейерных умножителей (см. § 6.14). Таким образом,
используется для построения быстрых конвейерных умножителей (см. § 6.14). Таким образом,  может использоваться для проектирования как конвейерных, так и обычных
может использоваться для проектирования как конвейерных, так и обычных  -разрядных быстрых умножителей.
-разрядных быстрых умножителей.
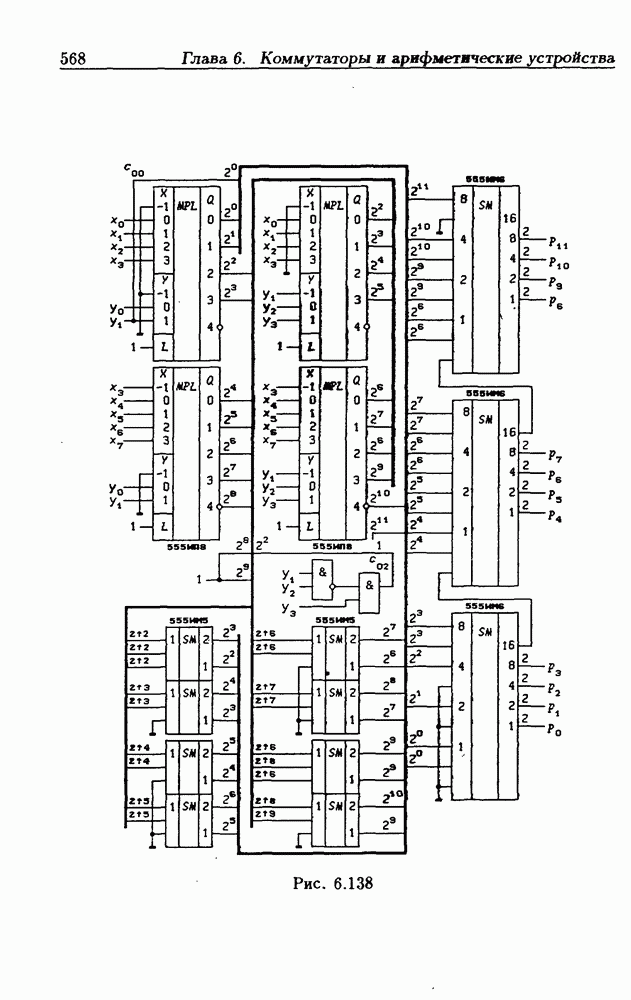
На рис. 6.138 показана схема быстрого умножителя  разряда. Четыре
разряда. Четыре  формируют два частичных произведения с весами разрядов от 2° до 29 и от 22 до 211 (сигналы
формируют два частичных произведения с весами разрядов от 2° до 29 и от 22 до 211 (сигналы  необходимы для преобразования обратного кода в дополнительный). Константы единица с весами 28, 29 и 211 добавляются для правильного суммирования частичных произведений в дополнительном коде с расширением разрядной сетки. Так как частичные произведения представляются в дополнительном коде, то и сомножители должны подаваться на умножитель в дополнительном коде. Понятно, что произведение
необходимы для преобразования обратного кода в дополнительный). Константы единица с весами 28, 29 и 211 добавляются для правильного суммирования частичных произведений в дополнительном коде с расширением разрядной сетки. Так как частичные произведения представляются в дополнительном коде, то и сомножители должны подаваться на умножитель в дополнительном коде. Понятно, что произведение  будет также представлено в
будет также представлено в

(кликните для просмотра скана)
дополнительном коде. Если  знаковые разряды сомножителей, то
знаковые разряды сомножителей, то  — знаковые разряды произведения
— знаковые разряды произведения  произведение положительное,
произведение положительное,  произведение отрицательное).
произведение отрицательное).
В табл. 6.28 указано число разрядов частичных произведений, имеющих одинаковый вес  Из табл. 6.28 видно, что даже два частичных произведения не могут быть просуммированы с помощью
Из табл. 6.28 видно, что даже два частичных произведения не могут быть просуммированы с помощью  -разрядного двоичного сумматора. Поэтому производится предварительное суммирование разрядов частичных произведений с помощью одноразрядных сумматоров (например,
-разрядного двоичного сумматора. Поэтому производится предварительное суммирование разрядов частичных произведений с помощью одноразрядных сумматоров (например,  После того, как таким способом будет получено не более, чем по два разряда с весами, большими 2°, суммирование сформированных двоичных чисел выполняется на
После того, как таким способом будет получено не более, чем по два разряда с весами, большими 2°, суммирование сформированных двоичных чисел выполняется на  -разрядном сумматоре, построенном, например, на трех
-разрядном сумматоре, построенном, например, на трех  Схема суммирования разрядов частичных произведений с помощью одноразрядных сумматоров называется деревом Уоллеса [9] (в данном случае имеется только основание дерева из-за малого числа частичных произведений).
Схема суммирования разрядов частичных произведений с помощью одноразрядных сумматоров называется деревом Уоллеса [9] (в данном случае имеется только основание дерева из-за малого числа частичных произведений).
Таблица 6.28. (см. скан) Число разрядов частичных произведений
Аналогично схеме на рис. 6.138 может быть построена схема быстрого умножителя при любом числеп и  разрядов сомножителей. При этом следует пользоваться правилом: две константы единица с весами
разрядов сомножителей. При этом следует пользоваться правилом: две константы единица с весами  и
и  добавляются к первому (младшему) частичному произведению, а к остальным частичным произведениям — только по одной константе единица с весами
добавляются к первому (младшему) частичному произведению, а к остальным частичным произведениям — только по одной константе единица с весами 
На основе рассмотренного выше принципа быстрого умножения (на два разряда множителя) построена и схема  (рис. 6.136), которая одновременно выполняет и суммирование частичных произведений. Схема, вычисляющая частичные произведения
(рис. 6.136), которая одновременно выполняет и суммирование частичных произведений. Схема, вычисляющая частичные произведения  разряда, описывается табл. 6.29. Функции и
разряда, описывается табл. 6.29. Функции и
Таблица 6.29. (см. скан) Вычисление частичных произведений
 введены для расширения разрядной сетки частичных произведений, а для преобразования обратного кода в дополнительный используется сигнал
введены для расширения разрядной сетки частичных произведений, а для преобразования обратного кода в дополнительный используется сигнал 
Выходы разрядов  суммы частичных произведений
суммы частичных произведений  описываются выражениями:
описываются выражениями:

где  частичное произведение, вычисленное другой
частичное произведение, вычисленное другой  вход управления полярностью, переключающей ИС на работу с инверсным множимым
вход управления полярностью, переключающей ИС на работу с инверсным множимым 
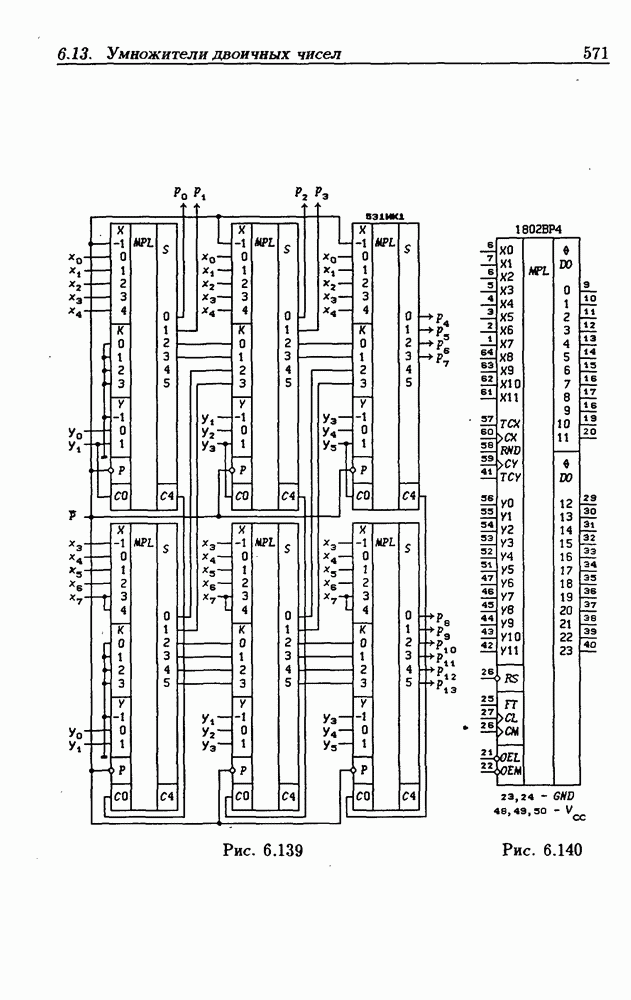
На рис. 6.139 показана схема быстрого умножителя  разрядов, выполненная на шести
разрядов, выполненная на шести  Сомножители, как и в схеме на рис. 6.138, подаются в дополнительном коде
Сомножители, как и в схеме на рис. 6.138, подаются в дополнительном коде  знаковые разряды), и результат произведения выдается в дополнительном коде
знаковые разряды), и результат произведения выдается в дополнительном коде  произведение положительное,
произведение положительное,  произведение отрицательное). При умножении
произведение отрицательное). При умножении  и m-разрядных отрицательных чисел
и m-разрядных отрицательных чисел  максимальной величины (
максимальной величины ( ), модуль которых равен
), модуль которых равен  и
и  при
при  получаются значения:
получаются значения:  что при использовании в качестве знакового разряда только
что при использовании в качестве знакового разряда только  дает правильный результат умножения.
дает правильный результат умножения.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Основы теории переключательных функций
- 1.2. Позиционные системы счисления
- 1.3. Переключательные функции
- 1.4. Принцип и закон двойственности
- 1.5. Теоремы разложения
- 1.6. Решение систем логических уравнений
- 1.7. Первичные термы, минтермы и макстермы
- 1.8. Совершенные нормальные формы представления функций
- 1.9. Конъюнктивные и дизъюнктивные термы
- 1.10. Минимизация переключательных функций
- 1.11. Диаграммы Вейча
- 1.12. Минимизация неполностью определенных функций, совместная минимизация нескольких функций
- 1.13. Скобочные формы функций
- 1.14. Закон двойственности для логических схем
- 1.15. Линейные функции
- Глава 2. Анализ и синтез логических схем
- 2.2. Модели логических элементов
- 2.3. Модели логических схем
- 2.4. Анализ логических схем
- 2.5. Синтез комбинационных схем, свободных от состязаний
- Глава 3. Синтез асинхронных потенциальных автоматов
- 3.2. Асинхронные потенциальные автоматы
- 3.3. Асинхронные потенциальные триггеры и элементы памяти
- Триггеры типа R-S
- Триггеры типа D-L
- Триггеры типа D-L-R с приоритетом входа R.
- Триггеры типа D-L-R с приоритетом входа L.
- Триггеры типа R-S-L.
- Триггеры типа DN-LN
- Аналитический метод синтеза и анализа триггеров.
- 3.4. Задание асинхронных потенциальных автоматов таблицами и графами переходов
- 3.5. Синтез асинхронных потенциальных счетчиков
- 3.6. Синтез асинхронных импульсных триггеров
- Триггеры типа dJ-dK.
- Классификация триггеров.
- 3.7. Синтез синхронных триггеров
- Триггеры типа J-K
- Синхронно-асинхронные триггеры.
- 3.8. Примеры синтеза асинхронных потенциальных автоматов
- Цифровые фазочастотные детекторы.
- Квантизатор временных интервалов.
- 3.9. Генераторы сигналов
- Автогенераторы.
- Управляемые автогенераторы.
- Глава 4. Синтез синхронных автоматов
- 4.2. Синхронные триггеры
- Триггеры типов D и R-S с импульсным тактовым сигналом.
- Синхронные триггеры типов R-S и D-L
- Синхронно-асинхронные триггеры.
- Синхронные триггеры типа J-K
- Триггеры типа Т.
- Классификация синхронных триггеров.
- Преобразования типов синхронных триггеров.
- Триггеры типов D-T-L и D-T-L/R
- Функции переходов синхронно-асинхронных триггеров.
- 4.3. Примеры синтеза синхронных автоматов
- 4.4. Сдвигающие регистры
- Синтез счетчиков на сдвигающих регистрах.
- Сдвигающие регистры с загрузкой данных.
- Реверсивные сдвигающие регистры.
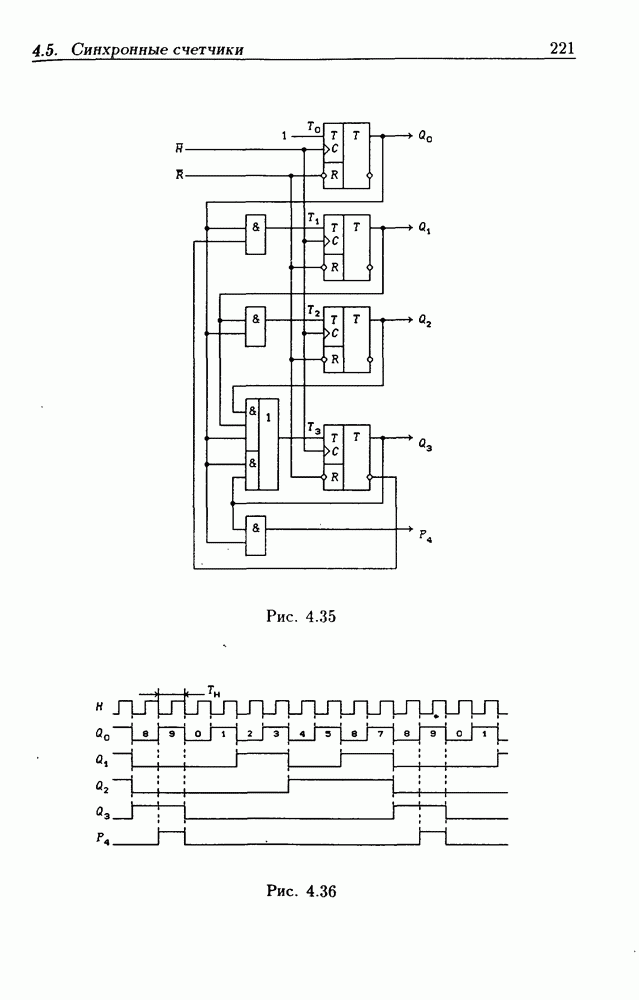
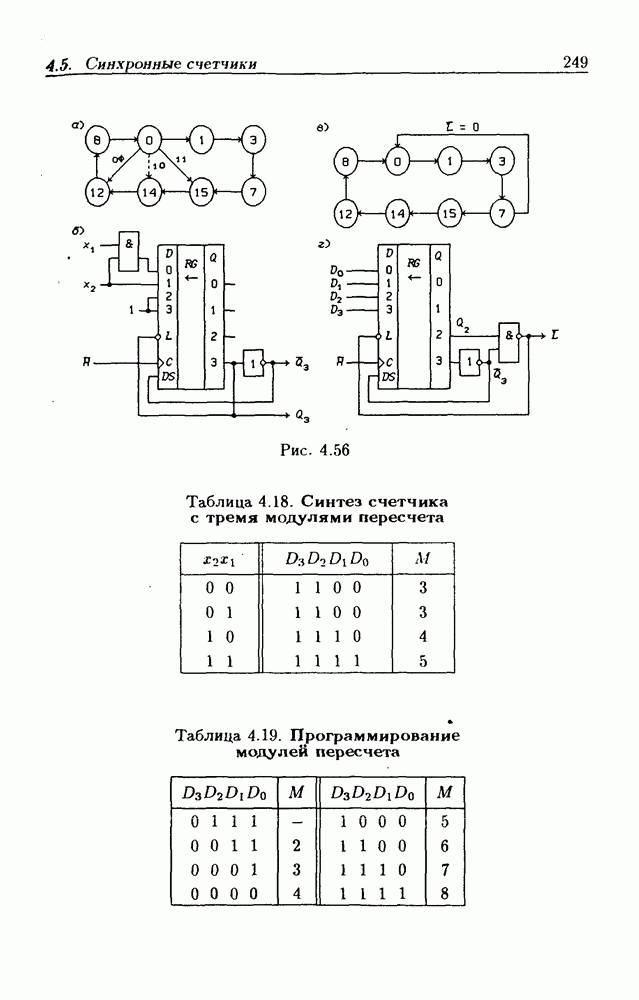
- 4.5. Синхронные счетчики
- Синхронные двоичные счетчики.
- Синхронные двоично-десятичные счетчики.
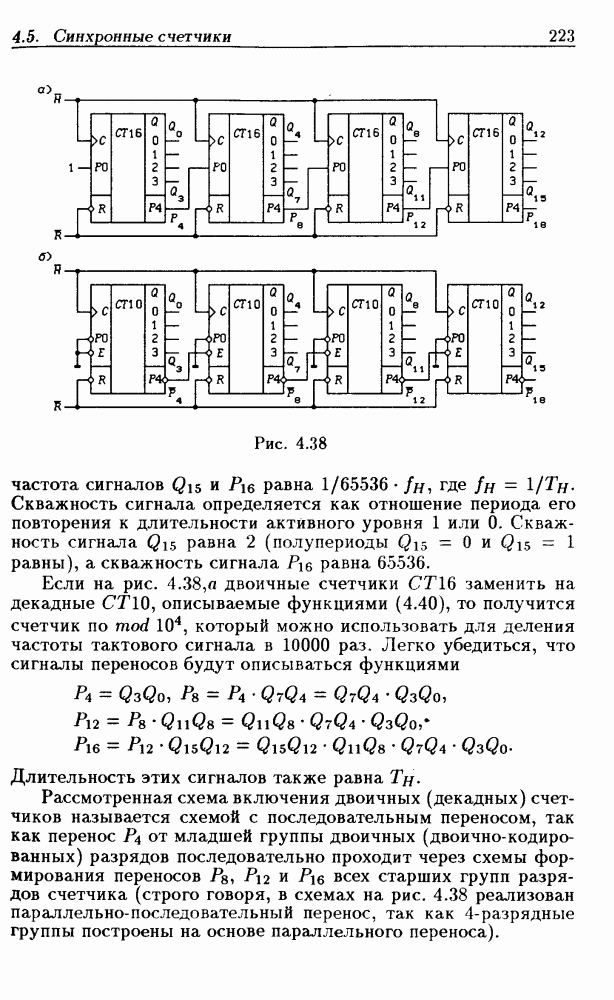
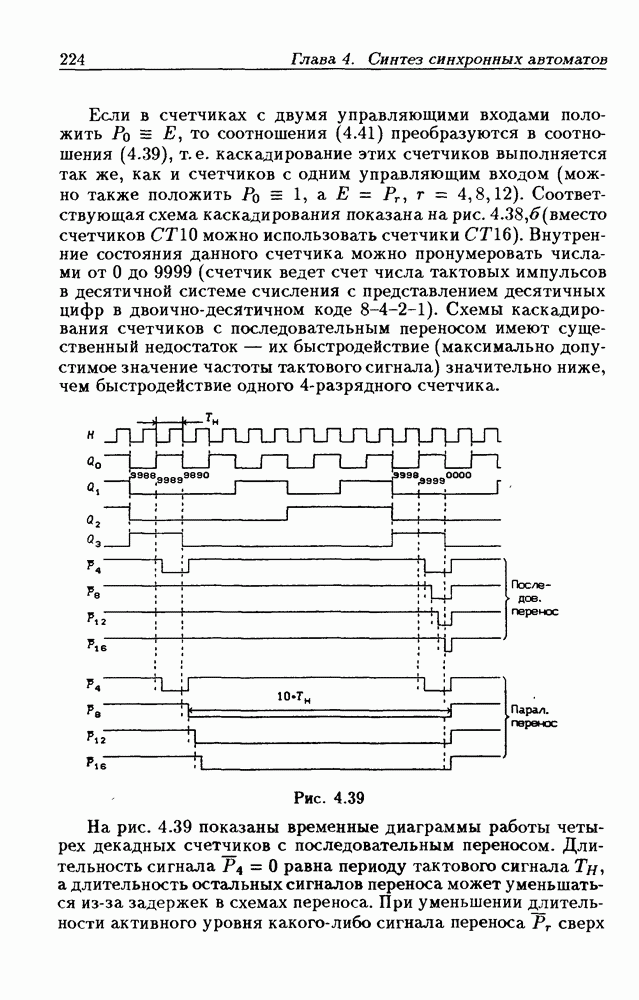
- Каскадирование двоичных и двоично-десятичных счетчиков.
- Синхронные двоичные реверсивные счетчики.
- Реверсивные двоично-десятичные счетчики.
- Каскадирование реверсивных счетчиков.
- Счетчики на сдвигающих регистрах.
- Кольцевые счетчики.
- Линейные счетчики.
- Программируемые счетчики.
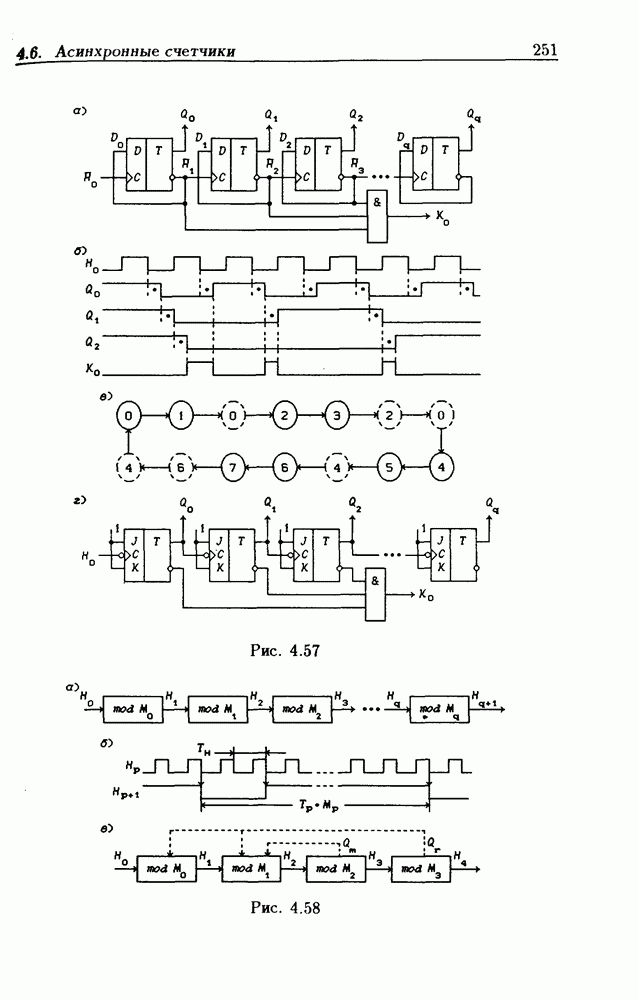
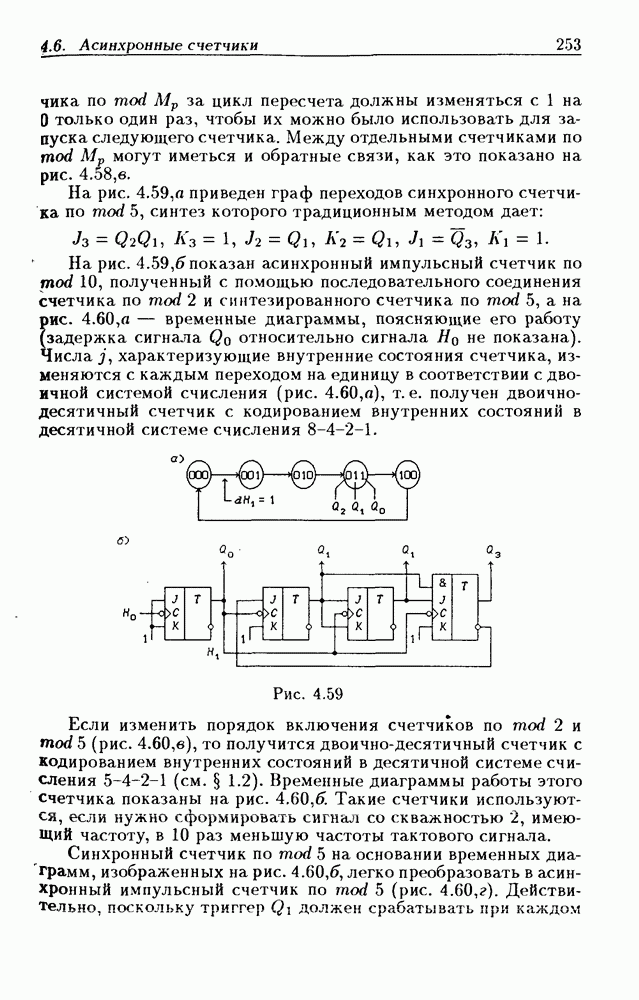
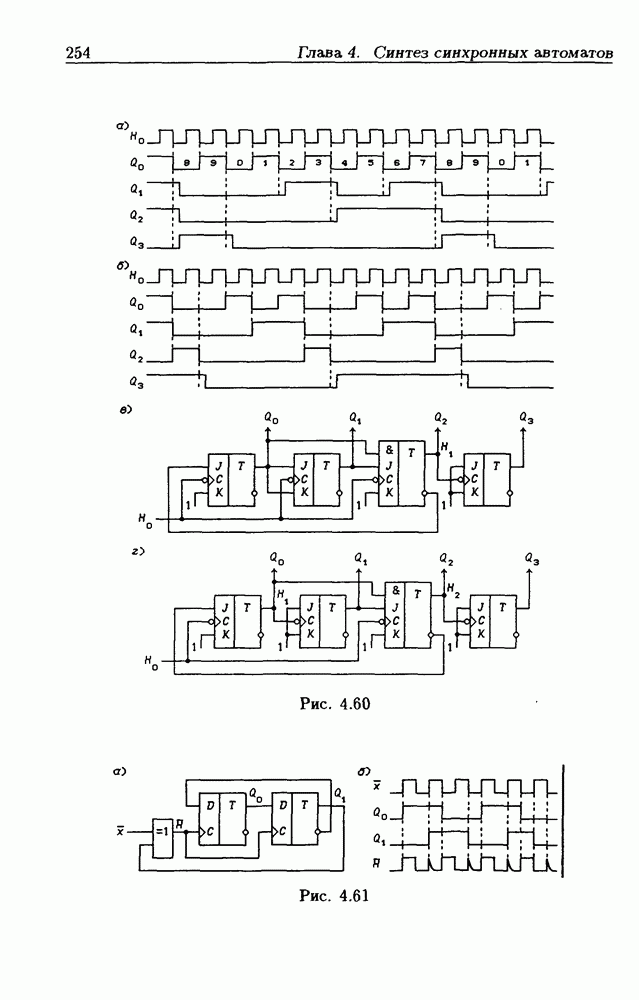
- 4.6. Асинхронные счетчики
- Асинхронные счетчики с умножением частоты счетного сигнала.
- Асинхронные импульсно-потенциальные счетчики.
- Асинхронное программирование модуля пересчета счетчиков.
- Глава 5. Логические элементы и триггеры
- Логические элементы.
- Классификация ИС по степени интеграции.
- 5.2. Интегральные схемы КМОП серий
- 5.3. Триггеры Шмитта
- 5.4. Логические элементы с открытым коллекторным выходом
- Логические элементы с открытым коллекторным выходом.
- Применения ЛЭ с открытым коллекторным выходом.
- Интерфейсные ЛЭ с открытым коллекторным выходом.
- Логические элементы с открытым стоковым выходом.
- Типовые цоколевки ИС.
- 5.5. Логические элементы с тремя состояниями выхода
- Шинные драйверы с Z-состоянием выхода.
- Основные правила графического изображения ИС.
- 5.6. Преобразователи уровней напряжения и тока
- 5.7. Асинхронные потенциальные триггеры и регистры памяти
- 5.8. Синхронные триггеры и регистры памяти
- 5.9. Шинные приемопередатчики
- Шинные приемопередатчики с Z-состоянием выхода.
- Шинные приемопередатчики с открытым коллекторным выходом.
- Шинные приемопередатчики с регистрами памяти.
- Шинные приемопередатчики со сдвигающим регистром.
- Шинные трехнаправленные приемопередатчики.
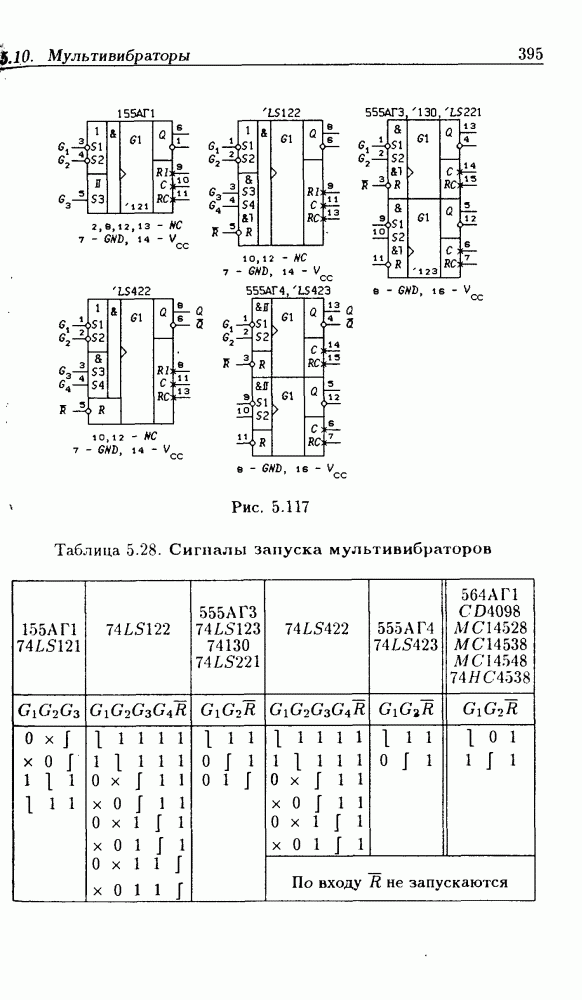
- 5.10. Мультивибраторы
- 5.11. Генераторы
- Схемы устранения «дребезга» механических контактов.
- Автогенераторы периодических сигналов.
- 5.12. Рекомендации по выбору серий ИС
- Глава 6. Коммутаторы и арифметические устройства
- 6.1. Дешифраторы
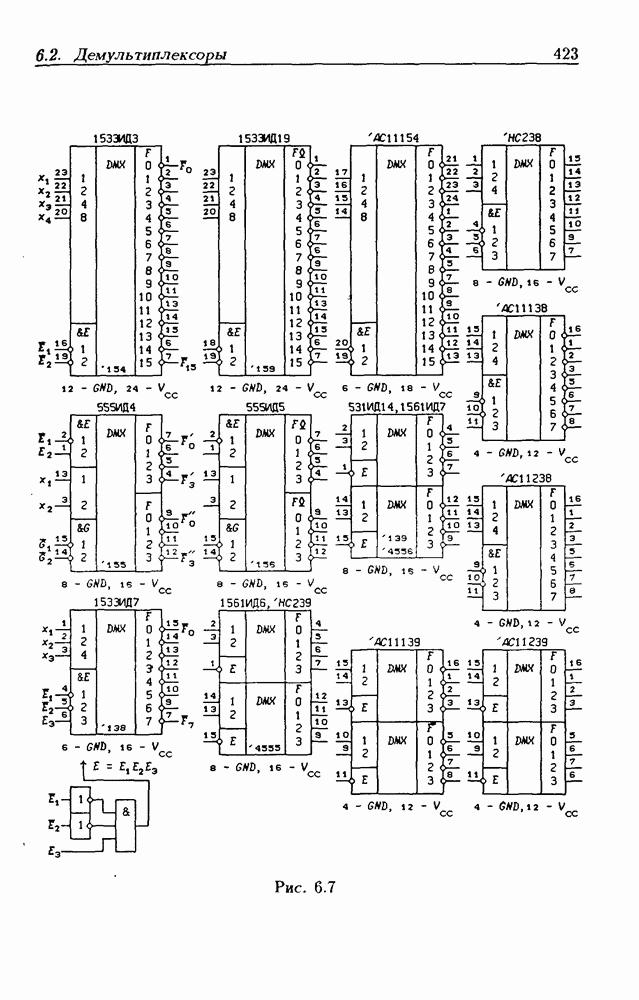
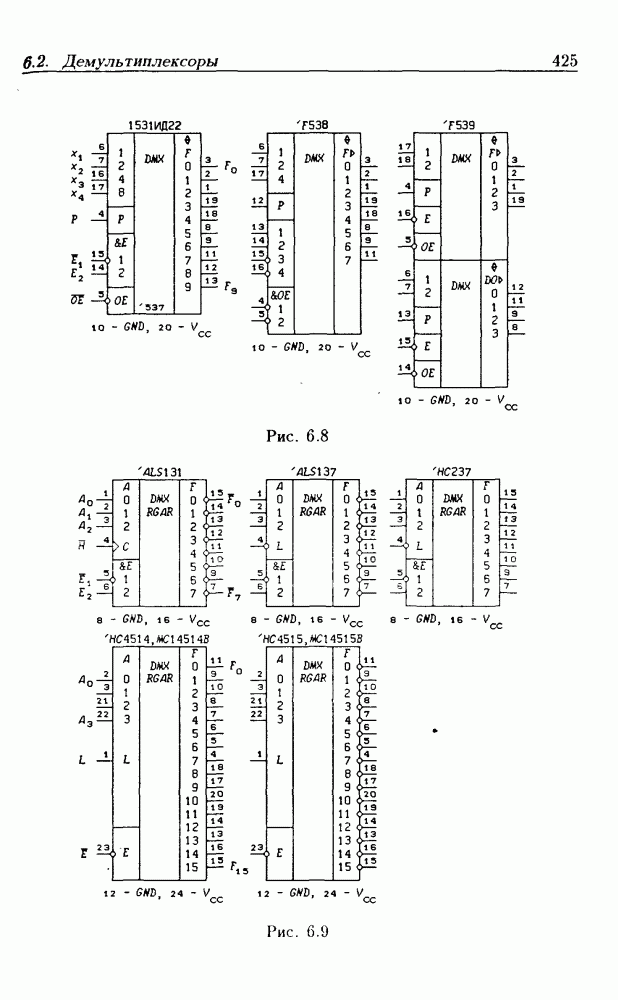
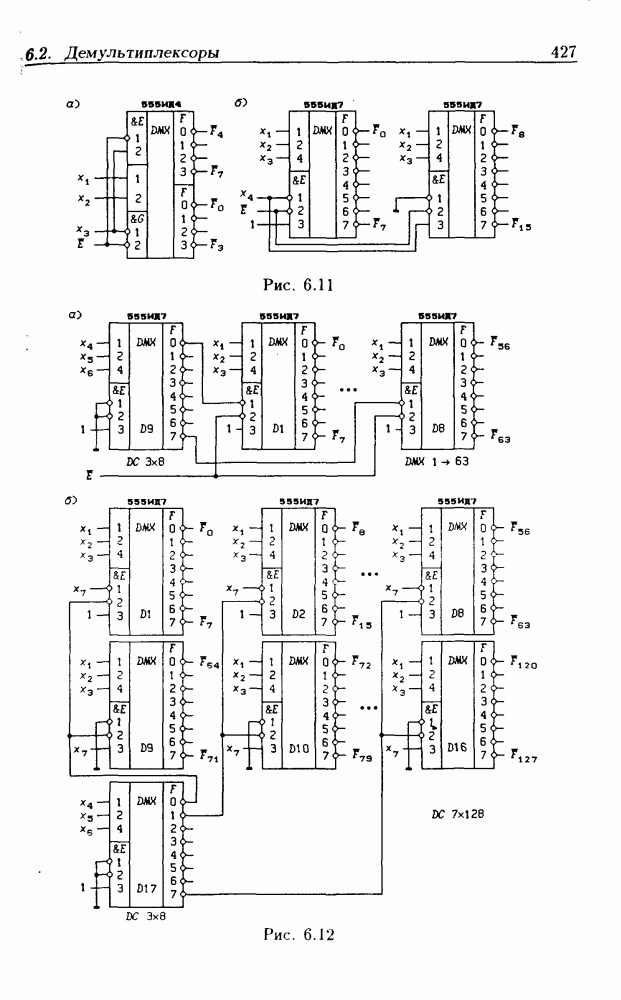
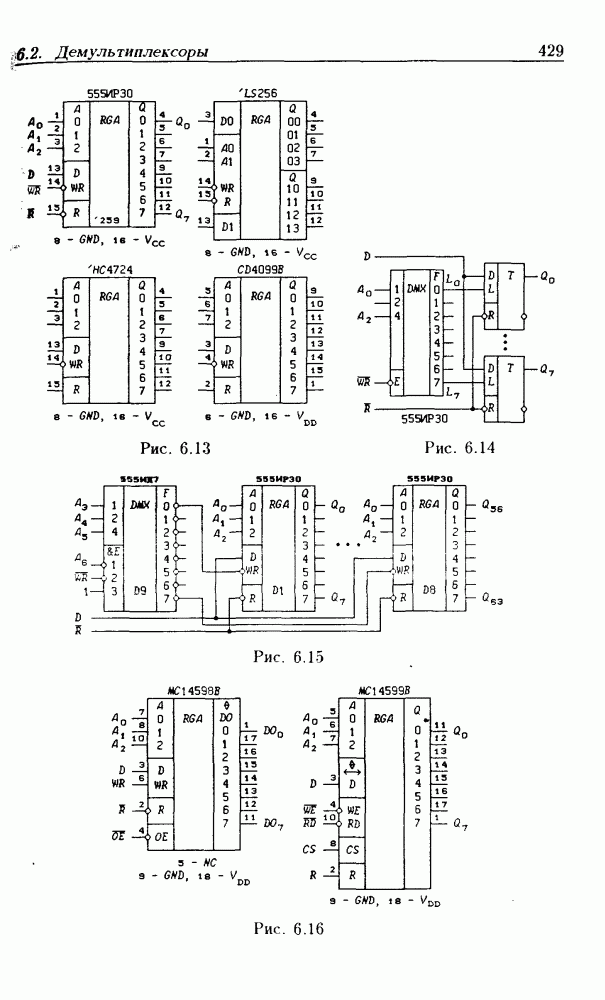
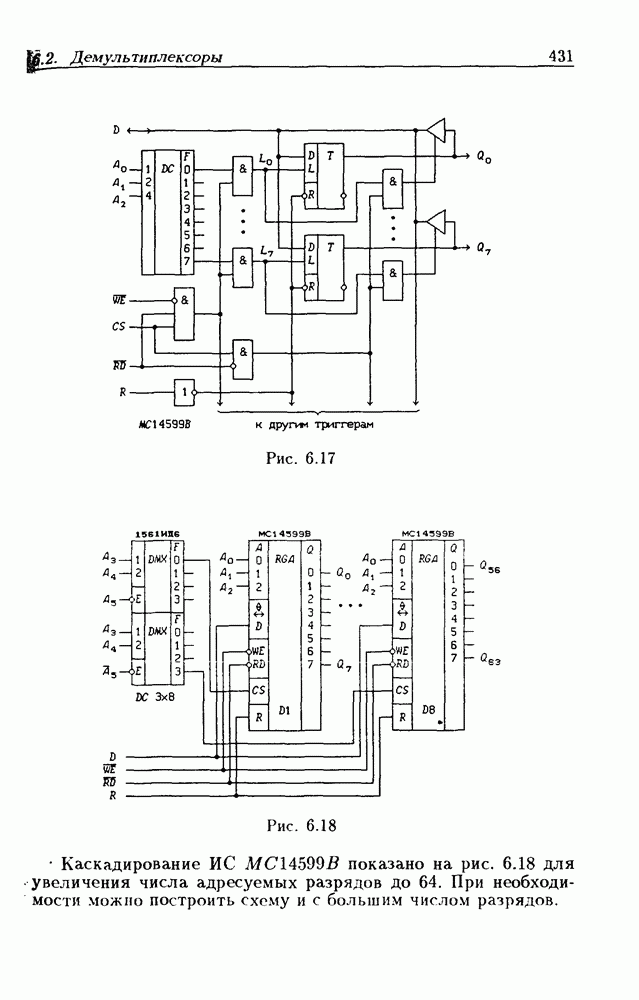
- 6.2. Демультиплексоры
- 6.3. Мультиплексоры
- Мультиплексоры без стробирования.
- Мультиплексоры со стробированием.
- Мультиплексоры с Z-состоянием выхода.
- Каскадирование мультиплексоров.
- Функциональные мультиплексоры.
- Регистры памяти с мультиплексными входами данных.
- Мультиплексоры с регистрами памяти данных и адреса.
- Сдвигающие мультиплексоры.
- 6.4. Синтез комбинационных схем и цифровых автоматов на мультиплексорах
- Синтез схем на 8-канальных мультиплексорах.
- Синтез на двухразрядных 4-канальных мультиплексорах.
- Синтез генератора синусоидальной функции на мультиплексорах.
- Синтез триггеров на мультиплексорах.
- Синтез счетчиков на мультиплексорах.
- 6.5. Аналоговые ключи и мультиплексоры-демультиплексоры
- 6.6. Шифраторы
- 6.7. Цифровые компараторы
- Программируемые цифровые компараторы.
- Адресные компараторы.
- Применения адресных компараторов.
- 6.8. Схемы сравнения двоичных чисел
- 8-разрядные схемы сравнения двоичных чисел.
- 6.9. Прямой, обратный и дополнительный коды
- Дополнительный код.
- Сложение чисел в обратном коде.
- Код с избытком 3.
- 6.10. Сумматоры
- Двоичные параллельные сумматоры с последовательным переносом.
- Двоичные сумматоры с параллельным переносом.
- Применения сумматоров.
- Десятичные сумматоры.
- Последовательные двоичные сумматоры.
- 6.11. Арифметическо-логические устройства
- 6.12. Пороговые схемы и мажоритарные элементы
- 6.13. Умножители двоичных чисел
- Быстрые умножители.
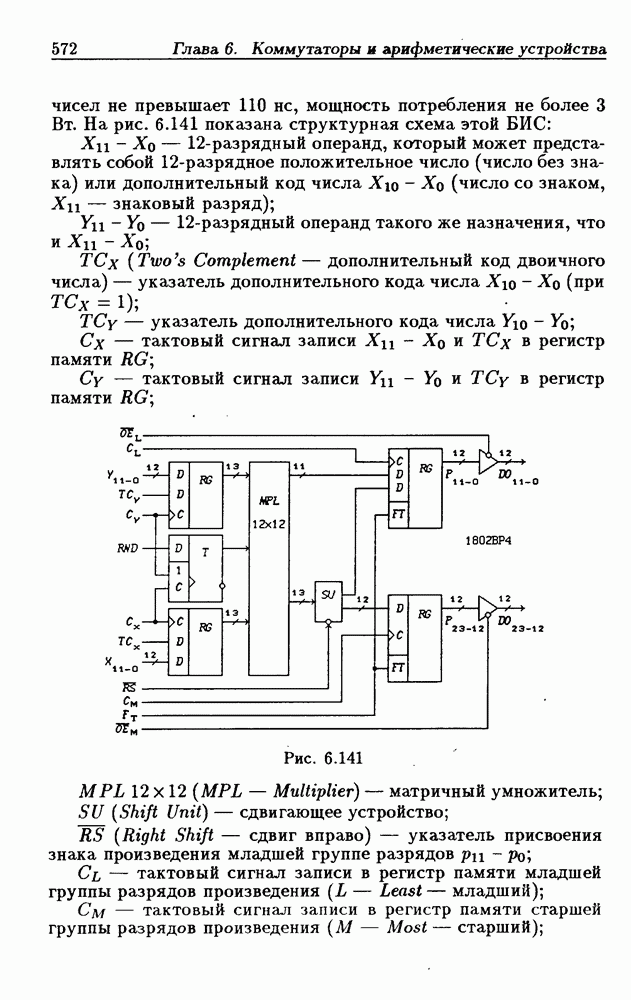
- БИС умножителя 12×12 разрядов 1802ВР4.
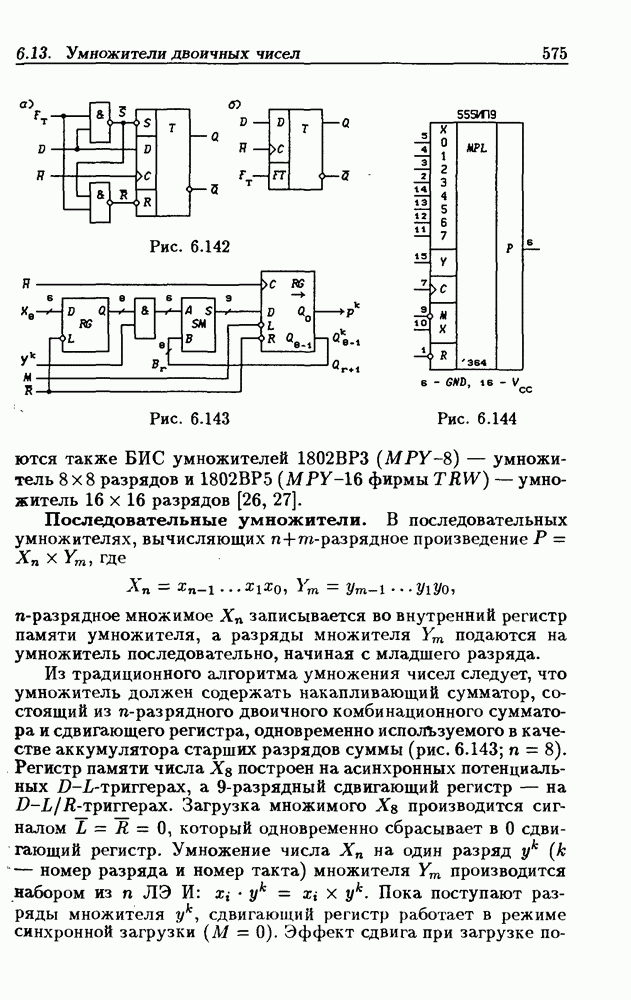
- Последовательные умножители.
- 6.14. Конвейерные устройства
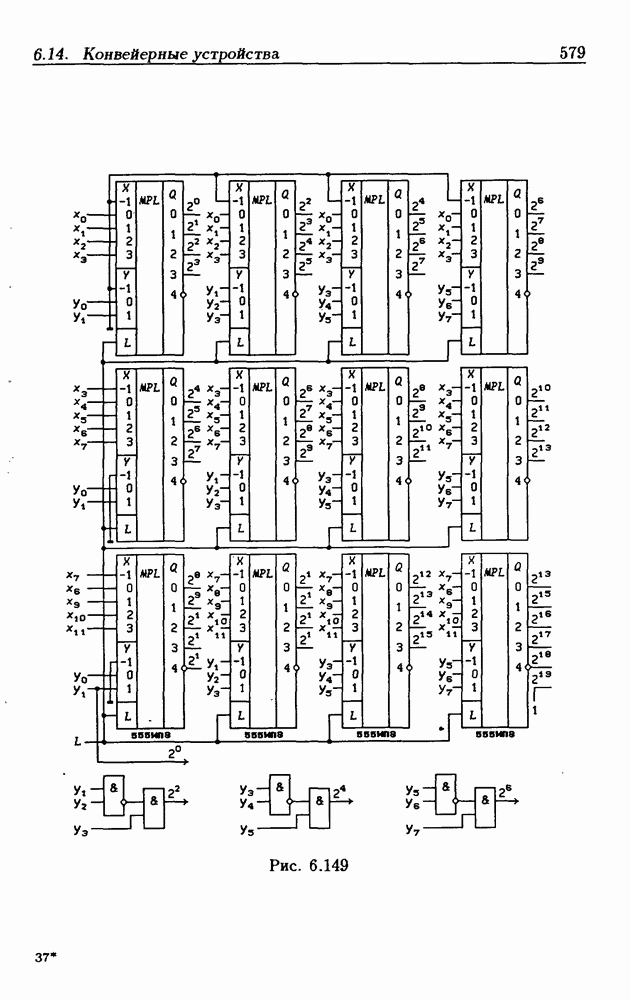
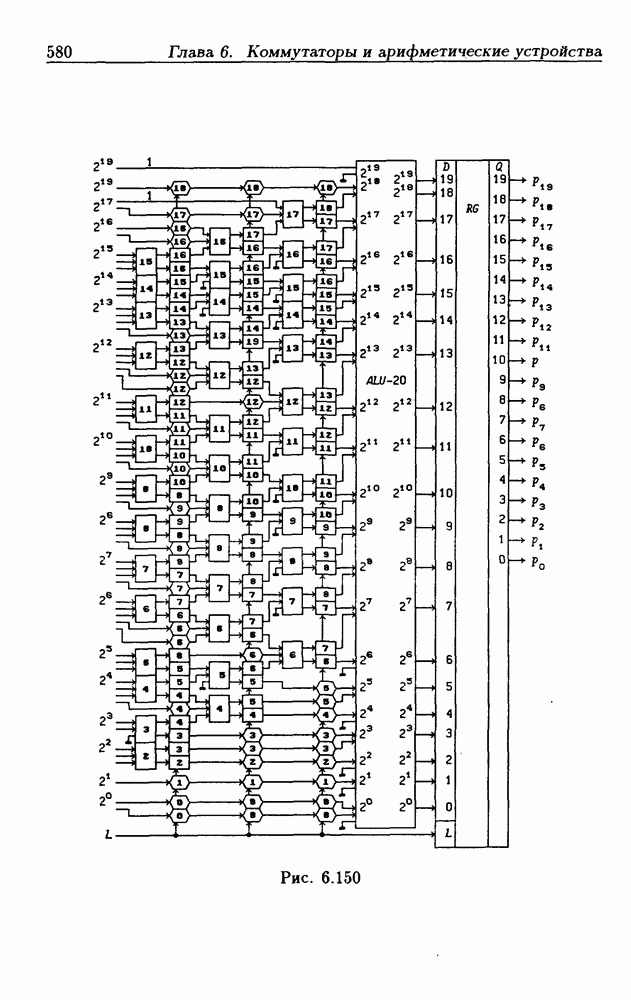
- Конвейерный быстрый умножитель.
- Конвейерные АЦП.
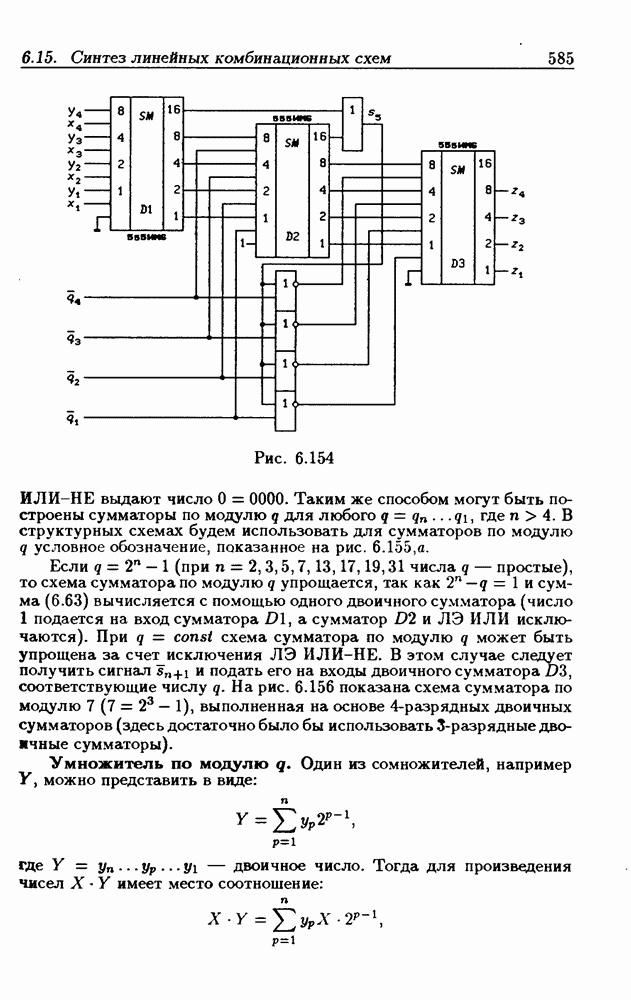
- 6.15. Синтез линейных комбинационных схем
- Сумматор по модулю q.
- Умножитель по модулю q.
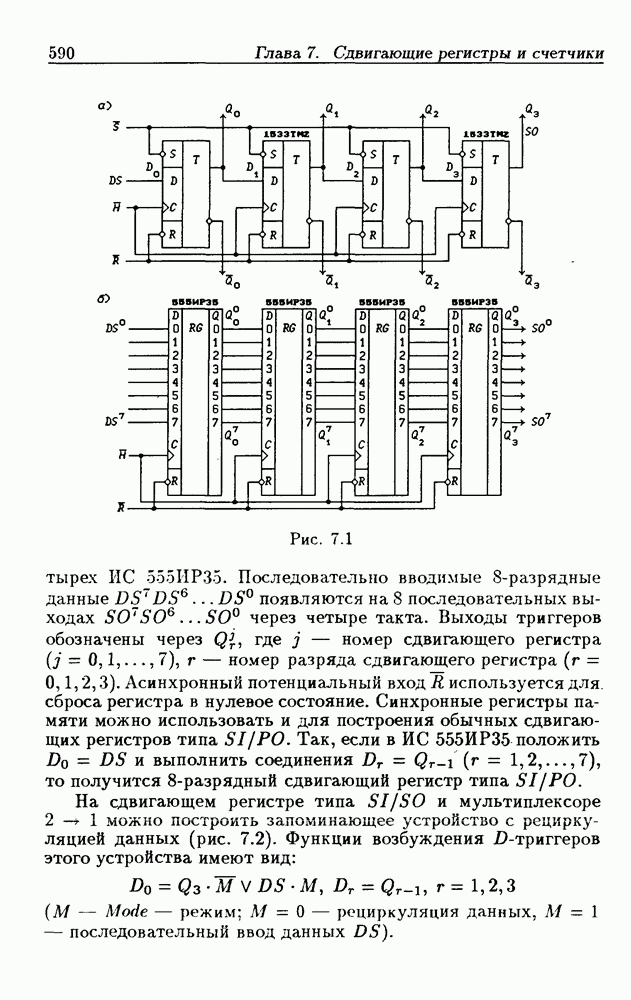
- Глава 7. Сдвигающие регистры и счетчики
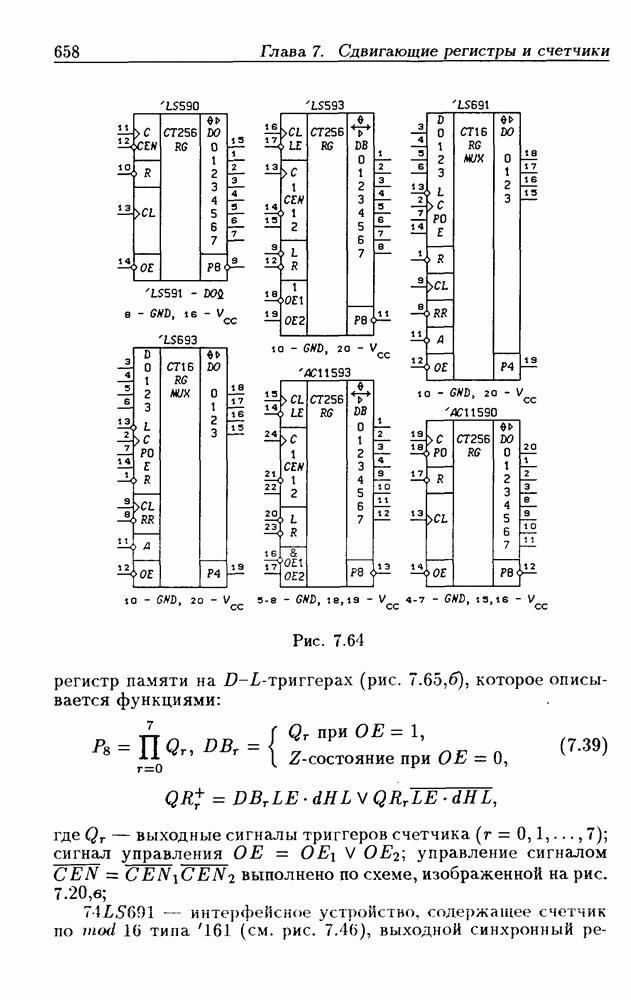
- 7.1. Сдвигающие регистры без параллельной записи данных
- Сдвигающие устройства с выходными регистрами памяти.
- 7.2. Сдвигающие регистры с параллельной записью данных
- Сдвигающие регистры с расширением знака.
- Сдвигающие регистры с входным регистром памяти.
- 7.3. Реверсивные сдвигающие регистры
- Реверсивные сдвигающие регистры типов PI/SO и PI/PO.
- Многофункциональные устройства на основе реверсивных сдвигающих регистров.
- 7.4. Асинхронные счетчики
- Двоично-десятичные асинхронные счетчики.
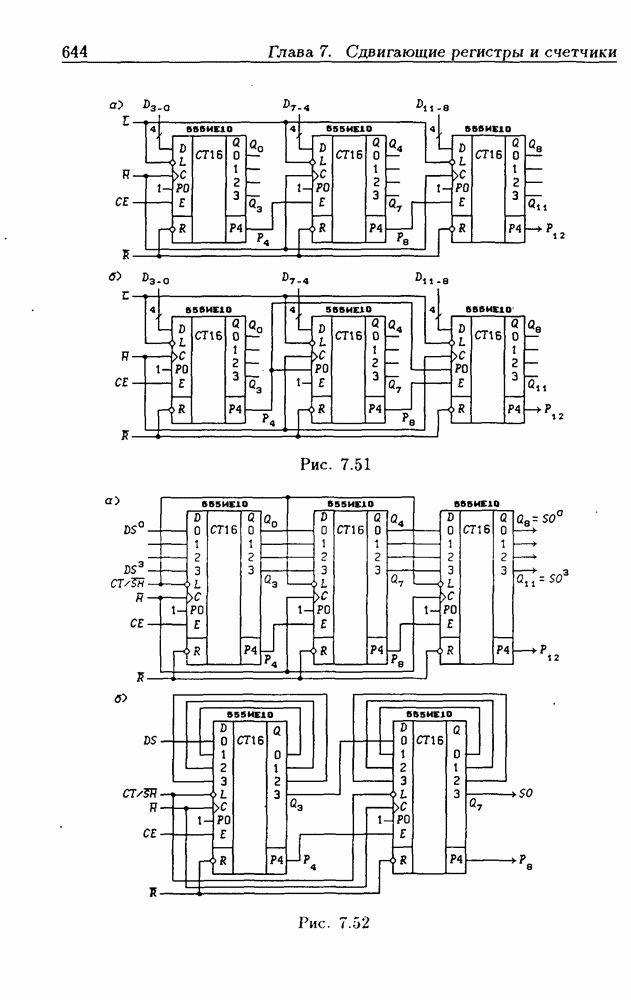
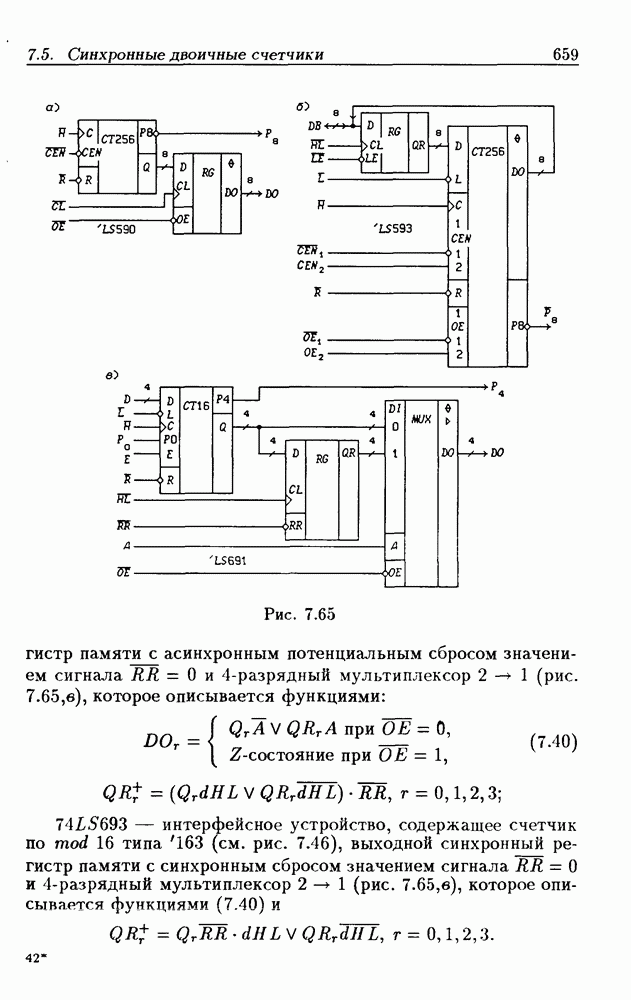
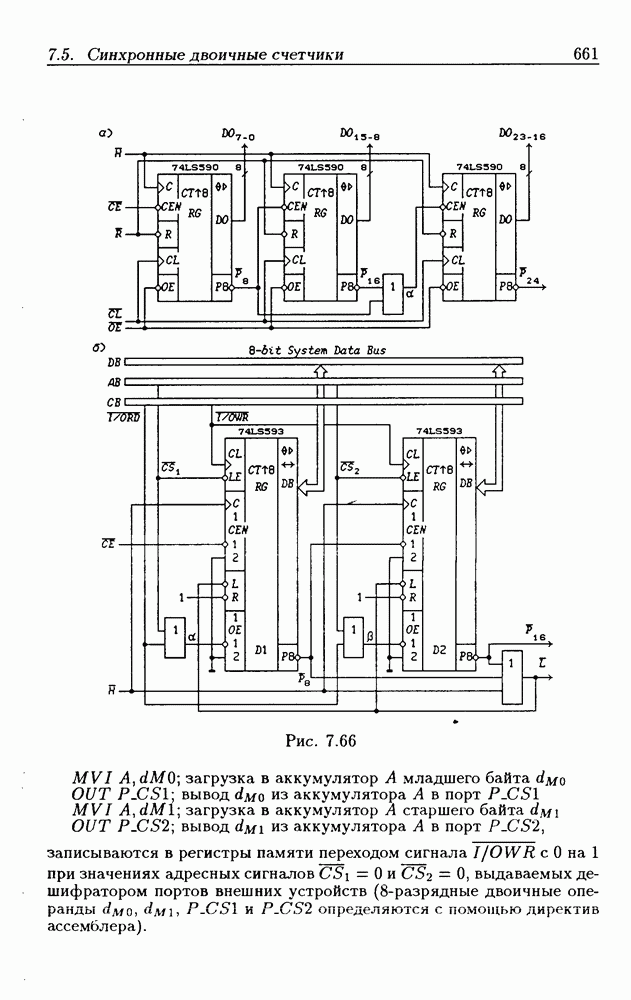
- 7.5. Синхронные двоичные счетчики
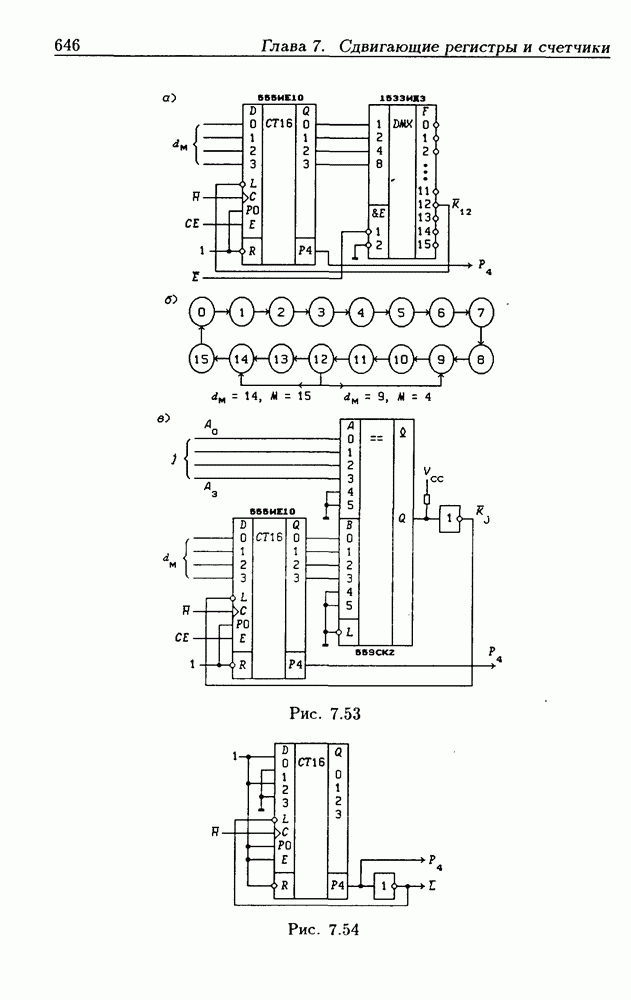
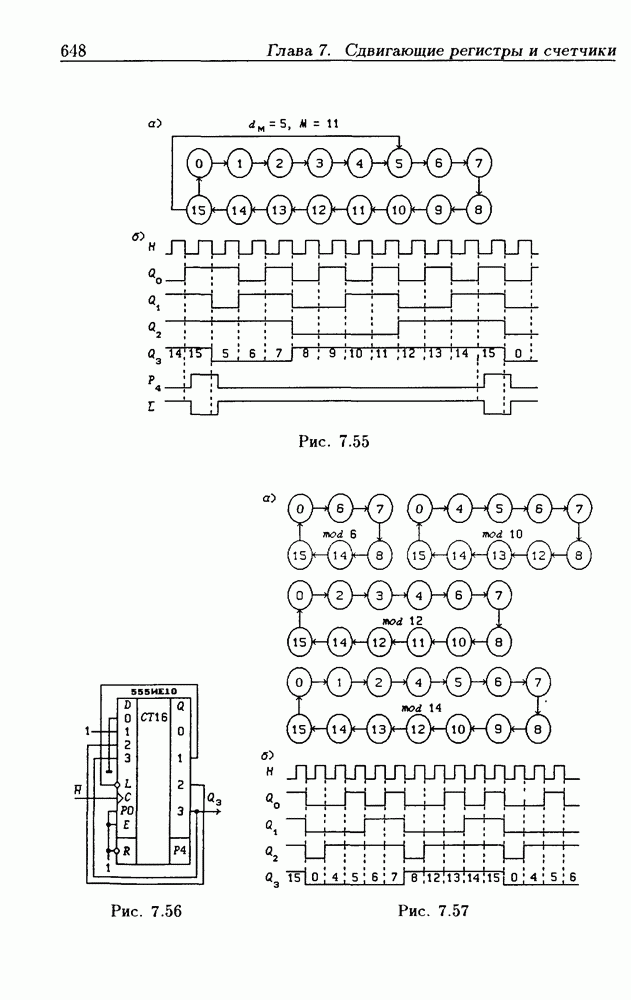
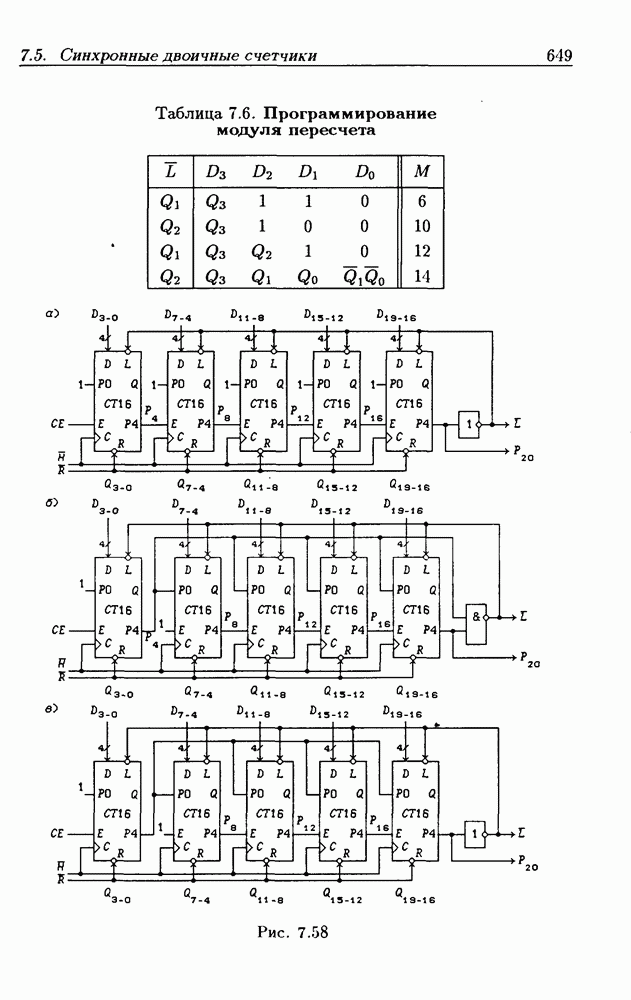
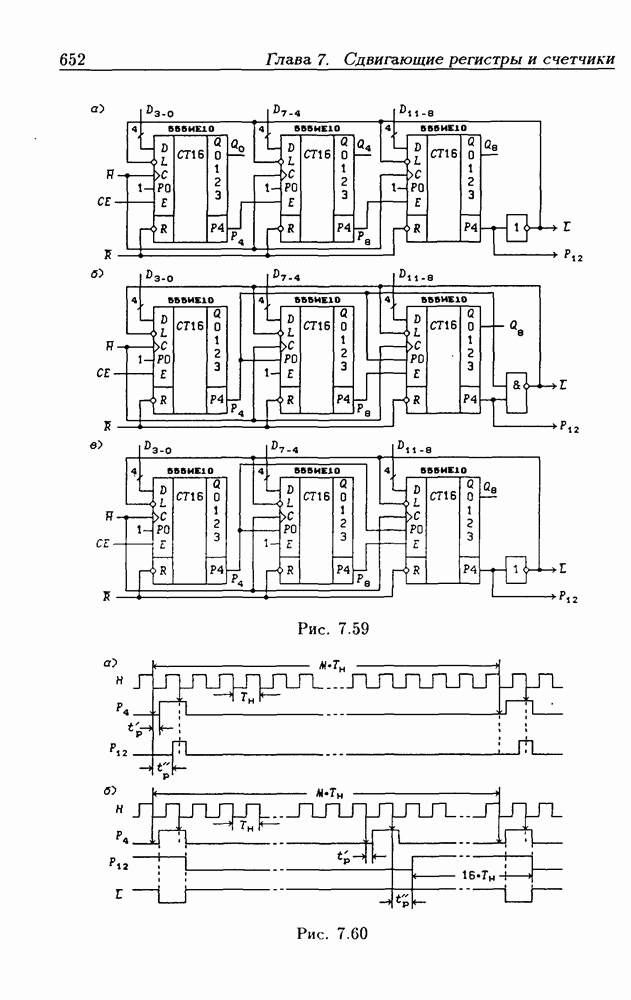
- Программирование модуля пересчета двоичных счетчиков.
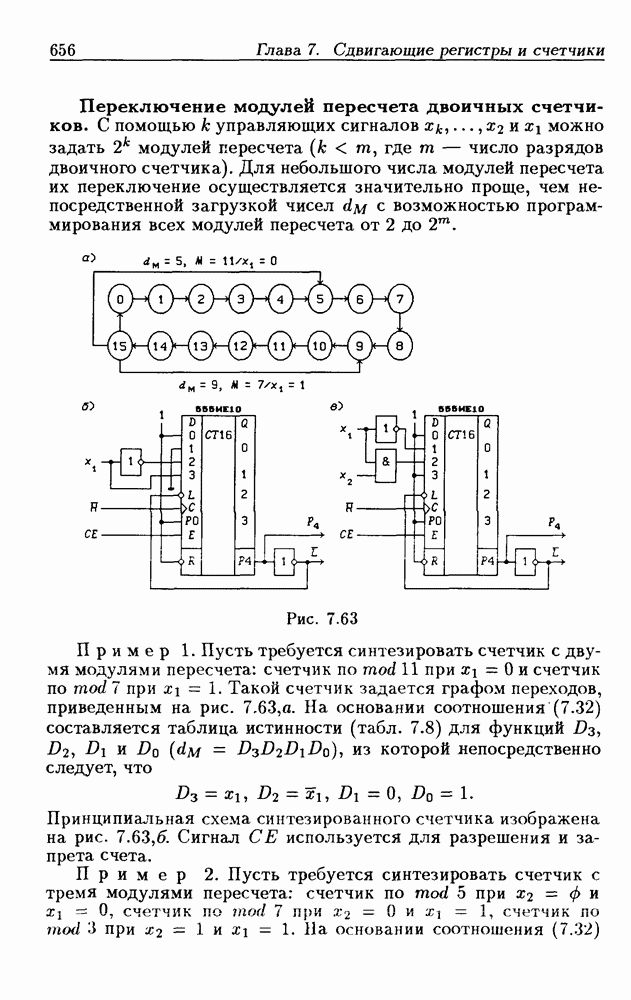
- Переключение модулей пересчета двоичных счетчиков.
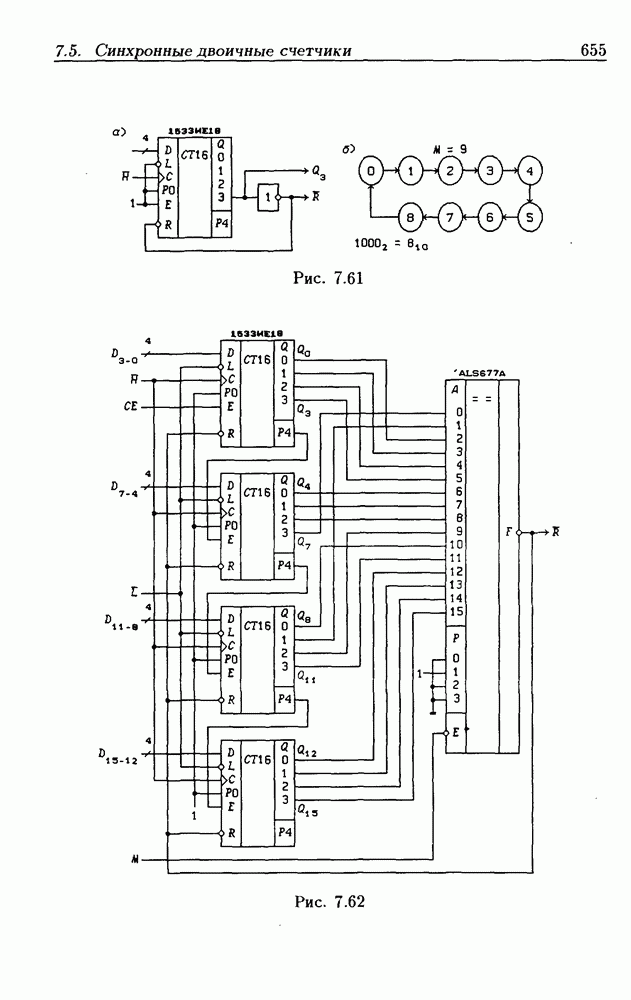
- Функциональные устройства на основе двоичных счетчиков.
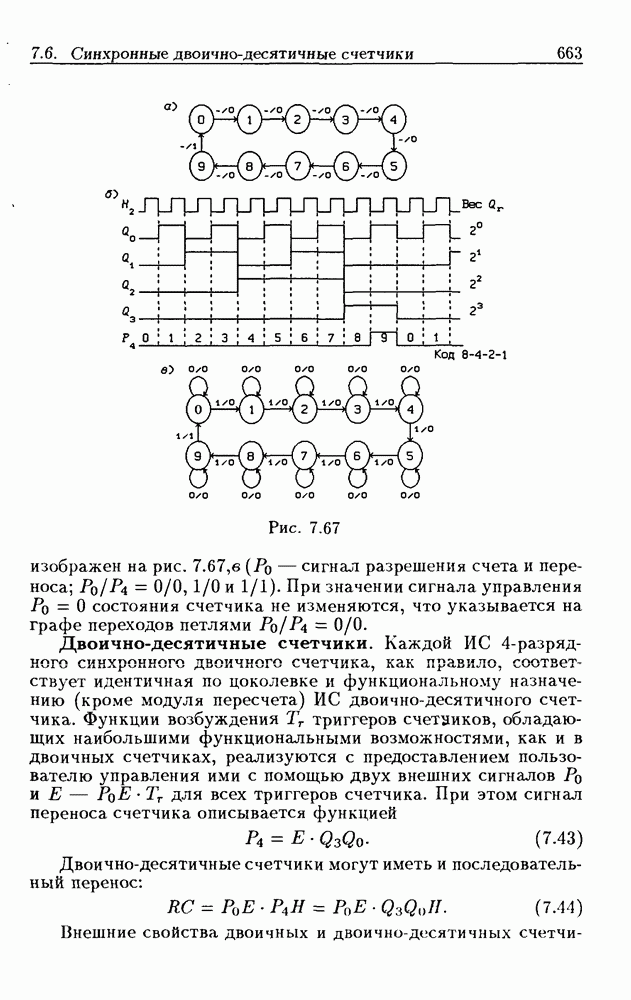
- 7.6. Синхронные двоично-десятичные счетчики
- 7.7. Синхронные реверсивные счетчики
- 7.8. Счетчики с расщепленным тактовым сигналом
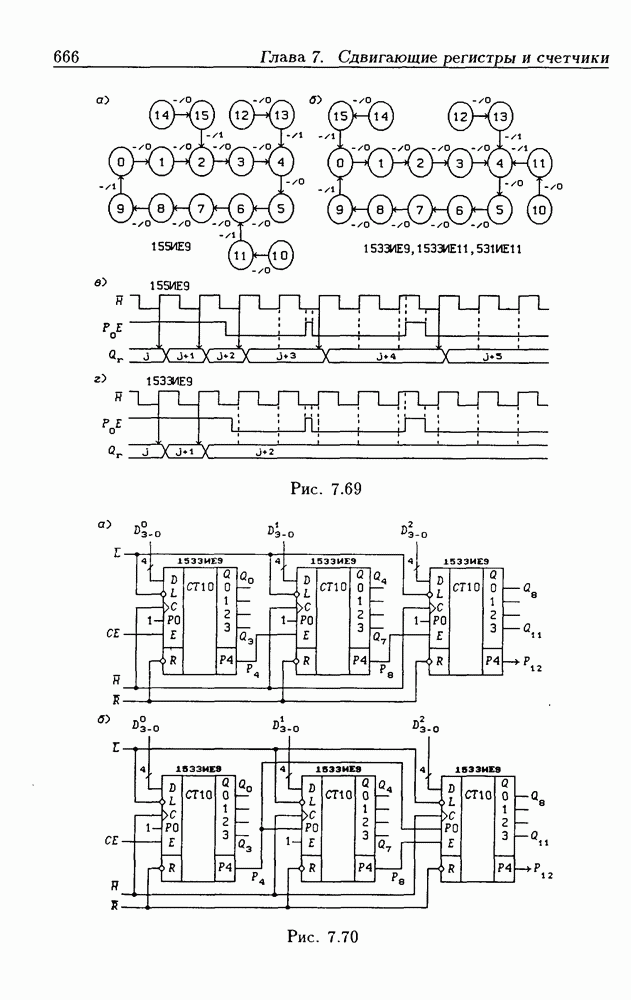
- 7.9. Счетчики на сдвигающих регистрах
- 7.10. Кольцевые счетчики
- 7.11. Делители частоты
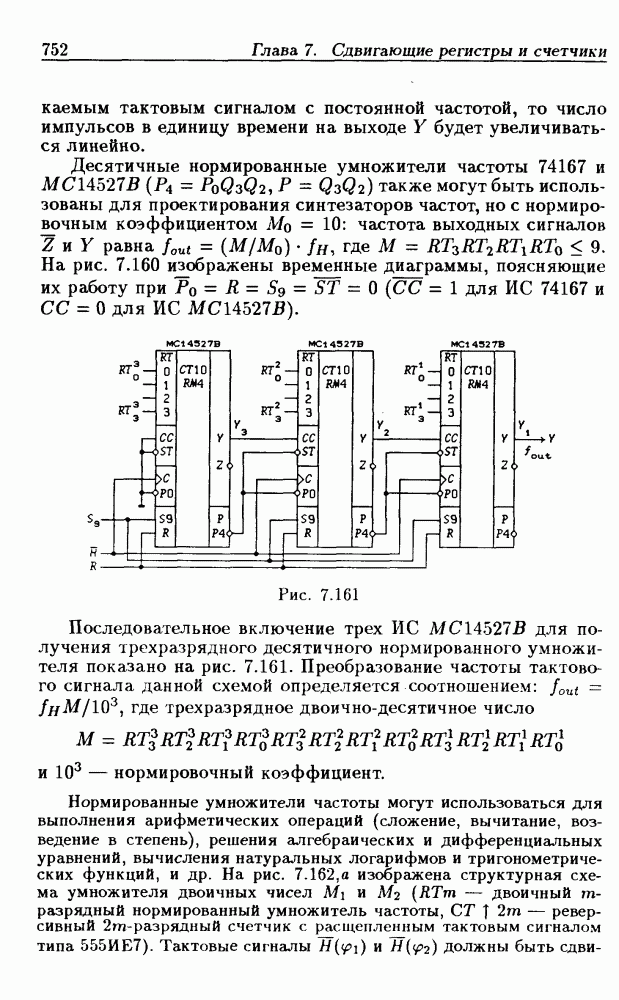
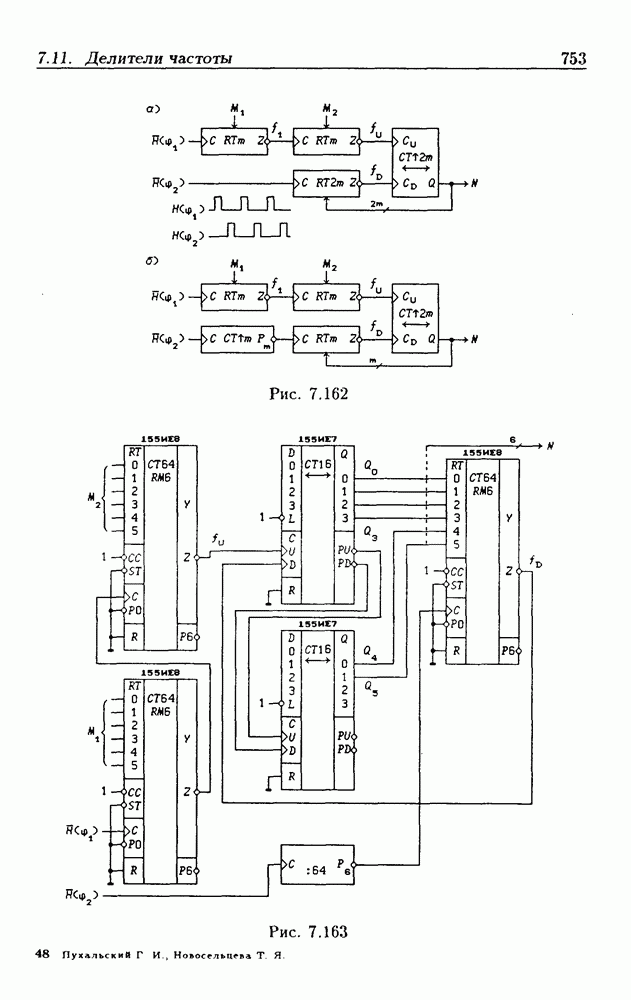
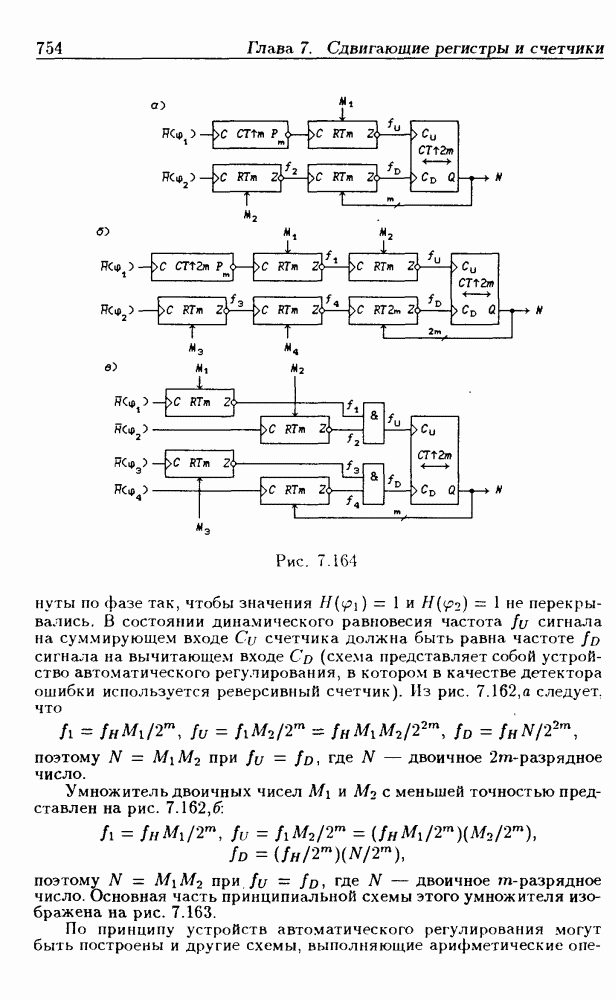
- Нормированные умножители частоты.
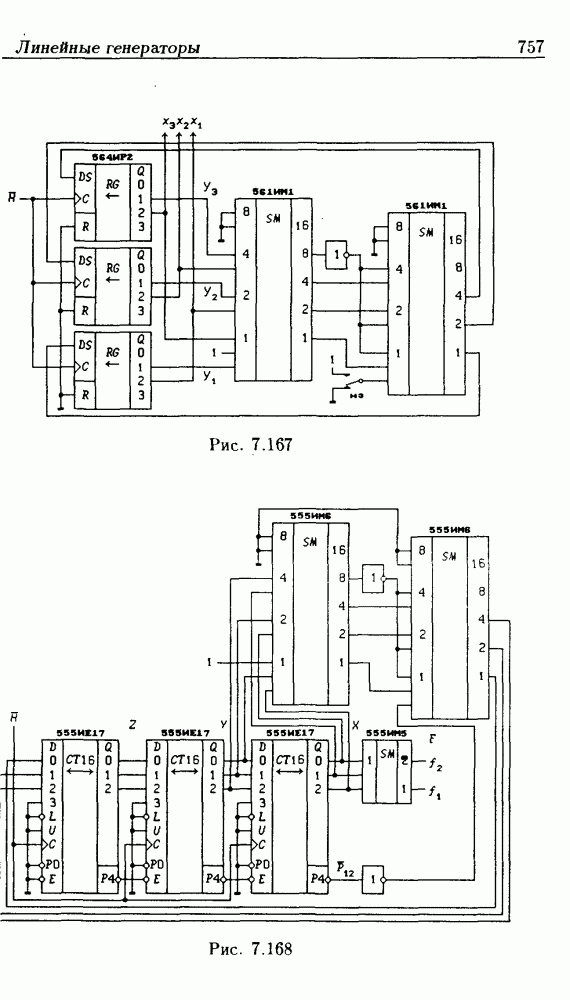
- 7.12. Линейные генераторы
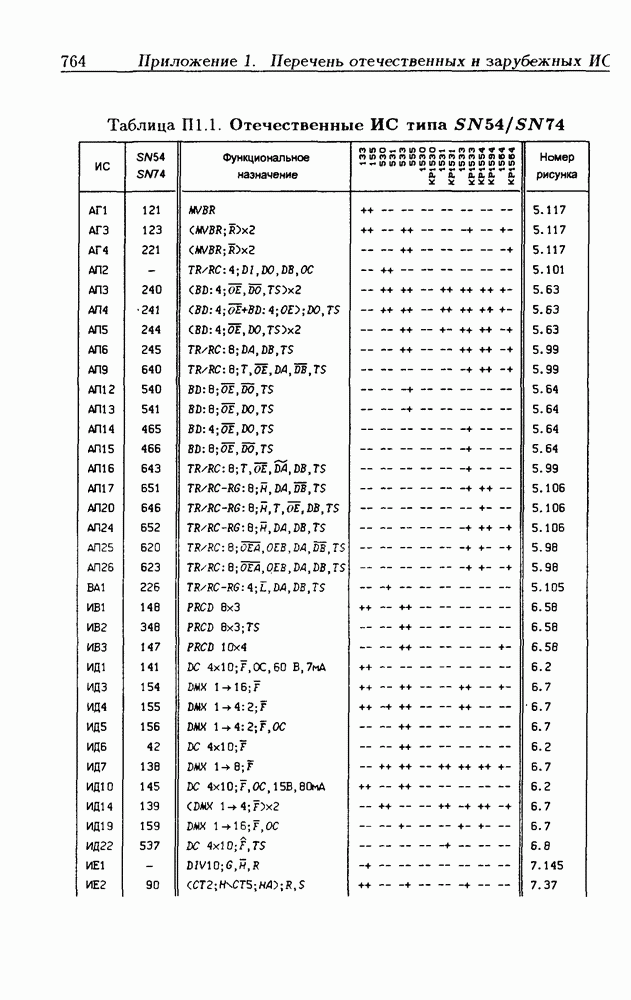
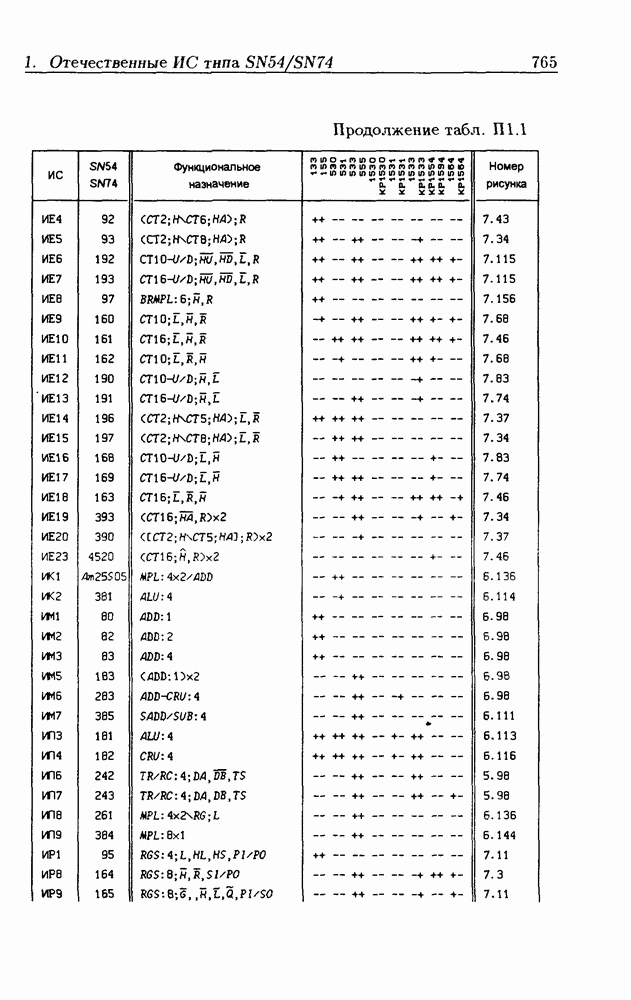
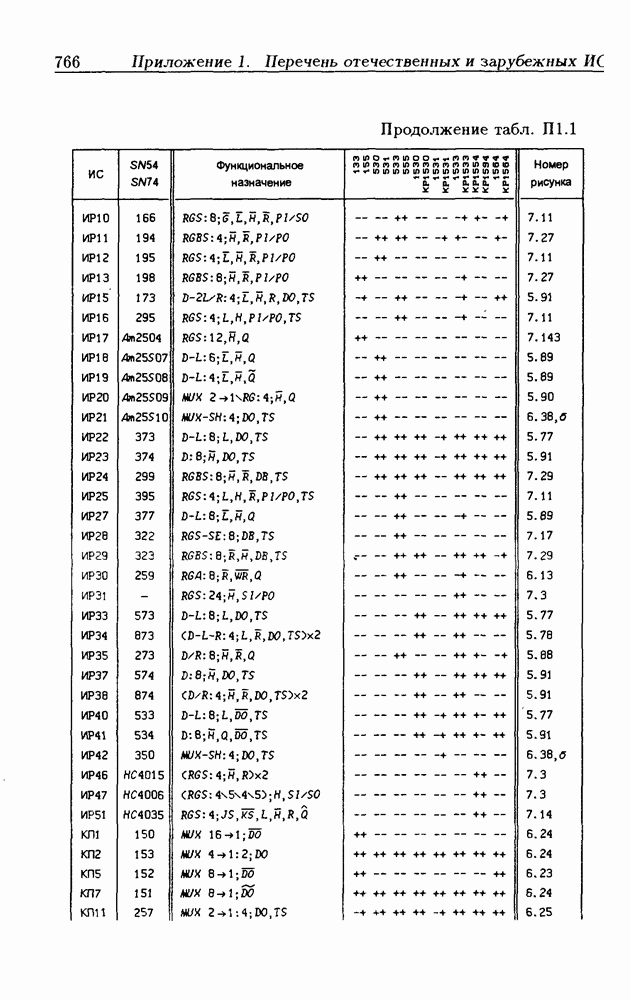
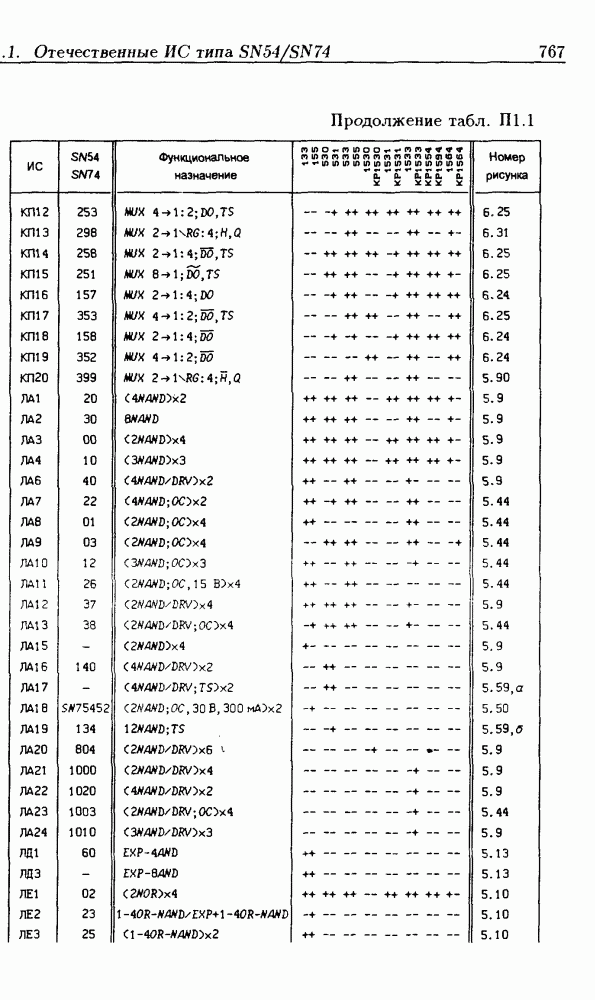
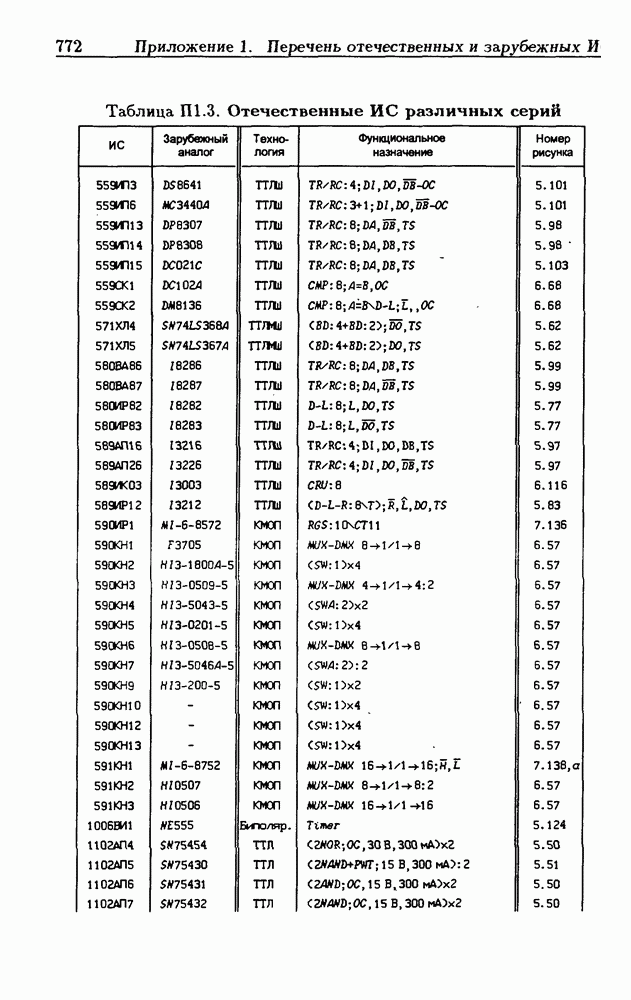
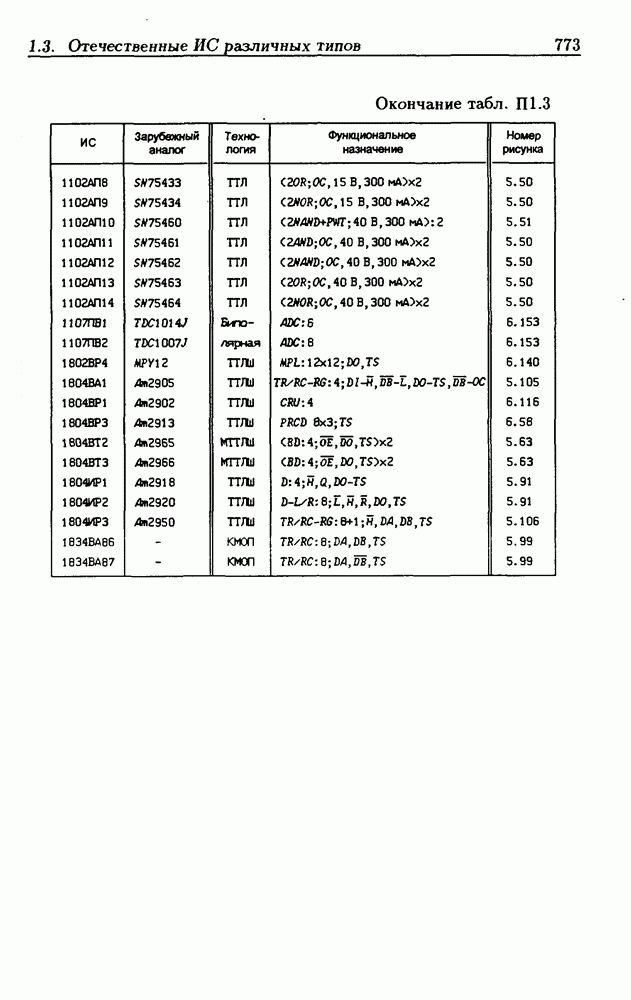
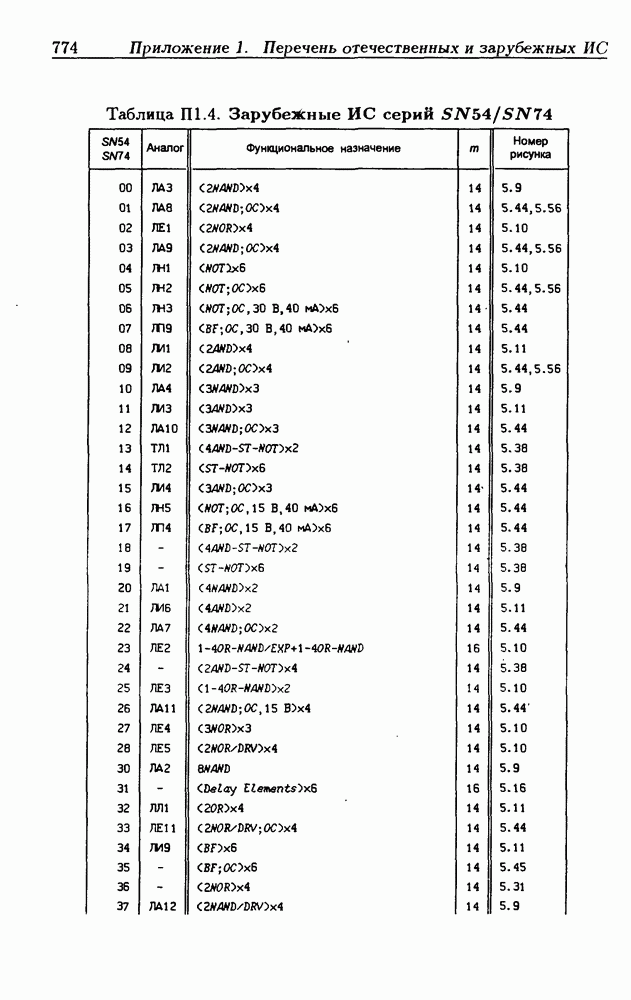
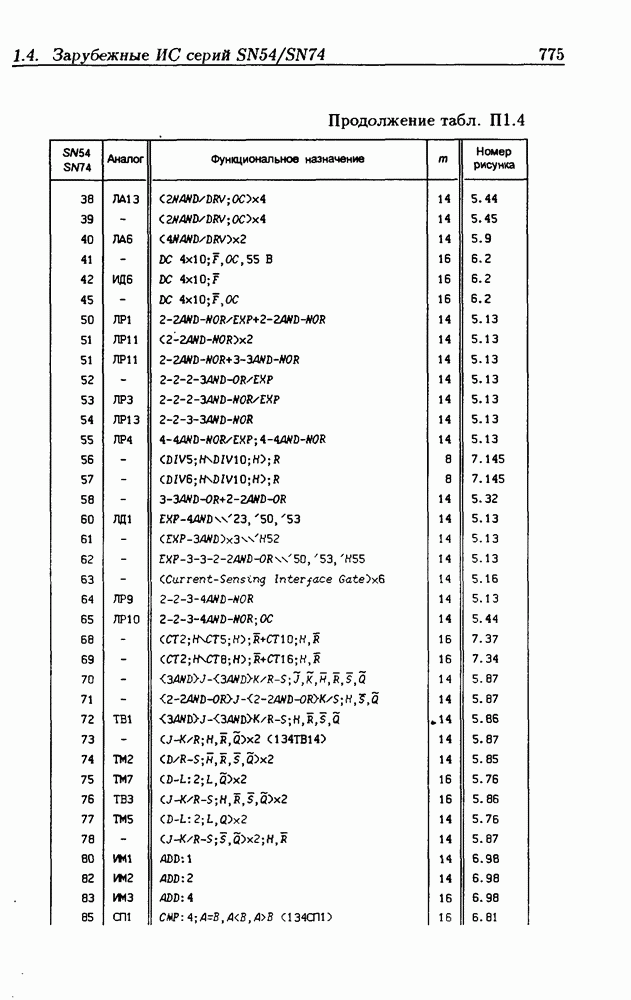
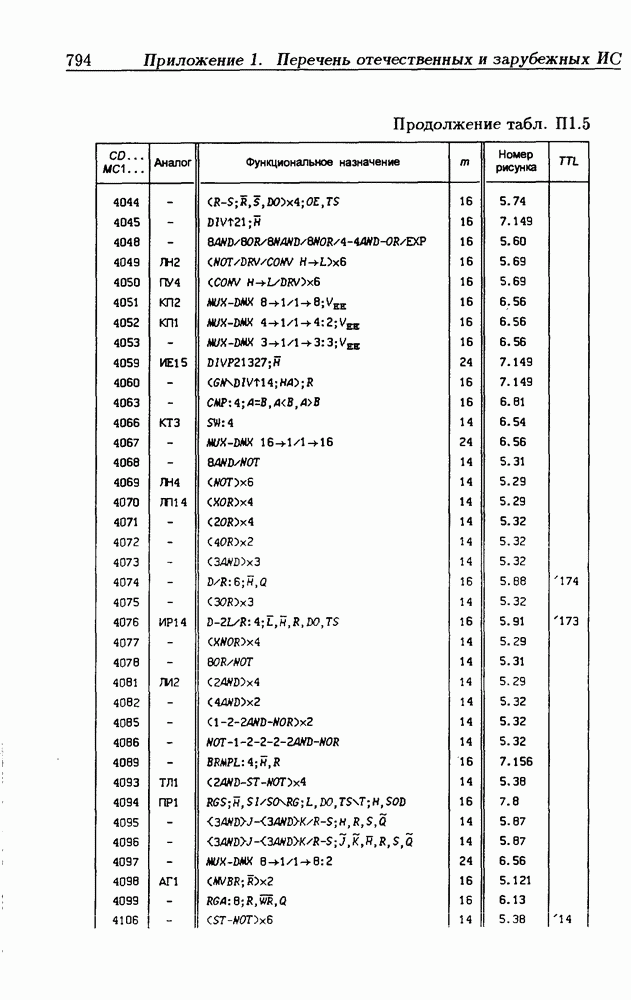
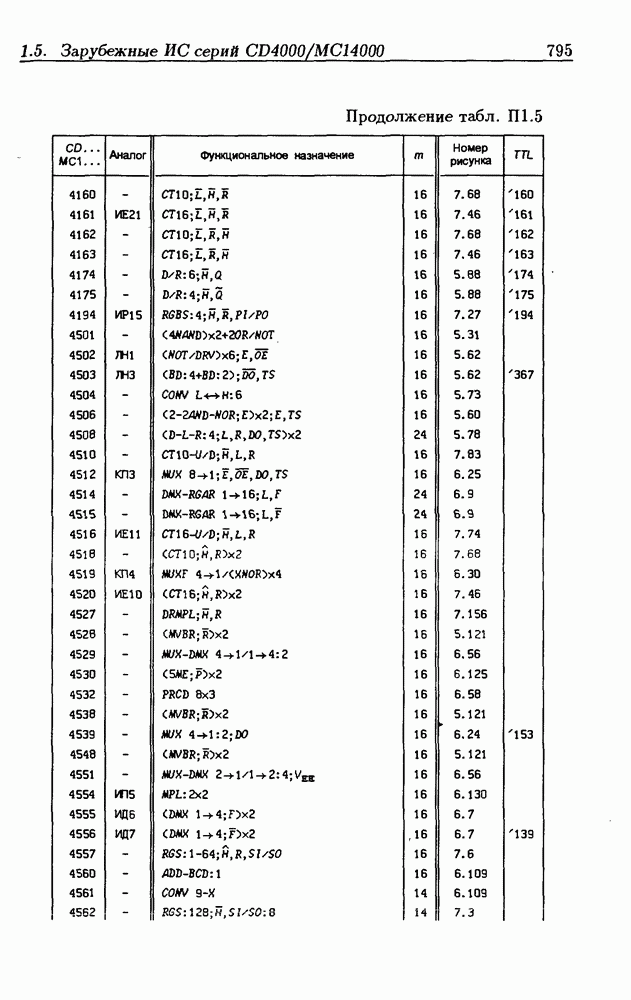
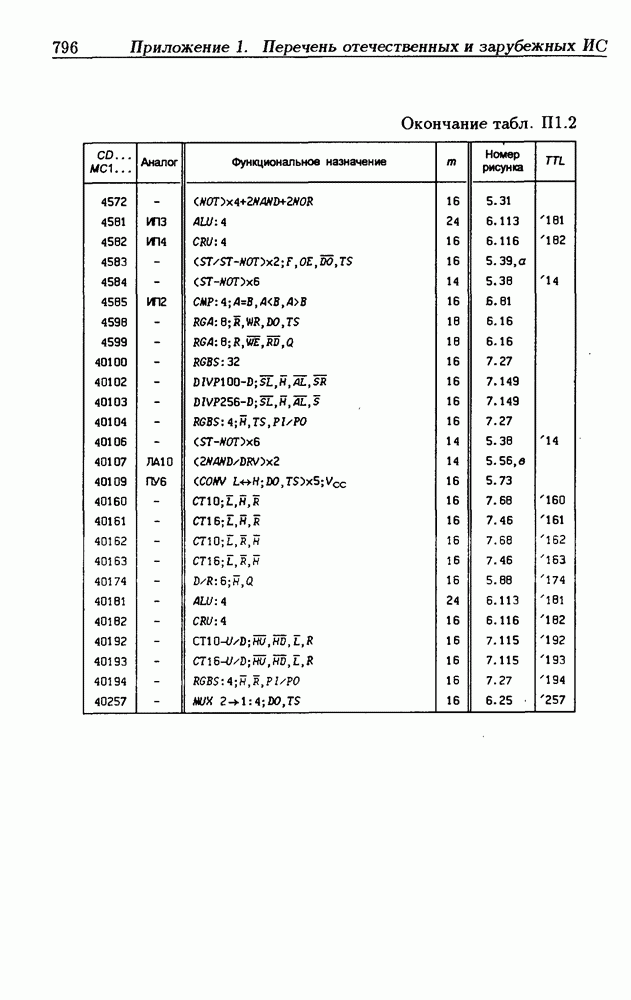
- Приложение 1. Перечень отечественных и зарубежных ИС
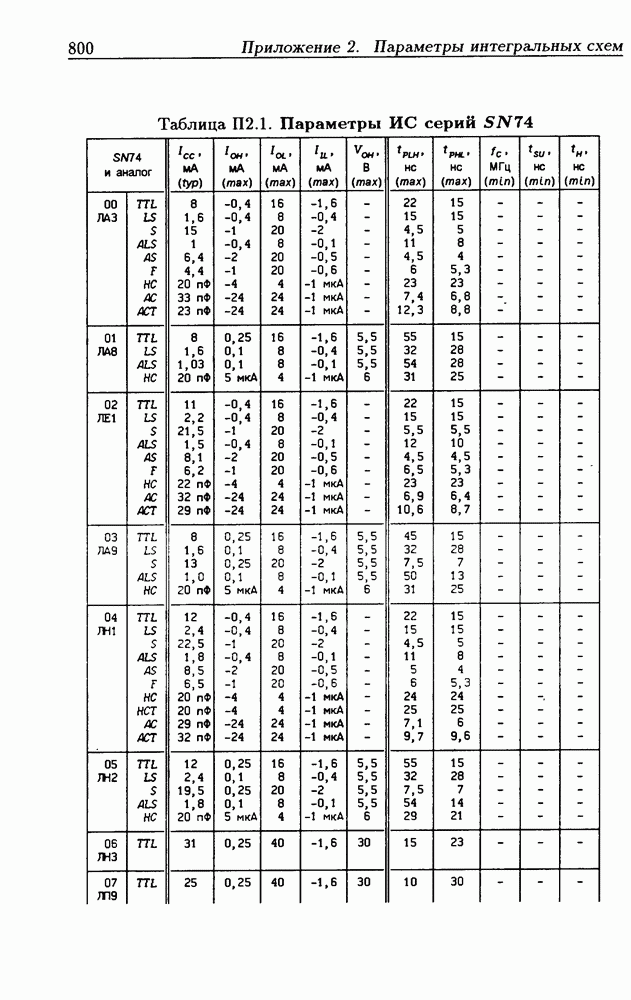
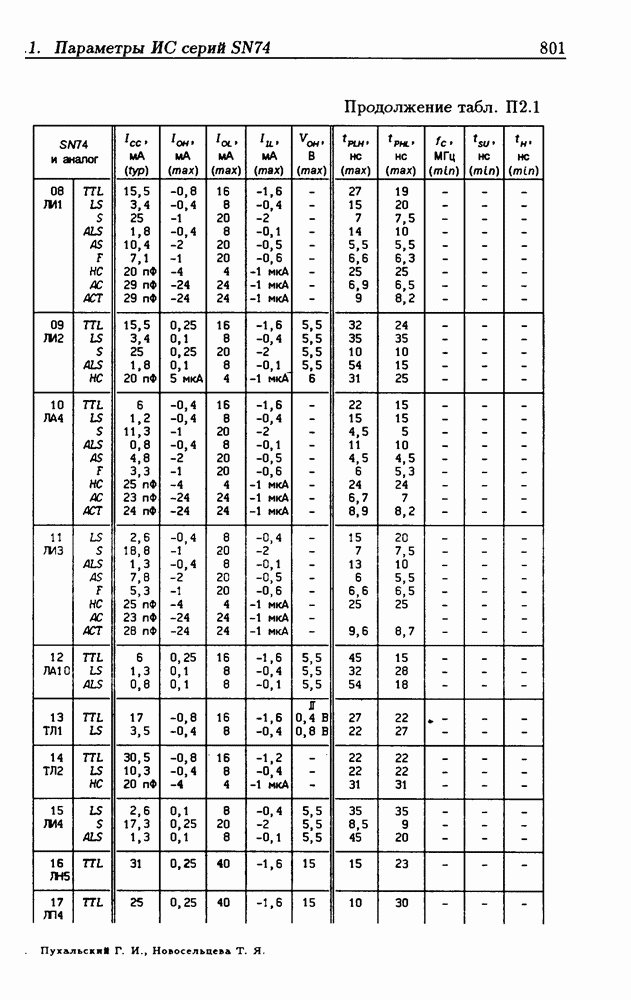
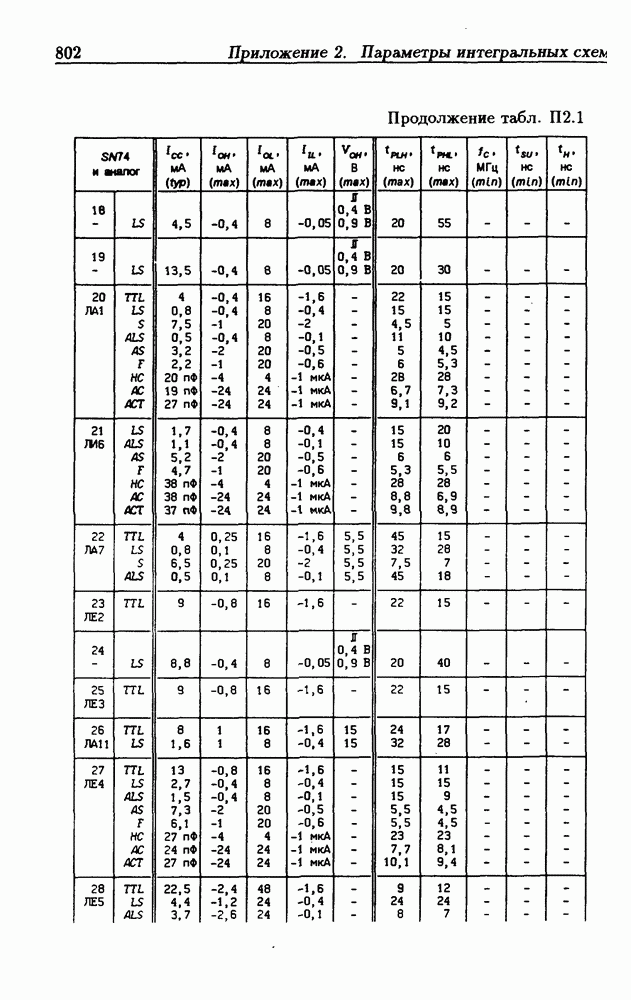
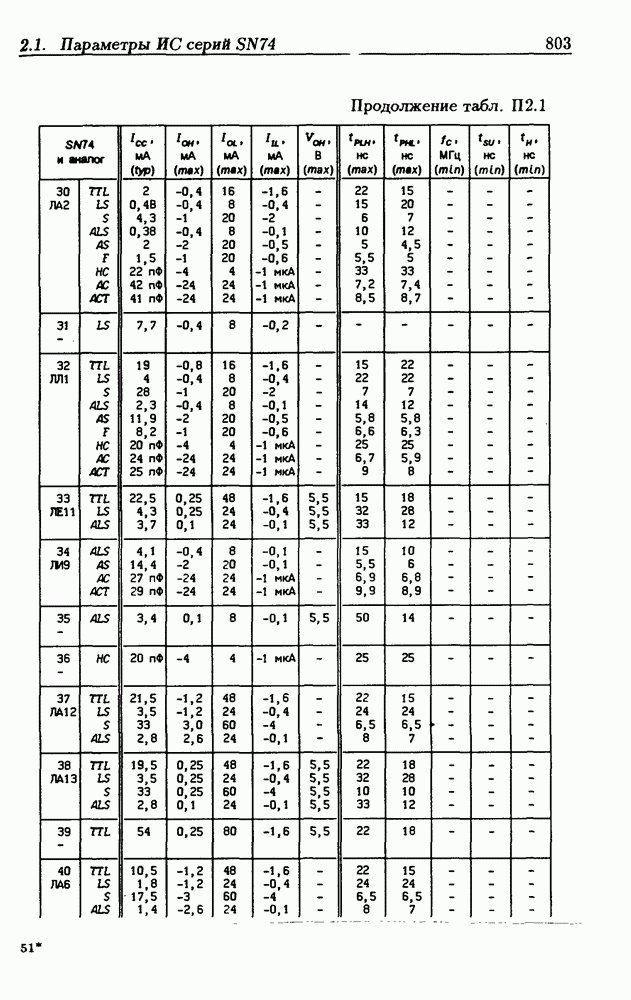
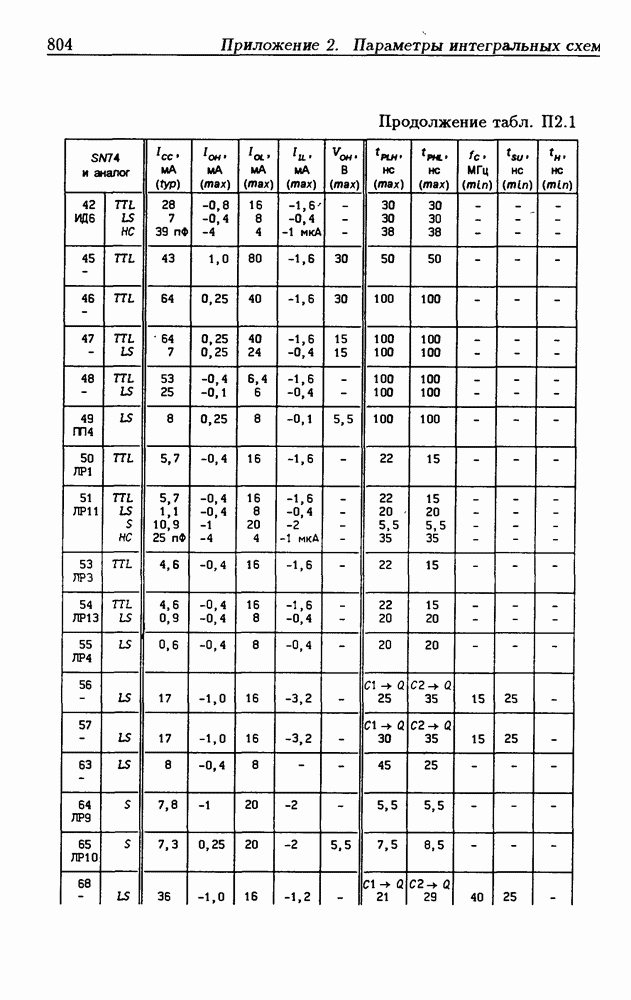
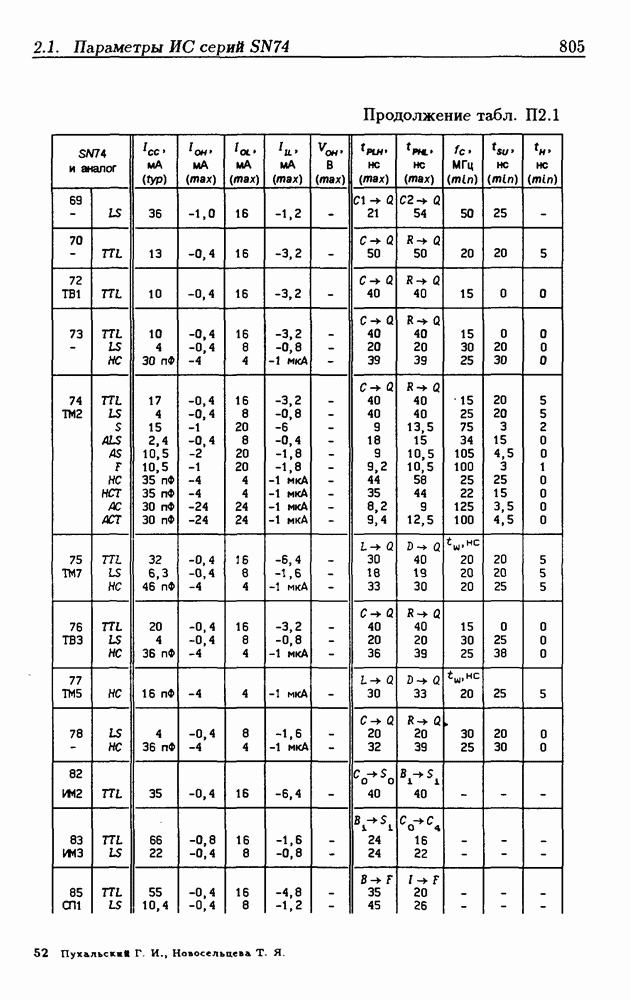
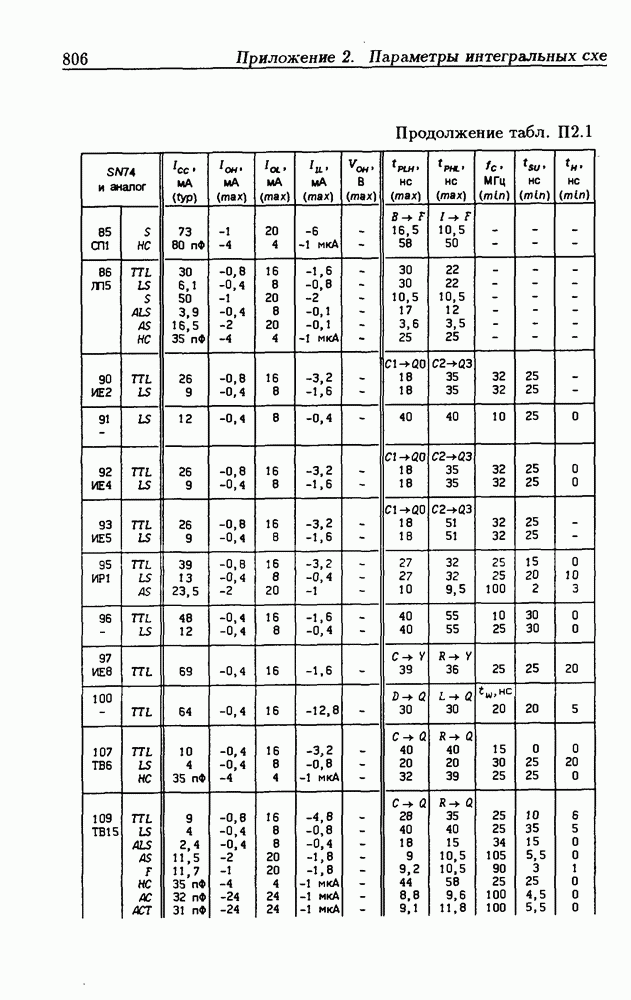
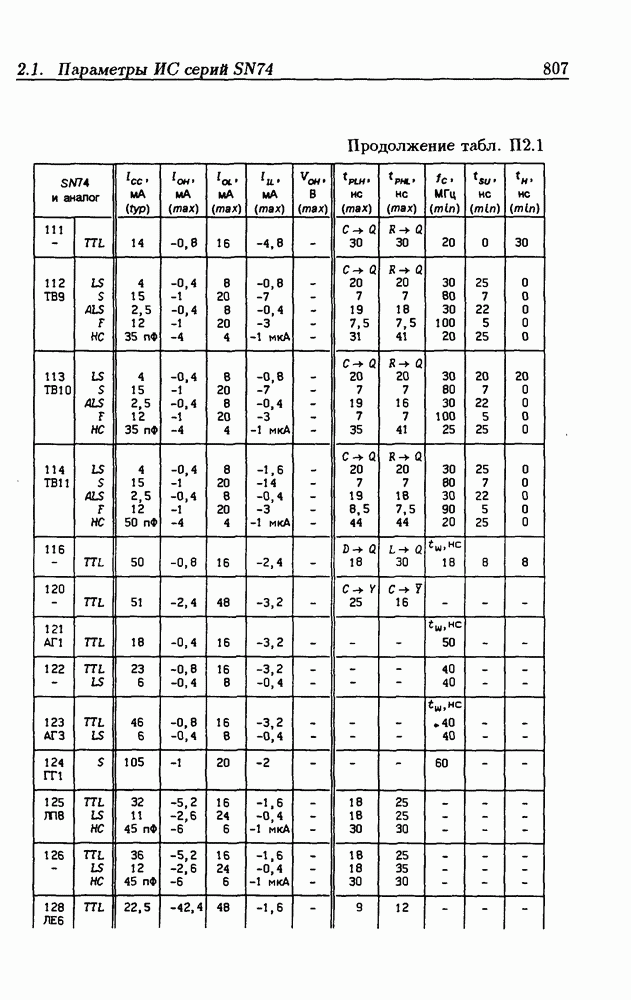
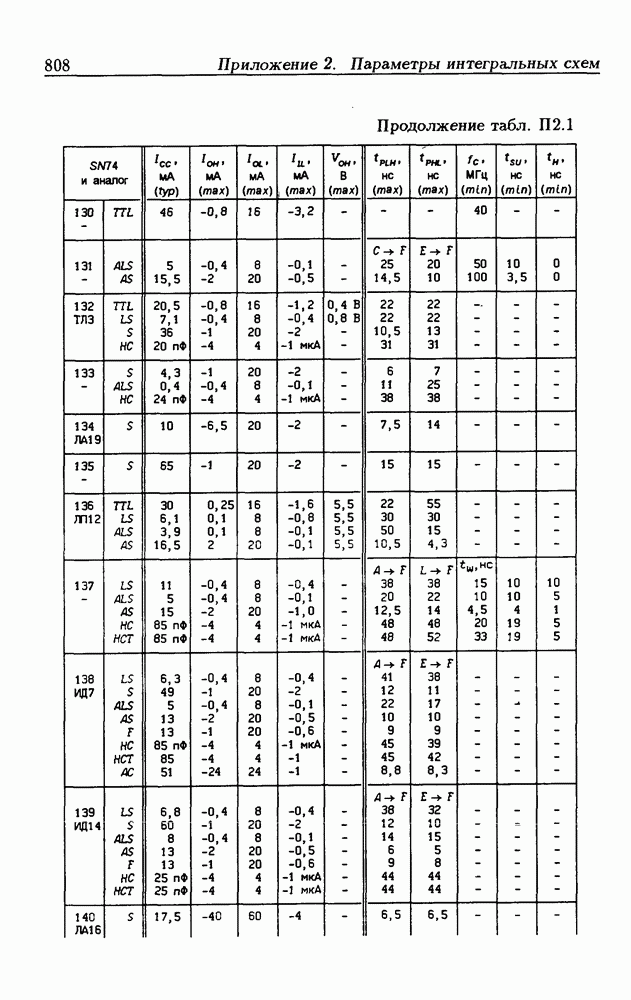
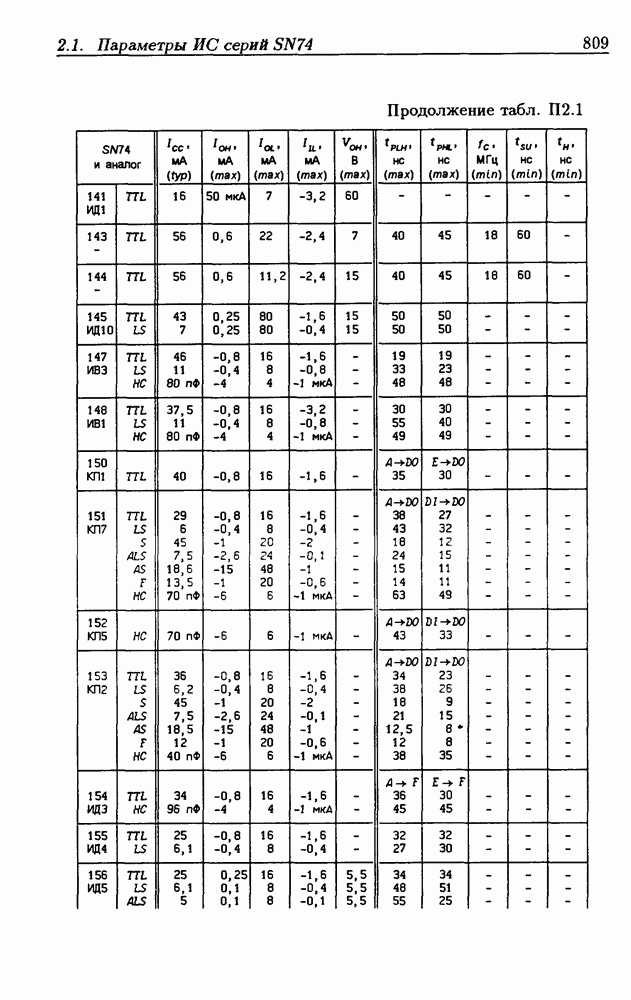
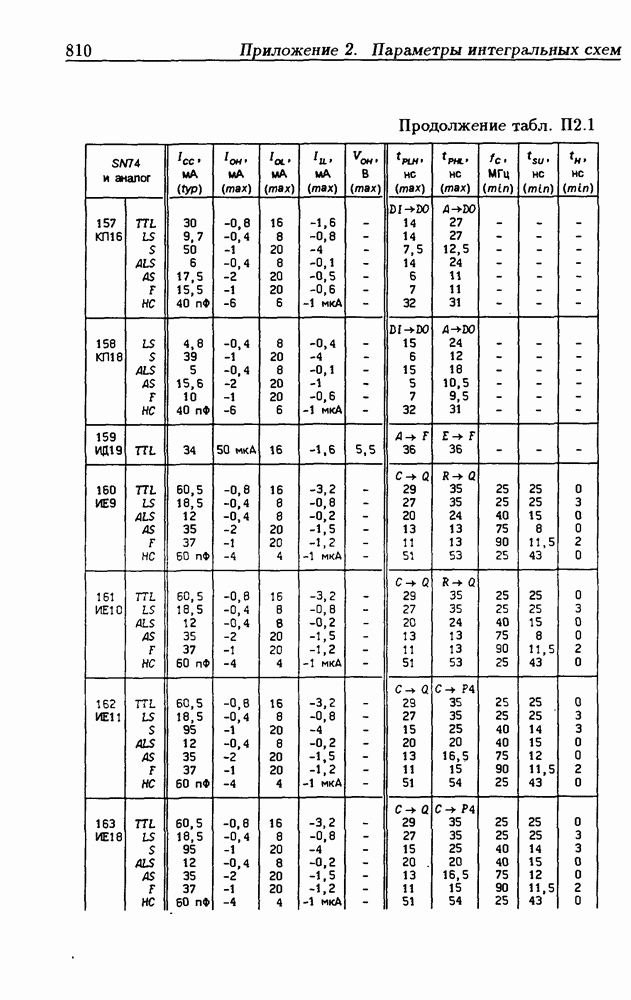
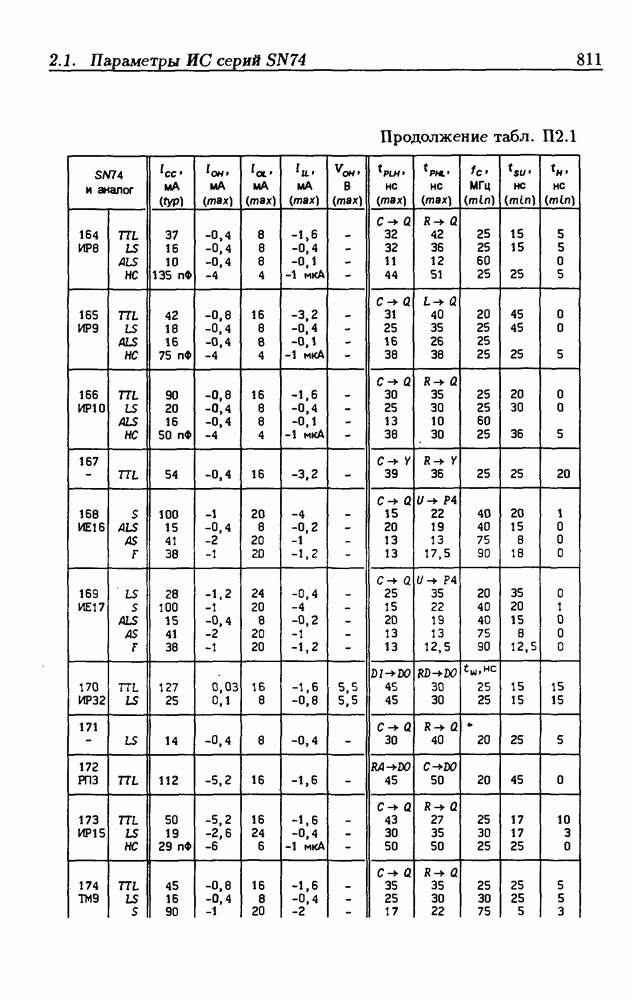
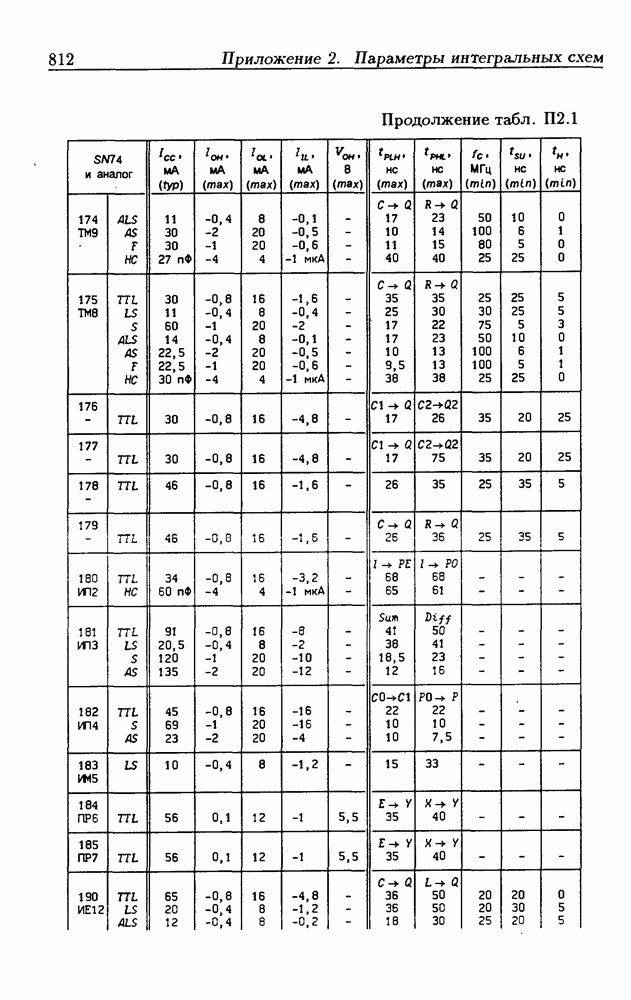
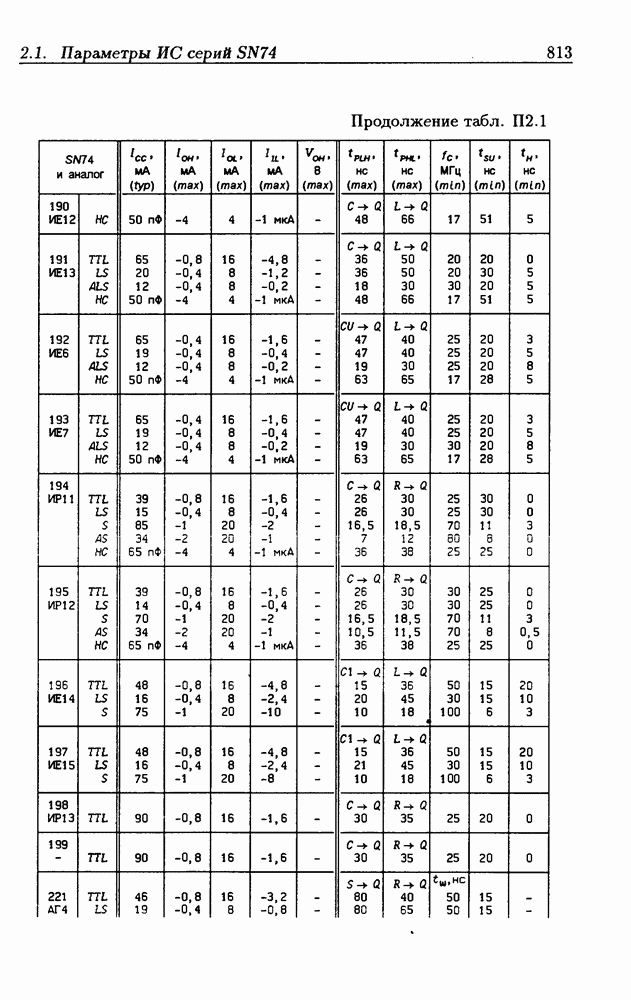
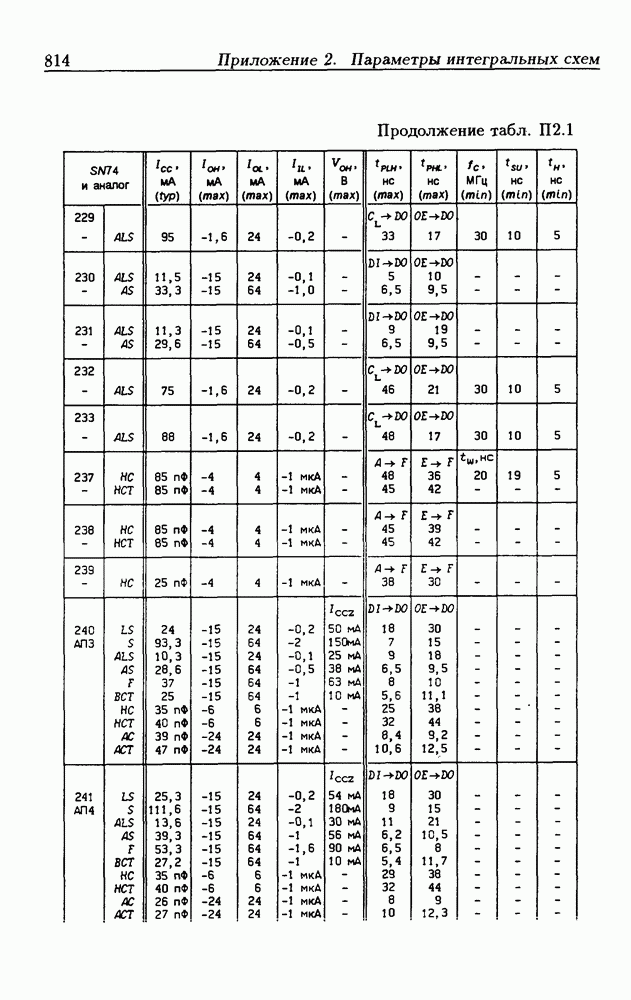
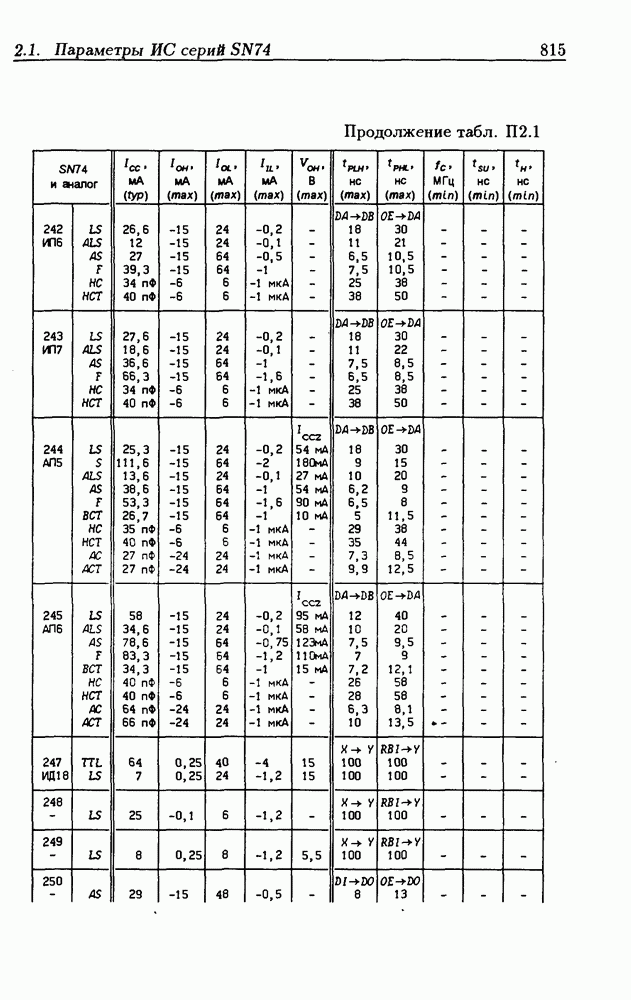
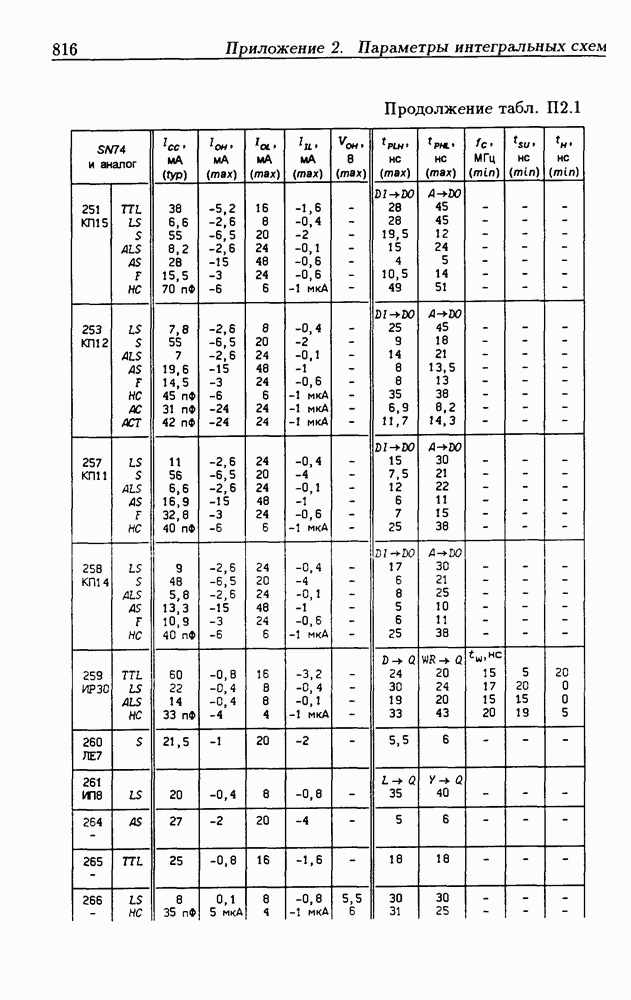
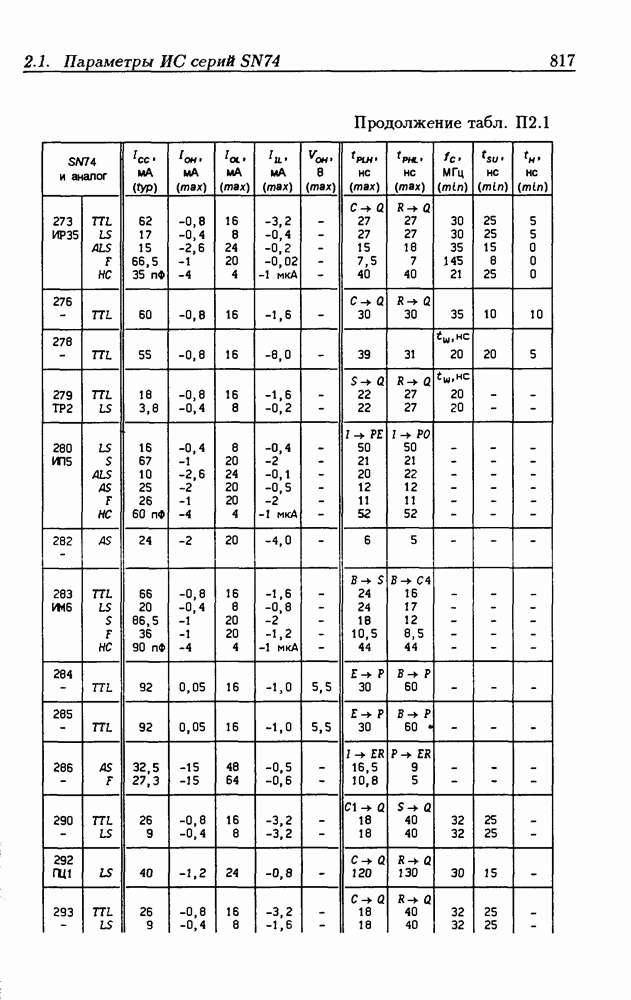
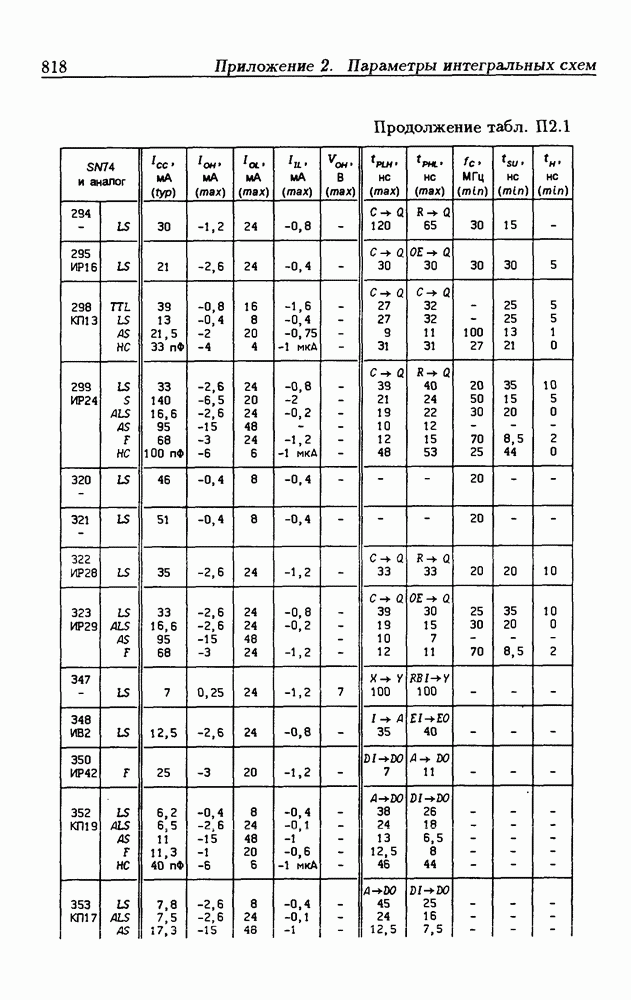
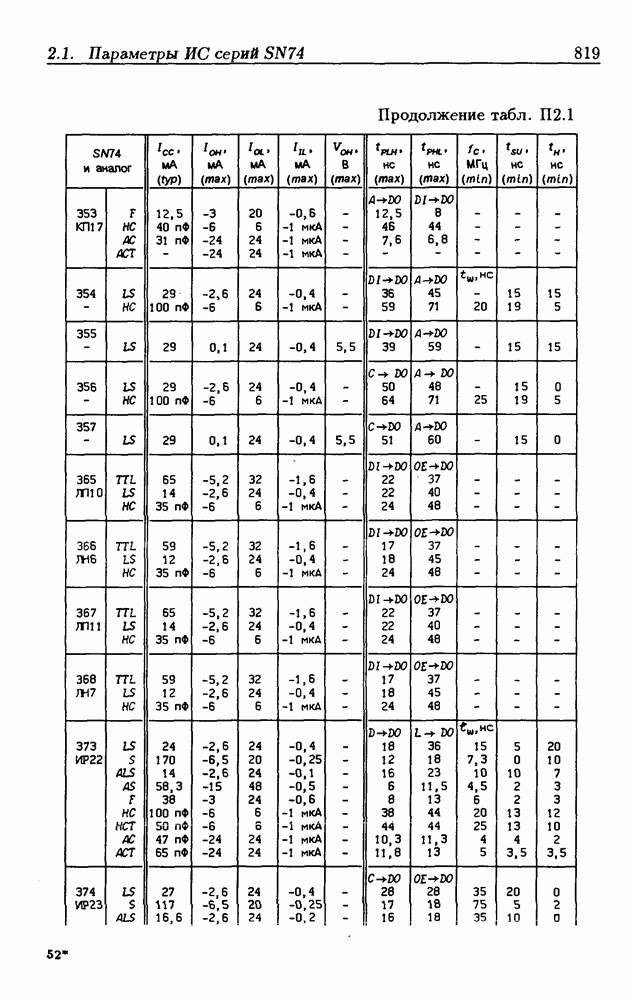
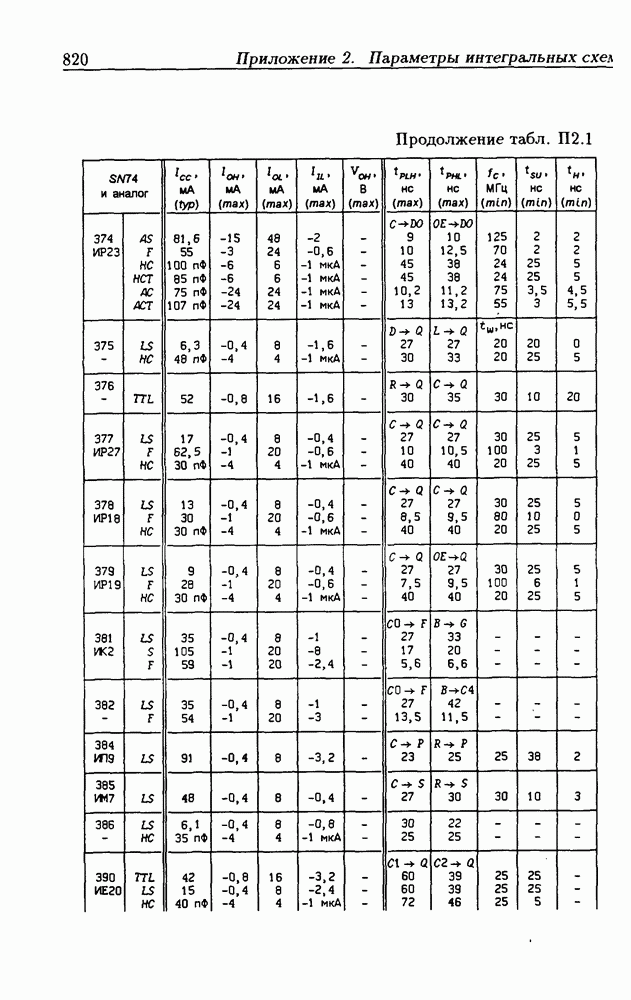
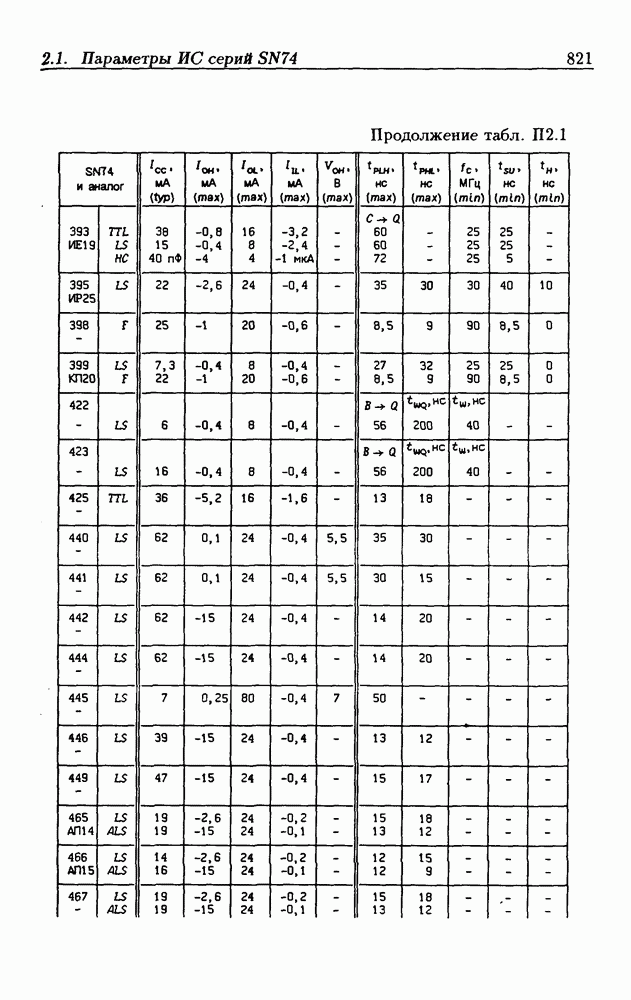
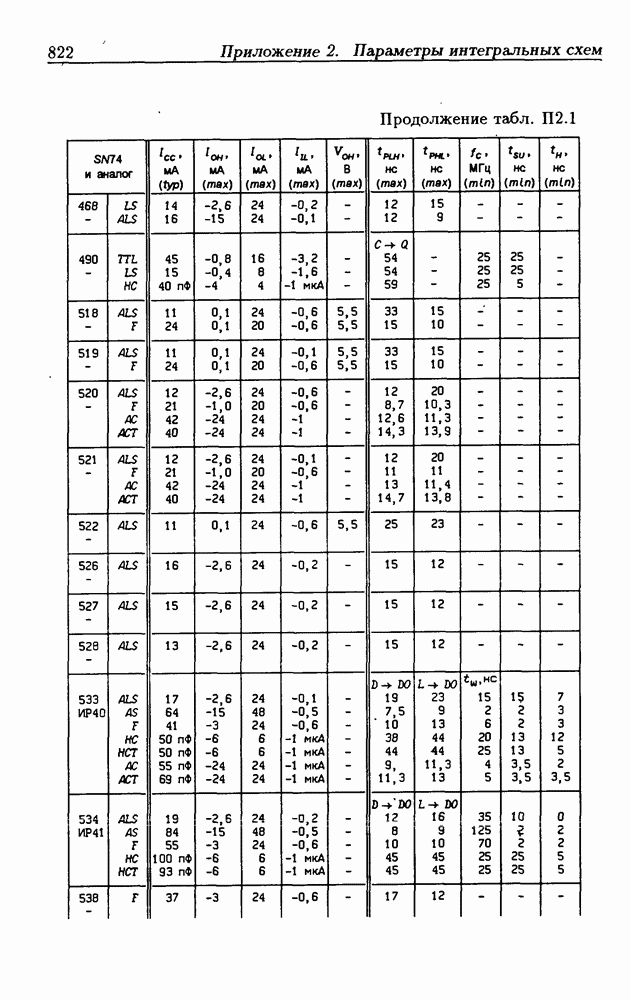
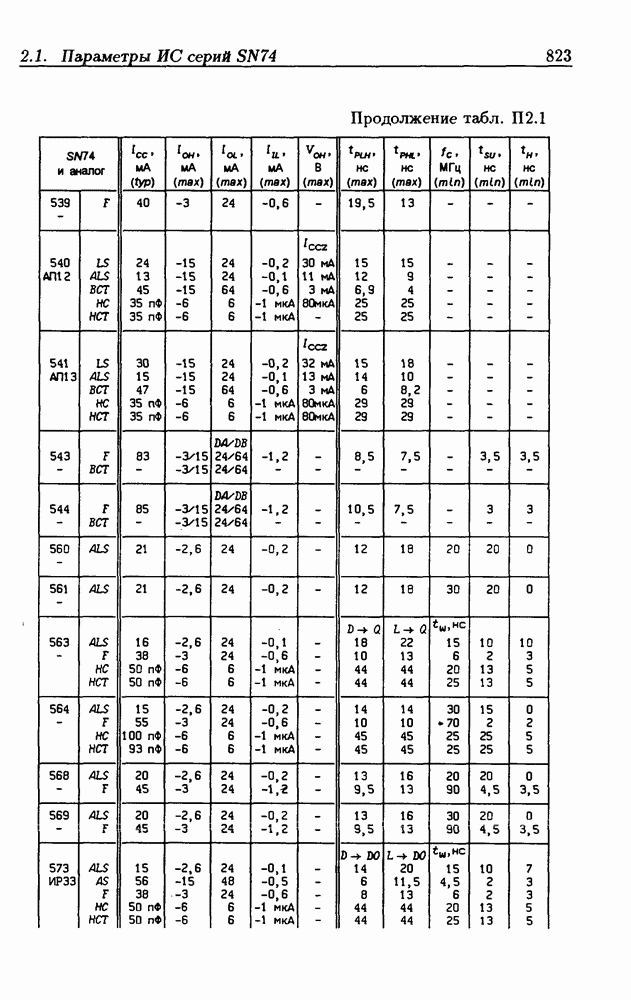
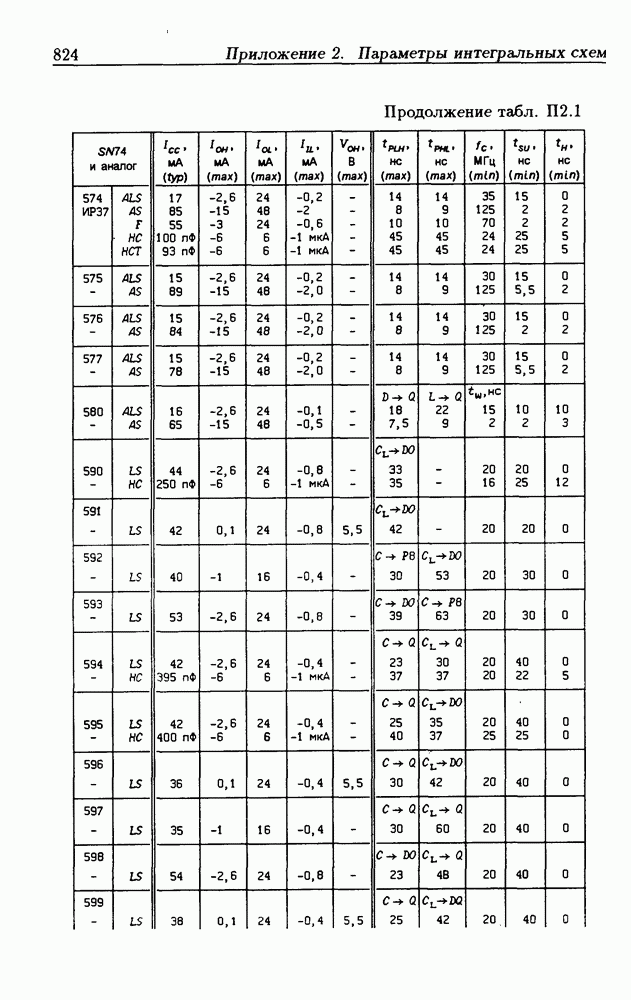
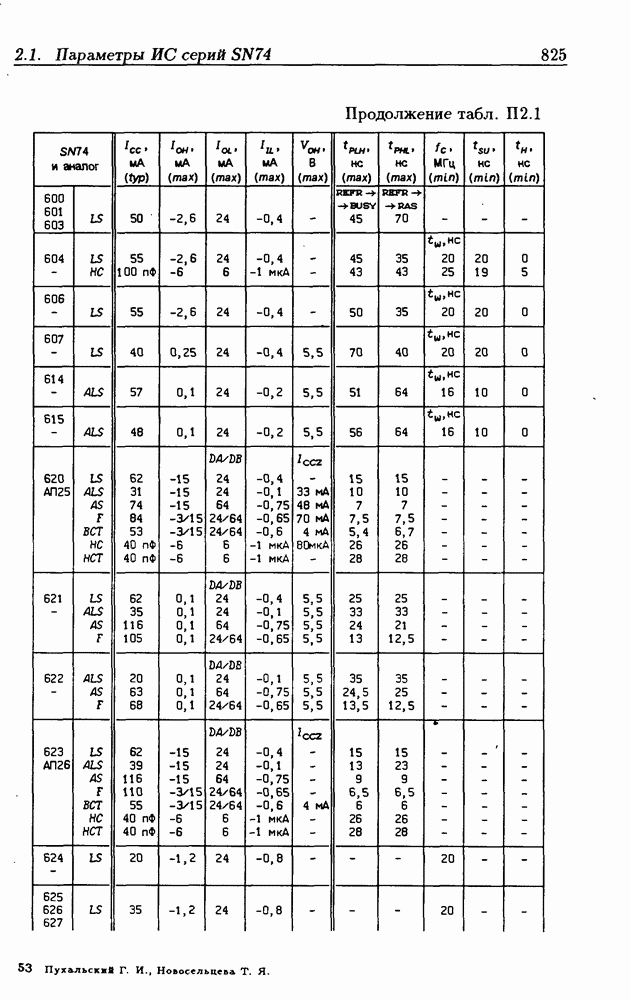
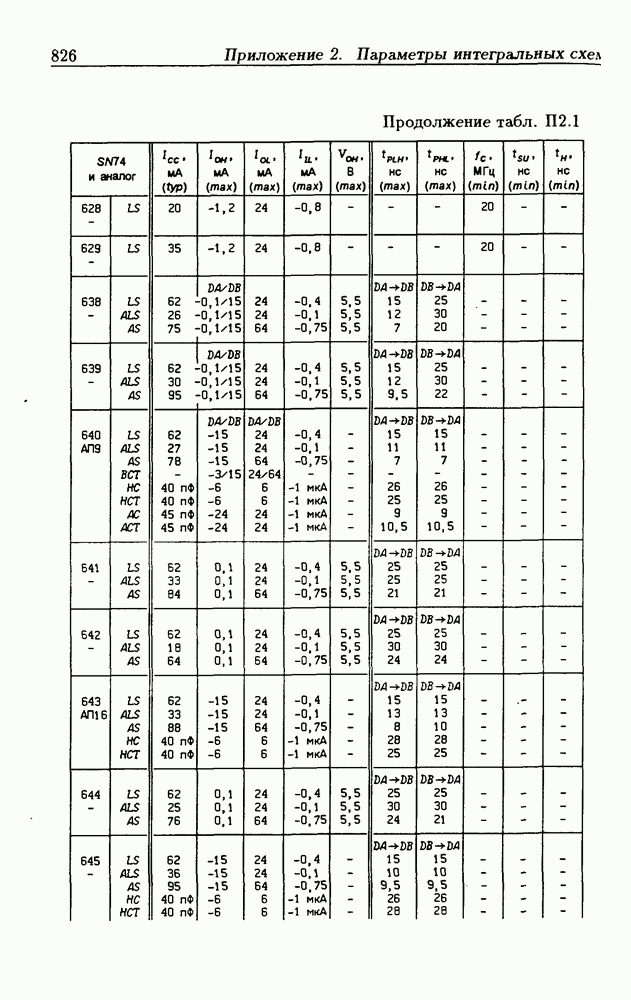
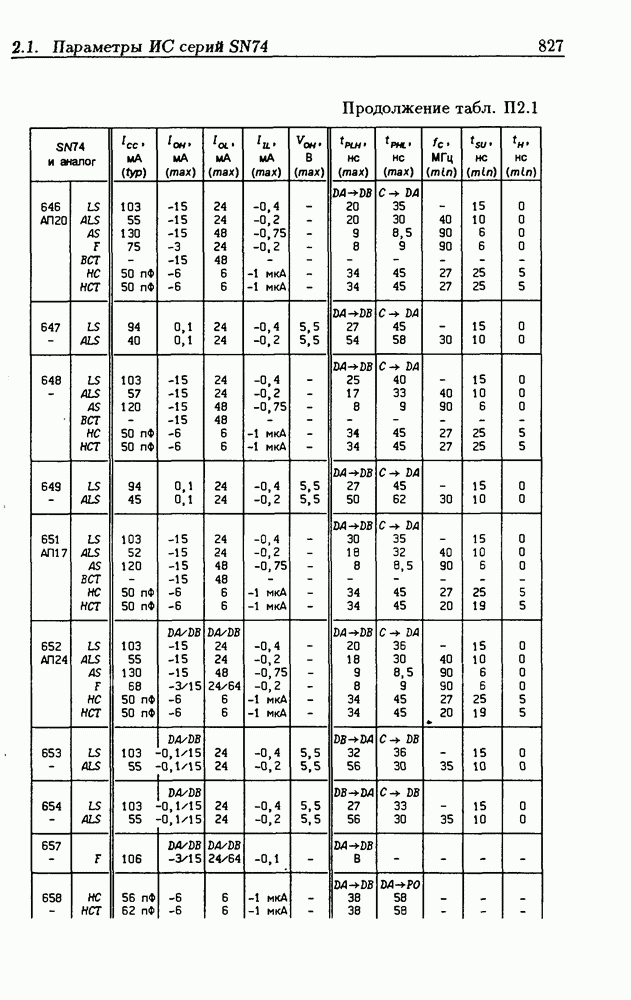
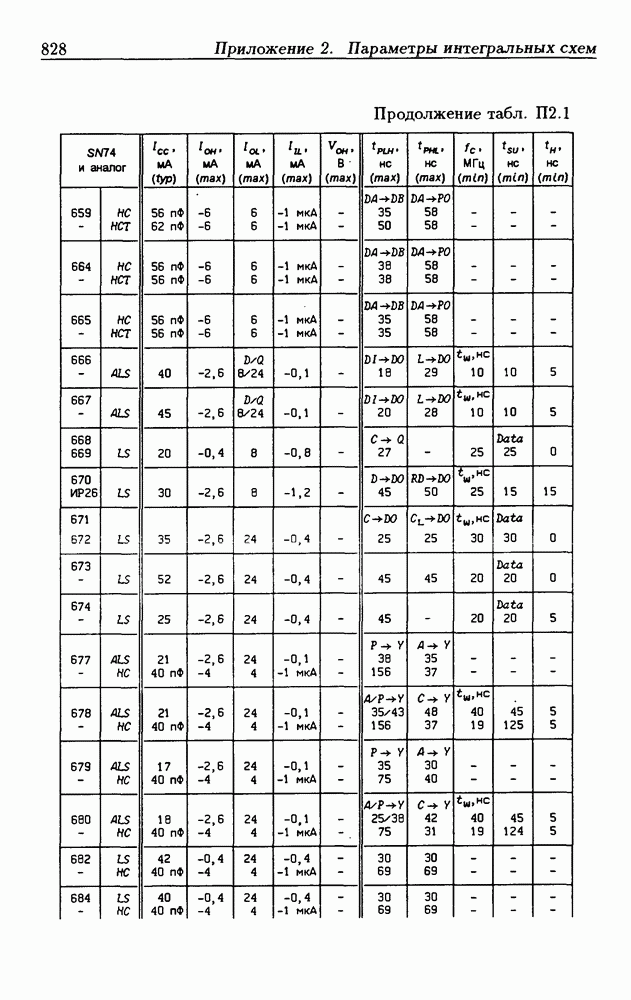
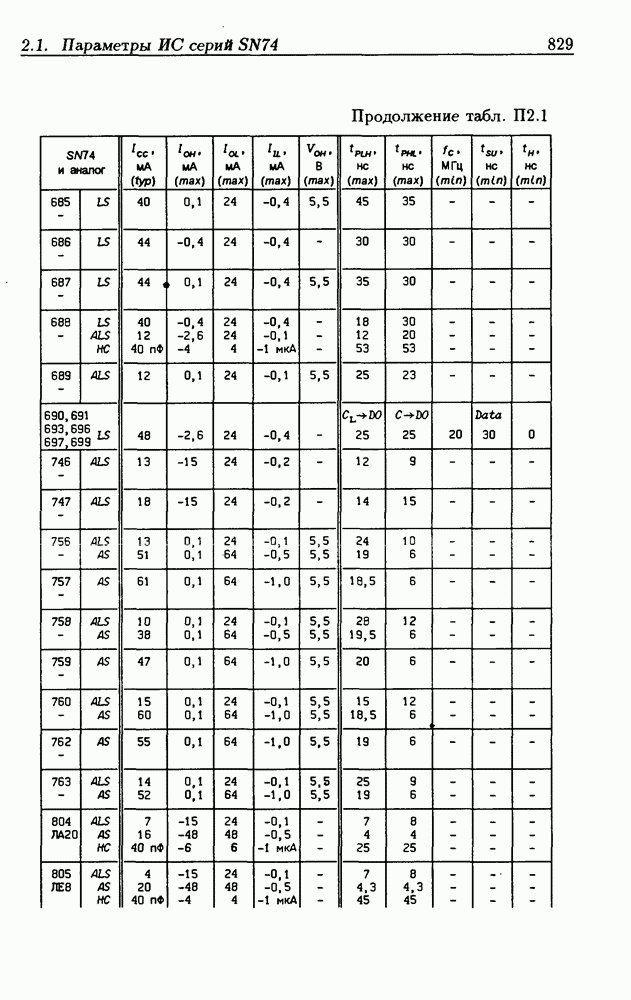
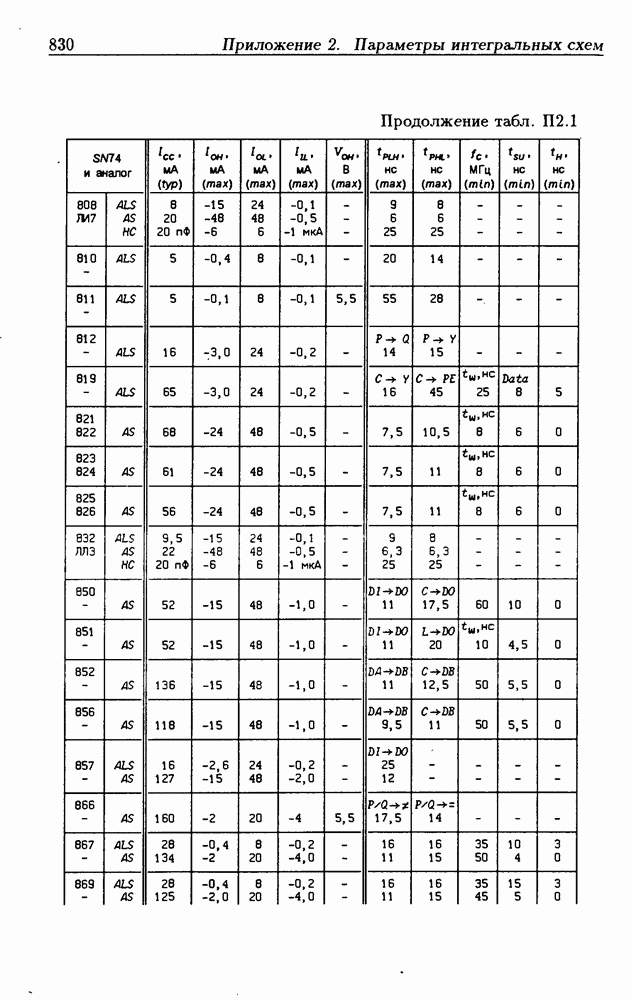
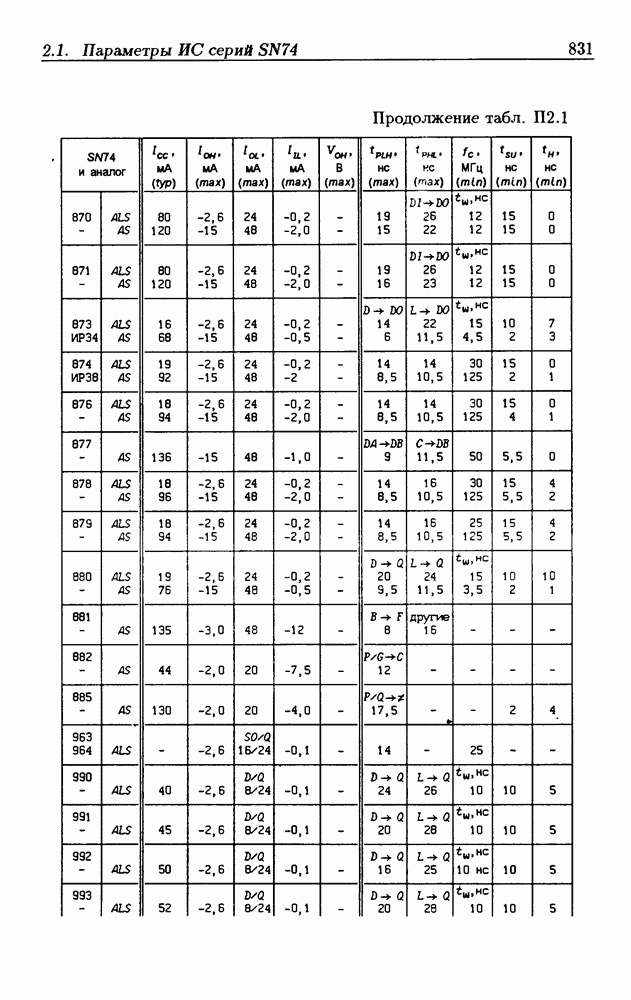
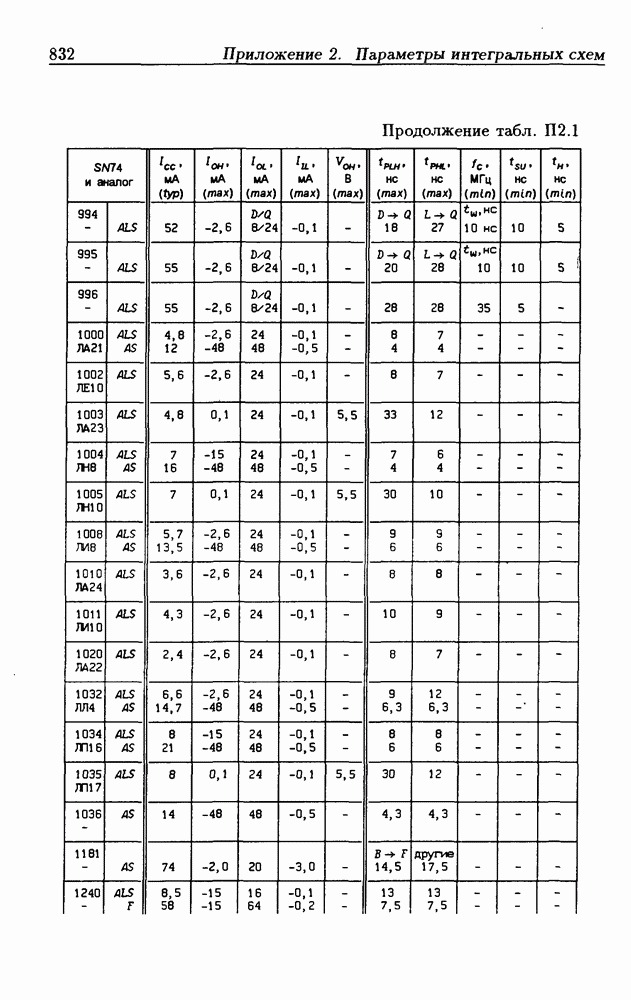
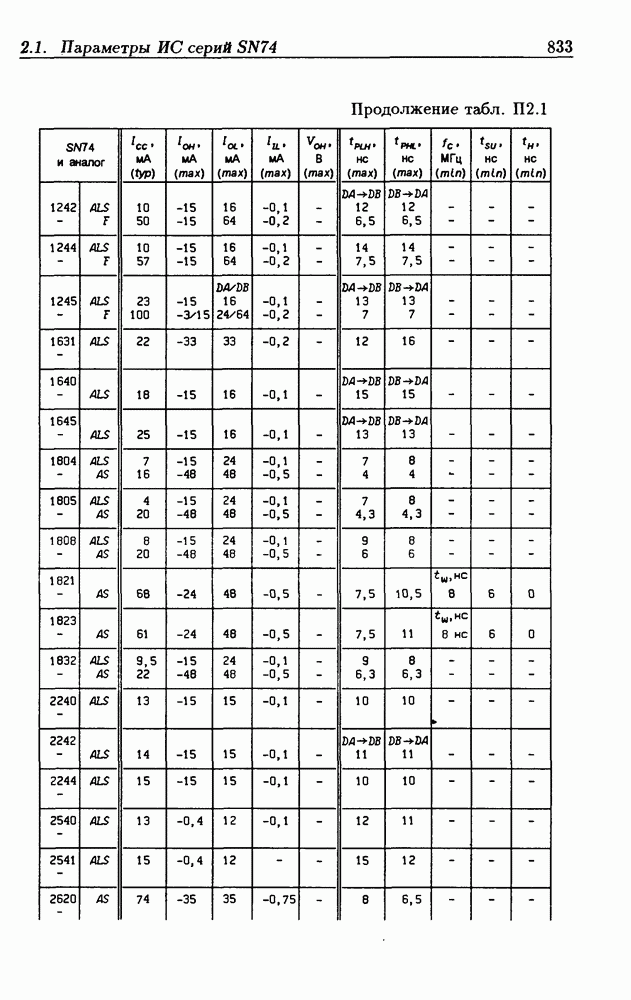
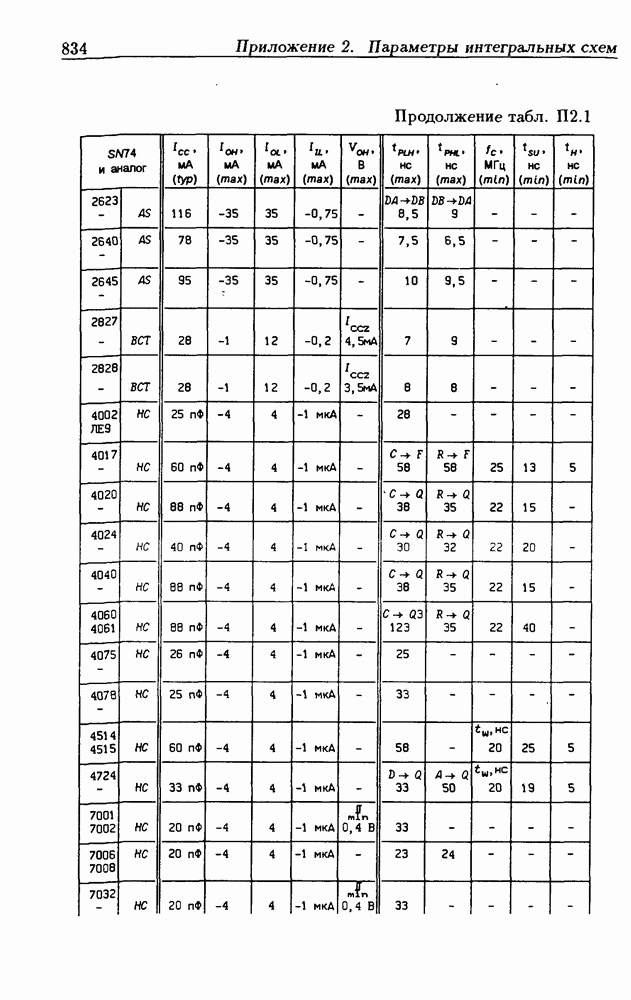
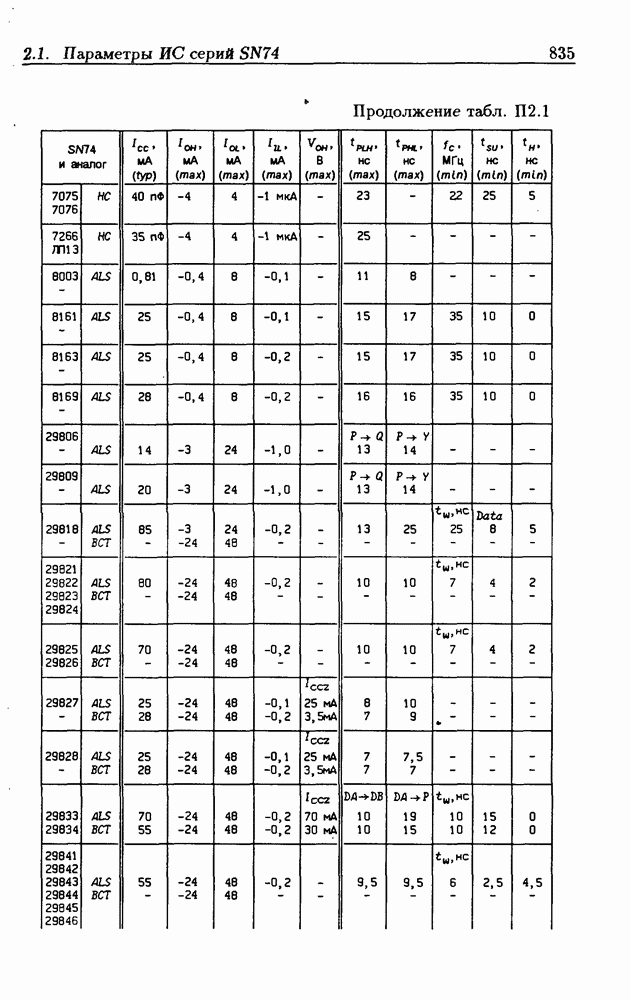
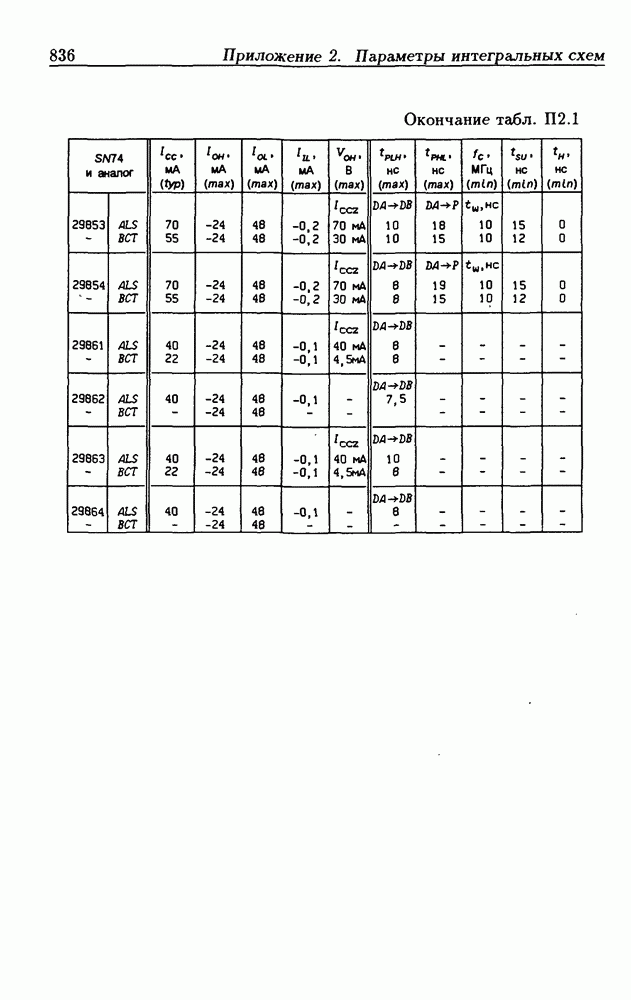
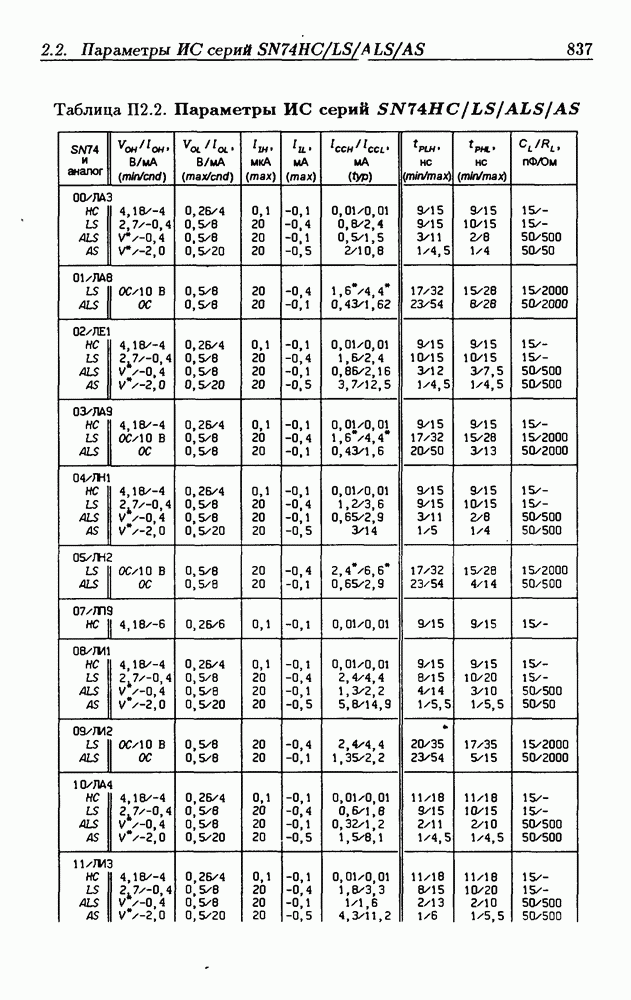
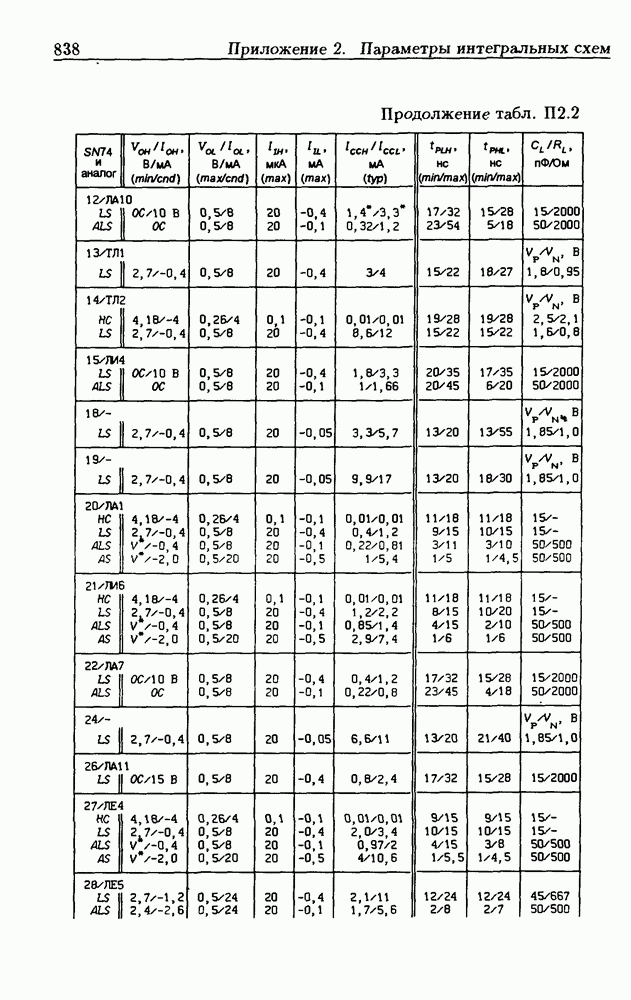
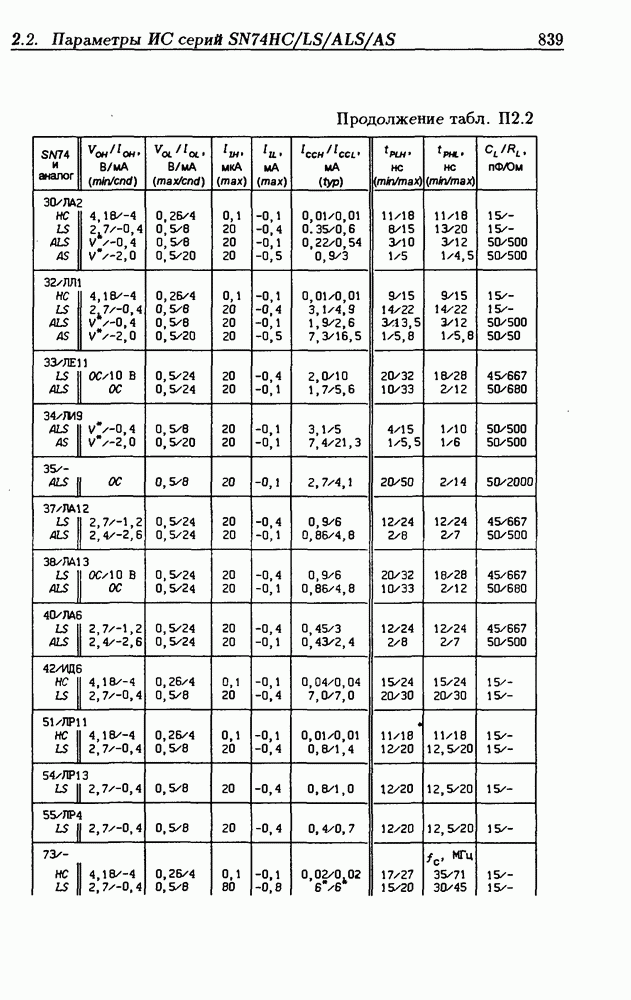
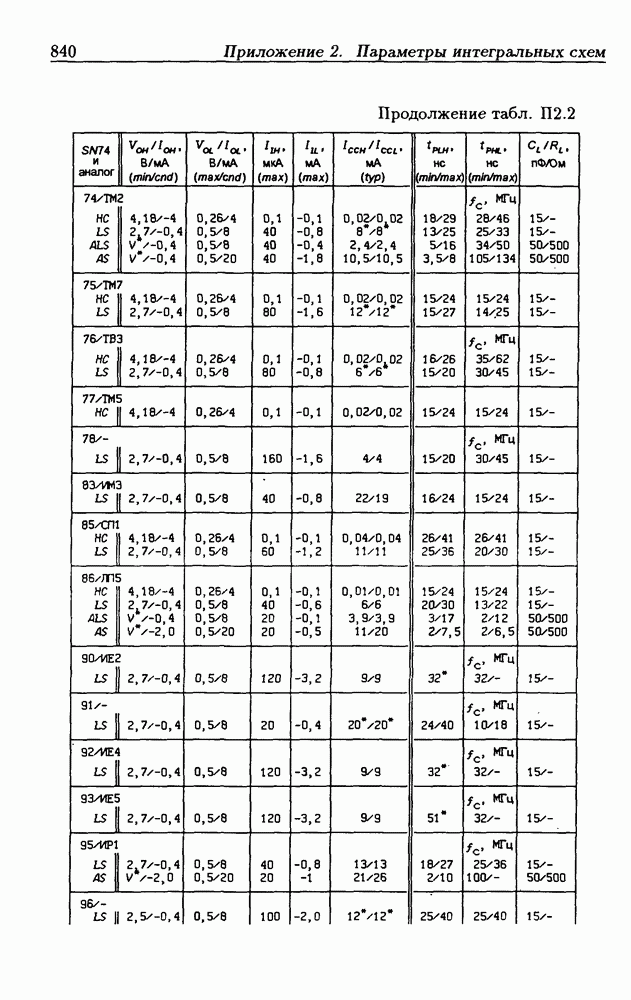
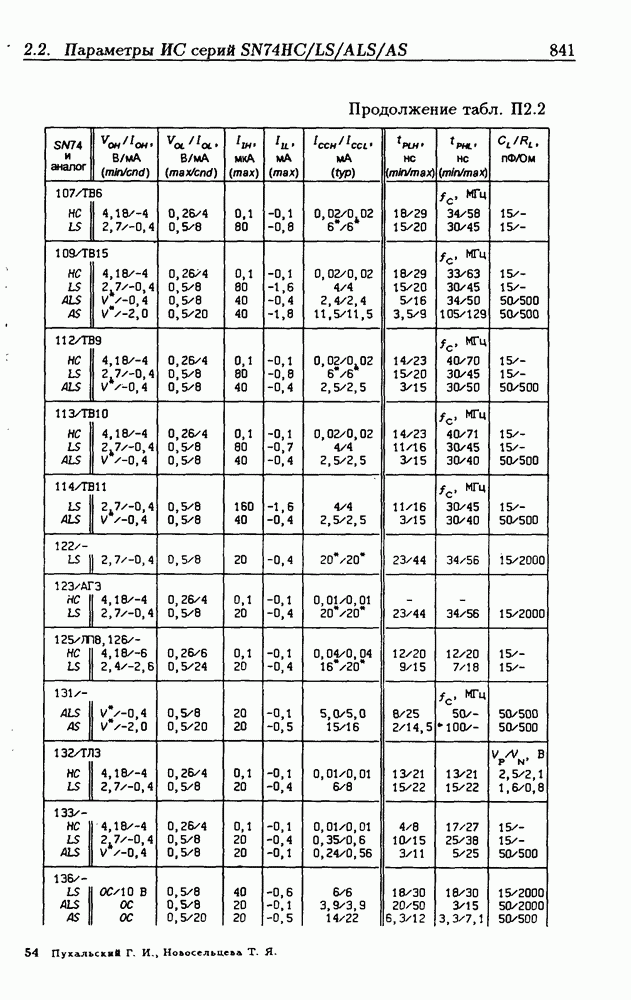
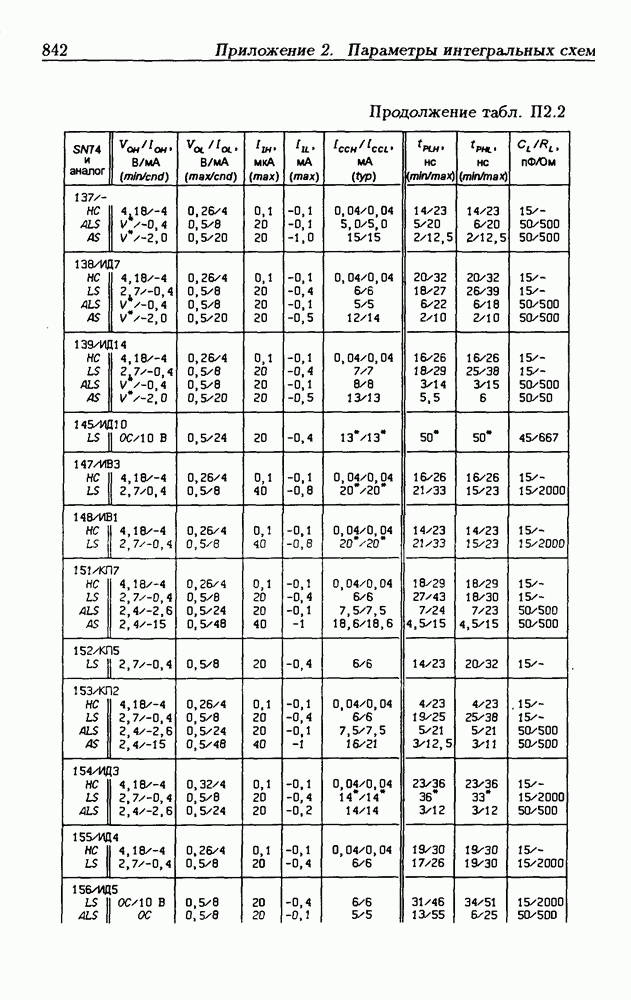
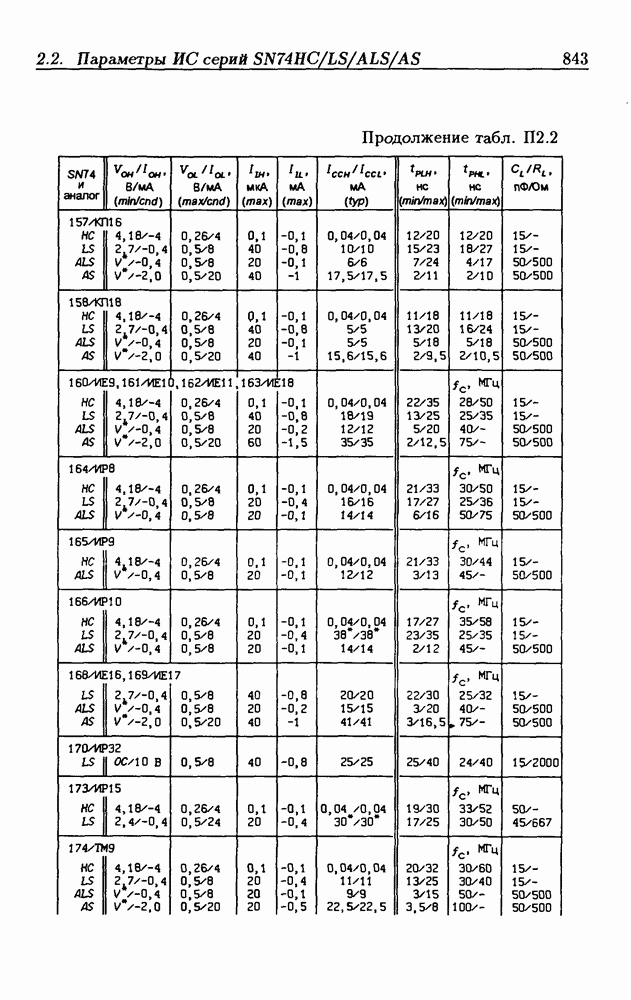
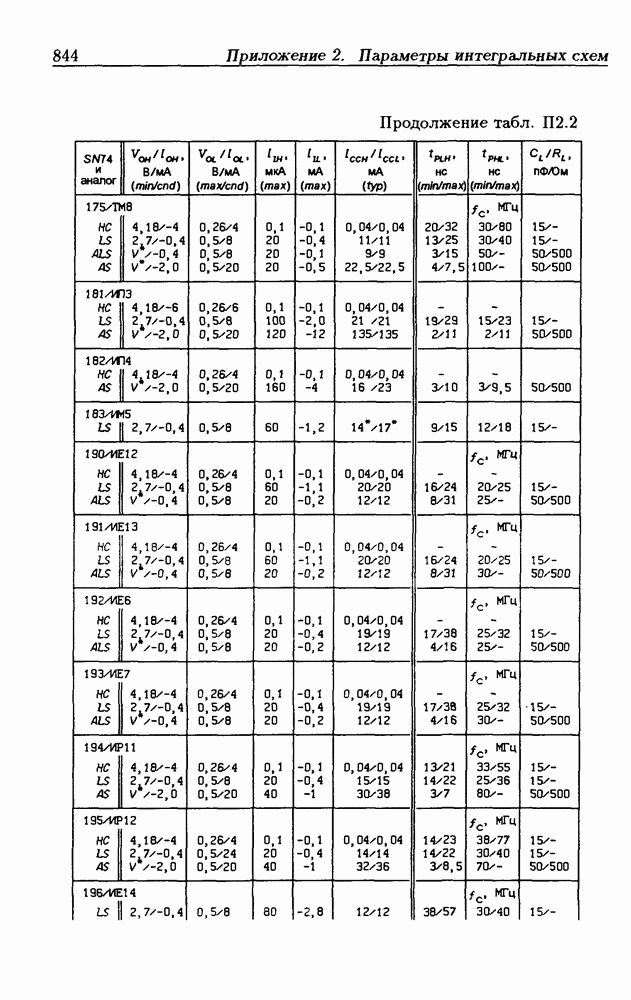
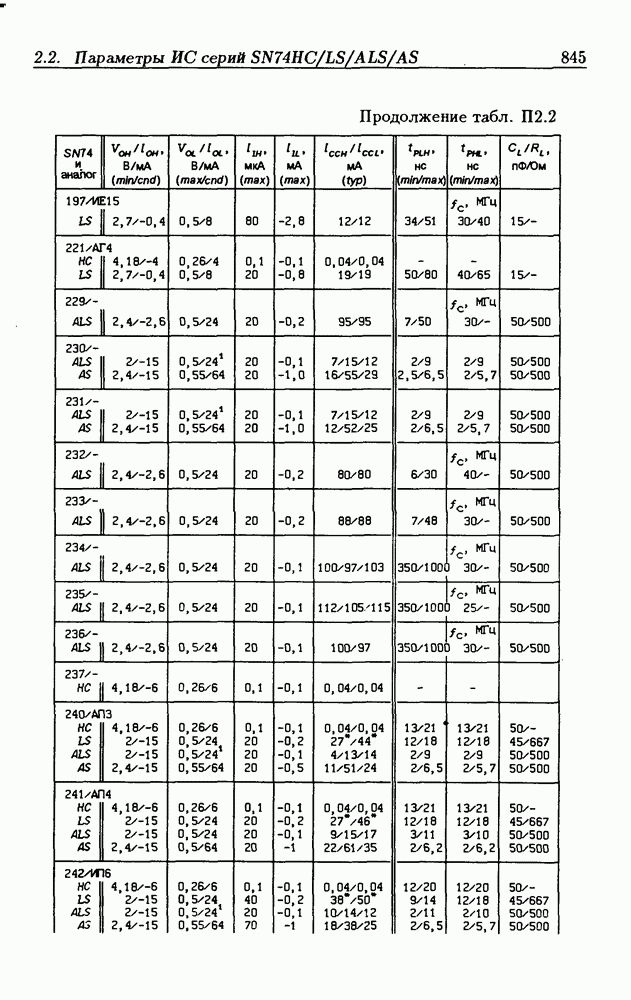
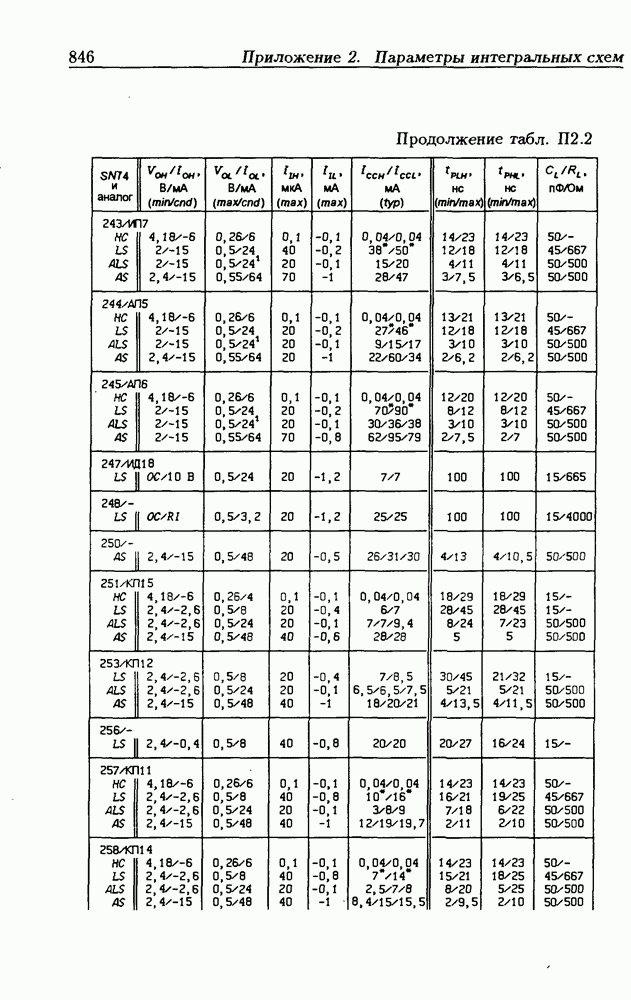
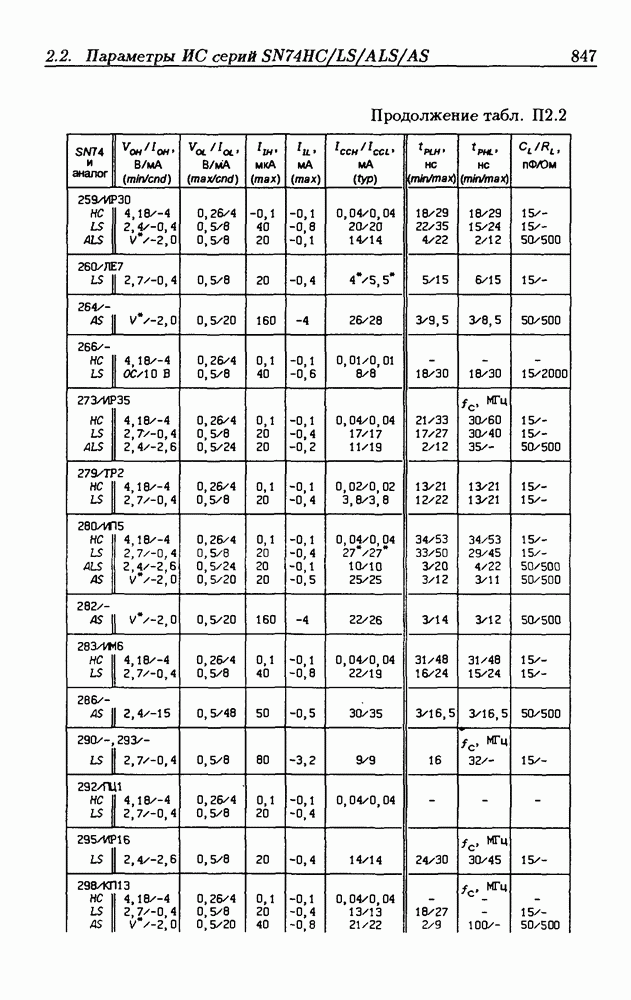
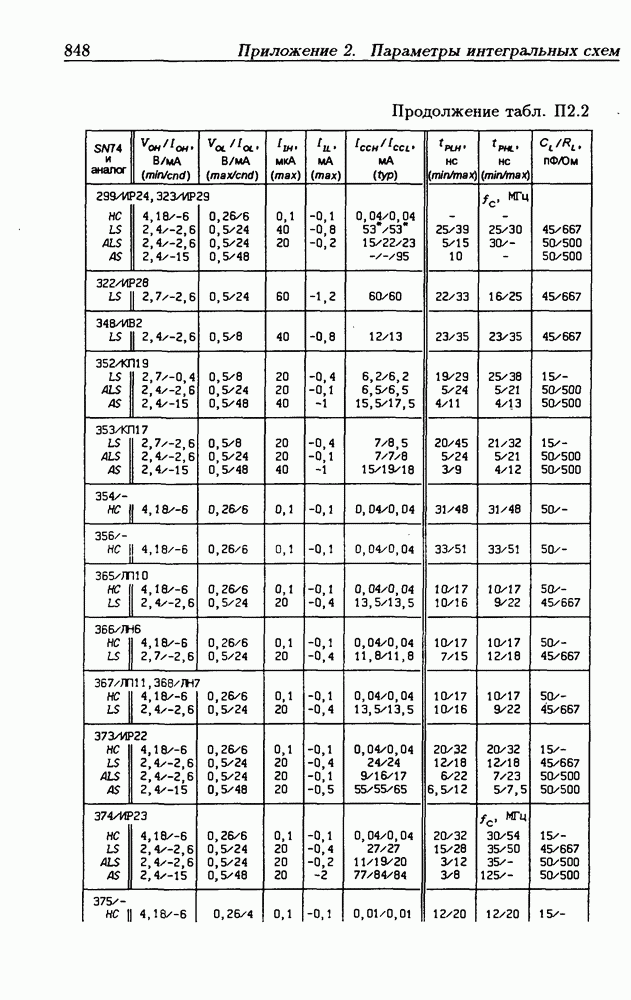
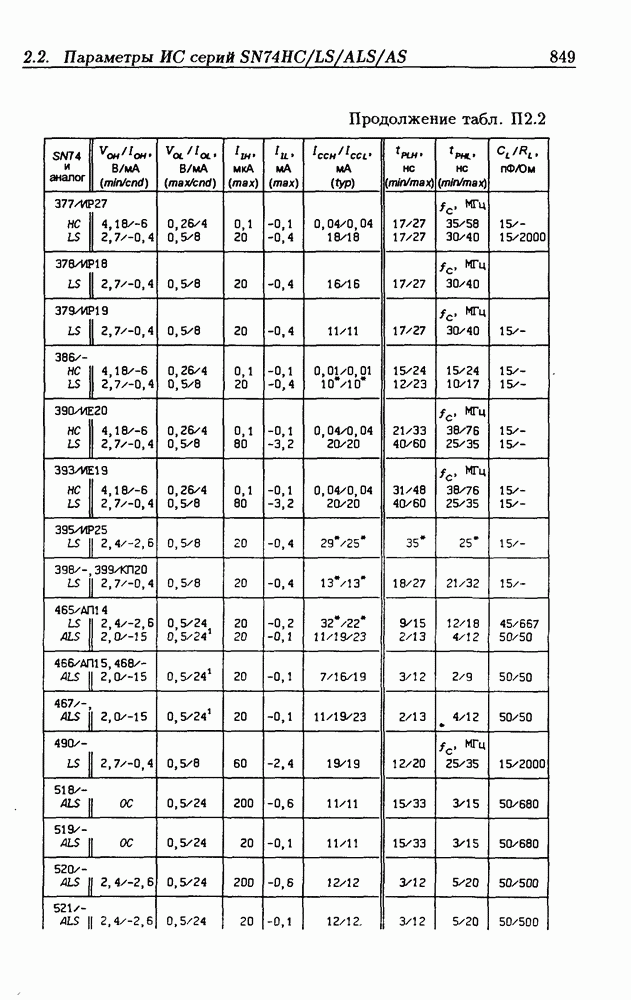
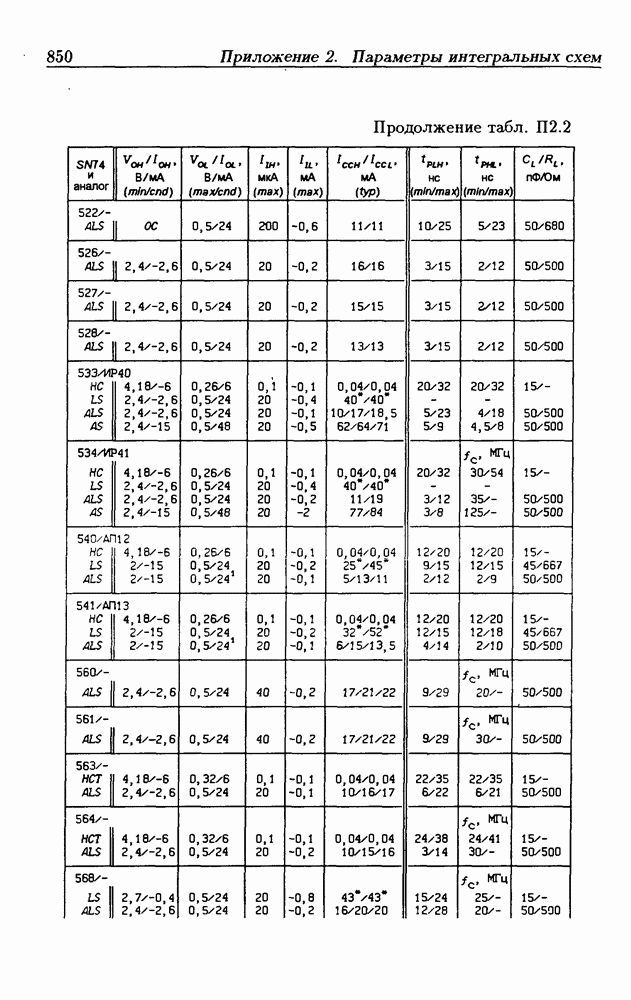
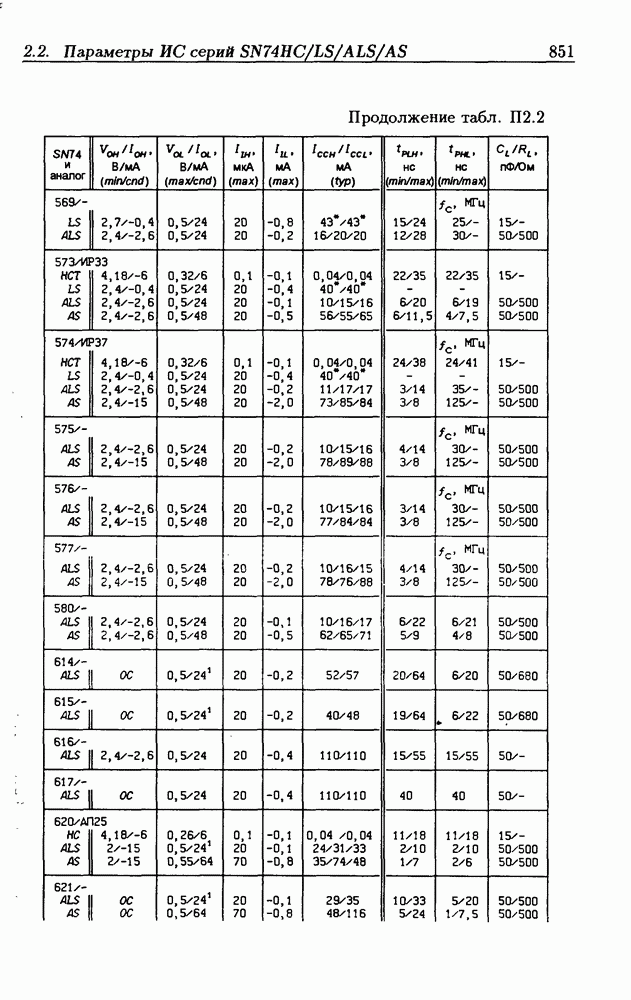
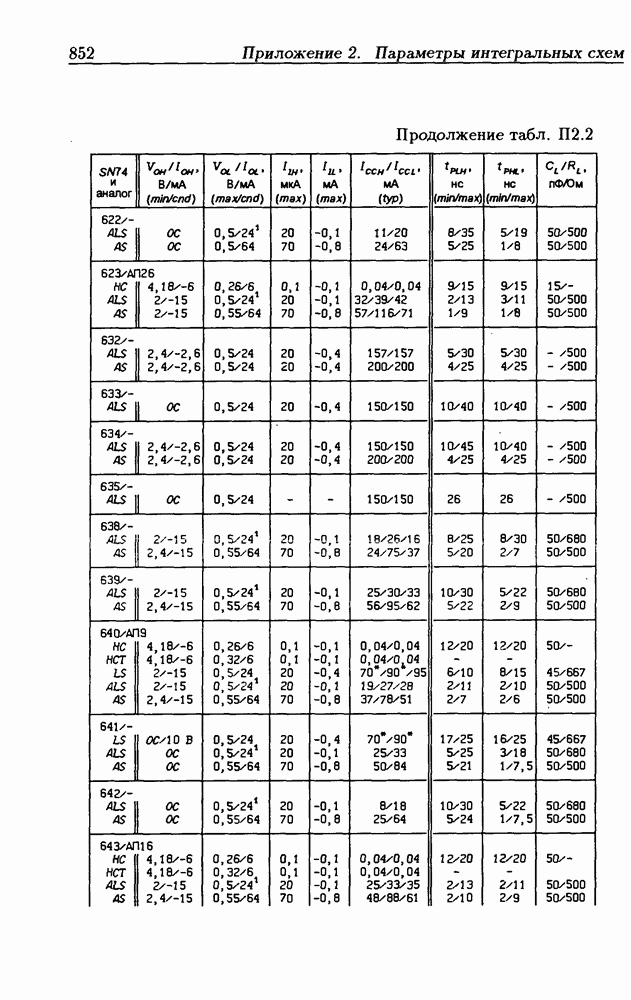
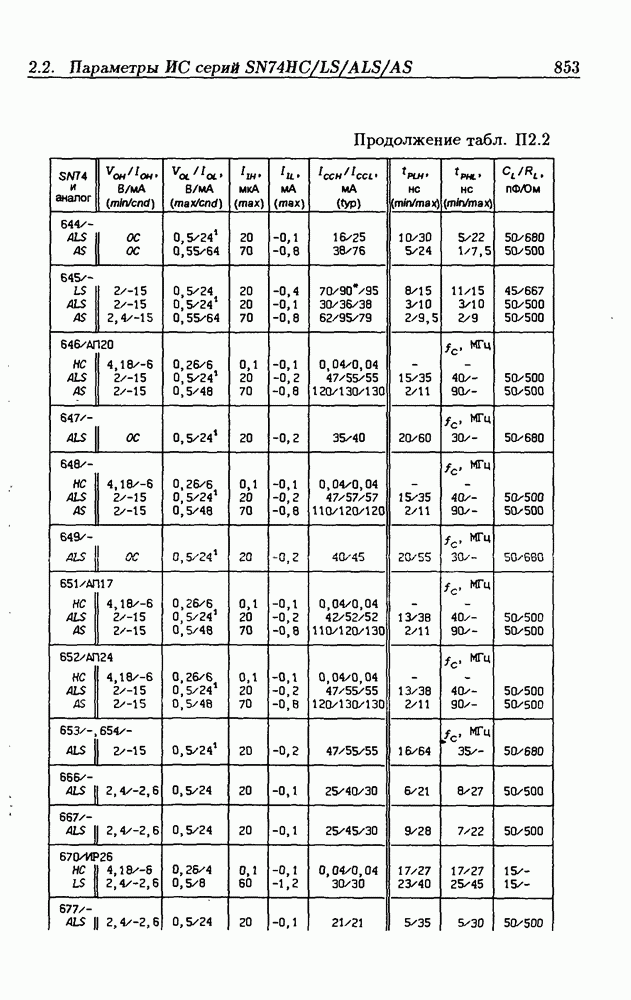
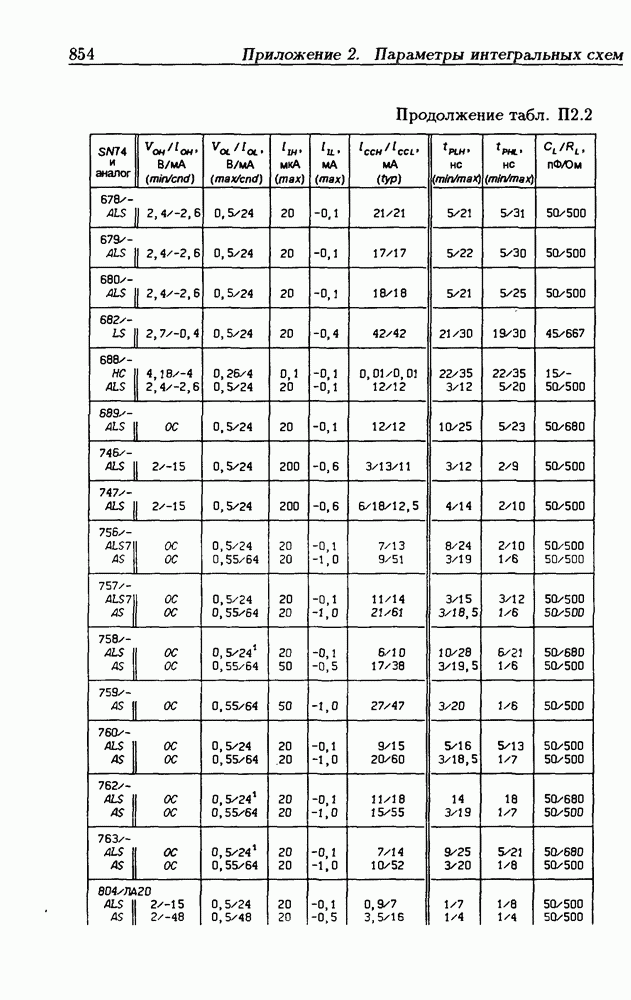
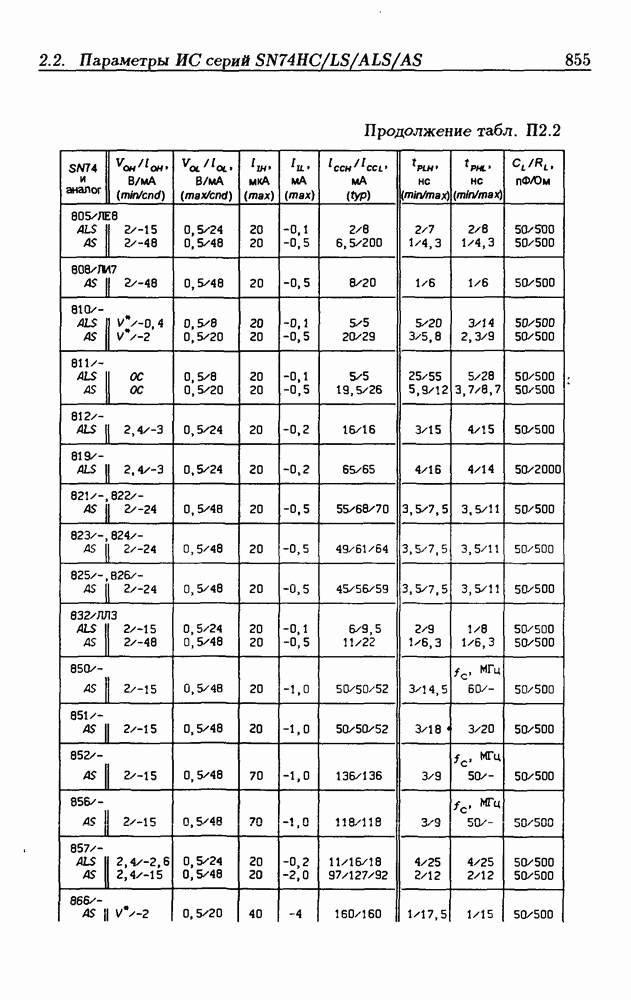
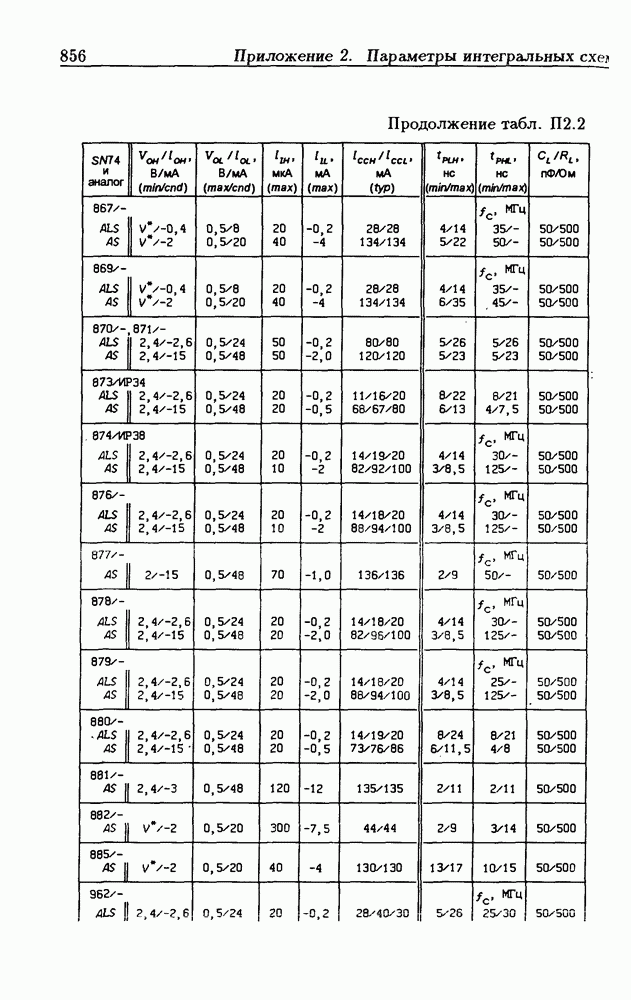
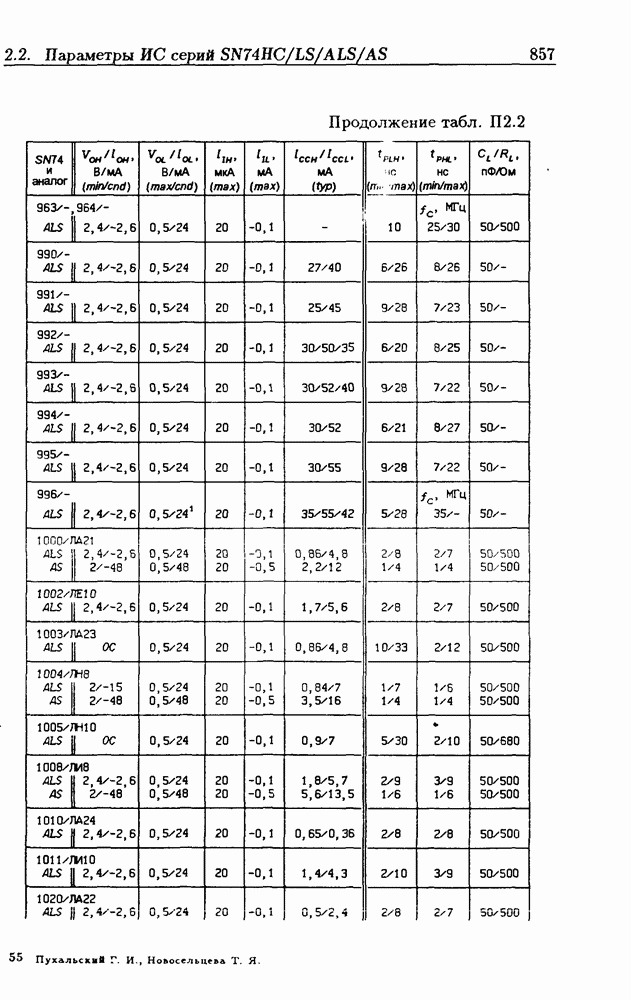
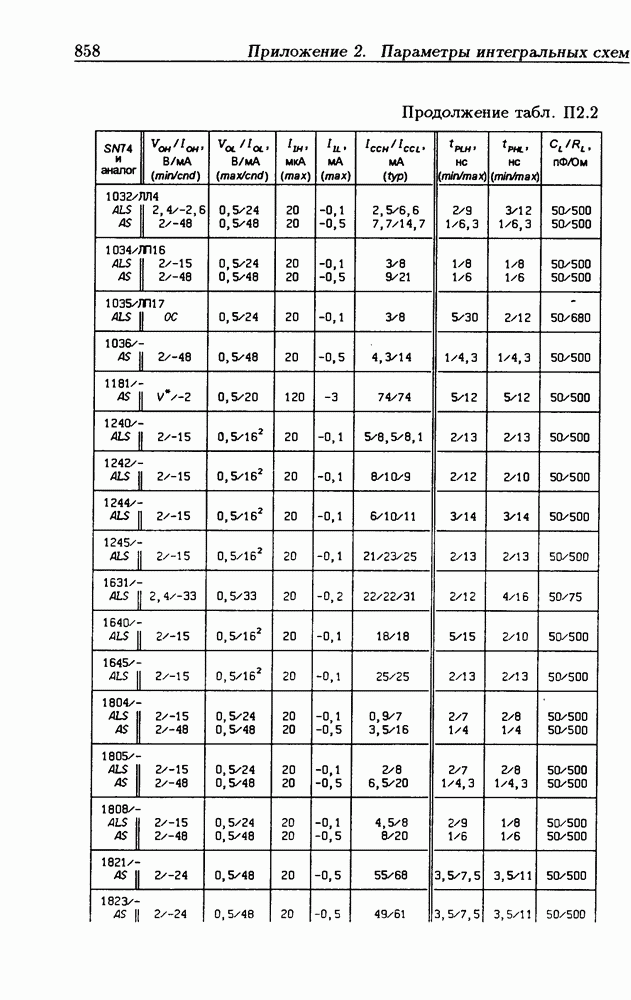
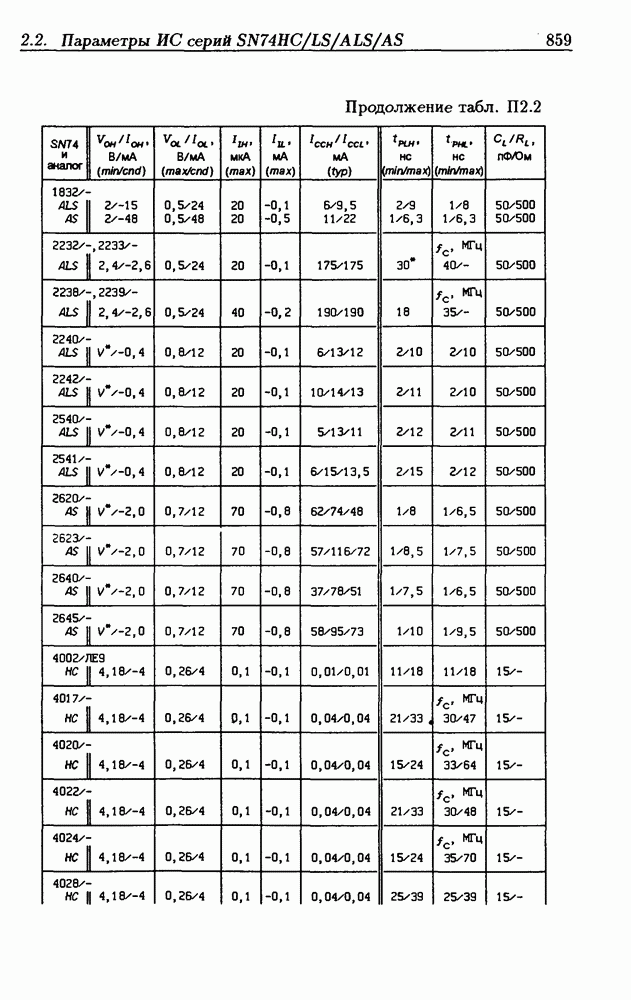
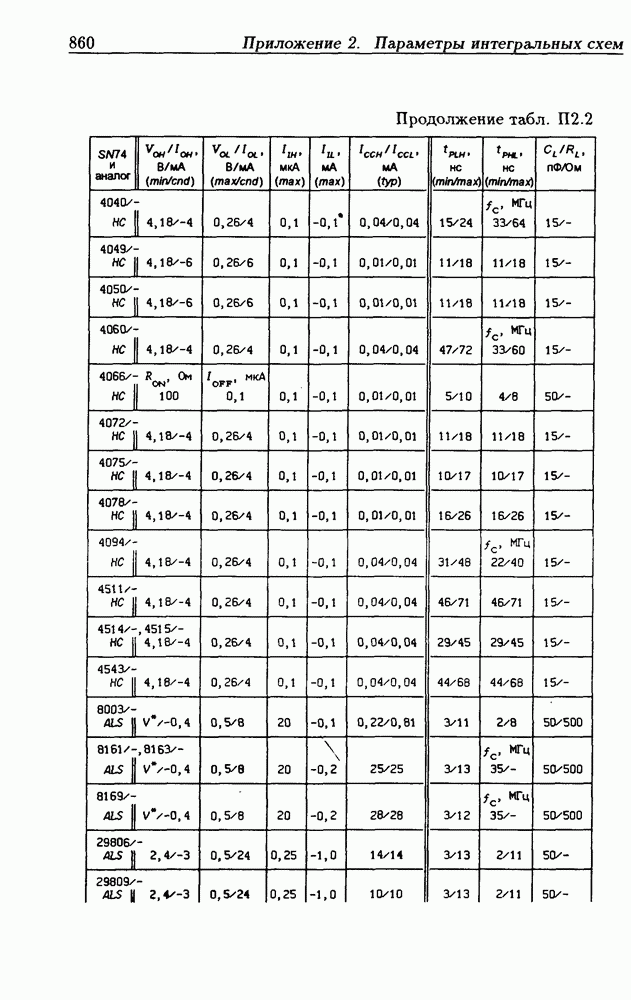
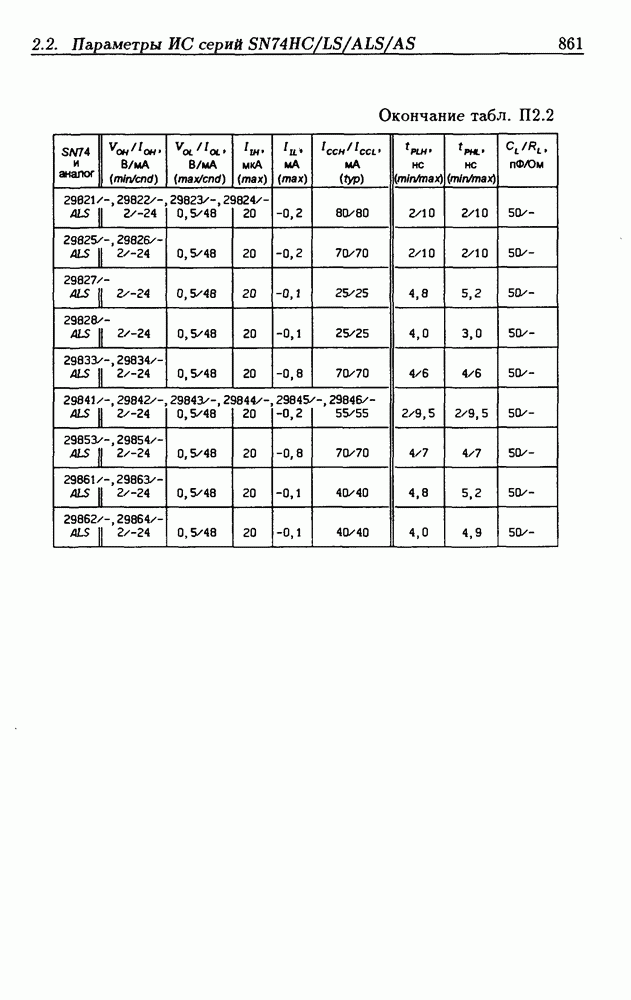
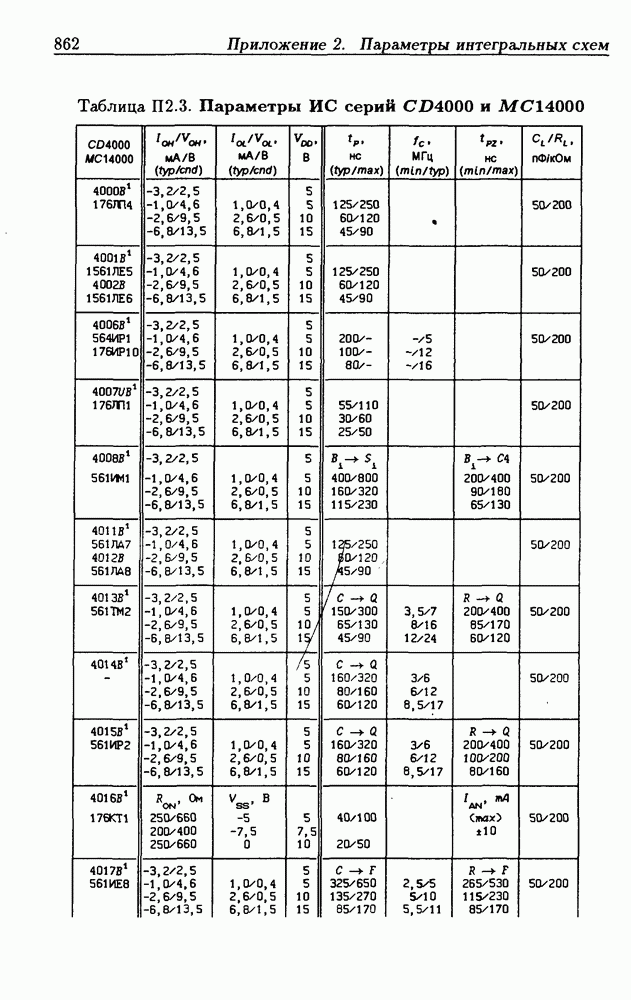
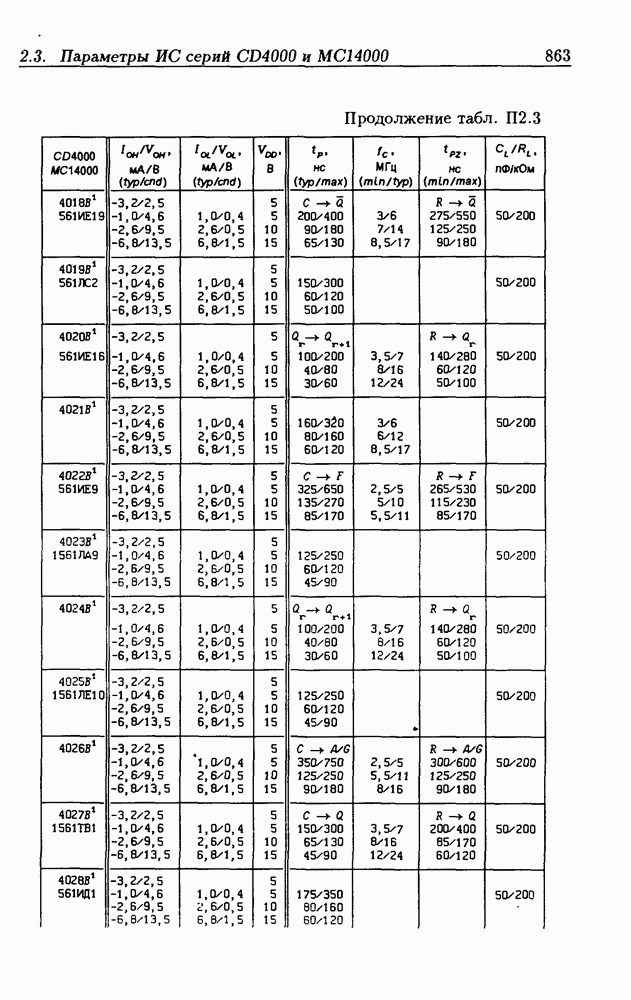
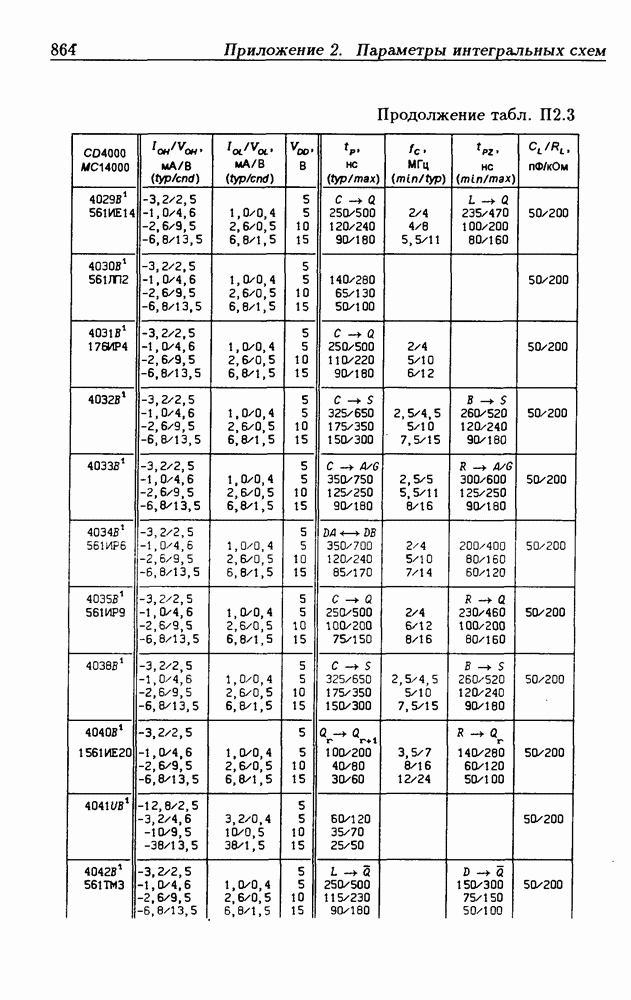
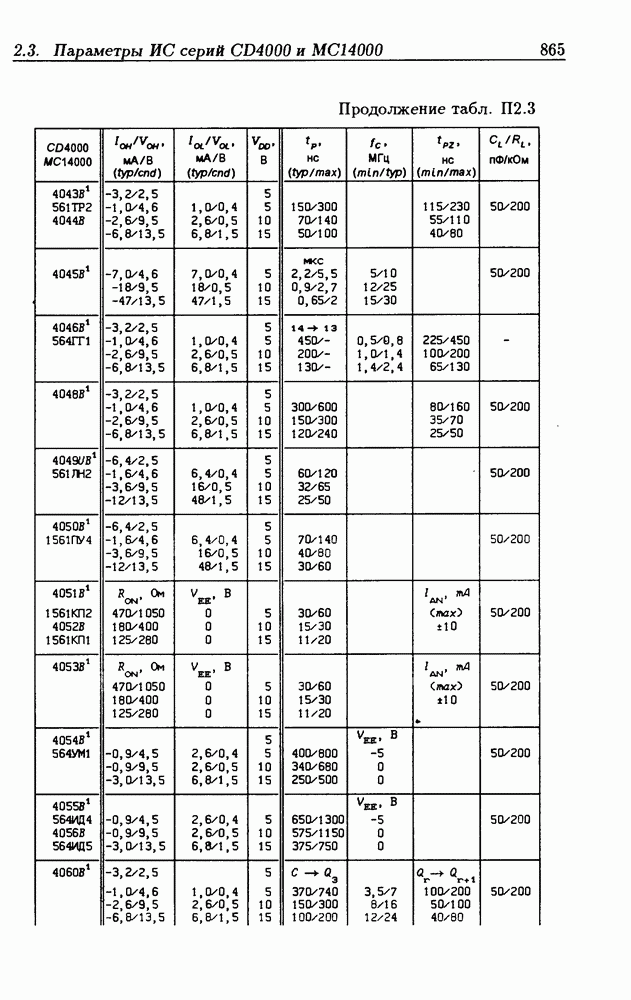
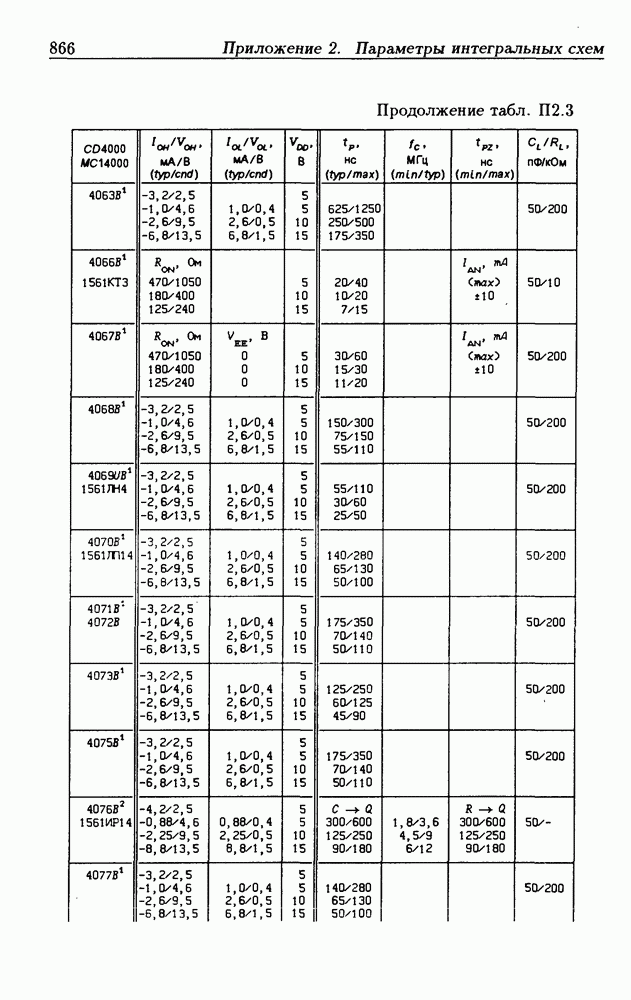
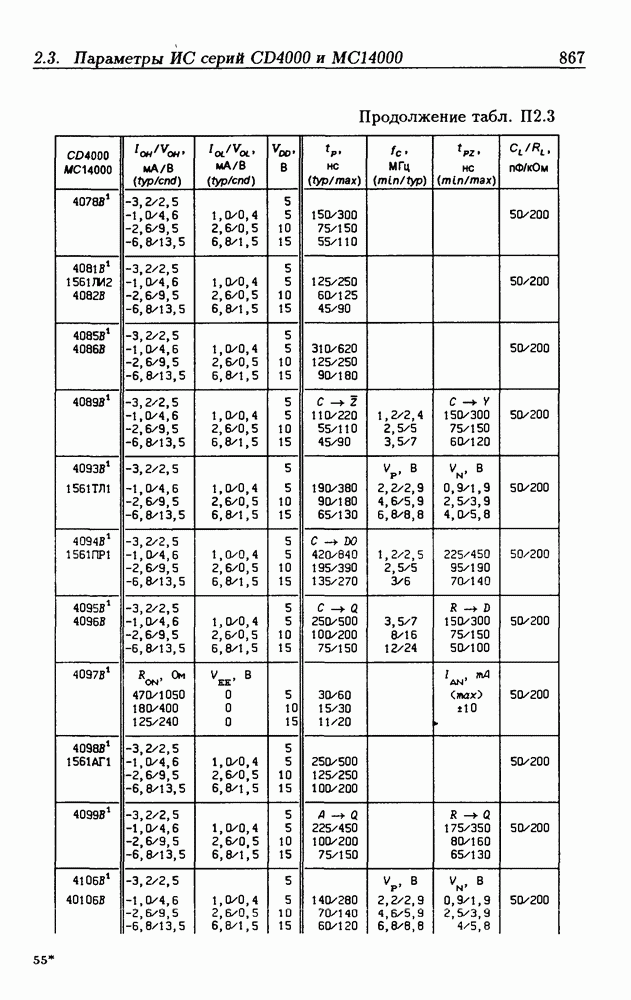
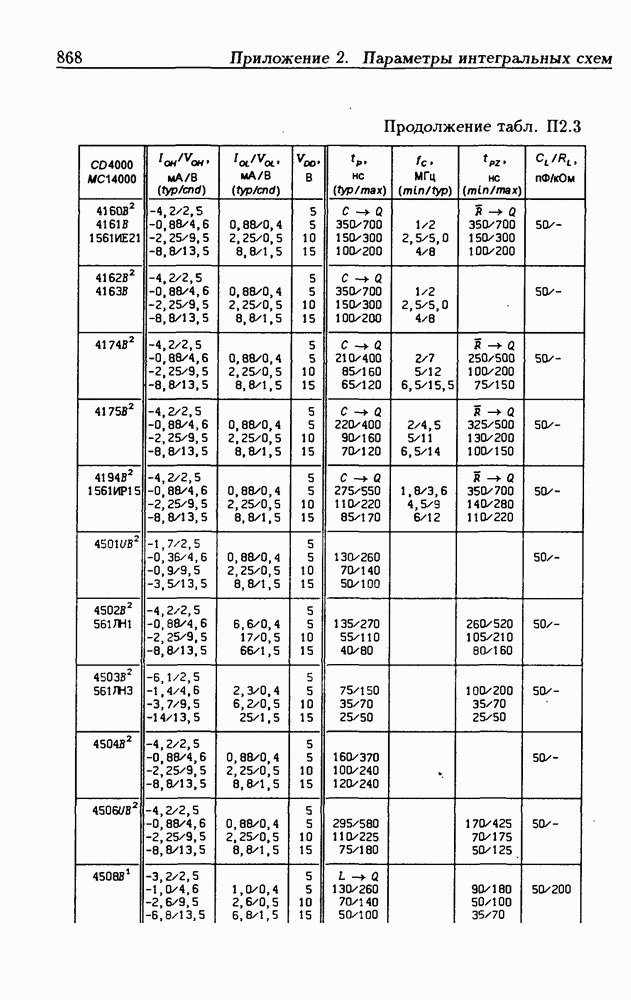
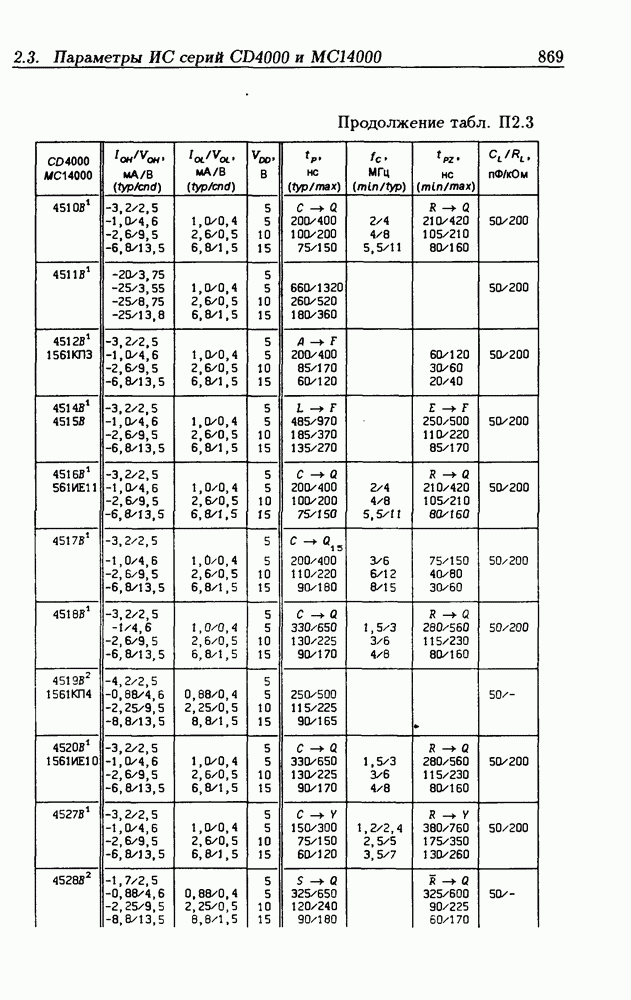
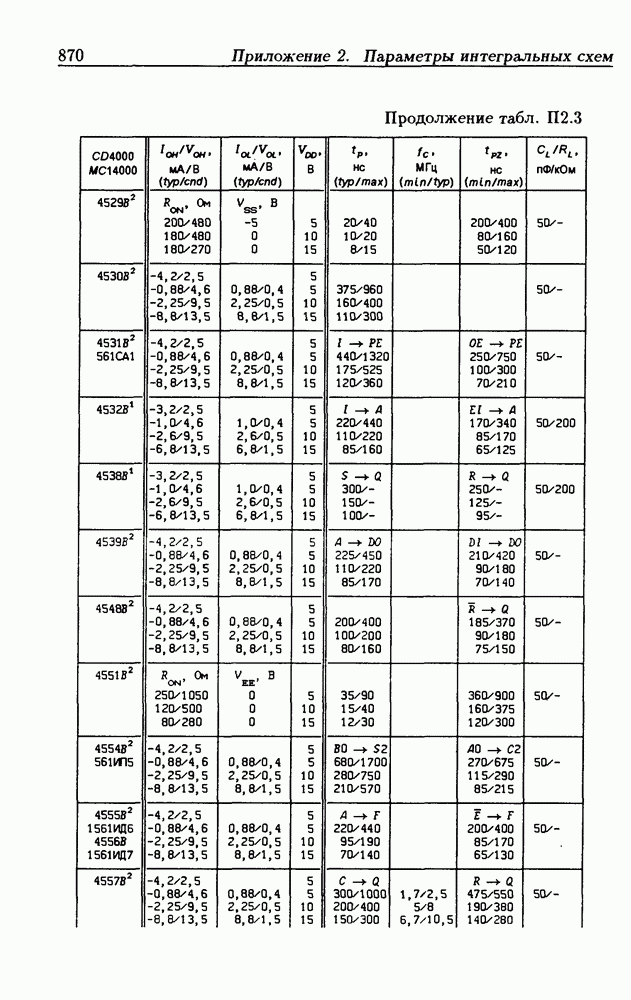
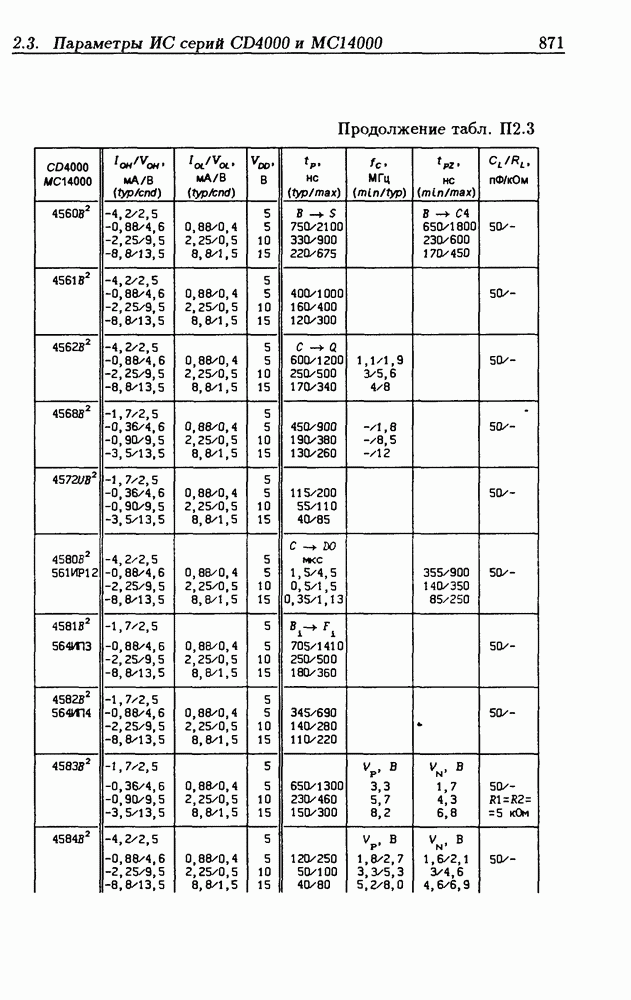
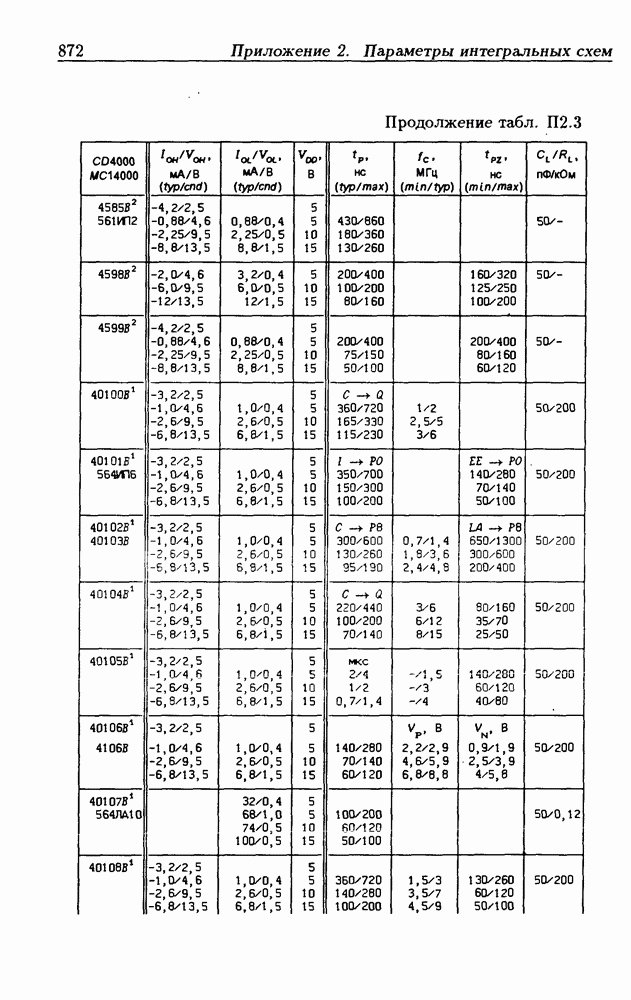
- Приложение 2. Параметры интегральных схем