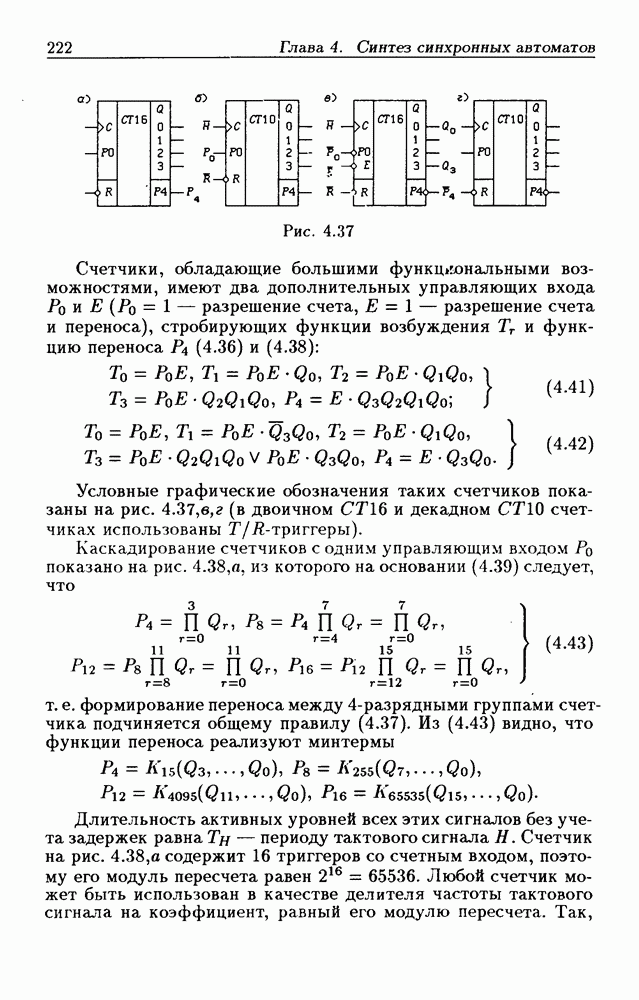| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Глава 2. Анализ и синтез логических схем
2.1. Потенциальные и импульсные сигналы
Сигнал называется потенциальным, если интервал времени  между соседними изменениями сигнала значительно больше времени реакции схемы
между соседними изменениями сигнала значительно больше времени реакции схемы  в которой он используется, т.е. сигнал
в которой он используется, т.е. сигнал  (рис. 2.1) потенциальный, если
(рис. 2.1) потенциальный, если  Сигнал называется импульсным, если длительность его активного уровня того же порядка, что и время реакции схемы (схема должна отреагировать на воздействие импульсного сигнала, а он должен закончиться сразу же после окончания в схеме переходного процесса).
Сигнал называется импульсным, если длительность его активного уровня того же порядка, что и время реакции схемы (схема должна отреагировать на воздействие импульсного сигнала, а он должен закончиться сразу же после окончания в схеме переходного процесса).

Рис. 2.1
При аналитическом описании схем, на которые воздействуют импульсные сигналы, используется понятие абстрактного импульсного сигнала, длительность которого бесконечно мала. Реальные импульсные сигналы всегда имеют конечную длительность, которая определяется временем реакции схемы. В зависимости от быстродействия ЛЭ, из которых построена схема, время реакции может изменяться в широких пределах. Понятие абстрактного импульсного сигнала позволяет абстрагироваться от физических параметров конкретных схем. Импульсные сигналы порождаются изменениями потенциальных сигналов с 1 на 0 и (или) с 0 на 1.
Для описания изменений потенциальных сигналов и порождаемых ими импульсных сигналов удобно использовать
математический аппарат, основанный на операторах переходов  [10]. Импульсные сигналы
[10]. Импульсные сигналы  с высоким активным уровнем, порождаемые изменениями потенциального сигнала х с 1 на 0 и с 0 на 1, показаны на рис. 2.1.
с высоким активным уровнем, порождаемые изменениями потенциального сигнала х с 1 на 0 и с 0 на 1, показаны на рис. 2.1.
Оператор переходов  определяется соотношением
определяется соотношением

где  импульсный сигнал, порождаемый изменениями потенциального сигнала с 1 на 0;
импульсный сигнал, порождаемый изменениями потенциального сигнала с 1 на 0;  значение потенциального сигнала в данный момент времени;
значение потенциального сигнала в данный момент времени;  значение потенциального сигнала в предыдущий момент времени.
значение потенциального сигнала в предыдущий момент времени.
Очевидно, что  только при изменении потенциального сигнала с 1 на 0. Считается, что абстрактный потенциальный сигнал имеет бесконечно крутые фронты, а для абстрактного импульсного сигнала в соотношении
только при изменении потенциального сигнала с 1 на 0. Считается, что абстрактный потенциальный сигнал имеет бесконечно крутые фронты, а для абстрактного импульсного сигнала в соотношении  Введя обозначения сигналов
Введя обозначения сигналов  получим:
получим:

Соотношение (2.2) учитывает время в явном виде и может использоваться не только для потенциальных сигналов, но и для переключательных функций от потенциальных сигналов:

где  значение функции в данный момент времени, — значение функции в предыдущий момент времени. Из соотношения (2.3) следует, что импульсные сигналы, порождаемые переключательными функциями от потенциальных сигналов, весьма просто могут быть получены с помощью основных операций алгебры логики. Так, если
значение функции в данный момент времени, — значение функции в предыдущий момент времени. Из соотношения (2.3) следует, что импульсные сигналы, порождаемые переключательными функциями от потенциальных сигналов, весьма просто могут быть получены с помощью основных операций алгебры логики. Так, если  то
то

где  только при изменении потенциального сигнала
только при изменении потенциального сигнала  на 1.
на 1.
Имеет место тождество  которое отражает тот факт, что потенциальный сигнал не может одновременно изменяться с 1 на 0 и с 0 на 1 (доказательство:
которое отражает тот факт, что потенциальный сигнал не может одновременно изменяться с 1 на 0 и с 0 на 1 (доказательство:  -хх-х
-хх-х  Следует всегда иметь в виду, что с точки зрения алгебры логики сигналы
Следует всегда иметь в виду, что с точки зрения алгебры логики сигналы  являются разными переменными, но поскольку их значения совпадают со значениями одного и того же сигнала, взятыми в различные моменты времени, то операторные соотношения учитывают время в явном виде.
являются разными переменными, но поскольку их значения совпадают со значениями одного и того же сигнала, взятыми в различные моменты времени, то операторные соотношения учитывают время в явном виде.
Оператор переходов V определяется соотношением

где  при изменении потенциального сигнала х как с 1 на 0, так и с 0 на 1.
при изменении потенциального сигнала х как с 1 на 0, так и с 0 на 1.
Легко доказать следующие основные операторные тождества:

Докажем, например, первое тождество:

Тождества (2.6) поясняются временными диаграммами, изображенными на рис. 2.2.

Рис. 2.2
Оператор переходов  от мультиплексной функции дает
от мультиплексной функции дает

В § 1.4 было показано, что для обычных тождеств алгебры логики справедлив принцип двойственности, устанавливающий правило, На основании которого для любого тождества можно получить двойственное ему тождество. В [22] доказана теорема, утверждающая, что и для операторных тождеств справедлив некоторый принцип, позволяющий разбить их на пары:
если справедливо операторное тождество

то имеет место также операторное тождество

где  некоторые переключательные функции
некоторые переключательные функции  переменных. Такие тождества будем называть сопряженными. Функции
переменных. Такие тождества будем называть сопряженными. Функции  и входящие во второе операторное тождество, получаются из функций
и входящие во второе операторное тождество, получаются из функций  входящих в первое операторное тождество, заменой
входящих в первое операторное тождество, заменой  на V, а и на V, т. е. заменой переменных
на V, а и на V, т. е. заменой переменных  на
на  на х, а переменных х на
на х, а переменных х на  на
на  Функции же
Функции же  входящие во второе тождество, получаются из функций
входящие во второе тождество, получаются из функций  входящих в первое тождество, взаимной заменой операций дизъюнкции
входящих в первое тождество, взаимной заменой операций дизъюнкции  и конъюнкции
и конъюнкции  Такое преобразование тождеств допустимо в силу того, что взаимная замена V на
Такое преобразование тождеств допустимо в силу того, что взаимная замена V на  эквивалентна изменению направления отсчета времени.
эквивалентна изменению направления отсчета времени.
Используя определение оператора перехода (2.3), не представляет труда доказать следующие операторные тождества:

Все тождества, за исключением последнего, записаны парами и могут быть получены одно из другого на основании приведенной теоремы. Последнее тождество является самосопряженным, так как оно по теореме не изменяется. Рассмотренные тождества наиболее часто используются для упрощения выражений, содержащих операторы переходов.
Для преобразования операторных выражений могут быть полезны следующие тождества:

При проектировании логических схем можно использовать и импульсные сигналы с низким активным уровнем  (инверсные импульсные сигналы).
(инверсные импульсные сигналы).
Операторные выражения, описывающие импульсные сигналы, могут быть применены для проектирования логических схем, формирующих такие сигналы. На рис. 2.3,а показана схема генератора импульсного сигнала  построенная в соответствии с (2.1), а на рис. 2.3,б - временные диаграммы, поясняющие ее работу (для простоты положили, что ЛЭ безынерционны). Инверсный импульсный сигнал
построенная в соответствии с (2.1), а на рис. 2.3,б - временные диаграммы, поясняющие ее работу (для простоты положили, что ЛЭ безынерционны). Инверсный импульсный сигнал  может быть получен с помощью ЛЭ НЕ. Генераторы импульсных сигналов называются разностными элементами.
может быть получен с помощью ЛЭ НЕ. Генераторы импульсных сигналов называются разностными элементами.
На рис. 2.3, в представлена схема удвоения частоты, выполненная в соответствии с (2.5), а на рис. 2.3,г - временные

Рис. 2.3
диаграммы, поясняющие ее работу. Вместо асинхронных потенциальных элементов задержки на время  можно использовать некоторое число последовательно включенных ЛЭ, обеспечивающих заданную задержку.
можно использовать некоторое число последовательно включенных ЛЭ, обеспечивающих заданную задержку.
Впервые операторы переходов были введены в работе [17]. Математический аппарат для синтеза и анализа цифровых схем, основанный на операторах переходов, разработан в [10].
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Глава 1. Основы теории переключательных функций
- 1.2. Позиционные системы счисления
- 1.3. Переключательные функции
- 1.4. Принцип и закон двойственности
- 1.5. Теоремы разложения
- 1.6. Решение систем логических уравнений
- 1.7. Первичные термы, минтермы и макстермы
- 1.8. Совершенные нормальные формы представления функций
- 1.9. Конъюнктивные и дизъюнктивные термы
- 1.10. Минимизация переключательных функций
- 1.11. Диаграммы Вейча
- 1.12. Минимизация неполностью определенных функций, совместная минимизация нескольких функций
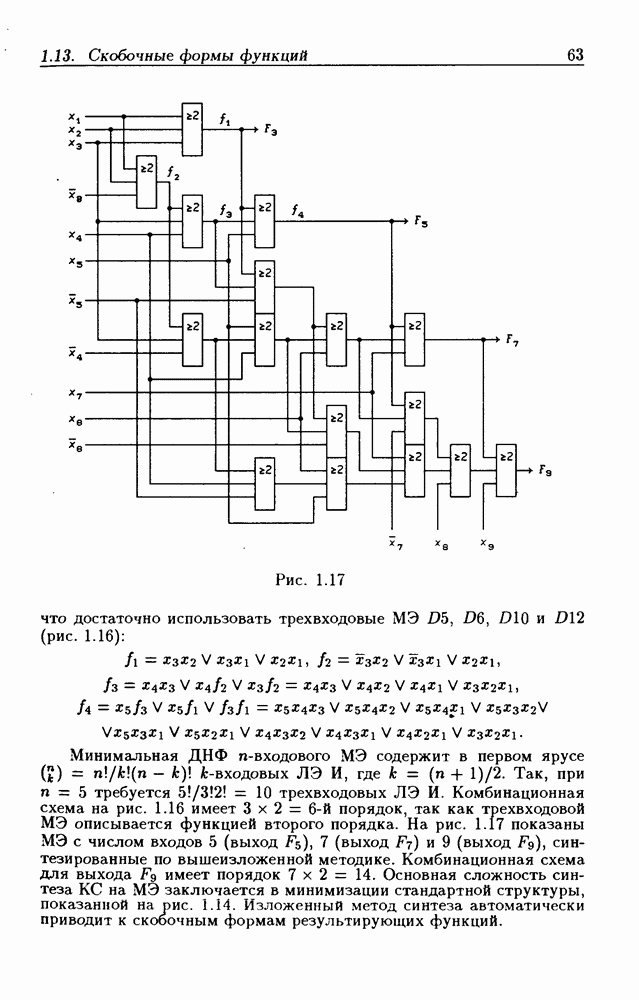
- 1.13. Скобочные формы функций
- 1.14. Закон двойственности для логических схем
- 1.15. Линейные функции
- Глава 2. Анализ и синтез логических схем
- 2.2. Модели логических элементов
- 2.3. Модели логических схем
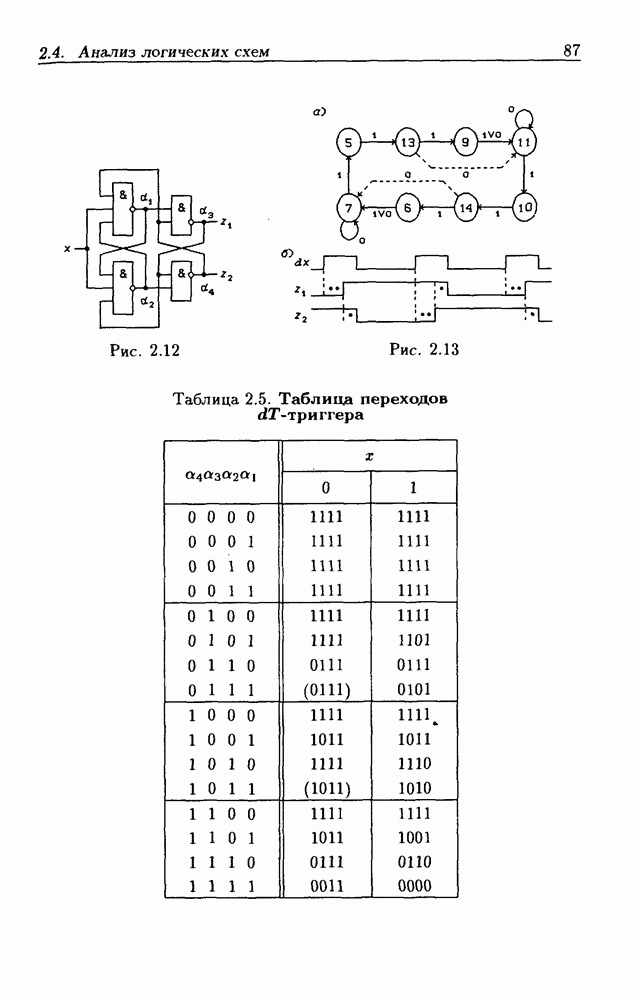
- 2.4. Анализ логических схем
- 2.5. Синтез комбинационных схем, свободных от состязаний
- Глава 3. Синтез асинхронных потенциальных автоматов
- 3.2. Асинхронные потенциальные автоматы
- 3.3. Асинхронные потенциальные триггеры и элементы памяти
- Триггеры типа R-S
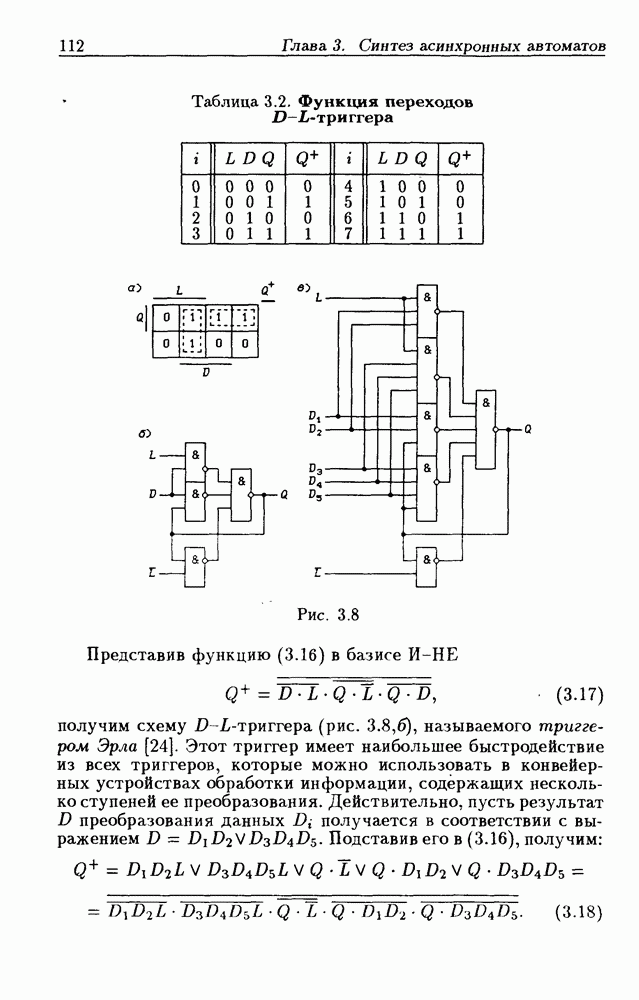
- Триггеры типа D-L
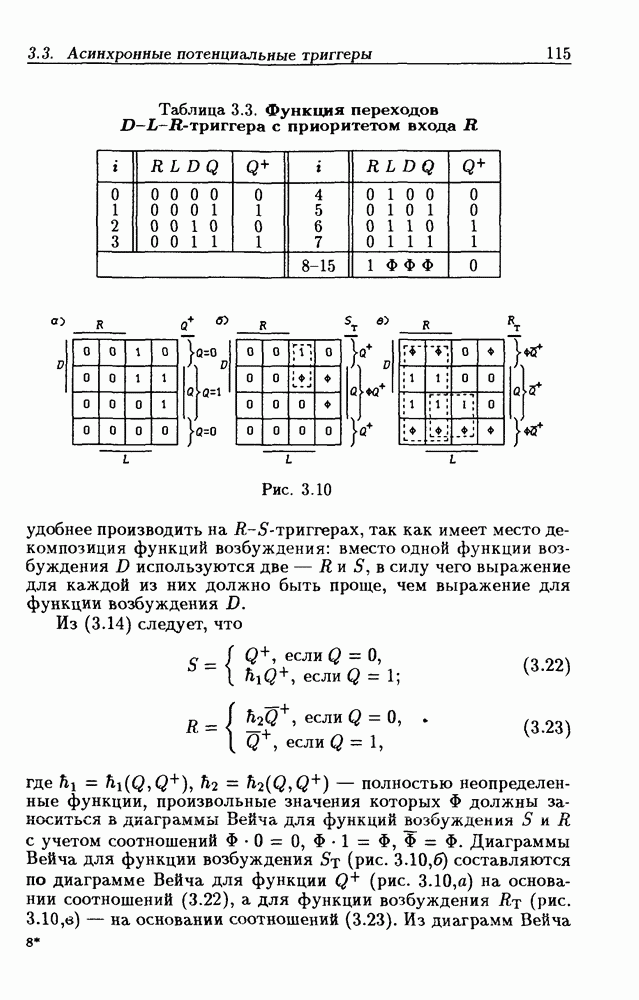
- Триггеры типа D-L-R с приоритетом входа R.
- Триггеры типа D-L-R с приоритетом входа L.
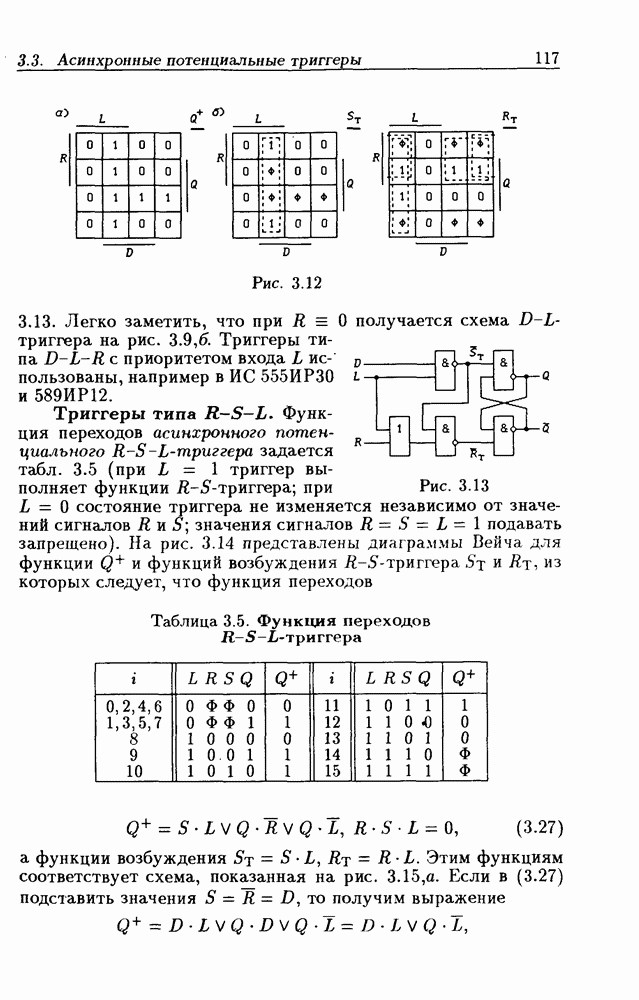
- Триггеры типа R-S-L.
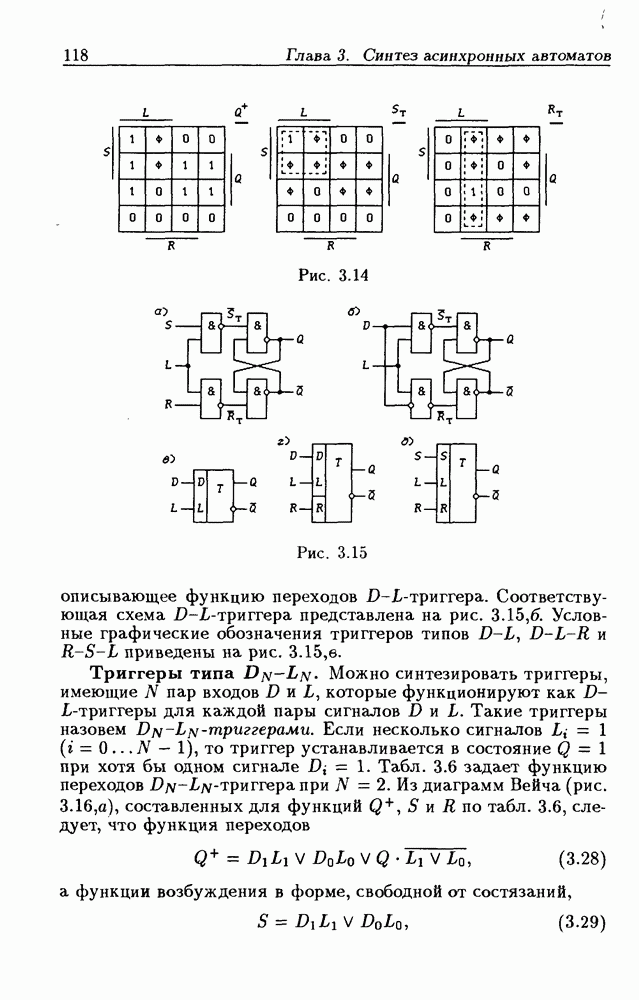
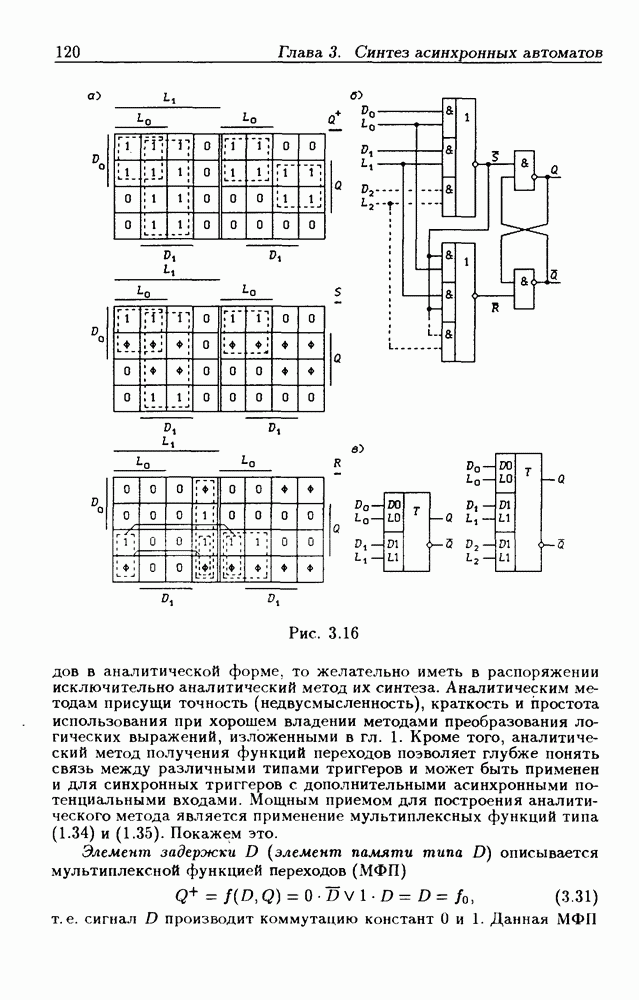
- Триггеры типа DN-LN
- Аналитический метод синтеза и анализа триггеров.
- 3.4. Задание асинхронных потенциальных автоматов таблицами и графами переходов
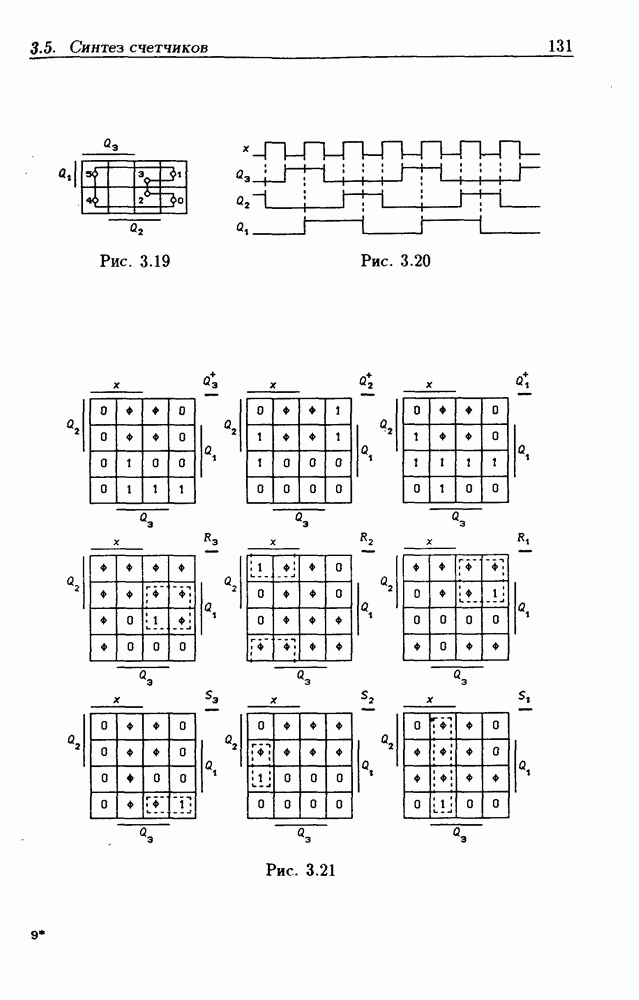
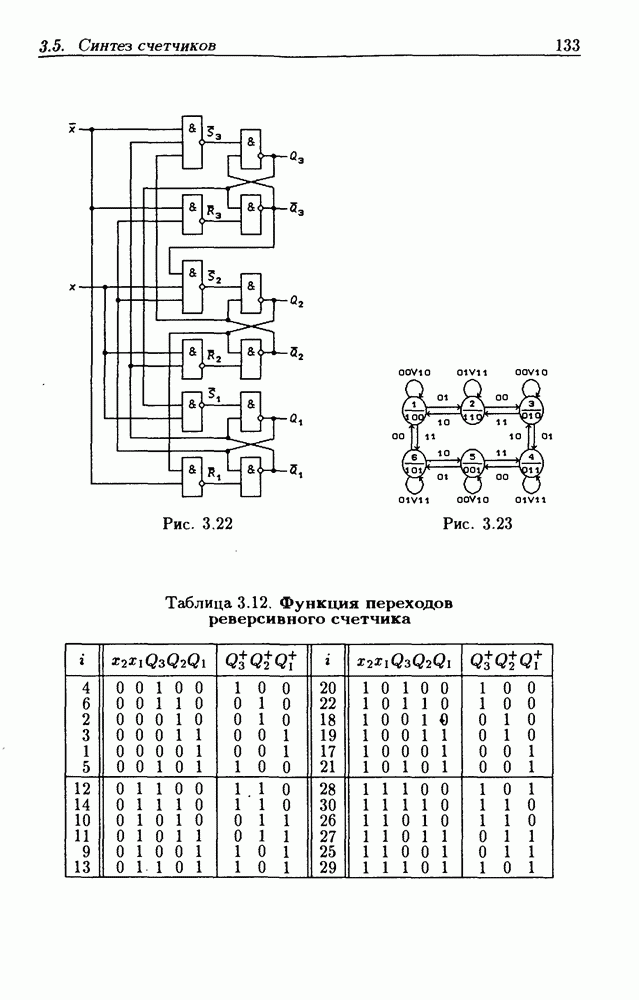
- 3.5. Синтез асинхронных потенциальных счетчиков
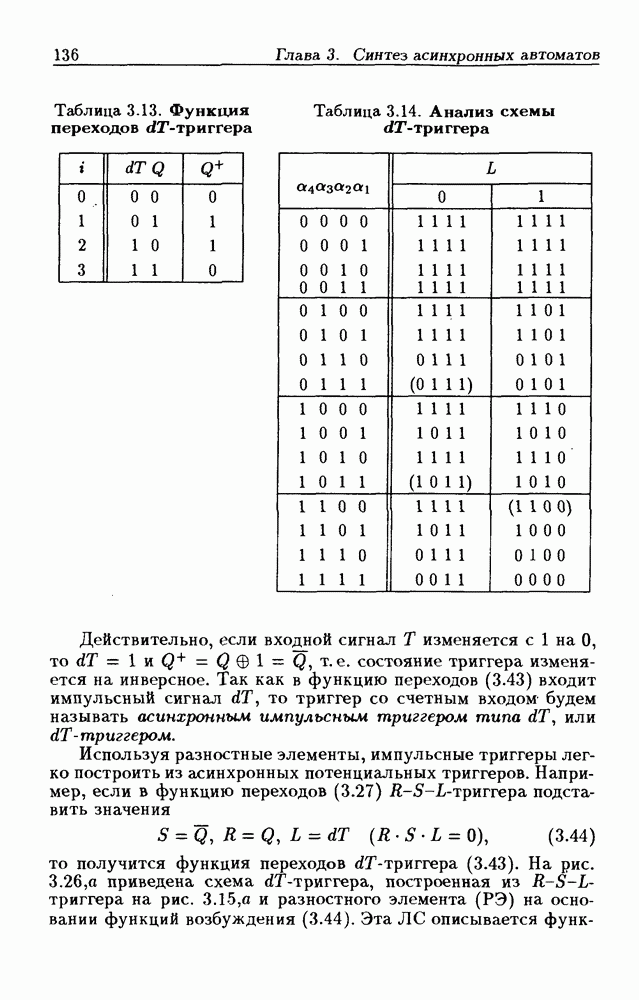
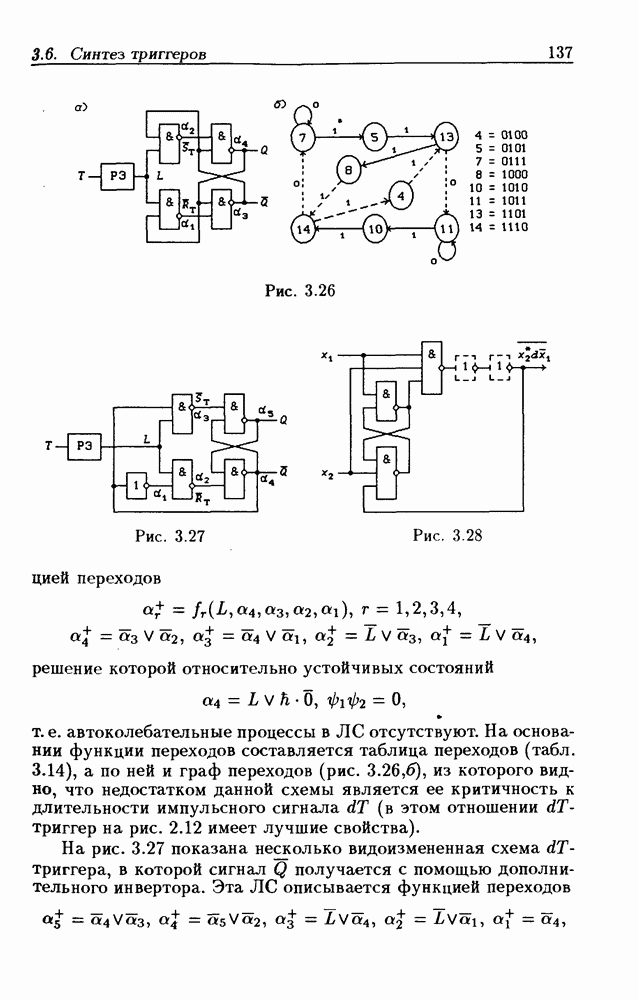
- 3.6. Синтез асинхронных импульсных триггеров
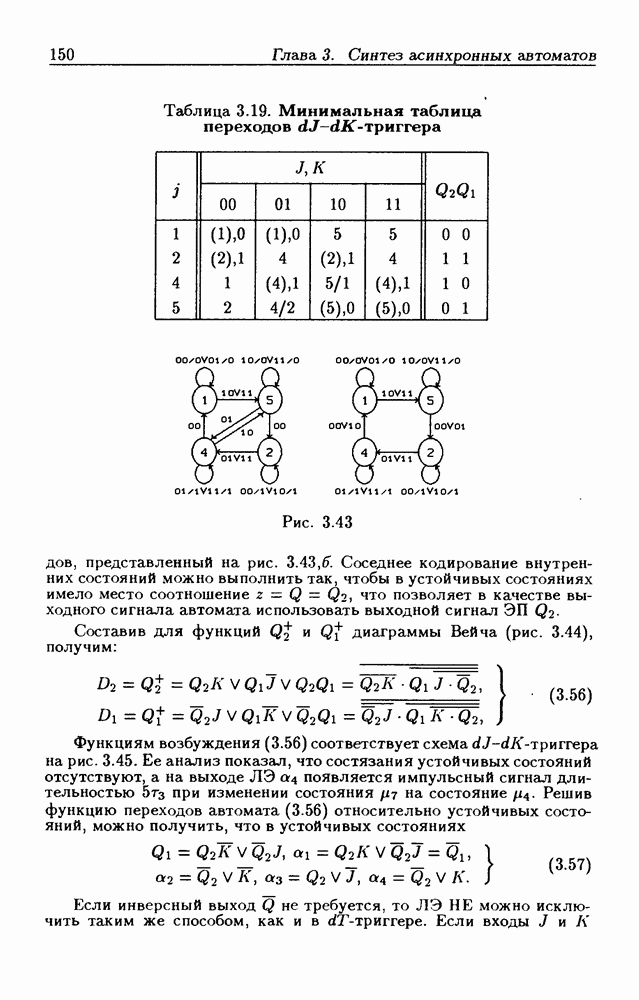
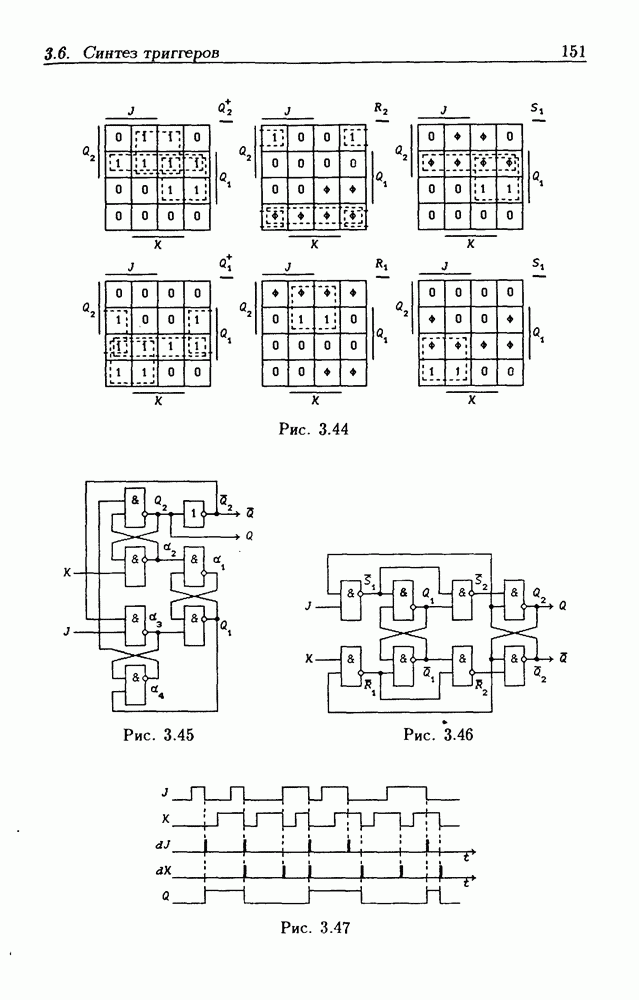
- Триггеры типа dJ-dK.
- Классификация триггеров.
- 3.7. Синтез синхронных триггеров
- Триггеры типа J-K
- Синхронно-асинхронные триггеры.
- 3.8. Примеры синтеза асинхронных потенциальных автоматов
- Цифровые фазочастотные детекторы.
- Квантизатор временных интервалов.
- 3.9. Генераторы сигналов
- Автогенераторы.
- Управляемые автогенераторы.
- Глава 4. Синтез синхронных автоматов
- 4.2. Синхронные триггеры
- Триггеры типов D и R-S с импульсным тактовым сигналом.
- Синхронные триггеры типов R-S и D-L
- Синхронно-асинхронные триггеры.
- Синхронные триггеры типа J-K
- Триггеры типа Т.
- Классификация синхронных триггеров.
- Преобразования типов синхронных триггеров.
- Триггеры типов D-T-L и D-T-L/R
- Функции переходов синхронно-асинхронных триггеров.
- 4.3. Примеры синтеза синхронных автоматов
- 4.4. Сдвигающие регистры
- Синтез счетчиков на сдвигающих регистрах.
- Сдвигающие регистры с загрузкой данных.
- Реверсивные сдвигающие регистры.
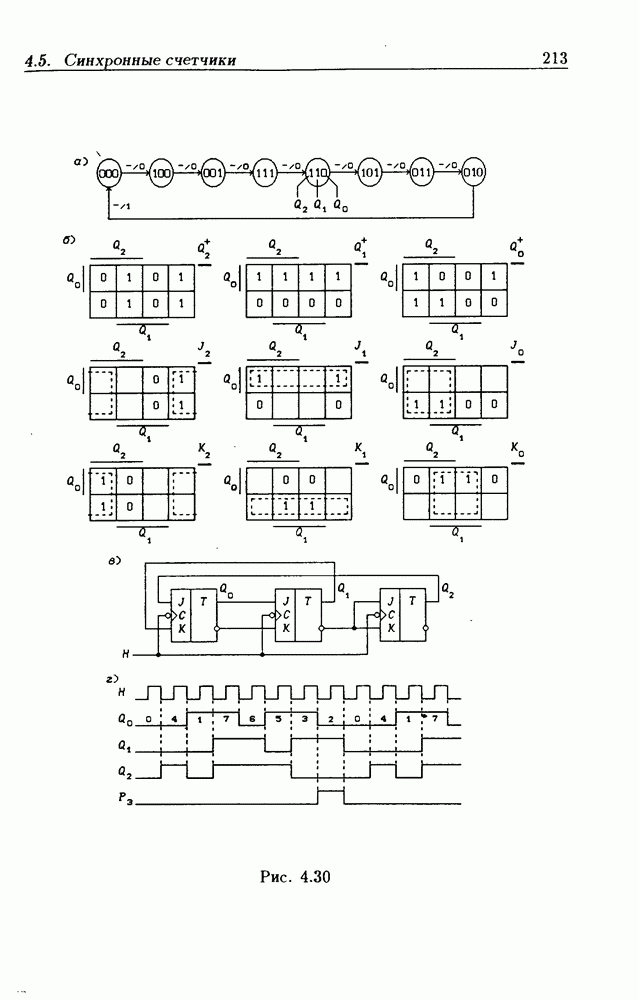
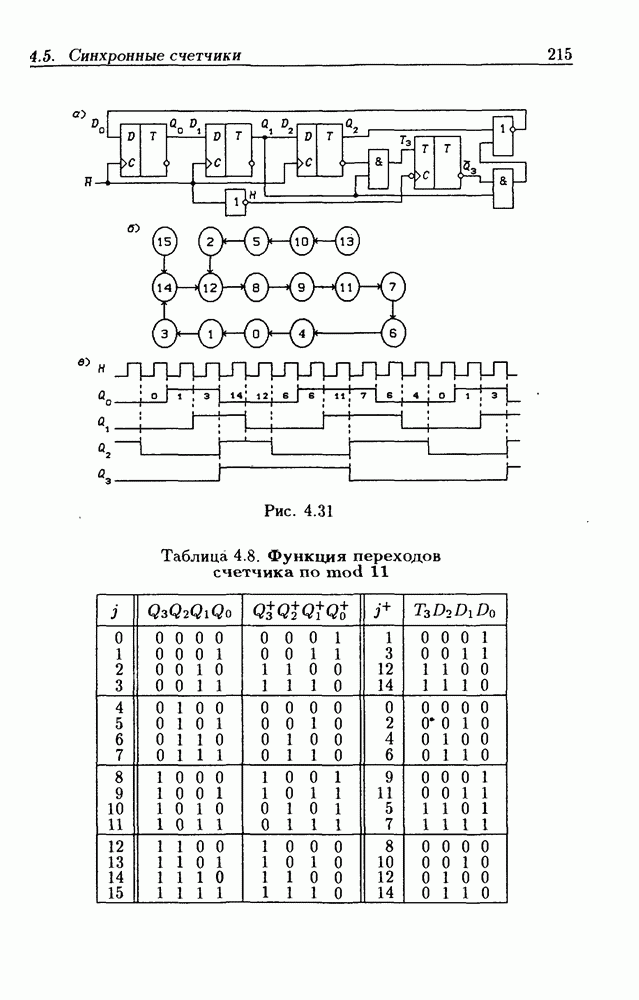
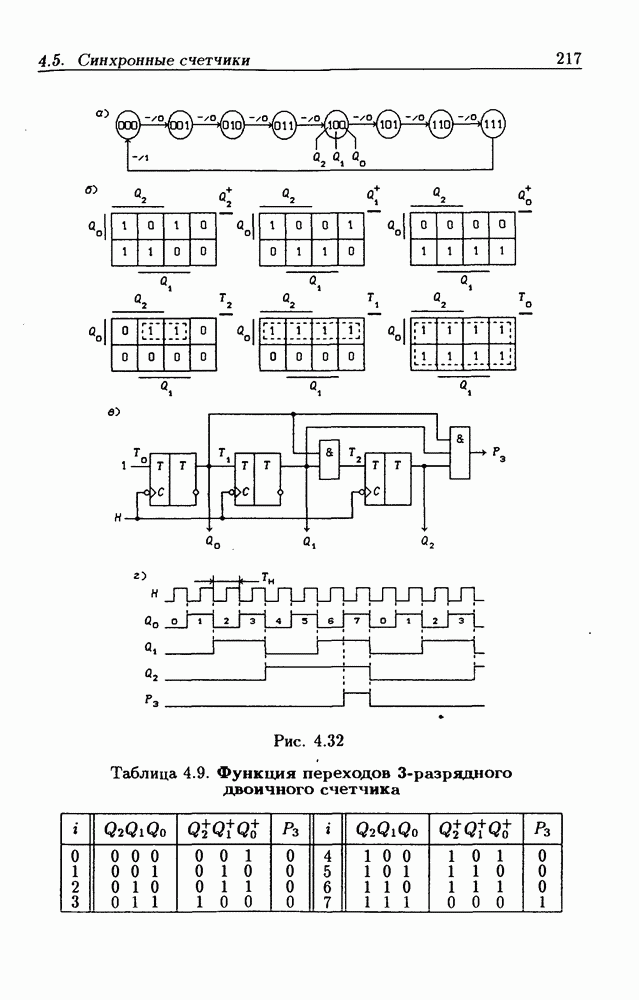
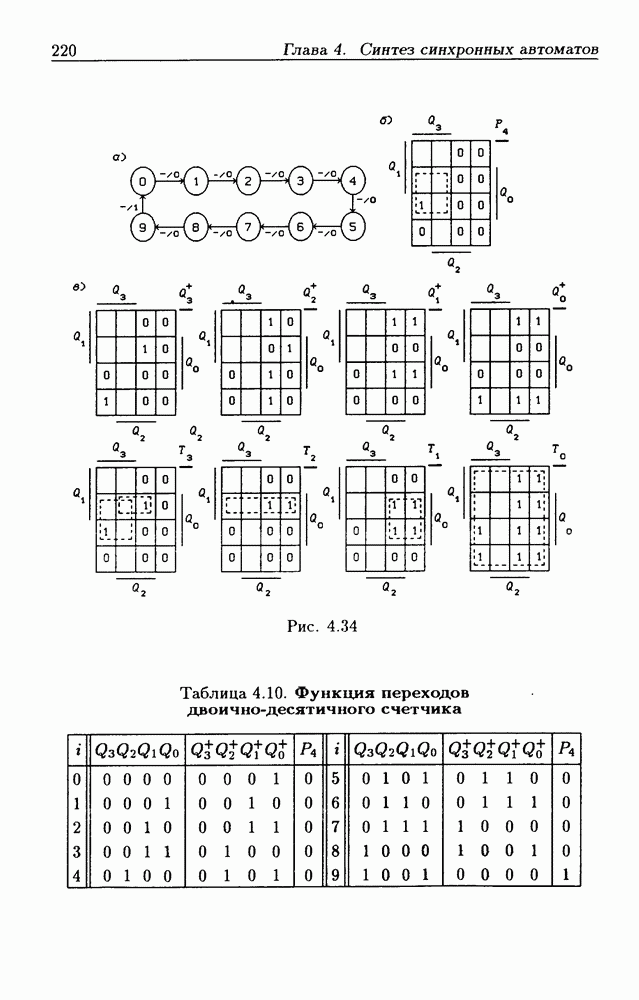
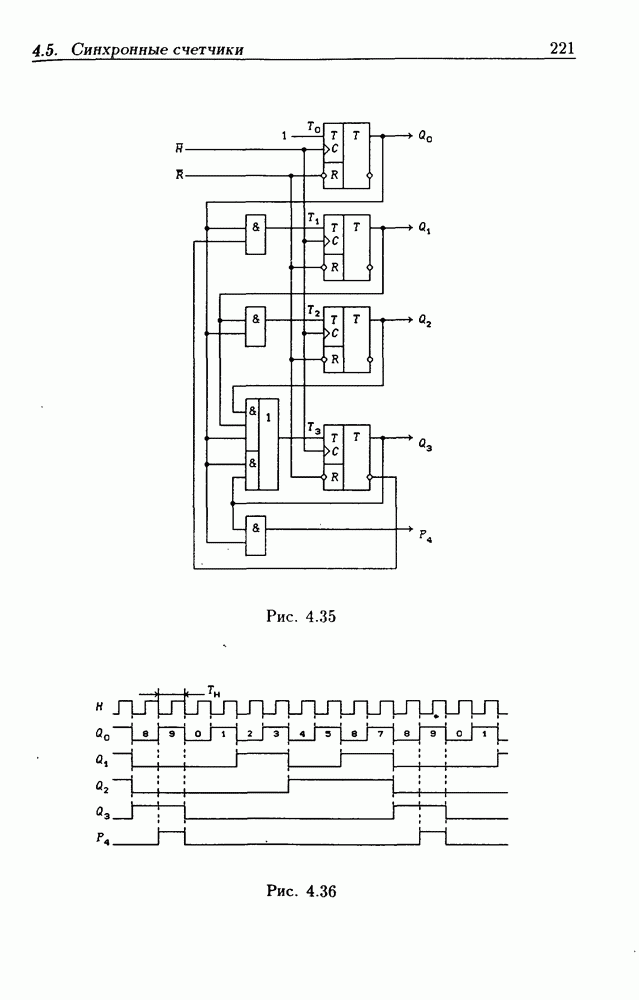
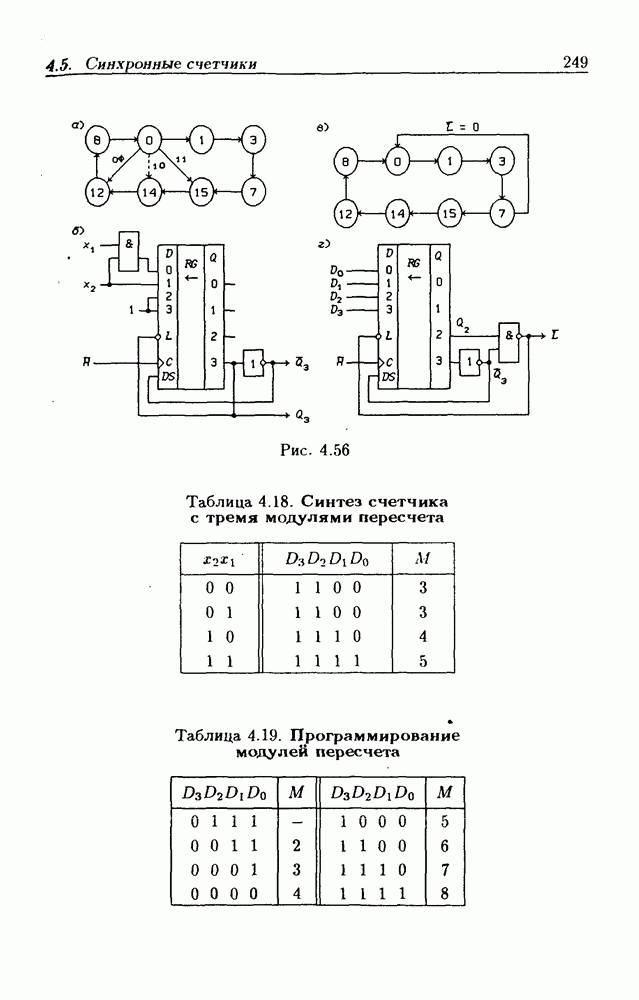
- 4.5. Синхронные счетчики
- Синхронные двоичные счетчики.
- Синхронные двоично-десятичные счетчики.
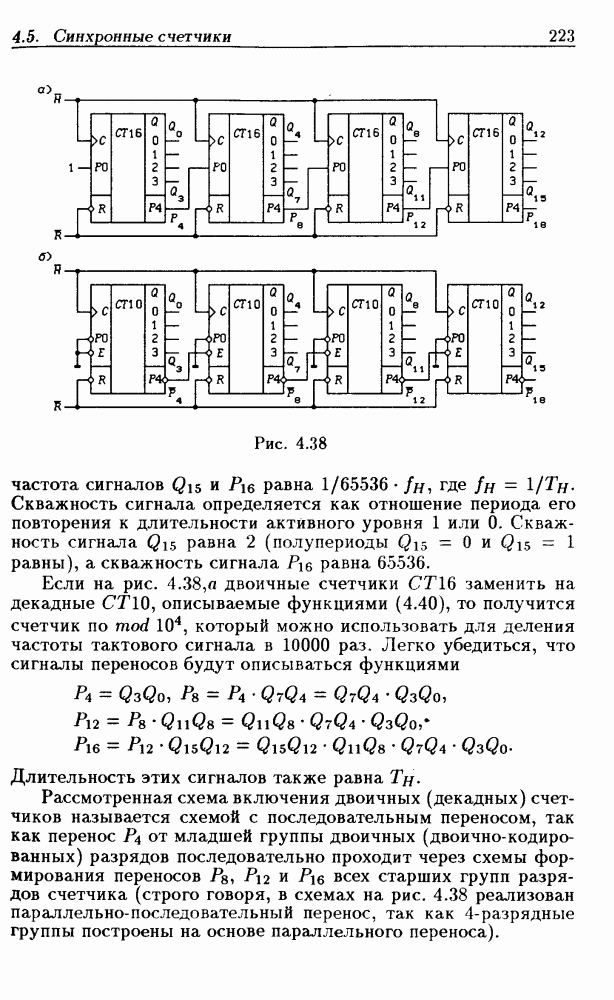
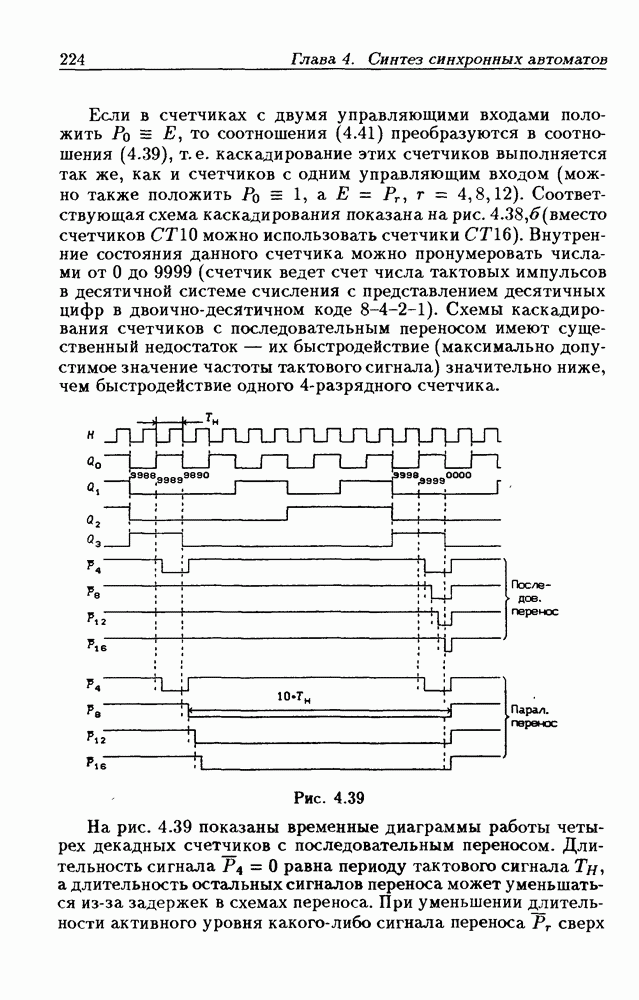
- Каскадирование двоичных и двоично-десятичных счетчиков.
- Синхронные двоичные реверсивные счетчики.
- Реверсивные двоично-десятичные счетчики.
- Каскадирование реверсивных счетчиков.
- Счетчики на сдвигающих регистрах.
- Кольцевые счетчики.
- Линейные счетчики.
- Программируемые счетчики.
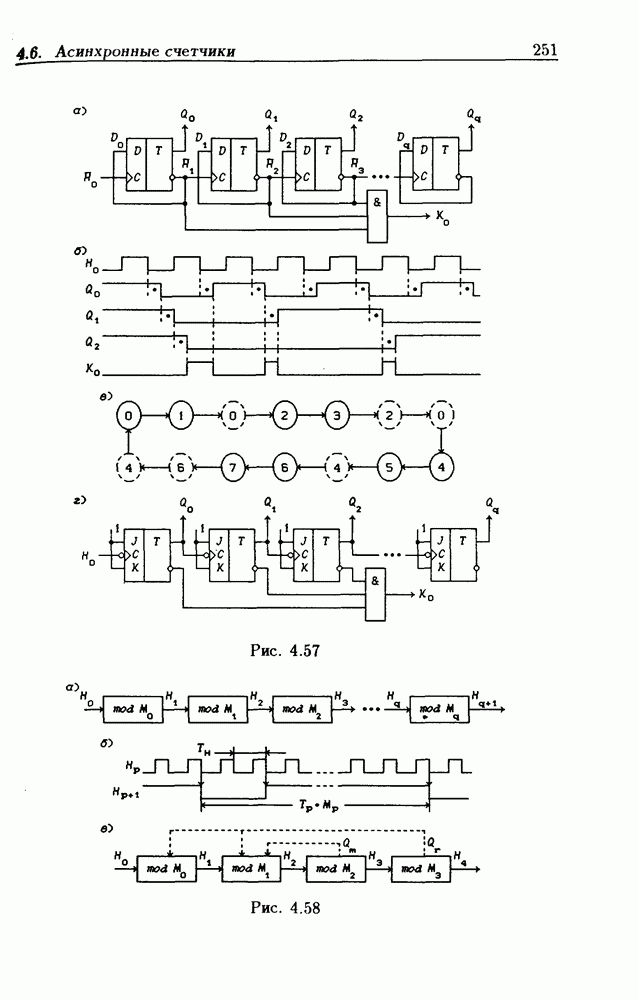
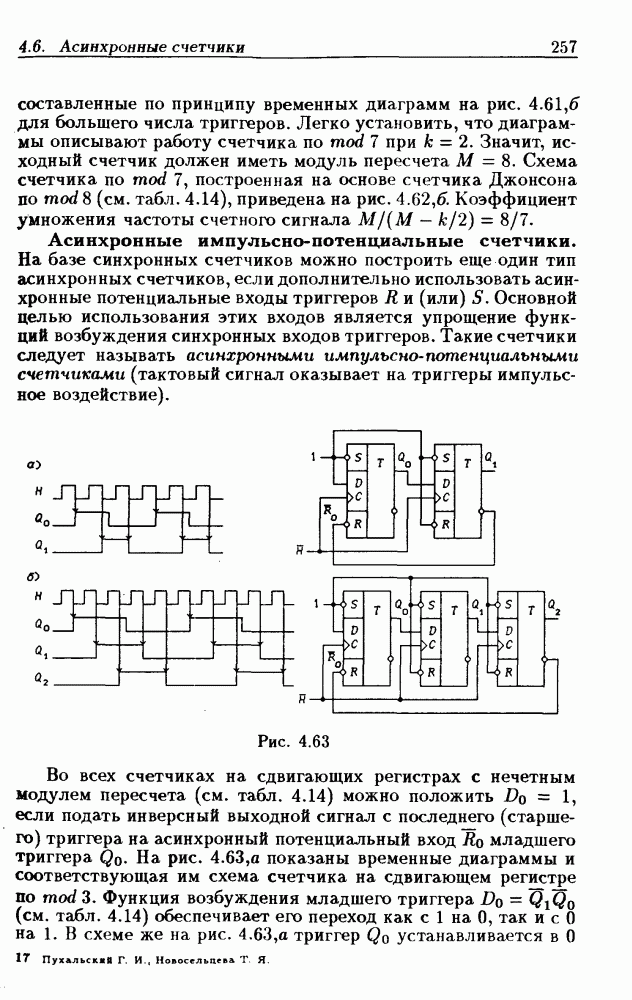
- 4.6. Асинхронные счетчики
- Асинхронные счетчики с умножением частоты счетного сигнала.
- Асинхронные импульсно-потенциальные счетчики.
- Асинхронное программирование модуля пересчета счетчиков.
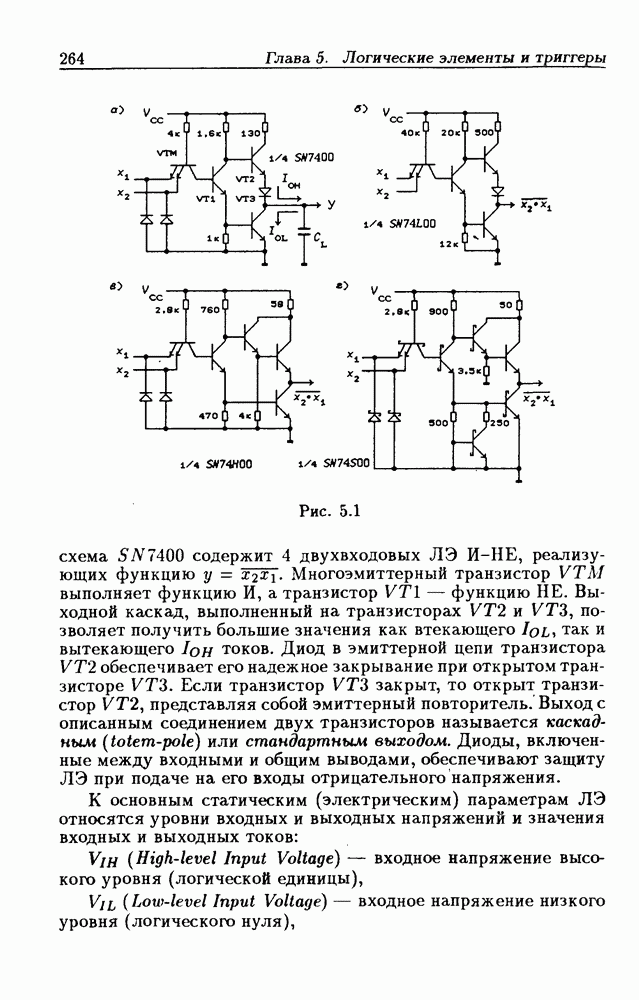
- Глава 5. Логические элементы и триггеры
- Логические элементы.
- Классификация ИС по степени интеграции.
- 5.2. Интегральные схемы КМОП серий
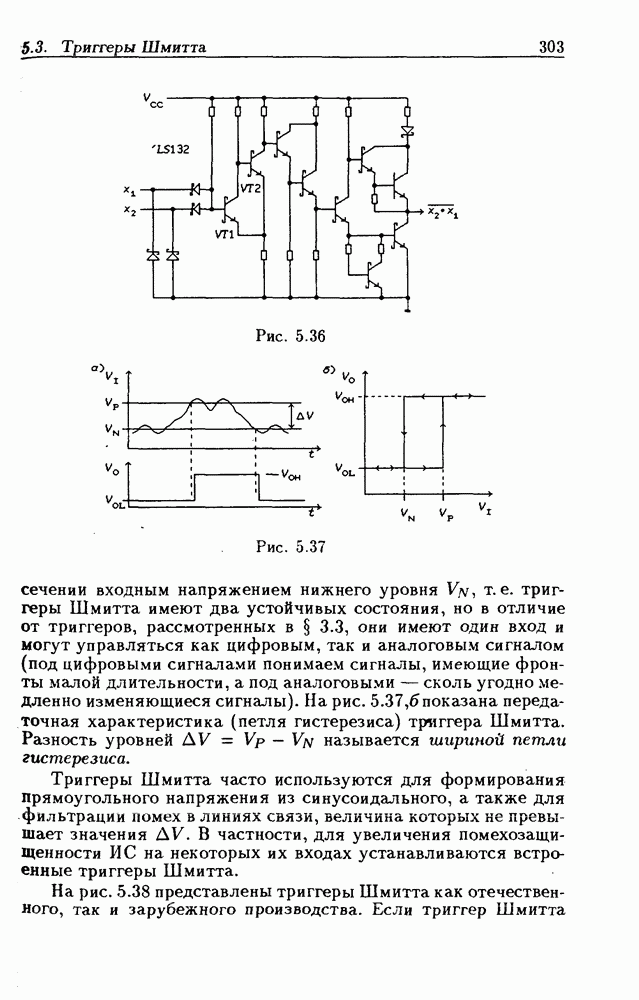
- 5.3. Триггеры Шмитта
- 5.4. Логические элементы с открытым коллекторным выходом
- Логические элементы с открытым коллекторным выходом.
- Применения ЛЭ с открытым коллекторным выходом.
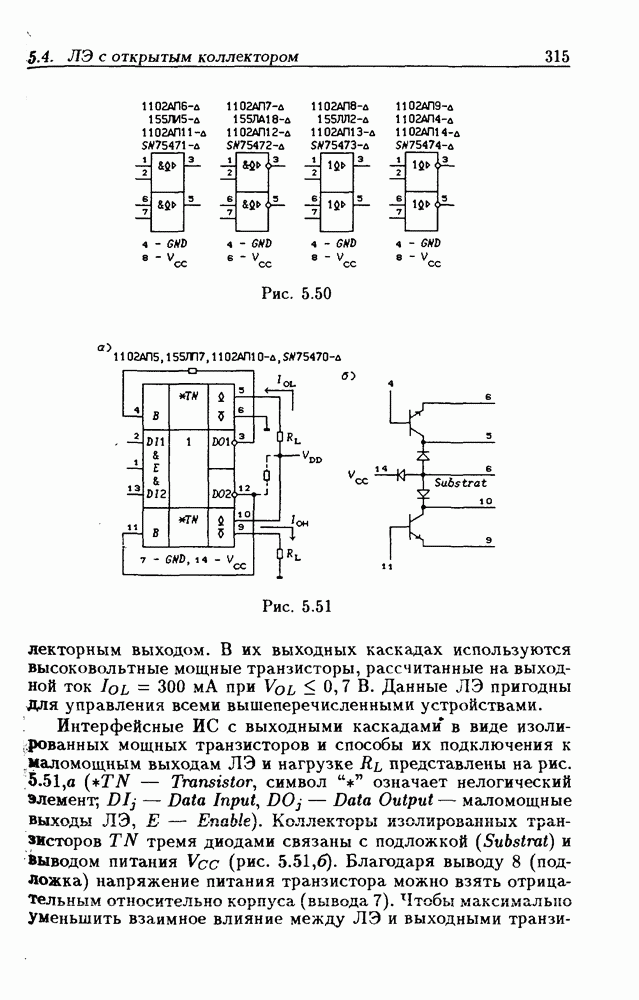
- Интерфейсные ЛЭ с открытым коллекторным выходом.
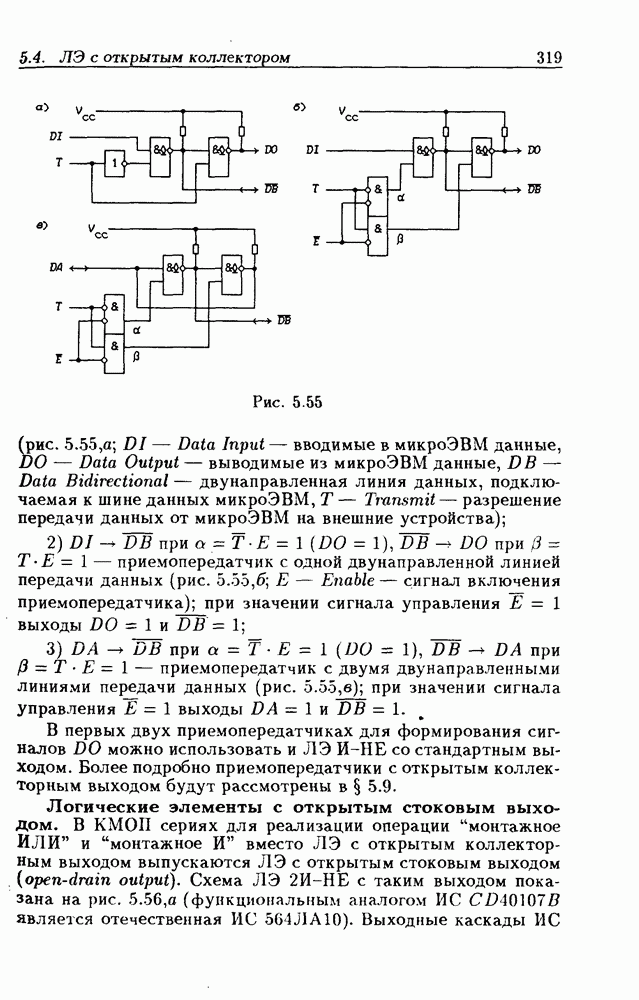
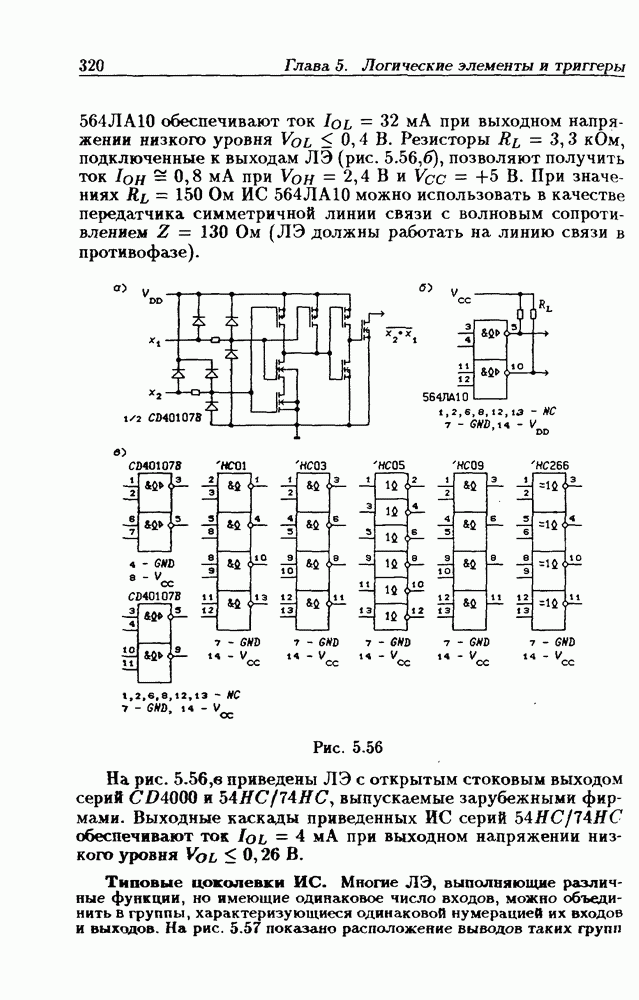
- Логические элементы с открытым стоковым выходом.
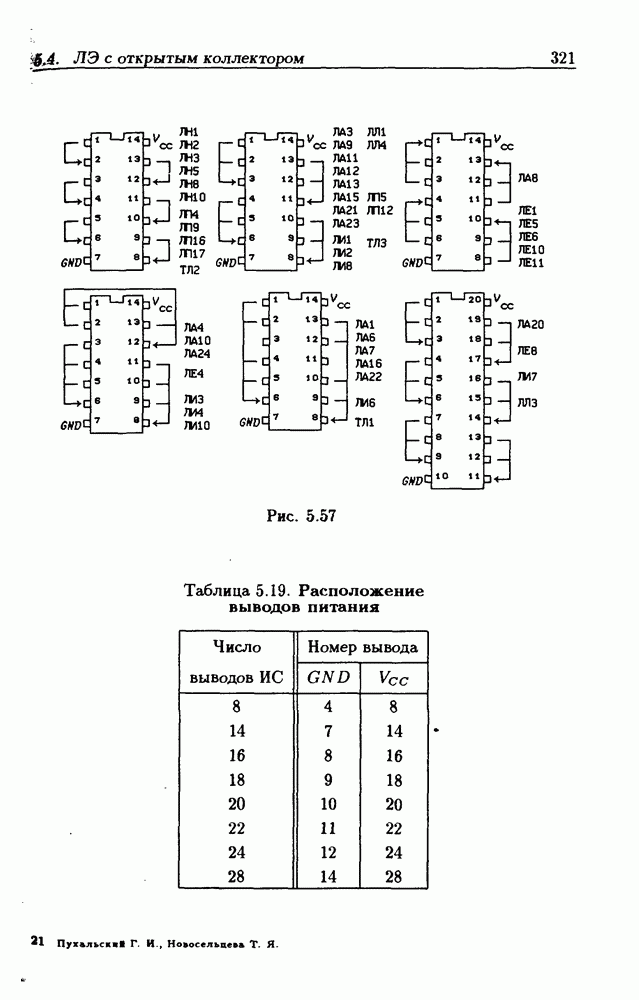
- Типовые цоколевки ИС.
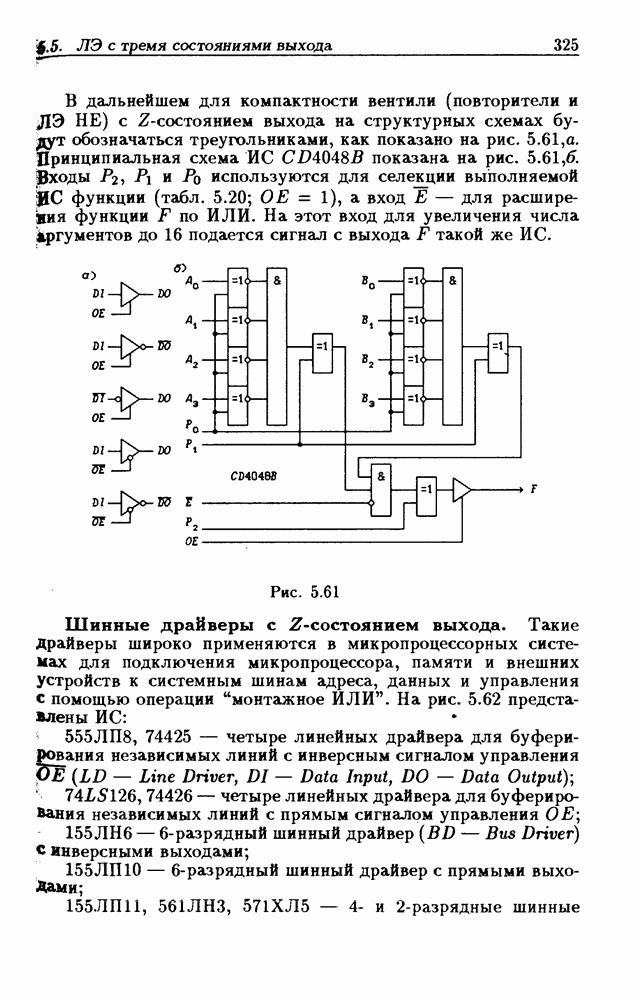
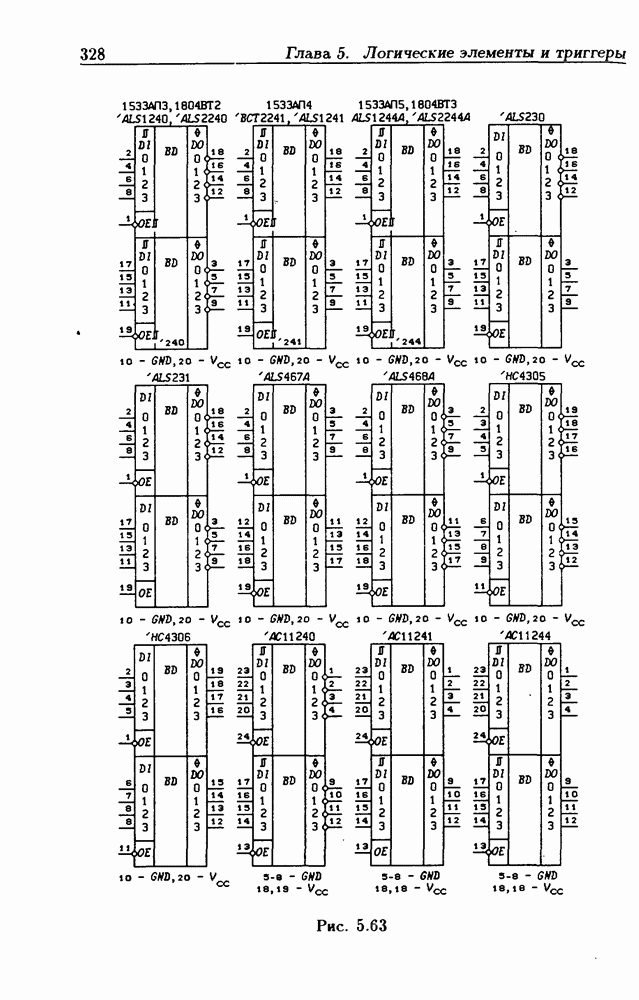
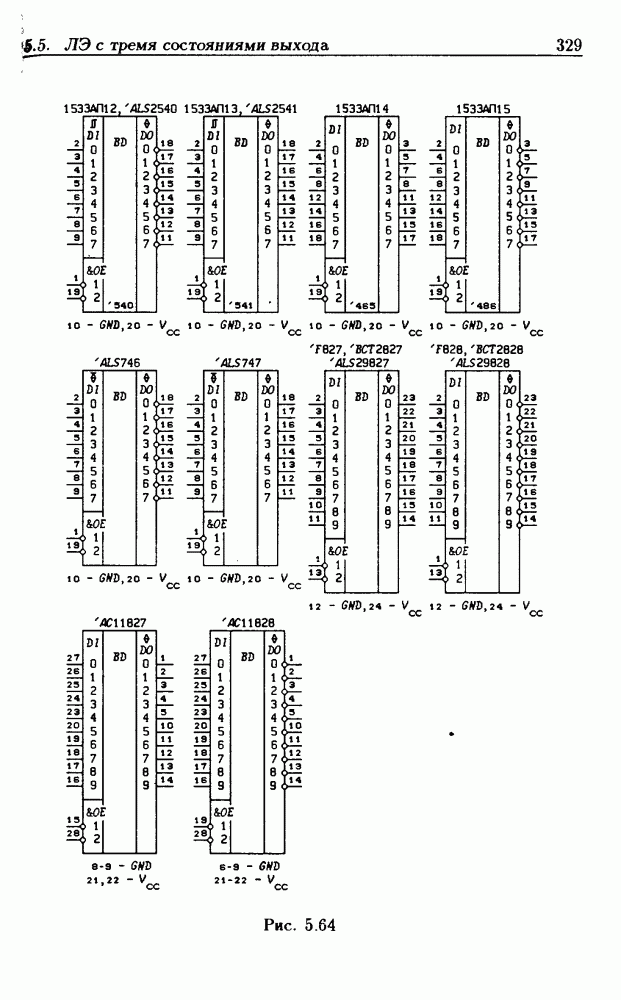
- 5.5. Логические элементы с тремя состояниями выхода
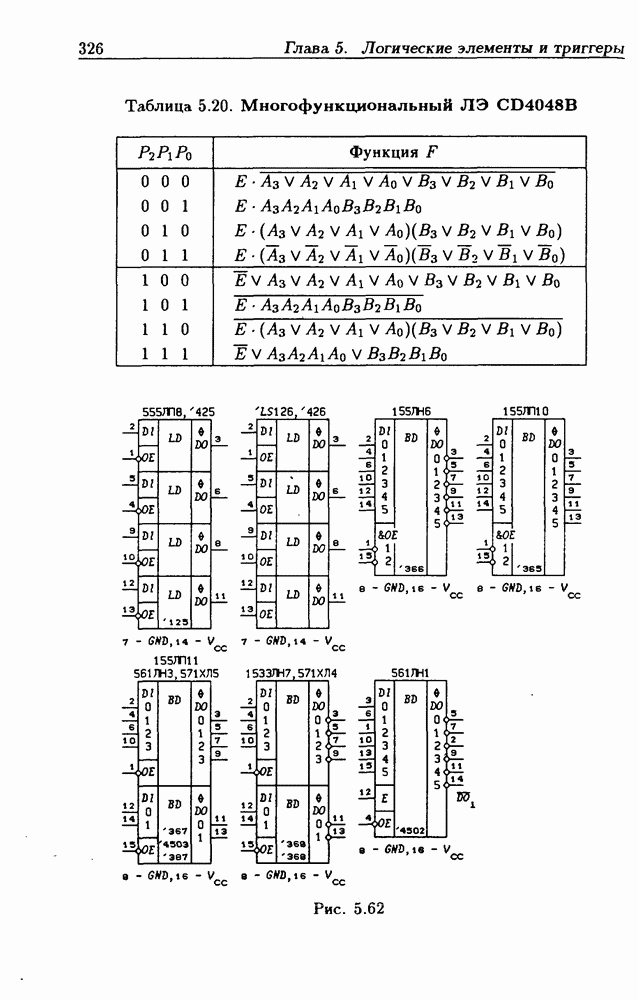
- Шинные драйверы с Z-состоянием выхода.
- Основные правила графического изображения ИС.
- 5.6. Преобразователи уровней напряжения и тока
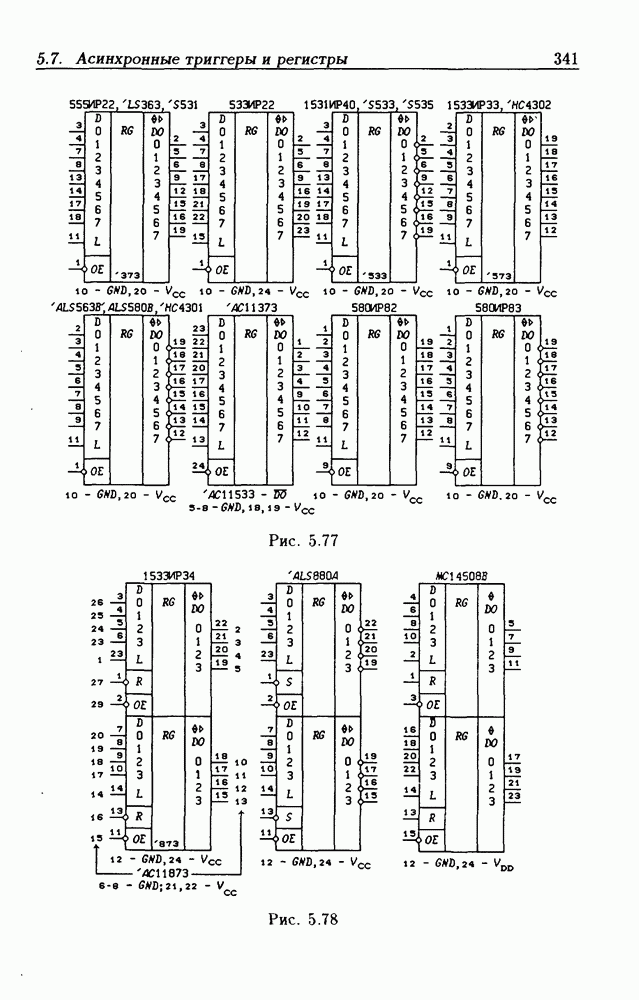
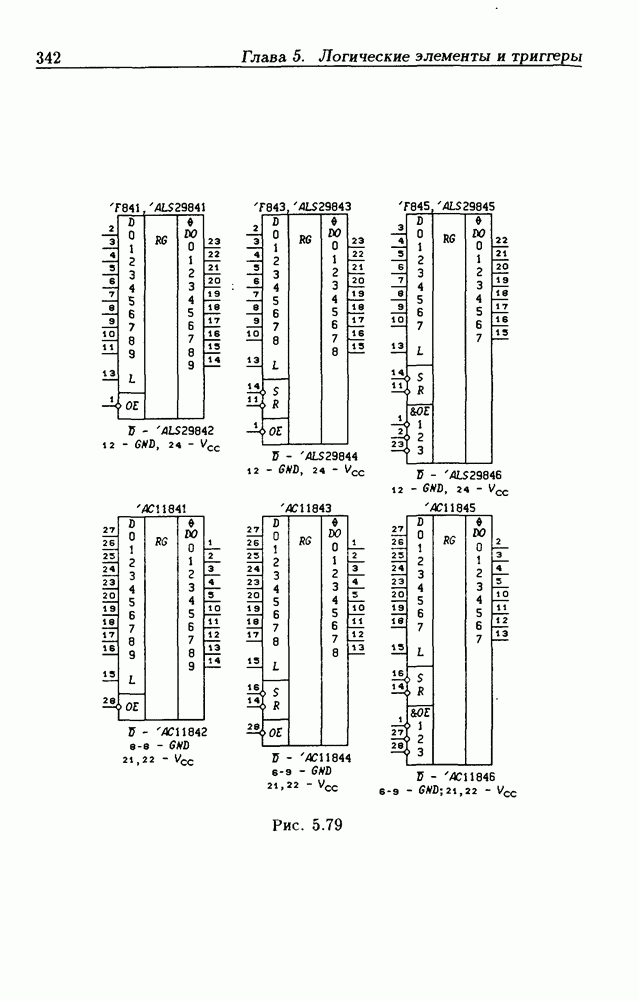
- 5.7. Асинхронные потенциальные триггеры и регистры памяти
- 5.8. Синхронные триггеры и регистры памяти
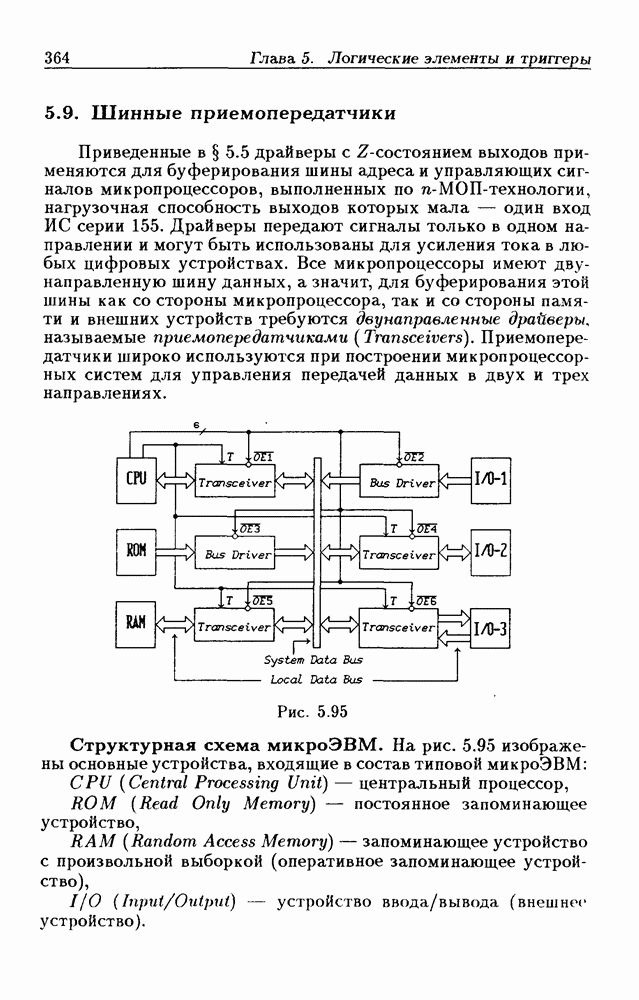
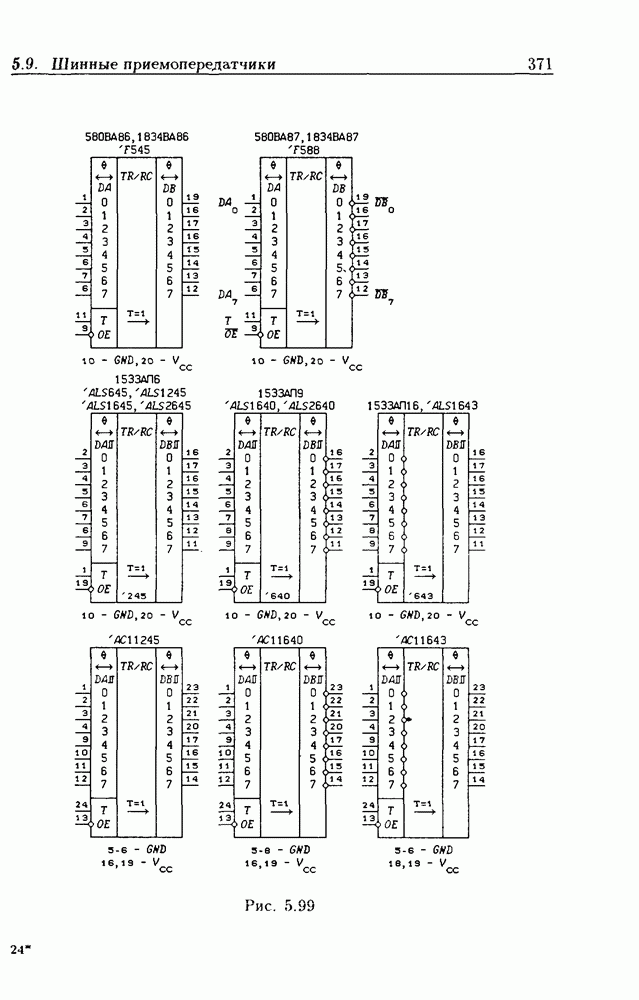
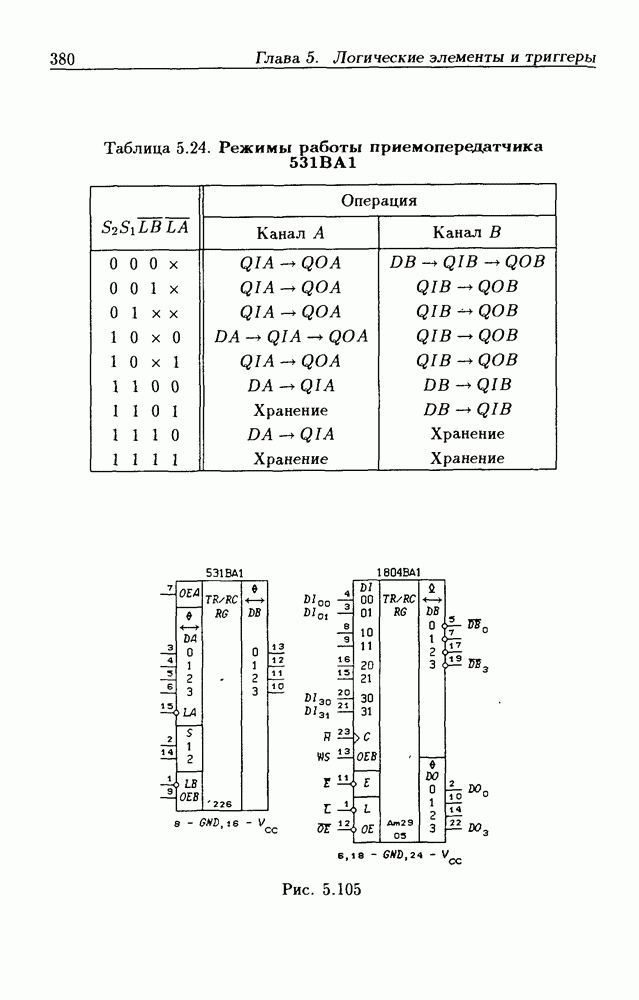
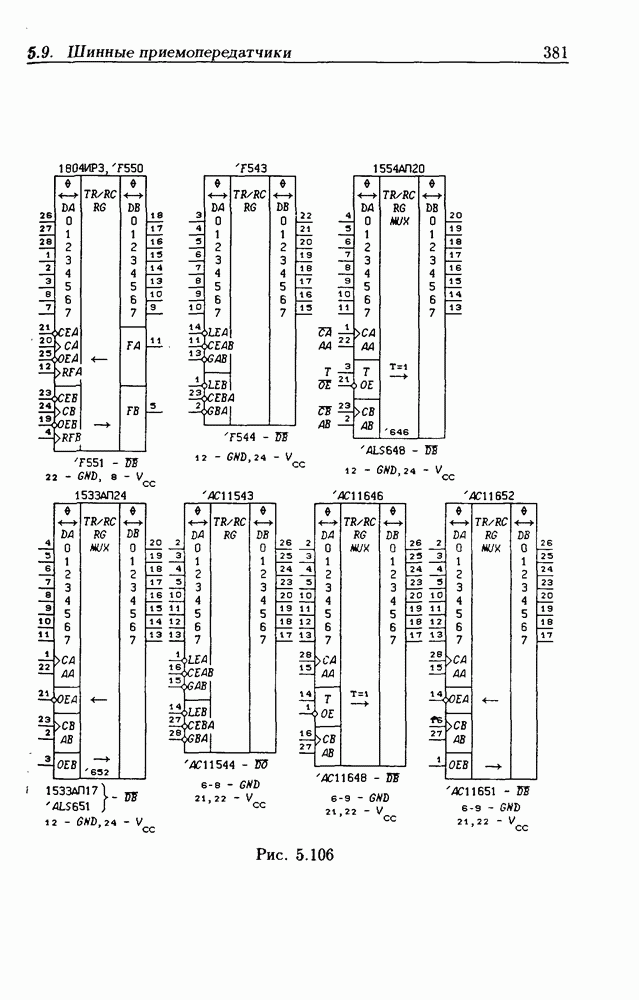
- 5.9. Шинные приемопередатчики
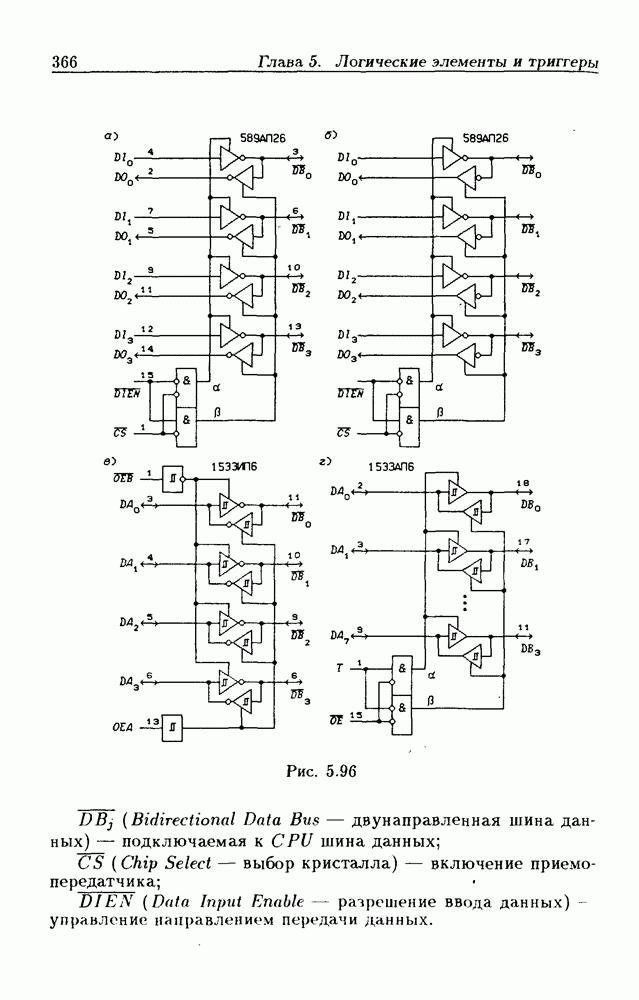
- Шинные приемопередатчики с Z-состоянием выхода.
- Шинные приемопередатчики с открытым коллекторным выходом.
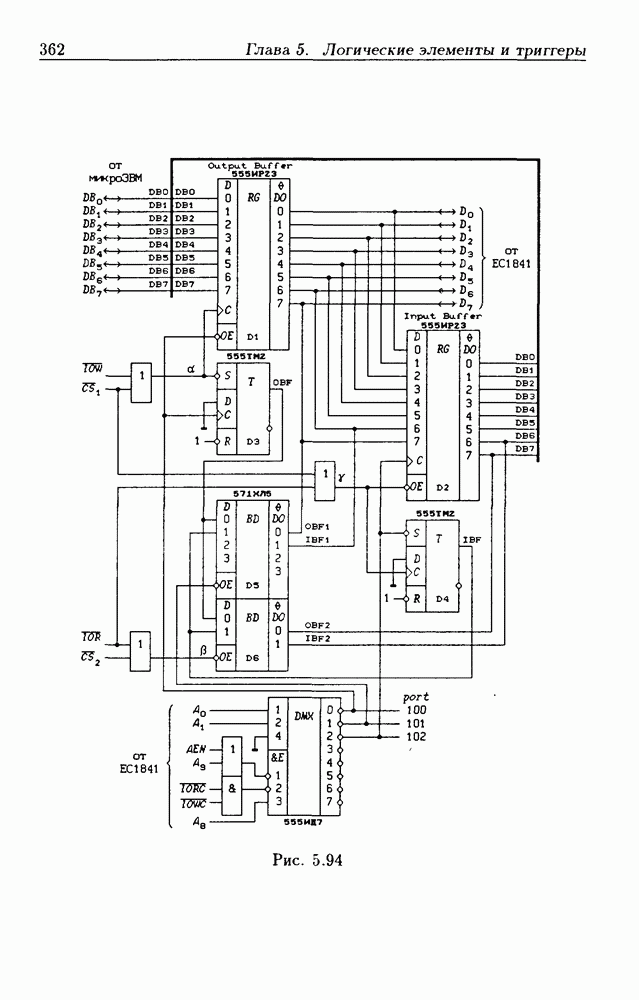
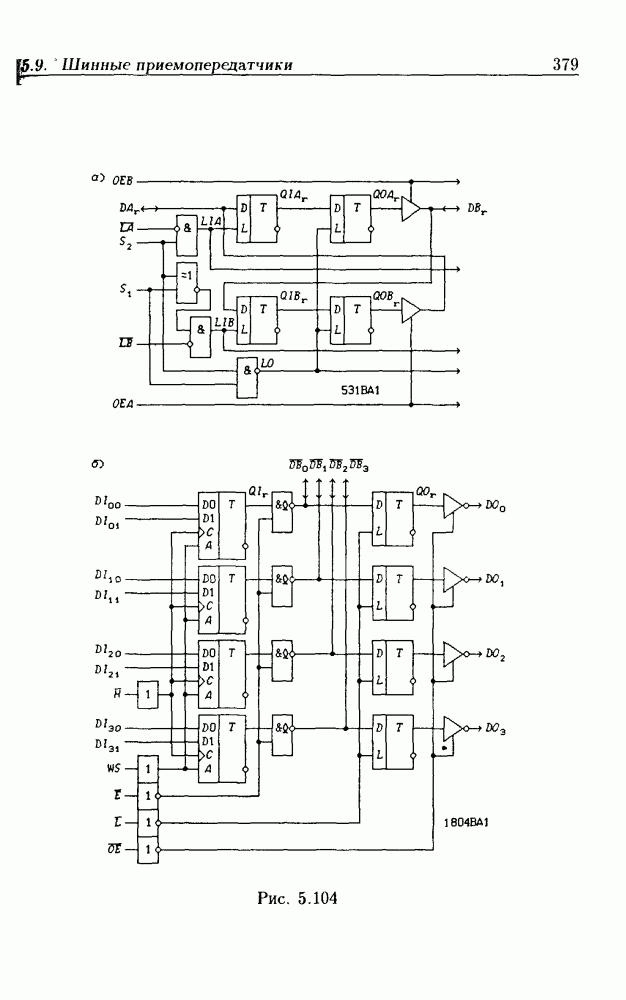
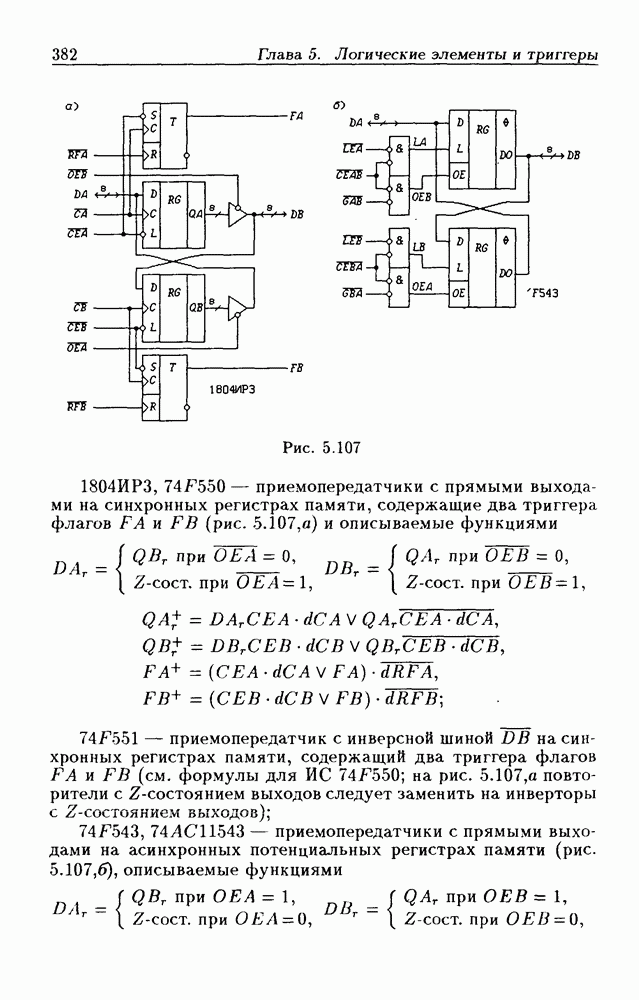
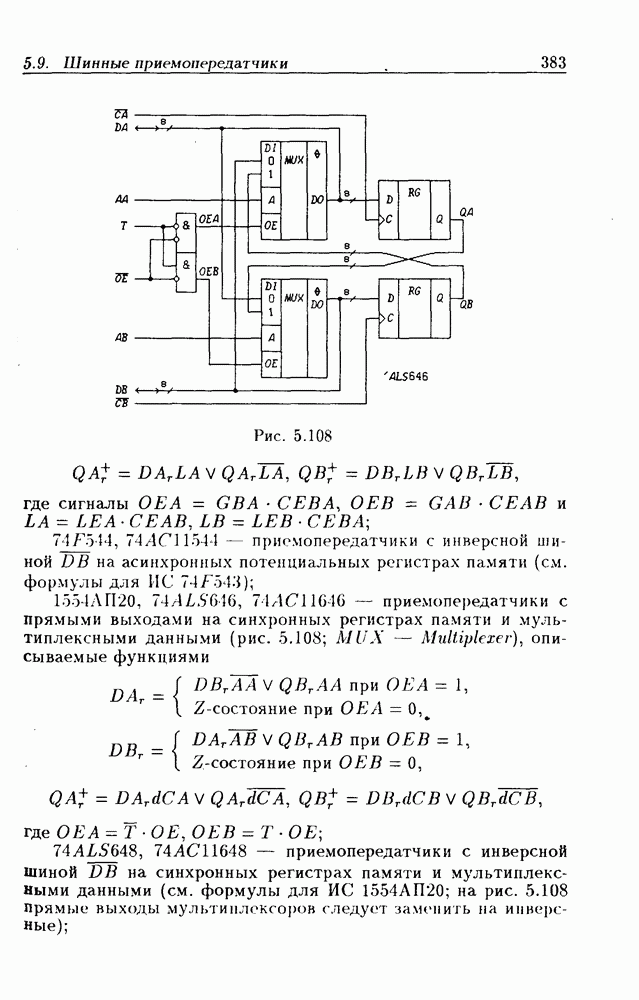
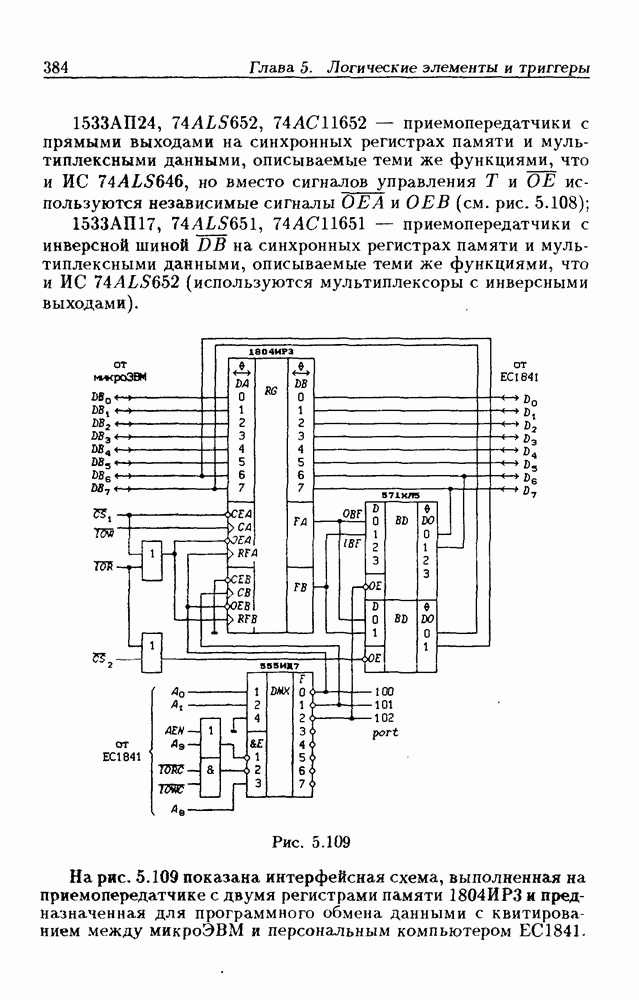
- Шинные приемопередатчики с регистрами памяти.
- Шинные приемопередатчики со сдвигающим регистром.
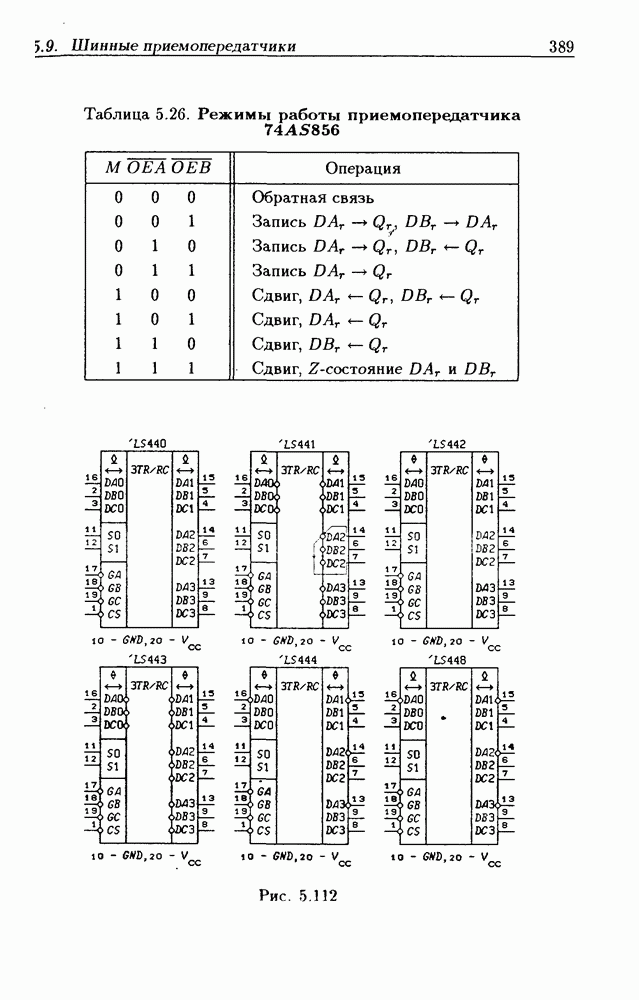
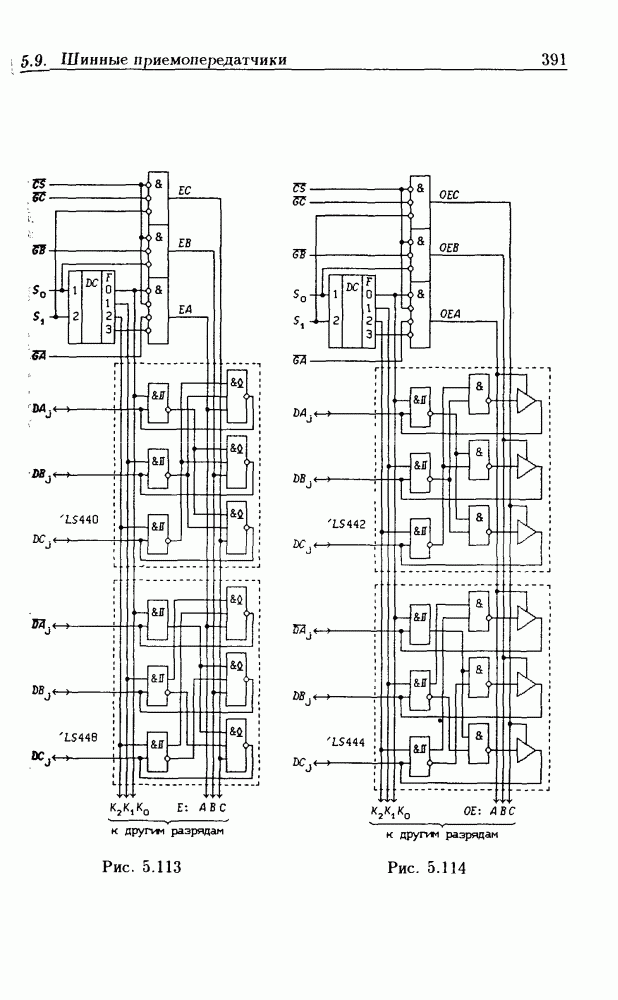
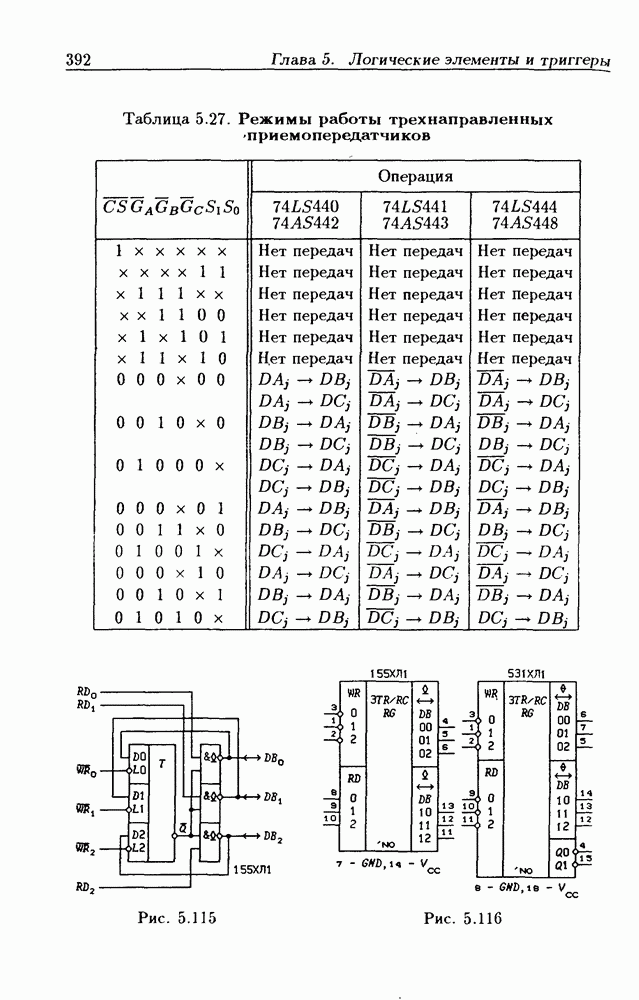
- Шинные трехнаправленные приемопередатчики.
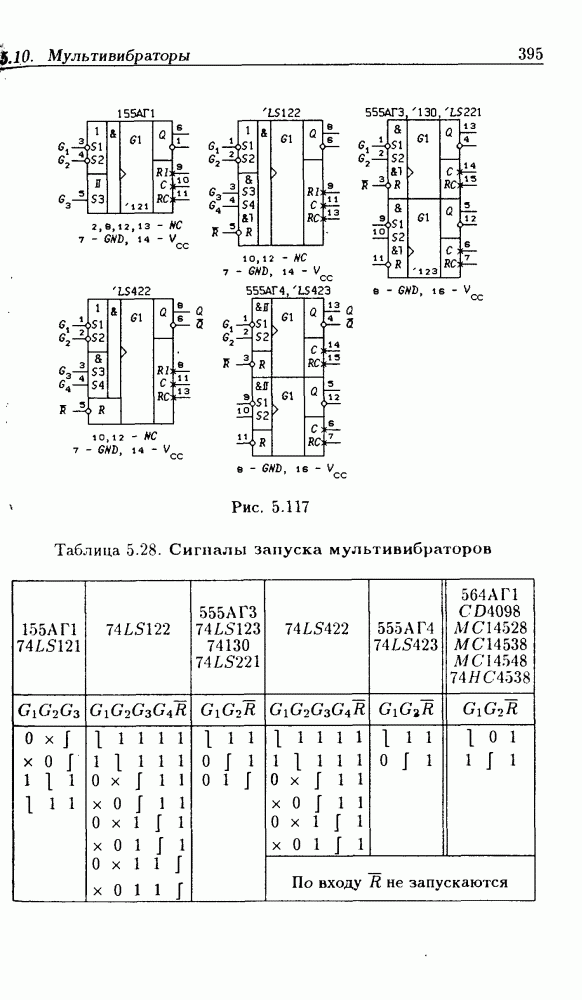
- 5.10. Мультивибраторы
- 5.11. Генераторы
- Схемы устранения «дребезга» механических контактов.
- Автогенераторы периодических сигналов.
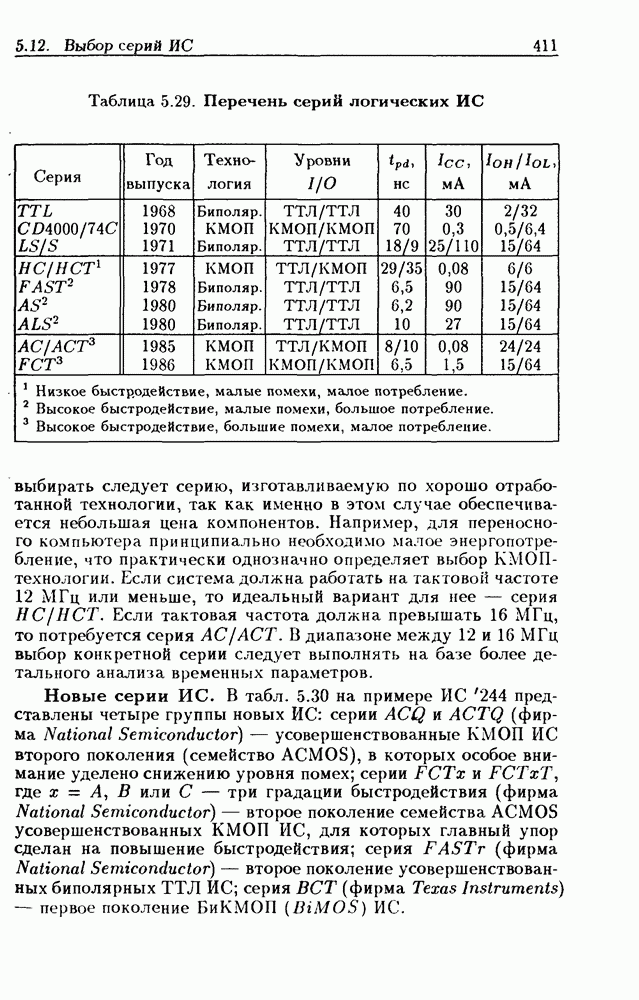
- 5.12. Рекомендации по выбору серий ИС
- Глава 6. Коммутаторы и арифметические устройства
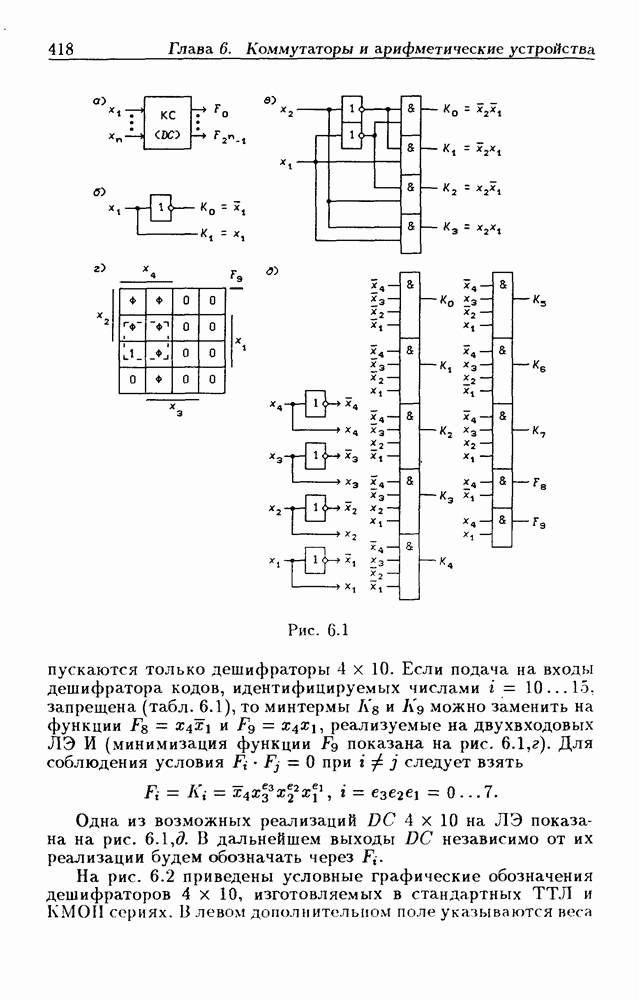
- 6.1. Дешифраторы
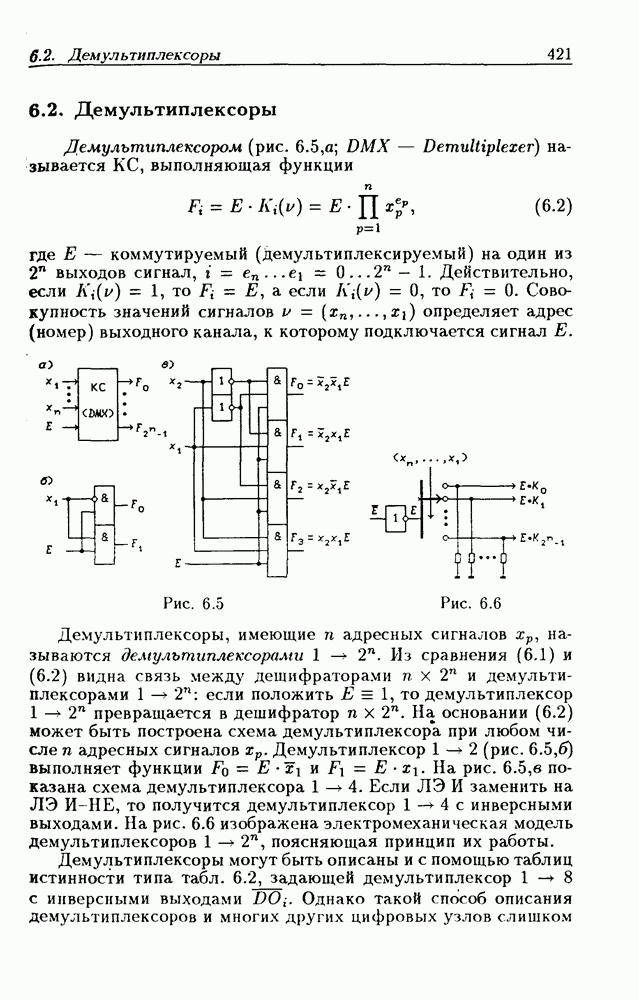
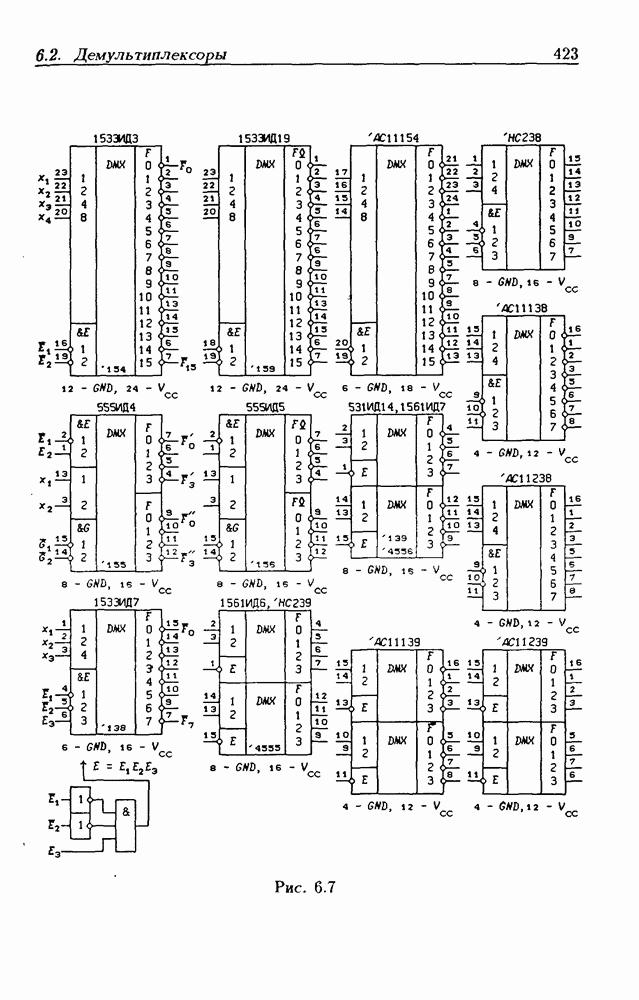
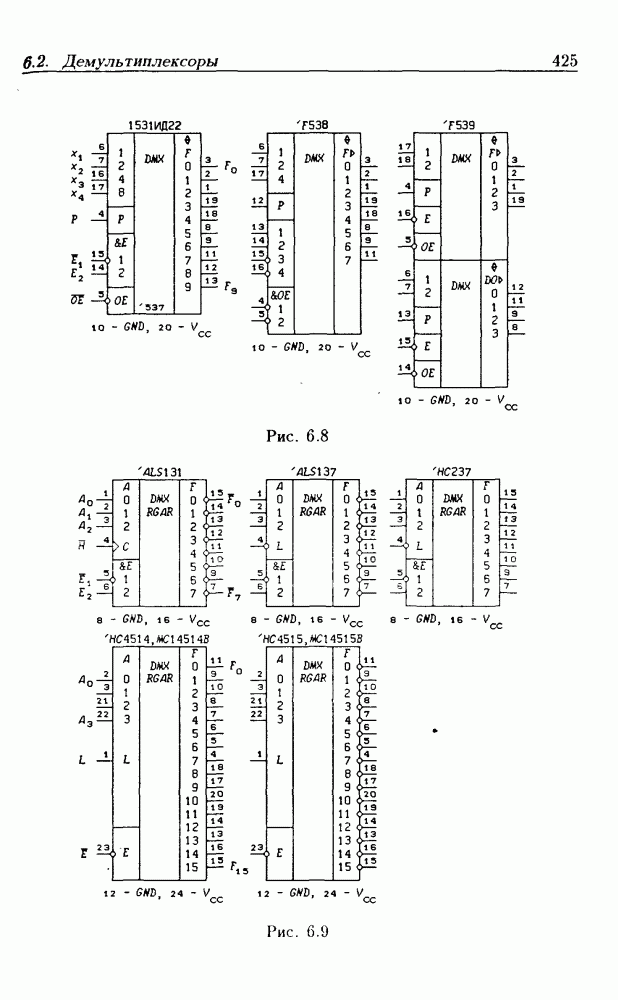
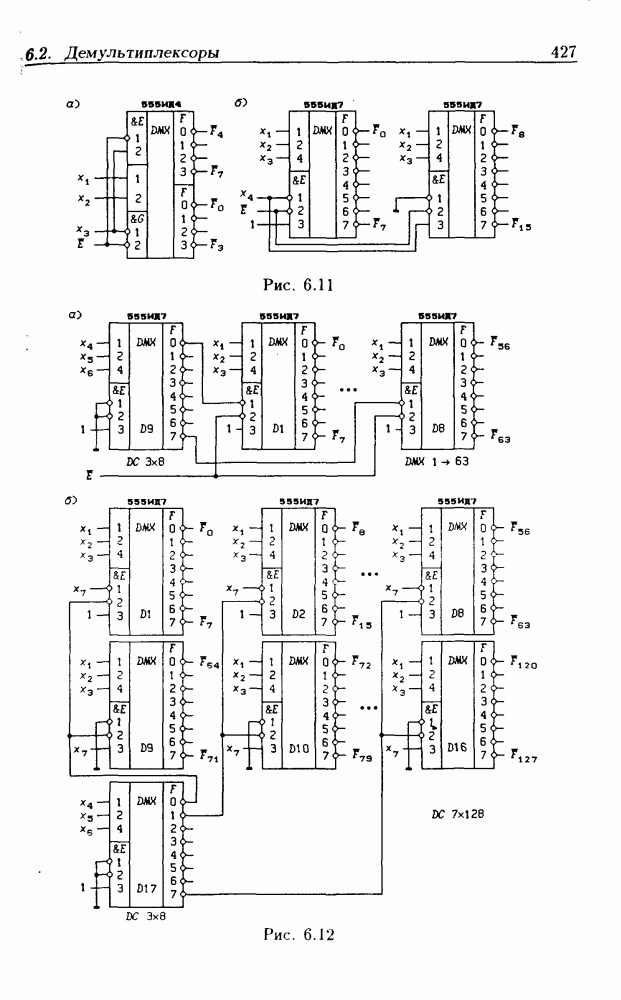
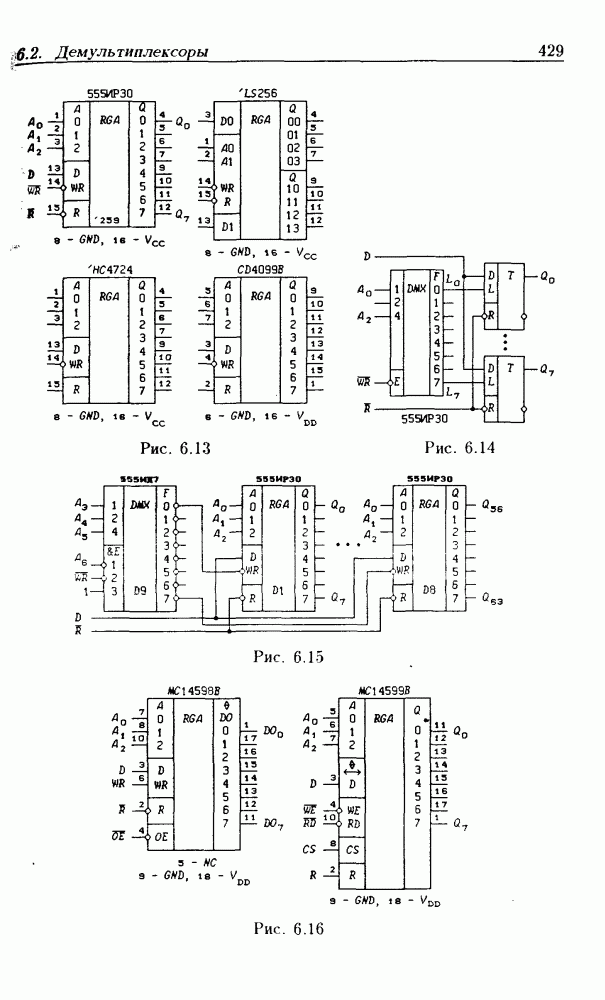
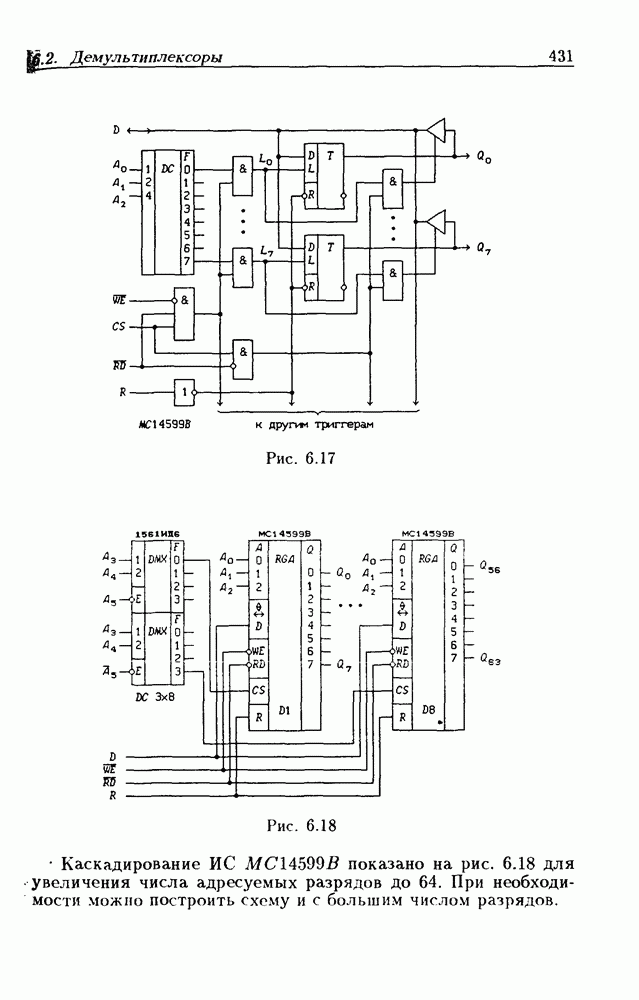
- 6.2. Демультиплексоры
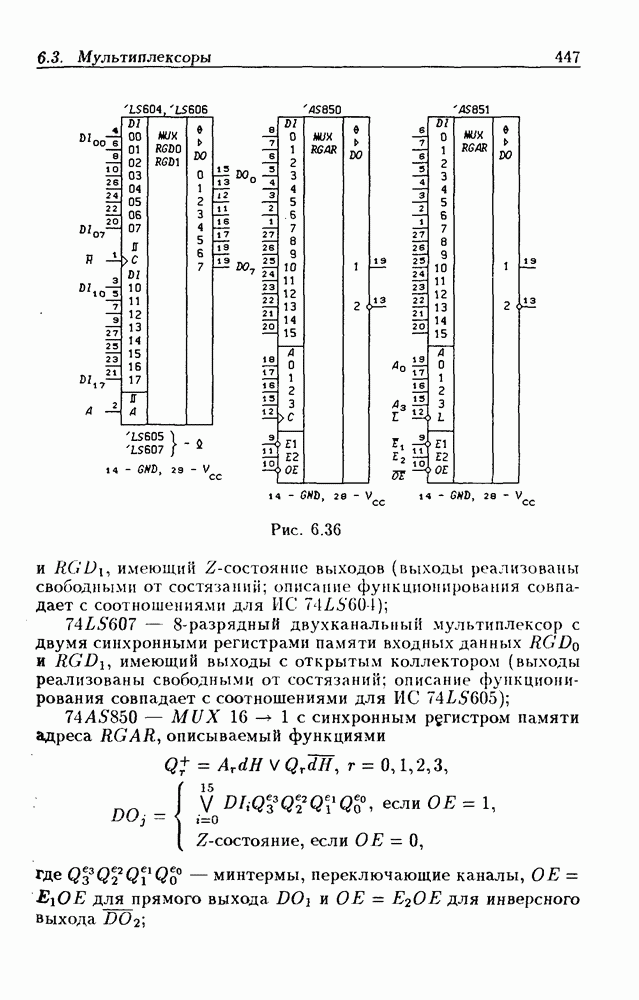
- 6.3. Мультиплексоры
- Мультиплексоры без стробирования.
- Мультиплексоры со стробированием.
- Мультиплексоры с Z-состоянием выхода.
- Каскадирование мультиплексоров.
- Функциональные мультиплексоры.
- Регистры памяти с мультиплексными входами данных.
- Мультиплексоры с регистрами памяти данных и адреса.
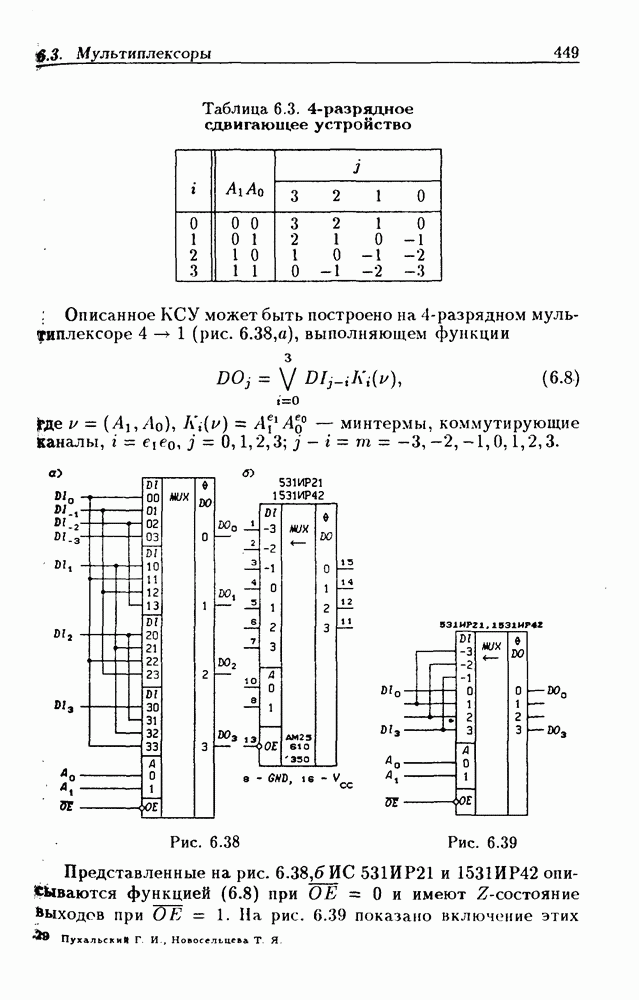
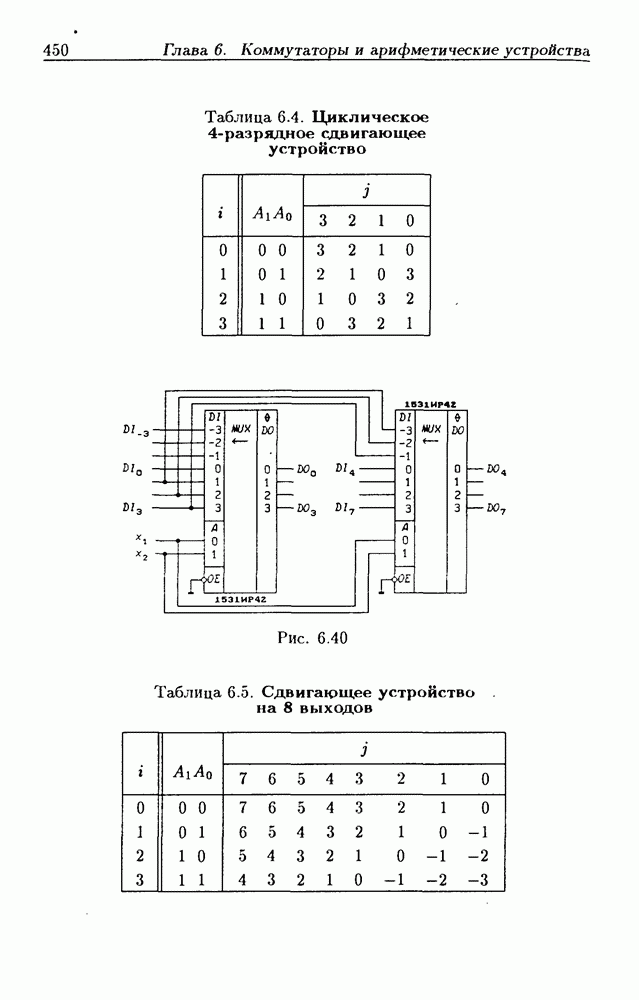
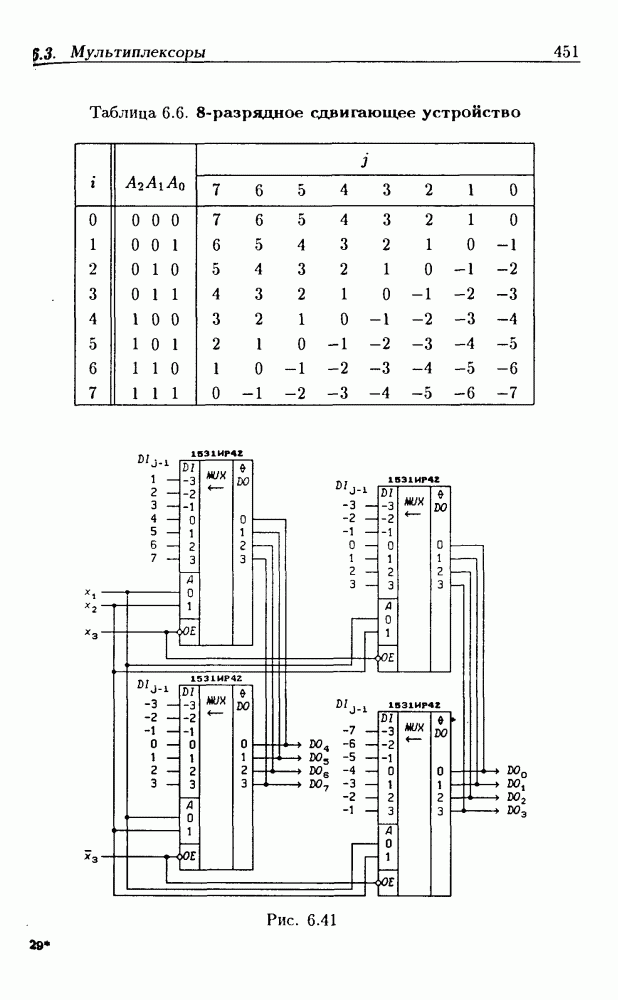
- Сдвигающие мультиплексоры.
- 6.4. Синтез комбинационных схем и цифровых автоматов на мультиплексорах
- Синтез схем на 8-канальных мультиплексорах.
- Синтез на двухразрядных 4-канальных мультиплексорах.
- Синтез генератора синусоидальной функции на мультиплексорах.
- Синтез триггеров на мультиплексорах.
- Синтез счетчиков на мультиплексорах.
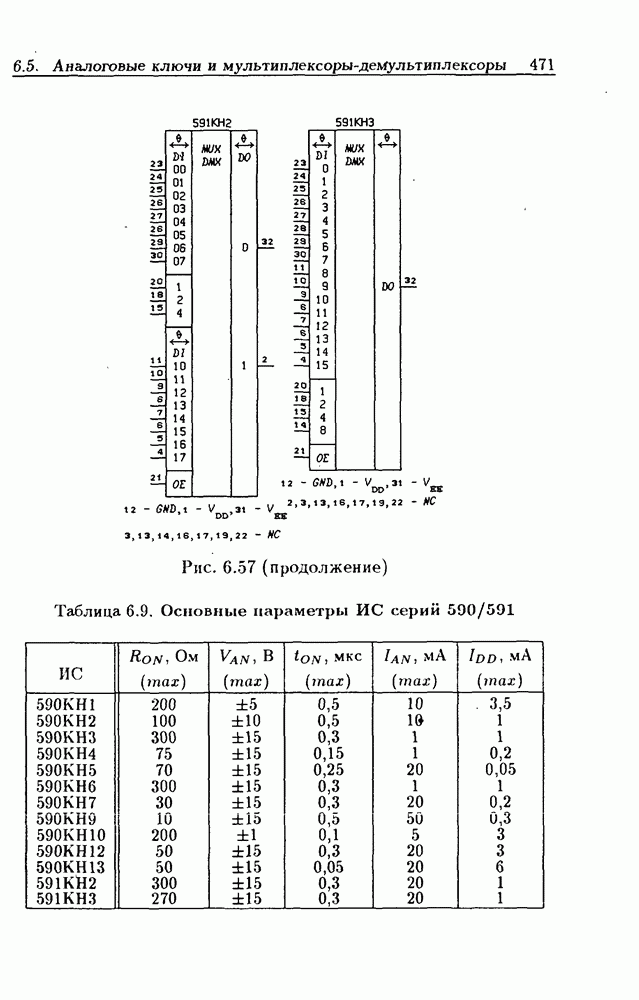
- 6.5. Аналоговые ключи и мультиплексоры-демультиплексоры
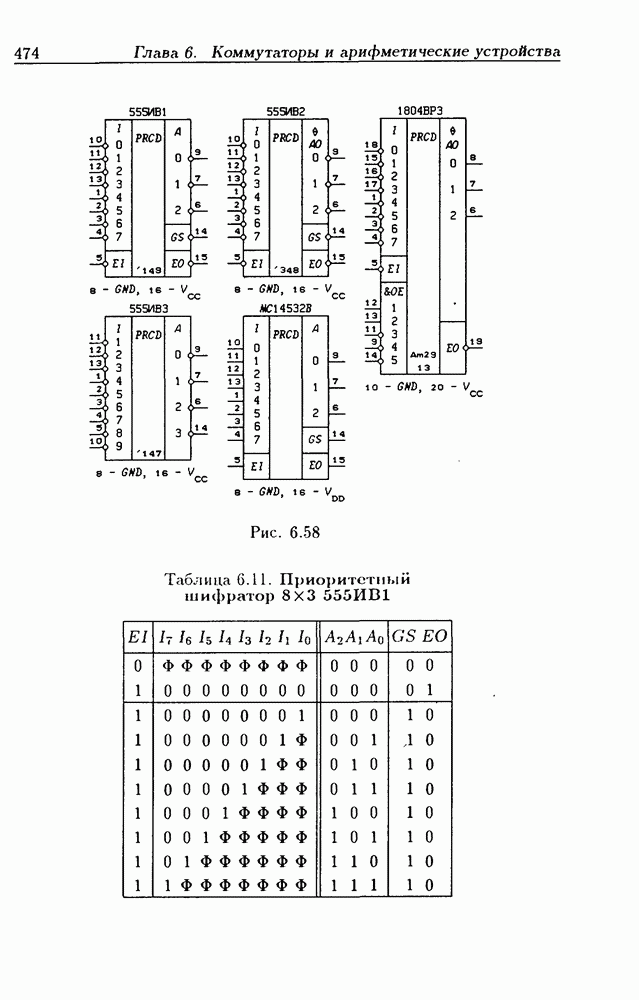
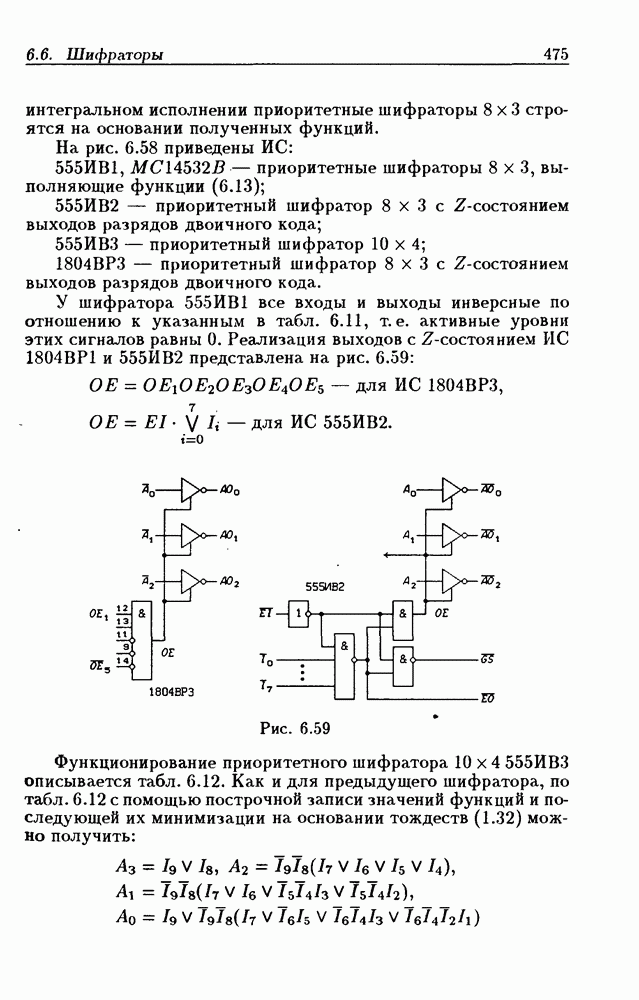
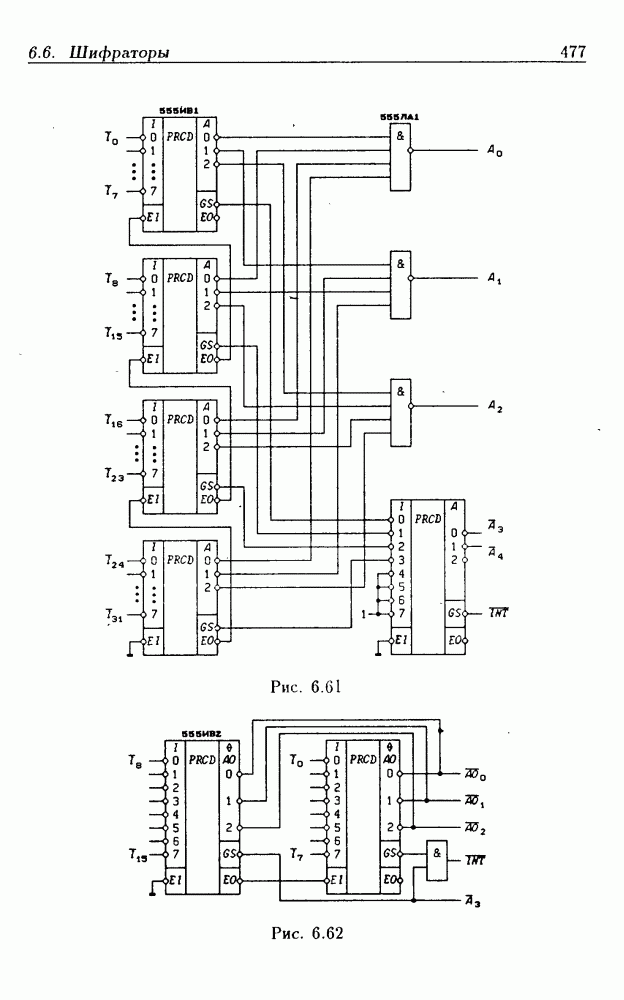
- 6.6. Шифраторы
- 6.7. Цифровые компараторы
- Программируемые цифровые компараторы.
- Адресные компараторы.
- Применения адресных компараторов.
- 6.8. Схемы сравнения двоичных чисел
- 8-разрядные схемы сравнения двоичных чисел.
- 6.9. Прямой, обратный и дополнительный коды
- Дополнительный код.
- Сложение чисел в обратном коде.
- Код с избытком 3.
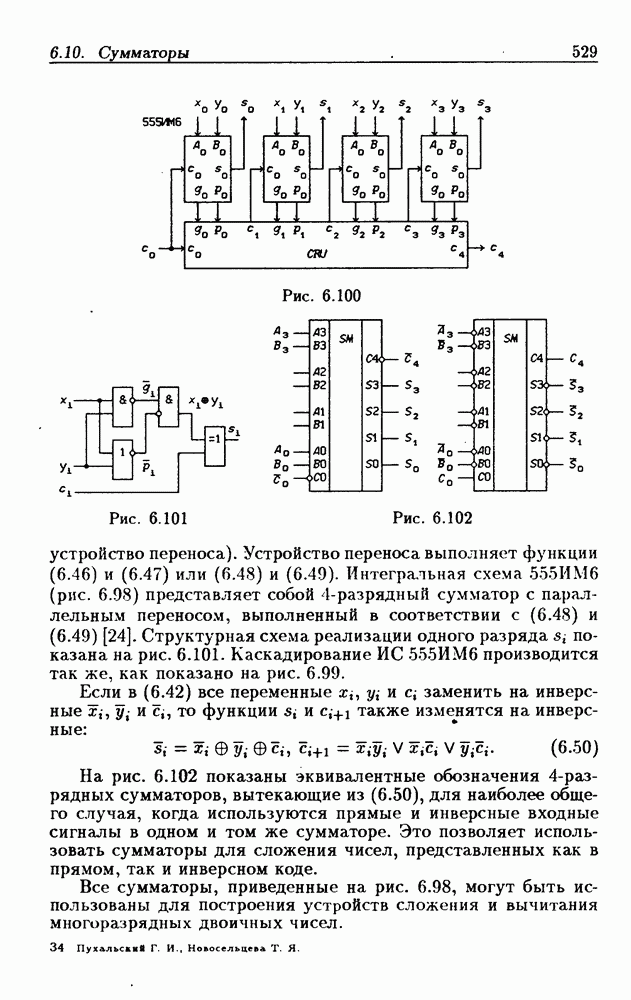
- 6.10. Сумматоры
- Двоичные параллельные сумматоры с последовательным переносом.
- Двоичные сумматоры с параллельным переносом.
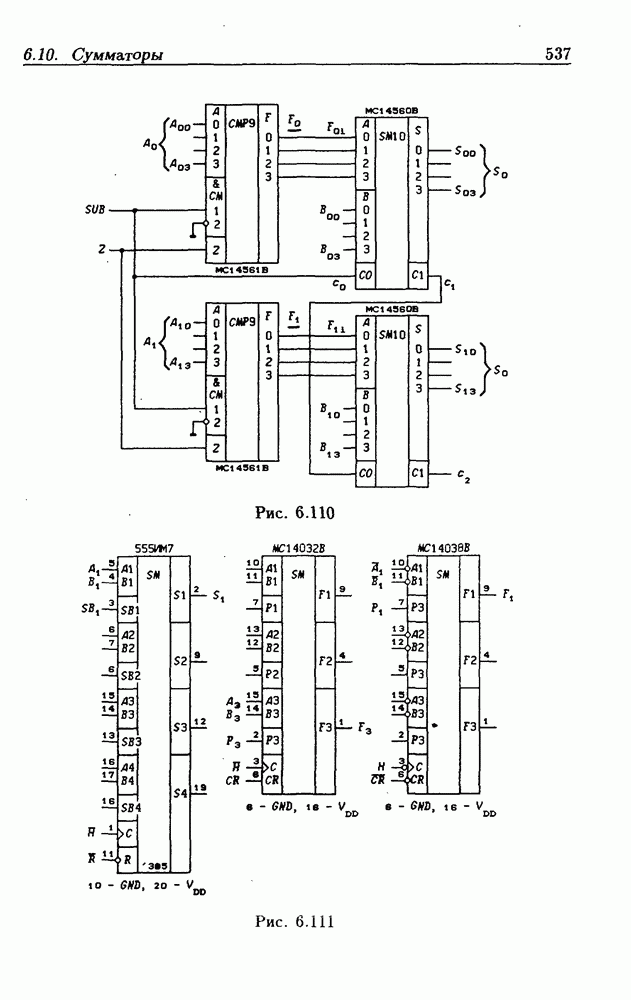
- Применения сумматоров.
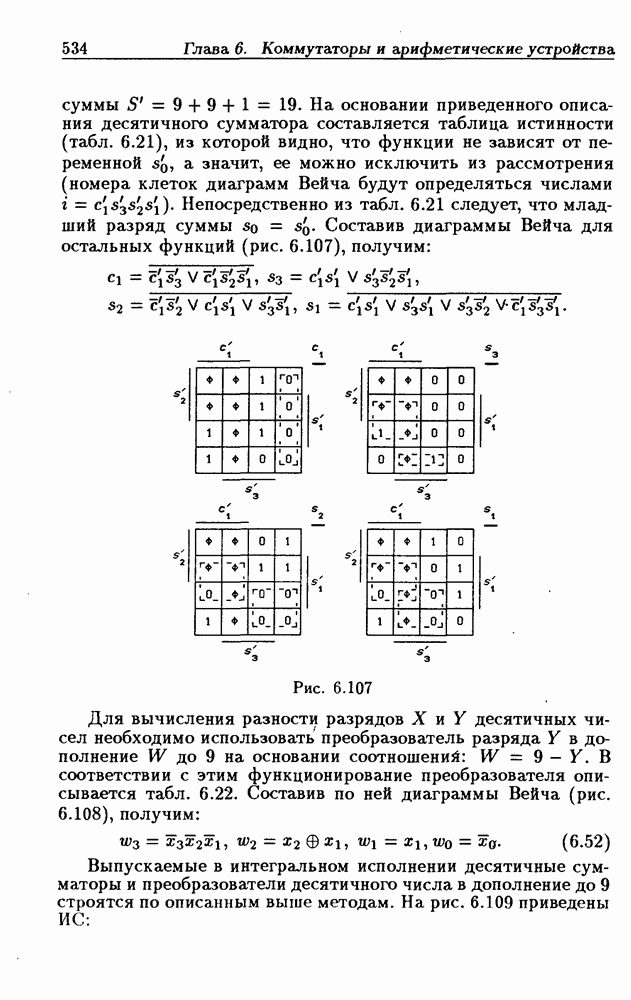
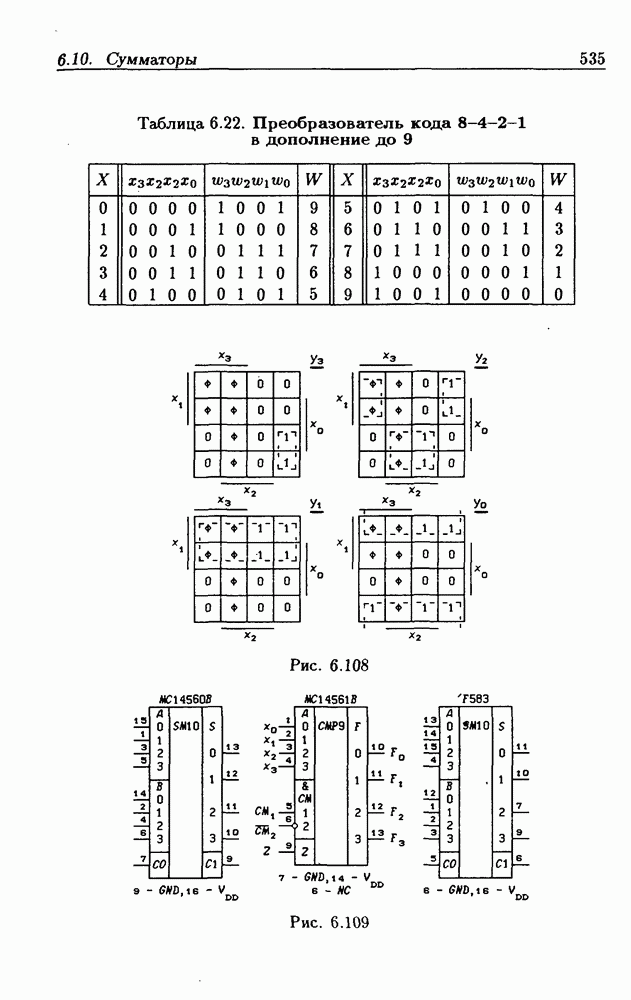
- Десятичные сумматоры.
- Последовательные двоичные сумматоры.
- 6.11. Арифметическо-логические устройства
- 6.12. Пороговые схемы и мажоритарные элементы
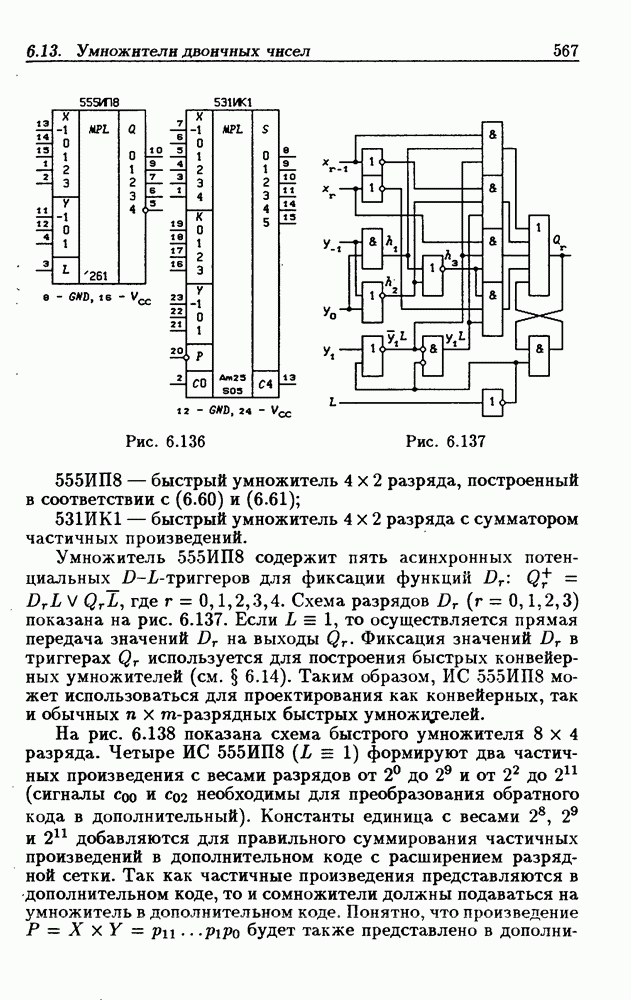
- 6.13. Умножители двоичных чисел
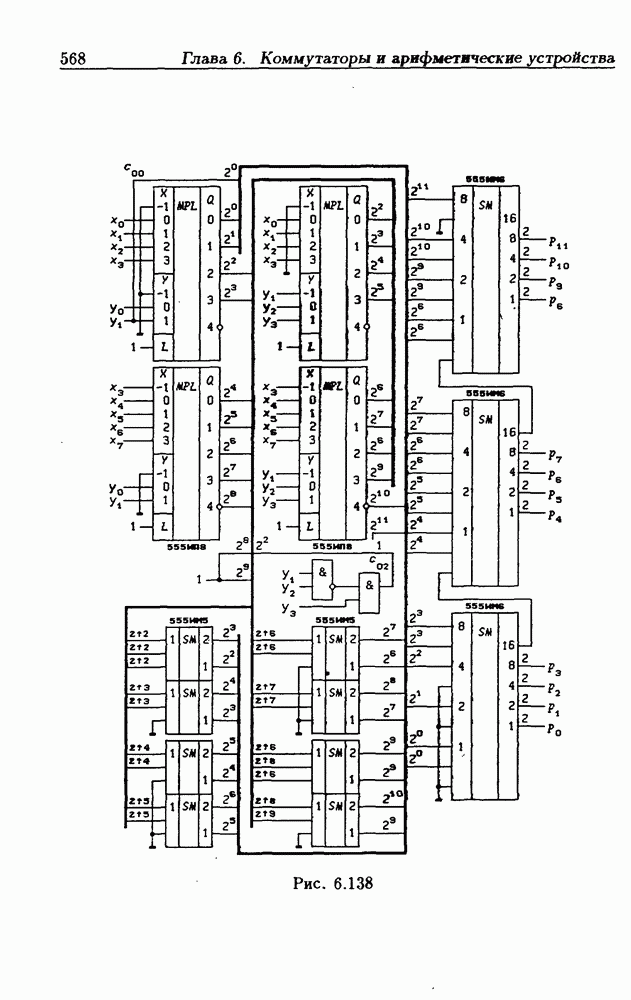
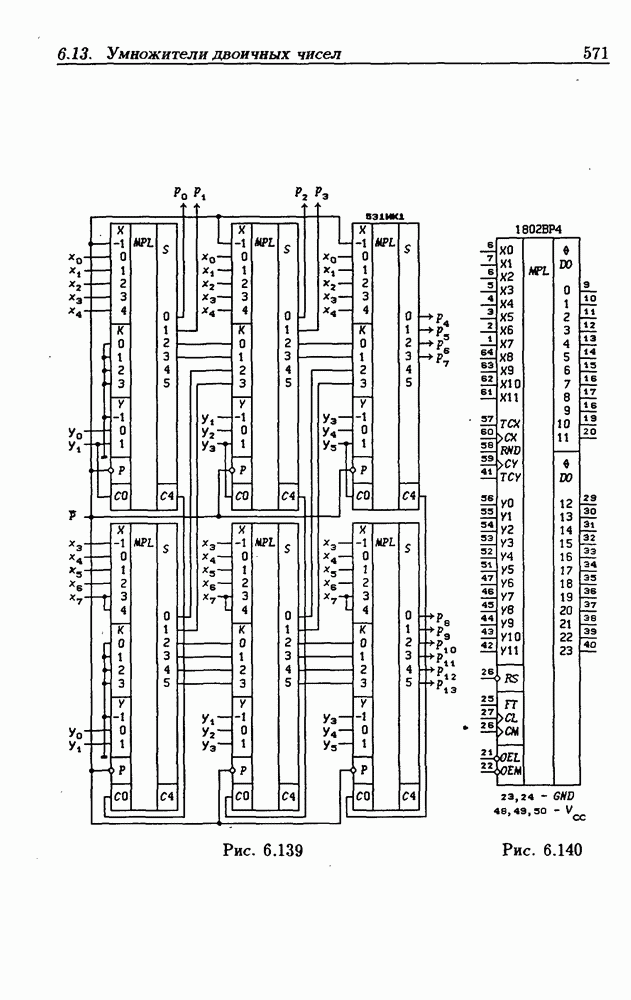
- Быстрые умножители.
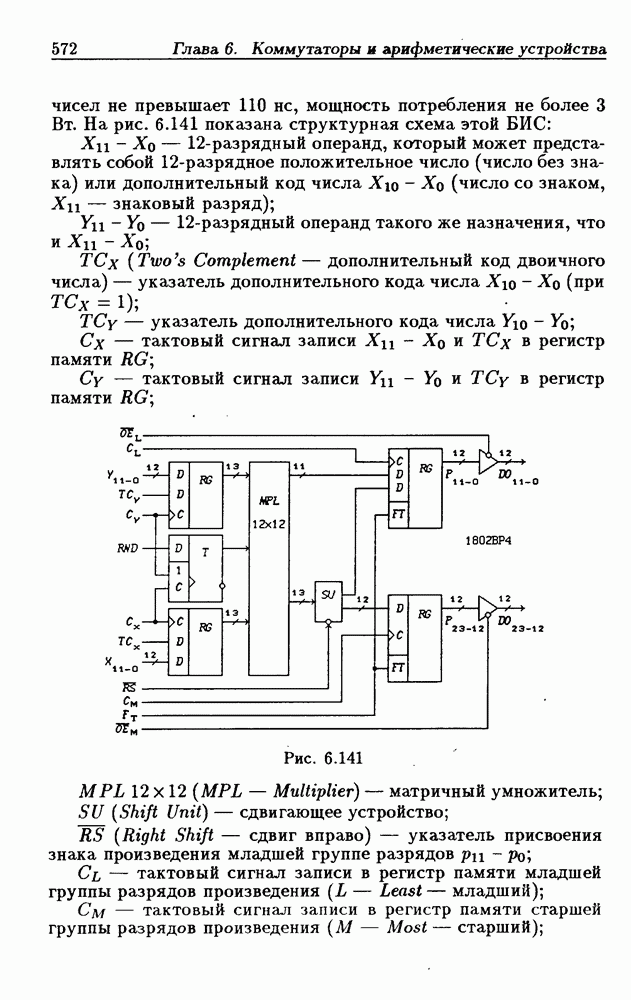
- БИС умножителя 12×12 разрядов 1802ВР4.
- Последовательные умножители.
- 6.14. Конвейерные устройства
- Конвейерный быстрый умножитель.
- Конвейерные АЦП.
- 6.15. Синтез линейных комбинационных схем
- Сумматор по модулю q.
- Умножитель по модулю q.
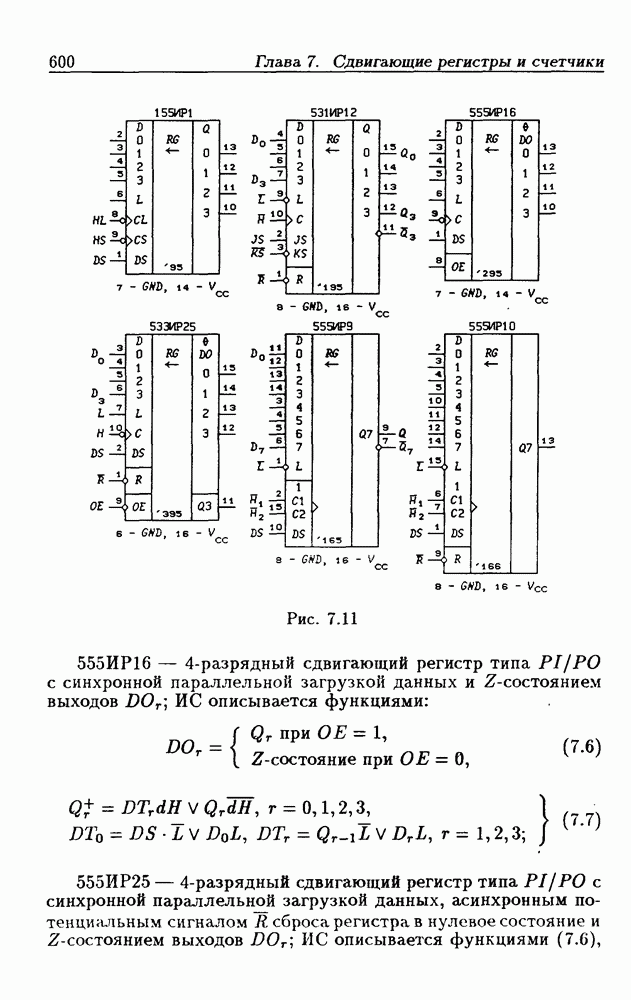
- Глава 7. Сдвигающие регистры и счетчики
- 7.1. Сдвигающие регистры без параллельной записи данных
- Сдвигающие устройства с выходными регистрами памяти.
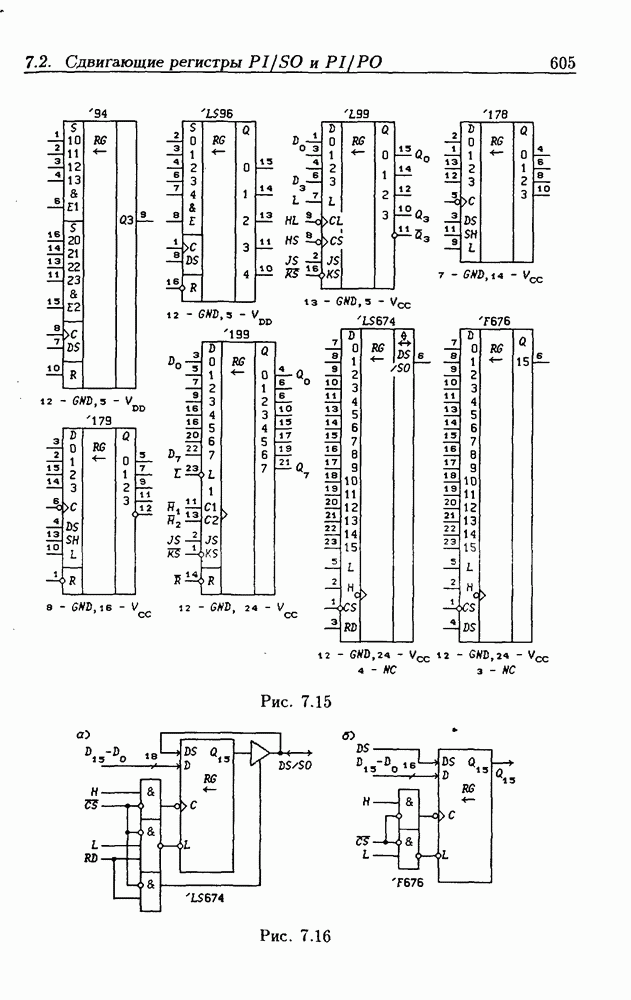
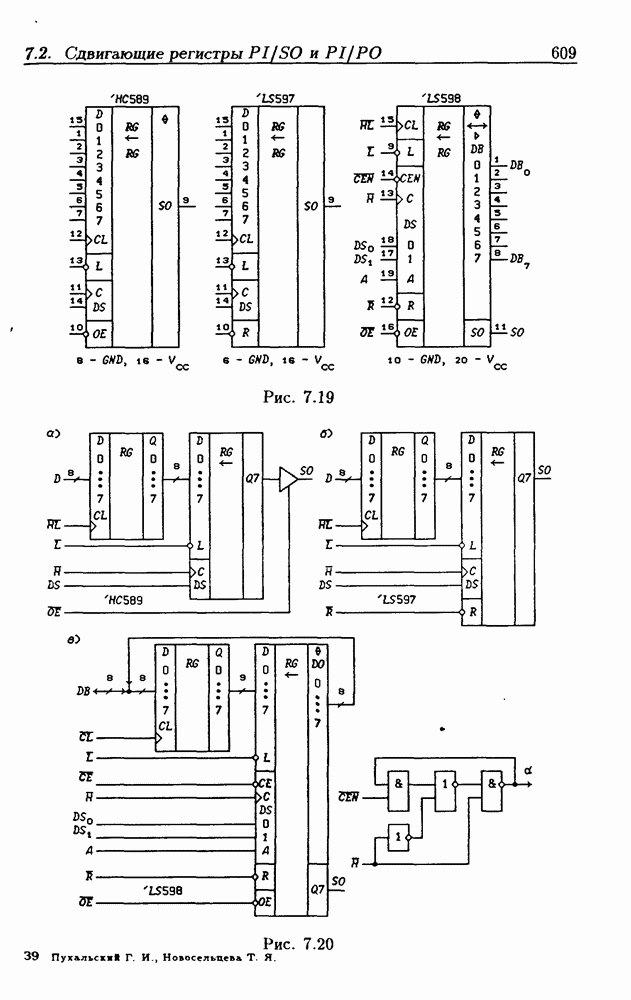
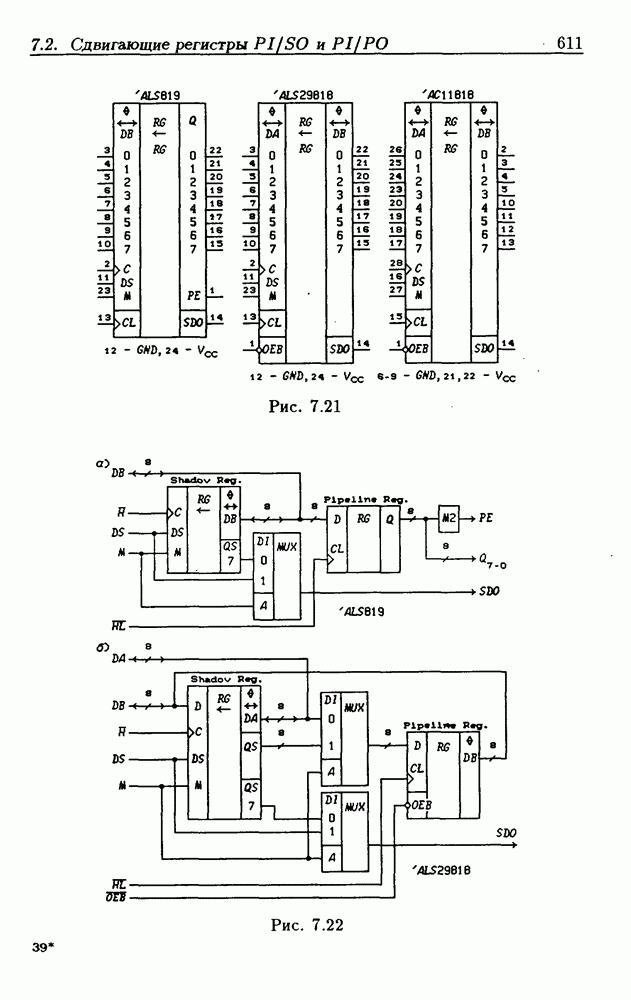
- 7.2. Сдвигающие регистры с параллельной записью данных
- Сдвигающие регистры с расширением знака.
- Сдвигающие регистры с входным регистром памяти.
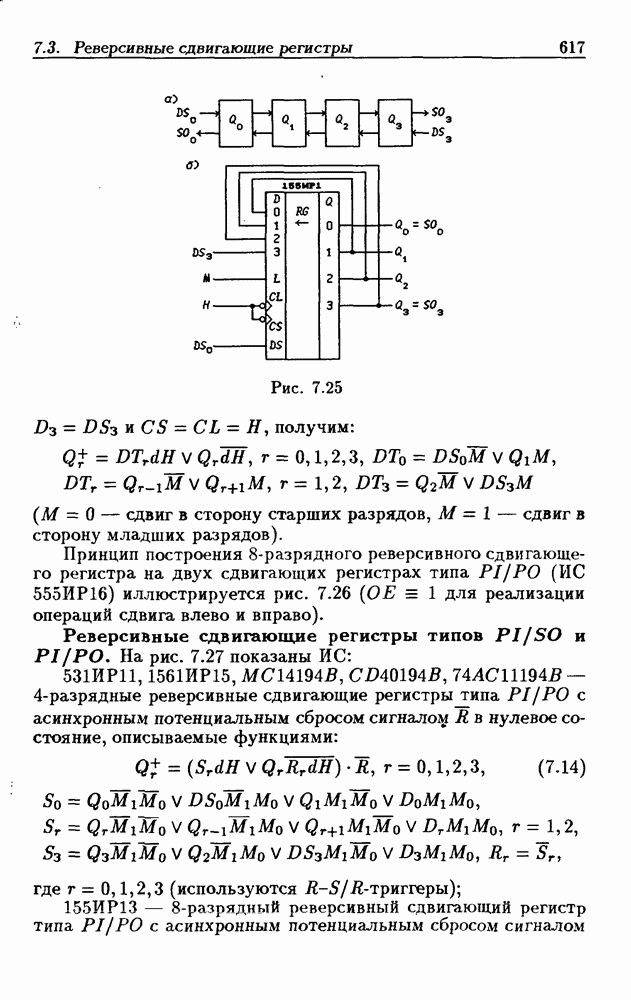
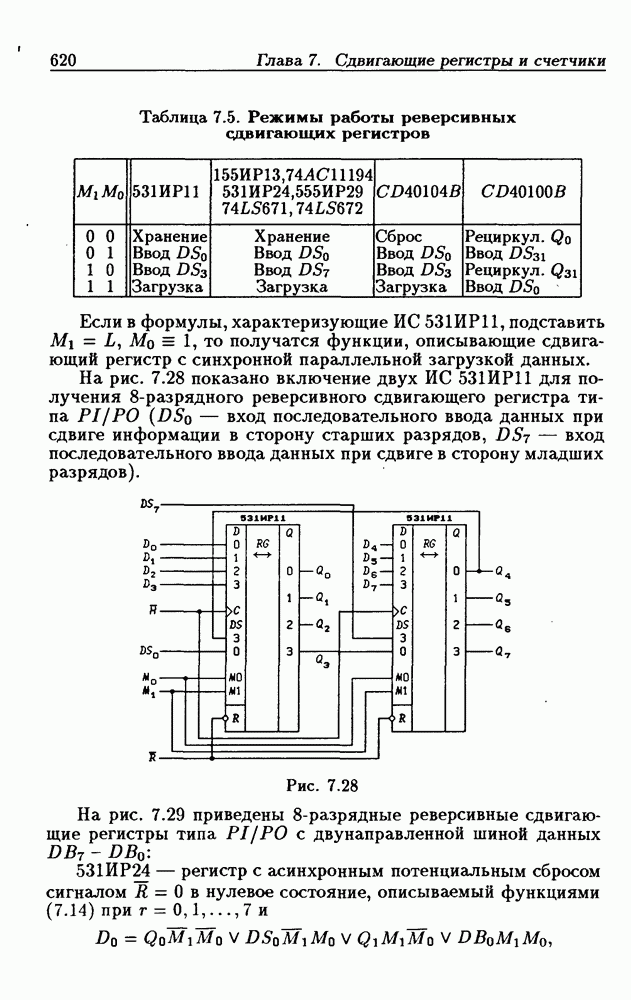
- 7.3. Реверсивные сдвигающие регистры
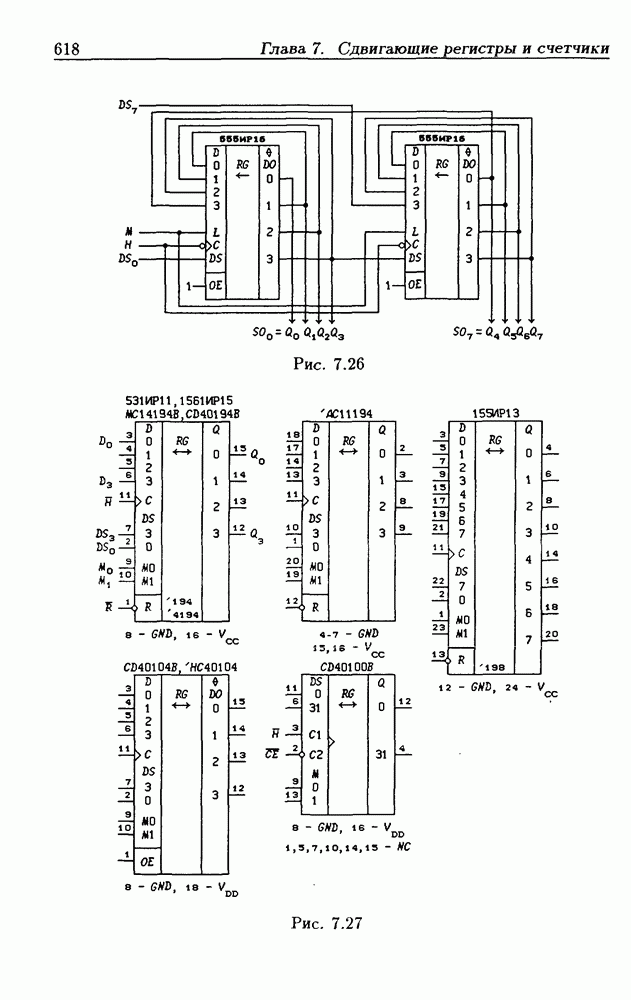
- Реверсивные сдвигающие регистры типов PI/SO и PI/PO.
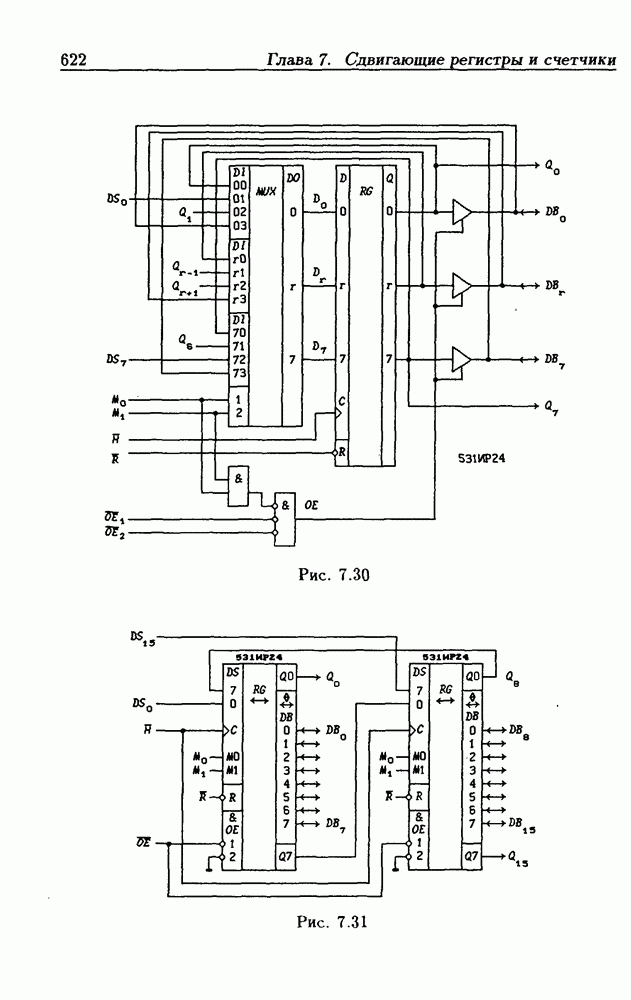
- Многофункциональные устройства на основе реверсивных сдвигающих регистров.
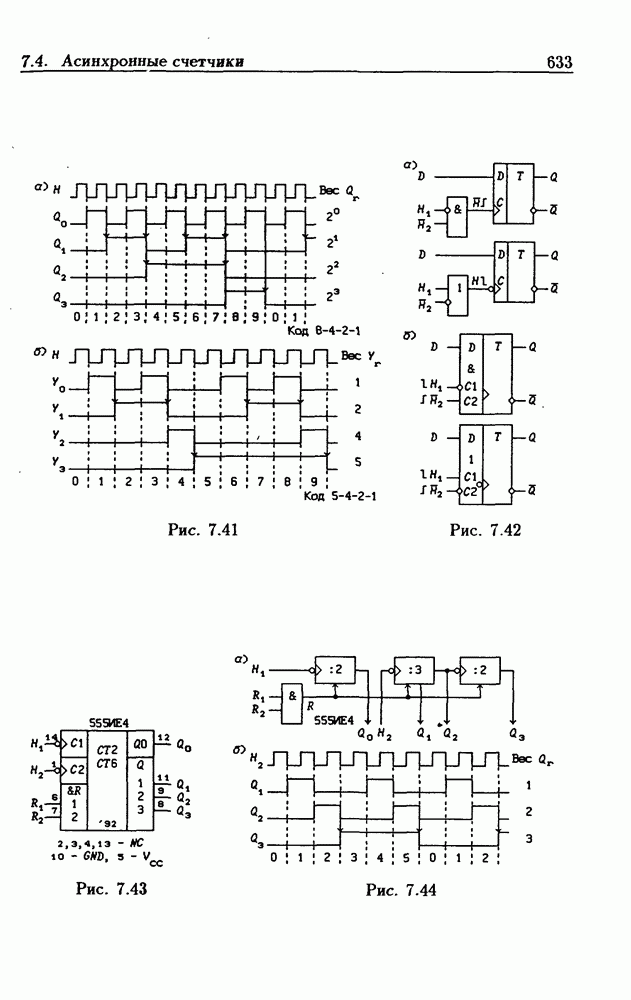
- 7.4. Асинхронные счетчики
- Двоично-десятичные асинхронные счетчики.
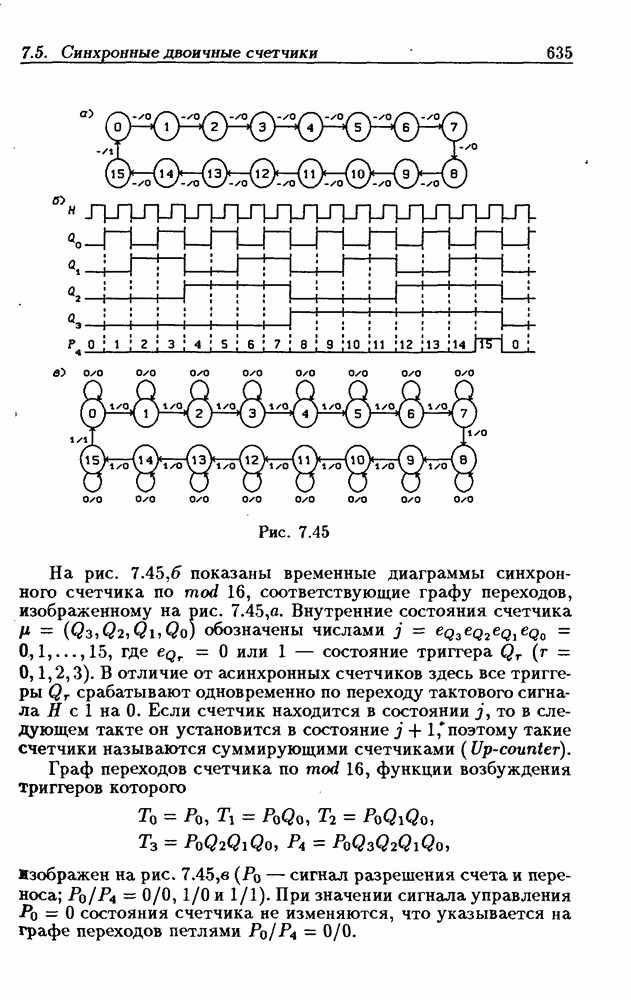
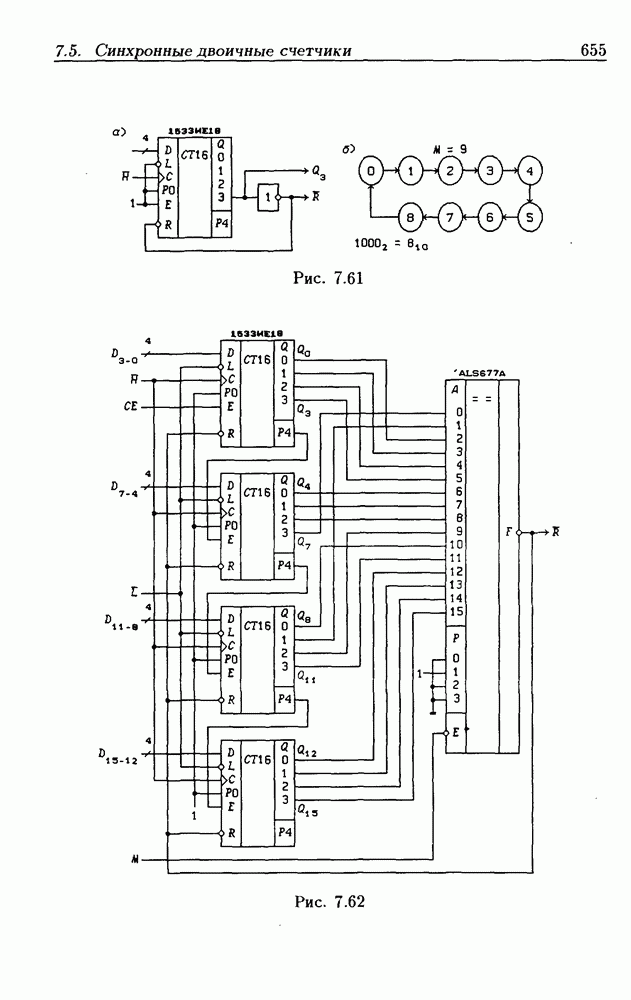
- 7.5. Синхронные двоичные счетчики
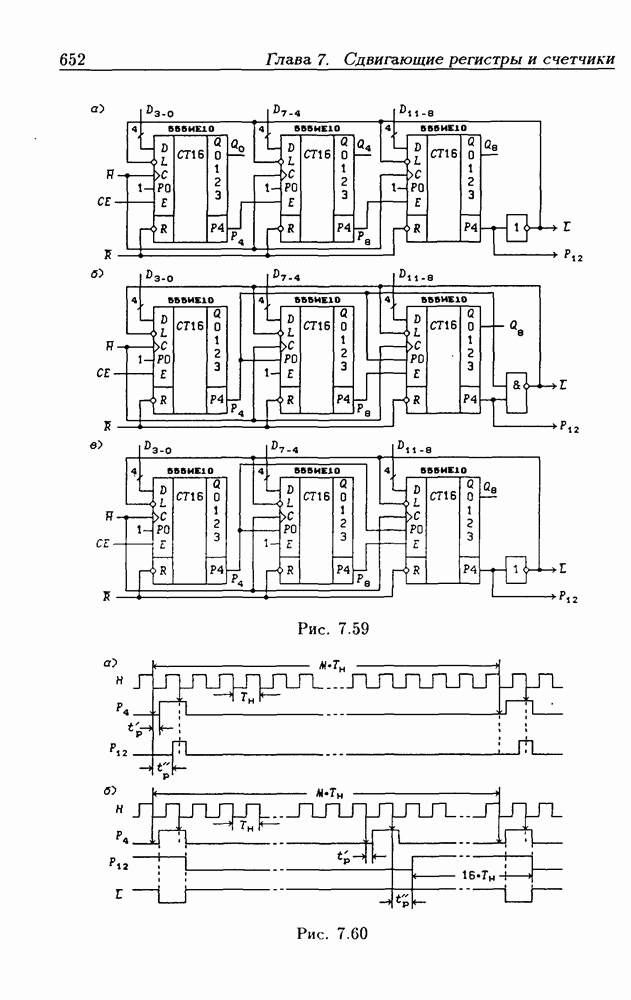
- Программирование модуля пересчета двоичных счетчиков.
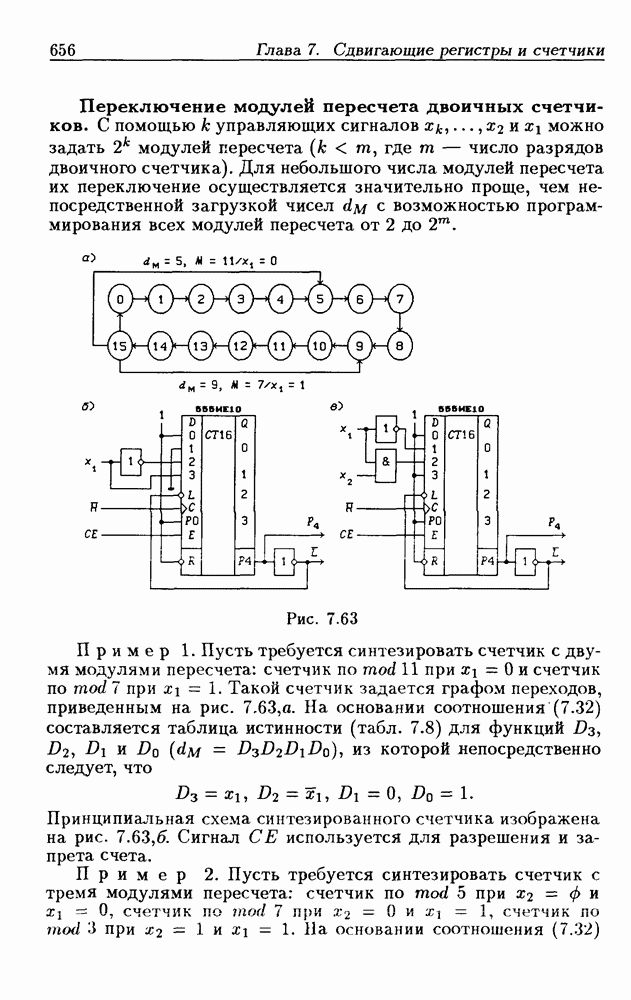
- Переключение модулей пересчета двоичных счетчиков.
- Функциональные устройства на основе двоичных счетчиков.
- 7.6. Синхронные двоично-десятичные счетчики
- 7.7. Синхронные реверсивные счетчики
- 7.8. Счетчики с расщепленным тактовым сигналом
- 7.9. Счетчики на сдвигающих регистрах
- 7.10. Кольцевые счетчики
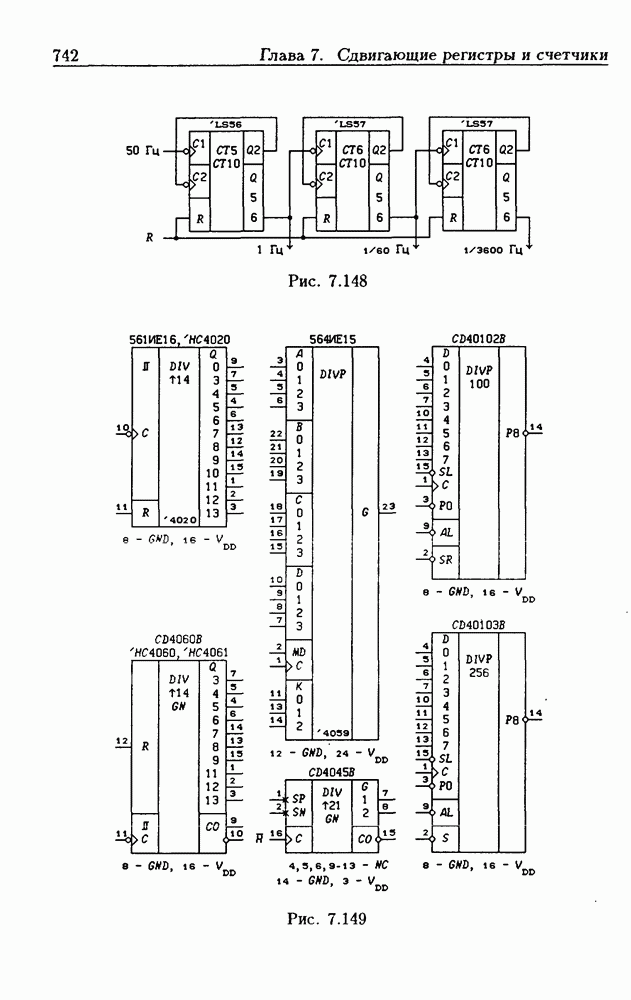
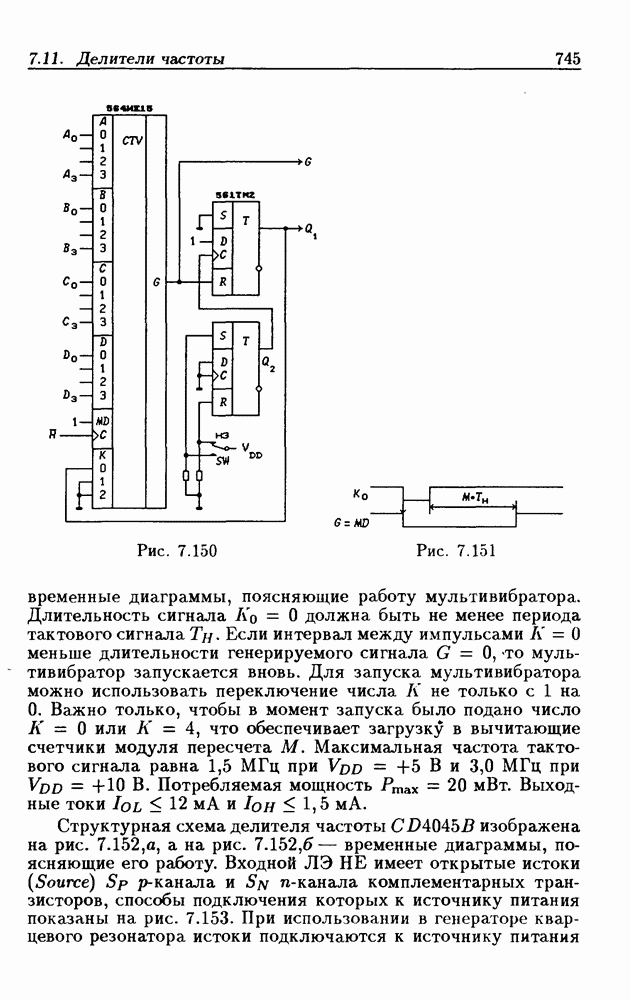
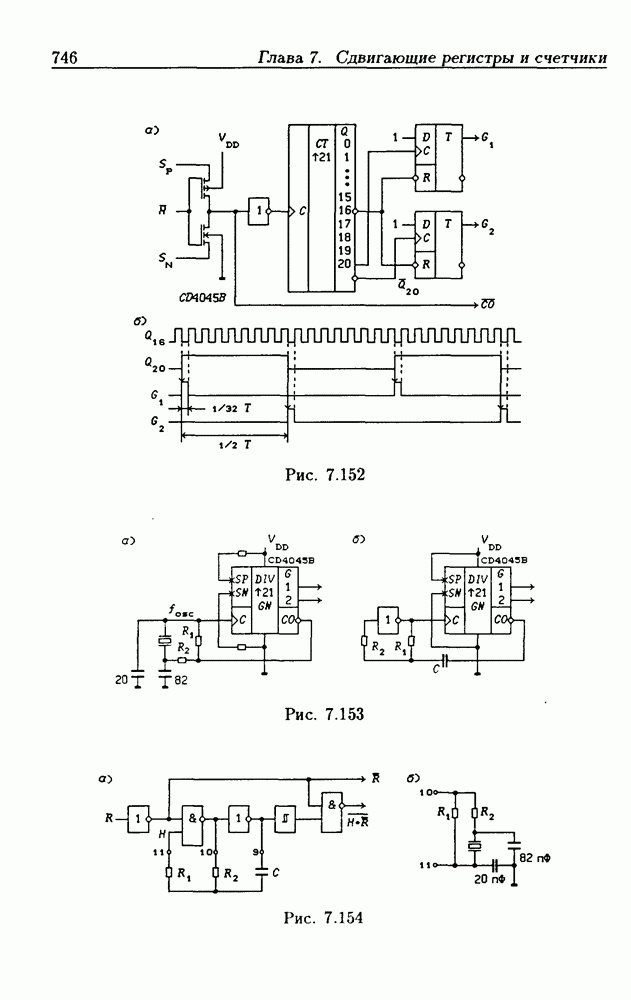
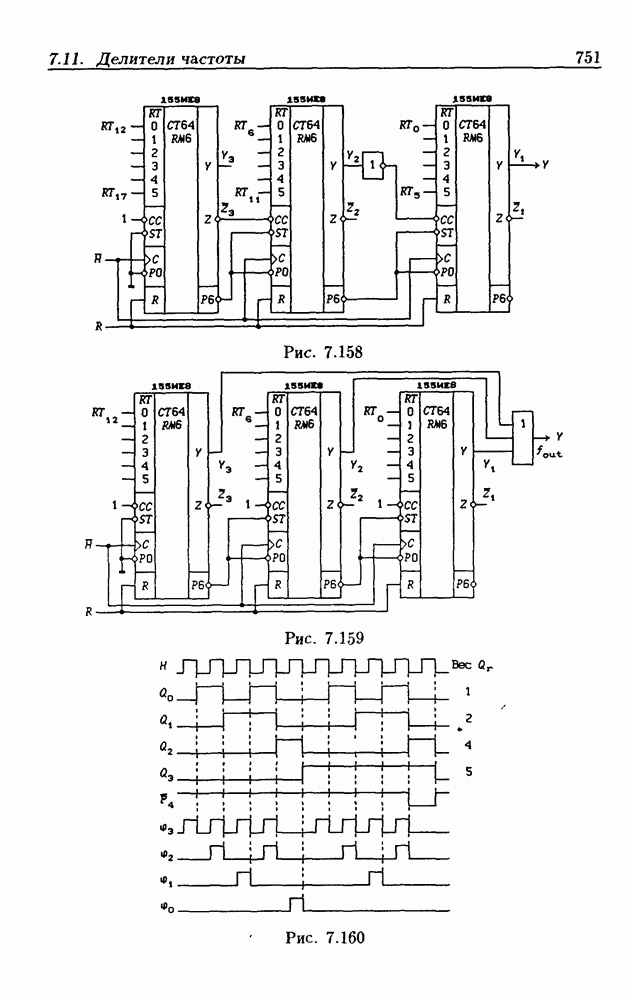
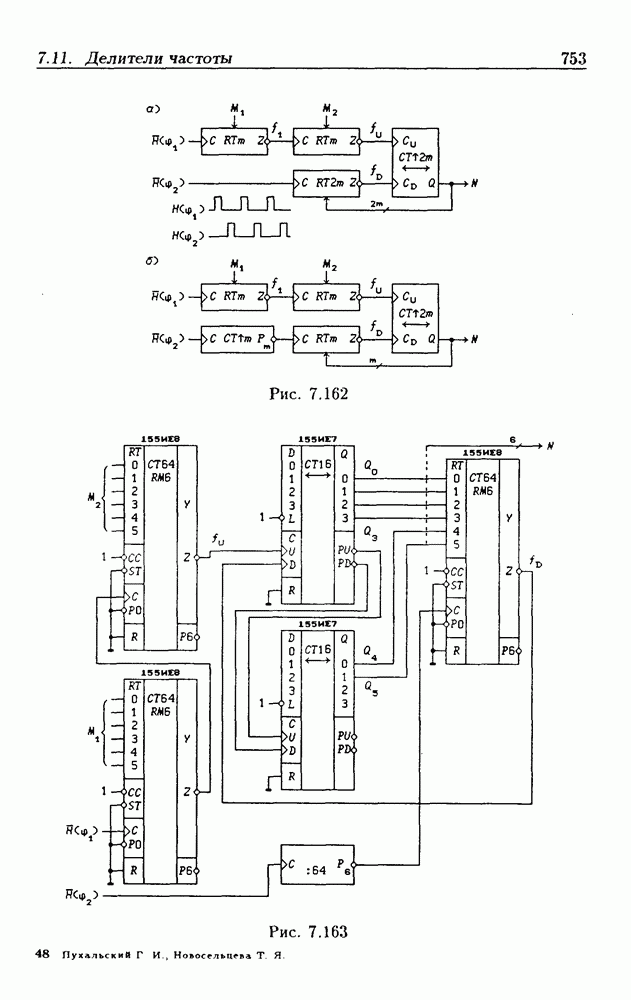
- 7.11. Делители частоты
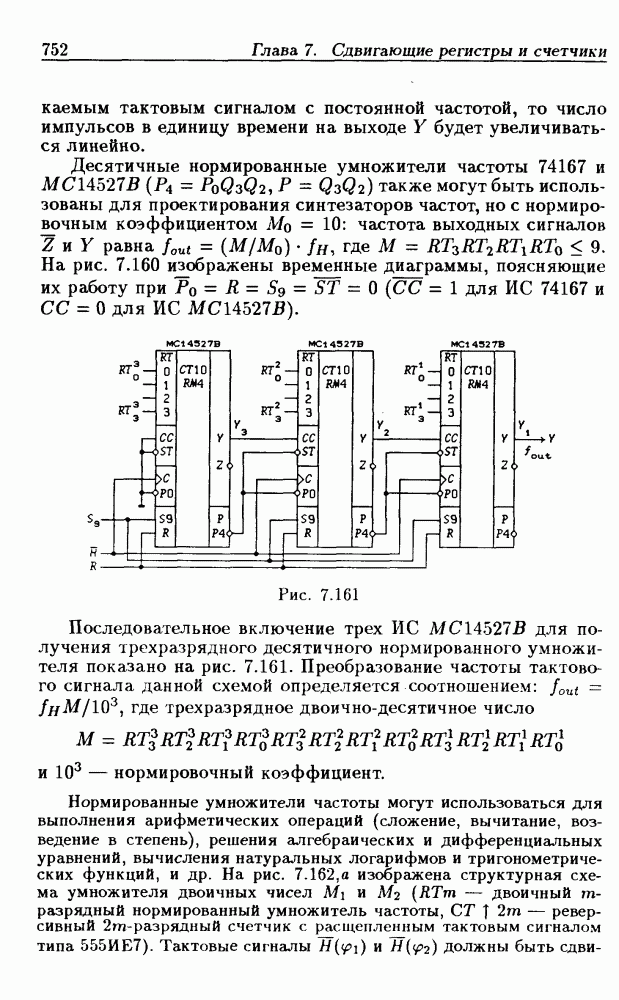
- Нормированные умножители частоты.
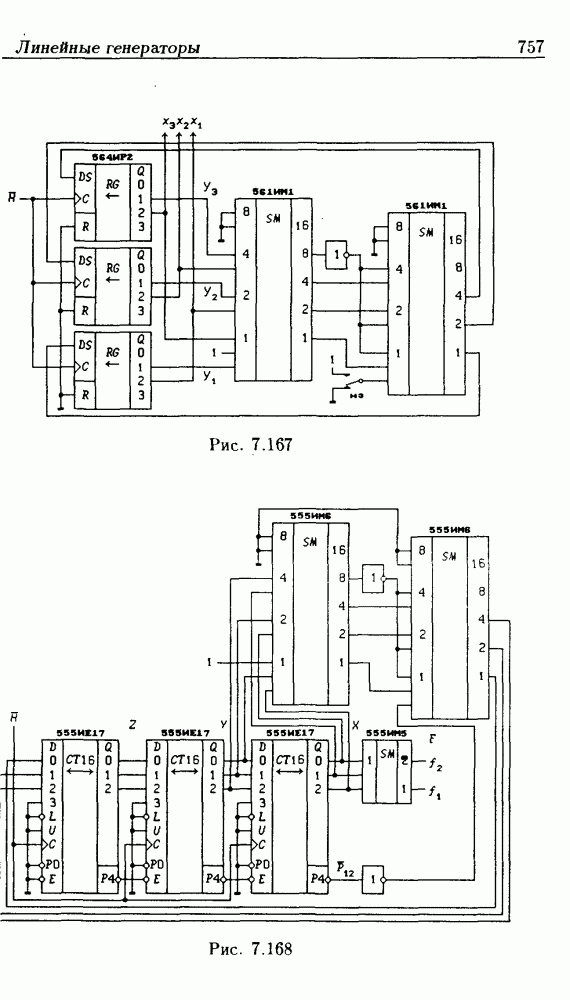
- 7.12. Линейные генераторы
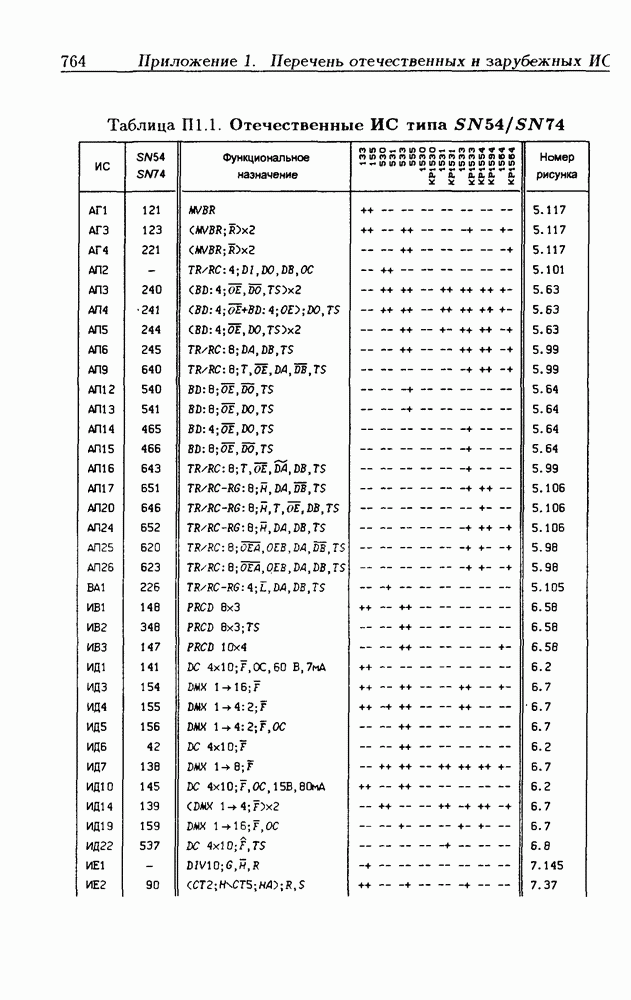
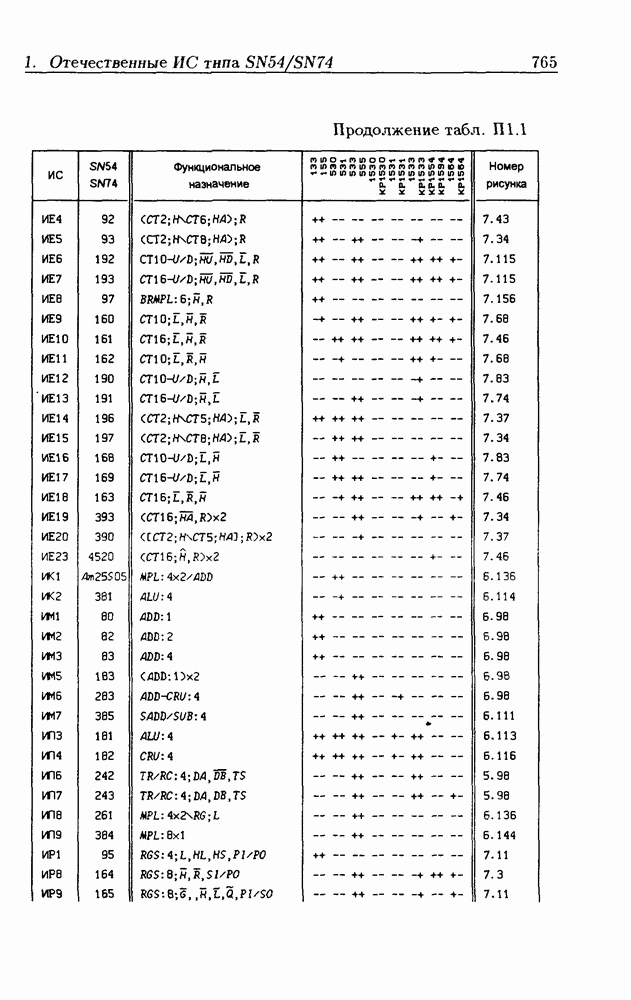
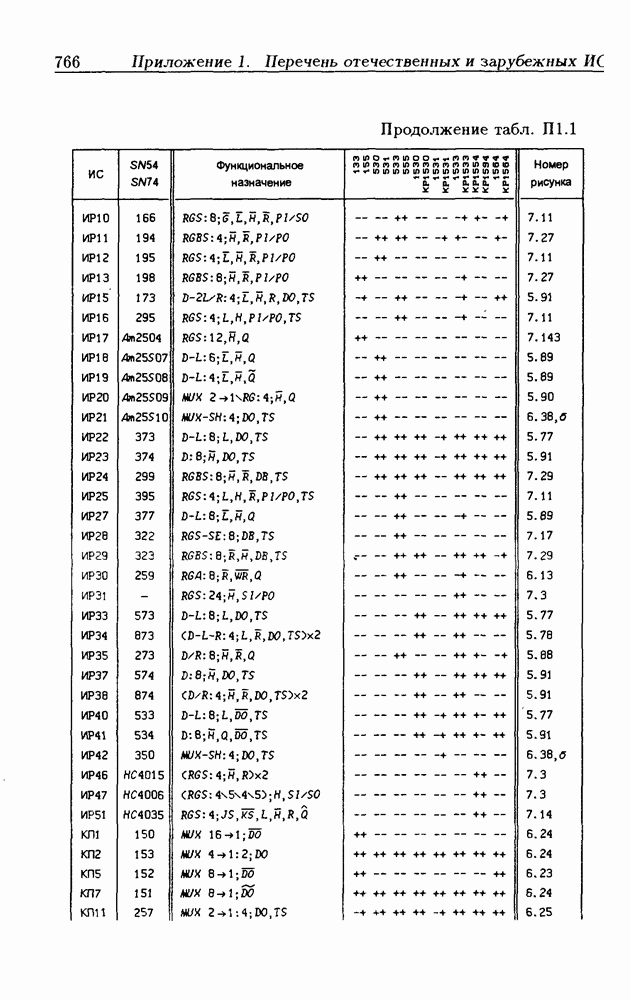
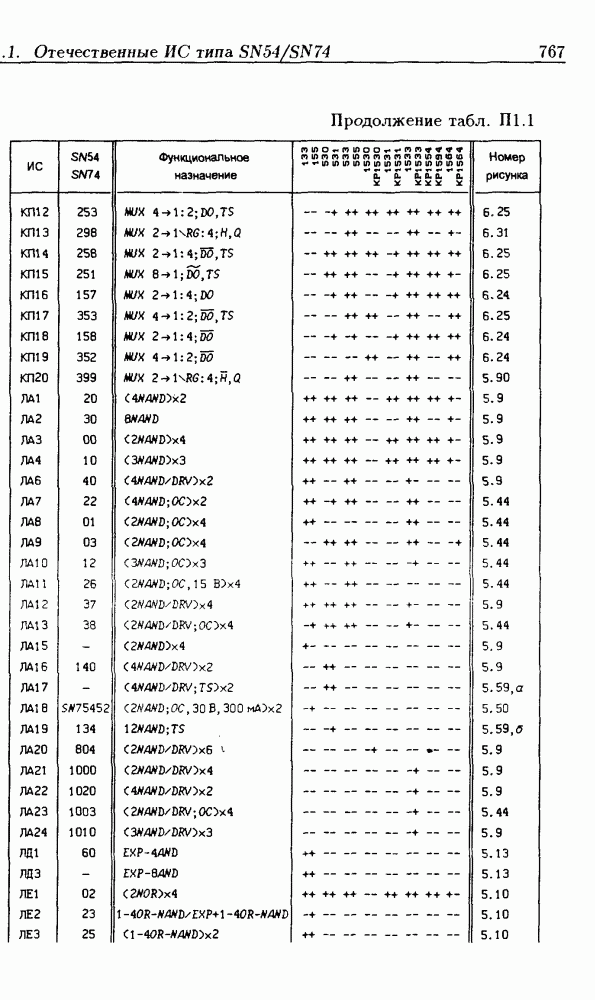
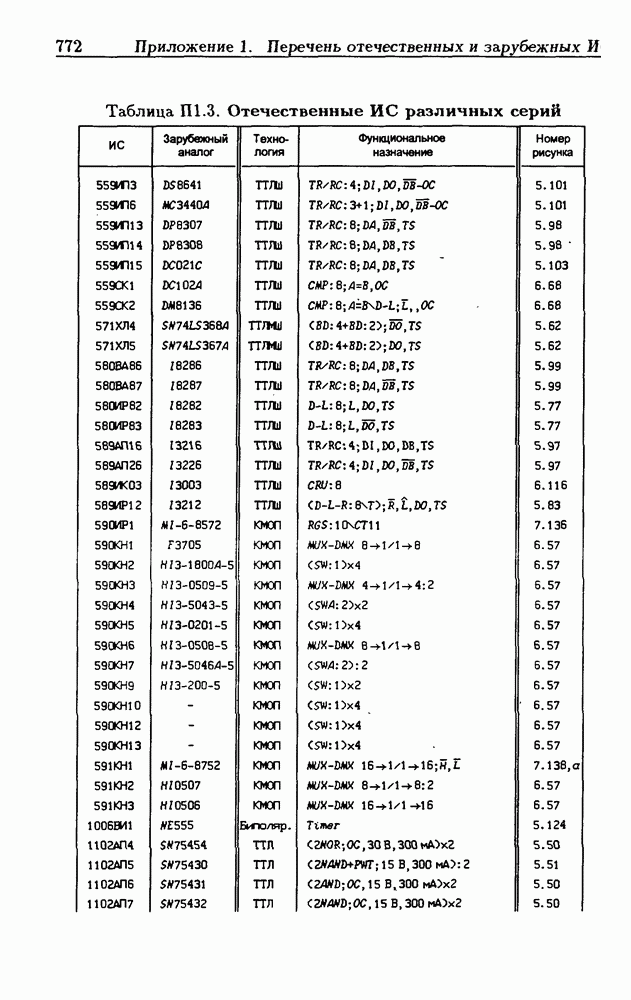
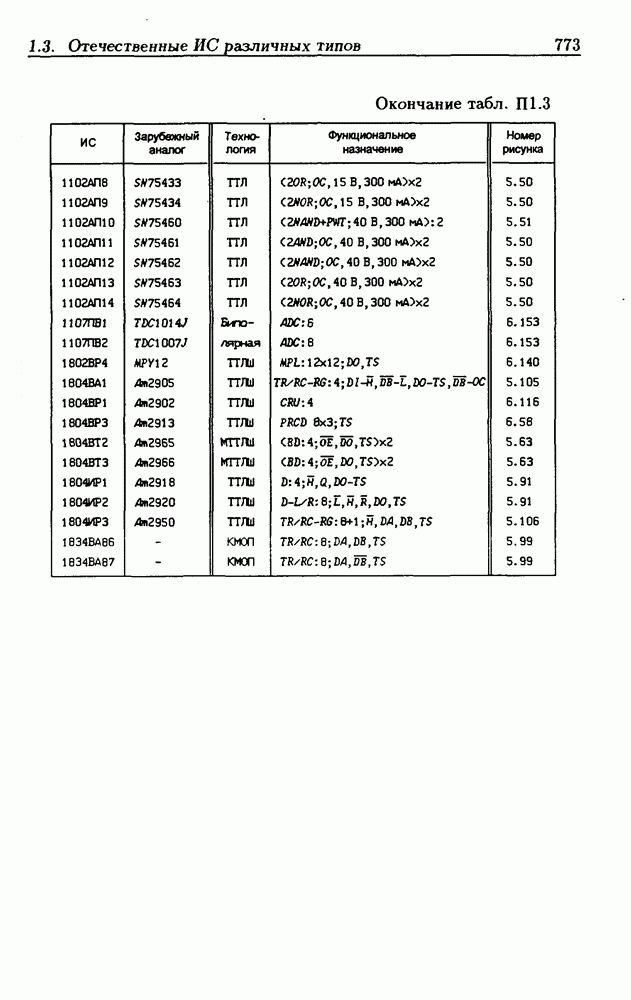
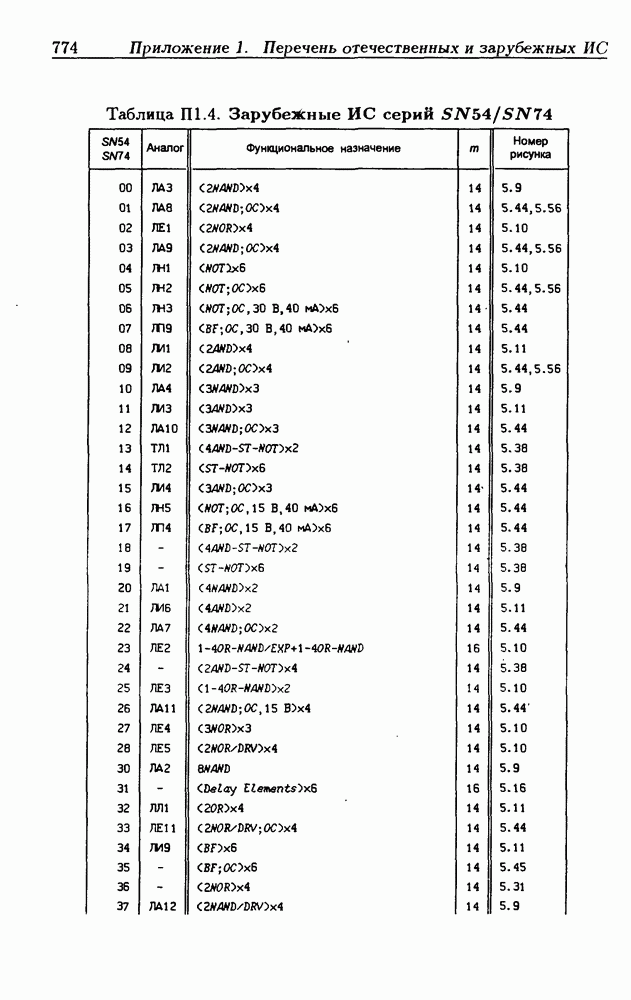
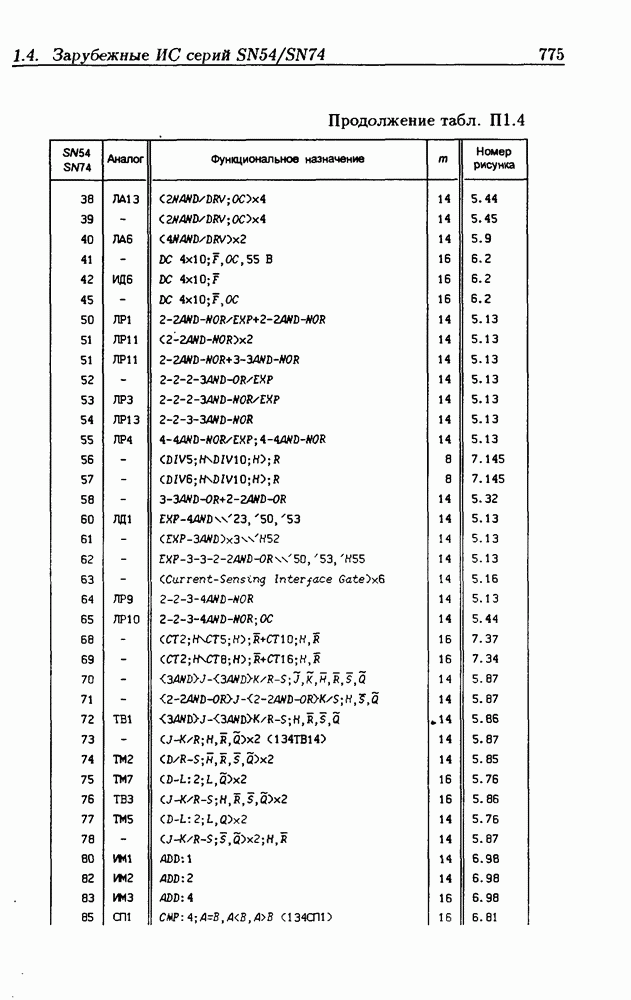
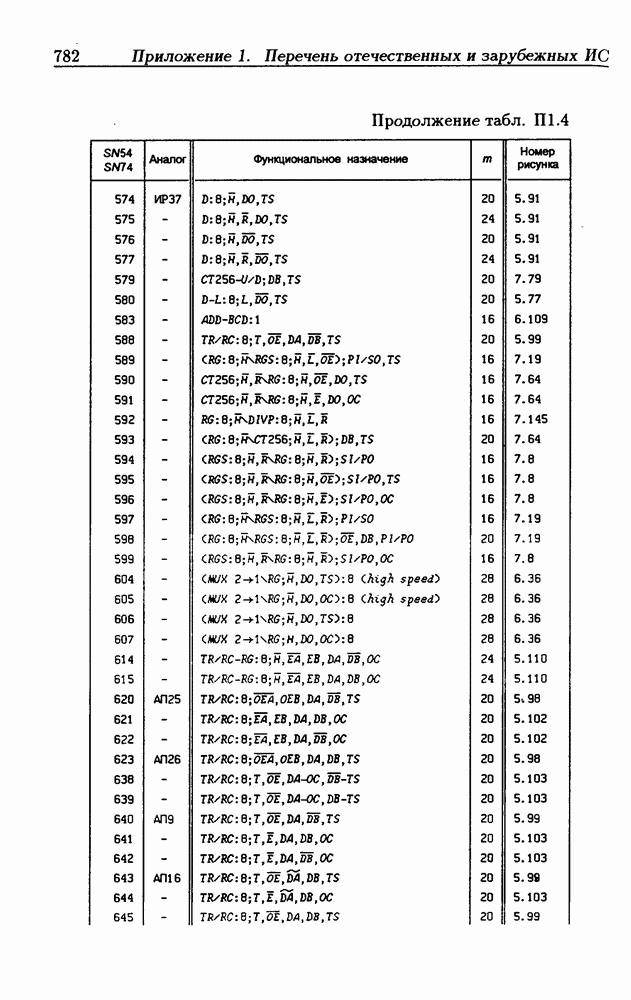
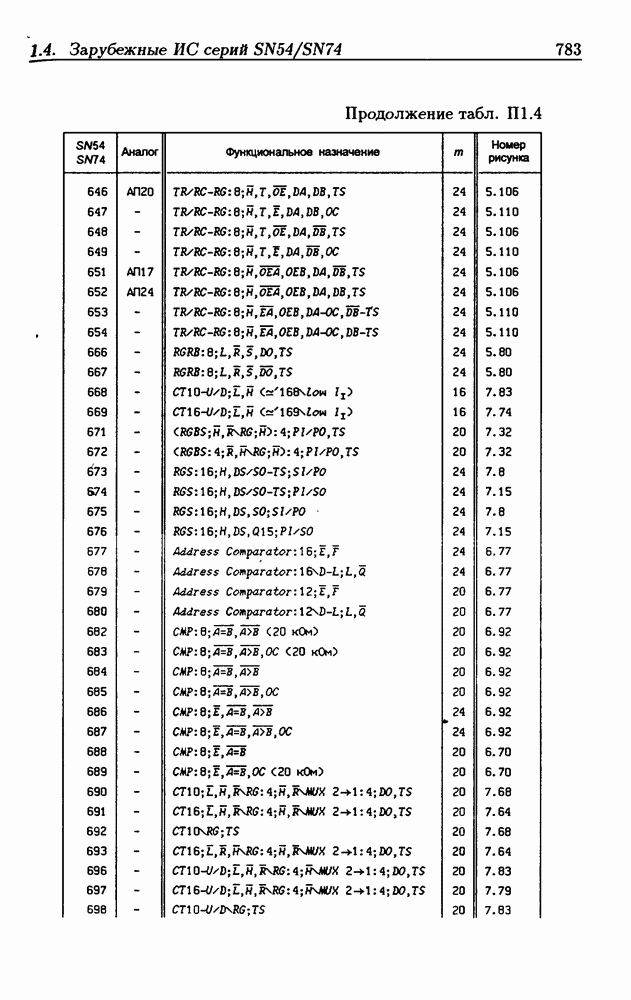
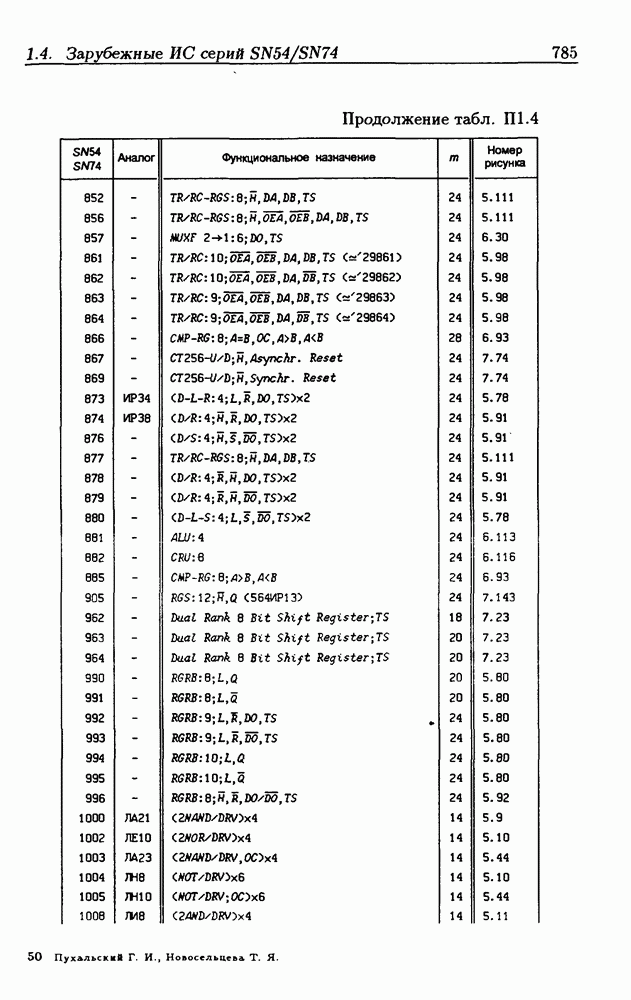
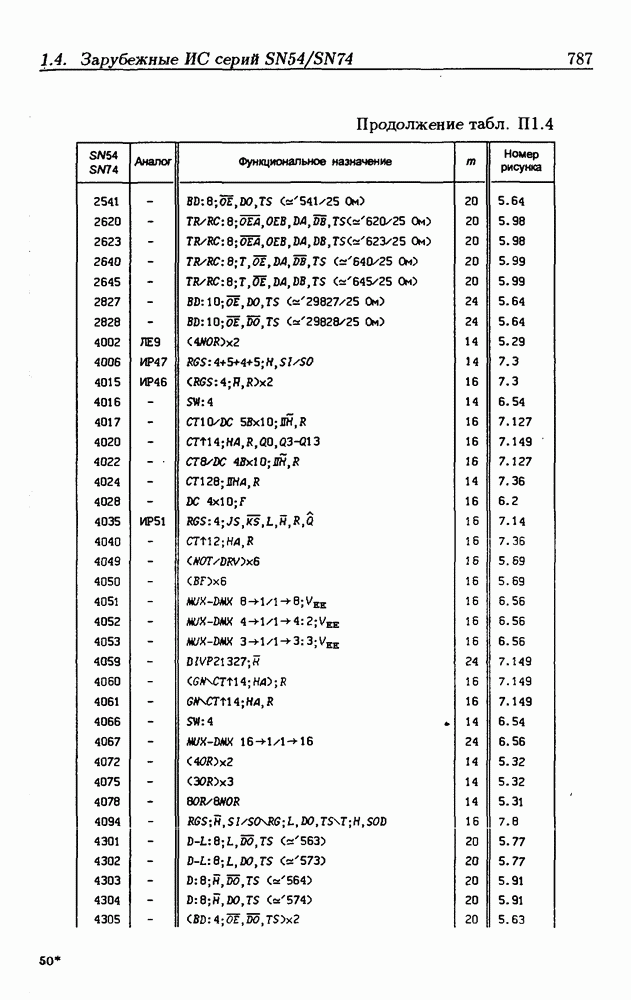
- Приложение 1. Перечень отечественных и зарубежных ИС
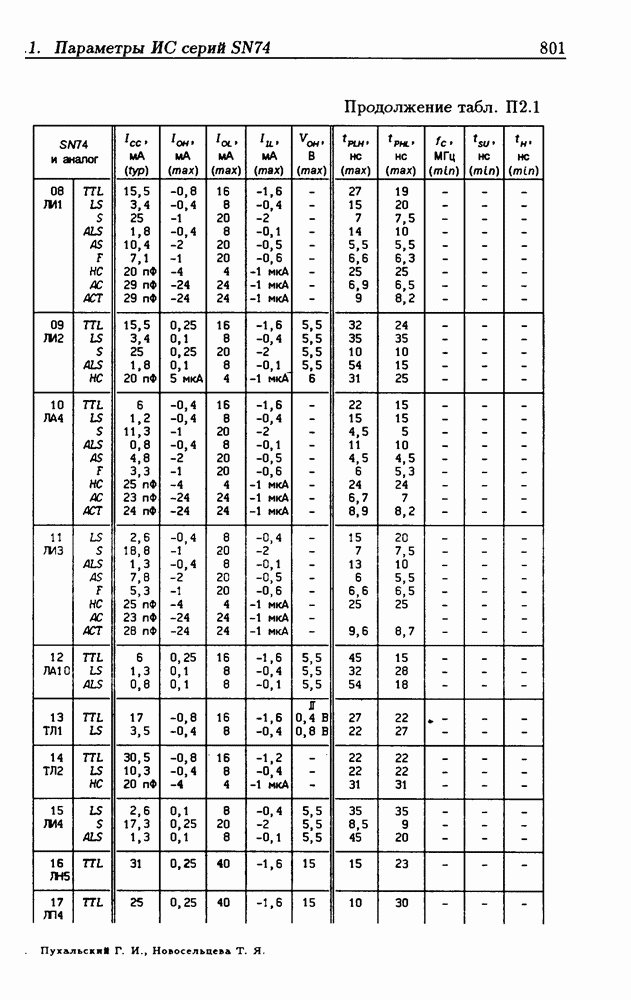
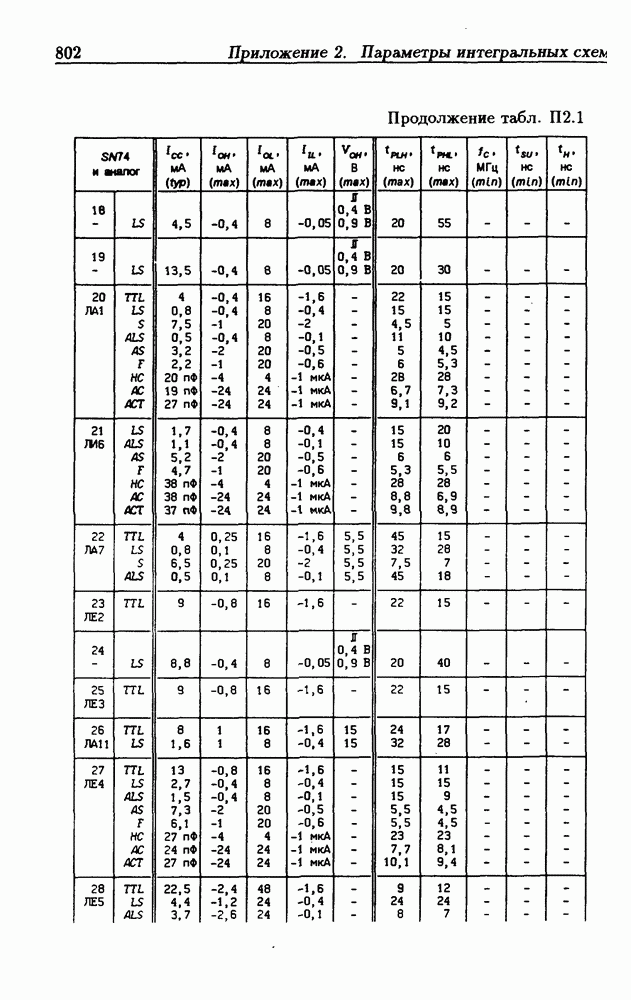
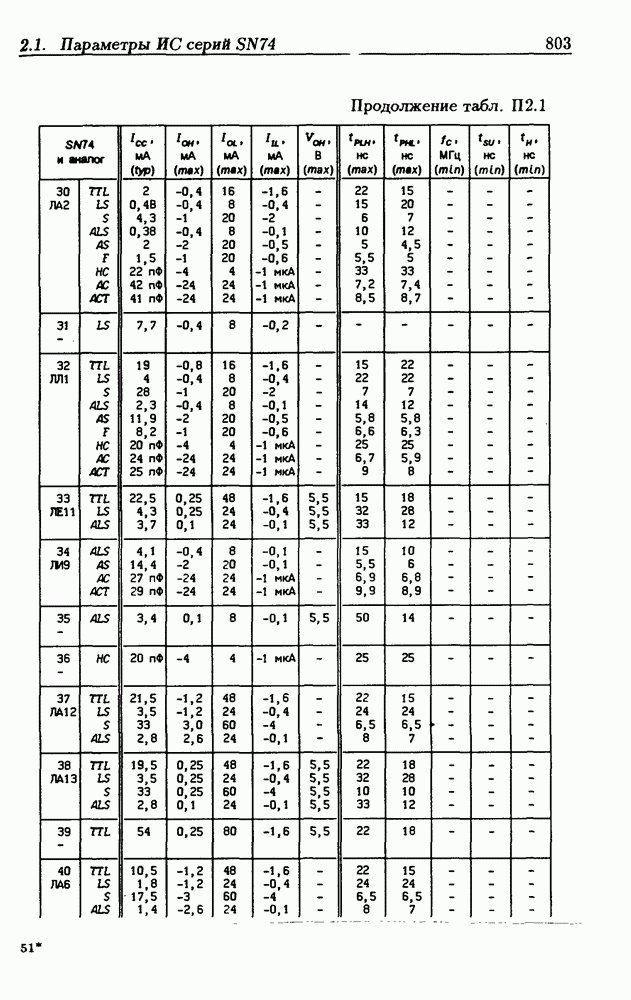
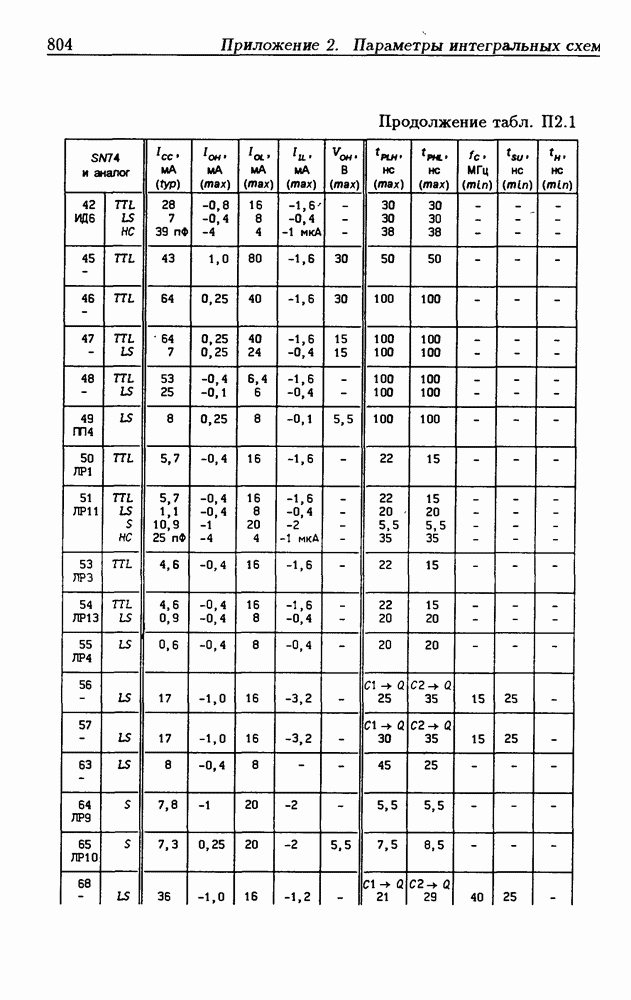
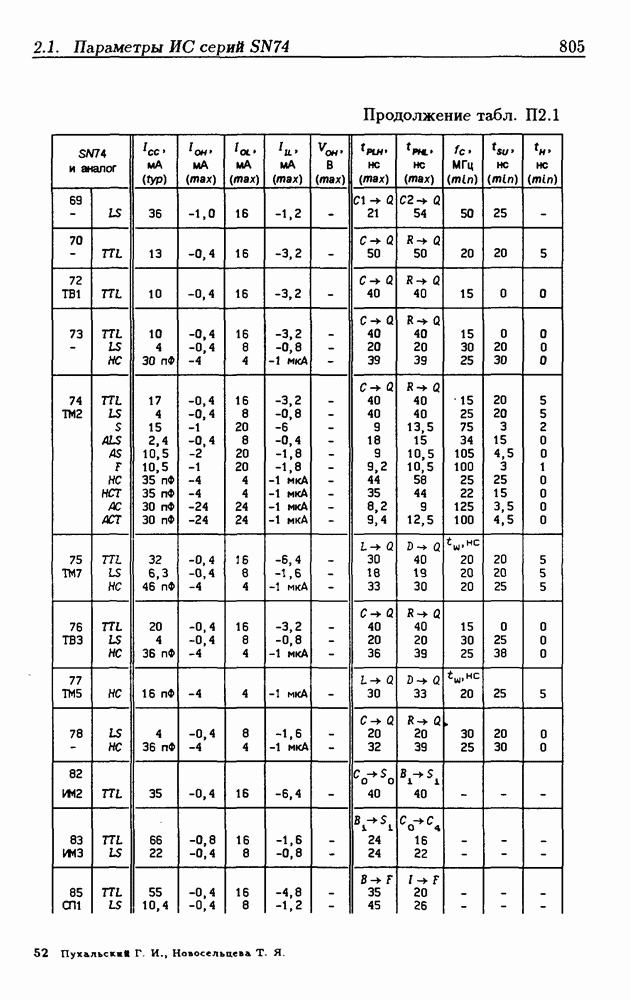
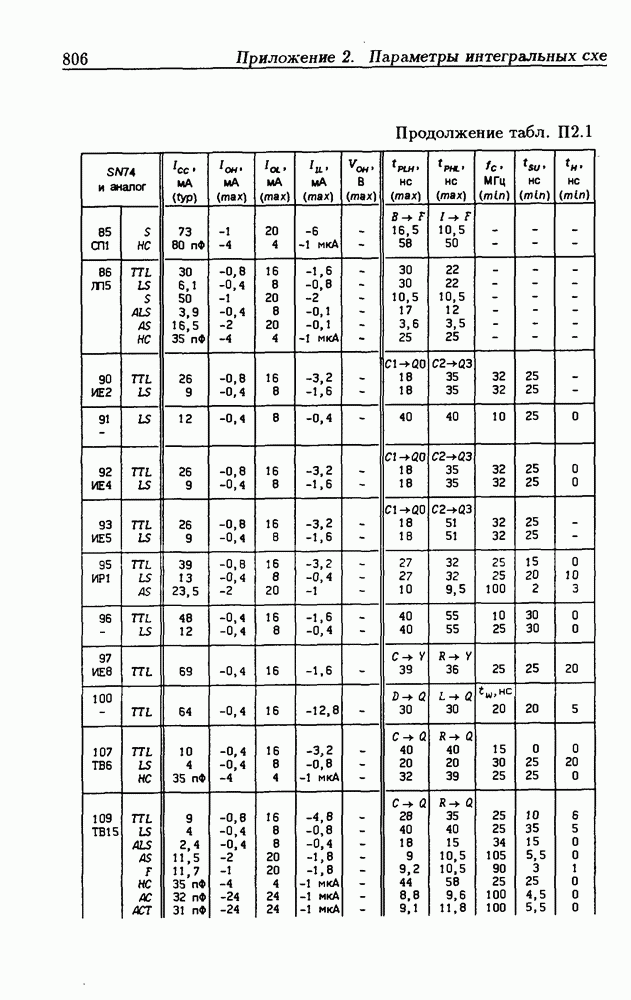
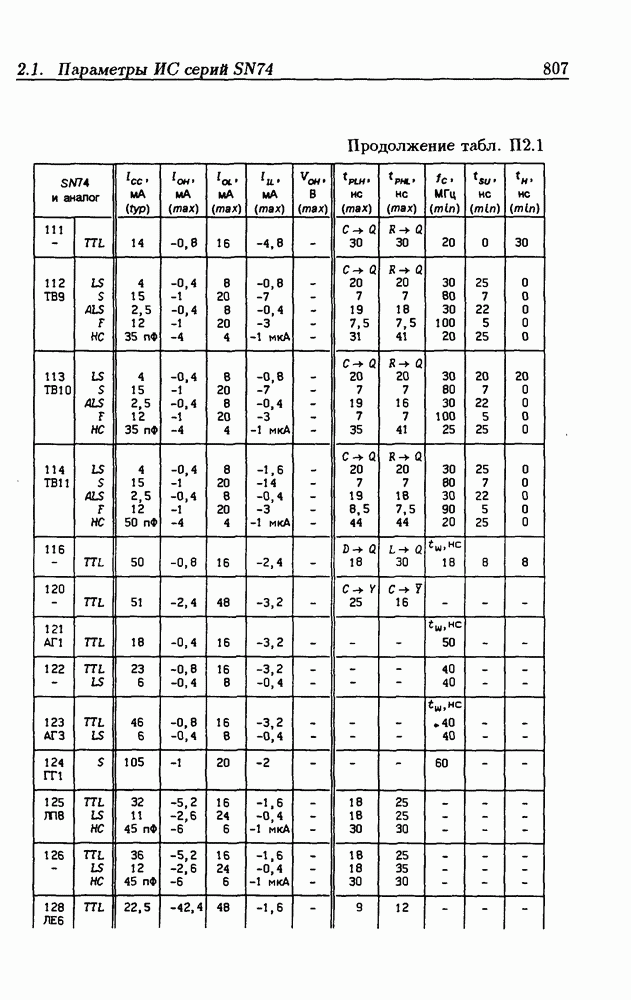
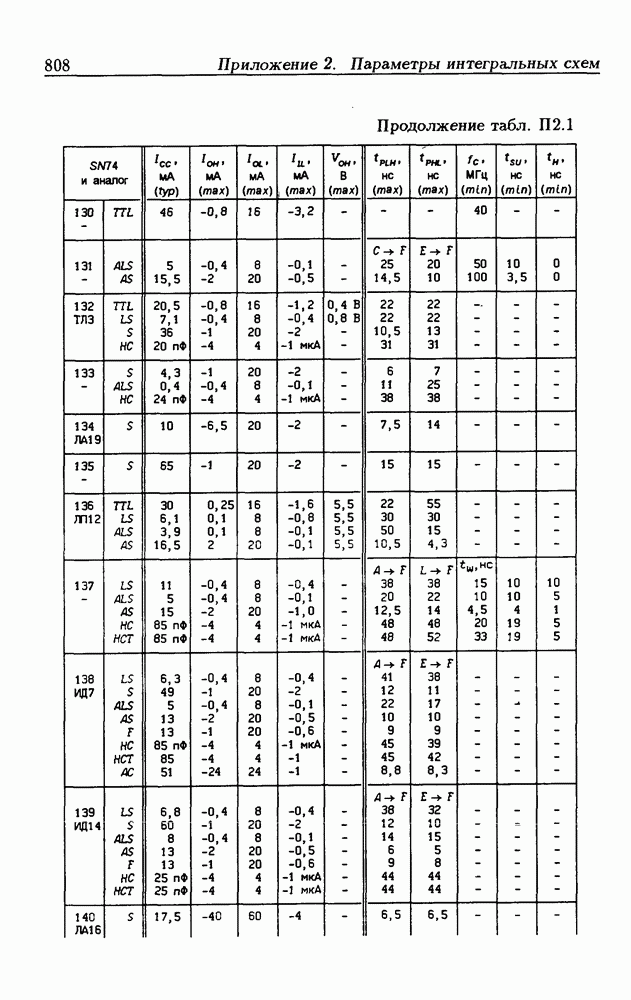
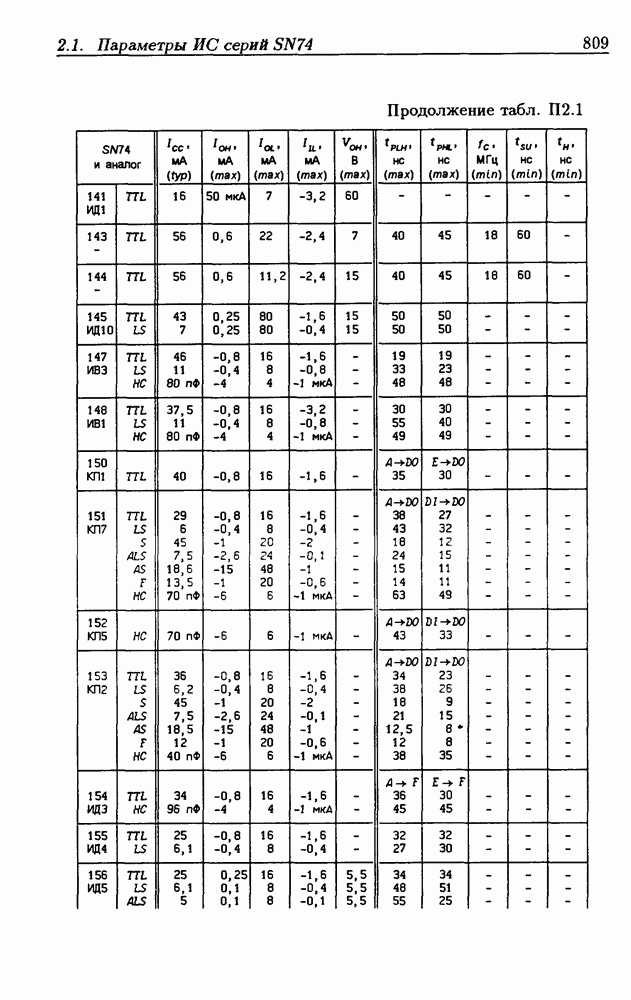
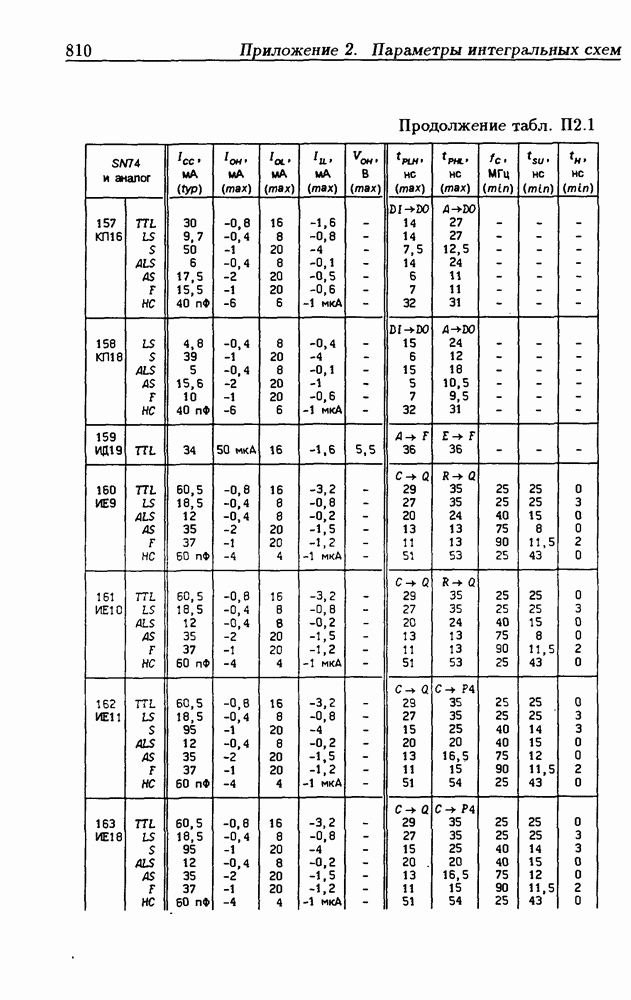
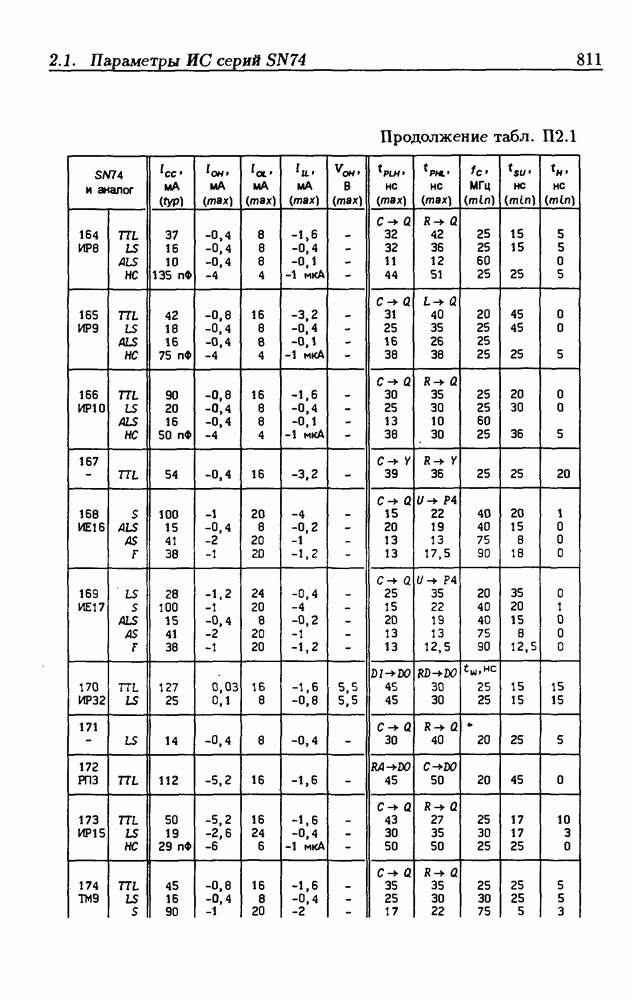
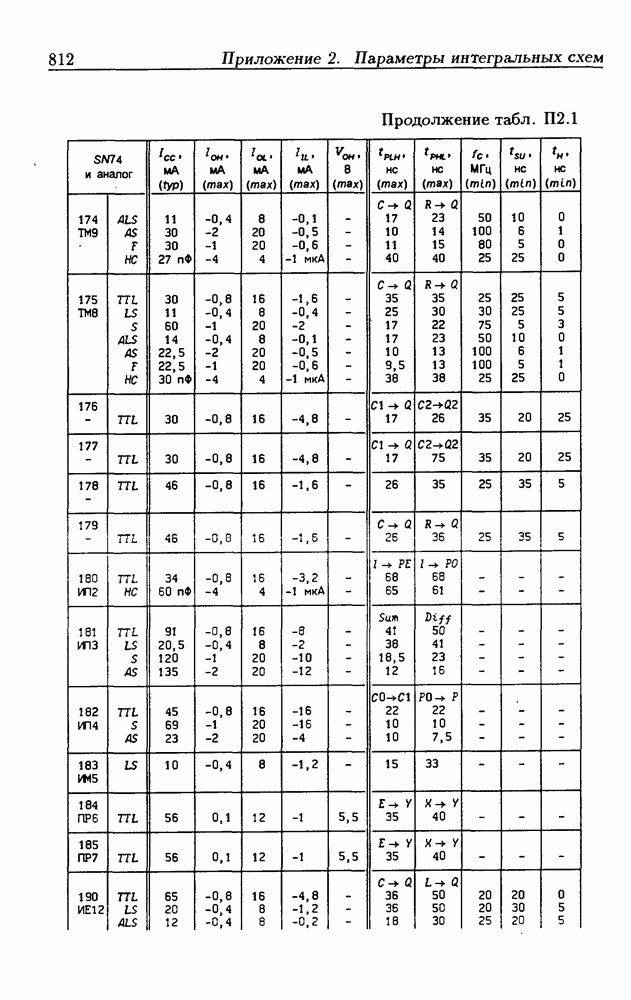
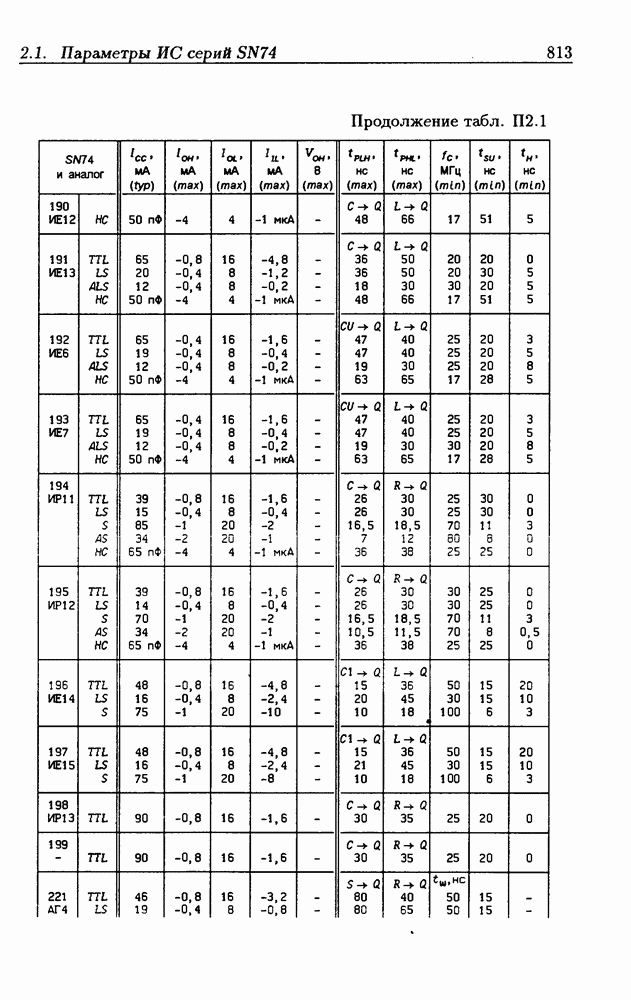
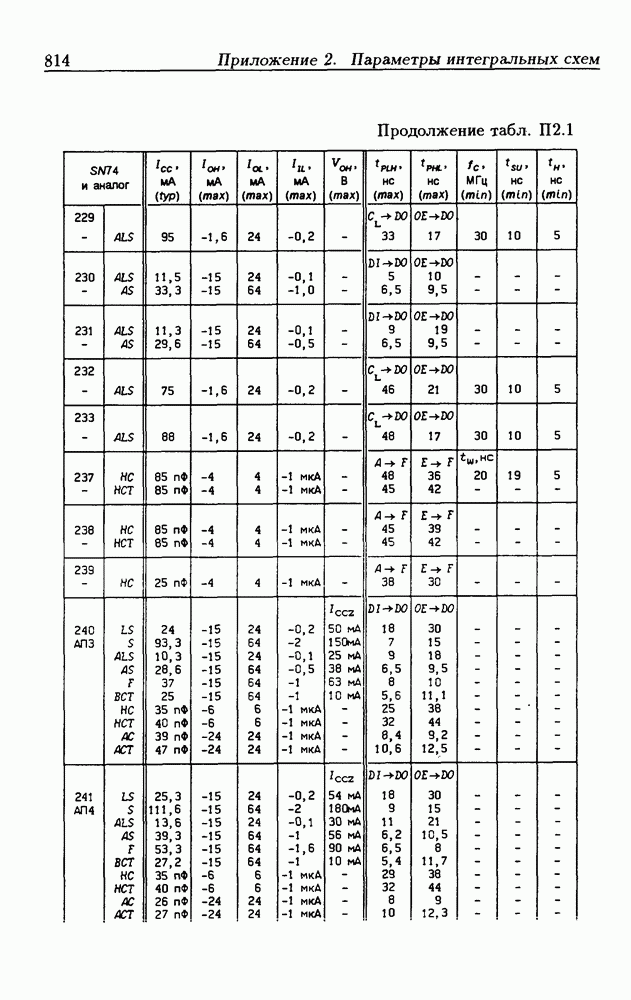
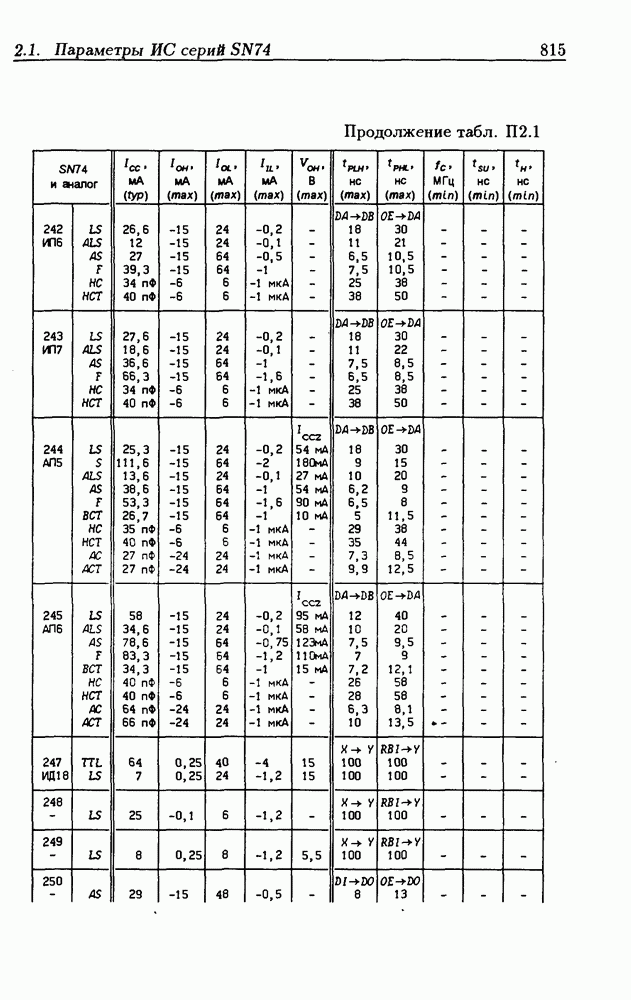
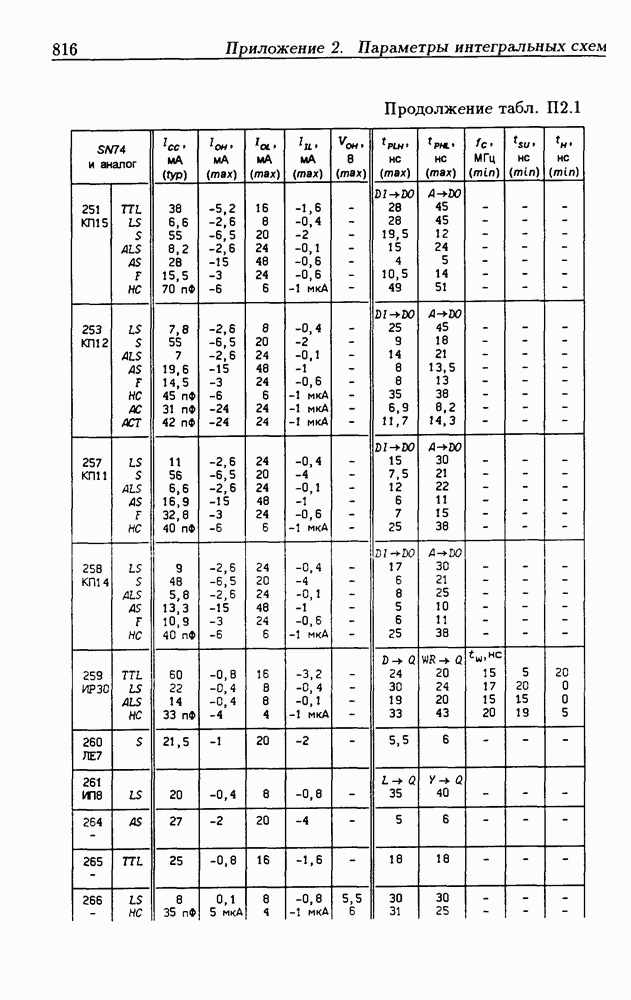
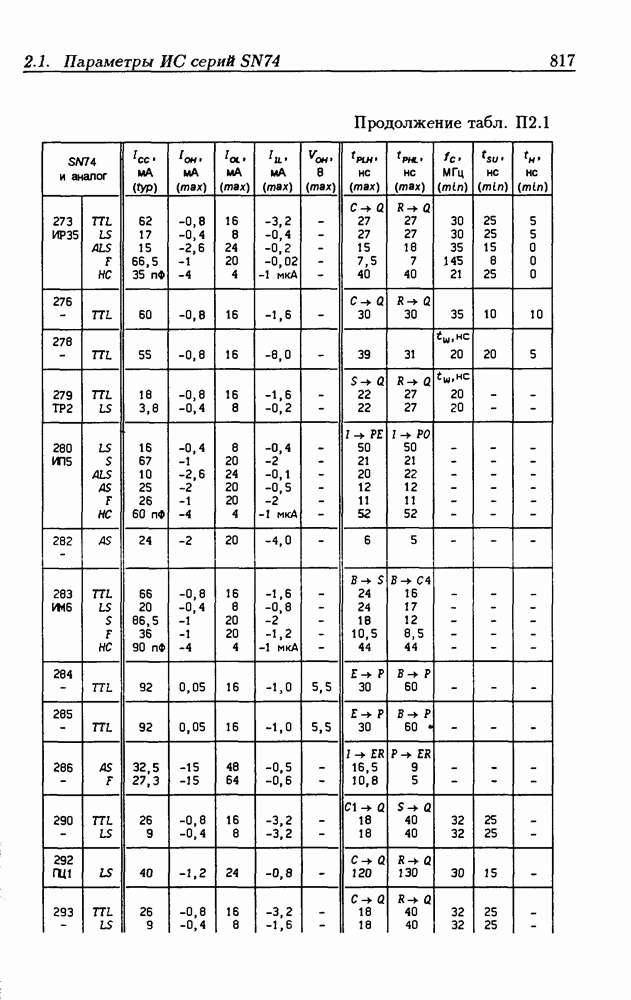
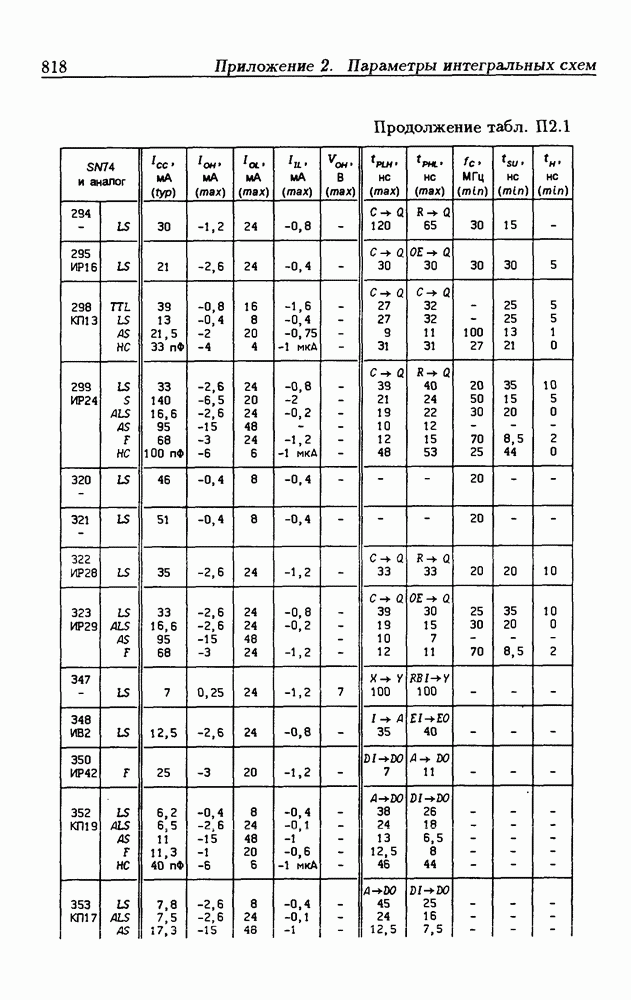
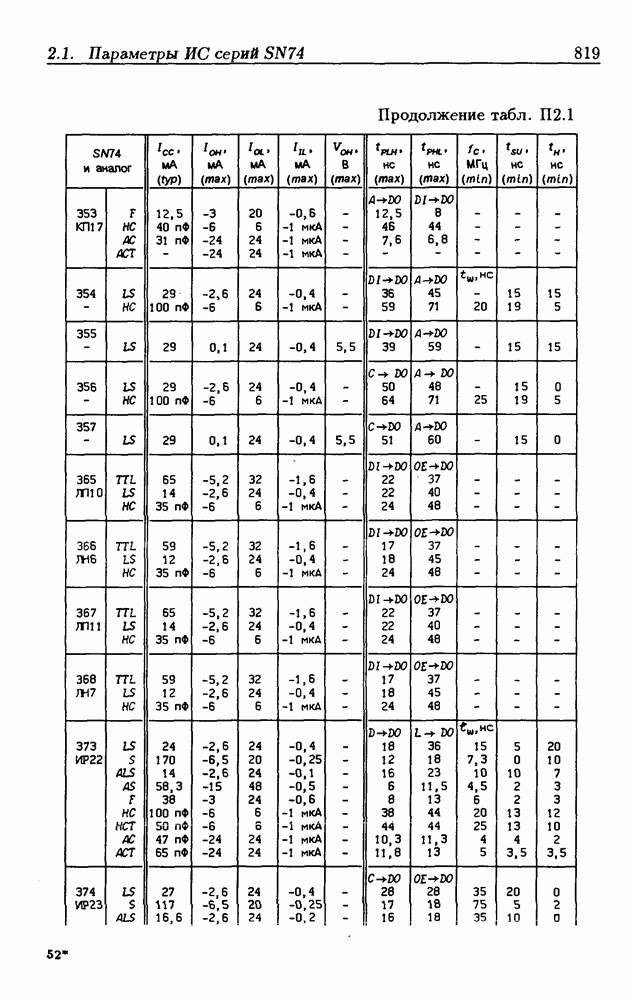
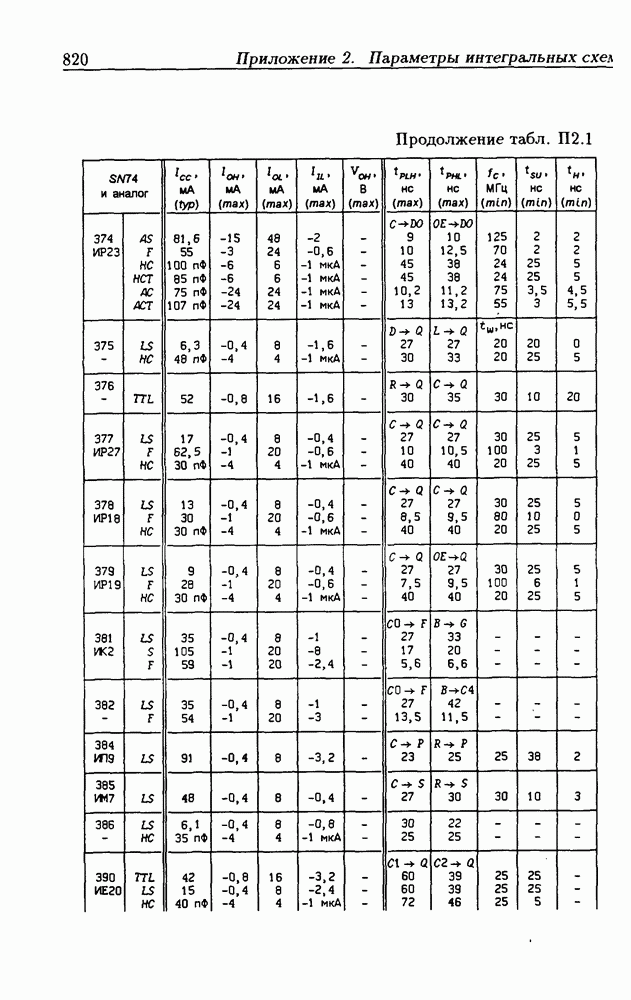
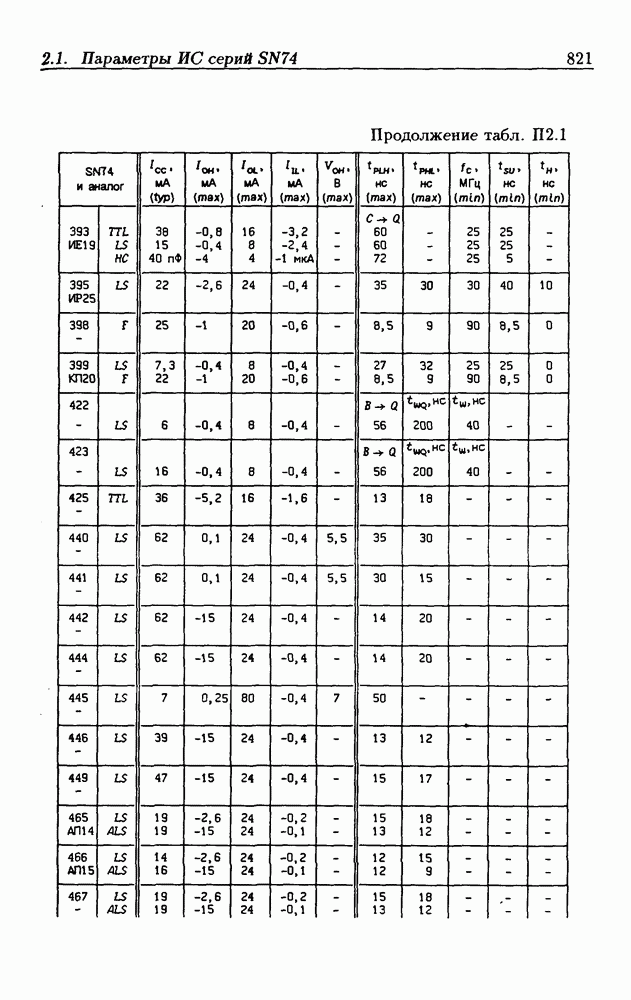
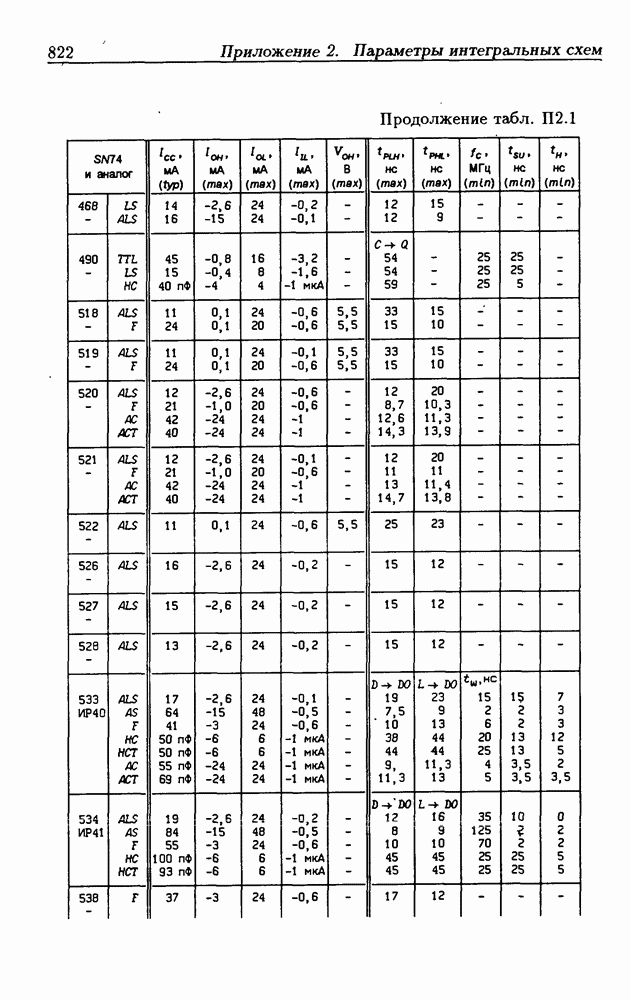
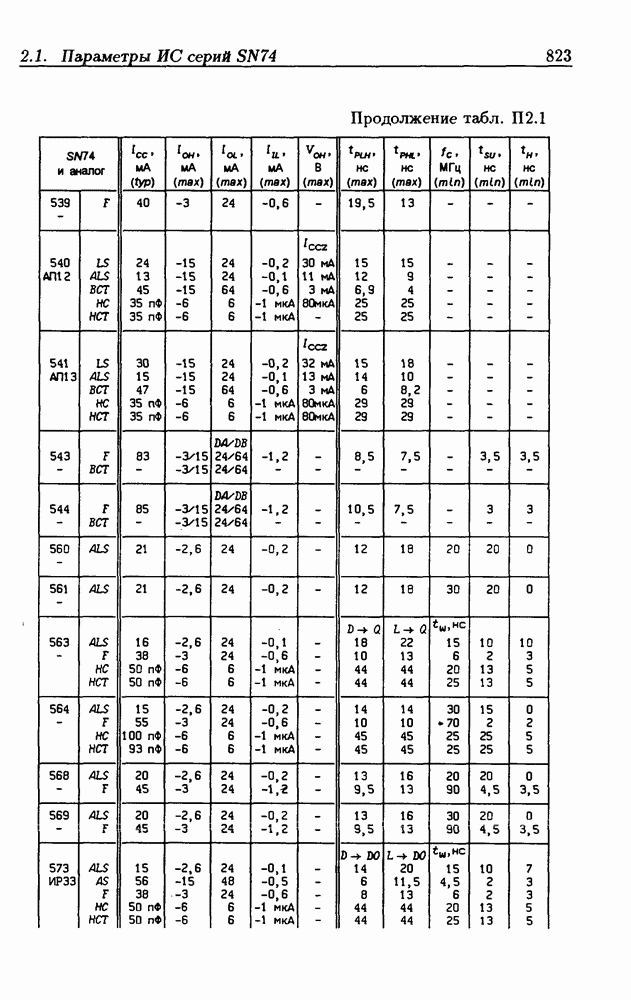
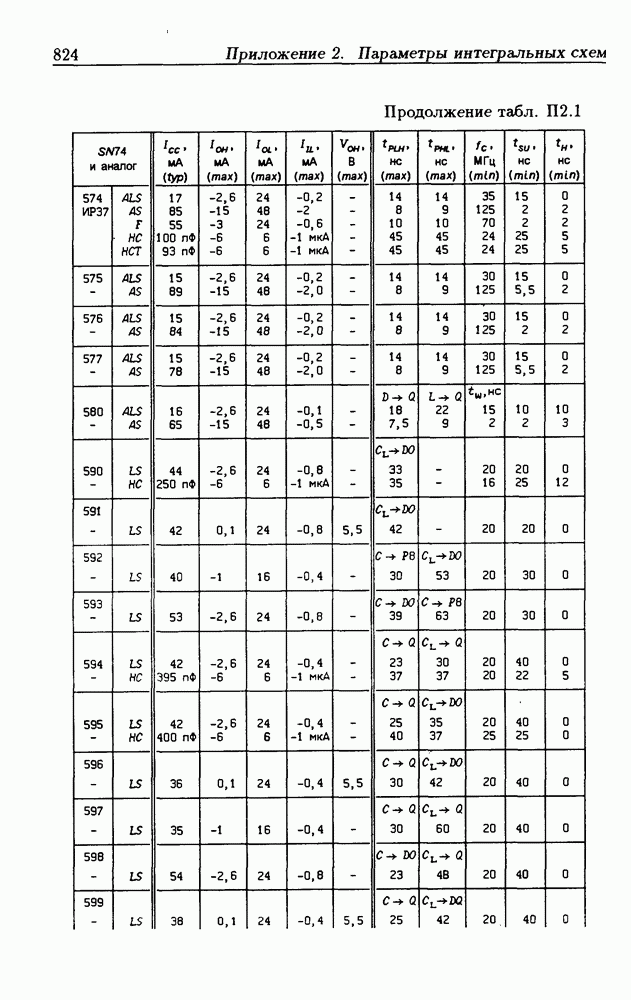
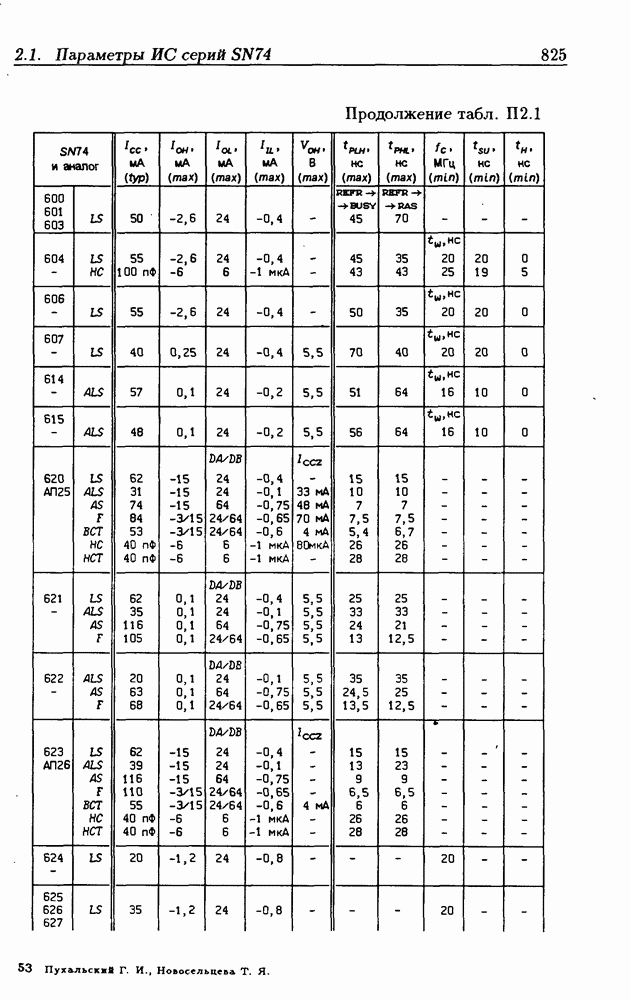
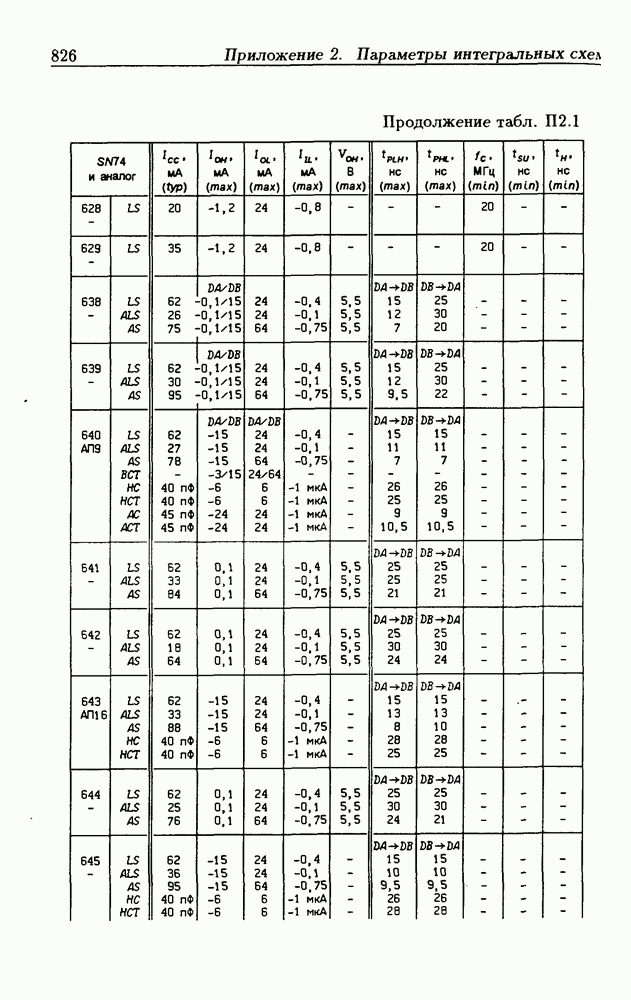
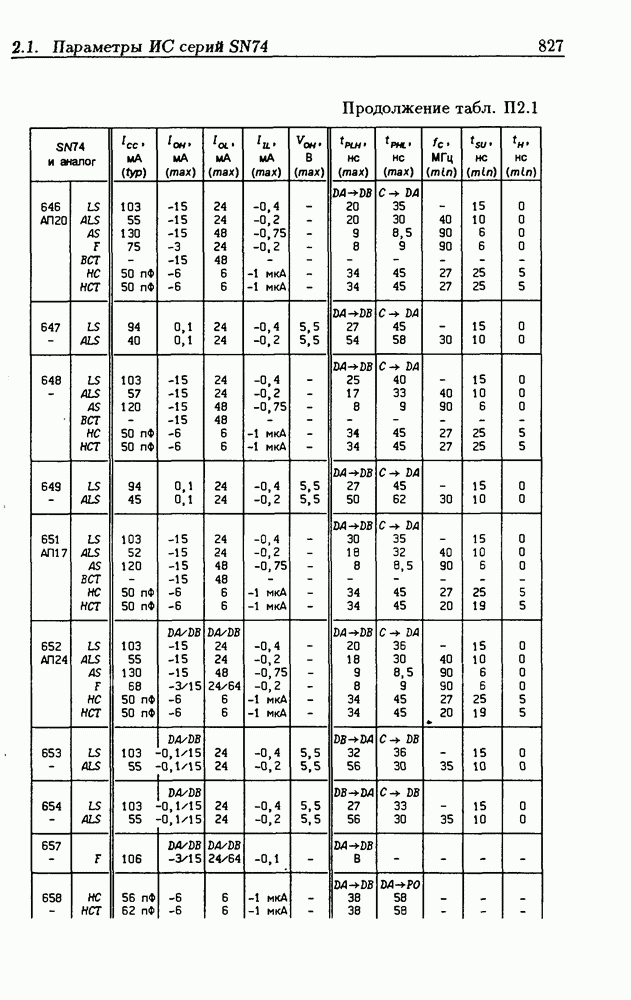
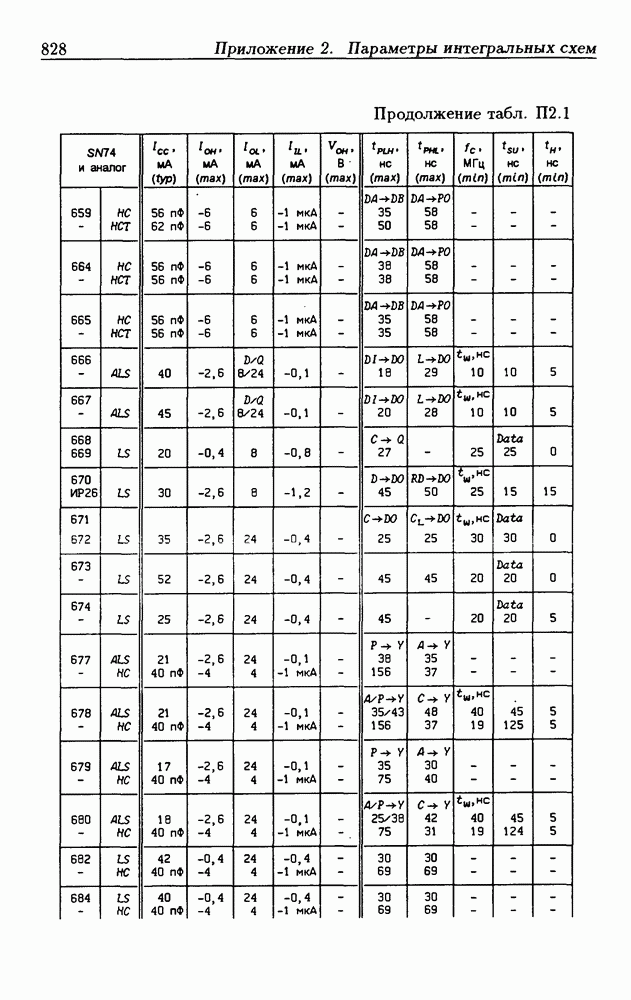
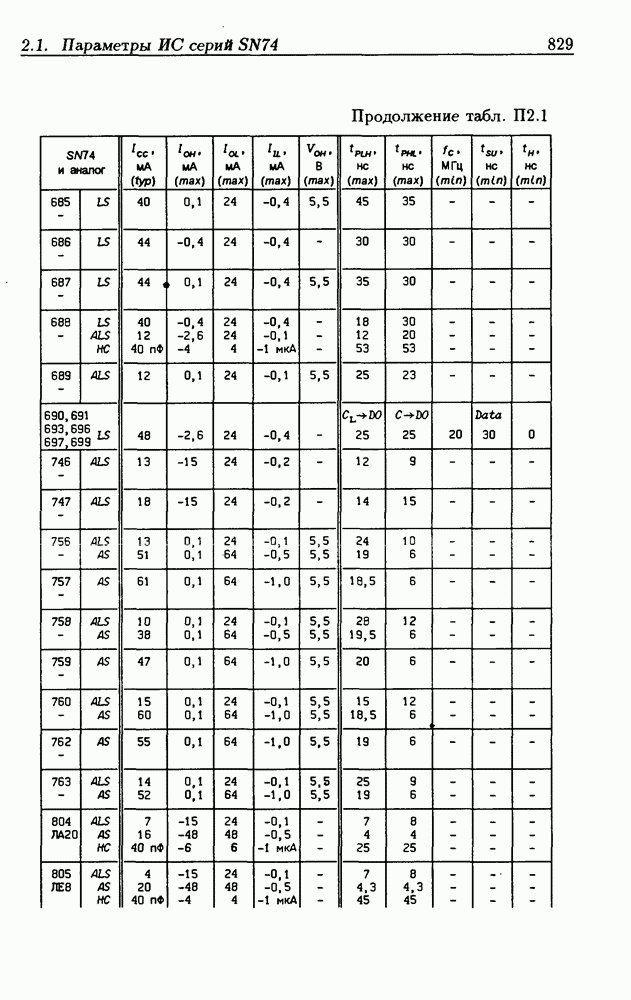
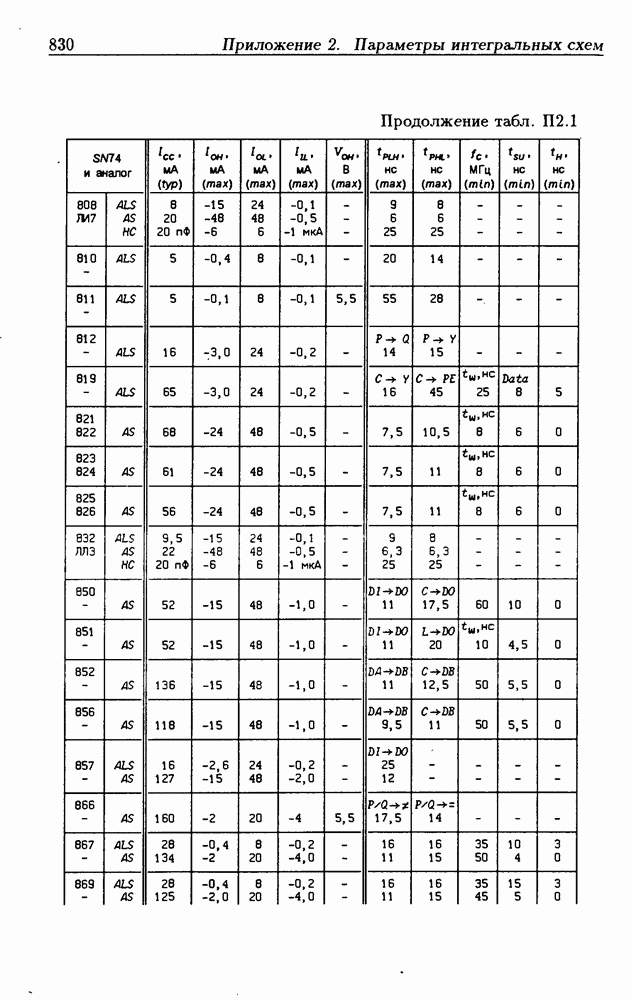
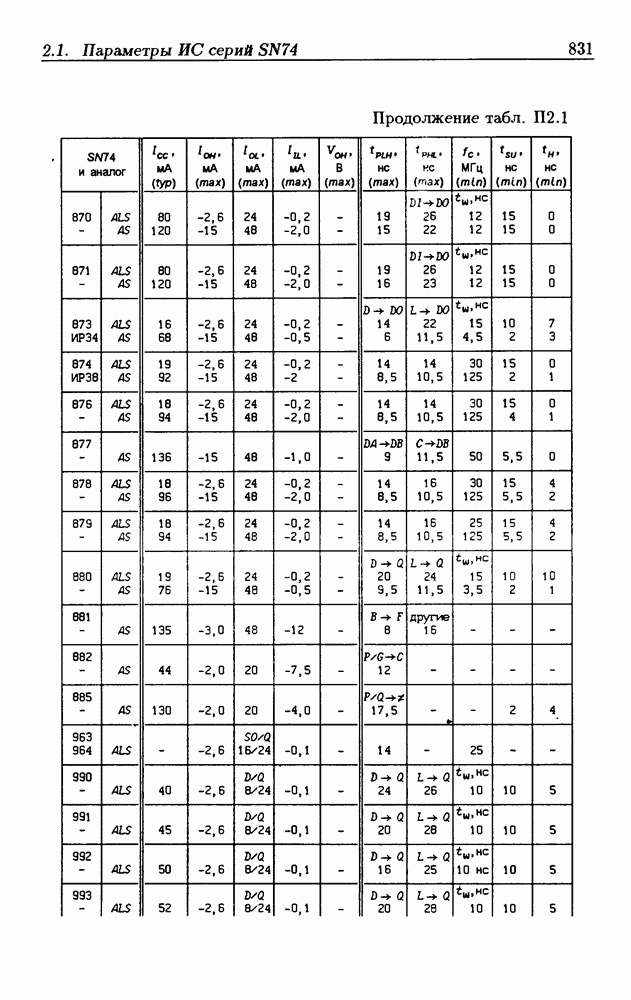
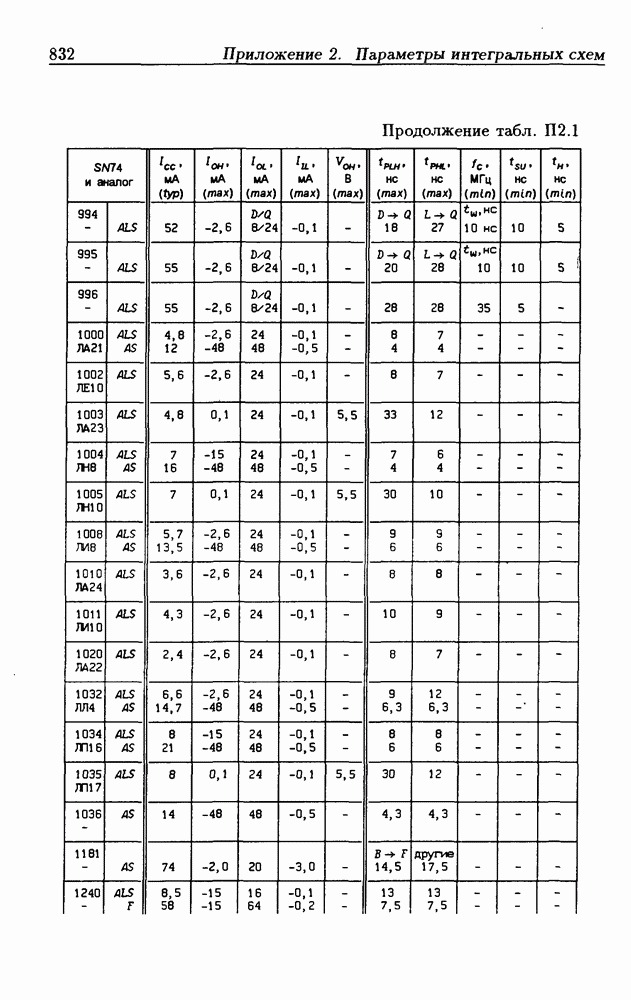
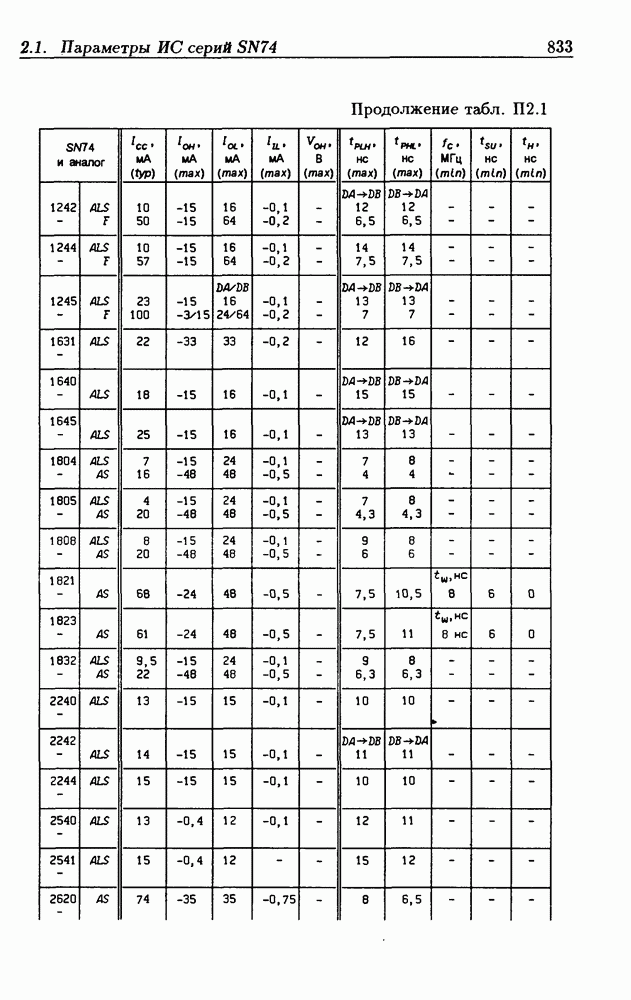
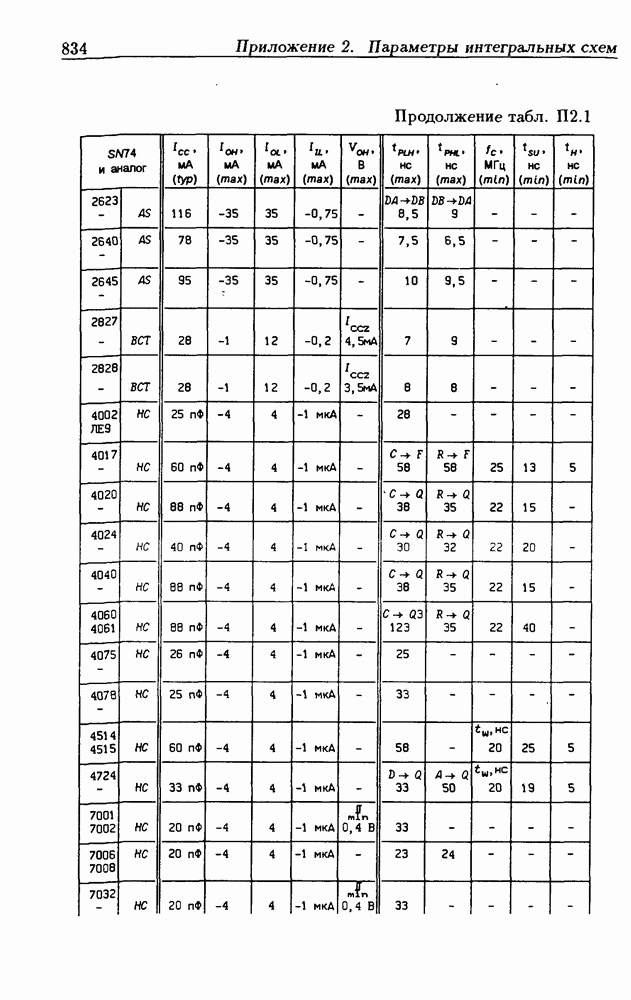
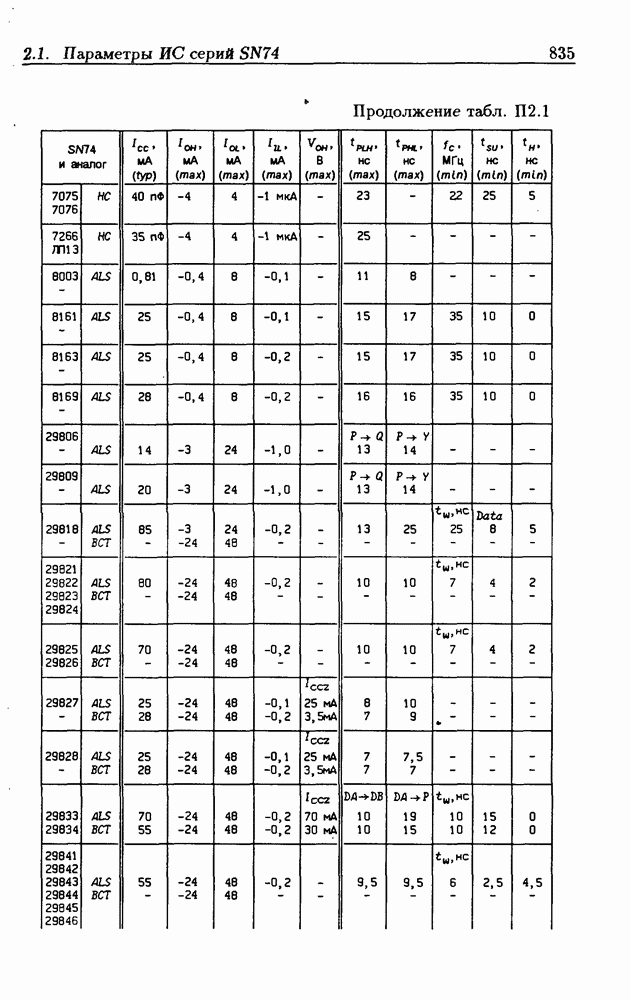
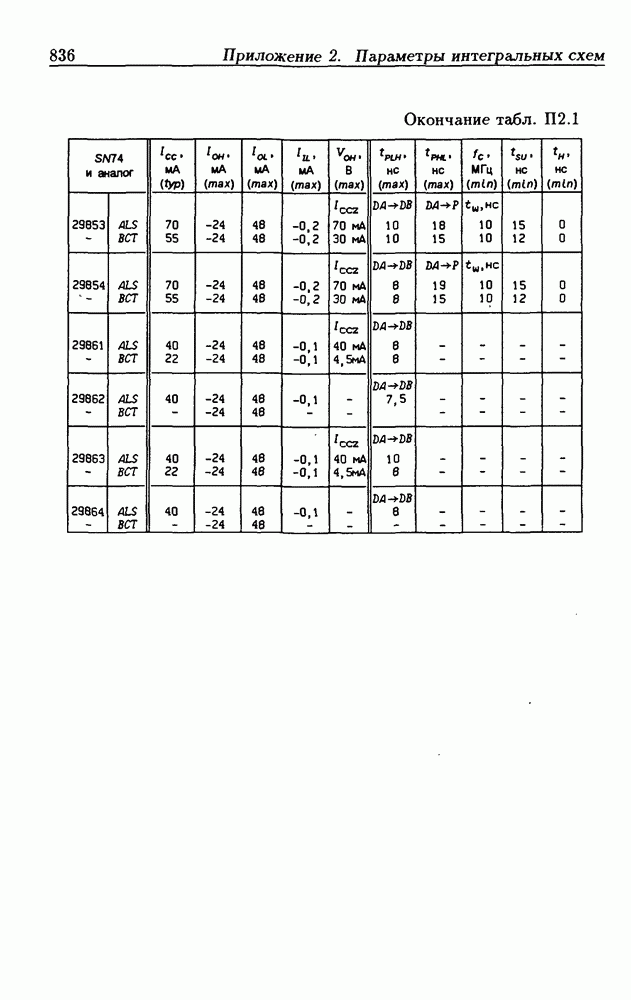
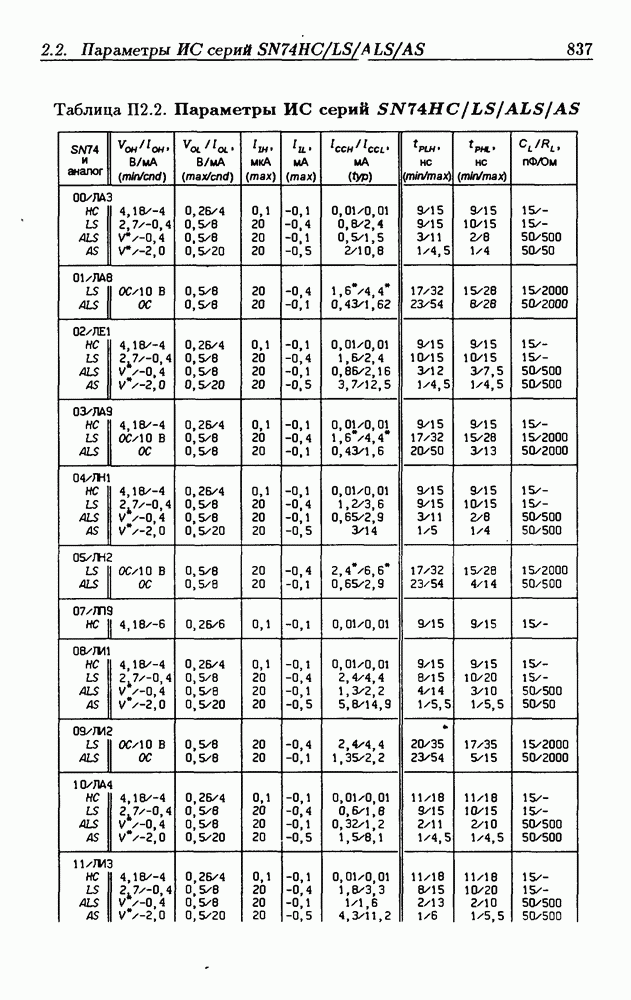
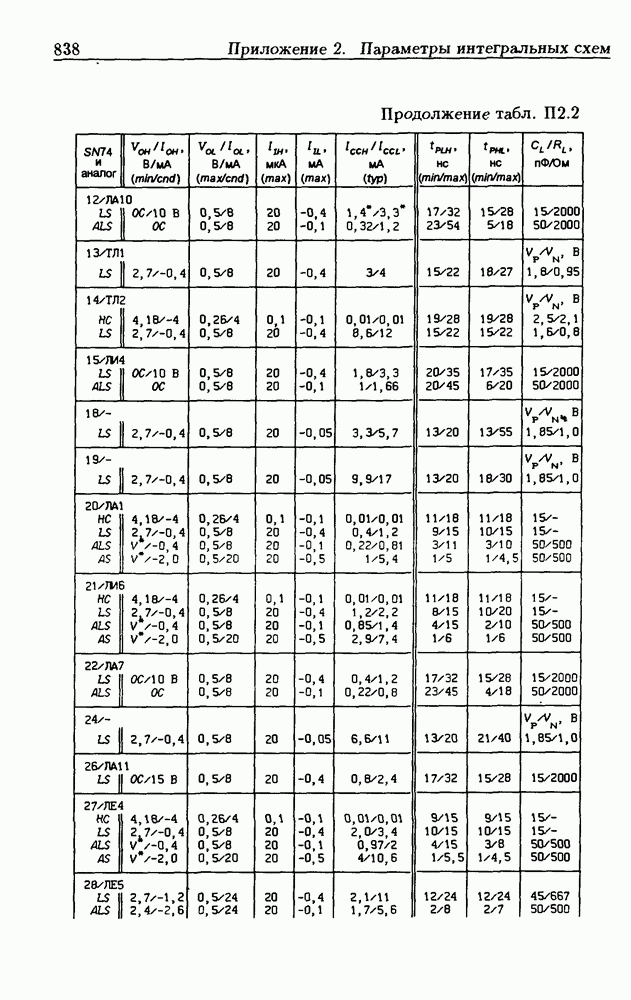
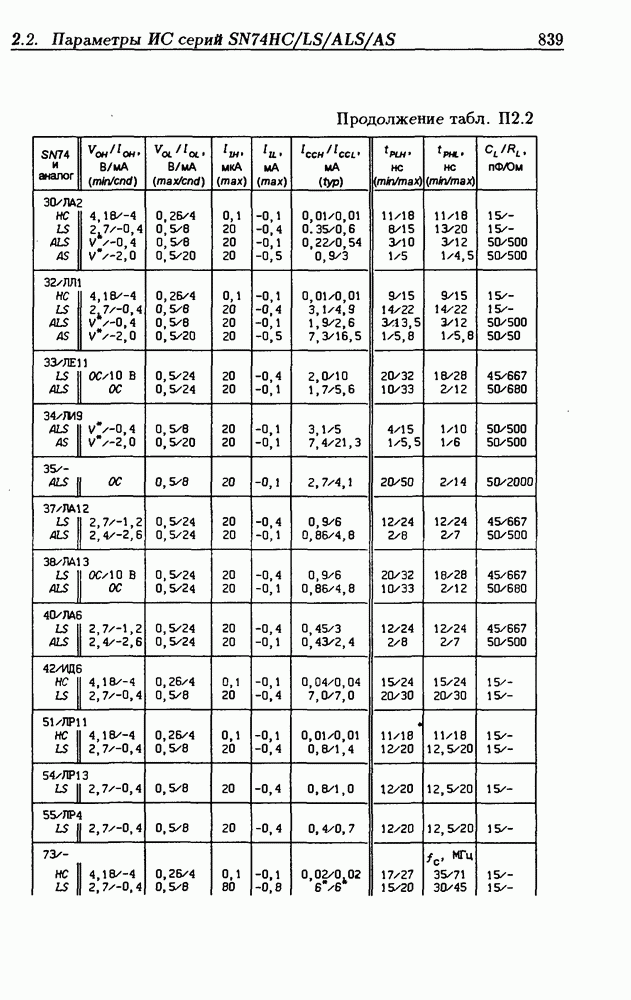
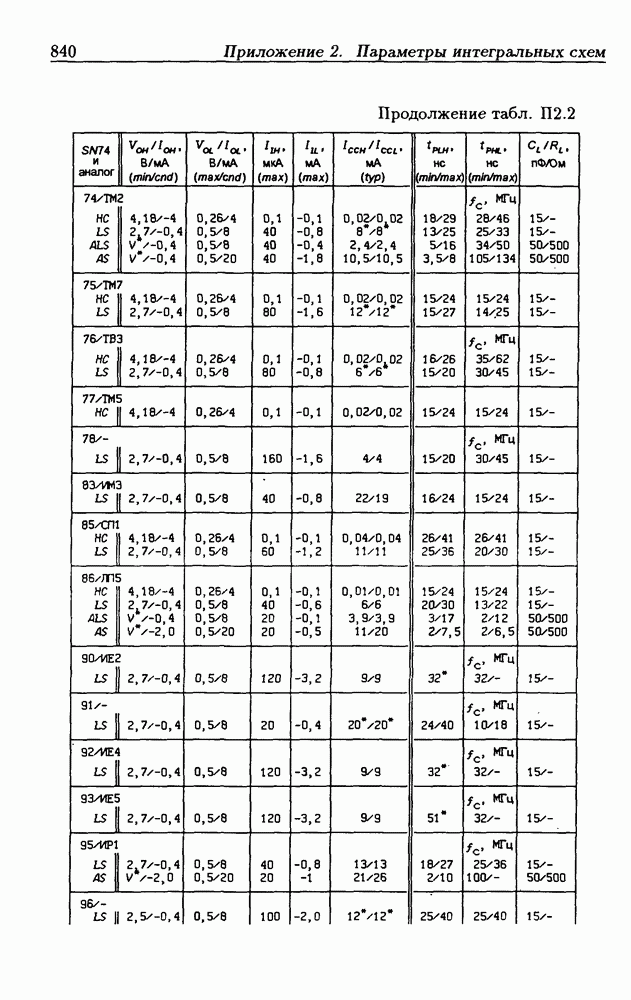
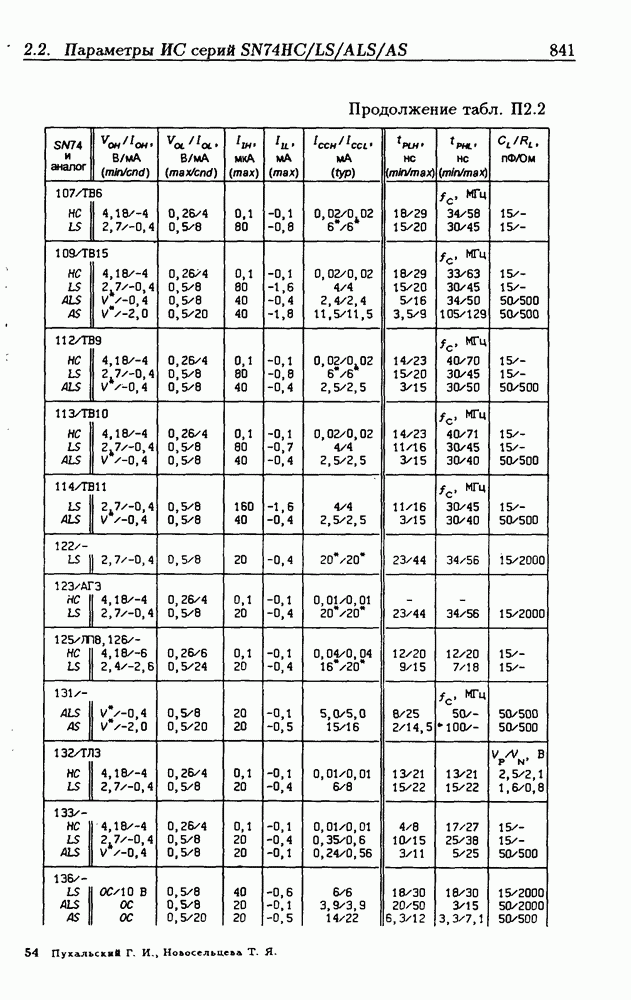
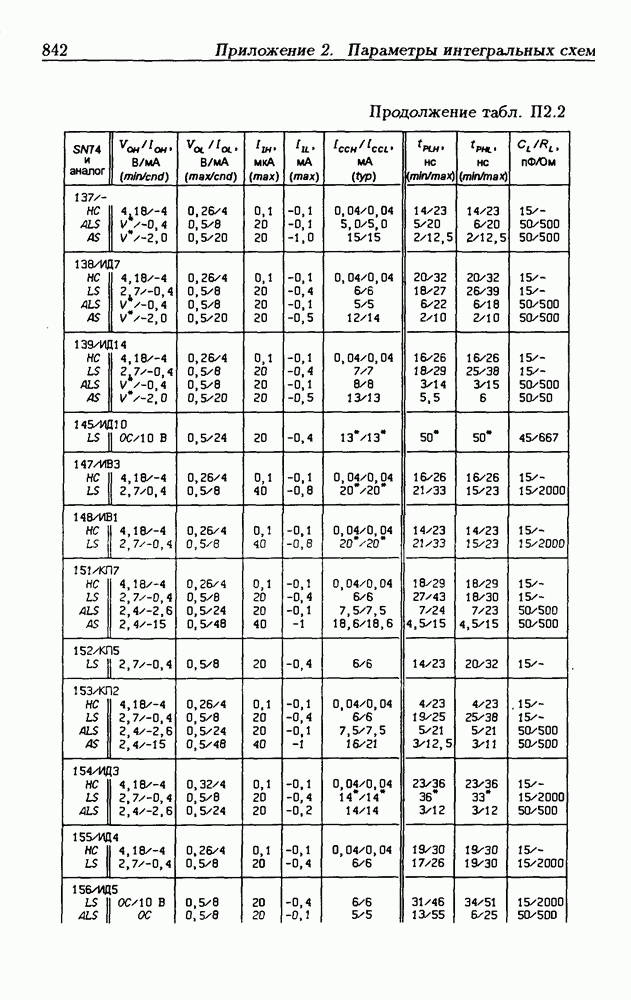
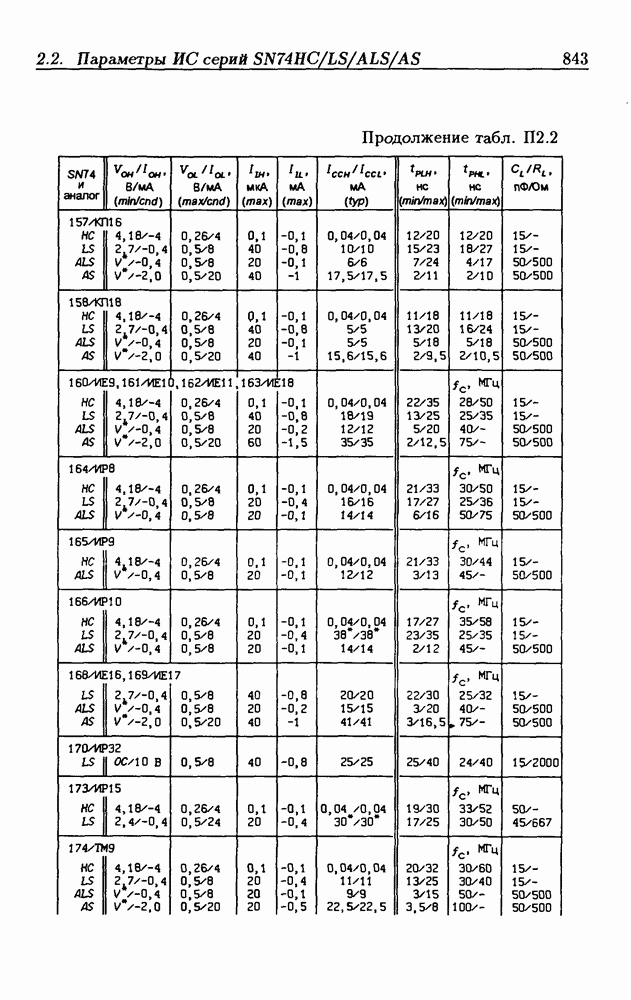
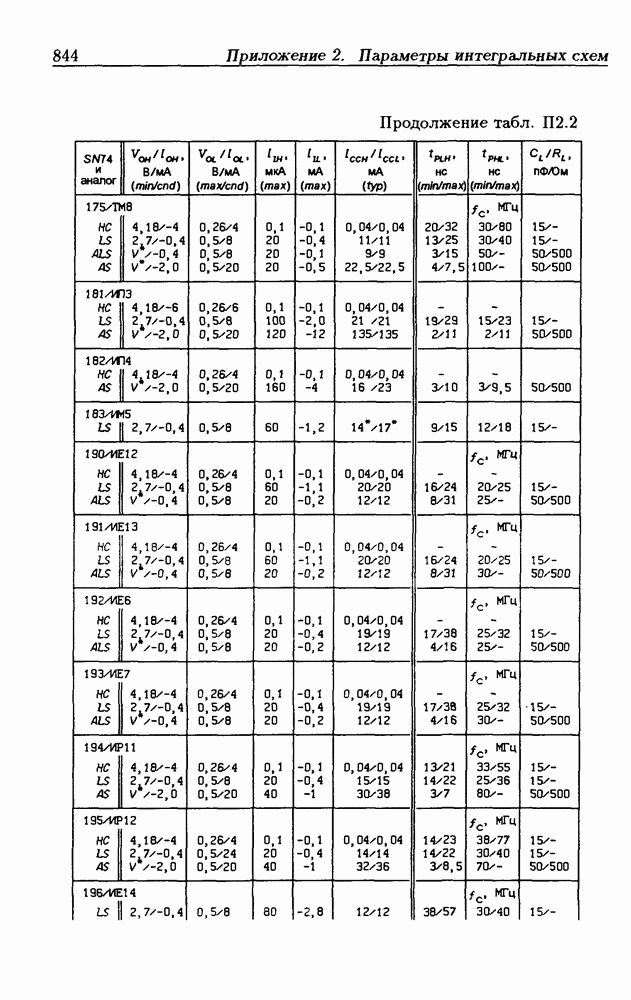
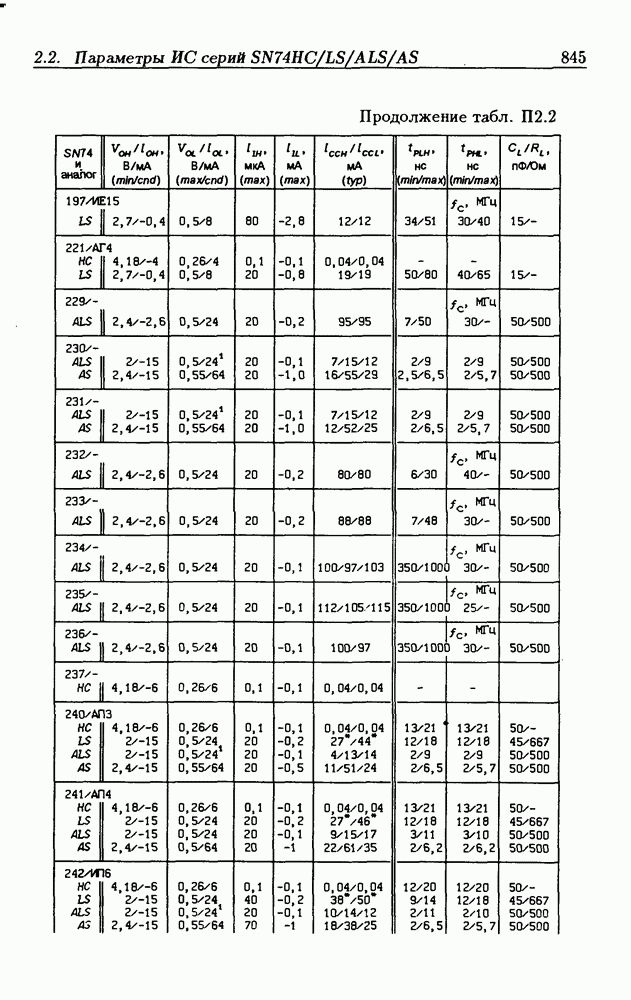
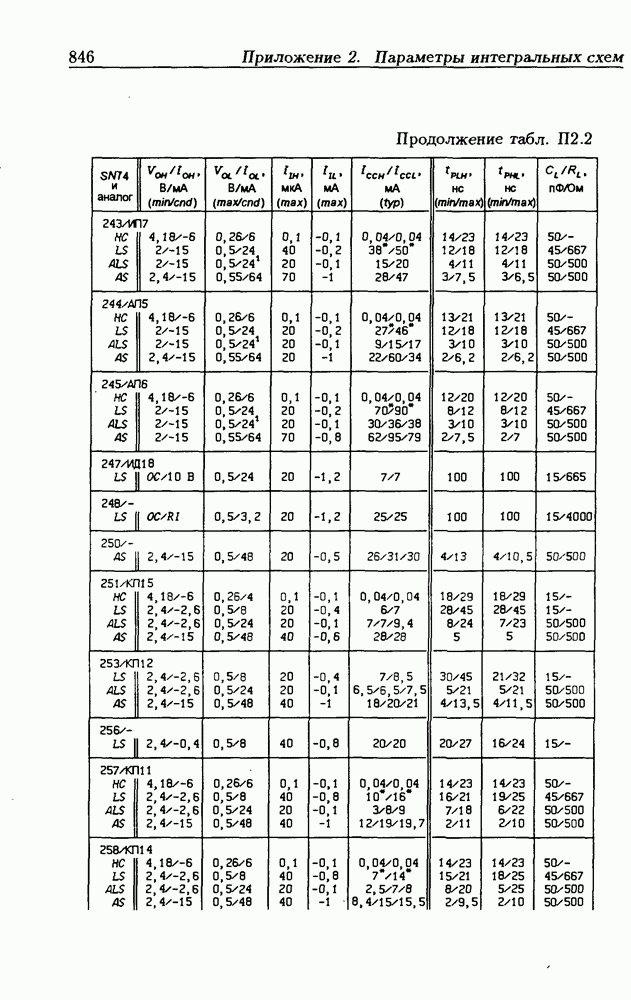
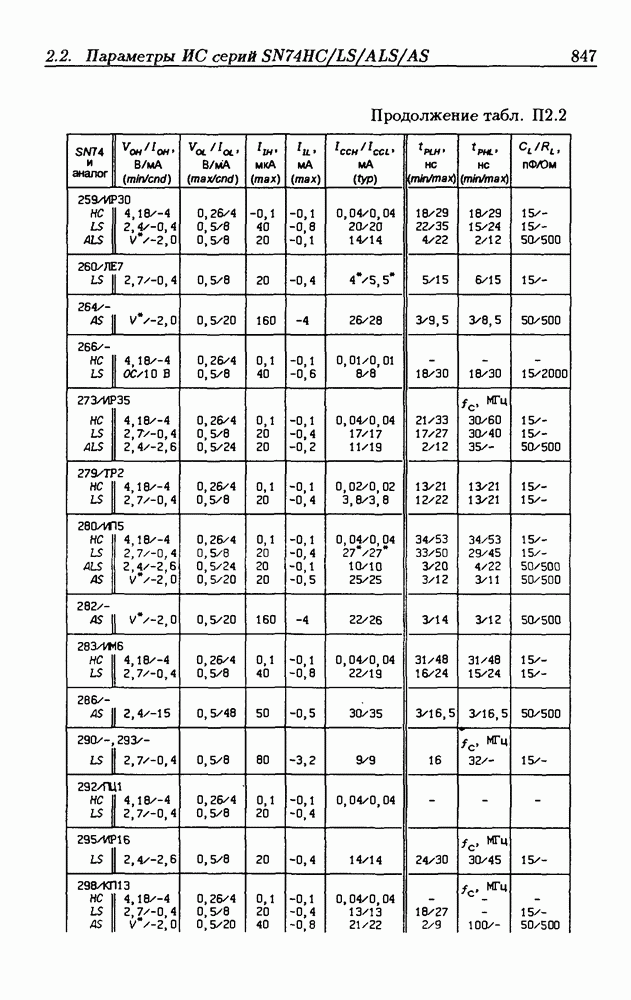
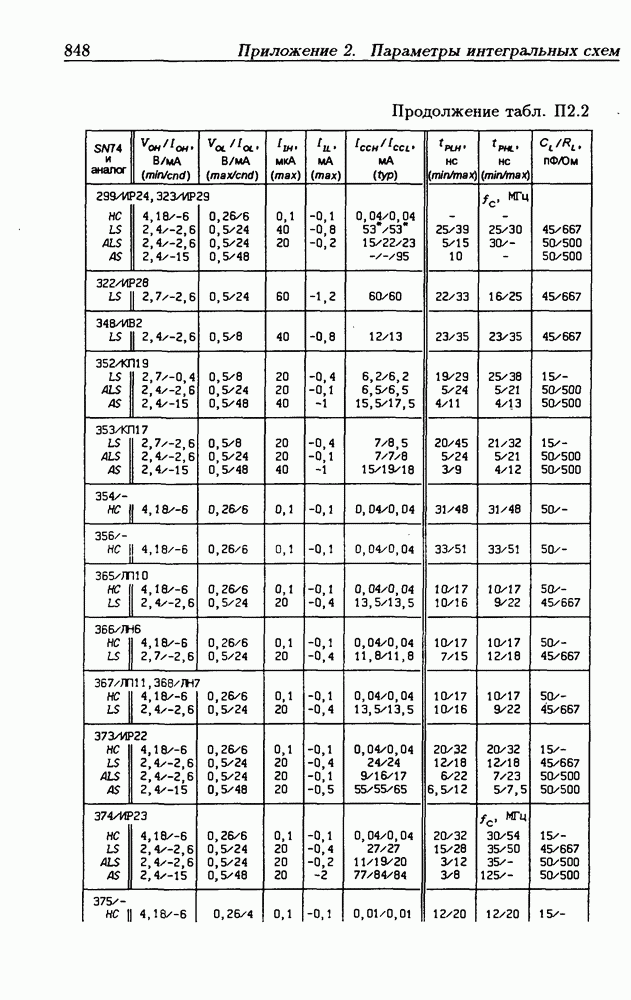
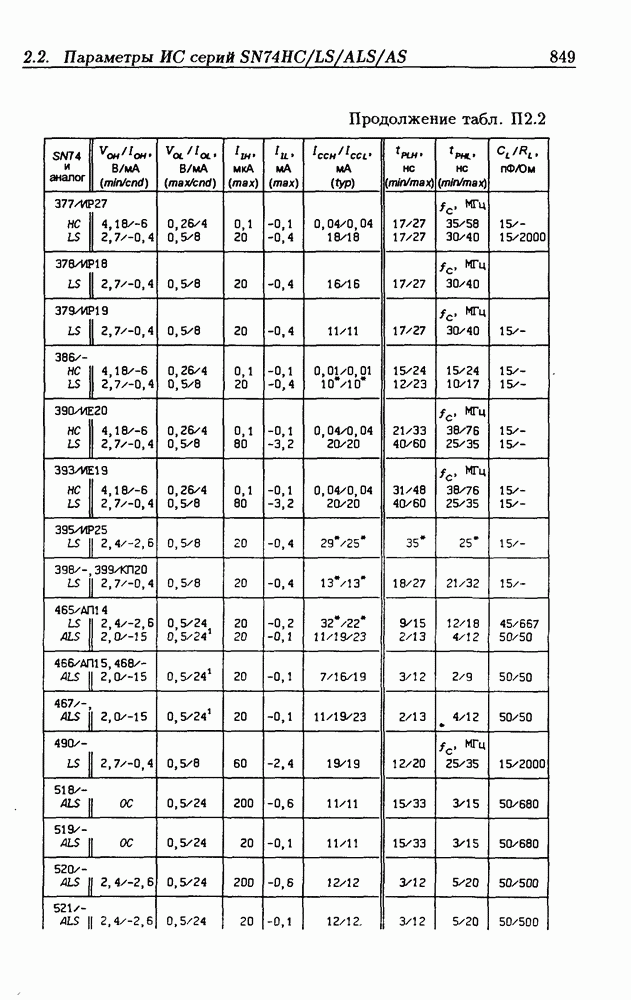
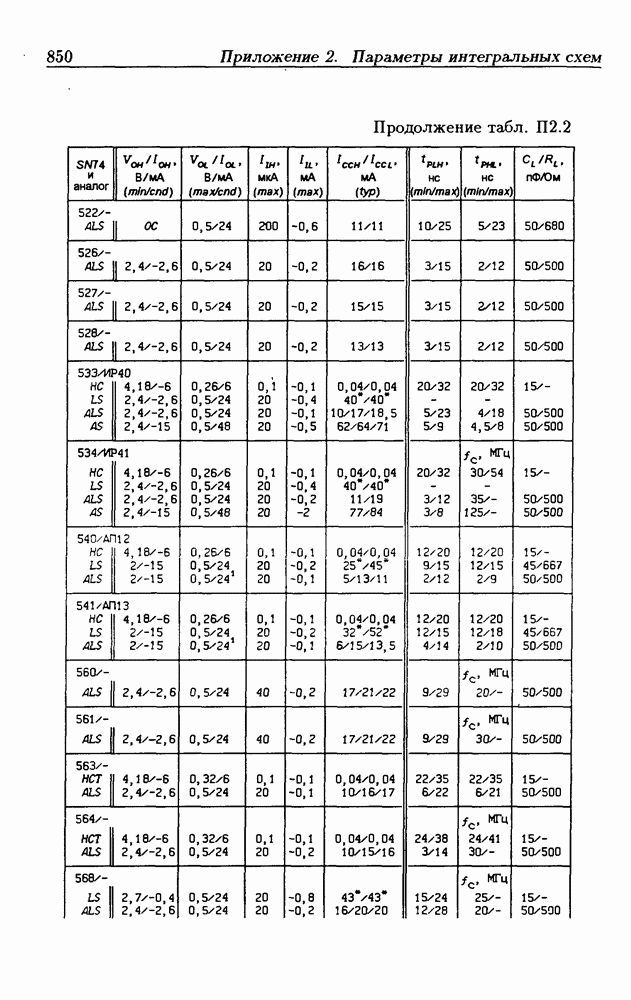
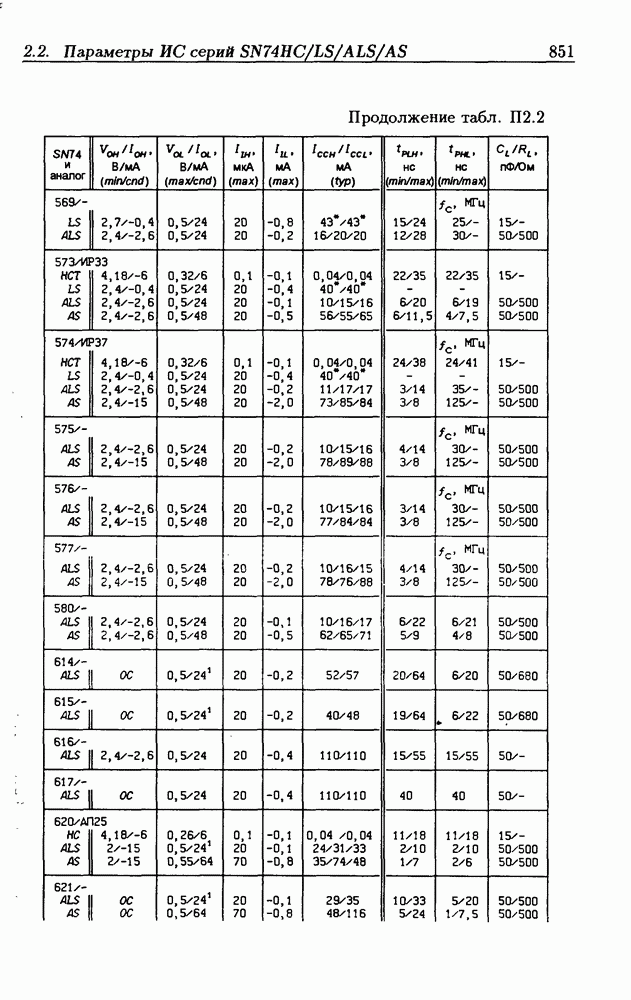
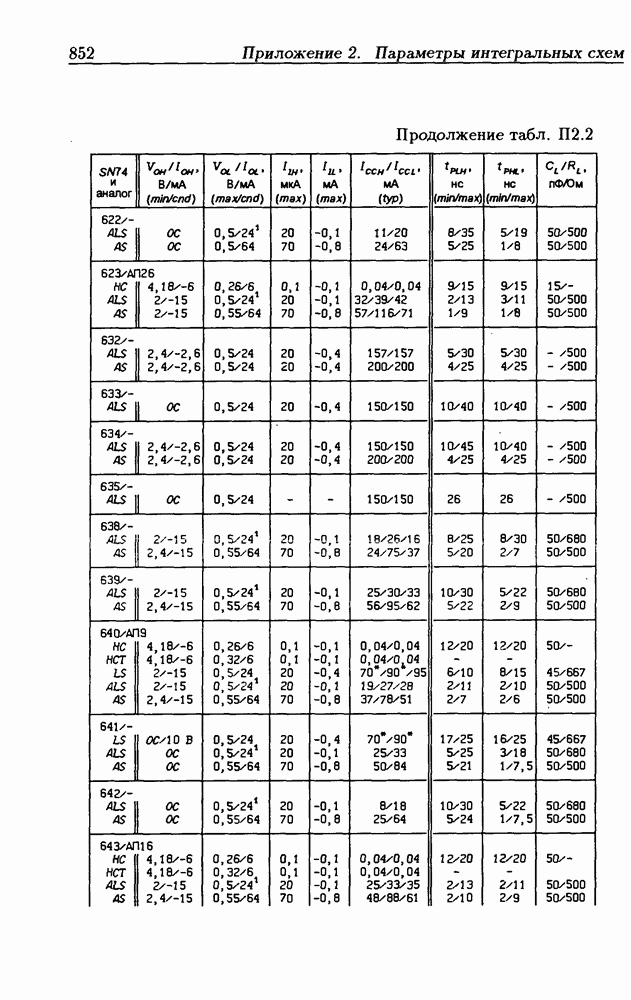
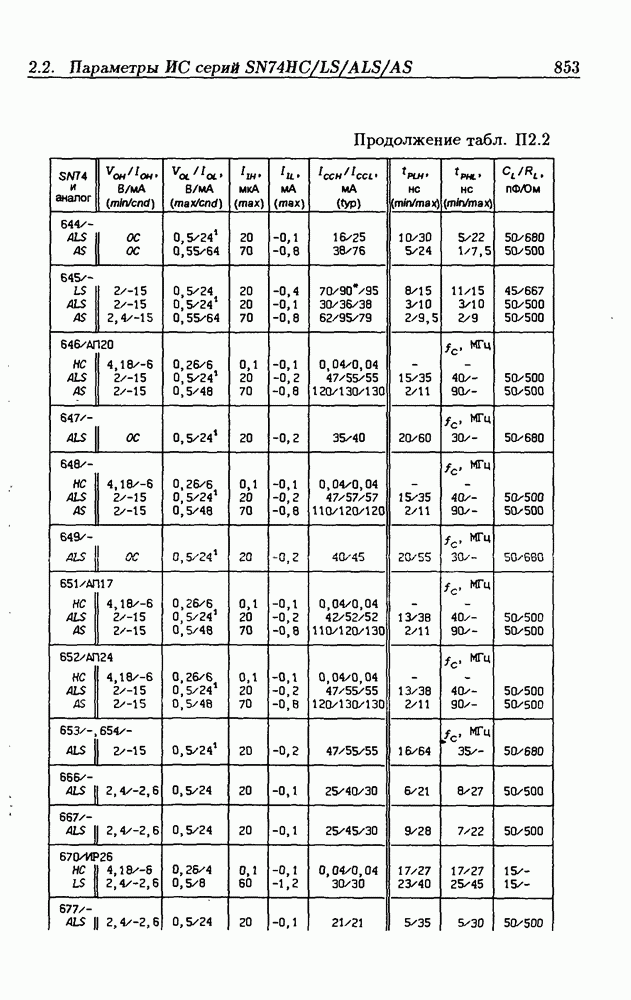
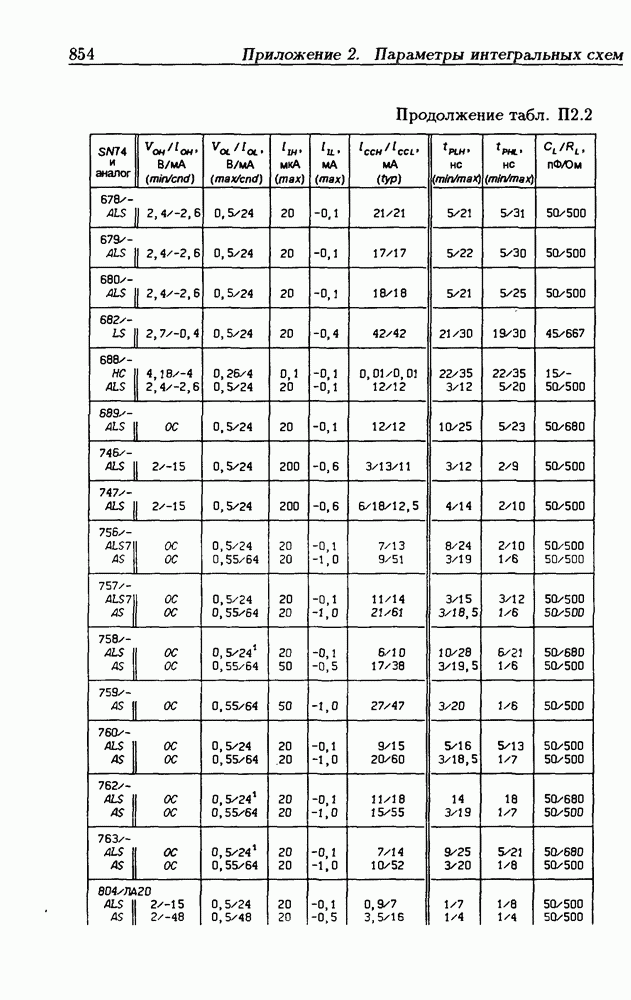
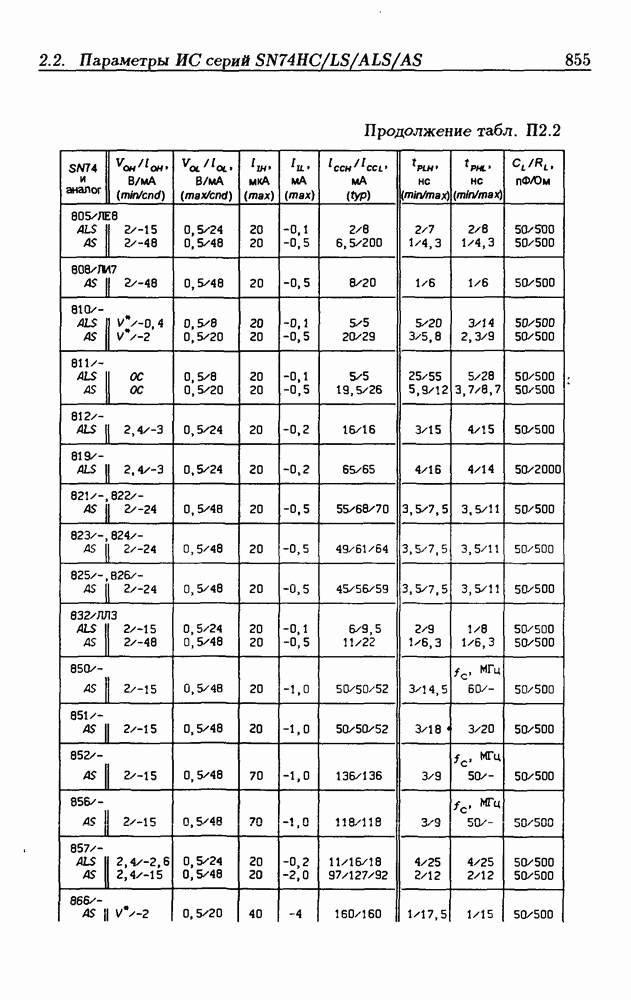
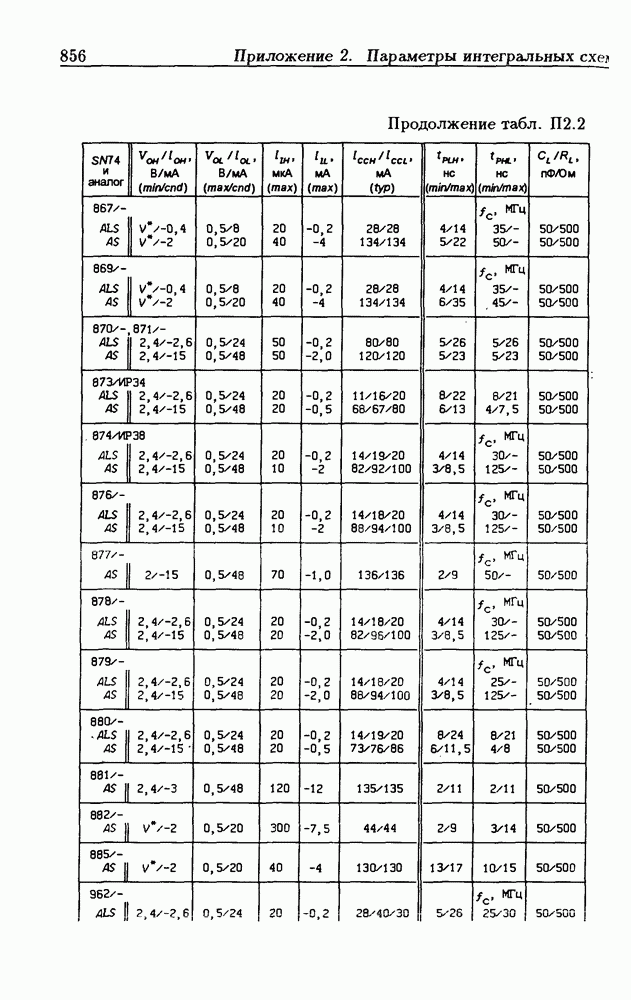
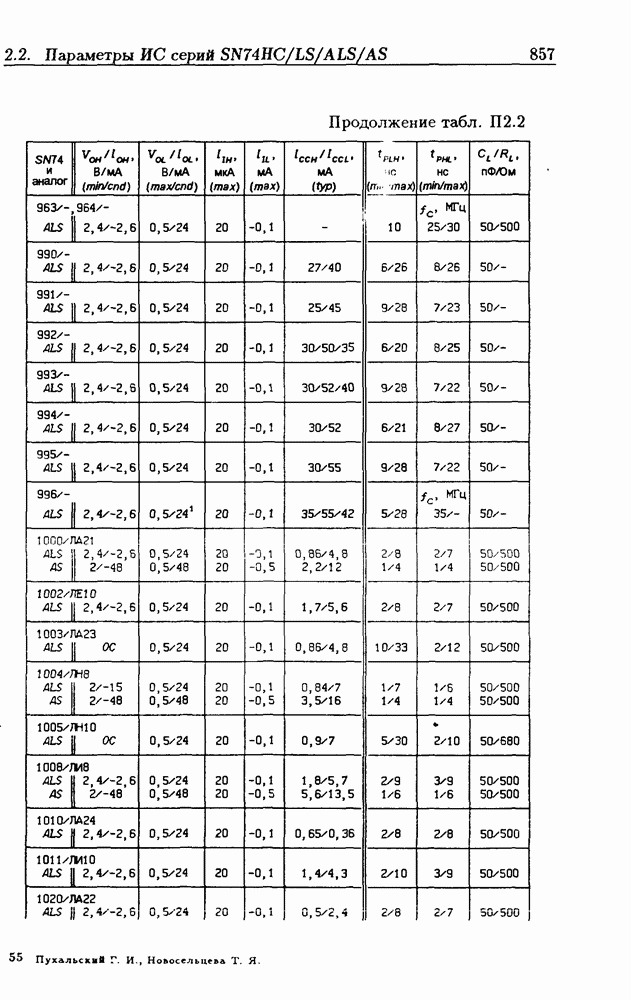
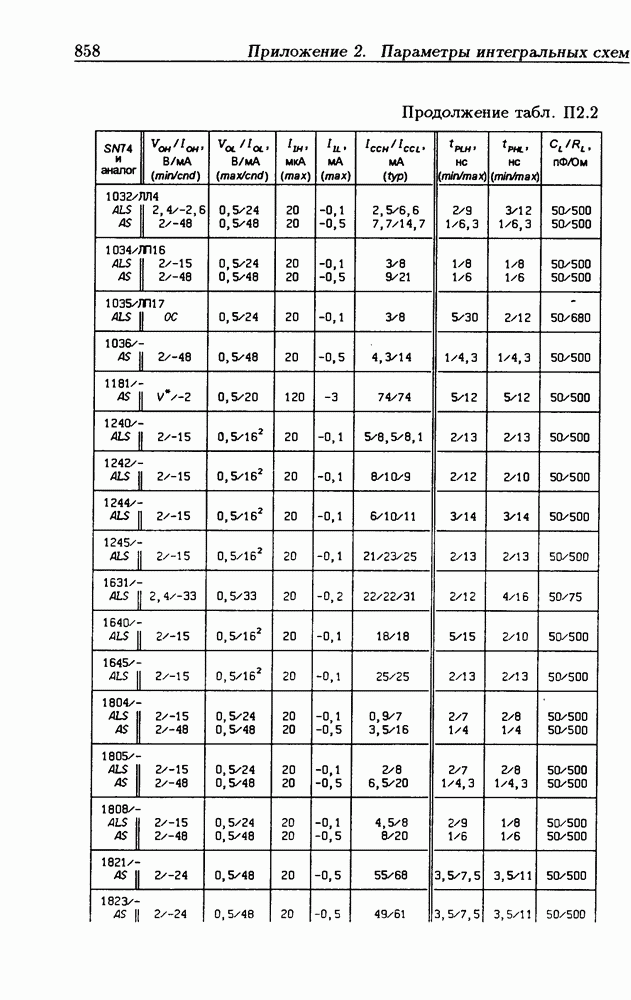
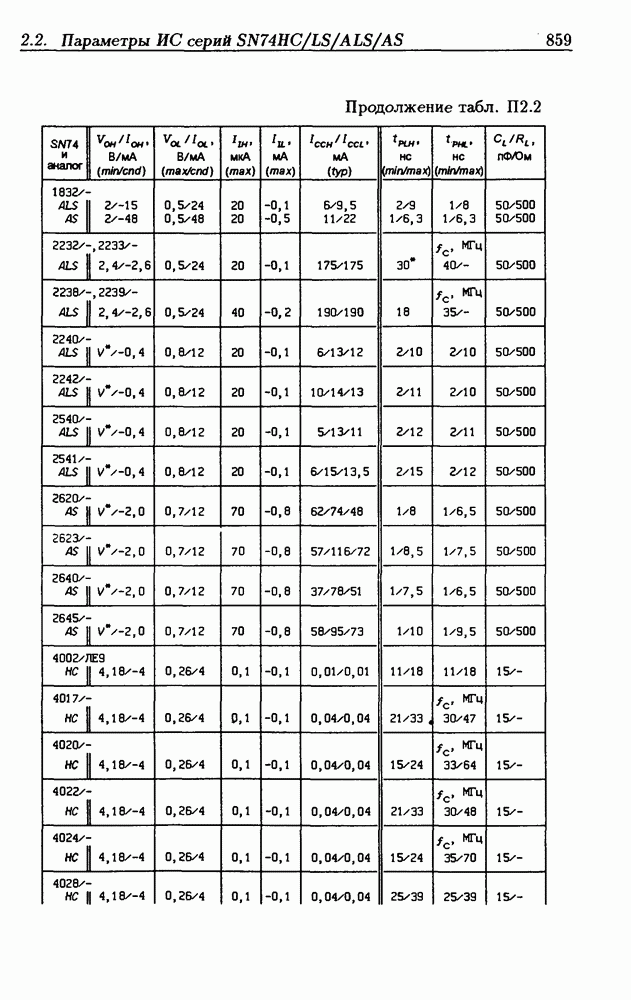
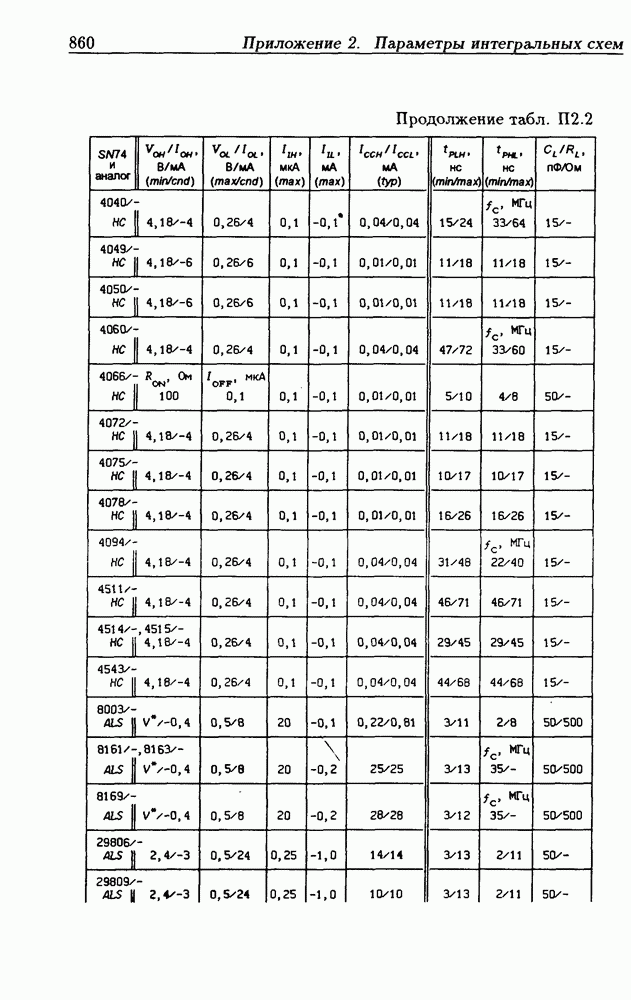
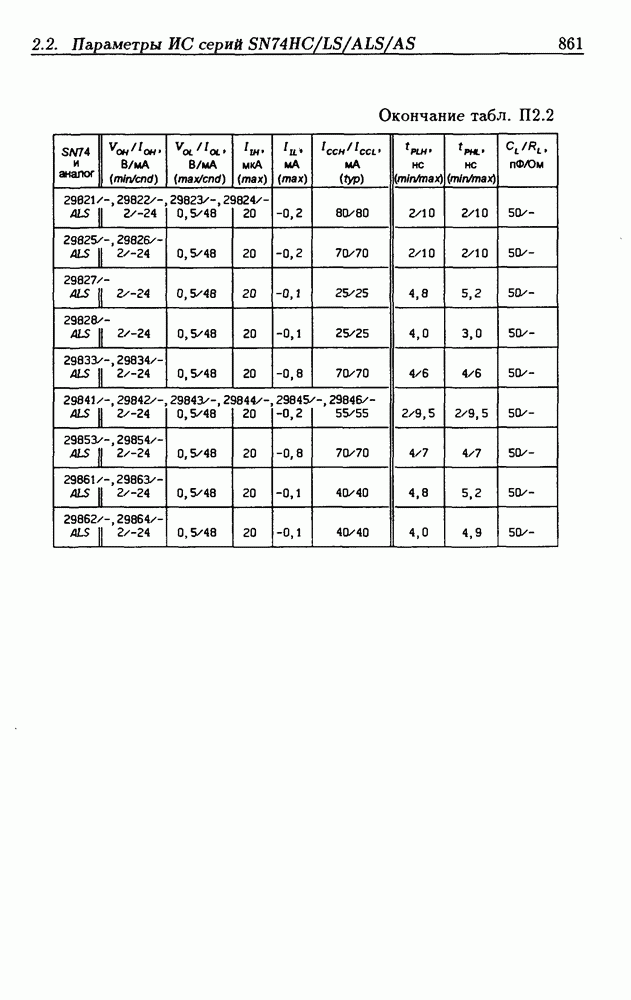
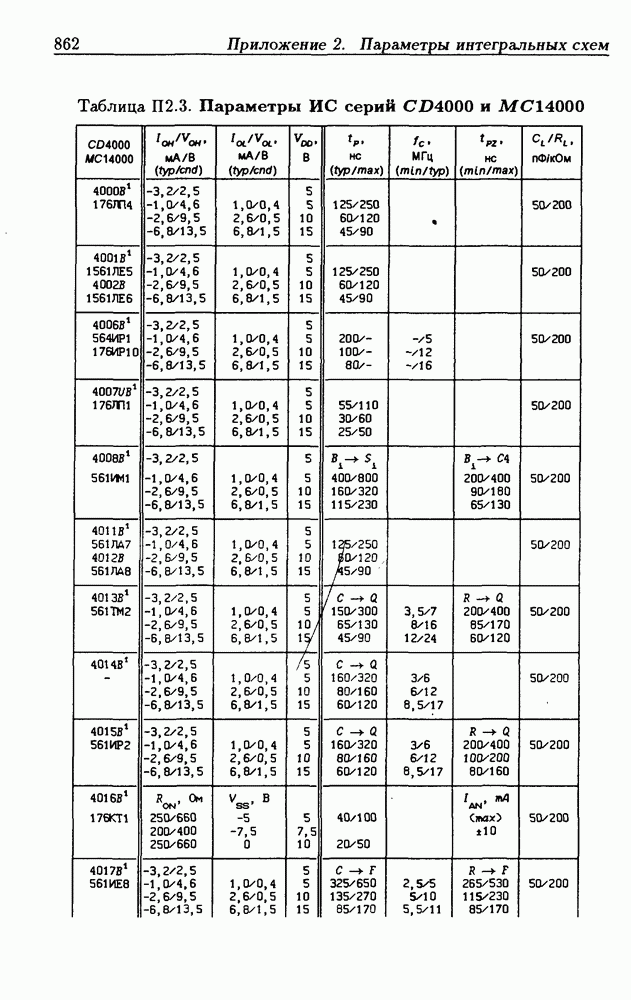
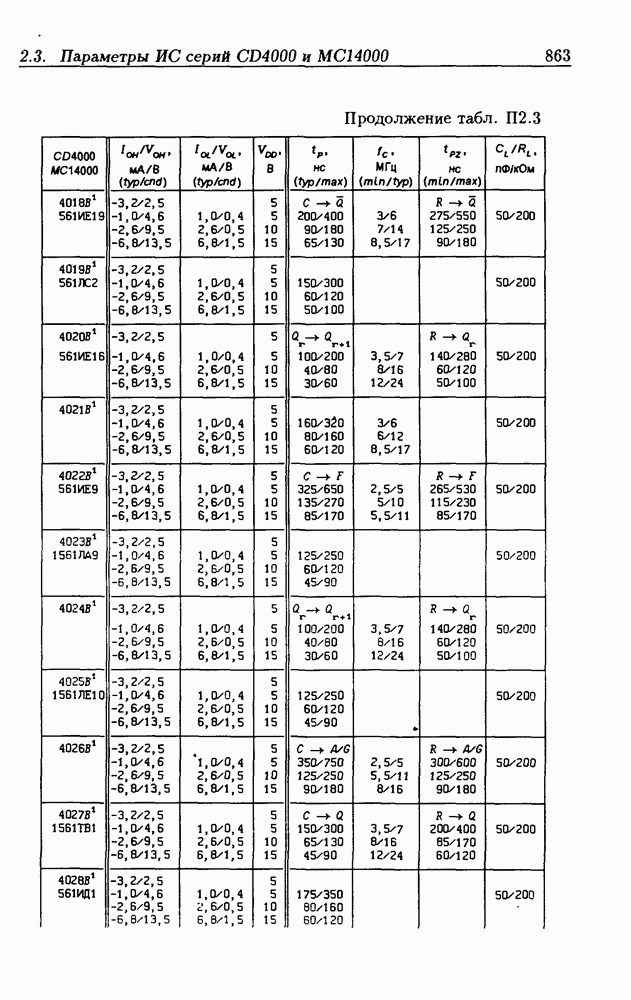
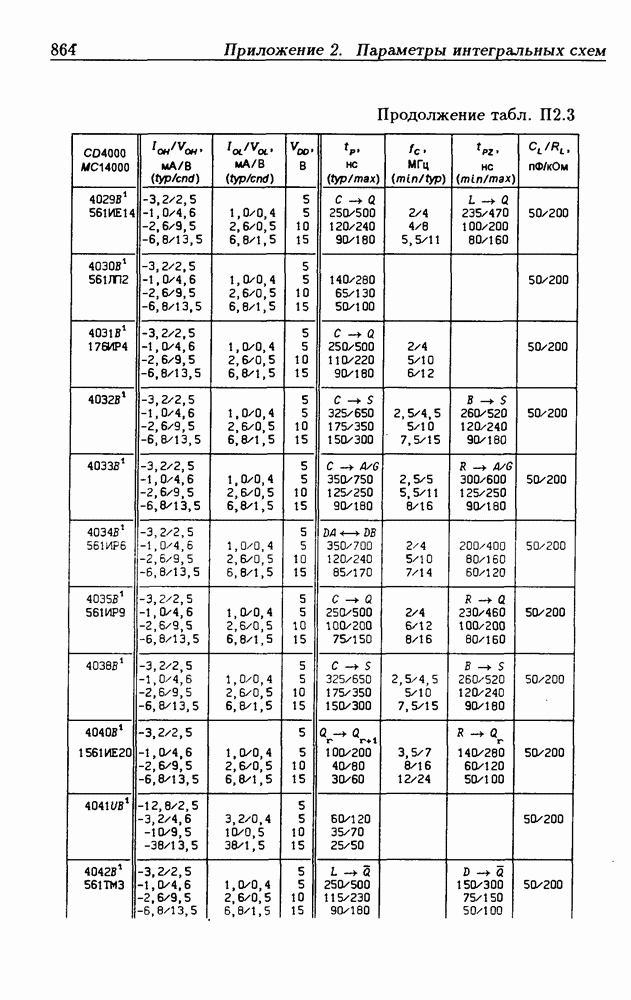
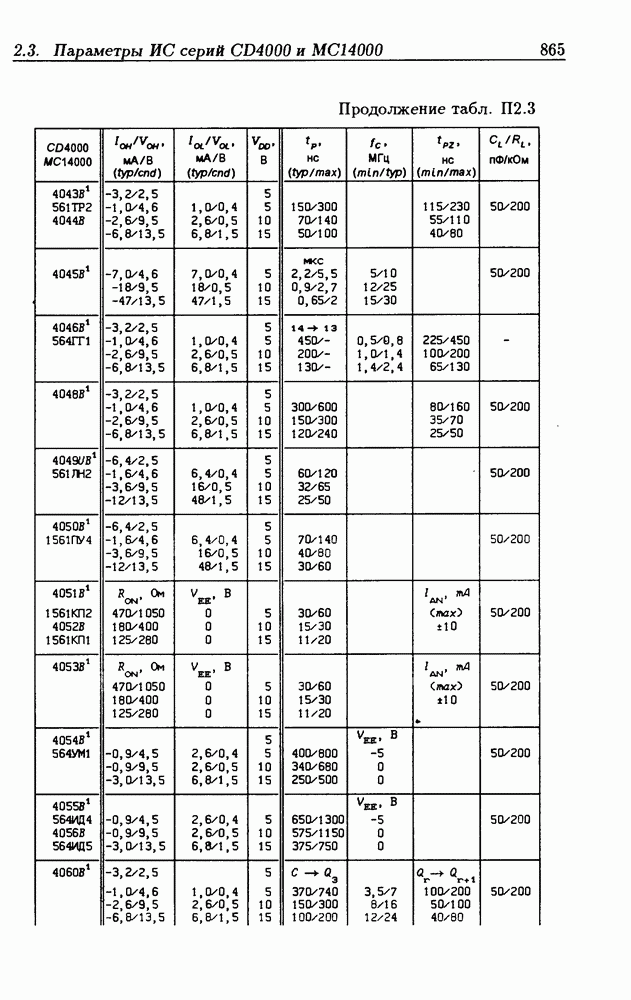
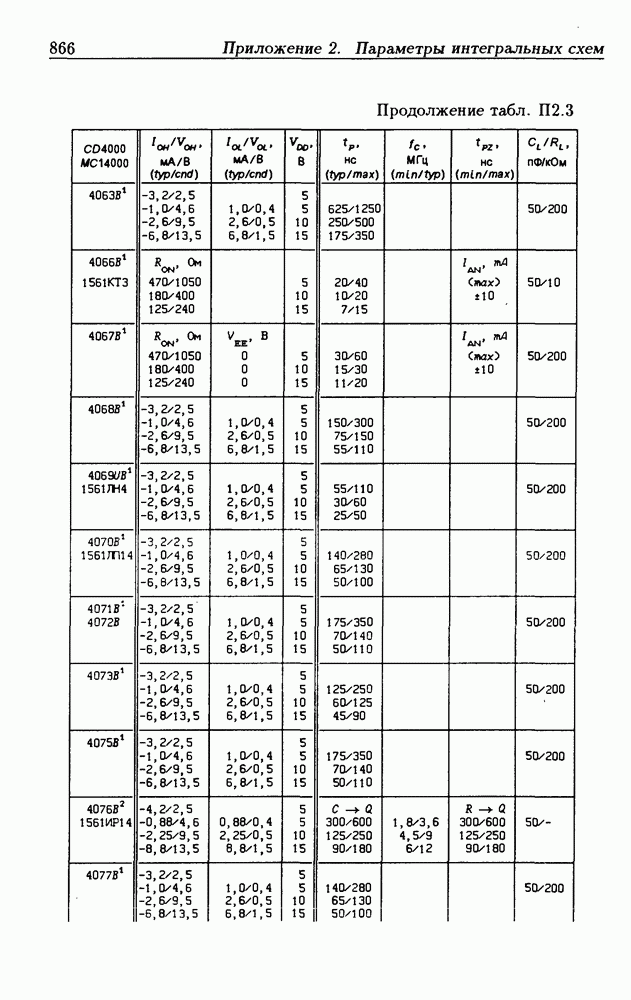
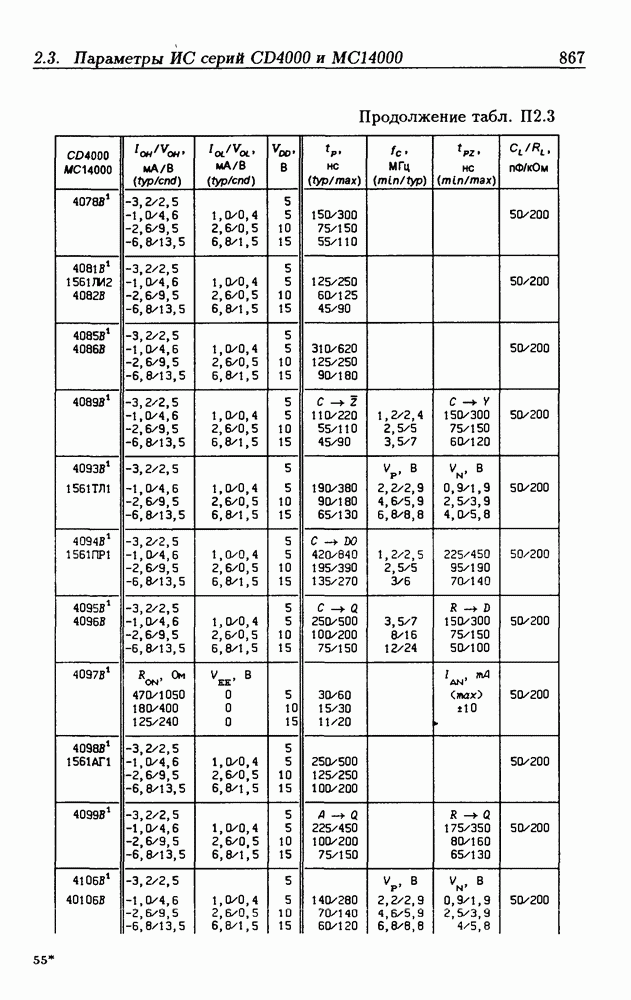
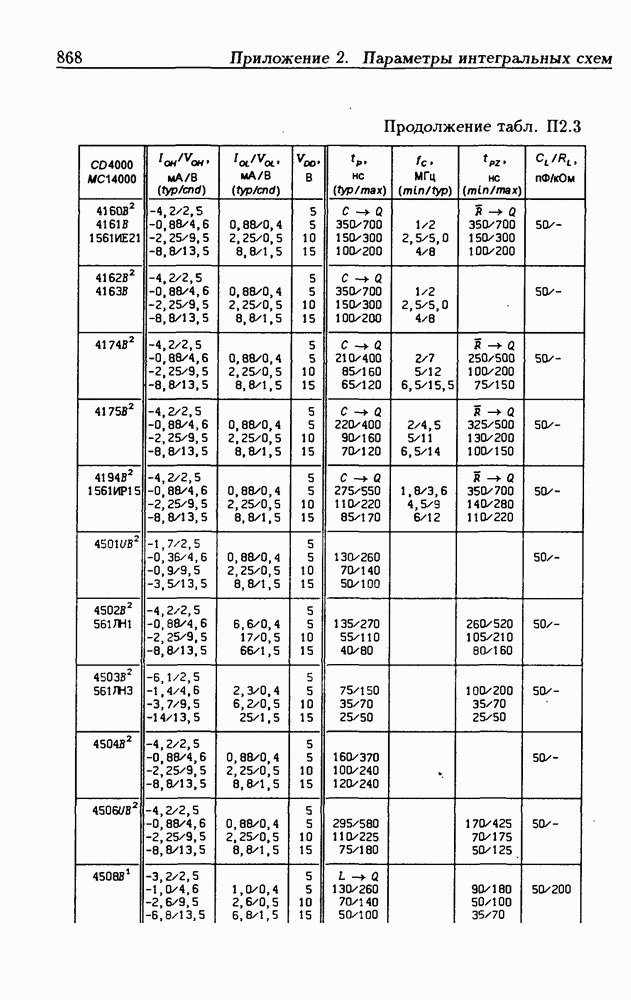
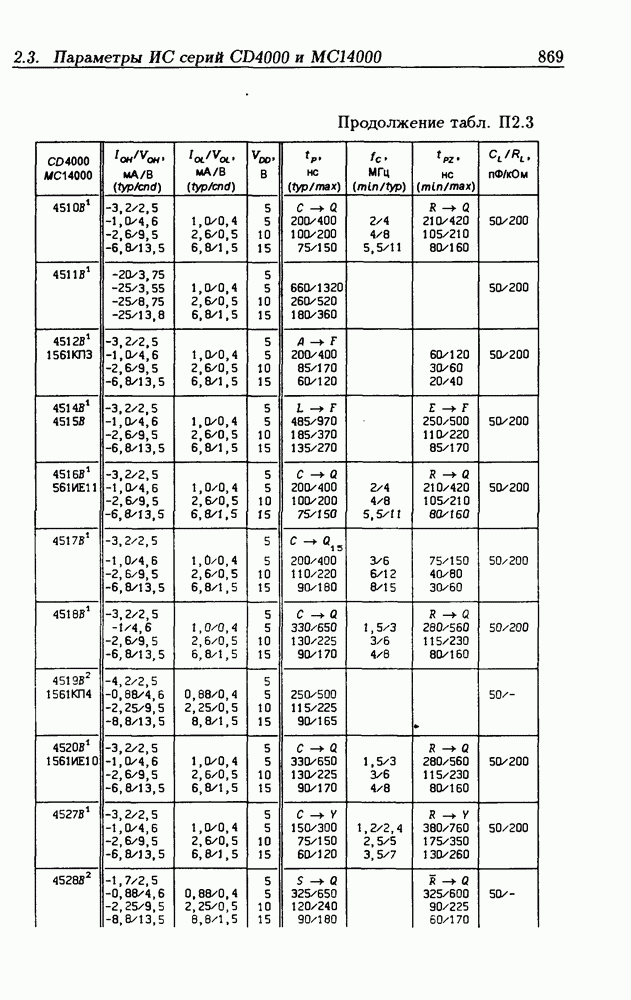
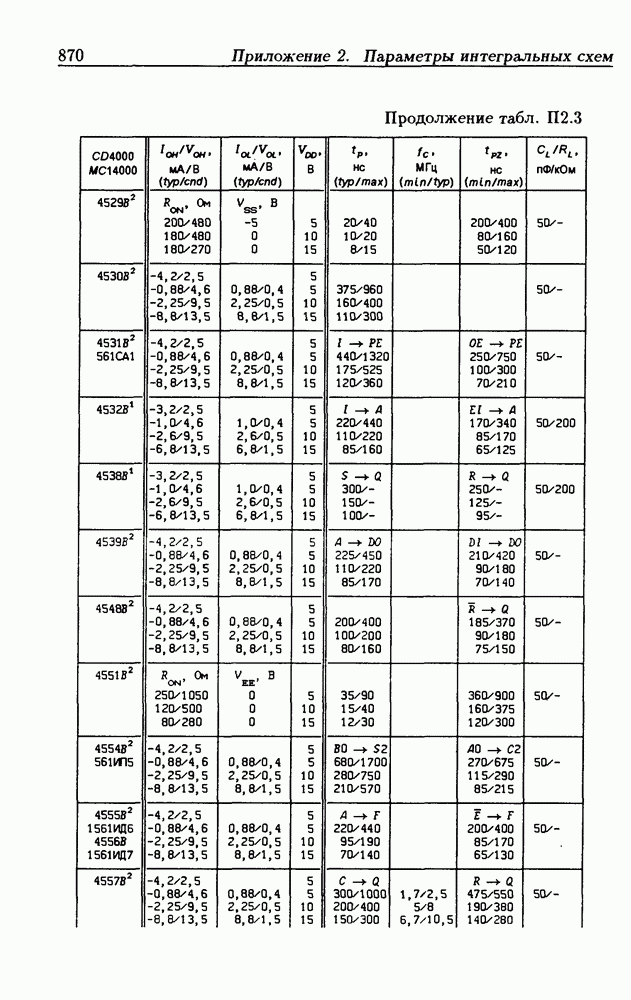
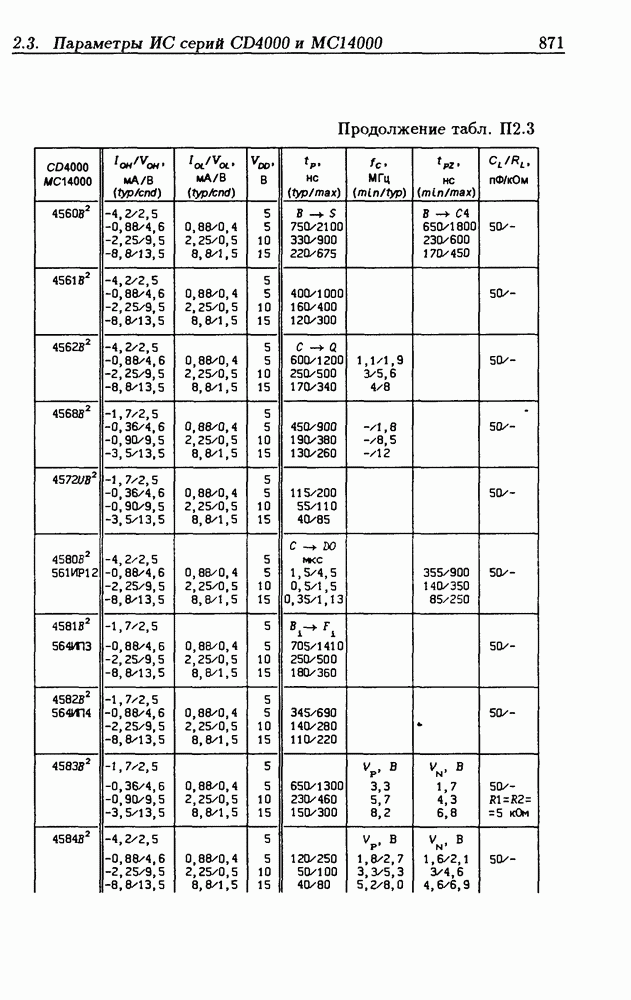
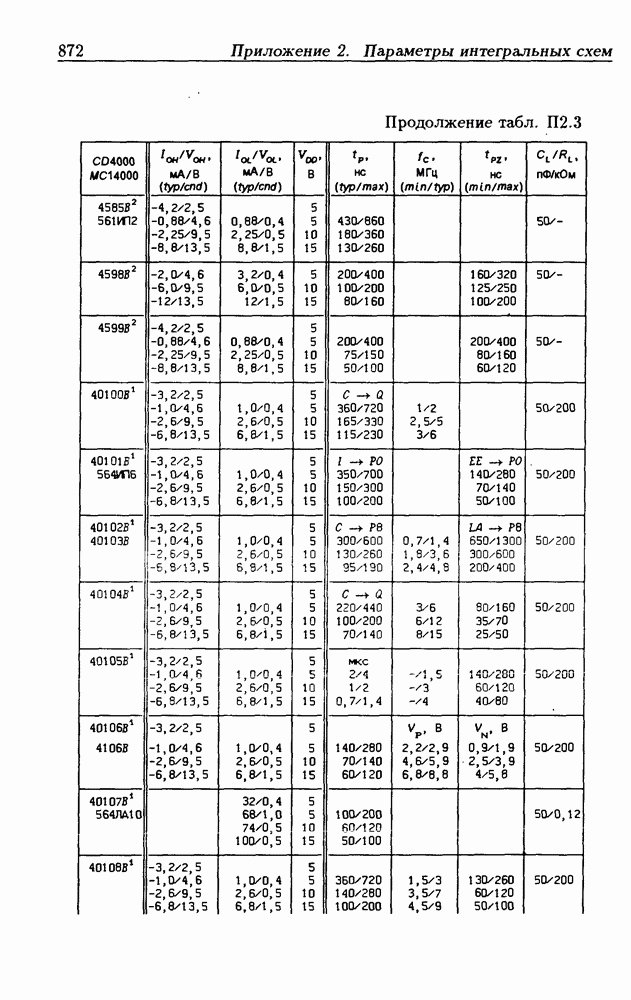
- Приложение 2. Параметры интегральных схем