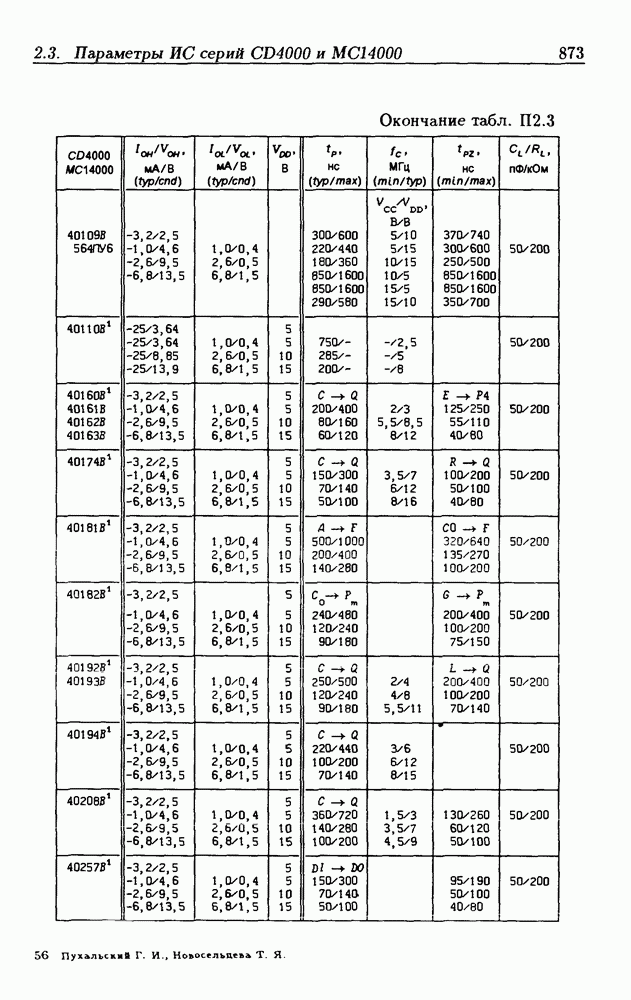
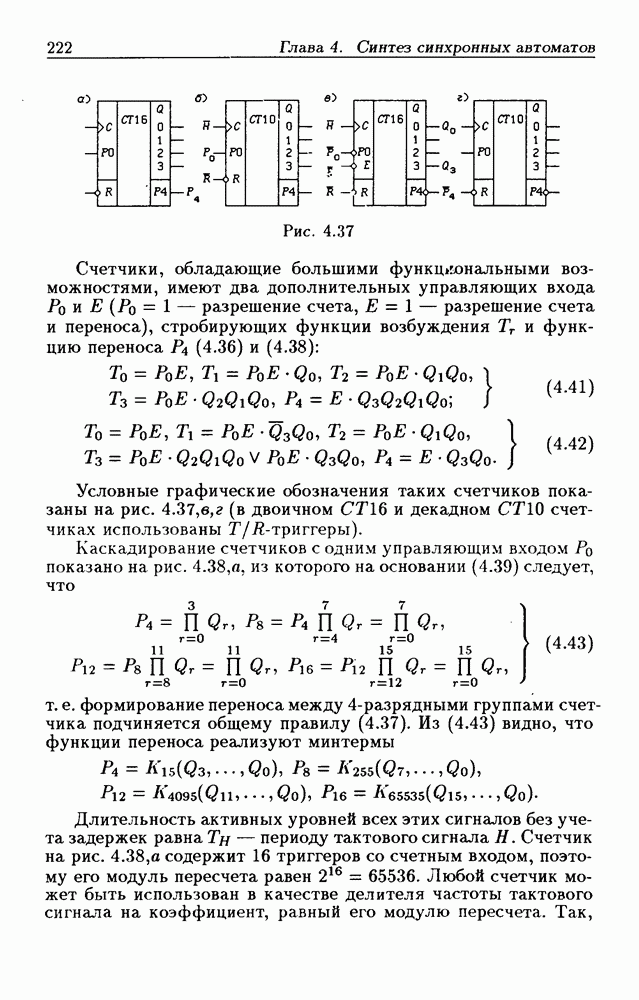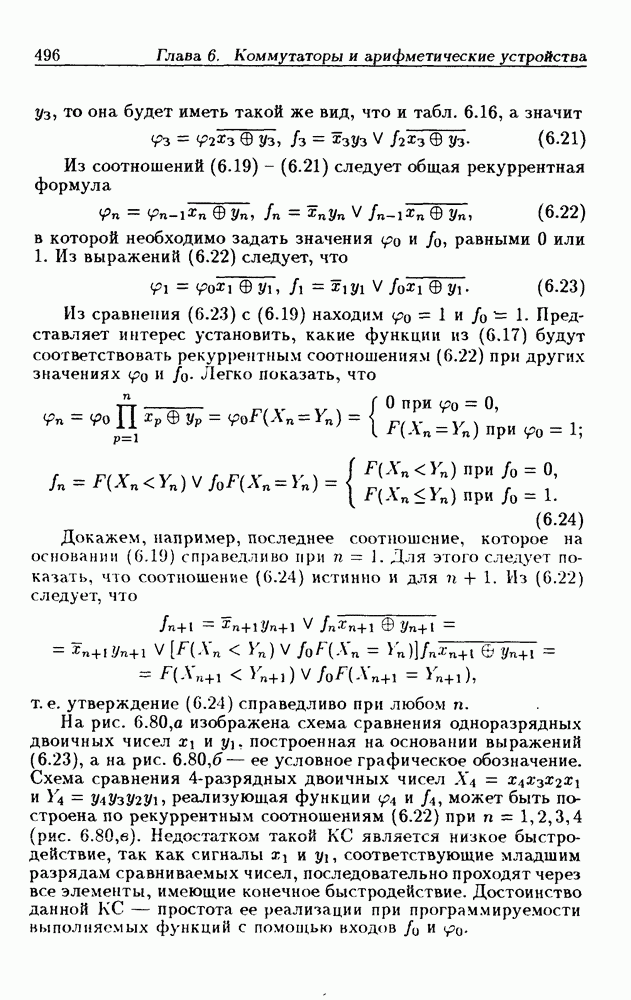| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2.3. Модели логических схем
Логической схемой называется схема, составленная из ЛЭ путем соединения выходов одних ЛЭ со входами других. Будем полагать, что построение ЛС основано на следующих правилах:
выход ЛЭ можно подсоединять ко входам нескольких ЛЭ;
на входы ЛЭ можно подавать сигналы, представляющие собой константы 0 и 1;
выходы ЛЭ нельзя соединять вместе;
выходы ЛЭ нельзя подключать к собственным входам;
ЛС может иметь любое число обратных связей, по которым выходные сигналы некоторых ЛЭ возвращаются на собственные входы, предварительно пройдя через некоторое число ЛЭ.
В дальнейшем ЛЭ и их выходные сигналы будем обозначать символами  где
где  Динамической моделью ЛС называется совокупность функций, описывающих сигналы всех ЛЭ, входящих в состав ЛС [10]. На рис. 2.6 приведена ЛС с обратными связями, в которой использована модель ЛЭ с переменной задержкой (см. рис.
Динамической моделью ЛС называется совокупность функций, описывающих сигналы всех ЛЭ, входящих в состав ЛС [10]. На рис. 2.6 приведена ЛС с обратными связями, в которой использована модель ЛЭ с переменной задержкой (см. рис.  Динамическая модель этой
Динамическая модель этой  описывается функциями
описывается функциями

Эти функции можно представить в более общем виде:

хотя и являются вырожденными функциями (зависят только от двух переменных).
Пусть ЛС состоит из  определенным образом связанных между собою, и имеет
определенным образом связанных между собою, и имеет  физических входов, на которые подаются сигналы
физических входов, на которые подаются сигналы  и к физических выходов, с которых снимаются сигналы
и к физических выходов, с которых снимаются сигналы  (рис. 2.7). Тогда динамическую модель ЛС на основании выражения (2.9) можно описать системой функций
(рис. 2.7). Тогда динамическую модель ЛС на основании выражения (2.9) можно описать системой функций

Данную систему функций можно представить в векторной форме:

где 
Введем некоторые определения. Состоянием входа  называется n-мерный вектор
называется n-мерный вектор

где  или 1 — значение входного сигнала
или 1 — значение входного сигнала  Всего может быть
Всего может быть  различных состояний входа
различных состояний входа 
Внутренним состоянием ЛС называется .ч-мерный вектор

где  или 1 — значение выходного сигнала
или 1 — значение выходного сигнала  Всего может быть
Всего может быть  различных внутренних состояний
различных внутренних состояний  В дальнейшем внутреннее состояние
В дальнейшем внутреннее состояние  часто будем называть просто состоянием
часто будем называть просто состоянием 
Два состояния входа  и (два внутренних состояния и
и (два внутренних состояния и  называются соседними, если они различаются значением только одного входного сигнала
называются соседними, если они различаются значением только одного входного сигнала  (выходного сигнала
(выходного сигнала  Соседним изменением состояний входа называется изменение некоторого состояния входа
Соседним изменением состояний входа называется изменение некоторого состояния входа  на любое соседнее состояние входа
на любое соседнее состояние входа  При соседних изменениях состояний входа изменяется только один входной сигнал ЛС. Изменения внутренних состояний называются переходами. Система функций (2.10), а также функция (2.11), называются функцией переходов ЛС. Функция переходов ЛС и представляет собой ее динамическую модель.
При соседних изменениях состояний входа изменяется только один входной сигнал ЛС. Изменения внутренних состояний называются переходами. Система функций (2.10), а также функция (2.11), называются функцией переходов ЛС. Функция переходов ЛС и представляет собой ее динамическую модель.
Так как выходными сигналами  являются выходные сигналы к ЛЭ, то можно считать, что
являются выходные сигналы к ЛЭ, то можно считать, что  Состоянием выхода ЛС называется
Состоянием выхода ЛС называется  -мерный вектор
-мерный вектор

где  или 1 — значение выходного сигнала
или 1 — значение выходного сигнала  Всего может быть
Всего может быть  различных состояний выхода
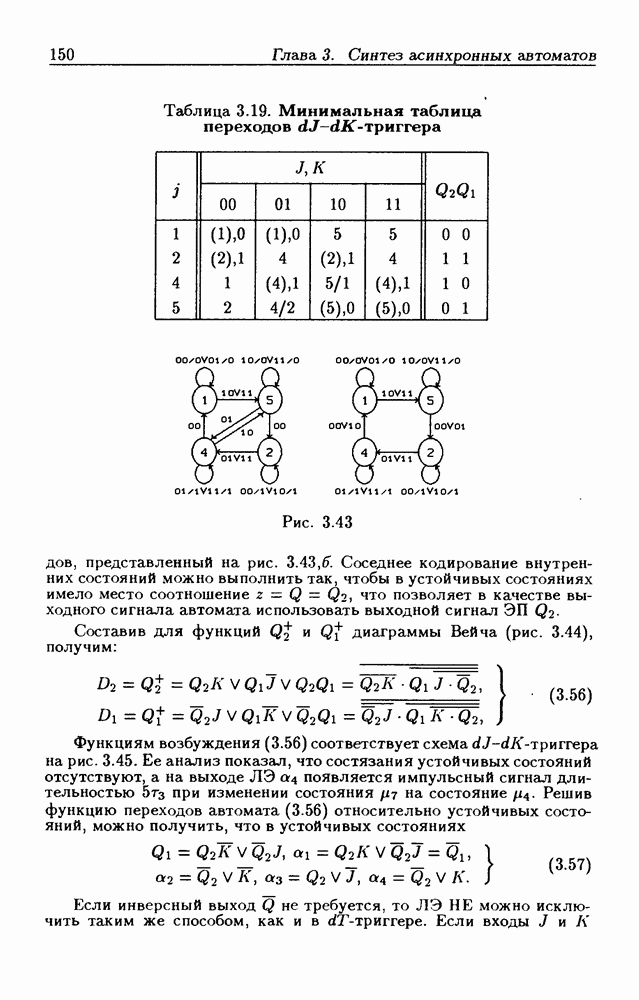
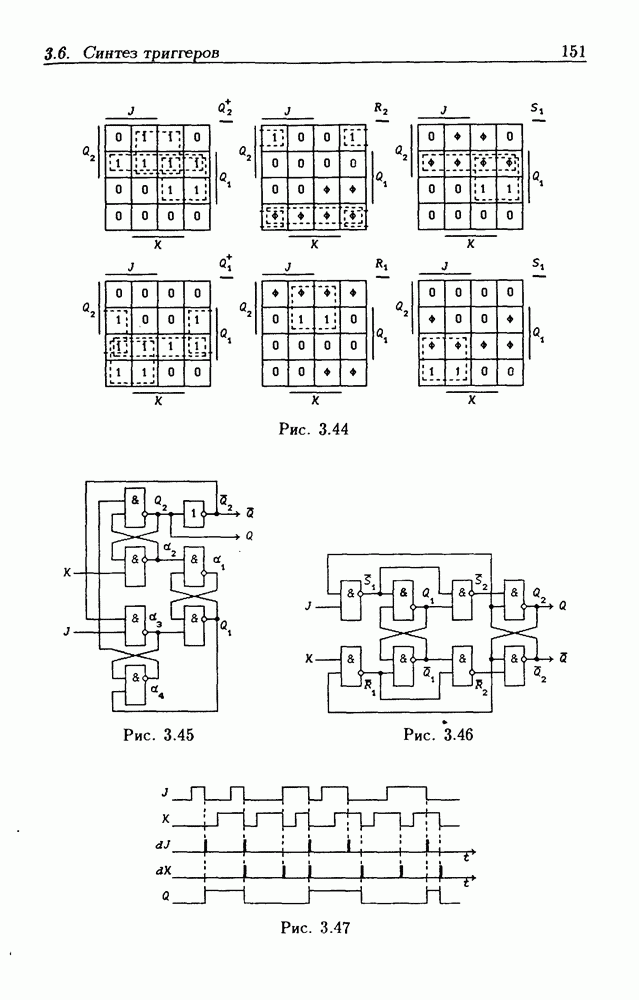
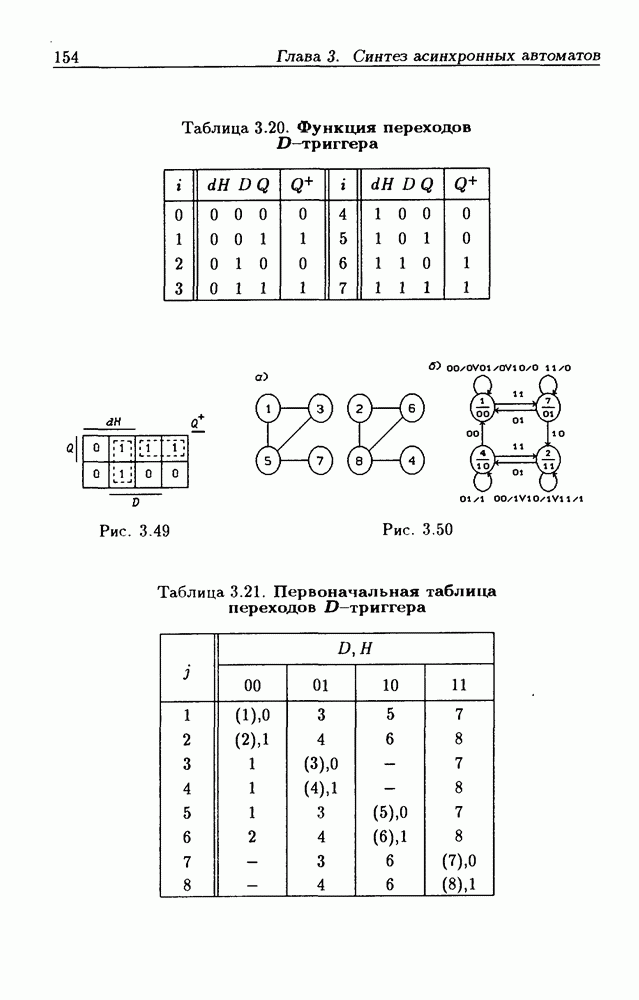
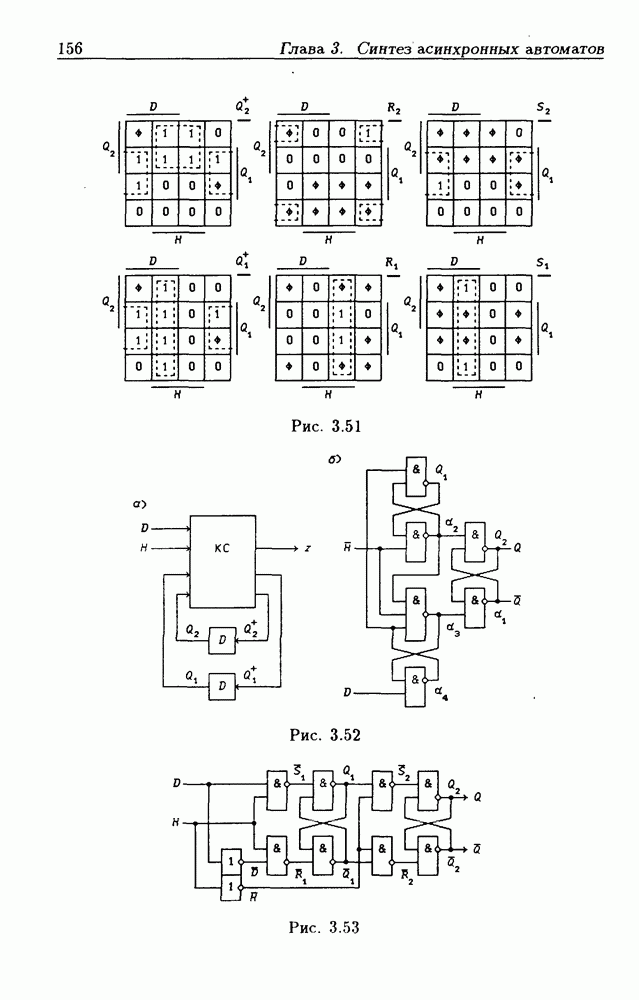
различных состояний выхода 
На основании вышеизложенного для  показанной на рис. 2.6, состояния
показанной на рис. 2.6, состояния  Функция переходов
Функция переходов  позволяет достаточно просто формальными методами проанализировать ее поведение при переходных процессах.
позволяет достаточно просто формальными методами проанализировать ее поведение при переходных процессах.
Логическая схема находится в устойчивом состоянии, если все ЛЭ, входящие в ее состав, находятся в устойчивом состоянии. Значит, в устойчивых состояниях должны выполняться равенства  для всех
для всех  т. е.
т. е.  Подставив эти значения сигналов
Подставив эти значения сигналов  в функцию переходов (2.10), получим систему логических уравнений
в функцию переходов (2.10), получим систему логических уравнений

 неизвестными
неизвестными  Данная система представляет собой статическую модель ЛС. Если решения системы логических уравнений (2.12) относительно неизвестных
Данная система представляет собой статическую модель ЛС. Если решения системы логических уравнений (2.12) относительно неизвестных  не существует, то это означает, что ЛС при некоторых или всех состояниях входа не имеет устойчивых состояний.
не существует, то это означает, что ЛС при некоторых или всех состояниях входа не имеет устойчивых состояний.
Логическая схема находится в неустойчивом состоянии, если хотя бы один ЛЭ находится в неустойчивом состоянии, т.е., если  Если ЛС находится в неустойчивом состоянии
Если ЛС находится в неустойчивом состоянии  то оно изменится на некоторое состояние
то оно изменится на некоторое состояние  через время, определяемое паразитными задержками тех
через время, определяемое паразитными задержками тех  которые находятся в неустойчивом состоянии. Поэтому отсутствие у ЛС при некоторых состояниях входа
которые находятся в неустойчивом состоянии. Поэтому отсутствие у ЛС при некоторых состояниях входа  устойчивых состояний означает наличие в ней автоколебательных процессов при данных состояниях входа (так как число ЛЭ, входящих в состав ЛС, конечно, то выходные сигналы некоторых из них должны самопроизвольно изменяться с некоторым периодом).
устойчивых состояний означает наличие в ней автоколебательных процессов при данных состояниях входа (так как число ЛЭ, входящих в состав ЛС, конечно, то выходные сигналы некоторых из них должны самопроизвольно изменяться с некоторым периодом).
Если ЛС является комбинационной схемой, то в устойчивых состояниях должно выполняться равенство

Действительно, из определения  следует, что ее выходные сигналы не зависят от внутреннего состояния
следует, что ее выходные сигналы не зависят от внутреннего состояния  поэтому к функций из
поэтому к функций из  не должны в устойчивых состояниях зависеть от состояния
не должны в устойчивых состояниях зависеть от состояния 
Равенства (2.13) всегда выполняются для ЛС без обратных связей. Для ЛС с обратными связями эти равенства также могут выполняться, т.е. отсутствие обратных связей не является необходимым
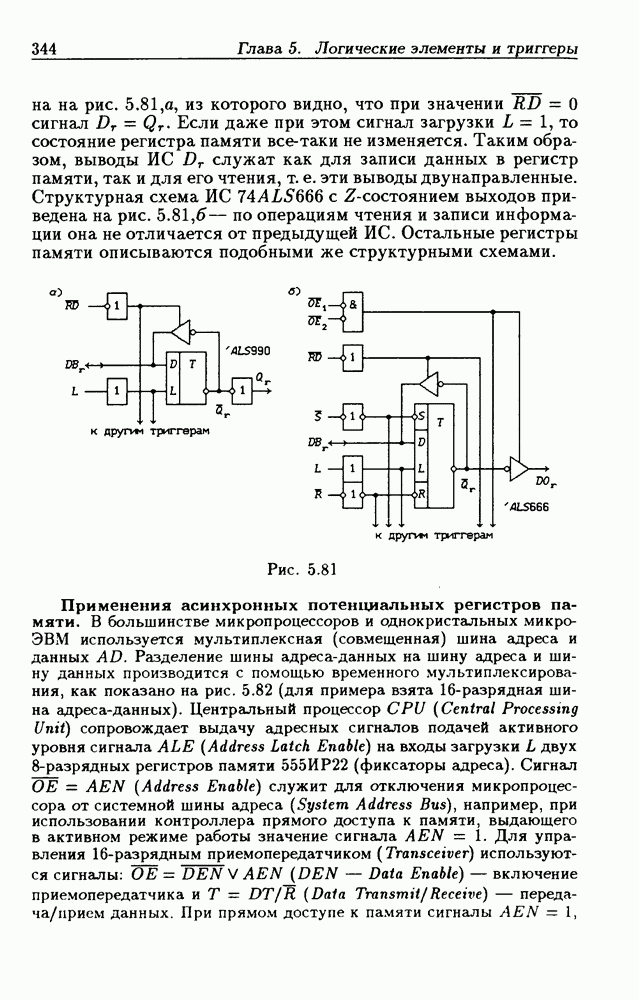
требованием для определения КС. Показанная на рис. 2.6 ЛС с обратными связями представляет собой комбинационную схему. Докажем это. Функция переходов (2.8) для устойчивых состояний  дает систему логических уравнений (статическую модель)
дает систему логических уравнений (статическую модель)

с тремя неизвестными  Подстановка
Подстановка  из первого уравнения во второе дает
из первого уравнения во второе дает  Подставив этот результат в третье уравнение, получим значение
Подставив этот результат в третье уравнение, получим значение  и поэтому
и поэтому  Итак, ЛС на рис. 2.6 реализует константу 1, т.е. ее выходной сигнал не зависит от внутреннего состояния, а значит ЛС является комбинационной схемой. Статическая модель (2.14) не позволяет получить большей информации о функционировании ЛС.
Итак, ЛС на рис. 2.6 реализует константу 1, т.е. ее выходной сигнал не зависит от внутреннего состояния, а значит ЛС является комбинационной схемой. Статическая модель (2.14) не позволяет получить большей информации о функционировании ЛС.
Систему логических уравнений (2.14) можно решить и формальным методом, изложенным в § 1.6. Решение систем уравнений типа (2.14) будем называть решением функции переходов относительно устойчивых состояний. Если при решении будут делаться ссылки на функцию переходов типа (2.8), то предполагается, что знаки  в ней опущены.
в ней опущены.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Глава 1. Основы теории переключательных функций
- 1.2. Позиционные системы счисления
- 1.3. Переключательные функции
- 1.4. Принцип и закон двойственности
- 1.5. Теоремы разложения
- 1.6. Решение систем логических уравнений
- 1.7. Первичные термы, минтермы и макстермы
- 1.8. Совершенные нормальные формы представления функций
- 1.9. Конъюнктивные и дизъюнктивные термы
- 1.10. Минимизация переключательных функций
- 1.11. Диаграммы Вейча
- 1.12. Минимизация неполностью определенных функций, совместная минимизация нескольких функций
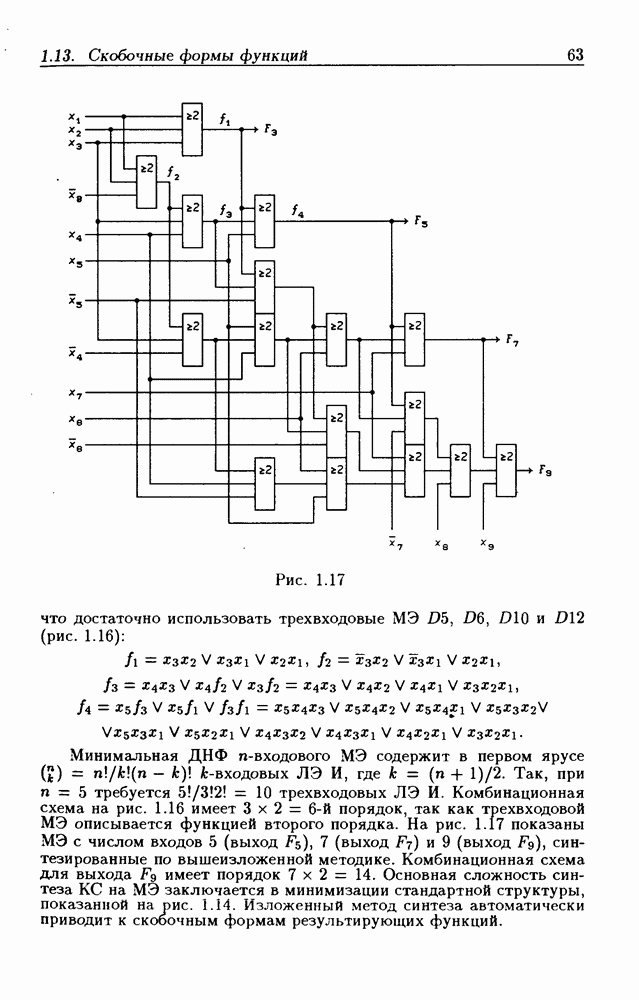
- 1.13. Скобочные формы функций
- 1.14. Закон двойственности для логических схем
- 1.15. Линейные функции
- Глава 2. Анализ и синтез логических схем
- 2.2. Модели логических элементов
- 2.3. Модели логических схем
- 2.4. Анализ логических схем
- 2.5. Синтез комбинационных схем, свободных от состязаний
- Глава 3. Синтез асинхронных потенциальных автоматов
- 3.2. Асинхронные потенциальные автоматы
- 3.3. Асинхронные потенциальные триггеры и элементы памяти
- Триггеры типа R-S
- Триггеры типа D-L
- Триггеры типа D-L-R с приоритетом входа R.
- Триггеры типа D-L-R с приоритетом входа L.
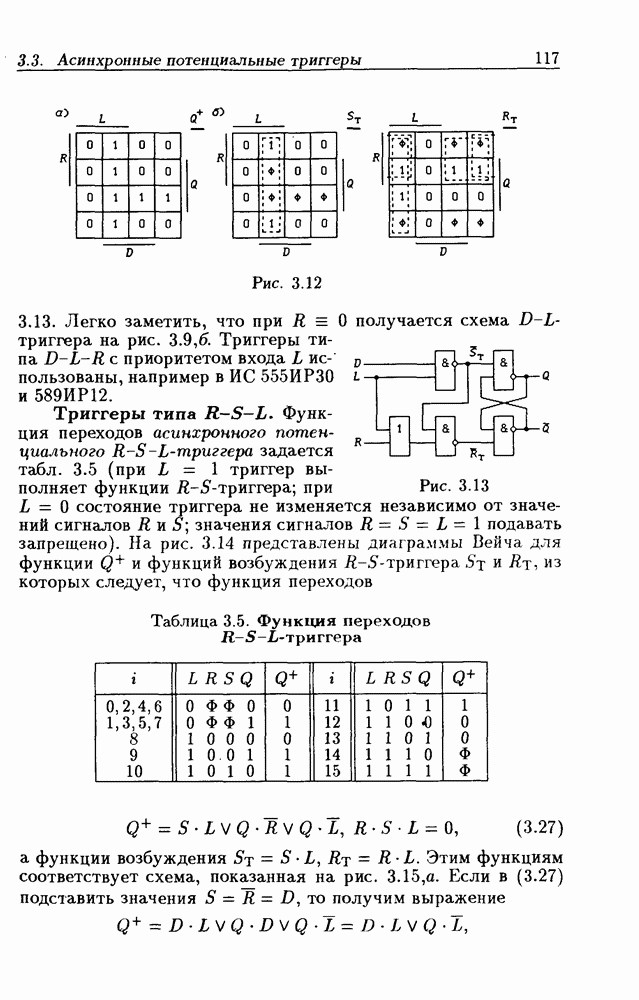
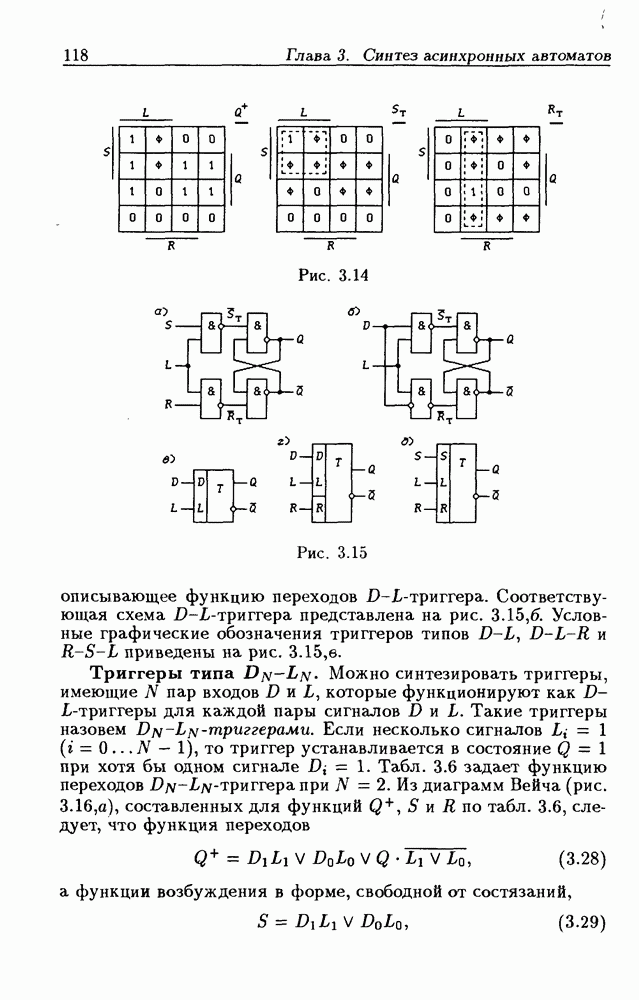
- Триггеры типа R-S-L.
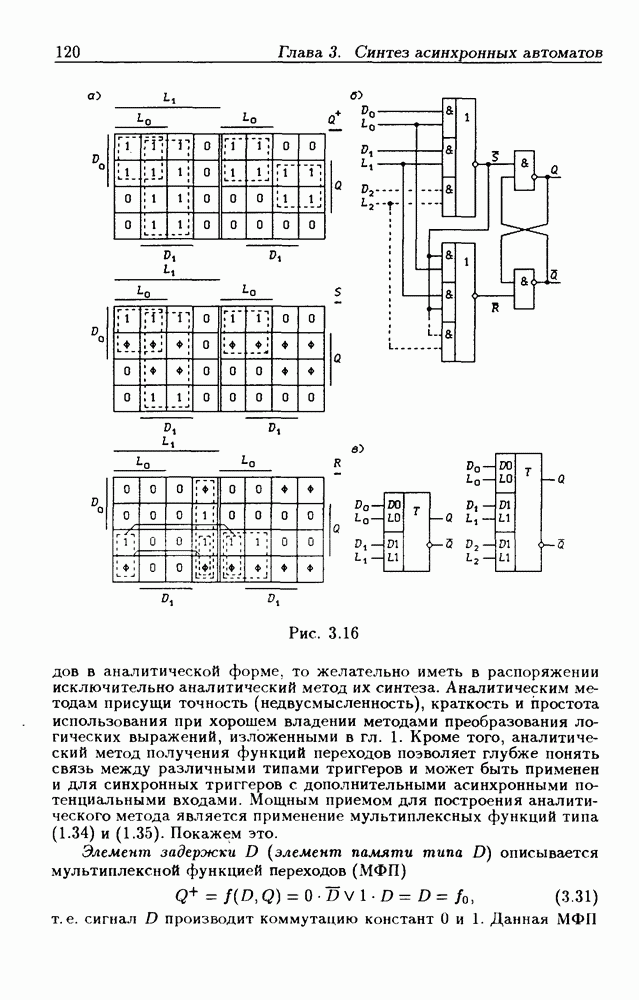
- Триггеры типа DN-LN
- Аналитический метод синтеза и анализа триггеров.
- 3.4. Задание асинхронных потенциальных автоматов таблицами и графами переходов
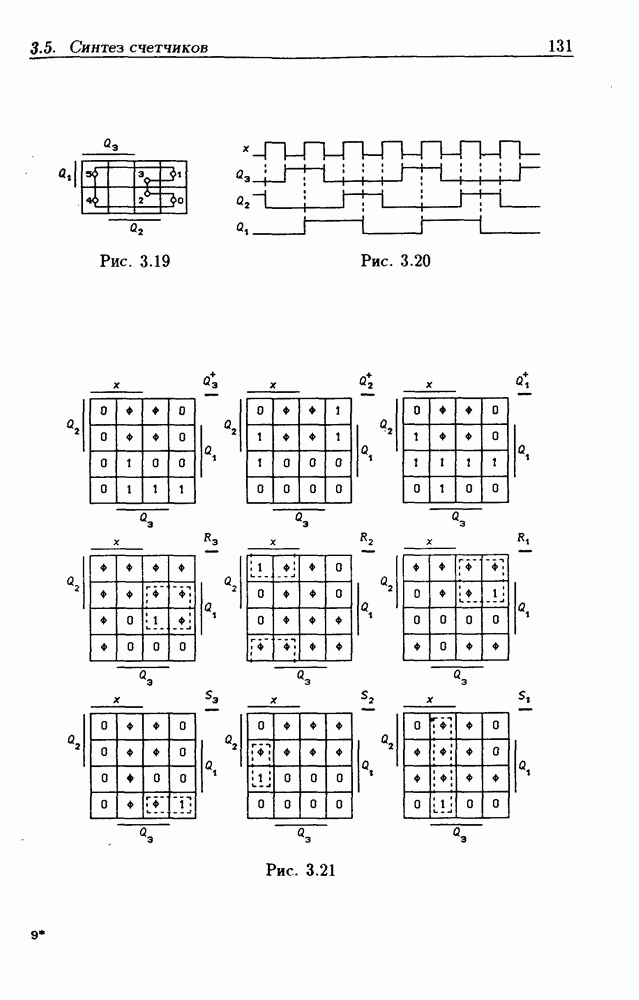
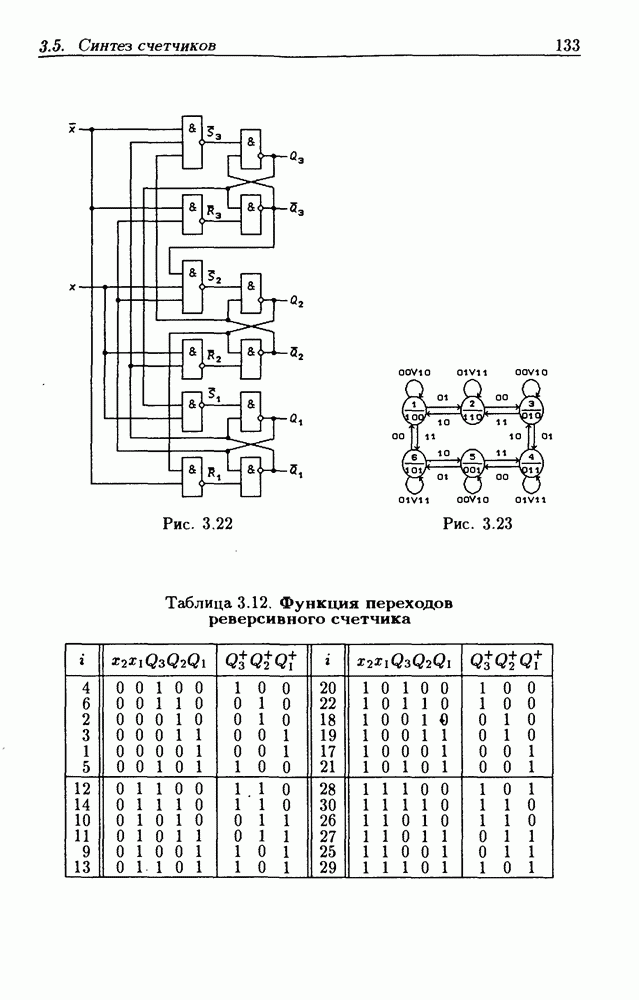
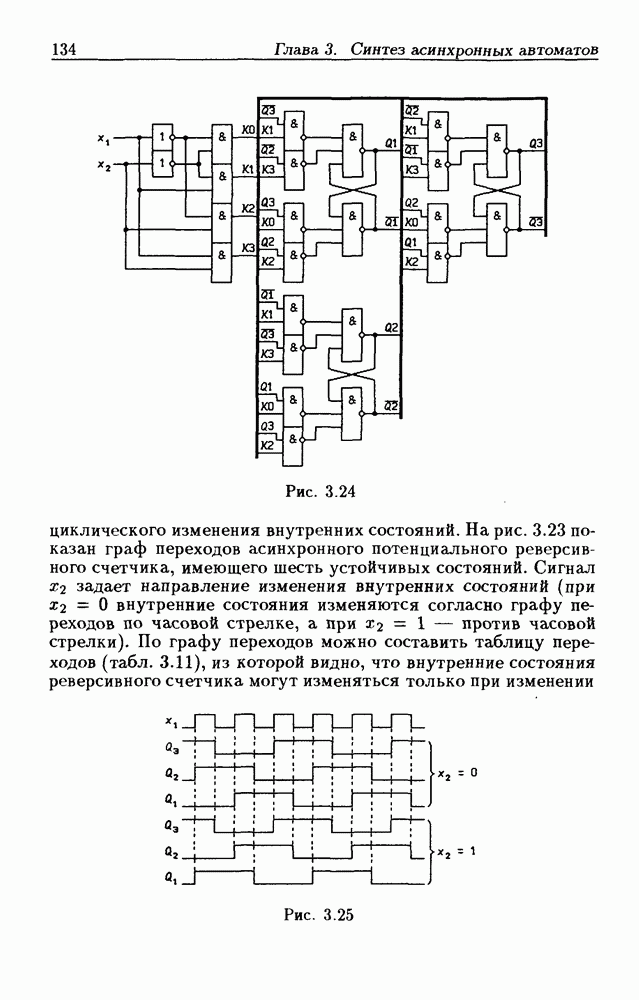
- 3.5. Синтез асинхронных потенциальных счетчиков
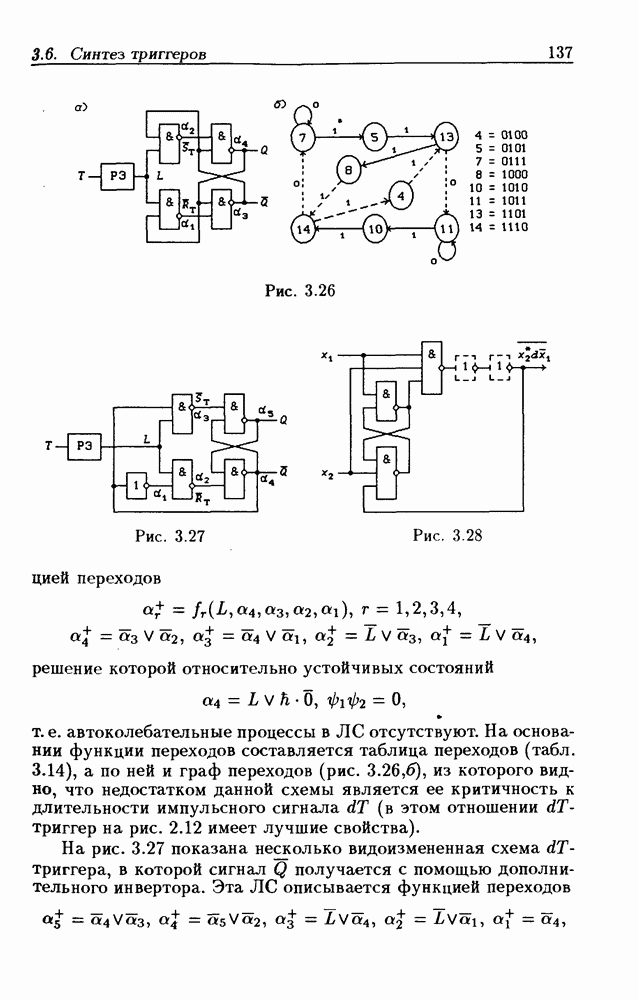
- 3.6. Синтез асинхронных импульсных триггеров
- Триггеры типа dJ-dK.
- Классификация триггеров.
- 3.7. Синтез синхронных триггеров
- Триггеры типа J-K
- Синхронно-асинхронные триггеры.
- 3.8. Примеры синтеза асинхронных потенциальных автоматов
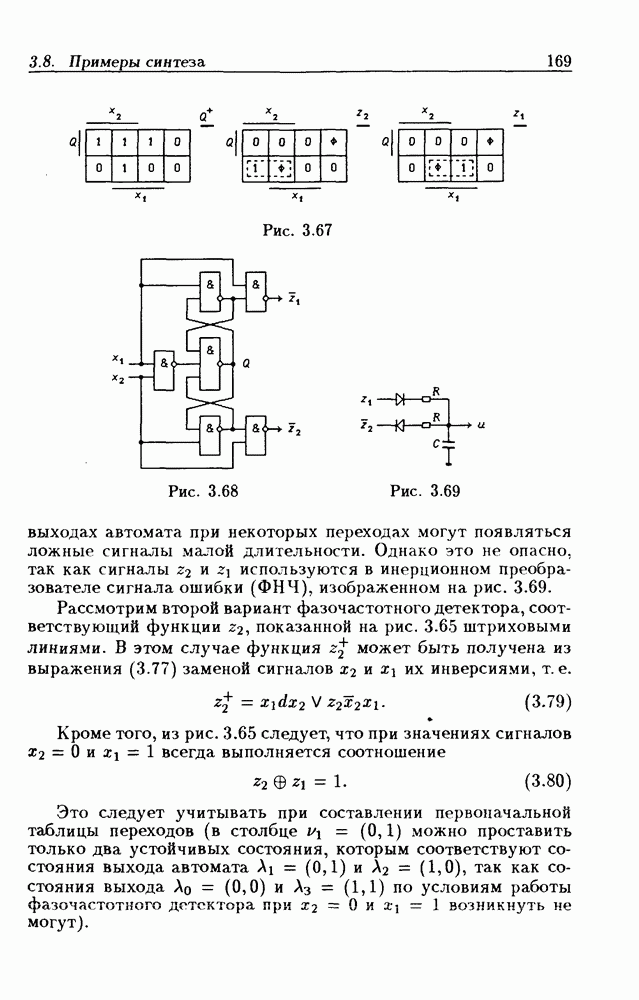
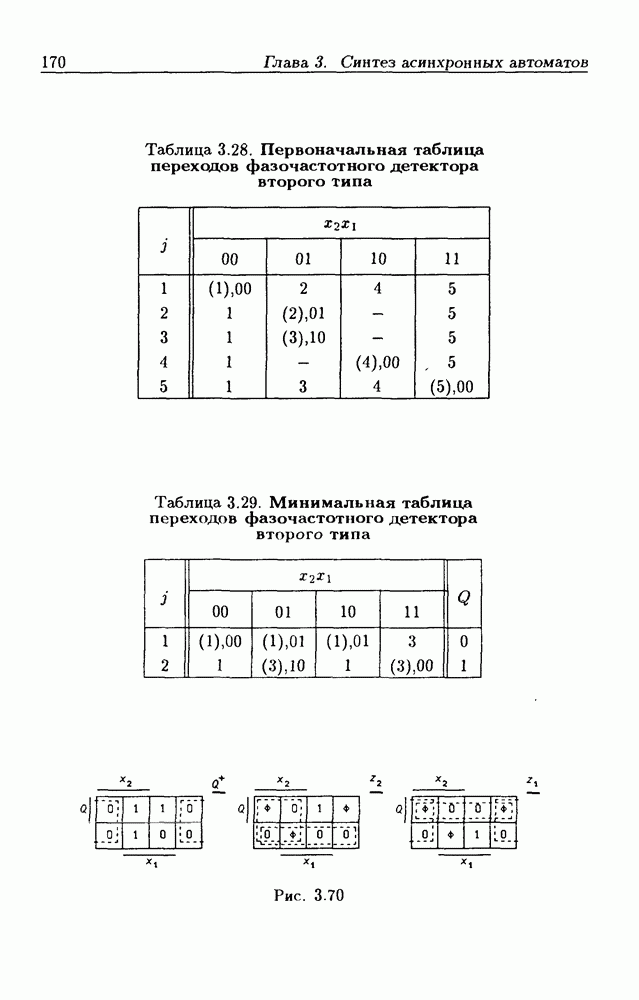
- Цифровые фазочастотные детекторы.
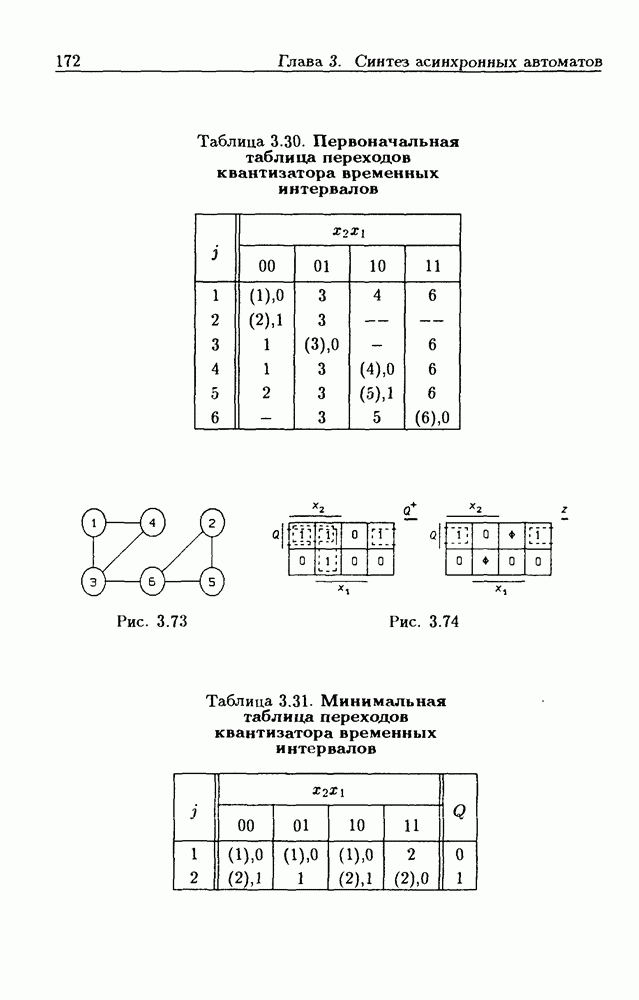
- Квантизатор временных интервалов.
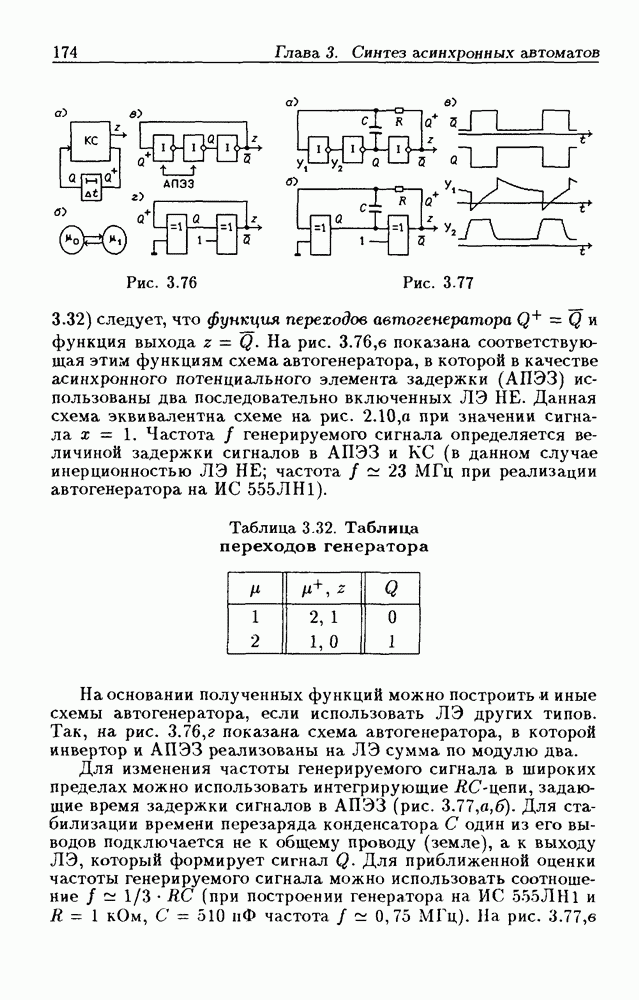
- 3.9. Генераторы сигналов
- Автогенераторы.
- Управляемые автогенераторы.
- Глава 4. Синтез синхронных автоматов
- 4.2. Синхронные триггеры
- Триггеры типов D и R-S с импульсным тактовым сигналом.
- Синхронные триггеры типов R-S и D-L
- Синхронно-асинхронные триггеры.
- Синхронные триггеры типа J-K
- Триггеры типа Т.
- Классификация синхронных триггеров.
- Преобразования типов синхронных триггеров.
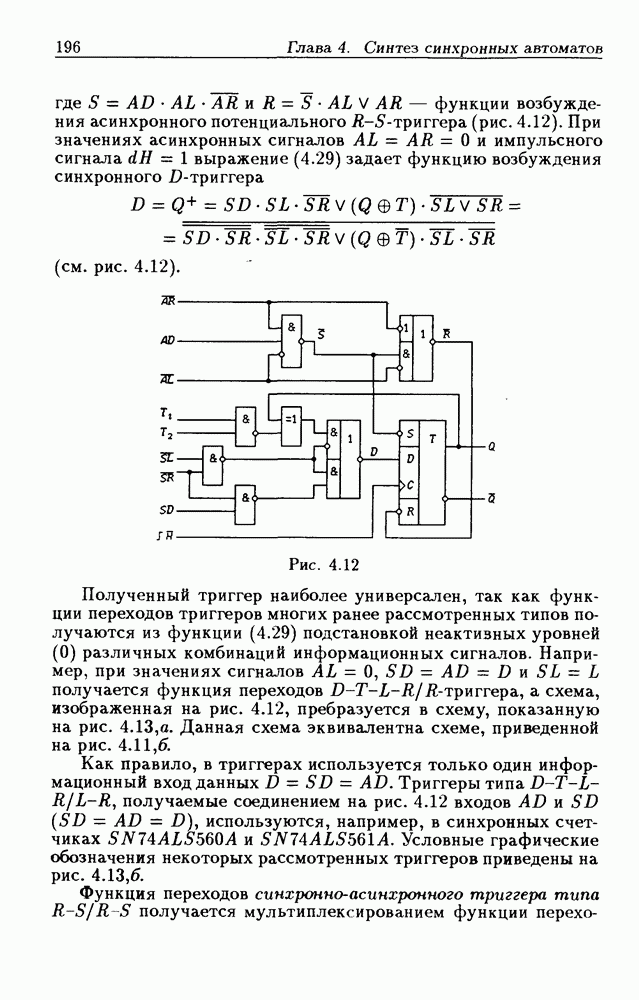
- Триггеры типов D-T-L и D-T-L/R
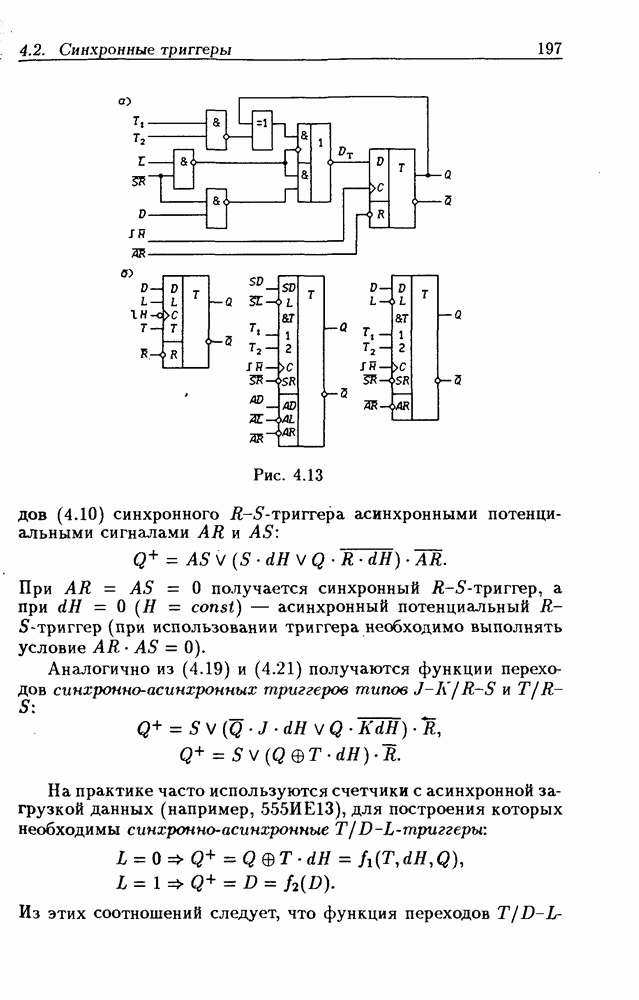
- Функции переходов синхронно-асинхронных триггеров.
- 4.3. Примеры синтеза синхронных автоматов
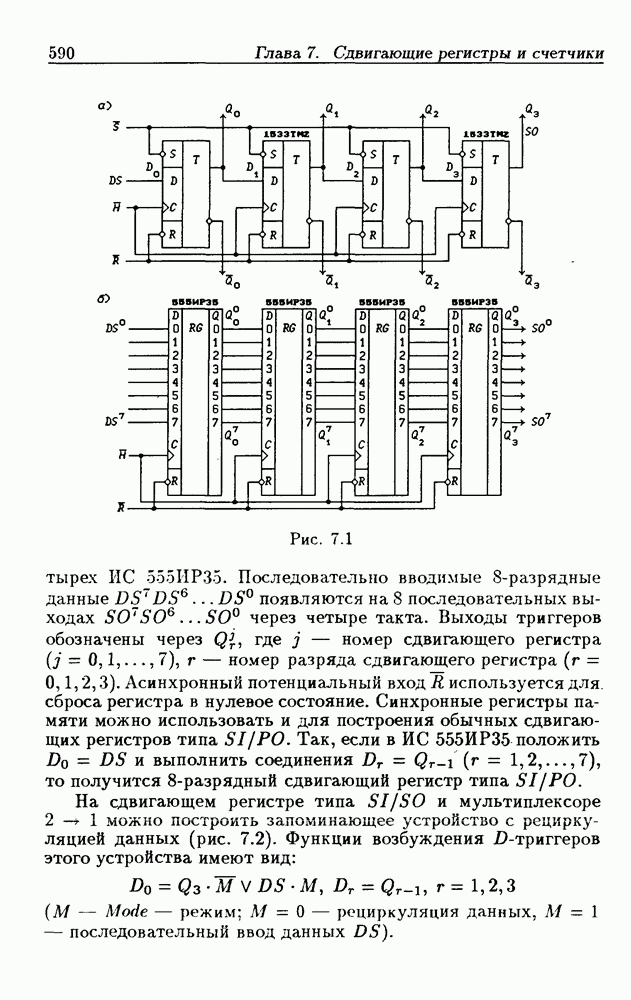
- 4.4. Сдвигающие регистры
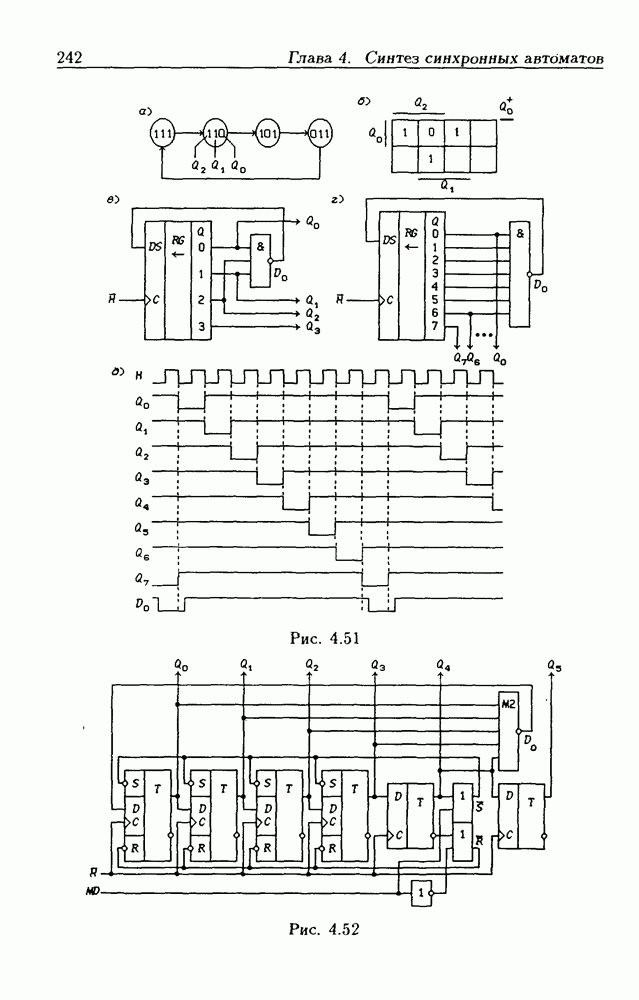
- Синтез счетчиков на сдвигающих регистрах.
- Сдвигающие регистры с загрузкой данных.
- Реверсивные сдвигающие регистры.
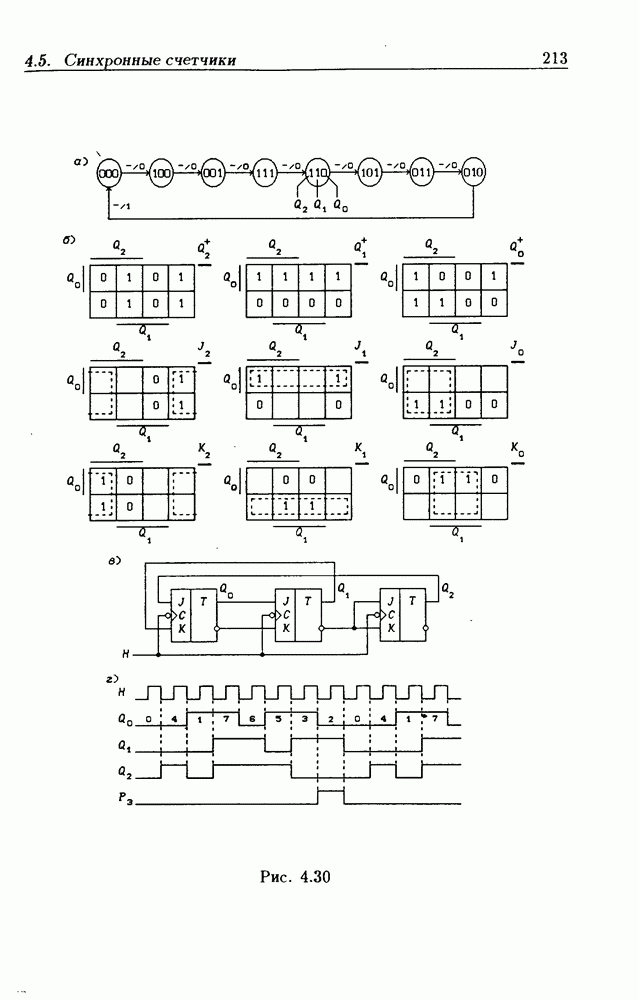
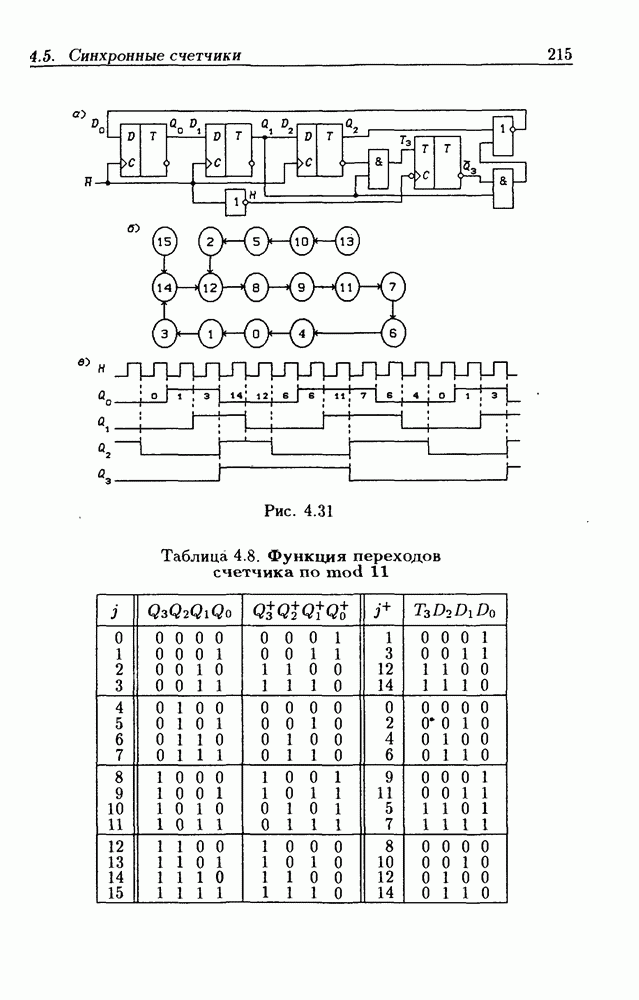
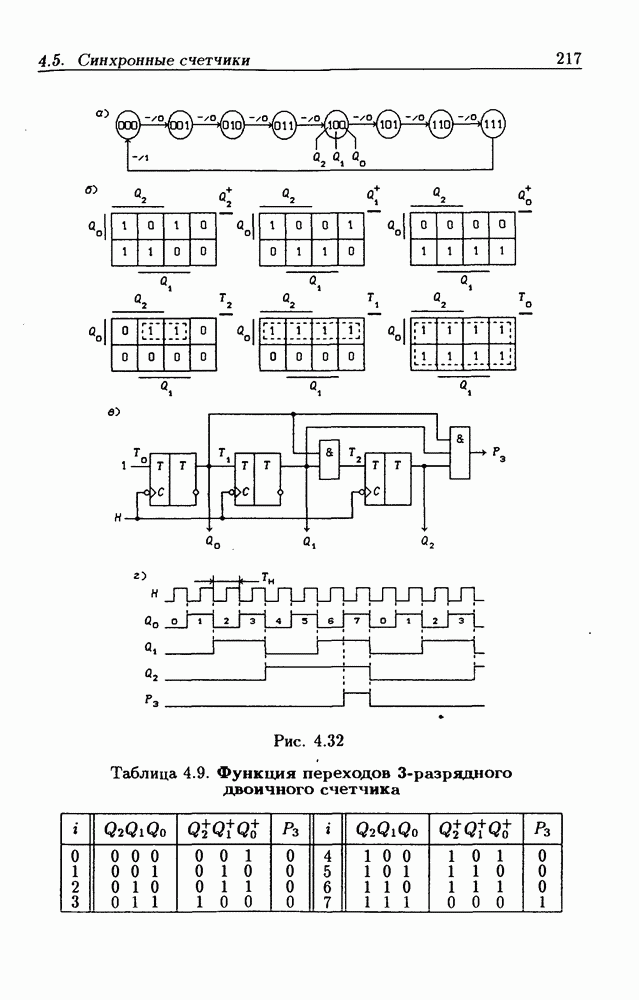
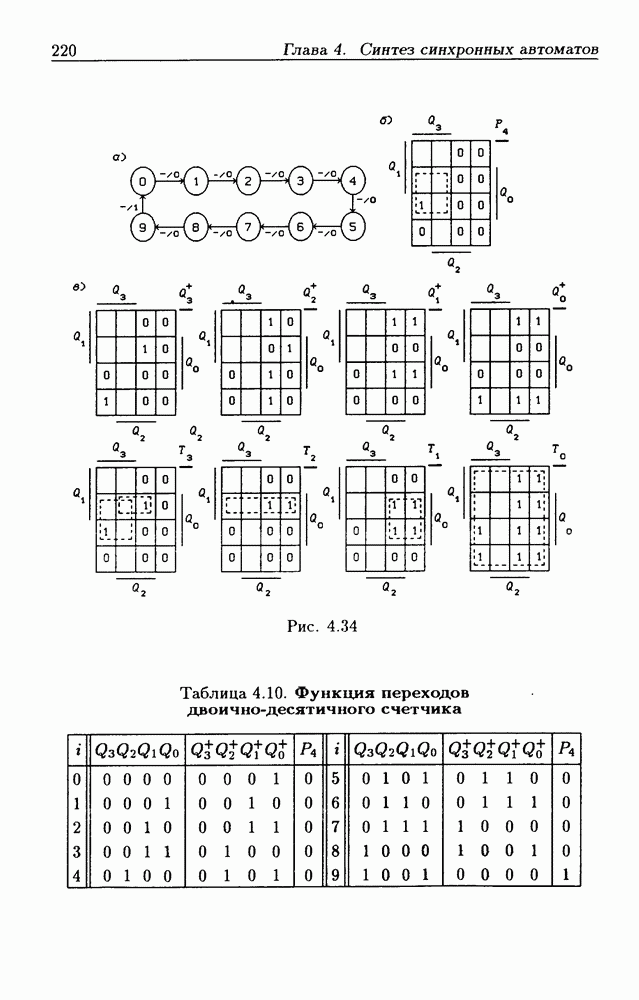
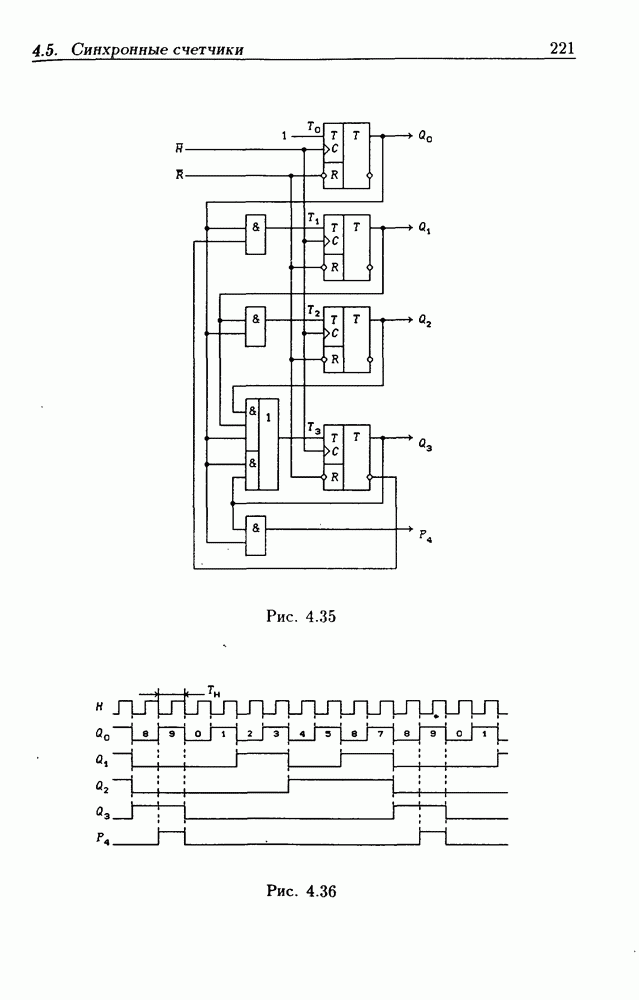
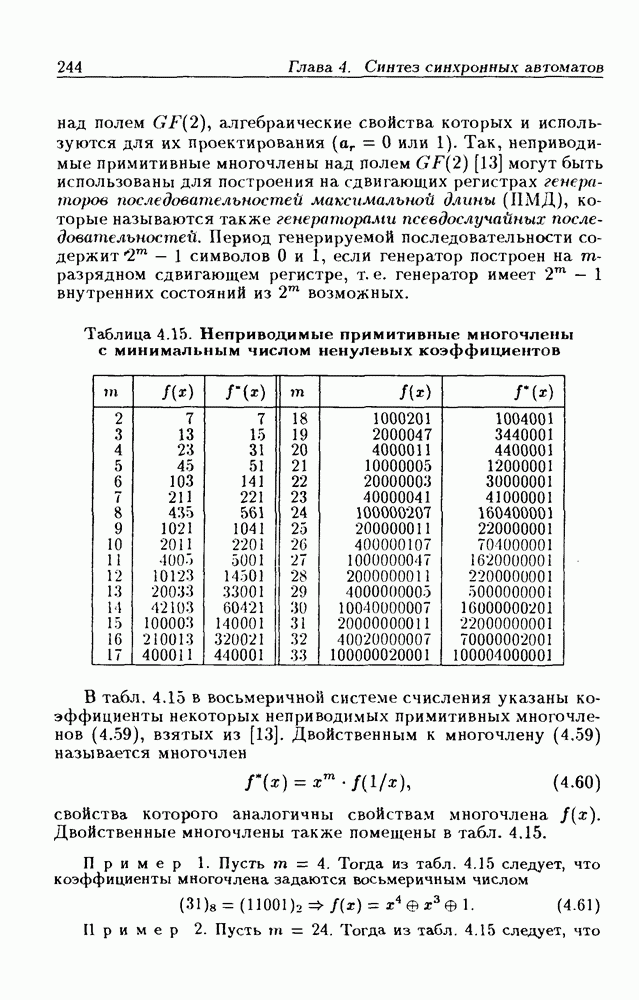
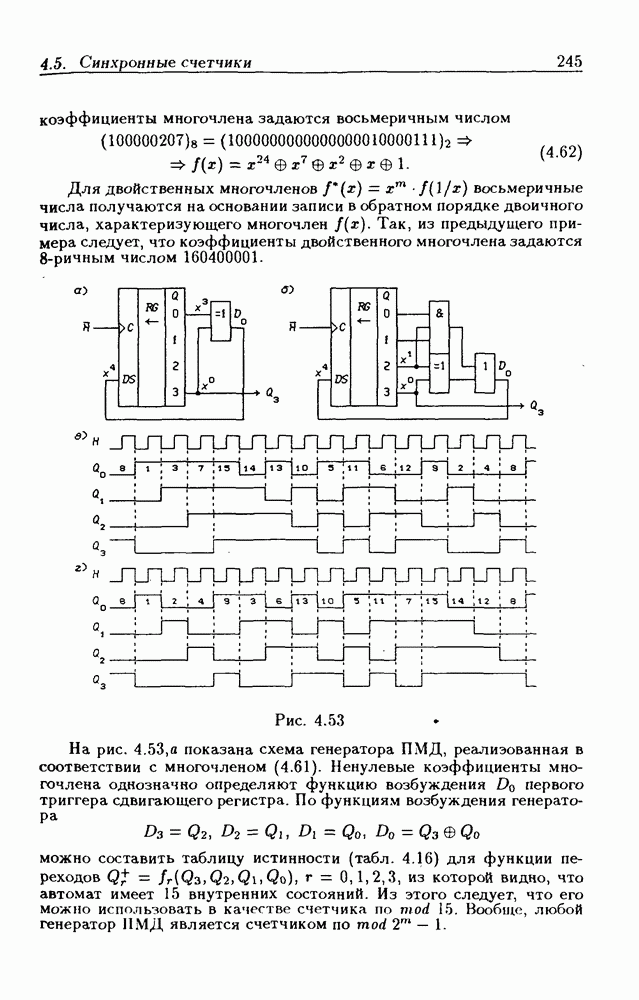
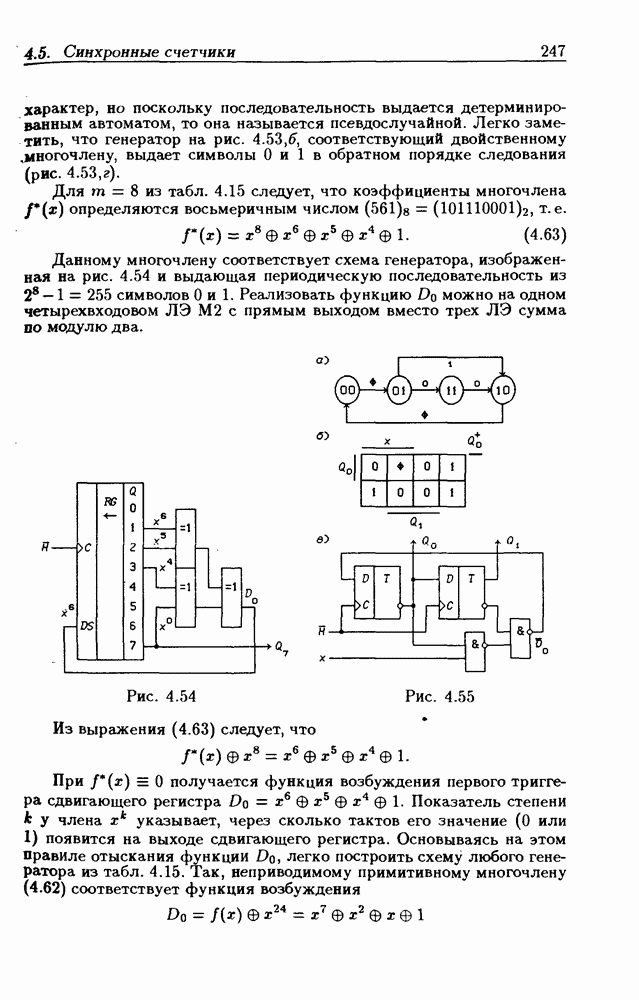
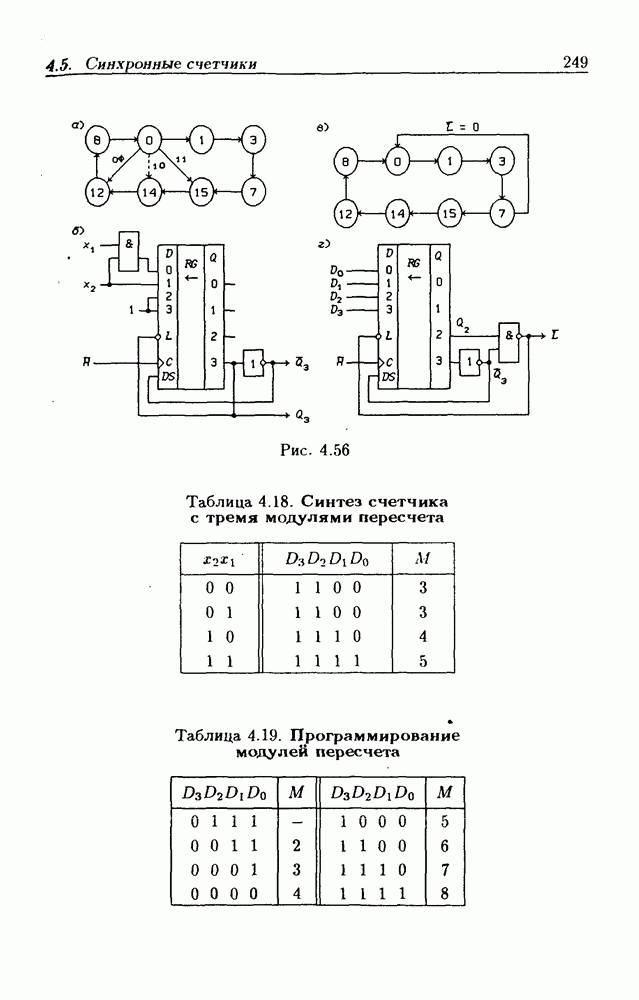
- 4.5. Синхронные счетчики
- Синхронные двоичные счетчики.
- Синхронные двоично-десятичные счетчики.
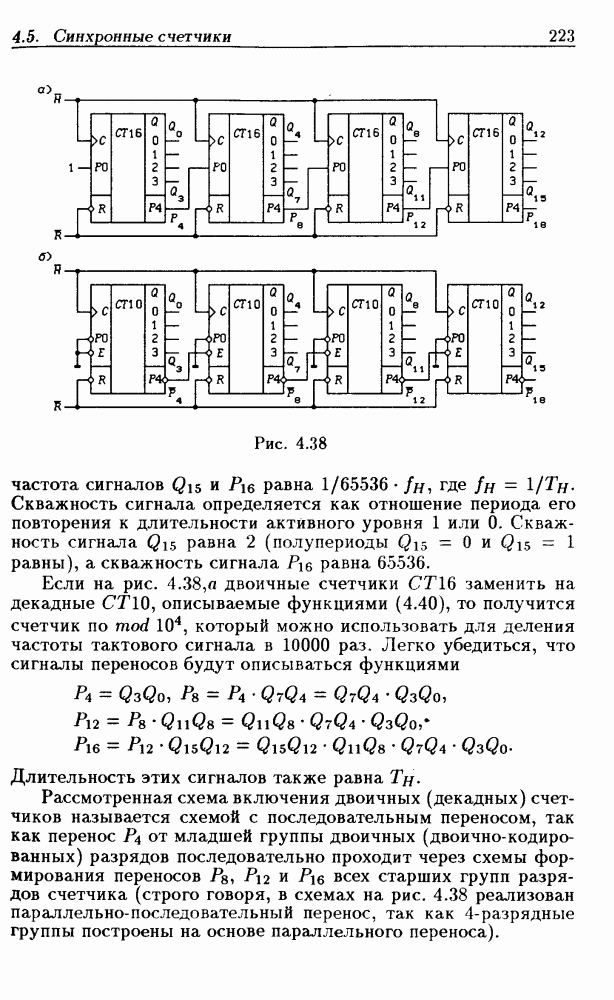
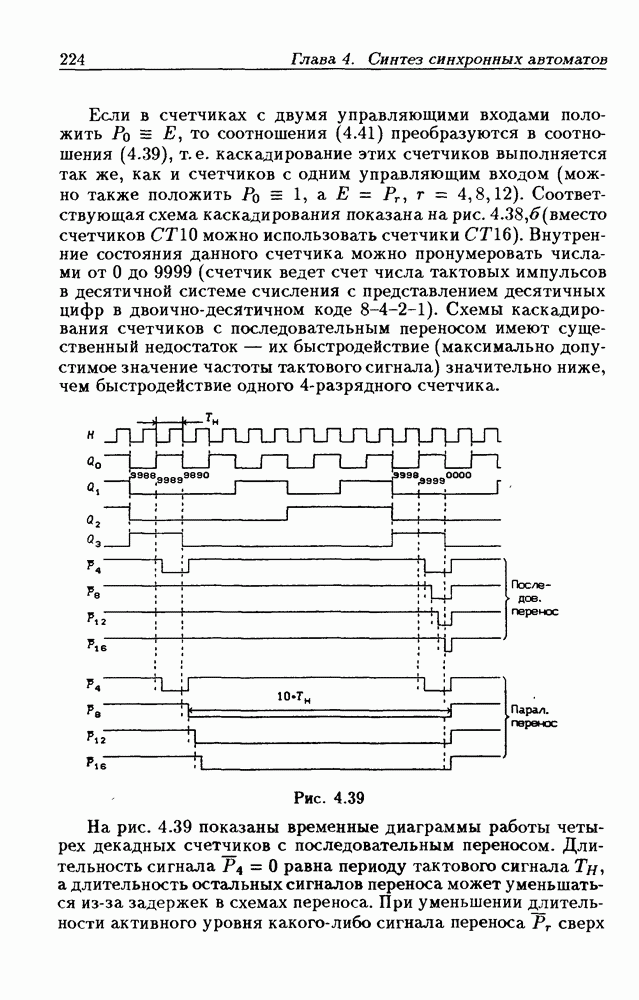
- Каскадирование двоичных и двоично-десятичных счетчиков.
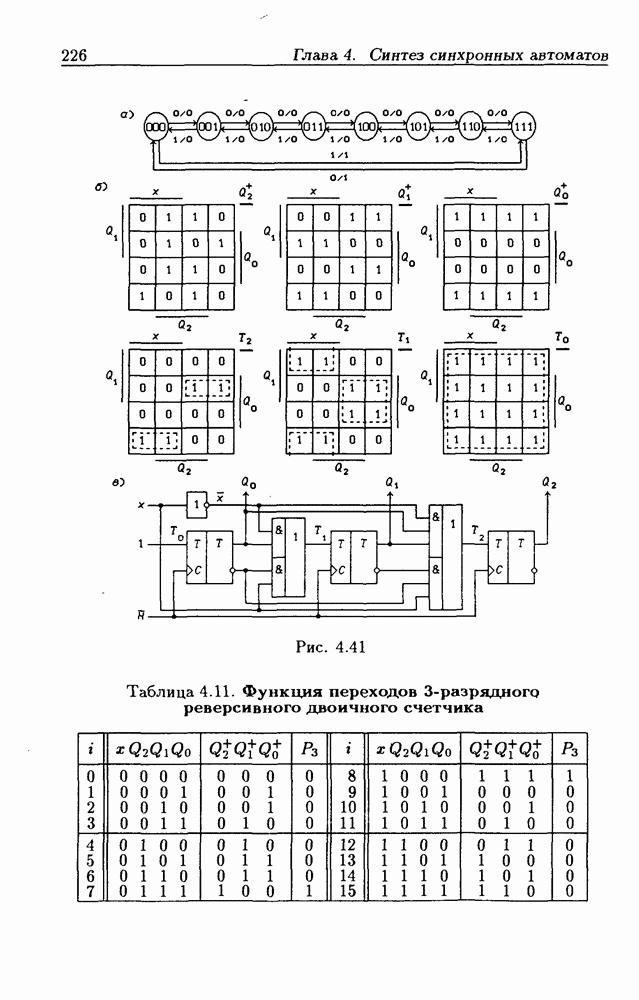
- Синхронные двоичные реверсивные счетчики.
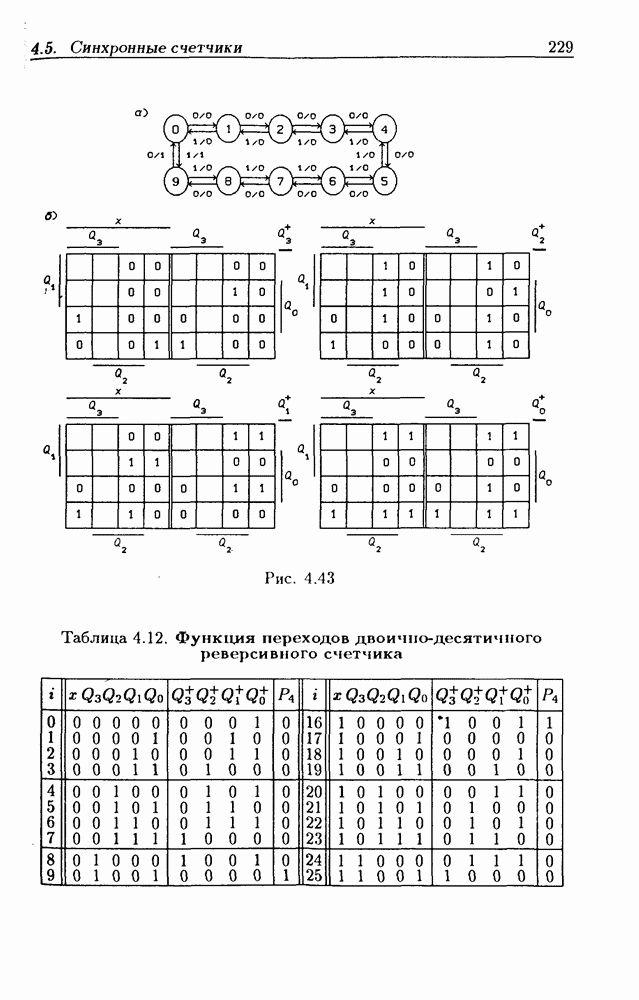
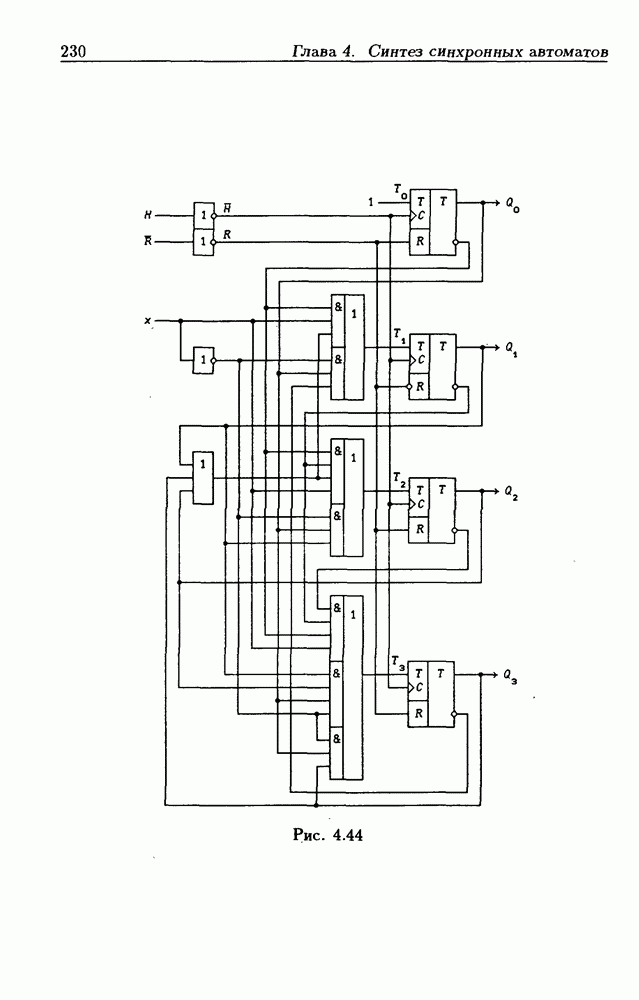
- Реверсивные двоично-десятичные счетчики.
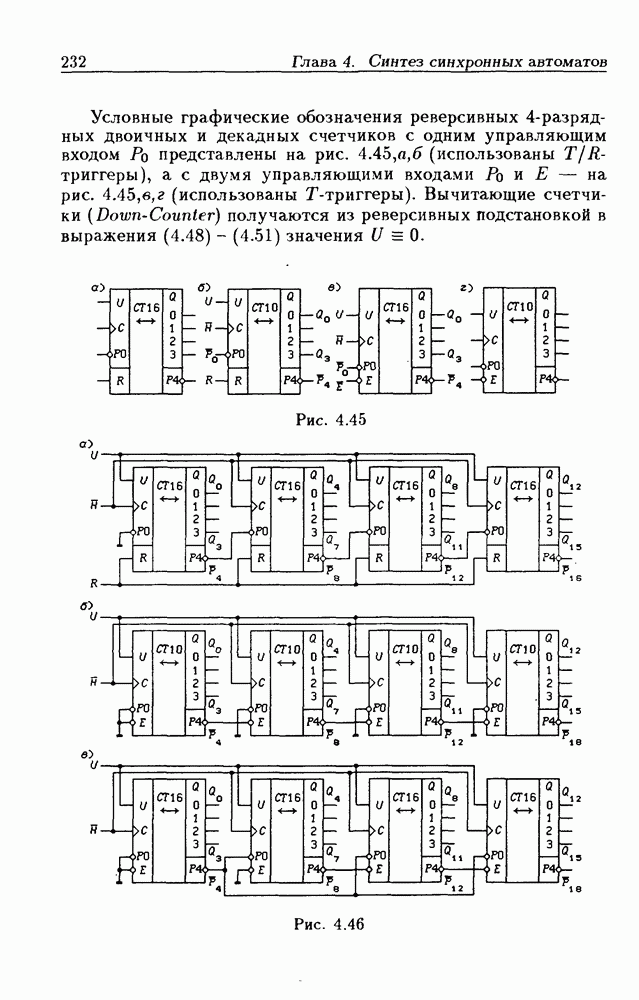
- Каскадирование реверсивных счетчиков.
- Счетчики на сдвигающих регистрах.
- Кольцевые счетчики.
- Линейные счетчики.
- Программируемые счетчики.
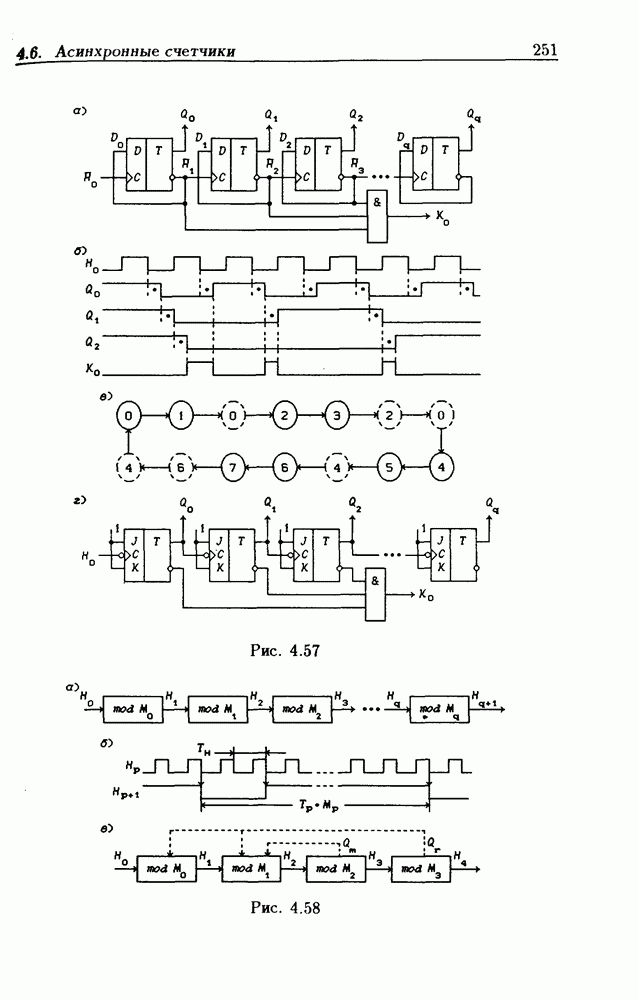
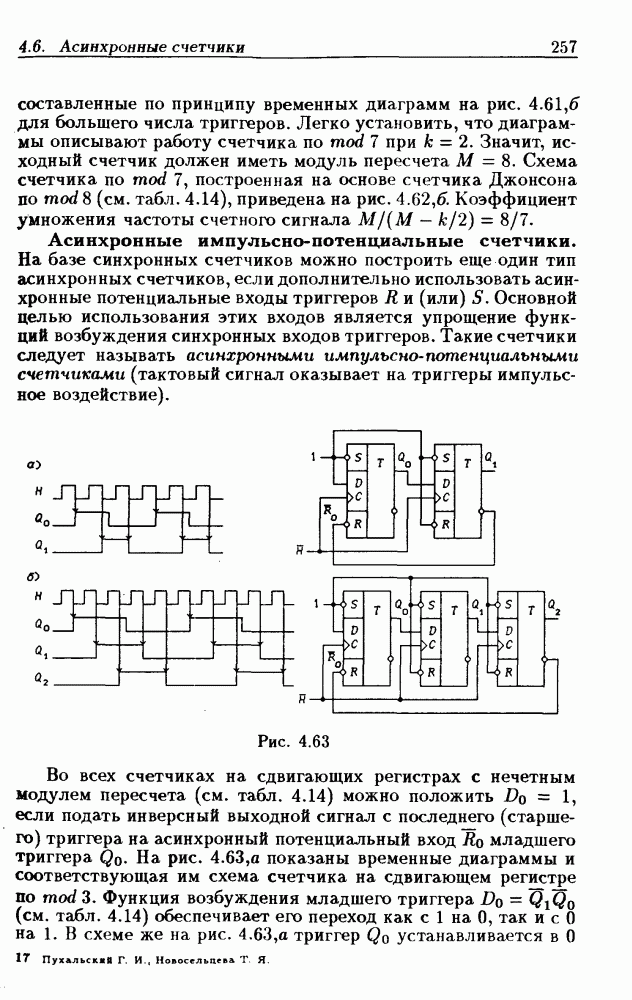
- 4.6. Асинхронные счетчики
- Асинхронные счетчики с умножением частоты счетного сигнала.
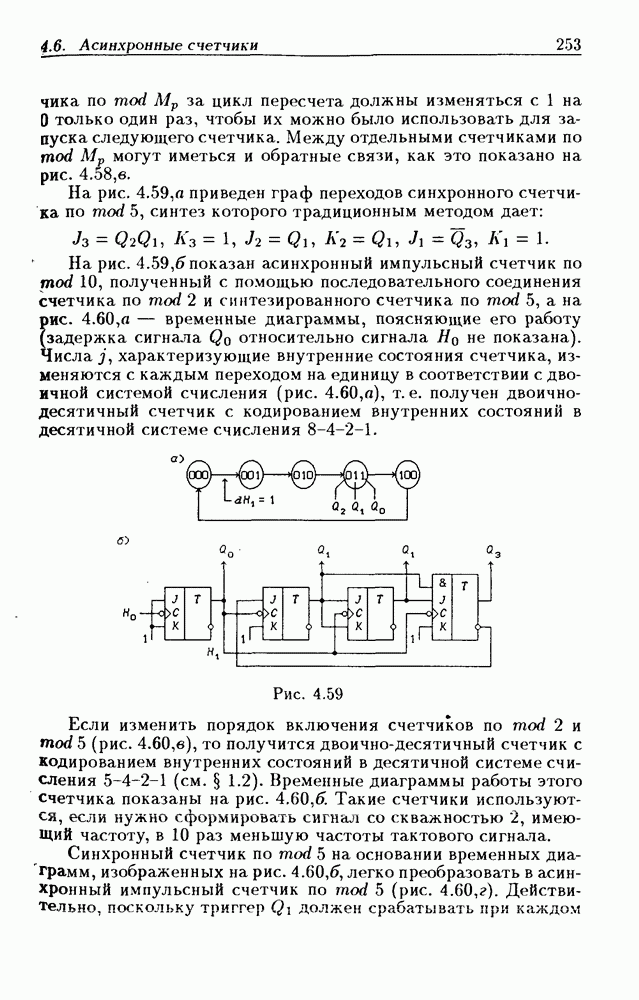
- Асинхронные импульсно-потенциальные счетчики.
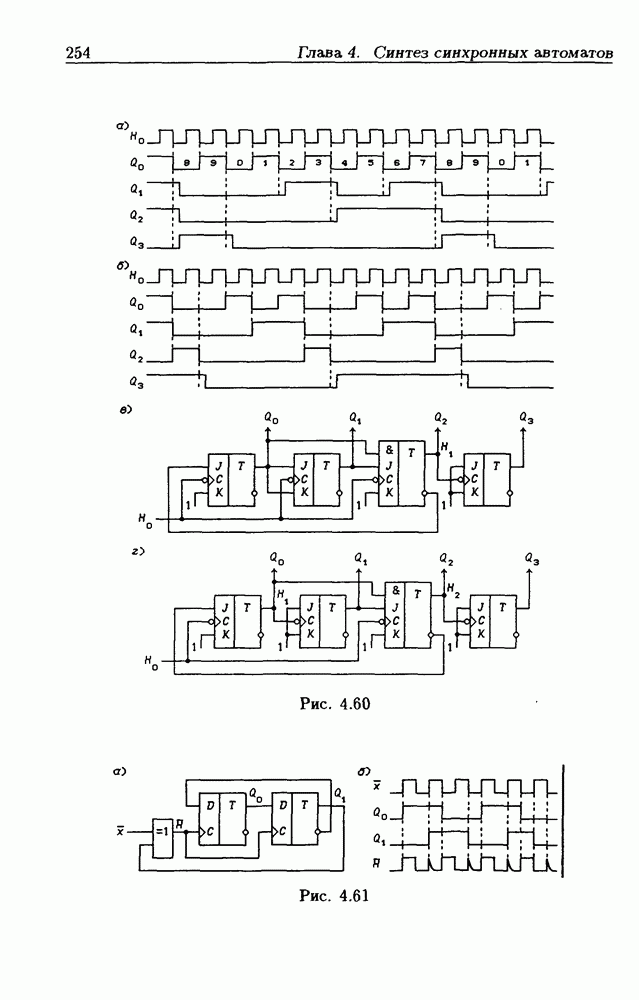
- Асинхронное программирование модуля пересчета счетчиков.
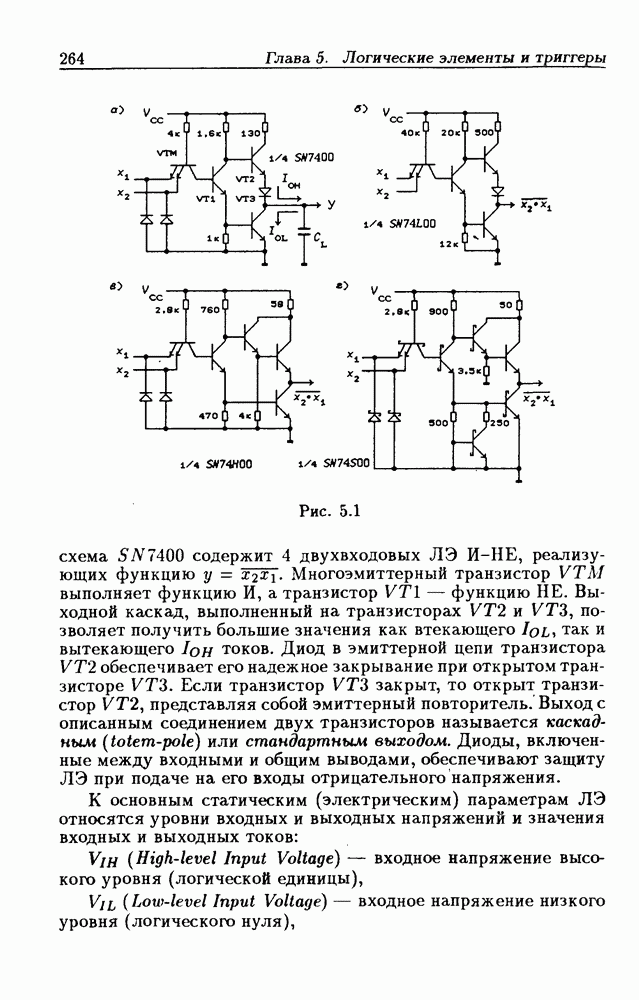
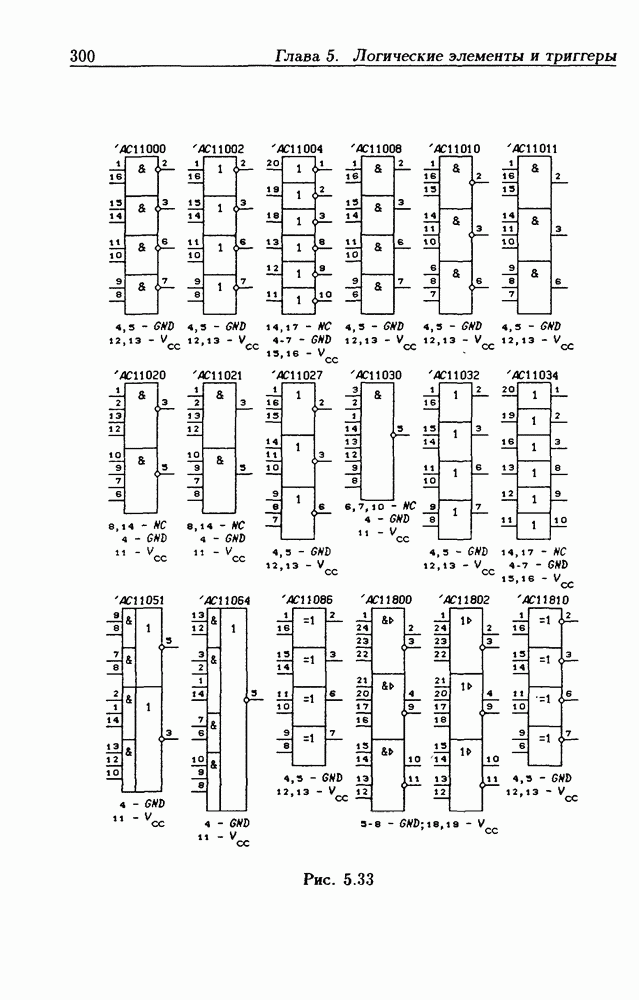
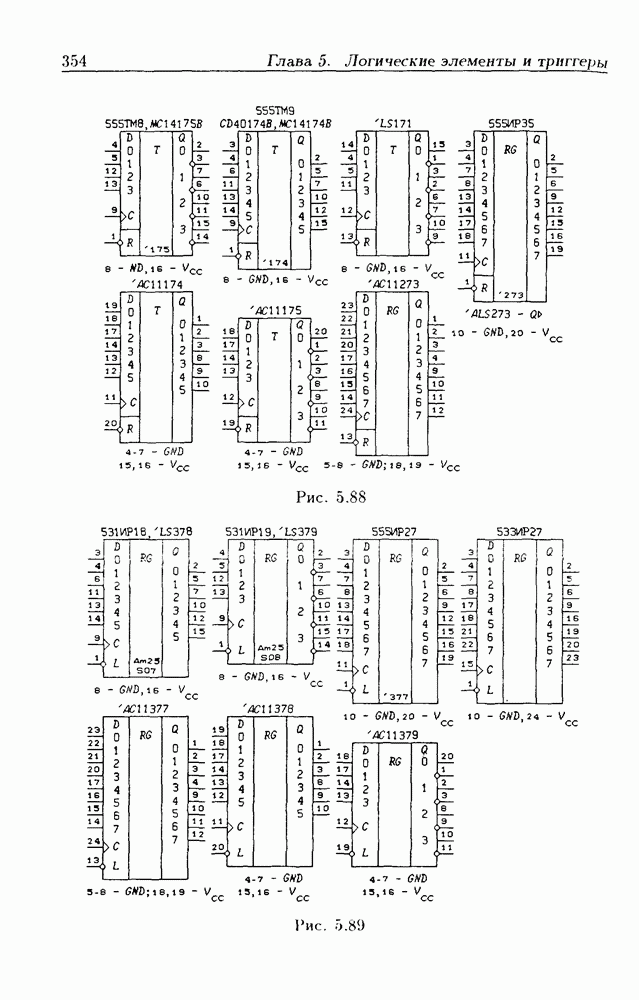
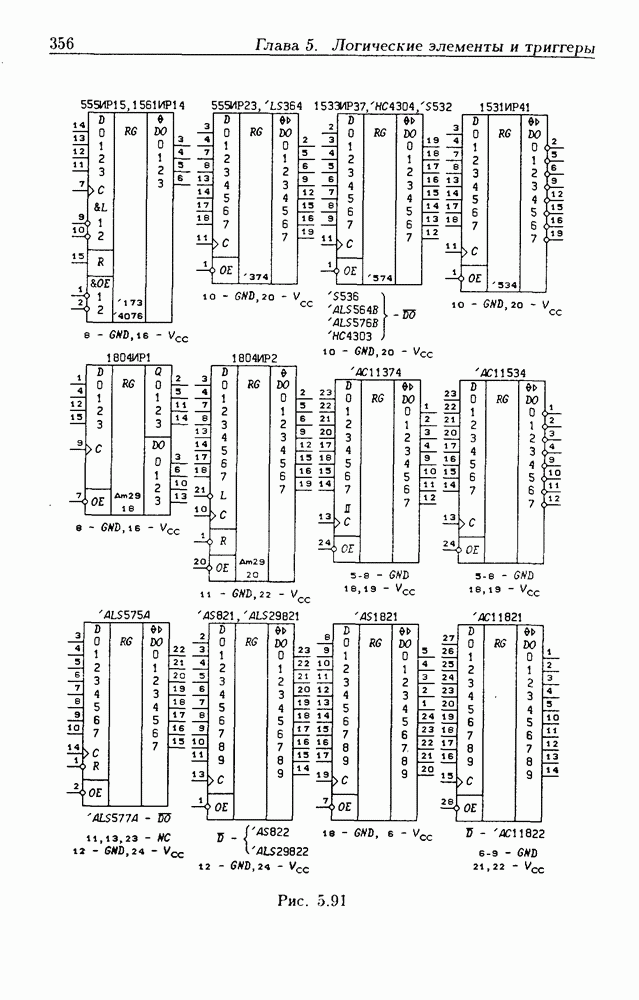
- Глава 5. Логические элементы и триггеры
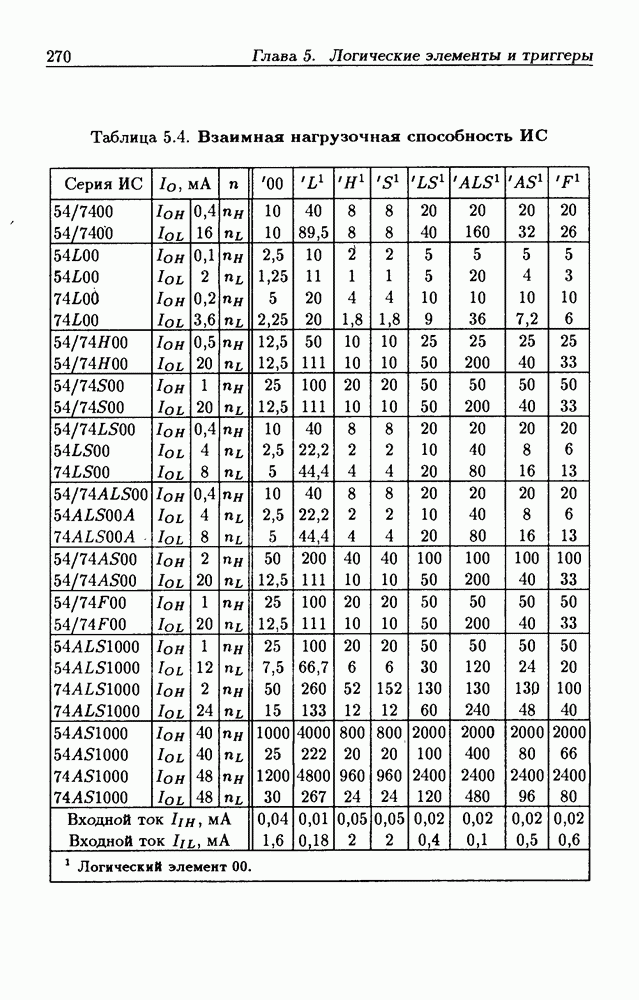
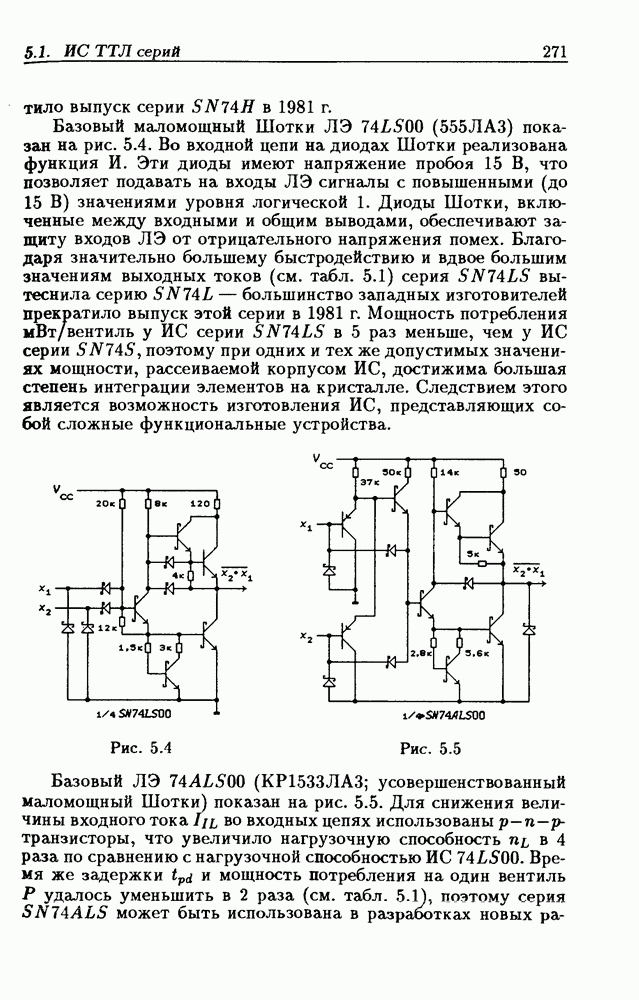
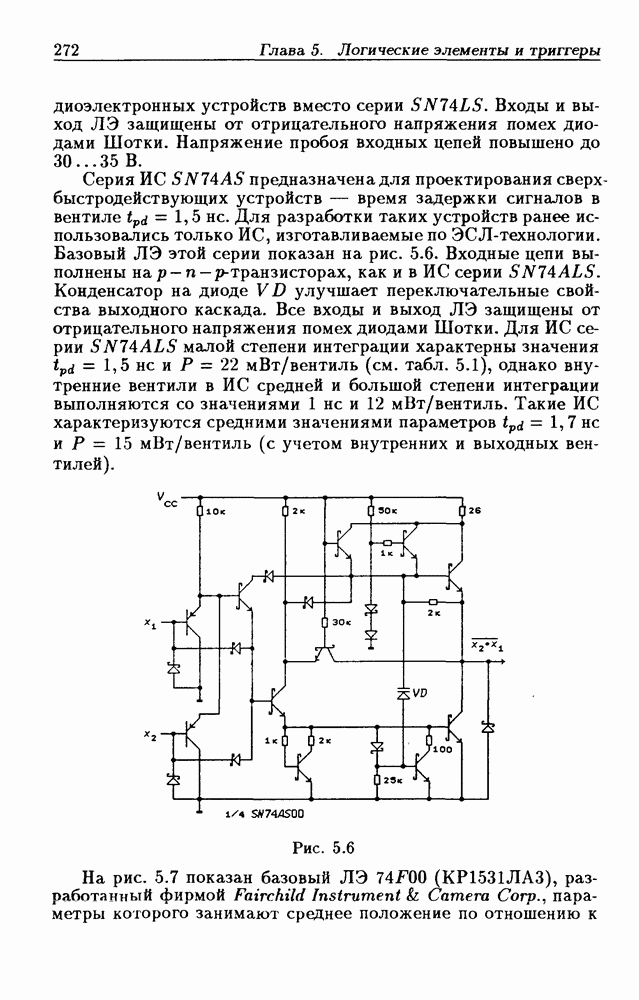
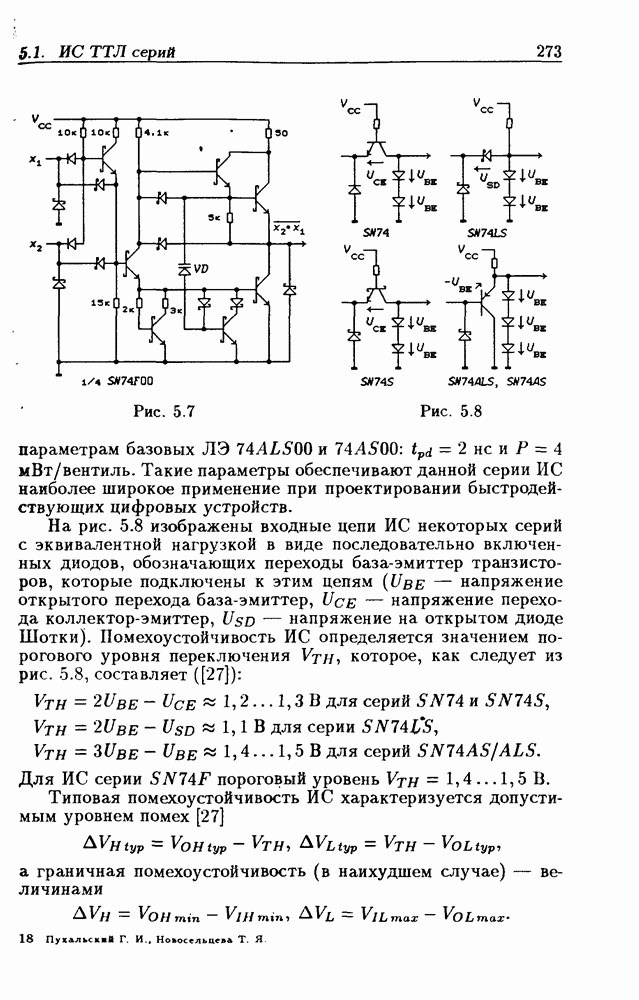
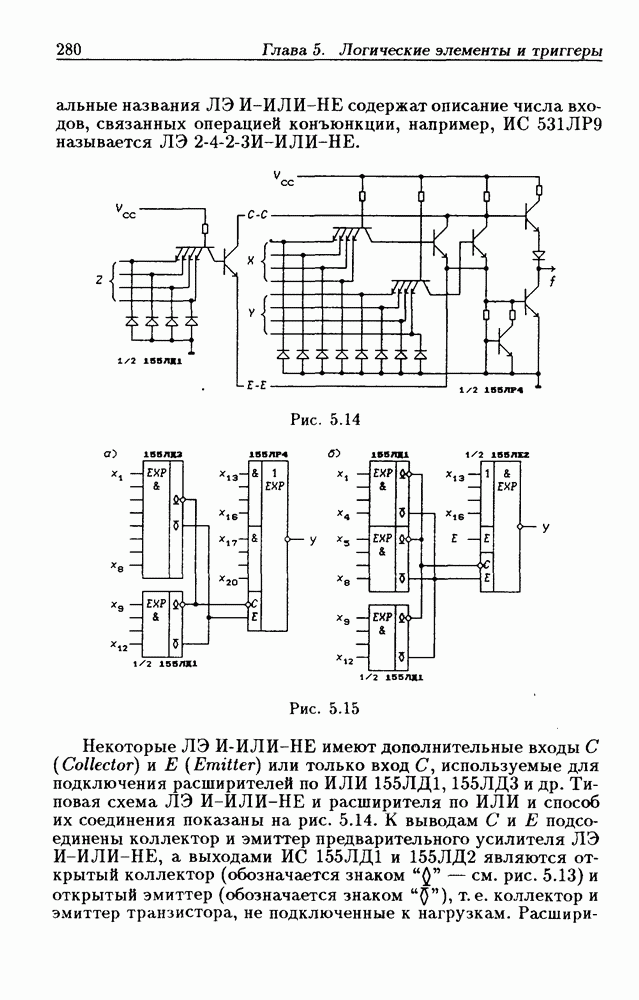
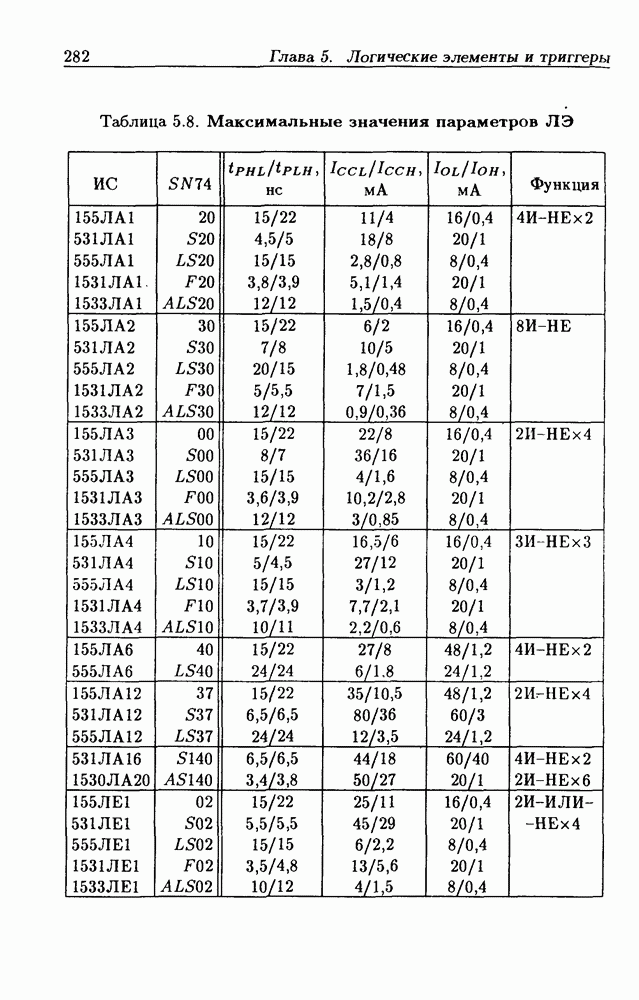
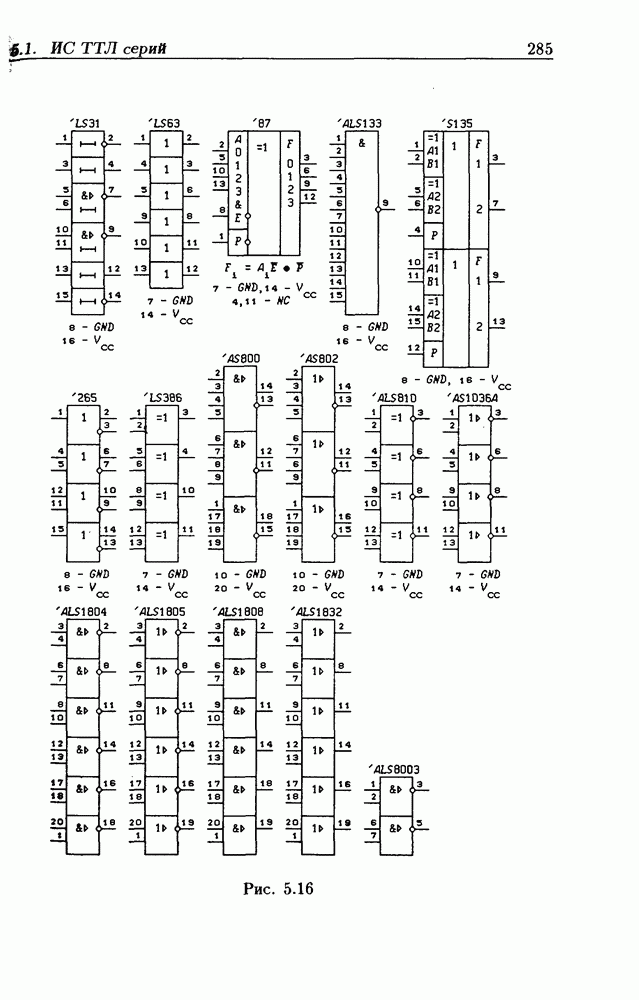
- Логические элементы.
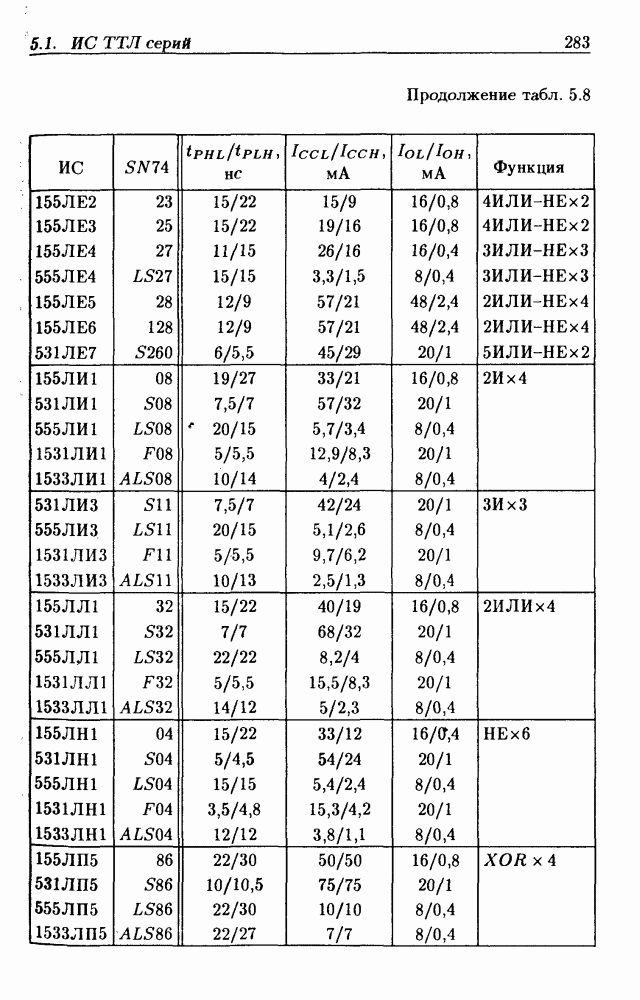
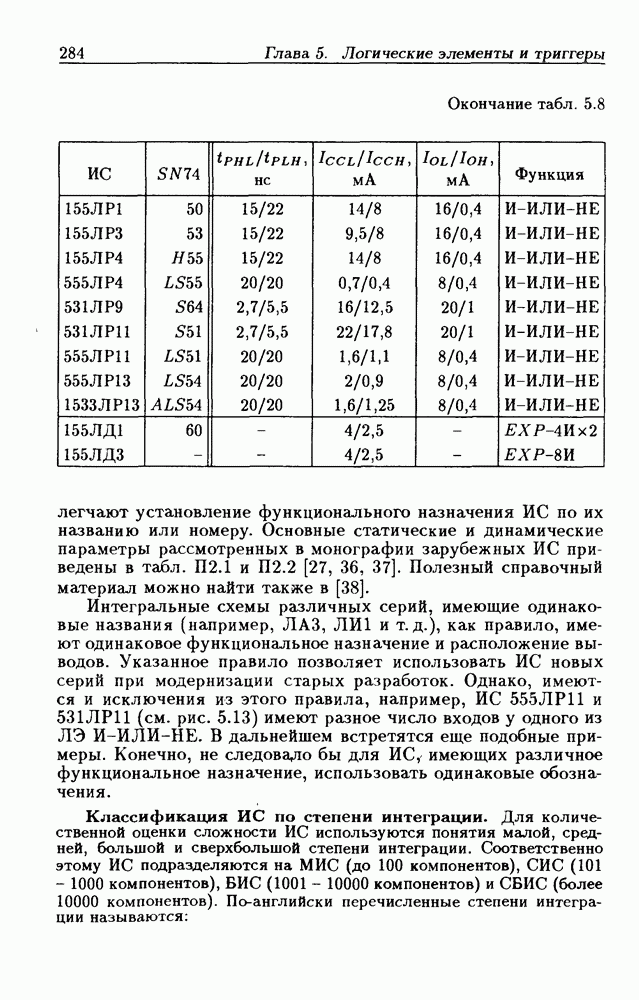
- Классификация ИС по степени интеграции.
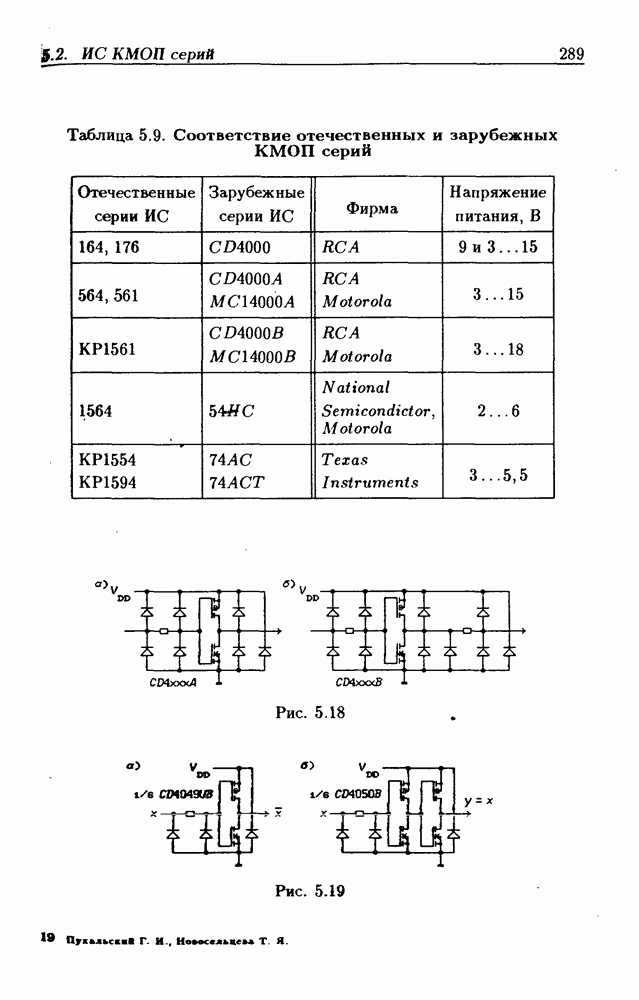
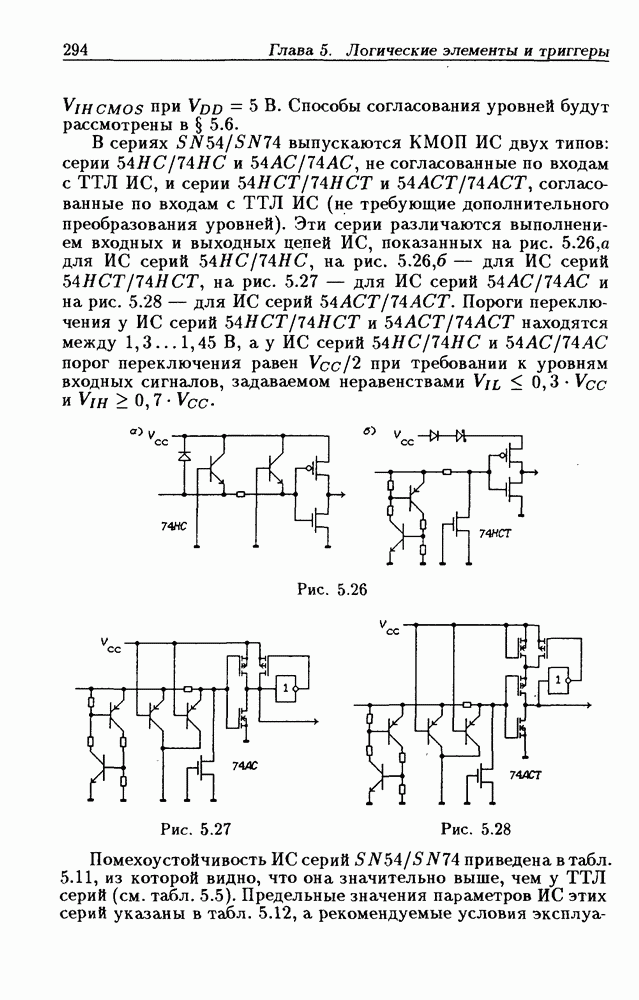
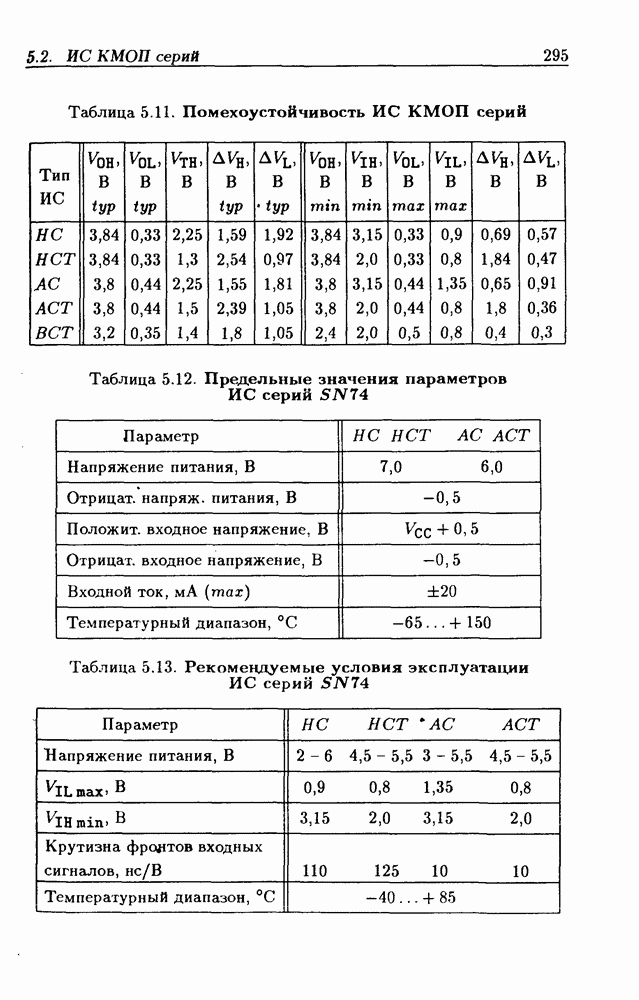
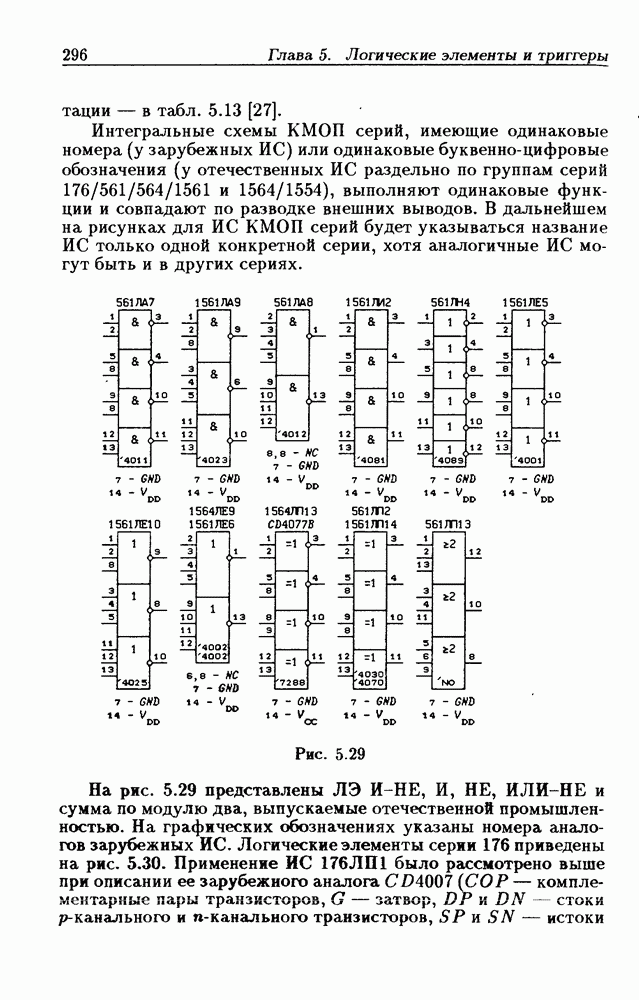
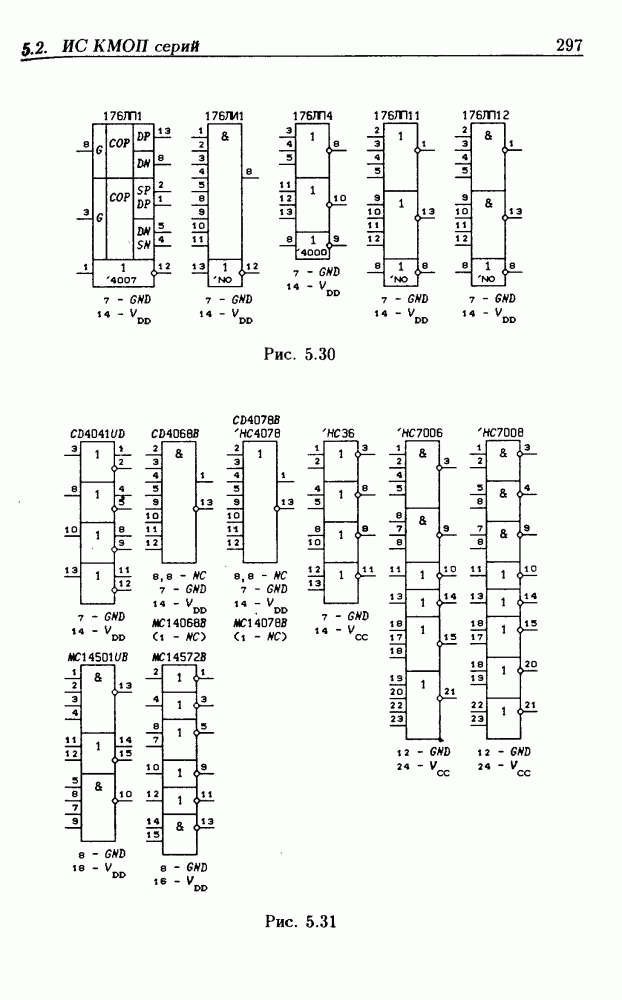
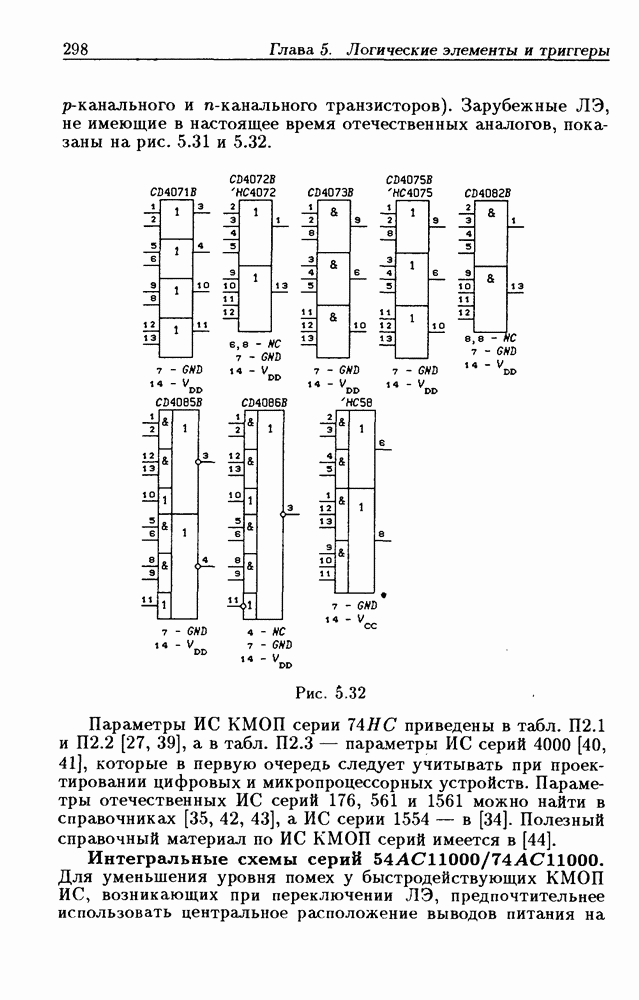
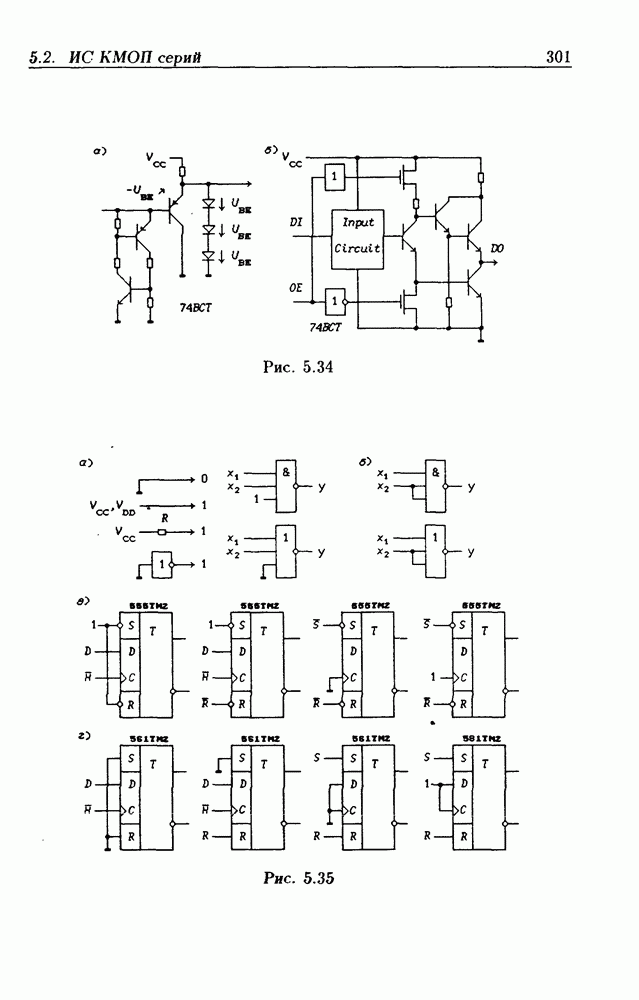
- 5.2. Интегральные схемы КМОП серий
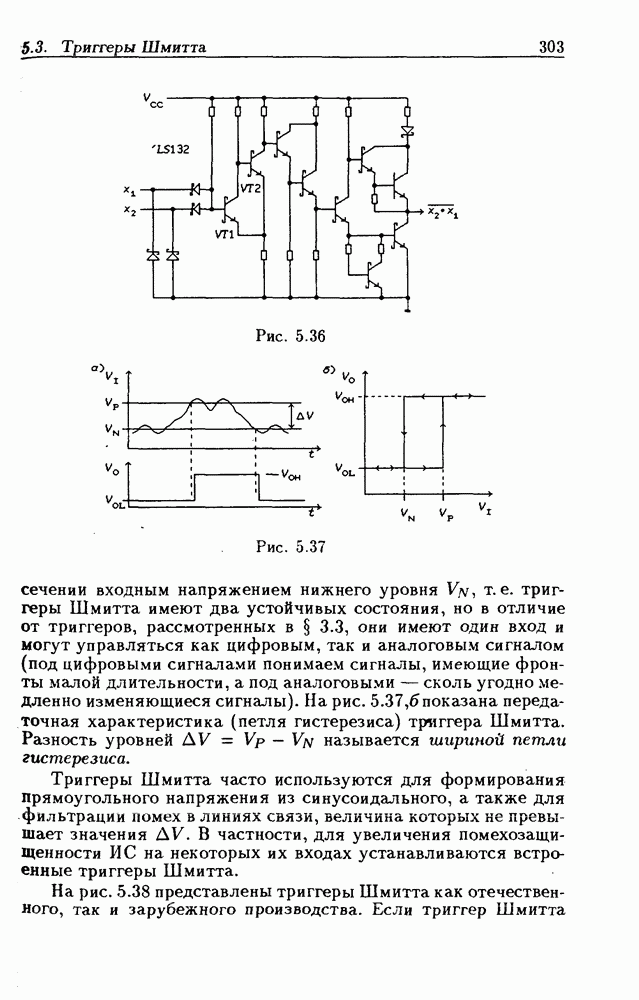
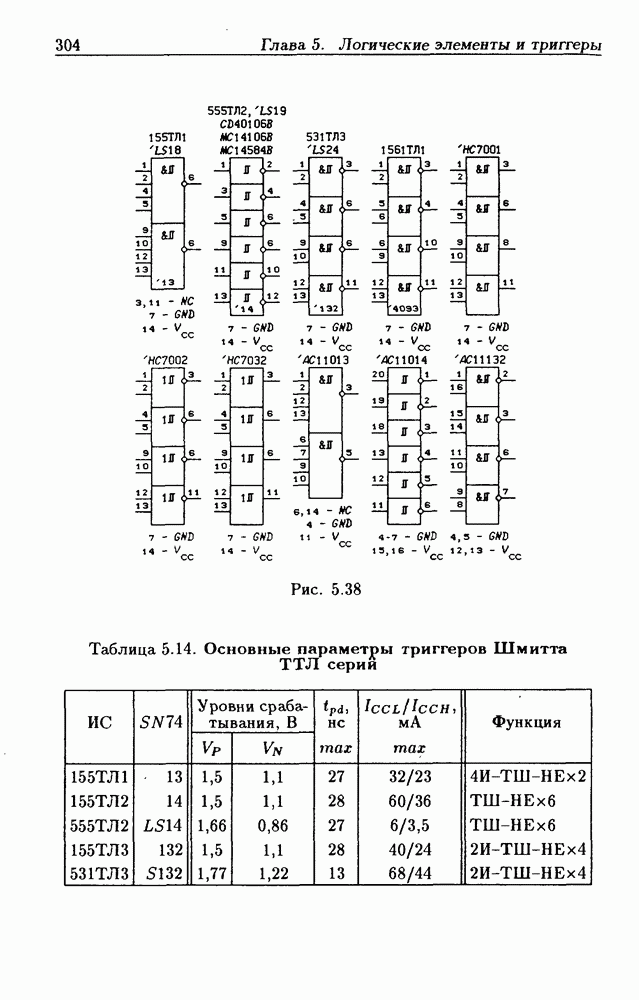
- 5.3. Триггеры Шмитта
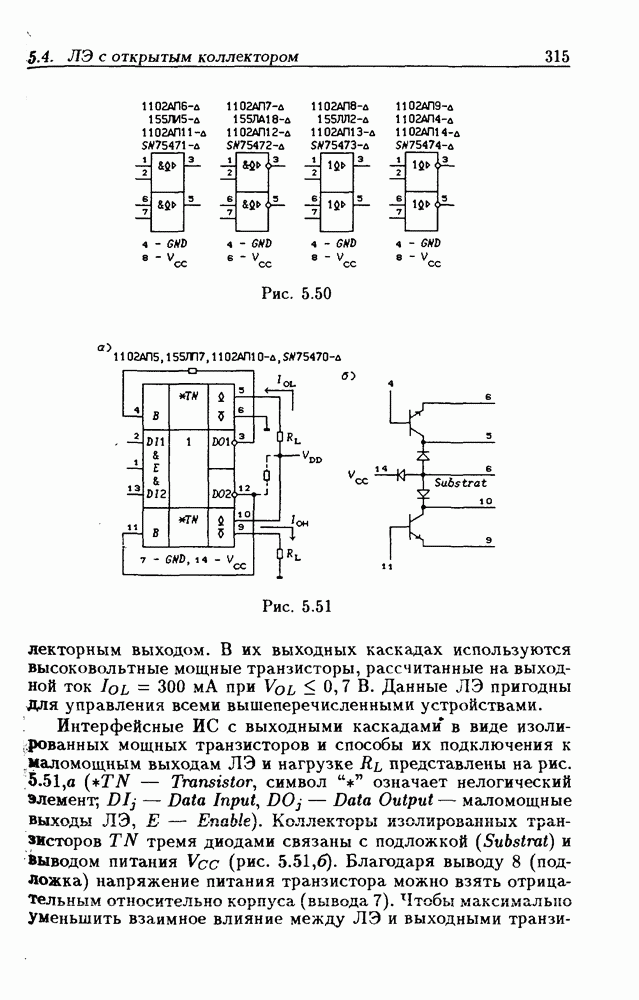
- 5.4. Логические элементы с открытым коллекторным выходом
- Логические элементы с открытым коллекторным выходом.
- Применения ЛЭ с открытым коллекторным выходом.
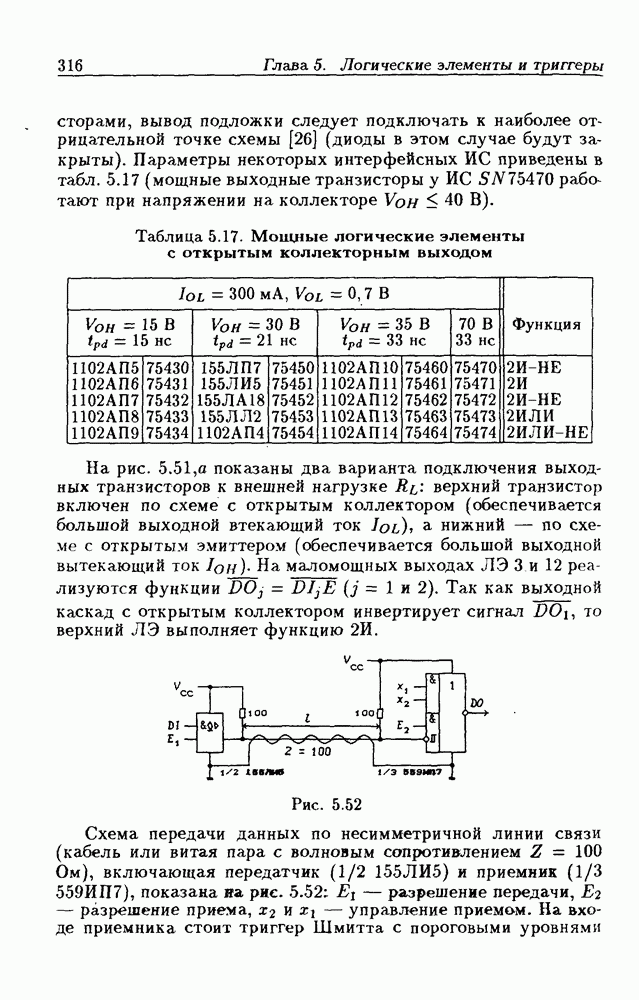
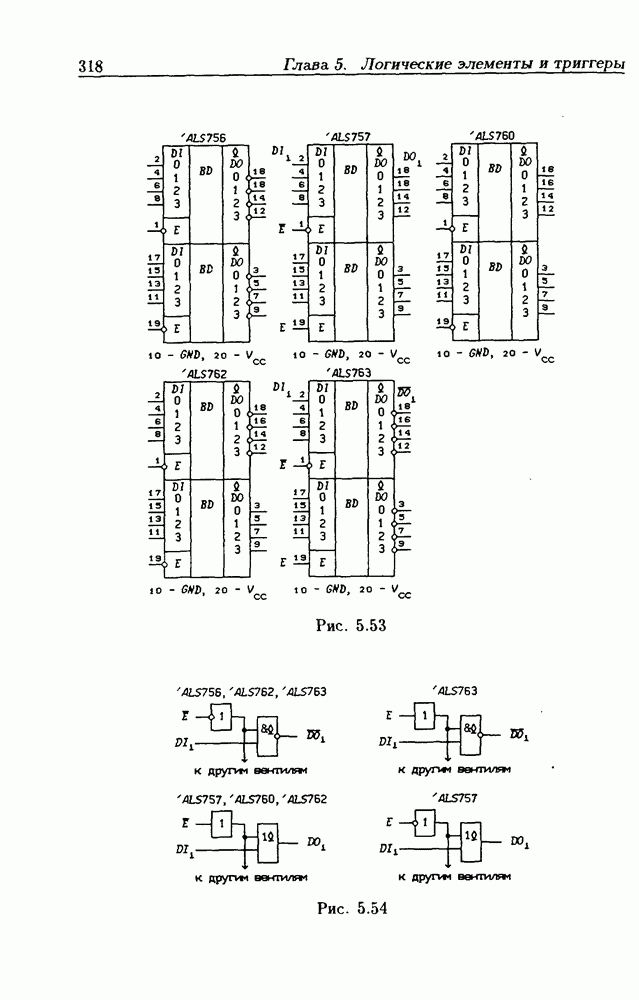
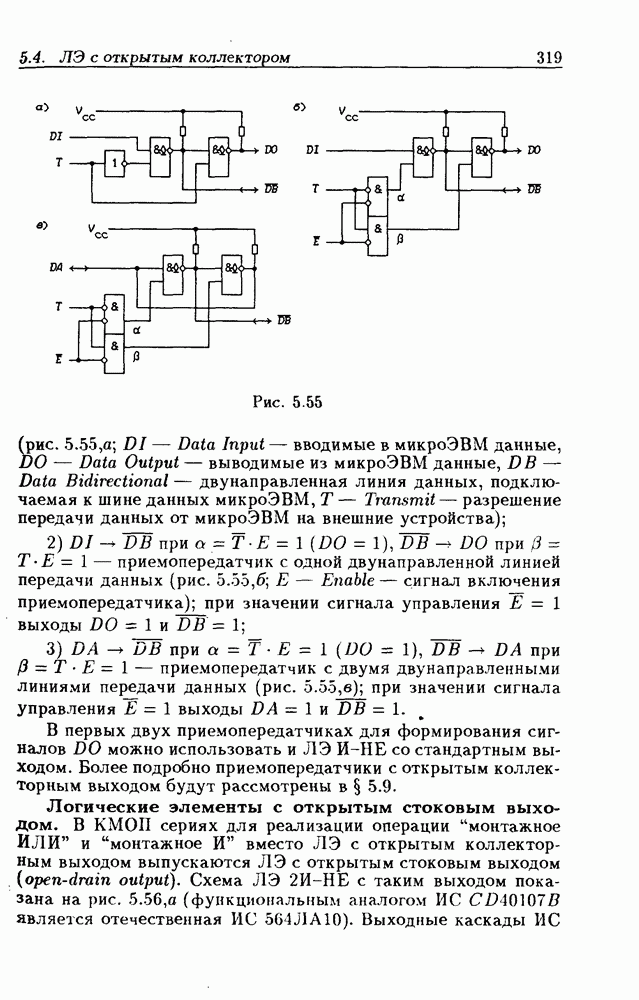
- Интерфейсные ЛЭ с открытым коллекторным выходом.
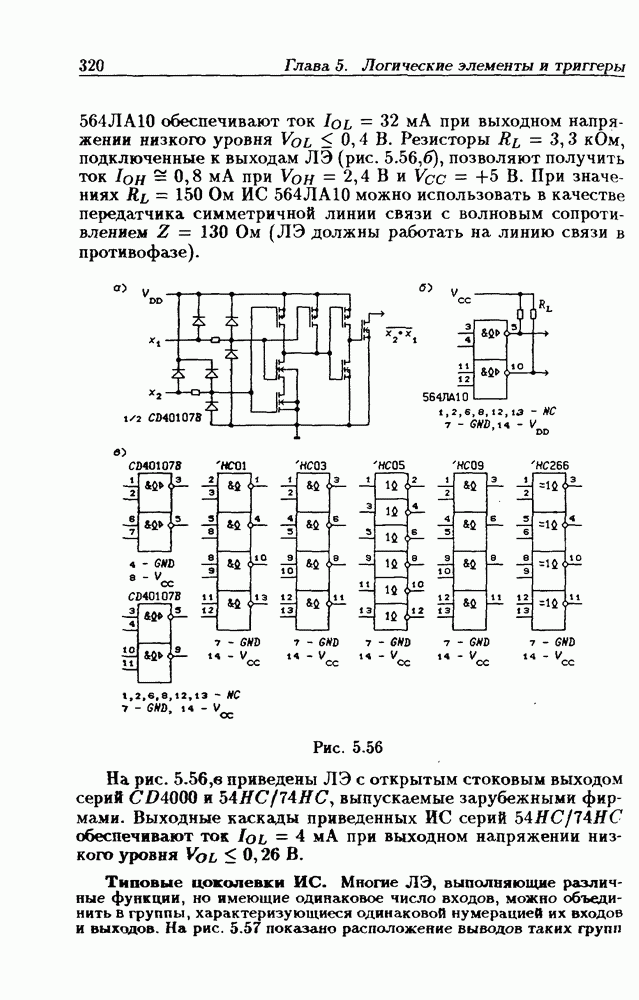
- Логические элементы с открытым стоковым выходом.
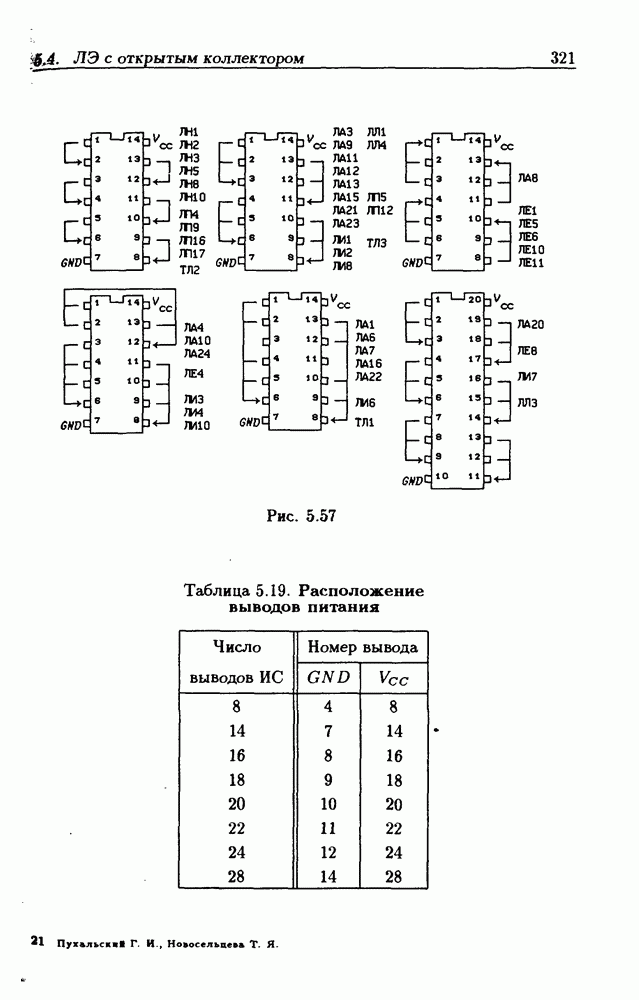
- Типовые цоколевки ИС.
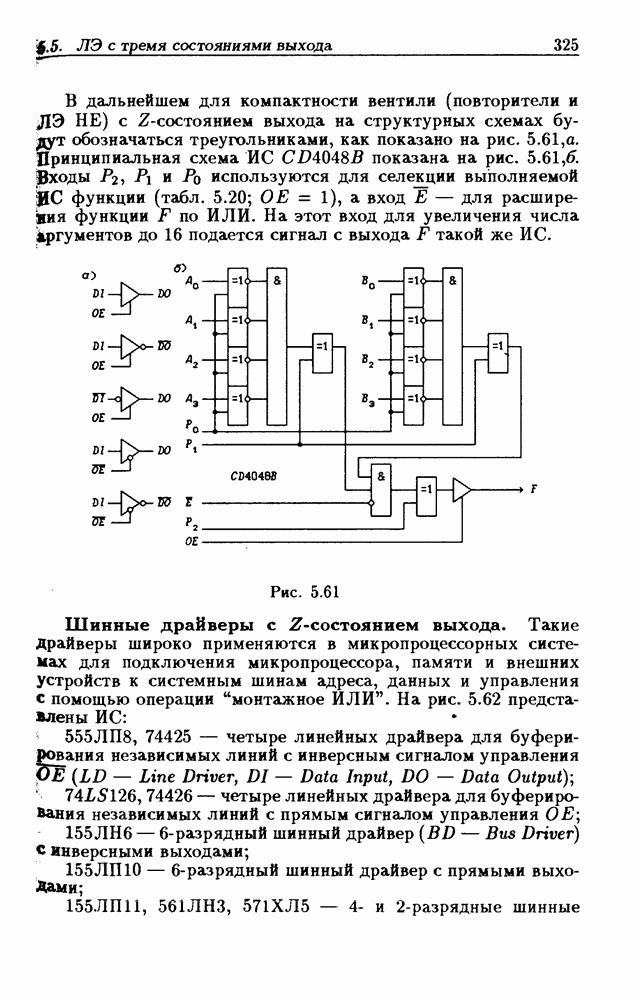
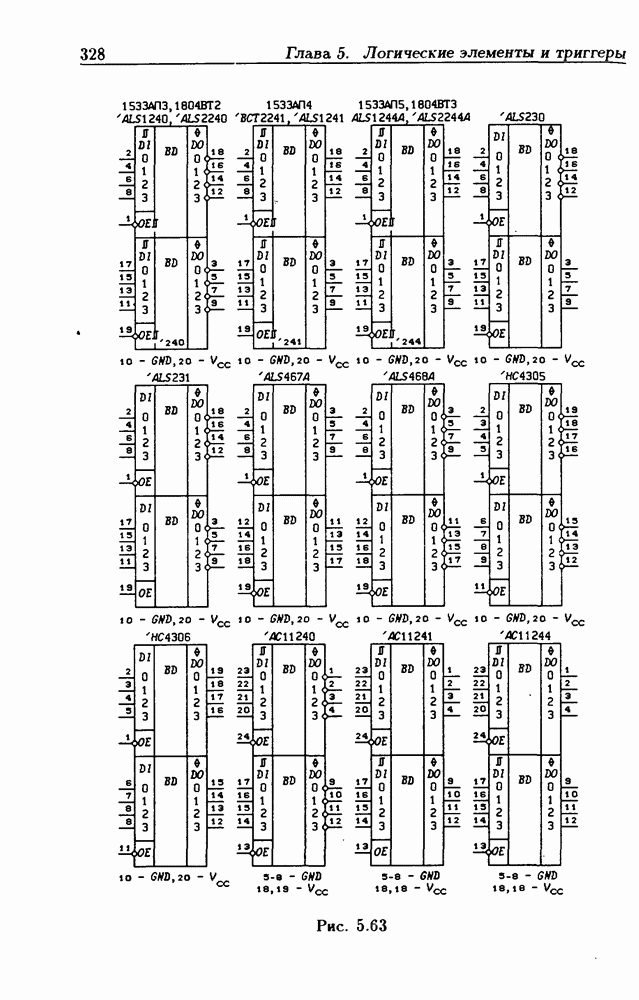
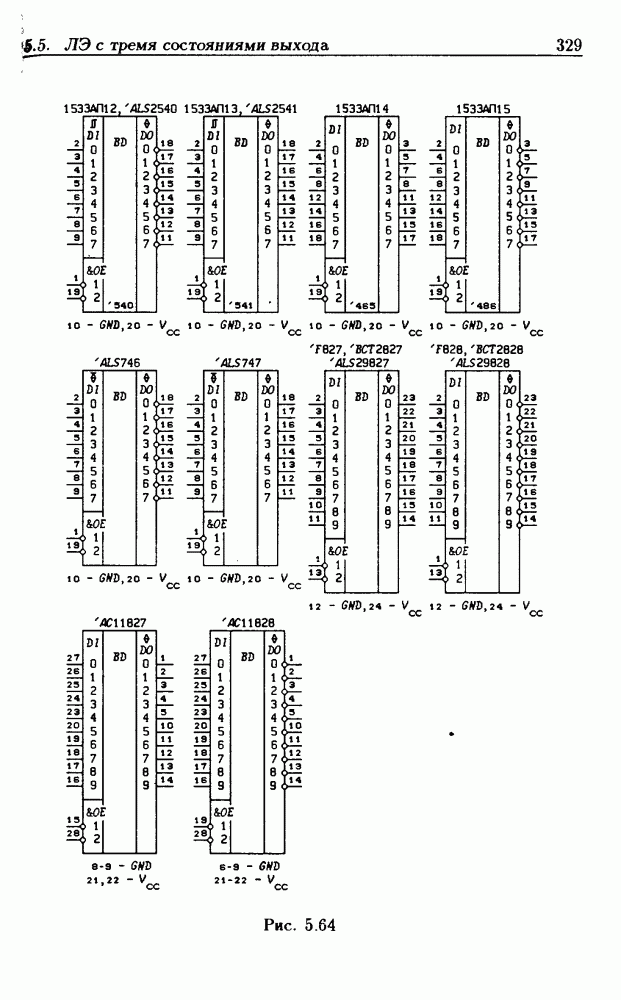
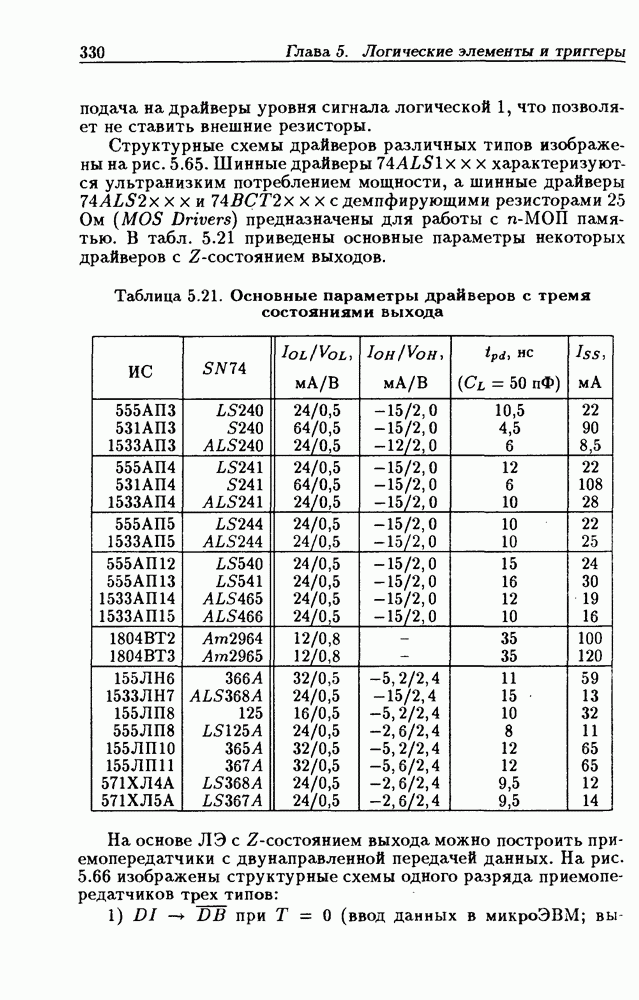
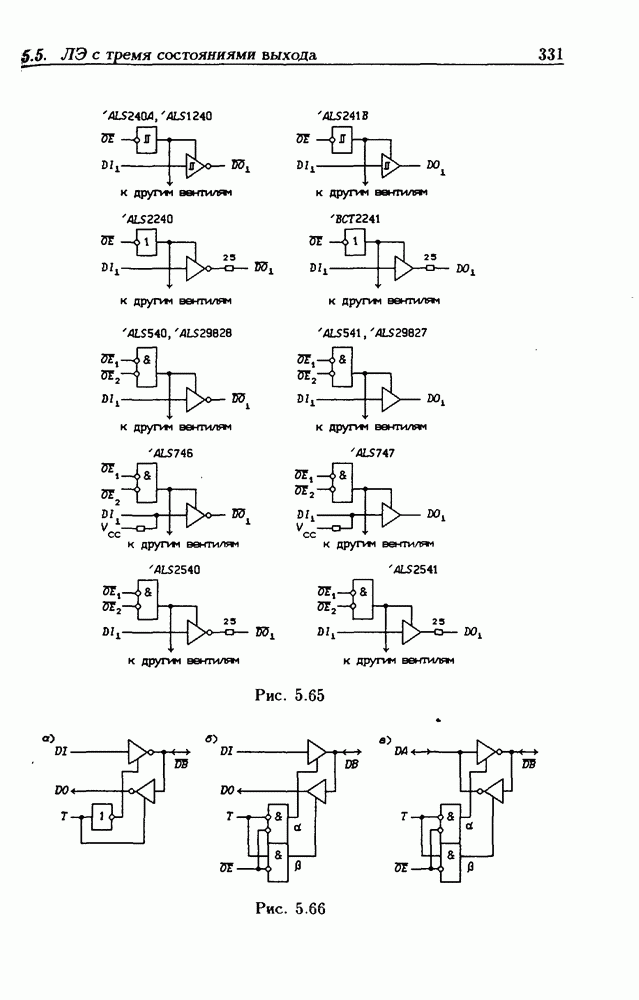
- 5.5. Логические элементы с тремя состояниями выхода
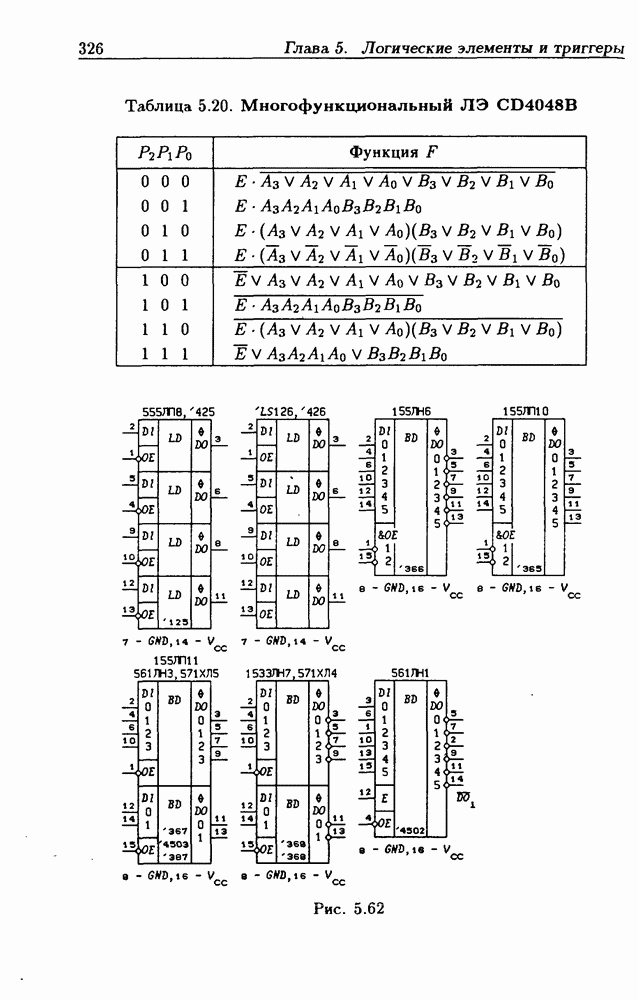
- Шинные драйверы с Z-состоянием выхода.
- Основные правила графического изображения ИС.
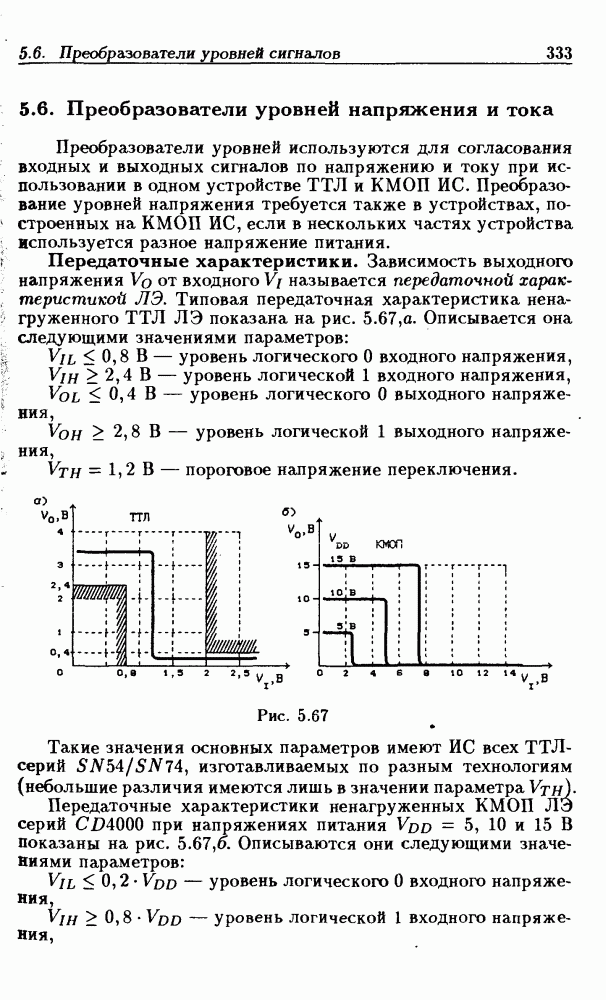
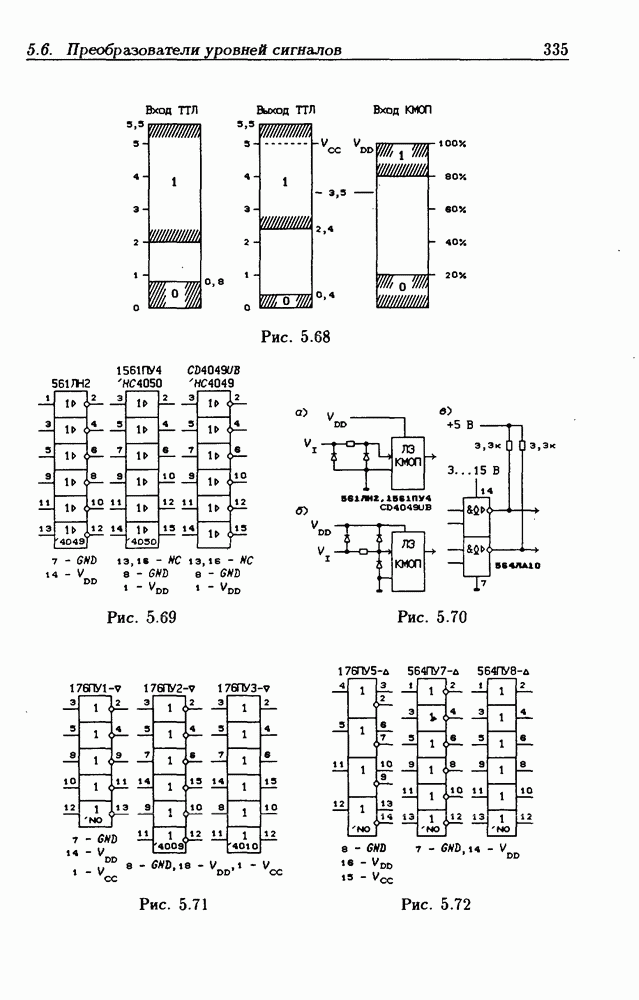
- 5.6. Преобразователи уровней напряжения и тока
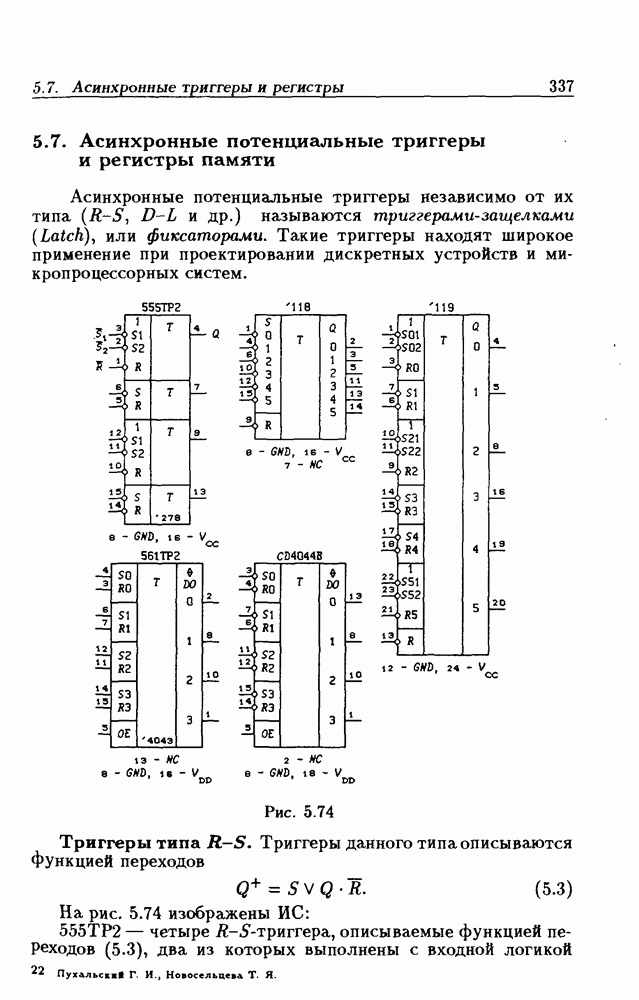
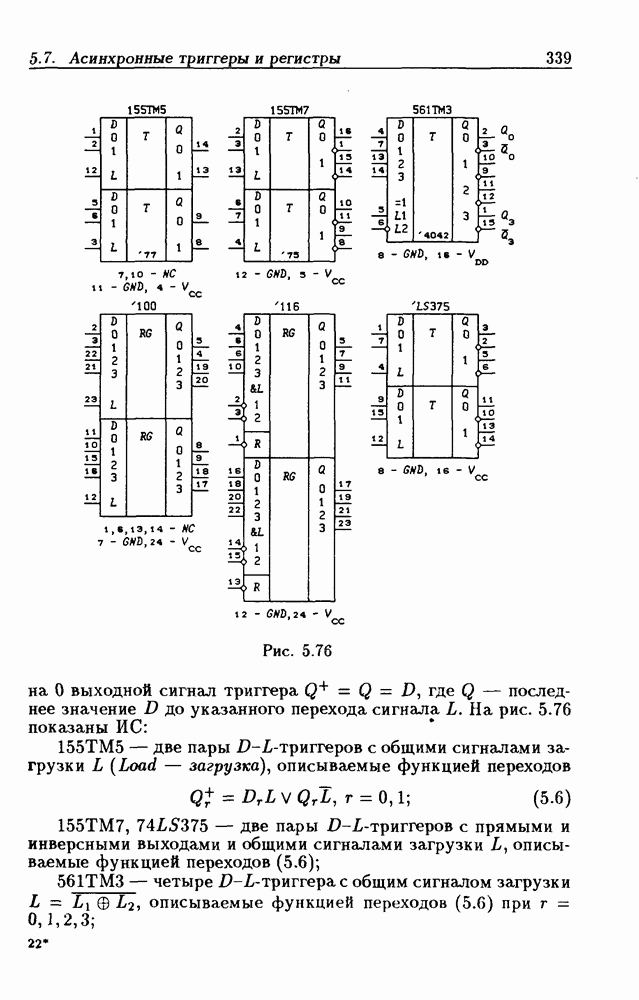
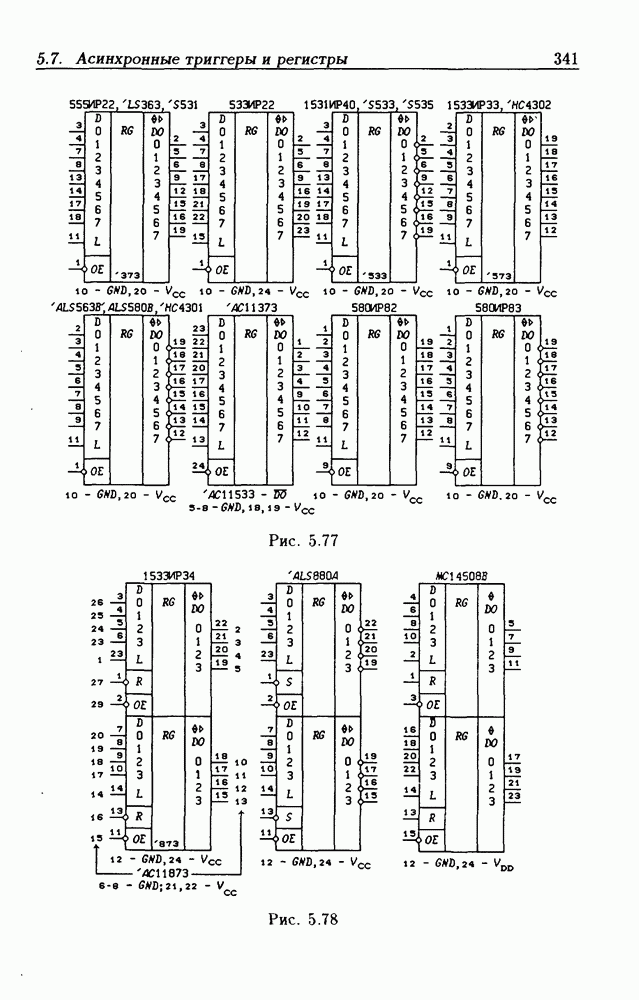
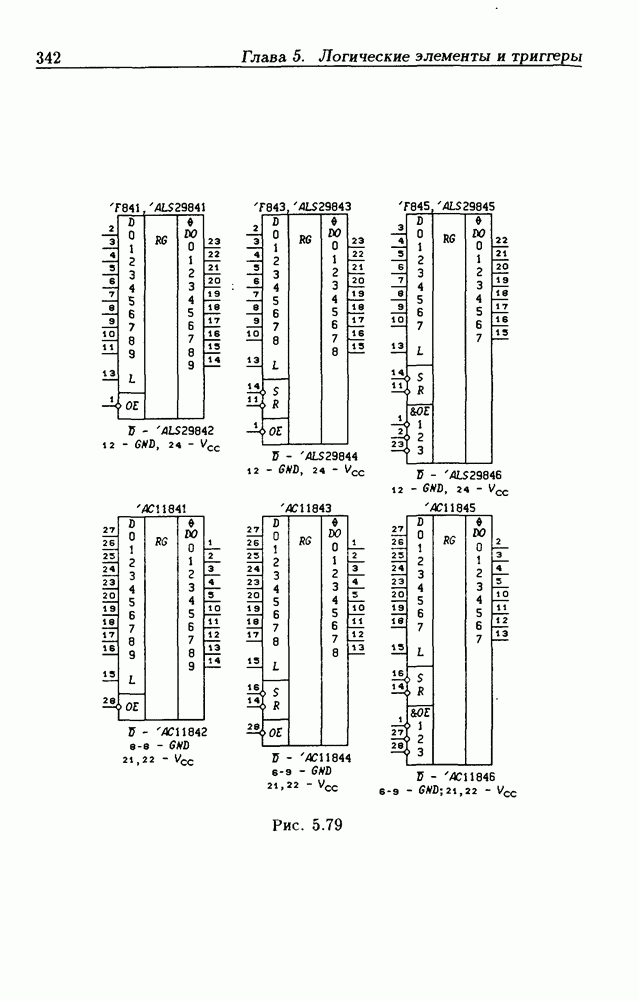
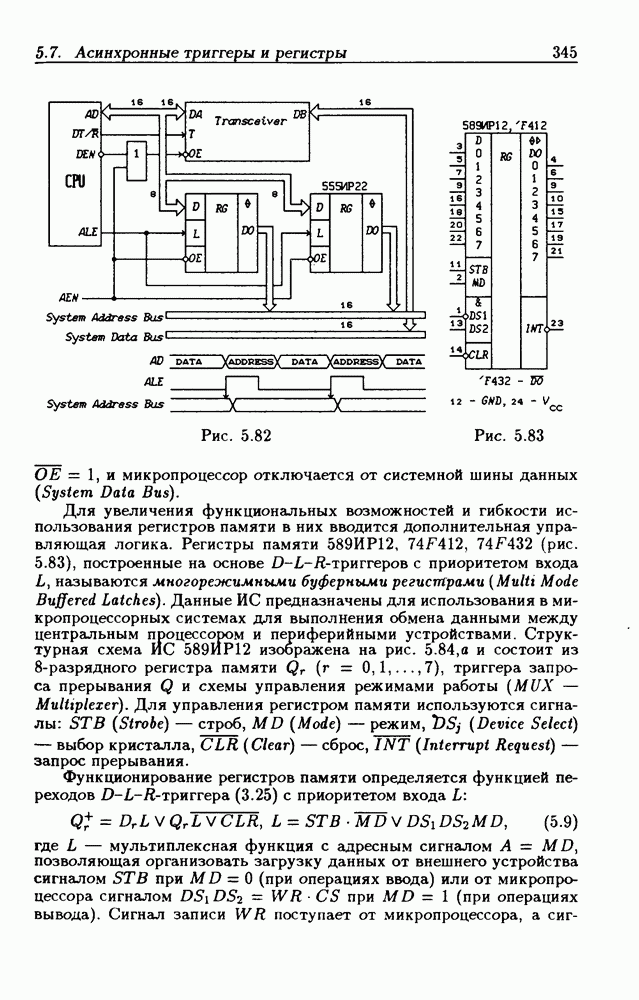
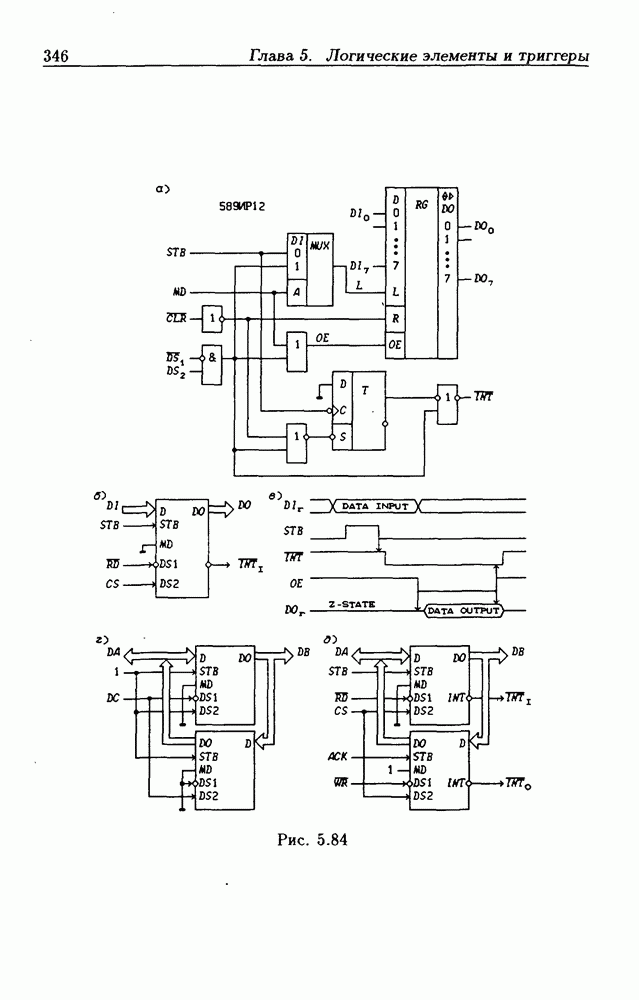
- 5.7. Асинхронные потенциальные триггеры и регистры памяти
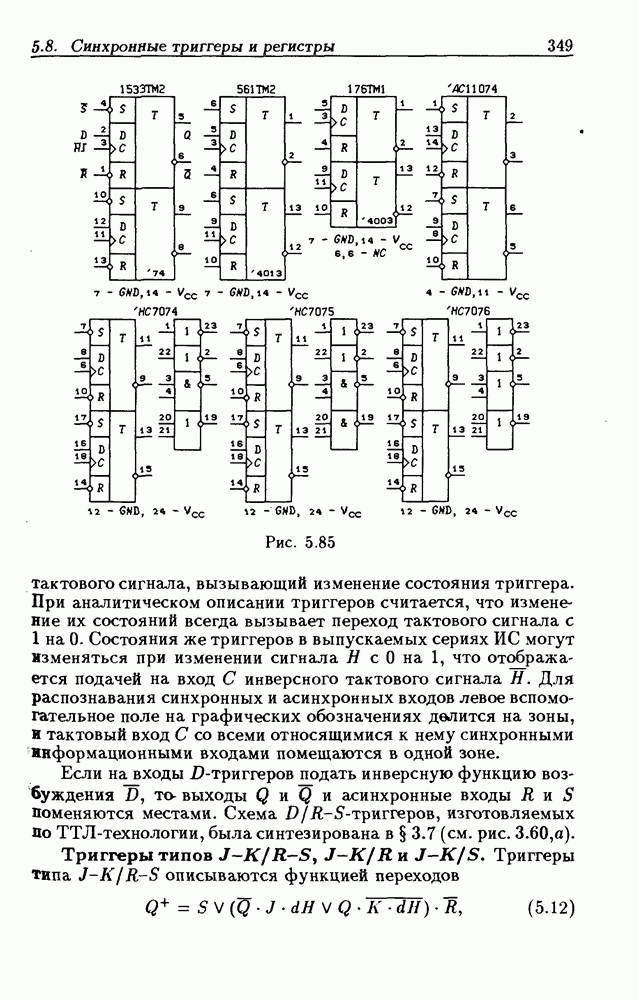
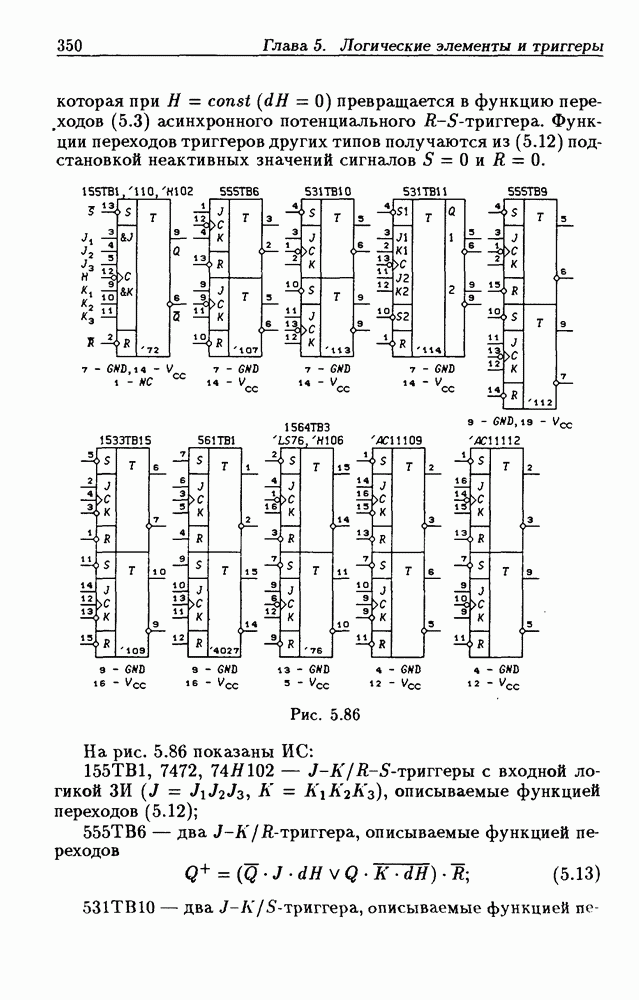
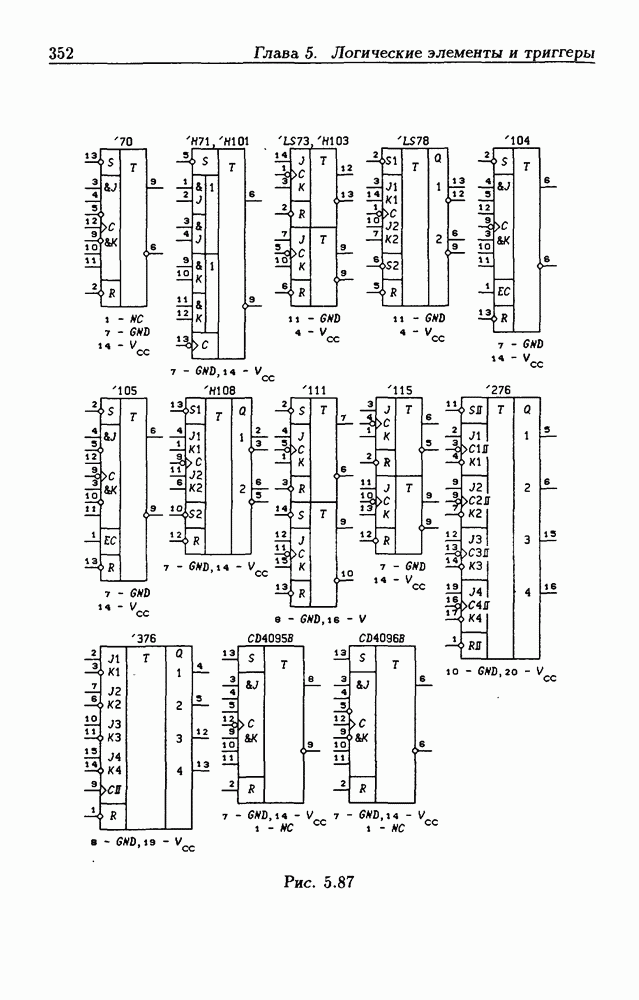
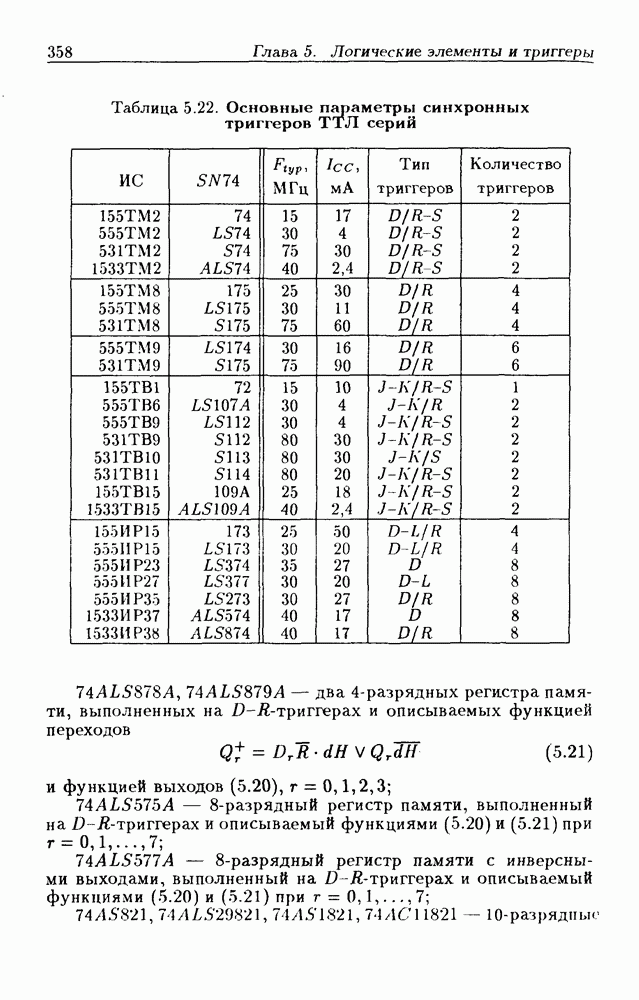
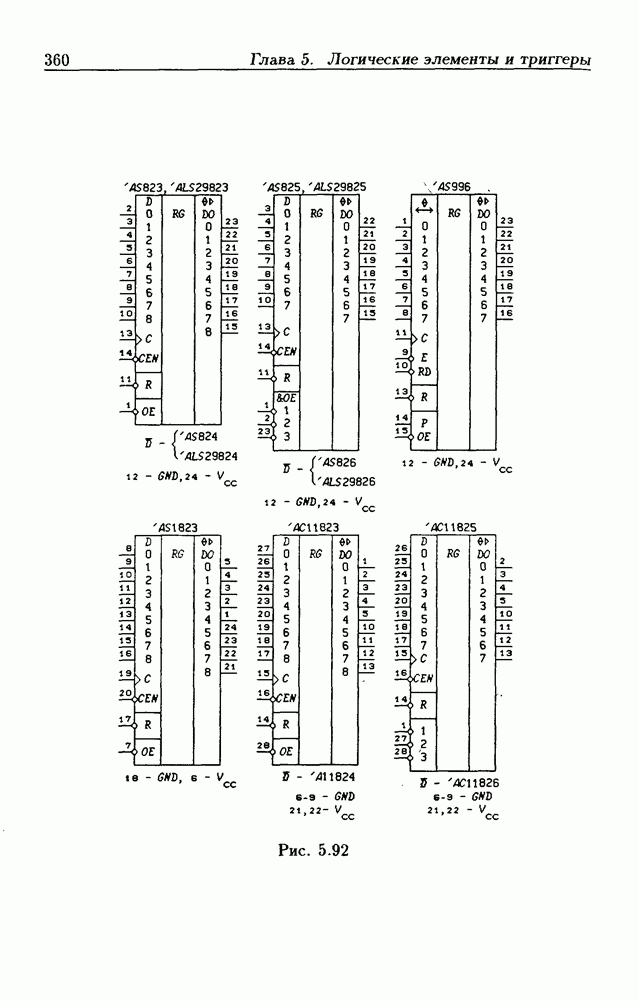
- 5.8. Синхронные триггеры и регистры памяти
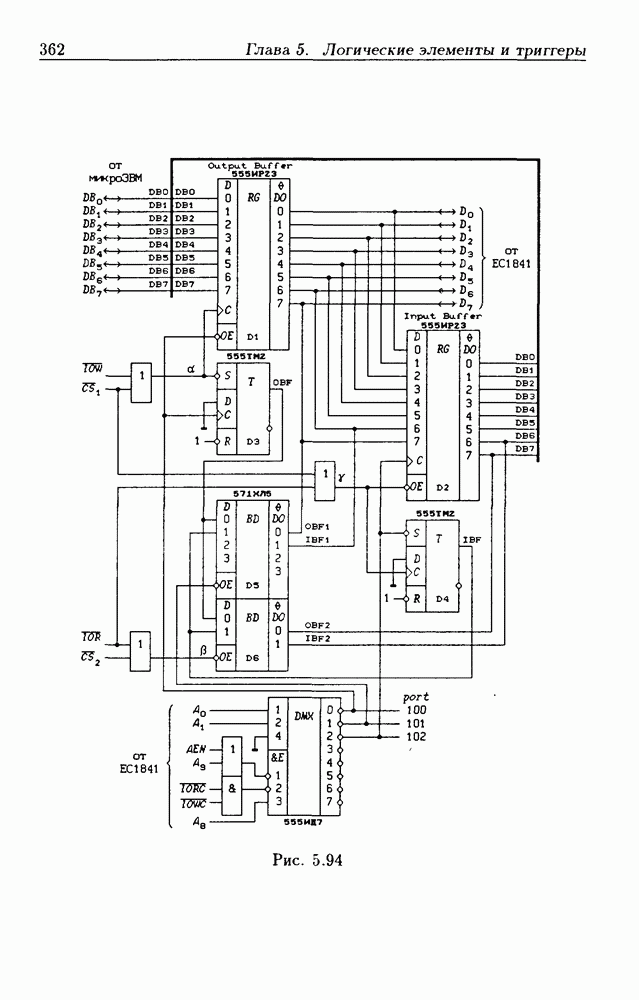
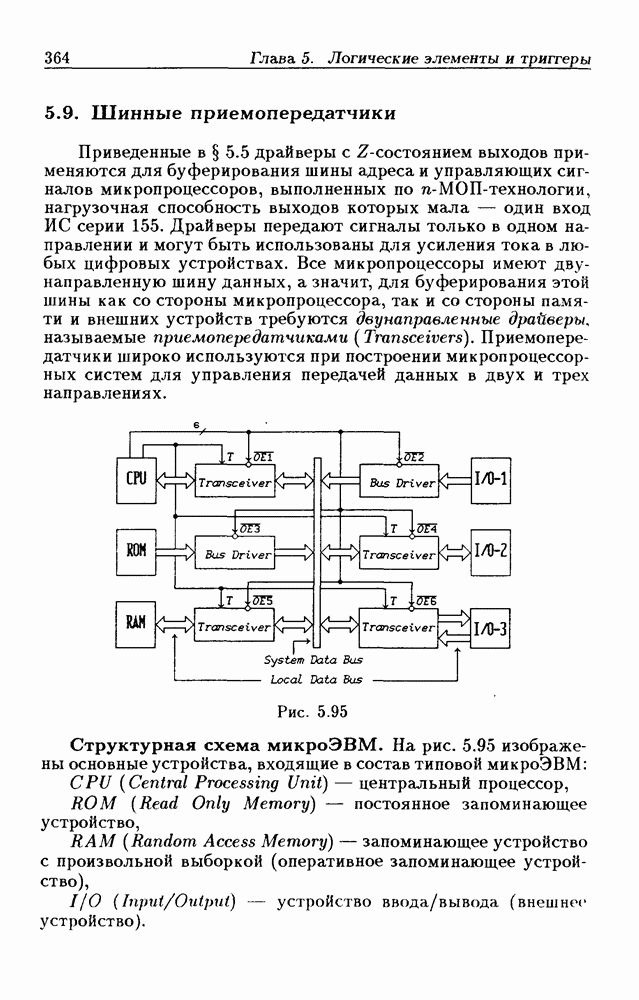
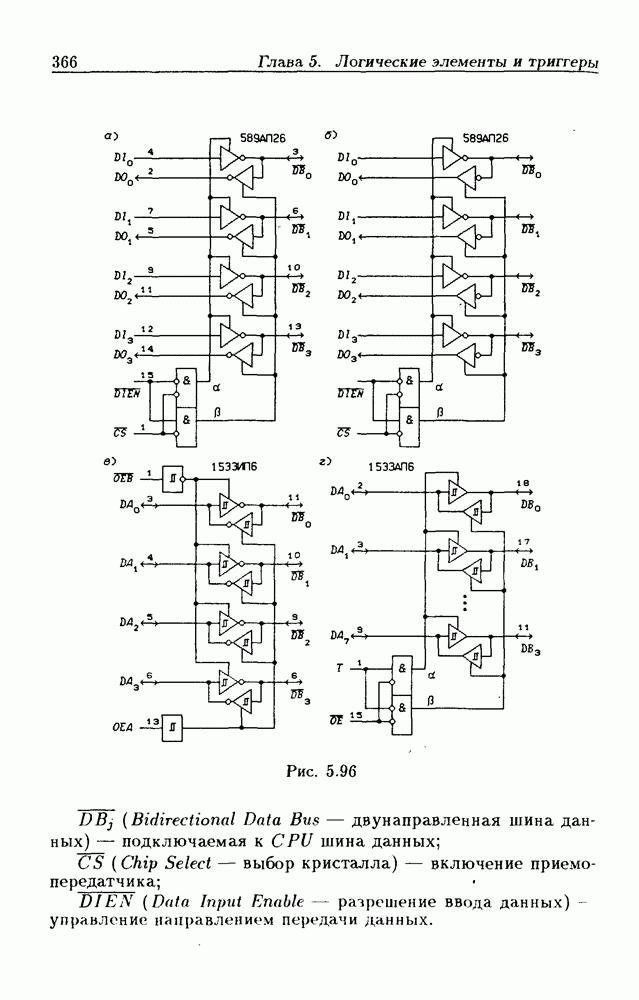
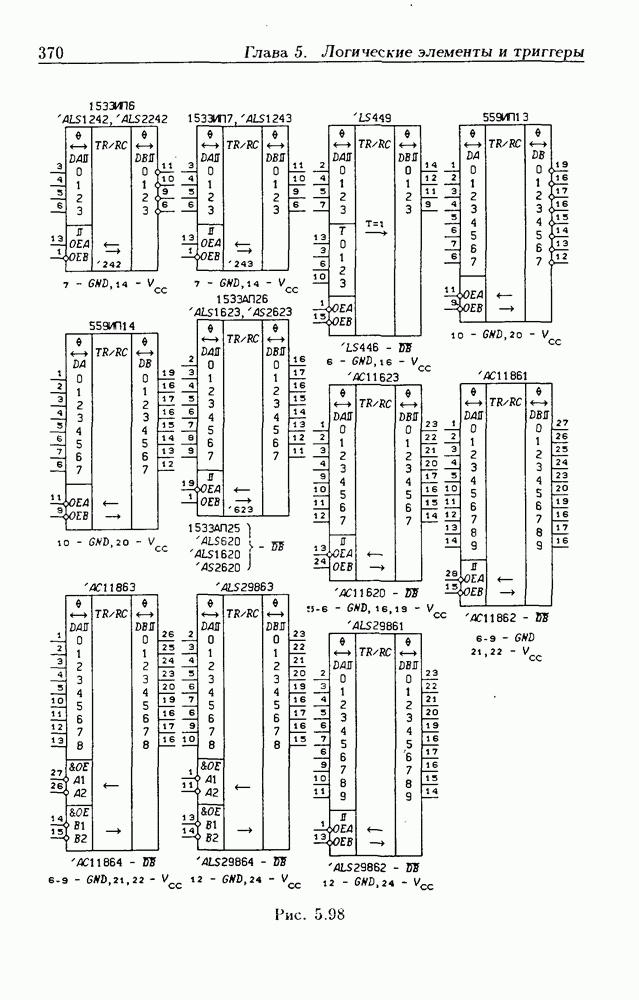
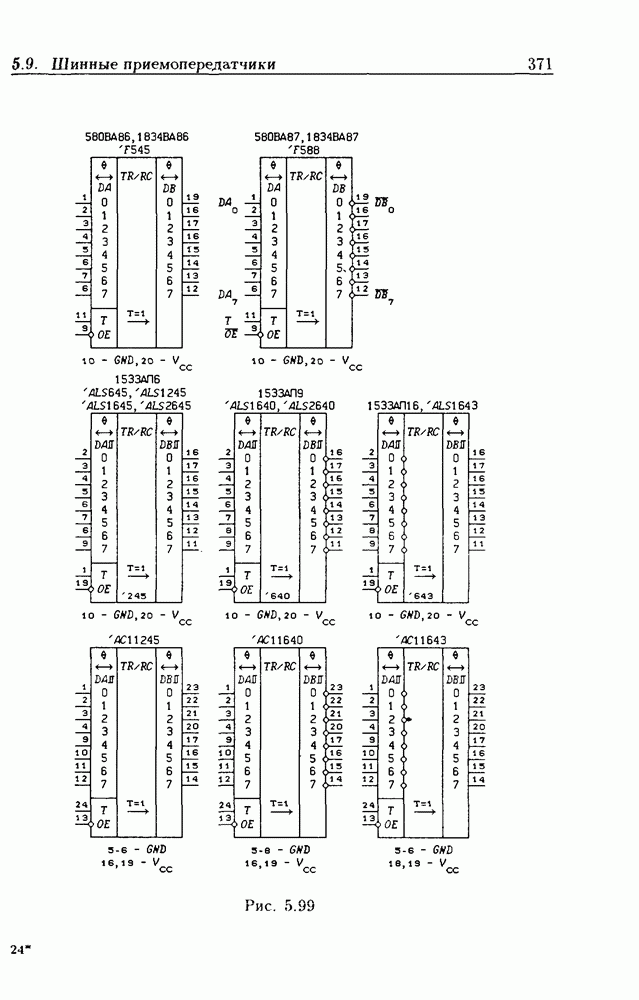
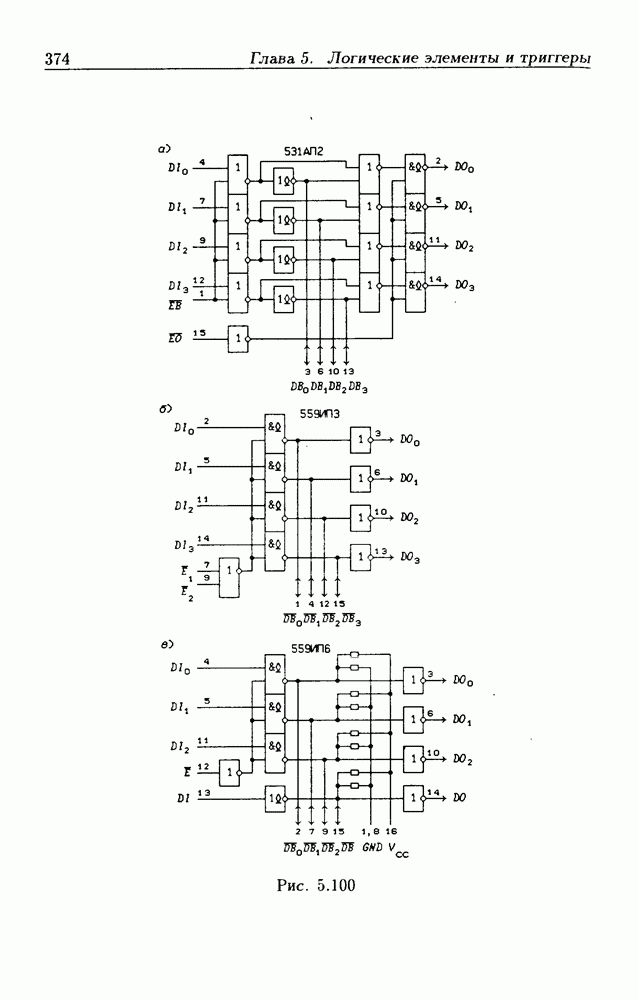
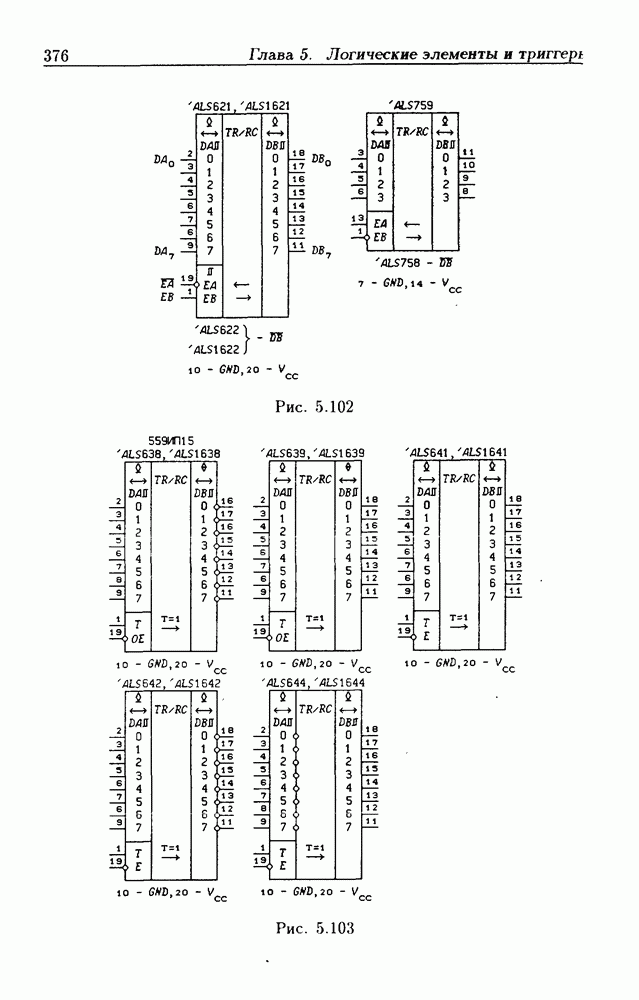
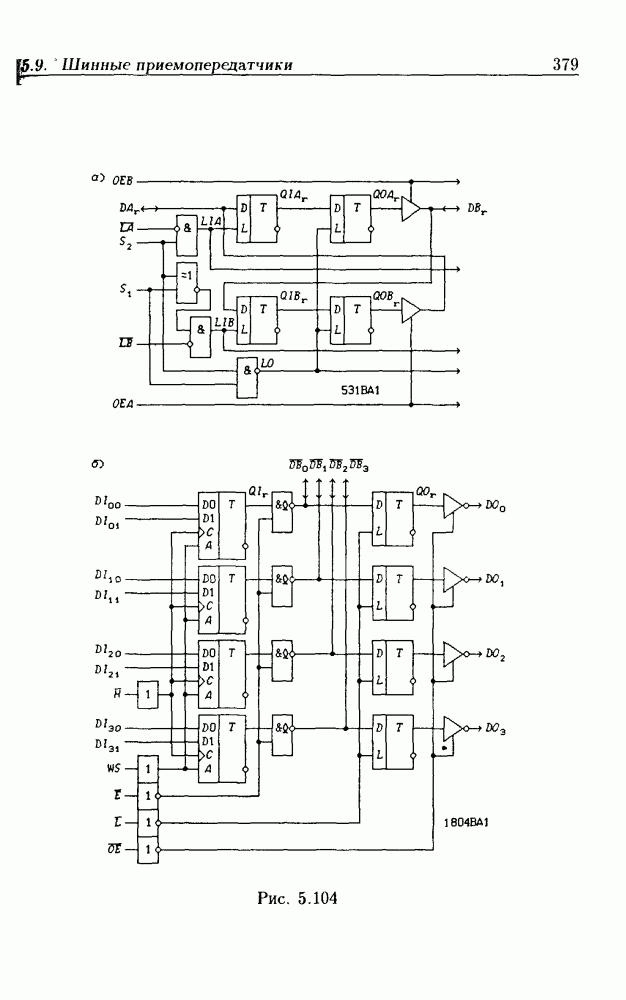
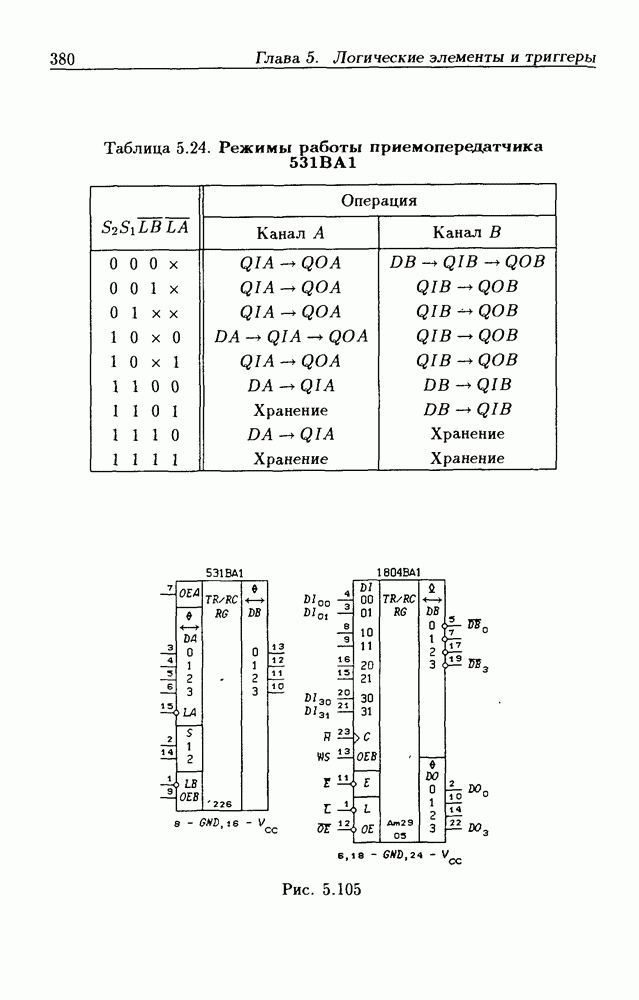
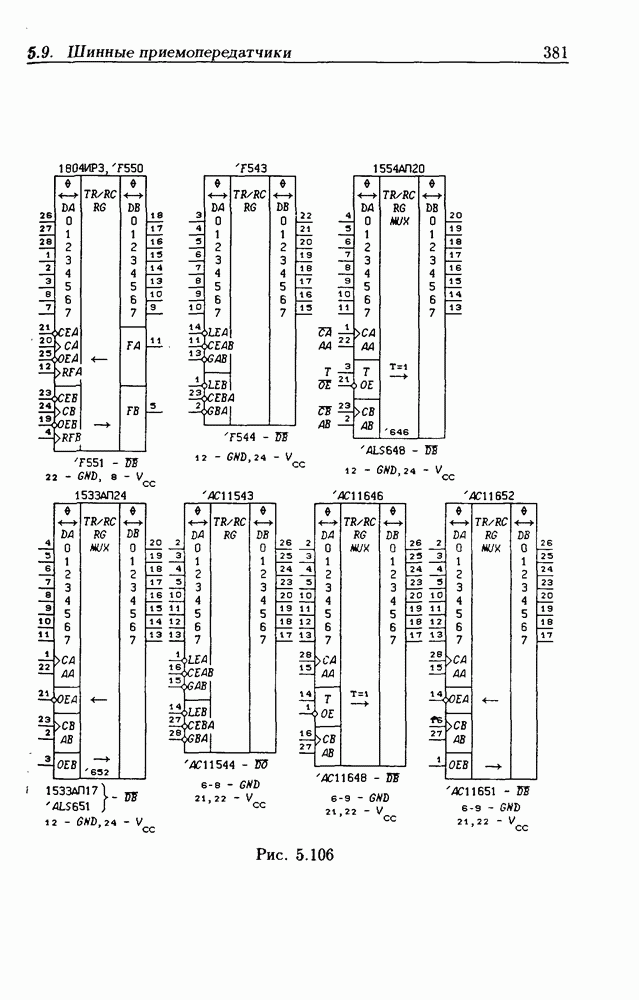
- 5.9. Шинные приемопередатчики
- Шинные приемопередатчики с Z-состоянием выхода.
- Шинные приемопередатчики с открытым коллекторным выходом.
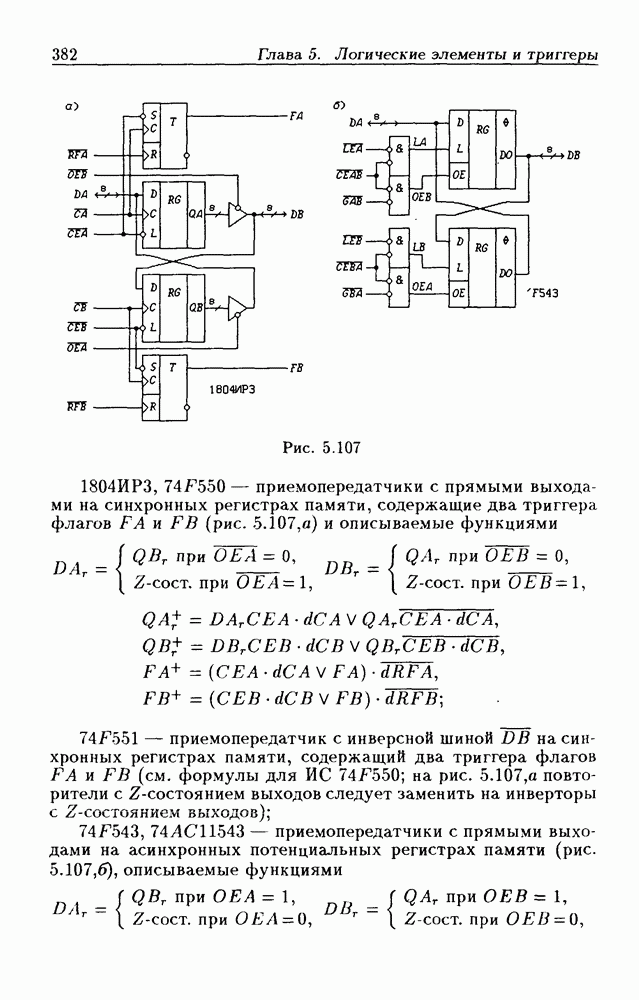
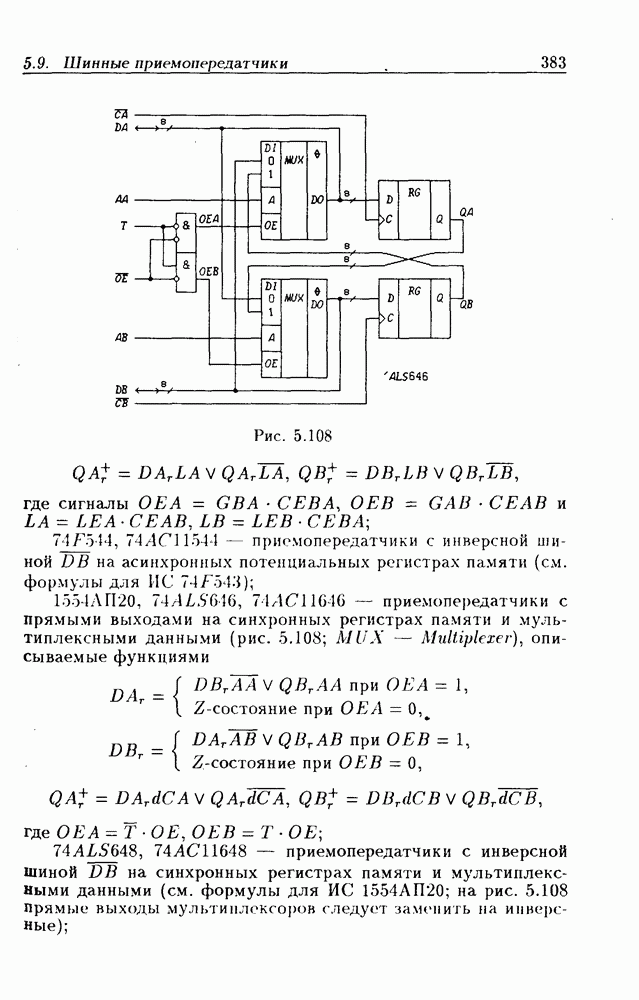
- Шинные приемопередатчики с регистрами памяти.
- Шинные приемопередатчики со сдвигающим регистром.
- Шинные трехнаправленные приемопередатчики.
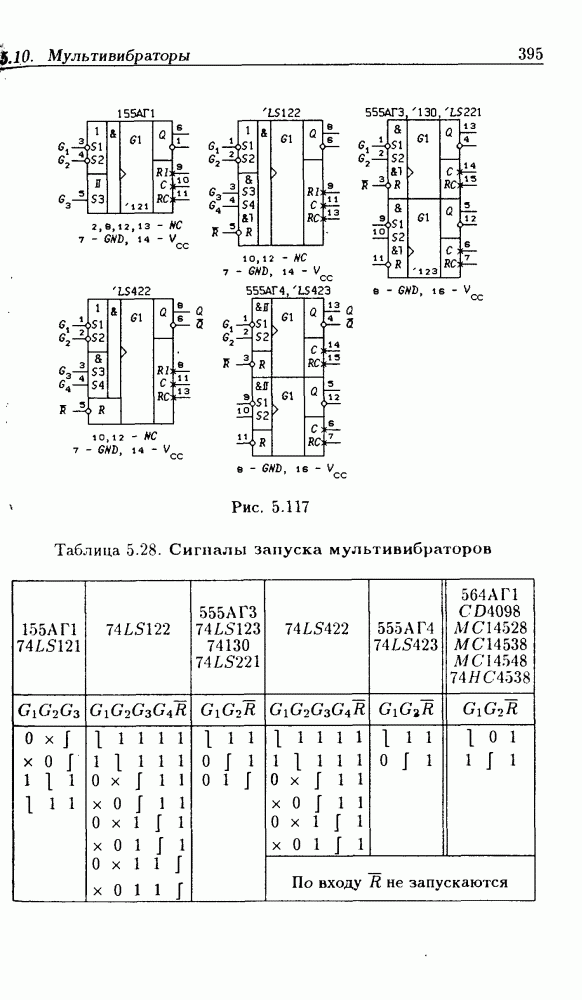
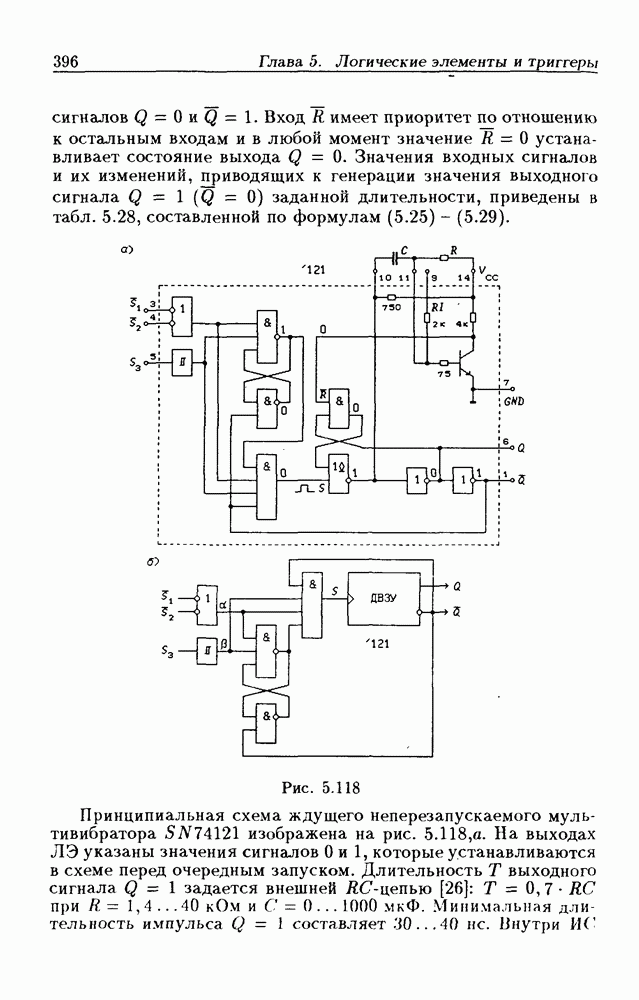
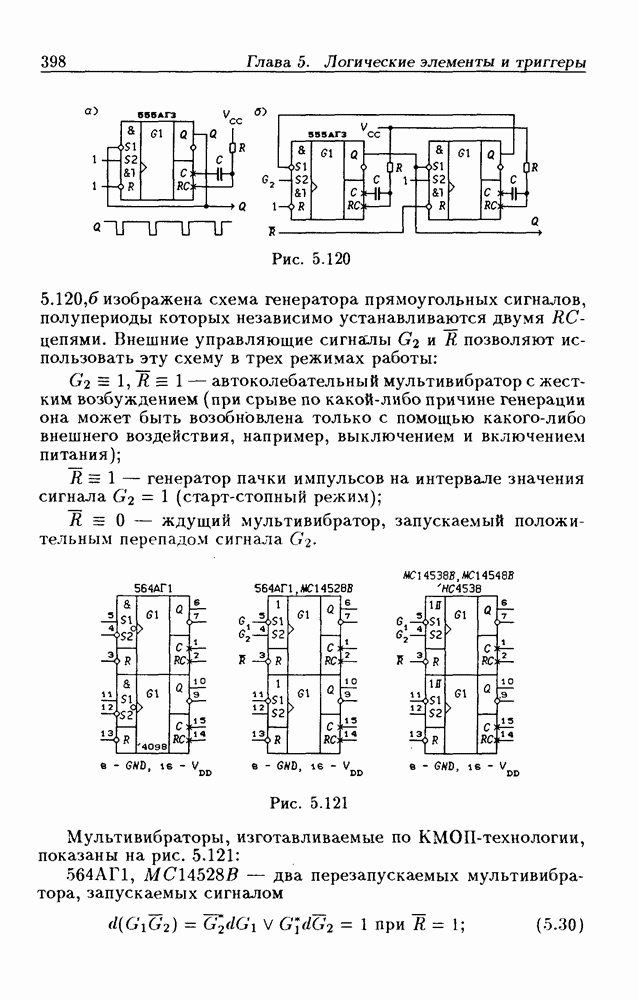
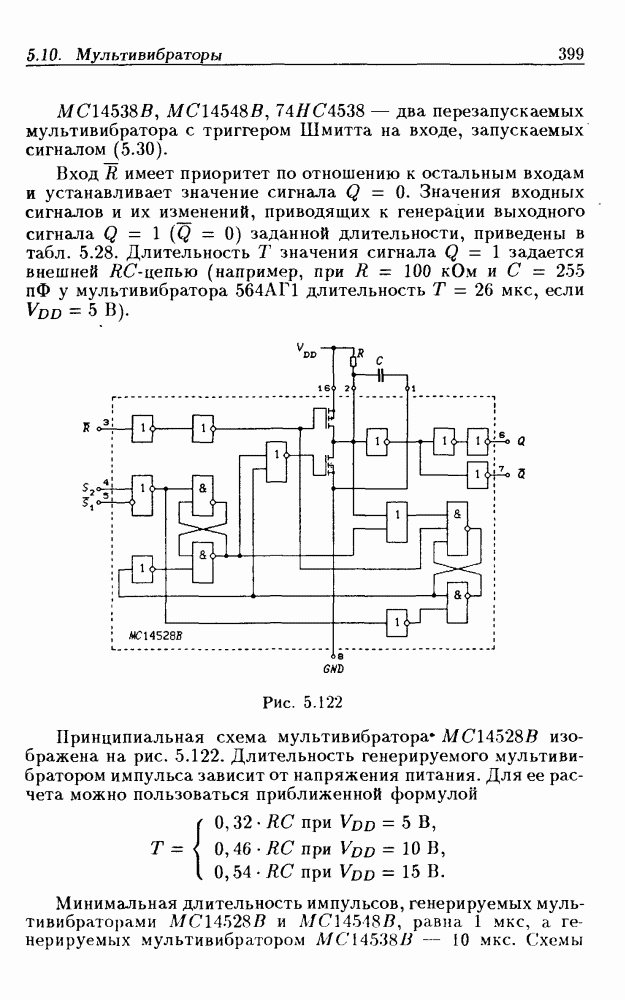
- 5.10. Мультивибраторы
- 5.11. Генераторы
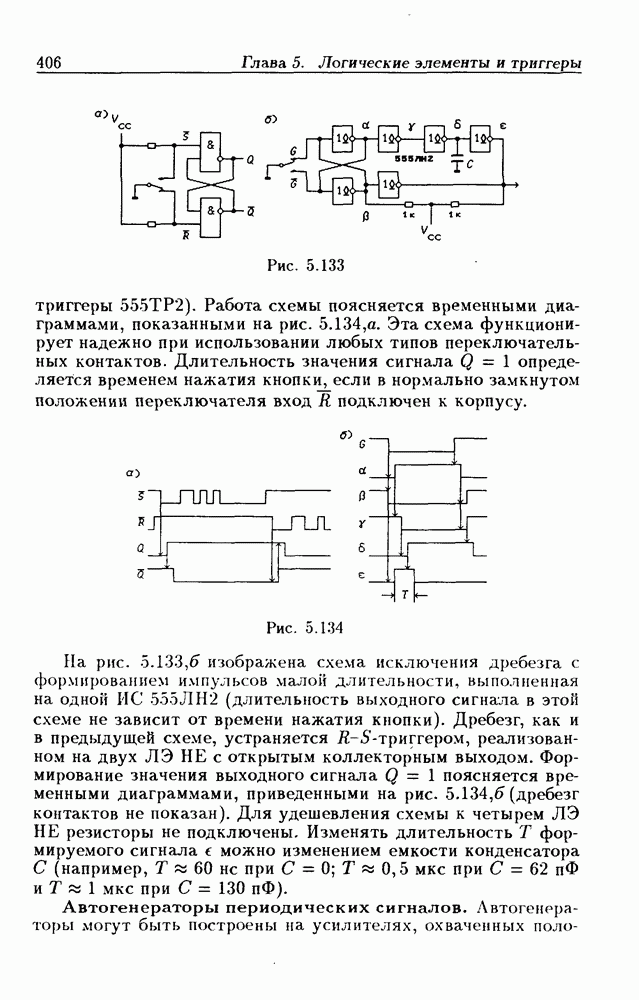
- Схемы устранения «дребезга» механических контактов.
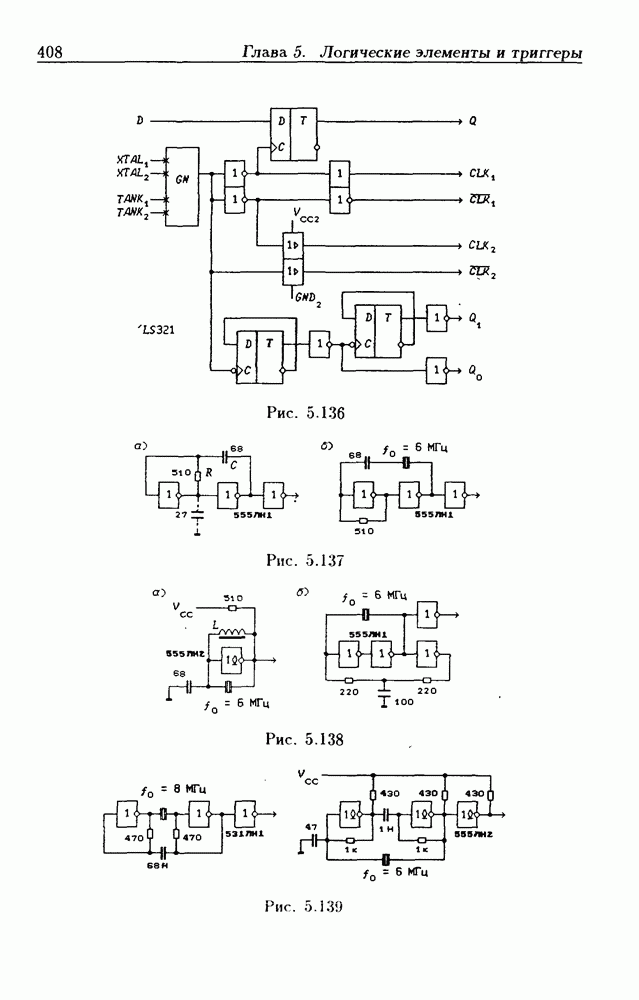
- Автогенераторы периодических сигналов.
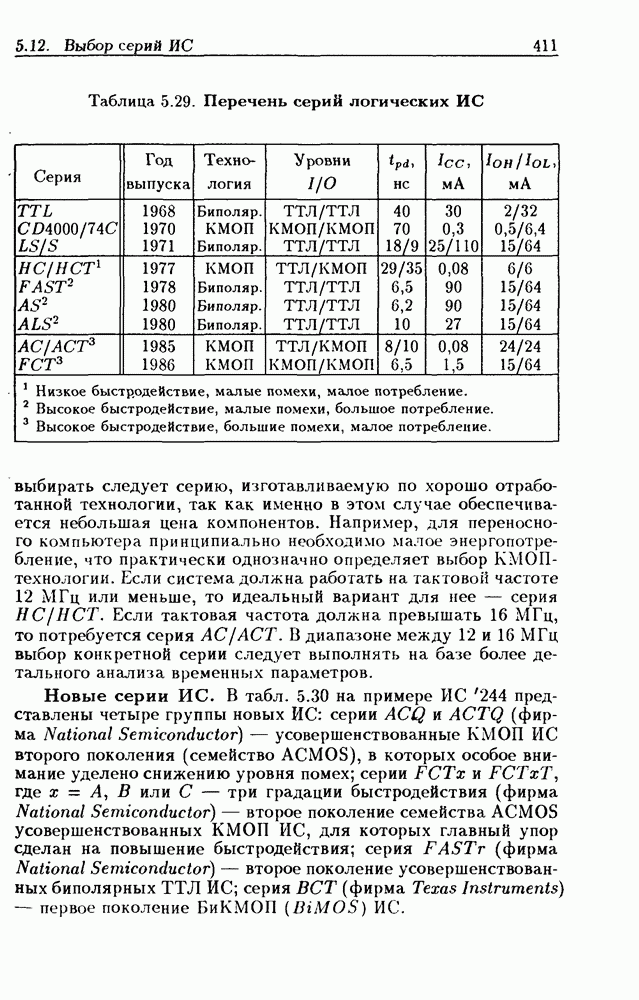
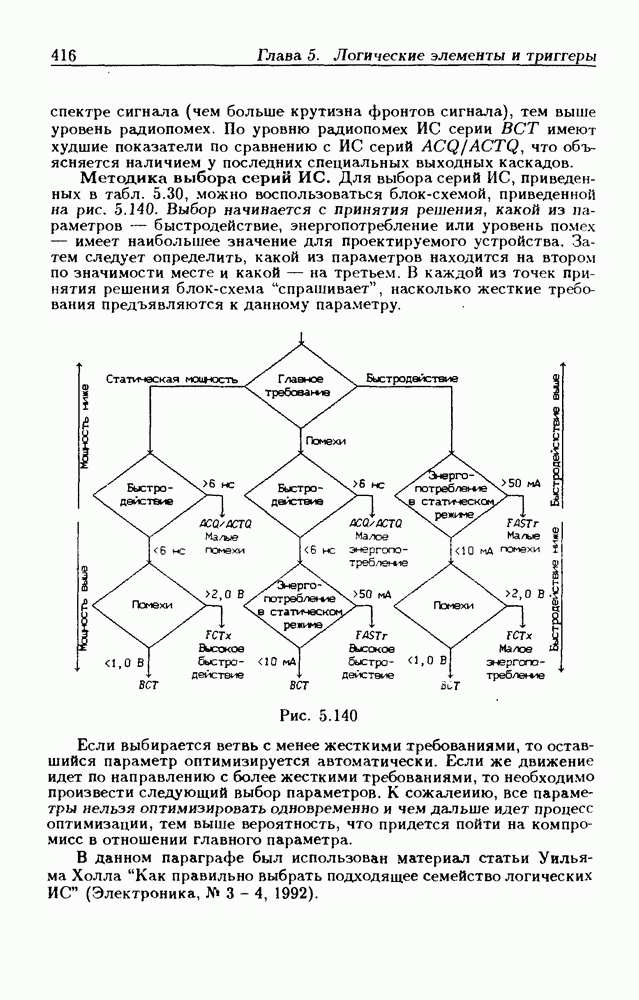
- 5.12. Рекомендации по выбору серий ИС
- Глава 6. Коммутаторы и арифметические устройства
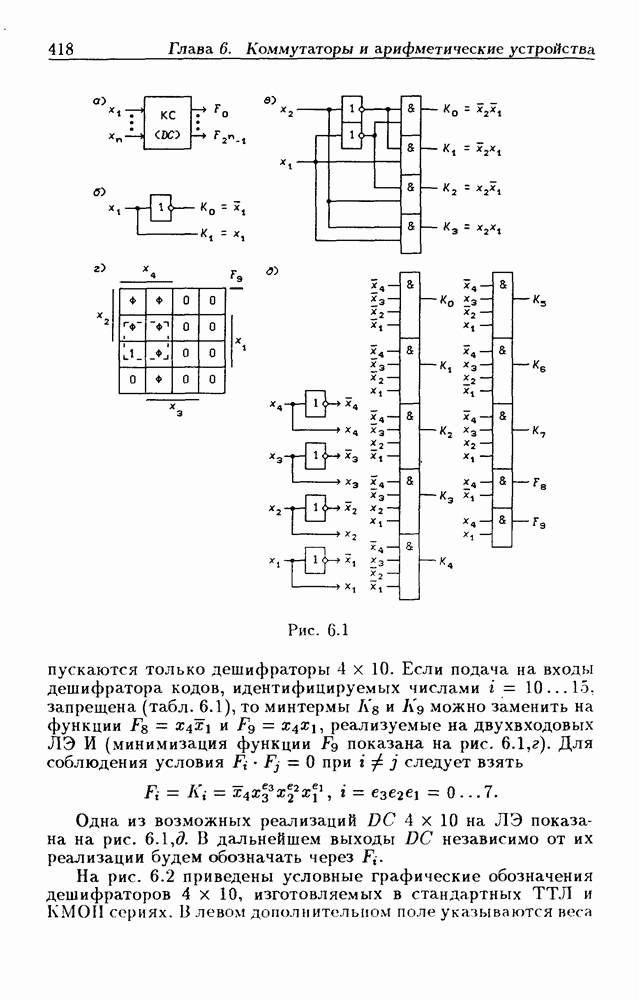
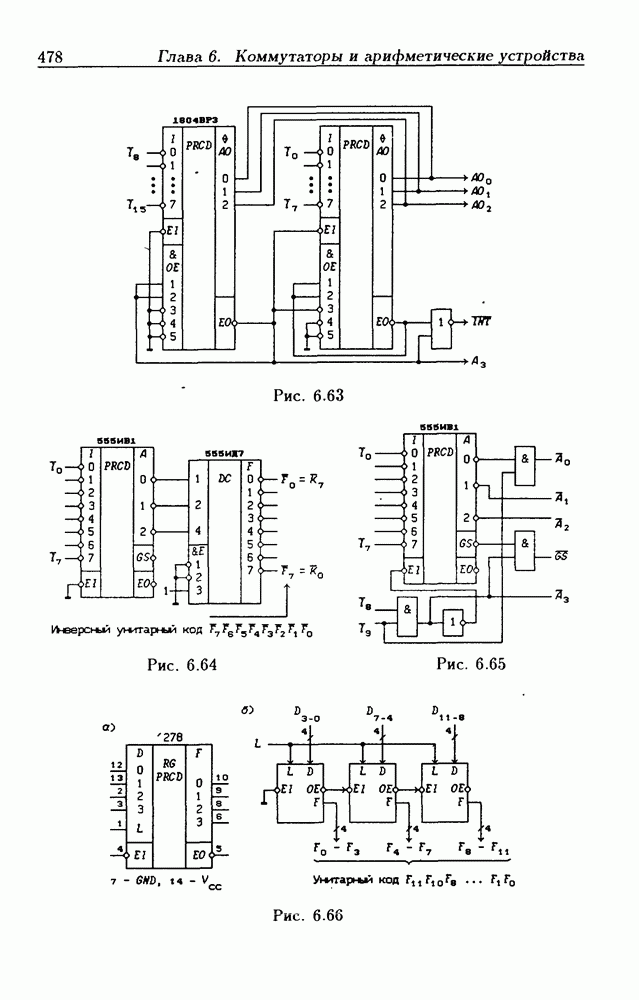
- 6.1. Дешифраторы
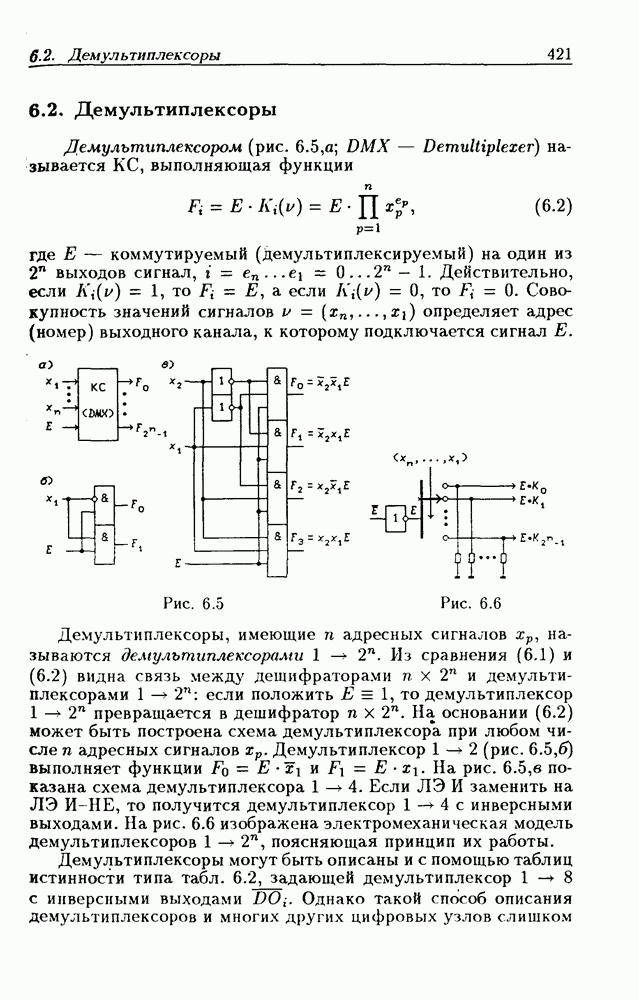
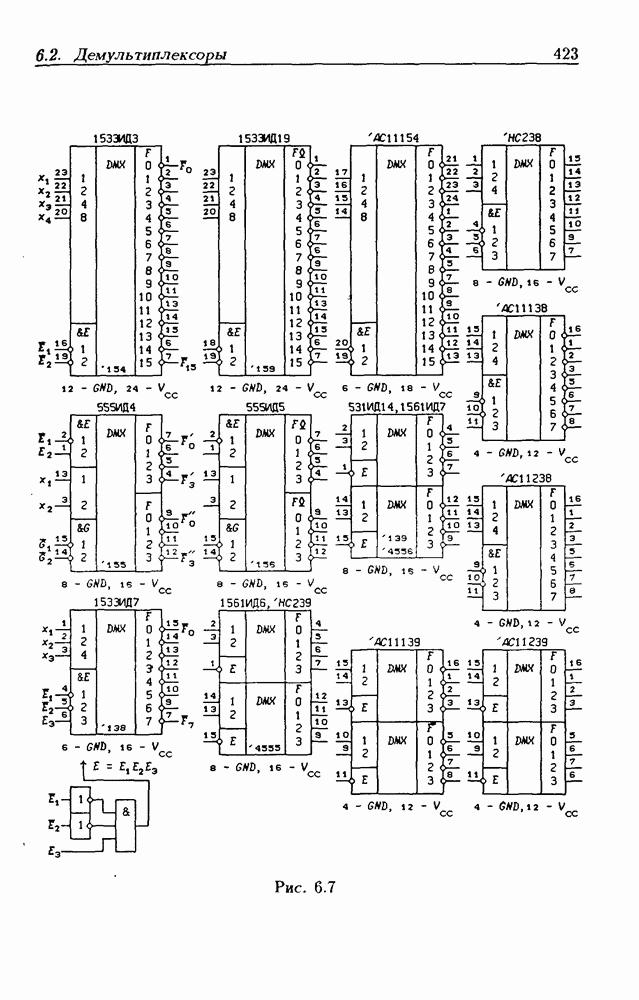
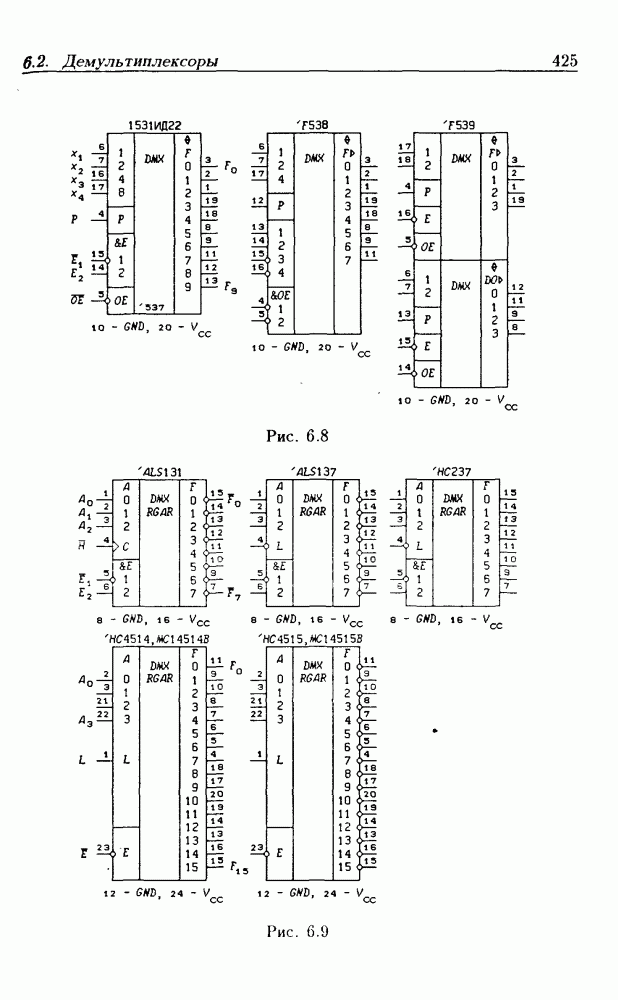
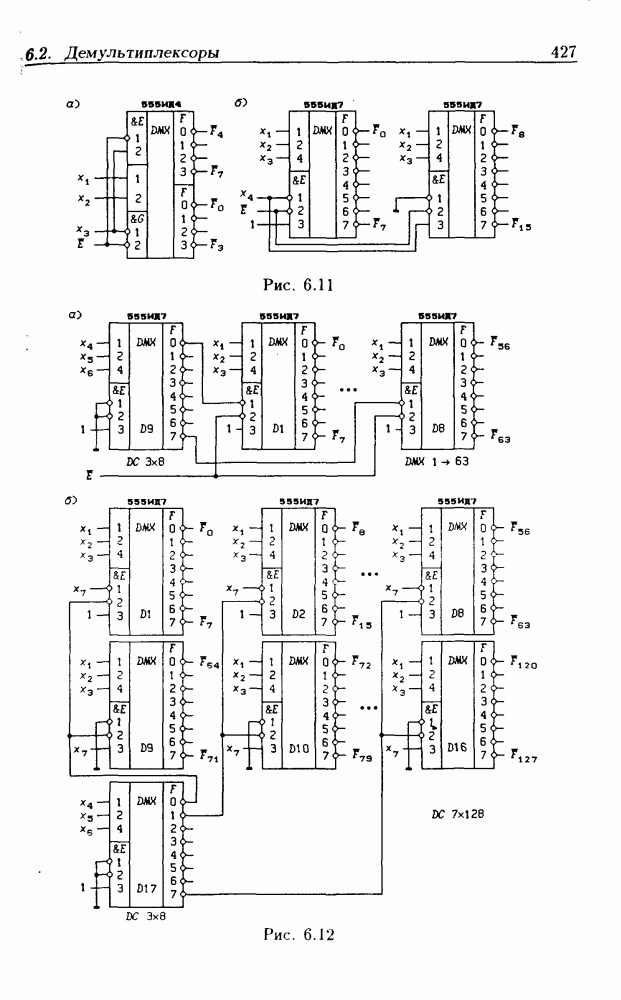
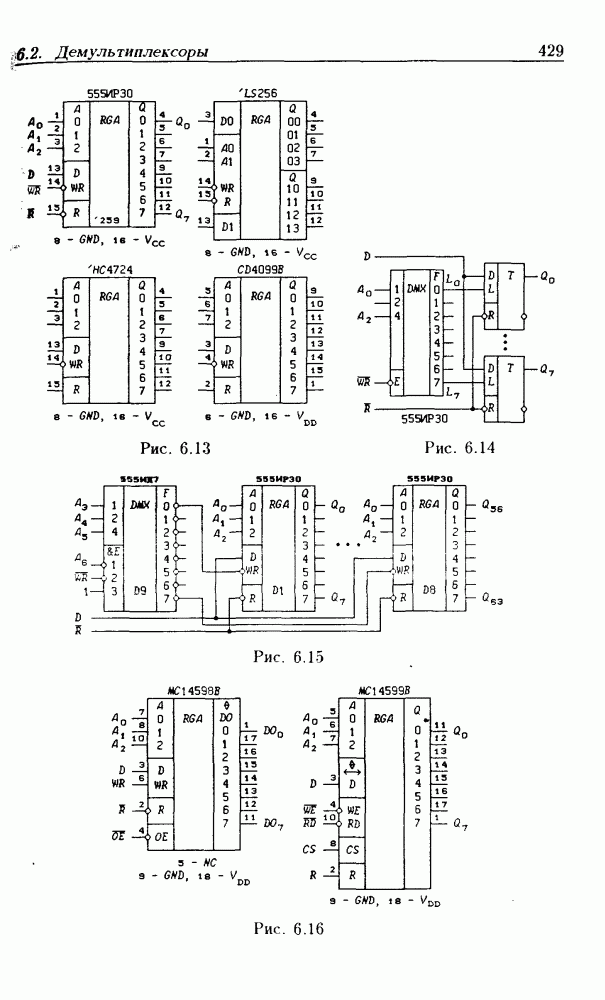
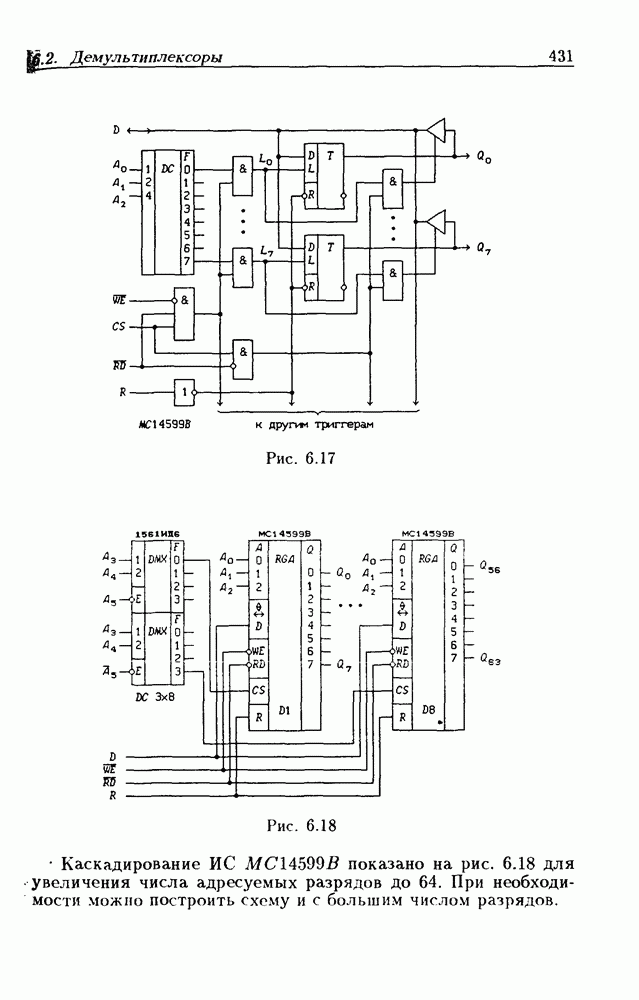
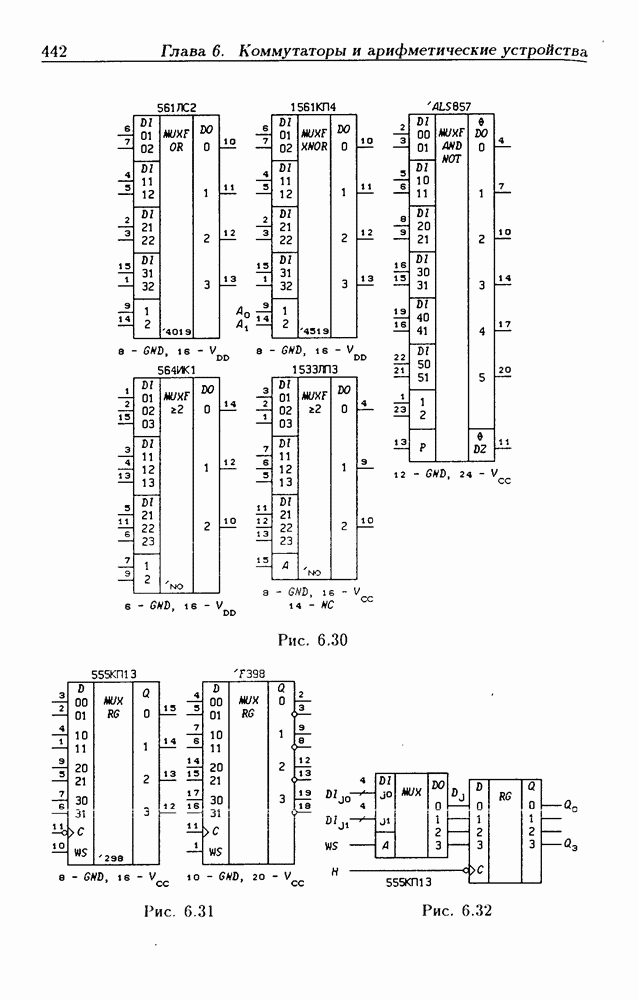
- 6.2. Демультиплексоры
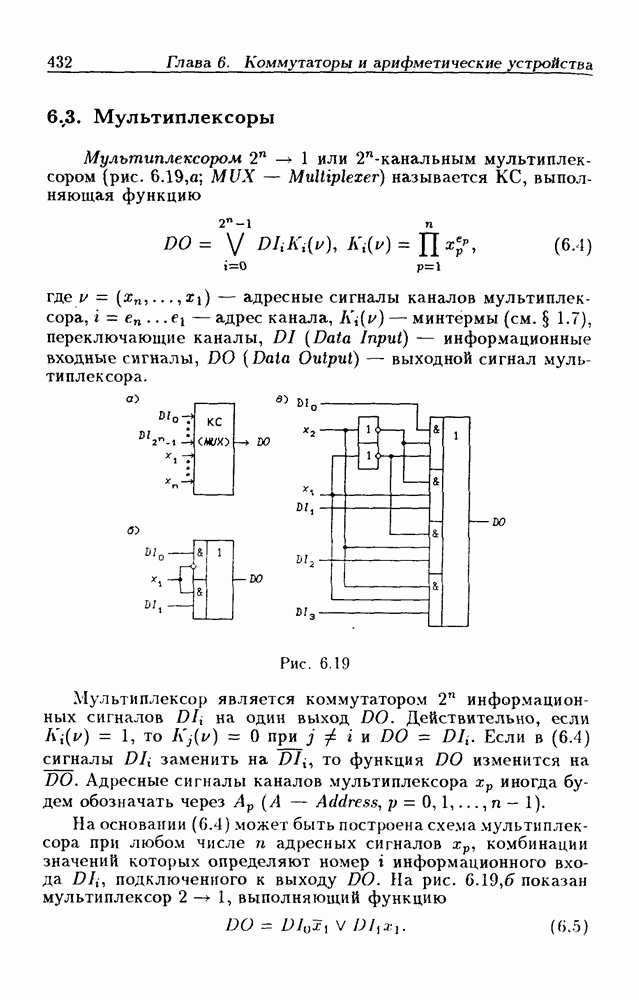
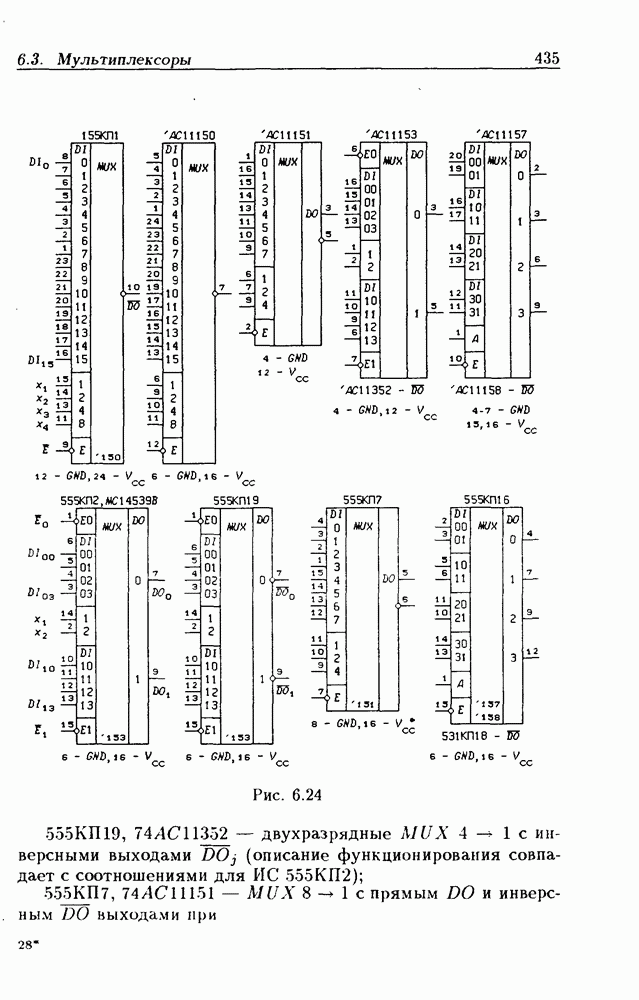
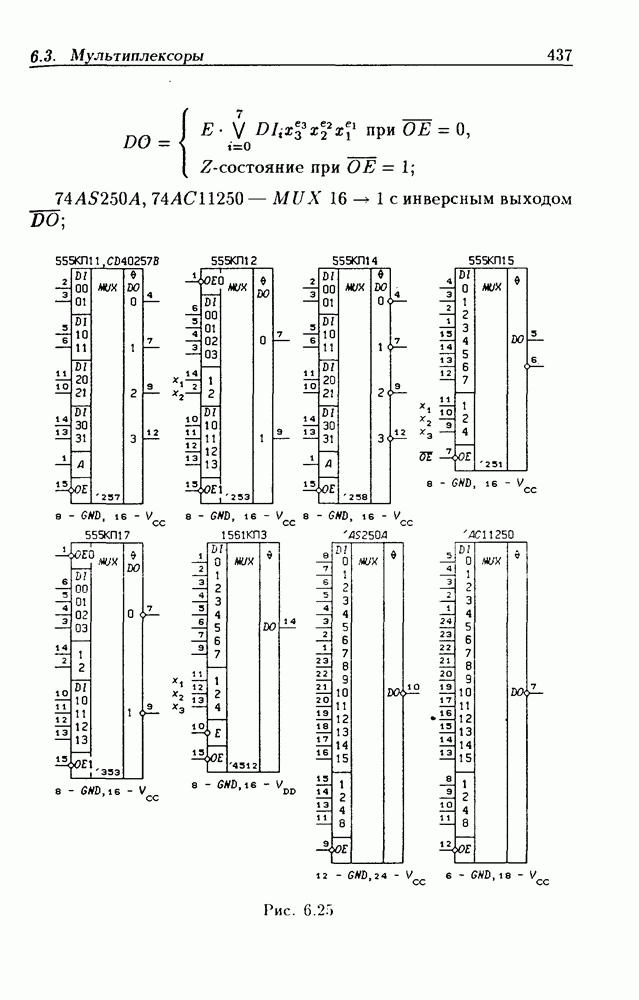
- 6.3. Мультиплексоры
- Мультиплексоры без стробирования.
- Мультиплексоры со стробированием.
- Мультиплексоры с Z-состоянием выхода.
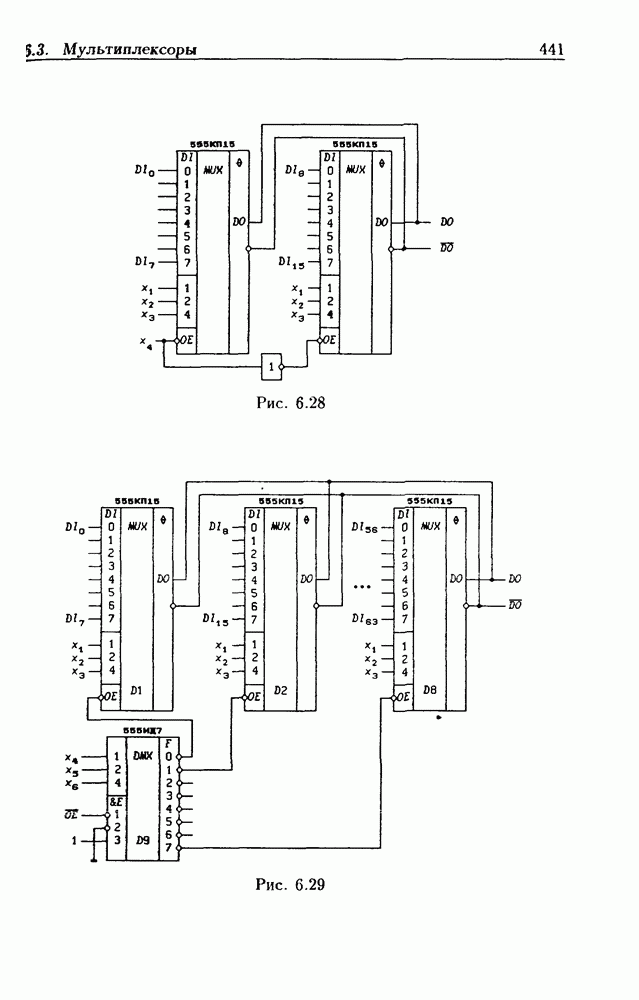
- Каскадирование мультиплексоров.
- Функциональные мультиплексоры.
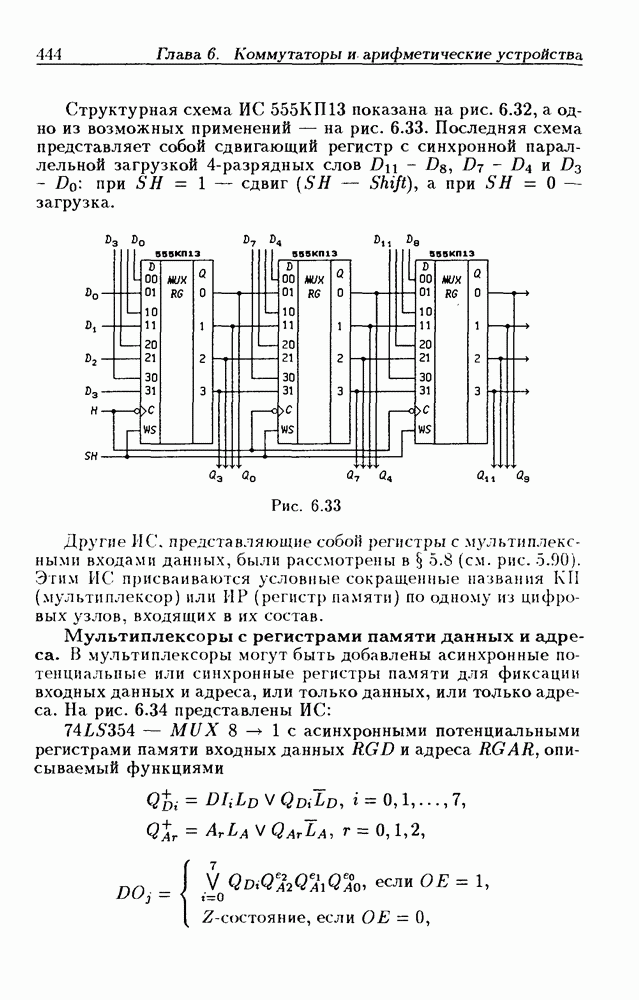
- Регистры памяти с мультиплексными входами данных.
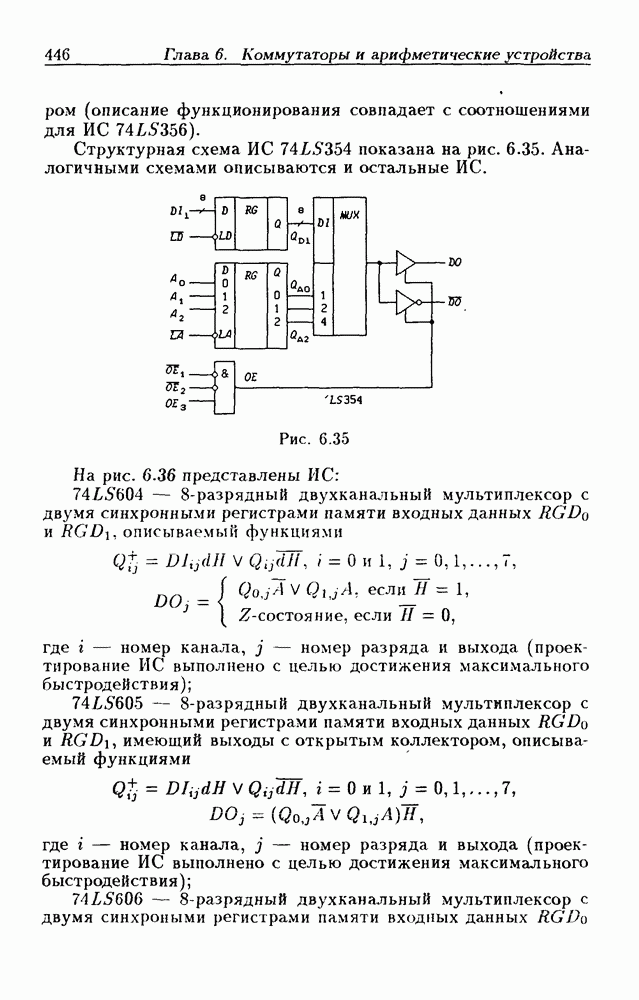
- Мультиплексоры с регистрами памяти данных и адреса.
- Сдвигающие мультиплексоры.
- 6.4. Синтез комбинационных схем и цифровых автоматов на мультиплексорах
- Синтез схем на 8-канальных мультиплексорах.
- Синтез на двухразрядных 4-канальных мультиплексорах.
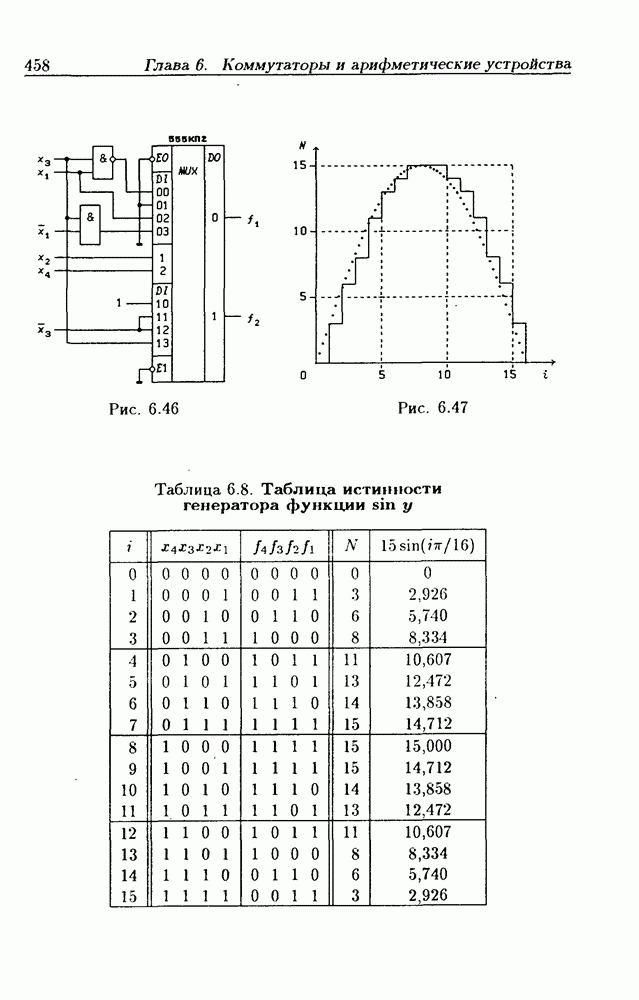
- Синтез генератора синусоидальной функции на мультиплексорах.
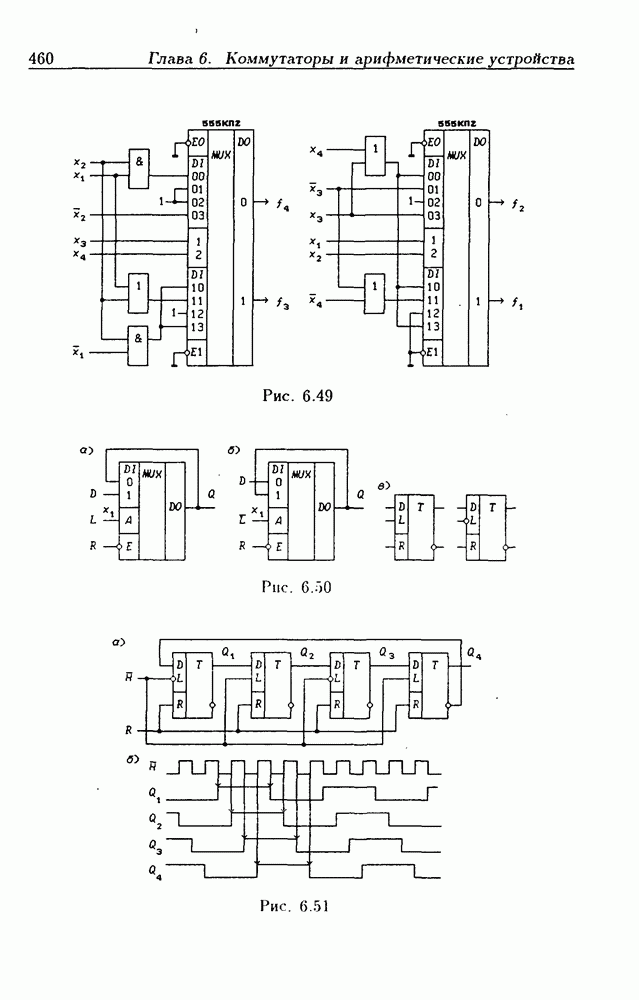
- Синтез триггеров на мультиплексорах.
- Синтез счетчиков на мультиплексорах.
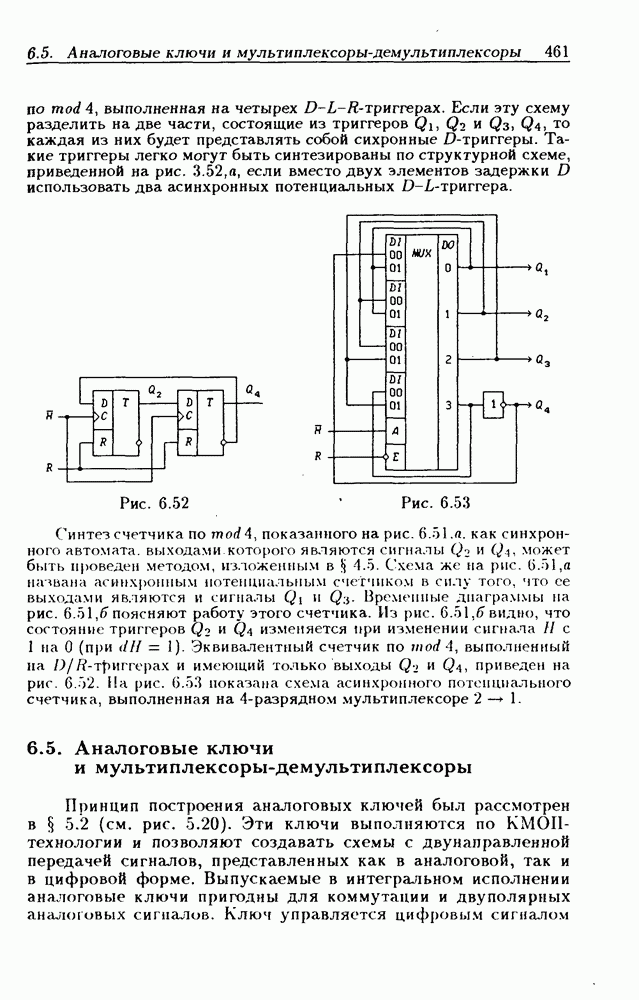
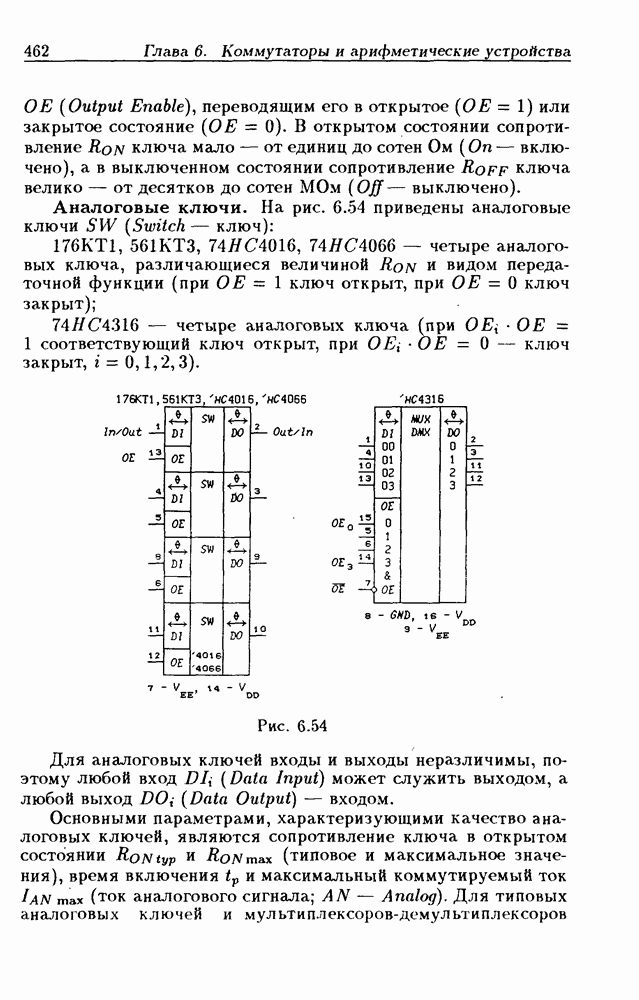
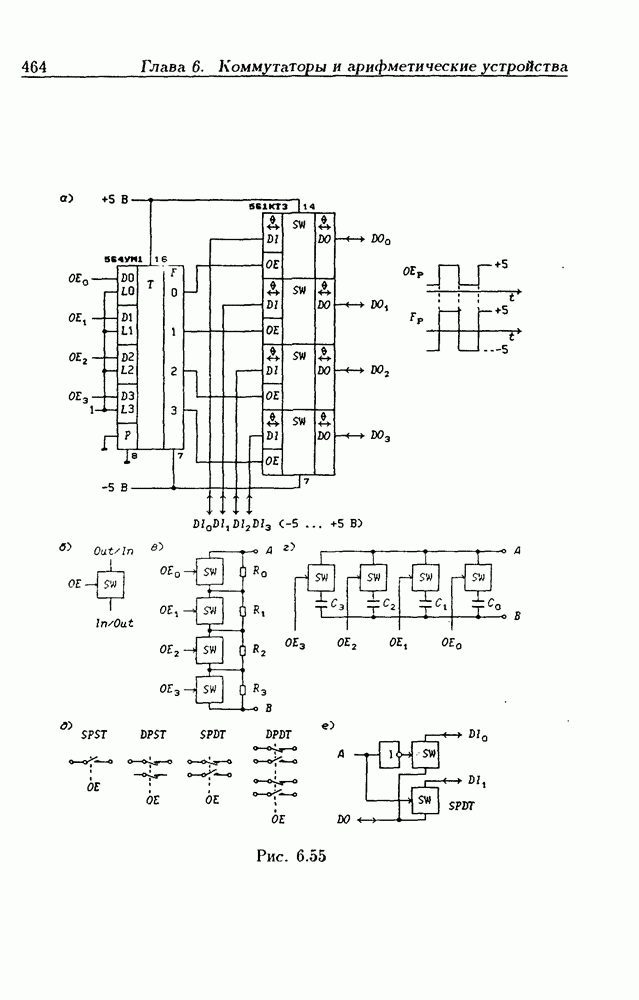
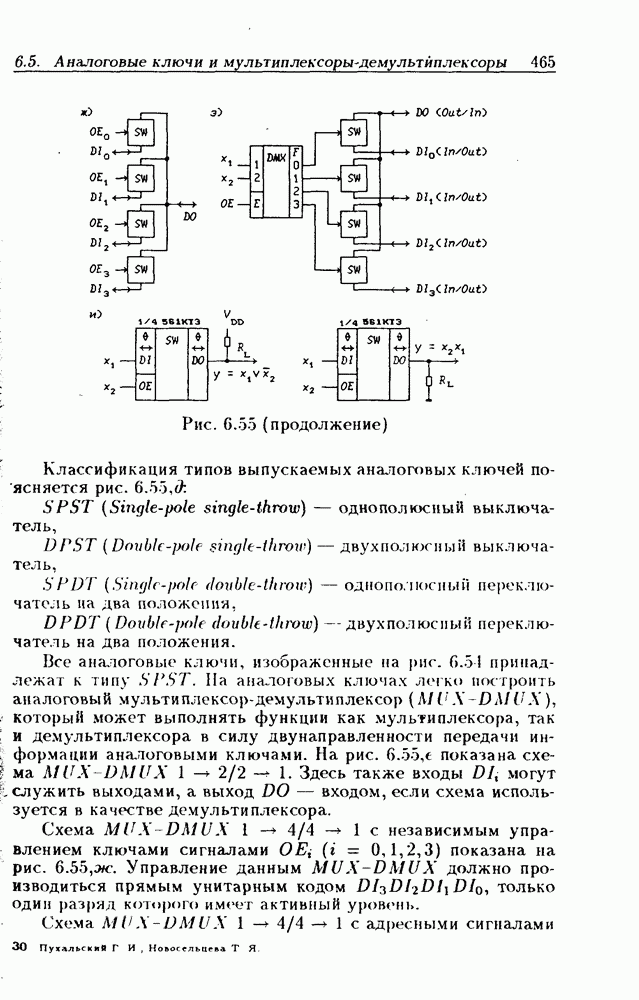
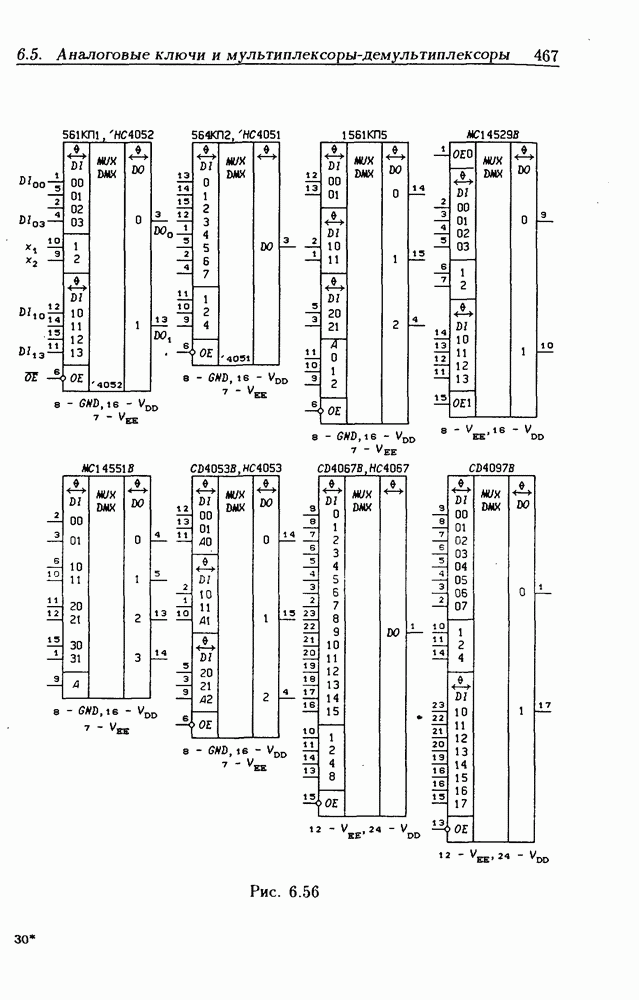
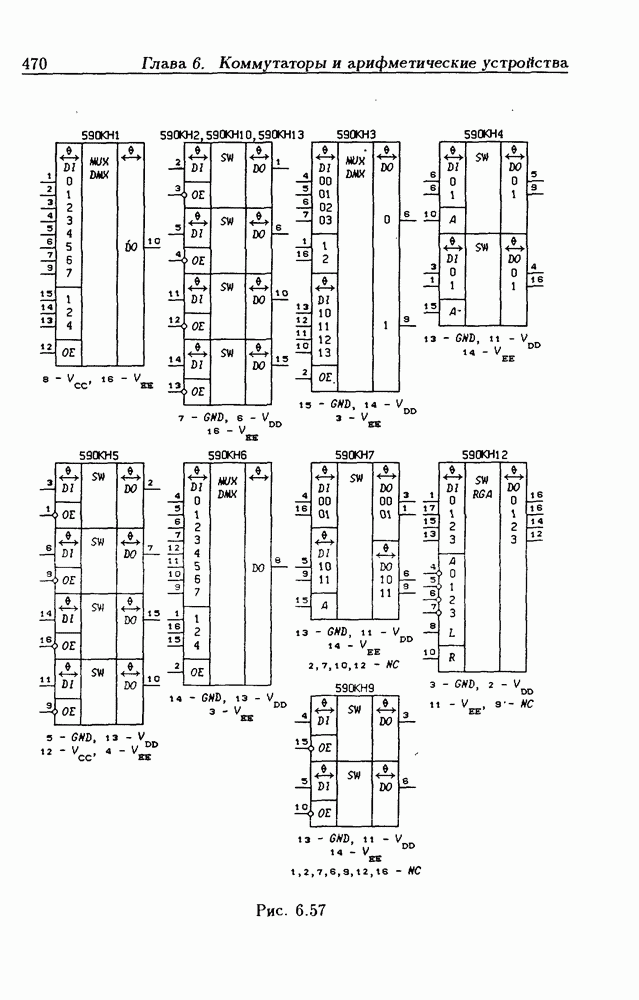
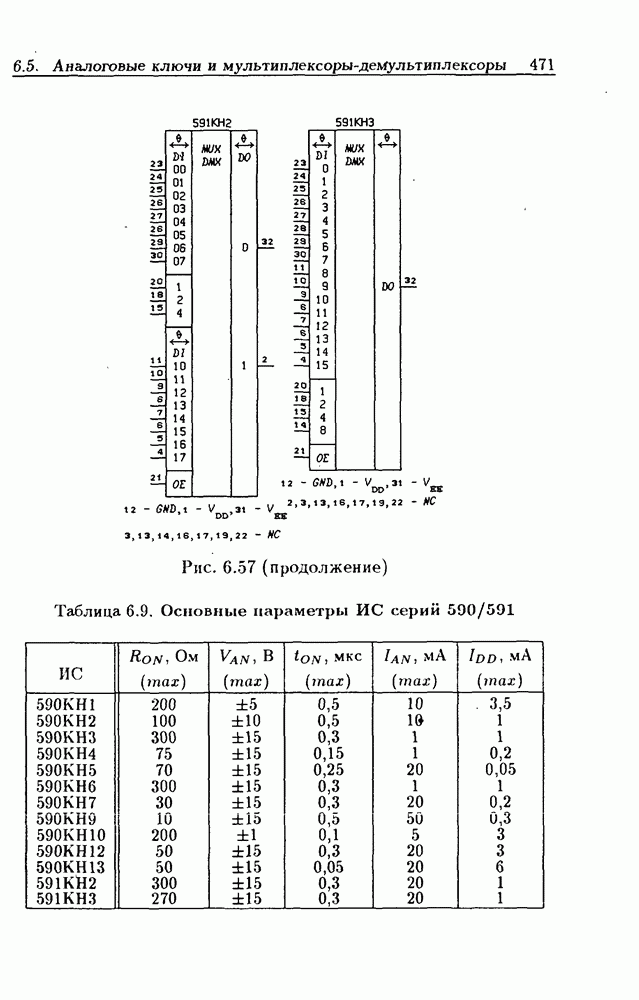
- 6.5. Аналоговые ключи и мультиплексоры-демультиплексоры
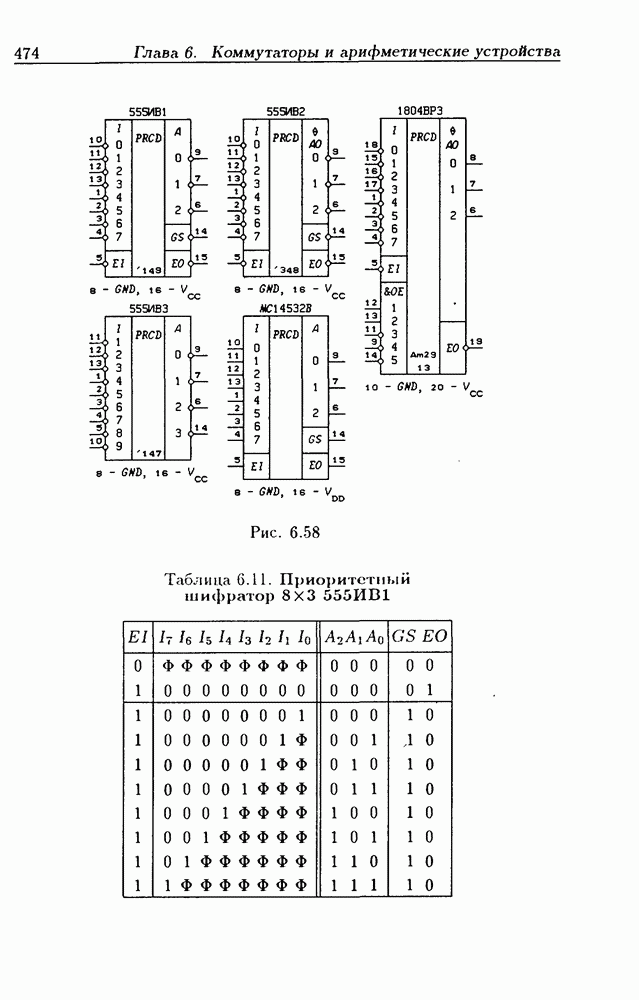
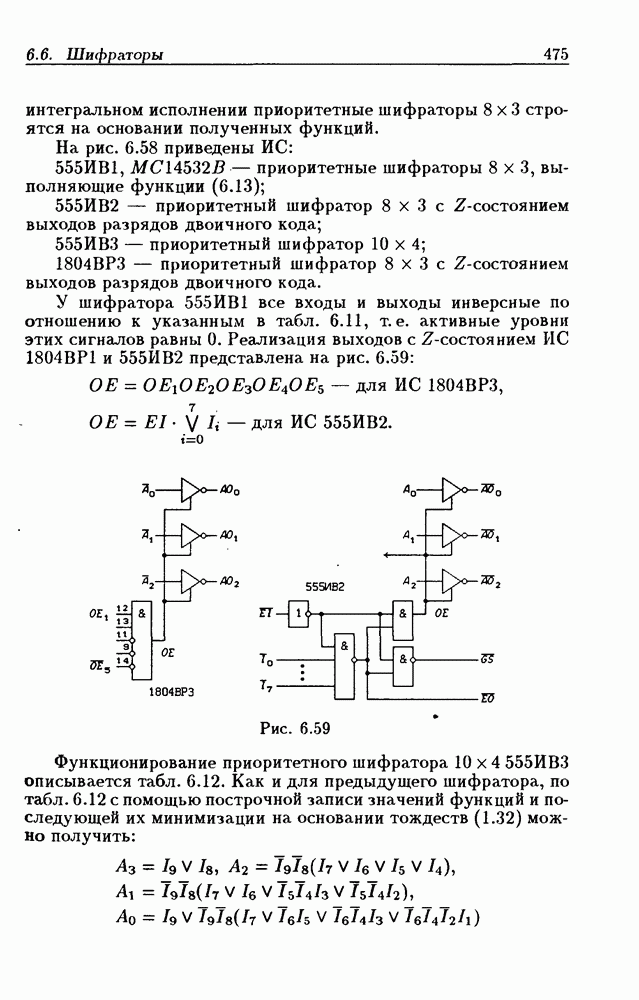
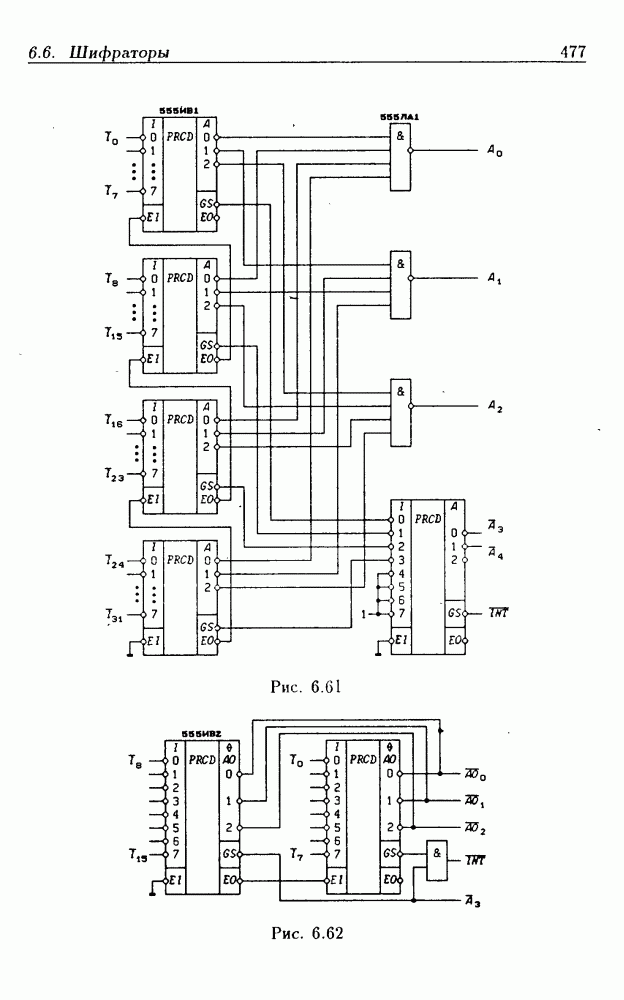
- 6.6. Шифраторы
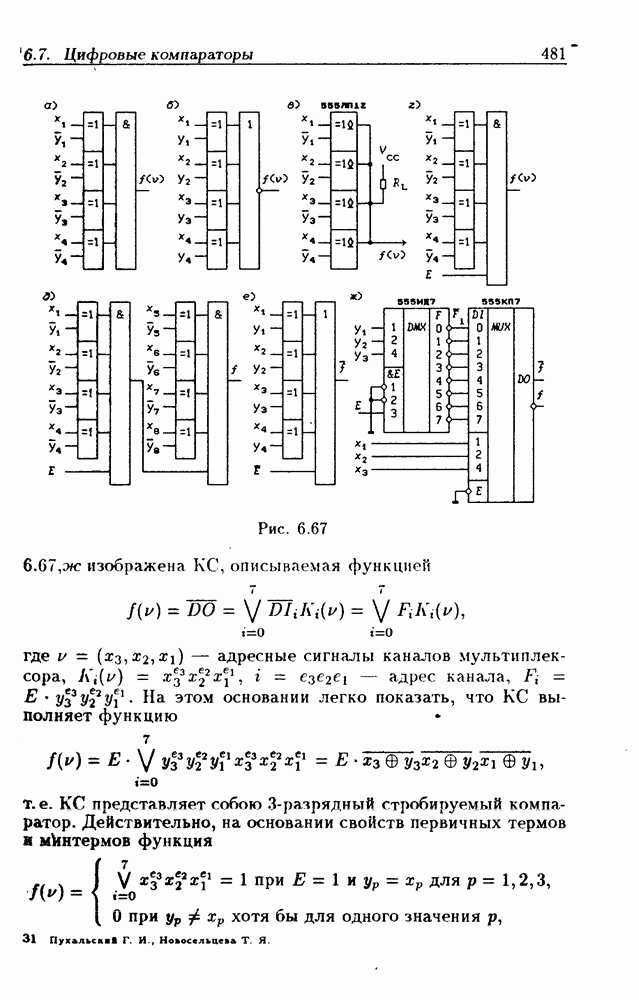
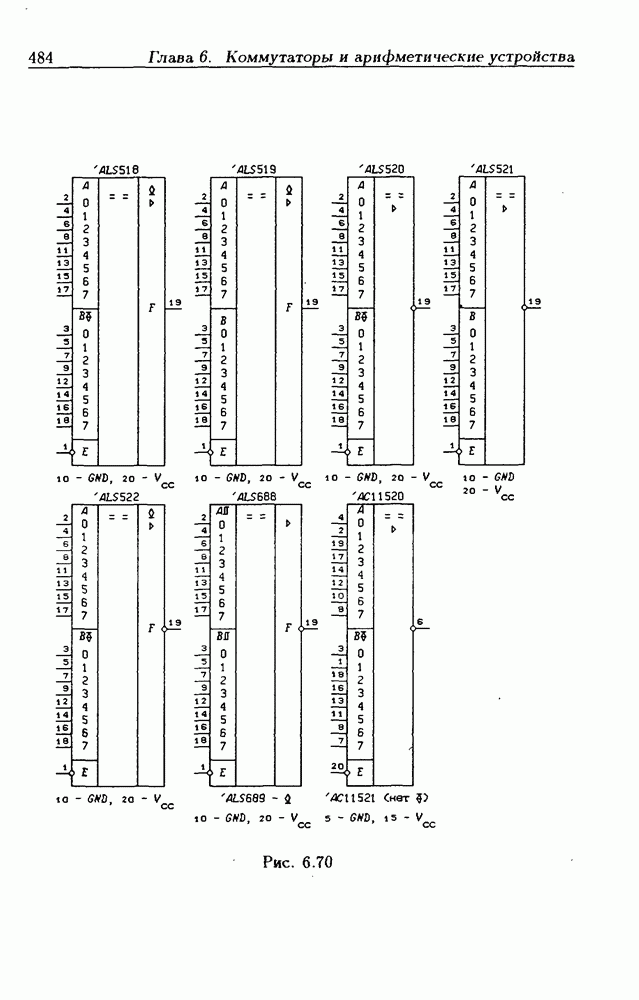
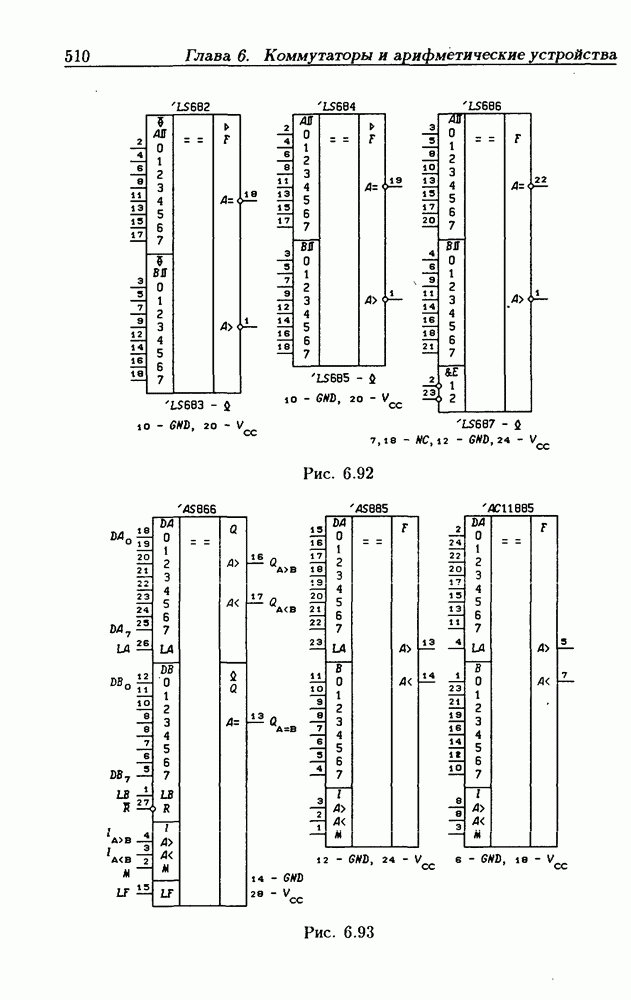
- 6.7. Цифровые компараторы
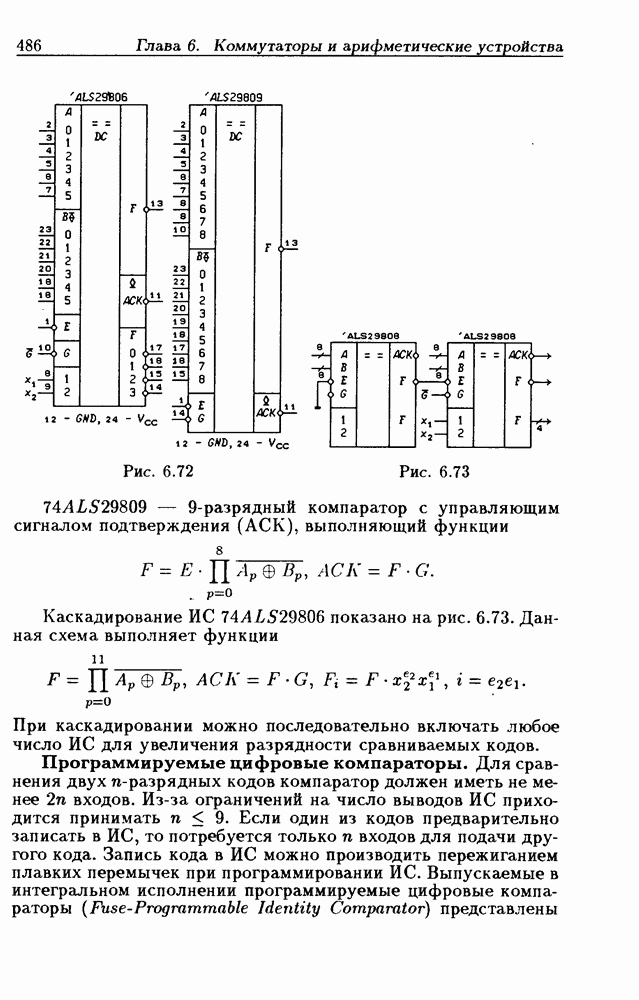
- Программируемые цифровые компараторы.
- Адресные компараторы.
- Применения адресных компараторов.
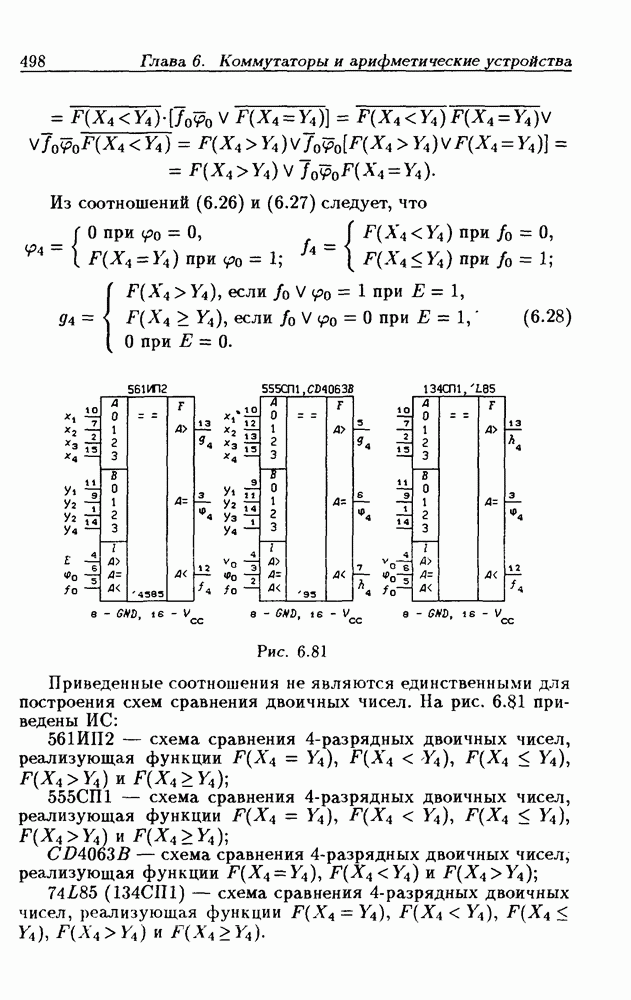
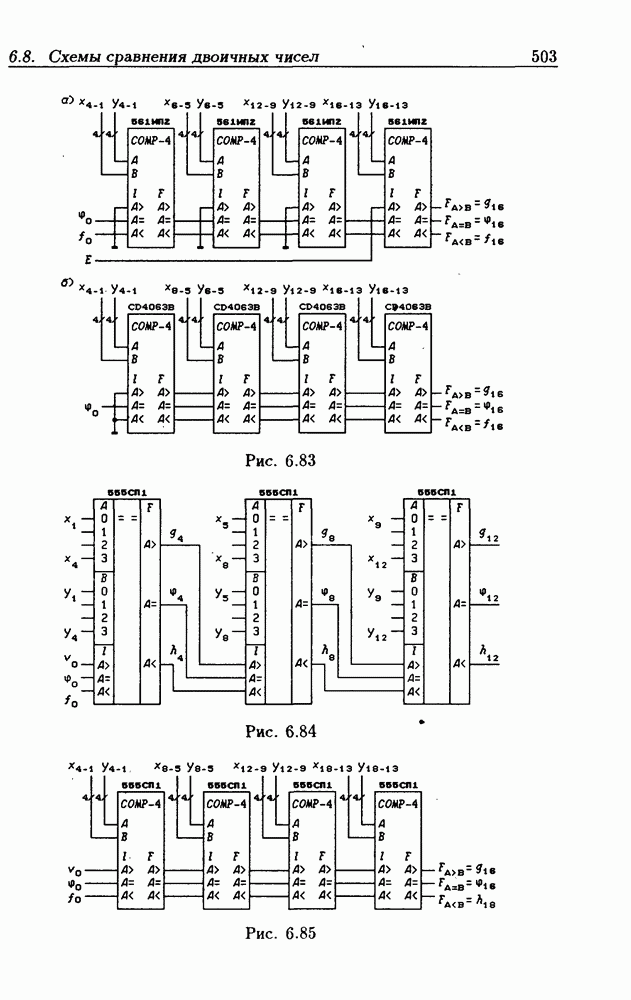
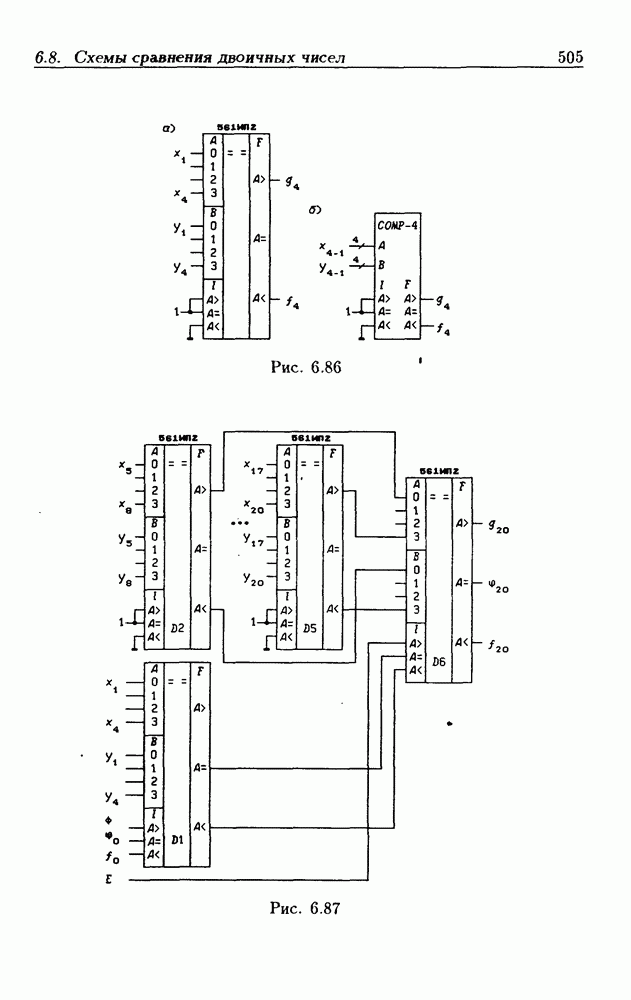
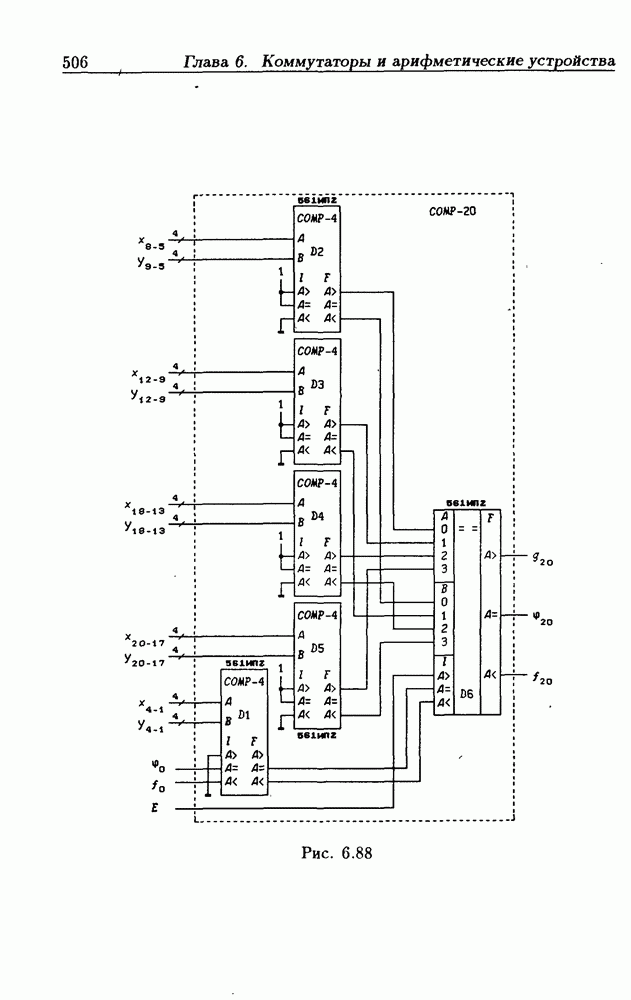
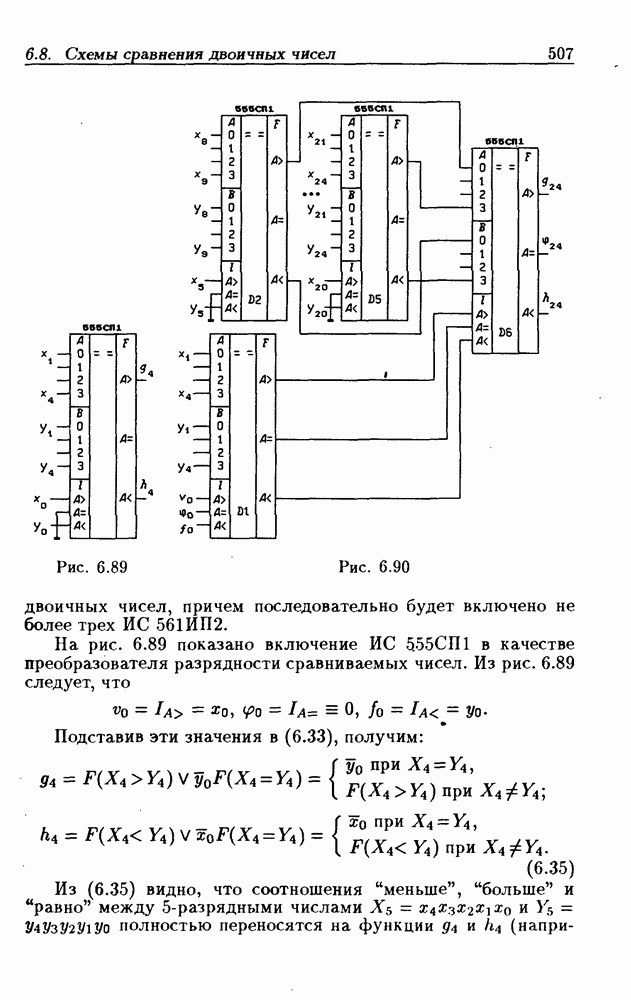
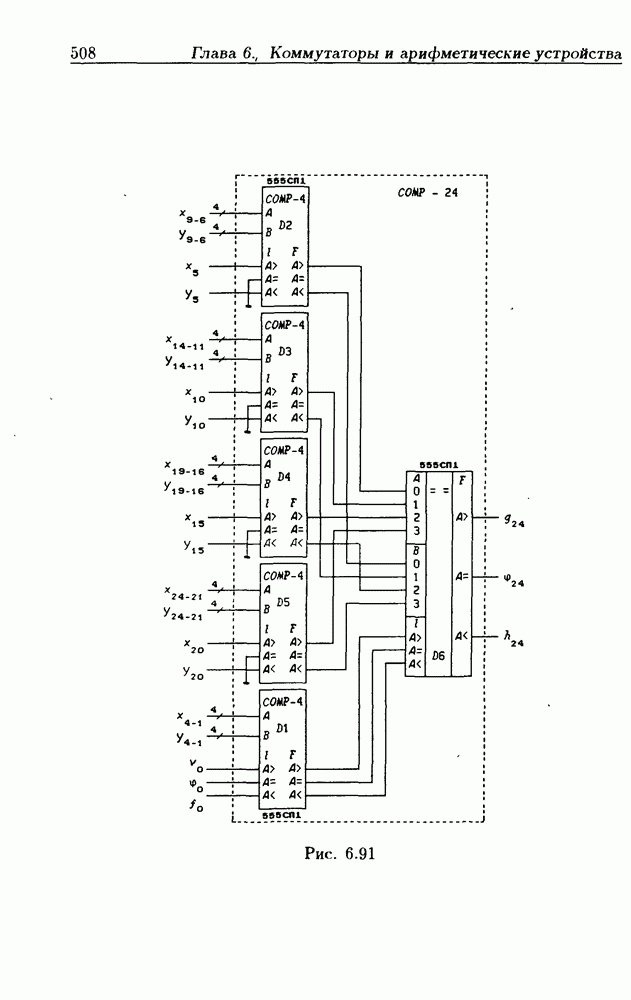
- 6.8. Схемы сравнения двоичных чисел
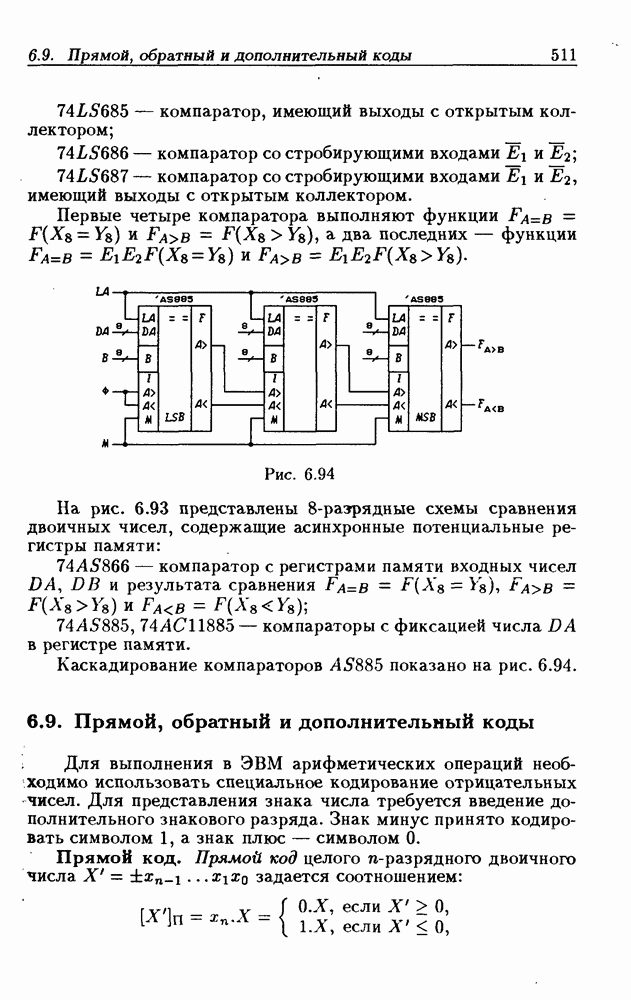
- 8-разрядные схемы сравнения двоичных чисел.
- 6.9. Прямой, обратный и дополнительный коды
- Дополнительный код.
- Сложение чисел в обратном коде.
- Код с избытком 3.
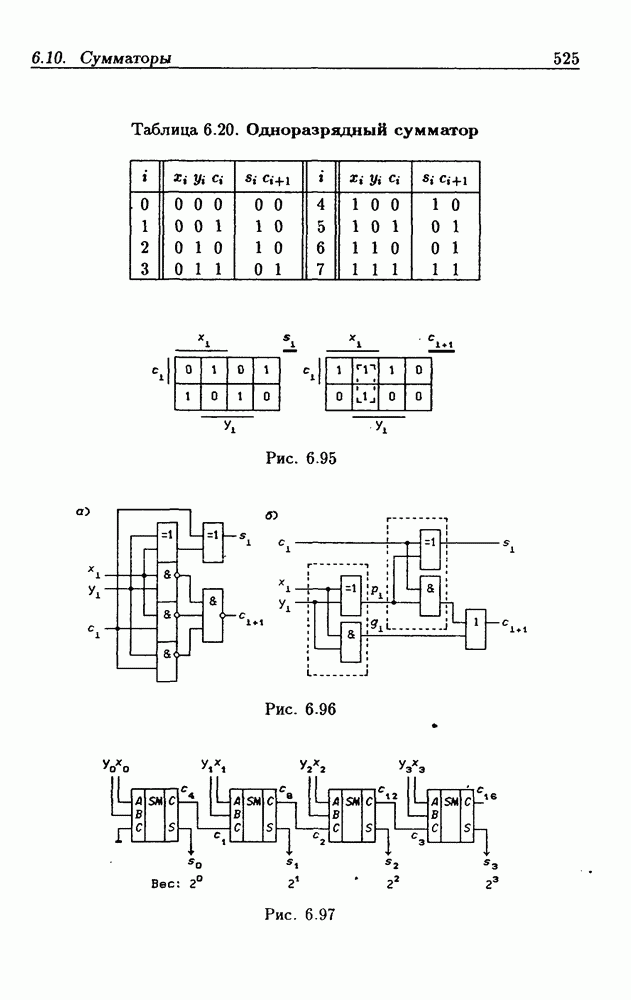
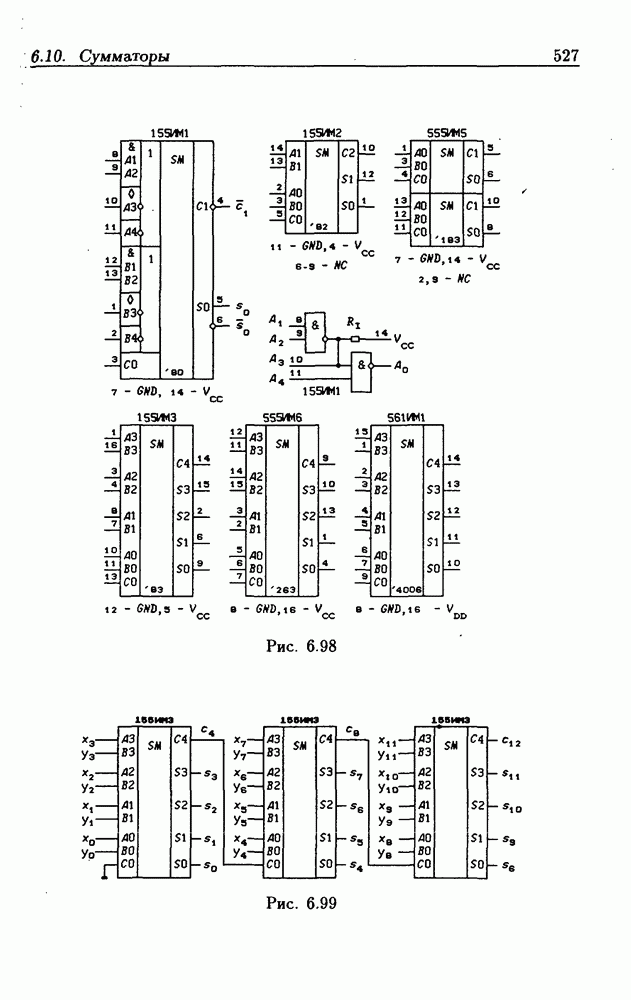
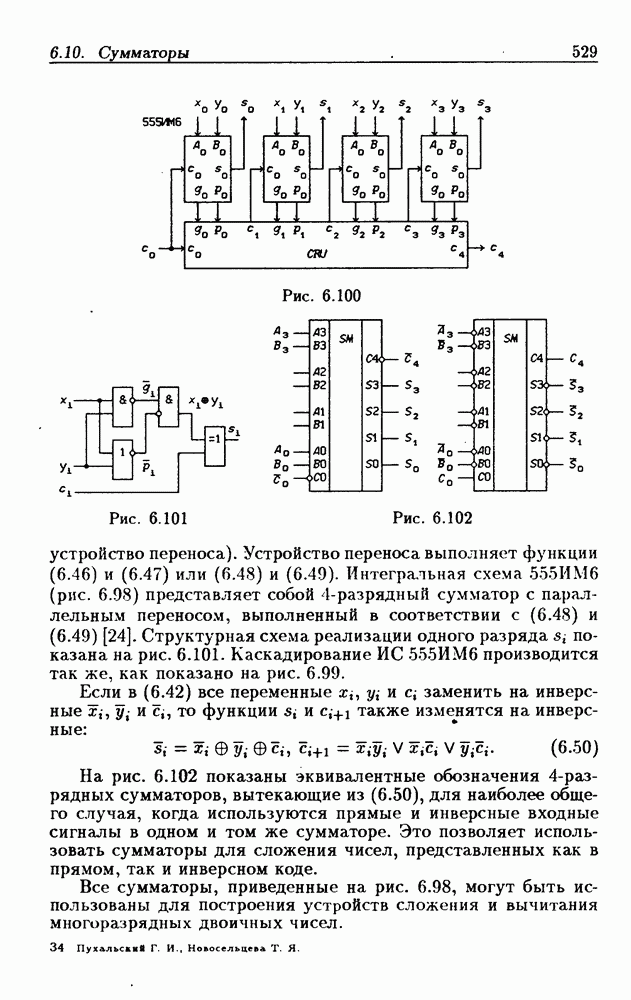
- 6.10. Сумматоры
- Двоичные параллельные сумматоры с последовательным переносом.
- Двоичные сумматоры с параллельным переносом.
- Применения сумматоров.
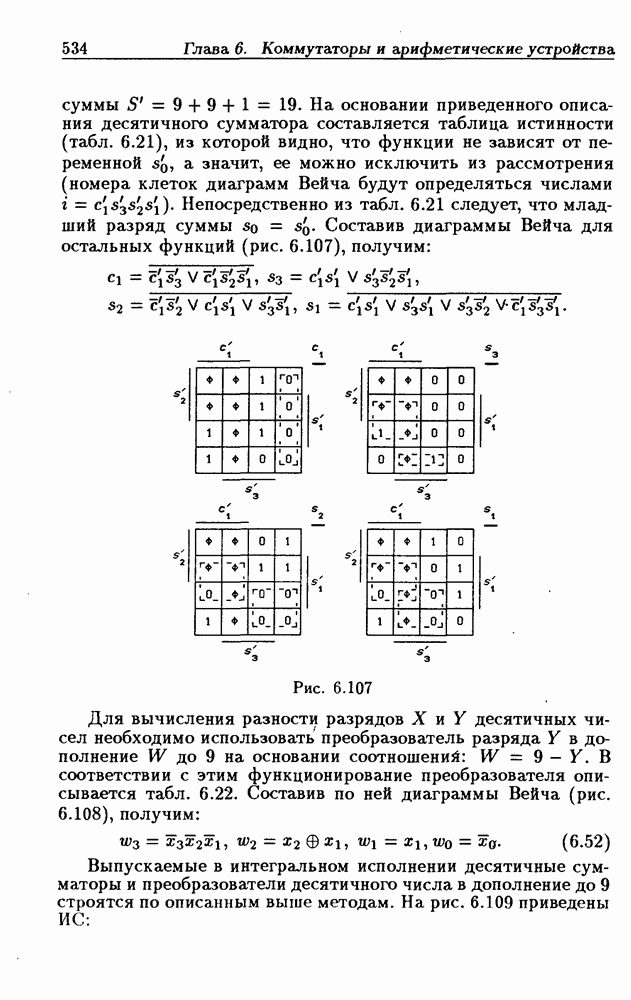
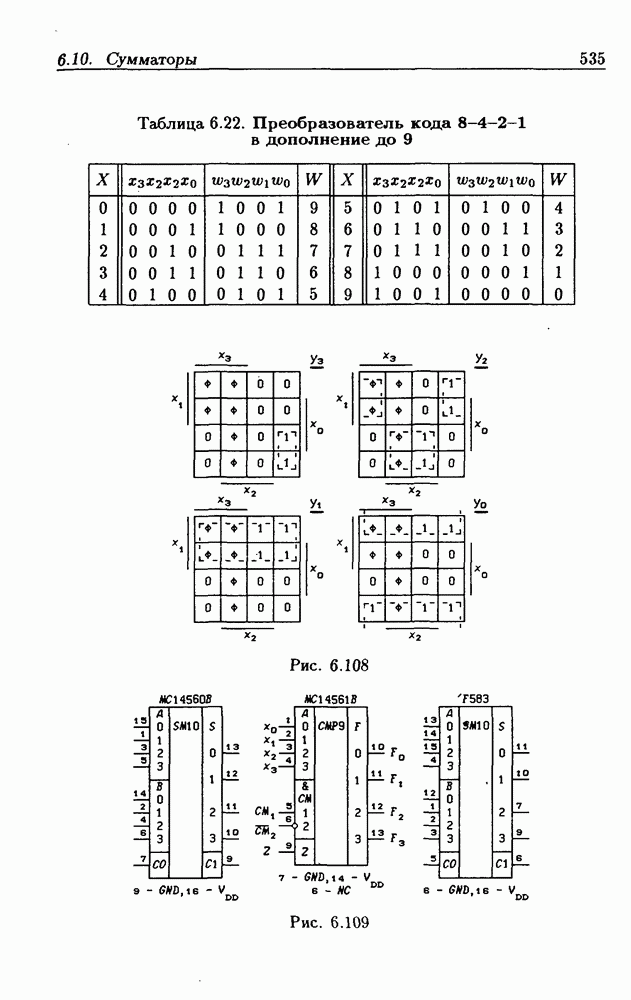
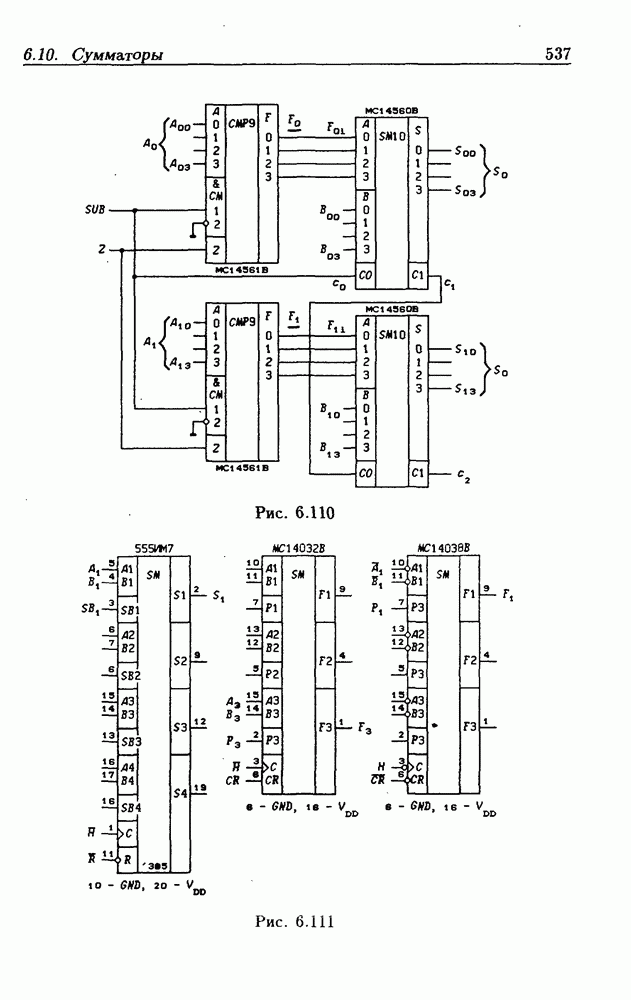
- Десятичные сумматоры.
- Последовательные двоичные сумматоры.
- 6.11. Арифметическо-логические устройства
- 6.12. Пороговые схемы и мажоритарные элементы
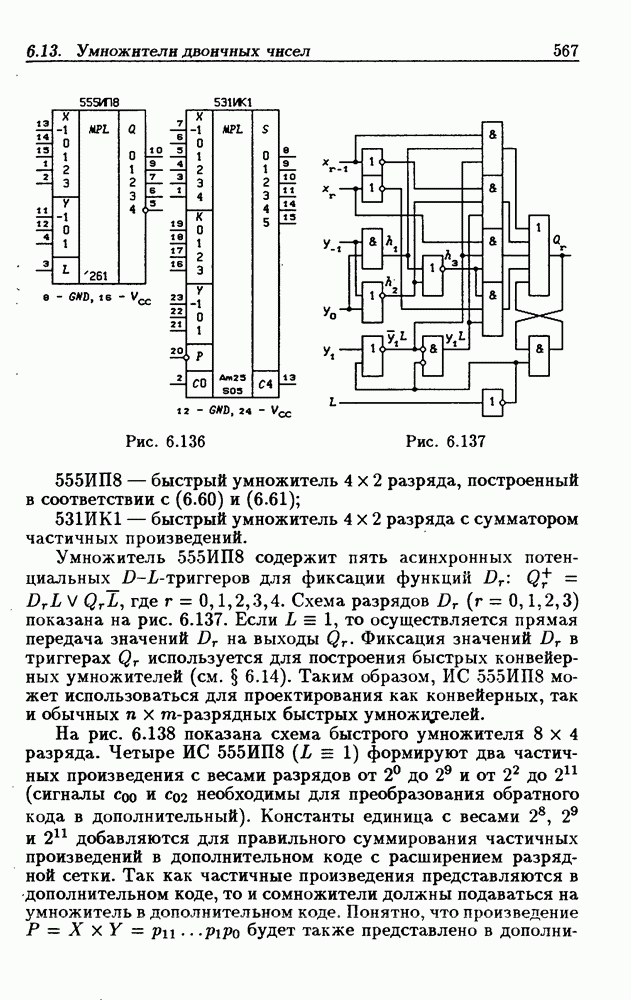
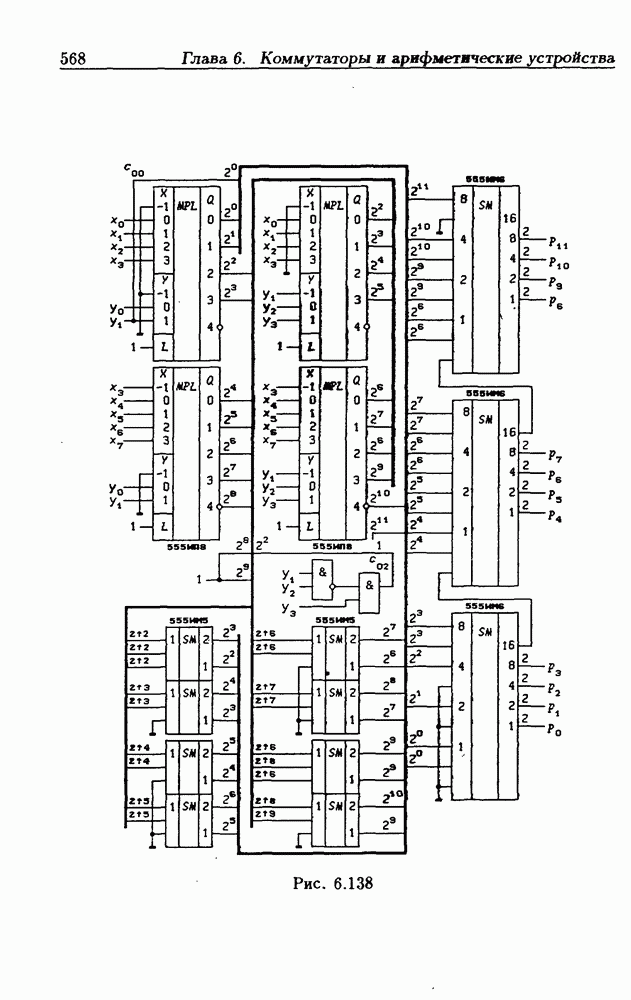
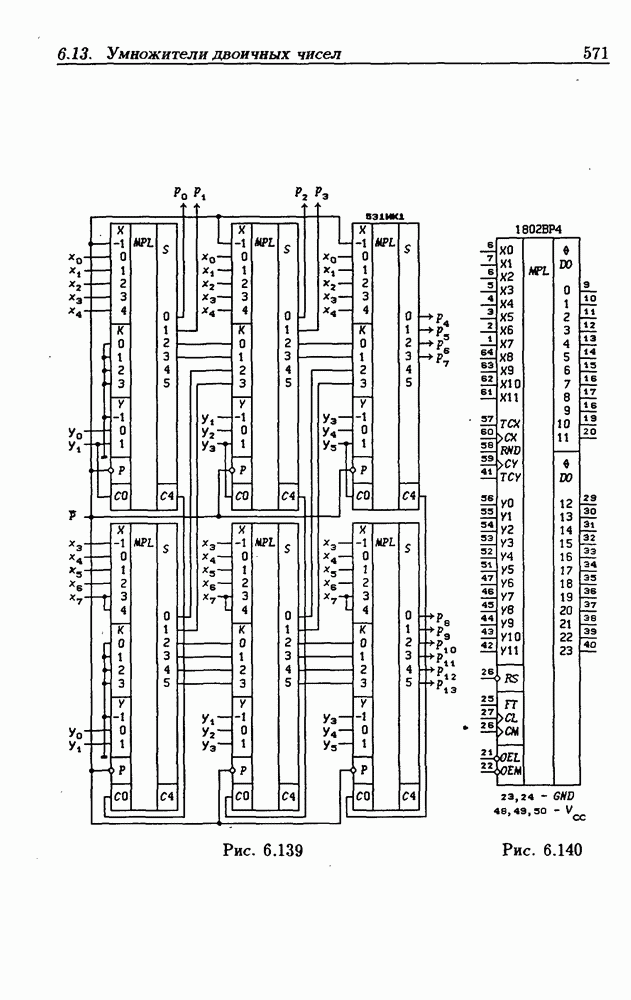
- 6.13. Умножители двоичных чисел
- Быстрые умножители.
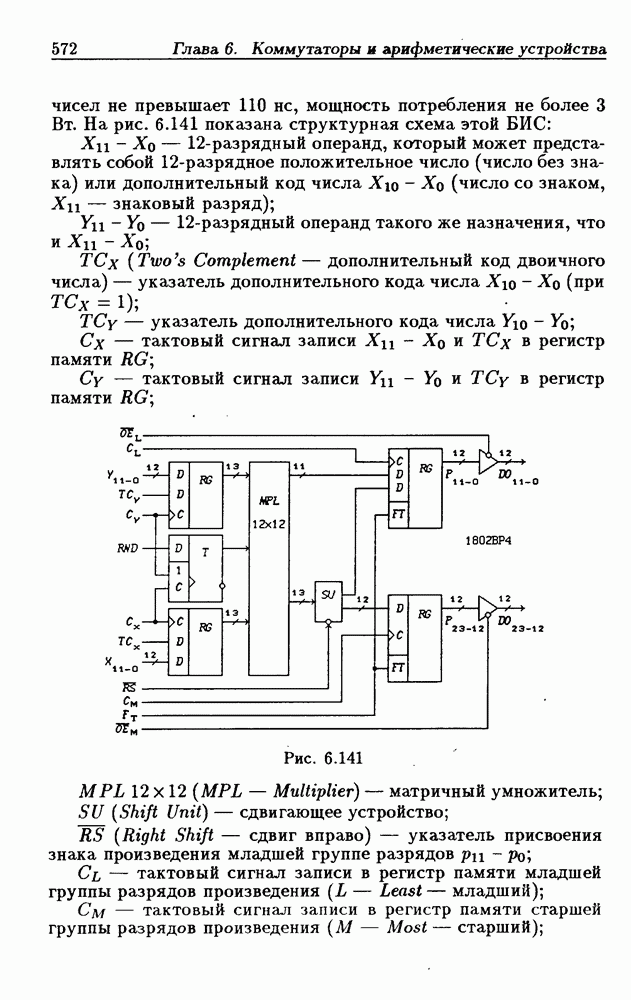
- БИС умножителя 12×12 разрядов 1802ВР4.
- Последовательные умножители.
- 6.14. Конвейерные устройства
- Конвейерный быстрый умножитель.
- Конвейерные АЦП.
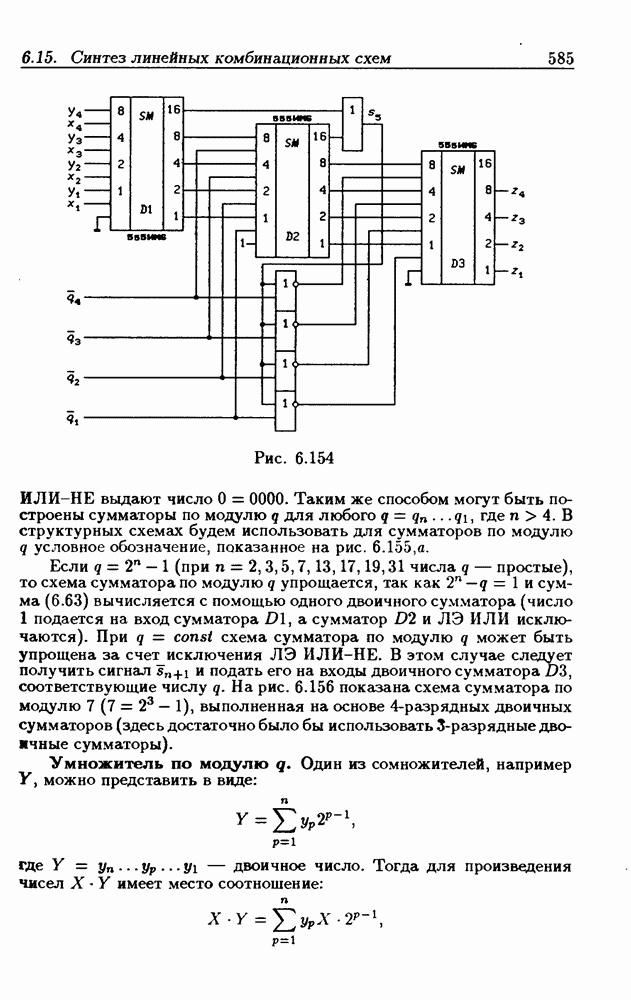
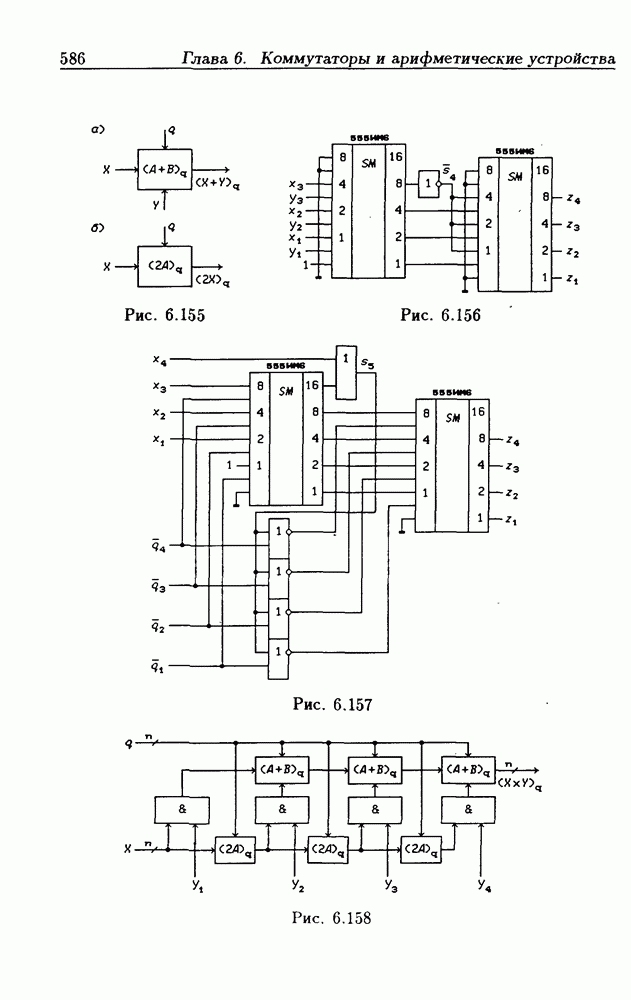
- 6.15. Синтез линейных комбинационных схем
- Сумматор по модулю q.
- Умножитель по модулю q.
- Глава 7. Сдвигающие регистры и счетчики
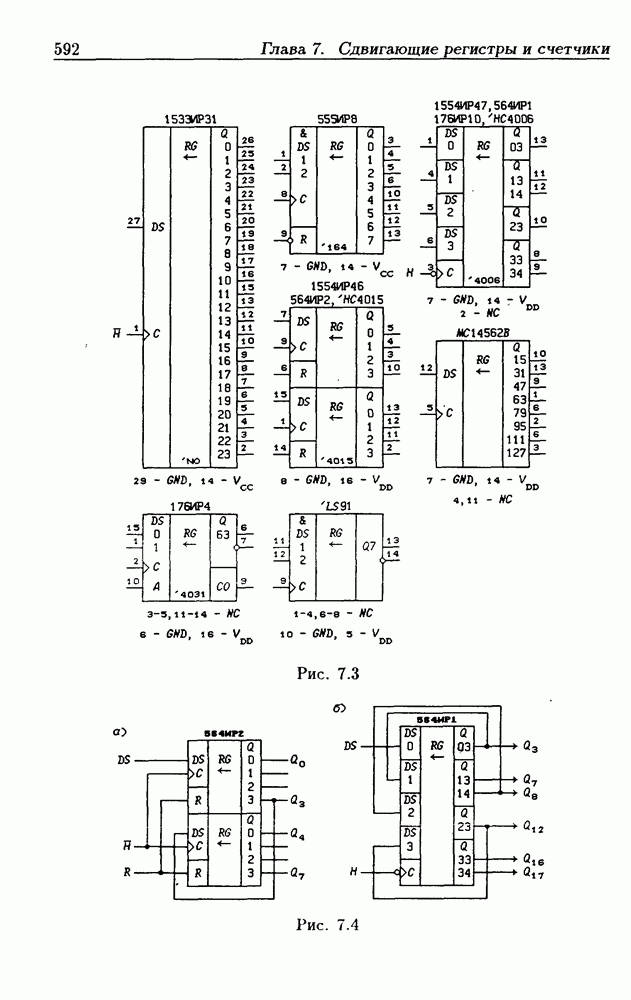
- 7.1. Сдвигающие регистры без параллельной записи данных
- Сдвигающие устройства с выходными регистрами памяти.
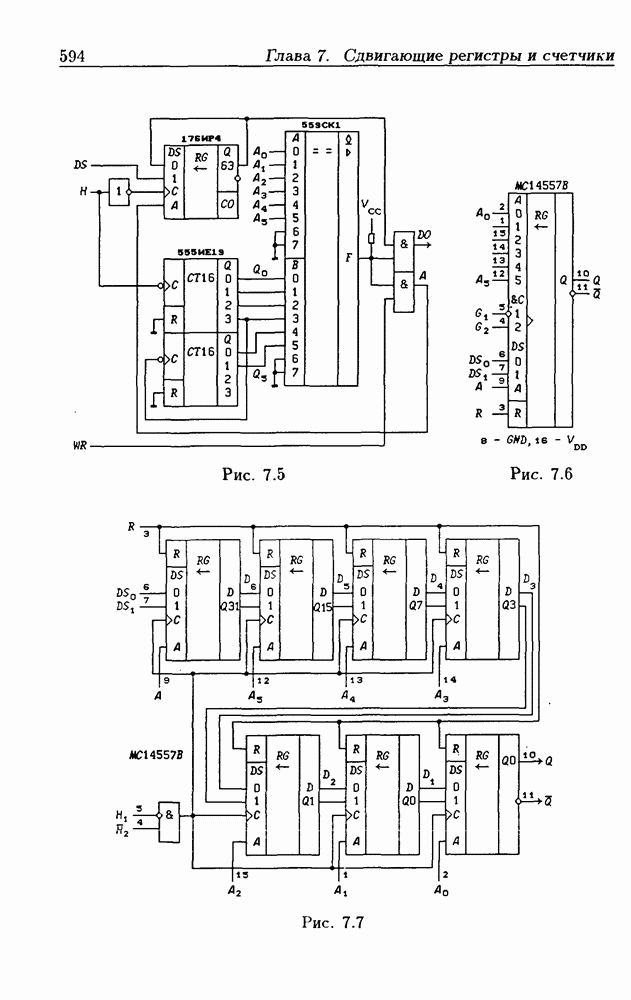
- 7.2. Сдвигающие регистры с параллельной записью данных
- Сдвигающие регистры с расширением знака.
- Сдвигающие регистры с входным регистром памяти.
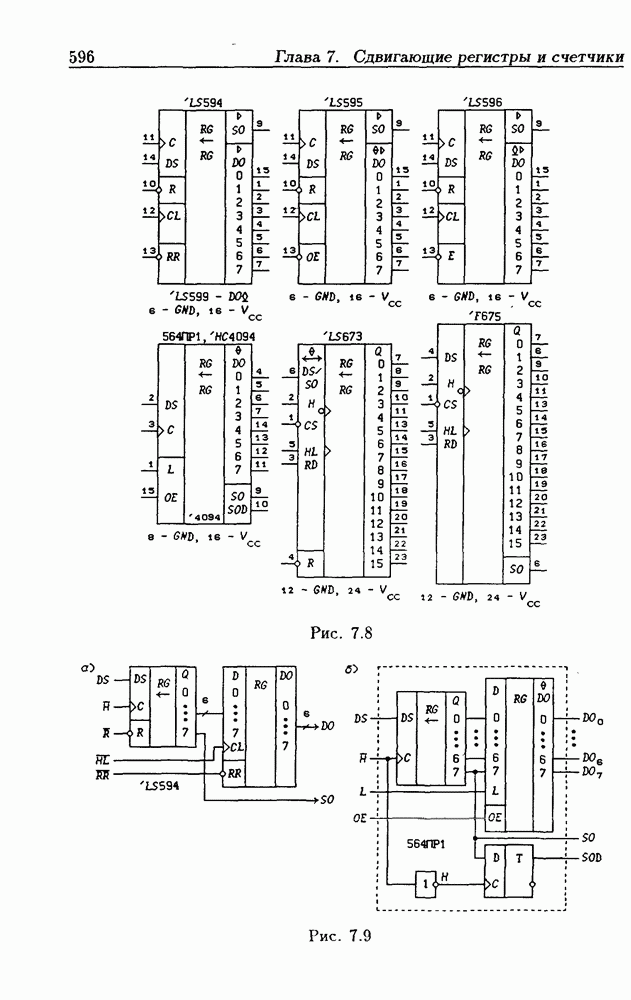
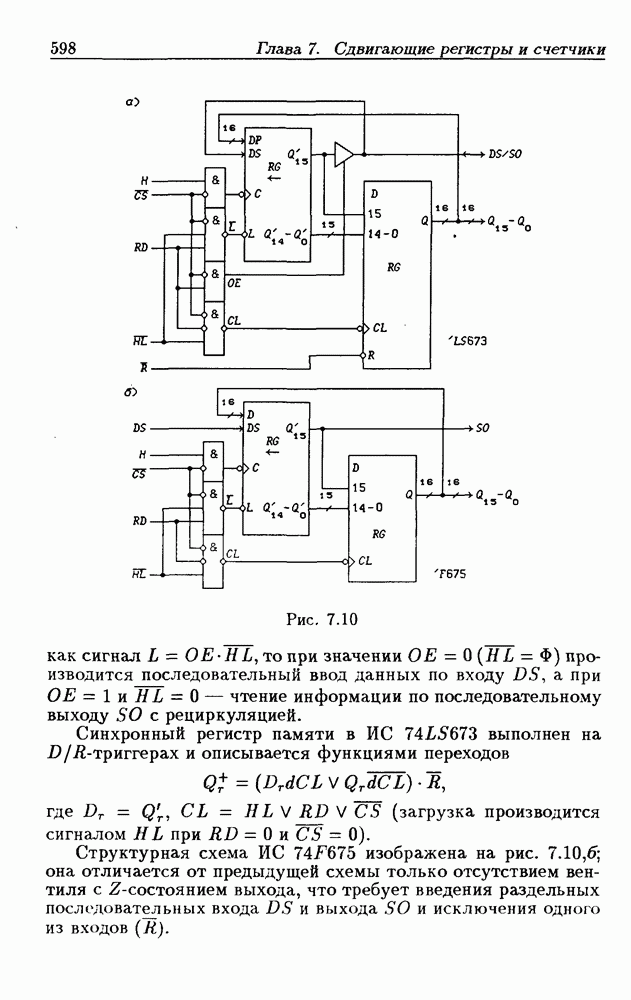
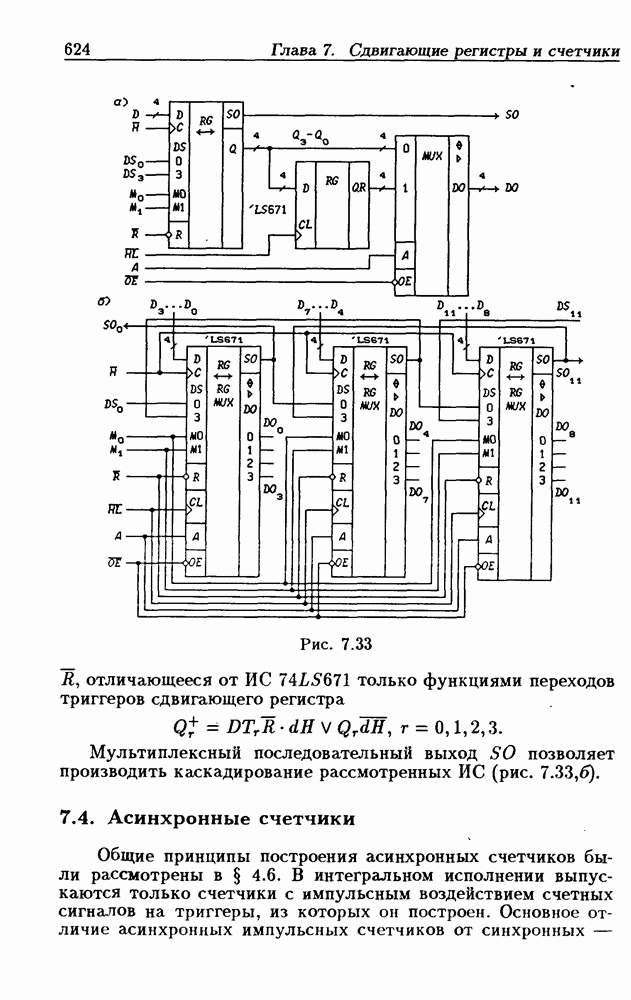
- 7.3. Реверсивные сдвигающие регистры
- Реверсивные сдвигающие регистры типов PI/SO и PI/PO.
- Многофункциональные устройства на основе реверсивных сдвигающих регистров.
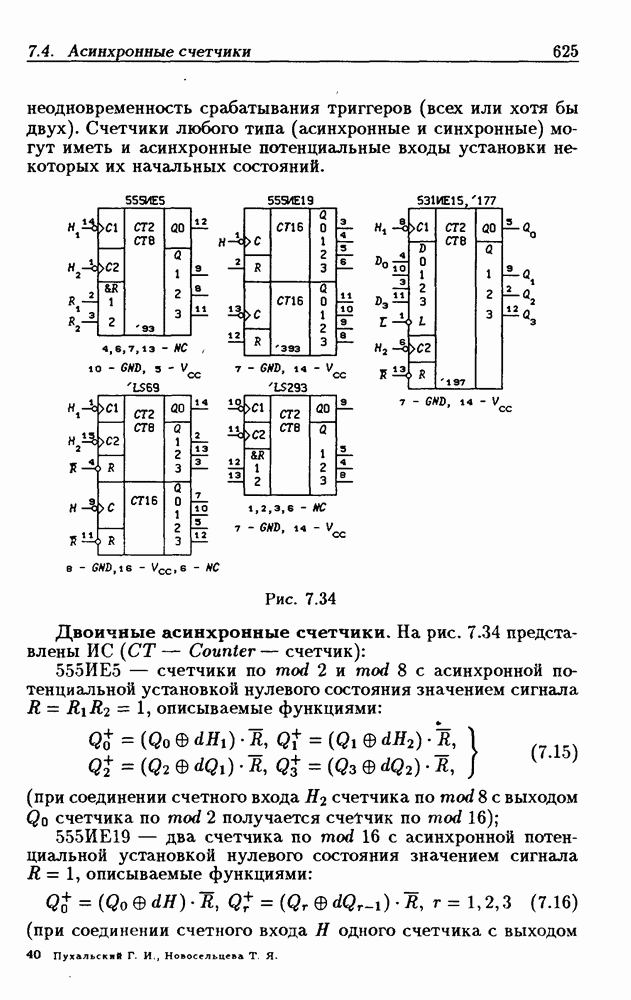
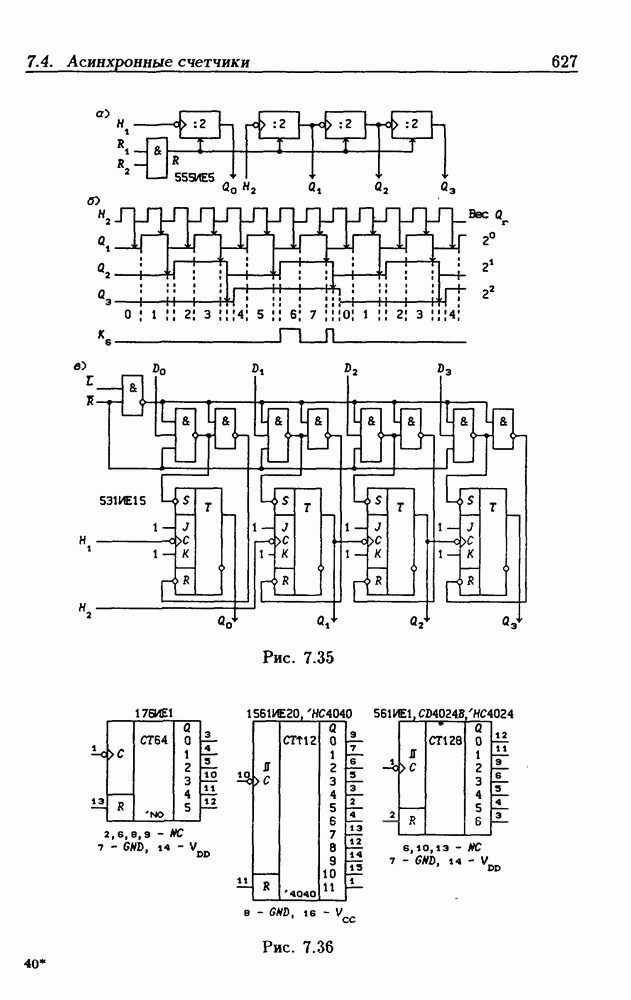
- 7.4. Асинхронные счетчики
- Двоично-десятичные асинхронные счетчики.
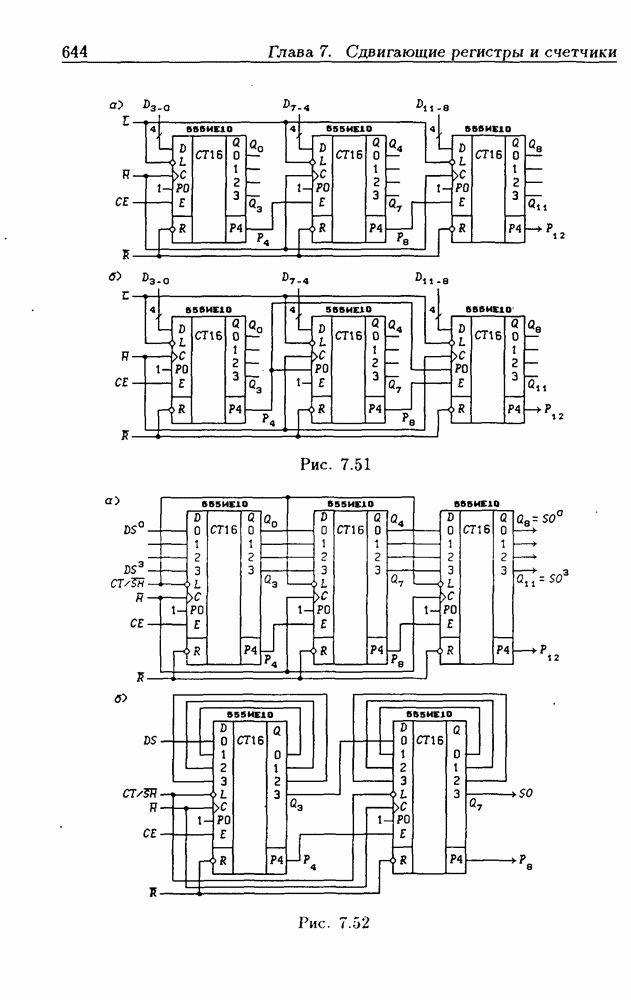
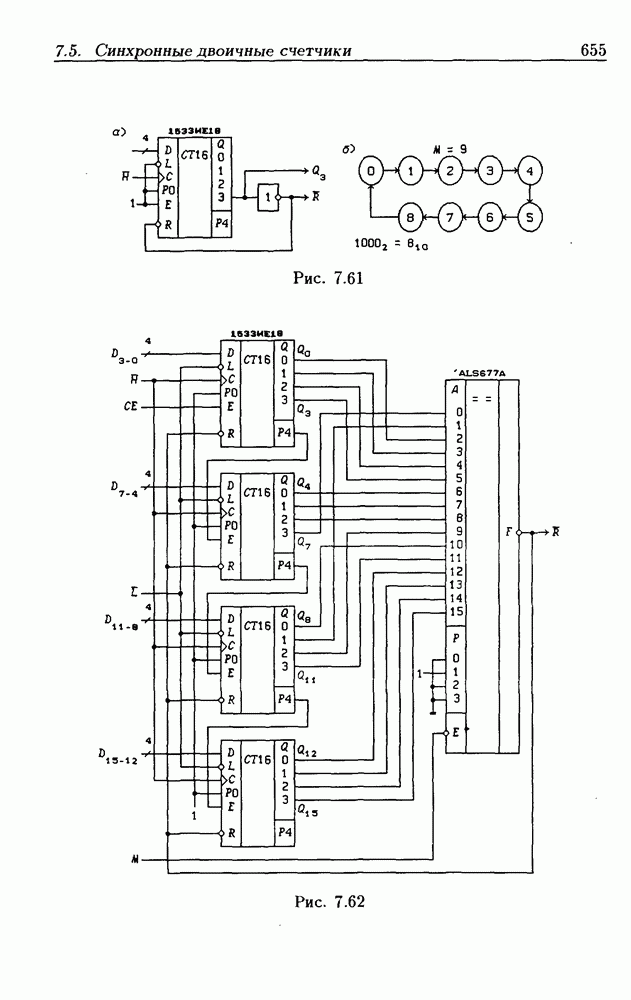
- 7.5. Синхронные двоичные счетчики
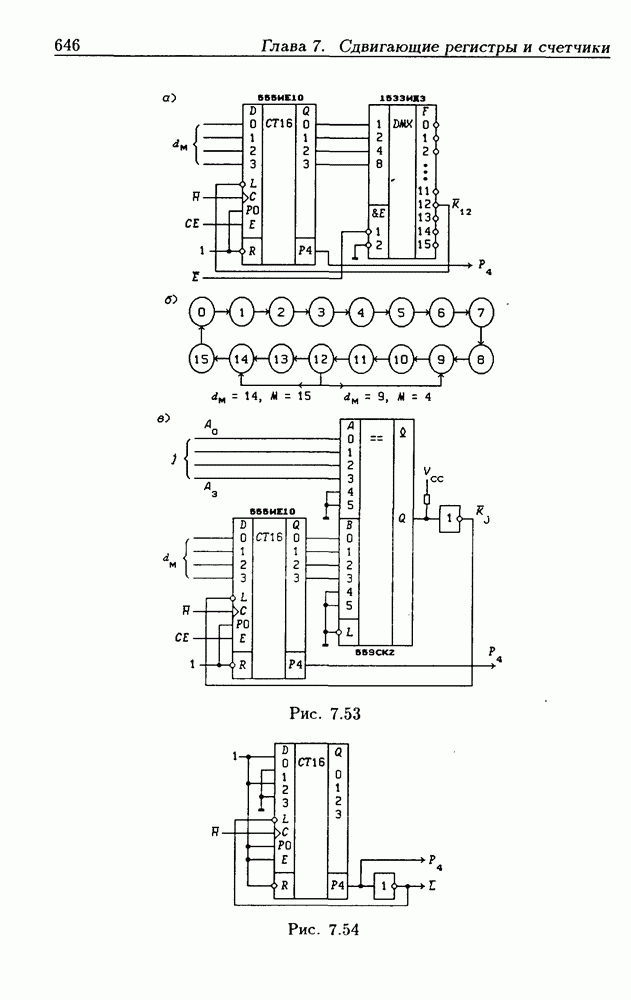
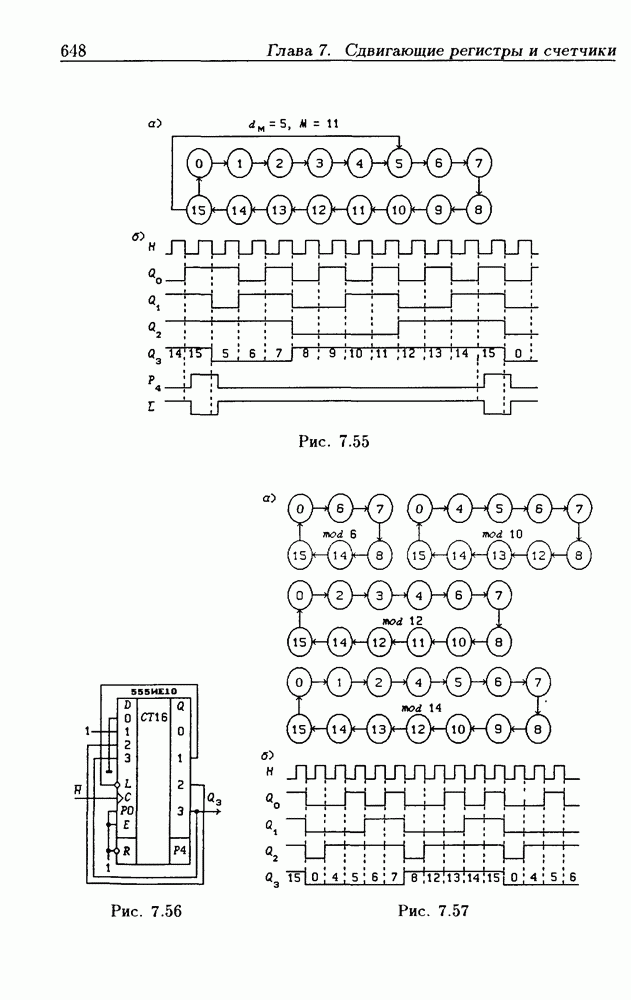
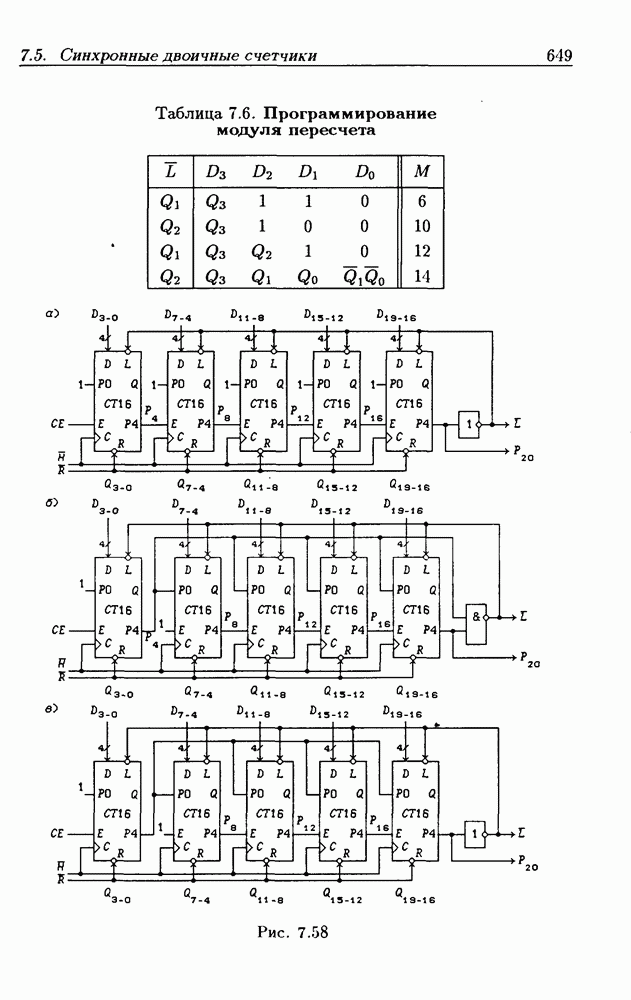
- Программирование модуля пересчета двоичных счетчиков.
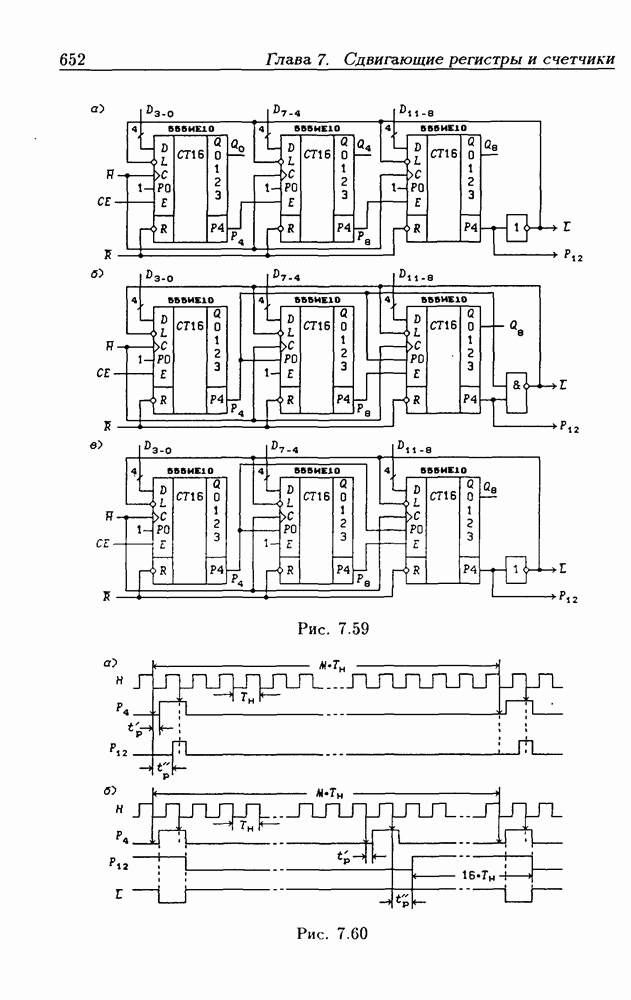
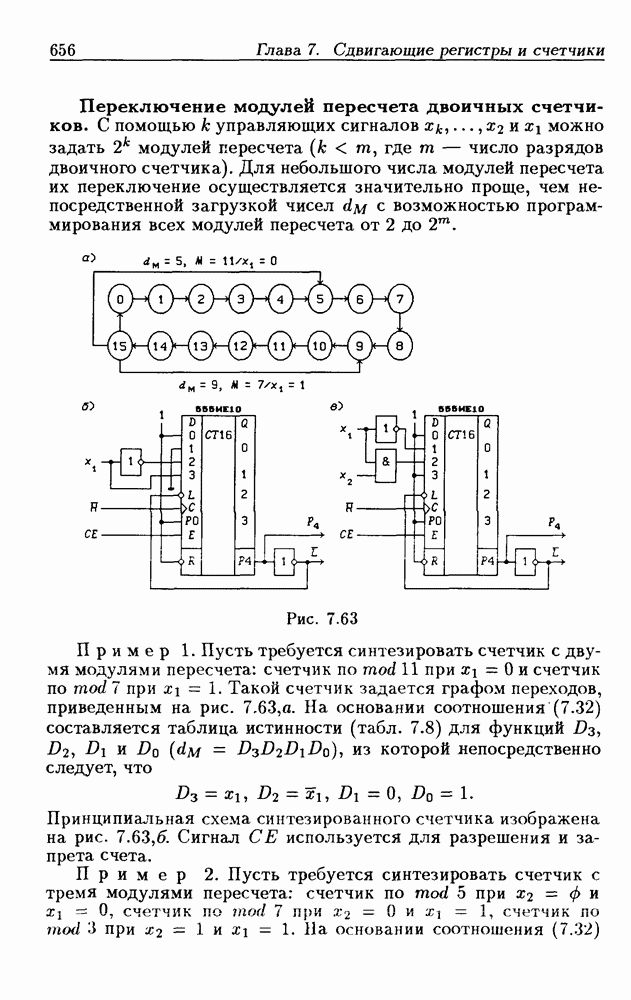
- Переключение модулей пересчета двоичных счетчиков.
- Функциональные устройства на основе двоичных счетчиков.
- 7.6. Синхронные двоично-десятичные счетчики
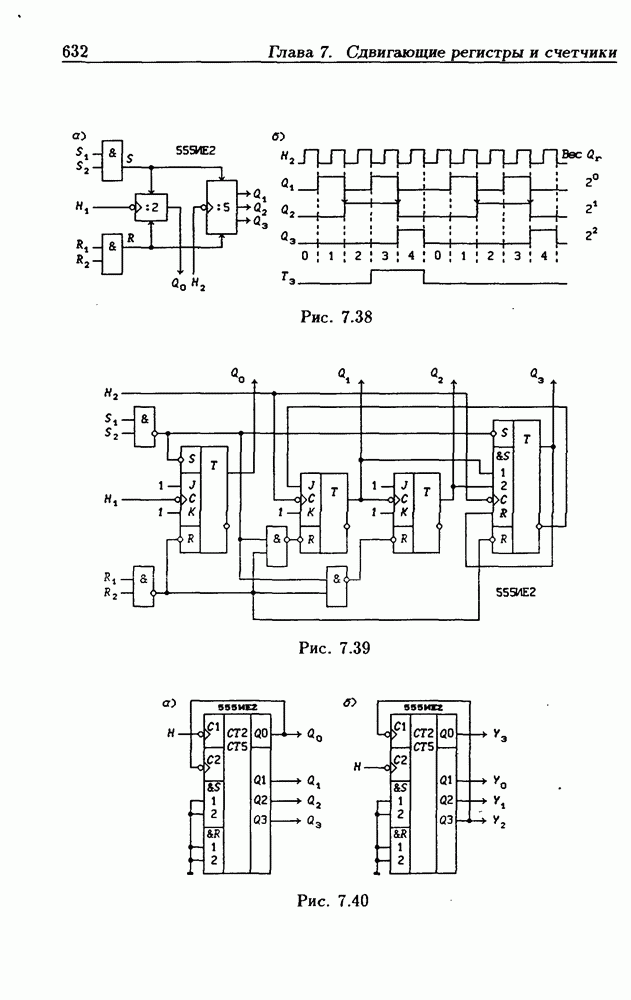
- 7.7. Синхронные реверсивные счетчики
- 7.8. Счетчики с расщепленным тактовым сигналом
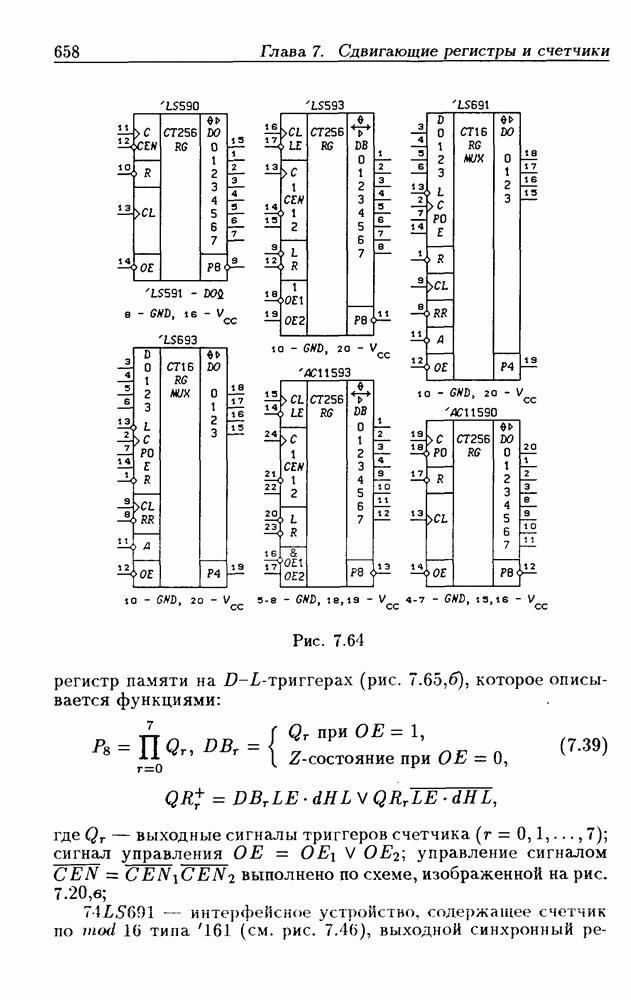
- 7.9. Счетчики на сдвигающих регистрах
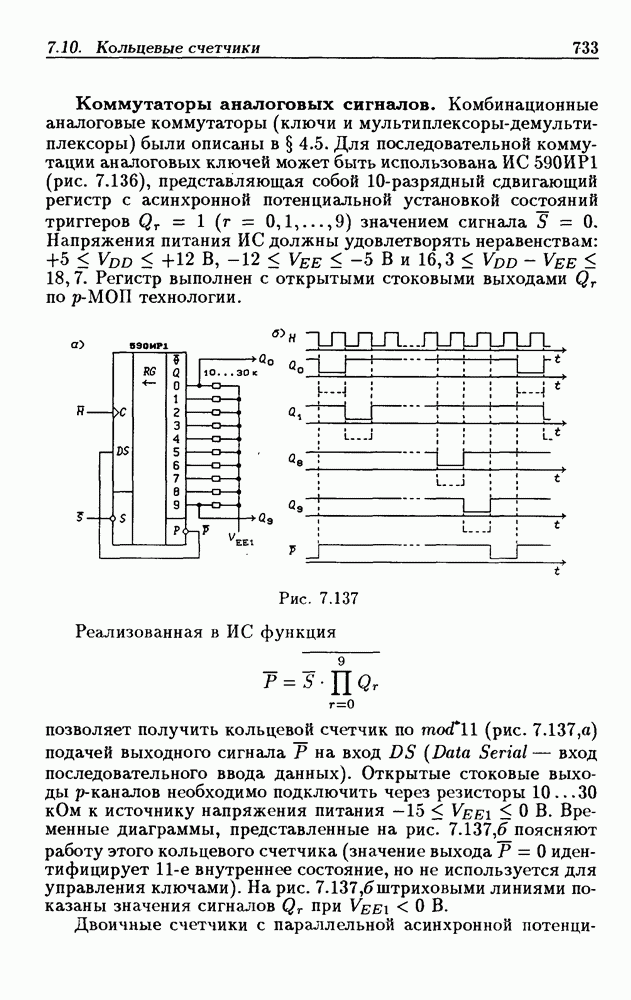
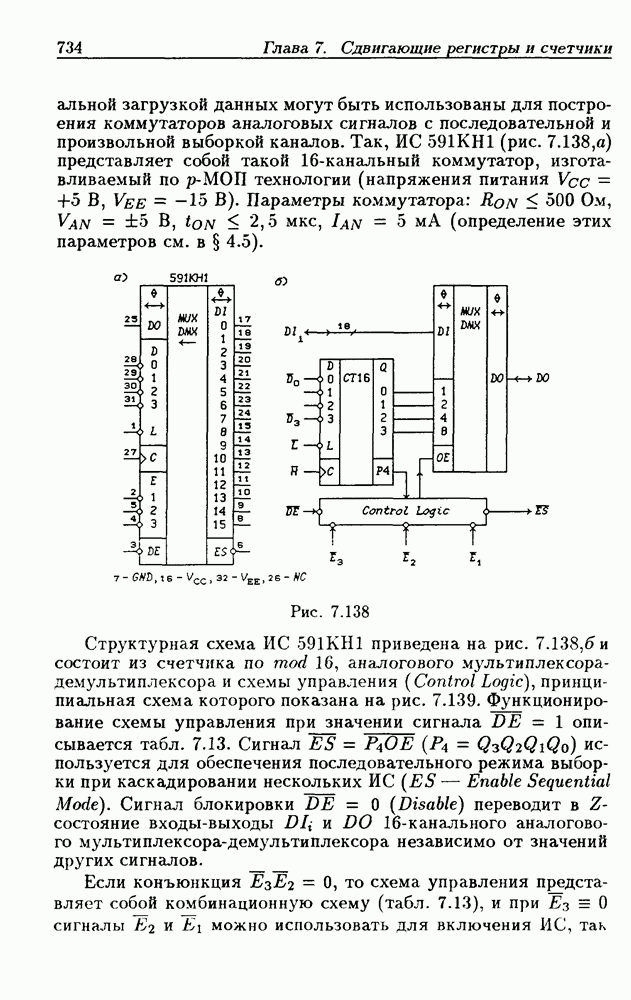
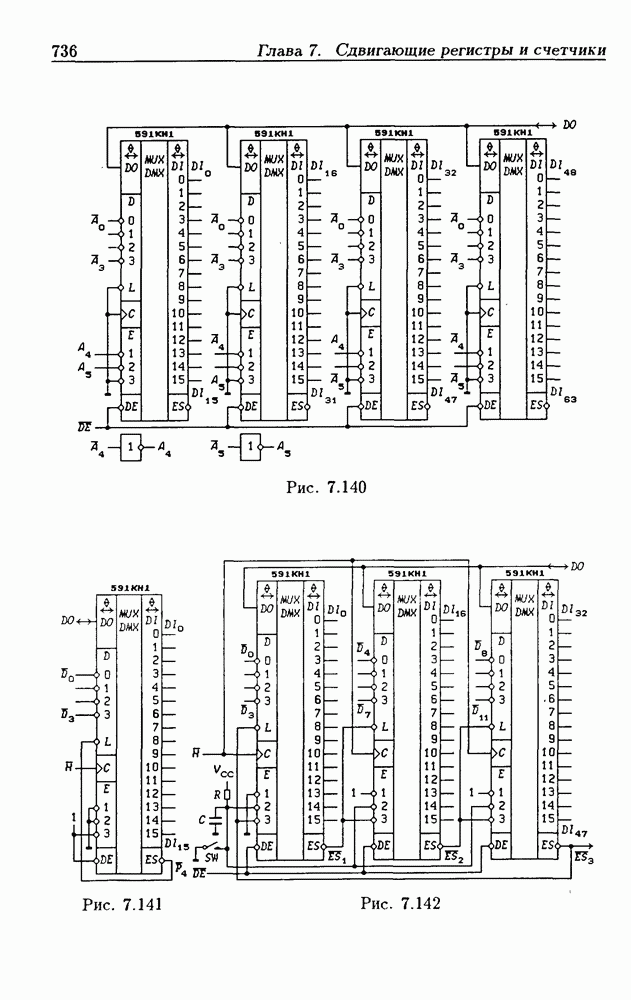
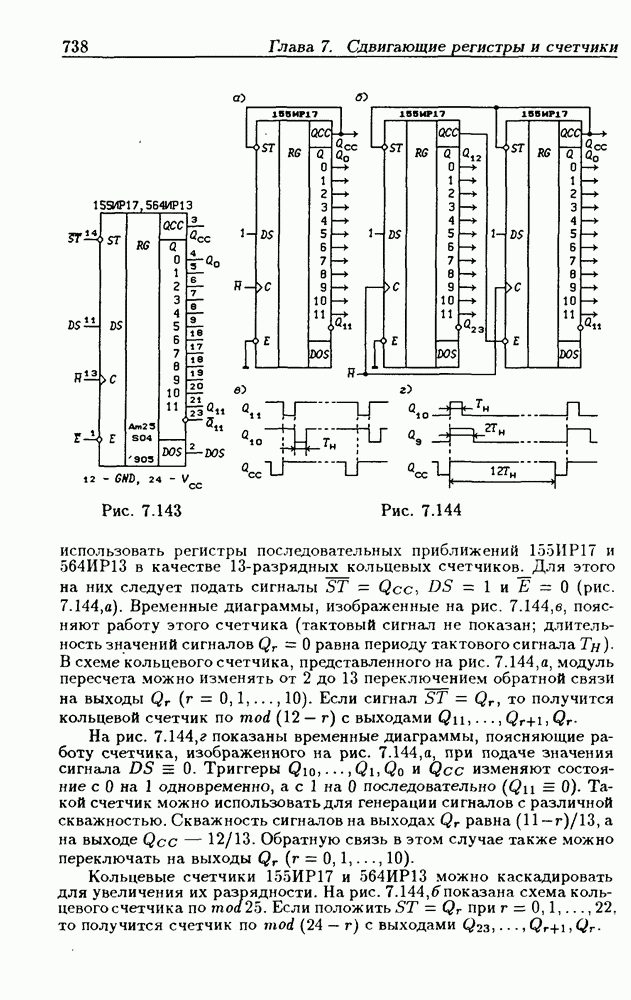
- 7.10. Кольцевые счетчики
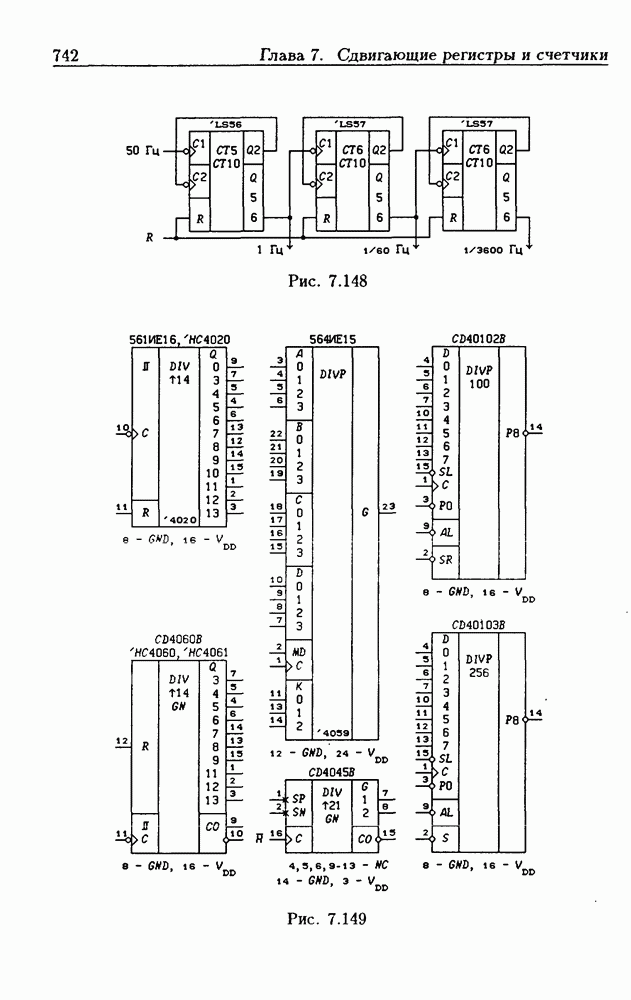
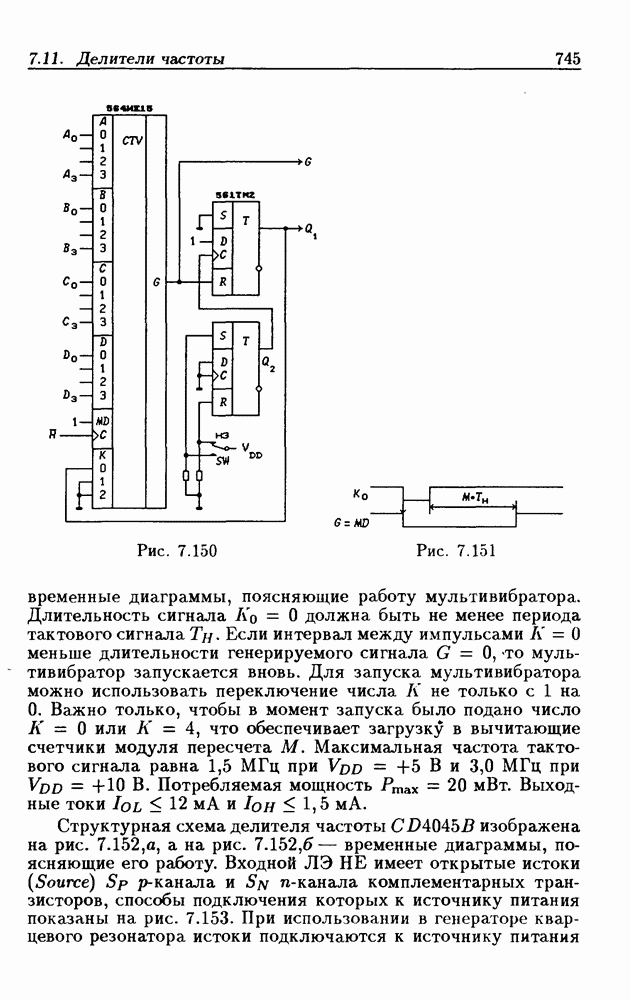
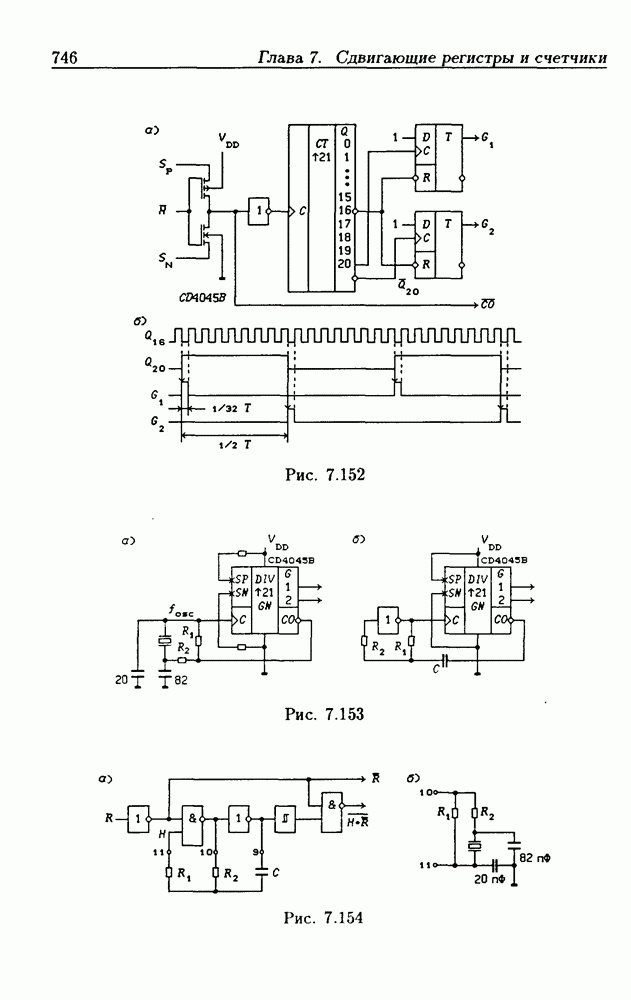
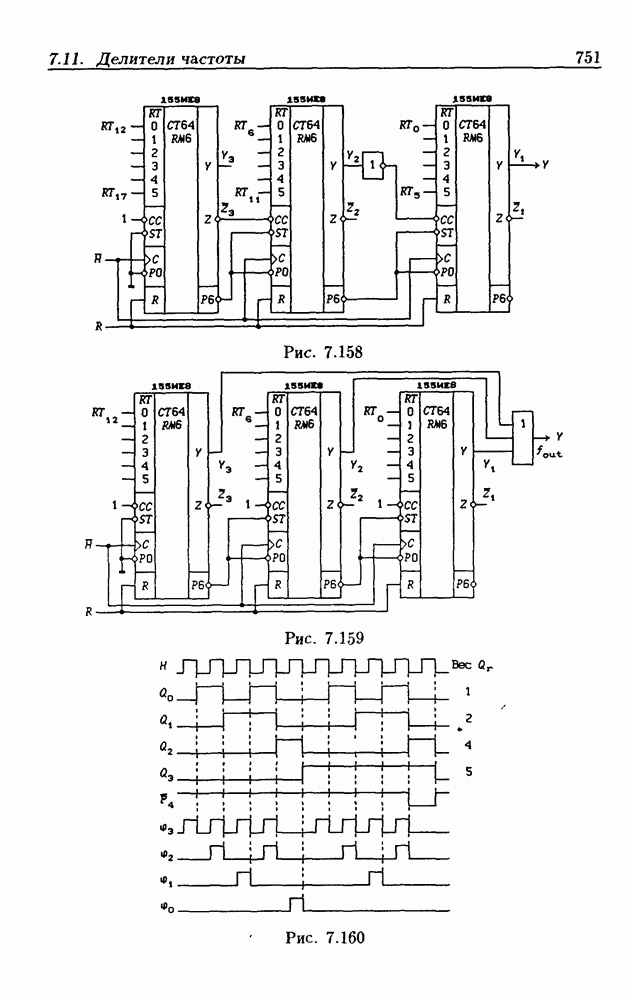
- 7.11. Делители частоты
- Нормированные умножители частоты.
- 7.12. Линейные генераторы
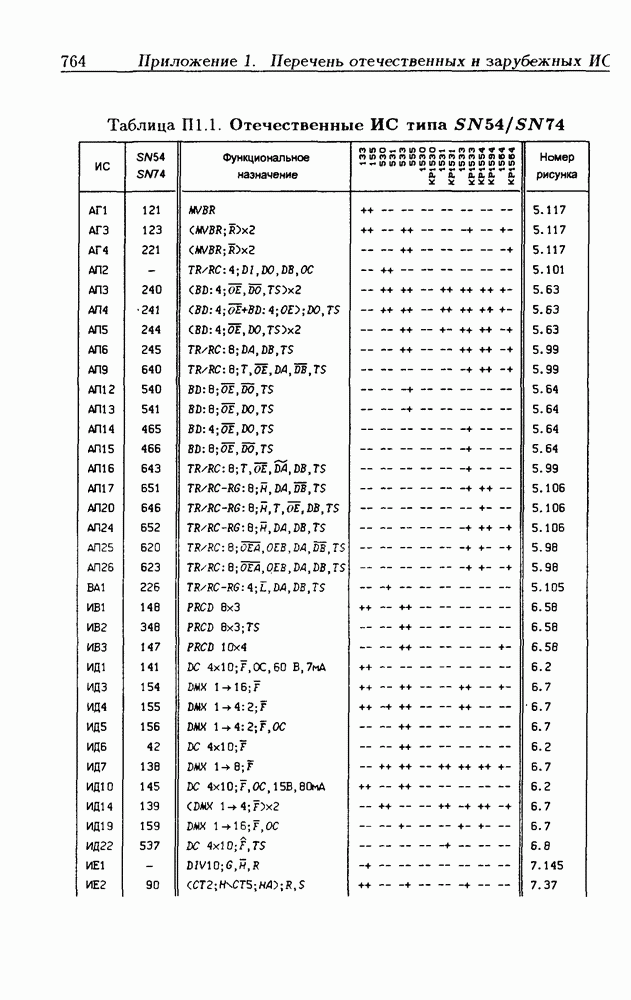
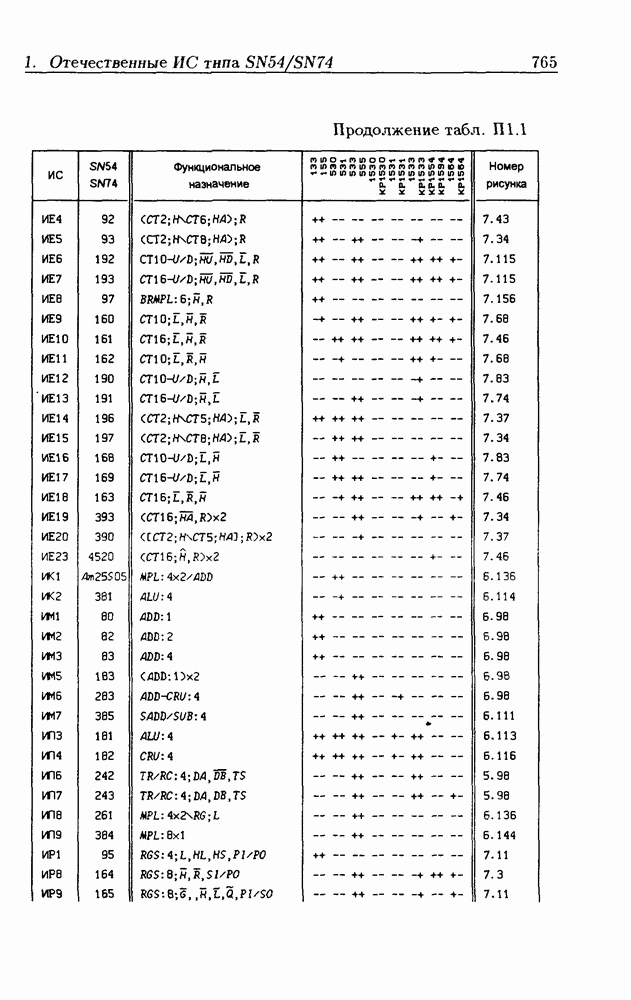
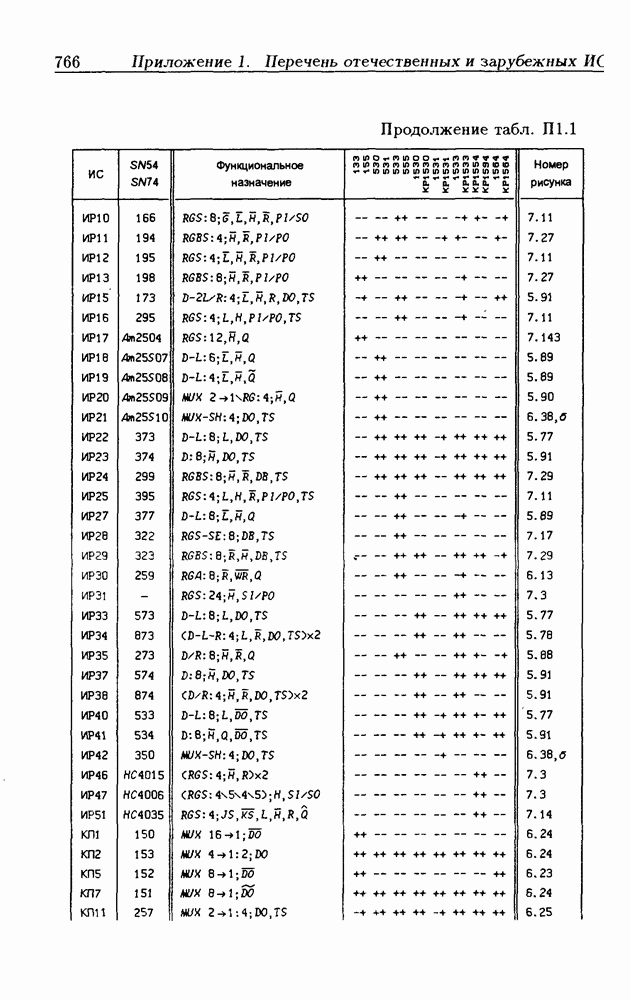
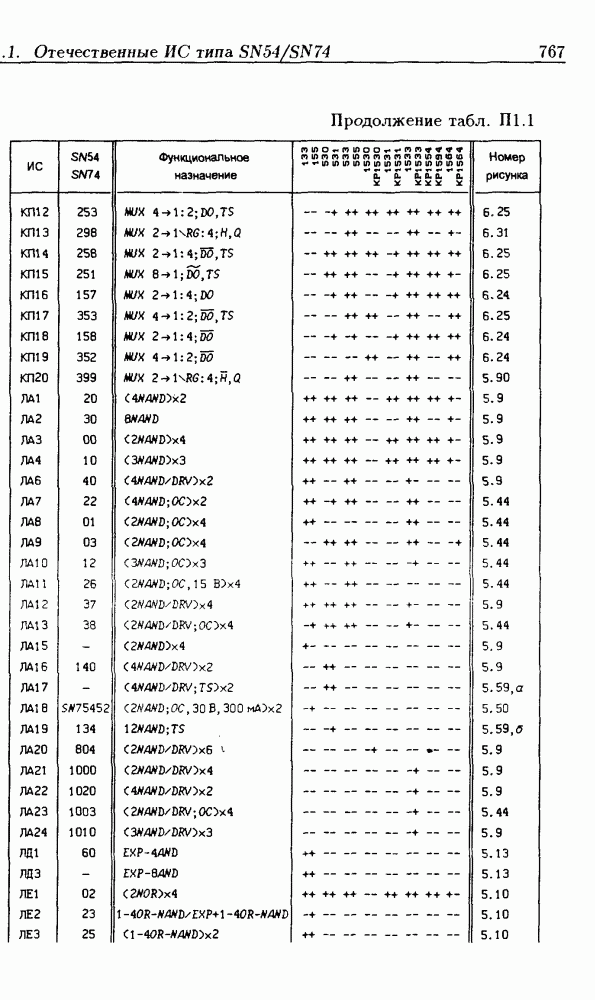
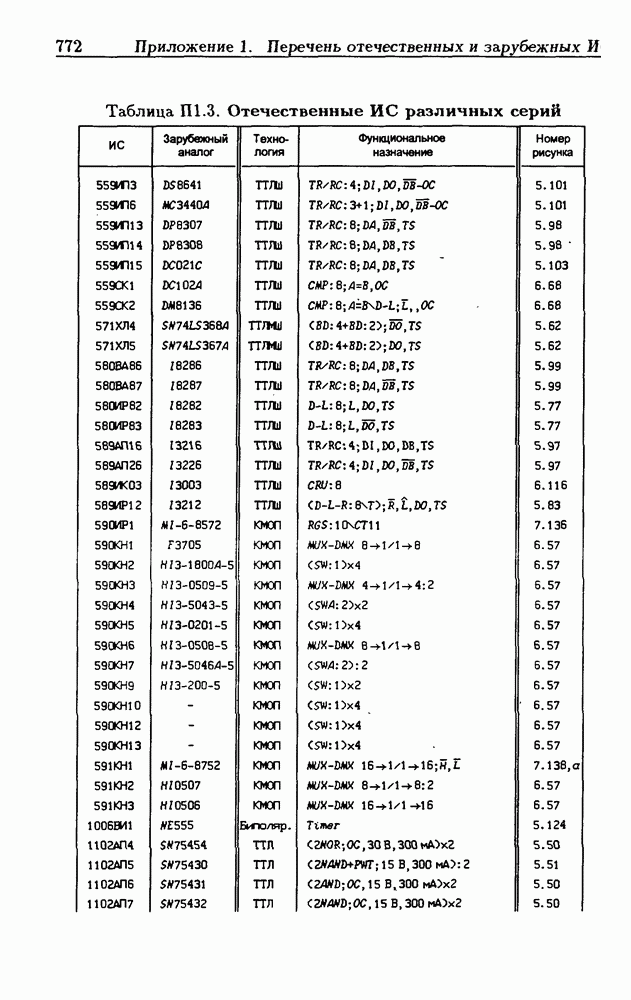
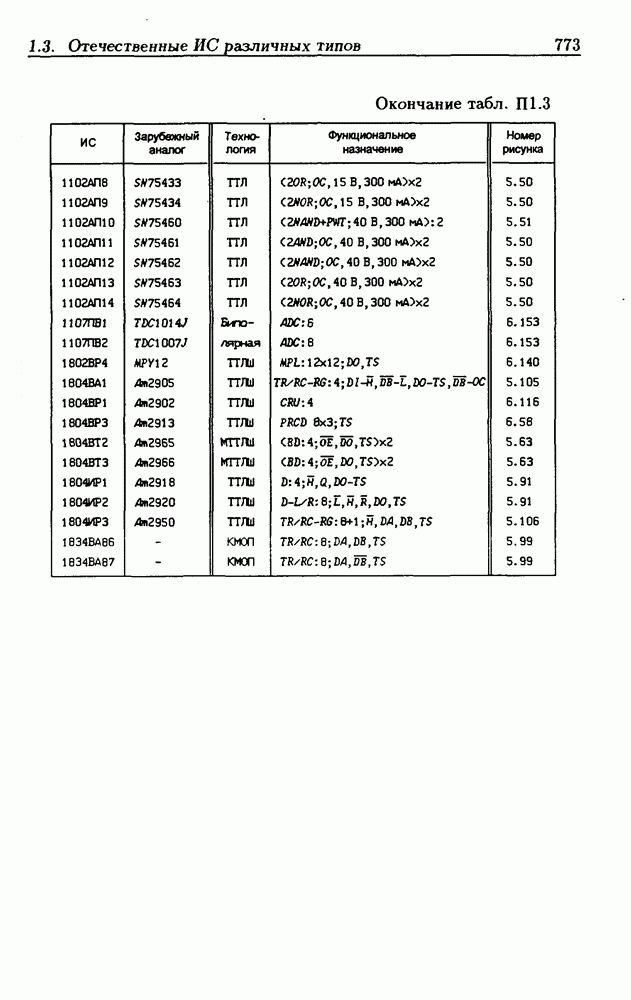
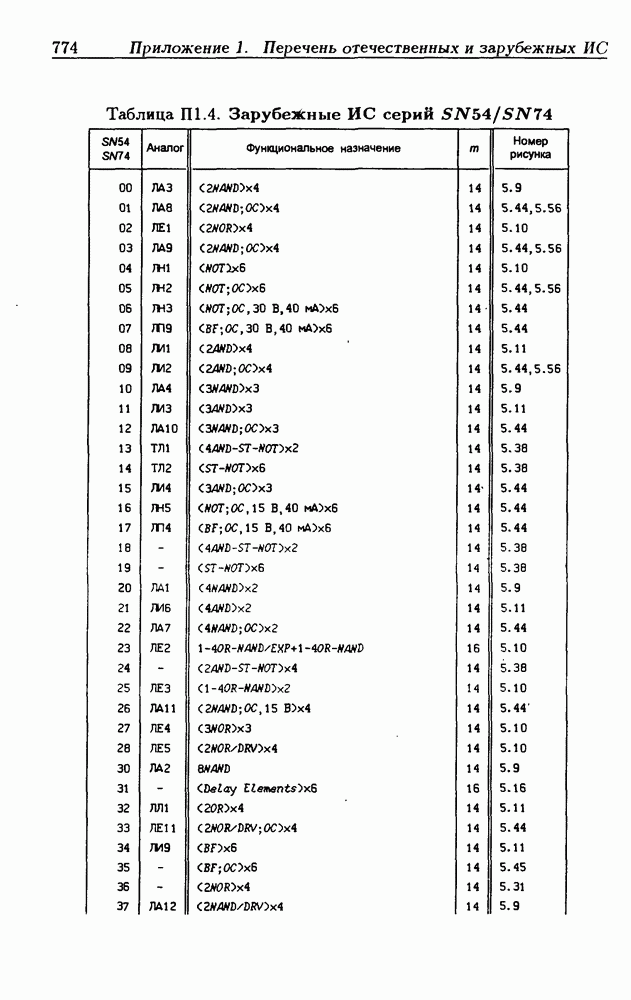
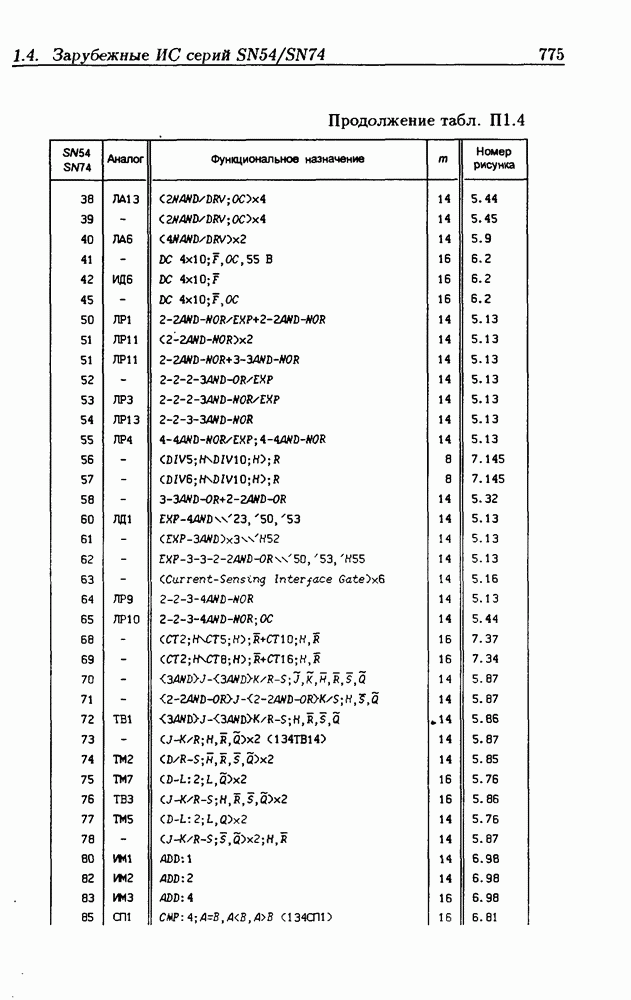
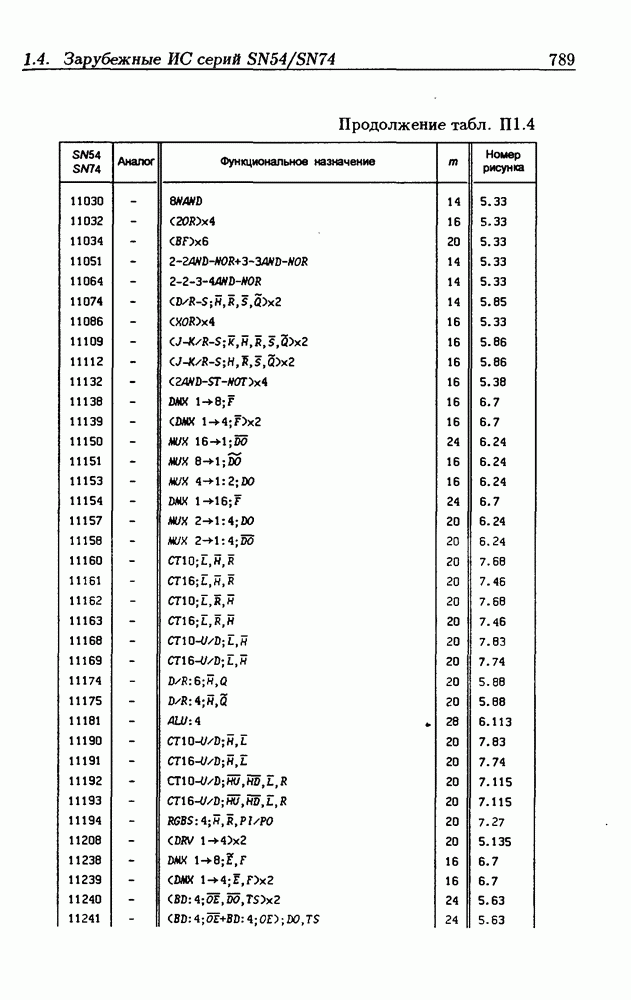
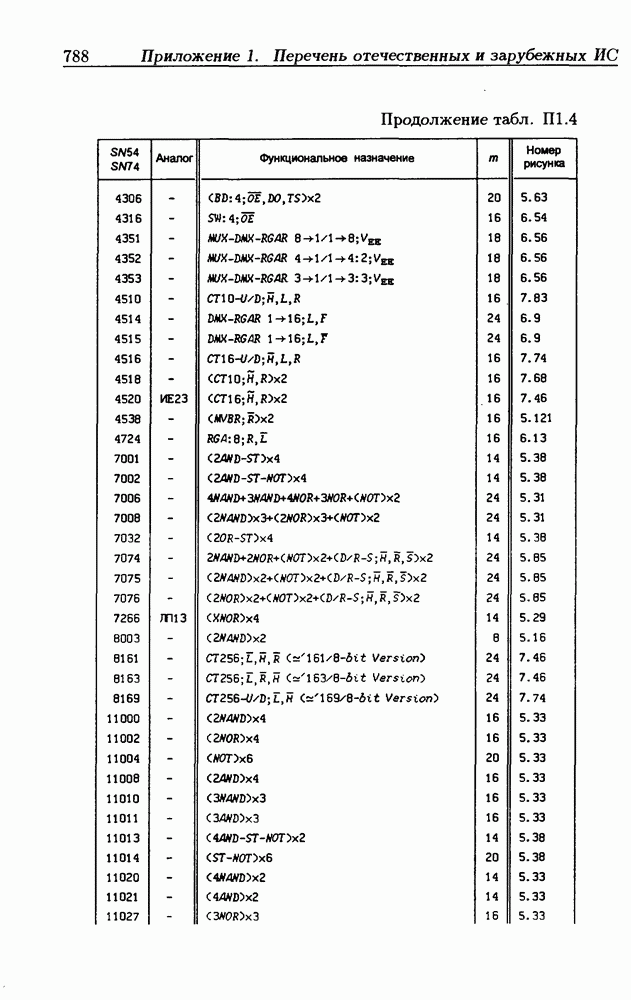
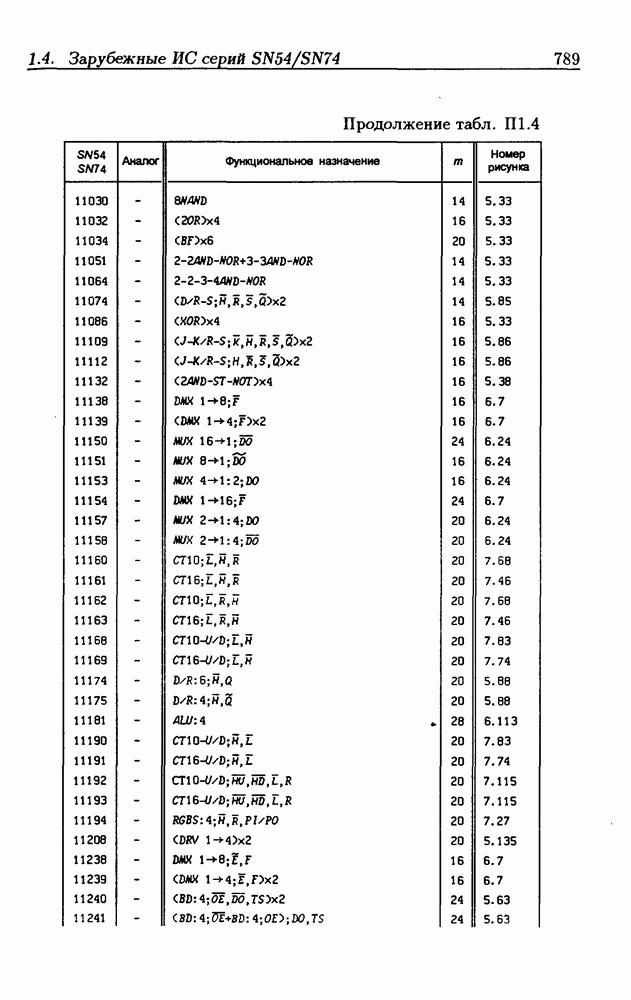
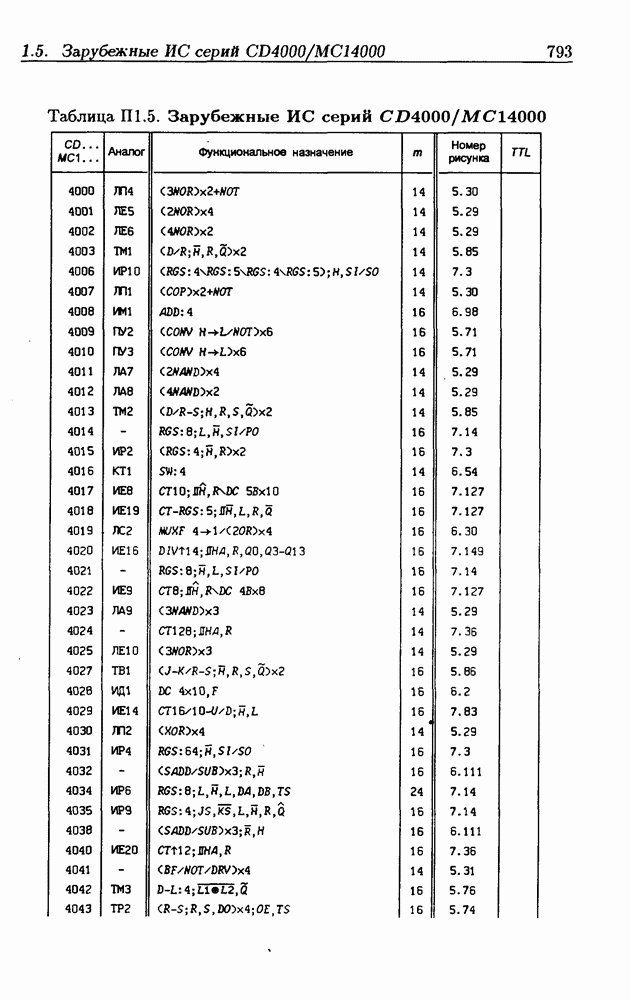
- Приложение 1. Перечень отечественных и зарубежных ИС
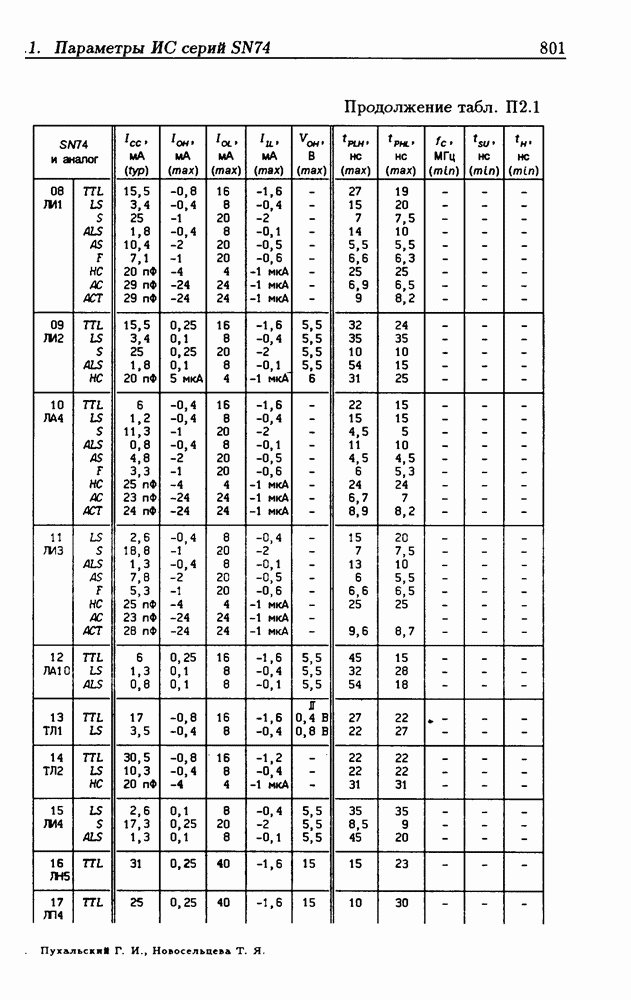
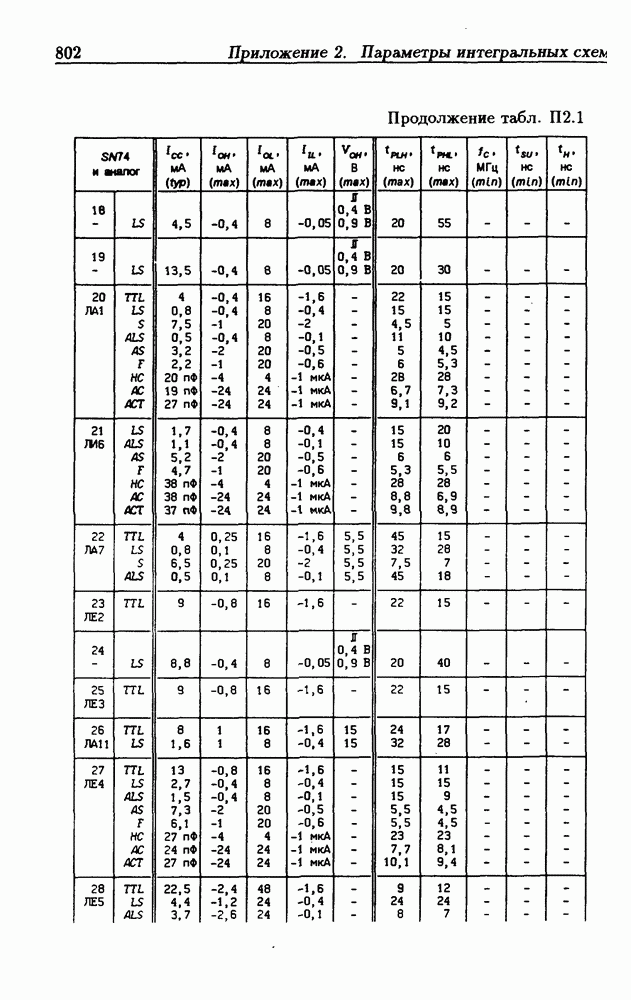
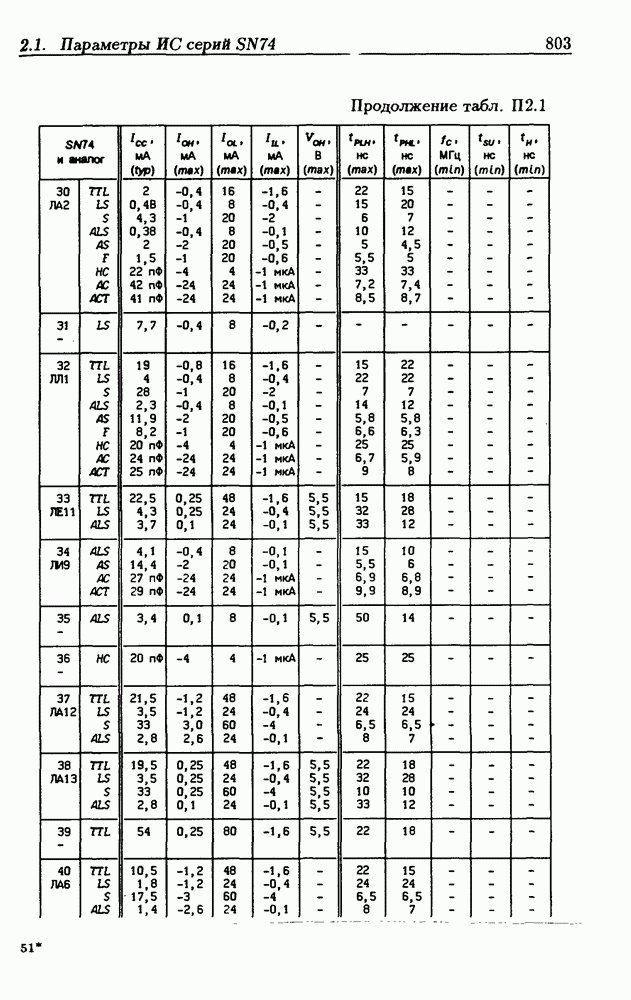
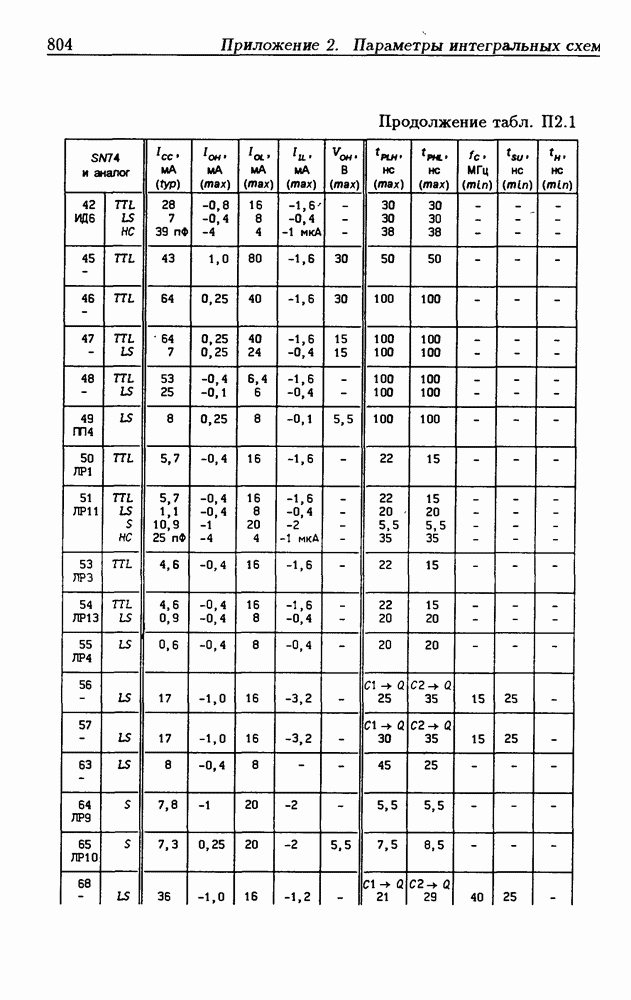
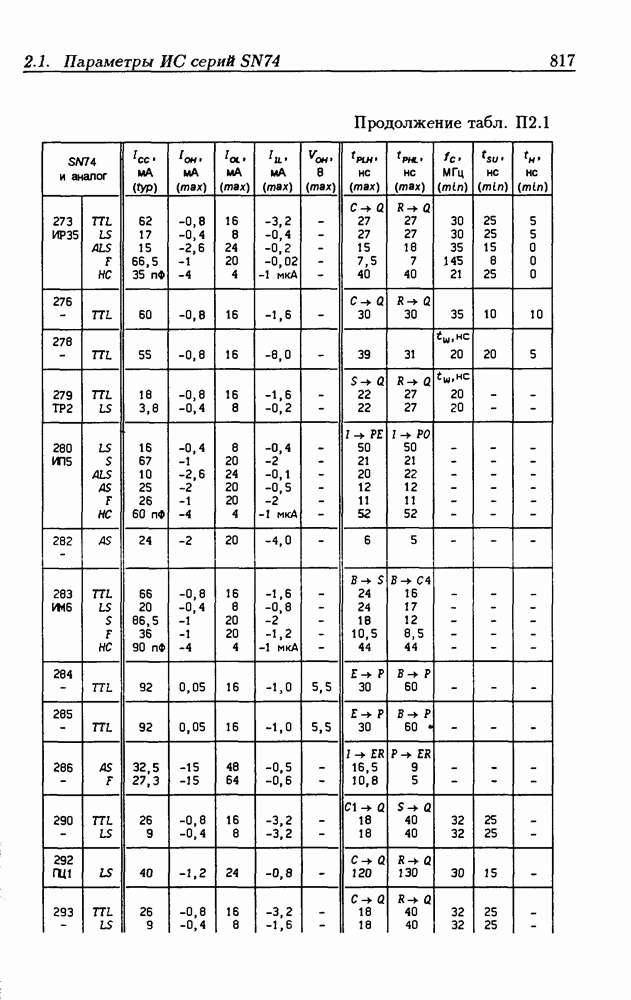
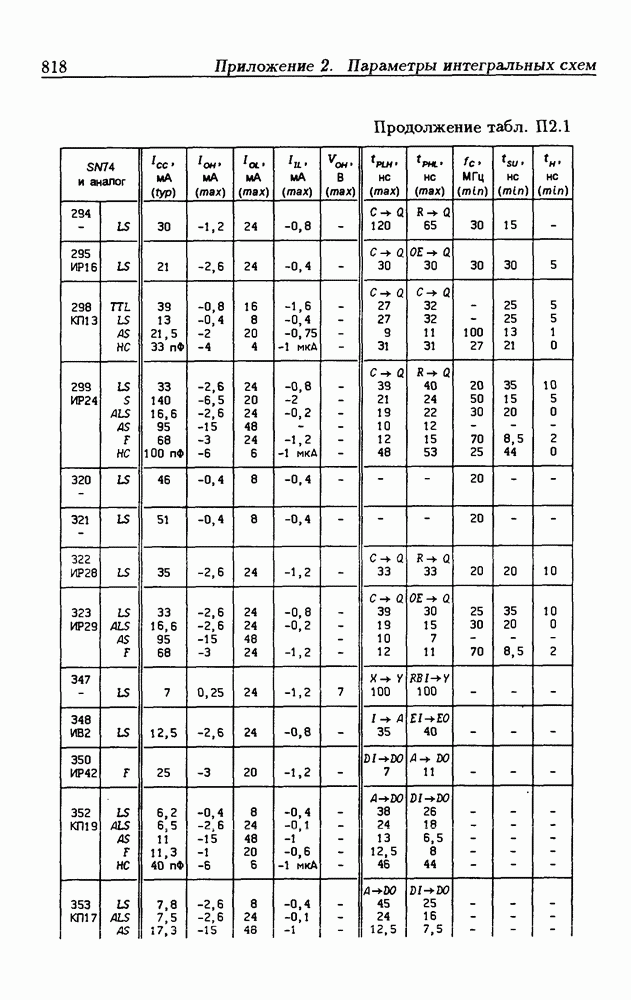
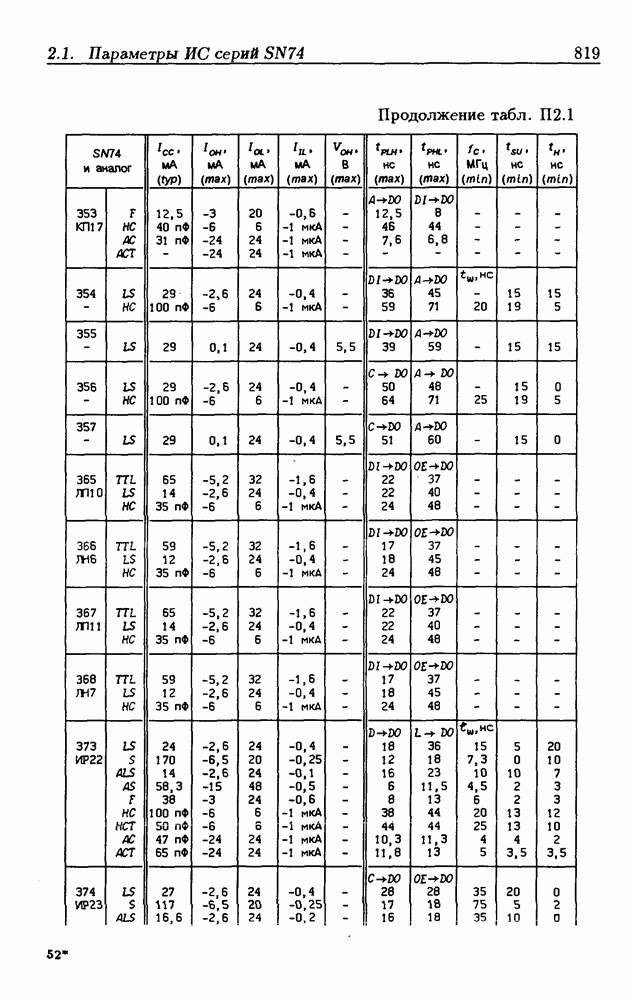
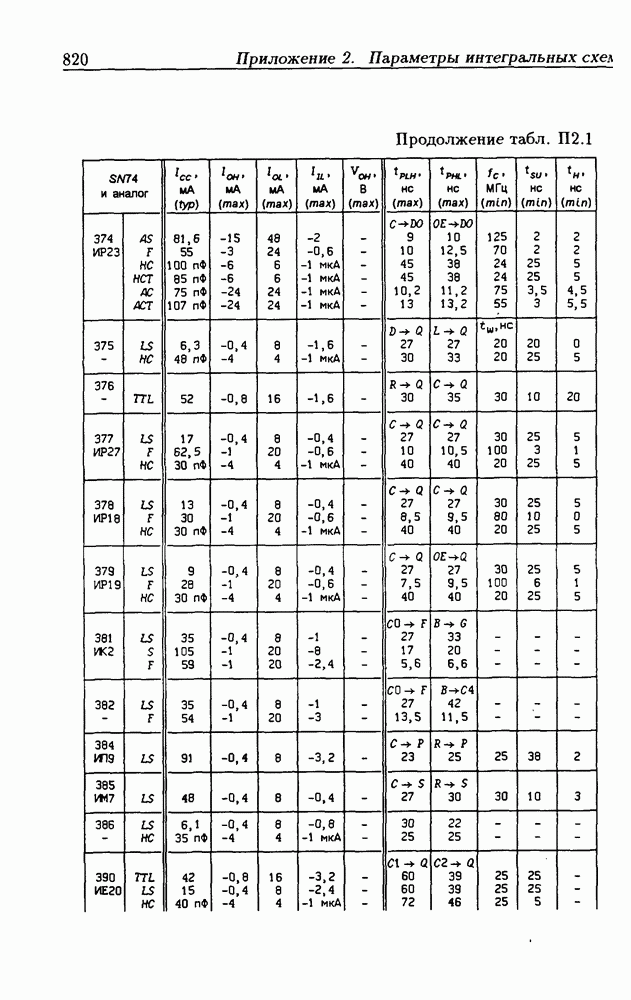
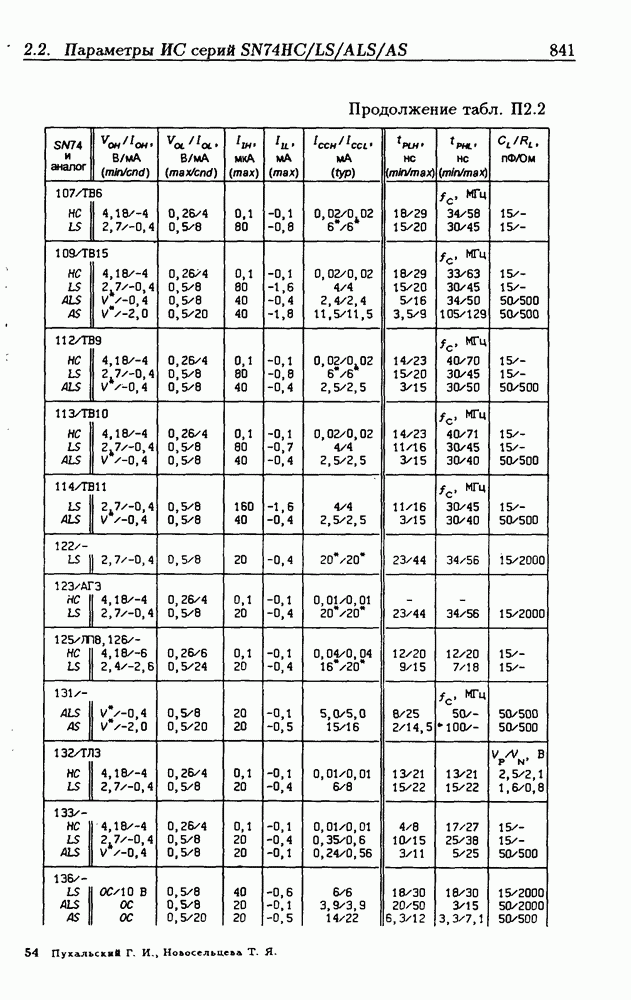
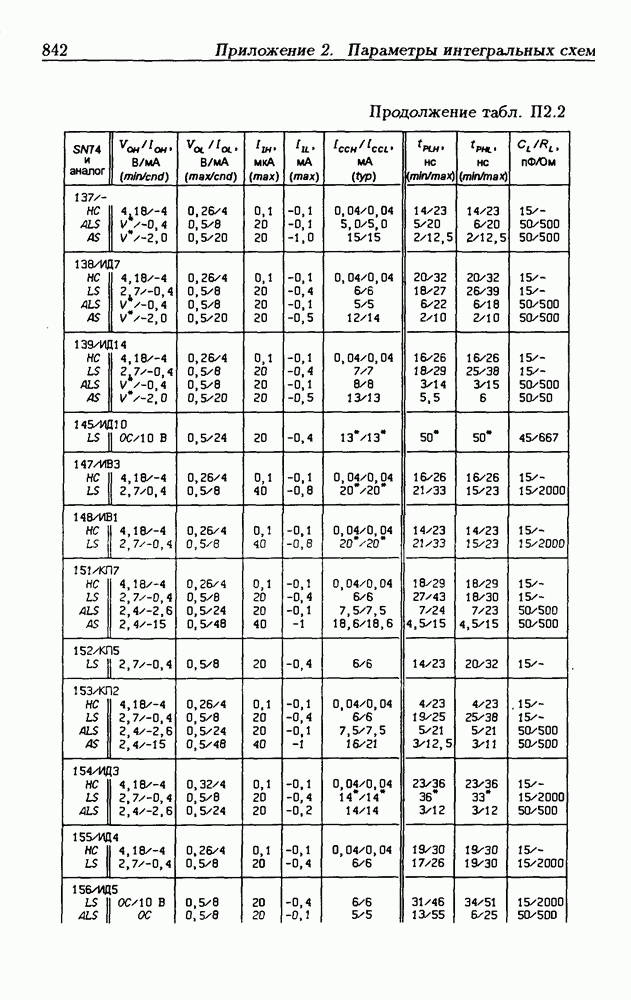
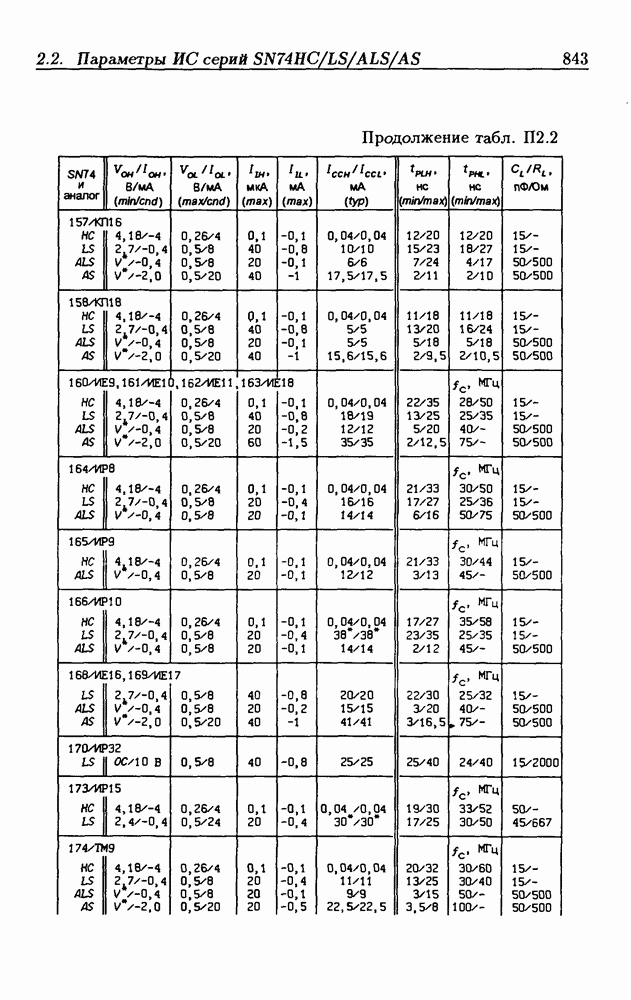
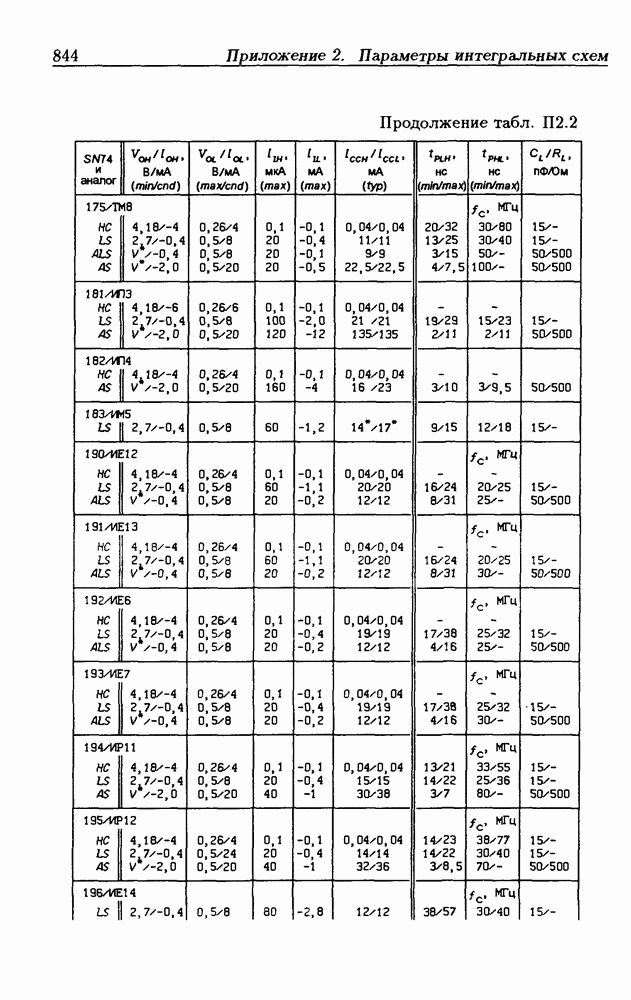
- Приложение 2. Параметры интегральных схем