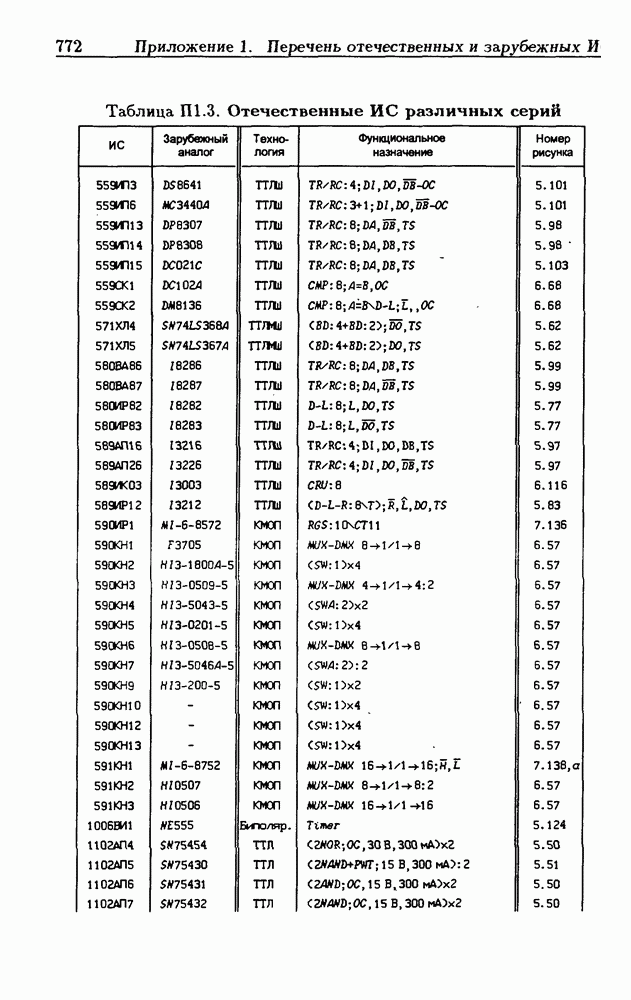
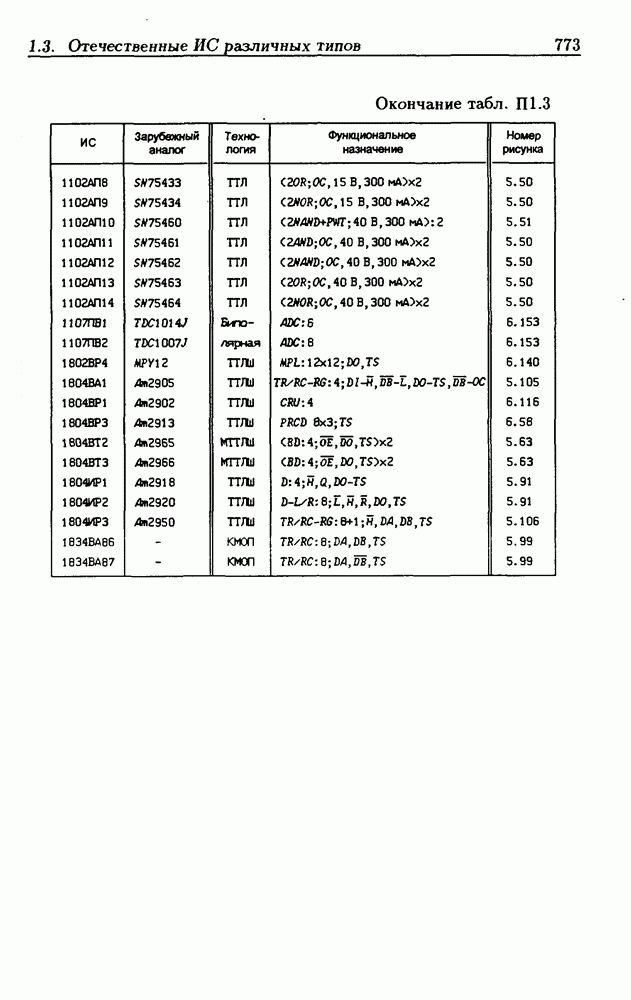
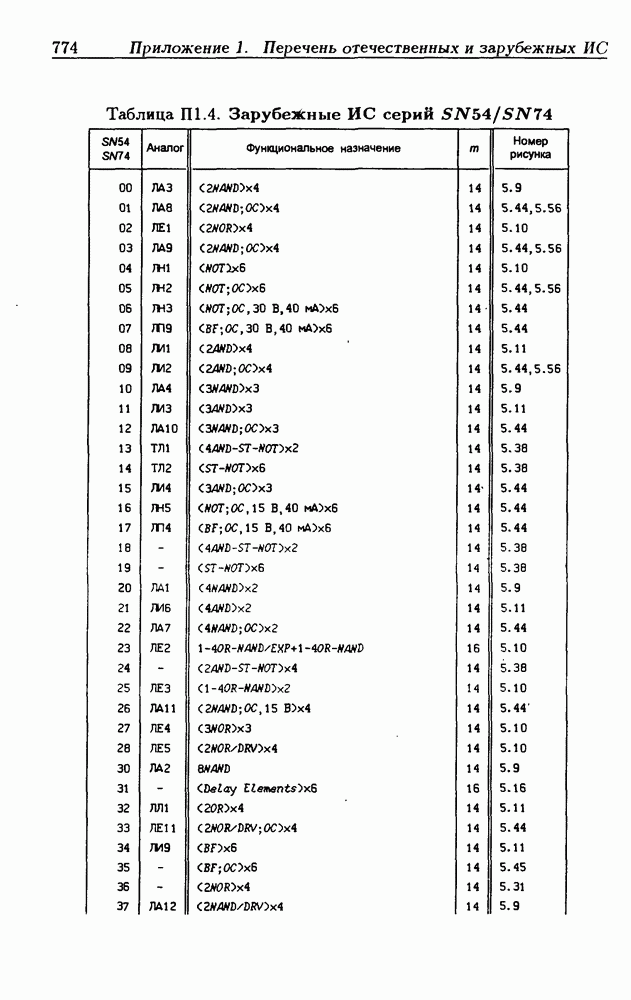
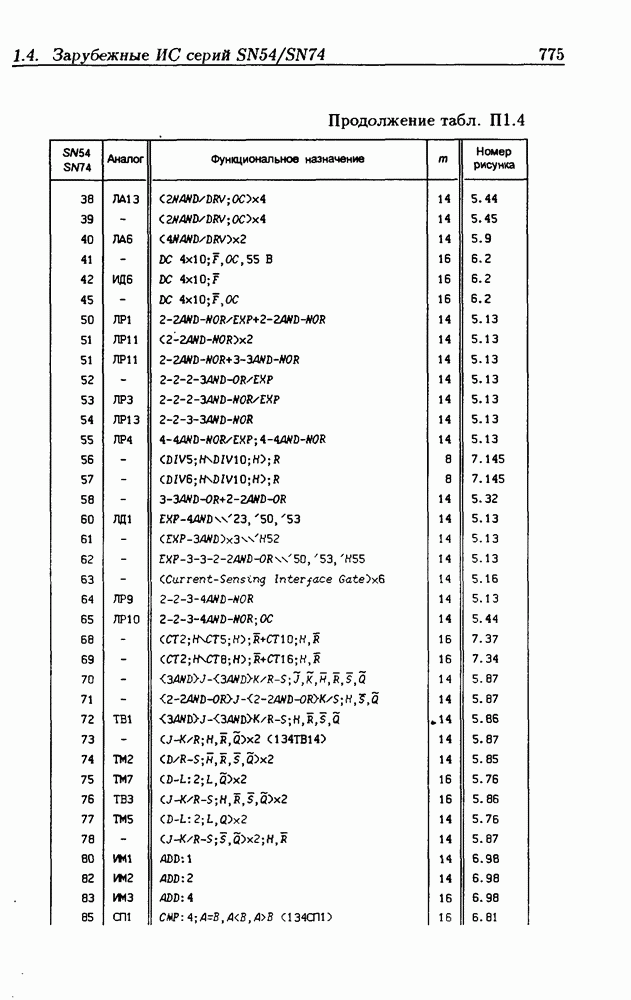
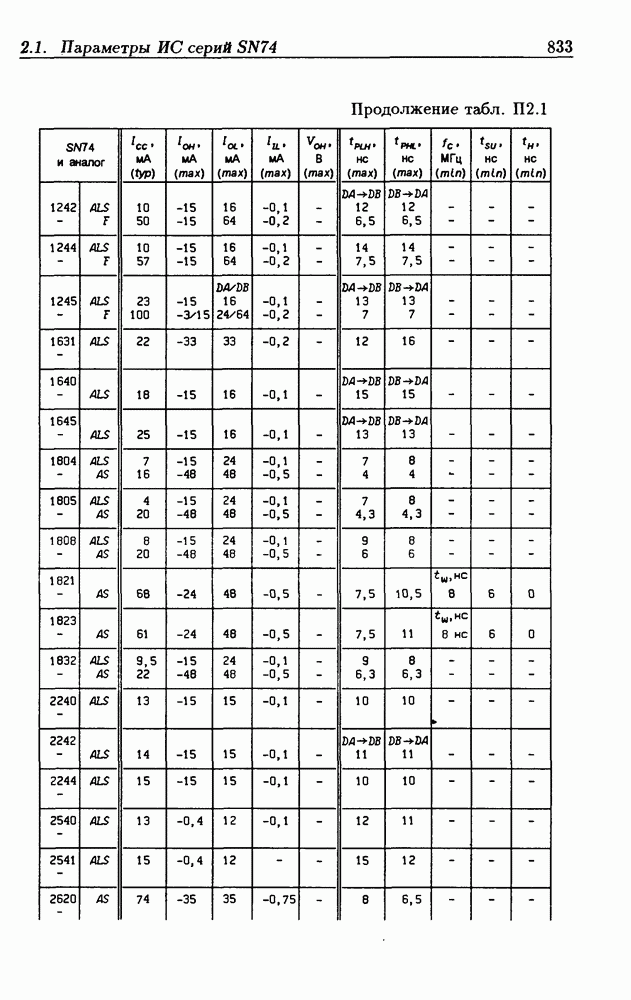
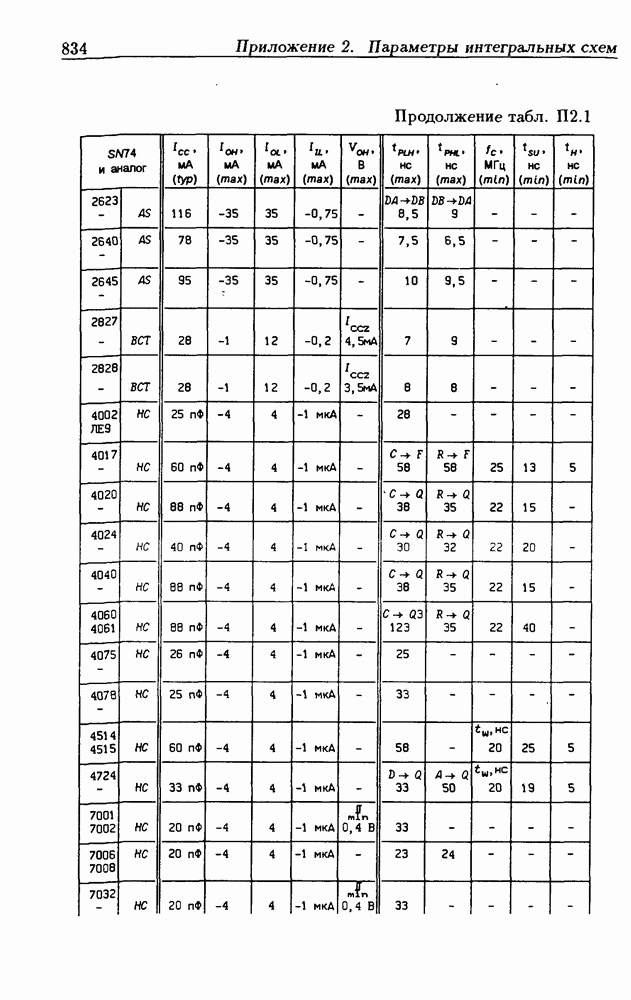
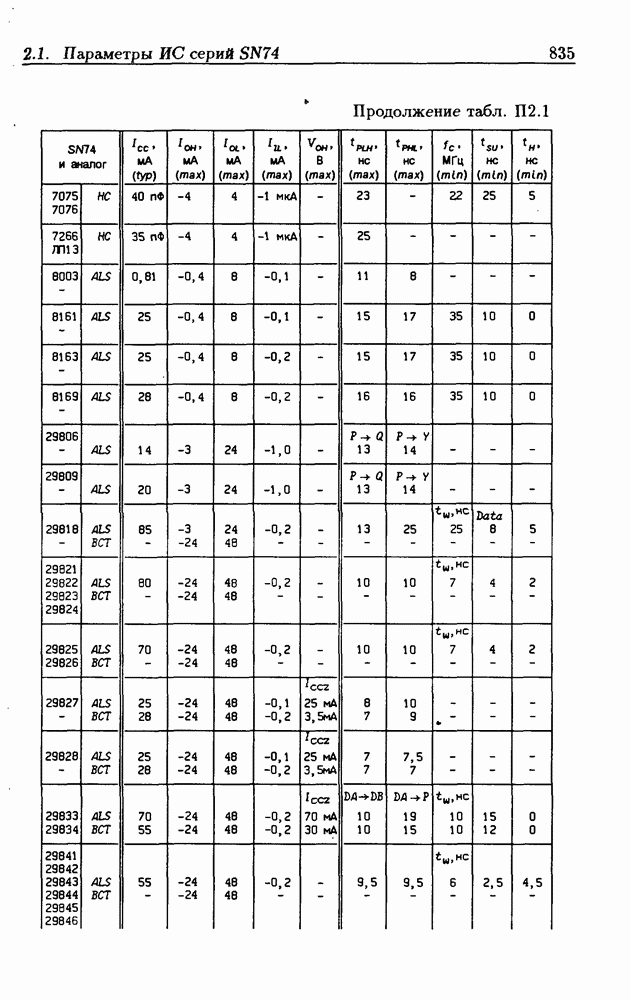
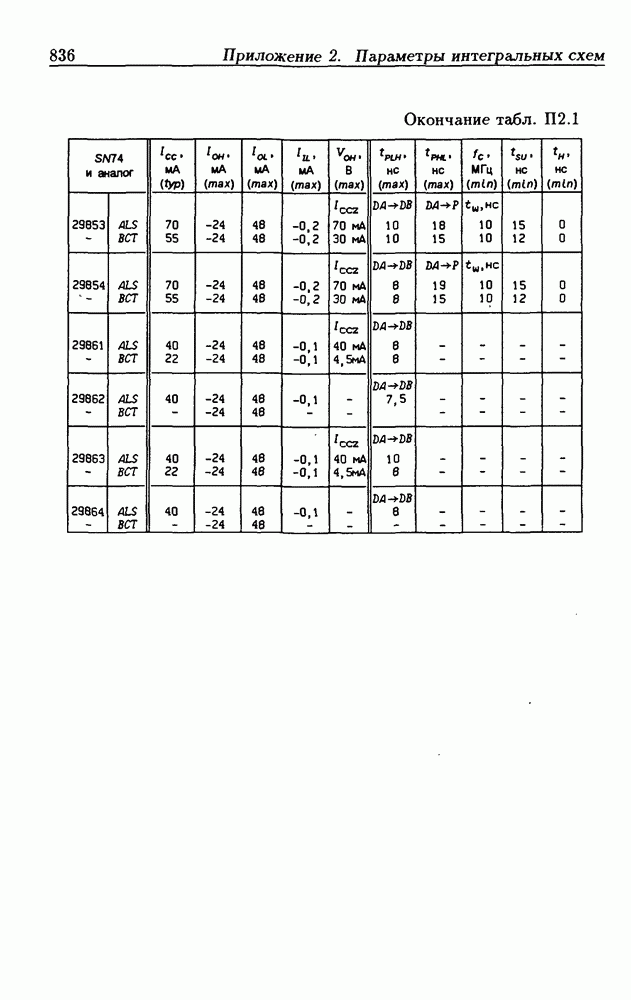
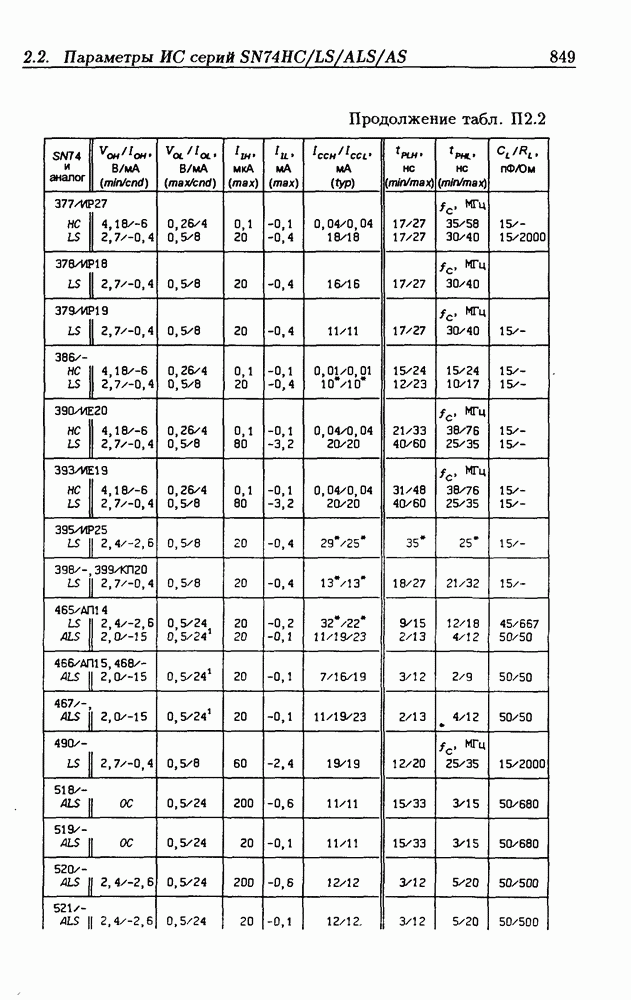
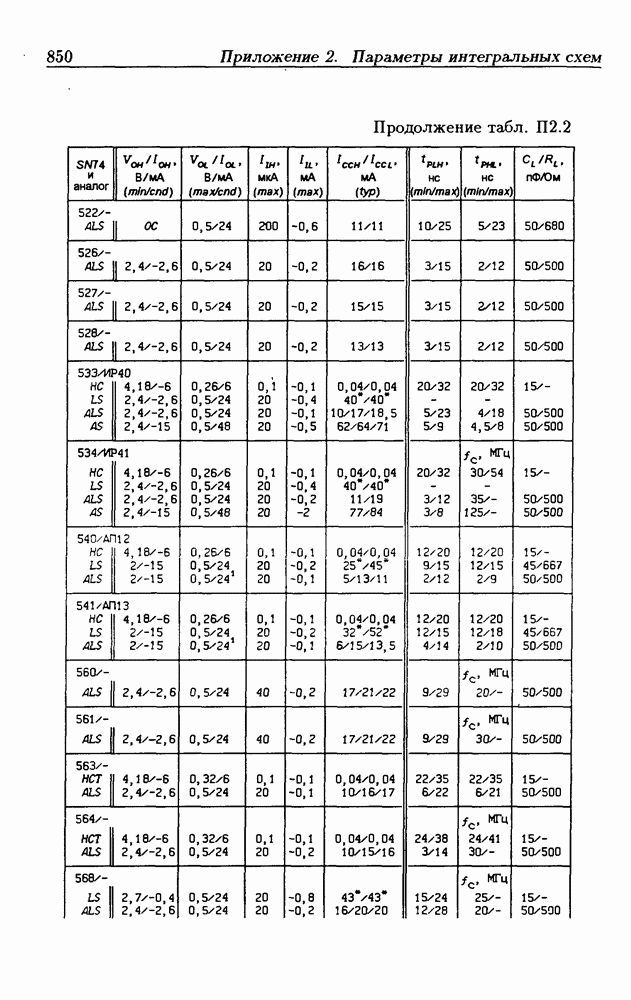
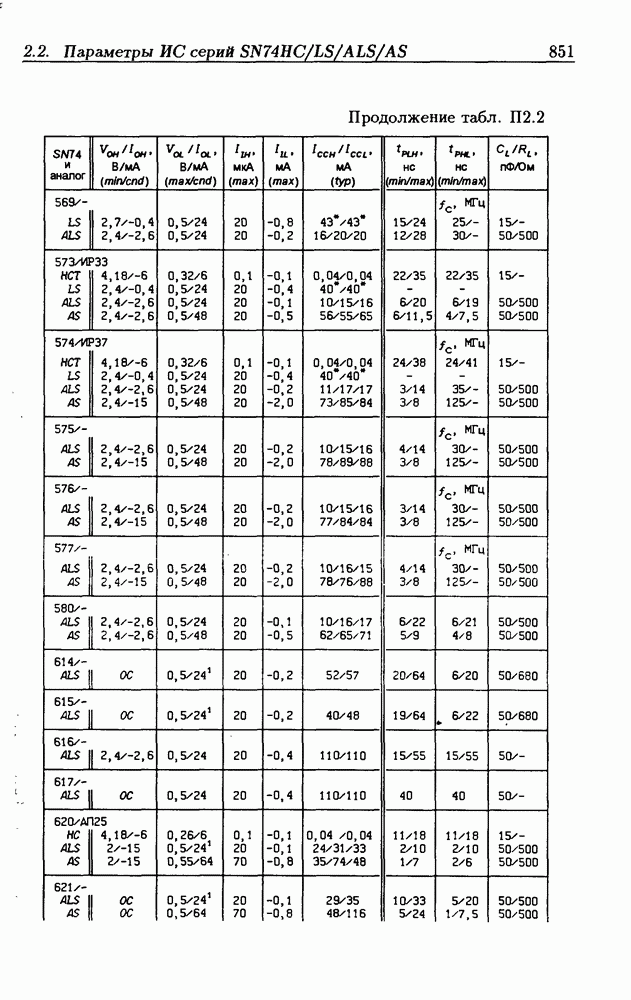
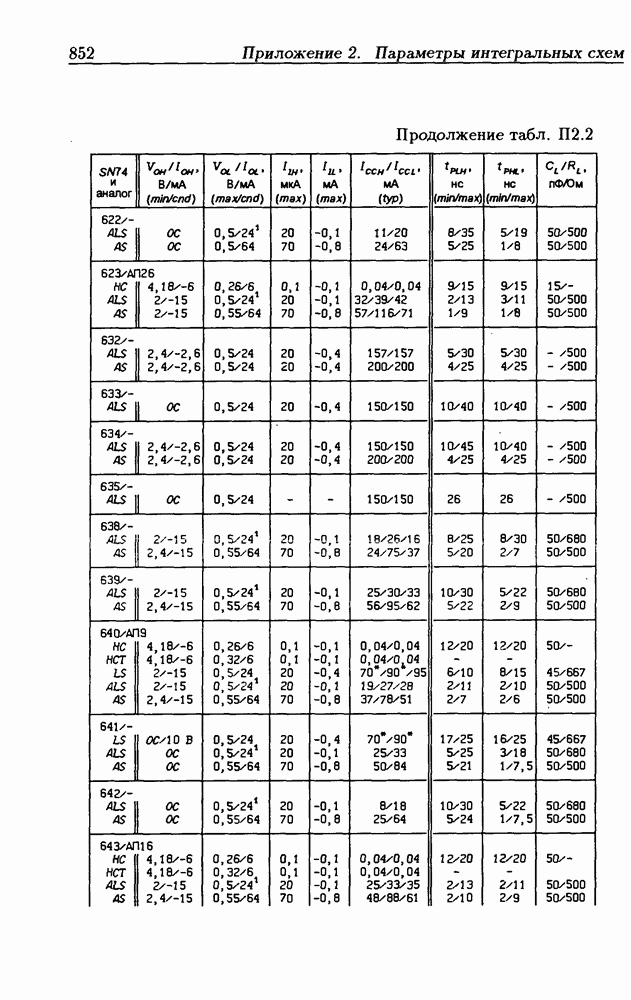
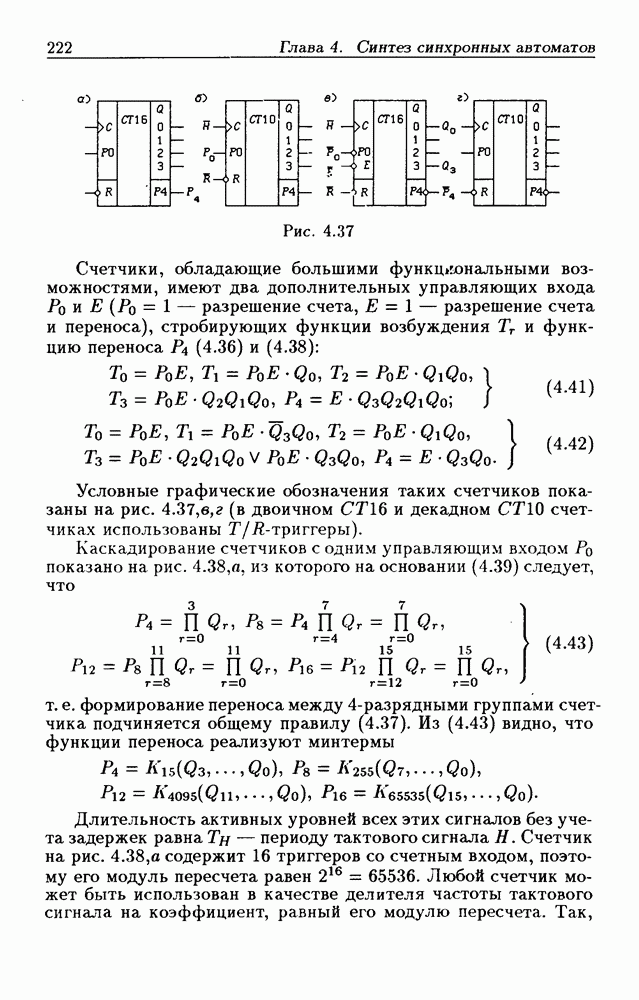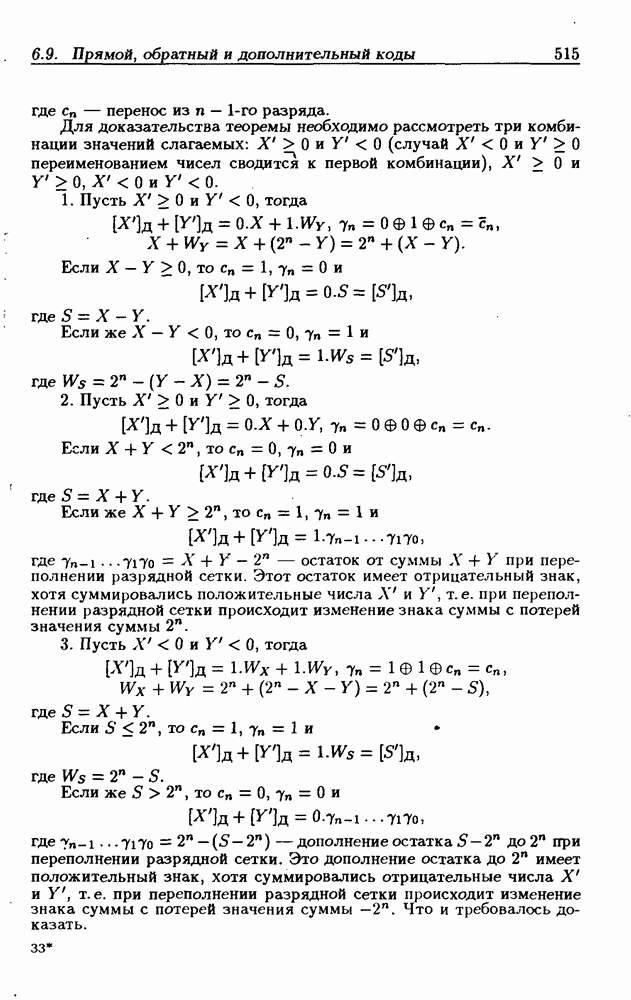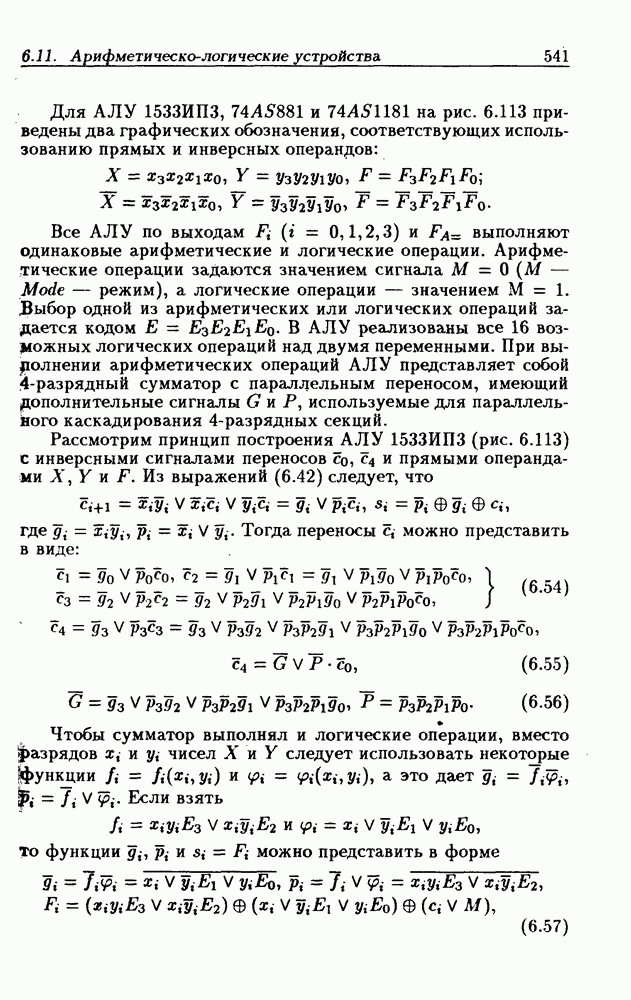| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
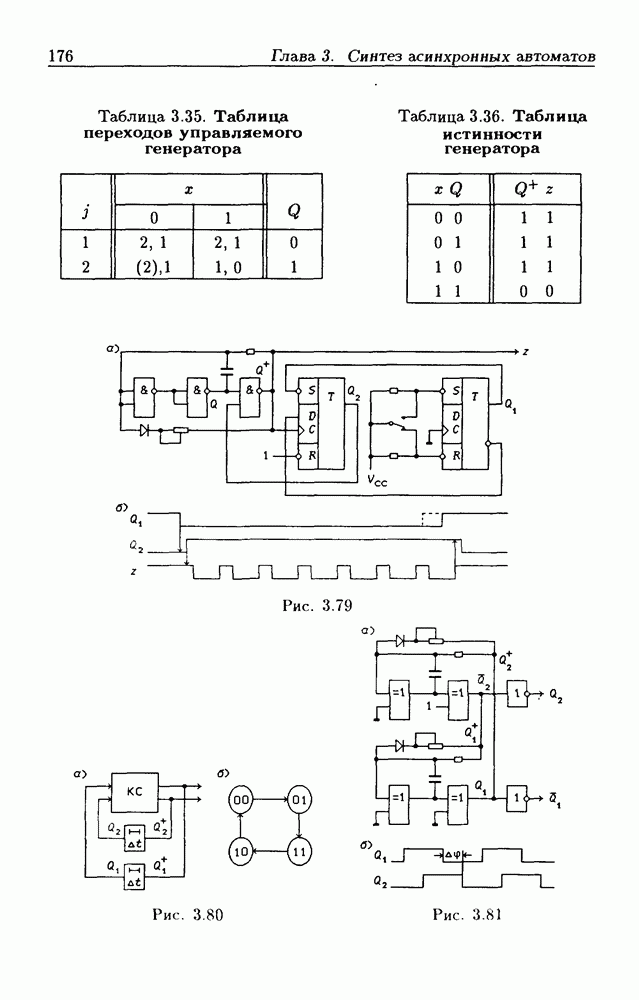
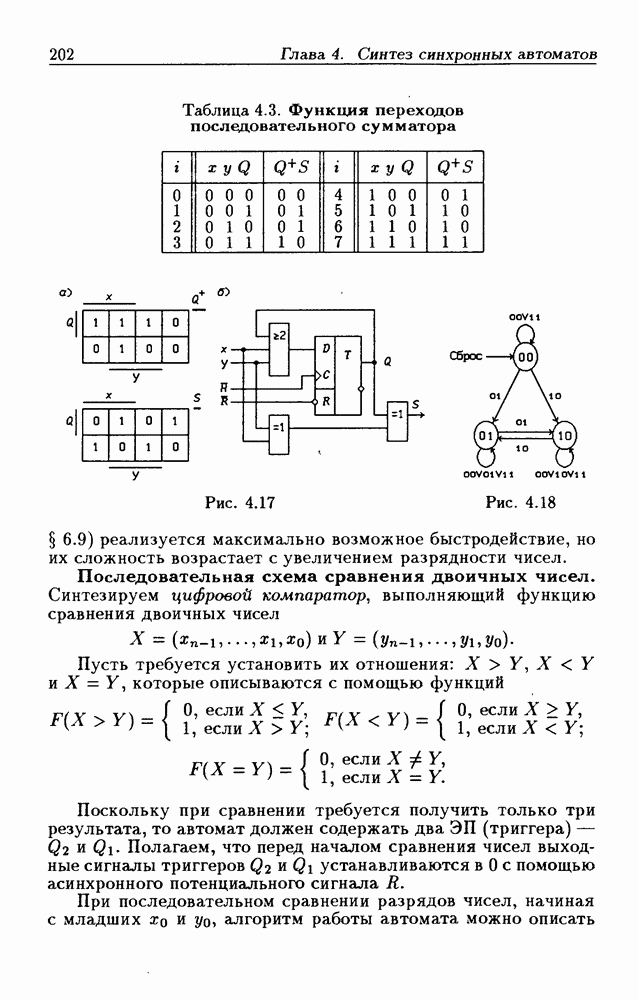
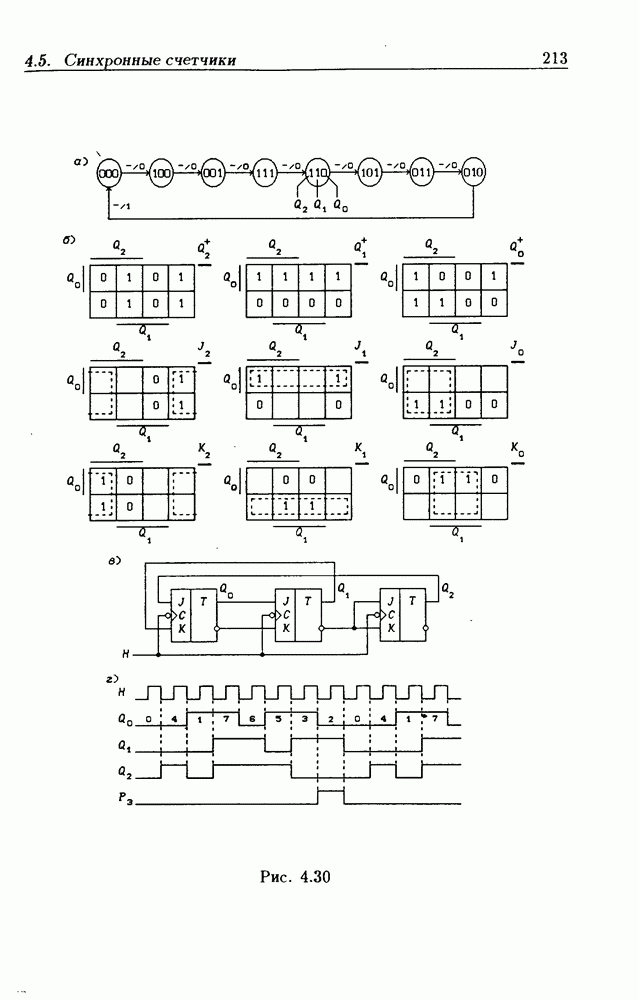
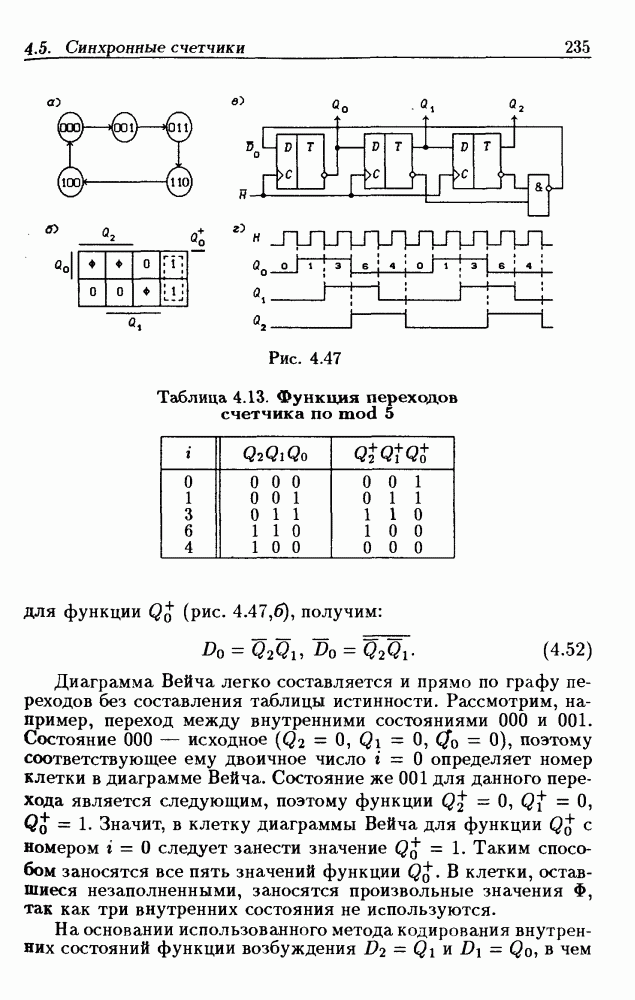
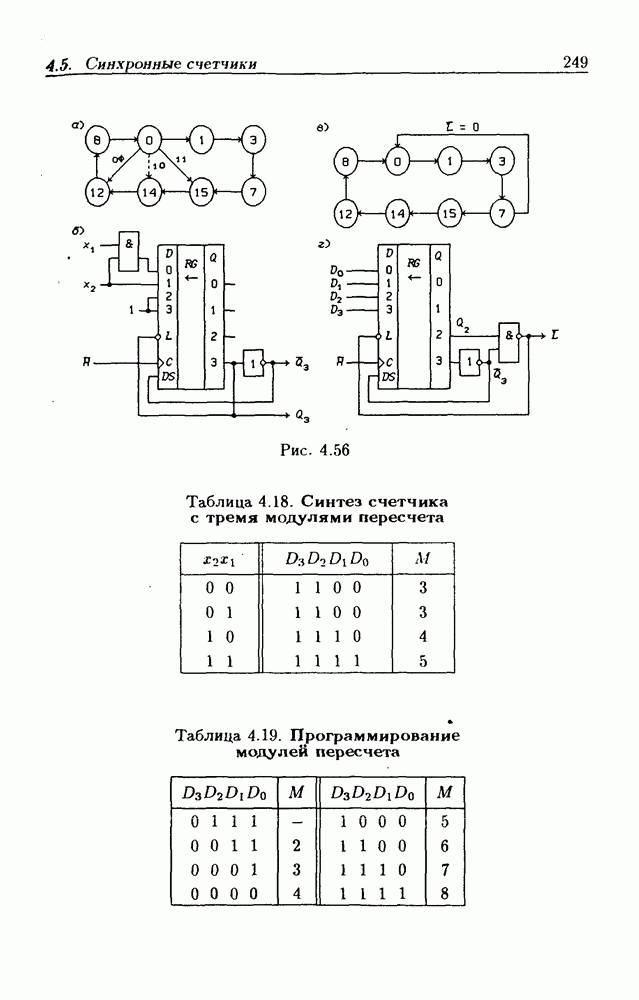
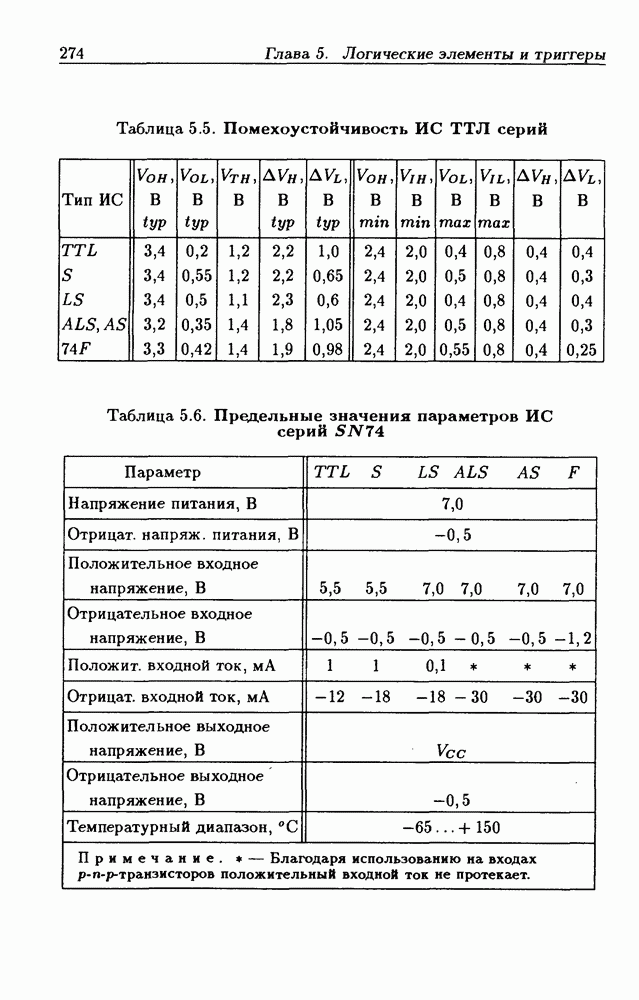
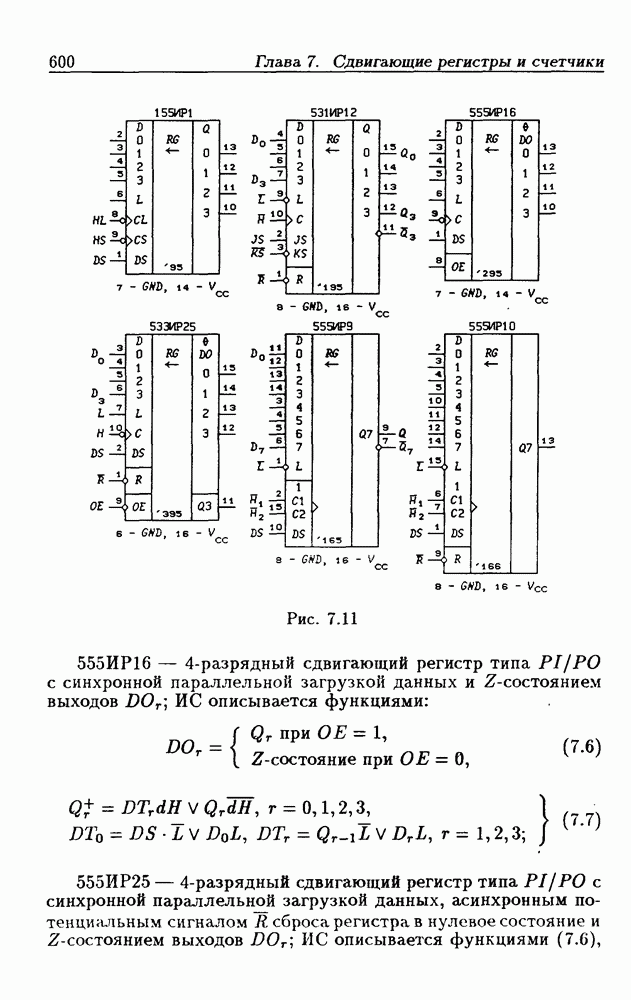
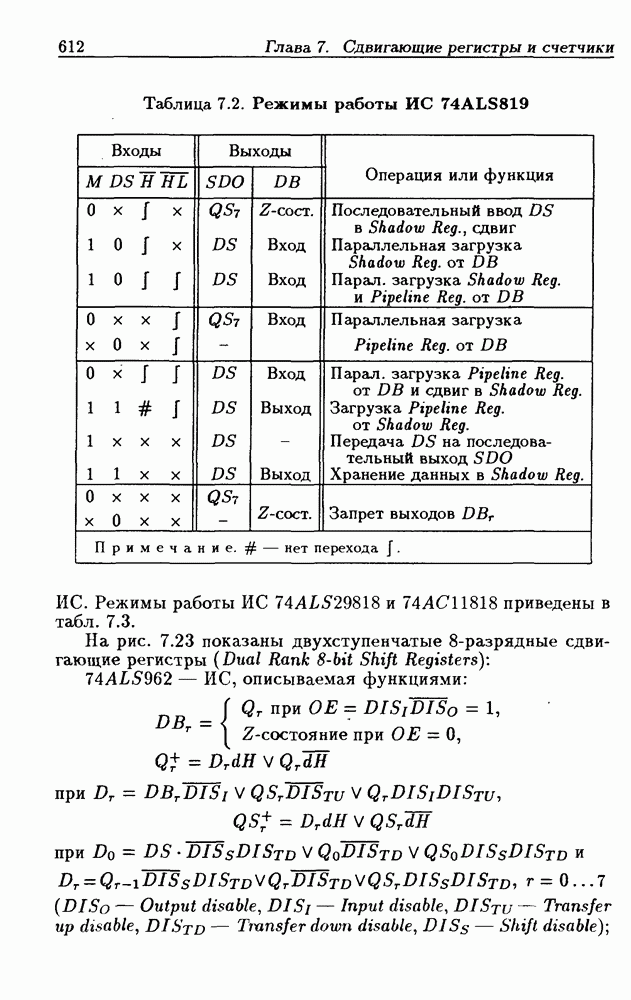
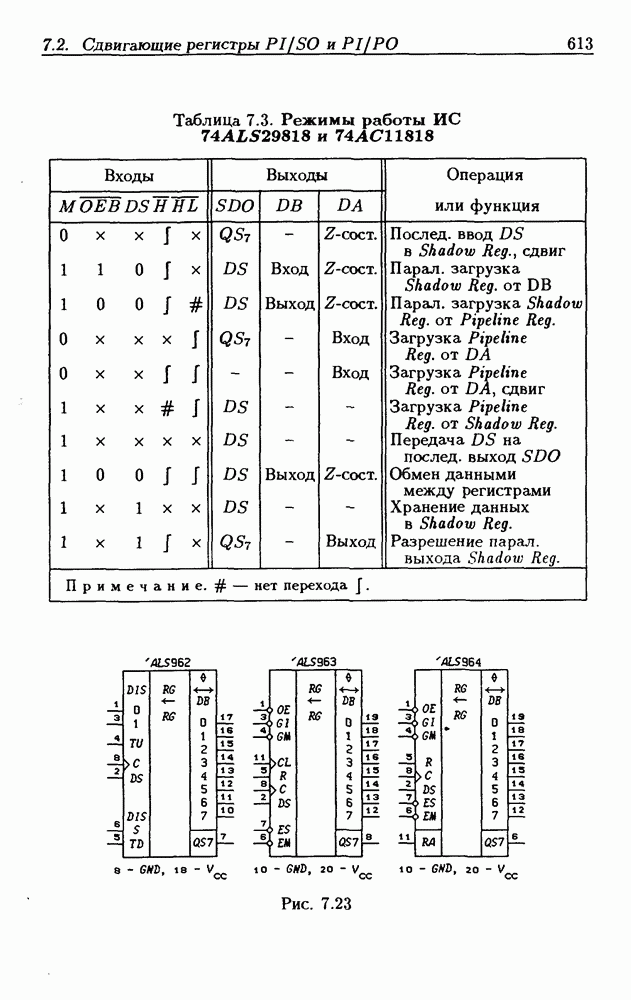
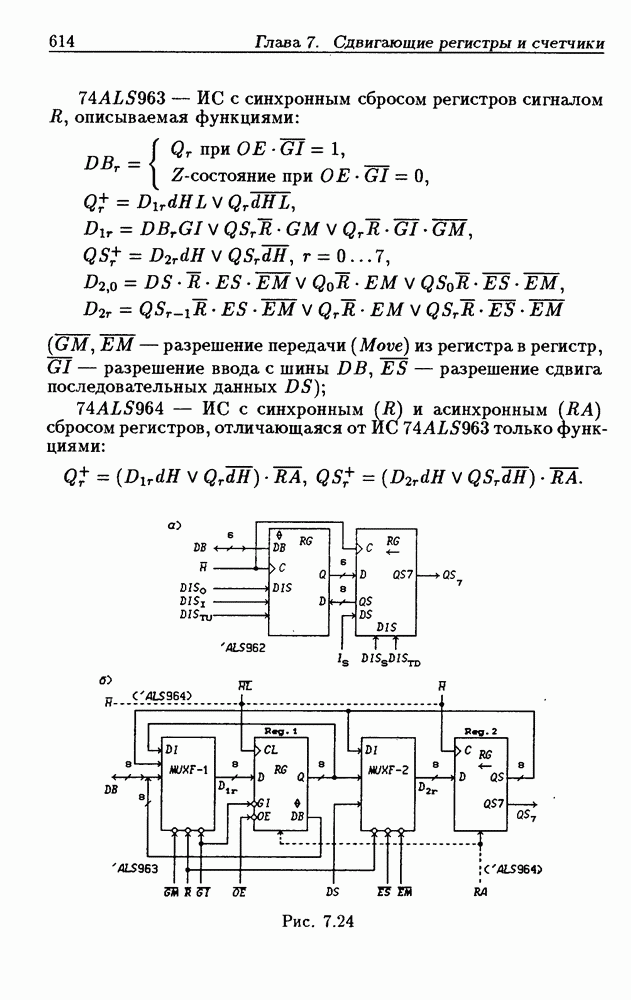
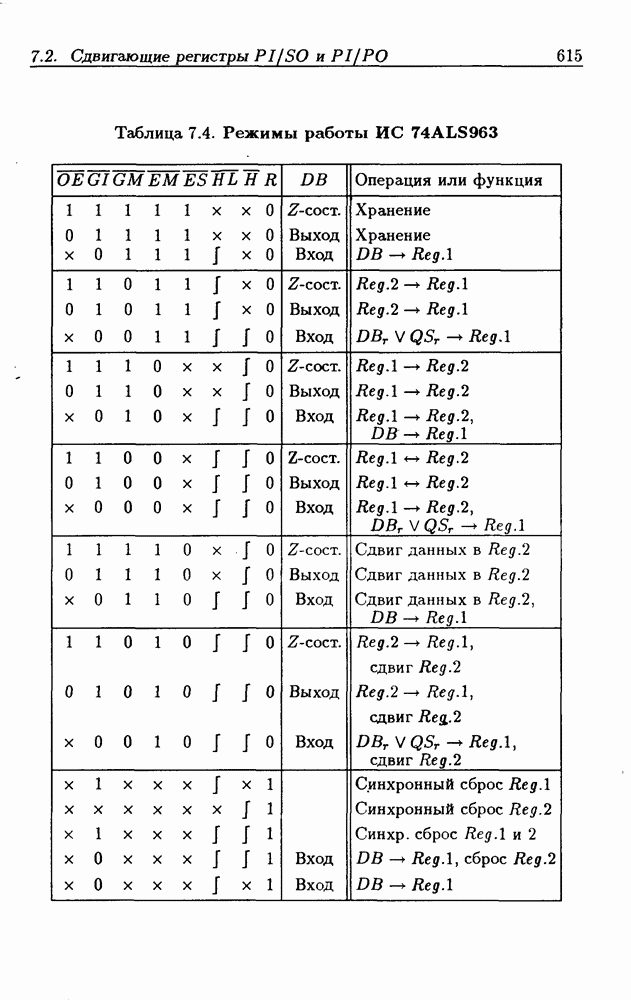
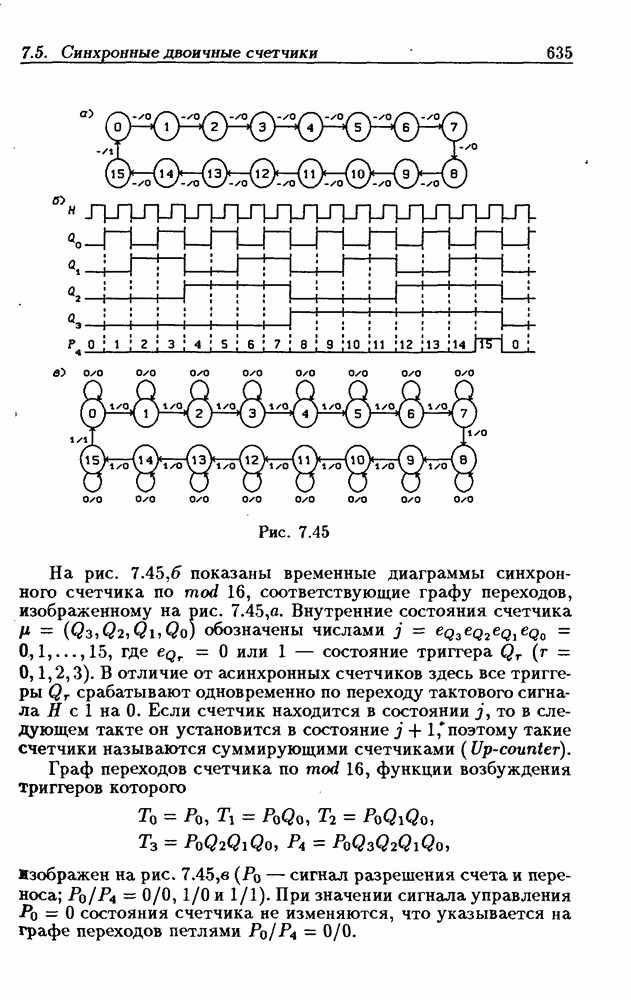
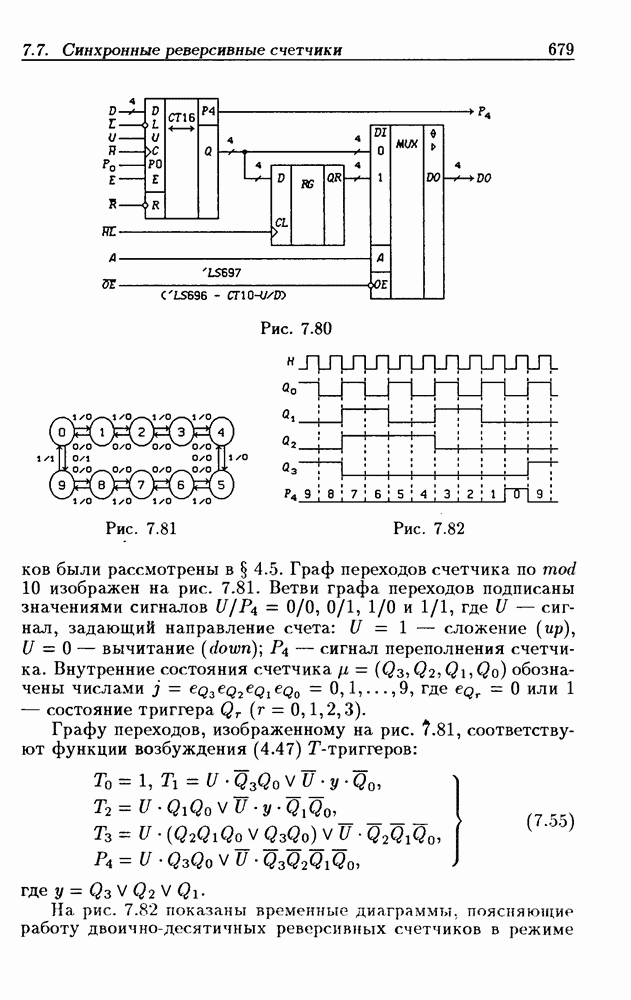
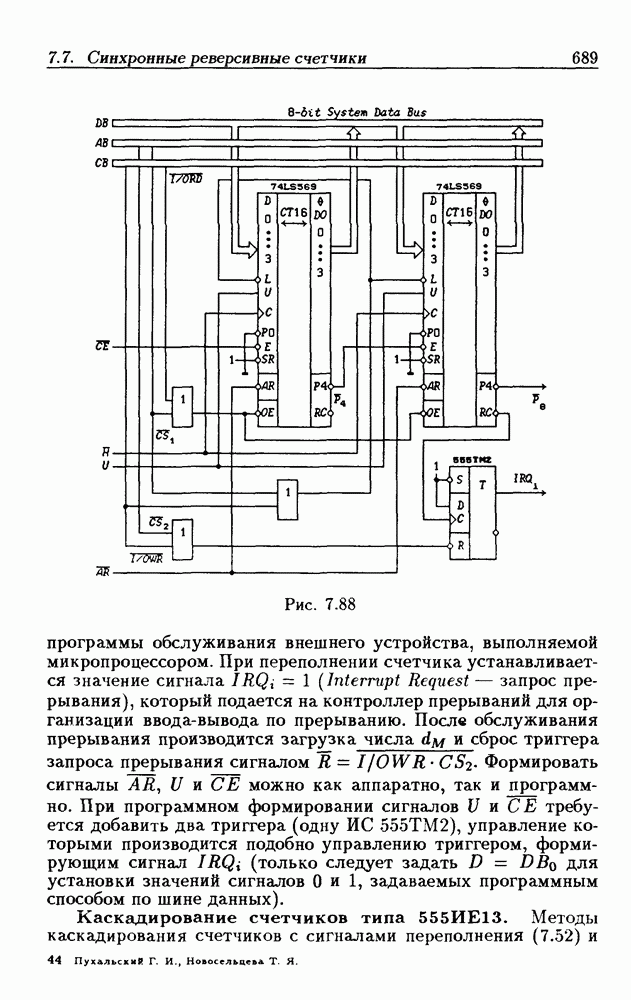
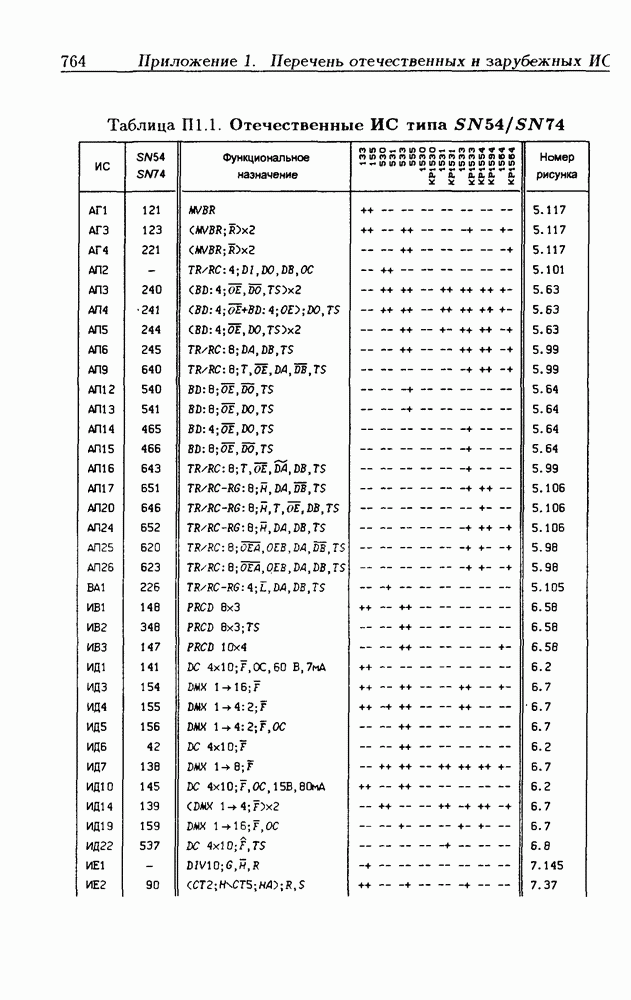
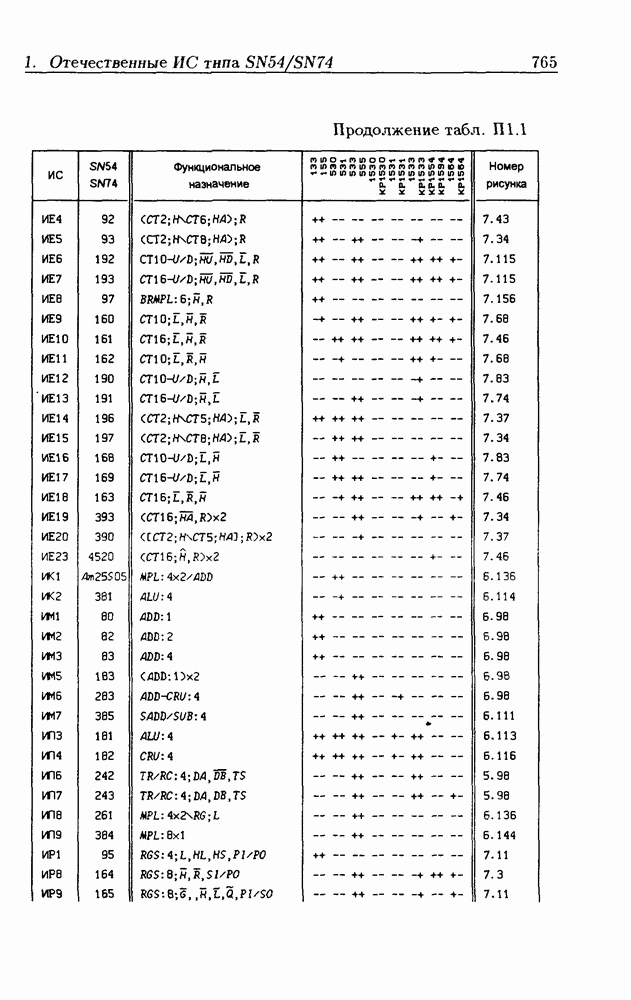
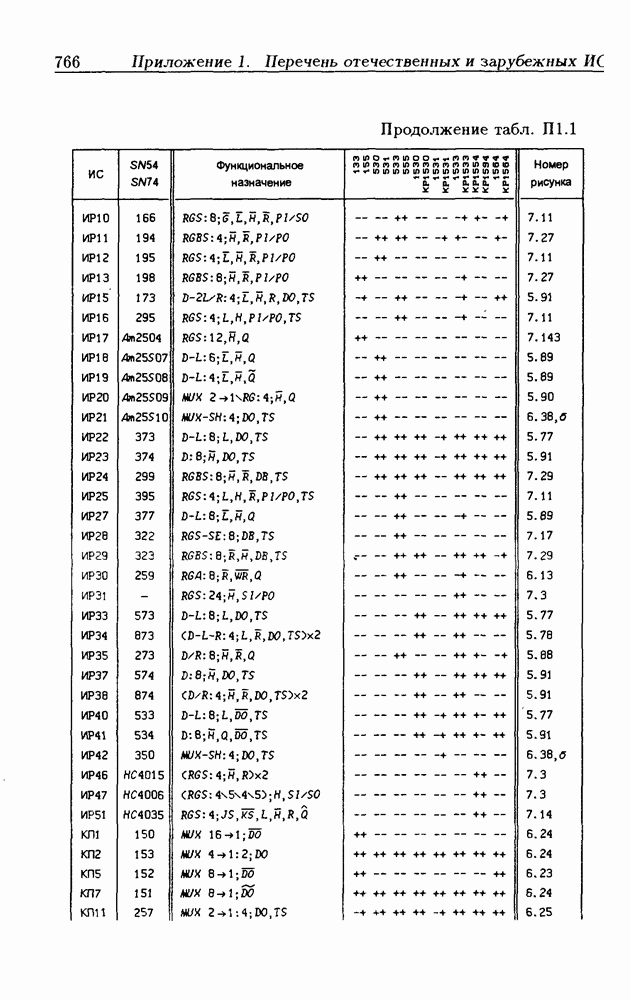
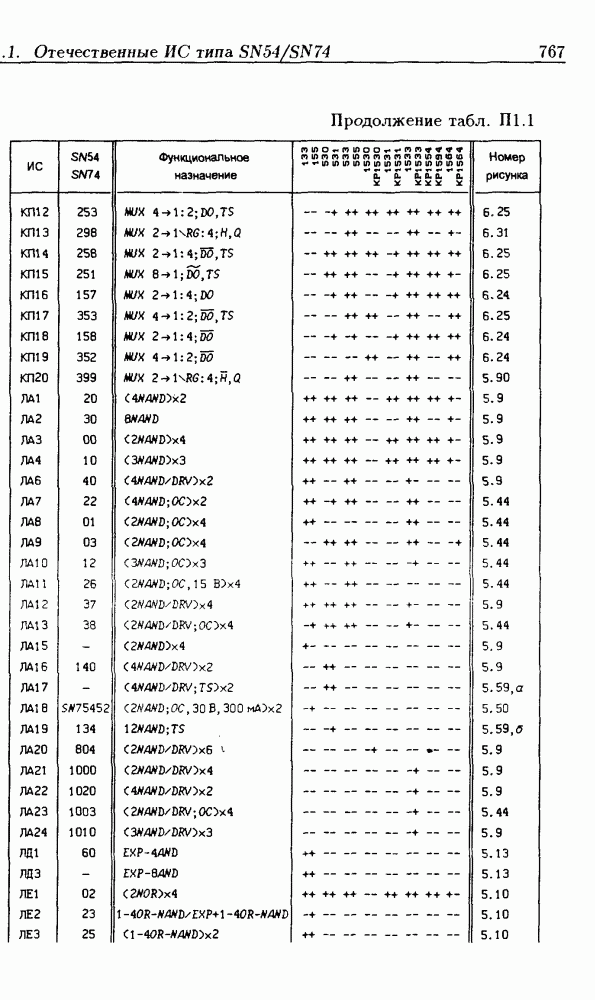
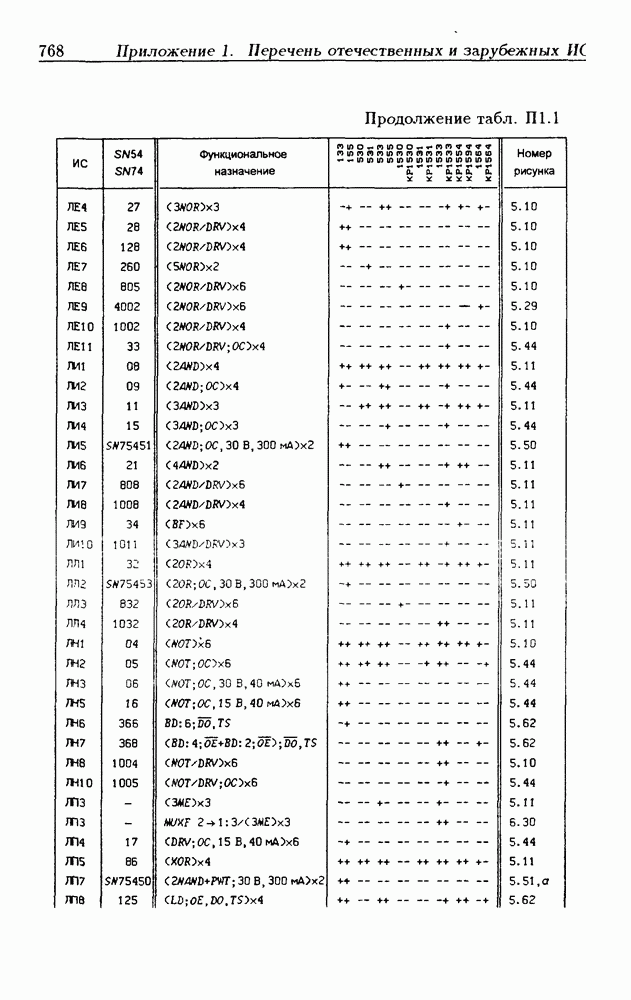
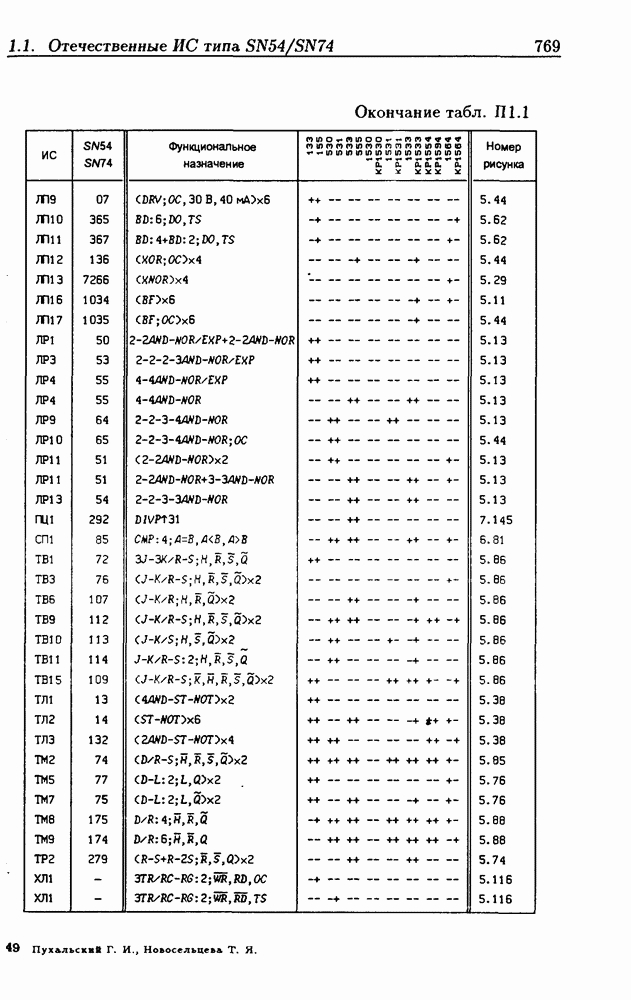
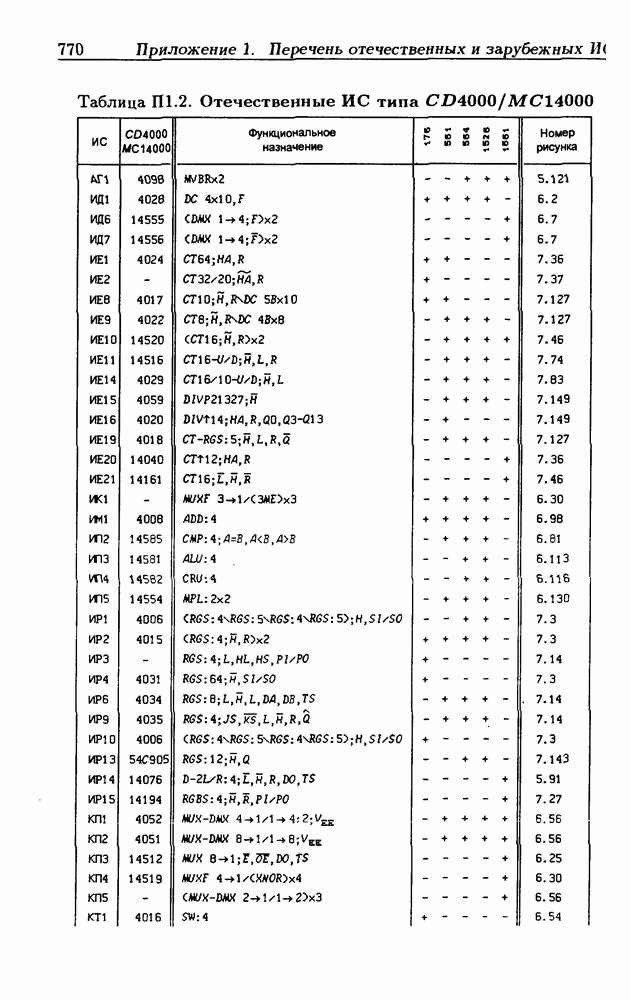
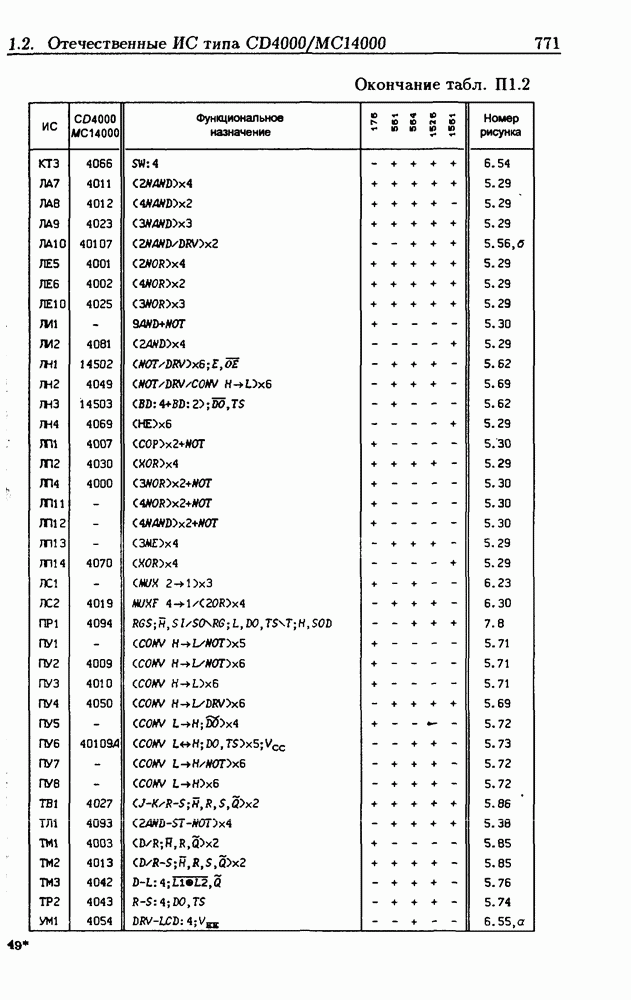
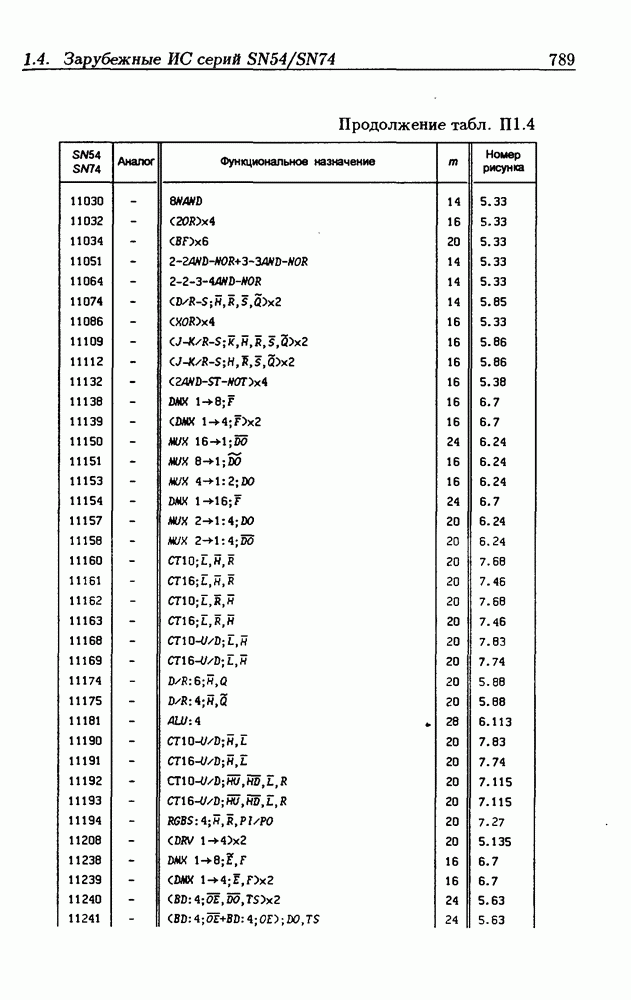
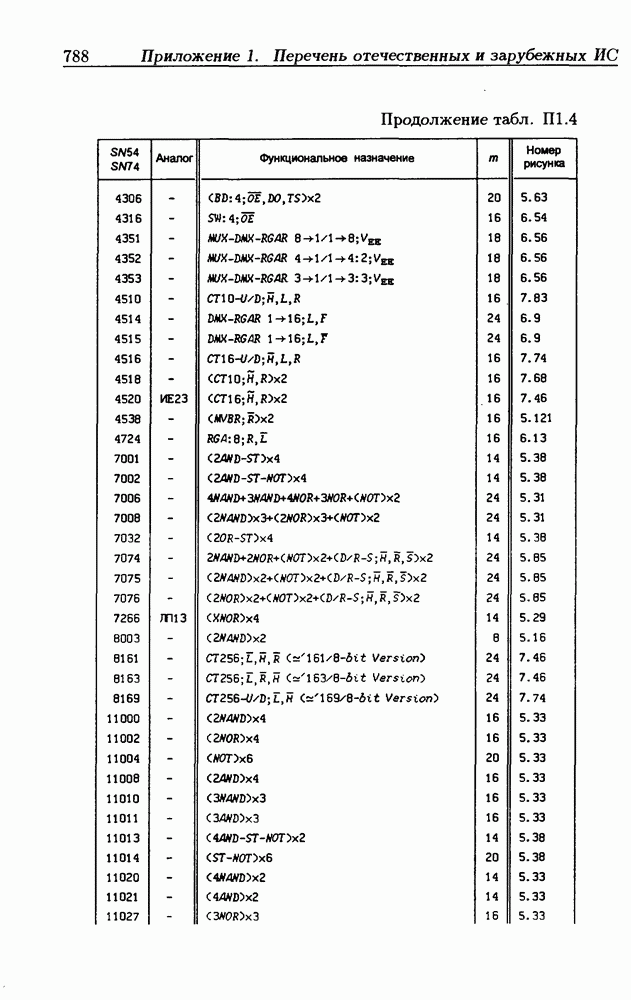
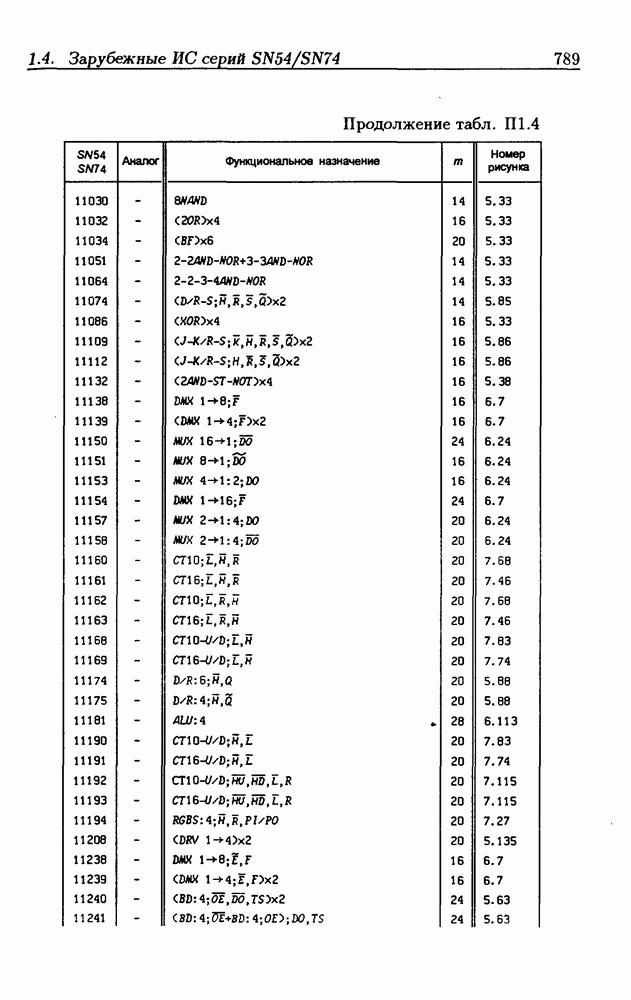
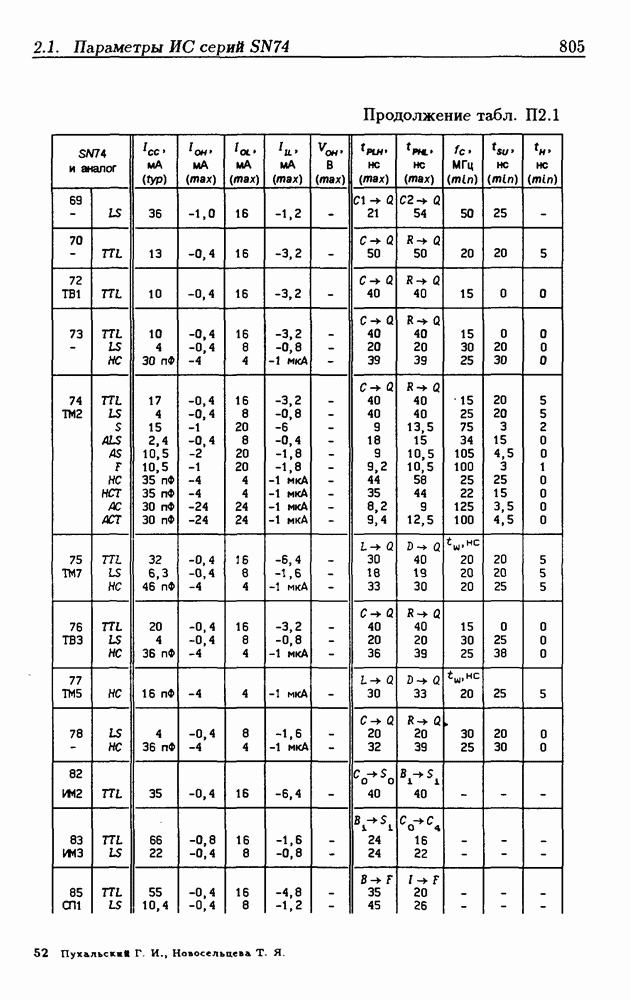
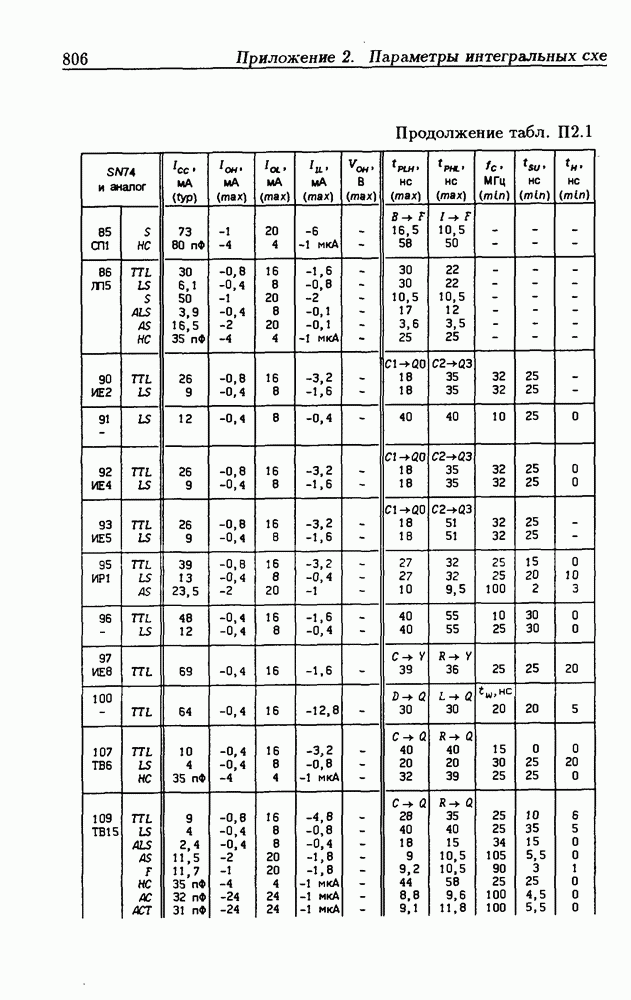
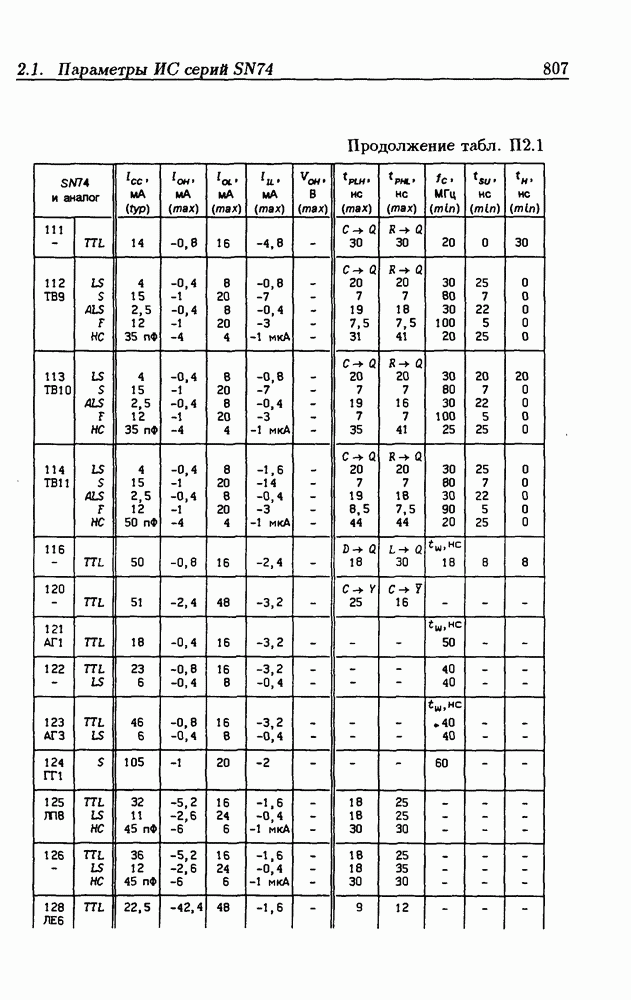
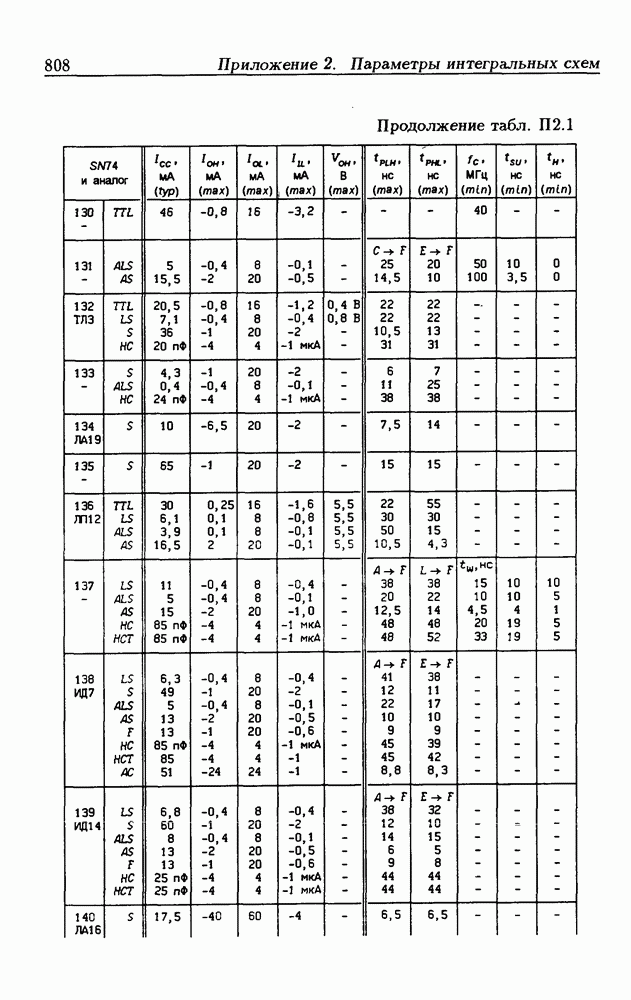
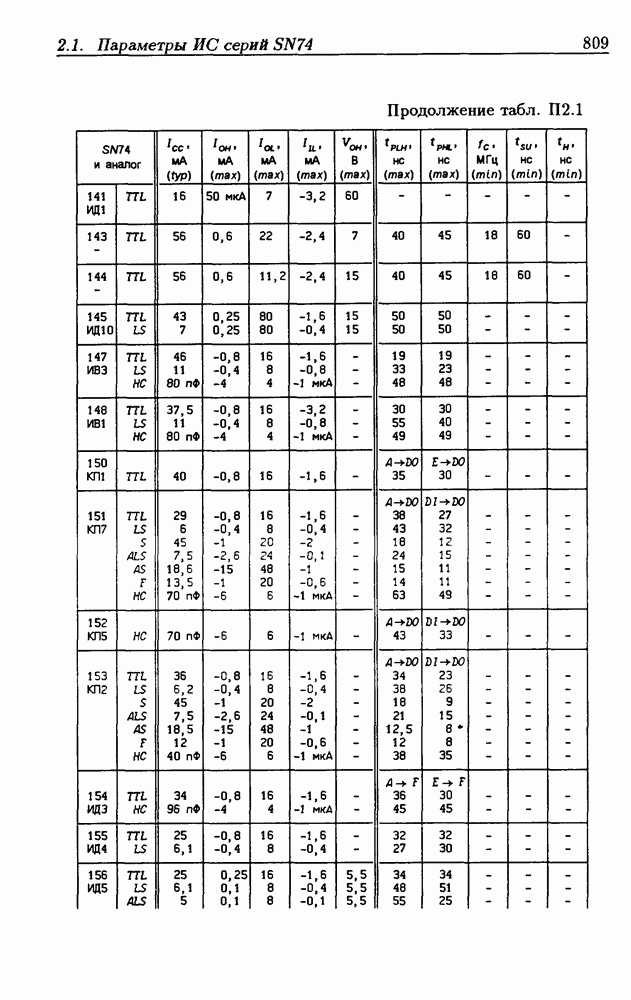
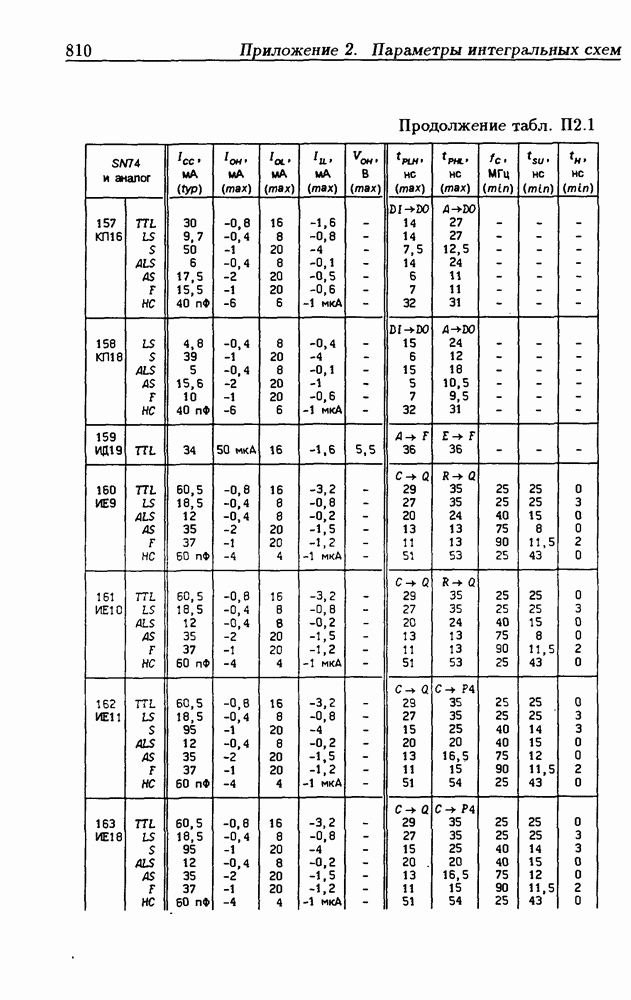
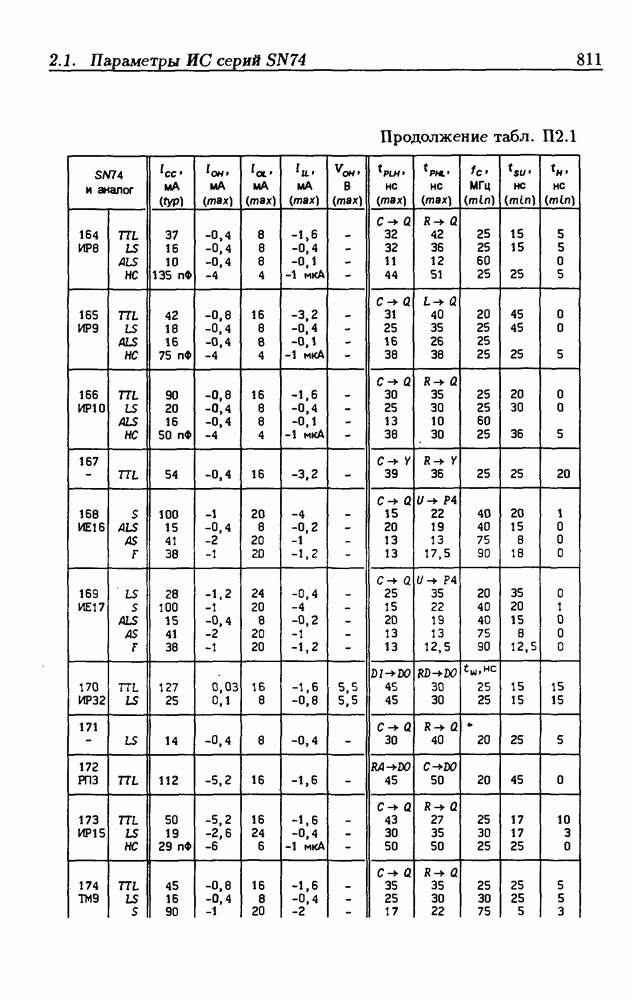
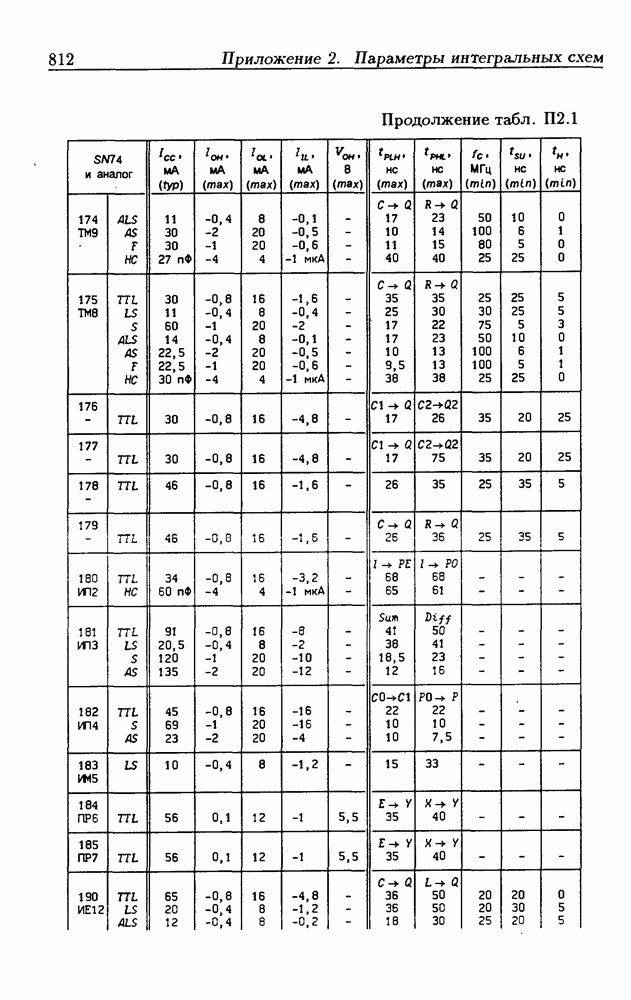
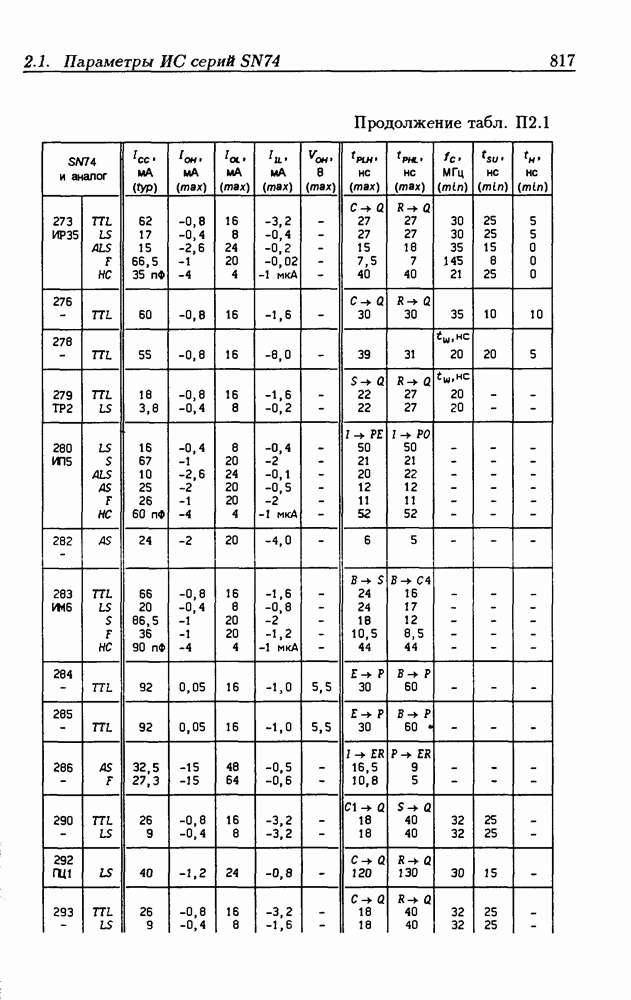
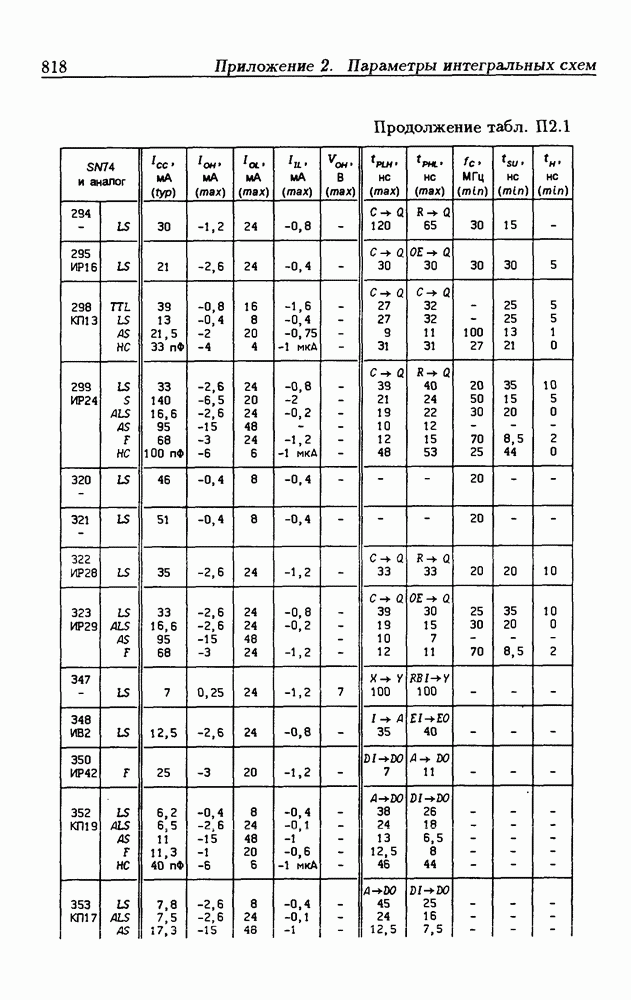
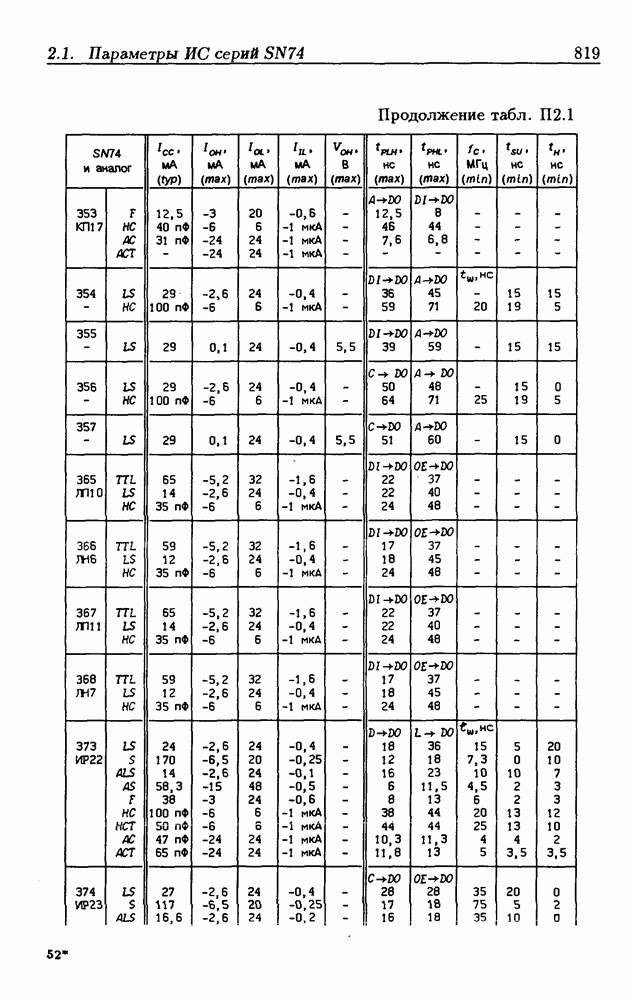
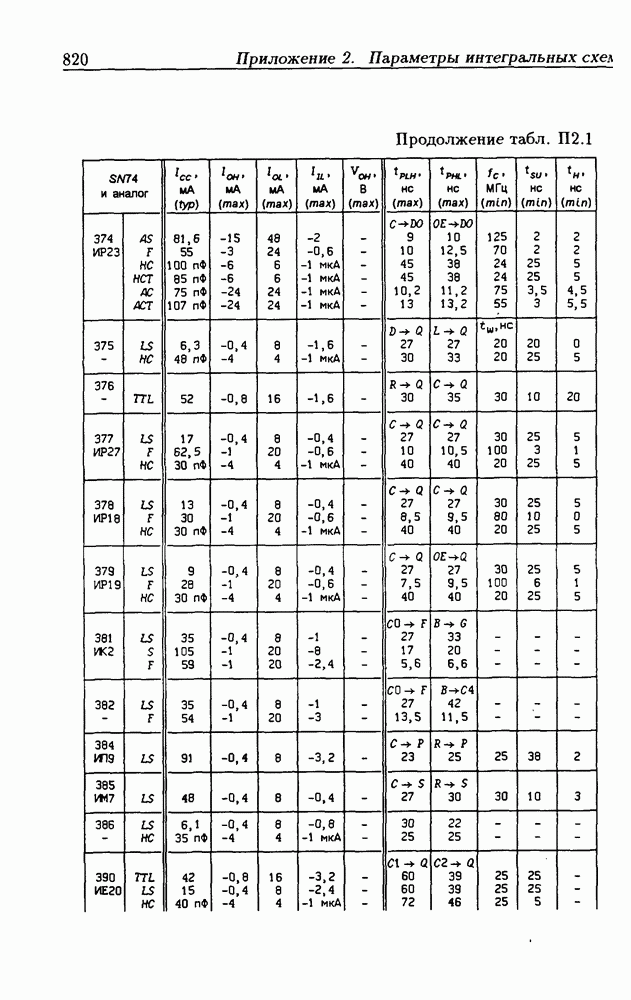
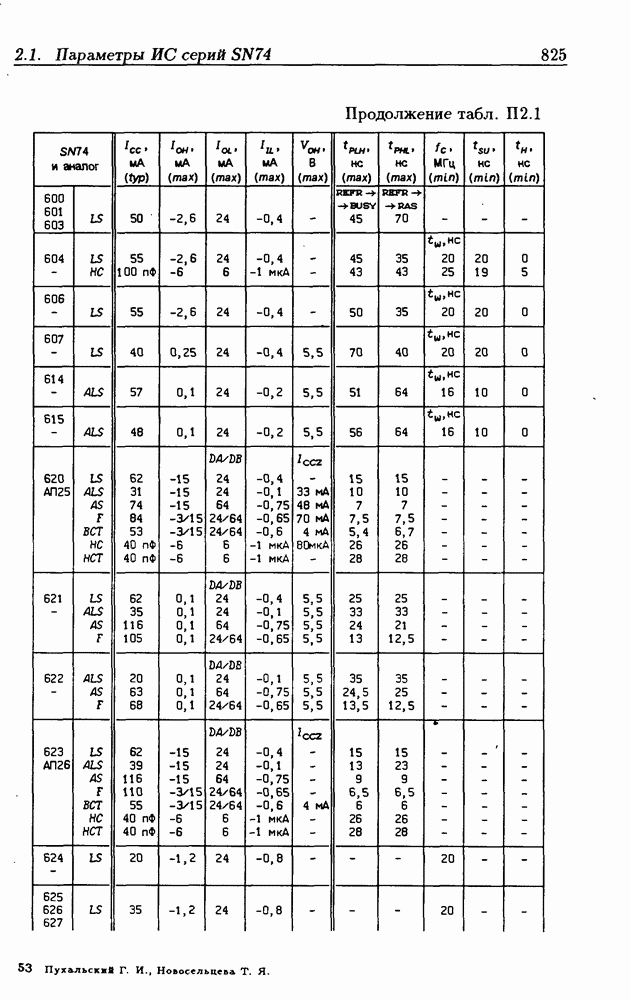
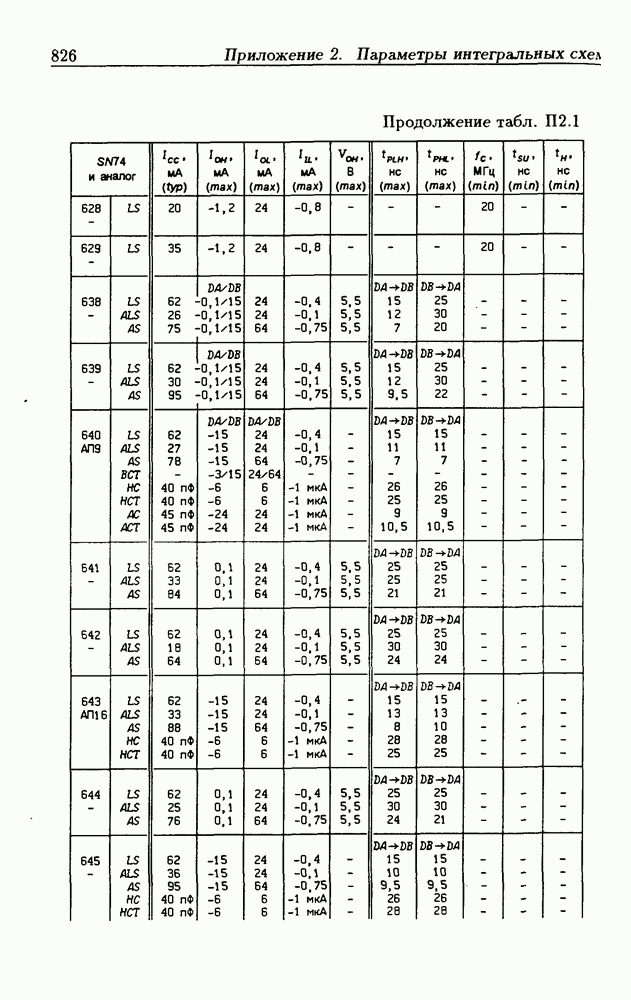
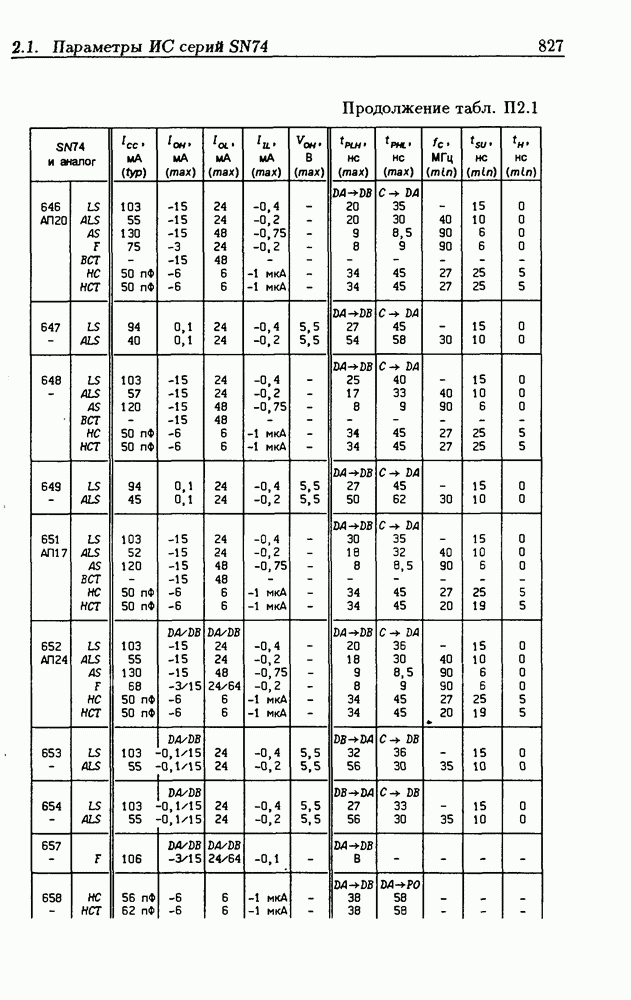
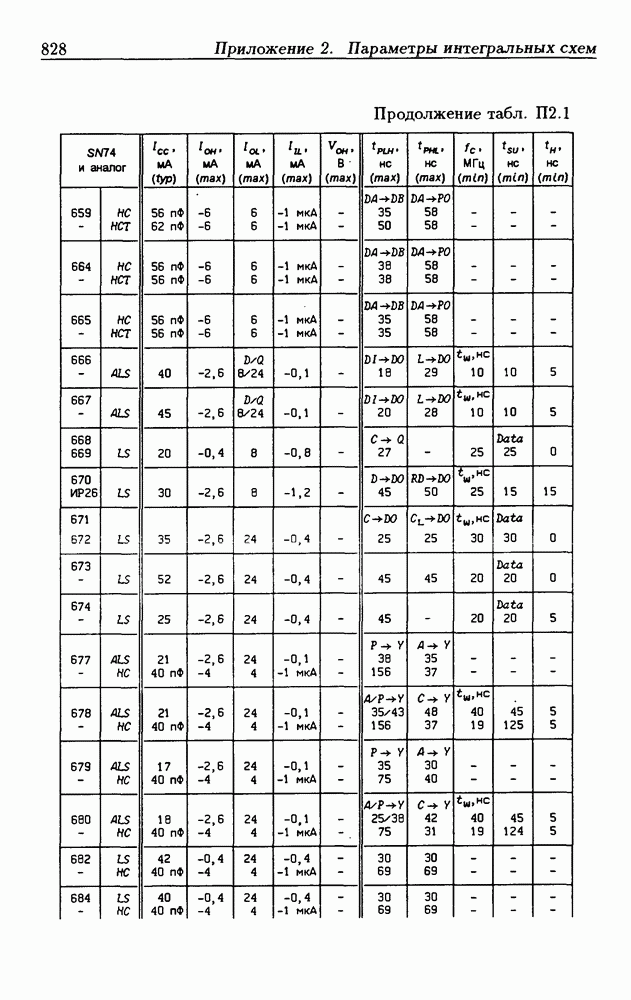
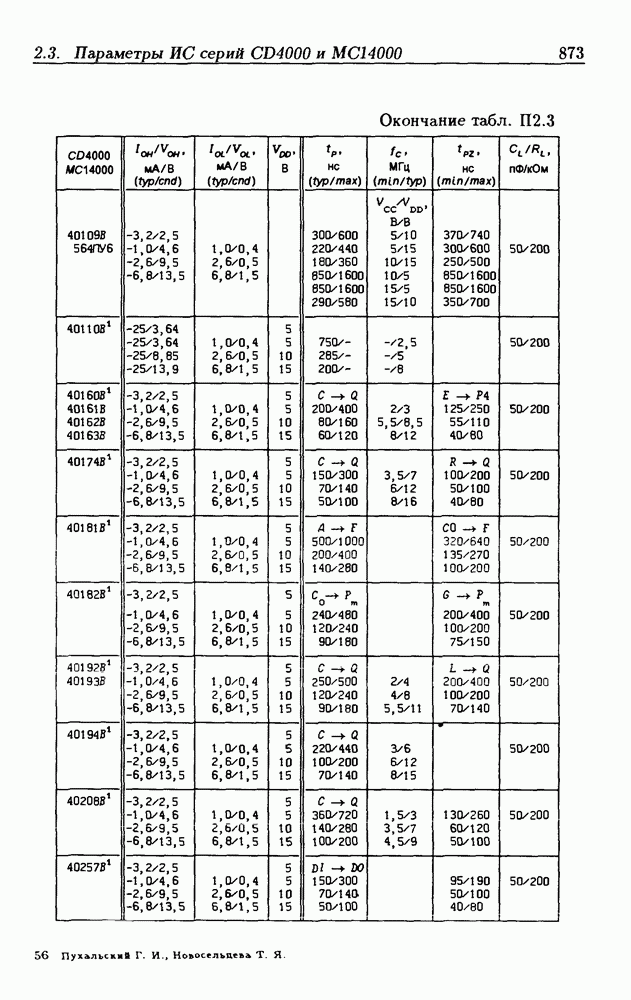
Синхронные двоичные счетчики.
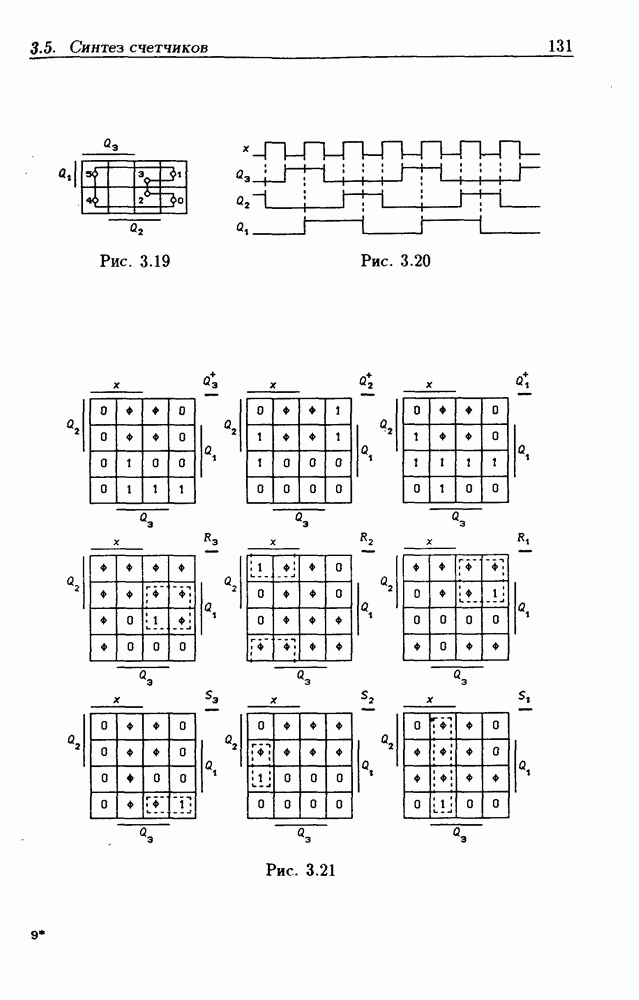
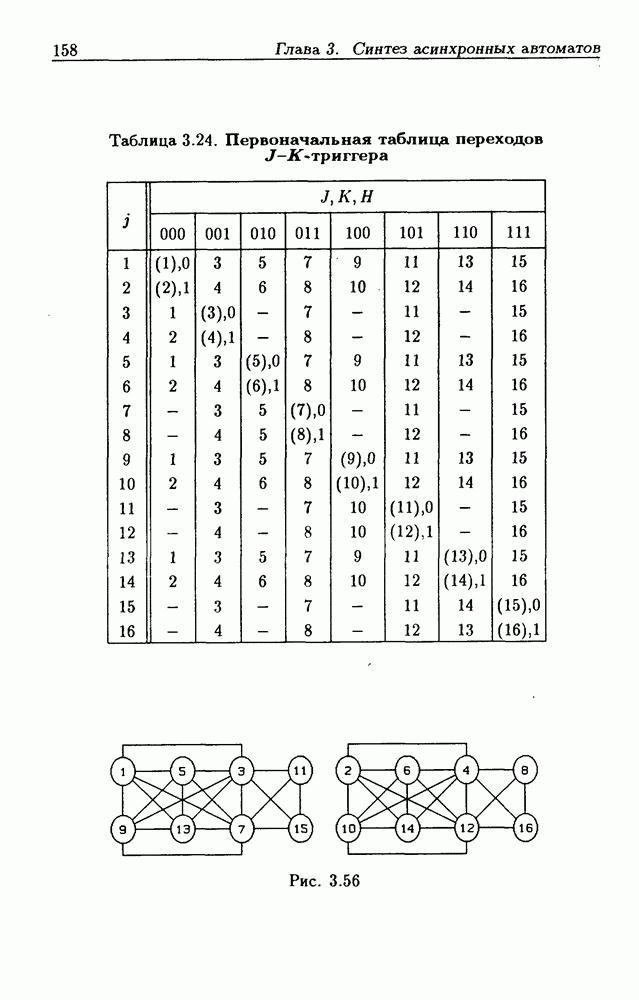
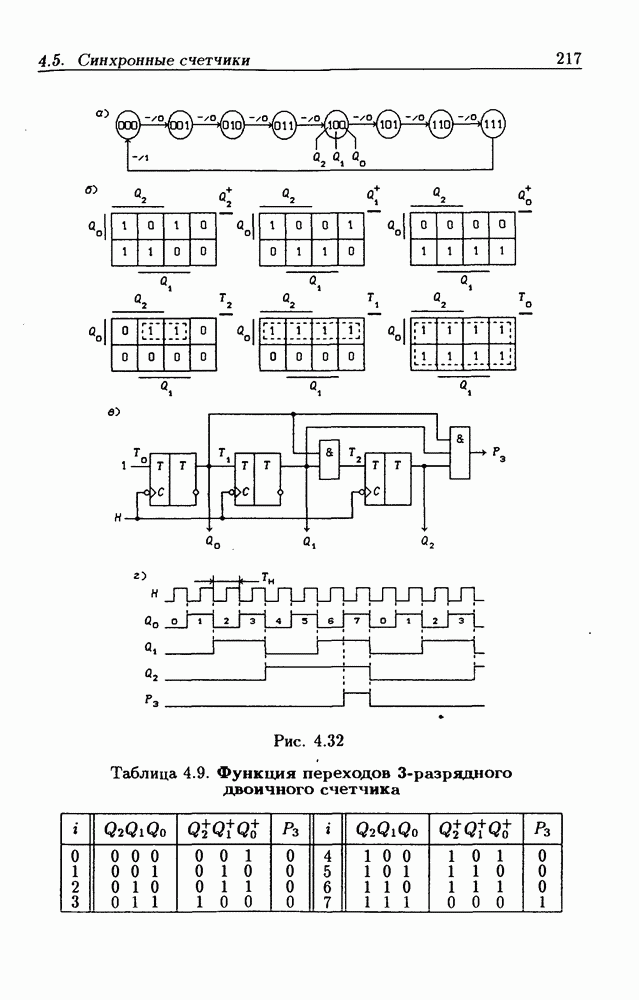
Внутренние состояния  -разрядного двоичного счетчика кодируются последовательными двоичными числами, десятичные эквиваленты которых
-разрядного двоичного счетчика кодируются последовательными двоичными числами, десятичные эквиваленты которых  (рис. 4.32,а). При каждом переходе счетчика число
(рис. 4.32,а). При каждом переходе счетчика число  увеличивается на 1 в соответствии с двоичной системой счисления и при достижении максимального значения
увеличивается на 1 в соответствии с двоичной системой счисления и при достижении максимального значения  возвращается в исходное (начальное нулевое) состояние
возвращается в исходное (начальное нулевое) состояние  Выходным сигналом счетчика, свидетельствующем о его переполнении, является сигнал
Выходным сигналом счетчика, свидетельствующем о его переполнении, является сигнал  По графу переходов на рис. 4.32,а составляется таблица истинности (табл. 4.9) для функции переходов
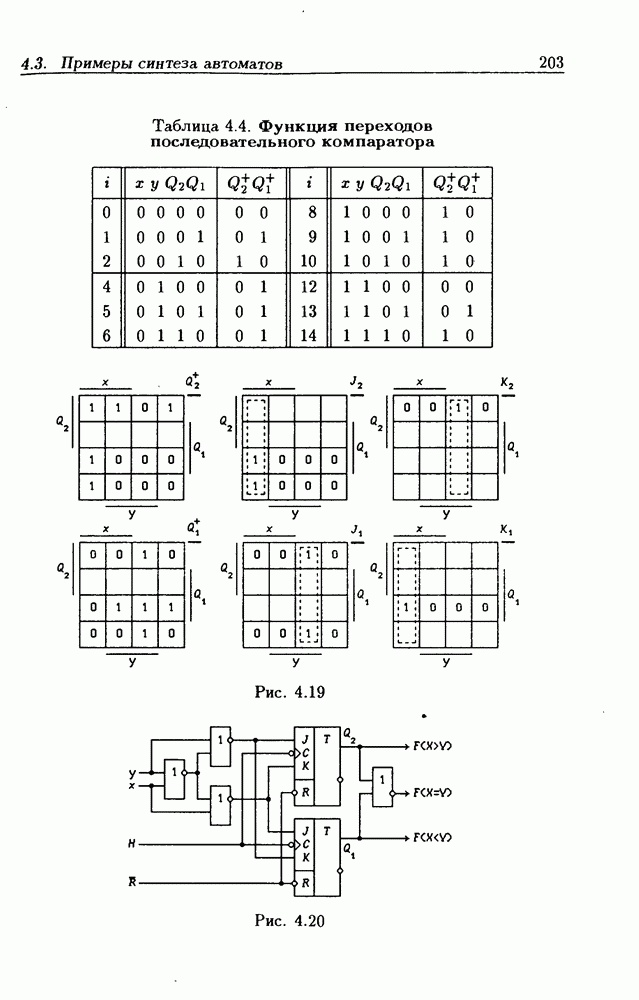
По графу переходов на рис. 4.32,а составляется таблица истинности (табл. 4.9) для функции переходов  а затем диаграммы Вейча (рис. 4.32, б) для функций
а затем диаграммы Вейча (рис. 4.32, б) для функций  Метод заполнения диаграмм Вейча для функций возбуждения
Метод заполнения диаграмм Вейча для функций возбуждения  вытекает из (1.59):
вытекает из (1.59):  при
при  при
при  Из диаграмм Вейча следует, что
Из диаграмм Вейча следует, что

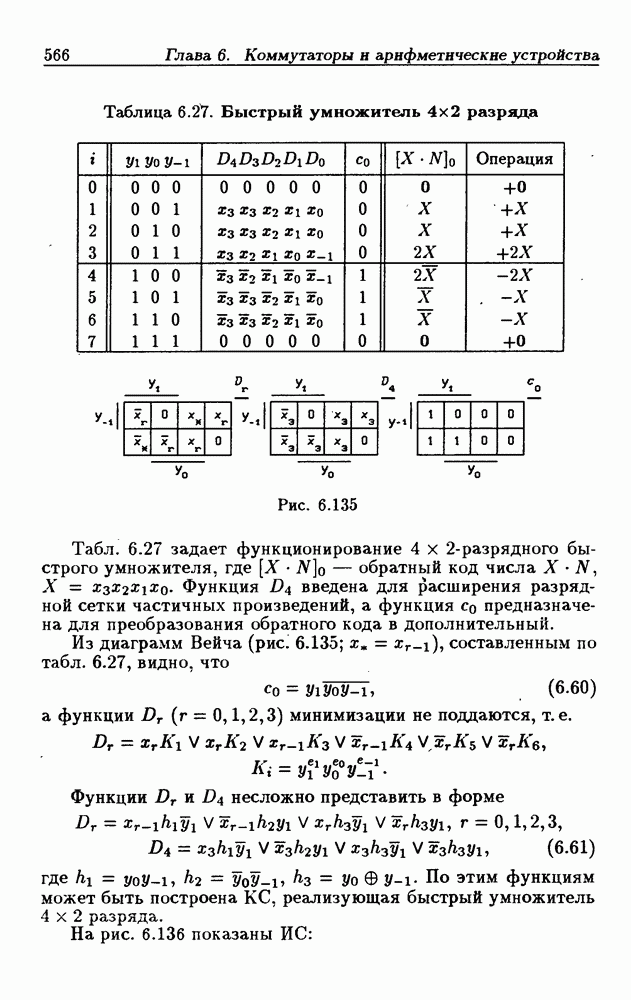
Функцию переполнения (переноса)  можно найти непосредственно из табл. 4.9:
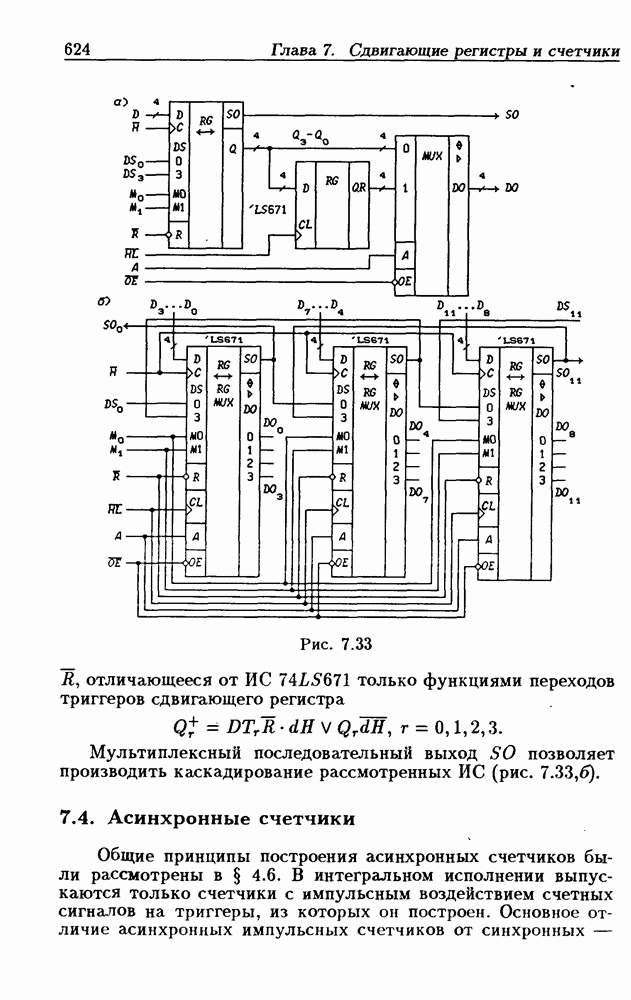
можно найти непосредственно из табл. 4.9:  Полученным функциям соответствует схема счетчика на рис. 4.32,е. Временные диаграммы, поясняющие его работу, показаны на рис.
Полученным функциям соответствует схема счетчика на рис. 4.32,е. Временные диаграммы, поясняющие его работу, показаны на рис. 
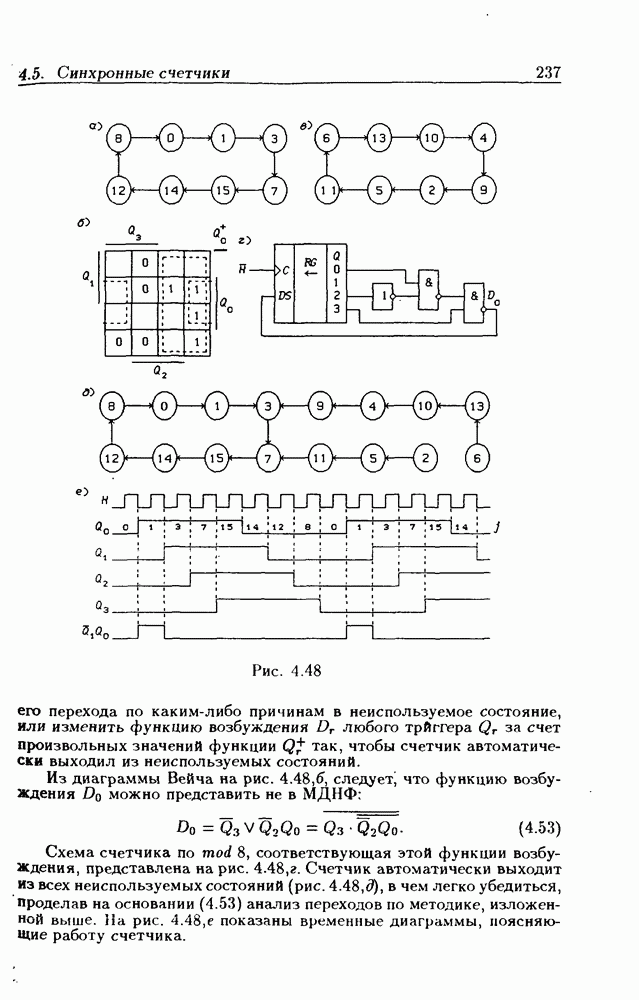
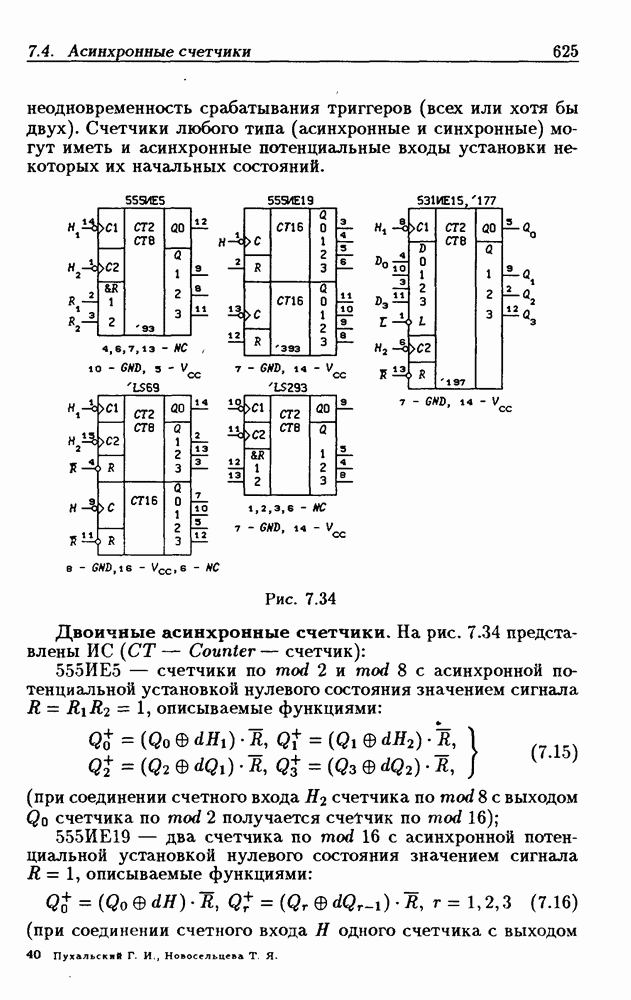
Легко показать, что двоичный счетчик по mod 16 описывается функциями:

Из сравнения (4.35) с (4.36) следует, что функции возбуждения  не изменились. Это дает основание сделать общий вывод, что функции возбуждения триггеров счетчика по
не изменились. Это дает основание сделать общий вывод, что функции возбуждения триггеров счетчика по  состоящего из m триггеров, определяются соотношениями
состоящего из m триггеров, определяются соотношениями

На основе этих функций строятся все синхронные двоичные счетчики. Длительность активного уровня сигнала  равна периоду тактового сигнала
равна периоду тактового сигнала 
Из (4.37) видно, что для триггера с номером m функция возбуждения  поэтому для переноса
поэтому для переноса  из предыдущего разряда и функции возбуждения
из предыдущего разряда и функции возбуждения  триггера следующего разряда можно было бы использовать единое обозначение —
триггера следующего разряда можно было бы использовать единое обозначение — 
(см. скан)
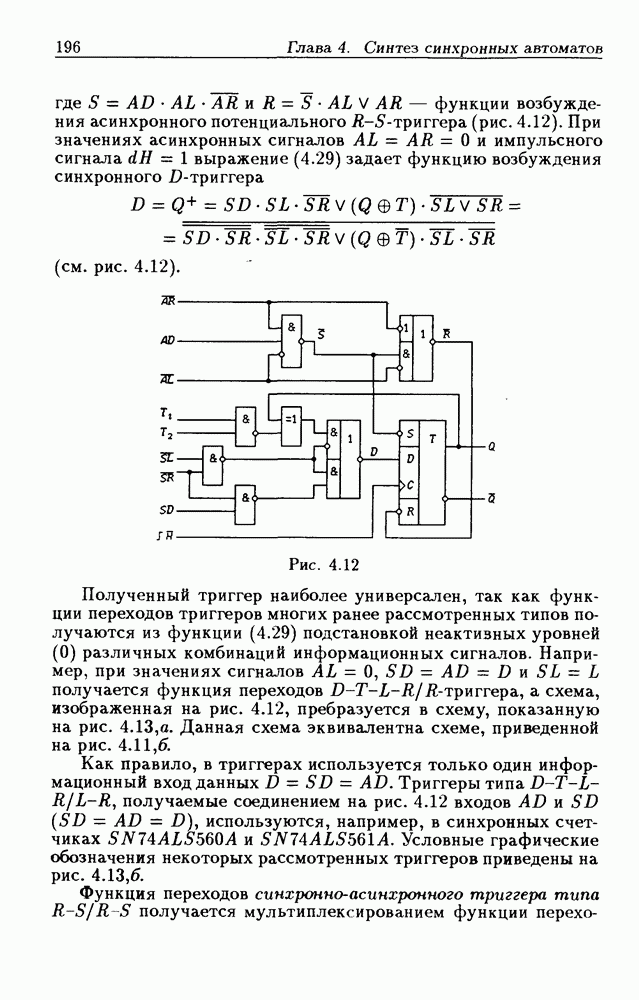
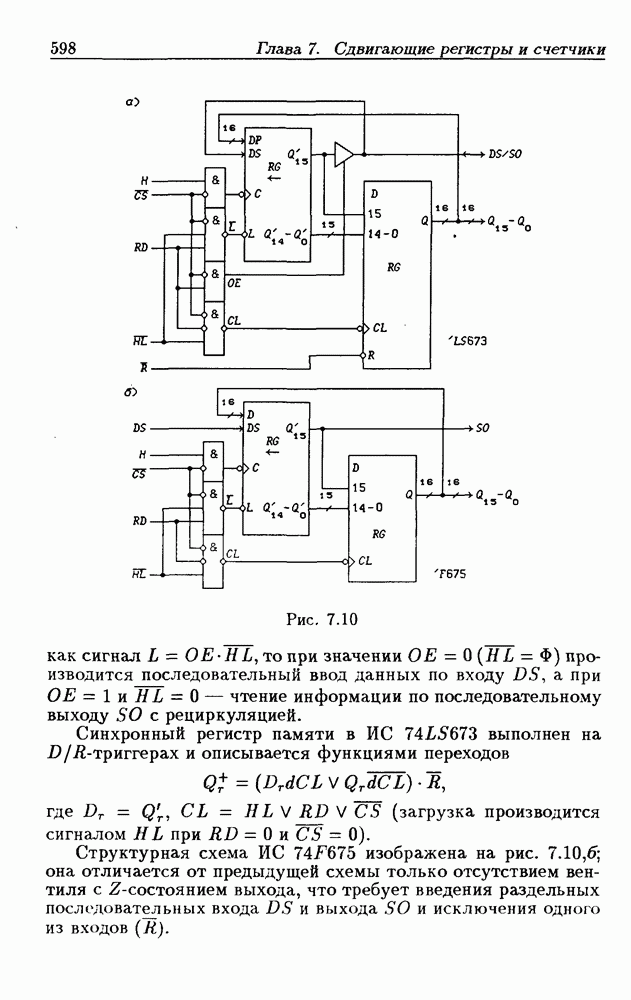
Однако, поскольку один сигнал является выходным, а другой — входным, то возникают трудности в восприятии аналитического описания счетчиков.
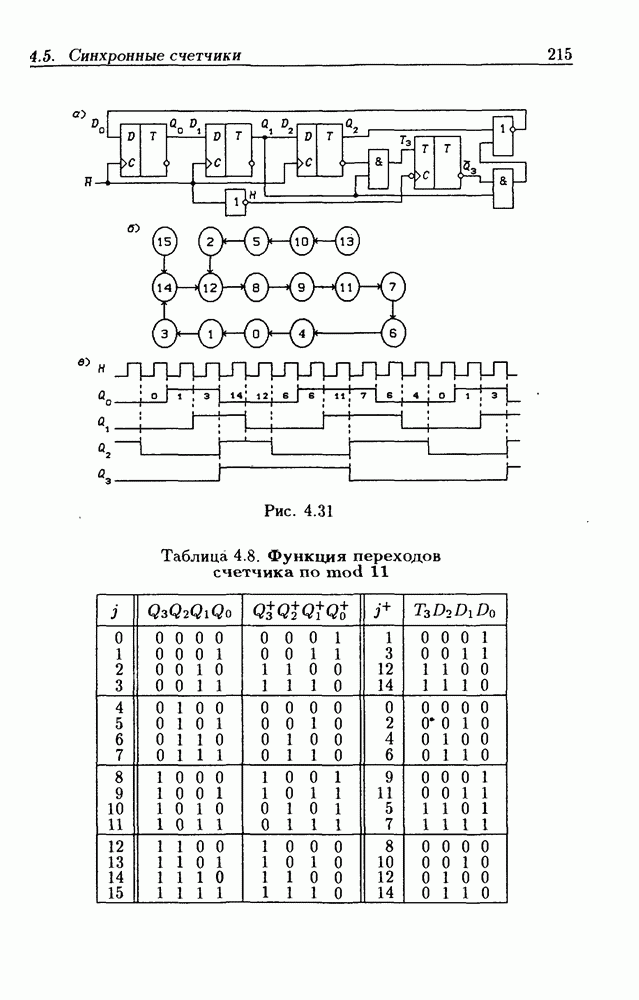
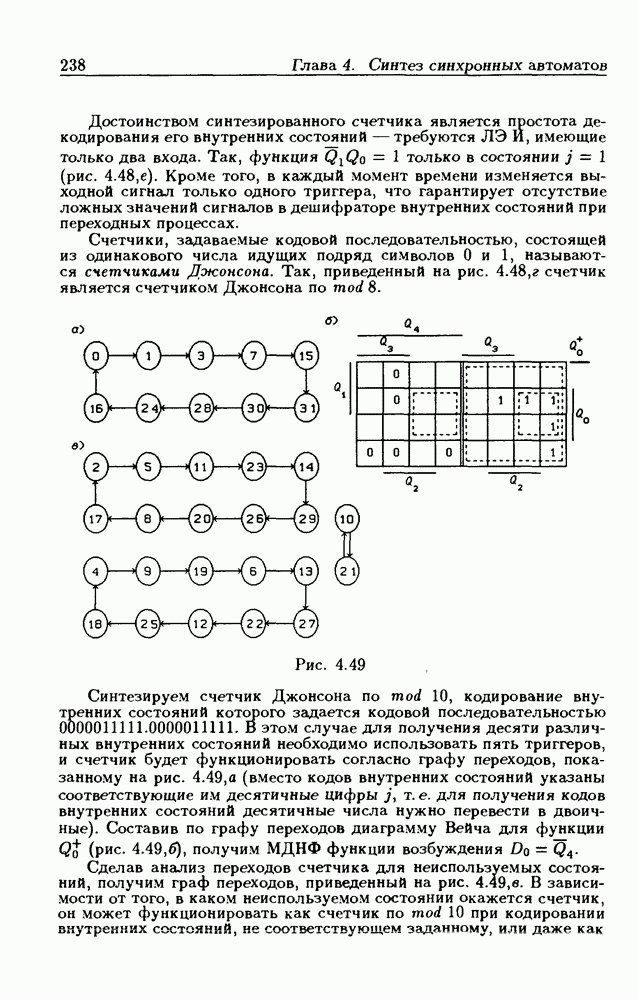
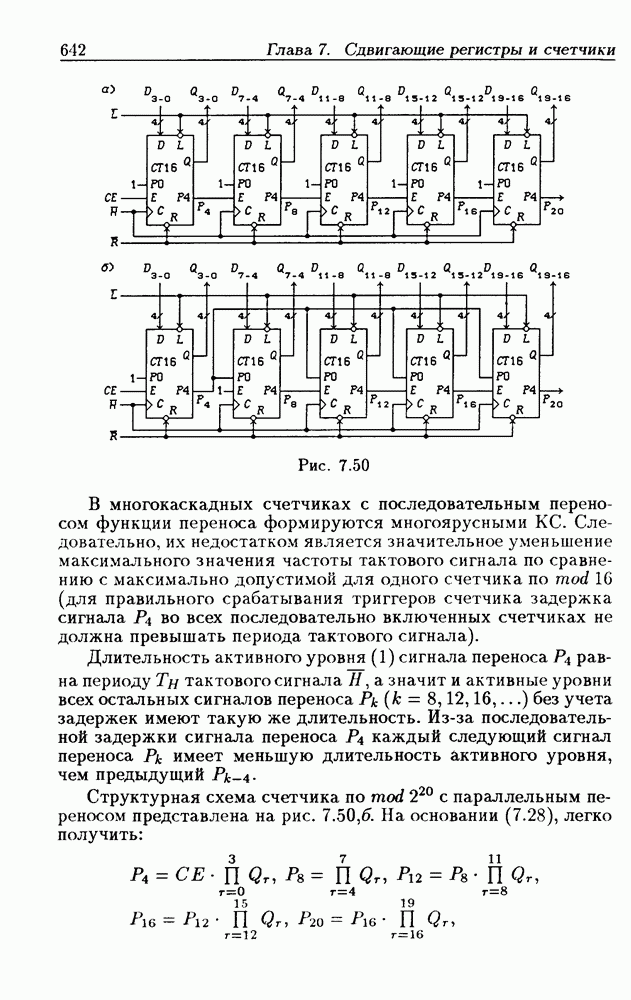
При большом числе  триггеров в счетчике функции возбуждения получаются весьма сложными, что является недостатком таких счетчиков. Соотношения (4.37) можно привести к виду
триггеров в счетчике функции возбуждения получаются весьма сложными, что является недостатком таких счетчиков. Соотношения (4.37) можно привести к виду


Рис. 4.33
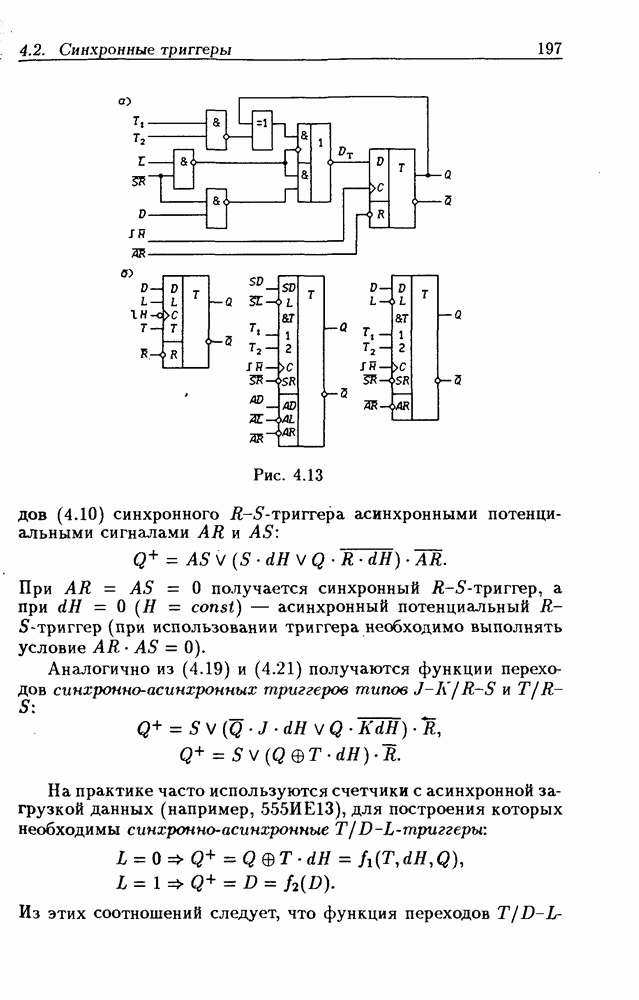
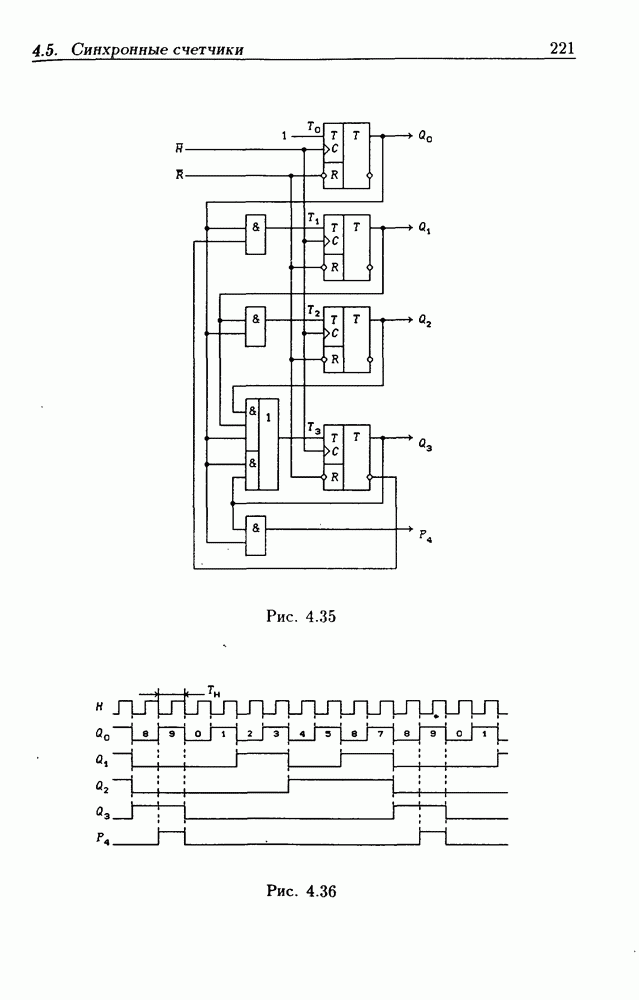
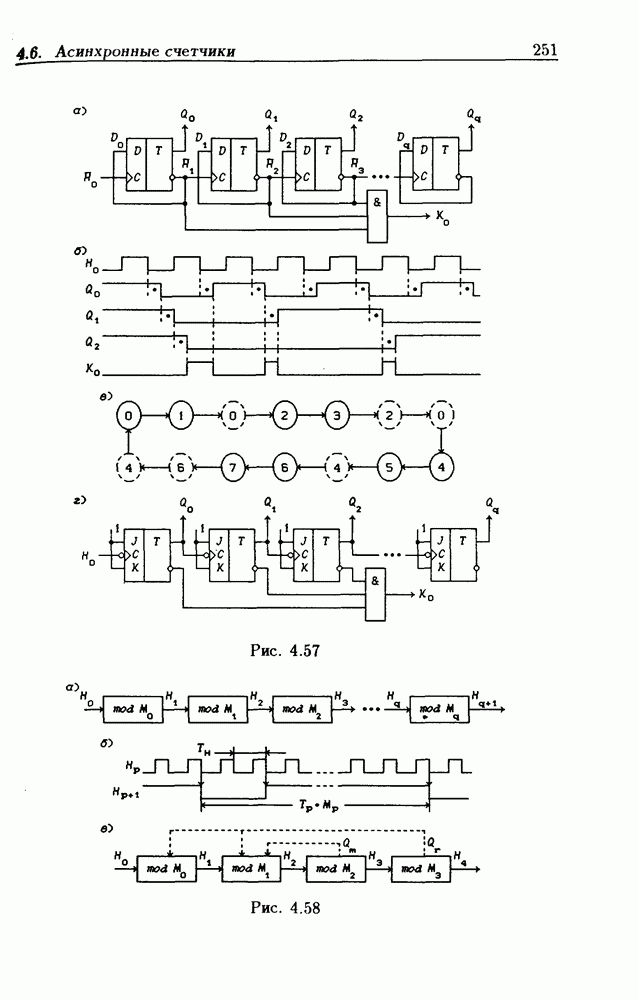
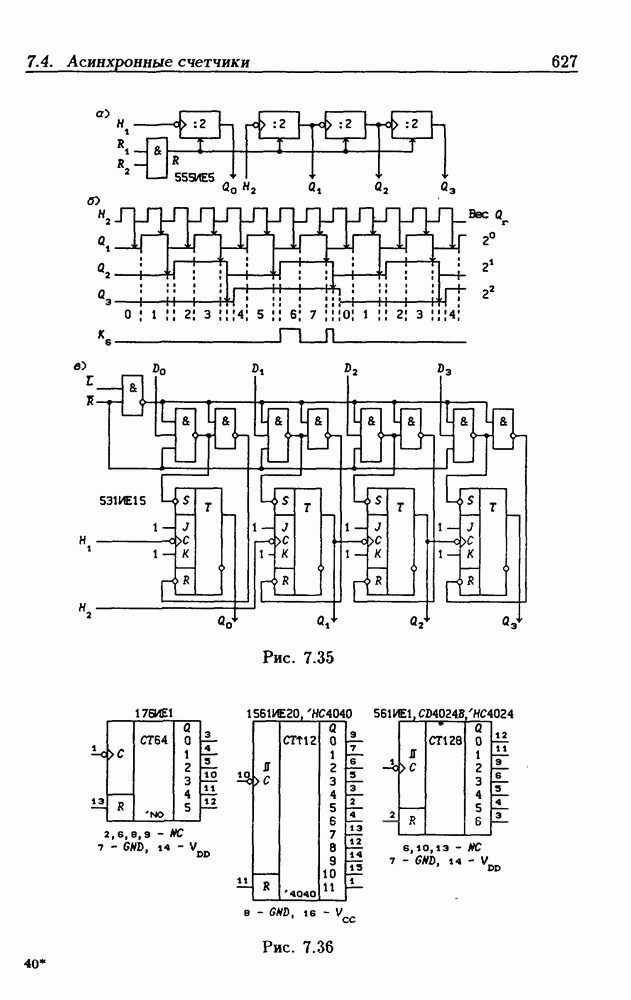
На рис. 4.33 показана схема двоичного 4-разрядного счетчика, соответствующая данным формам функций возбуждения  -триггеров. Ее недостаток — последовательное прохождение переносов от младших разрядов к старшим через ЛЭ И, что снижает быстродействие счетчика (функции возбуждения представлены скобочными формами порядка
-триггеров. Ее недостаток — последовательное прохождение переносов от младших разрядов к старшим через ЛЭ И, что снижает быстродействие счетчика (функции возбуждения представлены скобочными формами порядка  Схема на рис. 4.33 иллюстрирует метод каскадирования одноразрядных синхронных двоичных счетчиков. Действительно, узел, выделенный штриховой линией, описывается общими для всех таких узлов функциями
Схема на рис. 4.33 иллюстрирует метод каскадирования одноразрядных синхронных двоичных счетчиков. Действительно, узел, выделенный штриховой линией, описывается общими для всех таких узлов функциями  где
где  перенос из предыдущего разряда,
перенос из предыдущего разряда,  перенос в следующий разряд, и представляет собой одноразрядный счетчик. Первый разряд счетчика получается подстановкой
перенос в следующий разряд, и представляет собой одноразрядный счетчик. Первый разряд счетчика получается подстановкой  что дает
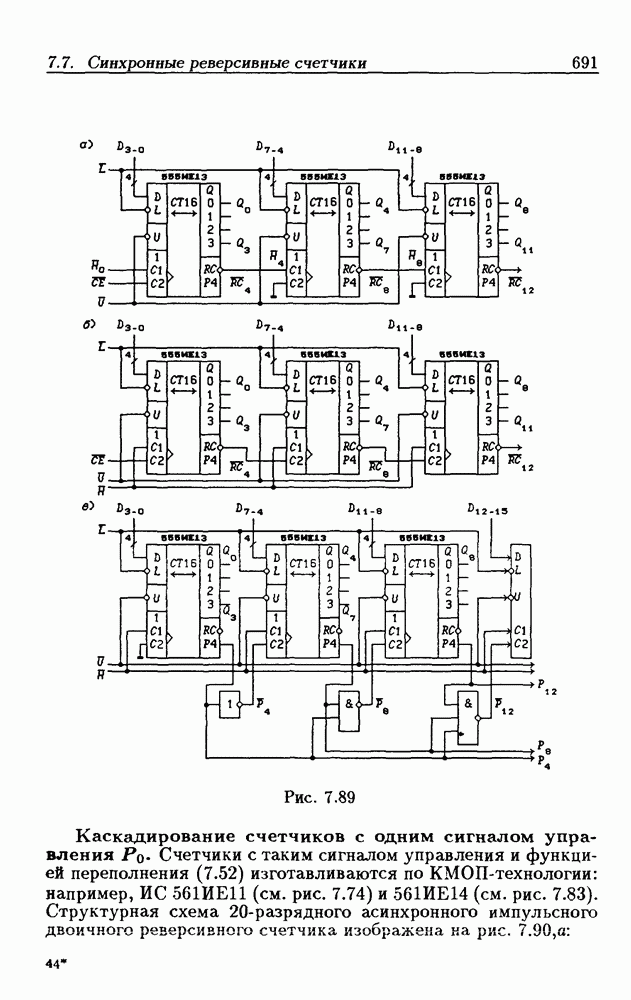
что дает  Таким образом, счетчик любой разрядности может быть построен с помощью последовательного соединения одноразрядных счетчиков. Такие счетчики называются счетчиками с последовательным переносом.
Таким образом, счетчик любой разрядности может быть построен с помощью последовательного соединения одноразрядных счетчиков. Такие счетчики называются счетчиками с последовательным переносом.
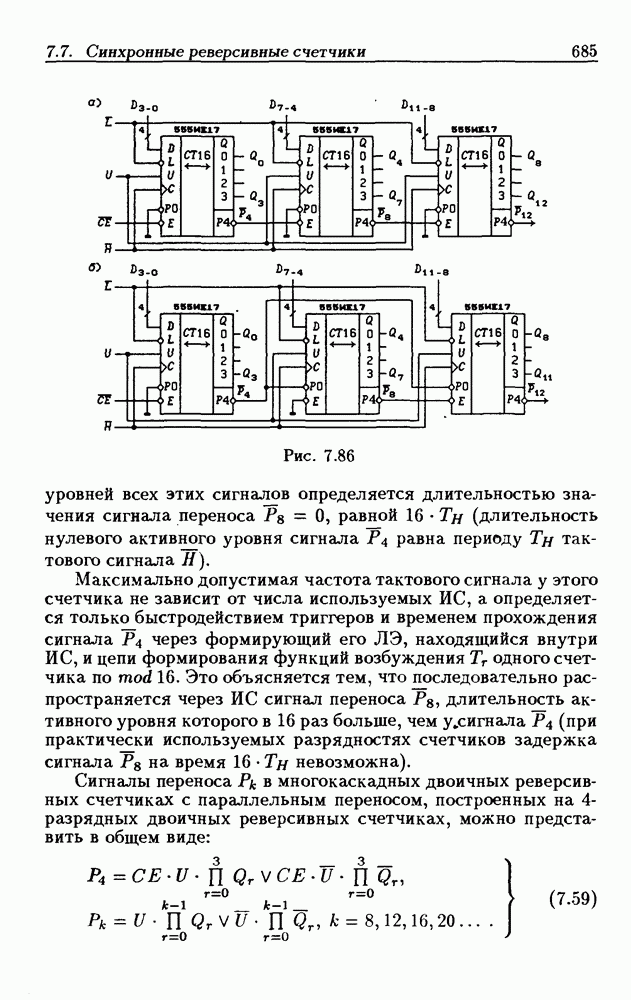
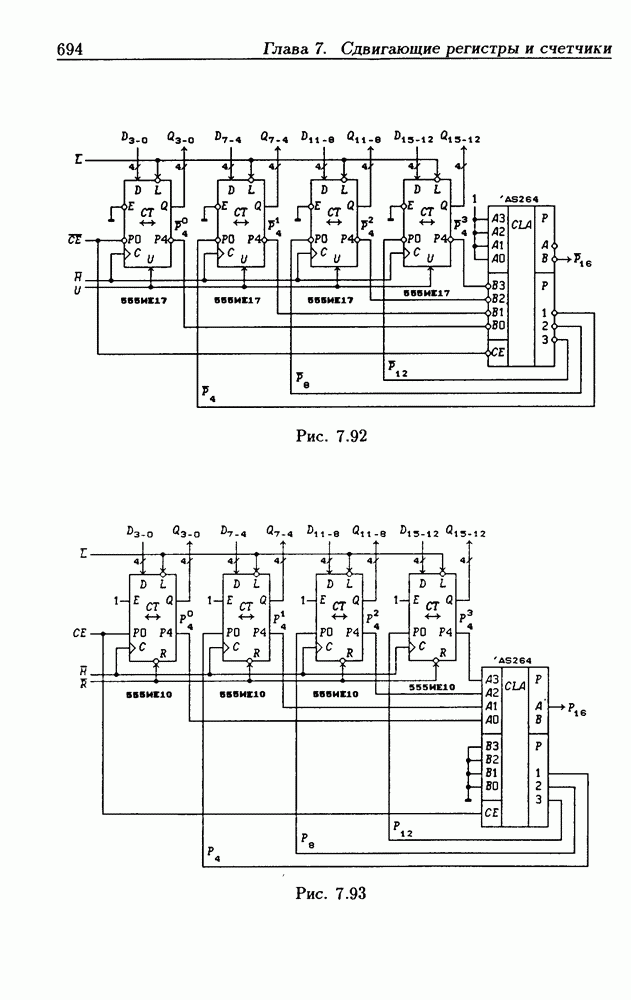
Функции (4.37) описывают синхронные двоичные счетчики с параллельным переносом. На практике широкое применение
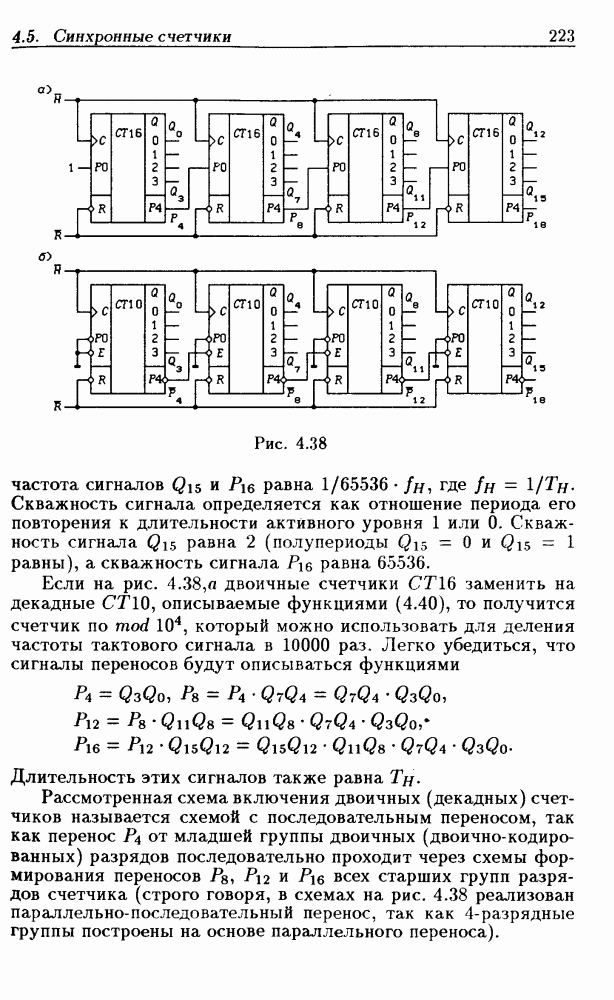
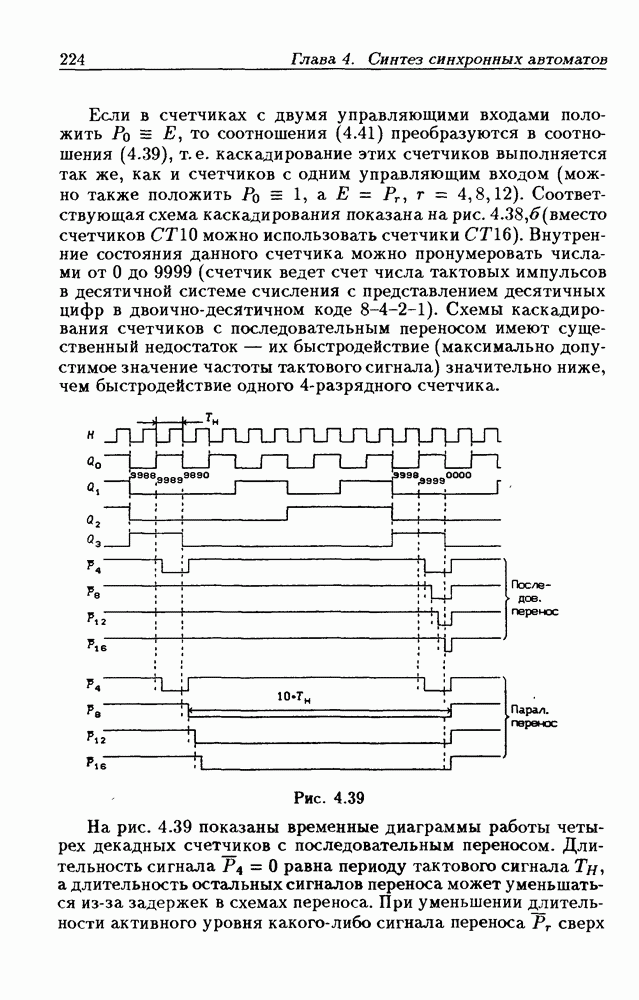
находят счетчики с параллельно-последовательным переносом, когда одинаковые  -разрядные (например, 4-разрядные) двоичные счетчики выполняются с параллельным переносом, а при соединении нескольких таких счетчиков используется последовательный перенос.
-разрядные (например, 4-разрядные) двоичные счетчики выполняются с параллельным переносом, а при соединении нескольких таких счетчиков используется последовательный перенос.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Глава 1. Основы теории переключательных функций
- 1.2. Позиционные системы счисления
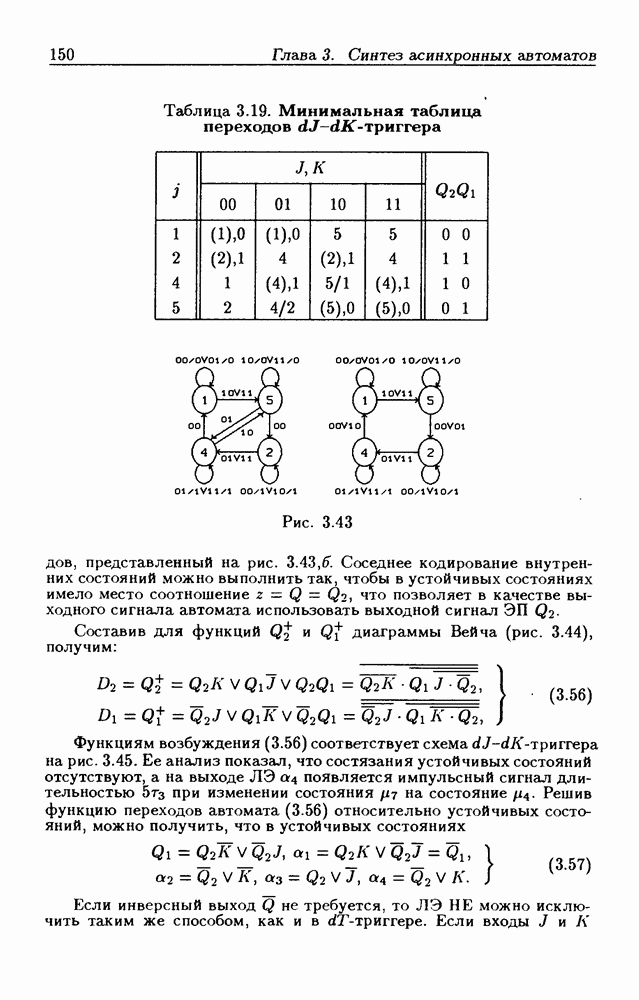
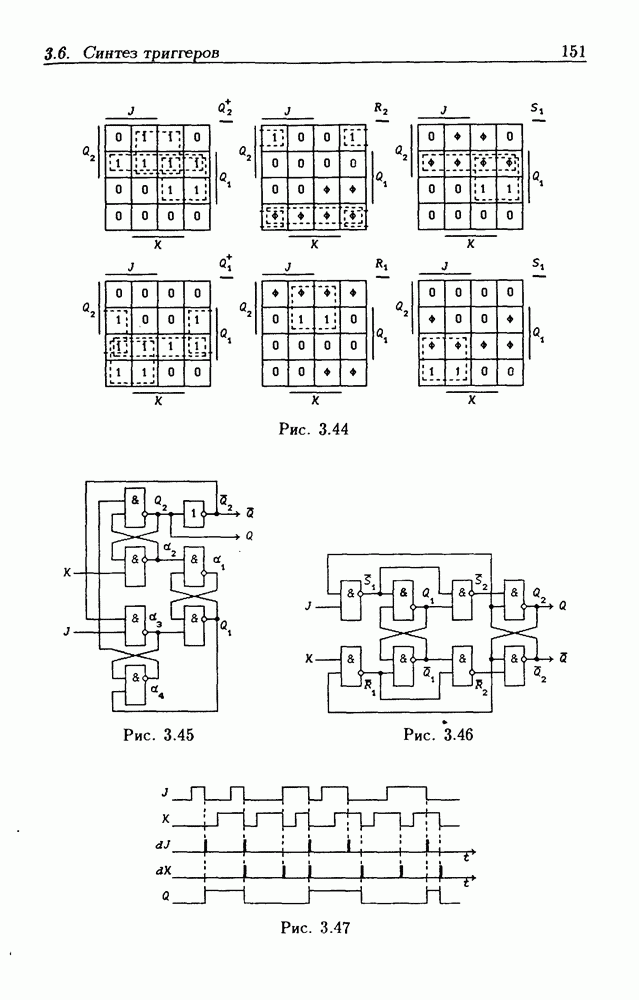
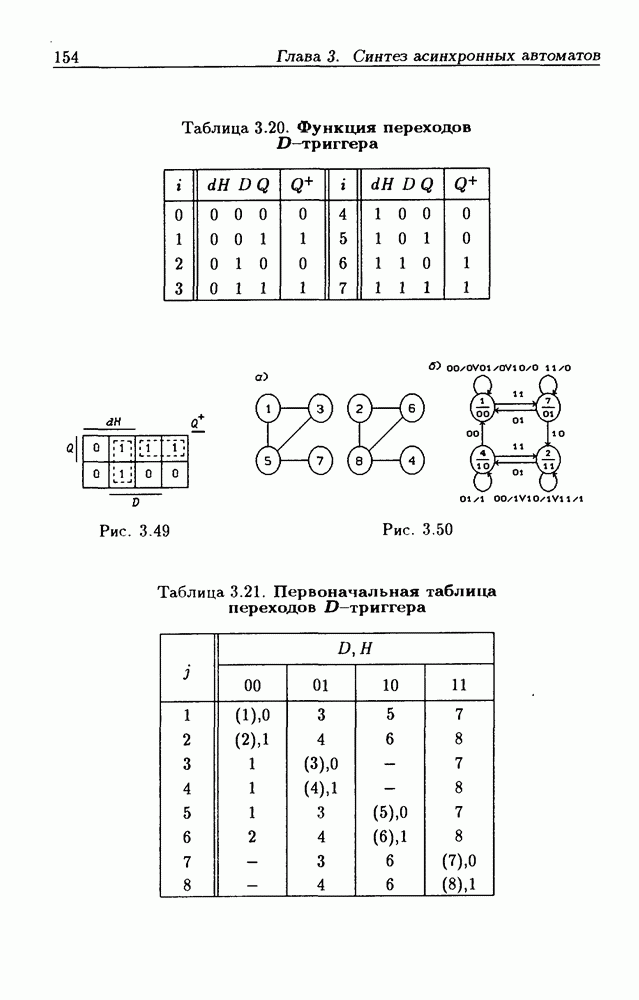
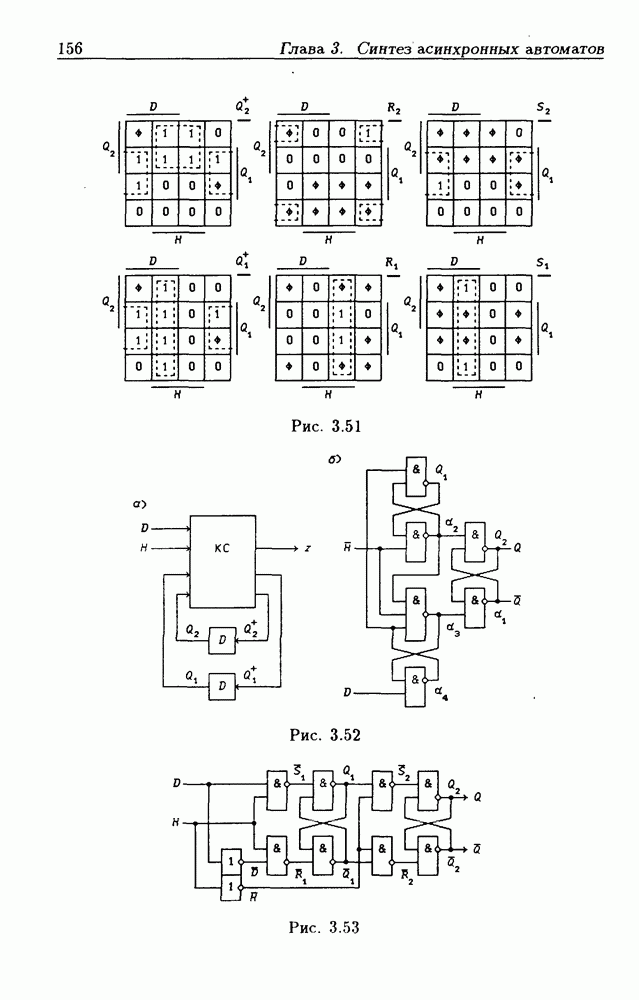
- 1.3. Переключательные функции
- 1.4. Принцип и закон двойственности
- 1.5. Теоремы разложения
- 1.6. Решение систем логических уравнений
- 1.7. Первичные термы, минтермы и макстермы
- 1.8. Совершенные нормальные формы представления функций
- 1.9. Конъюнктивные и дизъюнктивные термы
- 1.10. Минимизация переключательных функций
- 1.11. Диаграммы Вейча
- 1.12. Минимизация неполностью определенных функций, совместная минимизация нескольких функций
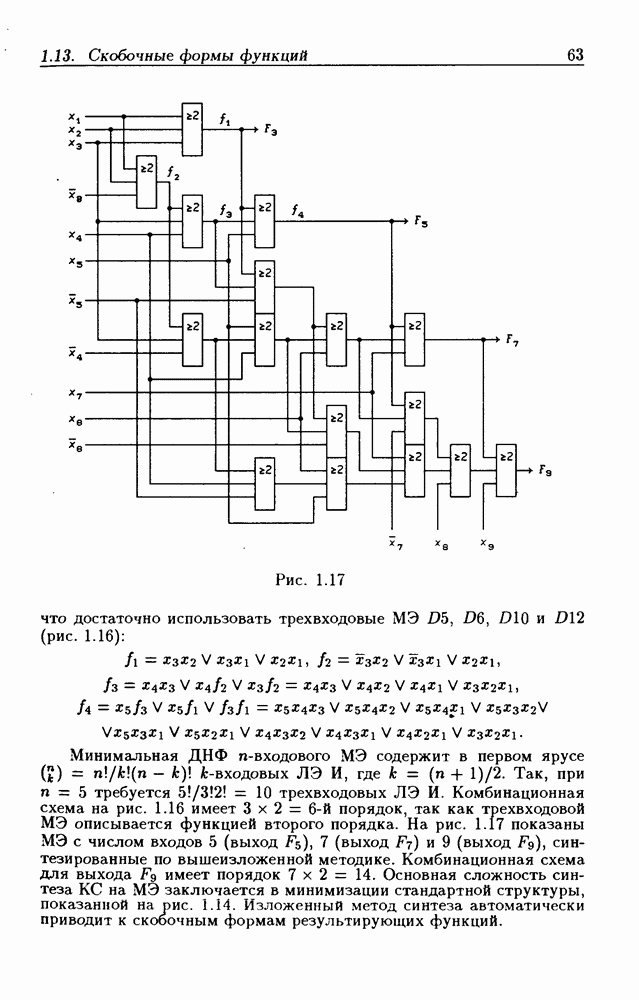
- 1.13. Скобочные формы функций
- 1.14. Закон двойственности для логических схем
- 1.15. Линейные функции
- Глава 2. Анализ и синтез логических схем
- 2.2. Модели логических элементов
- 2.3. Модели логических схем
- 2.4. Анализ логических схем
- 2.5. Синтез комбинационных схем, свободных от состязаний
- Глава 3. Синтез асинхронных потенциальных автоматов
- 3.2. Асинхронные потенциальные автоматы
- 3.3. Асинхронные потенциальные триггеры и элементы памяти
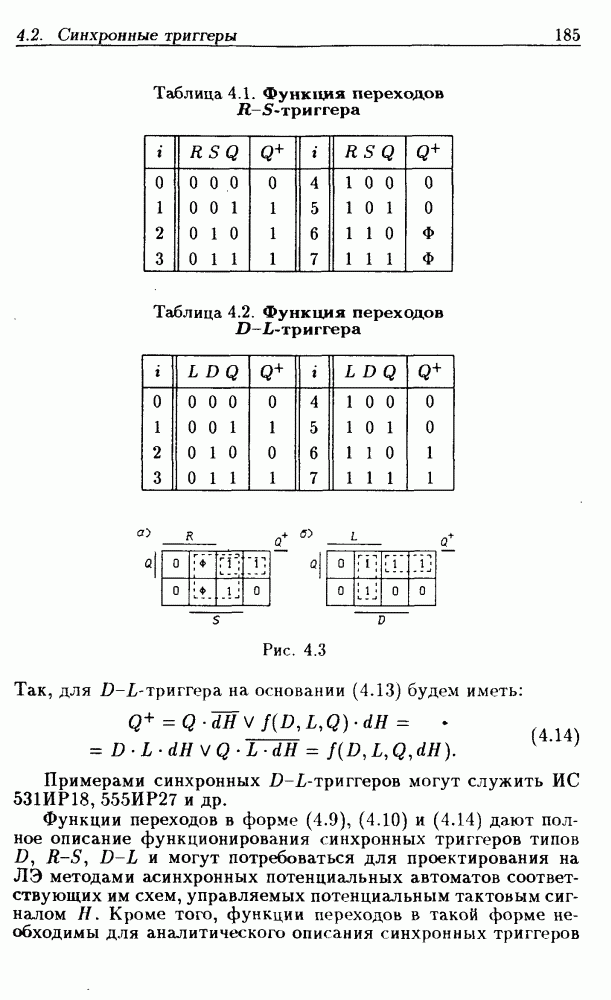
- Триггеры типа R-S
- Триггеры типа D-L
- Триггеры типа D-L-R с приоритетом входа R.
- Триггеры типа D-L-R с приоритетом входа L.
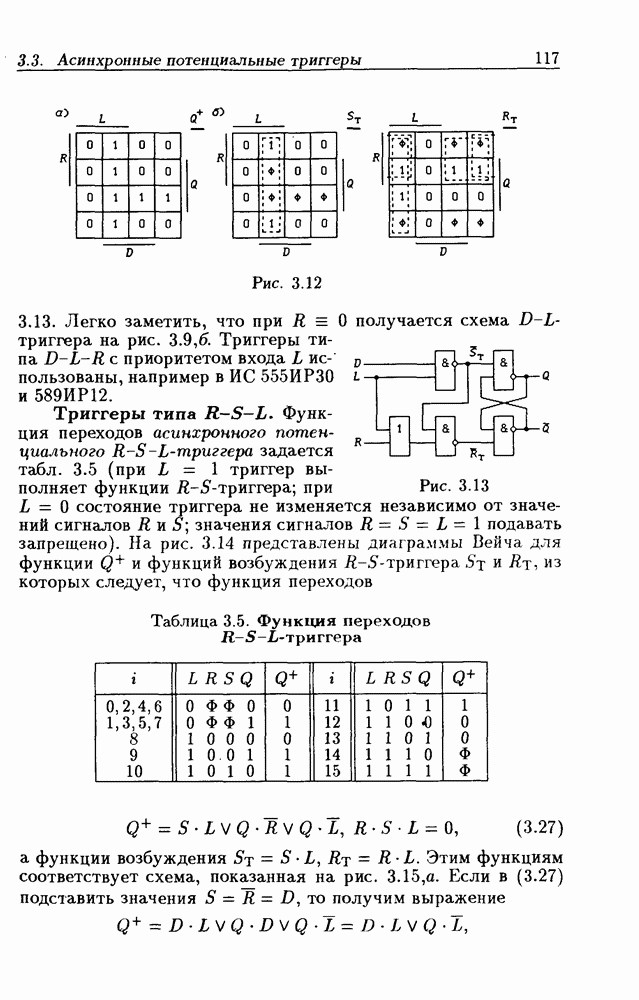
- Триггеры типа R-S-L.
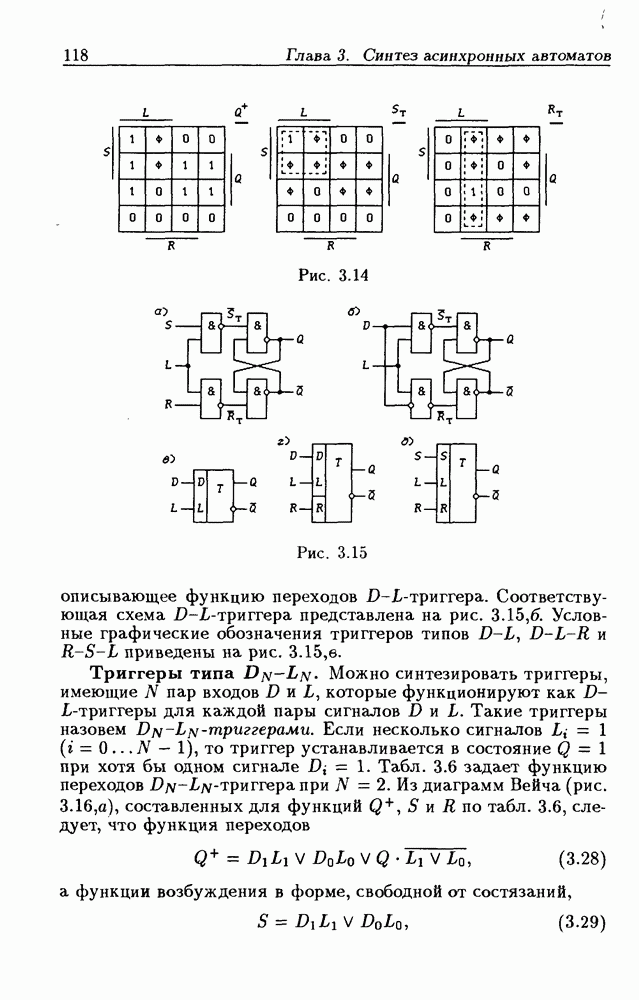
- Триггеры типа DN-LN
- Аналитический метод синтеза и анализа триггеров.
- 3.4. Задание асинхронных потенциальных автоматов таблицами и графами переходов
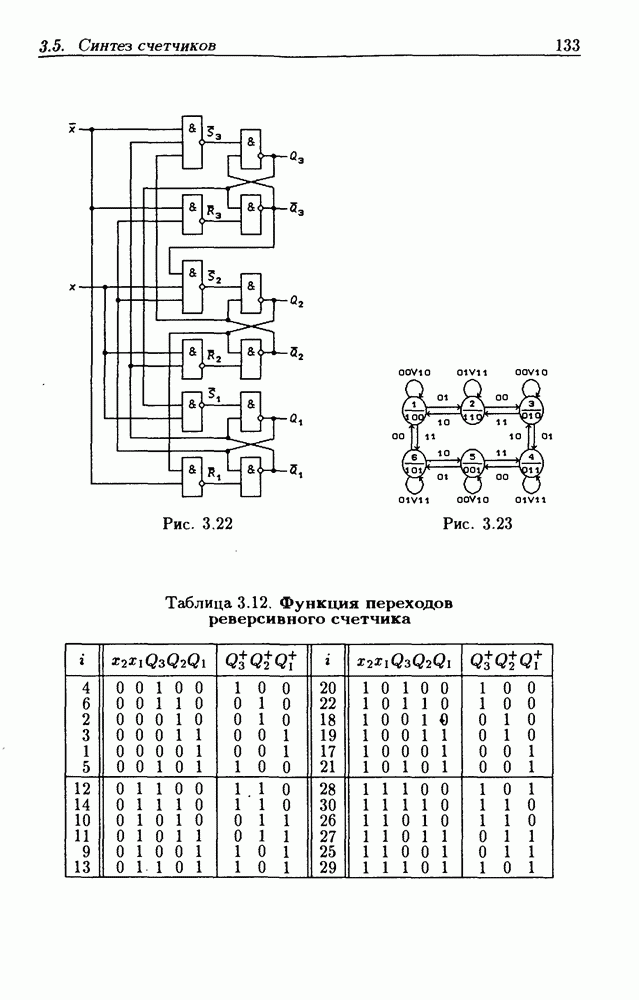
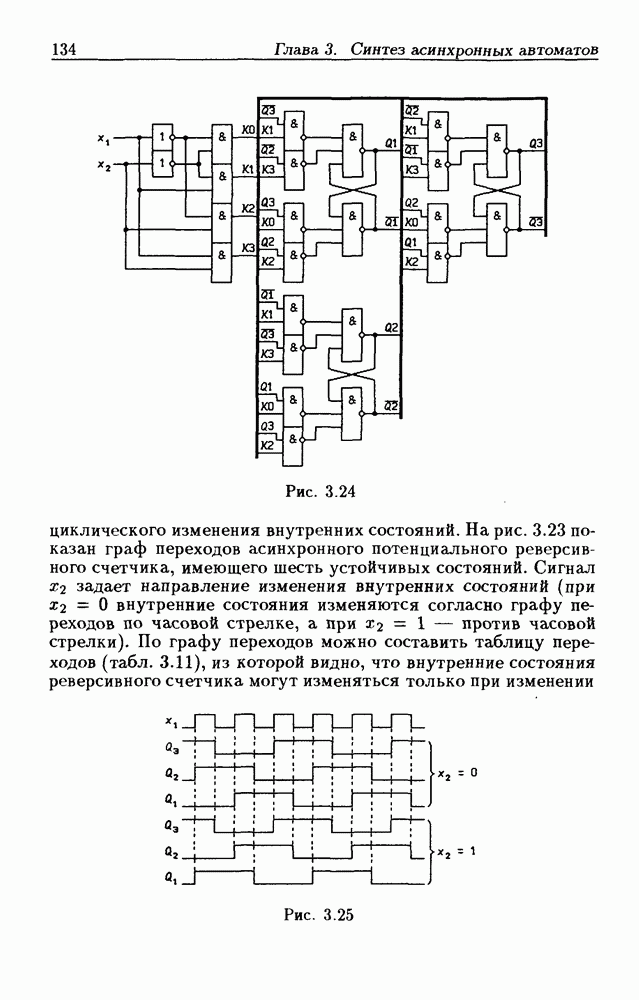
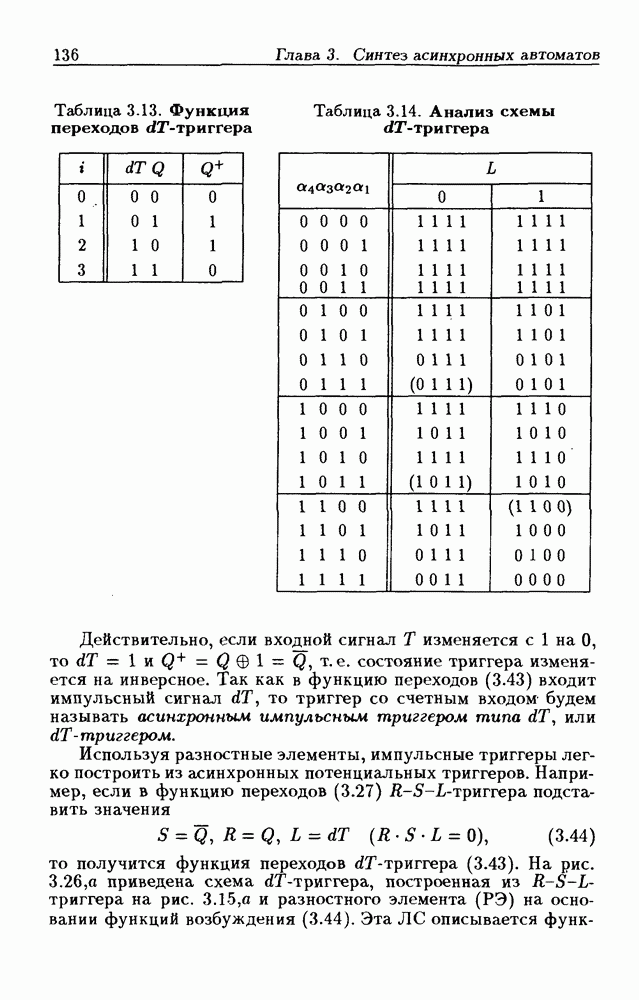
- 3.5. Синтез асинхронных потенциальных счетчиков
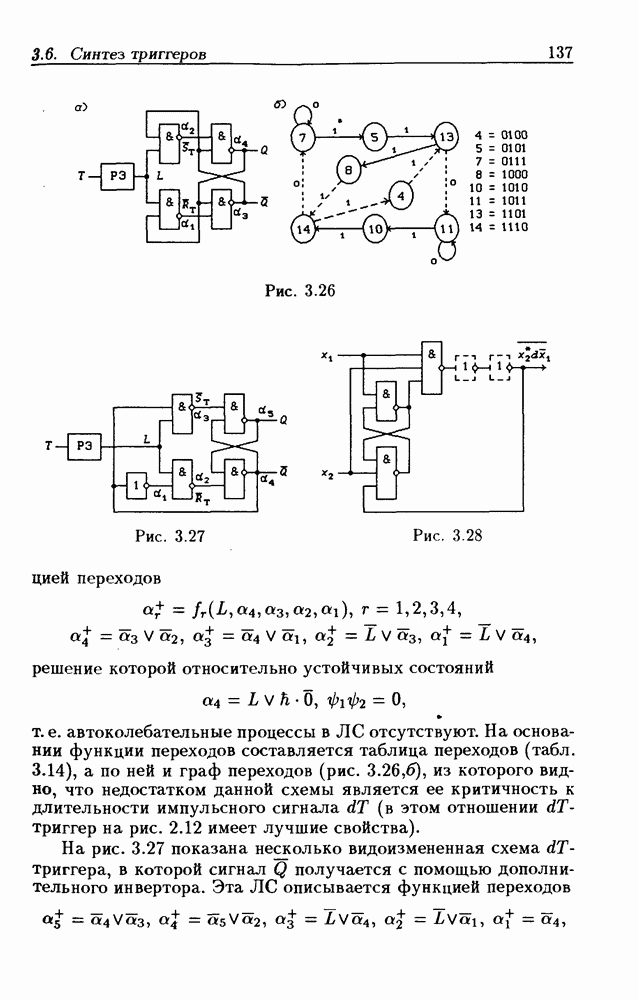
- 3.6. Синтез асинхронных импульсных триггеров
- Триггеры типа dJ-dK.
- Классификация триггеров.
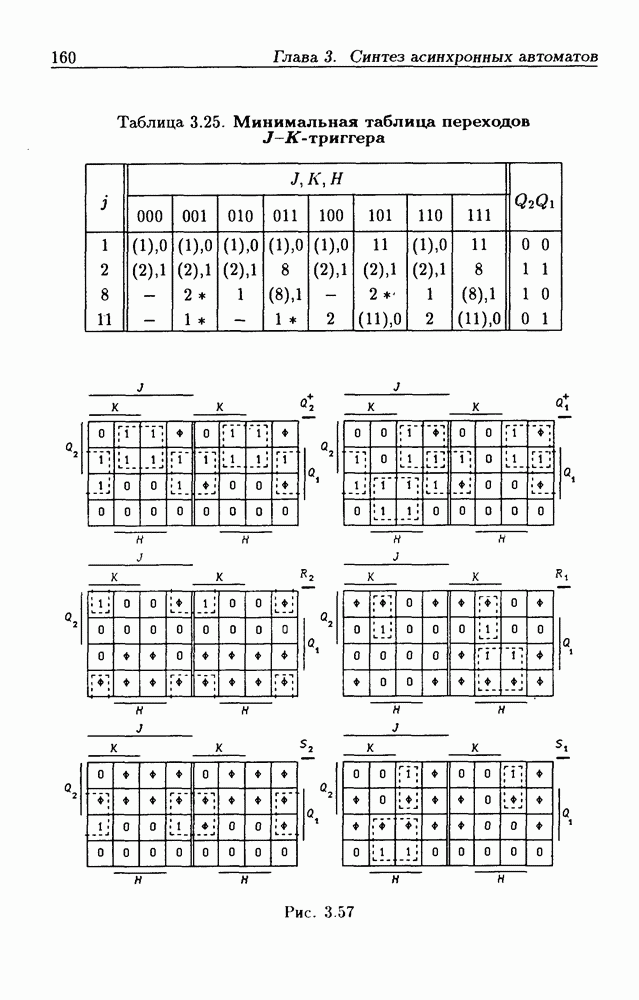
- 3.7. Синтез синхронных триггеров
- Триггеры типа J-K
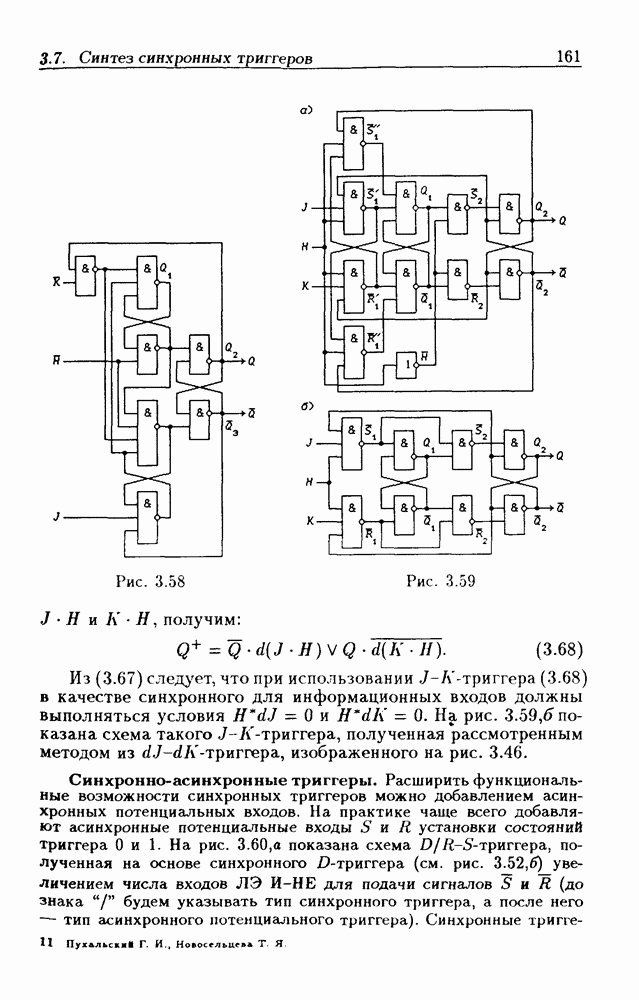
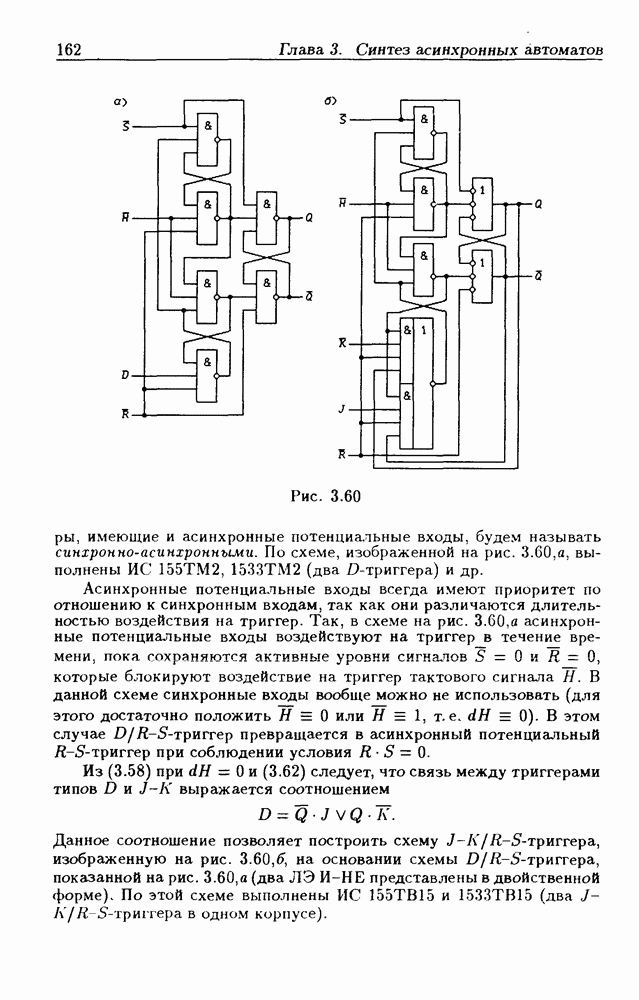
- Синхронно-асинхронные триггеры.
- 3.8. Примеры синтеза асинхронных потенциальных автоматов
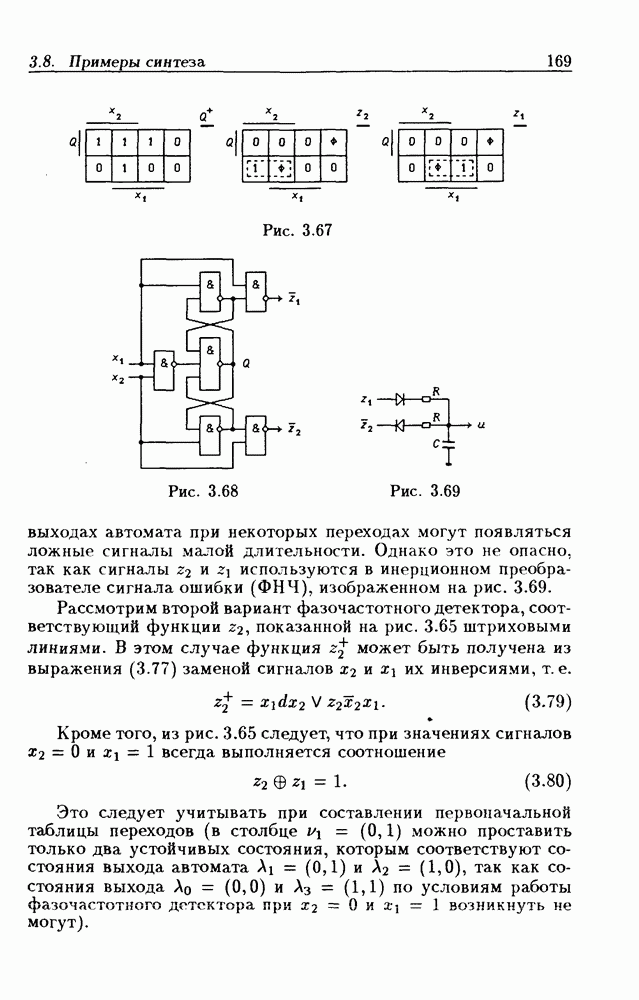
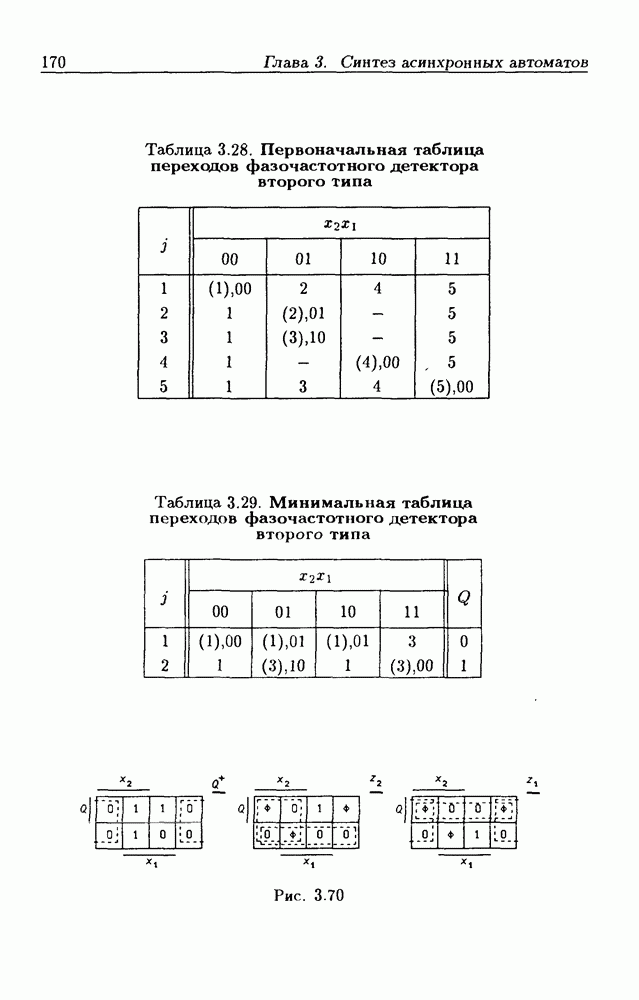
- Цифровые фазочастотные детекторы.
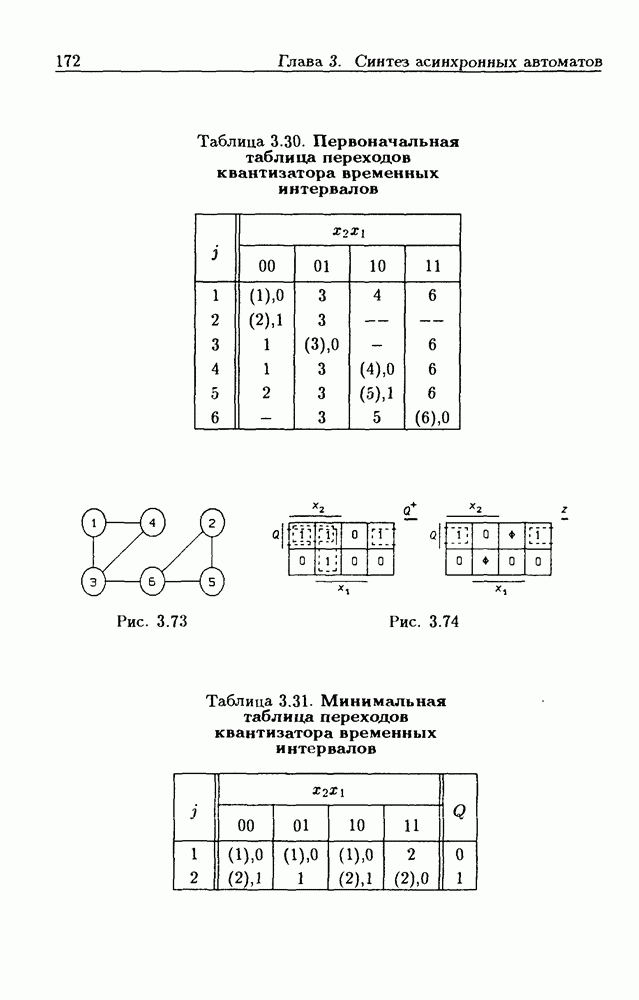
- Квантизатор временных интервалов.
- 3.9. Генераторы сигналов
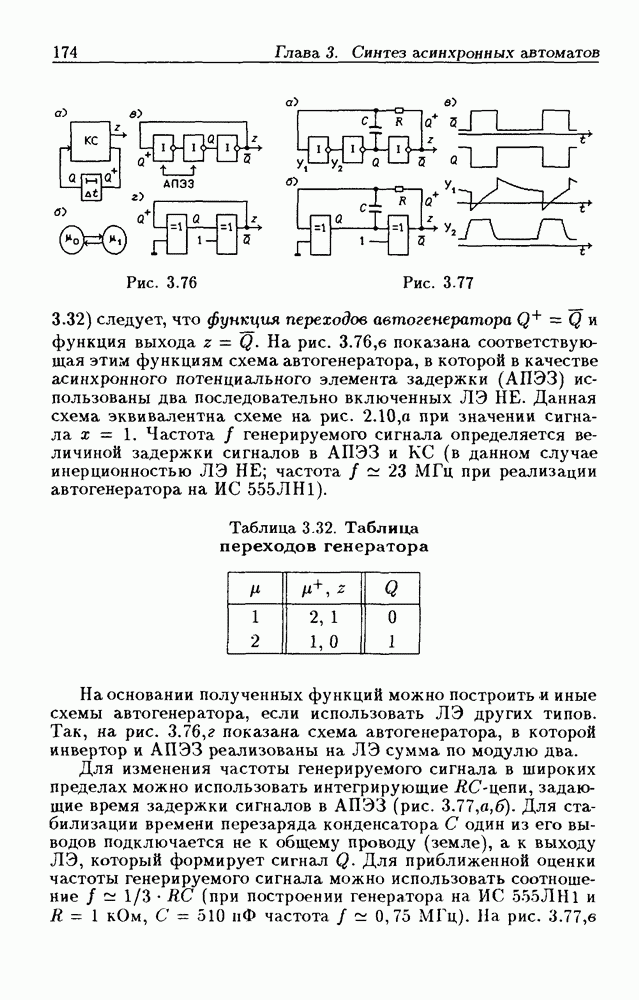
- Автогенераторы.
- Управляемые автогенераторы.
- Глава 4. Синтез синхронных автоматов
- 4.2. Синхронные триггеры
- Триггеры типов D и R-S с импульсным тактовым сигналом.
- Синхронные триггеры типов R-S и D-L
- Синхронно-асинхронные триггеры.
- Синхронные триггеры типа J-K
- Триггеры типа Т.
- Классификация синхронных триггеров.
- Преобразования типов синхронных триггеров.
- Триггеры типов D-T-L и D-T-L/R
- Функции переходов синхронно-асинхронных триггеров.
- 4.3. Примеры синтеза синхронных автоматов
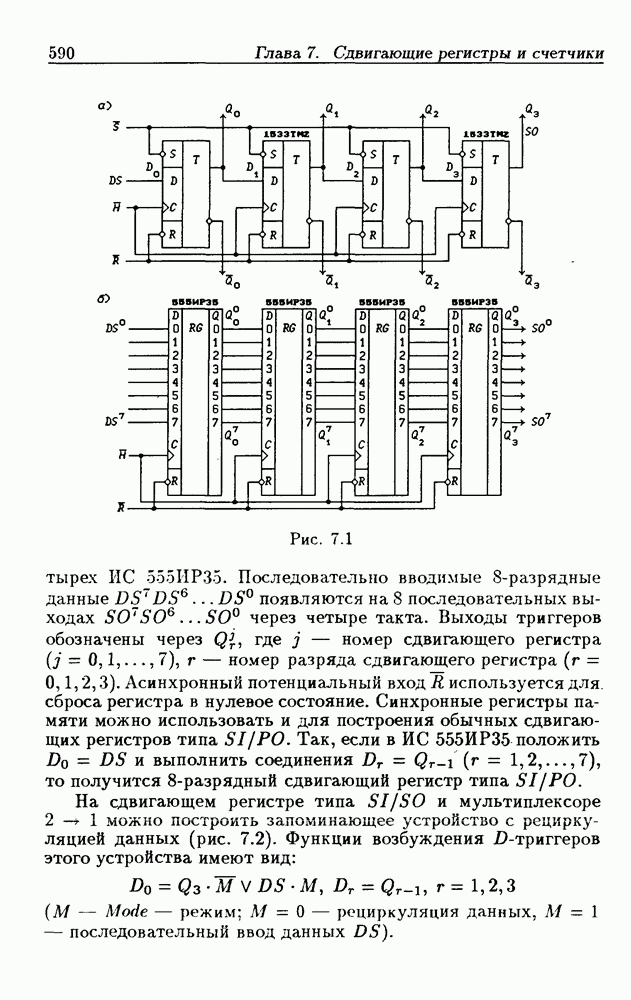
- 4.4. Сдвигающие регистры
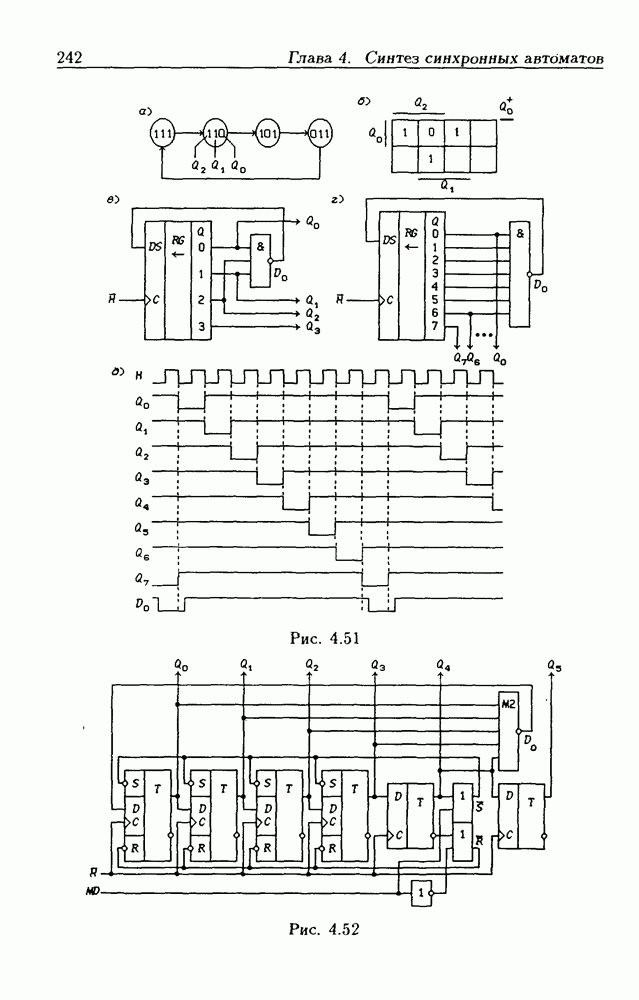
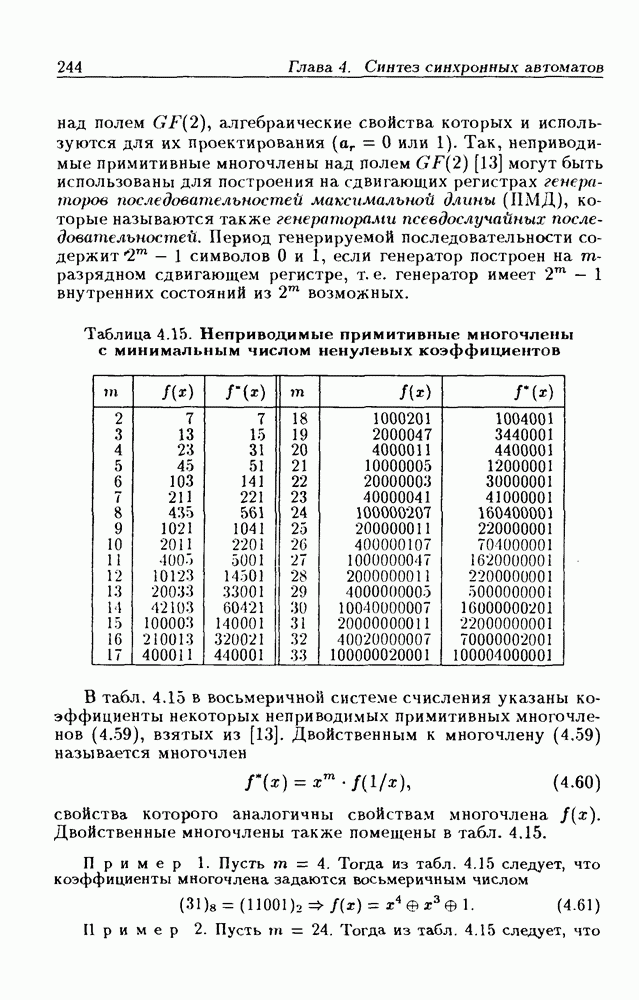
- Синтез счетчиков на сдвигающих регистрах.
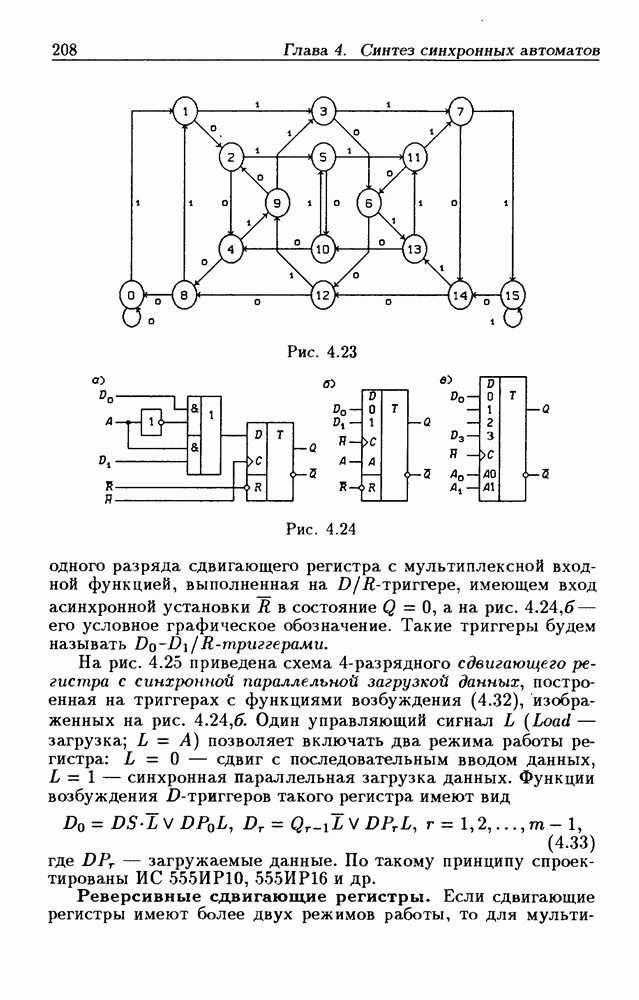
- Сдвигающие регистры с загрузкой данных.
- Реверсивные сдвигающие регистры.
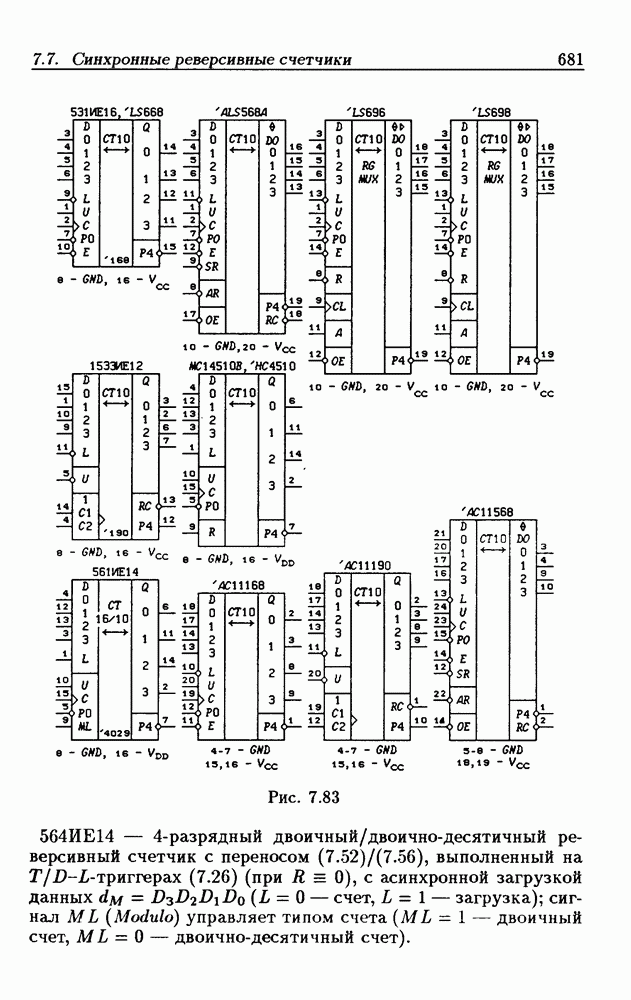
- 4.5. Синхронные счетчики
- Синхронные двоичные счетчики.
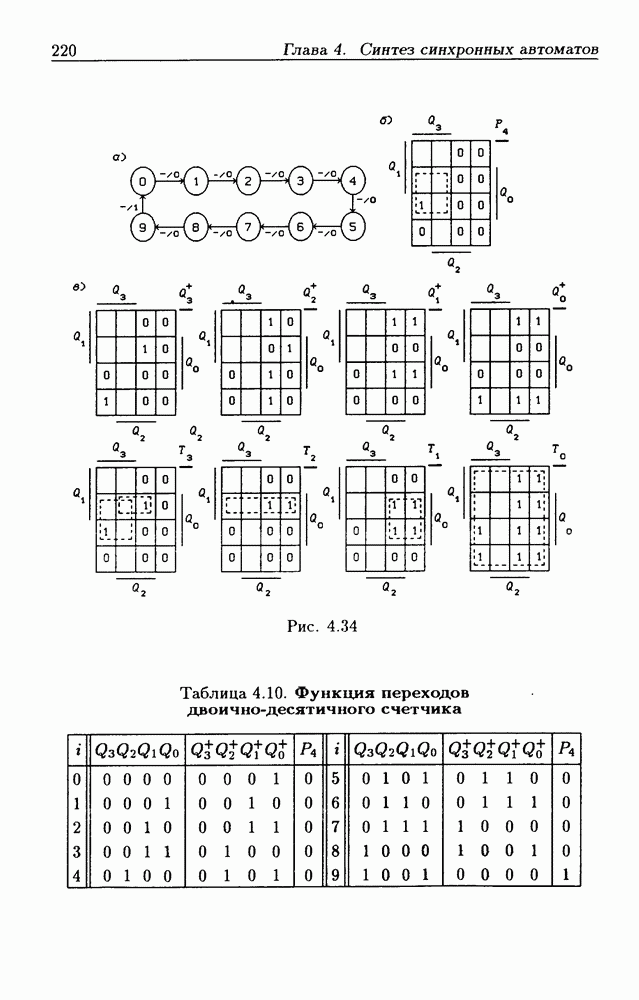
- Синхронные двоично-десятичные счетчики.
- Каскадирование двоичных и двоично-десятичных счетчиков.
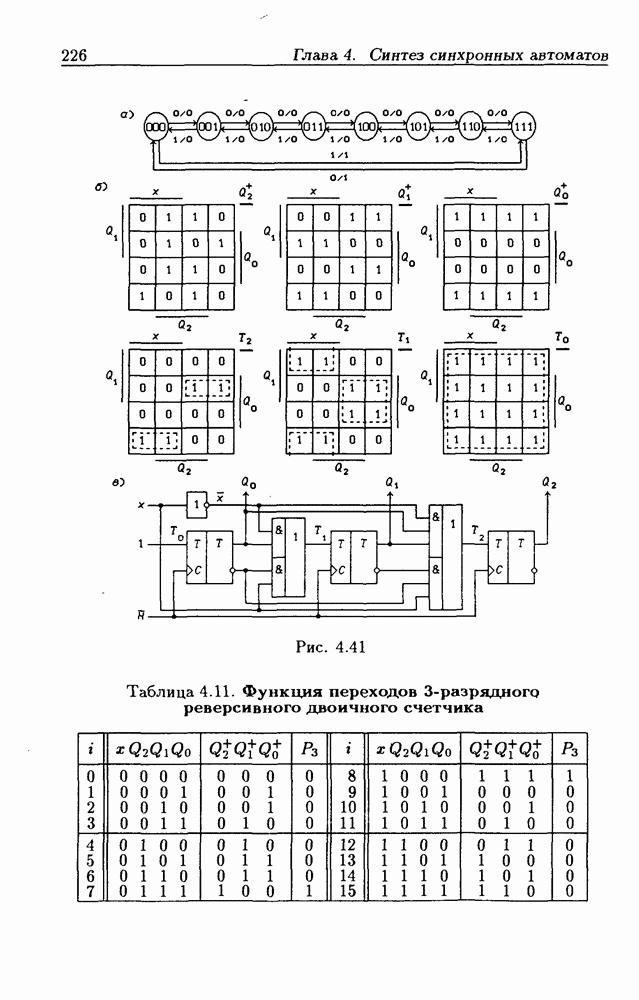
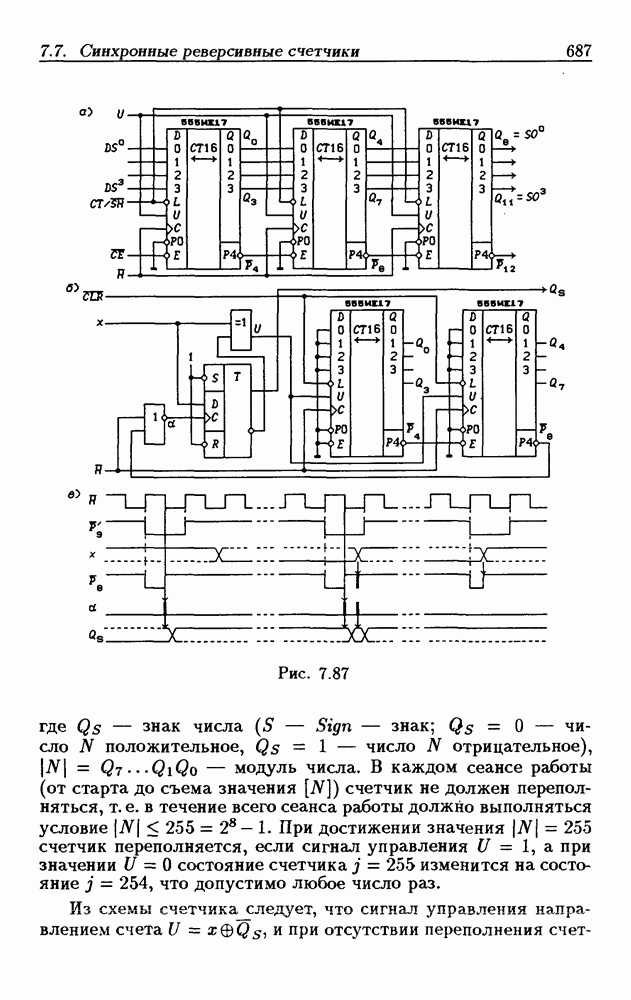
- Синхронные двоичные реверсивные счетчики.
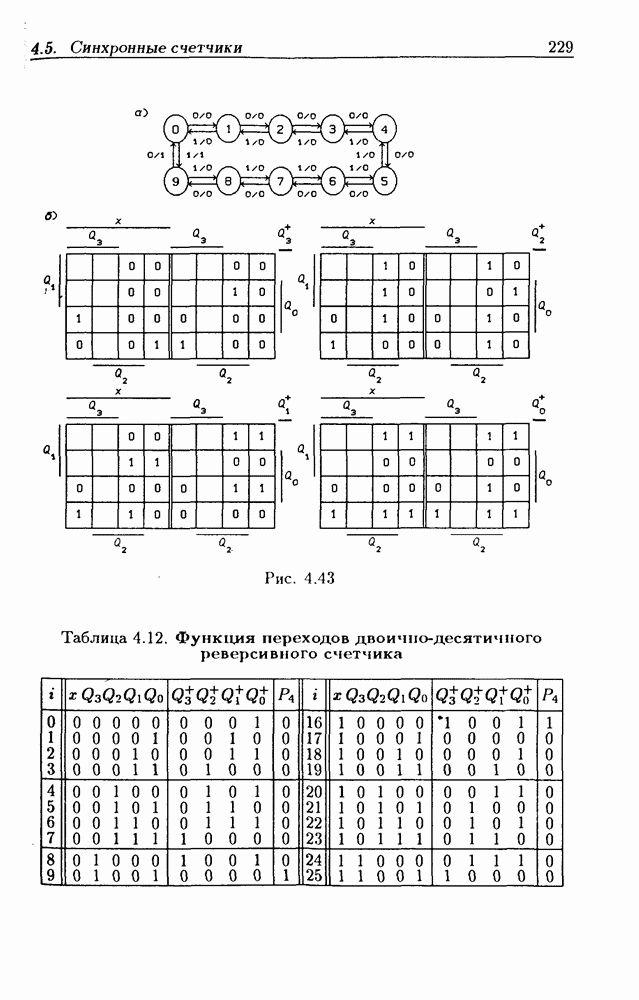
- Реверсивные двоично-десятичные счетчики.
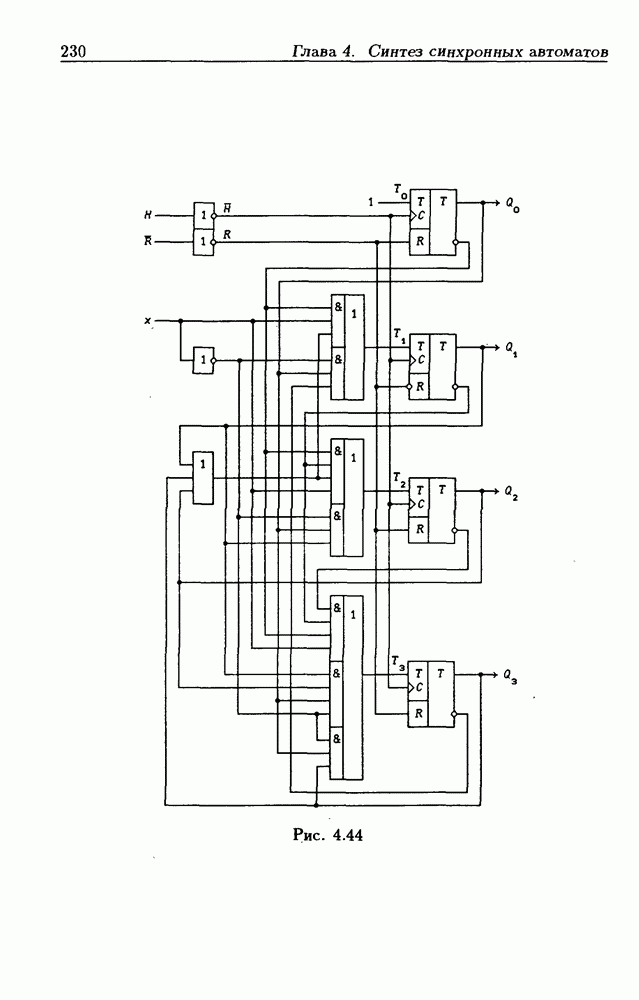
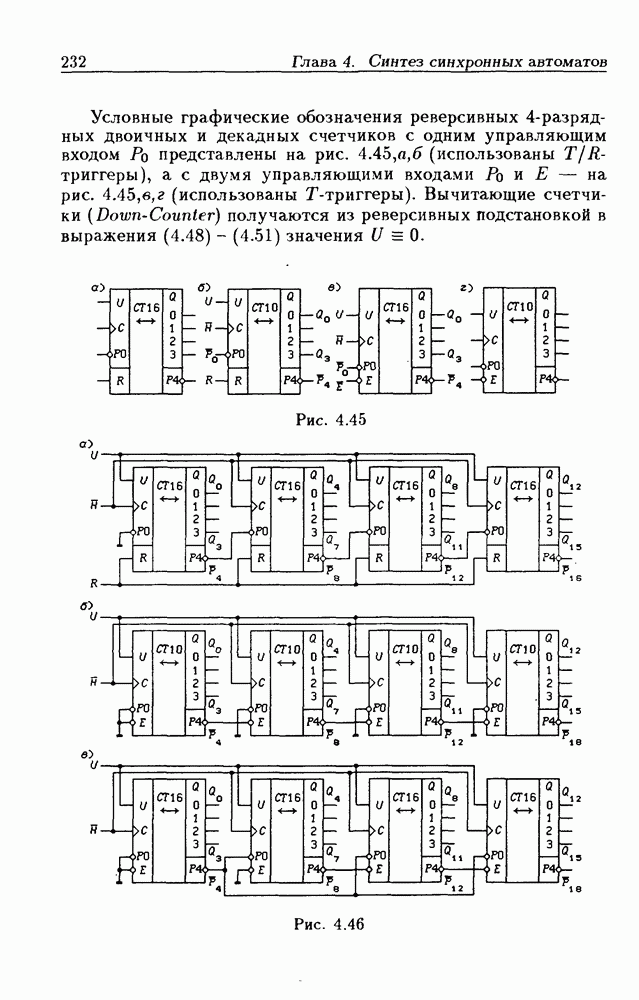
- Каскадирование реверсивных счетчиков.
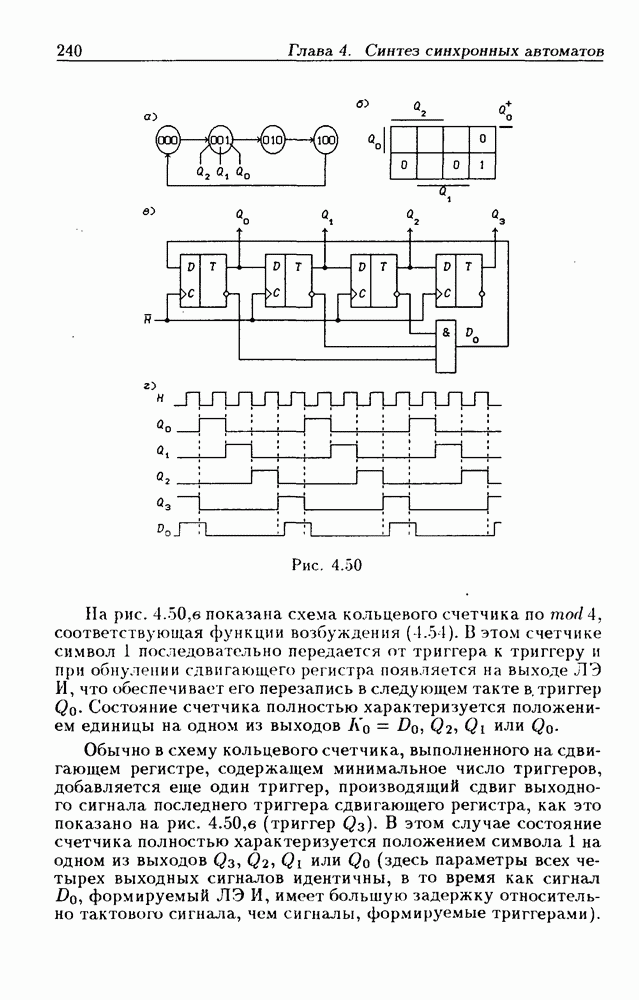
- Счетчики на сдвигающих регистрах.
- Кольцевые счетчики.
- Линейные счетчики.
- Программируемые счетчики.
- 4.6. Асинхронные счетчики
- Асинхронные счетчики с умножением частоты счетного сигнала.
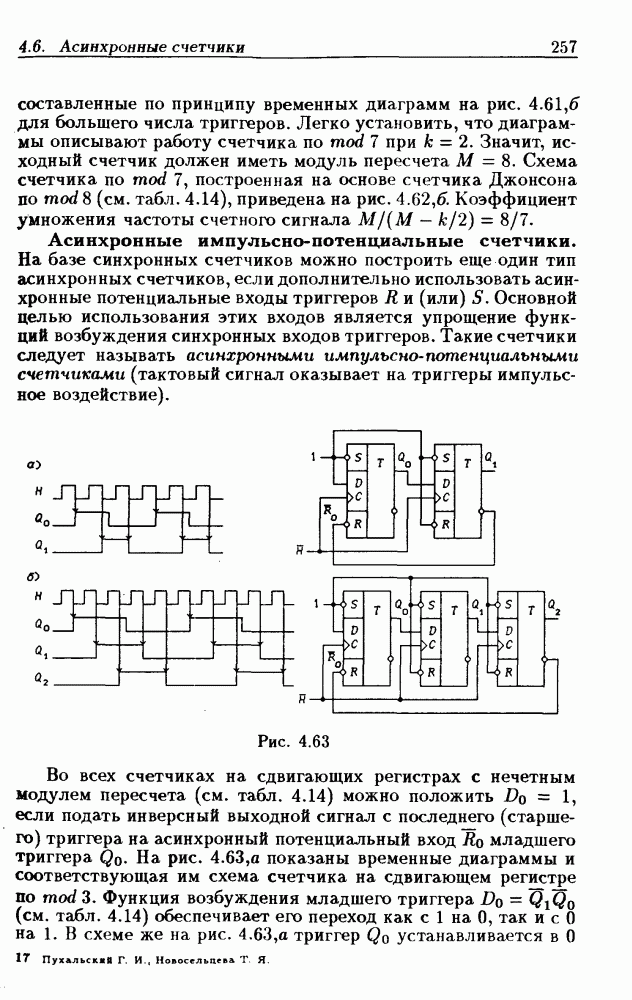
- Асинхронные импульсно-потенциальные счетчики.
- Асинхронное программирование модуля пересчета счетчиков.
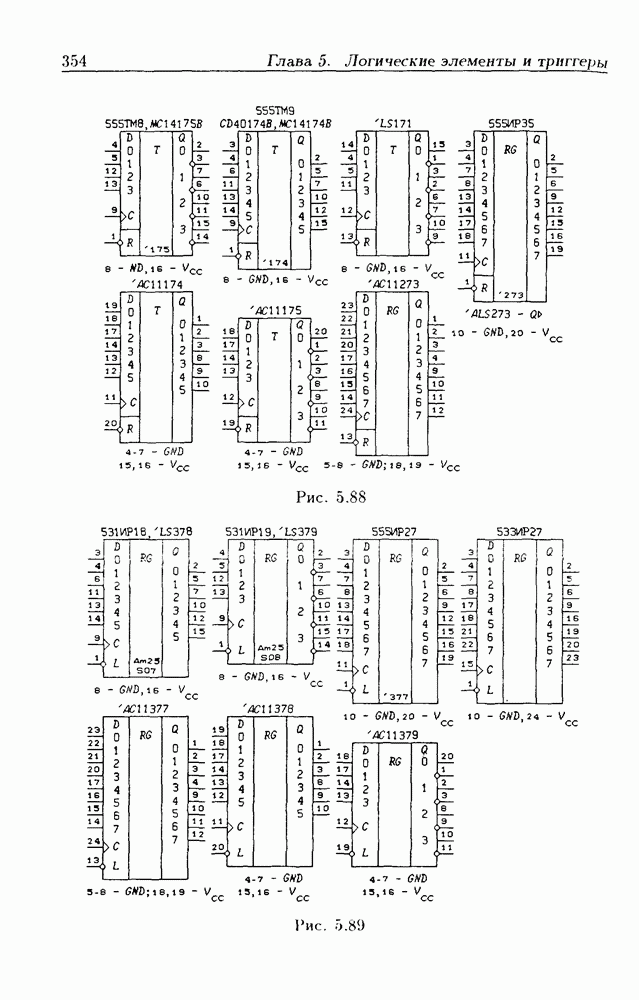
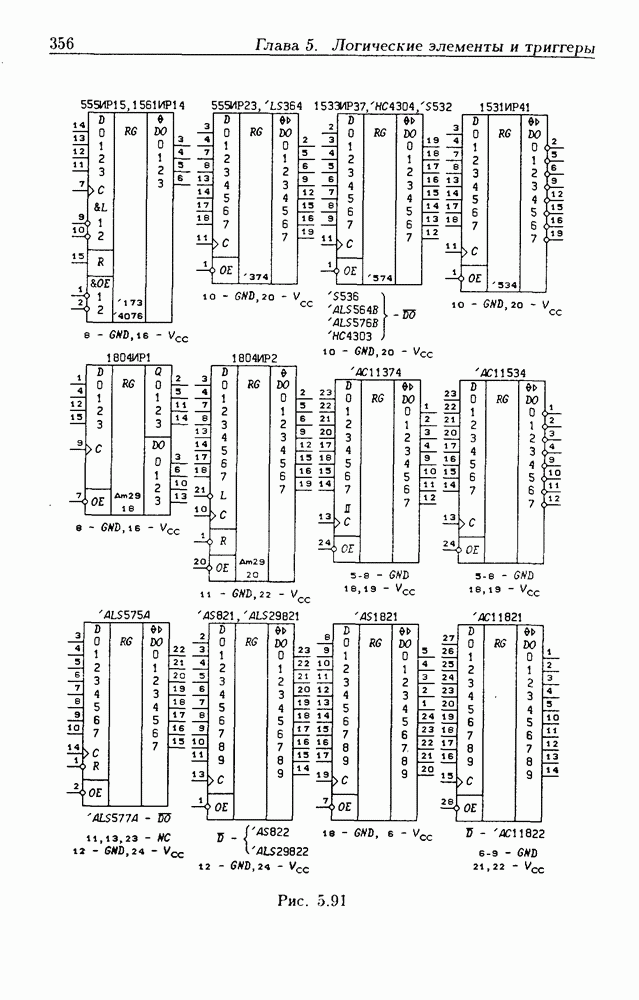
- Глава 5. Логические элементы и триггеры
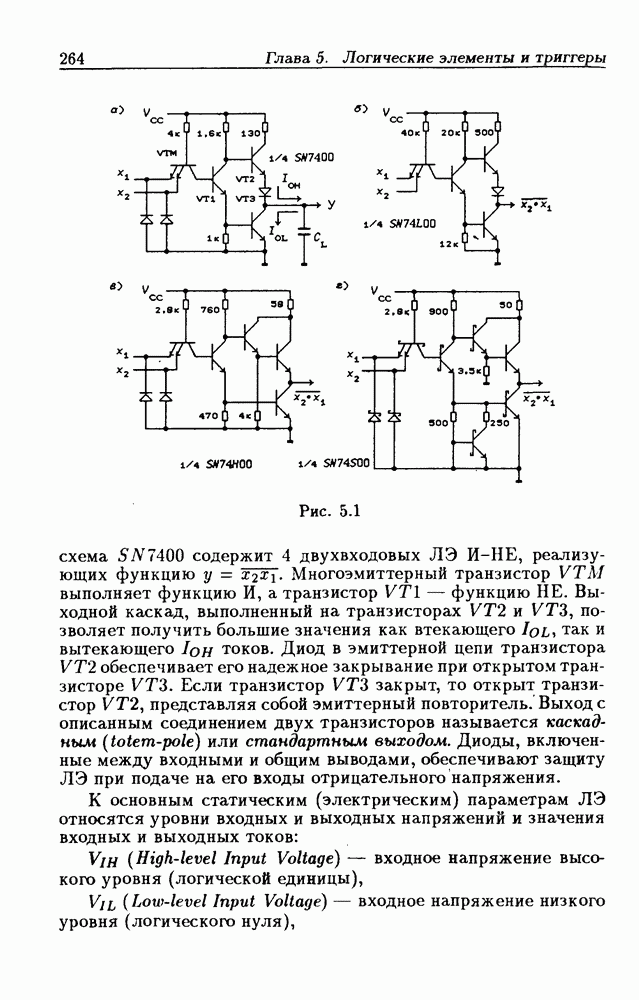
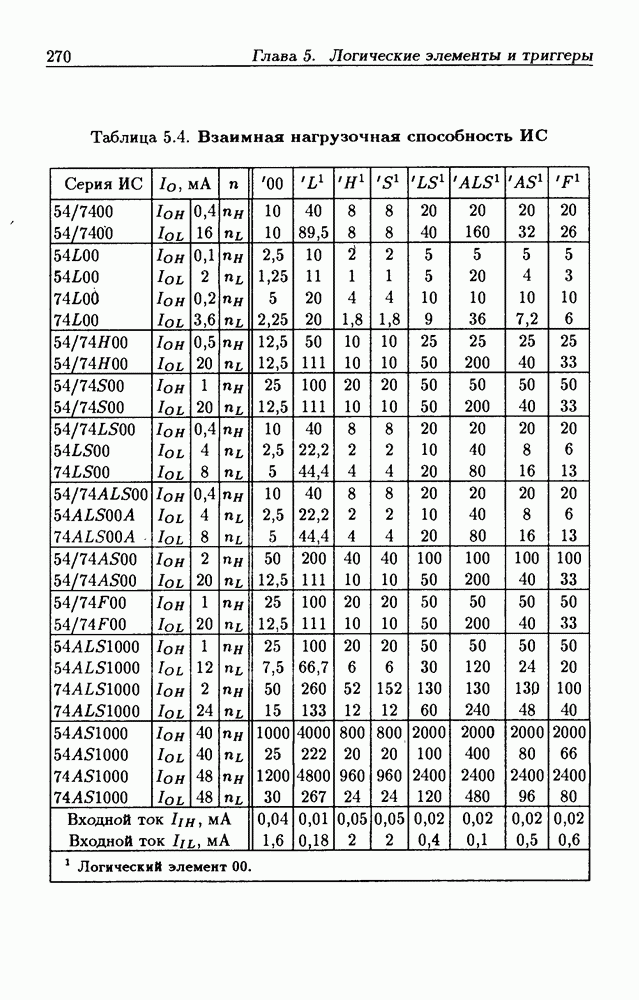
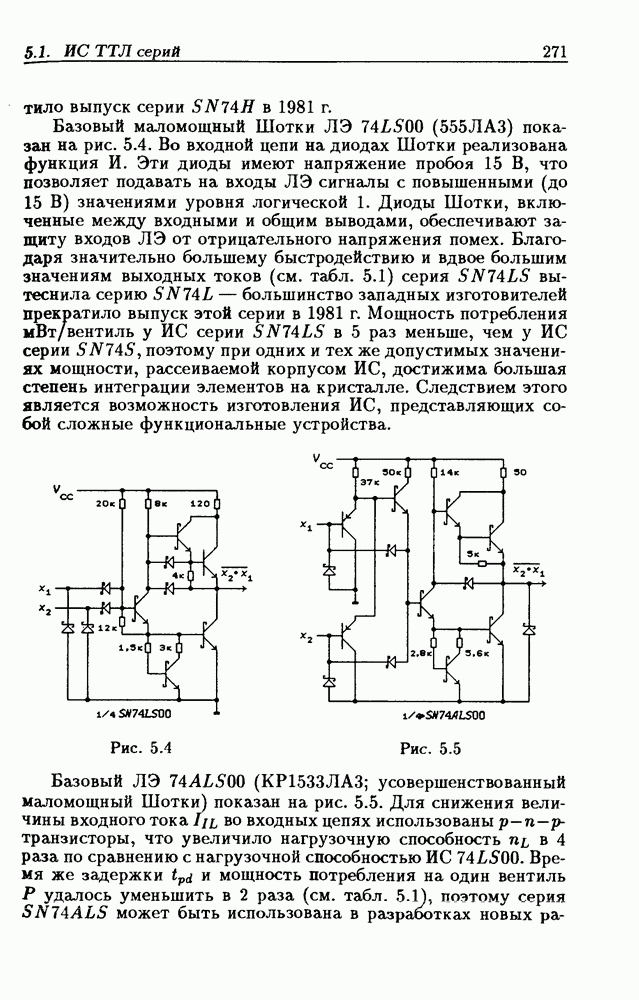
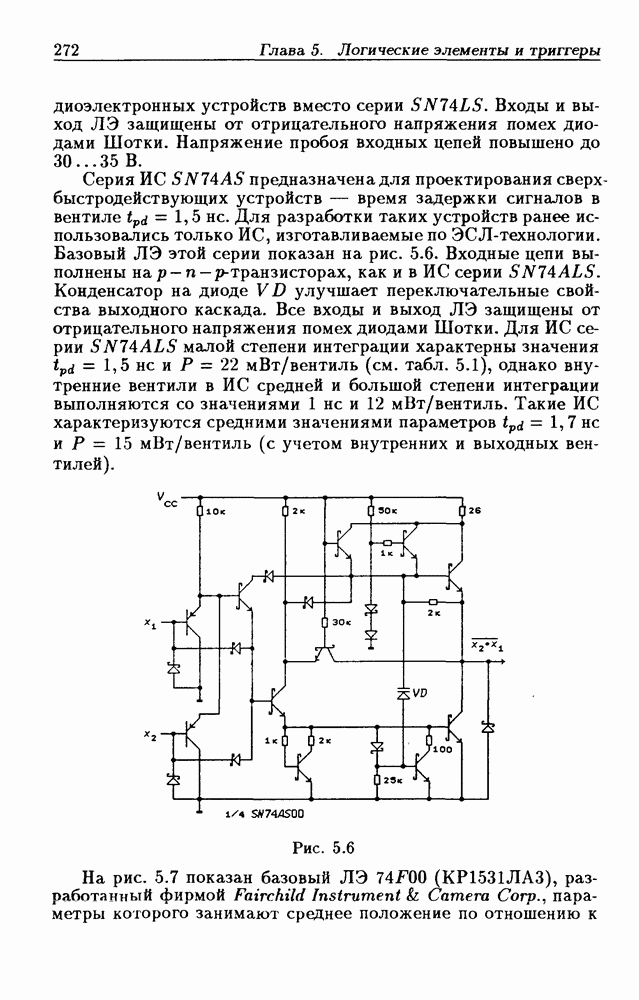
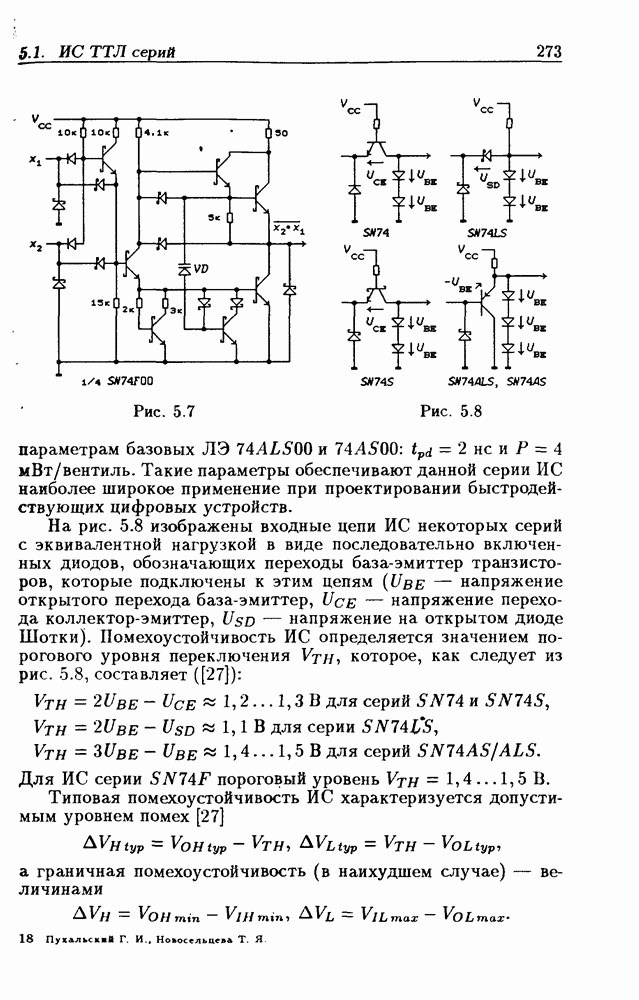
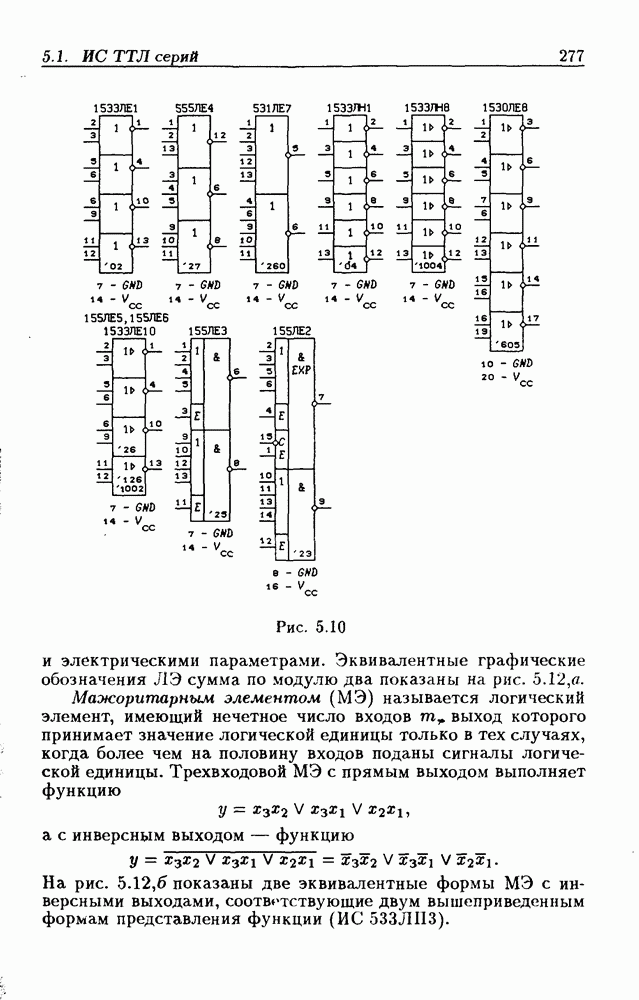
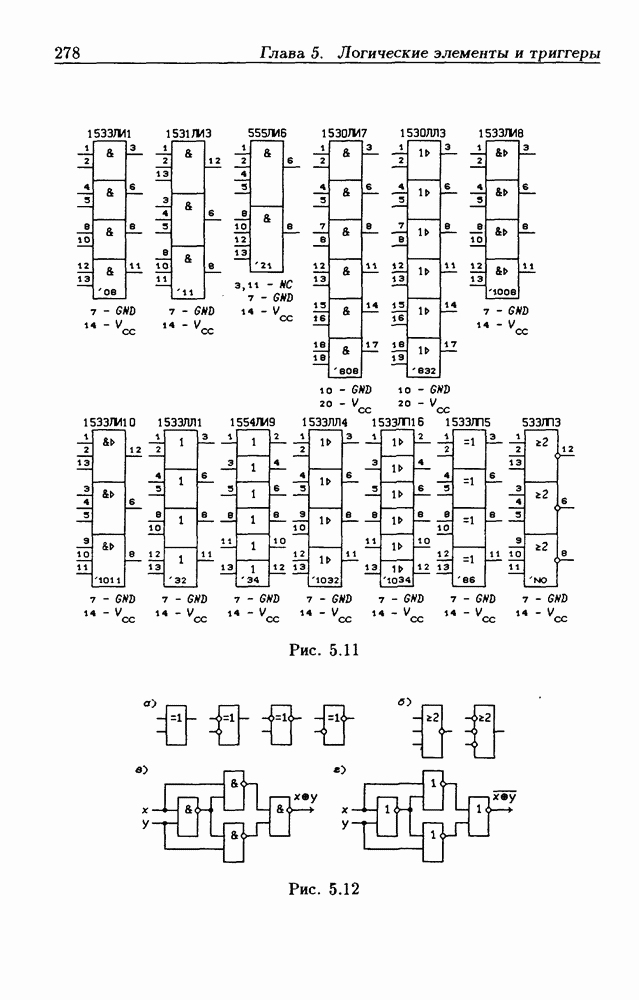
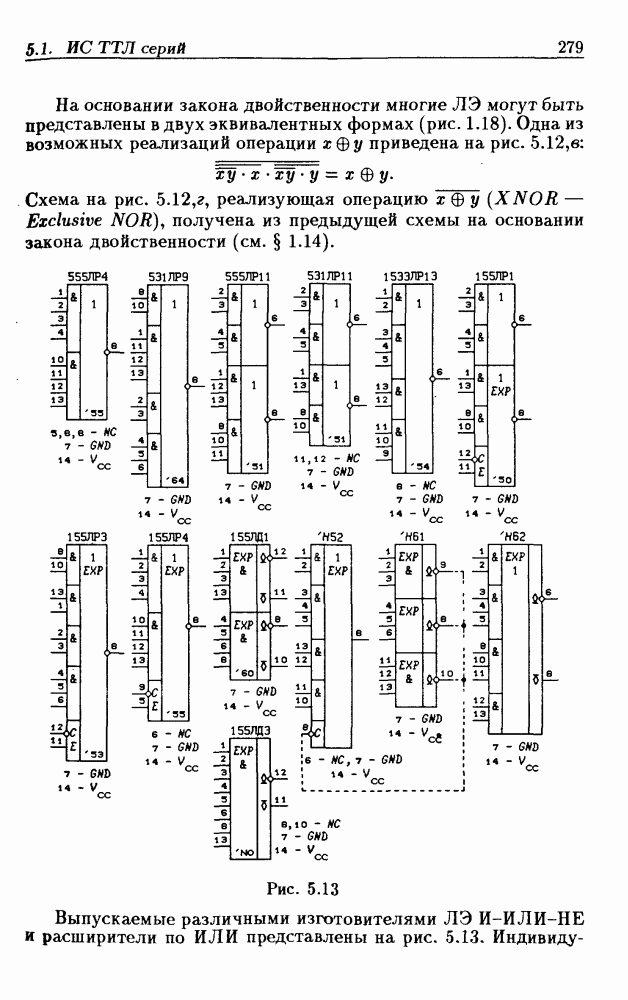
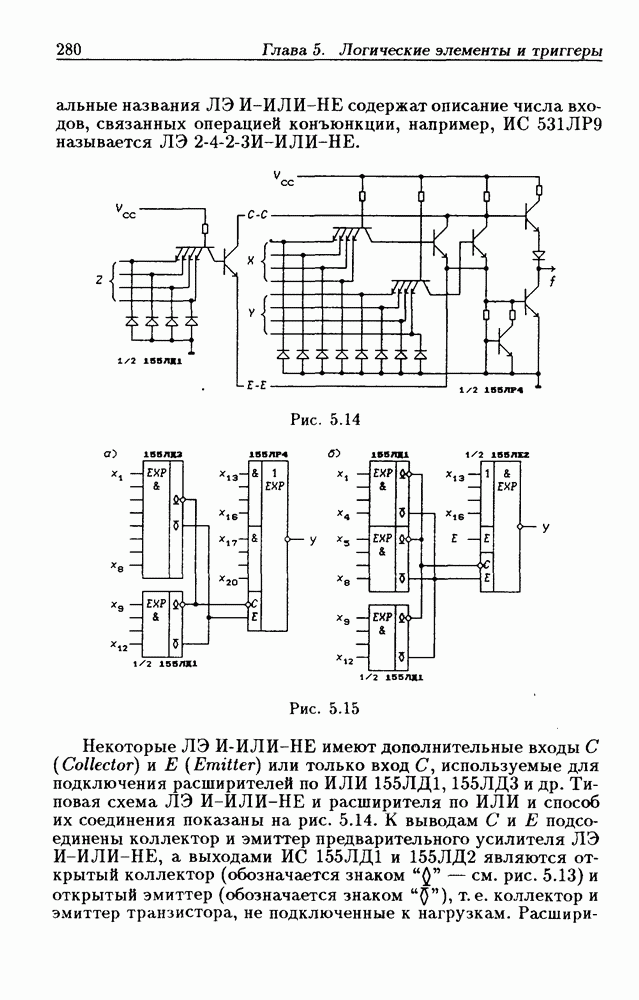
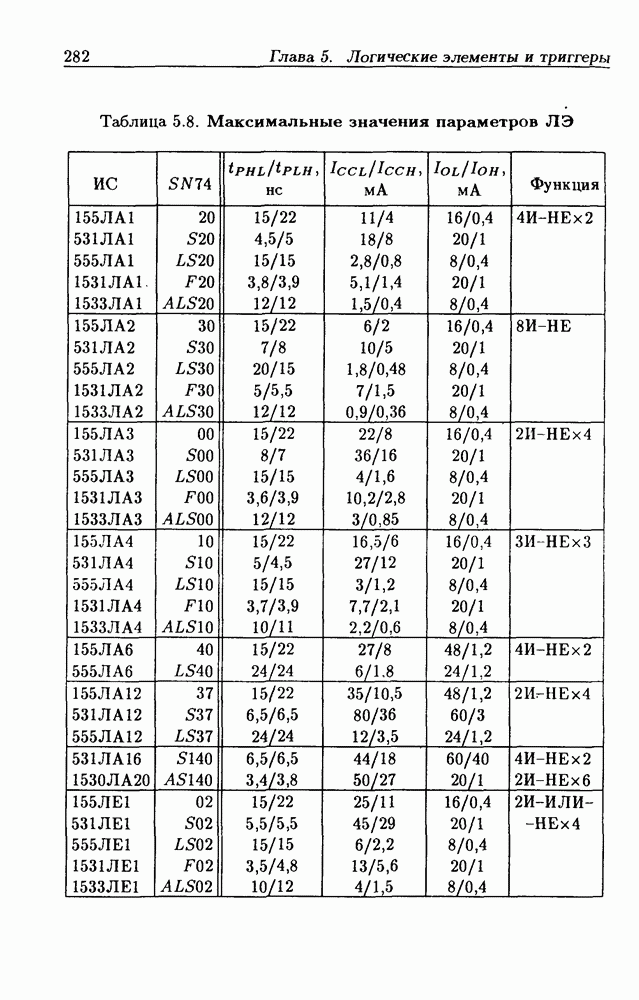
- Логические элементы.
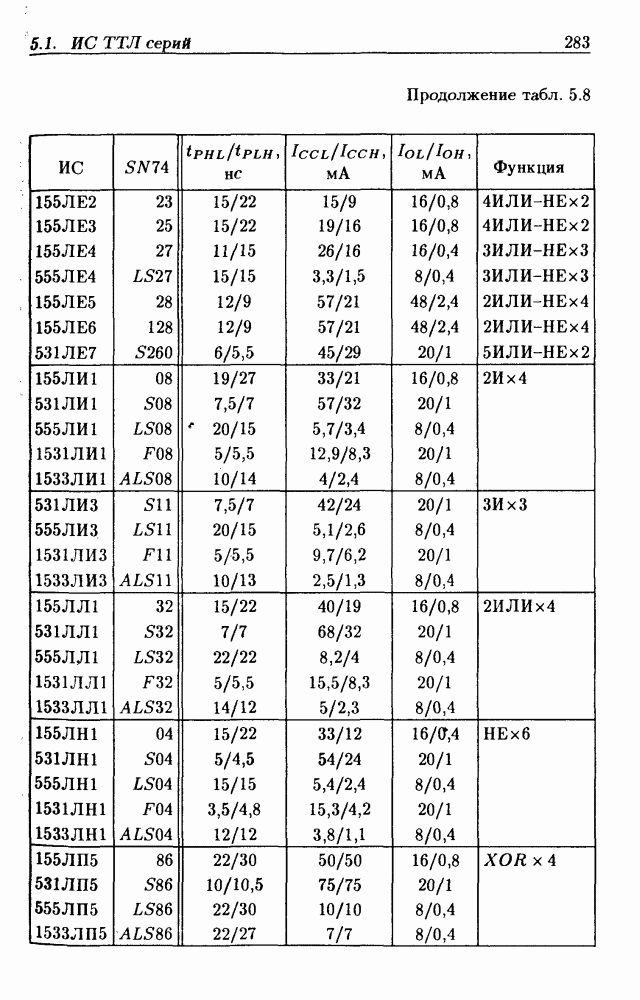
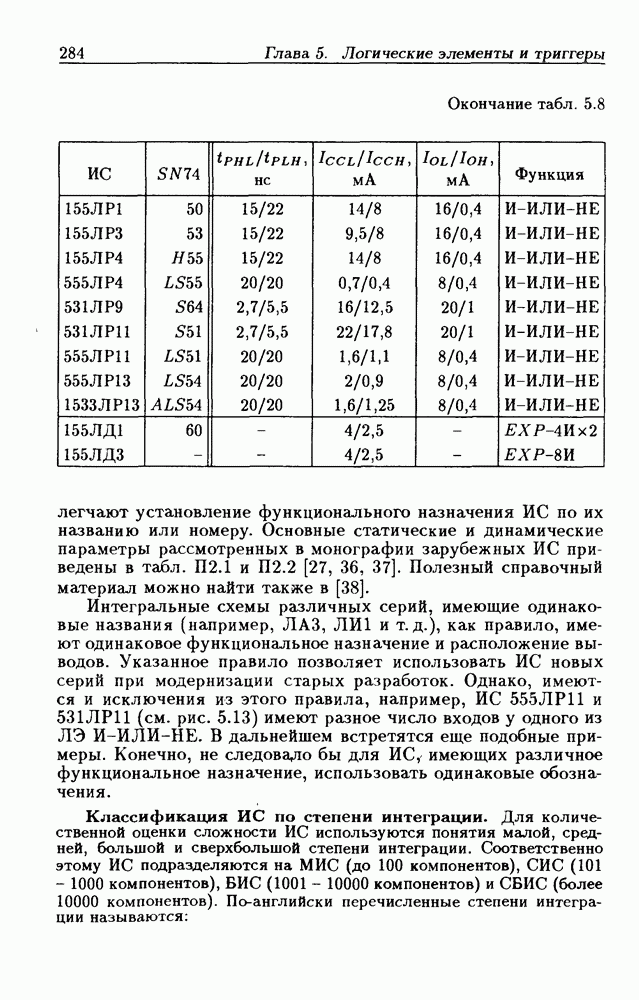
- Классификация ИС по степени интеграции.
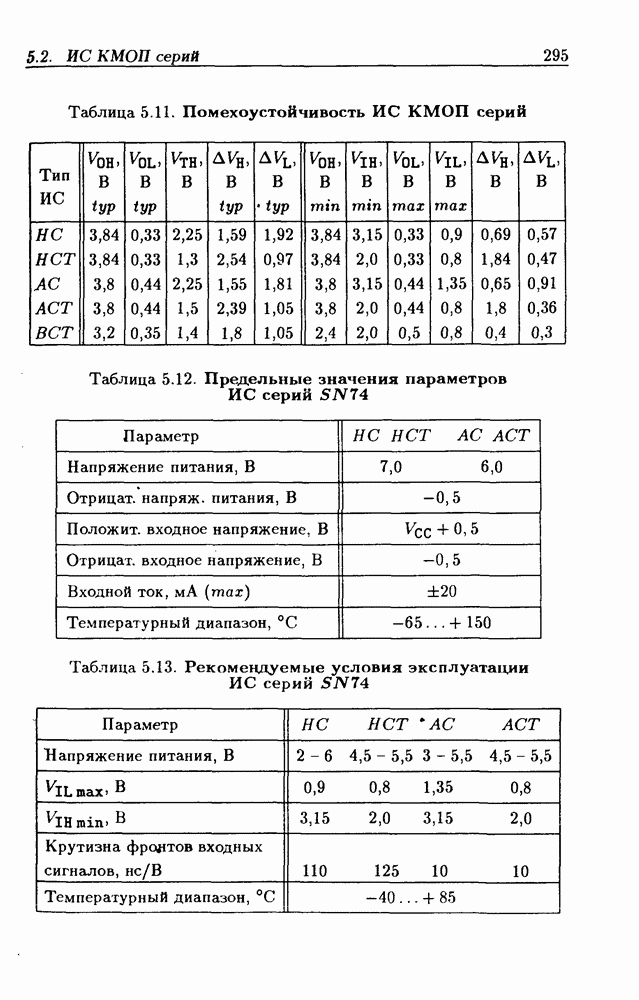
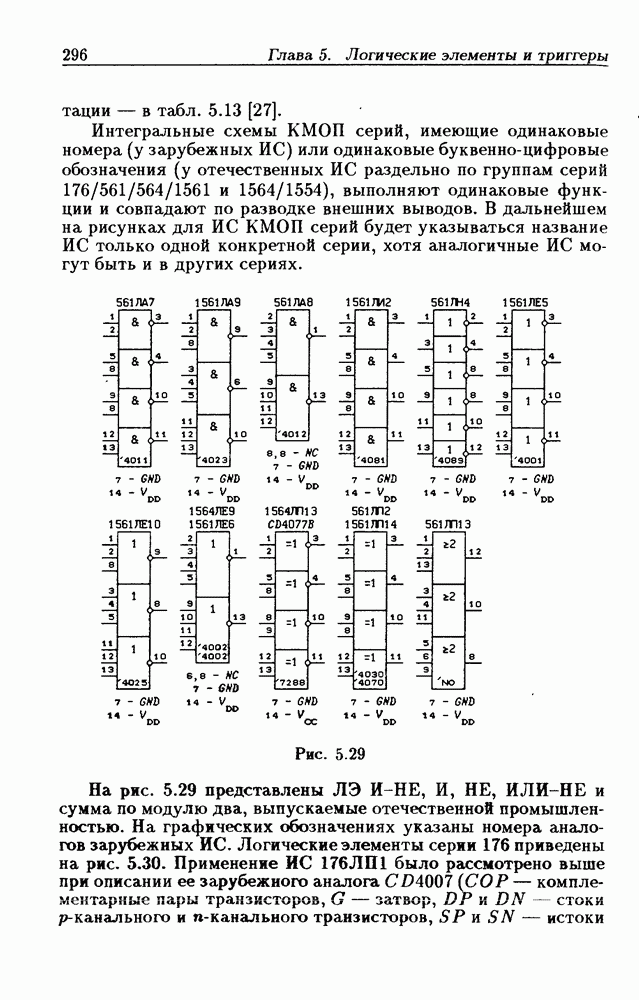
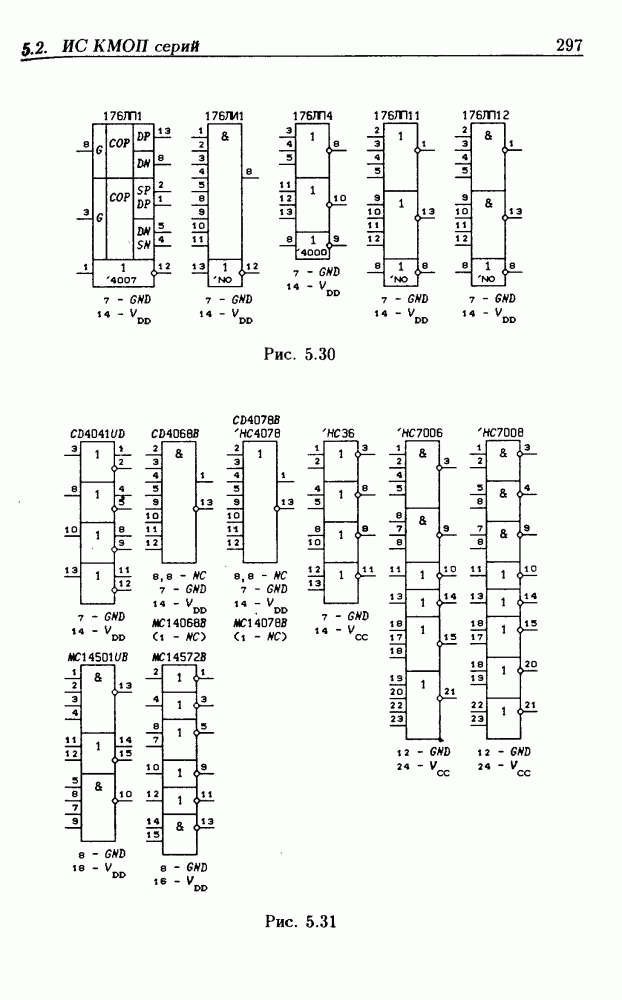
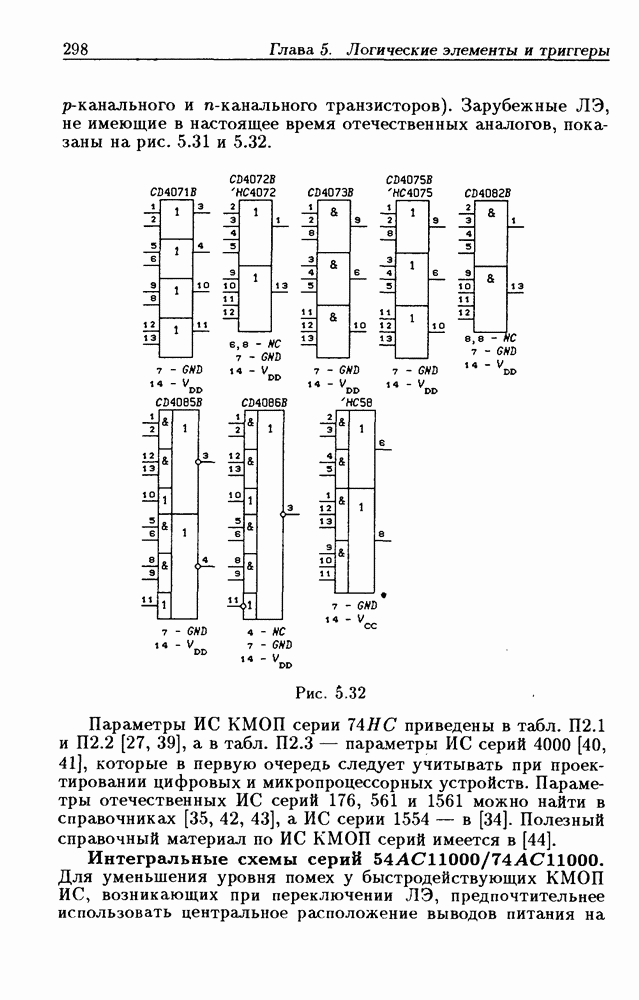
- 5.2. Интегральные схемы КМОП серий
- 5.3. Триггеры Шмитта
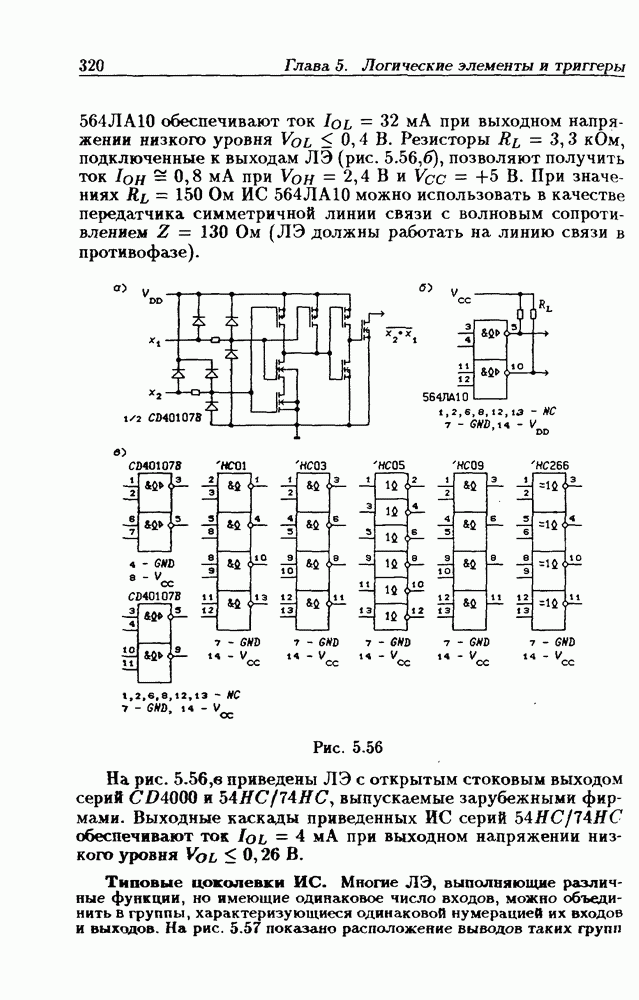
- 5.4. Логические элементы с открытым коллекторным выходом
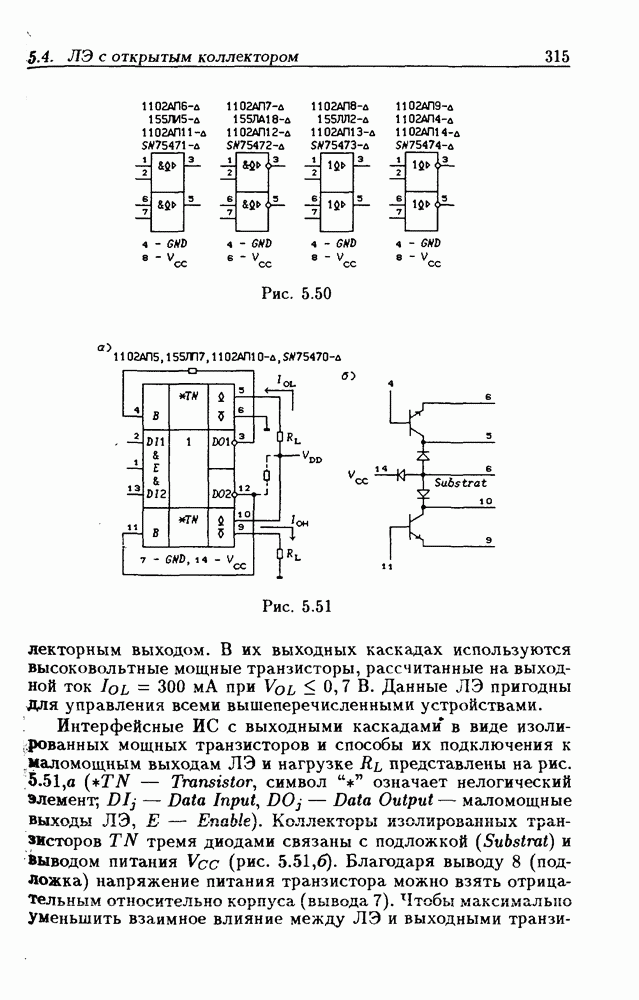
- Логические элементы с открытым коллекторным выходом.
- Применения ЛЭ с открытым коллекторным выходом.
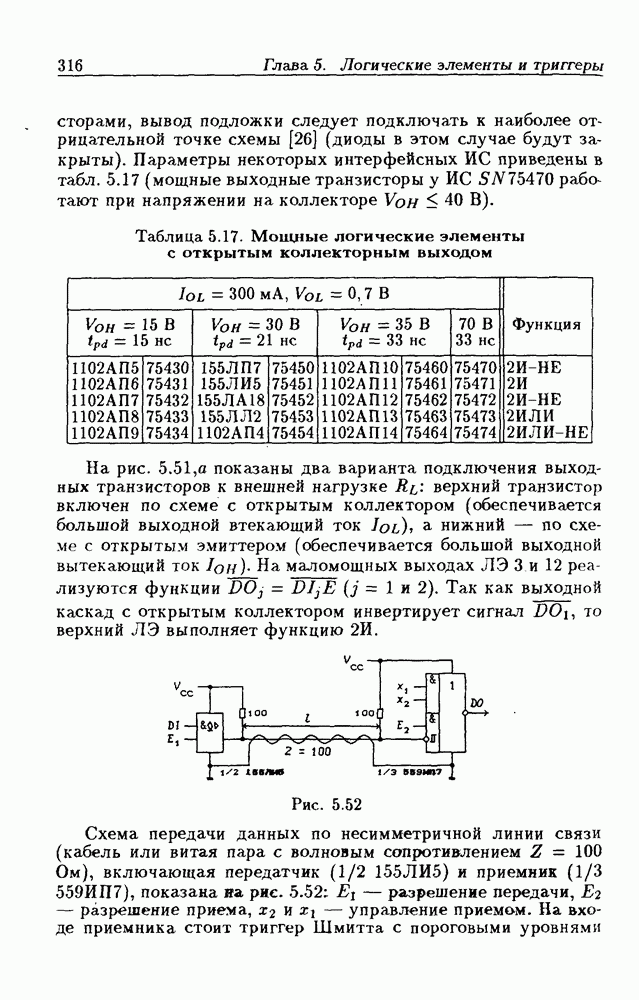
- Интерфейсные ЛЭ с открытым коллекторным выходом.
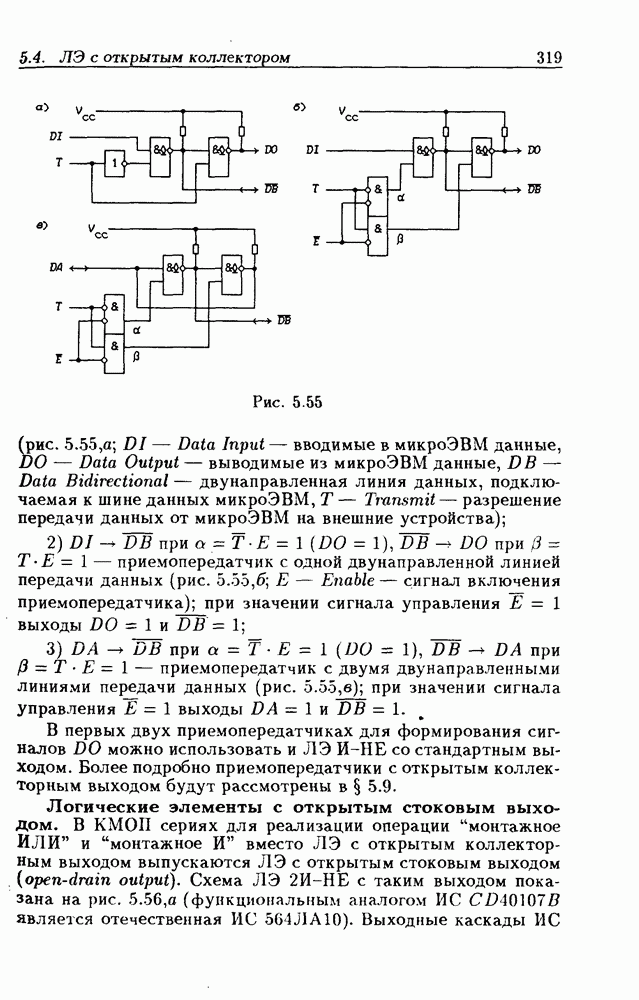
- Логические элементы с открытым стоковым выходом.
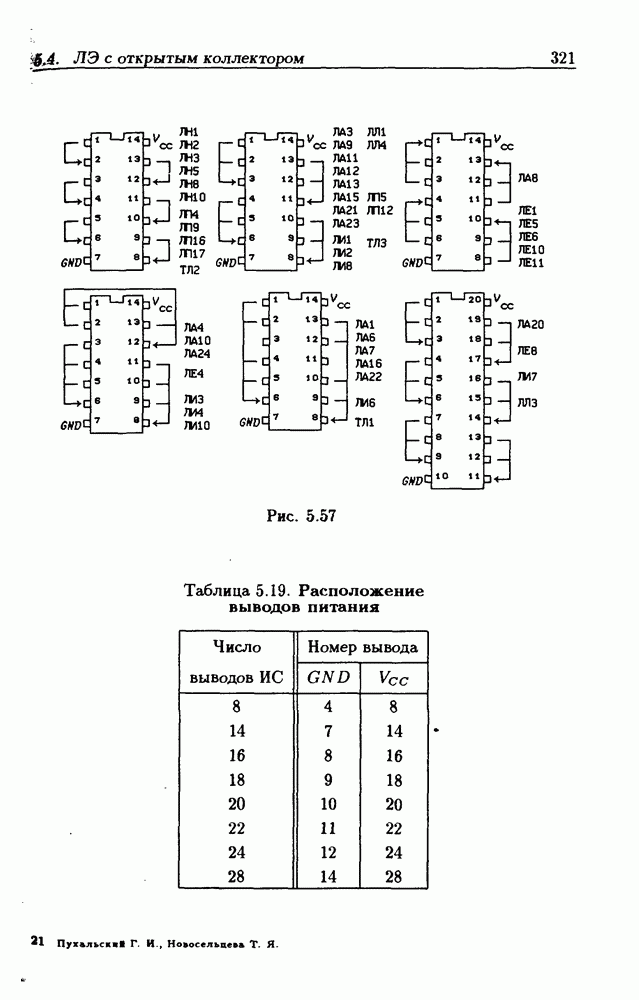
- Типовые цоколевки ИС.
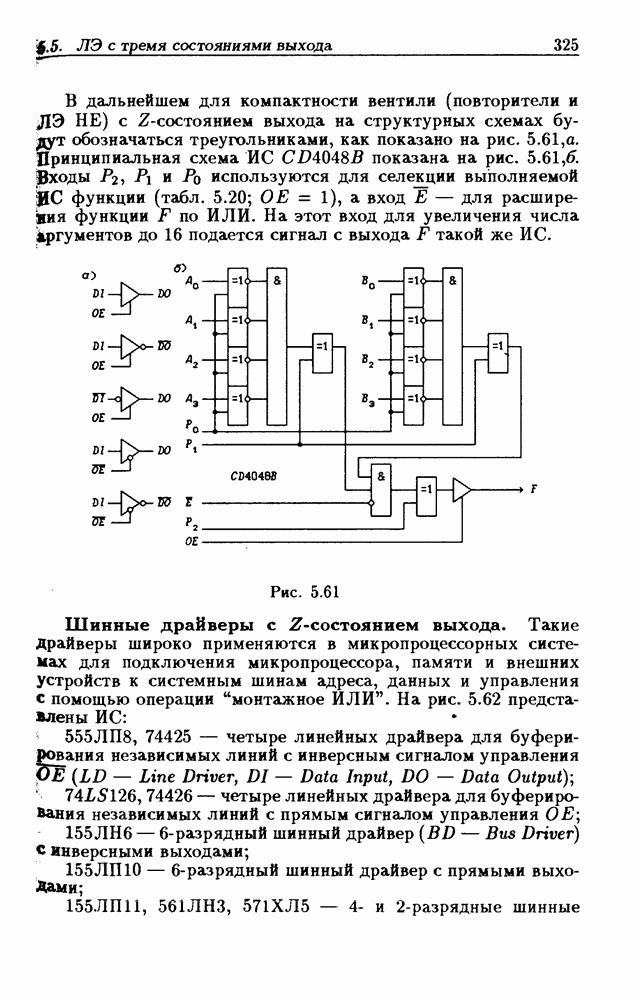
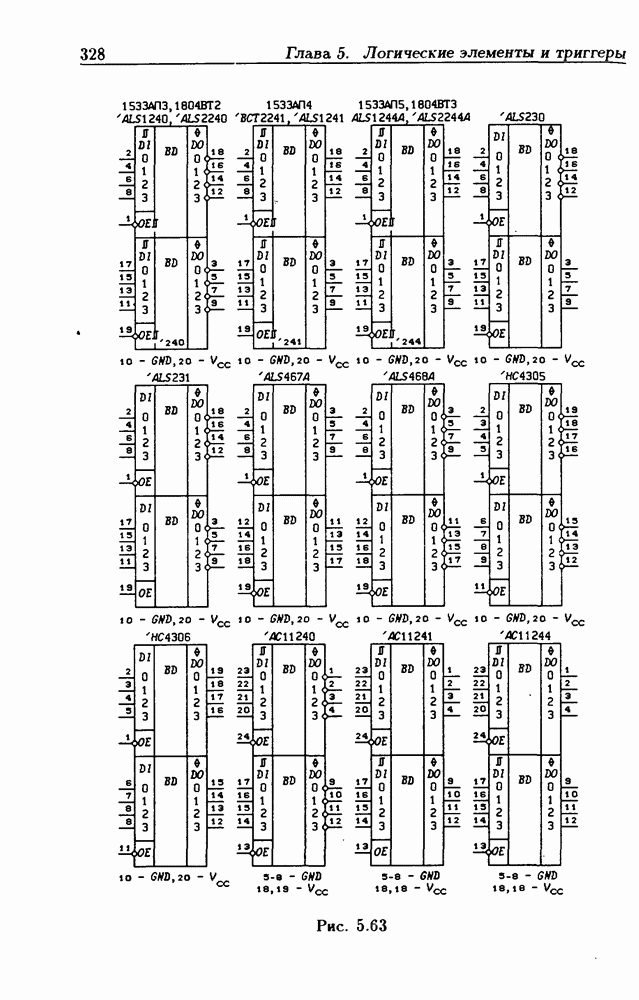
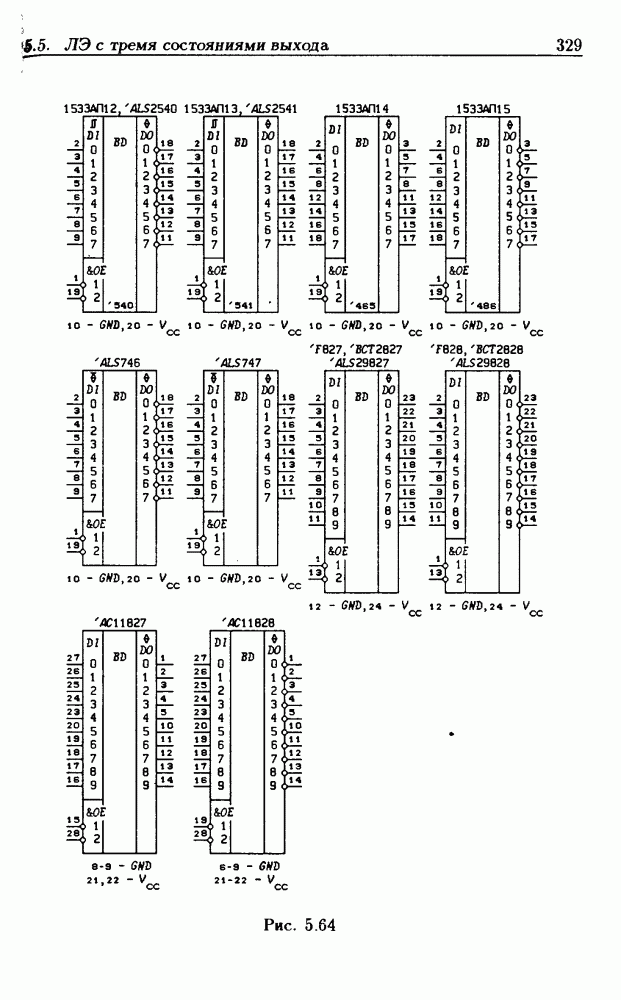
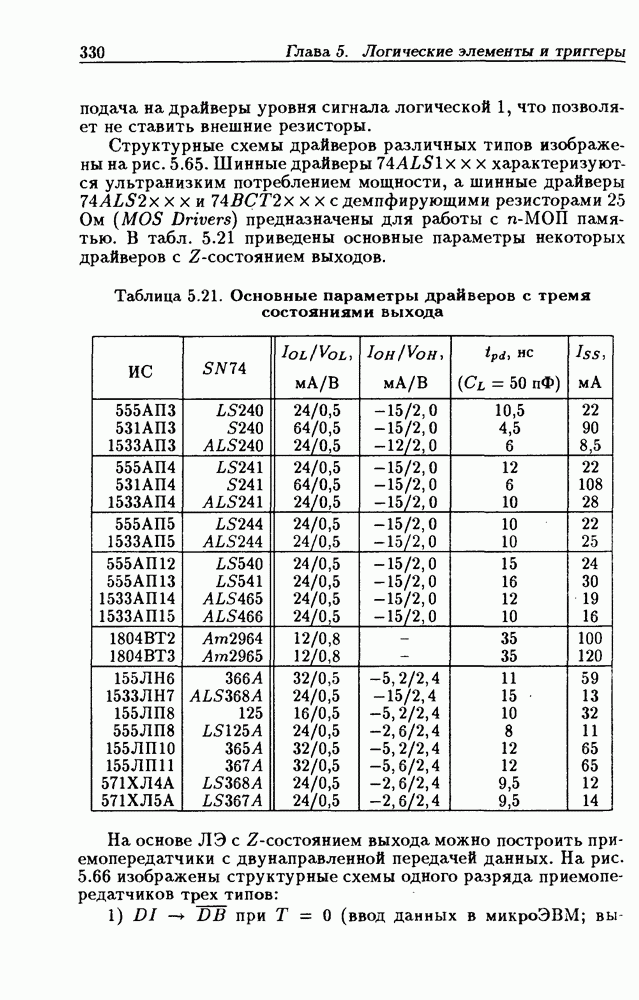
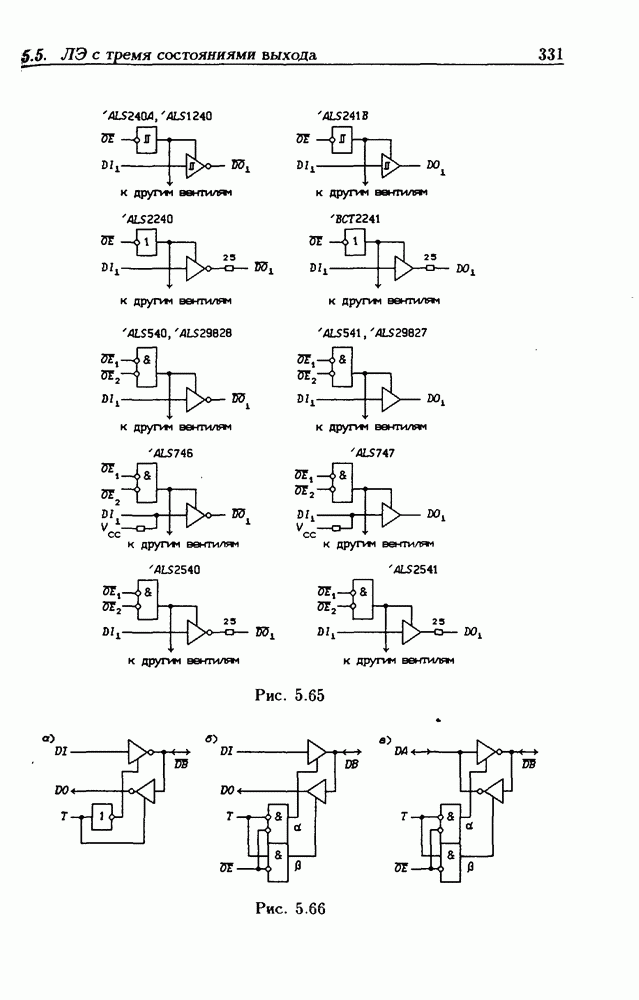
- 5.5. Логические элементы с тремя состояниями выхода
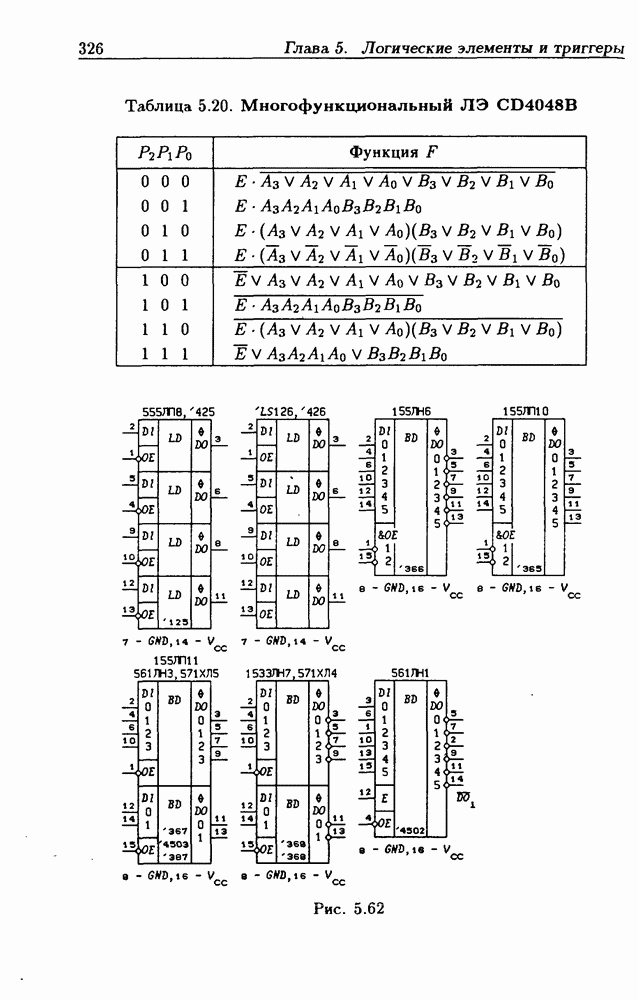
- Шинные драйверы с Z-состоянием выхода.
- Основные правила графического изображения ИС.
- 5.6. Преобразователи уровней напряжения и тока
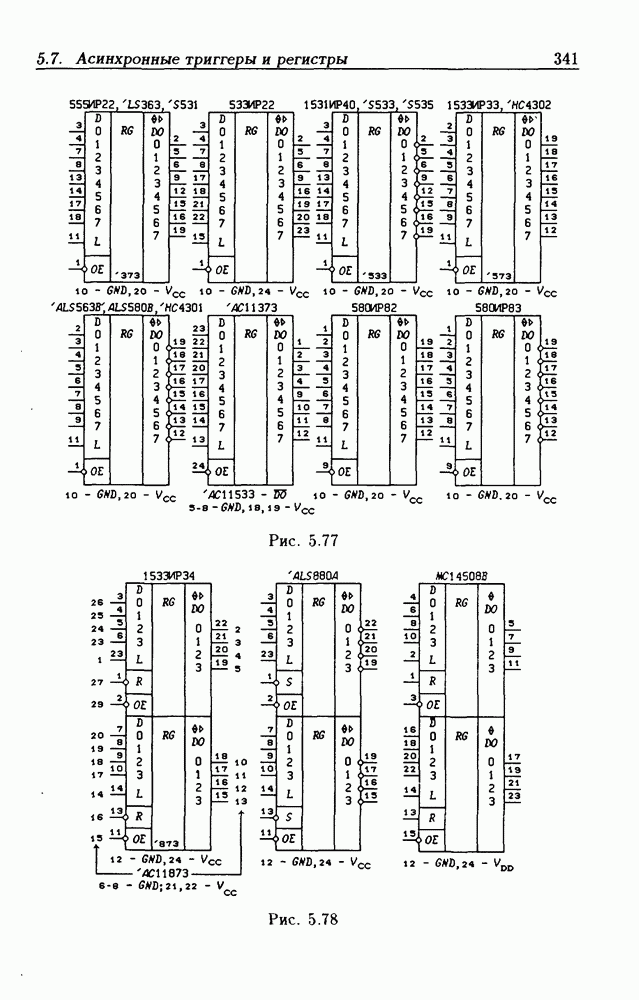
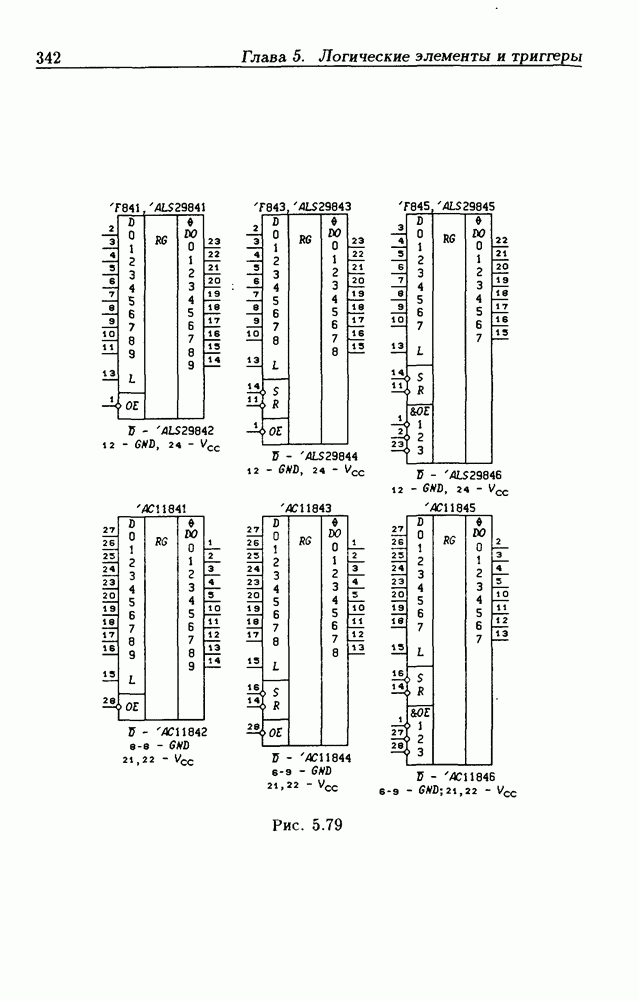
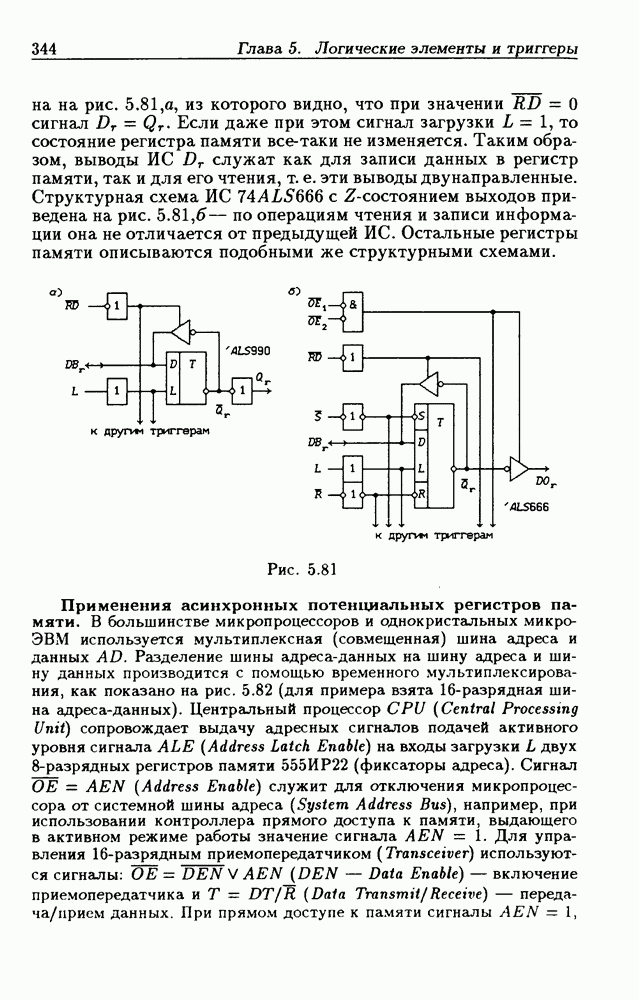
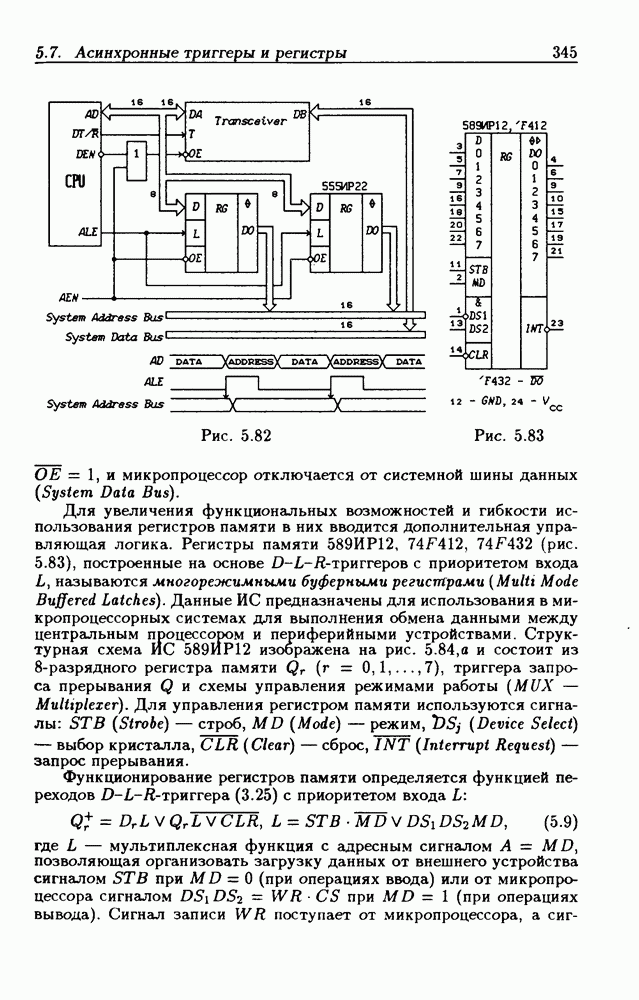
- 5.7. Асинхронные потенциальные триггеры и регистры памяти
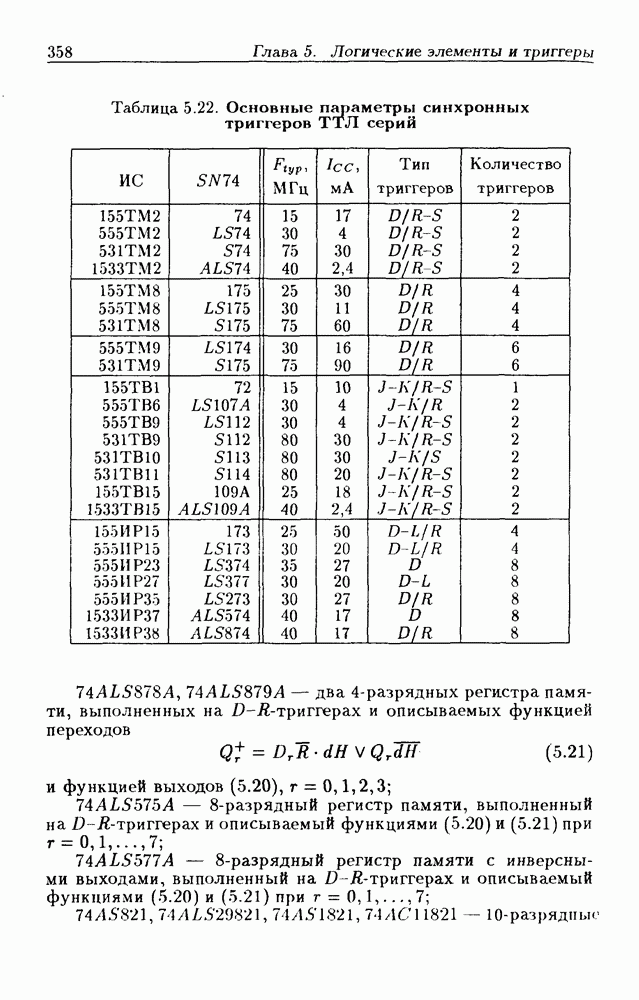
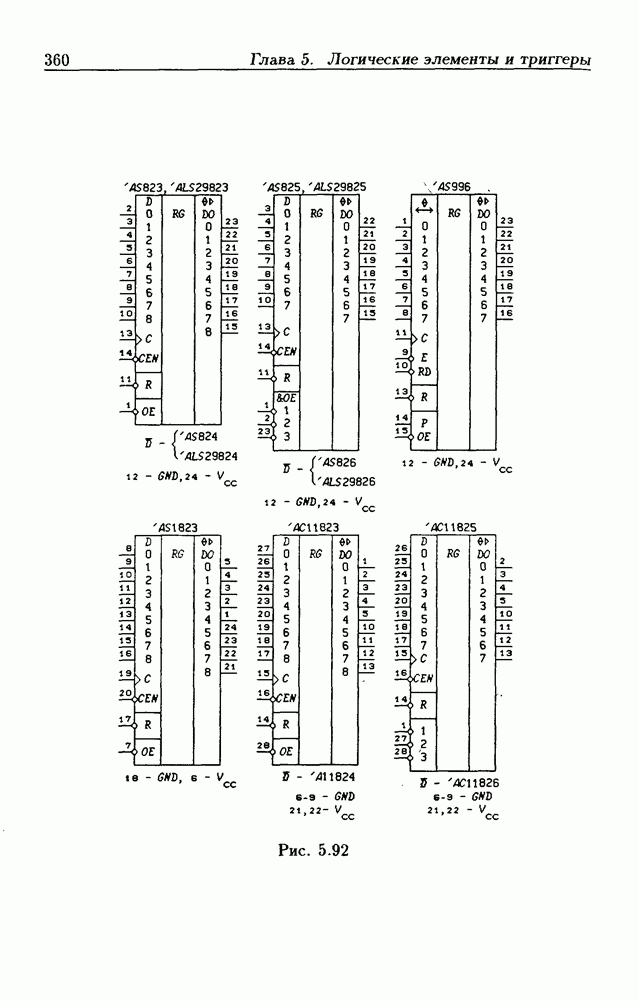
- 5.8. Синхронные триггеры и регистры памяти
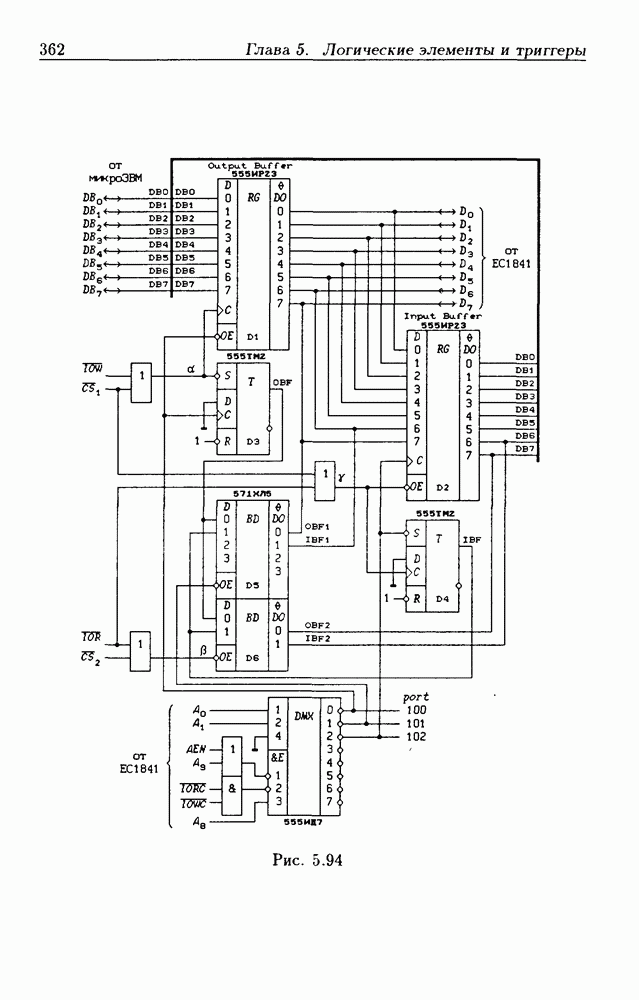
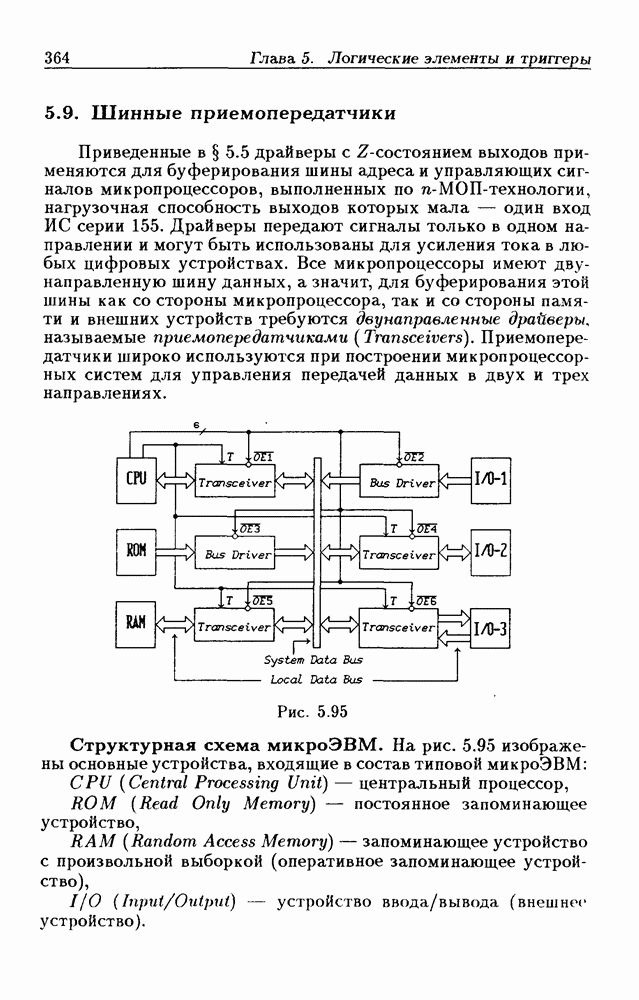
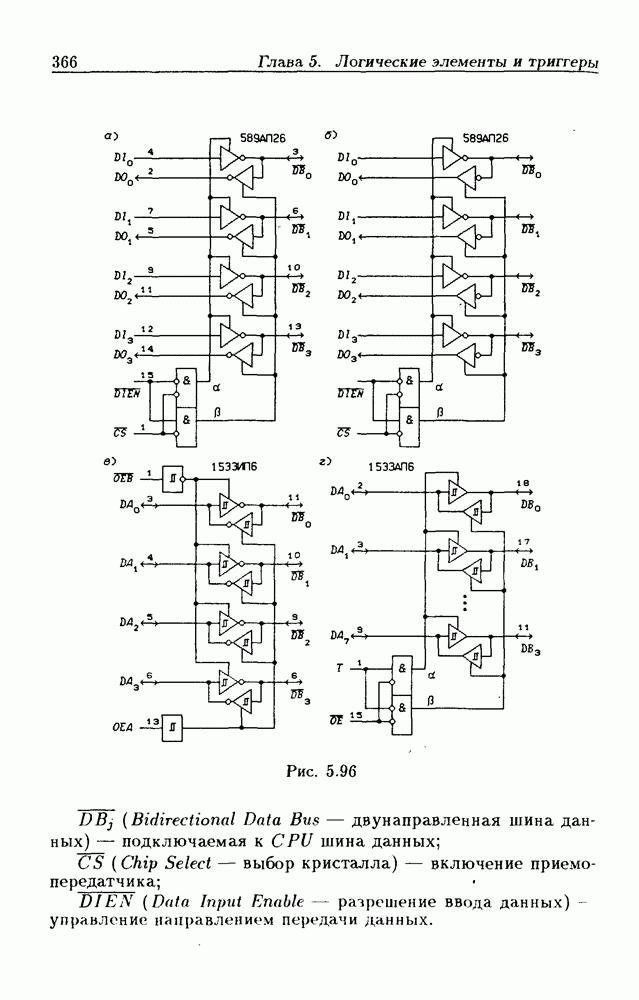
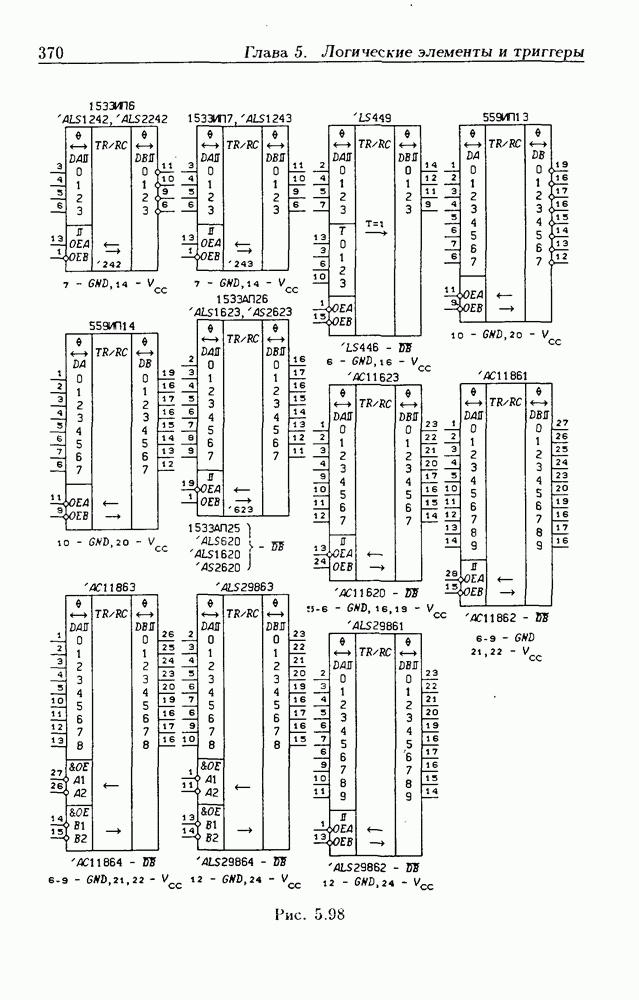
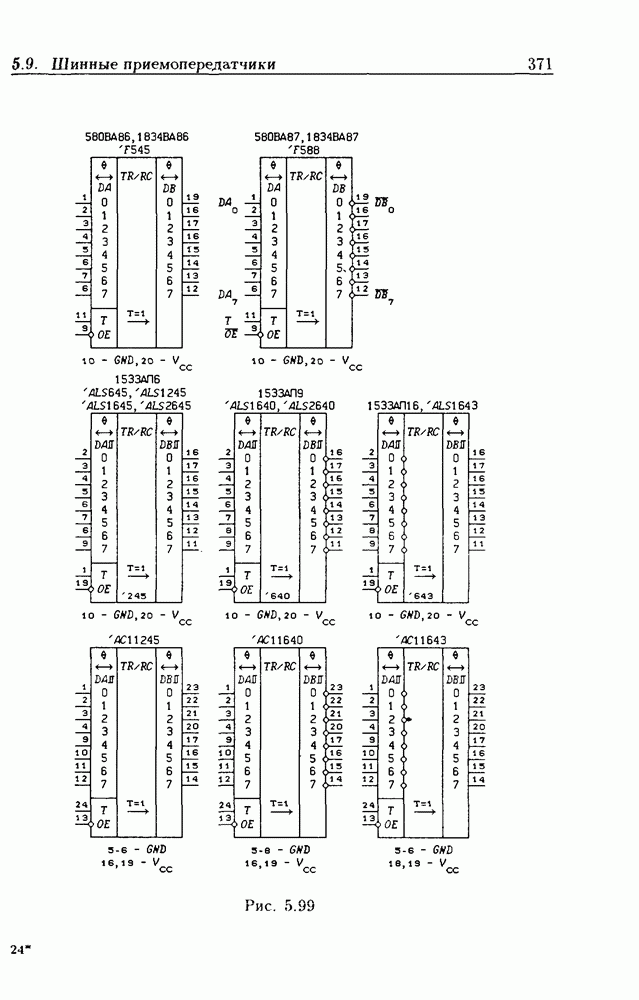
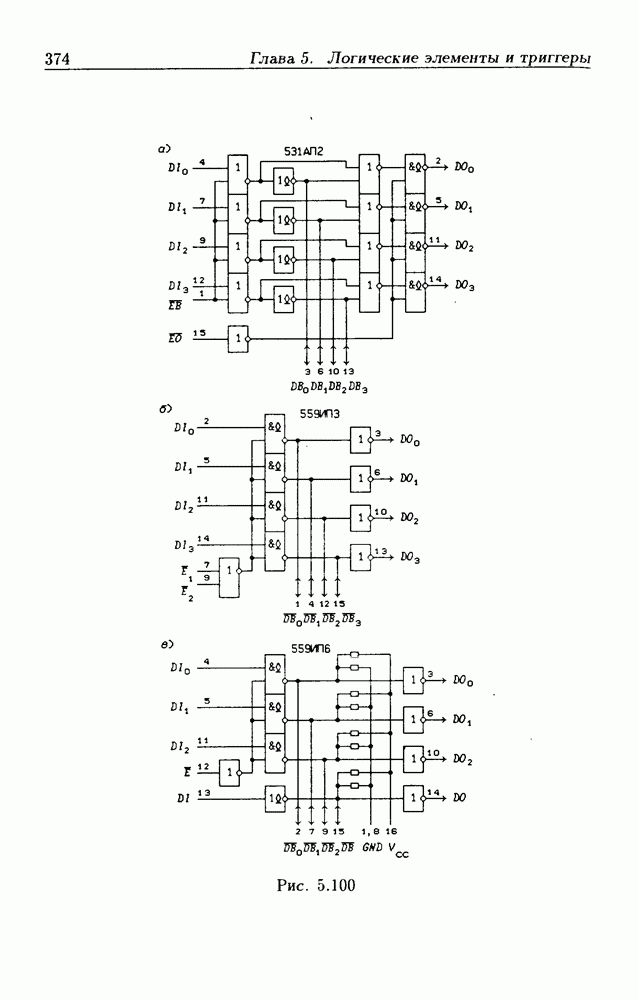
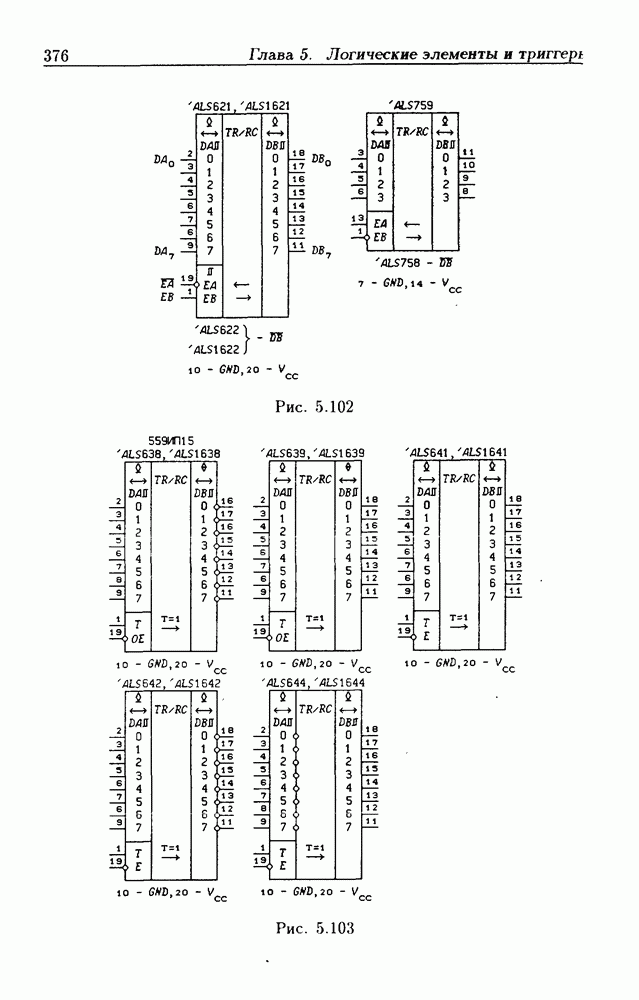
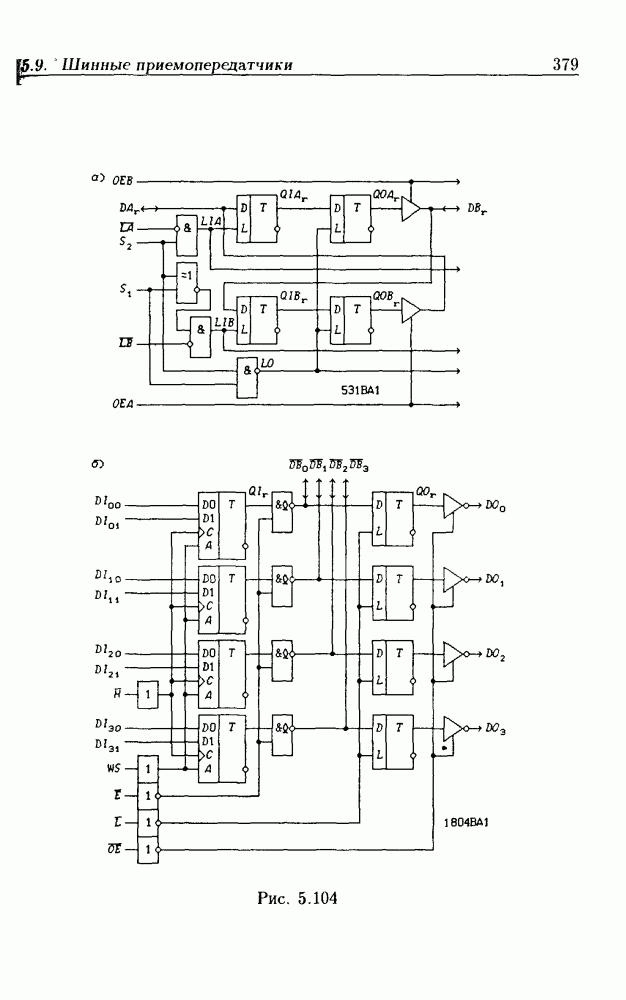
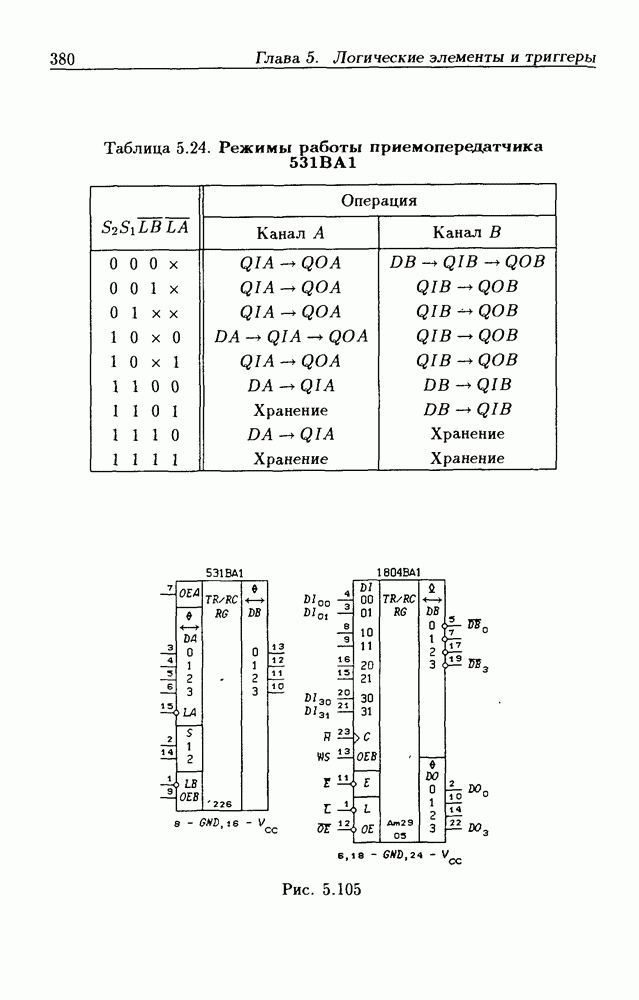
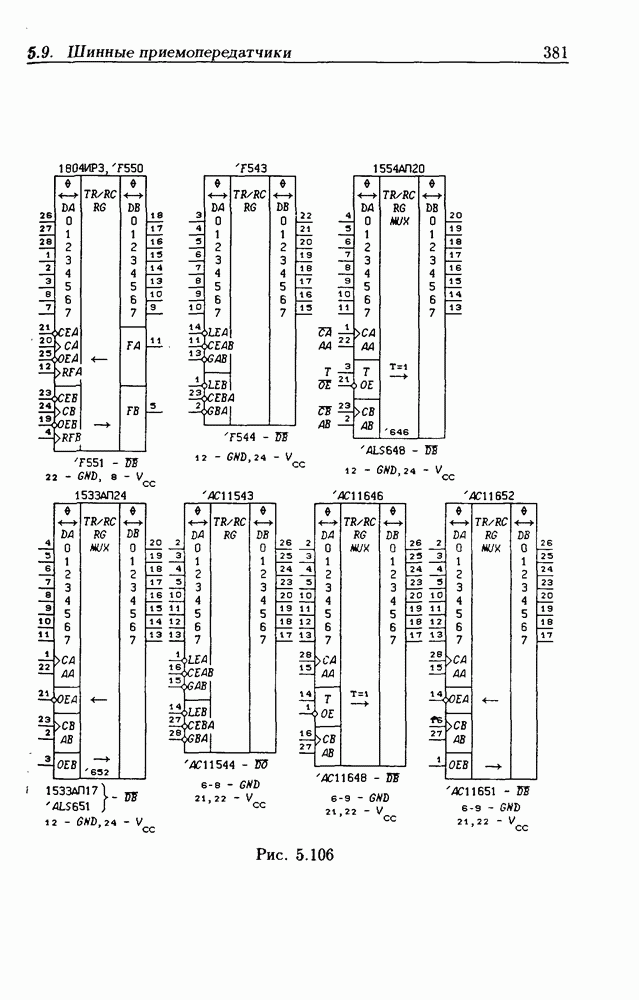
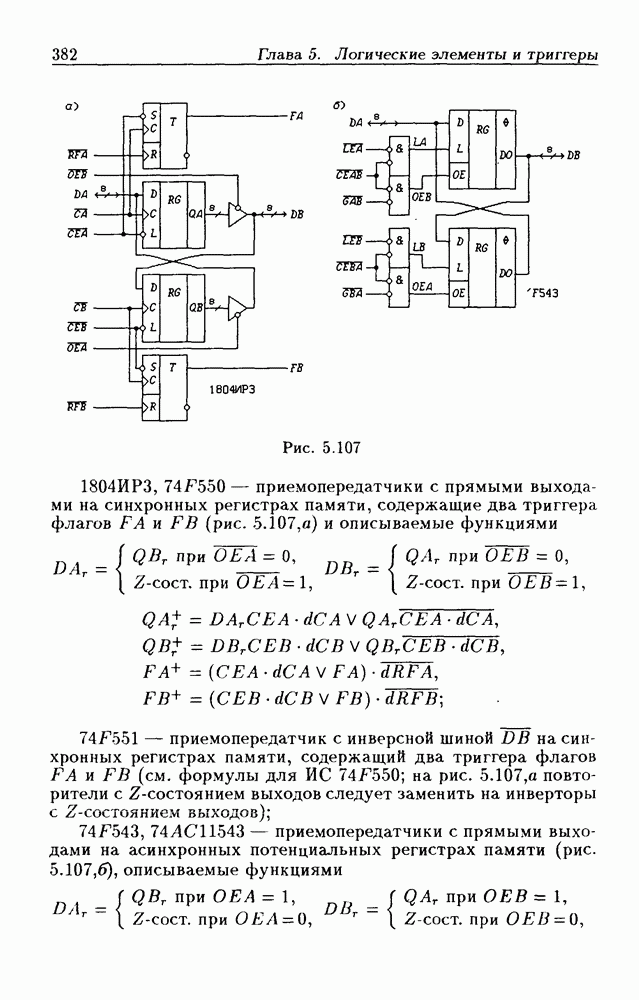
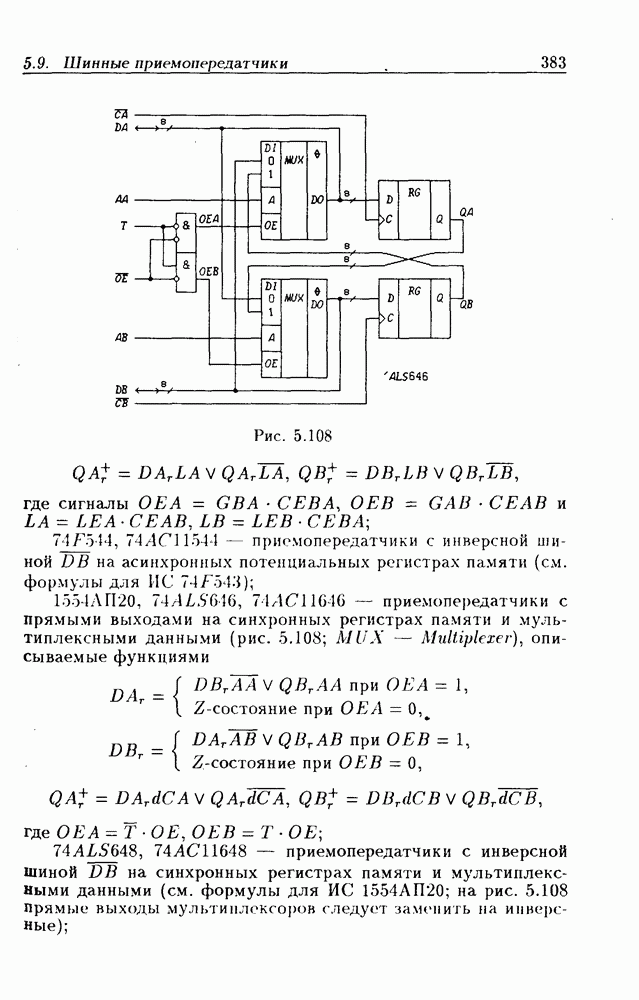
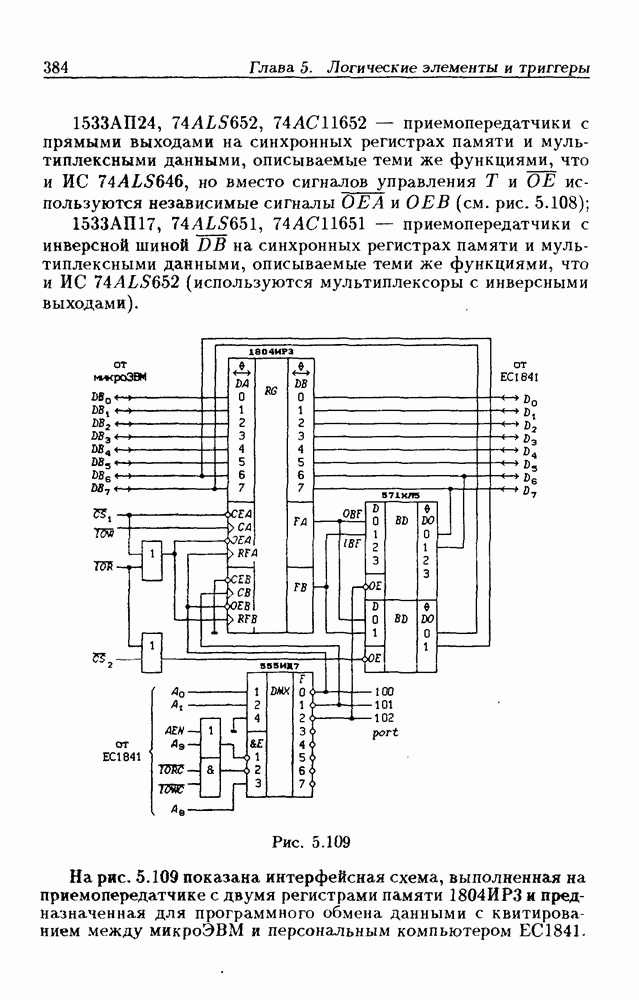
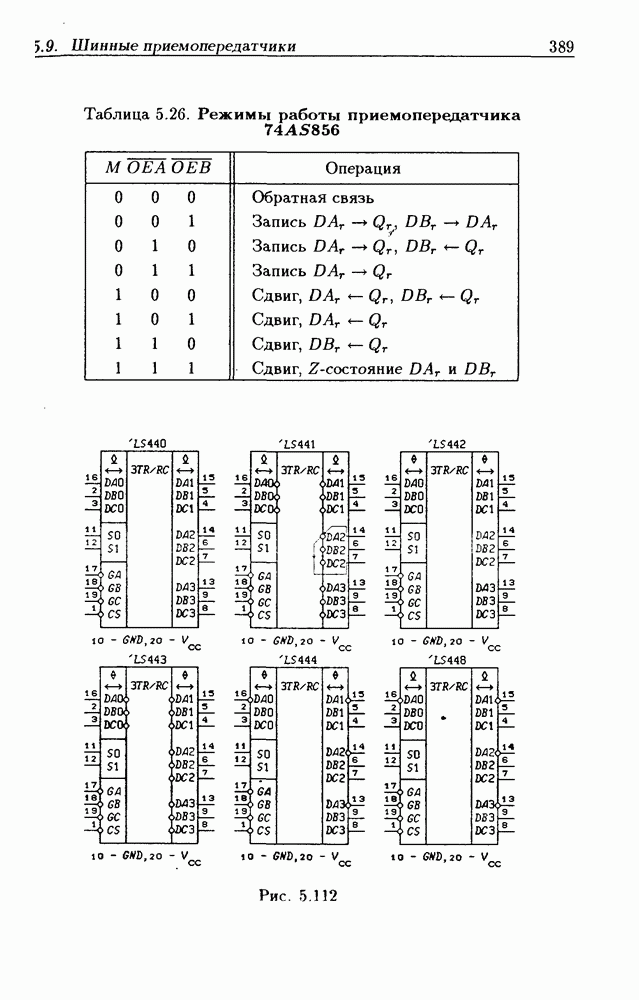
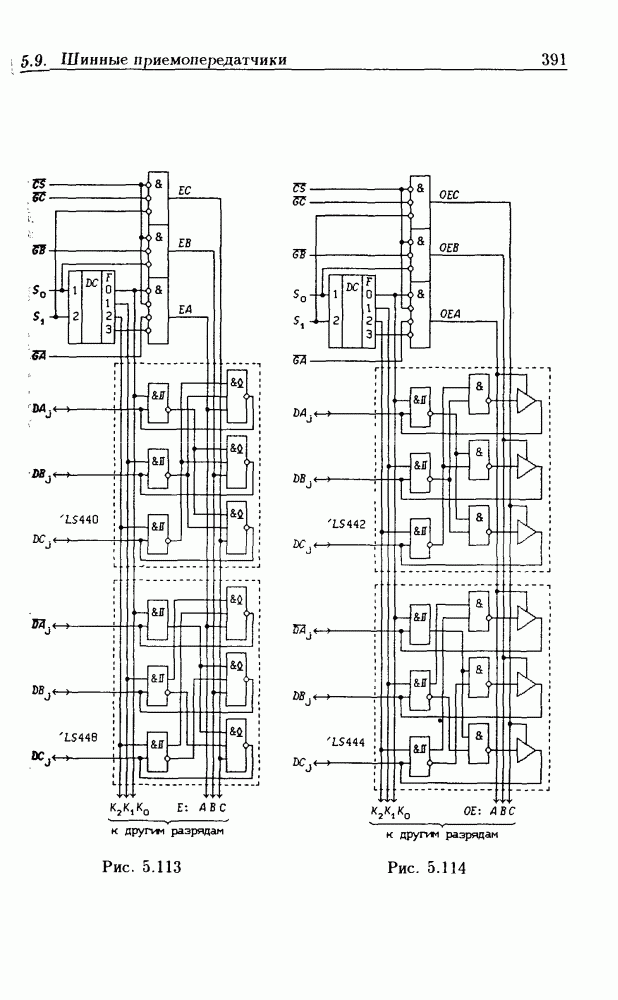
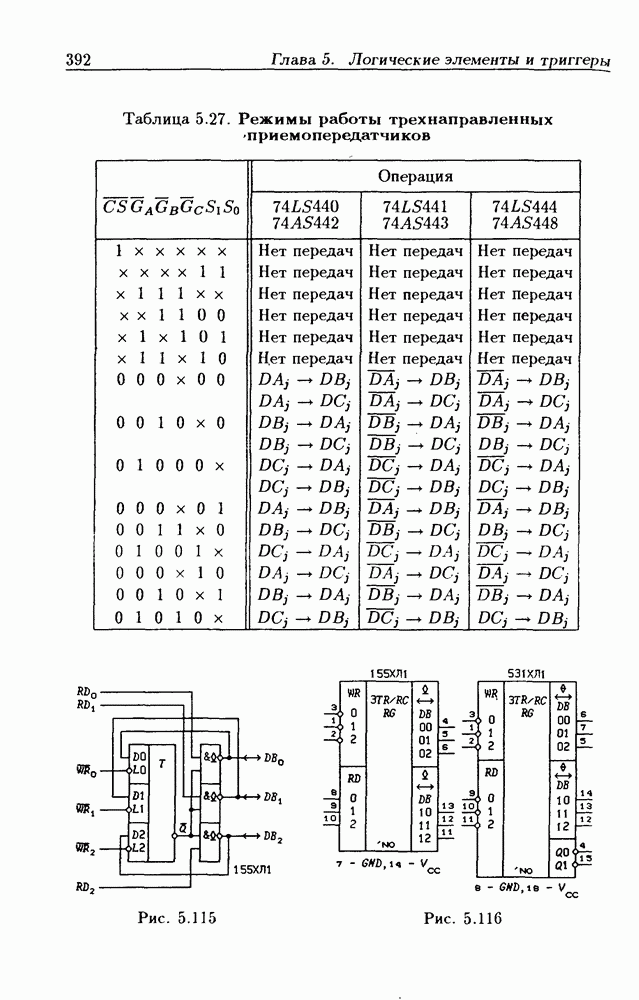
- 5.9. Шинные приемопередатчики
- Шинные приемопередатчики с Z-состоянием выхода.
- Шинные приемопередатчики с открытым коллекторным выходом.
- Шинные приемопередатчики с регистрами памяти.
- Шинные приемопередатчики со сдвигающим регистром.
- Шинные трехнаправленные приемопередатчики.
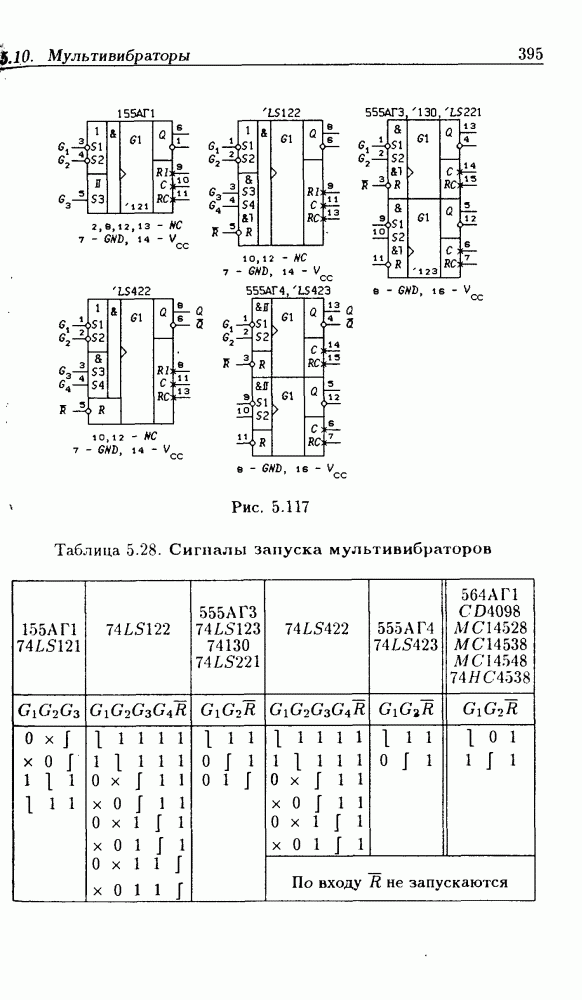
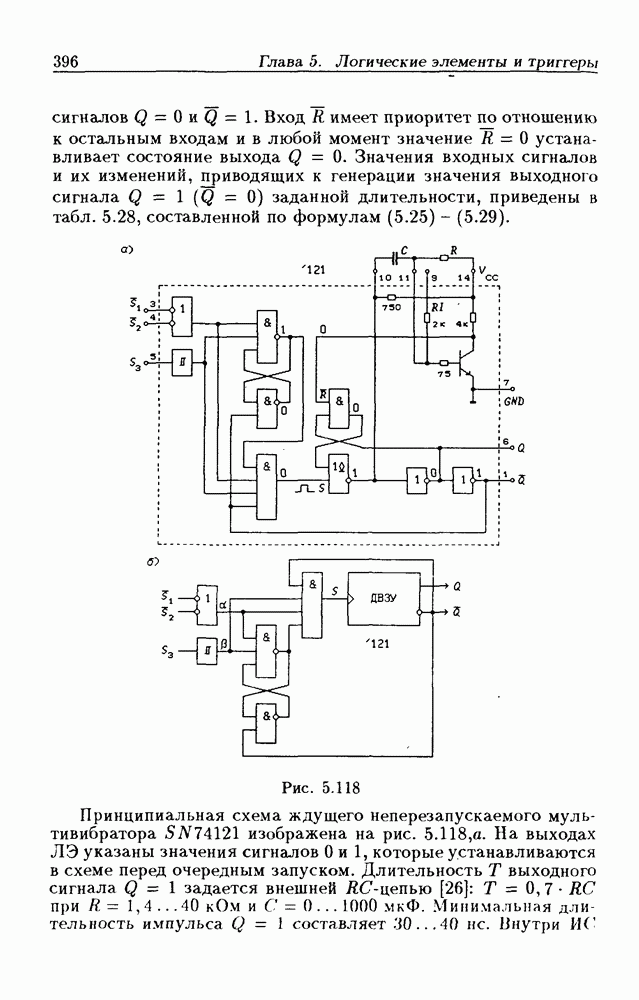
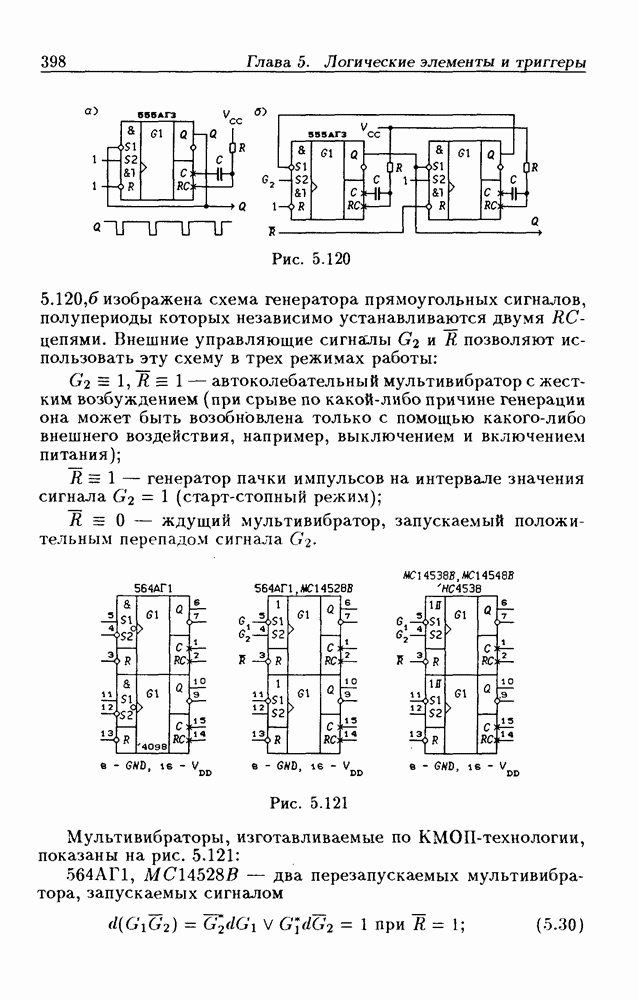
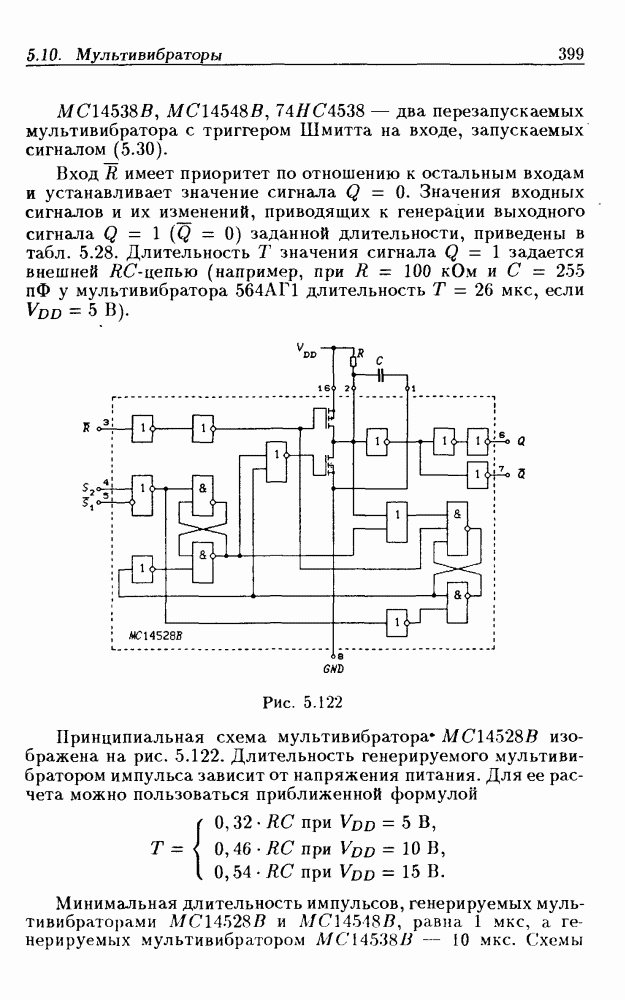
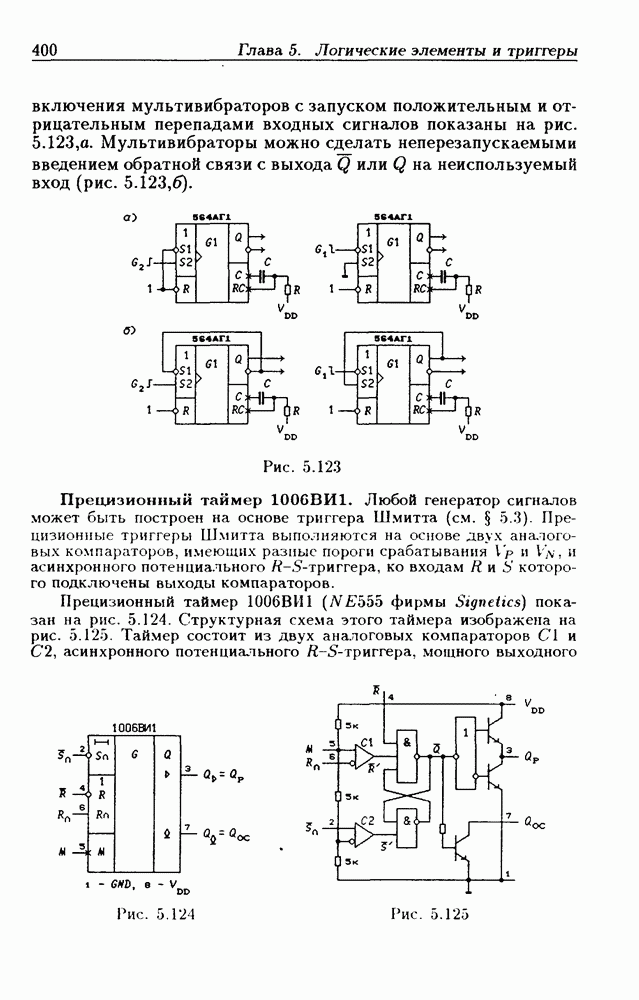
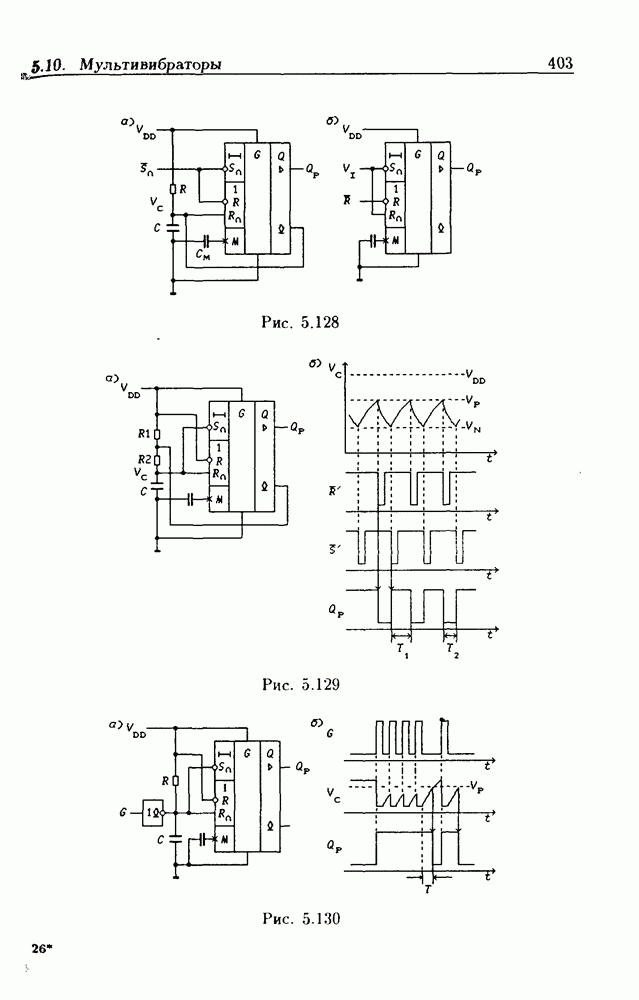
- 5.10. Мультивибраторы
- 5.11. Генераторы
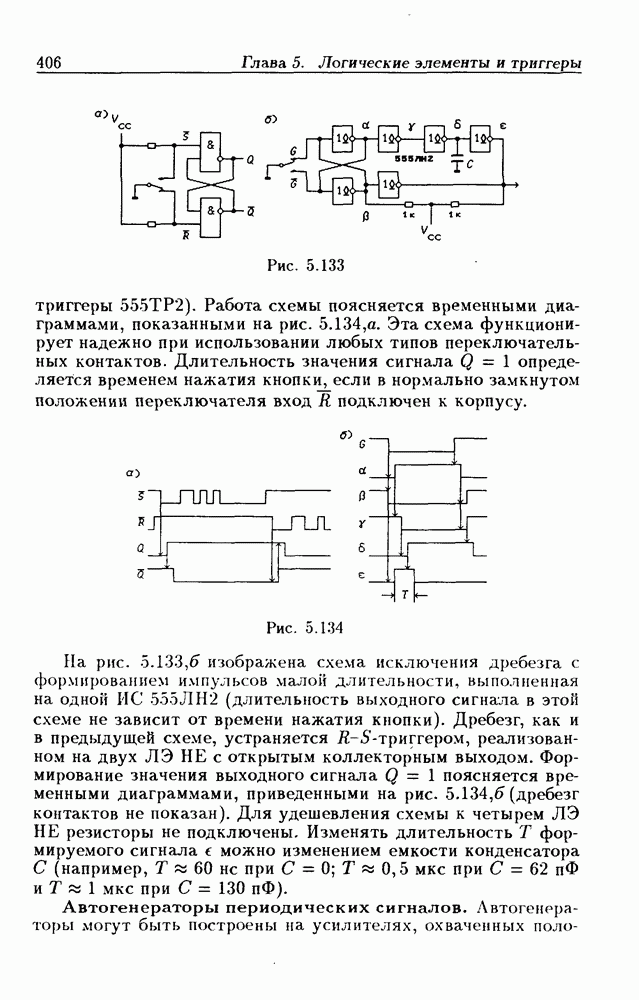
- Схемы устранения «дребезга» механических контактов.
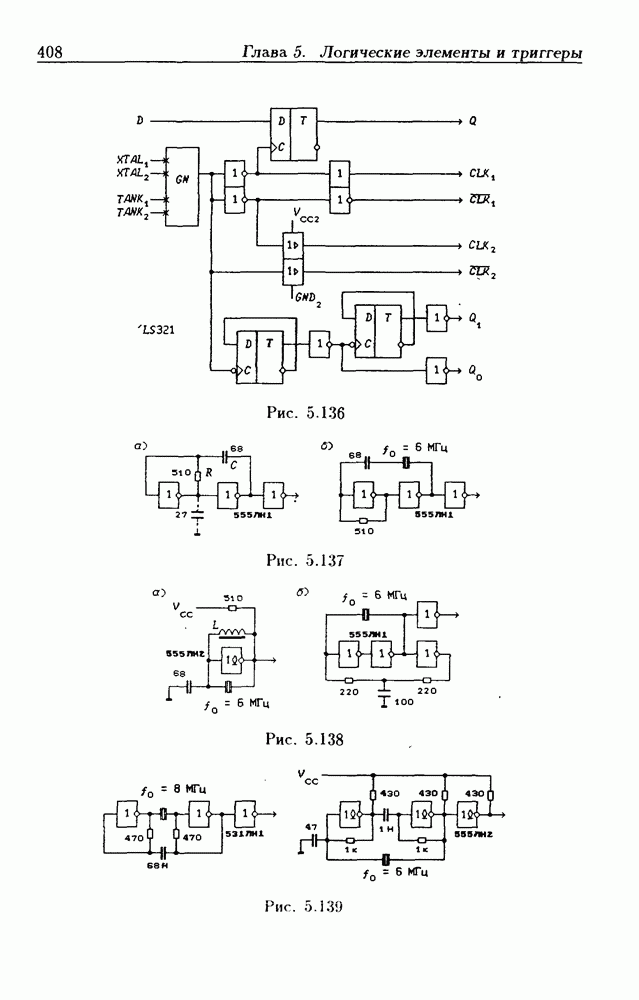
- Автогенераторы периодических сигналов.
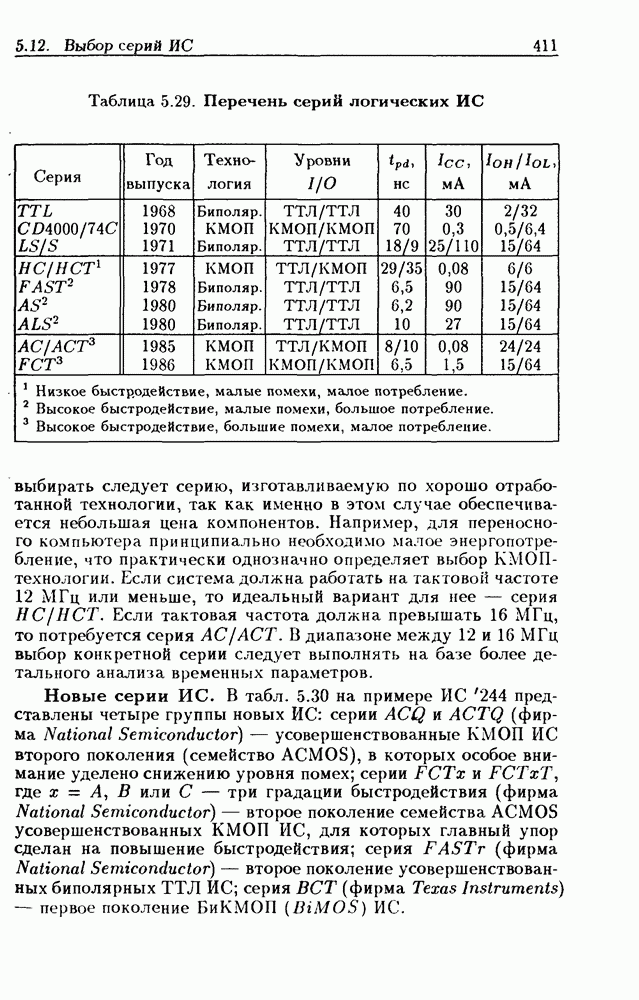
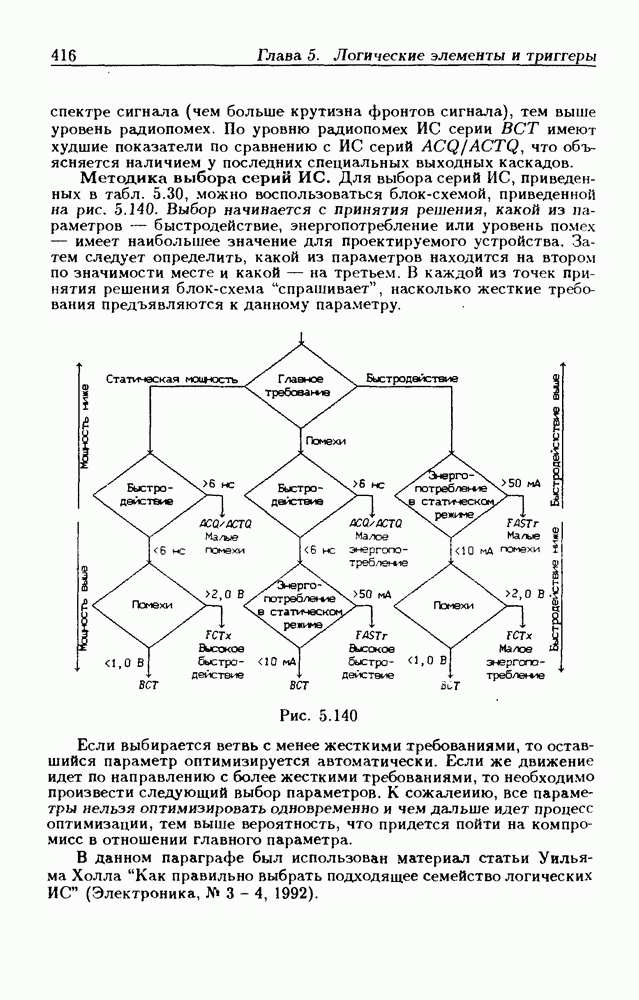
- 5.12. Рекомендации по выбору серий ИС
- Глава 6. Коммутаторы и арифметические устройства
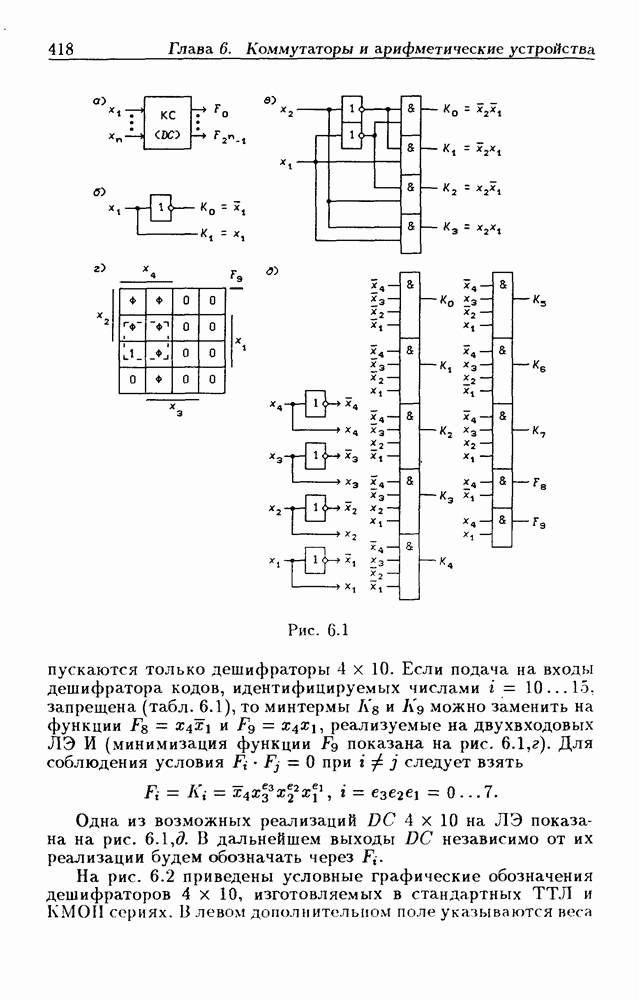
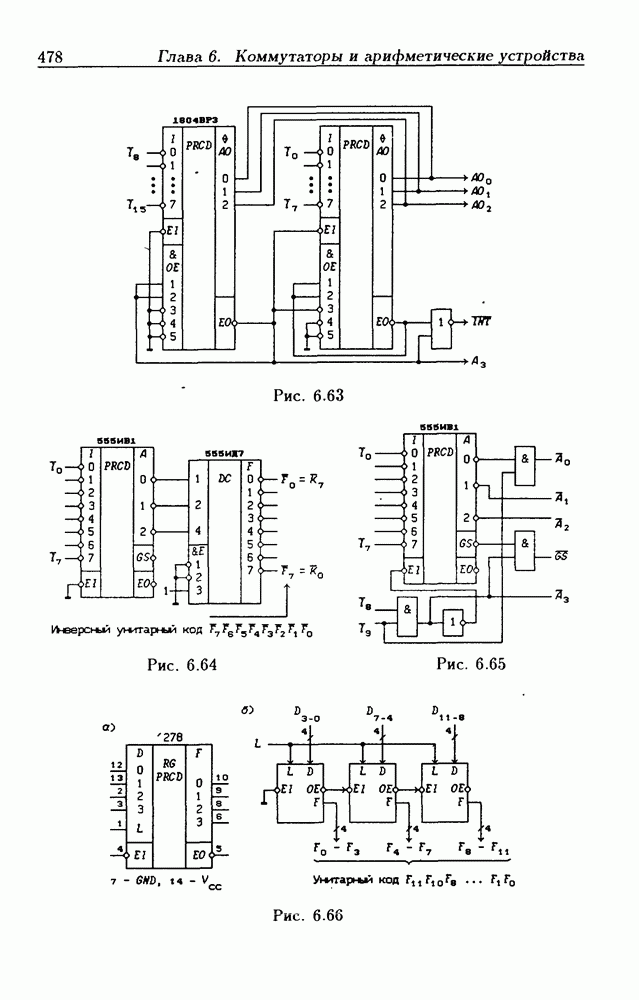
- 6.1. Дешифраторы
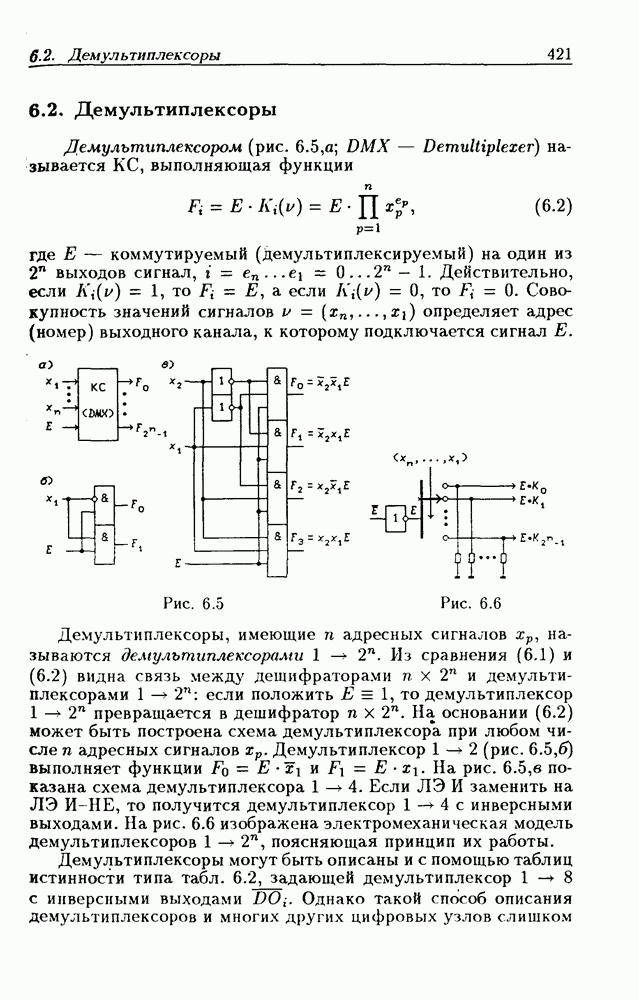
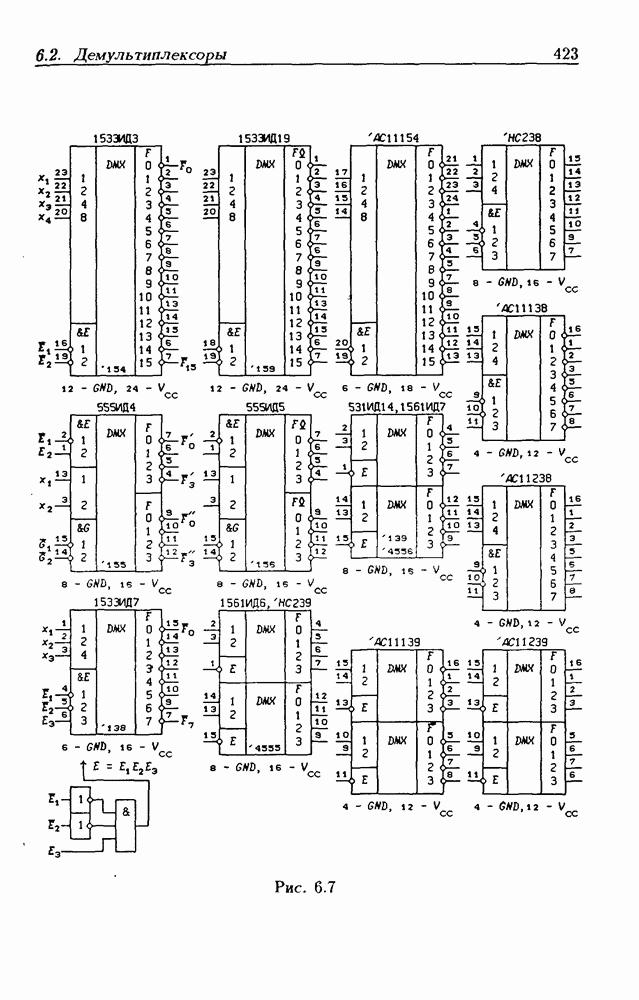
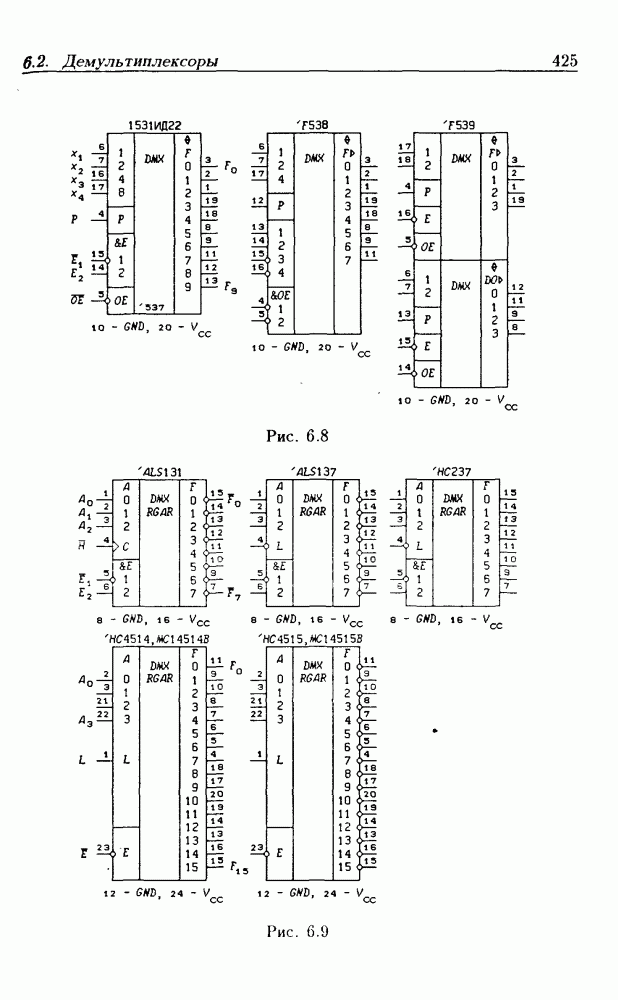
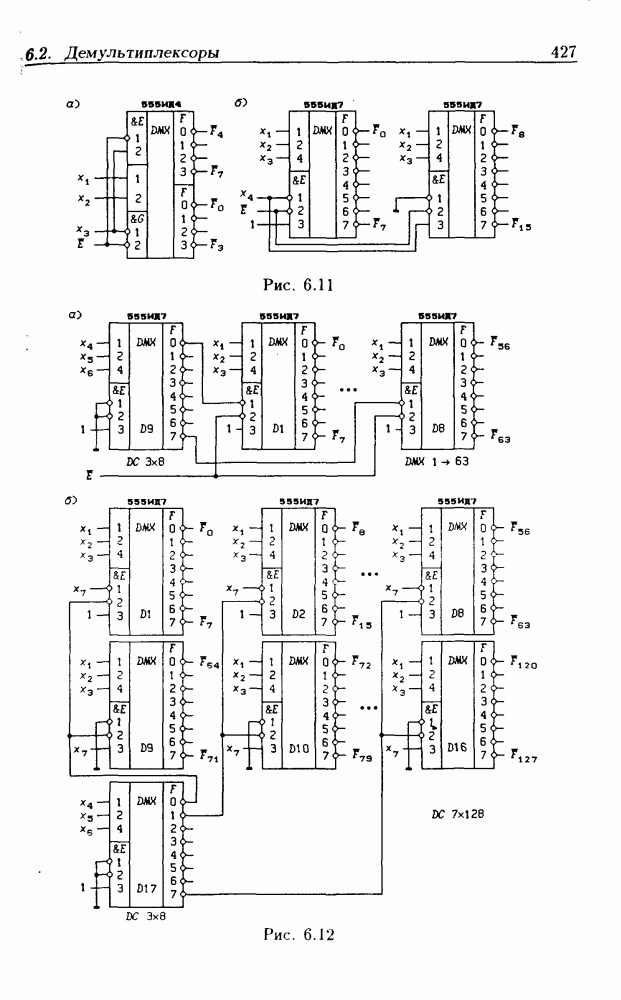
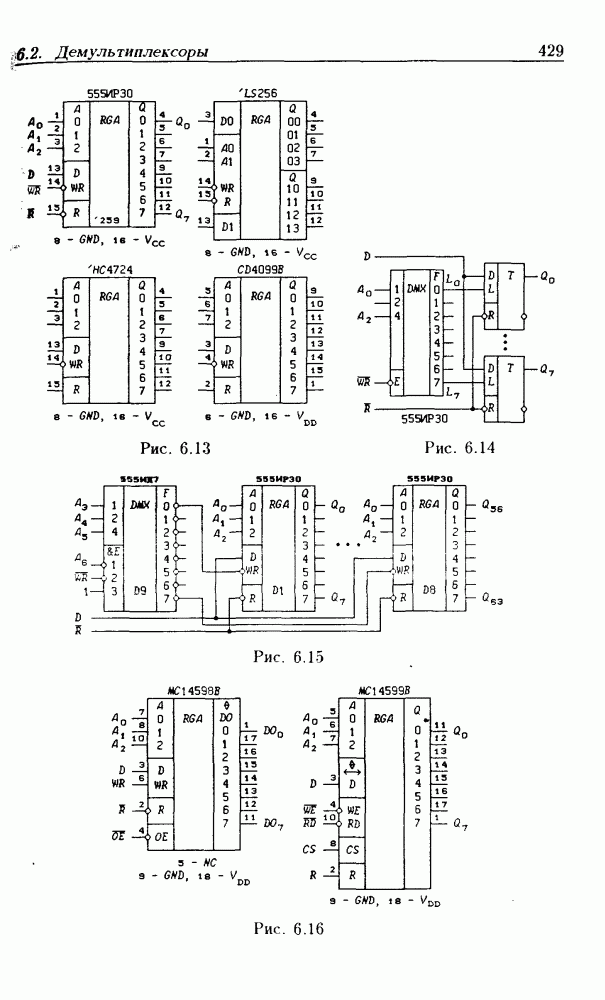
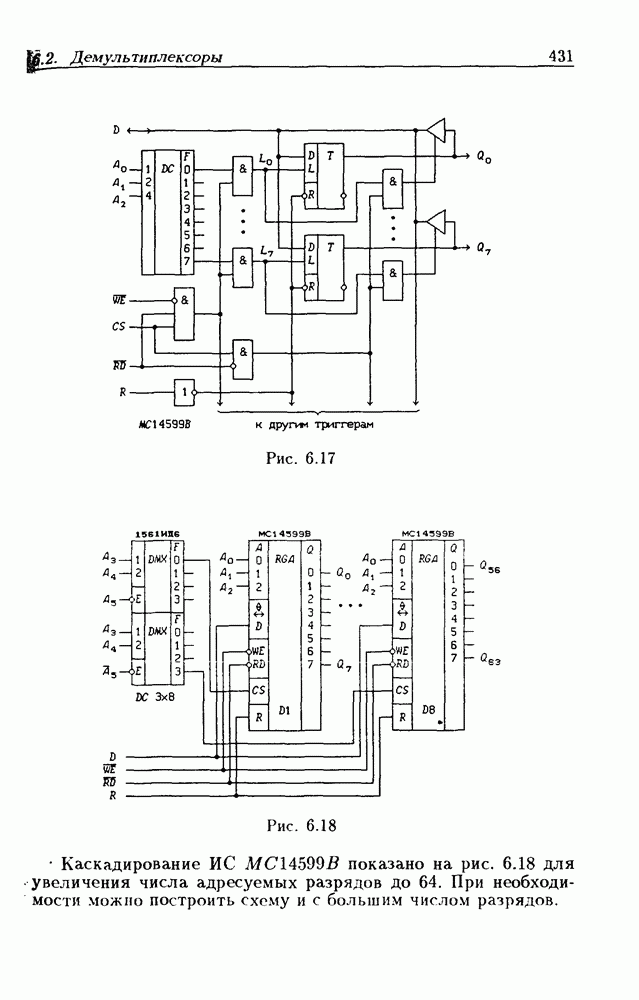
- 6.2. Демультиплексоры
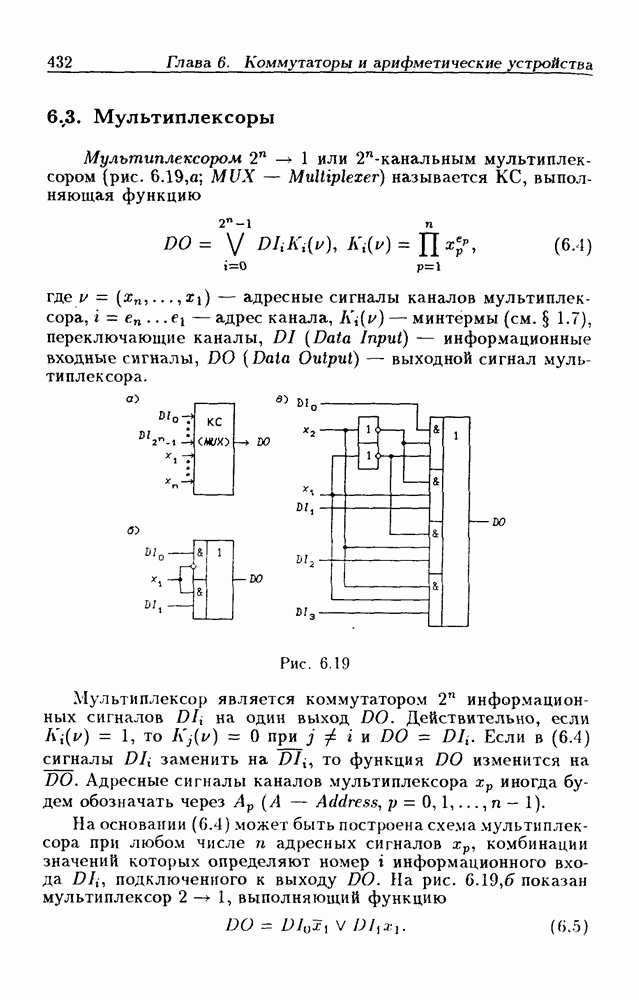
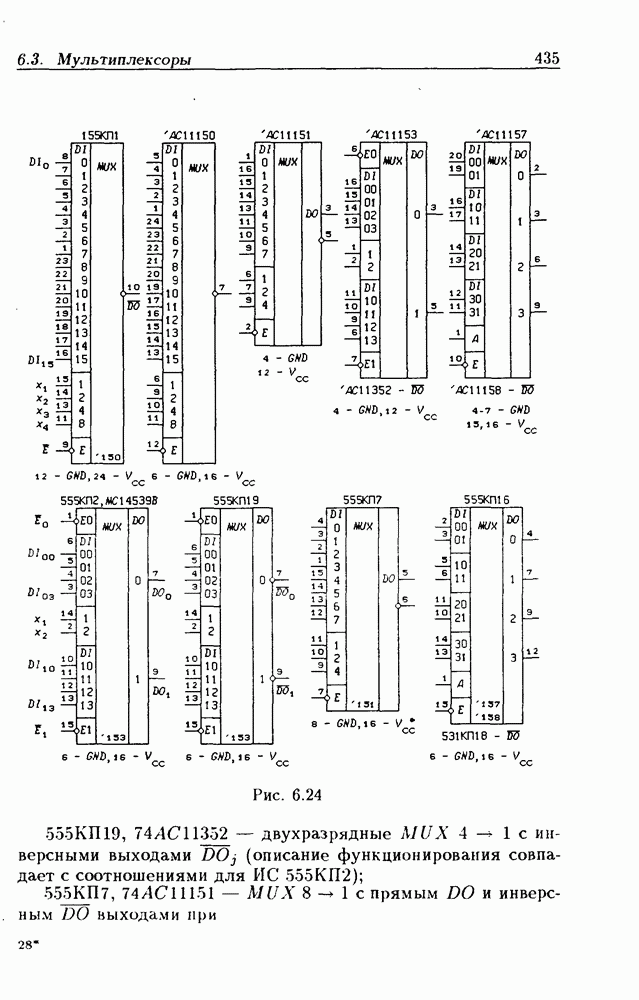
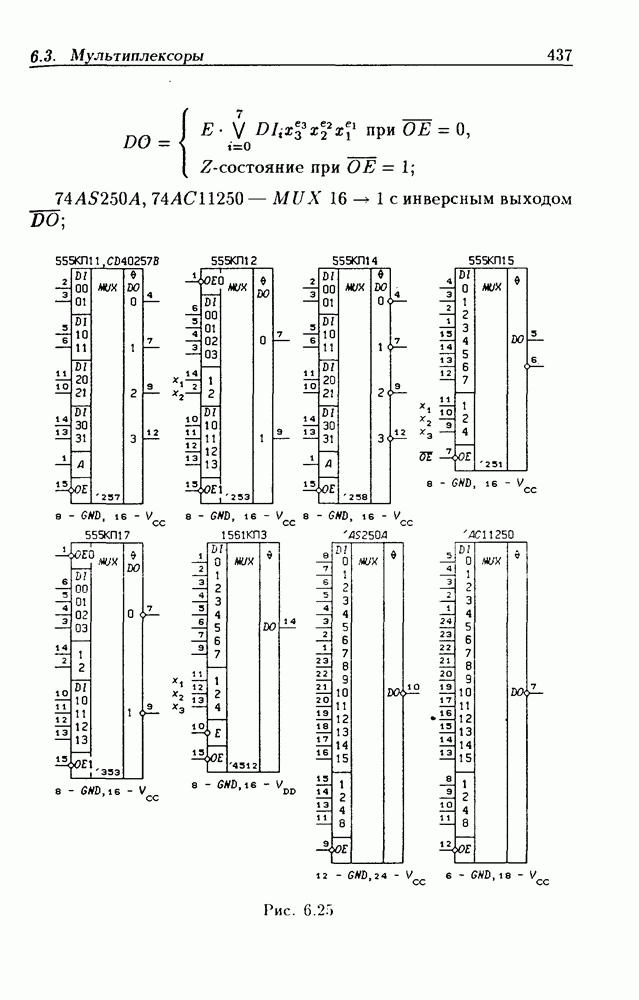
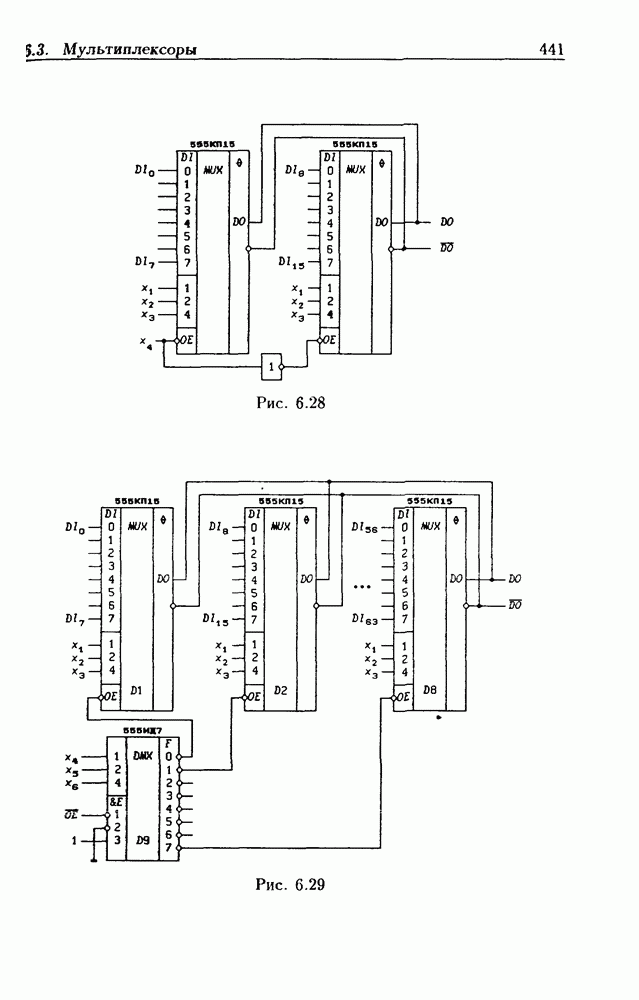
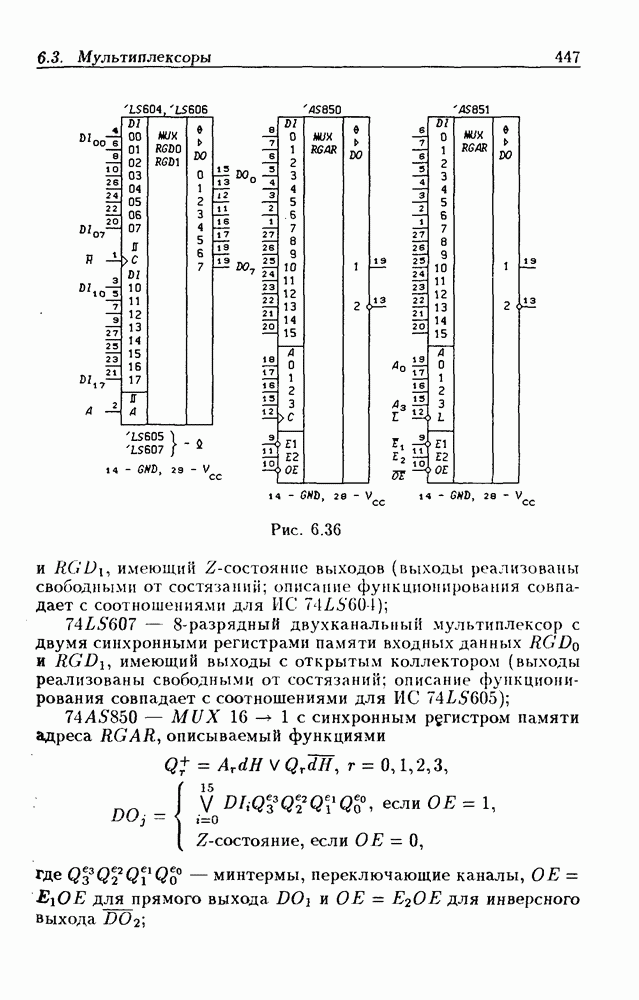
- 6.3. Мультиплексоры
- Мультиплексоры без стробирования.
- Мультиплексоры со стробированием.
- Мультиплексоры с Z-состоянием выхода.
- Каскадирование мультиплексоров.
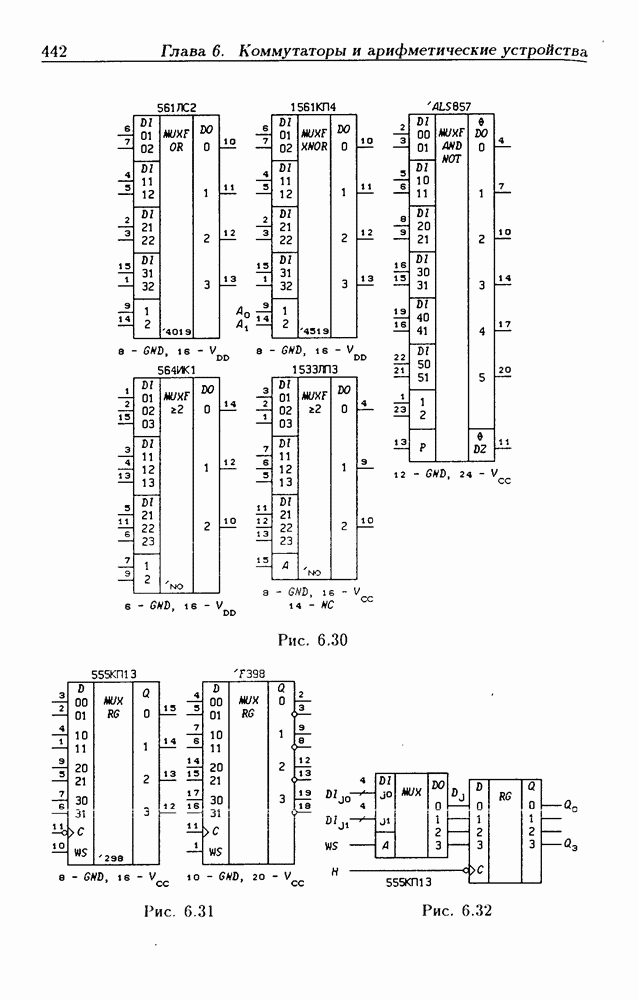
- Функциональные мультиплексоры.
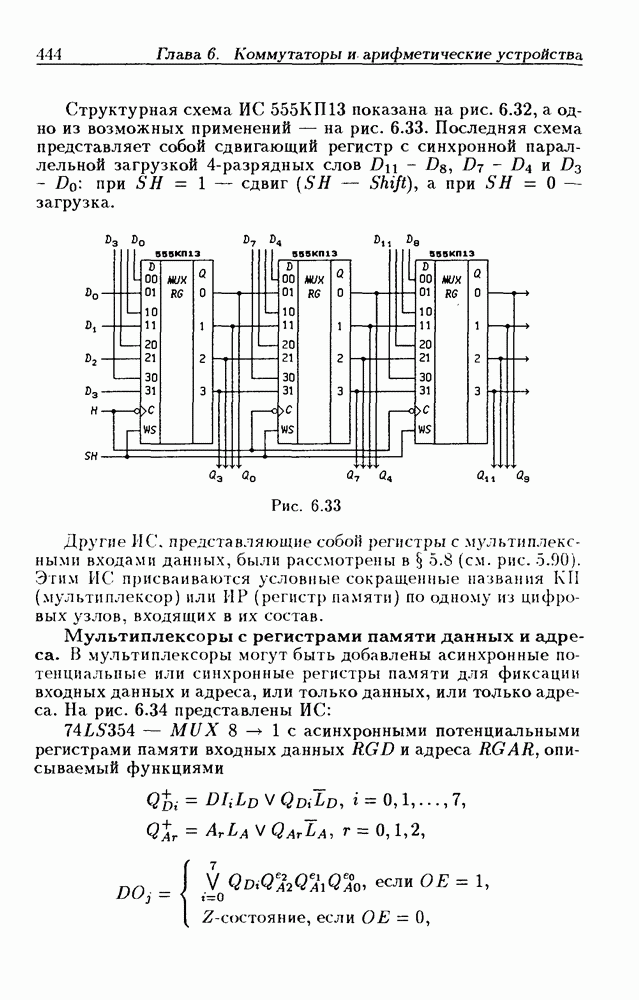
- Регистры памяти с мультиплексными входами данных.
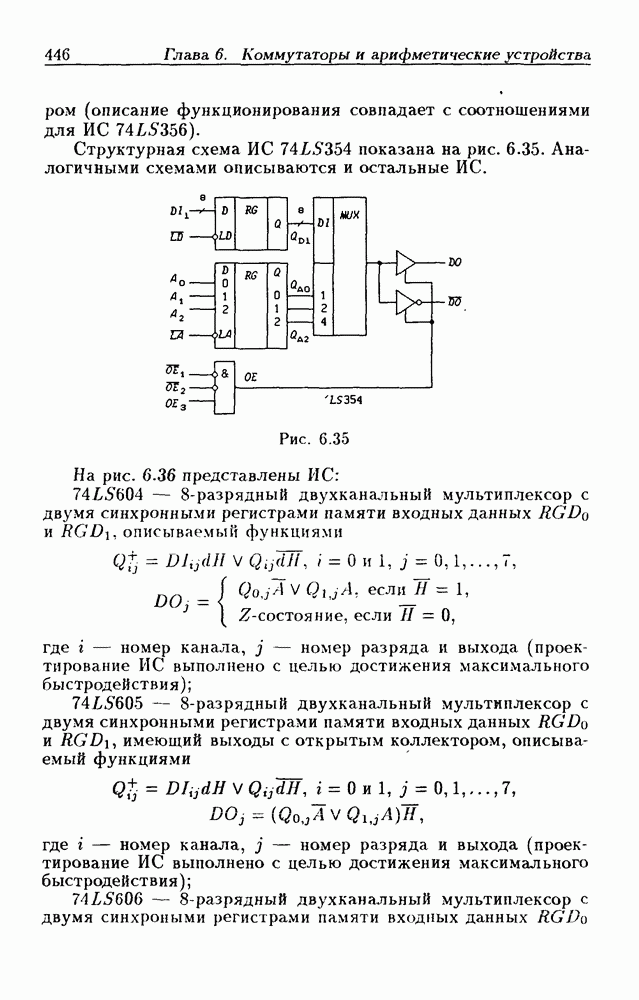
- Мультиплексоры с регистрами памяти данных и адреса.
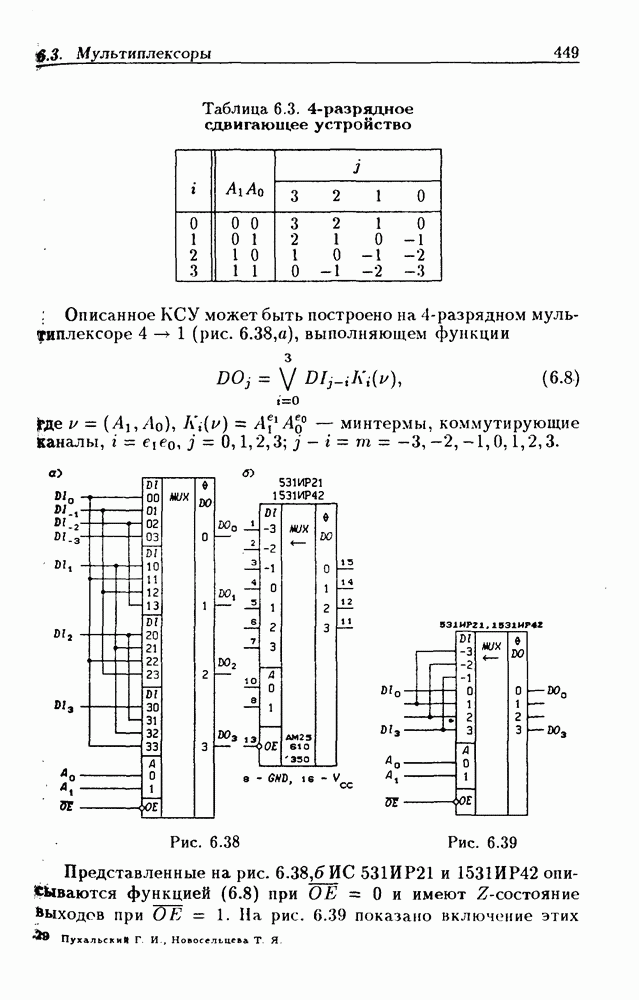
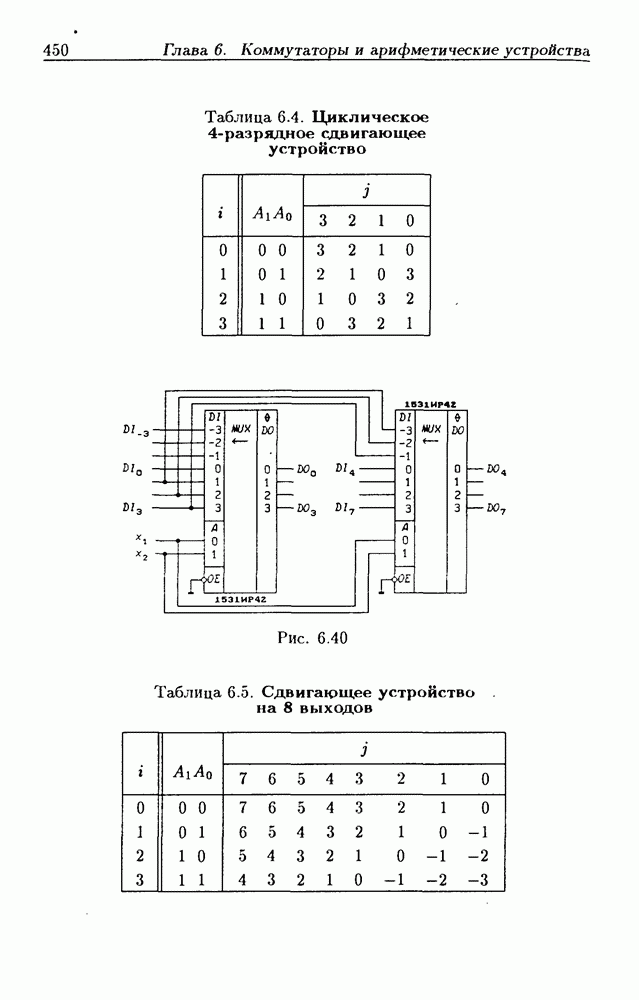
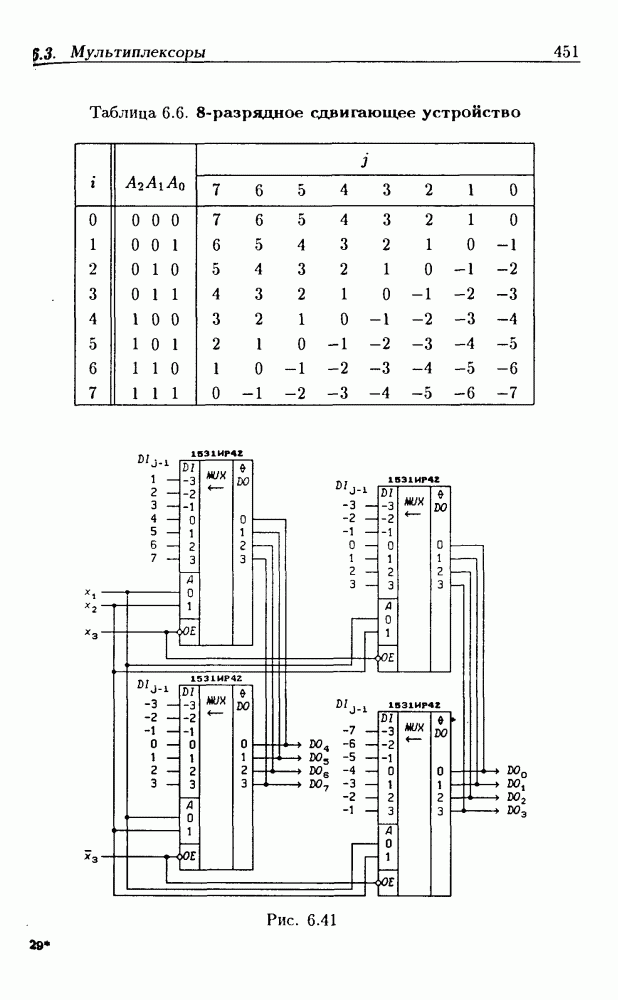
- Сдвигающие мультиплексоры.
- 6.4. Синтез комбинационных схем и цифровых автоматов на мультиплексорах
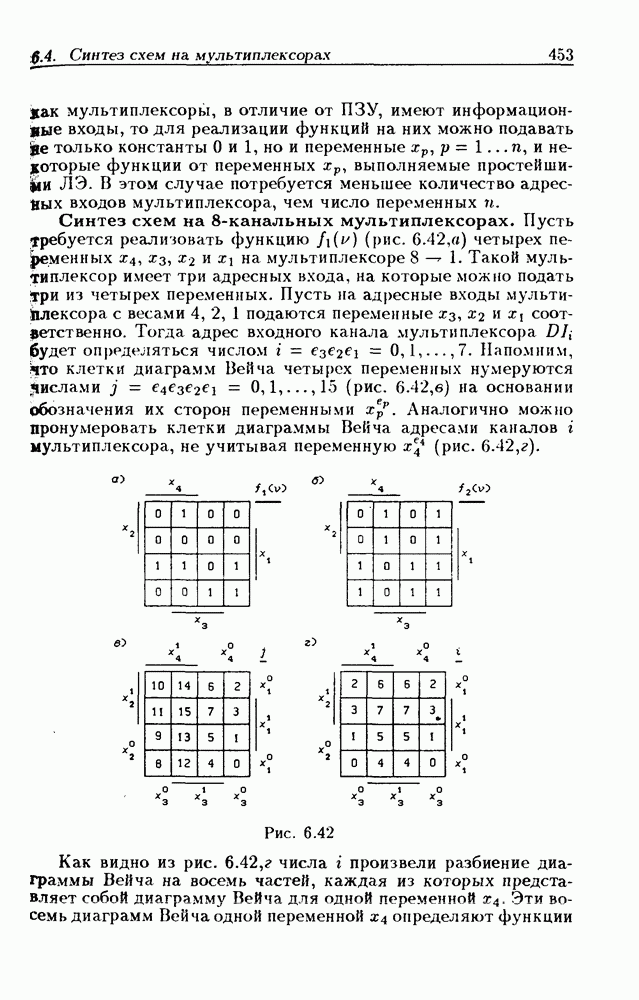
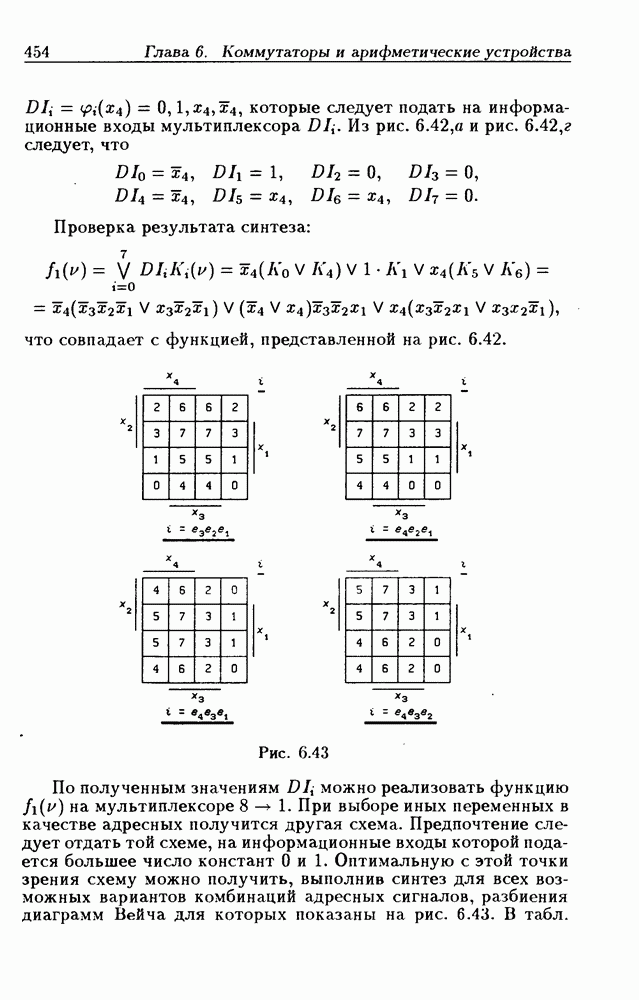
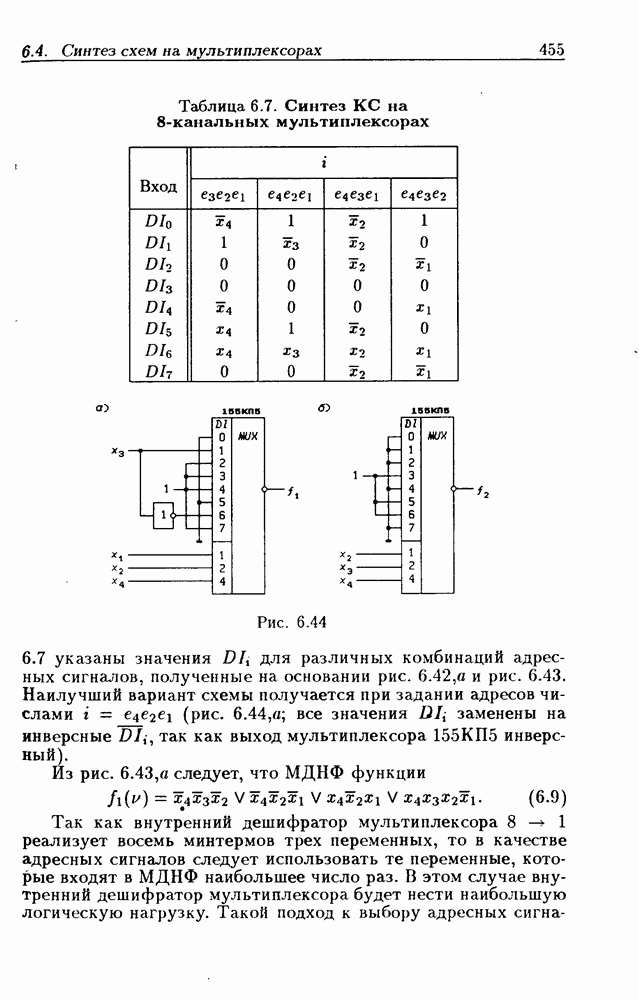
- Синтез схем на 8-канальных мультиплексорах.
- Синтез на двухразрядных 4-канальных мультиплексорах.
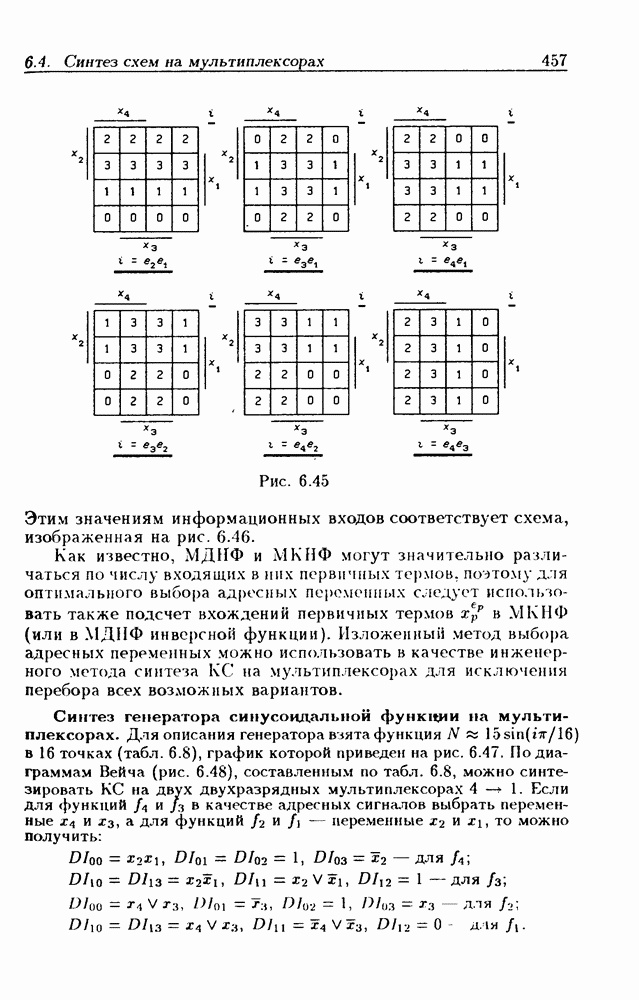
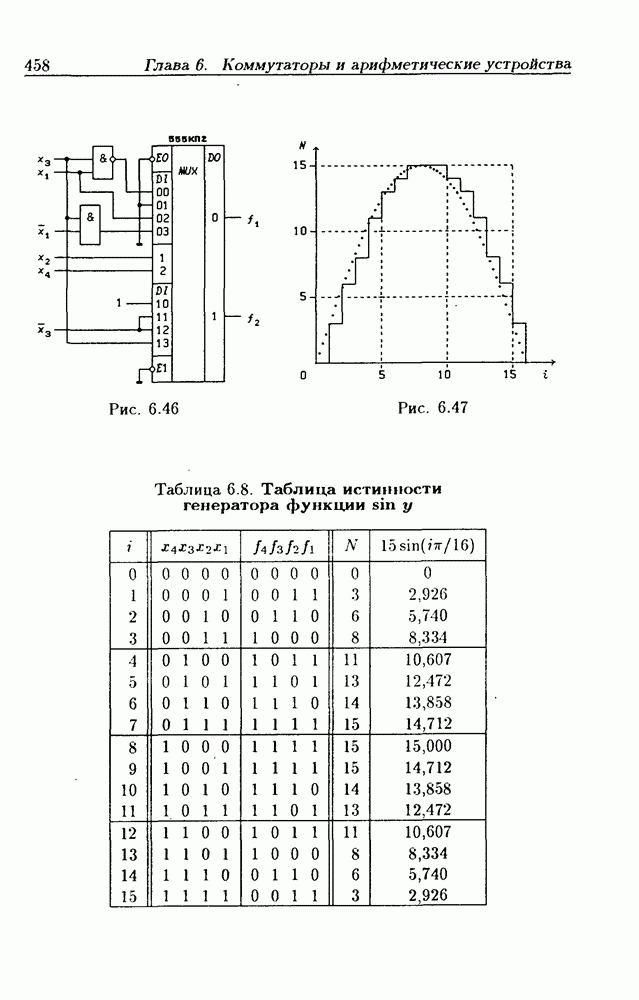
- Синтез генератора синусоидальной функции на мультиплексорах.
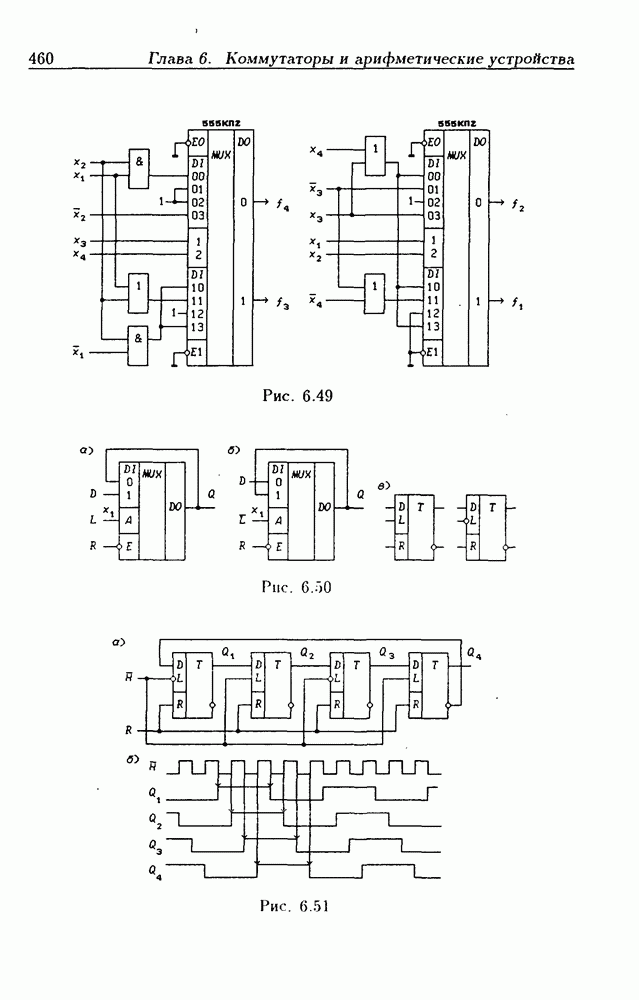
- Синтез триггеров на мультиплексорах.
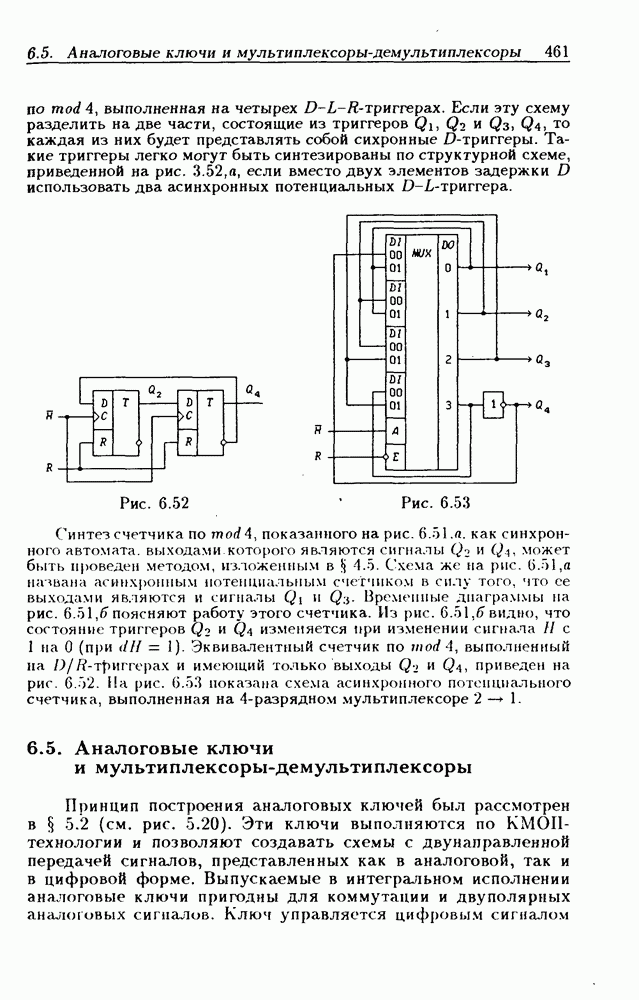
- Синтез счетчиков на мультиплексорах.
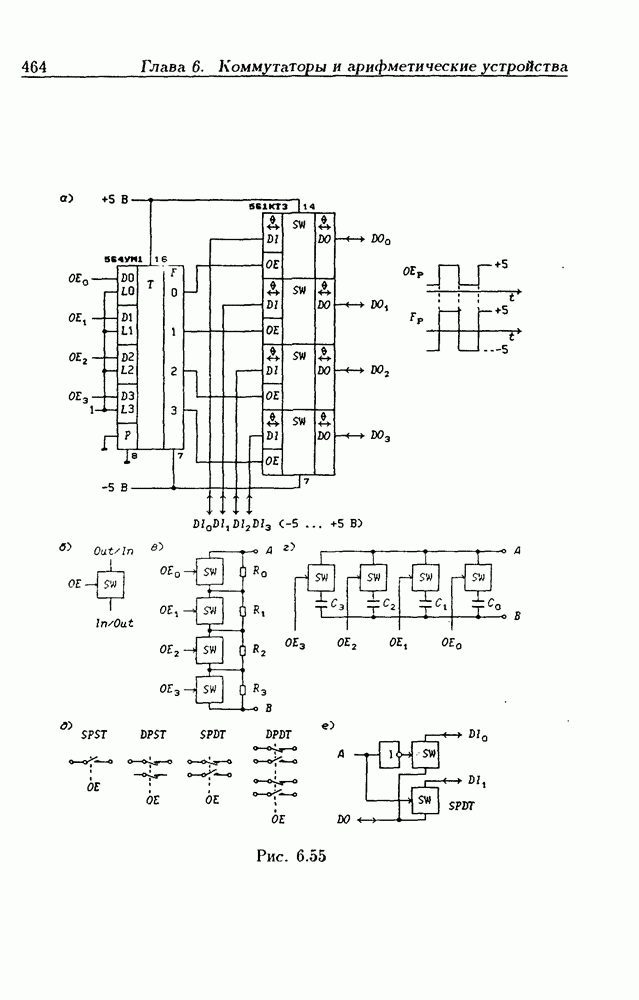
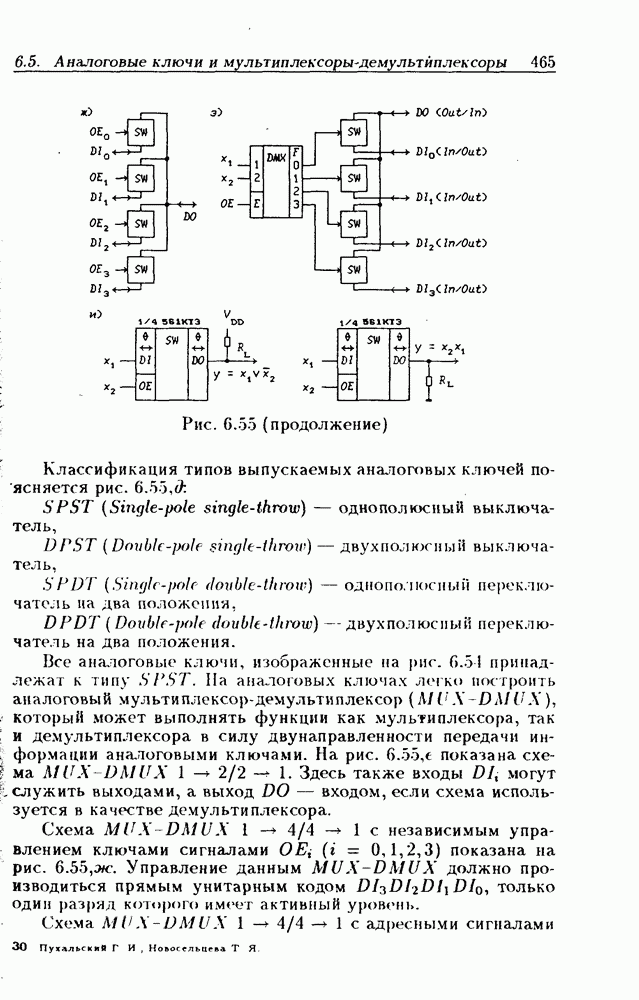
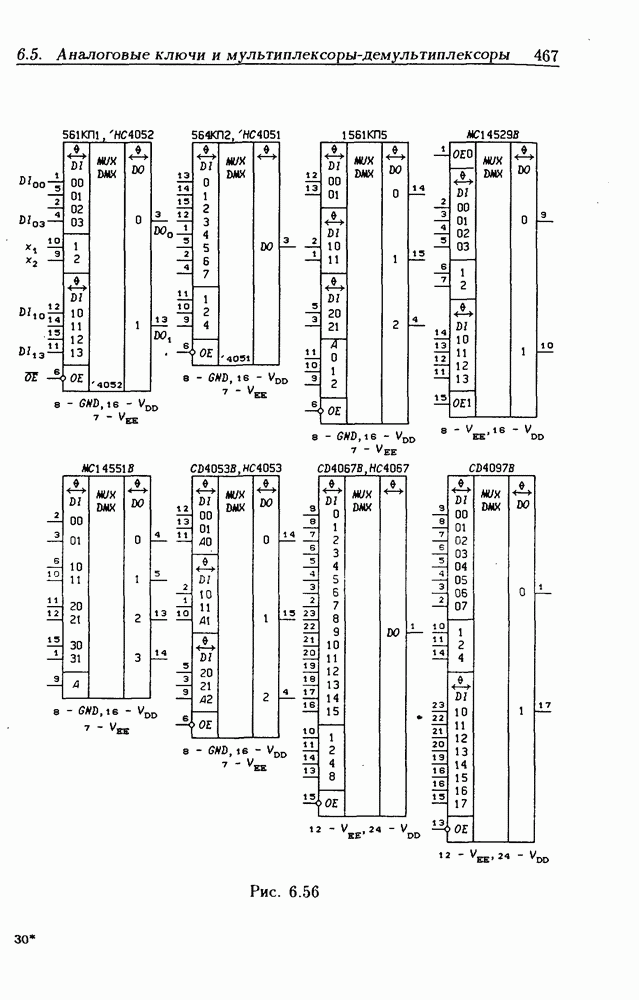
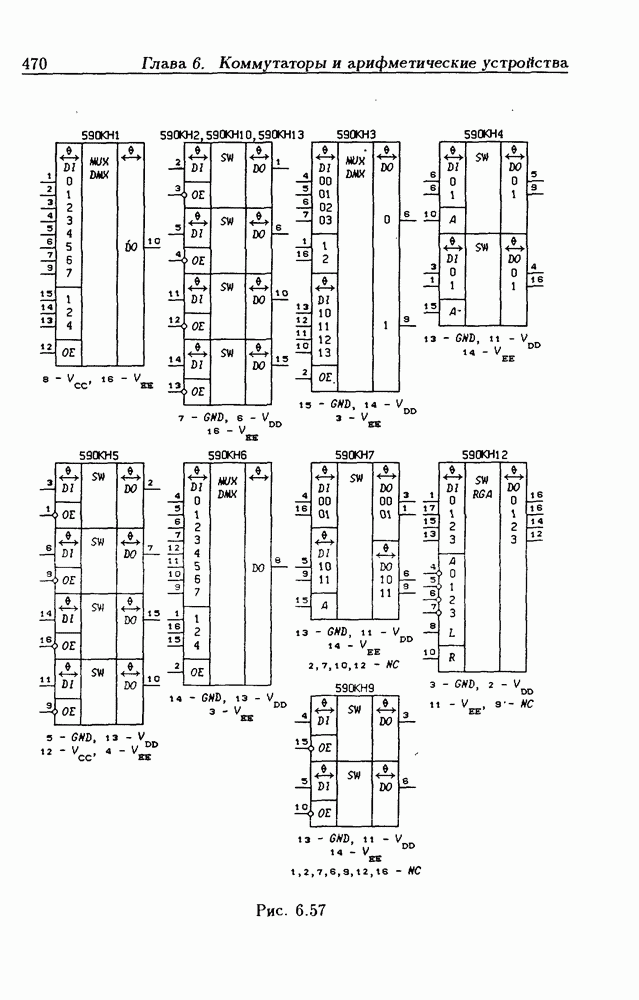
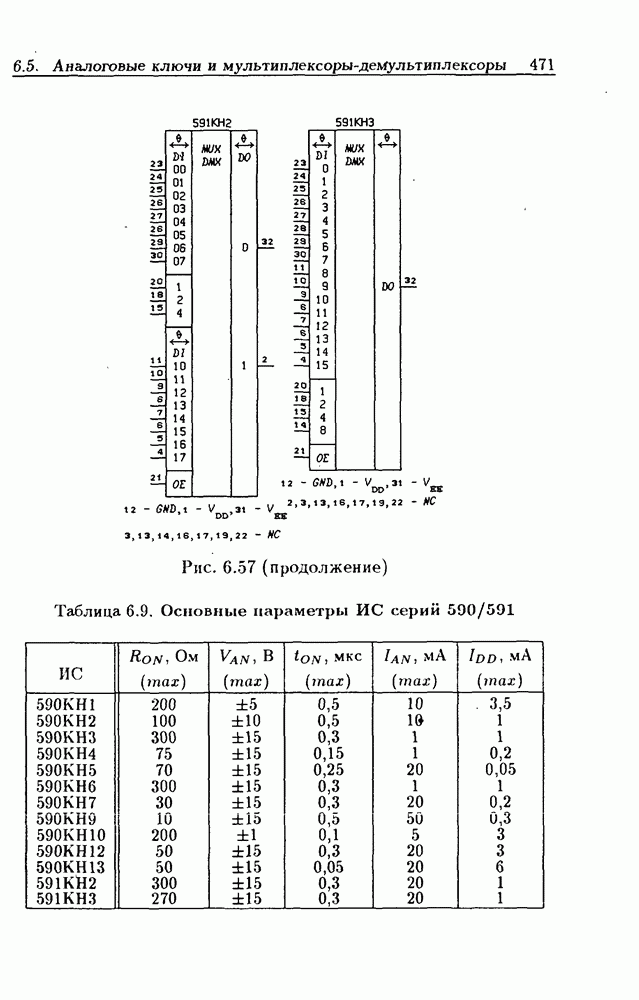
- 6.5. Аналоговые ключи и мультиплексоры-демультиплексоры
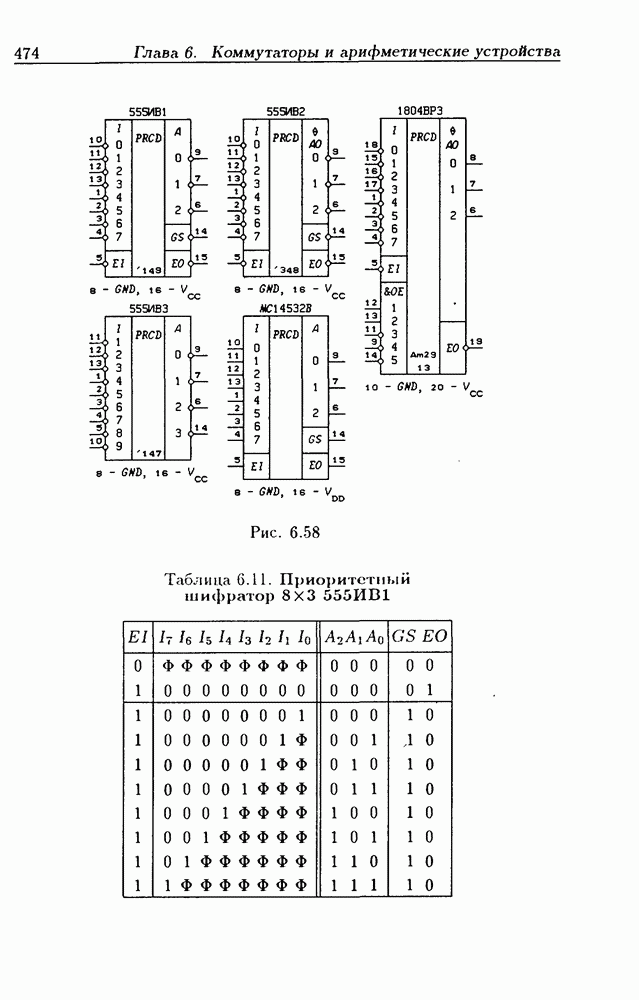
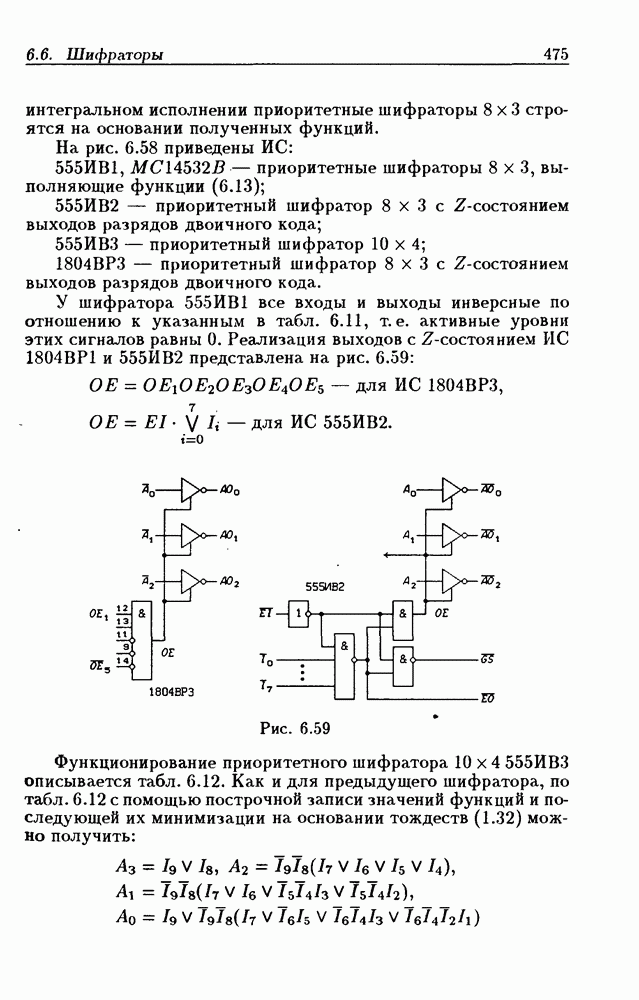
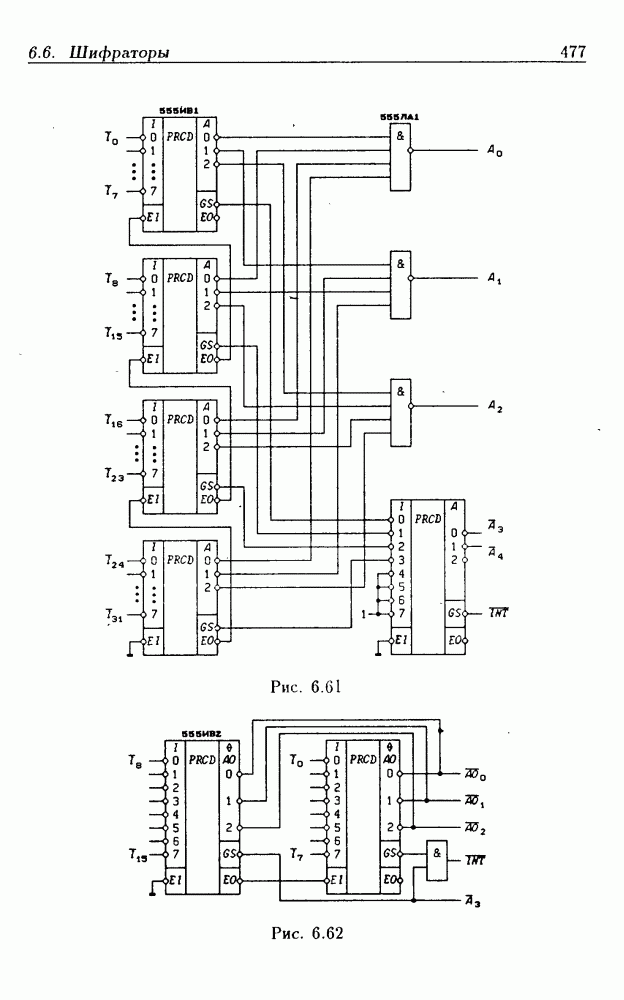
- 6.6. Шифраторы
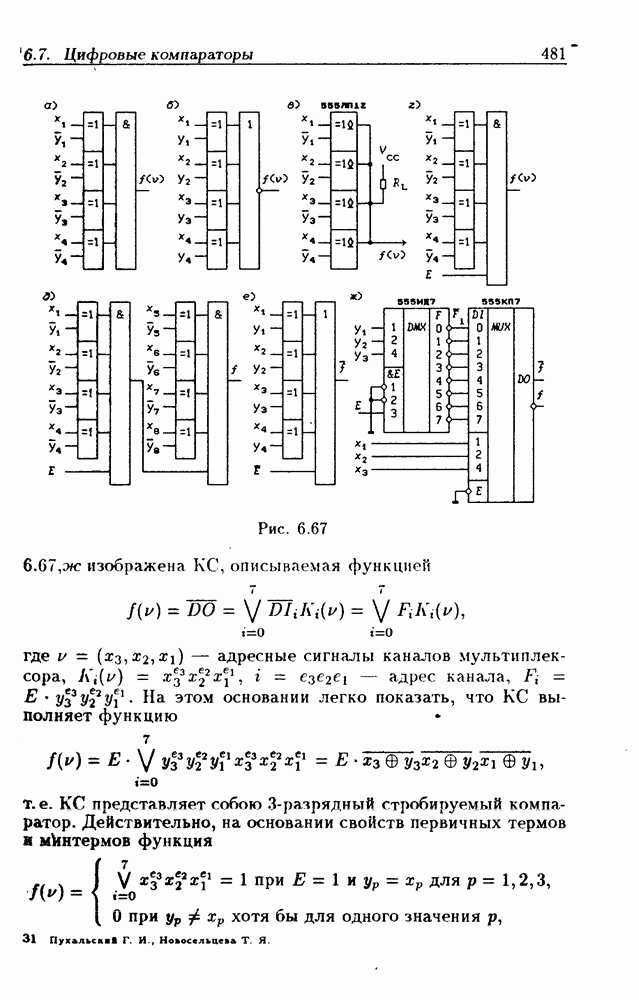
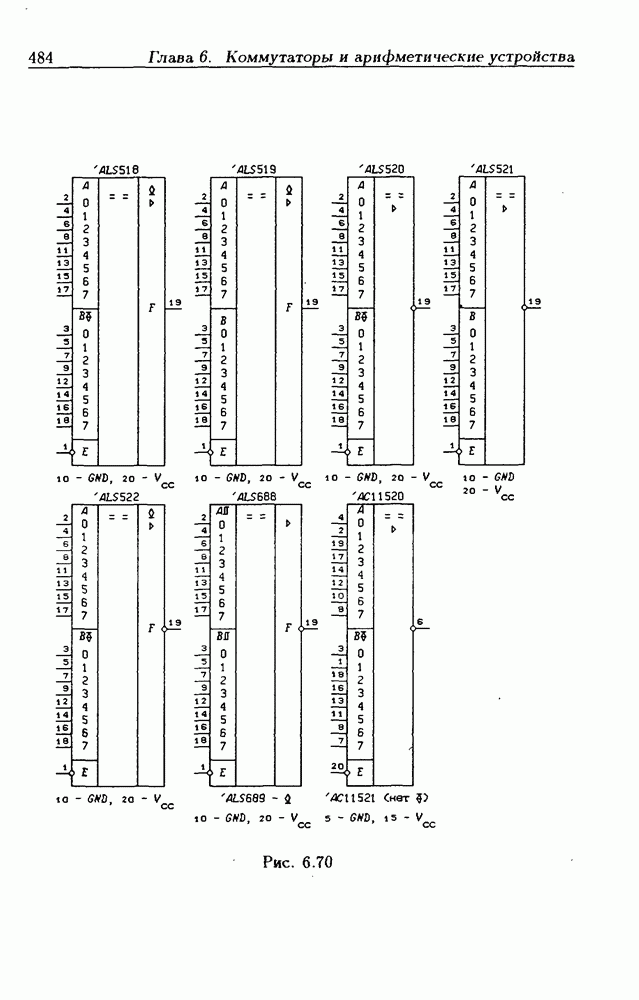
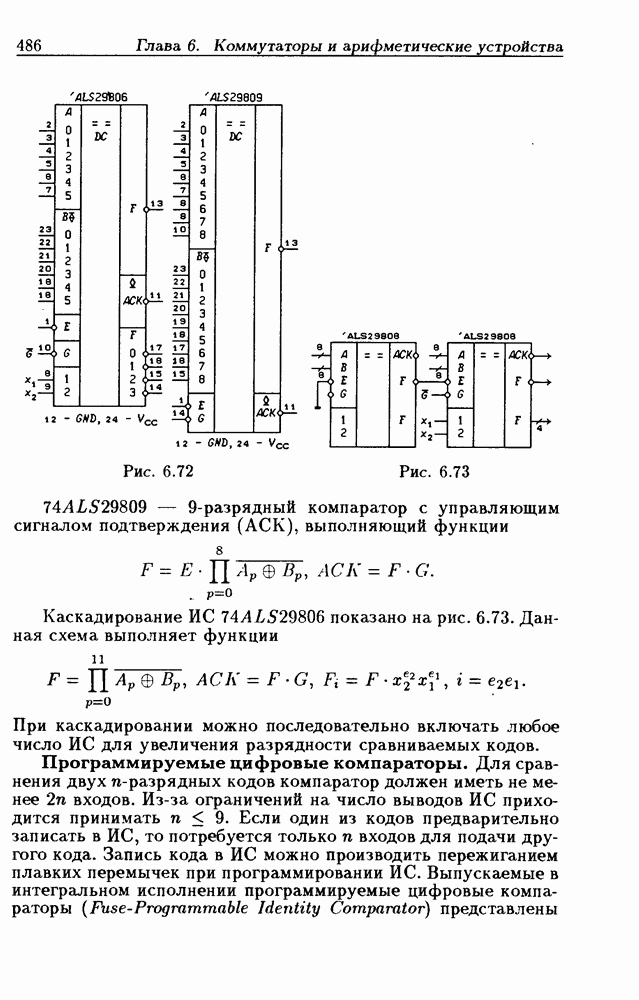
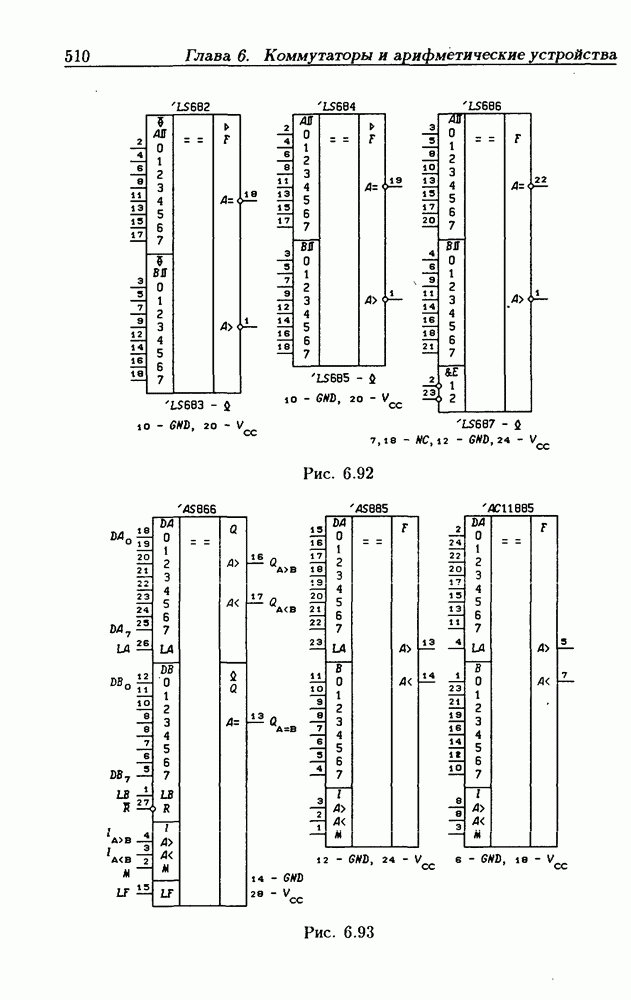
- 6.7. Цифровые компараторы
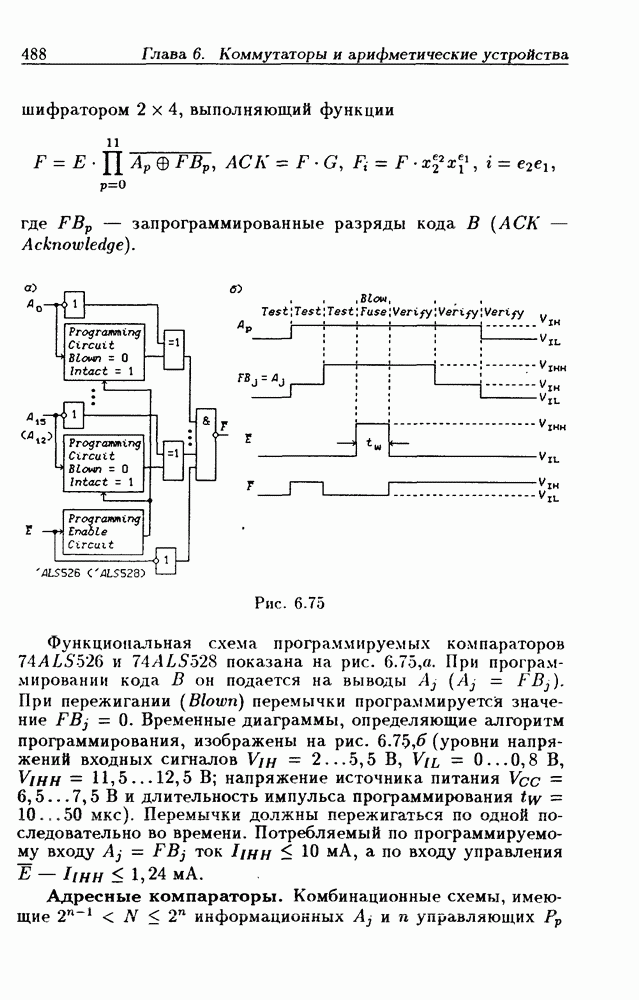
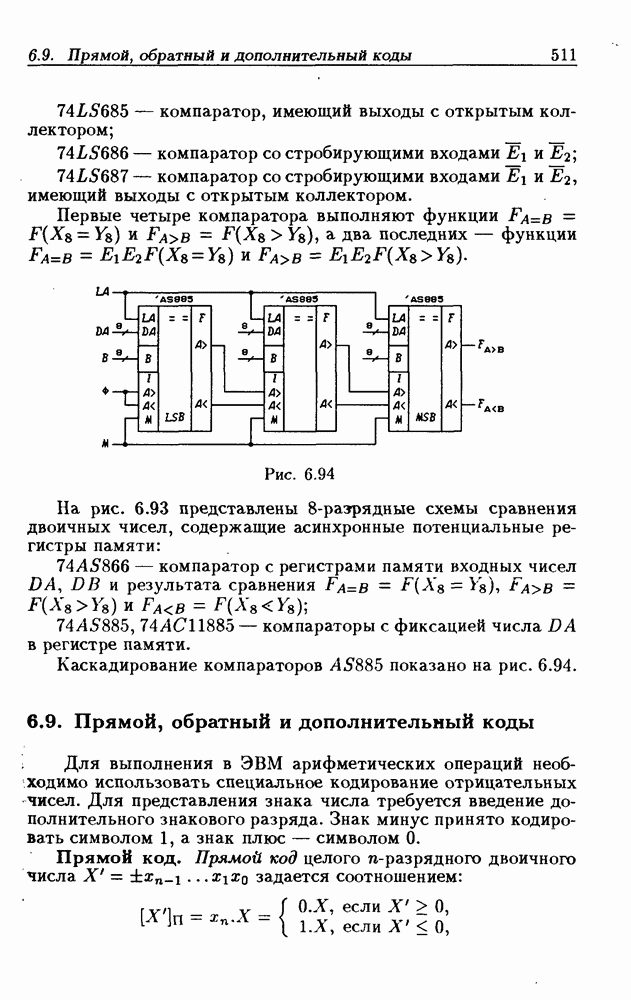
- Программируемые цифровые компараторы.
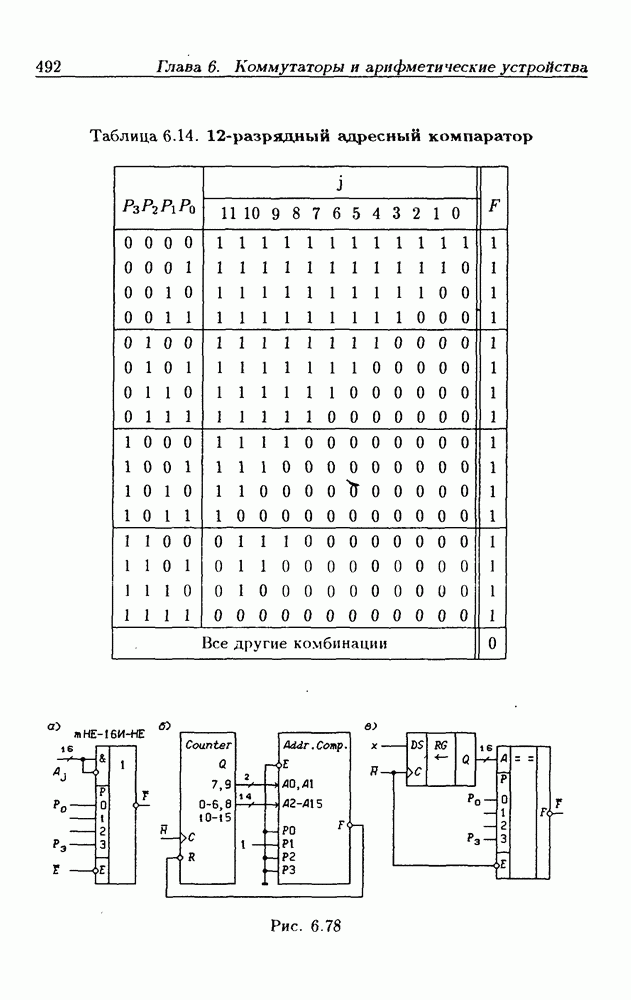
- Адресные компараторы.
- Применения адресных компараторов.
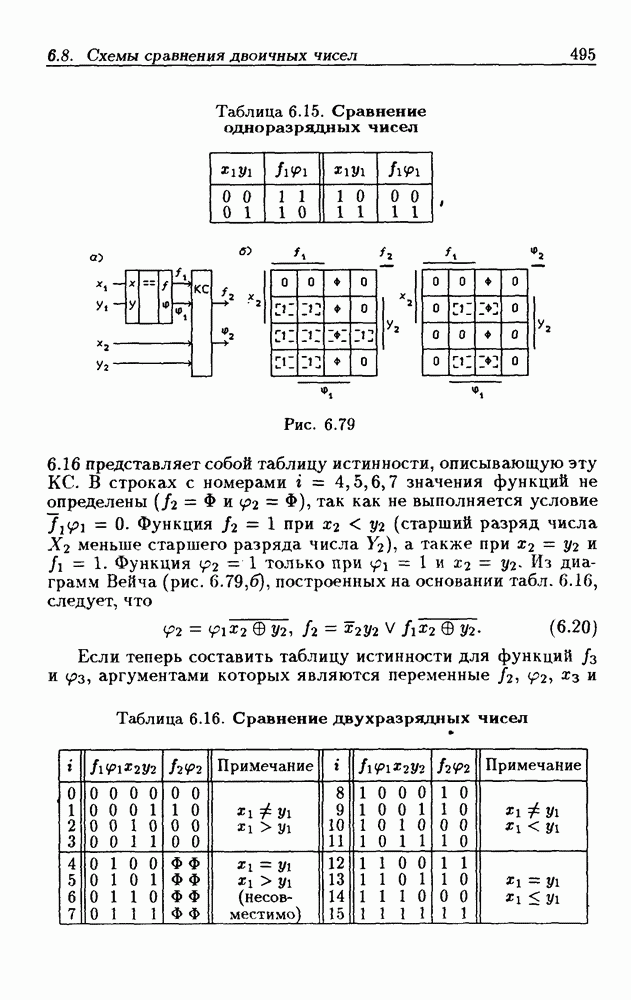
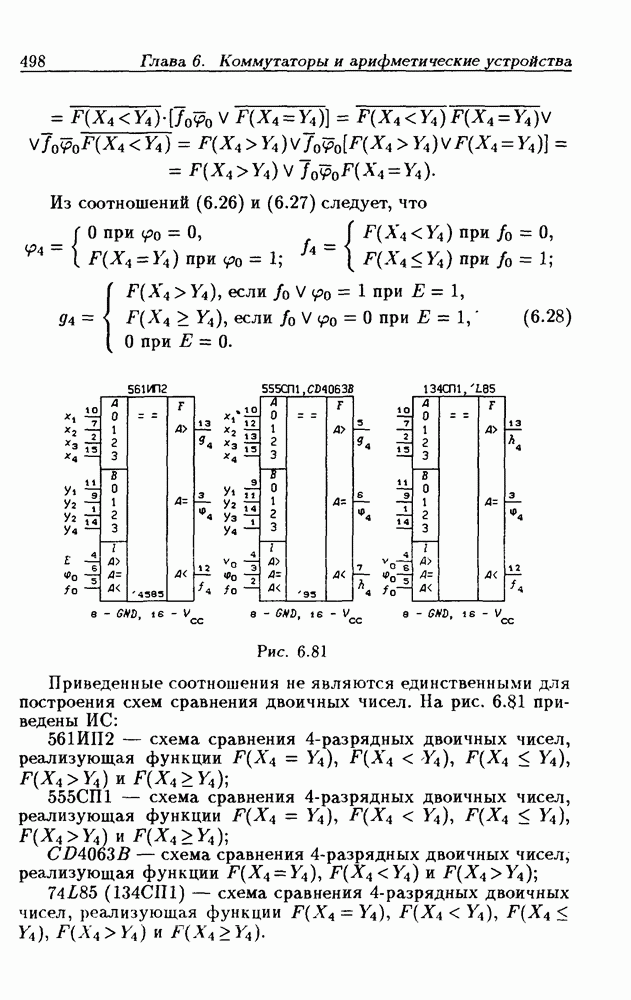
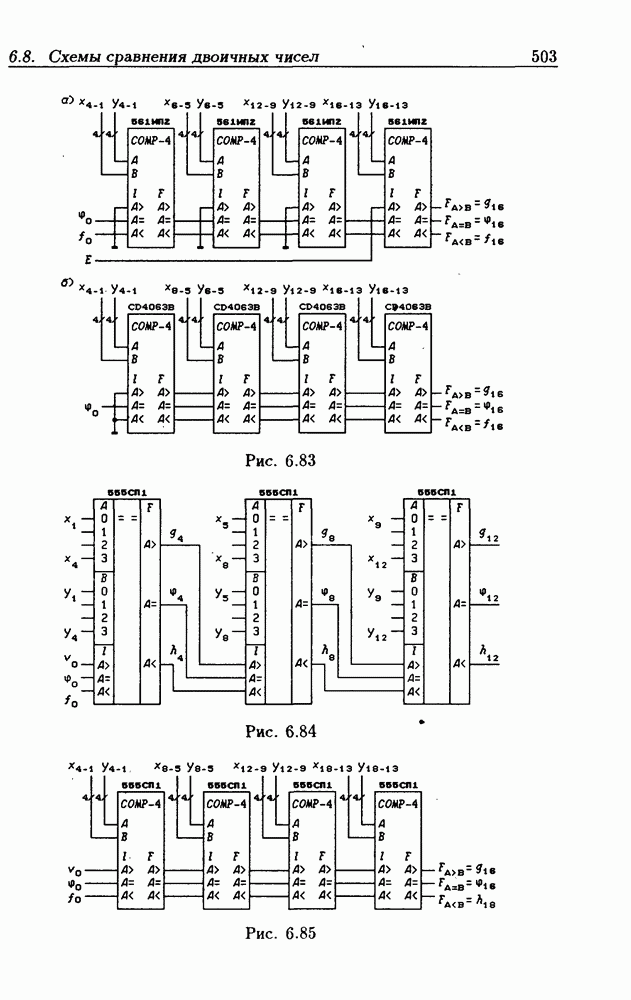
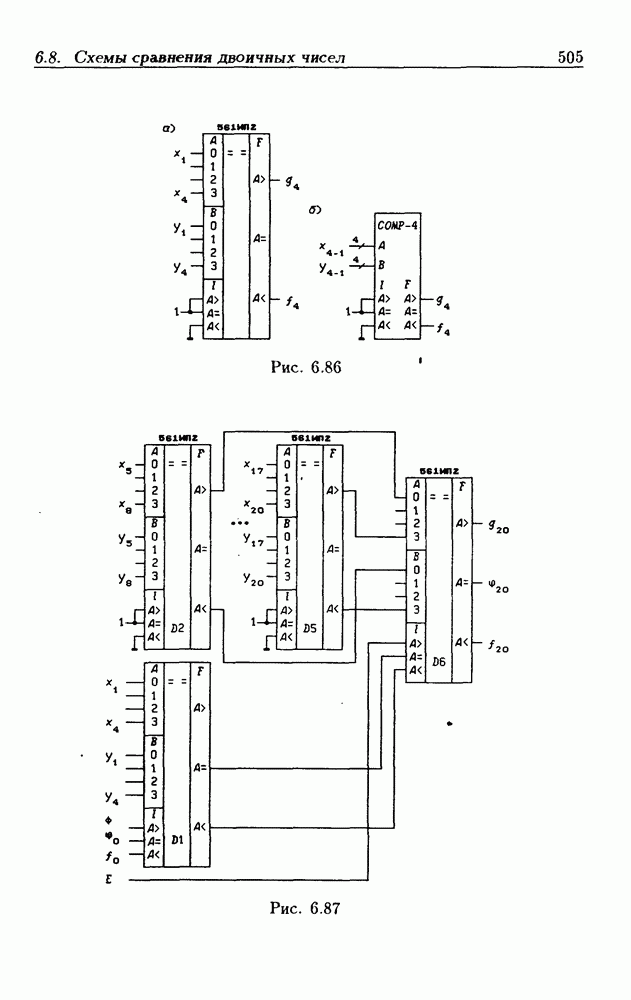
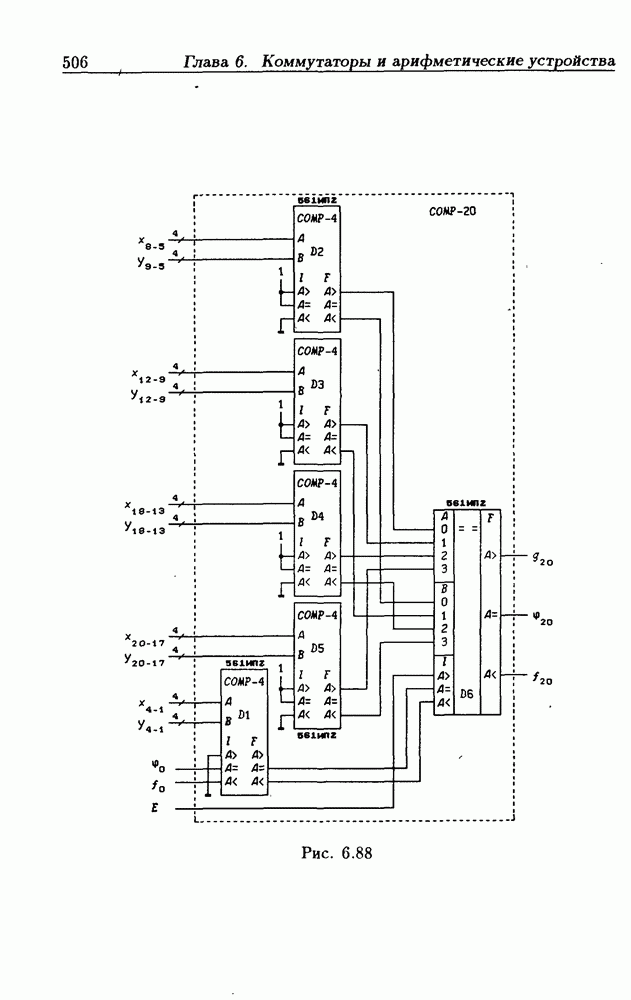
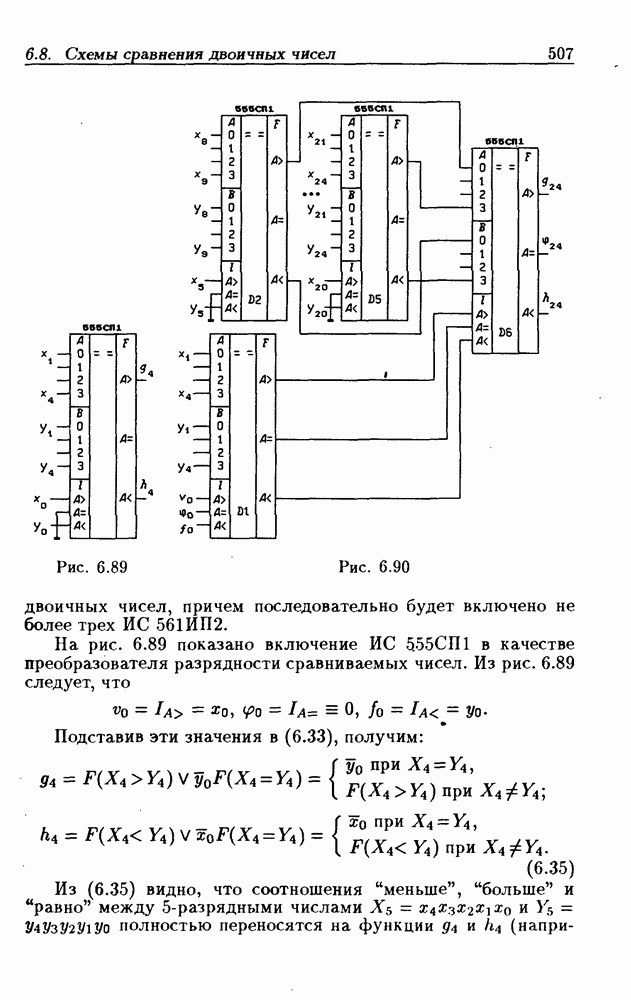
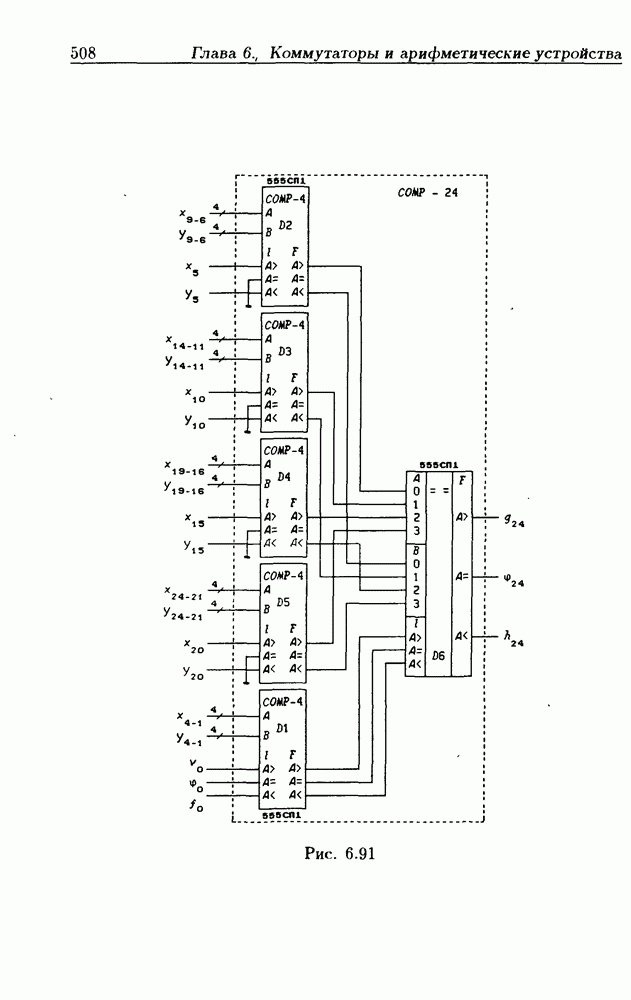
- 6.8. Схемы сравнения двоичных чисел
- 8-разрядные схемы сравнения двоичных чисел.
- 6.9. Прямой, обратный и дополнительный коды
- Дополнительный код.
- Сложение чисел в обратном коде.
- Код с избытком 3.
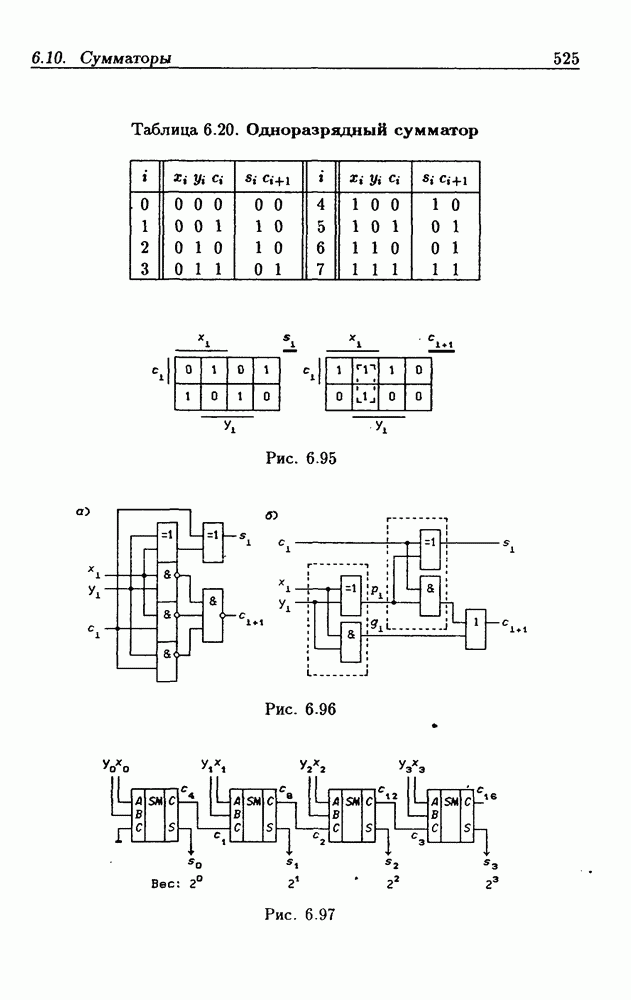
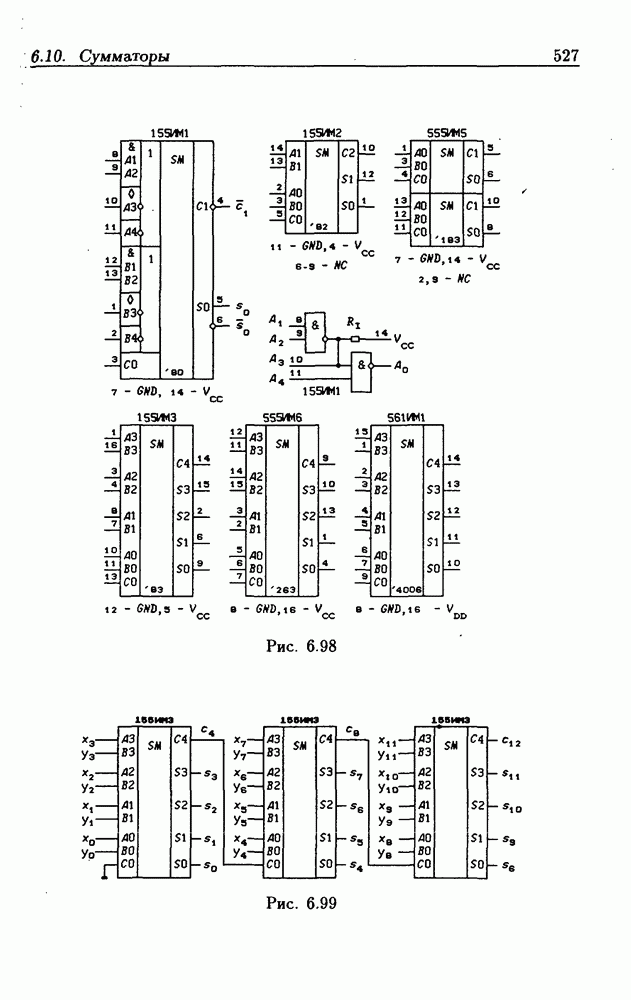
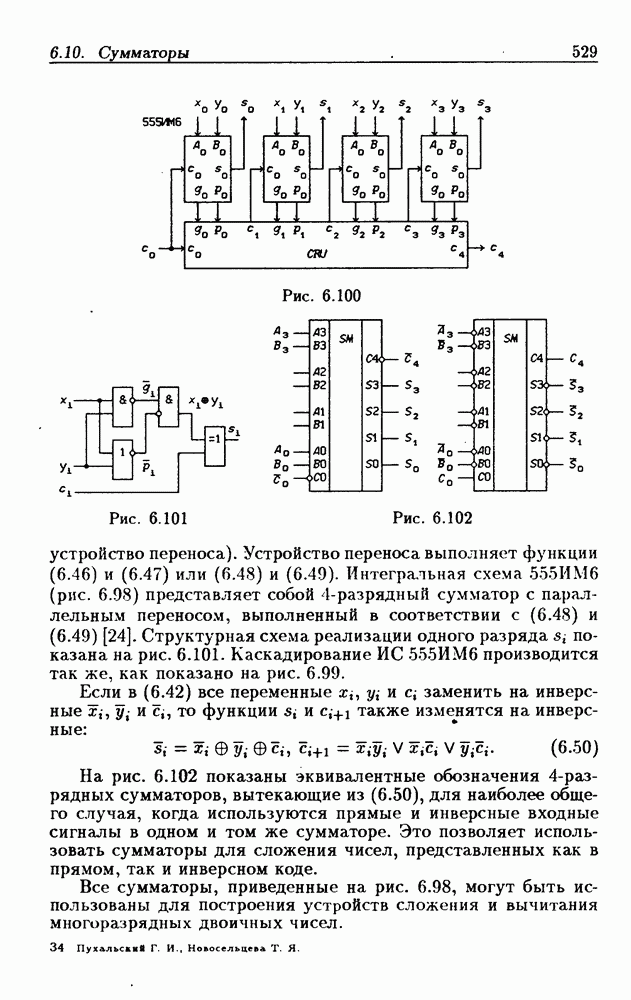
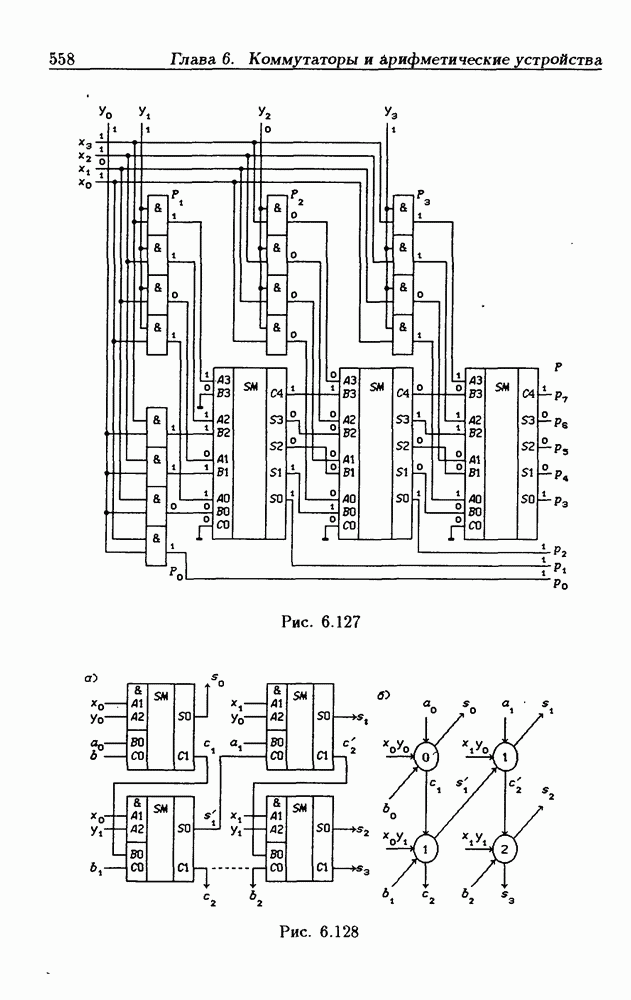
- 6.10. Сумматоры
- Двоичные параллельные сумматоры с последовательным переносом.
- Двоичные сумматоры с параллельным переносом.
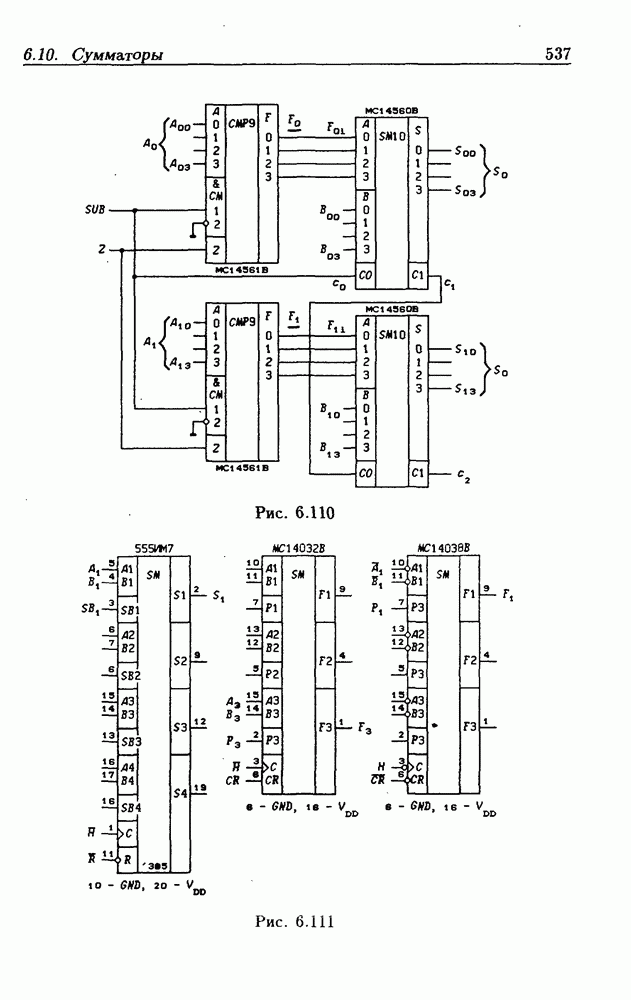
- Применения сумматоров.
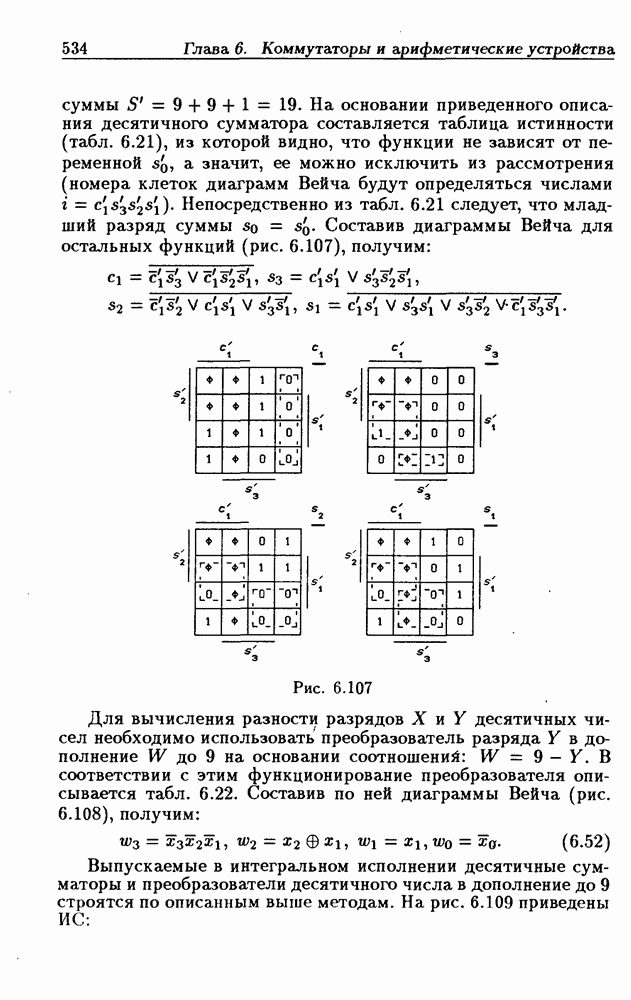
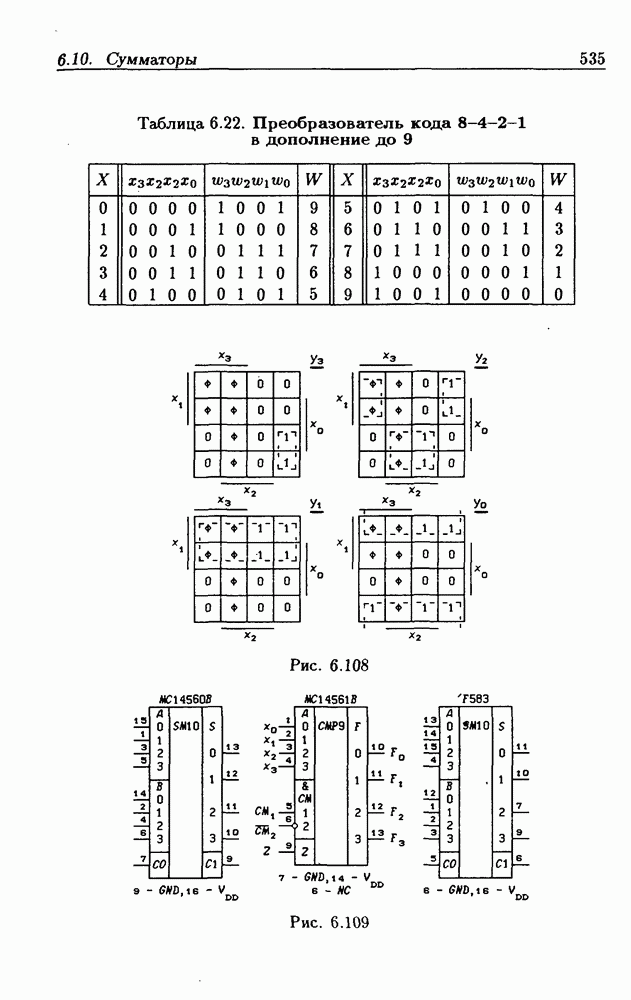
- Десятичные сумматоры.
- Последовательные двоичные сумматоры.
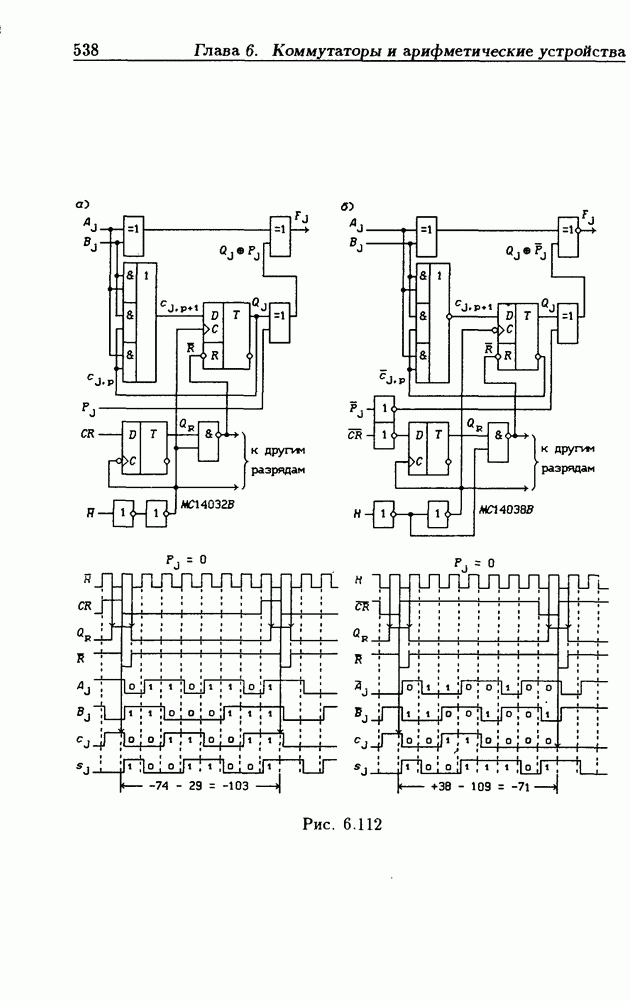
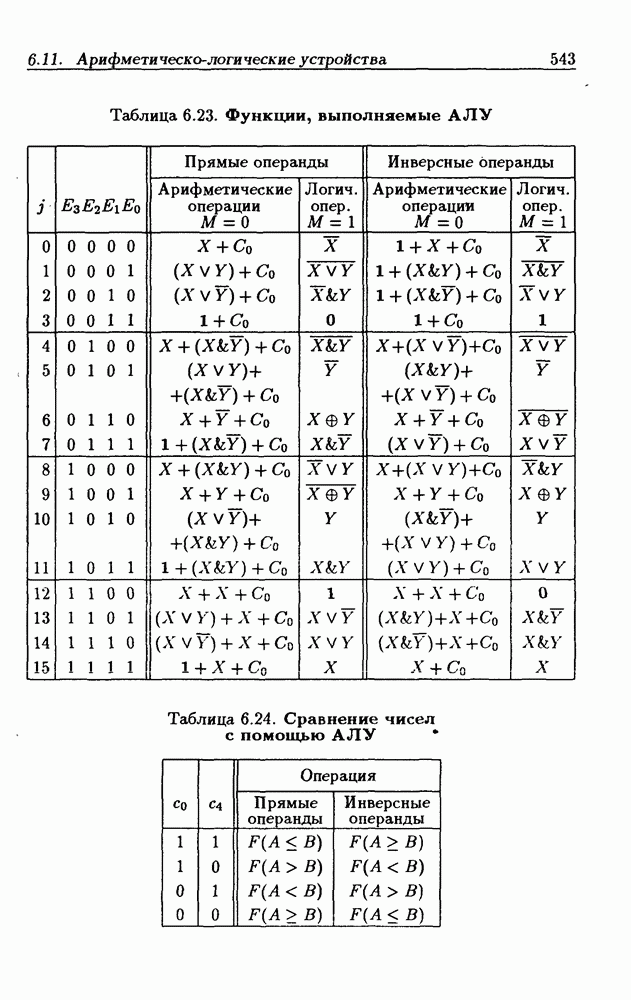
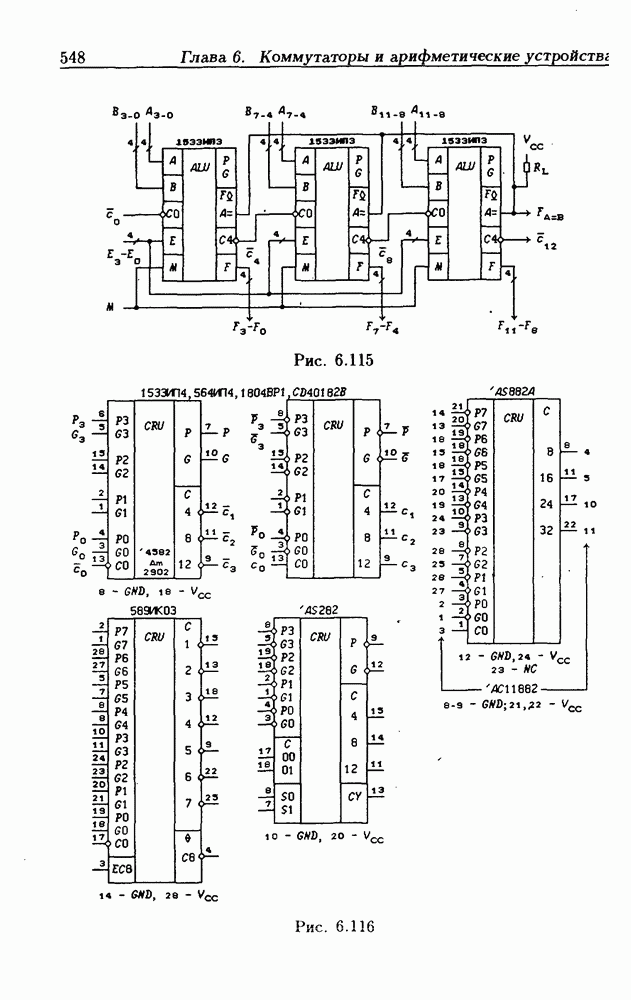
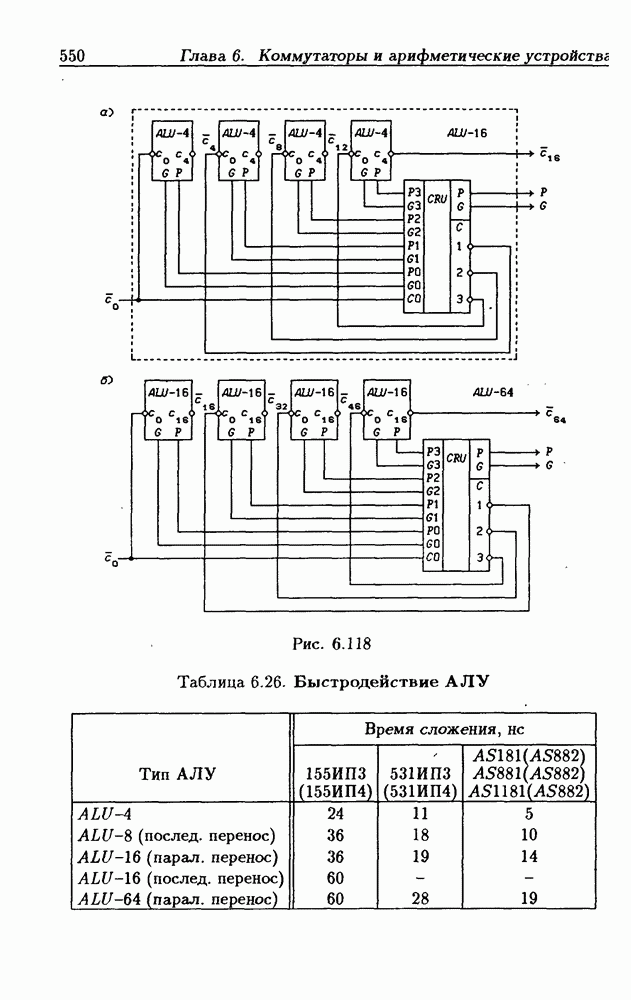
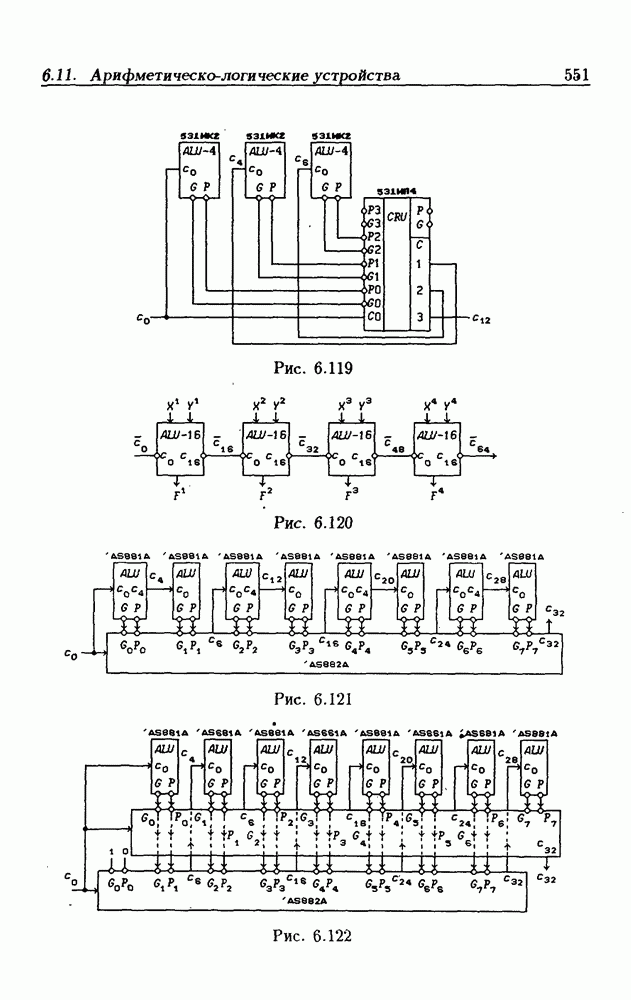
- 6.11. Арифметическо-логические устройства
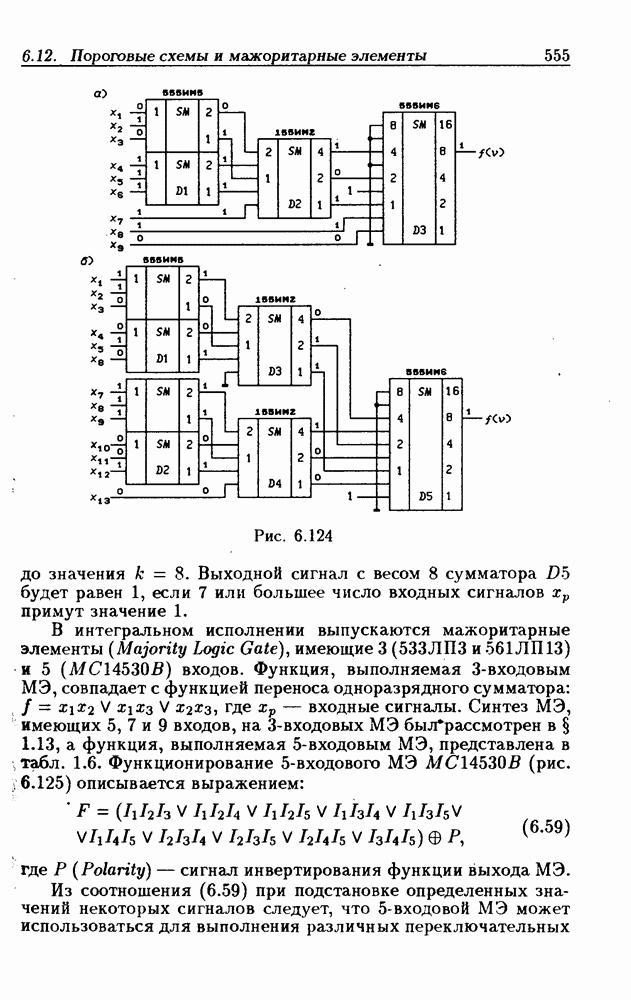
- 6.12. Пороговые схемы и мажоритарные элементы
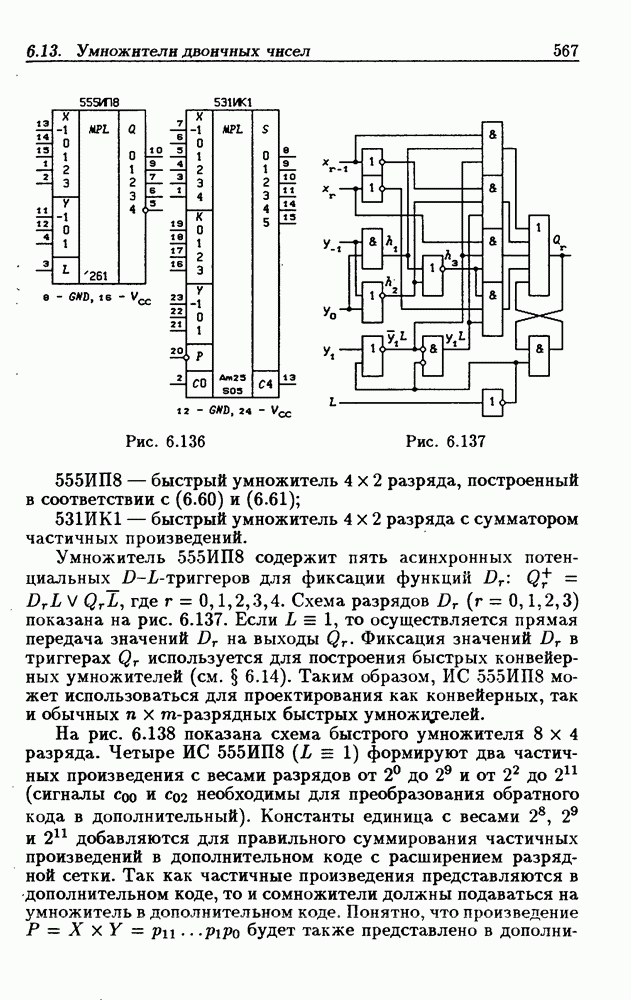
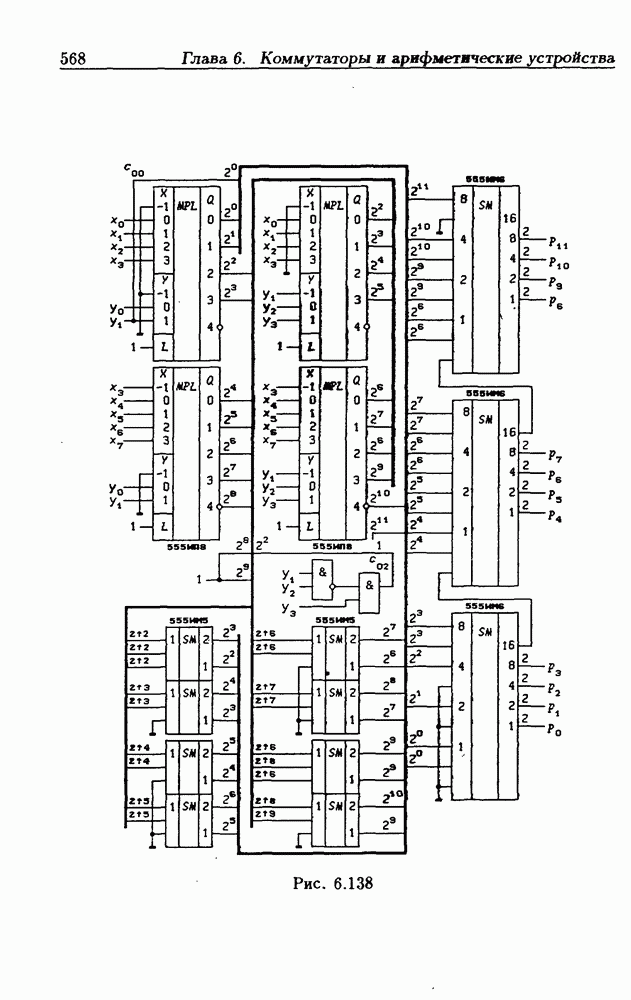
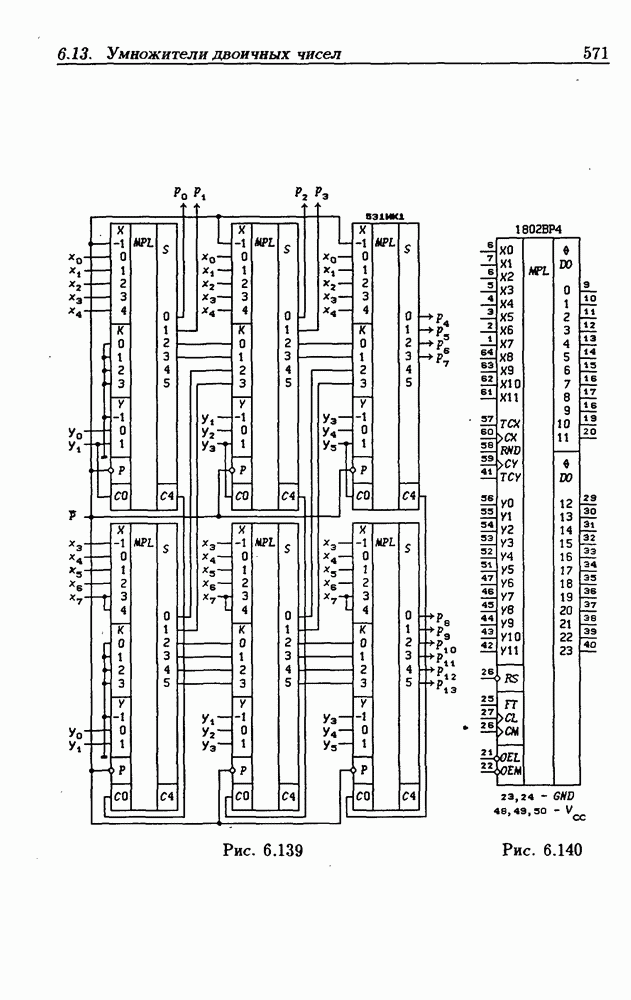
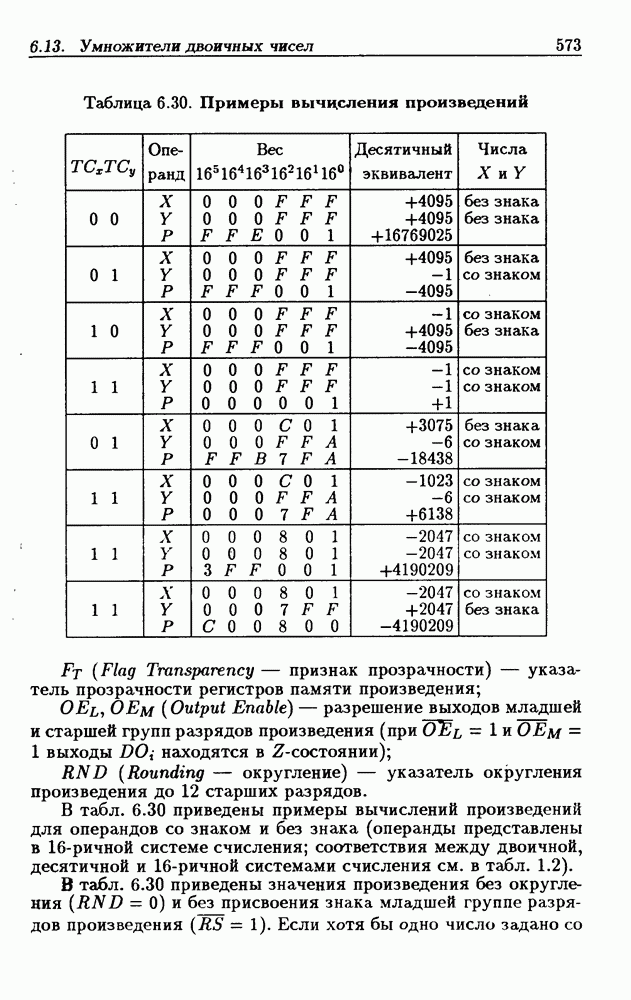
- 6.13. Умножители двоичных чисел
- Быстрые умножители.
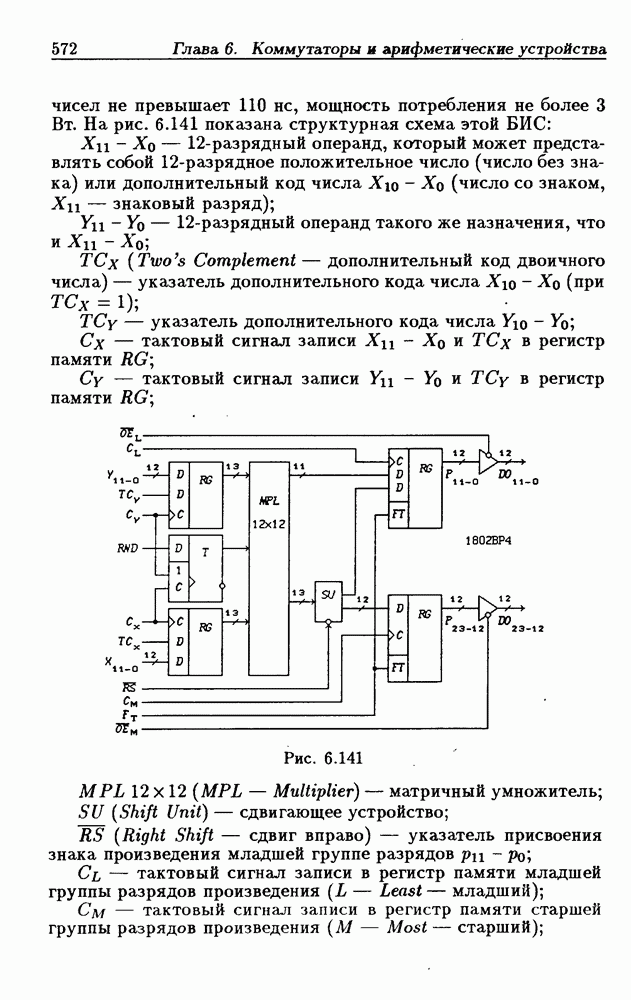
- БИС умножителя 12×12 разрядов 1802ВР4.
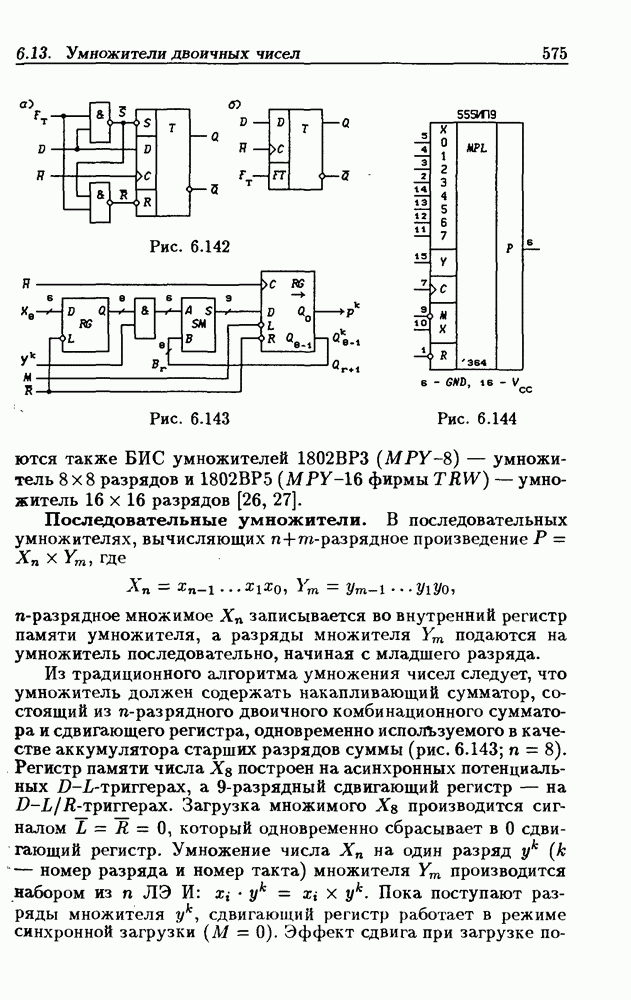
- Последовательные умножители.
- 6.14. Конвейерные устройства
- Конвейерный быстрый умножитель.
- Конвейерные АЦП.
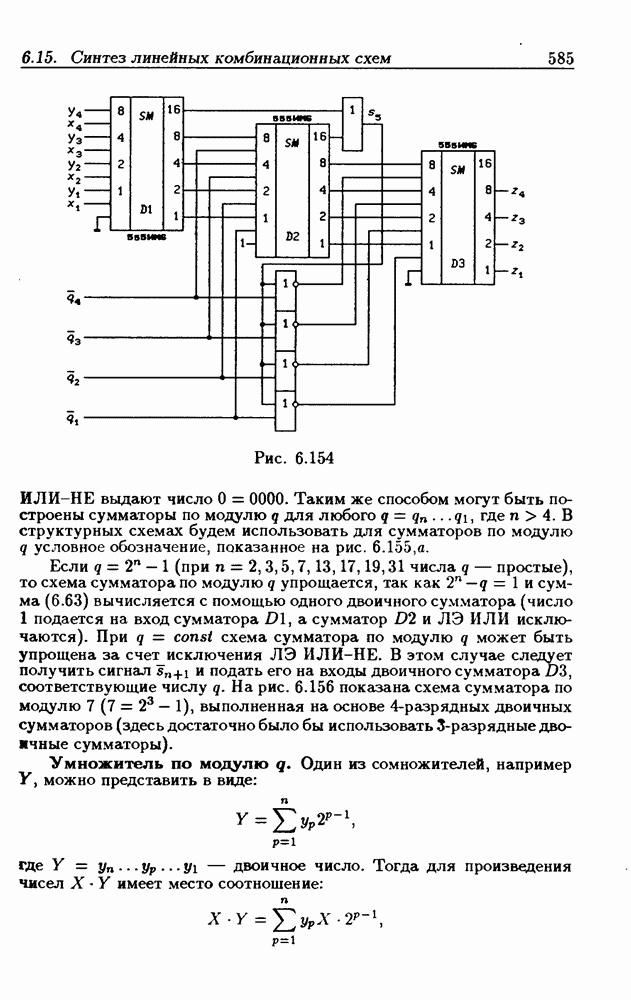
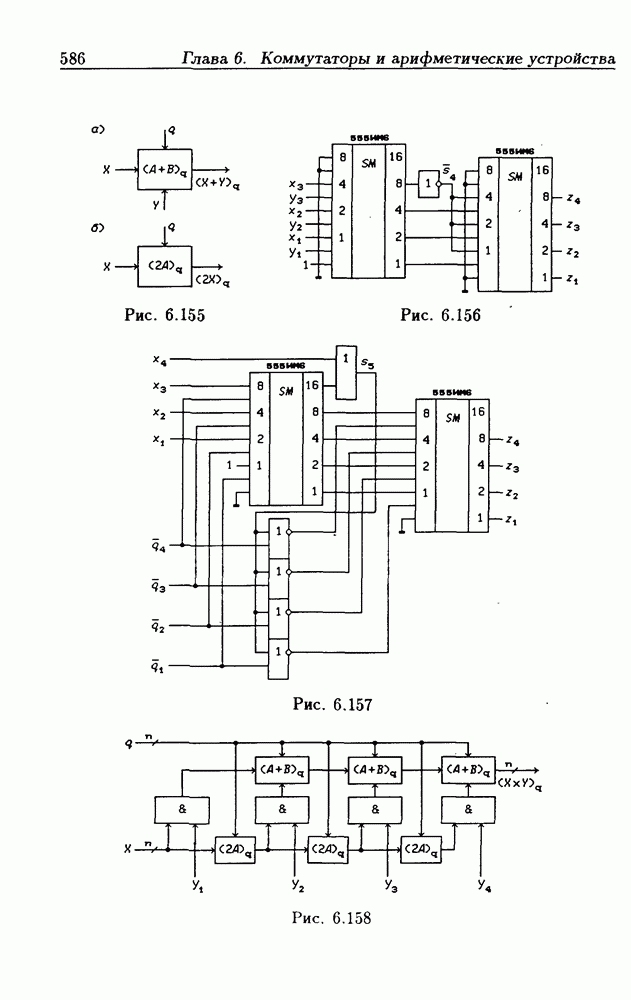
- 6.15. Синтез линейных комбинационных схем
- Сумматор по модулю q.
- Умножитель по модулю q.
- Глава 7. Сдвигающие регистры и счетчики
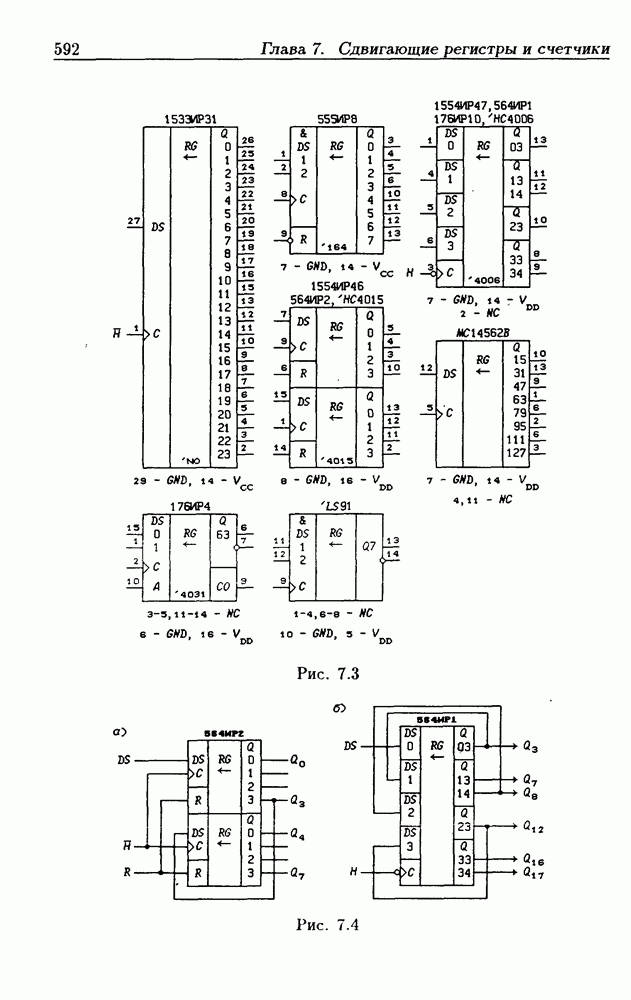
- 7.1. Сдвигающие регистры без параллельной записи данных
- Сдвигающие устройства с выходными регистрами памяти.
- 7.2. Сдвигающие регистры с параллельной записью данных
- Сдвигающие регистры с расширением знака.
- Сдвигающие регистры с входным регистром памяти.
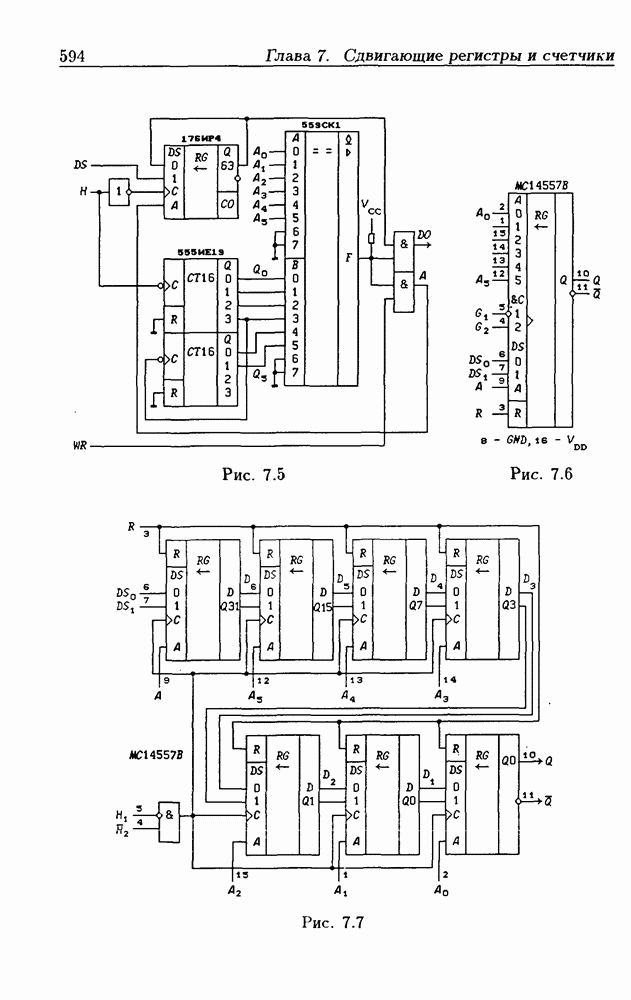
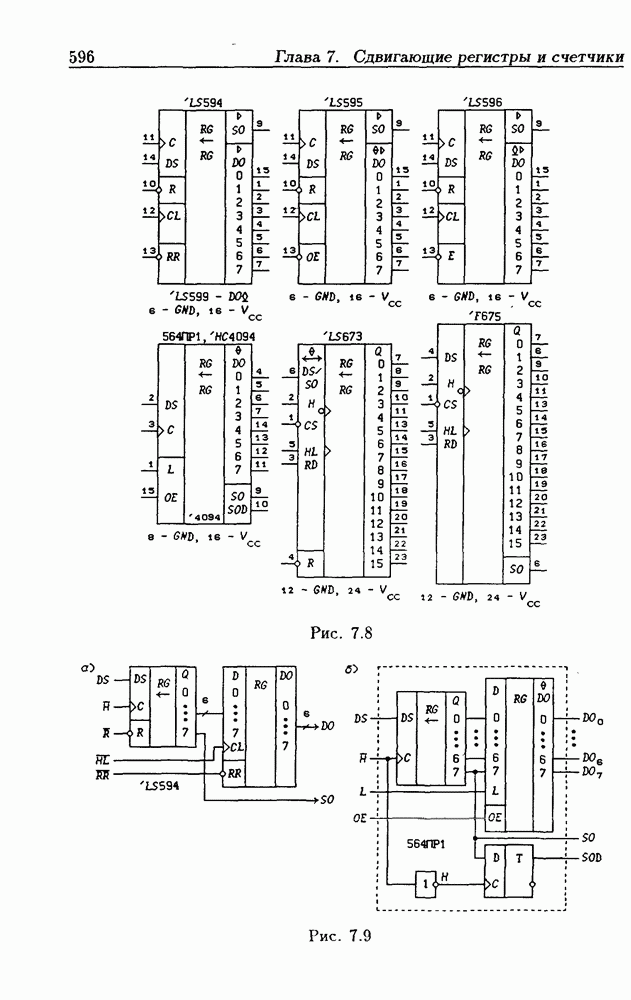
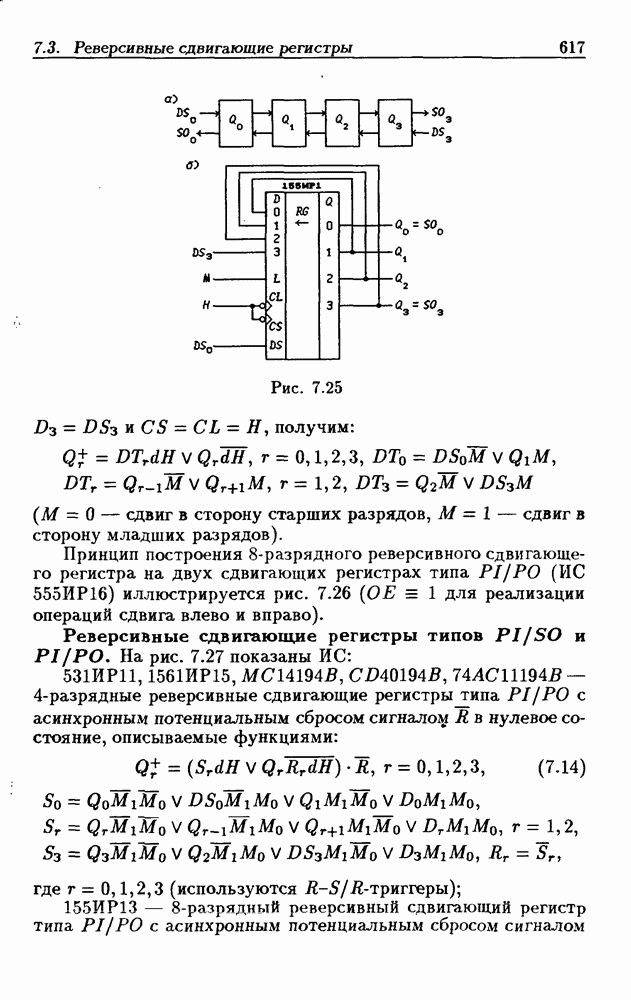
- 7.3. Реверсивные сдвигающие регистры
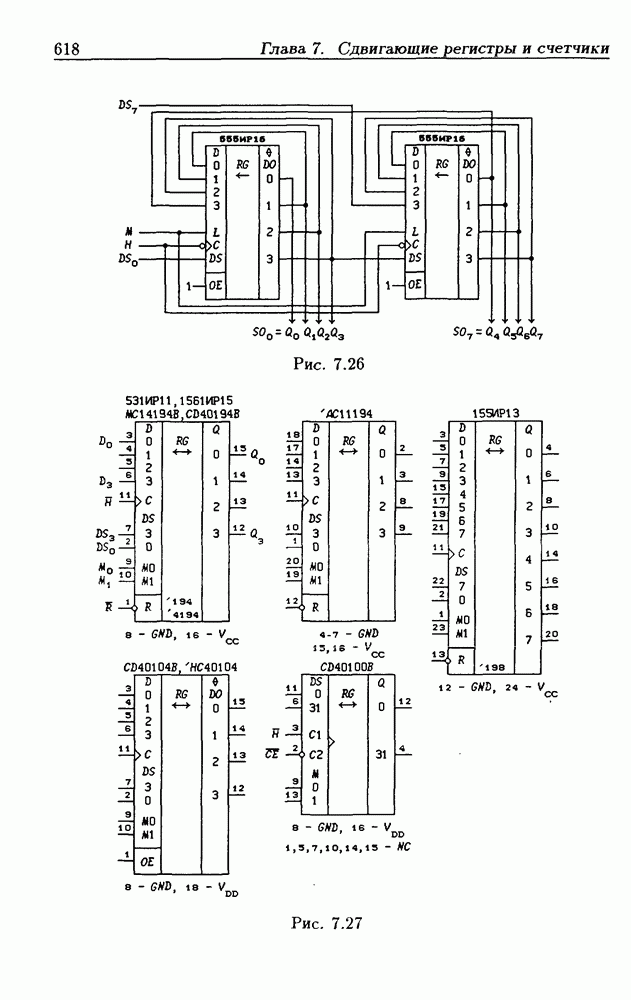
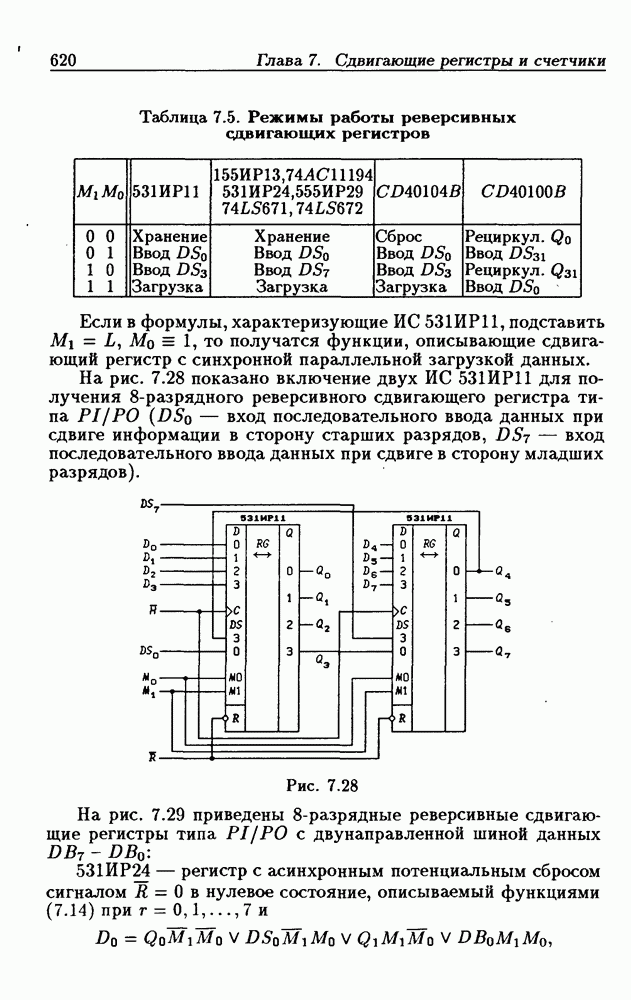
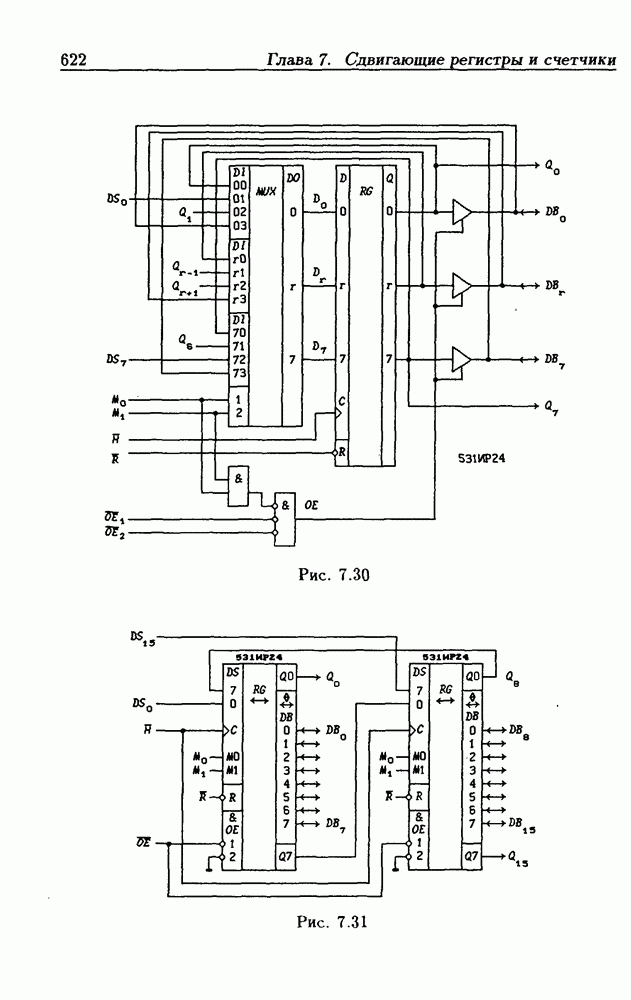
- Реверсивные сдвигающие регистры типов PI/SO и PI/PO.
- Многофункциональные устройства на основе реверсивных сдвигающих регистров.
- 7.4. Асинхронные счетчики
- Двоично-десятичные асинхронные счетчики.
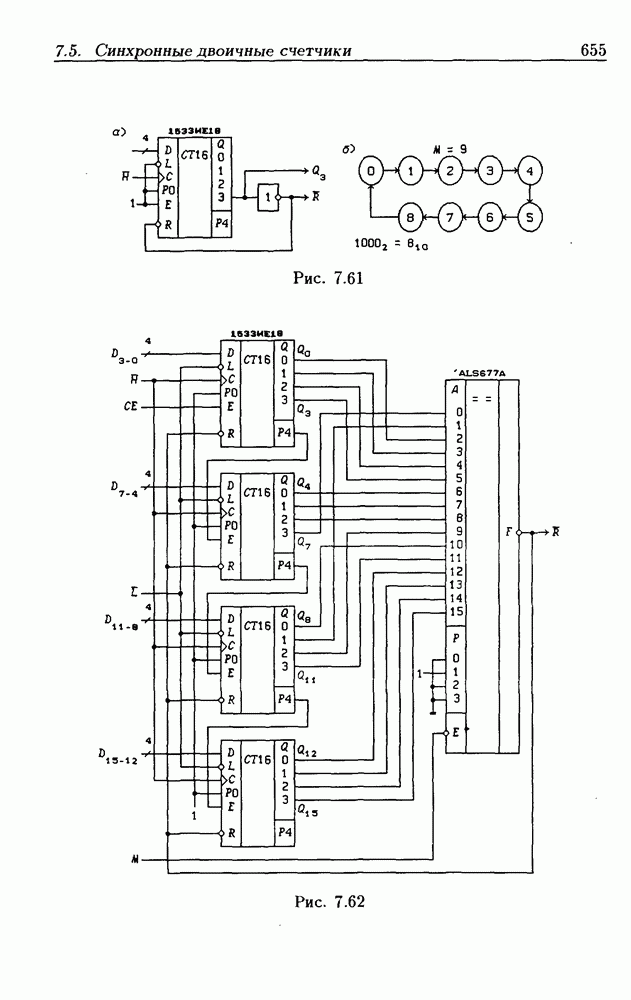
- 7.5. Синхронные двоичные счетчики
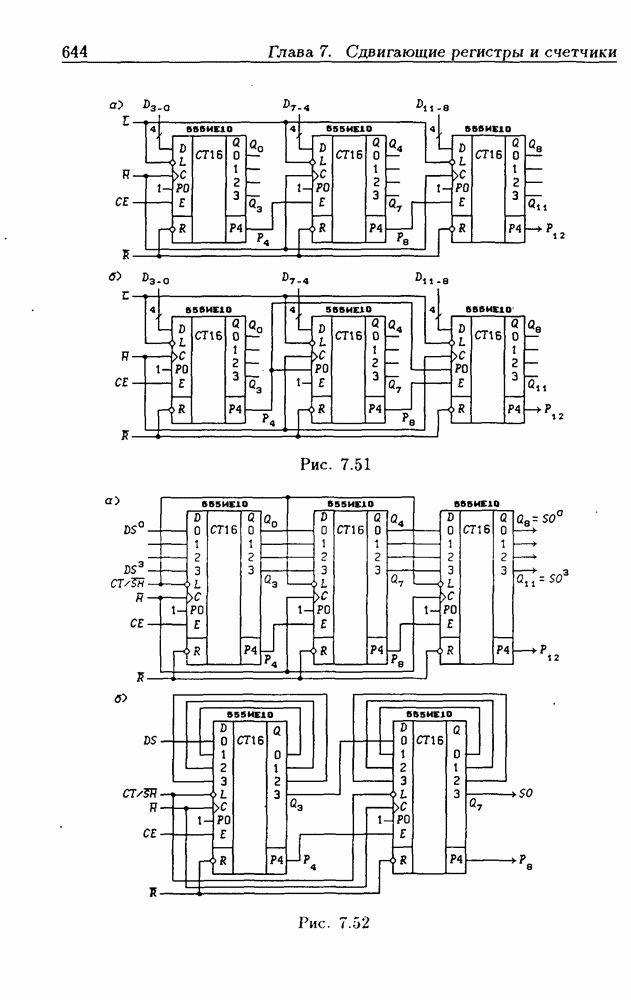
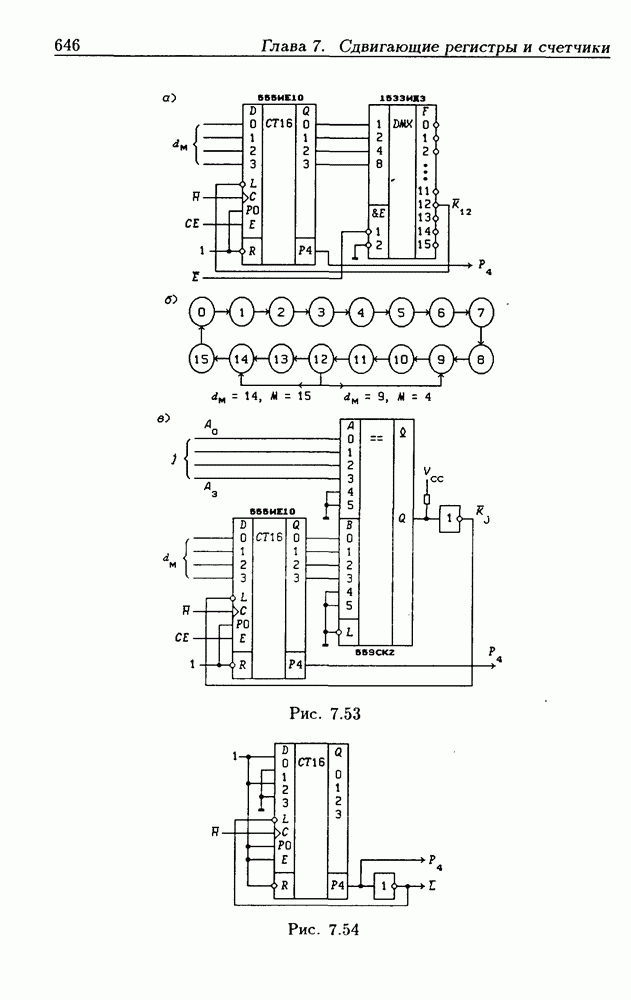
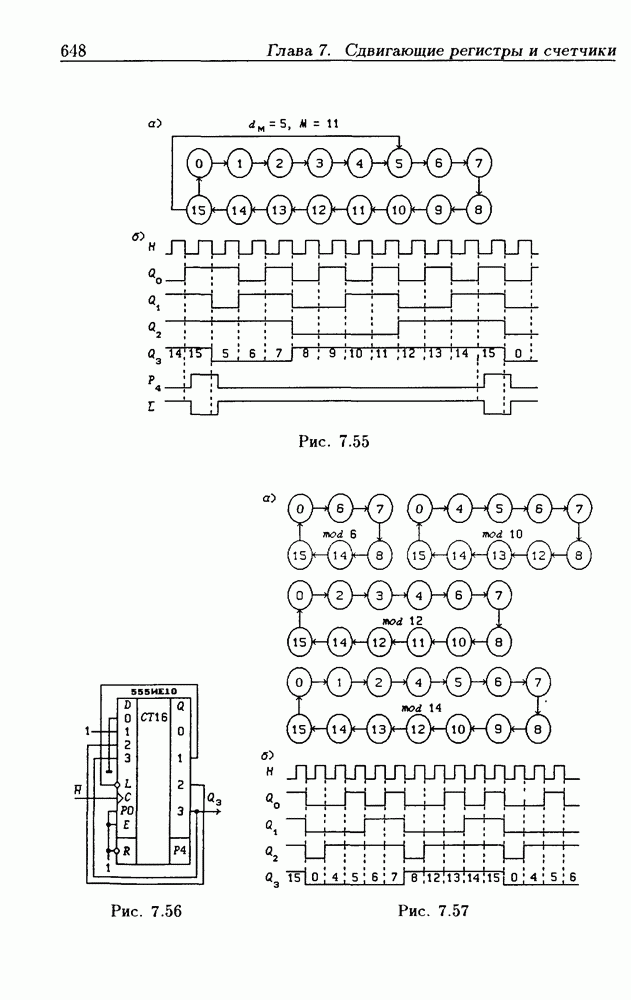
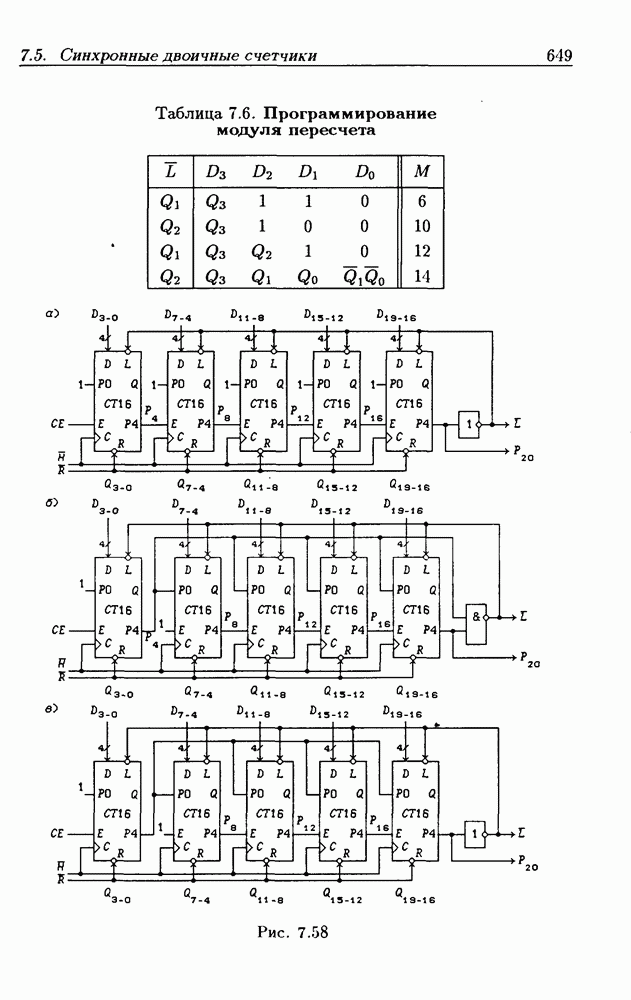
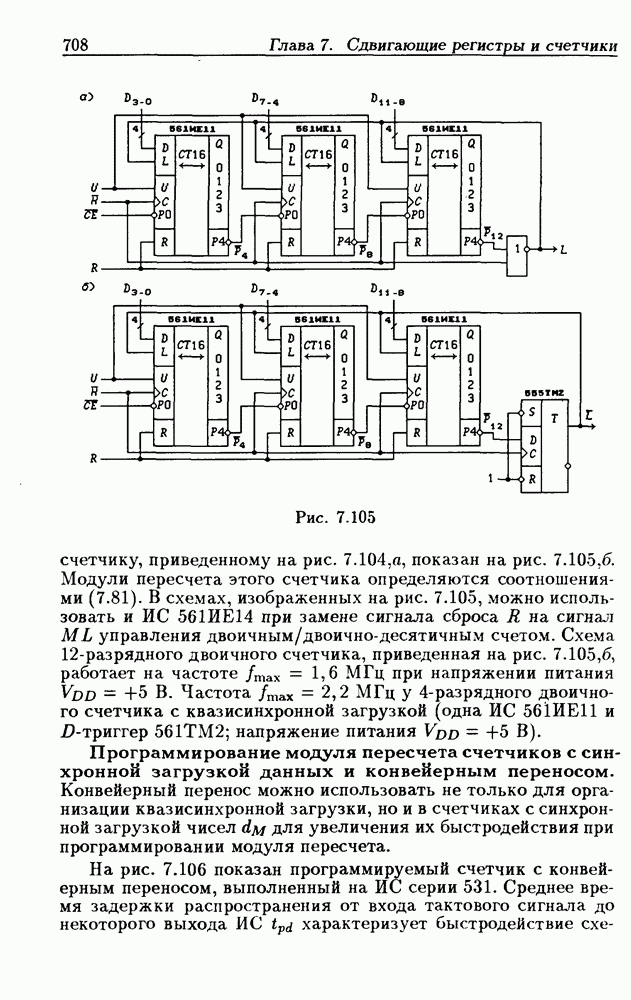
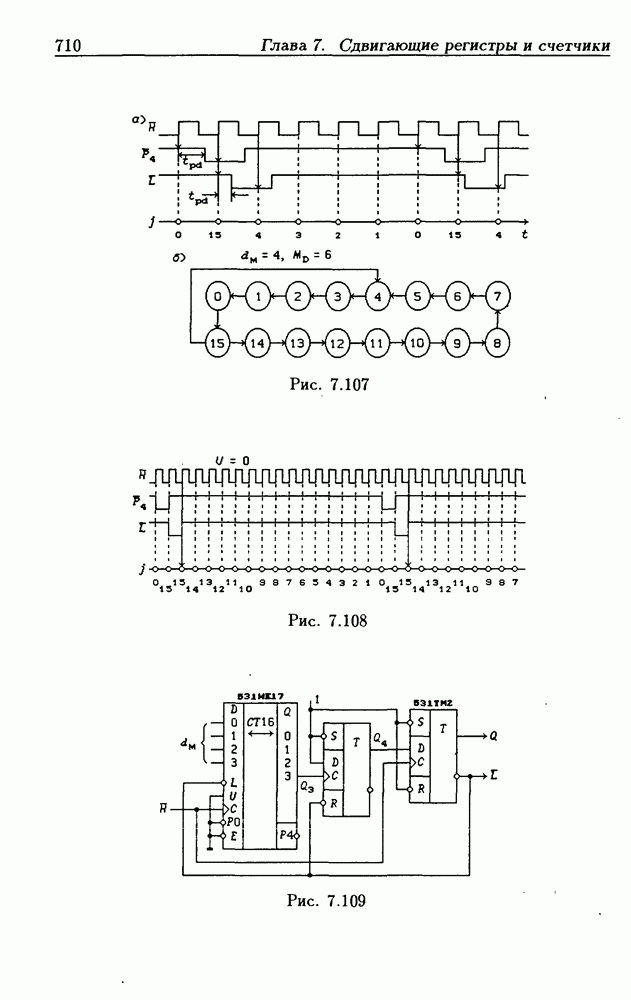
- Программирование модуля пересчета двоичных счетчиков.
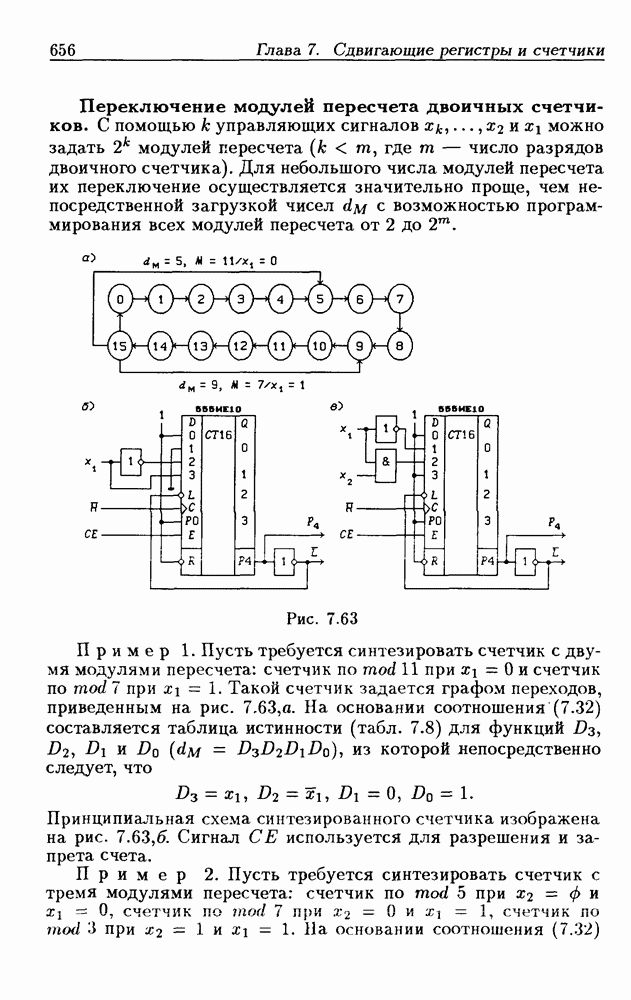
- Переключение модулей пересчета двоичных счетчиков.
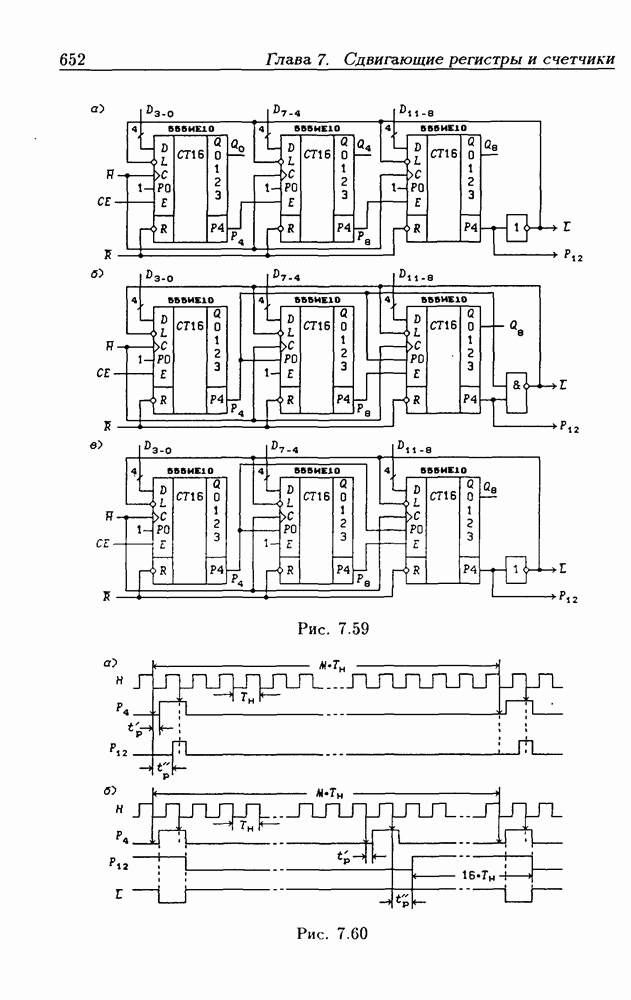
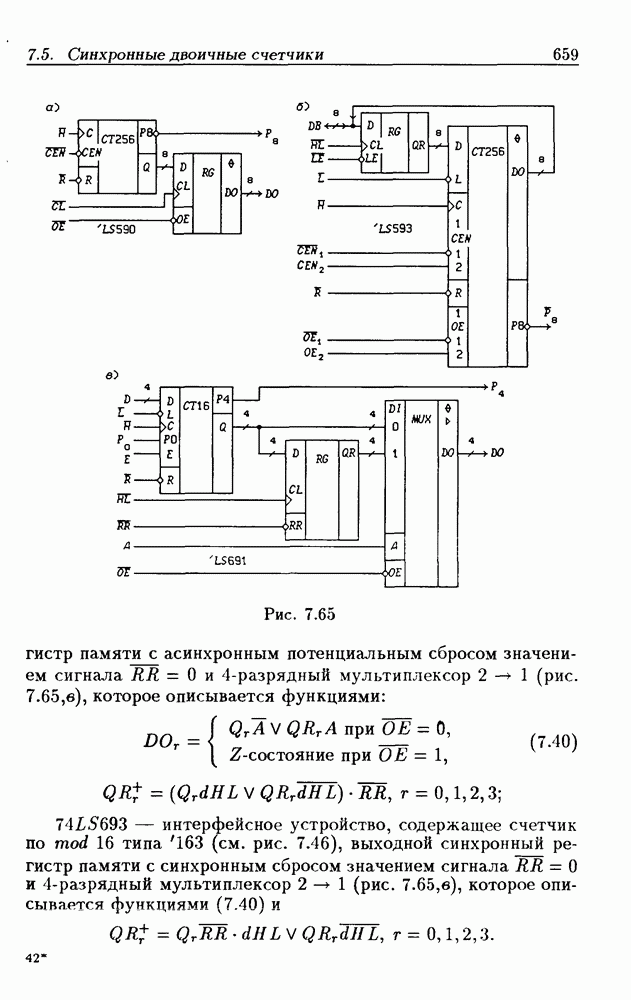
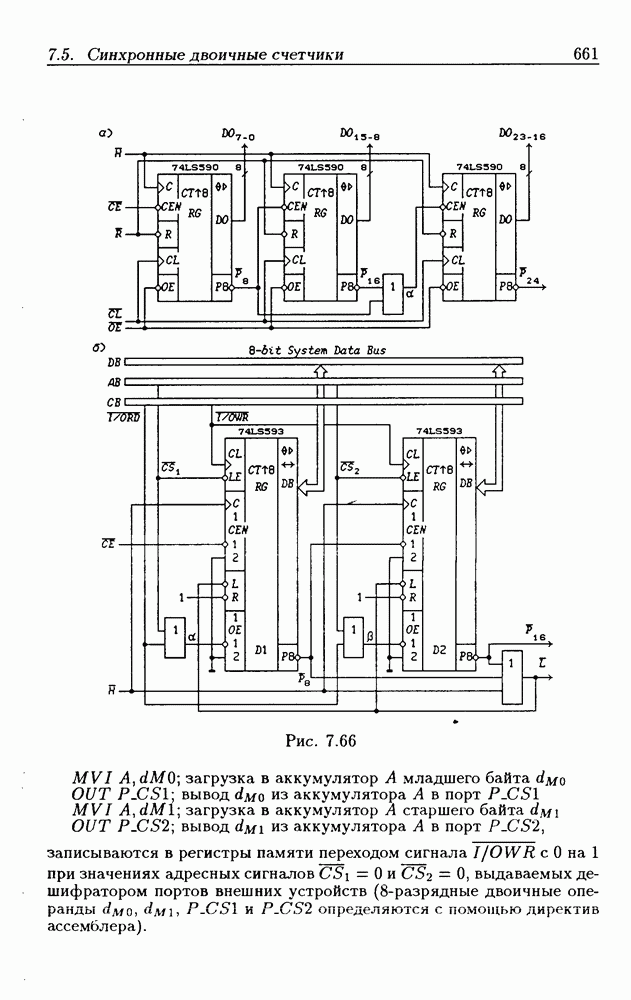
- Функциональные устройства на основе двоичных счетчиков.
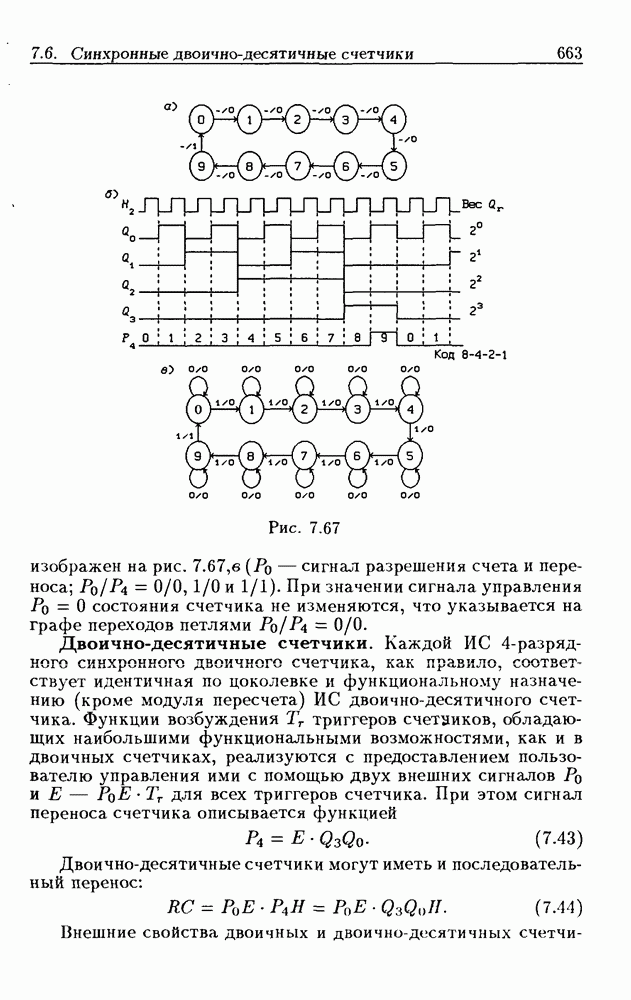
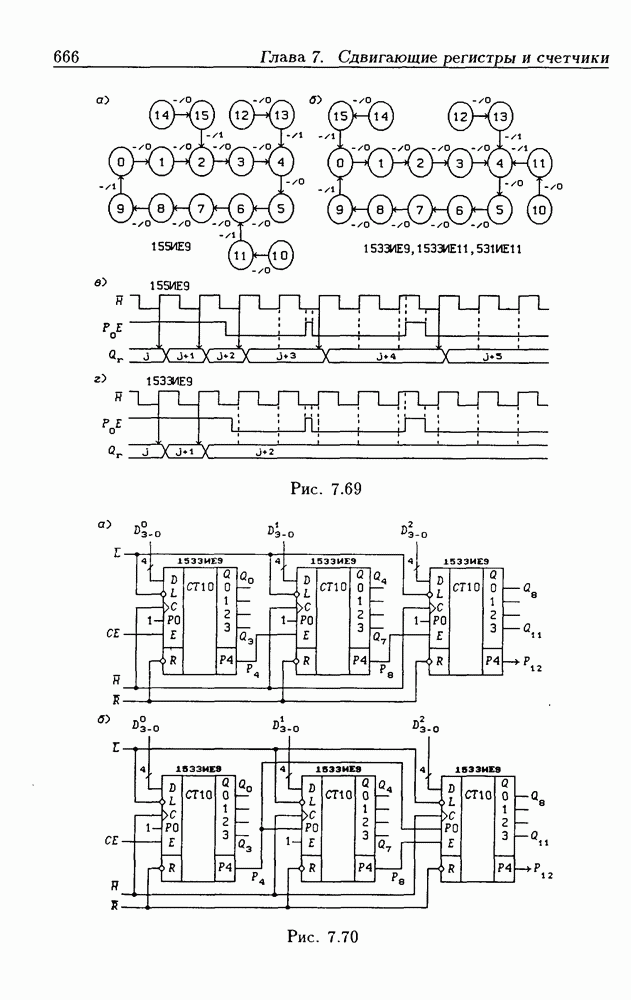
- 7.6. Синхронные двоично-десятичные счетчики
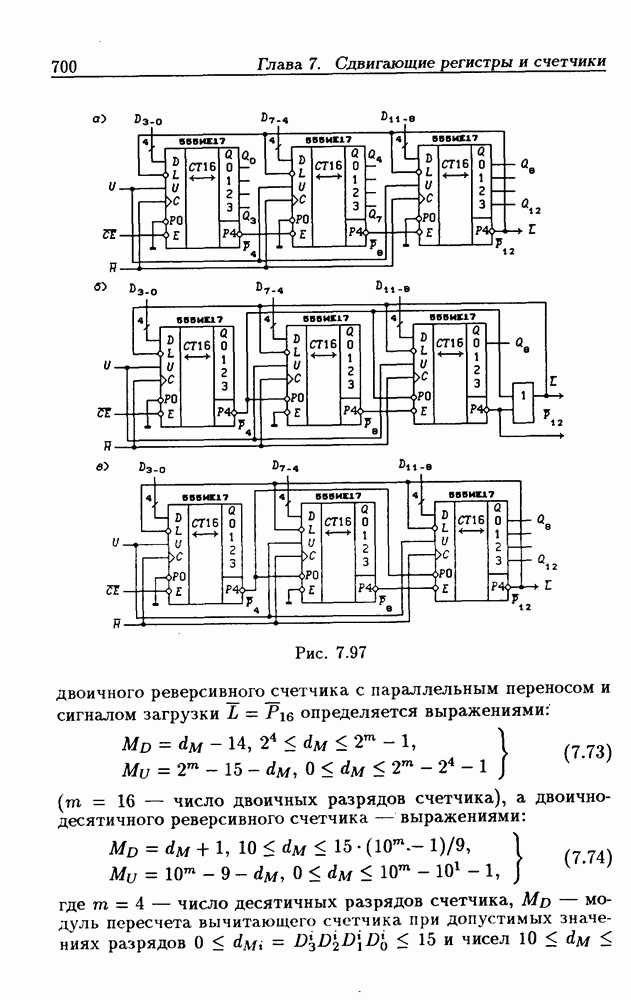
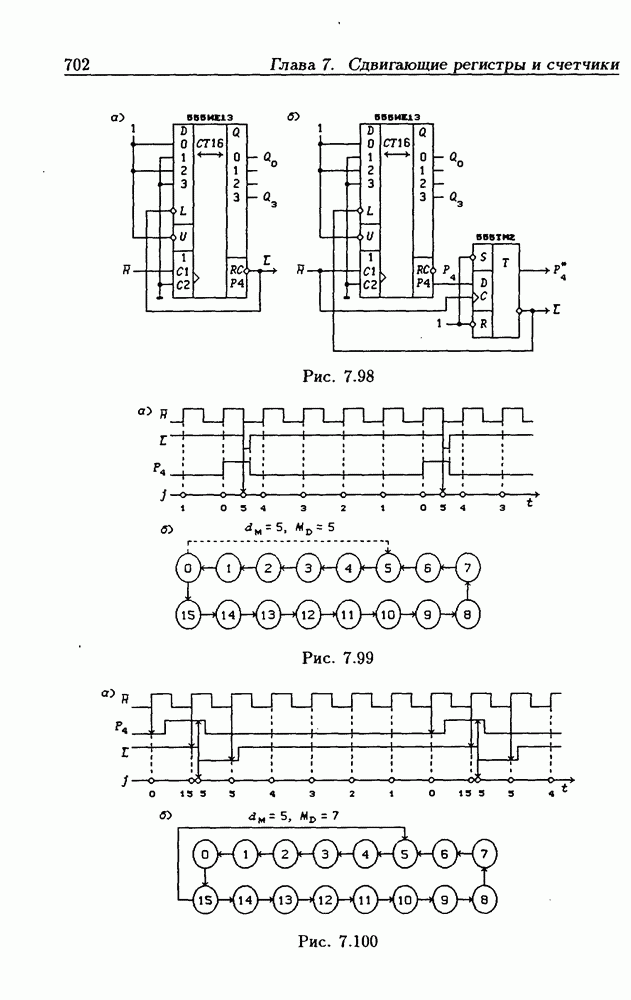
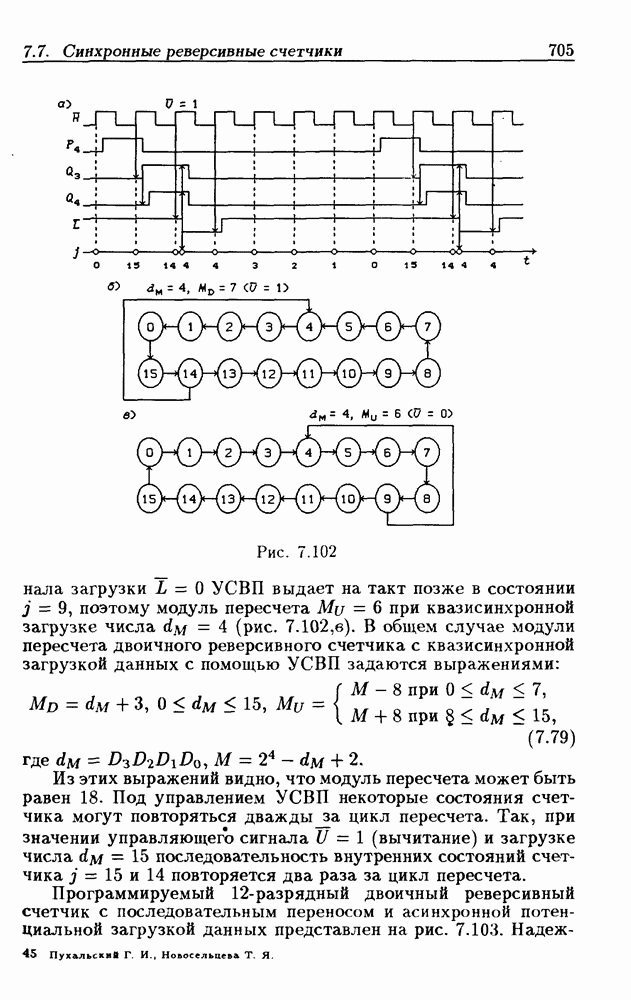
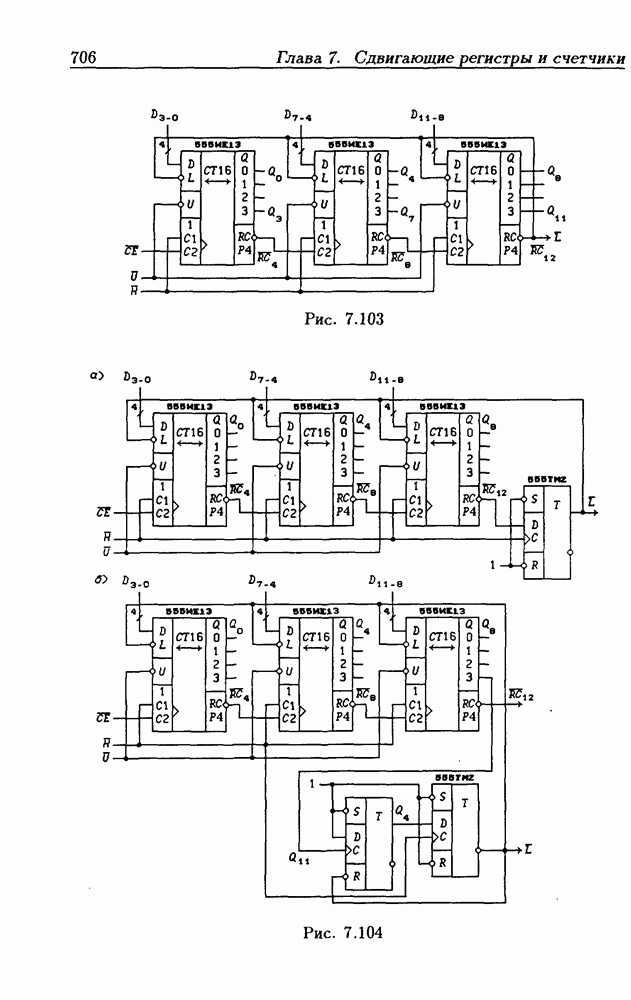
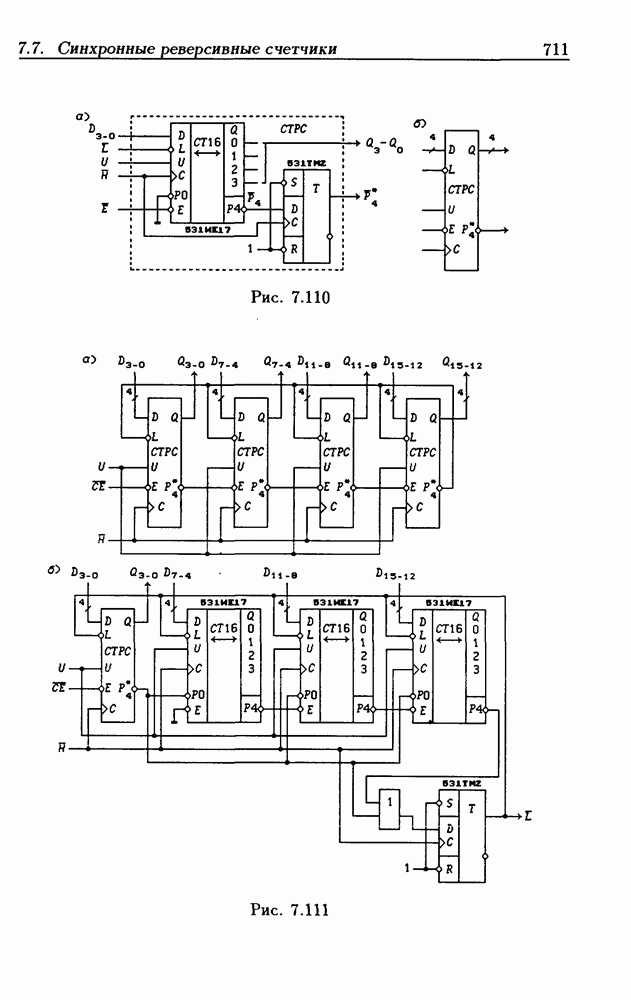
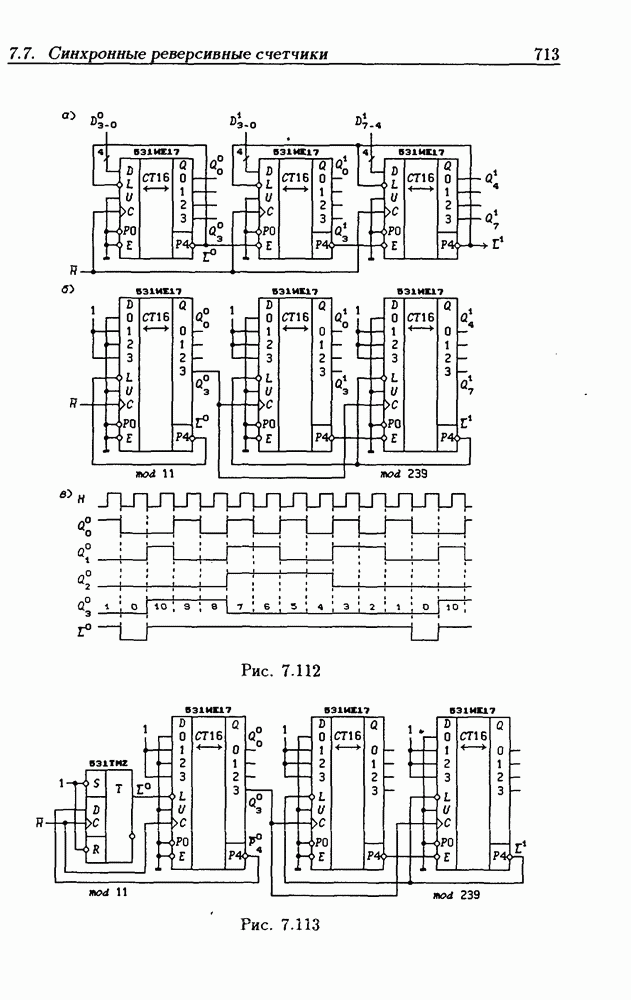
- 7.7. Синхронные реверсивные счетчики
- 7.8. Счетчики с расщепленным тактовым сигналом
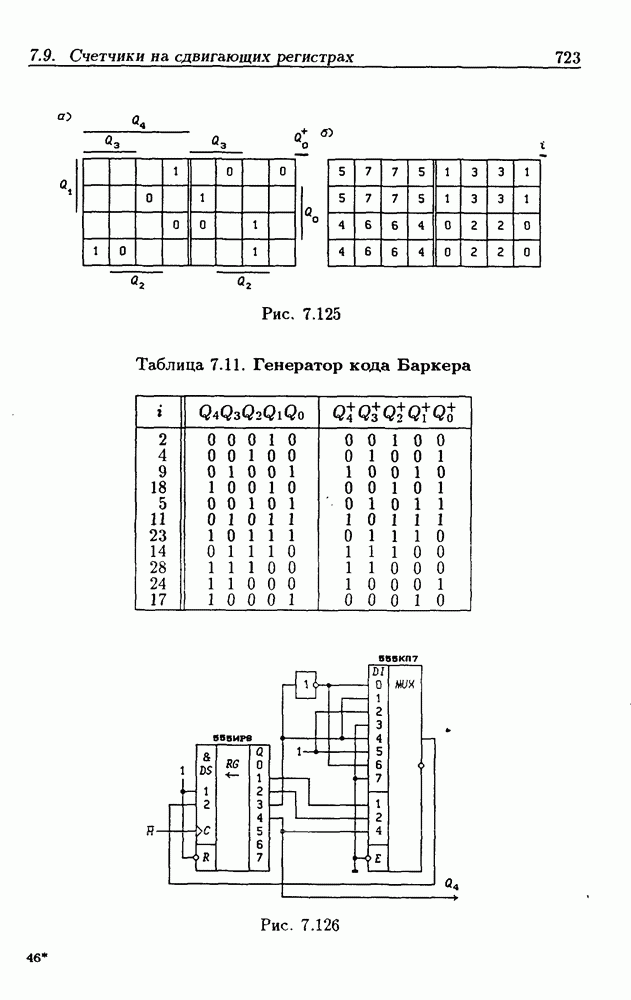
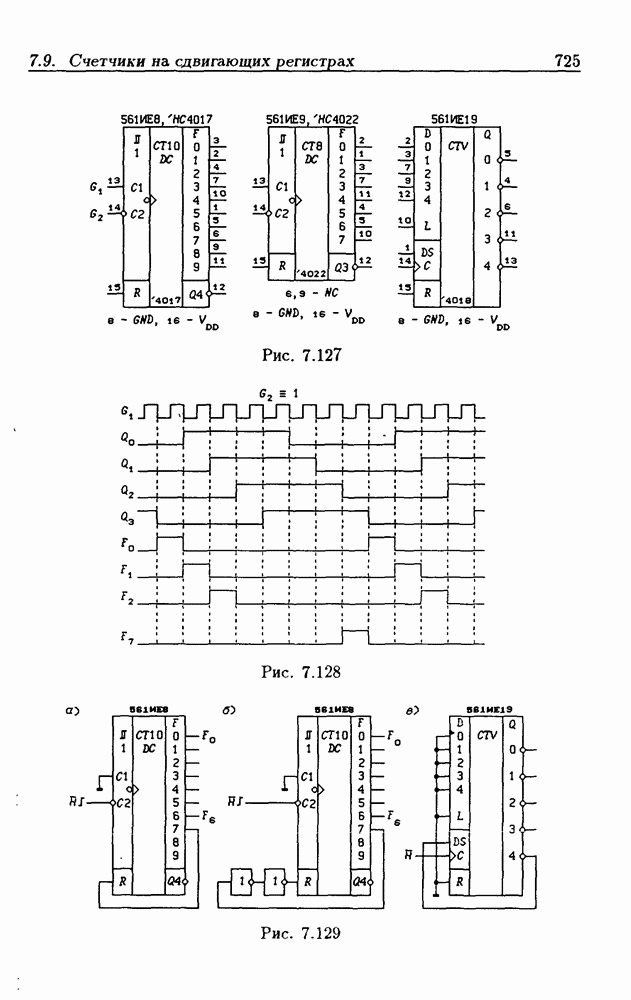
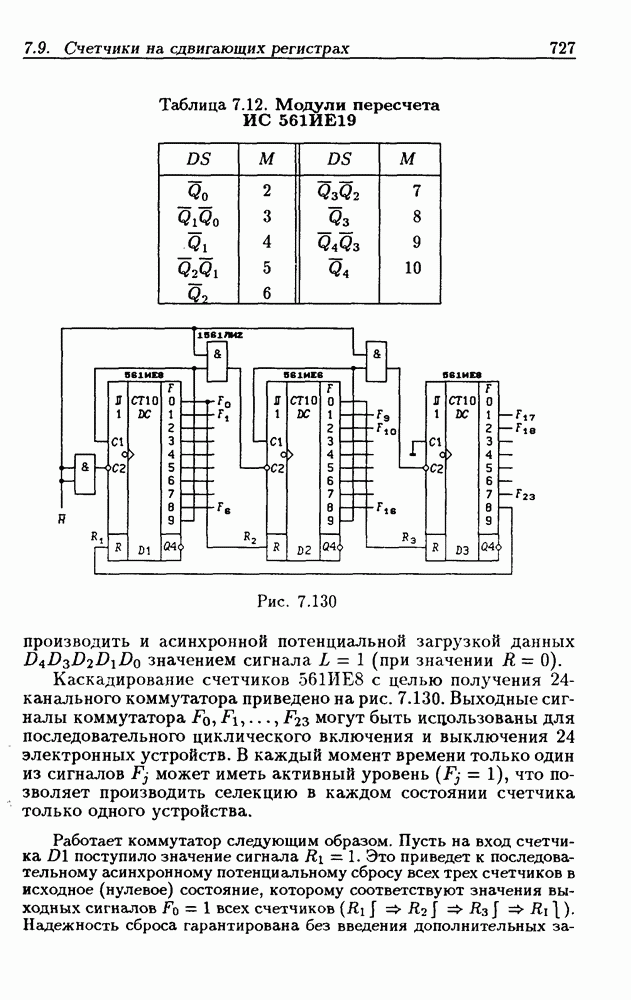
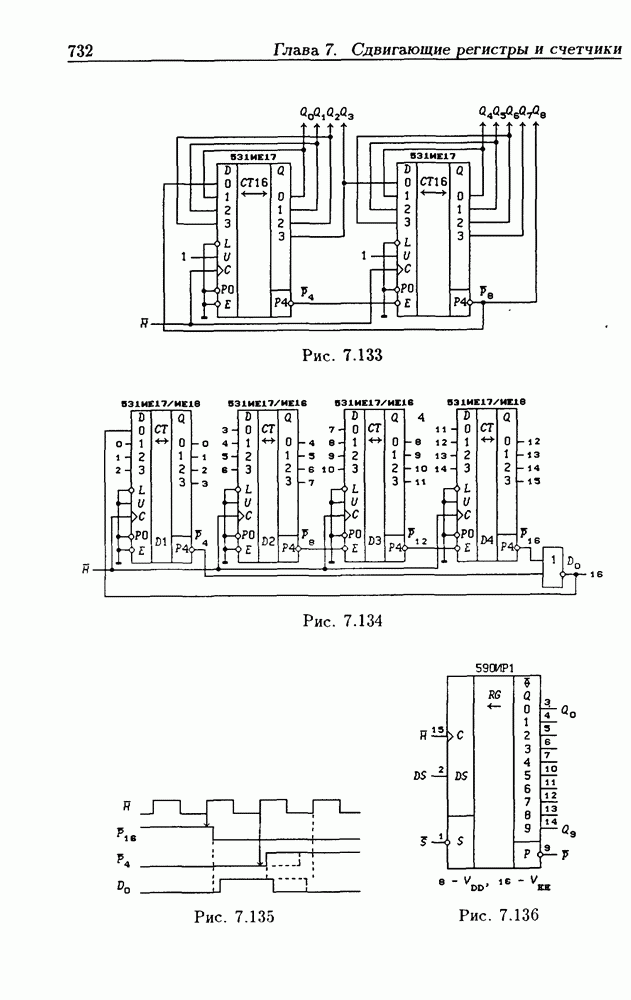
- 7.9. Счетчики на сдвигающих регистрах
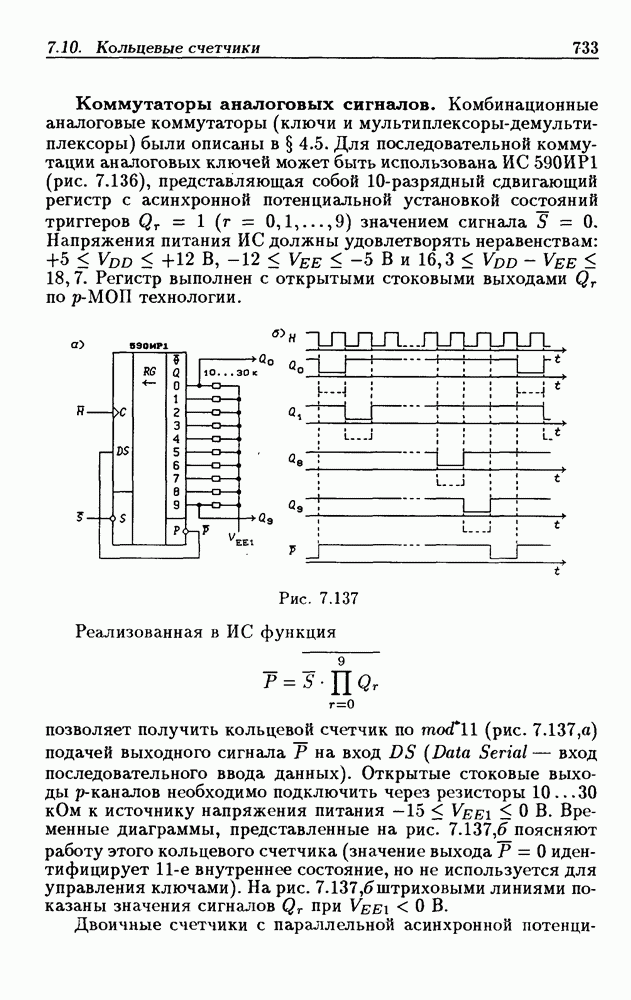
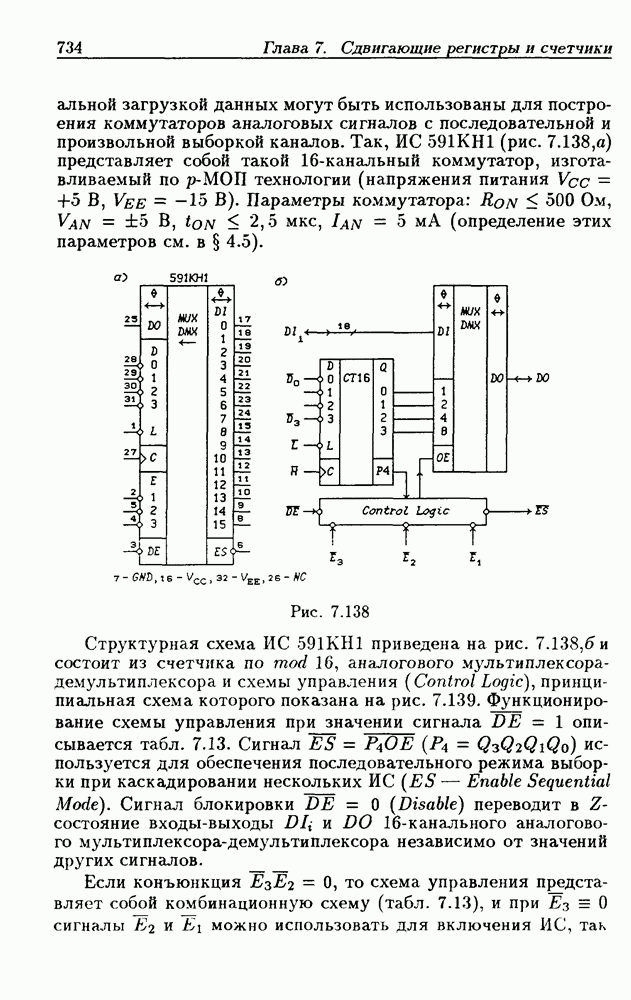
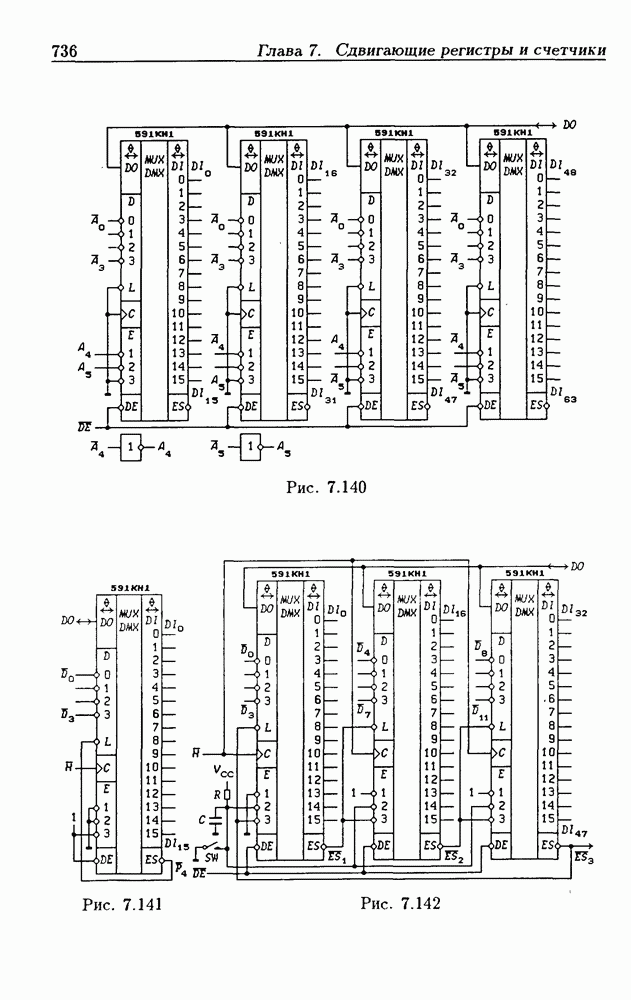
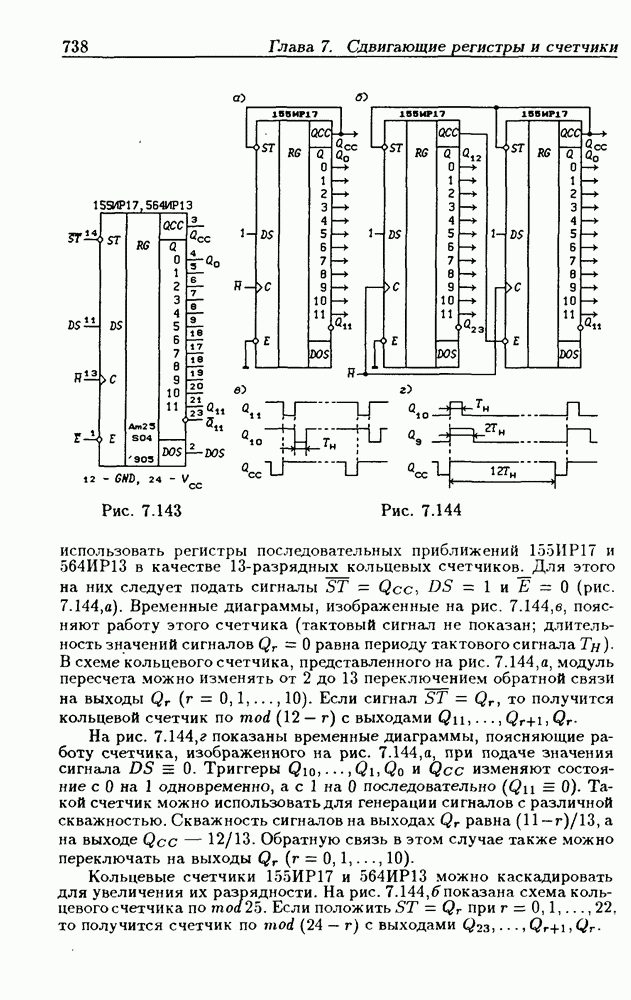
- 7.10. Кольцевые счетчики
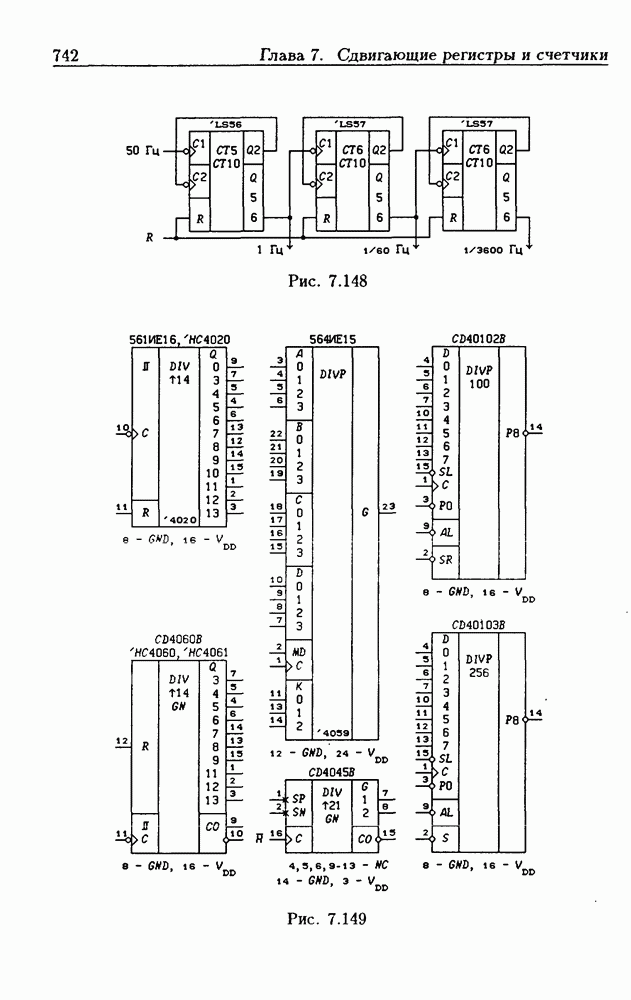
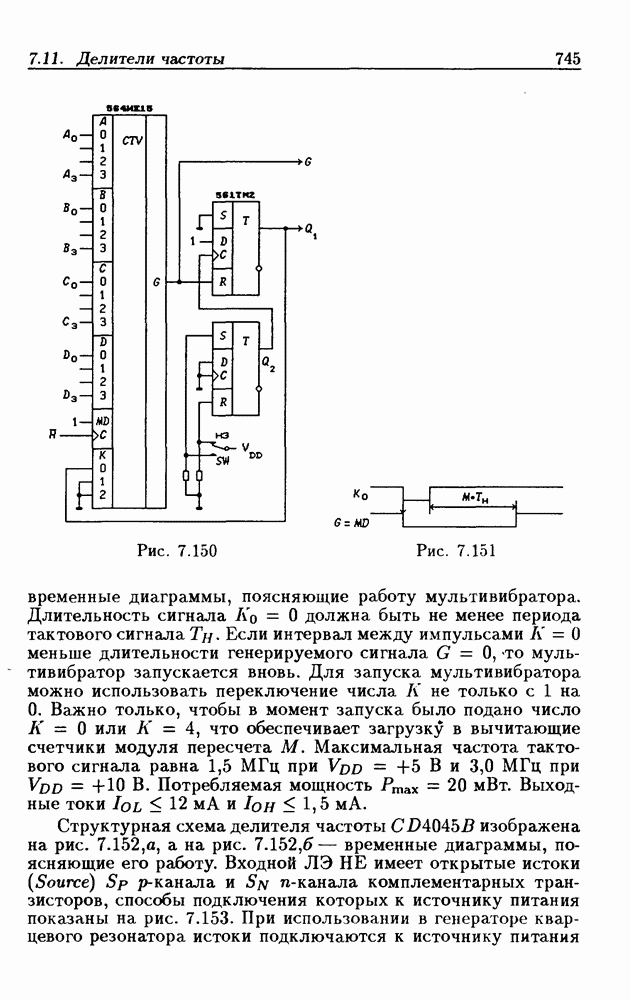
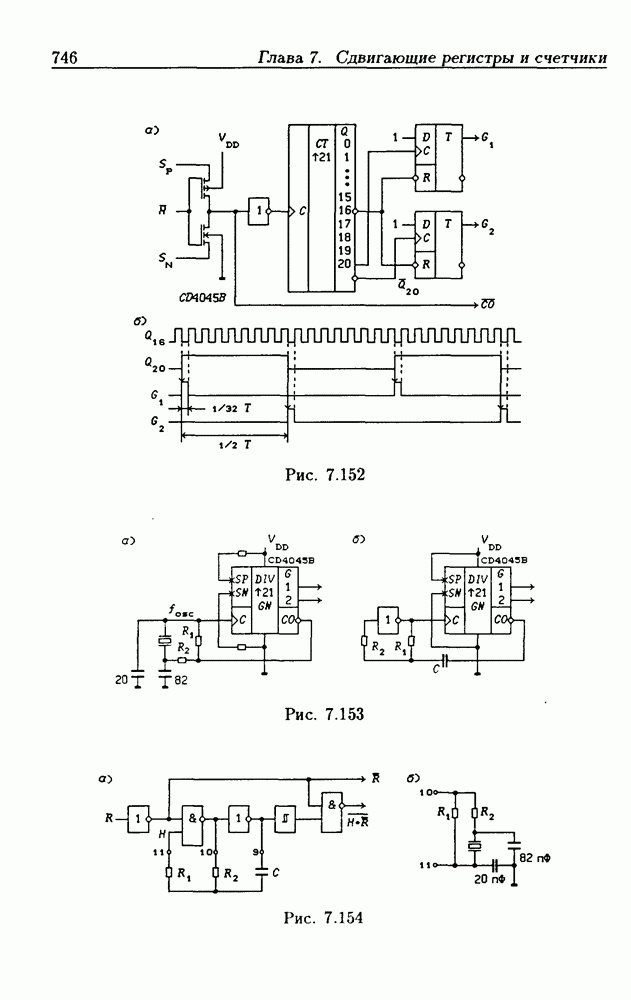
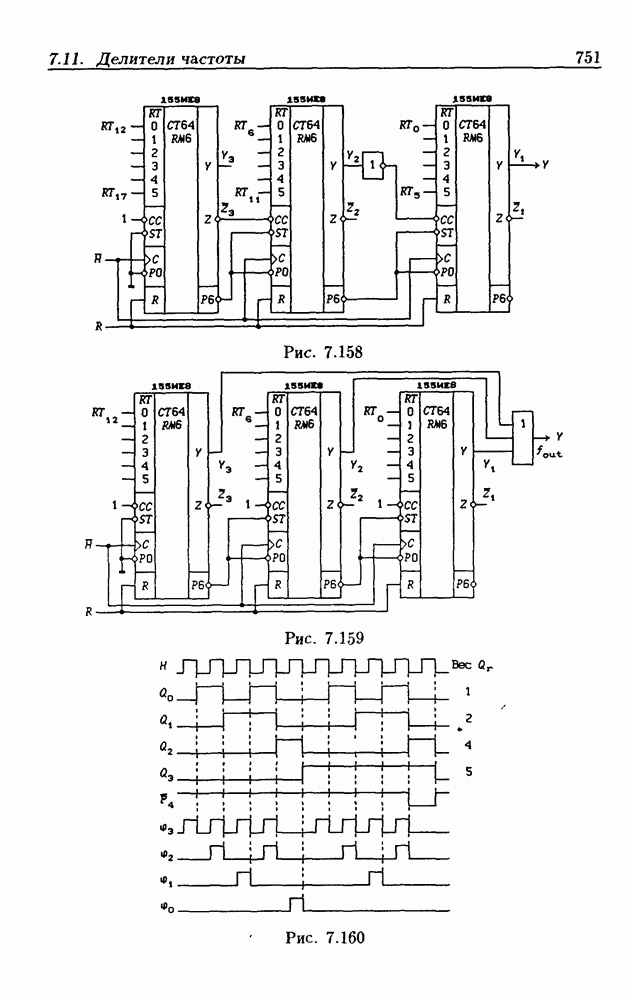
- 7.11. Делители частоты
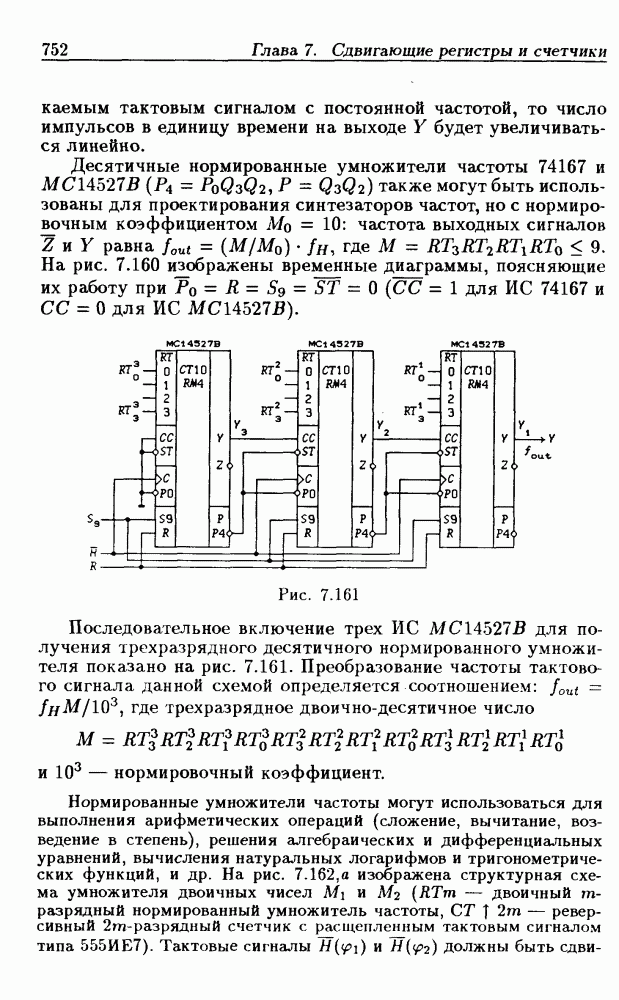
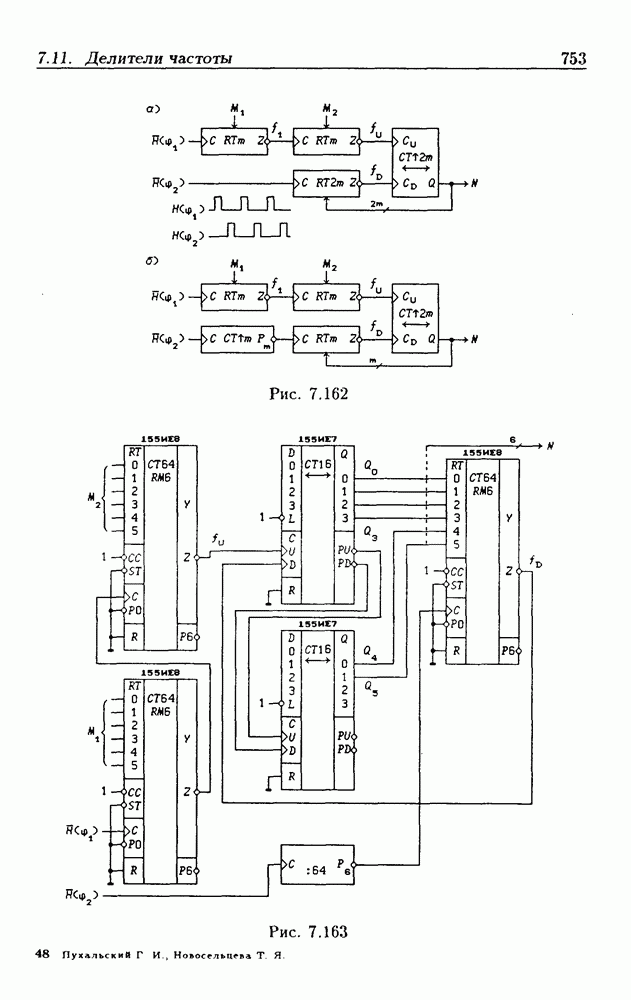
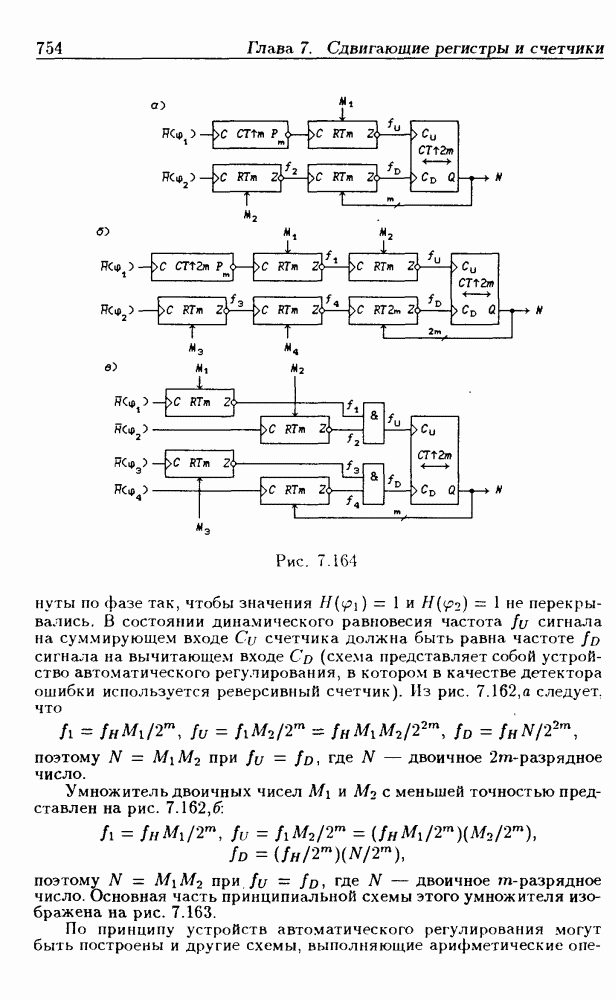
- Нормированные умножители частоты.
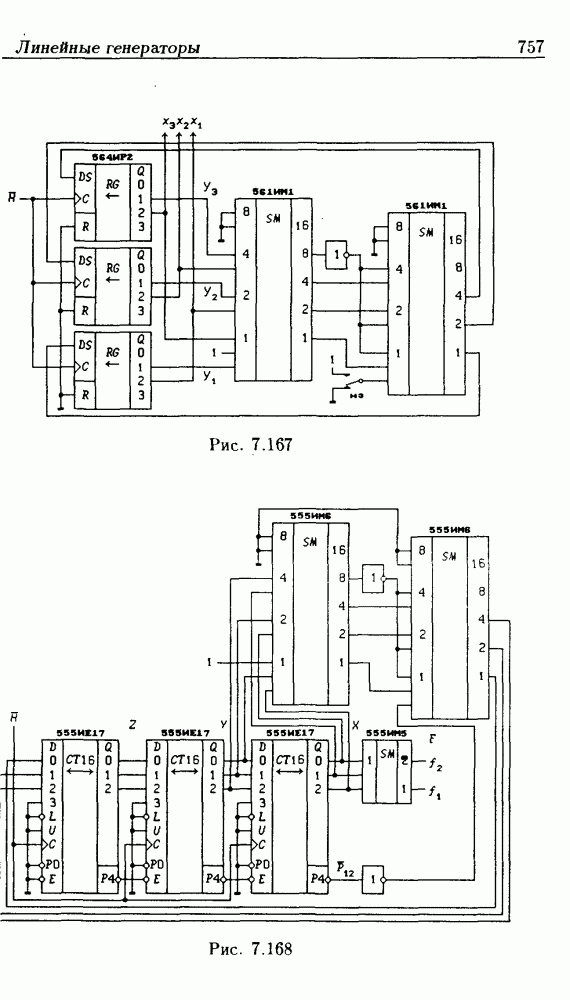
- 7.12. Линейные генераторы
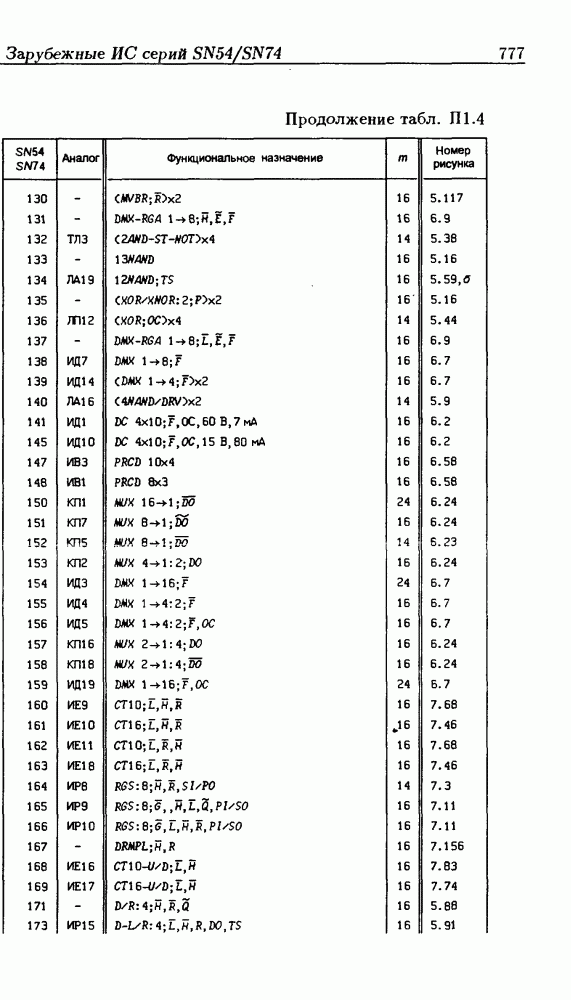
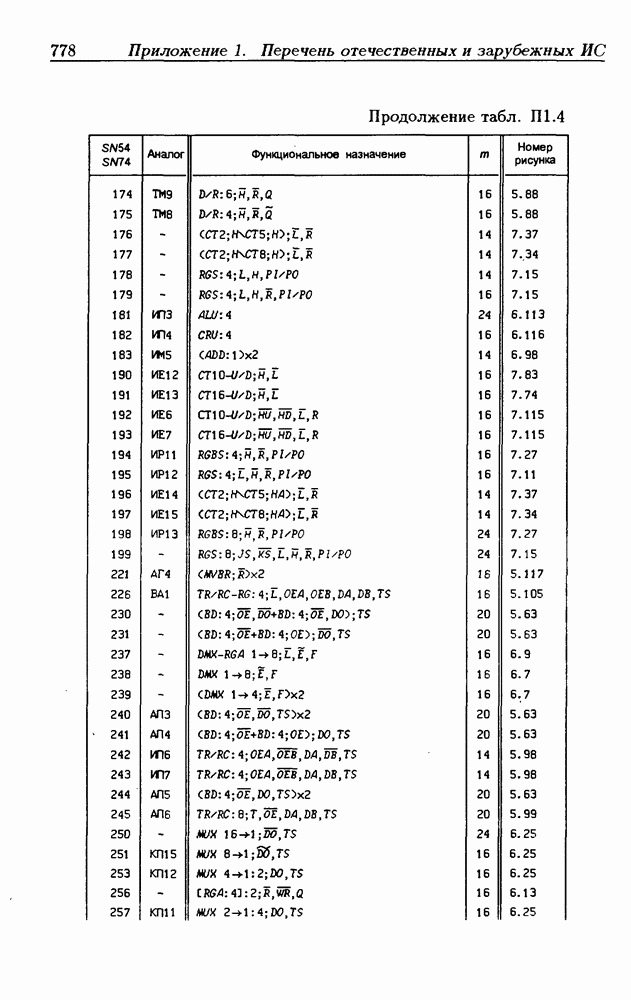
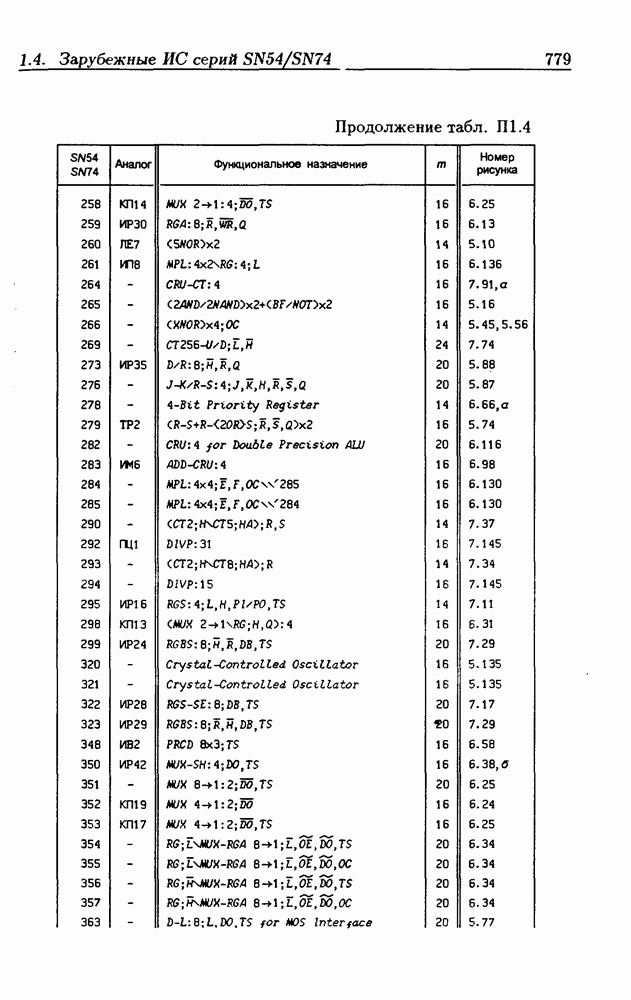
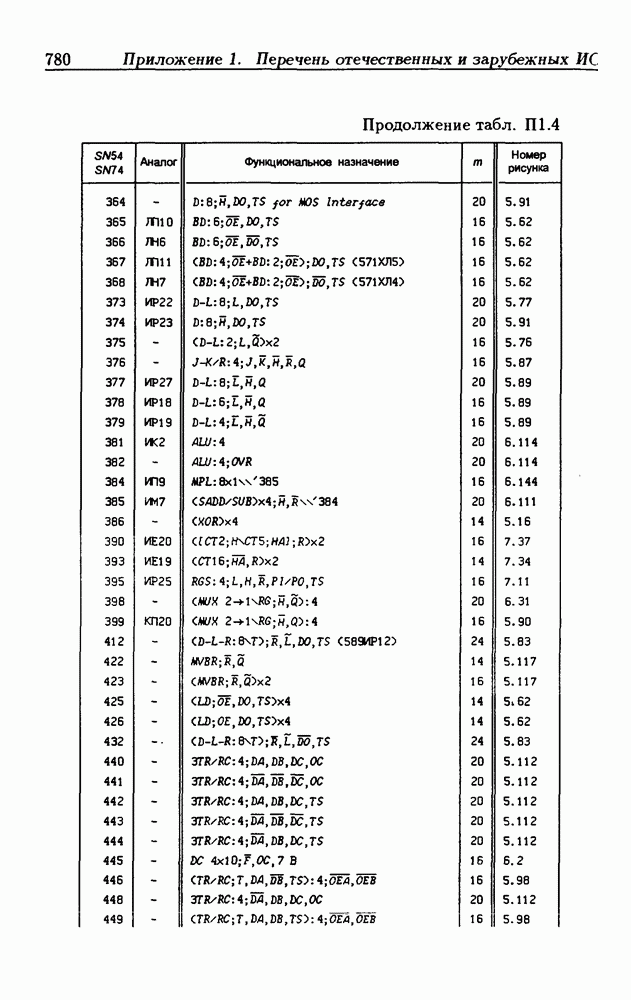
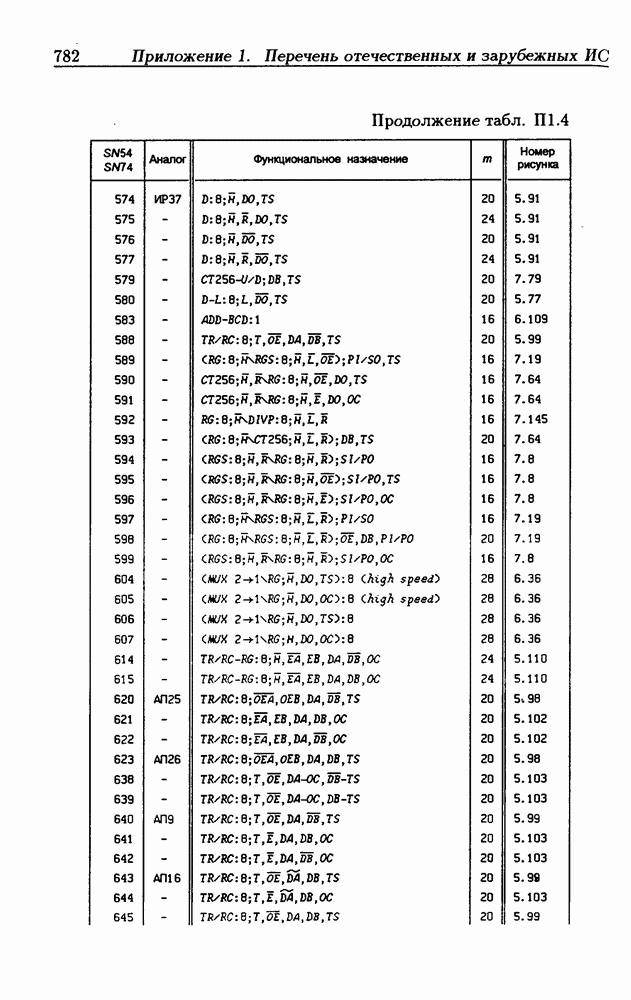
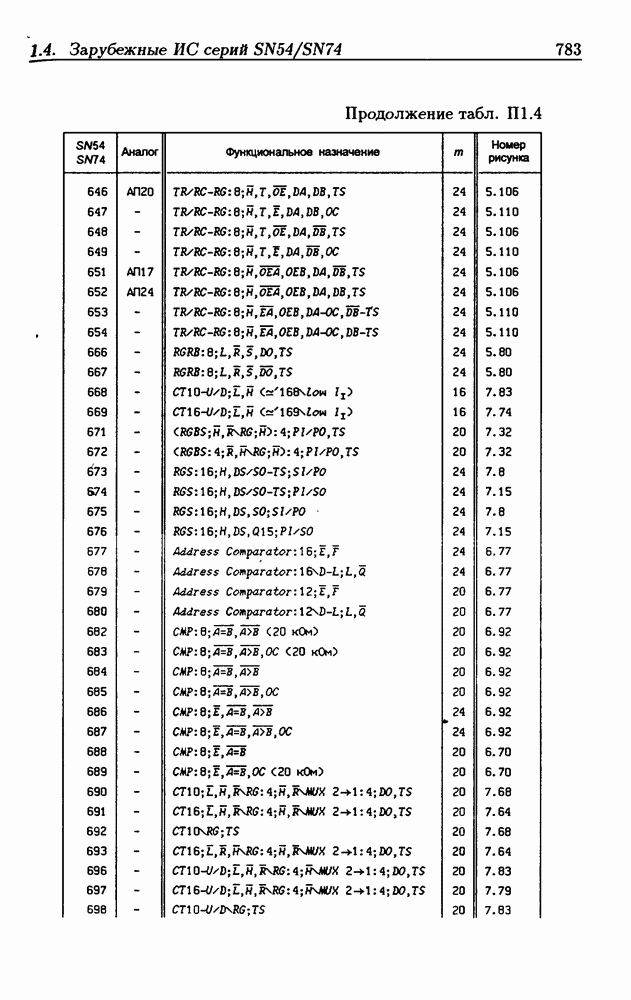
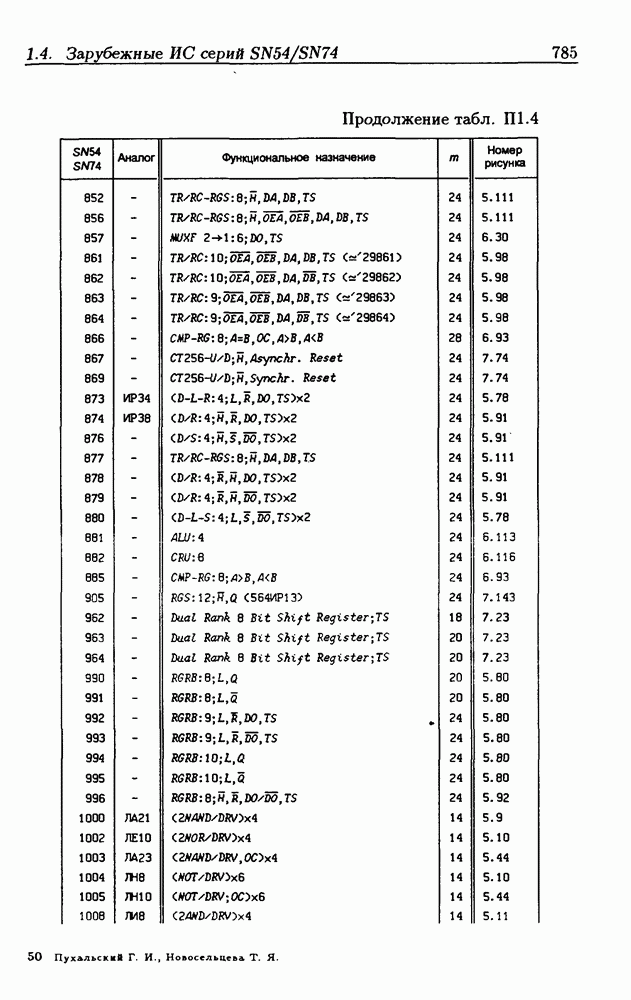
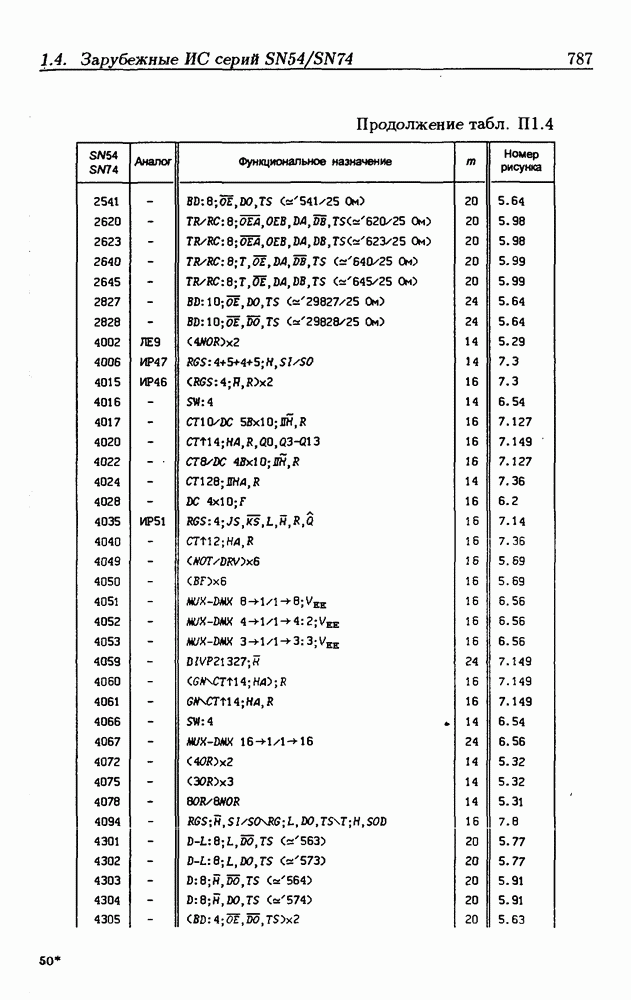
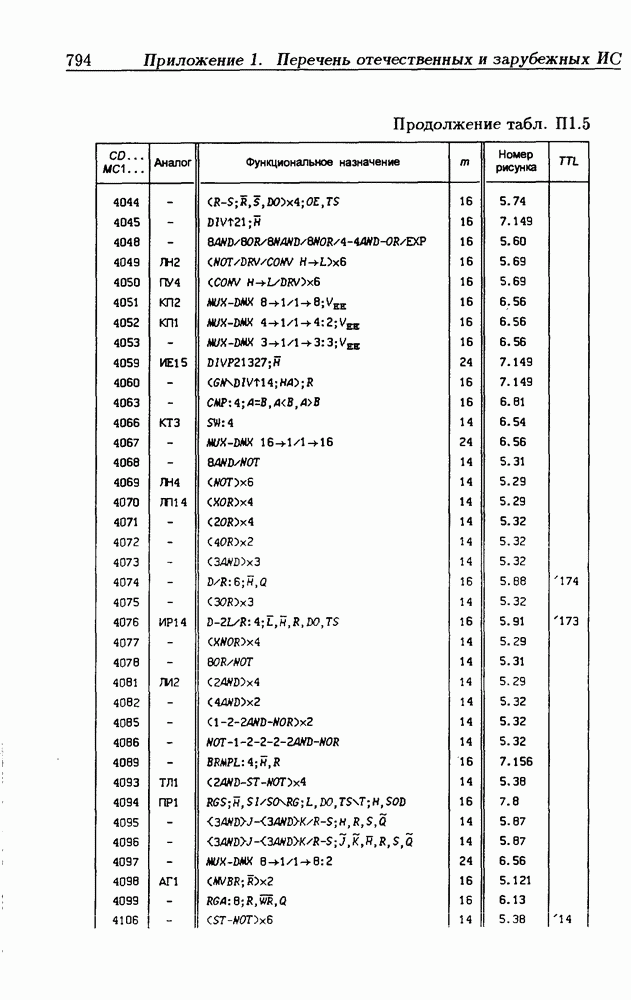
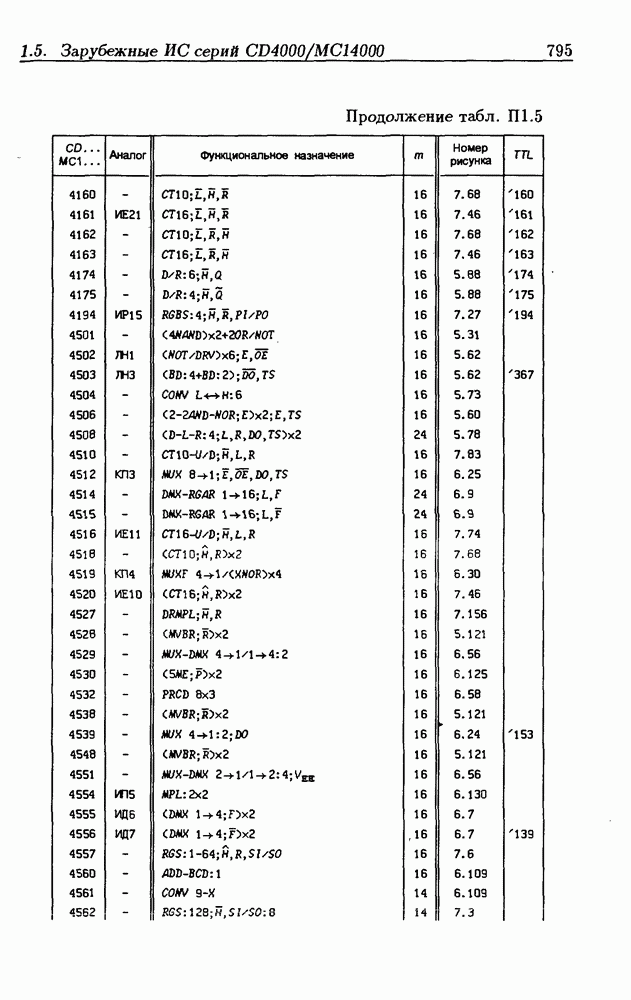
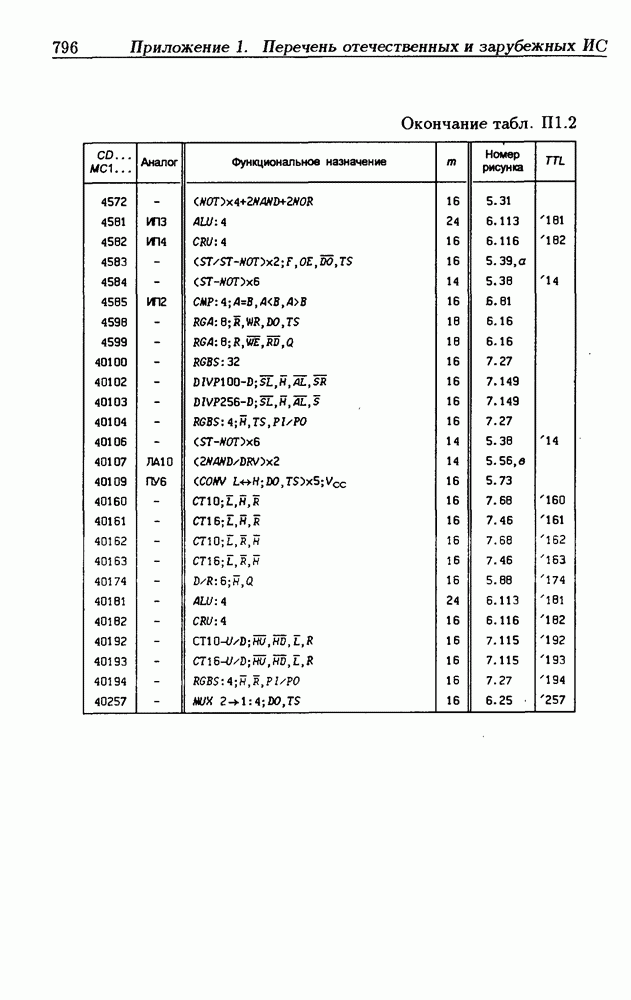
- Приложение 1. Перечень отечественных и зарубежных ИС
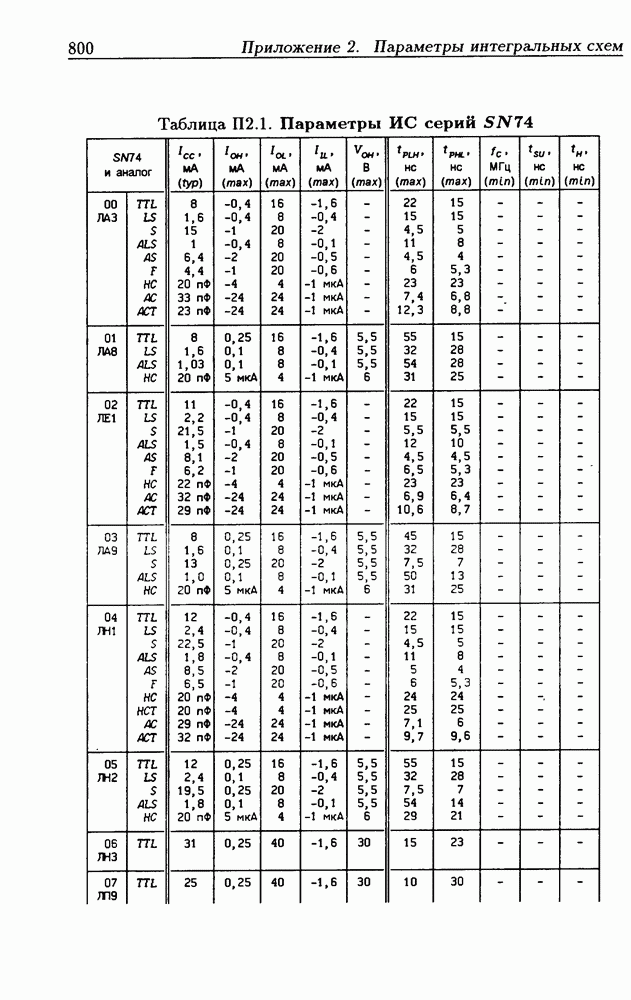
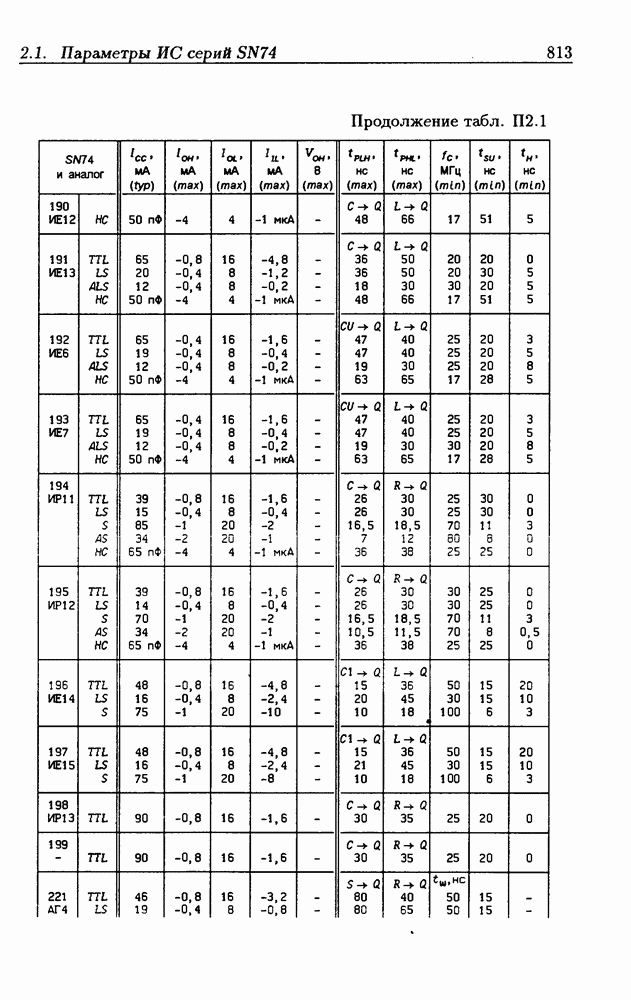
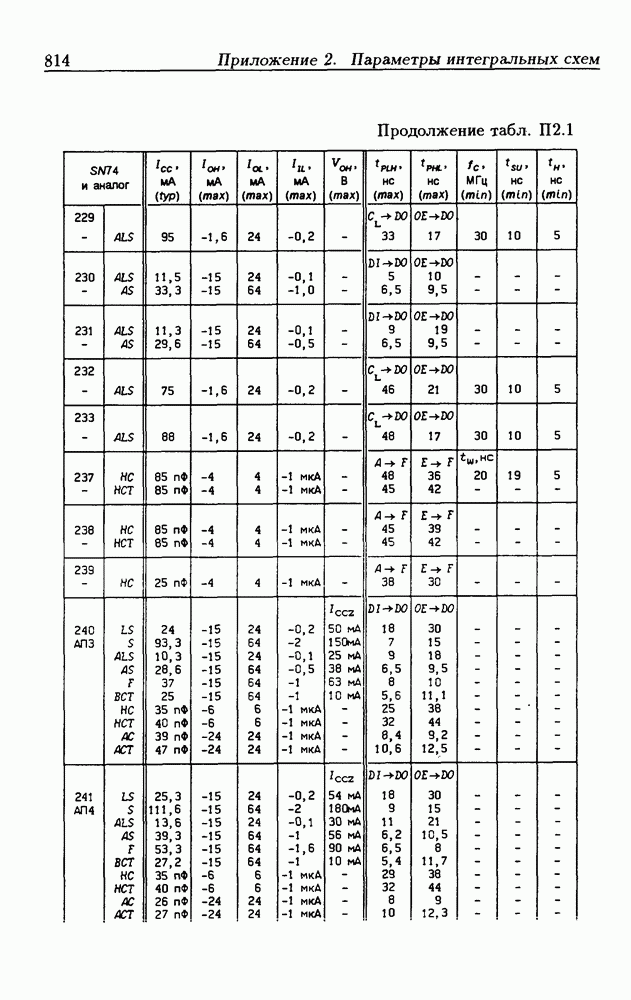
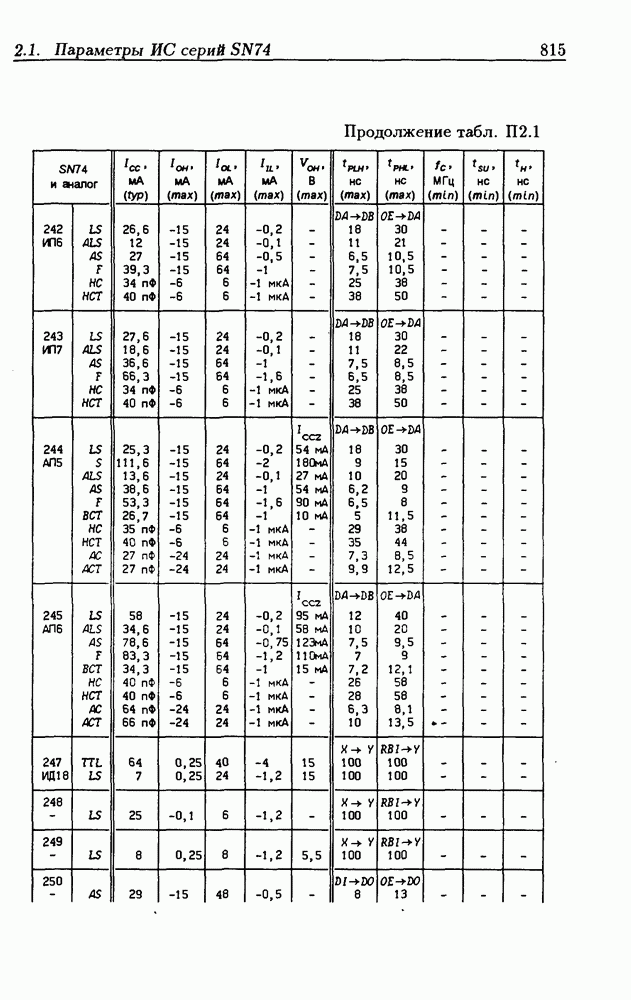
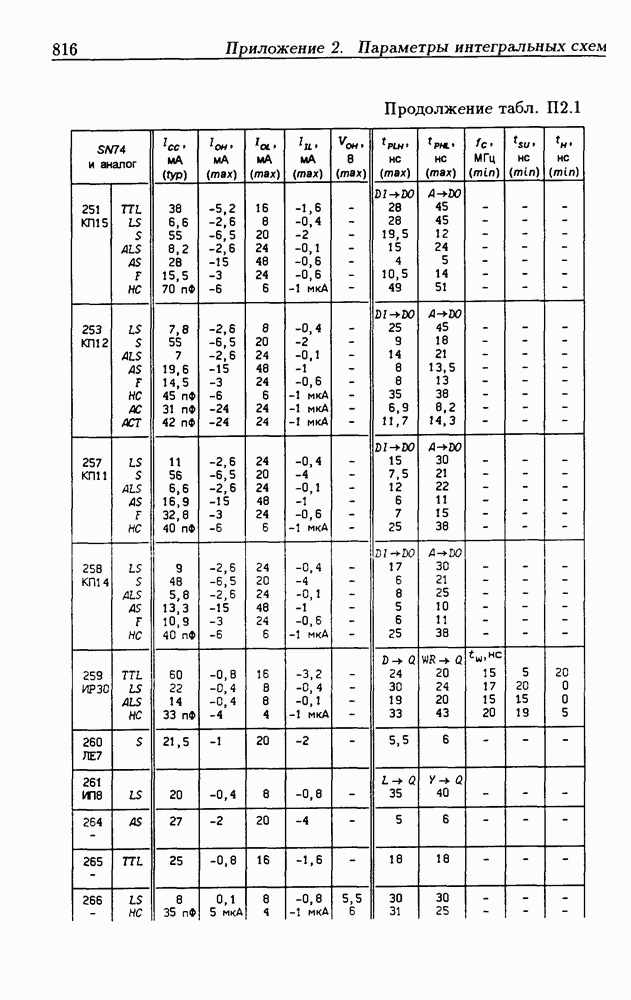
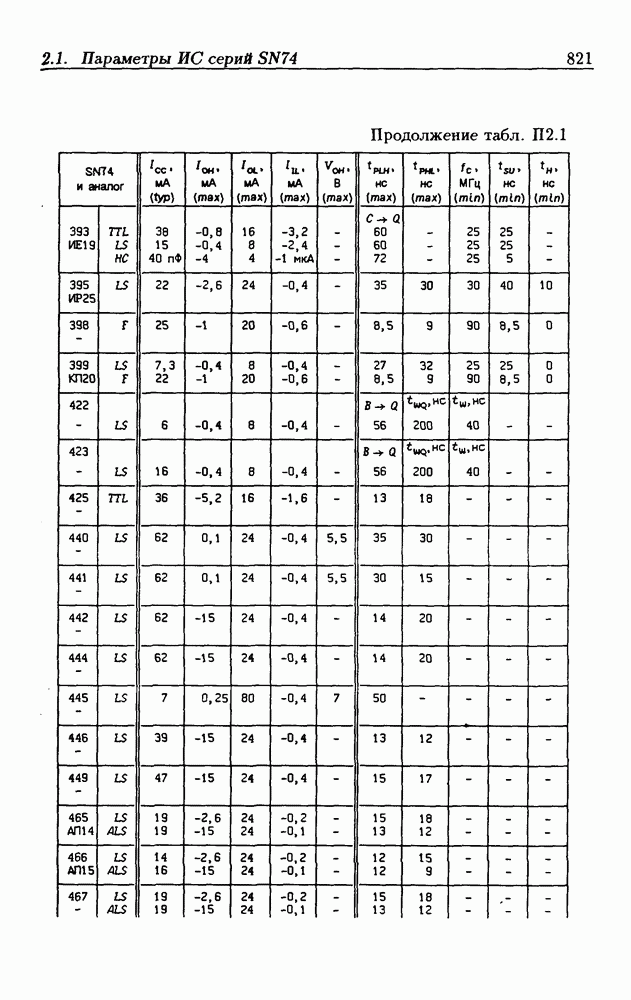
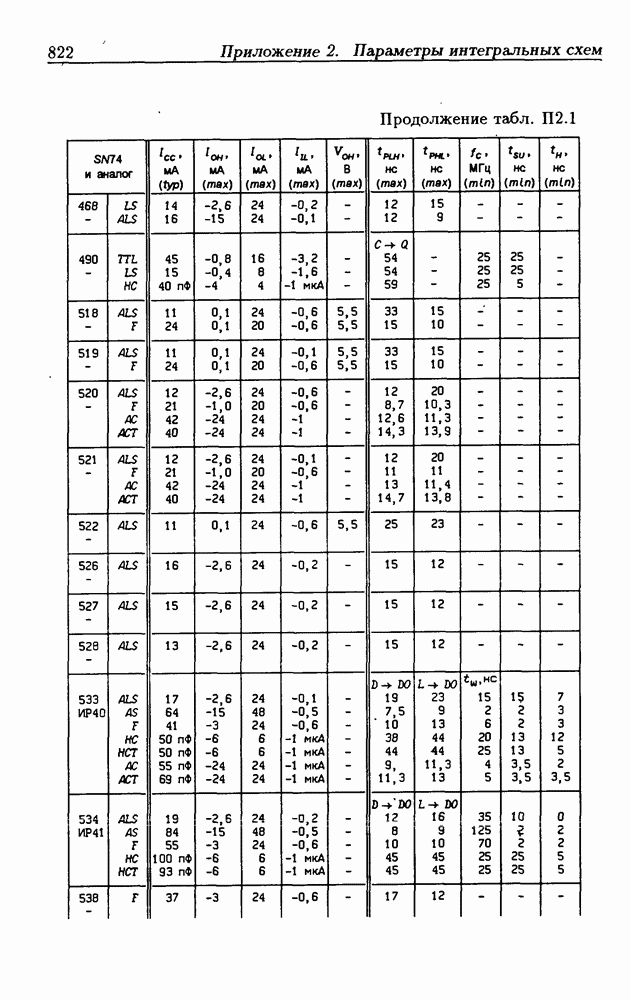
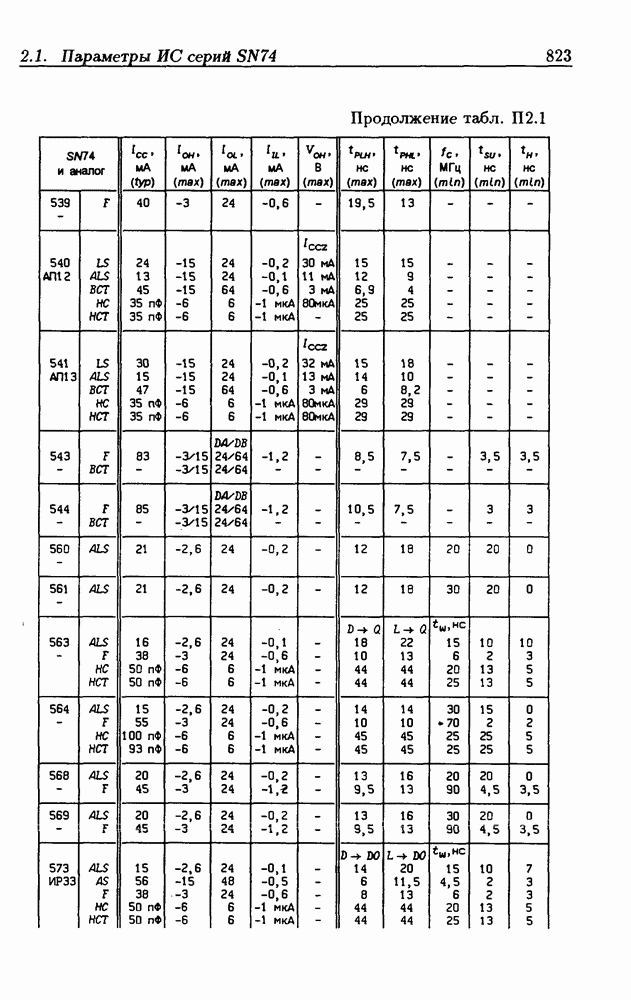
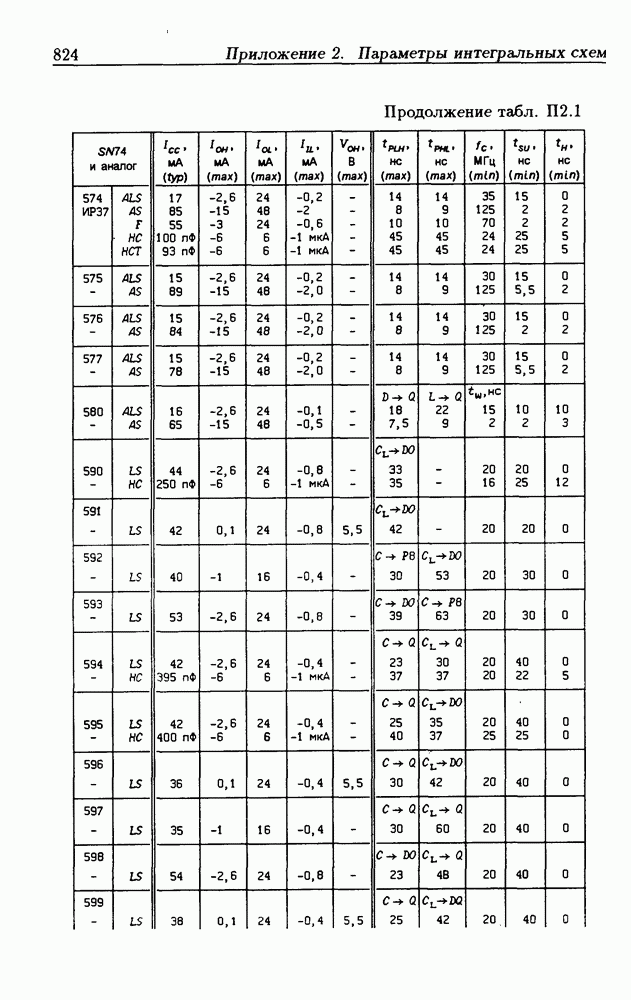
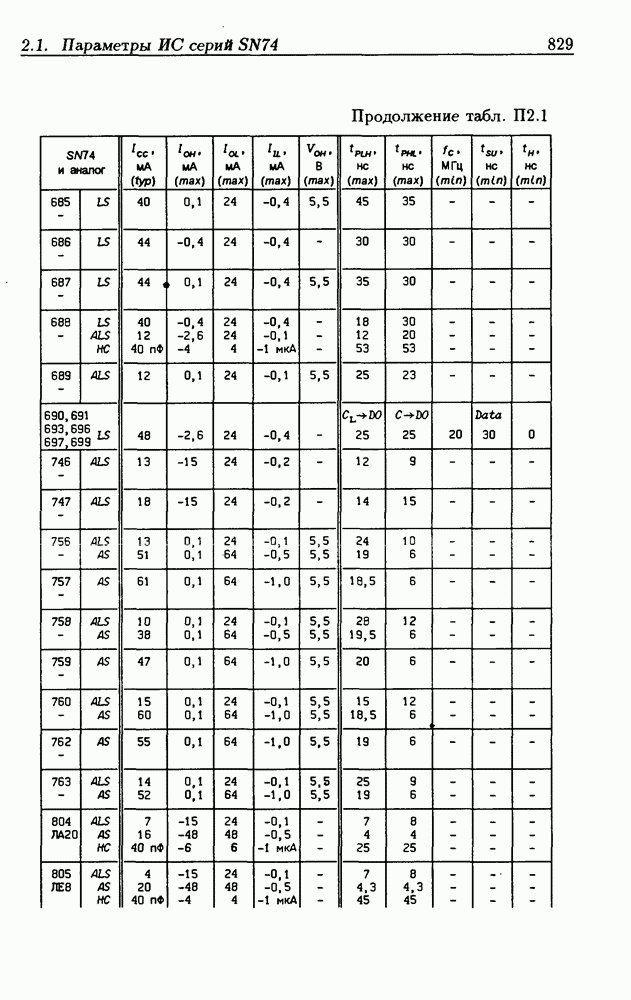
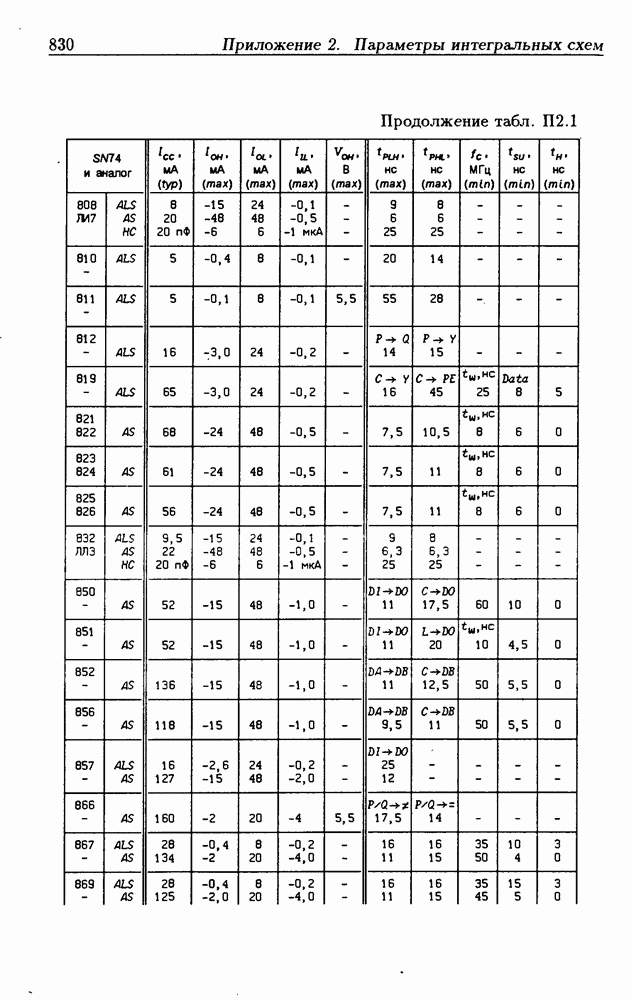
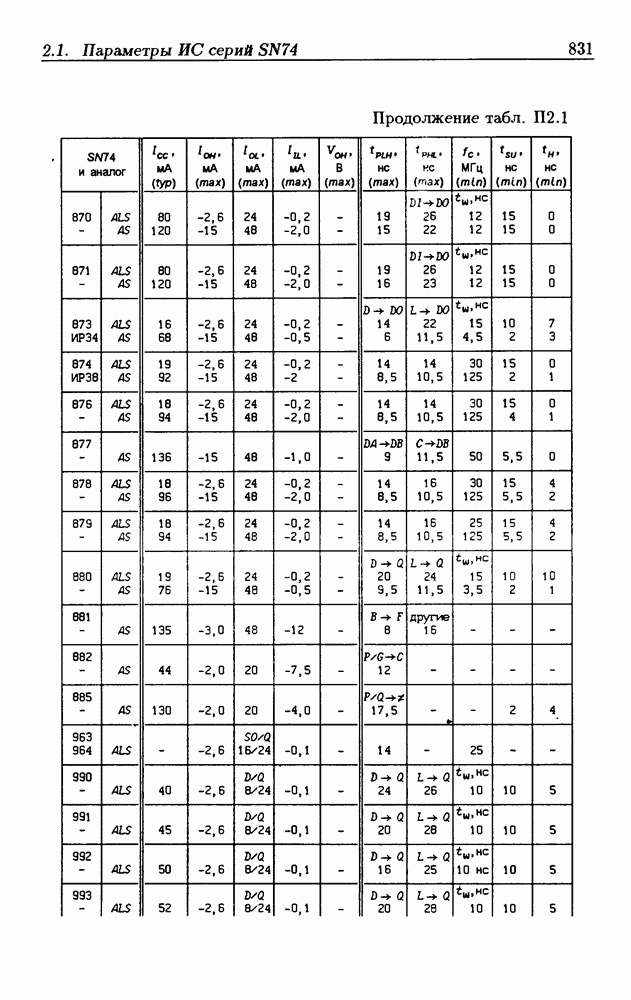
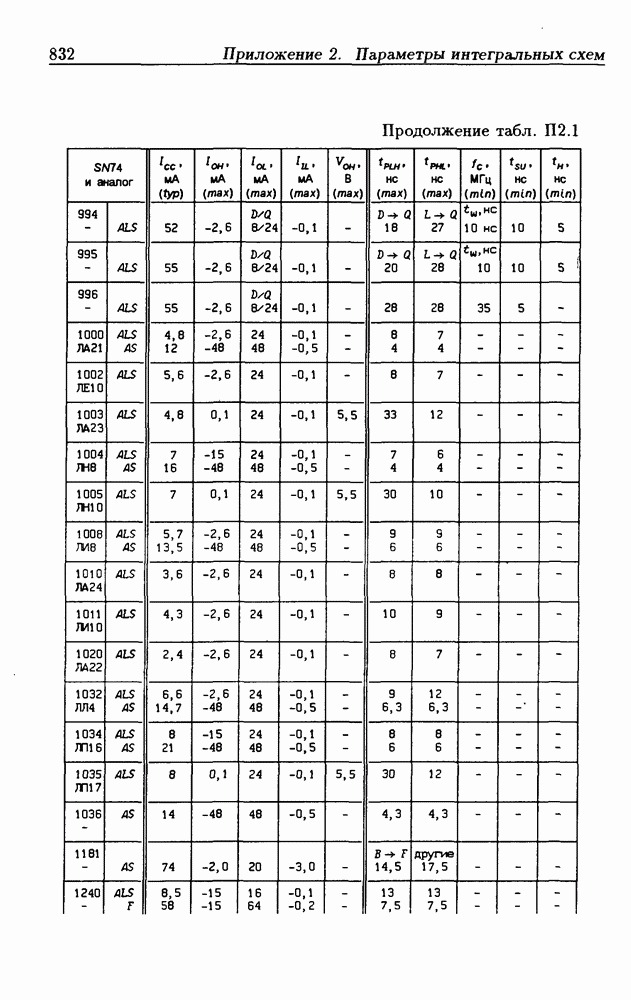
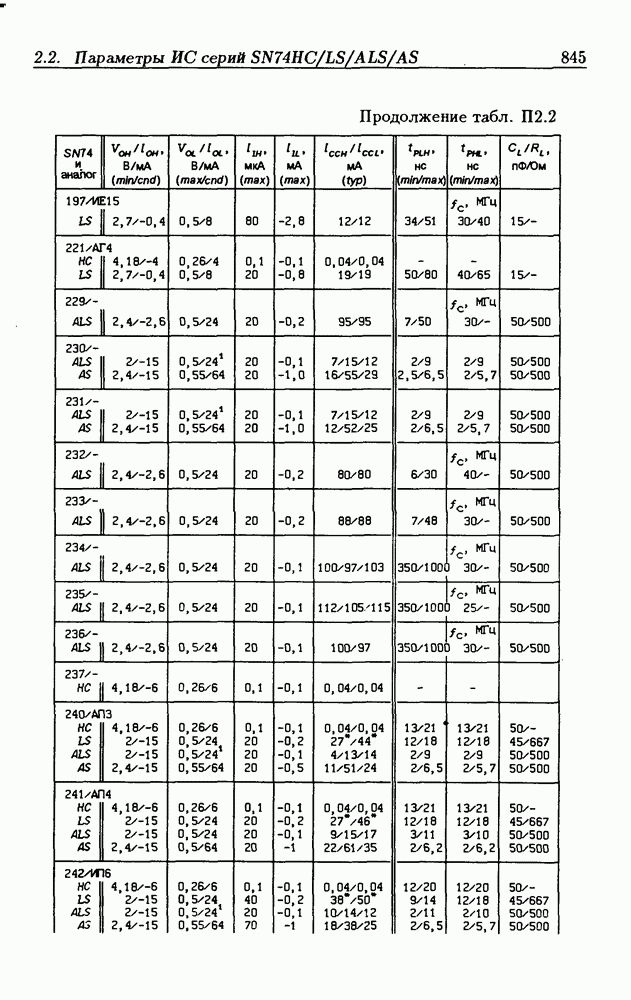
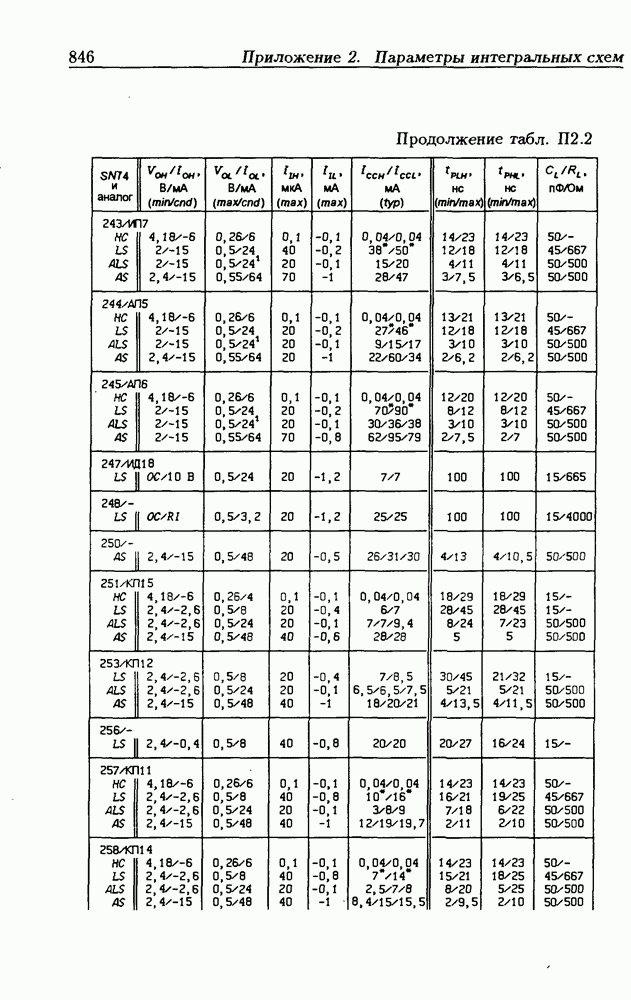
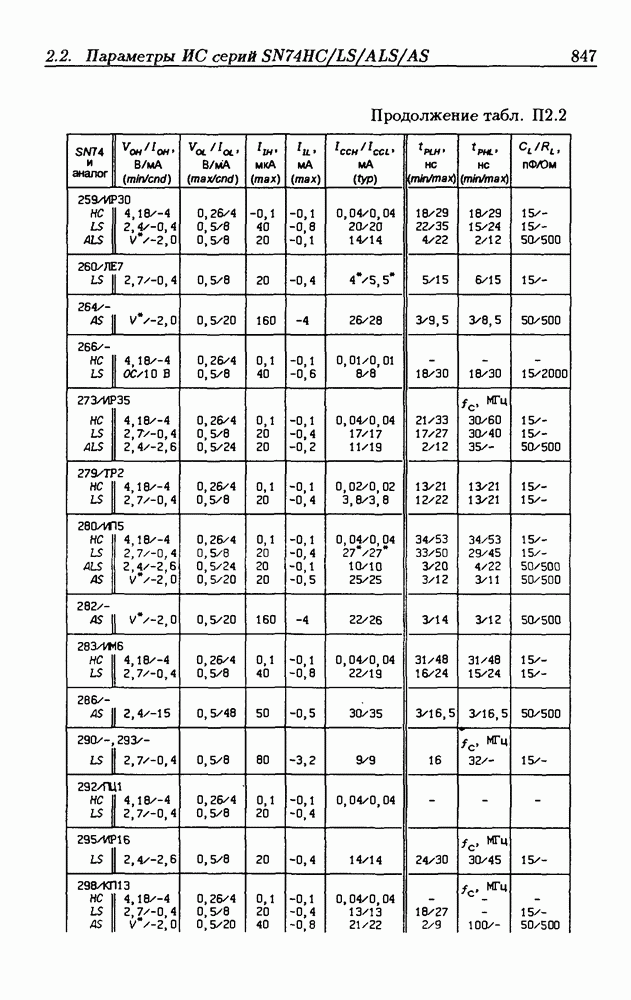
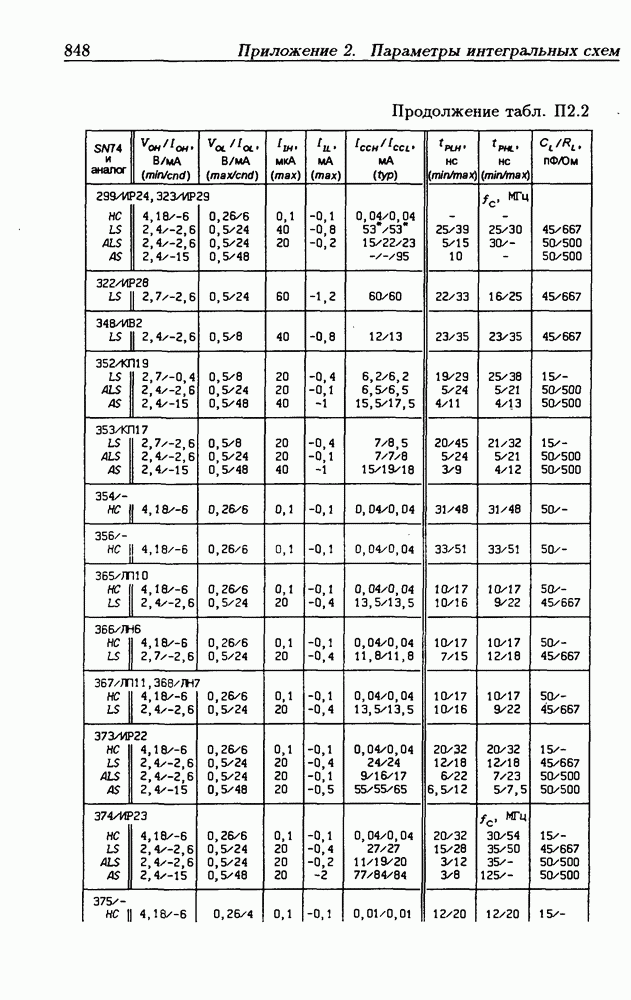
- Приложение 2. Параметры интегральных схем