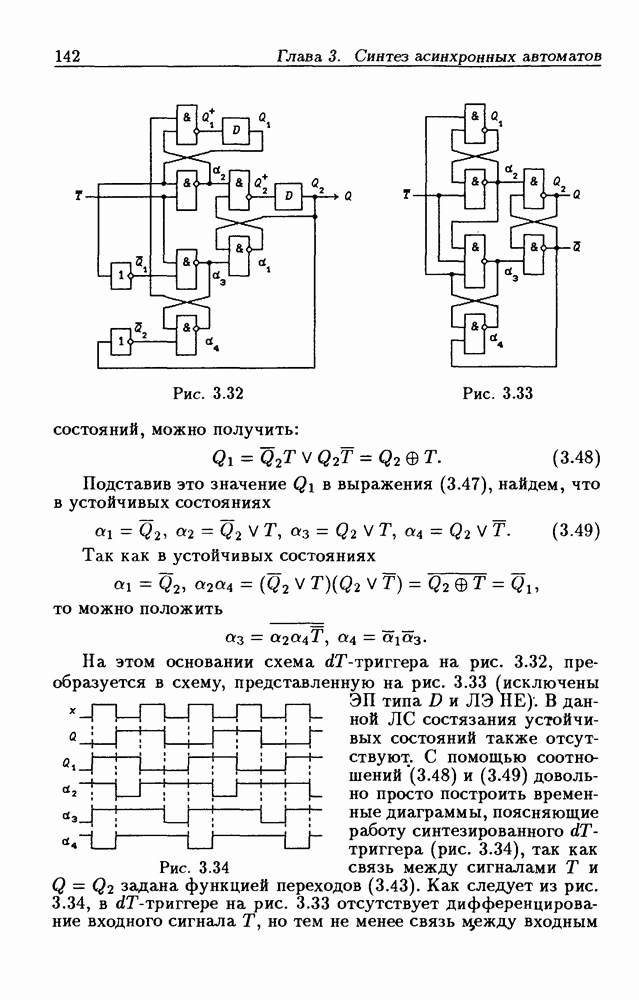
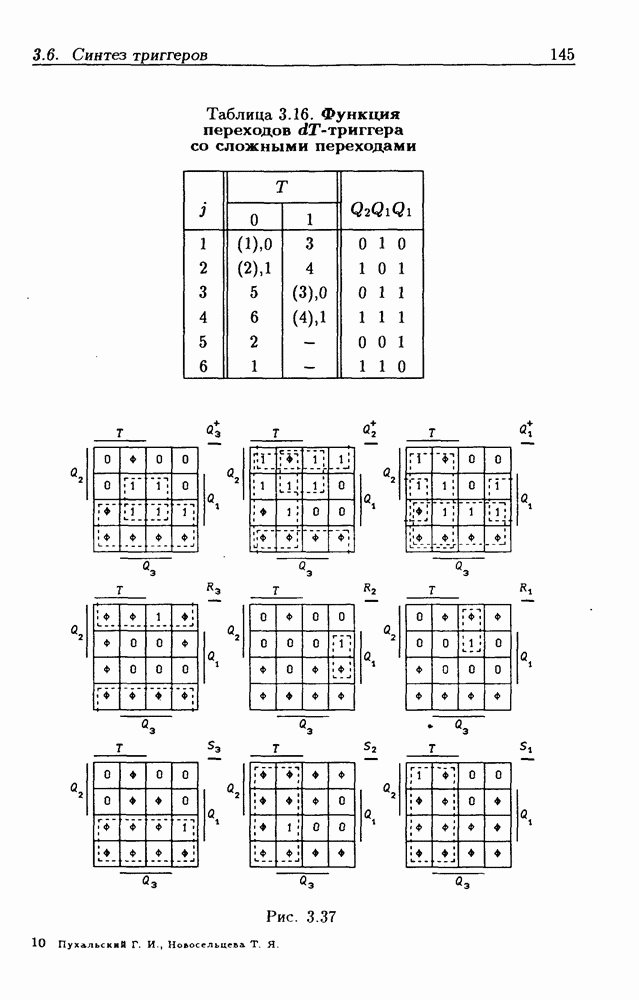
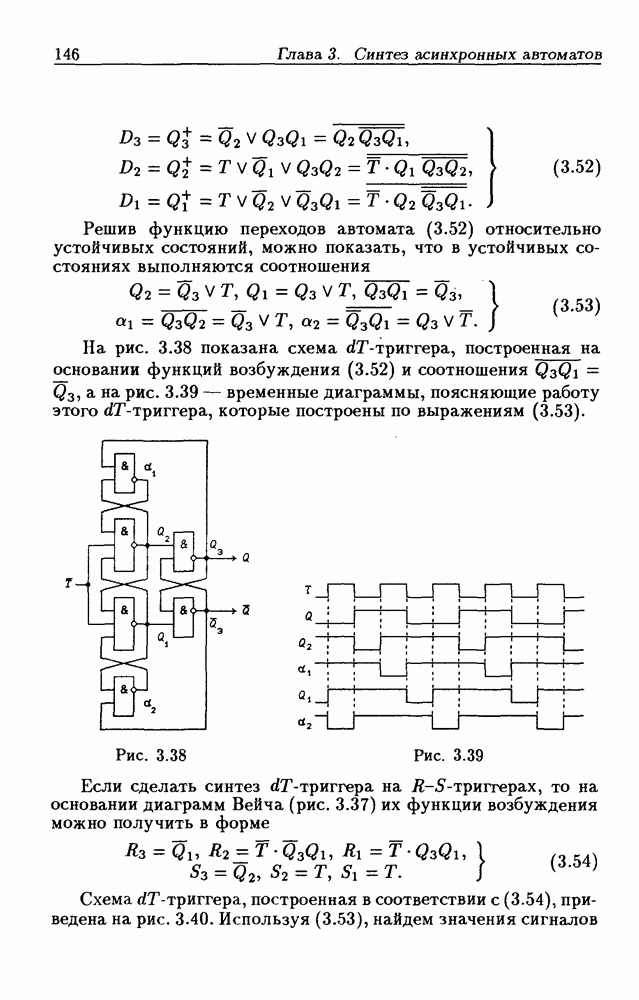
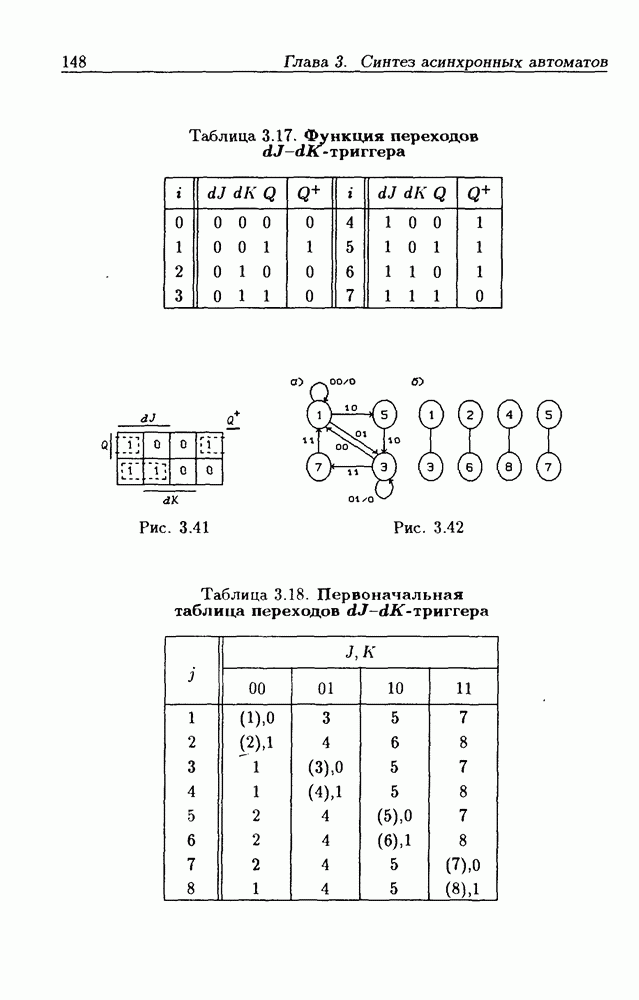
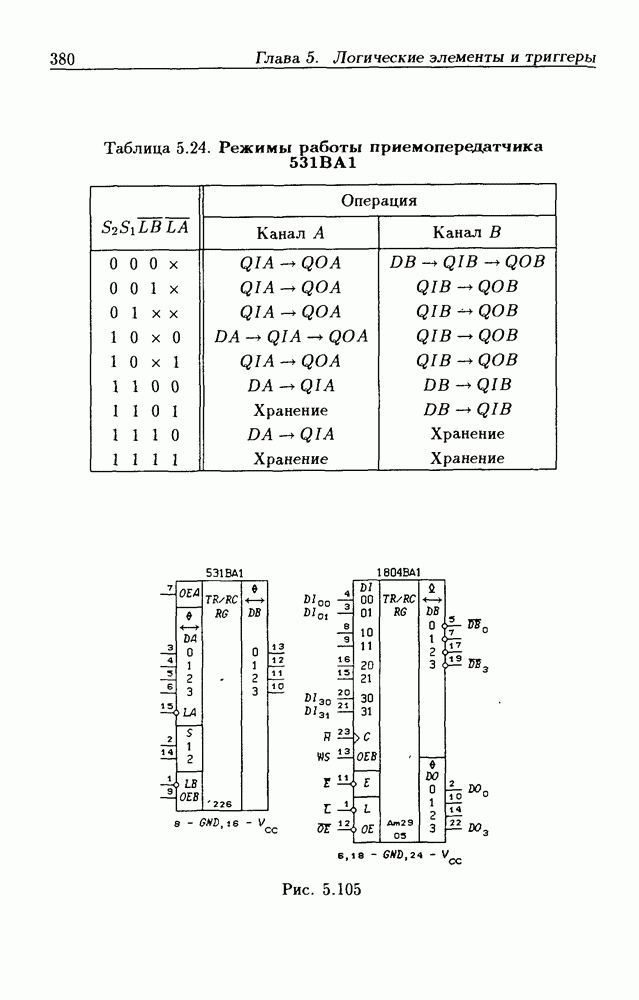
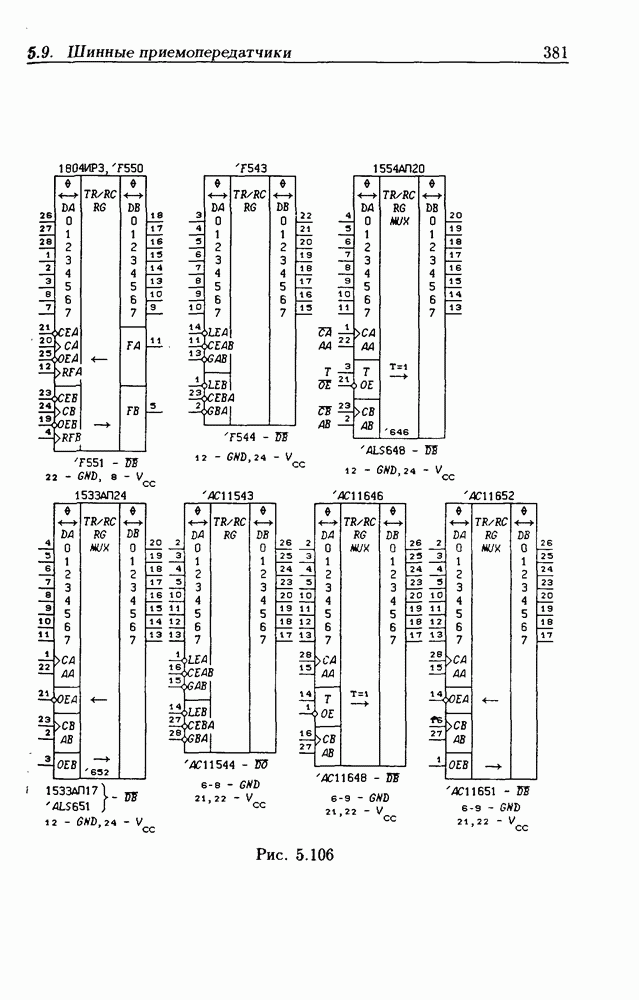
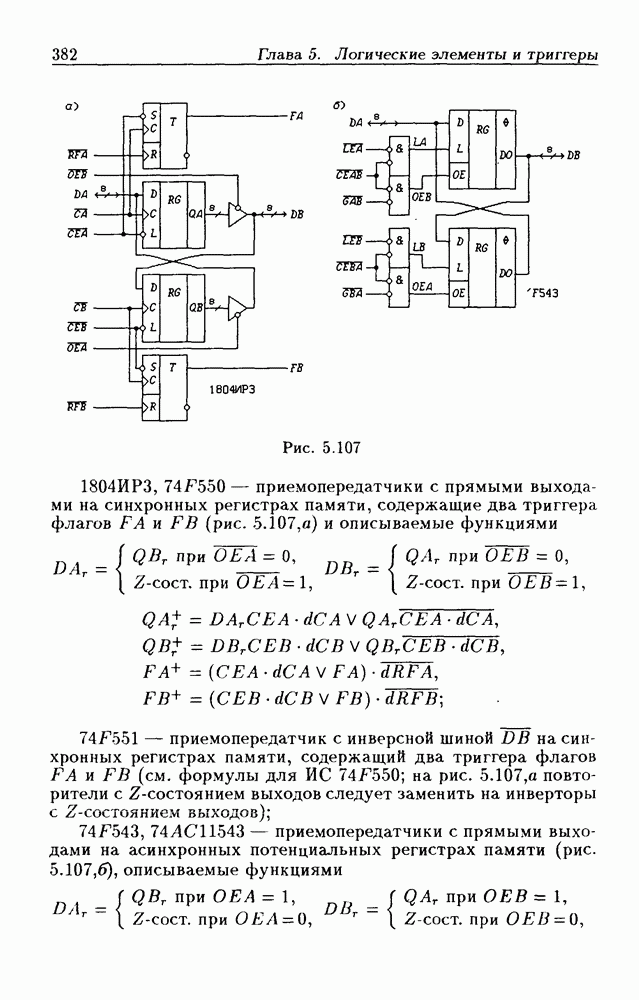
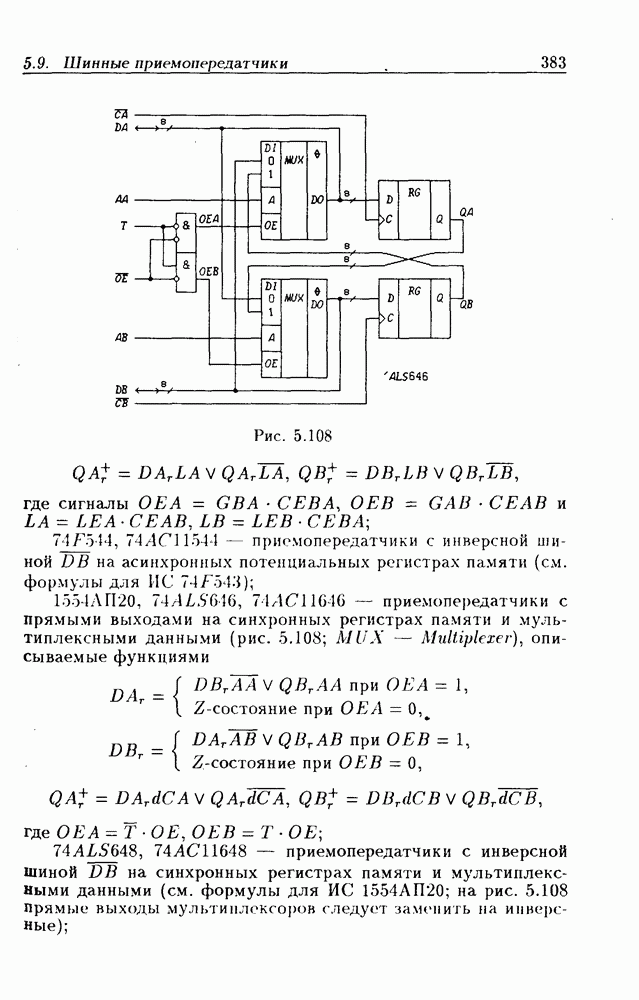
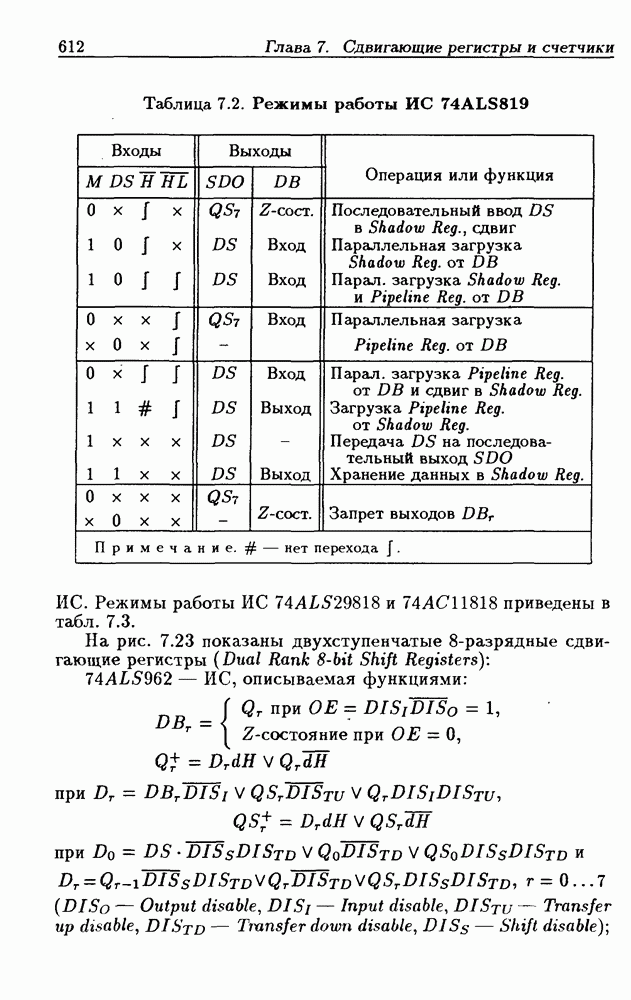
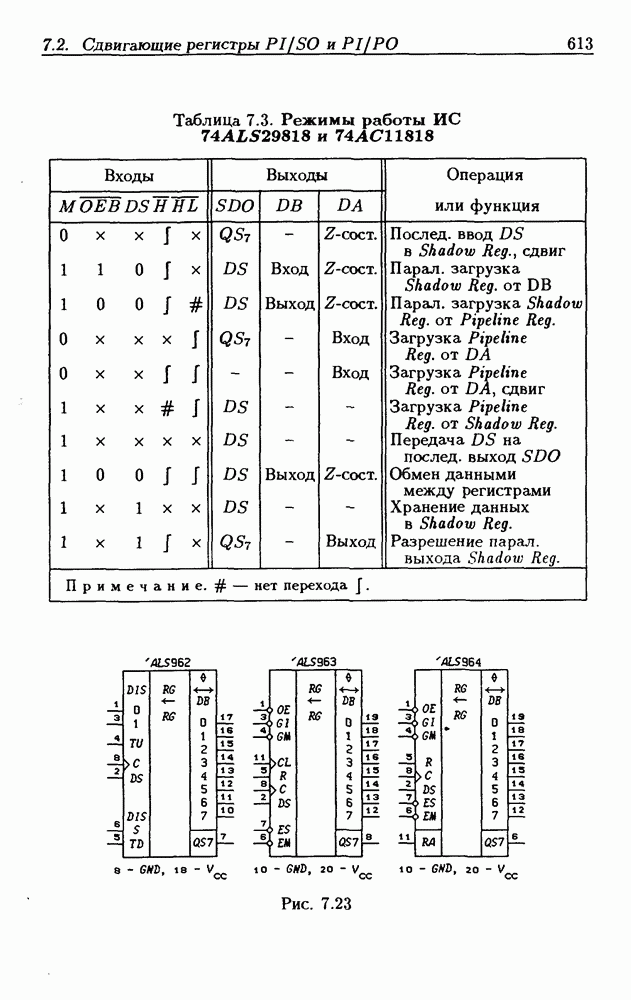
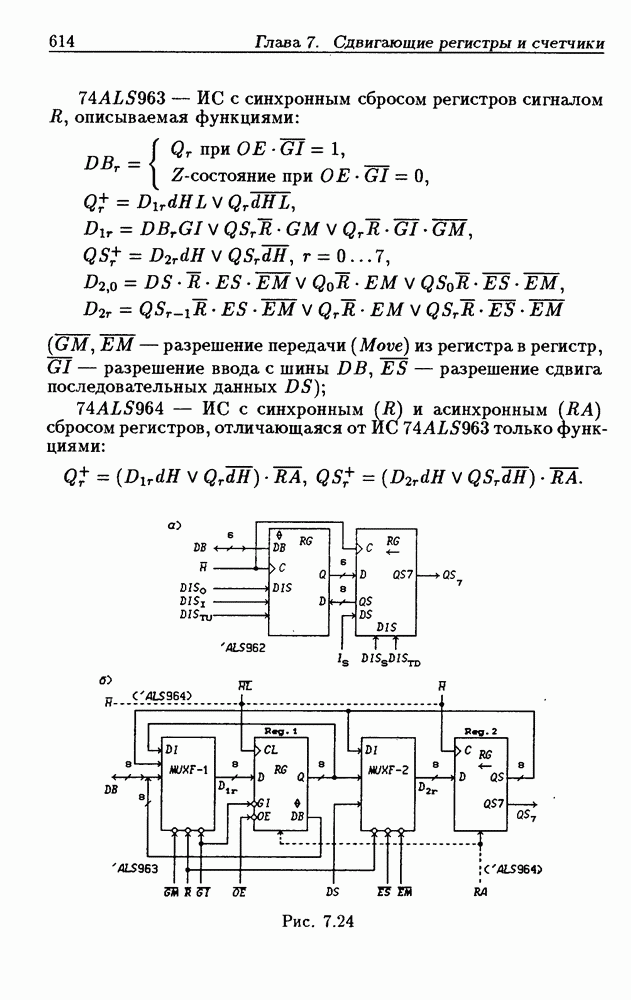
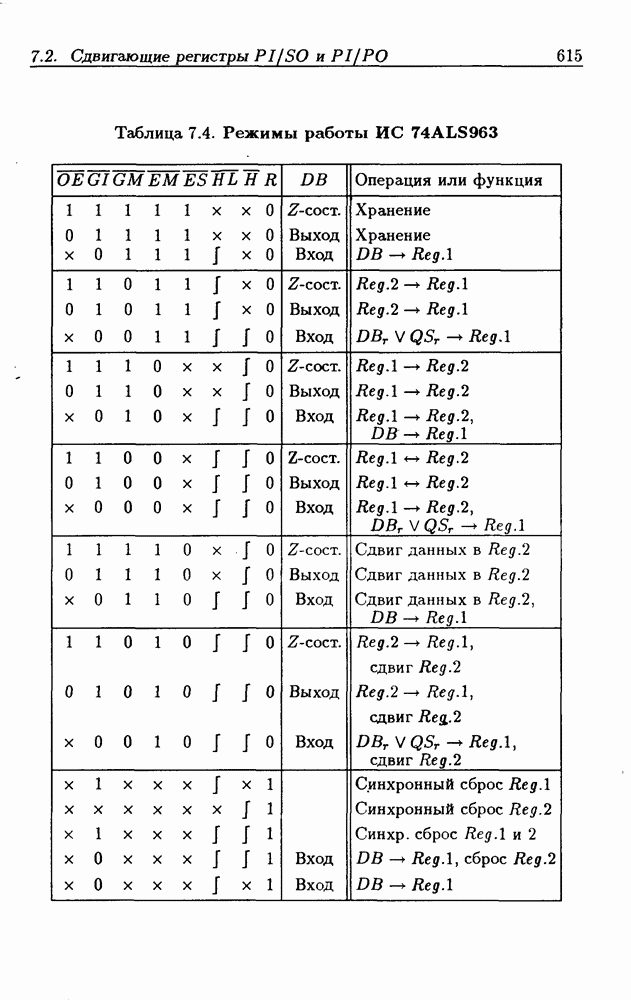
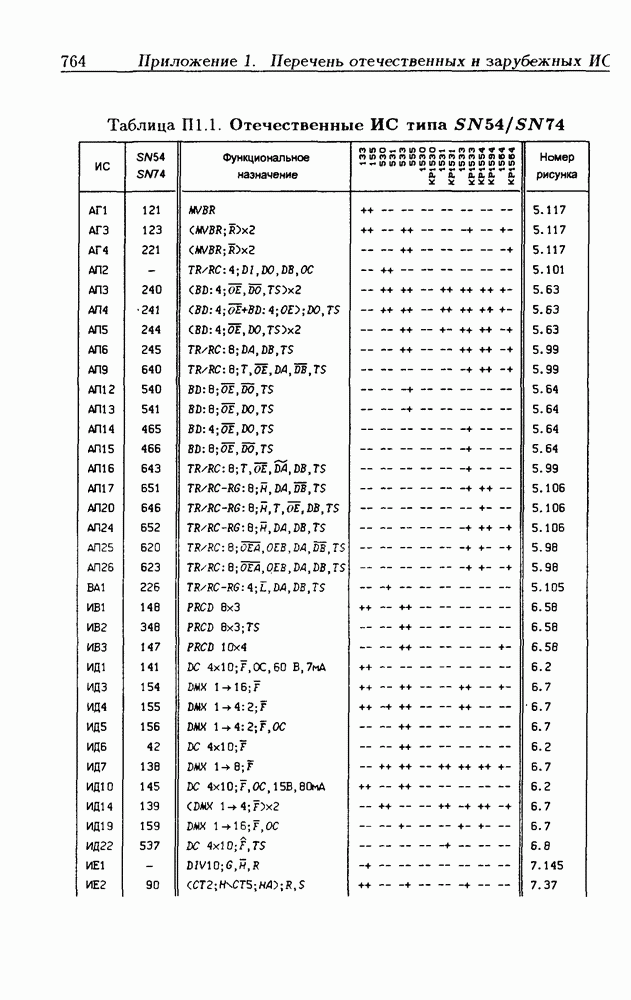
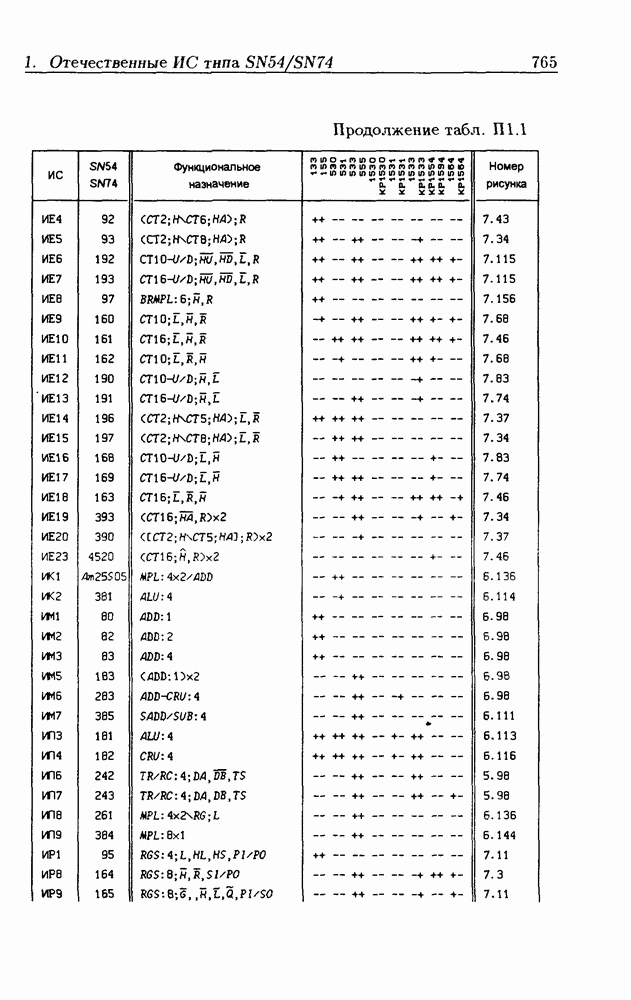
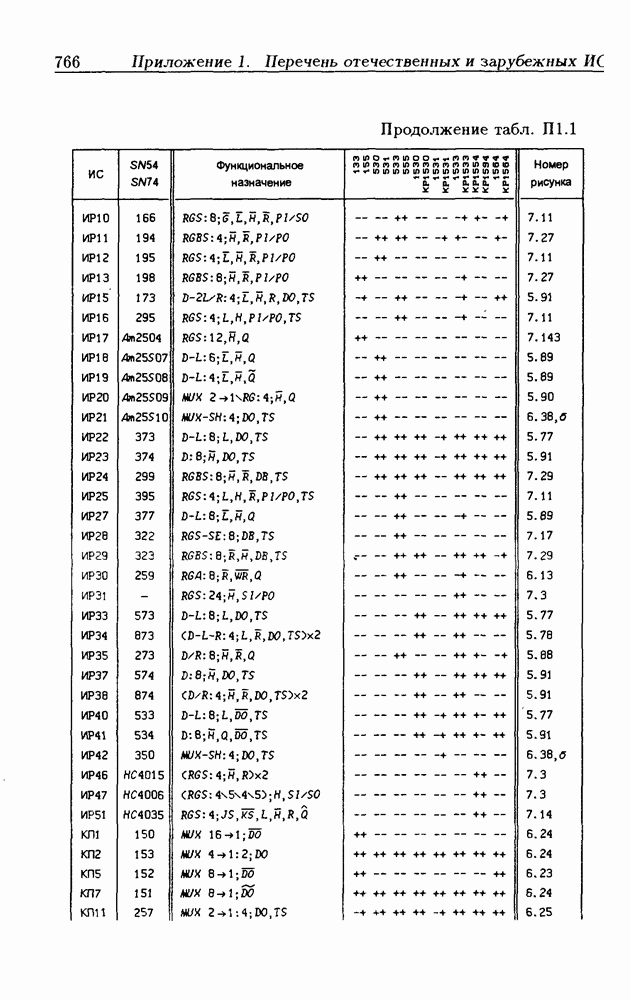
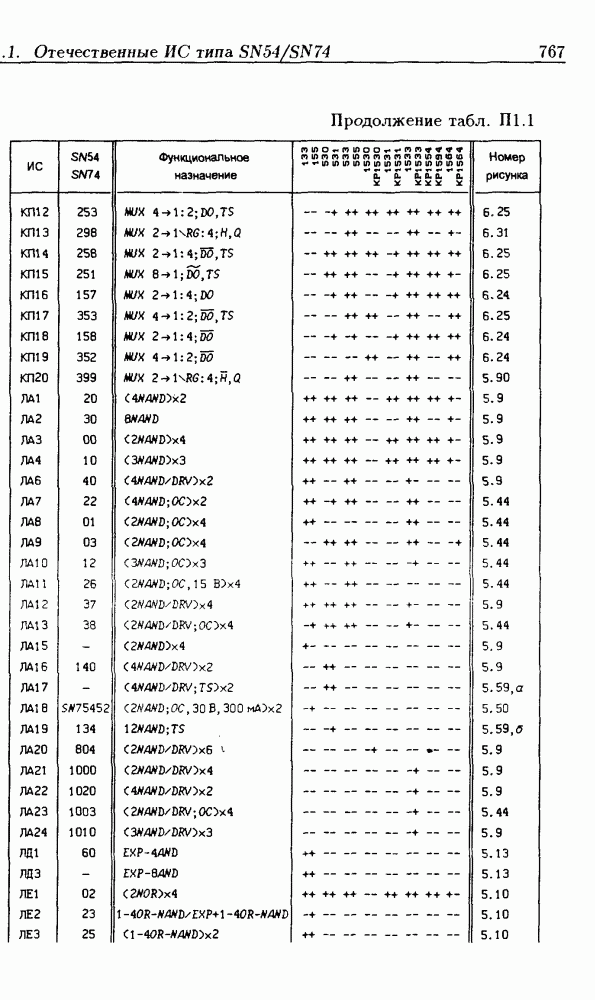
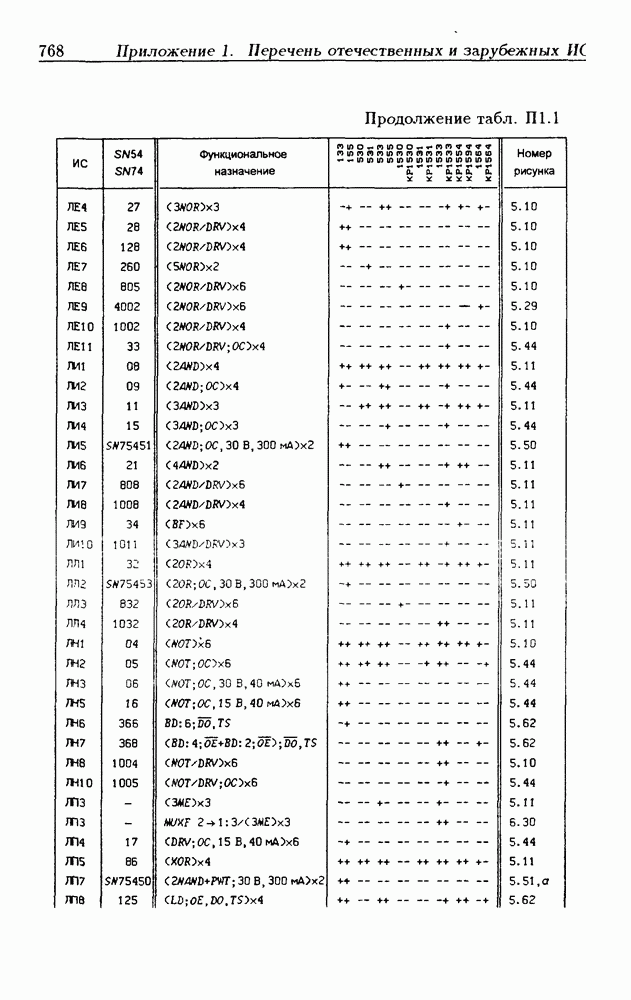
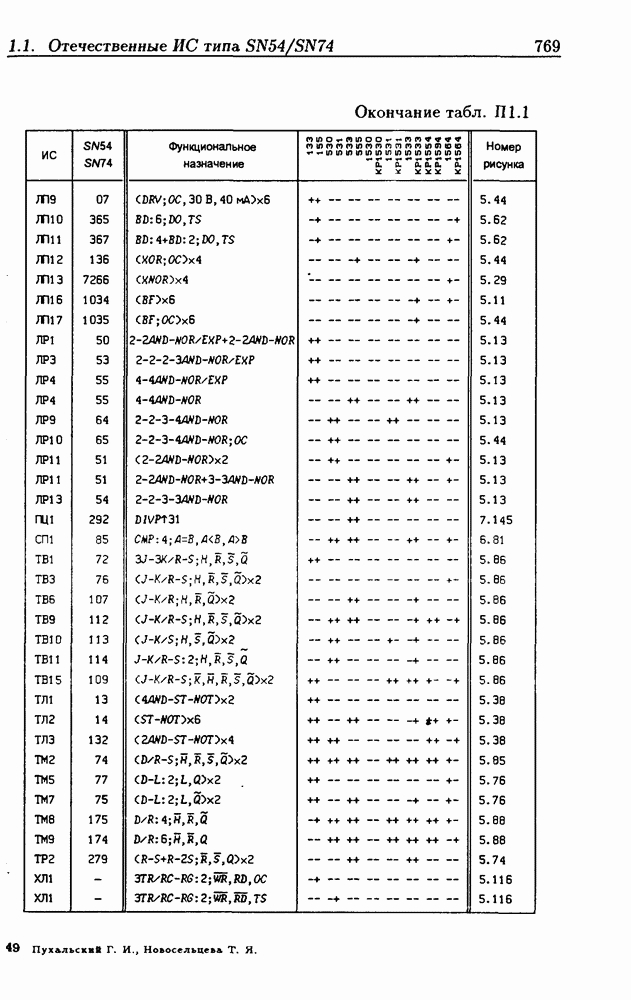
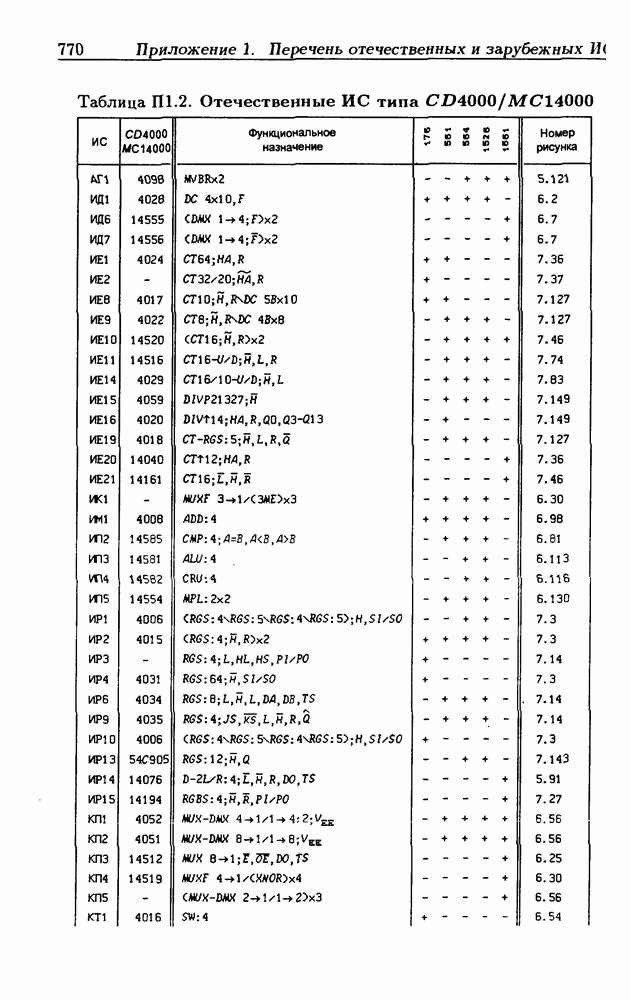
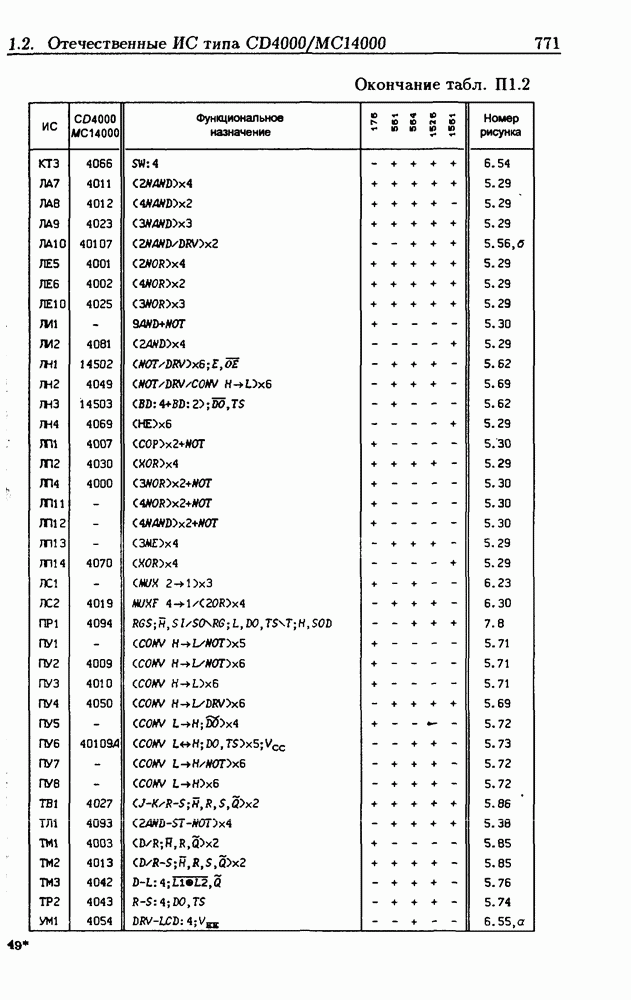
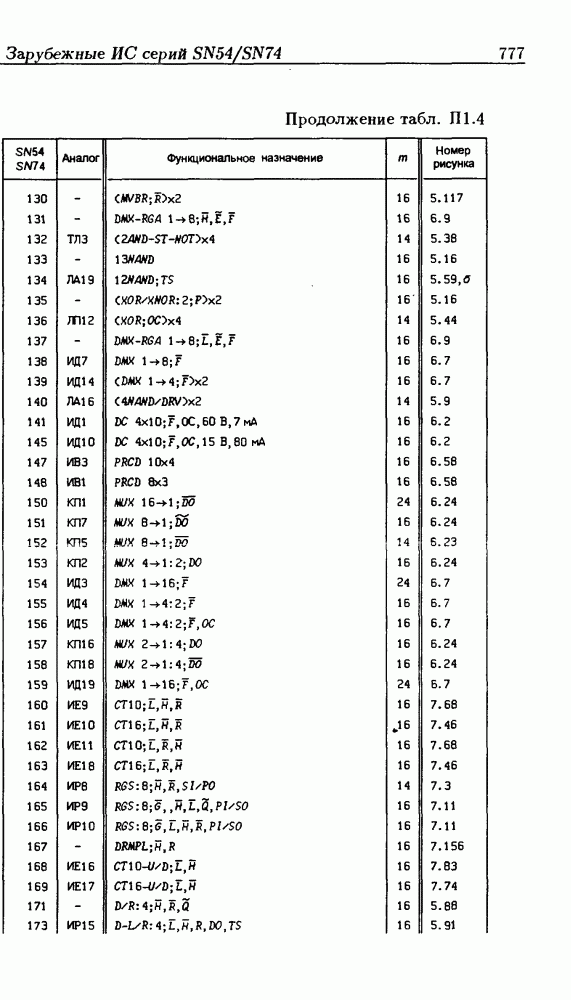
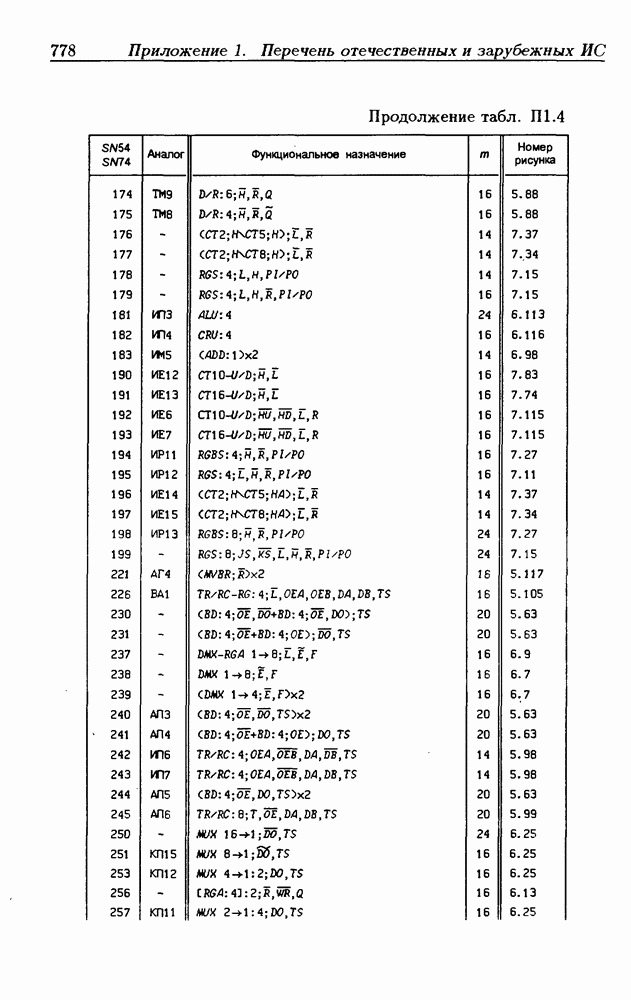
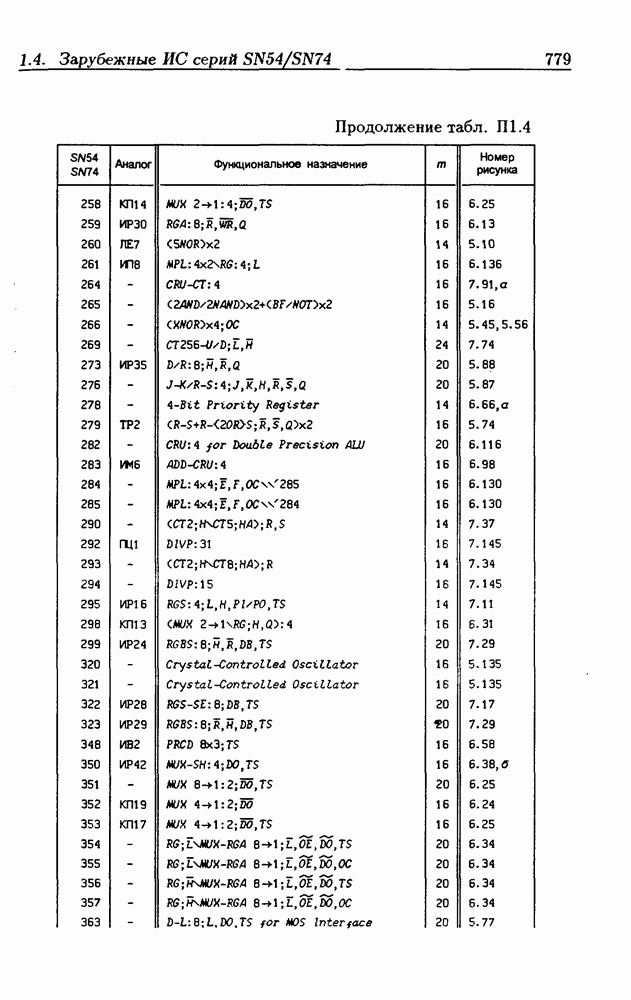
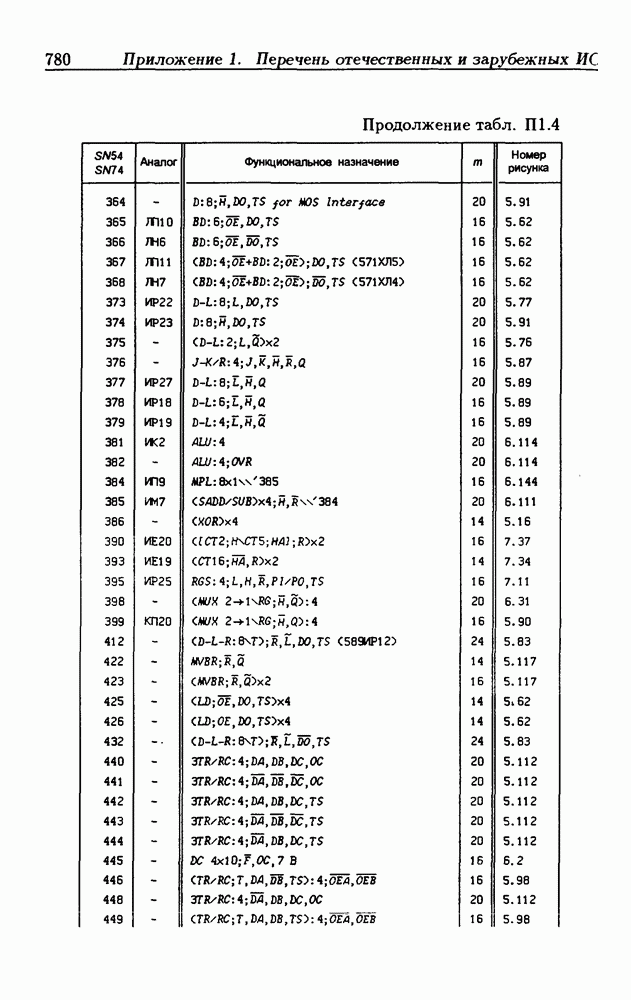
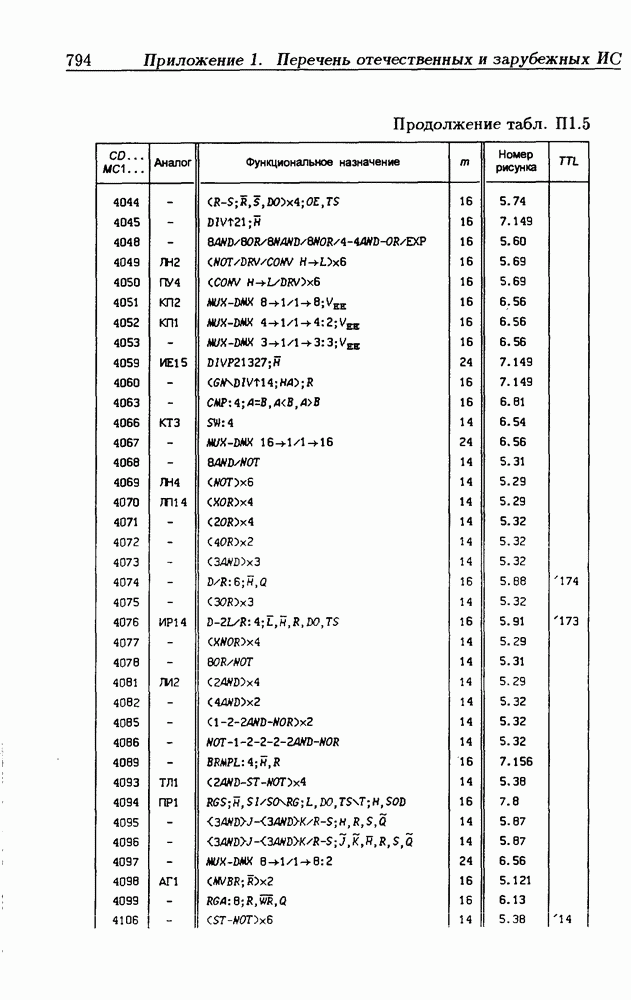
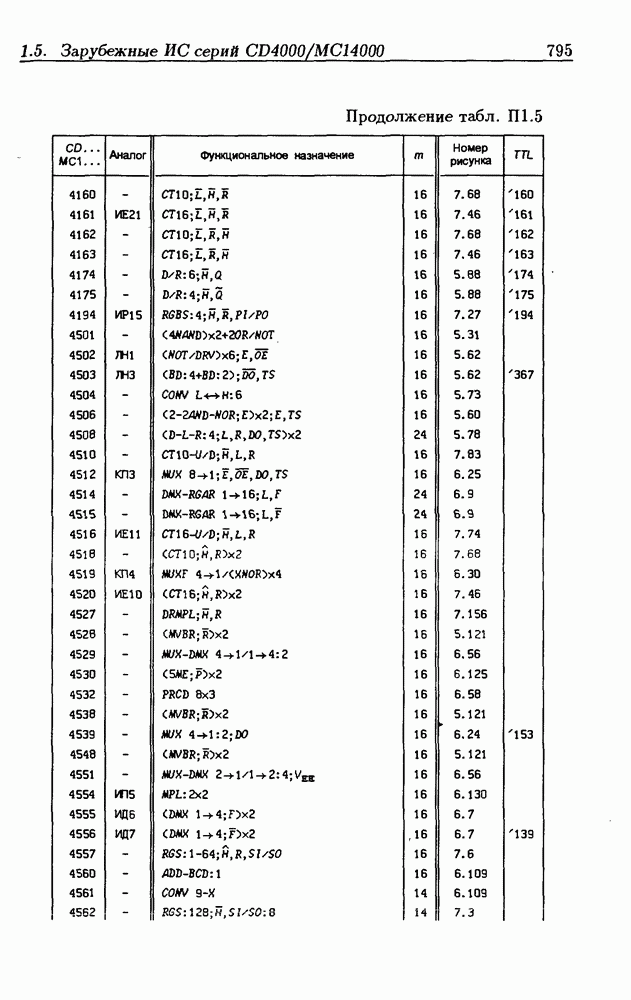
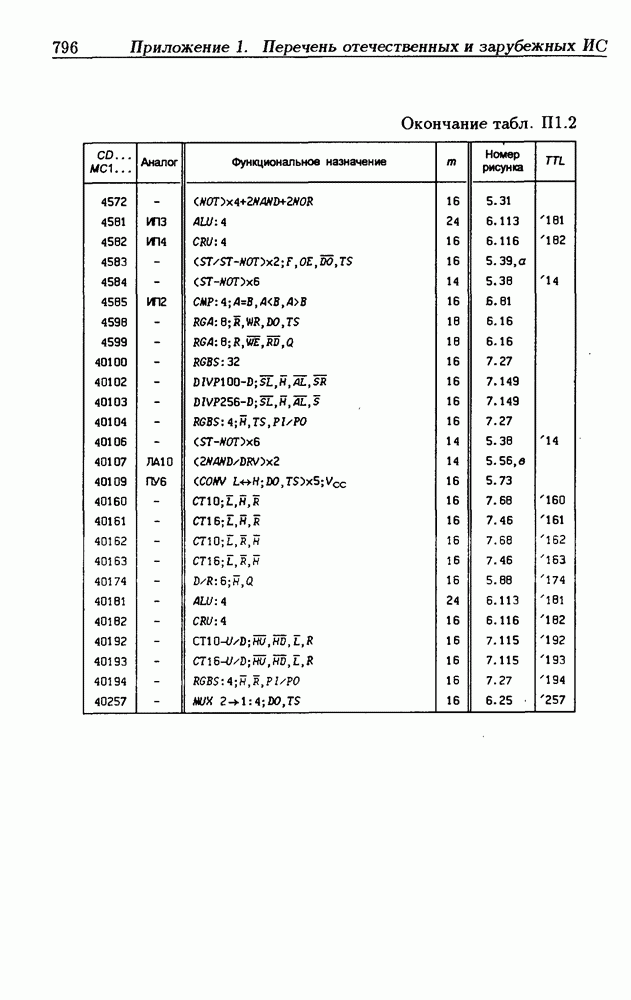
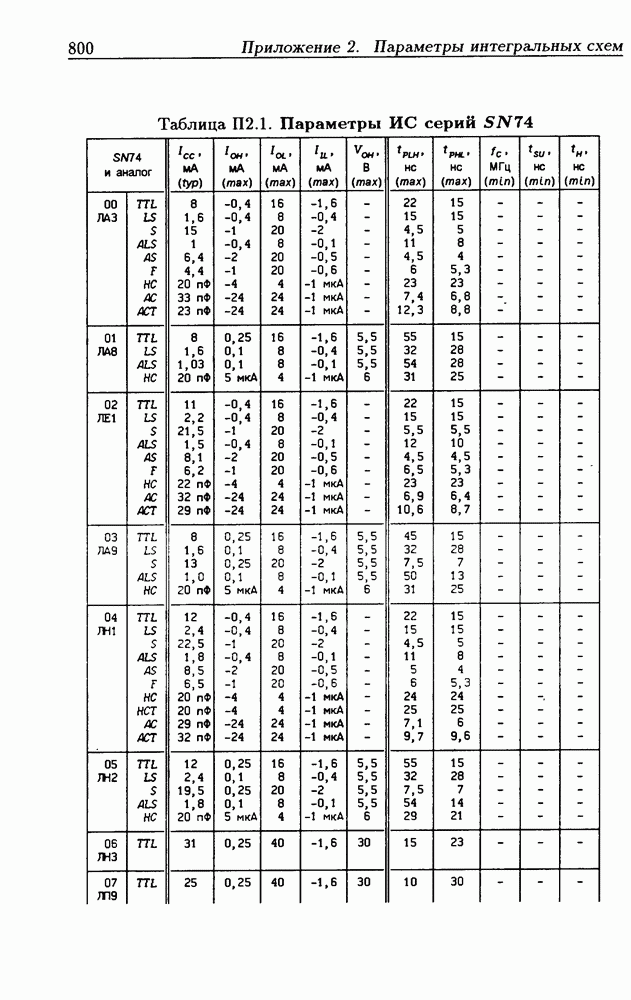
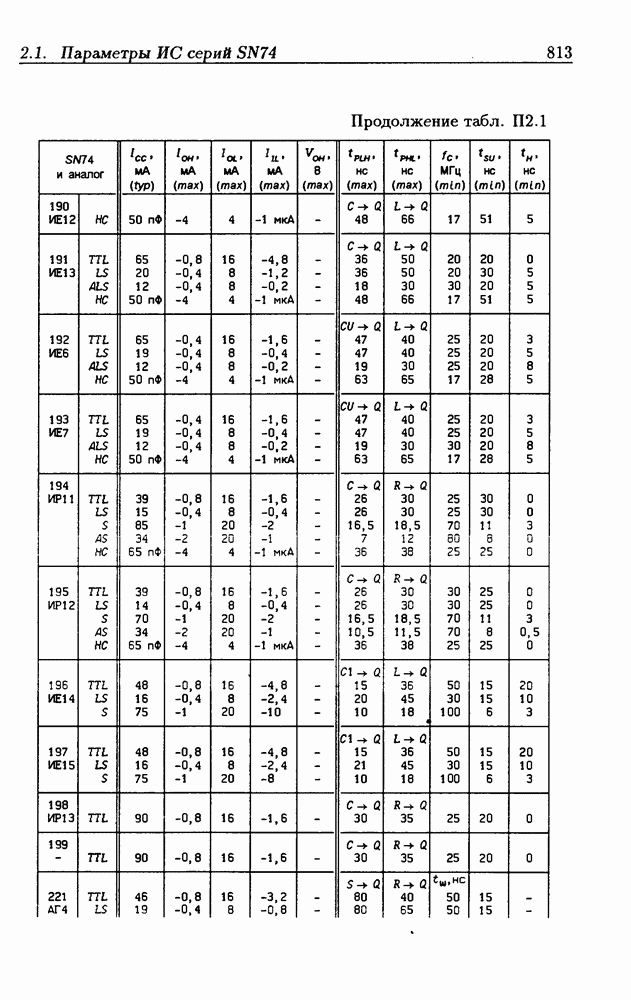
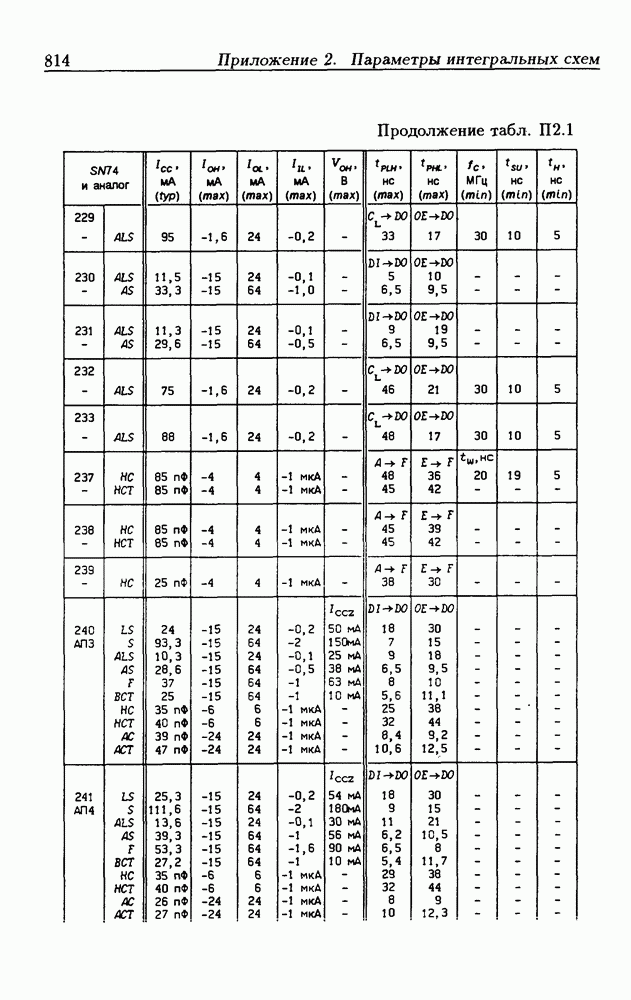
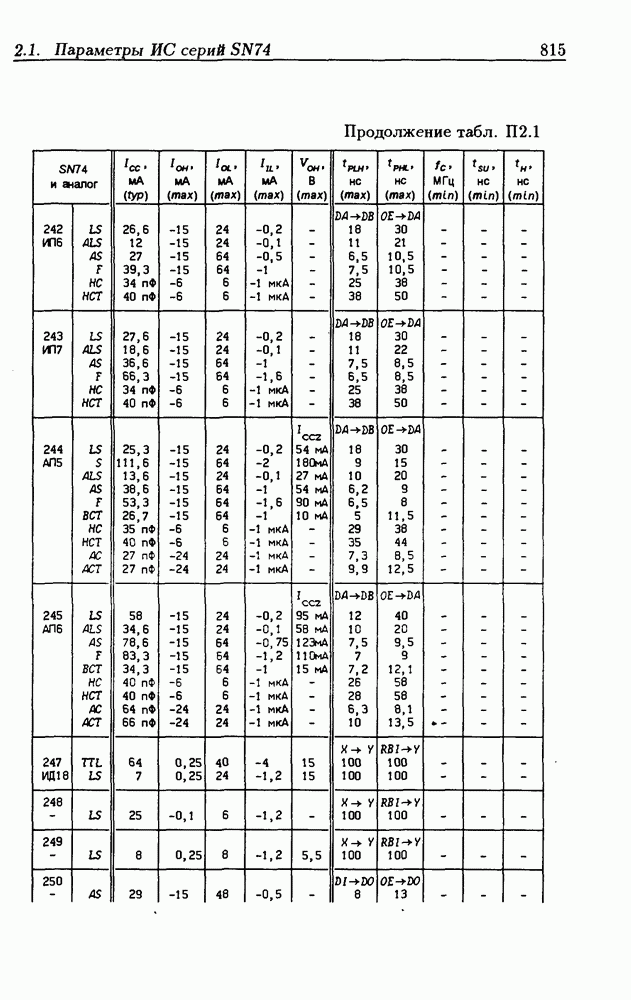
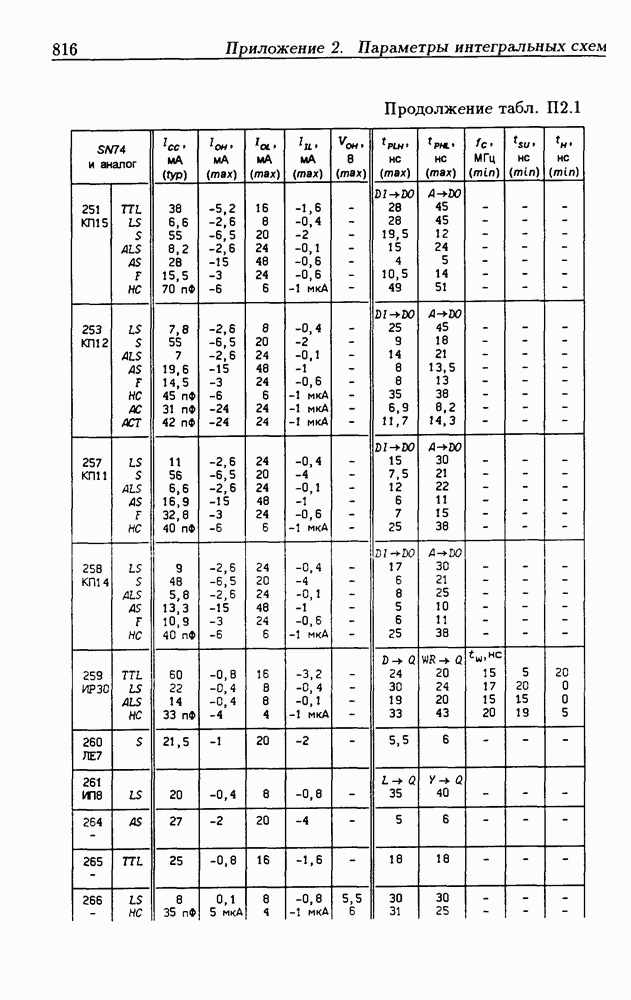
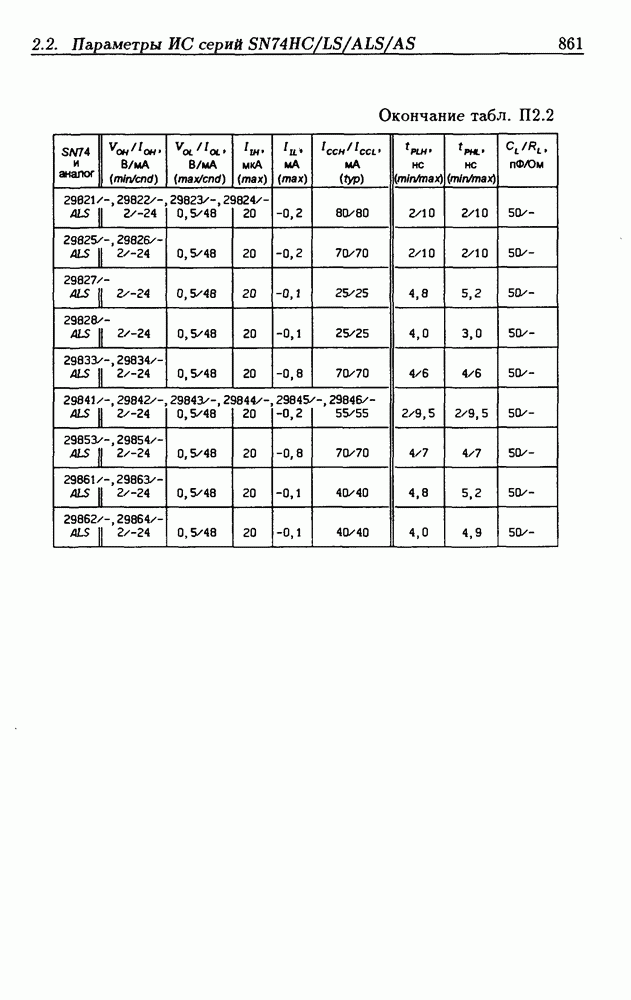
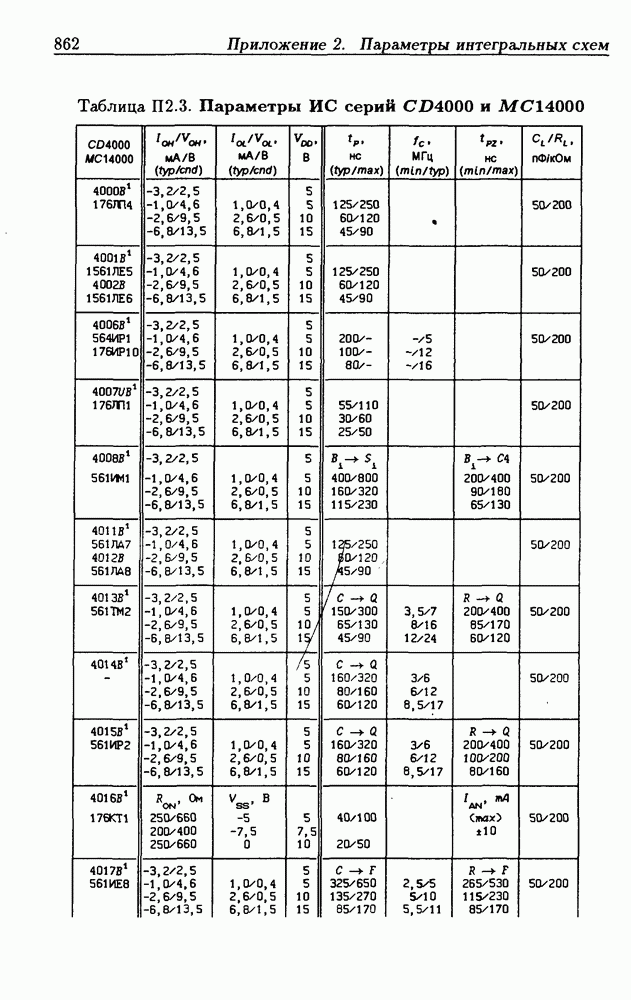
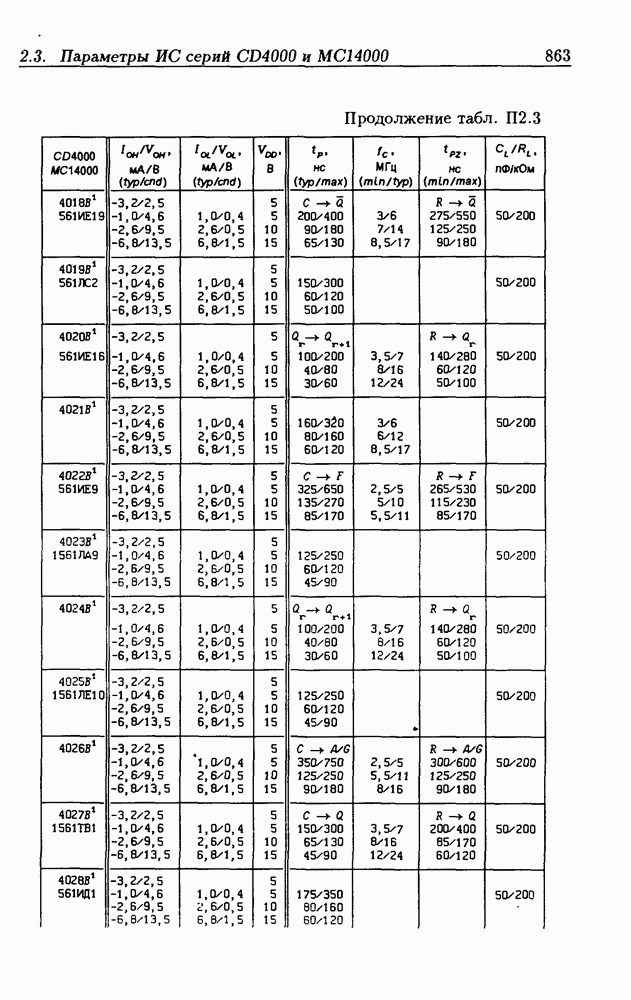
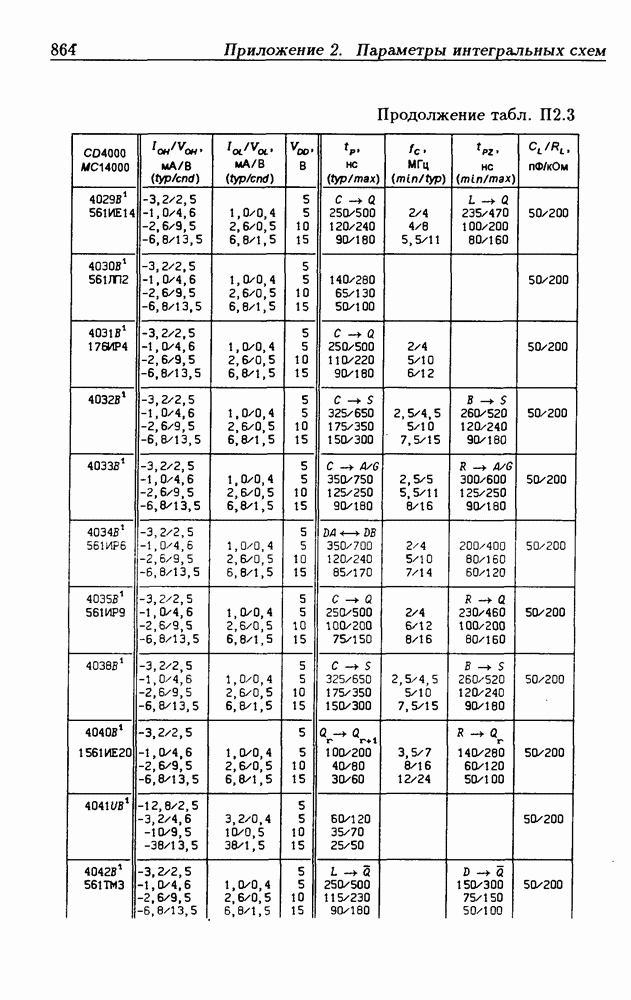
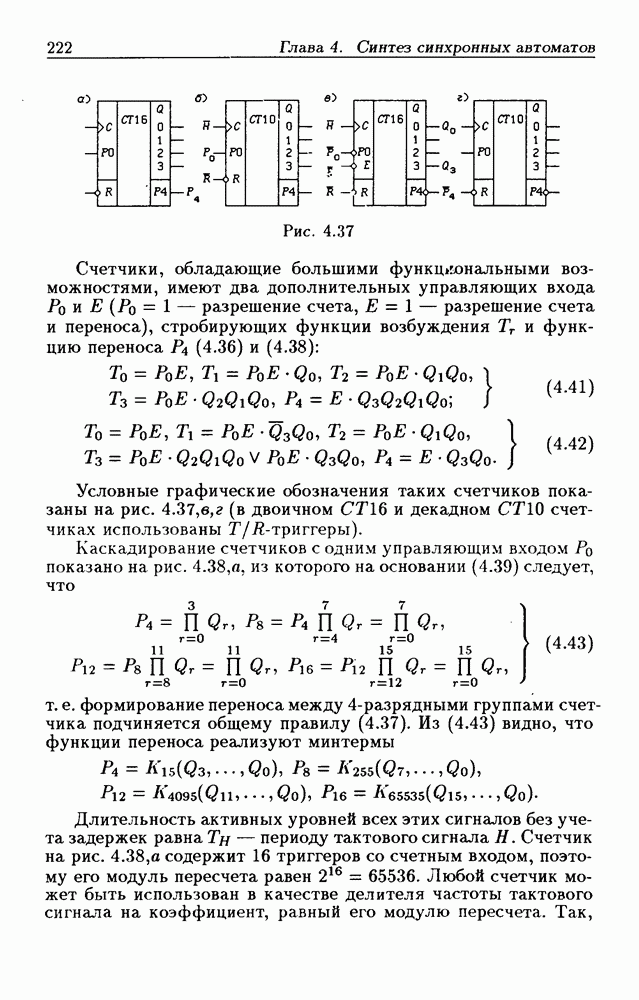| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.4. Анализ логических схем
Основной задачей анализа ЛС является исследование их поведения при переходных процессах (в неустойчивых состояниях). Такое исследование позволяет не только определить длительность переходных процессов при тех или иных входных воздействиях, но и установить закон функционирования ЛС, если он неизвестен. Понятно, что для исследования переходных процессов необходимо использовать динамическую модель ЛС, которая описывается функцией переходов (2.10) или (2.11).
Для любой ЛС функцию переходов  всегда можно записать в явном виде и вычислить все ее значения в зависимости от значений
всегда можно записать в явном виде и вычислить все ее значения в зависимости от значений  Пара
Пара  называется полным состоянием логической схемы. Значения функции переходов для конкретных значений пар
называется полным состоянием логической схемы. Значения функции переходов для конкретных значений пар  будем записывать в виде
будем записывать в виде  Вычисленные значения удобно представлять в виде таблицы, называемой таблицей переходов.
Вычисленные значения удобно представлять в виде таблицы, называемой таблицей переходов.
Таблица переходов состоит из  строк, каждой из которых соответствует одно из внутренних состояний
строк, каждой из которых соответствует одно из внутренних состояний  столбцов, каждому из которых соответствует одно из состояний входа
столбцов, каждому из которых соответствует одно из состояний входа  В каждую из клеток таблицы переходов, стоящую на пересечении столбца у, и строки
В каждую из клеток таблицы переходов, стоящую на пересечении столбца у, и строки  т. е. в клетки, соответствующие парам
т. е. в клетки, соответствующие парам  записывается вычисленное значение
записывается вычисленное значение  Если
Если  то это означает, что
то это означает, что
внутреннее состояние  для состояния входа их является устойчивым. Если же
для состояния входа их является устойчивым. Если же  то ЛС под воздействием состояния входа
то ЛС под воздействием состояния входа  перейдет через некоторое время из состояния
перейдет через некоторое время из состояния  в состояние
в состояние  , т. е. ЛС в данном случае находится в неустойчивом состоянии. Для большей наглядности устойчивые состояния в таблицах переходов отмечаются круглыми скобками.
, т. е. ЛС в данном случае находится в неустойчивом состоянии. Для большей наглядности устойчивые состояния в таблицах переходов отмечаются круглыми скобками.
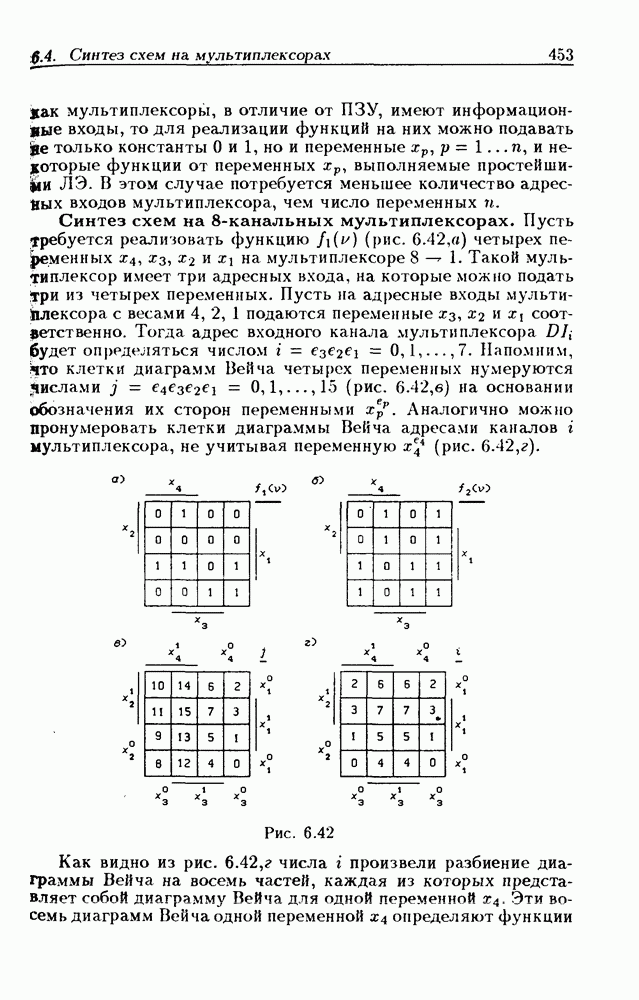
Методику анализа ЛС рассмотрим на пяти конкретных примерах, которые позволят не только освоить ее, но и ввести на физической основе некоторые новые понятия.
Пример  состоит из одного ЛЭ И-НЕ (см. рис. 2.4,6), описываемого функцией переходов (2.7), т.е.
состоит из одного ЛЭ И-НЕ (см. рис. 2.4,6), описываемого функцией переходов (2.7), т.е.

где  Таблица переходов в этом случае состоит из
Таблица переходов в этом случае состоит из  столбцов и
столбцов и  строк (табл. 2.1).
строк (табл. 2.1).
Таблица 2.1. (см. скан) Таблица переходов ЛЭ И-НЕ
Значения  довольно просто вычисляются на основании выражения (2.15). По таблице переходов легко установить, какие состояния входа
довольно просто вычисляются на основании выражения (2.15). По таблице переходов легко установить, какие состояния входа  при данном исходном устойчивом состоянии
при данном исходном устойчивом состоянии  вызывают в ЛС переходный процесс. Так, например, если
вызывают в ЛС переходный процесс. Так, например, если  то переходный процесс (изменение выходного сигнала а с 0 на 1) могут вызвать значения входа
то переходный процесс (изменение выходного сигнала а с 0 на 1) могут вызвать значения входа 
Функцию переходов можно представить и графически так называемым графом переходов (рис. 2.8), который легко может быть построен по таблице переходов. Граф переходов состоит из узлов, обозначаемых кружками, и ветвей, обозначаемых направленными линиями. Узлы указывают внутренние состояния  а ветви — переходы между ними, вызываемые состояниями входа
а ветви — переходы между ними, вызываемые состояниями входа  Ветви, исходящие из какого-либо узла и входящие в этот же узел, называются петлями. Ветви и петли подписываются состояниями входа вызывающими соответствующие переходы. Петли указывают, при каких состояниях входа
Ветви, исходящие из какого-либо узла и входящие в этот же узел, называются петлями. Ветви и петли подписываются состояниями входа вызывающими соответствующие переходы. Петли указывают, при каких состояниях входа  данное внутреннее состояние ЛС является устойчивым. С помощью графа переходов достигается большая наглядность изображения работы ЛС. Следует не забывать, что изменения внутренних состояний происходят не мгновенно, а через время
данное внутреннее состояние ЛС является устойчивым. С помощью графа переходов достигается большая наглядность изображения работы ЛС. Следует не забывать, что изменения внутренних состояний происходят не мгновенно, а через время  равное задержке сигналов в одном ЛЭ.
равное задержке сигналов в одном ЛЭ.

Рис. 2.8

Рис. 2.9
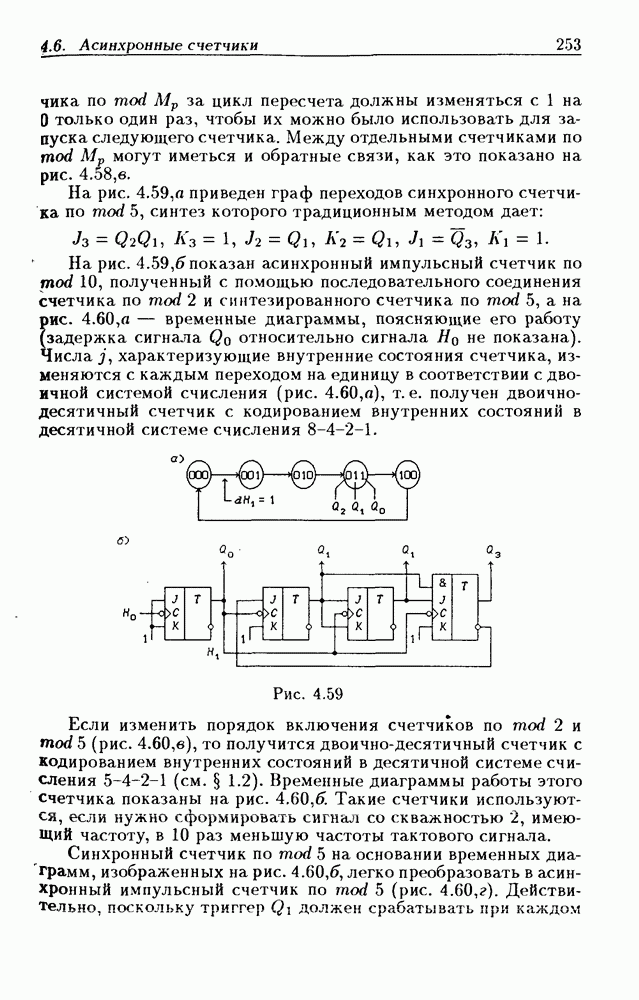
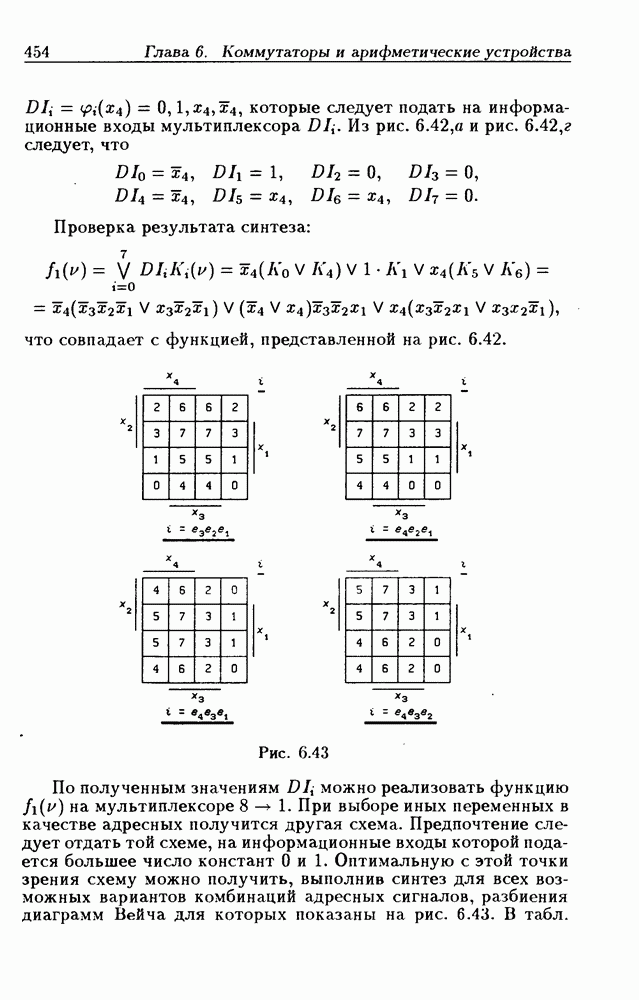
Пример 2. Установим закон функционирования ЛС с обратными связями (см. рис. 2.6), которая описывается функцией переходов (2.8). Составим по ней таблицу переходов (табл. 2.2) и отметим скобками устойчивые состояния. Как и в предыдущем примере, каждый столбец содержит по одному устойчивому состоянию. Наличие для каждого состояния входа  только одного устойчивого состояния является достаточным условием того, чтобы ЛС была комбинационной схемой.
только одного устойчивого состояния является достаточным условием того, чтобы ЛС была комбинационной схемой.
На рис. 2.9, в показан граф переходов, составленный по табл. 2.2. Поясним составление графа переходов. Пусть исходное состояние входа  т.е.
т.е.  Из табл. 2.2 следует, что ЛС находится в устойчивом состоянии
Из табл. 2.2 следует, что ЛС находится в устойчивом состоянии  т. е. полное ее состояние определяется парой
т. е. полное ее состояние определяется парой  При изменении сигнала
При изменении сигнала  на 1 (состояния входа
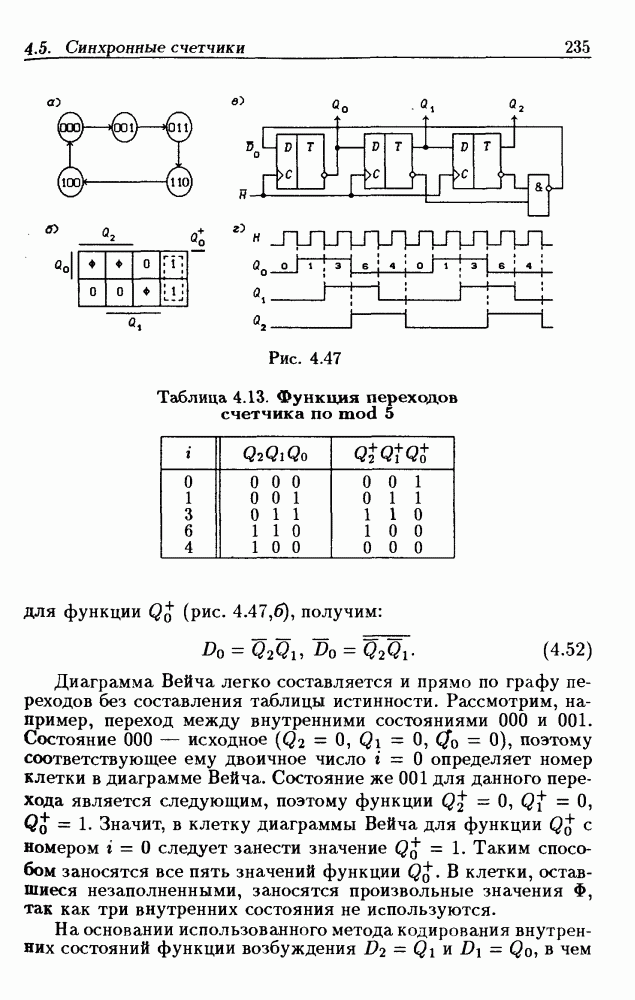
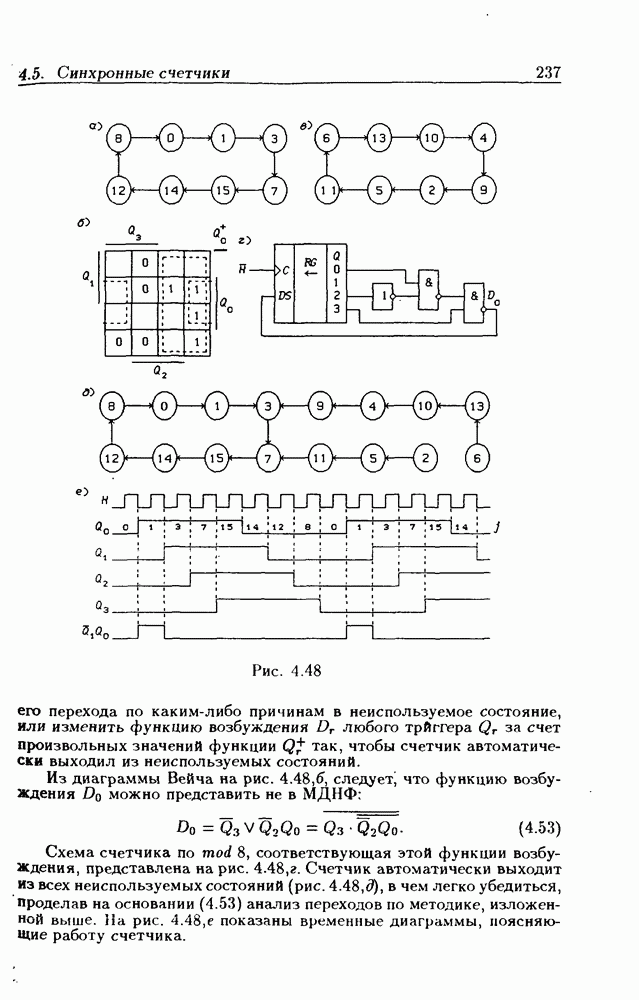
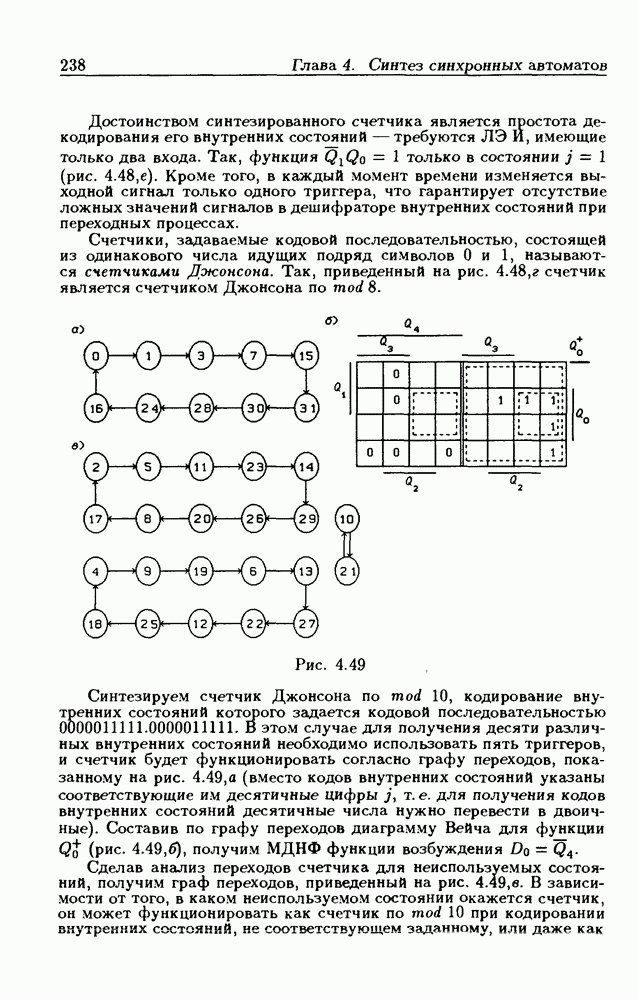
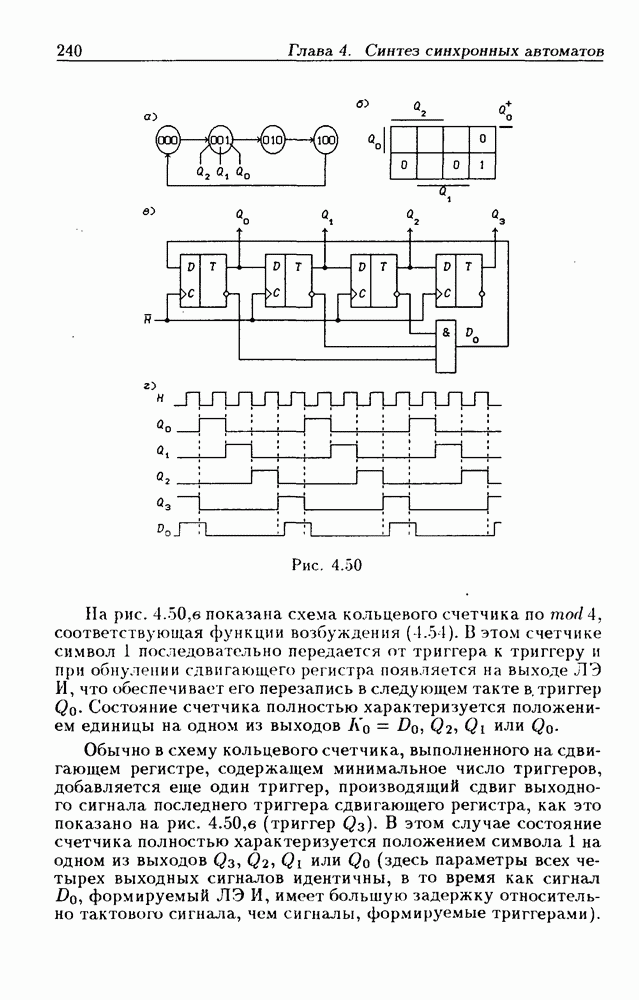
на 1 (состояния входа  на
на  состояние
состояние  должно измениться на состояние
должно измениться на состояние  так как оно находится в столбце
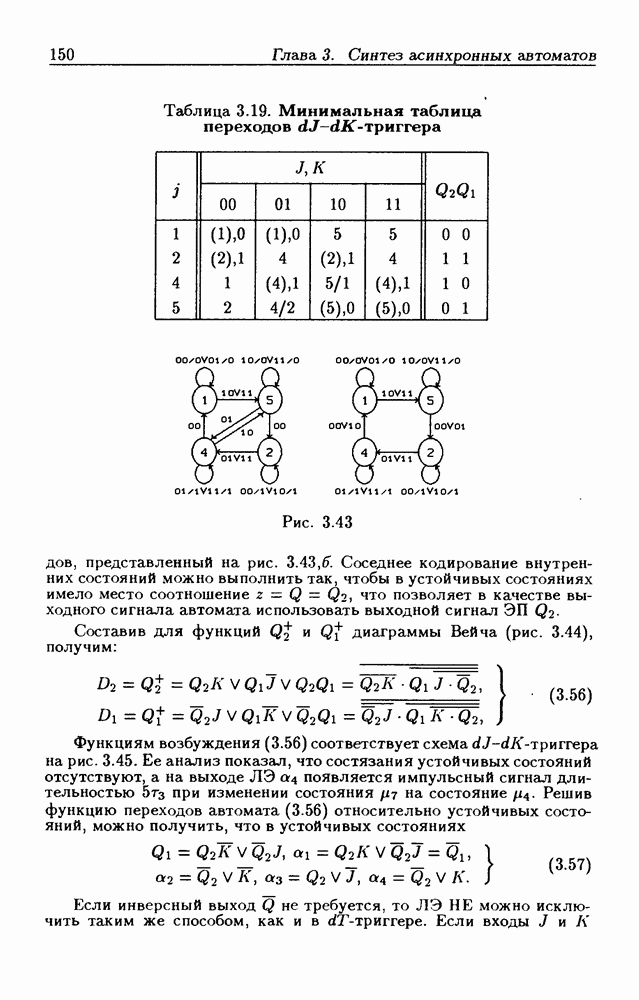
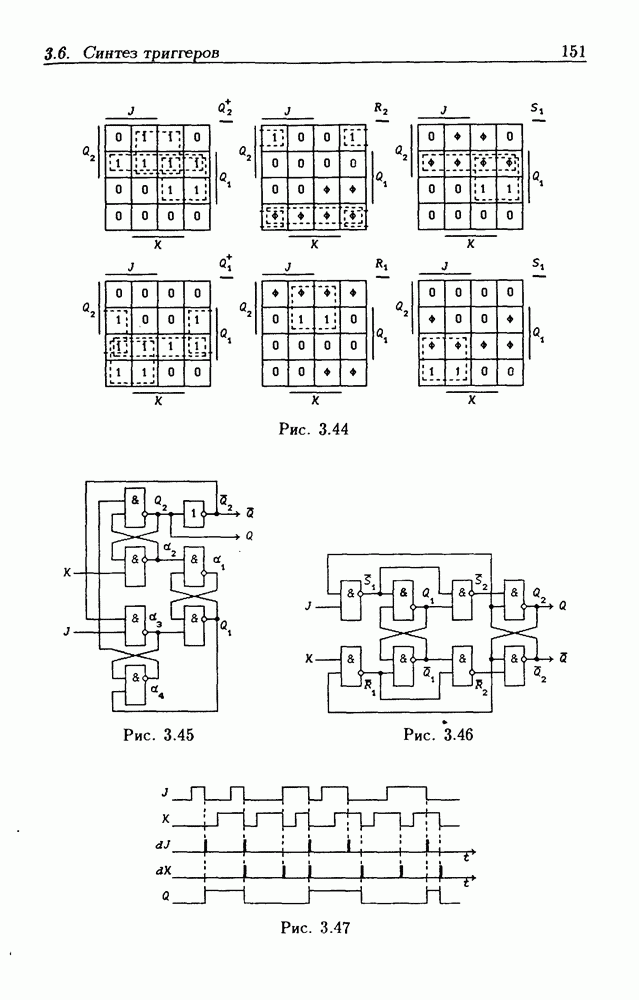
так как оно находится в столбце  и строке Изменение состояния произойдет через время
и строке Изменение состояния произойдет через время  поскольку при этом изменяется выходной сигнал только одного
поскольку при этом изменяется выходной сигнал только одного  Внутреннее состояние
Внутреннее состояние  при состоянии входа
при состоянии входа  как это видно из табл. 2.2, неустойчиво, поэтому оно должно измениться на следующее состояние
как это видно из табл. 2.2, неустойчиво, поэтому оно должно измениться на следующее состояние  соответствующее возникшей новой паре
соответствующее возникшей новой паре  Процесс изменения внутренних состояний продолжается до тех пор, пока ЛС не придет в устойчивое состояние. Из табл. 2.2 следует, что при этом реализуется следующая последовательность полных состояний:
Процесс изменения внутренних состояний продолжается до тех пор, пока ЛС не придет в устойчивое состояние. Из табл. 2.2 следует, что при этом реализуется следующая последовательность полных состояний:

Первый переход вызывается изменением состояния входа, а все остальные — изменениями внутренних состояний. Первое и последнее полные внутренние состояния устойчивые (отмечены круглыми скобками). Аналогично этому по табл. 2.2 отыскиваются переходы при изменении входного сигнала  с 1 на 0 (рис. 2.9,а). Граф переходов составлен только из тех состояний, которые возникают при переходах между устойчивыми внутренними состояниями.
с 1 на 0 (рис. 2.9,а). Граф переходов составлен только из тех состояний, которые возникают при переходах между устойчивыми внутренними состояниями.
Состояние  в которое есть переход под воздействием
в которое есть переход под воздействием
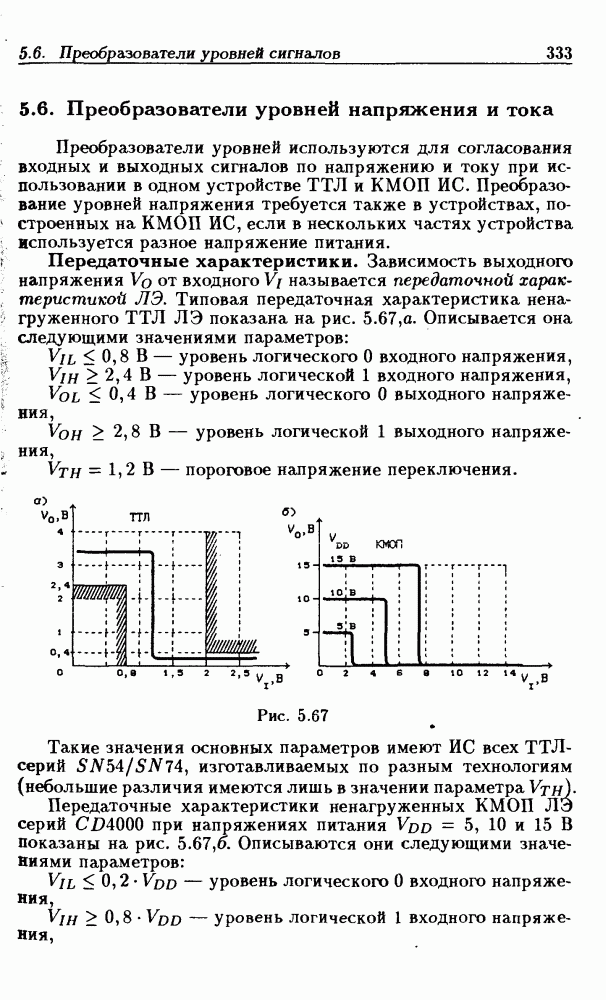
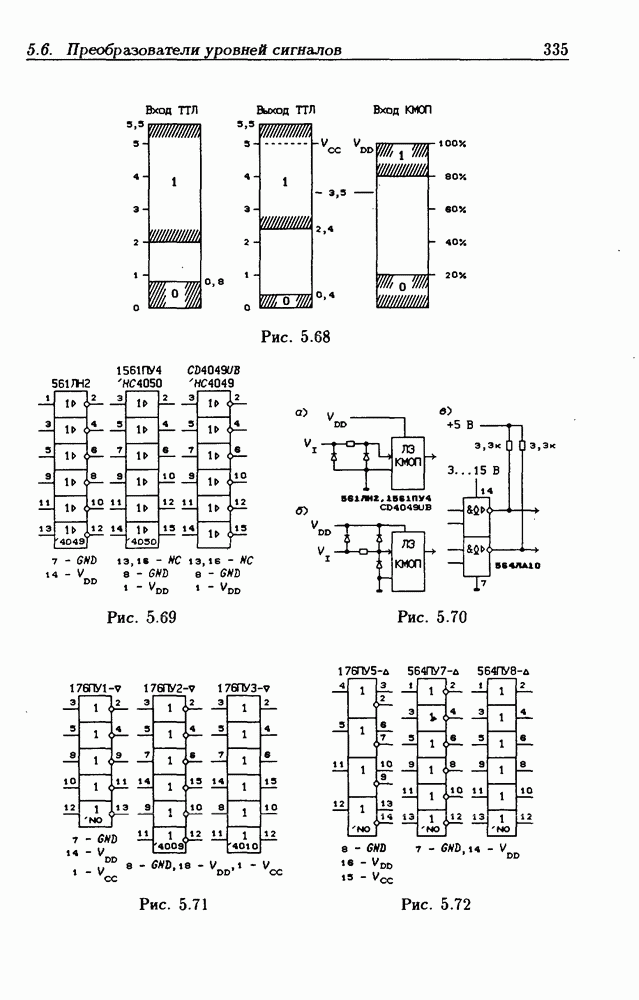
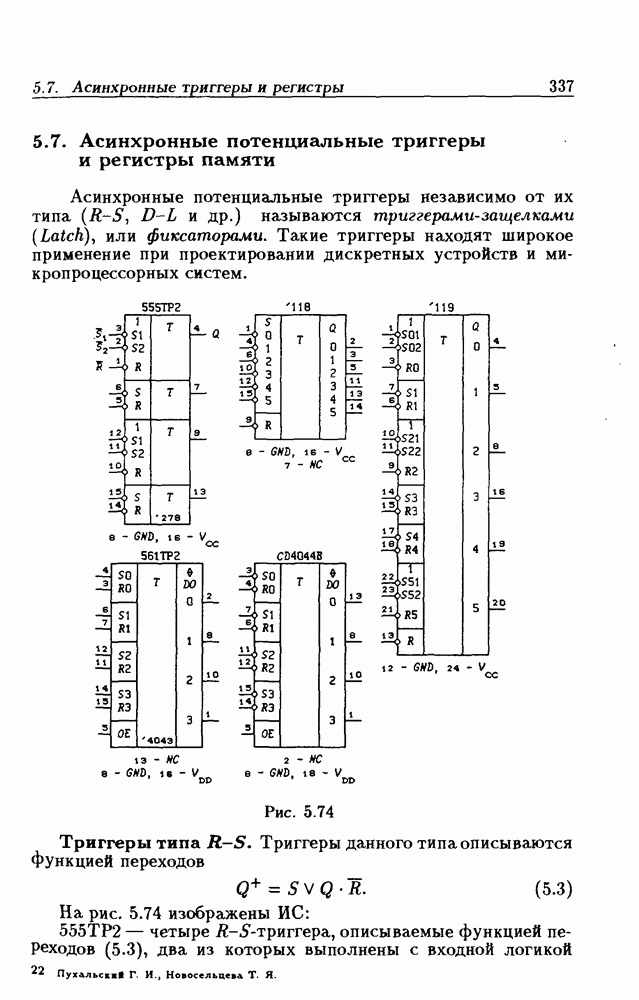
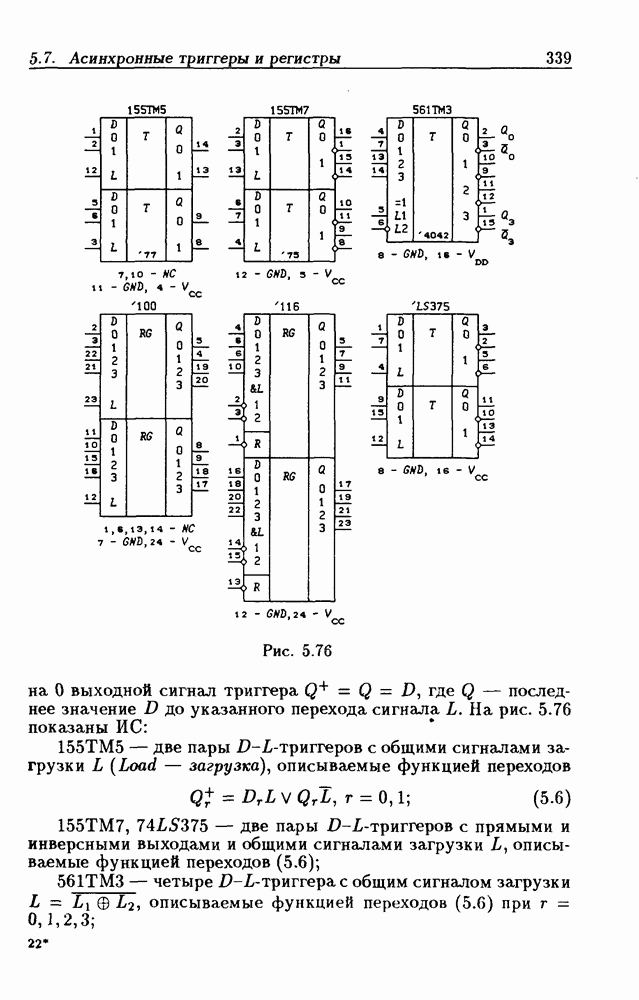
Таблица 2.2. (см. скан) Таблица переходов РЭ
Таблица 2.3. (см. скан) Таблица переходов генератора
какого-либо состояния входа  но не являющееся для него устойчивым, называется переходным состоянием. Так, состояния
но не являющееся для него устойчивым, называется переходным состоянием. Так, состояния  переходные.
переходные.
При практическом использовании любой ЛС частота изменения состояний входа должна быть ограничена некоторой величиной, гарантирующей надежный переход из одного устойчивого состояния в другое, т. е. состояние входа не должно изменяться до тех пор, пока в ЛС не закончится переходный процесс. В противном случае поведение ЛС будет недетерминированным.
Из графа переходов (рис. 2.9,а) видно, что при переходах внутренние состояния изменяются только на соседние (при каждом переходе изменяется выходной сигнал только одного  и на выходе
и на выходе  при изменении входного сигнала
при изменении входного сигнала  на 1 формируется сигнал, равный 0, длительностью
на 1 формируется сигнал, равный 0, длительностью  где
где  среднее время паразитной задержки сигналов в одном ЛЭ. На этом основании данная ЛС называется разностным элементом (элементом, формирующим импульсный сигнал при изменениях потенциального сигнала
среднее время паразитной задержки сигналов в одном ЛЭ. На этом основании данная ЛС называется разностным элементом (элементом, формирующим импульсный сигнал при изменениях потенциального сигнала 
На рис. 2.9, б показаны временные диаграммы, построенные по графу переходов на рис. 2.9,а (точками помечены интервалы времени  когда ЛС находится в неустойчивом состоянии). Из рис.
когда ЛС находится в неустойчивом состоянии). Из рис.  следует, что выходной импульсный сигнал ЛС описывается функцией
следует, что выходной импульсный сигнал ЛС описывается функцией  Если в обратную связь с
Если в обратную связь с  на
на  (см. рис. 2.6) последовательно включить
(см. рис. 2.6) последовательно включить  то длительность формируемого импульсного сигнала
то длительность формируемого импульсного сигнала  будет равна
будет равна 
Для приобретения навыков анализа ЛС рекомендуется самостоятельно произвести анализ двойственного разностного элемента, выполненного на ЛЭ ИЛИ-НЕ (см. рис. 1.19, в). Следует убедиться, что на его выходе формируется сигнал, равный 1, длительностью  при изменении входного сигнала с 1 на 0. Если входной и выходной сигналы этого разностного элемента обозначить через
при изменении входного сигнала с 1 на 0. Если входной и выходной сигналы этого разностного элемента обозначить через  то закон его функционирования будет описываться функцией
то закон его функционирования будет описываться функцией 
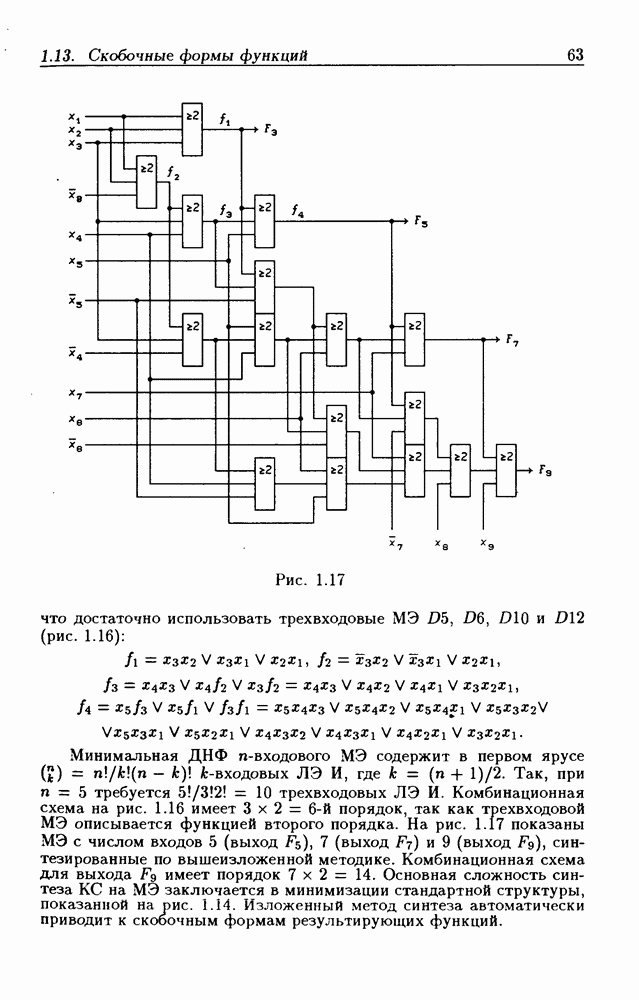
В § 1.13 было введено понятие порядка КС без обратных связей как максимальное число последовательно включенных ЛЭ. Для КС с обратными связями такое определение порядка непригодно. Действительно, по виду КС на рис. 2.6 ее порядок установить невозможно. Так как порядок КС характеризует максимальную длительность переходного процесса, вызываемого изменениями входных сигналов, то порядком КС с обратными связями следут считать максимальное число переходов внутренних состояний при изменении ее состояний входа. На этом основании КС, представляющая собой рассмотренный разностный элемент (рис. 2.6), имеет четвертый порядок.

Рис. 2.10
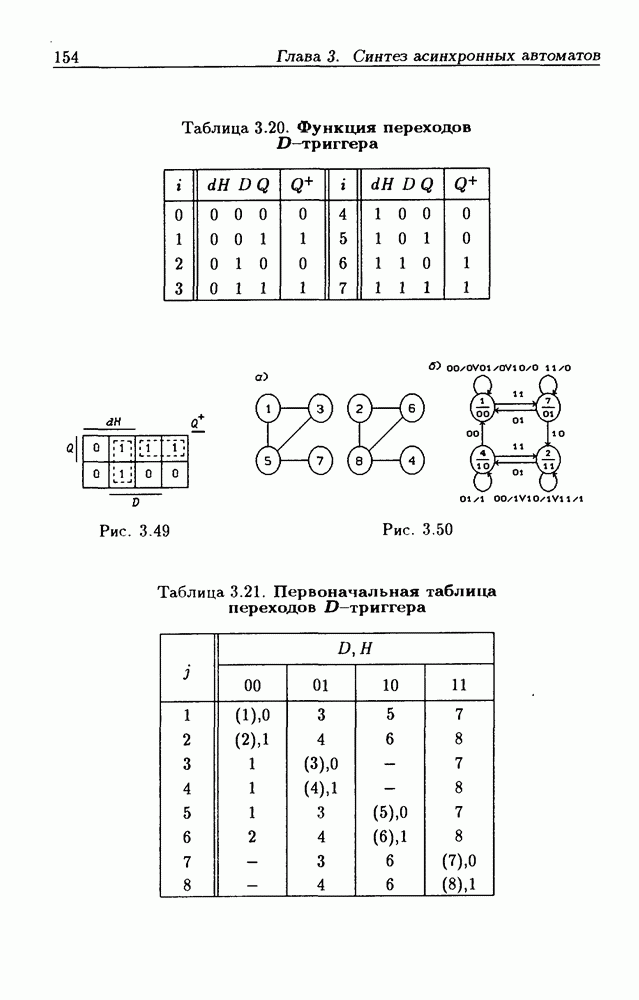
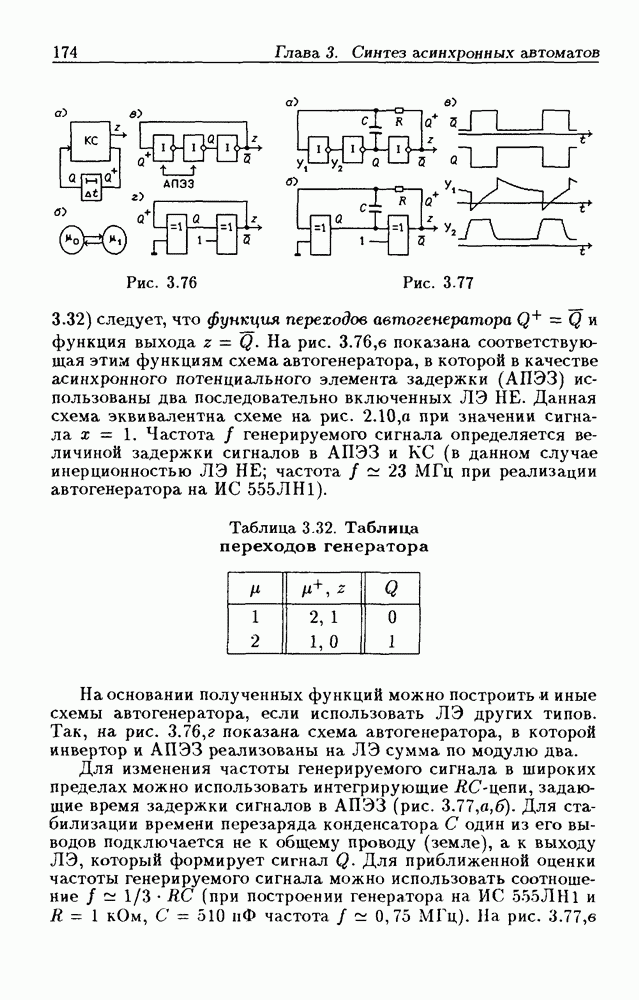
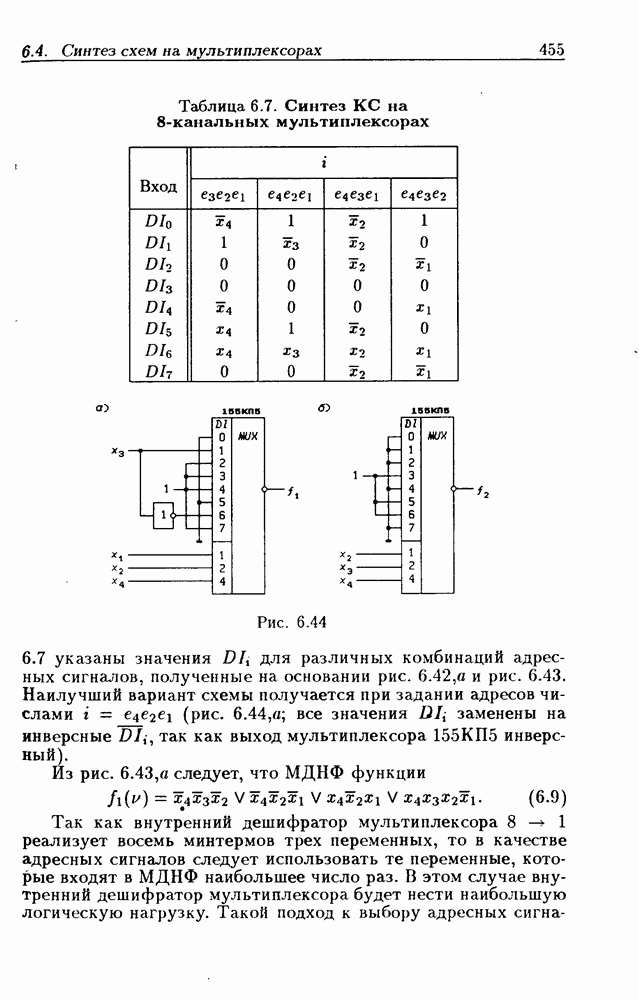
Пример 3. Исследуем ЛС с обратной связью, изображенную на рис. 2.10,а. Здесь (и в дальнейшем) для простоты паразитные элементы задержки не показаны. Для записи функции переходов ЛС

по ее структурной схеме (модели) все выходные сигналы  следует заменить на
следует заменить на  оставив неизменными обозначения их входных сигналов. Тогда из рис. 2.10,а следует, что функция переходов ЛС
оставив неизменными обозначения их входных сигналов. Тогда из рис. 2.10,а следует, что функция переходов ЛС

Опустив знаки  получим статическую модель
получим статическую модель  систему логических уравнений
систему логических уравнений

с тремя неизвестными  Благодаря тому, что неизвестные обычно не являются независимыми, имеется возможность сократить их число. Подстановкой значений одних неизвестных в другие данную систему можно свести к одному уравнению
Благодаря тому, что неизвестные обычно не являются независимыми, имеется возможность сократить их число. Подстановкой значений одних неизвестных в другие данную систему можно свести к одному уравнению  решение которого дает
решение которого дает

Из этого следует, что при значении входного сигнала  решения не существует, т. е. в ЛС при
решения не существует, т. е. в ЛС при  происходит автоколебательный процесс, так как отсутствуют устойчивые состояния. При
происходит автоколебательный процесс, так как отсутствуют устойчивые состояния. При  из системы (2.17) следует, что имеется одно устойчивое состояние, в котором сигналы
из системы (2.17) следует, что имеется одно устойчивое состояние, в котором сигналы  Таким образом, ЛС представляет собой управляемый сигналом х автогенератор.
Таким образом, ЛС представляет собой управляемый сигналом х автогенератор.
Эти же самые выводы можно сделать и из таблицы переходов (табл. 2.3), составленной на основании функции переходов (2.16). Действительно, в столбце, соответствующем значению входного сигнала
 не имеется ни одного устойчивого состояния. На рис. 2.10, б показан граф переходов, построенный по табл. 2.3, из которого видно, что при
не имеется ни одного устойчивого состояния. На рис. 2.10, б показан граф переходов, построенный по табл. 2.3, из которого видно, что при  внутренние состояния ЛС самопроизвольно изменяются на соседние, и период генерируемого сигнала равен
внутренние состояния ЛС самопроизвольно изменяются на соседние, и период генерируемого сигнала равен  По графу переходов легко построить временные диаграммы для сигналов
По графу переходов легко построить временные диаграммы для сигналов 
Из табл. 2.3 видно, что при  состояние
состояние  изменяется на
изменяется на  а на Эти переходы, отмеченные на рис.
а на Эти переходы, отмеченные на рис.  штриховыми ветвями, могут происходить длительное время только при равенстве задержек сигналов во всех трех ЛЭ, т. е. при
штриховыми ветвями, могут происходить длительное время только при равенстве задержек сигналов во всех трех ЛЭ, т. е. при  Даже при незначительном различии этих задержек в ЛС возникают состязания (гонки) ЛЭ. Так как истинное соотношение задержек неизвестно, то поведение ЛС в этом случае недетерминированно. Как бы близки ни были величины задержек, должен произойти переход в подграф, состоящий из шести состояний (рис. 2.10, б). Здесь внутренние состояния изменяются на соседние, а значит состязания ЛЭ отсутствуют, и автогенерация продолжается до тех пор, пока управляющий сигнал
Даже при незначительном различии этих задержек в ЛС возникают состязания (гонки) ЛЭ. Так как истинное соотношение задержек неизвестно, то поведение ЛС в этом случае недетерминированно. Как бы близки ни были величины задержек, должен произойти переход в подграф, состоящий из шести состояний (рис. 2.10, б). Здесь внутренние состояния изменяются на соседние, а значит состязания ЛЭ отсутствуют, и автогенерация продолжается до тех пор, пока управляющий сигнал 

Рис. 2.11
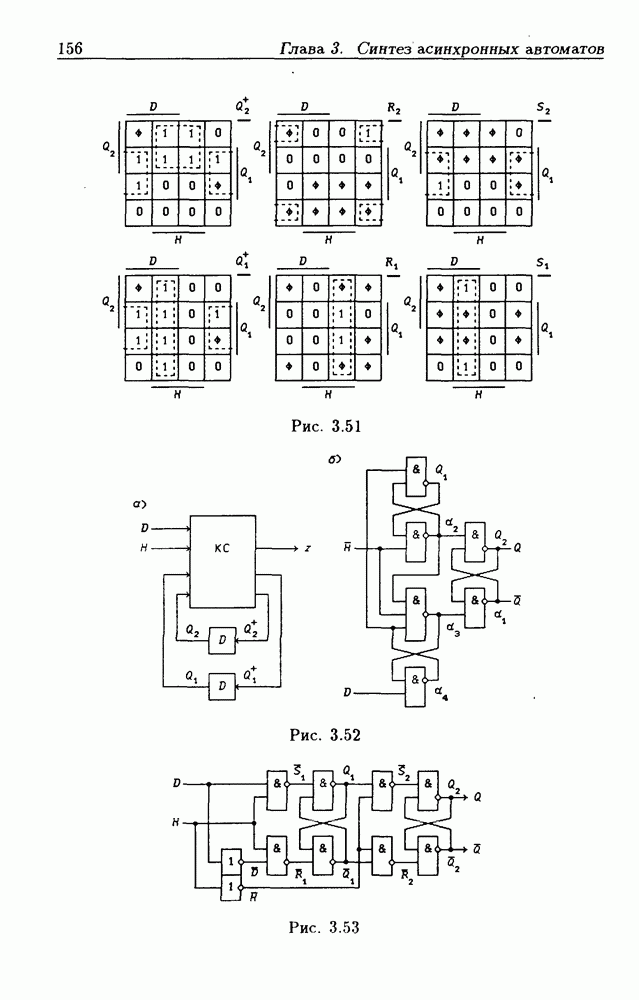
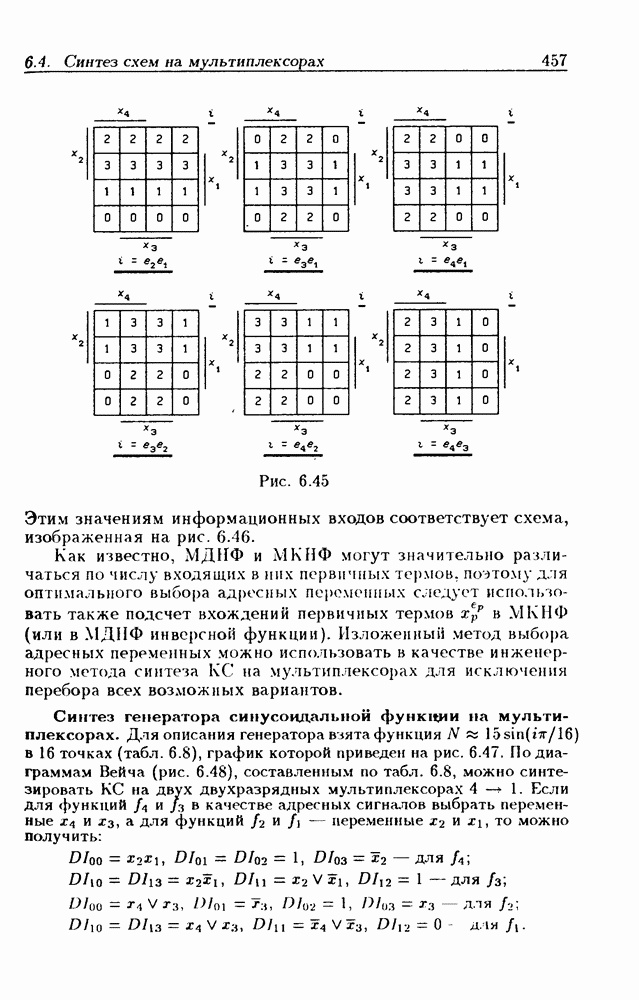
Пример 4. Установим закон функционирования ЛС, приведенной на рис. 2.11,а. В этом случае состояния  и функция переходов
и функция переходов

определяется выражениями:

Опустив знаки  получим статическую модель
получим статическую модель 

Подстановка значения  из второго уравнения в первое дает логическое уравнение
из второго уравнения в первое дает логическое уравнение  с одним неизвестным
с одним неизвестным  Решив его, получим:
Решив его, получим:

т. е. решение существует, а значит автоколебательные процессы в ЛС отсутствуют. Упростив полученное решение и подставив его во второе
уравнение (2.19), найдем:

Из этих выражений видно, что выходные сигналы  неоднозначно выражаются через входные сигналы
неоднозначно выражаются через входные сигналы  а это означает, что ЛС не является комбинационной схемой. В таблице переходов (табл. 2.4), составленной на основании функции переходов (2.18), в столбце
а это означает, что ЛС не является комбинационной схемой. В таблице переходов (табл. 2.4), составленной на основании функции переходов (2.18), в столбце  имеется два устойчивых состояния
имеется два устойчивых состояния  в отличие от предыдущих таблиц переходов, в которых было только по одному устойчивому состоянию. Из этого следует вывод: чтобы ЛС была комбинационной схемой, достаточно, чтобы во всех столбцах соответствующей ей таблицы переходов было только по одному устойчивому состоянию.
в отличие от предыдущих таблиц переходов, в которых было только по одному устойчивому состоянию. Из этого следует вывод: чтобы ЛС была комбинационной схемой, достаточно, чтобы во всех столбцах соответствующей ей таблицы переходов было только по одному устойчивому состоянию.
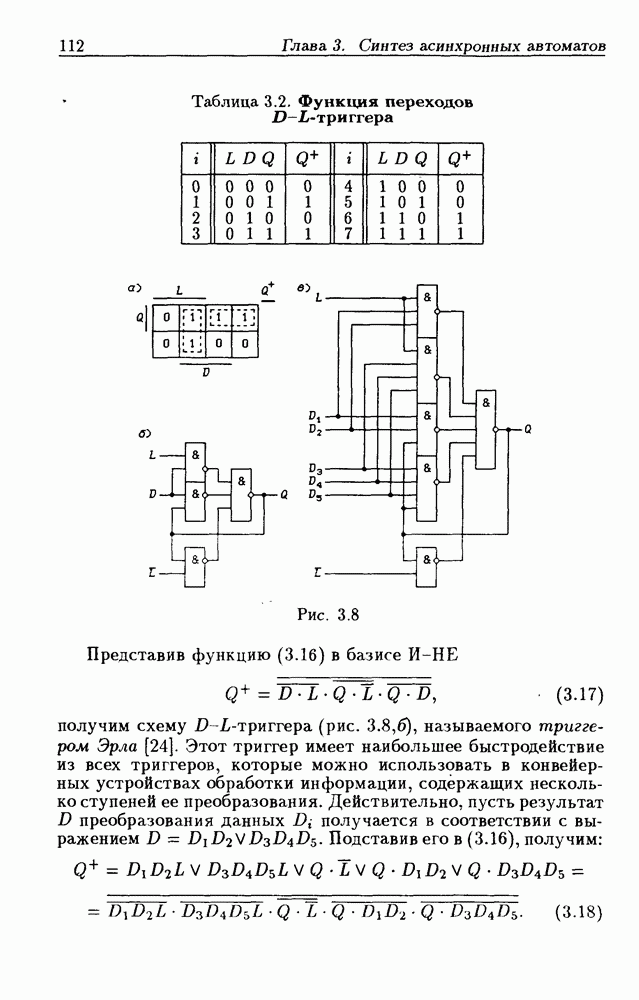
Таблица 2.4. (см. скан) Таблица переходов  -триггера
-триггера
В отличие от КС, которые в устойчивых состояниях реализуют однозначное соответствие между состояниями входа  и состояниями выхода
и состояниями выхода  в рассматриваемой ЛС реализуется соответствие между последовательностями состояний входа
в рассматриваемой ЛС реализуется соответствие между последовательностями состояний входа  (входными последовательностями) и последовательностями состояний выхода
(входными последовательностями) и последовательностями состояний выхода  (выходными последовательностями). По графу переходов (рис.
(выходными последовательностями). По графу переходов (рис.  составленному по табл. 2.4 для ЛС на рис. 2.11,а, легко установить такое соответствие. Так, например, входной последовательности
составленному по табл. 2.4 для ЛС на рис. 2.11,а, легко установить такое соответствие. Так, например, входной последовательности  соответствует выходная последовательность
соответствует выходная последовательность  откуда видно, что при одном и том
откуда видно, что при одном и том  «состоянии входа 1/3 получаются разные состояния выхода
«состоянии входа 1/3 получаются разные состояния выхода  Такие ЛС называются последовательностными схемами, или цифровыми автоматами. Для того, чтобы ЛС была последовательности ой, необходимо (но не достаточно), чтобы хотя бы в одном столбце имелось не менее двух устойчивых состояний.
Такие ЛС называются последовательностными схемами, или цифровыми автоматами. Для того, чтобы ЛС была последовательности ой, необходимо (но не достаточно), чтобы хотя бы в одном столбце имелось не менее двух устойчивых состояний.
При изменении состояния входа  на
на  возникают состязания ЛЭ (штриховые ветви на рис.
возникают состязания ЛЭ (штриховые ветви на рис.  так как состояние
так как состояние  изменяется на несоседнее состояние
изменяется на несоседнее состояние  зависимости от соотношений задержек
зависимости от соотношений задержек  может установиться в любое из двух устойчивых состояний:
может установиться в любое из двух устойчивых состояний:  или
или  (рис. 2.11,б), т. е. в этом случае переходы между устойчивыми состояниями являются недетерминированными. Таким образом, в
(рис. 2.11,б), т. е. в этом случае переходы между устойчивыми состояниями являются недетерминированными. Таким образом, в
рассматриваемой последовательностной схеме состязания ЛЭ приводят к состязаниям устойчивых состояний, которые недопустимы, так как разным устойчивым состояниям обычно соответствуют разные значения выходных сигналов автомата. Поэтому при практическом использовании ЛС состояние входа  должно быть запрещено, т.е. на входы никогда одновременно не должны подаваться значения сигналов
должно быть запрещено, т.е. на входы никогда одновременно не должны подаваться значения сигналов  При выполнении этого условия ЛС будет представлять собой асинхронный потенциальный триггер типа
При выполнении этого условия ЛС будет представлять собой асинхронный потенциальный триггер типа  имеющий прямой
имеющий прямой  и инверсный
и инверсный  выходы
выходы 
Из графа переходов (рис. 2.11, б) следует, что при изменении внутренних состояний триггера прямой и инверсный сигналы на время  или
или  одновременно становятся равными 1 (состояние
одновременно становятся равными 1 (состояние  является переходным для состояний входа и
является переходным для состояний входа и  Необходимо подчеркнуть, что понятие прямого и инверсного сигналов может быть определено только для устойчивых внутренних состояний, так как практически всегда "прямые" и "инверсные" сигналы в переходных режимах имеют одинаковые значения 0 или 1.
Необходимо подчеркнуть, что понятие прямого и инверсного сигналов может быть определено только для устойчивых внутренних состояний, так как практически всегда "прямые" и "инверсные" сигналы в переходных режимах имеют одинаковые значения 0 или 1.
Рассмотренные примеры позволяют разделить все ЛС на три класса: комбинационные схемы, последовательностные схемы (цифровые автоматы) и автогенераторы. В принципе, автогенераторы можно отнести к особым случаям комбинационных или последовательностных схем, поскольку ЛС с обратными связями могут быть как комбинационными, так и последовательностными схемами. Действительно, автогенератор можно рассматривать как КС, имеющую бесконечно высокий порядок, поскольку переходный процесс в автогенераторе длится бесконечно долго. Порядок КС, представляющей собой управляемый автогенератор, зависит от значения входного управляющего сигнала и от момента времени его изменения по отношению к внутреннему состоянию автогенератора. Но управляемый автогенератор можно считать и особым случаем цифрового автомата — автомата, не имеющего устойчивых внутренних состояний при некоторых состояниях входа.
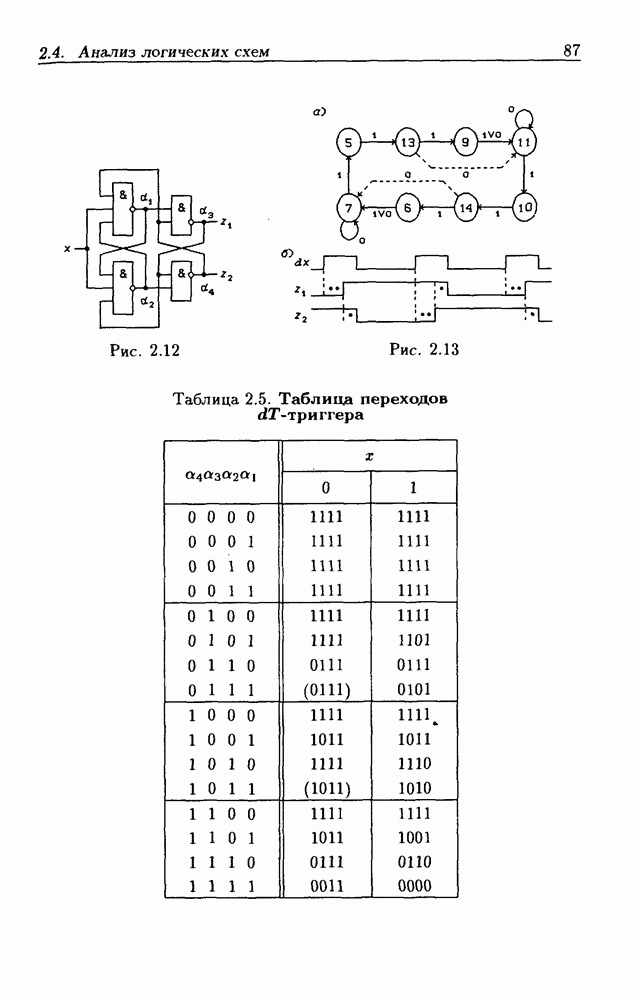
Пример 5. Требуется установить закон функционирования ЛС на рис. 2.12, функция переходов которой

описывается выражениями

Решение данной системы уравнений относительно устойчивых состояний дает  т. е. решение отсутствует при
т. е. решение отсутствует при  что подтверждается и таблицей переходов (табл. 2.5; в столбце
что подтверждается и таблицей переходов (табл. 2.5; в столбце  устойчивые состояния отсутствуют). При
устойчивые состояния отсутствуют). При  сигналы
сигналы  или
или  или
или  т.е. в этом случае имеется два устойчивых состояния
т.е. в этом случае имеется два устойчивых состояния  Для получения практических навыков в аналитических преобразованиях функций решение системы логических уравнений рекомендуется выполнить самостоятельно, сведя ее предварительно к одному логическому уравнению (число независимых уравнений обычно значительно меньше, чем их имеется в статической модели ЛС).
Для получения практических навыков в аналитических преобразованиях функций решение системы логических уравнений рекомендуется выполнить самостоятельно, сведя ее предварительно к одному логическому уравнению (число независимых уравнений обычно значительно меньше, чем их имеется в статической модели ЛС).
(см. скан)
Из графа переходов (рис.2.13,а), построенного на основании табл. 2.5, видно, что при значении входного  гнала
гнала  внутренние состояния ЛС циклически изменяются с периодом
внутренние состояния ЛС циклически изменяются с периодом  так как в этом случае не имеется ни одного устойчивого состояния. Внутренние состояния изменяются только на соседние, а значит состязания ЛЭ отсутствуют.
так как в этом случае не имеется ни одного устойчивого состояния. Внутренние состояния изменяются только на соседние, а значит состязания ЛЭ отсутствуют.
Покажем, что данную ЛС можно использовать в качестве асинхронного импульсного триггера со счетным входом  -триггера), если потенциальный сигнал х заменить импульсным сигналом
-триггера), если потенциальный сигнал х заменить импульсным сигналом  (
( входной информационный сигнал триггеров со счетным входом).
входной информационный сигнал триггеров со счетным входом).
Импульсный сигнал  характеризуется последовательностью значений
характеризуется последовательностью значений  Пусть при значении сигнала
Пусть при значении сигнала  находится в устойчивом состоянии
находится в устойчивом состоянии  затем его значение изменяется на 1. В ЛС при таком воздействии возникает переходный процесс, характеризующийся последовательностью изменений внутренних состояний
затем его значение изменяется на 1. В ЛС при таком воздействии возникает переходный процесс, характеризующийся последовательностью изменений внутренних состояний

Если импульсный сигнал  изменится с 1 на 0 в тот момент времени, когда ЛС перешла в состояние то переходный процесс на этом и закончится, так как данное внутреннее состояние является устойчивым для значения входного сигнала
изменится с 1 на 0 в тот момент времени, когда ЛС перешла в состояние то переходный процесс на этом и закончится, так как данное внутреннее состояние является устойчивым для значения входного сигнала  Часть ЛС, состоящая из
Часть ЛС, состоящая из  представляет собой рассмотренный выше асинхронный потенциальный
представляет собой рассмотренный выше асинхронный потенциальный  -триггер. Из графа переходов (рис. 2.13,а) видно, что данный триггер полностью переключается (сигналы
-триггер. Из графа переходов (рис. 2.13,а) видно, что данный триггер полностью переключается (сигналы  в момент времени, в который ЛС переходит в неустойчивое состояние
в момент времени, в который ЛС переходит в неустойчивое состояние  и состояние
и состояние  изменяется на
изменяется на  при любых значениях входного сигнала. Длительность перехода из устойчивого состояния
при любых значениях входного сигнала. Длительность перехода из устойчивого состояния  в неустойчивое состояние
в неустойчивое состояние  равна
равна  где
где  среднее время паразитной задержки сигналов в одном ЛЭ.
среднее время паразитной задержки сигналов в одном ЛЭ.
Если импульсный сикнал  изменится с 1 на 0, когда ЛС находится в неустойчивом состоянии
изменится с 1 на 0, когда ЛС находится в неустойчивом состоянии  то возникнут состязания ЛЭ, которые приведут к состязаниям устойчивых состояний (подробный анализ состязаний можно произвести с помощью табл. 2.5). Длительность перехода ЛС из устойчивого состояния
то возникнут состязания ЛЭ, которые приведут к состязаниям устойчивых состояний (подробный анализ состязаний можно произвести с помощью табл. 2.5). Длительность перехода ЛС из устойчивого состояния  в состояние
в состояние  равна
равна  а в состояние
а в состояние  Поэтому длительность импульсного сигнала
Поэтому длительность импульсного сигнала  при использовании ЛС на рис. 2.12 в качестве триггера со счетным входом
при использовании ЛС на рис. 2.12 в качестве триггера со счетным входом  -триггера) должна удовлетворять соотношению
-триггера) должна удовлетворять соотношению

Переход из устойчивого состояния  под воздействием активного уровня импульсного сигнала
под воздействием активного уровня импульсного сигнала  в состояние
в состояние  в силу симметричности схемы подчиняется тем же закономерностям, что и рассмотренный выше переход из состояния
в силу симметричности схемы подчиняется тем же закономерностям, что и рассмотренный выше переход из состояния  в состояние
в состояние  поэтому при поступлении на вход триггера каждого нового импульса его состояние (сигнал
поэтому при поступлении на вход триггера каждого нового импульса его состояние (сигнал  будет изменяться на инверсное (0 на 1, а 1 на 0).
будет изменяться на инверсное (0 на 1, а 1 на 0).
Таким образом, действительно, рассмотренная ЛС при соответствующем выборе длительности импульсного сигнала  может быть использована в качестве триггера со счетным входом. На рис.
может быть использована в качестве триггера со счетным входом. На рис.  изображены временные диаграммы, поясняющие его работу (интервалы времени
изображены временные диаграммы, поясняющие его работу (интервалы времени  обозначены одной точкой, а
обозначены одной точкой, а  двумя точками).
двумя точками).
Импульсный сигнал  длительностью
длительностью  можно получить с помощью разностного элемента, показанного на рис. 2.6 (перед подачей на вход триггера выходной сигнал разностного элемента необходимо проинвертировать).
можно получить с помощью разностного элемента, показанного на рис. 2.6 (перед подачей на вход триггера выходной сигнал разностного элемента необходимо проинвертировать).
Если на вход триггера подать сигнал  имеющий длительность
имеющий длительность  то триггер сработает два раза, т. е. один импульс будет воспринят как два импульса, длительность которых определяется соотношением (2.21). Рассмотренный триггер можно использовать и без разностного элемента, если период
то триггер сработает два раза, т. е. один импульс будет воспринят как два импульса, длительность которых определяется соотношением (2.21). Рассмотренный триггер можно использовать и без разностного элемента, если период  подаваемого на его вход сигнала (полагаем, что полупериоды равны) удовлетворяет соотношению
подаваемого на его вход сигнала (полагаем, что полупериоды равны) удовлетворяет соотношению 
Изложенная формальная методика анализа ЛС дает ясное представление о физических процессах, протекающих в них при изменении входных воздействий, и достаточно проста в применении, если ЛС состоит из небольшого числа  и имеет мало физических входов
и имеет мало физических входов  Анализ же более сложных ЛС необходимо проводить с помощью компьютера. Все понятия, введенные при выполнении анализа ЛС, естественным образом используются в теории асинхронных потенциальных автоматов.
Анализ же более сложных ЛС необходимо проводить с помощью компьютера. Все понятия, введенные при выполнении анализа ЛС, естественным образом используются в теории асинхронных потенциальных автоматов.
Один из упрощенных методов анализа ЛС с обратными связями заключается в отыскании минимального числа обратных связей, при разрыве которых получается ЛС без обратных связей. Это позволяет найти минимальное число переменных  для описания динамической модели ЛС. Так, если в разностном элементе (см. рис. 2.6) разорвать связь с выхода ЛЭ
для описания динамической модели ЛС. Так, если в разностном элементе (см. рис. 2.6) разорвать связь с выхода ЛЭ  на вход
на вход  то получится ЛС без обратных связей. Тогда паразитные элементы задержки
то получится ЛС без обратных связей. Тогда паразитные элементы задержки  можно вынести на выход а полученной ЛС и получить упрощенную динамическую модель ЛС с восстановленной обратной связью (рис. 2.14):
можно вынести на выход а полученной ЛС и получить упрощенную динамическую модель ЛС с восстановленной обратной связью (рис. 2.14):

Упрощенная динамическая модель ЛС позволяет значительно проще установить закон ее функционирования,  переходные процессы на ее основе исследовать невозможно.
переходные процессы на ее основе исследовать невозможно.

Рис. 2.14
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Основы теории переключательных функций
- 1.2. Позиционные системы счисления
- 1.3. Переключательные функции
- 1.4. Принцип и закон двойственности
- 1.5. Теоремы разложения
- 1.6. Решение систем логических уравнений
- 1.7. Первичные термы, минтермы и макстермы
- 1.8. Совершенные нормальные формы представления функций
- 1.9. Конъюнктивные и дизъюнктивные термы
- 1.10. Минимизация переключательных функций
- 1.11. Диаграммы Вейча
- 1.12. Минимизация неполностью определенных функций, совместная минимизация нескольких функций
- 1.13. Скобочные формы функций
- 1.14. Закон двойственности для логических схем
- 1.15. Линейные функции
- Глава 2. Анализ и синтез логических схем
- 2.2. Модели логических элементов
- 2.3. Модели логических схем
- 2.4. Анализ логических схем
- 2.5. Синтез комбинационных схем, свободных от состязаний
- Глава 3. Синтез асинхронных потенциальных автоматов
- 3.2. Асинхронные потенциальные автоматы
- 3.3. Асинхронные потенциальные триггеры и элементы памяти
- Триггеры типа R-S
- Триггеры типа D-L
- Триггеры типа D-L-R с приоритетом входа R.
- Триггеры типа D-L-R с приоритетом входа L.
- Триггеры типа R-S-L.
- Триггеры типа DN-LN
- Аналитический метод синтеза и анализа триггеров.
- 3.4. Задание асинхронных потенциальных автоматов таблицами и графами переходов
- 3.5. Синтез асинхронных потенциальных счетчиков
- 3.6. Синтез асинхронных импульсных триггеров
- Триггеры типа dJ-dK.
- Классификация триггеров.
- 3.7. Синтез синхронных триггеров
- Триггеры типа J-K
- Синхронно-асинхронные триггеры.
- 3.8. Примеры синтеза асинхронных потенциальных автоматов
- Цифровые фазочастотные детекторы.
- Квантизатор временных интервалов.
- 3.9. Генераторы сигналов
- Автогенераторы.
- Управляемые автогенераторы.
- Глава 4. Синтез синхронных автоматов
- 4.2. Синхронные триггеры
- Триггеры типов D и R-S с импульсным тактовым сигналом.
- Синхронные триггеры типов R-S и D-L
- Синхронно-асинхронные триггеры.
- Синхронные триггеры типа J-K
- Триггеры типа Т.
- Классификация синхронных триггеров.
- Преобразования типов синхронных триггеров.
- Триггеры типов D-T-L и D-T-L/R
- Функции переходов синхронно-асинхронных триггеров.
- 4.3. Примеры синтеза синхронных автоматов
- 4.4. Сдвигающие регистры
- Синтез счетчиков на сдвигающих регистрах.
- Сдвигающие регистры с загрузкой данных.
- Реверсивные сдвигающие регистры.
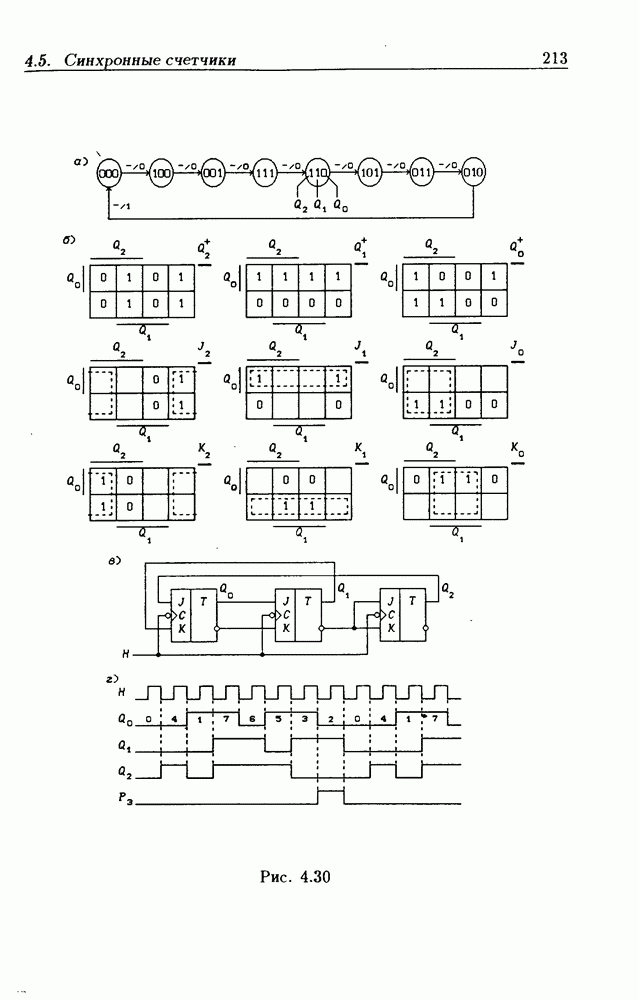
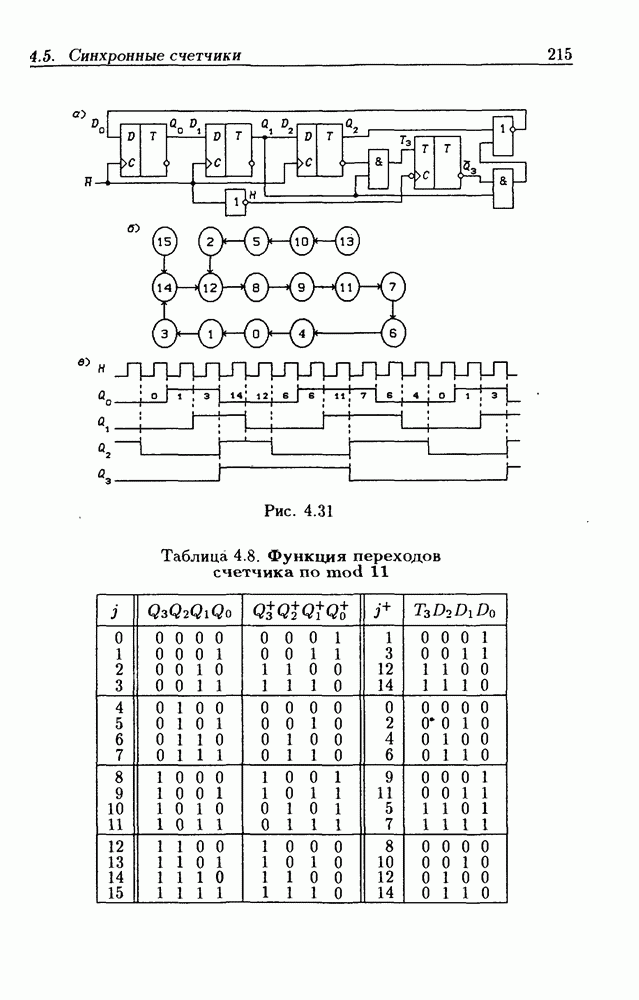
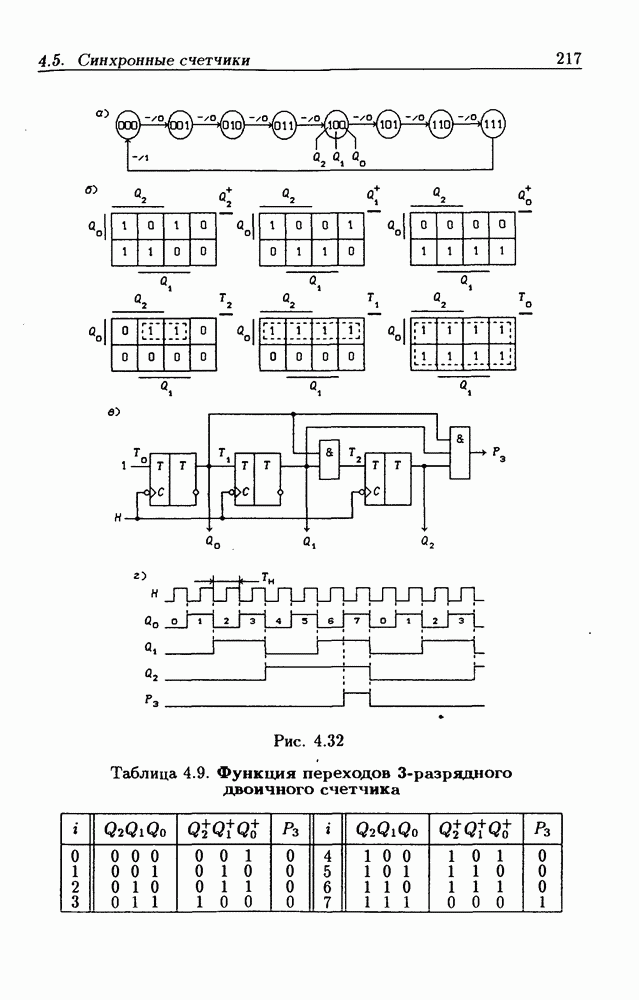
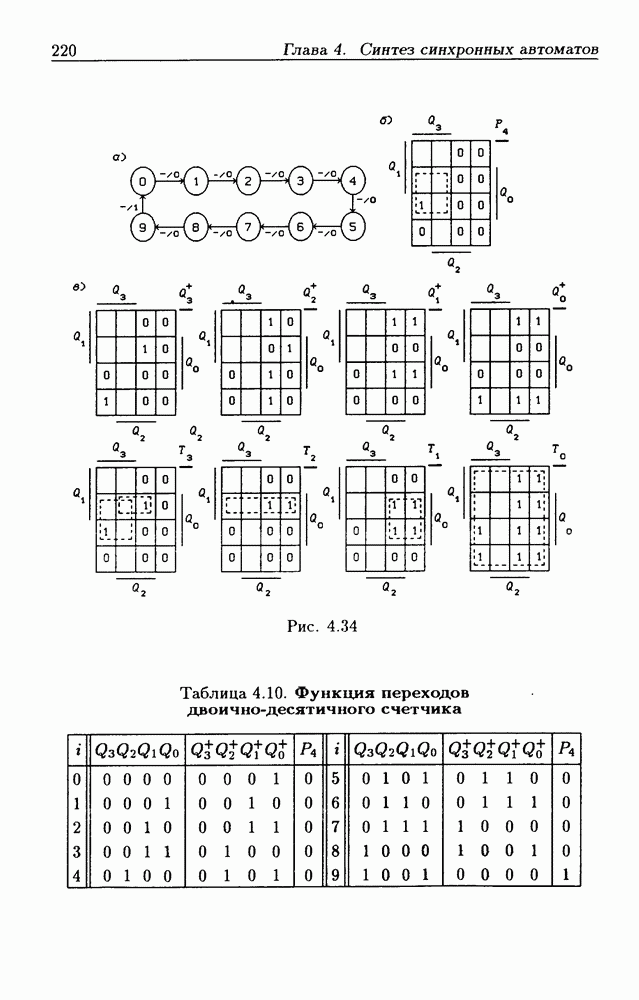
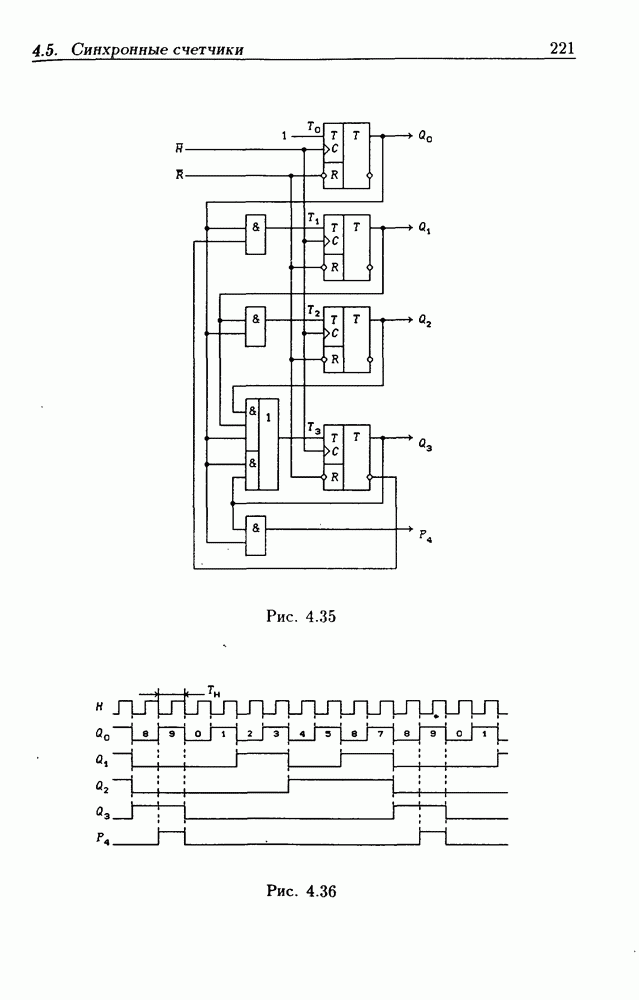
- 4.5. Синхронные счетчики
- Синхронные двоичные счетчики.
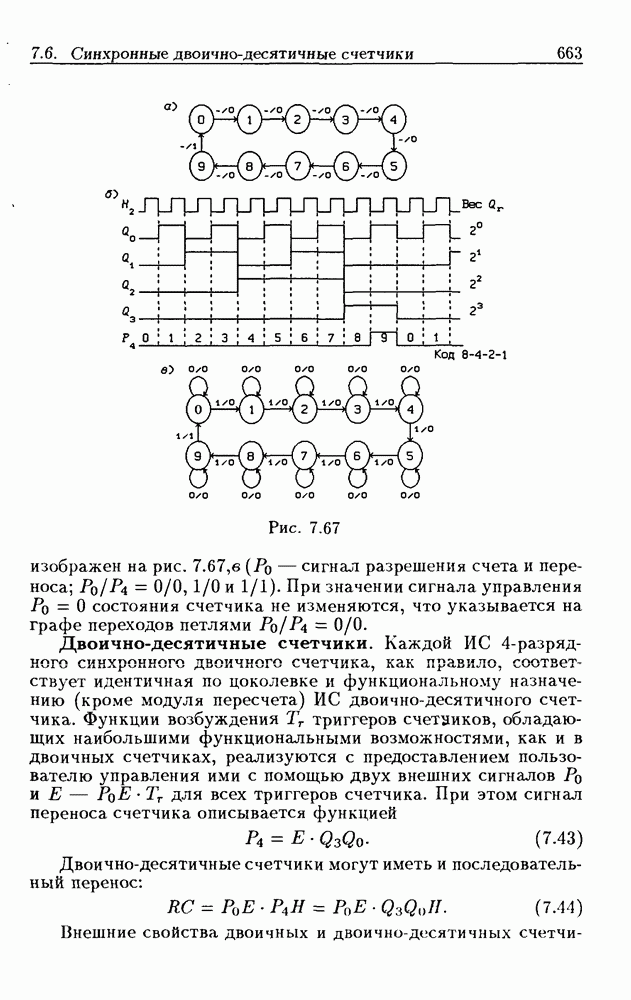
- Синхронные двоично-десятичные счетчики.
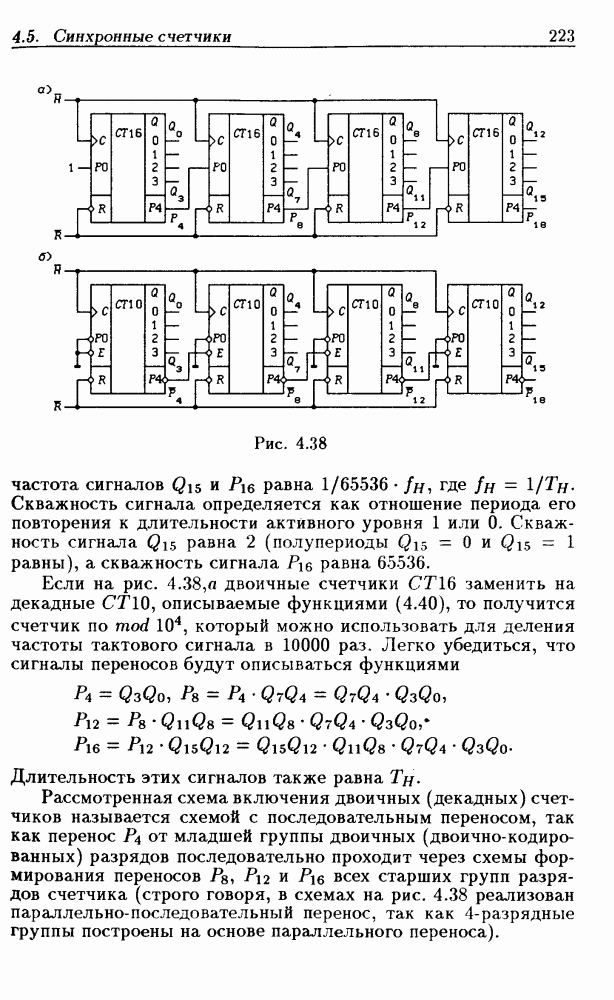
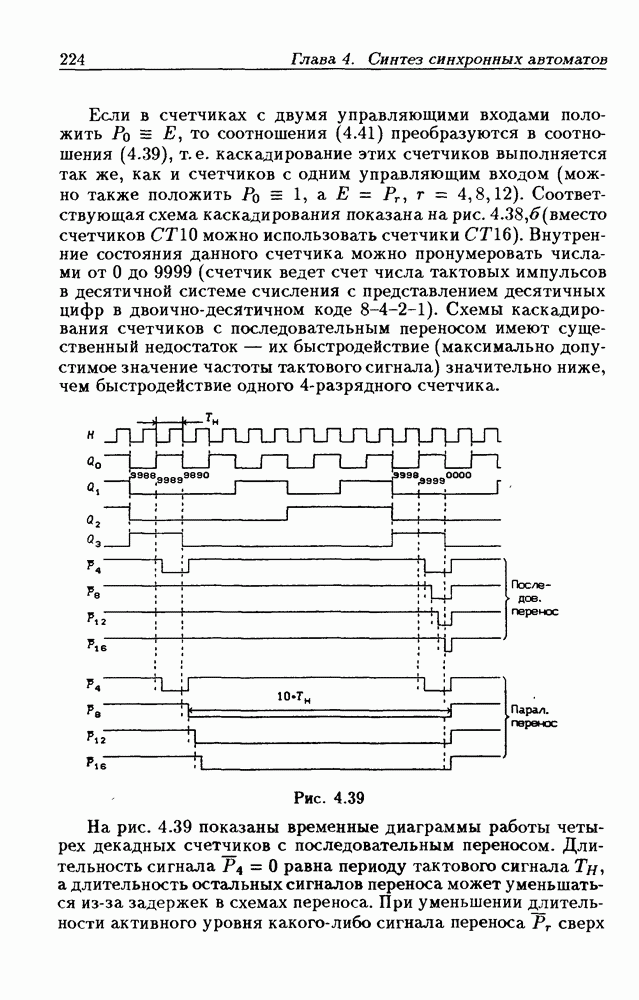
- Каскадирование двоичных и двоично-десятичных счетчиков.
- Синхронные двоичные реверсивные счетчики.
- Реверсивные двоично-десятичные счетчики.
- Каскадирование реверсивных счетчиков.
- Счетчики на сдвигающих регистрах.
- Кольцевые счетчики.
- Линейные счетчики.
- Программируемые счетчики.
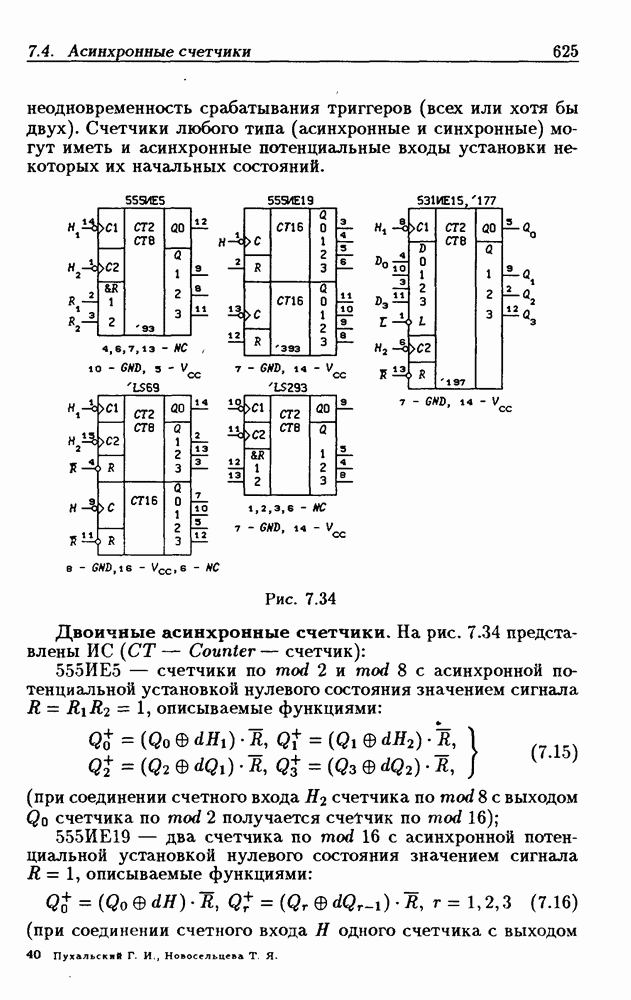
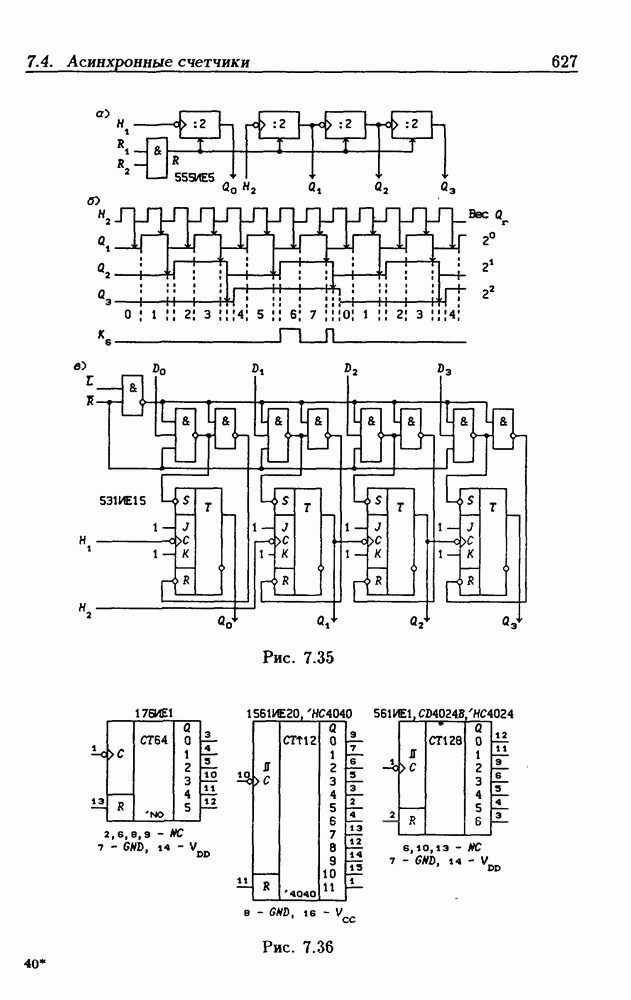
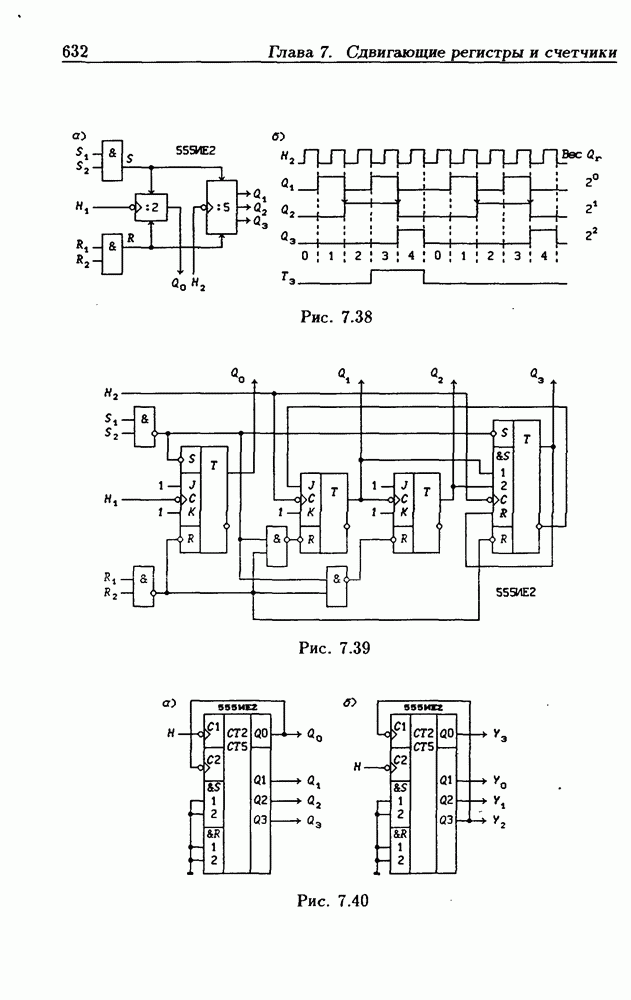
- 4.6. Асинхронные счетчики
- Асинхронные счетчики с умножением частоты счетного сигнала.
- Асинхронные импульсно-потенциальные счетчики.
- Асинхронное программирование модуля пересчета счетчиков.
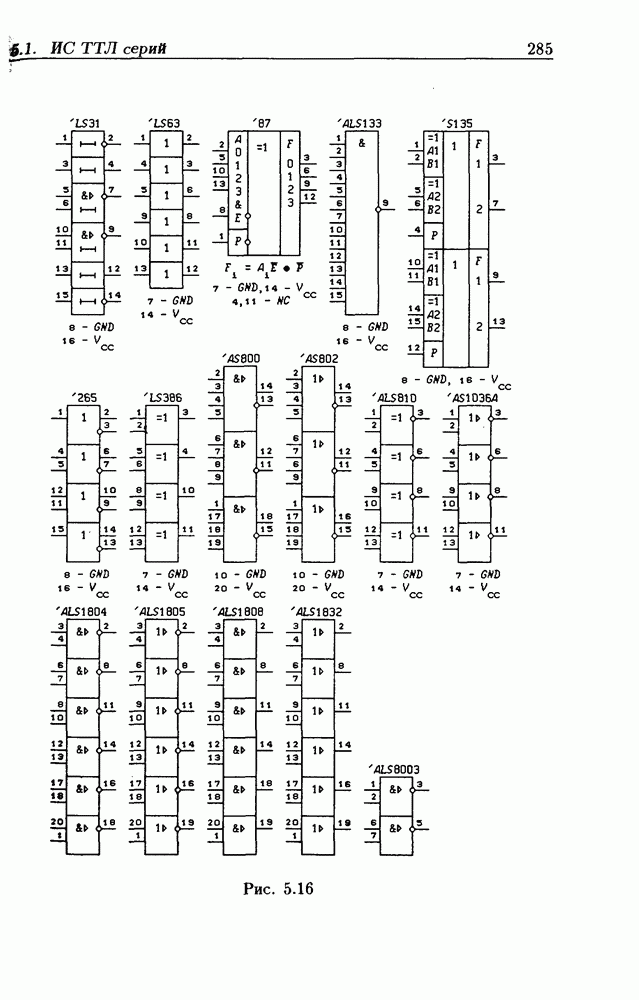
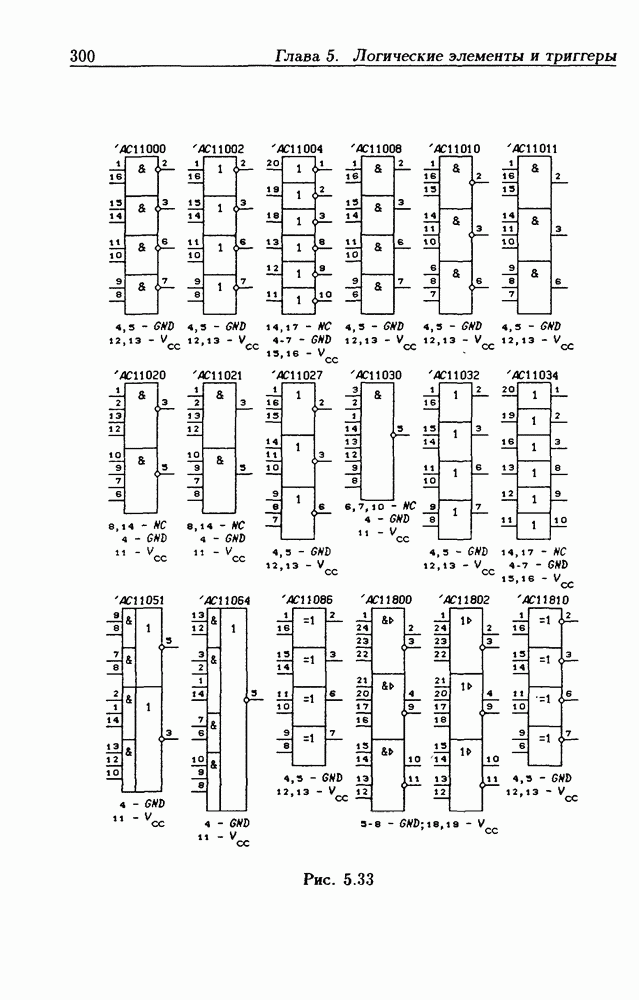
- Глава 5. Логические элементы и триггеры
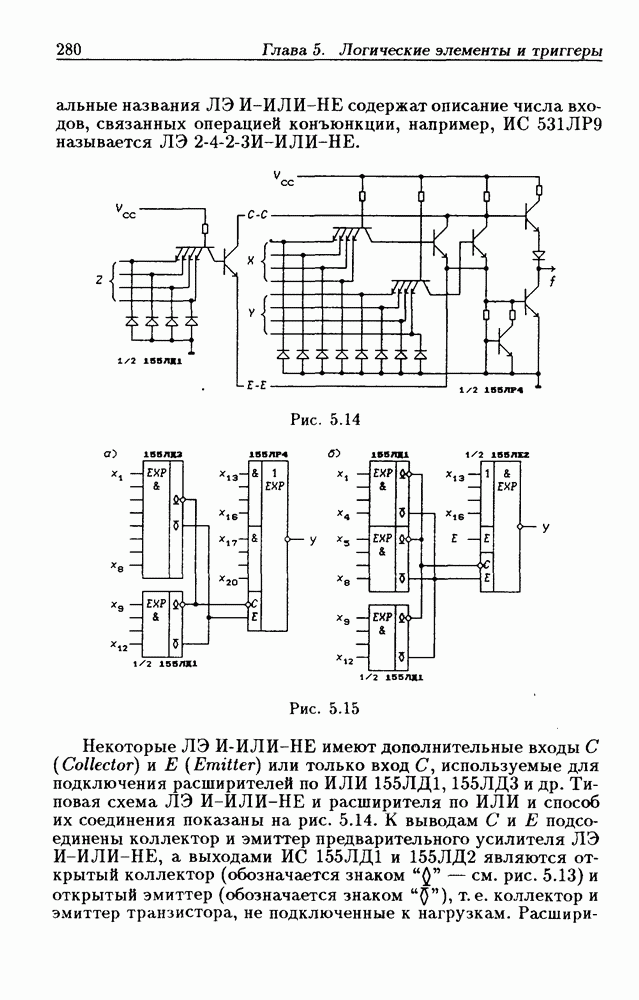
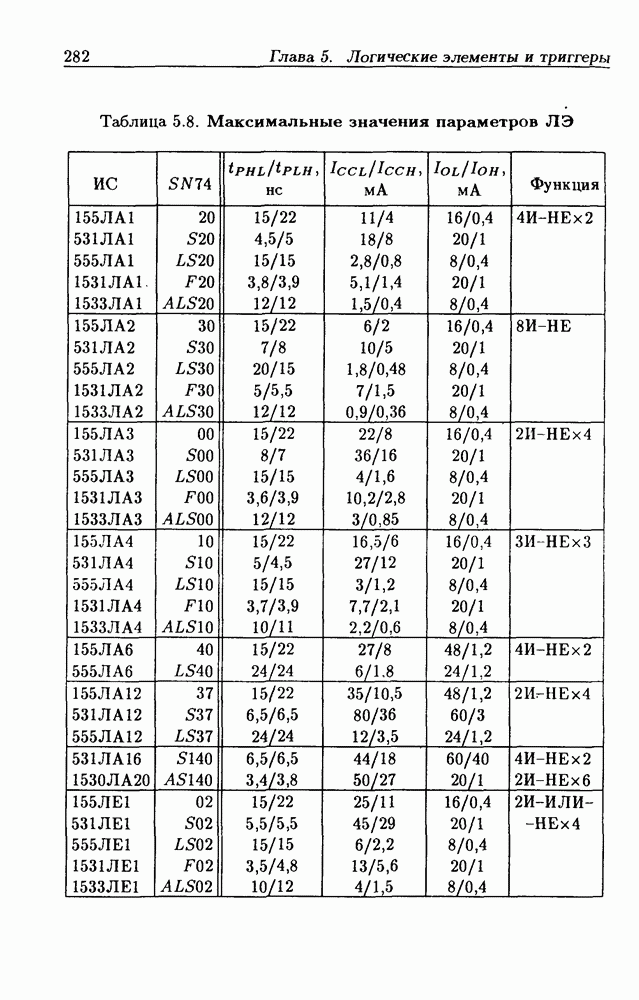
- Логические элементы.
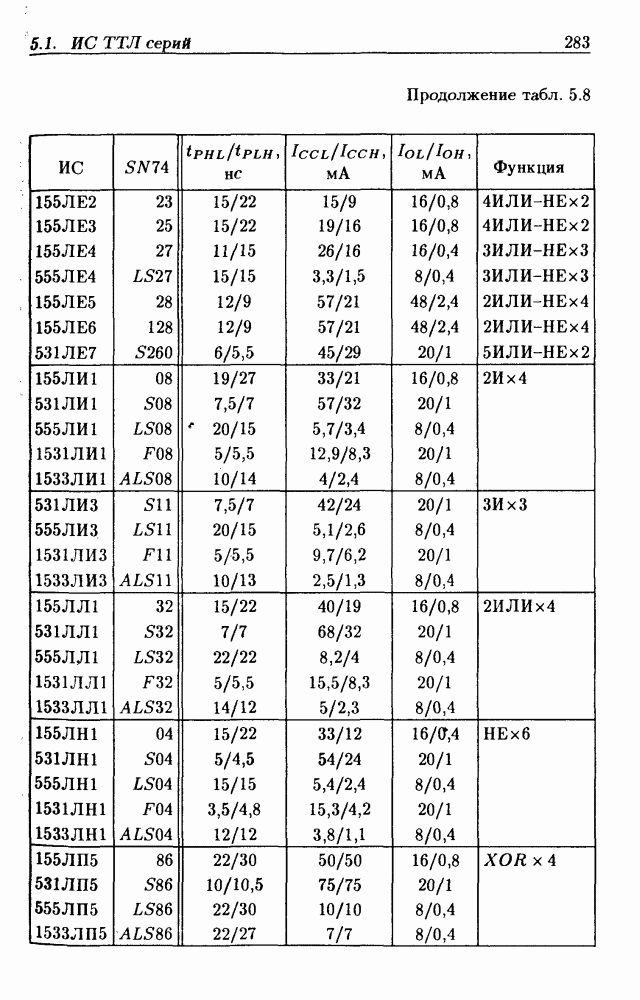
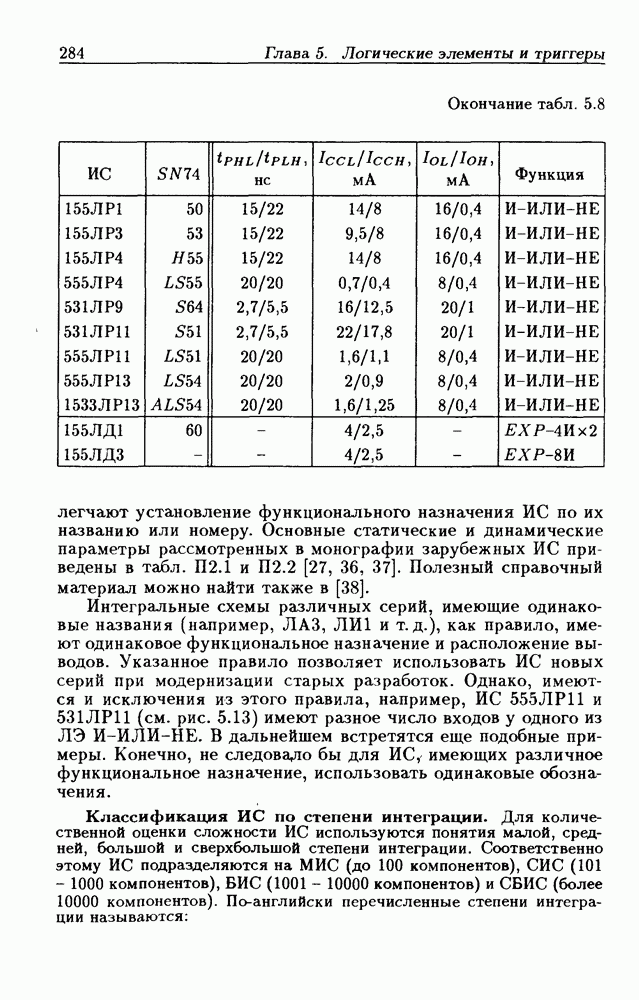
- Классификация ИС по степени интеграции.
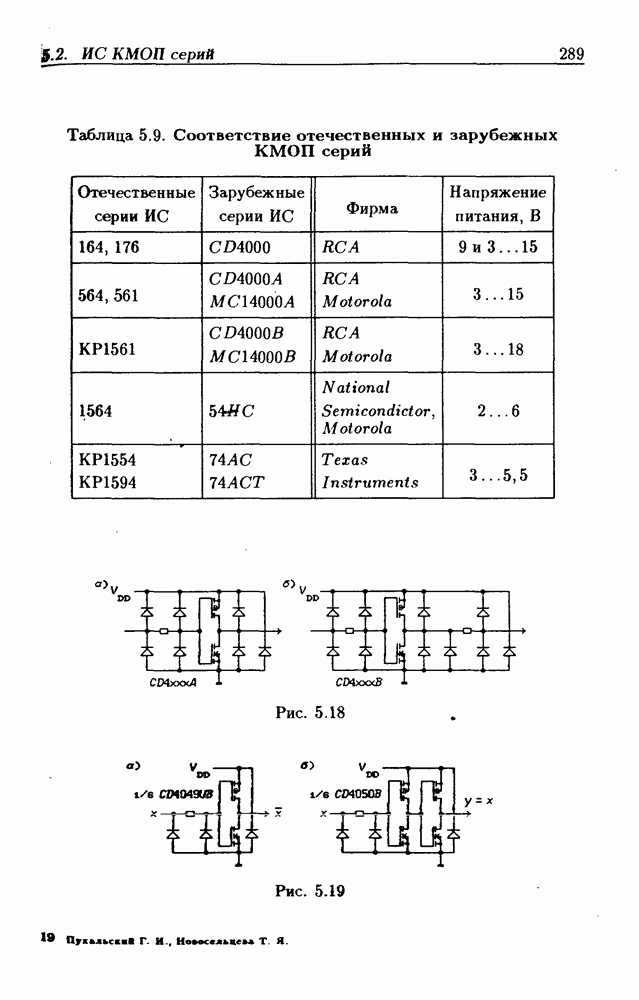
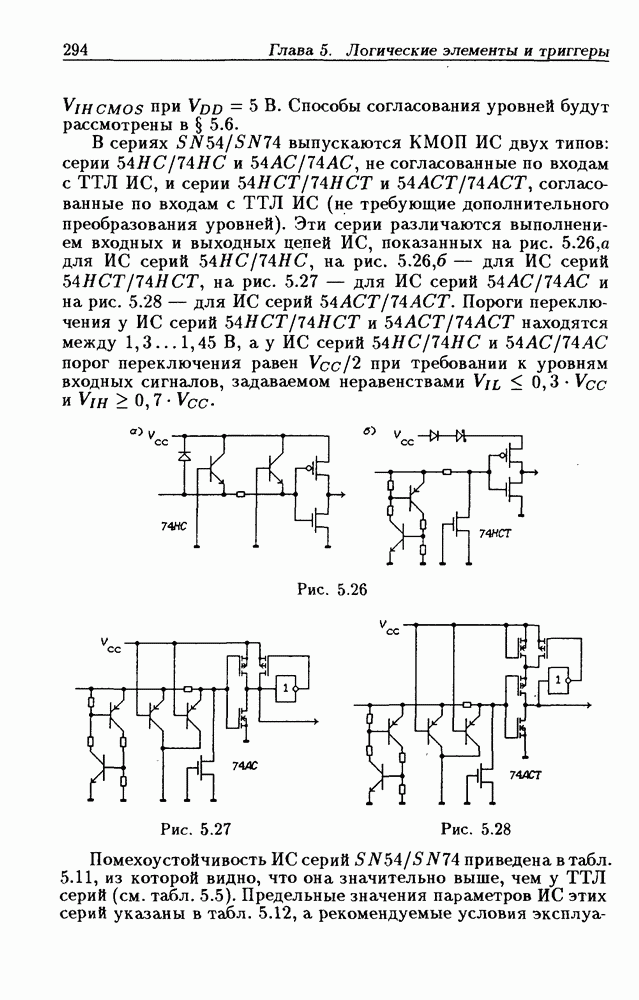
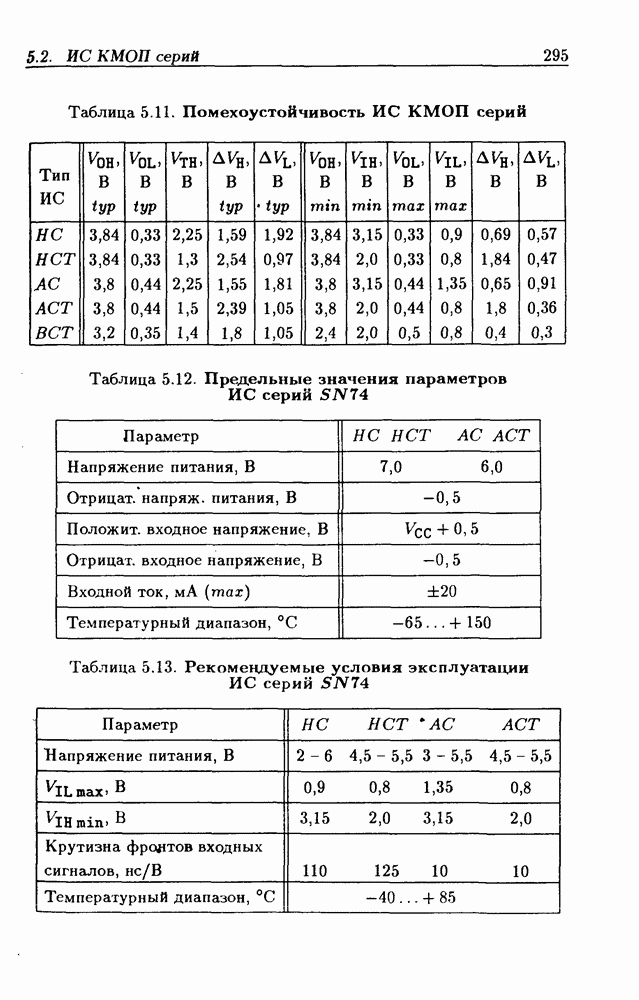
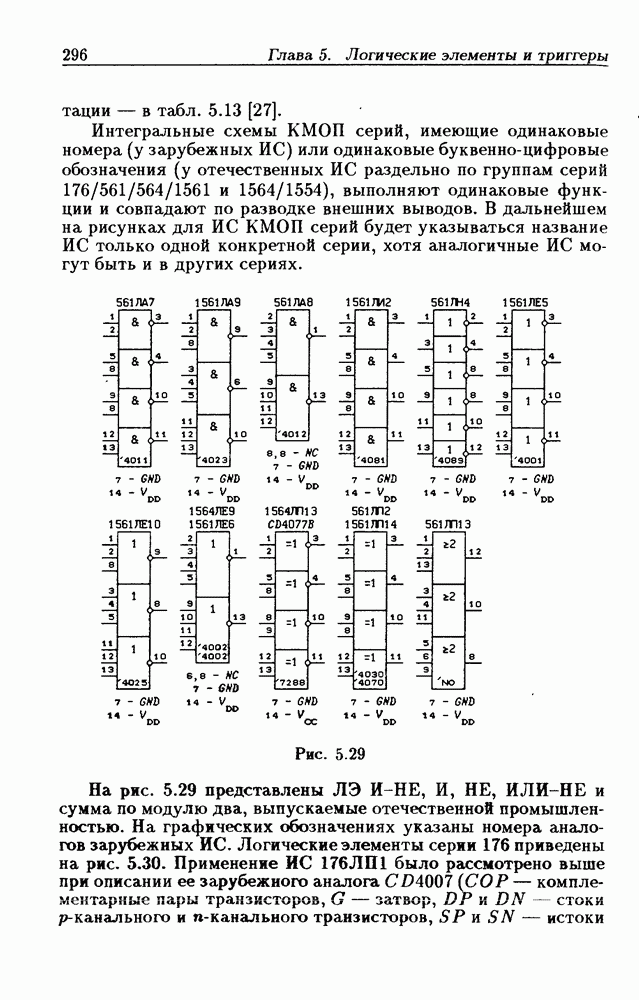
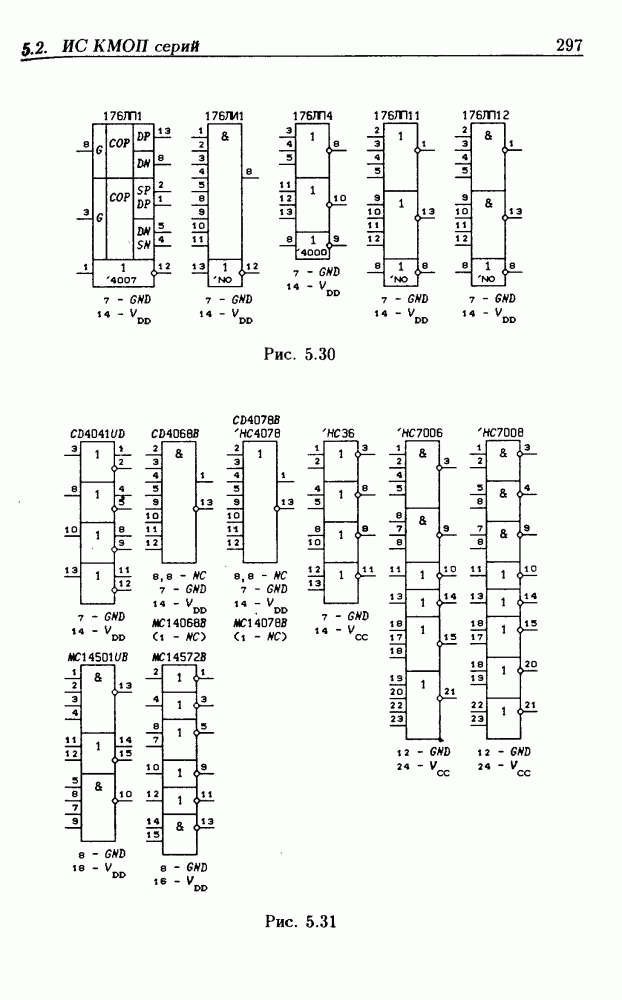
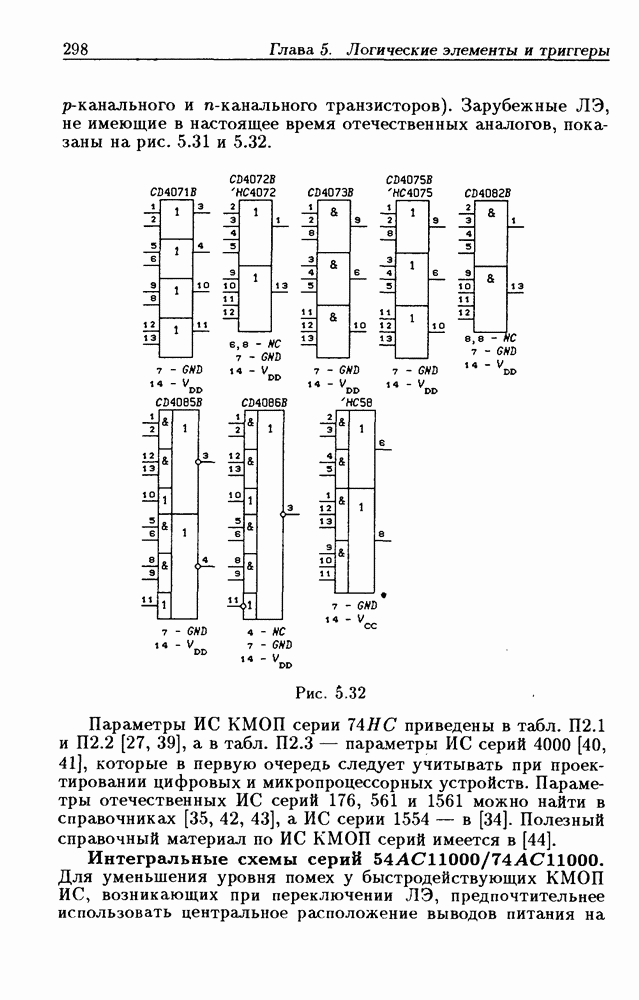
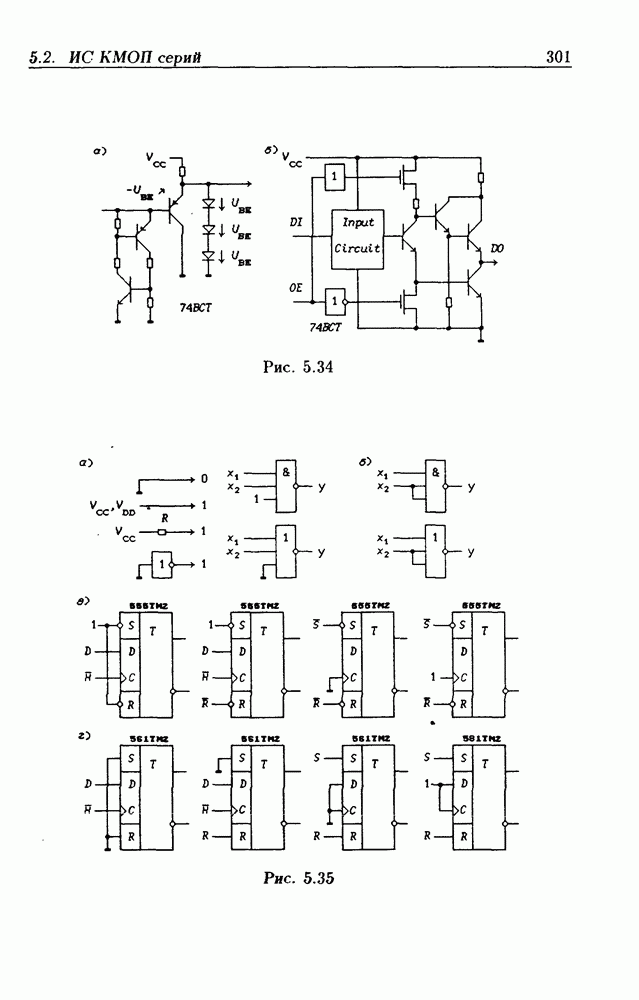
- 5.2. Интегральные схемы КМОП серий
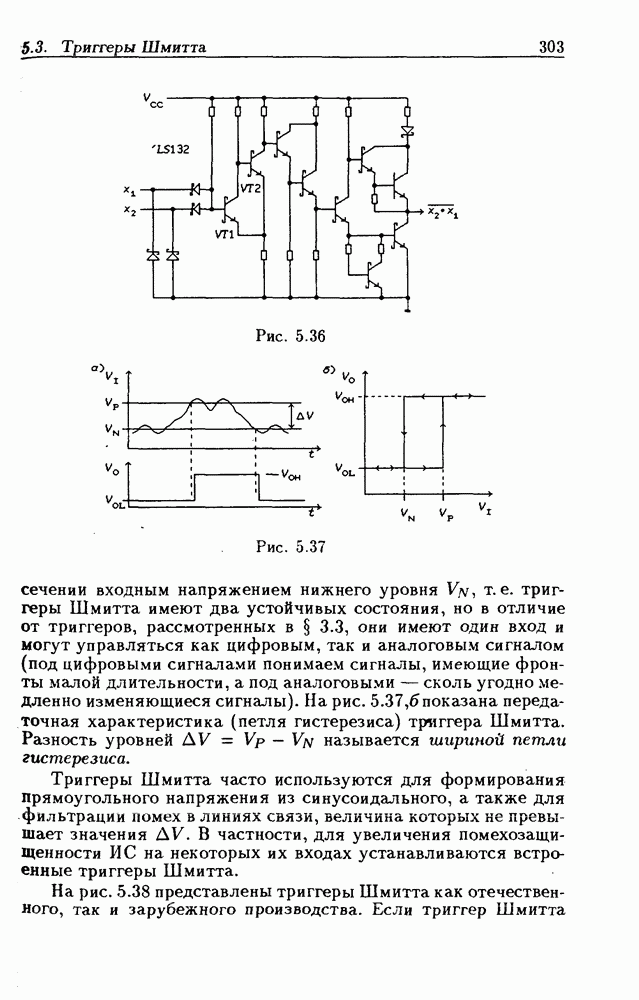
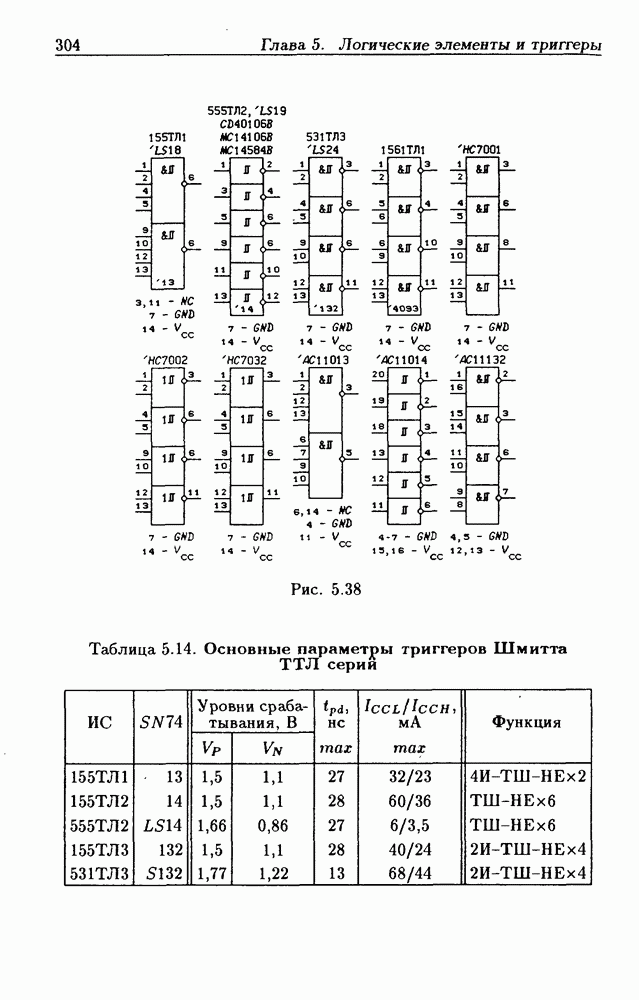
- 5.3. Триггеры Шмитта
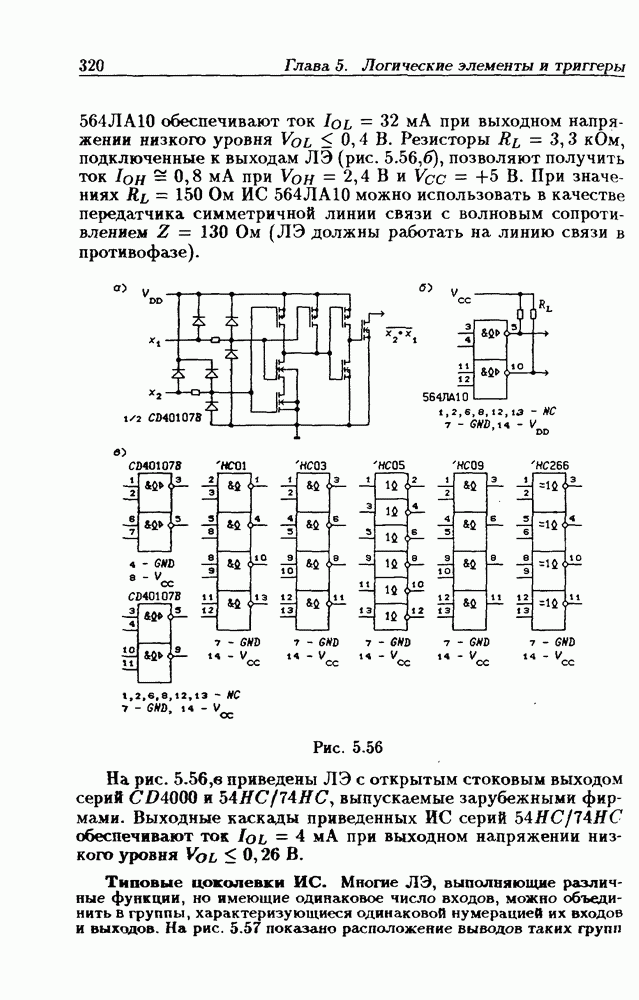
- 5.4. Логические элементы с открытым коллекторным выходом
- Логические элементы с открытым коллекторным выходом.
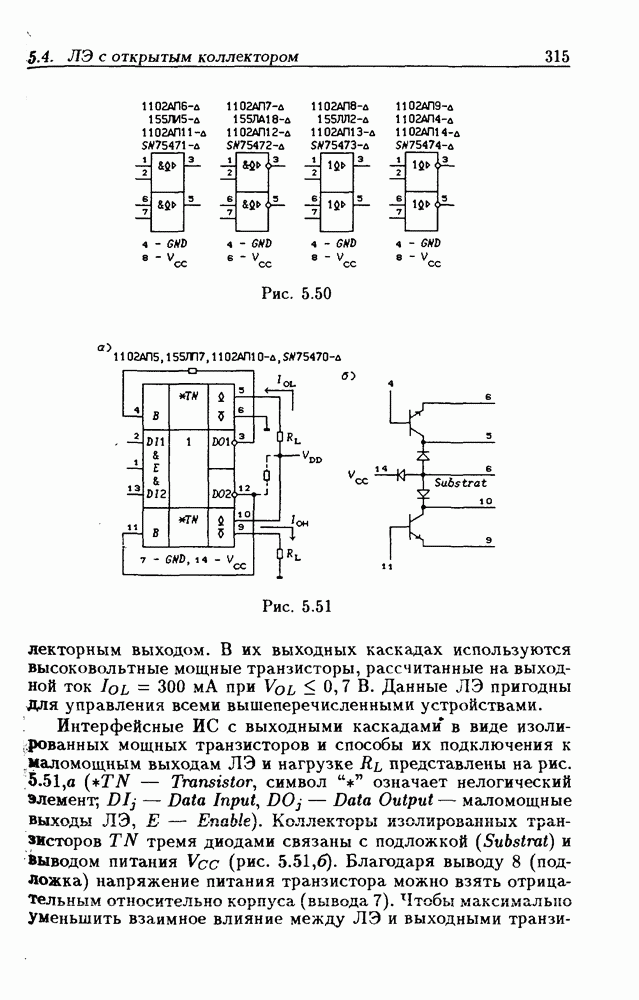
- Применения ЛЭ с открытым коллекторным выходом.
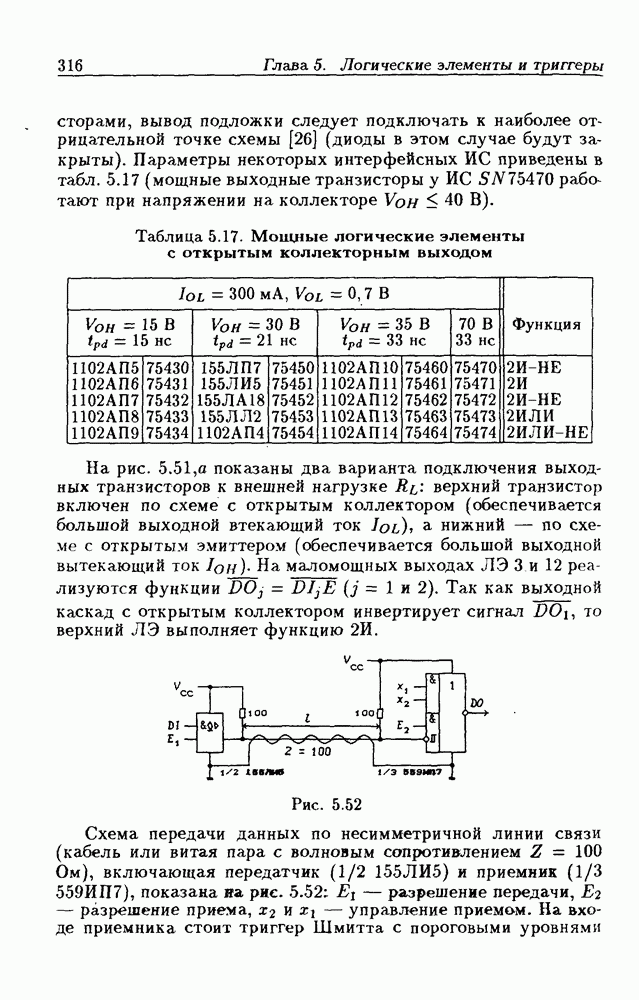
- Интерфейсные ЛЭ с открытым коллекторным выходом.
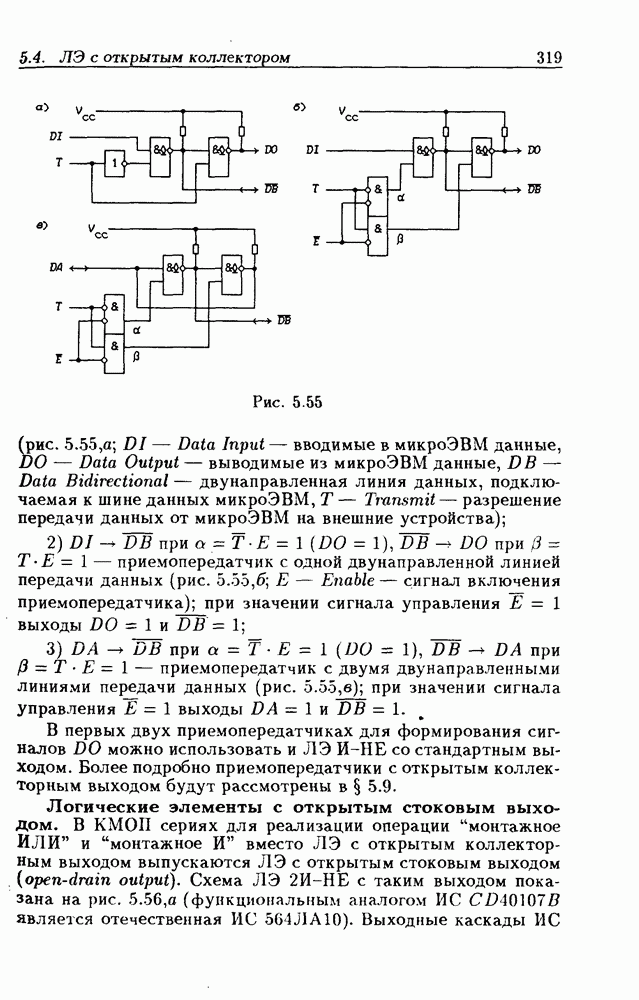
- Логические элементы с открытым стоковым выходом.
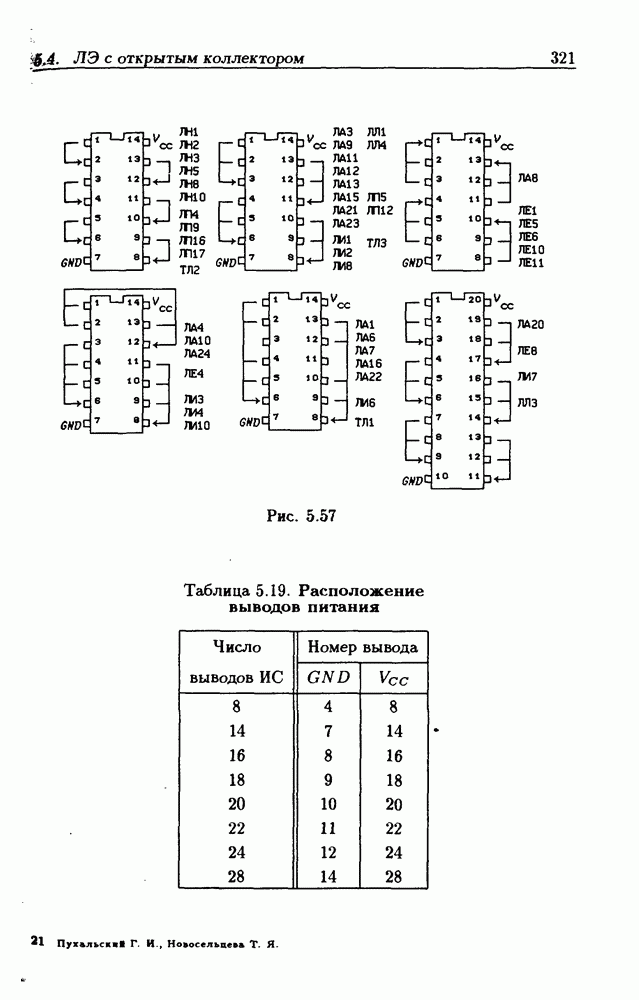
- Типовые цоколевки ИС.
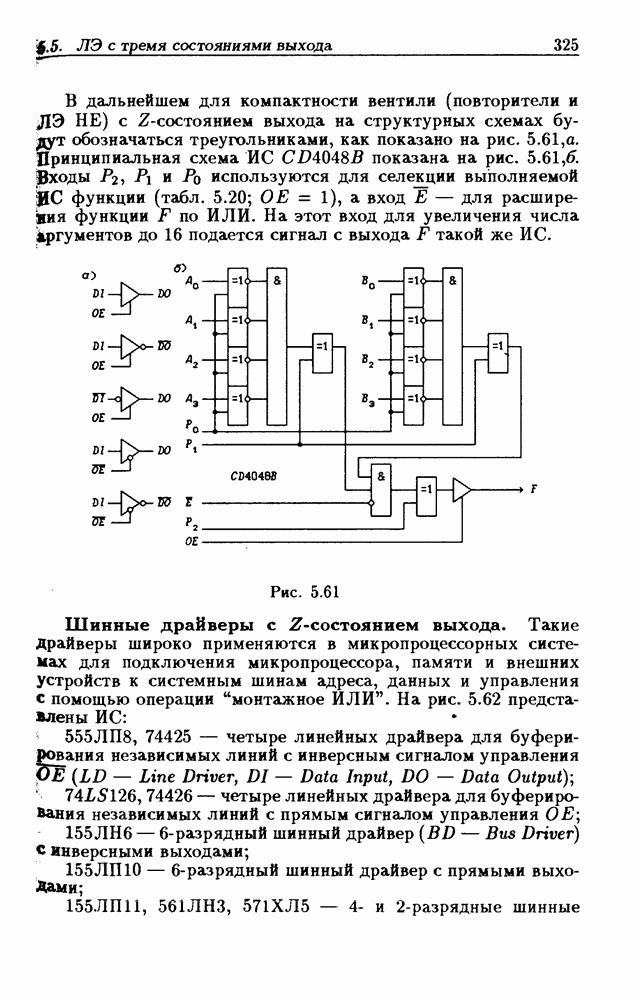
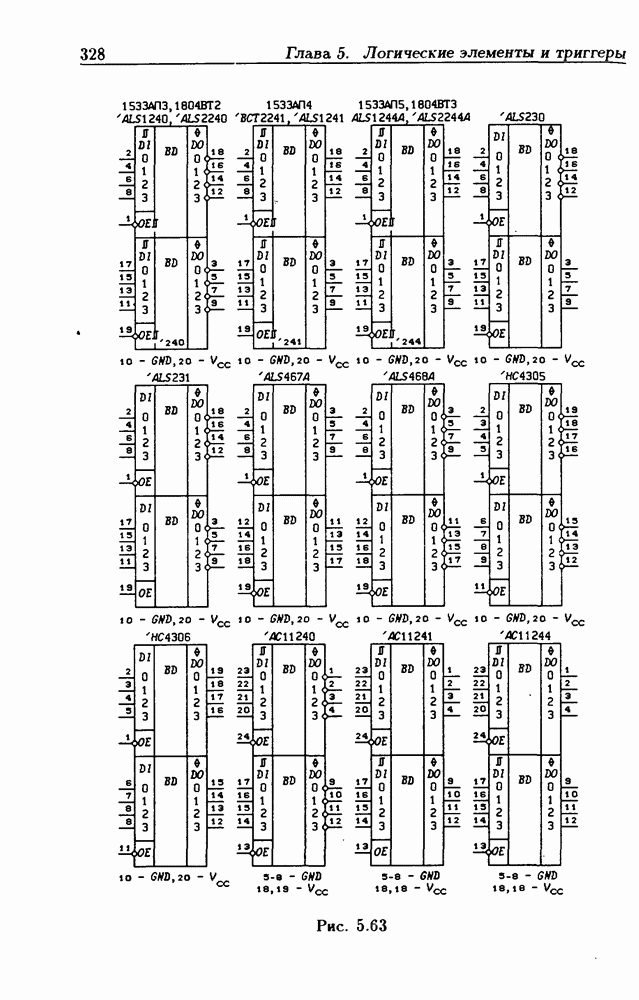
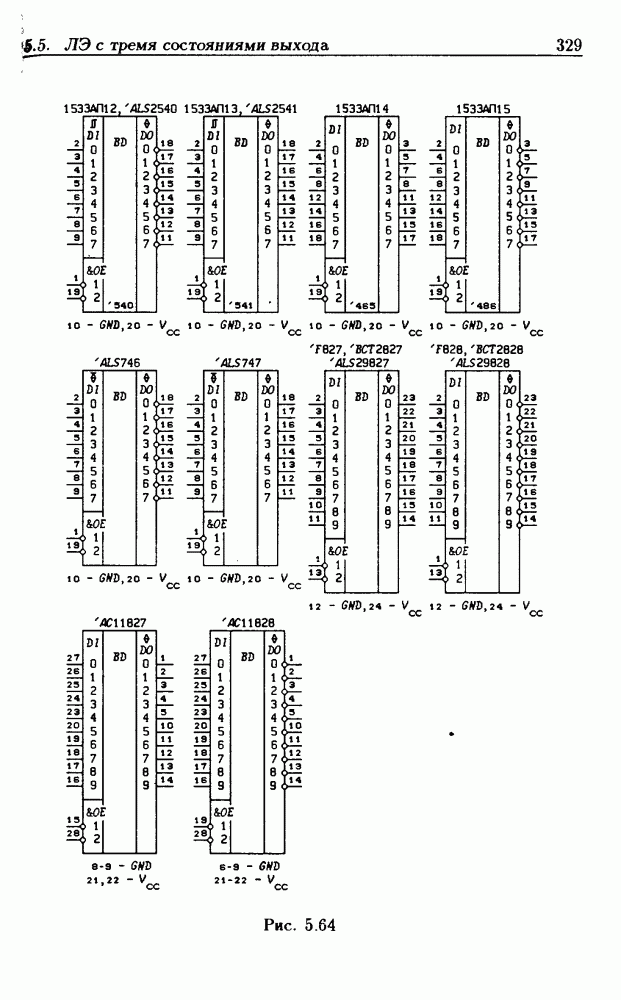
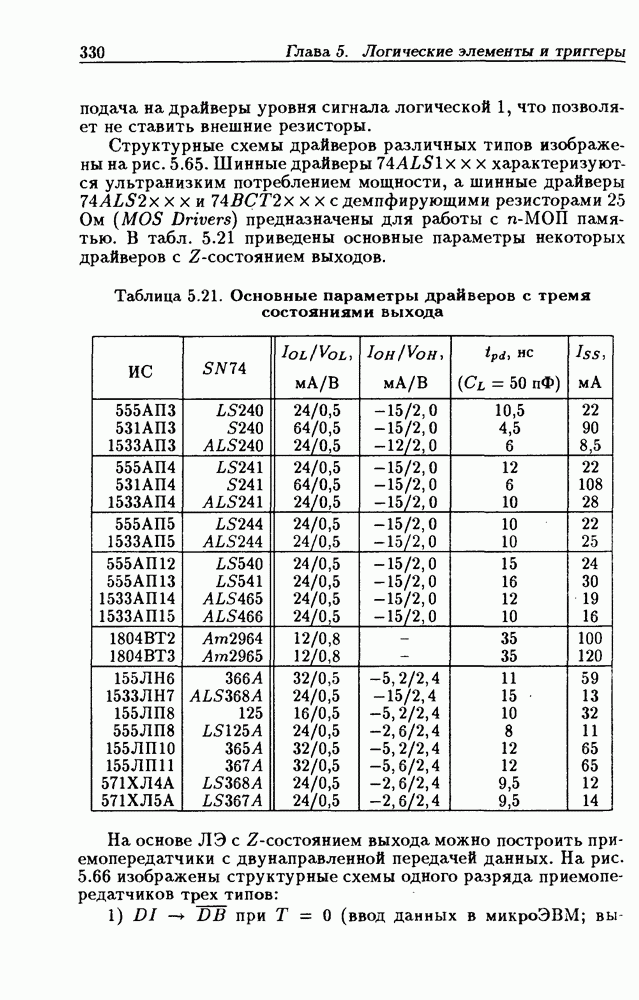
- 5.5. Логические элементы с тремя состояниями выхода
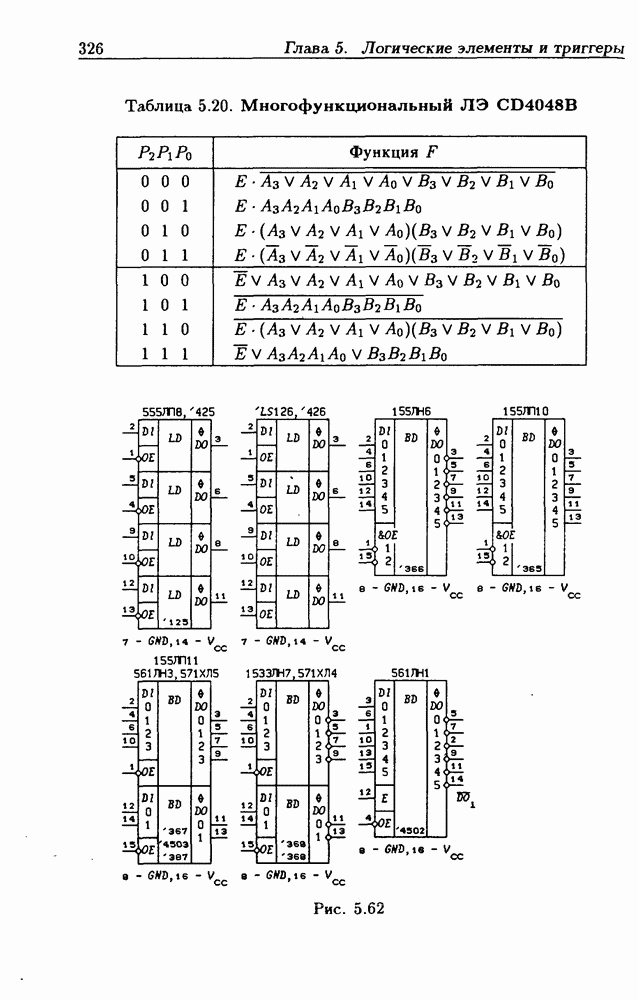
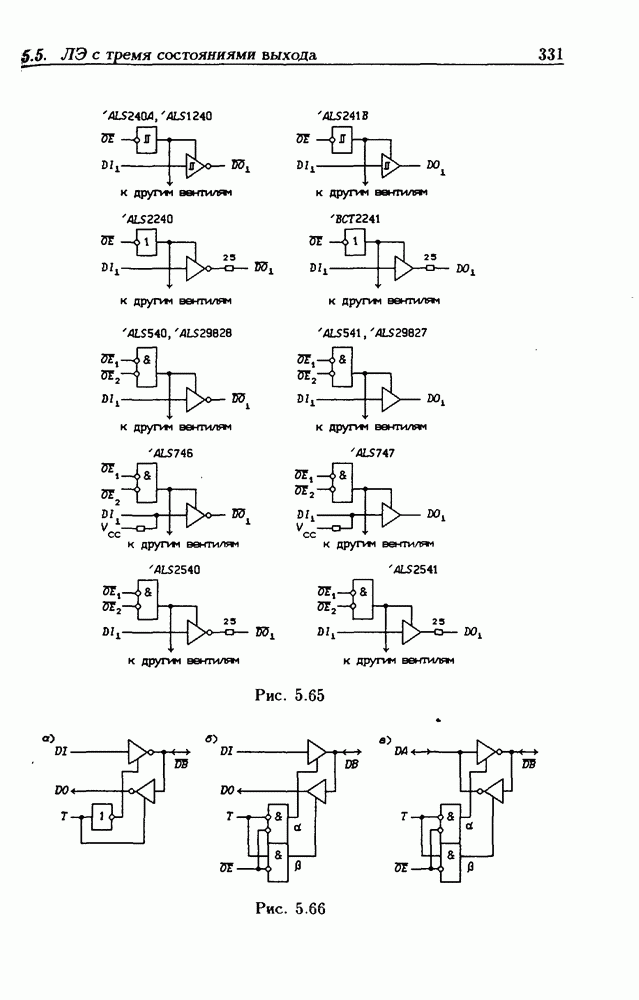
- Шинные драйверы с Z-состоянием выхода.
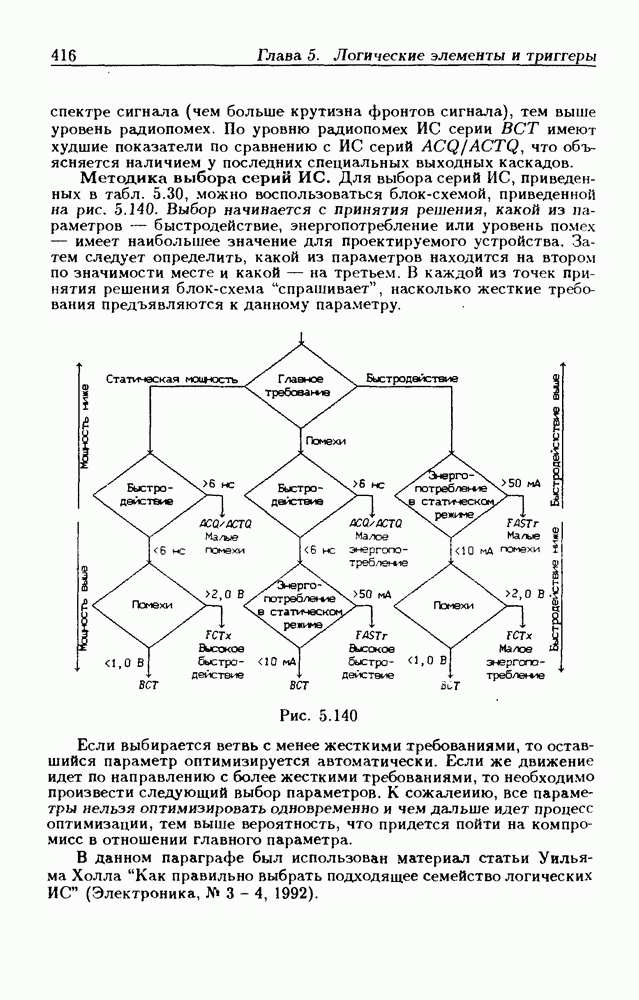
- Основные правила графического изображения ИС.
- 5.6. Преобразователи уровней напряжения и тока
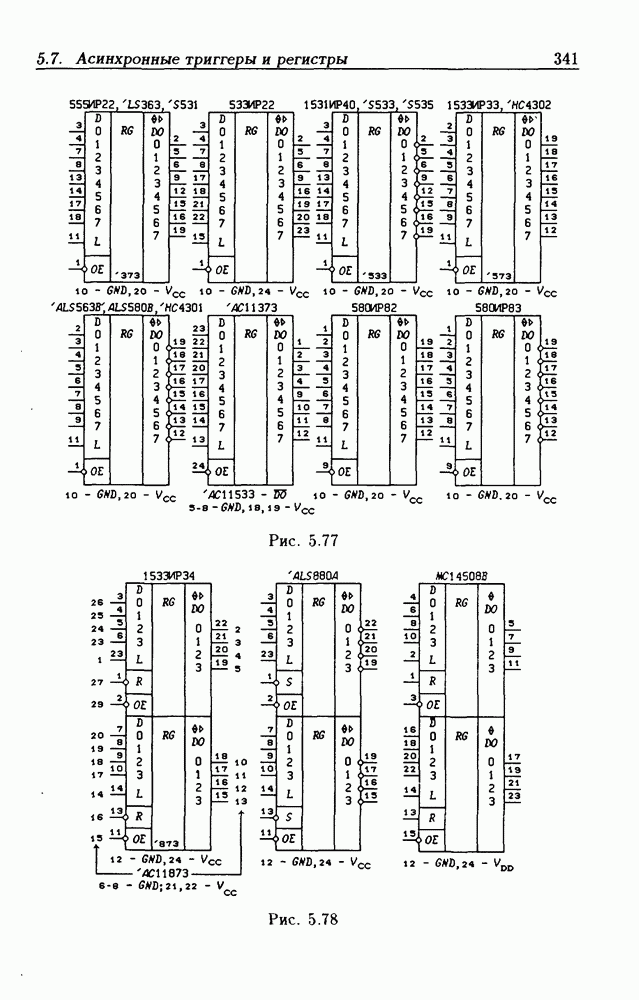
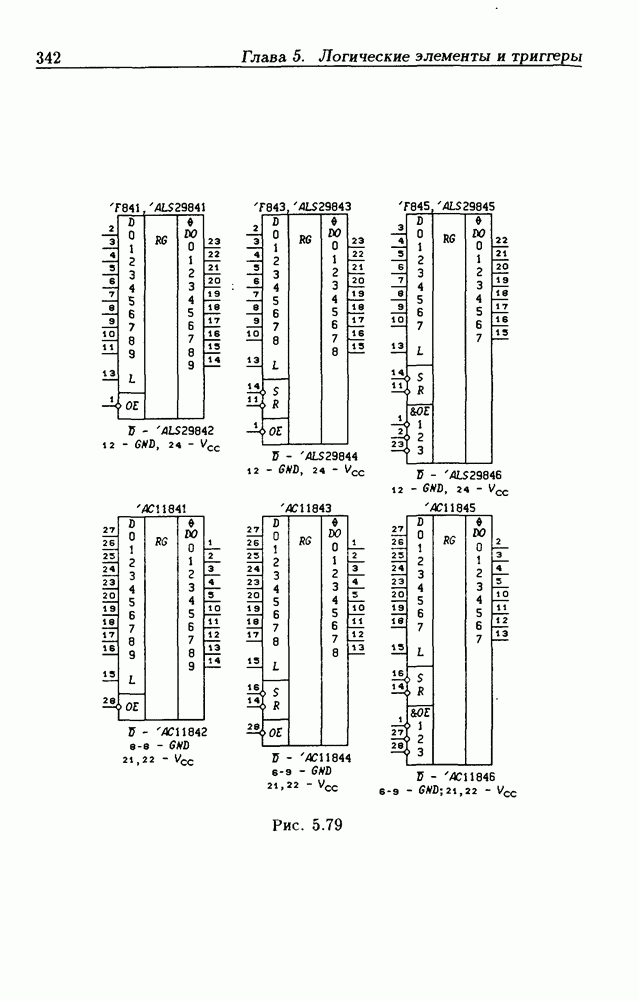
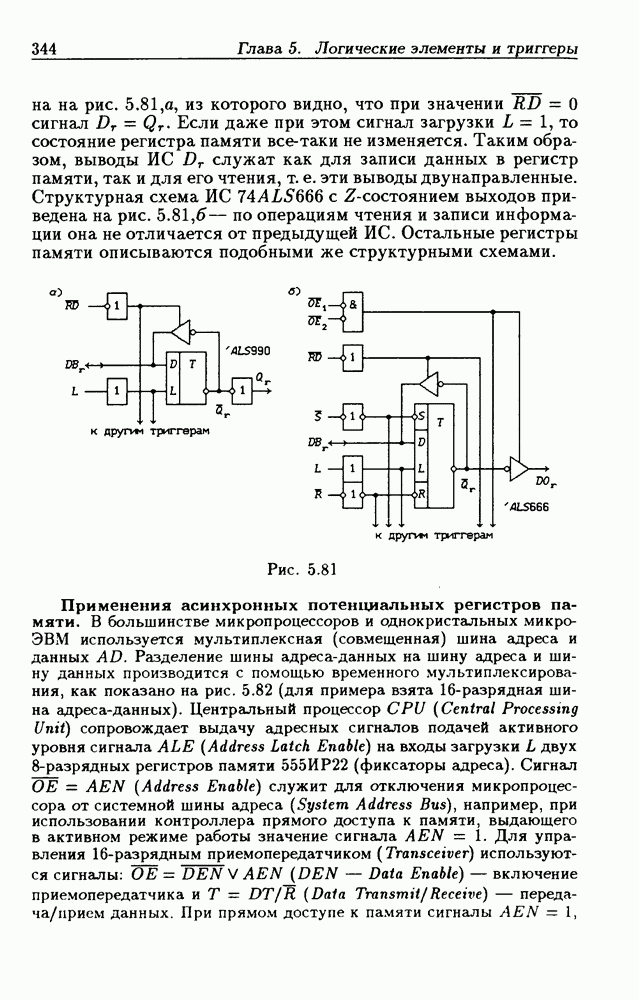
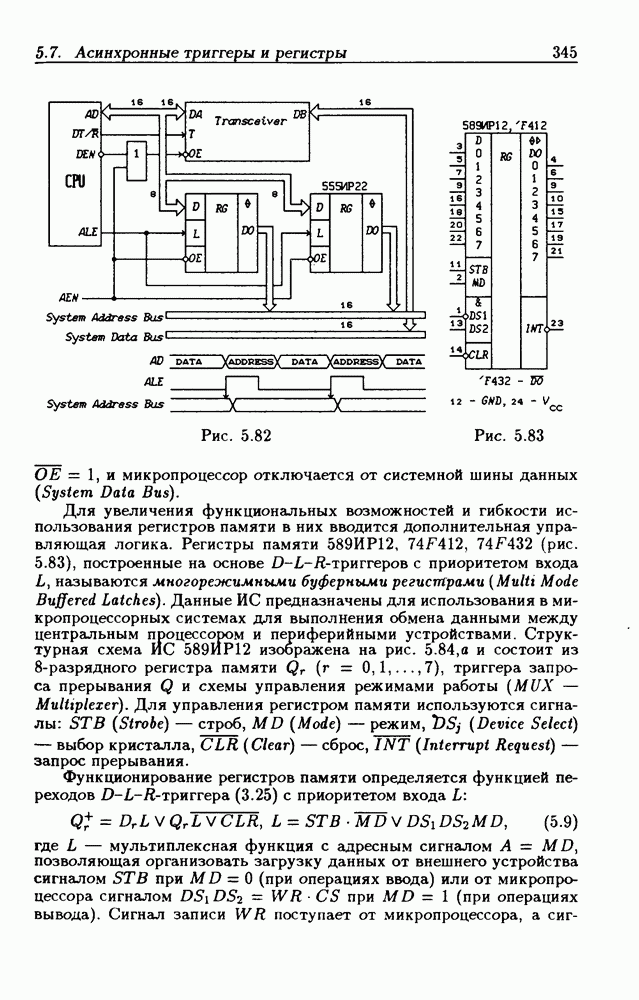
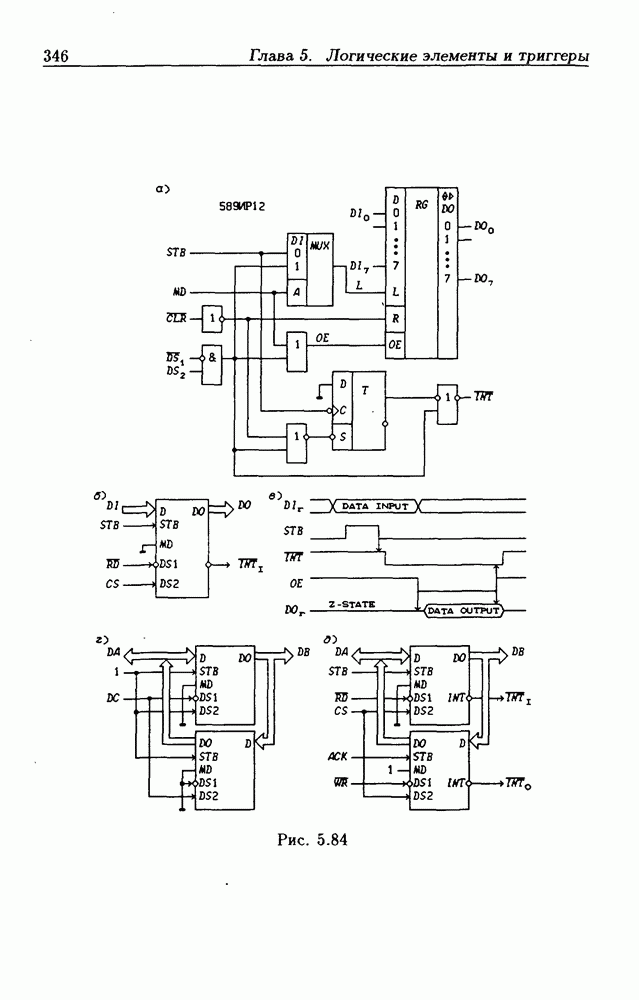
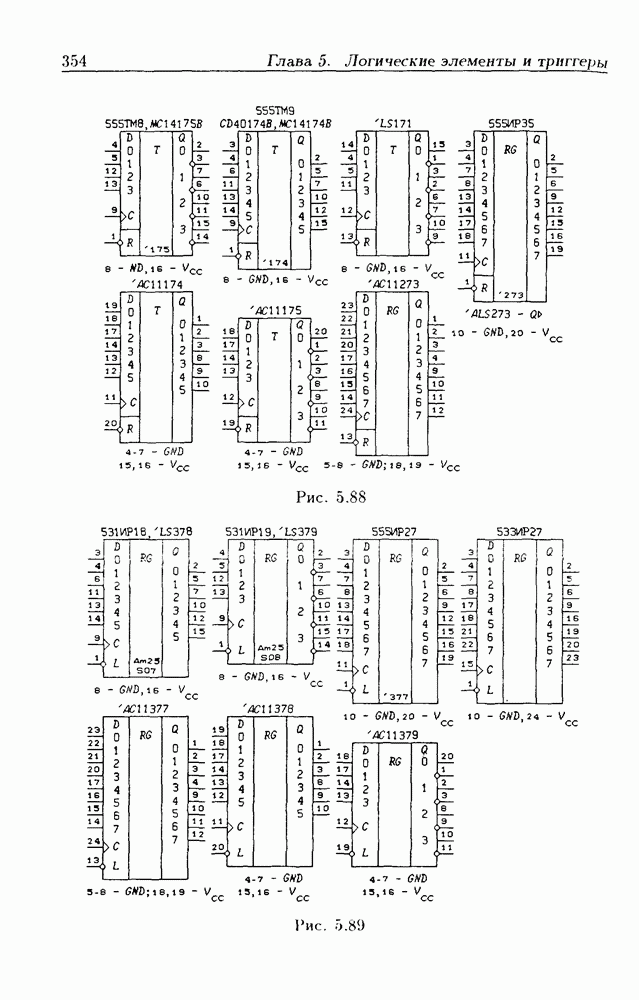
- 5.7. Асинхронные потенциальные триггеры и регистры памяти
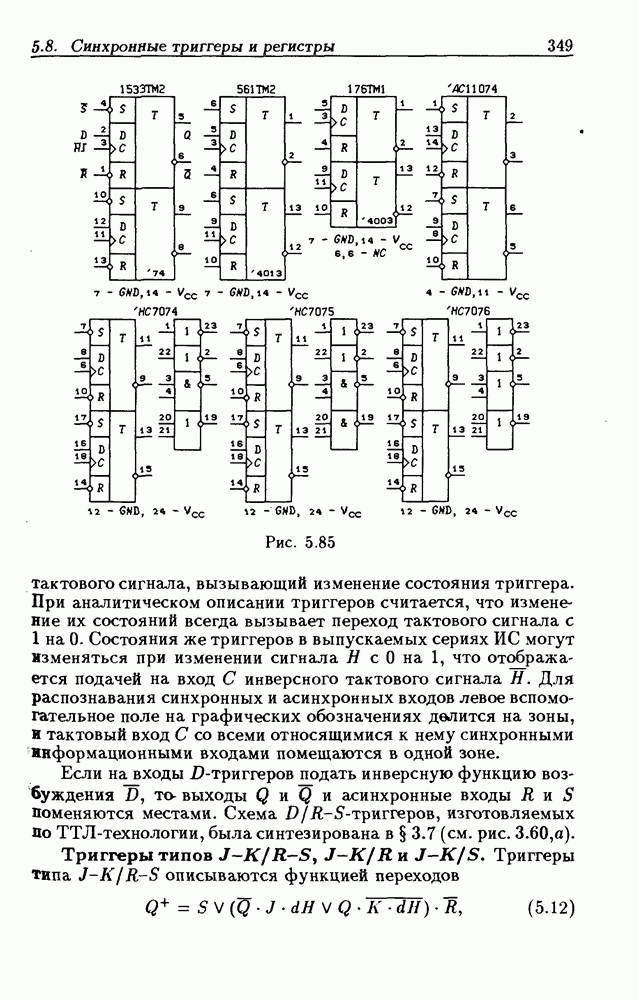
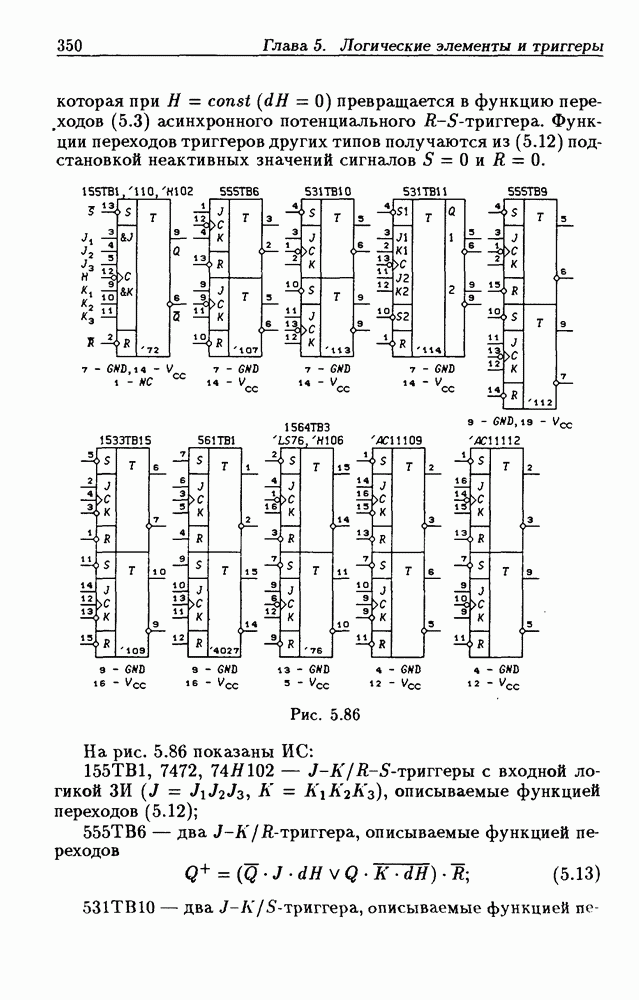
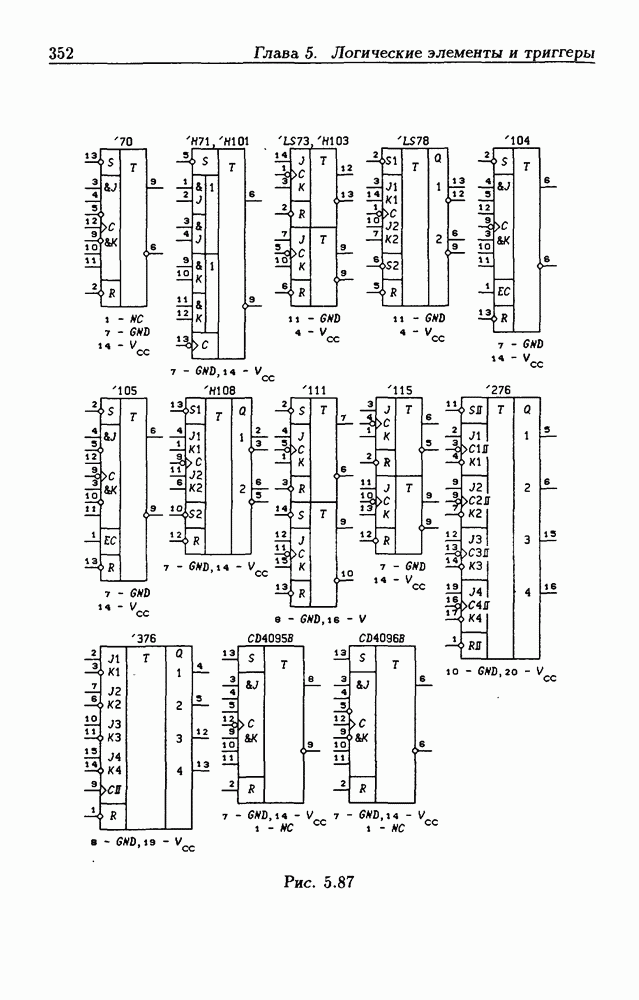
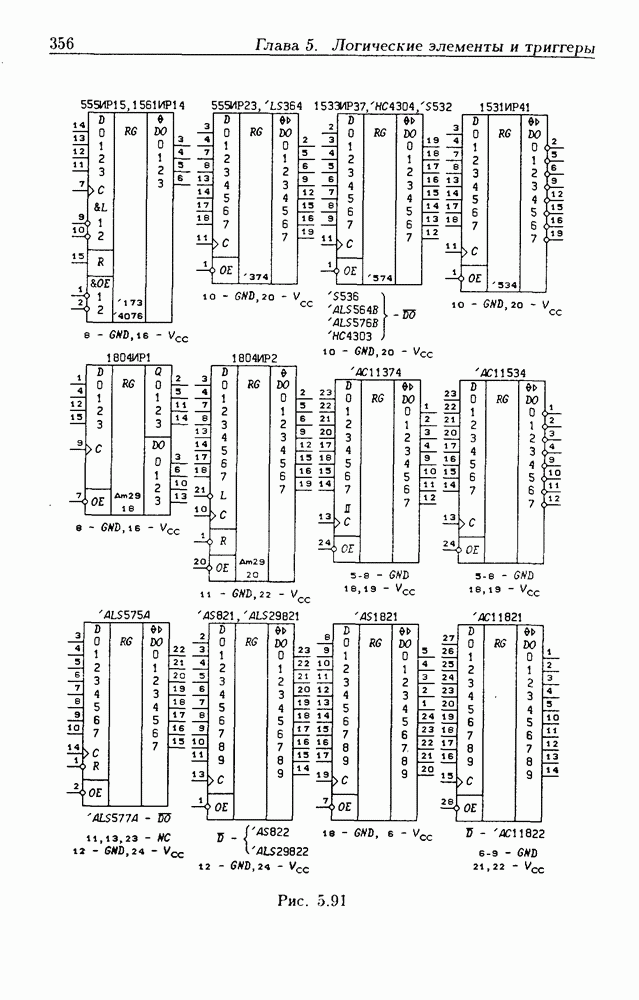
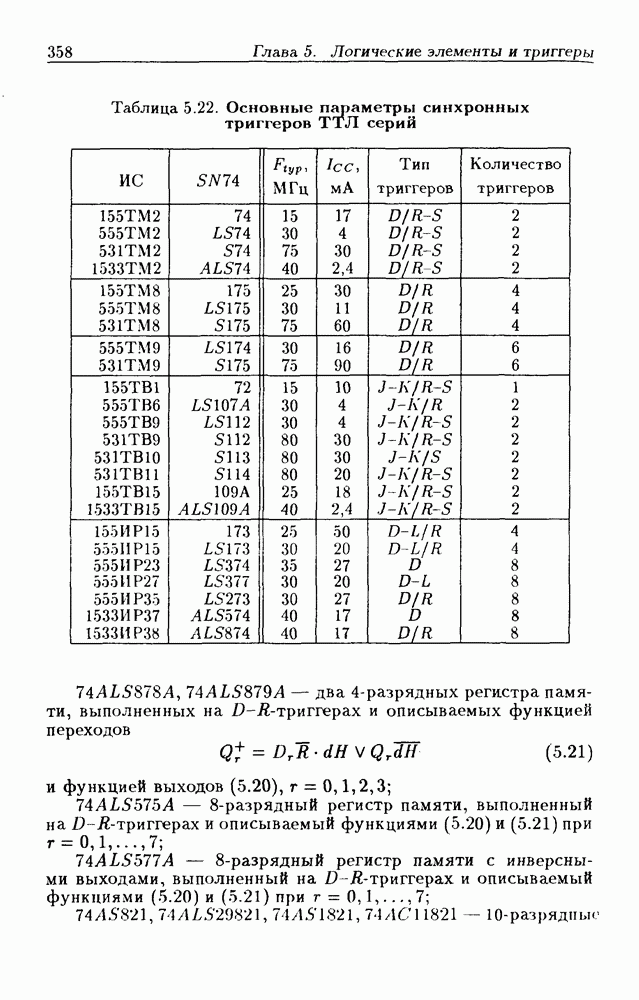
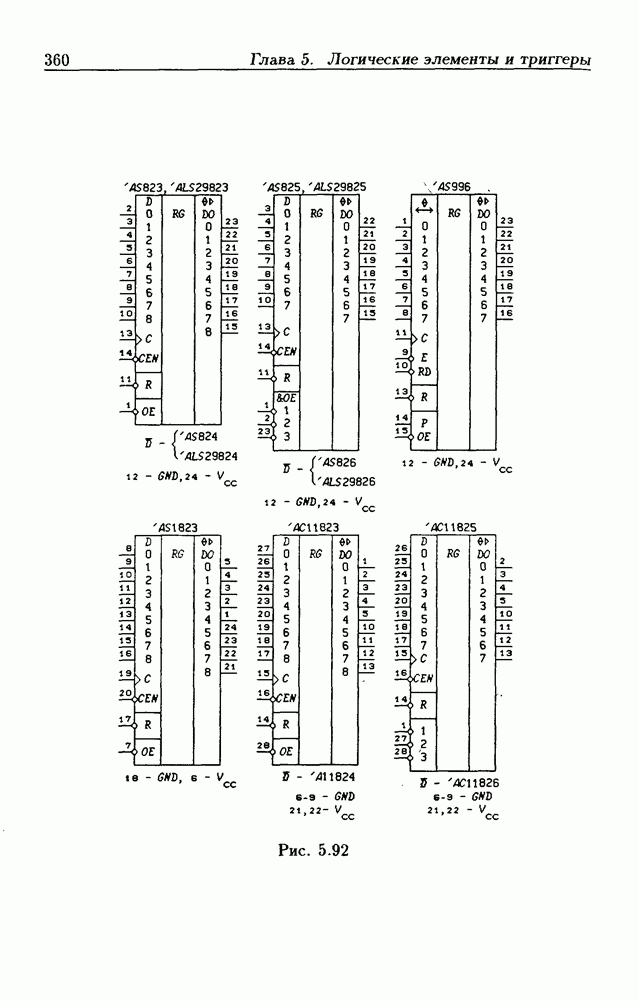
- 5.8. Синхронные триггеры и регистры памяти
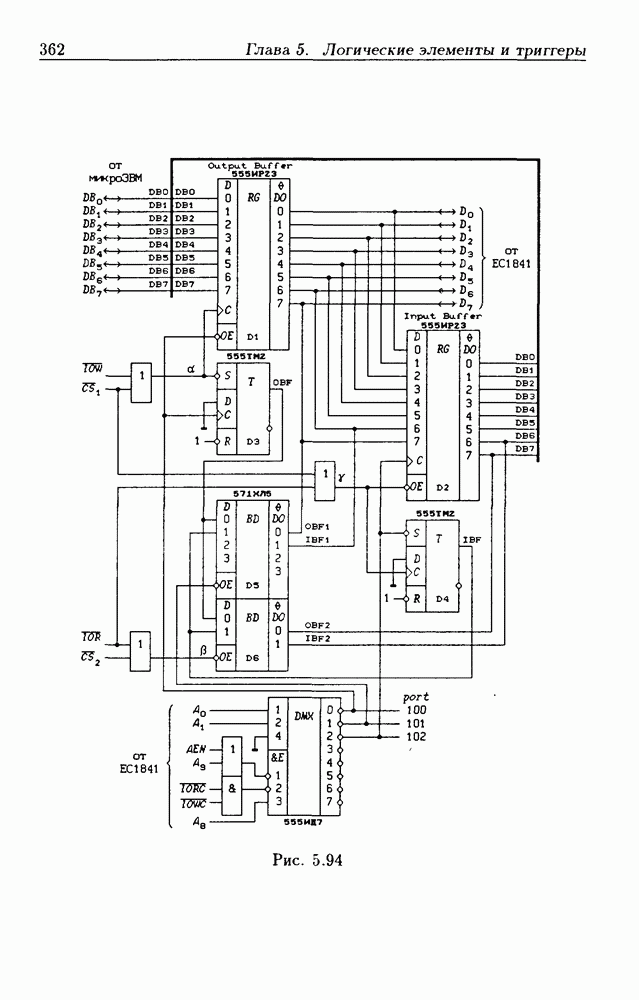
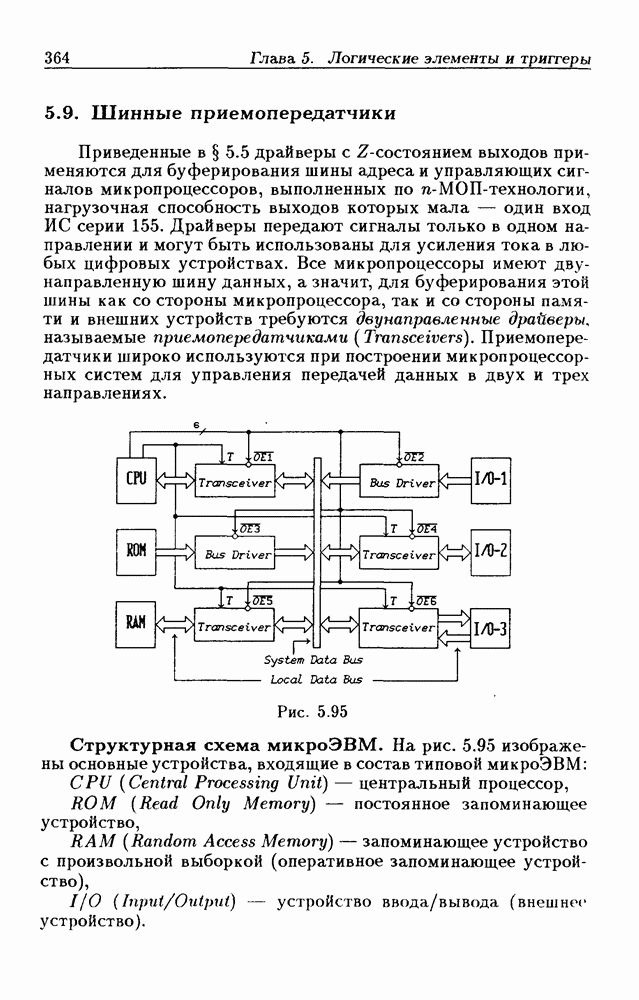
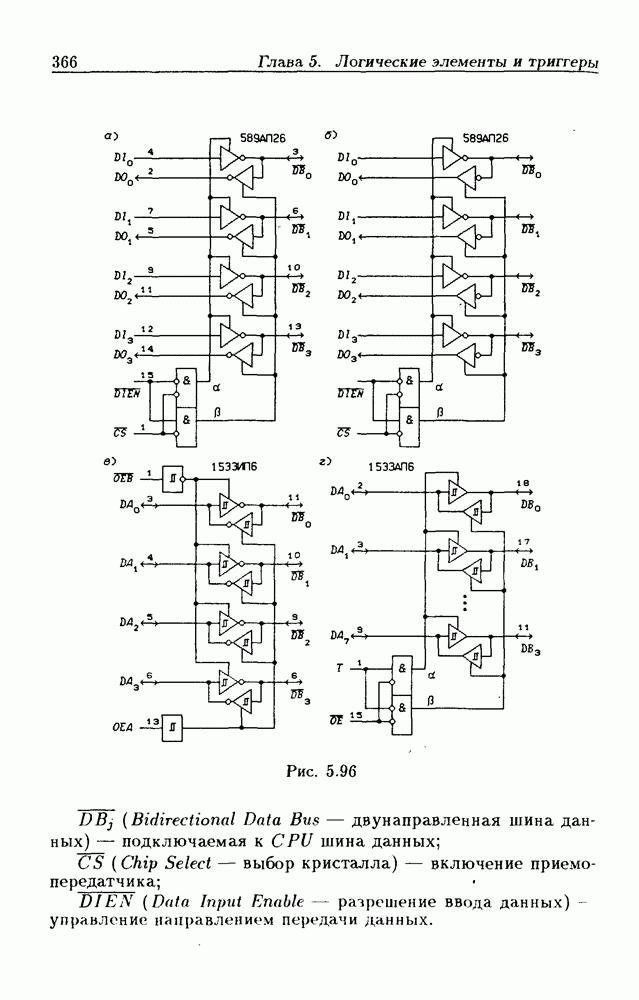
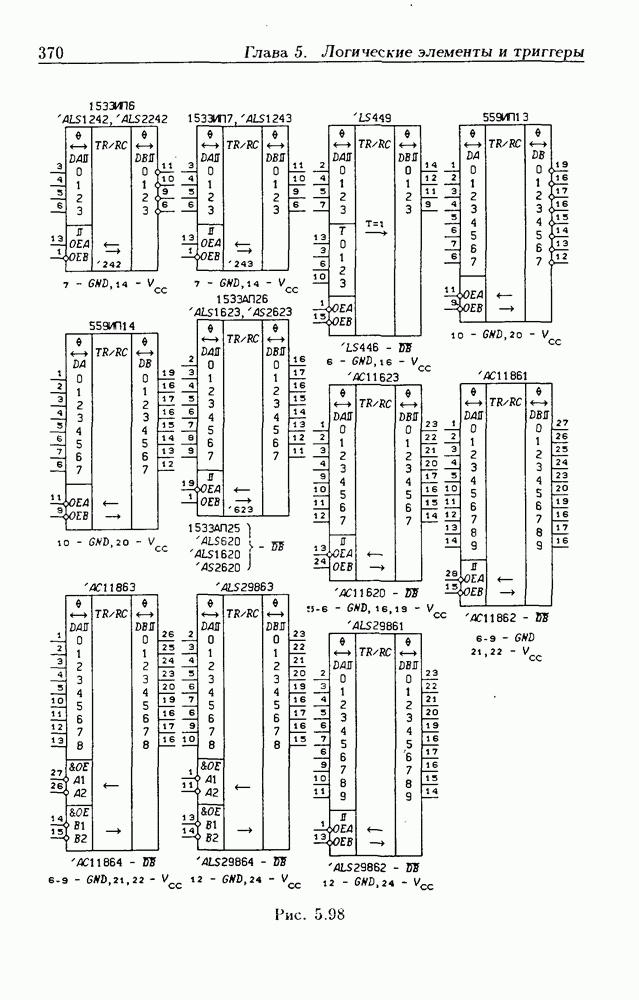
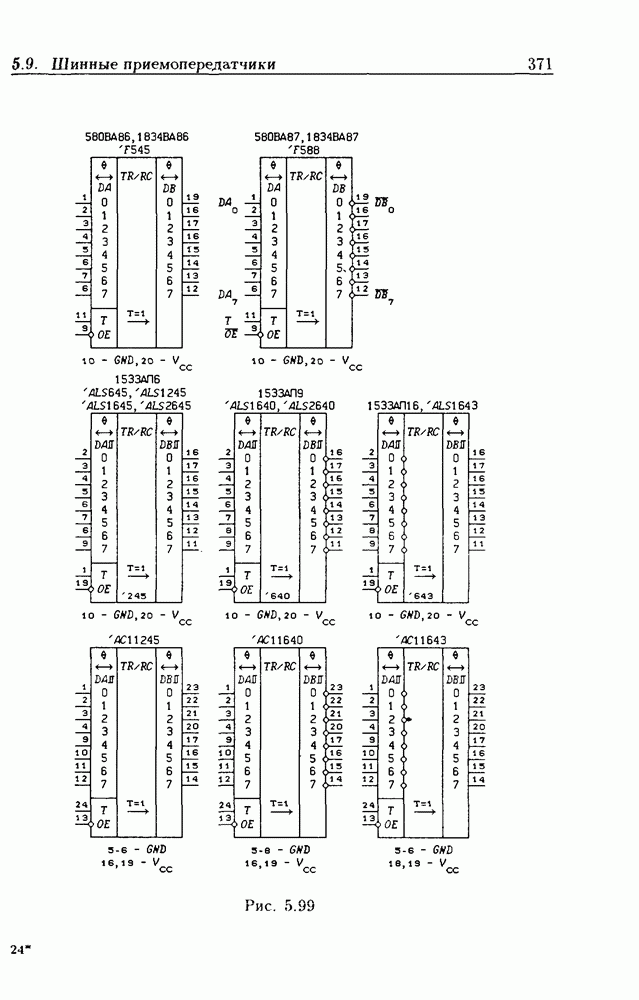
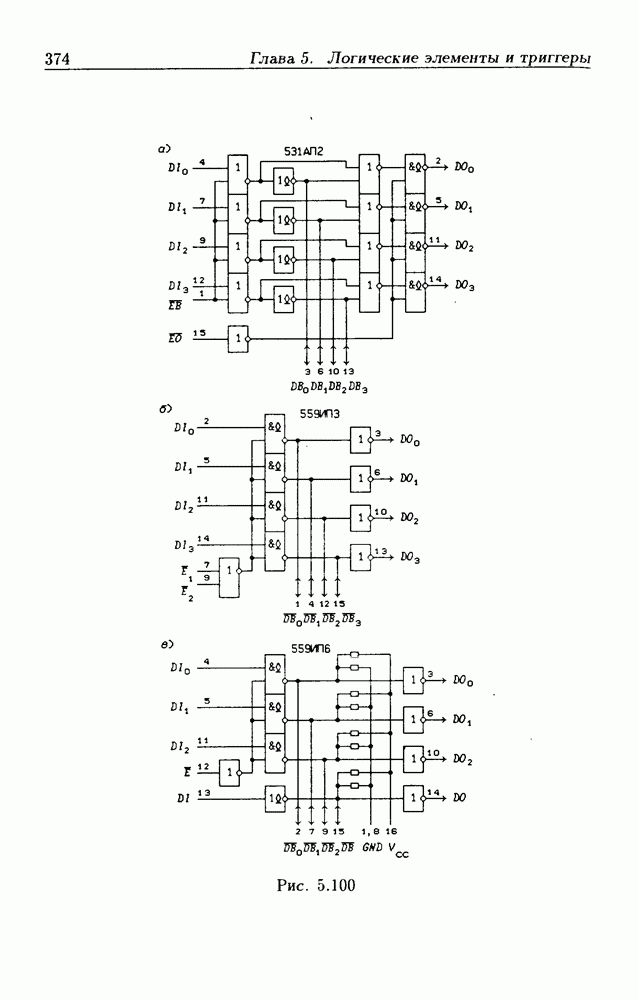
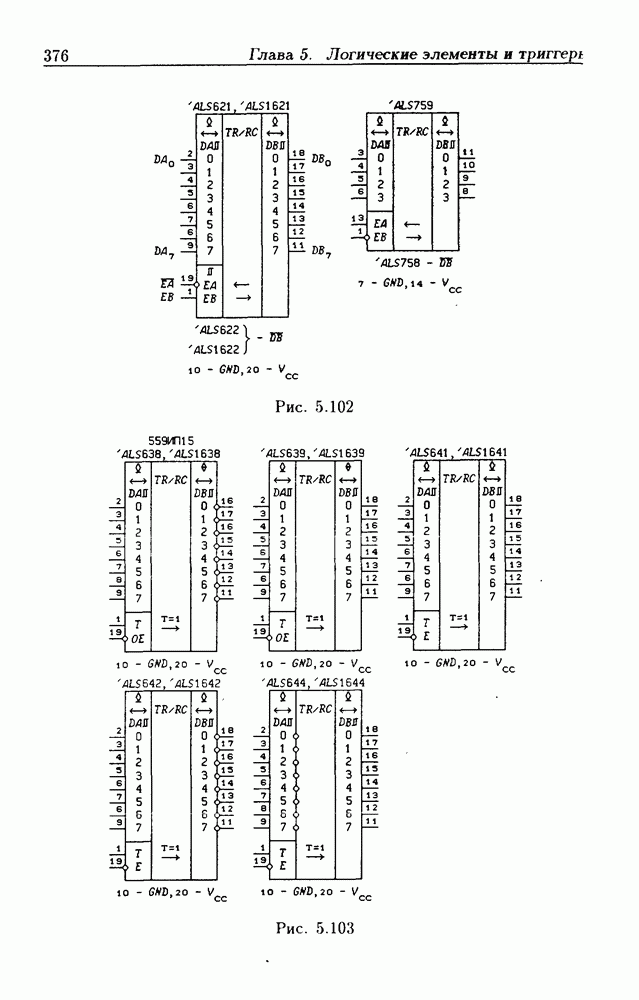
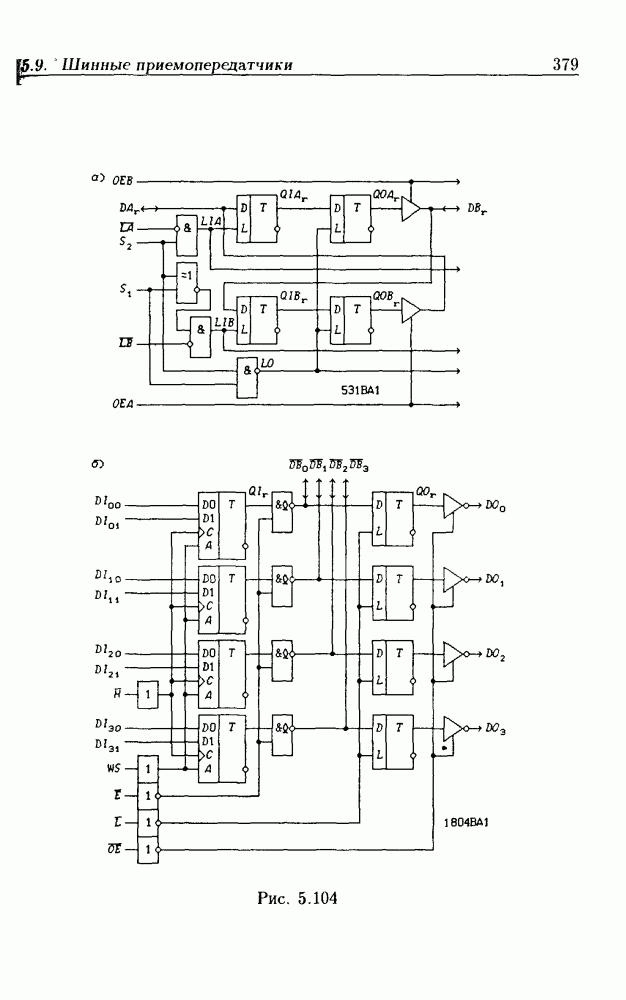
- 5.9. Шинные приемопередатчики
- Шинные приемопередатчики с Z-состоянием выхода.
- Шинные приемопередатчики с открытым коллекторным выходом.
- Шинные приемопередатчики с регистрами памяти.
- Шинные приемопередатчики со сдвигающим регистром.
- Шинные трехнаправленные приемопередатчики.
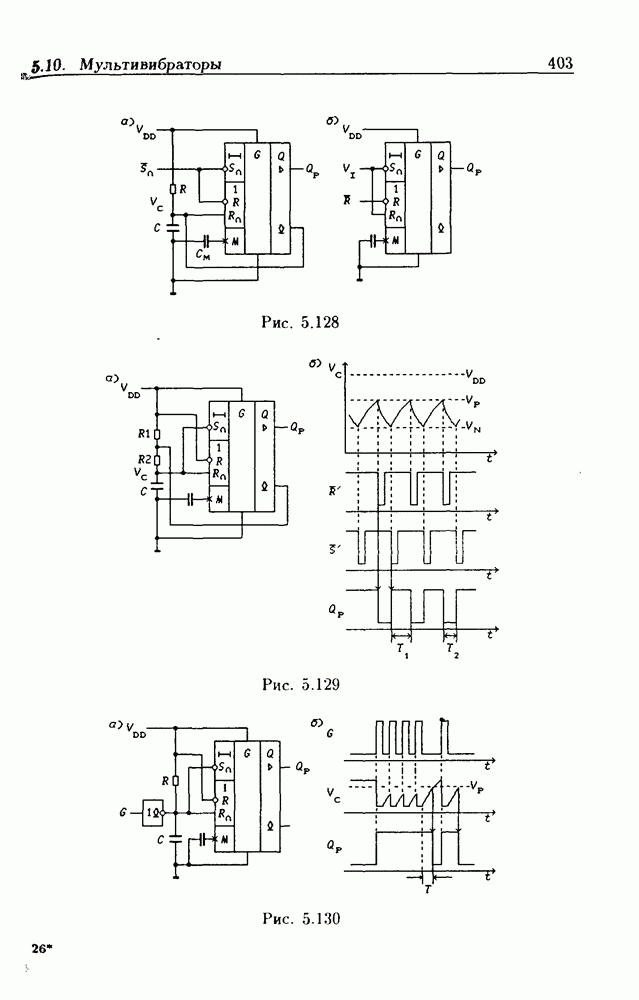
- 5.10. Мультивибраторы
- 5.11. Генераторы
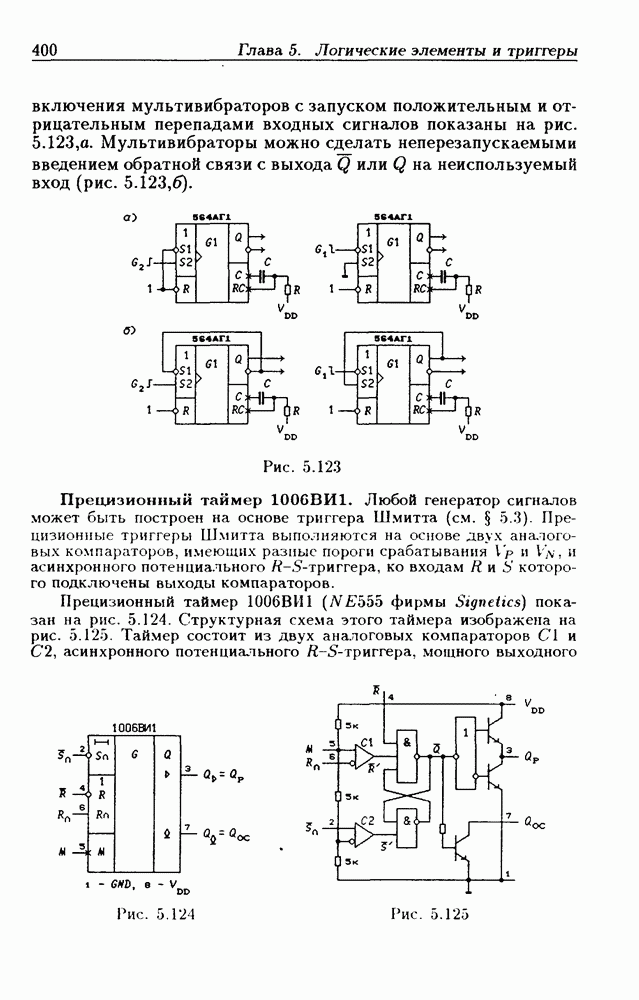
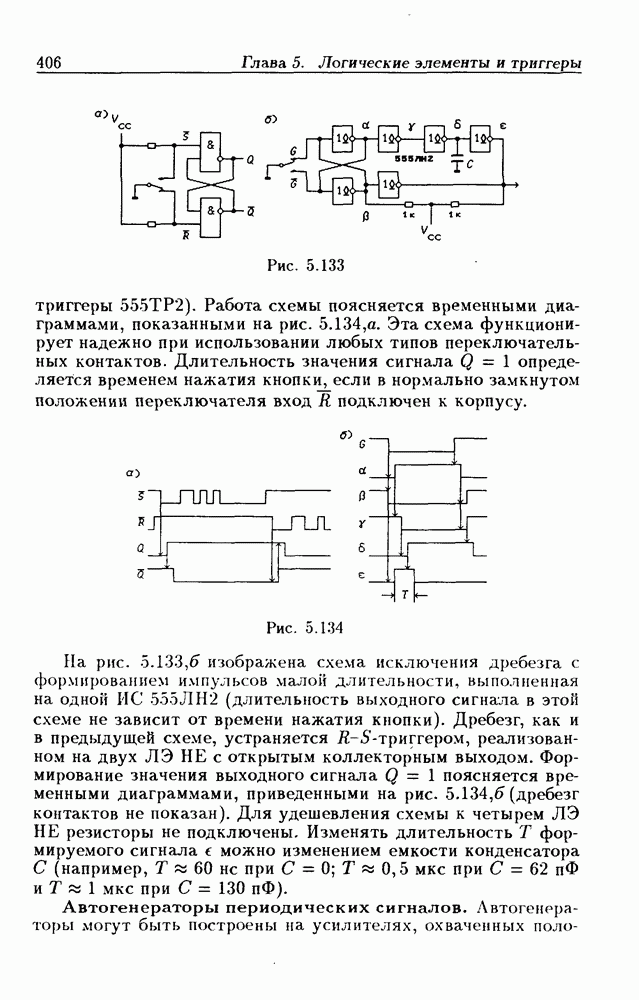
- Схемы устранения «дребезга» механических контактов.
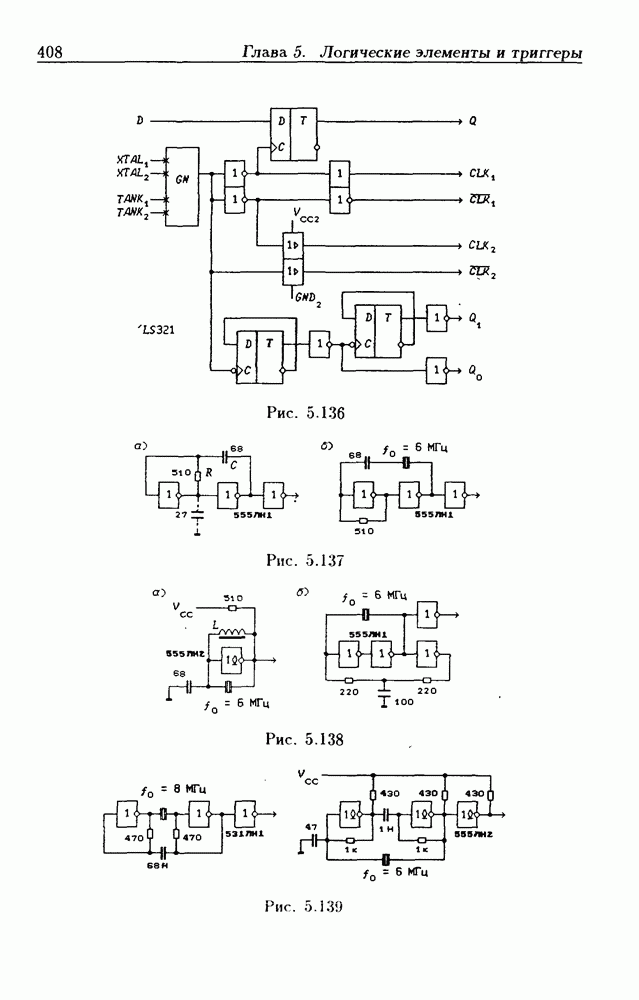
- Автогенераторы периодических сигналов.
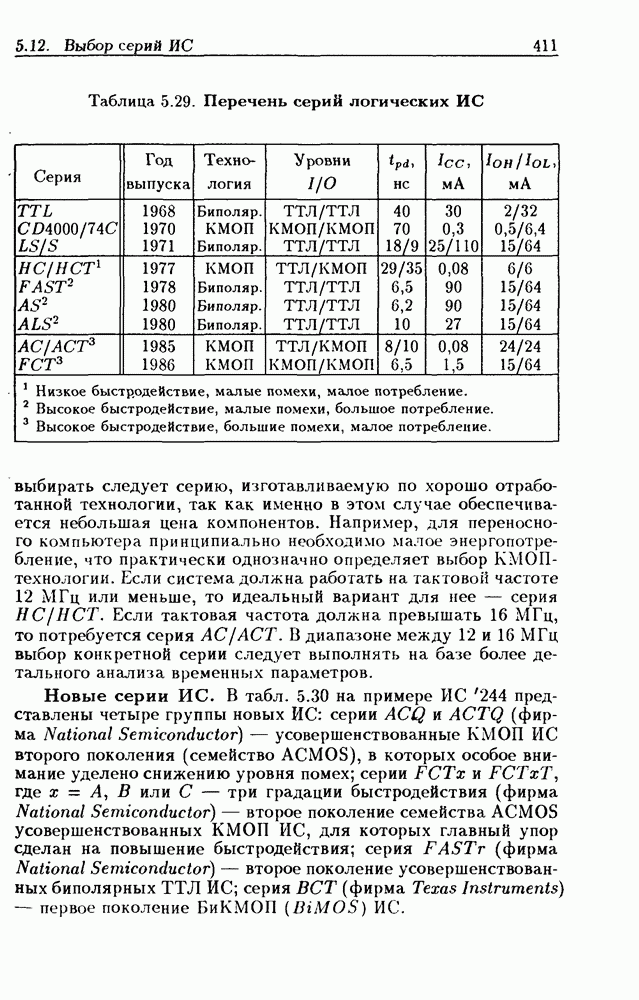
- 5.12. Рекомендации по выбору серий ИС
- Глава 6. Коммутаторы и арифметические устройства
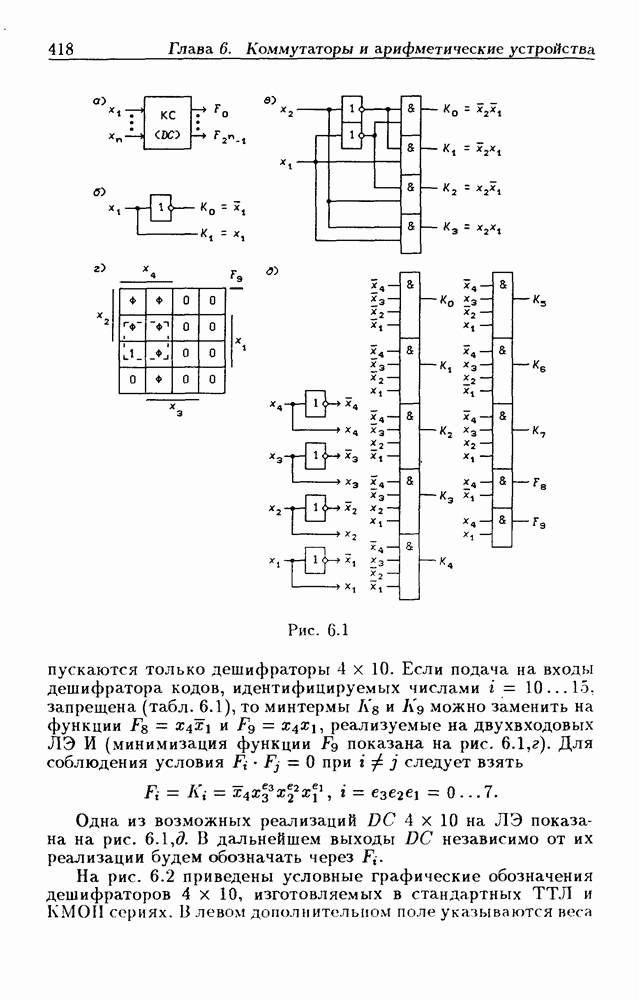
- 6.1. Дешифраторы
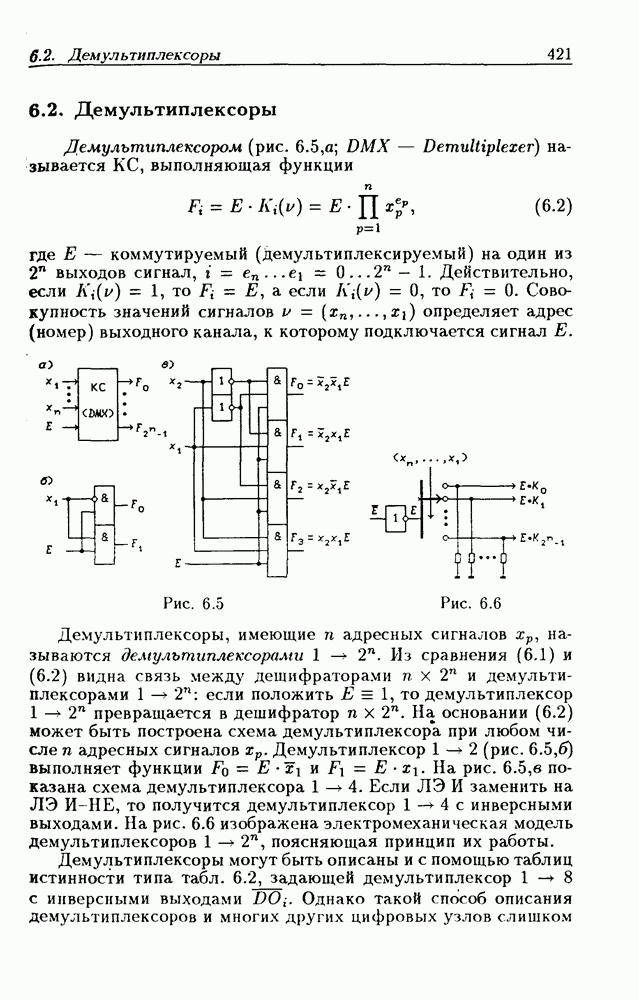
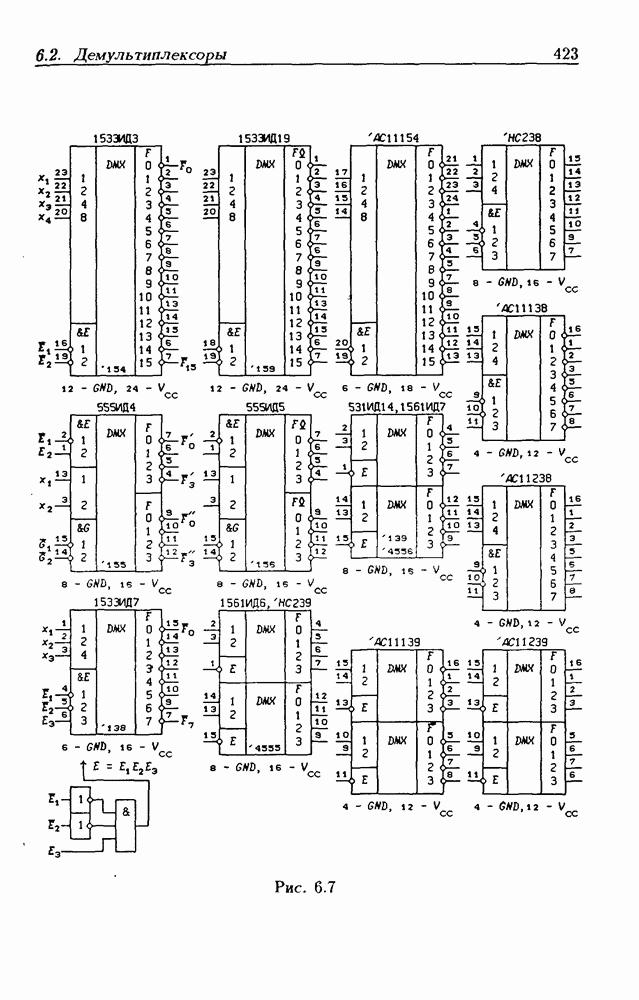
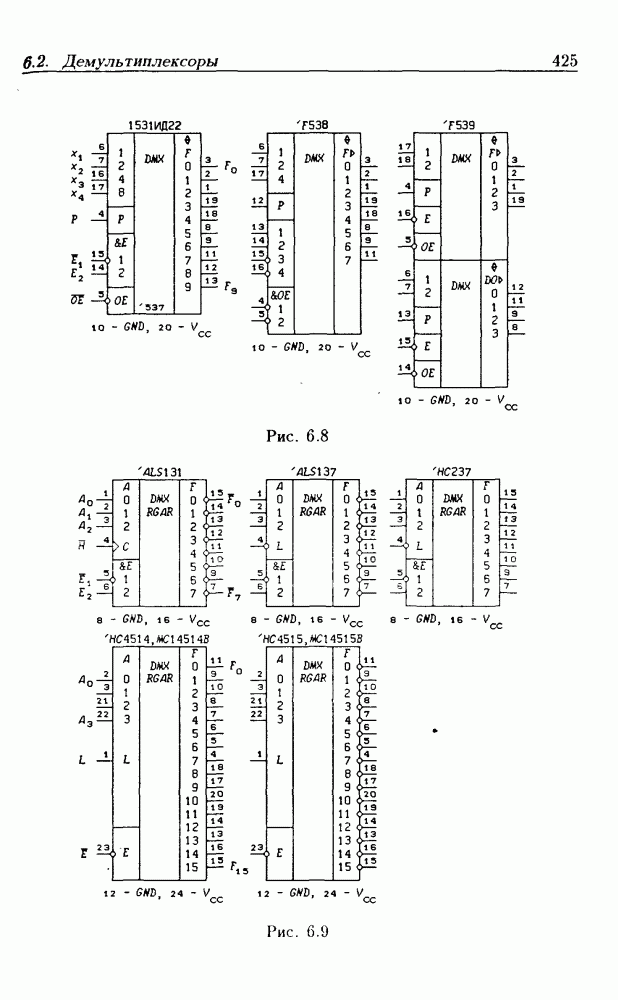
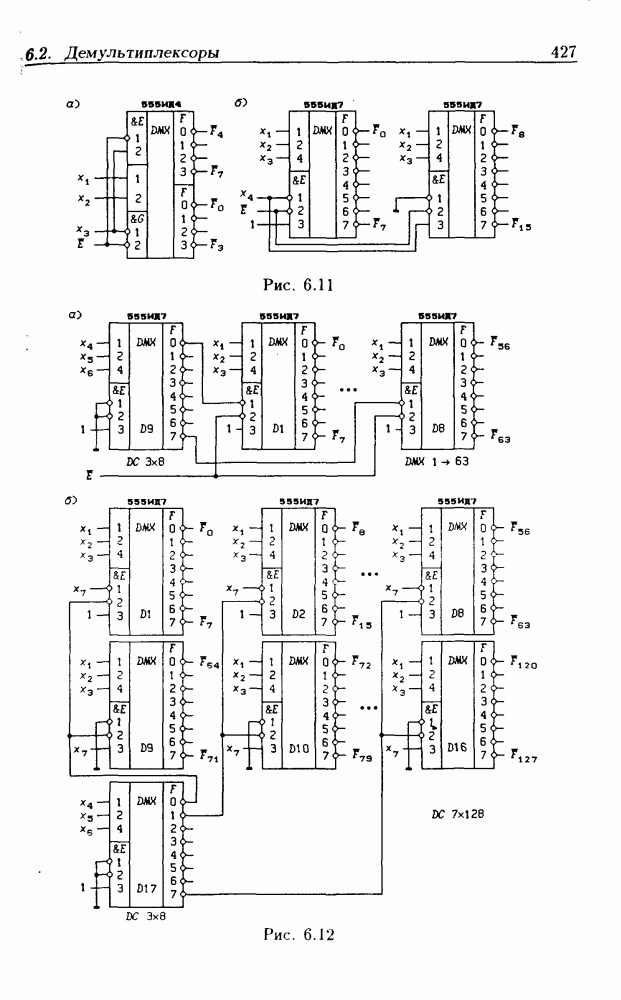
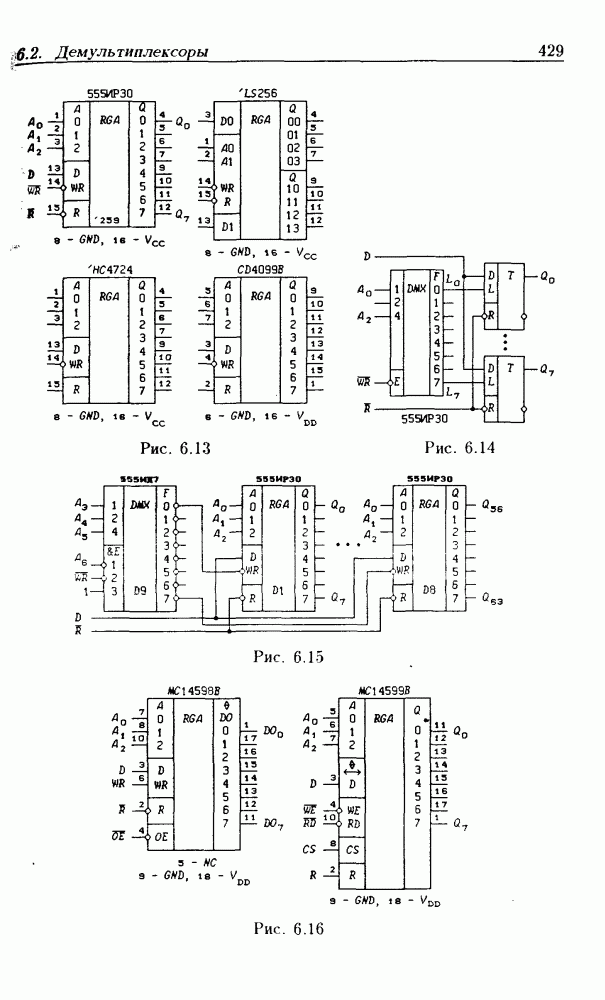
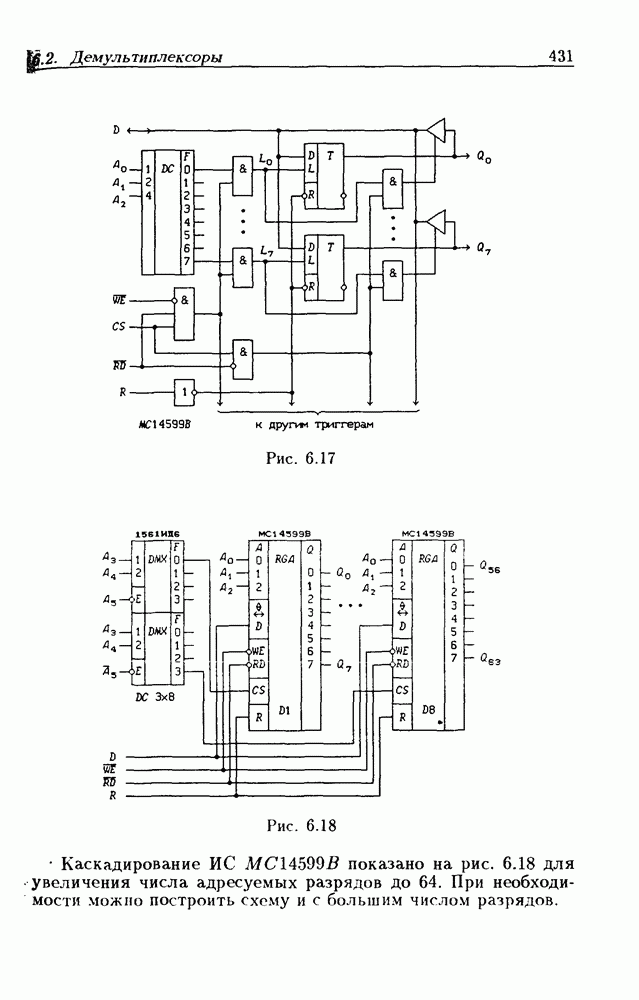
- 6.2. Демультиплексоры
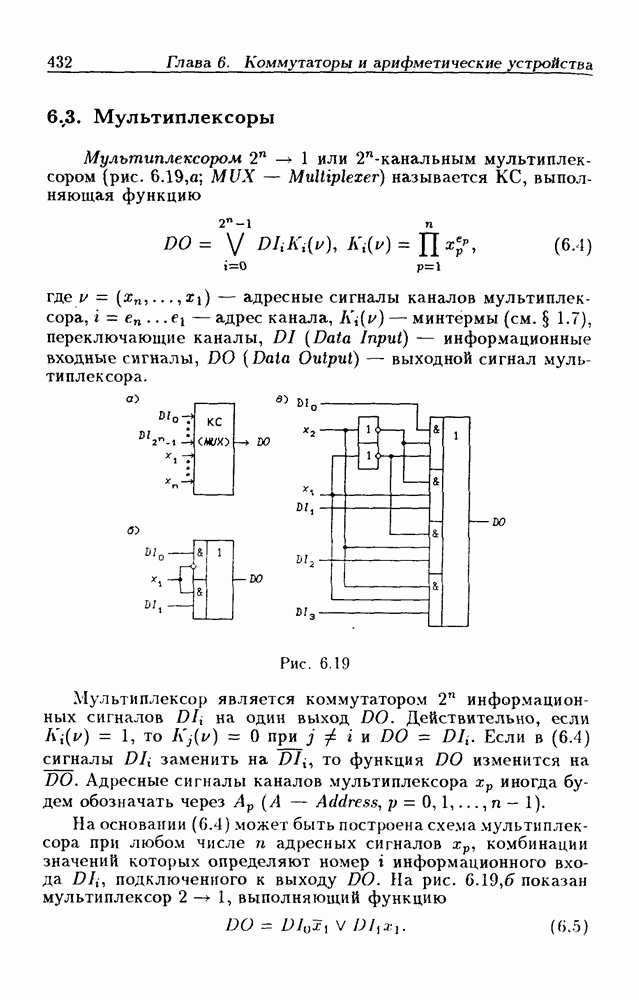
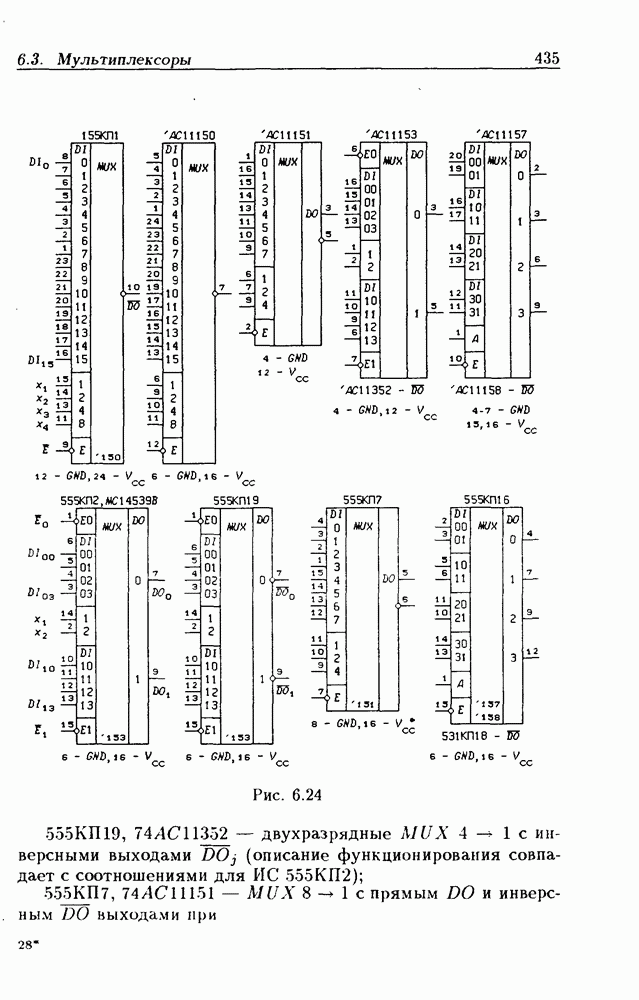
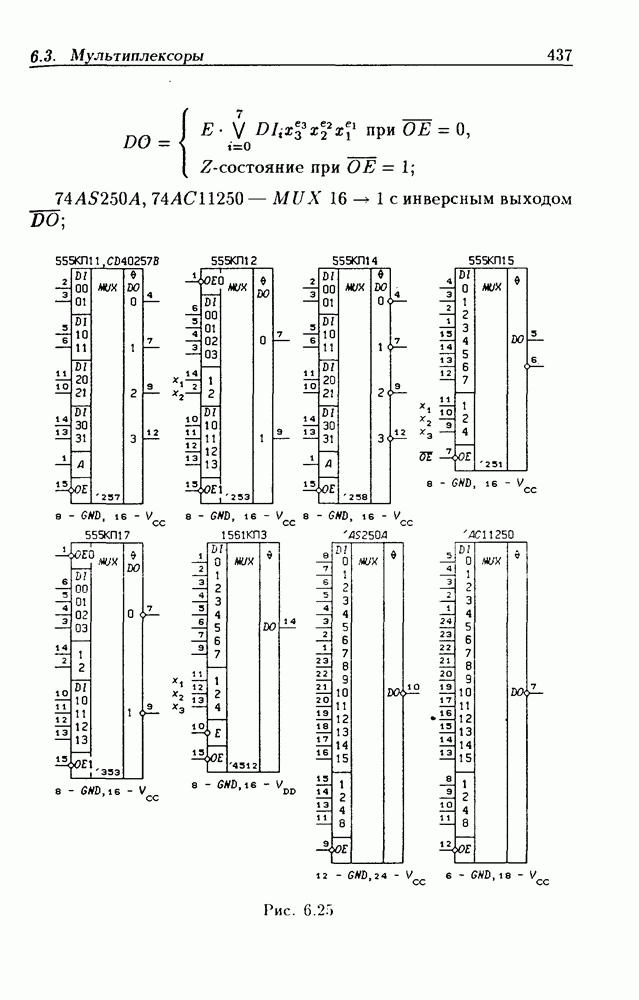
- 6.3. Мультиплексоры
- Мультиплексоры без стробирования.
- Мультиплексоры со стробированием.
- Мультиплексоры с Z-состоянием выхода.
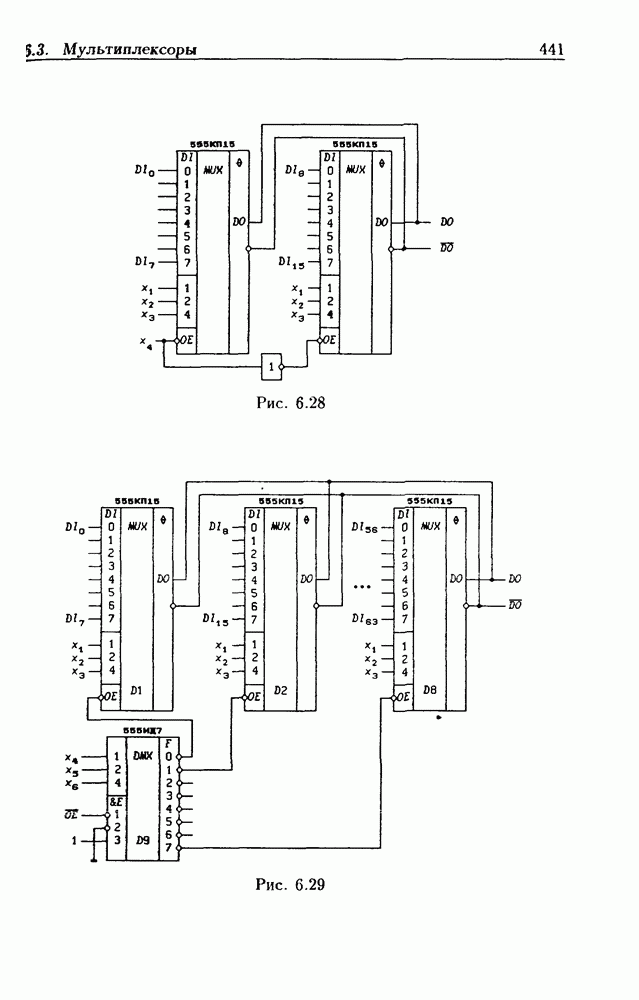
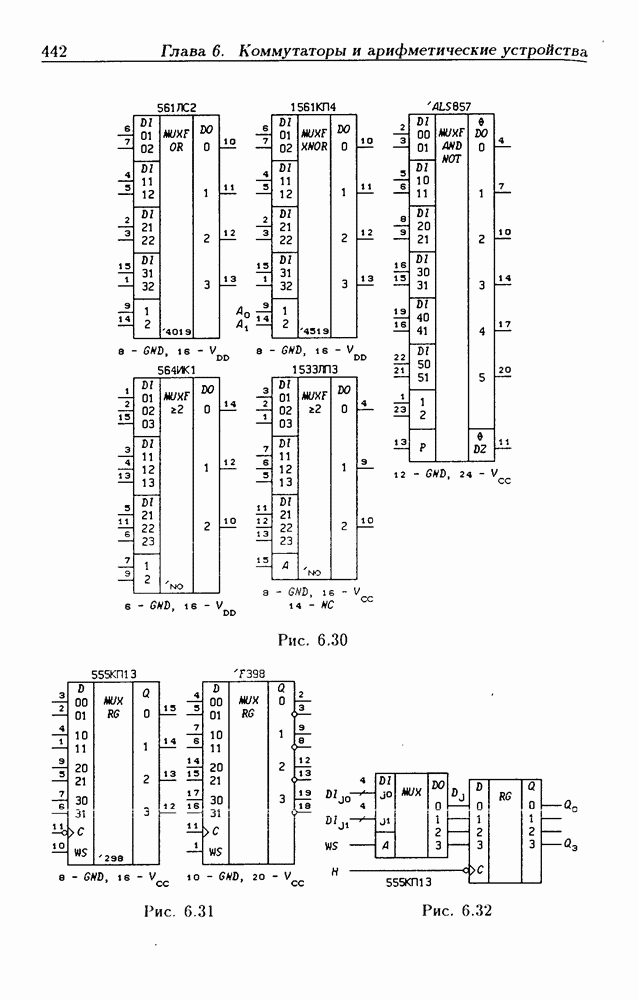
- Каскадирование мультиплексоров.
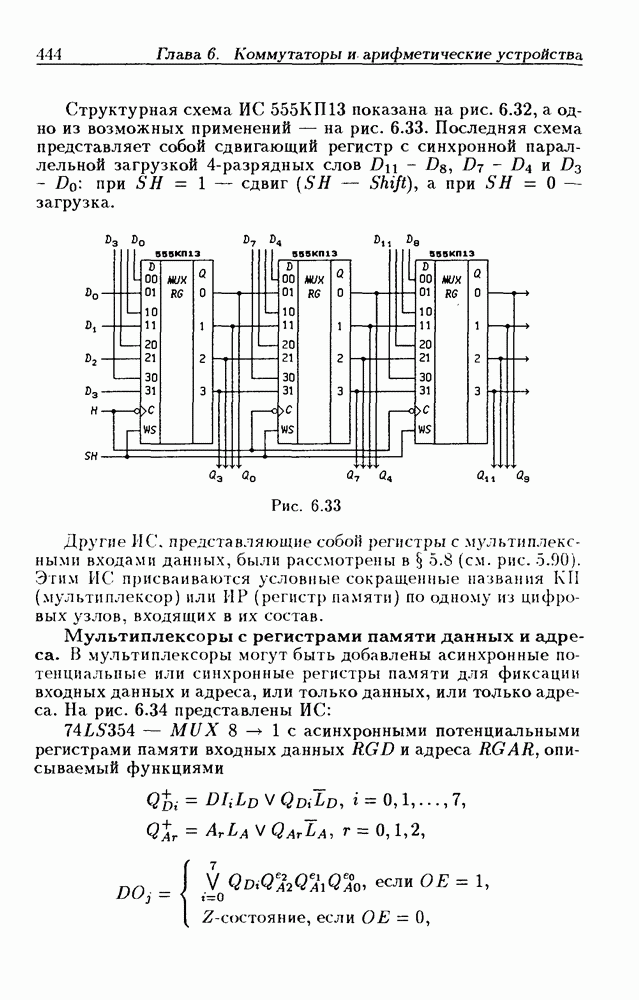
- Функциональные мультиплексоры.
- Регистры памяти с мультиплексными входами данных.
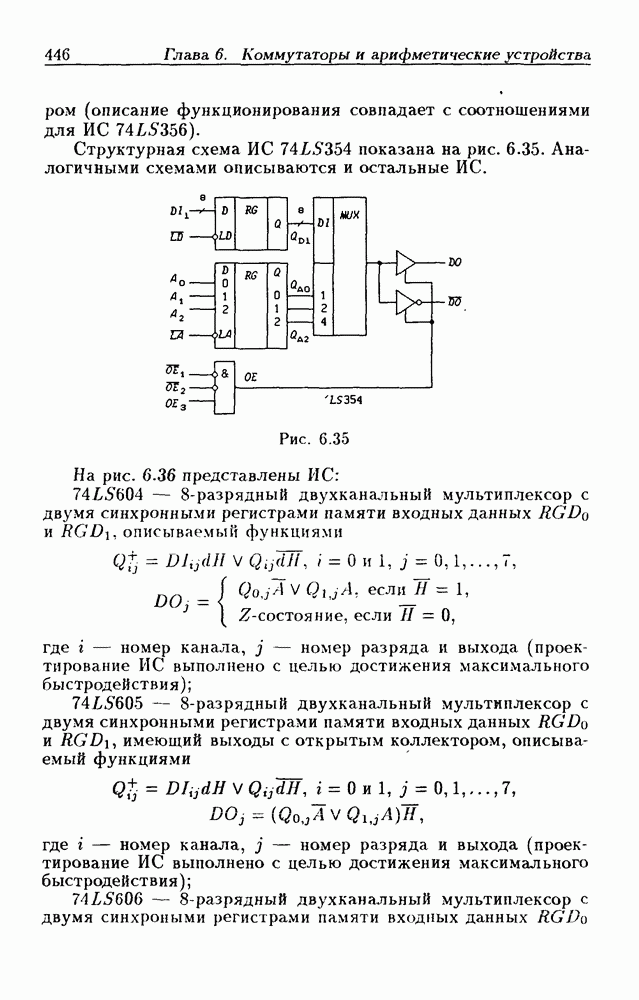
- Мультиплексоры с регистрами памяти данных и адреса.
- Сдвигающие мультиплексоры.
- 6.4. Синтез комбинационных схем и цифровых автоматов на мультиплексорах
- Синтез схем на 8-канальных мультиплексорах.
- Синтез на двухразрядных 4-канальных мультиплексорах.
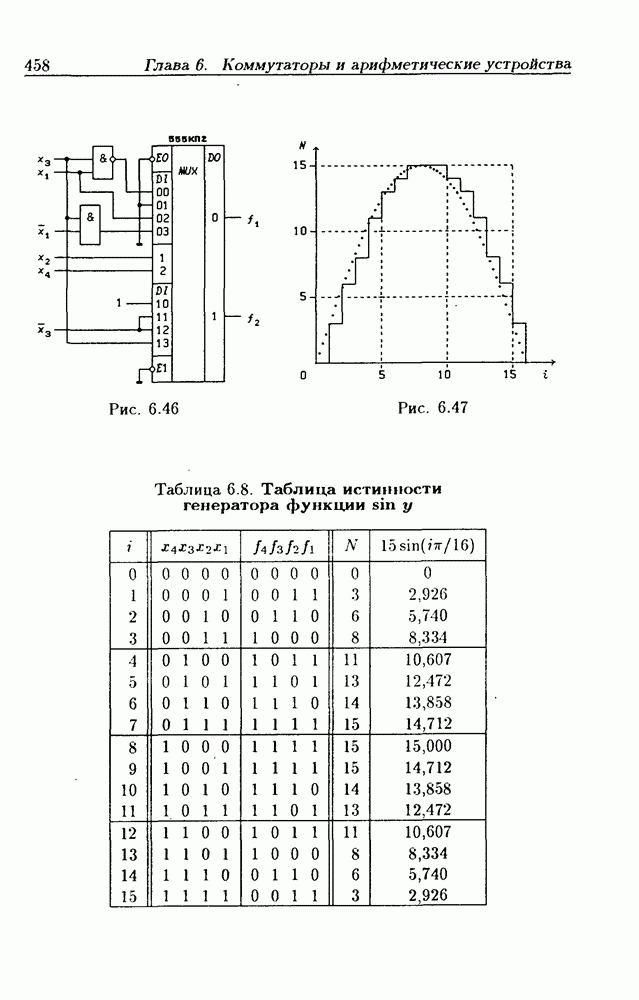
- Синтез генератора синусоидальной функции на мультиплексорах.
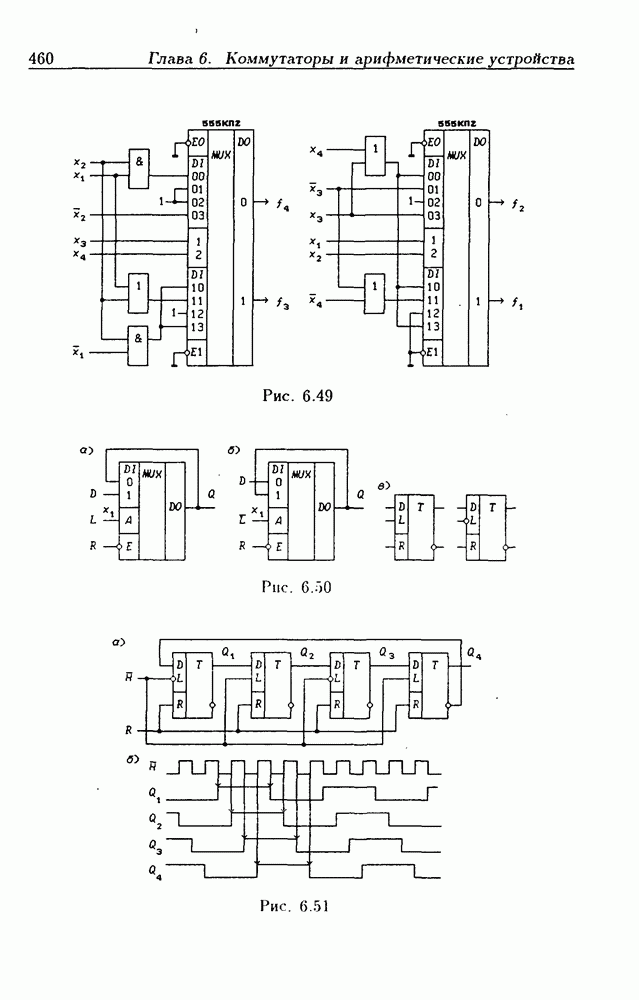
- Синтез триггеров на мультиплексорах.
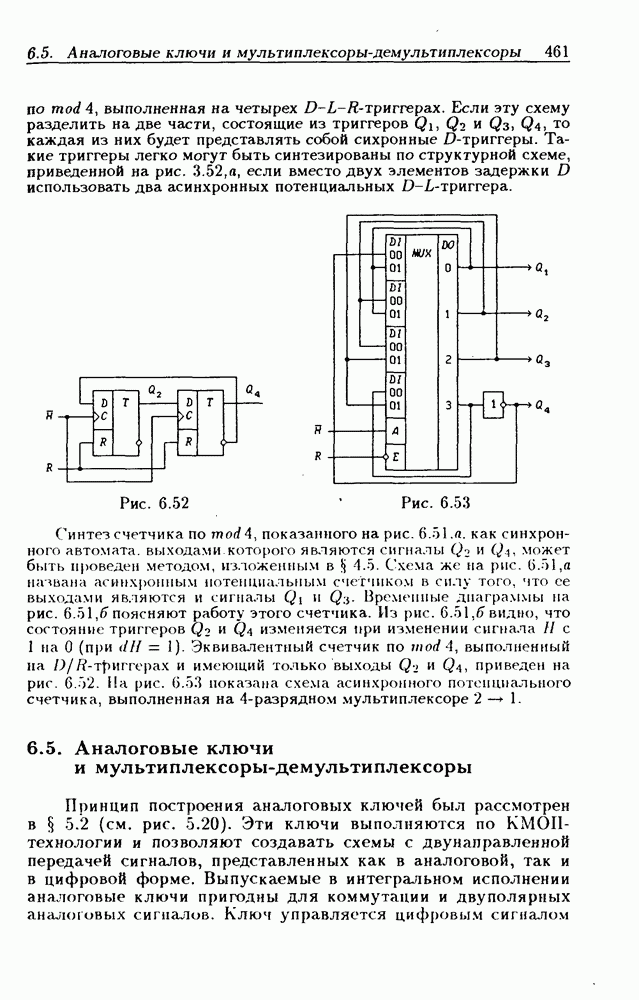
- Синтез счетчиков на мультиплексорах.
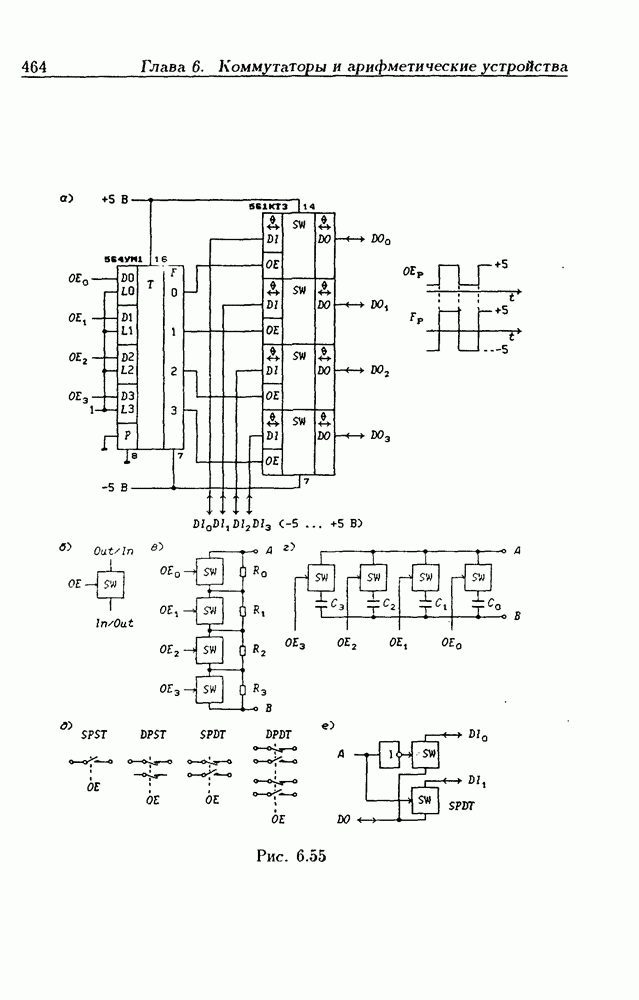
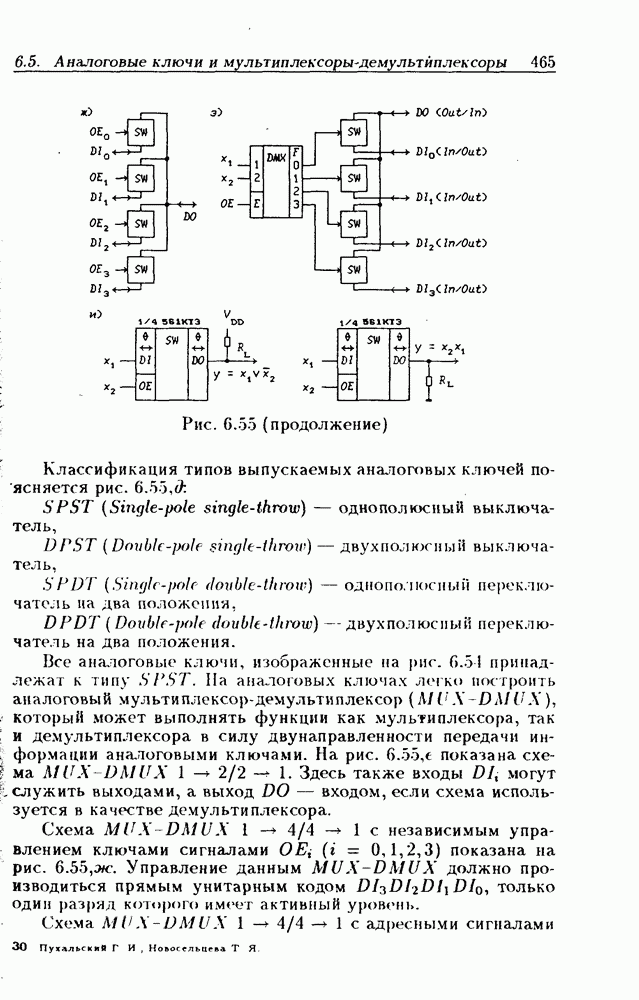
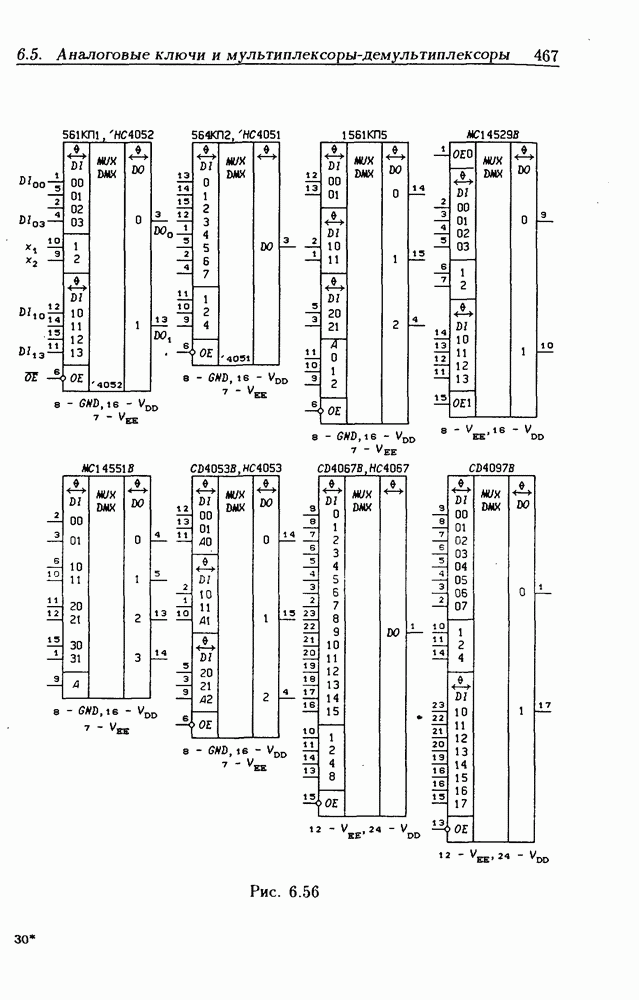
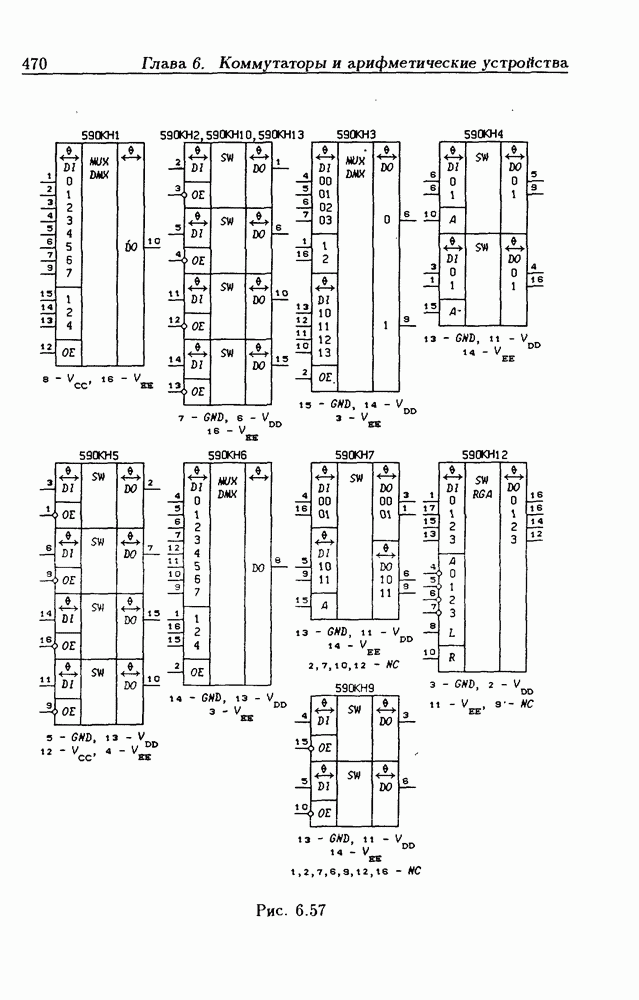
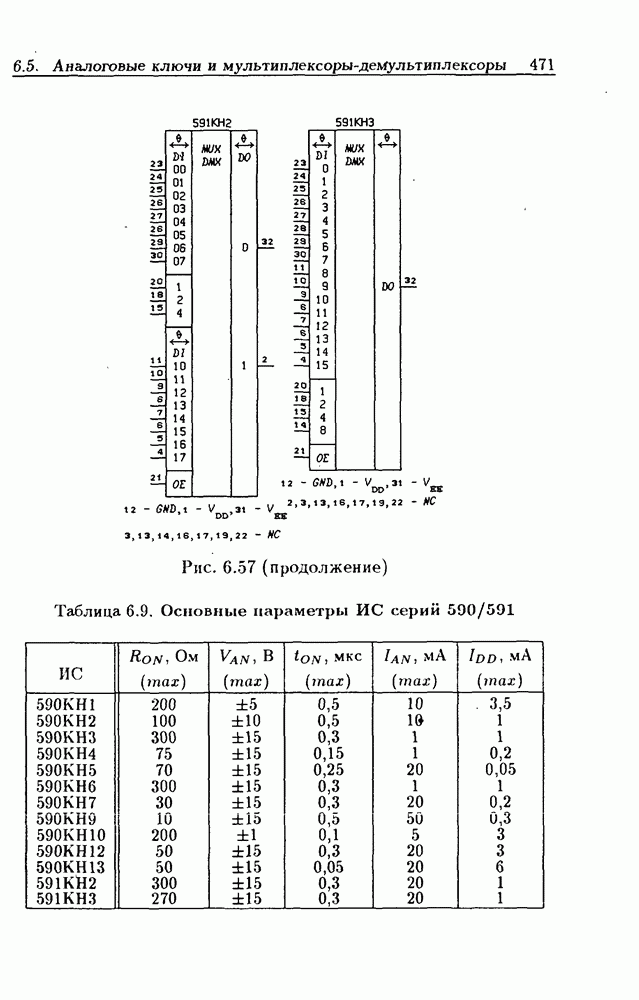
- 6.5. Аналоговые ключи и мультиплексоры-демультиплексоры
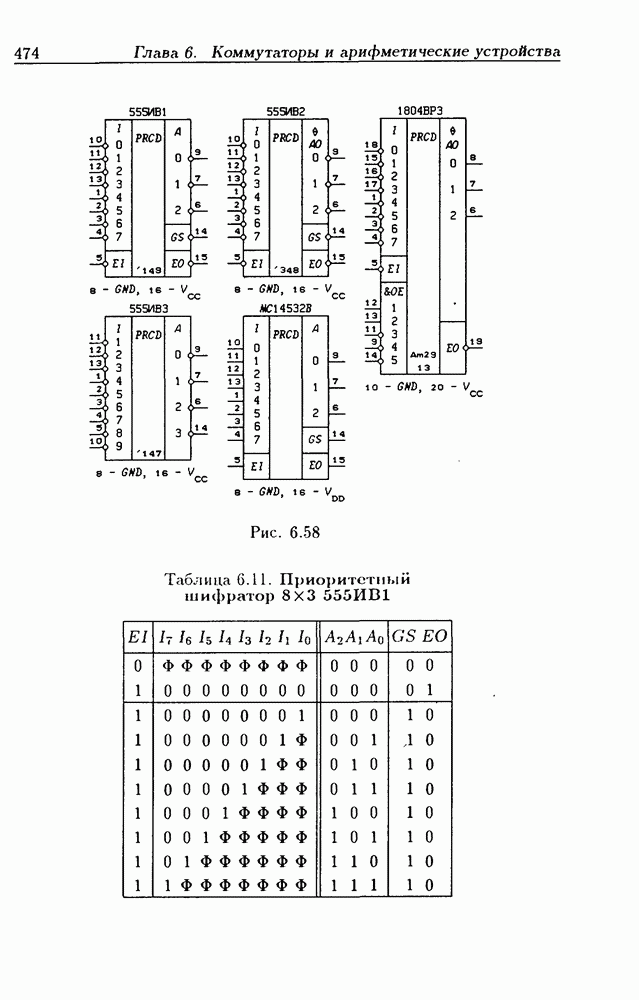
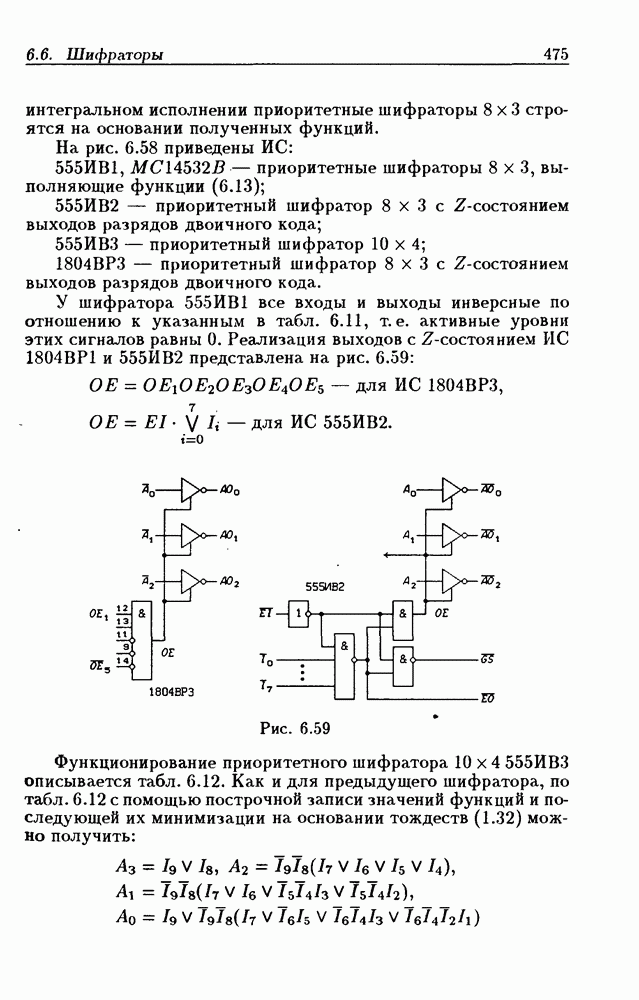
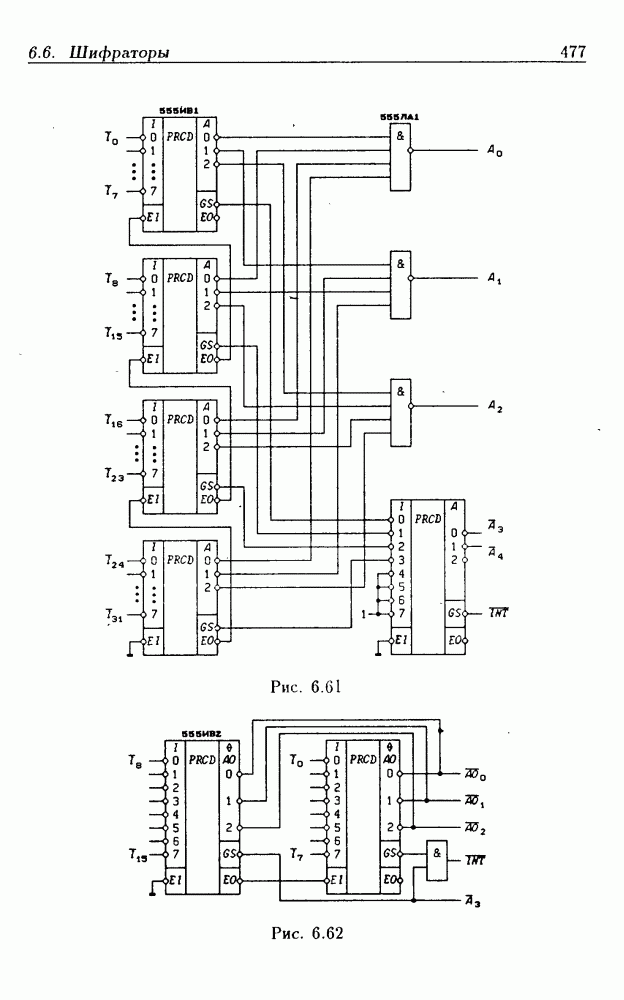
- 6.6. Шифраторы
- 6.7. Цифровые компараторы
- Программируемые цифровые компараторы.
- Адресные компараторы.
- Применения адресных компараторов.
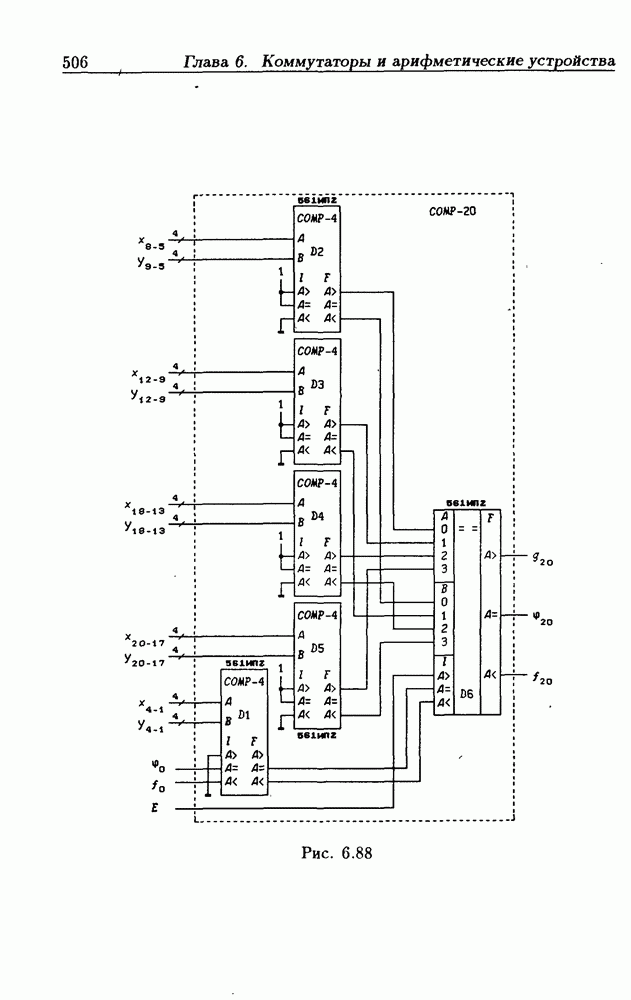
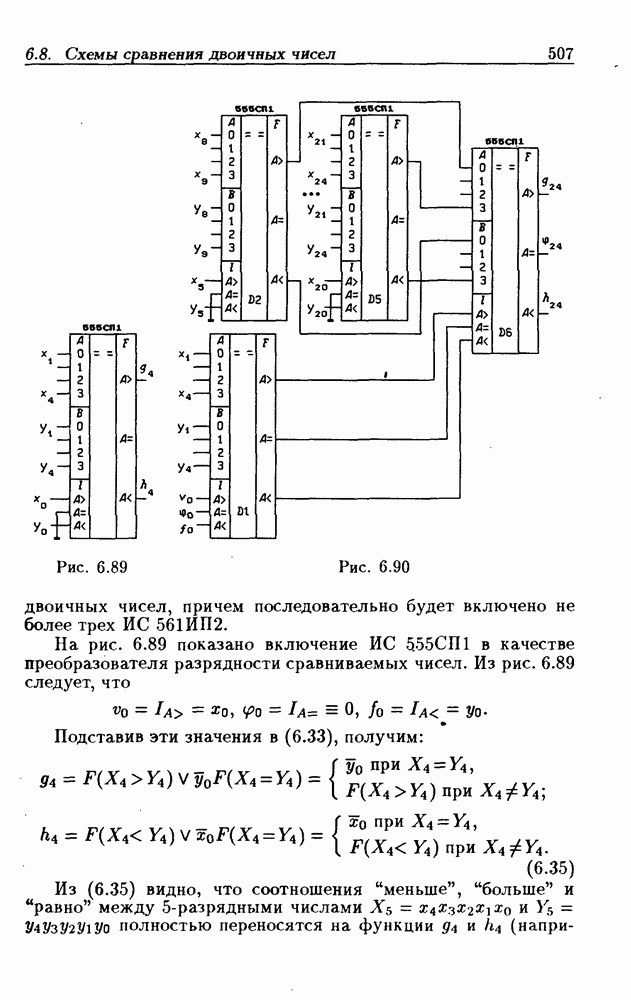
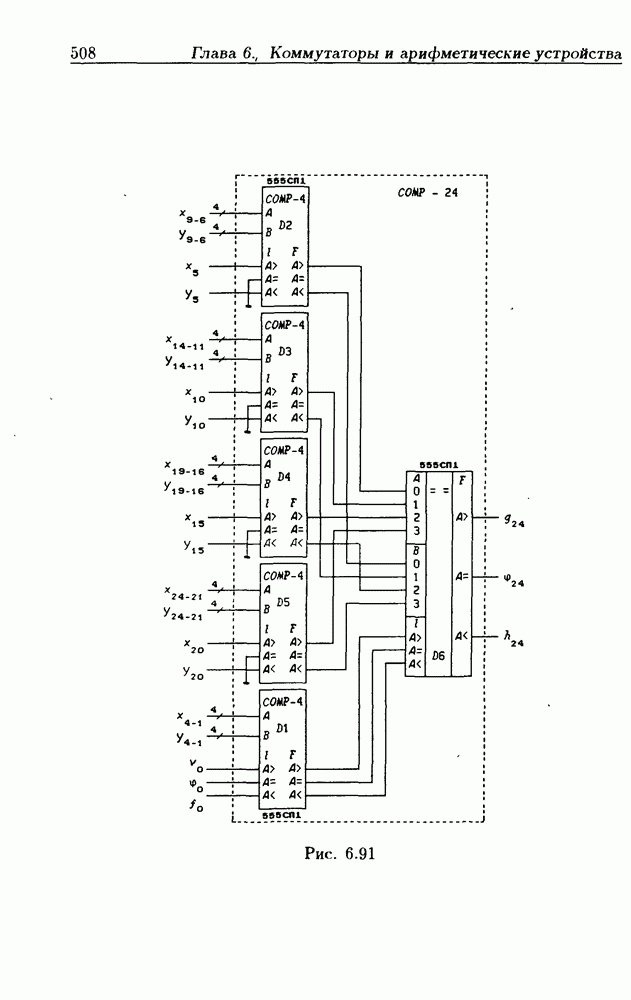
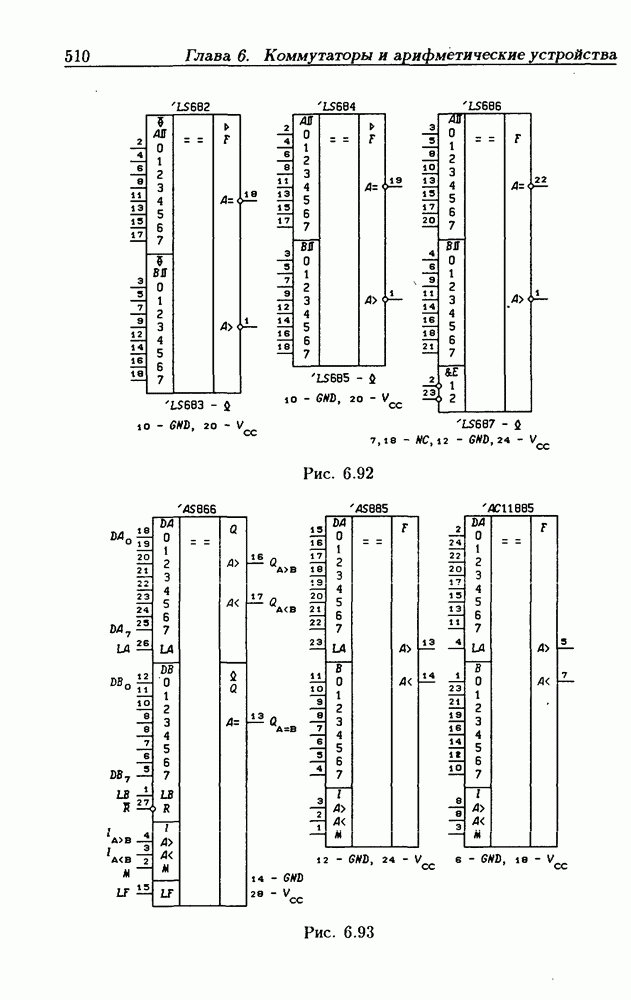
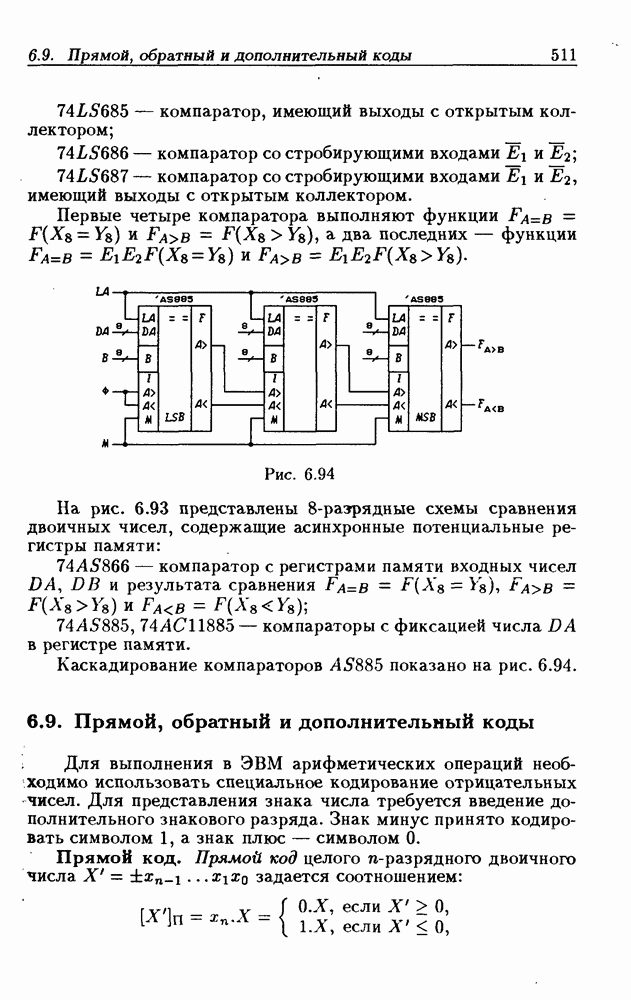
- 6.8. Схемы сравнения двоичных чисел
- 8-разрядные схемы сравнения двоичных чисел.
- 6.9. Прямой, обратный и дополнительный коды
- Дополнительный код.
- Сложение чисел в обратном коде.
- Код с избытком 3.
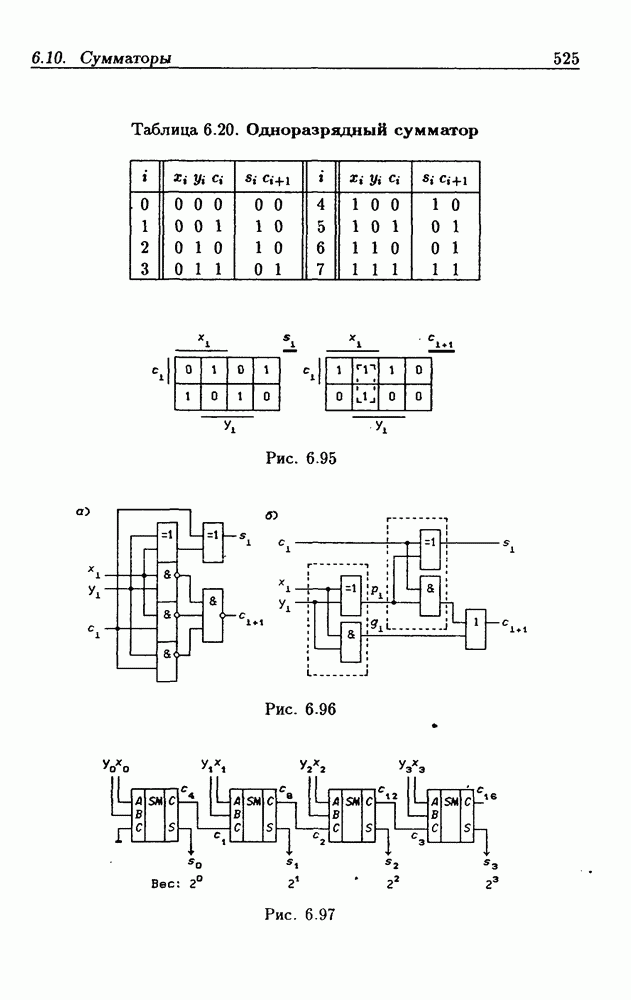
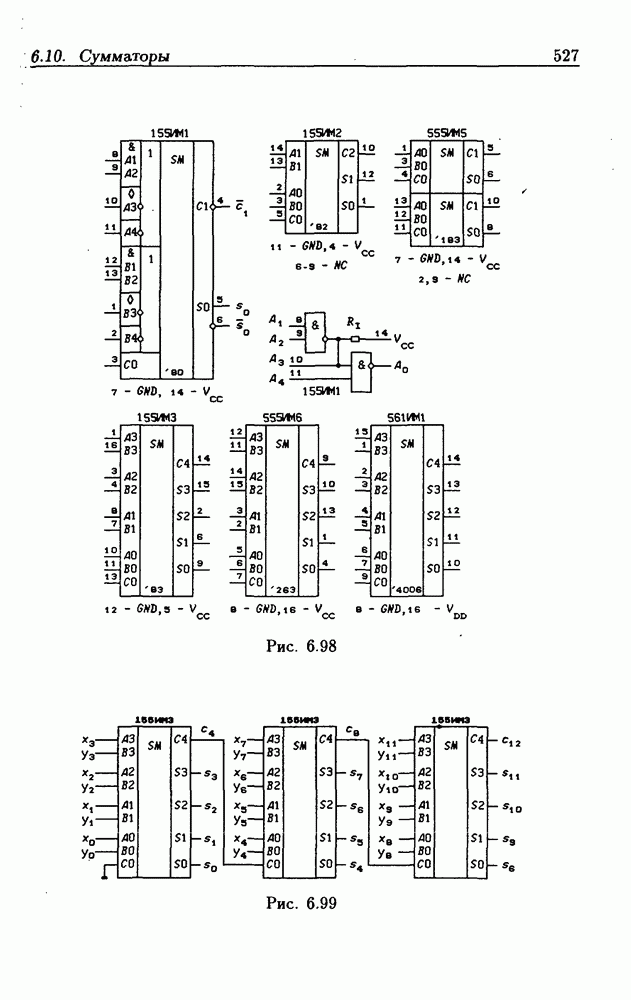
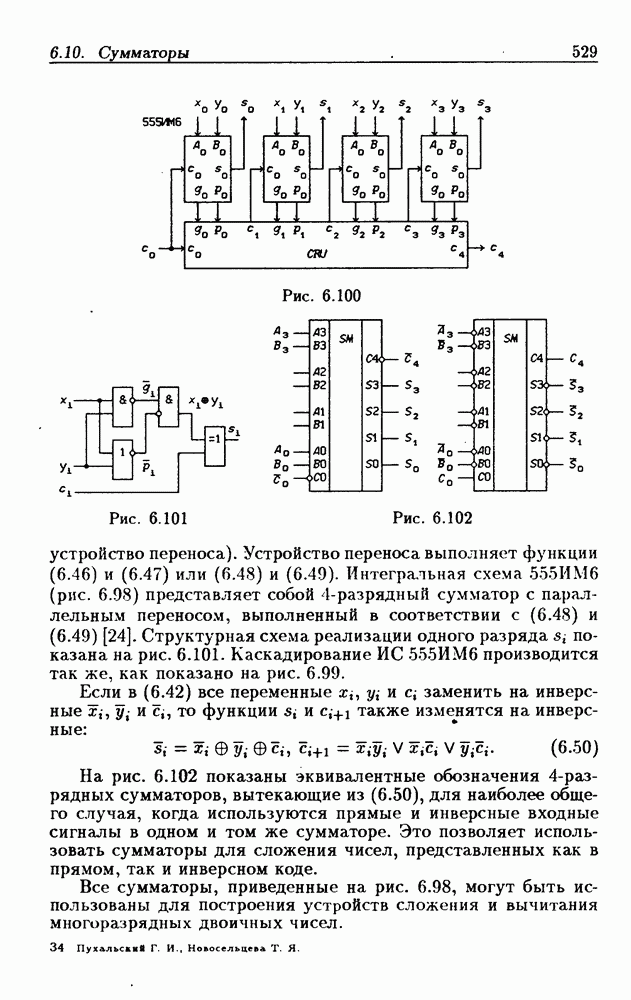
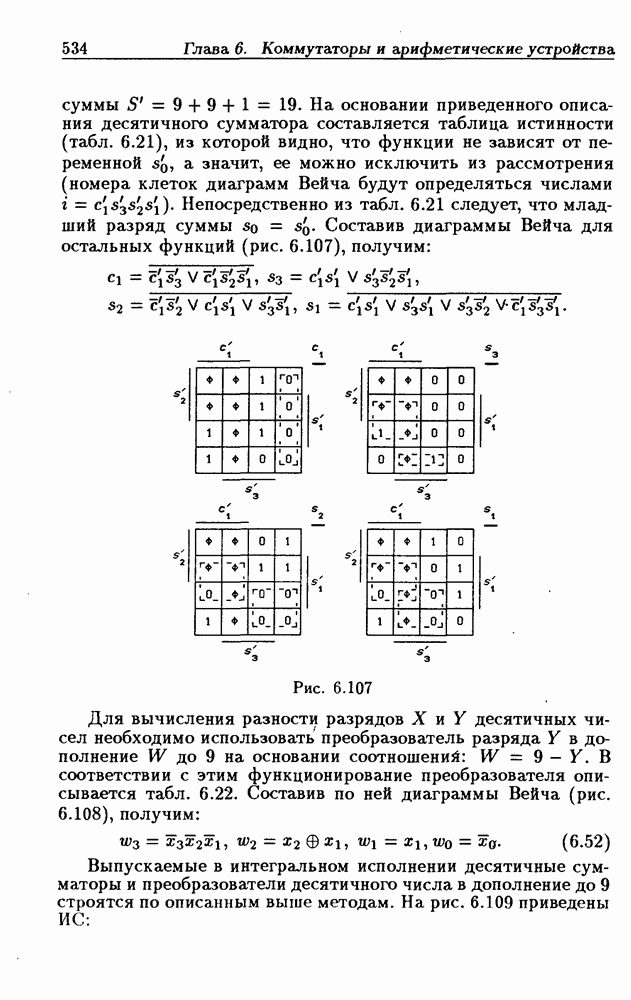
- 6.10. Сумматоры
- Двоичные параллельные сумматоры с последовательным переносом.
- Двоичные сумматоры с параллельным переносом.
- Применения сумматоров.
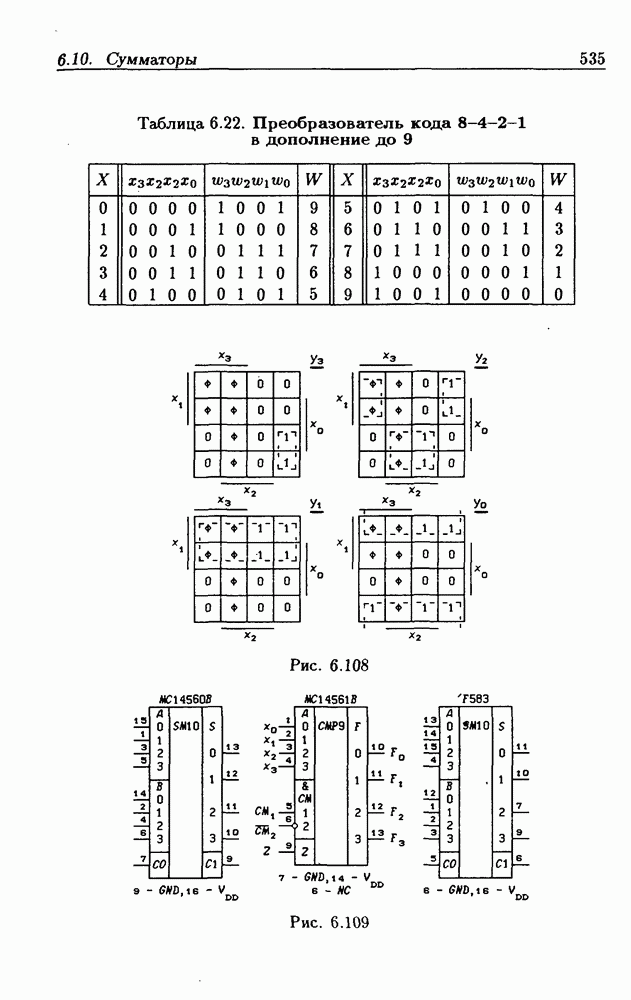
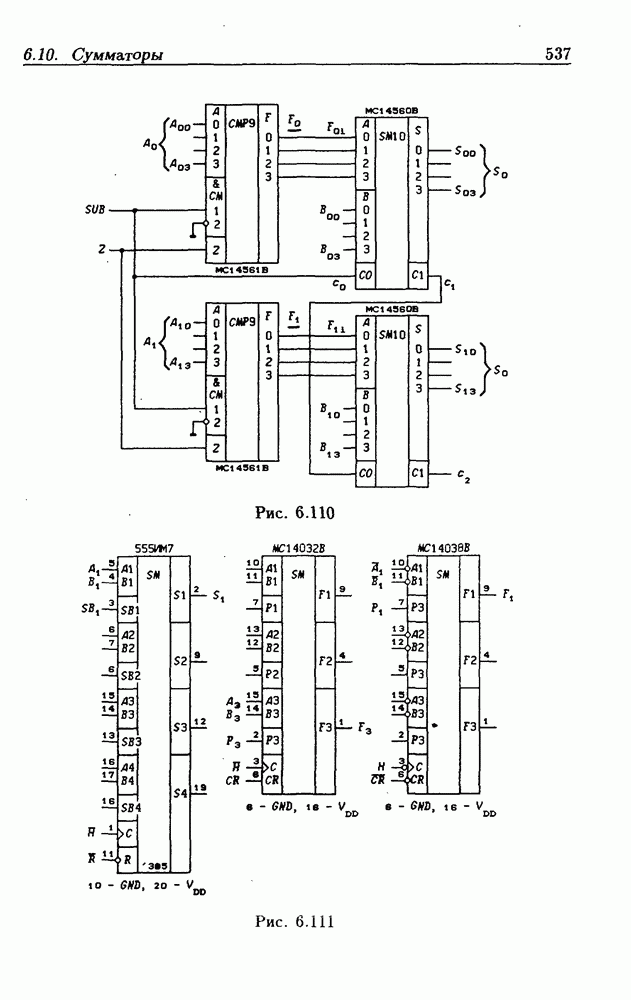
- Десятичные сумматоры.
- Последовательные двоичные сумматоры.
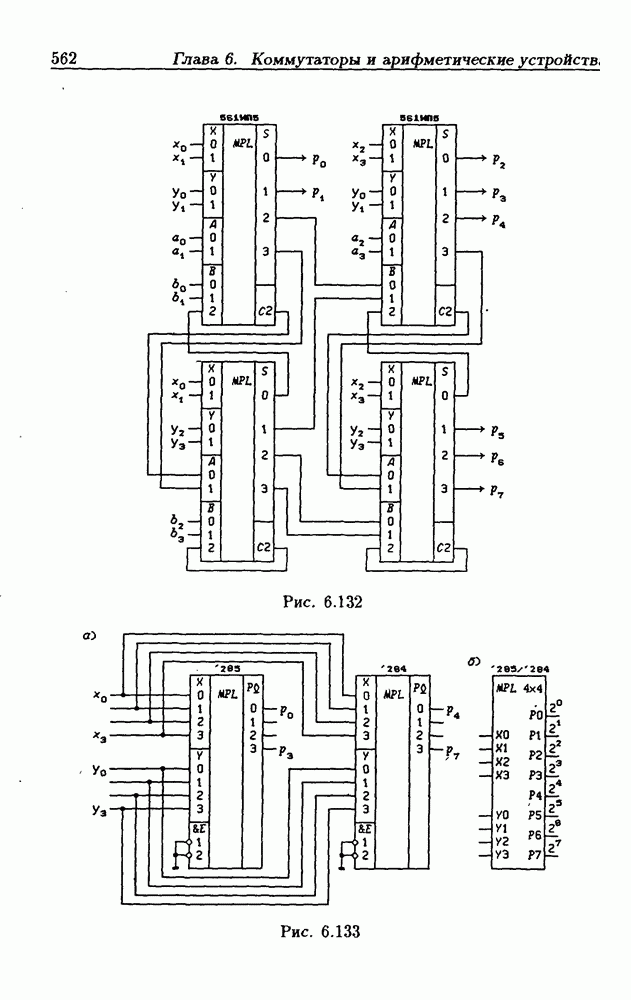
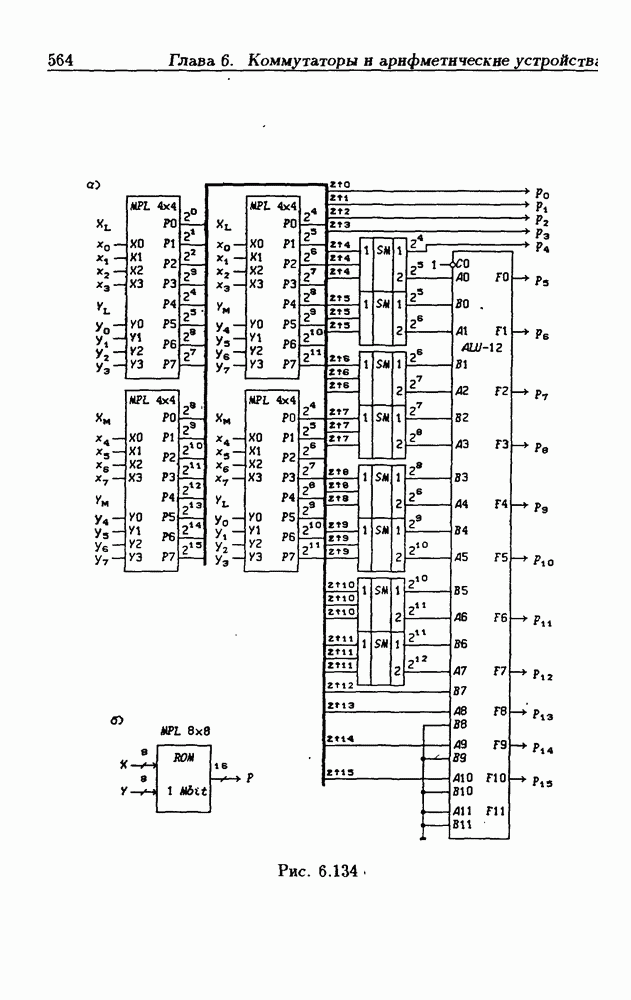
- 6.11. Арифметическо-логические устройства
- 6.12. Пороговые схемы и мажоритарные элементы
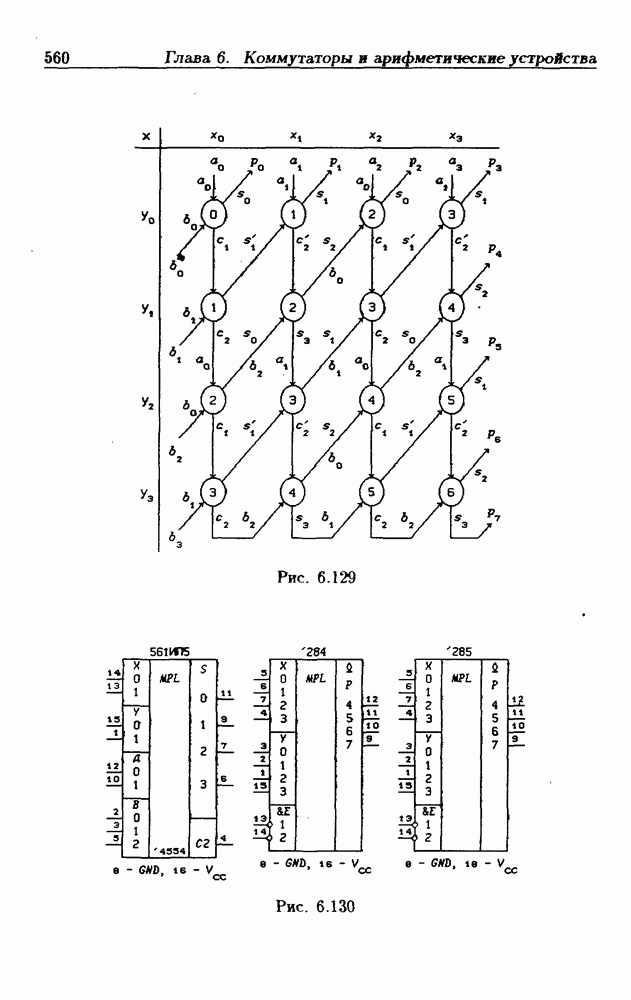
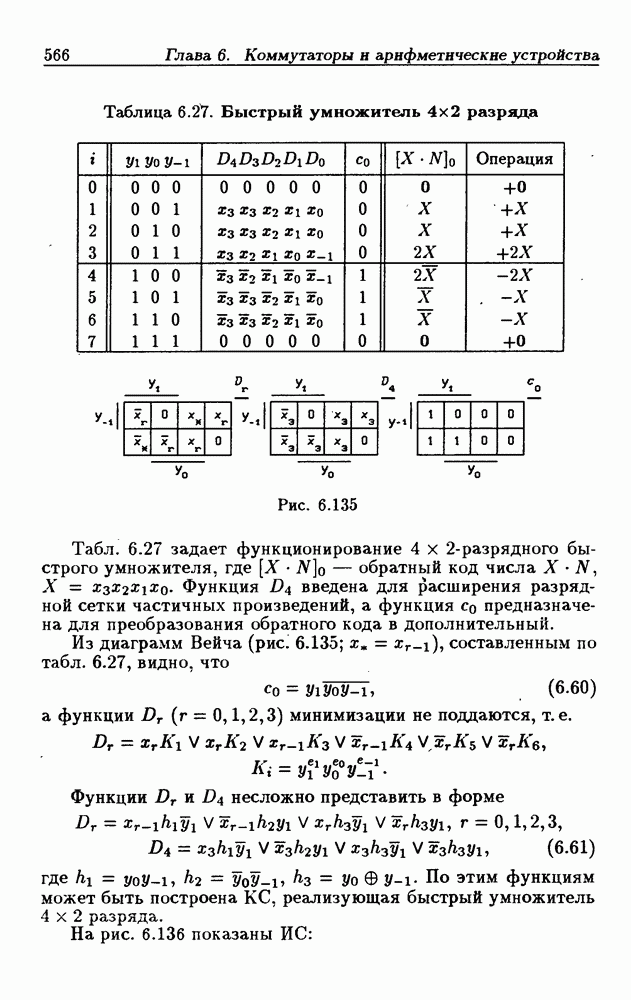
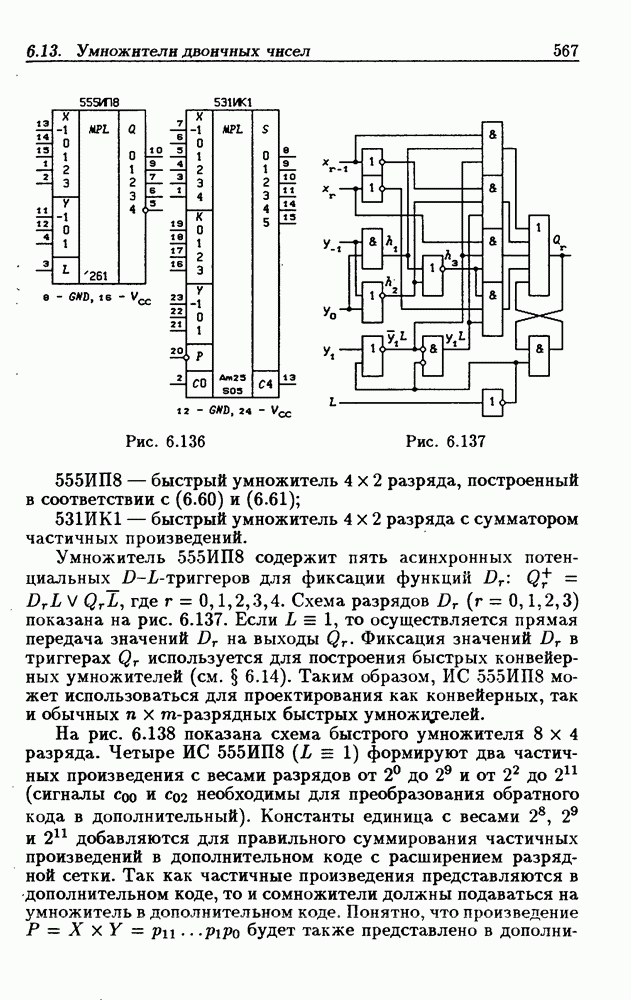
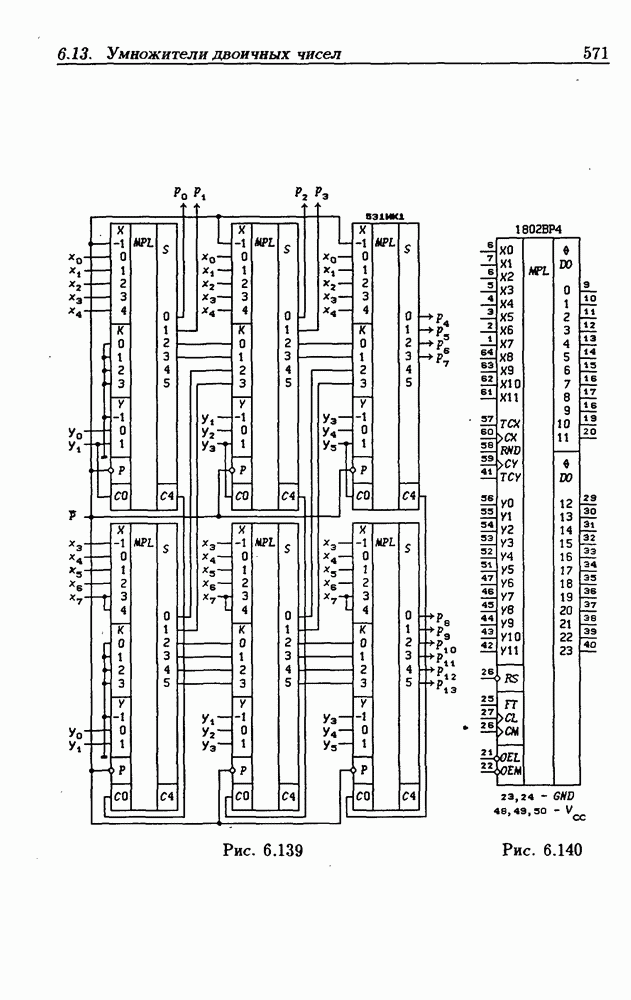
- 6.13. Умножители двоичных чисел
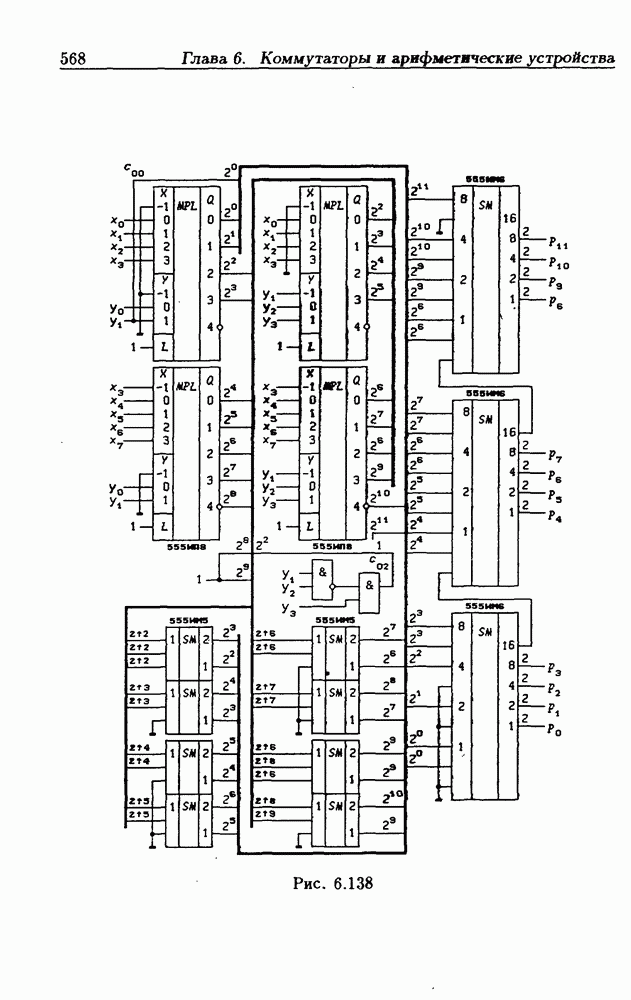
- Быстрые умножители.
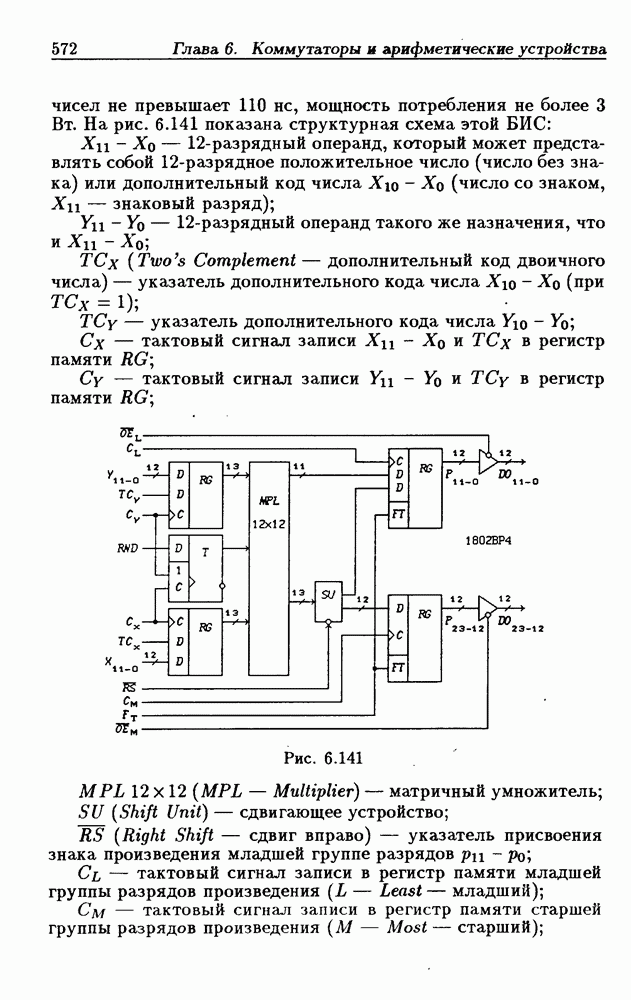
- БИС умножителя 12×12 разрядов 1802ВР4.
- Последовательные умножители.
- 6.14. Конвейерные устройства
- Конвейерный быстрый умножитель.
- Конвейерные АЦП.
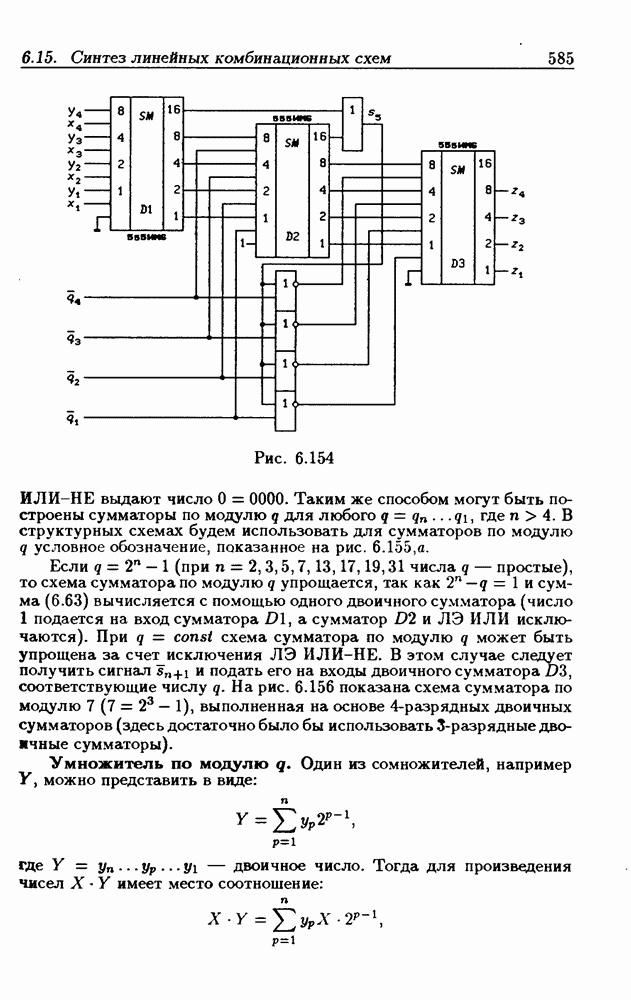
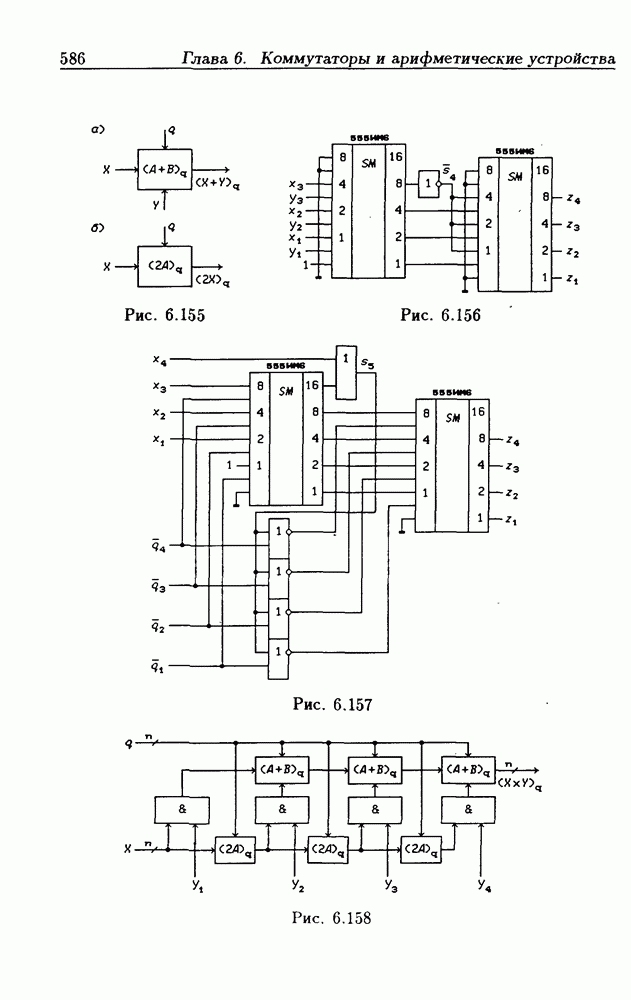
- 6.15. Синтез линейных комбинационных схем
- Сумматор по модулю q.
- Умножитель по модулю q.
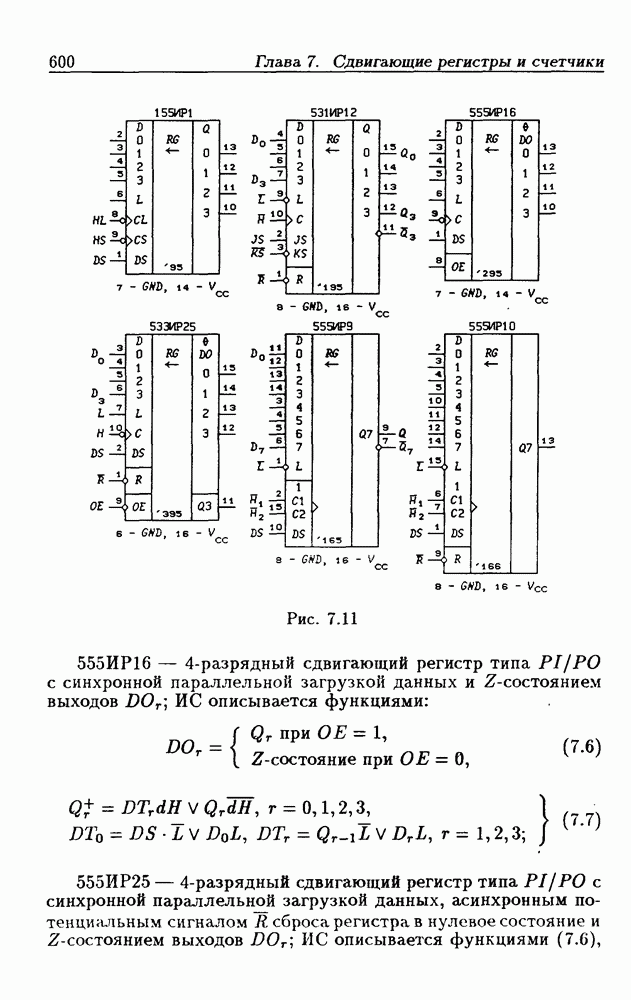
- Глава 7. Сдвигающие регистры и счетчики
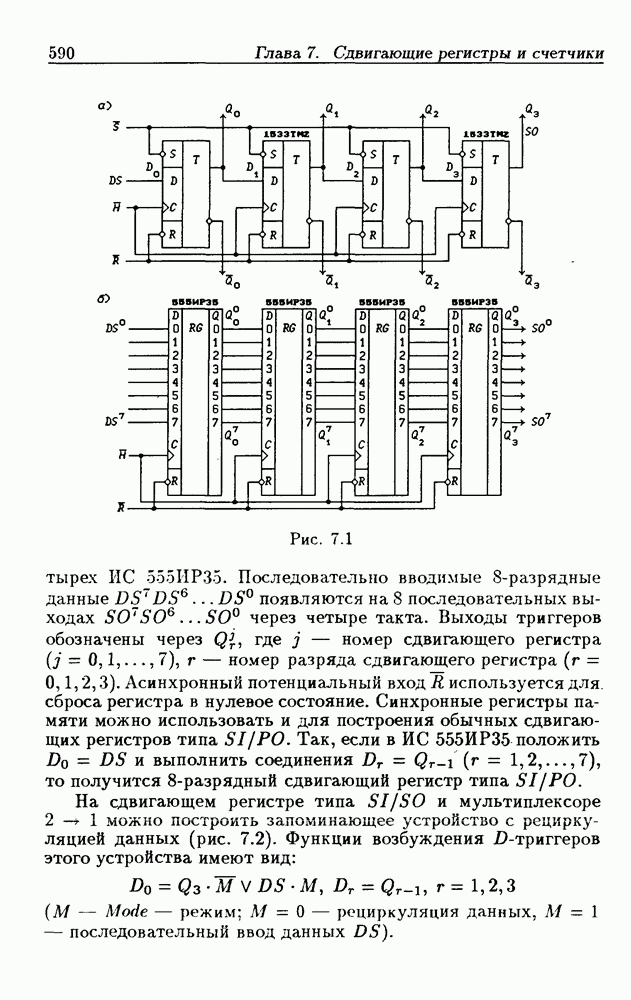
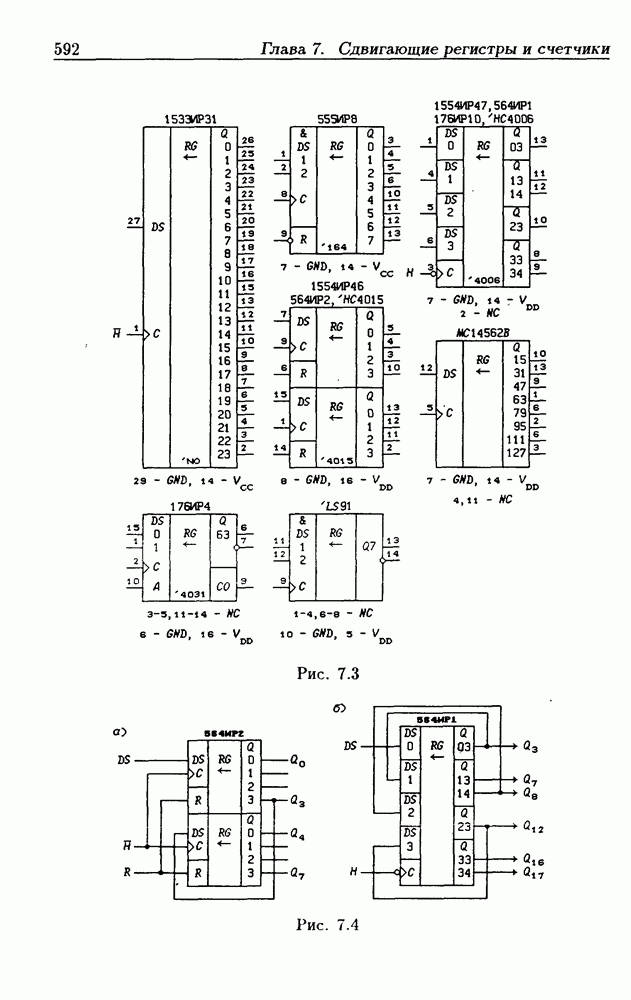
- 7.1. Сдвигающие регистры без параллельной записи данных
- Сдвигающие устройства с выходными регистрами памяти.
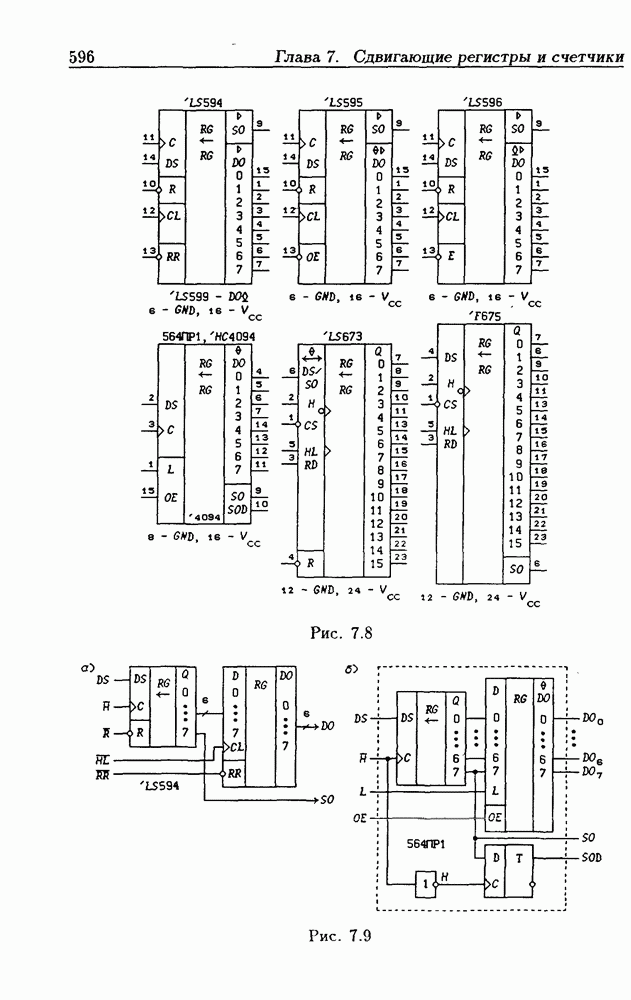
- 7.2. Сдвигающие регистры с параллельной записью данных
- Сдвигающие регистры с расширением знака.
- Сдвигающие регистры с входным регистром памяти.
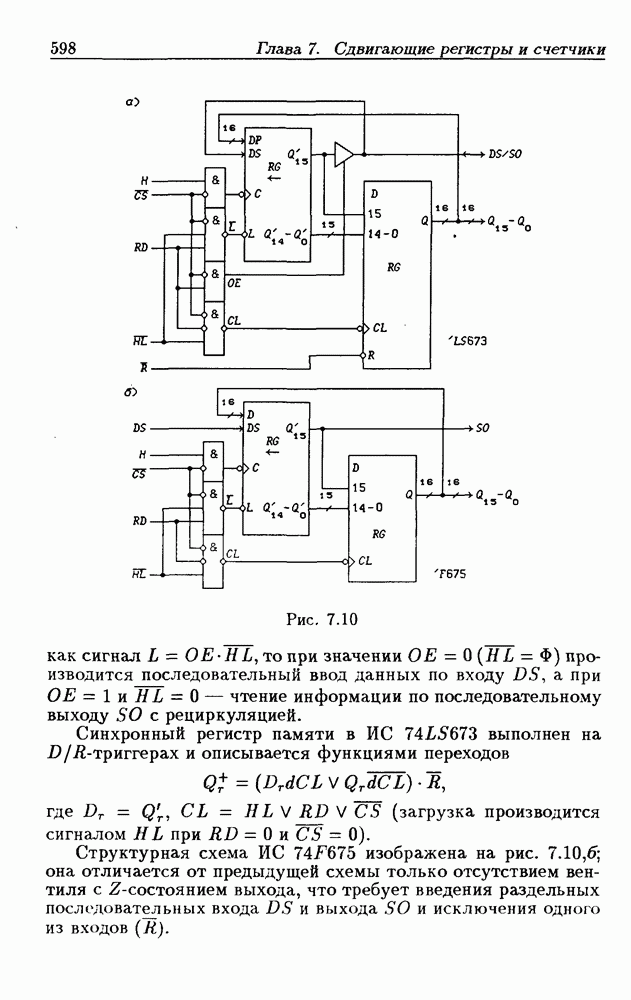
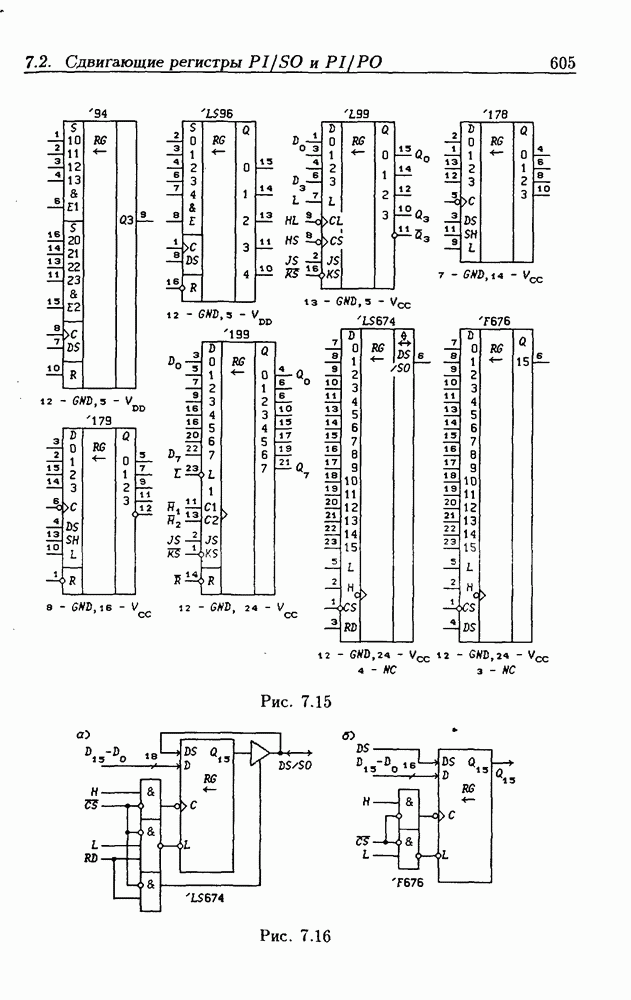
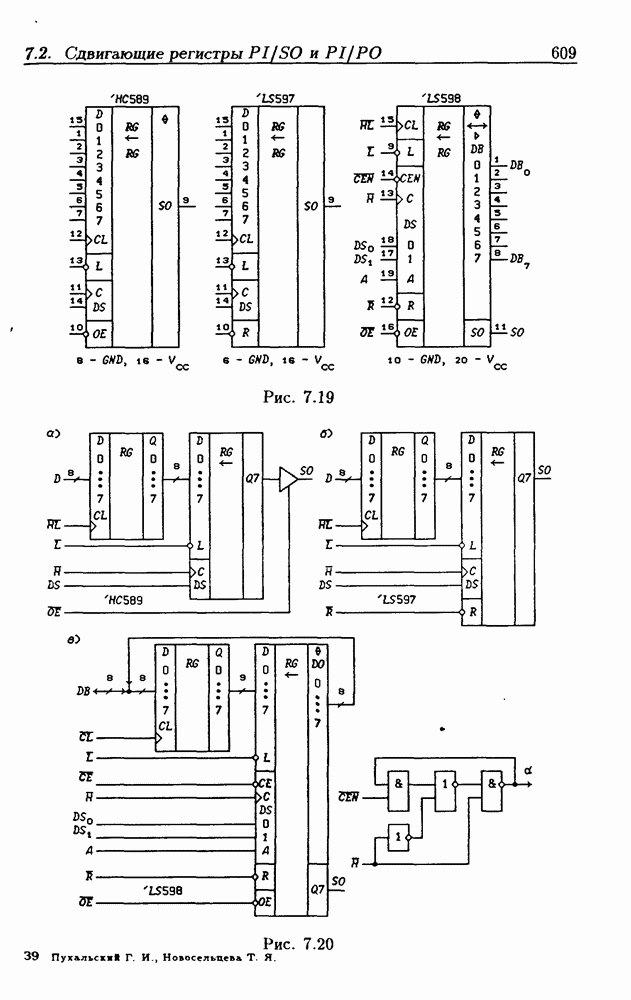
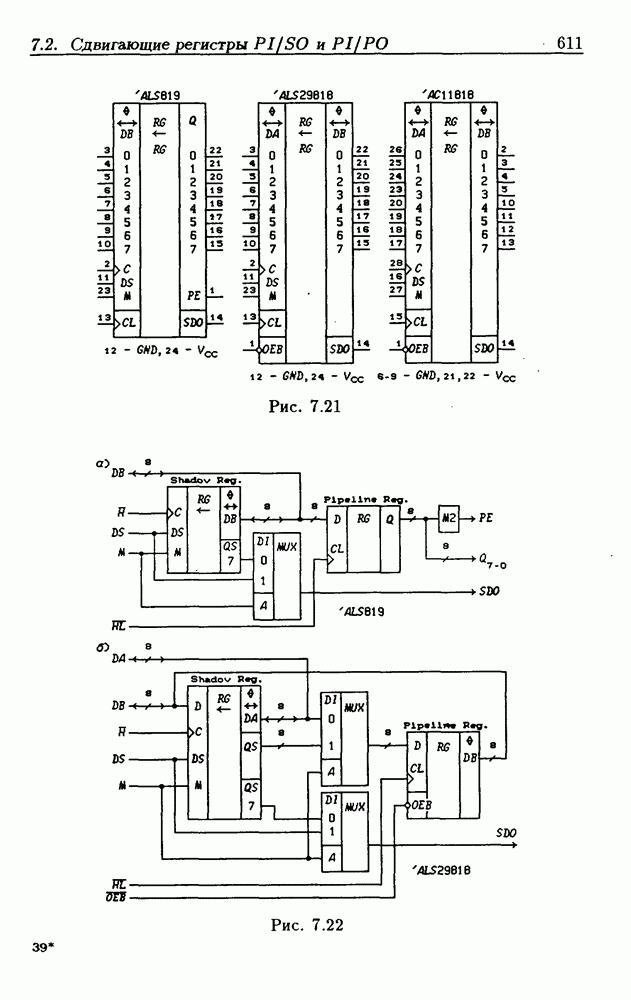
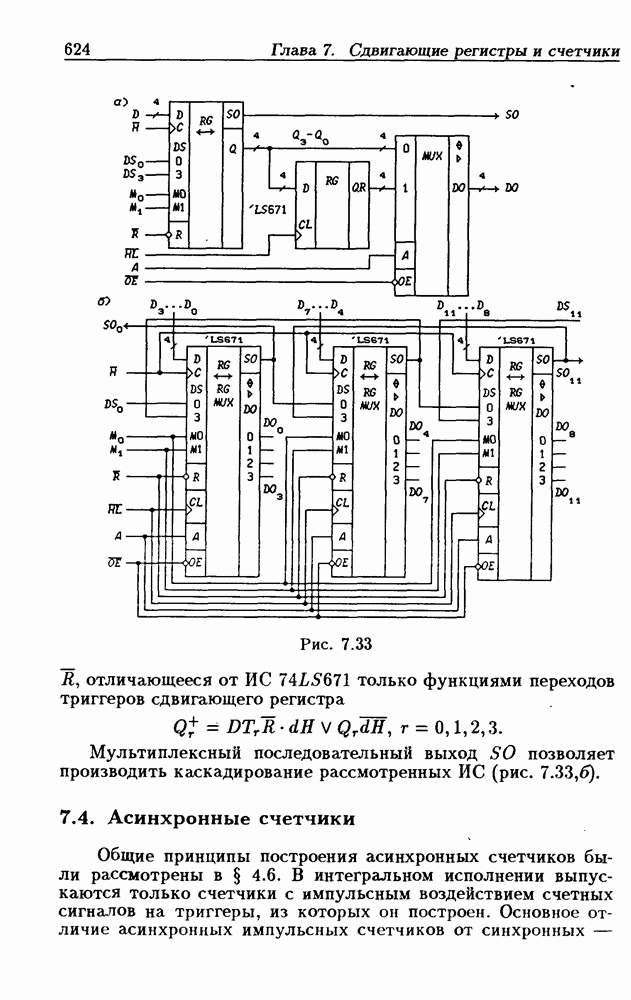
- 7.3. Реверсивные сдвигающие регистры
- Реверсивные сдвигающие регистры типов PI/SO и PI/PO.
- Многофункциональные устройства на основе реверсивных сдвигающих регистров.
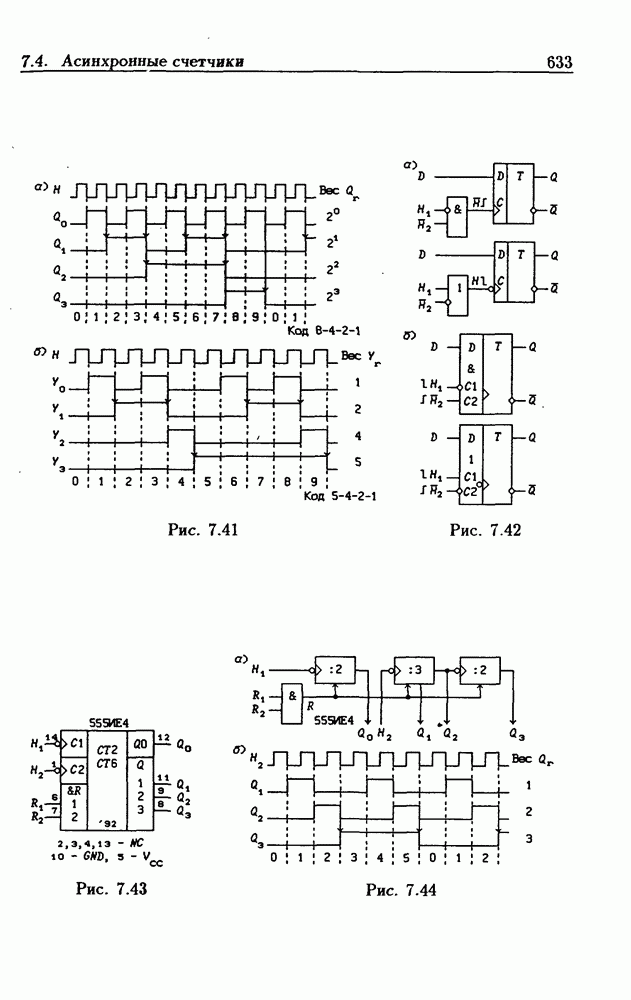
- 7.4. Асинхронные счетчики
- Двоично-десятичные асинхронные счетчики.
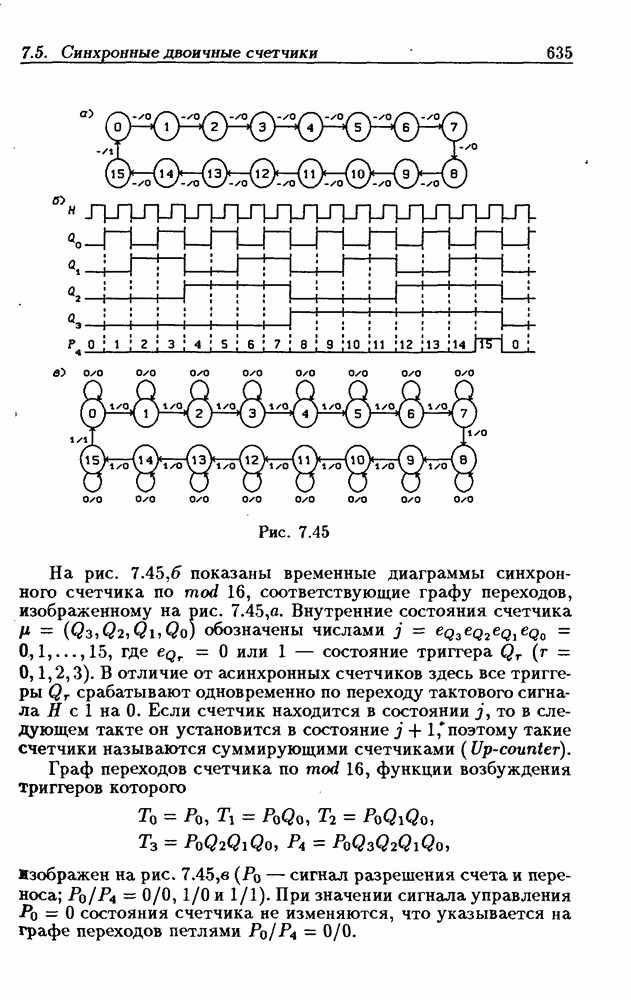
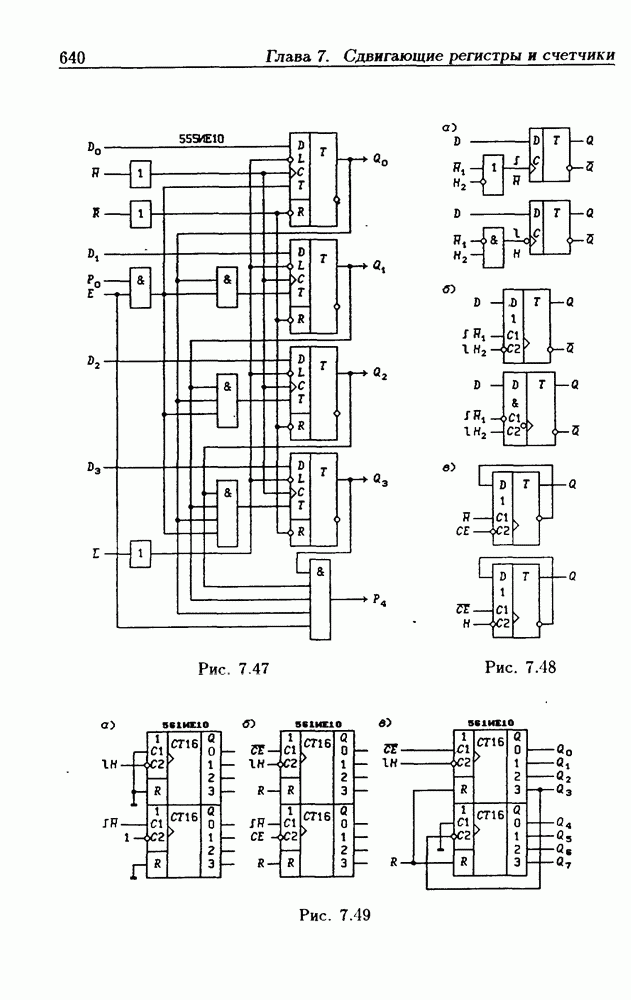
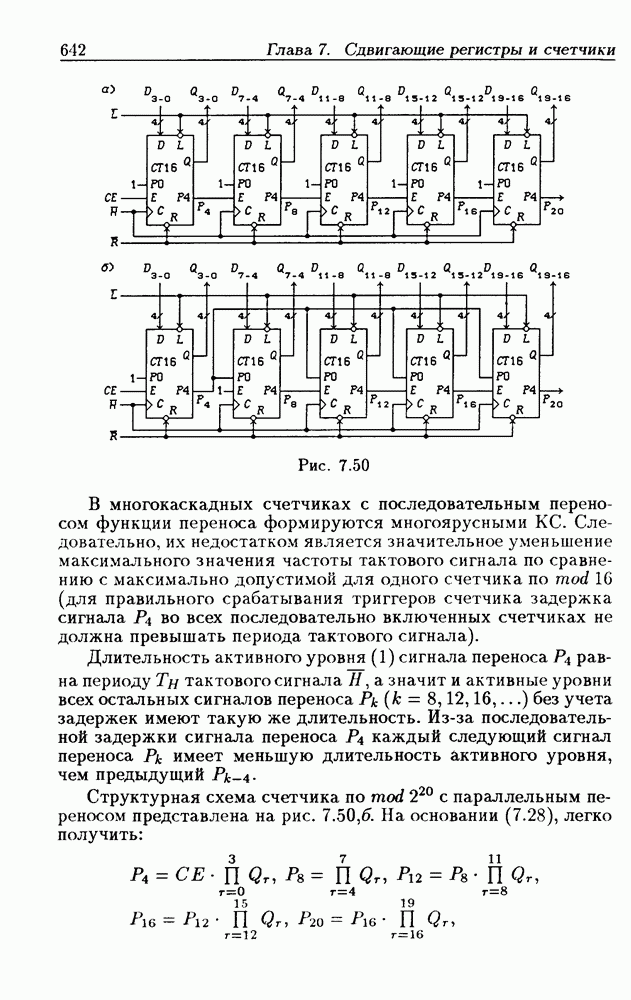
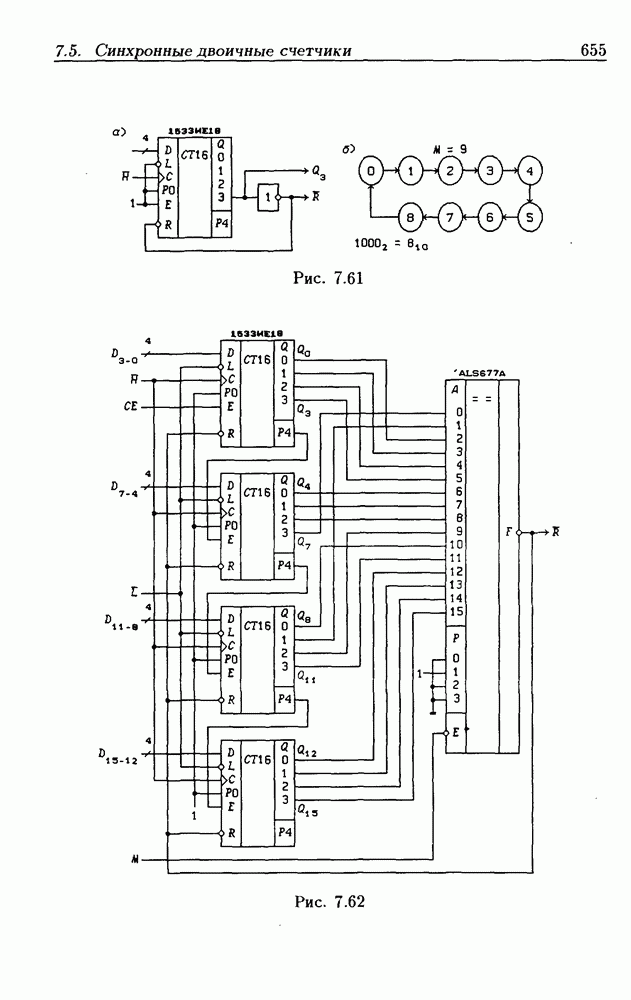
- 7.5. Синхронные двоичные счетчики
- Программирование модуля пересчета двоичных счетчиков.
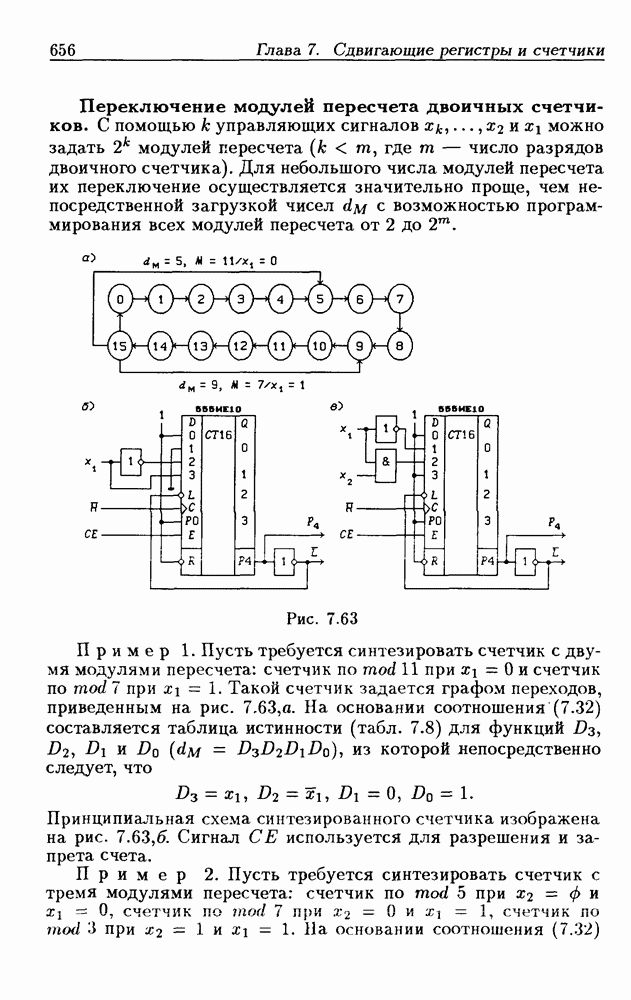
- Переключение модулей пересчета двоичных счетчиков.
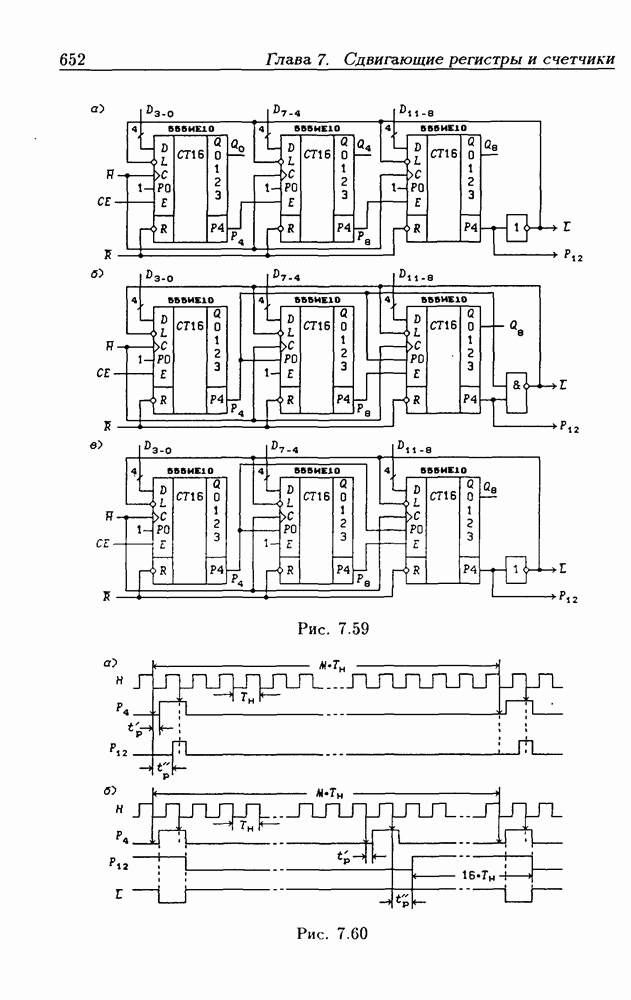
- Функциональные устройства на основе двоичных счетчиков.
- 7.6. Синхронные двоично-десятичные счетчики
- 7.7. Синхронные реверсивные счетчики
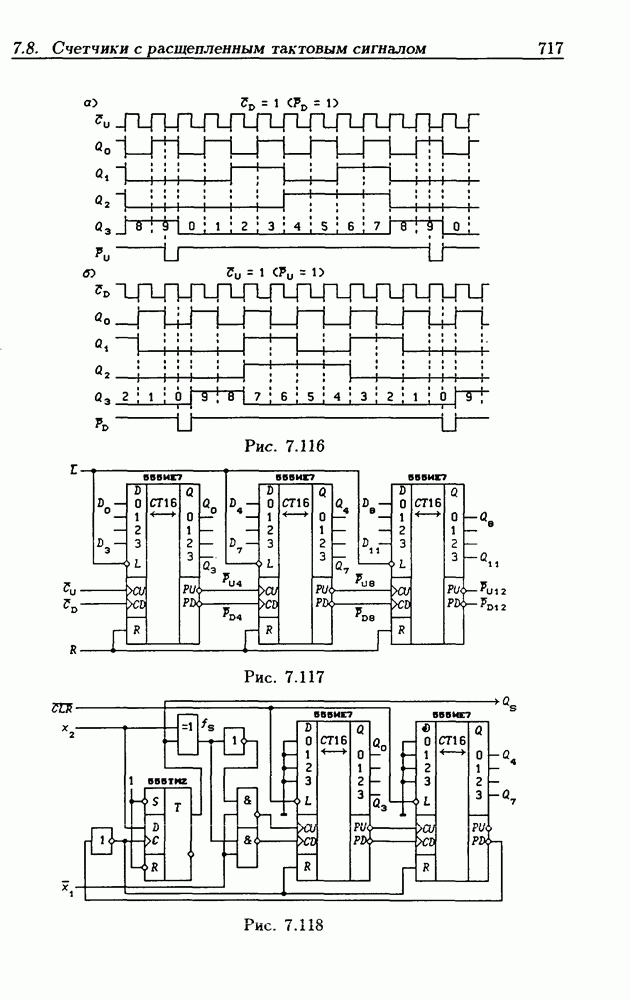
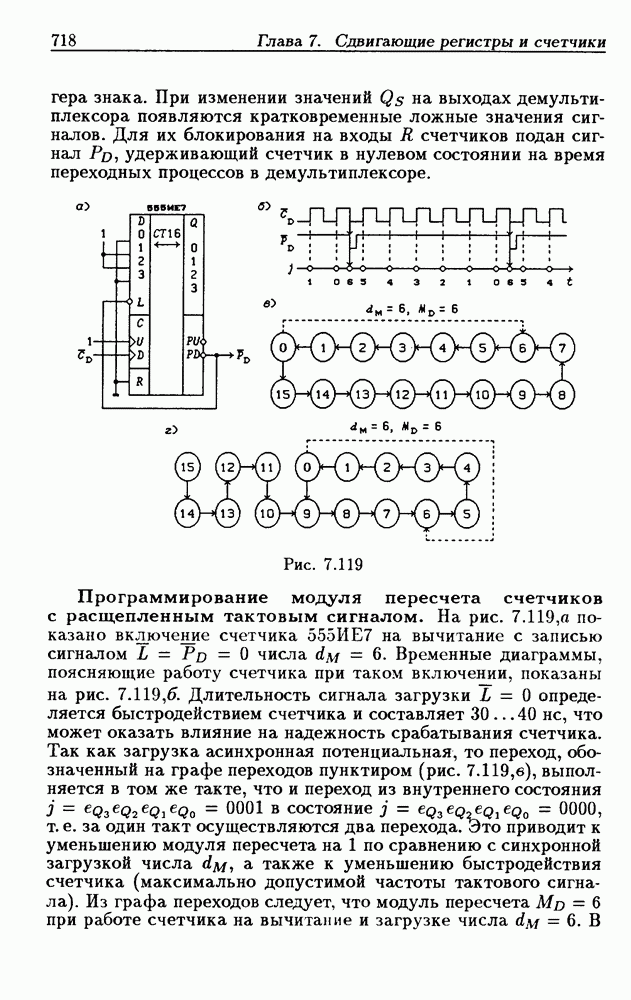
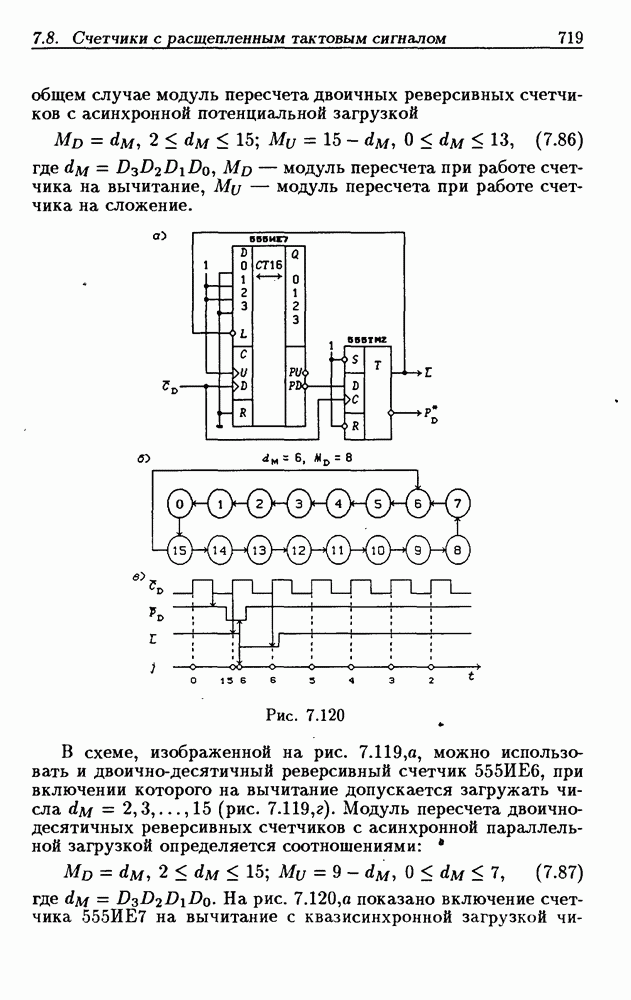
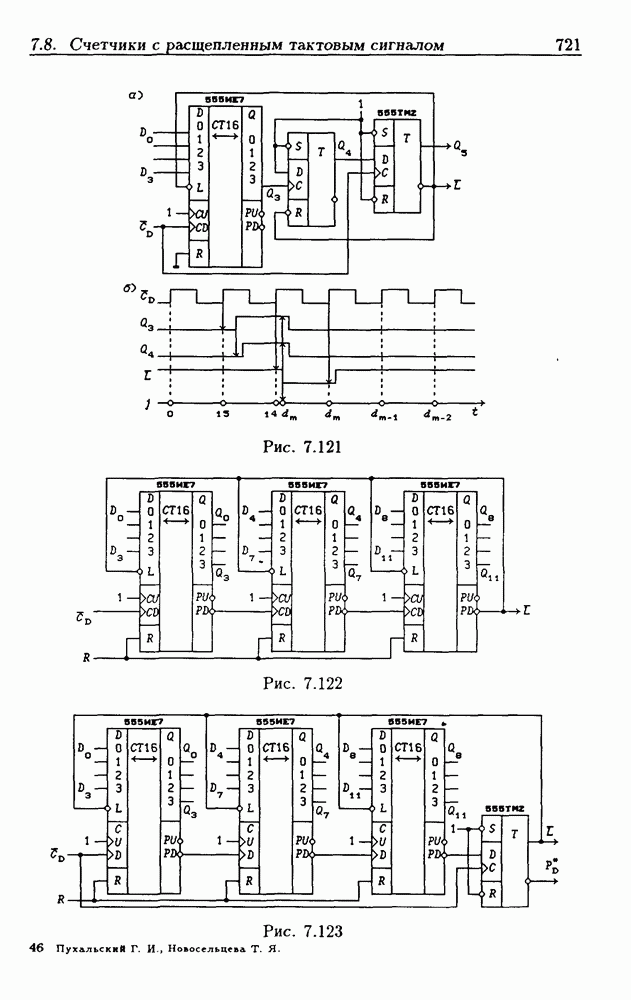
- 7.8. Счетчики с расщепленным тактовым сигналом
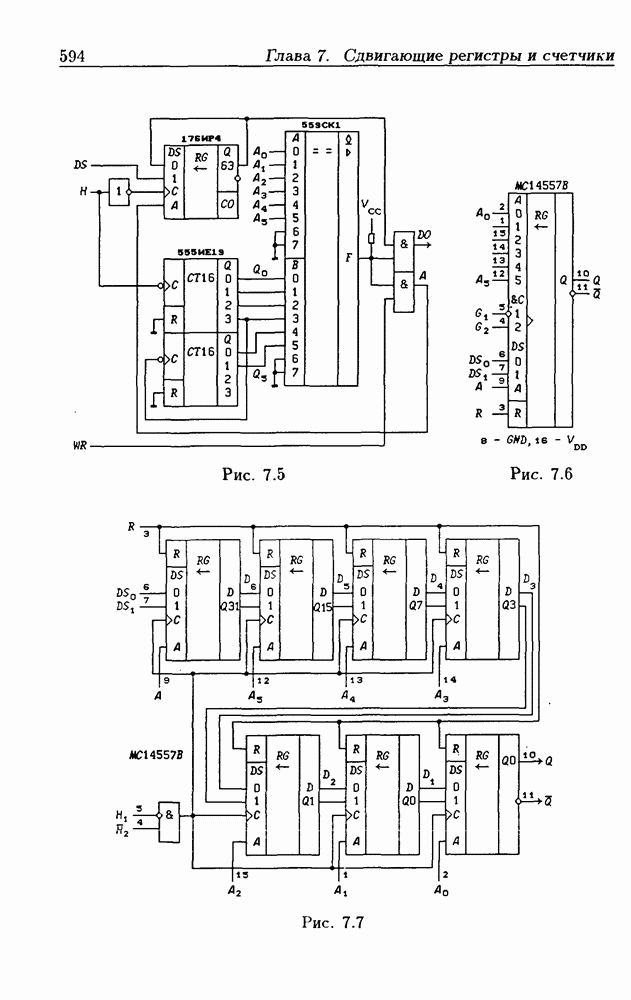
- 7.9. Счетчики на сдвигающих регистрах
- 7.10. Кольцевые счетчики
- 7.11. Делители частоты
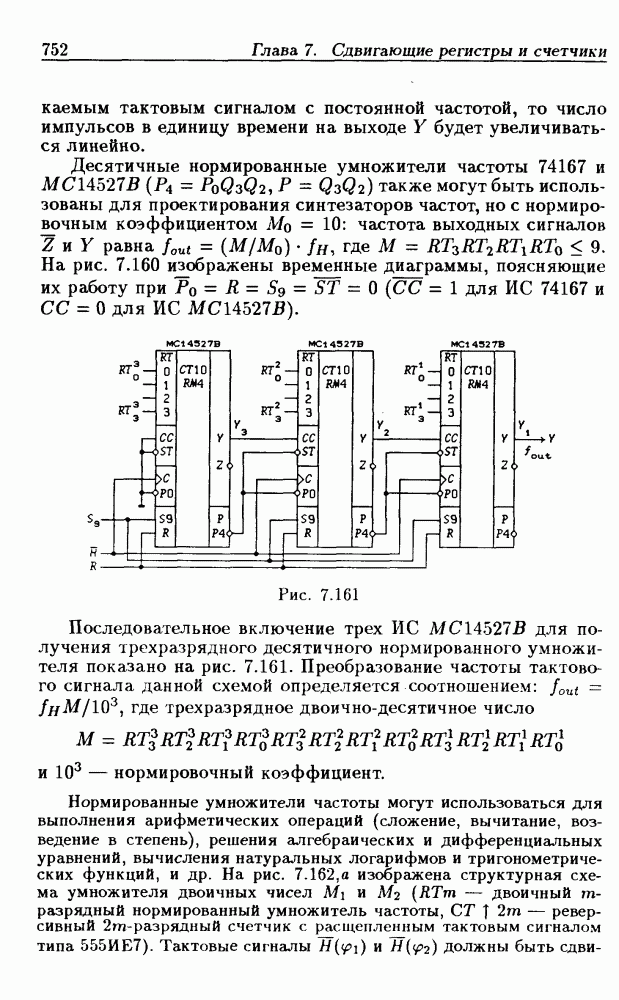
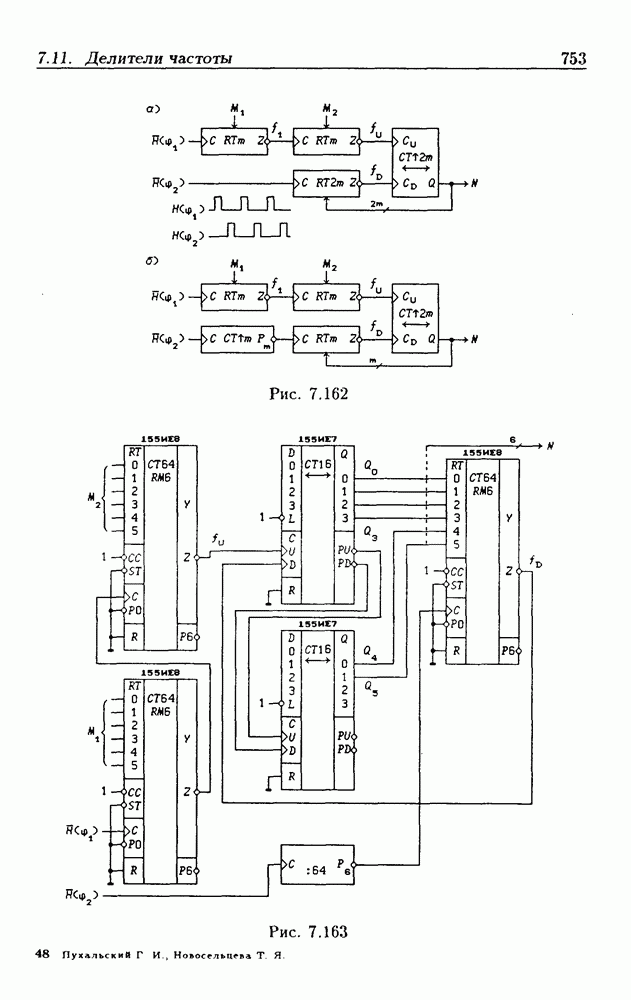
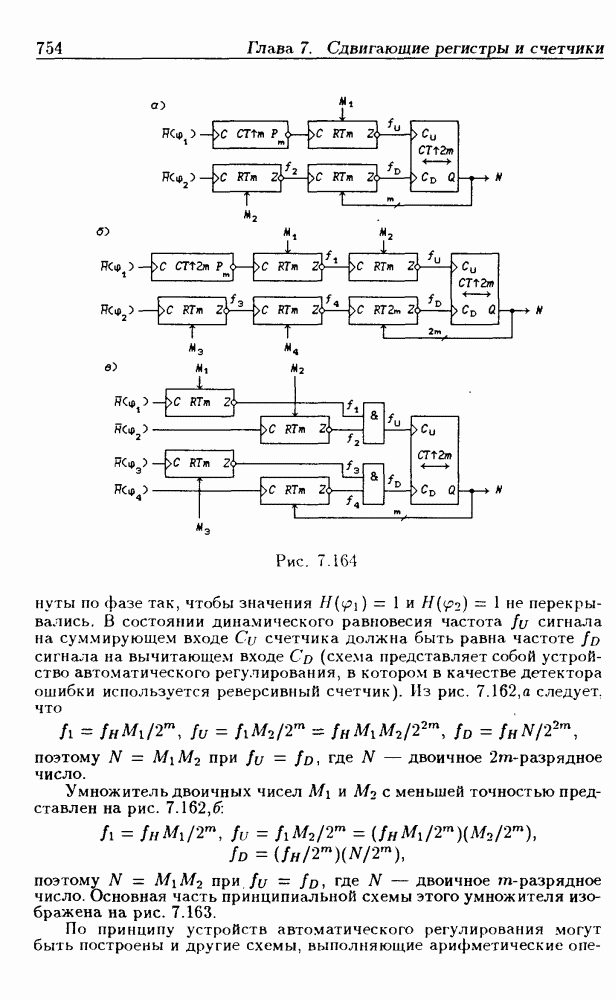
- Нормированные умножители частоты.
- 7.12. Линейные генераторы
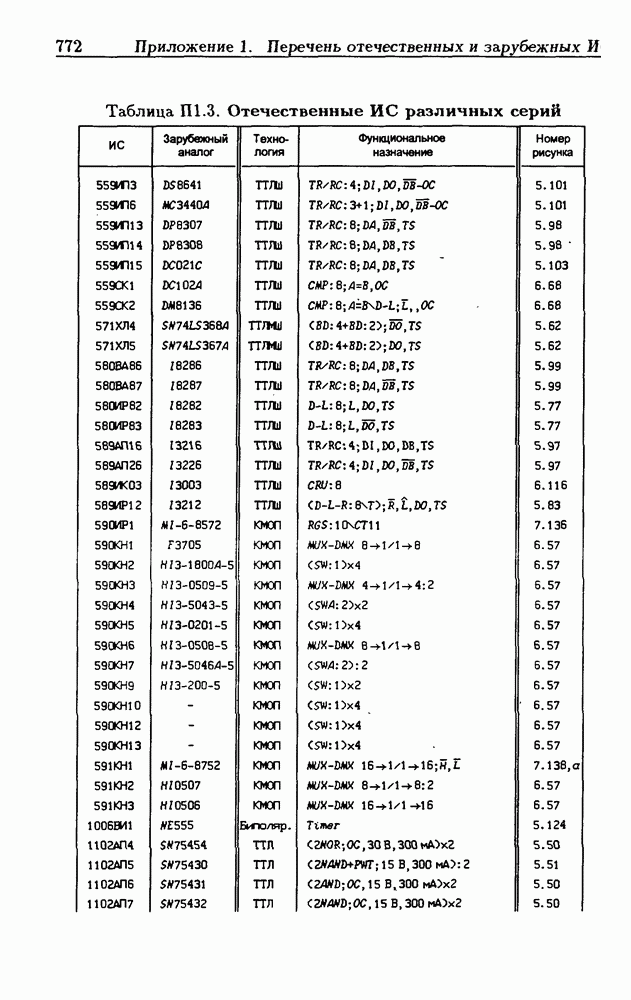
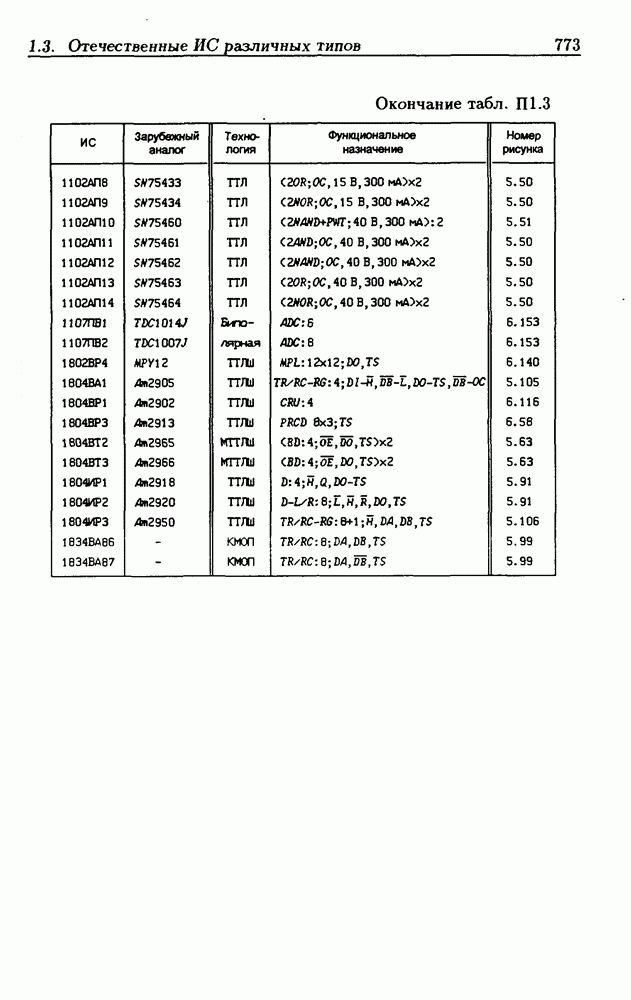
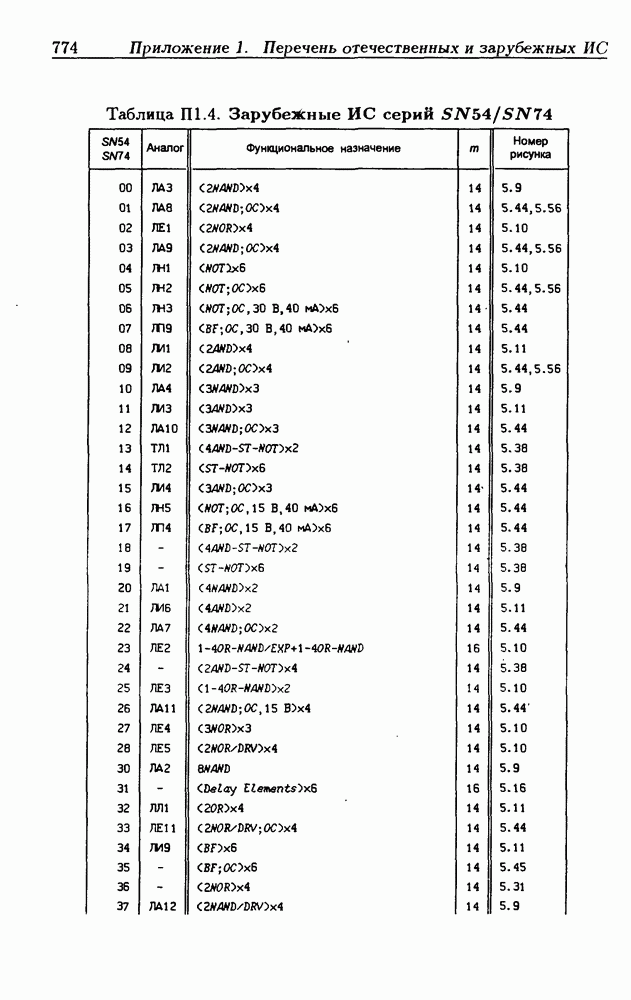
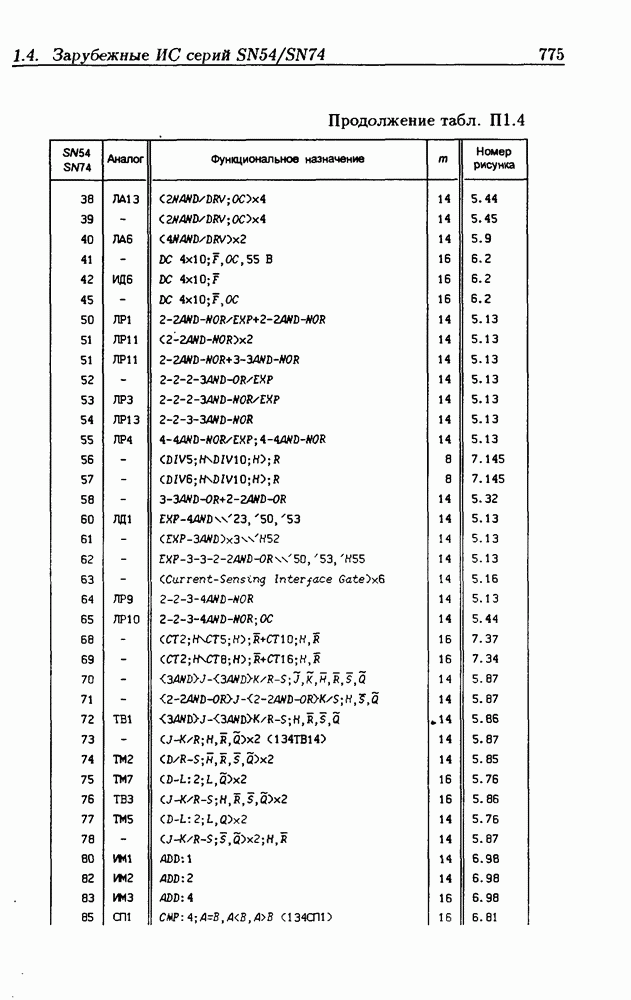
- Приложение 1. Перечень отечественных и зарубежных ИС
- Приложение 2. Параметры интегральных схем