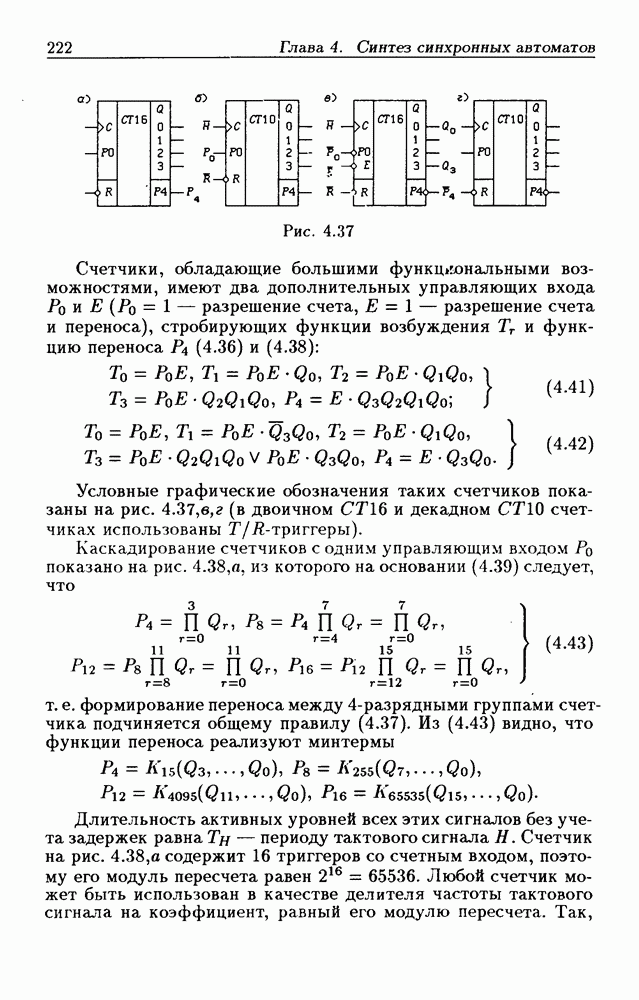| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
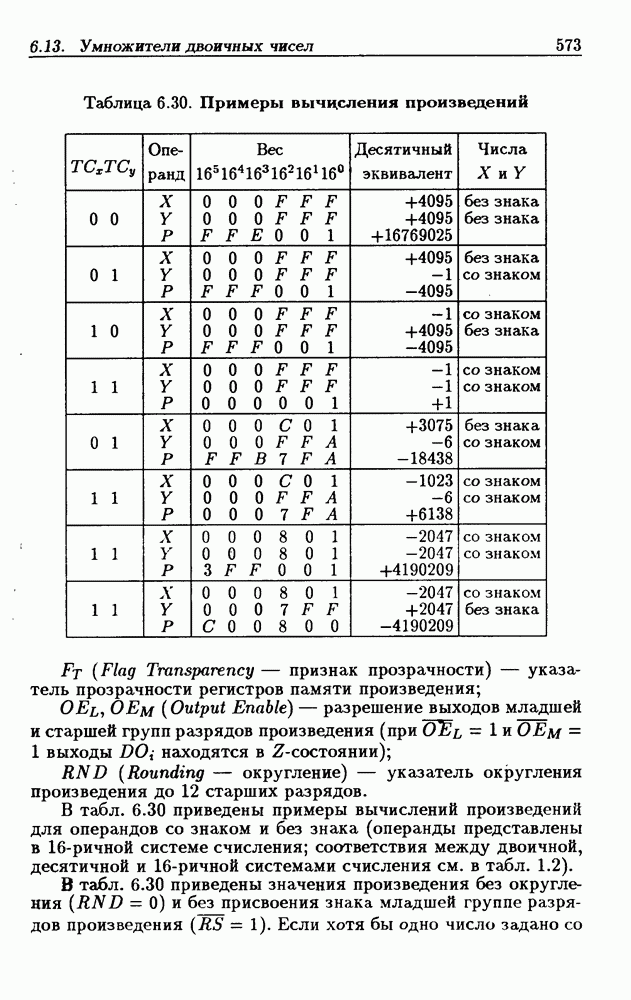
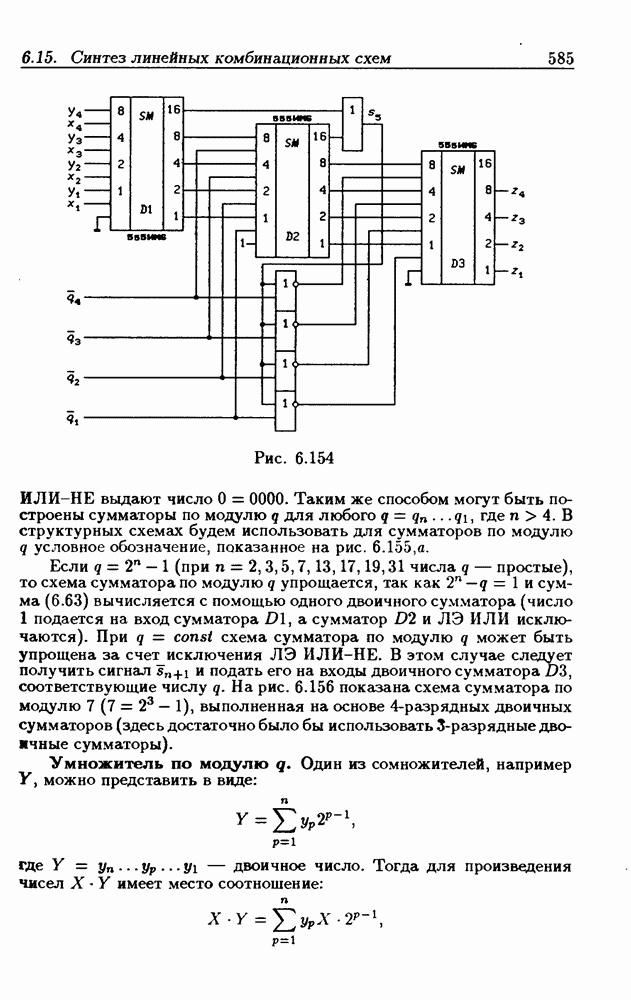
Умножитель по модулю q.
Один из сомножителей, например У, можно представить в виде:

где  двоичное число. Тогда для произведения чисел
двоичное число. Тогда для произведения чисел  имеет место соотношение:
имеет место соотношение:


(кликните для просмотра скана)
где  или 1. Из этого следует, что для построения умножителя по модулю
или 1. Из этого следует, что для построения умножителя по модулю  необходимо синтезировать типовую схему, выполняющую операцию
необходимо синтезировать типовую схему, выполняющую операцию  умножение на 2 по модулю
умножение на 2 по модулю  Действительно, так как
Действительно, так как  величины
величины  могут быть получены последовательным использованием умножителей на 2 по модулю
могут быть получены последовательным использованием умножителей на 2 по модулю 
Правило построения схемы умножителя на 2 по модулю  следует из соотношений (6.63) и (6.64), если в них положить
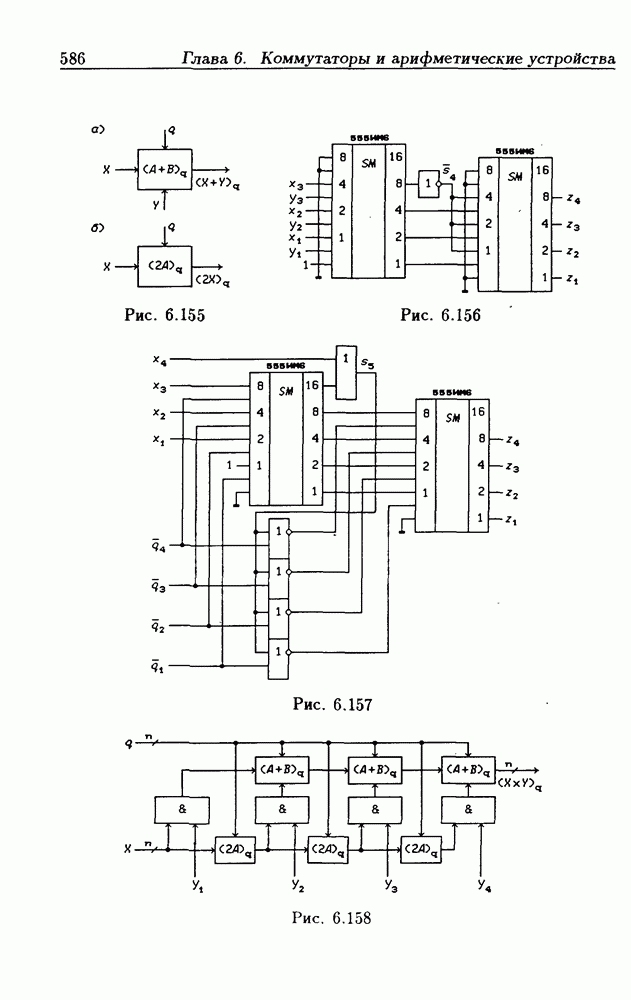
следует из соотношений (6.63) и (6.64), если в них положить  На рис. 6.157 показана схема умножителя на 2 по модулю
На рис. 6.157 показана схема умножителя на 2 по модулю  при 4-разрядном двоичном представлении
при 4-разрядном двоичном представлении  Умножение числа X на 2 достигается сдвигом разрядов числа X на один разряд относительно входов левого сумматора, поэтому для вычисления двоичной суммы
Умножение числа X на 2 достигается сдвигом разрядов числа X на один разряд относительно входов левого сумматора, поэтому для вычисления двоичной суммы  требуется всего один двоичный сумматор. На выходе правого сумматора получается величина
требуется всего один двоичный сумматор. На выходе правого сумматора получается величина  На рис.
На рис.  приведено условное обозначение умножителя на 2 по модулю
приведено условное обозначение умножителя на 2 по модулю  которое будет использоваться в
которое будет использоваться в  структурных схемах умножителей чисел
структурных схемах умножителей чисел  по модулю
по модулю 
На рис. 6.158 показана структурная схема умножителя по модулю  вычисляющего величину
вычисляющего величину

Здесь числа  и X представляют собой n-мерные векторы, а узел
и X представляют собой n-мерные векторы, а узел  совокупность
совокупность  И для поразрядного логического умножения числа X на разряды
И для поразрядного логического умножения числа X на разряды  где
где  (на рис.
(на рис. 
Схема умножителя чисел  по модулю
по модулю  существенно упрощается, если
существенно упрощается, если  Покажем, что в этом случае
Покажем, что в этом случае  где
где  т.е. умножение на 2 по модулю
т.е. умножение на 2 по модулю  реализуется циклическим сдвигом разрядов числа А на один разряд в сторону старших разрядов. Действительно, при
реализуется циклическим сдвигом разрядов числа А на один разряд в сторону старших разрядов. Действительно, при  сумма
сумма  Если
Если  то
то  т.е.
т.е.  так как
так как  только при
только при  Если же
Если же  то
то  т.е.
т.е.  так как
так как  только при
только при 
При построении линейных цифровых автоматов требуется произ-, водить умножение чисел X не на произвольные числа У, а на постоянные коэффициенты  задающие структуру линейного автомата. В этом случае значения
задающие структуру линейного автомата. В этом случае значения  (0 или
(0 или  ) не изменяются во времени, поэтому узлы
) не изменяются во времени, поэтому узлы  на рис. 6.158 имеют чисто символическое значение, указывающее на наличие или отсутствие связей. Например, при
на рис. 6.158 имеют чисто символическое значение, указывающее на наличие или отсутствие связей. Например, при  или
или  два первых сумматора по модулю
два первых сумматора по модулю  отсутствуют, а сигнал X и сигнал с выхода последнего умножителя на 2 по модулю
отсутствуют, а сигнал X и сигнал с выхода последнего умножителя на 2 по модулю  следует подать на входы последнего сумматора
следует подать на входы последнего сумматора  (рис. 6.159).
(рис. 6.159).
На рис. 6.160 показана схема умножителя 

Рис. 6.159

Рис. 6.160
построенная на основании очевидного соотношения:

Здесь для получения величины  использован циклический сдвиг разрядов числа
использован циклический сдвиг разрядов числа  на два разряда в сторону старших разрядов. Чем меньше в двоичном представлении константы
на два разряда в сторону старших разрядов. Чем меньше в двоичном представлении константы  содержится единиц, тем проще получается схема умножителя по модулю
содержится единиц, тем проще получается схема умножителя по модулю 
Таблица 6.34. Сумматор и умножитель по модулю 3
Синтезированные выше сумматор и умножитель по модулю  позволяют реализовать любой линейный автомат над полем
позволяют реализовать любой линейный автомат над полем  Сумматор и умножитель по модулю
Сумматор и умножитель по модулю  легко синтезировать традиционными методами. Для этого по табл. 1.8 составляется таблица истинности (табл. 6.34) для функций
легко синтезировать традиционными методами. Для этого по табл. 1.8 составляется таблица истинности (табл. 6.34) для функций  определяющих искомые разряды чисел
определяющих искомые разряды чисел

где  Если по табл. 6.34 составить диаграммы Вейча, то можно получить:
Если по табл. 6.34 составить диаграммы Вейча, то можно получить:

При больших значениях  задача синтеза сильно усложняется, а схемы получаются более громоздкими, чем при использовании сумматоров.
задача синтеза сильно усложняется, а схемы получаются более громоздкими, чем при использовании сумматоров.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Глава 1. Основы теории переключательных функций
- 1.2. Позиционные системы счисления
- 1.3. Переключательные функции
- 1.4. Принцип и закон двойственности
- 1.5. Теоремы разложения
- 1.6. Решение систем логических уравнений
- 1.7. Первичные термы, минтермы и макстермы
- 1.8. Совершенные нормальные формы представления функций
- 1.9. Конъюнктивные и дизъюнктивные термы
- 1.10. Минимизация переключательных функций
- 1.11. Диаграммы Вейча
- 1.12. Минимизация неполностью определенных функций, совместная минимизация нескольких функций
- 1.13. Скобочные формы функций
- 1.14. Закон двойственности для логических схем
- 1.15. Линейные функции
- Глава 2. Анализ и синтез логических схем
- 2.2. Модели логических элементов
- 2.3. Модели логических схем
- 2.4. Анализ логических схем
- 2.5. Синтез комбинационных схем, свободных от состязаний
- Глава 3. Синтез асинхронных потенциальных автоматов
- 3.2. Асинхронные потенциальные автоматы
- 3.3. Асинхронные потенциальные триггеры и элементы памяти
- Триггеры типа R-S
- Триггеры типа D-L
- Триггеры типа D-L-R с приоритетом входа R.
- Триггеры типа D-L-R с приоритетом входа L.
- Триггеры типа R-S-L.
- Триггеры типа DN-LN
- Аналитический метод синтеза и анализа триггеров.
- 3.4. Задание асинхронных потенциальных автоматов таблицами и графами переходов
- 3.5. Синтез асинхронных потенциальных счетчиков
- 3.6. Синтез асинхронных импульсных триггеров
- Триггеры типа dJ-dK.
- Классификация триггеров.
- 3.7. Синтез синхронных триггеров
- Триггеры типа J-K
- Синхронно-асинхронные триггеры.
- 3.8. Примеры синтеза асинхронных потенциальных автоматов
- Цифровые фазочастотные детекторы.
- Квантизатор временных интервалов.
- 3.9. Генераторы сигналов
- Автогенераторы.
- Управляемые автогенераторы.
- Глава 4. Синтез синхронных автоматов
- 4.2. Синхронные триггеры
- Триггеры типов D и R-S с импульсным тактовым сигналом.
- Синхронные триггеры типов R-S и D-L
- Синхронно-асинхронные триггеры.
- Синхронные триггеры типа J-K
- Триггеры типа Т.
- Классификация синхронных триггеров.
- Преобразования типов синхронных триггеров.
- Триггеры типов D-T-L и D-T-L/R
- Функции переходов синхронно-асинхронных триггеров.
- 4.3. Примеры синтеза синхронных автоматов
- 4.4. Сдвигающие регистры
- Синтез счетчиков на сдвигающих регистрах.
- Сдвигающие регистры с загрузкой данных.
- Реверсивные сдвигающие регистры.
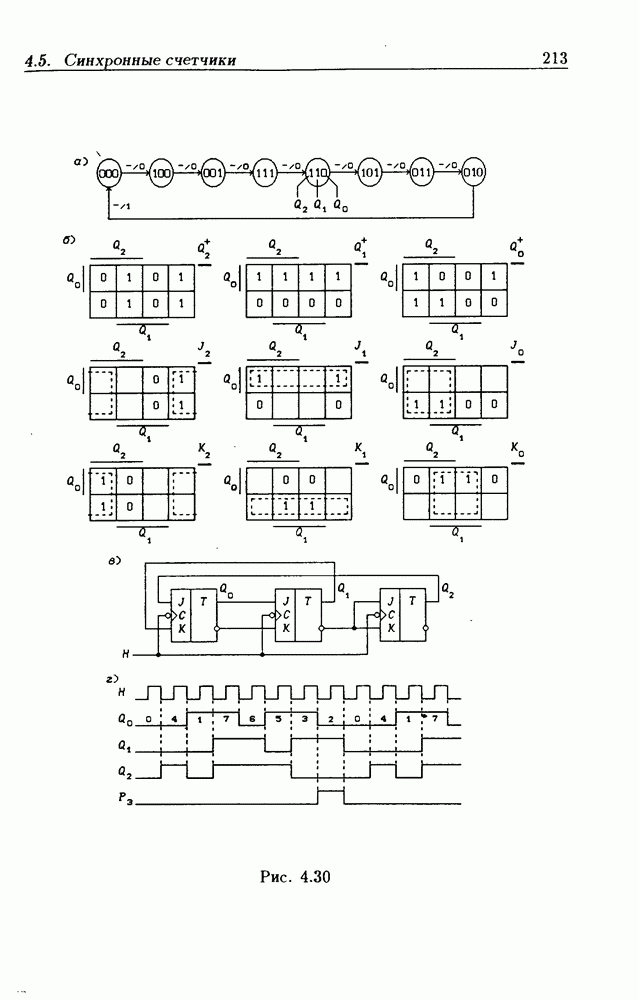
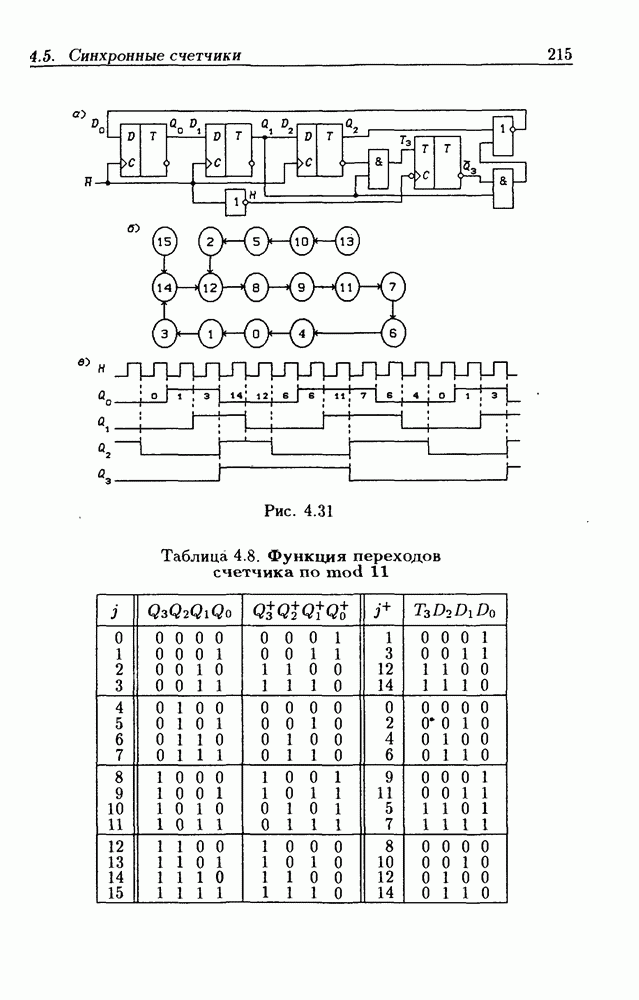
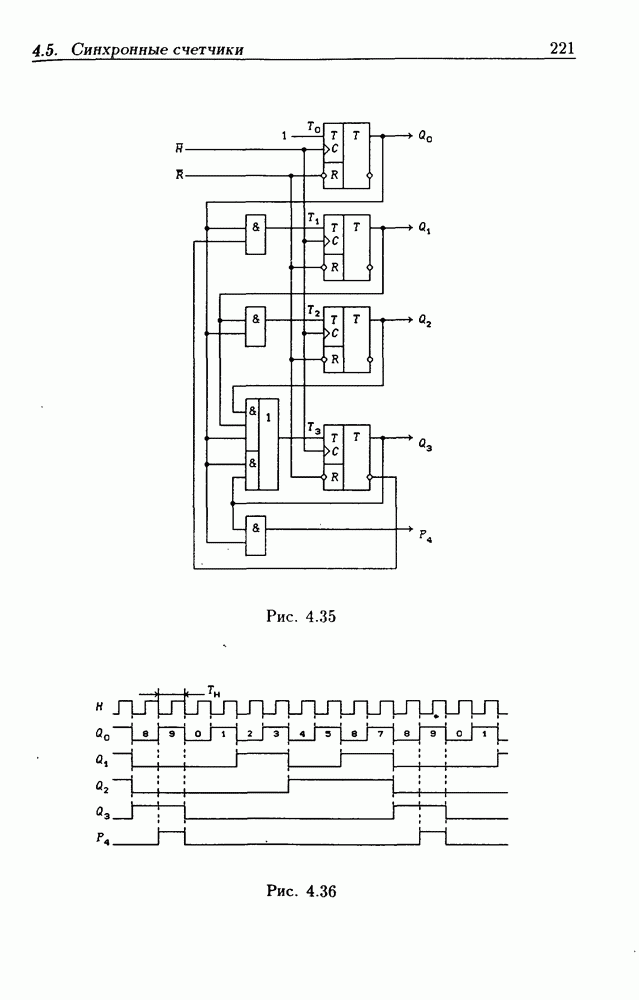
- 4.5. Синхронные счетчики
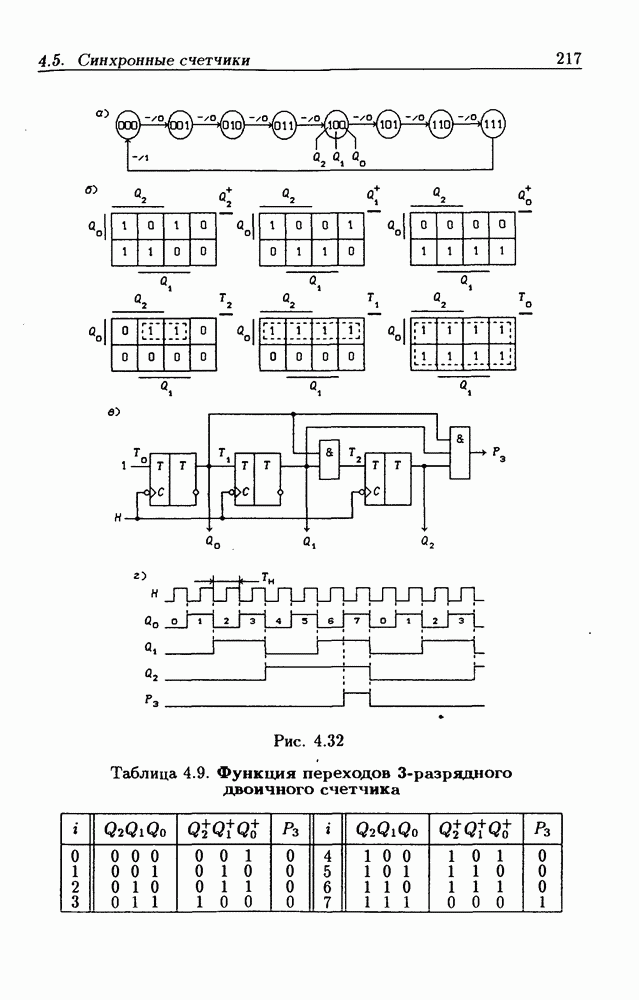
- Синхронные двоичные счетчики.
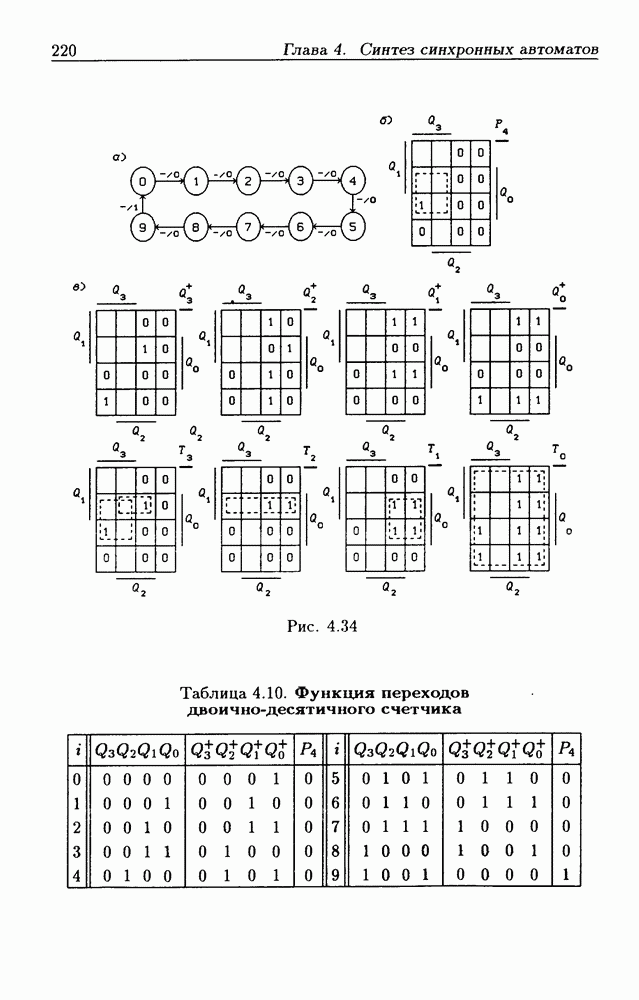
- Синхронные двоично-десятичные счетчики.
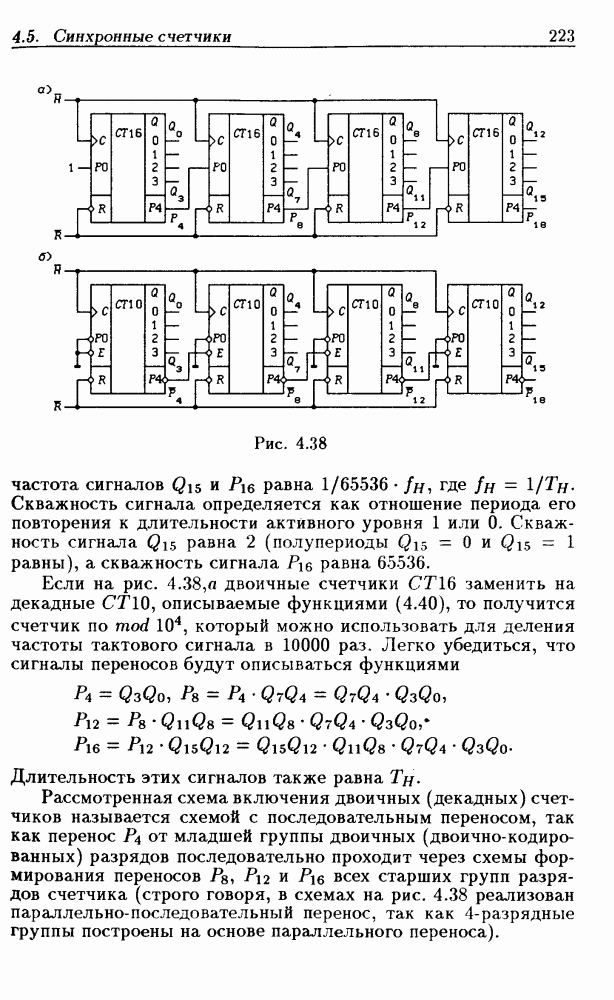
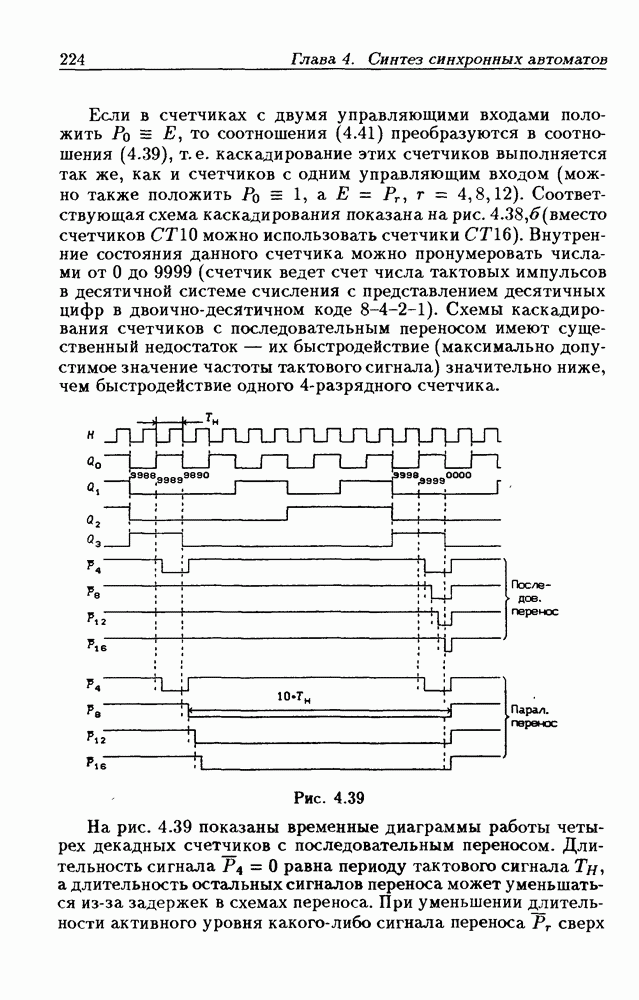
- Каскадирование двоичных и двоично-десятичных счетчиков.
- Синхронные двоичные реверсивные счетчики.
- Реверсивные двоично-десятичные счетчики.
- Каскадирование реверсивных счетчиков.
- Счетчики на сдвигающих регистрах.
- Кольцевые счетчики.
- Линейные счетчики.
- Программируемые счетчики.
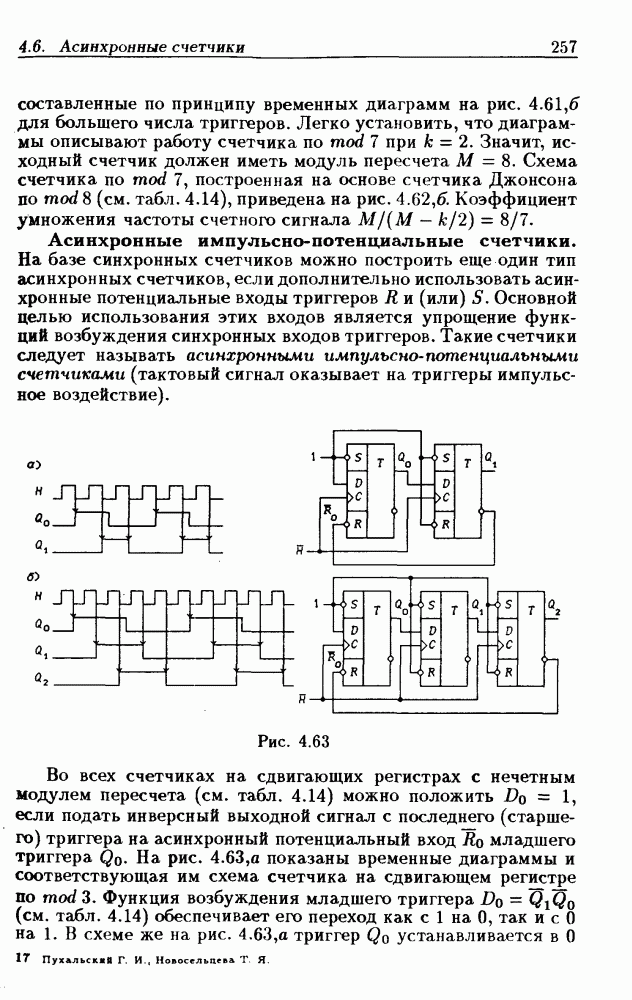
- 4.6. Асинхронные счетчики
- Асинхронные счетчики с умножением частоты счетного сигнала.
- Асинхронные импульсно-потенциальные счетчики.
- Асинхронное программирование модуля пересчета счетчиков.
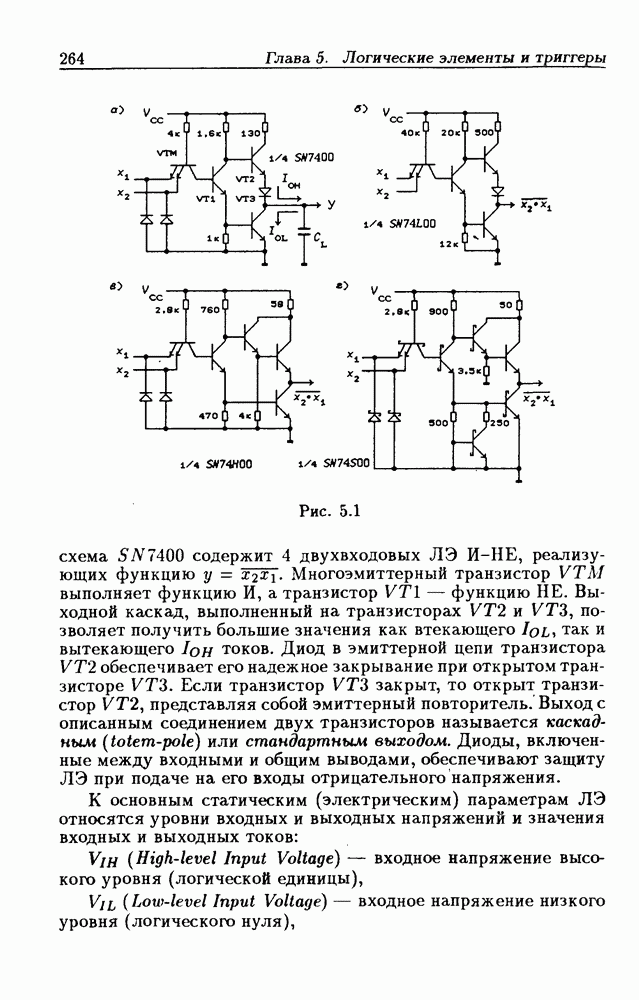
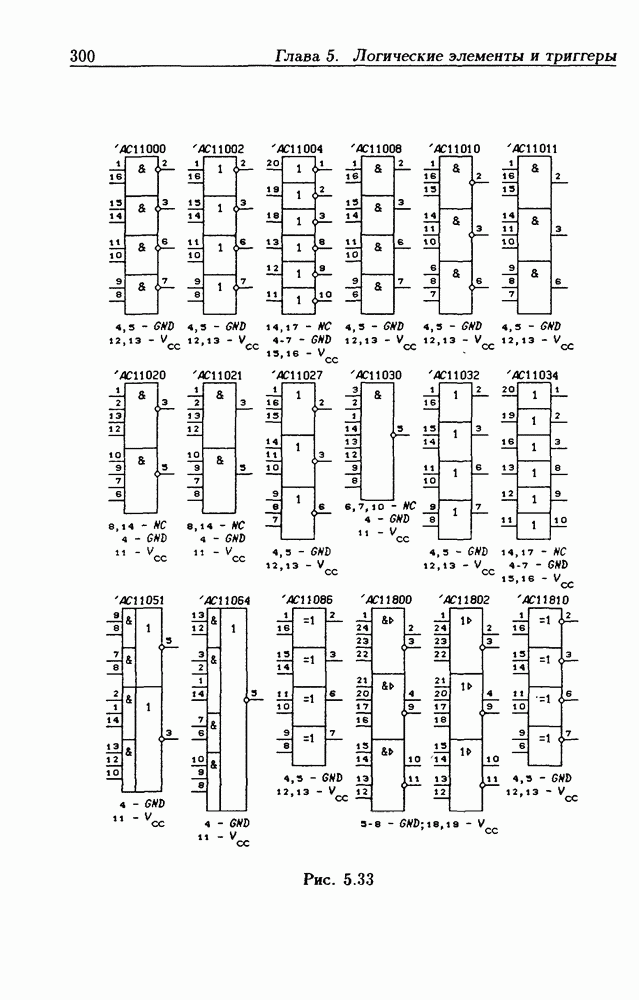
- Глава 5. Логические элементы и триггеры
- Логические элементы.
- Классификация ИС по степени интеграции.
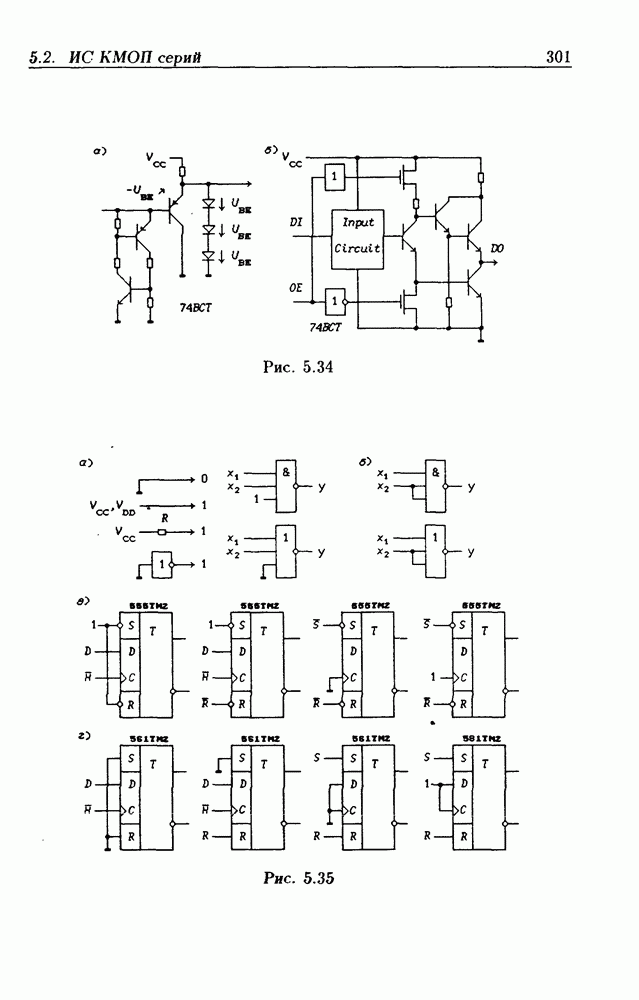
- 5.2. Интегральные схемы КМОП серий
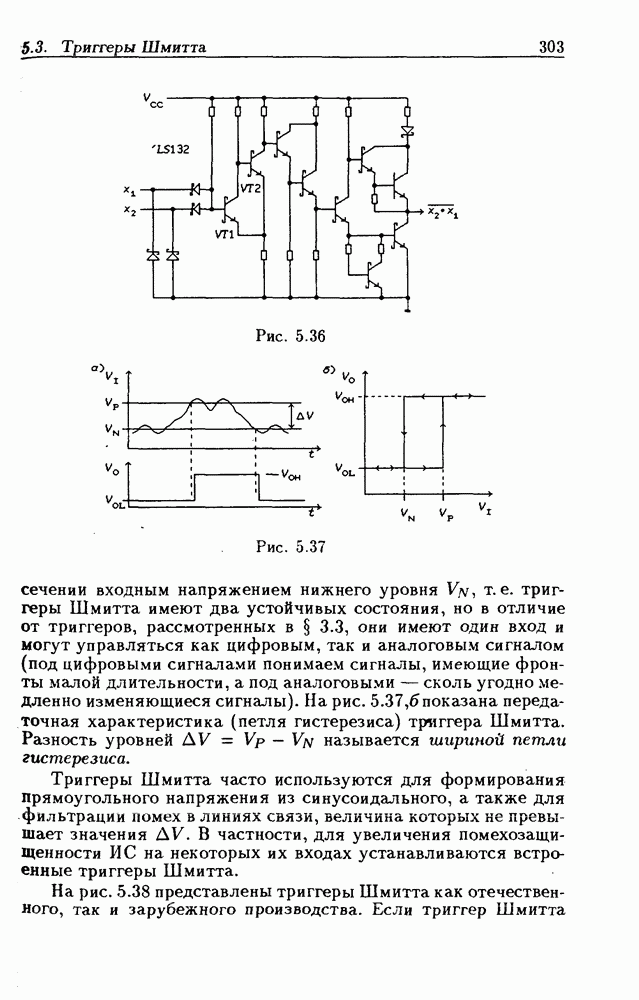
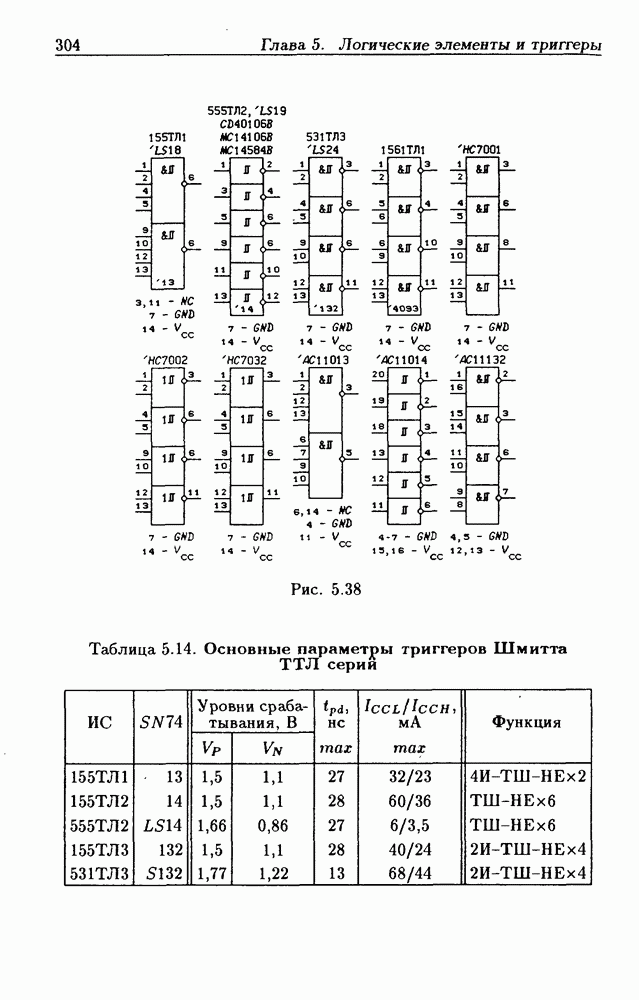
- 5.3. Триггеры Шмитта
- 5.4. Логические элементы с открытым коллекторным выходом
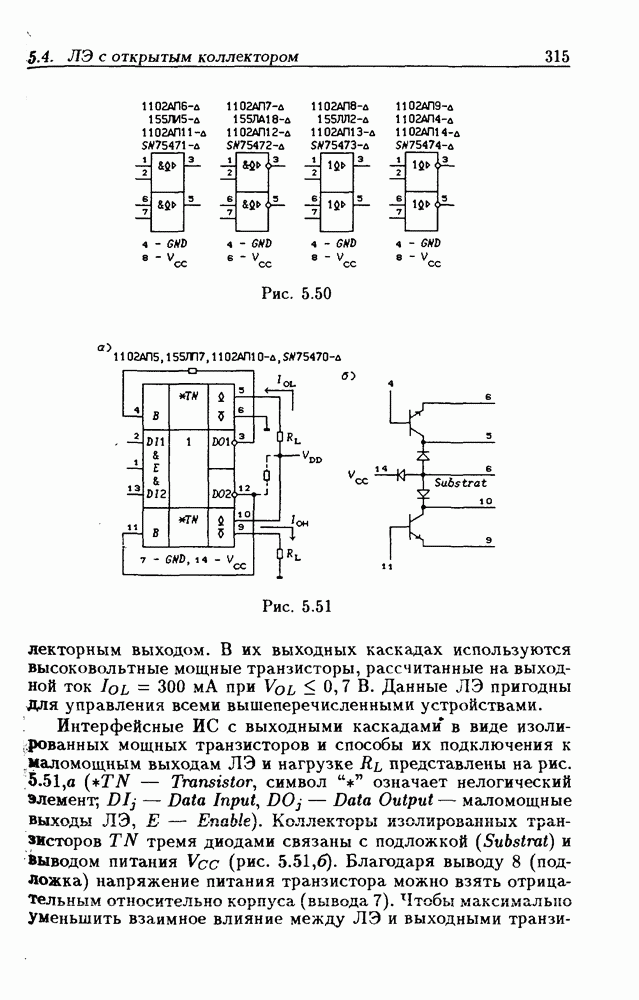
- Логические элементы с открытым коллекторным выходом.
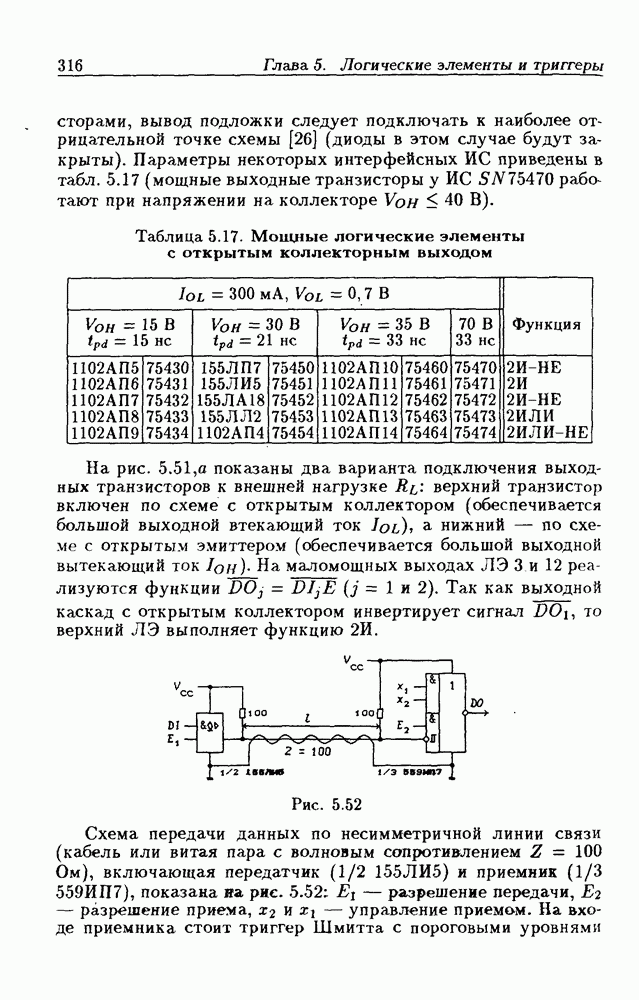
- Применения ЛЭ с открытым коллекторным выходом.
- Интерфейсные ЛЭ с открытым коллекторным выходом.
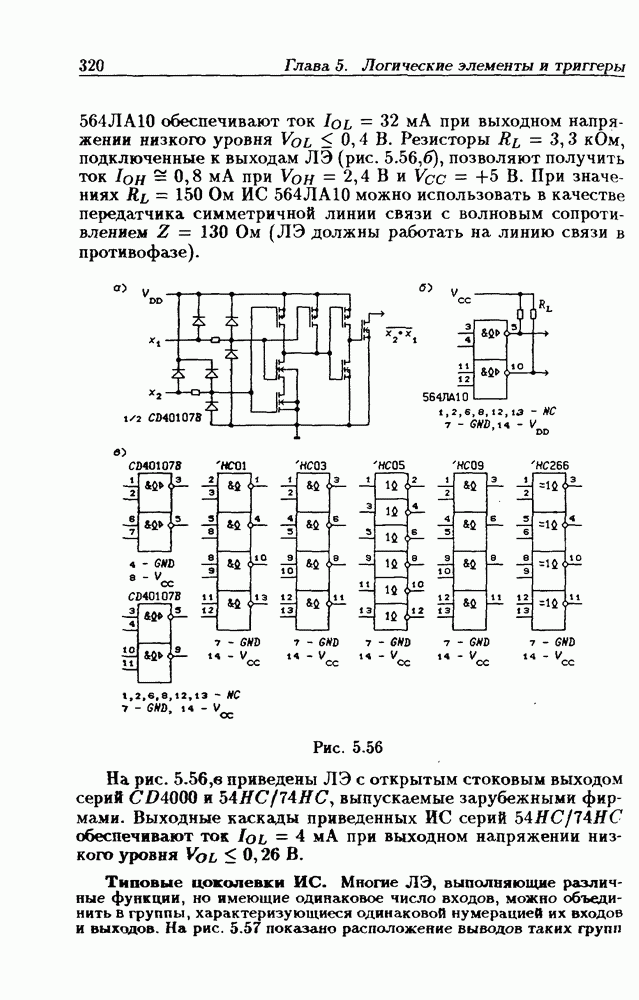
- Логические элементы с открытым стоковым выходом.
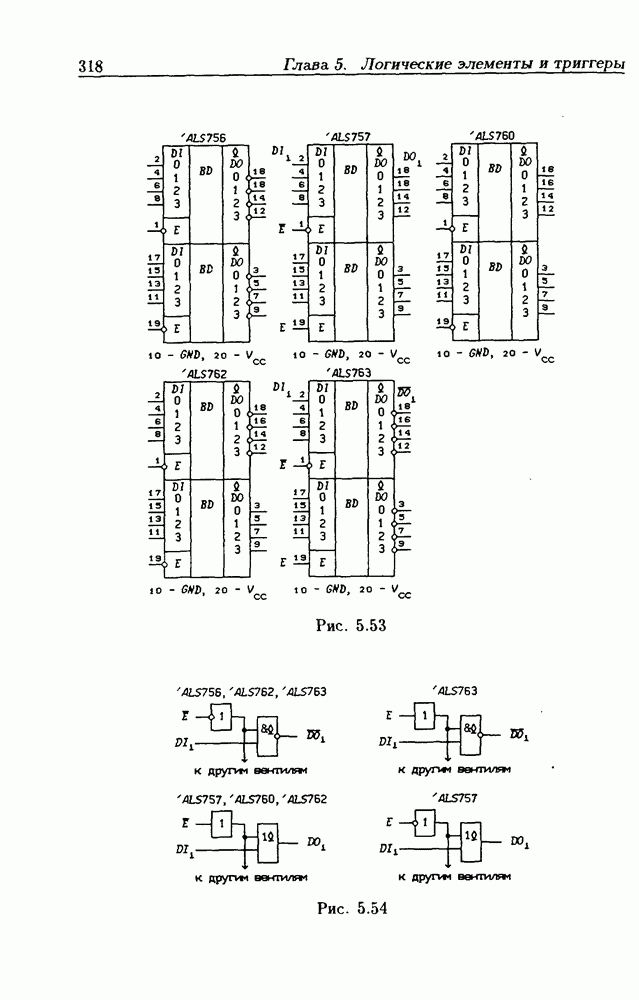
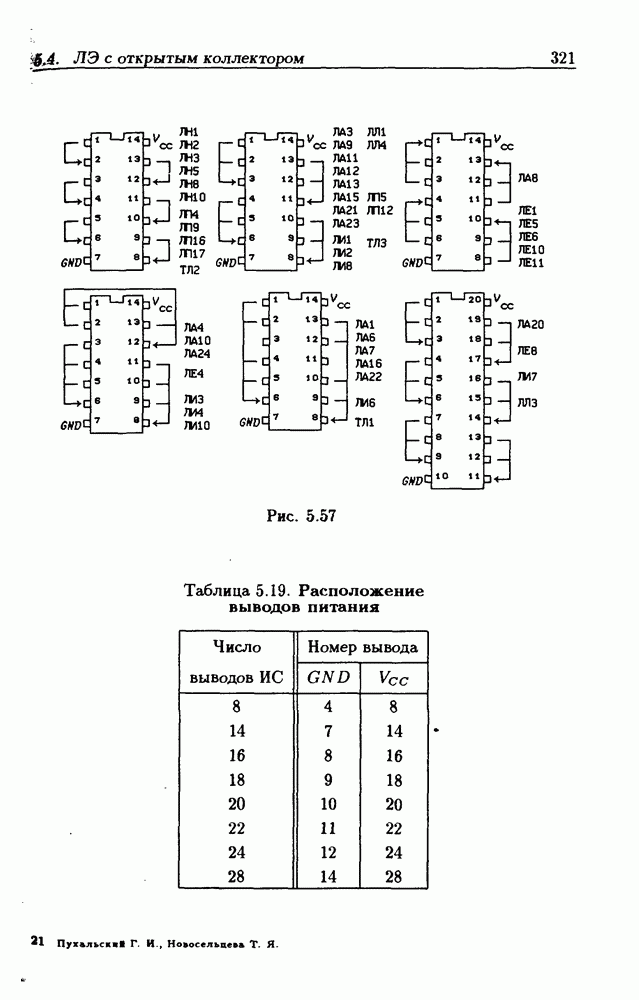
- Типовые цоколевки ИС.
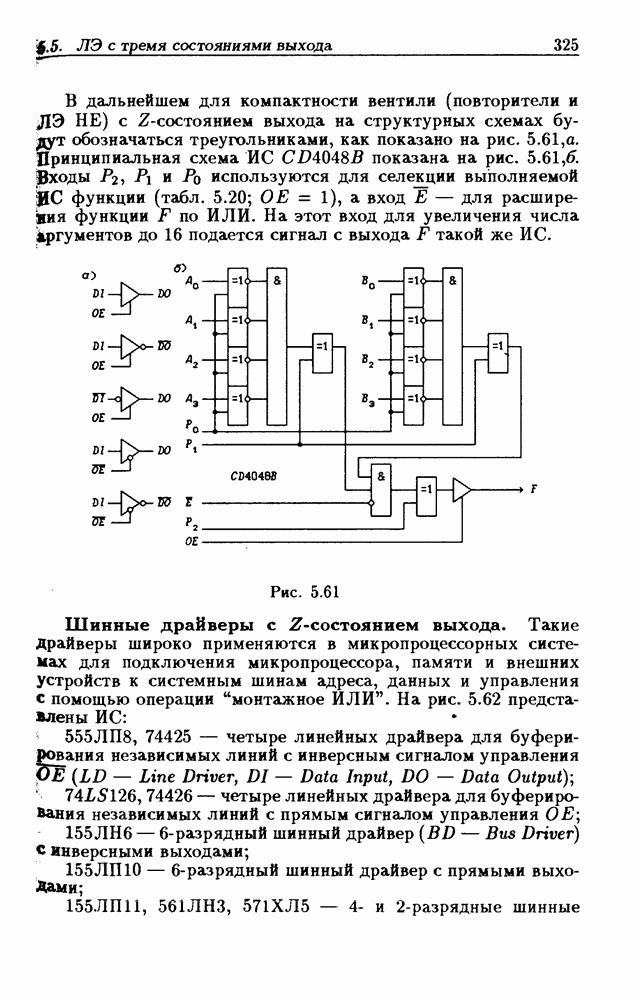
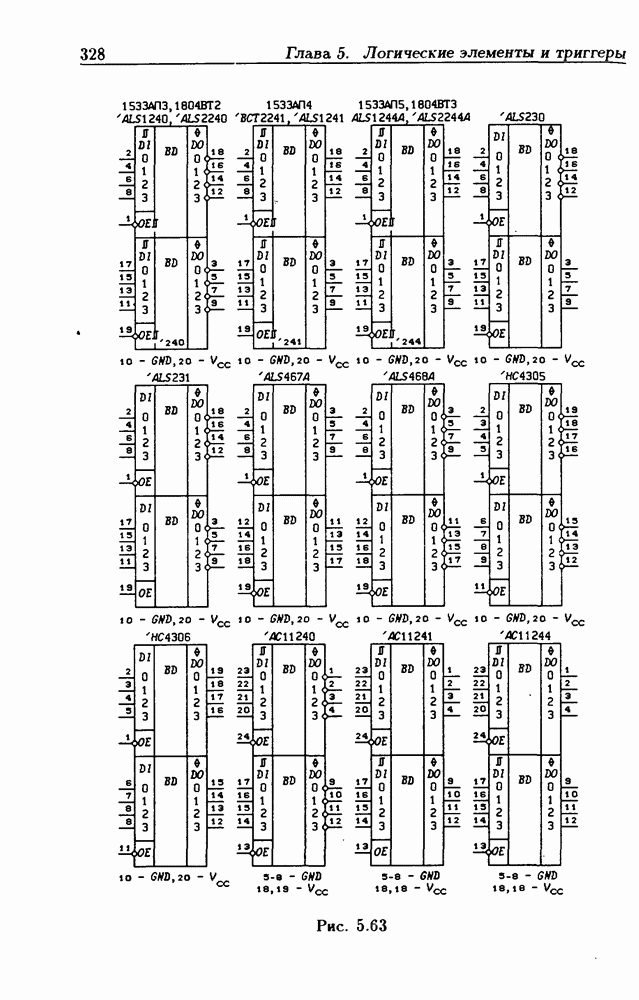
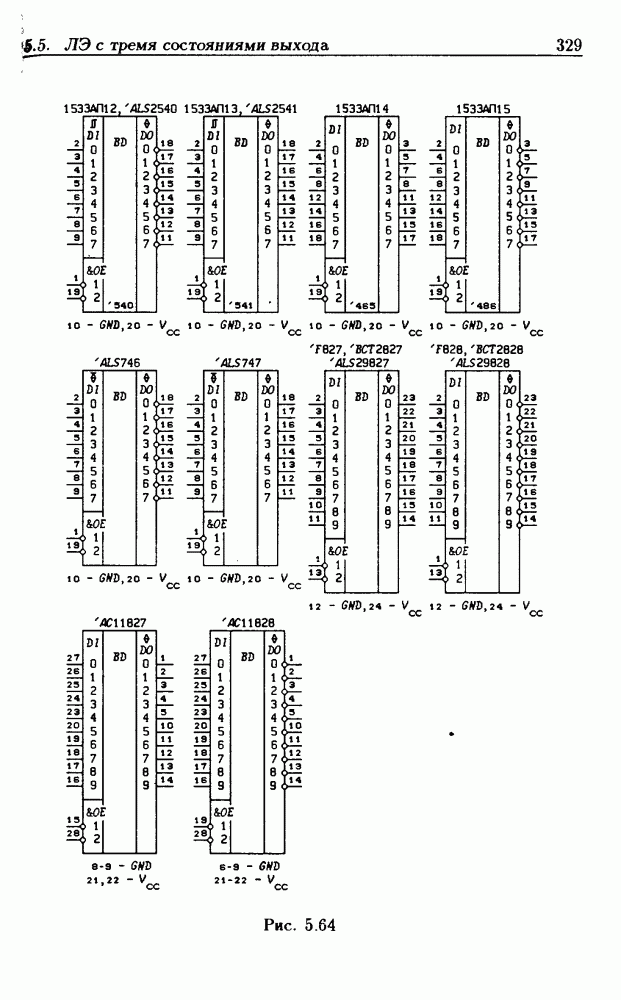
- 5.5. Логические элементы с тремя состояниями выхода
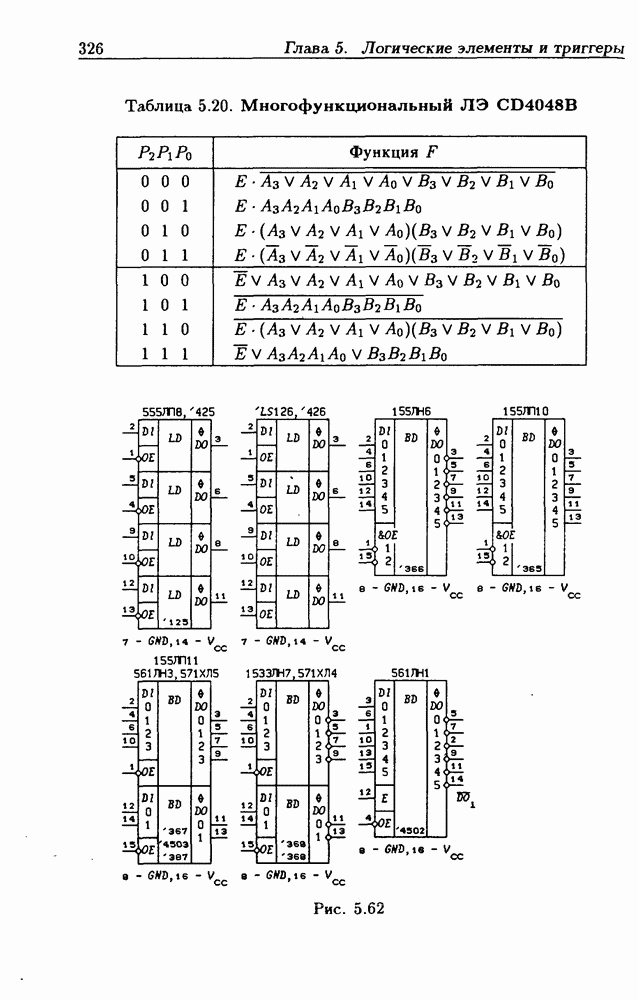
- Шинные драйверы с Z-состоянием выхода.
- Основные правила графического изображения ИС.
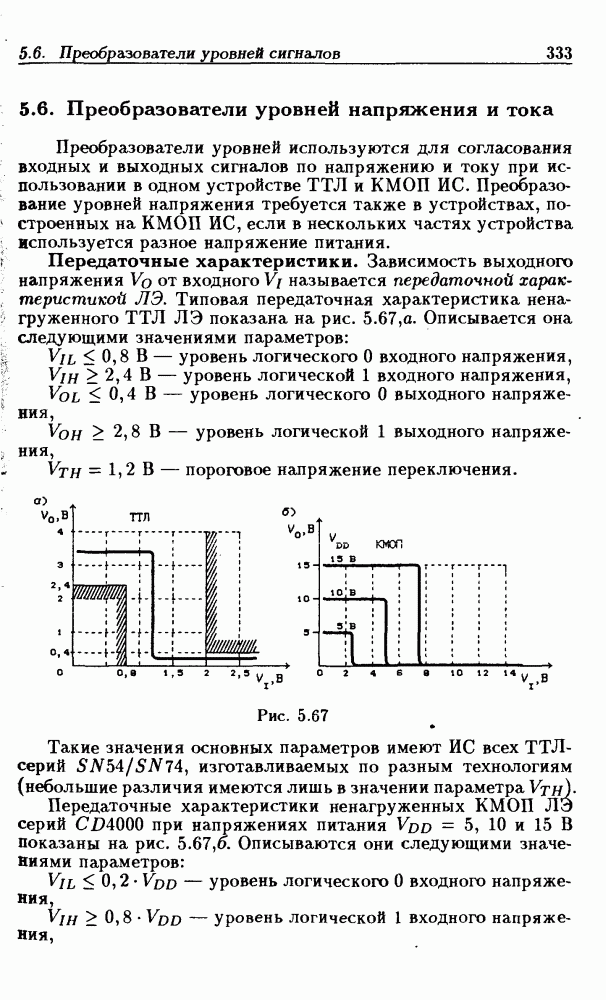
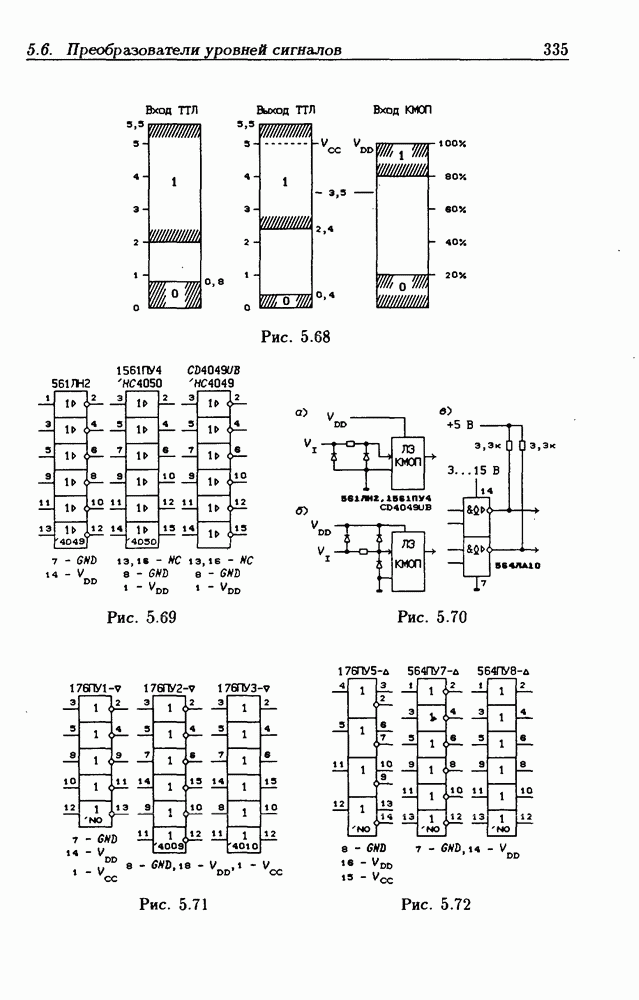
- 5.6. Преобразователи уровней напряжения и тока
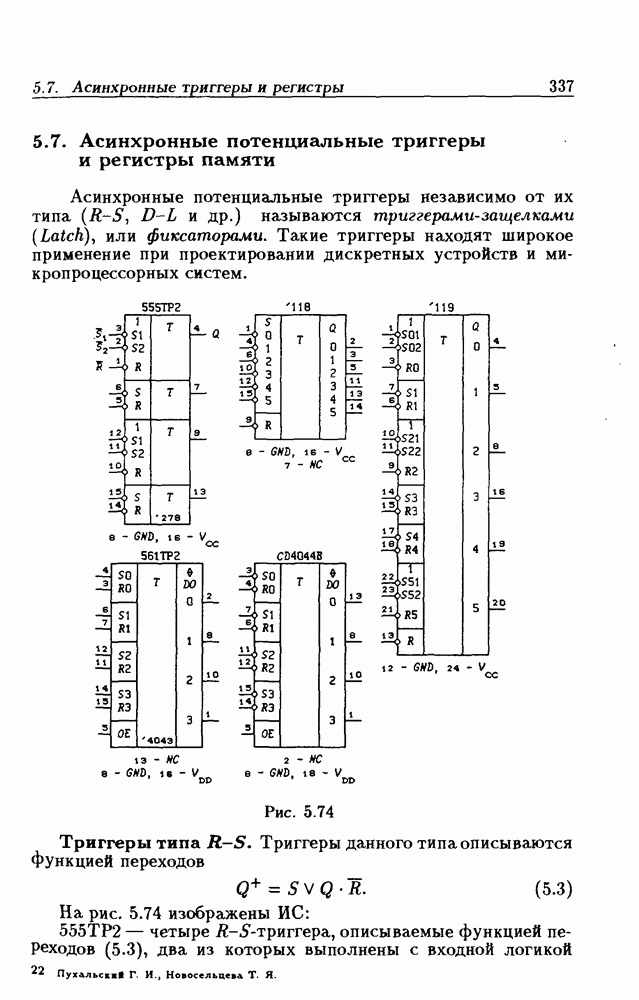
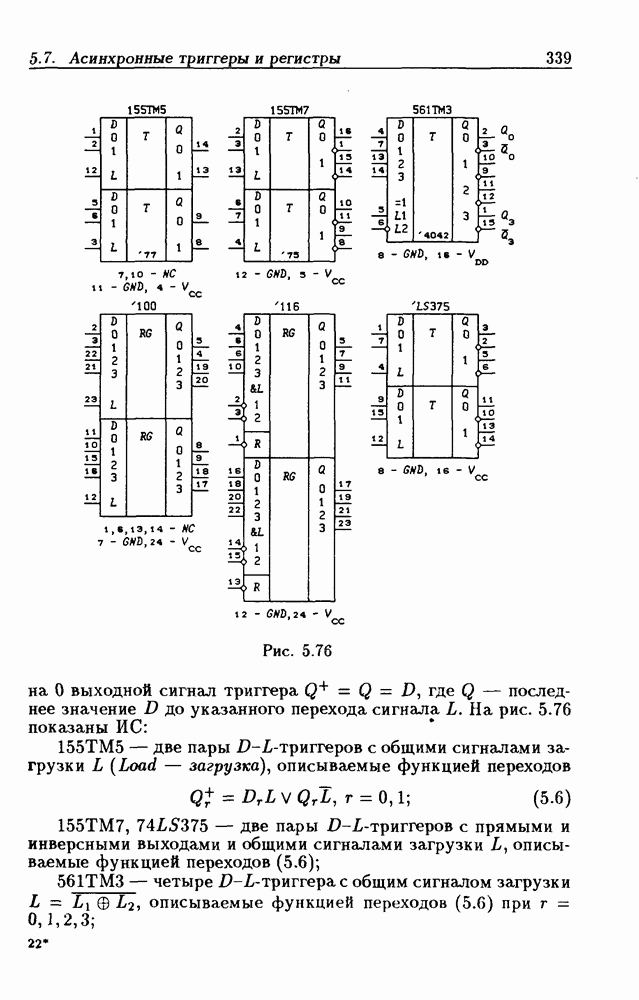
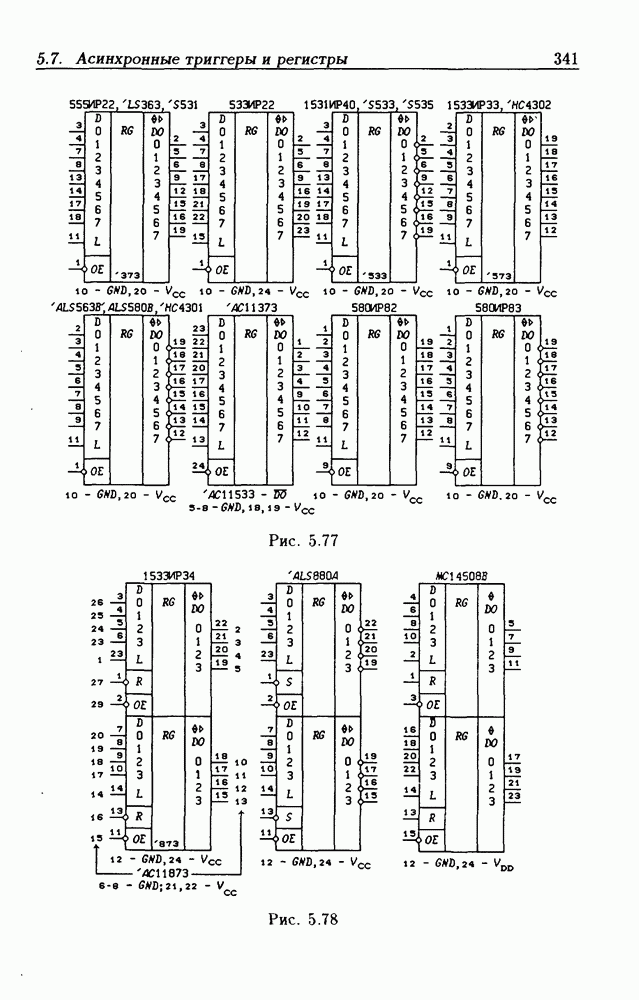
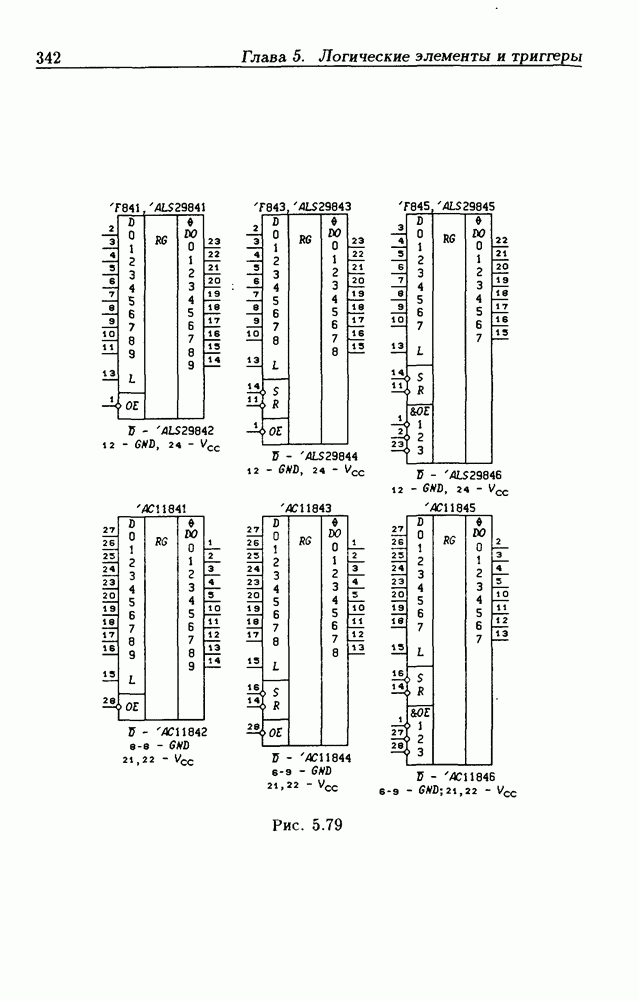
- 5.7. Асинхронные потенциальные триггеры и регистры памяти
- 5.8. Синхронные триггеры и регистры памяти
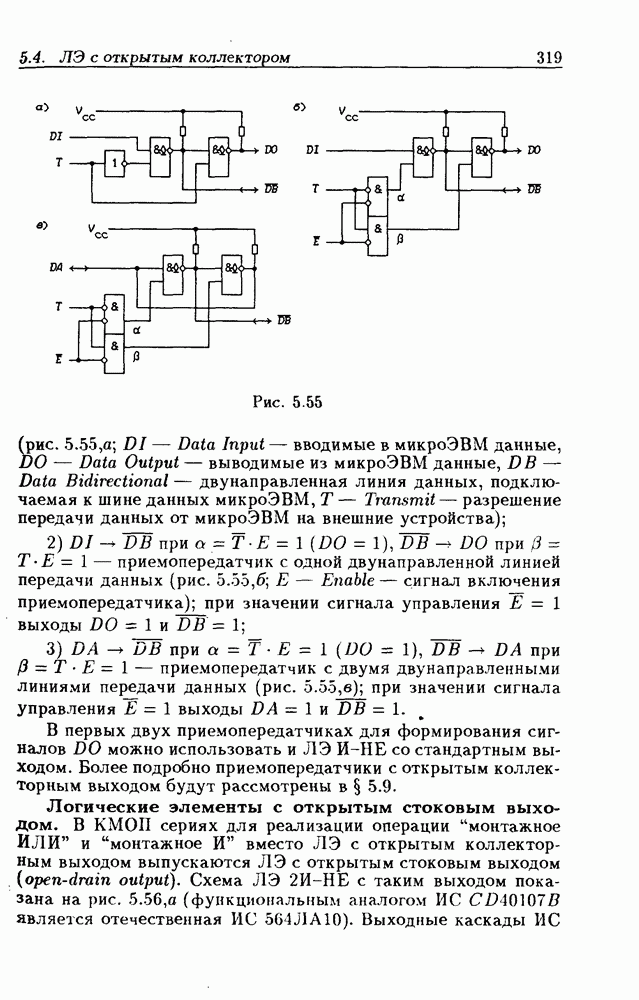
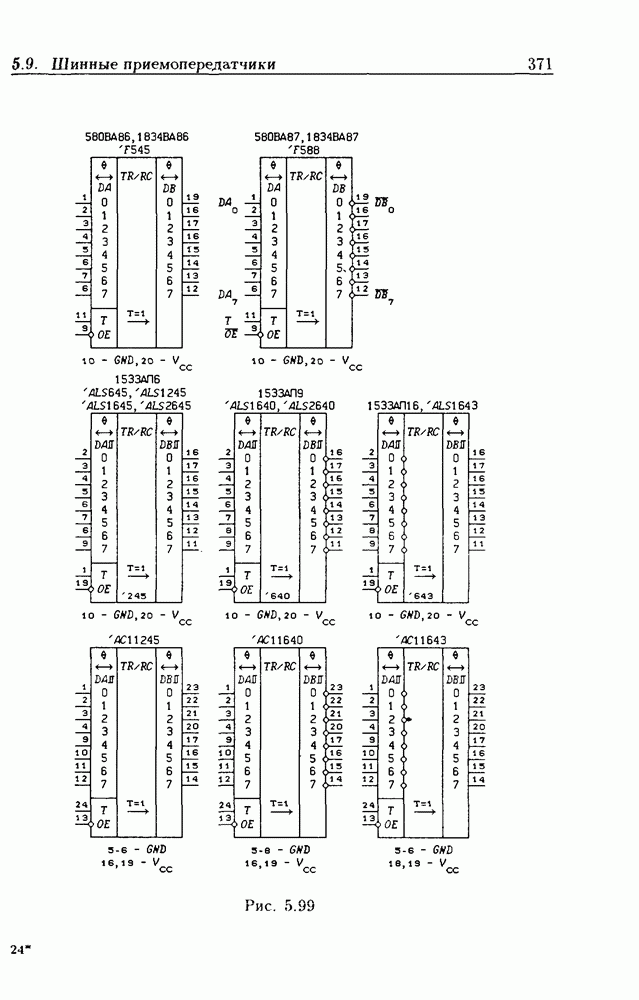
- 5.9. Шинные приемопередатчики
- Шинные приемопередатчики с Z-состоянием выхода.
- Шинные приемопередатчики с открытым коллекторным выходом.
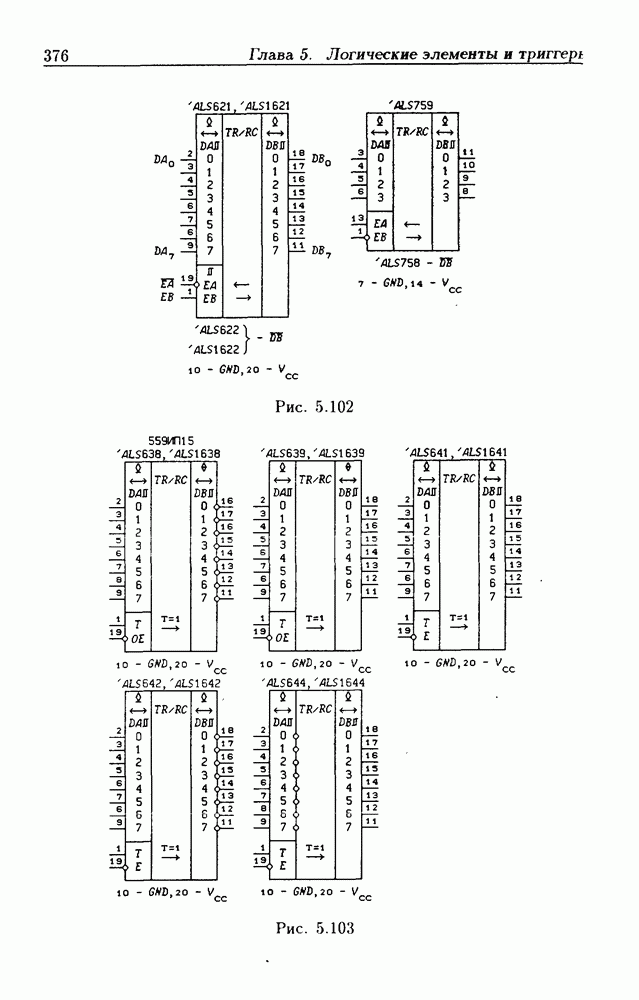
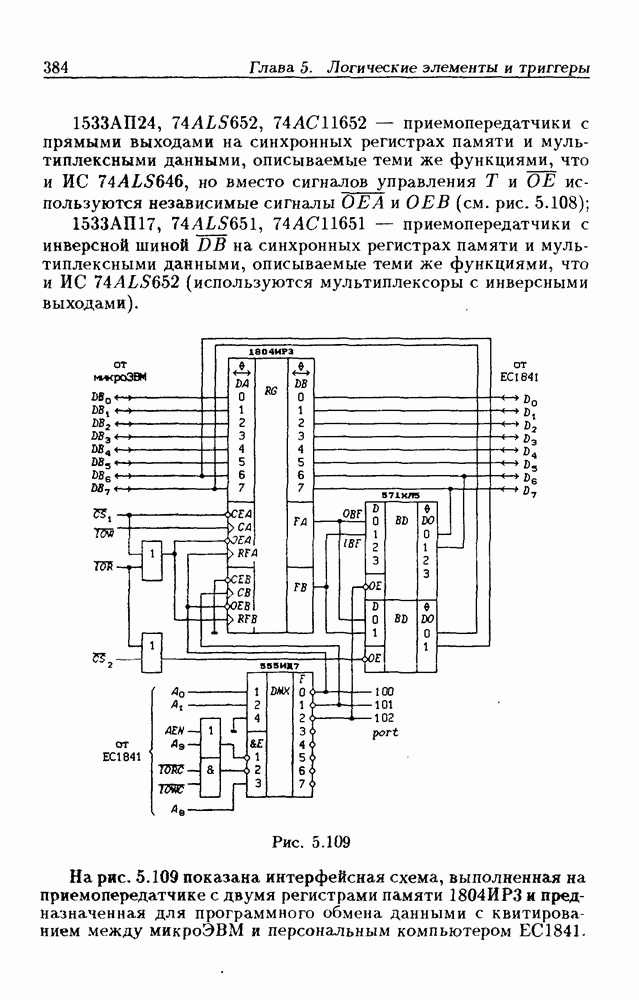
- Шинные приемопередатчики с регистрами памяти.
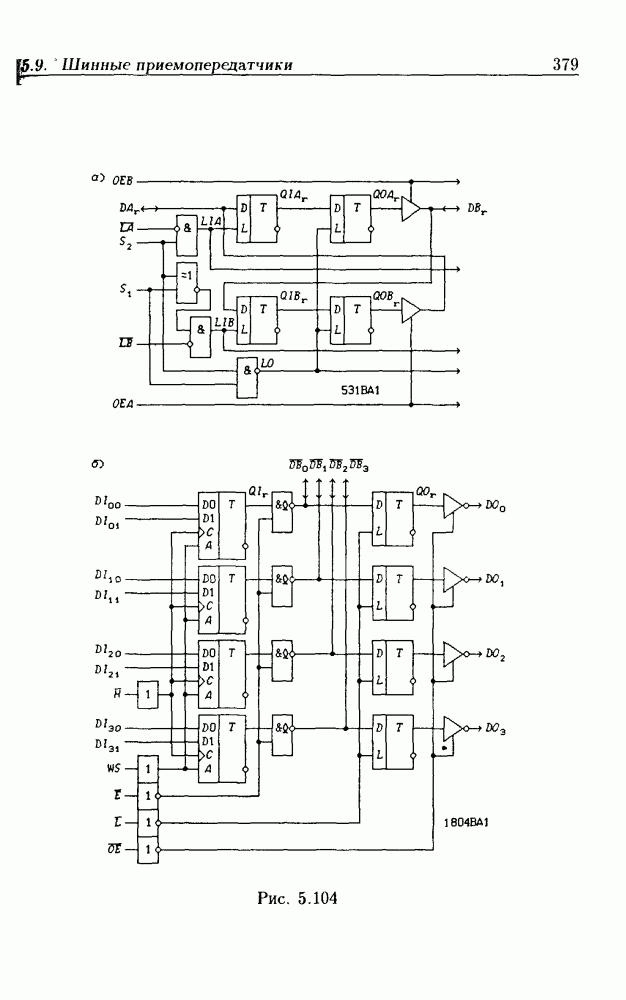
- Шинные приемопередатчики со сдвигающим регистром.
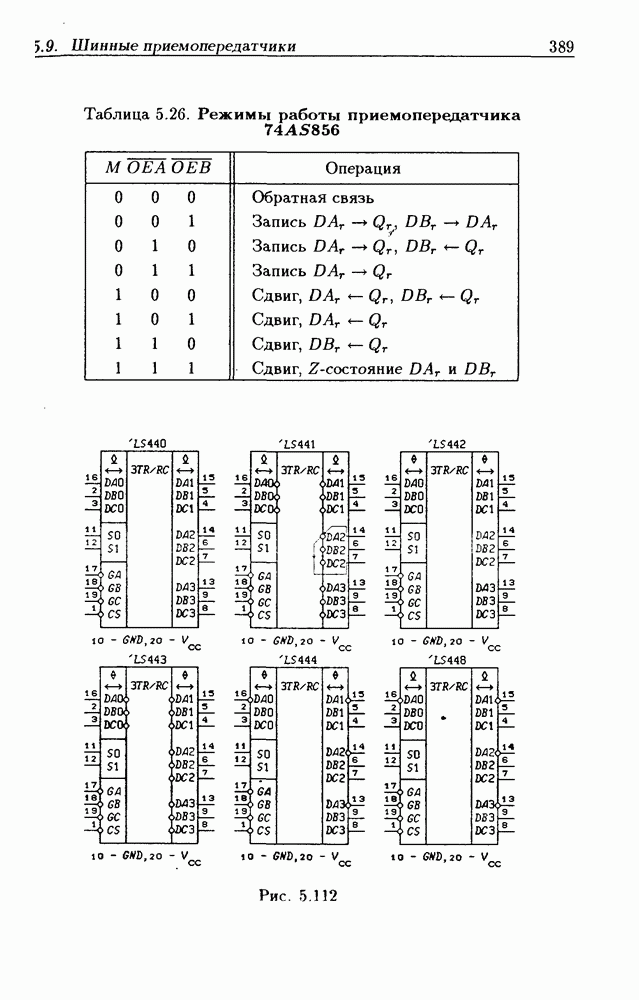
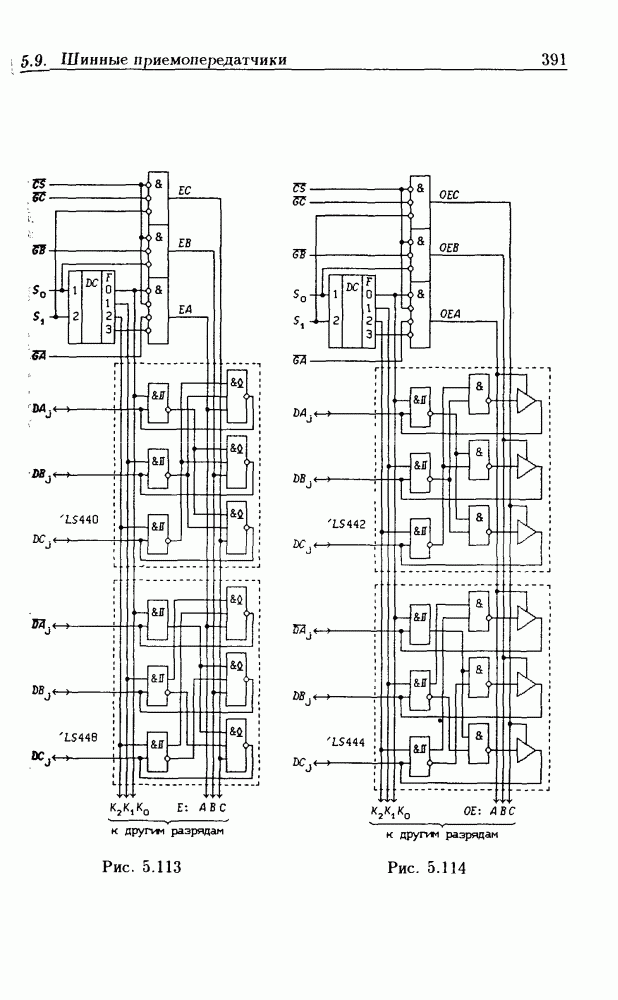
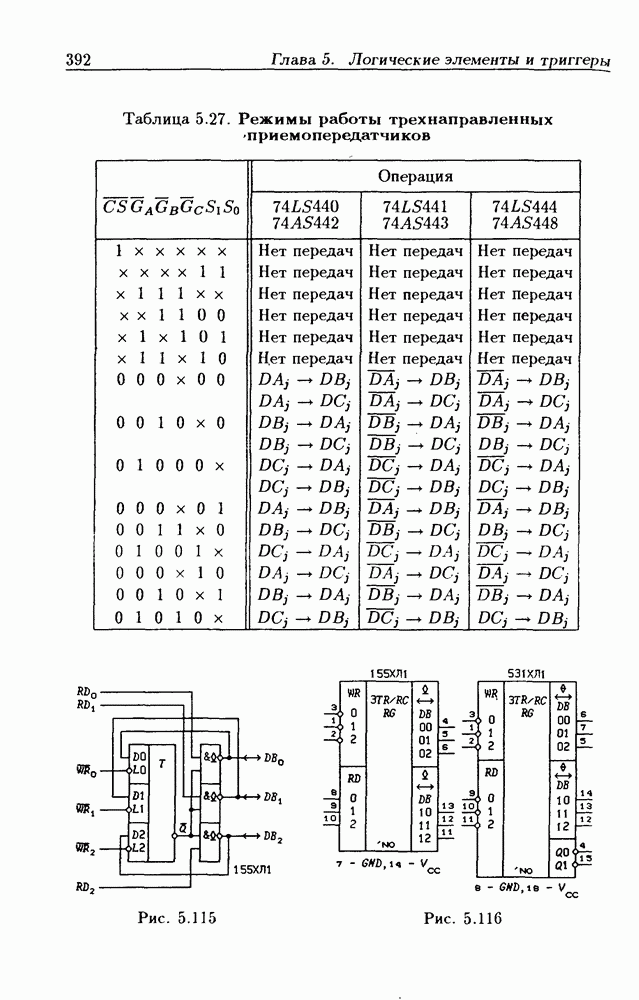
- Шинные трехнаправленные приемопередатчики.
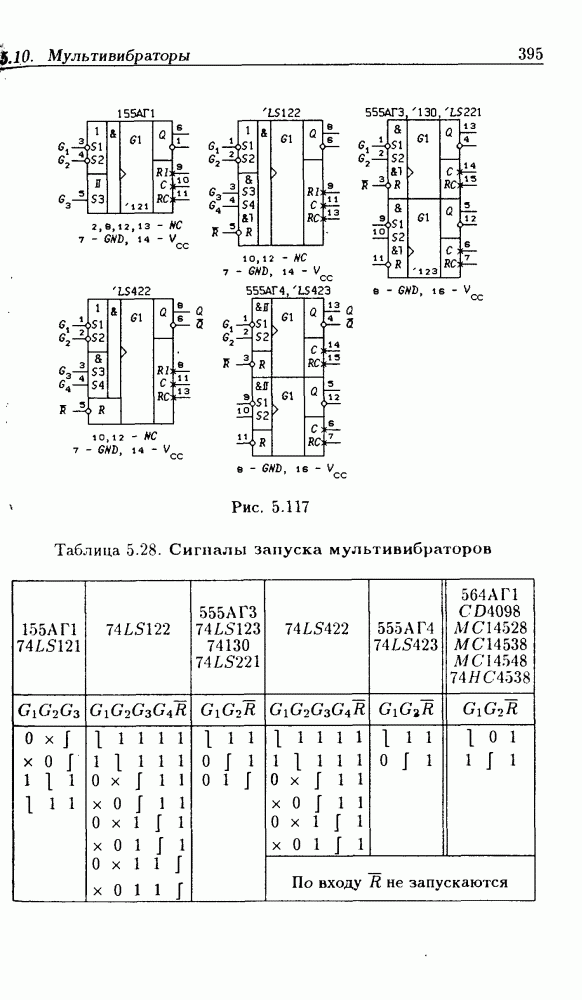
- 5.10. Мультивибраторы
- 5.11. Генераторы
- Схемы устранения «дребезга» механических контактов.
- Автогенераторы периодических сигналов.
- 5.12. Рекомендации по выбору серий ИС
- Глава 6. Коммутаторы и арифметические устройства
- 6.1. Дешифраторы
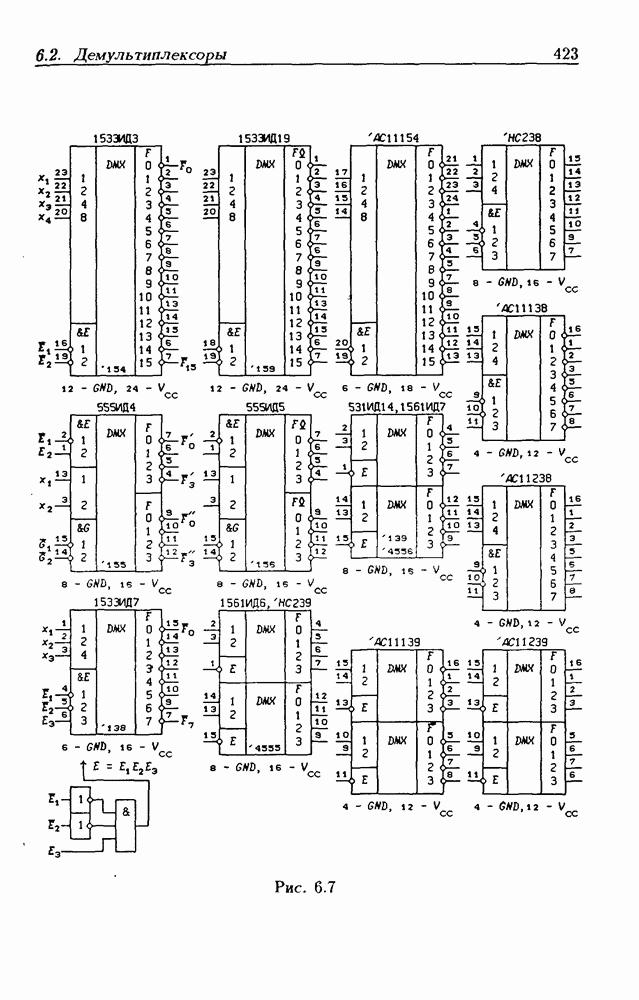
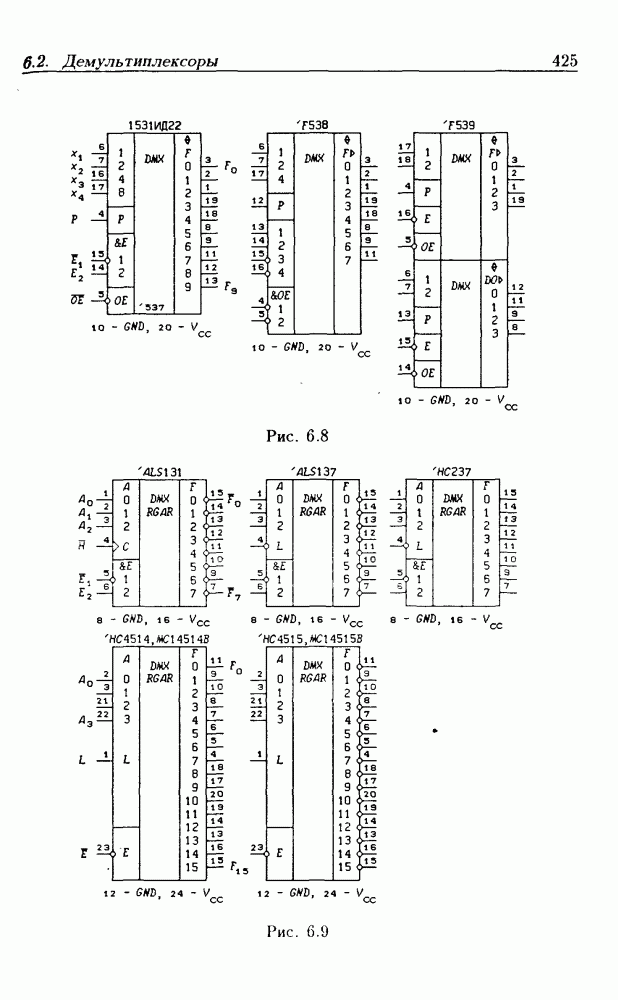
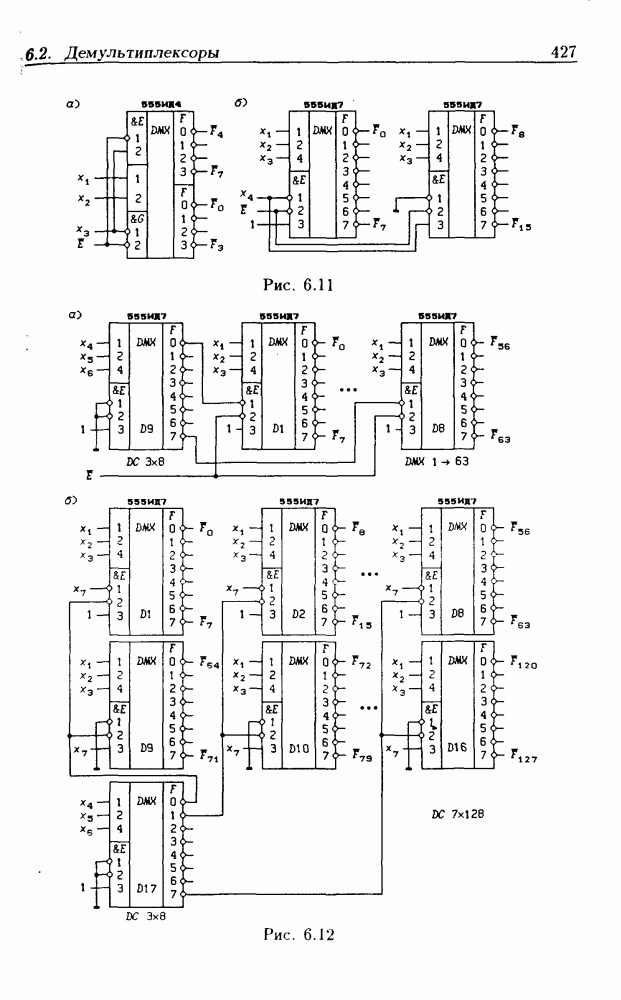
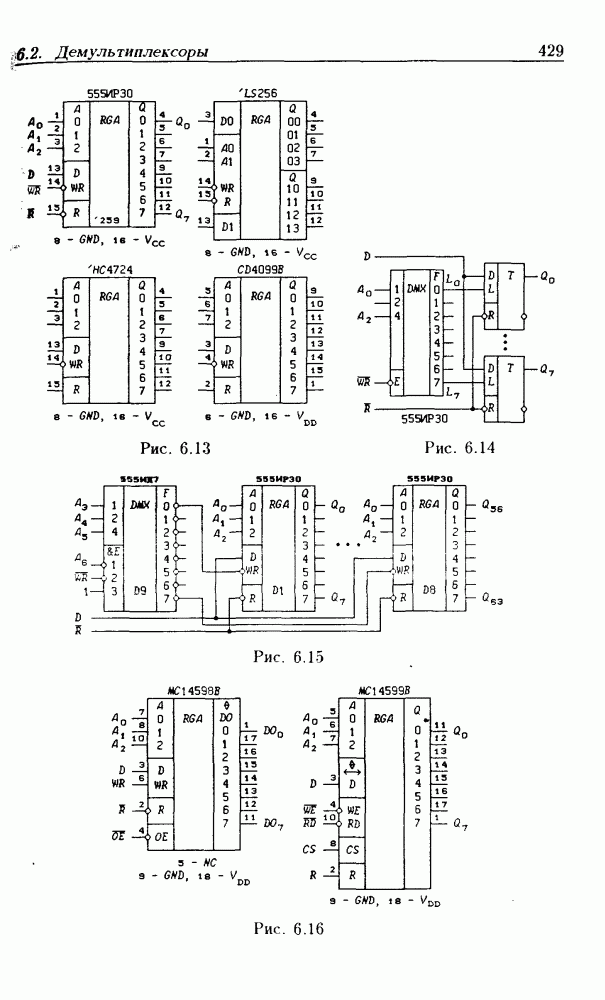
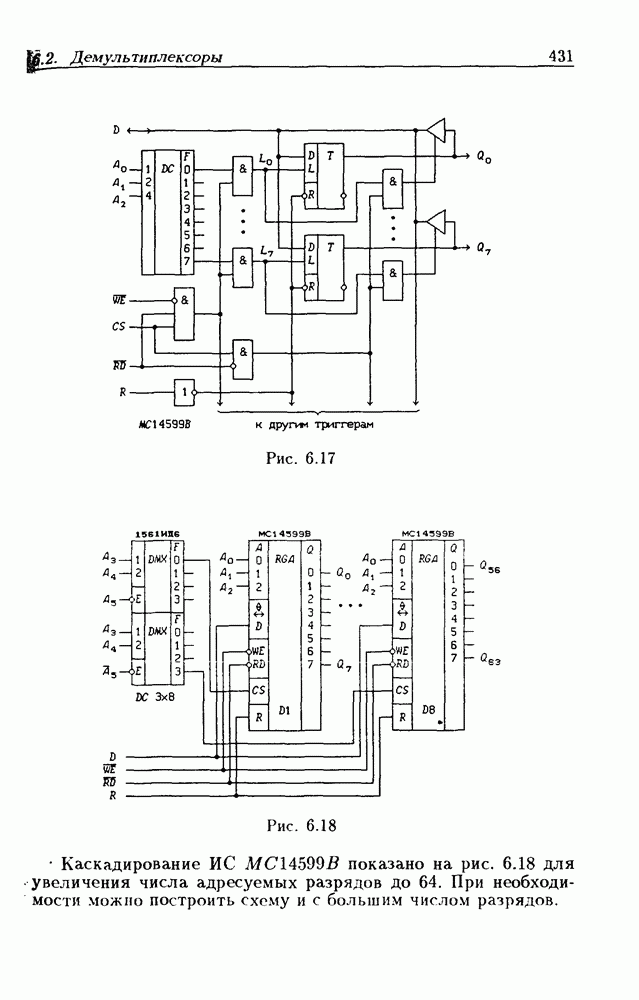
- 6.2. Демультиплексоры
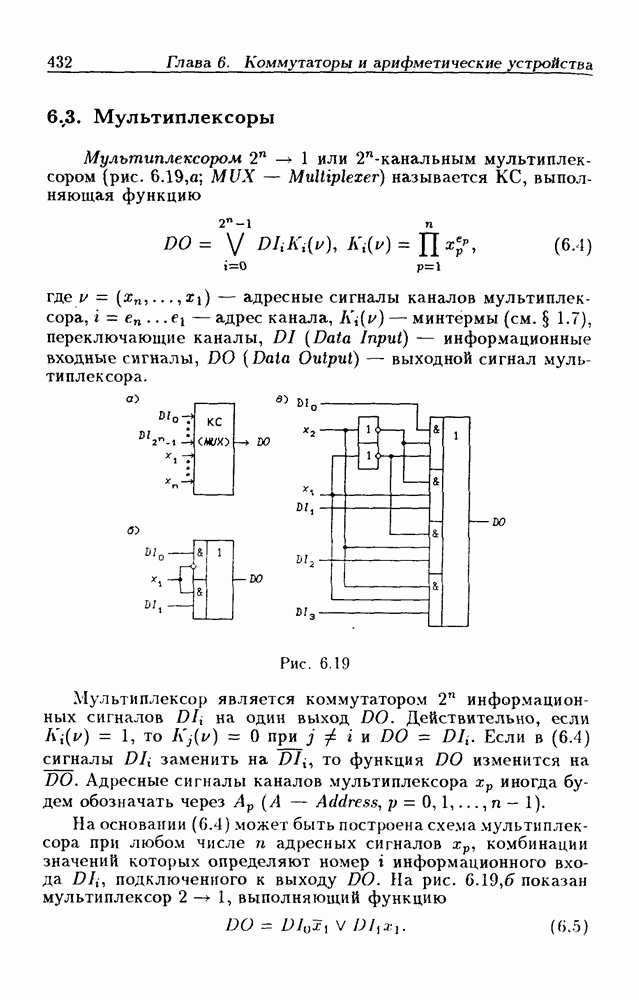
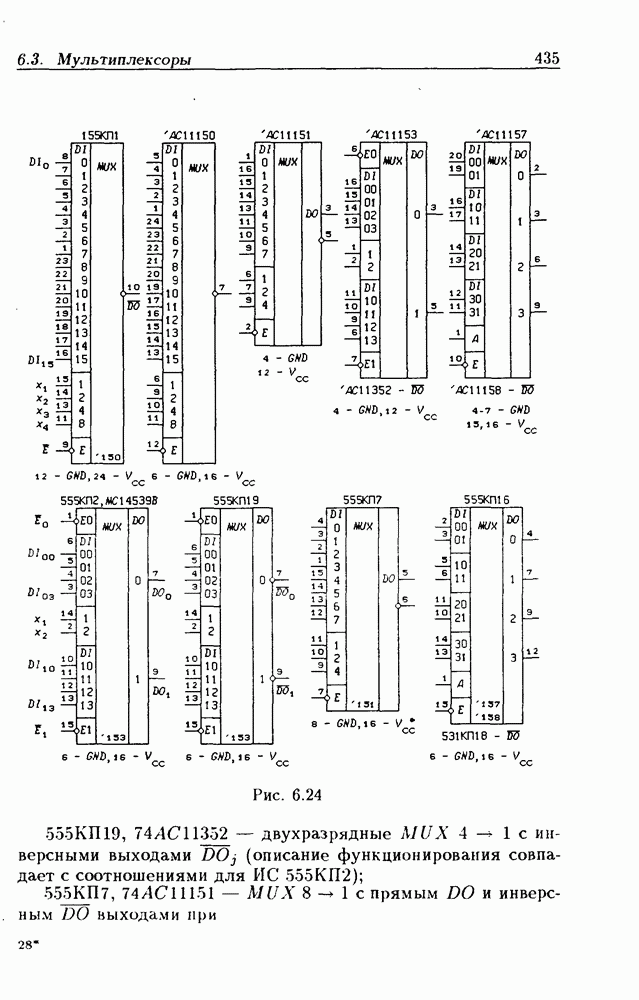
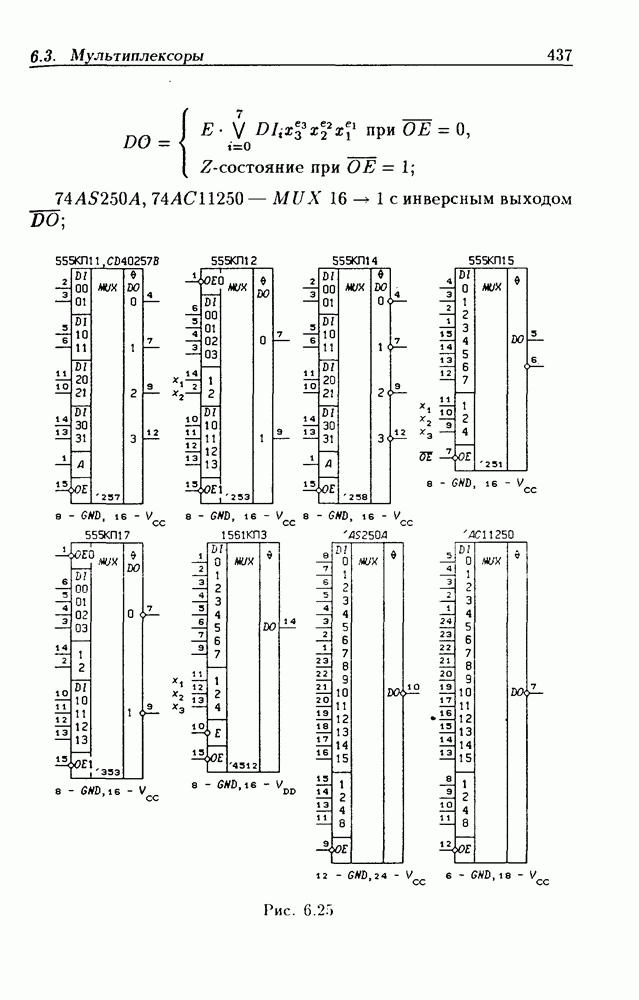
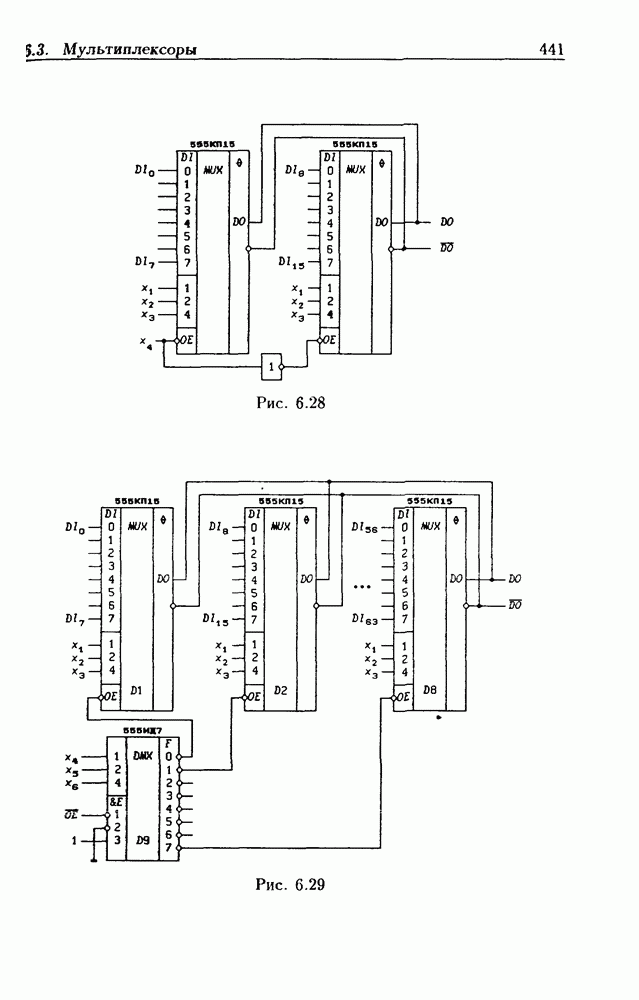
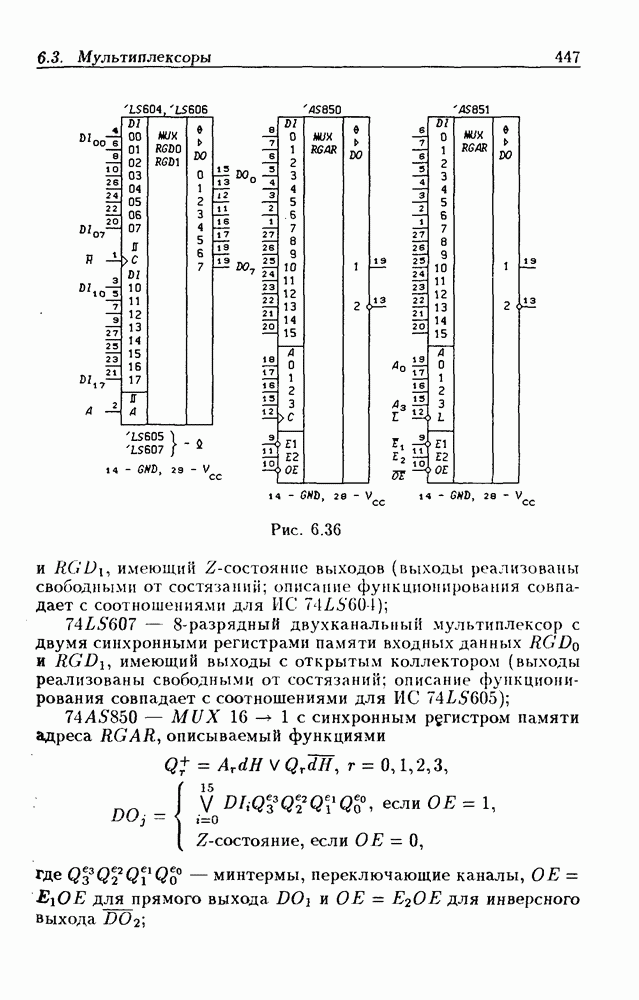
- 6.3. Мультиплексоры
- Мультиплексоры без стробирования.
- Мультиплексоры со стробированием.
- Мультиплексоры с Z-состоянием выхода.
- Каскадирование мультиплексоров.
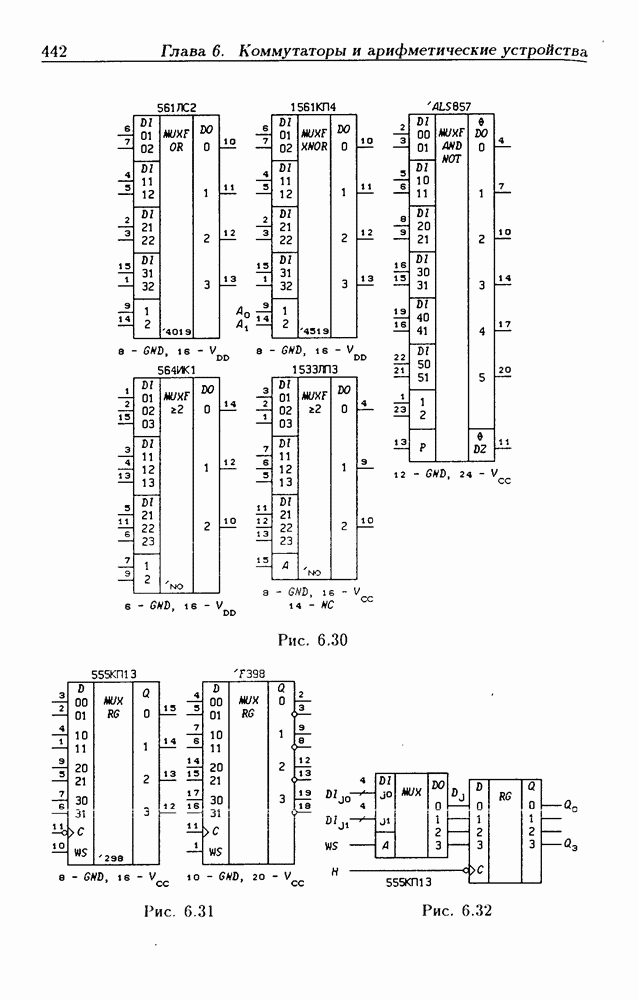
- Функциональные мультиплексоры.
- Регистры памяти с мультиплексными входами данных.
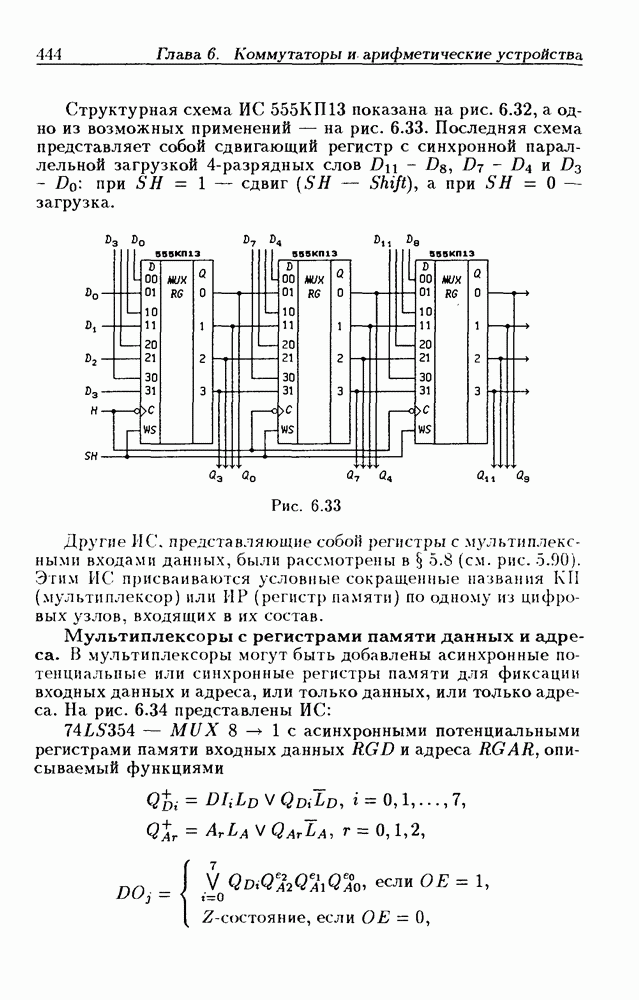
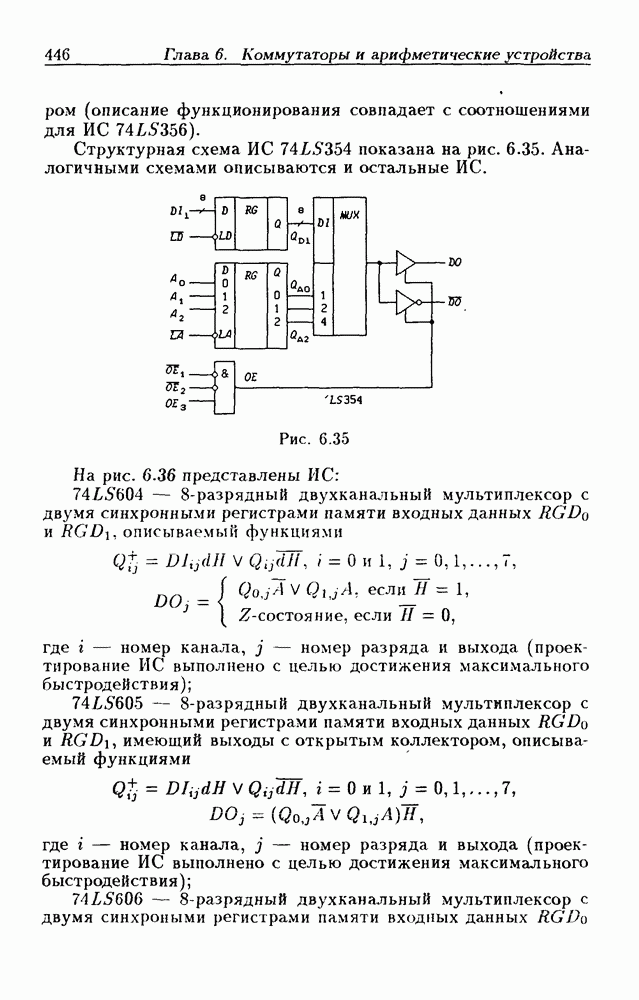
- Мультиплексоры с регистрами памяти данных и адреса.
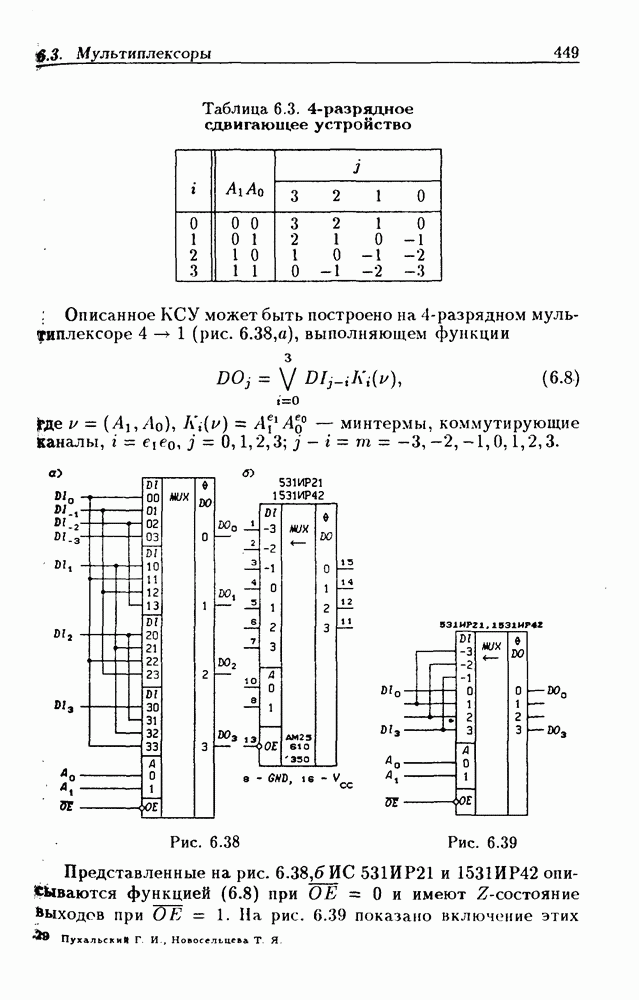
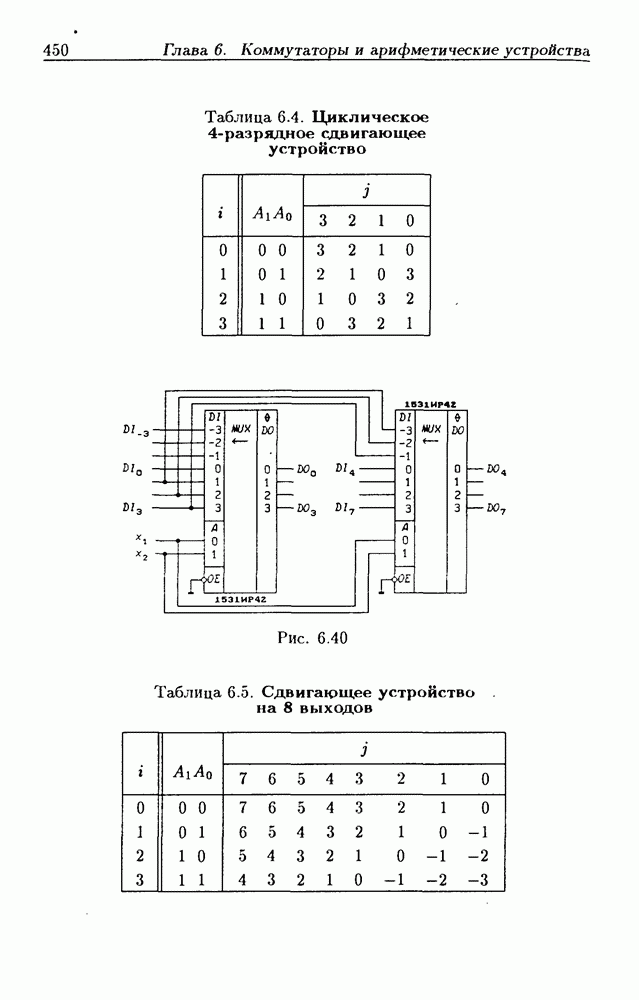
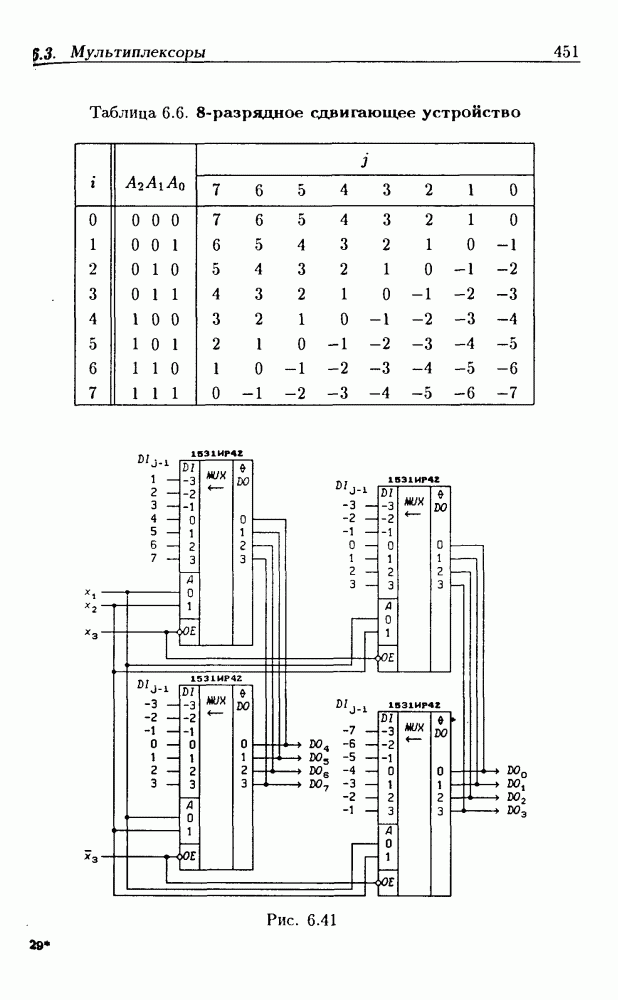
- Сдвигающие мультиплексоры.
- 6.4. Синтез комбинационных схем и цифровых автоматов на мультиплексорах
- Синтез схем на 8-канальных мультиплексорах.
- Синтез на двухразрядных 4-канальных мультиплексорах.
- Синтез генератора синусоидальной функции на мультиплексорах.
- Синтез триггеров на мультиплексорах.
- Синтез счетчиков на мультиплексорах.
- 6.5. Аналоговые ключи и мультиплексоры-демультиплексоры
- 6.6. Шифраторы
- 6.7. Цифровые компараторы
- Программируемые цифровые компараторы.
- Адресные компараторы.
- Применения адресных компараторов.
- 6.8. Схемы сравнения двоичных чисел
- 8-разрядные схемы сравнения двоичных чисел.
- 6.9. Прямой, обратный и дополнительный коды
- Дополнительный код.
- Сложение чисел в обратном коде.
- Код с избытком 3.
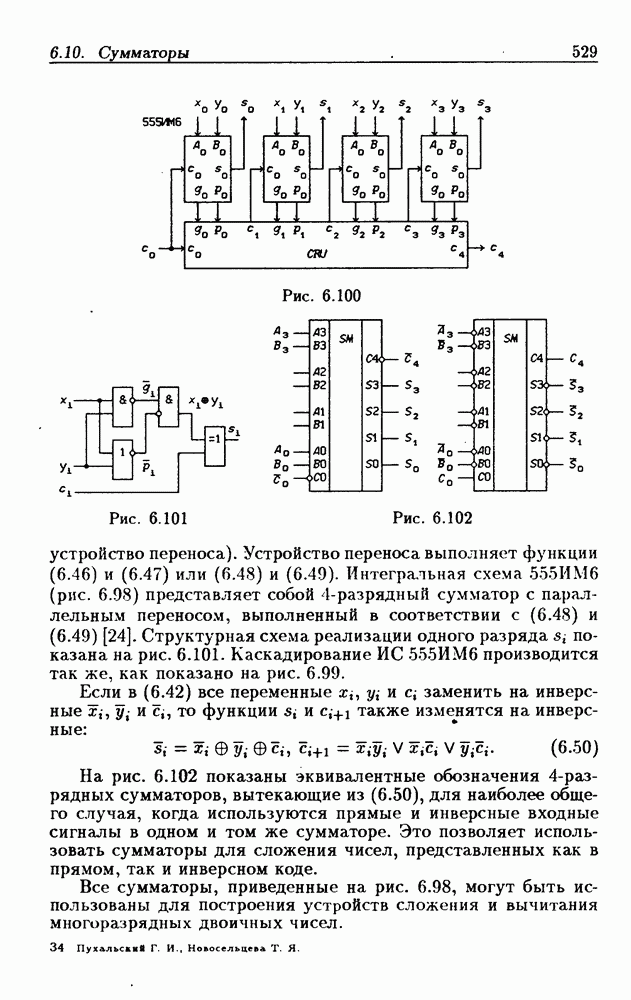
- 6.10. Сумматоры
- Двоичные параллельные сумматоры с последовательным переносом.
- Двоичные сумматоры с параллельным переносом.
- Применения сумматоров.
- Десятичные сумматоры.
- Последовательные двоичные сумматоры.
- 6.11. Арифметическо-логические устройства
- 6.12. Пороговые схемы и мажоритарные элементы
- 6.13. Умножители двоичных чисел
- Быстрые умножители.
- БИС умножителя 12×12 разрядов 1802ВР4.
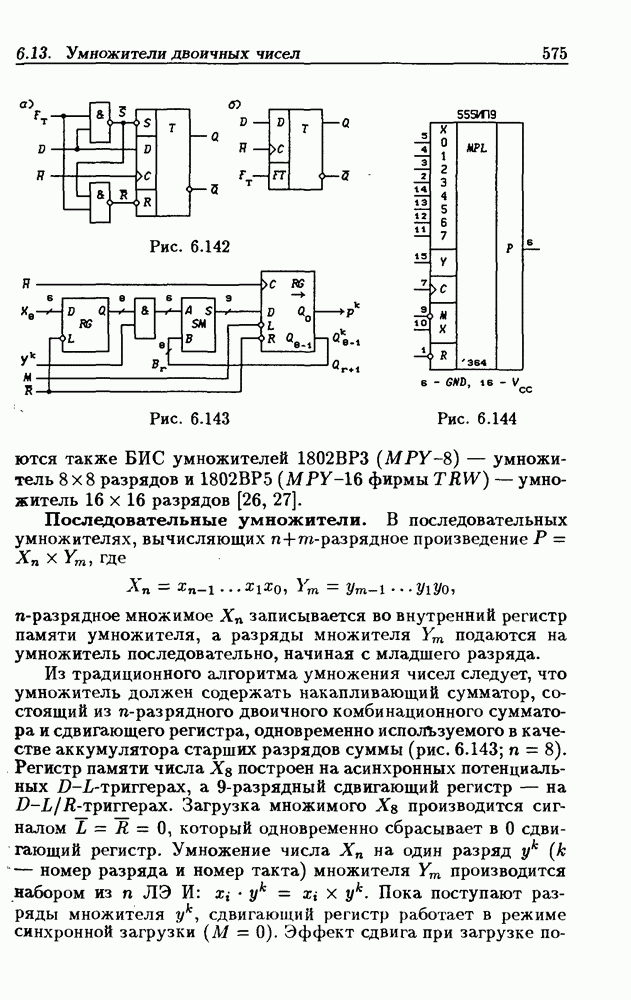
- Последовательные умножители.
- 6.14. Конвейерные устройства
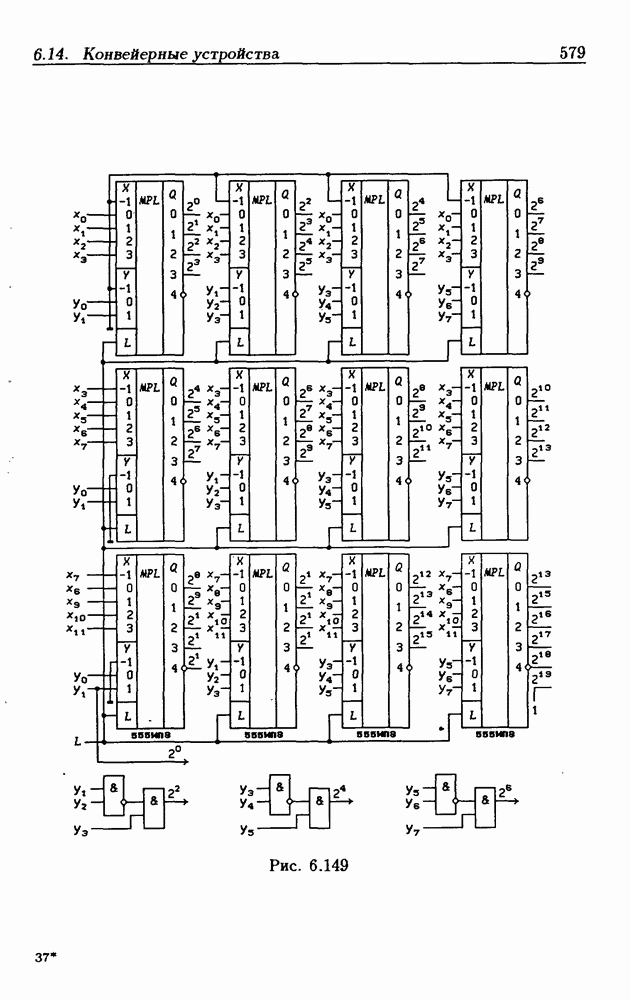
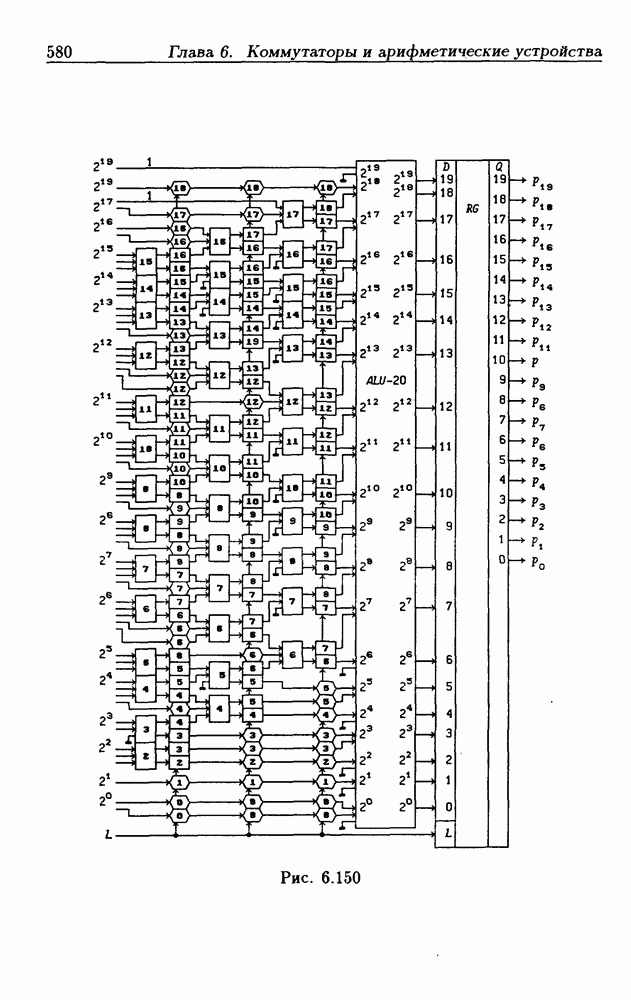
- Конвейерный быстрый умножитель.
- Конвейерные АЦП.
- 6.15. Синтез линейных комбинационных схем
- Сумматор по модулю q.
- Умножитель по модулю q.
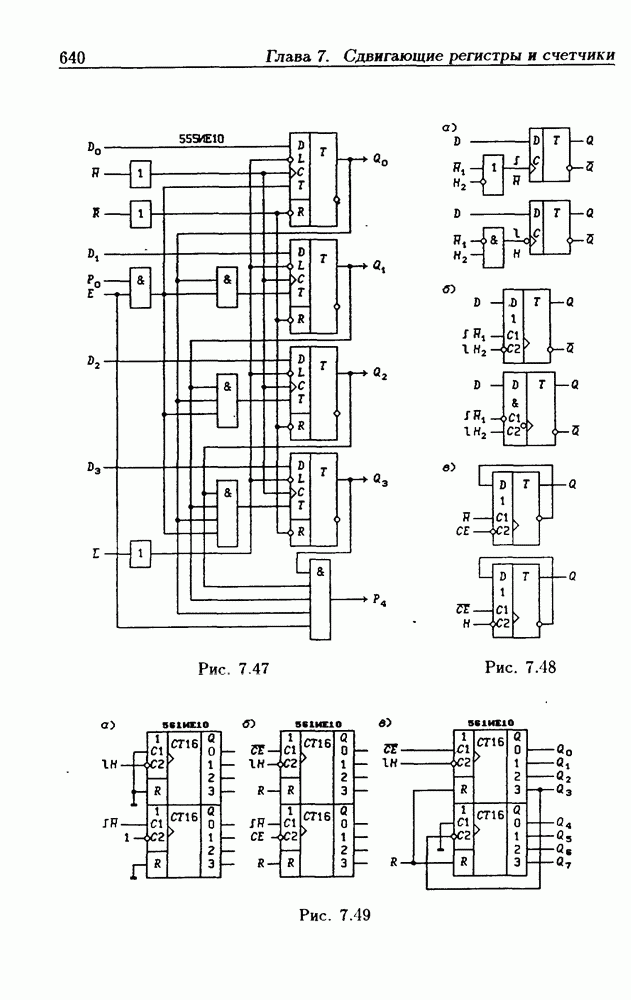
- Глава 7. Сдвигающие регистры и счетчики
- 7.1. Сдвигающие регистры без параллельной записи данных
- Сдвигающие устройства с выходными регистрами памяти.
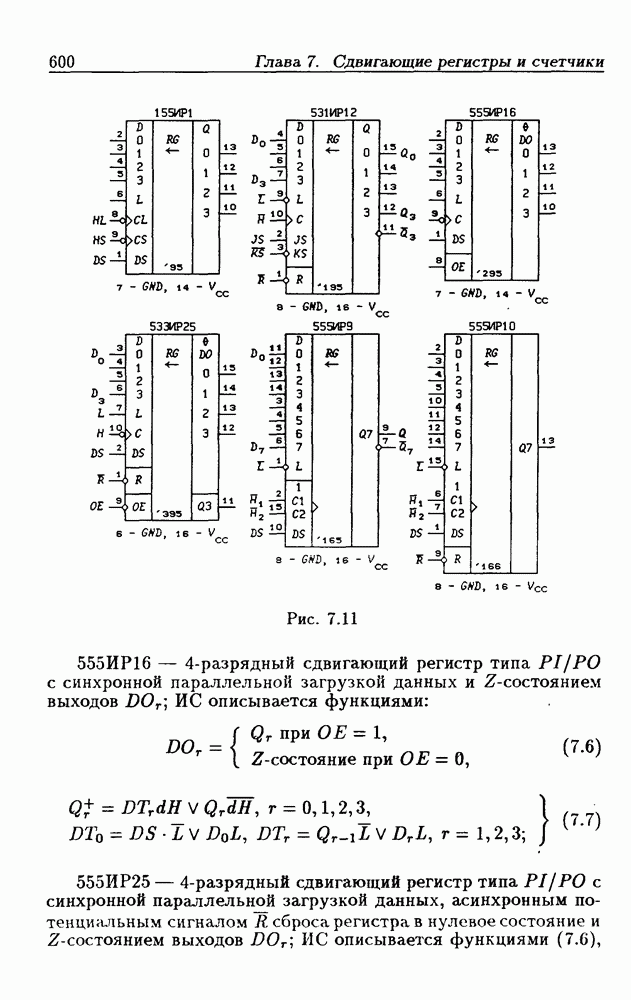
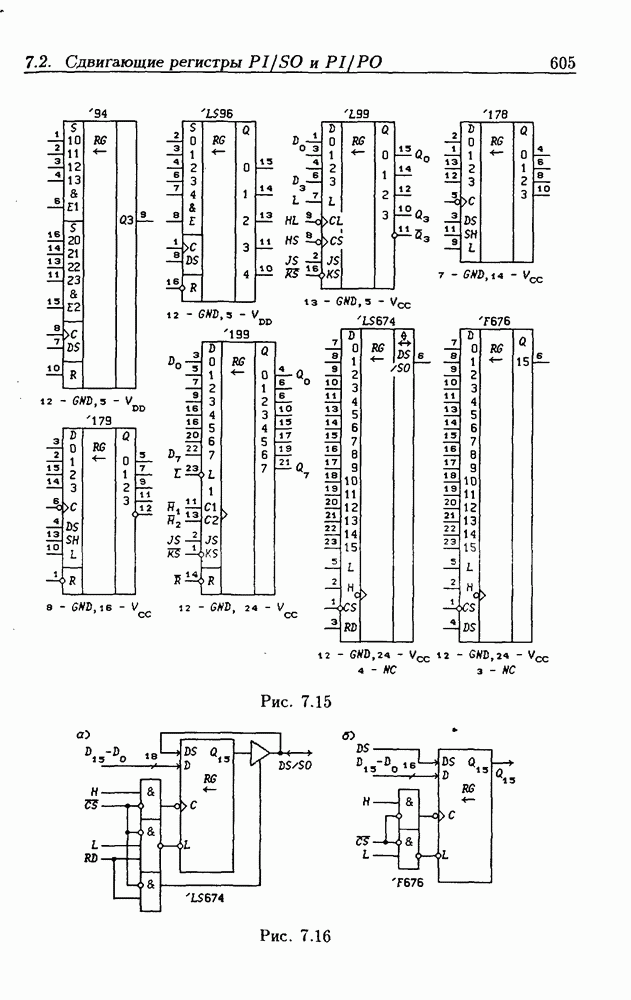
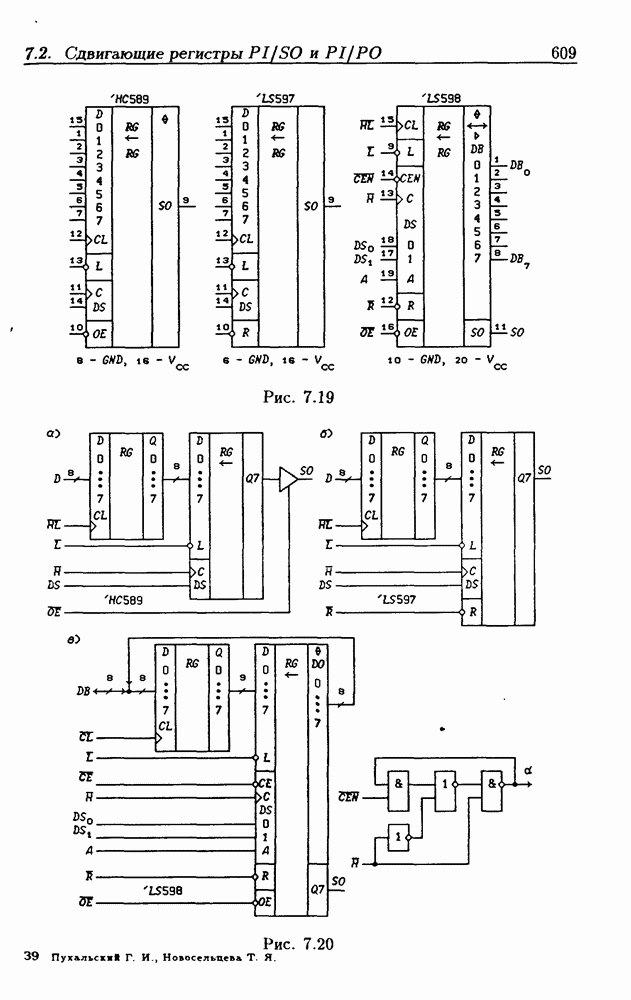
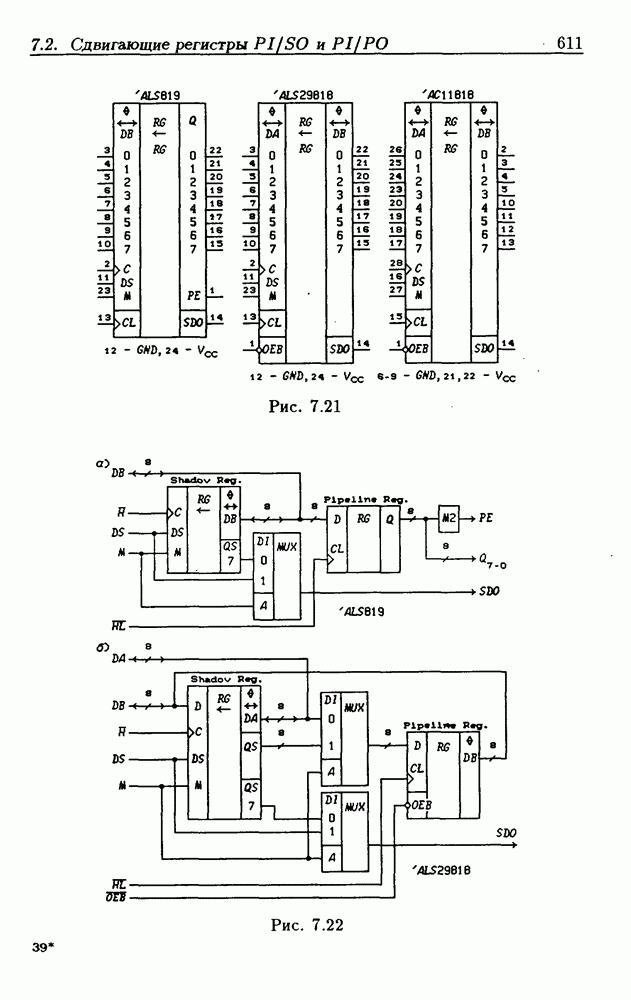
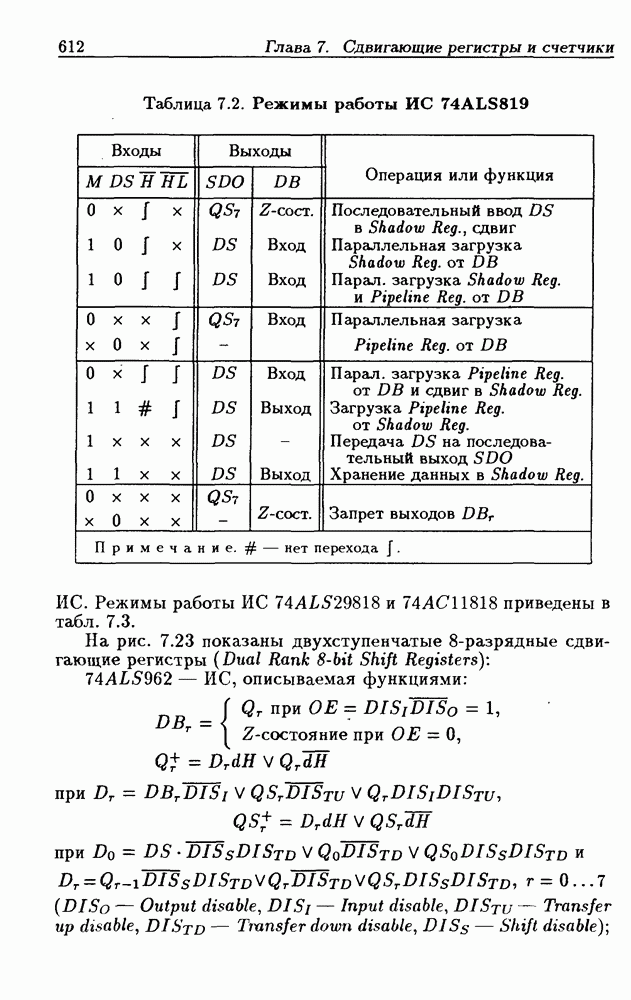
- 7.2. Сдвигающие регистры с параллельной записью данных
- Сдвигающие регистры с расширением знака.
- Сдвигающие регистры с входным регистром памяти.
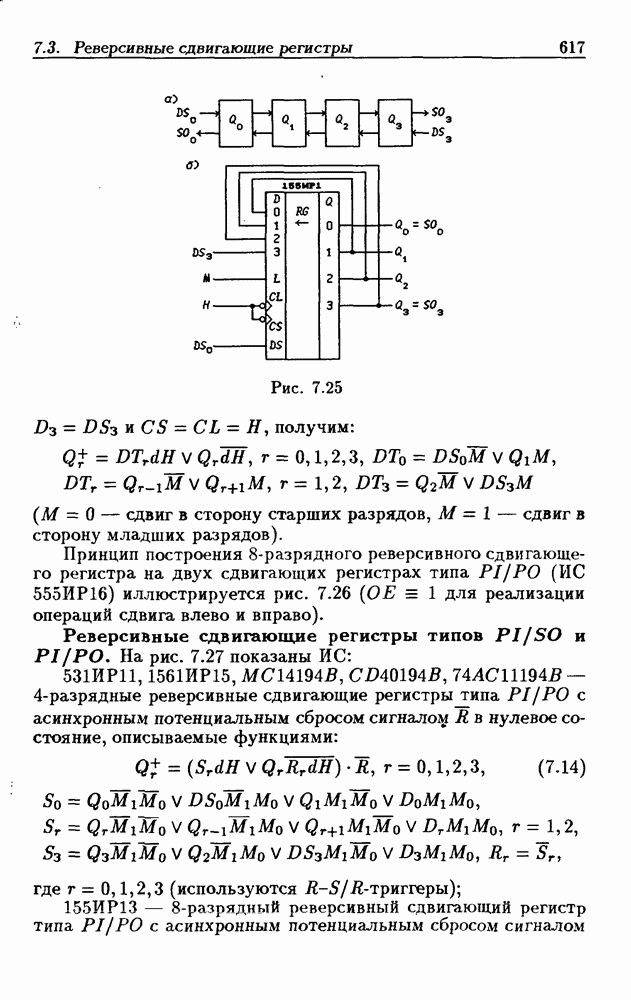
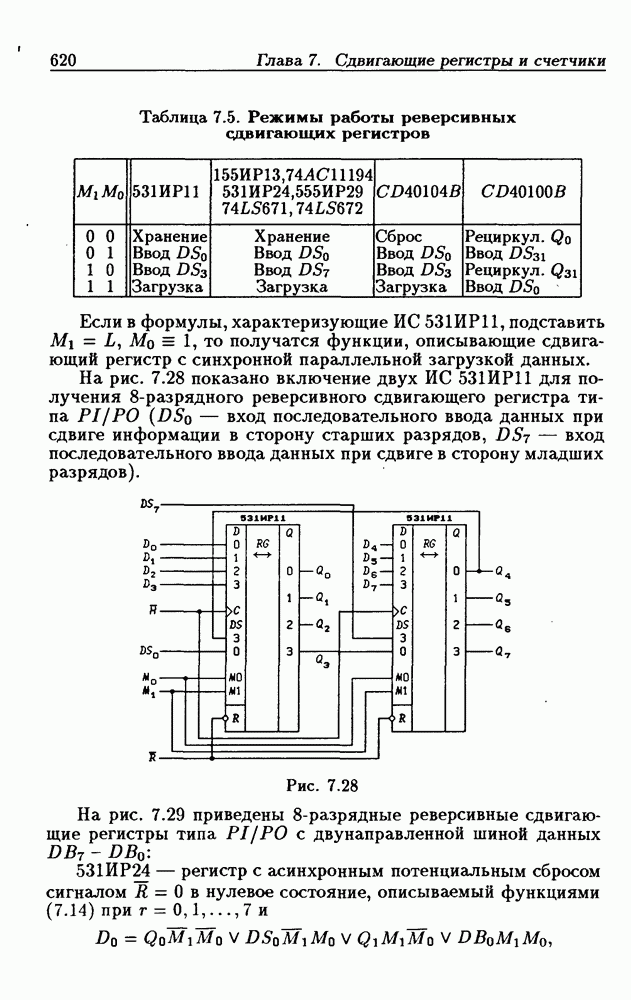
- 7.3. Реверсивные сдвигающие регистры
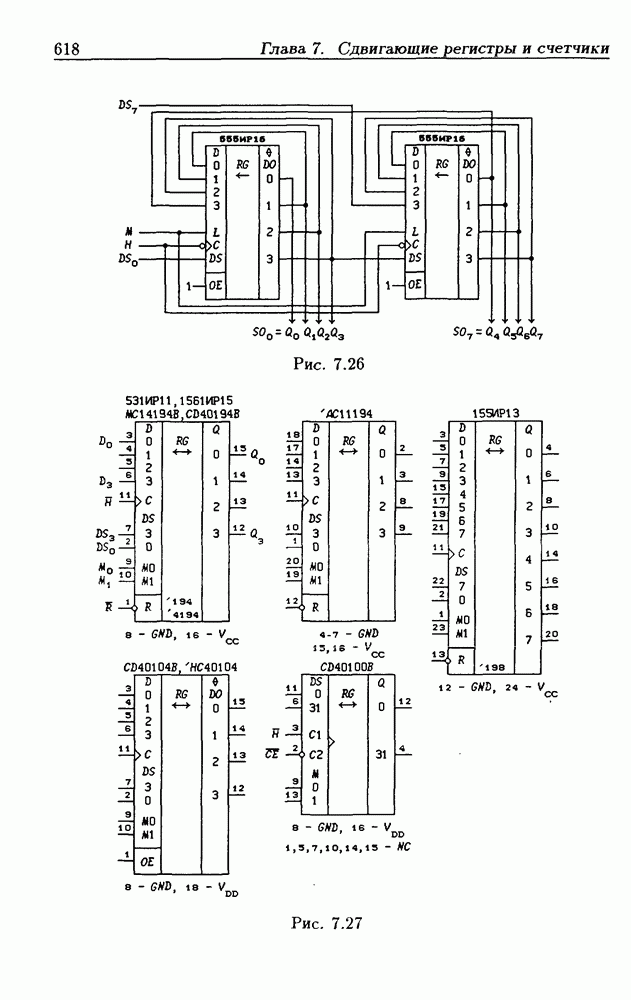
- Реверсивные сдвигающие регистры типов PI/SO и PI/PO.
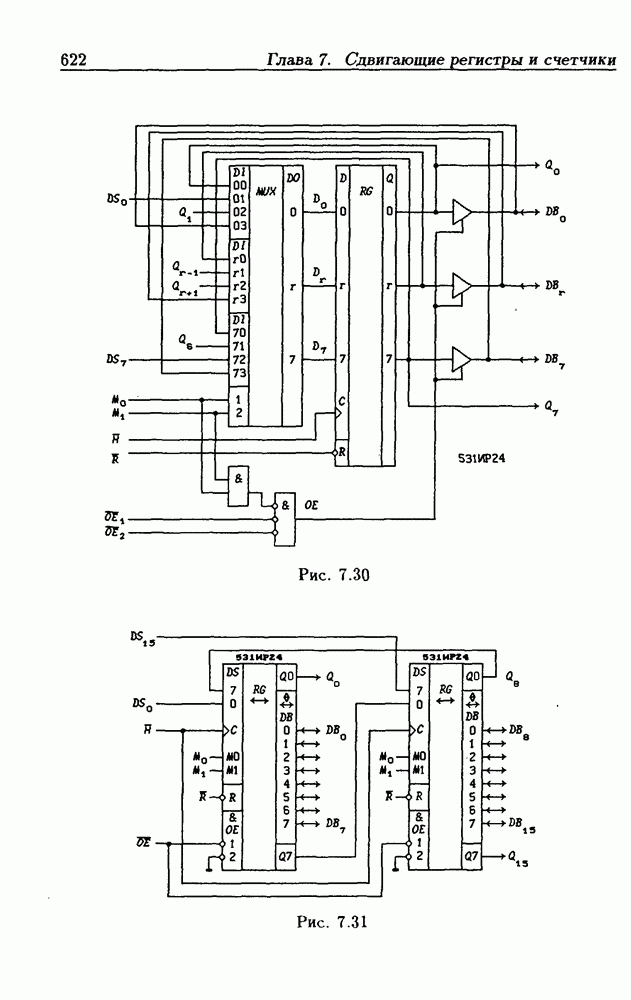
- Многофункциональные устройства на основе реверсивных сдвигающих регистров.
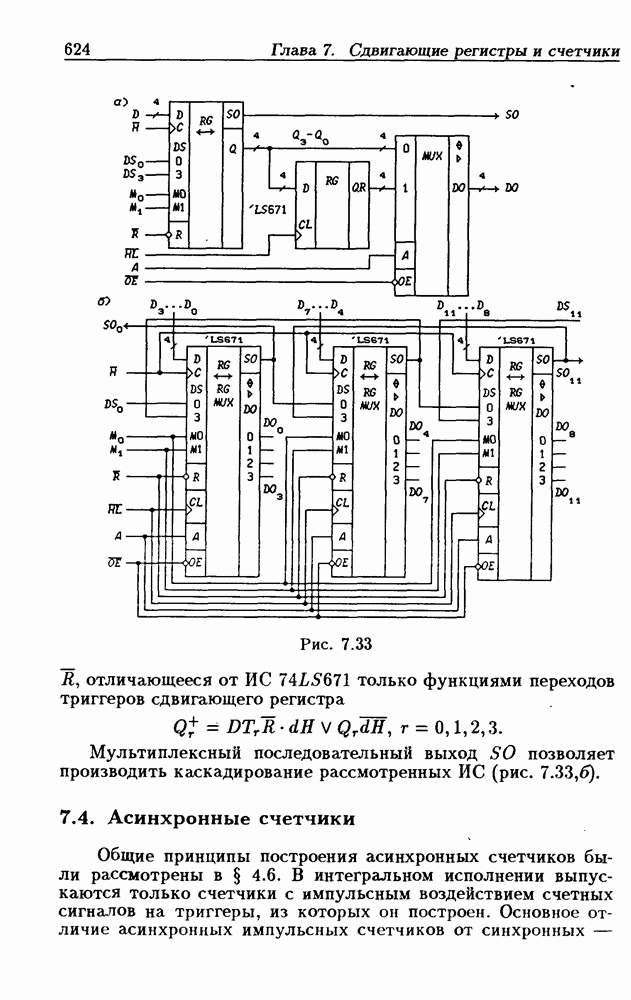
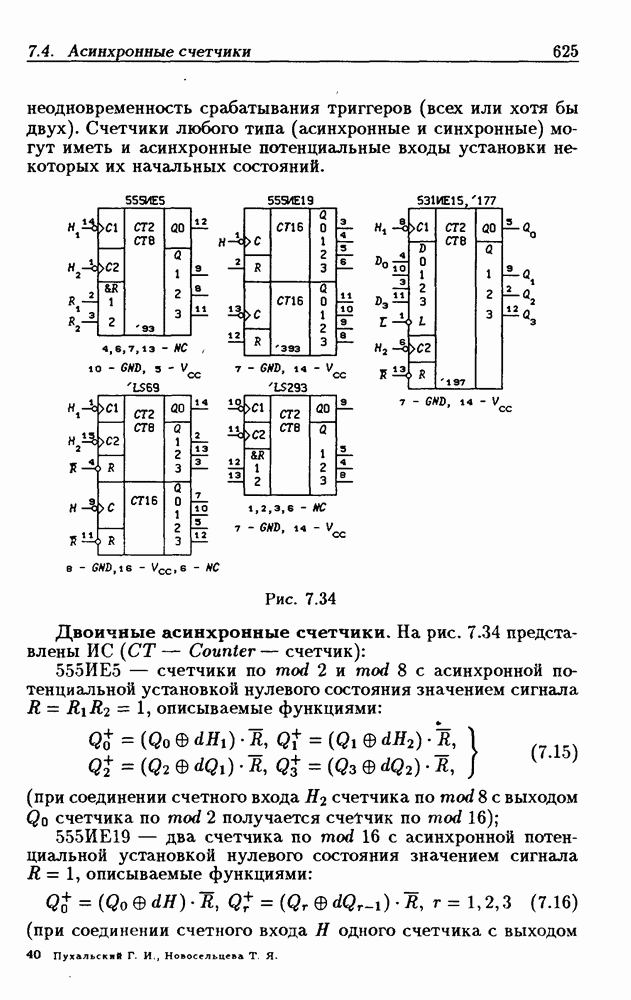
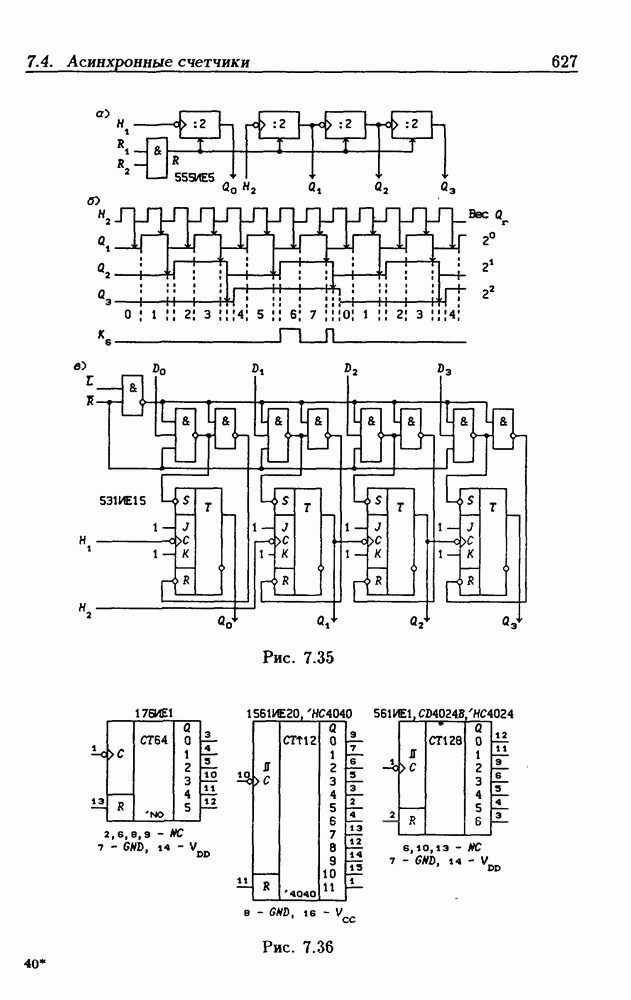
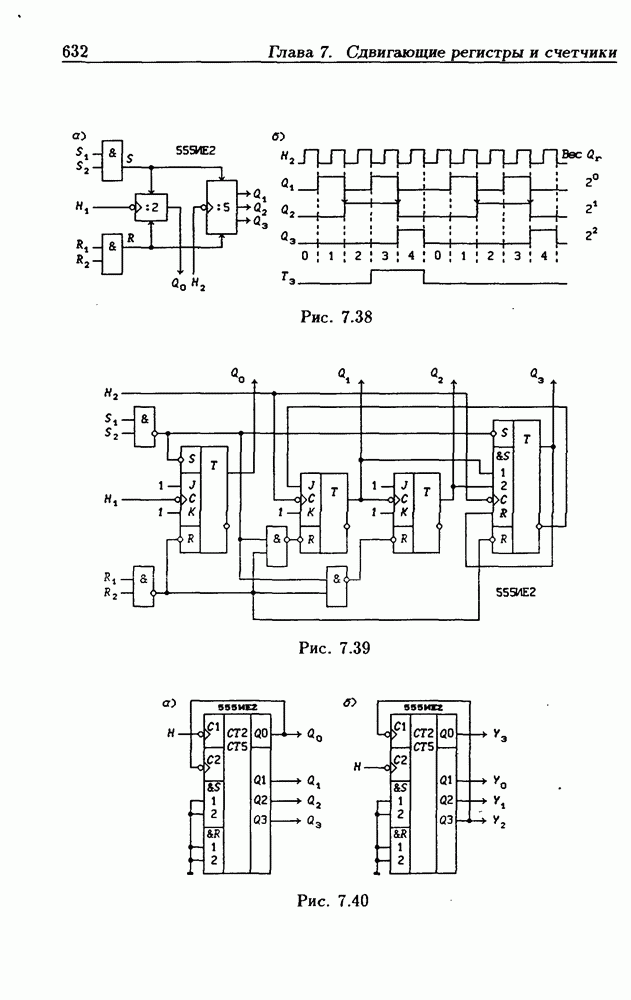
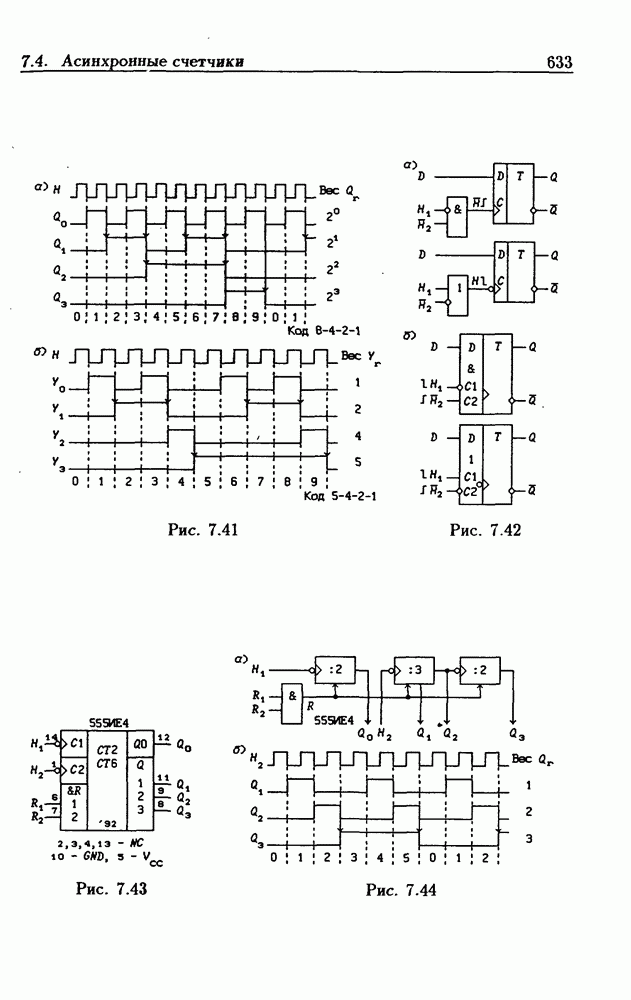
- 7.4. Асинхронные счетчики
- Двоично-десятичные асинхронные счетчики.
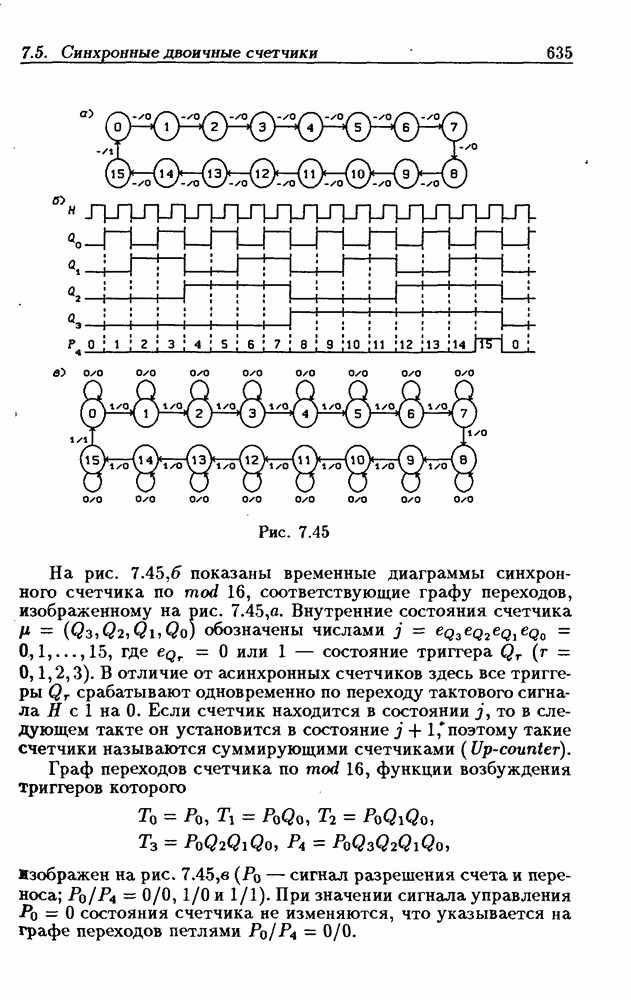
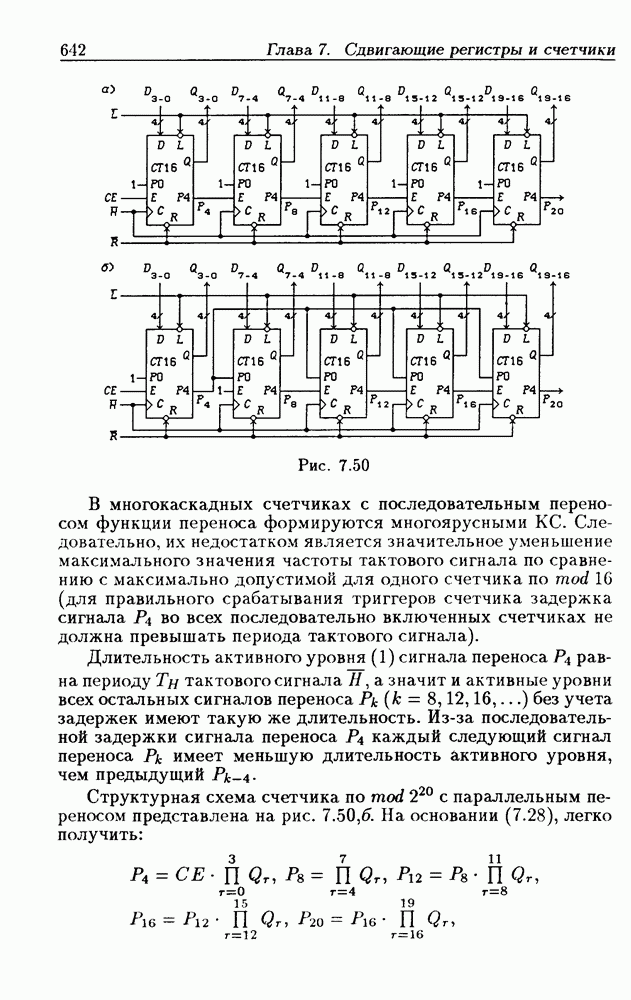
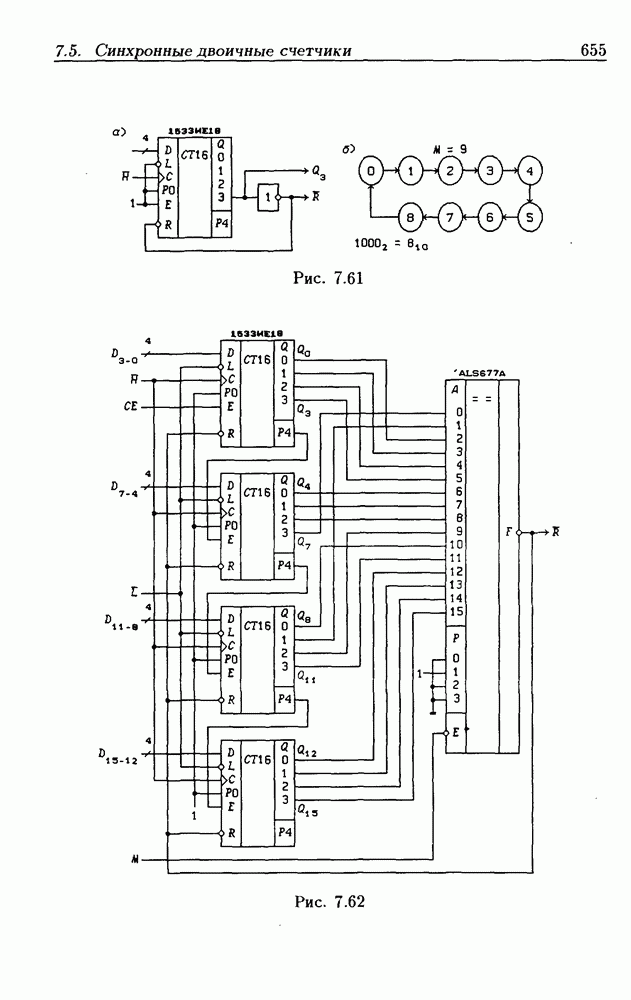
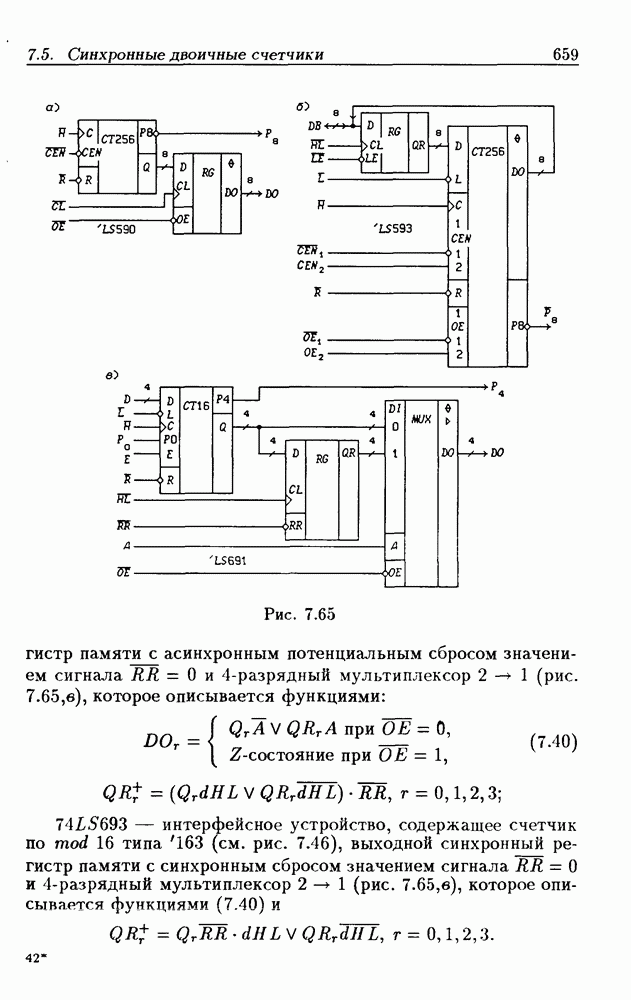
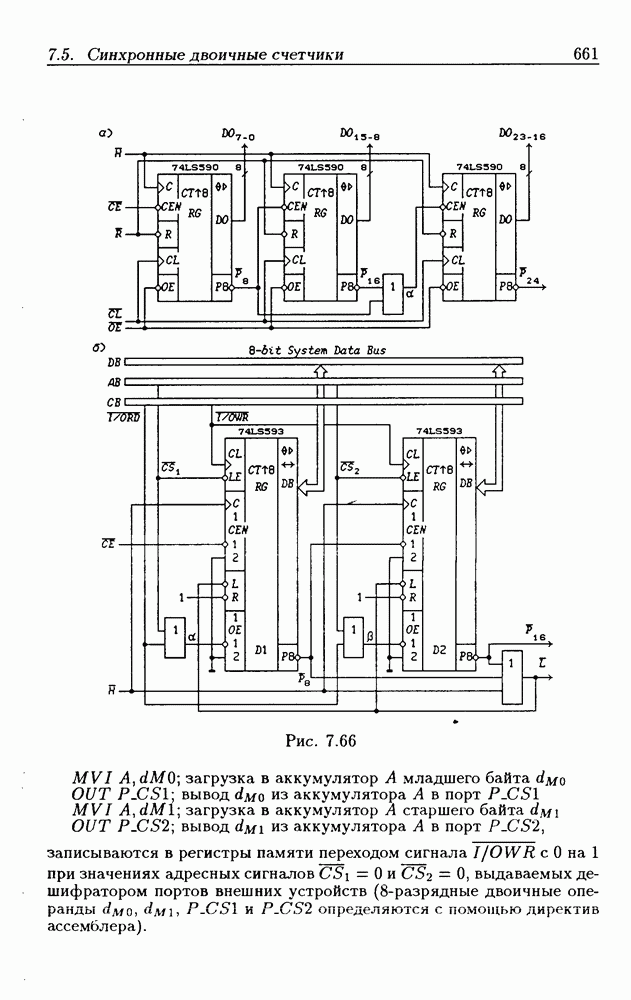
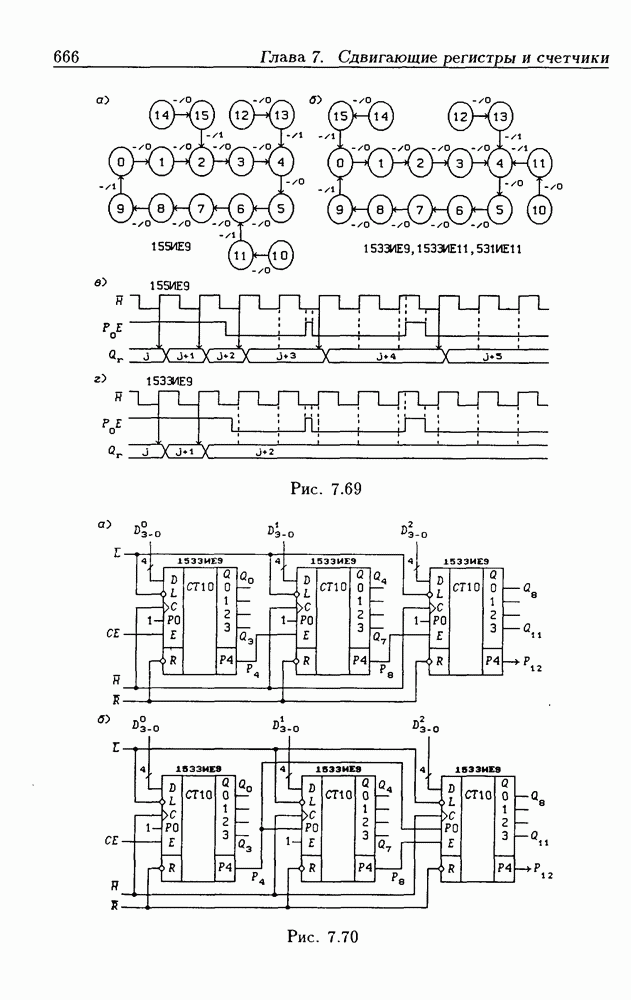
- 7.5. Синхронные двоичные счетчики
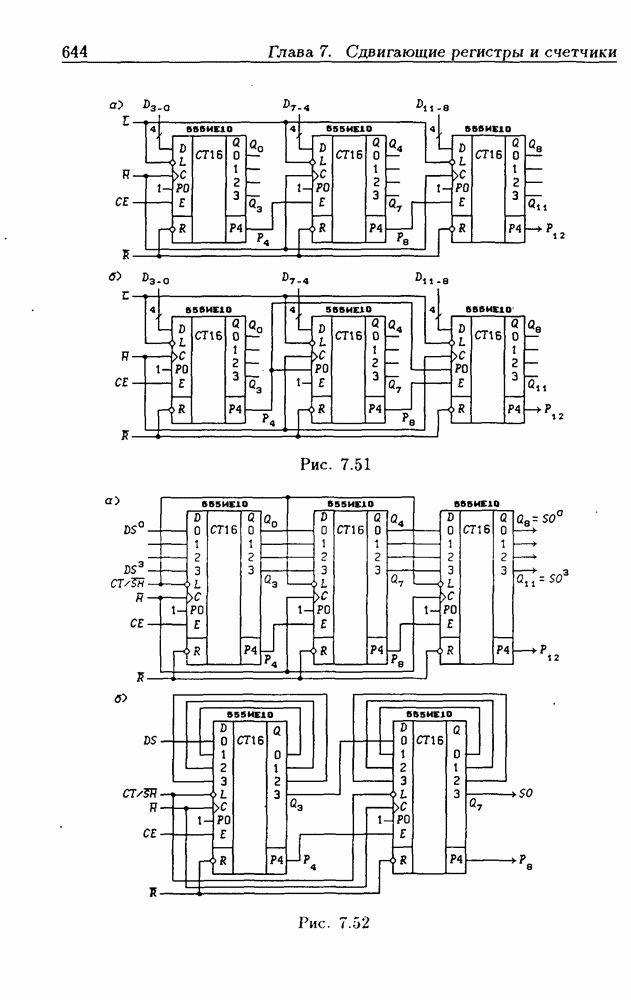
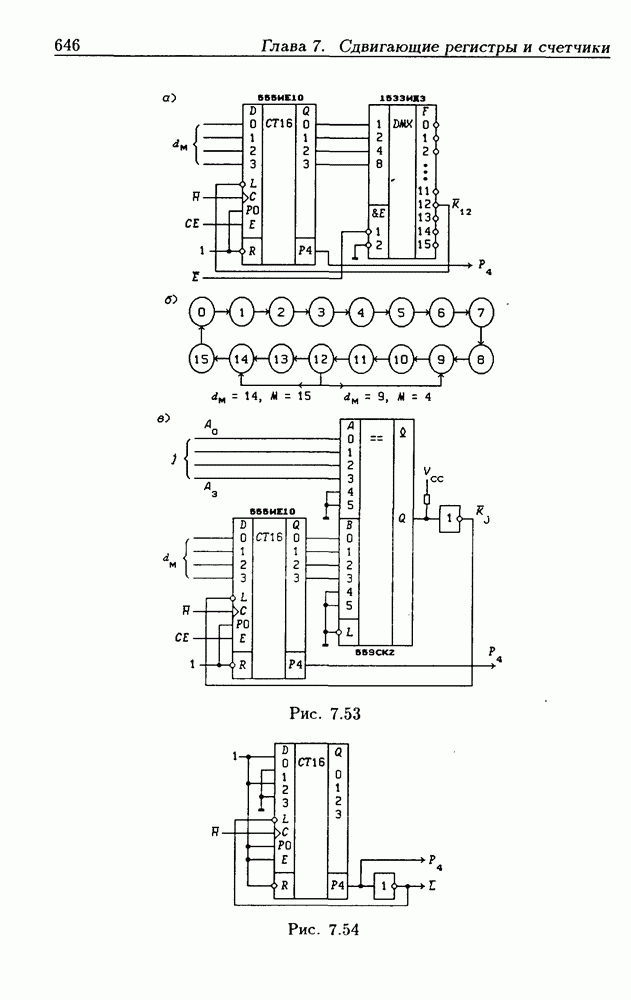
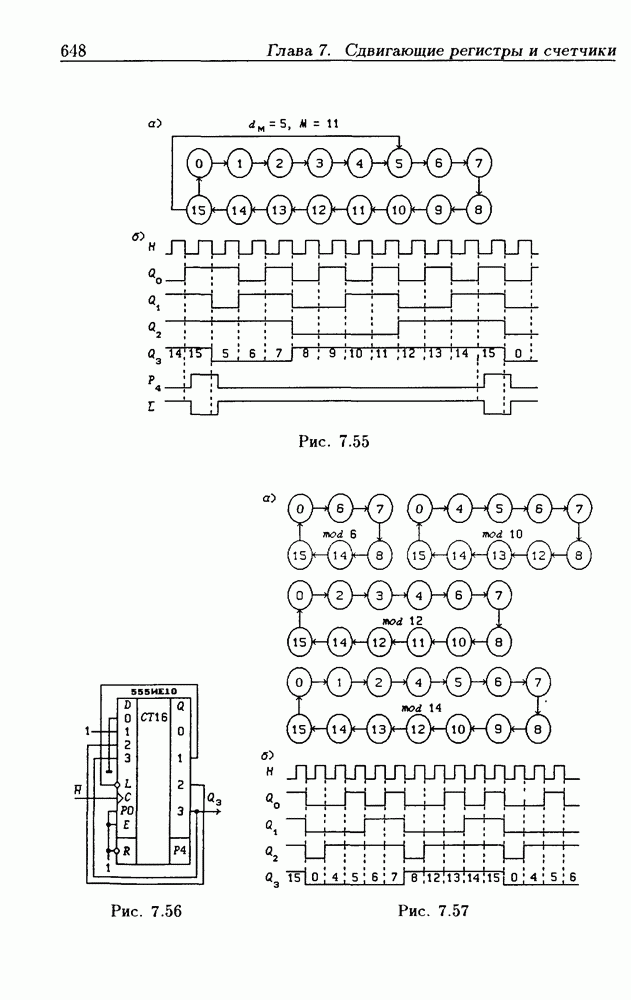
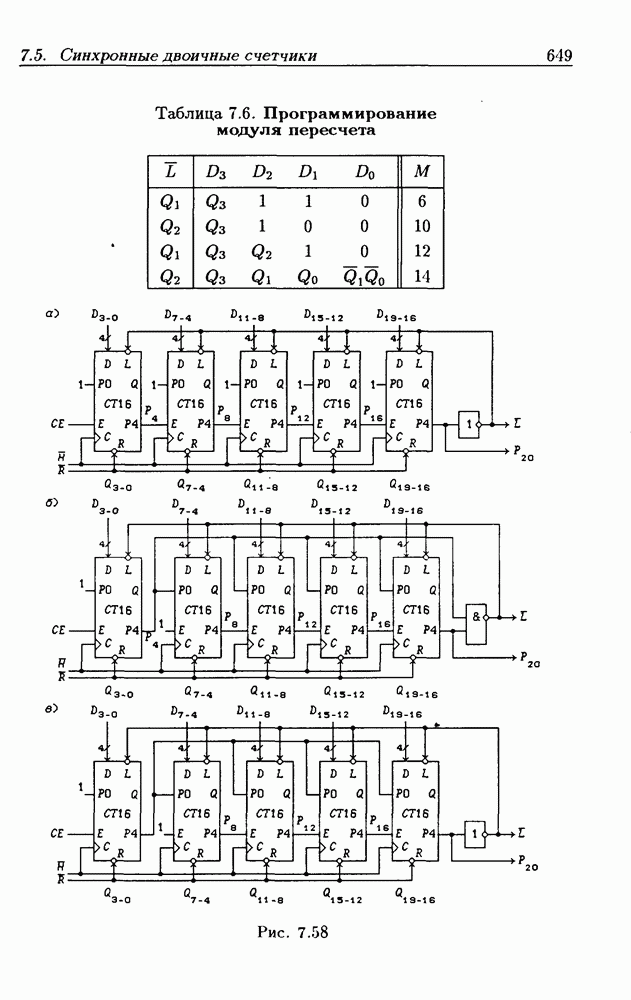
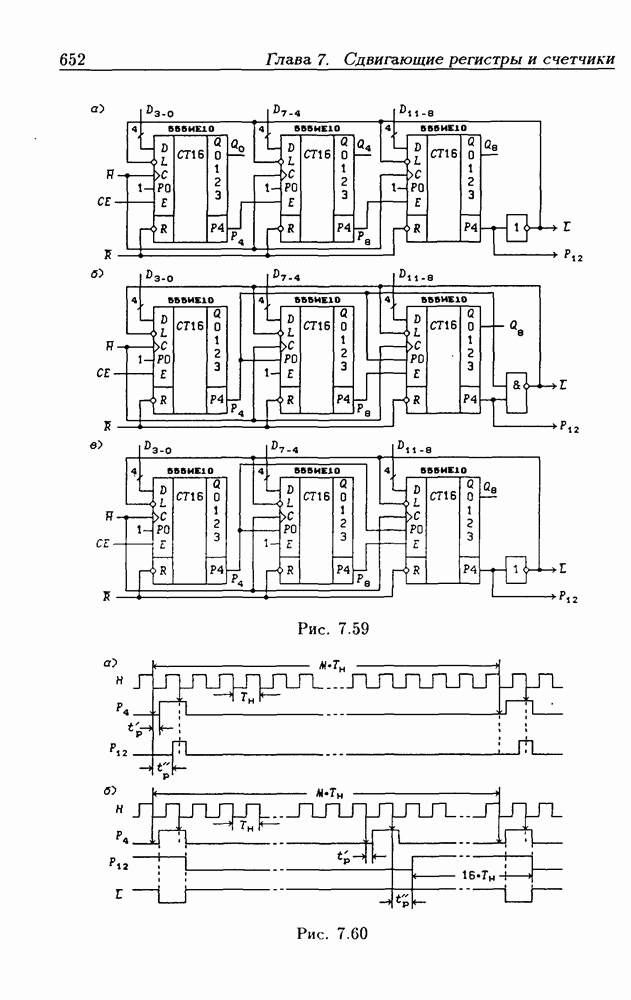
- Программирование модуля пересчета двоичных счетчиков.
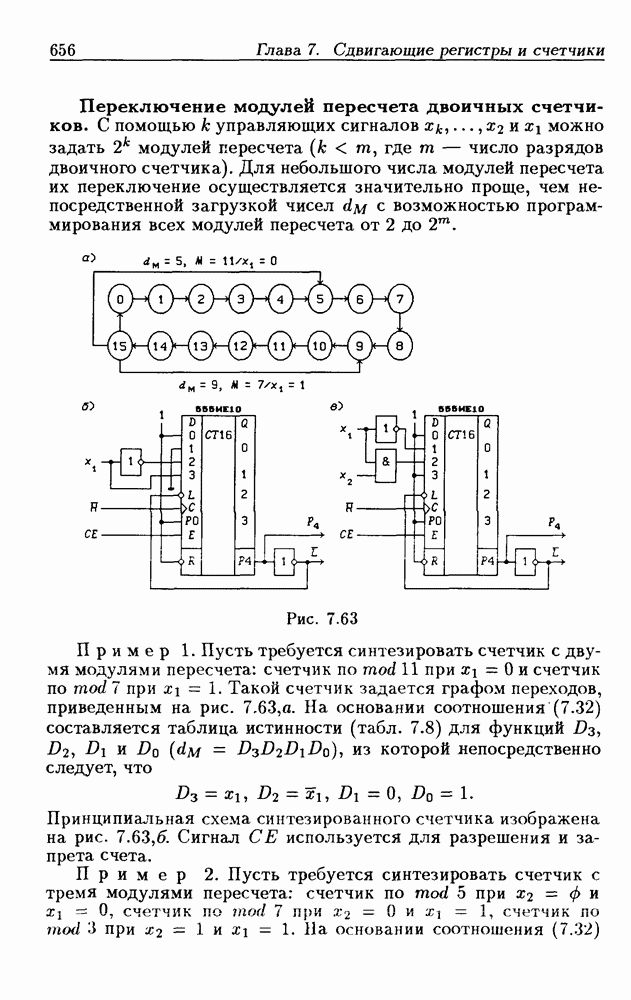
- Переключение модулей пересчета двоичных счетчиков.
- Функциональные устройства на основе двоичных счетчиков.
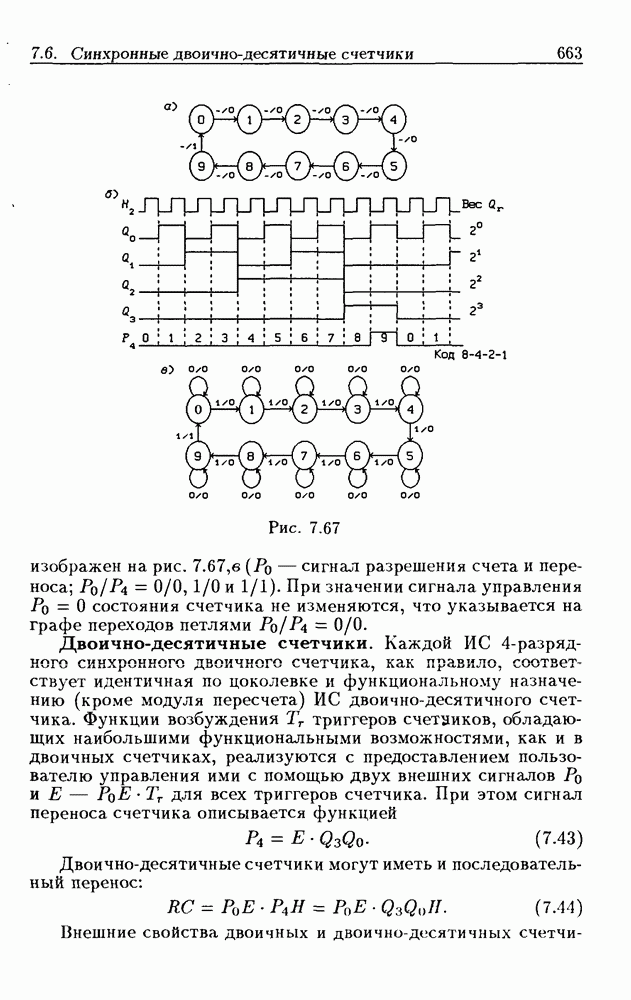
- 7.6. Синхронные двоично-десятичные счетчики
- 7.7. Синхронные реверсивные счетчики
- 7.8. Счетчики с расщепленным тактовым сигналом
- 7.9. Счетчики на сдвигающих регистрах
- 7.10. Кольцевые счетчики
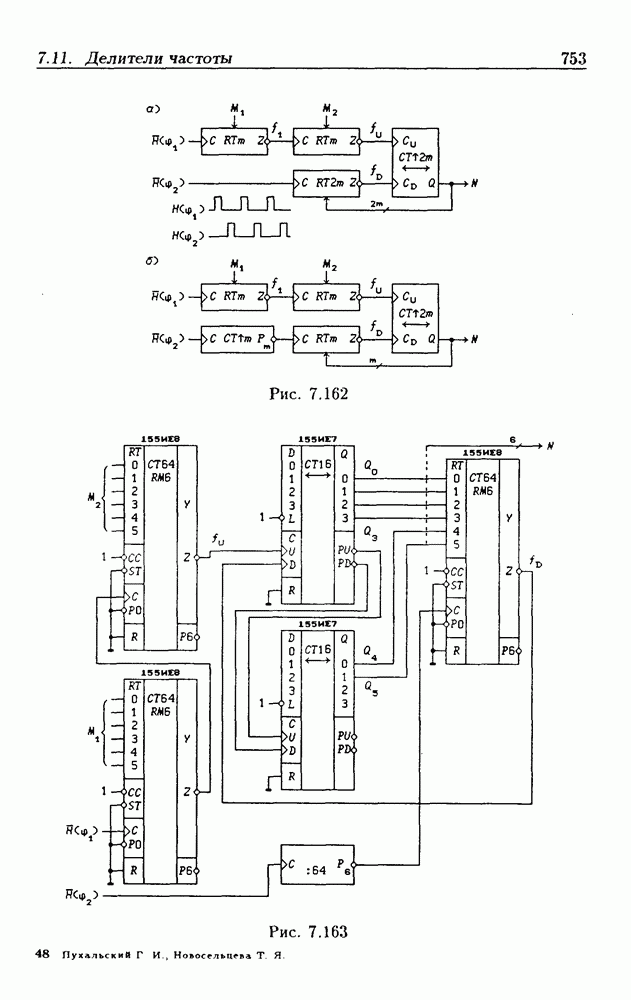
- 7.11. Делители частоты
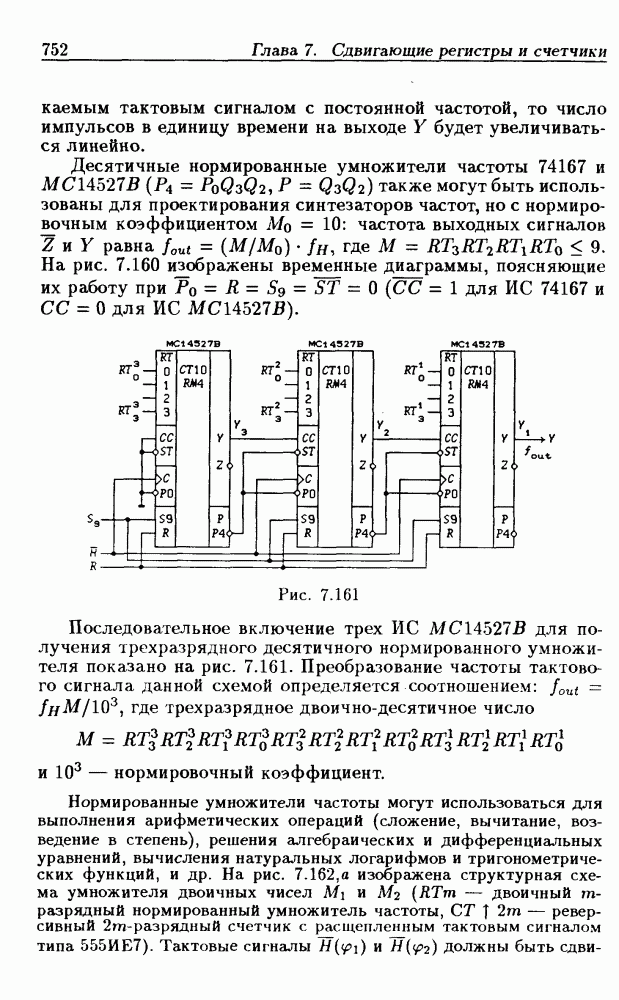
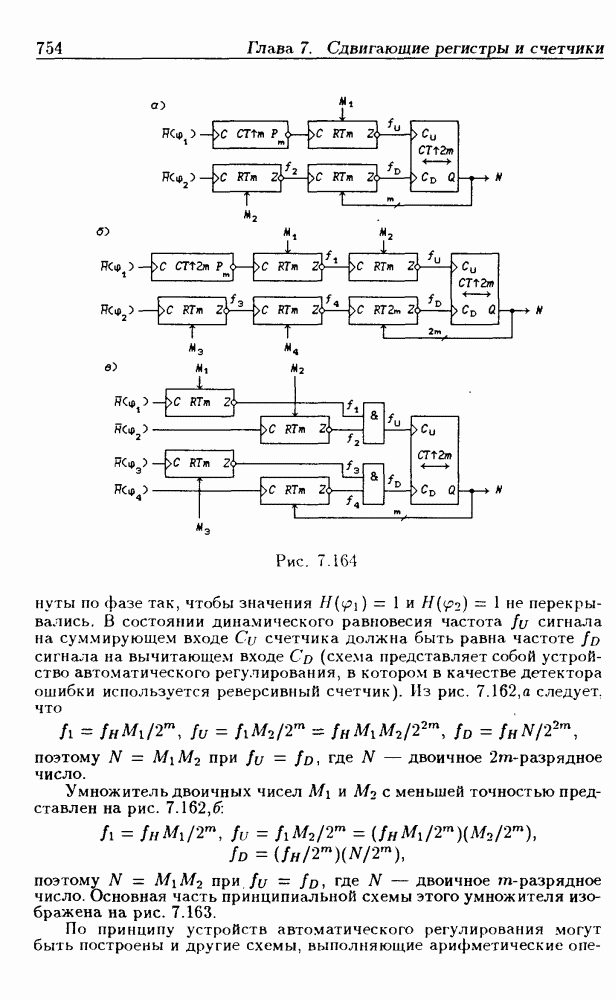
- Нормированные умножители частоты.
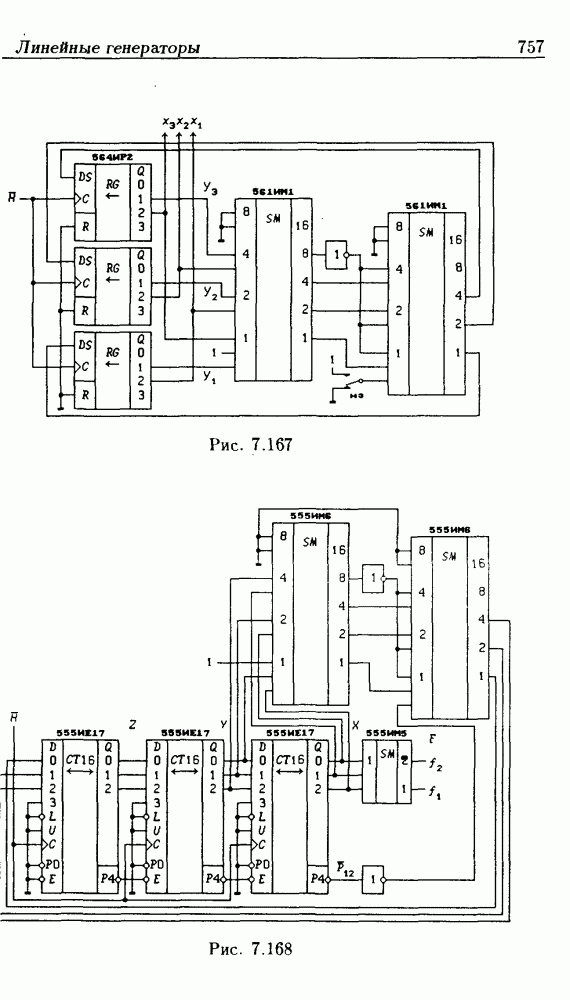
- 7.12. Линейные генераторы
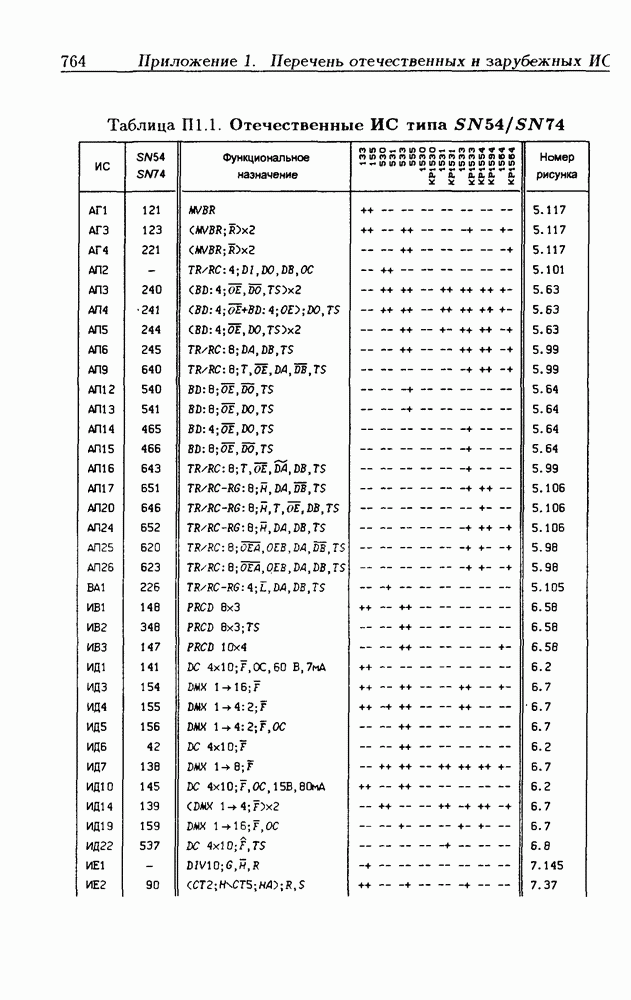
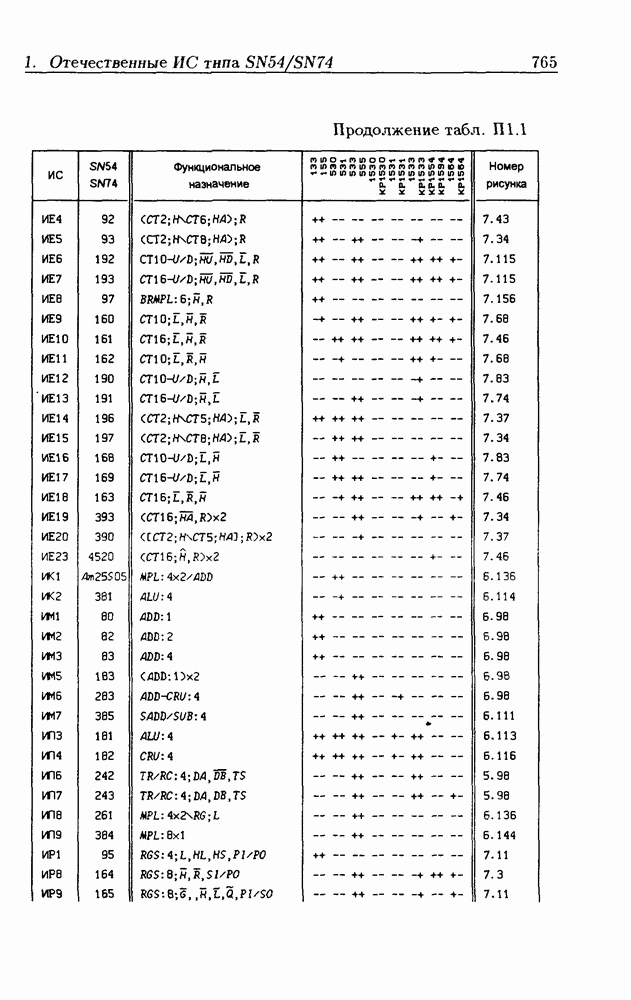
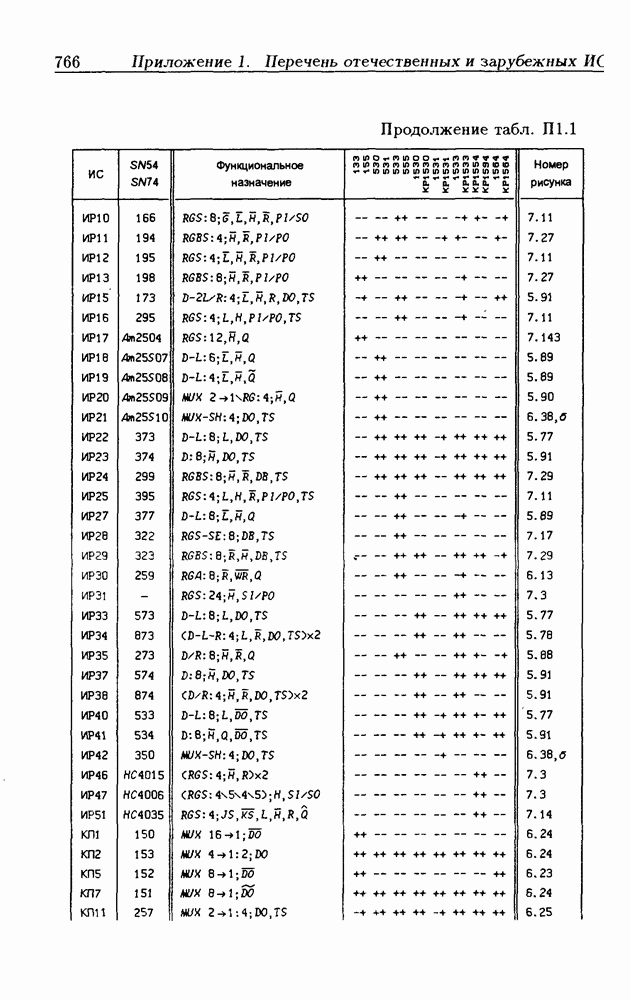
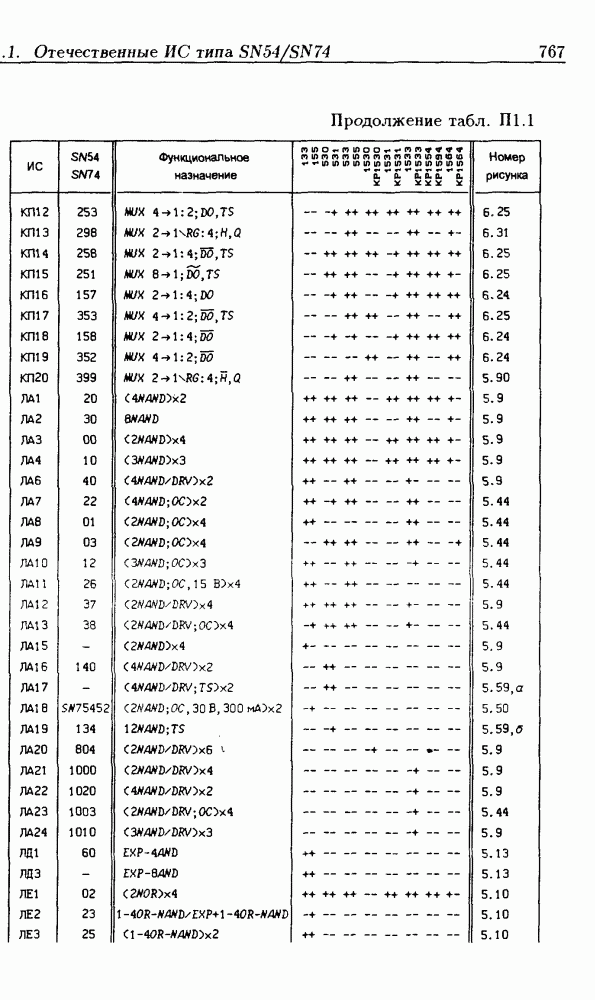
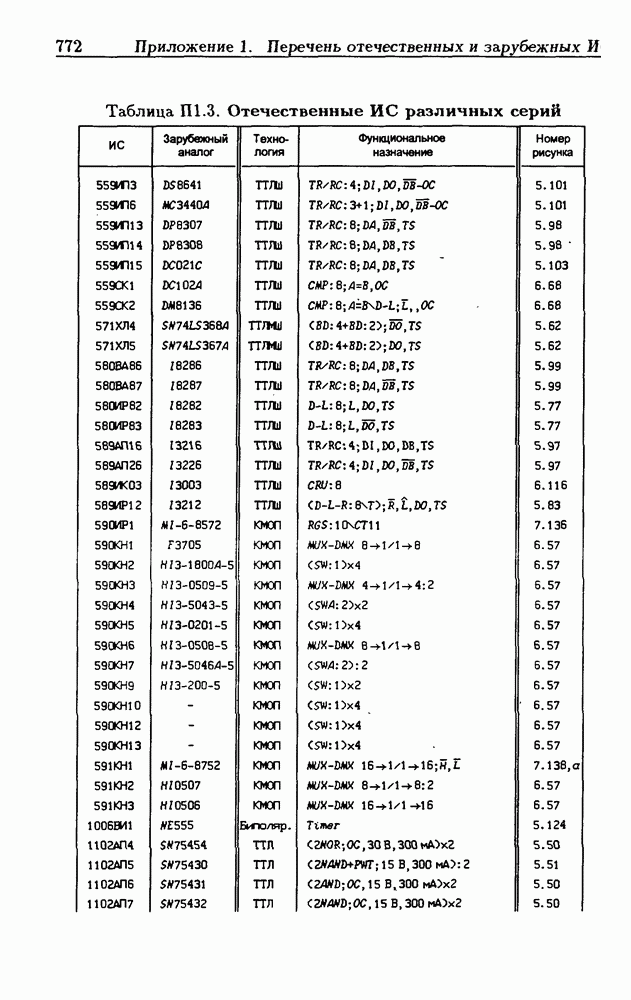
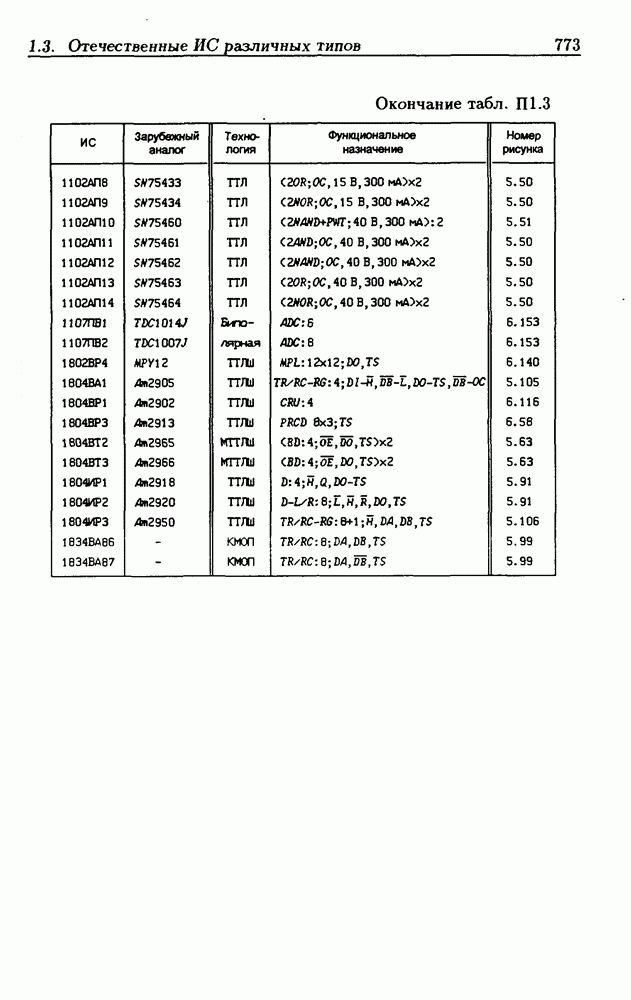
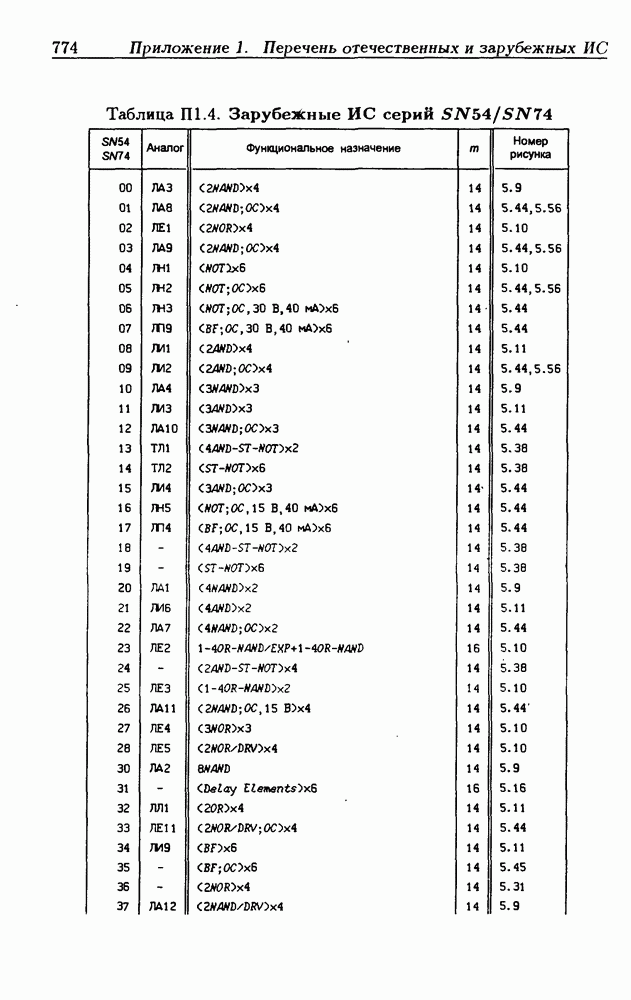
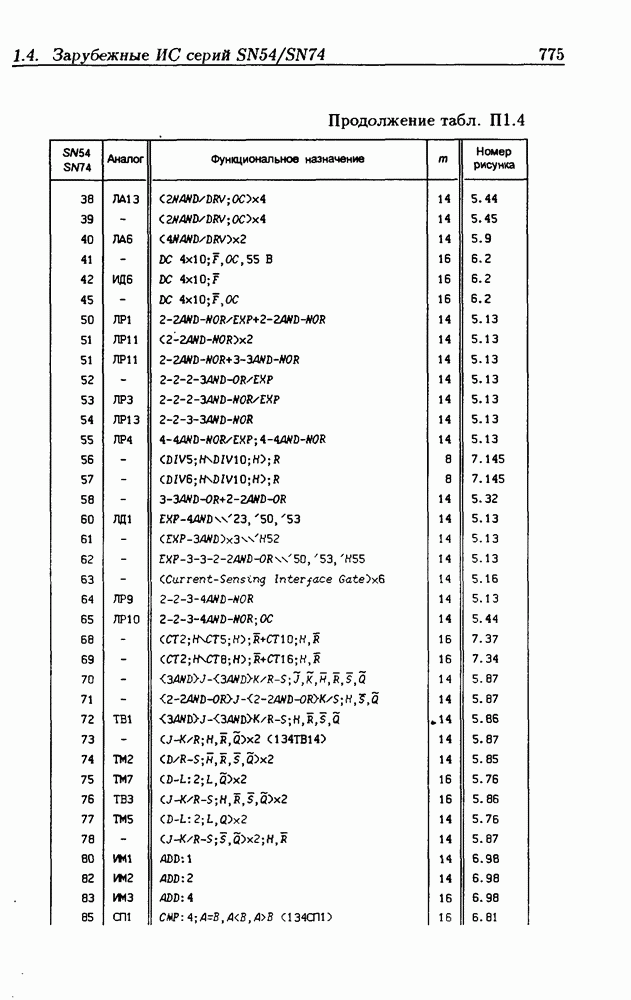
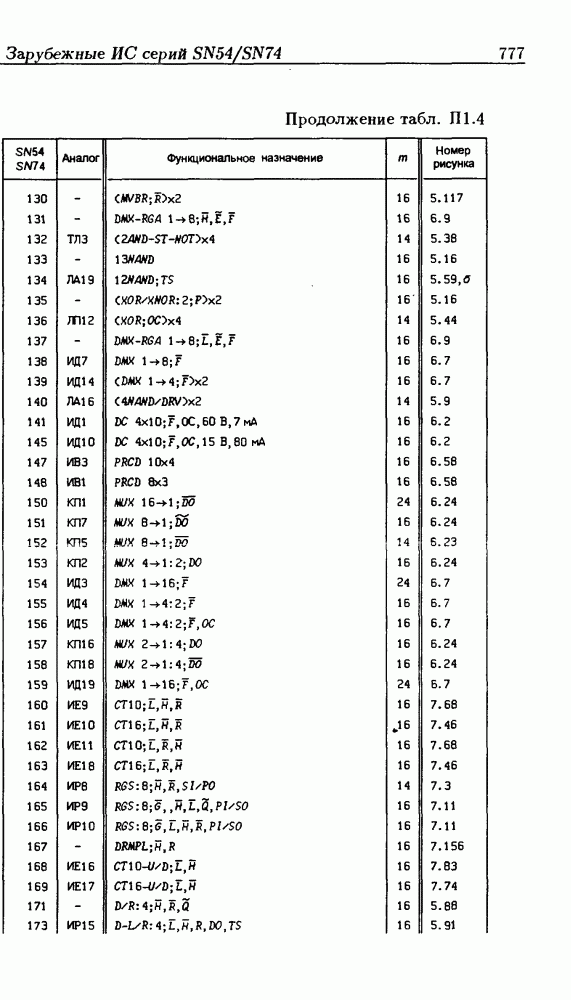
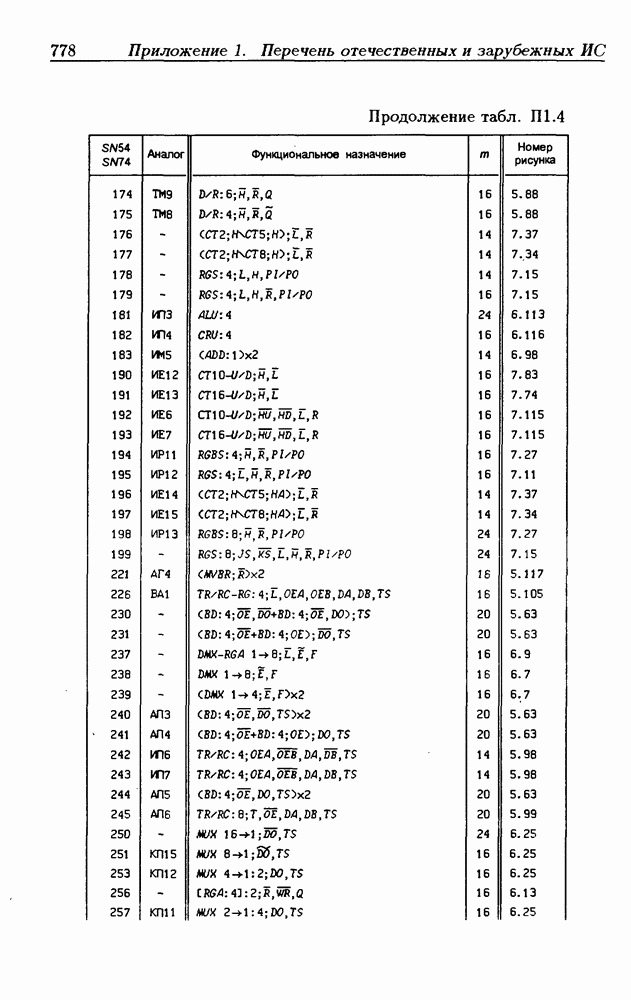
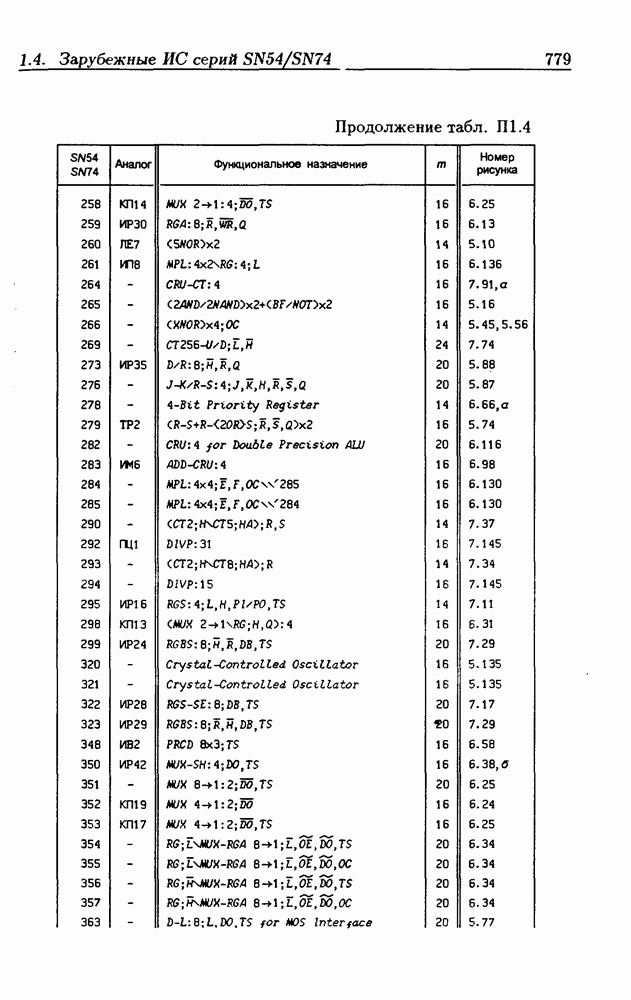
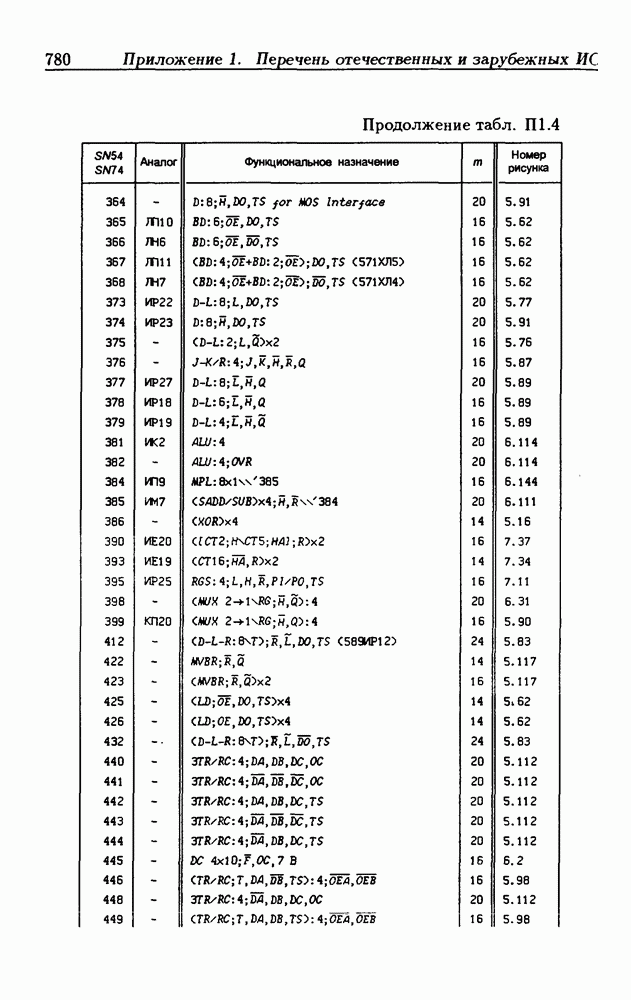
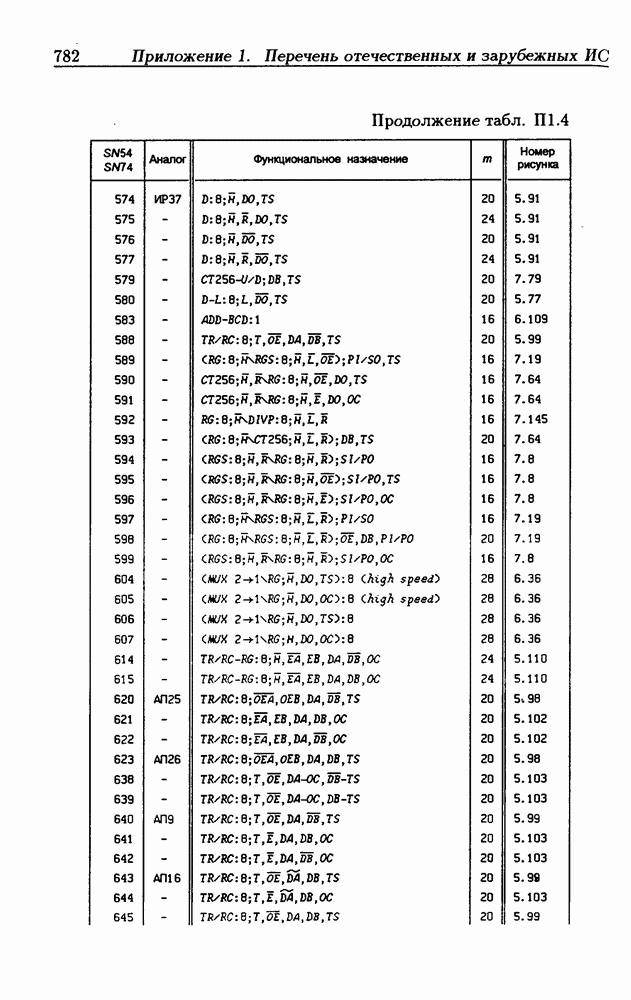
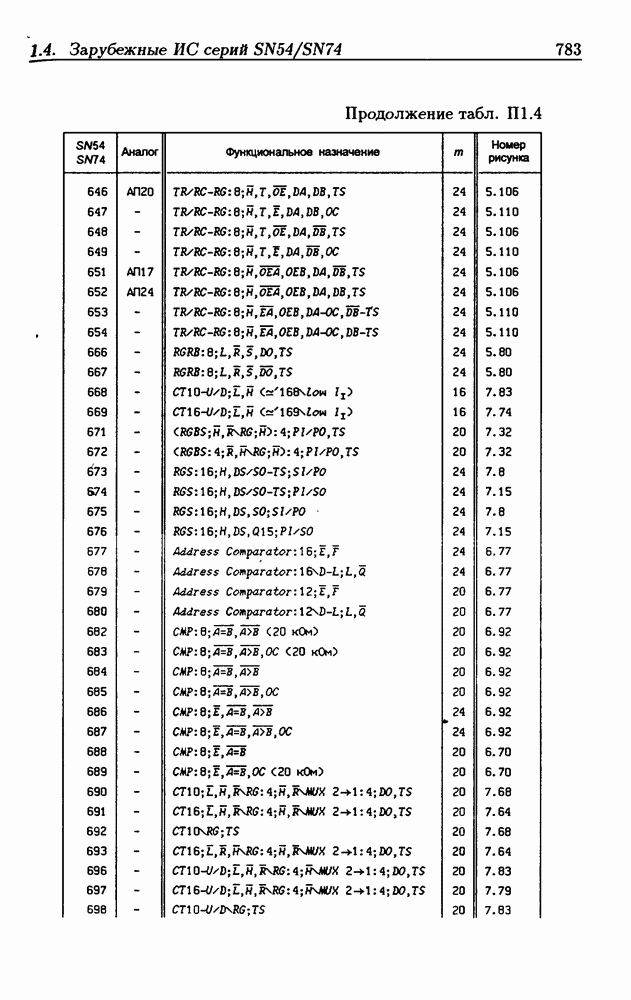
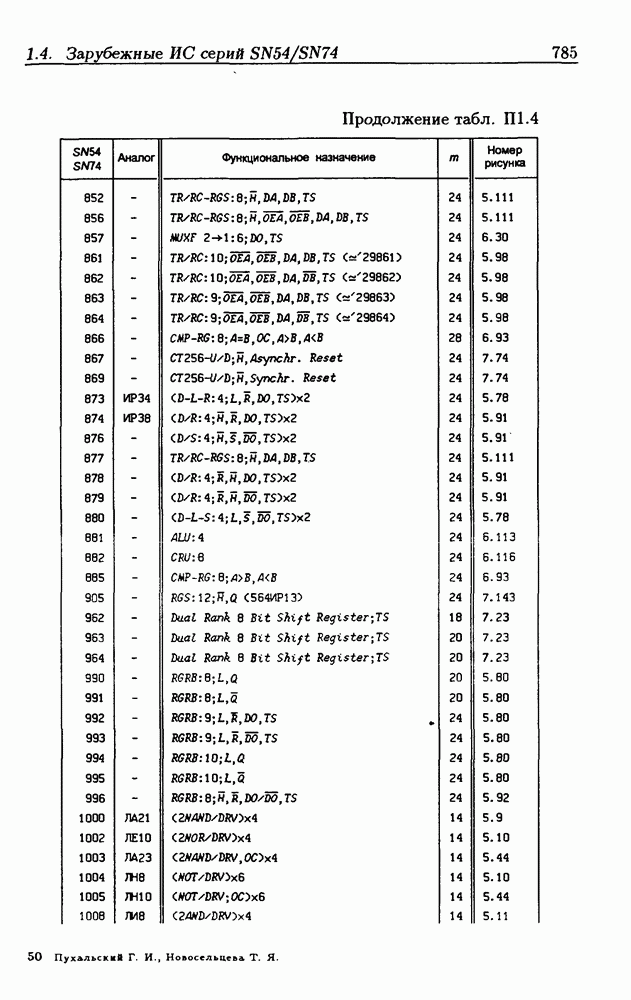
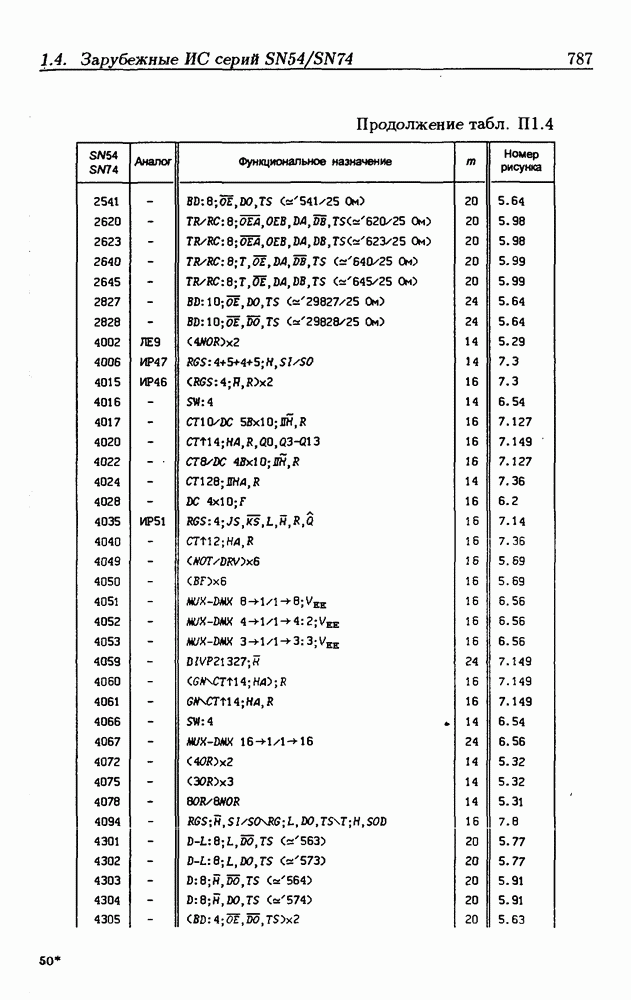
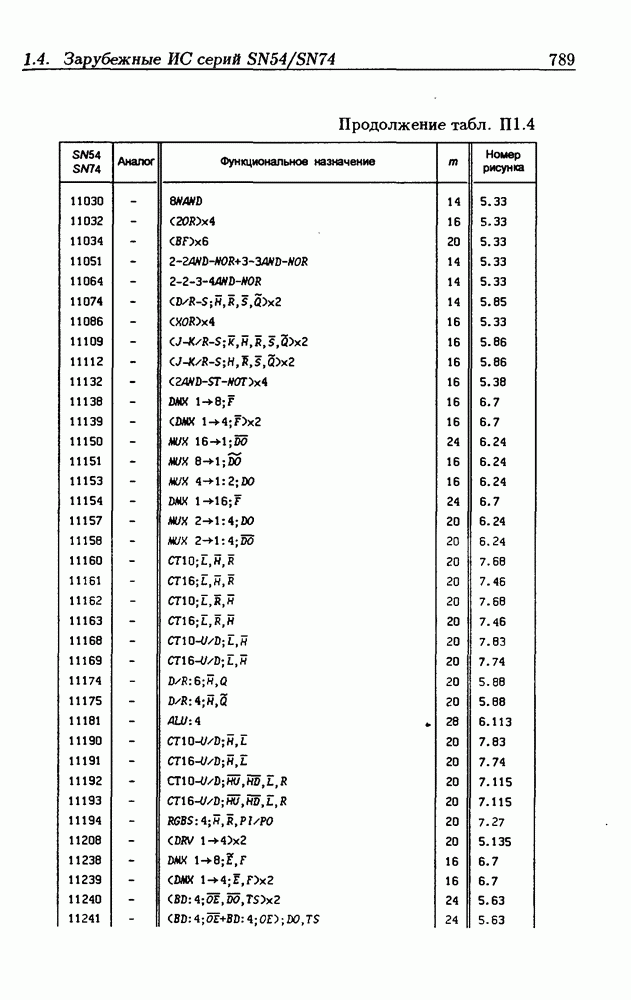
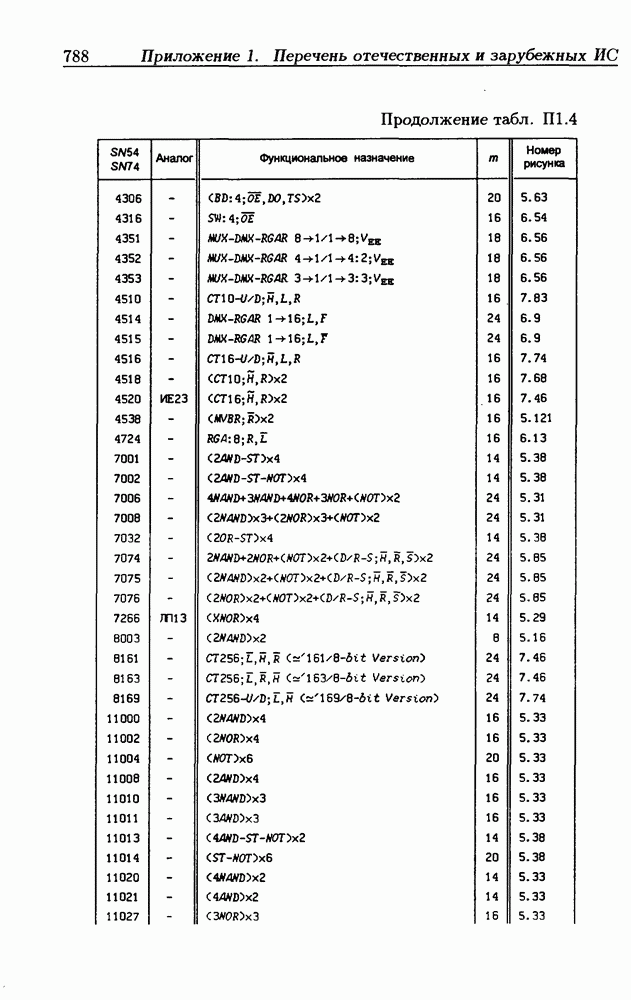
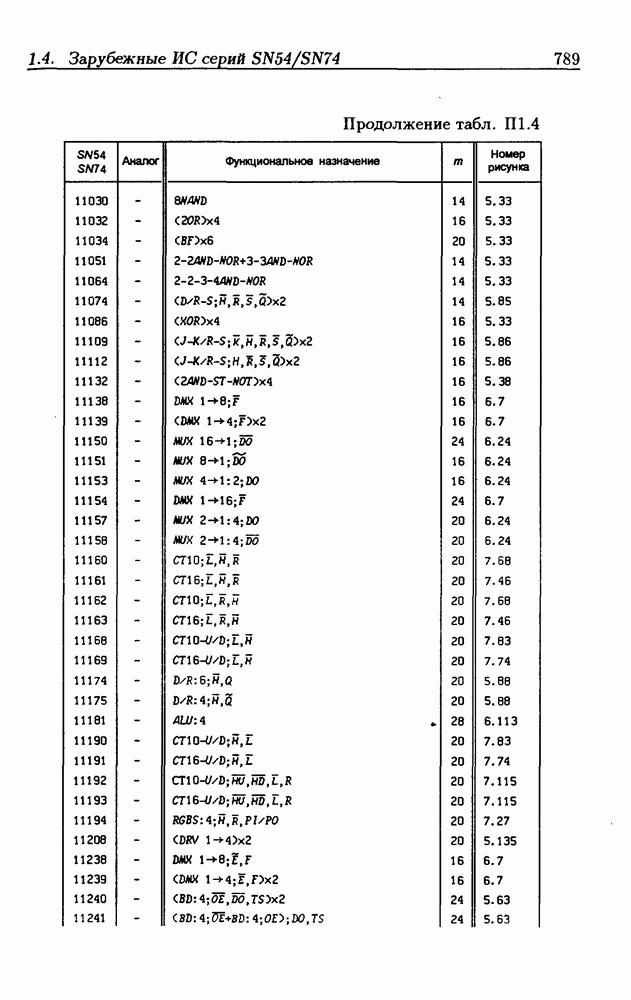
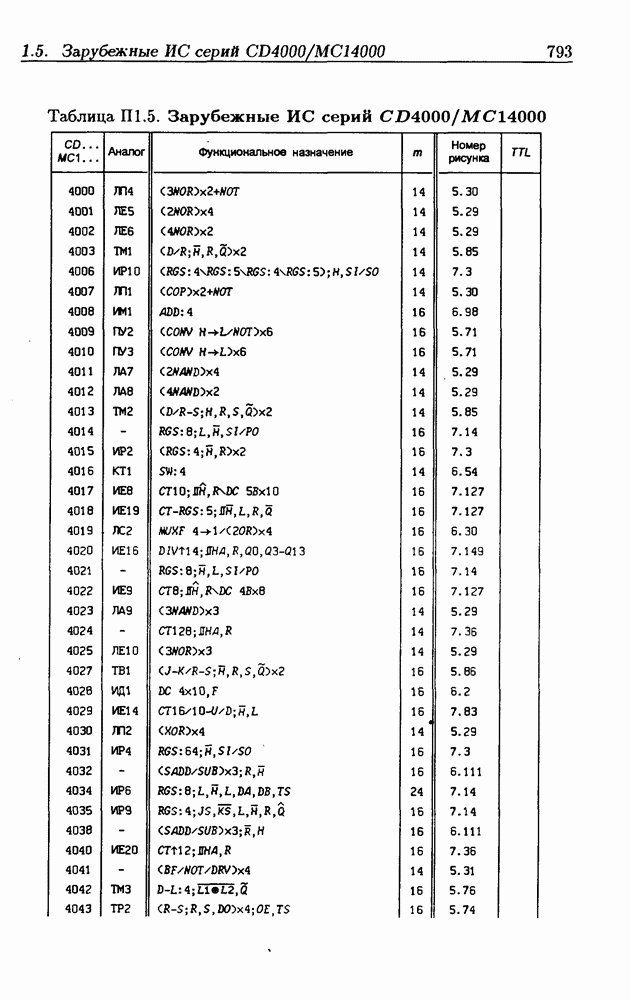
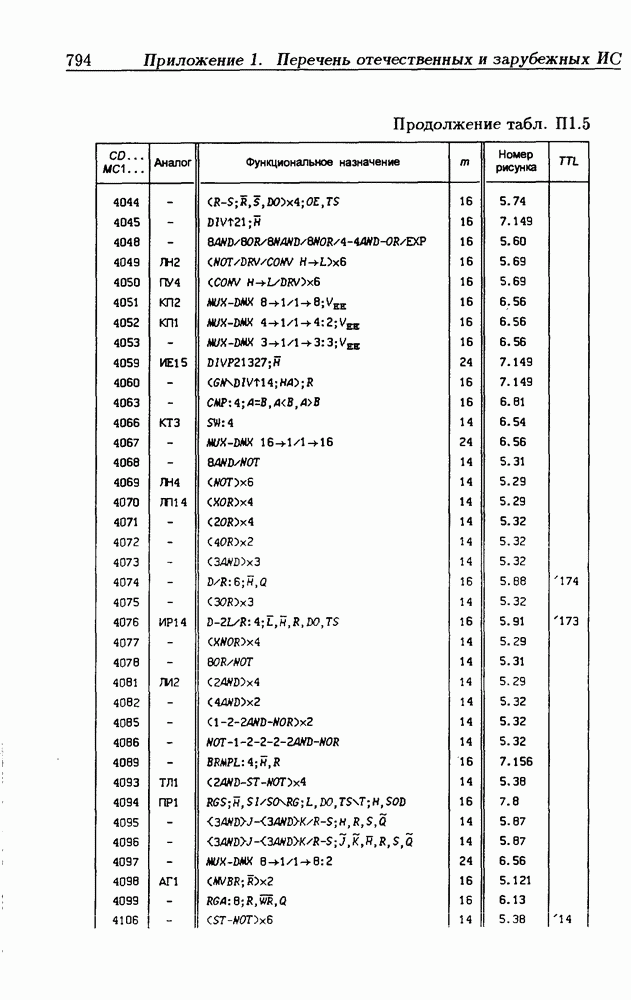
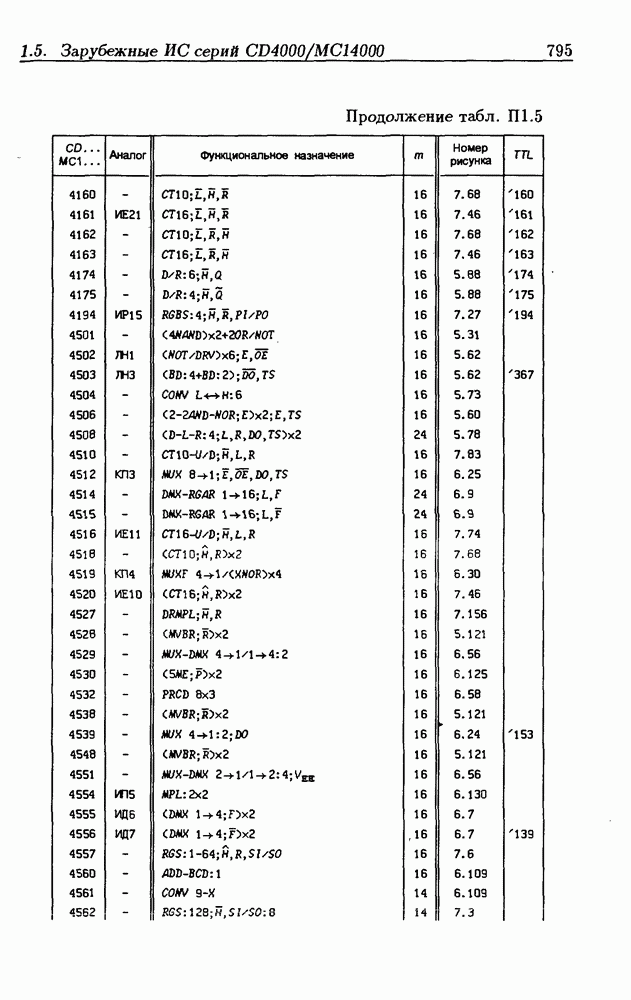
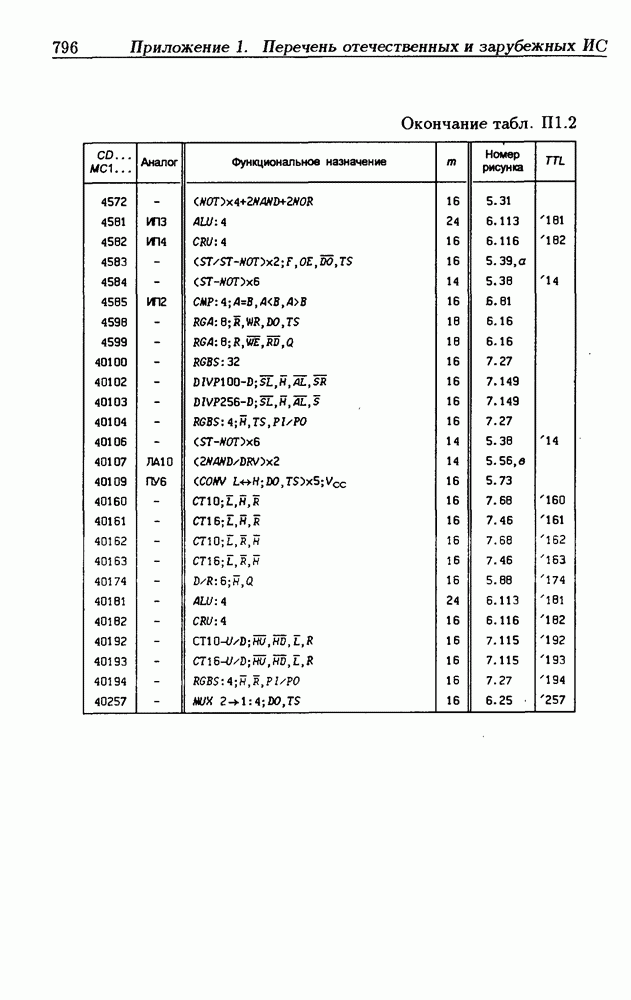
- Приложение 1. Перечень отечественных и зарубежных ИС
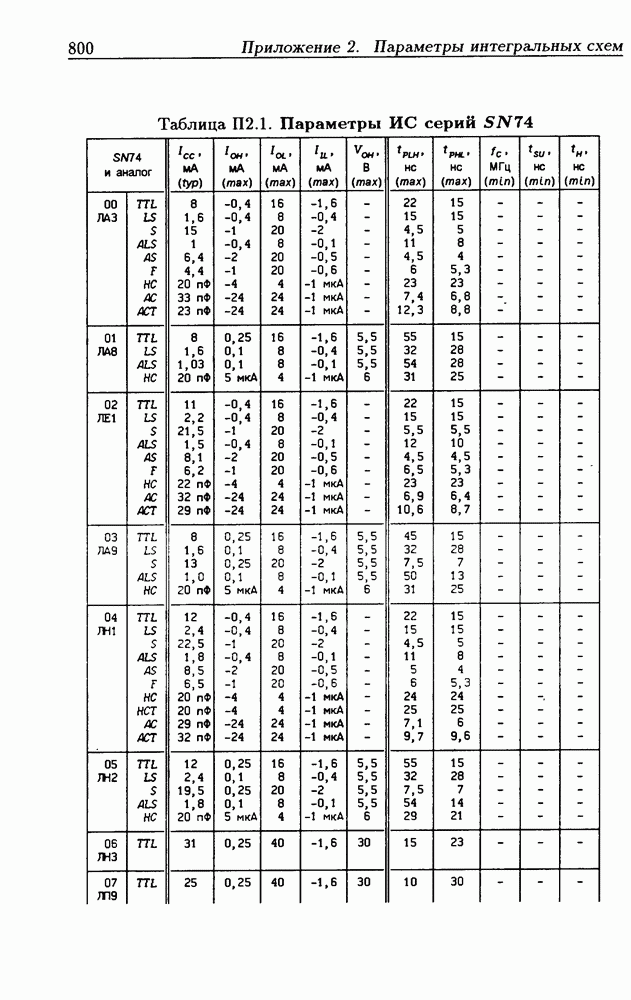
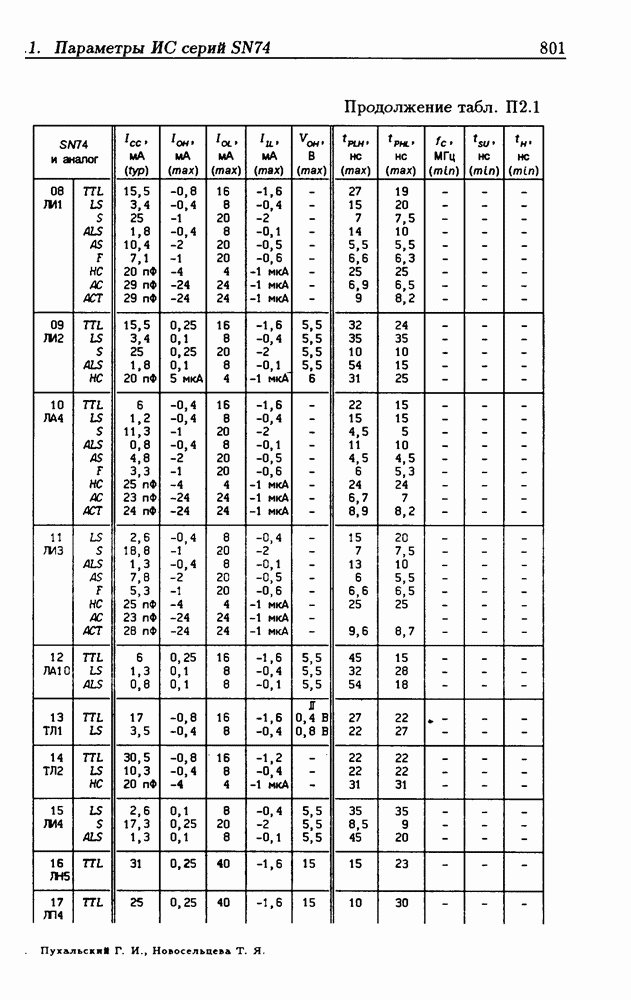
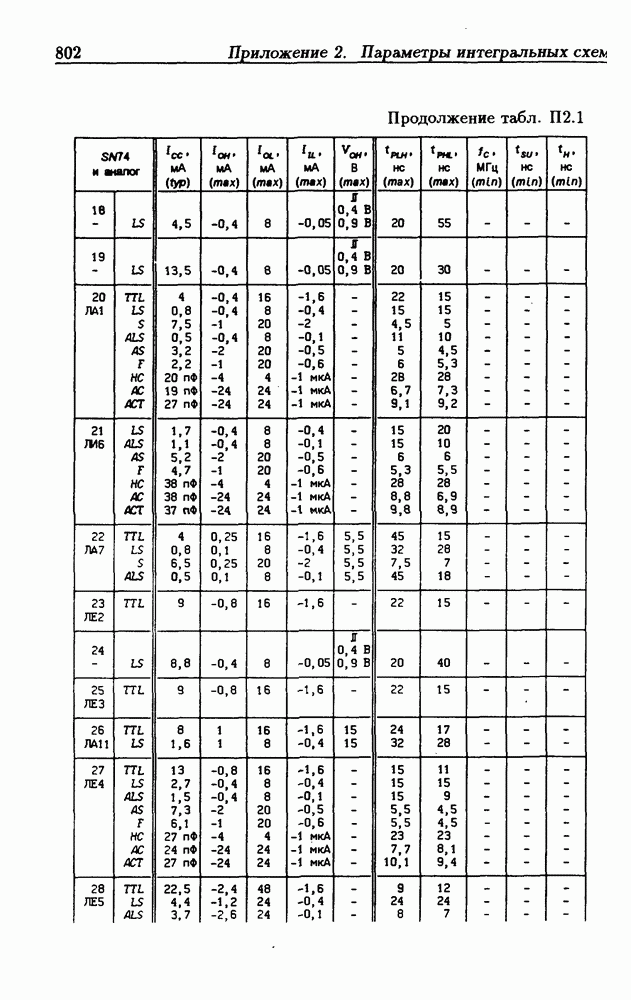
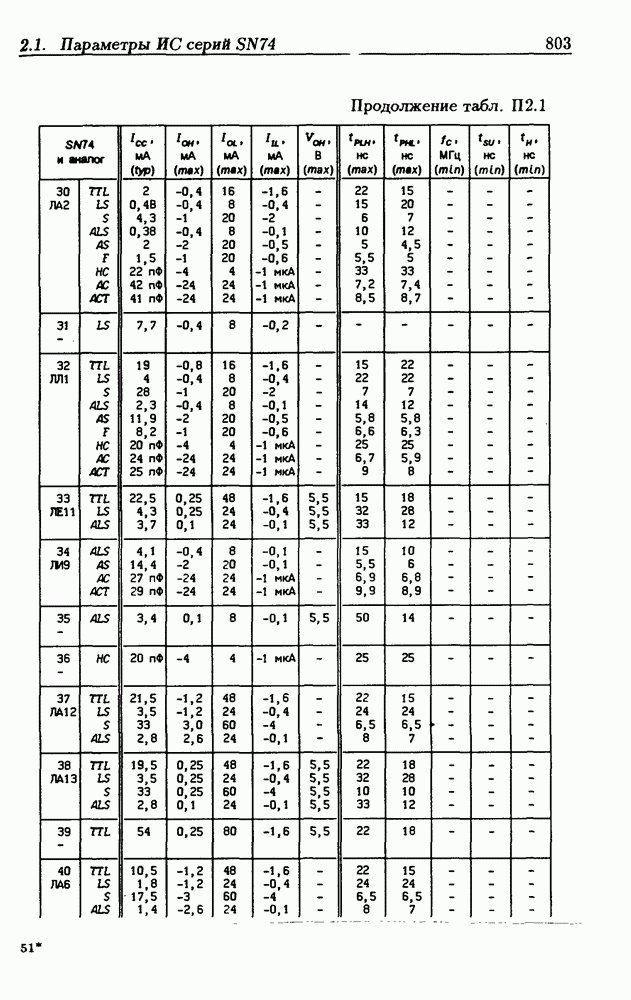
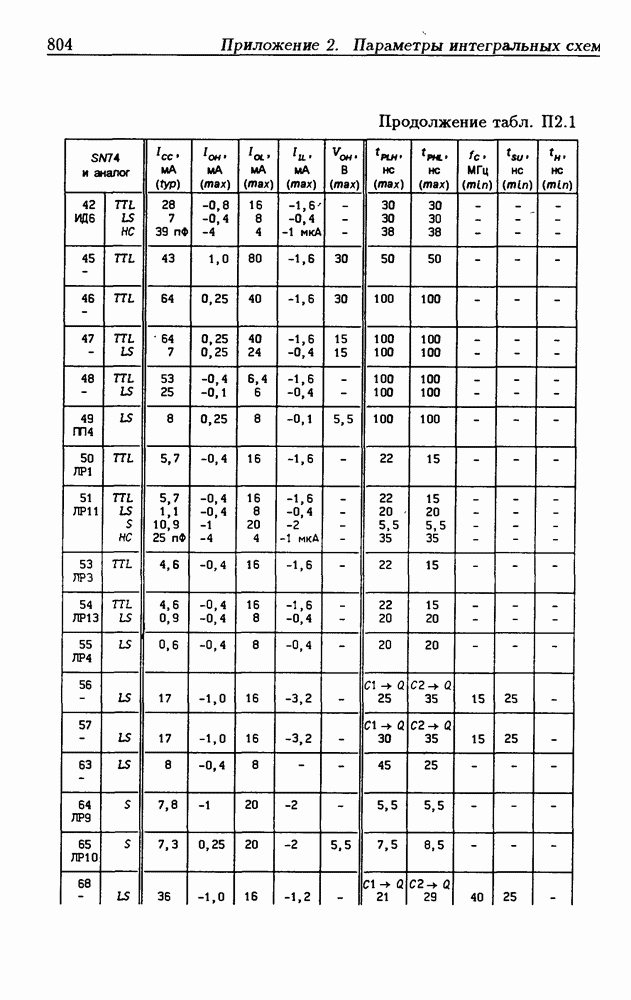
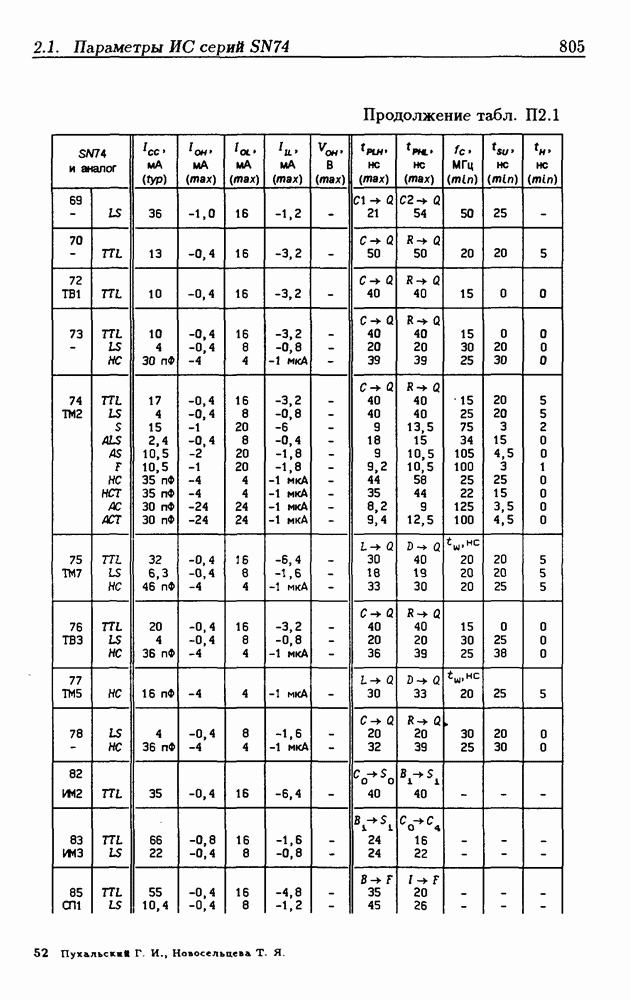
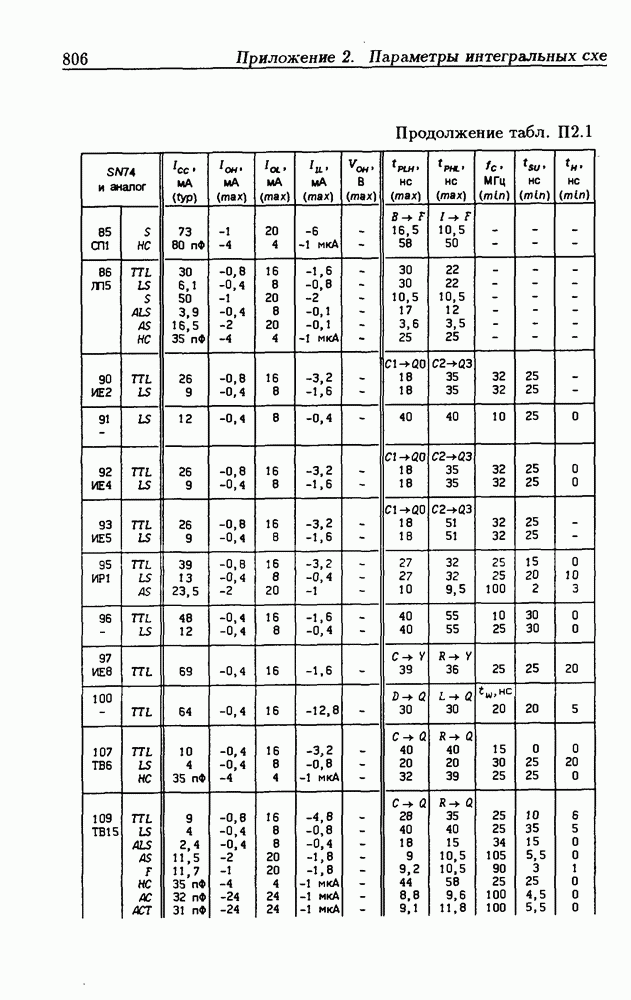
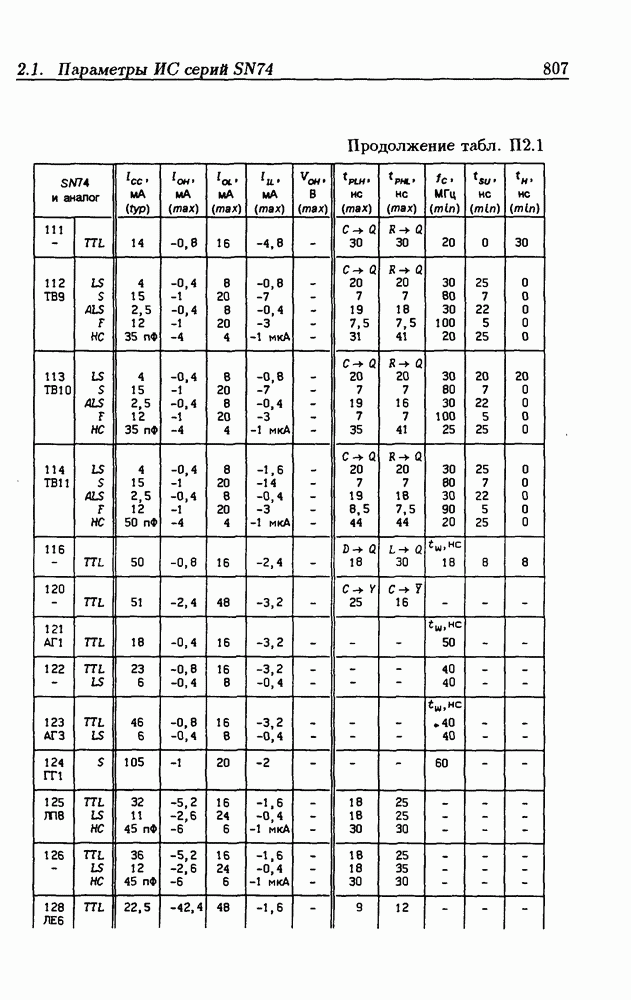
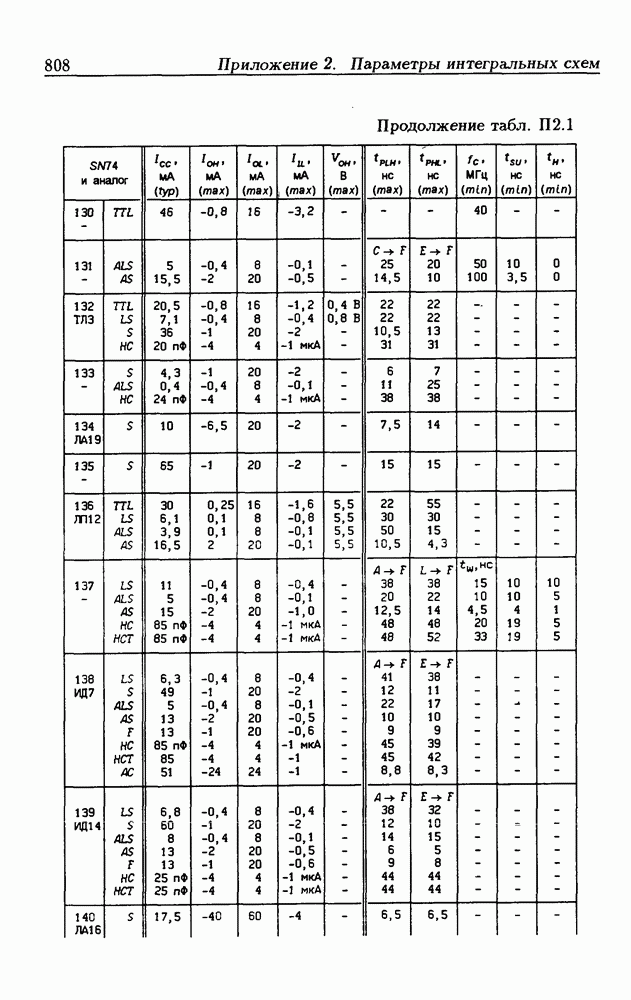
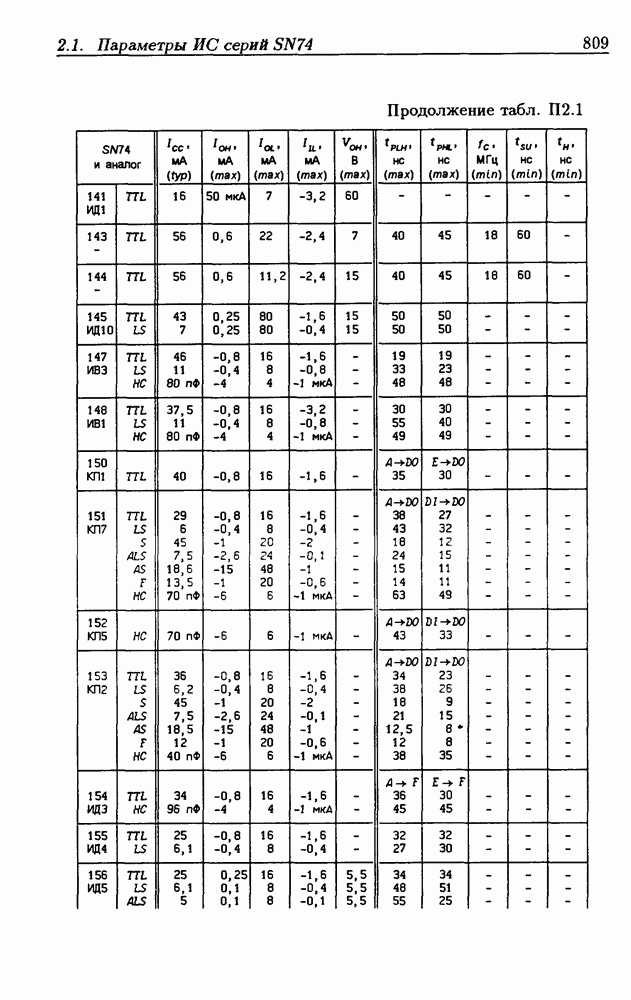
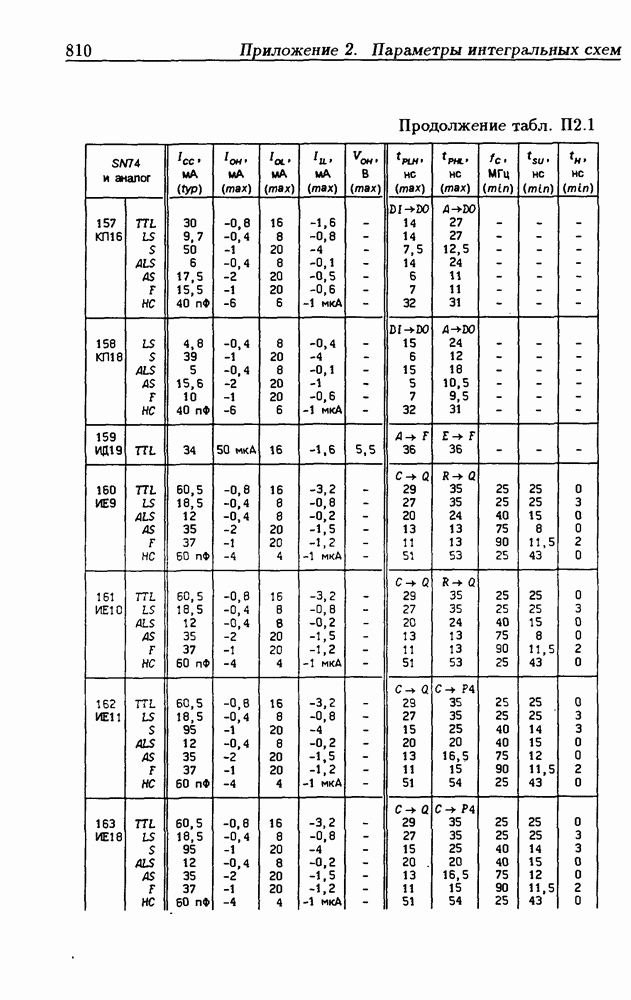
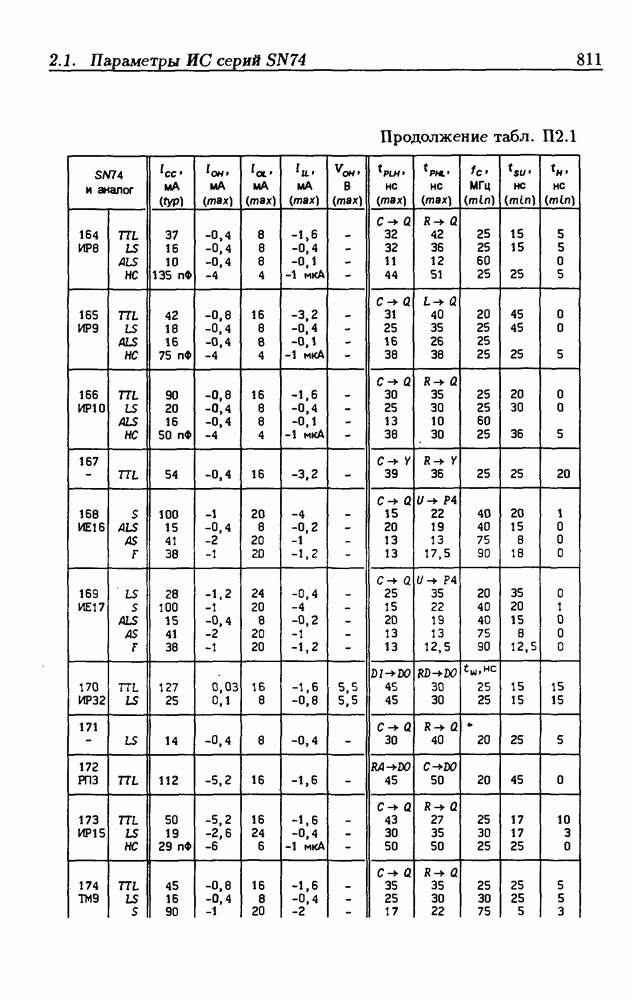
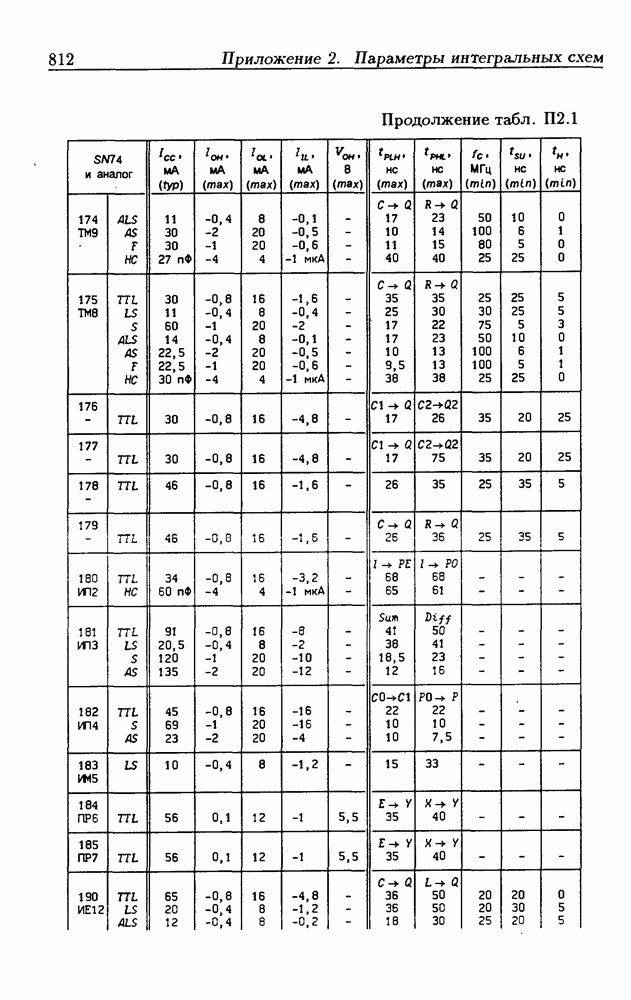
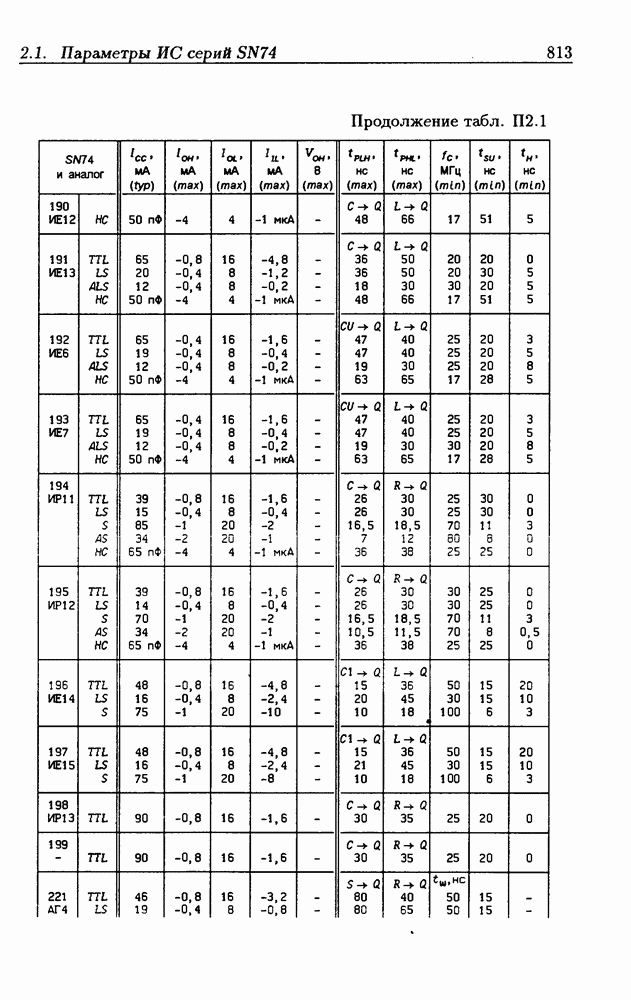
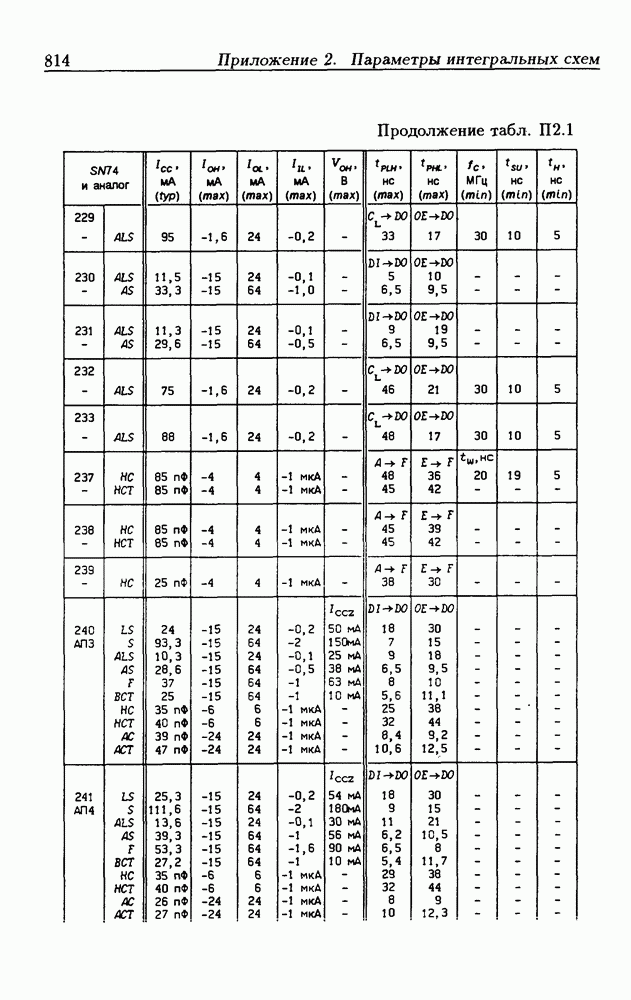
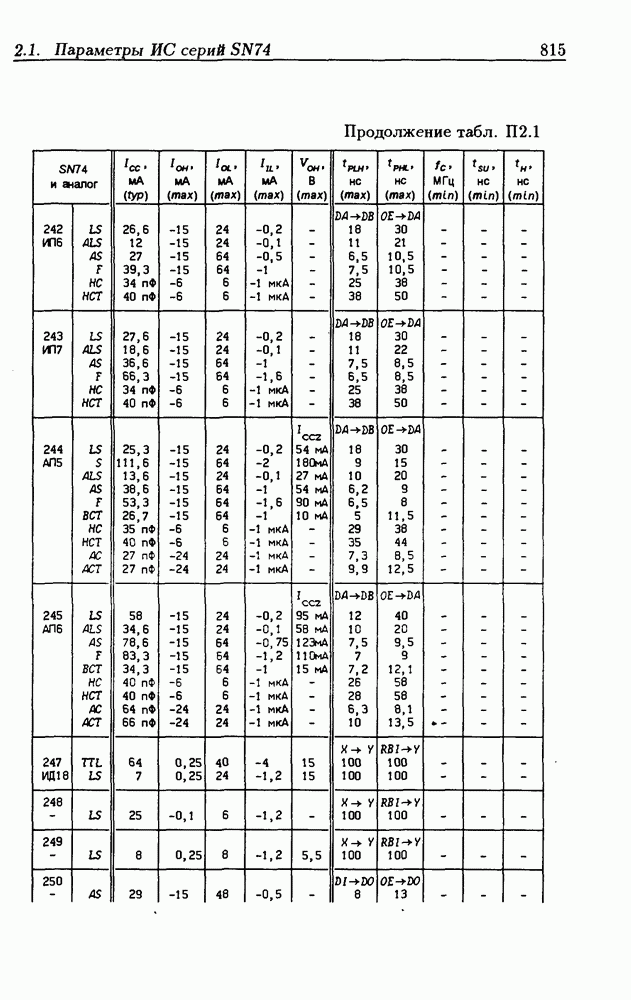
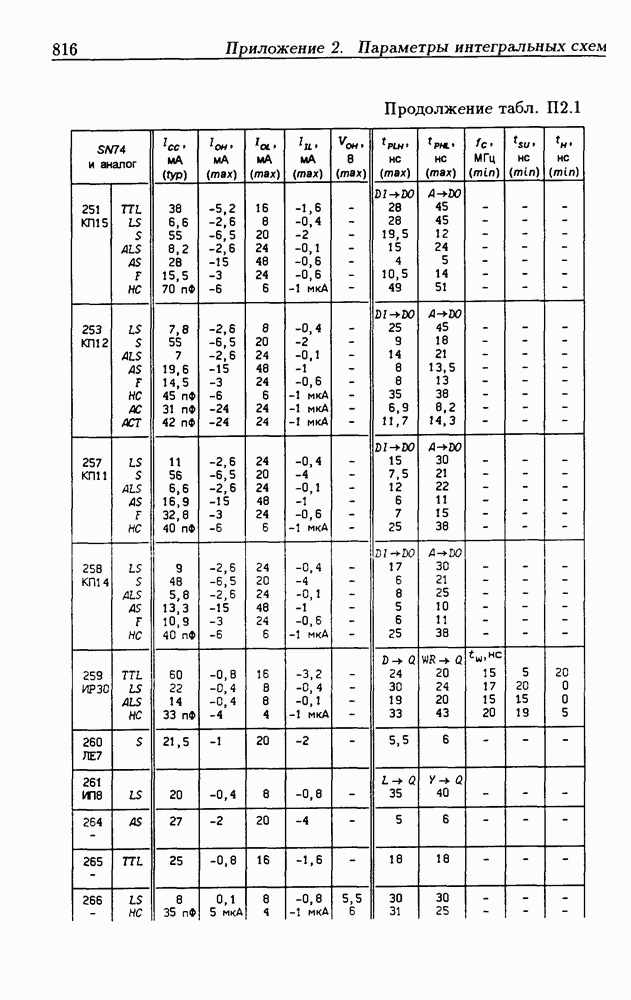
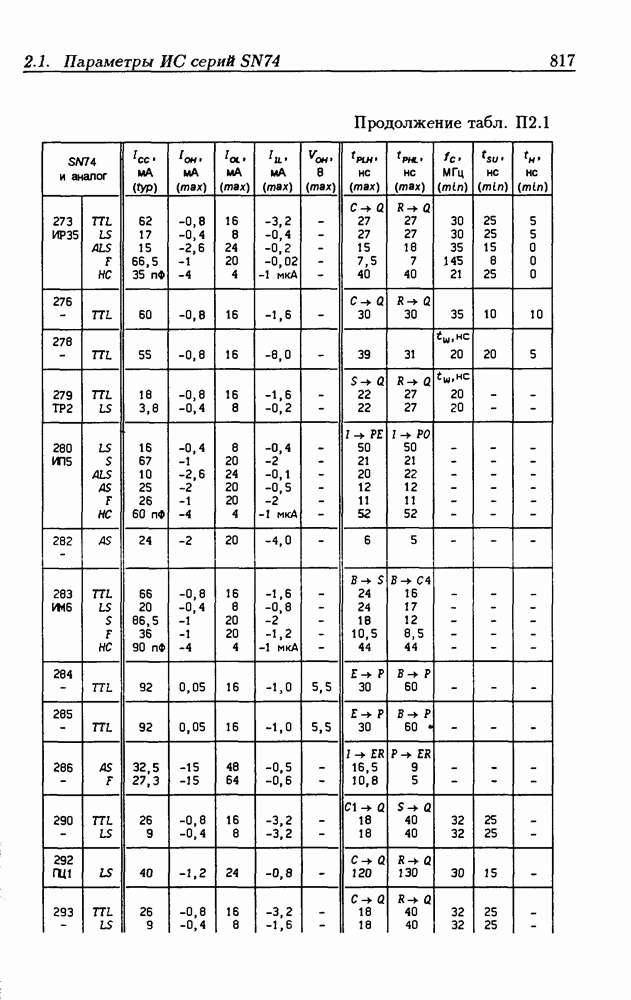
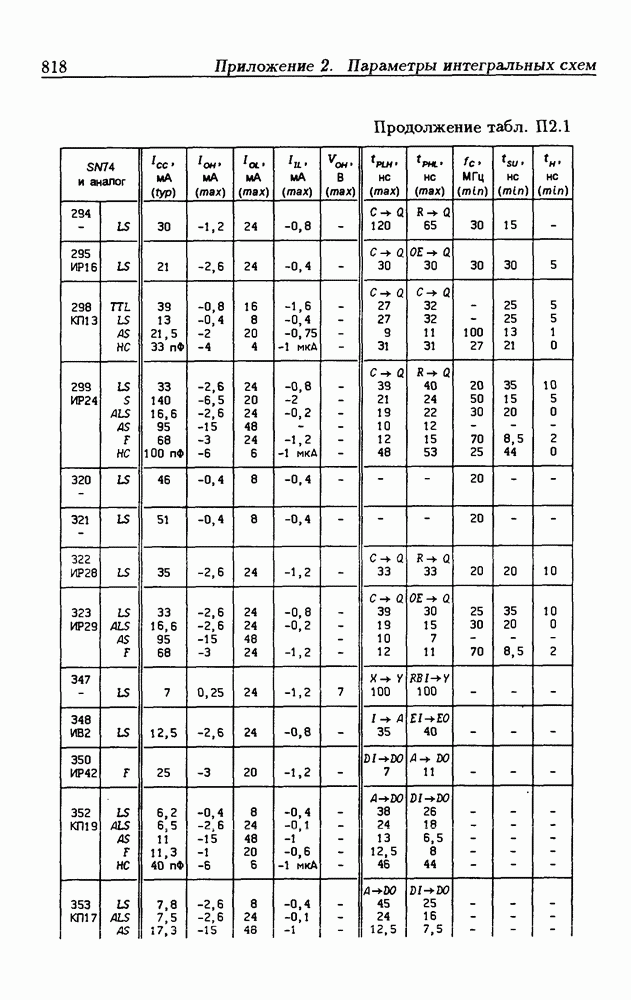
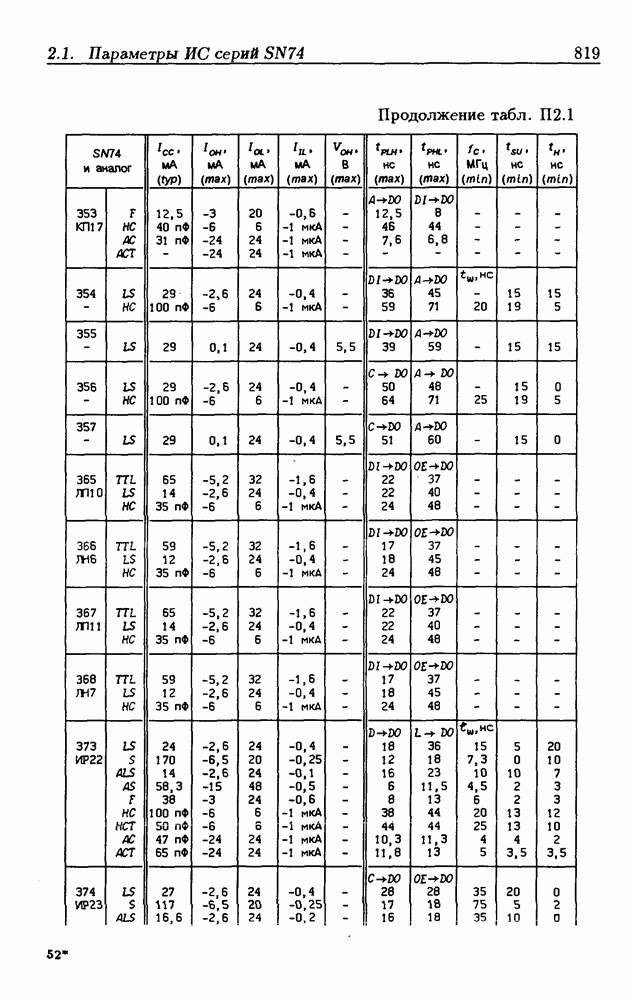
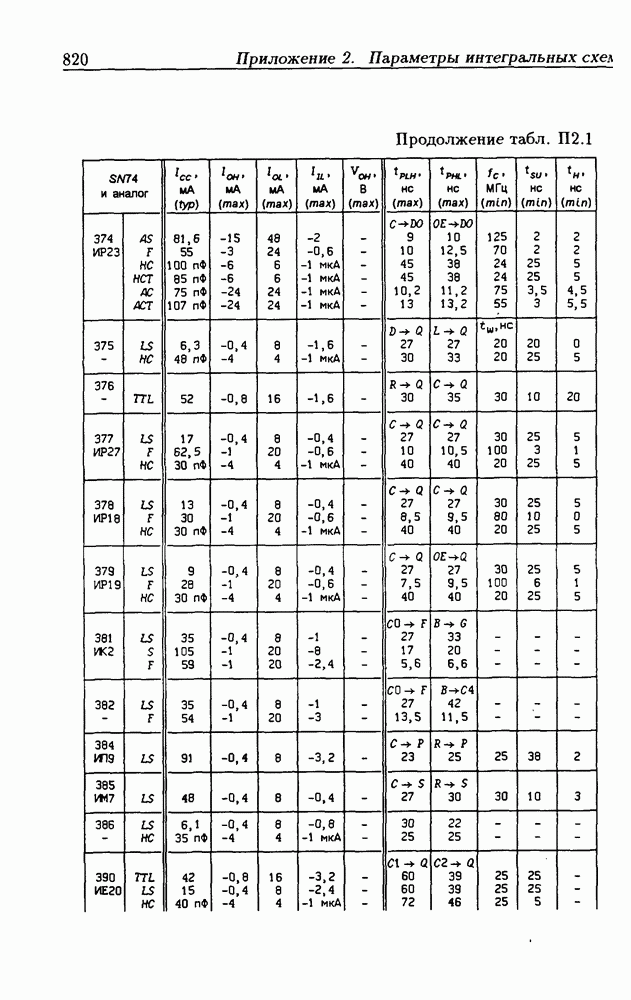
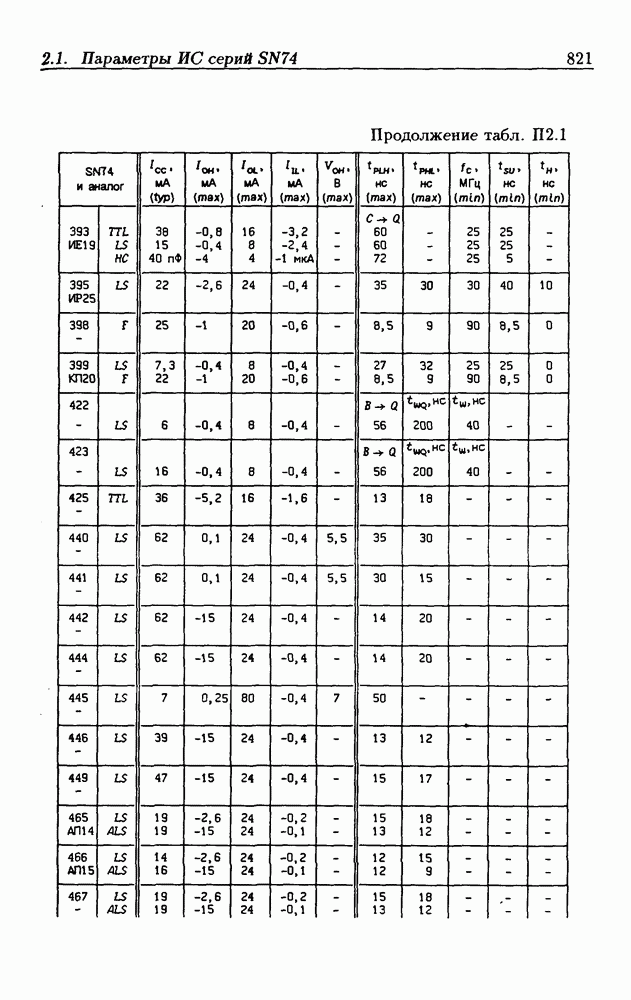
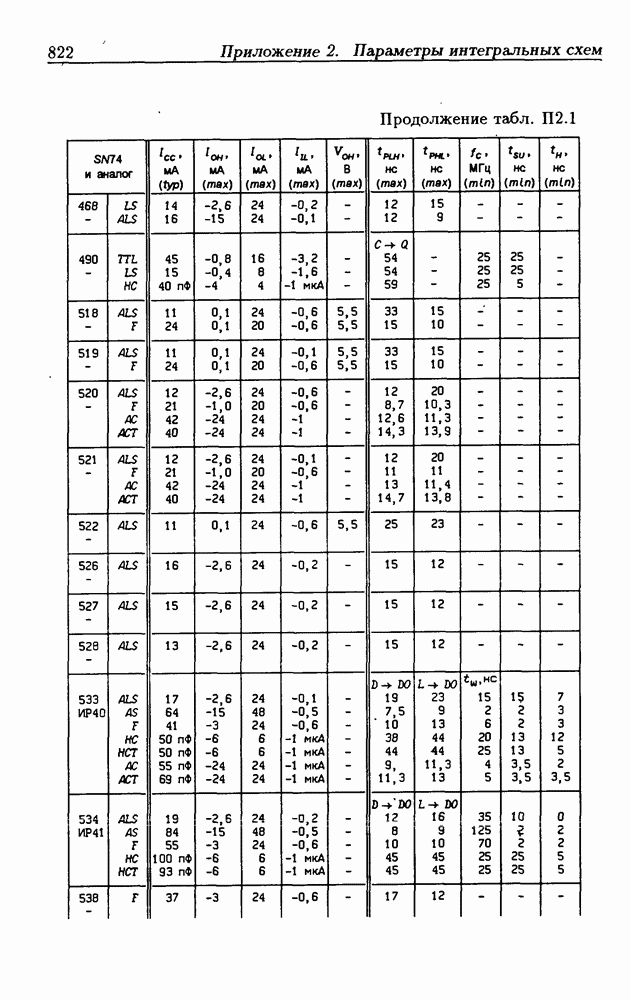
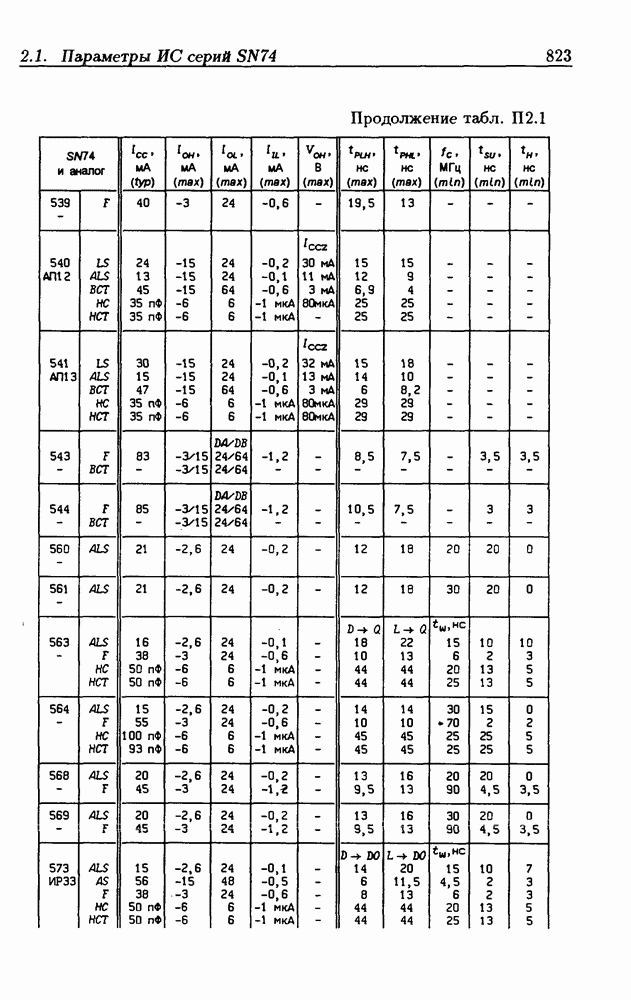
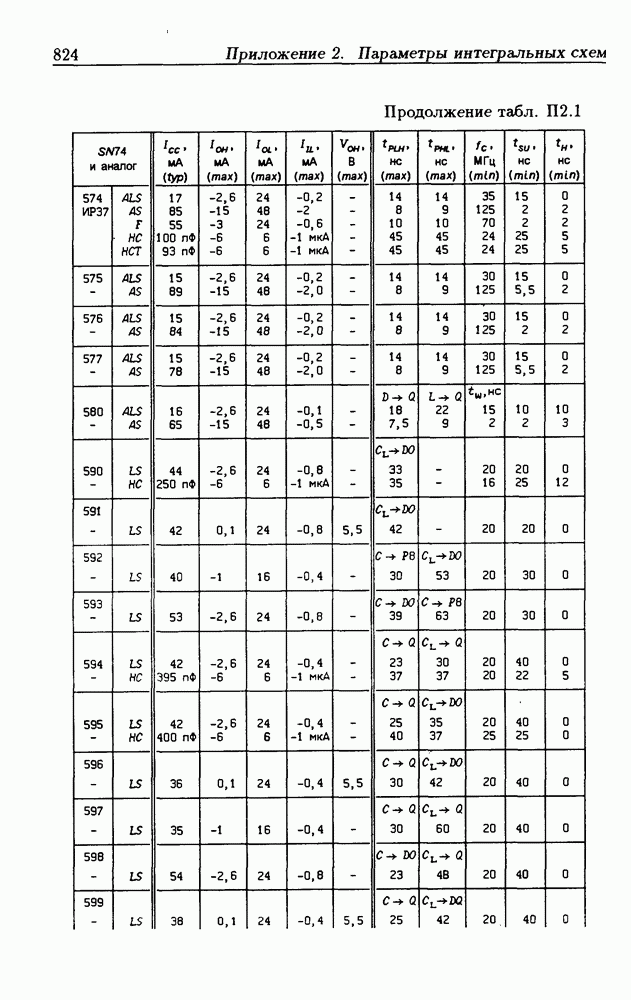
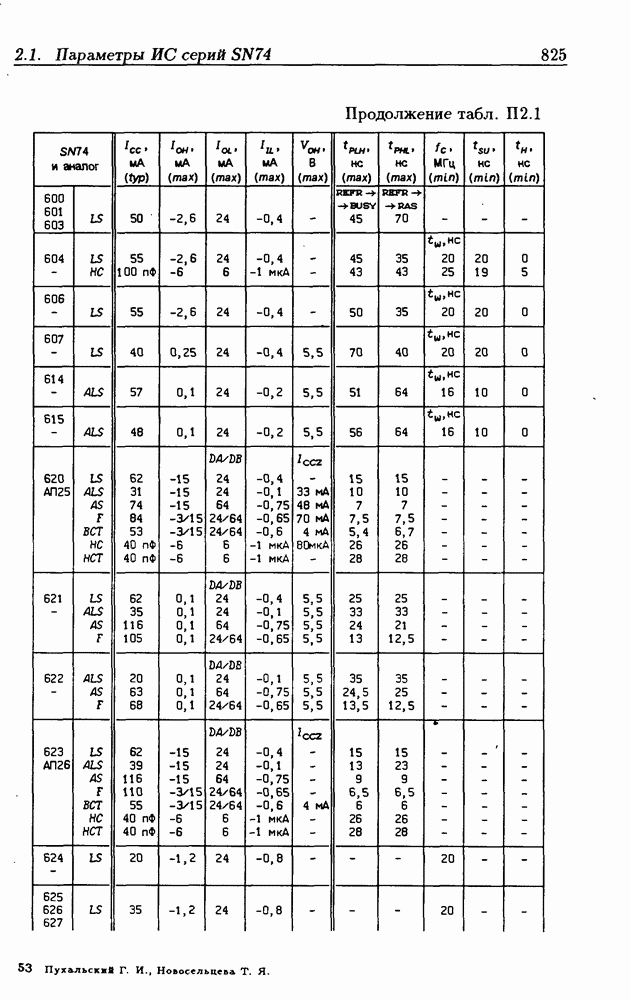
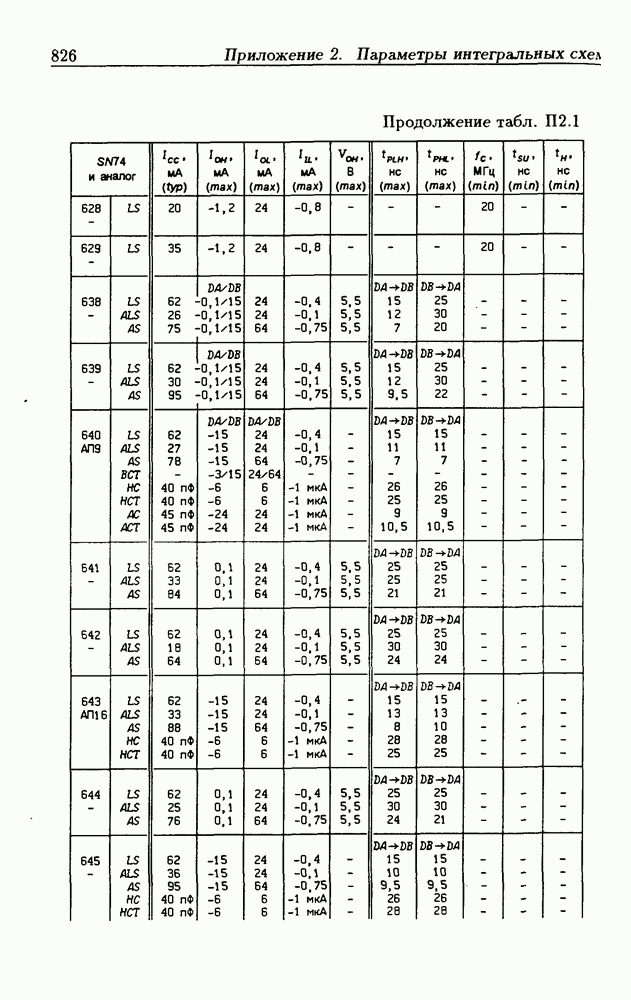
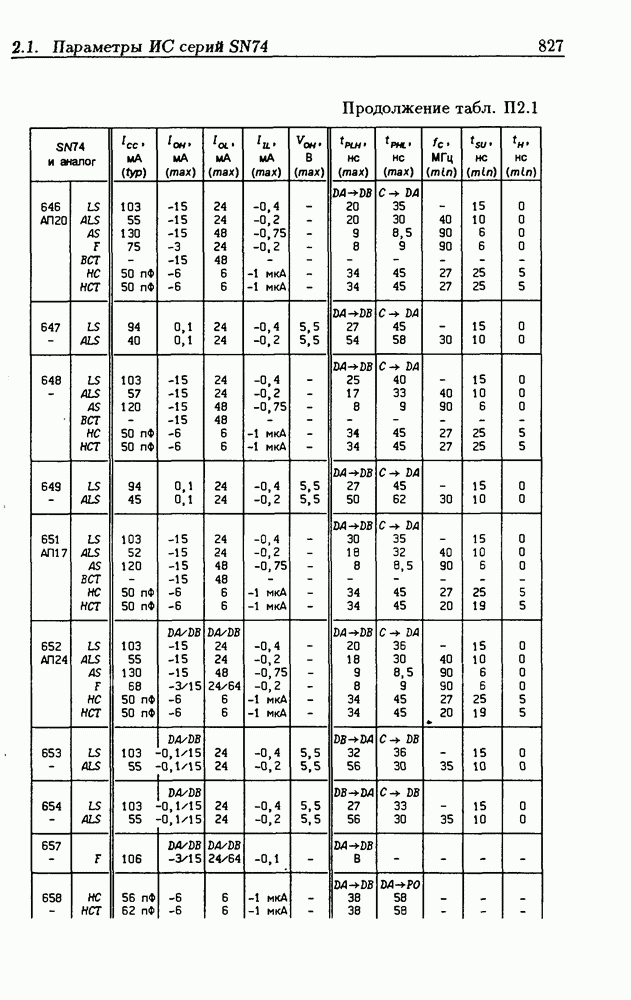
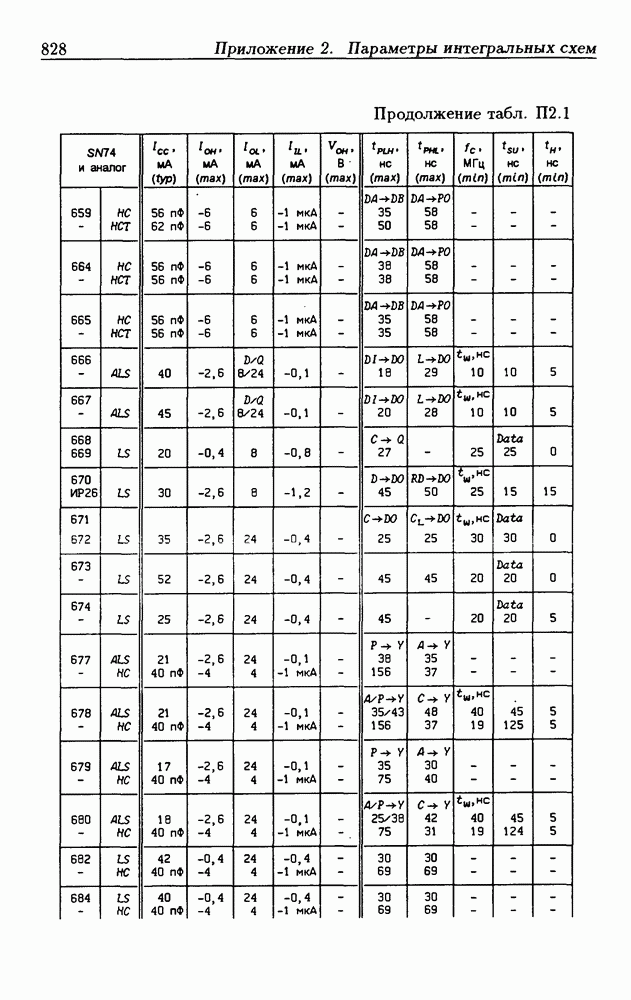
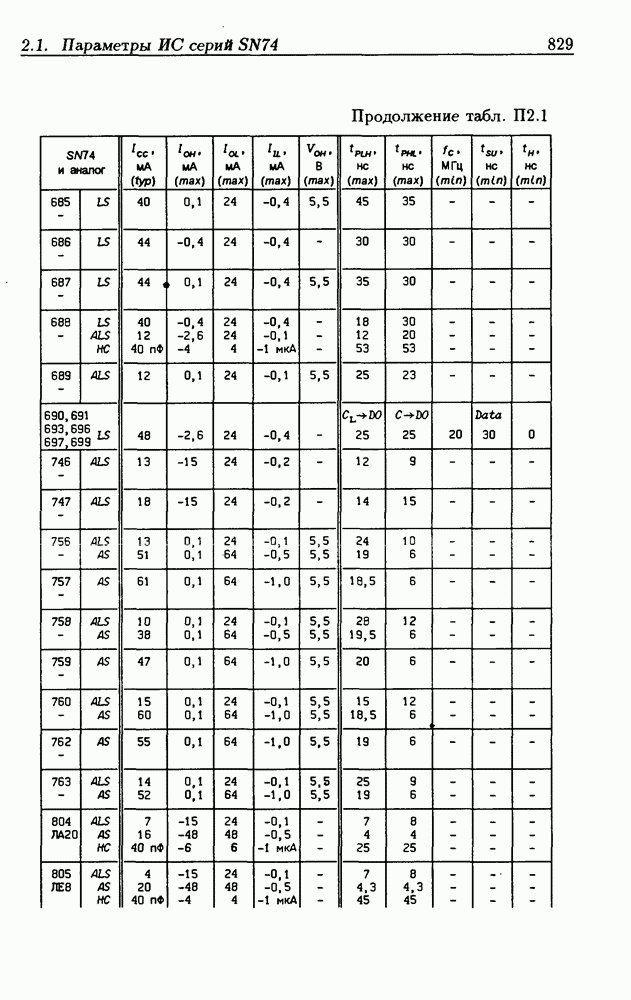
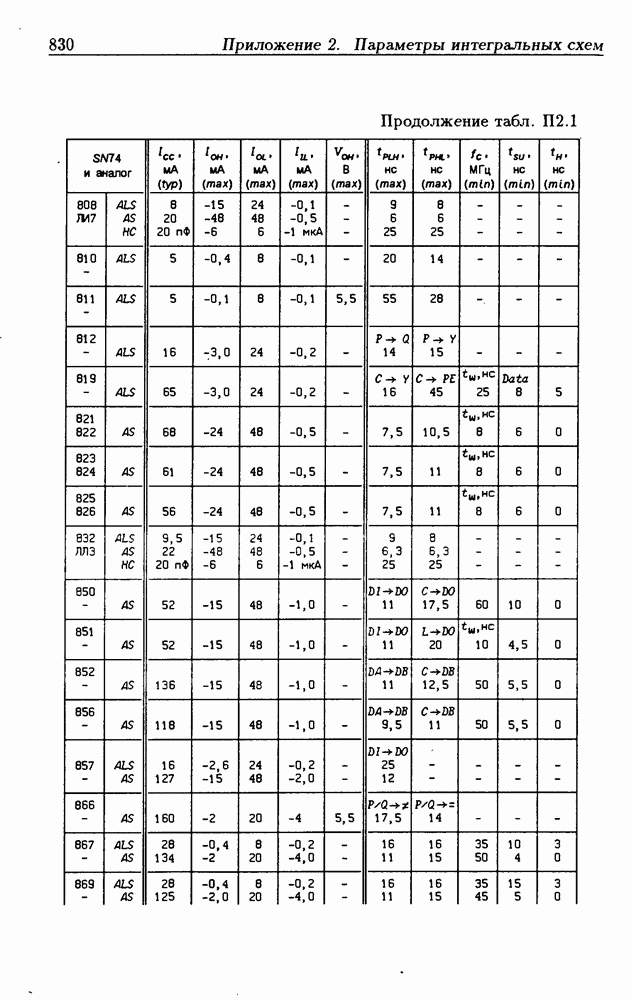
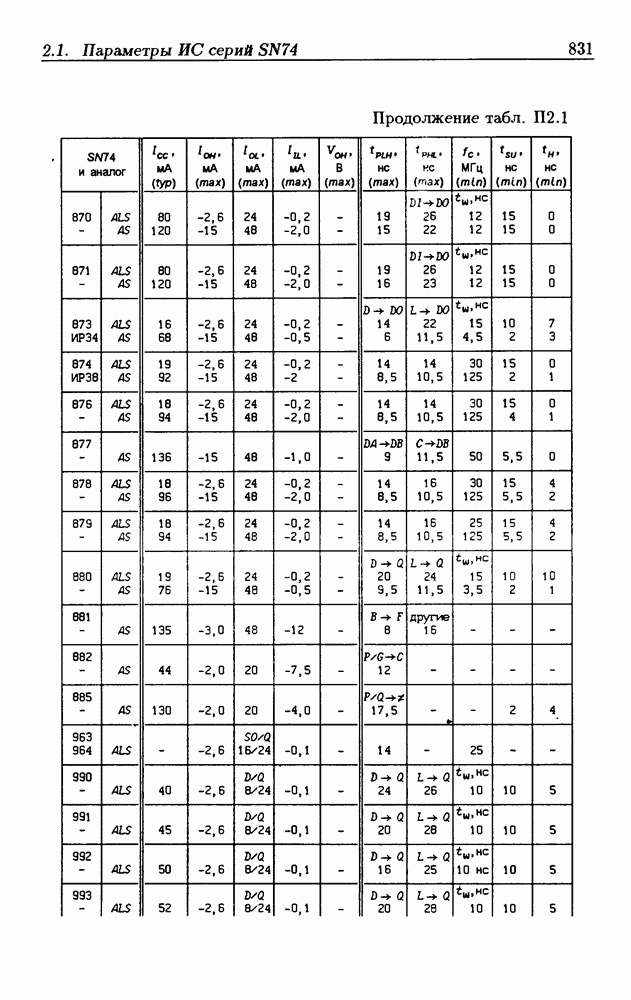
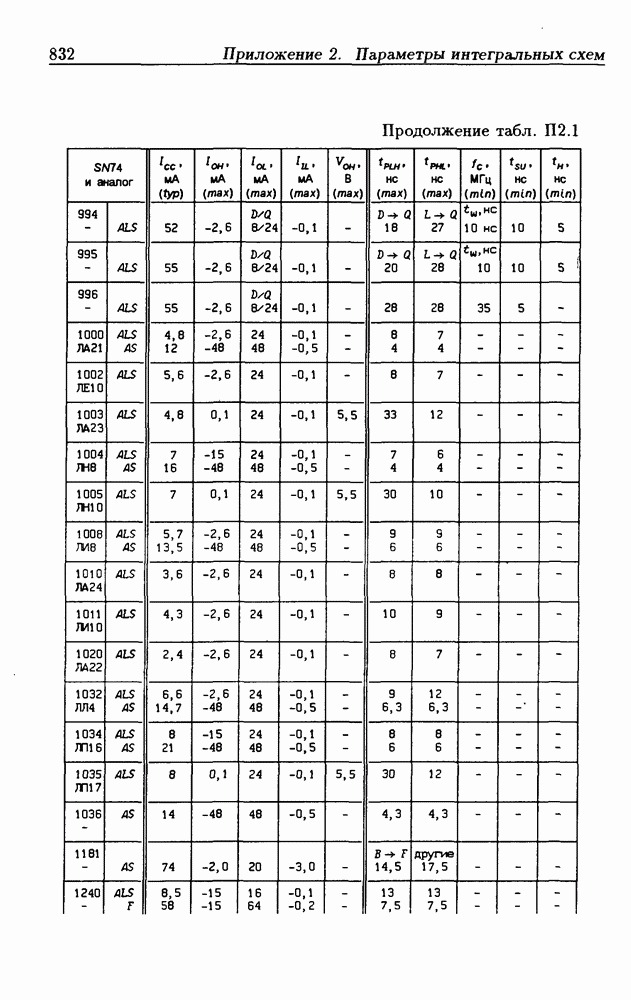
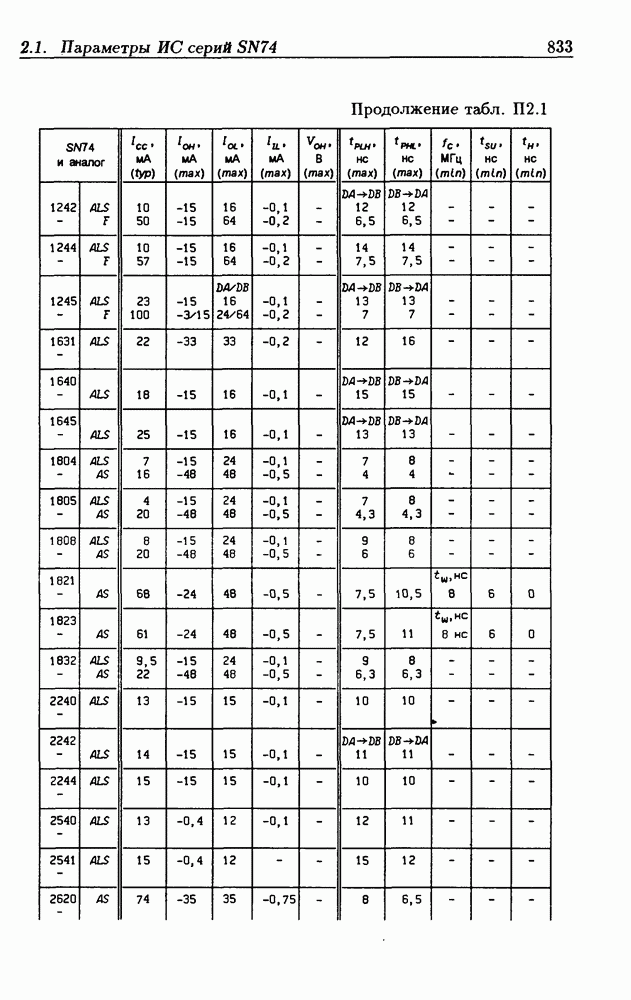
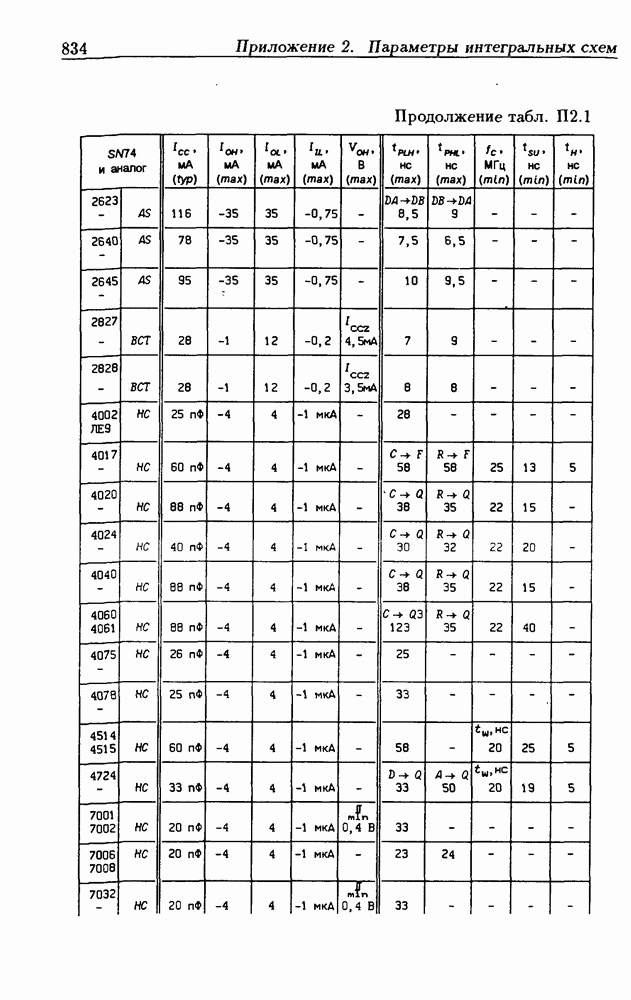
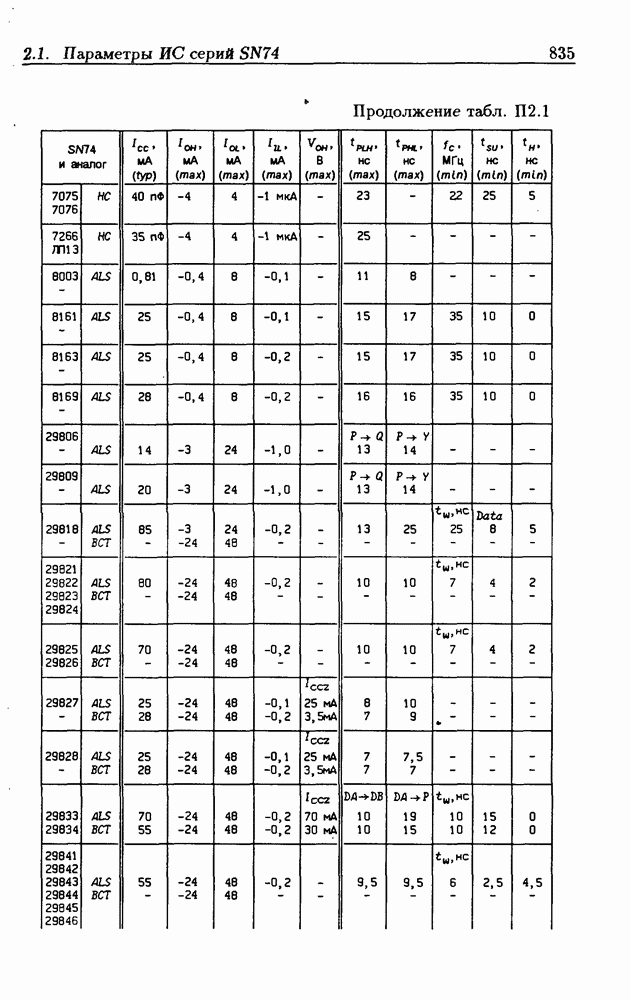
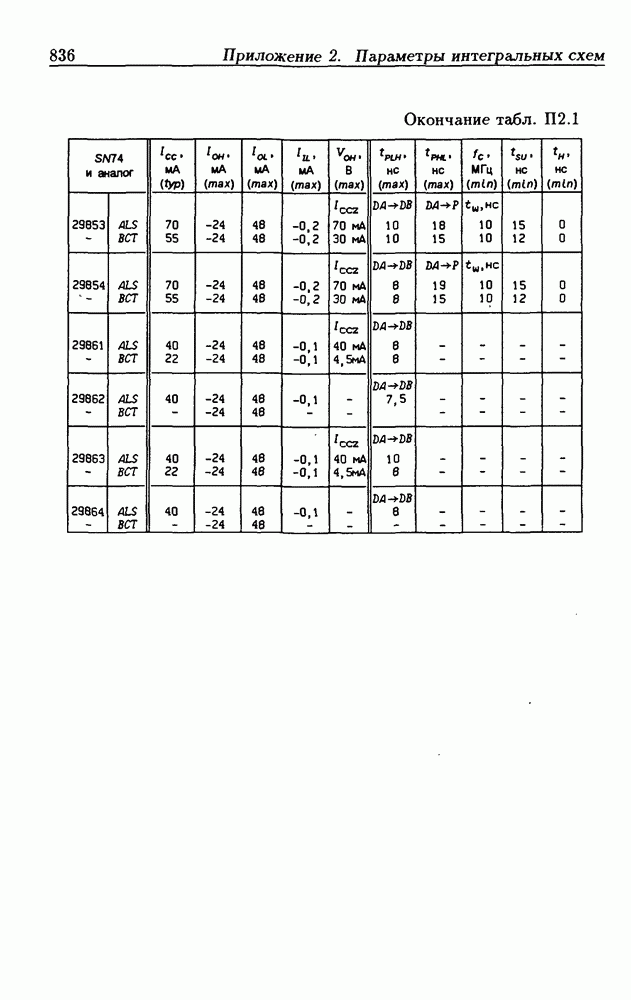
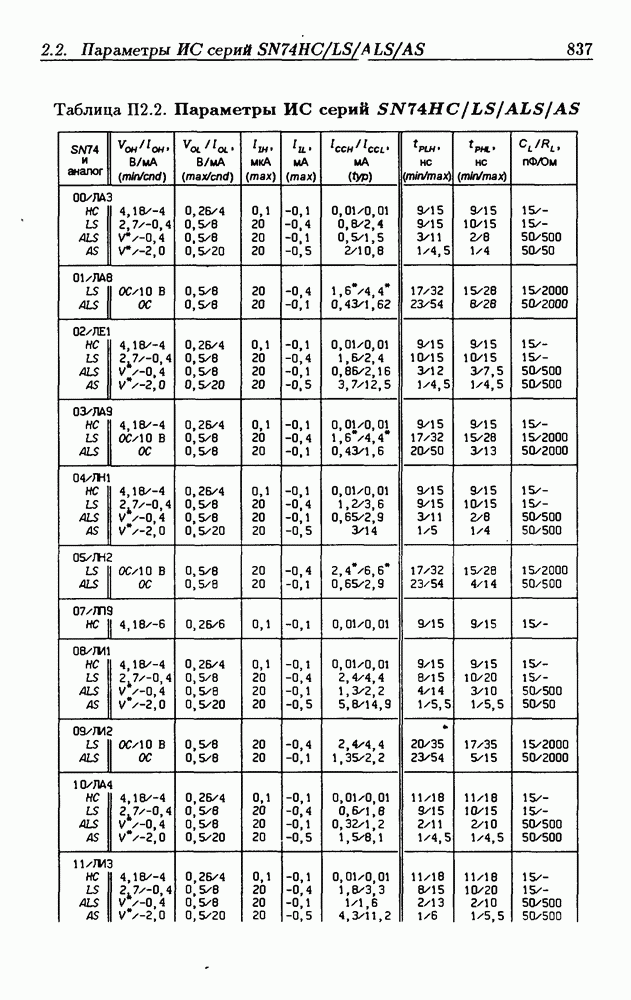
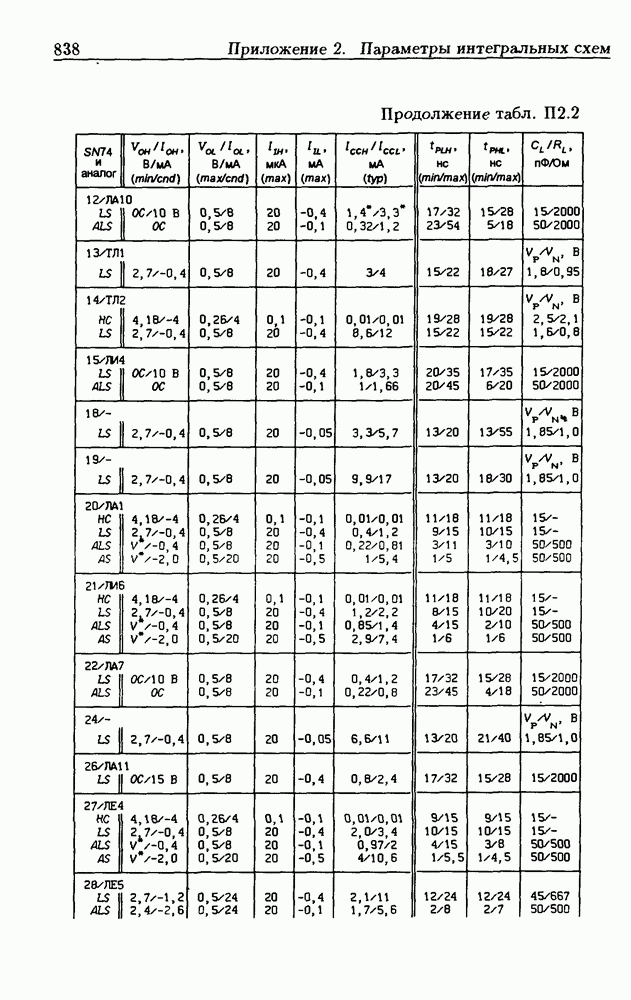
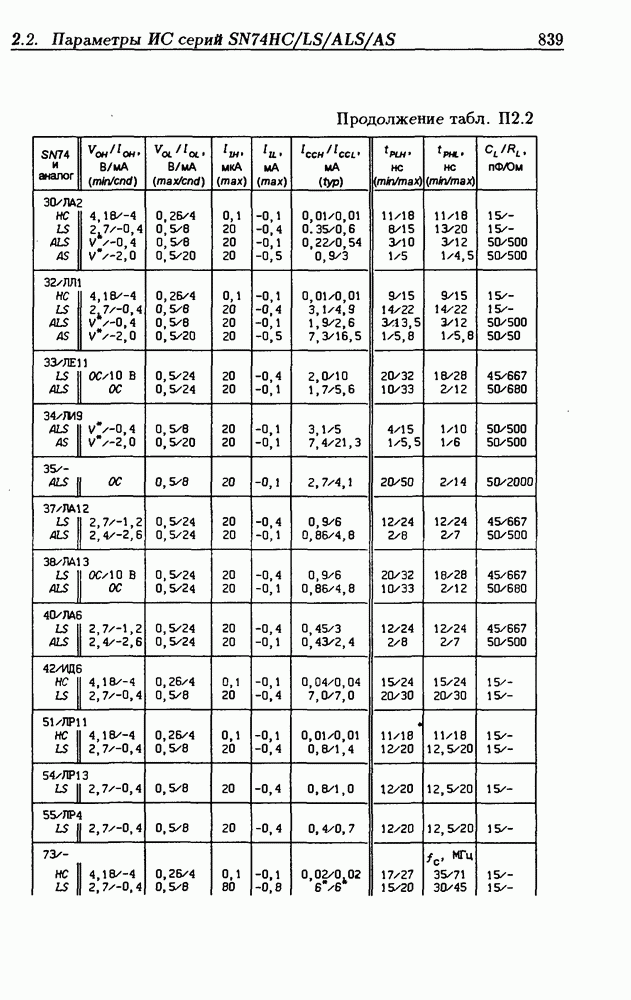
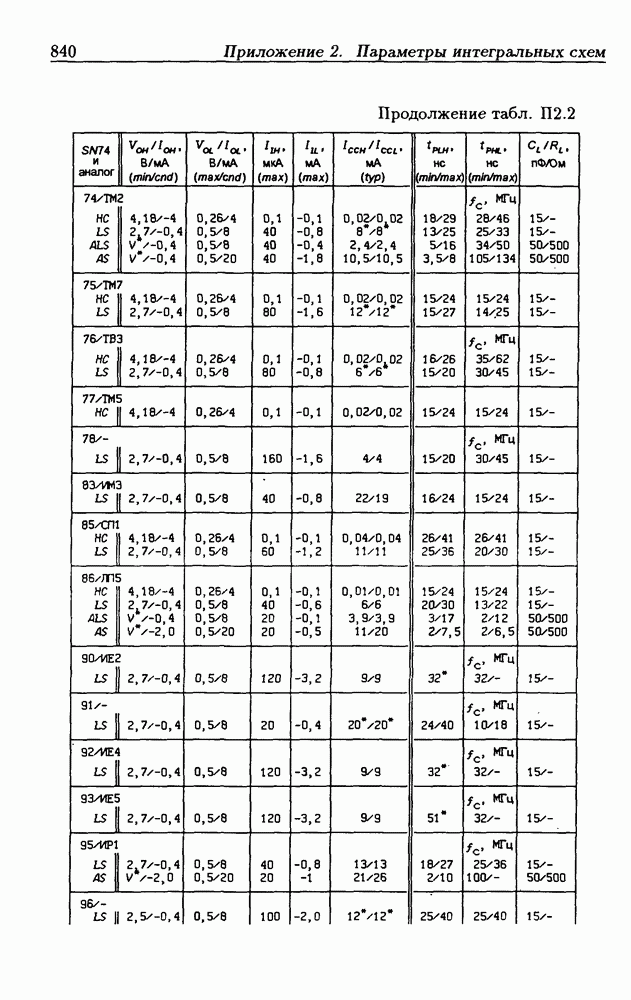
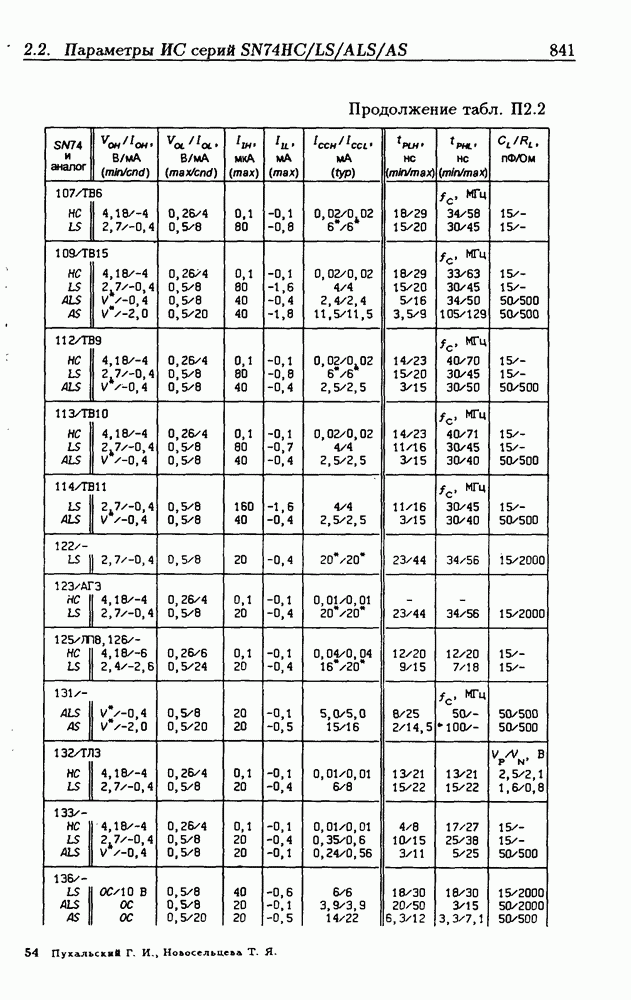
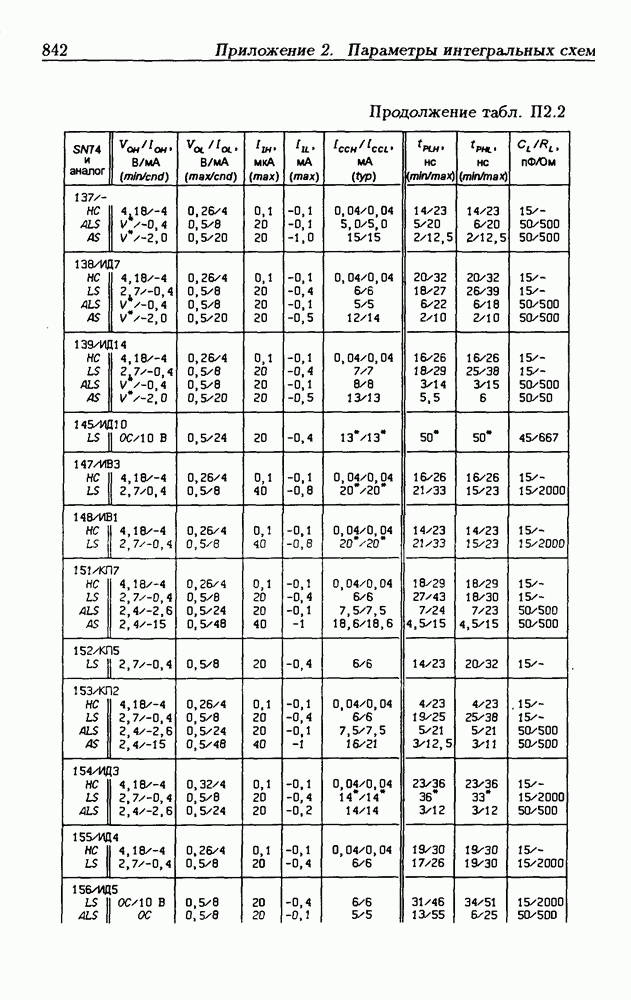
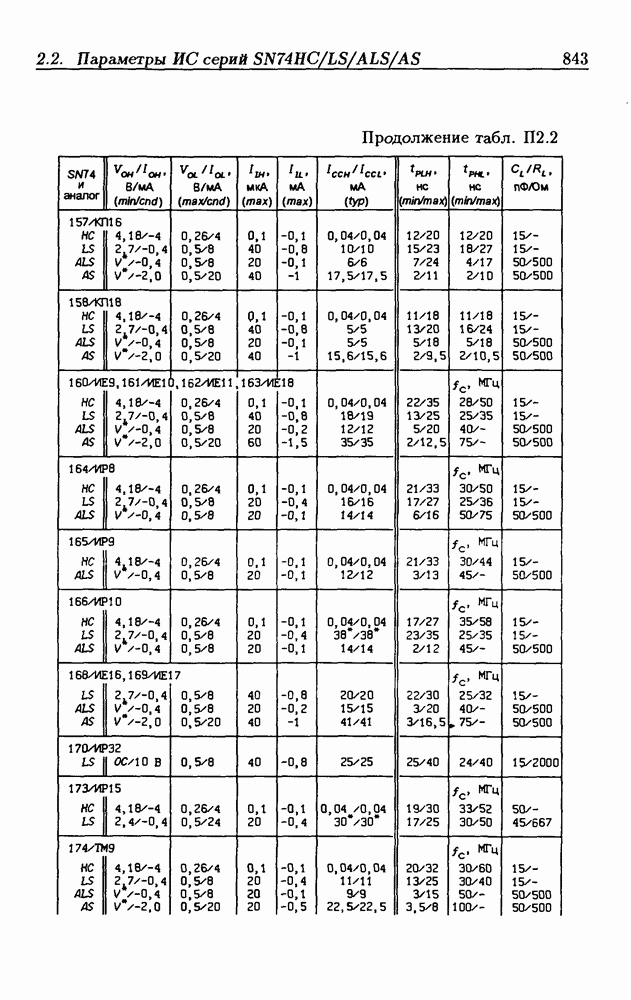
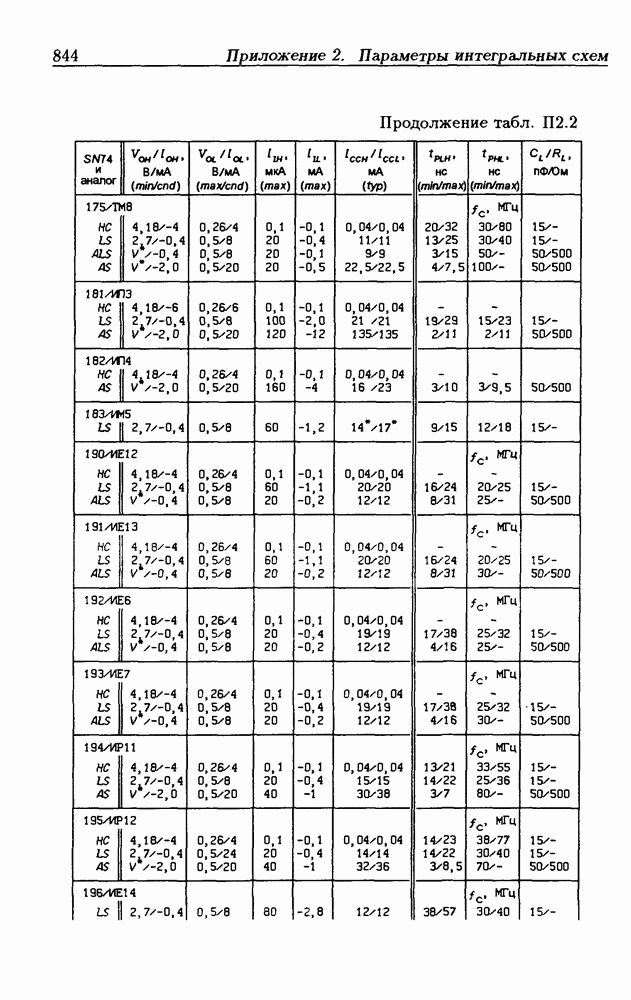
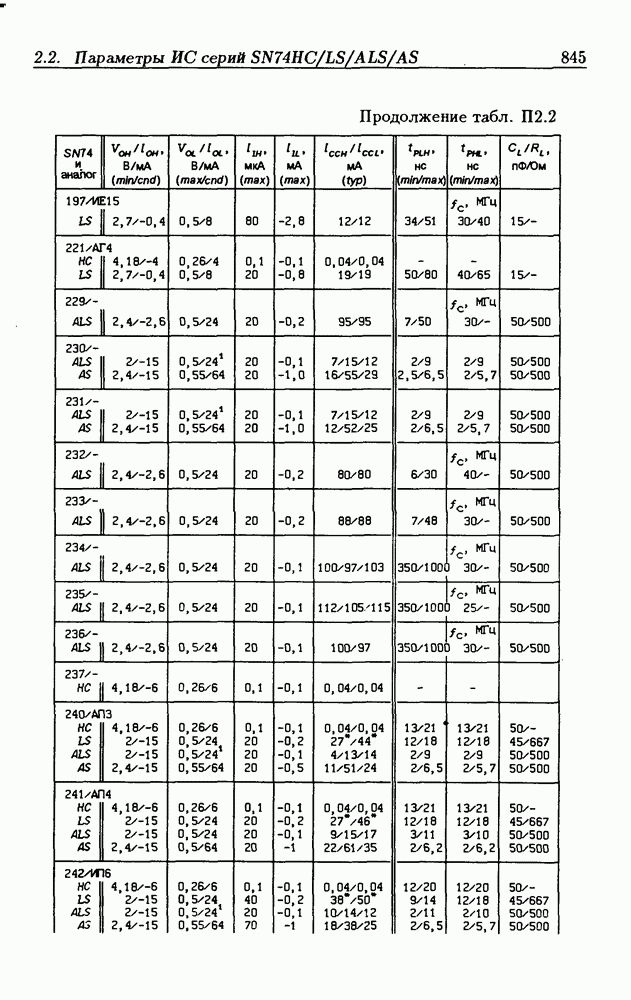
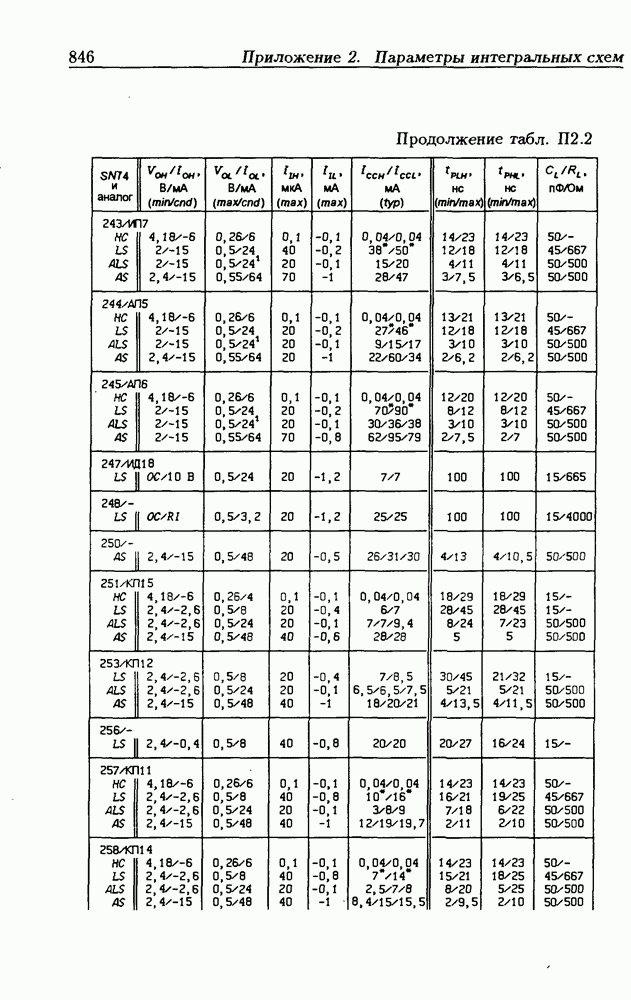
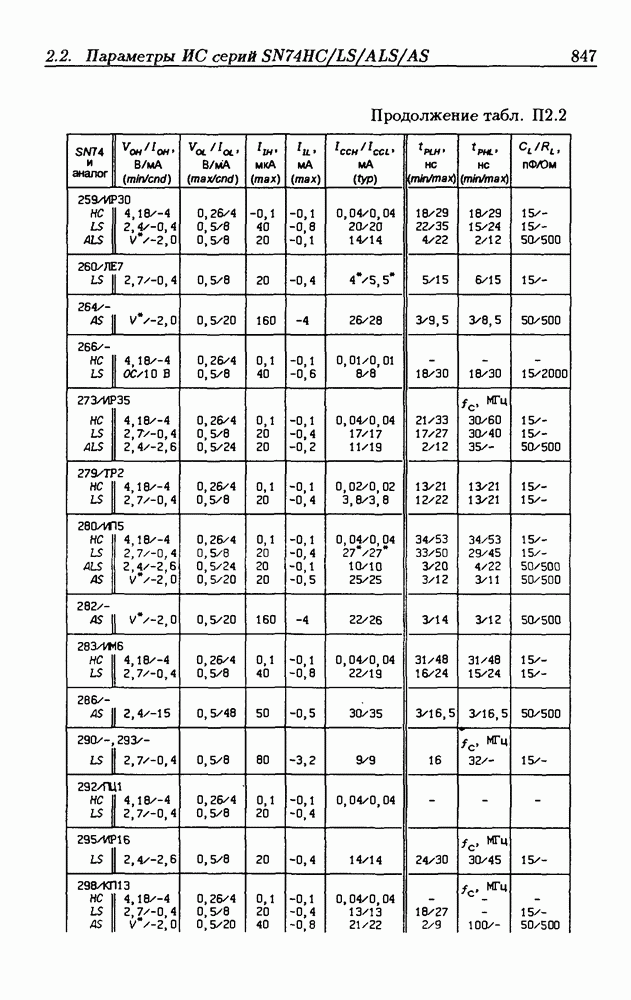
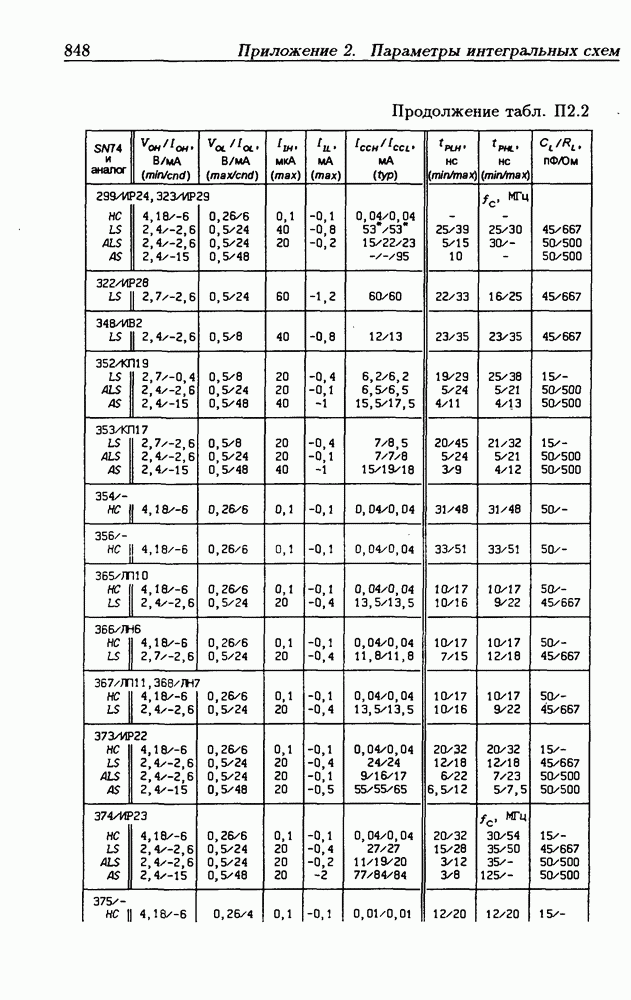
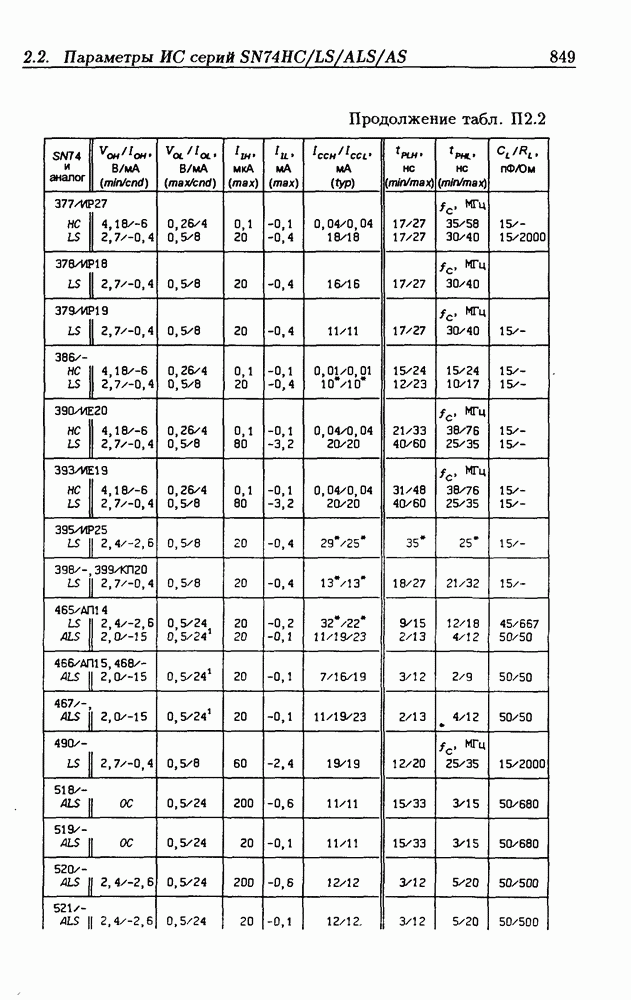
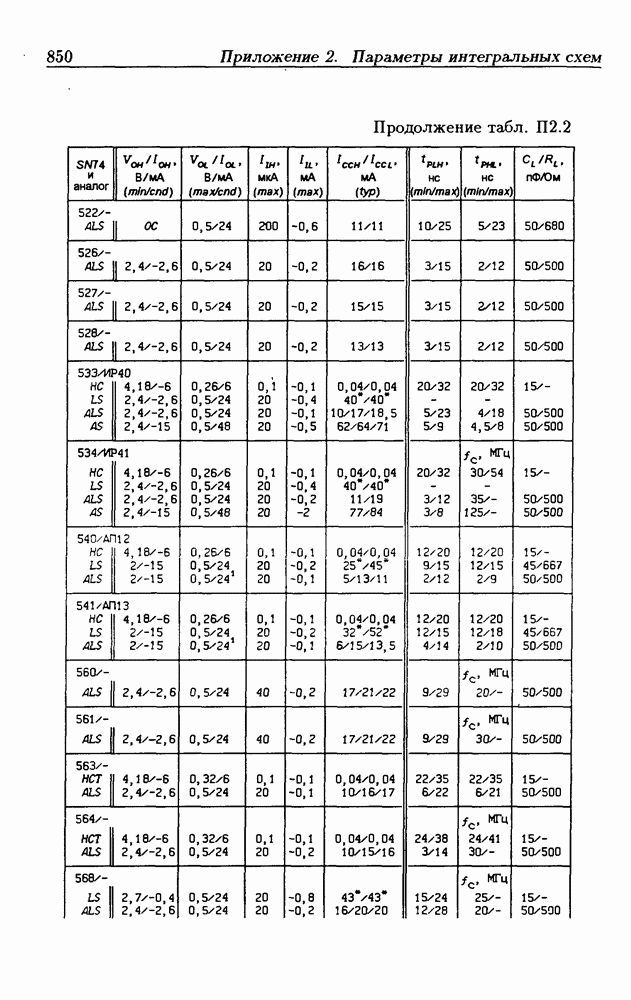
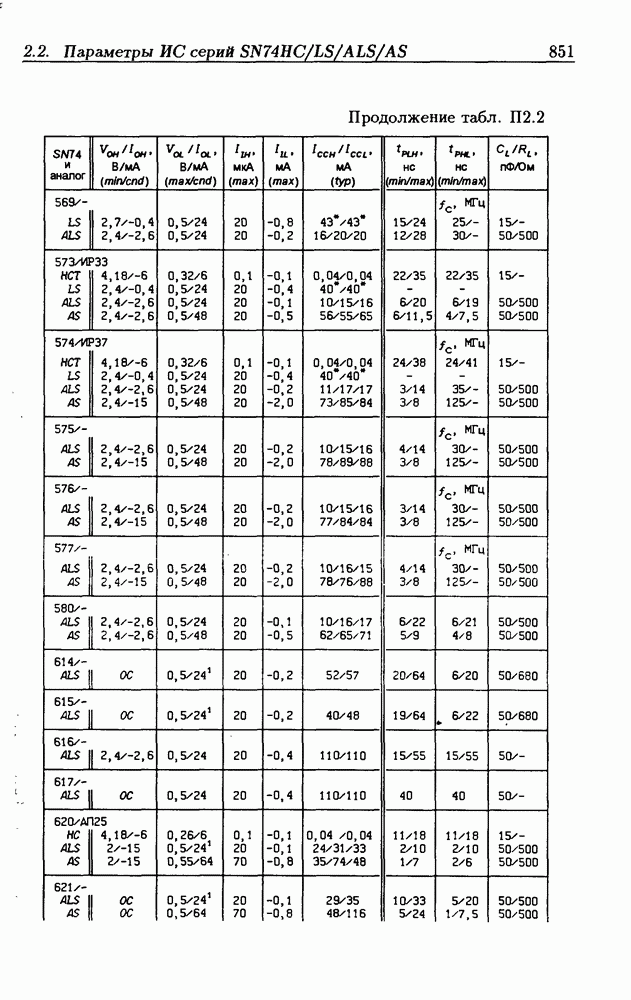
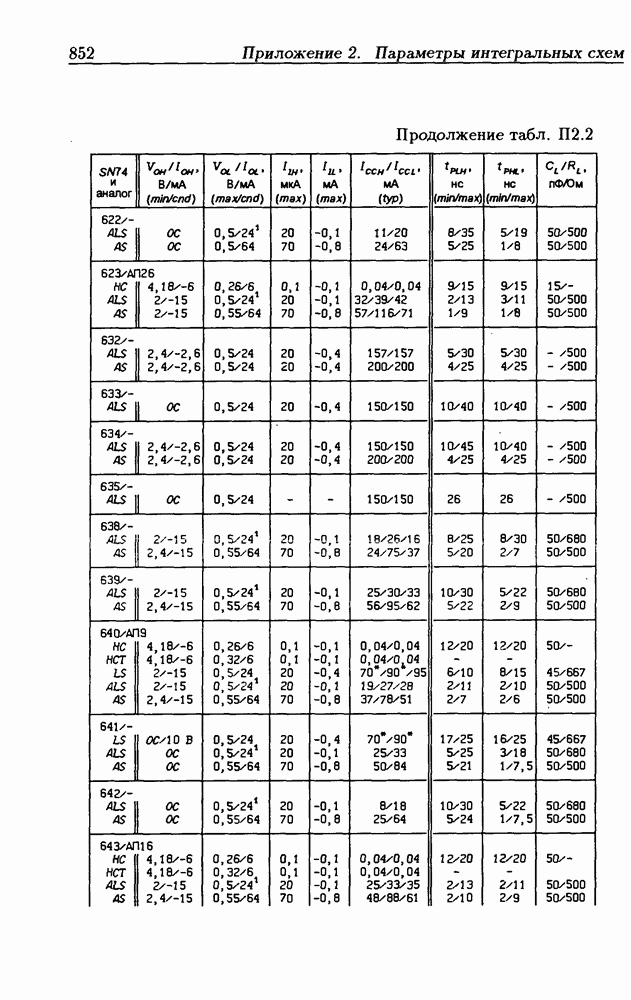
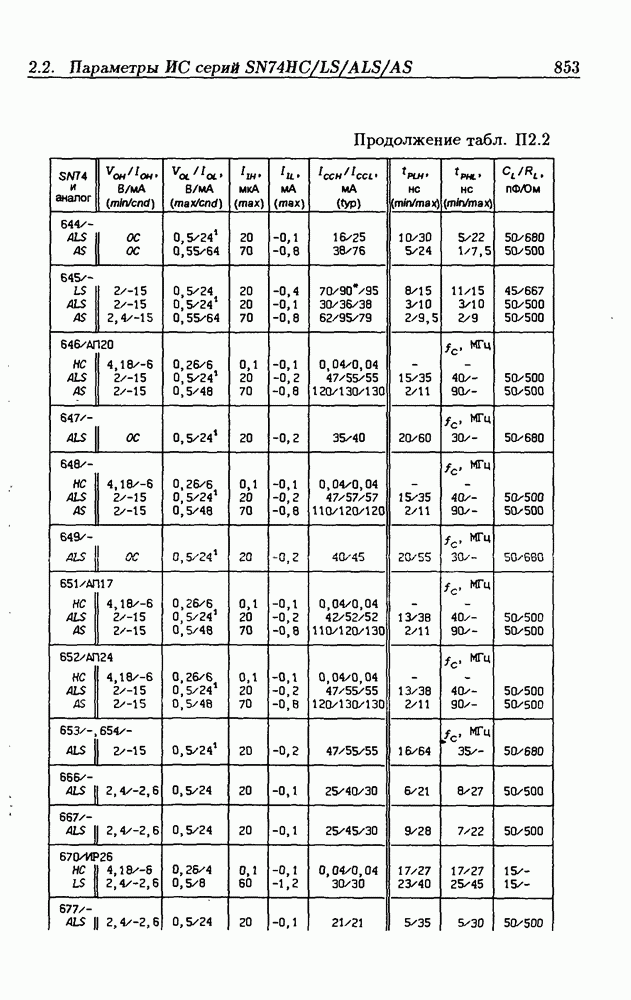
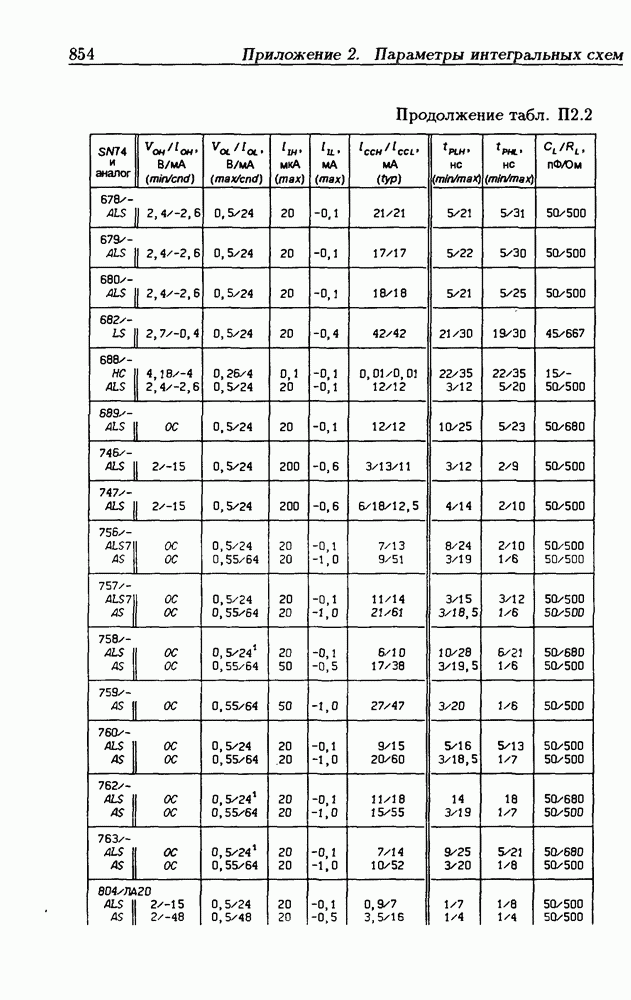
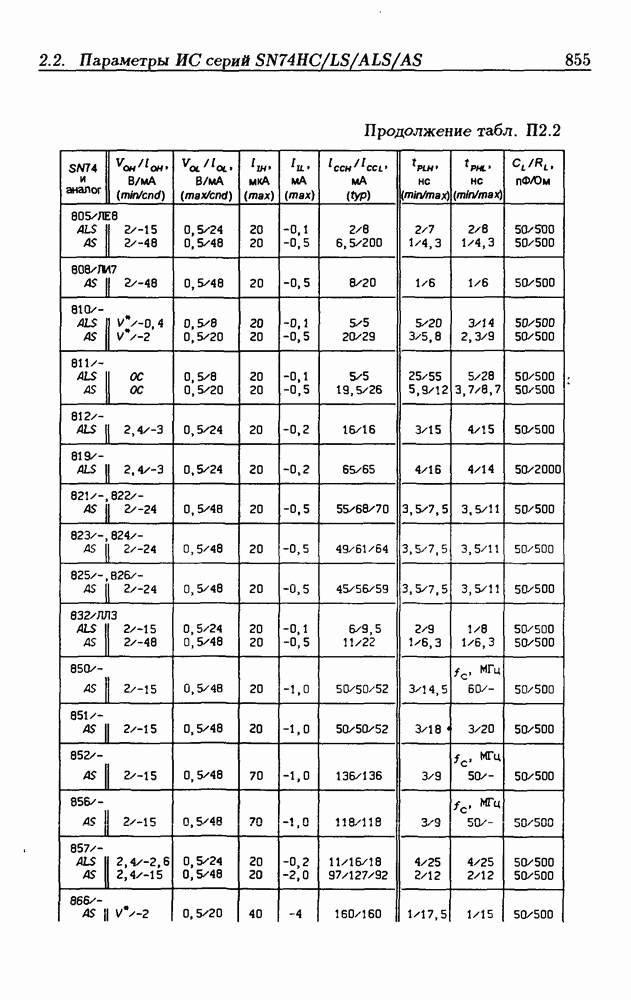
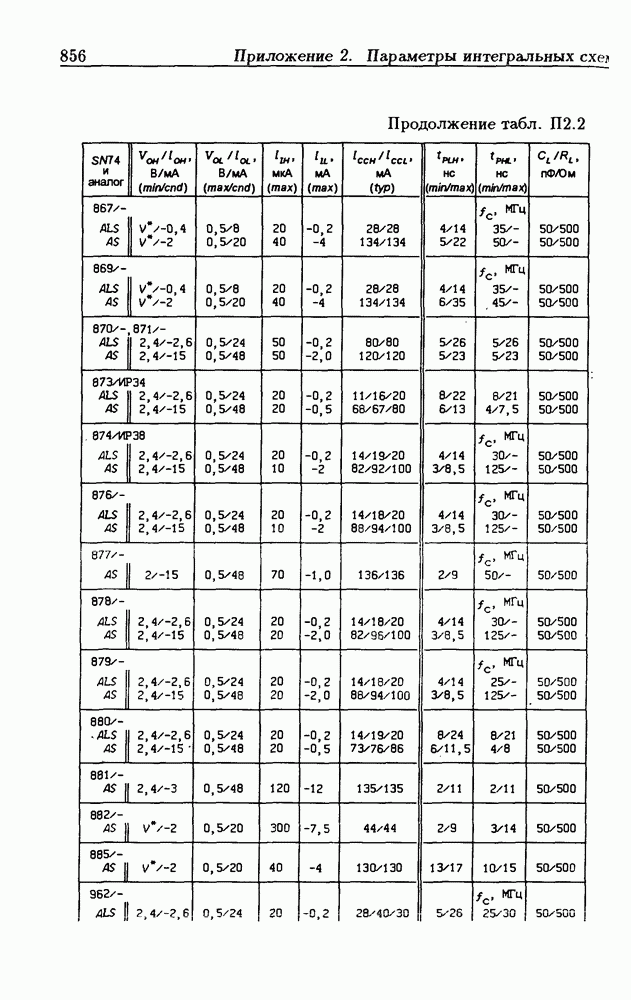
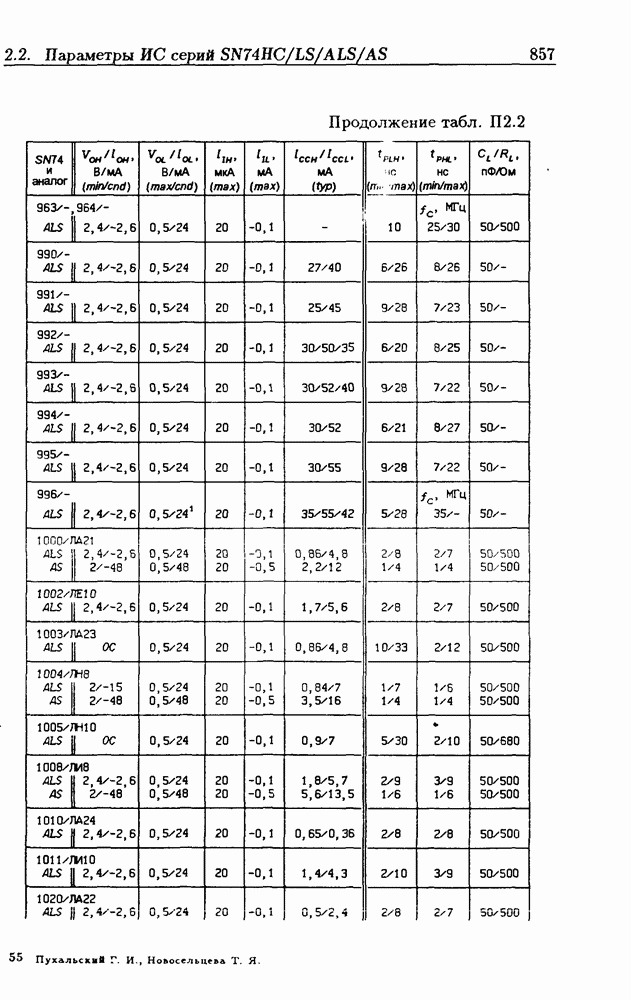
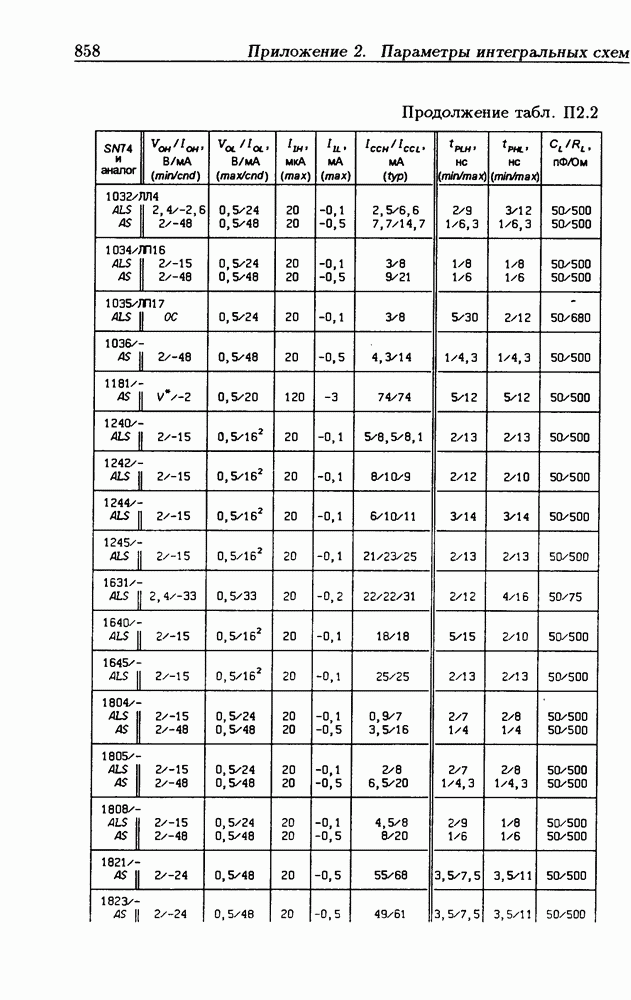
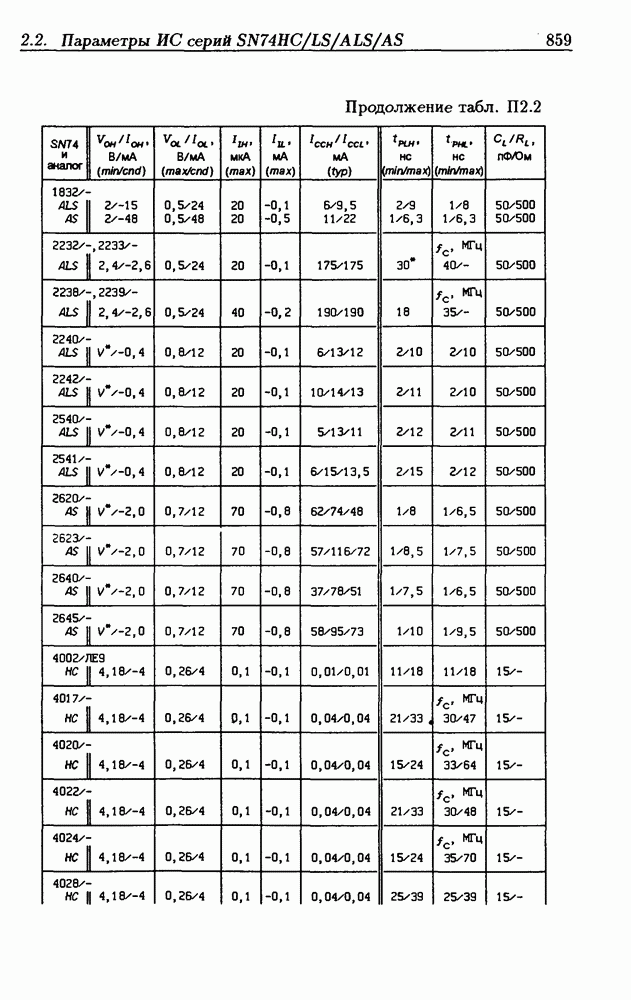
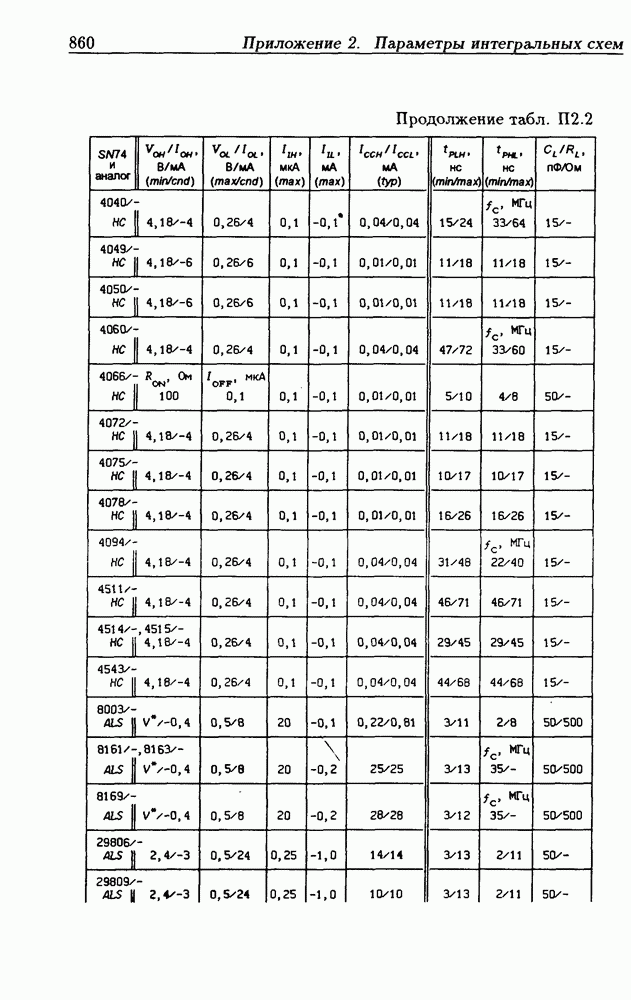
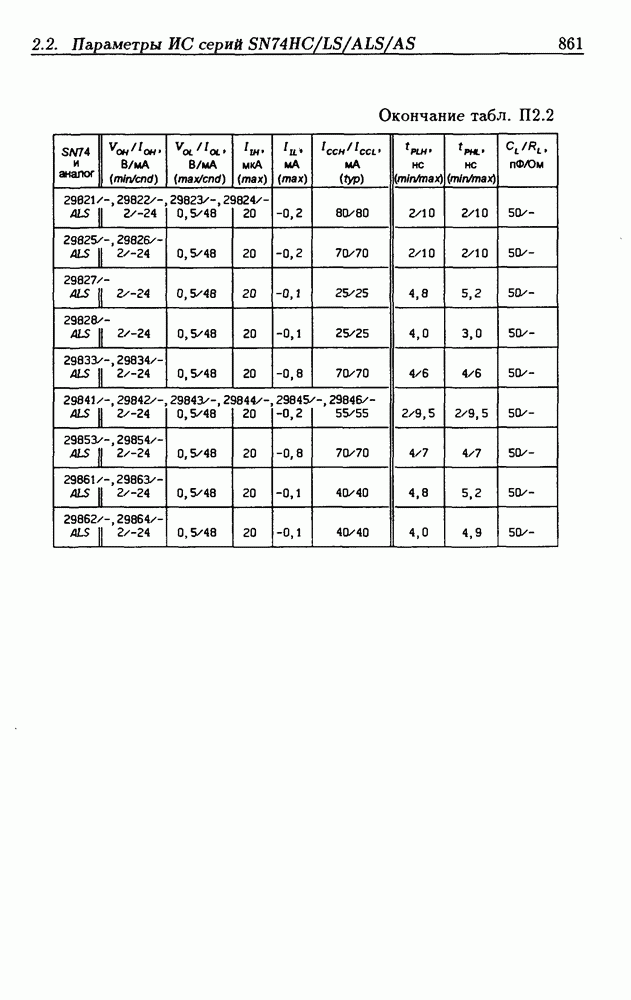
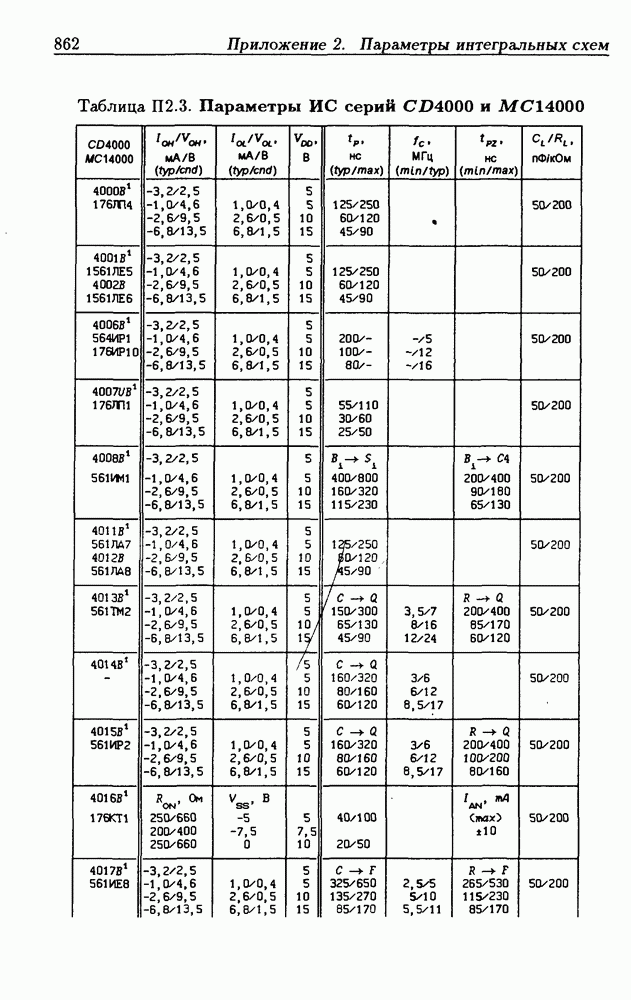
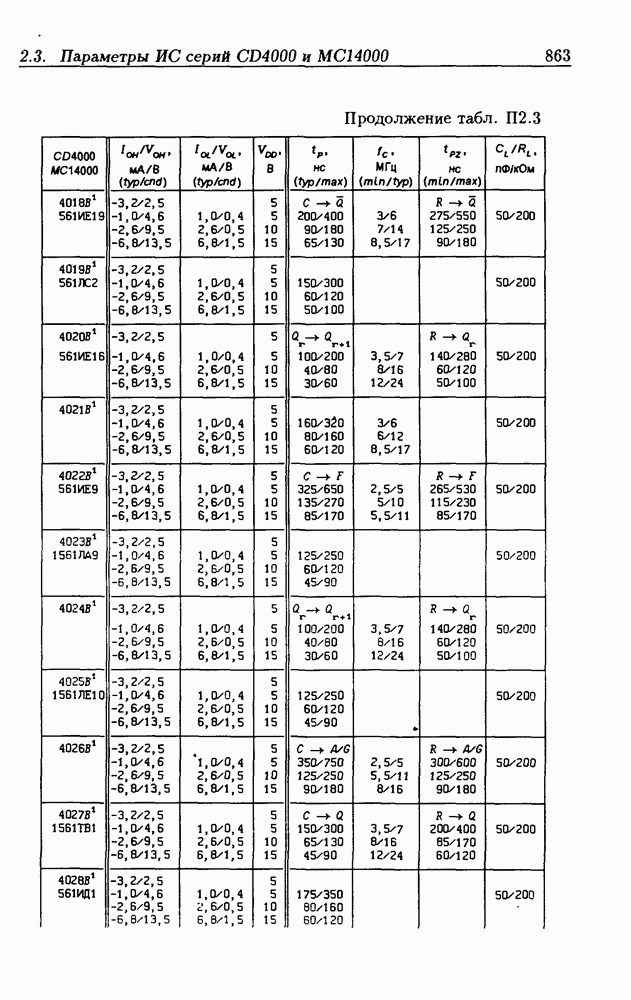
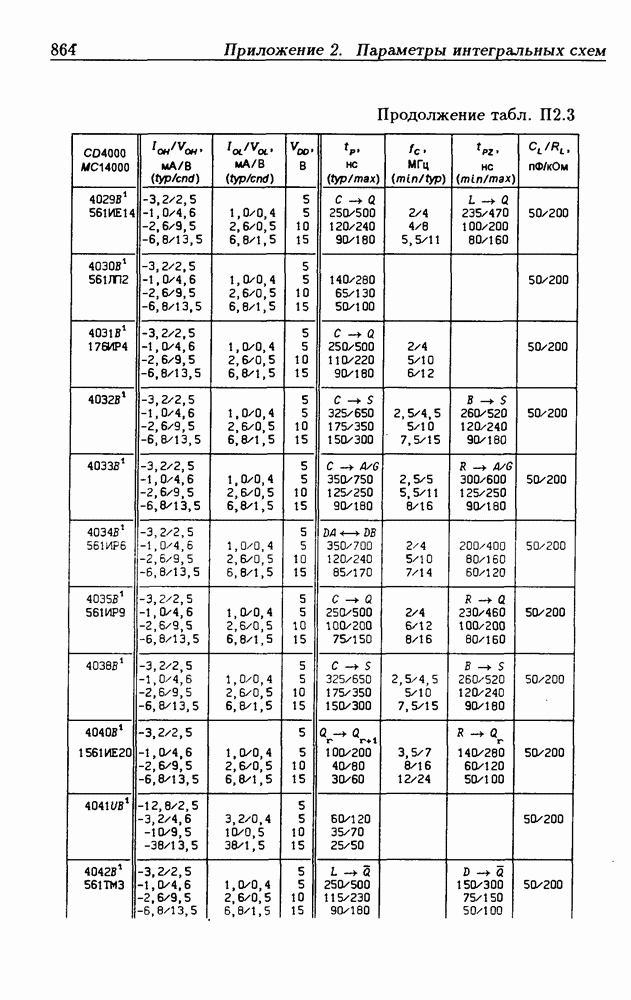
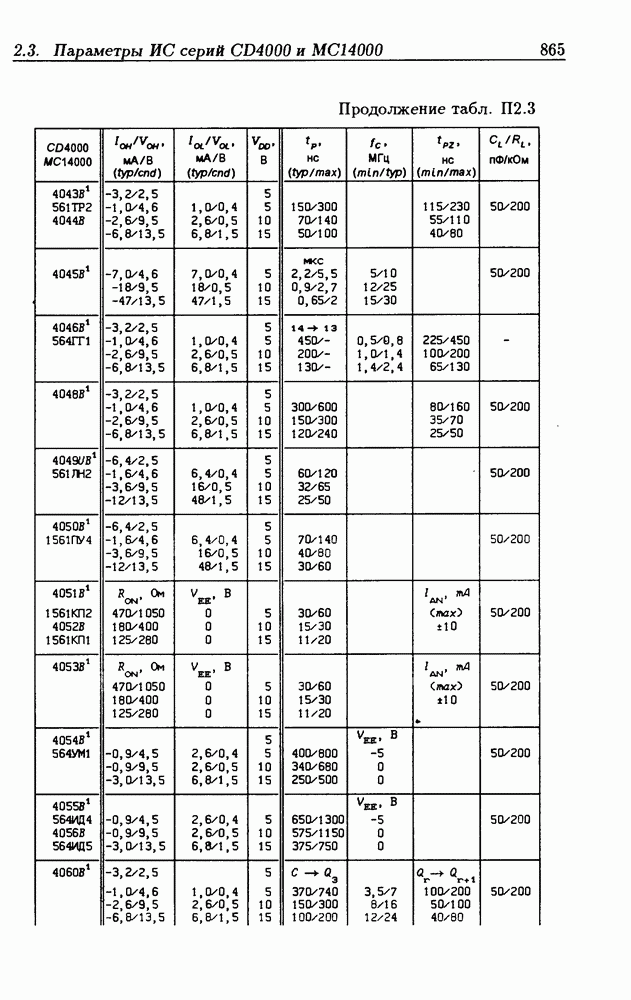
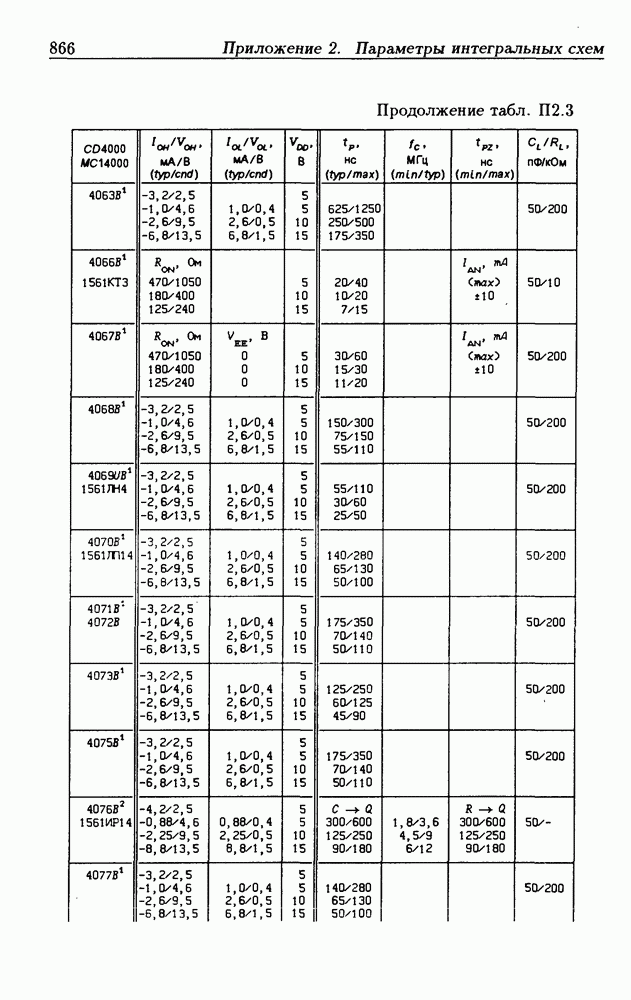
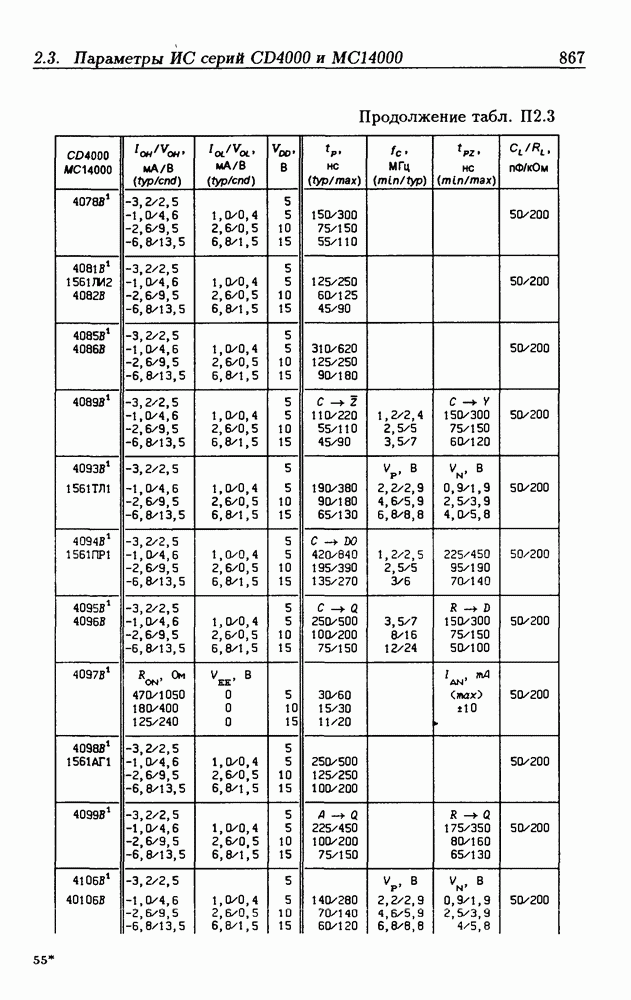
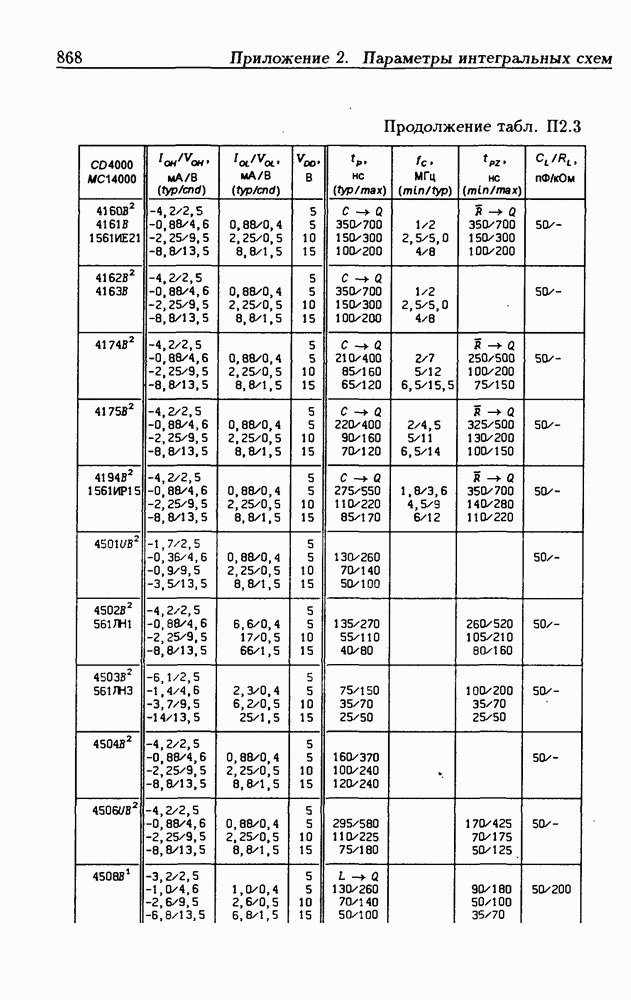
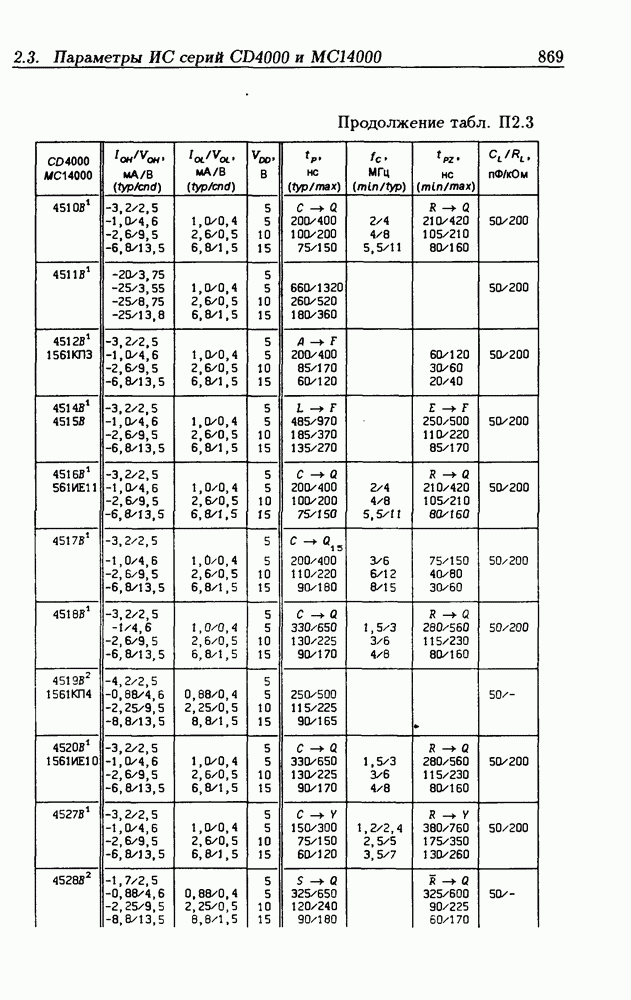
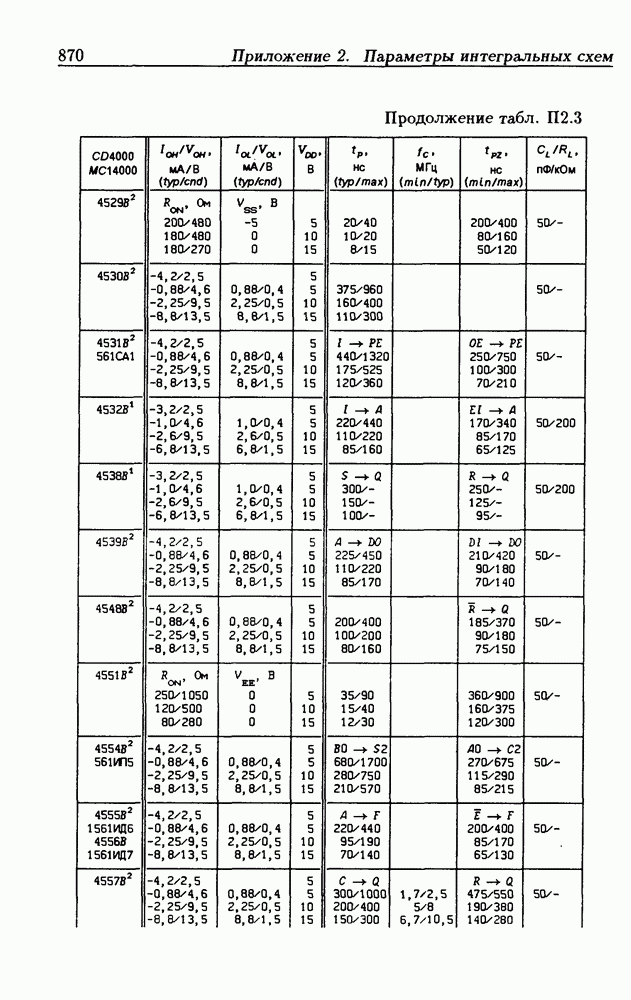
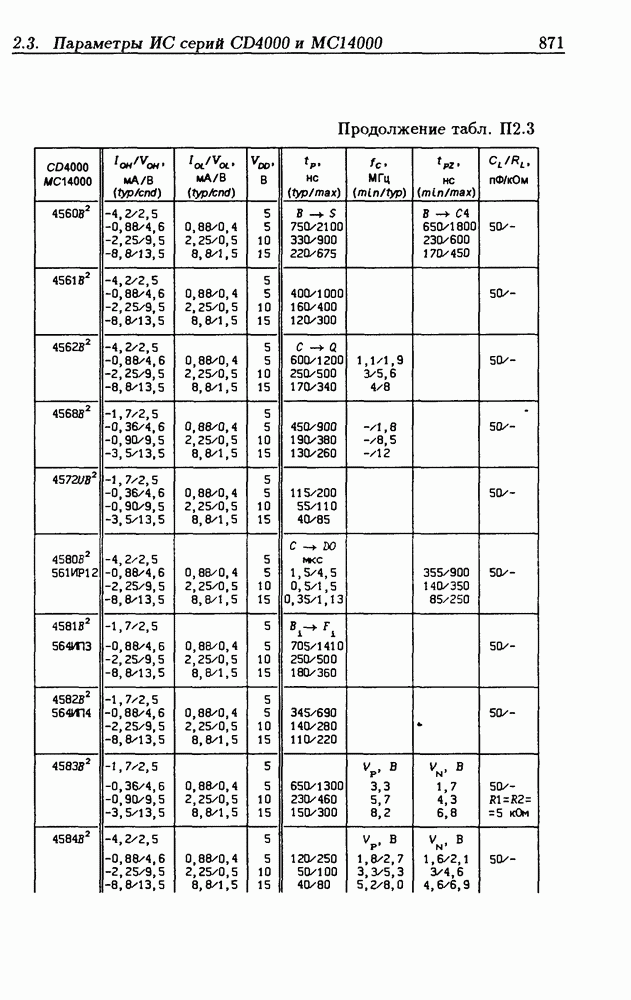
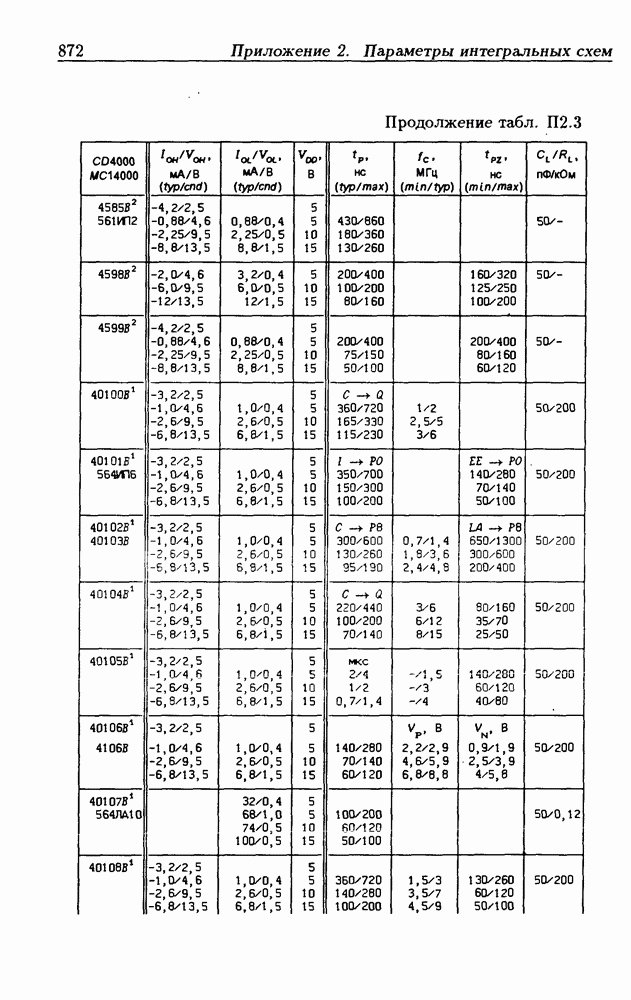
- Приложение 2. Параметры интегральных схем