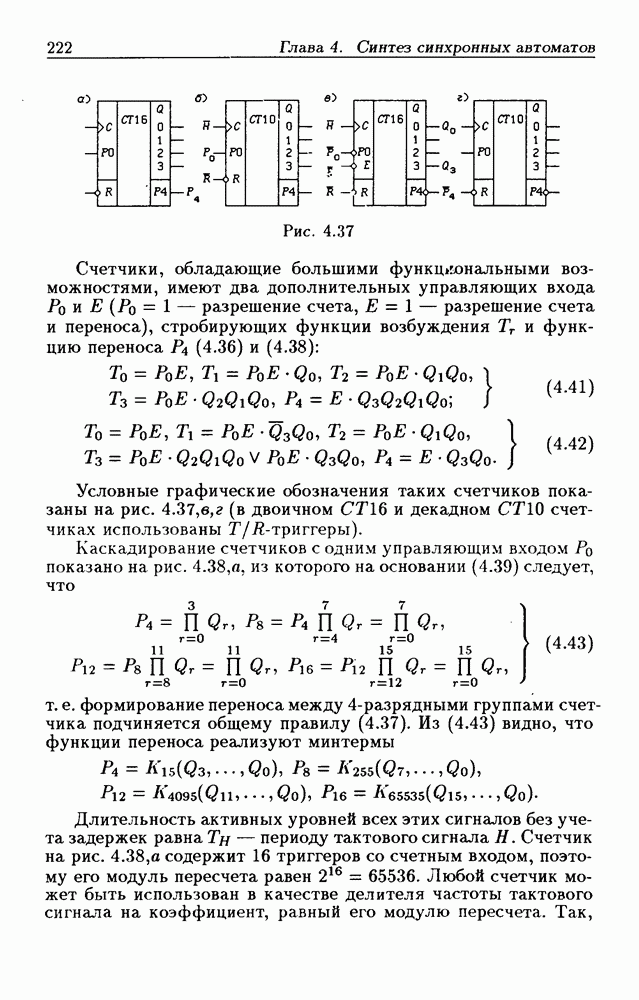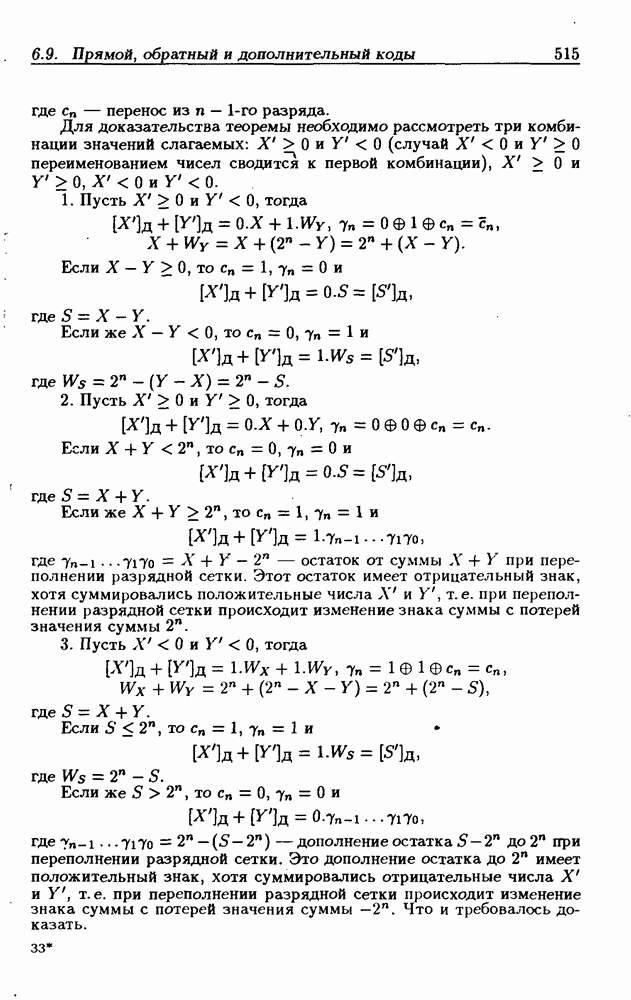| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.6. Синтез асинхронных импульсных триггеров
Асинхронными импульсными триггерами, или просто импульсными триггерами, называются такие триггеры, на которые входные сигналы производят лишь кратковременное воздействие в момент их изменения с 1 на 0 или с 0 на 1. Импульсные триггеры являются простейшими асинхронными импульсными автоматами, поэтому строгое описание законов функционирования данных триггеров возможно только на основе их логических свойств, определяемых функциями переходов.
Триггеры типа dT.
Рассмотрим триггер со счетным входом  Состояние (выходной сигнал
Состояние (выходной сигнал  такого триггера должно изменяться при каждом изменении входного сигнала
такого триггера должно изменяться при каждом изменении входного сигнала  с 1 на 0, т.е. при
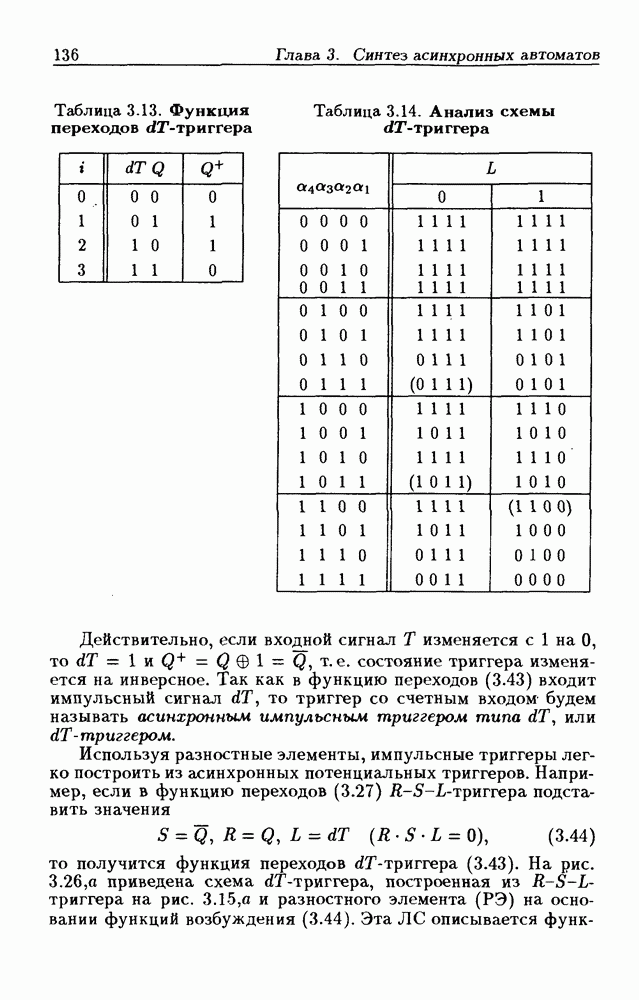
с 1 на 0, т.е. при  На основании данного словесного описания закона функционирования триггера составим таблицу истинности (табл. 3.13), задающую его функцию переходов
На основании данного словесного описания закона функционирования триггера составим таблицу истинности (табл. 3.13), задающую его функцию переходов  Из табл. 3.13 следует, что функция переходов триггера со счетным входом
Из табл. 3.13 следует, что функция переходов триггера со счетным входом

Таблица 3.13. (см. скан) Функция переходов  -триггера
-триггера
Таблица 3.14. (см. скан) Анализ схемы  -триггера
-триггера
Действительно, если входной сигнал  изменяется с 1 на 0, то
изменяется с 1 на 0, то  т.е. состояние триггера изменяется на инверсное. Так как в функцию переходов (3.43) входит импульсный сигнал
т.е. состояние триггера изменяется на инверсное. Так как в функцию переходов (3.43) входит импульсный сигнал  то триггер со счетным входом будем называть асинхронным импульсным триггером типа
то триггер со счетным входом будем называть асинхронным импульсным триггером типа  или
или  -триггером.
-триггером.
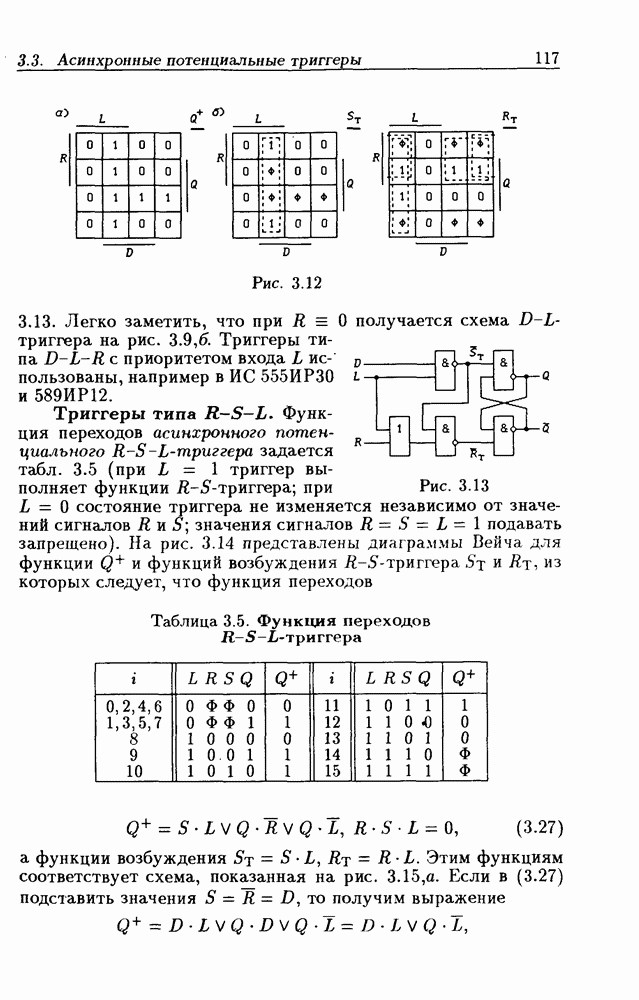
Используя разностные элементы, импульсные триггеры легко построить из асинхронных потенциальных триггеров. Например, если в функцию переходов (3.27)  -триггера подставить значения
-триггера подставить значения

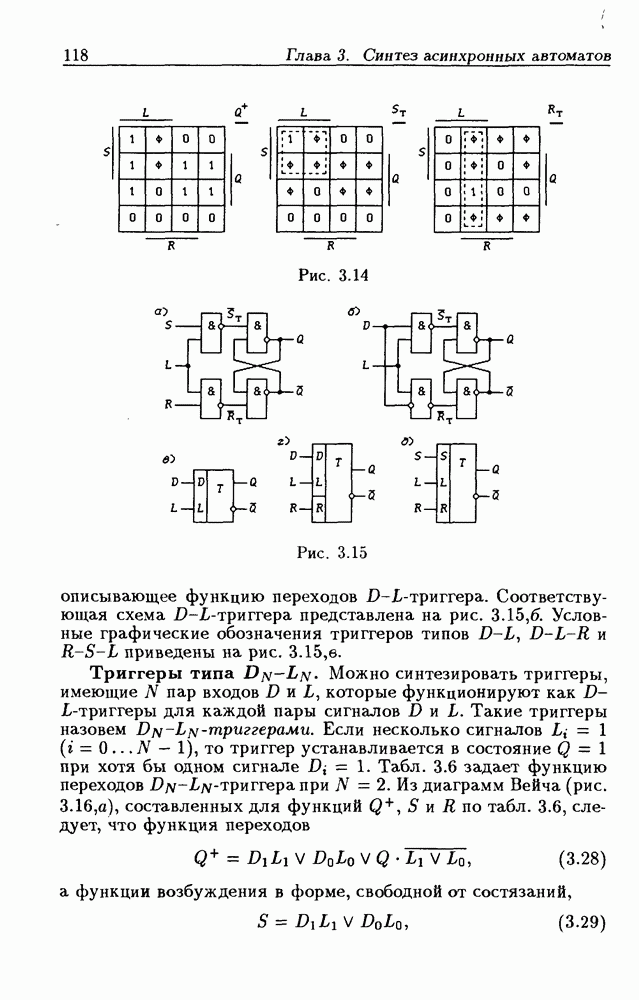
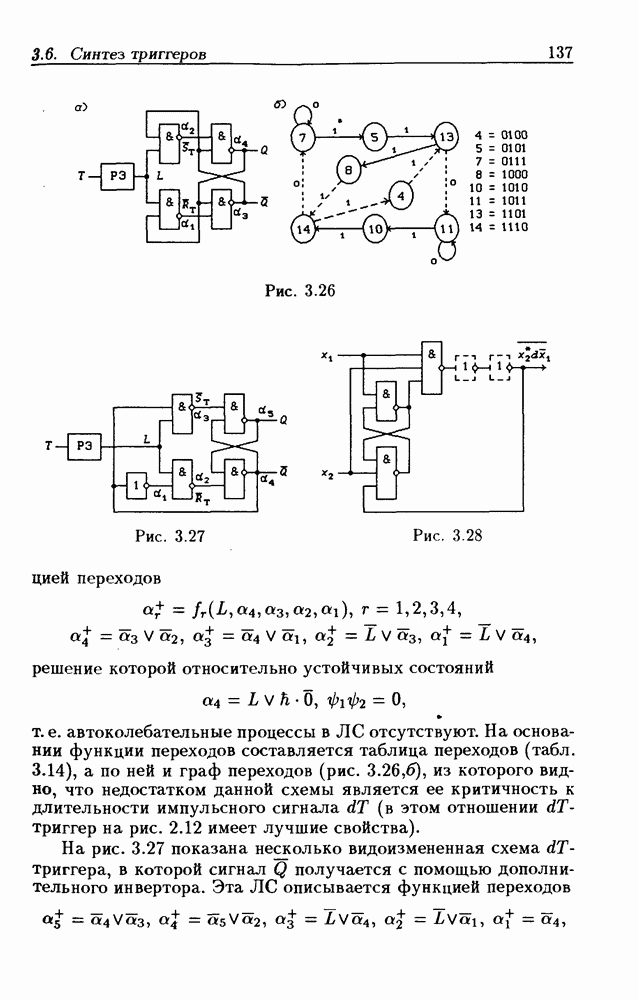
то получится функция переходов  -триггера (3.43). На рис. 3.26,а приведена схема
-триггера (3.43). На рис. 3.26,а приведена схема  -триггера, построенная из
-триггера, построенная из  -триггера на рис. 3.15,а и разностного элемента
-триггера на рис. 3.15,а и разностного элемента  на основании функций возбуждения (3.44). Эта ЛС описывается
на основании функций возбуждения (3.44). Эта ЛС описывается

Рис. 3.26

Рис. 3.27

Рис. 3.28
функцией переходов

решение которой относительно устойчивых состояний 

т.е. автоколебательные процессы в ЛС отсутствуют. На основании функции переходов составляется таблица переходов (табл. 3.14), а по ней и граф переходов (рис. 3.26, б), из которого видно, что недостатком данной схемы является ее критичность к длительности импульсного сигнала  (в этом отношении
(в этом отношении  -триггер на рис. 2.12 имеет лучшие свойства).
-триггер на рис. 2.12 имеет лучшие свойства).
На рис. 3.27 показана несколько видоизмененная схема  -триггера, в которой сигнал
-триггера, в которой сигнал  получается с помощью дополнительного инвертора. Эта ЛС описывается функцией переходов
получается с помощью дополнительного инвертора. Эта ЛС описывается функцией переходов

решение которой относительно устойчивых состояний

т. е. при  в схеме возникает автоколебательный процесс.
в схеме возникает автоколебательный процесс.
В силу описанных явлений принцип построения импульсных триггеров, основанный на разделении функций дифференцирования входных сигналов (разностный элемент) и запоминания входных воздействий  -триггер), практически не нашел применения. Но при использовании двух разностных элементов можно построить схемы импульсных триггеров, обладающие высокой надежностью работы.
-триггер), практически не нашел применения. Но при использовании двух разностных элементов можно построить схемы импульсных триггеров, обладающие высокой надежностью работы.

Рис. 3.29
На рис. 3.28 показана схема управляемого сигналом  разностного элемента, выполняющего функцию
разностного элемента, выполняющего функцию  При
При  длительность активного нулевого уровня выходного сигнала равна
длительность активного нулевого уровня выходного сигнала равна  без ЛЭ НЕ и
без ЛЭ НЕ и  при включении в разностный элемент двух инверторов
при включении в разностный элемент двух инверторов  среднее время задержки сигналов в одном ЛЭ). Анализ данного разностного элемента приведен в [10]. На рис. 3.29 показана схема
среднее время задержки сигналов в одном ЛЭ). Анализ данного разностного элемента приведен в [10]. На рис. 3.29 показана схема  -триггера, выполненного на двух таких разностных элементах и
-триггера, выполненного на двух таких разностных элементах и  -триггере. Действительно, на основании функции переходов
-триггере. Действительно, на основании функции переходов  -триггера (3.10)
-триггера (3.10)

так как  до воздействия импульсного сигнала
до воздействия импульсного сигнала  Логические элементы И-НЕ, составляющие
Логические элементы И-НЕ, составляющие  -триггер, фактически входят в разностный элемент подобно ЛЭ НЕ на рис.
-триггер, фактически входят в разностный элемент подобно ЛЭ НЕ на рис.  Для одного и
Для одного и  для другого разностного элемента).
для другого разностного элемента).
Функция переходов (3.43) задает некоторый автомат, поэтому вполне естественно предположить, что его можно реализовать в виде асинхронного потенциального автомата. Эту задачу можно рассматривать как преобразование импульсного автомата в эквивалентный ему потенциальный автомат. Для ее решения необходимо разработать метод преобразования функции переходов, в которую входят операторы  в функции переходов и выходов (3.3), не содержащие их. Такое преобразование будем
в функции переходов и выходов (3.3), не содержащие их. Такое преобразование будем
называть интегрированием функции переходов импульсного автомата или просто интегрированием импульсного автомата.
Наиболее просто интегрирование импульсных триггеров выполняется табличным методом, так как оказывается возможным построить таблицу переходов асинхронного потенциального автомата непосредственно по функции переходов импульсного триггера. Автомат, выполняющий функции dT-триггера, должен иметь один вход  и один выход
и один выход  причем закон изменения выходного сигнала задается функцией переходов (3.43). Собственно, задание функции выхода автомата не в виде переключательной функции, а в форме функции переходов и позволяет составить первоначальную таблицу переходов, характерную тем, что в каждой строке таблицы проставляется только по одному устойчивому состоянию, а все переходы между ними задаются простыми. Примитивность структуры первоначальной таблицы переходов обеспечивает возможность ее построения без особых затруднений для любого автомата, функции выхода которого заданы в операторной форме.
причем закон изменения выходного сигнала задается функцией переходов (3.43). Собственно, задание функции выхода автомата не в виде переключательной функции, а в форме функции переходов и позволяет составить первоначальную таблицу переходов, характерную тем, что в каждой строке таблицы проставляется только по одному устойчивому состоянию, а все переходы между ними задаются простыми. Примитивность структуры первоначальной таблицы переходов обеспечивает возможность ее построения без особых затруднений для любого автомата, функции выхода которого заданы в операторной форме.
Таблица 3.15. (см. скан) Функция переходов  -триггера с простыми переходами
-триггера с простыми переходами
Рассмотрим методику построения первоначальной таблицы переходов (табл. 3.15) на примере  -триггера, описываемого функцией (3.43). Если входной сигнал триггера не изменяется
-триггера, описываемого функцией (3.43). Если входной сигнал триггера не изменяется  или 1), то импульсный сигнал
или 1), то импульсный сигнал  или 1. Из этого следует, что при каждом состоянии входа
или 1. Из этого следует, что при каждом состоянии входа  и 1 автомат должен иметь по два устойчивых состояния, которым соответствуют различные значения функции выхода автомата
и 1 автомат должен иметь по два устойчивых состояния, которым соответствуют различные значения функции выхода автомата  и 1. На основании этого в каждый столбец первоначальной таблицы переходов (табл. 3.15) необходимо занести по два устойчивых состояния, различающихся состояниями выхода
и 1. На основании этого в каждый столбец первоначальной таблицы переходов (табл. 3.15) необходимо занести по два устойчивых состояния, различающихся состояниями выхода  и 1.
и 1.
Далее с помощью функции переходов (3.43) можно найти переходы между устойчивыми состояниями. Пусть сигнал  изменяется с 0 на 1. В этом случае
изменяется с 0 на 1. В этом случае  при таком изменении состояния входа выходной сигнал
при таком изменении состояния входа выходной сигнал  не должен изменяться
не должен изменяться  а это возможно только при переходе автомата из состояния
а это возможно только при переходе автомата из состояния  в состояние
в состояние  и из состояния
и из состояния  в состояние Аналитически это можно записать так:
в состояние Аналитически это можно записать так:

На этом основании проставляются неустойчивые состояния в столбце  (табл. 3.15).
(табл. 3.15).
Если же сигнал  изменяется с 1 на 0, то импульсный сигнал
изменяется с 1 на 0, то импульсный сигнал  т. е. в этом случае значение выходного сигнала автомата
т. е. в этом случае значение выходного сигнала автомата  должно измениться на инверсное
должно измениться на инверсное  а это возможно только при переходе автомата из состояния
а это возможно только при переходе автомата из состояния  в состояние
в состояние  и из состояния
и из состояния  в состояние
в состояние  Таким образом,
Таким образом,

На этом основании проставляются неустойчивые состояния в столбце  (табл. 3.15).
(табл. 3.15).

Рис. 3.30
Полученная таким способом первоначальная таблица переходов полностью определяет закон функционирования асинхронного потенциального автомата, выполняющего функции  -триггера. Для кодирования внутренних состояний автомата необходимо использовать два
-триггера. Для кодирования внутренних состояний автомата необходимо использовать два  Структурная схема асинхронного импульсного
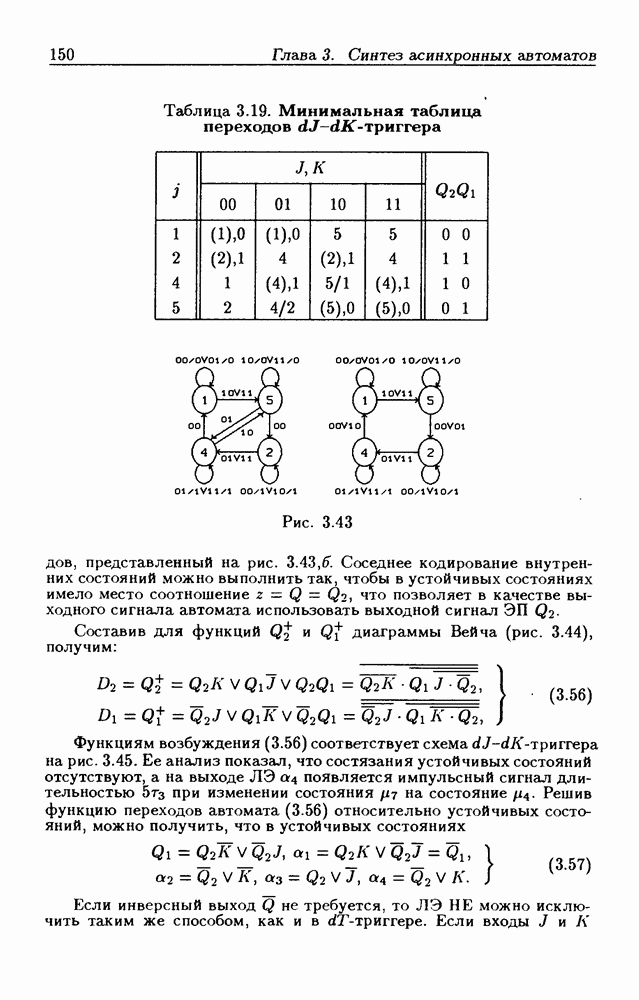
Структурная схема асинхронного импульсного  -триггера как асинхронного потенциального автомата показана на рис. 3.30,а. Из графа переходов (рис. 3.30, б), построенного по табл. 3.15, следует, что соседнее кодирование внутренних состояний автомата можно выполнить без преобразования таблицы переходовю Из табл. 3.15. видно, что кодирование осуществлено так, что функция выхода
-триггера как асинхронного потенциального автомата показана на рис. 3.30,а. Из графа переходов (рис. 3.30, б), построенного по табл. 3.15, следует, что соседнее кодирование внутренних состояний автомата можно выполнить без преобразования таблицы переходовю Из табл. 3.15. видно, что кодирование осуществлено так, что функция выхода

Рис. 3.31
автомата  (значения
(значения  в устойчивых состояниях совпадают). Это позволяет в качестве выходного сигнала автомата использовать выходной сигнал
в устойчивых состояниях совпадают). Это позволяет в качестве выходного сигнала автомата использовать выходной сигнал 
Выполним структурный синтез  -триггера из ЭП типов
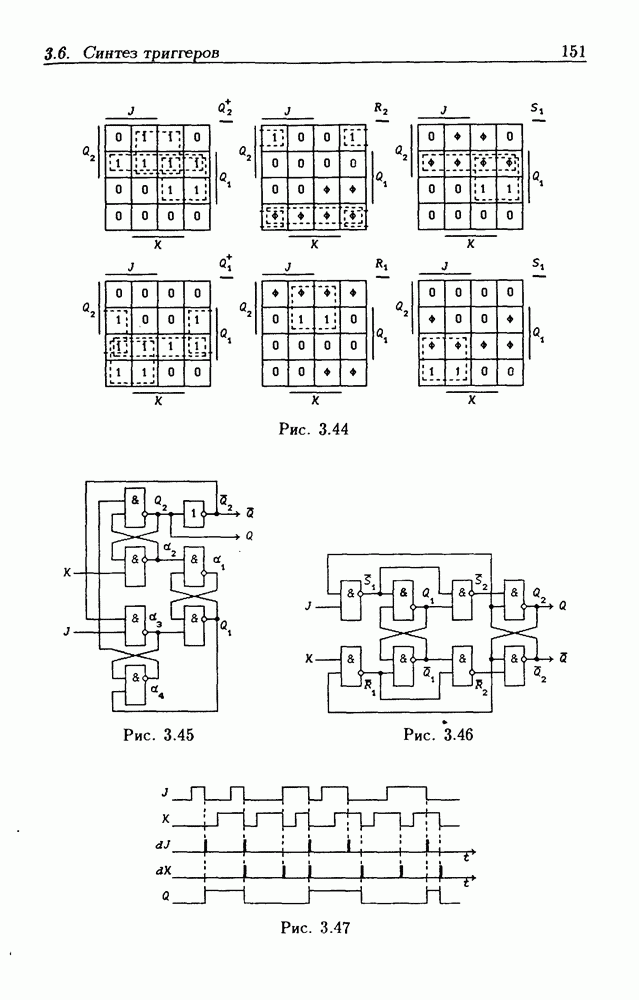
-триггера из ЭП типов  На рис. 3.31,а показаны диаграммы Вейча для функций
На рис. 3.31,а показаны диаграммы Вейча для функций  из которых следует, что МДНФС функций возбуждения
из которых следует, что МДНФС функций возбуждения  можно представить в форме
можно представить в форме

С помощью элементарных преобразований можно получить

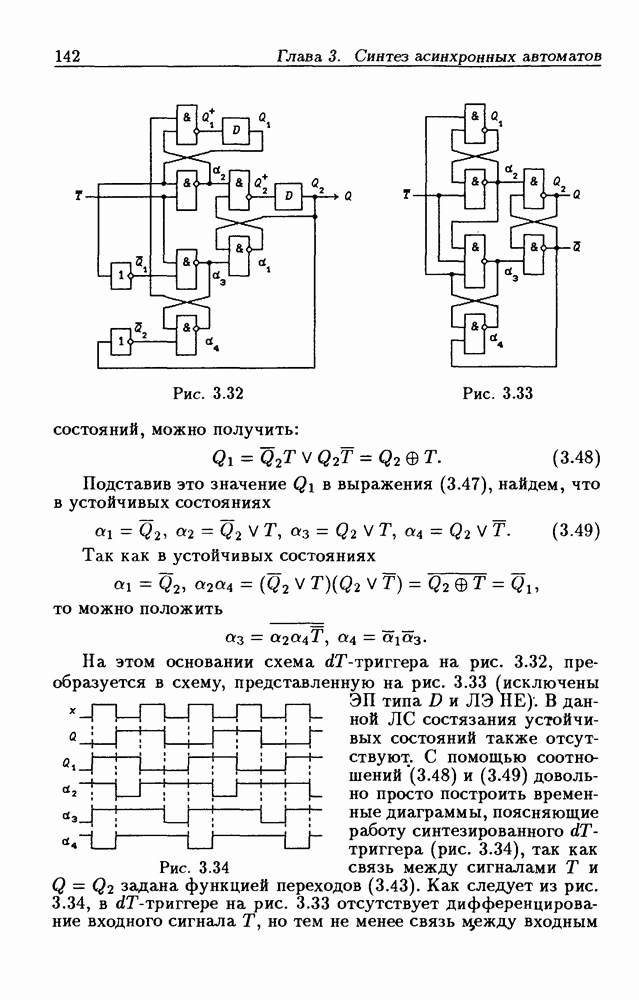
На рис. 3.32 изображена схема  -триггера, построенная на основании соотношений (3.46). Если из данной ЛС исключить оба ЭП типа
-триггера, построенная на основании соотношений (3.46). Если из данной ЛС исключить оба ЭП типа  то, как показывает анализ, ее закон функционирования не изменится (состязания устойчивых состояний не возникнут).
то, как показывает анализ, ее закон функционирования не изменится (состязания устойчивых состояний не возникнут).
Из рис. 3.32 следует, что выходные сигналы ЛЭ И-НЕ  определяются соотношениями:
определяются соотношениями:

Найдем значения сигналов  в устойчивых состояниях в зависимости от значений сигналов
в устойчивых состояниях в зависимости от значений сигналов  Решив функцию переходов автомата (3.45) относительно устойчивых
Решив функцию переходов автомата (3.45) относительно устойчивых

Рис. 3.32

Рис. 3.33
состояний, можно получить:

Подставив это значение  в выражения (3.47), найдем, что в устойчивых состояниях
в выражения (3.47), найдем, что в устойчивых состояниях

Так как в устойчивых состояниях

то можно положить

На этом основании схема  -триггера на рис. 3.32, преобразуется в схему, представленную на рис. 3.33 (исключены ЭП типа
-триггера на рис. 3.32, преобразуется в схему, представленную на рис. 3.33 (исключены ЭП типа  и ЛЭ НЕ). В данной ЛС состязания устойчивых состояний также отсутствуют. С помощью соотношений (3.48) и (3.49) довольно просто построить временные диаграммы, поясняющие работу синтезированного
и ЛЭ НЕ). В данной ЛС состязания устойчивых состояний также отсутствуют. С помощью соотношений (3.48) и (3.49) довольно просто построить временные диаграммы, поясняющие работу синтезированного  -триггера (рис. 3.34), так как связь между сигналами
-триггера (рис. 3.34), так как связь между сигналами  задана функцией переходов (3.43). Как следует из рис. 3.34, в
задана функцией переходов (3.43). Как следует из рис. 3.34, в  -триггере на рис. 3.33 отсутствует дифференцирование входного сигнала
-триггере на рис. 3.33 отсутствует дифференцирование входного сигнала  но тем не менее связь цежду входным
но тем не менее связь цежду входным

Рис. 3.34
сигналом  и выходным сигналом
и выходным сигналом  описывается функцией переходов (3.43), в которую входит импульсный сигнал
описывается функцией переходов (3.43), в которую входит импульсный сигнал 
В общем случае в некоторых точках схем потенциальных автоматов, получаемых в результате интегрирования импульсных автоматов, могут возникать и импульсные сигналы (продифференцированные входные сигналы). Такое дифференцирование будем называть логическим, так как оно достигается исключительно за счет логического построения схем автоматов, и его особенностью является то, что на выходах ни одного ЛЭ импульсные сигналы вообще могут не появиться. Дифференцирование же с помощью разностных элементов будем называть физическим, так как оно основано на физических свойствах ЛЭ (на паразитных задержках). Таким образом, дифференцирование сигналов в автоматах следует рассматривать в более широком смысле, чем физическое дифференцирование, в результате которого порождаются импульсные сигналы.
Возникает вопрос, каким автоматом является ЛС на рис. 3.33 — импульсным или потенциальным. Ответ зависит от точки зрения, с которой рассматривается данная ЛС. Если нас интересует внутренняя структура автомата, то ЛС следует считать асинхронным потенциальным автоматом. Если же интересоваться только внешним поведением ЛС (зависимостью выходного сигнала  от входного сигнала
от входного сигнала  то ее следует считать асинхронным импульсным автоматом. Действительно, если данный автомат рассматривать как "черный ящик", имеющий один вход
то ее следует считать асинхронным импульсным автоматом. Действительно, если данный автомат рассматривать как "черный ящик", имеющий один вход  и один выход
и один выход  то никакими экспериментами нельзя установить, производится в нем, физическое дифференцирование сигнала
то никакими экспериментами нельзя установить, производится в нем, физическое дифференцирование сигнала  или нет.
или нет.
Может показаться, что если в логической схеме (рис. 3.33) отсутствуют импульсные сигналы, то входной сигнал  оказывает на триггер длительное воздействие. Однако воздействие входного сигнала нужно рассматривать с точки зрения функционирования автомата в качестве
оказывает на триггер длительное воздействие. Однако воздействие входного сигнала нужно рассматривать с точки зрения функционирования автомата в качестве  -триггера. Так, если какой-либо кратковременный сигнал помехи, возникший, например, в цепях питания, изменит состояние
-триггера. Так, если какой-либо кратковременный сигнал помехи, возникший, например, в цепях питания, изменит состояние  -триггера, то он не вернется в прежнее состояние после окончания воздействия этого сигнала независимо от значения
-триггера, то он не вернется в прежнее состояние после окончания воздействия этого сигнала независимо от значения  Если же взять асинхронный потенциальный
Если же взять асинхронный потенциальный  -триггер, то входные сигналы
-триггер, то входные сигналы  возвращают триггер в прежнее состояние после окончания воздействия сигнала помехи, т.е. входные сигналы оказывают на потенциальные триггеры длительное воздействие (не только изменяют состояние триггера, но и удерживают его в новом состоянии). В импульсных же триггерах сигнал помехи может быть скомпенсирован только в момент изменения входных
возвращают триггер в прежнее состояние после окончания воздействия сигнала помехи, т.е. входные сигналы оказывают на потенциальные триггеры длительное воздействие (не только изменяют состояние триггера, но и удерживают его в новом состоянии). В импульсных же триггерах сигнал помехи может быть скомпенсирован только в момент изменения входных
информационных сигналов.
Синтезируем  -триггер на
-триггер на  -триггерах. На рис. 3.31,6 приведены диаграммы Вейча для функций возбуждения триггеров
-триггерах. На рис. 3.31,6 приведены диаграммы Вейча для функций возбуждения триггеров  составленные на основании диаграмм Вейча для функций и
составленные на основании диаграмм Вейча для функций и  по методике, изложенной в § 3.4. Из диаграмм следует, что функции возбуждения можно представить в виде
по методике, изложенной в § 3.4. Из диаграмм следует, что функции возбуждения можно представить в виде

Схема  -триггера, выполненная в соответствии с выражениями (3.50), приведена на рис. 3.35,а.
-триггера, выполненная в соответствии с выражениями (3.50), приведена на рис. 3.35,а.

Рис. 3.35
Используя 1-кубы, отмеченные на рис.  штриховыми линиями, функции возбуждения триггера
штриховыми линиями, функции возбуждения триггера  можно получить в форме
можно получить в форме

Схема  -триггера, соответствующая функциям возбуждения (3.51) триггера
-триггера, соответствующая функциям возбуждения (3.51) триггера  изображена на рис. 3.35, б.
изображена на рис. 3.35, б.
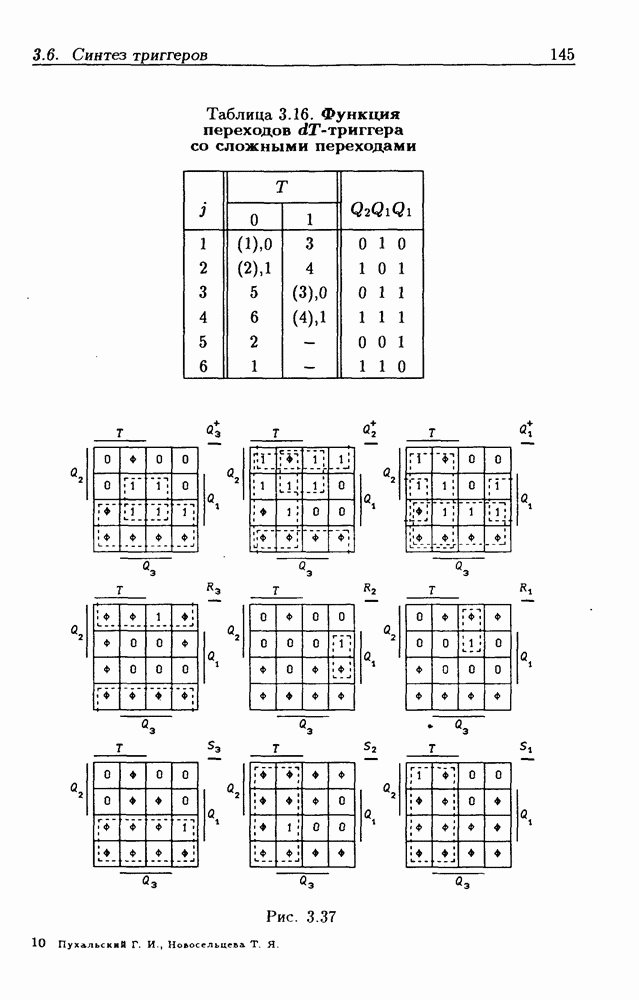
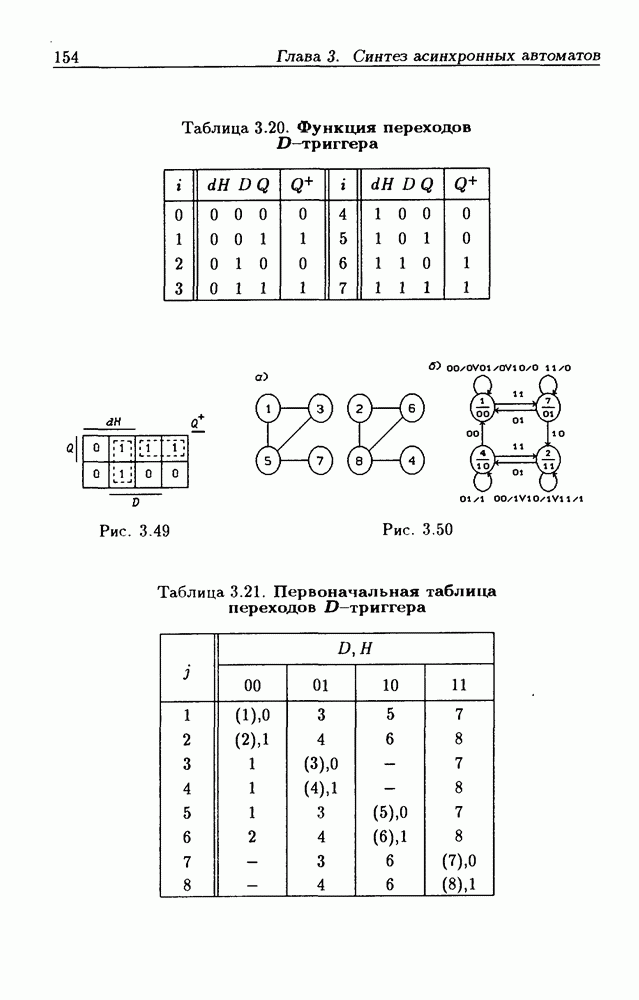
Можно синтезировать еще некоторые схемы  -триггеров, если преобразовать табл. 3.15. Введя два переходных состояния, можно получить таблицу переходов (табл. 3.16), содержащую шесть внутренних состояний, для реализации которых требуются три ЭП. На рис. 3.36 приведен граф переходов, на котором указан принятый вариант соседнего кодирования внутренних состояний автомата. Составив диаграммы Вейча для функций
-триггеров, если преобразовать табл. 3.15. Введя два переходных состояния, можно получить таблицу переходов (табл. 3.16), содержащую шесть внутренних состояний, для реализации которых требуются три ЭП. На рис. 3.36 приведен граф переходов, на котором указан принятый вариант соседнего кодирования внутренних состояний автомата. Составив диаграммы Вейча для функций  (рис. 3.37), получаем:
(рис. 3.37), получаем:

Рис. 3.36
(см. скан)

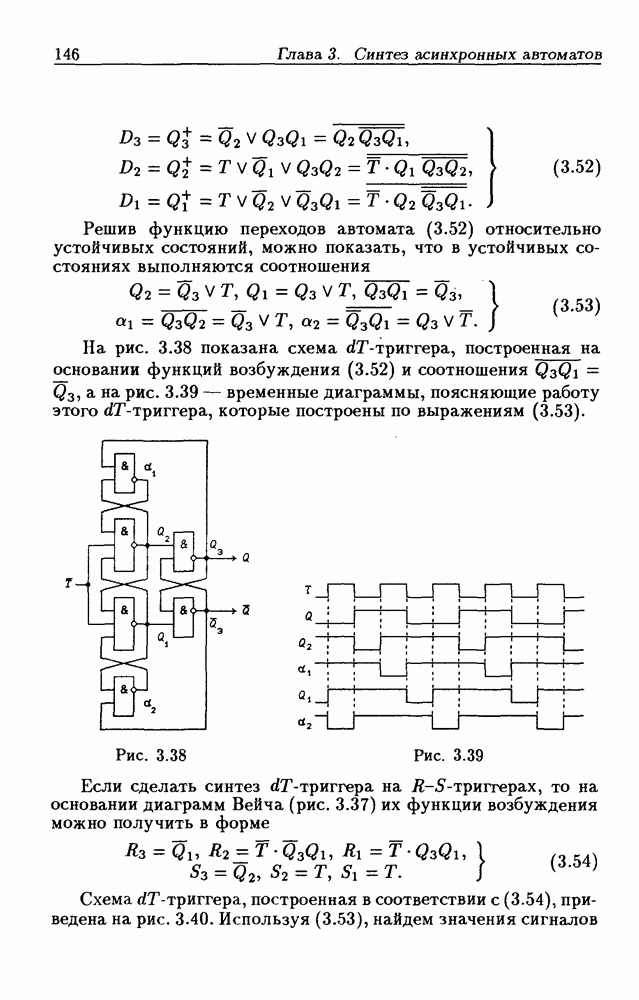
Решив функцию переходов автомата (3.52) относительно устойчивых состояний, можно показать, что в устойчивых состояниях выполняются соотношения

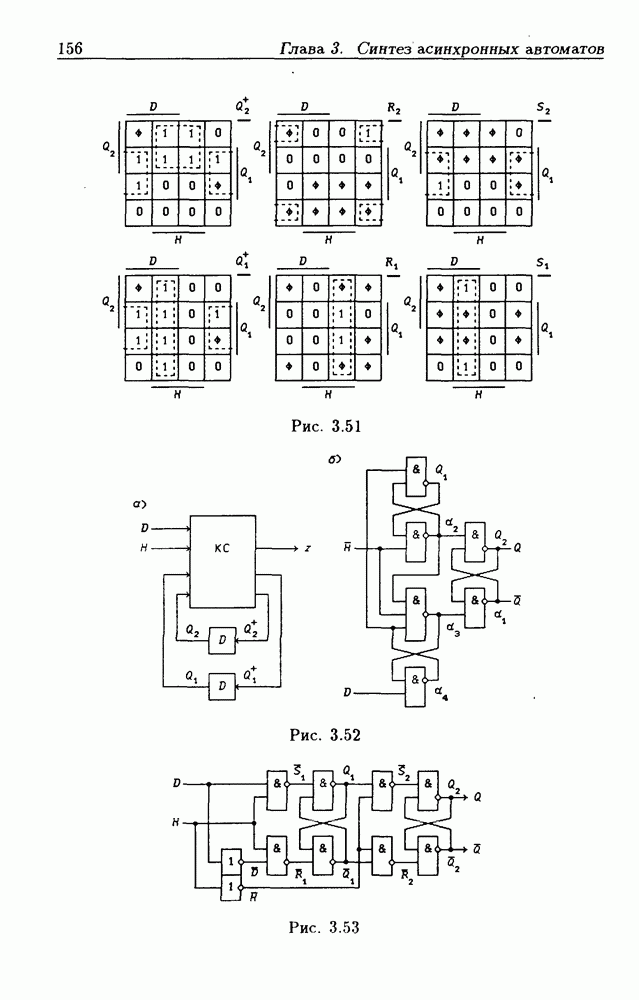
На рис. 3.38 показана схема  -триггера, построенная на основании функций возбуждения (3.52) и соотношения
-триггера, построенная на основании функций возбуждения (3.52) и соотношения  а на рис. 3.39 — временные диаграммы, поясняющие работу этого
а на рис. 3.39 — временные диаграммы, поясняющие работу этого  -триггера, которые построены по выражениям (3.53).
-триггера, которые построены по выражениям (3.53).

Рис. 3.38

Рис. 3.39
Если сделать синтез  -триггера на
-триггера на  -триггерах, то на основании диаграмм Вейча (рис. 3.37) их функции возбуждения можно получить в форме
-триггерах, то на основании диаграмм Вейча (рис. 3.37) их функции возбуждения можно получить в форме

Схема  -триггера, построенная в соответствии с (3.54), приведена на рис. 3.40. Используя (3.53), найдем значения сигналов
-триггера, построенная в соответствии с (3.54), приведена на рис. 3.40. Используя (3.53), найдем значения сигналов
 в устойчивых состояниях:
в устойчивых состояниях:

Из этого следует, что в переходных режимах на выходах ЛЭ  должны появляться импульсные сигналы (длительность активных уровней сигналов
должны появляться импульсные сигналы (длительность активных уровней сигналов  равна
равна  где
где  среднее время задержки сигналов в одном ЛЭ И-НЕ).
среднее время задержки сигналов в одном ЛЭ И-НЕ).
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Основы теории переключательных функций
- 1.2. Позиционные системы счисления
- 1.3. Переключательные функции
- 1.4. Принцип и закон двойственности
- 1.5. Теоремы разложения
- 1.6. Решение систем логических уравнений
- 1.7. Первичные термы, минтермы и макстермы
- 1.8. Совершенные нормальные формы представления функций
- 1.9. Конъюнктивные и дизъюнктивные термы
- 1.10. Минимизация переключательных функций
- 1.11. Диаграммы Вейча
- 1.12. Минимизация неполностью определенных функций, совместная минимизация нескольких функций
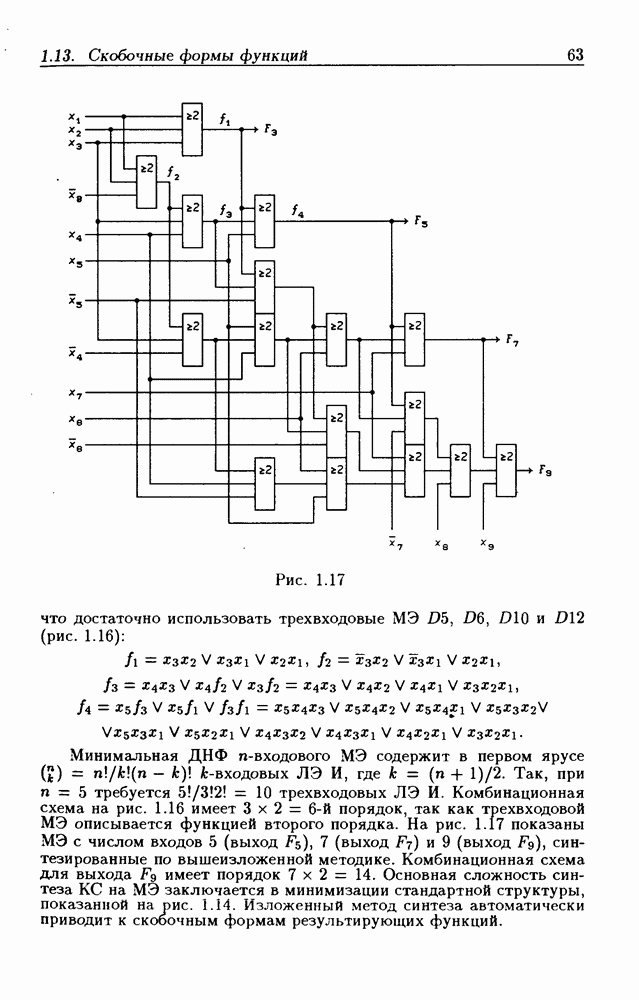
- 1.13. Скобочные формы функций
- 1.14. Закон двойственности для логических схем
- 1.15. Линейные функции
- Глава 2. Анализ и синтез логических схем
- 2.2. Модели логических элементов
- 2.3. Модели логических схем
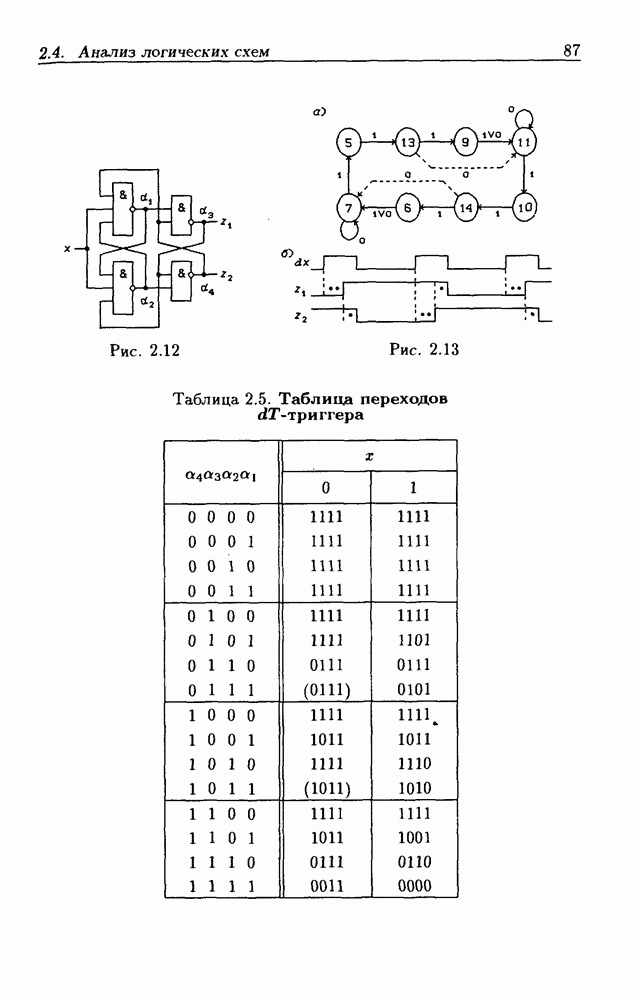
- 2.4. Анализ логических схем
- 2.5. Синтез комбинационных схем, свободных от состязаний
- Глава 3. Синтез асинхронных потенциальных автоматов
- 3.2. Асинхронные потенциальные автоматы
- 3.3. Асинхронные потенциальные триггеры и элементы памяти
- Триггеры типа R-S
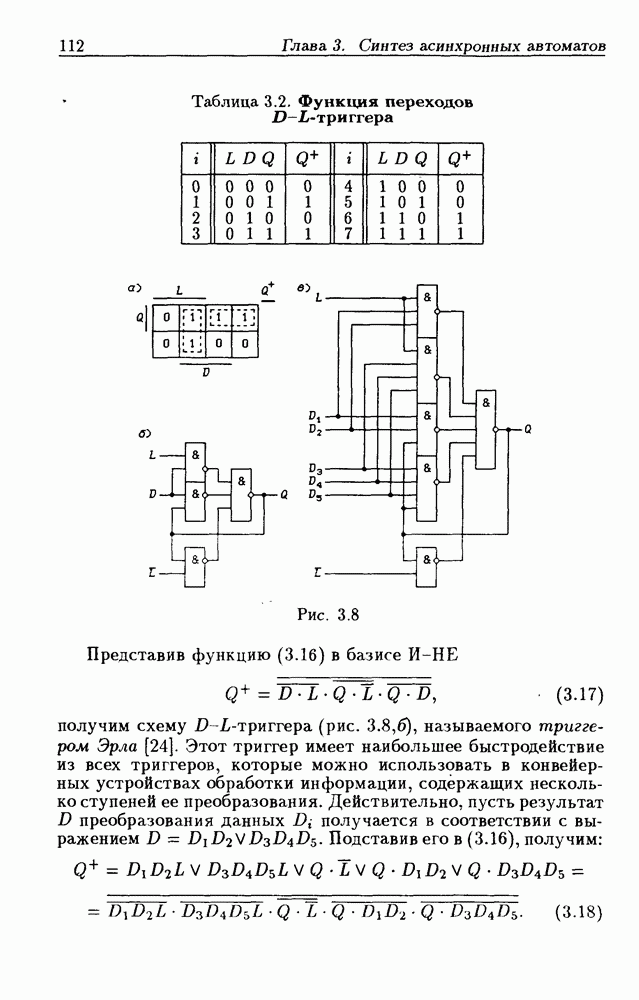
- Триггеры типа D-L
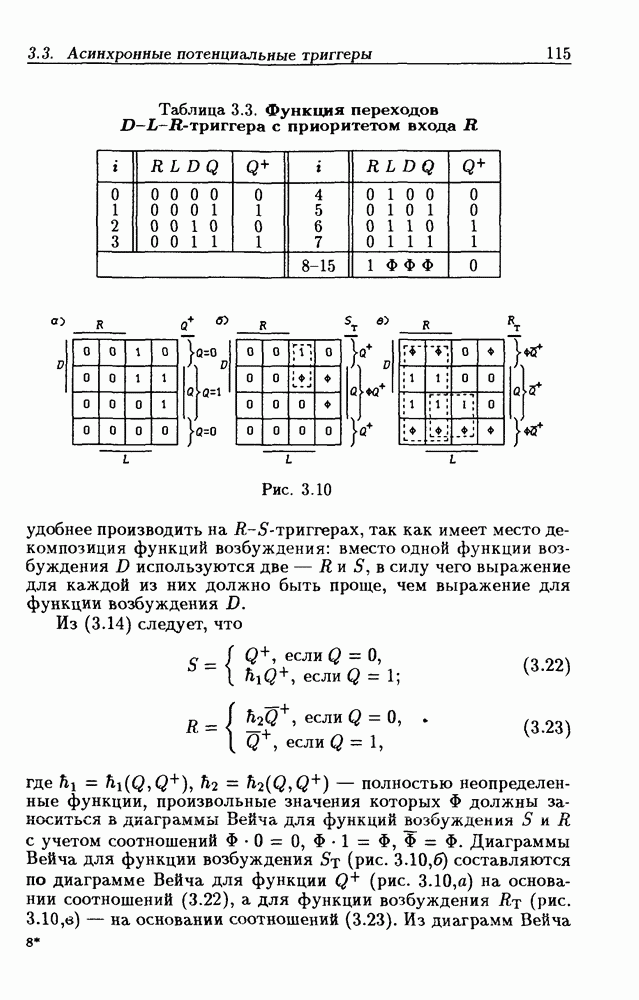
- Триггеры типа D-L-R с приоритетом входа R.
- Триггеры типа D-L-R с приоритетом входа L.
- Триггеры типа R-S-L.
- Триггеры типа DN-LN
- Аналитический метод синтеза и анализа триггеров.
- 3.4. Задание асинхронных потенциальных автоматов таблицами и графами переходов
- 3.5. Синтез асинхронных потенциальных счетчиков
- 3.6. Синтез асинхронных импульсных триггеров
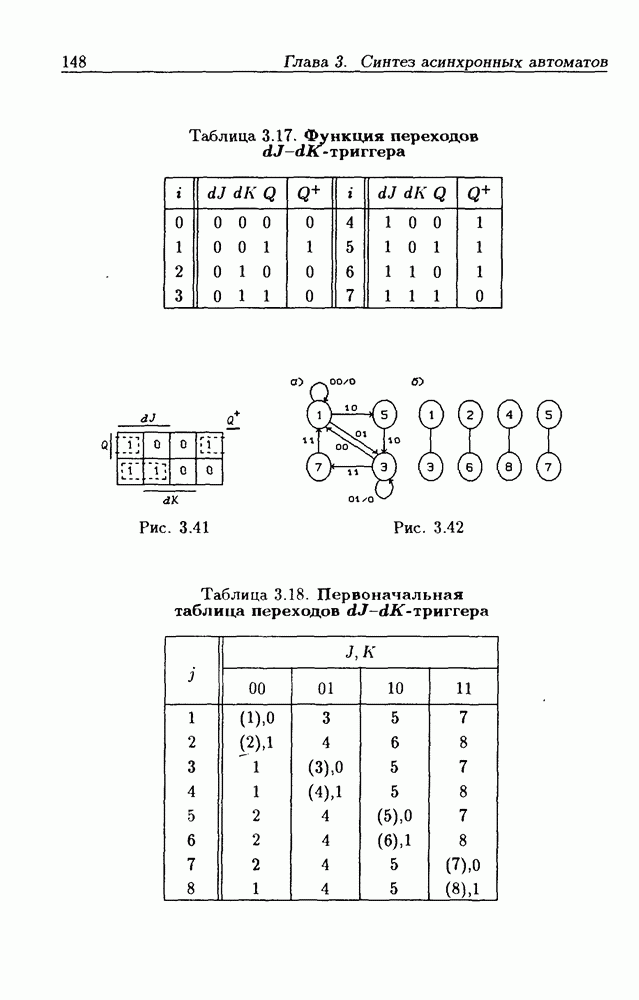
- Триггеры типа dJ-dK.
- Классификация триггеров.
- 3.7. Синтез синхронных триггеров
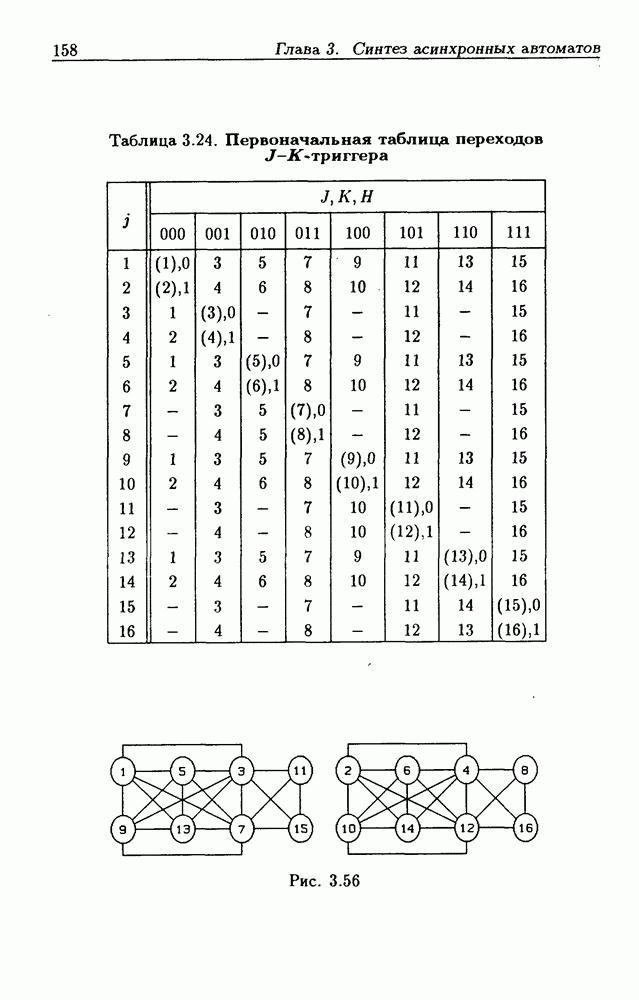
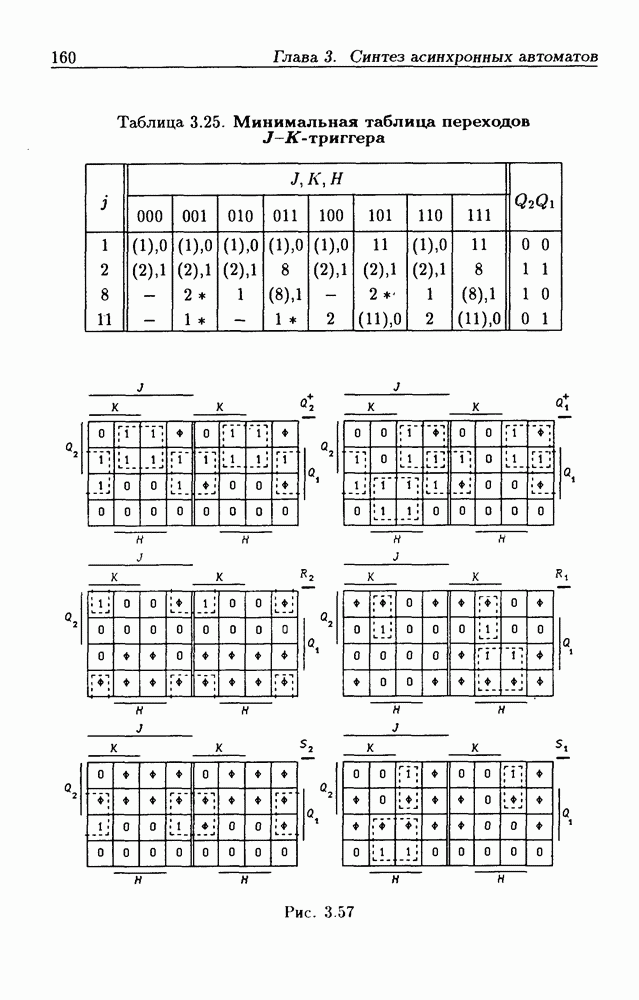
- Триггеры типа J-K
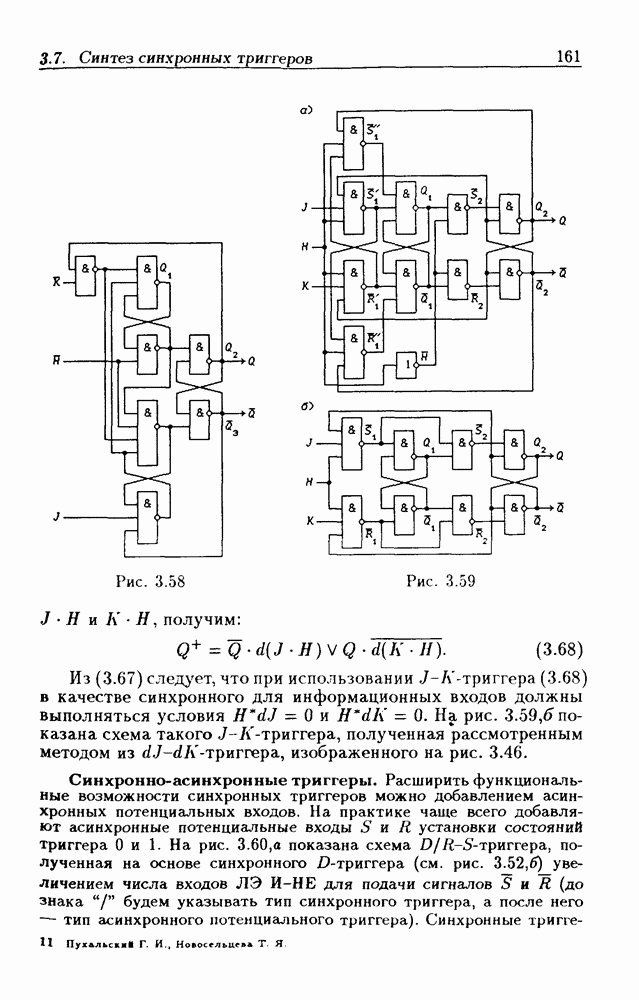
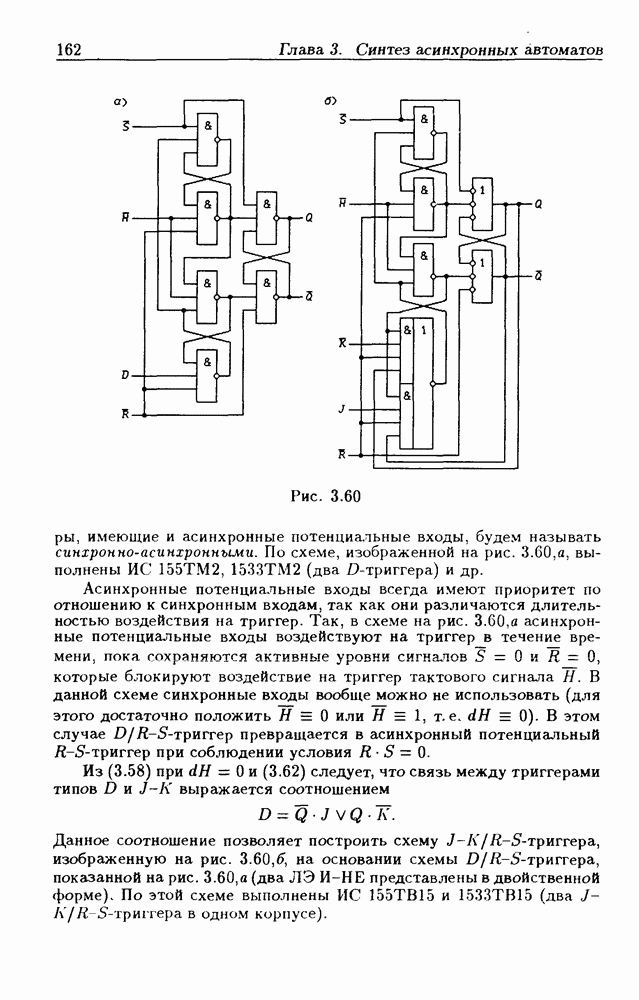
- Синхронно-асинхронные триггеры.
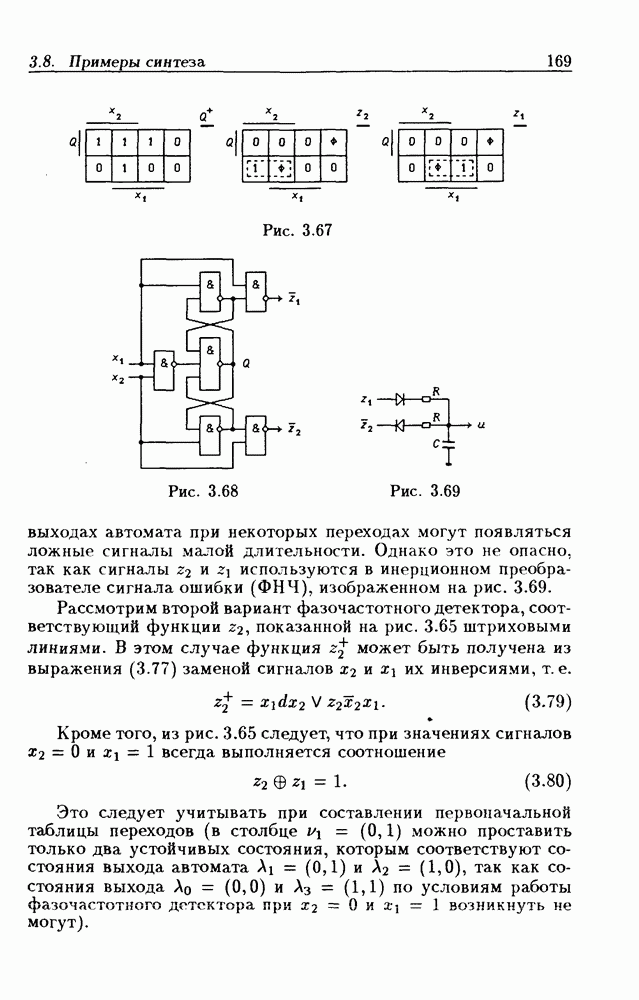
- 3.8. Примеры синтеза асинхронных потенциальных автоматов
- Цифровые фазочастотные детекторы.
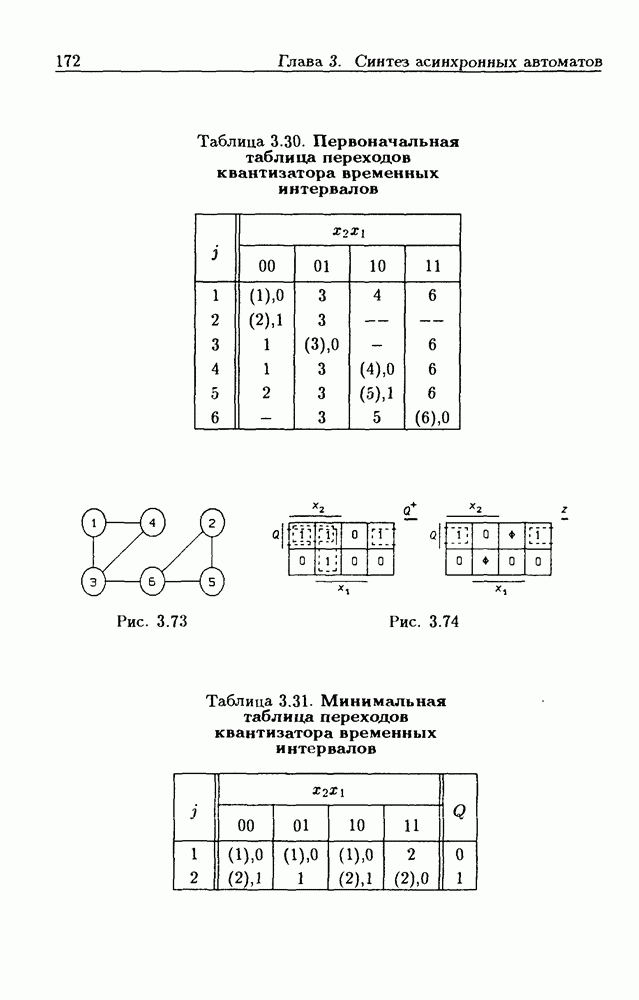
- Квантизатор временных интервалов.
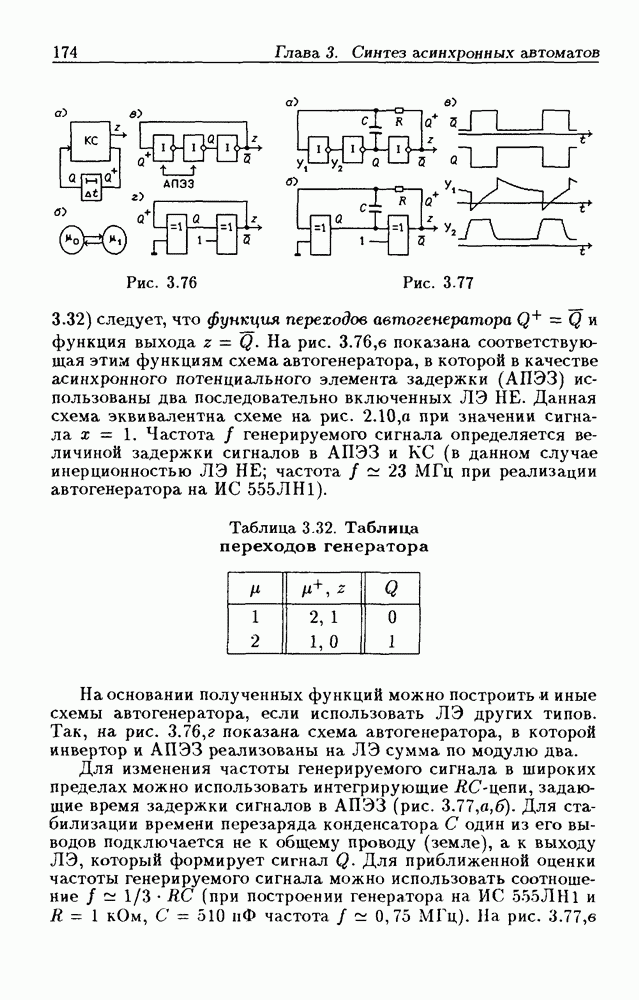
- 3.9. Генераторы сигналов
- Автогенераторы.
- Управляемые автогенераторы.
- Глава 4. Синтез синхронных автоматов
- 4.2. Синхронные триггеры
- Триггеры типов D и R-S с импульсным тактовым сигналом.
- Синхронные триггеры типов R-S и D-L
- Синхронно-асинхронные триггеры.
- Синхронные триггеры типа J-K
- Триггеры типа Т.
- Классификация синхронных триггеров.
- Преобразования типов синхронных триггеров.
- Триггеры типов D-T-L и D-T-L/R
- Функции переходов синхронно-асинхронных триггеров.
- 4.3. Примеры синтеза синхронных автоматов
- 4.4. Сдвигающие регистры
- Синтез счетчиков на сдвигающих регистрах.
- Сдвигающие регистры с загрузкой данных.
- Реверсивные сдвигающие регистры.
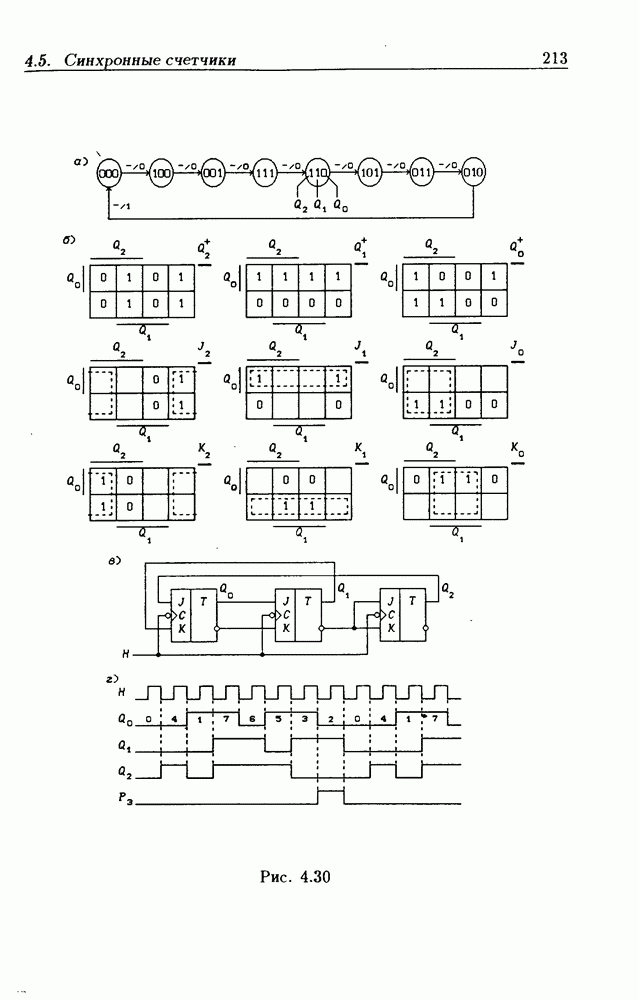
- 4.5. Синхронные счетчики
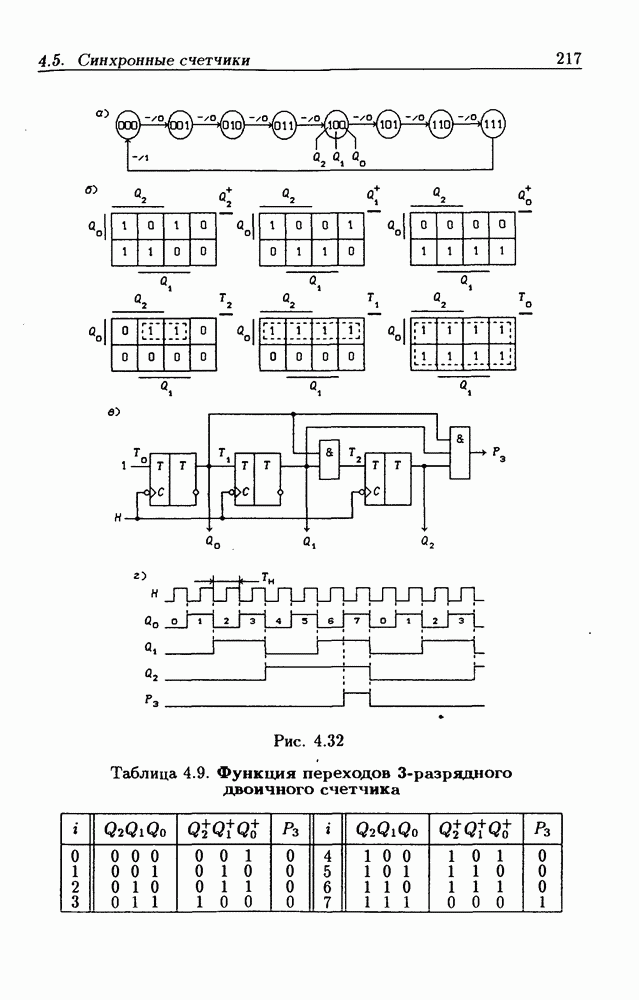
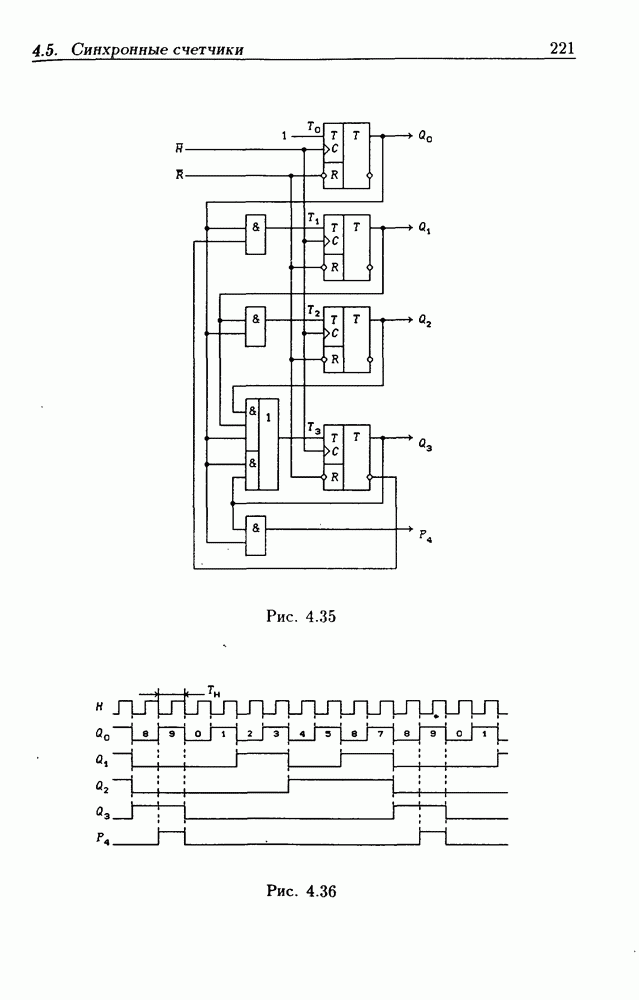
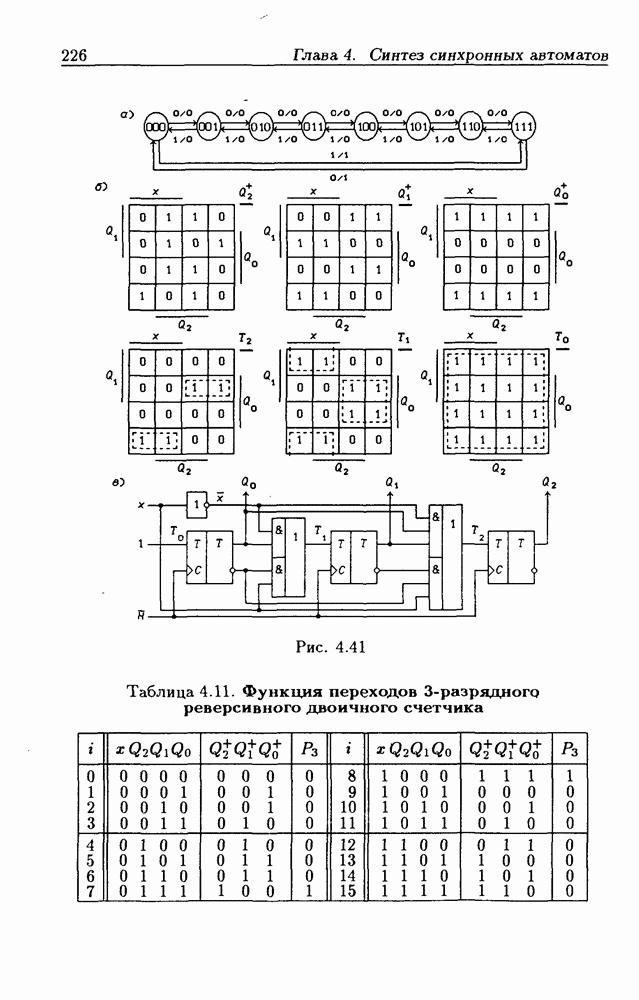
- Синхронные двоичные счетчики.
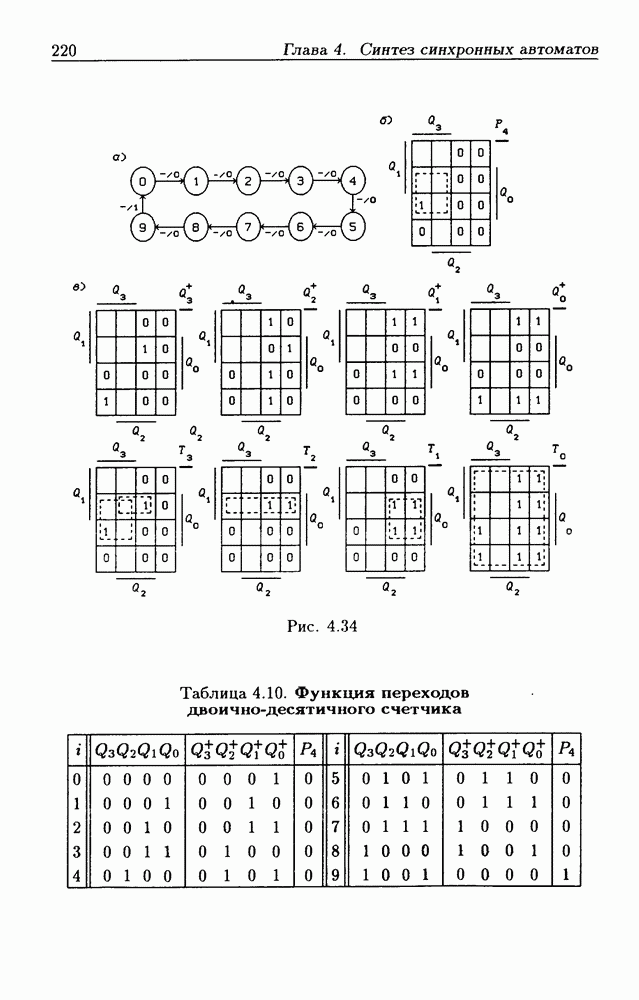
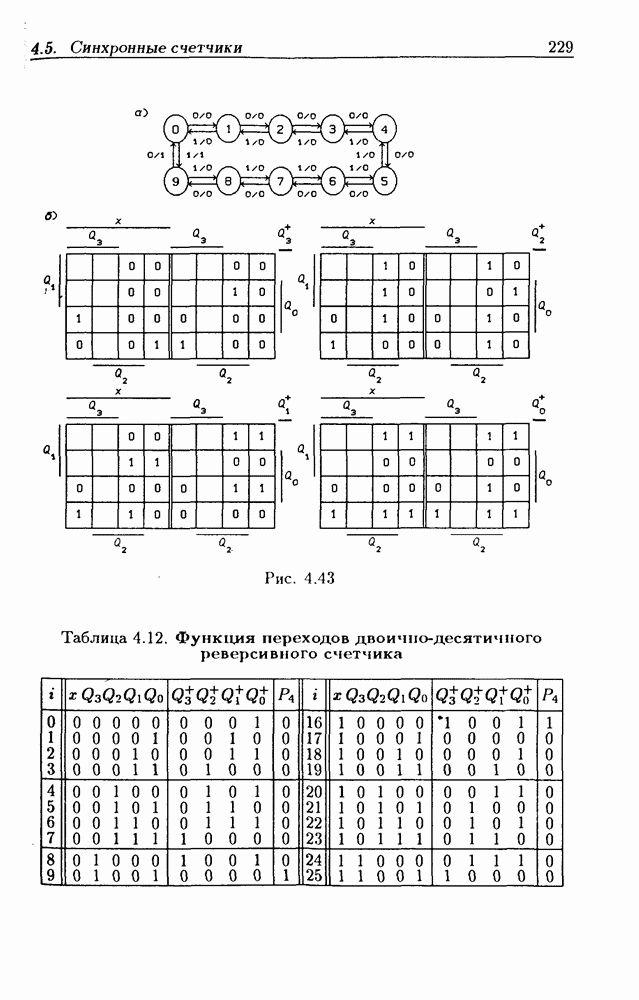
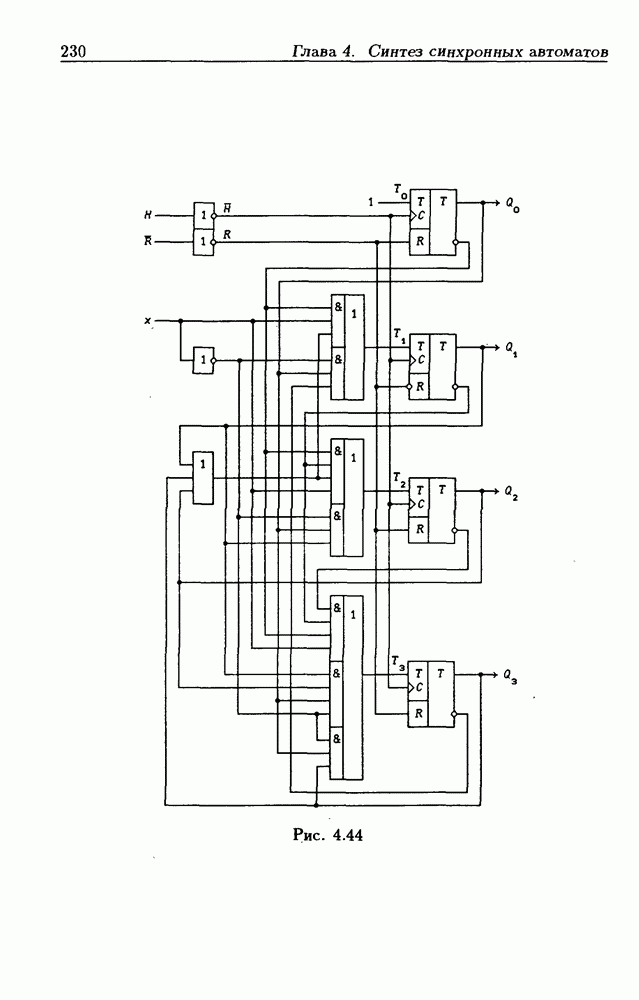
- Синхронные двоично-десятичные счетчики.
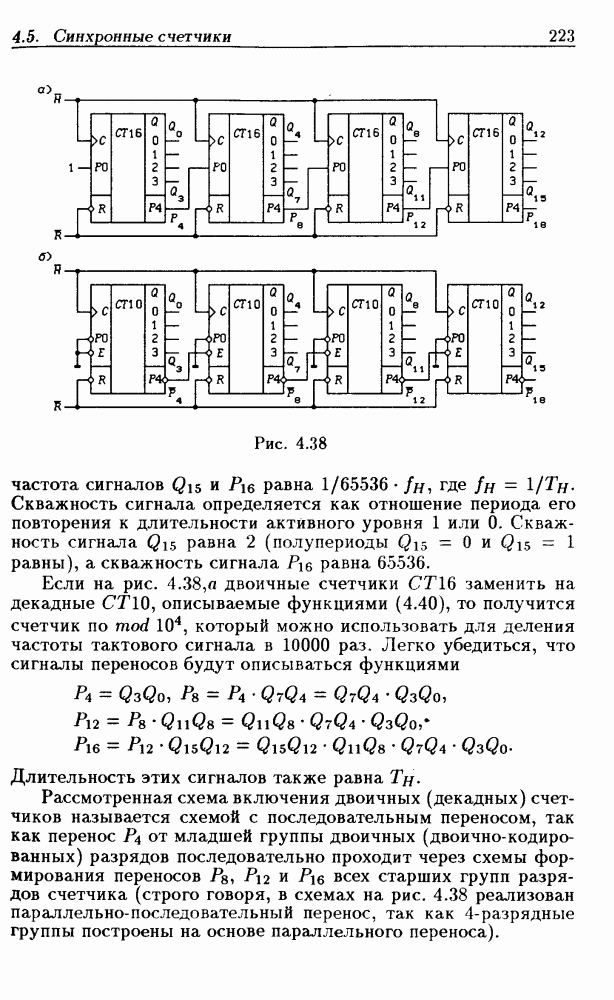
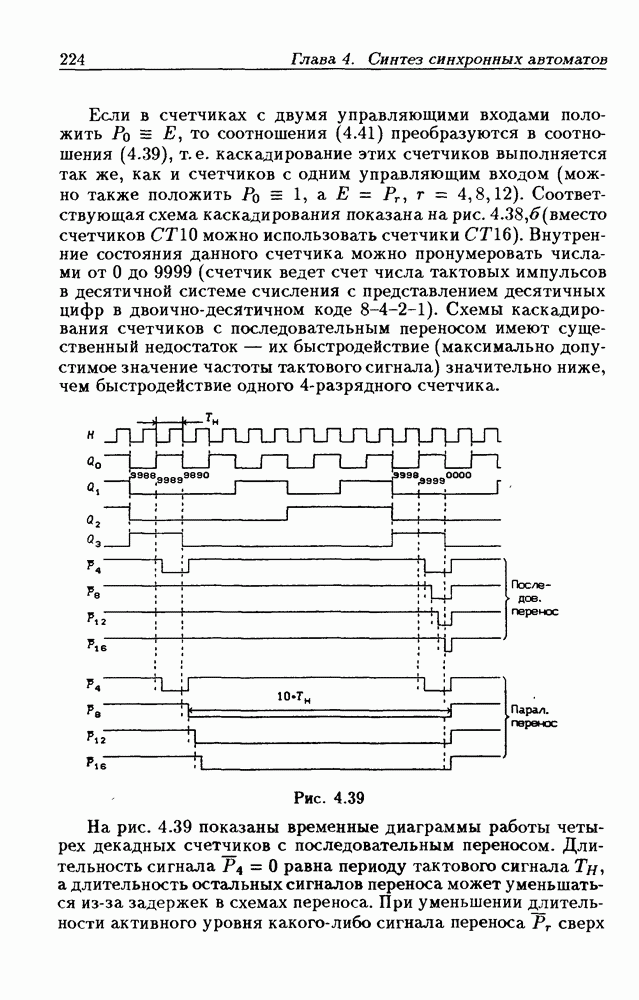
- Каскадирование двоичных и двоично-десятичных счетчиков.
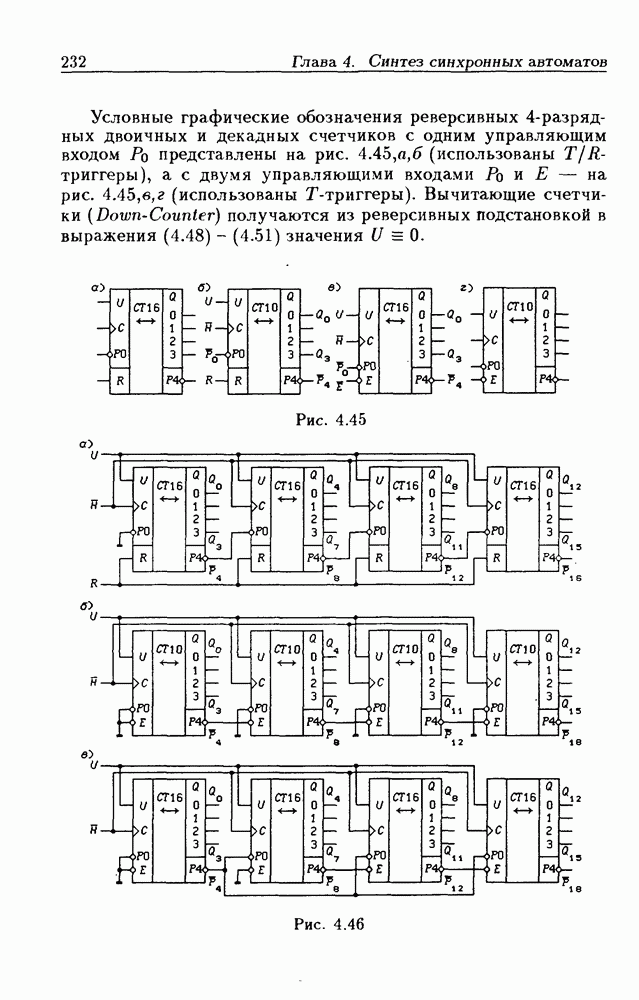
- Синхронные двоичные реверсивные счетчики.
- Реверсивные двоично-десятичные счетчики.
- Каскадирование реверсивных счетчиков.
- Счетчики на сдвигающих регистрах.
- Кольцевые счетчики.
- Линейные счетчики.
- Программируемые счетчики.
- 4.6. Асинхронные счетчики
- Асинхронные счетчики с умножением частоты счетного сигнала.
- Асинхронные импульсно-потенциальные счетчики.
- Асинхронное программирование модуля пересчета счетчиков.
- Глава 5. Логические элементы и триггеры
- Логические элементы.
- Классификация ИС по степени интеграции.
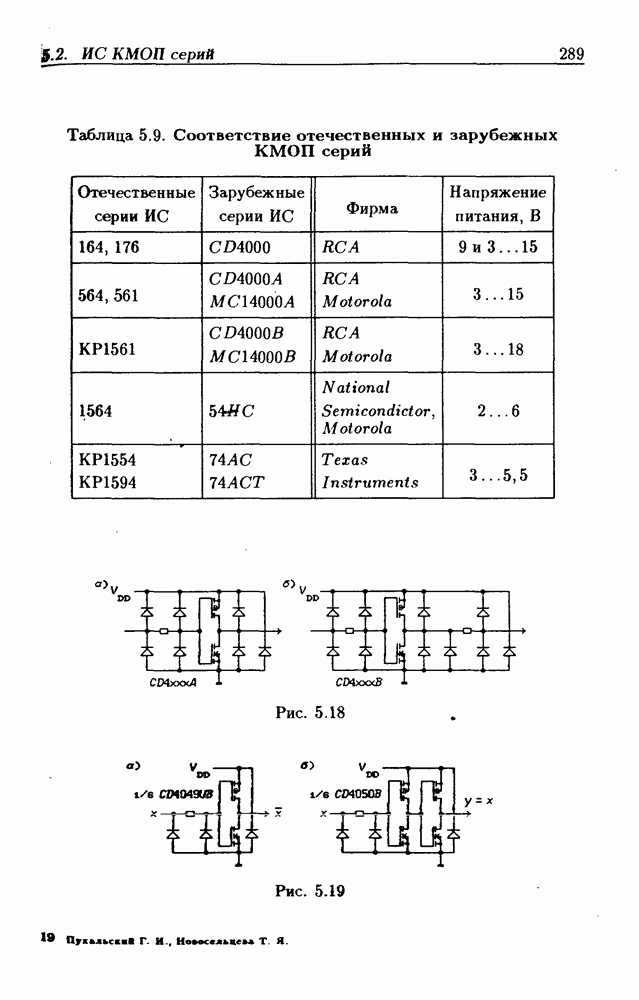
- 5.2. Интегральные схемы КМОП серий
- 5.3. Триггеры Шмитта
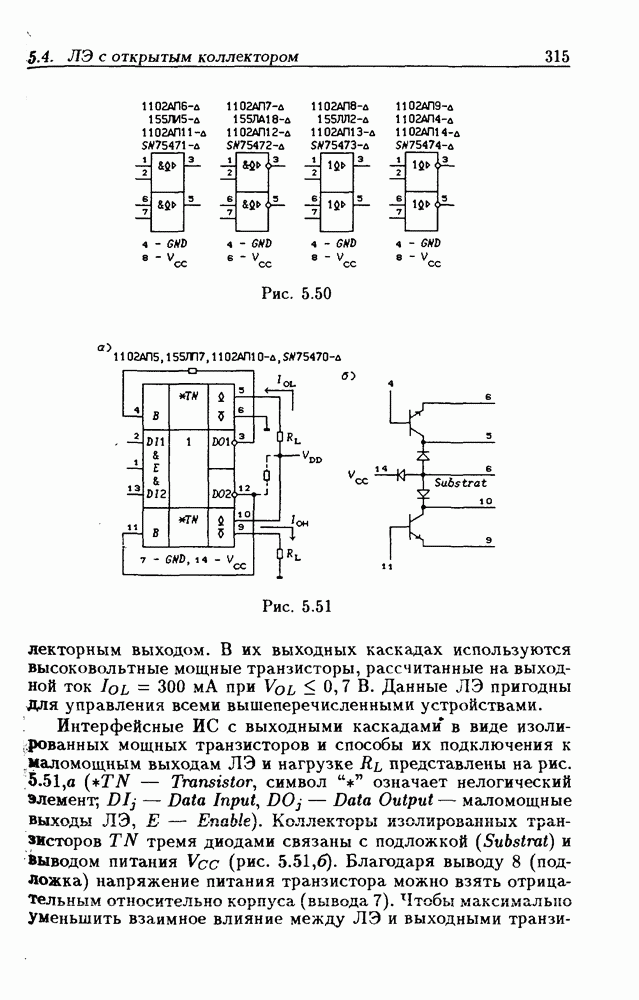
- 5.4. Логические элементы с открытым коллекторным выходом
- Логические элементы с открытым коллекторным выходом.
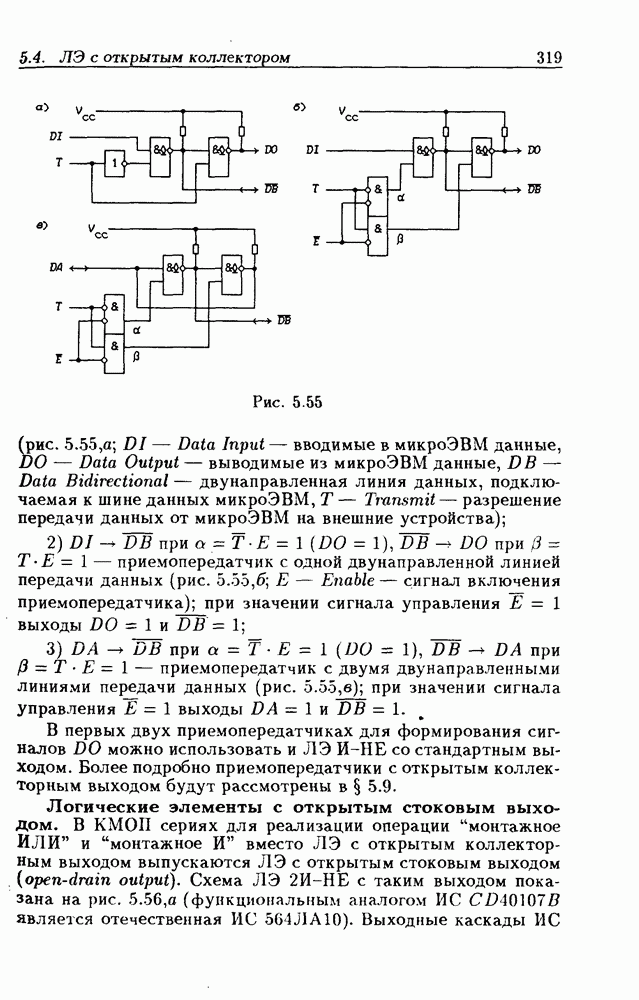
- Применения ЛЭ с открытым коллекторным выходом.
- Интерфейсные ЛЭ с открытым коллекторным выходом.
- Логические элементы с открытым стоковым выходом.
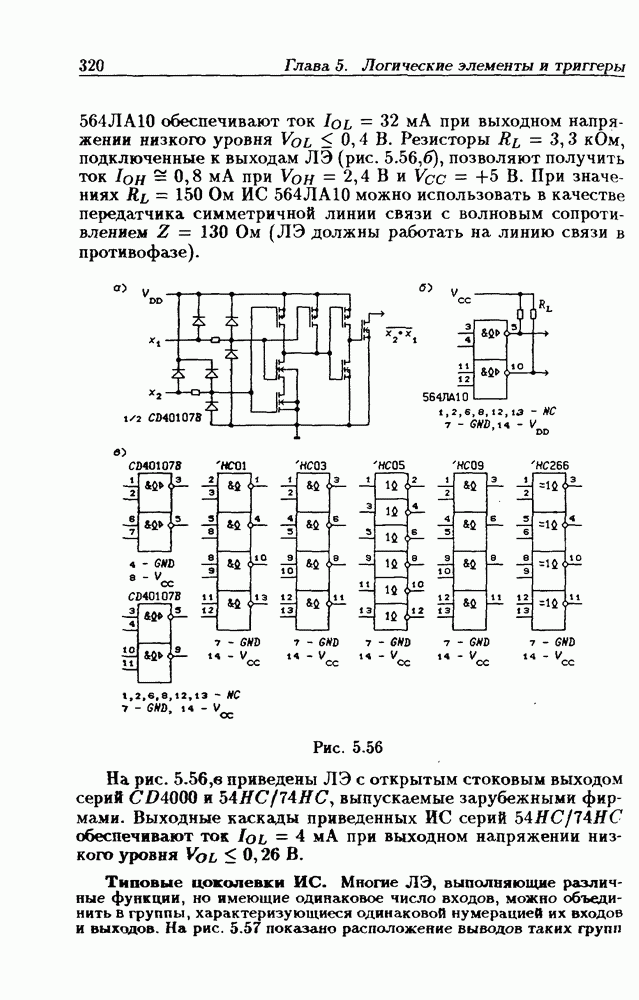
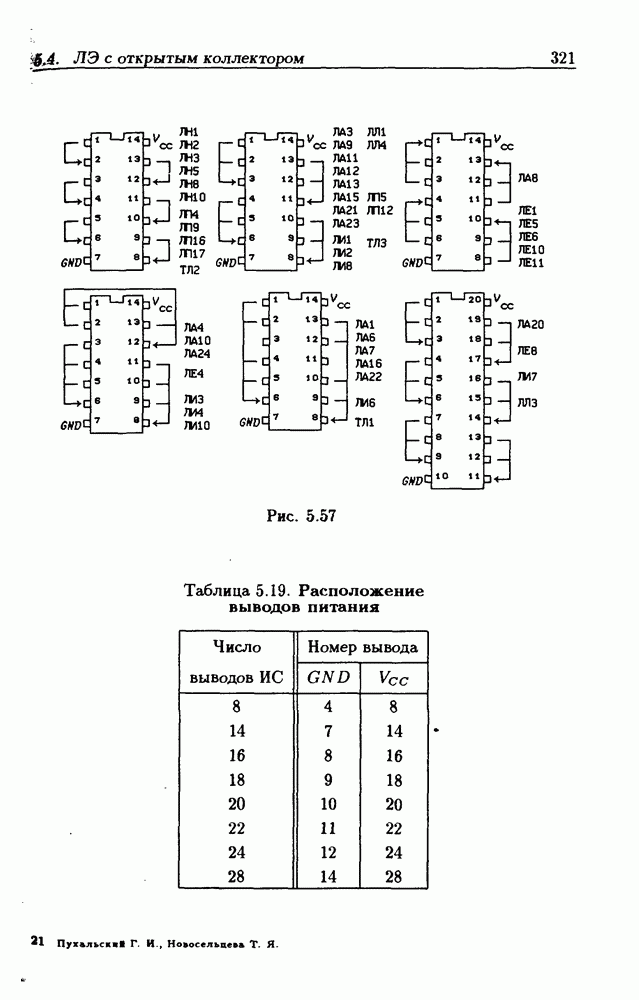
- Типовые цоколевки ИС.
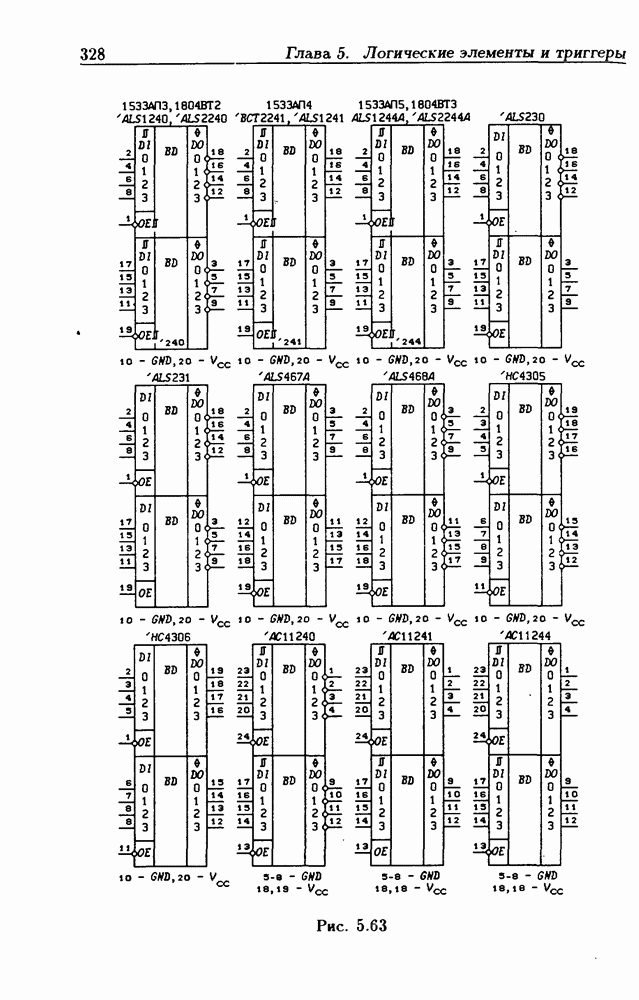
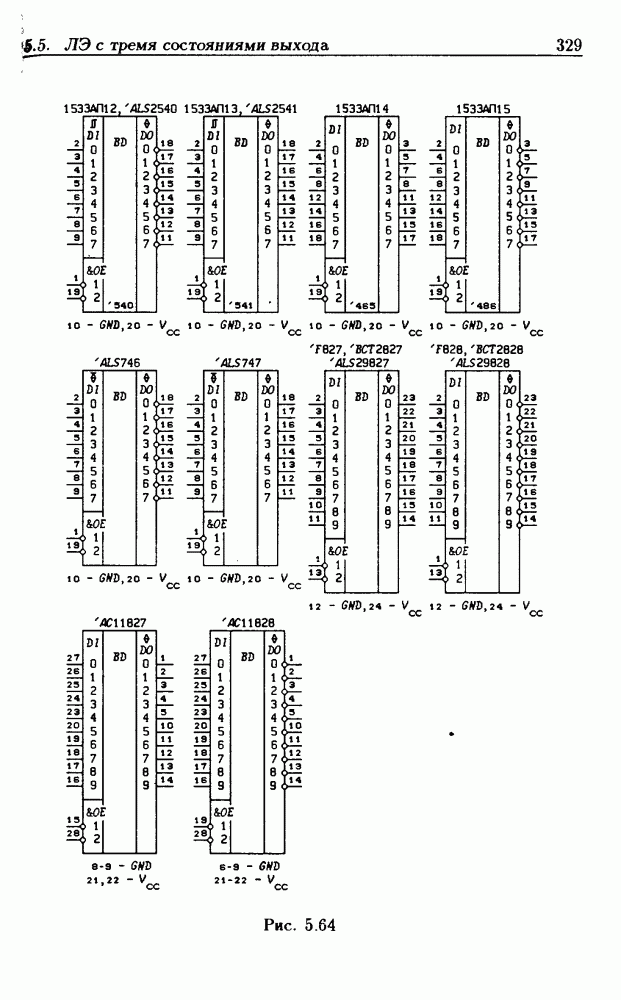
- 5.5. Логические элементы с тремя состояниями выхода
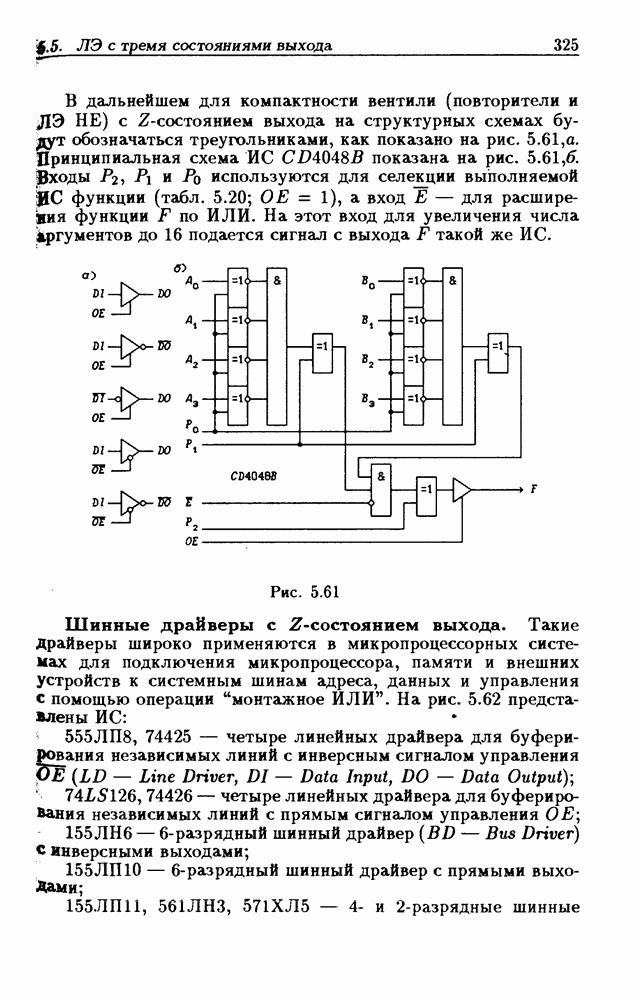
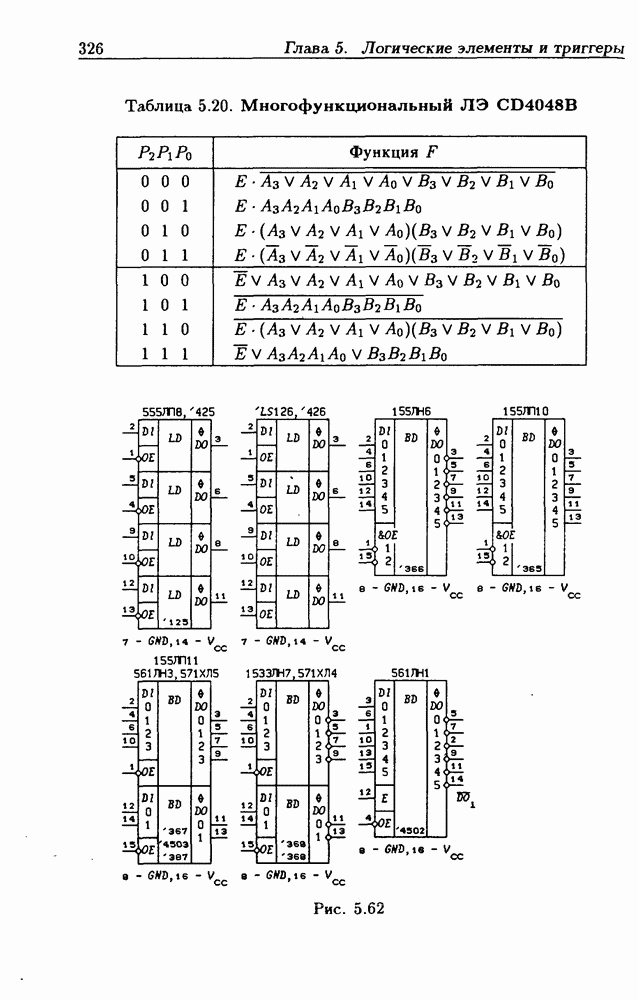
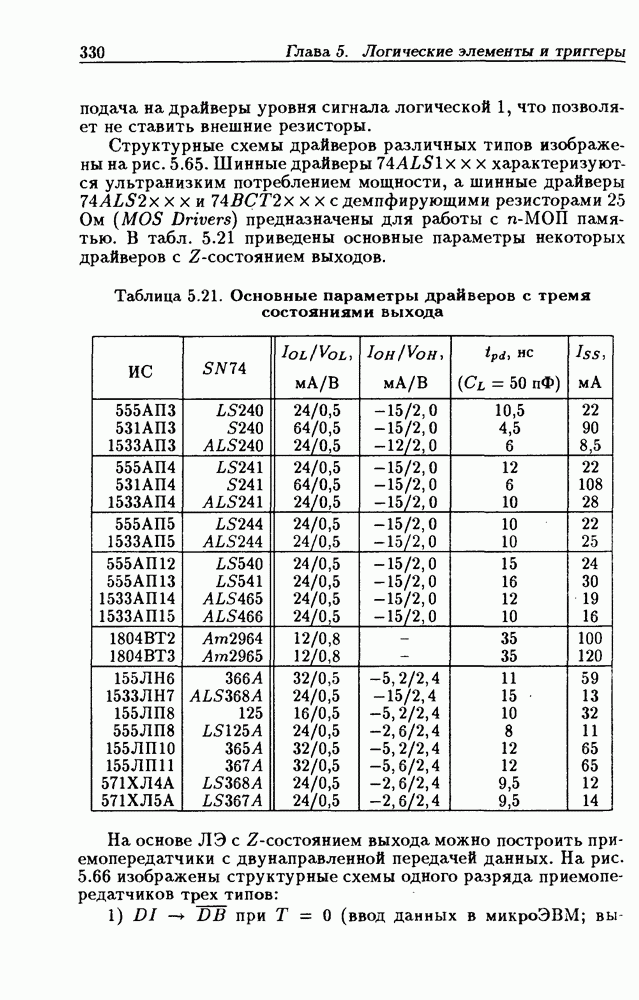
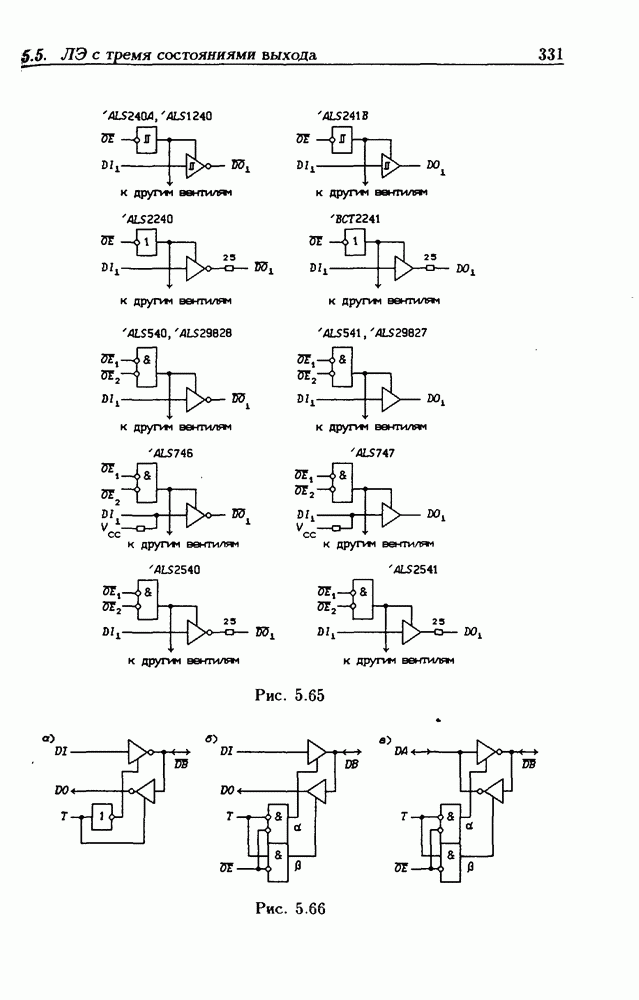
- Шинные драйверы с Z-состоянием выхода.
- Основные правила графического изображения ИС.
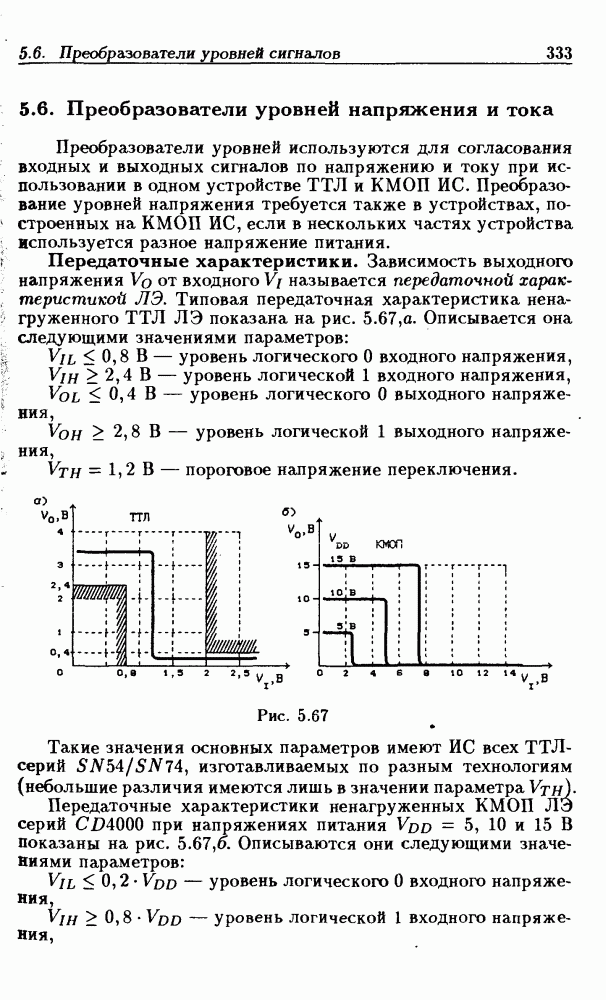
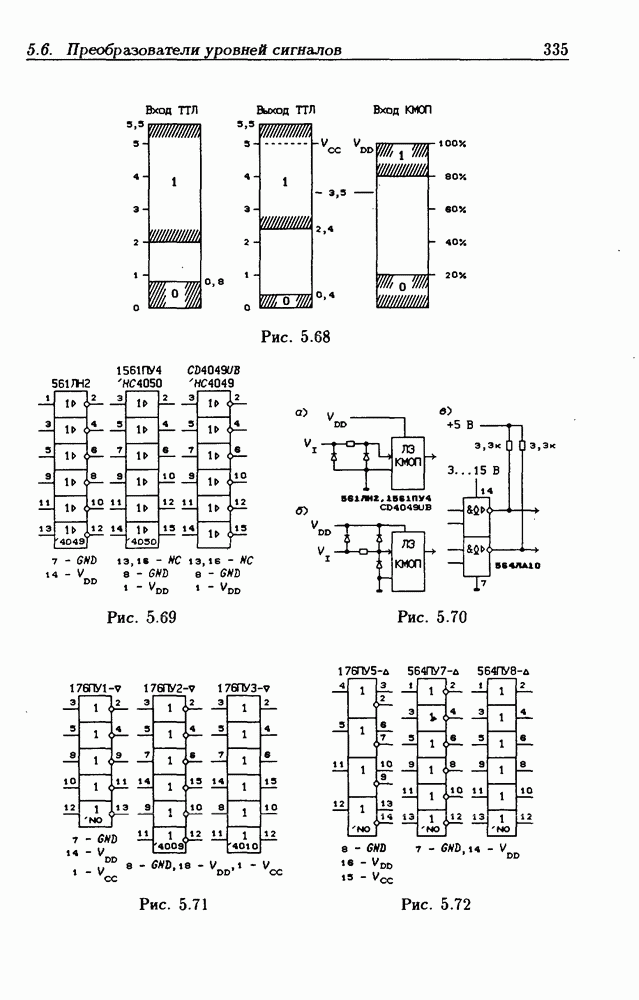
- 5.6. Преобразователи уровней напряжения и тока
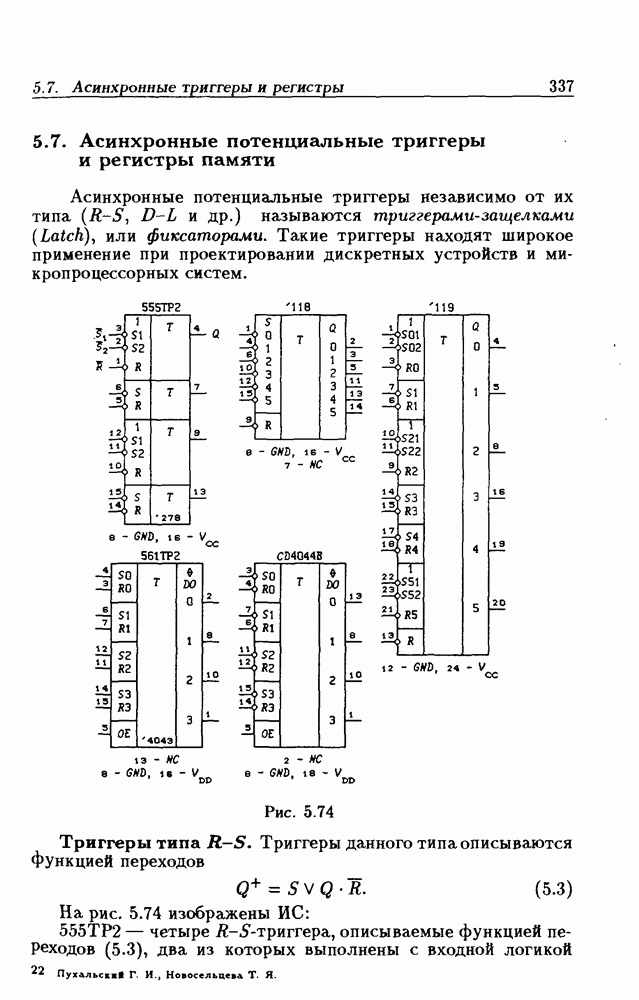
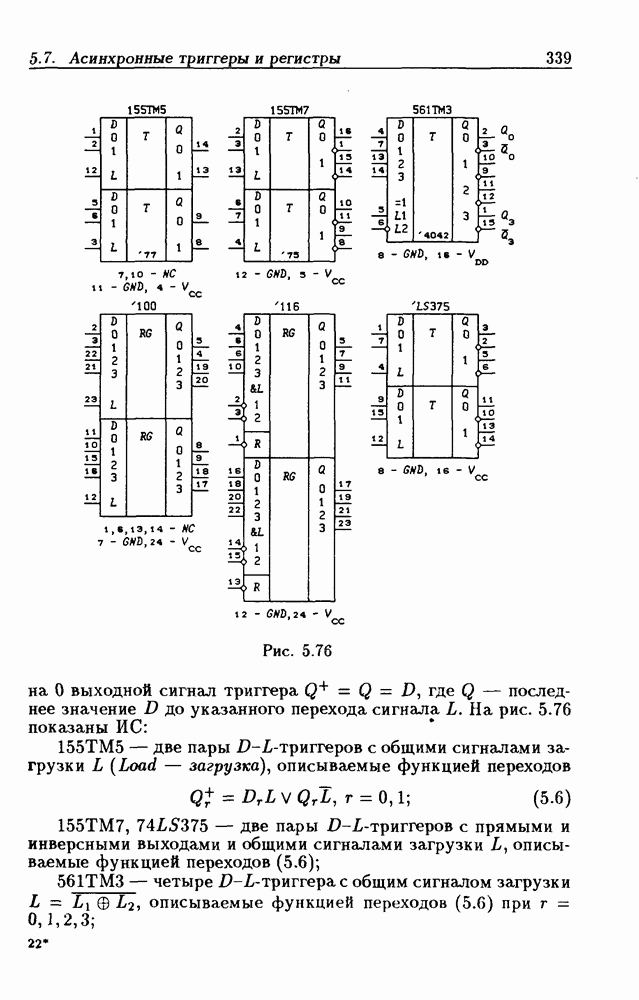
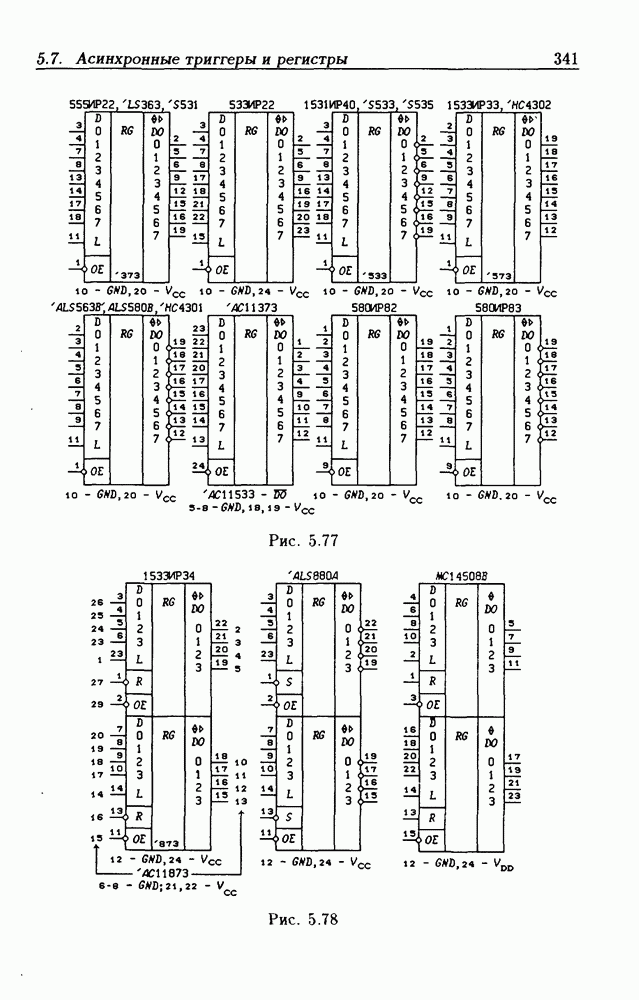
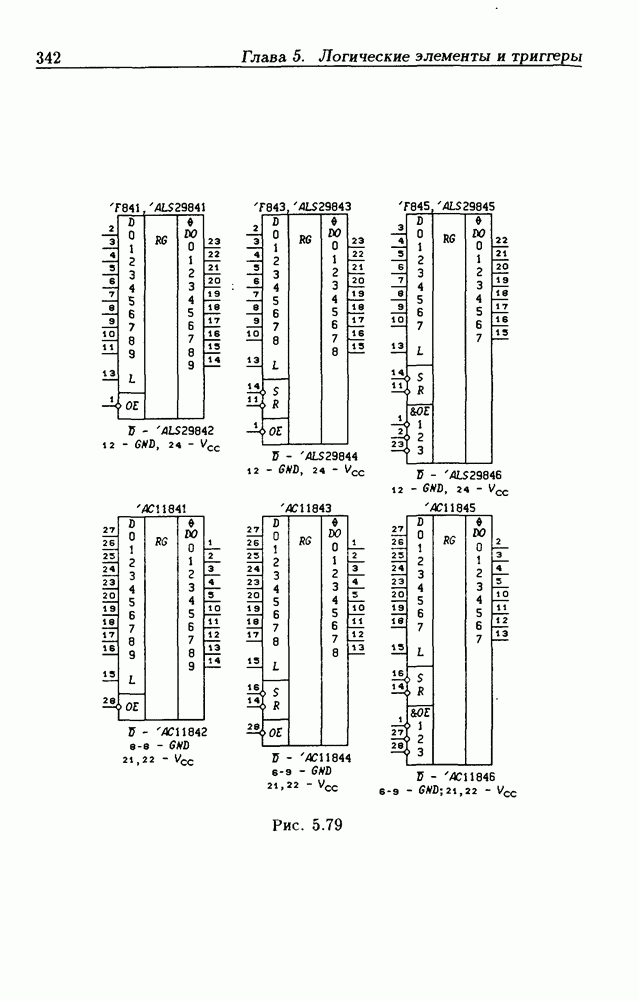
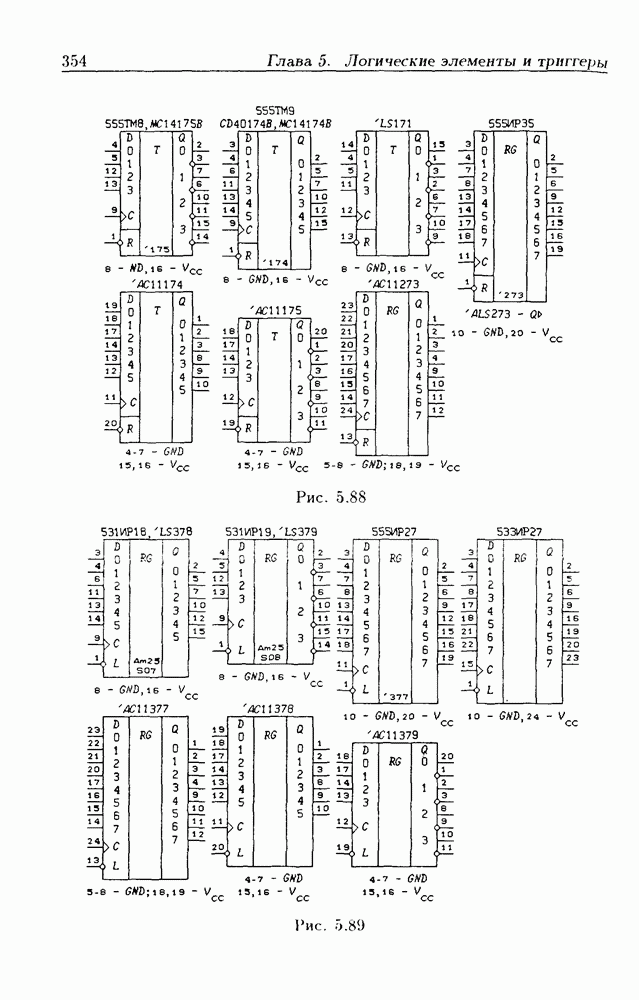
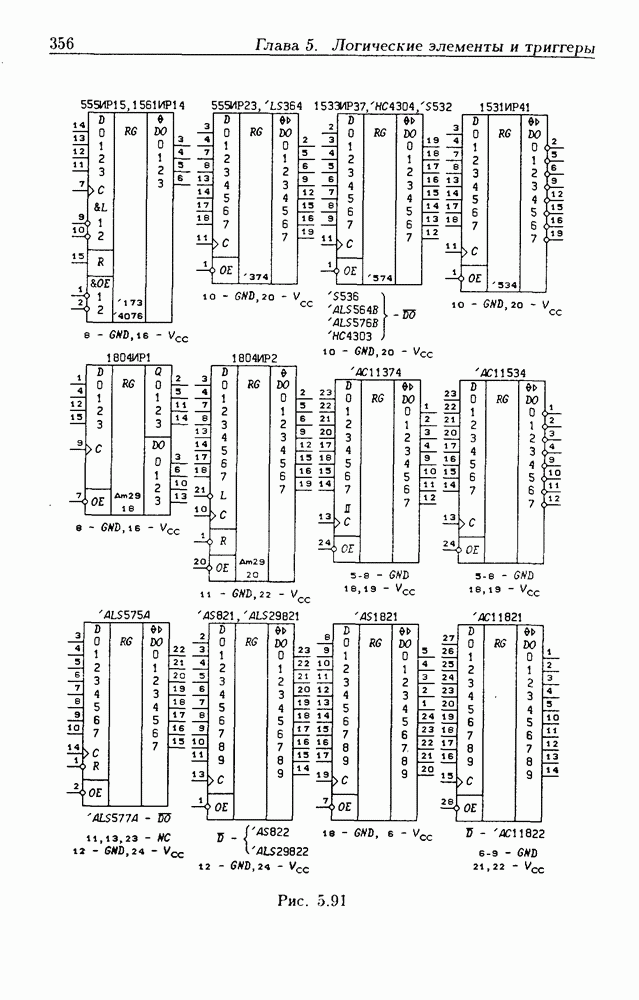
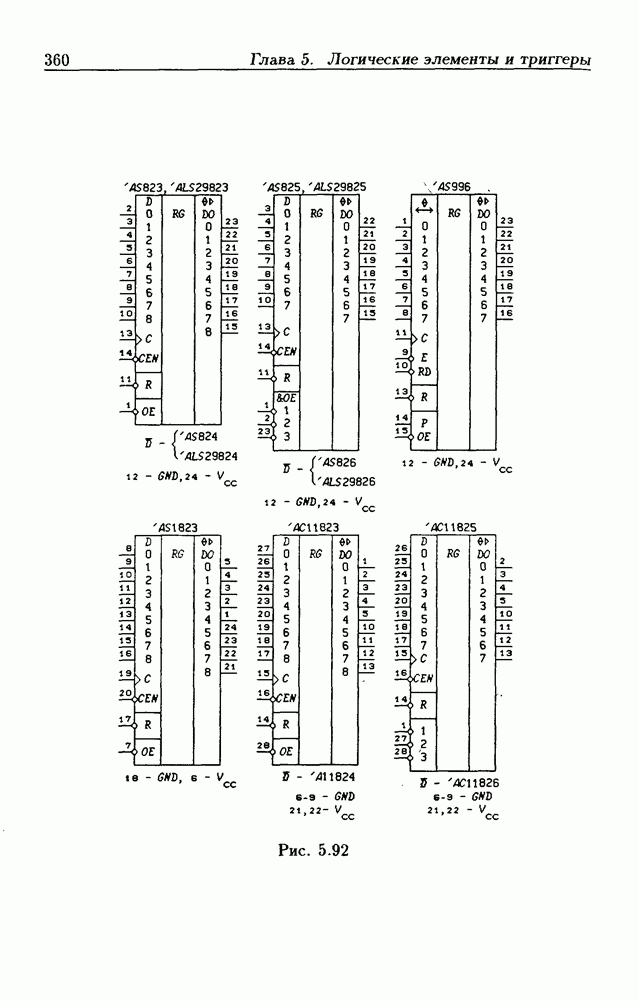
- 5.7. Асинхронные потенциальные триггеры и регистры памяти
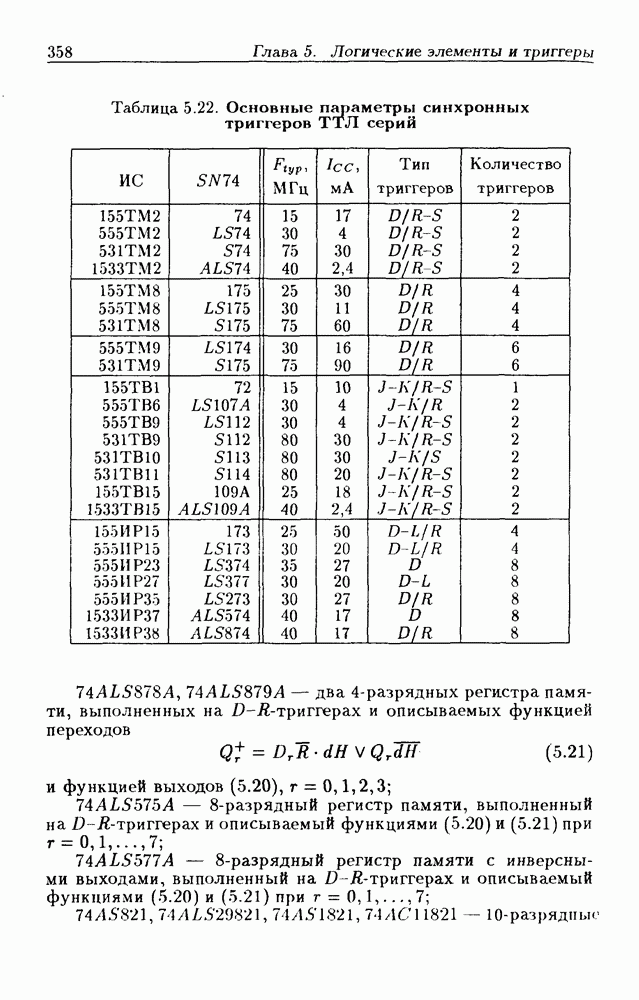
- 5.8. Синхронные триггеры и регистры памяти
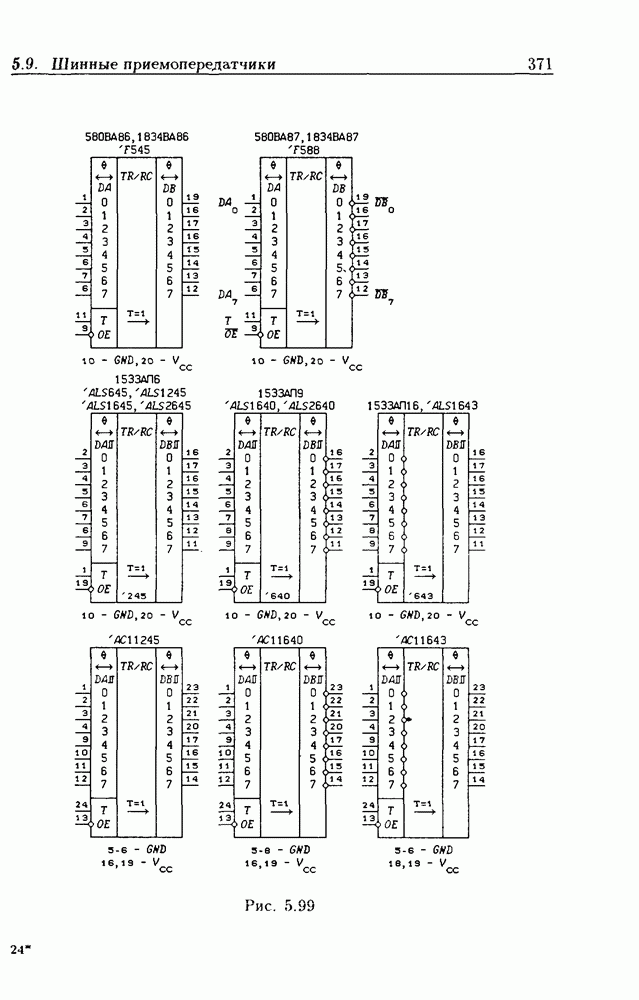
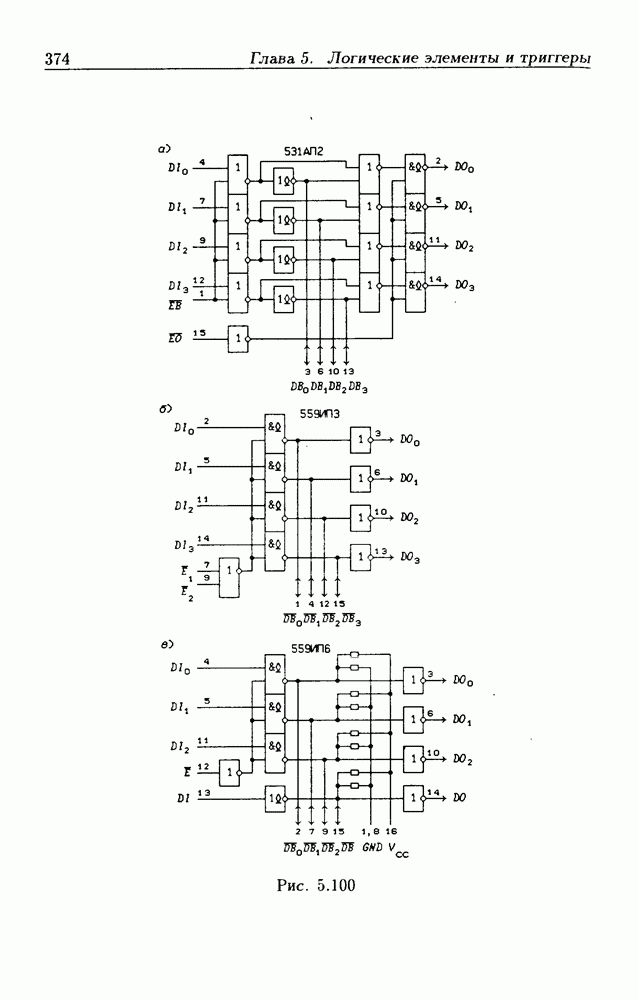
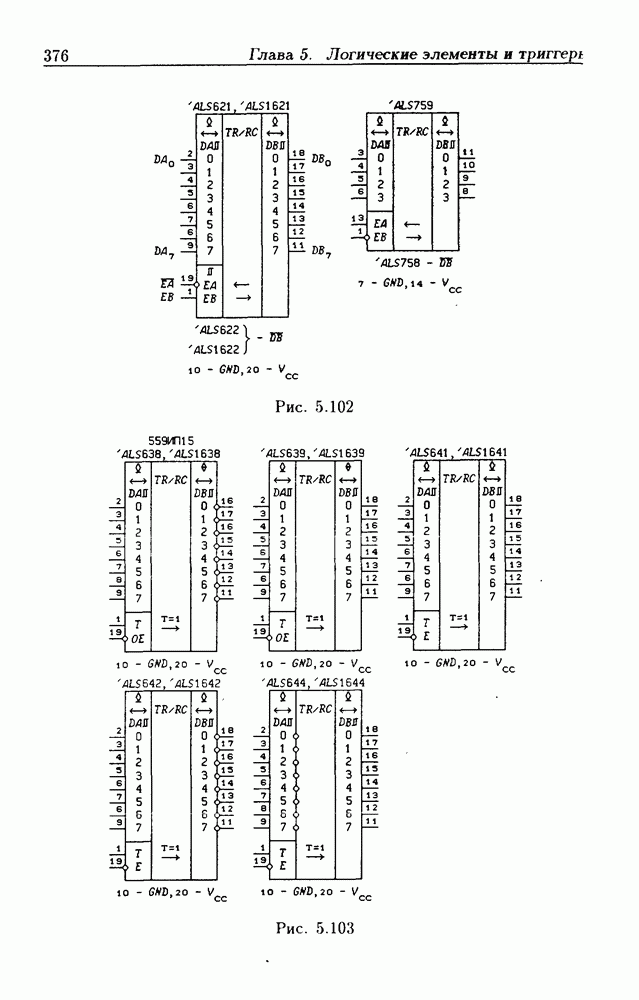
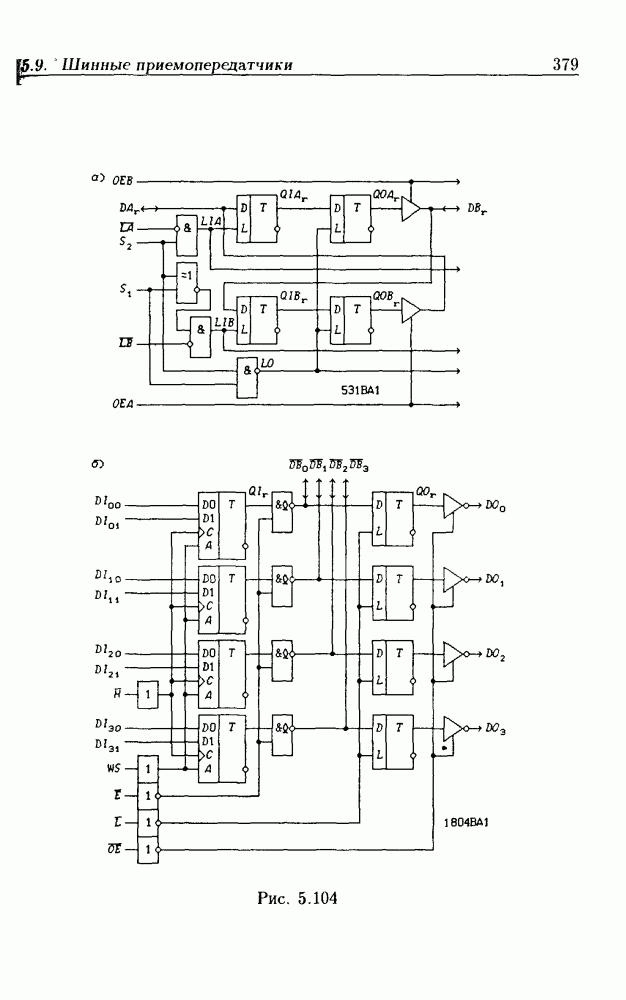
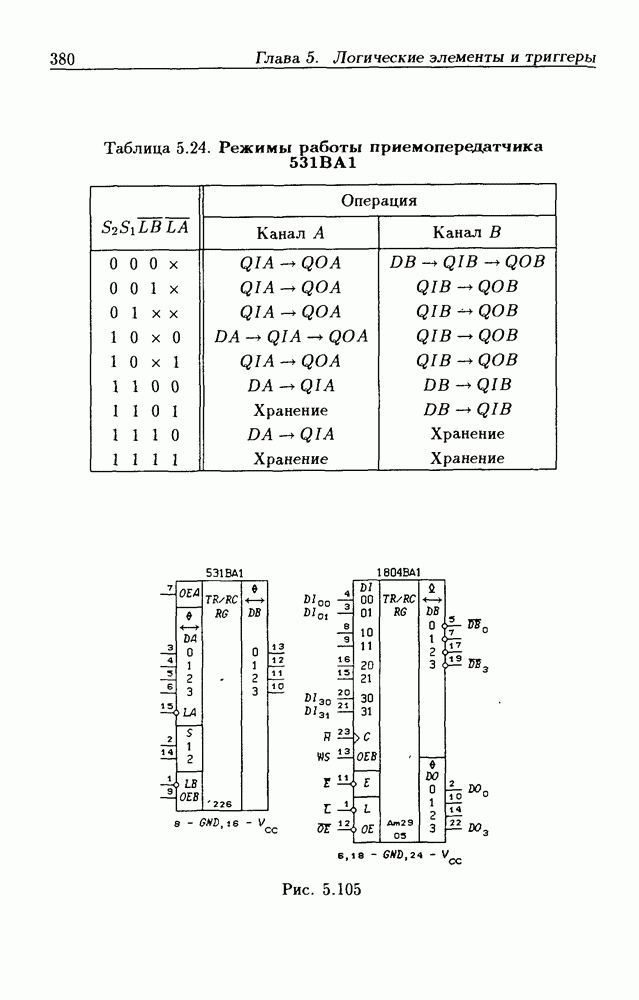
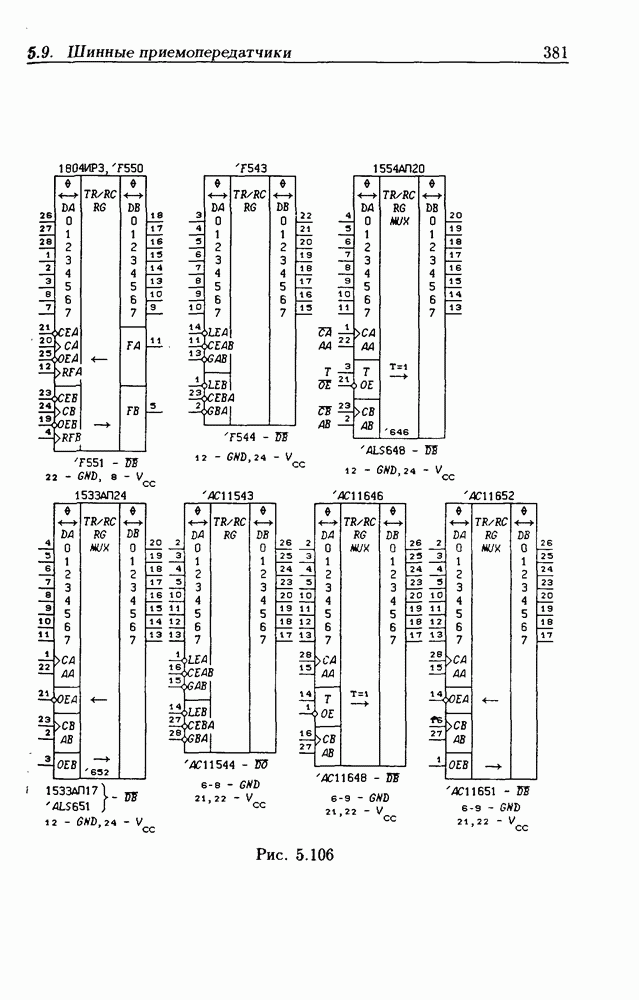
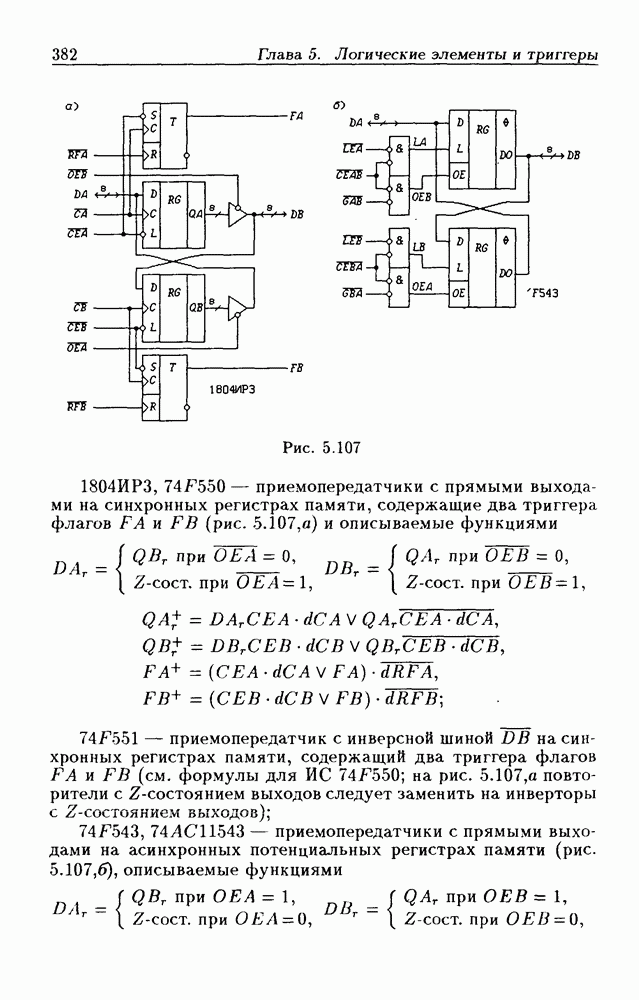
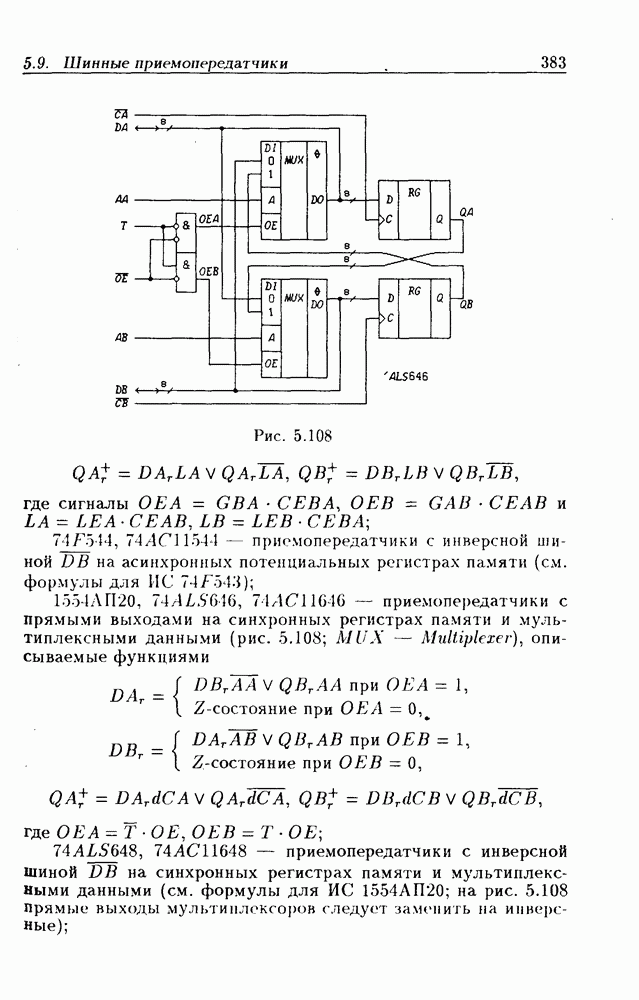
- 5.9. Шинные приемопередатчики
- Шинные приемопередатчики с Z-состоянием выхода.
- Шинные приемопередатчики с открытым коллекторным выходом.
- Шинные приемопередатчики с регистрами памяти.
- Шинные приемопередатчики со сдвигающим регистром.
- Шинные трехнаправленные приемопередатчики.
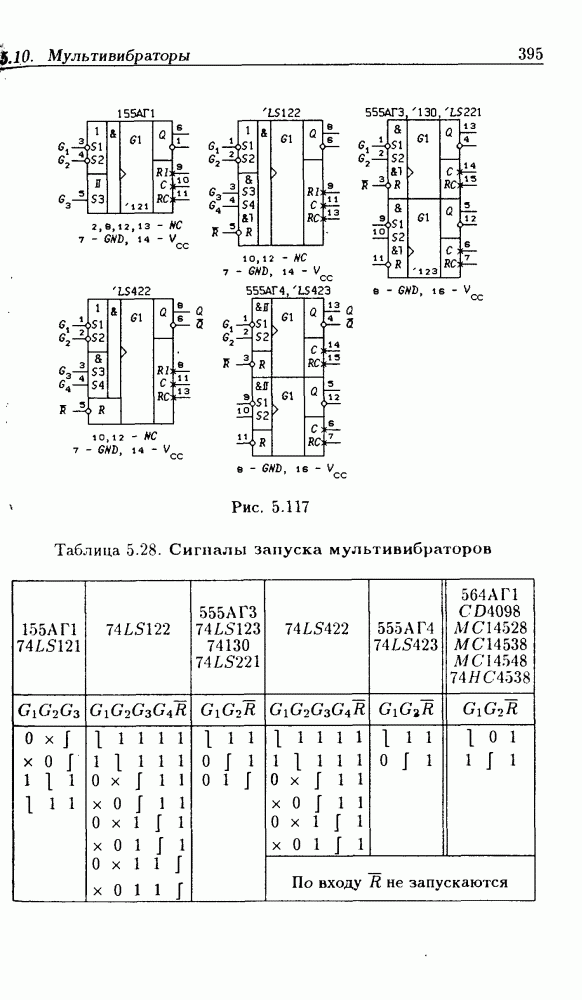
- 5.10. Мультивибраторы
- 5.11. Генераторы
- Схемы устранения «дребезга» механических контактов.
- Автогенераторы периодических сигналов.
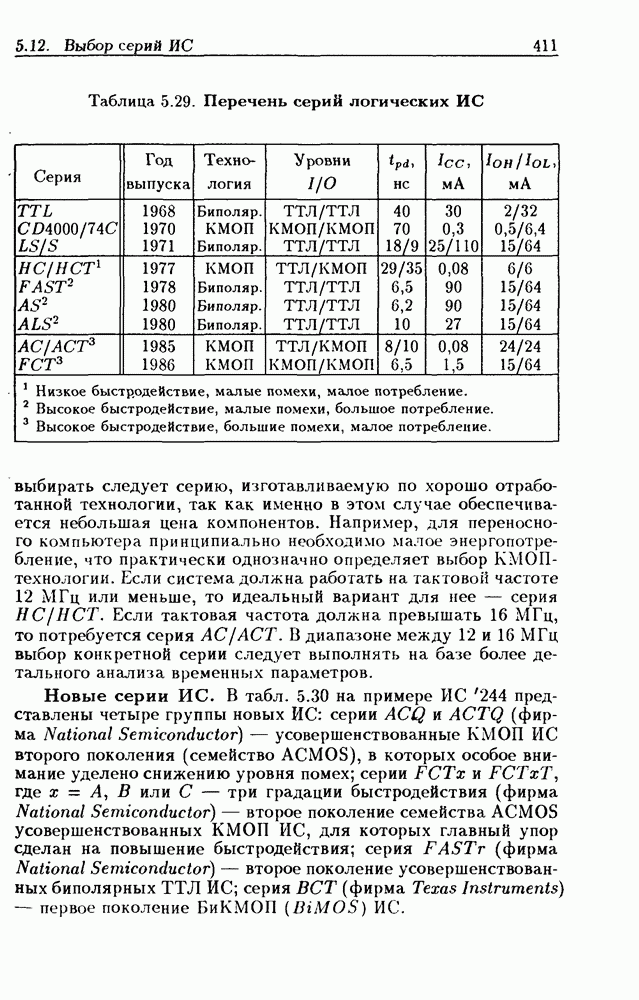
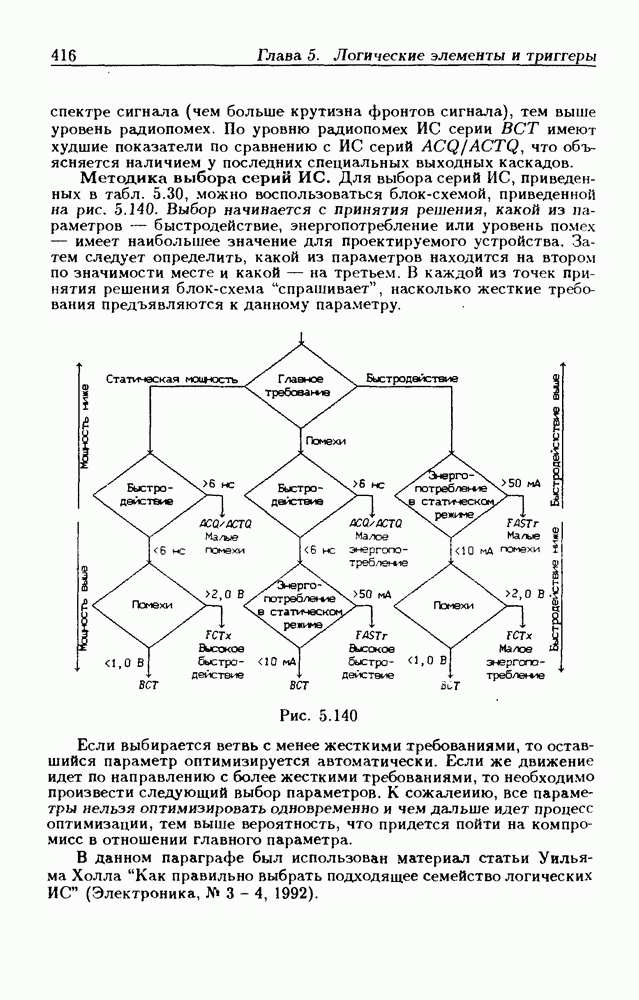
- 5.12. Рекомендации по выбору серий ИС
- Глава 6. Коммутаторы и арифметические устройства
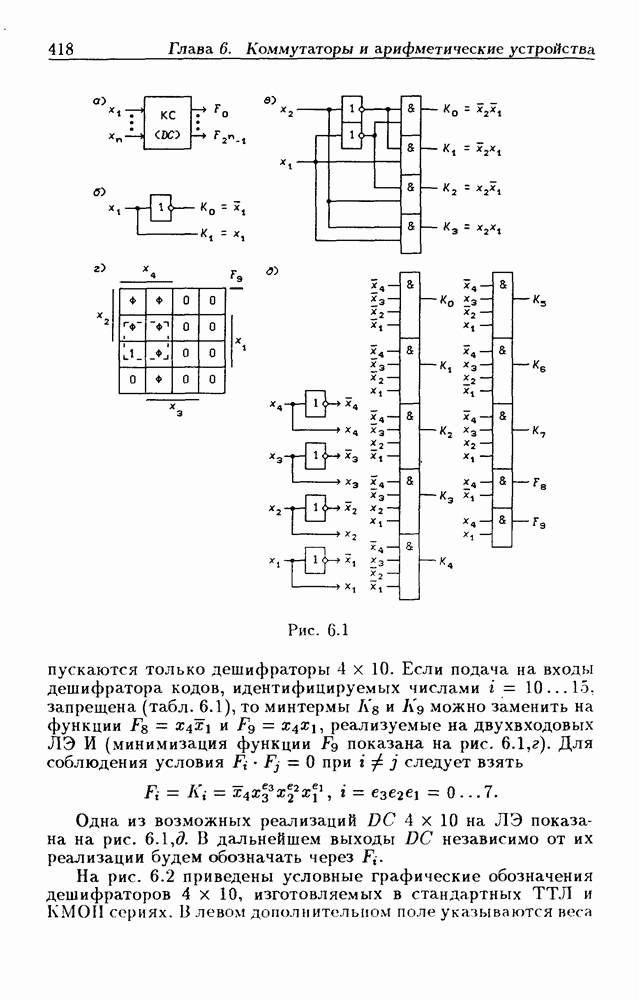
- 6.1. Дешифраторы
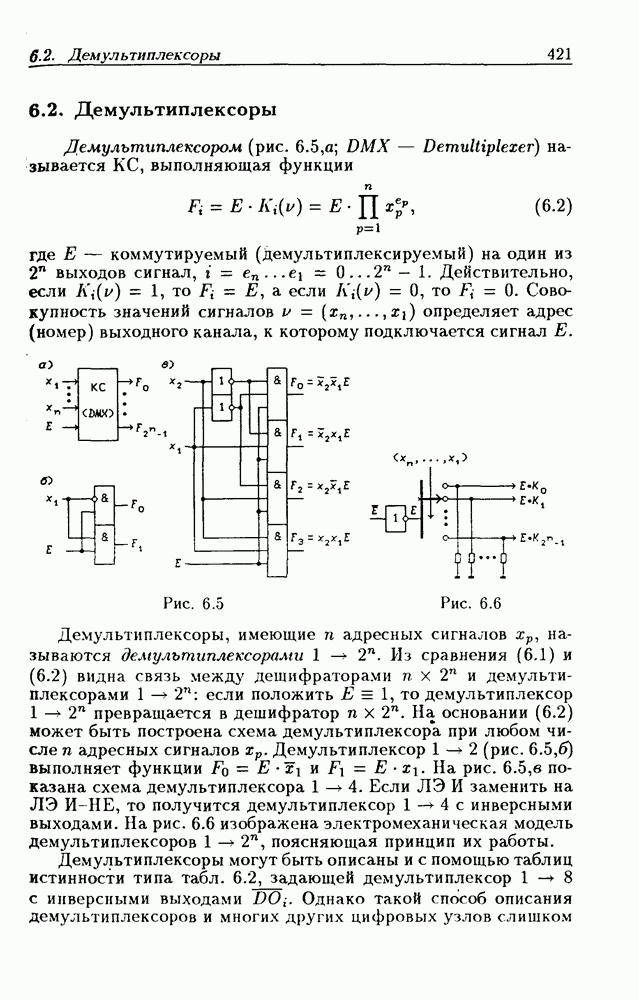
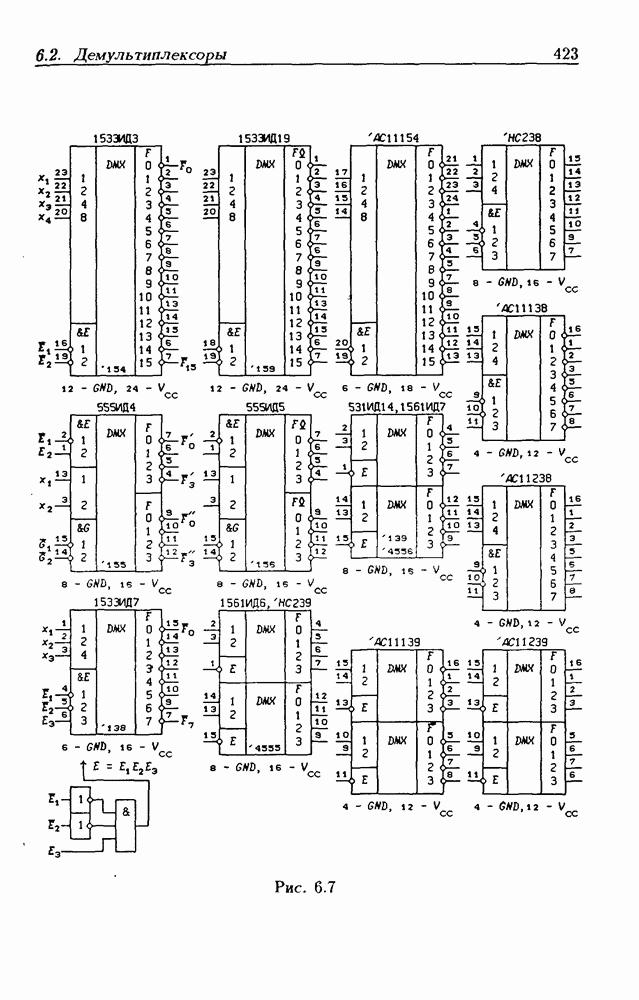
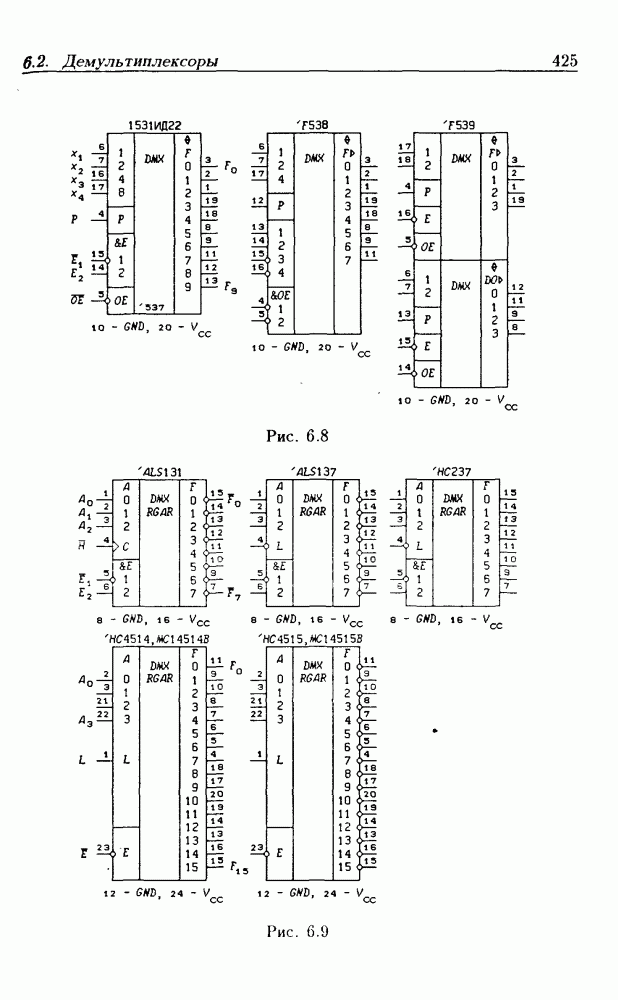
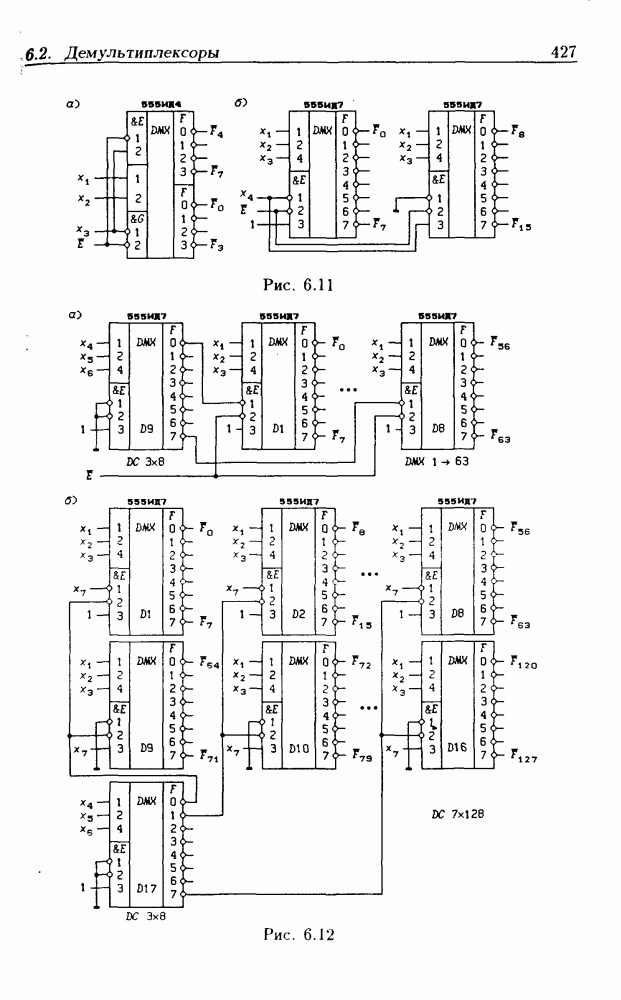
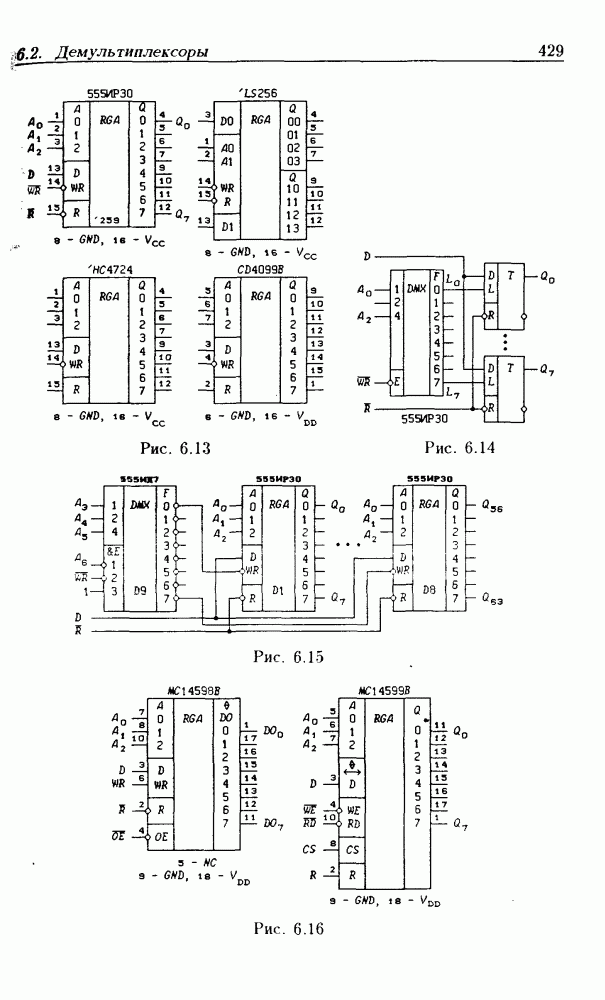
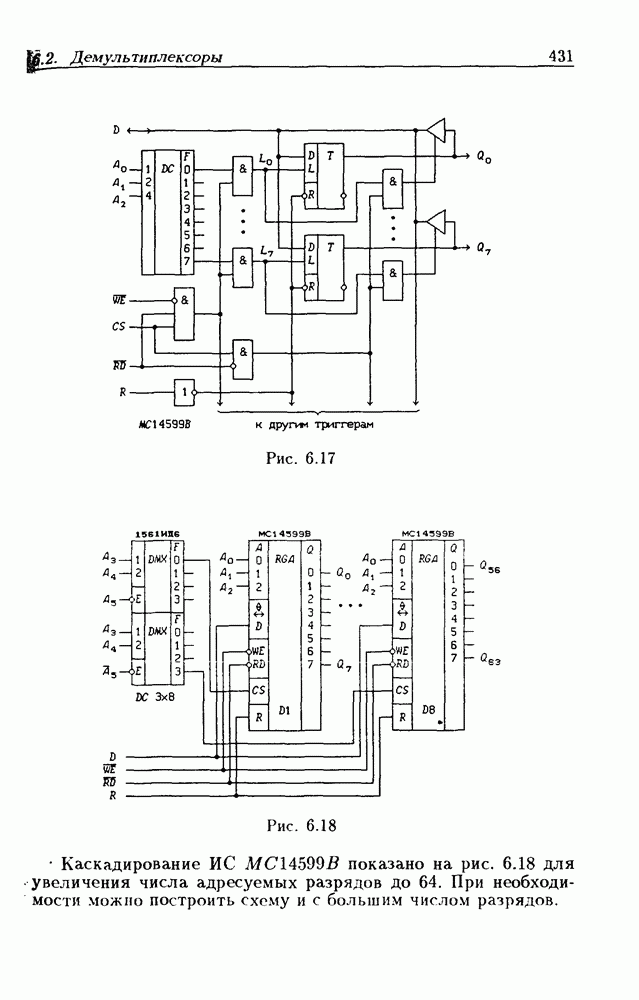
- 6.2. Демультиплексоры
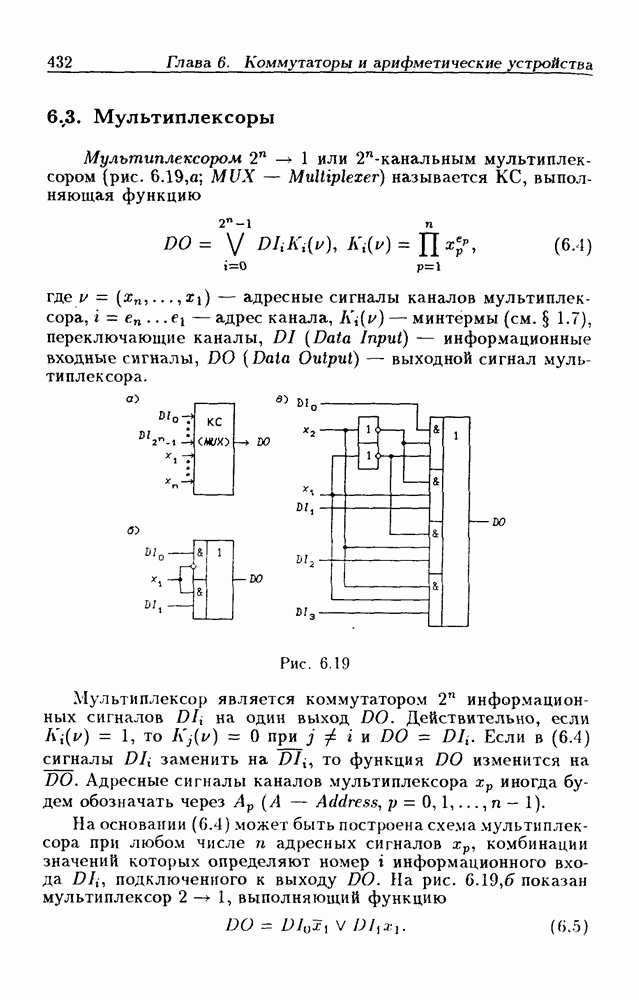
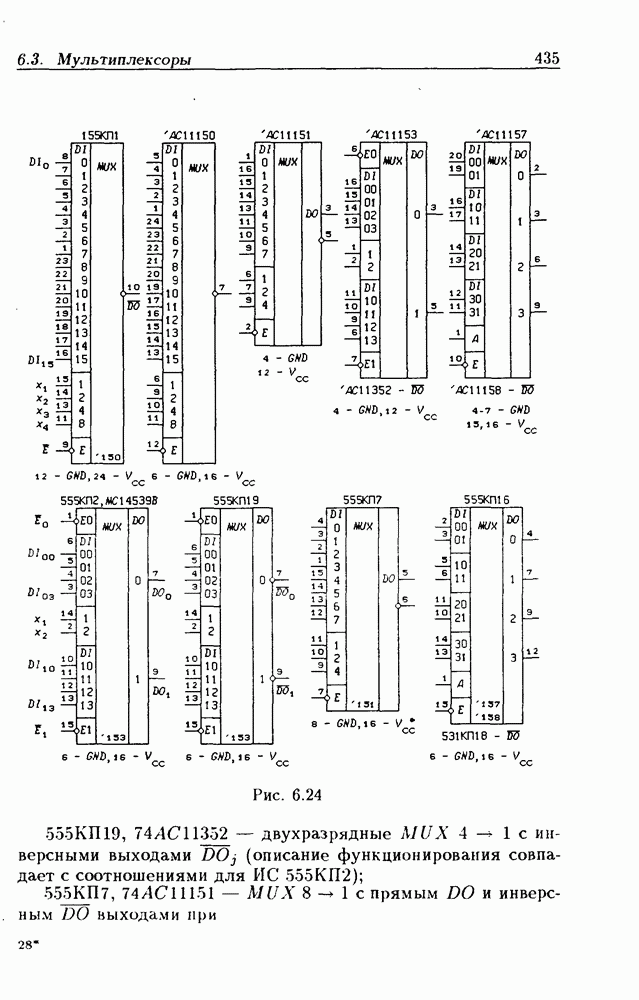
- 6.3. Мультиплексоры
- Мультиплексоры без стробирования.
- Мультиплексоры со стробированием.
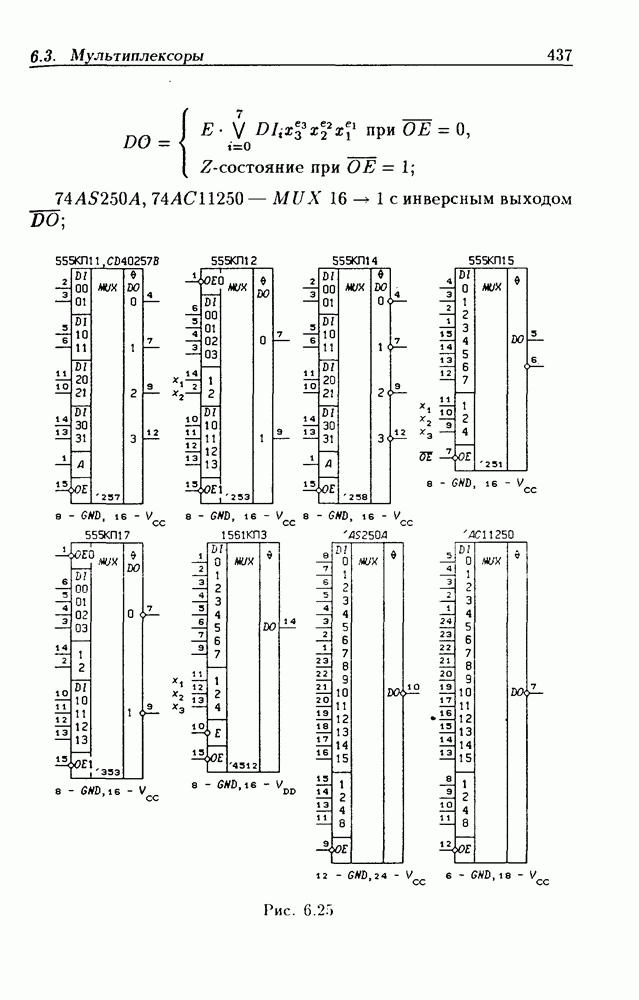
- Мультиплексоры с Z-состоянием выхода.
- Каскадирование мультиплексоров.
- Функциональные мультиплексоры.
- Регистры памяти с мультиплексными входами данных.
- Мультиплексоры с регистрами памяти данных и адреса.
- Сдвигающие мультиплексоры.
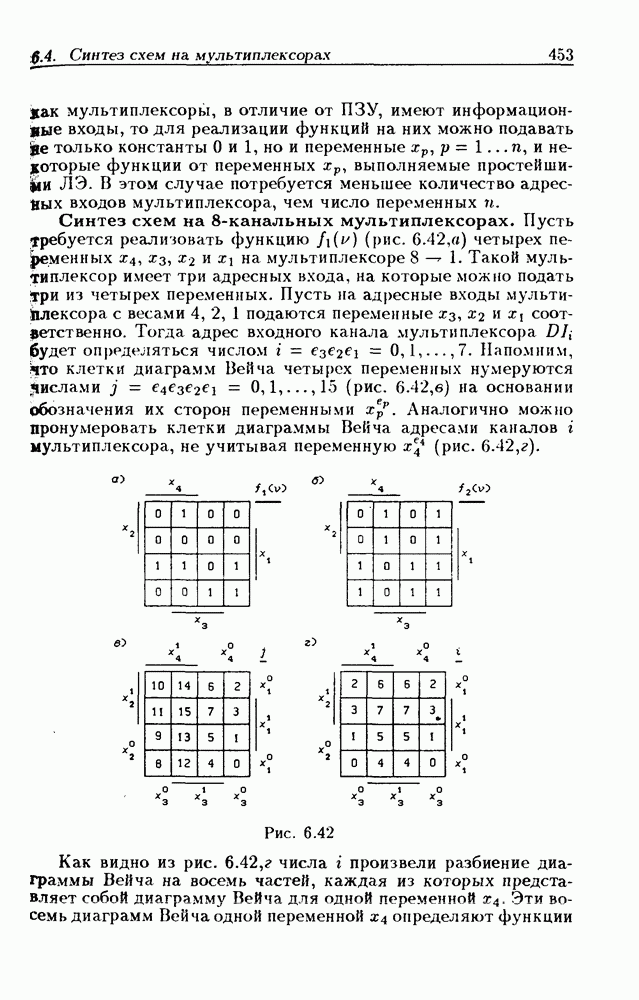
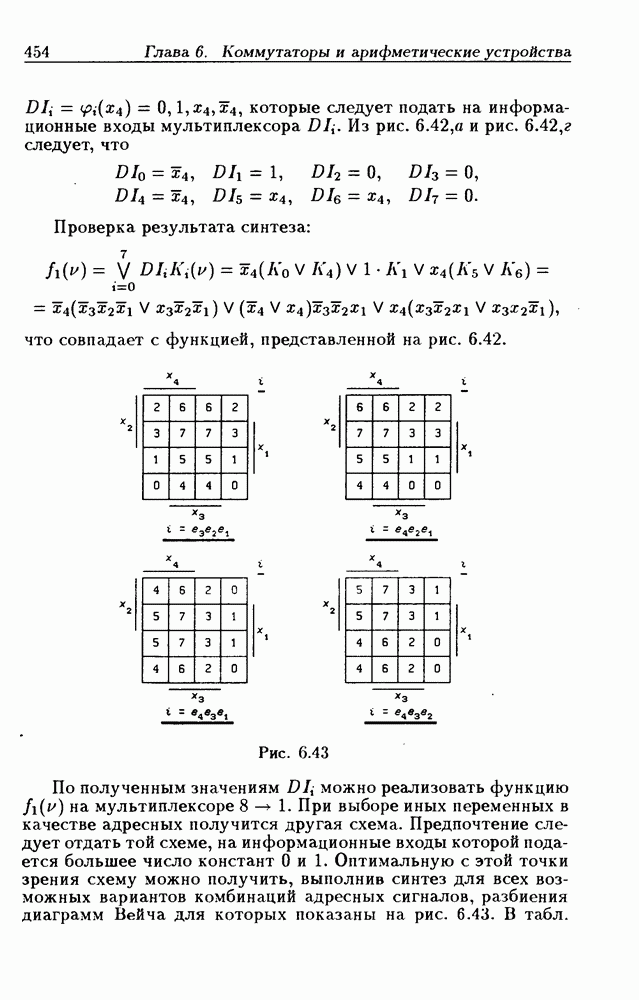
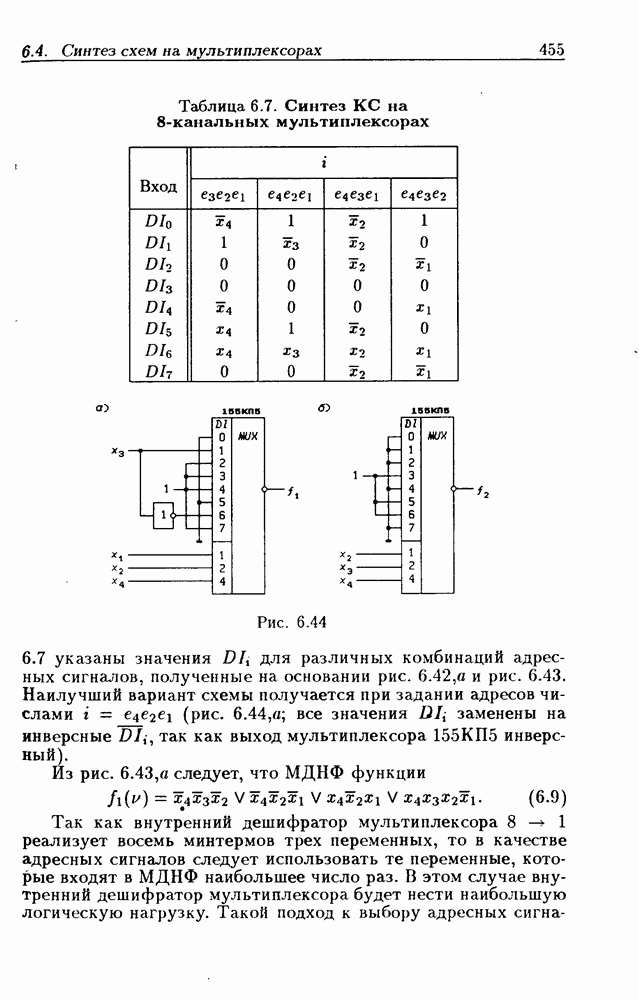
- 6.4. Синтез комбинационных схем и цифровых автоматов на мультиплексорах
- Синтез схем на 8-канальных мультиплексорах.
- Синтез на двухразрядных 4-канальных мультиплексорах.
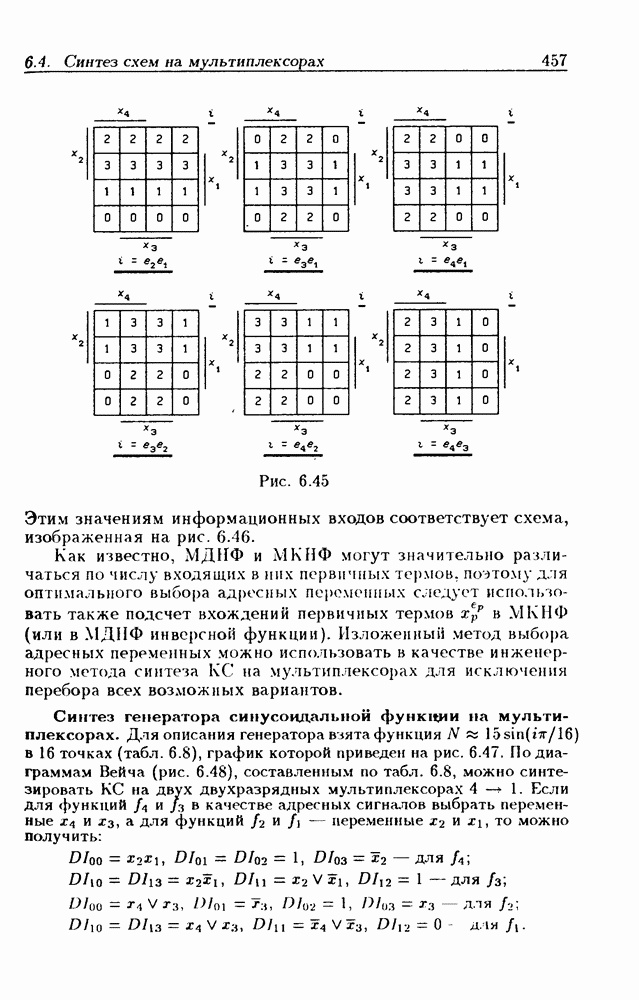
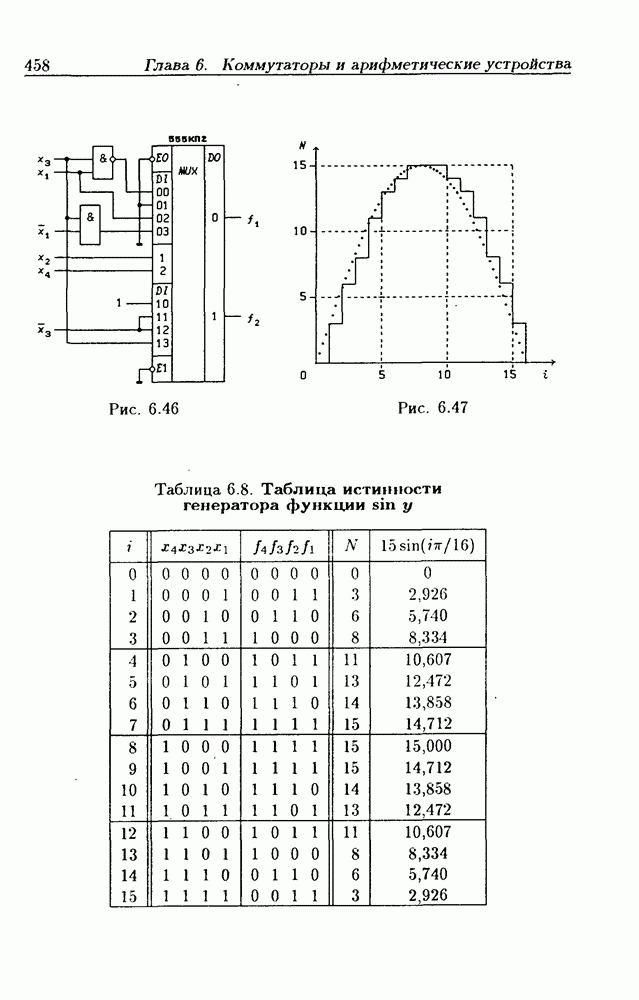
- Синтез генератора синусоидальной функции на мультиплексорах.
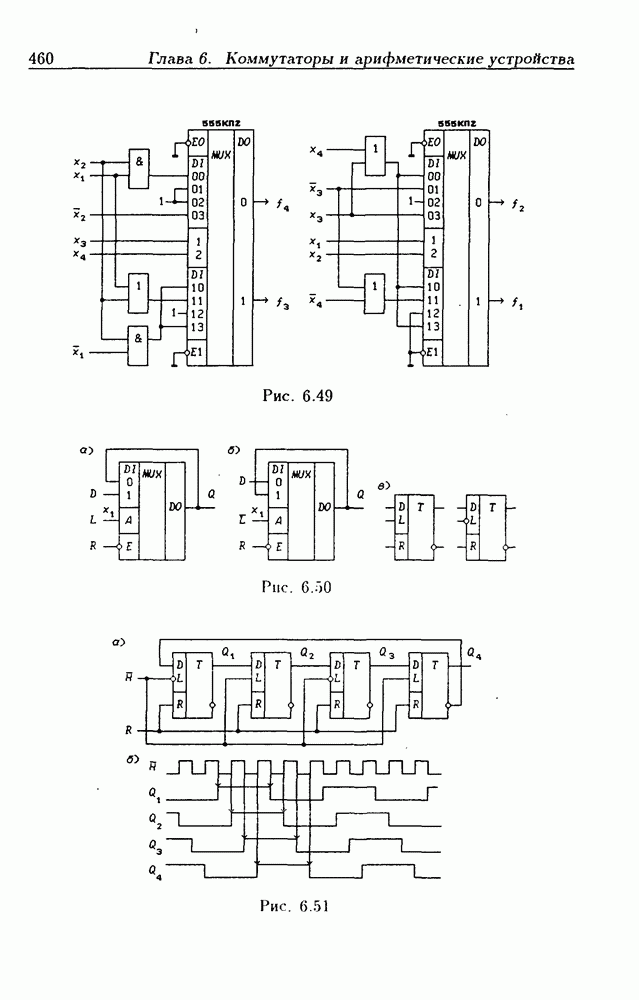
- Синтез триггеров на мультиплексорах.
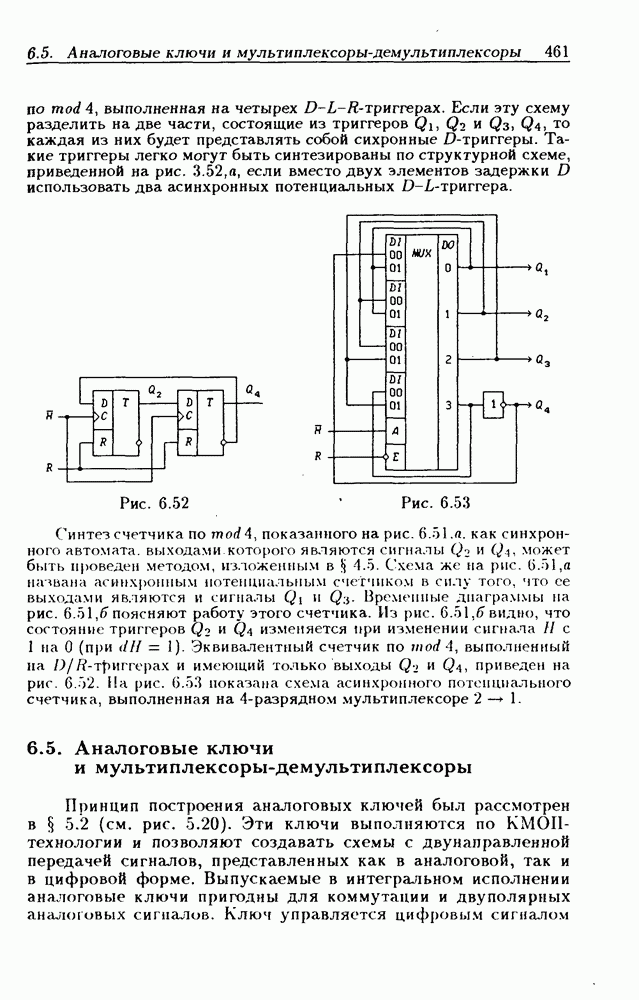
- Синтез счетчиков на мультиплексорах.
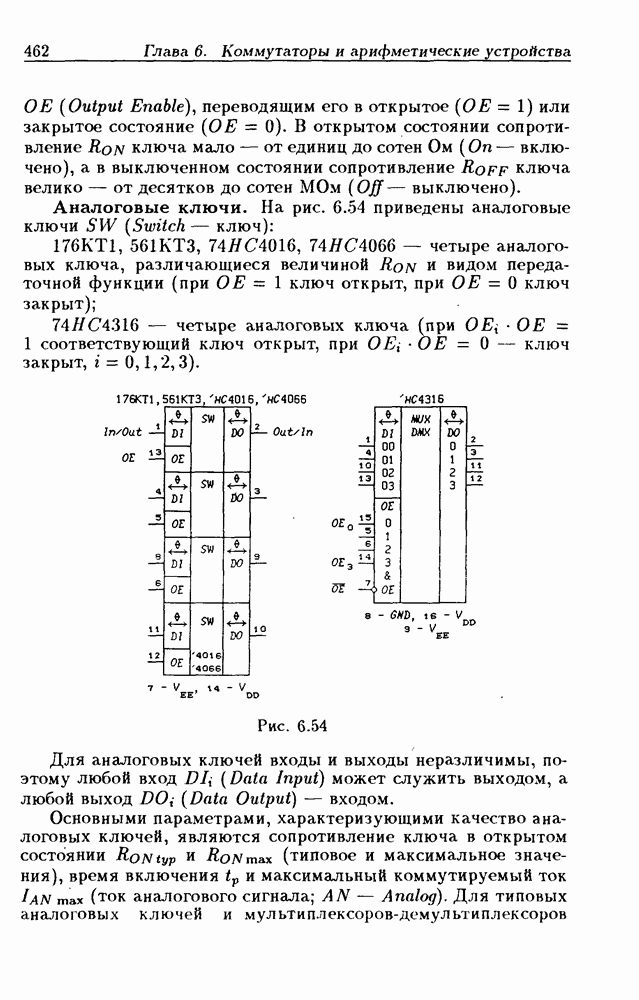
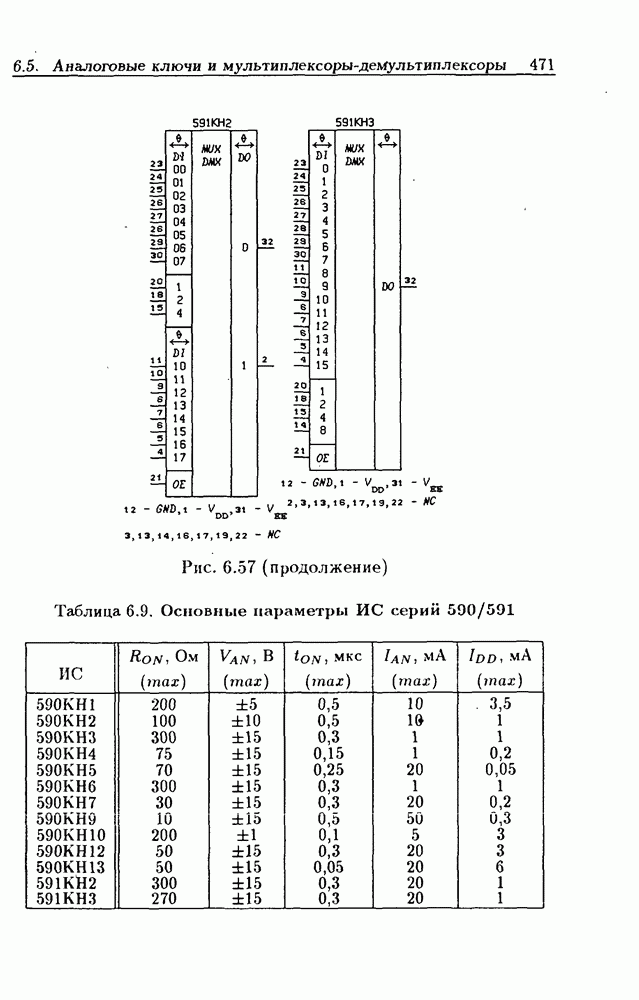
- 6.5. Аналоговые ключи и мультиплексоры-демультиплексоры
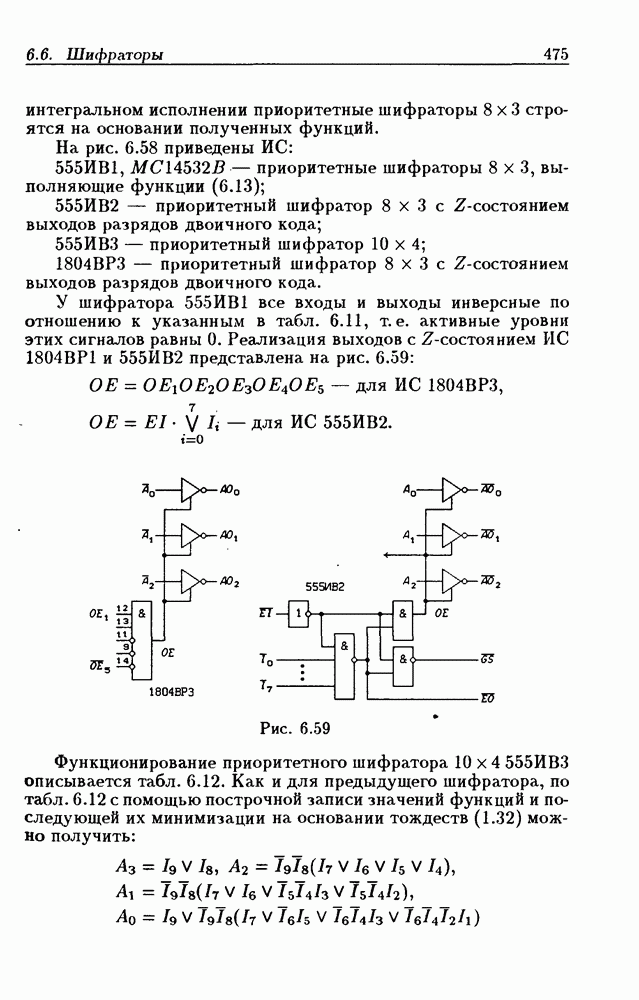
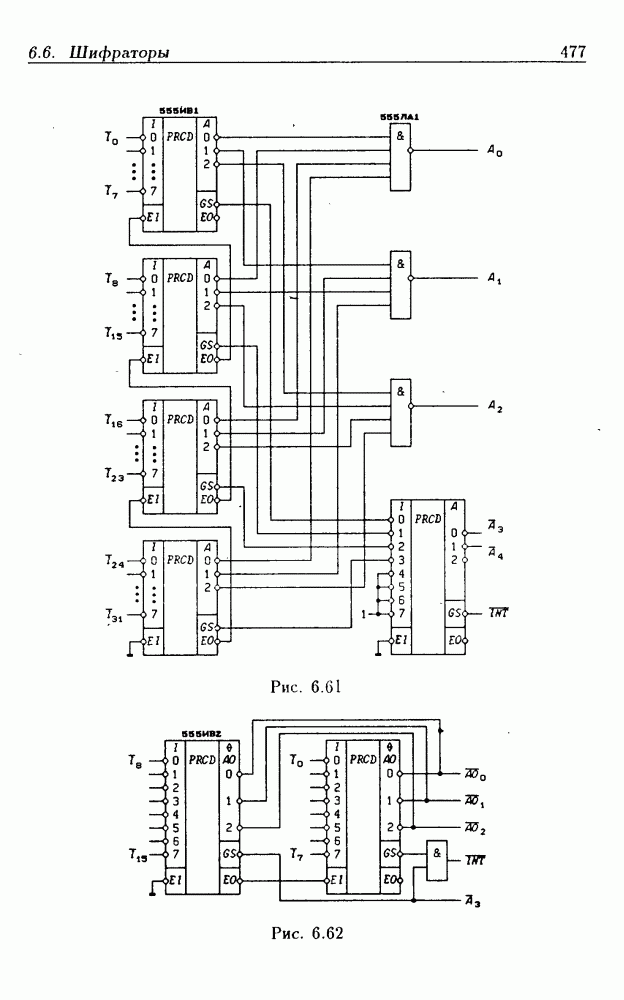
- 6.6. Шифраторы
- 6.7. Цифровые компараторы
- Программируемые цифровые компараторы.
- Адресные компараторы.
- Применения адресных компараторов.
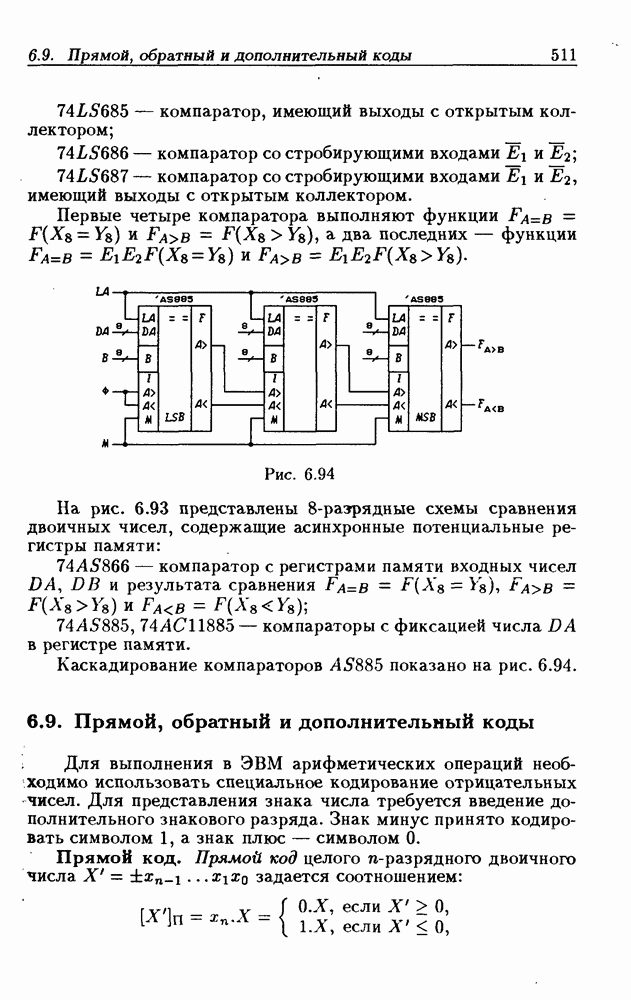
- 6.8. Схемы сравнения двоичных чисел
- 8-разрядные схемы сравнения двоичных чисел.
- 6.9. Прямой, обратный и дополнительный коды
- Дополнительный код.
- Сложение чисел в обратном коде.
- Код с избытком 3.
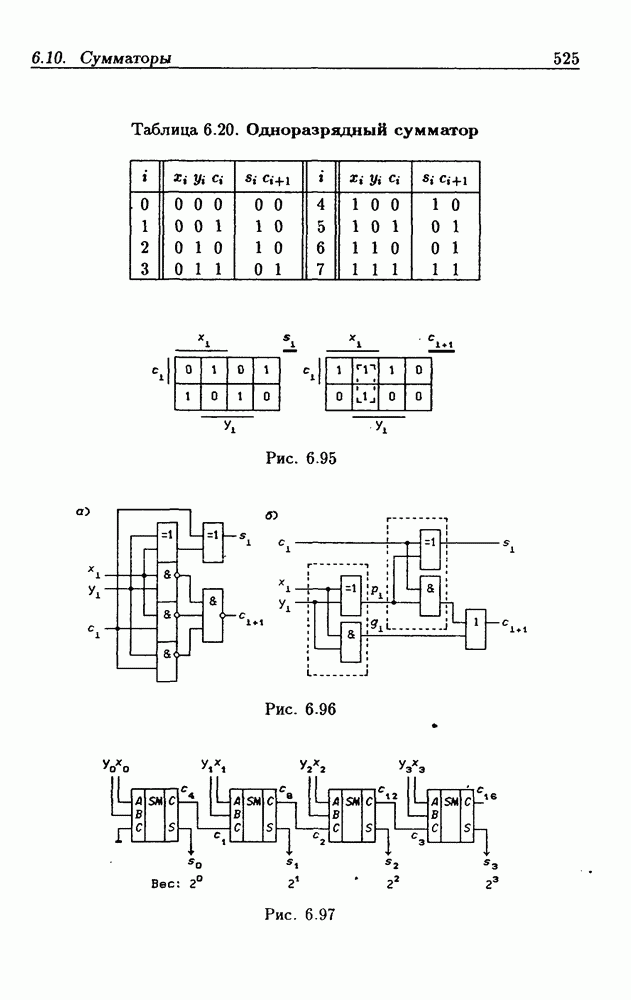
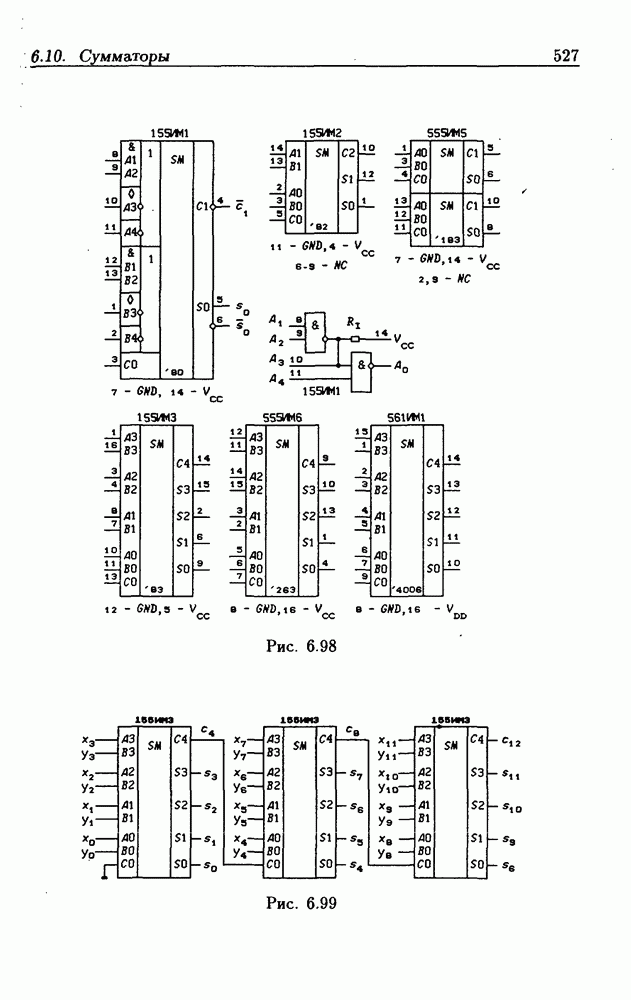
- 6.10. Сумматоры
- Двоичные параллельные сумматоры с последовательным переносом.
- Двоичные сумматоры с параллельным переносом.
- Применения сумматоров.
- Десятичные сумматоры.
- Последовательные двоичные сумматоры.
- 6.11. Арифметическо-логические устройства
- 6.12. Пороговые схемы и мажоритарные элементы
- 6.13. Умножители двоичных чисел
- Быстрые умножители.
- БИС умножителя 12×12 разрядов 1802ВР4.
- Последовательные умножители.
- 6.14. Конвейерные устройства
- Конвейерный быстрый умножитель.
- Конвейерные АЦП.
- 6.15. Синтез линейных комбинационных схем
- Сумматор по модулю q.
- Умножитель по модулю q.
- Глава 7. Сдвигающие регистры и счетчики
- 7.1. Сдвигающие регистры без параллельной записи данных
- Сдвигающие устройства с выходными регистрами памяти.
- 7.2. Сдвигающие регистры с параллельной записью данных
- Сдвигающие регистры с расширением знака.
- Сдвигающие регистры с входным регистром памяти.
- 7.3. Реверсивные сдвигающие регистры
- Реверсивные сдвигающие регистры типов PI/SO и PI/PO.
- Многофункциональные устройства на основе реверсивных сдвигающих регистров.
- 7.4. Асинхронные счетчики
- Двоично-десятичные асинхронные счетчики.
- 7.5. Синхронные двоичные счетчики
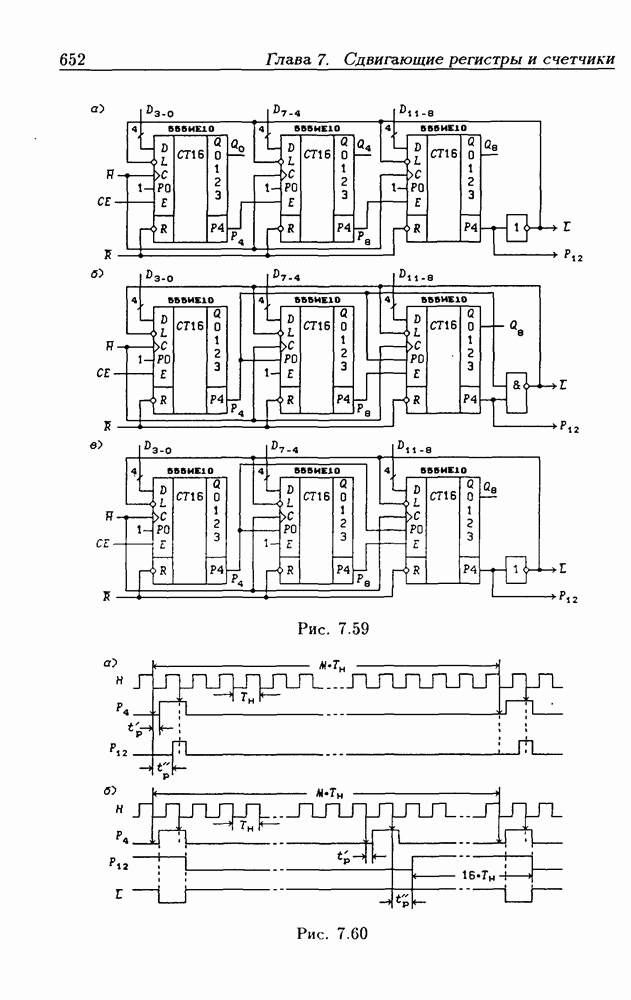
- Программирование модуля пересчета двоичных счетчиков.
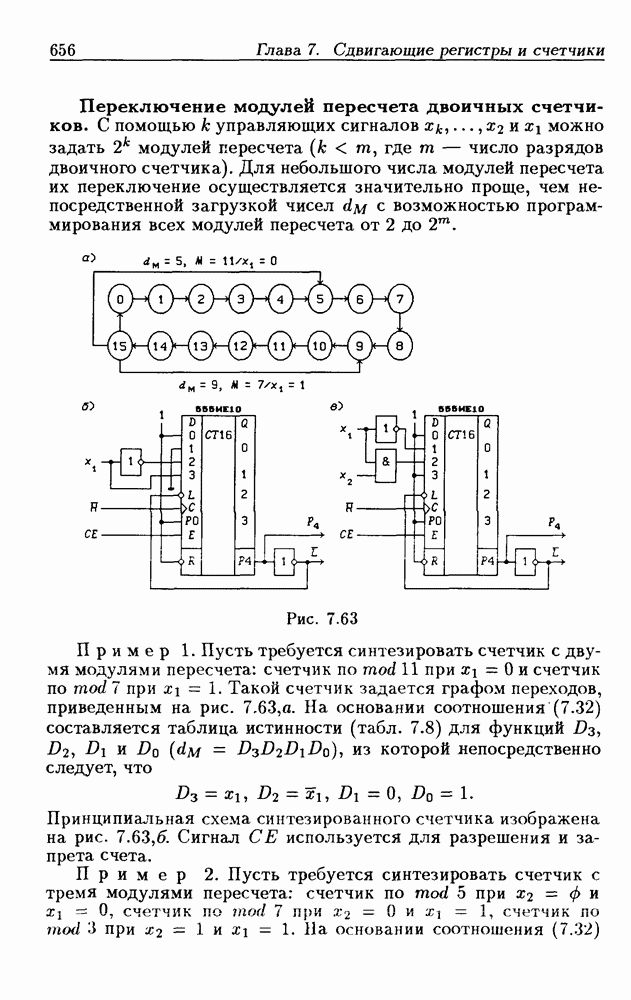
- Переключение модулей пересчета двоичных счетчиков.
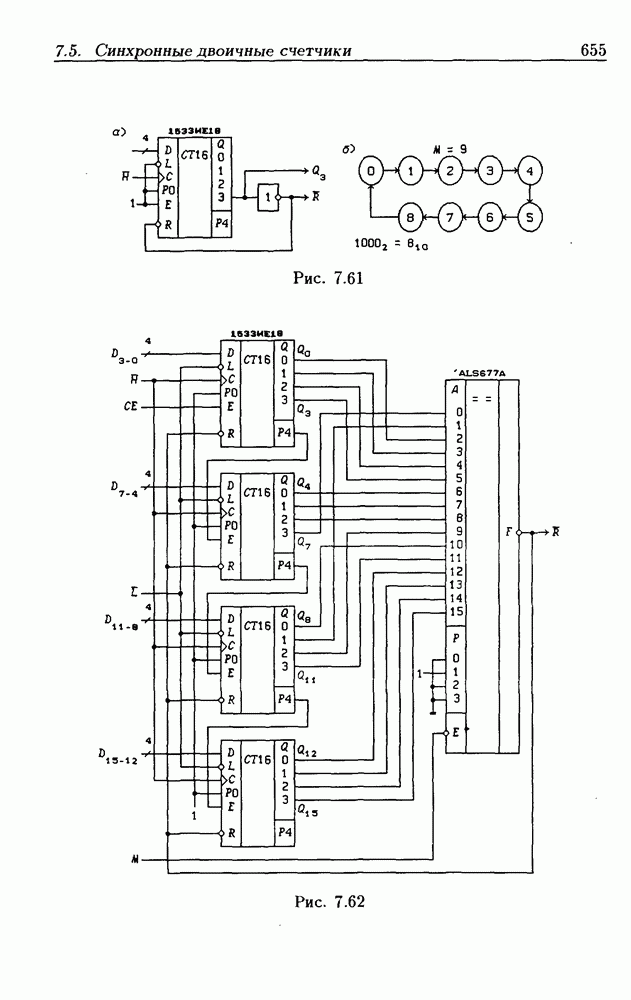
- Функциональные устройства на основе двоичных счетчиков.
- 7.6. Синхронные двоично-десятичные счетчики
- 7.7. Синхронные реверсивные счетчики
- 7.8. Счетчики с расщепленным тактовым сигналом
- 7.9. Счетчики на сдвигающих регистрах
- 7.10. Кольцевые счетчики
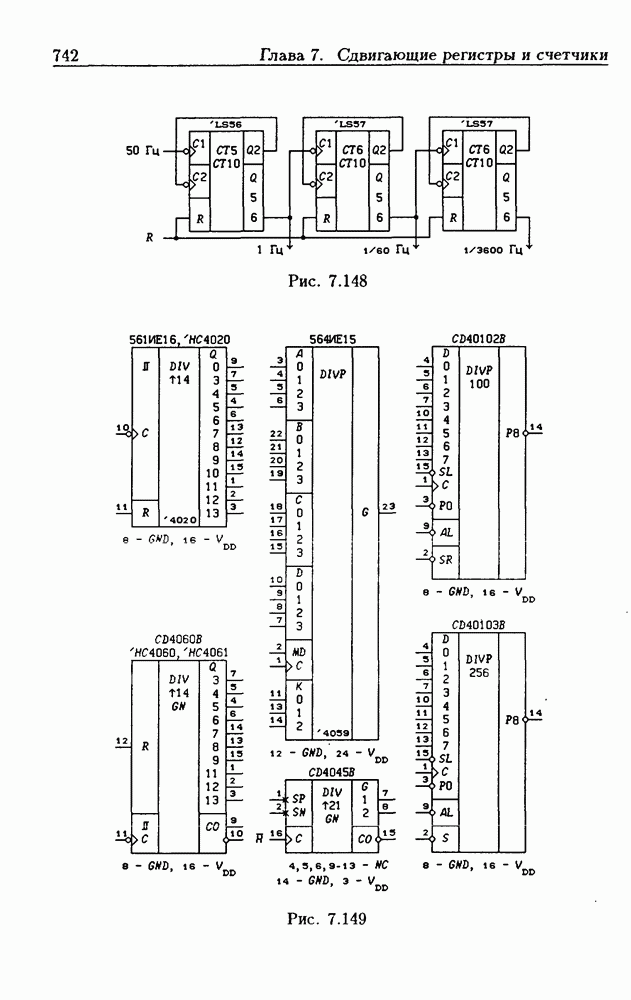
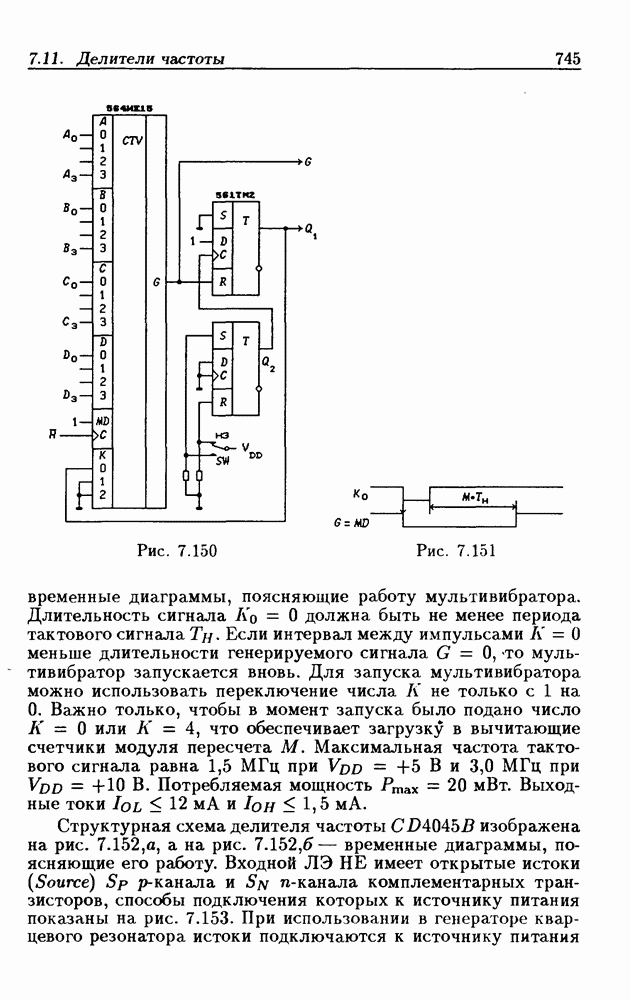
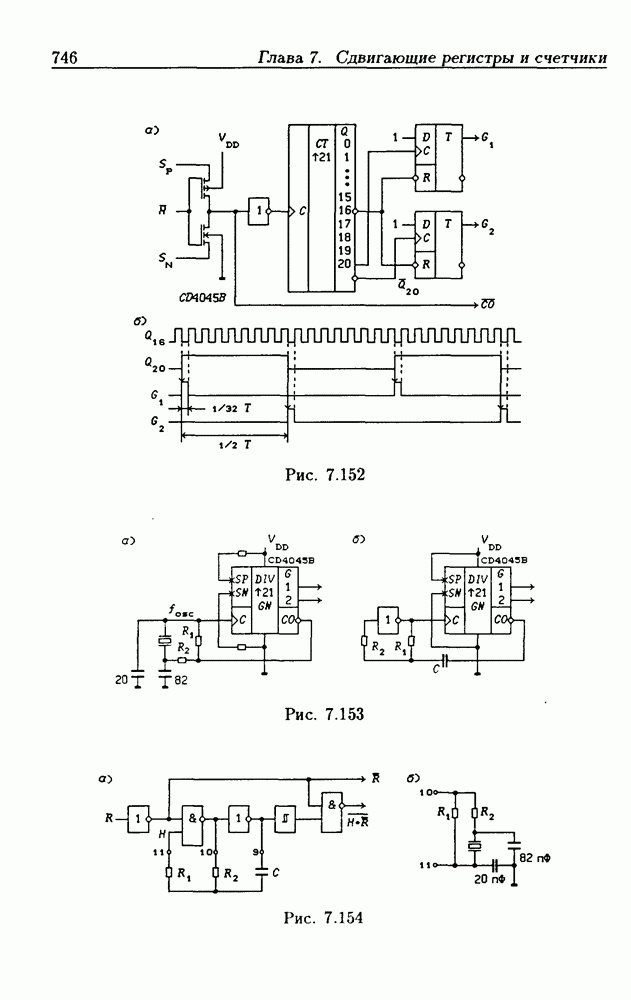
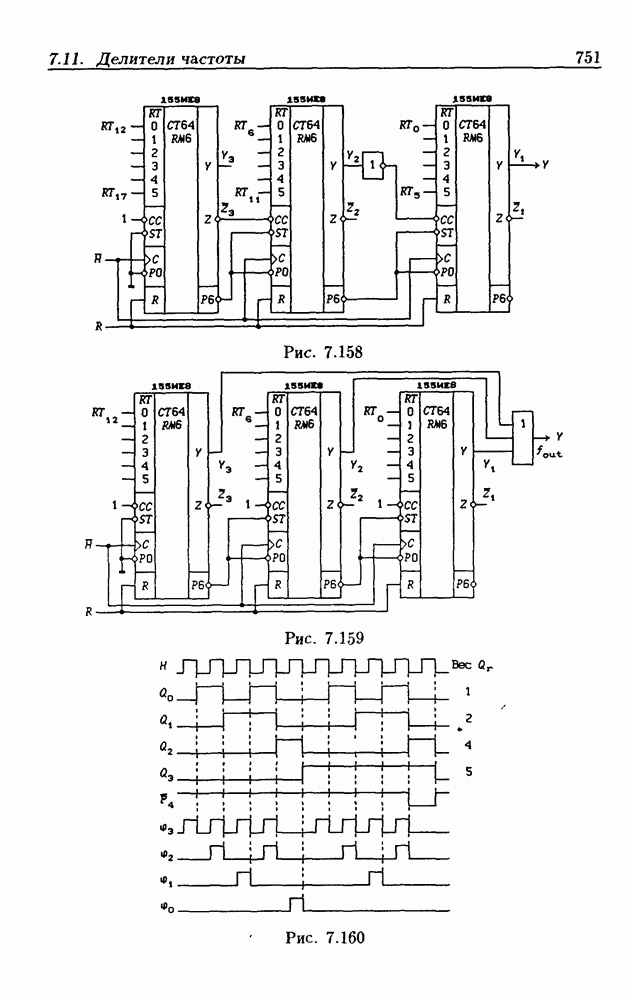
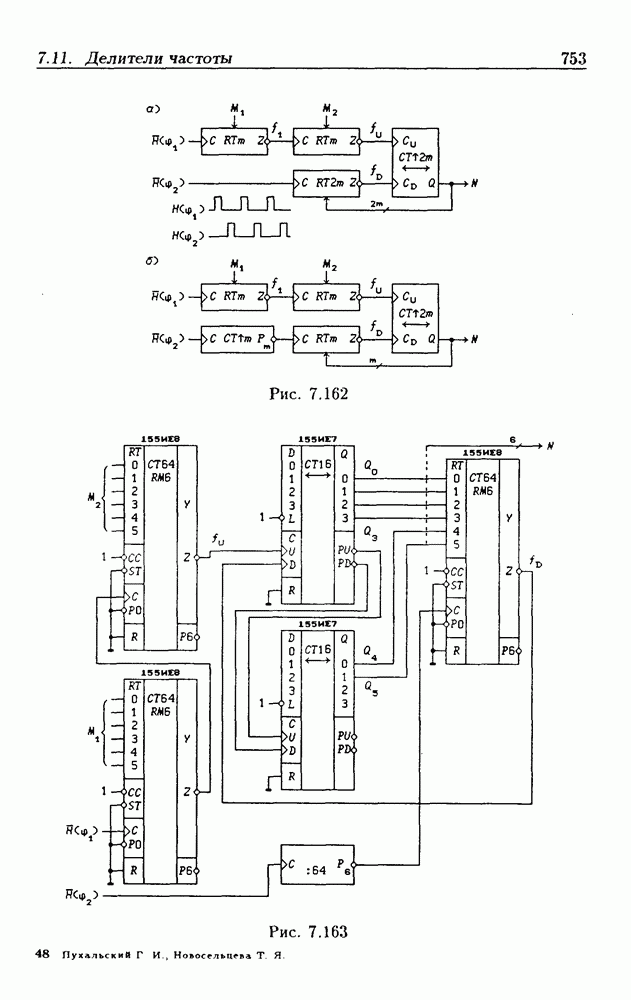
- 7.11. Делители частоты
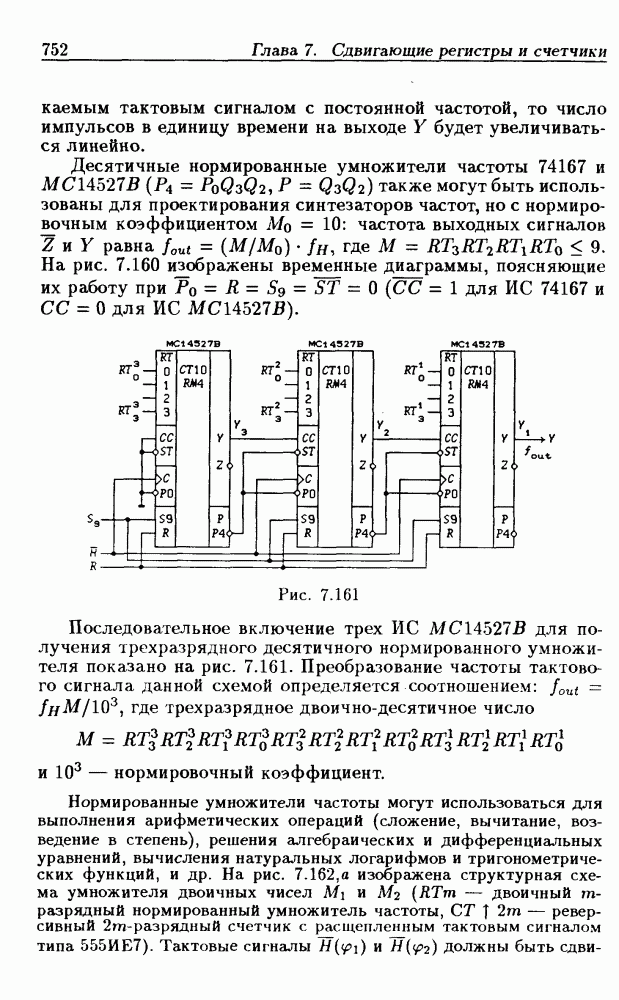
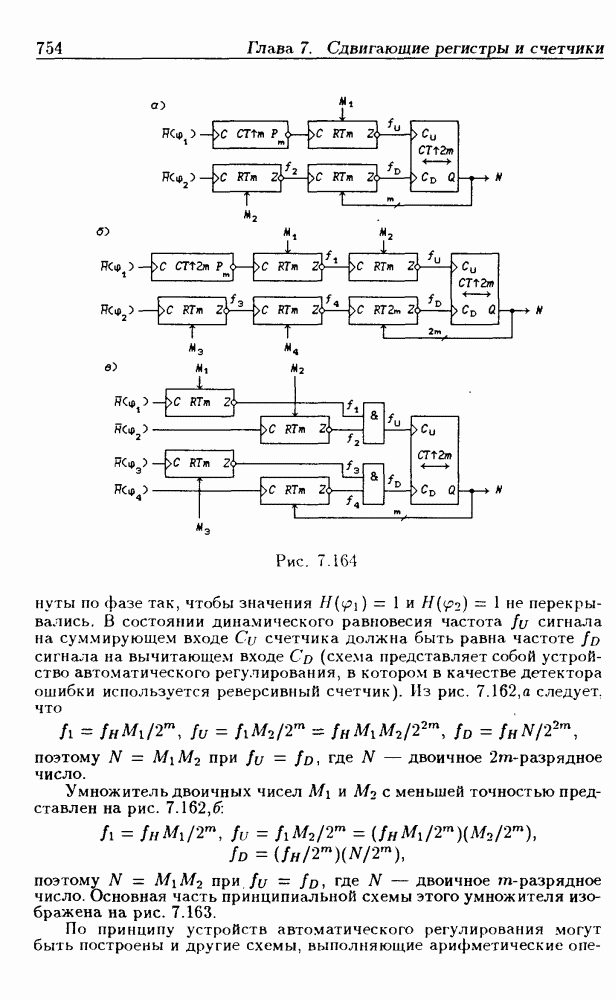
- Нормированные умножители частоты.
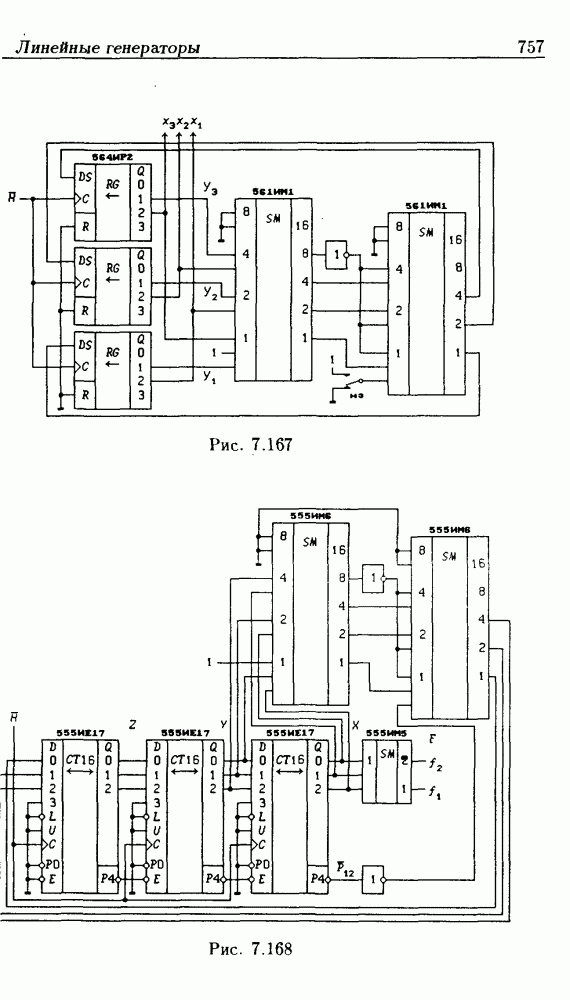
- 7.12. Линейные генераторы
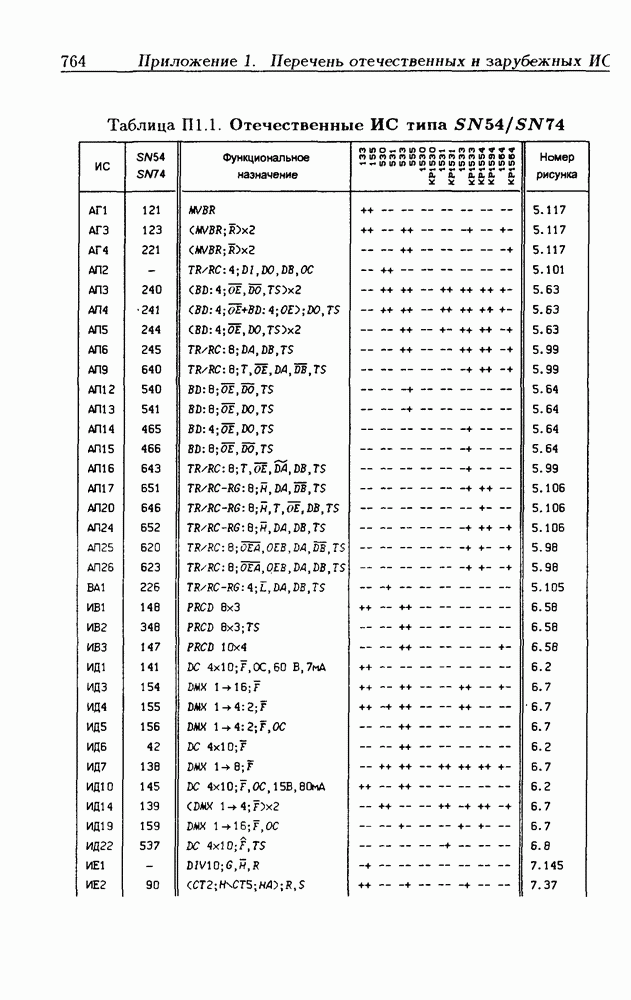
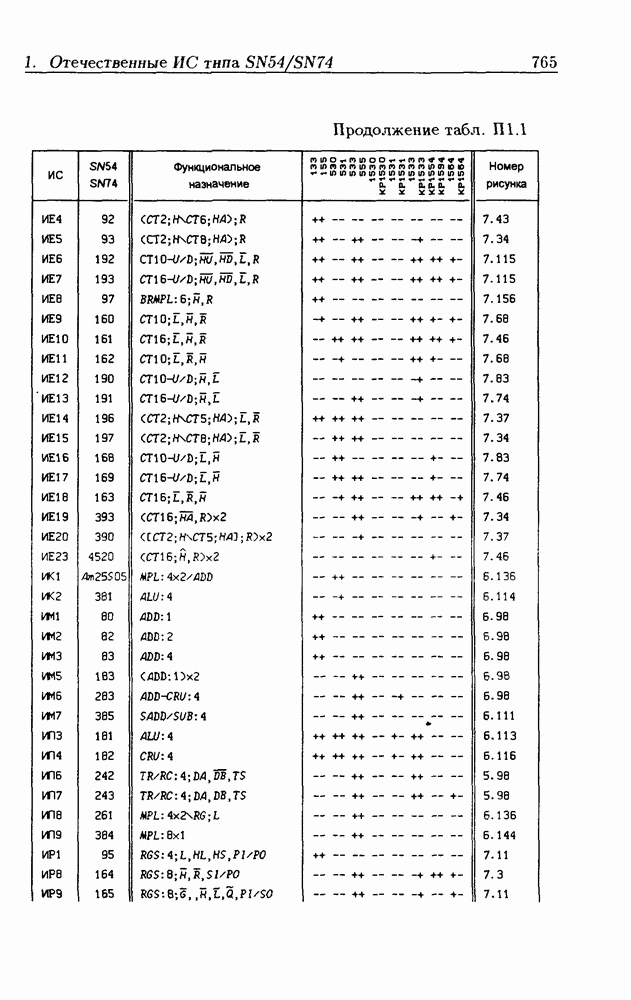
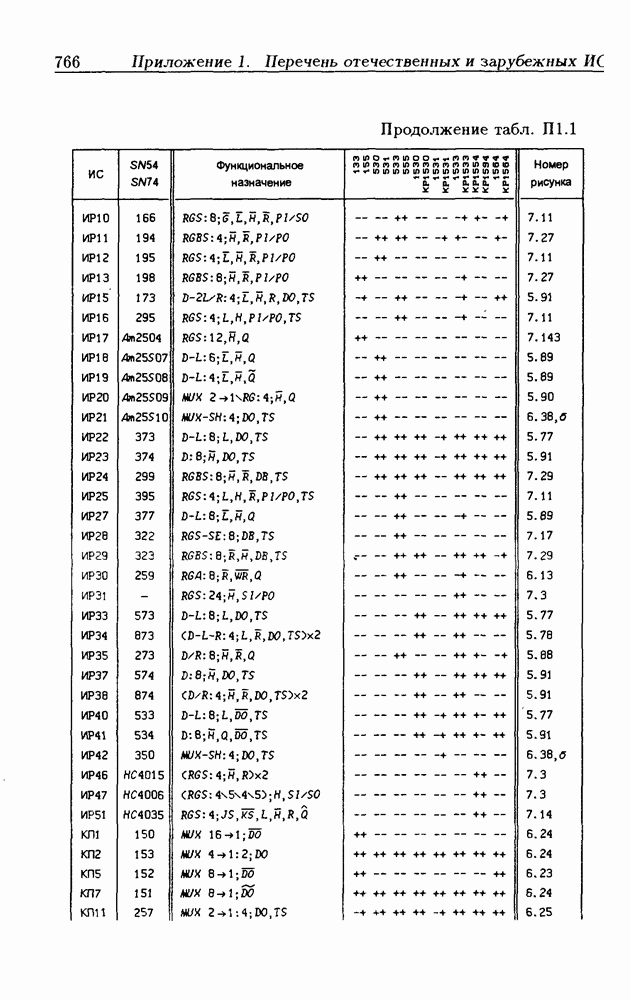
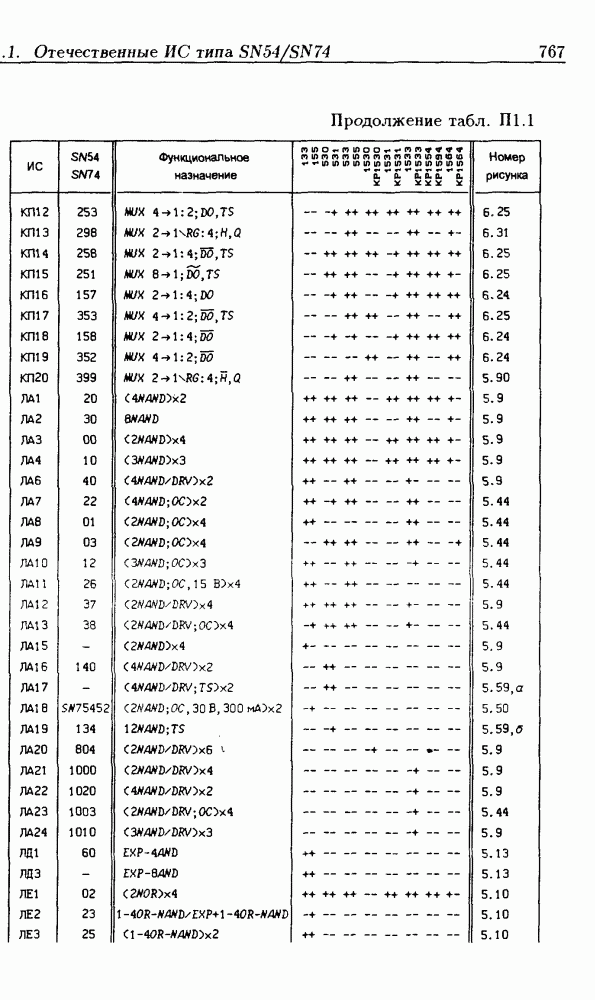
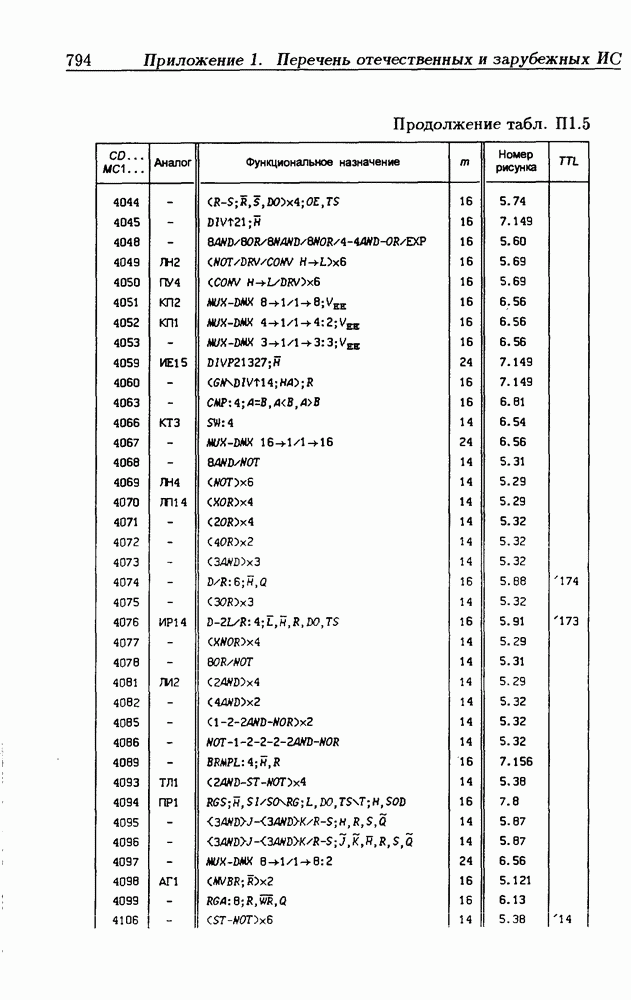
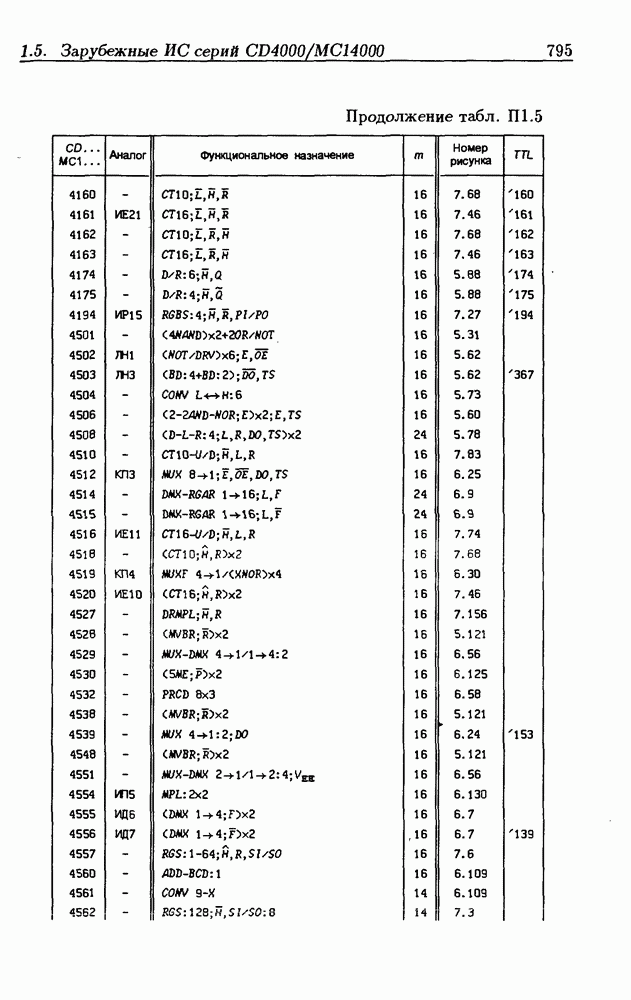
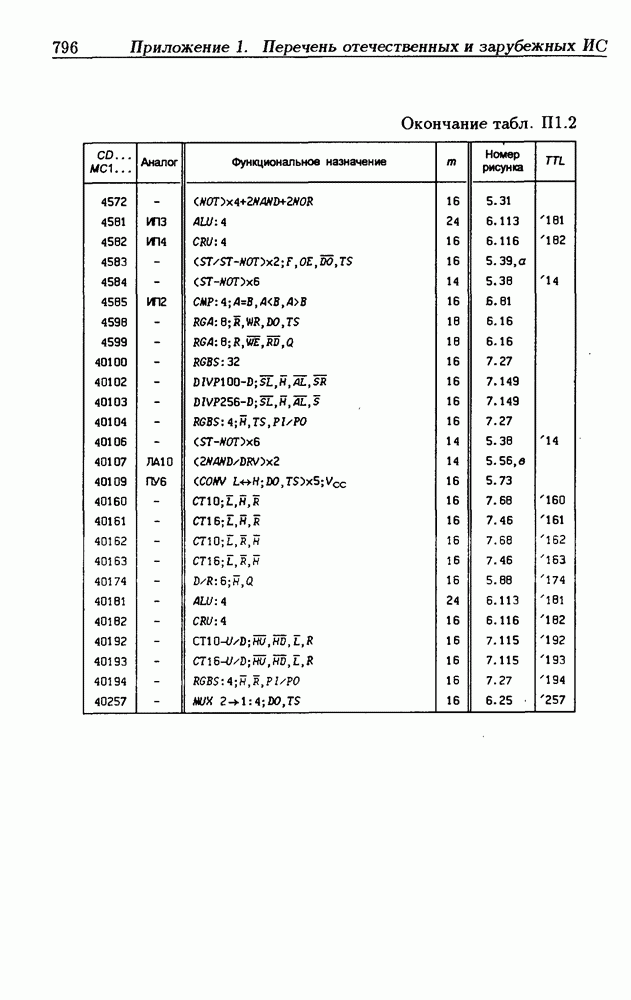
- Приложение 1. Перечень отечественных и зарубежных ИС
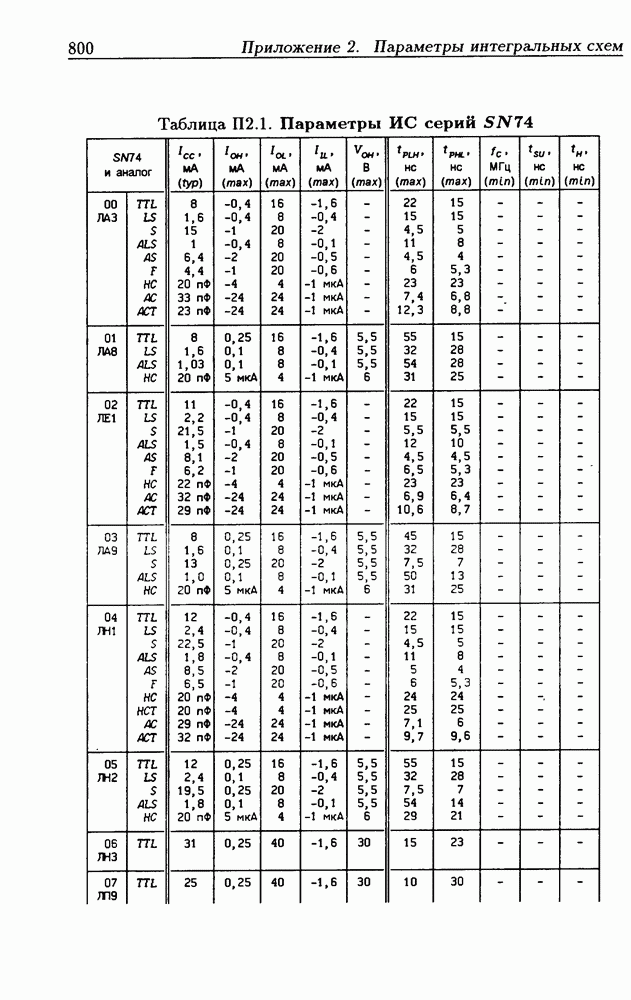
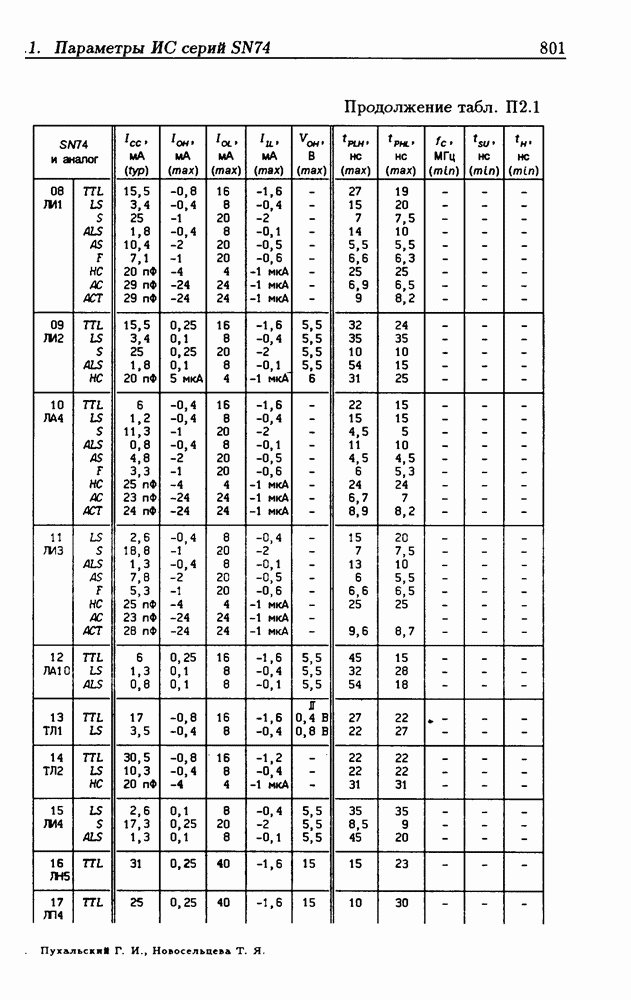
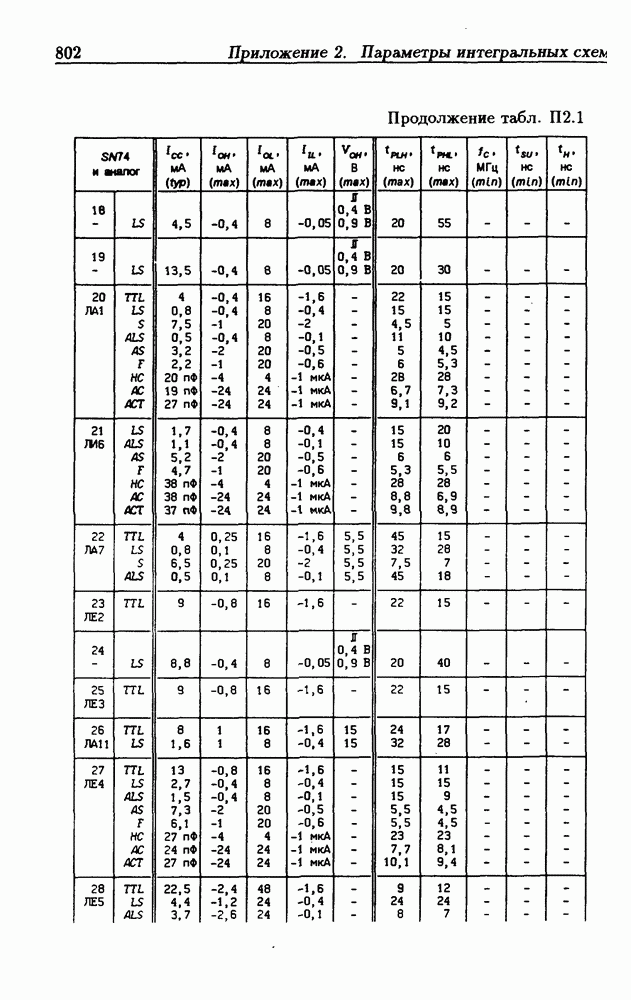
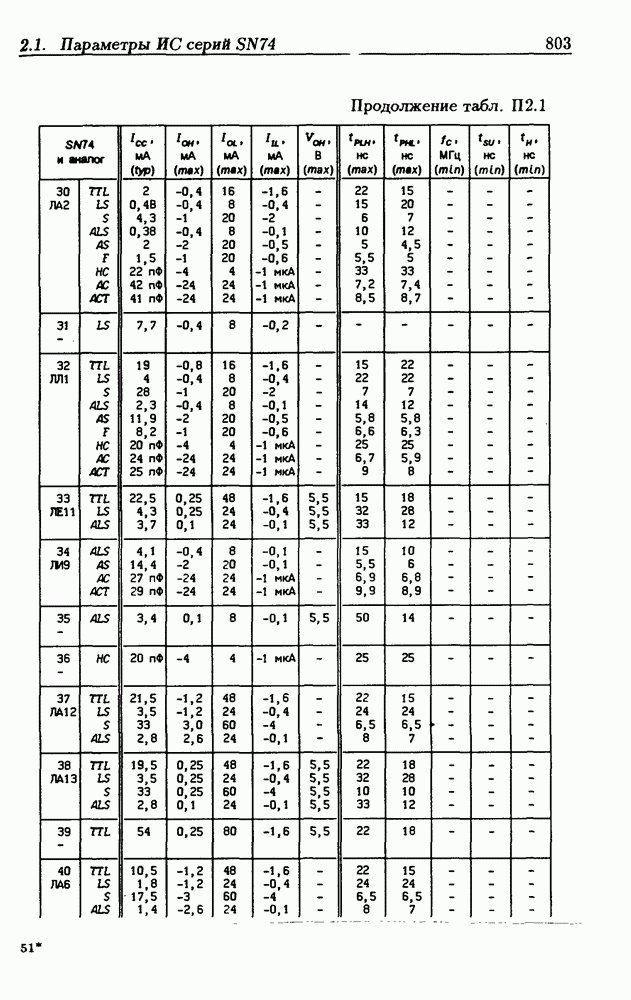
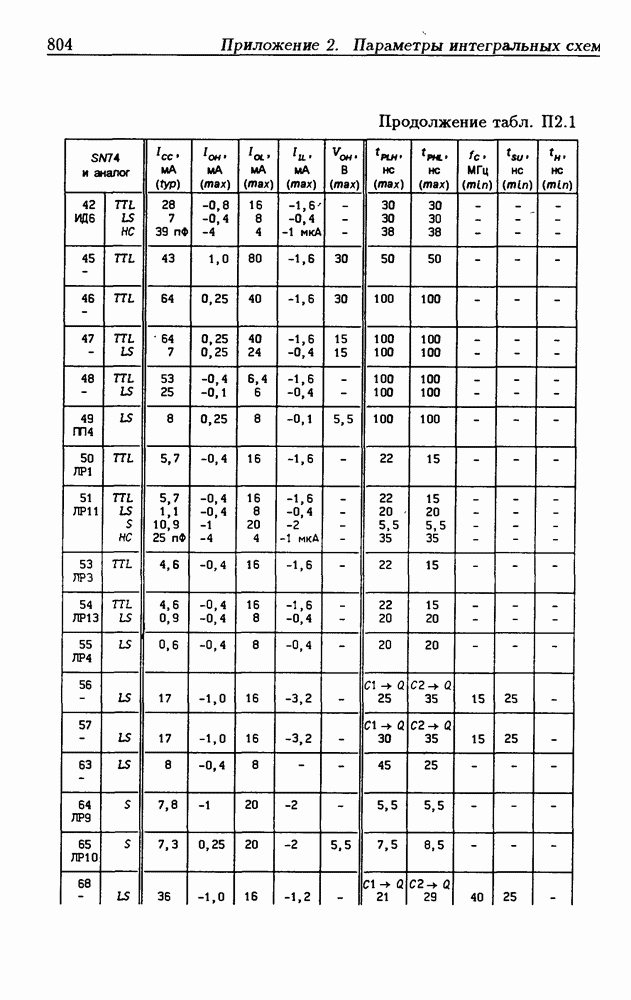
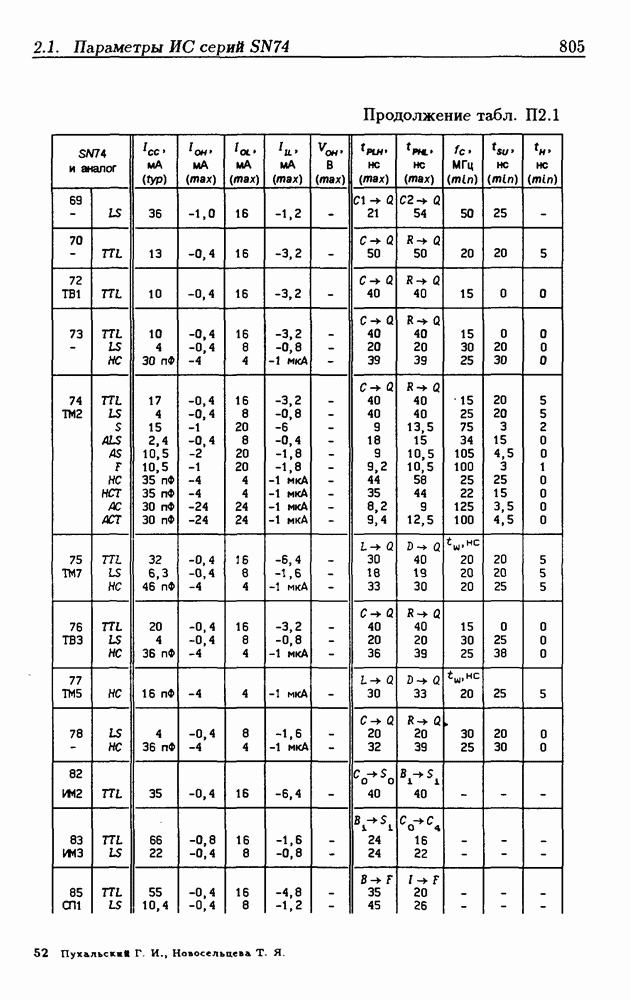
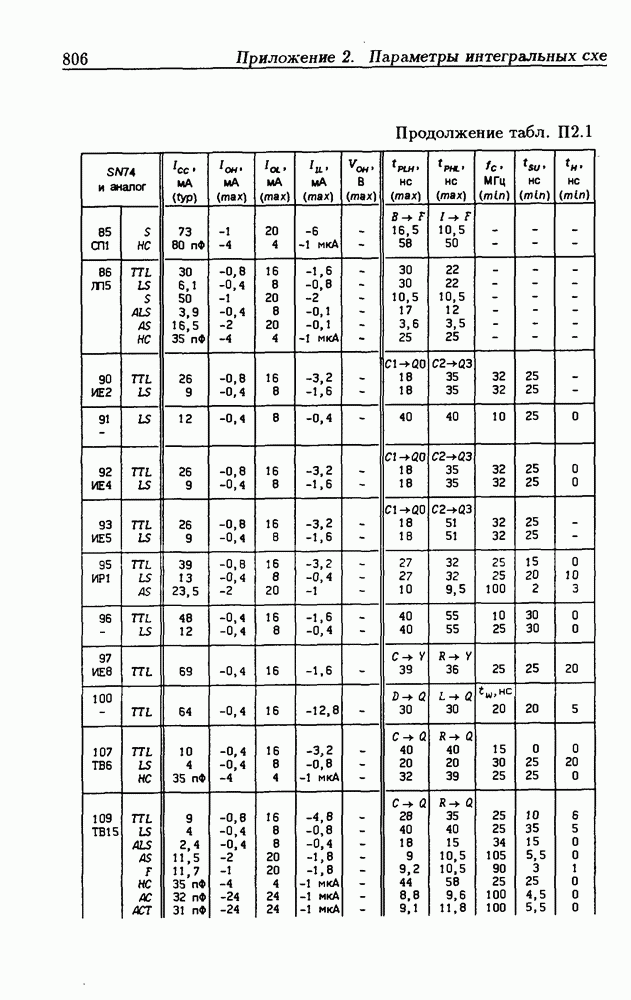
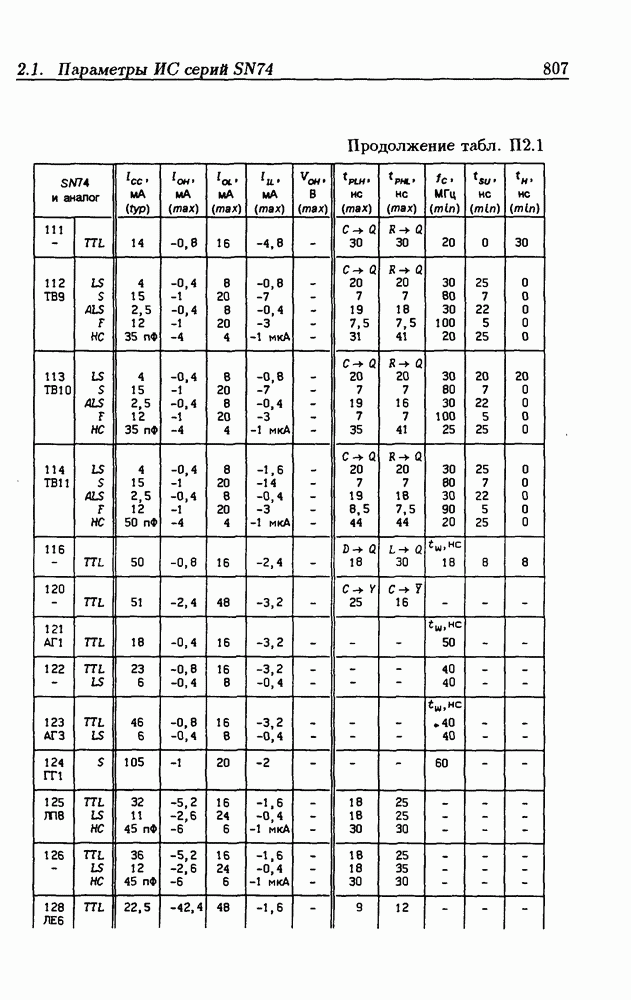
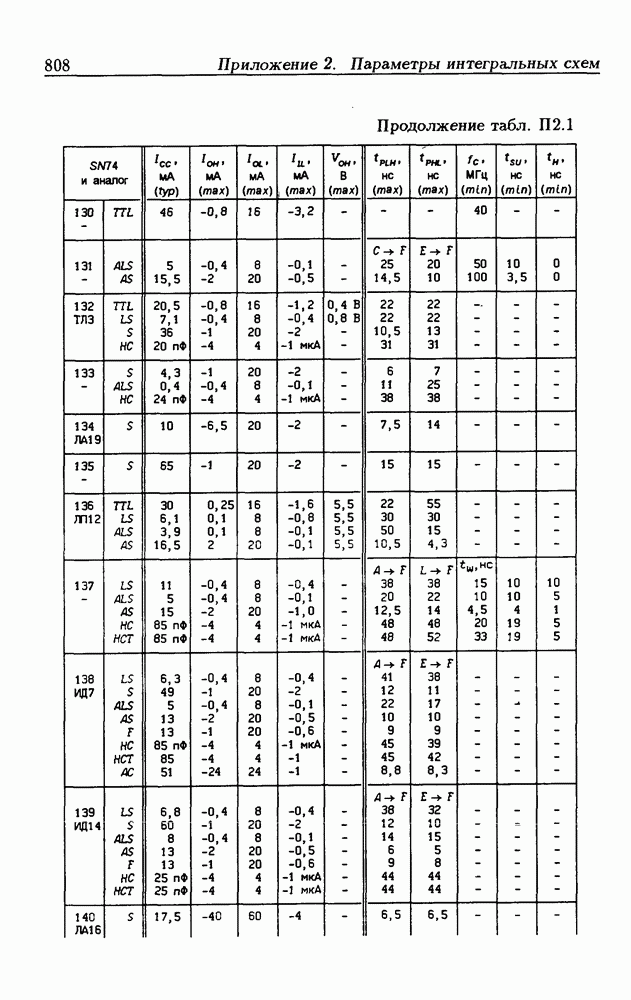
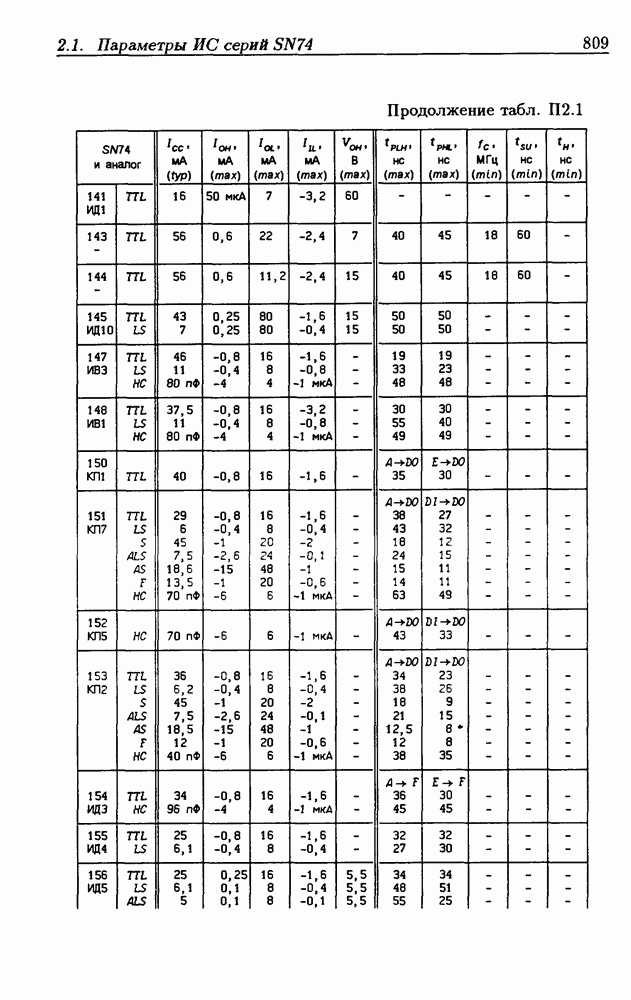
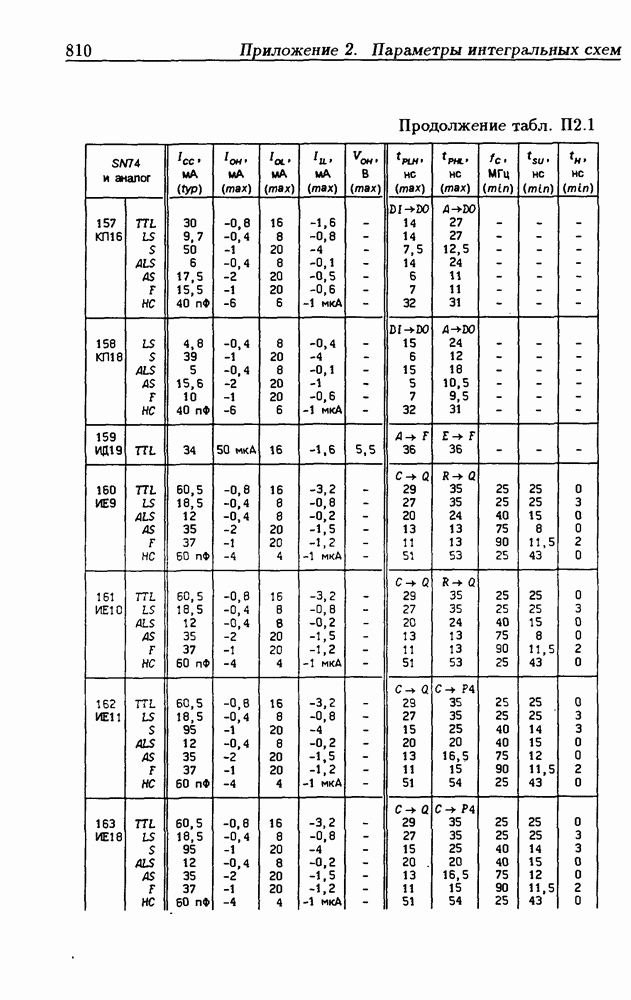
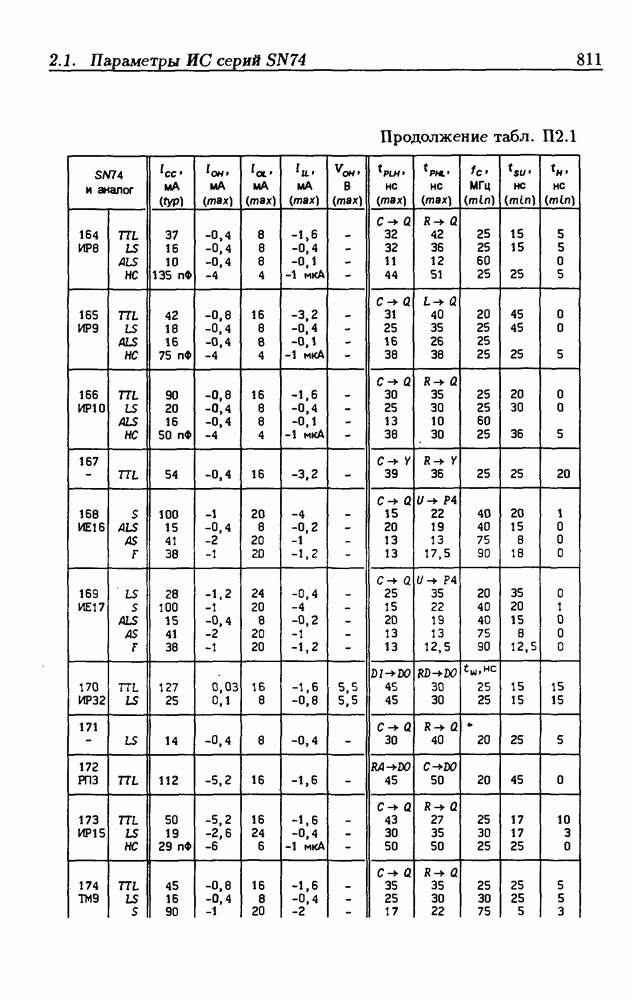
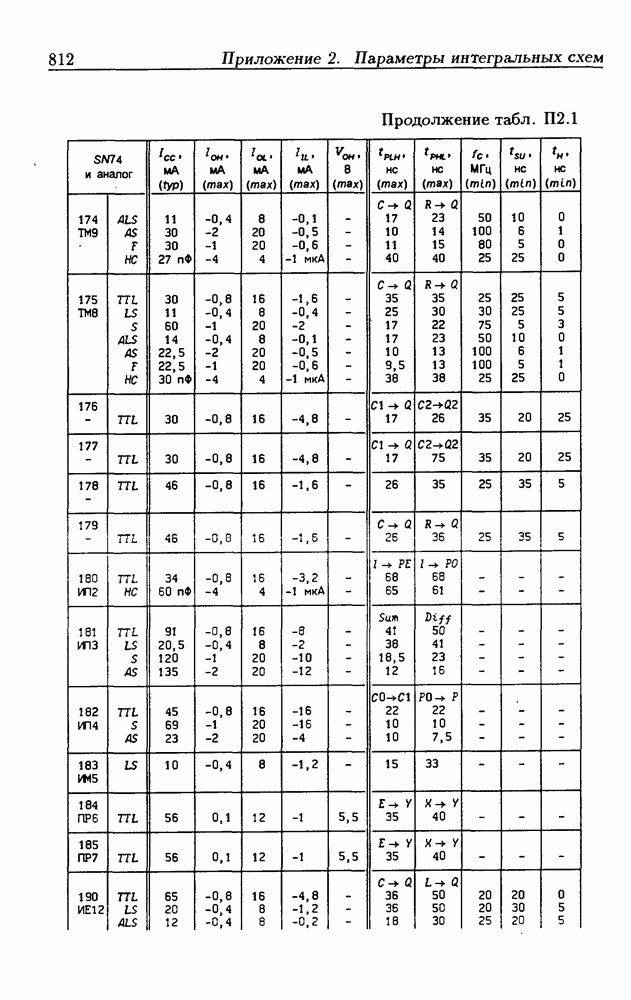
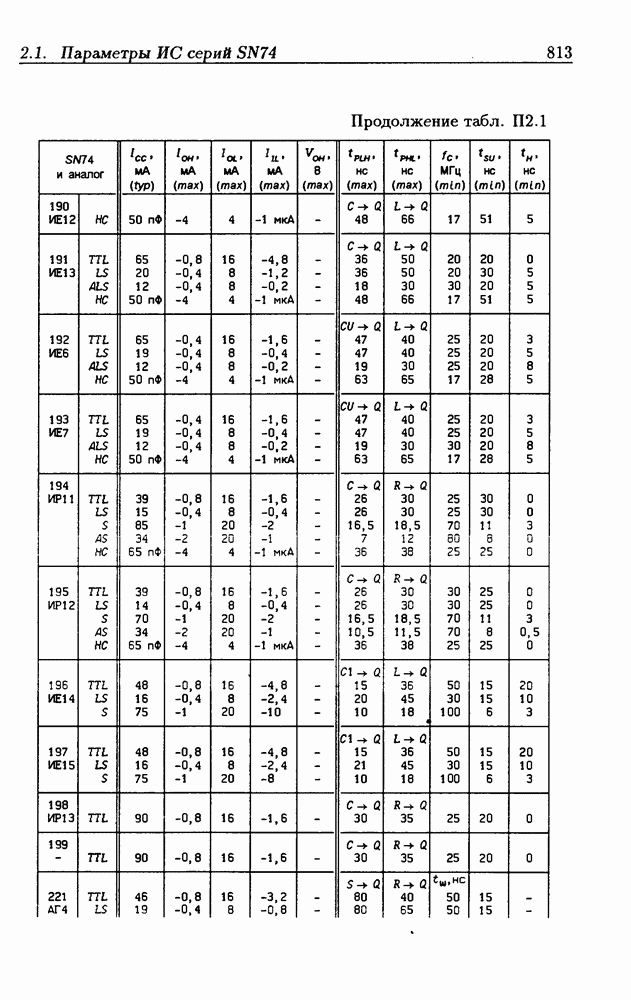
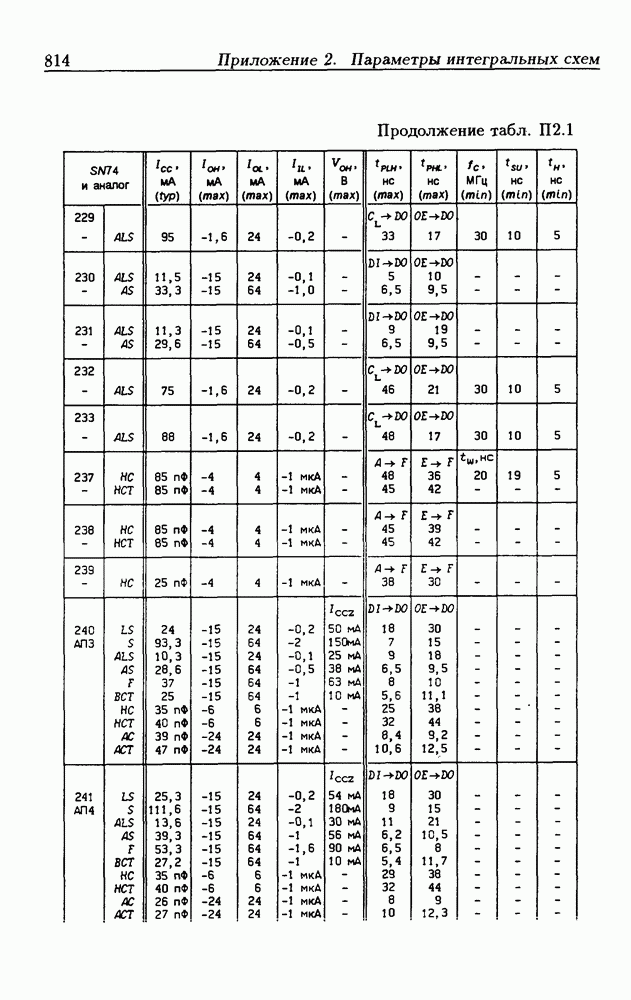
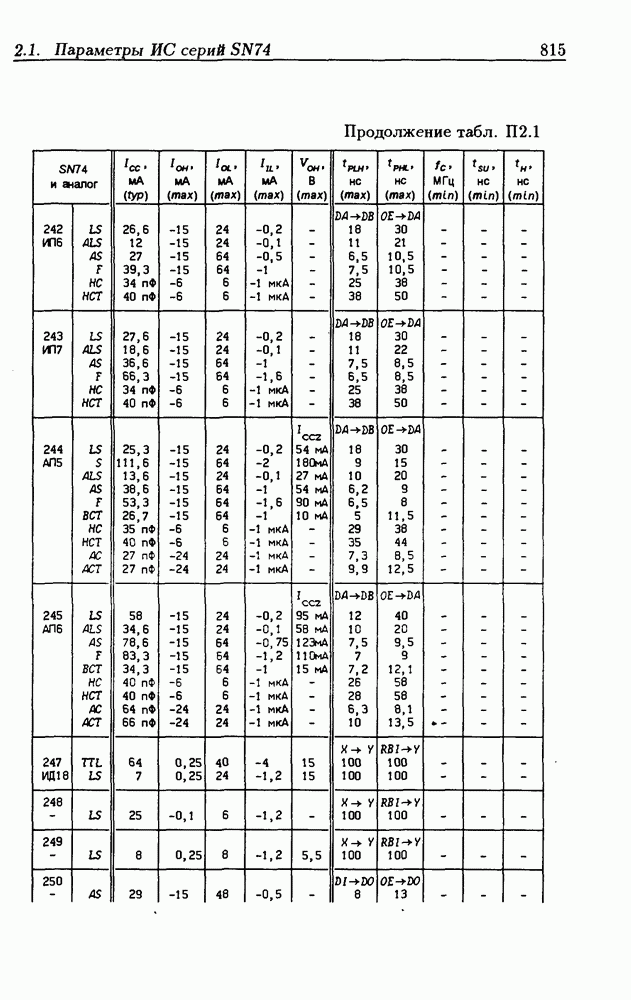
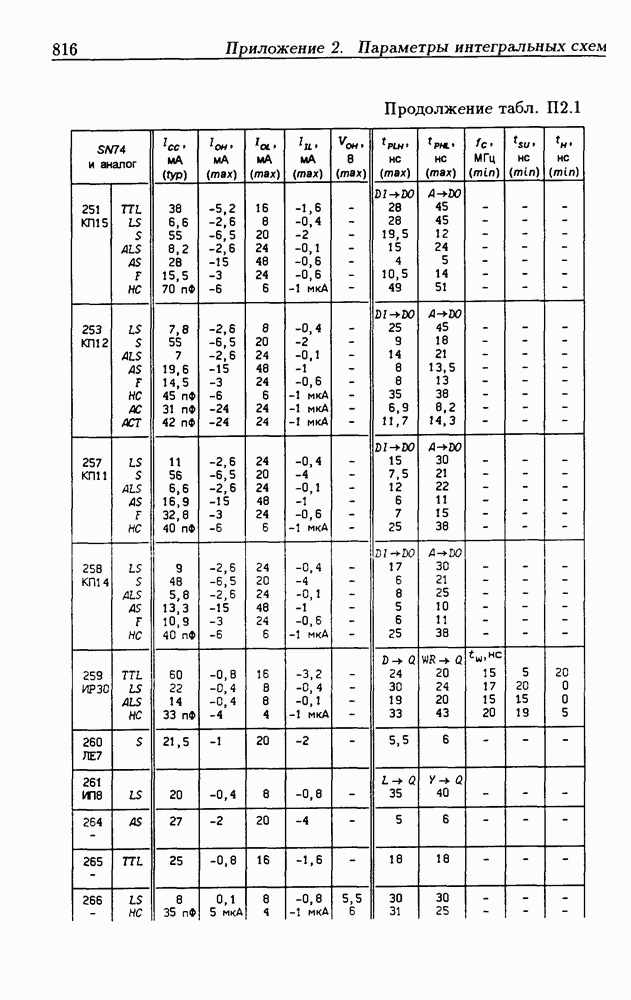
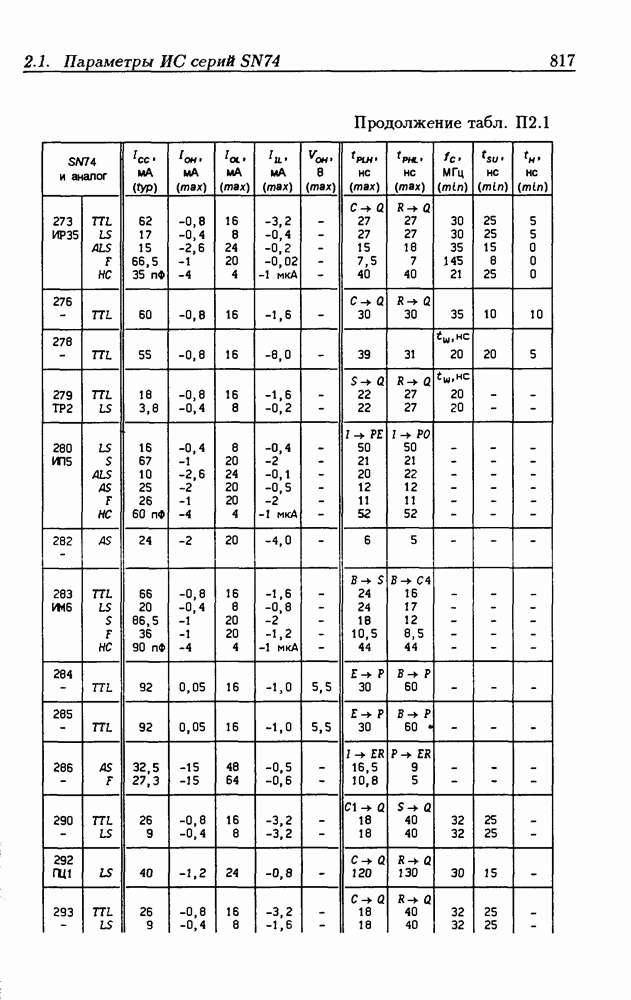
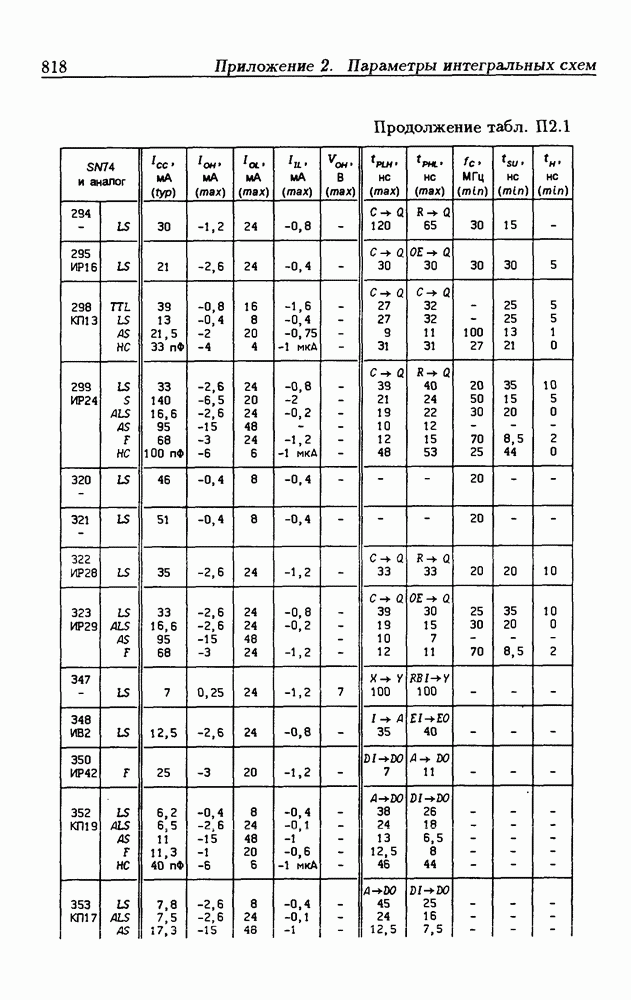
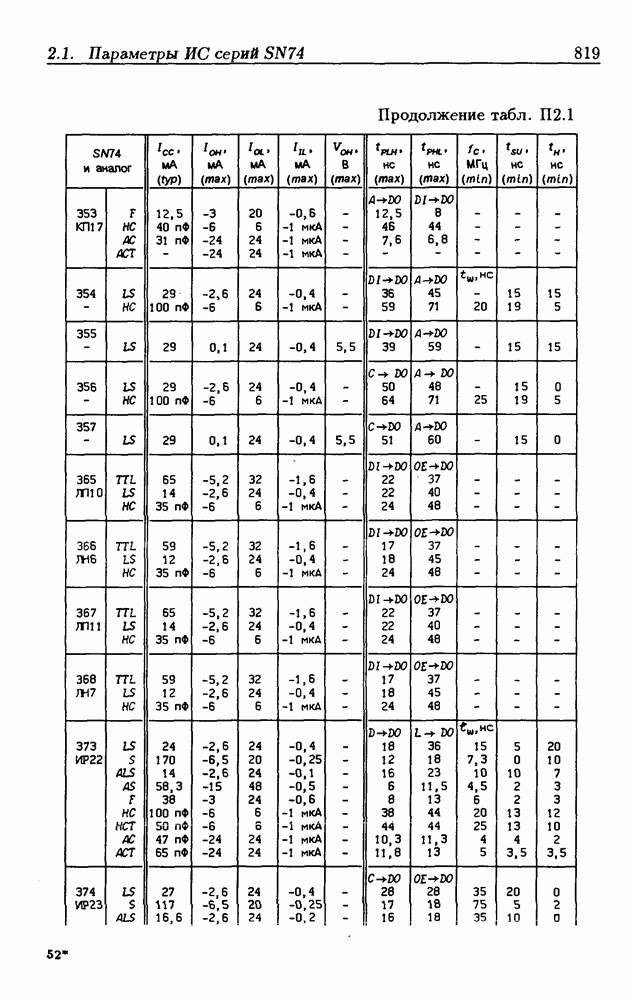
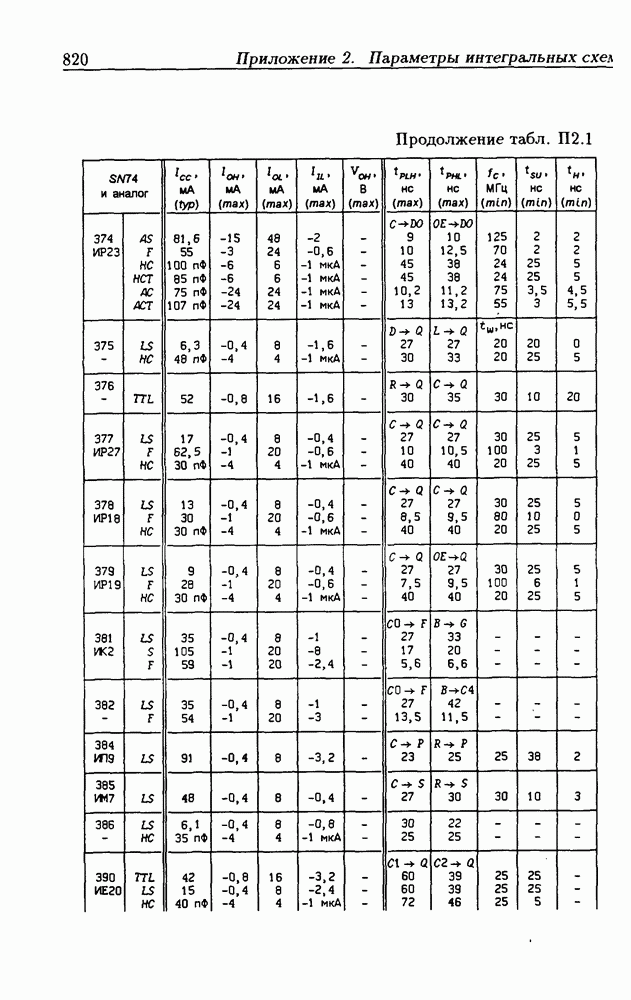
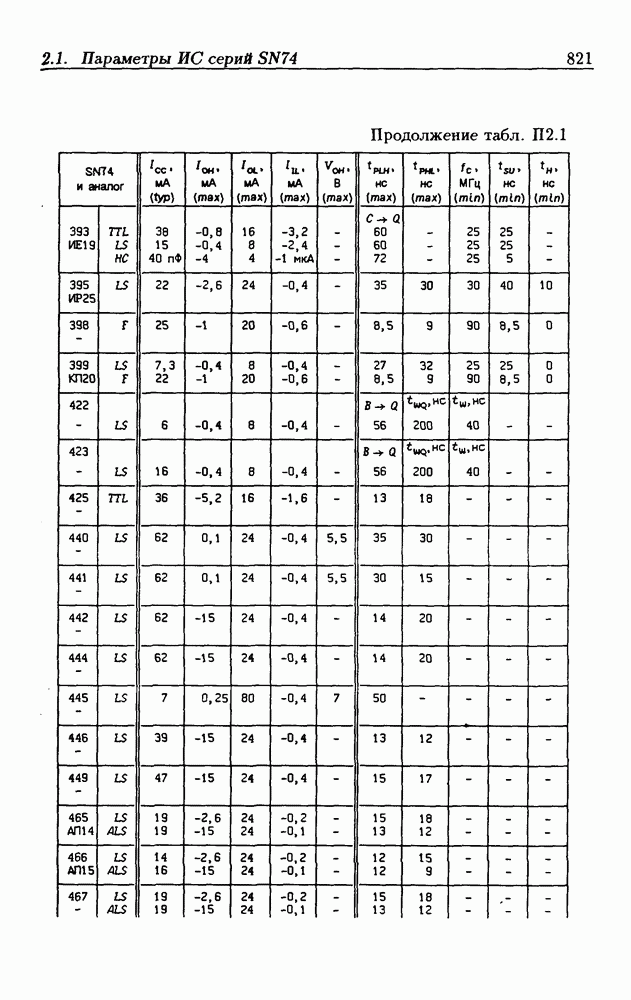
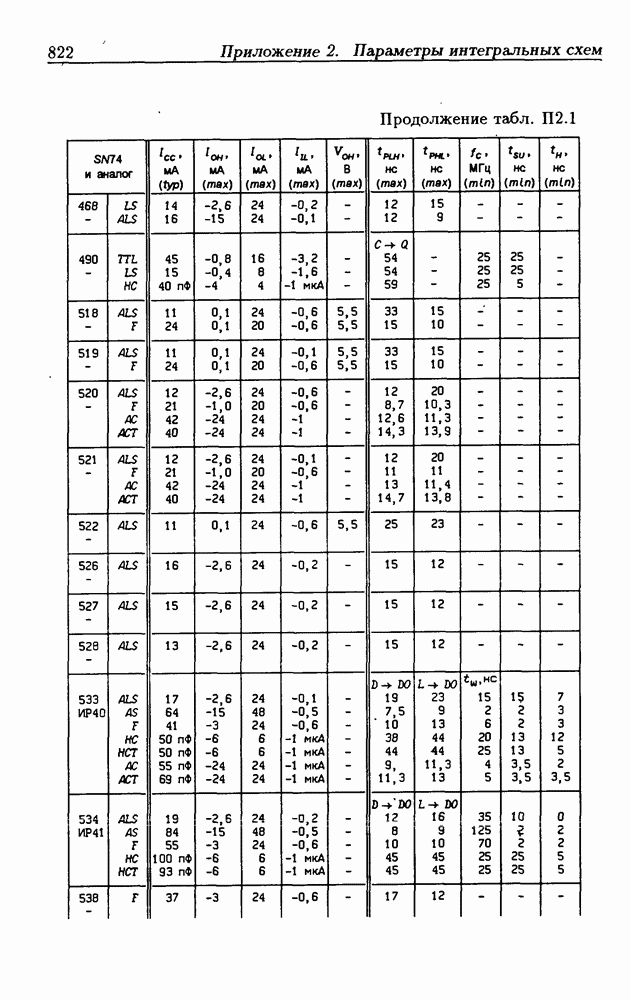
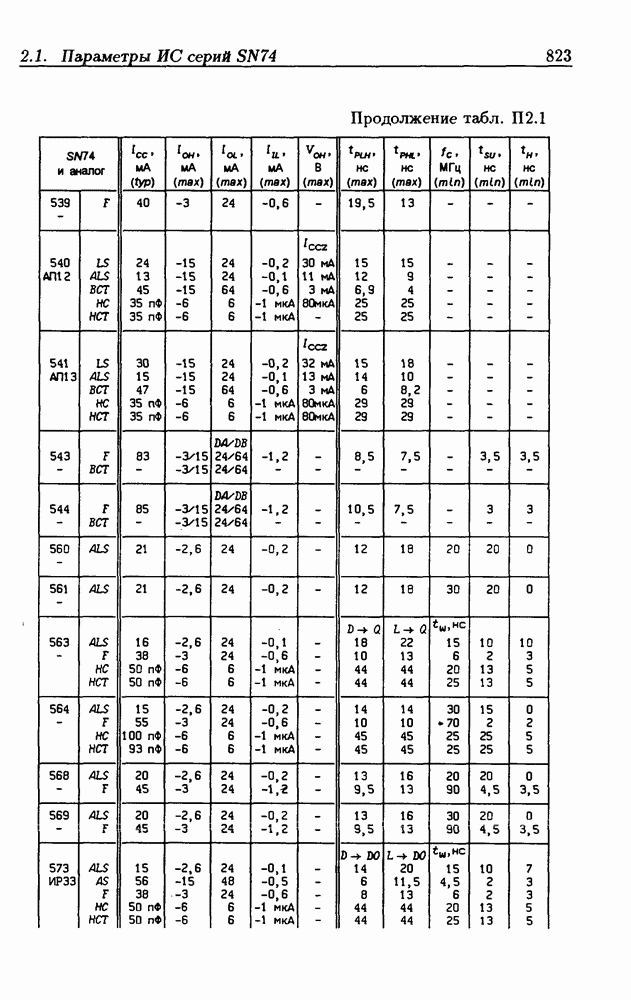
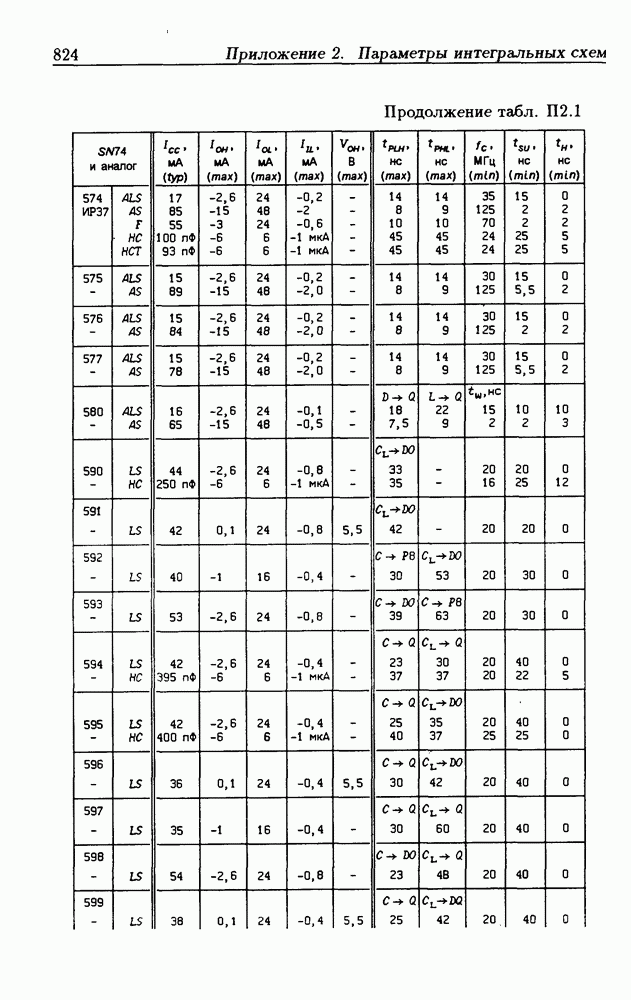
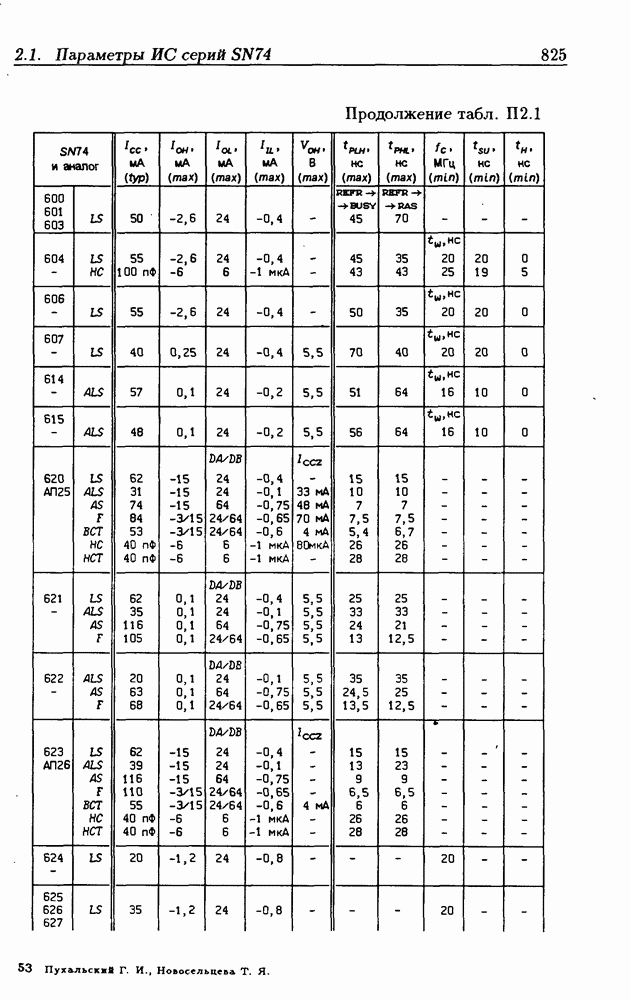
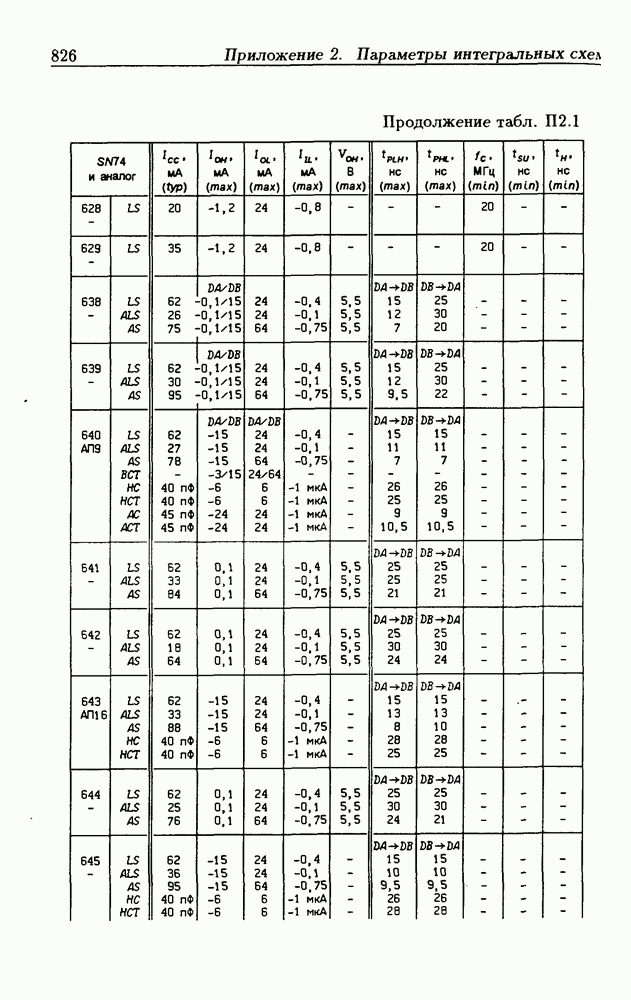
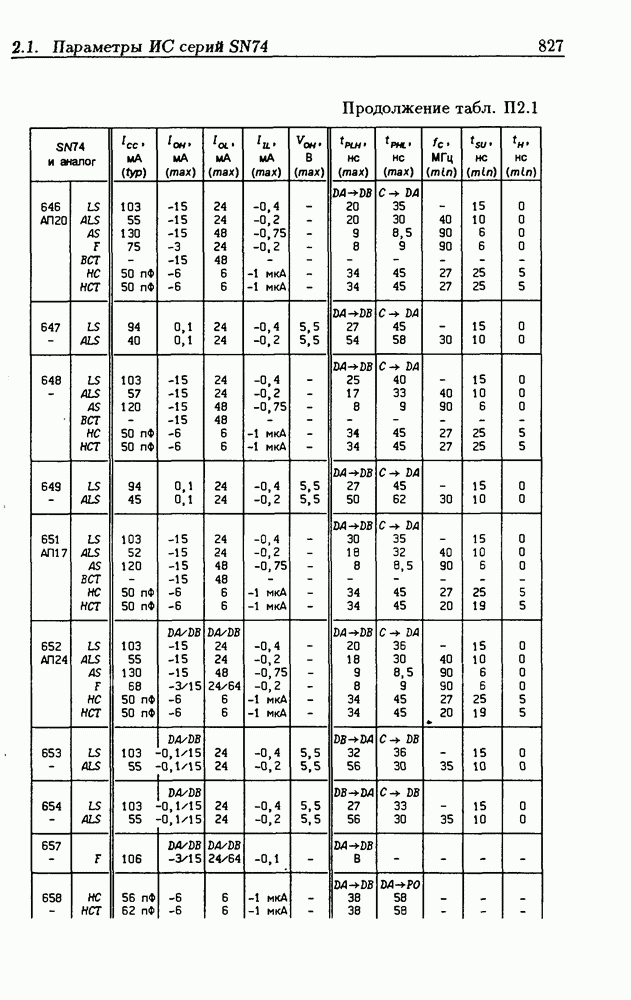
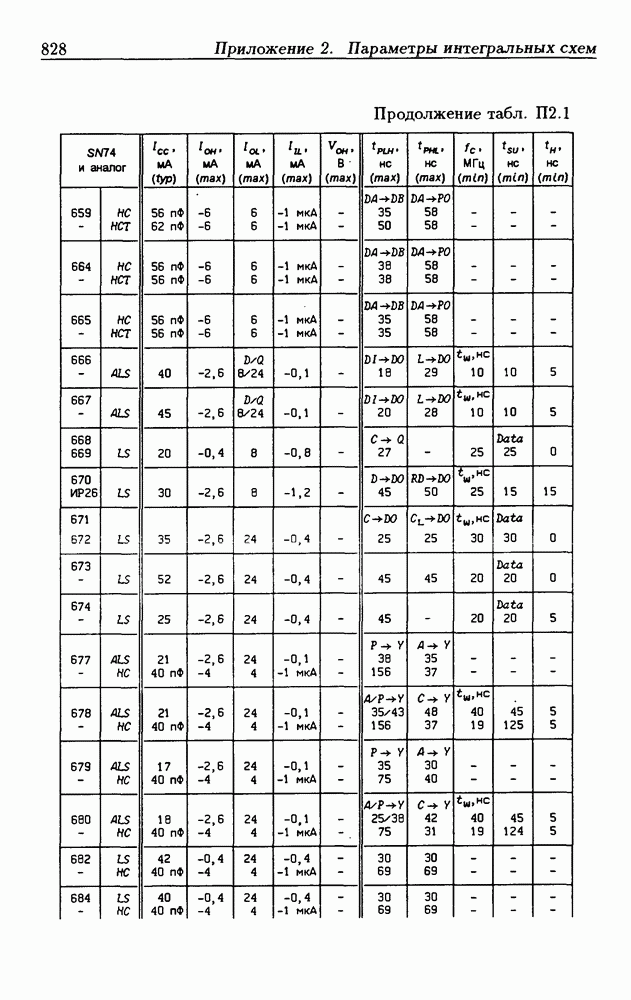
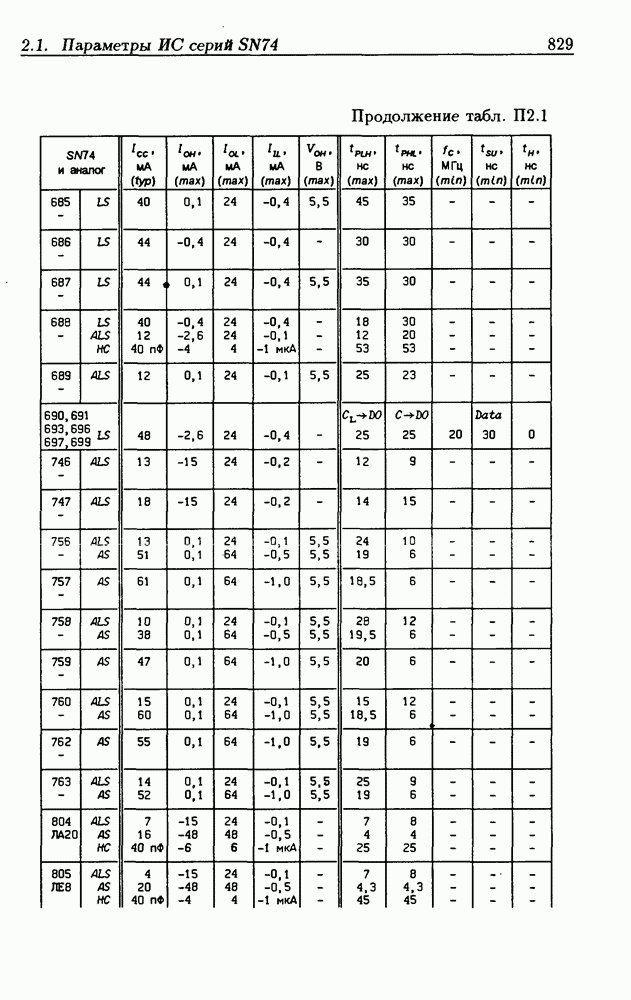
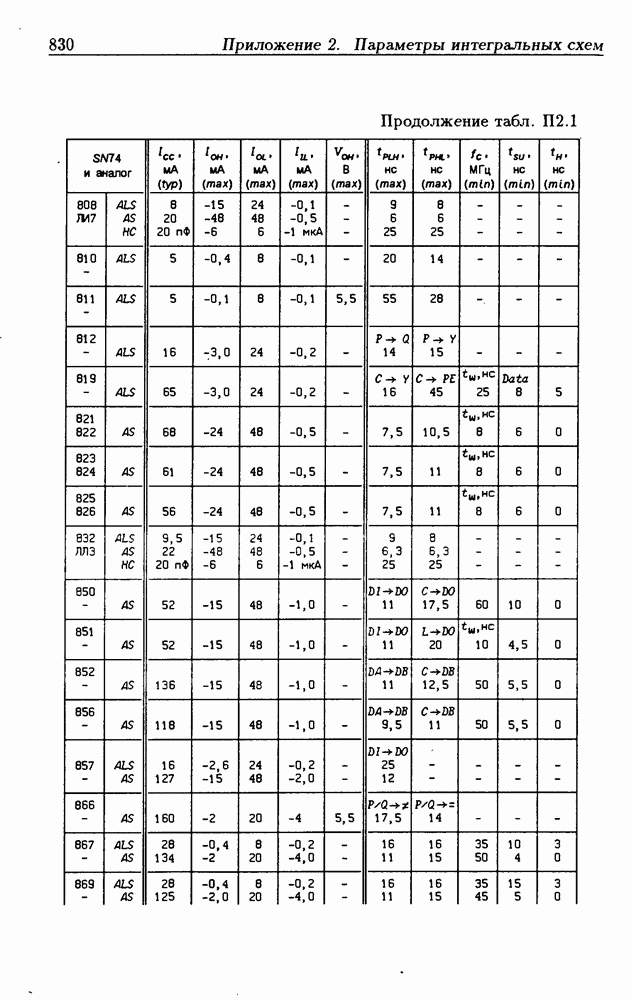
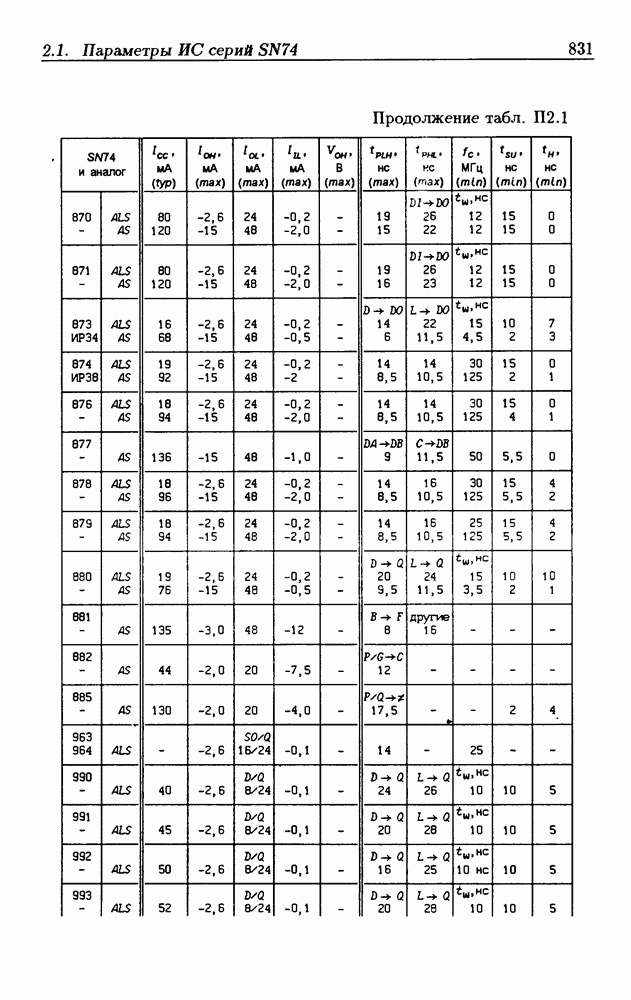
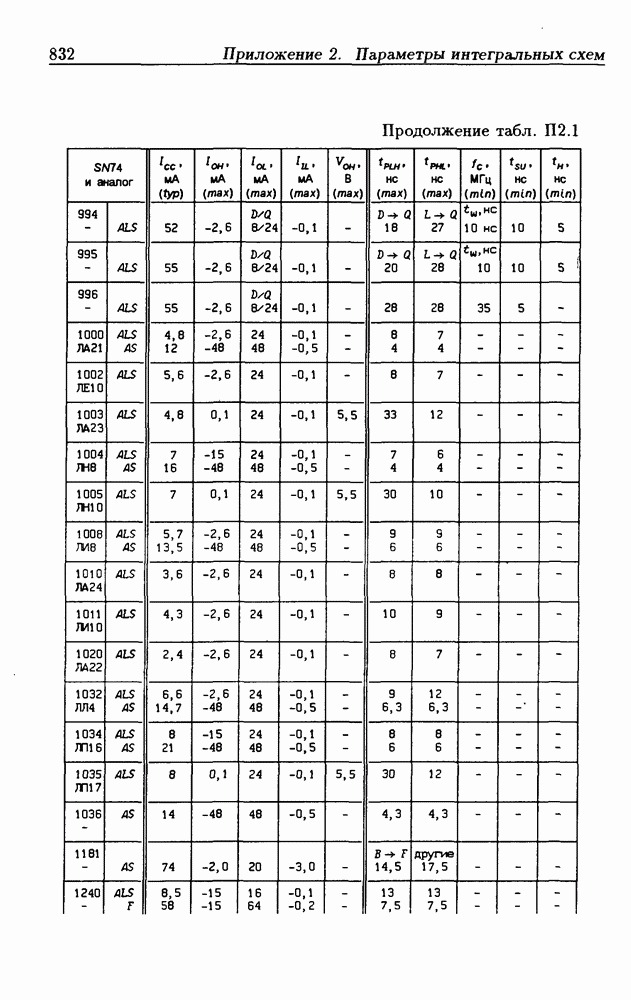
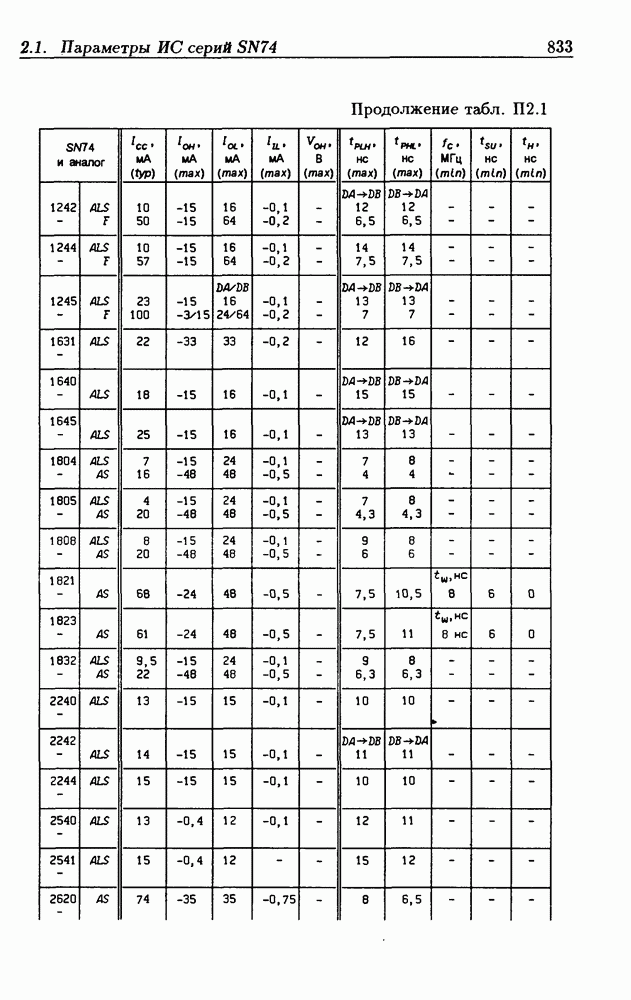
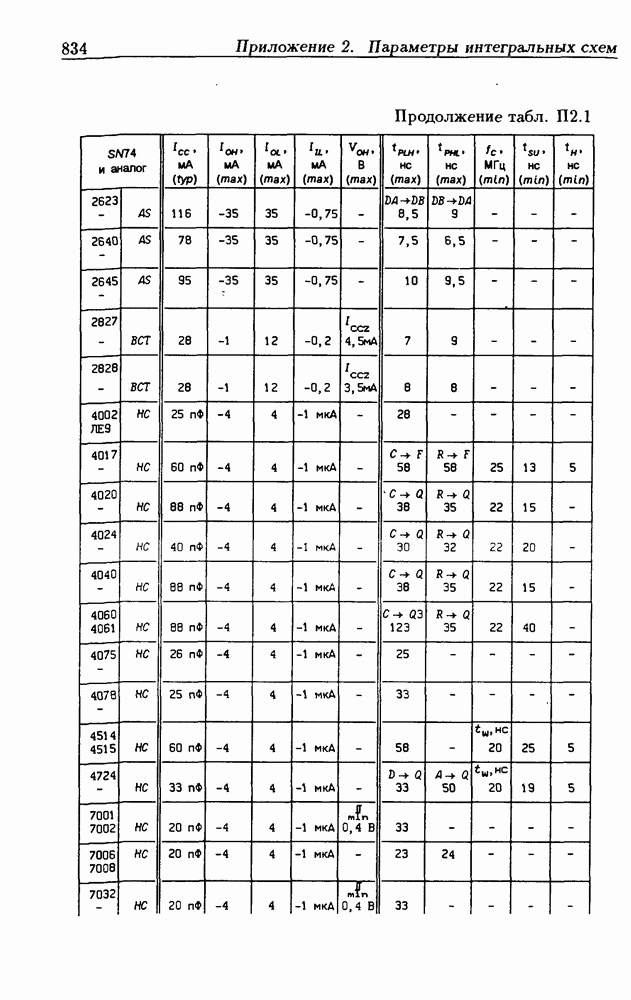
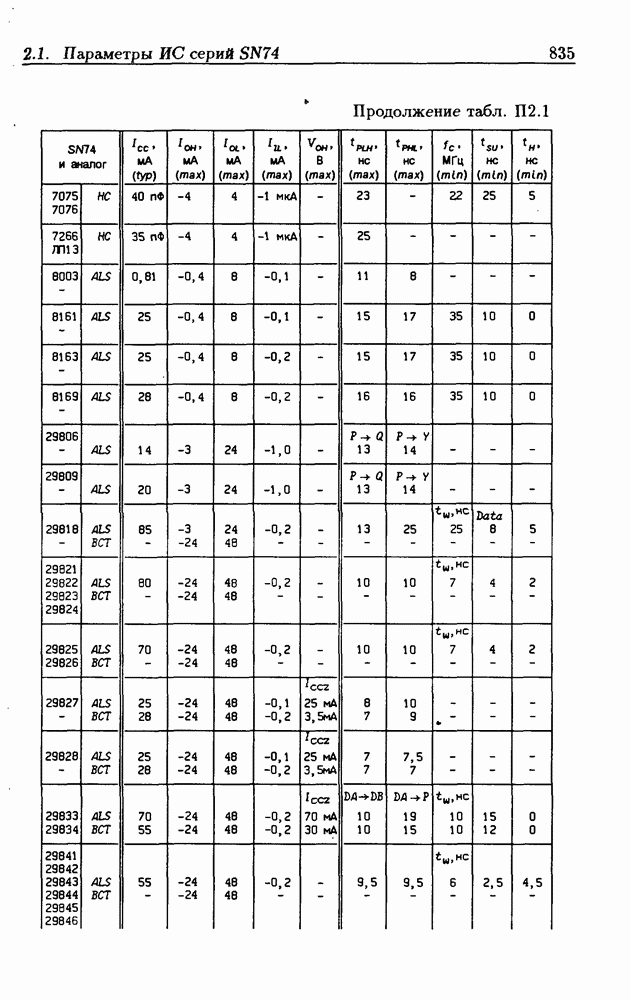
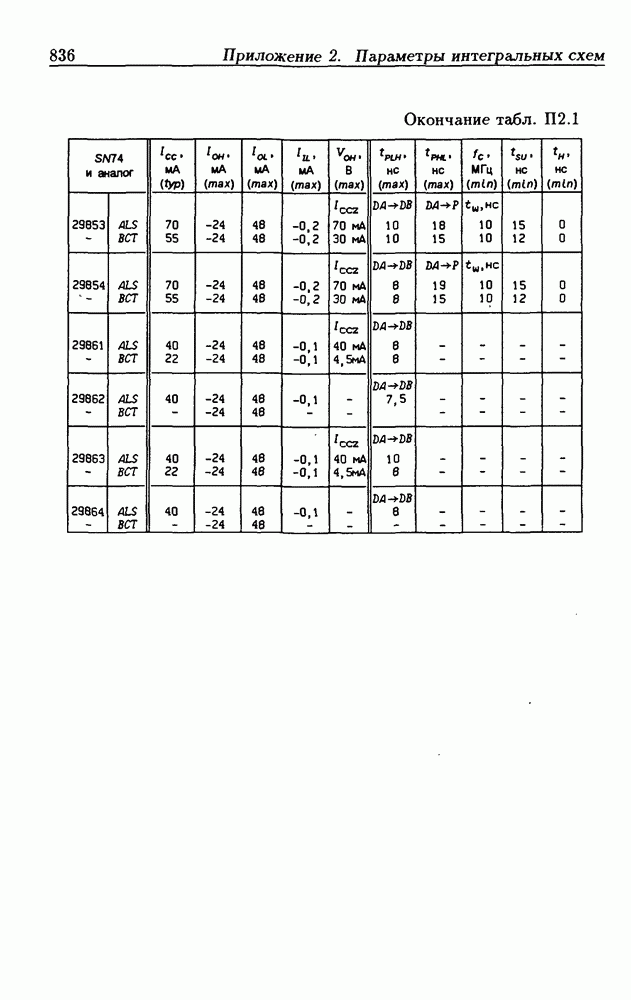
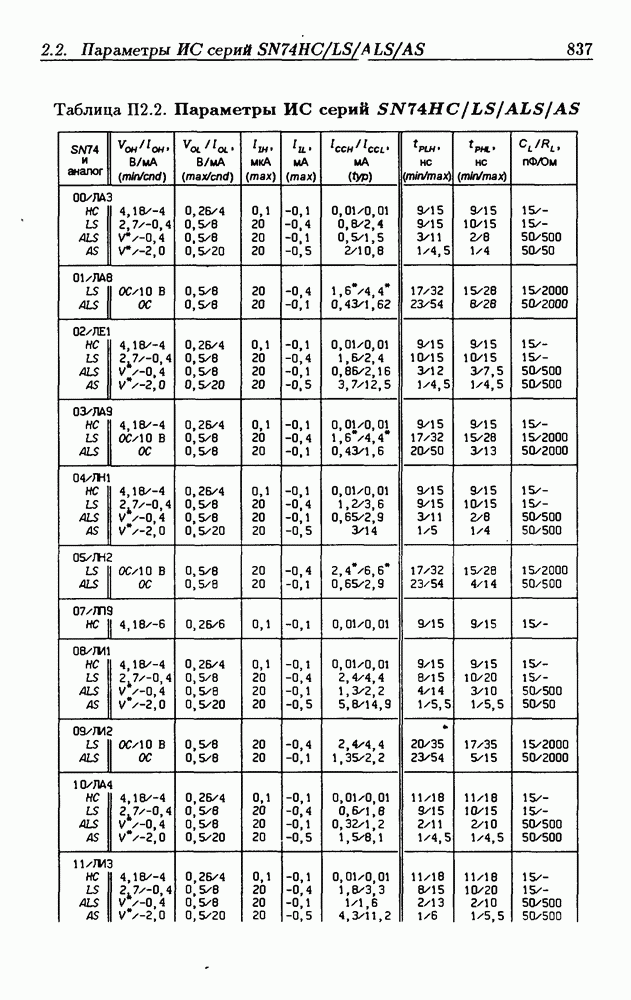
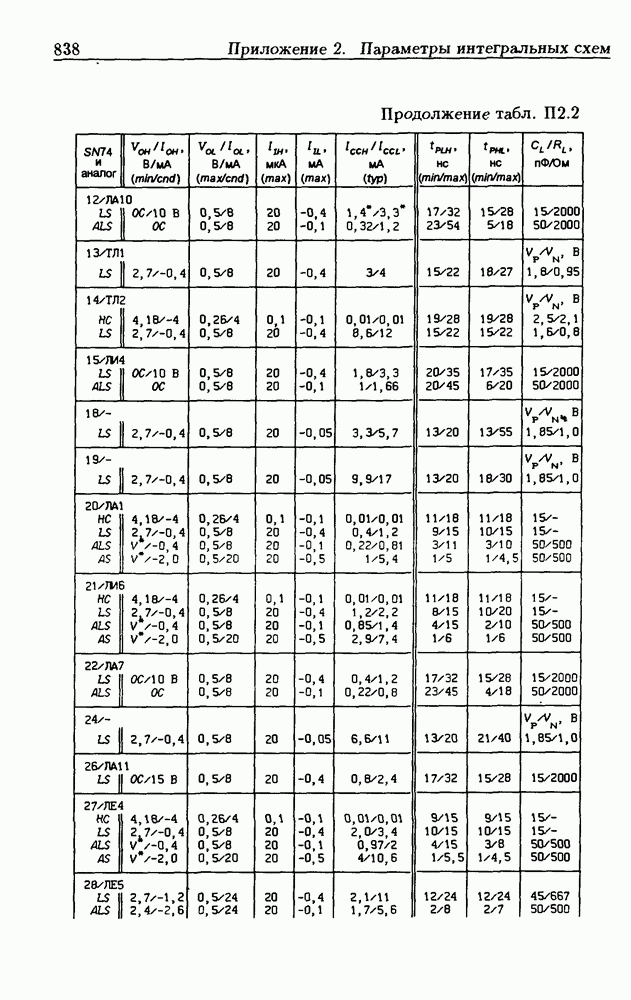
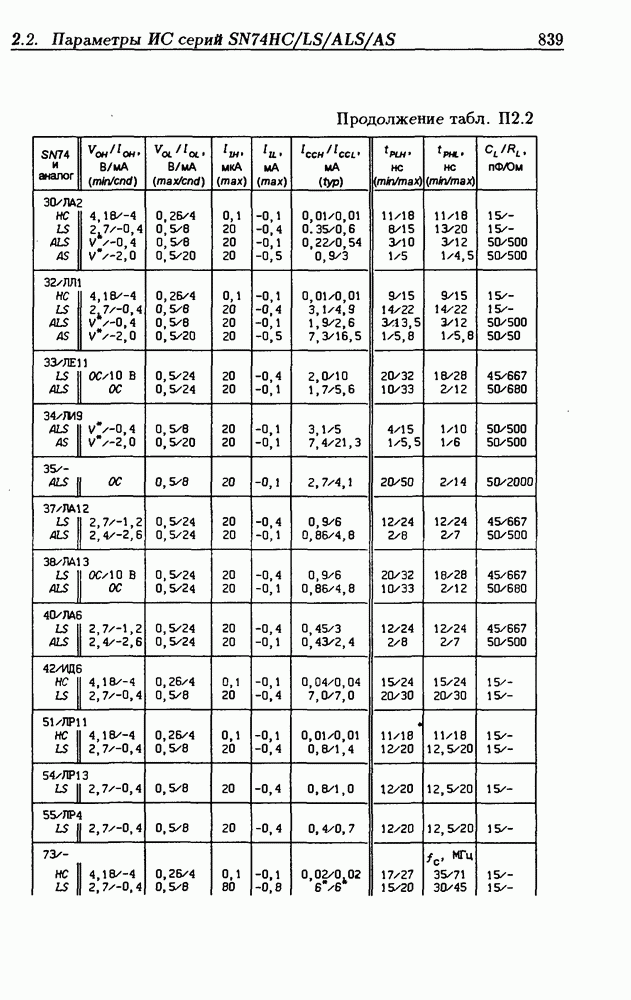
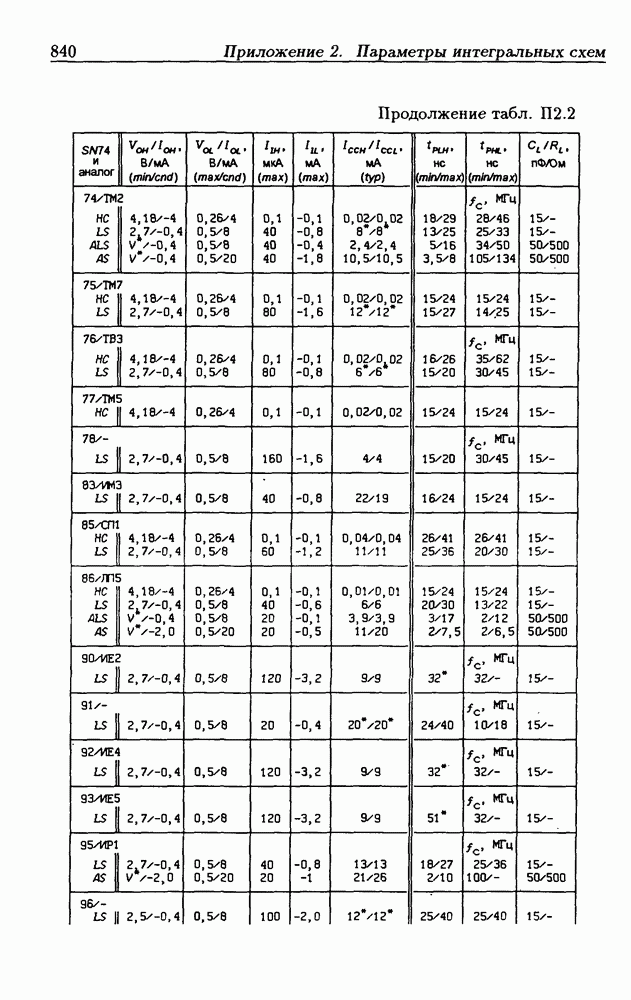
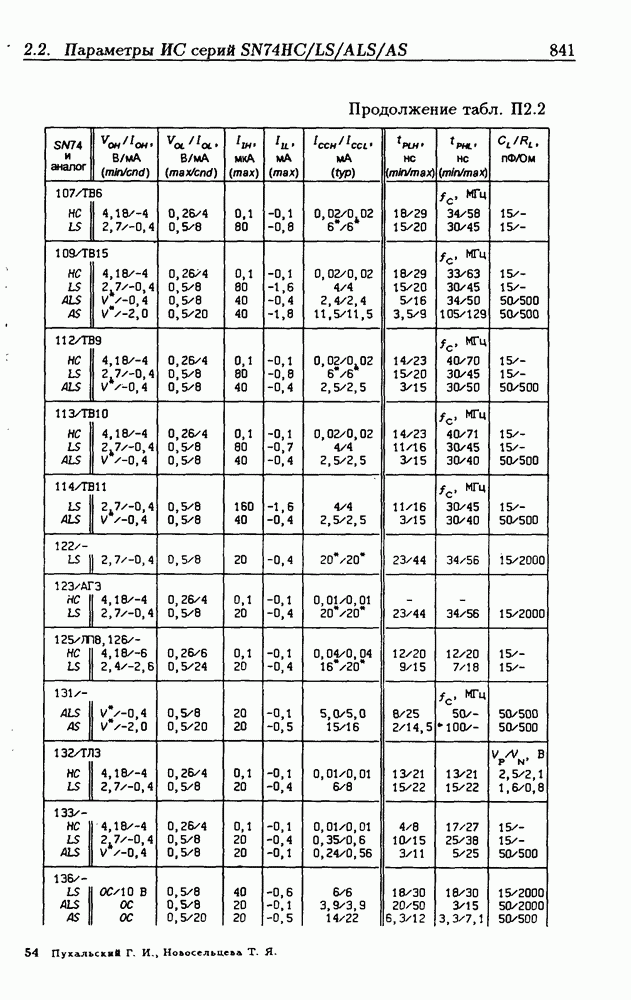
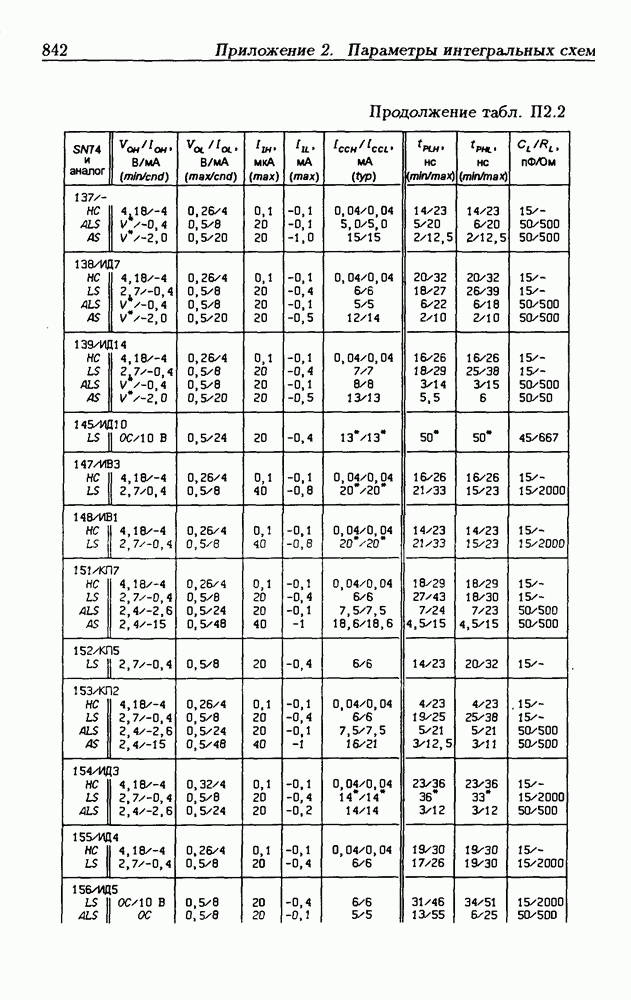
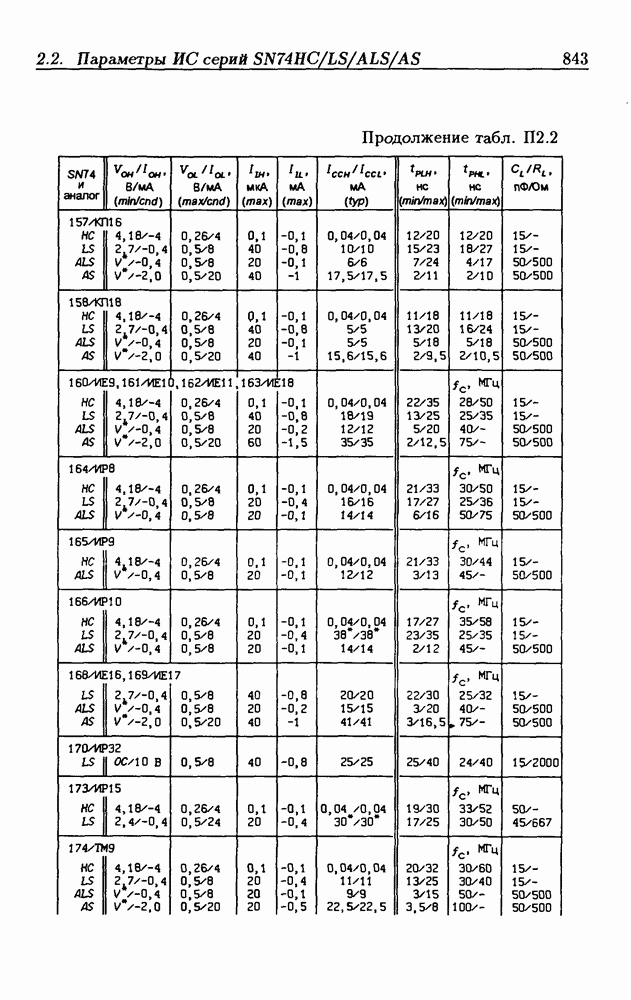
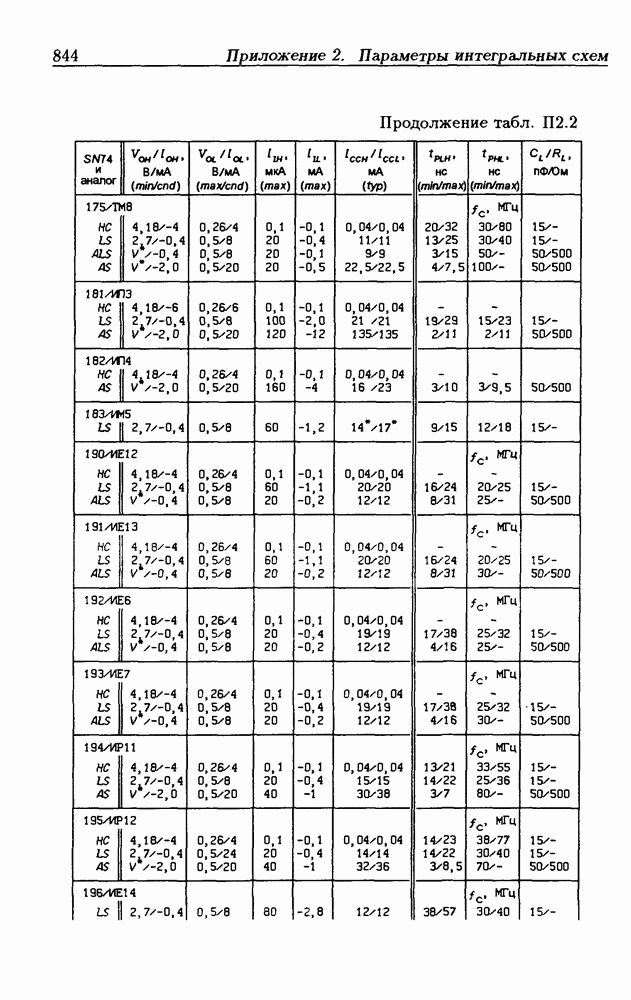
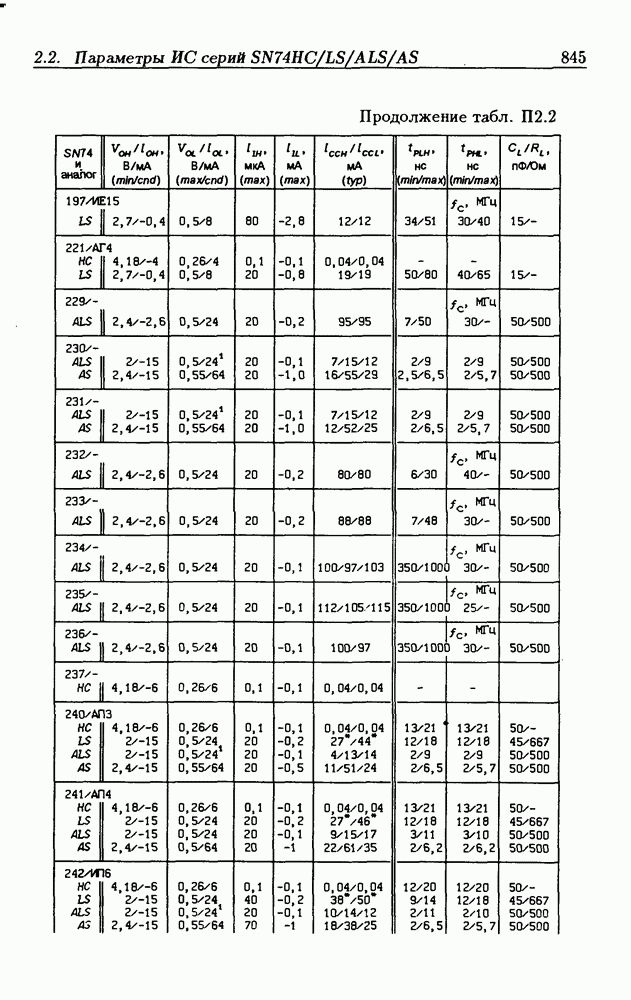
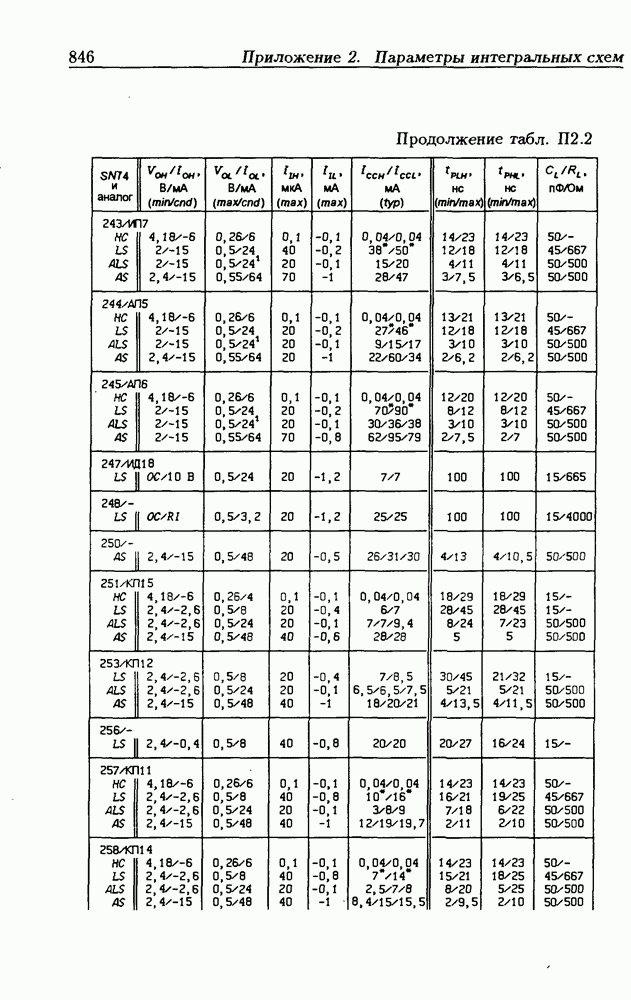
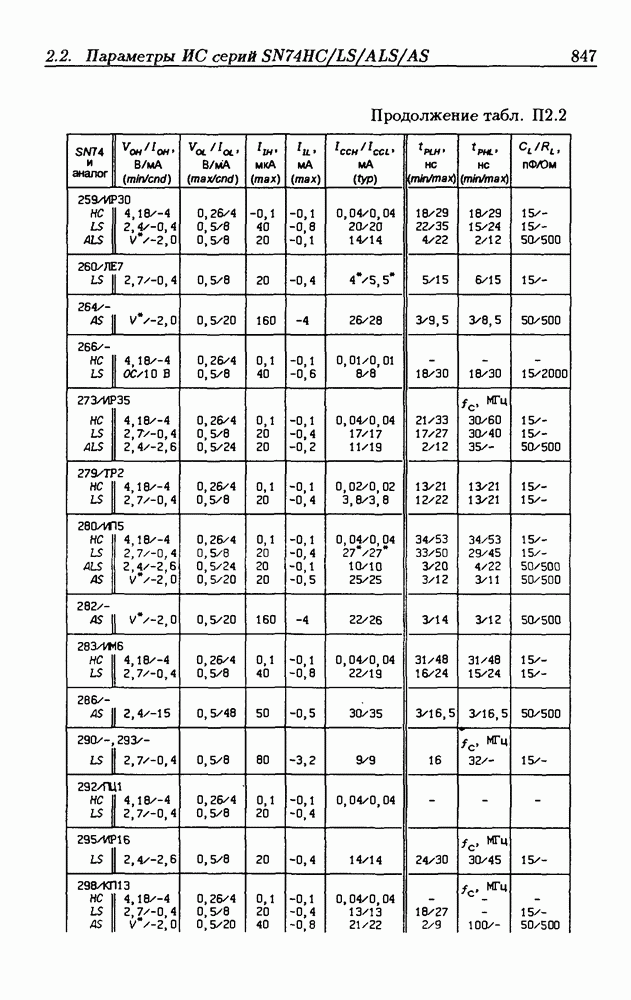
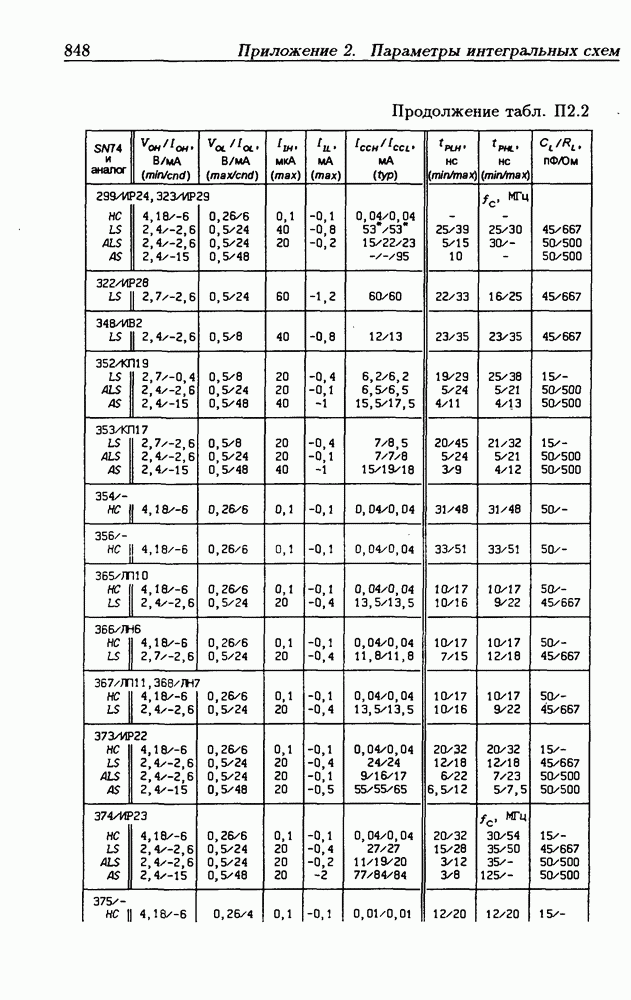
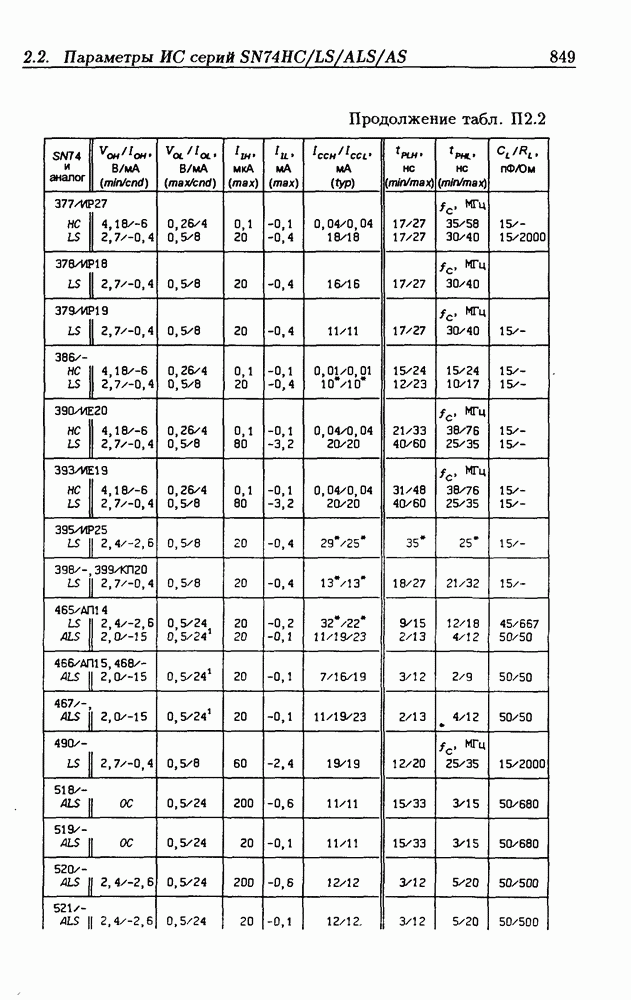
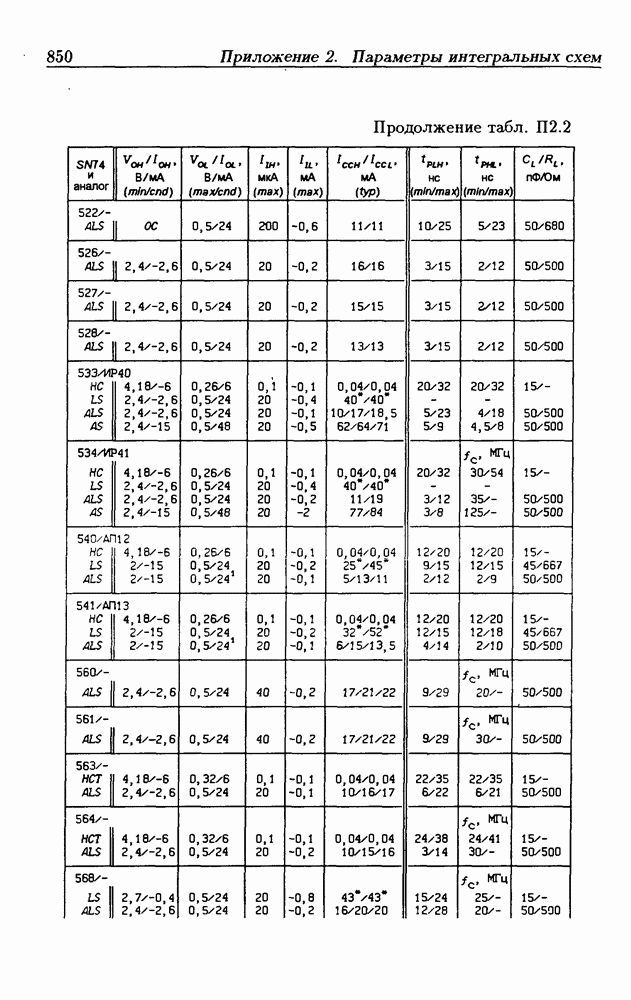
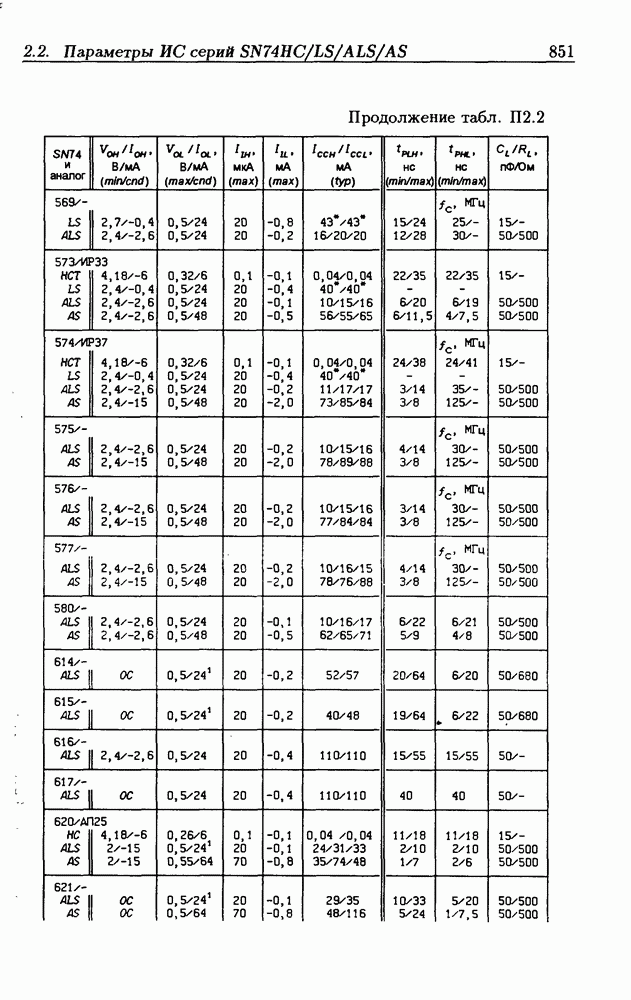
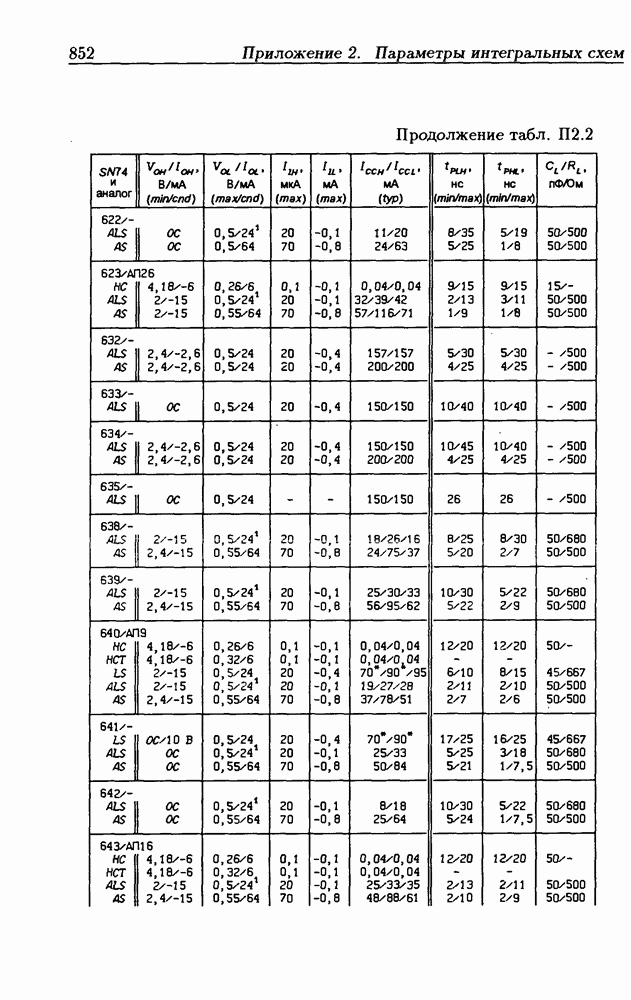
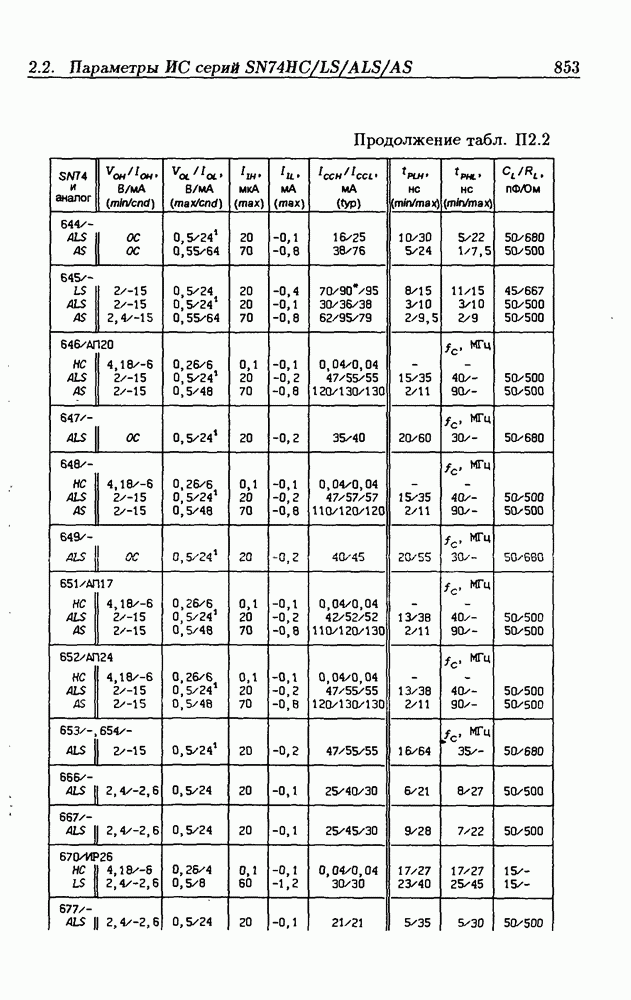
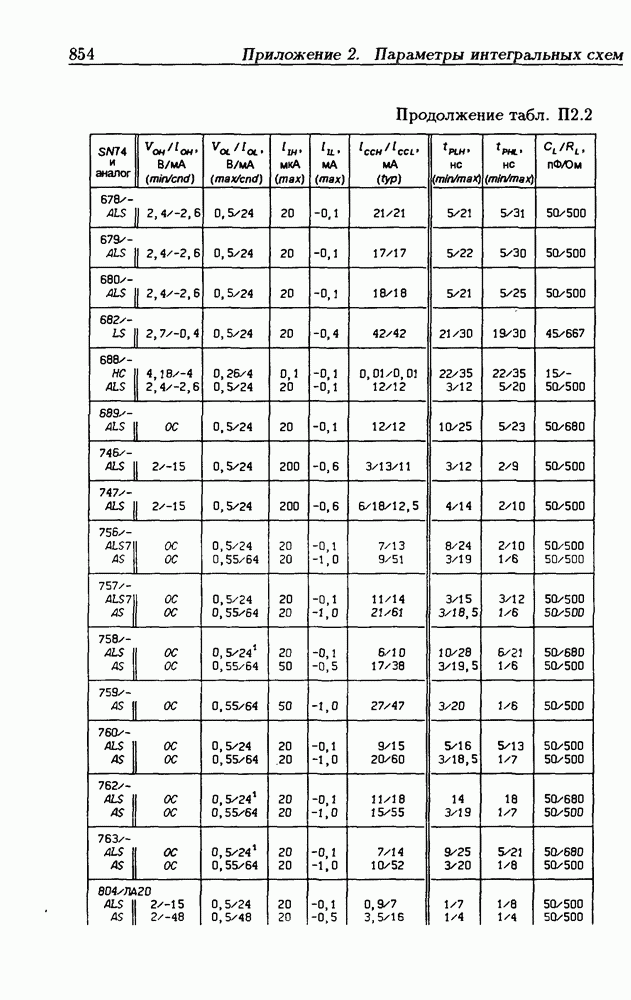
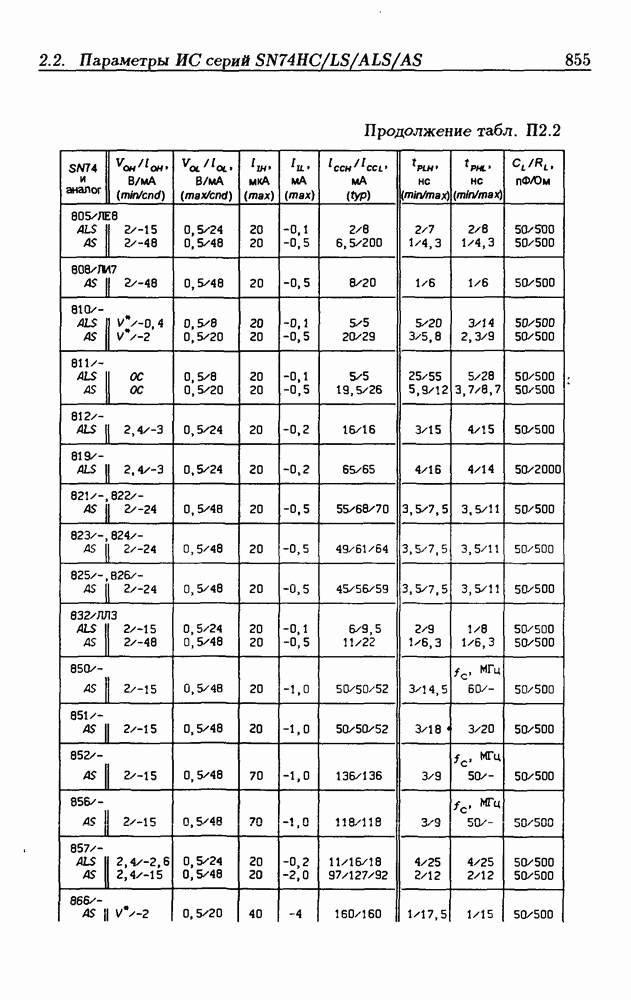
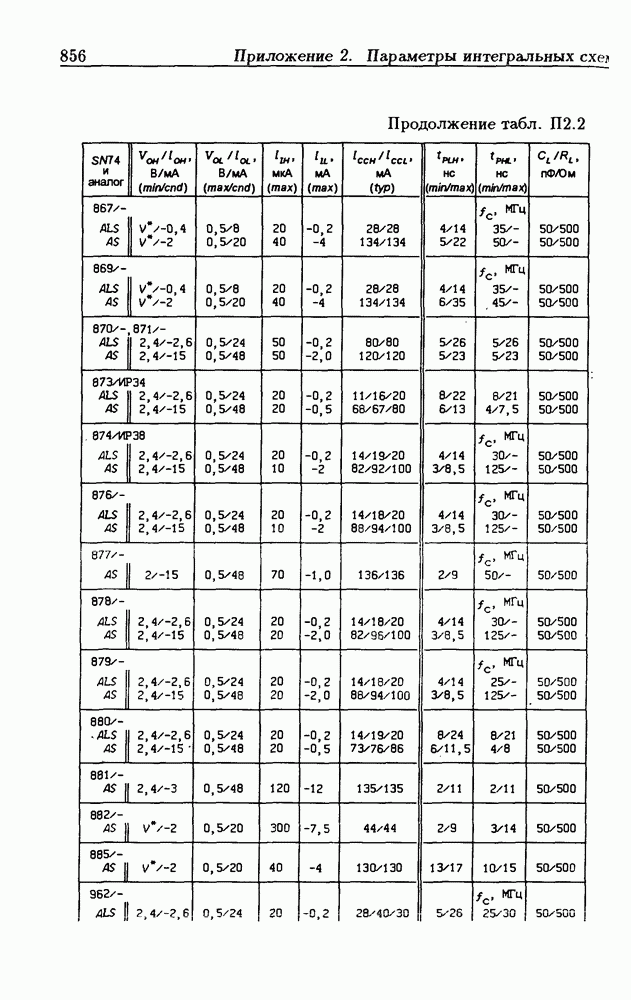
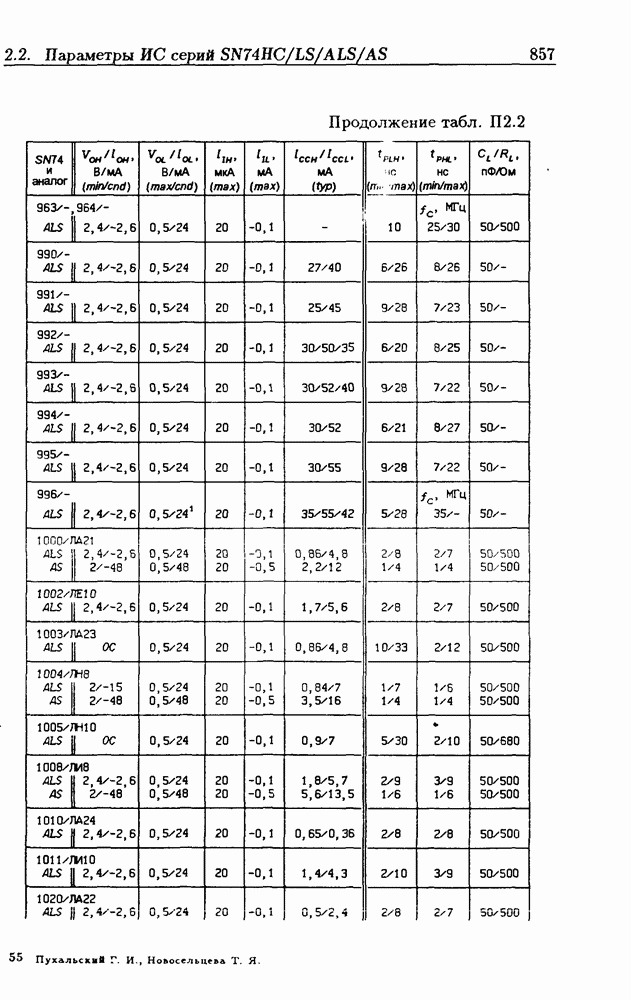
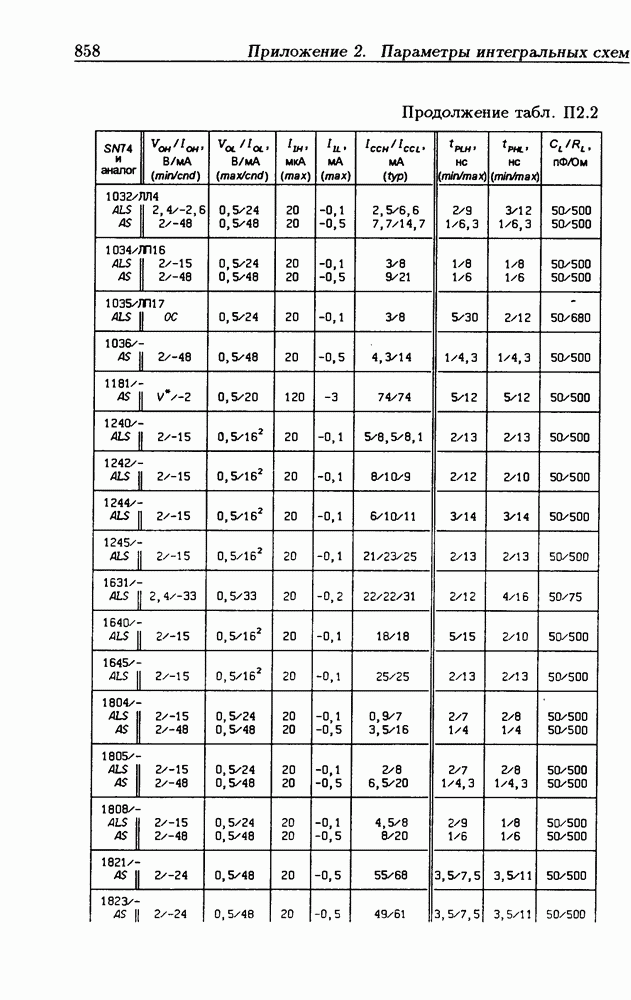
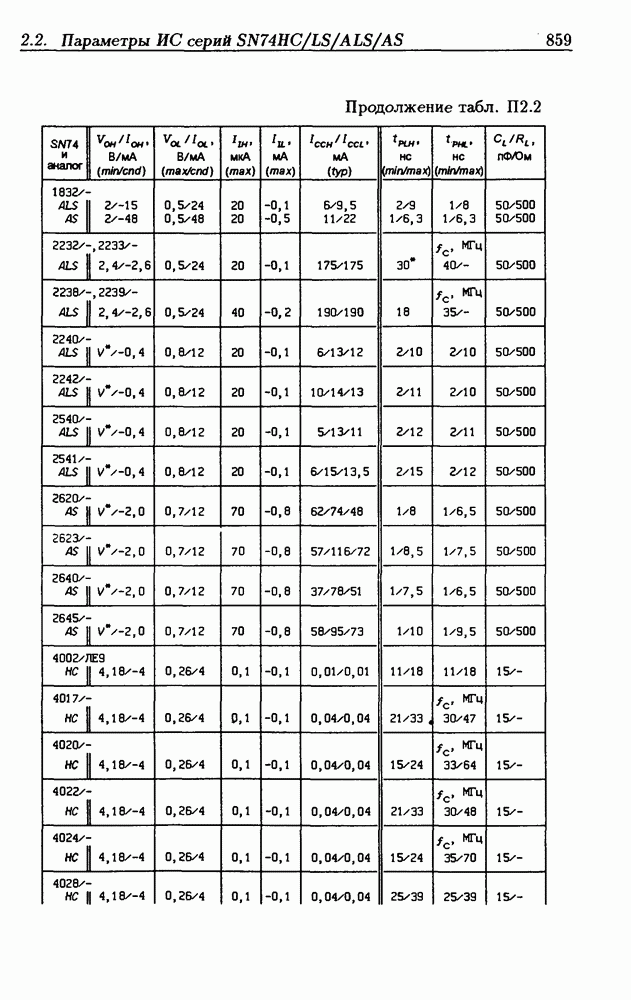
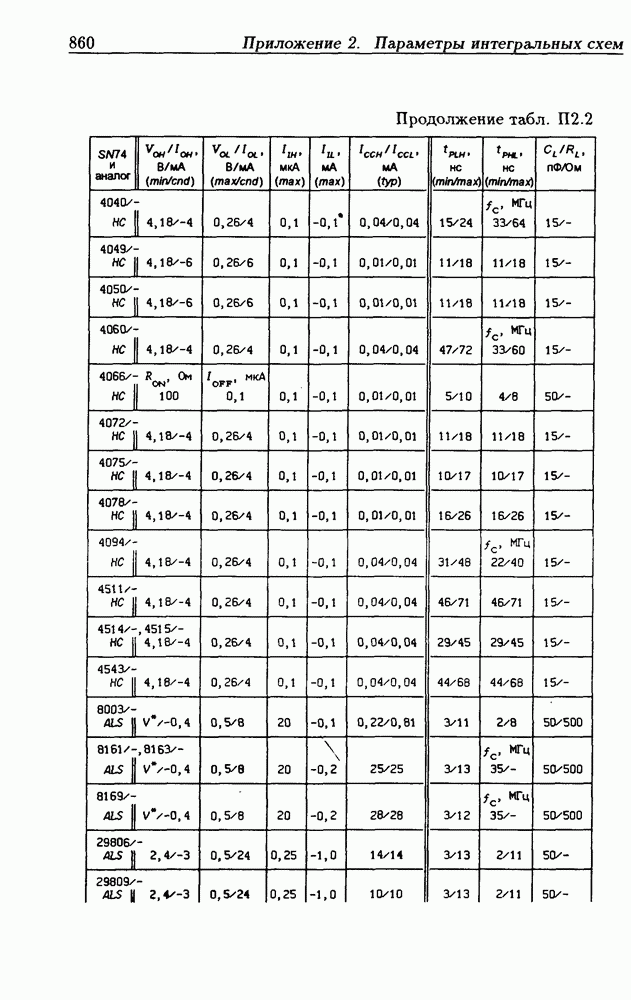
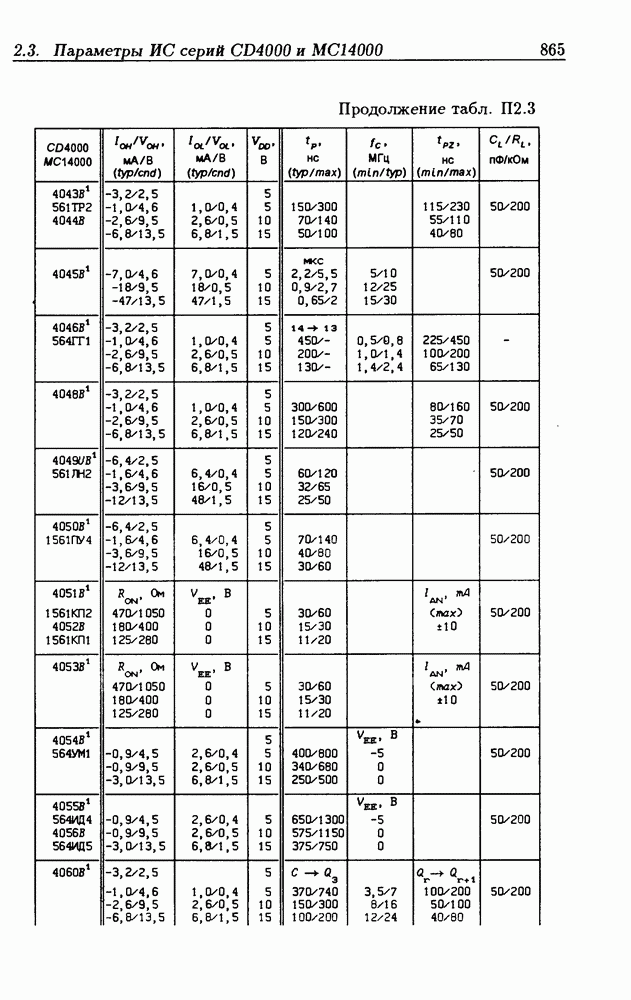
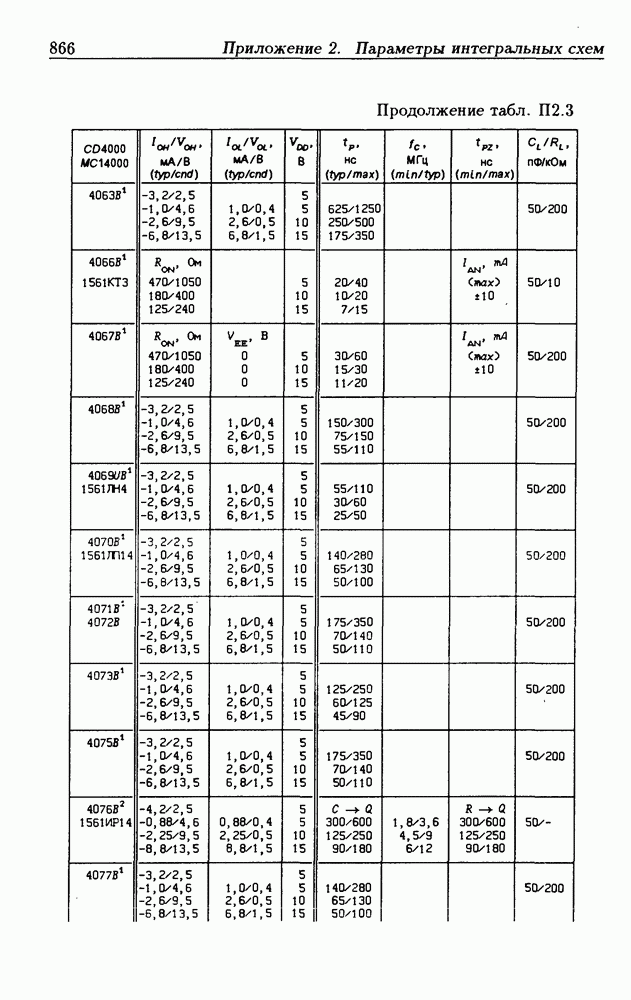
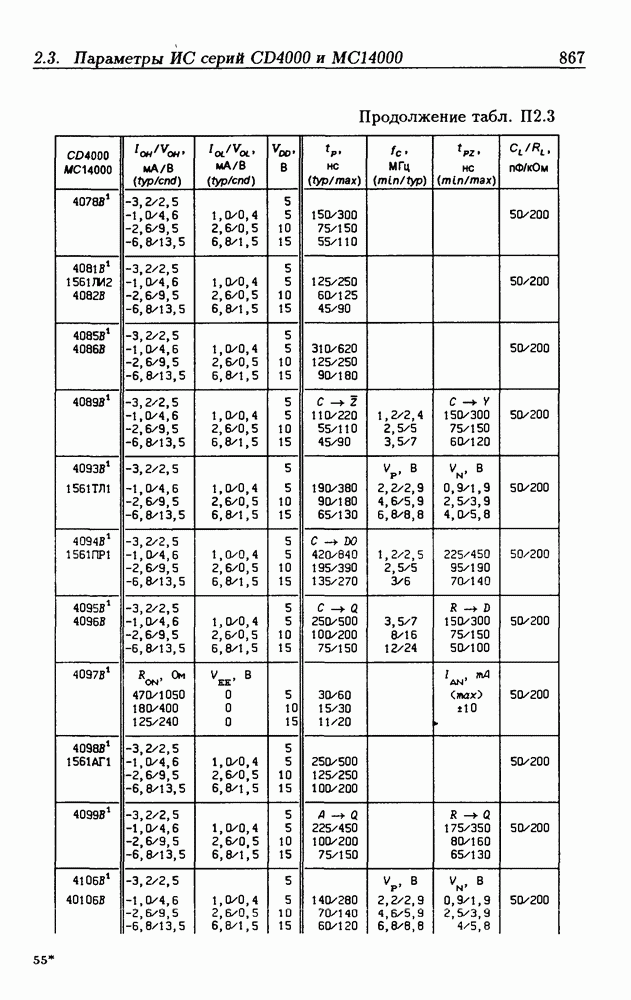
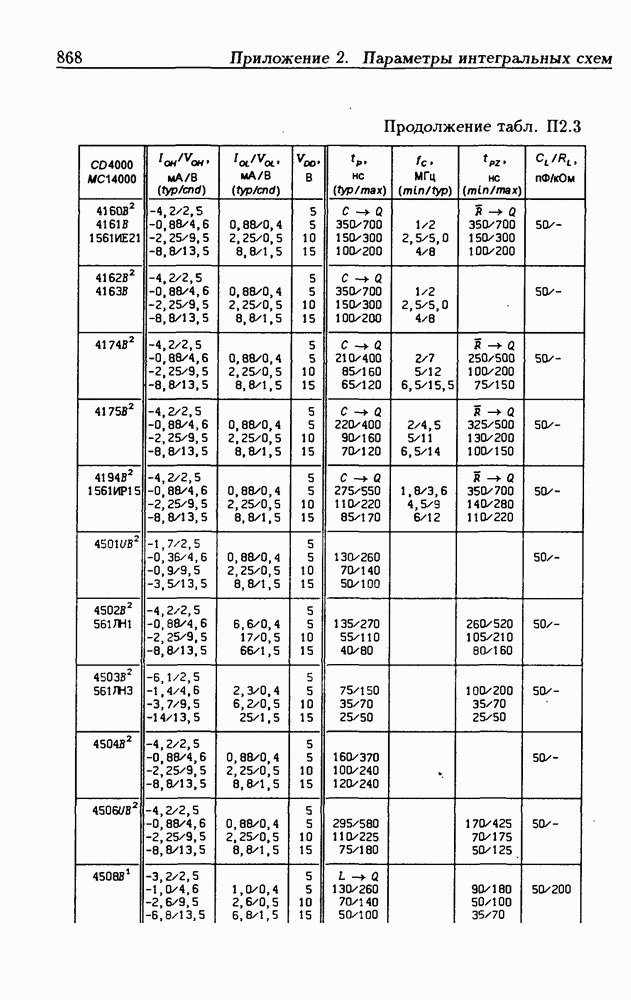
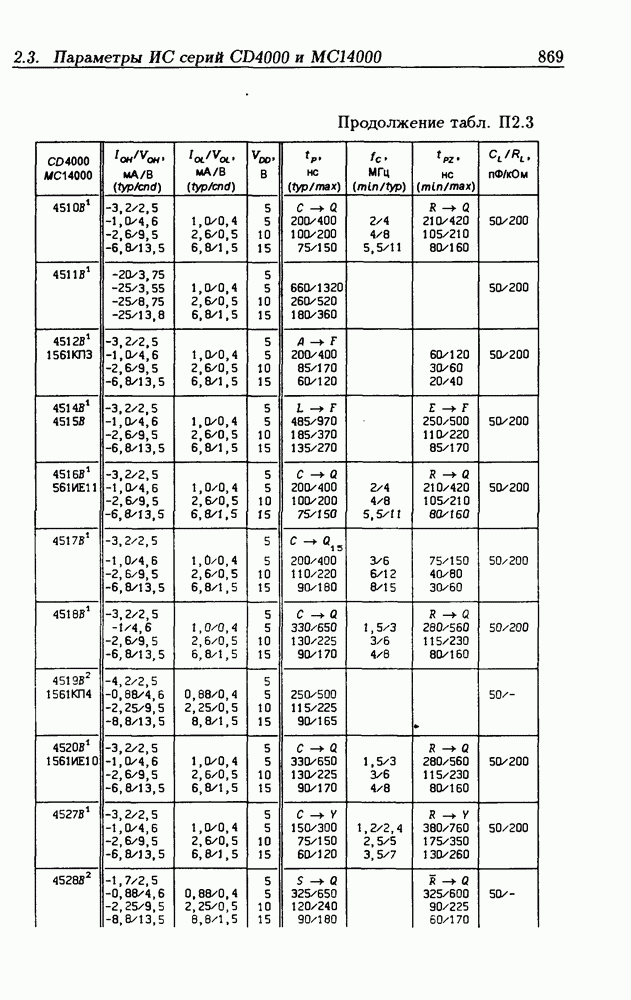
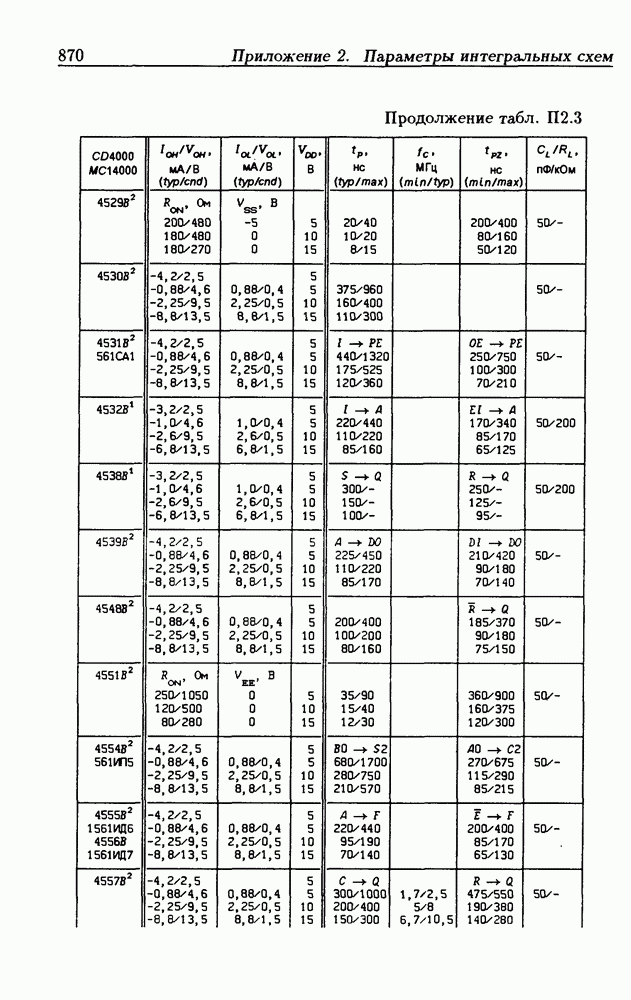
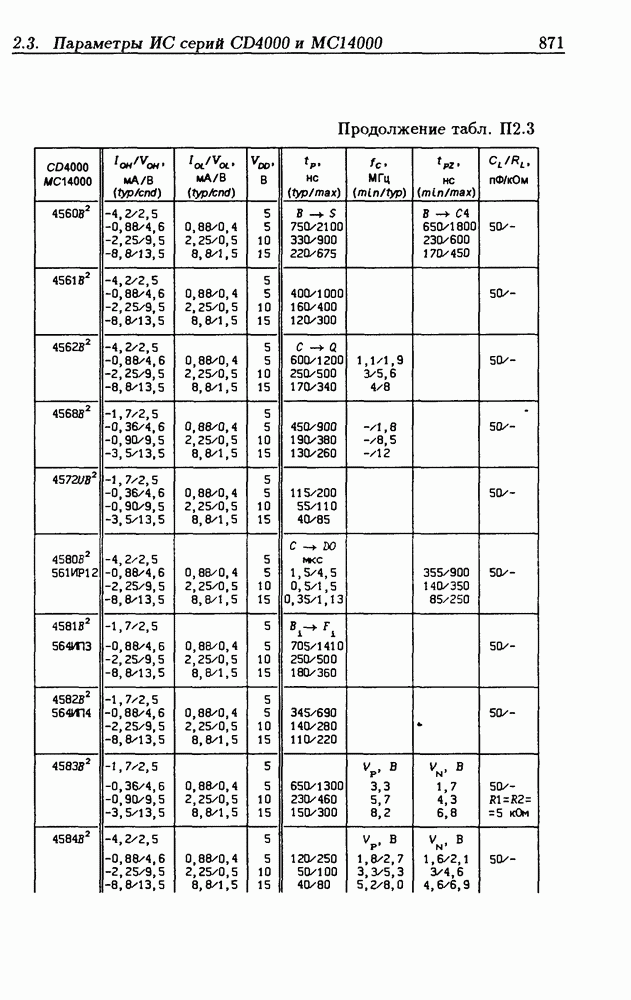
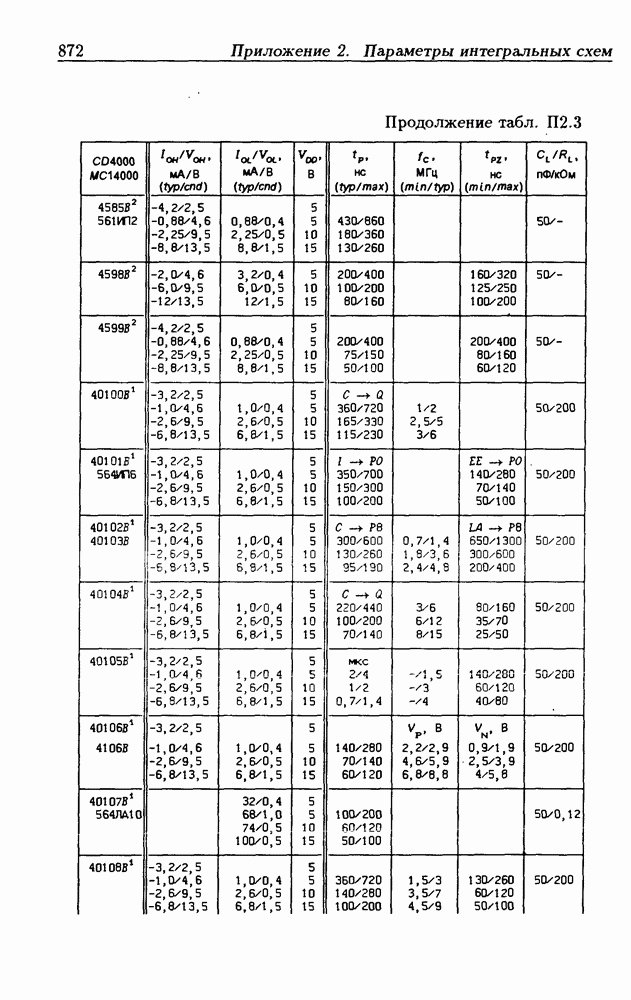
- Приложение 2. Параметры интегральных схем