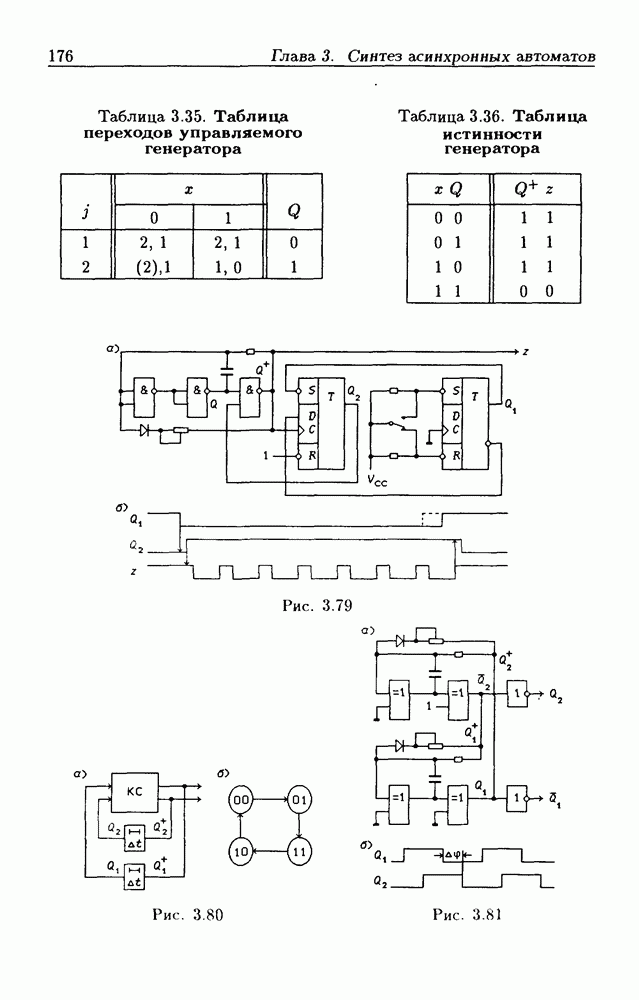
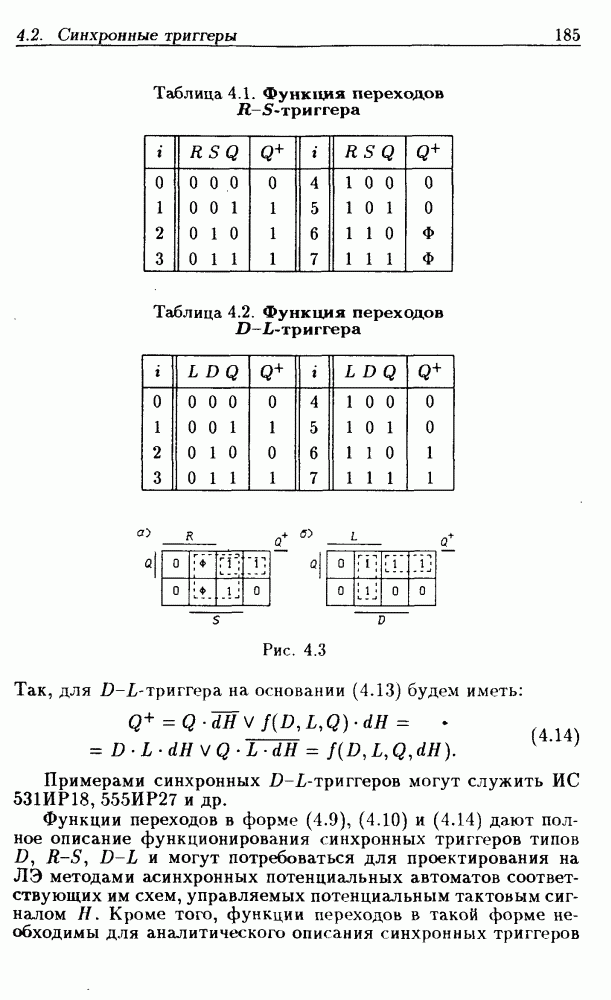
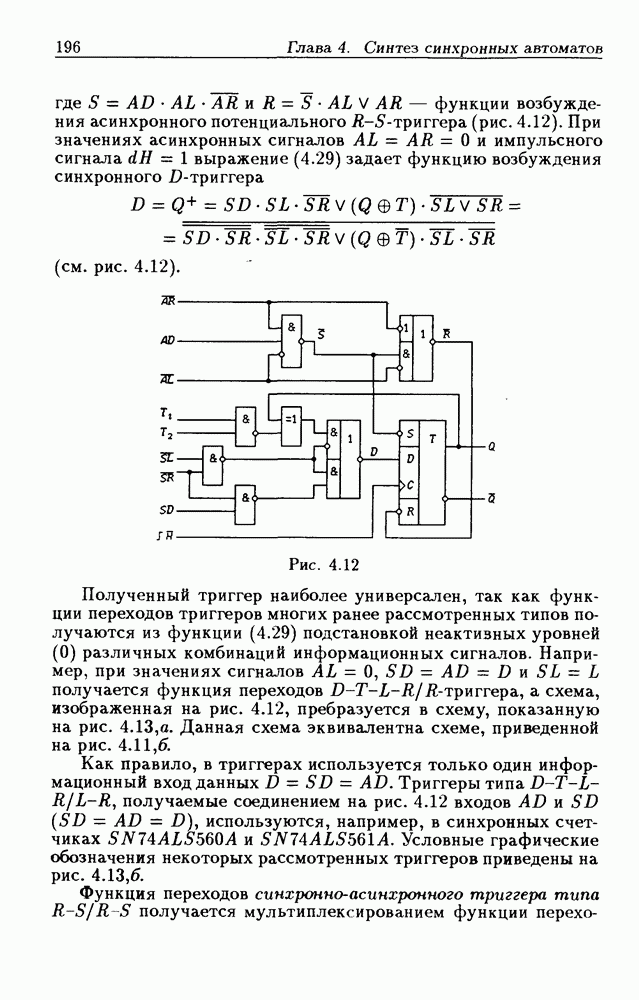
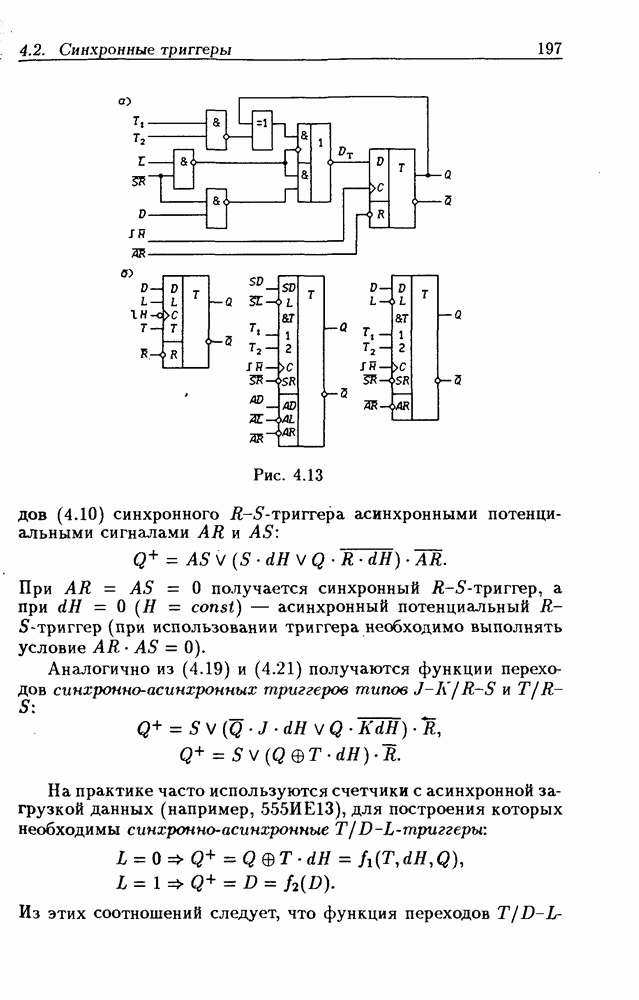
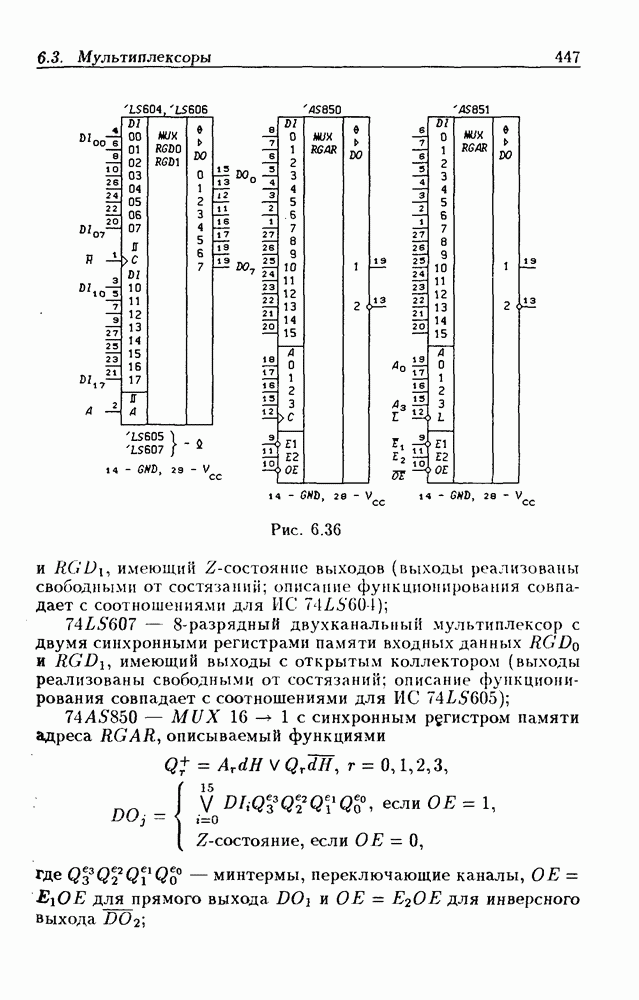
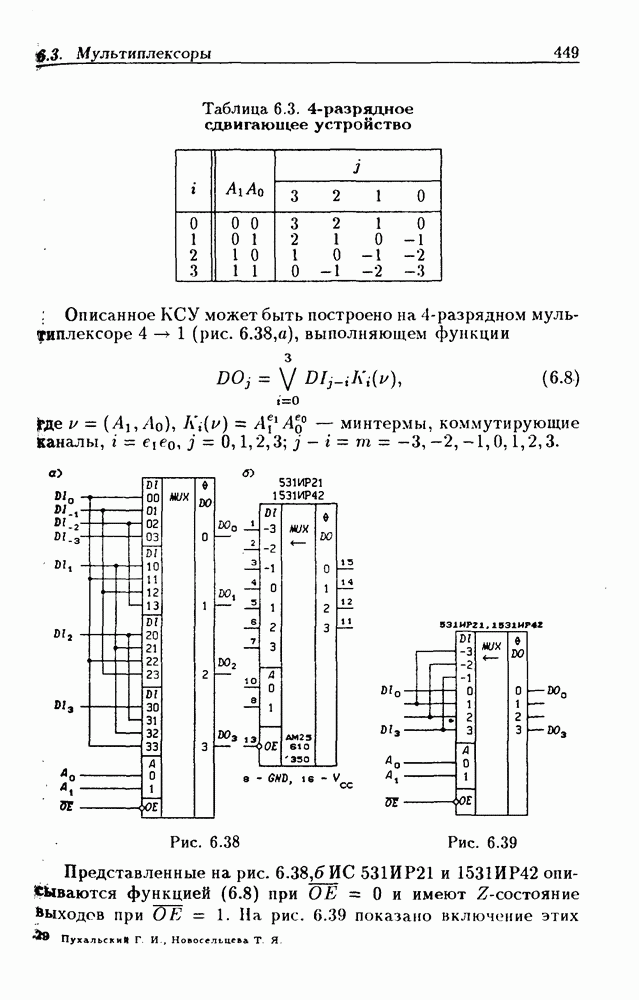
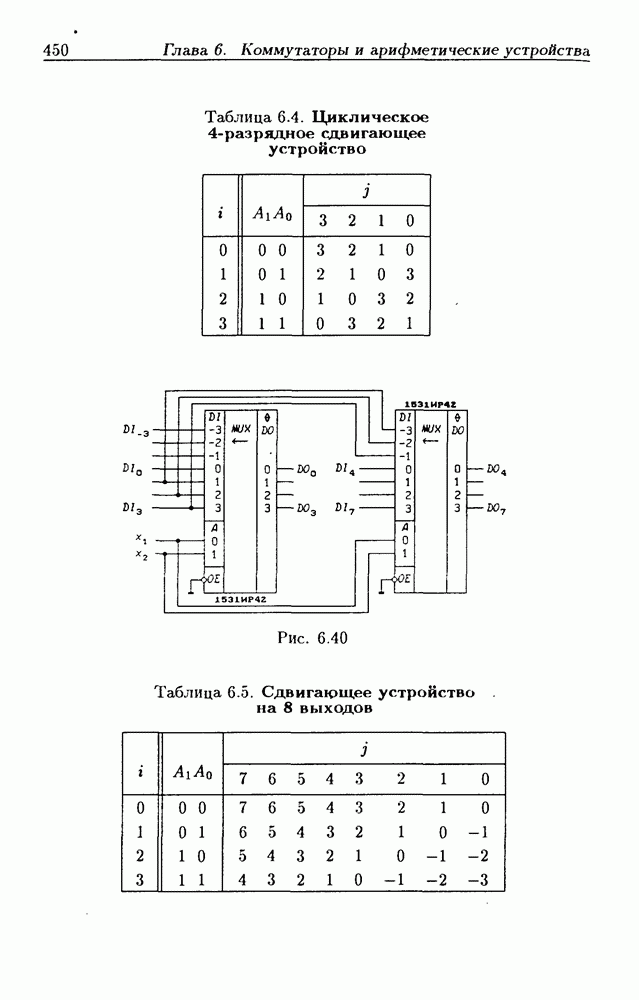
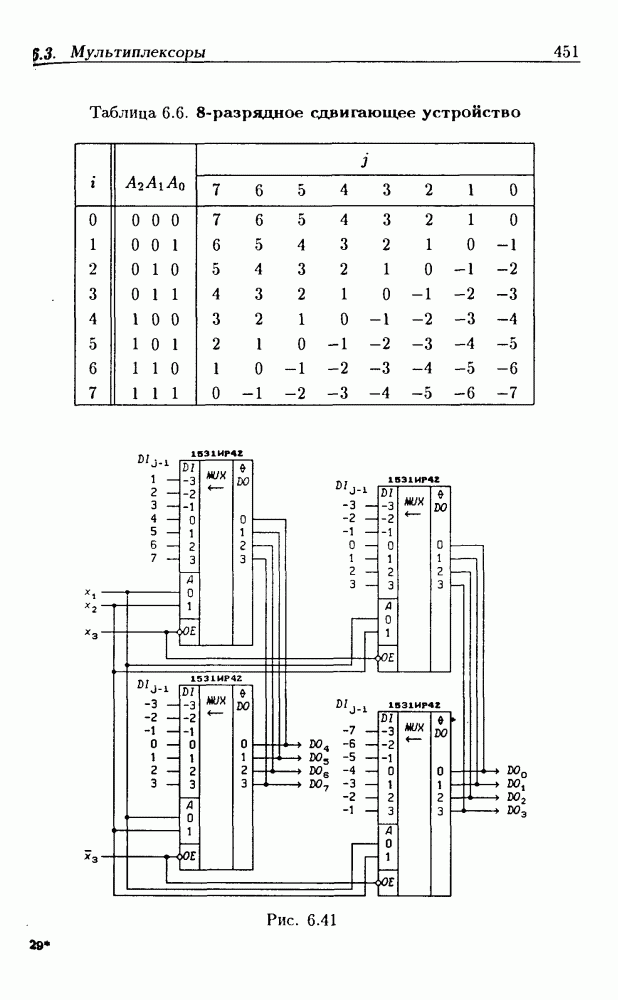
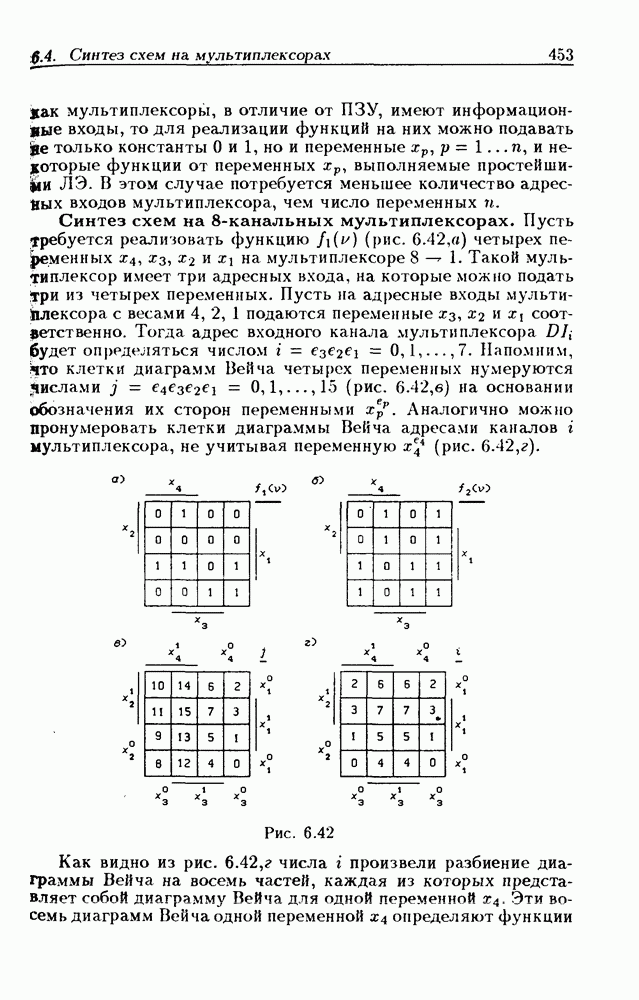
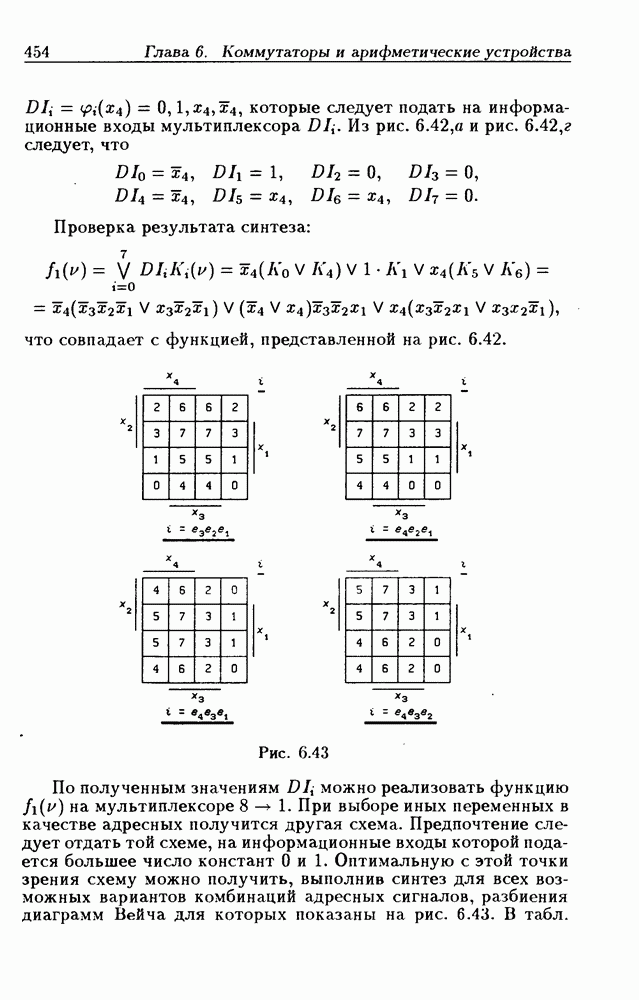
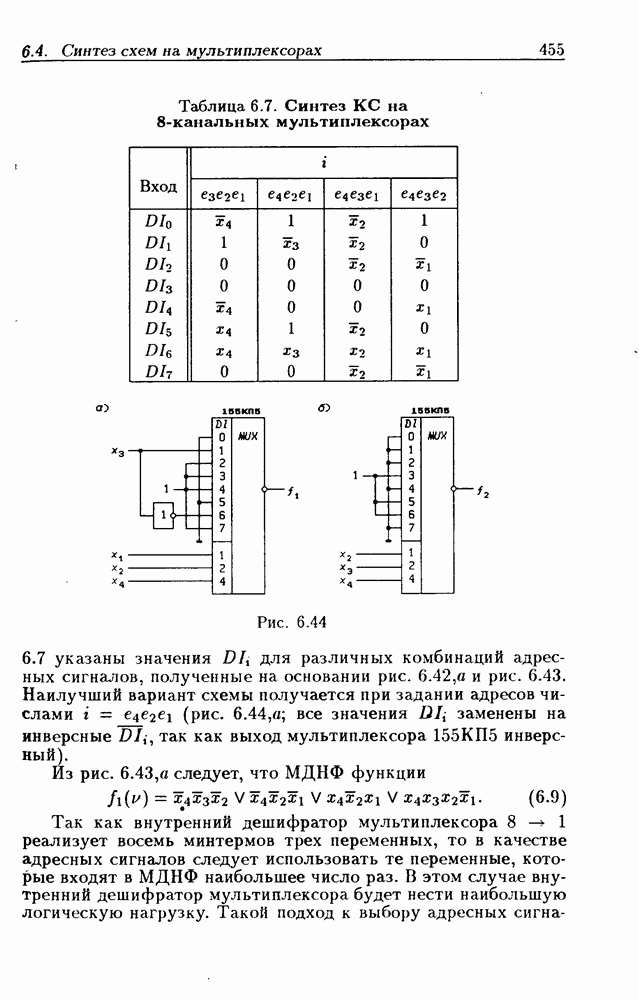
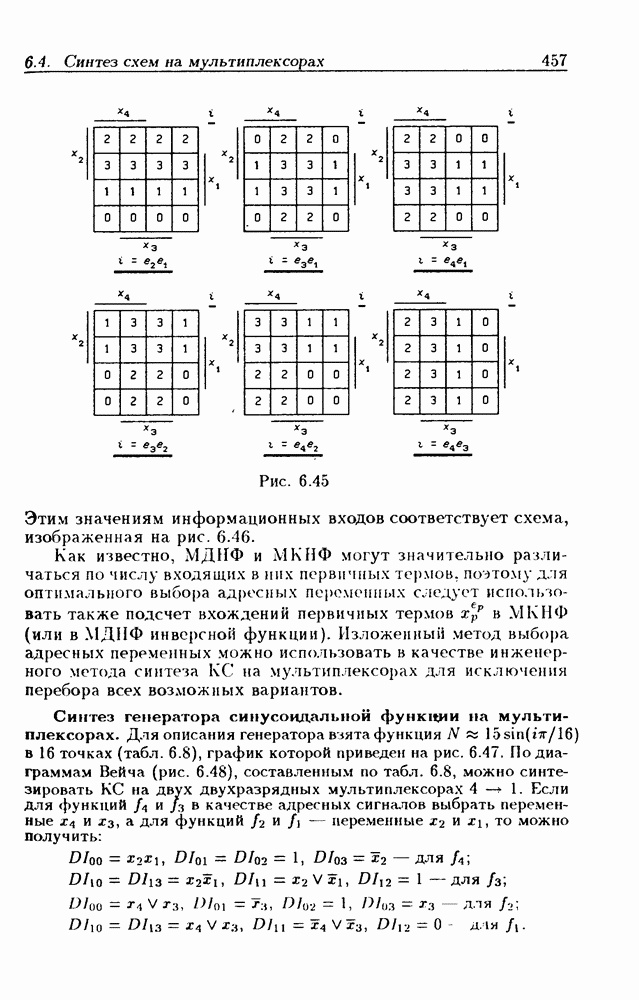
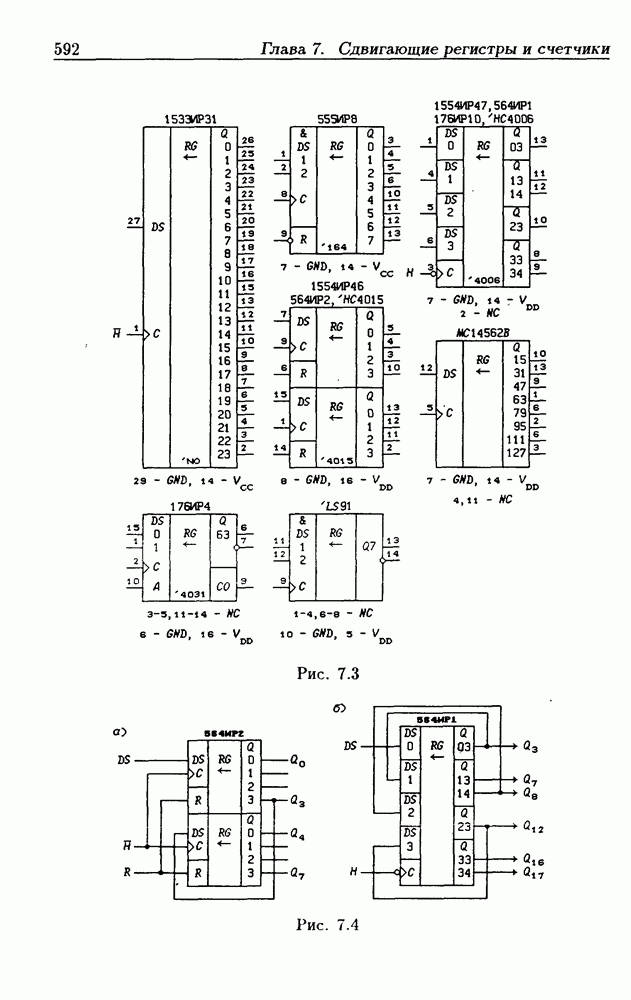
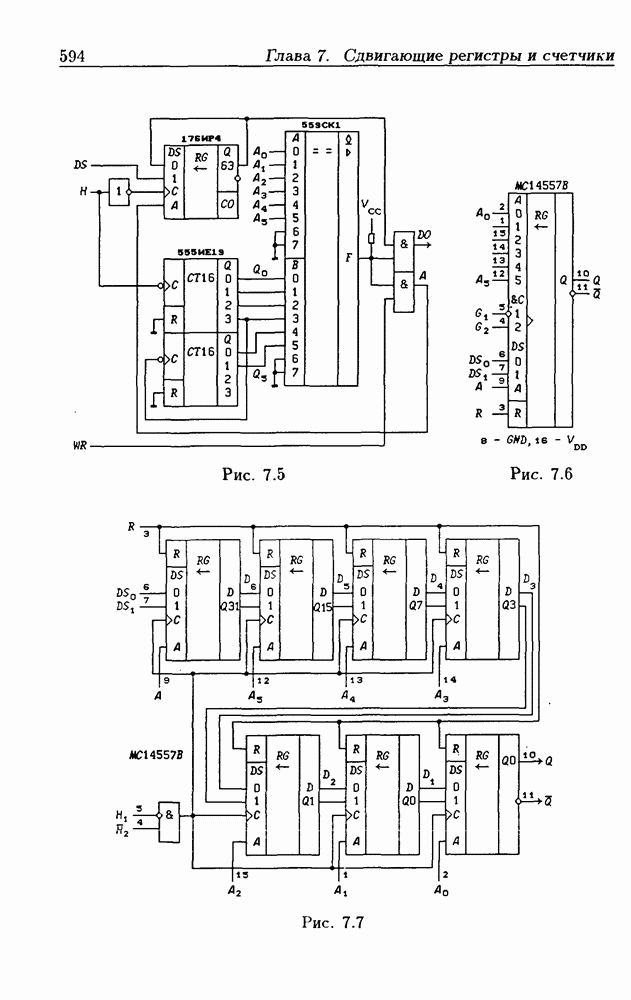
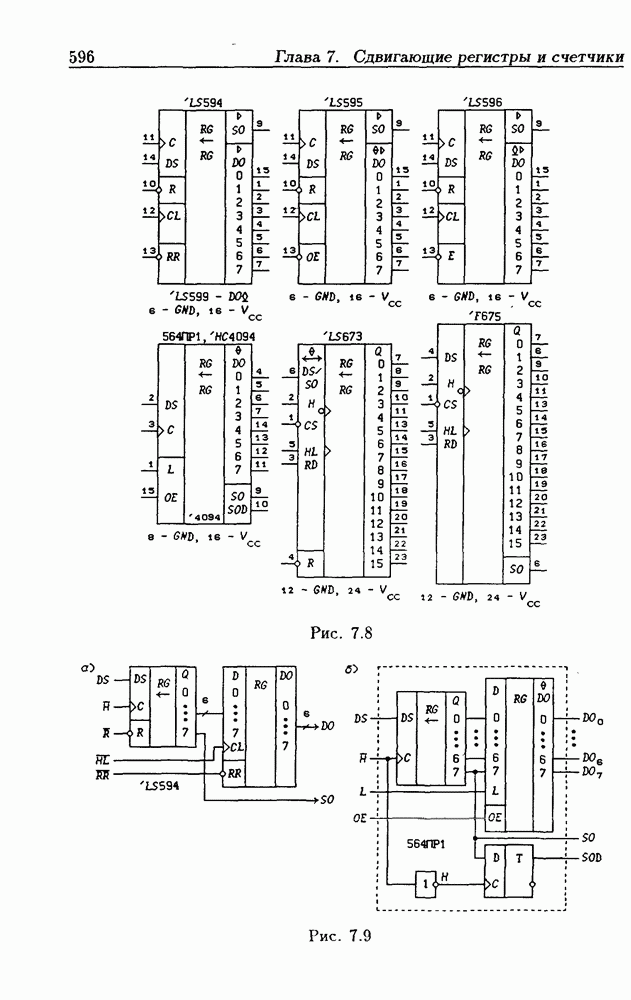
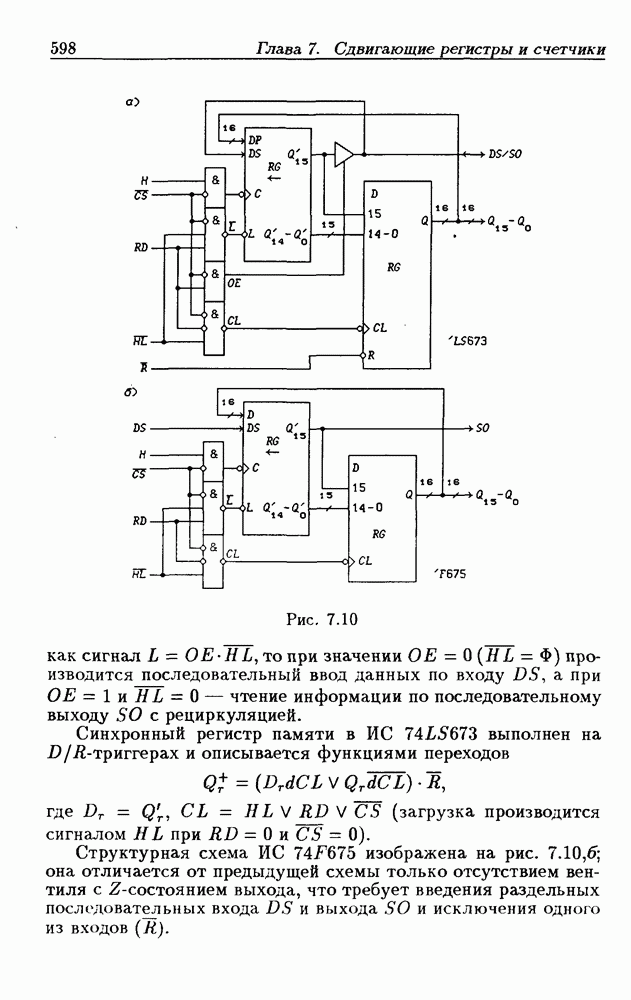
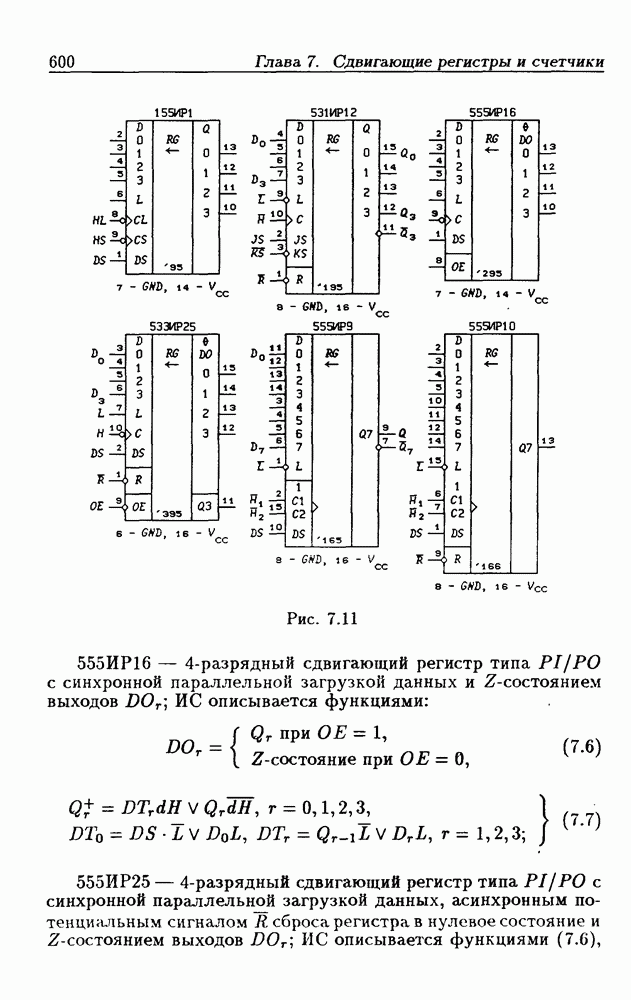
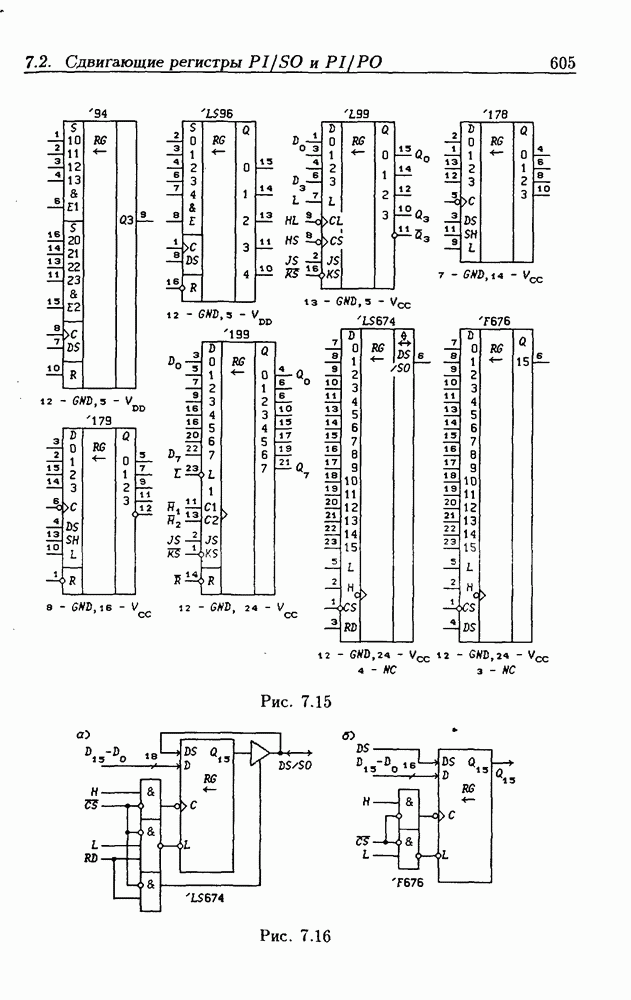
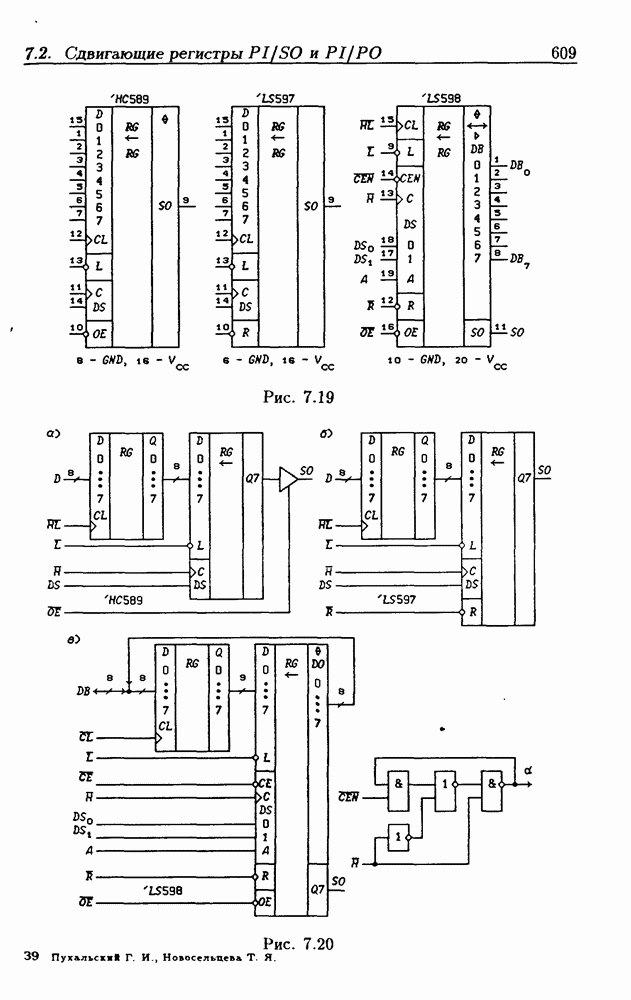
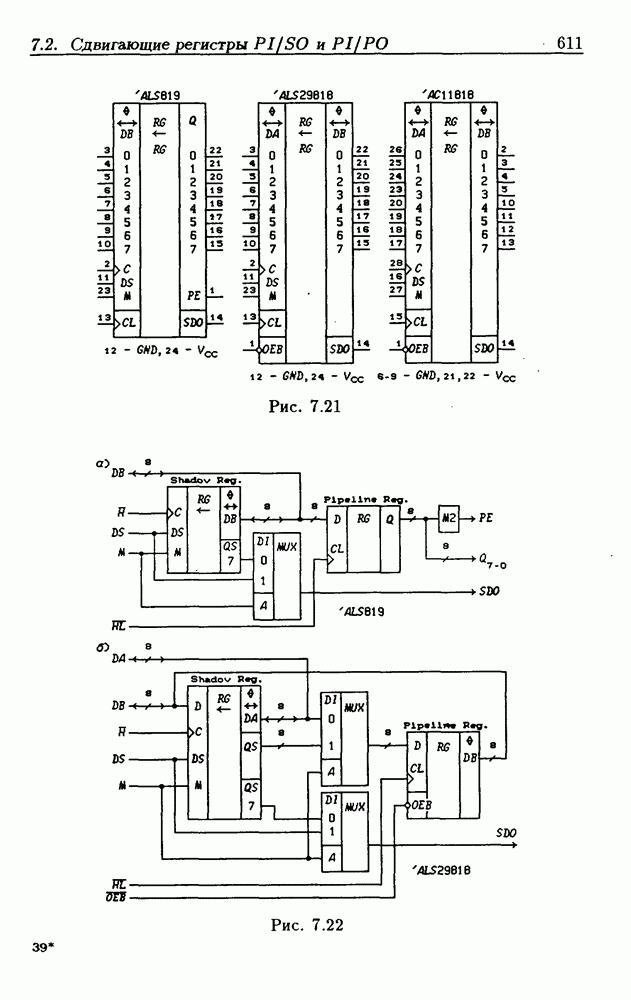
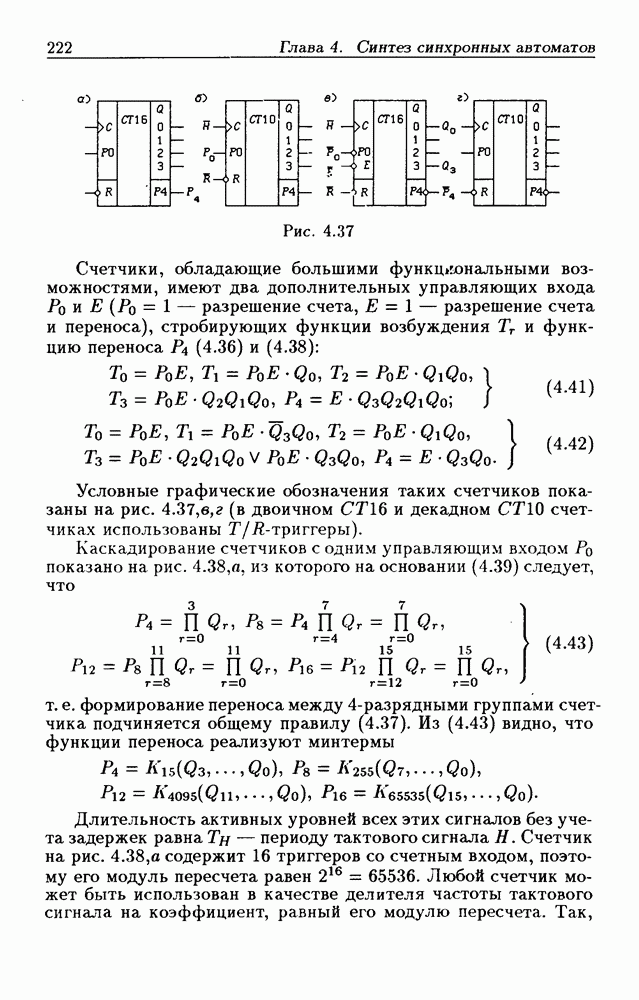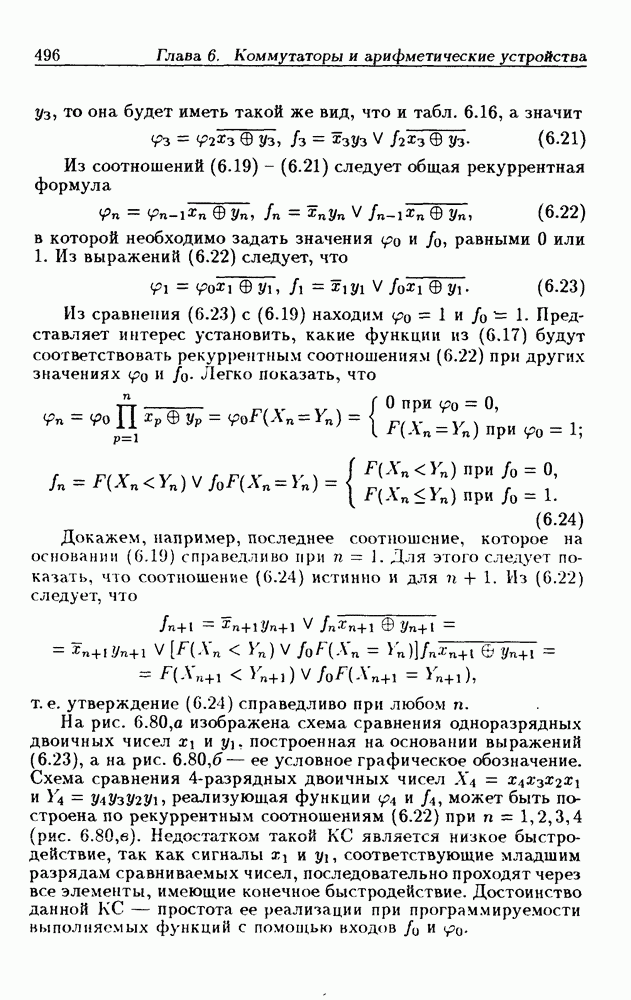| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
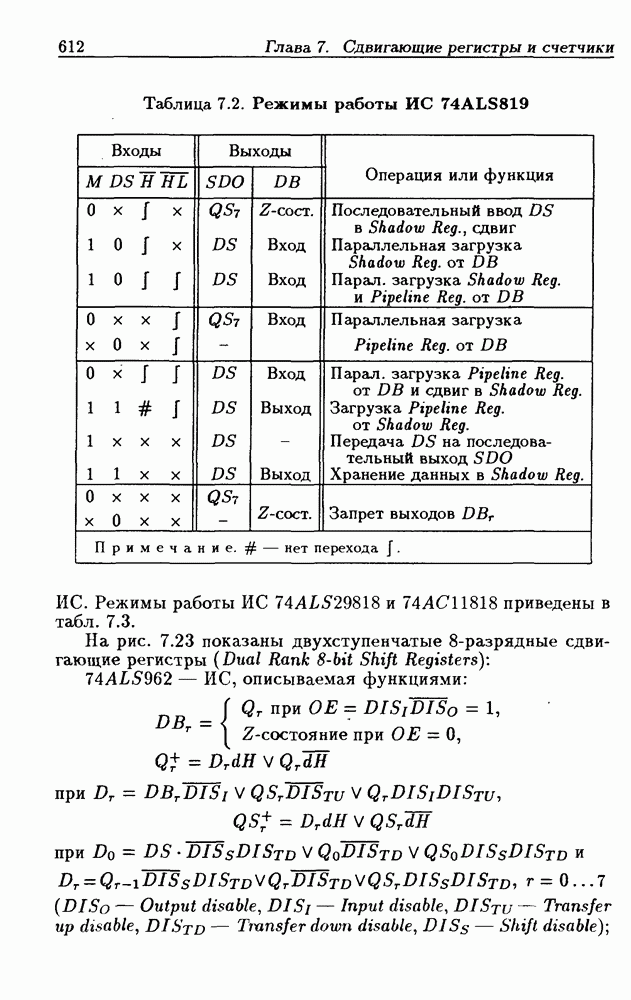
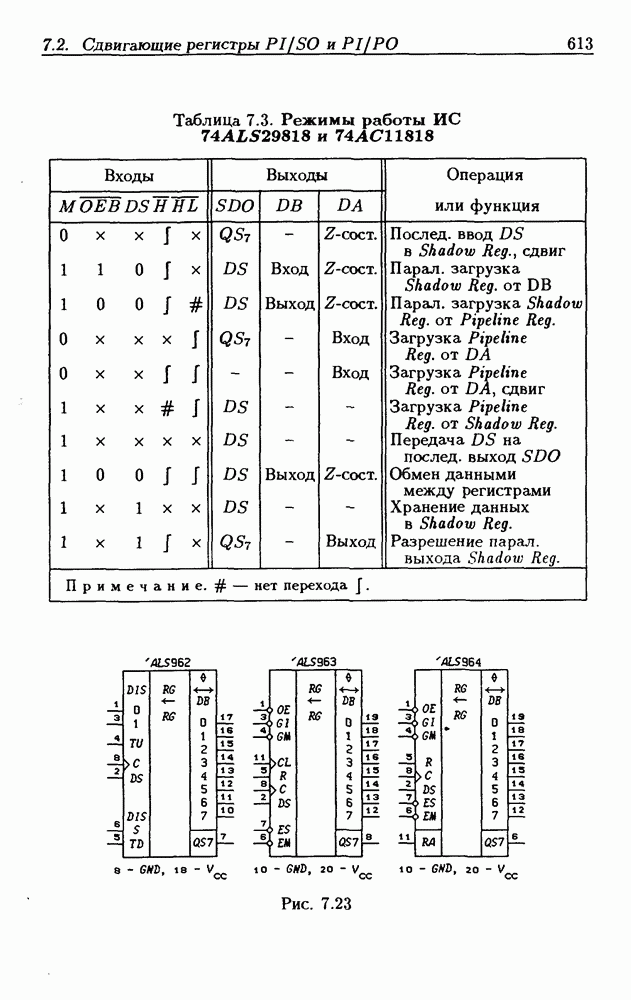
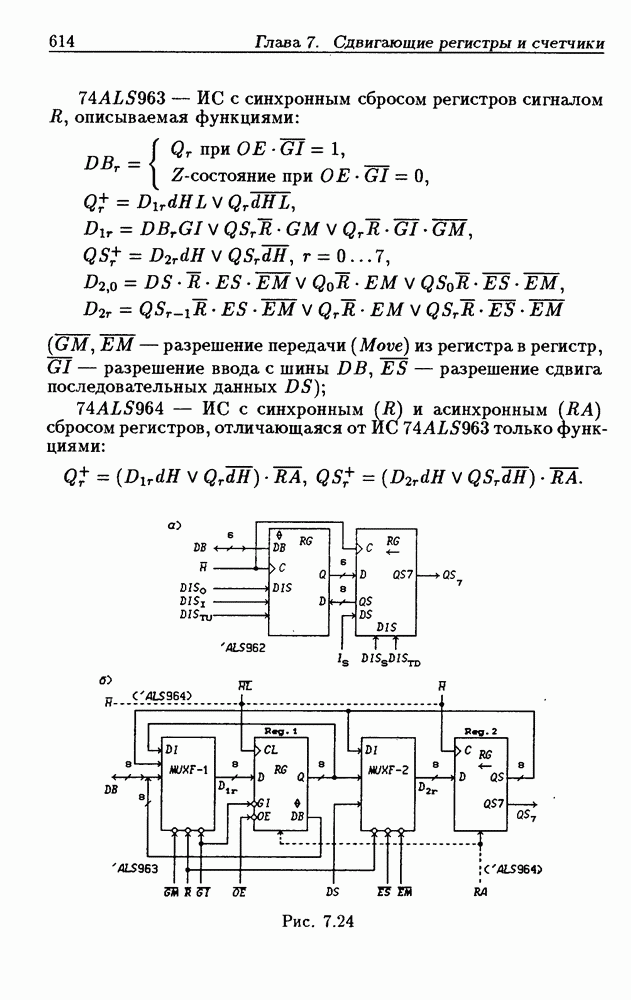
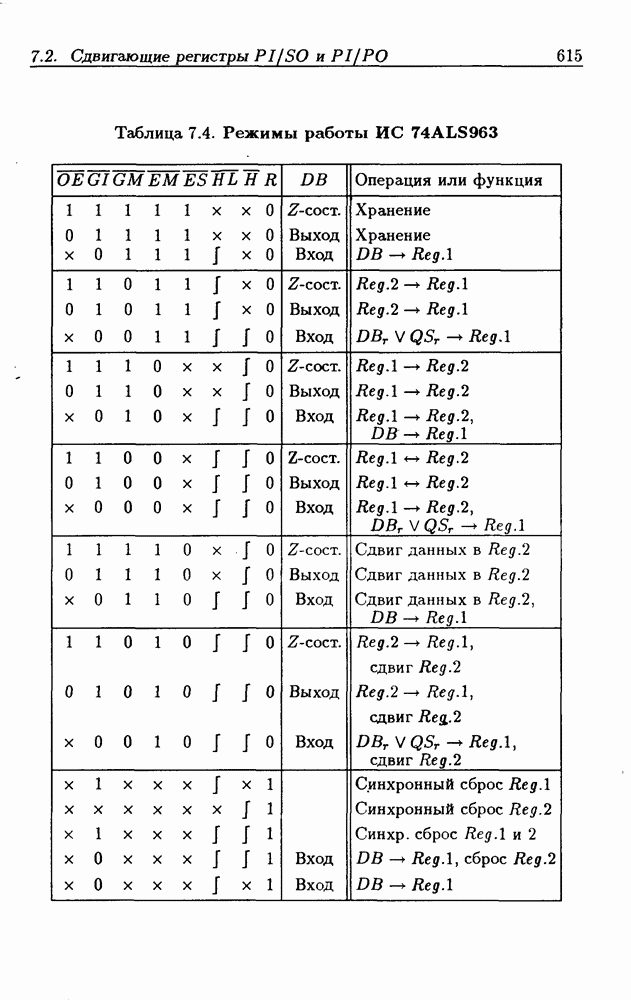
1.2. Позиционные системы счисления
Совокупность правил записи чисел называется системой счисления. Наиболее часто используются позиционные системы, в которых целое положительное число записывается в виде последовательности символов  а вес каждого символа
а вес каждого символа  равен
равен  где
где  основание системы счисления,
основание системы счисления,  Тогда любое целое положительное число
Тогда любое целое положительное число  в системе счисления с основанием
в системе счисления с основанием  можно записать в виде:
можно записать в виде: 

При вычислении суммы полагаем, что все значения  представлены в привычной десятичной системе счисления. Максимальное n-разрядное число получается при
представлены в привычной десятичной системе счисления. Максимальное n-разрядное число получается при  для всех
для всех  :
:

Таким образом, существует  различных n-разрядных чисел (с учетом нуля). В табл. 1.2 показан перевод 16 чисел из одной системы счисления в другую для наиболее часто используемых оснований
различных n-разрядных чисел (с учетом нуля). В табл. 1.2 показан перевод 16 чисел из одной системы счисления в другую для наиболее часто используемых оснований 
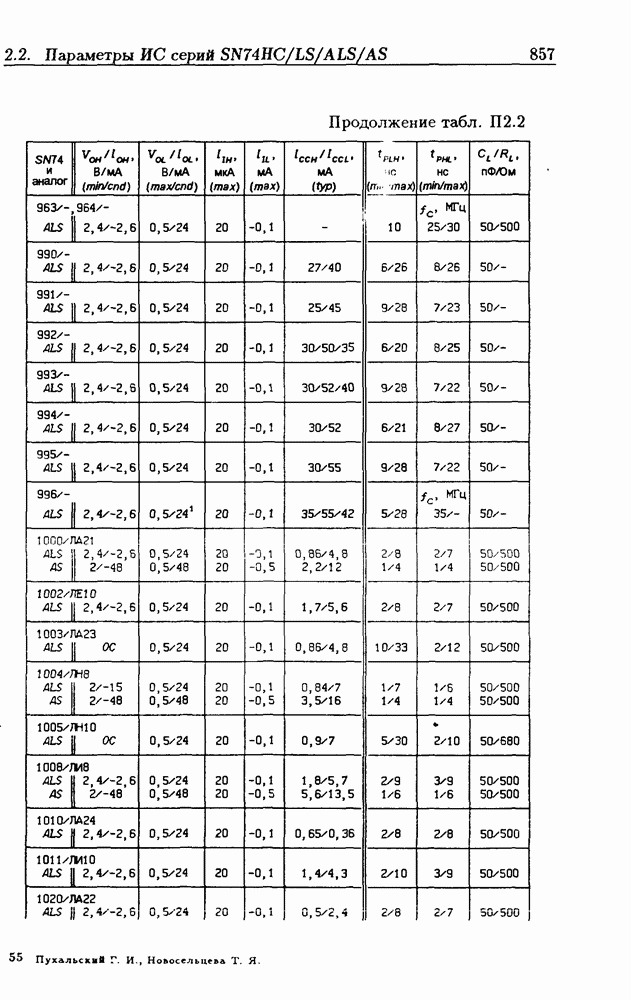
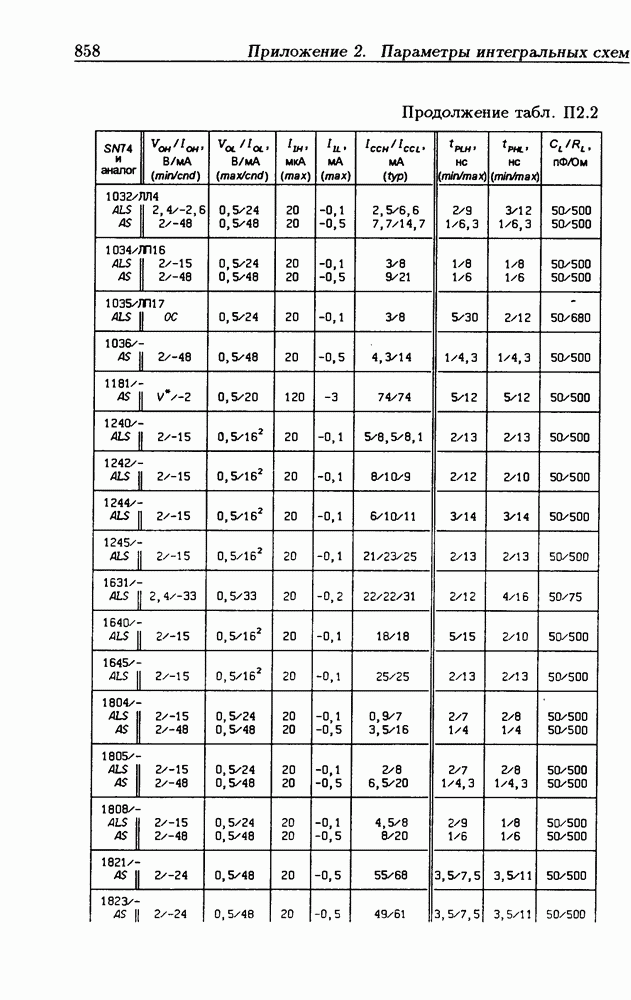
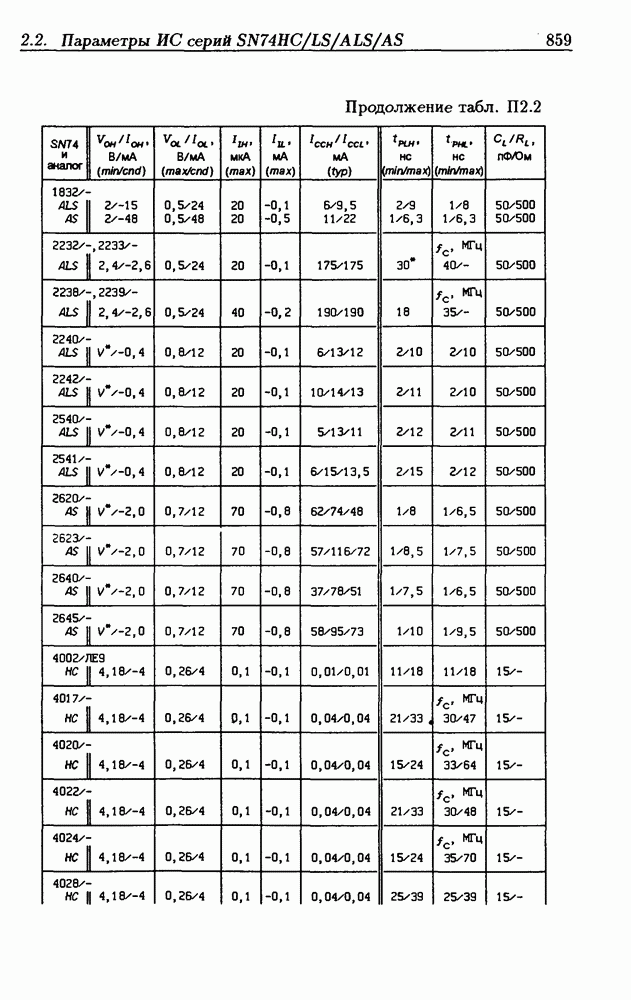
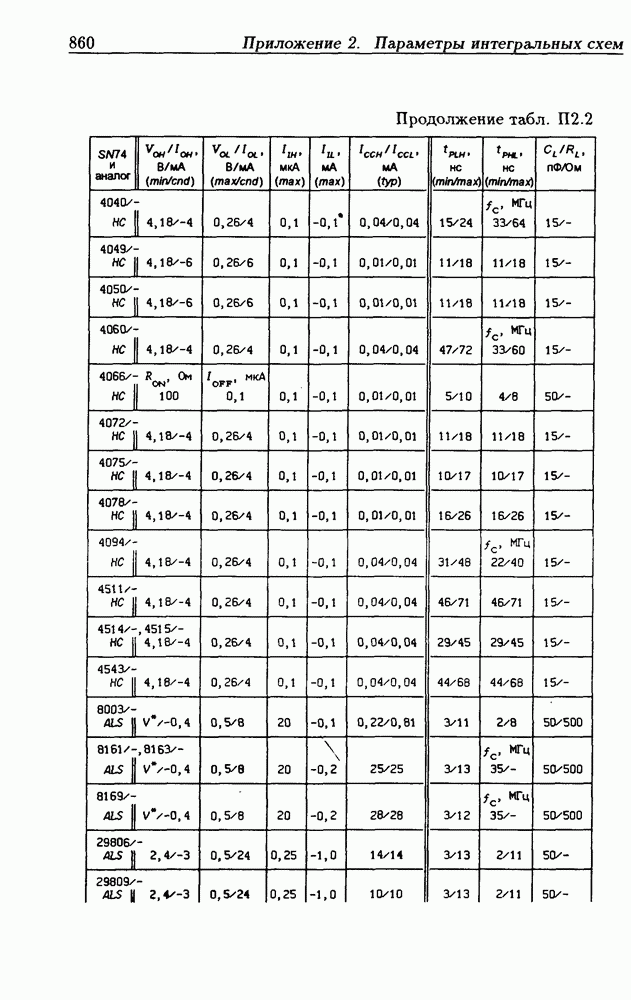
Таблица 1.2. Запись чисел в основных системах счисления
Двоичная система счисления  используется для представления информации в ЭВМ, что обусловлено легкостью реализации двоичных электронных элементов (требуется высоконадежное различение только двух состояний элементов). Восприятие же человеком информации, представленной в двоичной системе счисления, сильно затруднено как из-за ее монотонности, так и из-за большого числа разрядов, необходимых для ее представления.
используется для представления информации в ЭВМ, что обусловлено легкостью реализации двоичных электронных элементов (требуется высоконадежное различение только двух состояний элементов). Восприятие же человеком информации, представленной в двоичной системе счисления, сильно затруднено как из-за ее монотонности, так и из-за большого числа разрядов, необходимых для ее представления.
В некоторых случаях нумерацию разрядов n-разрядного числа удобнее производить числами от 1 до  :
:

Перевод чисел из системы счисления с произвольным основанием  в десятичную систему счисления
в десятичную систему счисления  выполняется по вышеприведенным формулам, для чего требуется перевести в десятичную систему счисления только числа
выполняется по вышеприведенным формулам, для чего требуется перевести в десятичную систему счисления только числа  Несколько сложнее перевести числа из десятичной системы счисления в систему счисления с основанием
Несколько сложнее перевести числа из десятичной системы счисления в систему счисления с основанием  Наиболее просто такая операция выполняется для
Наиболее просто такая операция выполняется для 
Пусть требуется перевести число (1993) в указанные системы, счисления. Перевод в восьмеричную систему счисления осуществляется последовательным делением десятичного числа на основание системы счисления 

Таким образом,  Для перевода полученного числа в двоичную систему счисления достаточно каждую цифру представить в двоичном коде:
Для перевода полученного числа в двоичную систему счисления достаточно каждую цифру представить в двоичном коде:  (точки введены только для удобства чтения двоичного числа в 8-ричной системе счисления). Перевод двоичного числа в 16-ричную систему счисления выполняется его разбиением на тетрады (тетрада — четыре разряда) и переводом каждой тетрады в 16-ричную систему счисления:
(точки введены только для удобства чтения двоичного числа в 8-ричной системе счисления). Перевод двоичного числа в 16-ричную систему счисления выполняется его разбиением на тетрады (тетрада — четыре разряда) и переводом каждой тетрады в 16-ричную систему счисления:  Итак,
Итак, 
В общем случае числа имеют целую и дробную части. Такие числа в позиционных системах счисления с основанием  можно записать в виде
можно записать в виде

Целой частью числа  называется наибольшее целое число, не превосходящее
называется наибольшее целое число, не превосходящее  Целая часть числа
Целая часть числа  обозначается через
обозначается через  (так [13,25]
(так [13,25]  ). Дробной частью числа называется разность
). Дробной частью числа называется разность  Всегда
Всегда 
Системы счисления с основаниями  при
при  жестко связаны с двоичной системой счисления
жестко связаны с двоичной системой счисления  Для перевода чисел из этих систем в двоичную запись достаточно цифры
Для перевода чисел из этих систем в двоичную запись достаточно цифры  всех разрядов числа представить
всех разрядов числа представить  -разрядным двоичным кодом. Не более сложно и взаимное преобразование чисел из одной системы счисления в другую. Для общения человека с ЭВМ наиболее удобна система счисления с основанием
-разрядным двоичным кодом. Не более сложно и взаимное преобразование чисел из одной системы счисления в другую. Для общения человека с ЭВМ наиболее удобна система счисления с основанием  что обусловлено большей компактностью записи чисел, чем в системах счисления с
что обусловлено большей компактностью записи чисел, чем в системах счисления с  при приемлемом для запоминания человеком числе различных цифр (символов), используемых для обозначения всех значений разрядов.
при приемлемом для запоминания человеком числе различных цифр (символов), используемых для обозначения всех значений разрядов.
Для представления в ЭВМ десятичных чисел также необходимо использовать их двоичное кодирование. С этой целью наиболее часто применяется код прямого замещения, называемый
иначе двоично-десятичным кодом 8-4-2-1 (каждая десятичная цифра  заменяется прямым двоичным эквивалентом
заменяется прямым двоичным эквивалентом  двоичной тетрадой; шесть двоичных тетрад 1010, 1011, 1100, 1101, 1110 и 1111 не используются). Так, можно записать, что
двоичной тетрадой; шесть двоичных тетрад 1010, 1011, 1100, 1101, 1110 и 1111 не используются). Так, можно записать, что

Десятичные числа в цифровых устройствах (например, в декадных счетчиках) иногда представляются в двоично-десятинном коде 5-4-2-1, который отличается от кода прямого замещения весом старшего разряда тетрады. Числа от 0 до 9 в этом коде имеют представление:

В принципе, на основании приведенного выше выражения для записи чисел  в позиционных системах счисления можно определить унитарную систему счисления, в которой используется основание
в позиционных системах счисления можно определить унитарную систему счисления, в которой используется основание  а ее единственный символ обозначить через
а ее единственный символ обозначить через  (формально следовало бы положить
(формально следовало бы положить  Так как
Так как  то вес разряда не зависит от его положения в записи числа, т. е. система счисления, по существу, превращается в непозиционную. Это самая древняя система счисления, используемая до сих пор, например, охотниками, делающими зарубки на стволе ружья. В электронике унитарная система счисления применяется довольно часто для представления чисел количеством импульсов, подаваемых на вход устройства (например,
то вес разряда не зависит от его положения в записи числа, т. е. система счисления, по существу, превращается в непозиционную. Это самая древняя система счисления, используемая до сих пор, например, охотниками, делающими зарубки на стволе ружья. В электронике унитарная система счисления применяется довольно часто для представления чисел количеством импульсов, подаваемых на вход устройства (например,  где символ 1 означает один импульс).
где символ 1 означает один импульс).
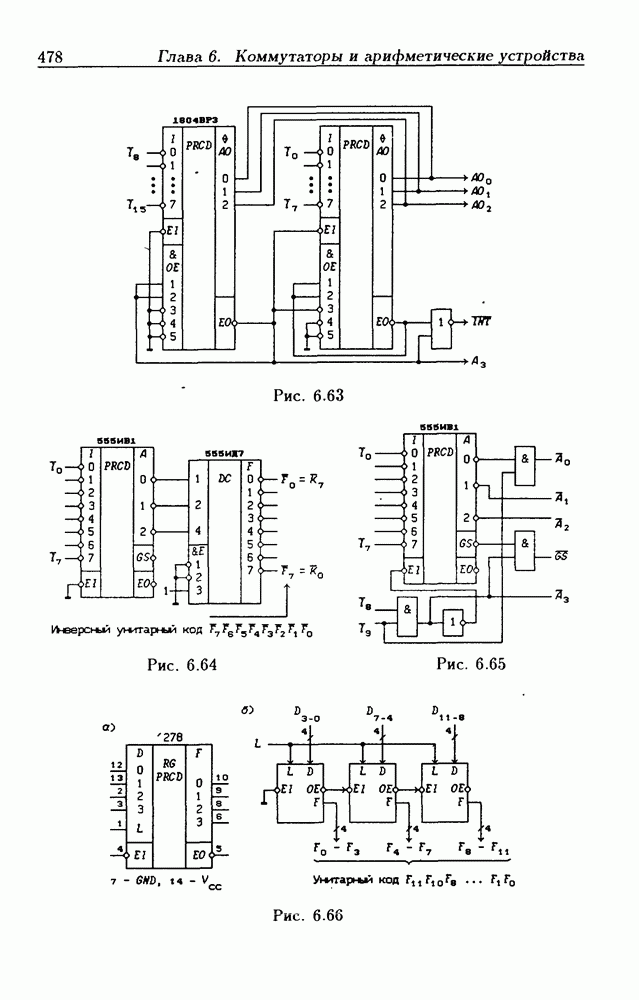
Для кодирования информации в электронных схемах широкое применение находит унитарный код, содержащий символ 1 только в одной позиции n-разрядного кода (в остальных позициях проставляются символы 0), т.е. для представления информации используется специальное двоичное ее кодирование. Так, например, числа от 0 до 7 можно записать с помощью унитарного кода:

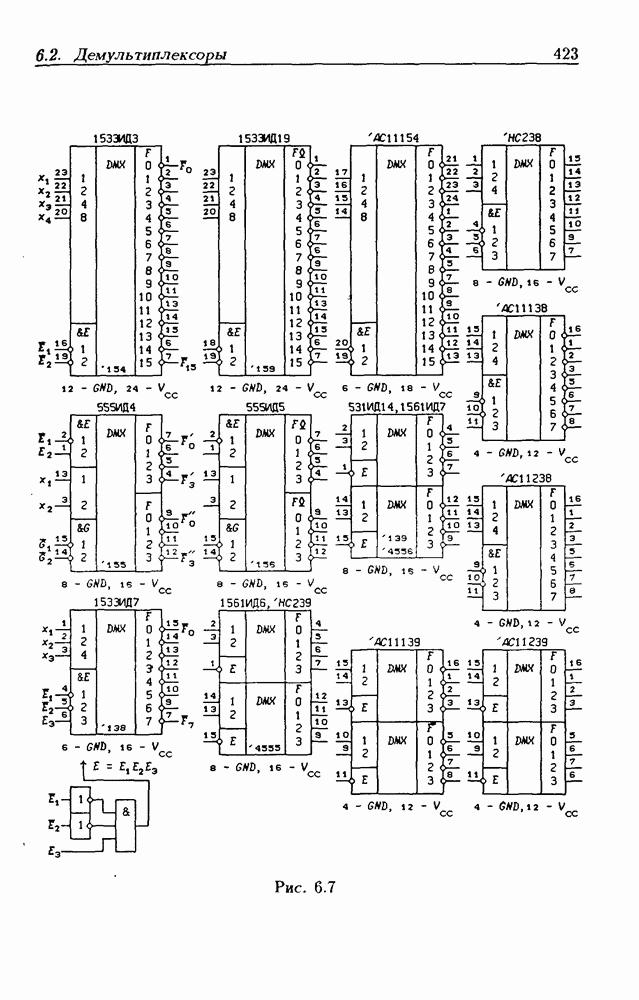
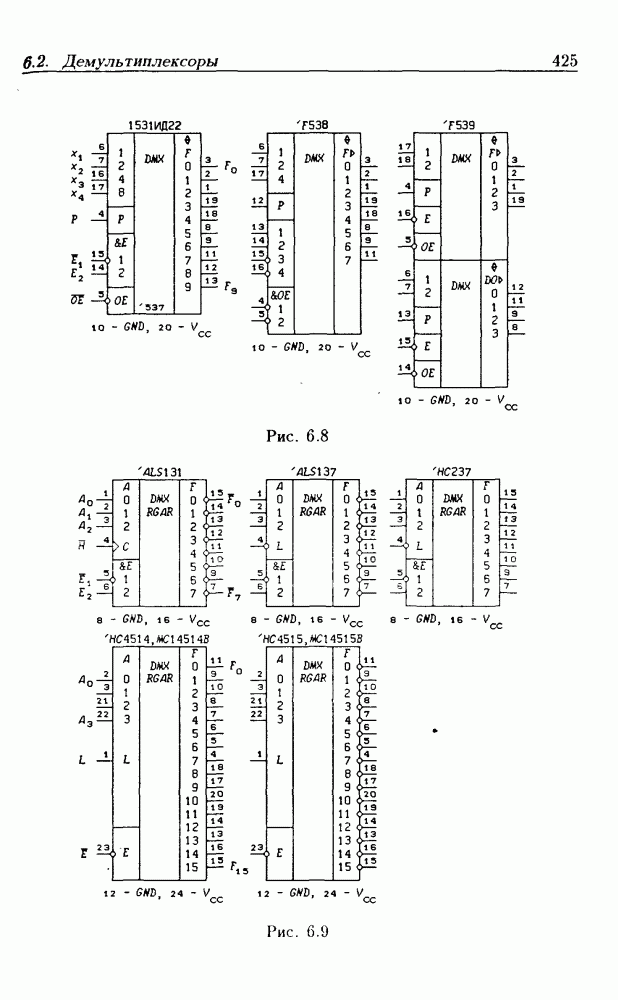
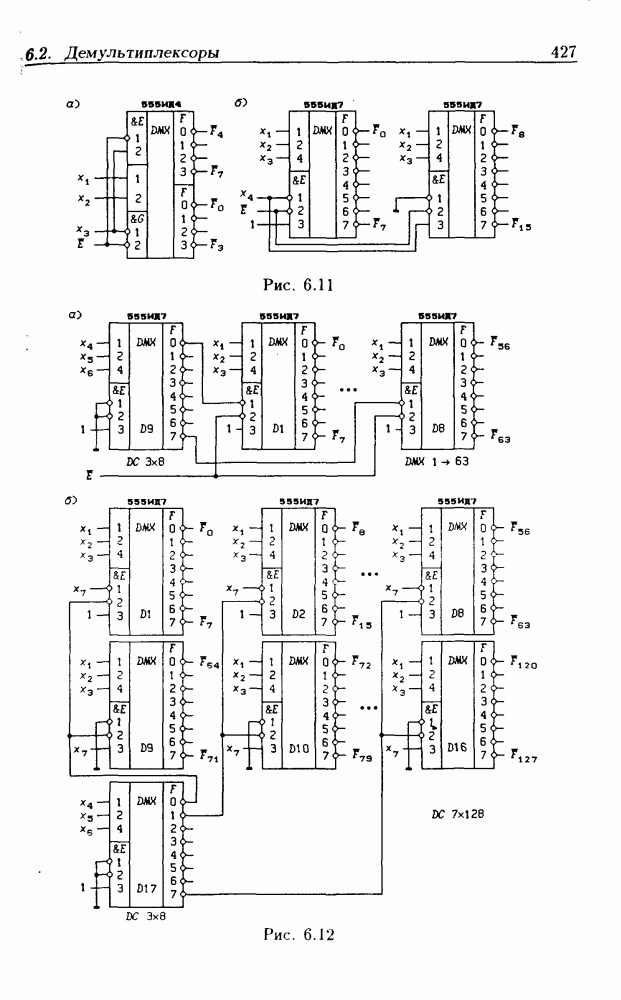
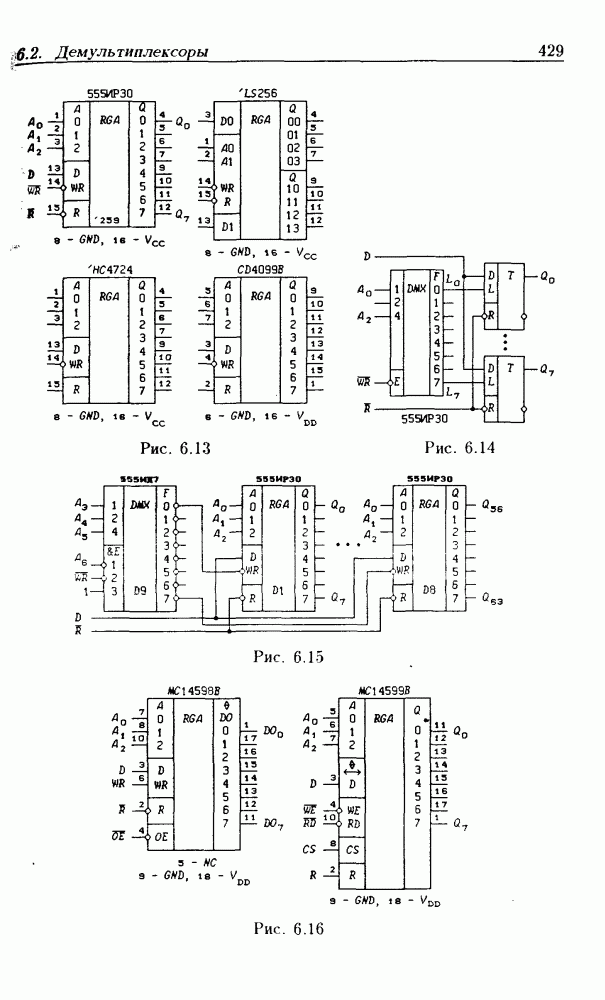
Унитарный код чаще всего применяется для кодирования нечисловой информации. В частности, на выходах полных дешифраторов (см. § 6.1) всегда реализуется унитарный код.
Дополнительные полезные сведения по системам счисления и кодированию числовой информации можно найти в [6].
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Глава 1. Основы теории переключательных функций
- 1.2. Позиционные системы счисления
- 1.3. Переключательные функции
- 1.4. Принцип и закон двойственности
- 1.5. Теоремы разложения
- 1.6. Решение систем логических уравнений
- 1.7. Первичные термы, минтермы и макстермы
- 1.8. Совершенные нормальные формы представления функций
- 1.9. Конъюнктивные и дизъюнктивные термы
- 1.10. Минимизация переключательных функций
- 1.11. Диаграммы Вейча
- 1.12. Минимизация неполностью определенных функций, совместная минимизация нескольких функций
- 1.13. Скобочные формы функций
- 1.14. Закон двойственности для логических схем
- 1.15. Линейные функции
- Глава 2. Анализ и синтез логических схем
- 2.2. Модели логических элементов
- 2.3. Модели логических схем
- 2.4. Анализ логических схем
- 2.5. Синтез комбинационных схем, свободных от состязаний
- Глава 3. Синтез асинхронных потенциальных автоматов
- 3.2. Асинхронные потенциальные автоматы
- 3.3. Асинхронные потенциальные триггеры и элементы памяти
- Триггеры типа R-S
- Триггеры типа D-L
- Триггеры типа D-L-R с приоритетом входа R.
- Триггеры типа D-L-R с приоритетом входа L.
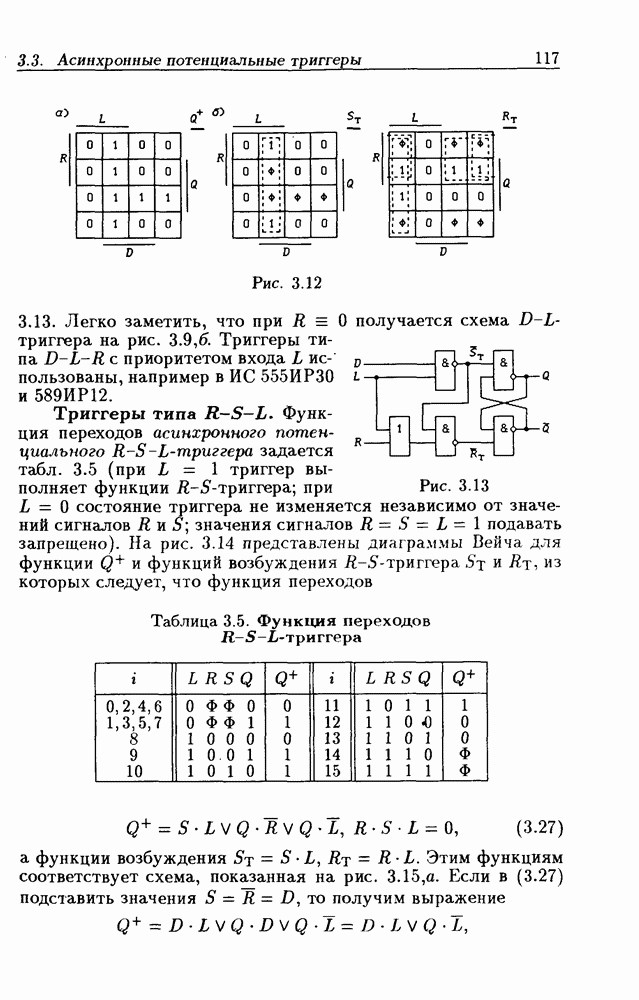
- Триггеры типа R-S-L.
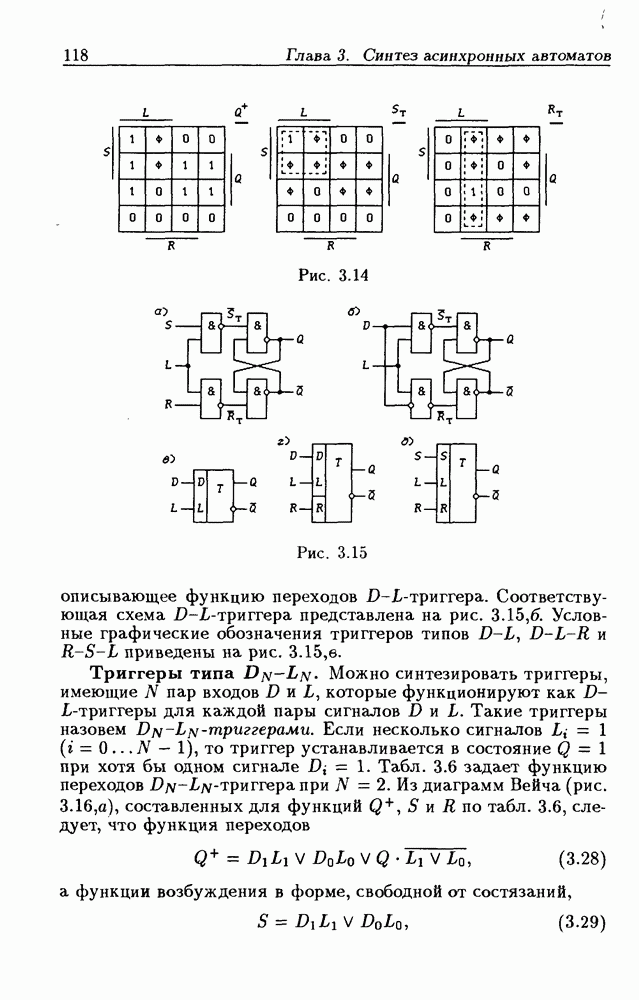
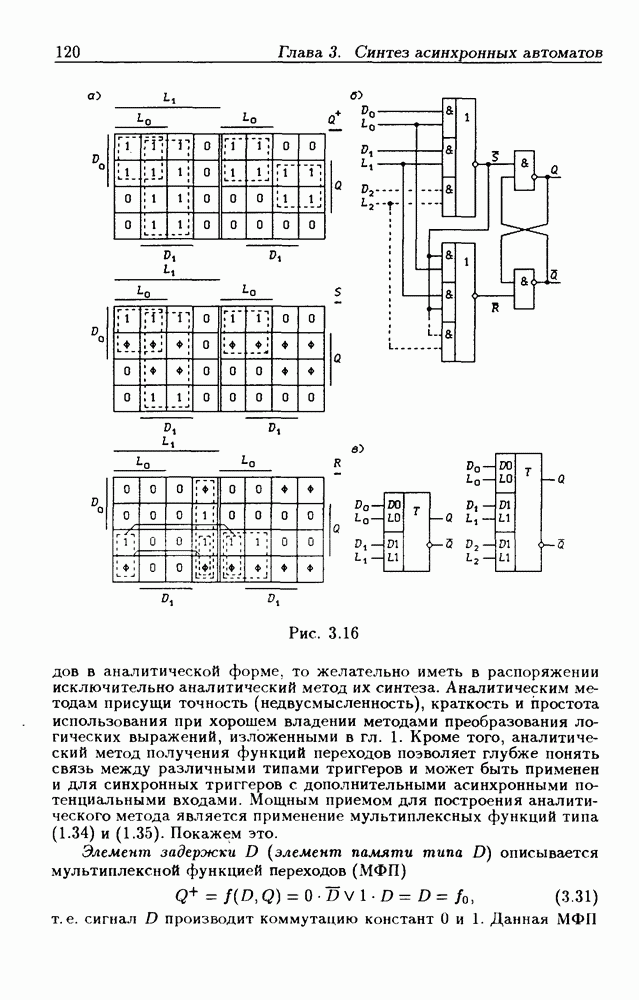
- Триггеры типа DN-LN
- Аналитический метод синтеза и анализа триггеров.
- 3.4. Задание асинхронных потенциальных автоматов таблицами и графами переходов
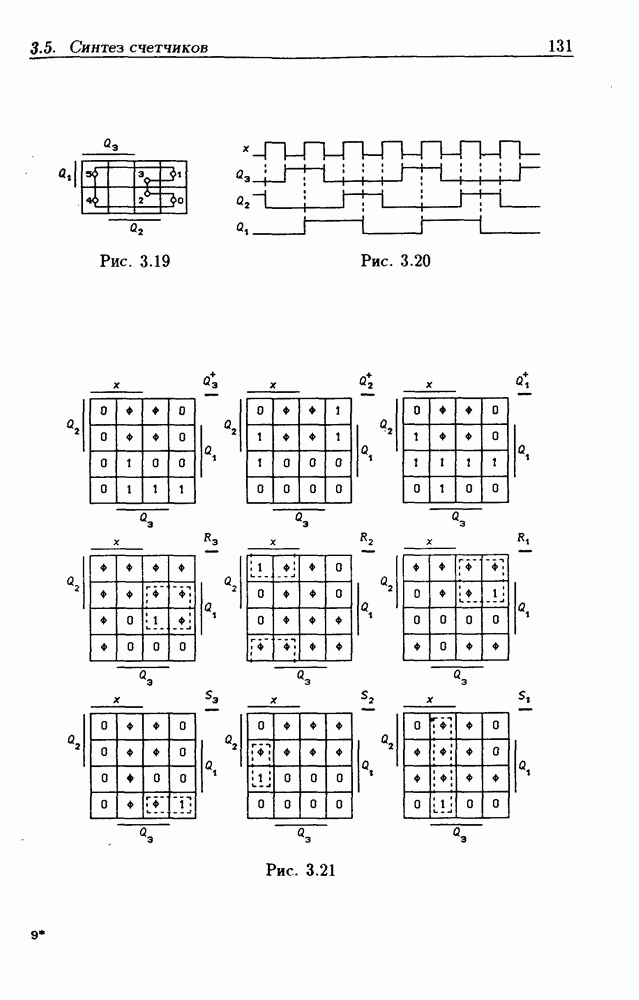
- 3.5. Синтез асинхронных потенциальных счетчиков
- 3.6. Синтез асинхронных импульсных триггеров
- Триггеры типа dJ-dK.
- Классификация триггеров.
- 3.7. Синтез синхронных триггеров
- Триггеры типа J-K
- Синхронно-асинхронные триггеры.
- 3.8. Примеры синтеза асинхронных потенциальных автоматов
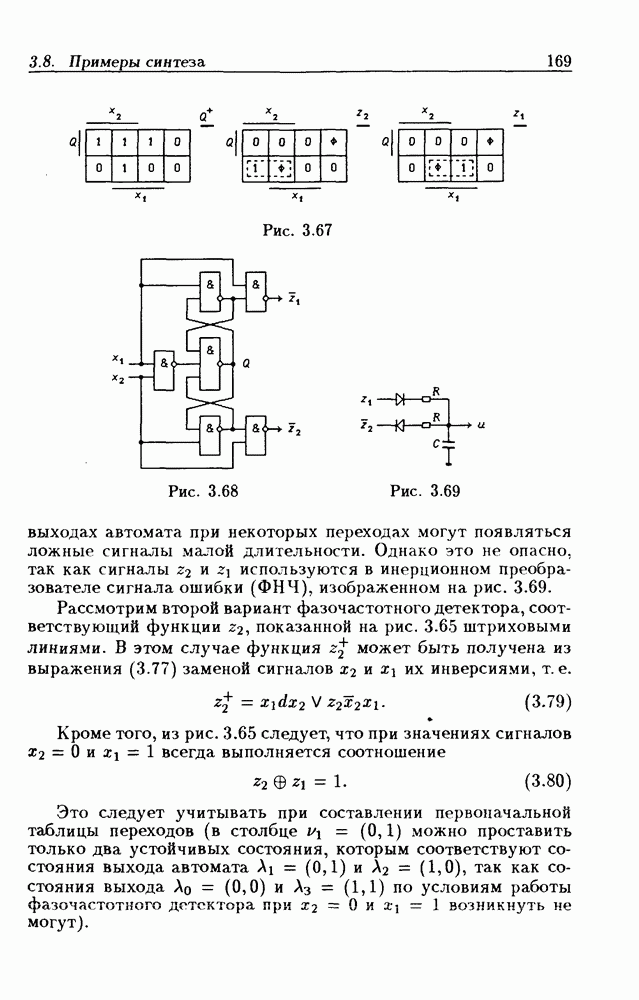
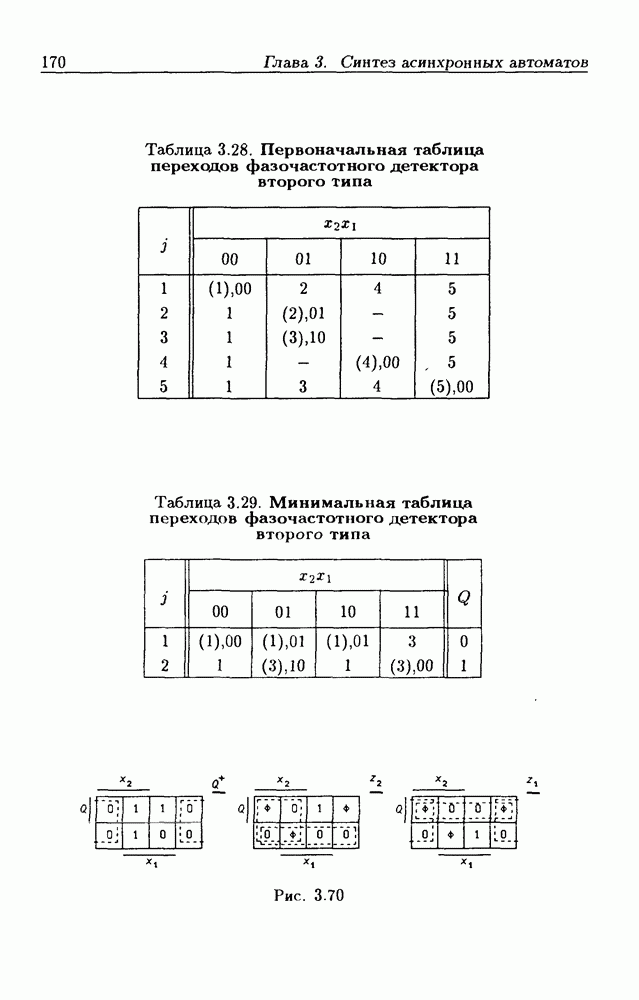
- Цифровые фазочастотные детекторы.
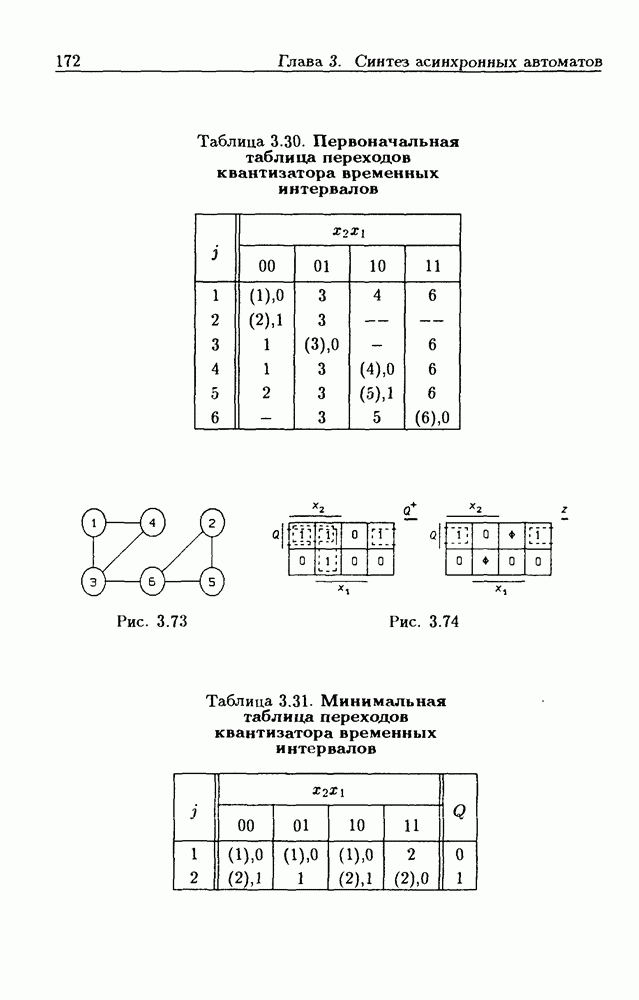
- Квантизатор временных интервалов.
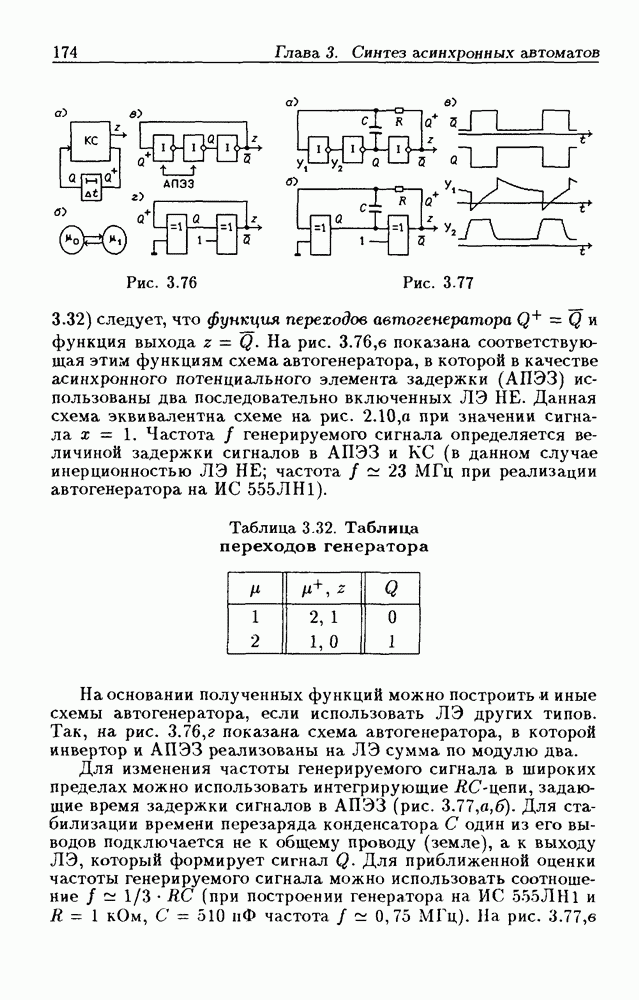
- 3.9. Генераторы сигналов
- Автогенераторы.
- Управляемые автогенераторы.
- Глава 4. Синтез синхронных автоматов
- 4.2. Синхронные триггеры
- Триггеры типов D и R-S с импульсным тактовым сигналом.
- Синхронные триггеры типов R-S и D-L
- Синхронно-асинхронные триггеры.
- Синхронные триггеры типа J-K
- Триггеры типа Т.
- Классификация синхронных триггеров.
- Преобразования типов синхронных триггеров.
- Триггеры типов D-T-L и D-T-L/R
- Функции переходов синхронно-асинхронных триггеров.
- 4.3. Примеры синтеза синхронных автоматов
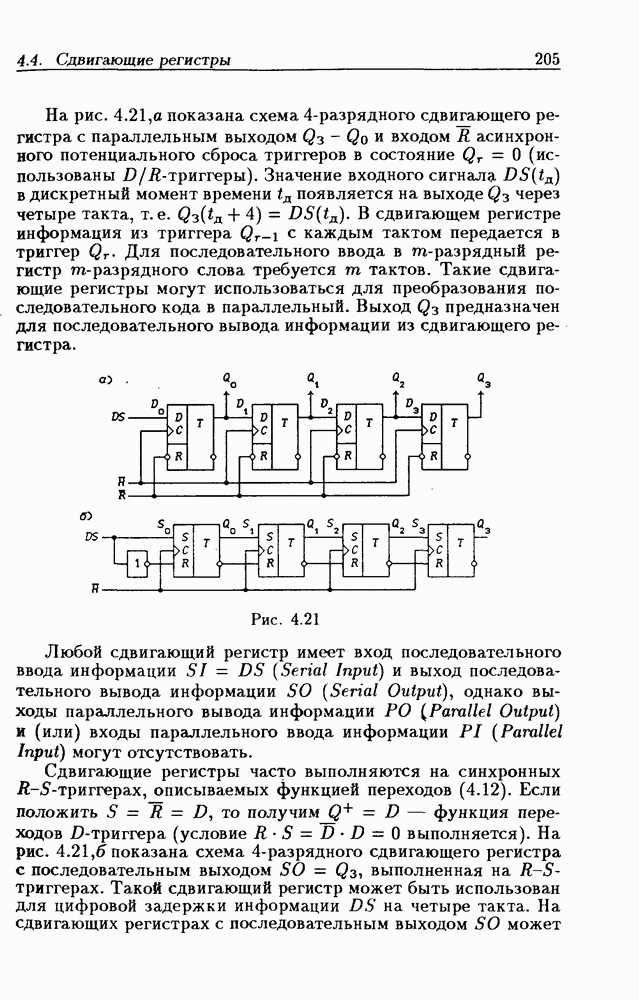
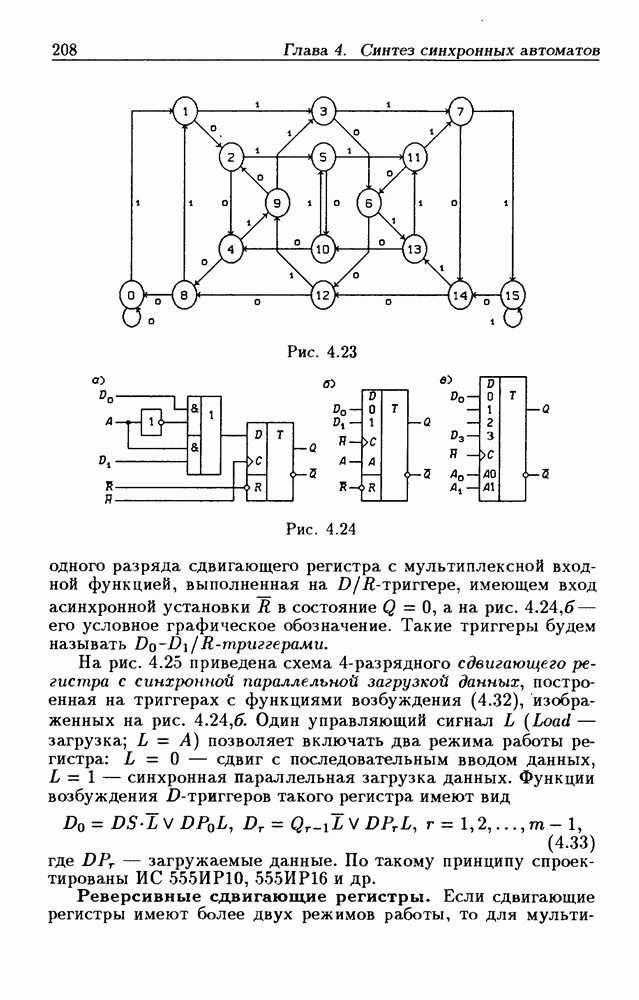
- 4.4. Сдвигающие регистры
- Синтез счетчиков на сдвигающих регистрах.
- Сдвигающие регистры с загрузкой данных.
- Реверсивные сдвигающие регистры.
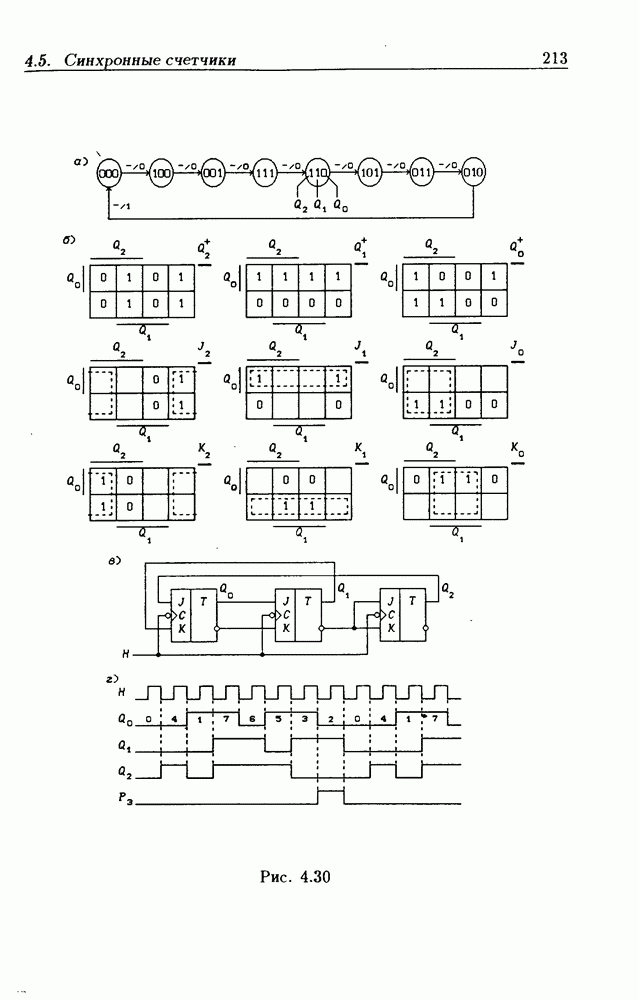
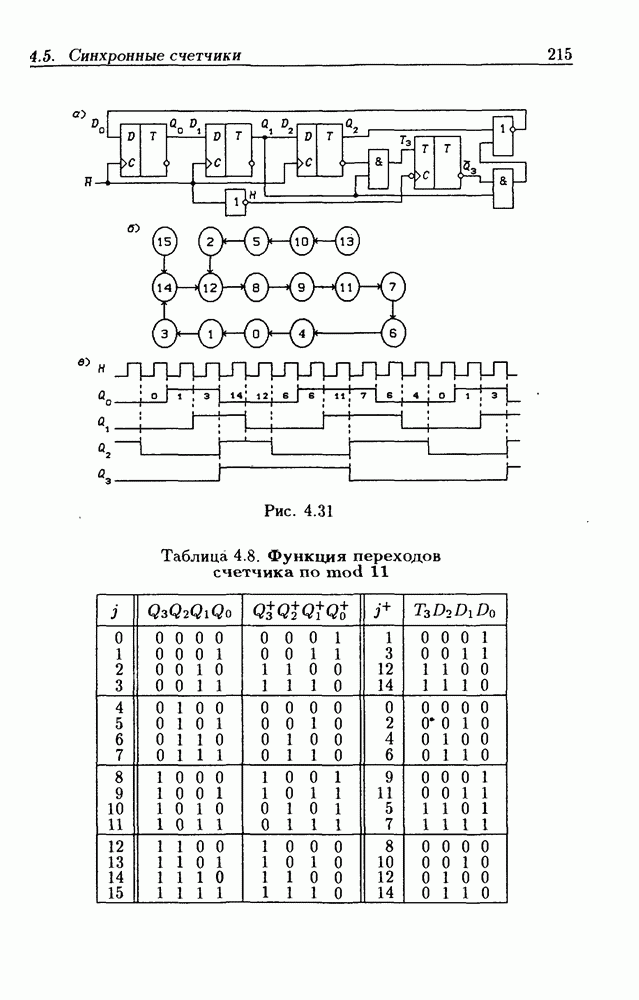
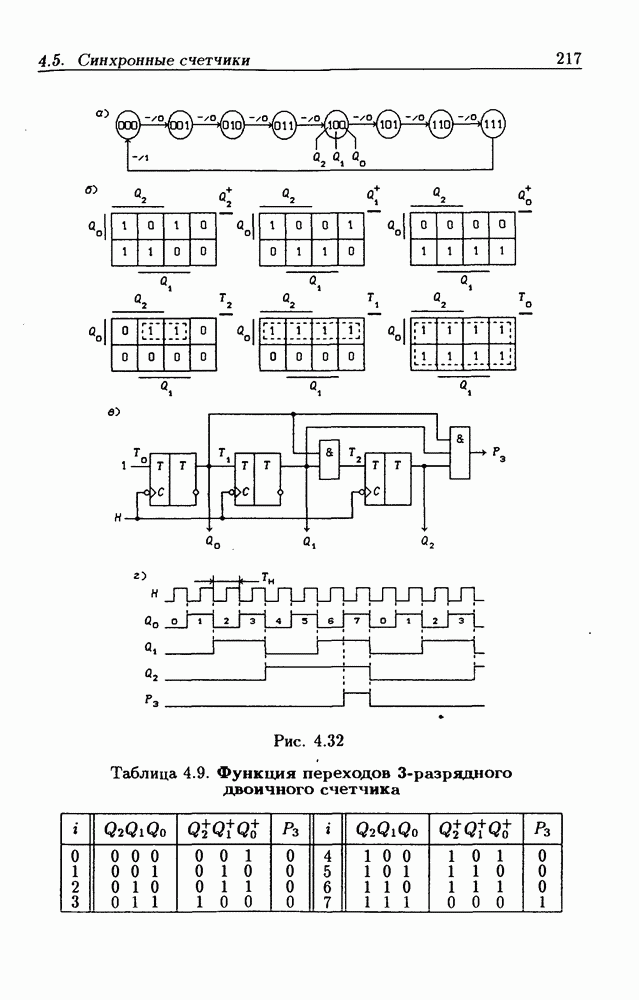
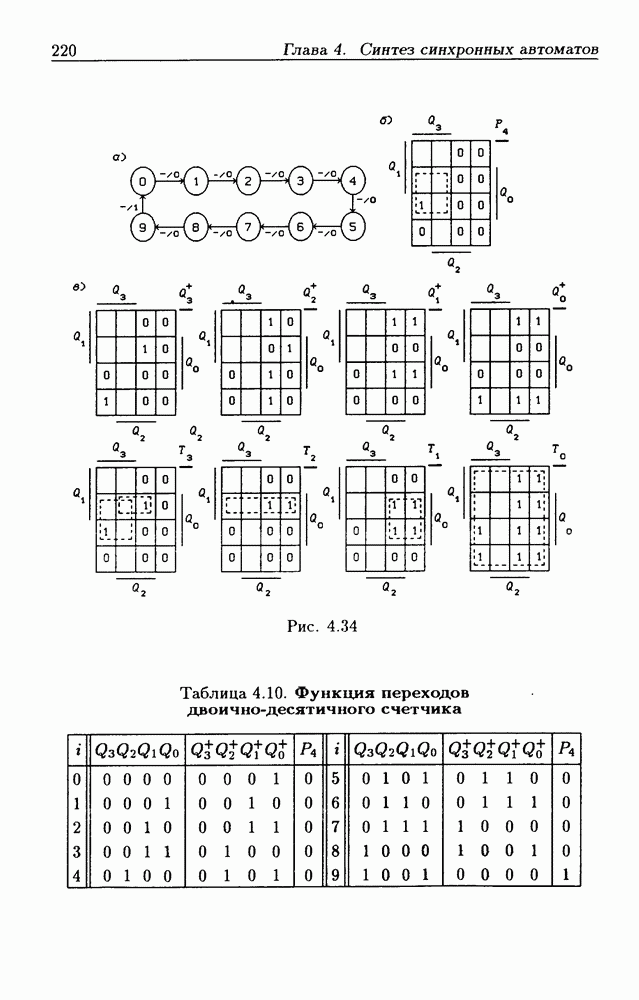
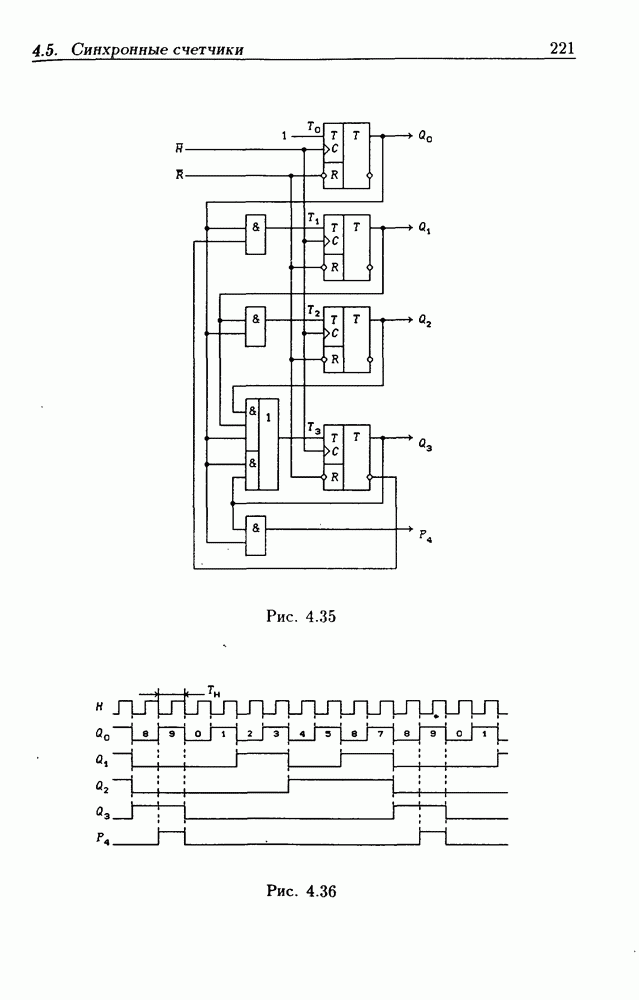
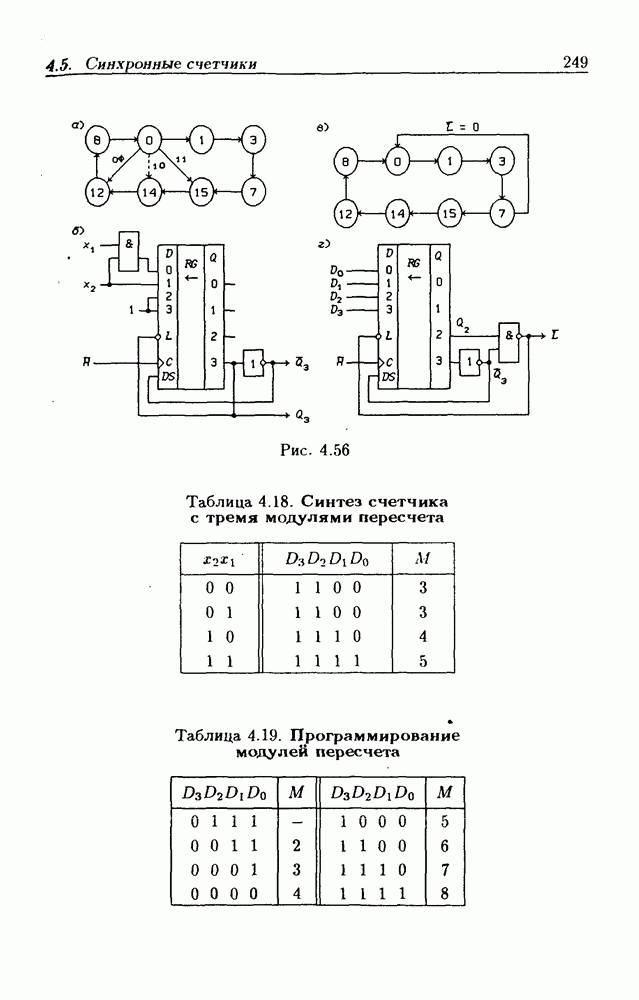
- 4.5. Синхронные счетчики
- Синхронные двоичные счетчики.
- Синхронные двоично-десятичные счетчики.
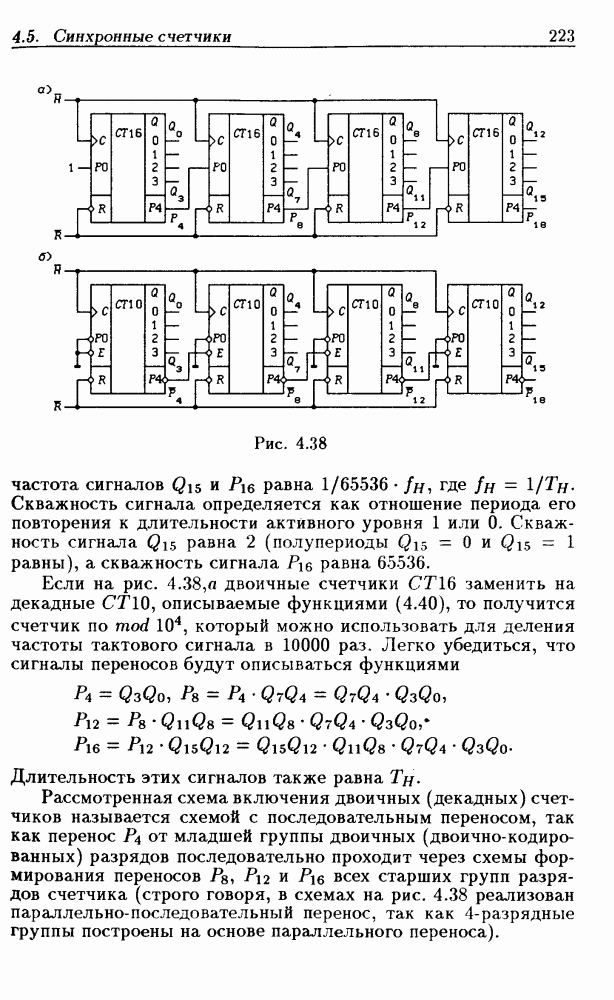
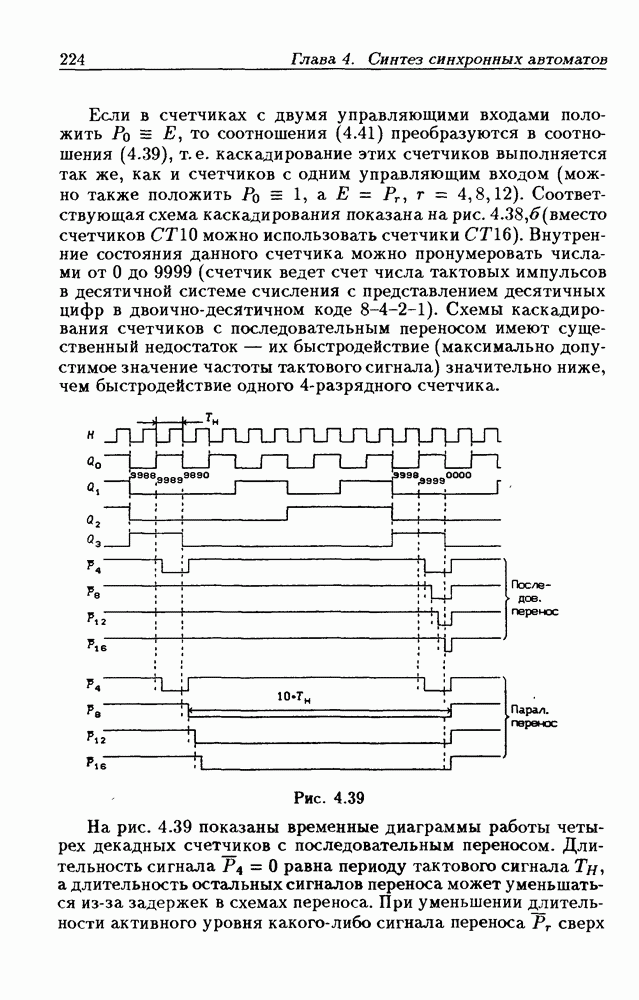
- Каскадирование двоичных и двоично-десятичных счетчиков.
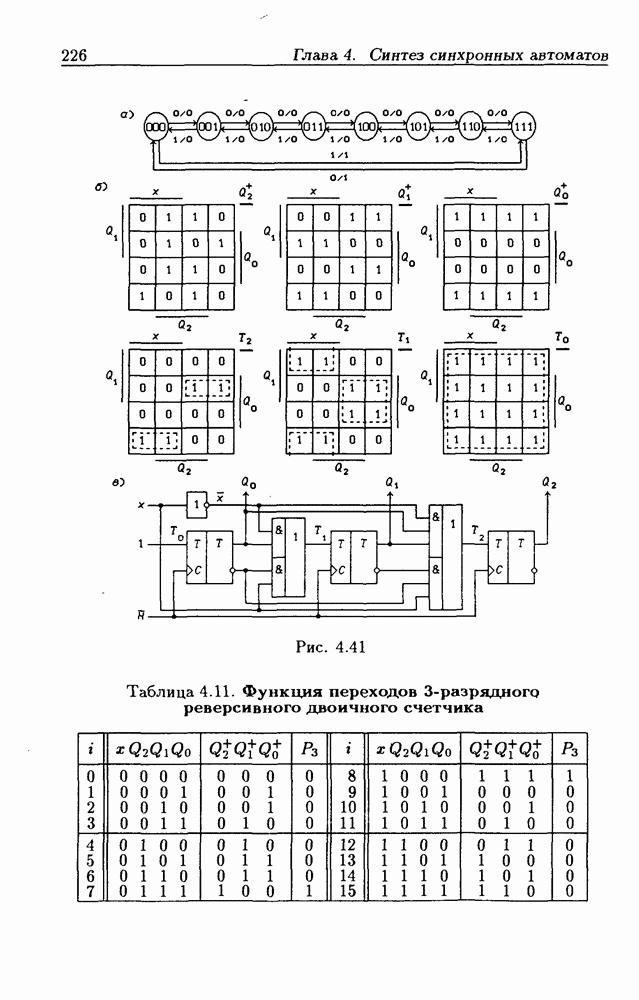
- Синхронные двоичные реверсивные счетчики.
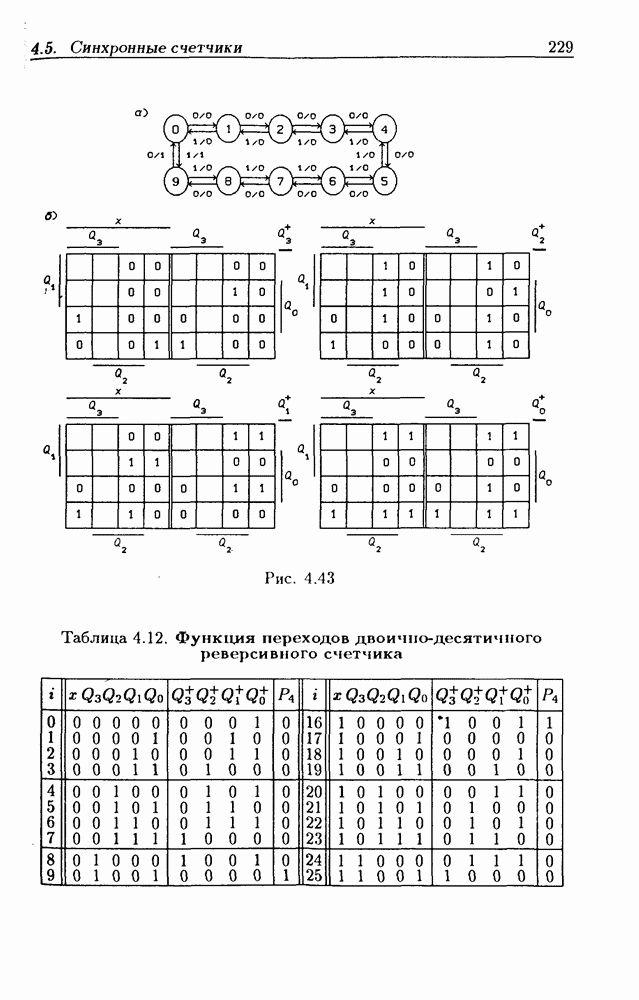
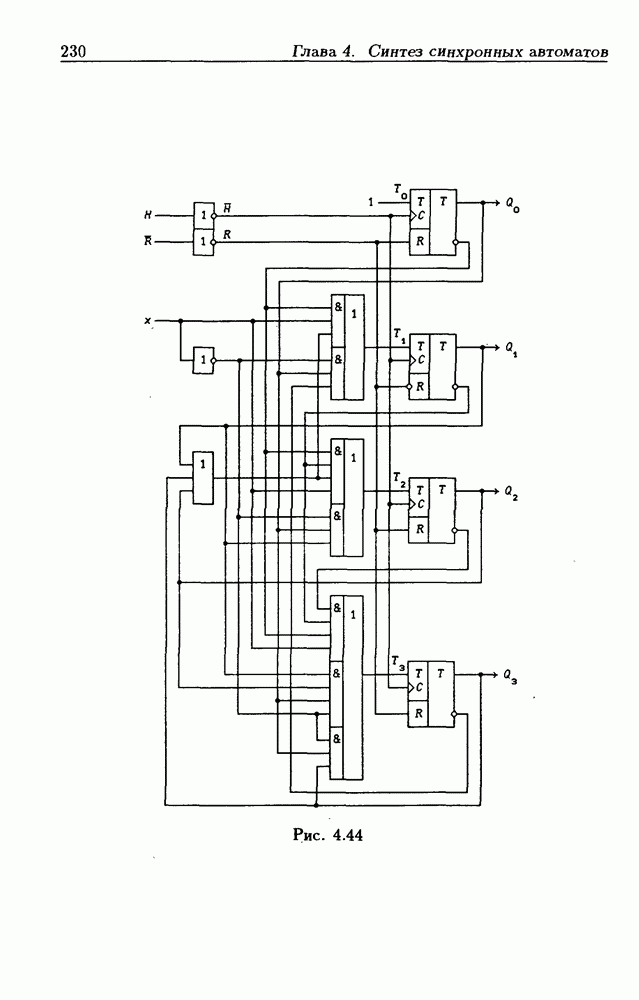
- Реверсивные двоично-десятичные счетчики.
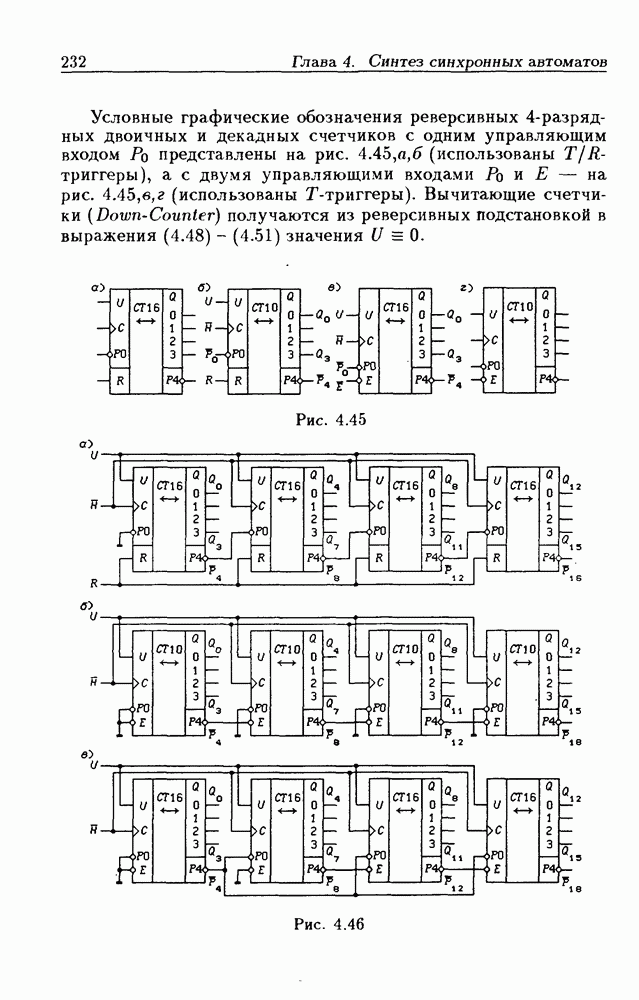
- Каскадирование реверсивных счетчиков.
- Счетчики на сдвигающих регистрах.
- Кольцевые счетчики.
- Линейные счетчики.
- Программируемые счетчики.
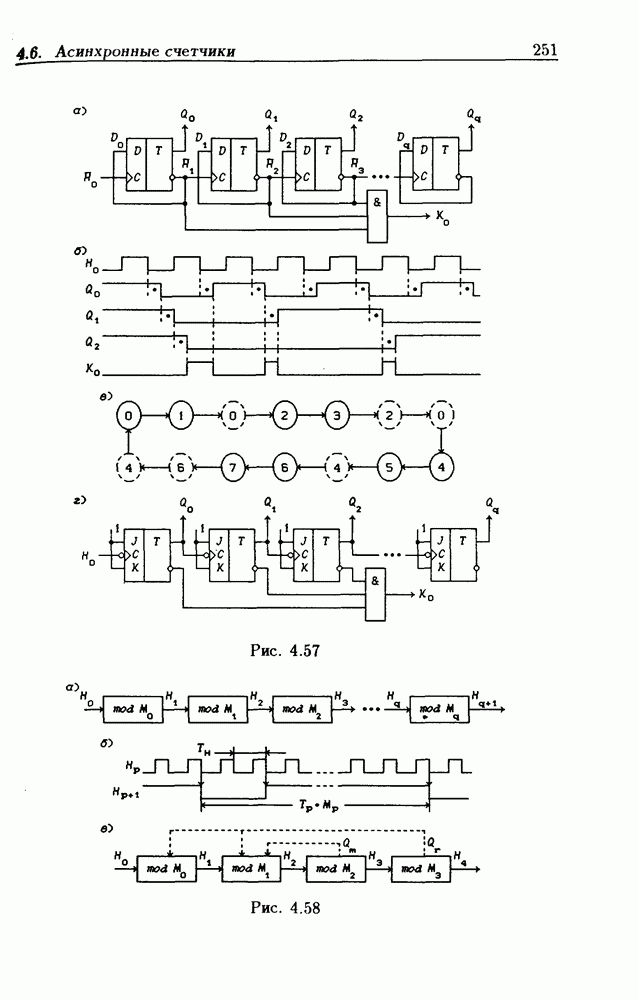
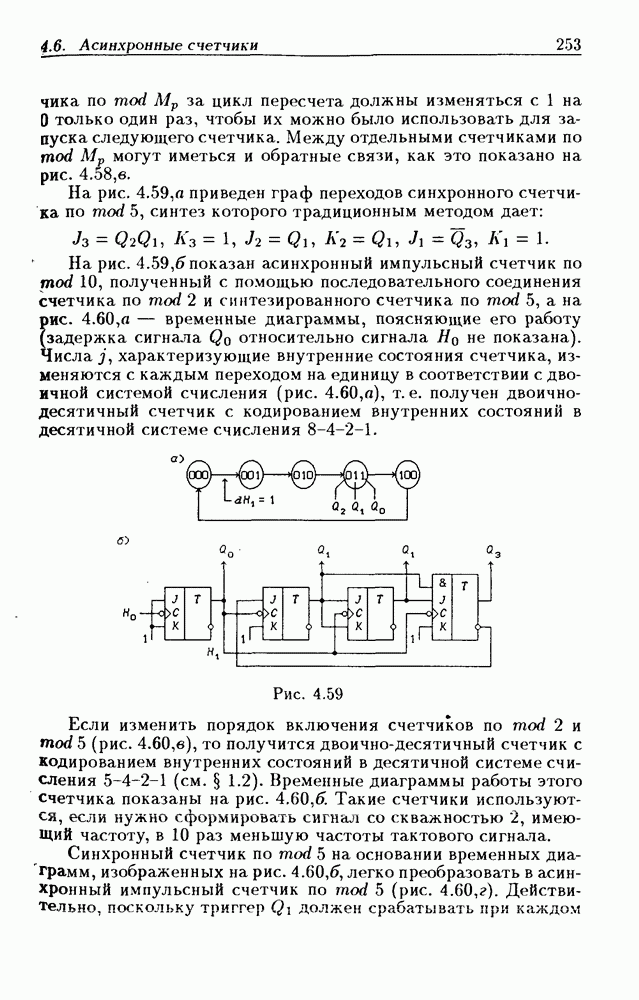
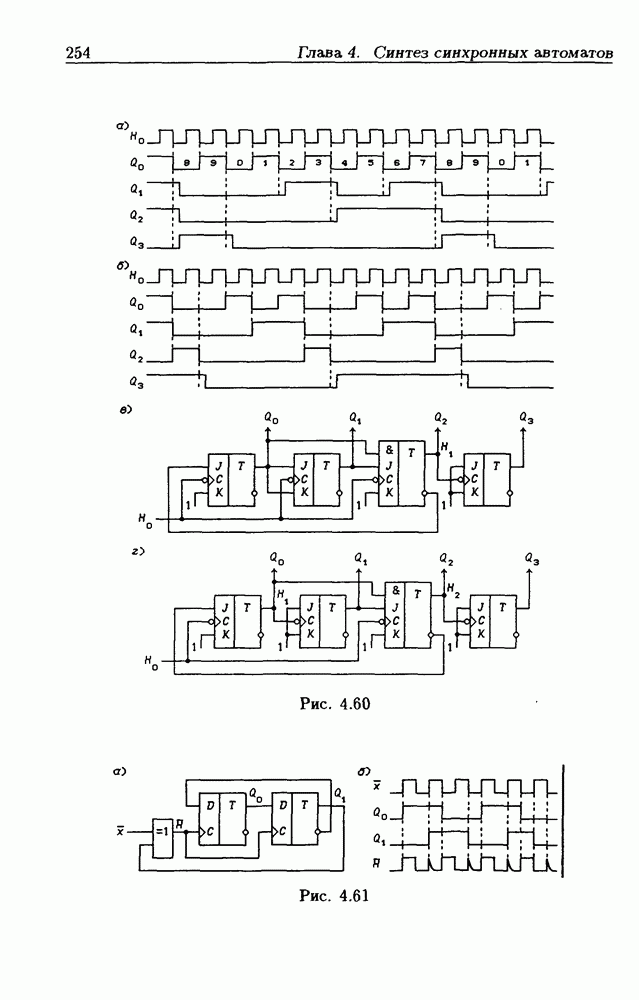
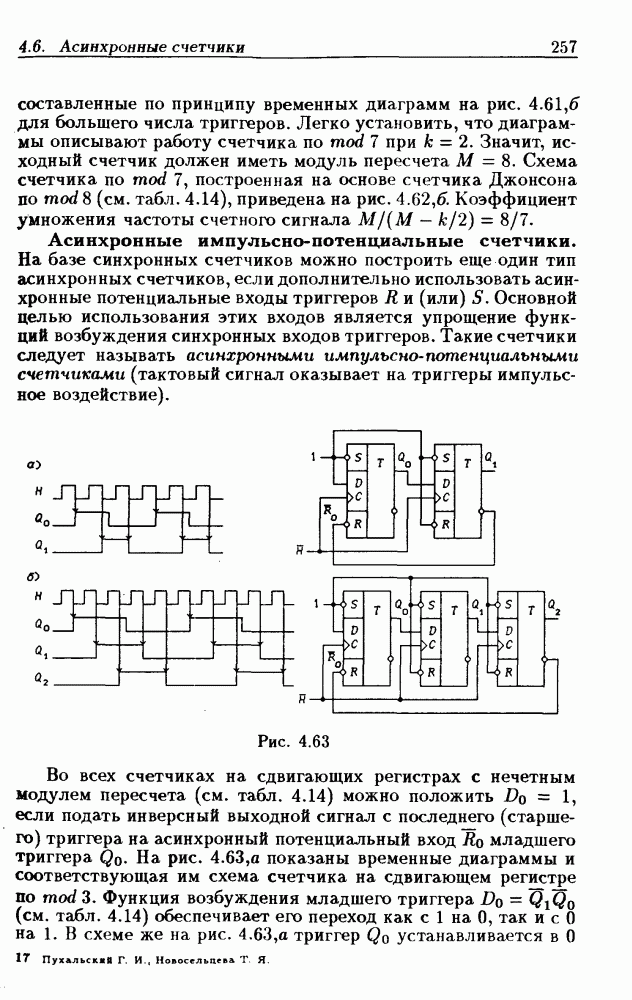
- 4.6. Асинхронные счетчики
- Асинхронные счетчики с умножением частоты счетного сигнала.
- Асинхронные импульсно-потенциальные счетчики.
- Асинхронное программирование модуля пересчета счетчиков.
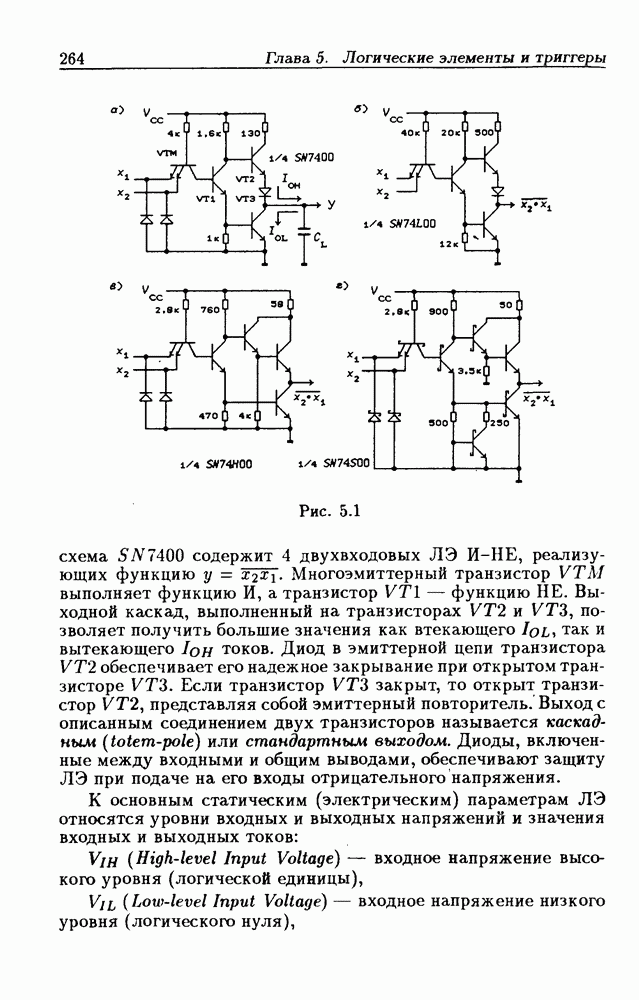
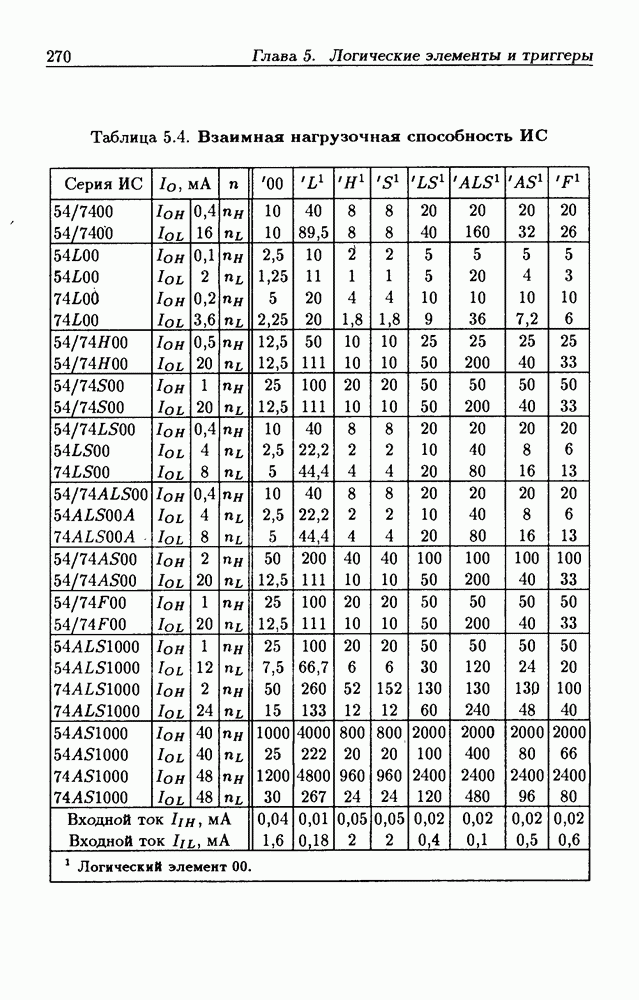
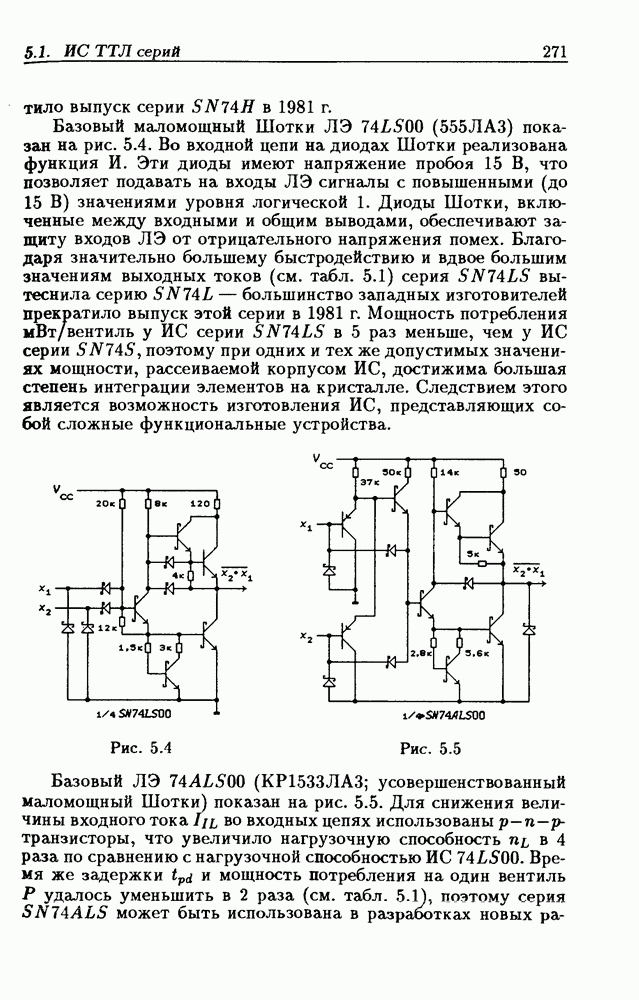
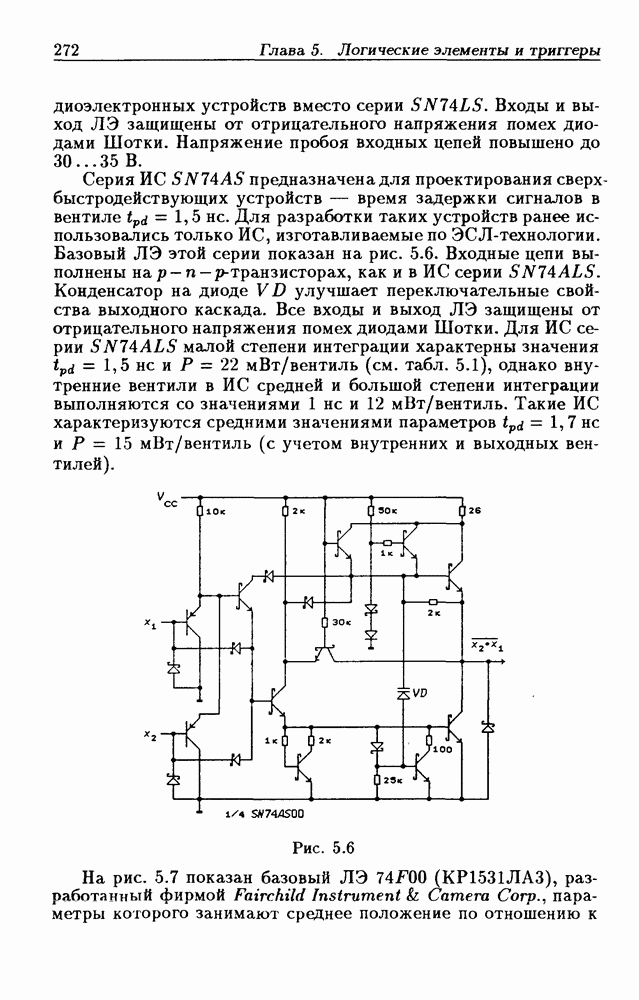
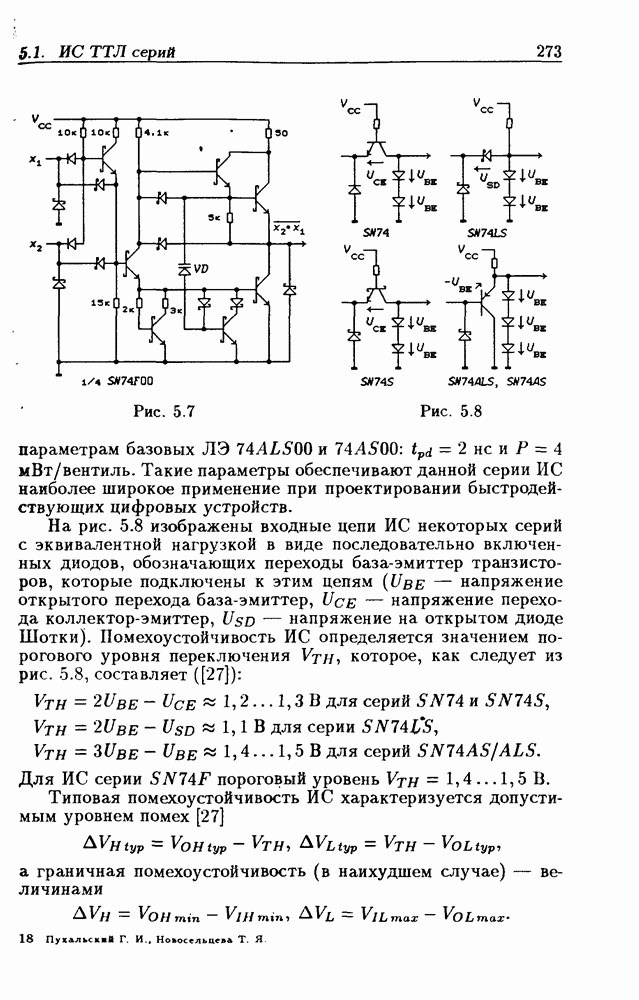
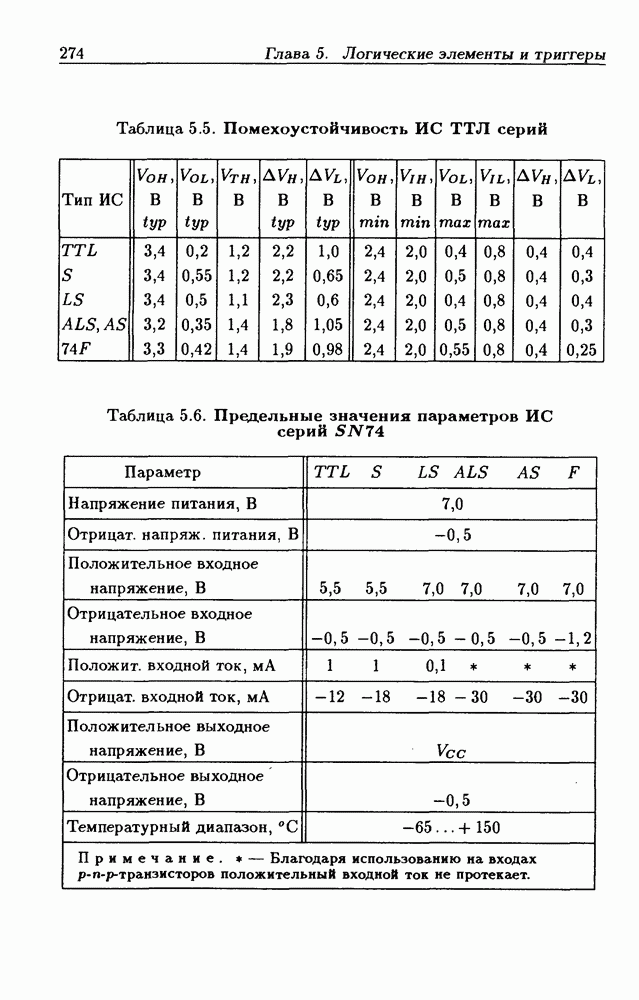
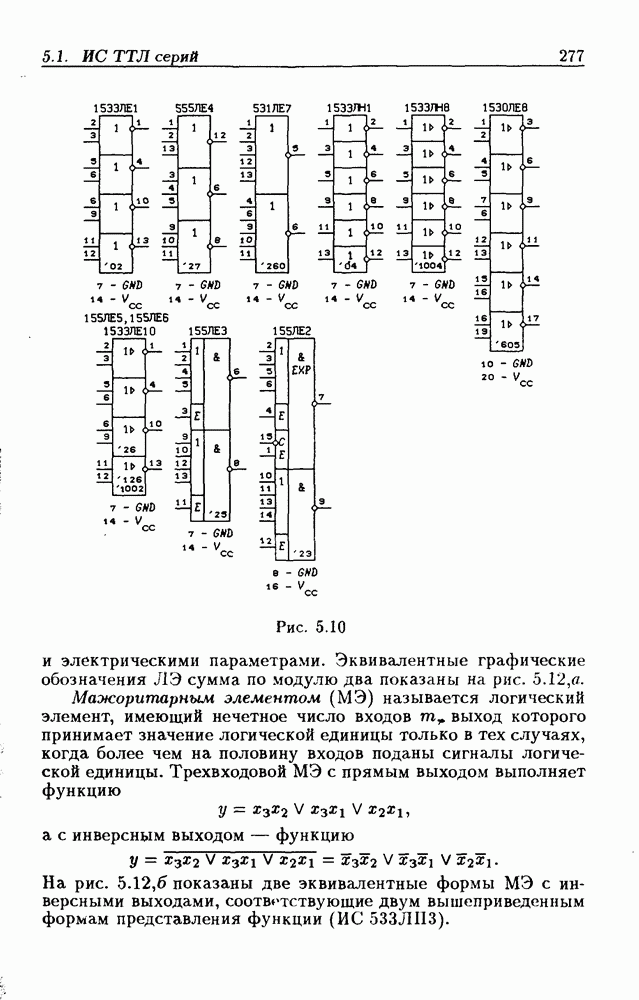
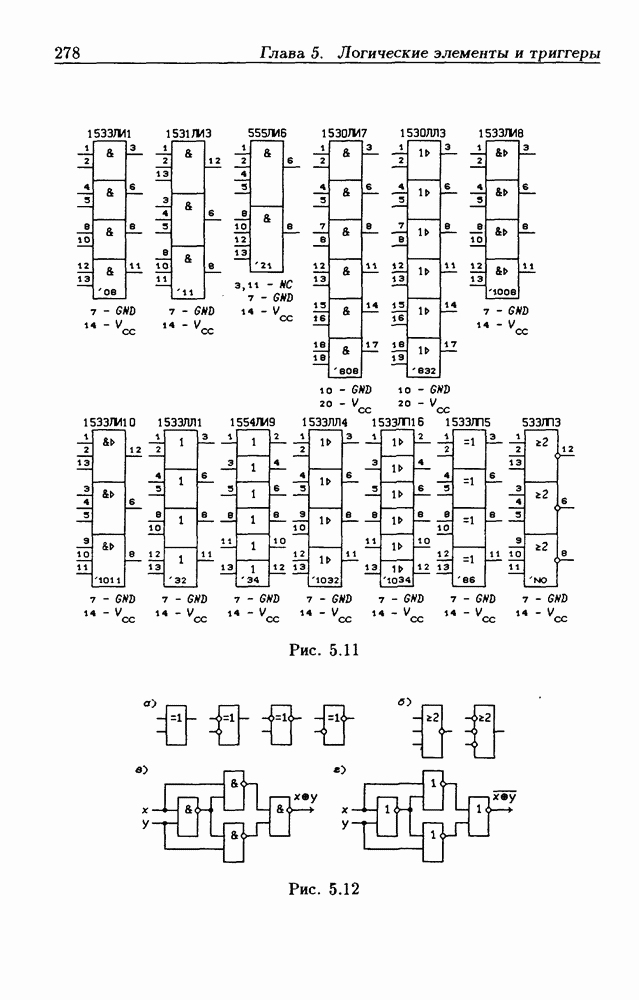
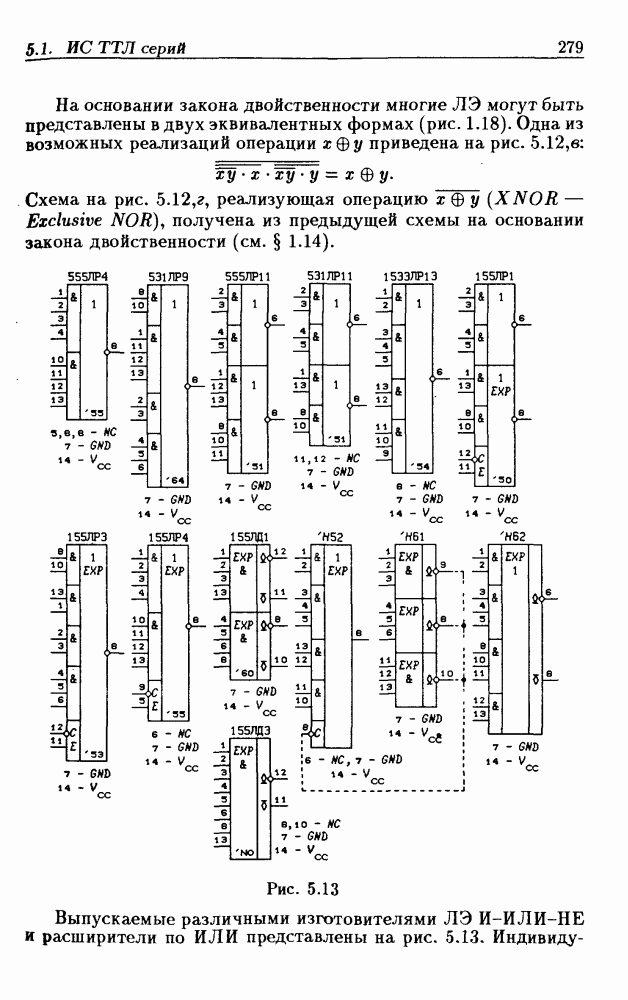
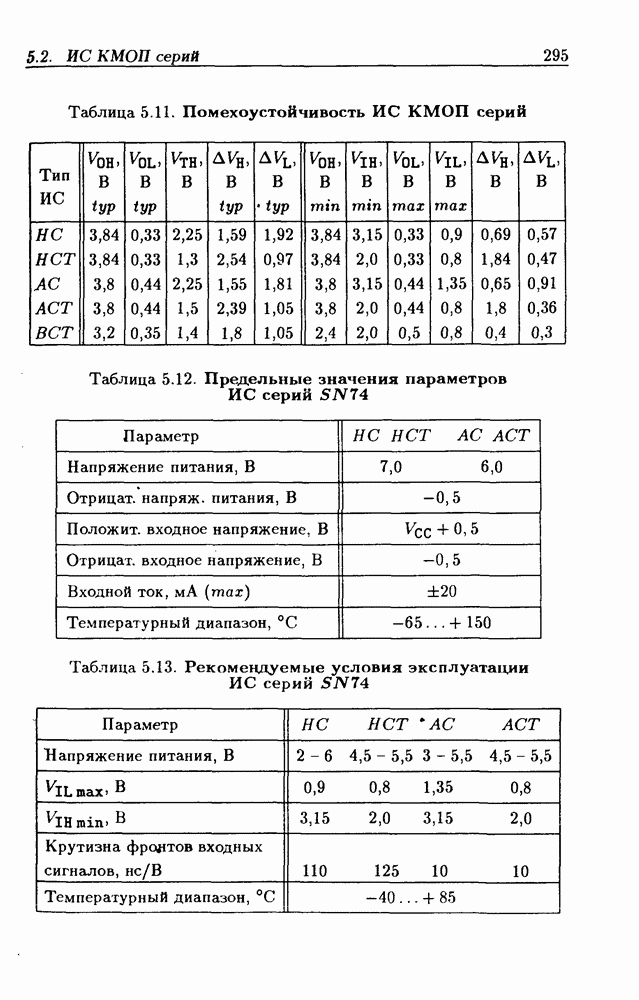
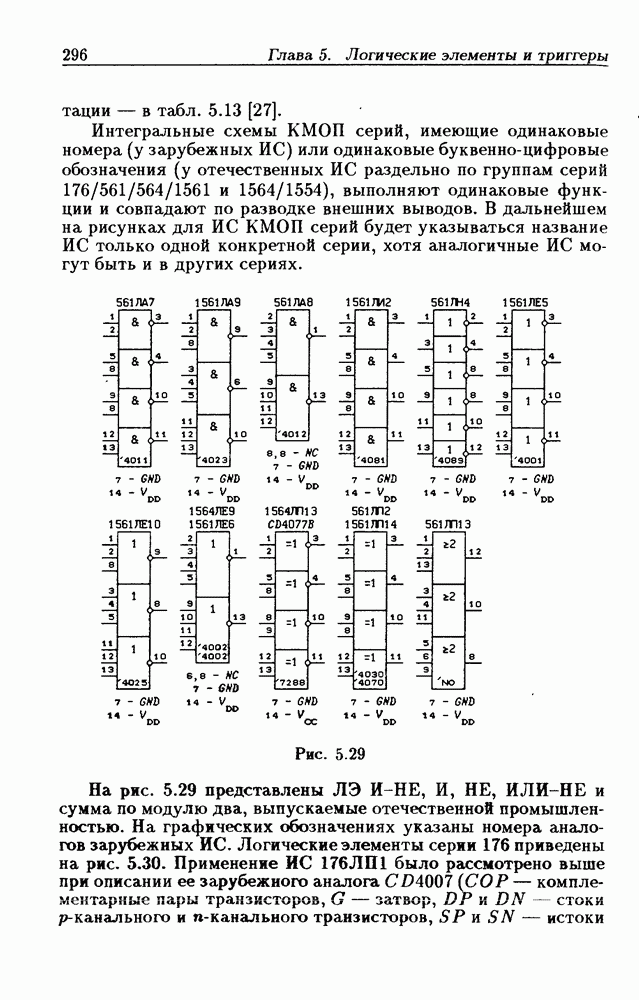
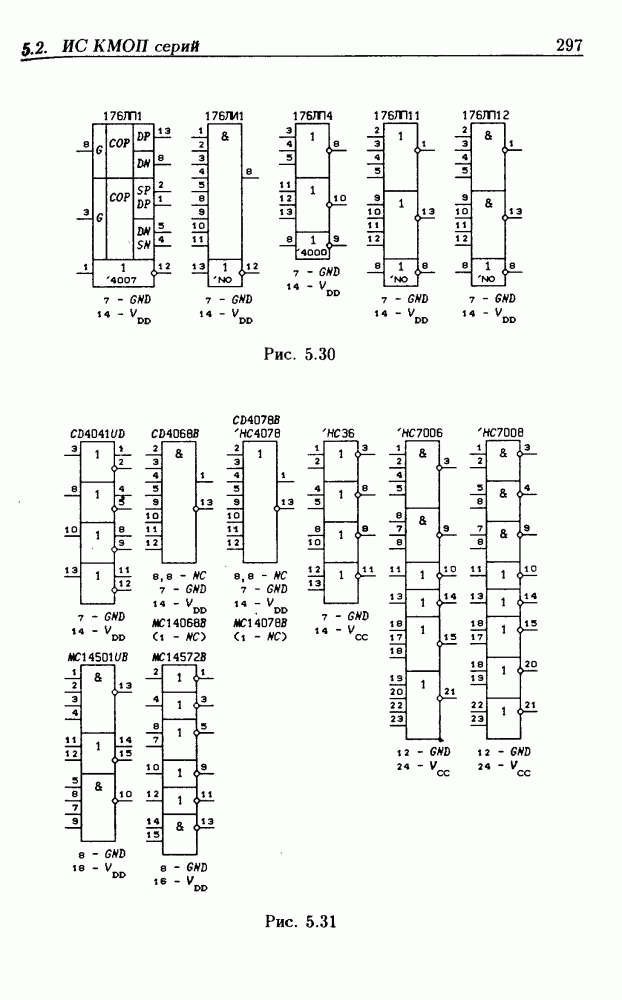
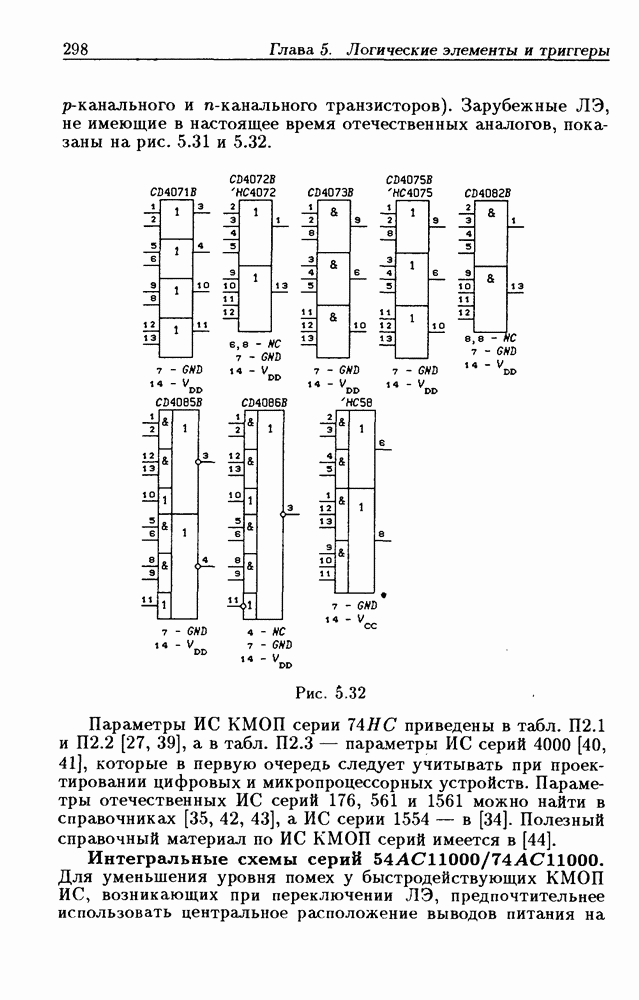
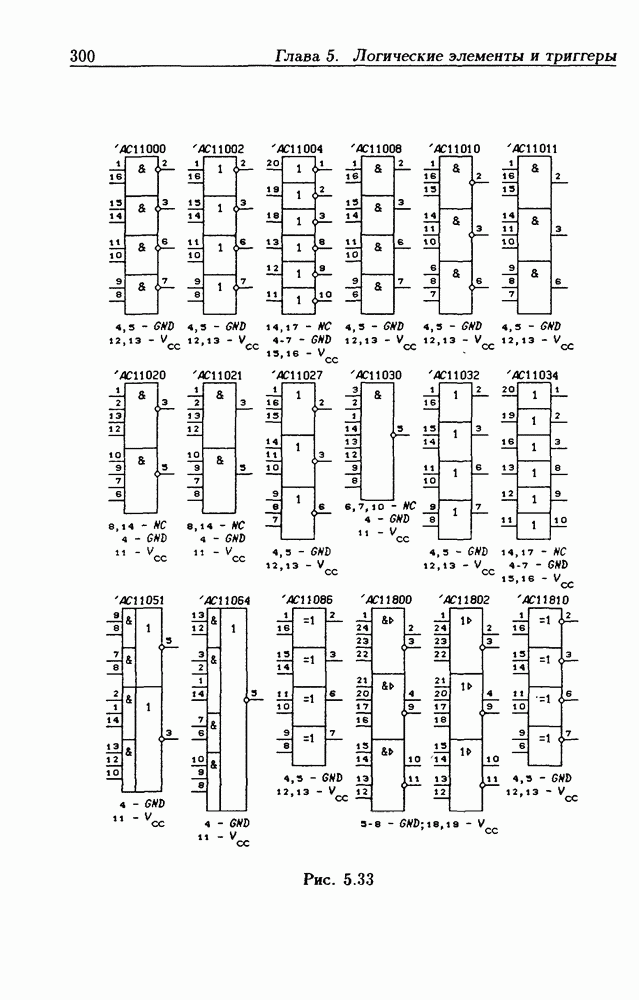
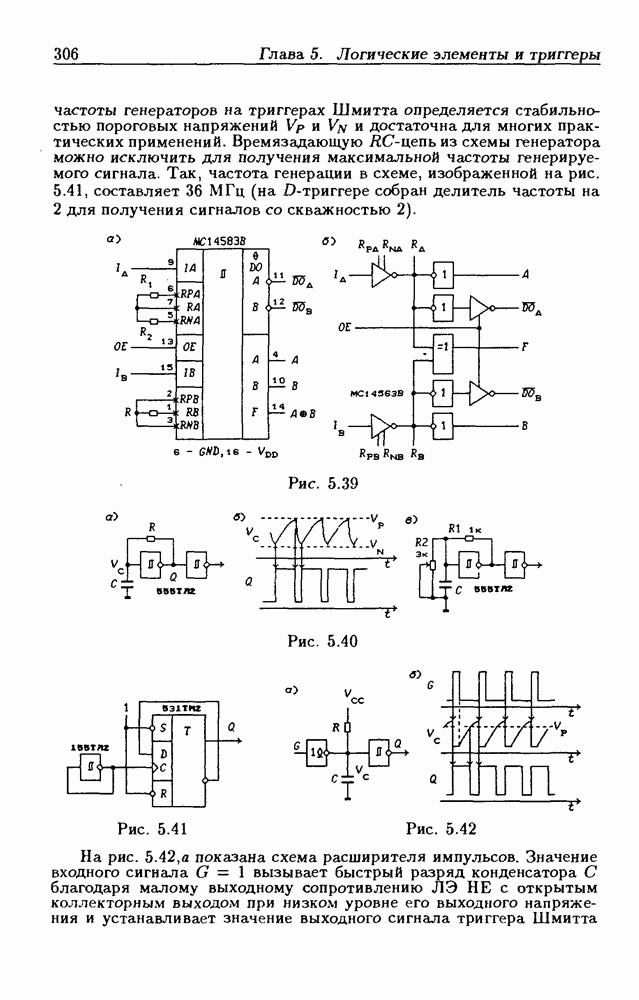
- Глава 5. Логические элементы и триггеры
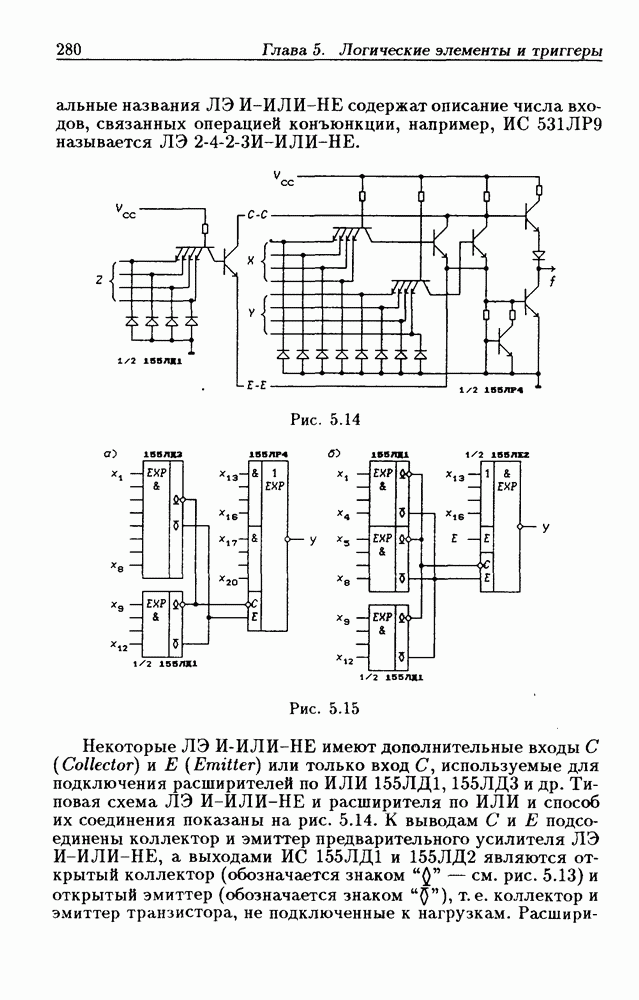
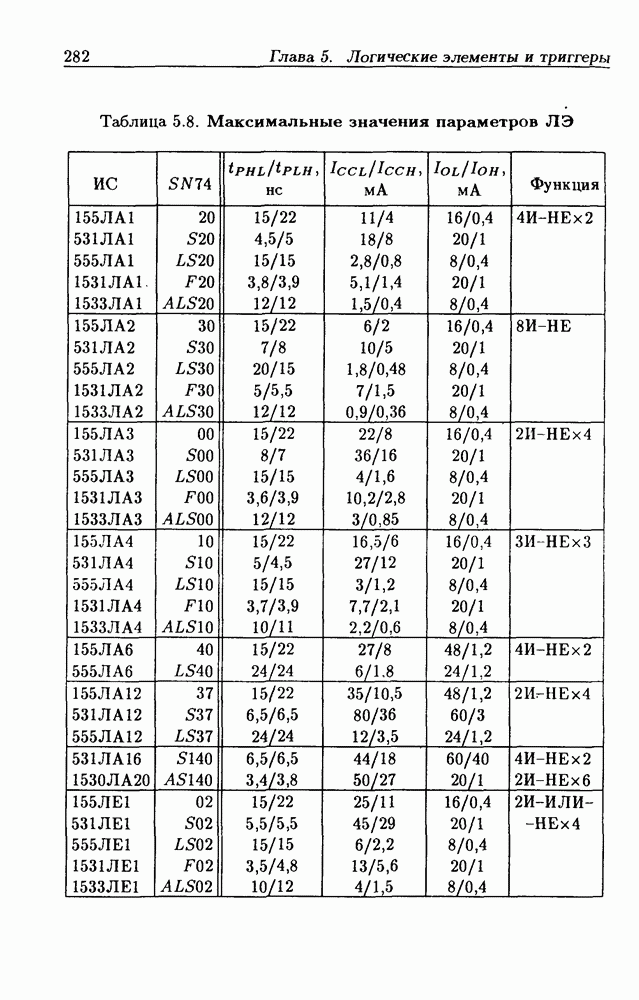
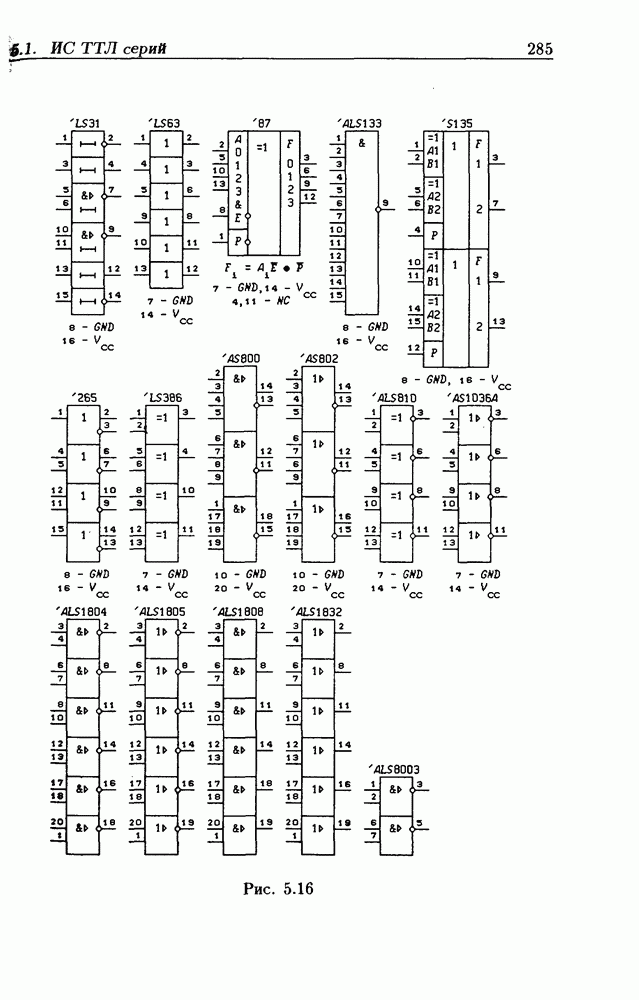
- Логические элементы.
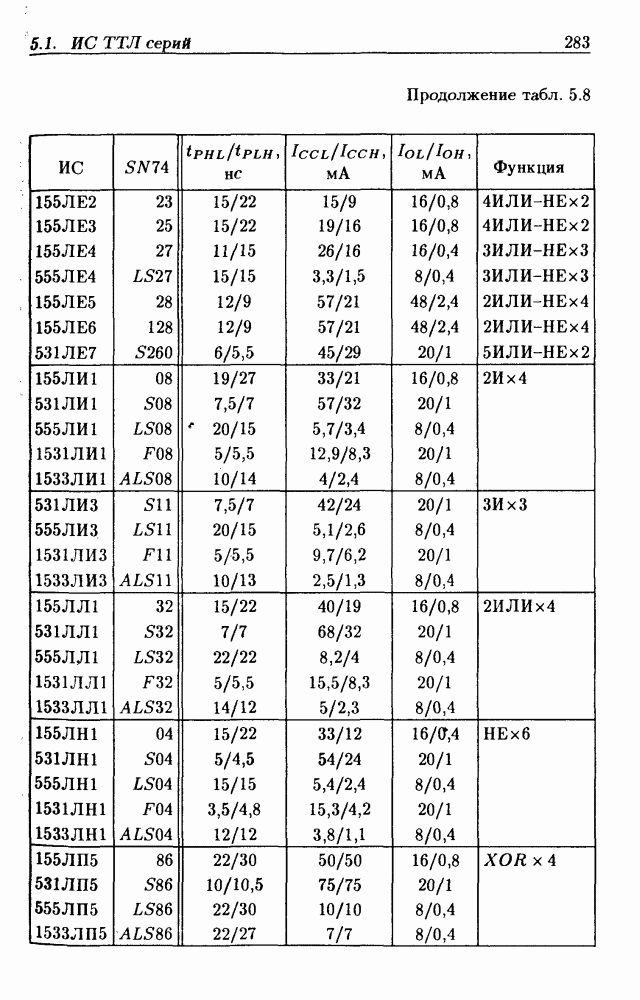
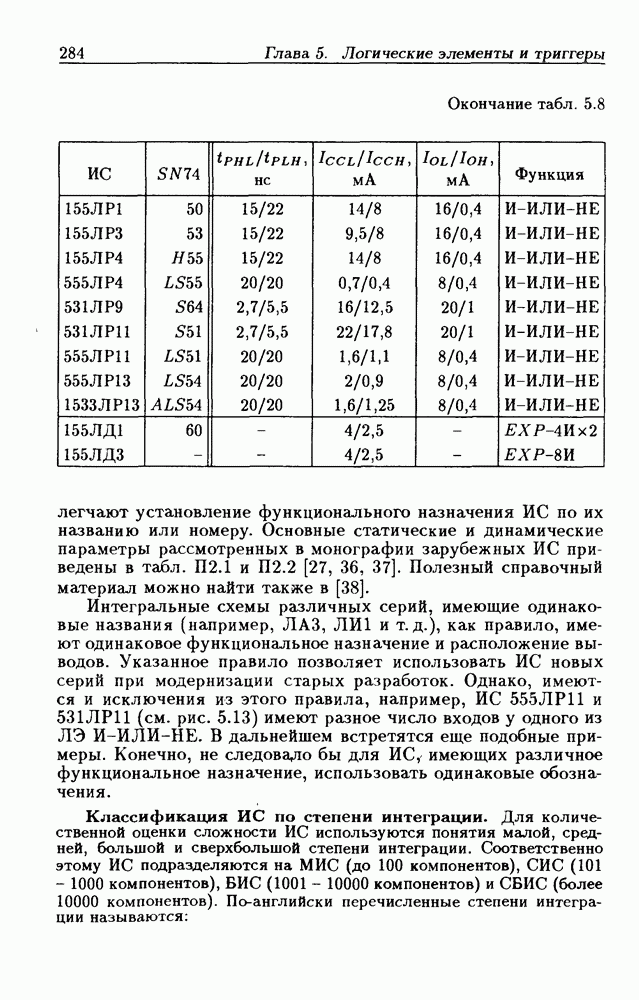
- Классификация ИС по степени интеграции.
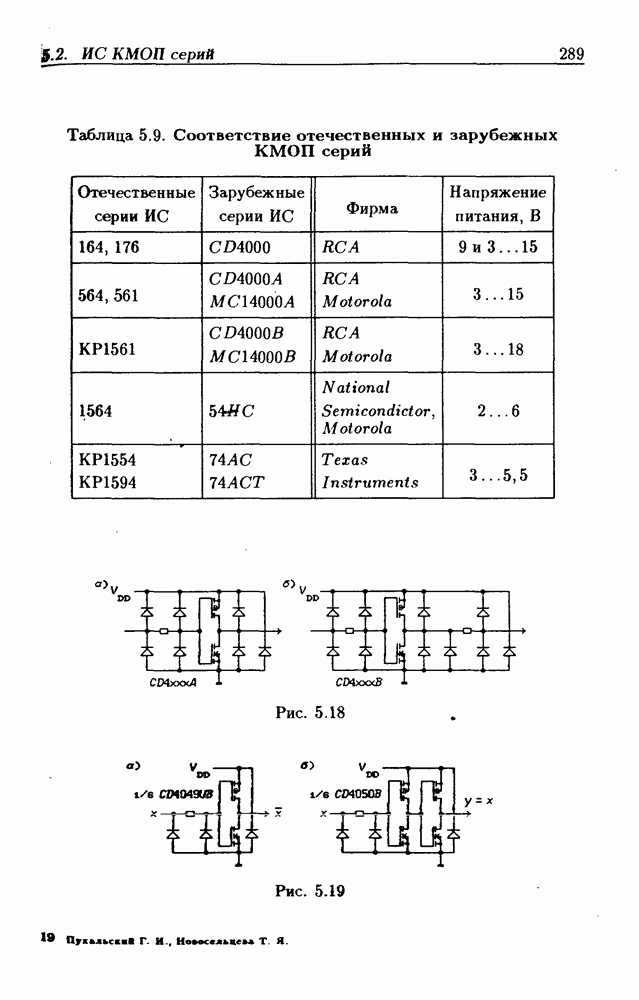
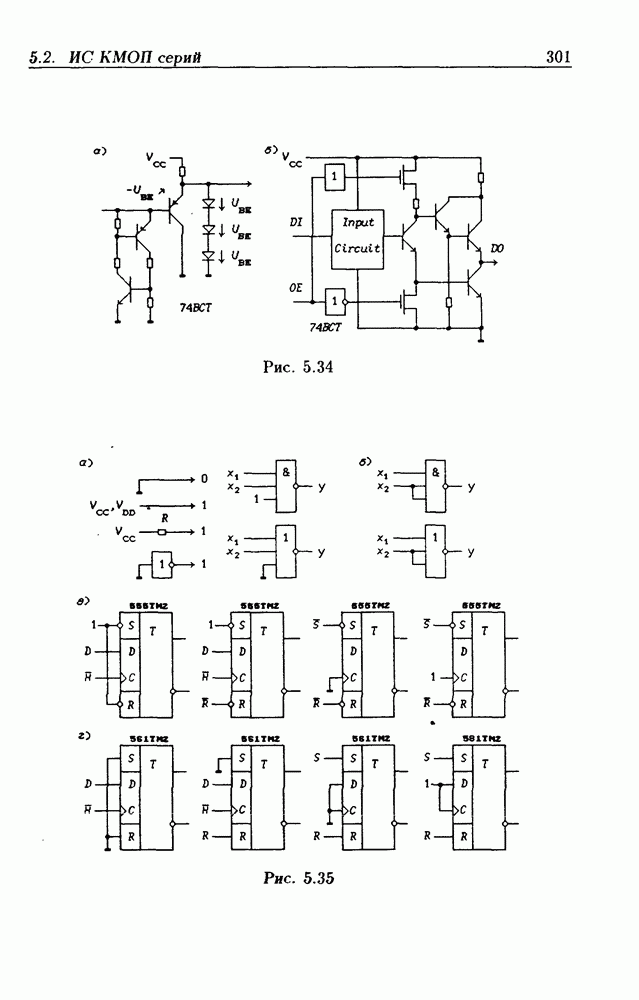
- 5.2. Интегральные схемы КМОП серий
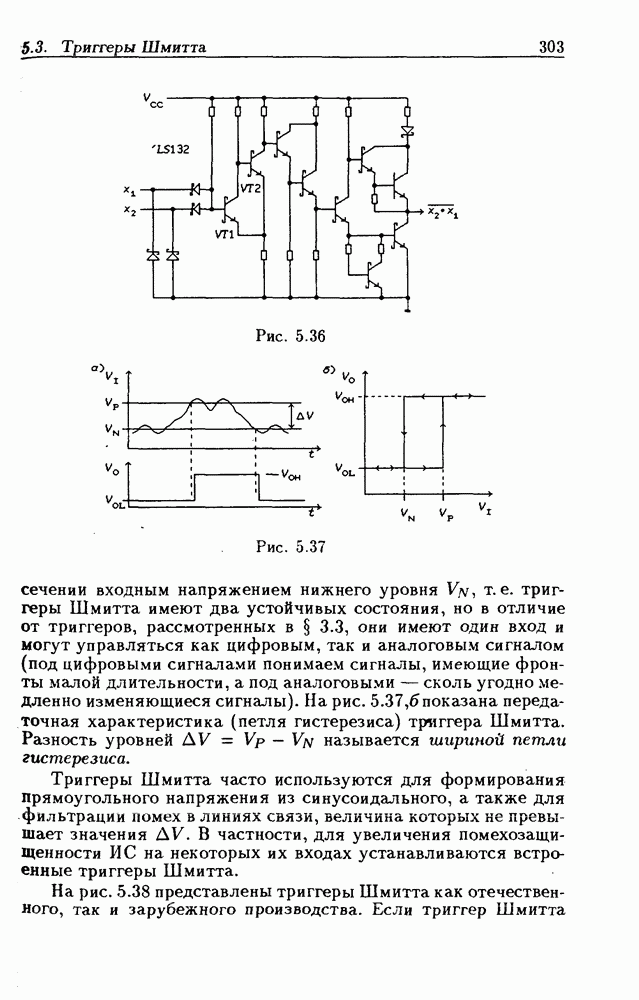
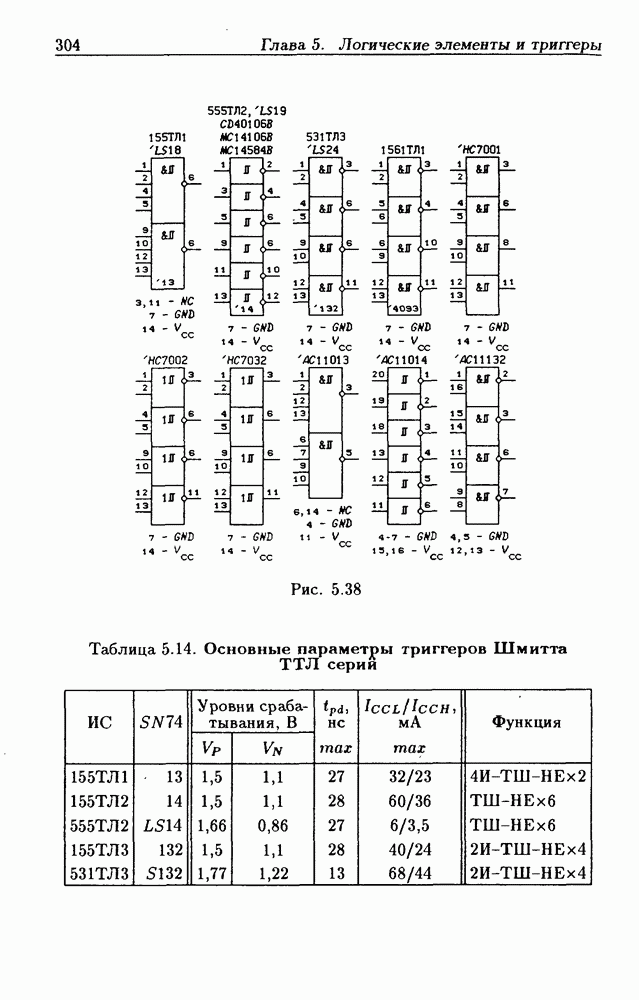
- 5.3. Триггеры Шмитта
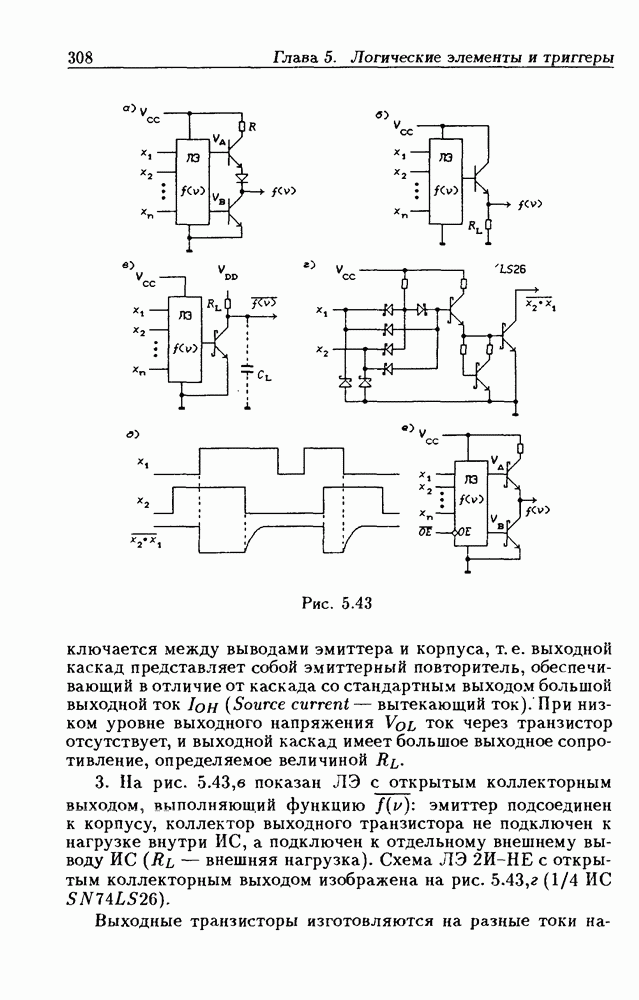
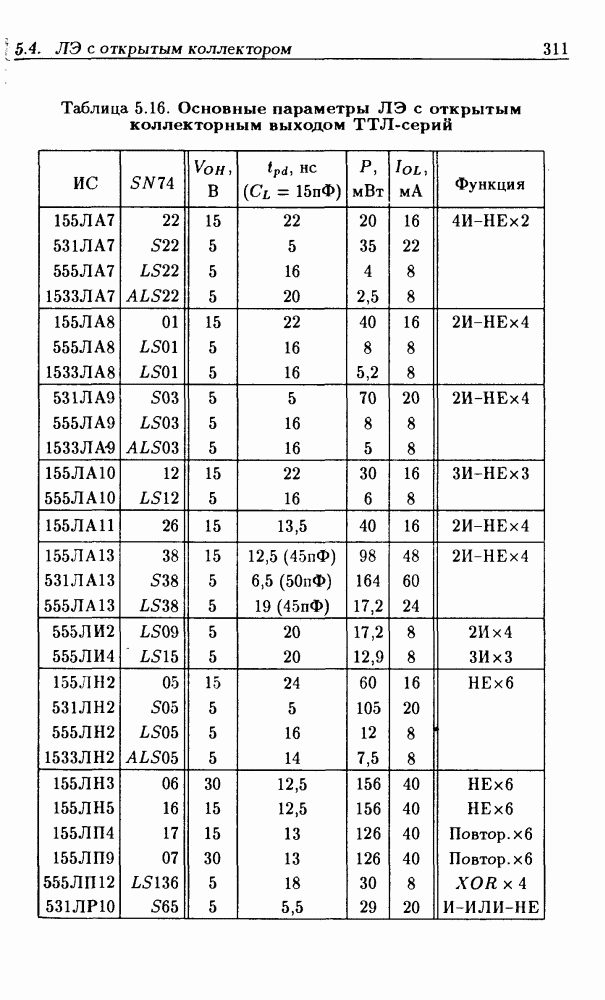
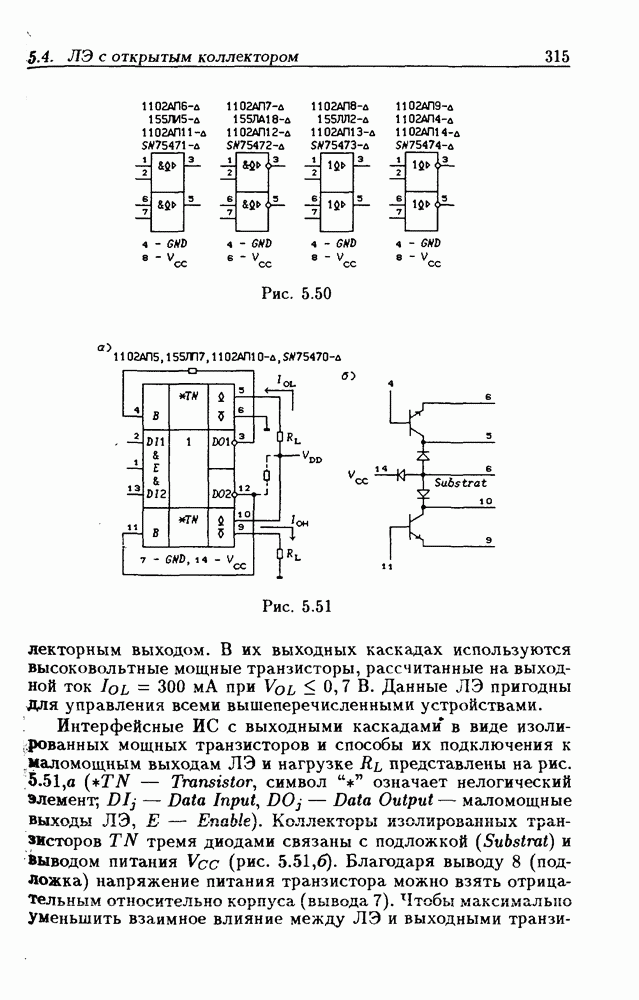
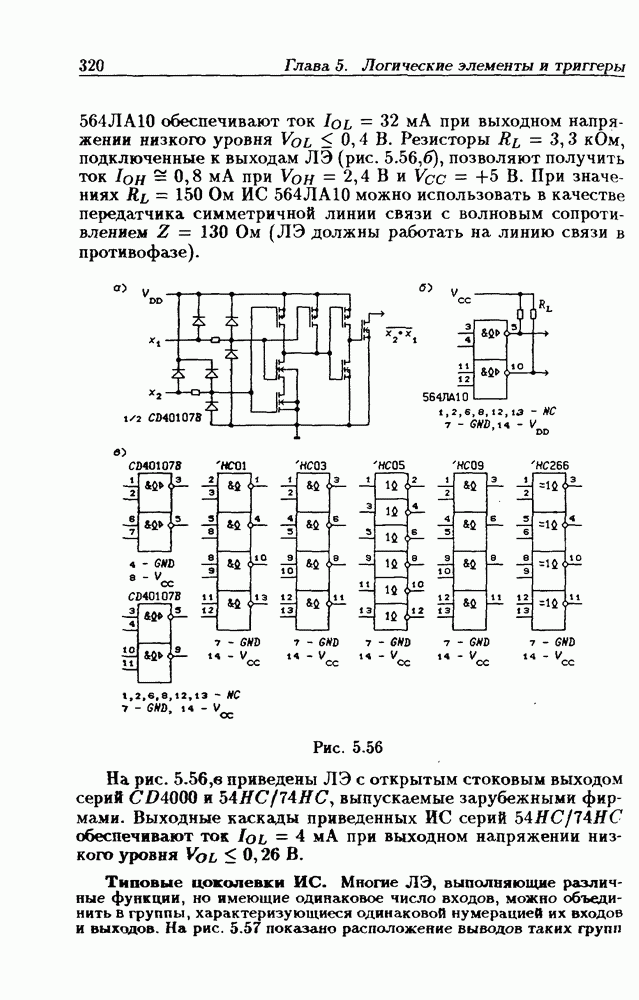
- 5.4. Логические элементы с открытым коллекторным выходом
- Логические элементы с открытым коллекторным выходом.
- Применения ЛЭ с открытым коллекторным выходом.
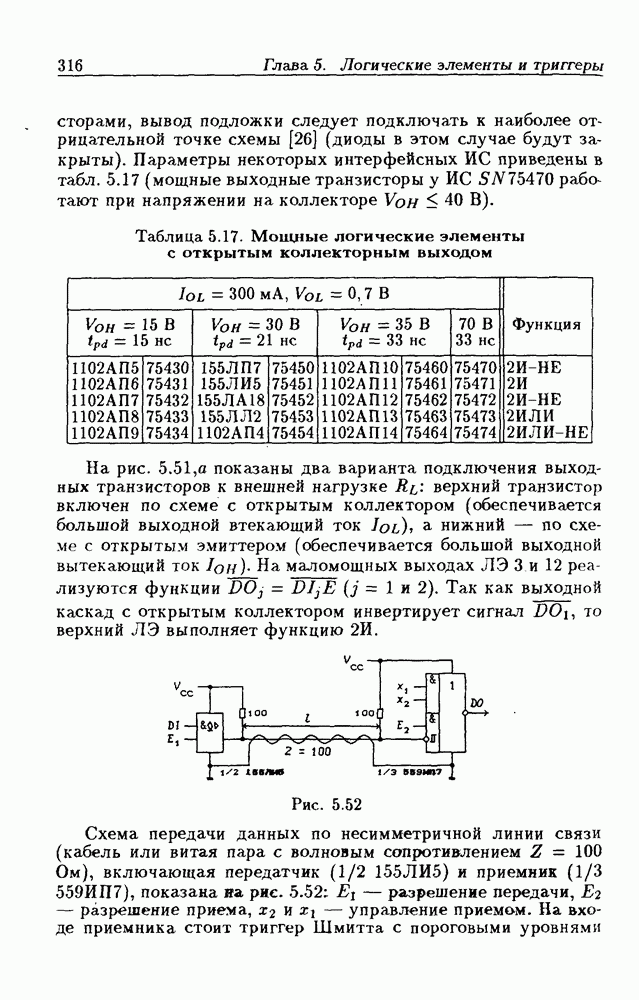
- Интерфейсные ЛЭ с открытым коллекторным выходом.
- Логические элементы с открытым стоковым выходом.
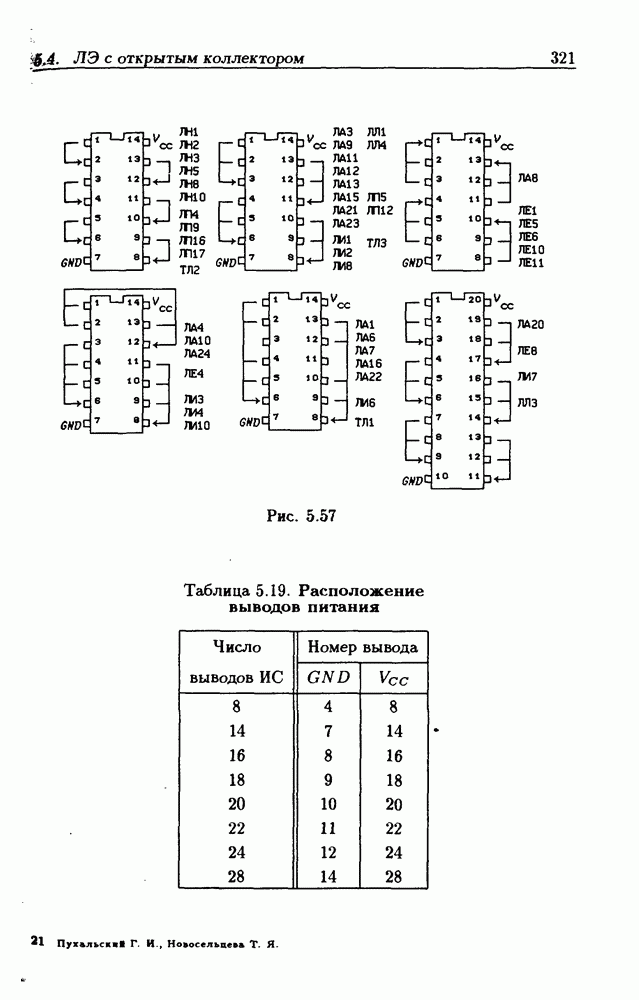
- Типовые цоколевки ИС.
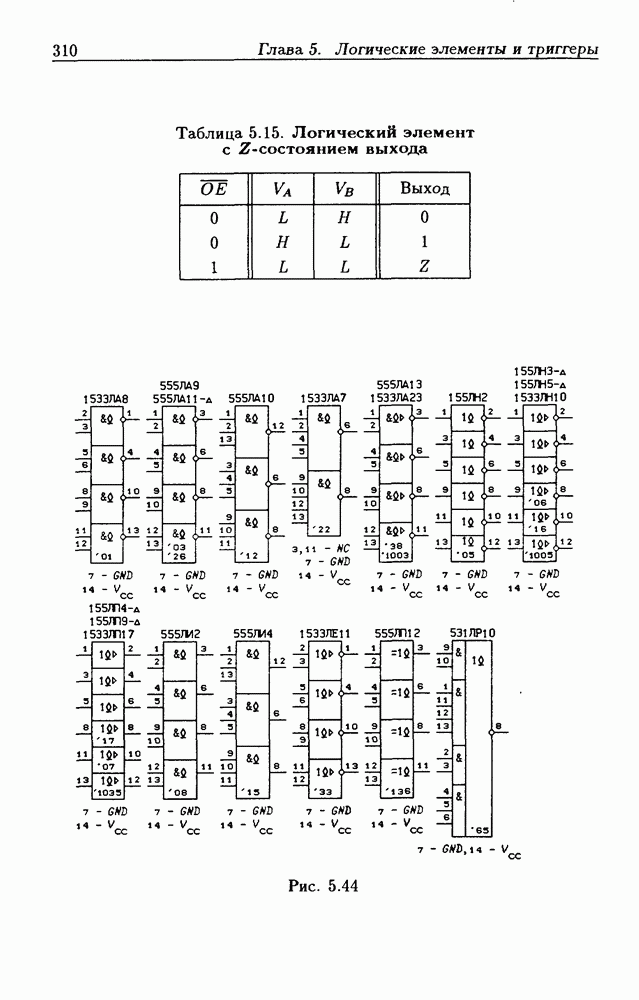
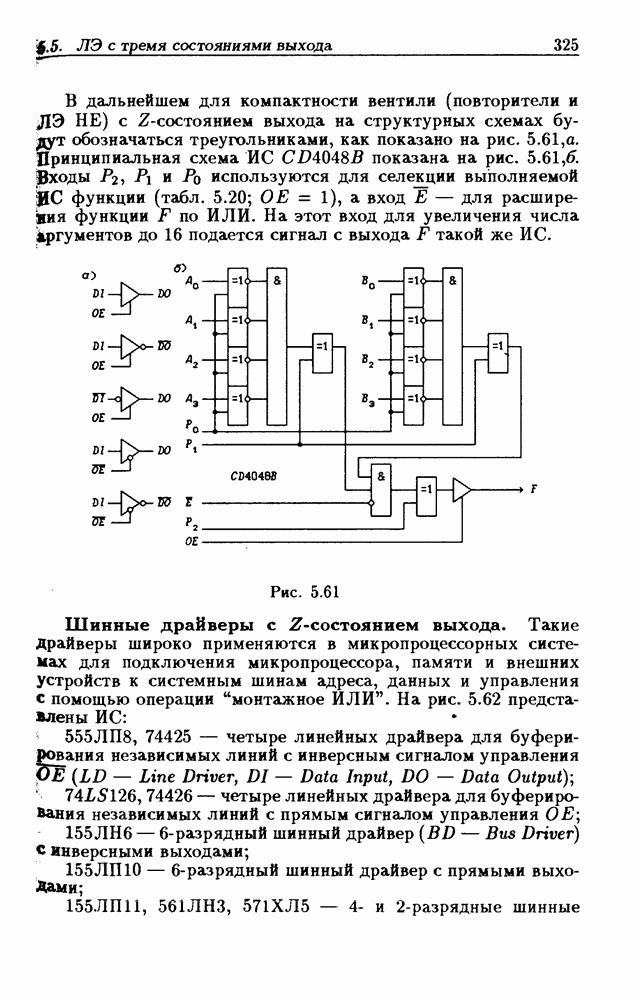
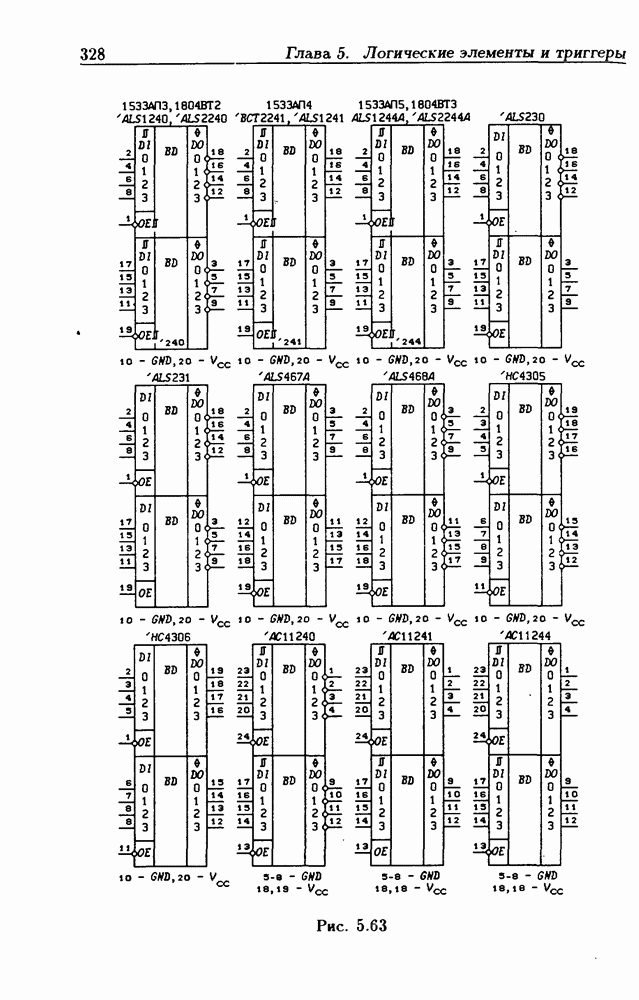
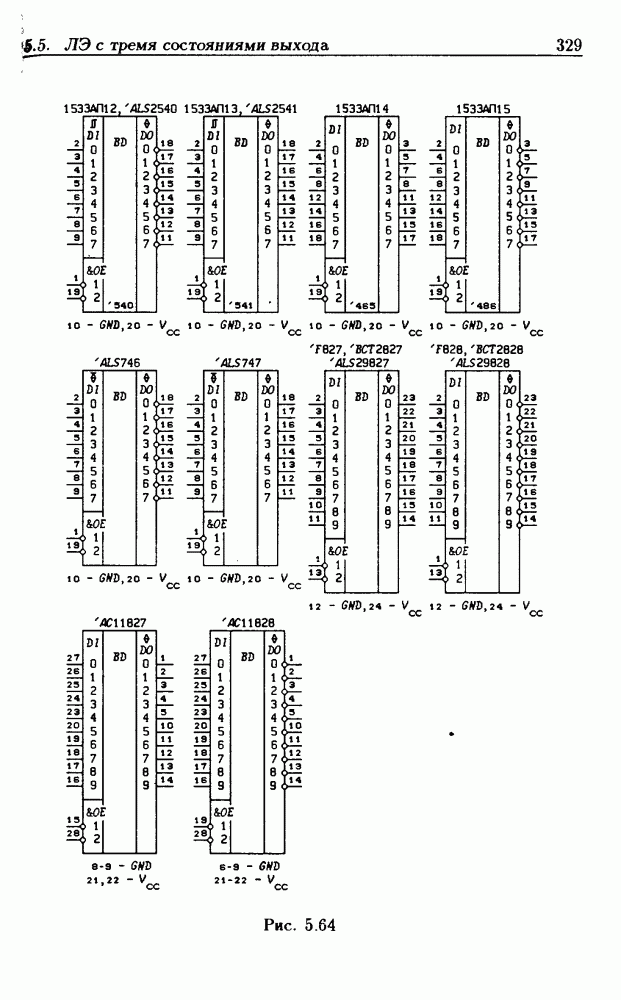
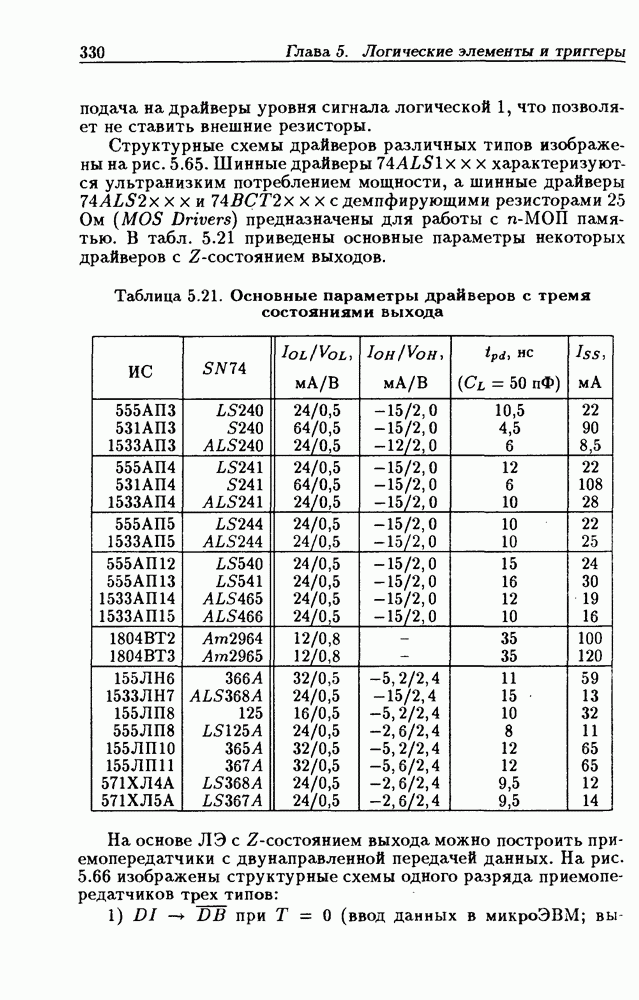
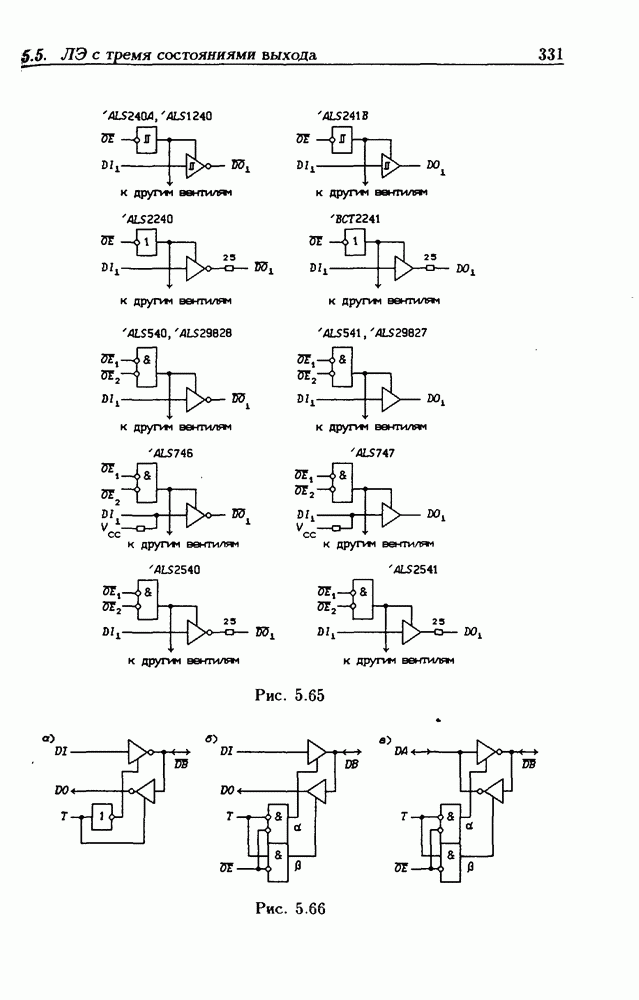
- 5.5. Логические элементы с тремя состояниями выхода
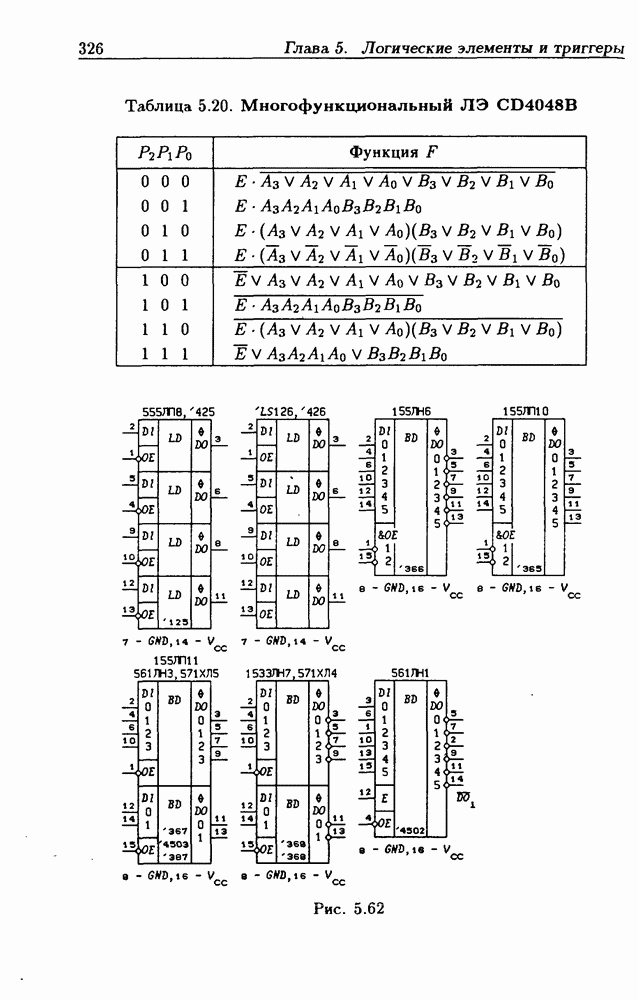
- Шинные драйверы с Z-состоянием выхода.
- Основные правила графического изображения ИС.
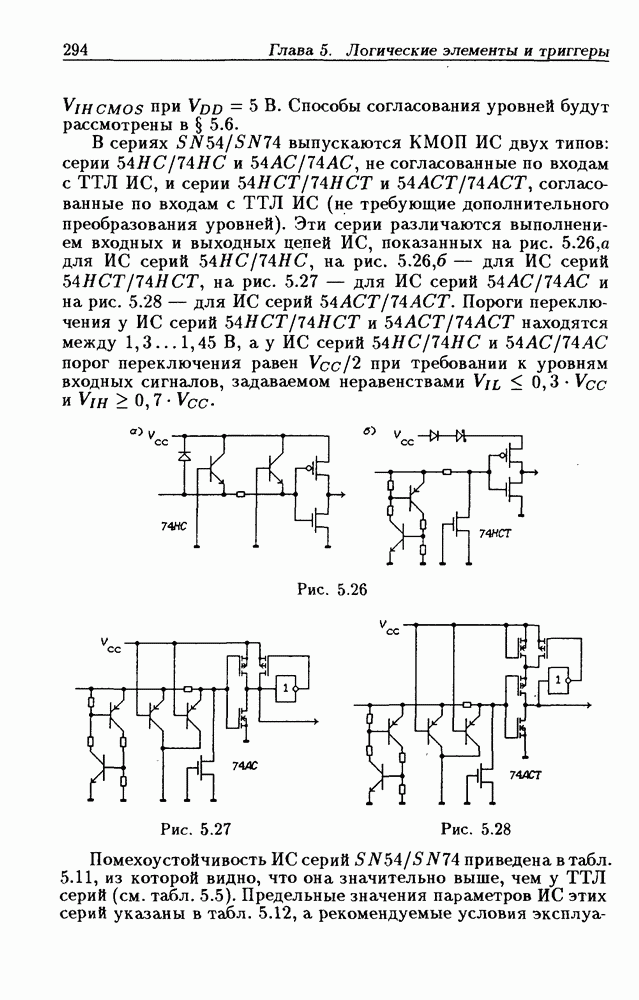
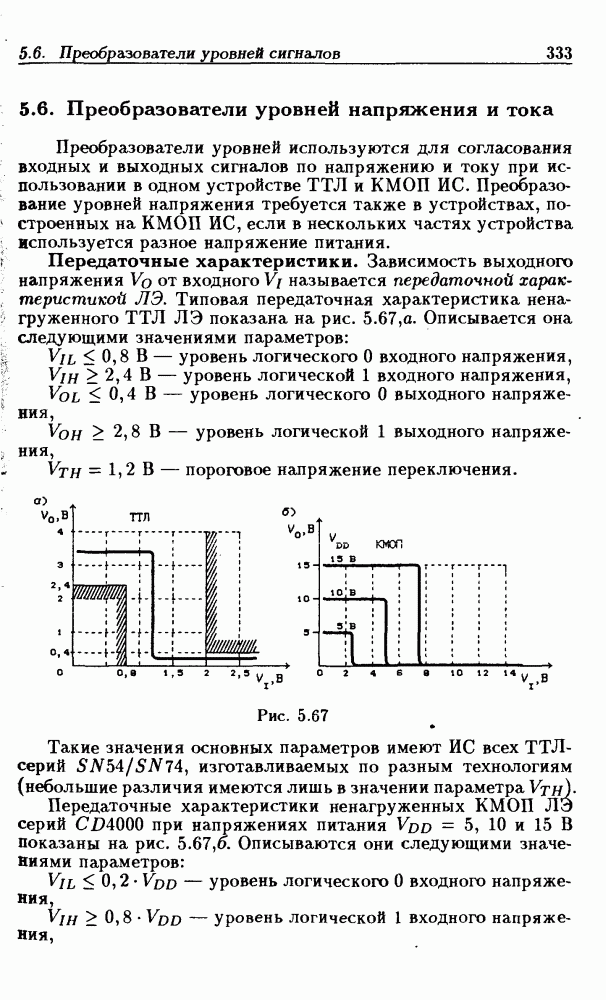
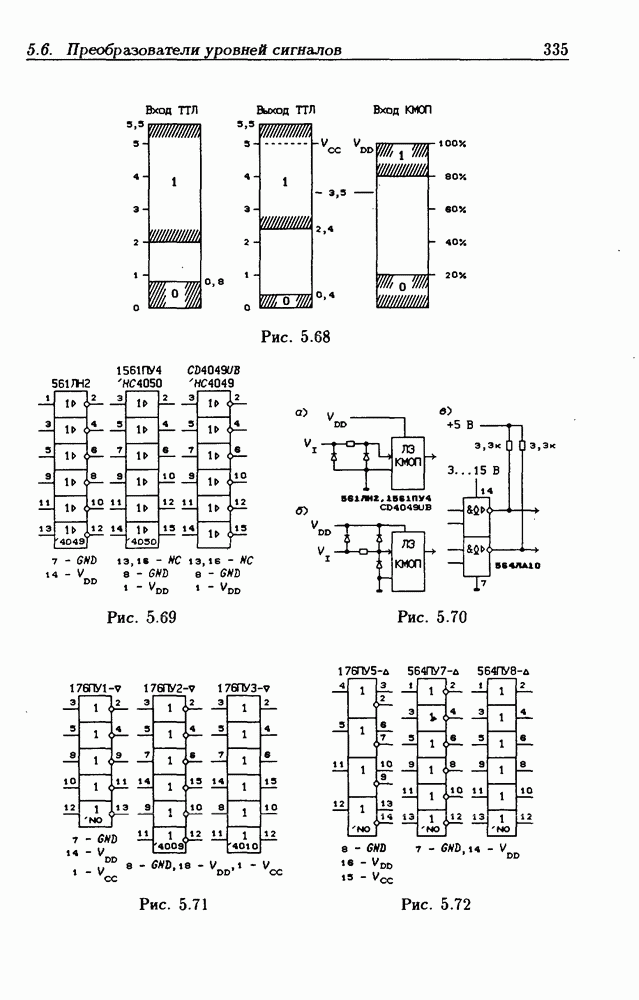
- 5.6. Преобразователи уровней напряжения и тока
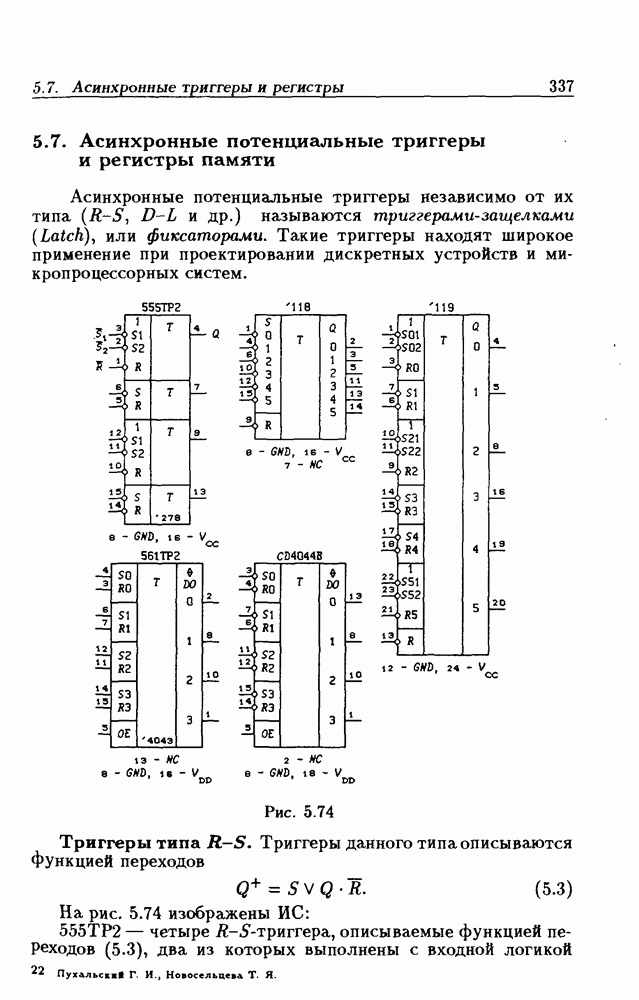
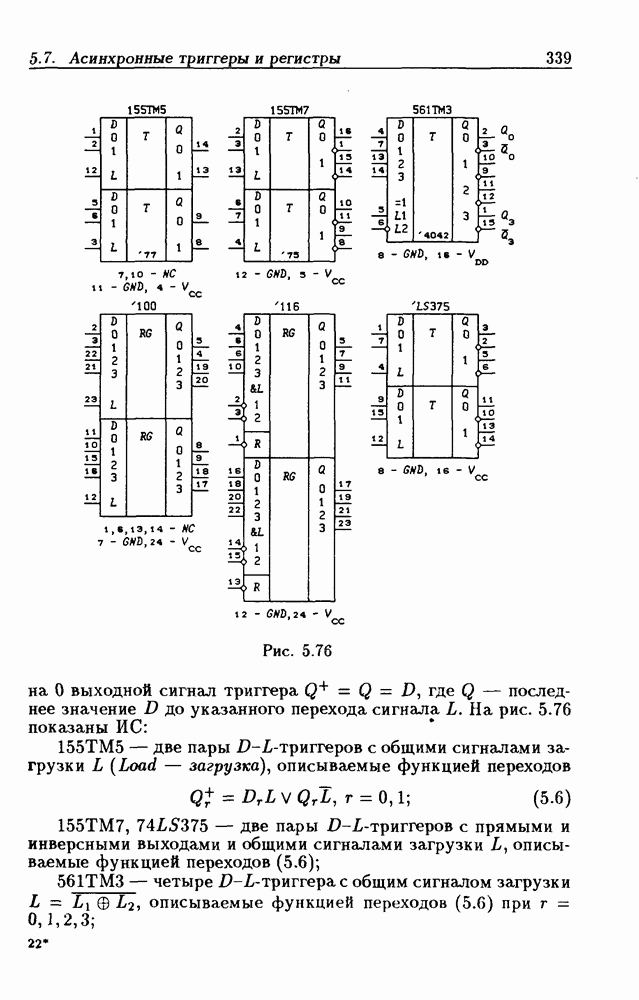
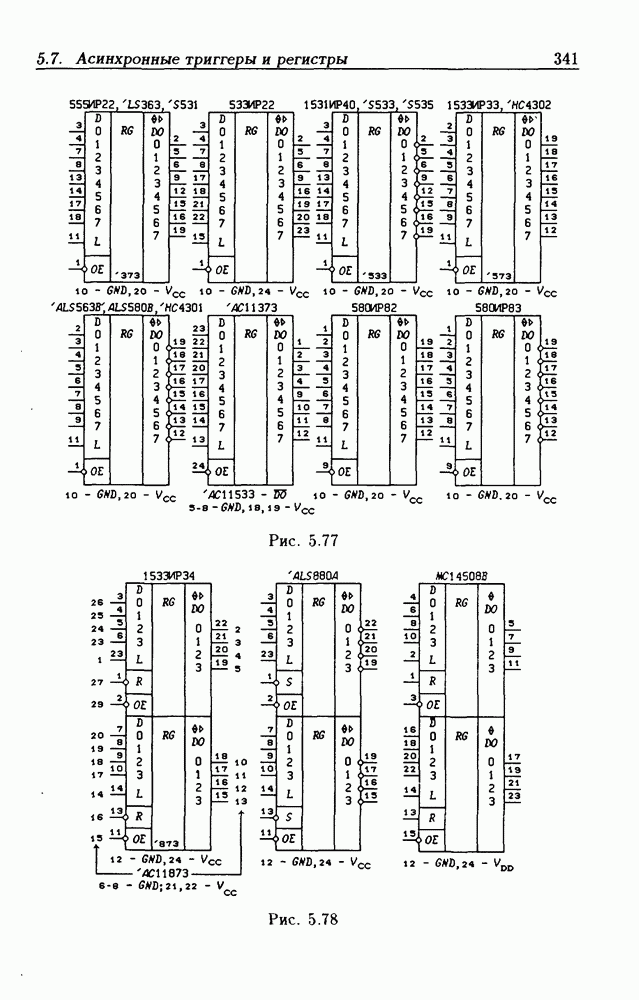
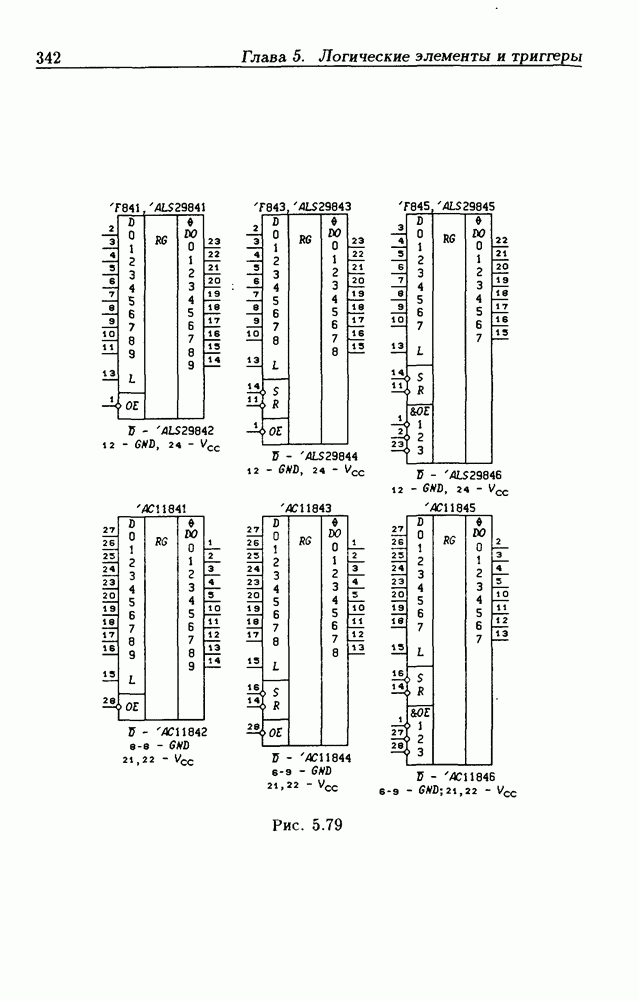
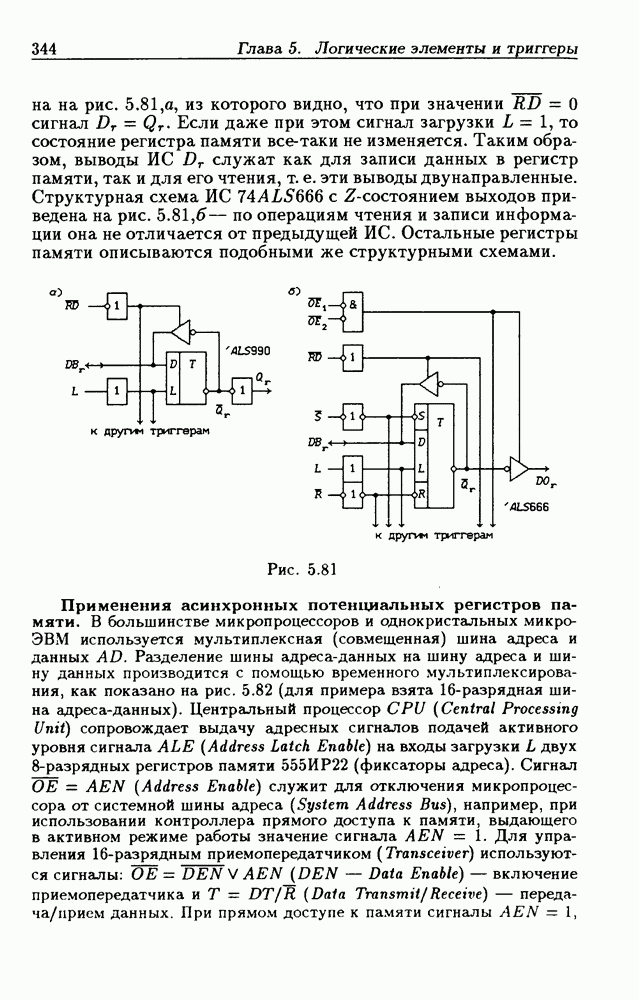
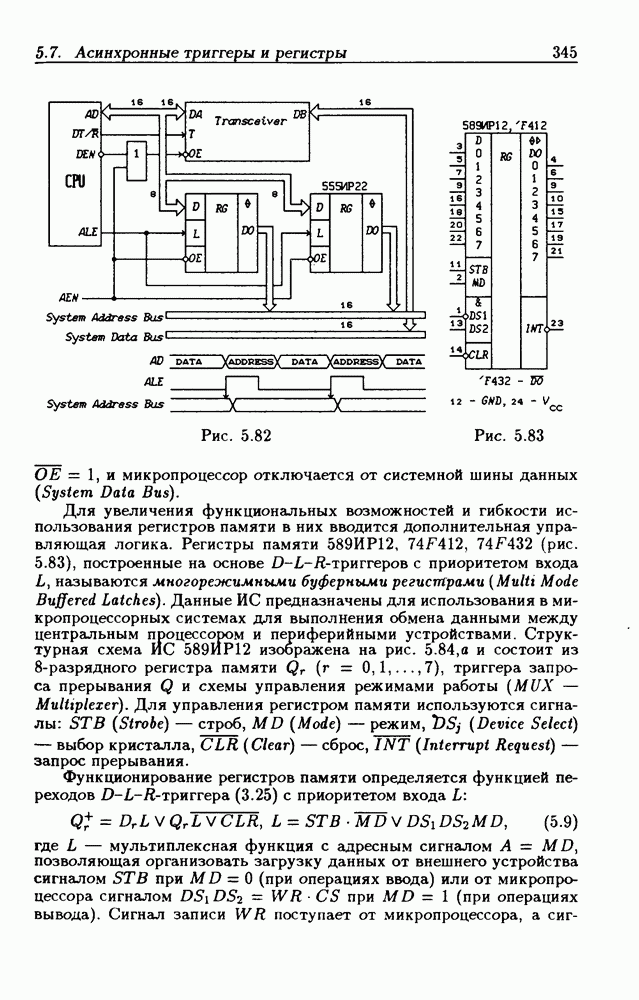
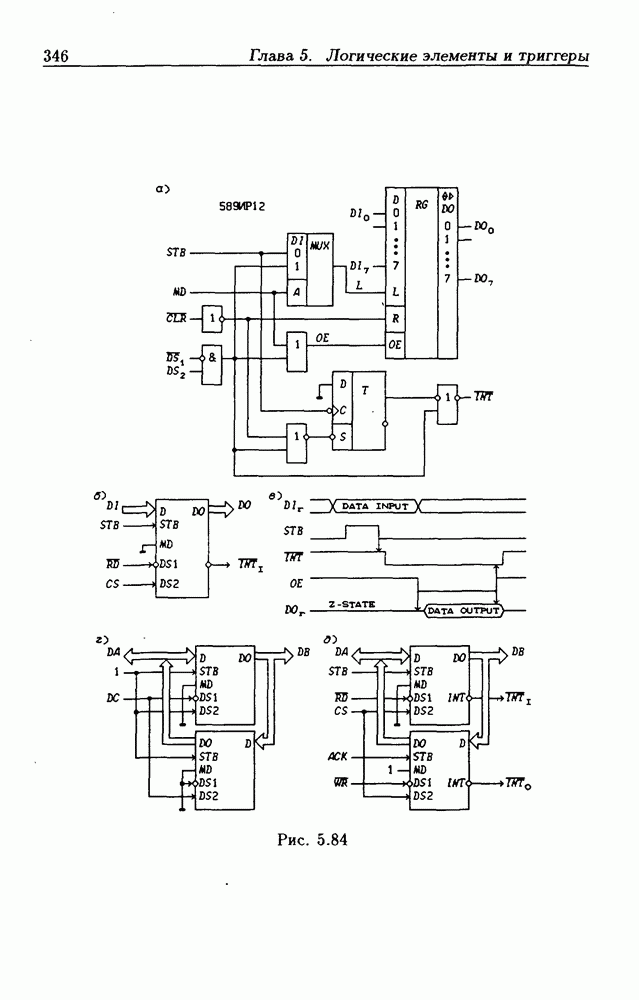
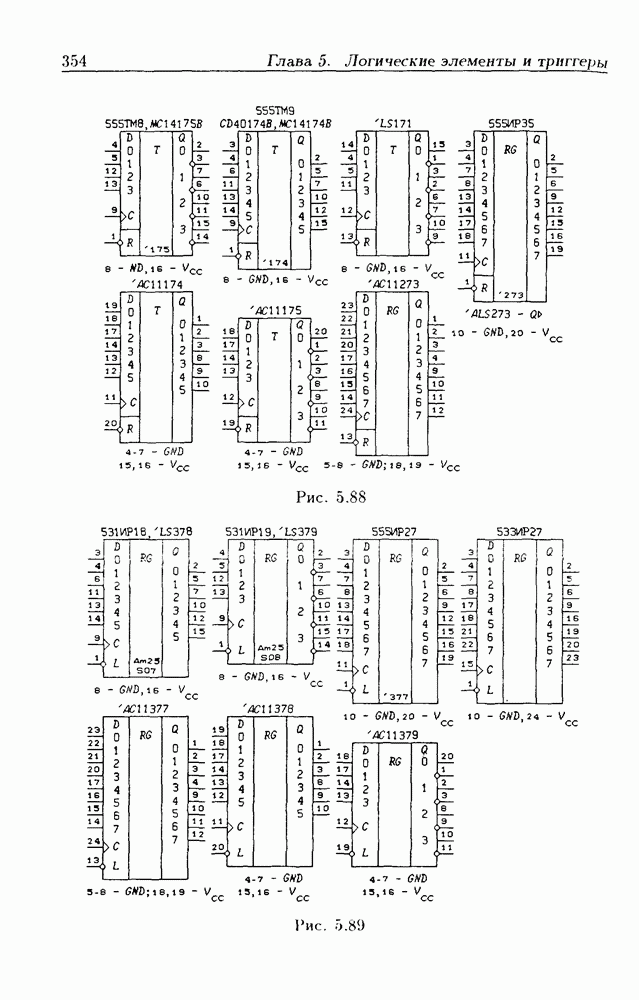
- 5.7. Асинхронные потенциальные триггеры и регистры памяти
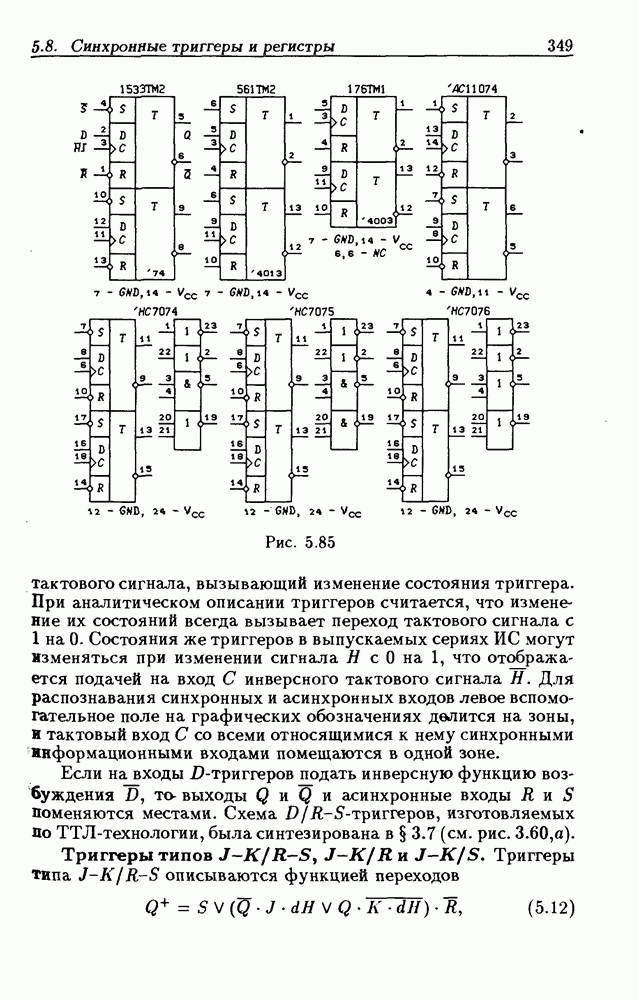
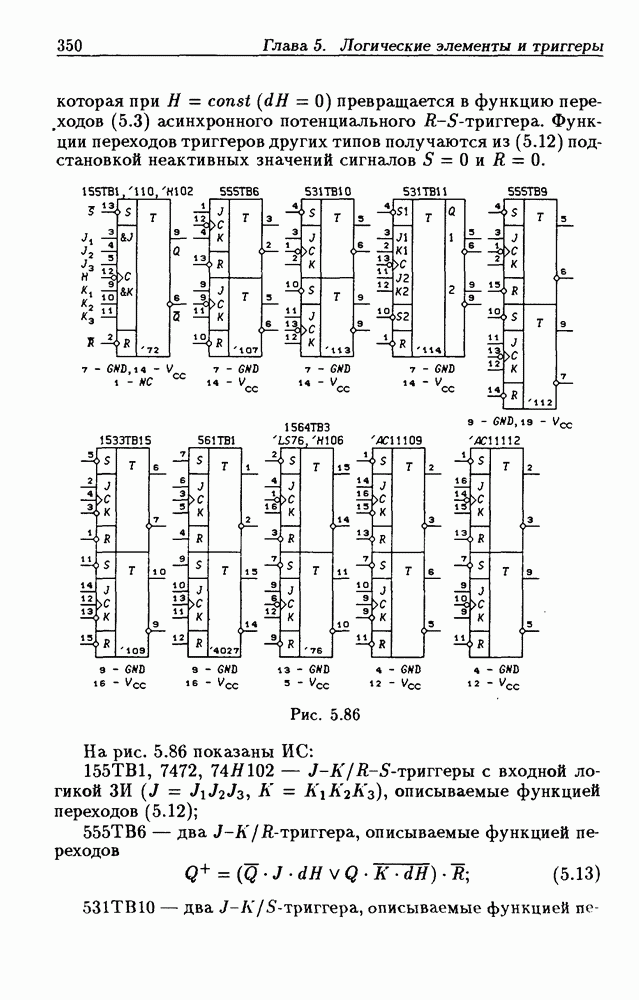
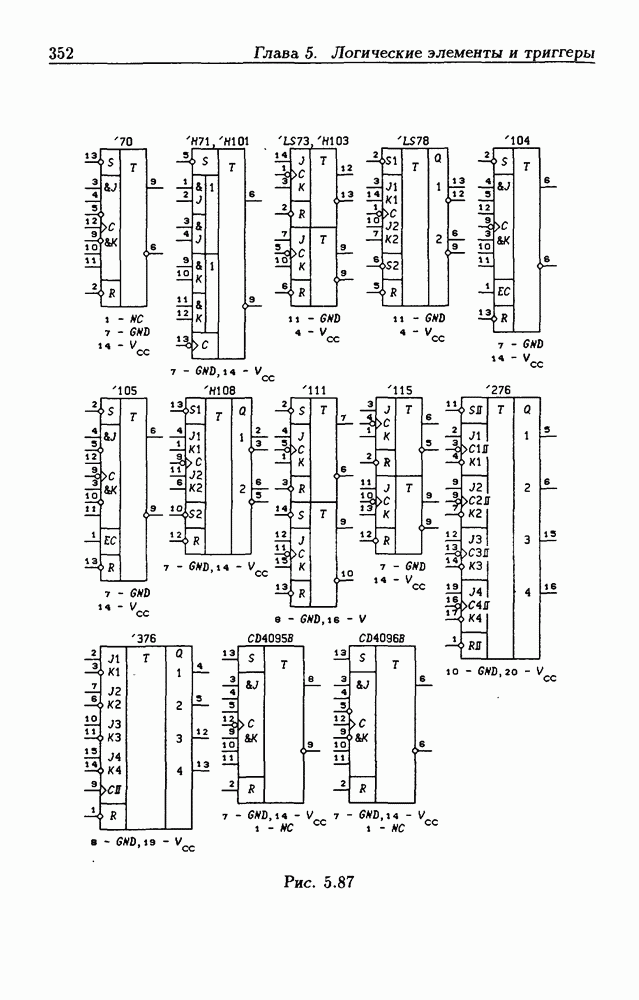
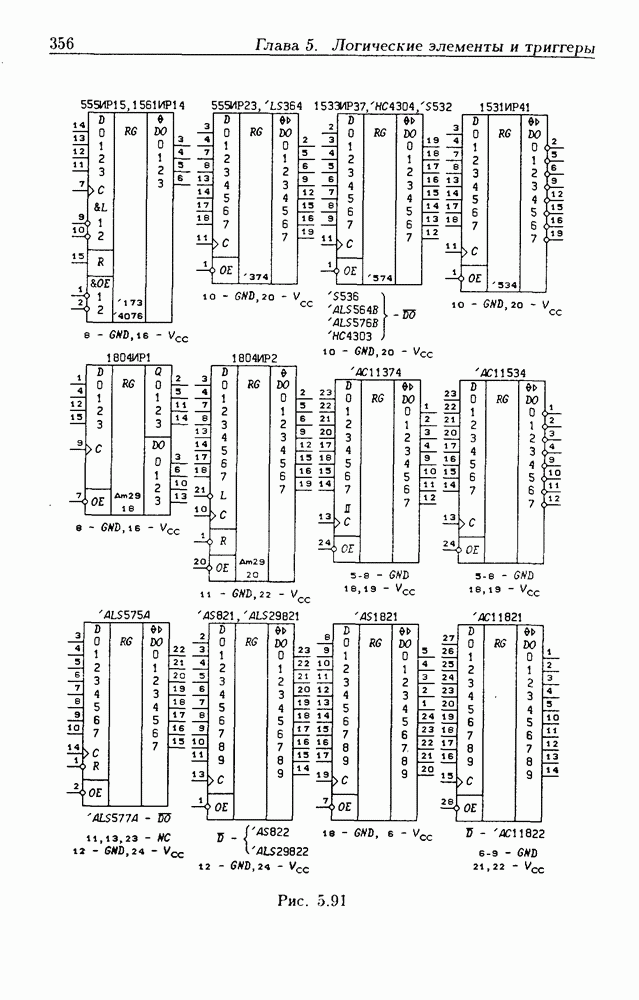
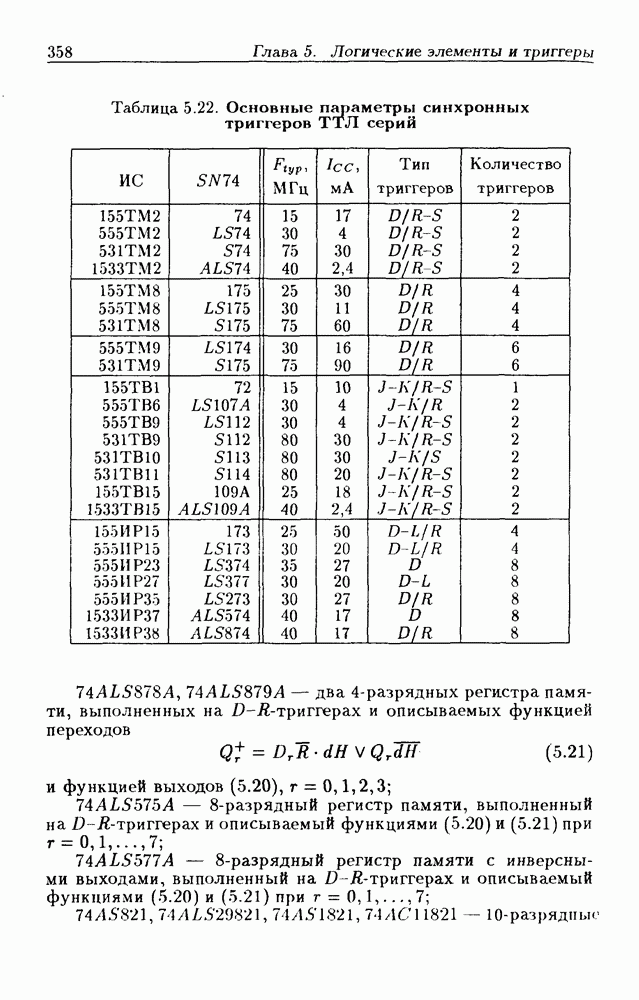
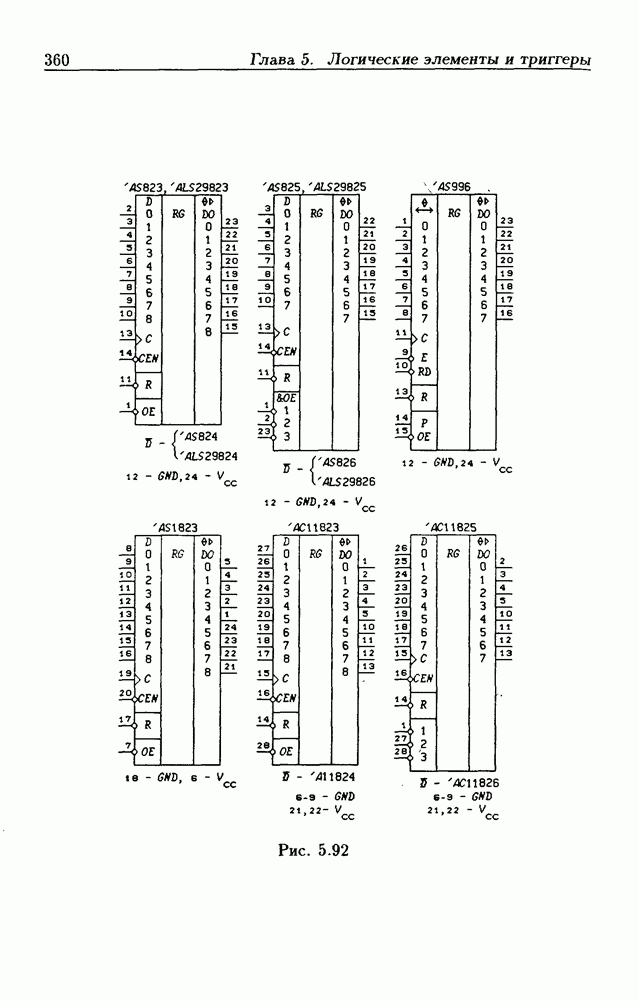
- 5.8. Синхронные триггеры и регистры памяти
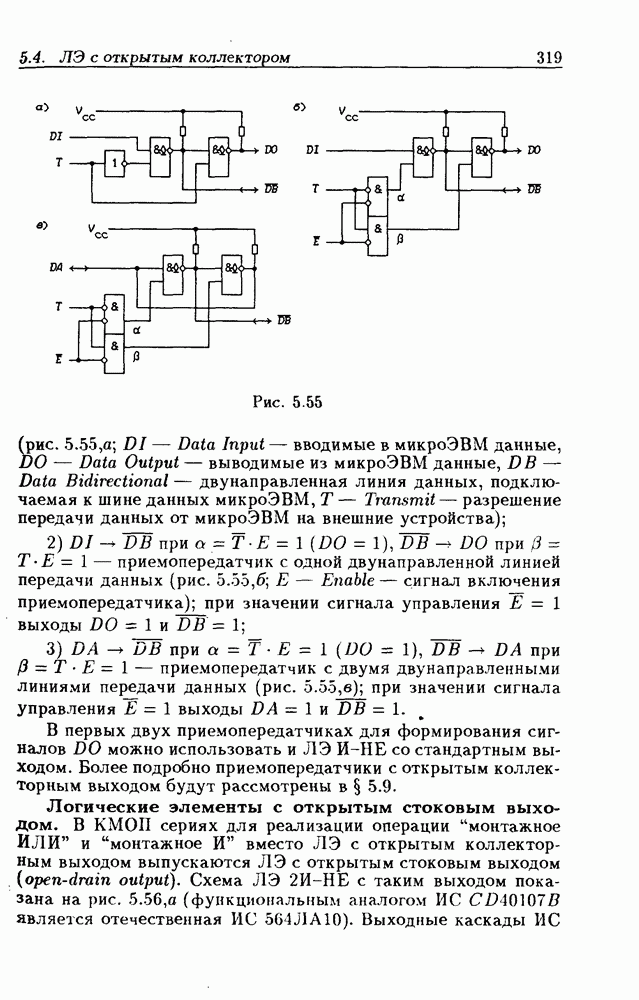
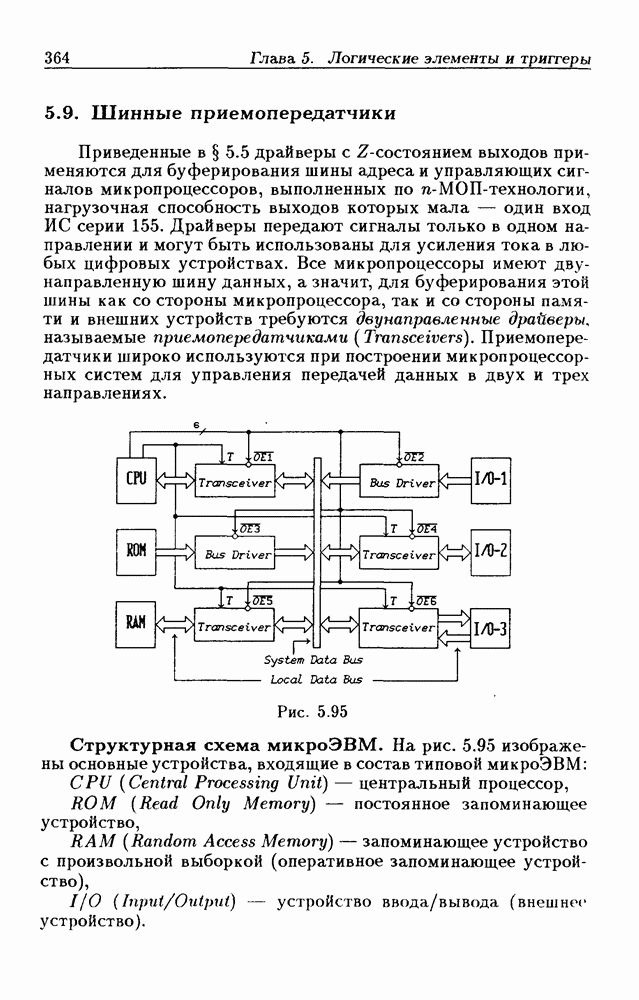
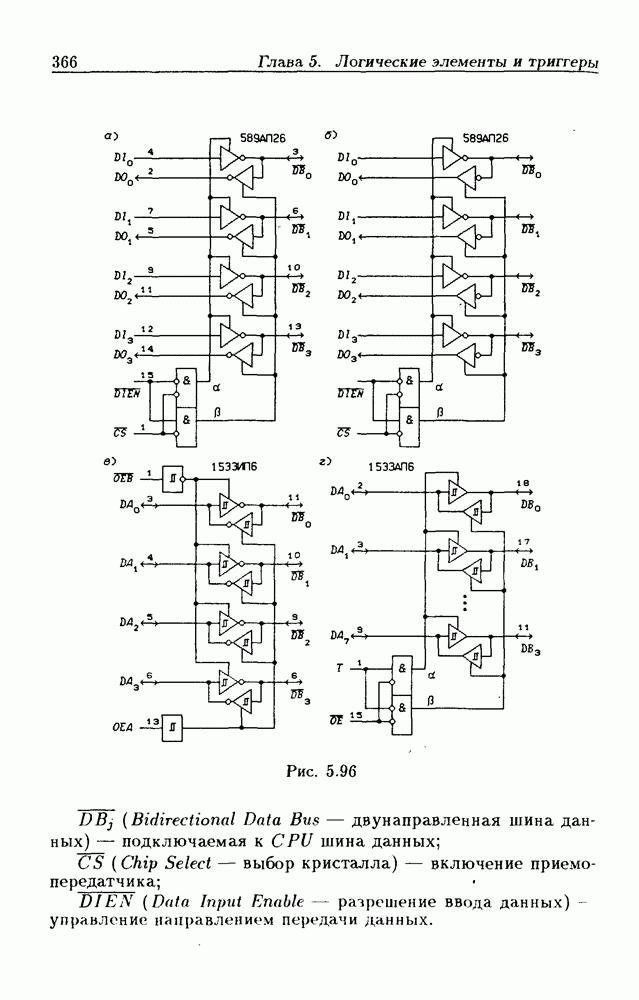
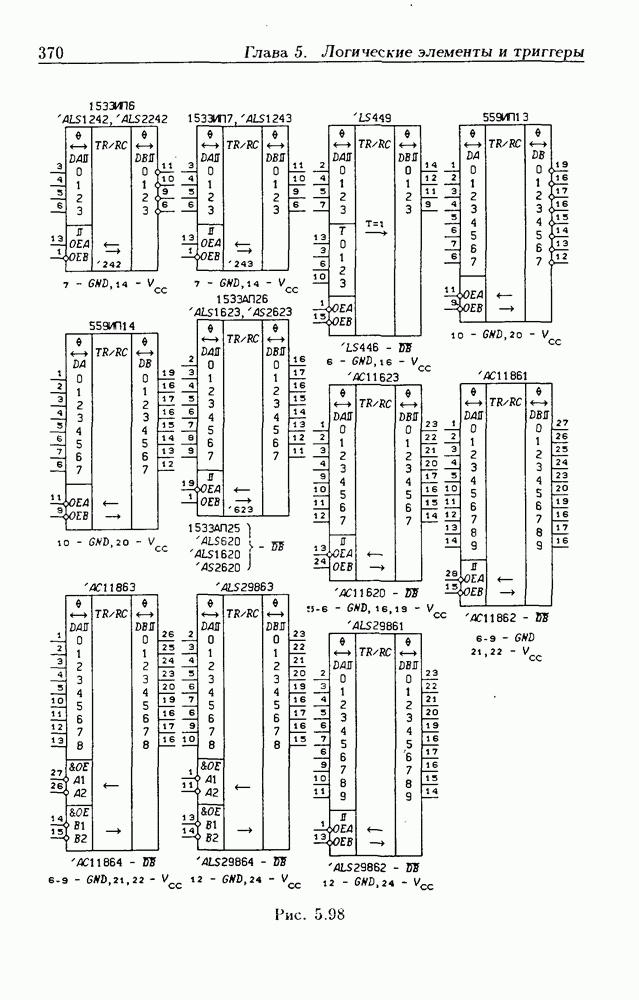
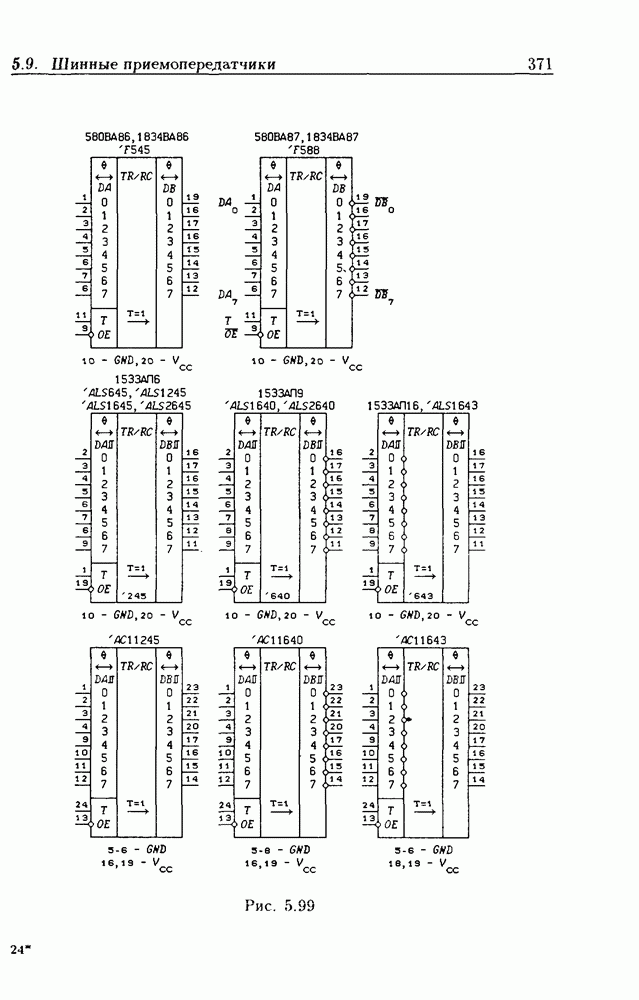
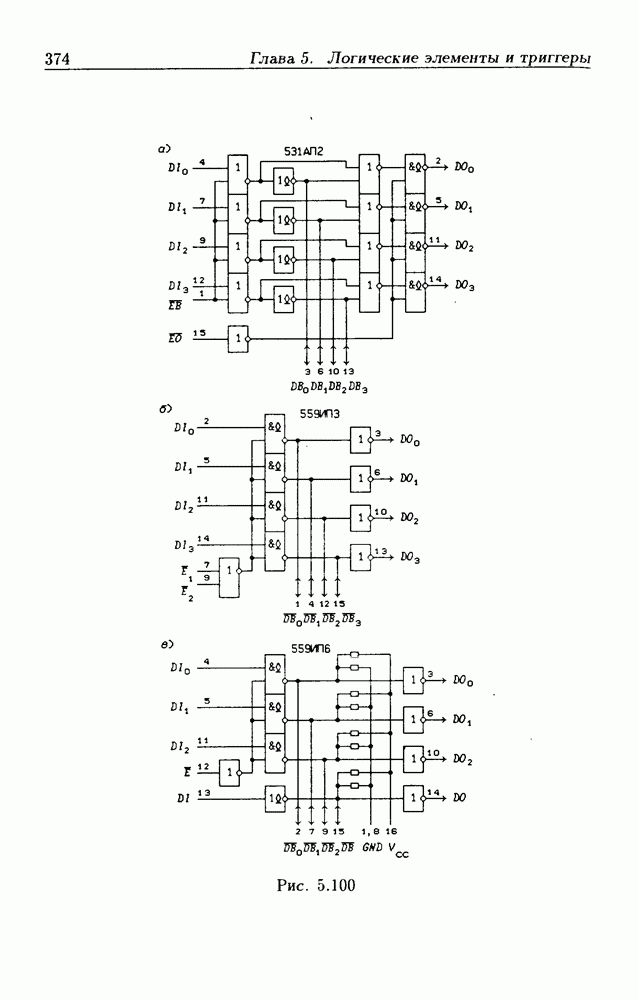
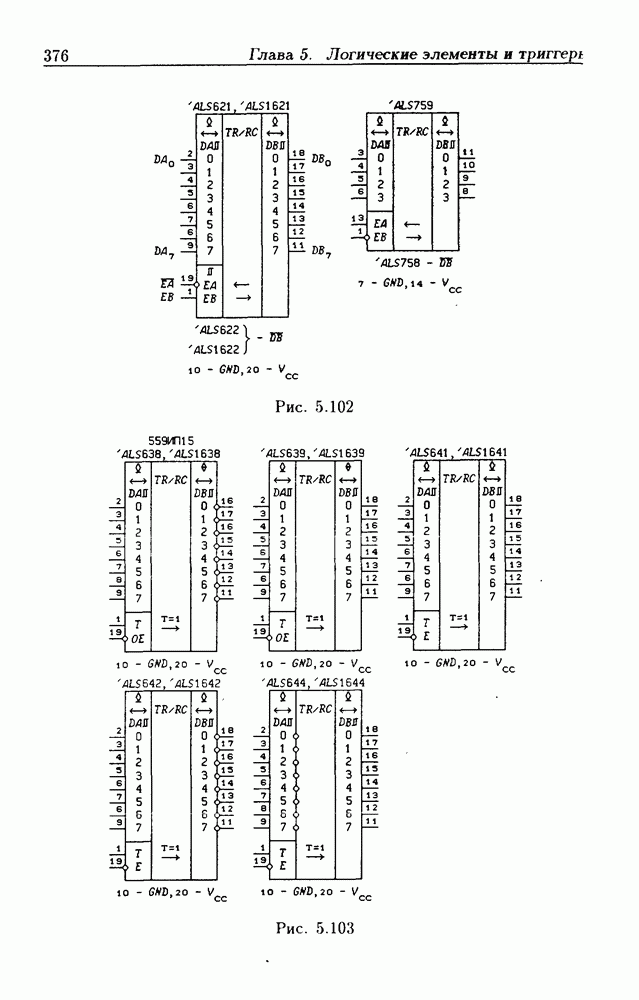
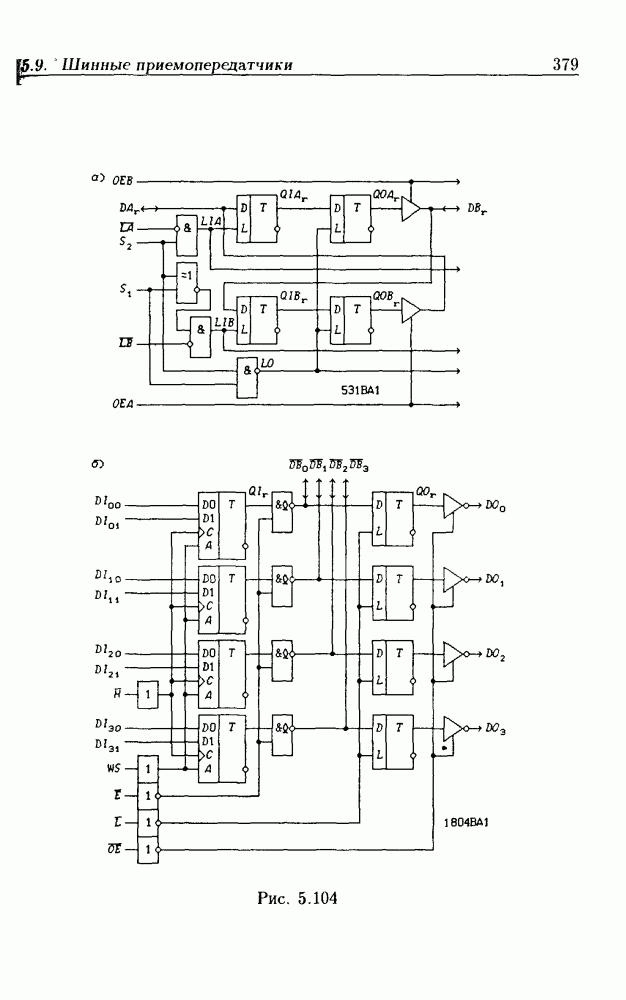
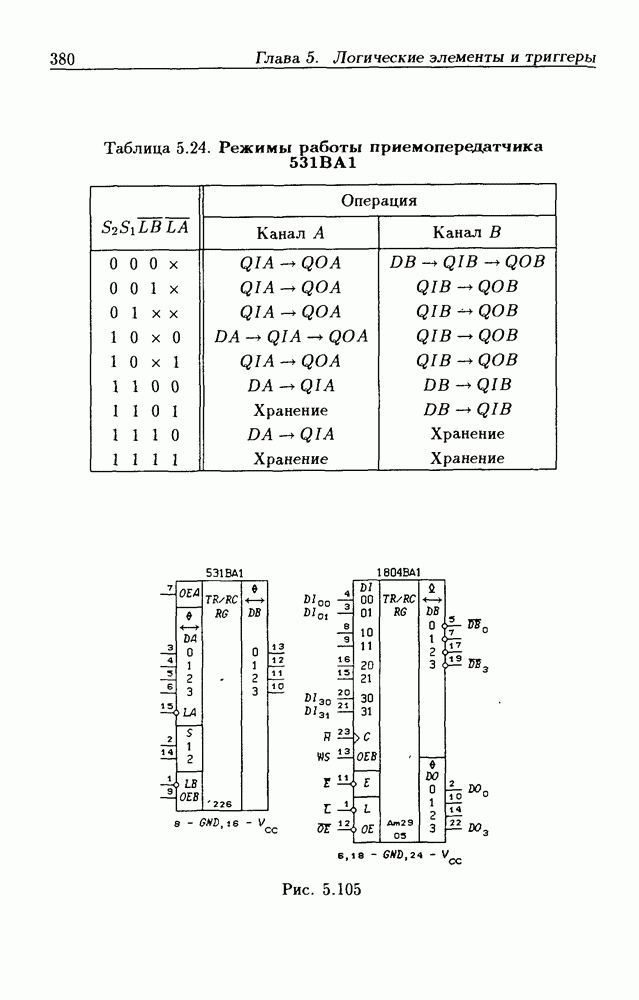
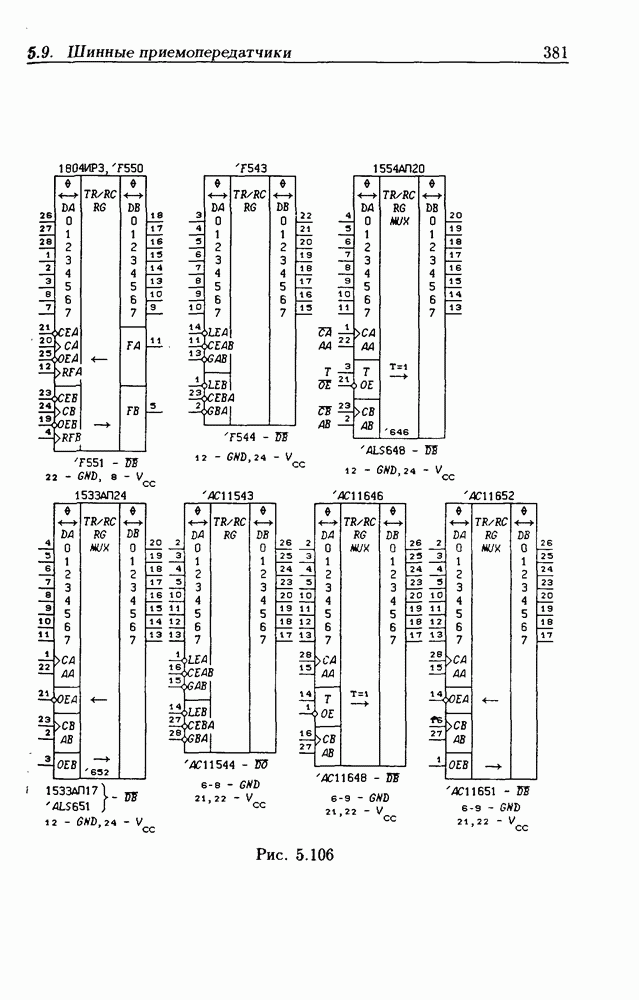
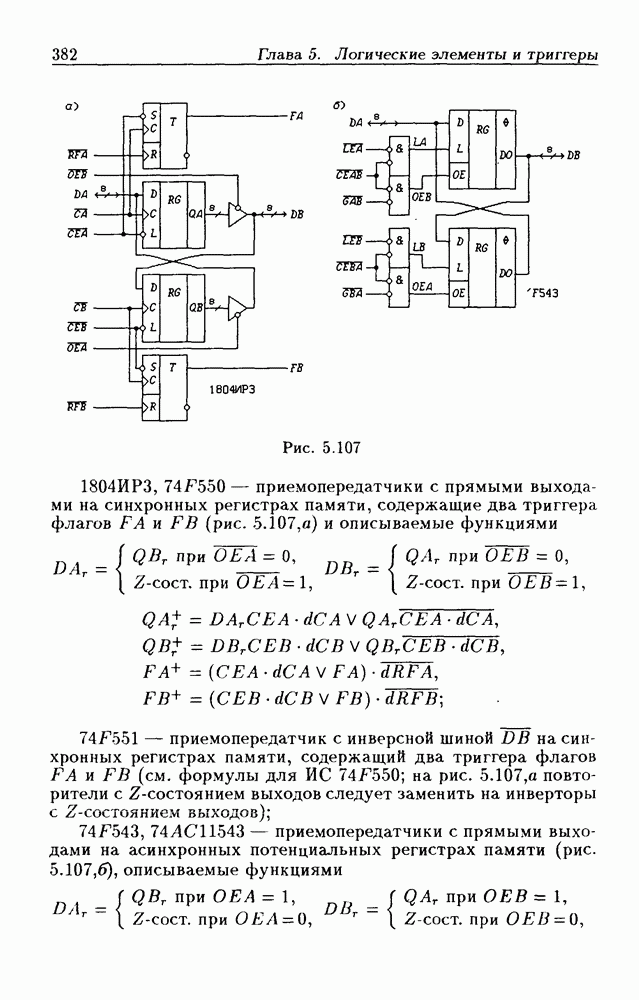
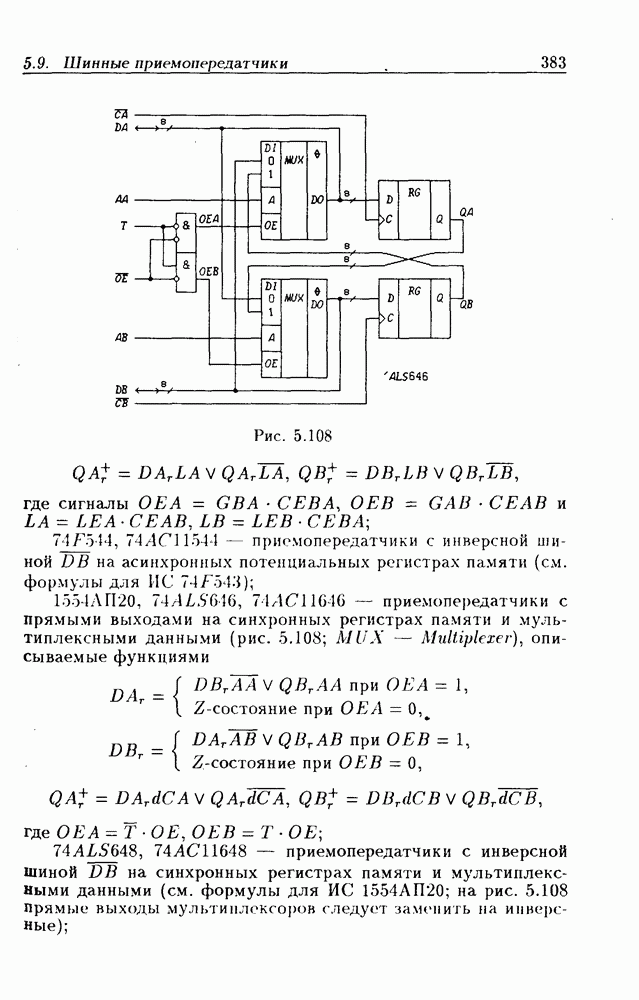
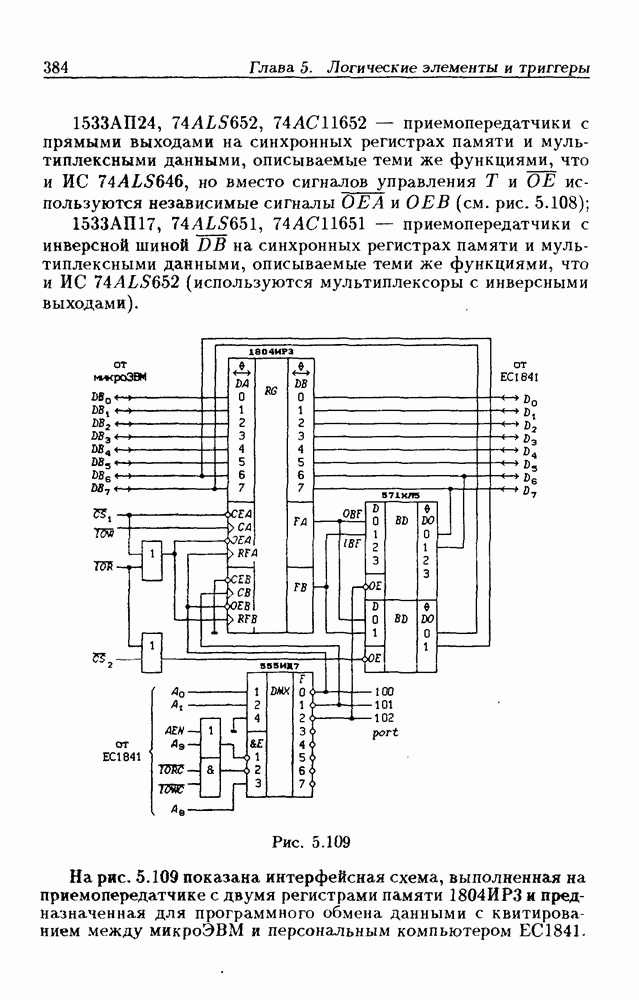
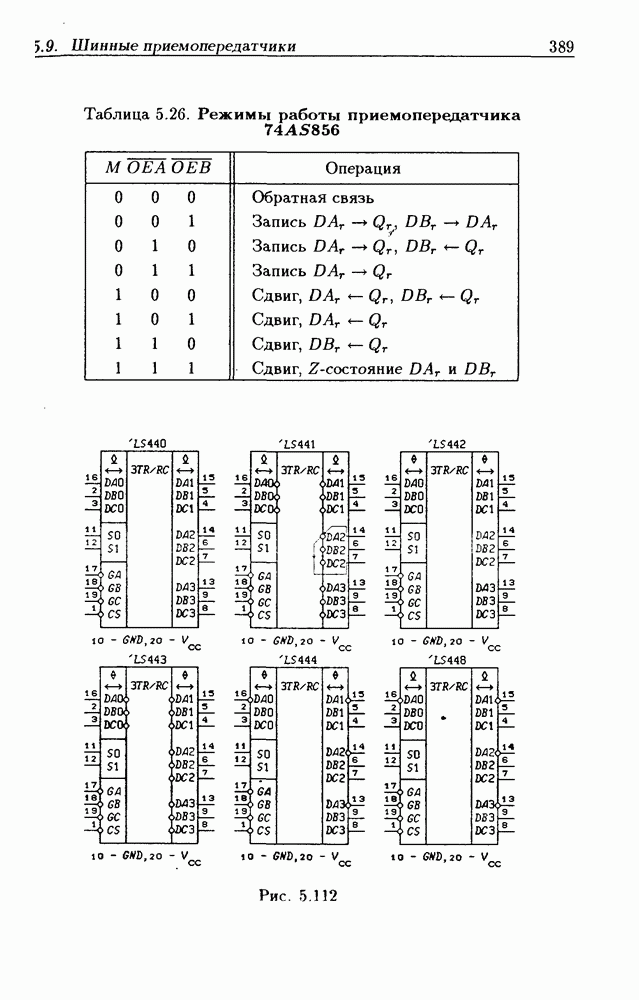
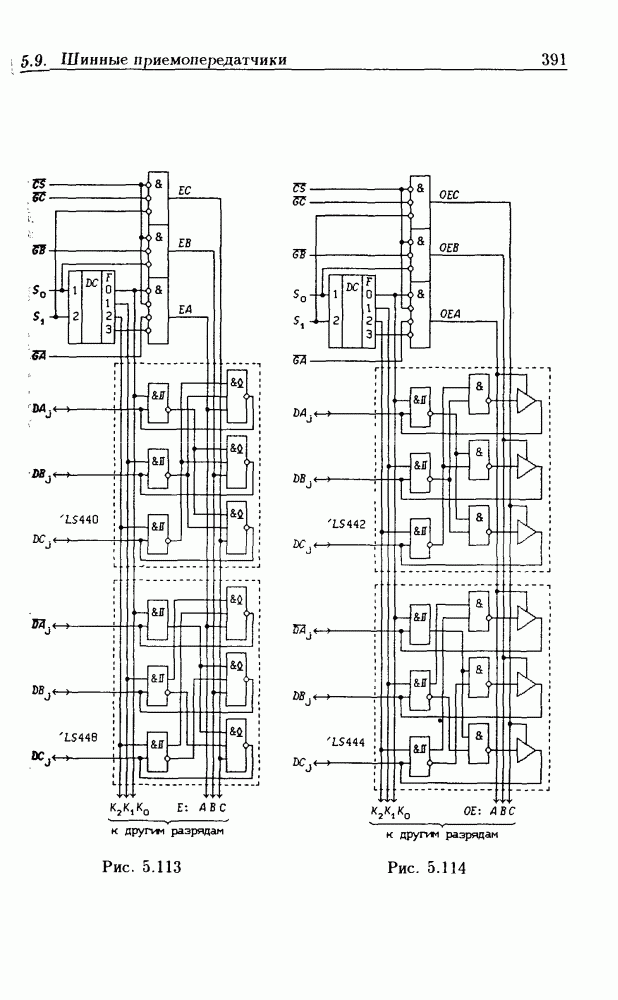
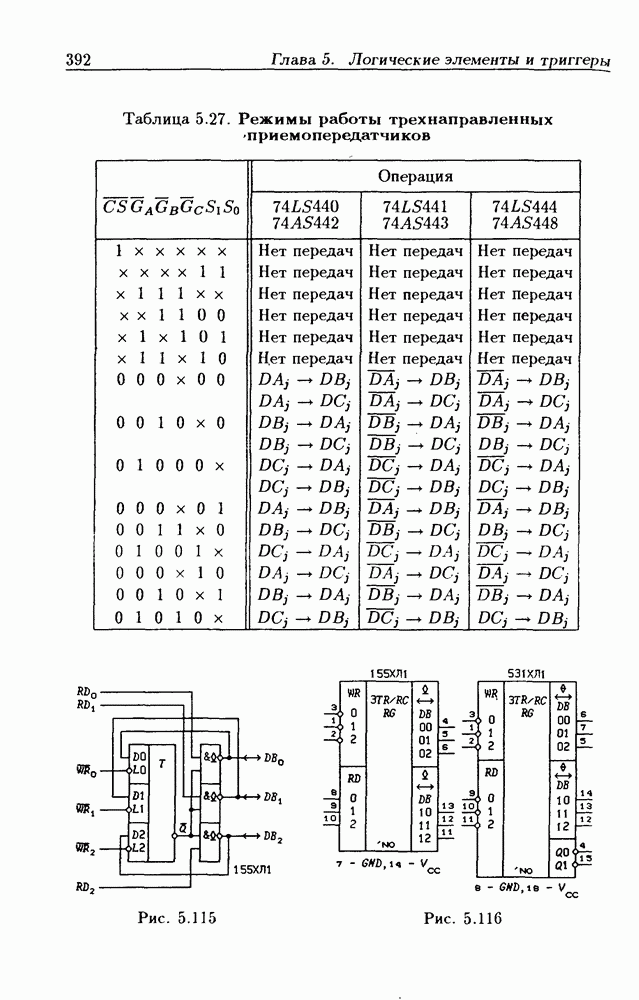
- 5.9. Шинные приемопередатчики
- Шинные приемопередатчики с Z-состоянием выхода.
- Шинные приемопередатчики с открытым коллекторным выходом.
- Шинные приемопередатчики с регистрами памяти.
- Шинные приемопередатчики со сдвигающим регистром.
- Шинные трехнаправленные приемопередатчики.
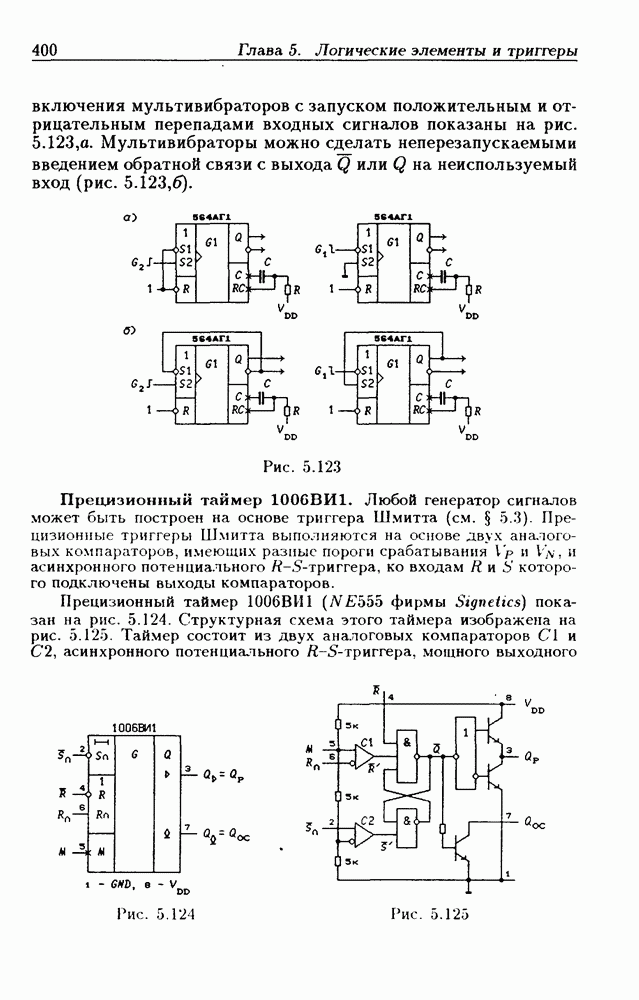
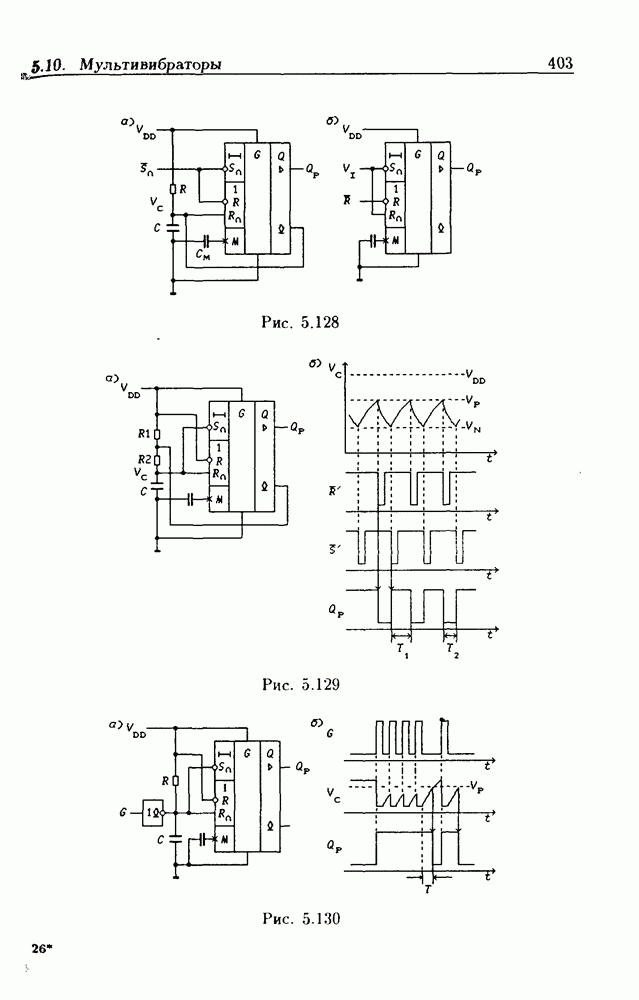
- 5.10. Мультивибраторы
- 5.11. Генераторы
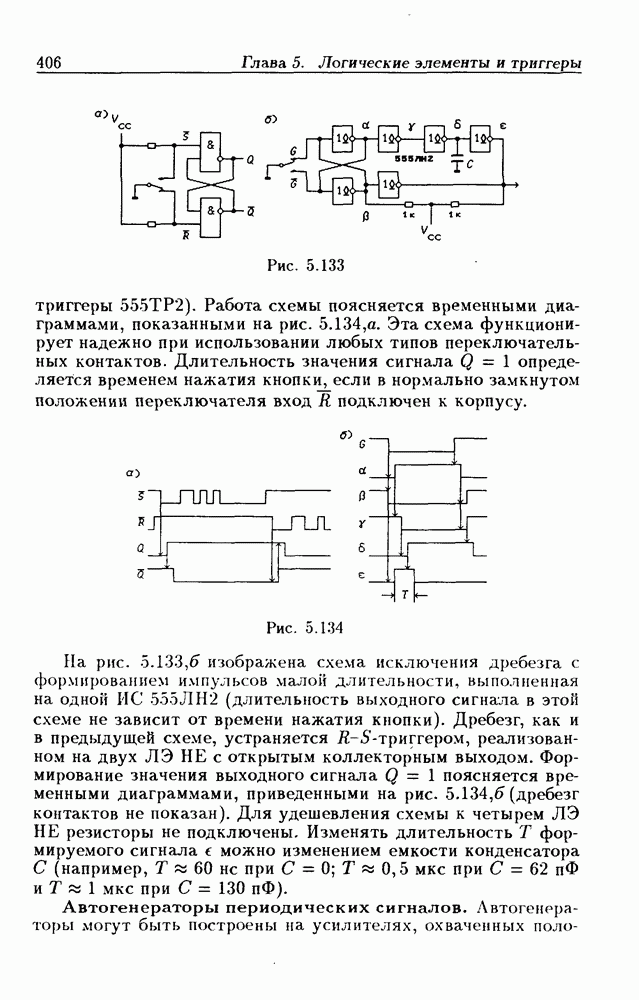
- Схемы устранения «дребезга» механических контактов.
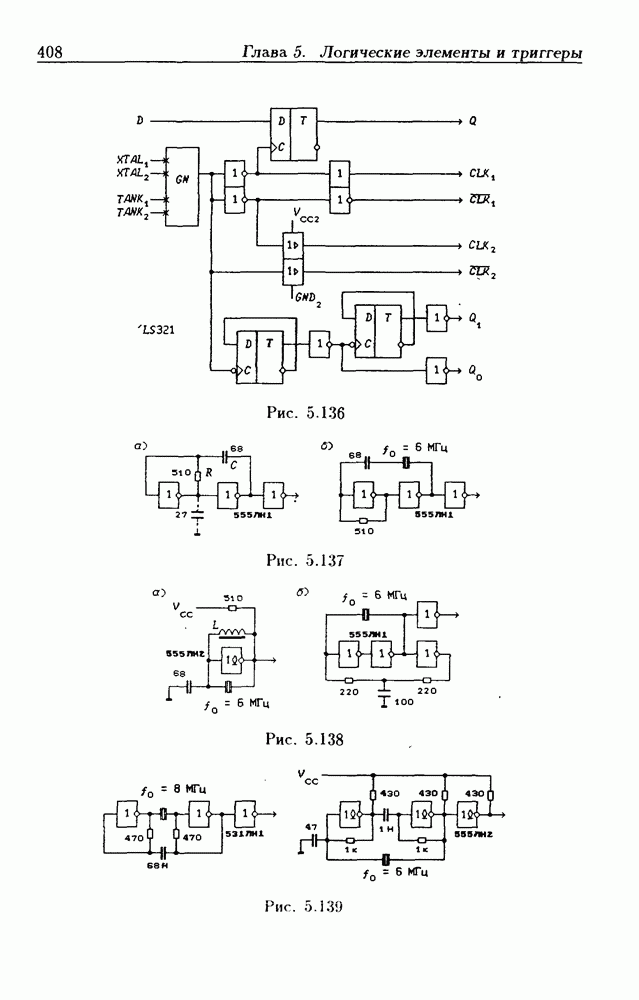
- Автогенераторы периодических сигналов.
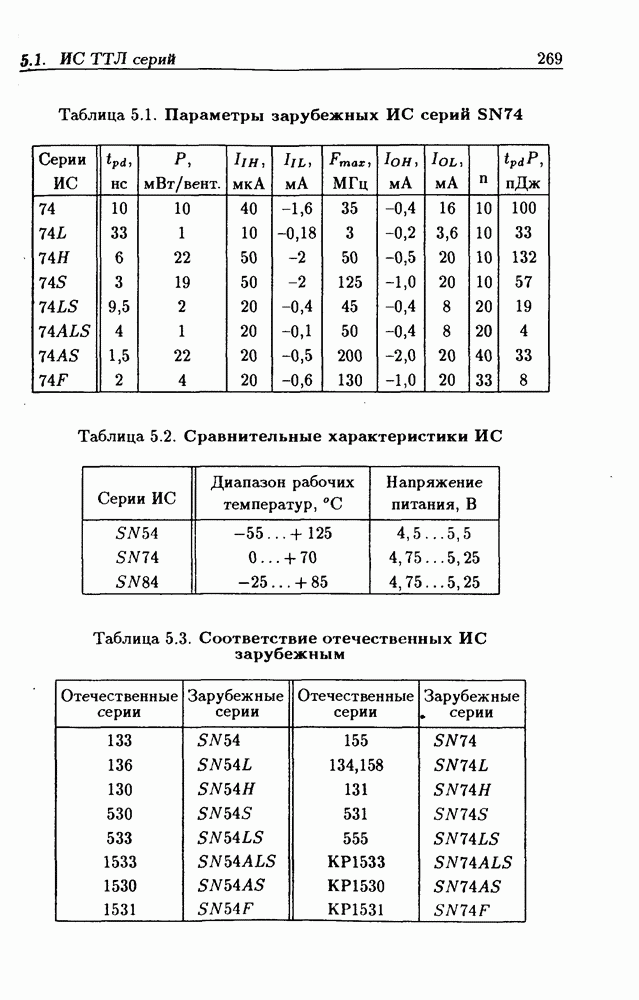
- 5.12. Рекомендации по выбору серий ИС
- Глава 6. Коммутаторы и арифметические устройства
- 6.1. Дешифраторы
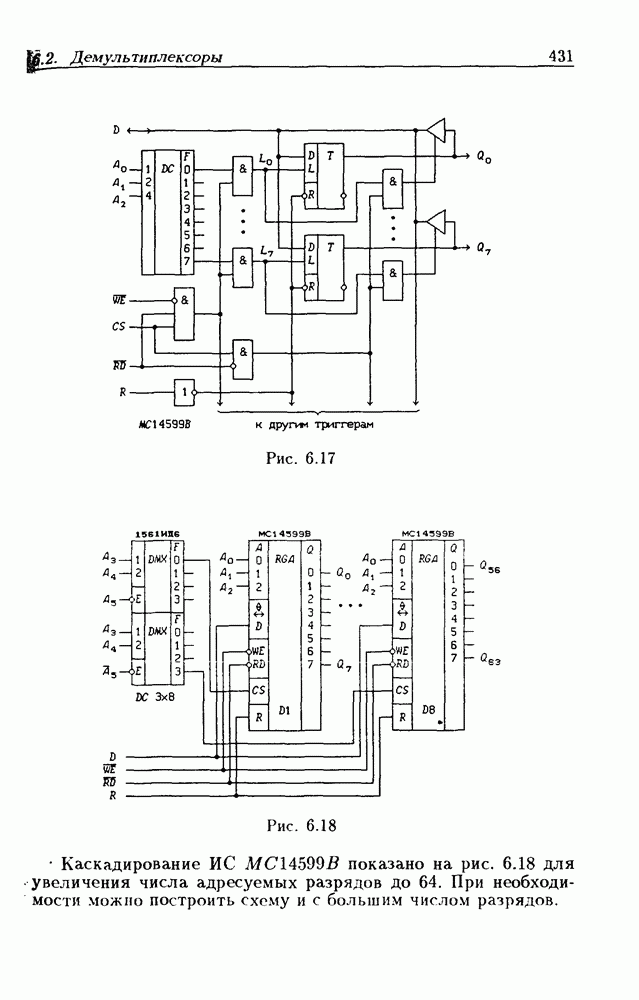
- 6.2. Демультиплексоры
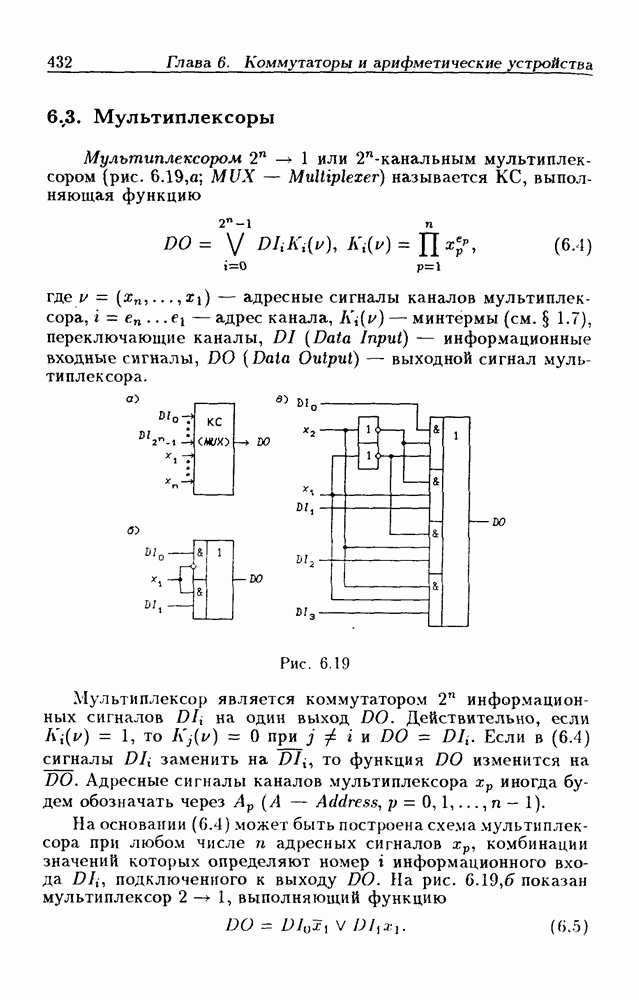
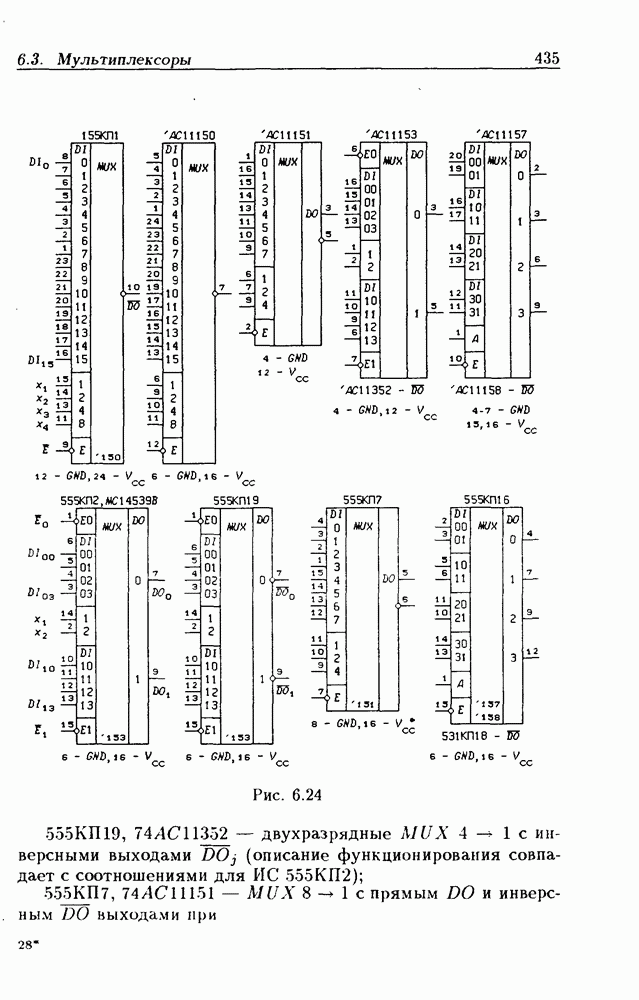
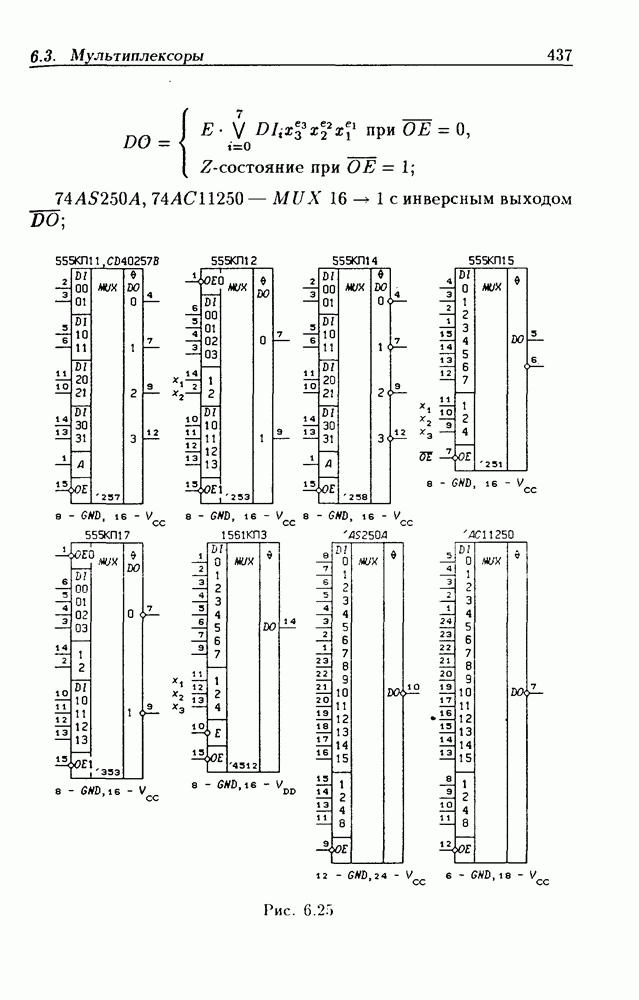
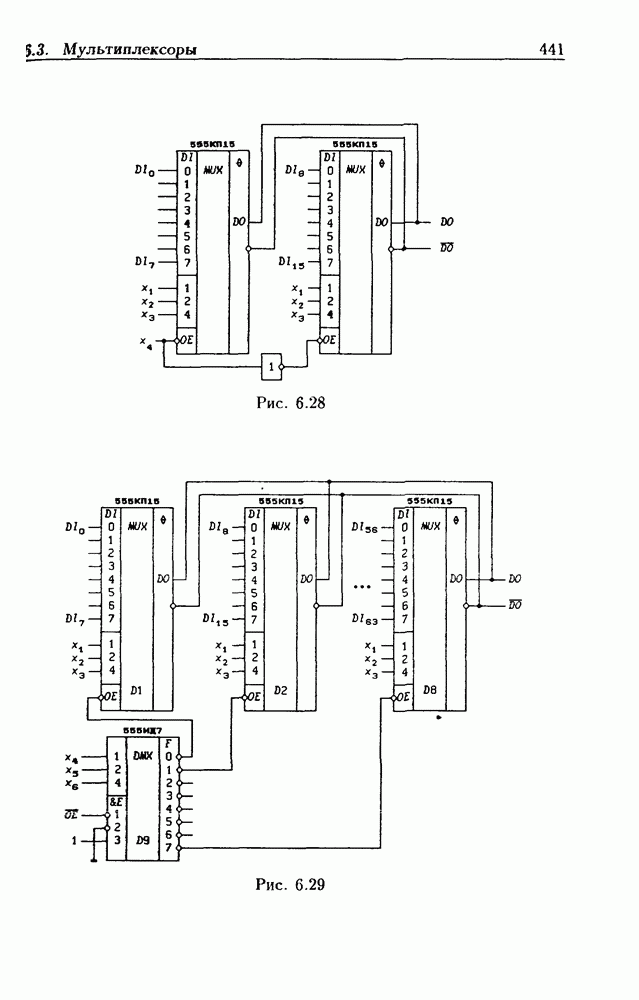
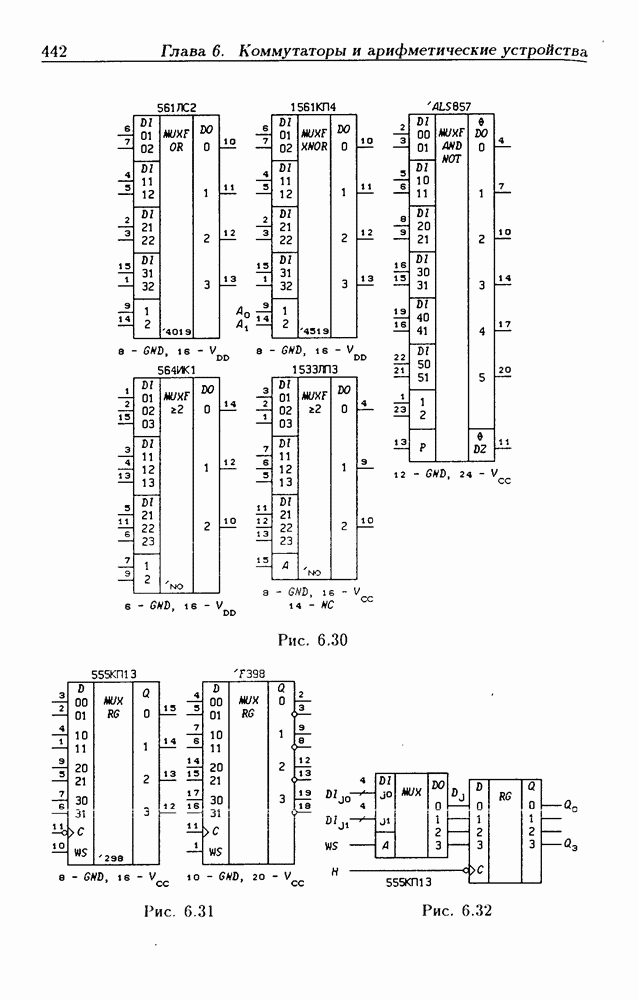
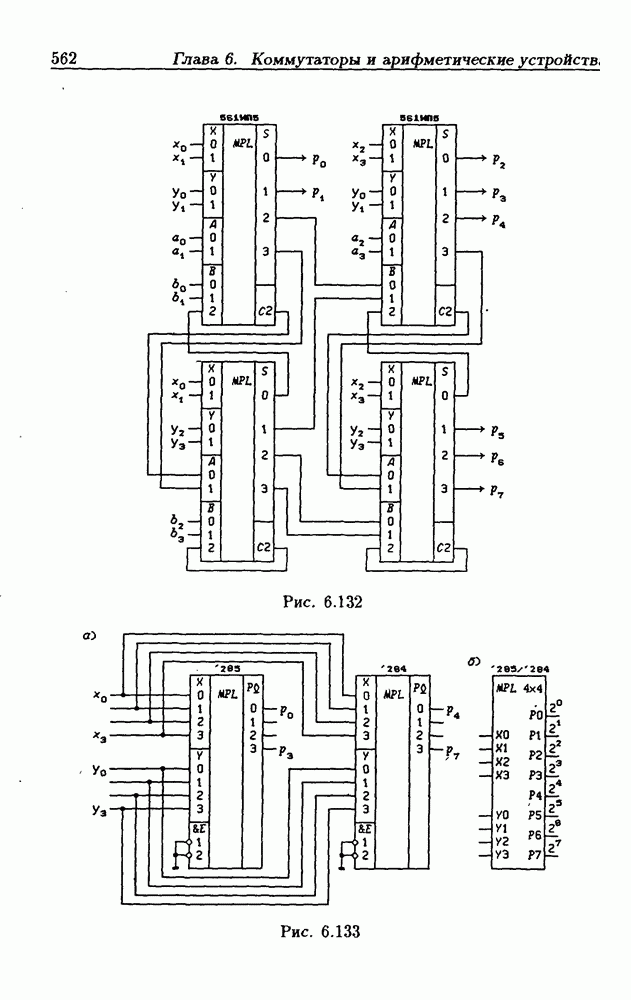
- 6.3. Мультиплексоры
- Мультиплексоры без стробирования.
- Мультиплексоры со стробированием.
- Мультиплексоры с Z-состоянием выхода.
- Каскадирование мультиплексоров.
- Функциональные мультиплексоры.
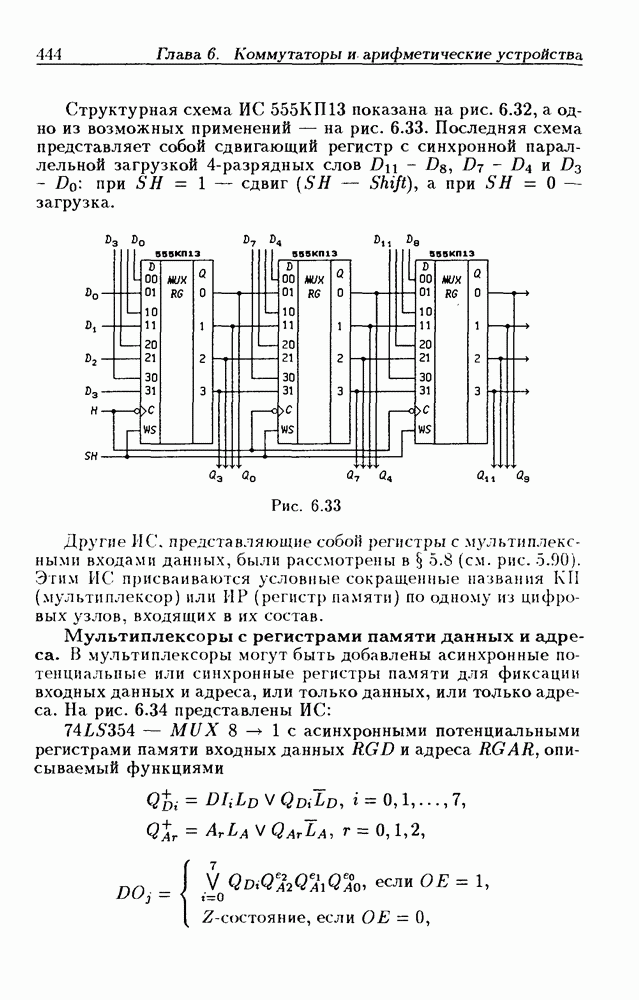
- Регистры памяти с мультиплексными входами данных.
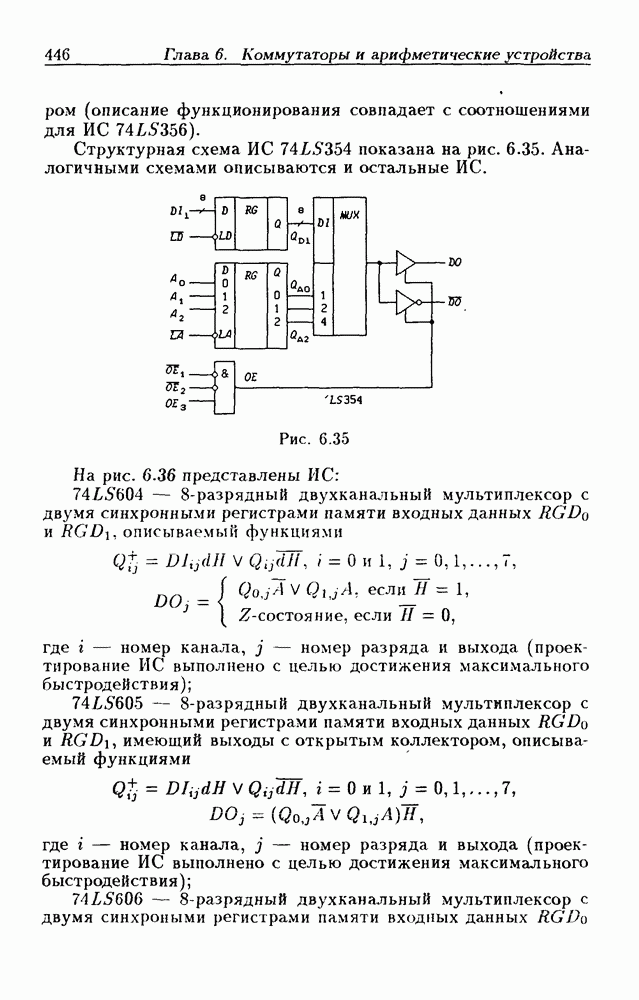
- Мультиплексоры с регистрами памяти данных и адреса.
- Сдвигающие мультиплексоры.
- 6.4. Синтез комбинационных схем и цифровых автоматов на мультиплексорах
- Синтез схем на 8-канальных мультиплексорах.
- Синтез на двухразрядных 4-канальных мультиплексорах.
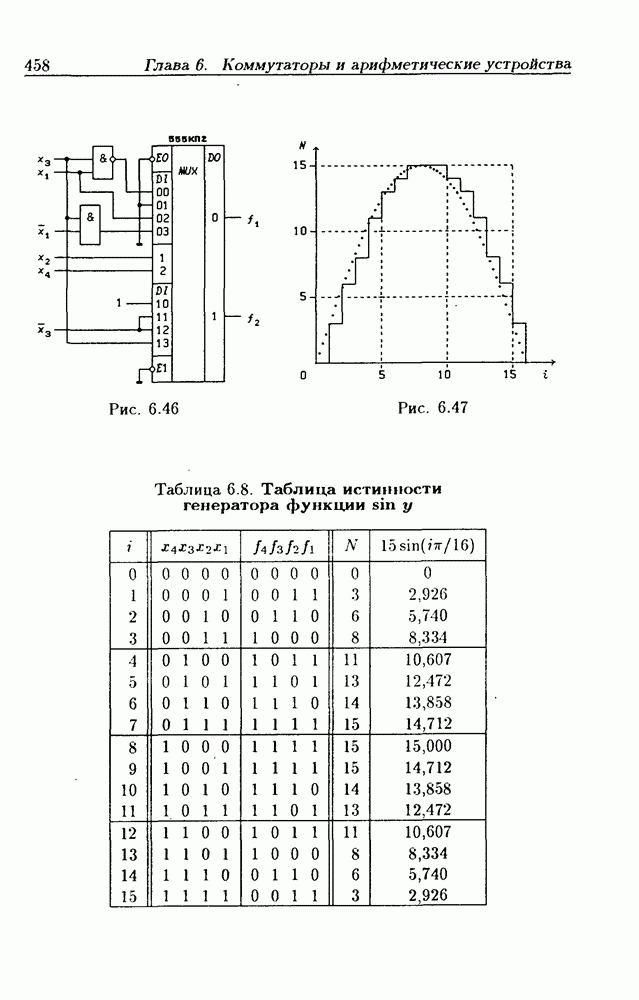
- Синтез генератора синусоидальной функции на мультиплексорах.
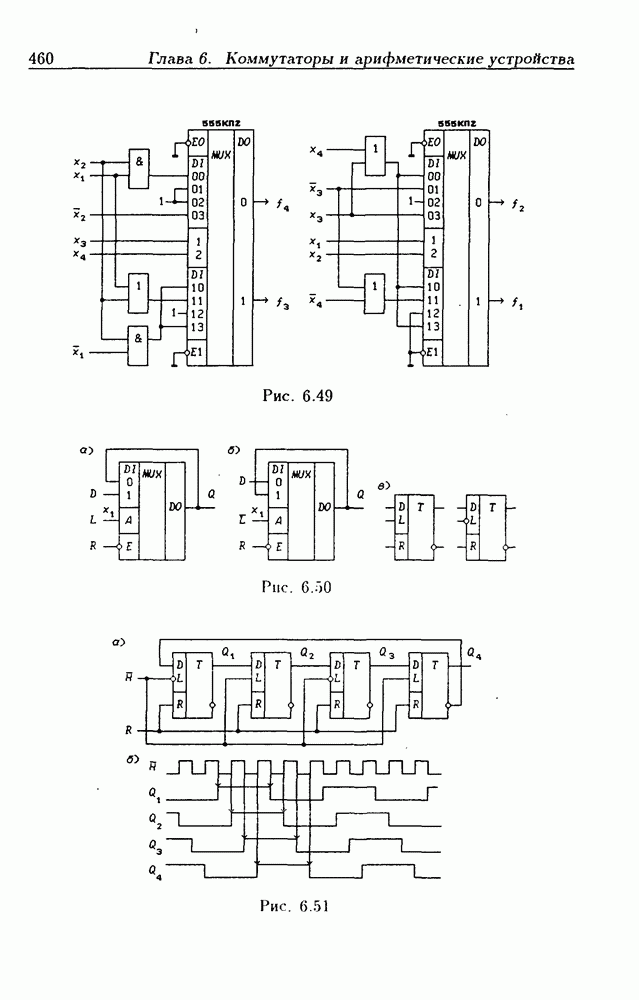
- Синтез триггеров на мультиплексорах.
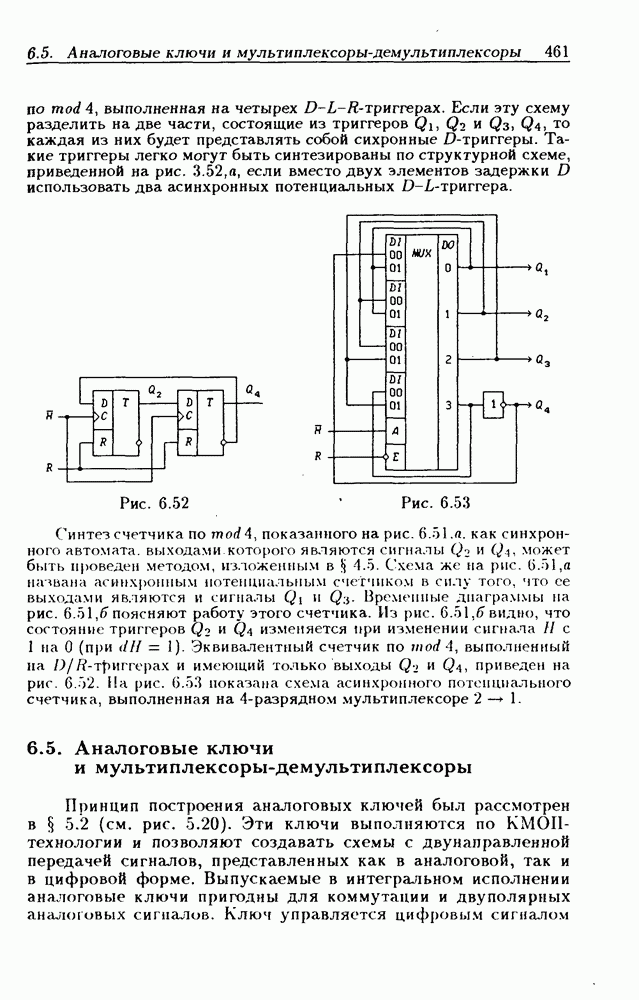
- Синтез счетчиков на мультиплексорах.
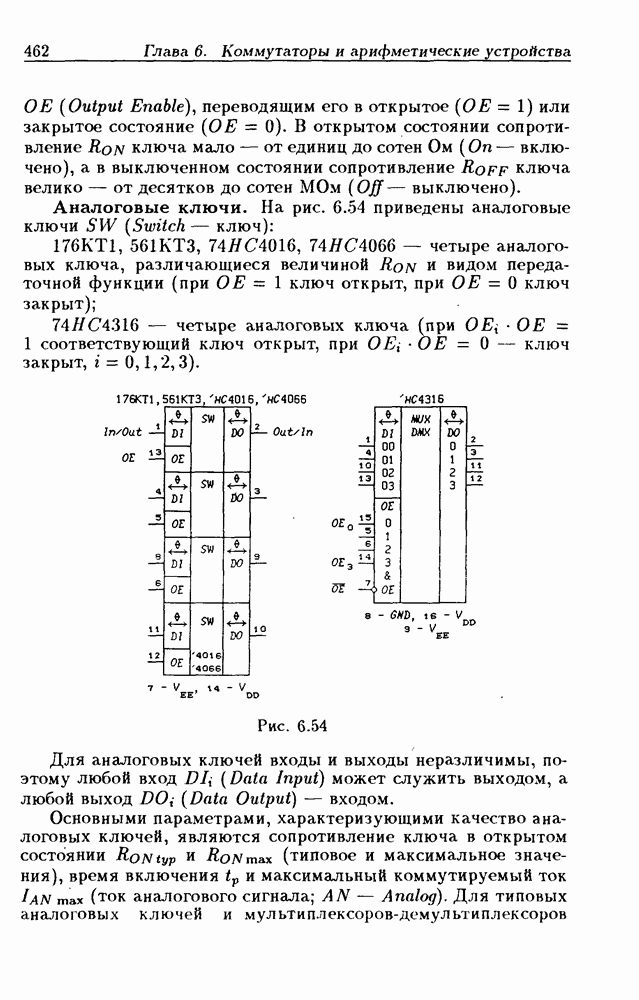
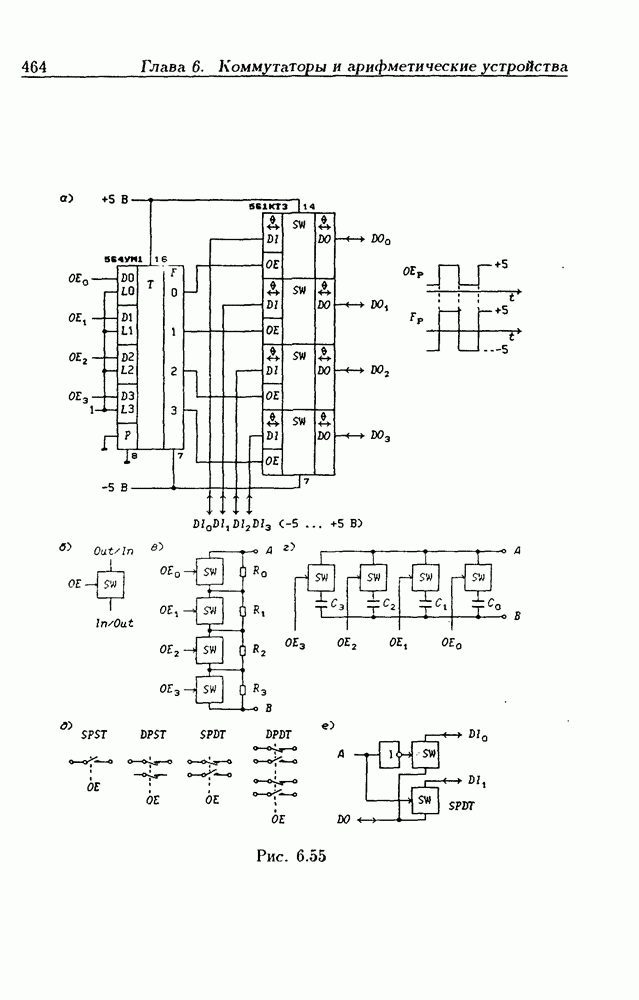
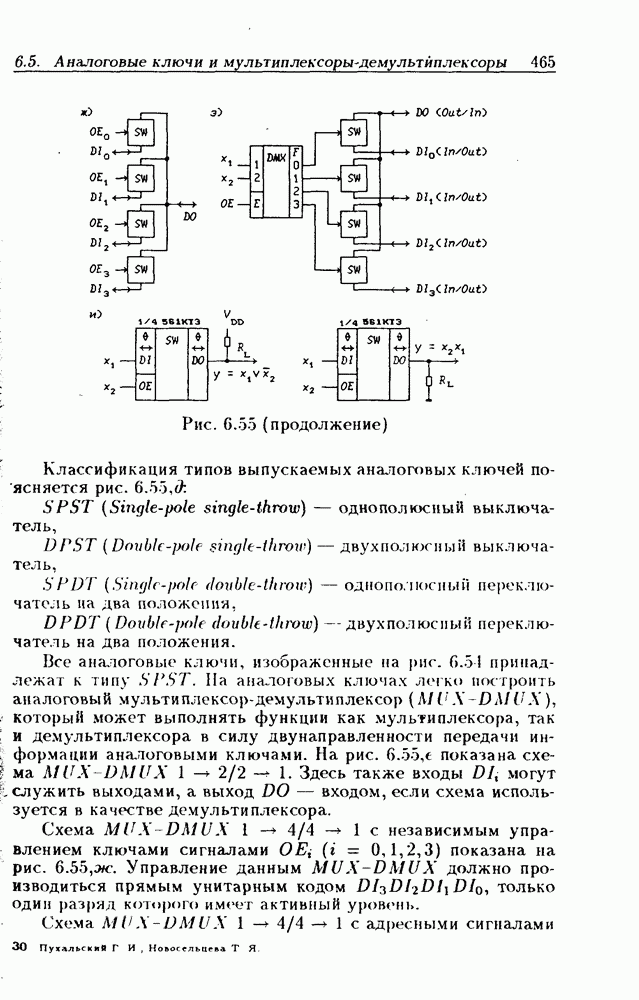
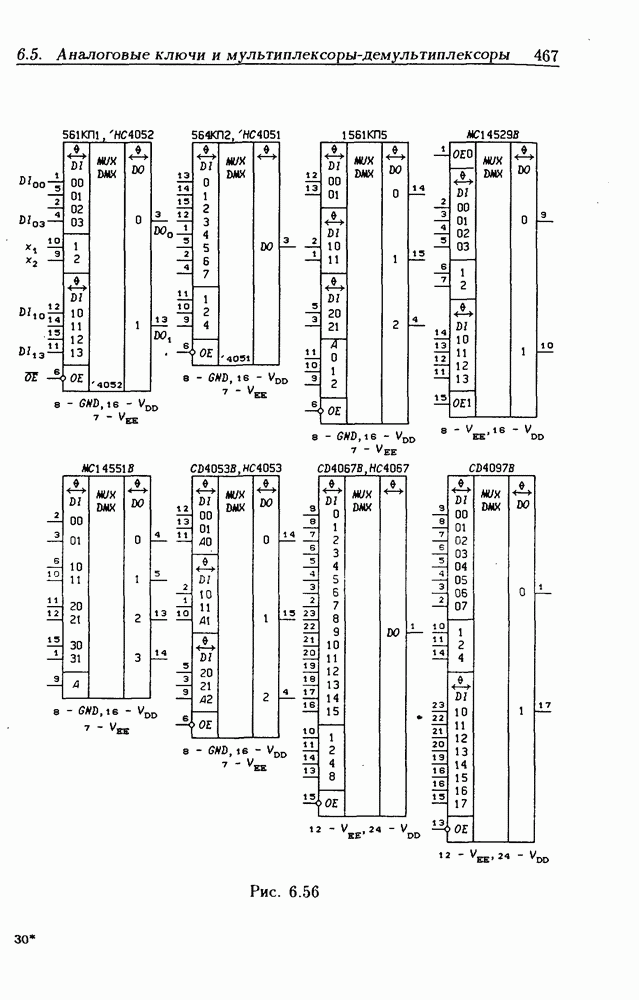
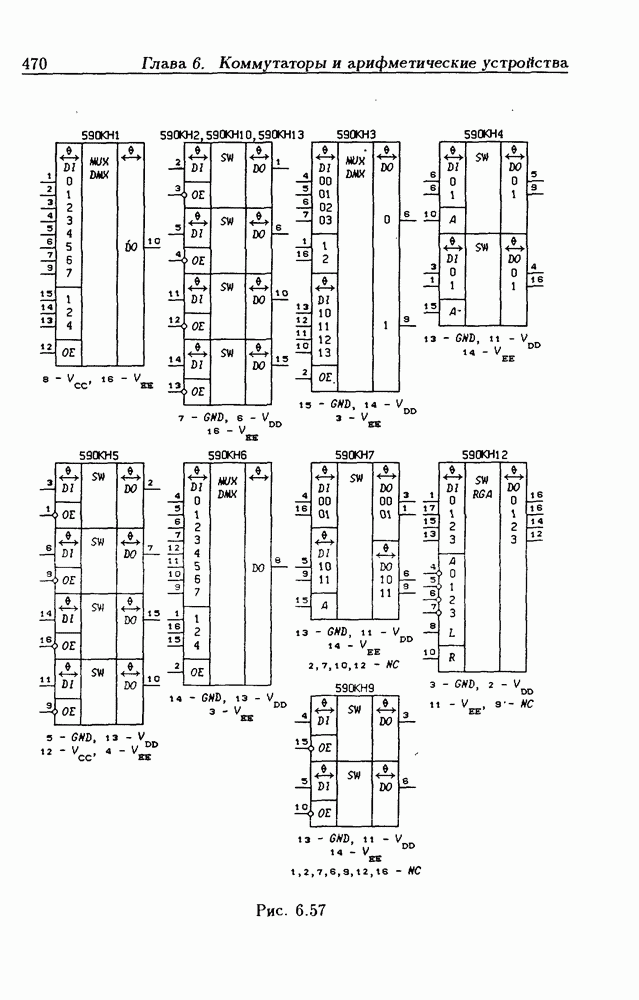
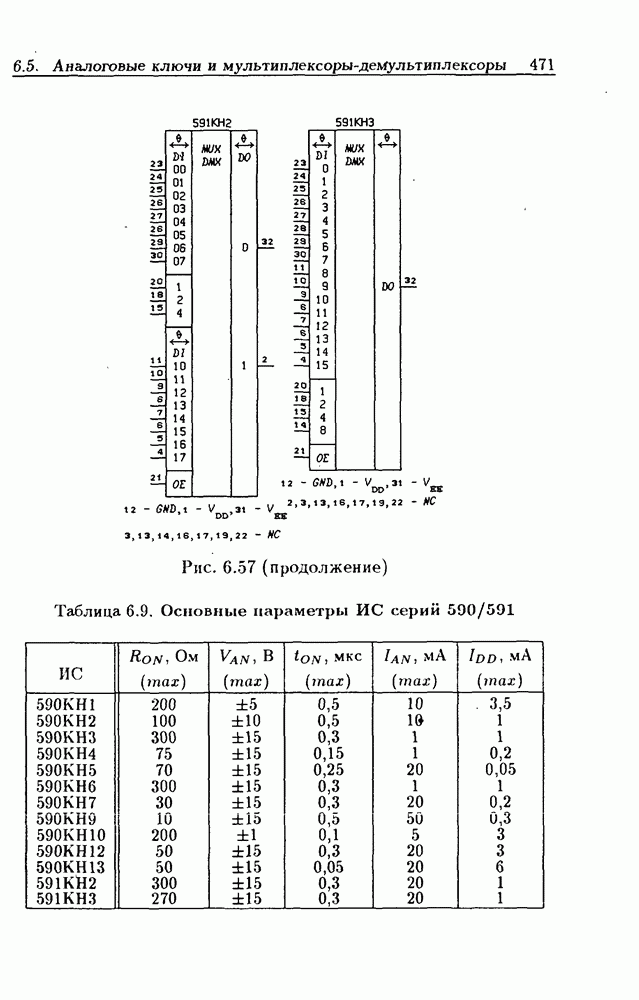
- 6.5. Аналоговые ключи и мультиплексоры-демультиплексоры
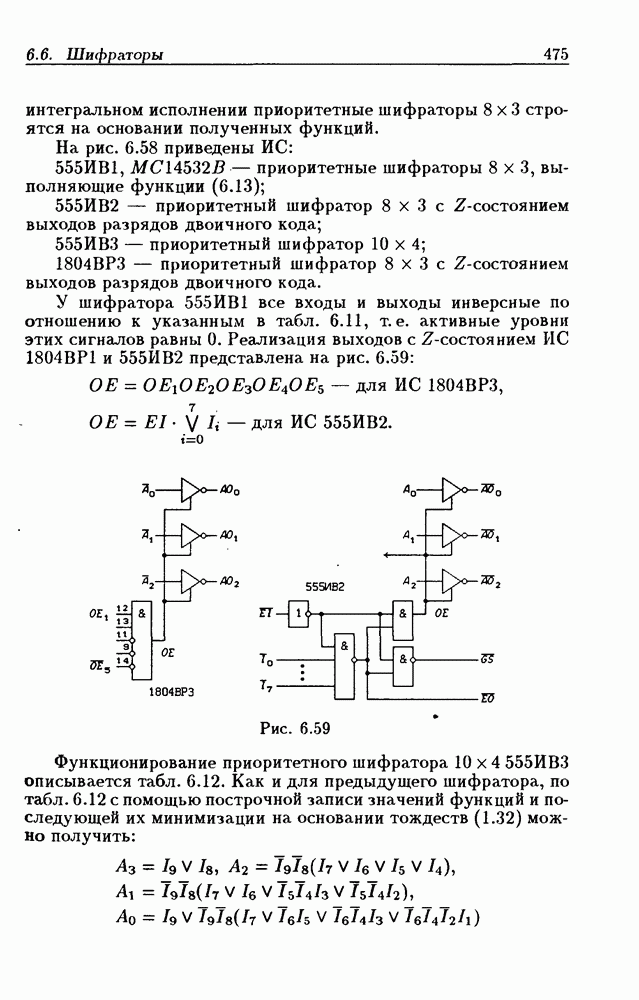
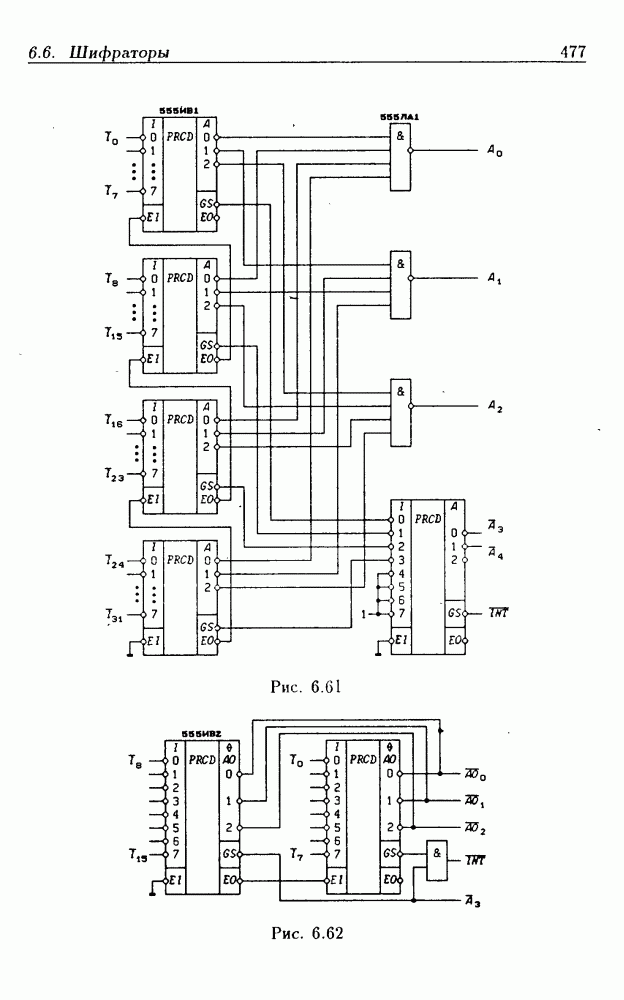
- 6.6. Шифраторы
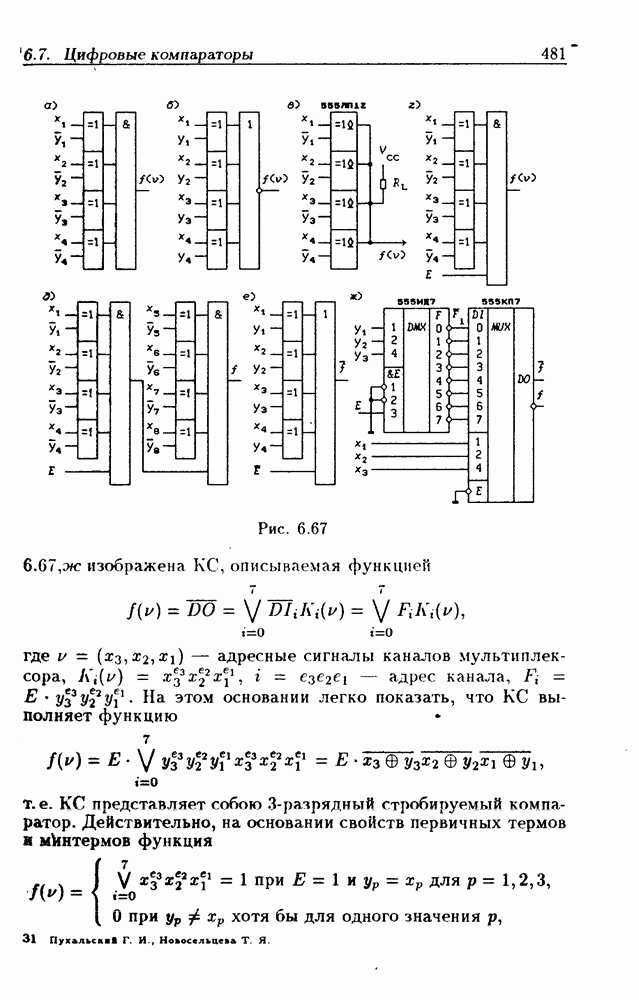
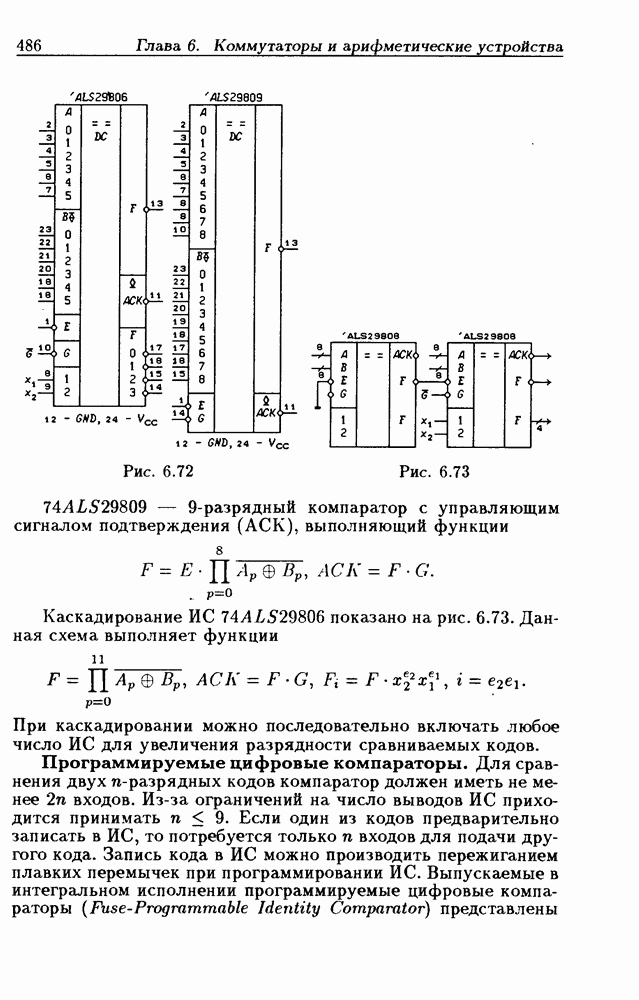
- 6.7. Цифровые компараторы
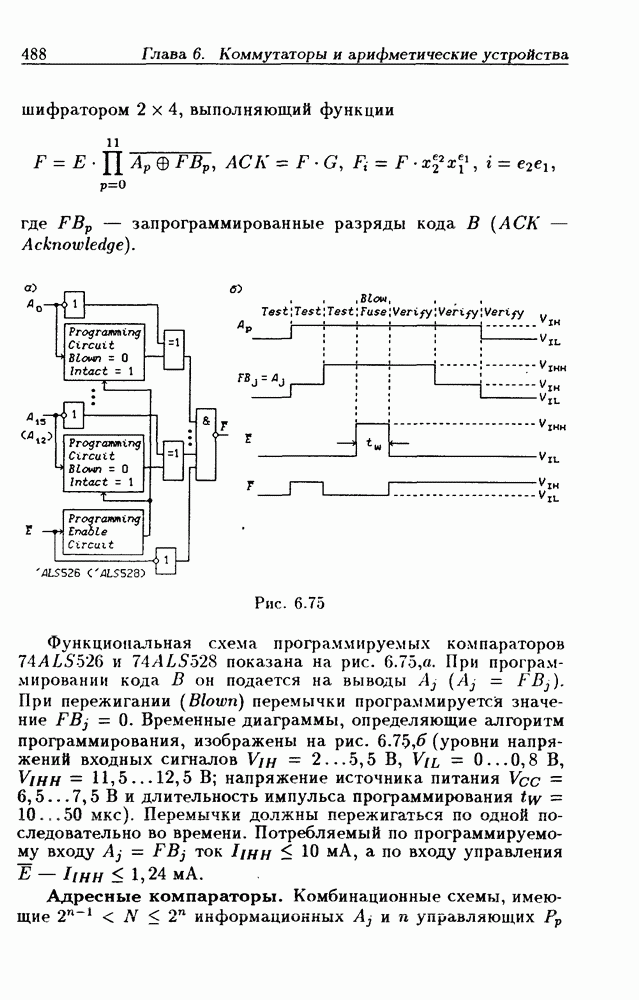
- Программируемые цифровые компараторы.
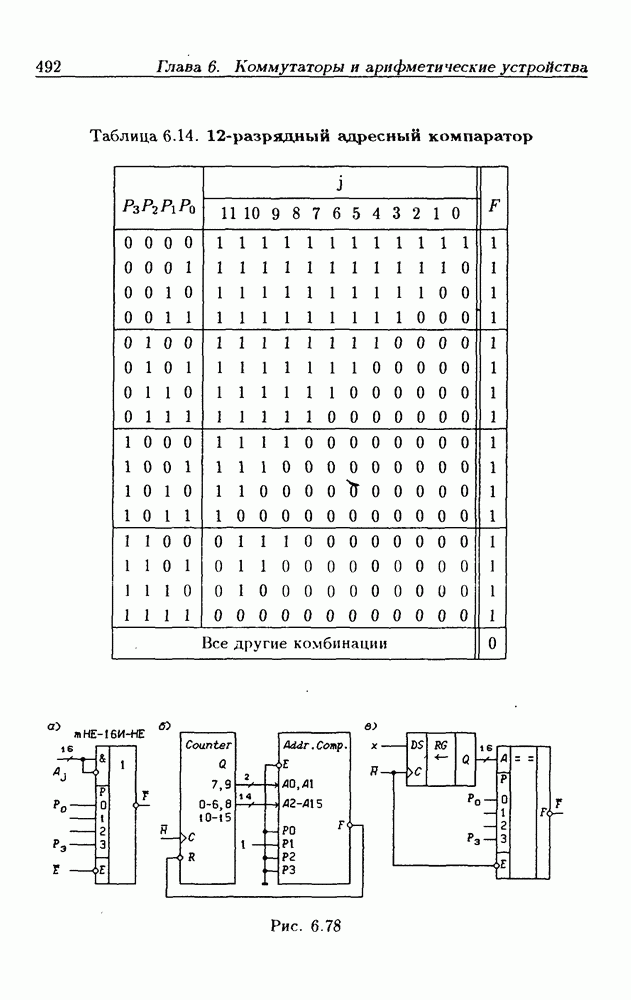
- Адресные компараторы.
- Применения адресных компараторов.
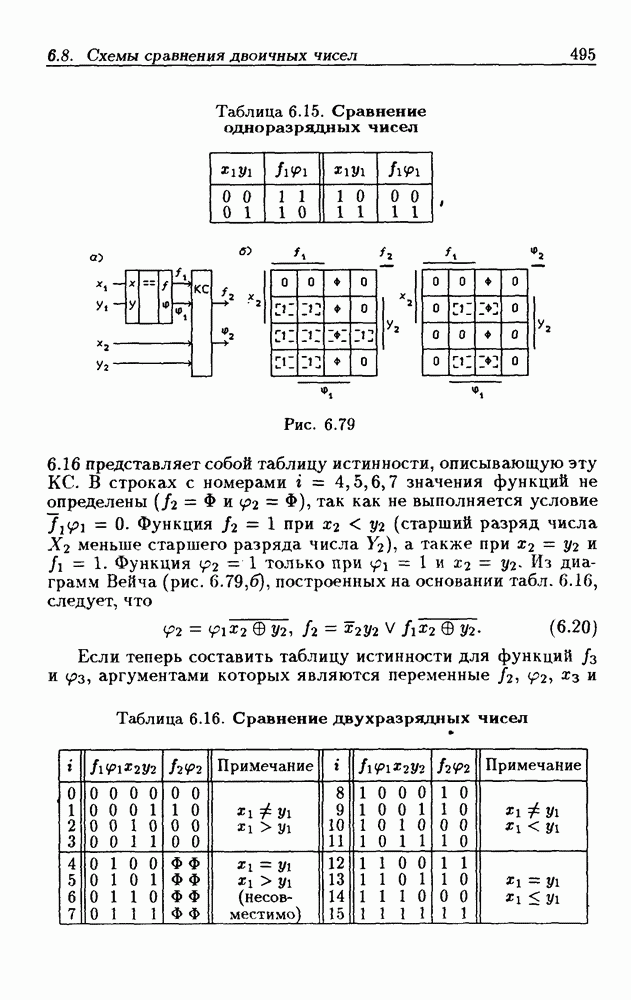
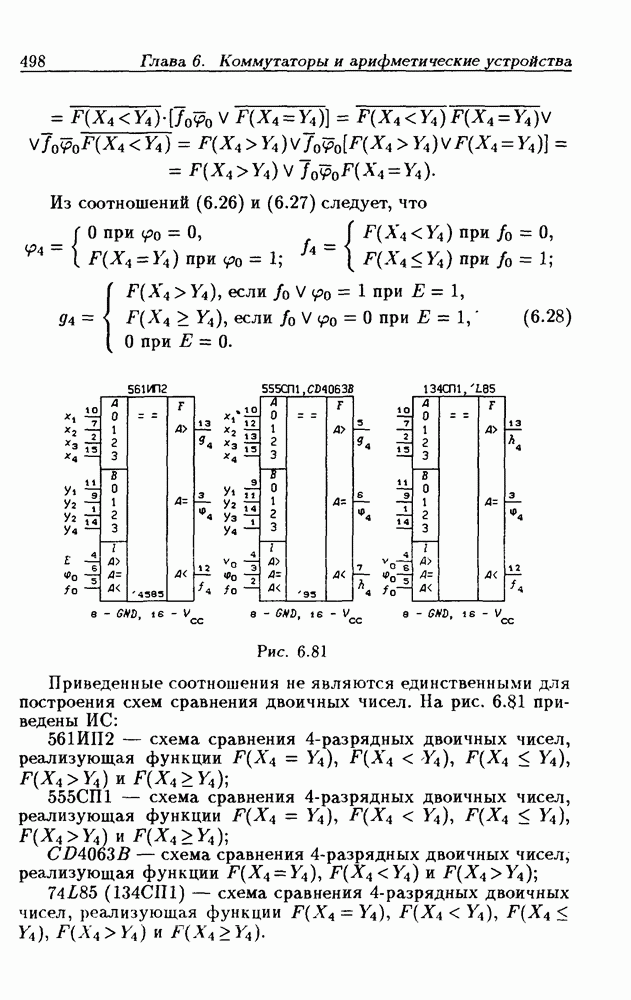
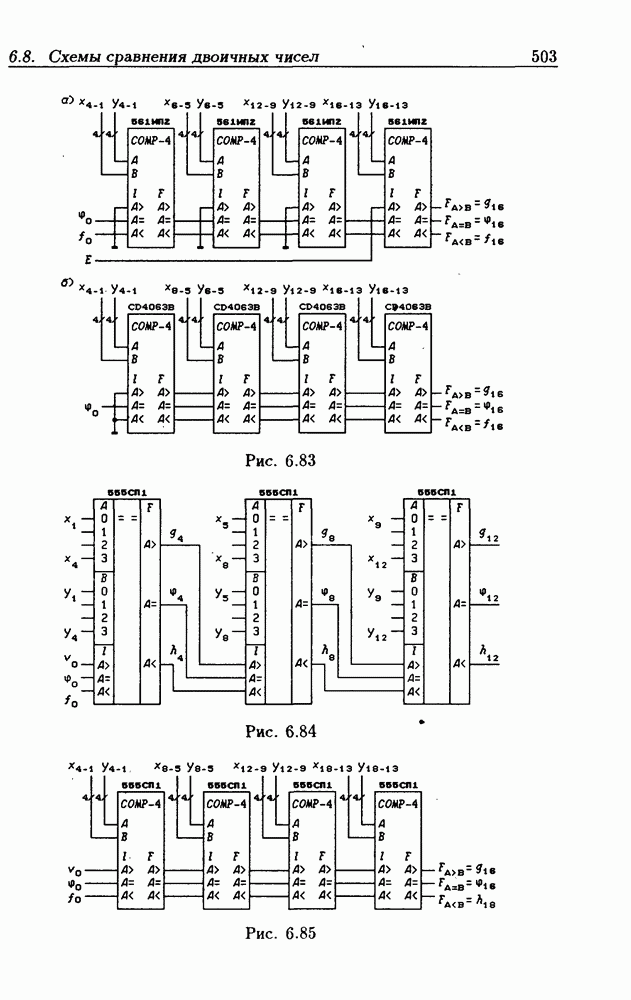
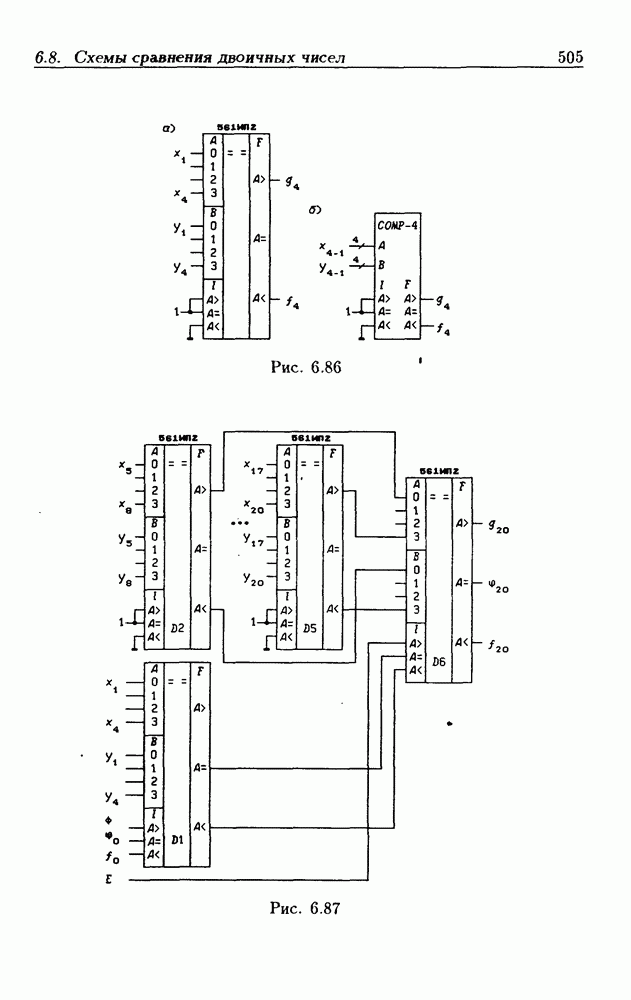
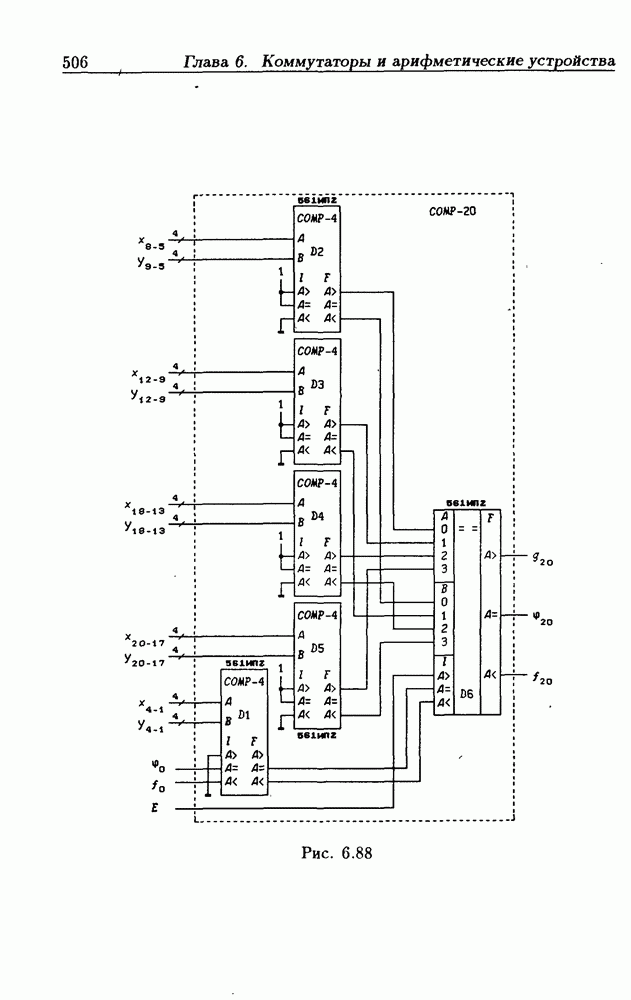
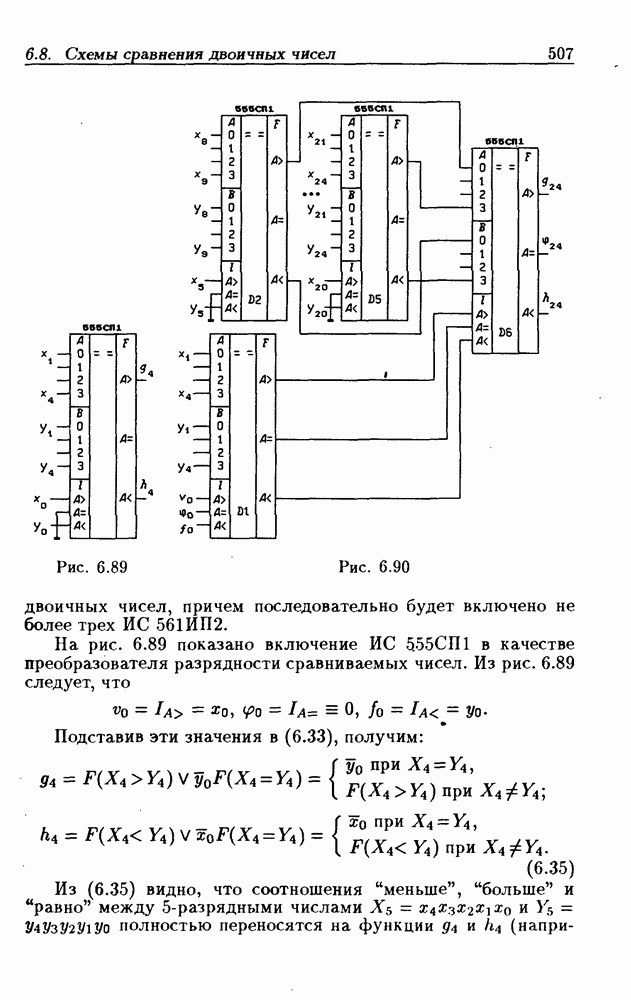
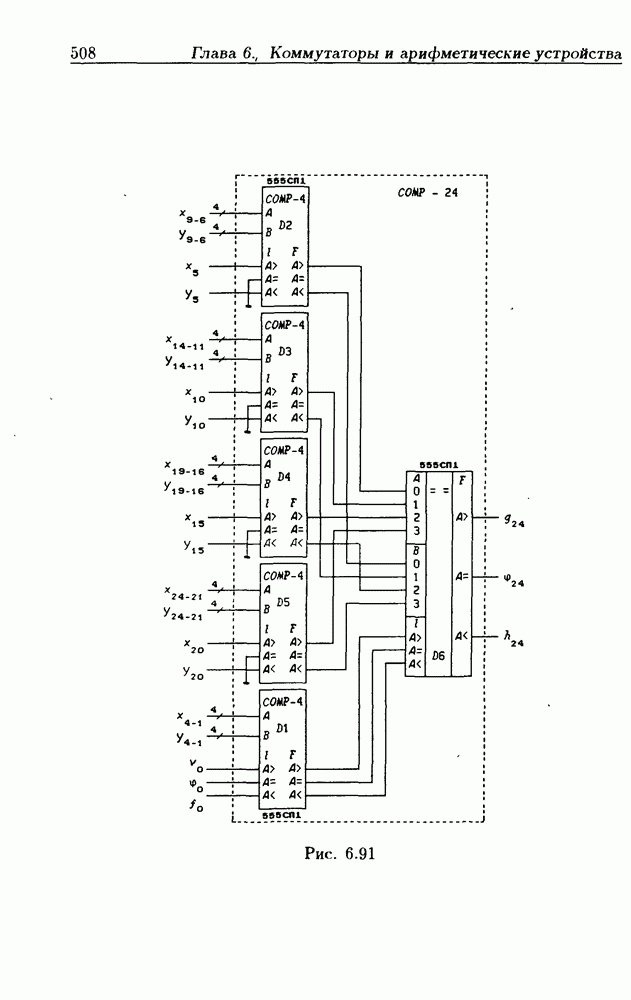
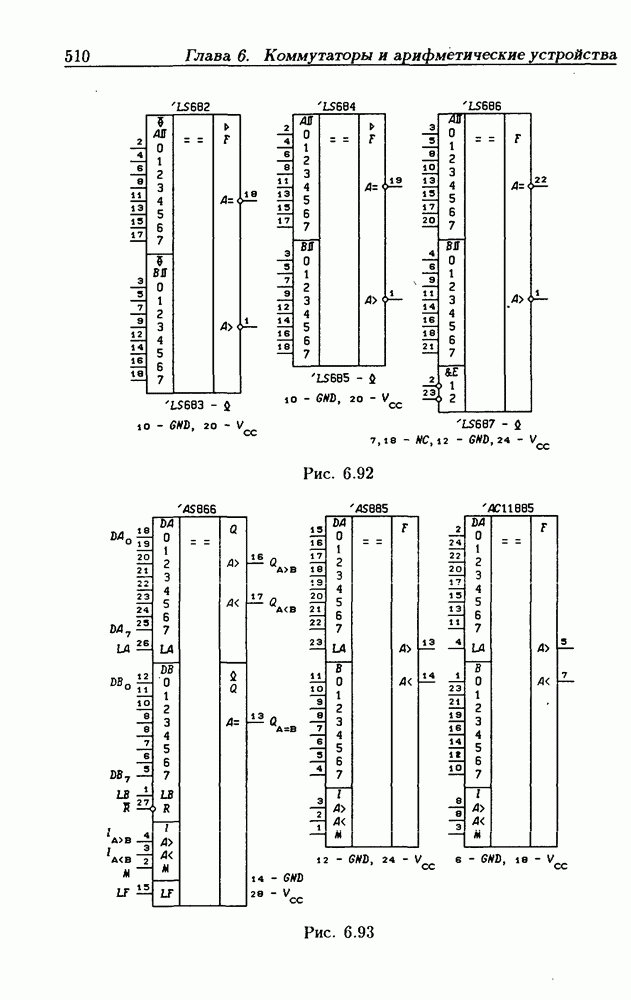
- 6.8. Схемы сравнения двоичных чисел
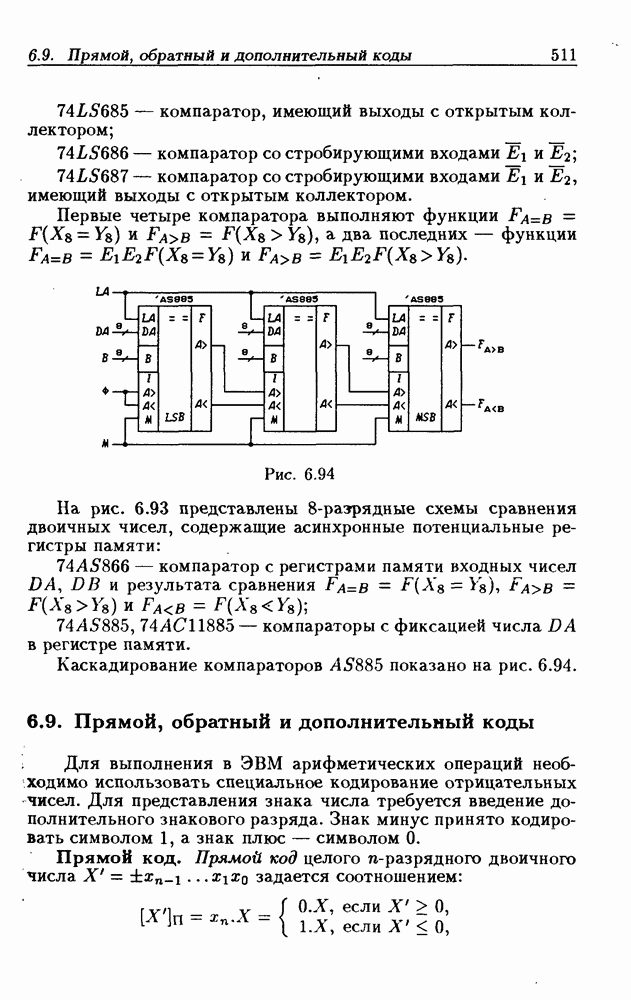
- 8-разрядные схемы сравнения двоичных чисел.
- 6.9. Прямой, обратный и дополнительный коды
- Дополнительный код.
- Сложение чисел в обратном коде.
- Код с избытком 3.
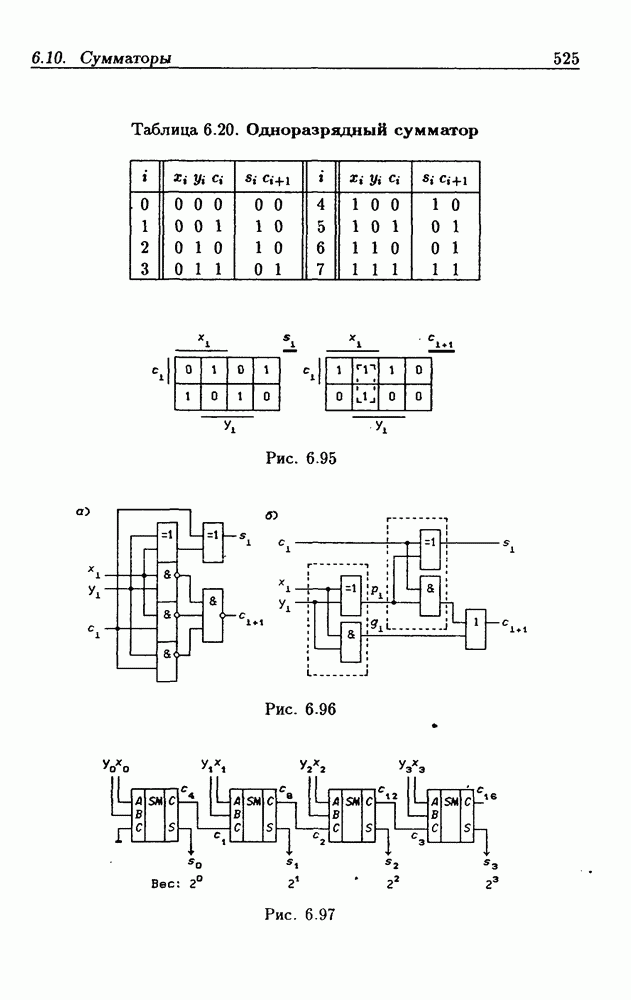
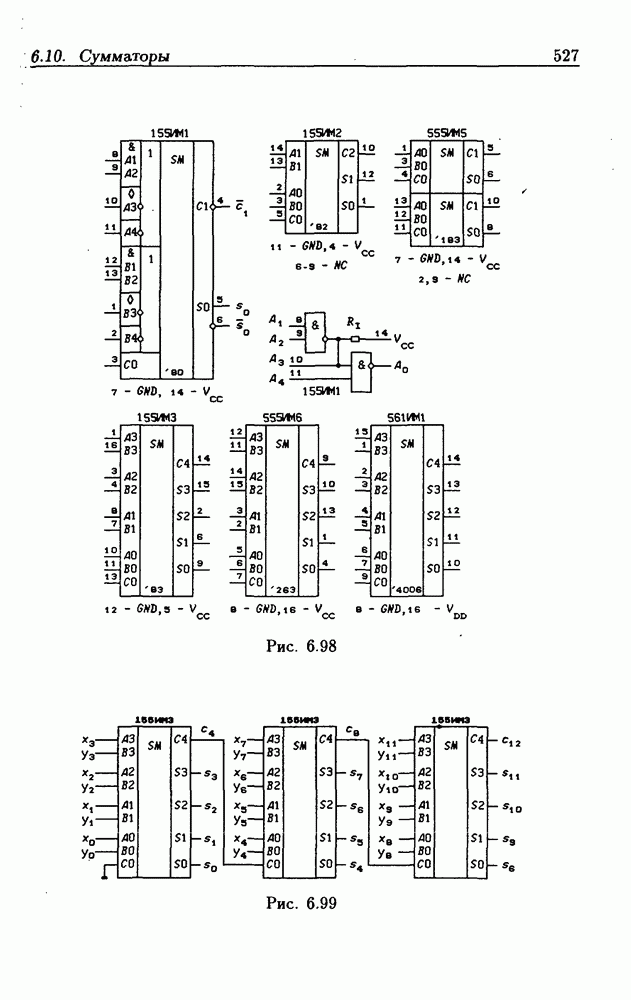
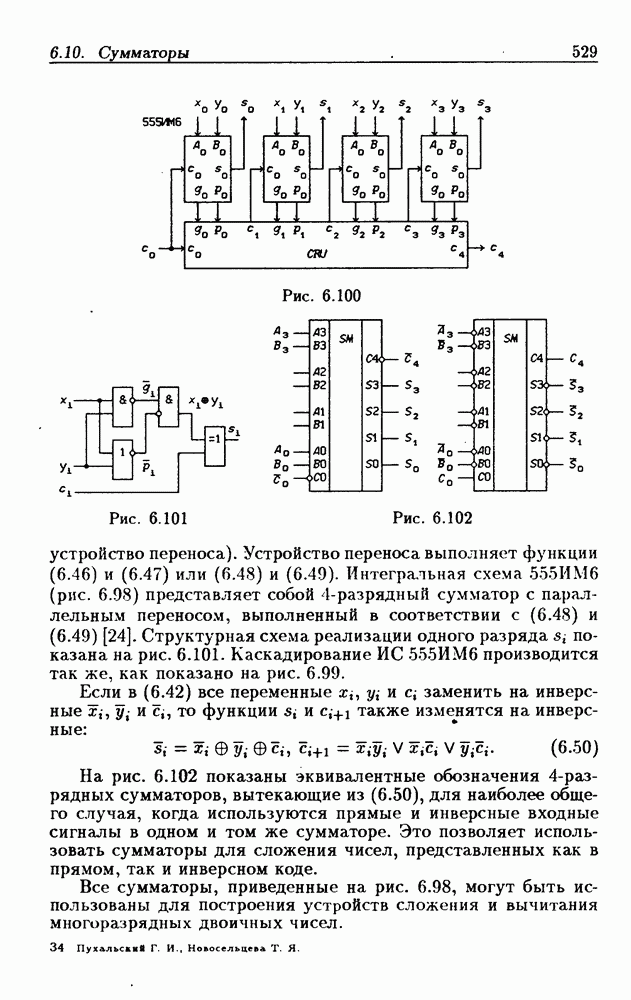
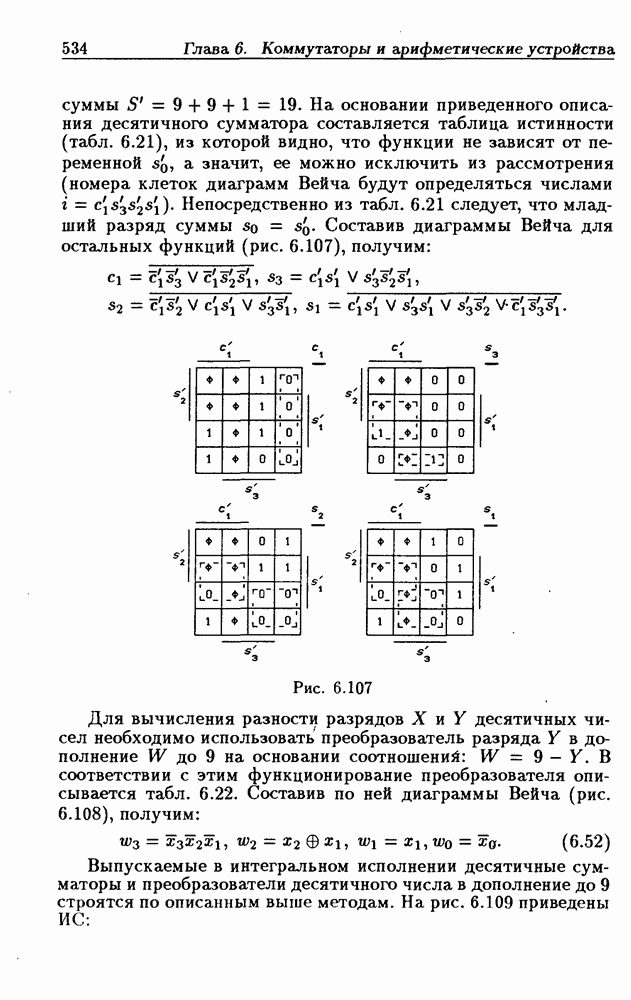
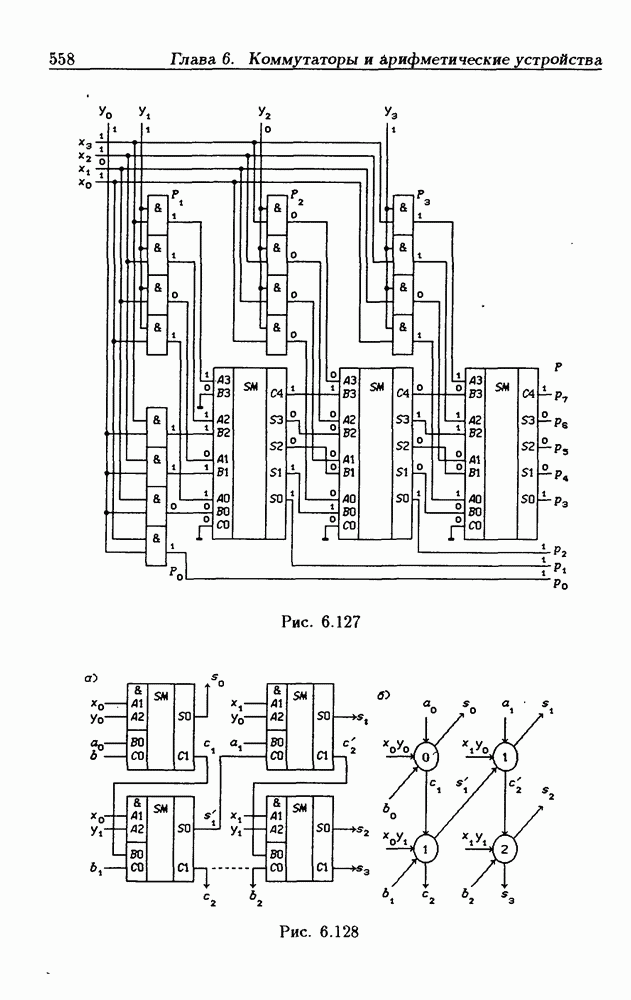
- 6.10. Сумматоры
- Двоичные параллельные сумматоры с последовательным переносом.
- Двоичные сумматоры с параллельным переносом.
- Применения сумматоров.
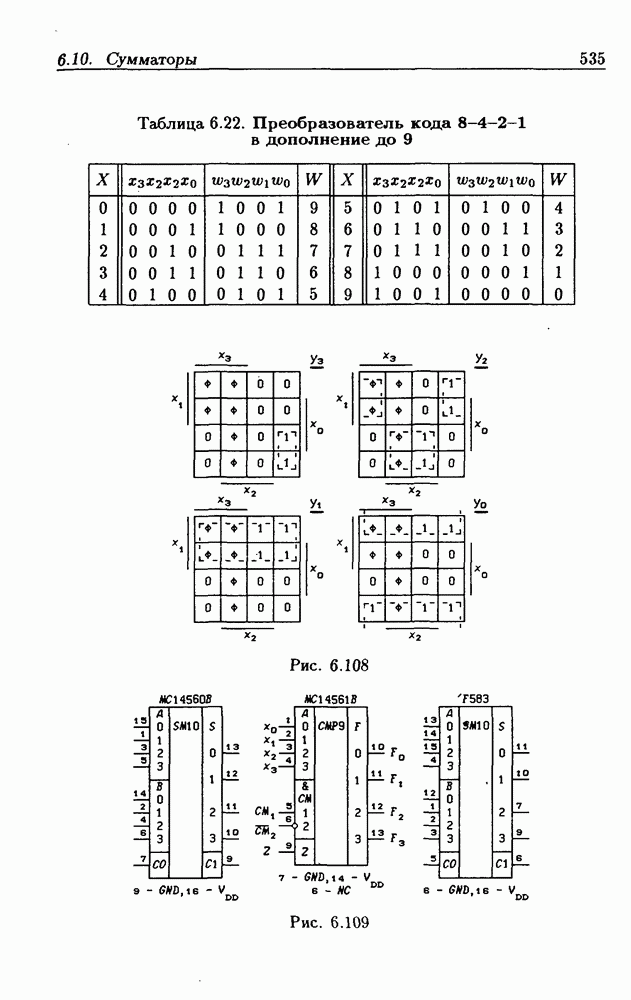
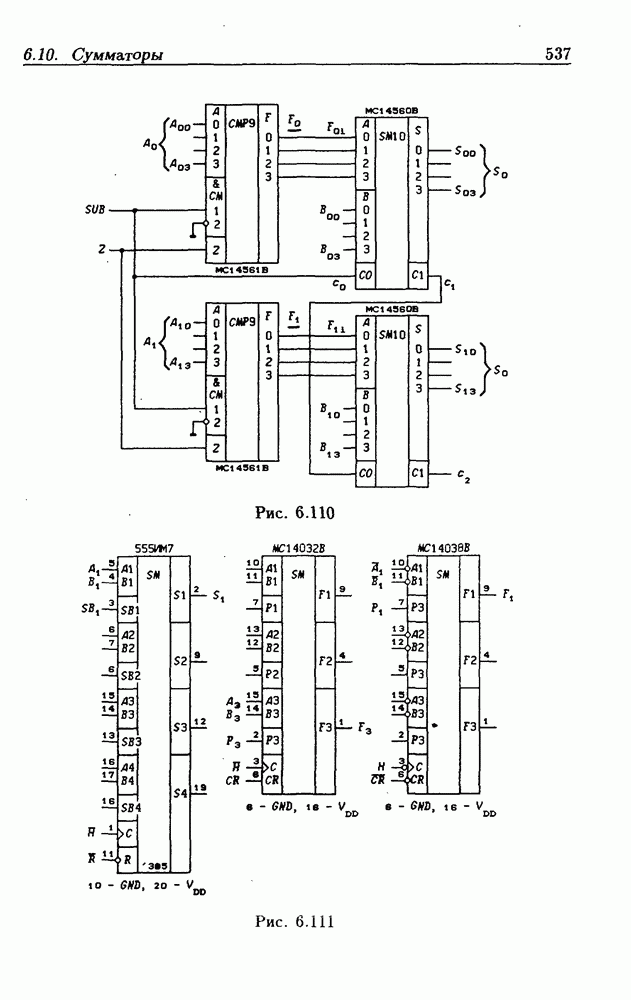
- Десятичные сумматоры.
- Последовательные двоичные сумматоры.
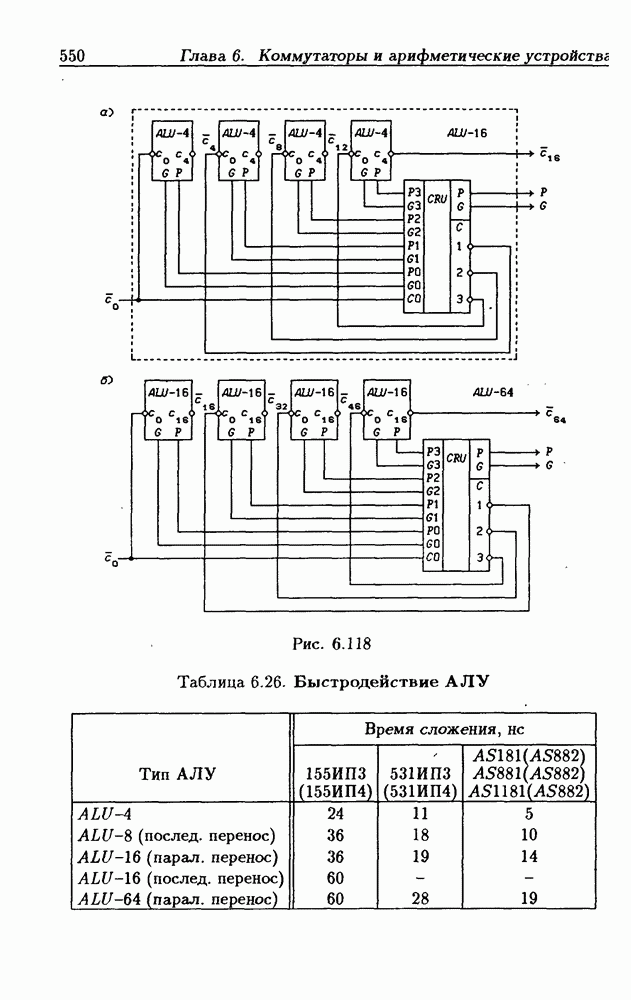
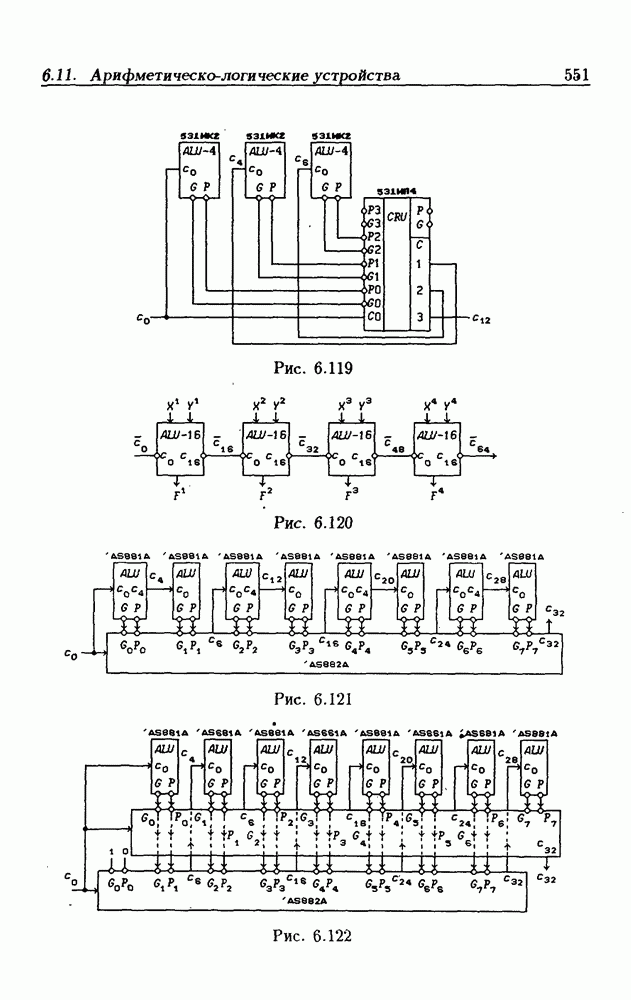
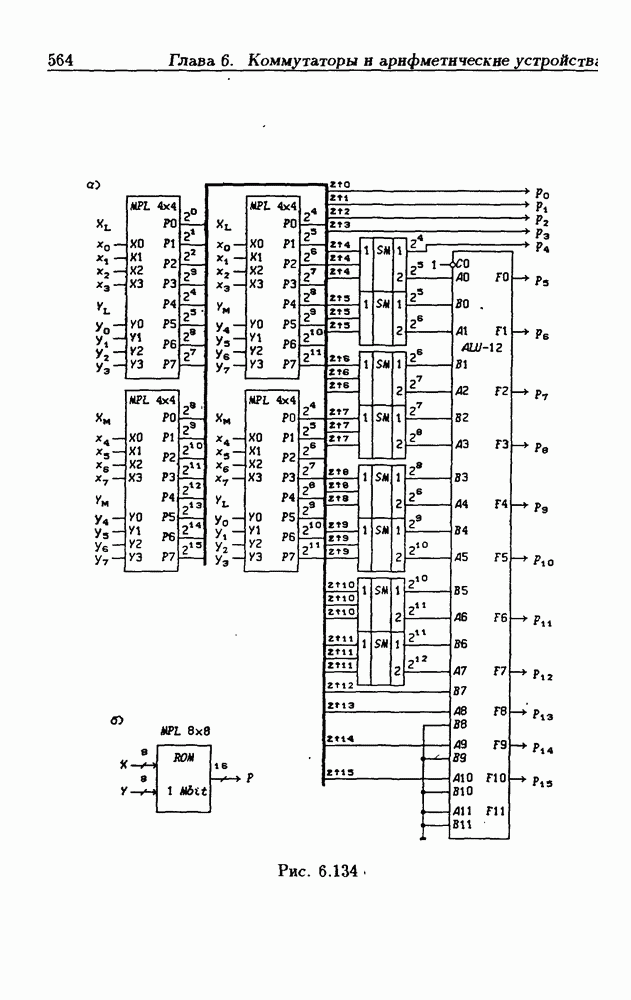
- 6.11. Арифметическо-логические устройства
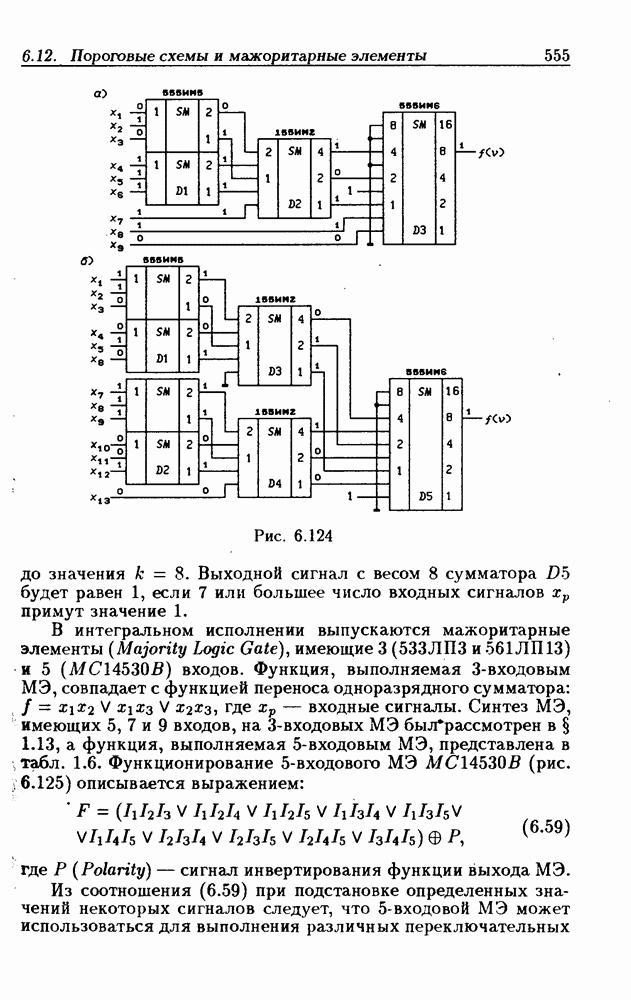
- 6.12. Пороговые схемы и мажоритарные элементы
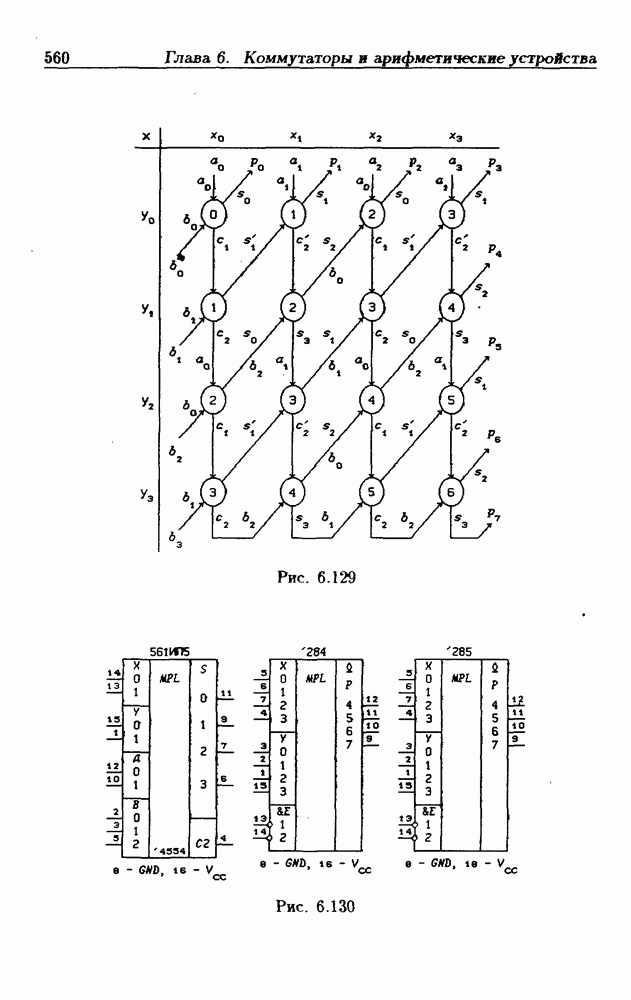
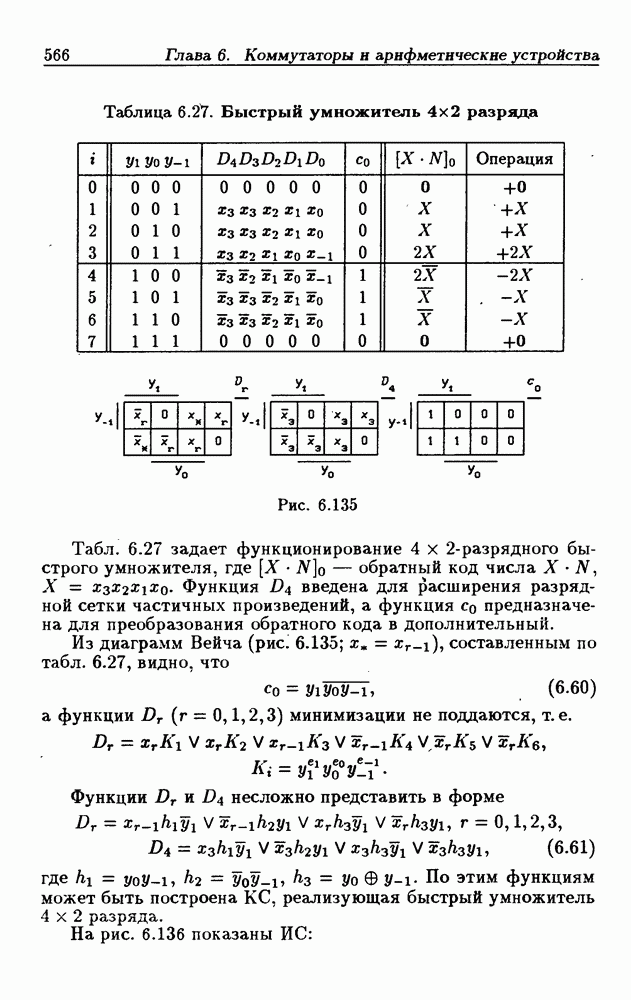
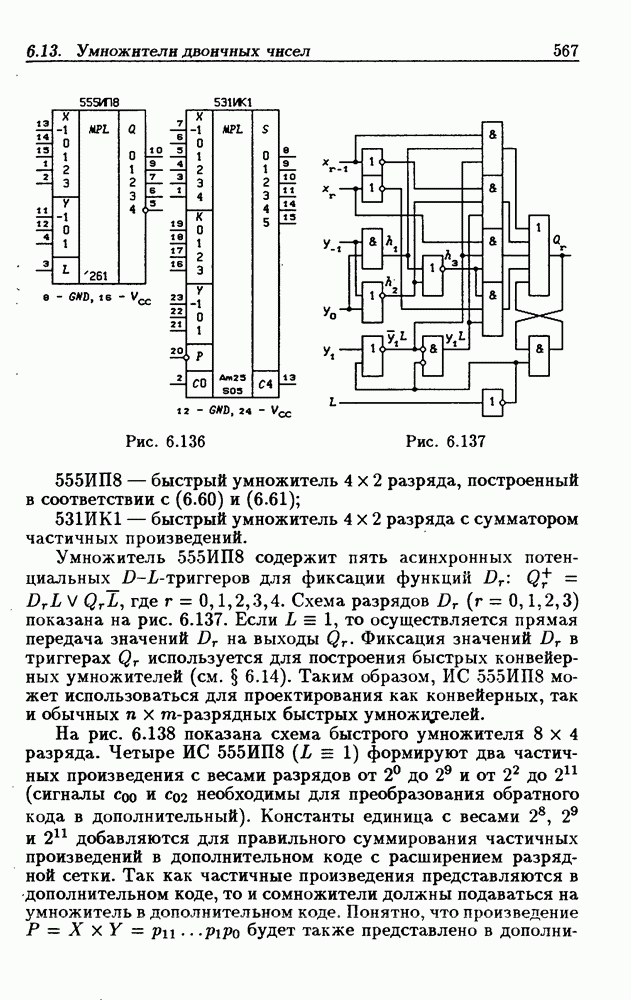
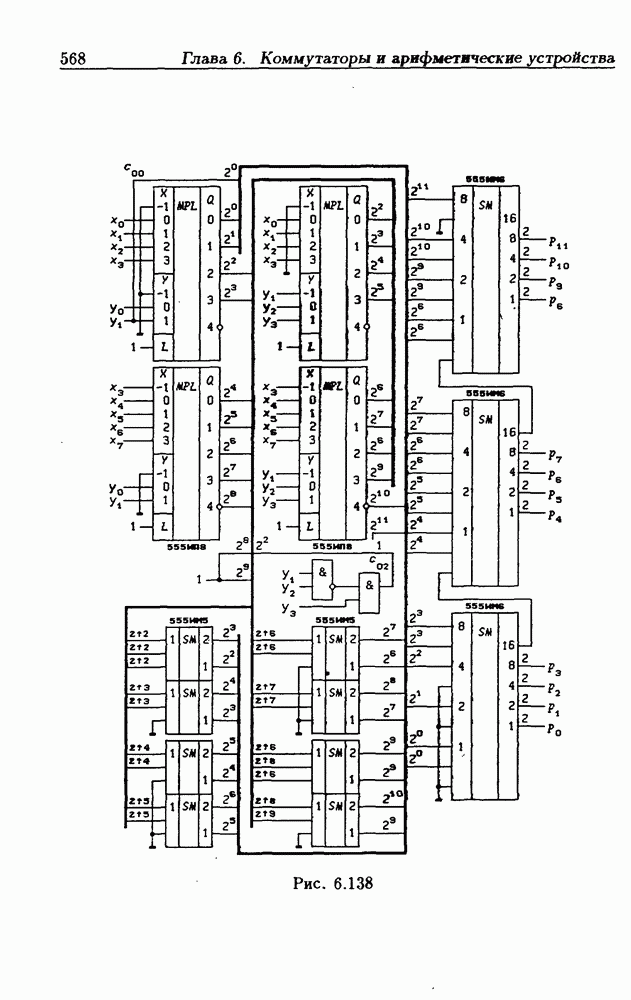
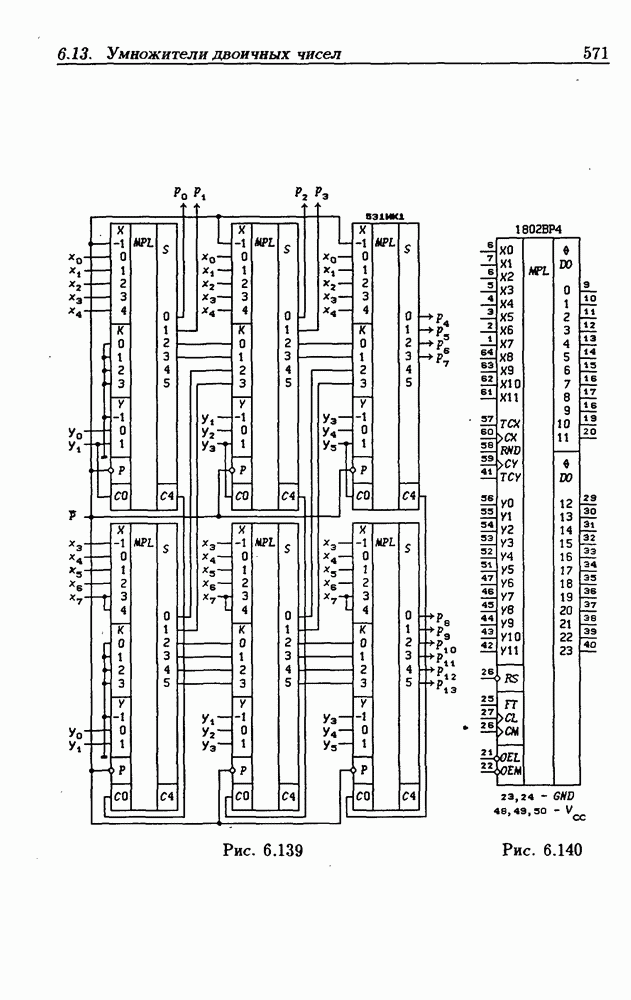
- 6.13. Умножители двоичных чисел
- Быстрые умножители.
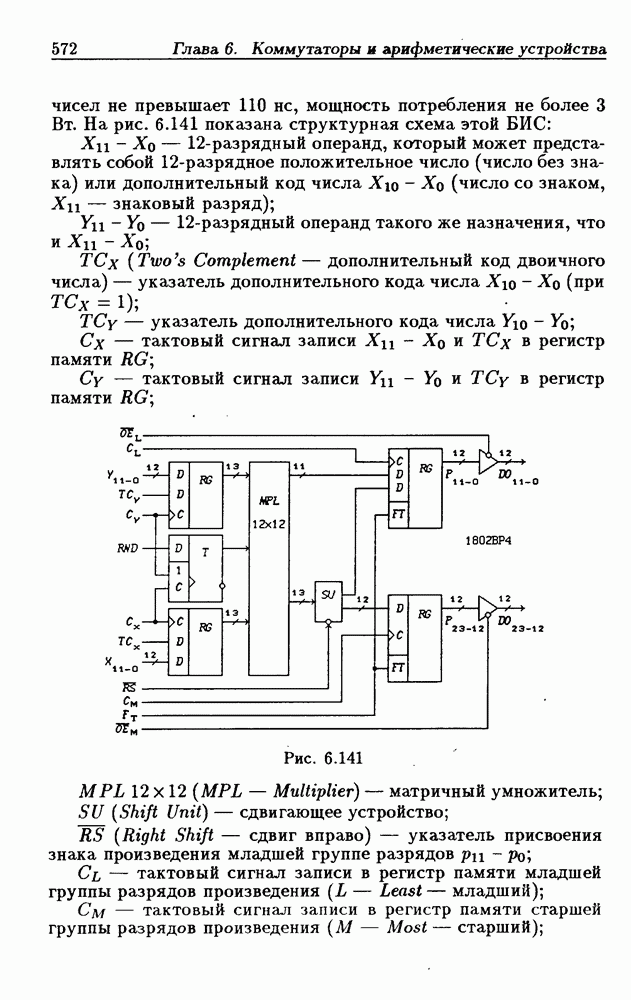
- БИС умножителя 12×12 разрядов 1802ВР4.
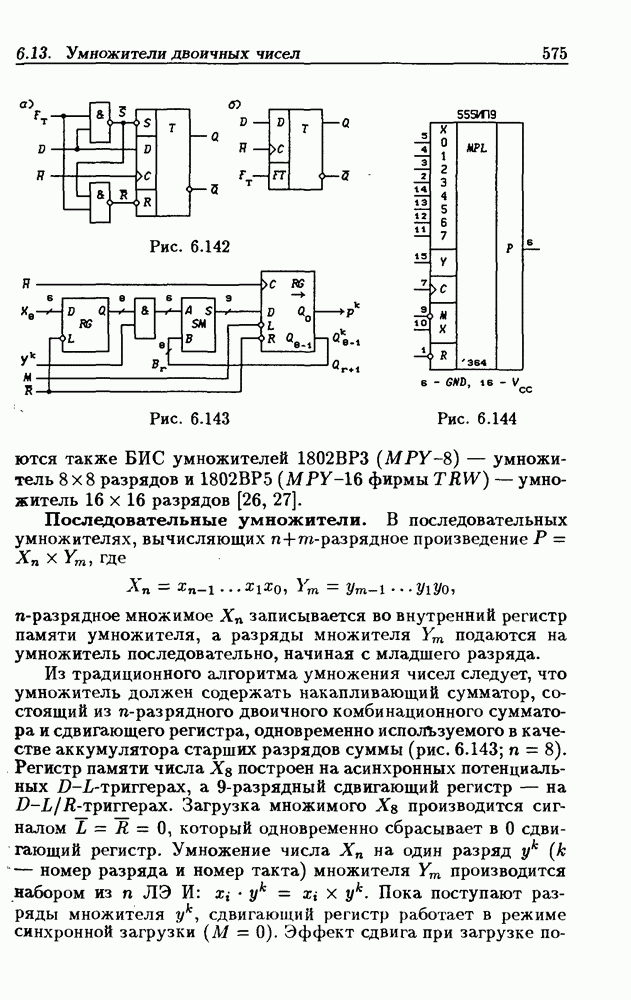
- Последовательные умножители.
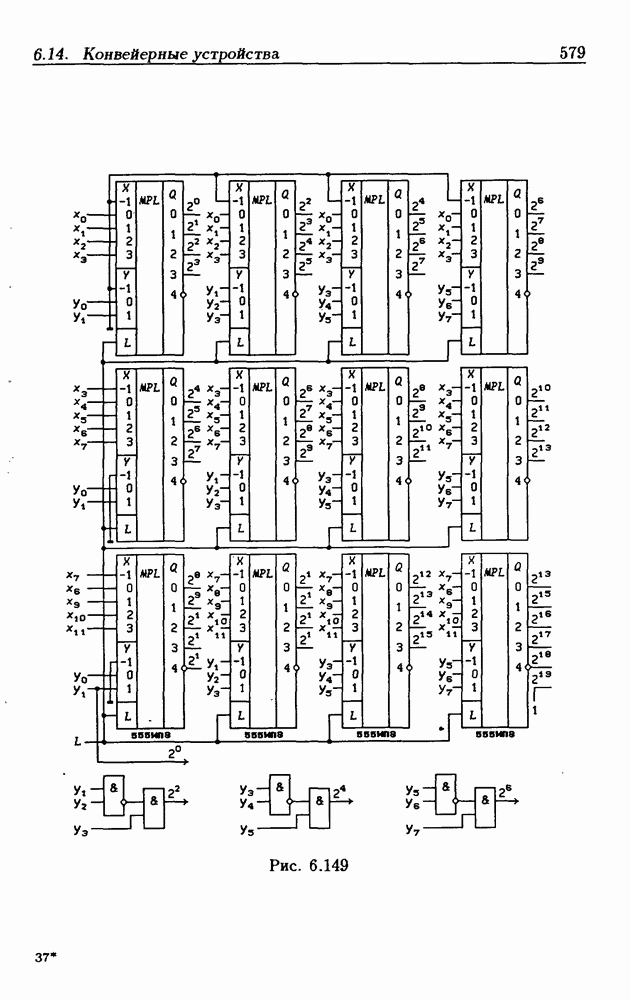
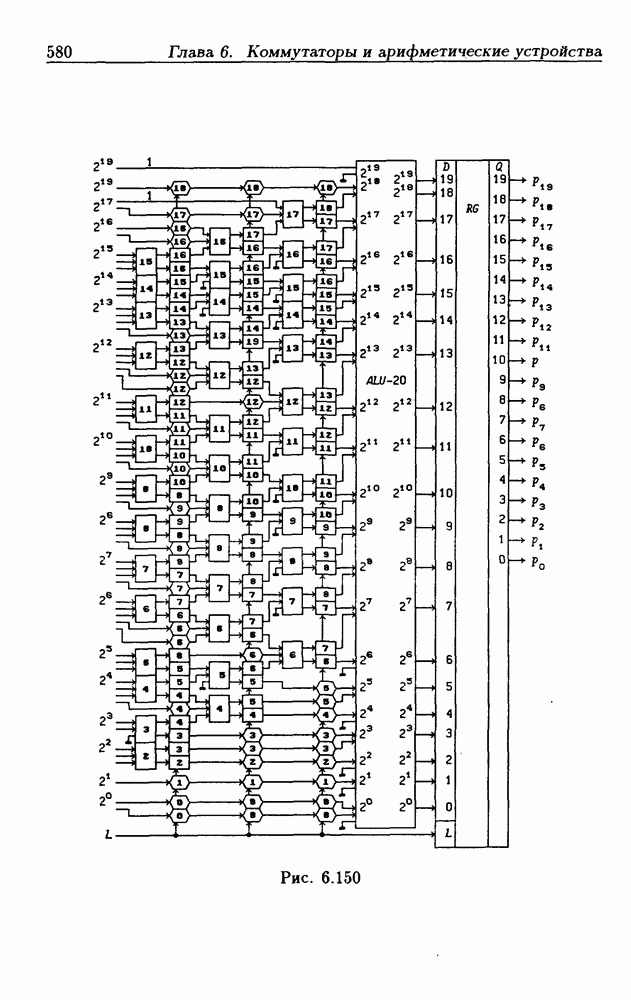
- 6.14. Конвейерные устройства
- Конвейерный быстрый умножитель.
- Конвейерные АЦП.
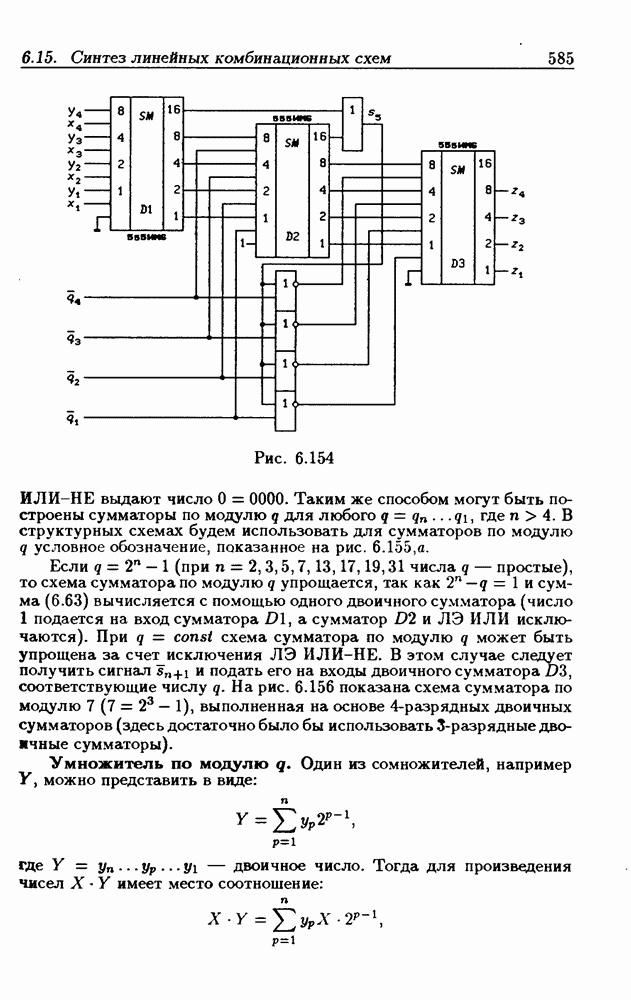
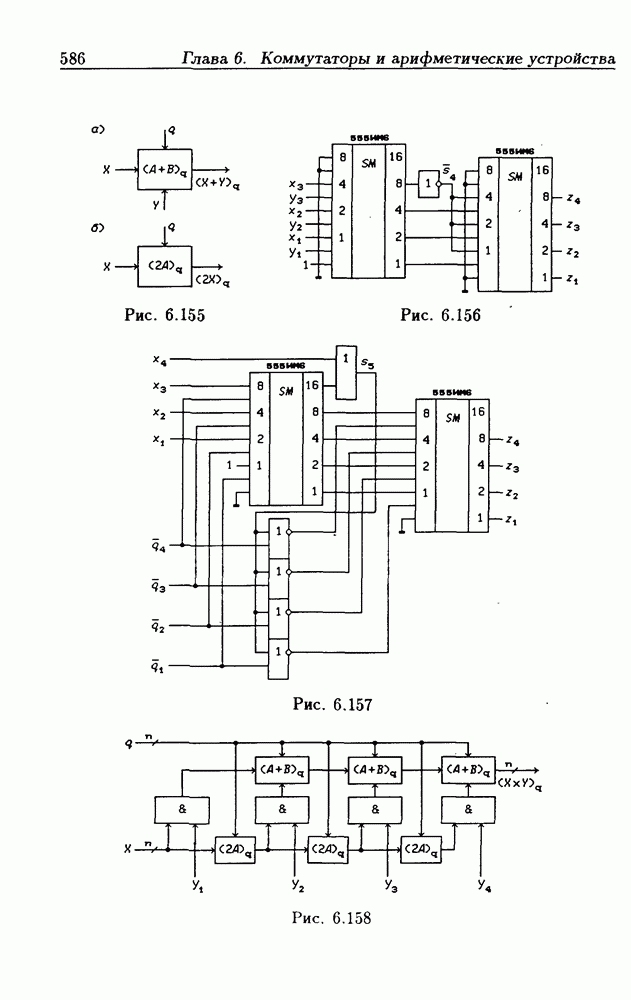
- 6.15. Синтез линейных комбинационных схем
- Сумматор по модулю q.
- Умножитель по модулю q.
- Глава 7. Сдвигающие регистры и счетчики
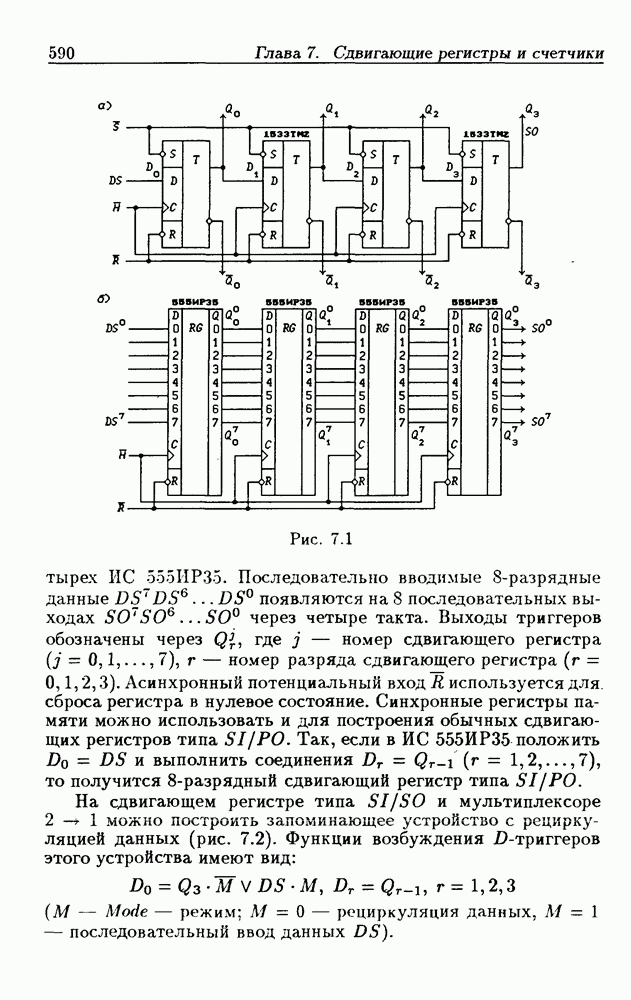
- 7.1. Сдвигающие регистры без параллельной записи данных
- Сдвигающие устройства с выходными регистрами памяти.
- 7.2. Сдвигающие регистры с параллельной записью данных
- Сдвигающие регистры с расширением знака.
- Сдвигающие регистры с входным регистром памяти.
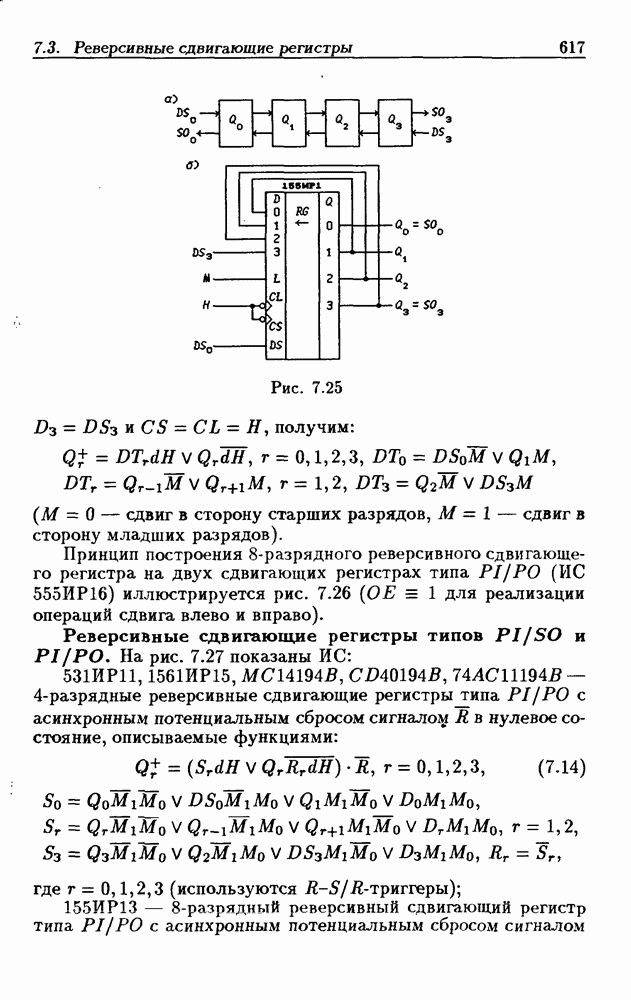
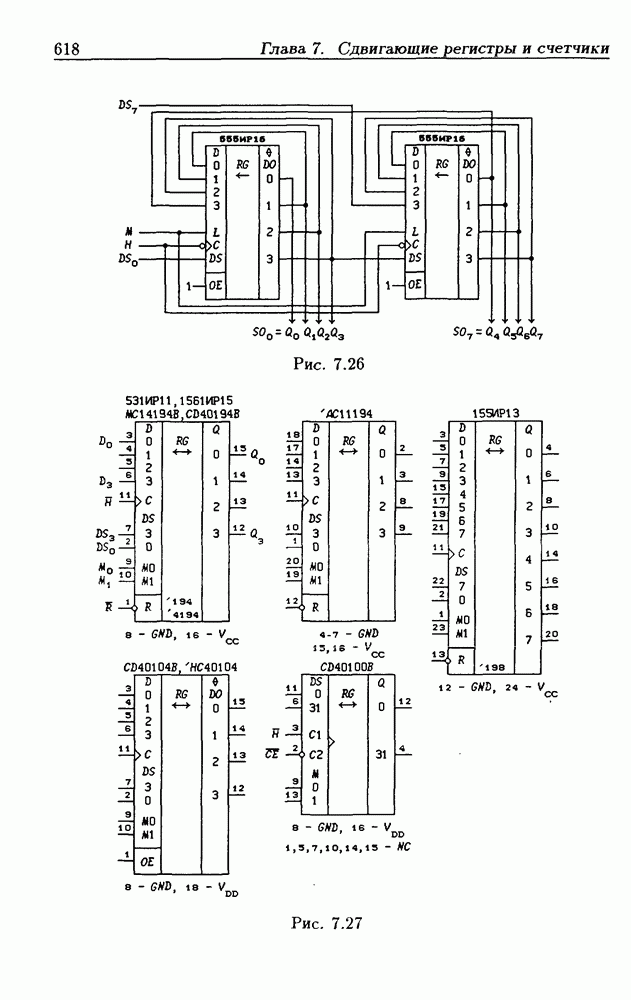
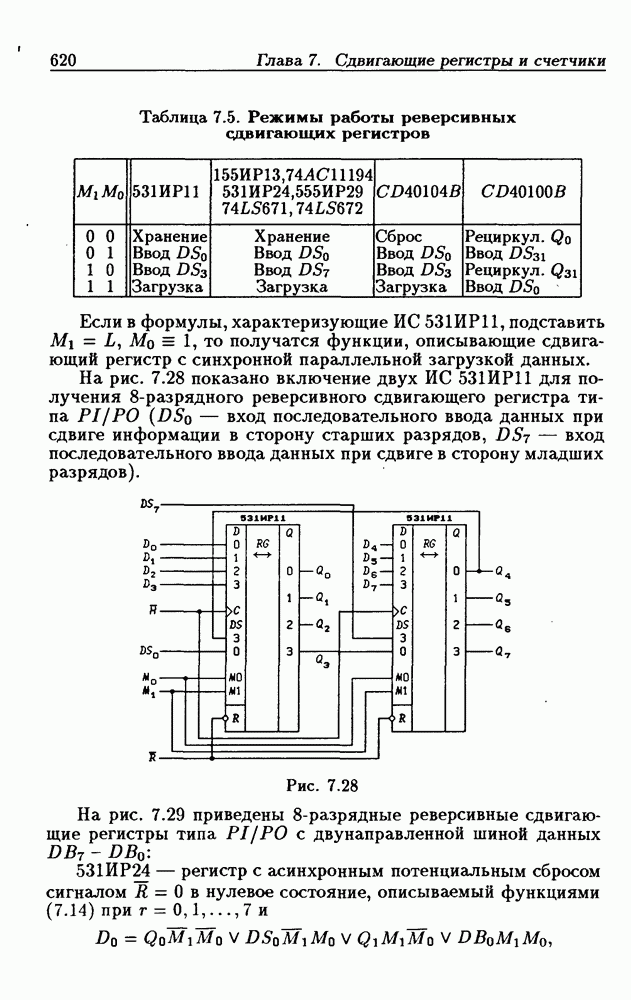
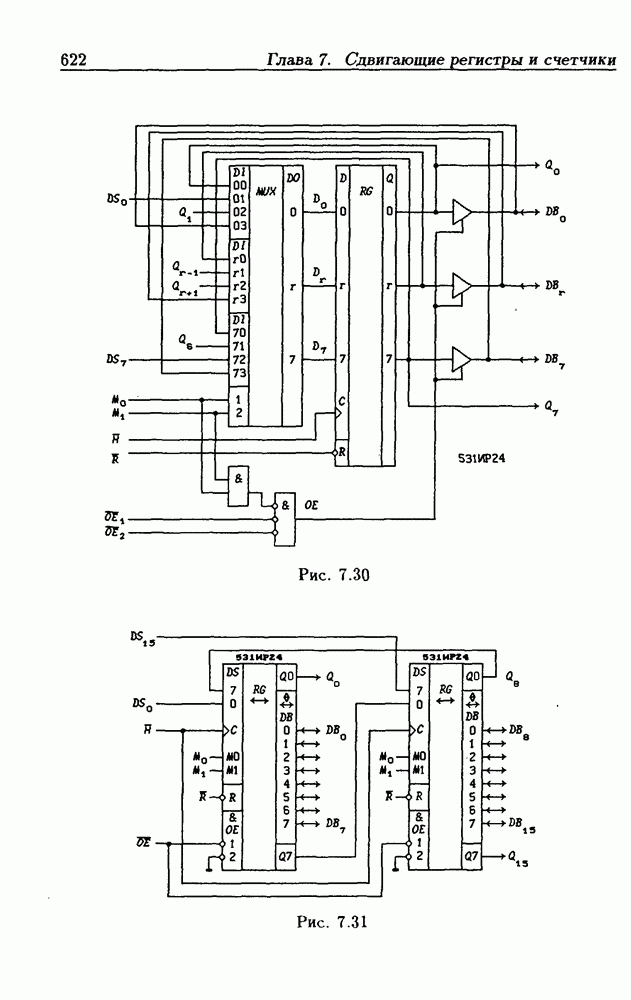
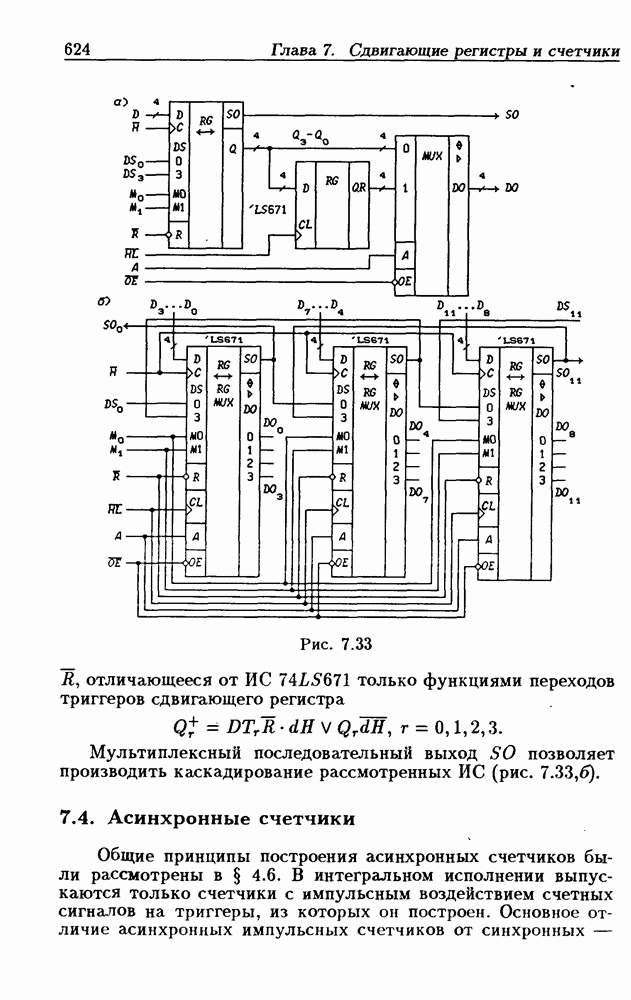
- 7.3. Реверсивные сдвигающие регистры
- Реверсивные сдвигающие регистры типов PI/SO и PI/PO.
- Многофункциональные устройства на основе реверсивных сдвигающих регистров.
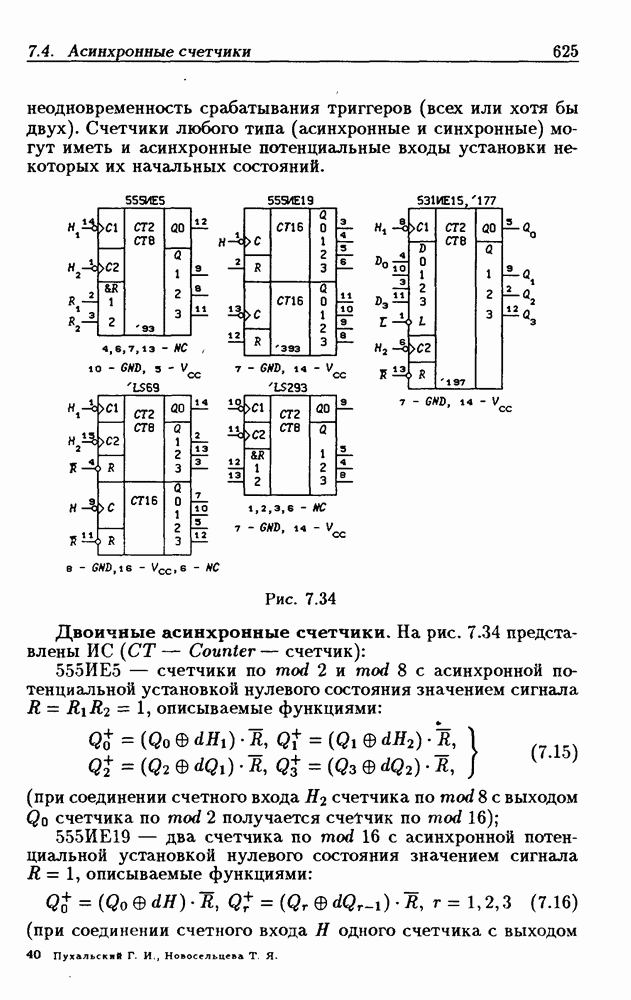
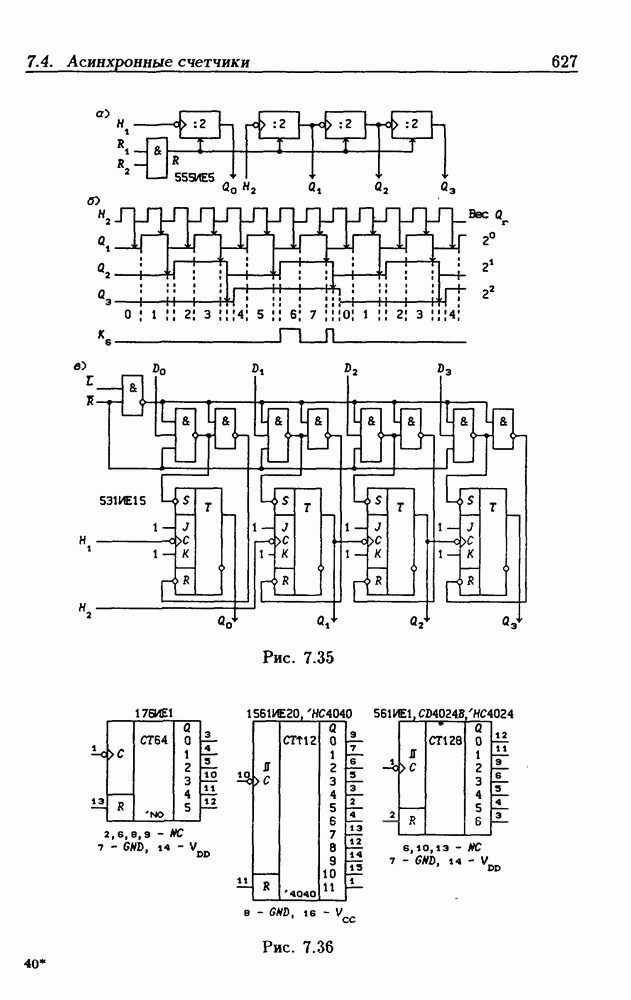
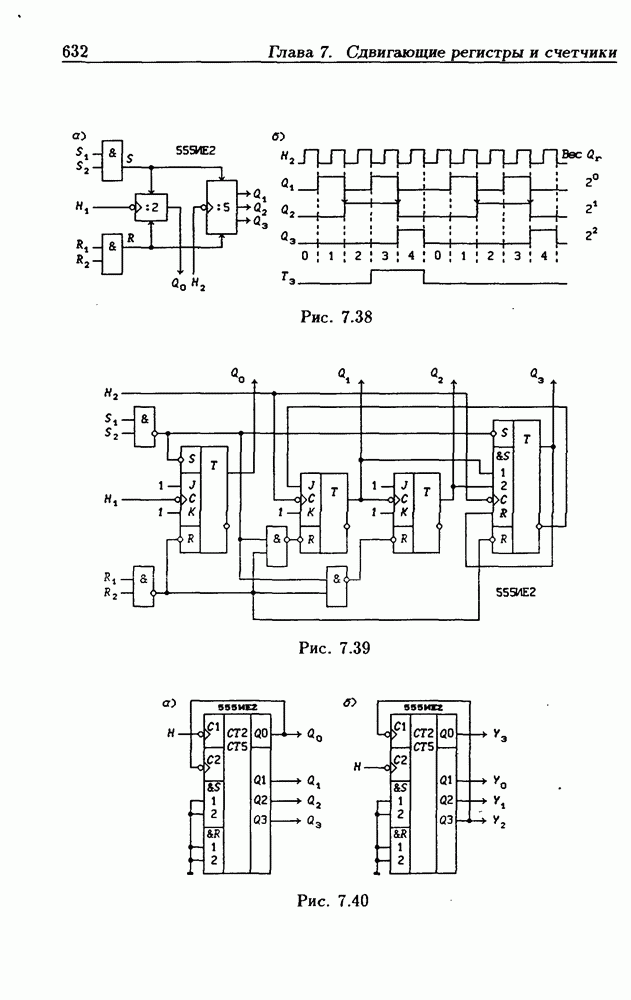
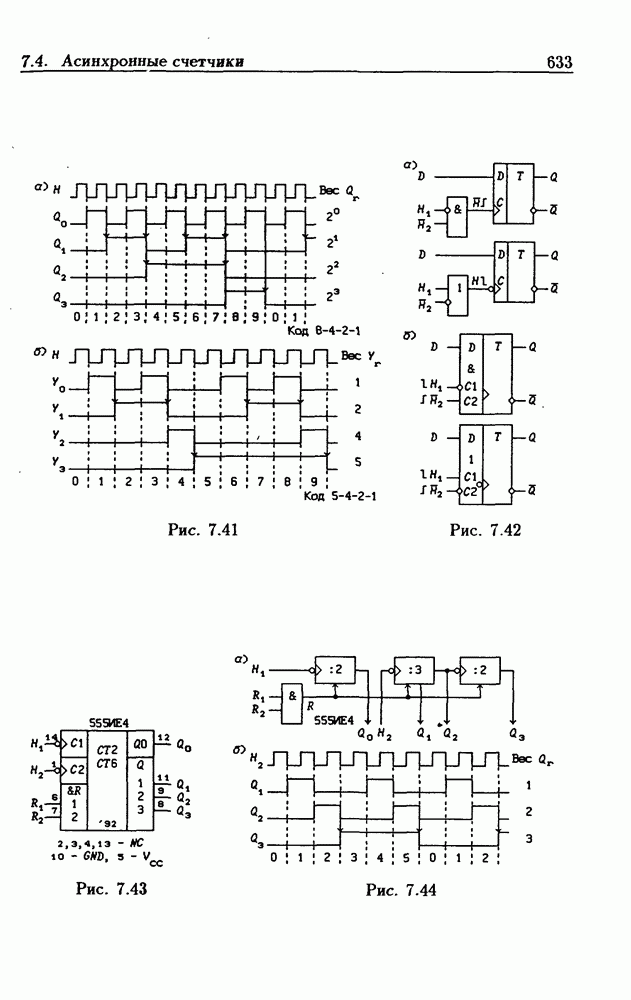
- 7.4. Асинхронные счетчики
- Двоично-десятичные асинхронные счетчики.
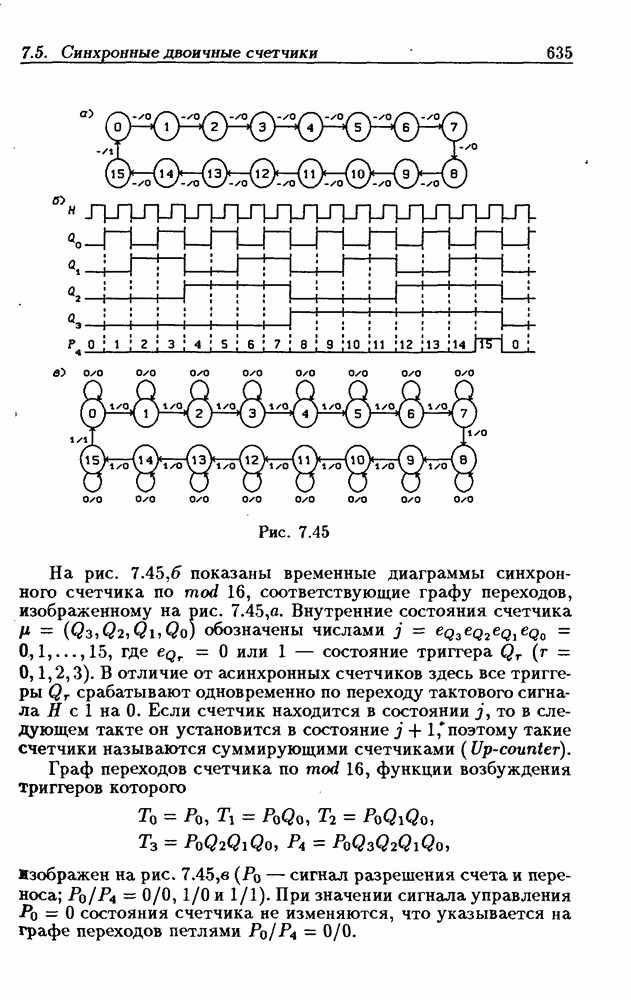
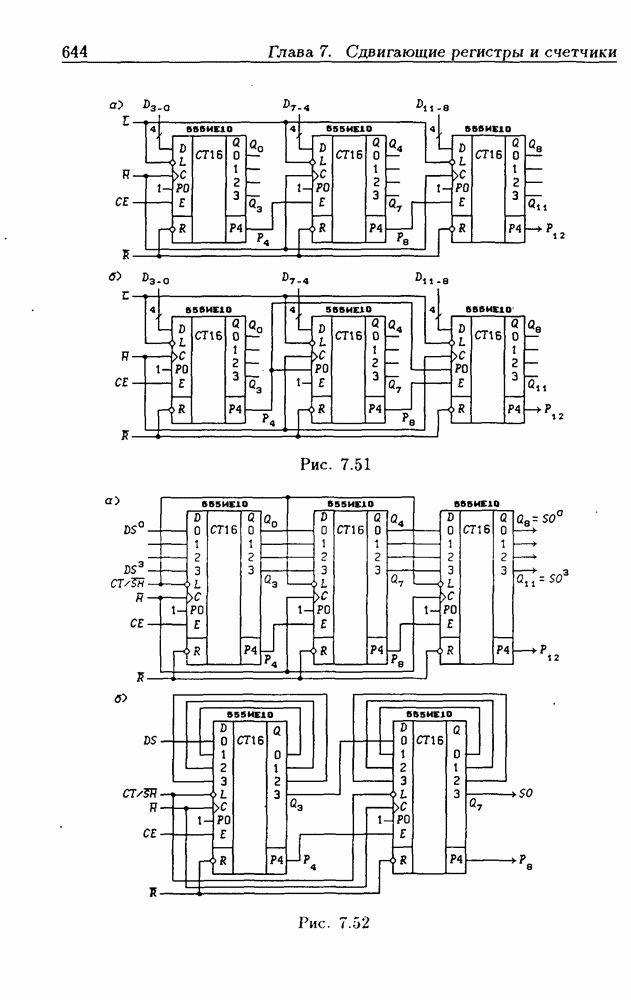
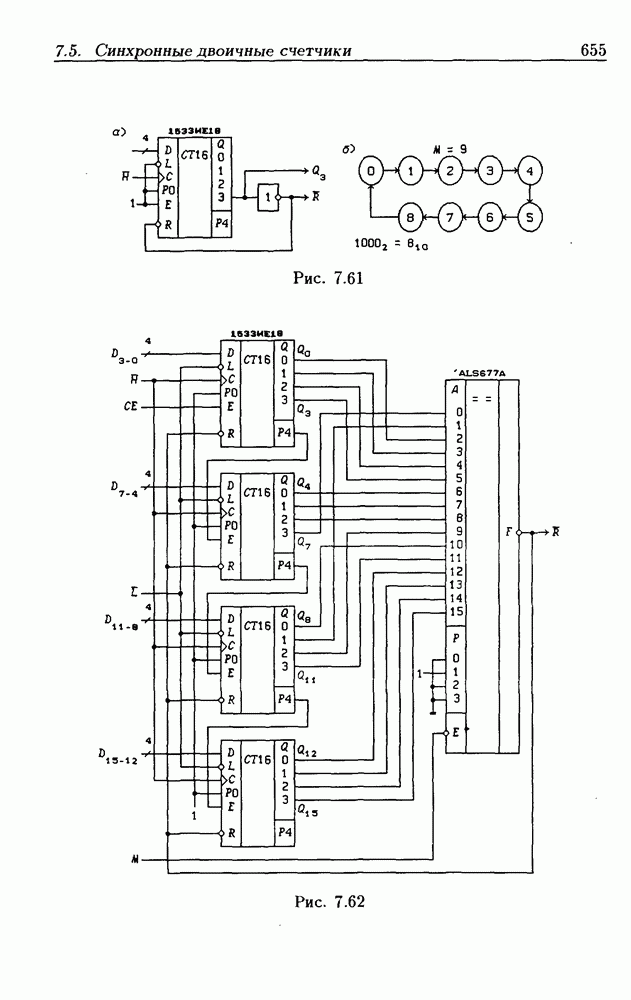
- 7.5. Синхронные двоичные счетчики
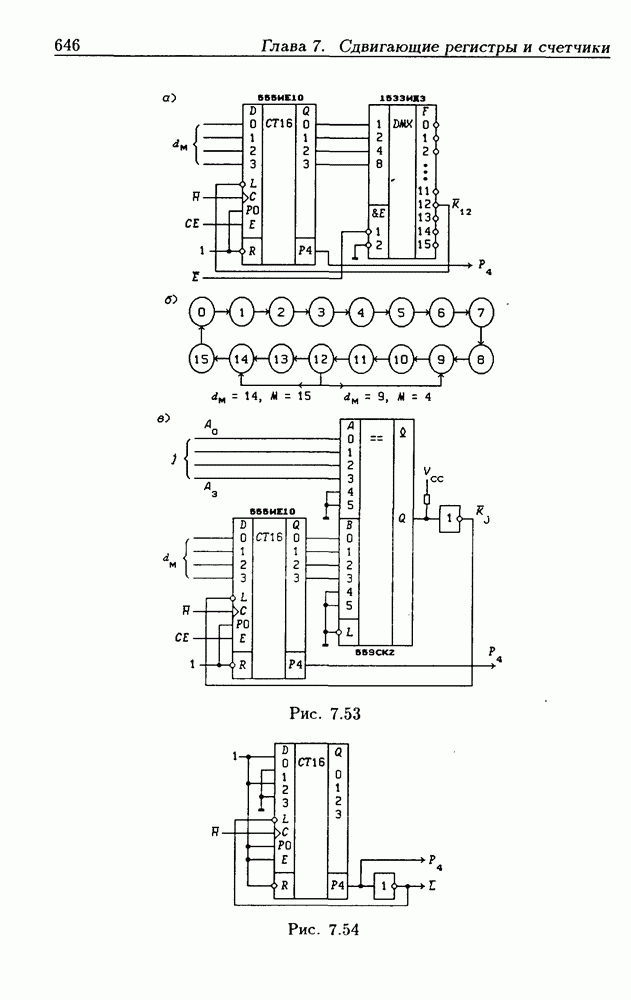
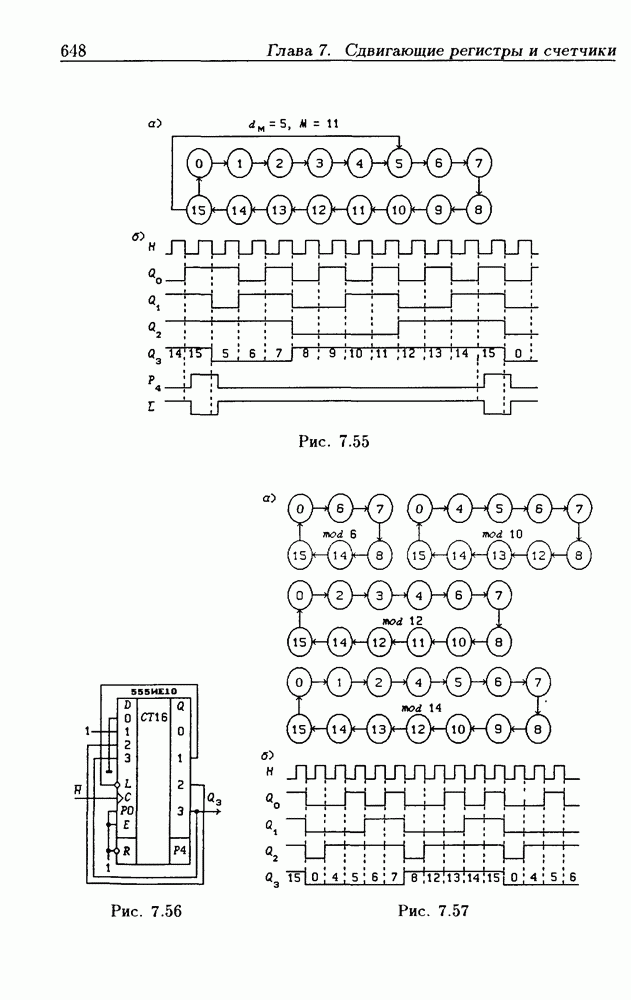
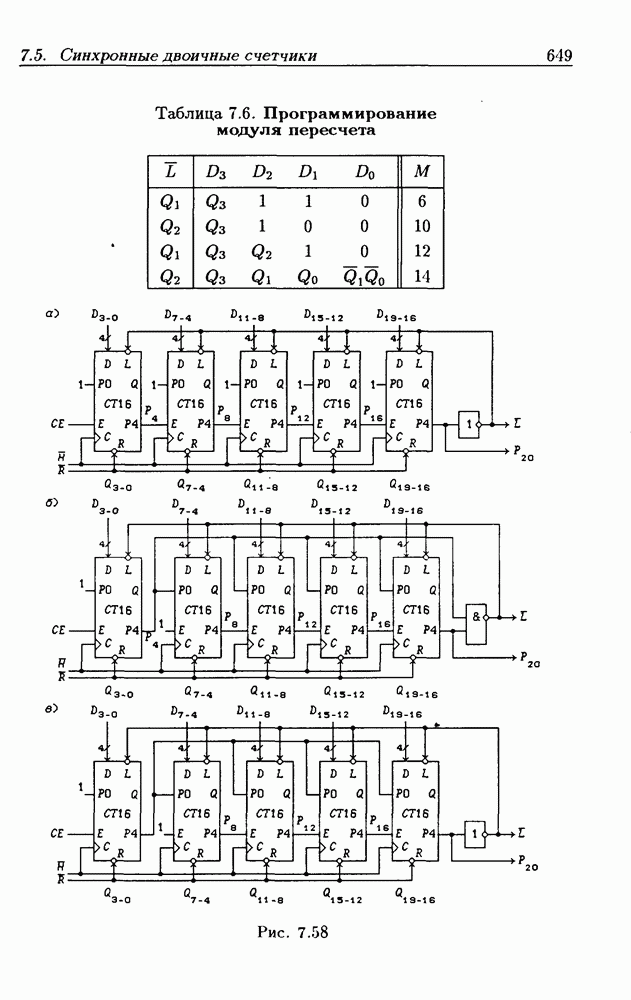
- Программирование модуля пересчета двоичных счетчиков.
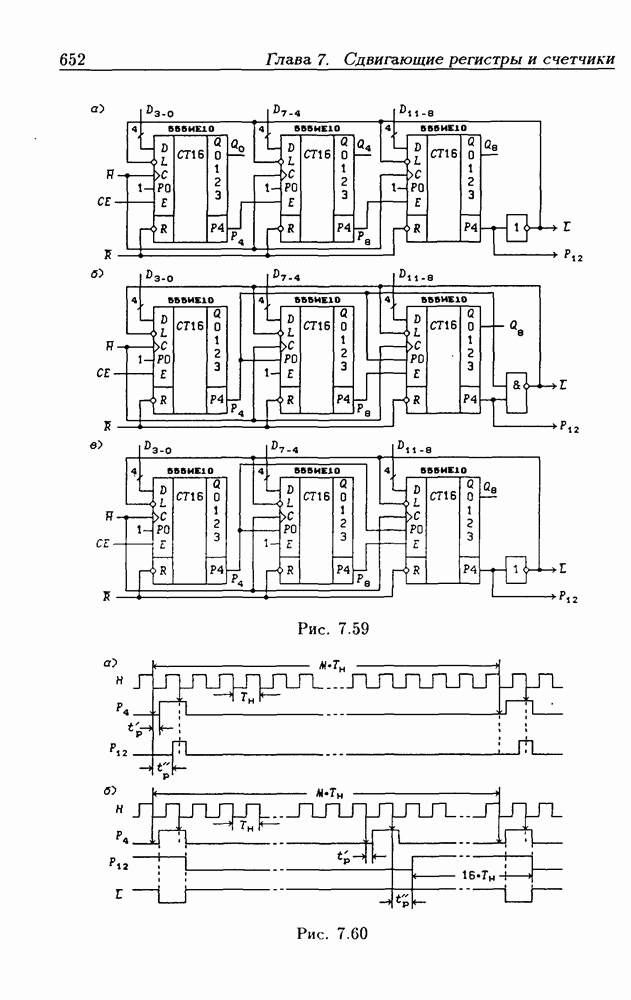
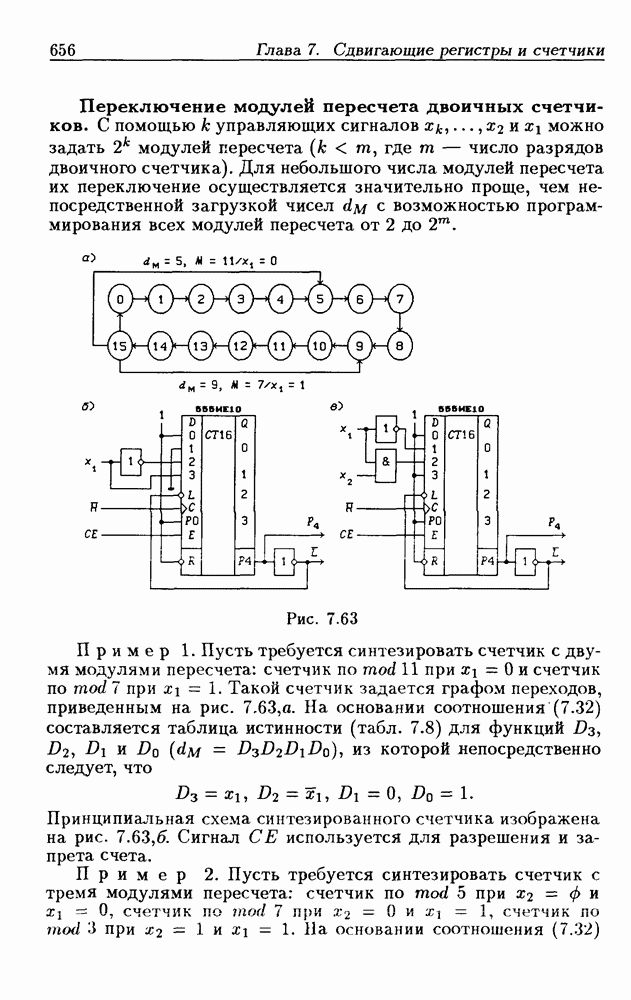
- Переключение модулей пересчета двоичных счетчиков.
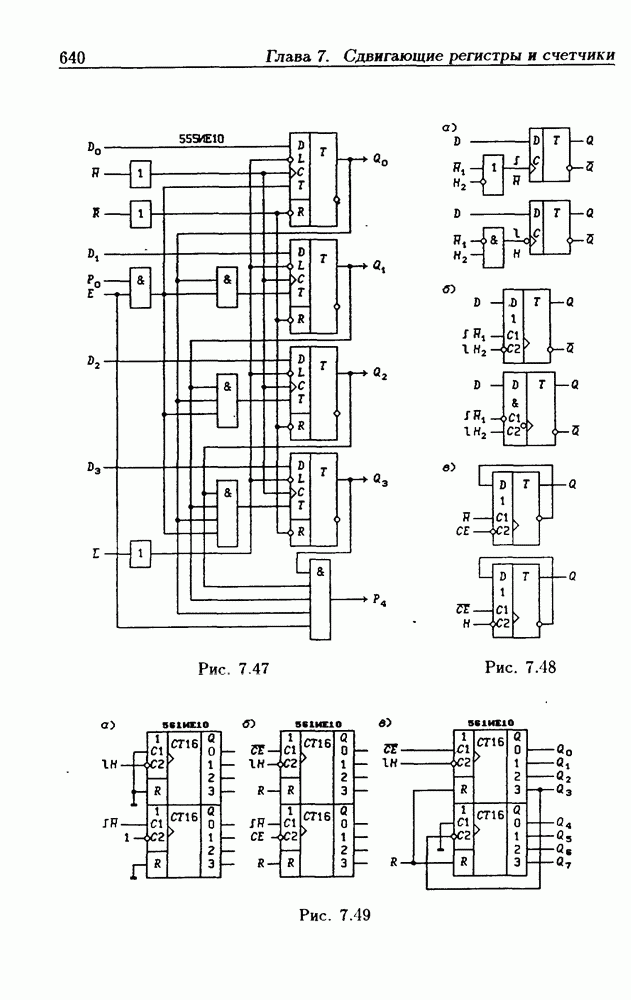
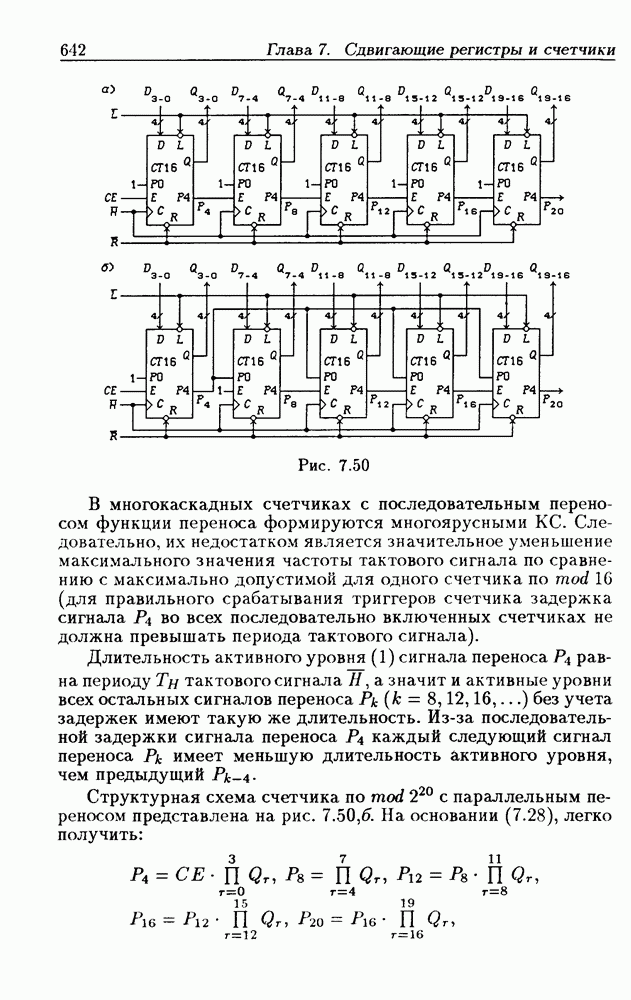
- Функциональные устройства на основе двоичных счетчиков.
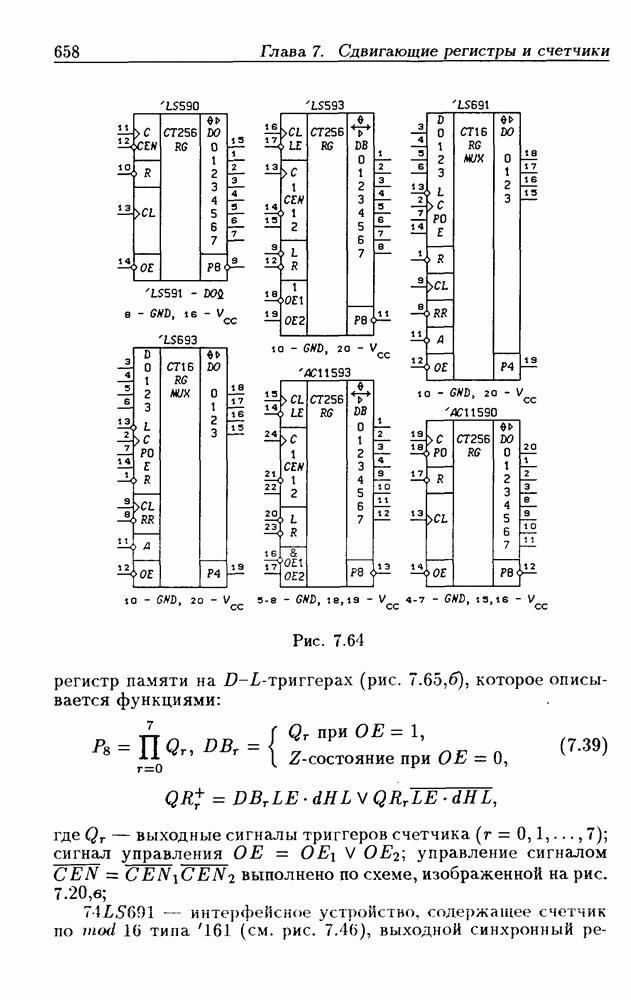
- 7.6. Синхронные двоично-десятичные счетчики
- 7.7. Синхронные реверсивные счетчики
- 7.8. Счетчики с расщепленным тактовым сигналом
- 7.9. Счетчики на сдвигающих регистрах
- 7.10. Кольцевые счетчики
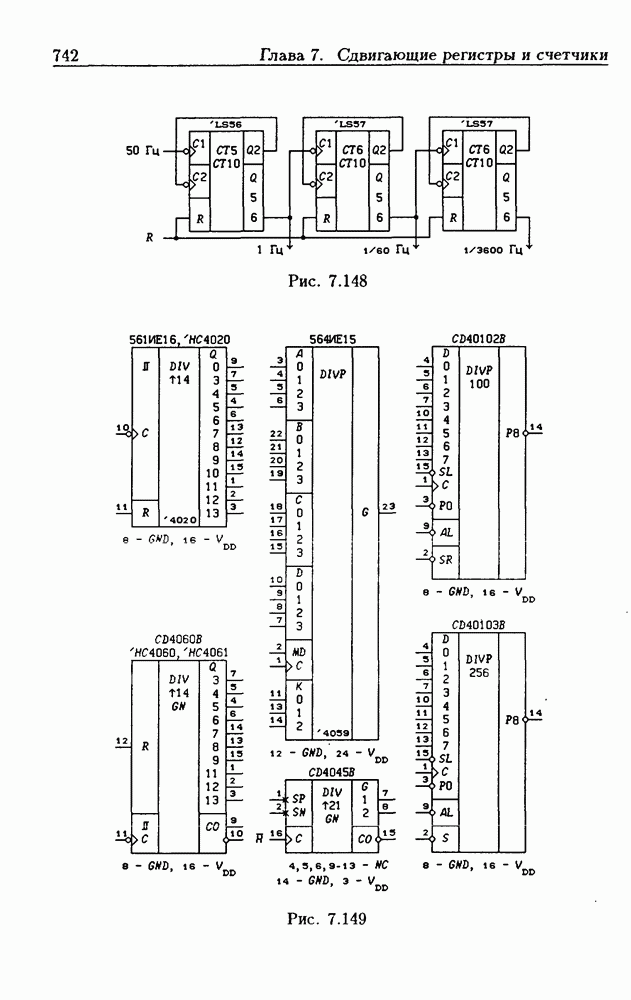
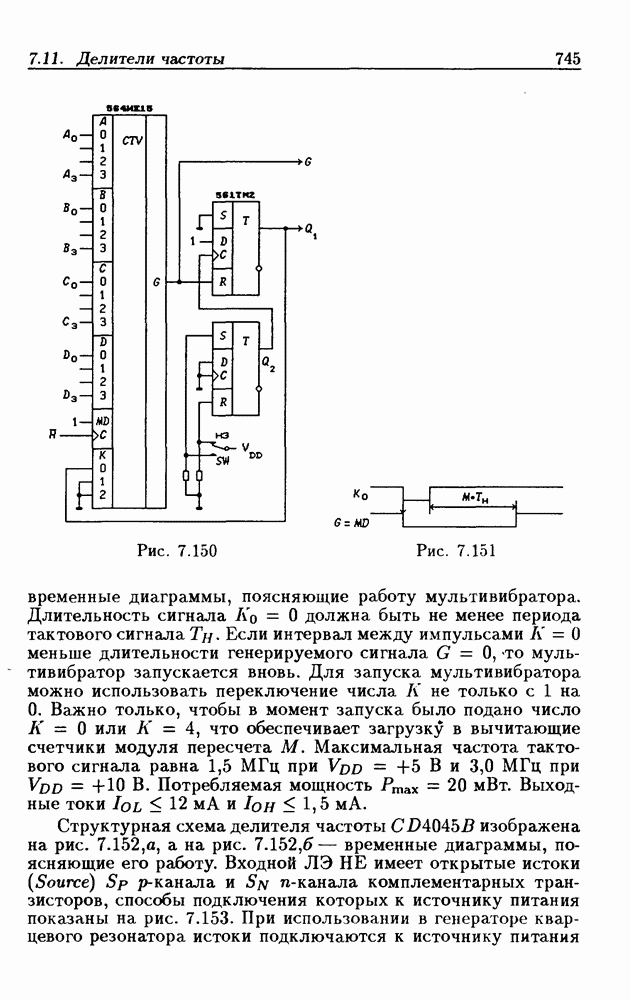
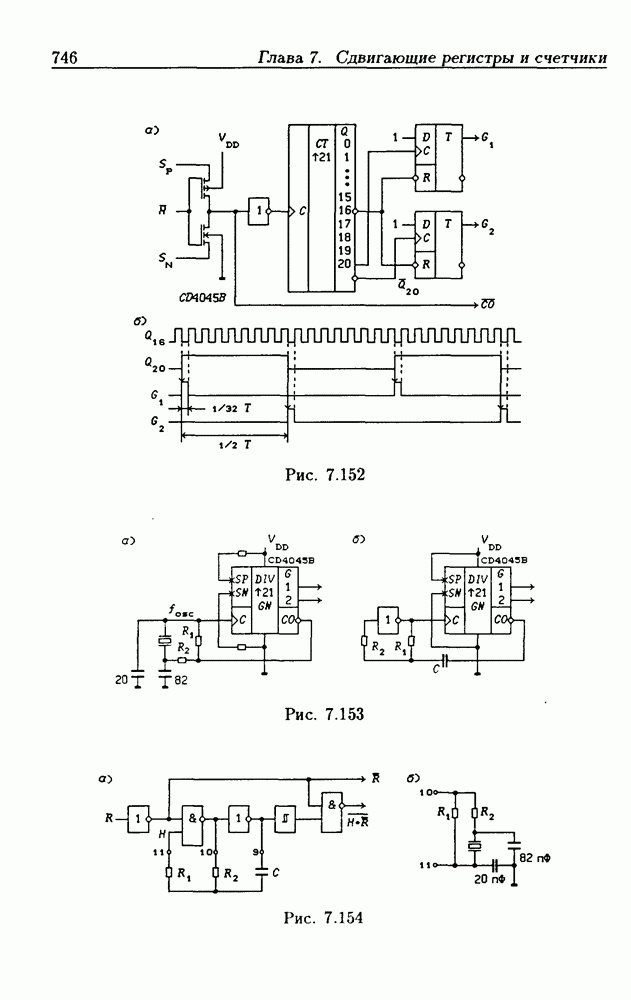
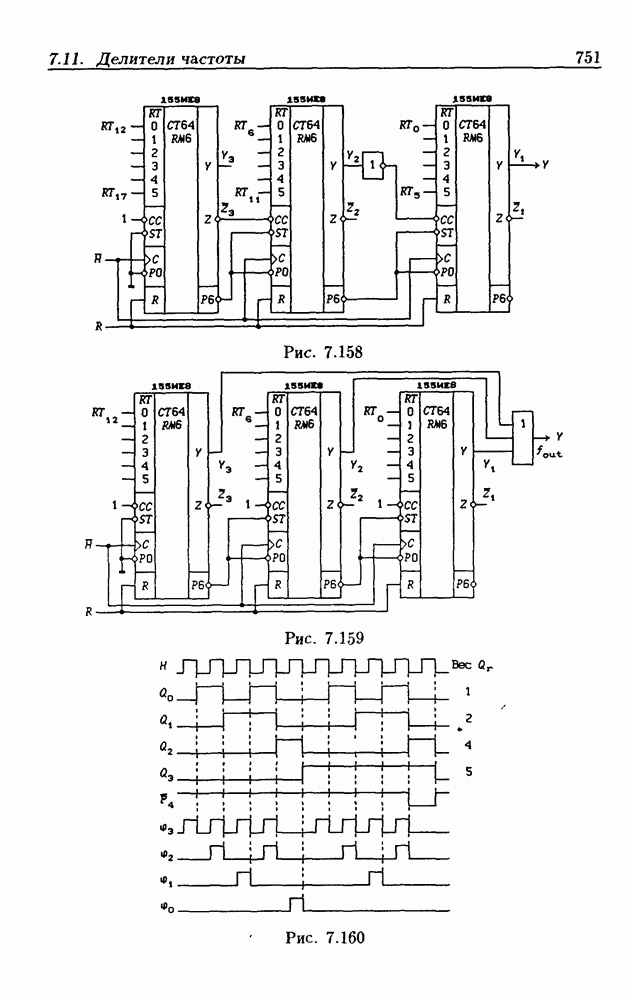
- 7.11. Делители частоты
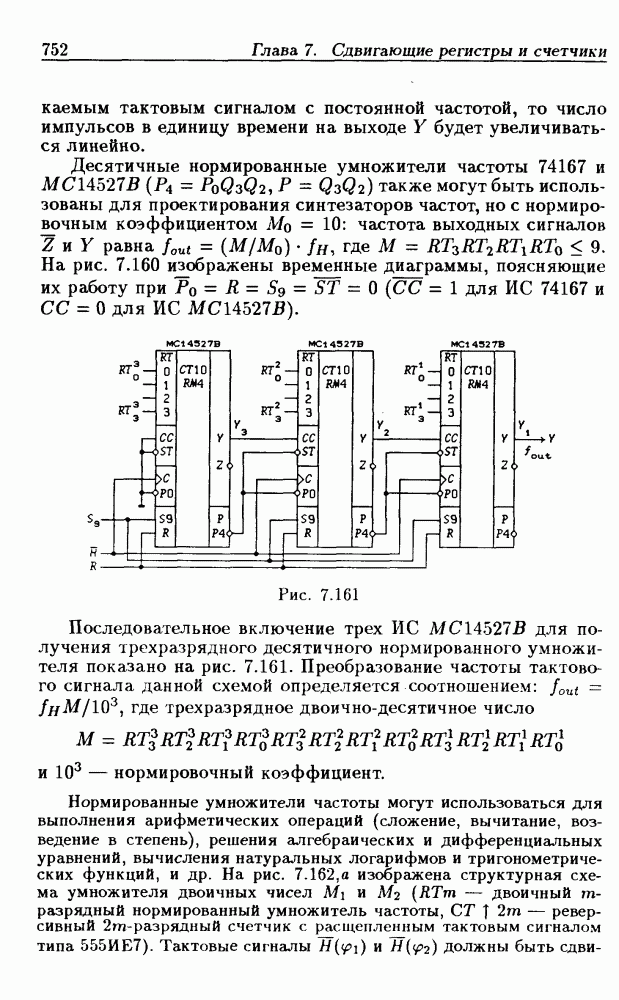
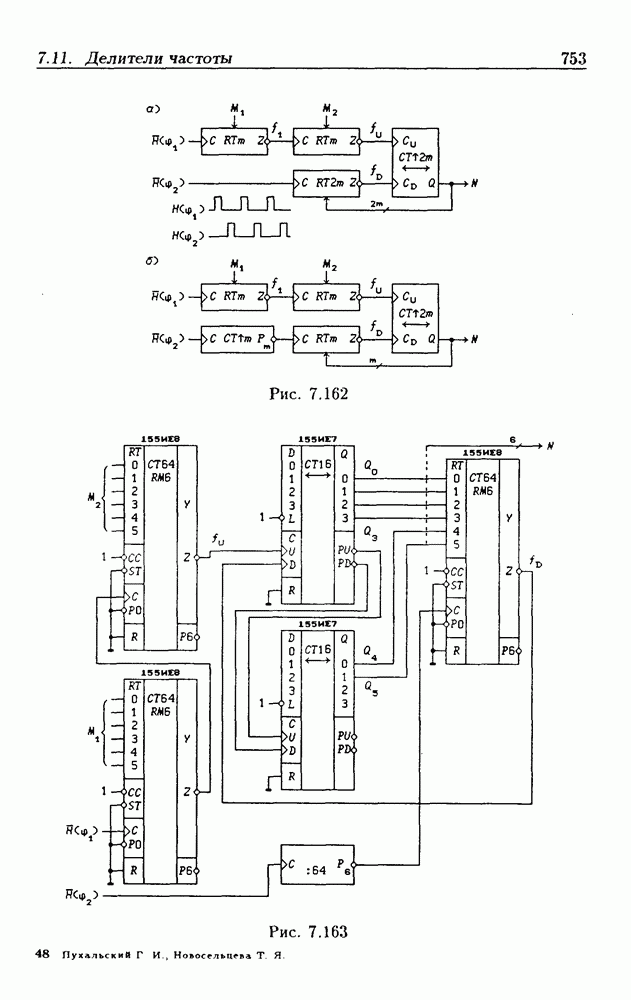
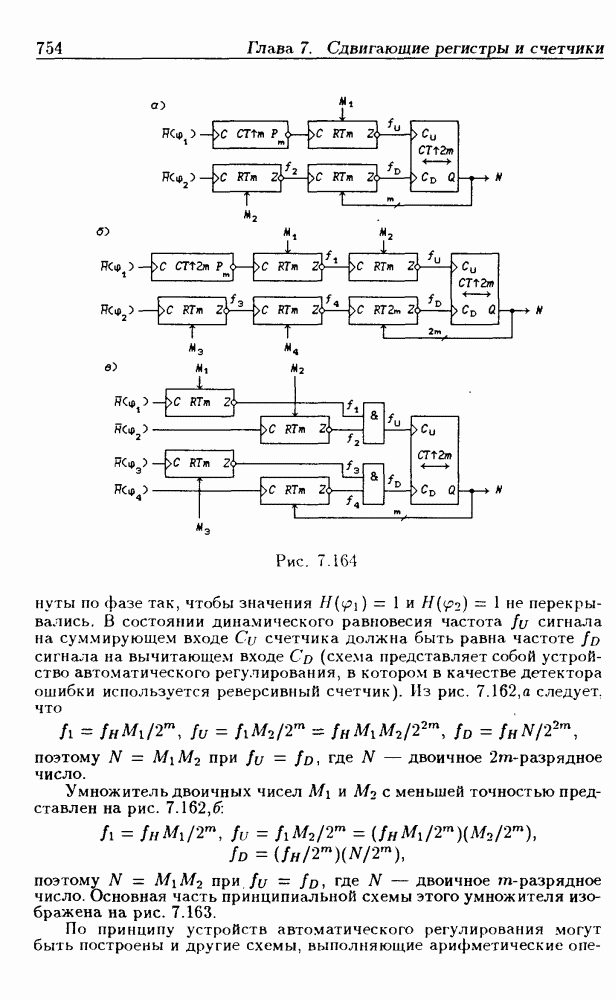
- Нормированные умножители частоты.
- 7.12. Линейные генераторы
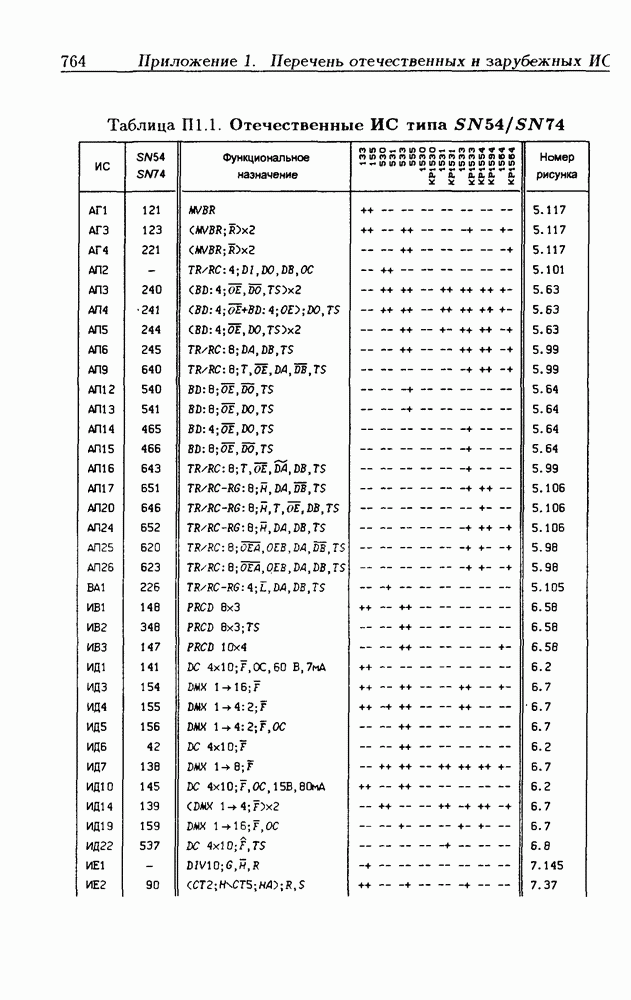
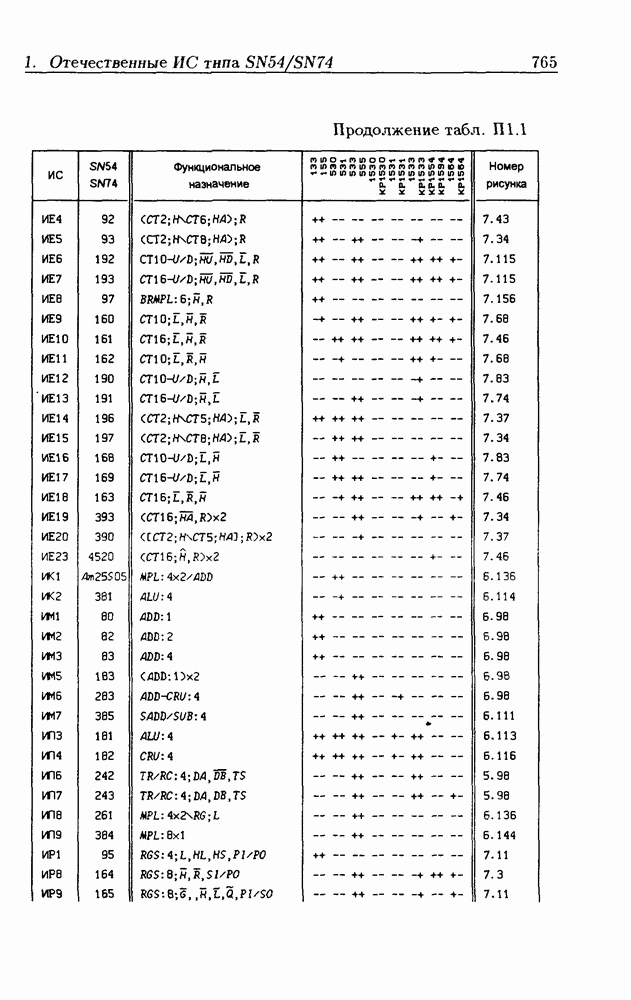
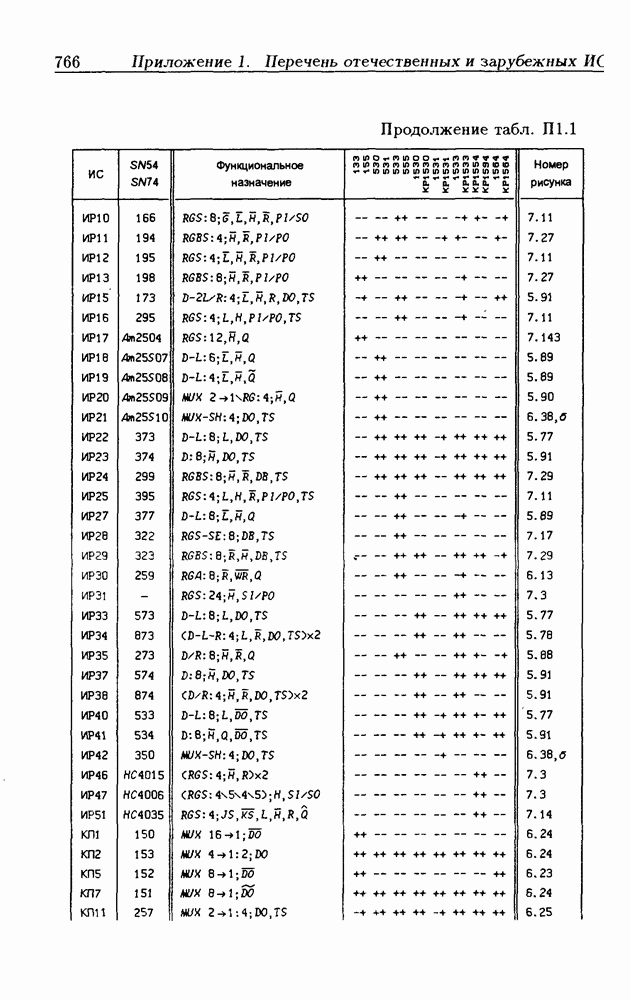
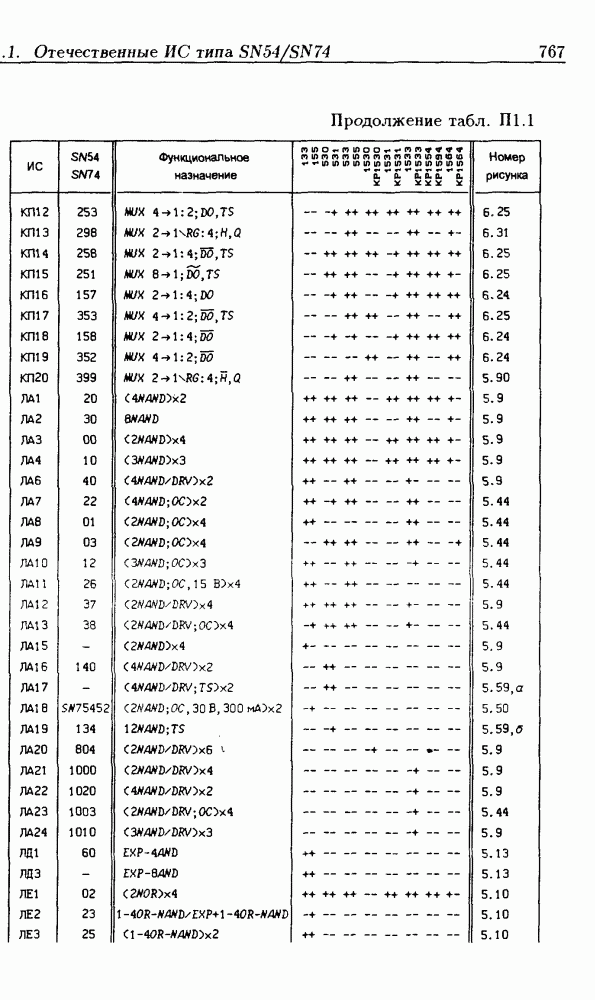
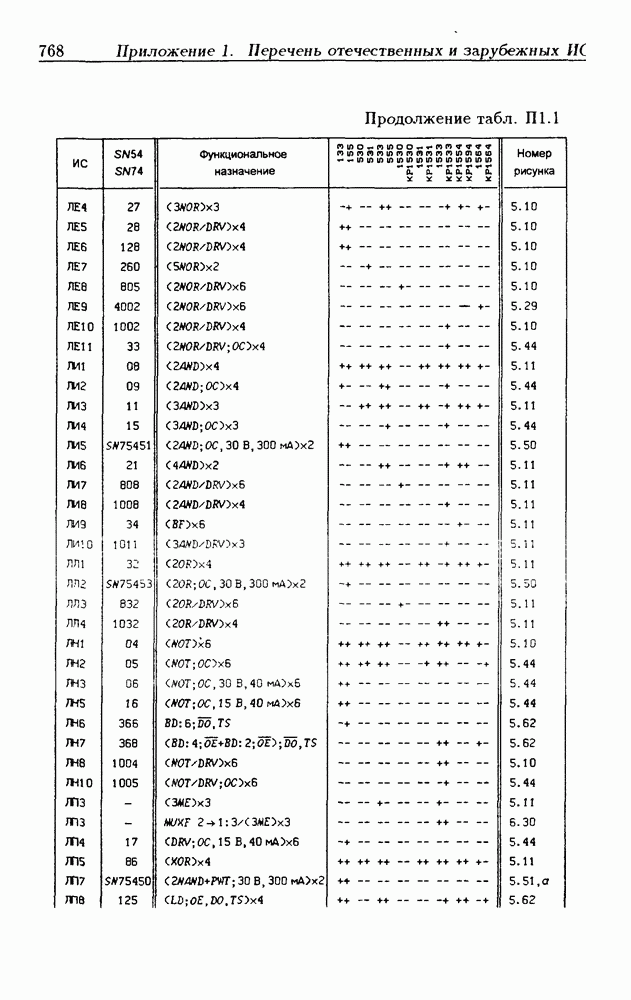
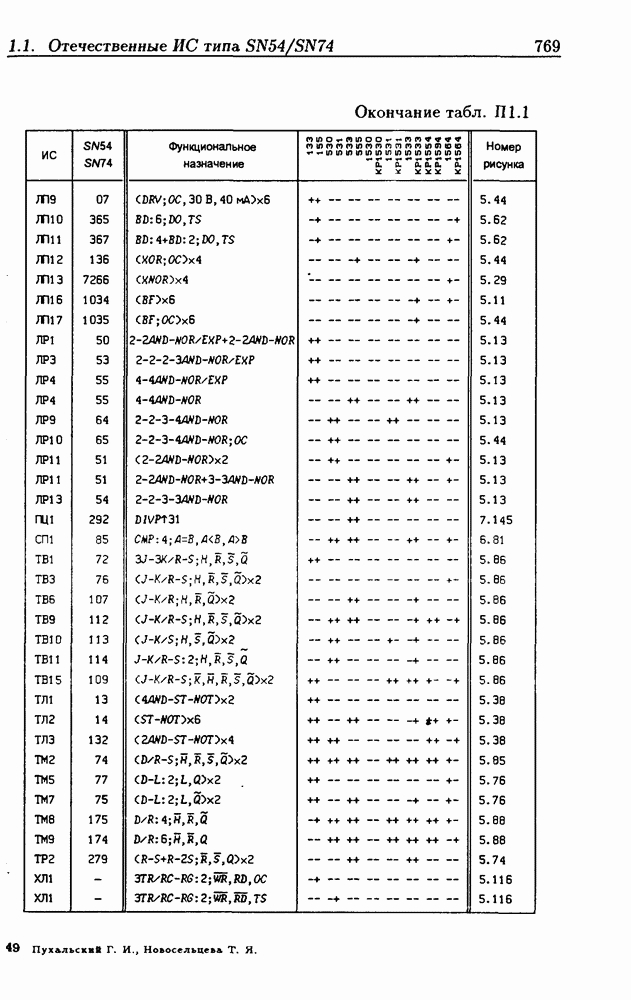
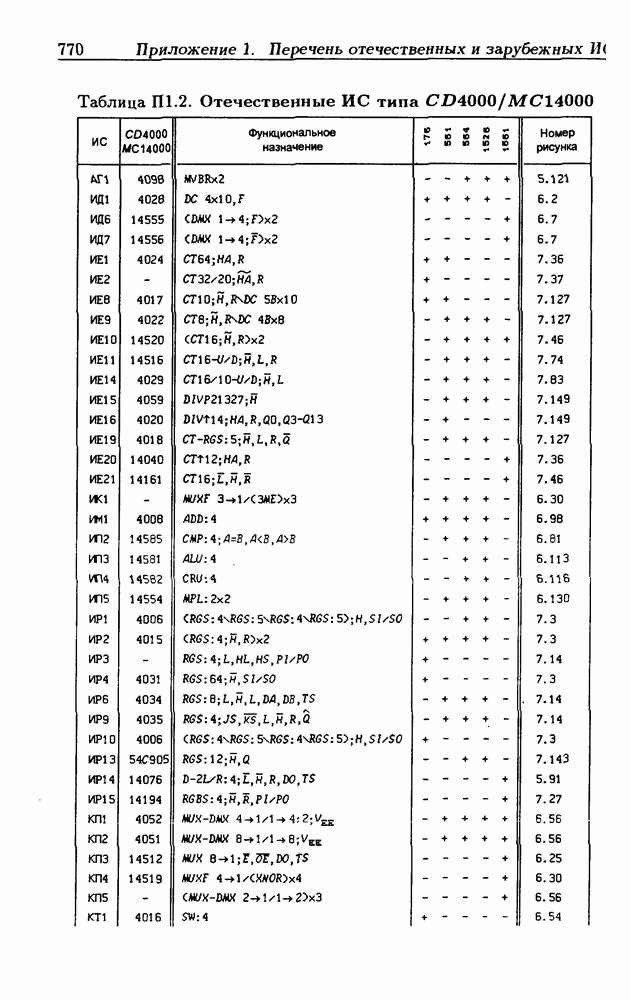
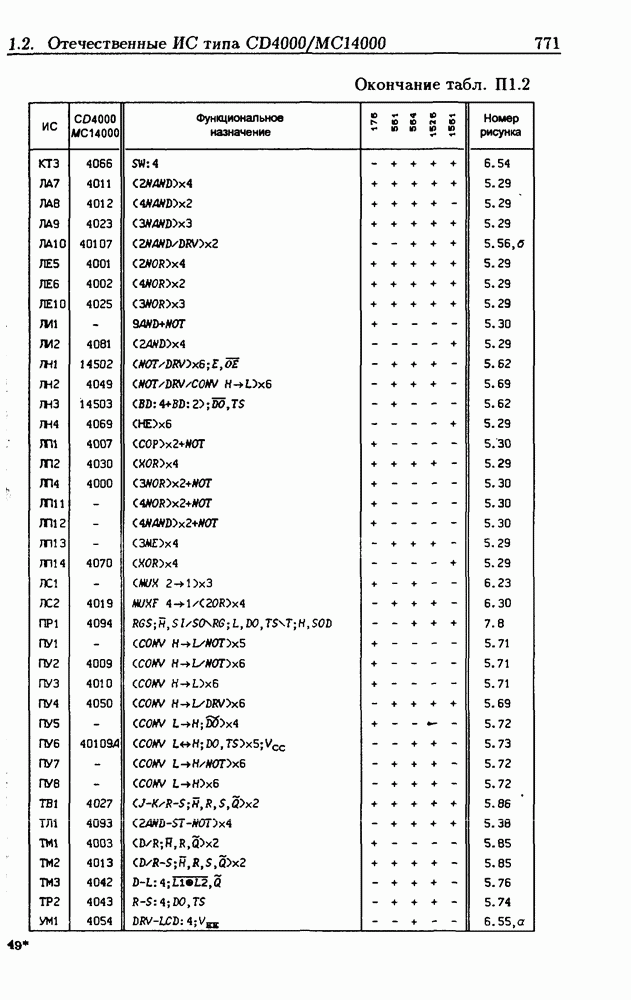
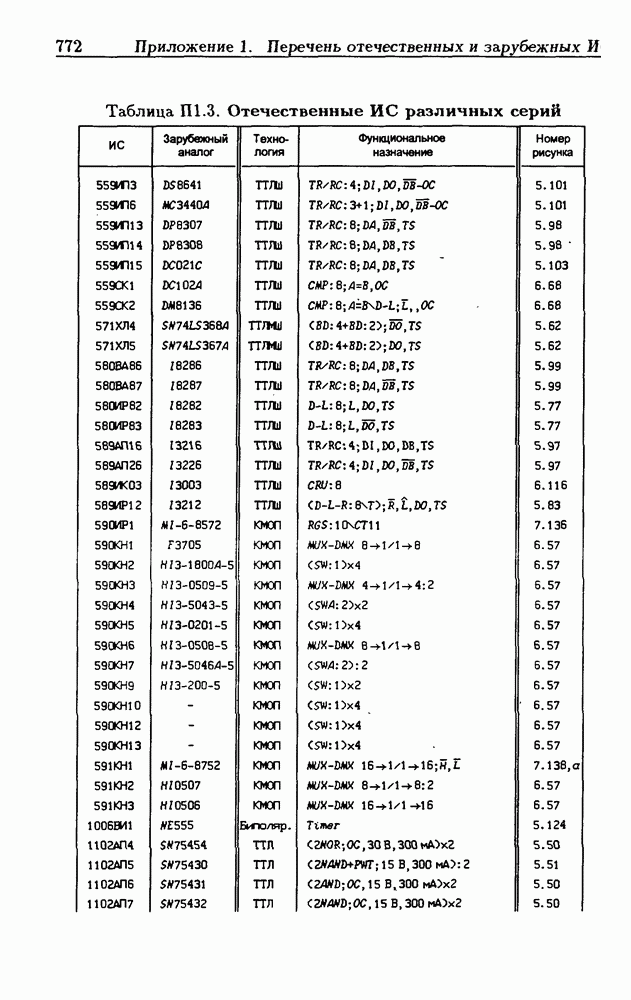
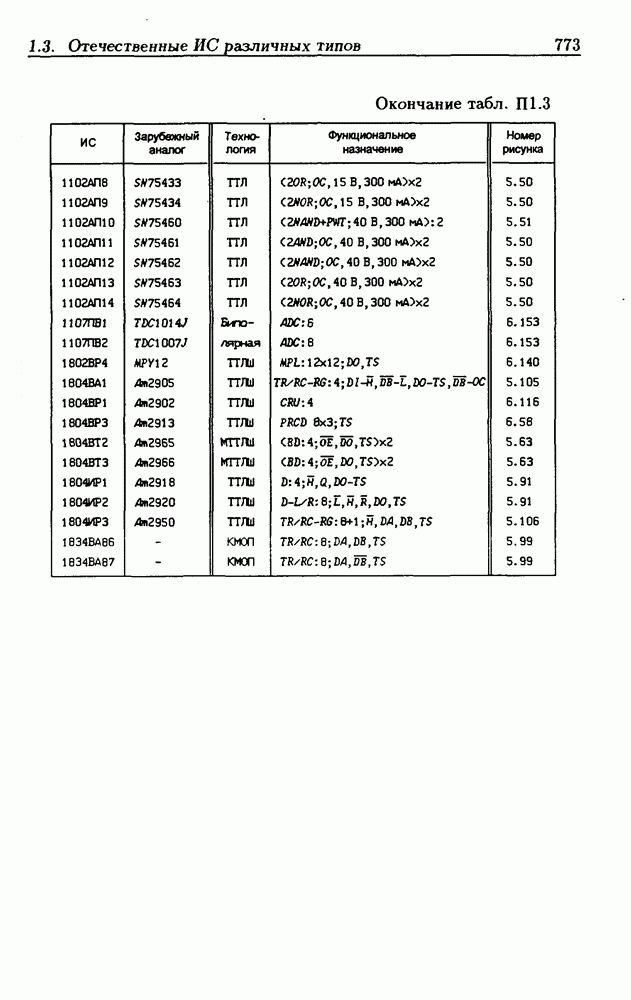
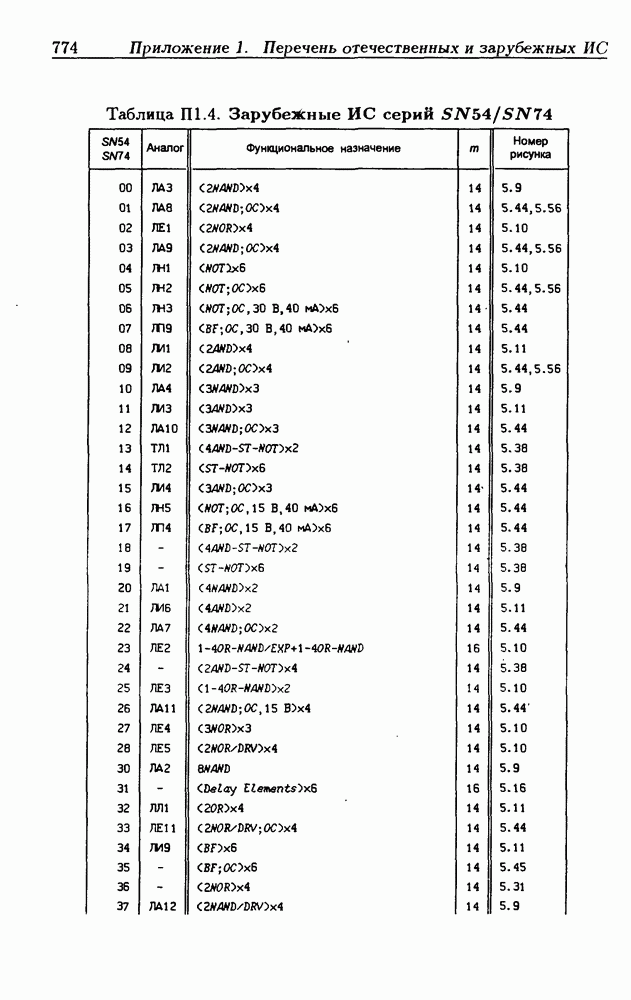
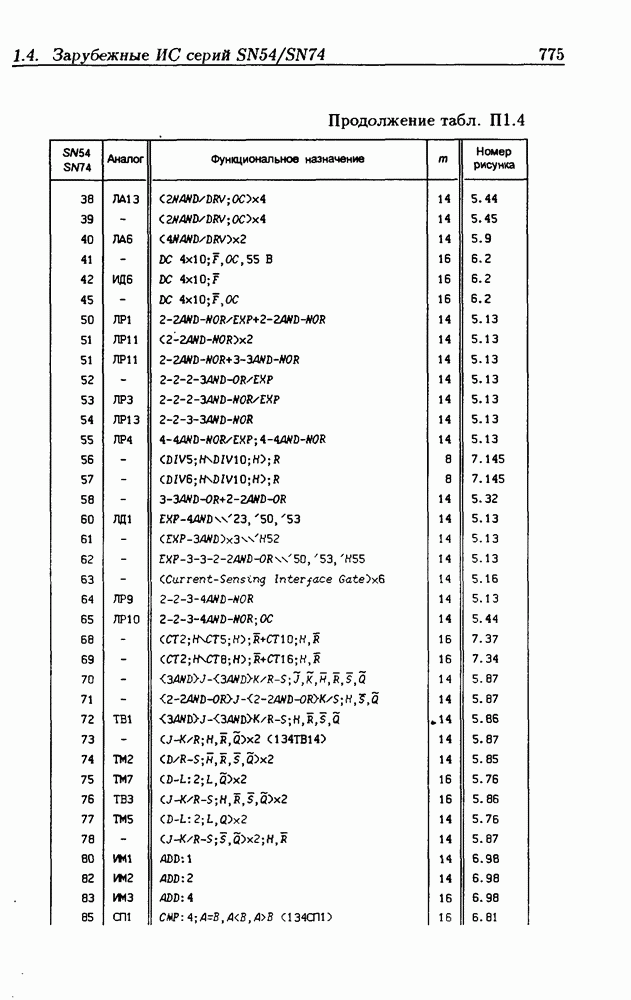
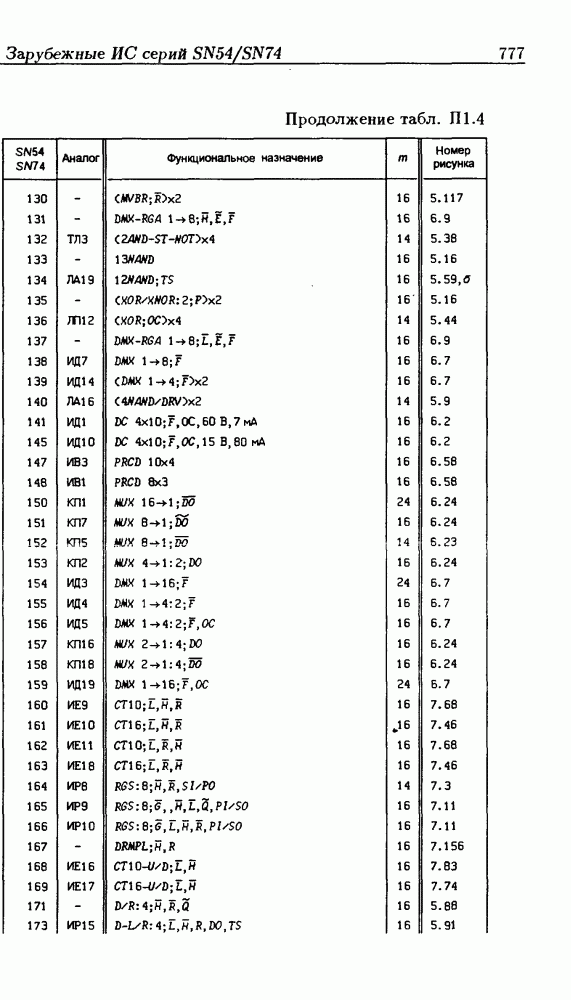
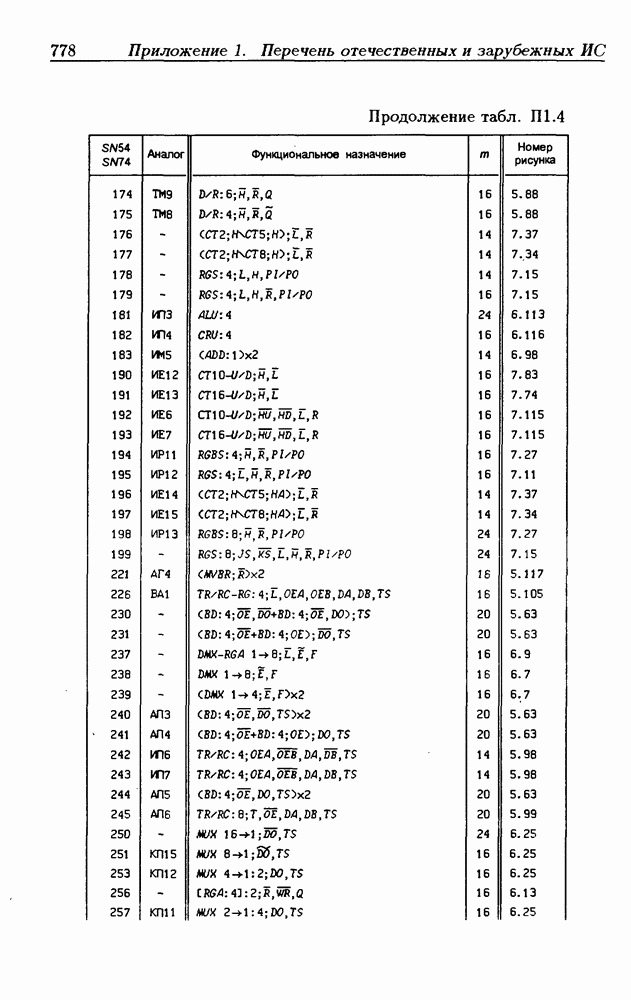
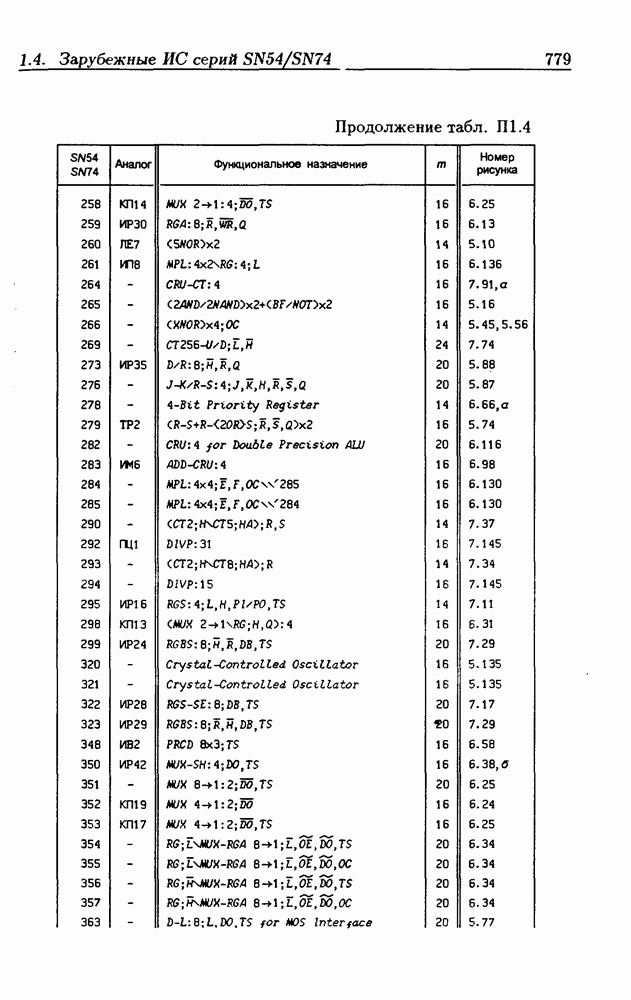
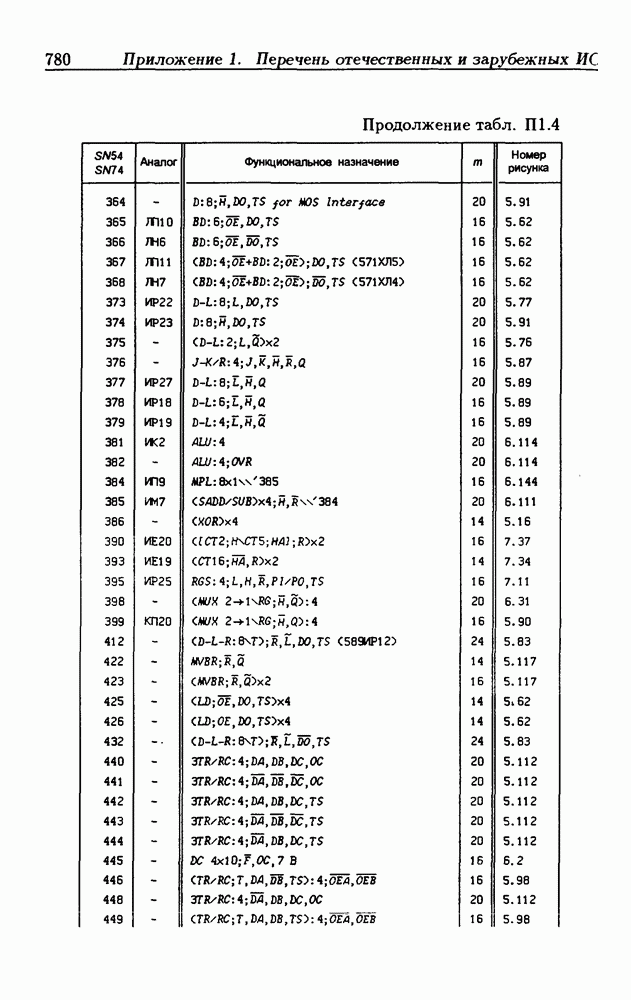
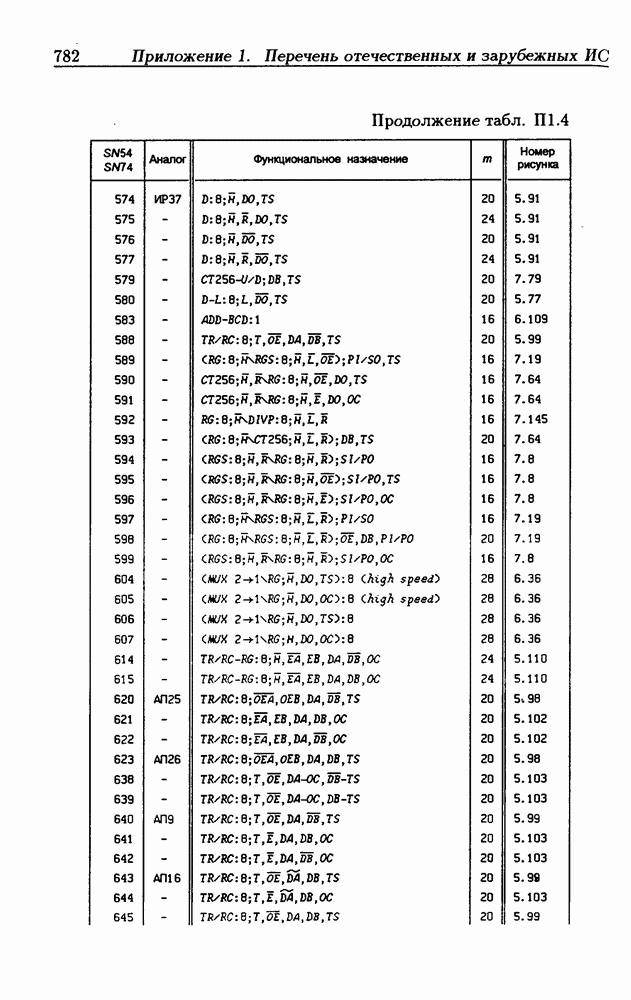
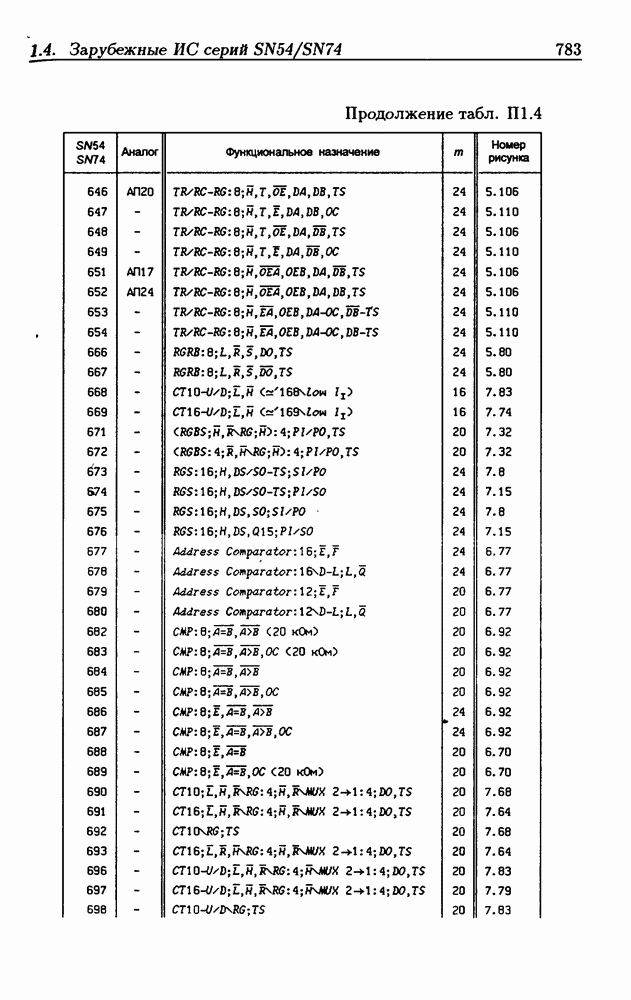
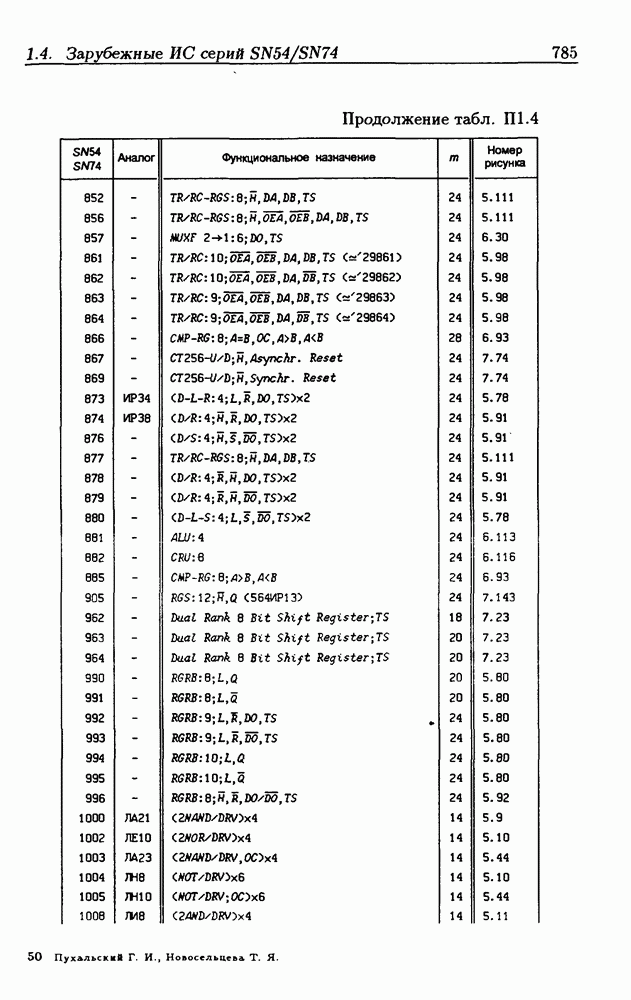
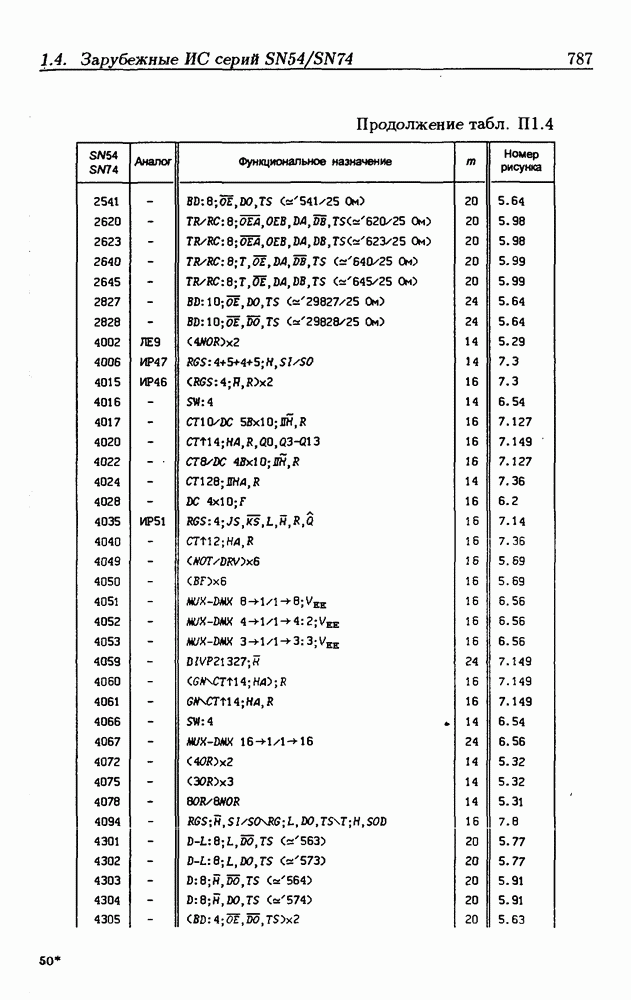
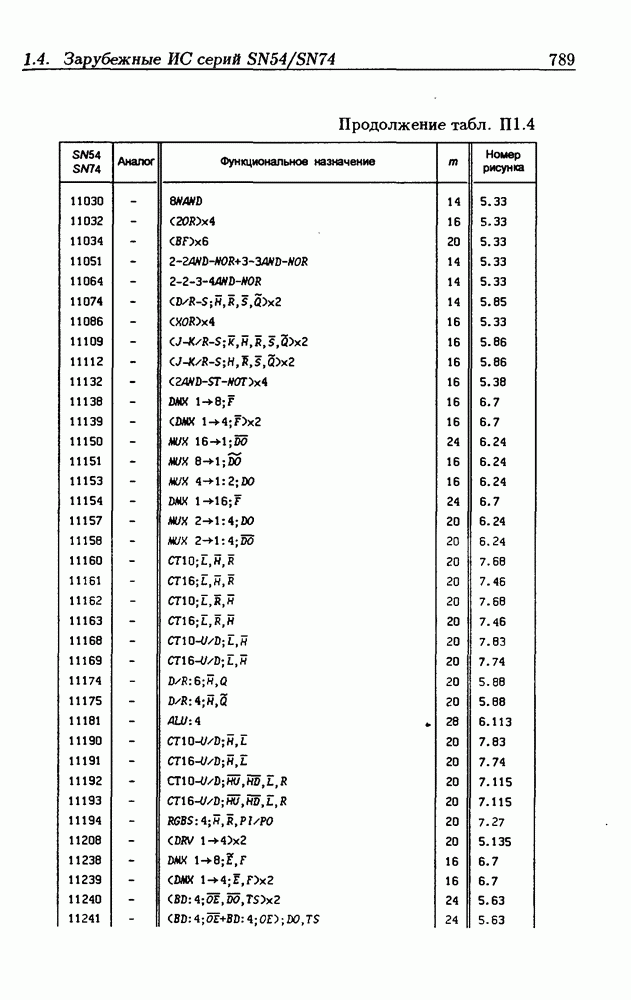
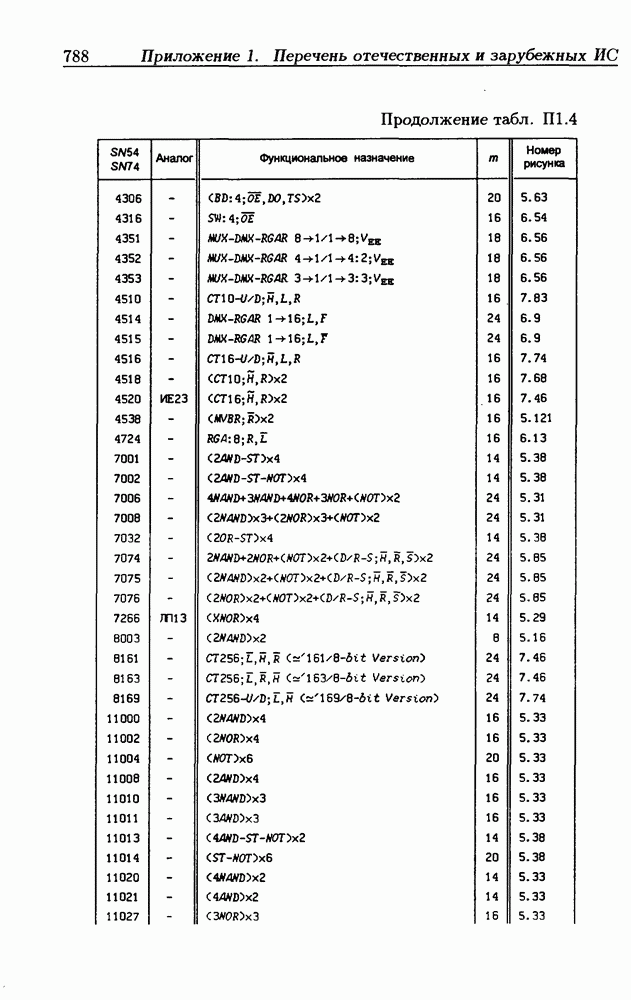
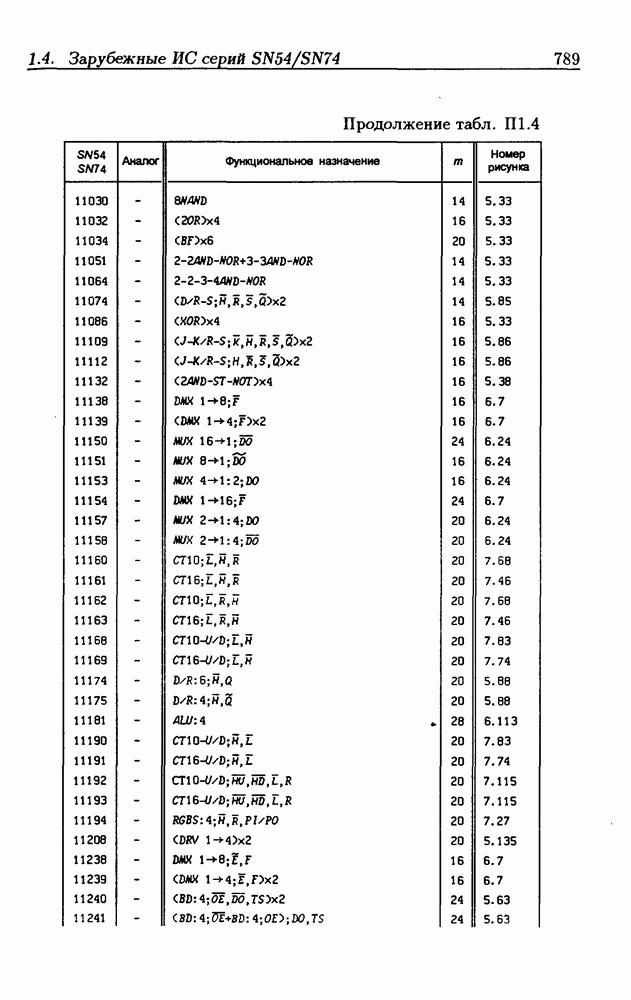
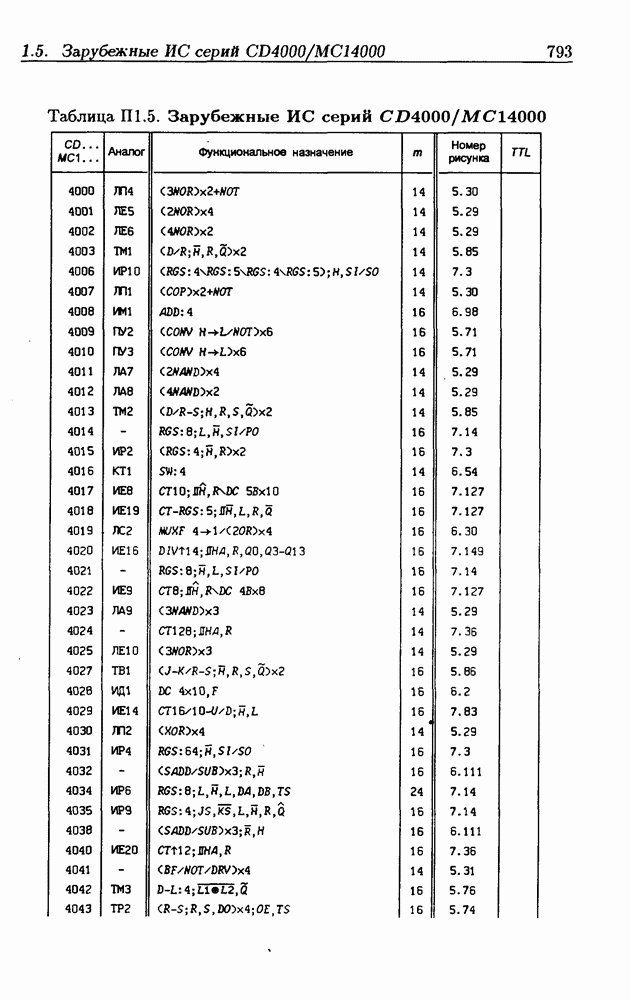
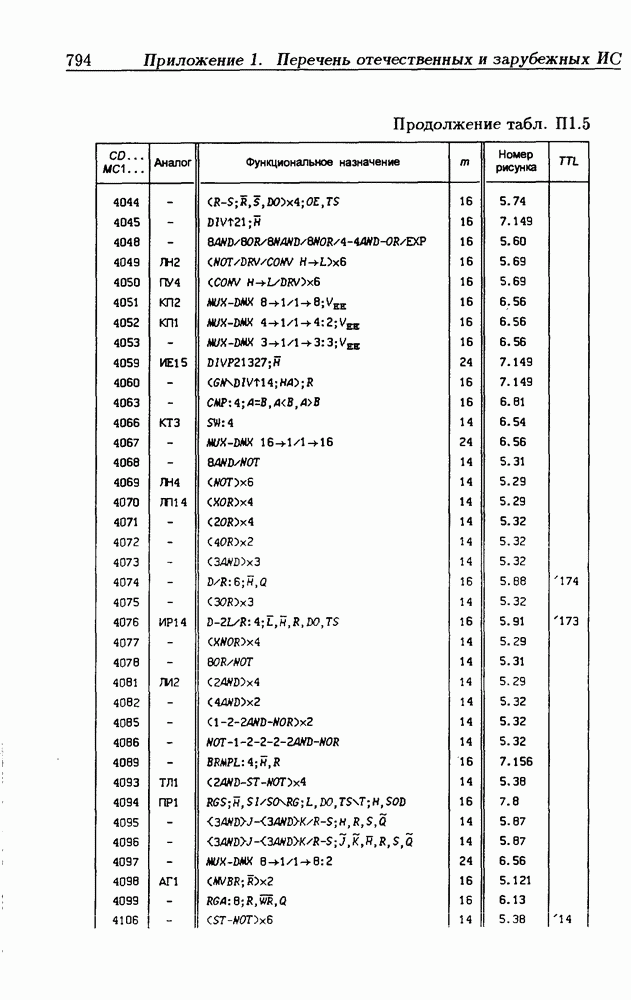
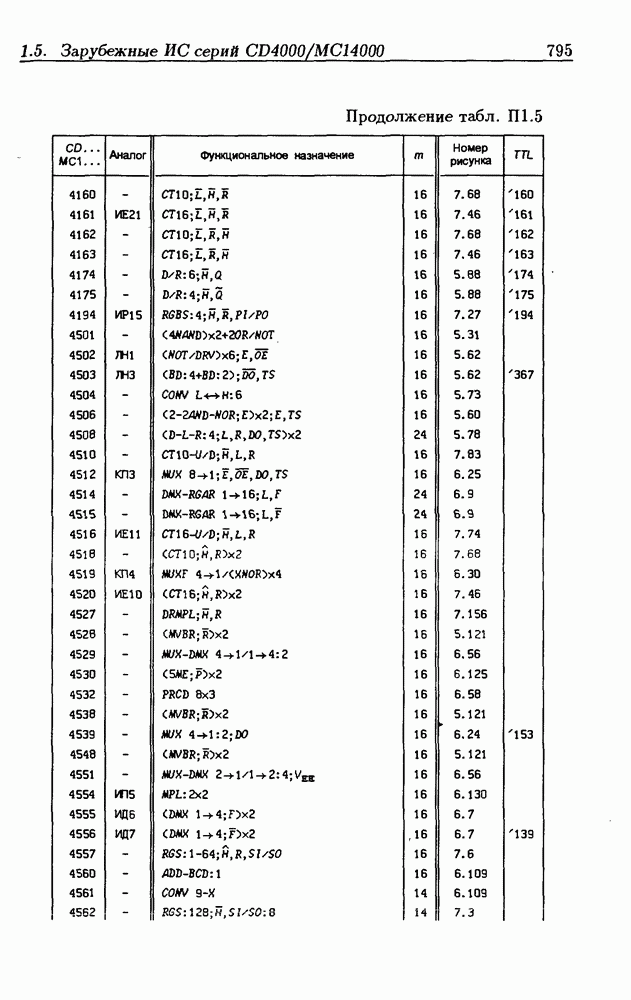
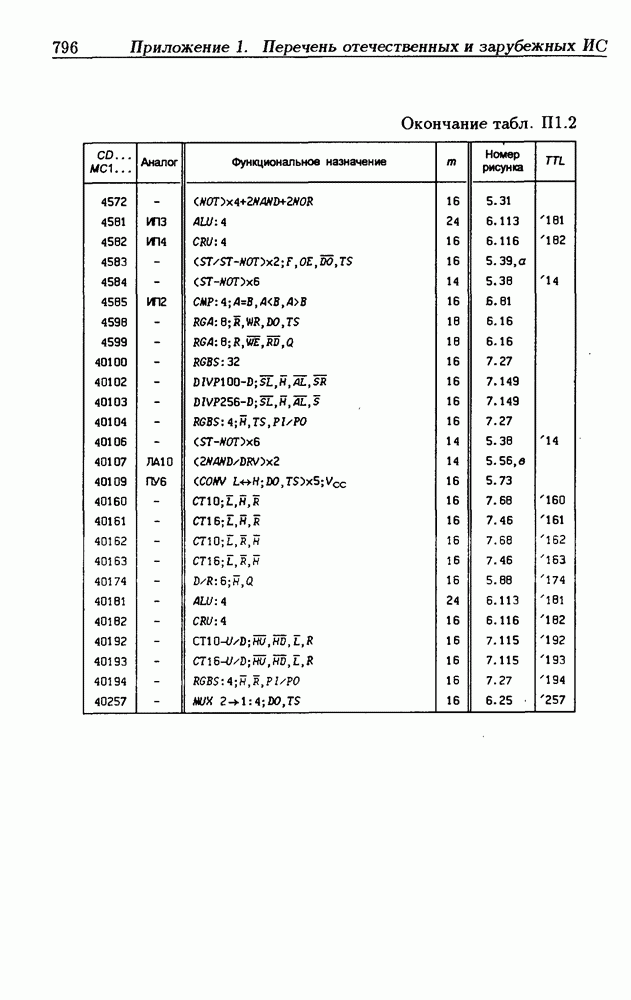
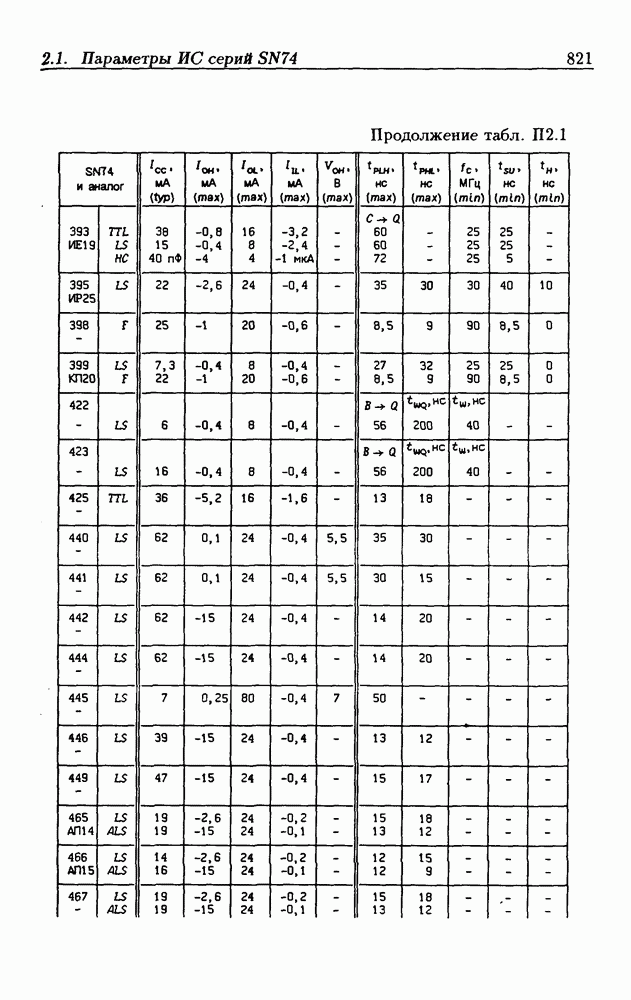
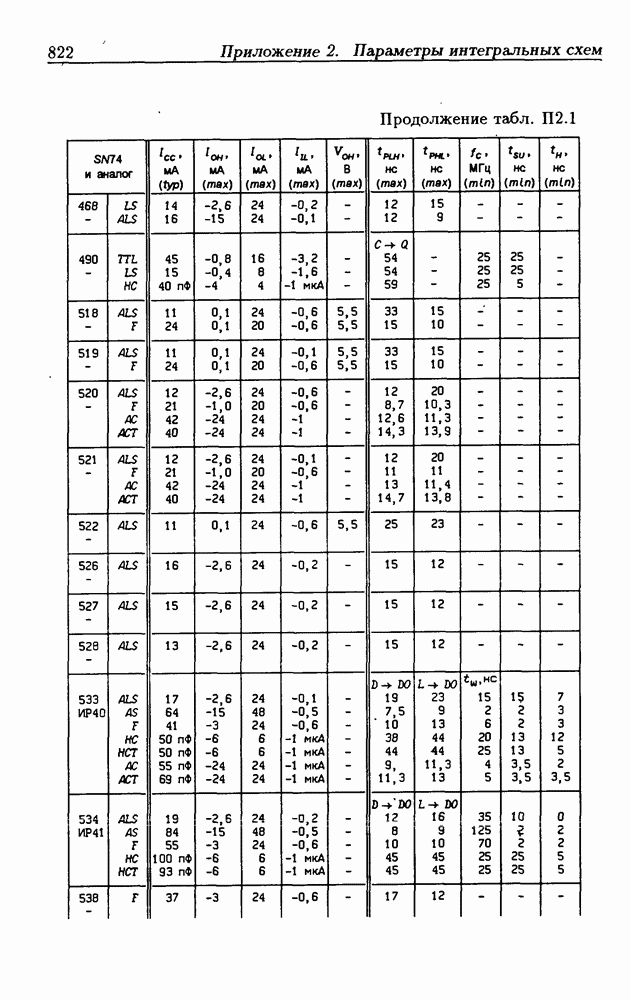
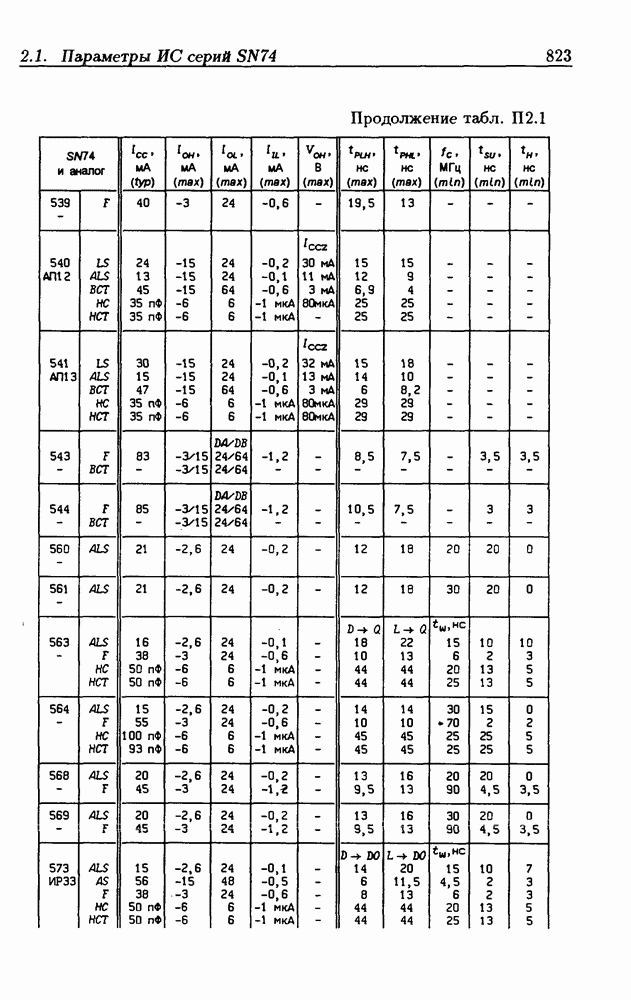
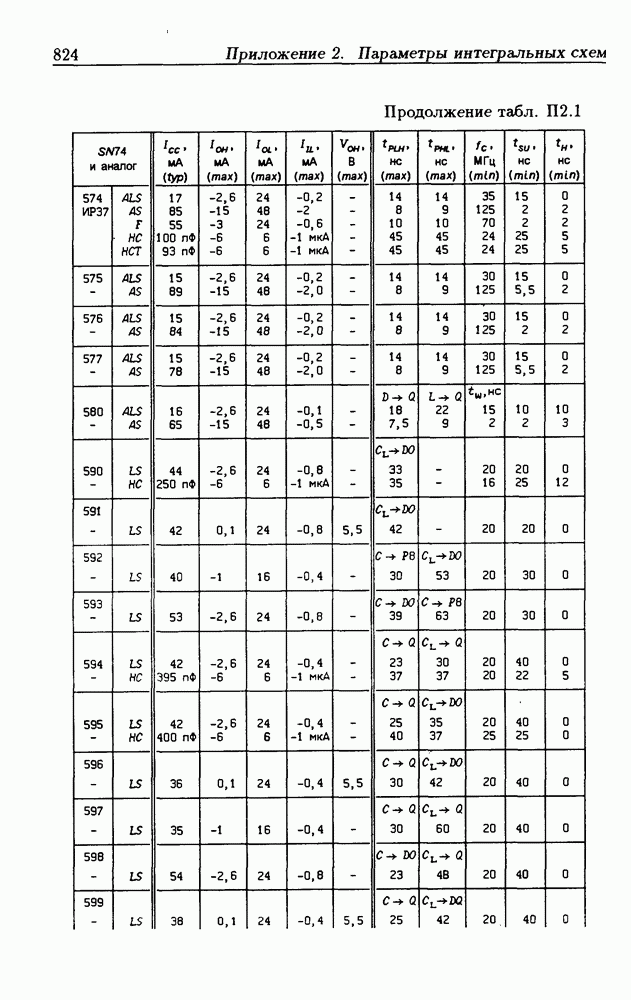
- Приложение 1. Перечень отечественных и зарубежных ИС
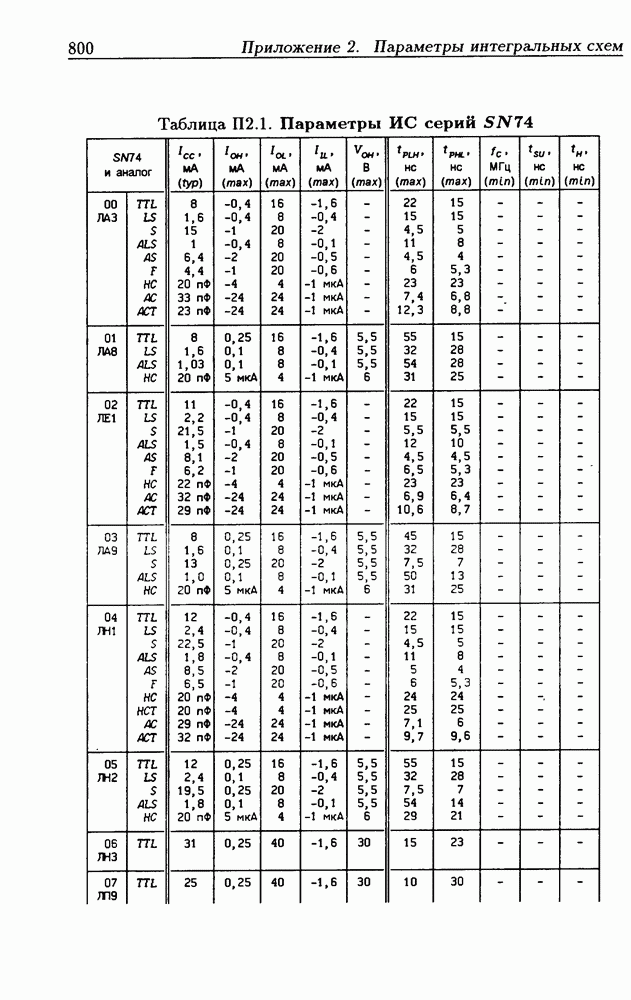
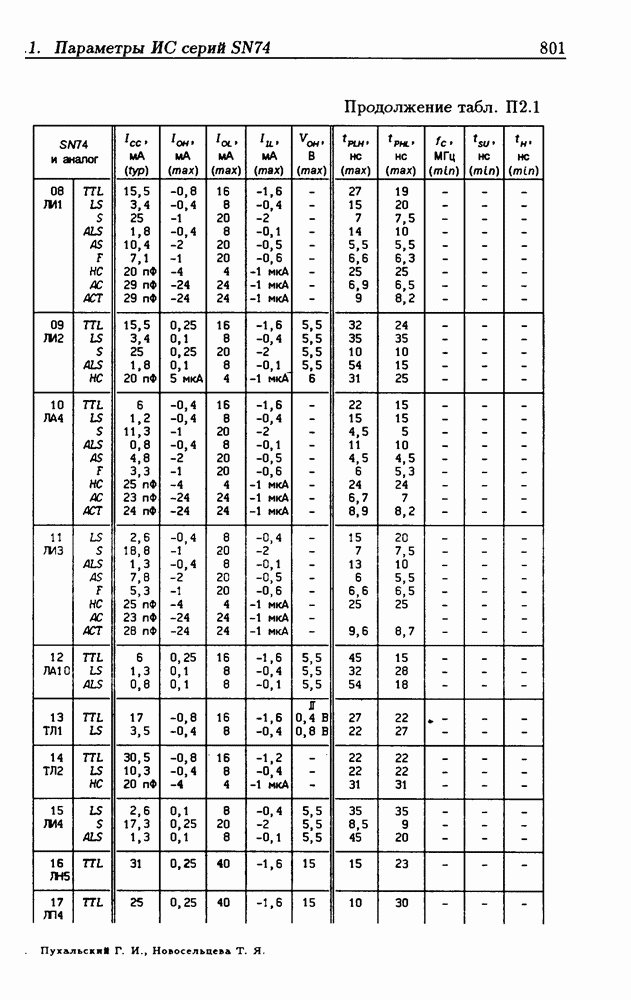
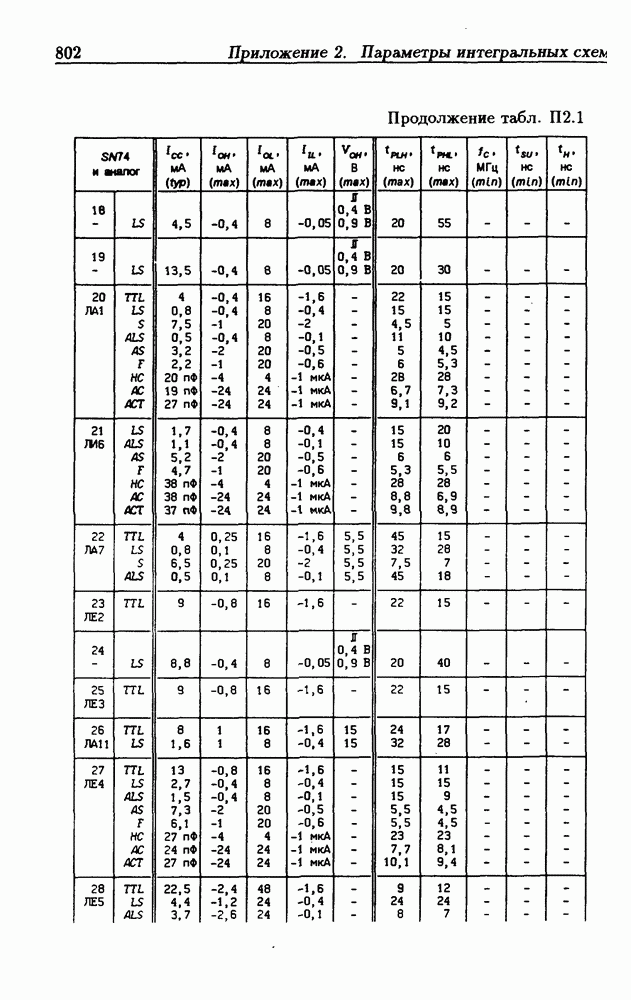
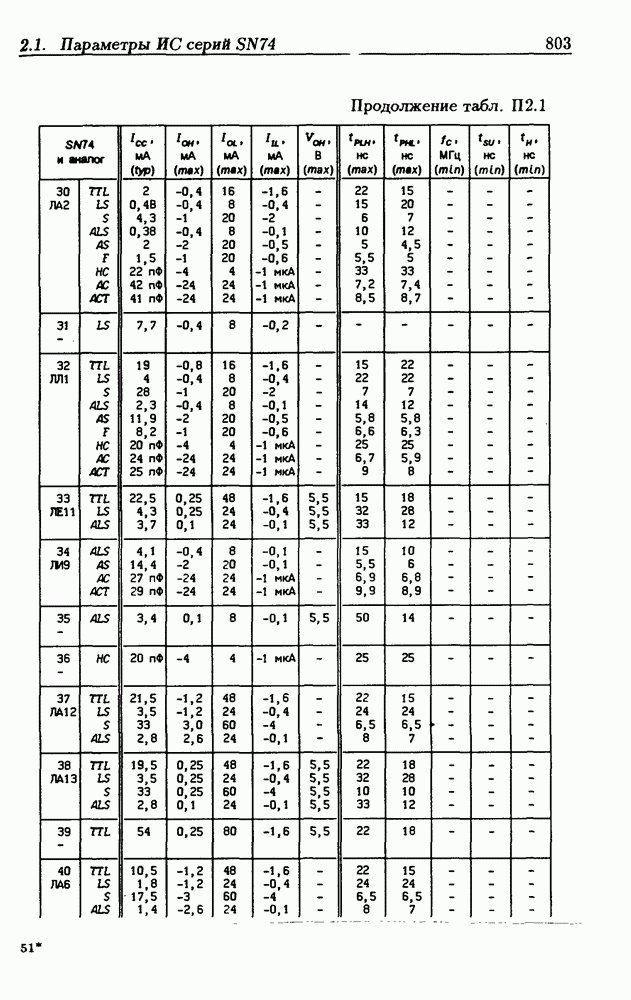
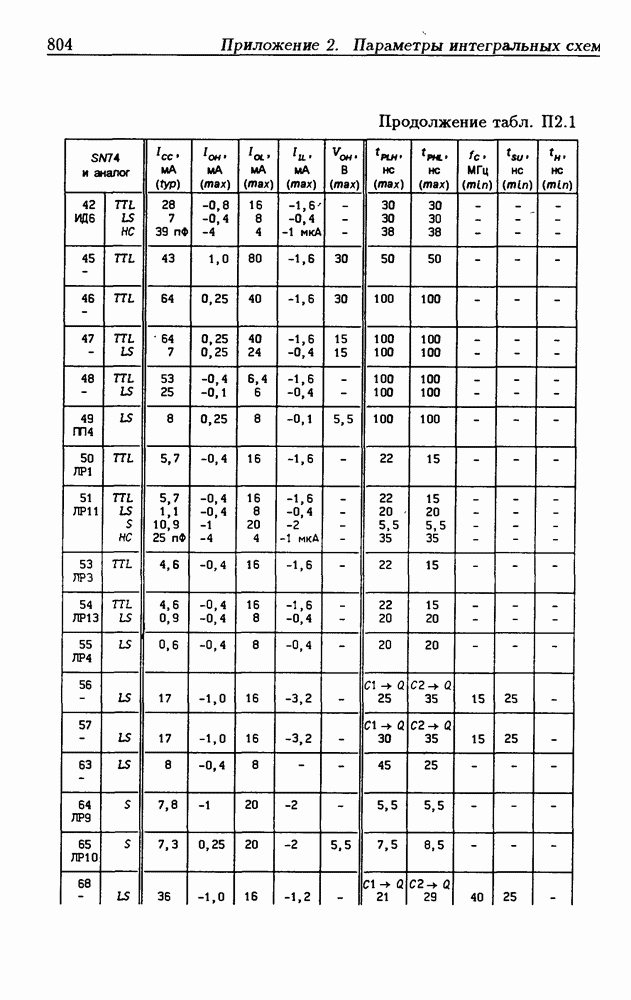
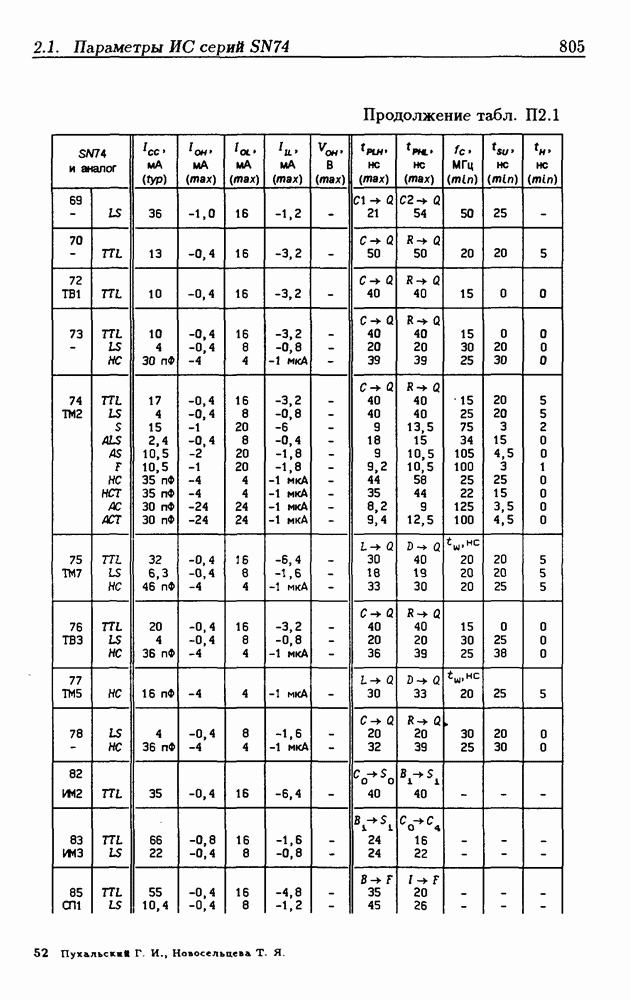
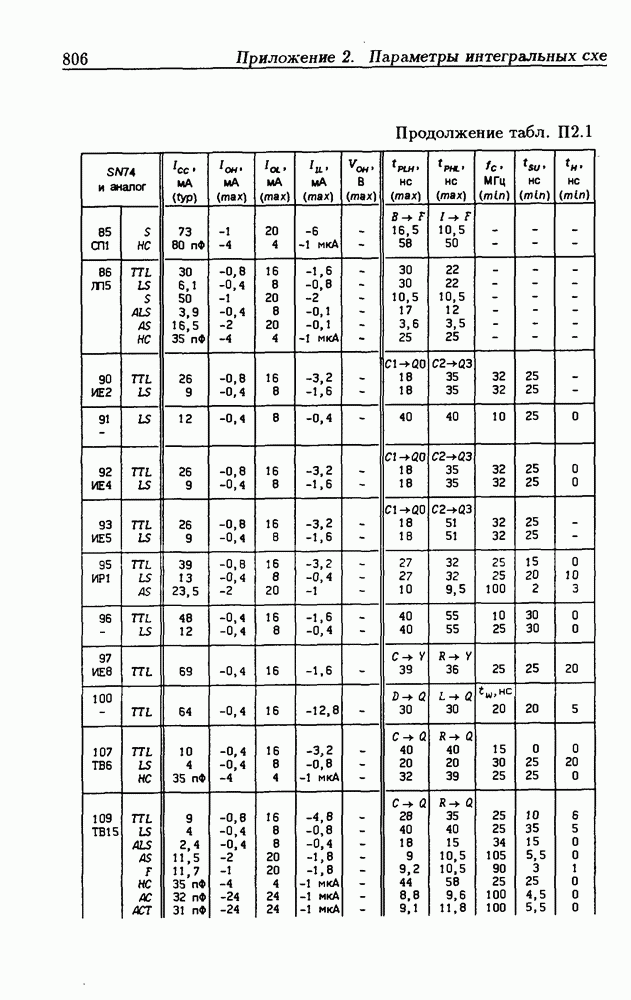
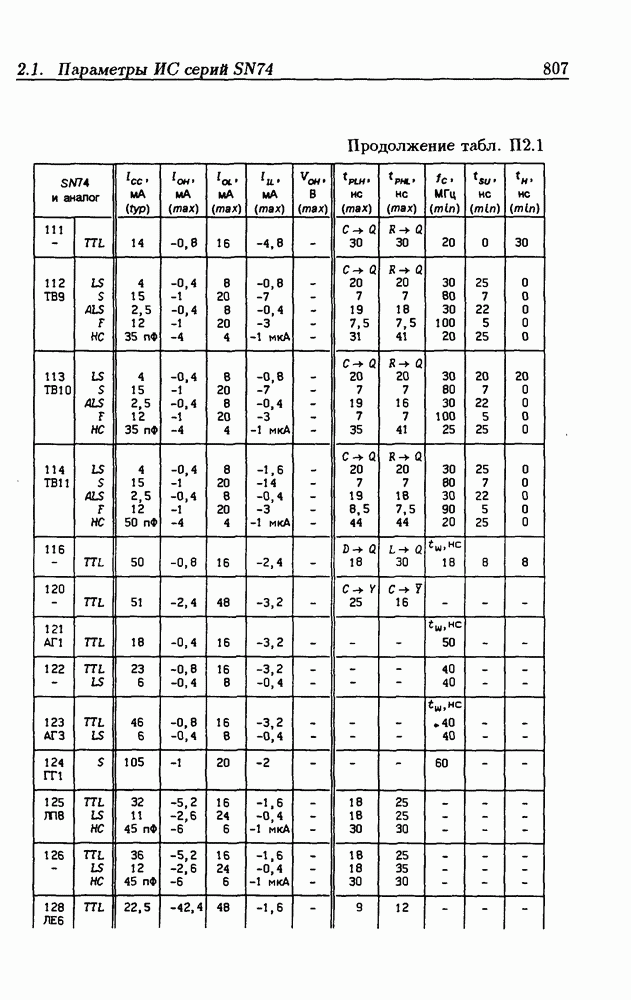
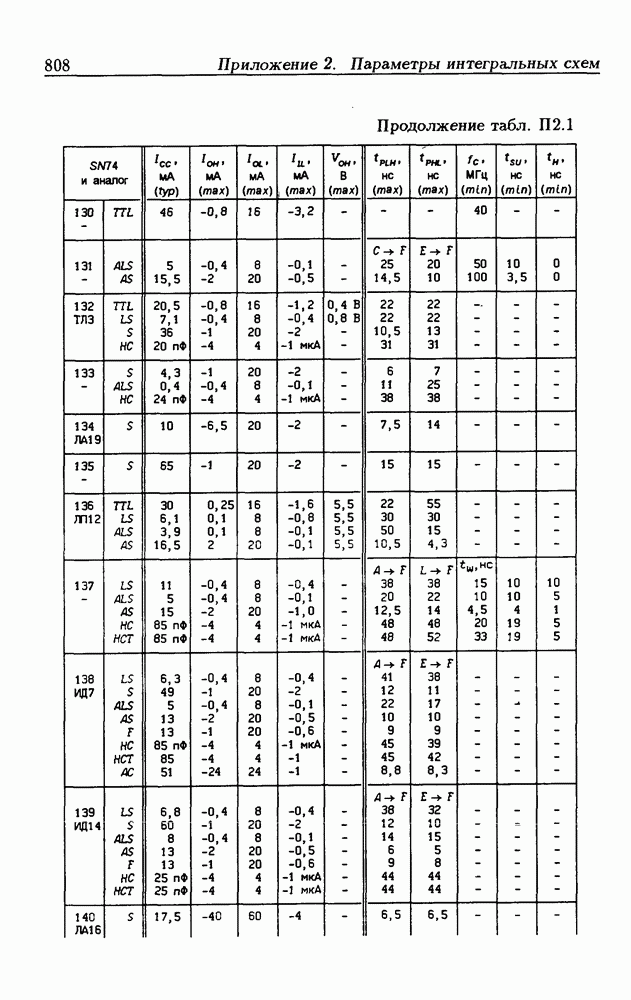
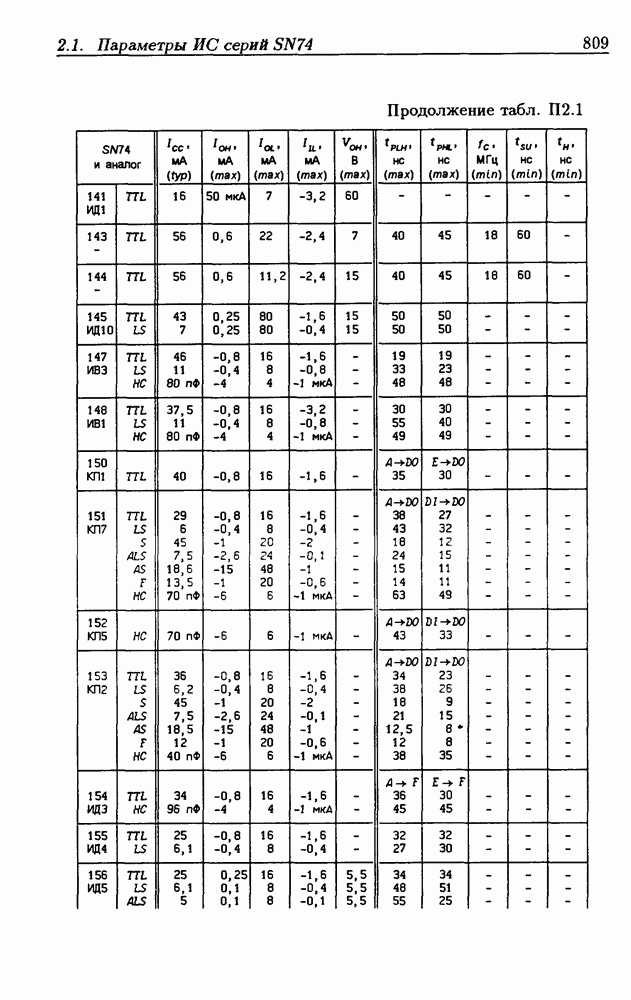
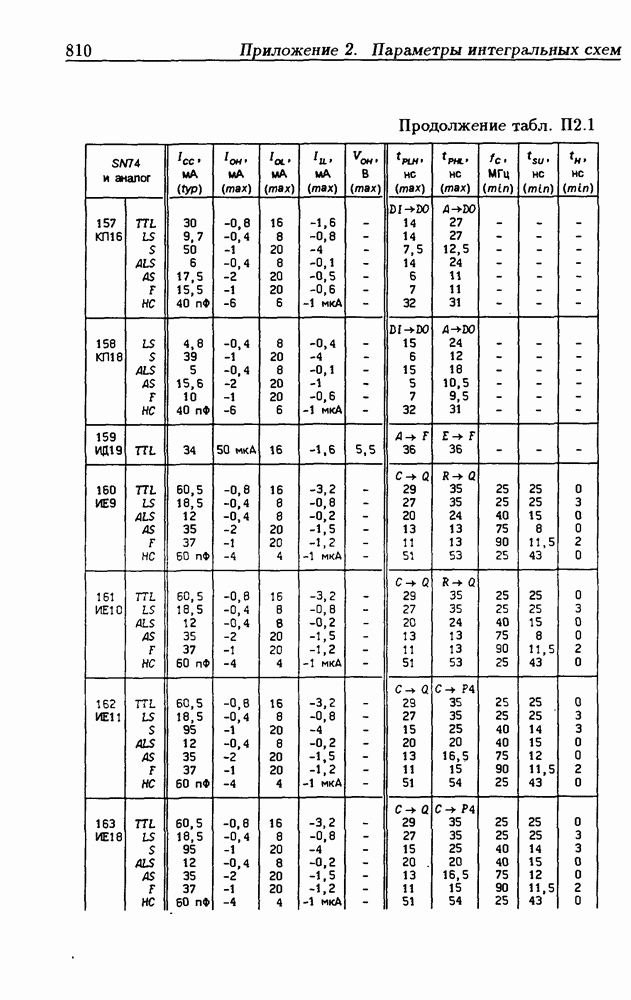
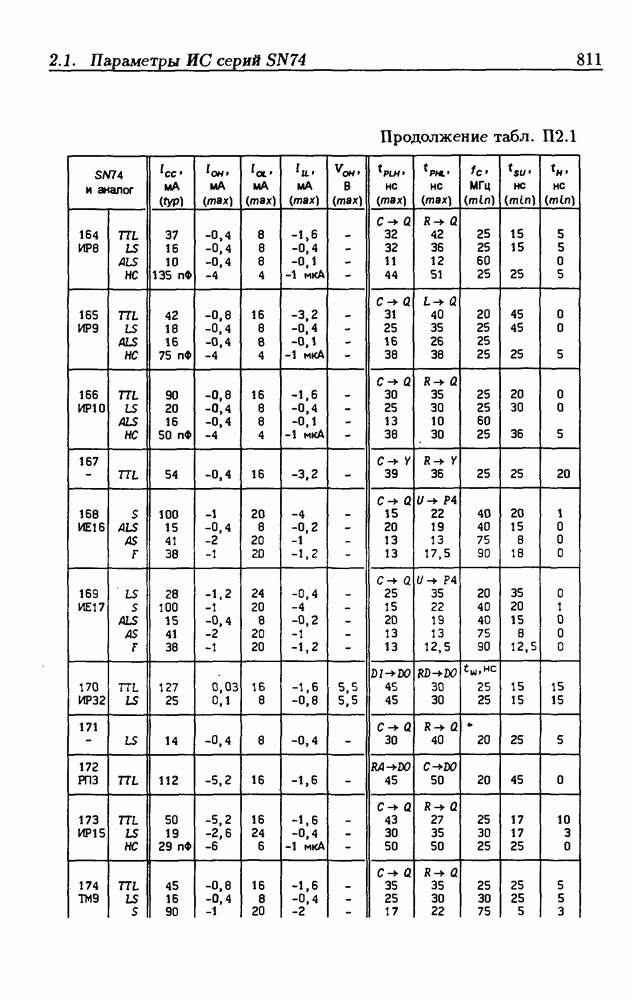
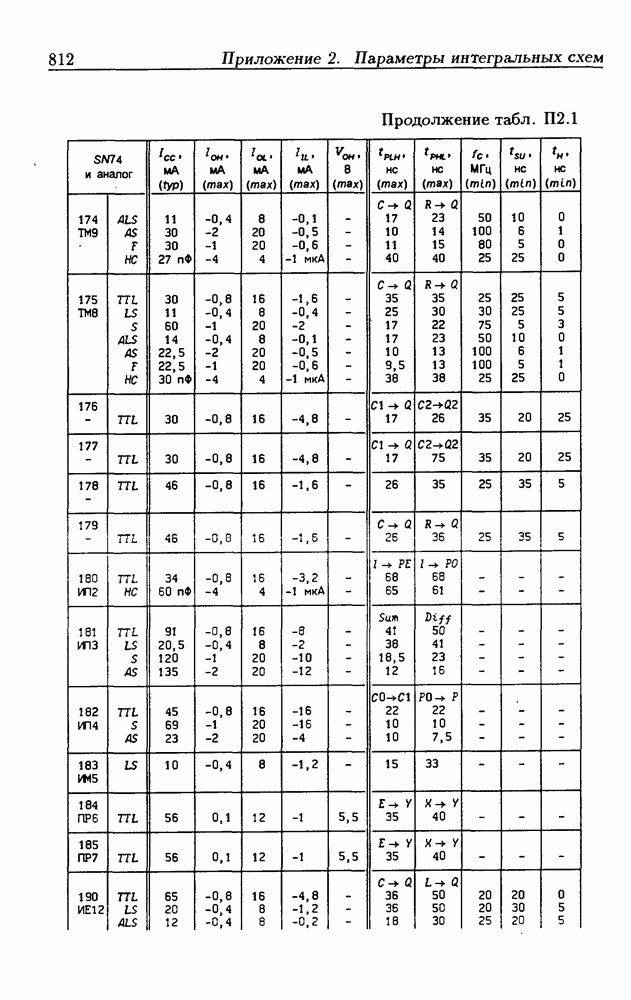
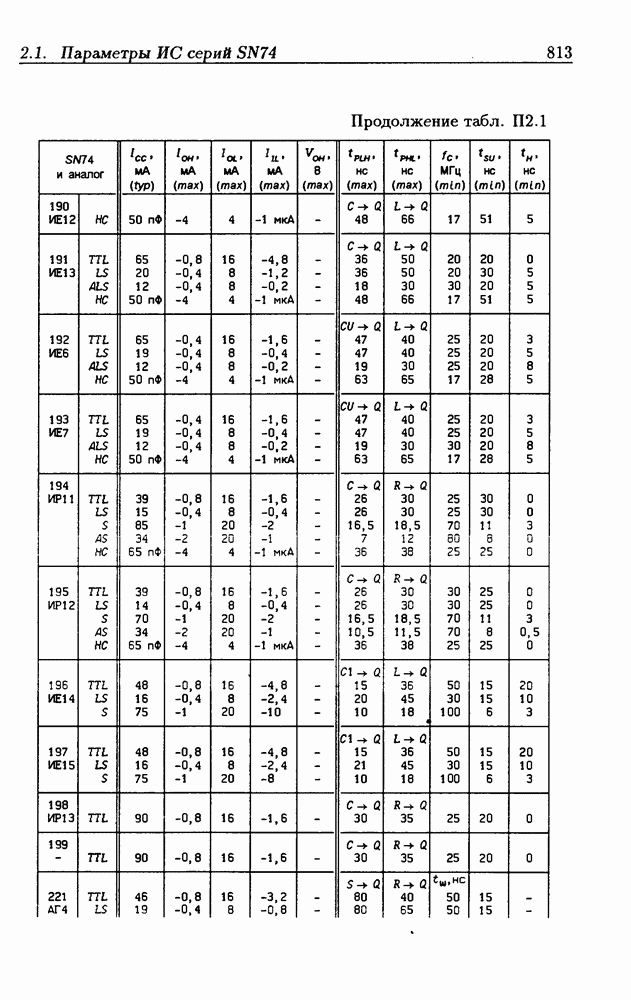
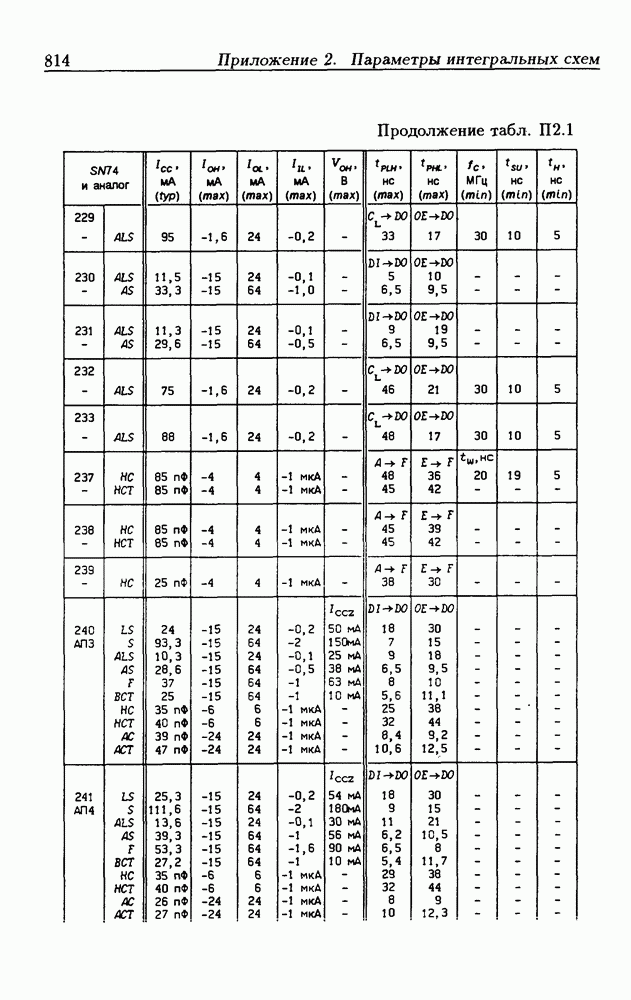
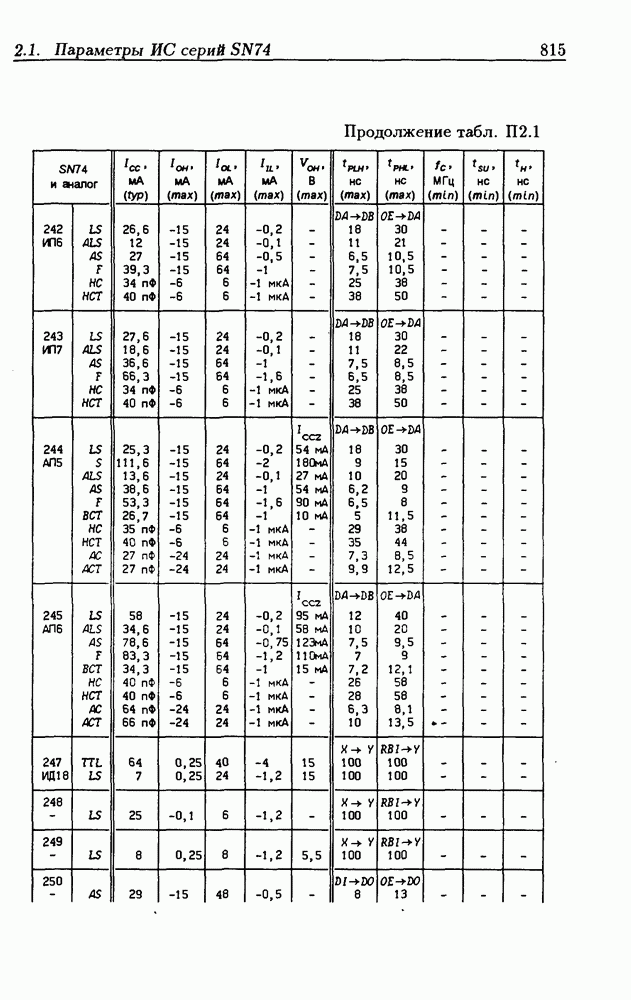
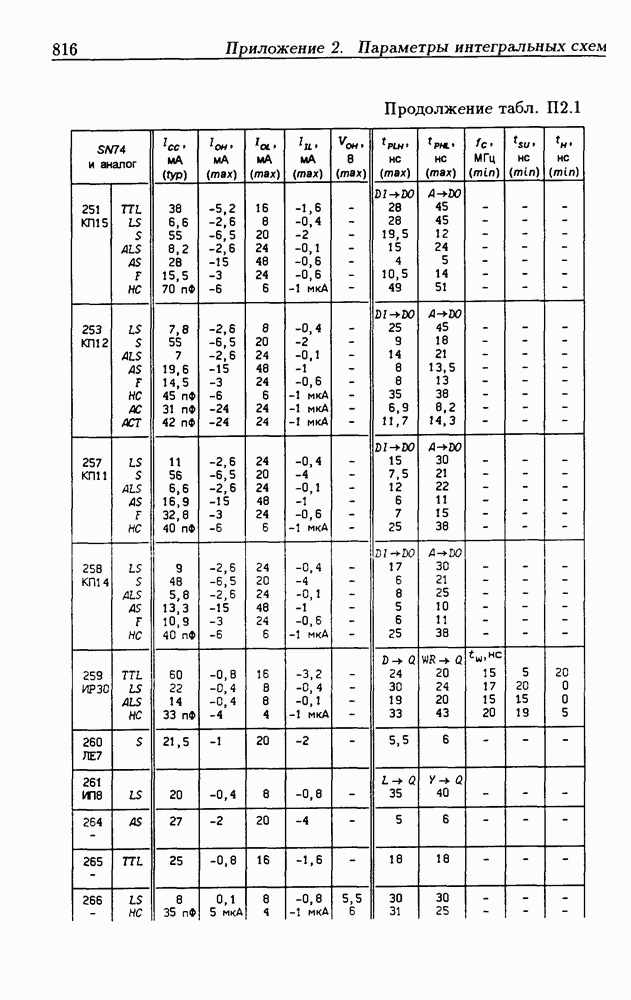
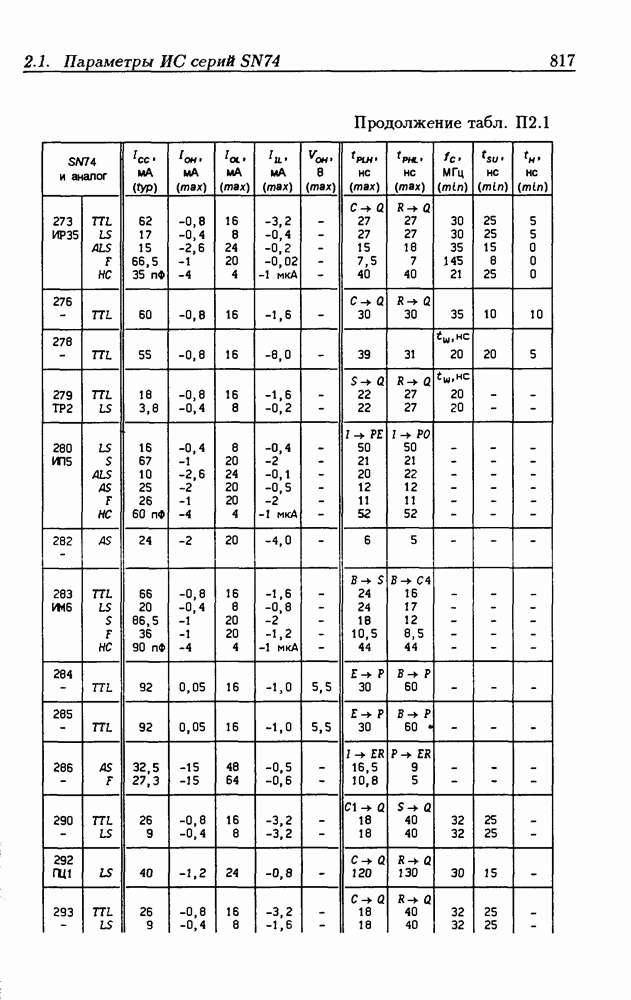
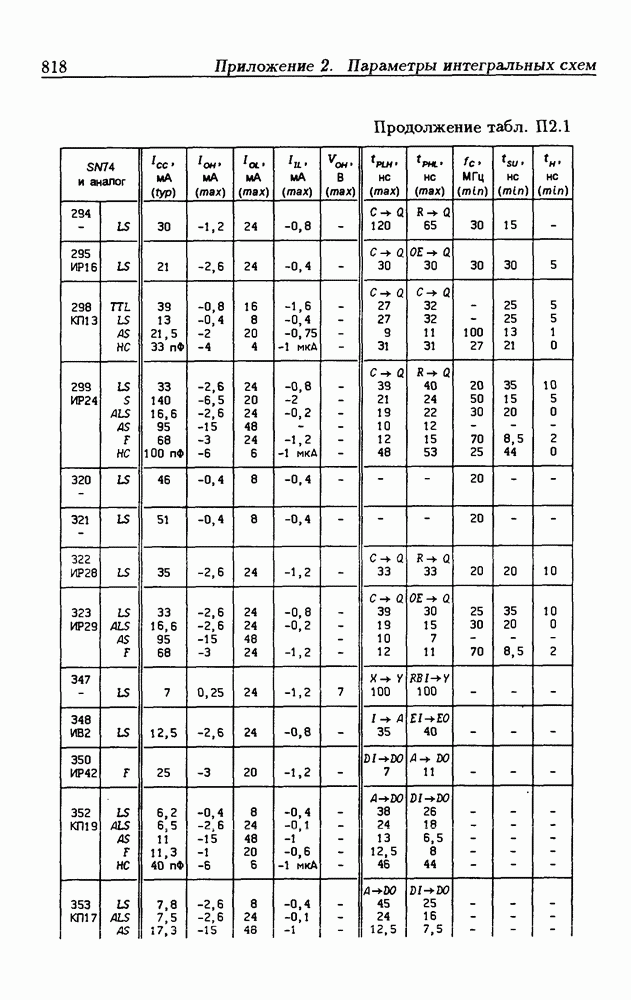
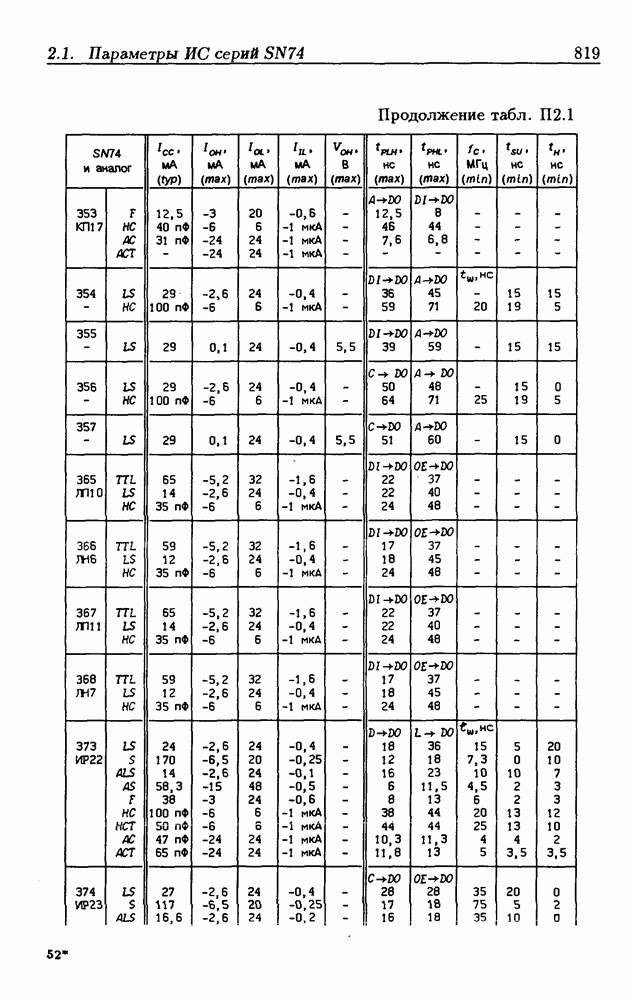
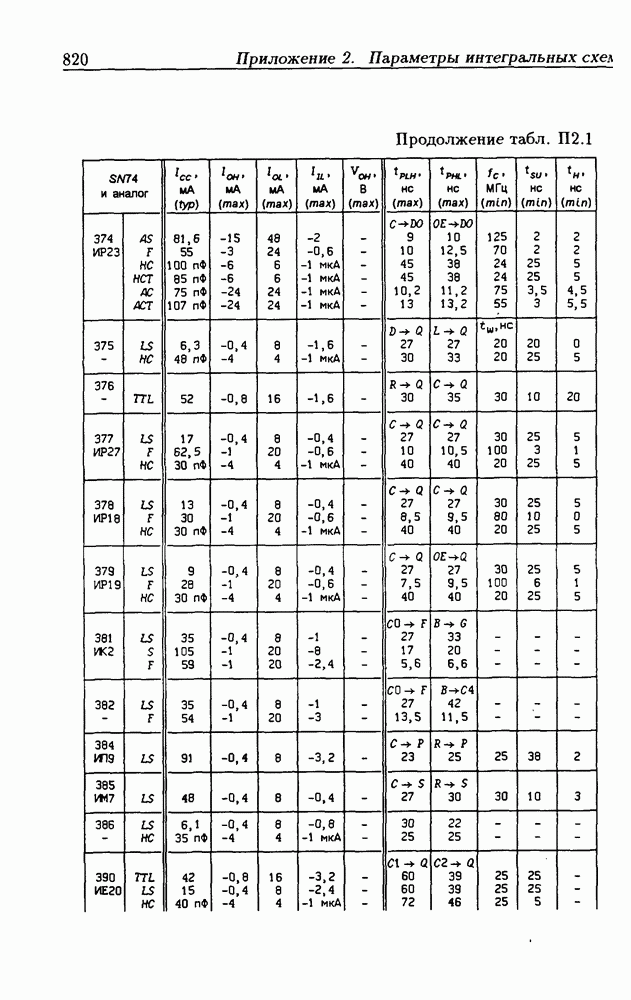
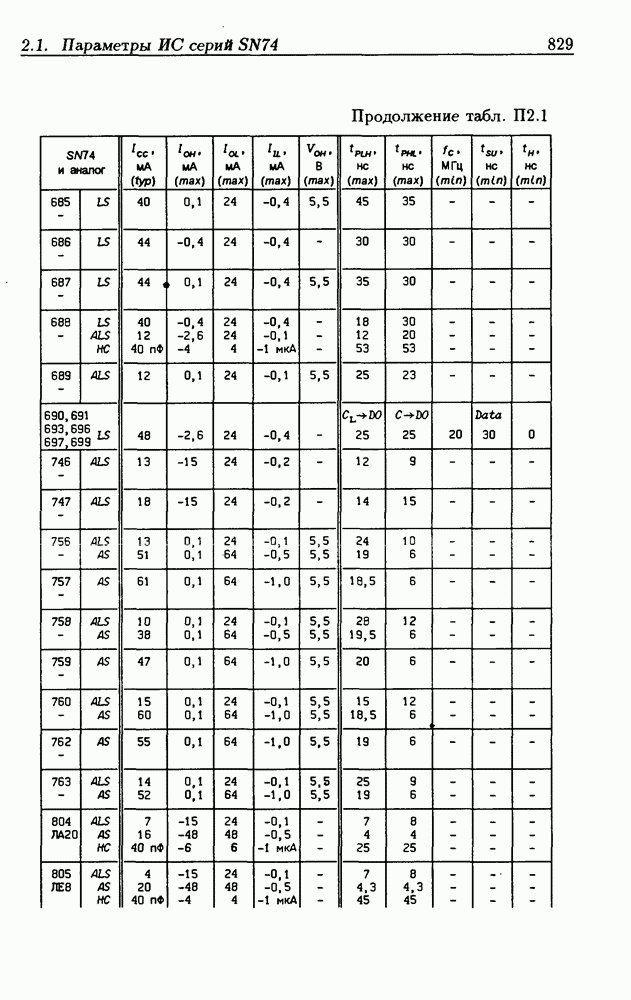
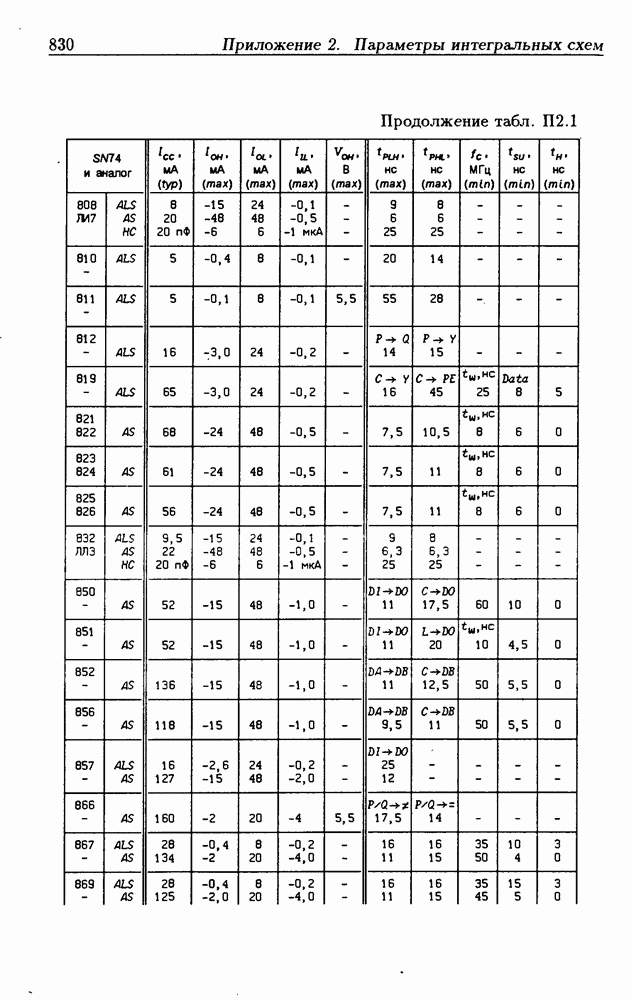
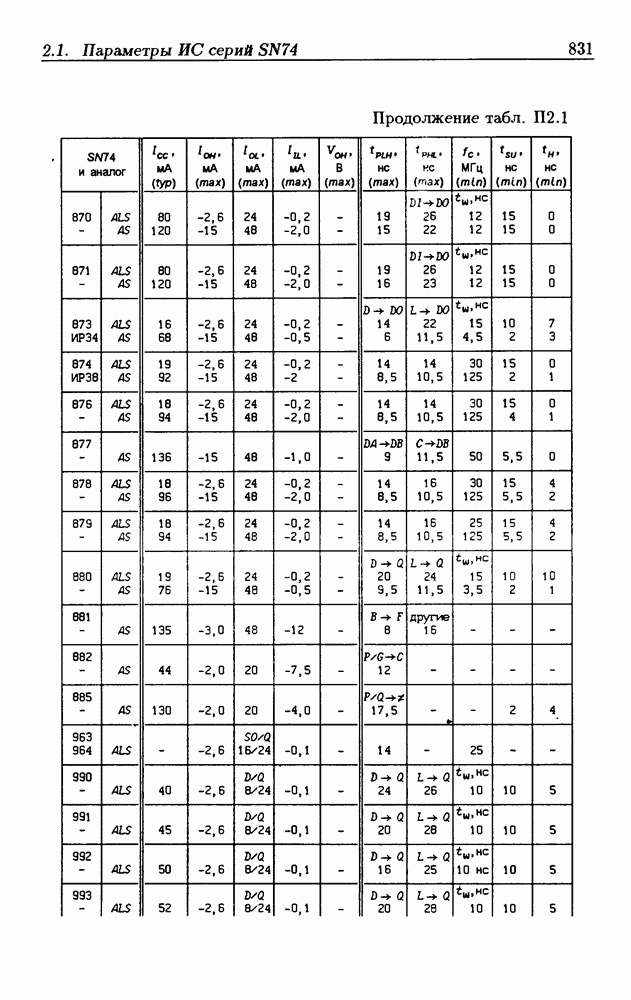
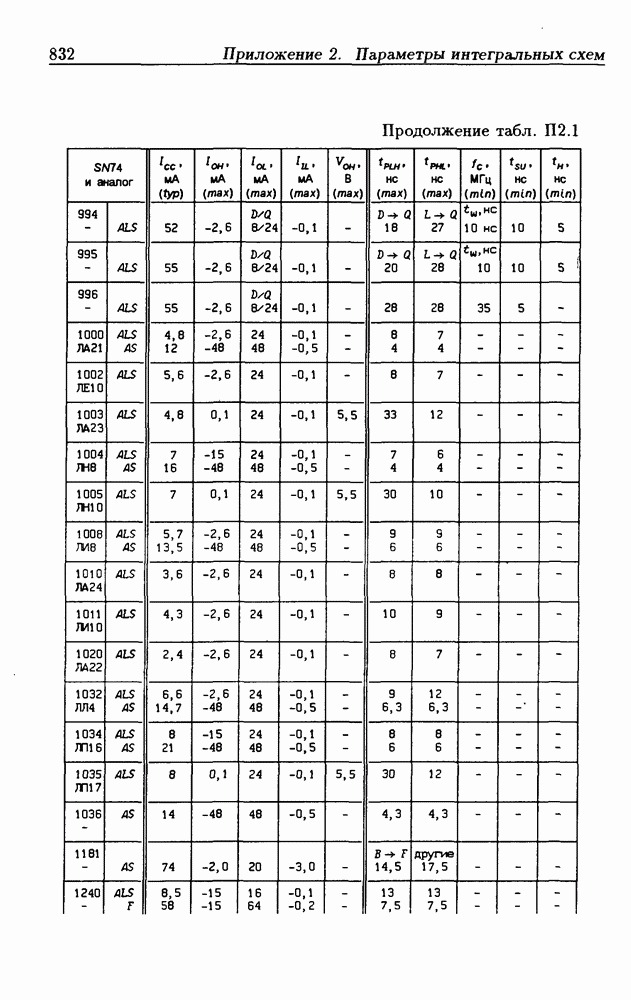
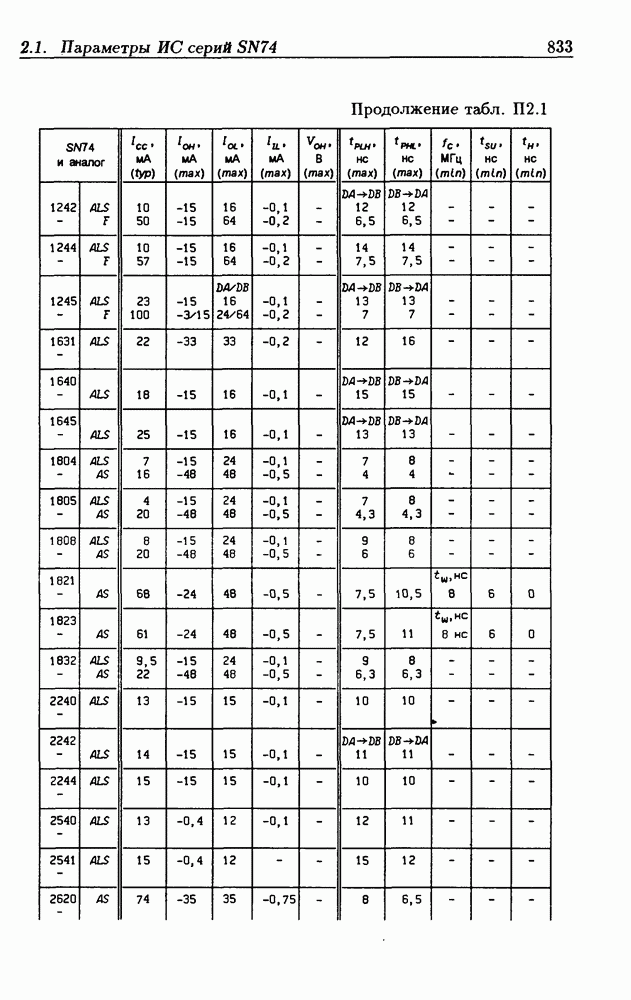
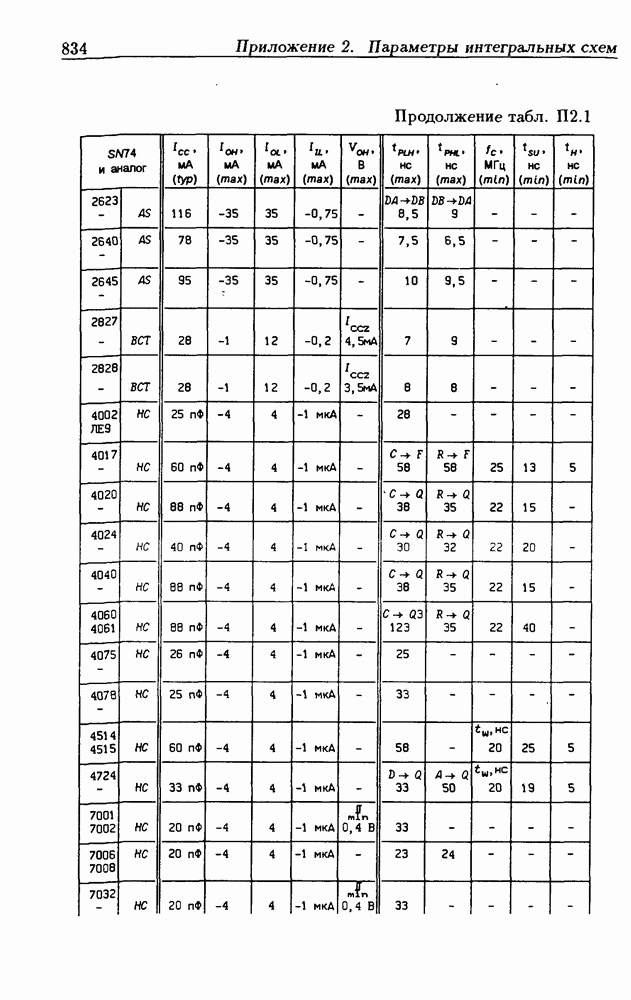
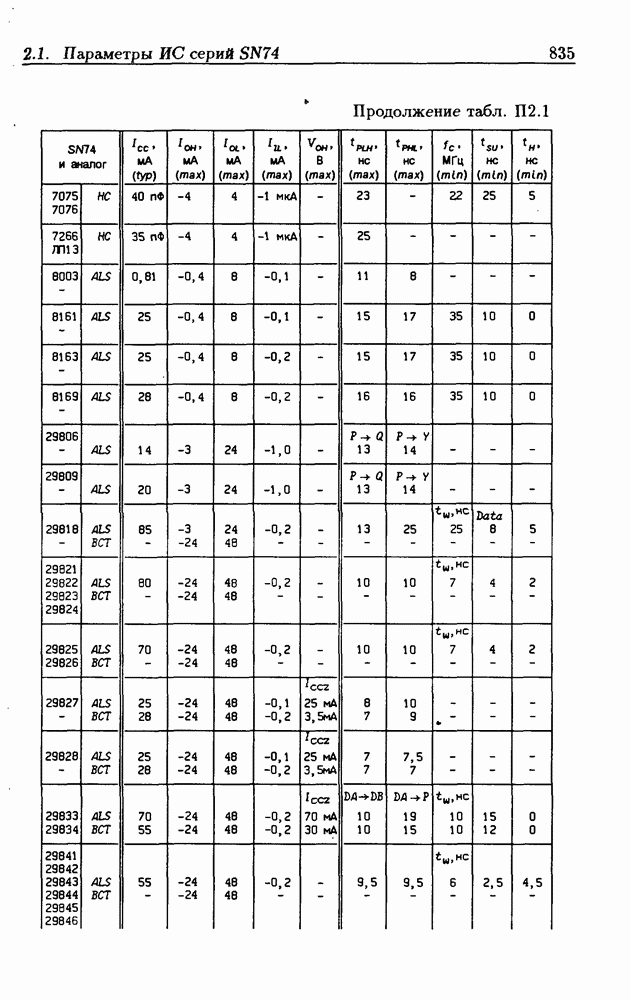
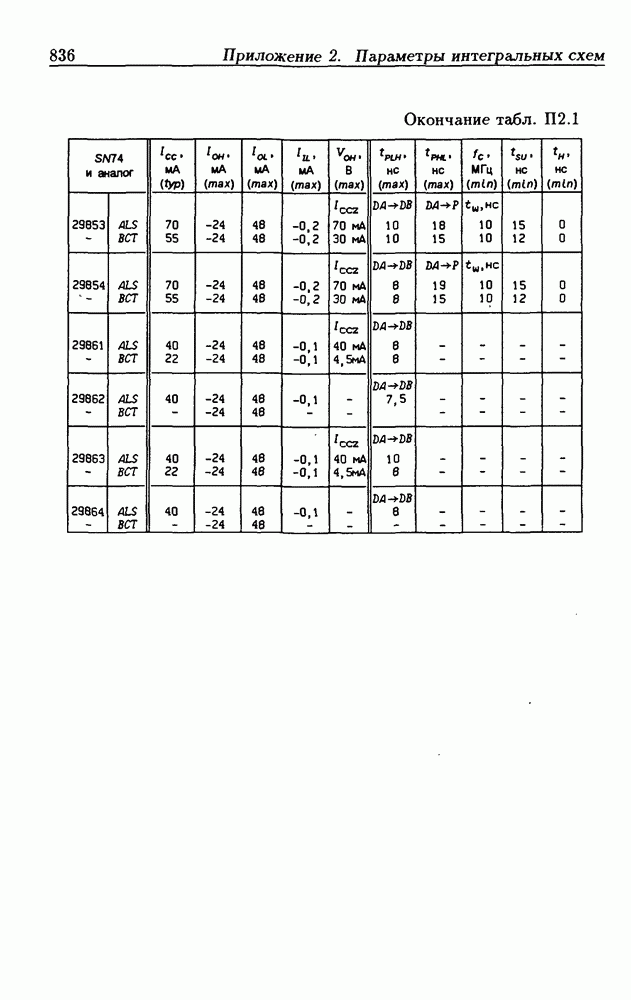
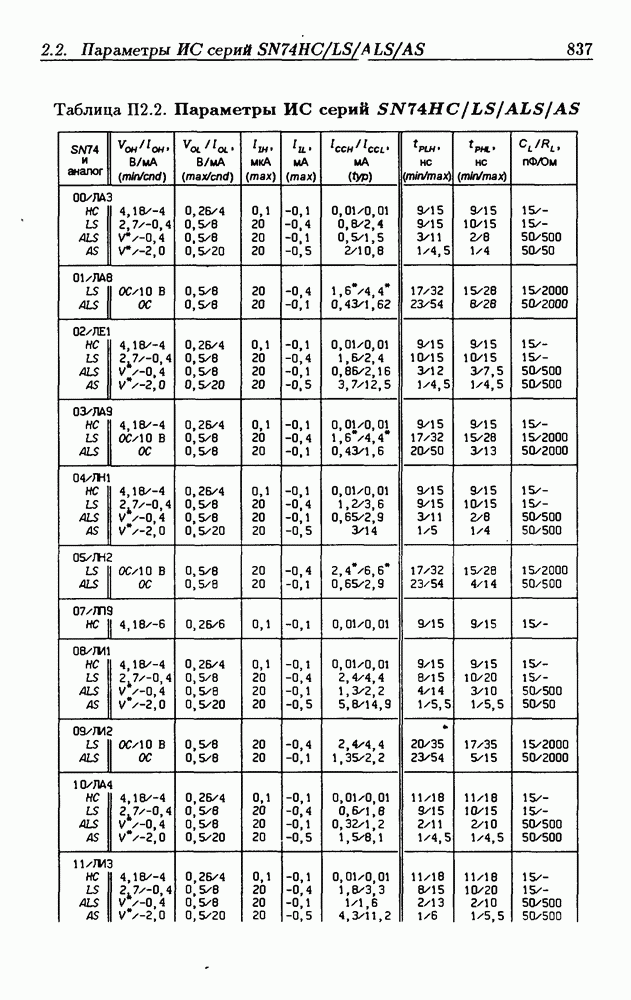
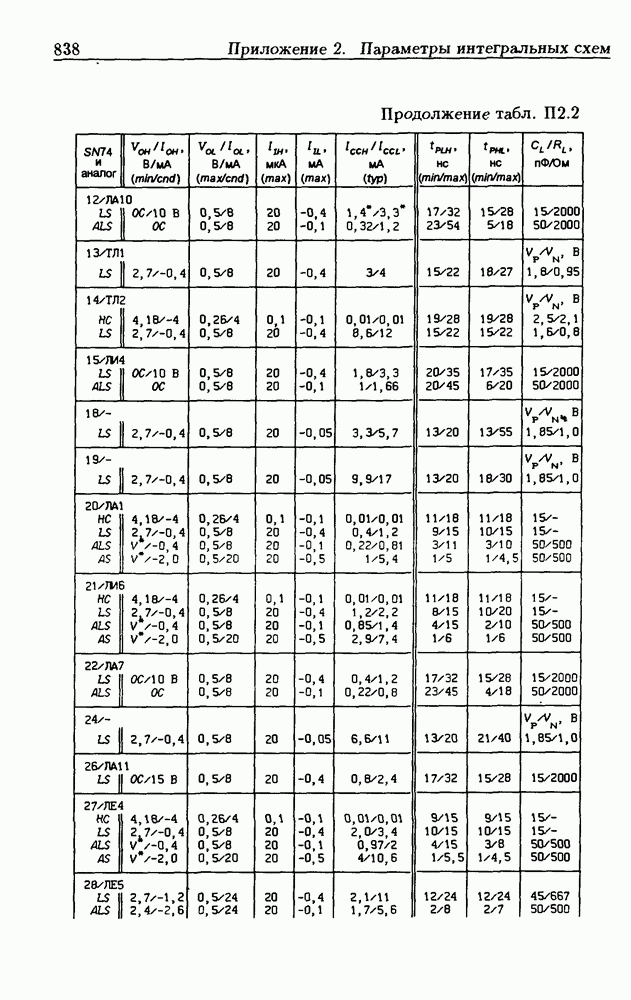
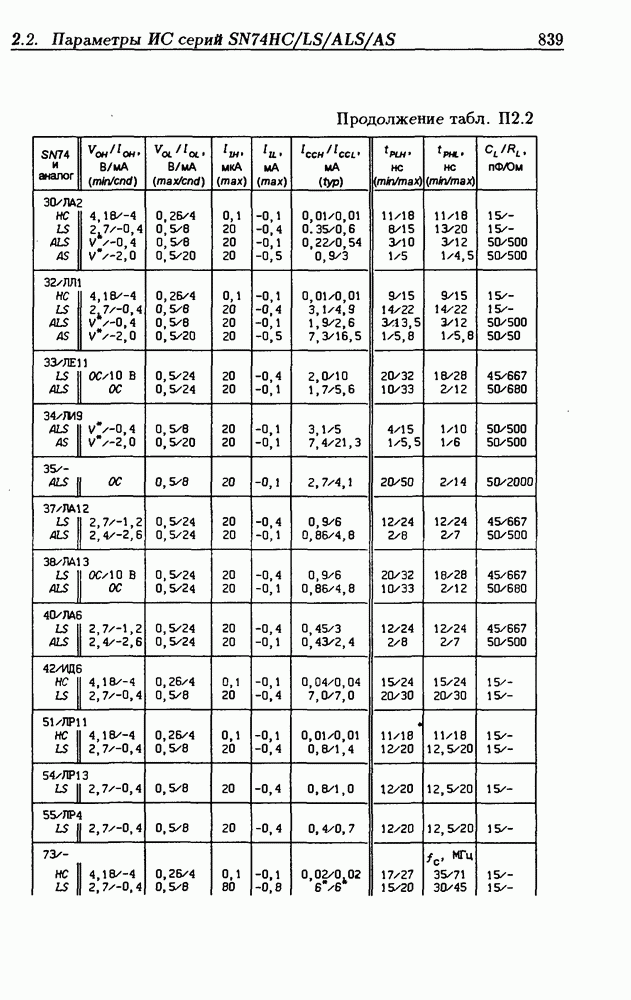
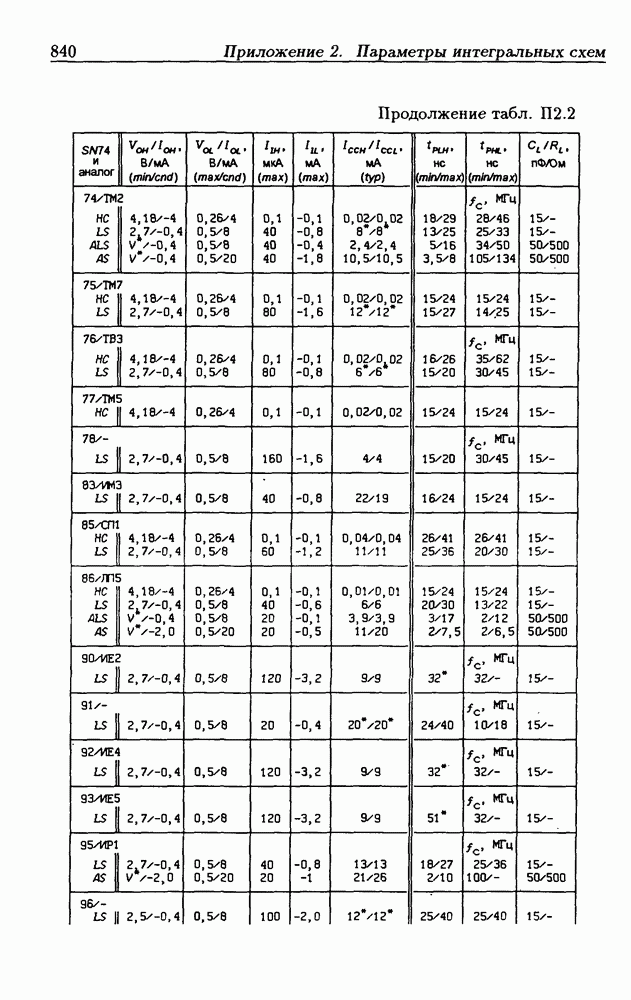
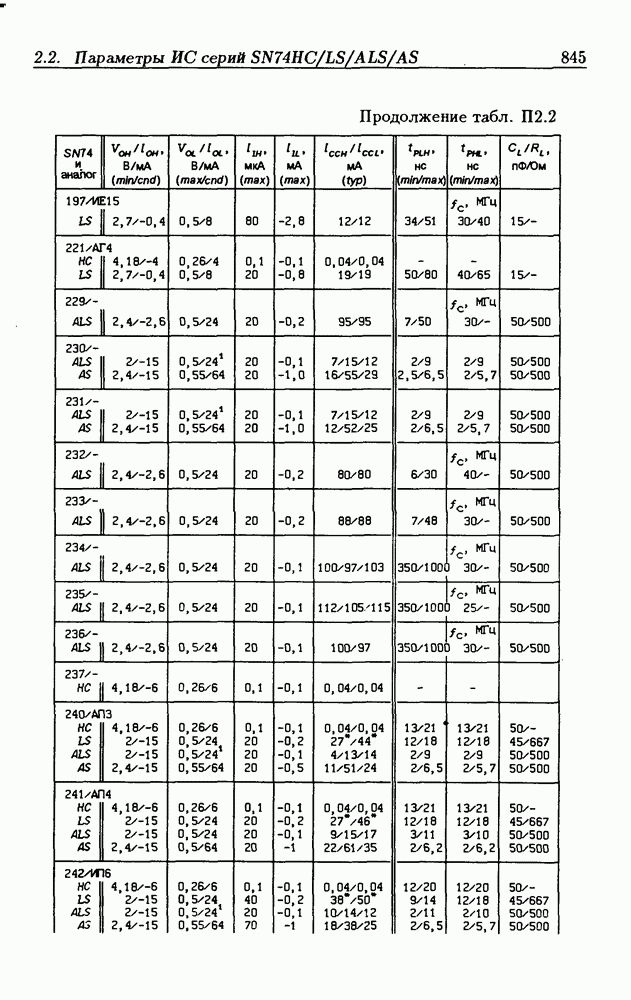
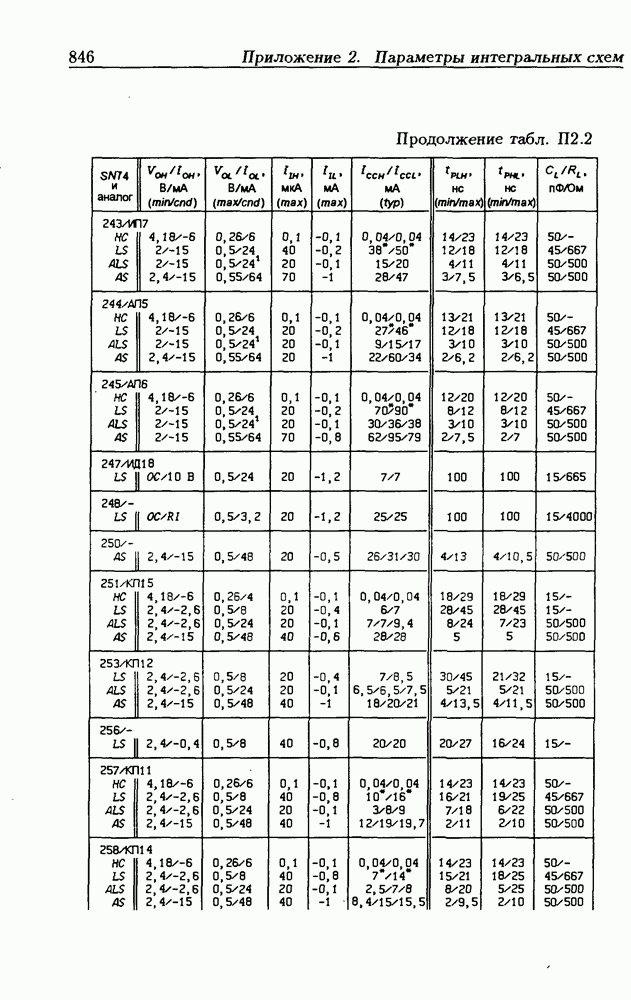
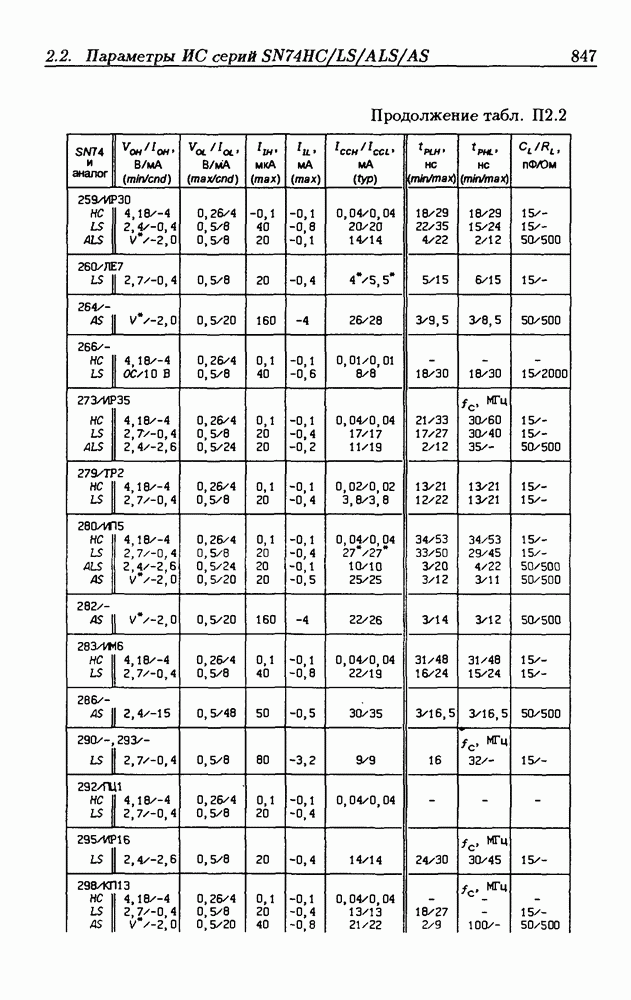
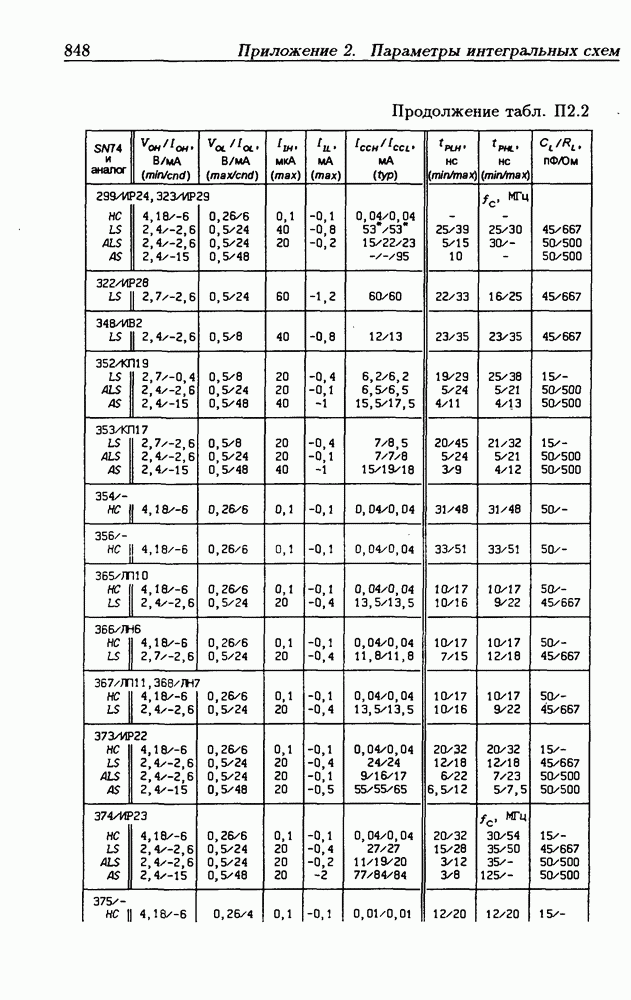
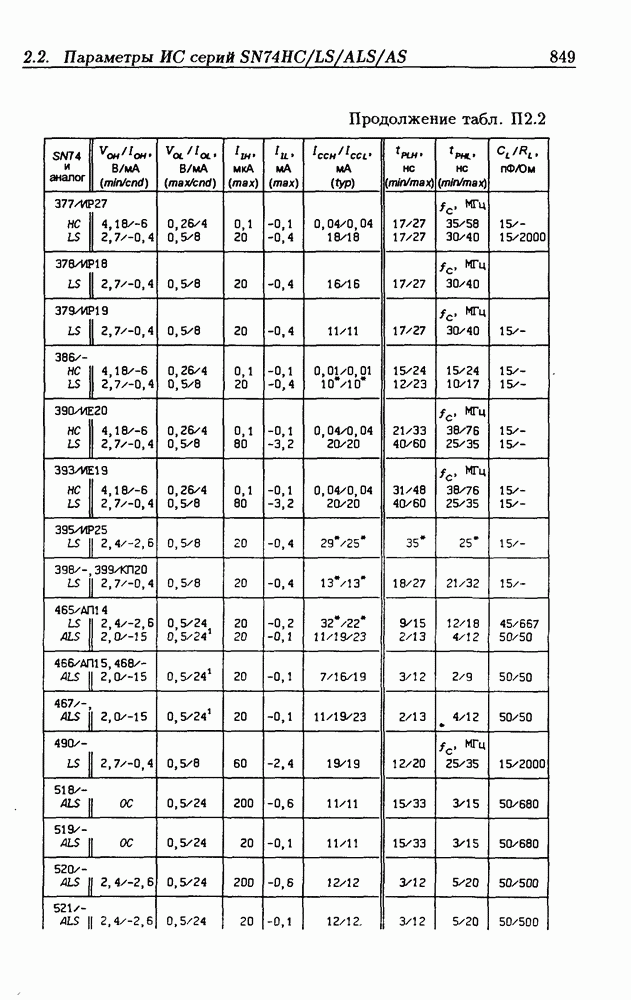
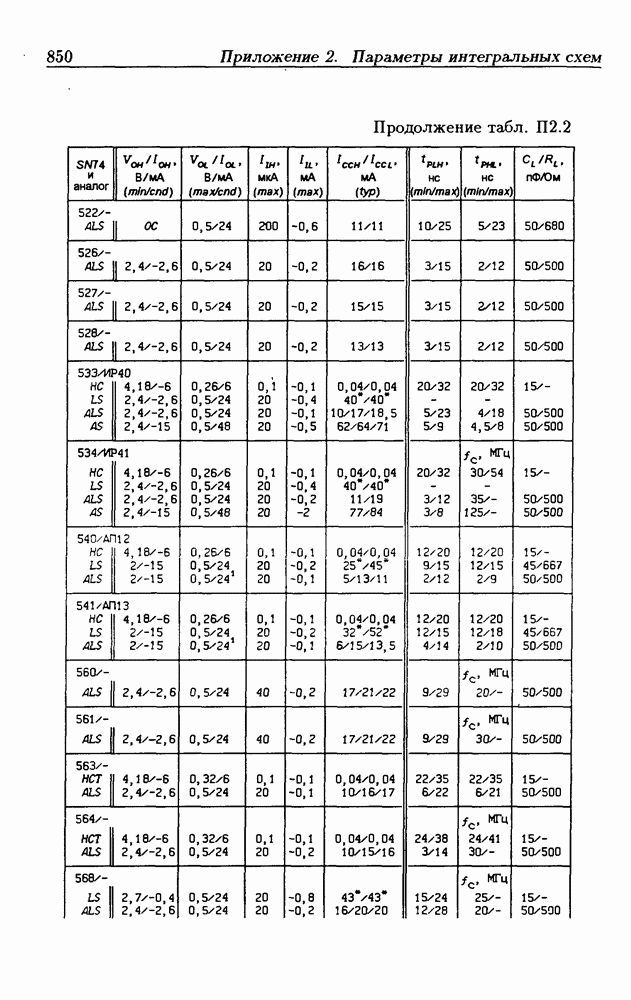
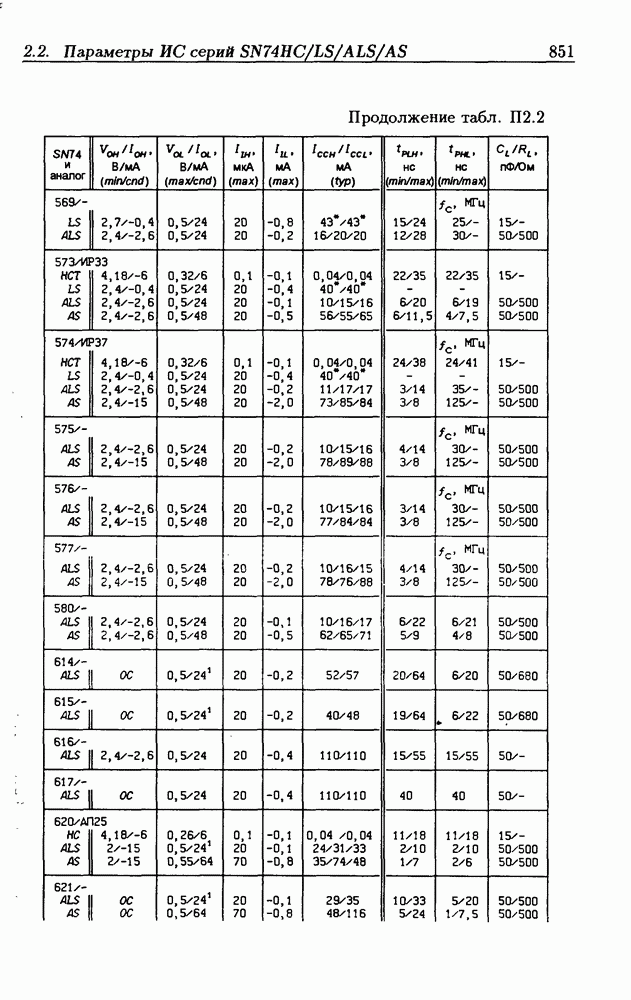
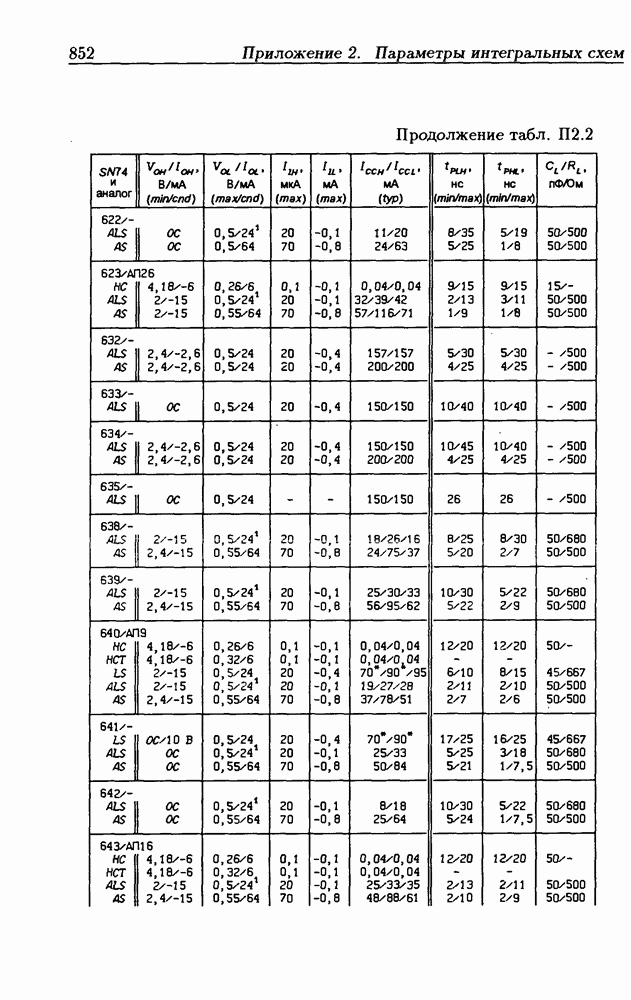
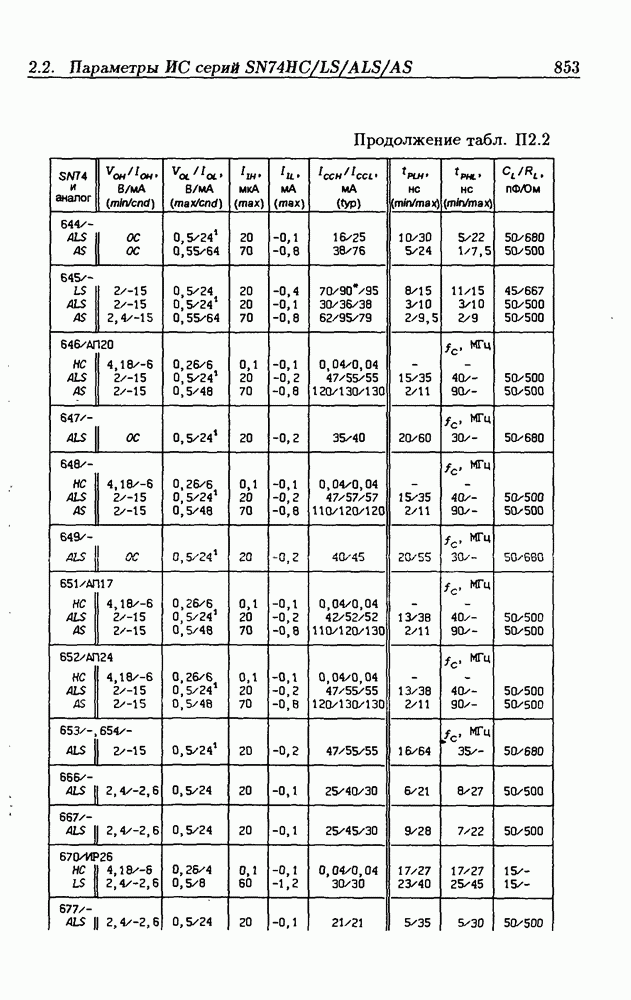
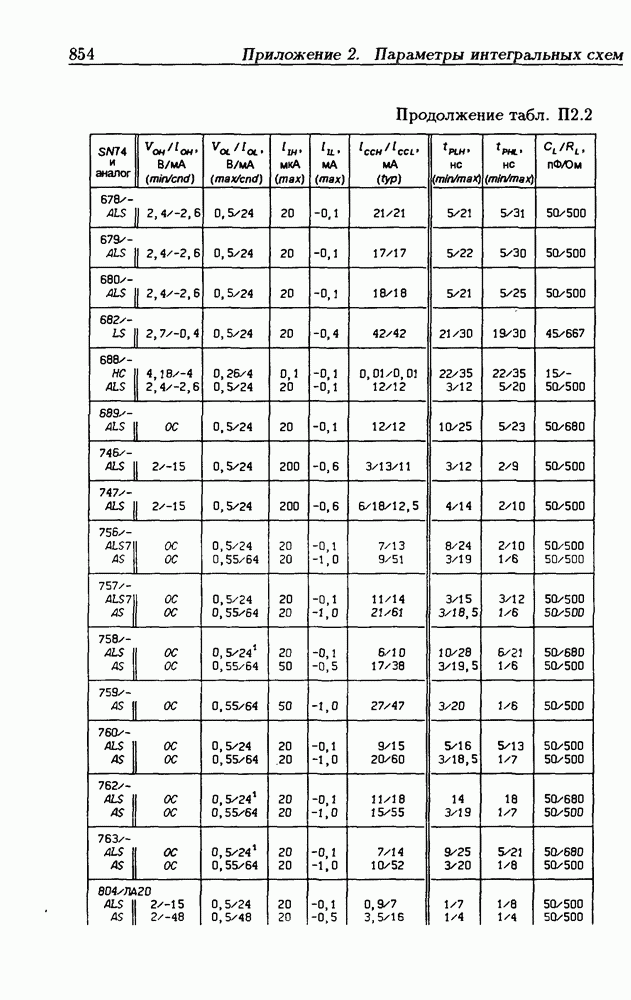
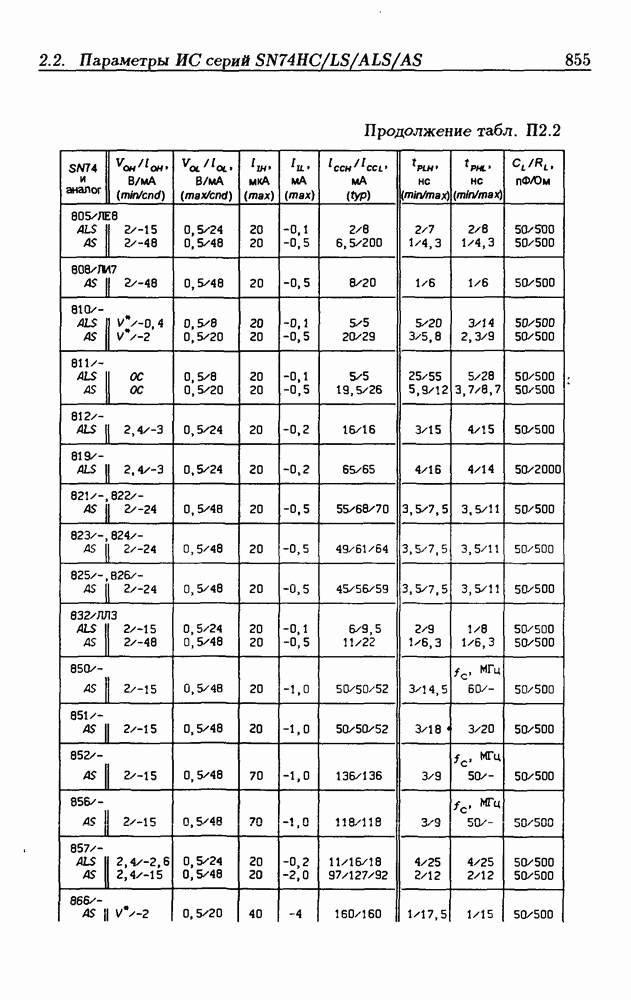
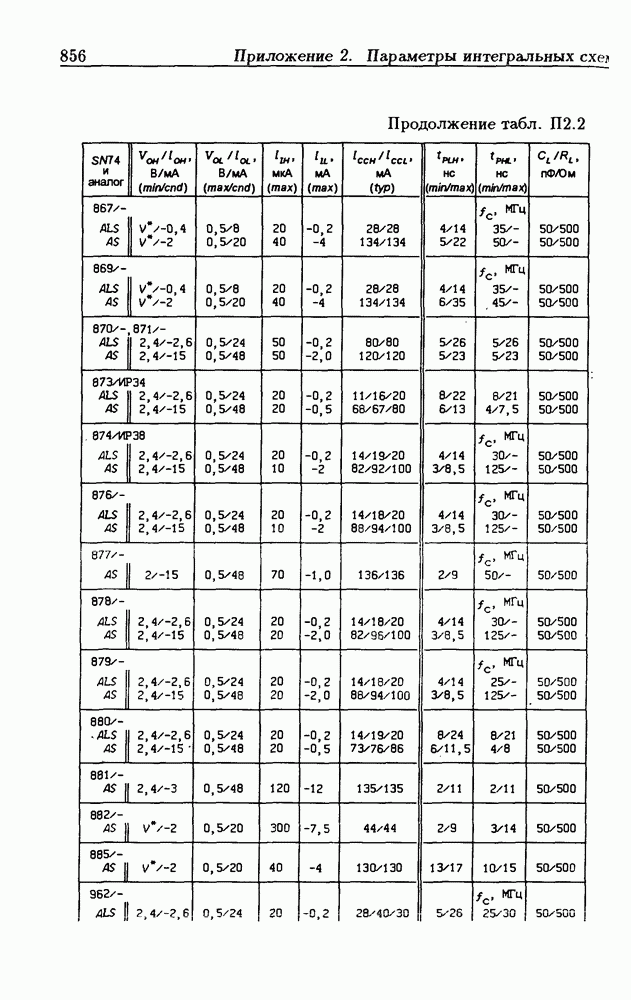
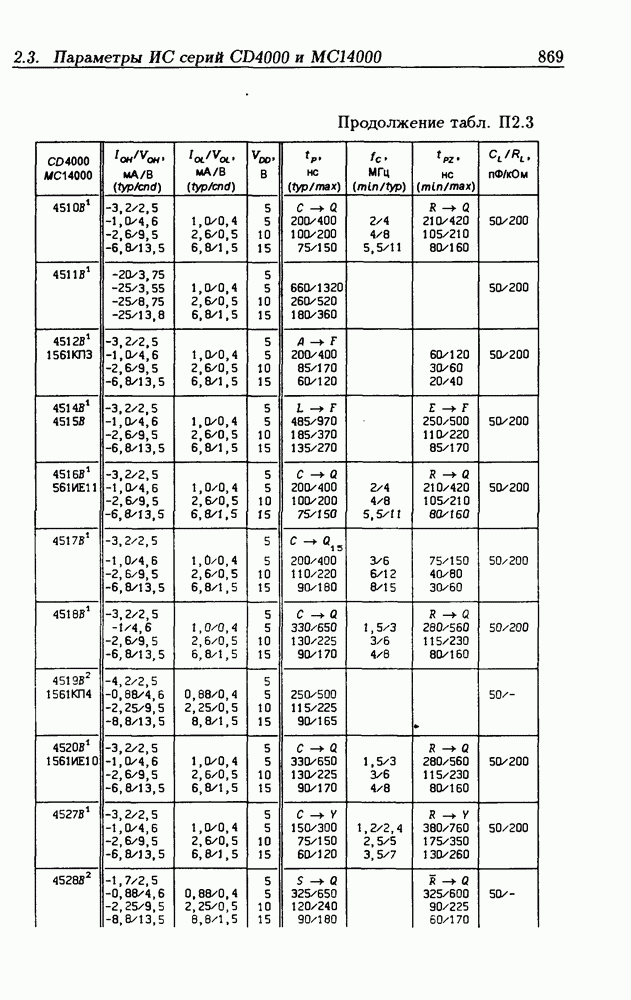
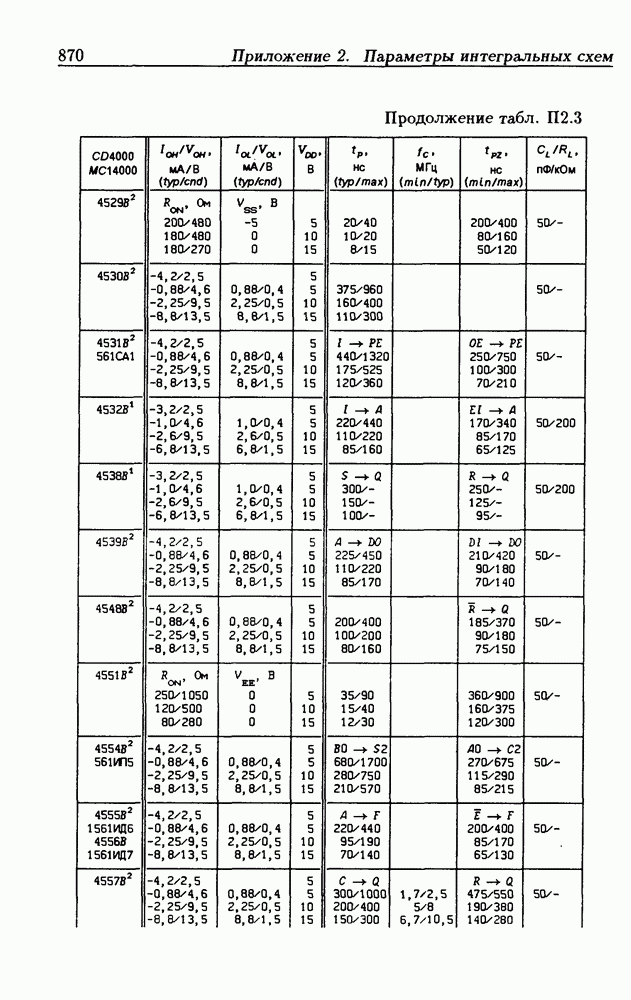
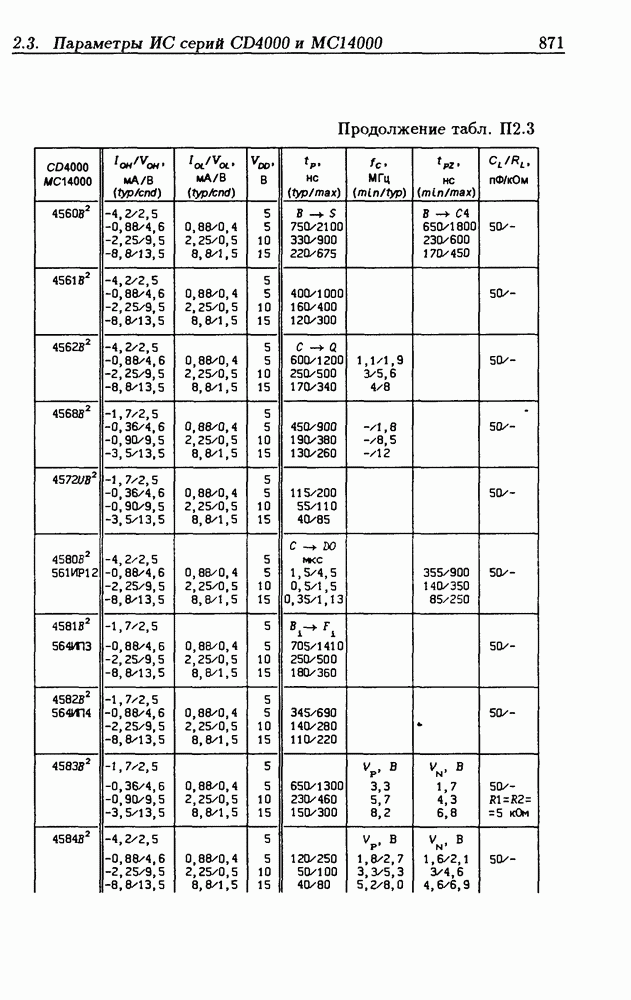
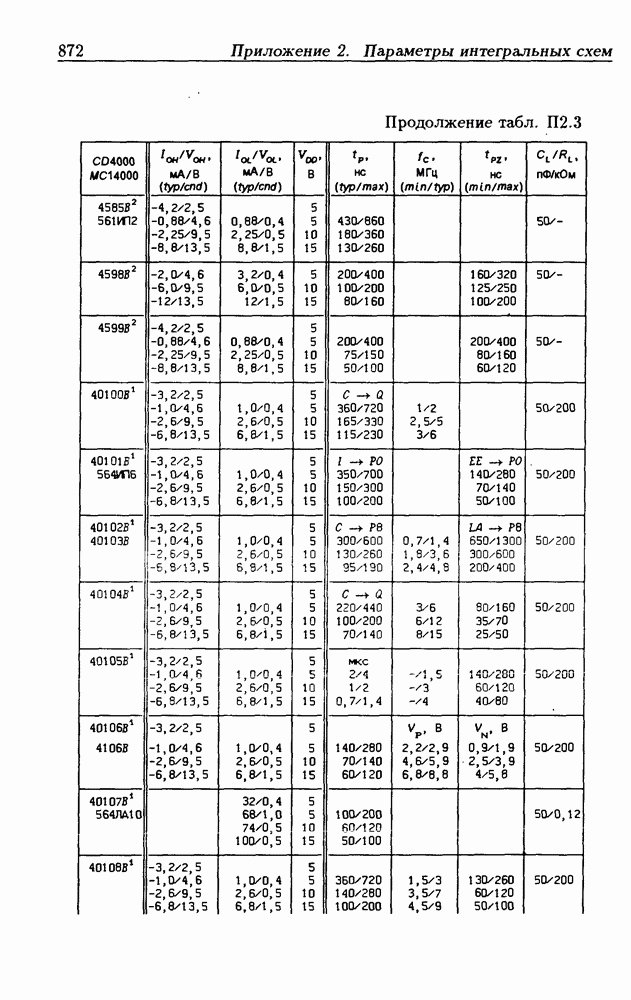
- Приложение 2. Параметры интегральных схем