| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 3. Синтез асинхронных потенциальных автоматов
3.1. Основная модель цифровых автоматов
Цифровые автоматы (последовательностные схемы), элементарные примеры которых были рассмотрены в § 2.4, по способу воздействия на них входных информационных сигналов подразделяются на три основных класса: асинхронные потенциальные автоматы, синхронные автоматы и асинхронные импульсные автоматы. Каждый, из классов автоматов можно разделить на несколько типов по другим признакам.
На асинхронный потенциальный автомат воздействия производят непосредственно его входные информационные сигналы до тех пор, пока сохраняется их активный уровень.
В синхронном автомате используется единый для всего автомата тактовый сигнал, который осуществляет на него импульсное воздействие в соответствии с уровнями входных информационных сигналов, т. е. в синхронном автомате последние только управляют воздействиями, а момент времени воздействия полностью определяется тактовым сигналом. Далее информационные сигналы будут называться просто входными сигналами автомата.
Асинхронный импульсный автомат отличается от потенциального тем, что входные потенциальные сигналы производят на него импульсные воздействия в момент их изменения. Такие воздействия в синхронных автоматах производит только один сигнал — тактовый, а в асинхронных импульсных автоматах любой из входных сигналов может управлять воздействиями и производить их.
Так как воздействия активных уровней входных сигналов на асинхронный потенциальный автомат происходят
непрерывно, то при их синтезе необходим учет переходных процессов, вызываемых этими воздействиями. В синхронных же автоматах изменения входных сигналов не могут вызвать переходного процесса без участия тактового сигнала, который задает моменты времени, в которые автомат воспринимает значения входных сигналов. Тактовый сигнал поступает на синхронный автомат от внешнего генератора, не синхронизированного с его входными сигналами. Поэтому в момент воздействия на автомат тактового сигнала входные сигналы не должны изменяться. При выполнении этого требования переходные процессы в синхронных автоматах можно не рассматривать, обеспечив выбором соответствующей частоты тактового сигнала окончание переходного процесса к следующему моменту его воздействия. Таким образом, в синхронных автоматах вместо непрерывного времени вводится в рассмотрение дискретное время, задаваемое генератором тактового сигнала.
Для проектирования цифровых автоматов используются не только ЛЭ, но и элементы памяти (ЭП), в качестве которых чаще всего используются триггеры (анализ работы двух типов триггеров был выполнен в § 2.4). Элементы памяти и триггеры являются элементарными автоматами, поэтому они, как и цифровые автоматы, делятся на те же три класса. Классы автоматов различаются только типом используемых в них ЭП: с потенциальным воздействием входных сигналов, импульсным воздействием только одного тактового сигнала или с импульсным воздействием нескольких входных сигналов (может быть и одного).
Наиболее фундаментальной и сложной является теория асинхронных потенциальных автоматов, и только ее методами можно синтезировать триггеры с импульсным восприятием изменений входных потенциальных сигналов, например тактового. Такие триггеры необходимы для структурного синтеза автоматов, принадлежащих к другим классам. Основные понятия теории автоматов являются общими для всех классов автоматов, различия же появляются в основном на этапе их структурного синтеза из-за особенностей законов функционирования используемых триггеров.
В отличие от КС значения выходных сигналов автомата в данный момент времени зависят не только от значений входных сигналов в этот же момент времени, но и от предыдущих их значений. Из этого следует, что цифровые автоматы реализуют функциональную связь уже не между отдельными значениями входных и выходных сигналов, а между их последовательностями. Таким образом, в отличие от КС работу автоматов следует
рассматривать во времени. Чтобы значения выходных сигналов зависели от предыдущих значений входных сигналов, автомат должен обладать памятью, в которой сохраняется информация о предыдущих входных воздействиях. Эта информация используется в автомате в виде совокупности сигналов, вырабатываемых памятью и называемых внутренними сигналами.

Рис. 3.1
На рис. 3.1 показана основная модель асинхронного потенциального автомата, которая состоит из КС и элементов задержки  входных сигналов
входных сигналов  на время
на время  включенных в обратных связях КС (основная модель синхронного автомата отличается от показанной на рис. 3.1 только тем, что на ЭП типа
включенных в обратных связях КС (основная модель синхронного автомата отличается от показанной на рис. 3.1 только тем, что на ЭП типа  подается еще тактовый сигнал). Элементы задержки производят запоминание внутренних сигналов
подается еще тактовый сигнал). Элементы задержки производят запоминание внутренних сигналов  на время
на время  т. е. они являются элементами памяти. Эти сигналы появляются на входах КС (выходах ЭП) через время
т. е. они являются элементами памяти. Эти сигналы появляются на входах КС (выходах ЭП) через время  и могут вызвать изменение ее выходных сигналов. Понятно, что если сигнал
и могут вызвать изменение ее выходных сигналов. Понятно, что если сигнал  то сигнал
то сигнал 
В общем случае автомат содержит  и имеет
и имеет  физических входов, на которые подаются сигналы
физических входов, на которые подаются сигналы  и к физических выходов, с которых снимаются сигналы
и к физических выходов, с которых снимаются сигналы  При фиксированных значениях внутренних сигналов
При фиксированных значениях внутренних сигналов  автомат ведет себя подобно некоторой КС, т. е. реализует однозначное соответствие между значениями входных и выходных сигналов. Однако при изменении входных сигналов его реакция может выразиться в изменении внутренних сигналов. Если затем подать прежние значения входных сигналов, то соответствие между значениями входных и выходных сигналов может оказаться совсем другим.
автомат ведет себя подобно некоторой КС, т. е. реализует однозначное соответствие между значениями входных и выходных сигналов. Однако при изменении входных сигналов его реакция может выразиться в изменении внутренних сигналов. Если затем подать прежние значения входных сигналов, то соответствие между значениями входных и выходных сигналов может оказаться совсем другим.
На основании основной модели автомата его внутренние  и выходные
и выходные  сигналы можно задать некоторыми системами переключательных функций:
сигналы можно задать некоторыми системами переключательных функций:

где 
Система функций (3.1) называется функцией переходов автомата, а система функций (3.2) — функцией выхода. Эти системы функций можно представить в векторной форме:

где
Введем основные определения. Состоянием входа автомата называется n-мерный вектор  где
где  или 1 — значение входного сигнала автомата
или 1 — значение входного сигнала автомата  Всего может быть
Всего может быть  различных состояний входа
различных состояний входа  т. е. множество
т. е. множество  возможных состояний входа состоит из
возможных состояний входа состоит из  элементов:
элементов:

Внутренним состоянием автомата называется m-мерный вектор  где
где  или 1 — значение выходного сигнала
или 1 — значение выходного сигнала  Всего может быть
Всего может быть  различных внутренних состояний
различных внутренних состояний  т. е. множество
т. е. множество  возможных внутренних состояний состоит из
возможных внутренних состояний состоит из  элементов:
элементов:

В дальнейшем внутреннее состояние  часто будем называть просто состоянием автомата.
часто будем называть просто состоянием автомата.
Состоянием выхода автомата называется  -мерный вектор
-мерный вектор  где
где  или 1 — значение выходного сигнала автомата
или 1 — значение выходного сигнала автомата  Всего может быть 2 различных состояний выхода
Всего может быть 2 различных состояний выхода  т.е. множество
т.е. множество  возможных состояний выхода состоит из
возможных состояний выхода состоит из  элементов:
элементов:

Так как множества  конечны, то цифровые автоматы называют также конечными автоматами. В конкретных автоматах множества
конечны, то цифровые автоматы называют также конечными автоматами. В конкретных автоматах множества  могут использоваться не полностью. Так, если есть какие-либо ограничения на значения входных сигналов, то некоторые состояния входа будут запрещенными (не могут появиться при работе автомата). Таким образом, в конкретных автоматах могут использоваться подмножества
могут использоваться не полностью. Так, если есть какие-либо ограничения на значения входных сигналов, то некоторые состояния входа будут запрещенными (не могут появиться при работе автомата). Таким образом, в конкретных автоматах могут использоваться подмножества 
Для формального задания автомата необходимо задать множества  и функции переходов и выхода (3.3), определенные на этих множествах. Для задания этих функций каждой
и функции переходов и выхода (3.3), определенные на этих множествах. Для задания этих функций каждой
паре  необходимо поставить в соответствие определенные значения
необходимо поставить в соответствие определенные значения  необходимо задать соотношения
необходимо задать соотношения

где
Каждая пара  называется полным состоянием автомата, а совокупность всех возможных пар
называется полным состоянием автомата, а совокупность всех возможных пар  представляет собой множество
представляет собой множество  Функции переходов и выхода автомата можно задать аналитически, графически и с помощью таблиц, так как множества
Функции переходов и выхода автомата можно задать аналитически, графически и с помощью таблиц, так как множества  конечны.
конечны.
Автоматы могут быть полностью определенными и недоопределенными. Полностью определенными, или полными, называются такие автоматы, для которых функции переходов и выхода определены на всем множестве  т.е. значения функций переходов и выхода заданы на всех парах
т.е. значения функций переходов и выхода заданы на всех парах  Если же функции переходов и выхода или функция выхода определены только на подмножестве
Если же функции переходов и выхода или функция выхода определены только на подмножестве  С
С  т.е. значения этих функций заданы не на всех парах
т.е. значения этих функций заданы не на всех парах  то автомат называется недоопределенным, или неполным.
то автомат называется недоопределенным, или неполным.
Хотя назначением автоматов является преобразование входных последовательностей в выходные, иногда удобно рассматривать автоматы без выхода, задаваемые только множествами  и функцией переходов, определенной на этих множествах. Автоматы без выхода появляются при решении задач, в которых интересуются только внутренним его поведением. В таких случаях не имеет смысла усложнять задачу рассмотрением функции выхода. В качестве выходных сигналов автомата
и функцией переходов, определенной на этих множествах. Автоматы без выхода появляются при решении задач, в которых интересуются только внутренним его поведением. В таких случаях не имеет смысла усложнять задачу рассмотрением функции выхода. В качестве выходных сигналов автомата  всегда можно использовать выходные сигналы ЭП
всегда можно использовать выходные сигналы ЭП  . В этом случае множество
. В этом случае множество  и функция выхода
и функция выхода 
Два состояния входа  (два внутренних состояния и
(два внутренних состояния и  называются соседними, если они различаются значением только одного входного сигнала
называются соседними, если они различаются значением только одного входного сигнала  (выходного сигнала
(выходного сигнала  Соседним изменением состояний входа называется изменение некоторого состояния входа
Соседним изменением состояний входа называется изменение некоторого состояния входа  на любое соседнее состояние входа
на любое соседнее состояние входа  При соседних изменениях состояний входа изменяется только один входной сигнал автомата
При соседних изменениях состояний входа изменяется только один входной сигнал автомата  Изменения внутренних состояний называются переходами. Переходы являются соседними, если при этом внутреннее состояние изменяется на соседнее состояние
Изменения внутренних состояний называются переходами. Переходы являются соседними, если при этом внутреннее состояние изменяется на соседнее состояние 
Все приведенные выше определения в равной степени относятся как к асинхронным потенциальным автоматам, так и к синхронным, а в большей своей части — и к асинхронным импульсным автоматам. Для краткости цифровые автоматы,
принадлежащие к разным классам, будем называть просто автоматами без указания принадлежности к тому или иному классу, если ясно, о каких автоматах идет речь.
Теории автоматов посвящена обширная литература различного уровня сложности. Абстрактная теория автоматов достаточно полно изложена в [5, 7, 18, 19], а практические вопросы ее реализации — в [8, 20]. В указанной литературе рассматриваются в основном синхронные и асинхронные потенциальные автоматы. Основы теории асинхронных импульсных автоматов приведены в [21]. Аналитическая теория этих автоматов разработана в [10, 22, 23].
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Основы теории переключательных функций
- 1.2. Позиционные системы счисления
- 1.3. Переключательные функции
- 1.4. Принцип и закон двойственности
- 1.5. Теоремы разложения
- 1.6. Решение систем логических уравнений
- 1.7. Первичные термы, минтермы и макстермы
- 1.8. Совершенные нормальные формы представления функций
- 1.9. Конъюнктивные и дизъюнктивные термы
- 1.10. Минимизация переключательных функций
- 1.11. Диаграммы Вейча
- 1.12. Минимизация неполностью определенных функций, совместная минимизация нескольких функций
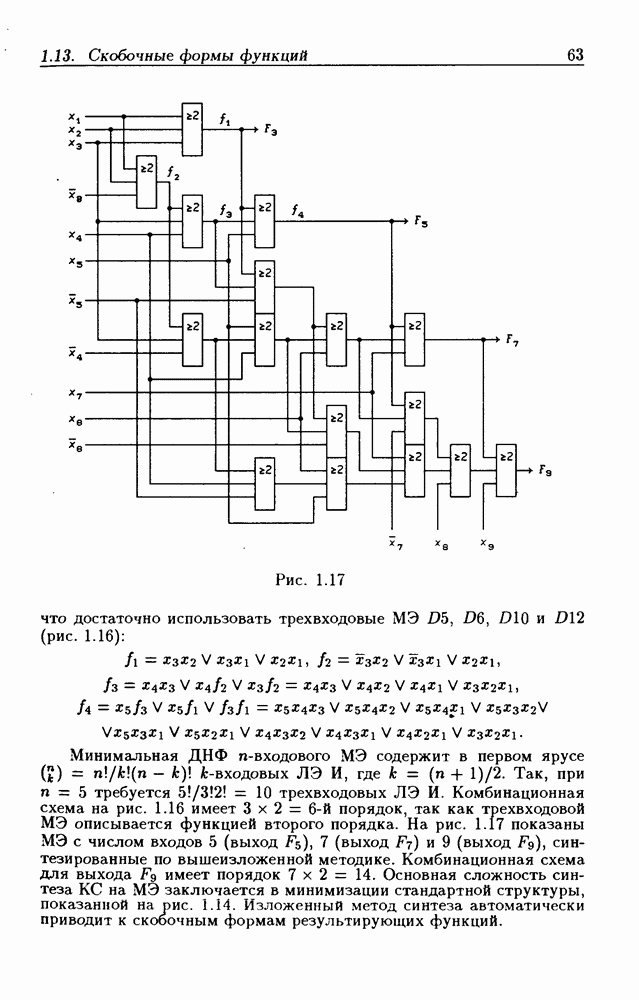
- 1.13. Скобочные формы функций
- 1.14. Закон двойственности для логических схем
- 1.15. Линейные функции
- Глава 2. Анализ и синтез логических схем
- 2.2. Модели логических элементов
- 2.3. Модели логических схем
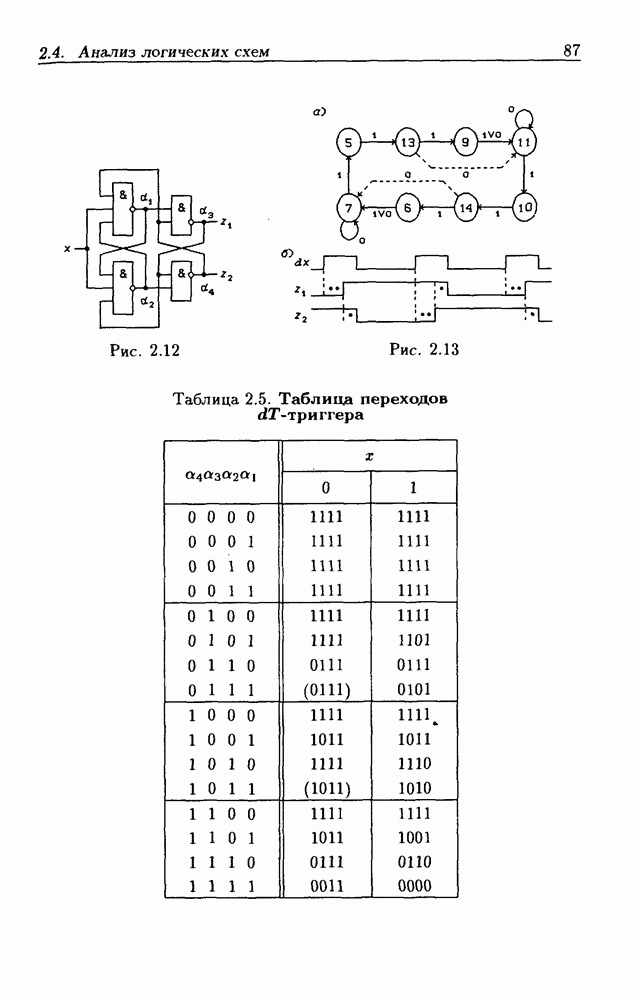
- 2.4. Анализ логических схем
- 2.5. Синтез комбинационных схем, свободных от состязаний
- Глава 3. Синтез асинхронных потенциальных автоматов
- 3.2. Асинхронные потенциальные автоматы
- 3.3. Асинхронные потенциальные триггеры и элементы памяти
- Триггеры типа R-S
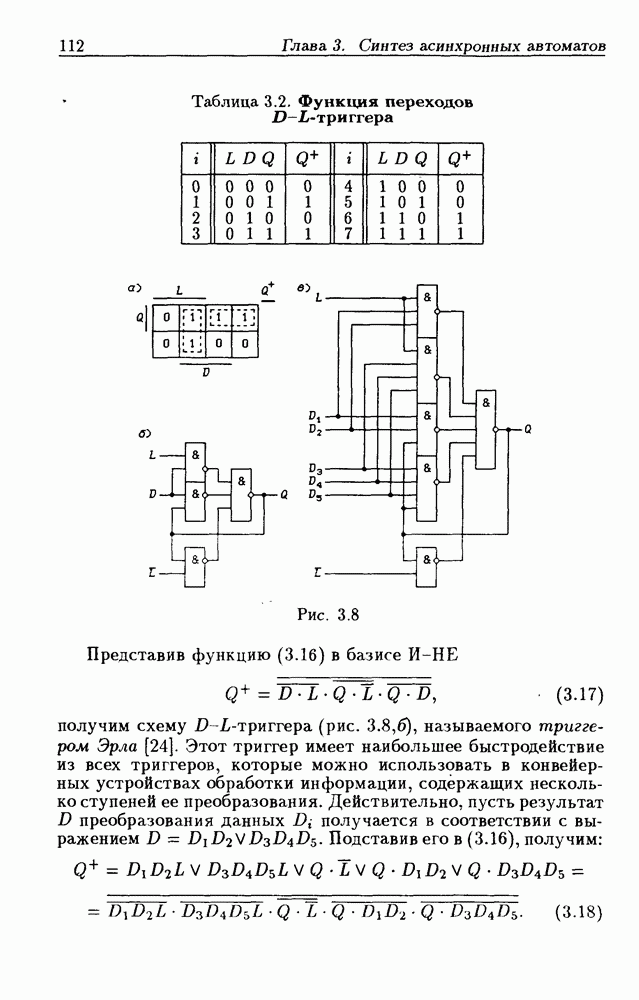
- Триггеры типа D-L
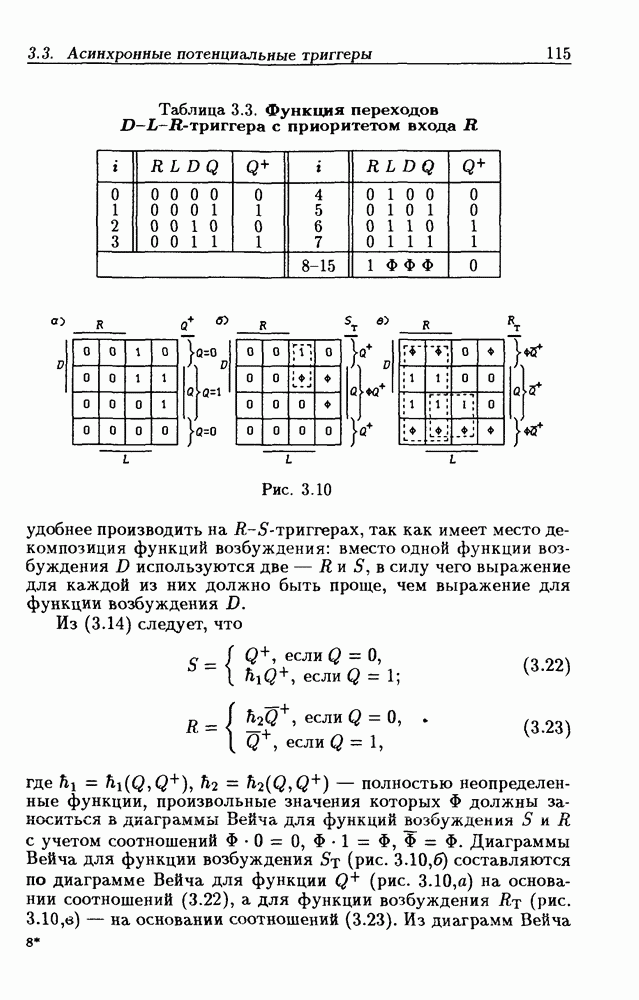
- Триггеры типа D-L-R с приоритетом входа R.
- Триггеры типа D-L-R с приоритетом входа L.
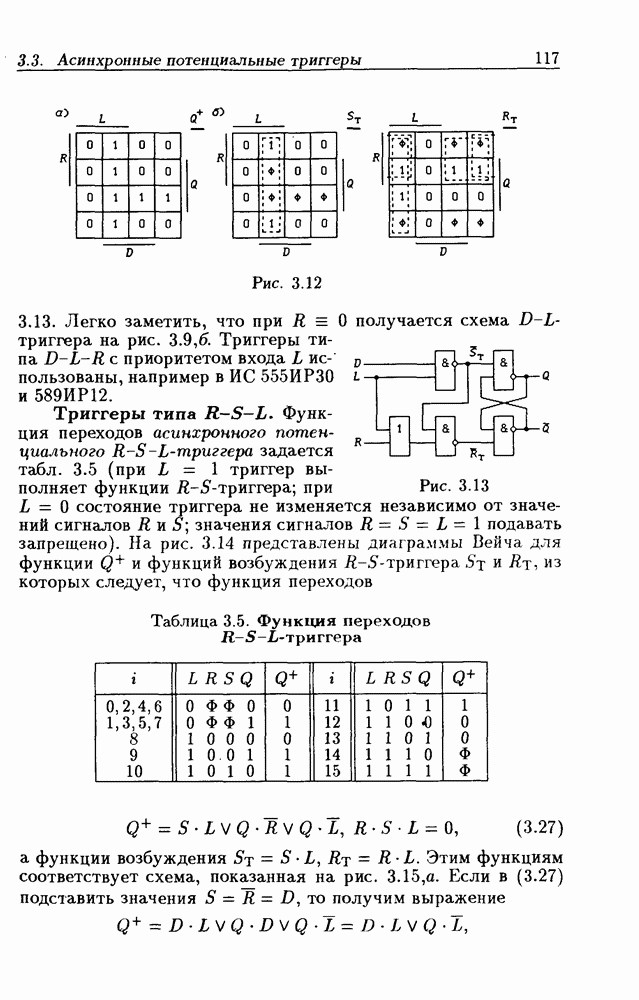
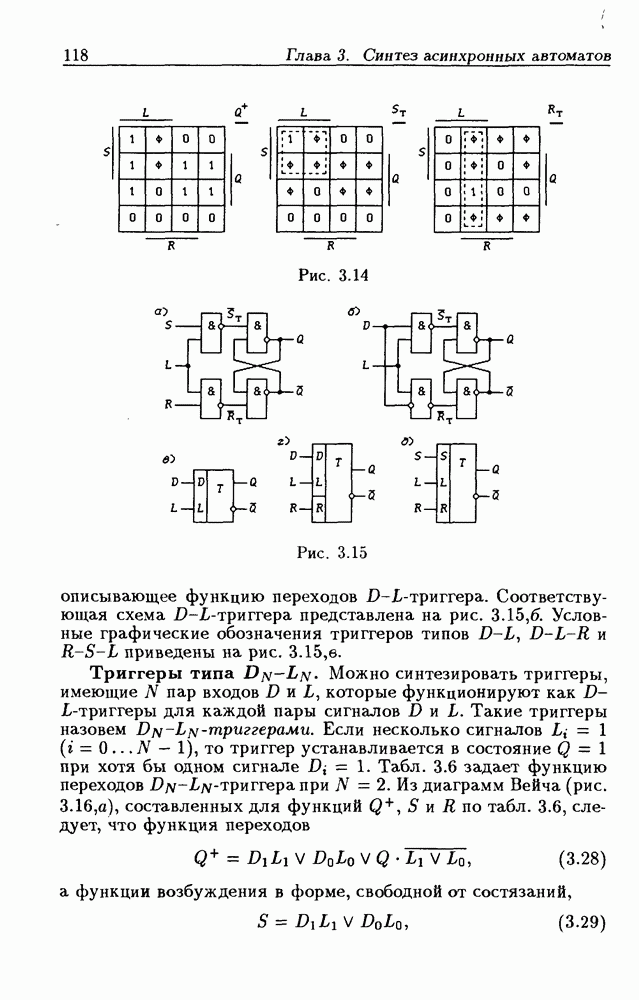
- Триггеры типа R-S-L.
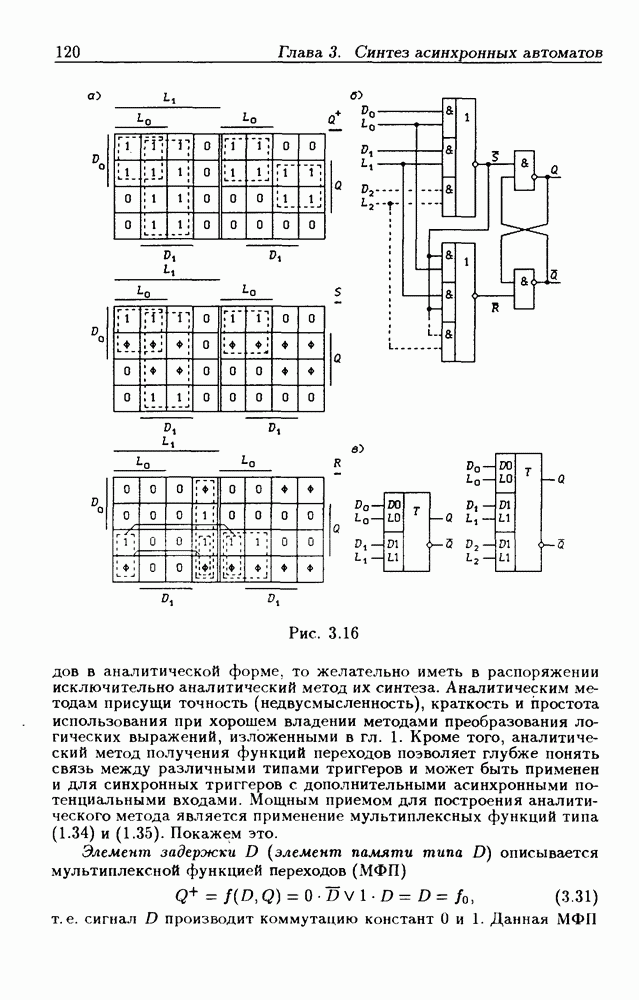
- Триггеры типа DN-LN
- Аналитический метод синтеза и анализа триггеров.
- 3.4. Задание асинхронных потенциальных автоматов таблицами и графами переходов
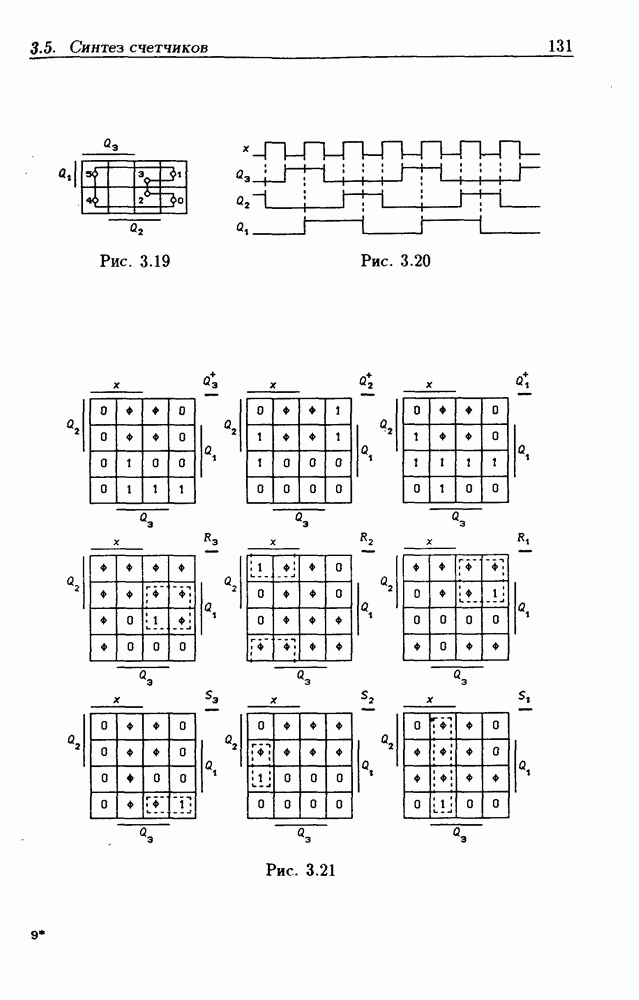
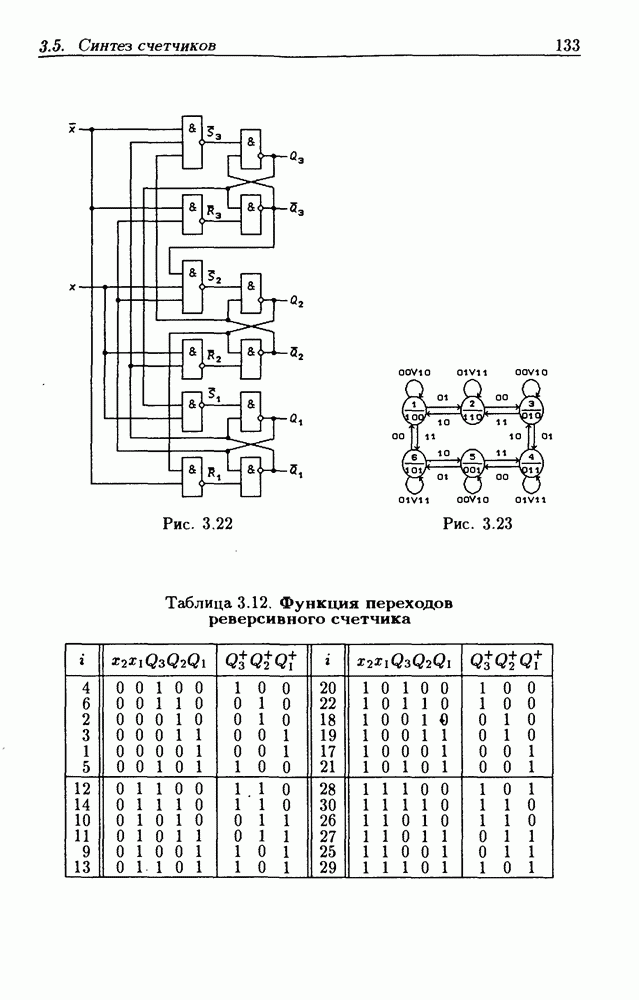
- 3.5. Синтез асинхронных потенциальных счетчиков
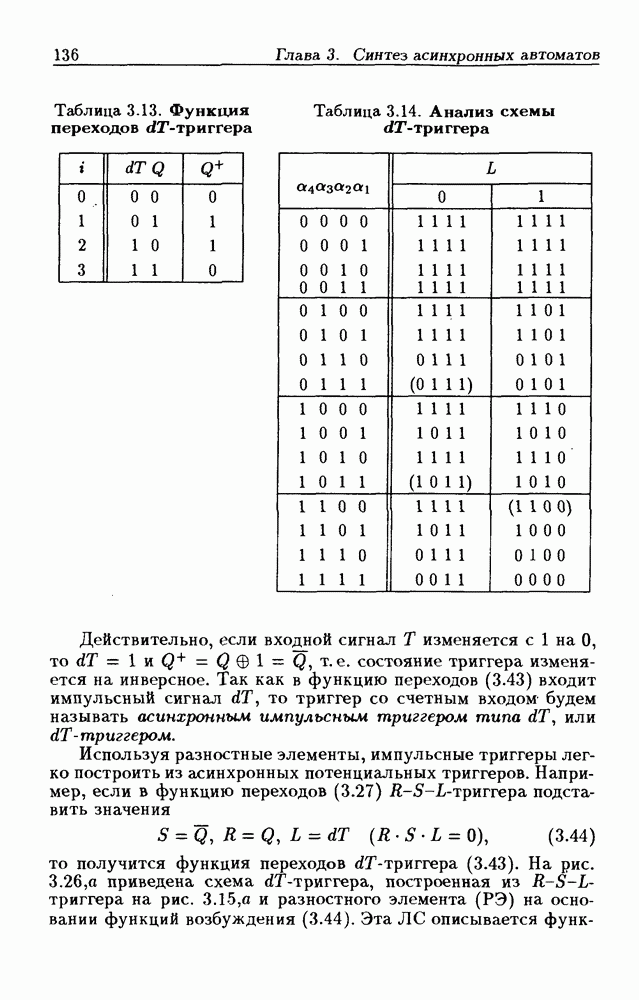
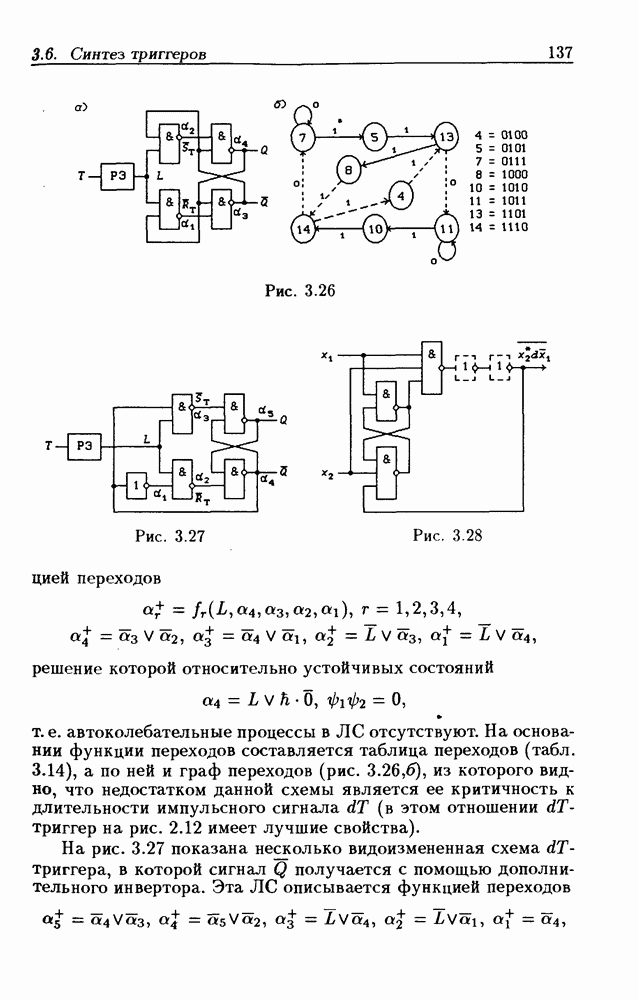
- 3.6. Синтез асинхронных импульсных триггеров
- Триггеры типа dJ-dK.
- Классификация триггеров.
- 3.7. Синтез синхронных триггеров
- Триггеры типа J-K
- Синхронно-асинхронные триггеры.
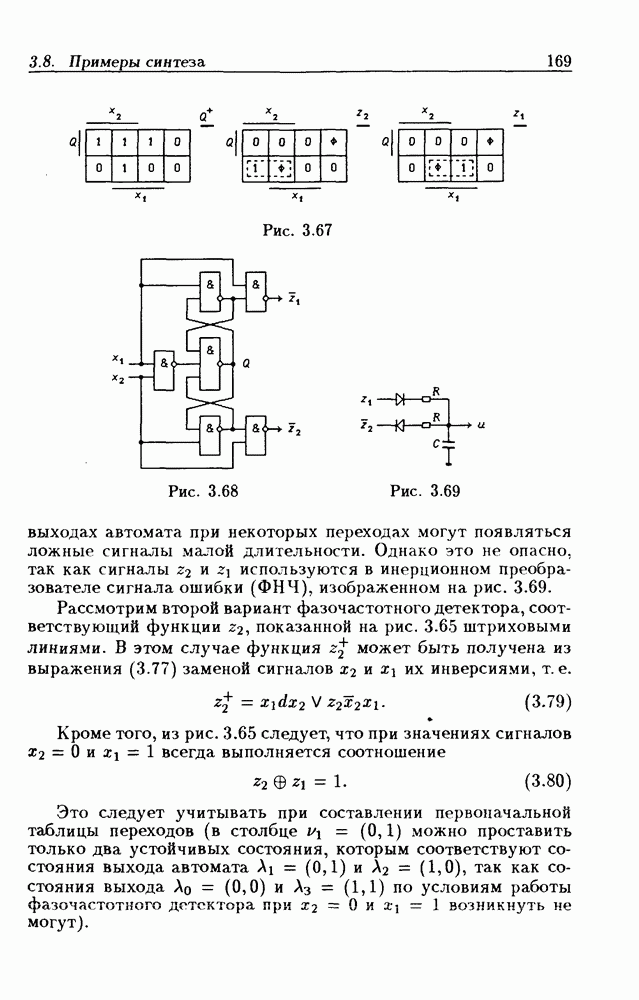
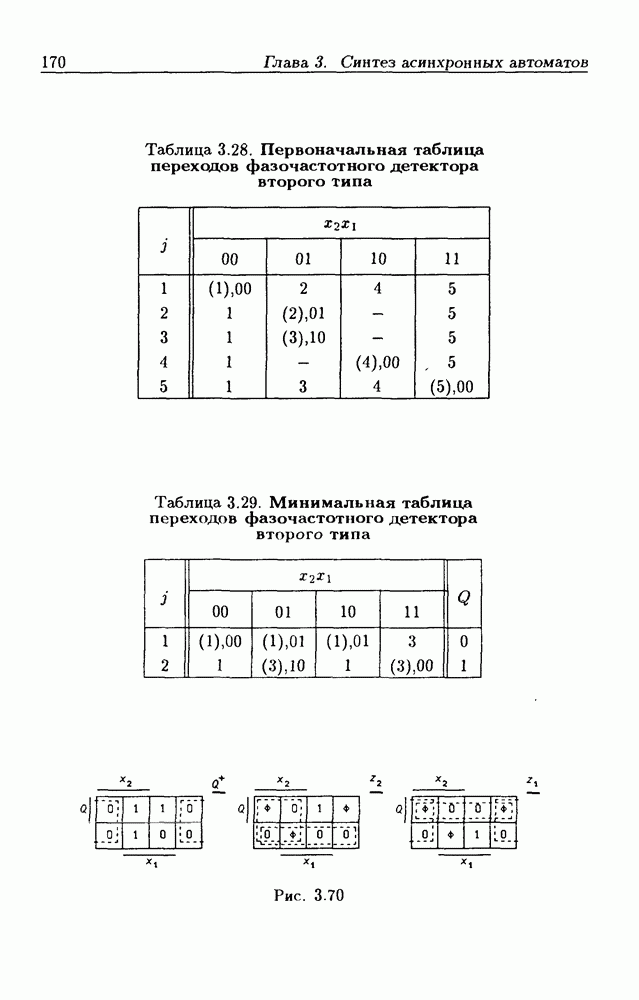
- 3.8. Примеры синтеза асинхронных потенциальных автоматов
- Цифровые фазочастотные детекторы.
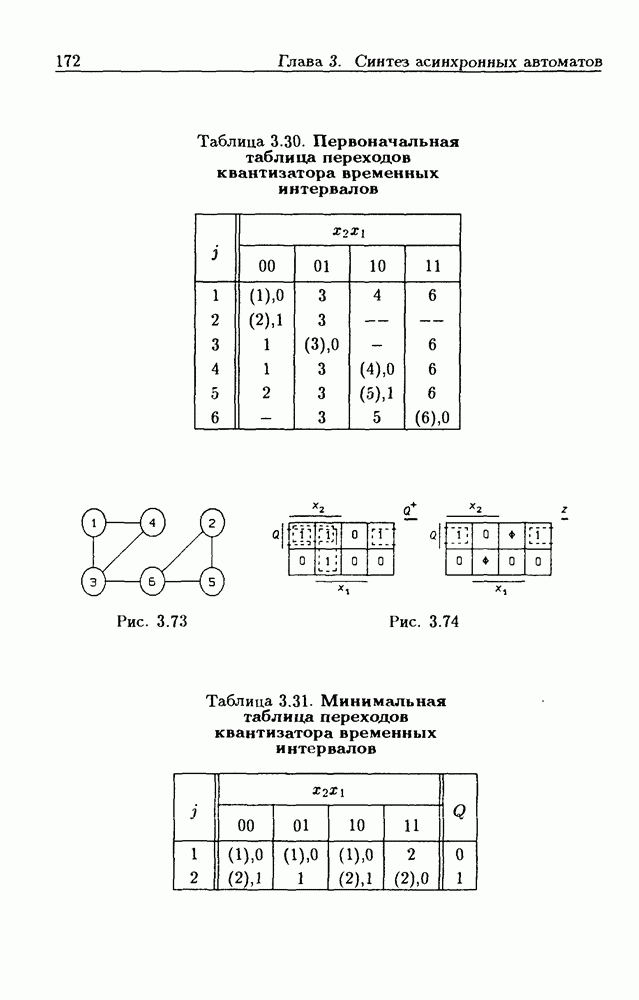
- Квантизатор временных интервалов.
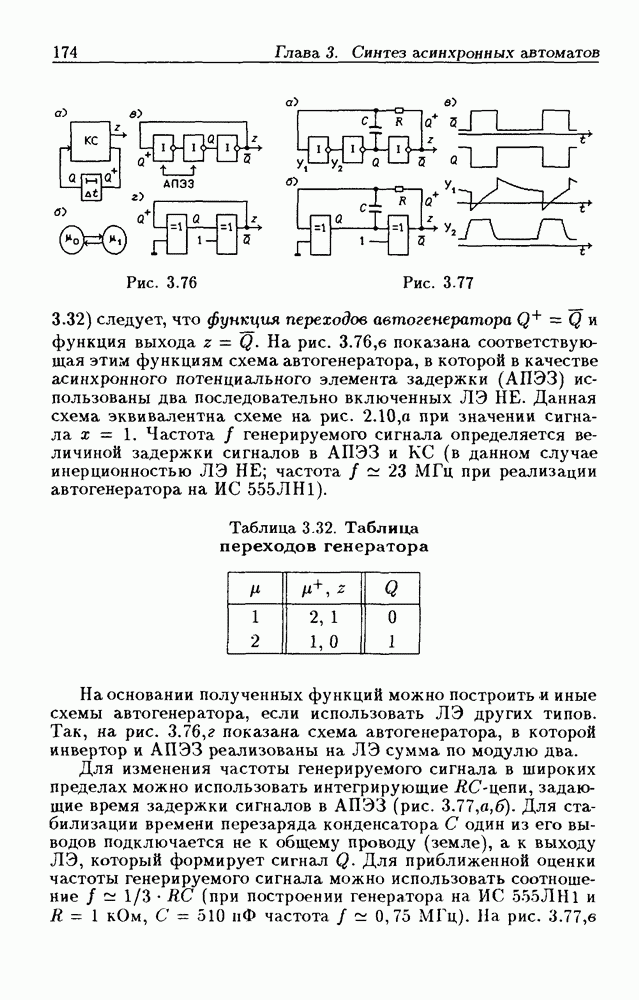
- 3.9. Генераторы сигналов
- Автогенераторы.
- Управляемые автогенераторы.
- Глава 4. Синтез синхронных автоматов
- 4.2. Синхронные триггеры
- Триггеры типов D и R-S с импульсным тактовым сигналом.
- Синхронные триггеры типов R-S и D-L
- Синхронно-асинхронные триггеры.
- Синхронные триггеры типа J-K
- Триггеры типа Т.
- Классификация синхронных триггеров.
- Преобразования типов синхронных триггеров.
- Триггеры типов D-T-L и D-T-L/R
- Функции переходов синхронно-асинхронных триггеров.
- 4.3. Примеры синтеза синхронных автоматов
- 4.4. Сдвигающие регистры
- Синтез счетчиков на сдвигающих регистрах.
- Сдвигающие регистры с загрузкой данных.
- Реверсивные сдвигающие регистры.
- 4.5. Синхронные счетчики
- Синхронные двоичные счетчики.
- Синхронные двоично-десятичные счетчики.
- Каскадирование двоичных и двоично-десятичных счетчиков.
- Синхронные двоичные реверсивные счетчики.
- Реверсивные двоично-десятичные счетчики.
- Каскадирование реверсивных счетчиков.
- Счетчики на сдвигающих регистрах.
- Кольцевые счетчики.
- Линейные счетчики.
- Программируемые счетчики.
- 4.6. Асинхронные счетчики
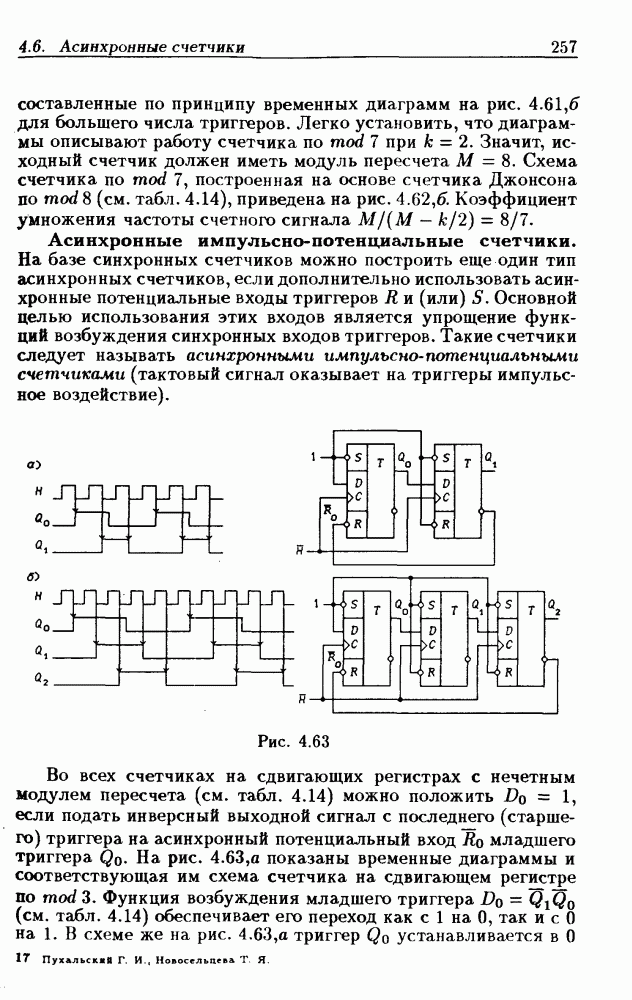
- Асинхронные счетчики с умножением частоты счетного сигнала.
- Асинхронные импульсно-потенциальные счетчики.
- Асинхронное программирование модуля пересчета счетчиков.
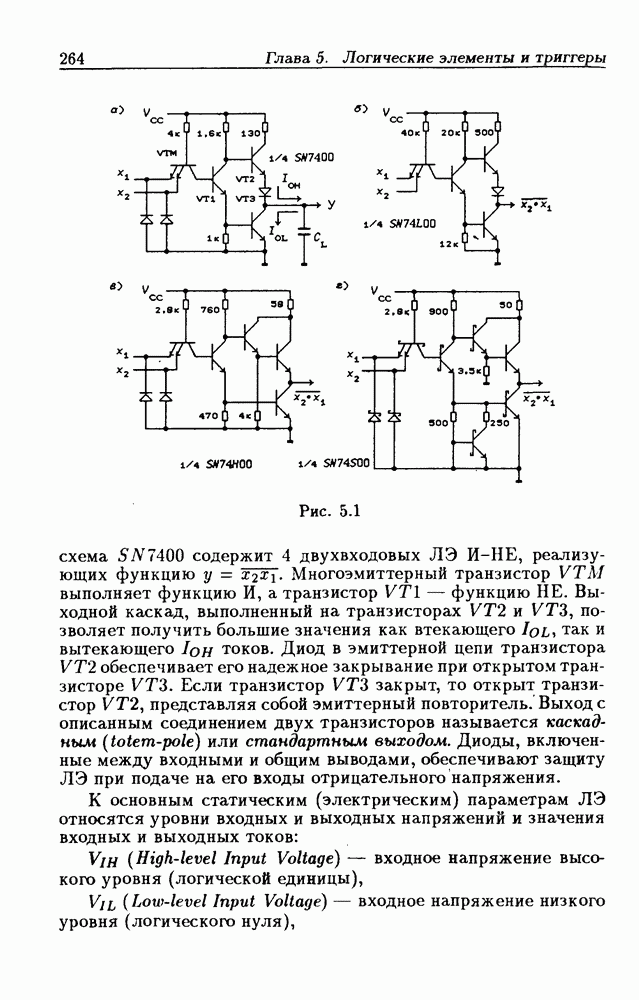
- Глава 5. Логические элементы и триггеры
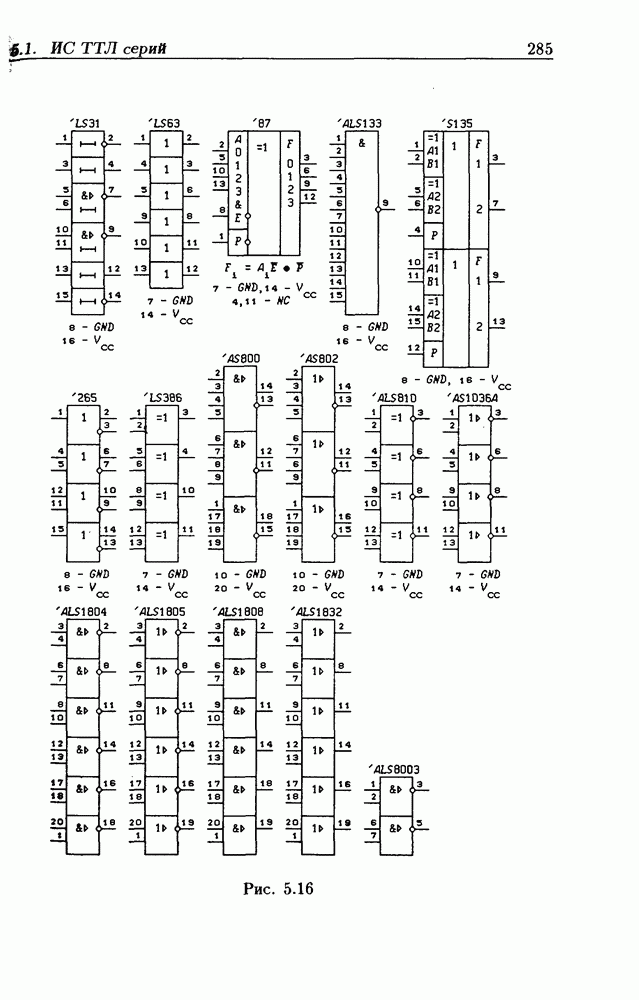
- Логические элементы.
- Классификация ИС по степени интеграции.
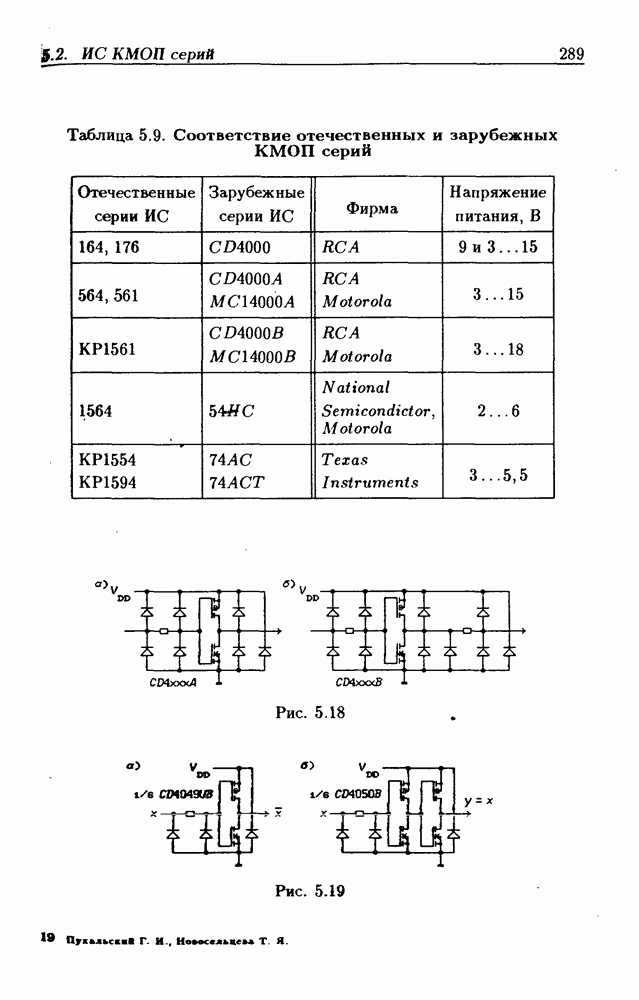
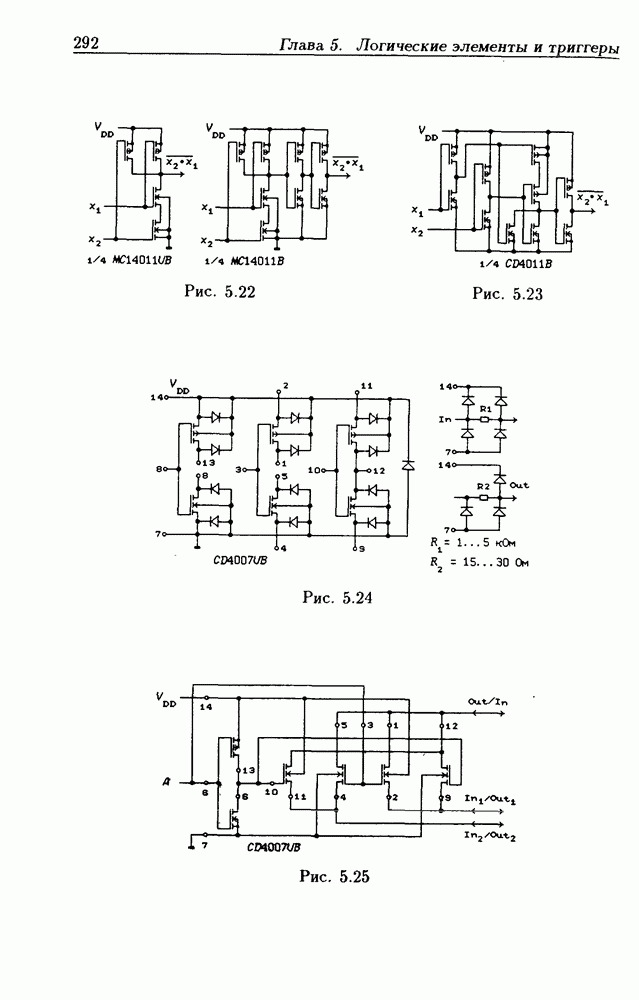
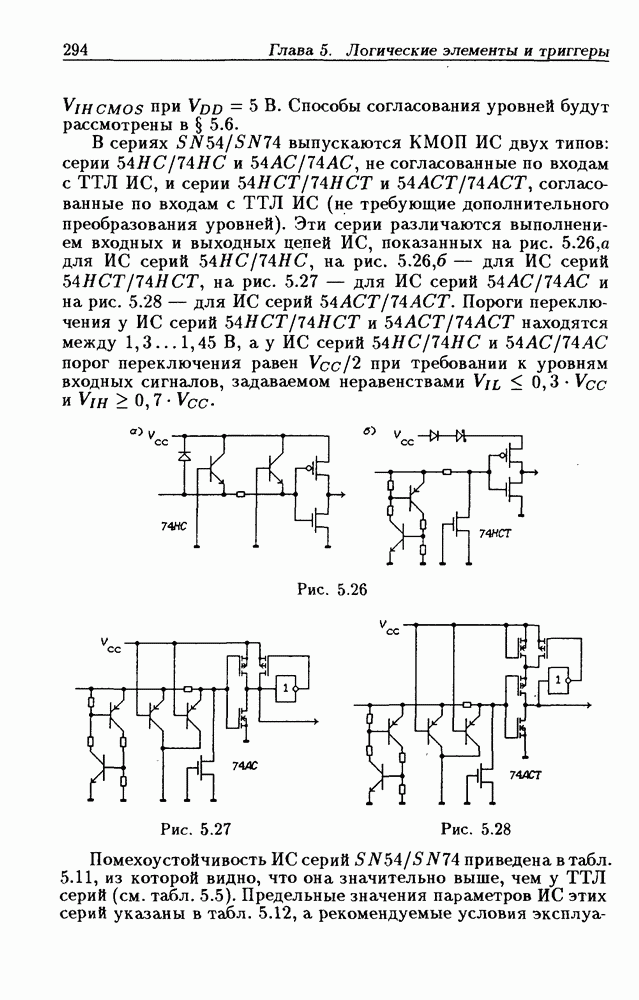
- 5.2. Интегральные схемы КМОП серий
- 5.3. Триггеры Шмитта
- 5.4. Логические элементы с открытым коллекторным выходом
- Логические элементы с открытым коллекторным выходом.
- Применения ЛЭ с открытым коллекторным выходом.
- Интерфейсные ЛЭ с открытым коллекторным выходом.
- Логические элементы с открытым стоковым выходом.
- Типовые цоколевки ИС.
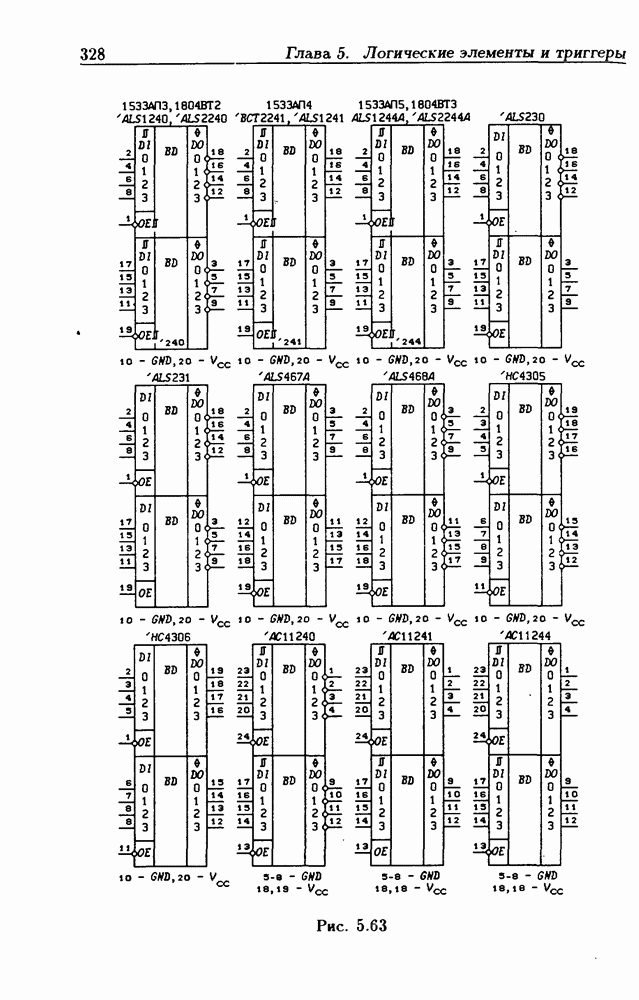
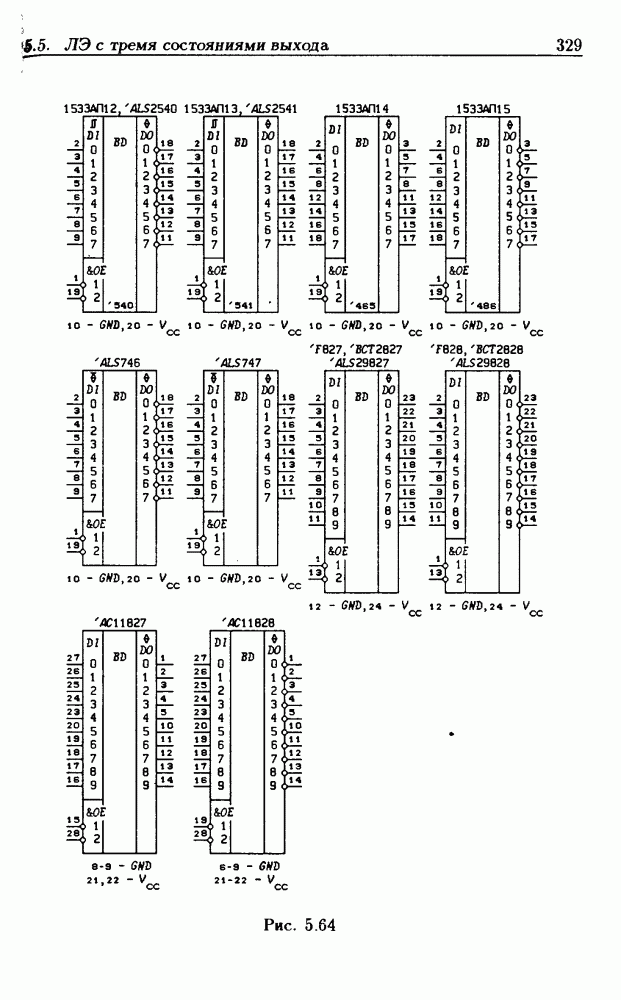
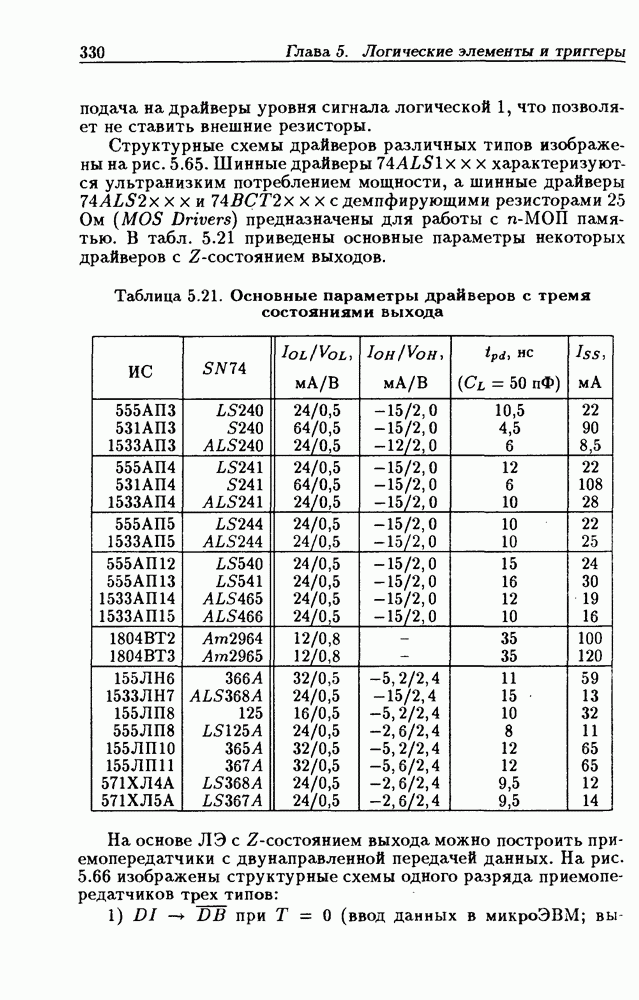
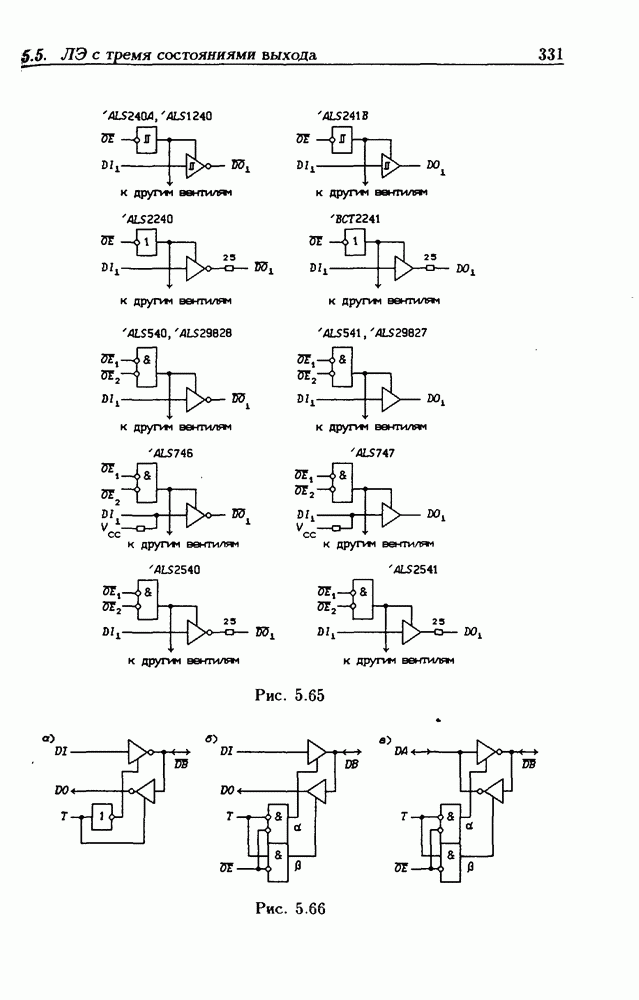
- 5.5. Логические элементы с тремя состояниями выхода
- Шинные драйверы с Z-состоянием выхода.
- Основные правила графического изображения ИС.
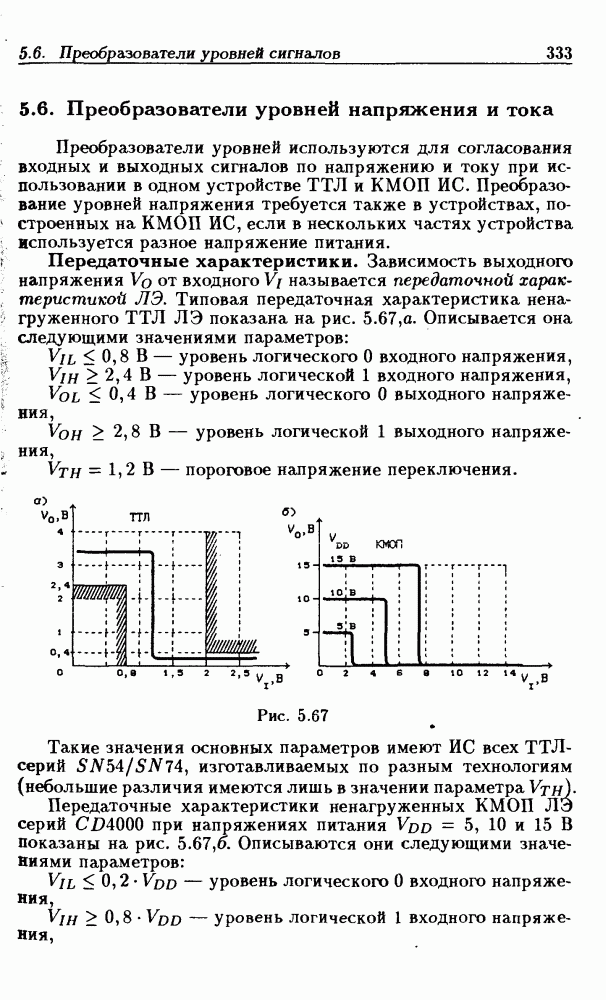
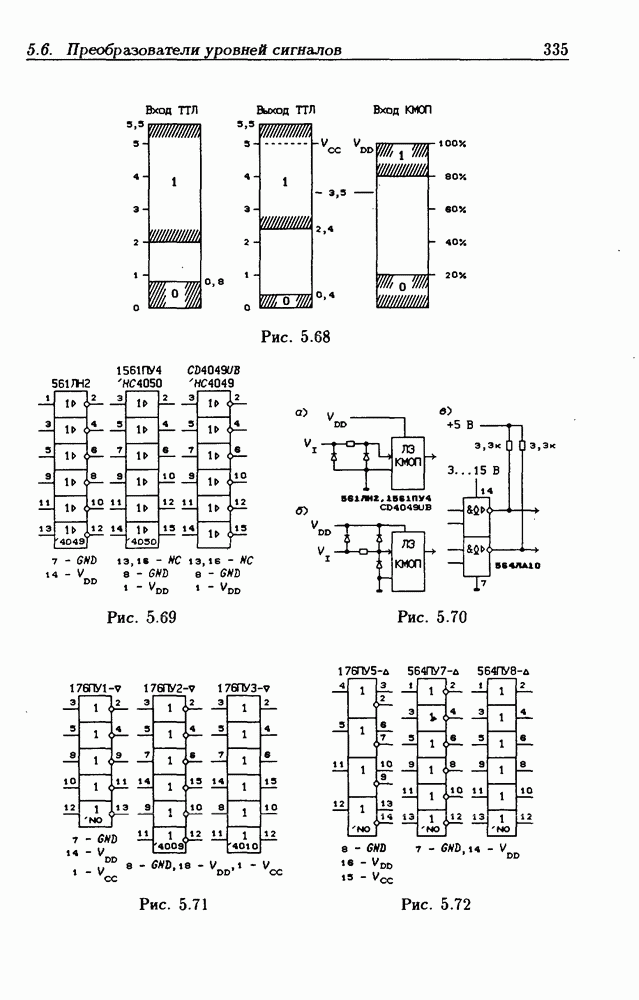
- 5.6. Преобразователи уровней напряжения и тока
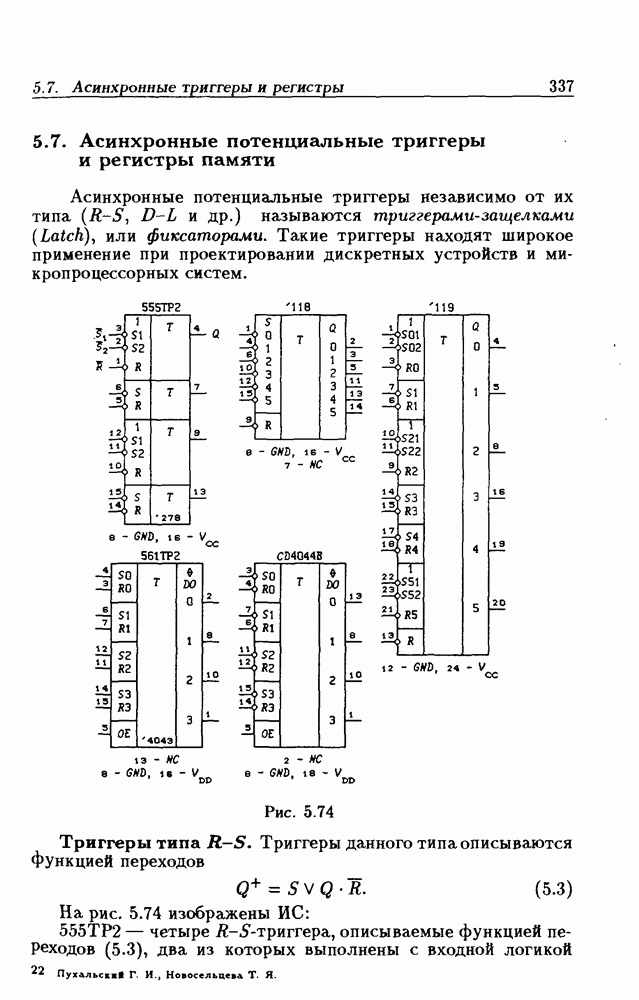
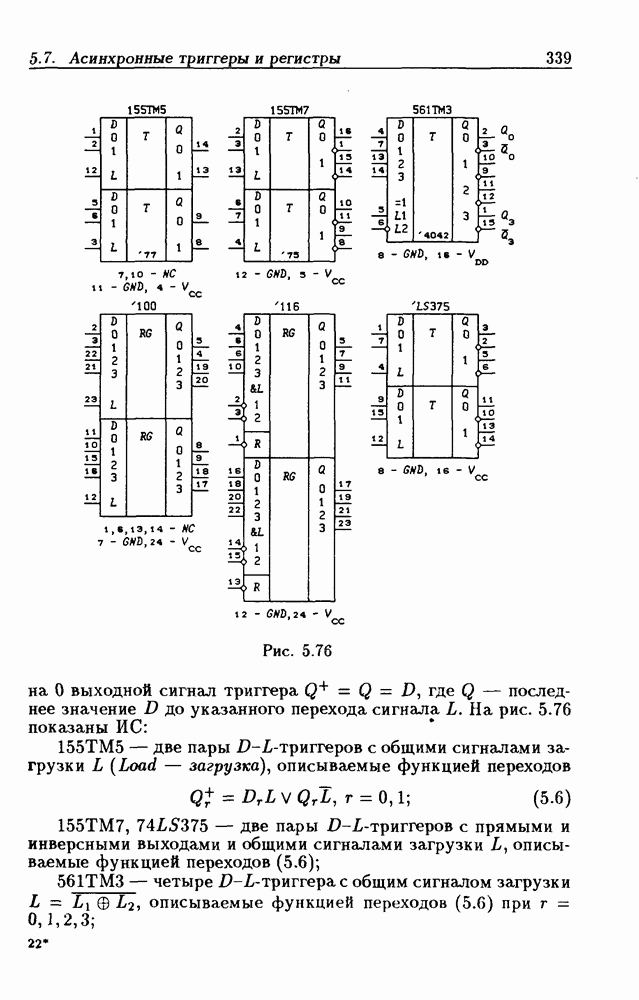
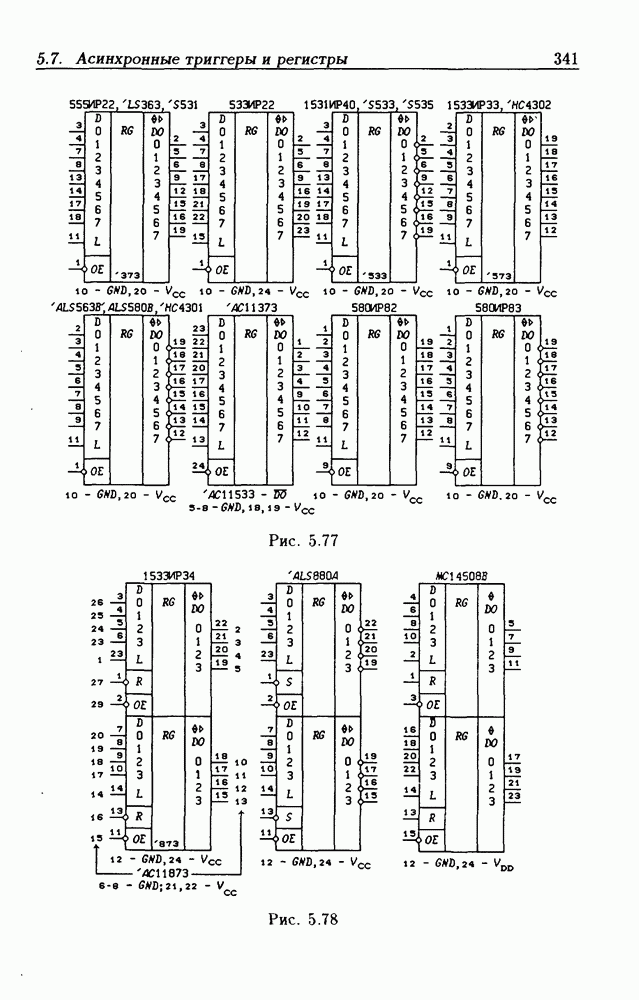
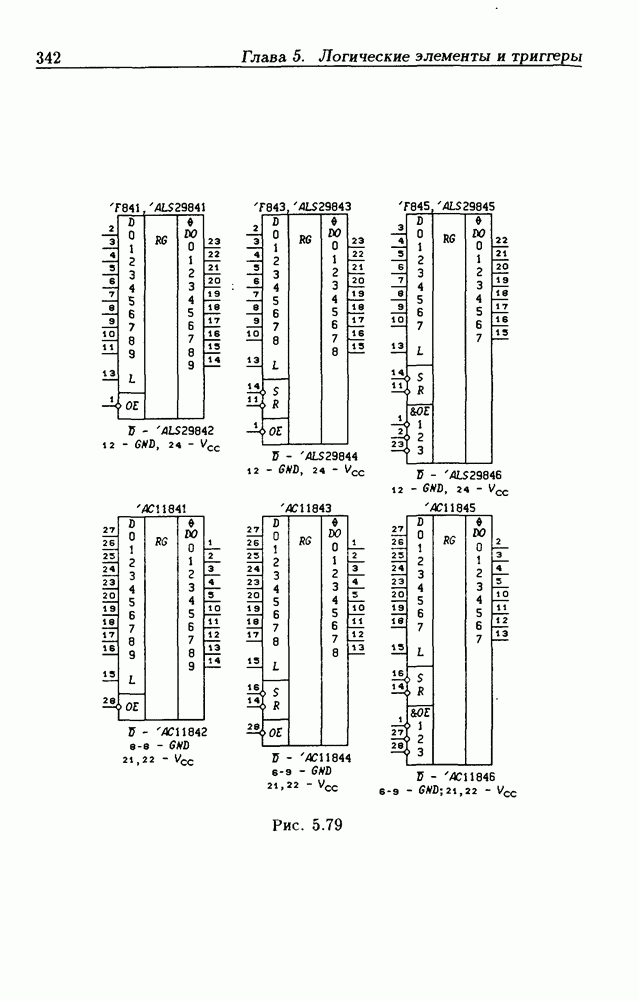
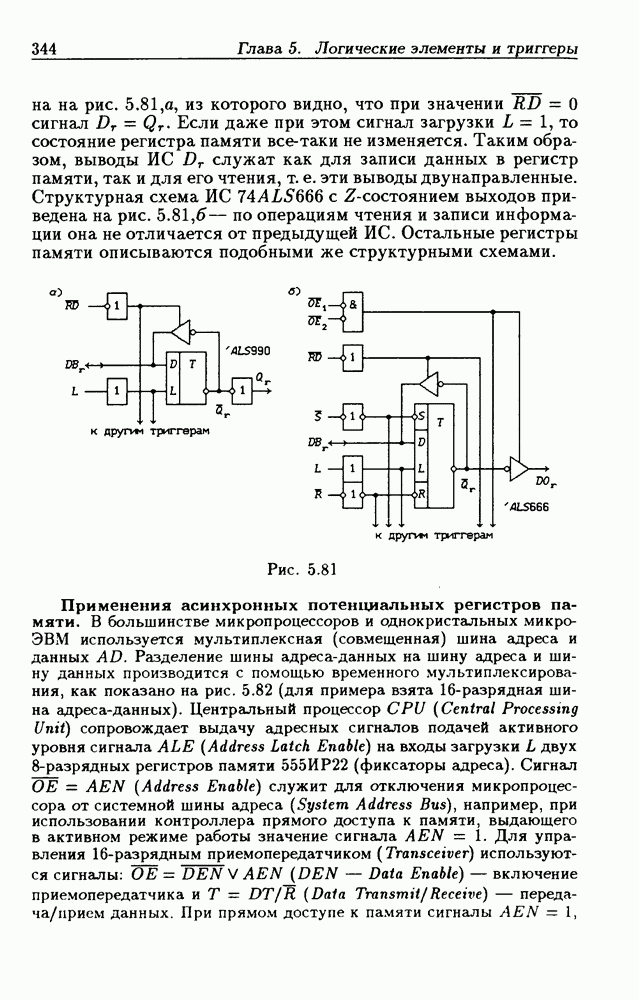
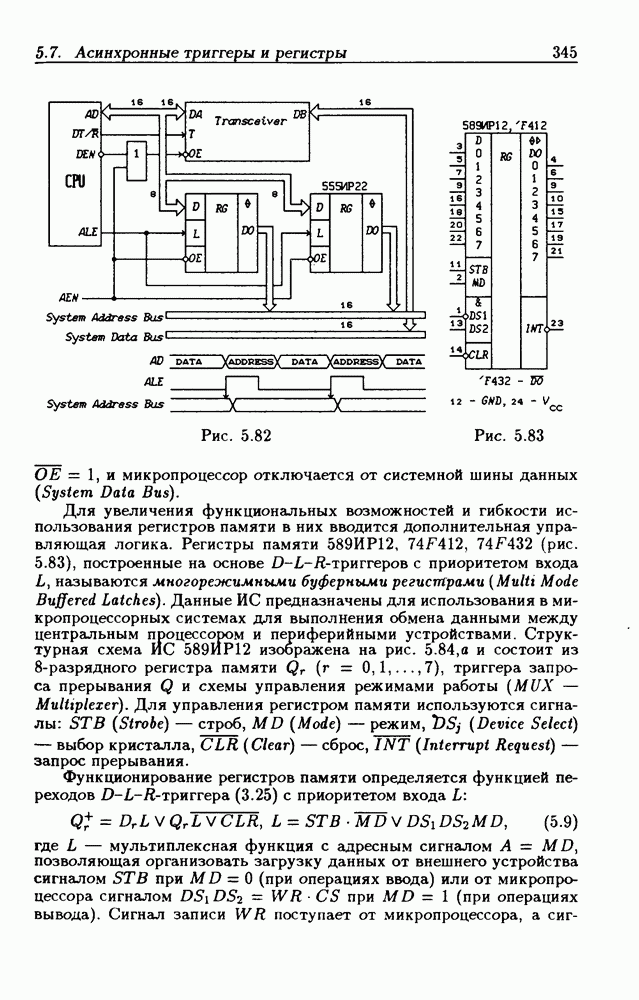
- 5.7. Асинхронные потенциальные триггеры и регистры памяти
- 5.8. Синхронные триггеры и регистры памяти
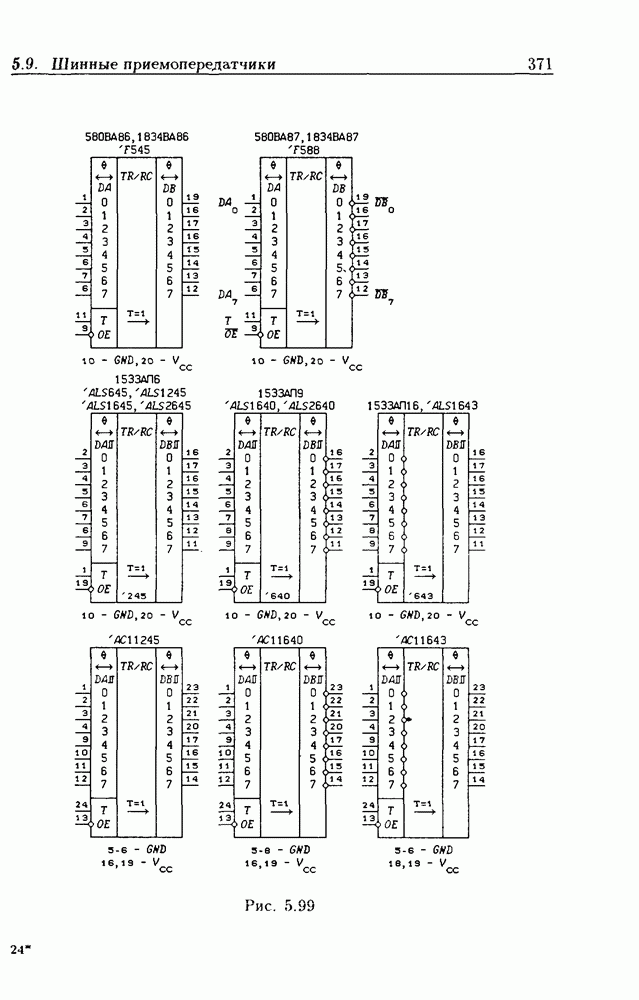
- 5.9. Шинные приемопередатчики
- Шинные приемопередатчики с Z-состоянием выхода.
- Шинные приемопередатчики с открытым коллекторным выходом.
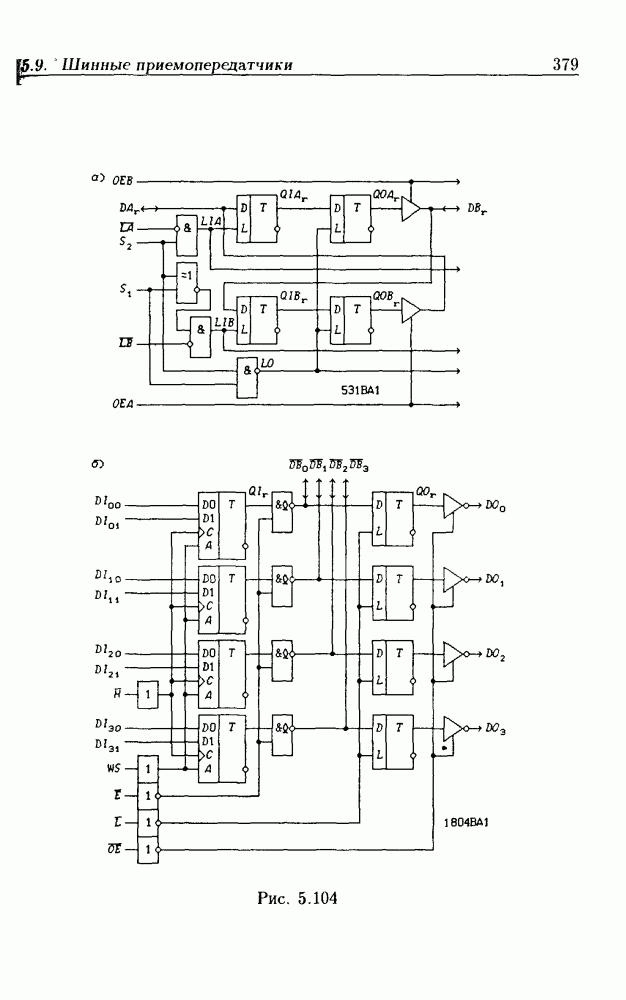
- Шинные приемопередатчики с регистрами памяти.
- Шинные приемопередатчики со сдвигающим регистром.
- Шинные трехнаправленные приемопередатчики.
- 5.10. Мультивибраторы
- 5.11. Генераторы
- Схемы устранения «дребезга» механических контактов.
- Автогенераторы периодических сигналов.
- 5.12. Рекомендации по выбору серий ИС
- Глава 6. Коммутаторы и арифметические устройства
- 6.1. Дешифраторы
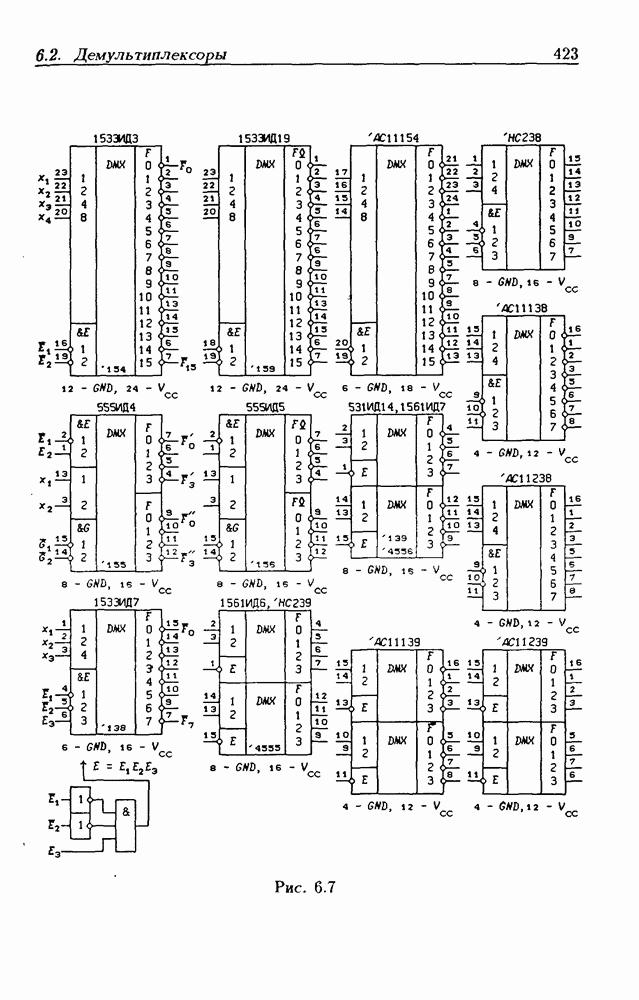
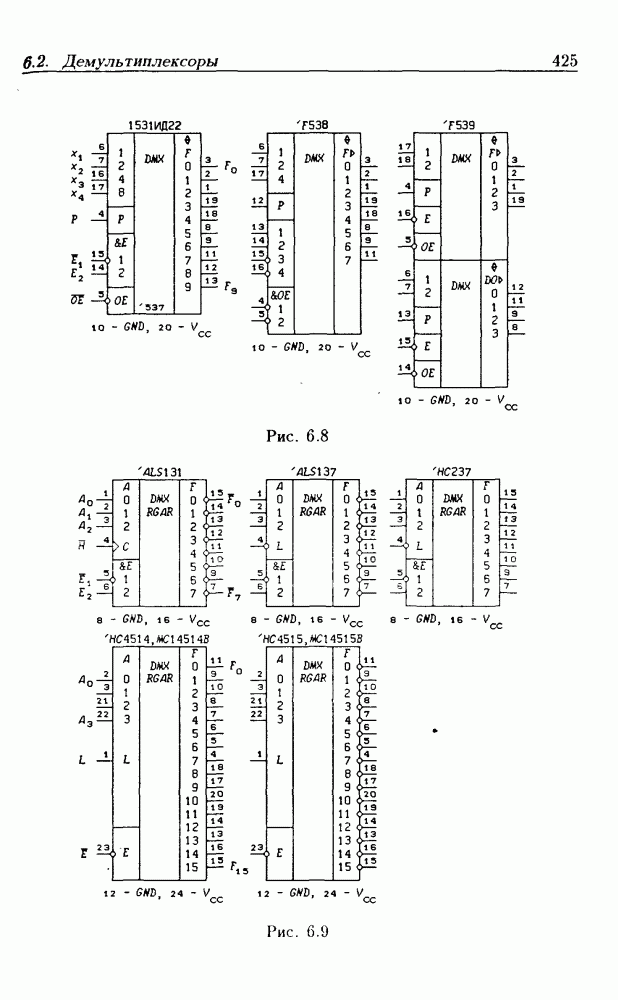
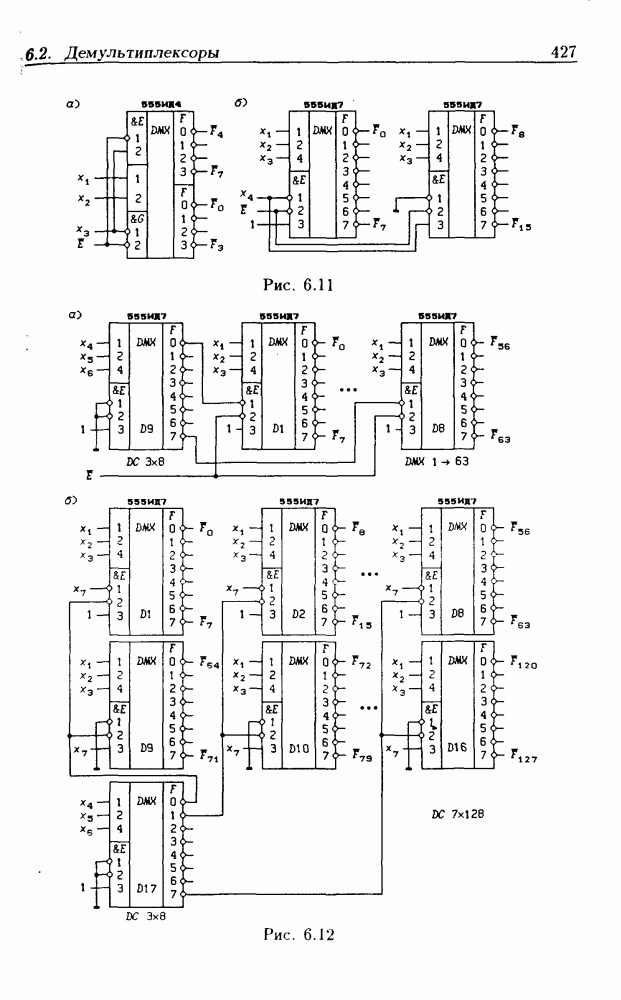
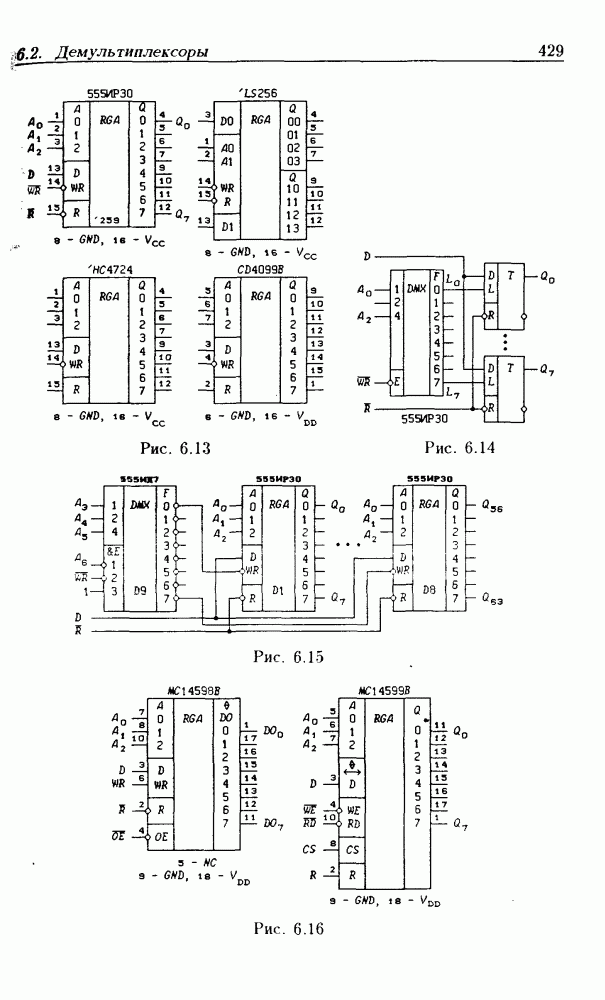
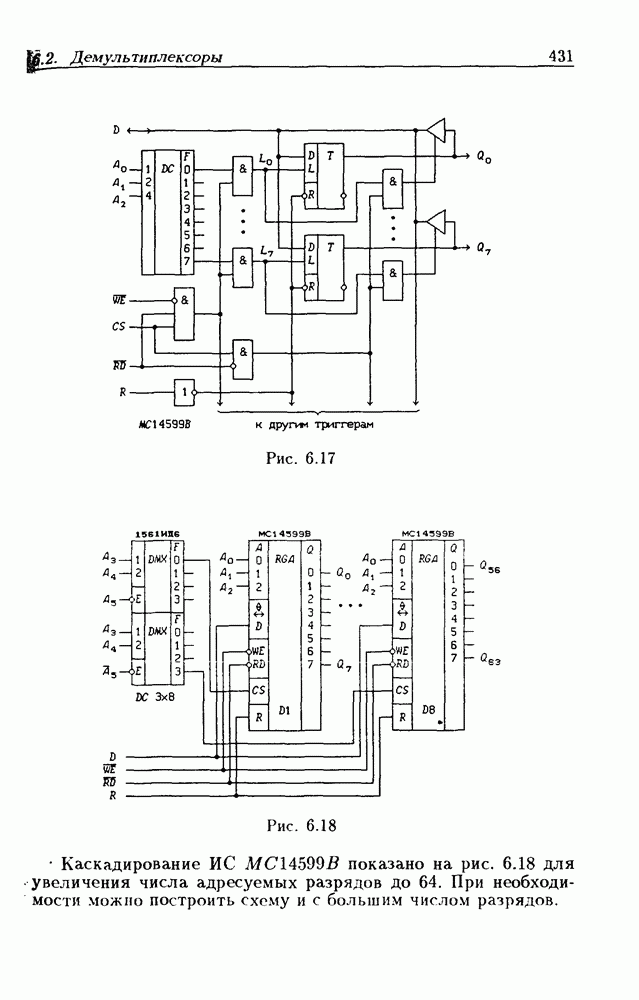
- 6.2. Демультиплексоры
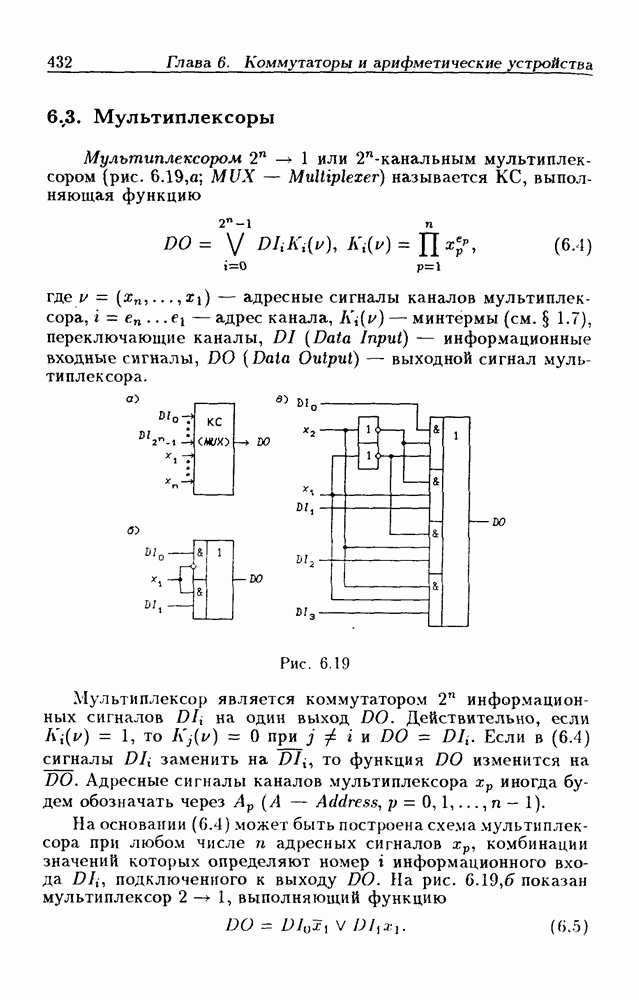
- 6.3. Мультиплексоры
- Мультиплексоры без стробирования.
- Мультиплексоры со стробированием.
- Мультиплексоры с Z-состоянием выхода.
- Каскадирование мультиплексоров.
- Функциональные мультиплексоры.
- Регистры памяти с мультиплексными входами данных.
- Мультиплексоры с регистрами памяти данных и адреса.
- Сдвигающие мультиплексоры.
- 6.4. Синтез комбинационных схем и цифровых автоматов на мультиплексорах
- Синтез схем на 8-канальных мультиплексорах.
- Синтез на двухразрядных 4-канальных мультиплексорах.
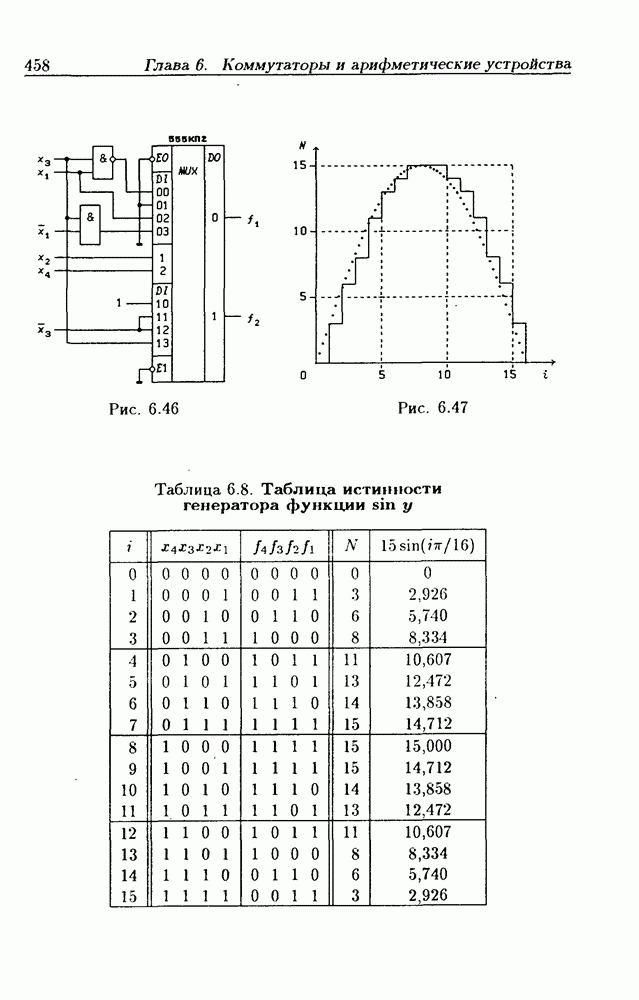
- Синтез генератора синусоидальной функции на мультиплексорах.
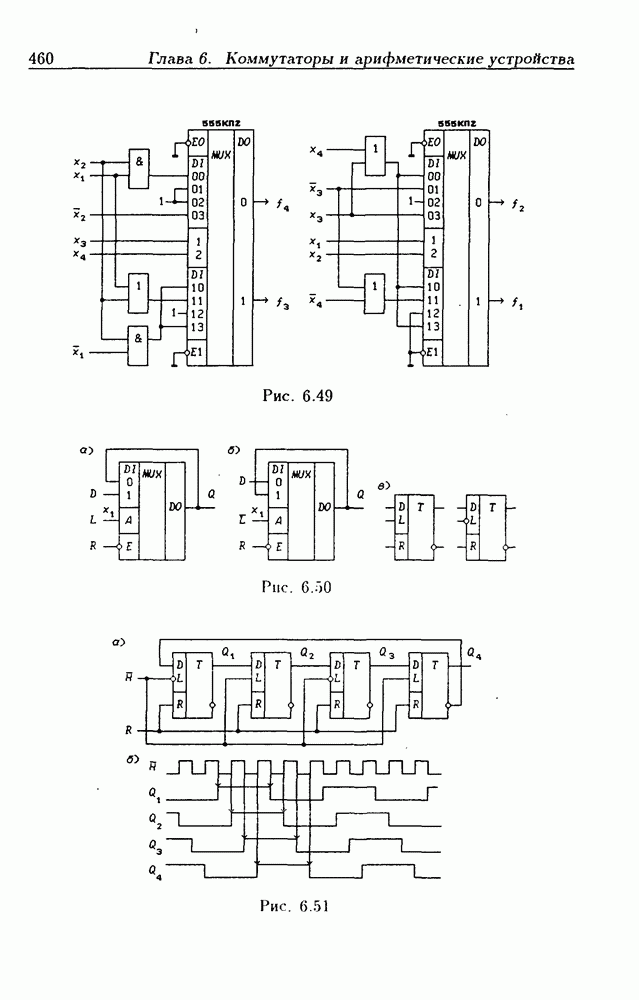
- Синтез триггеров на мультиплексорах.
- Синтез счетчиков на мультиплексорах.
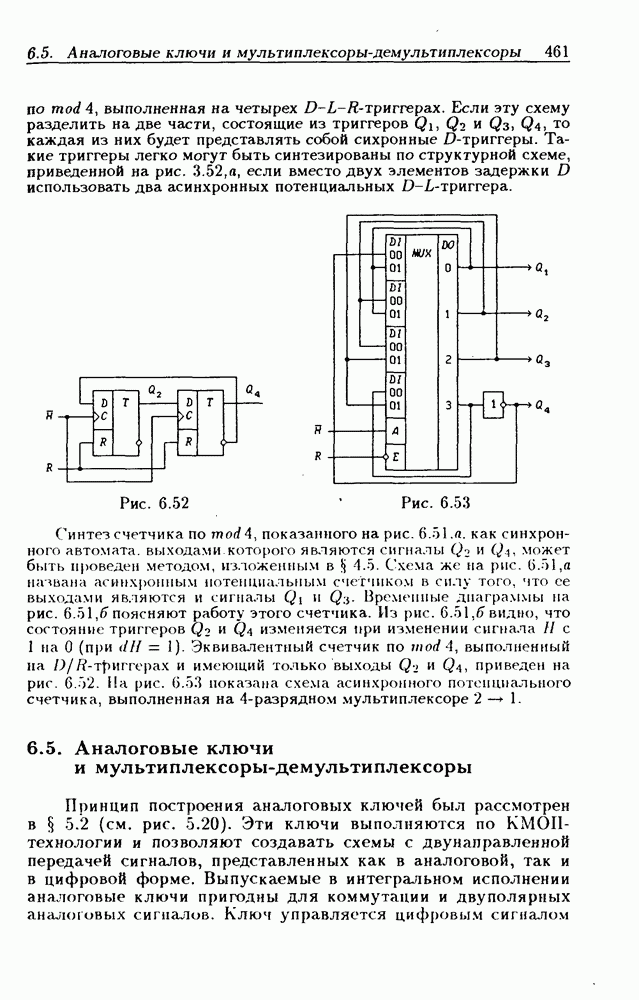
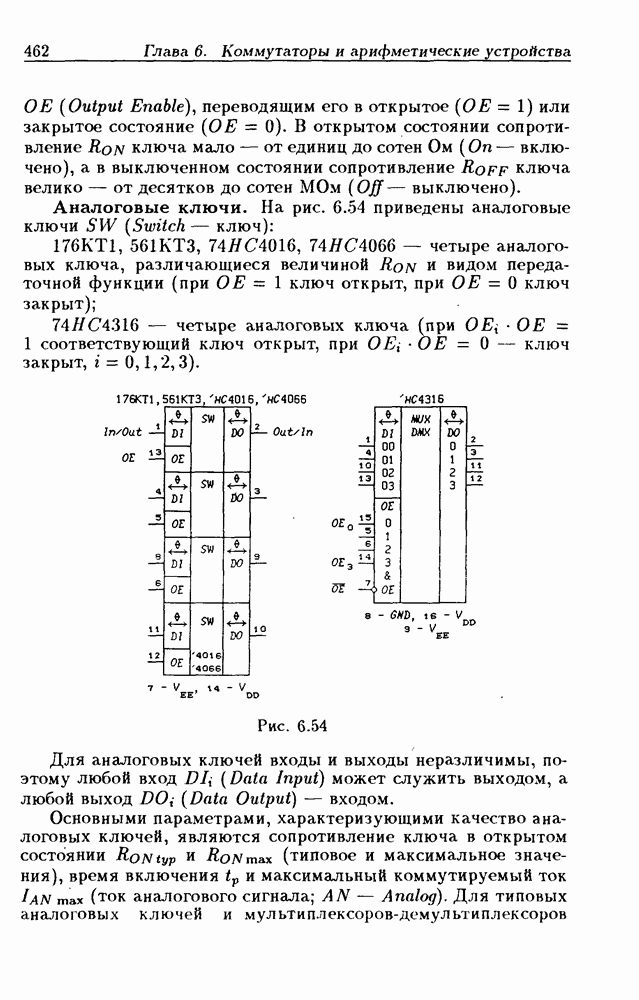
- 6.5. Аналоговые ключи и мультиплексоры-демультиплексоры
- 6.6. Шифраторы
- 6.7. Цифровые компараторы
- Программируемые цифровые компараторы.
- Адресные компараторы.
- Применения адресных компараторов.
- 6.8. Схемы сравнения двоичных чисел
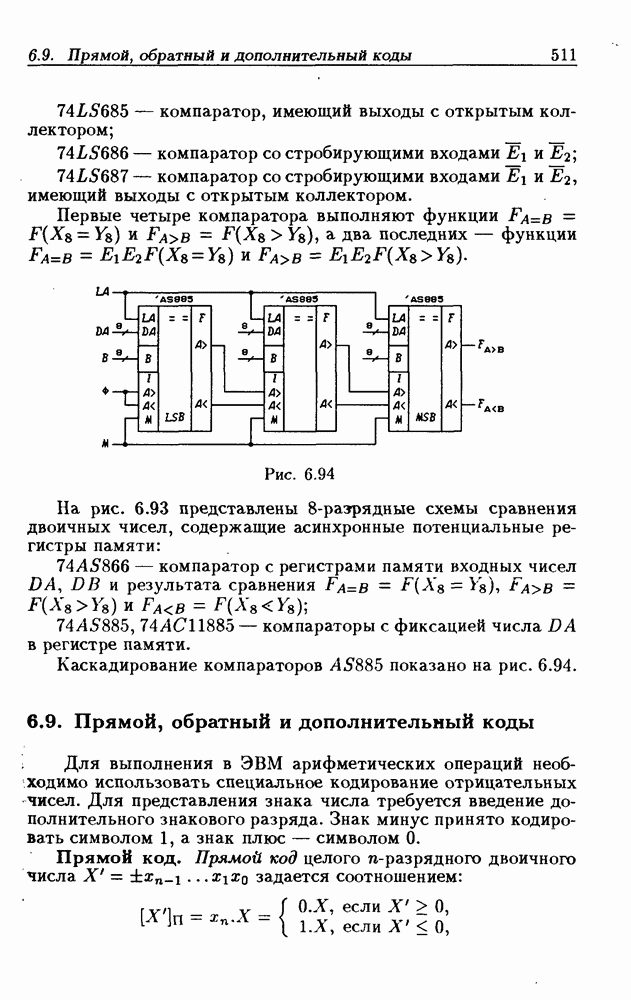
- 8-разрядные схемы сравнения двоичных чисел.
- 6.9. Прямой, обратный и дополнительный коды
- Дополнительный код.
- Сложение чисел в обратном коде.
- Код с избытком 3.
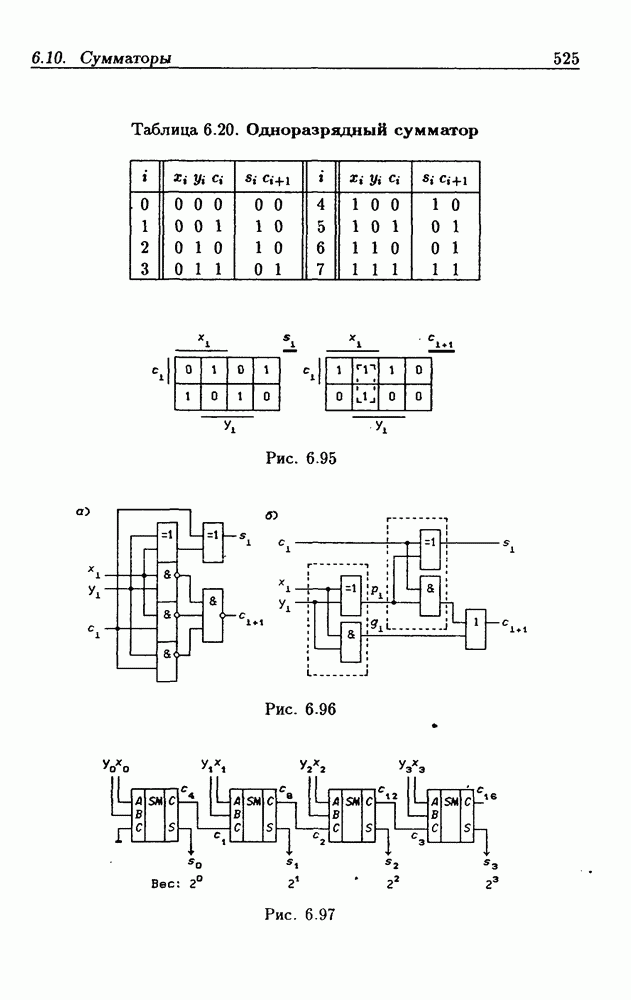
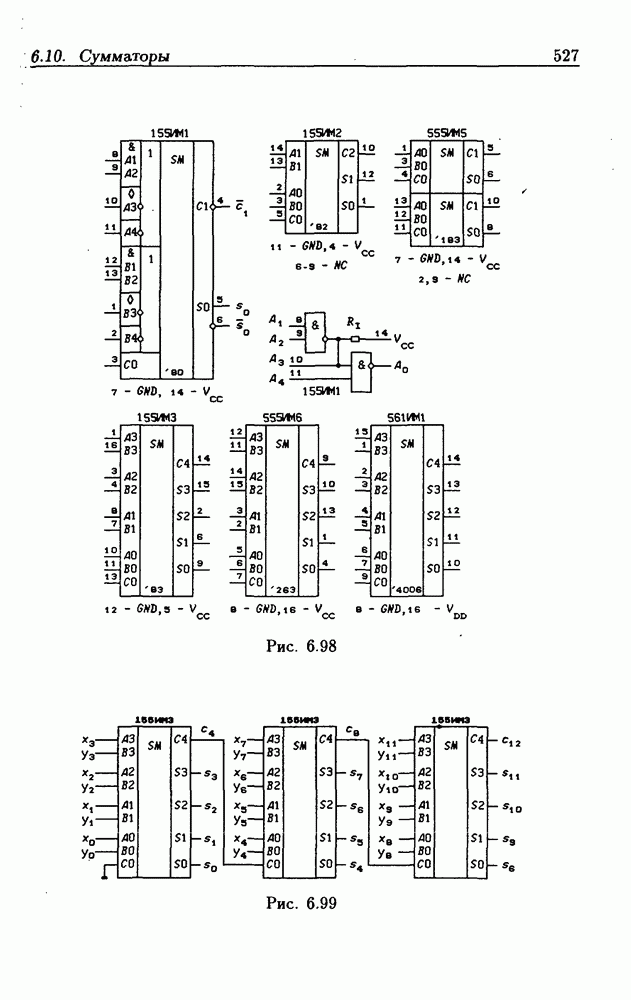
- 6.10. Сумматоры
- Двоичные параллельные сумматоры с последовательным переносом.
- Двоичные сумматоры с параллельным переносом.
- Применения сумматоров.
- Десятичные сумматоры.
- Последовательные двоичные сумматоры.
- 6.11. Арифметическо-логические устройства
- 6.12. Пороговые схемы и мажоритарные элементы
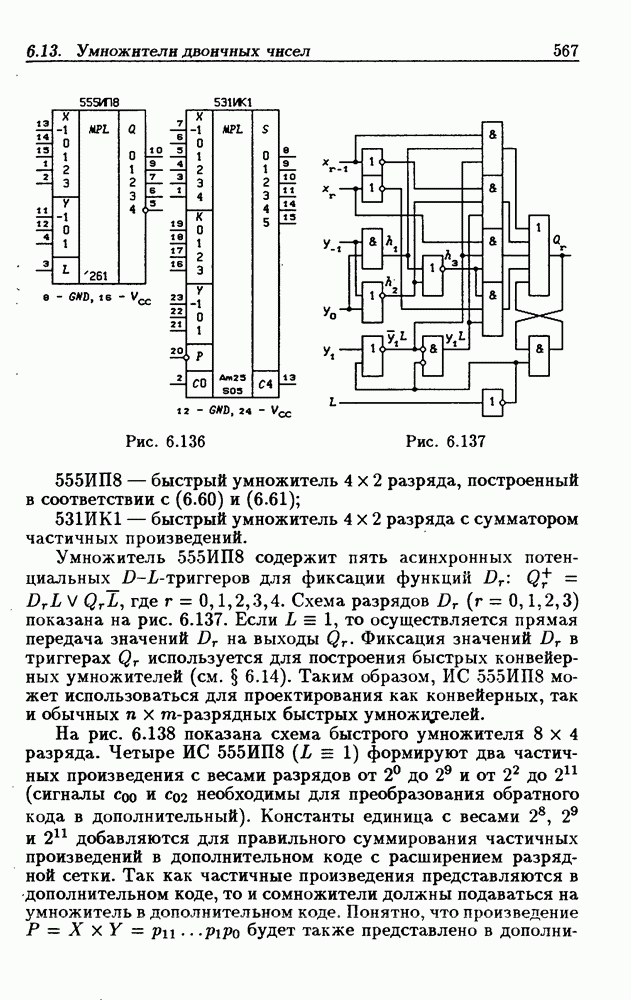
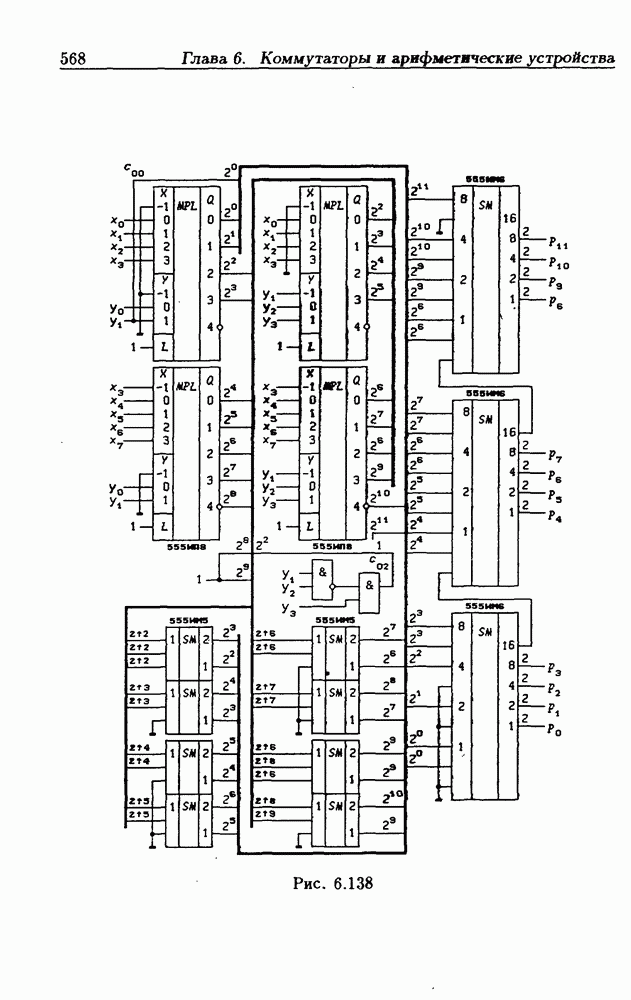
- 6.13. Умножители двоичных чисел
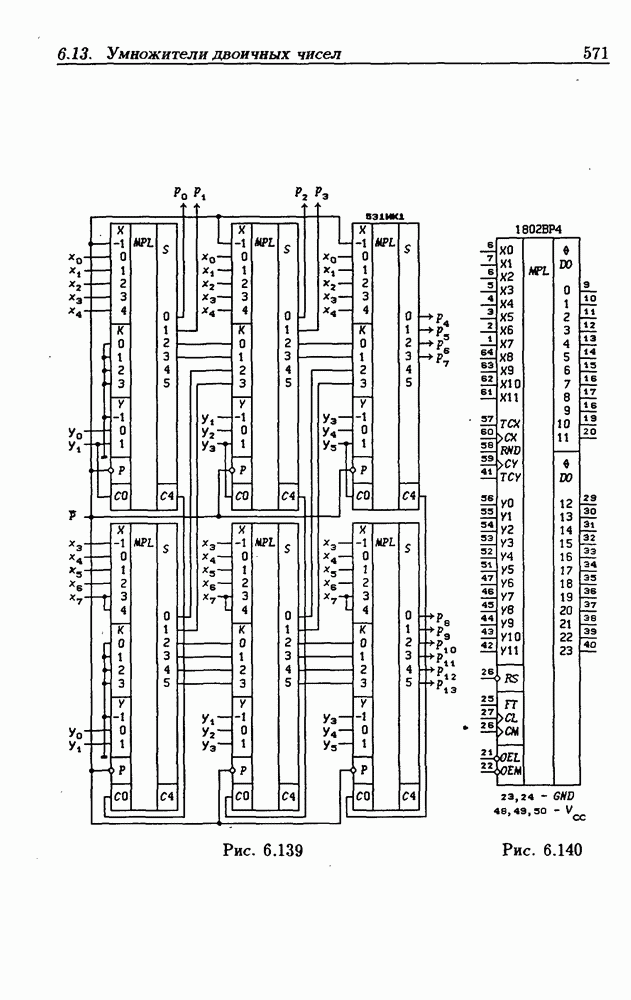
- Быстрые умножители.
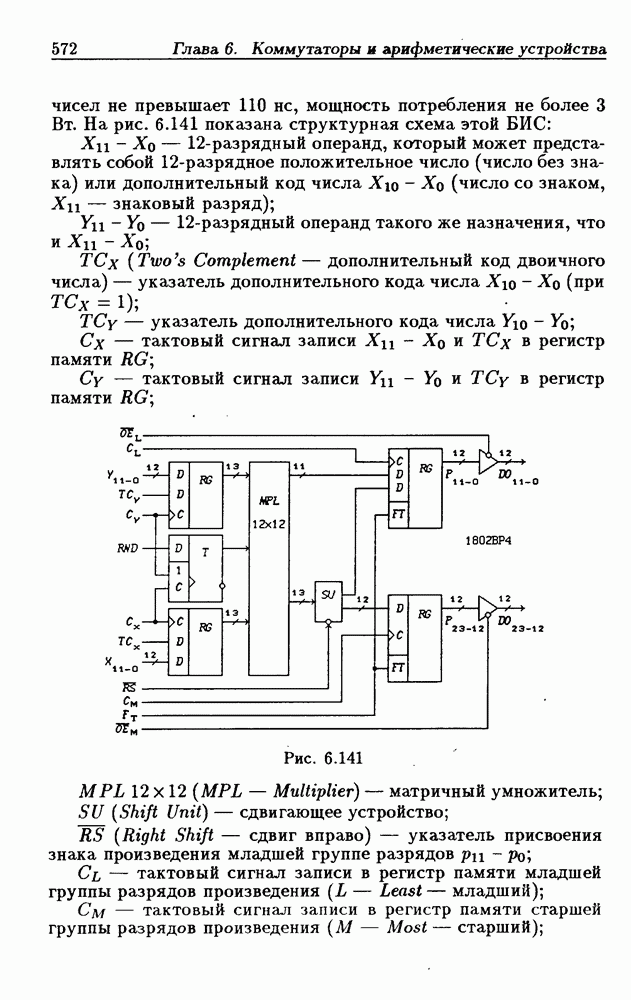
- БИС умножителя 12×12 разрядов 1802ВР4.
- Последовательные умножители.
- 6.14. Конвейерные устройства
- Конвейерный быстрый умножитель.
- Конвейерные АЦП.
- 6.15. Синтез линейных комбинационных схем
- Сумматор по модулю q.
- Умножитель по модулю q.
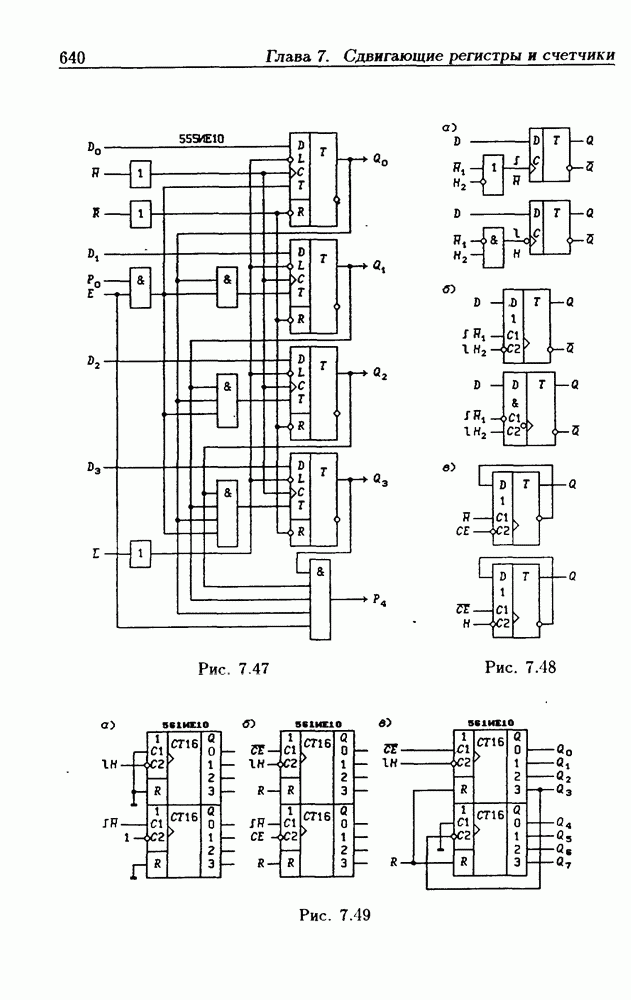
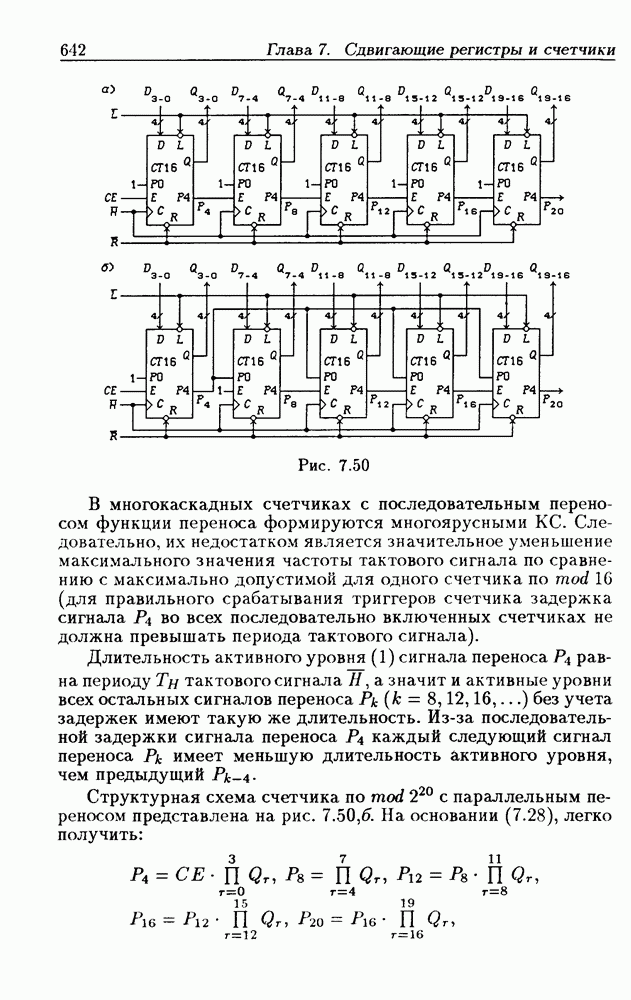
- Глава 7. Сдвигающие регистры и счетчики
- 7.1. Сдвигающие регистры без параллельной записи данных
- Сдвигающие устройства с выходными регистрами памяти.
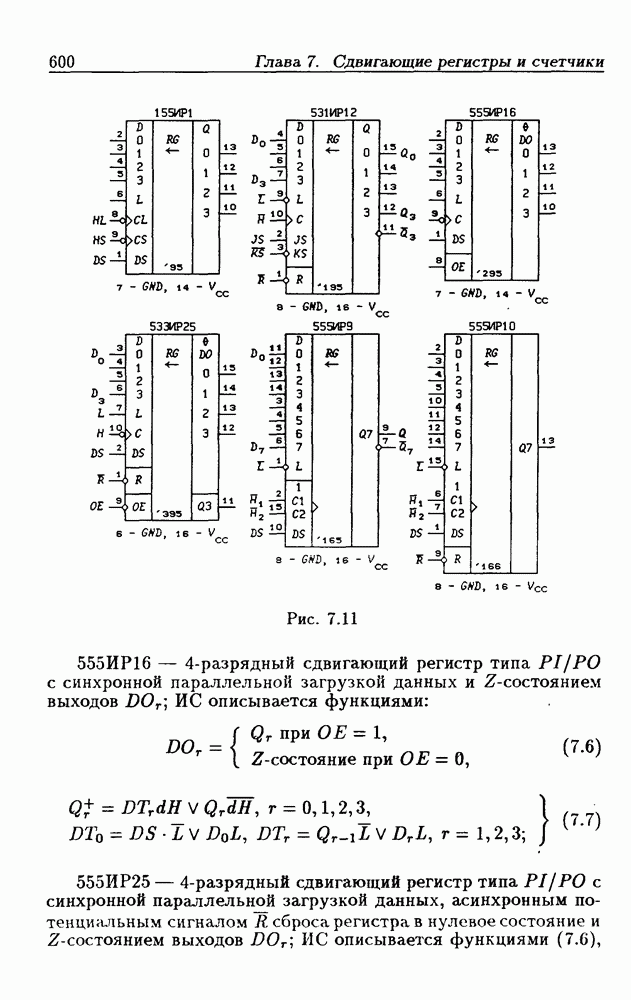
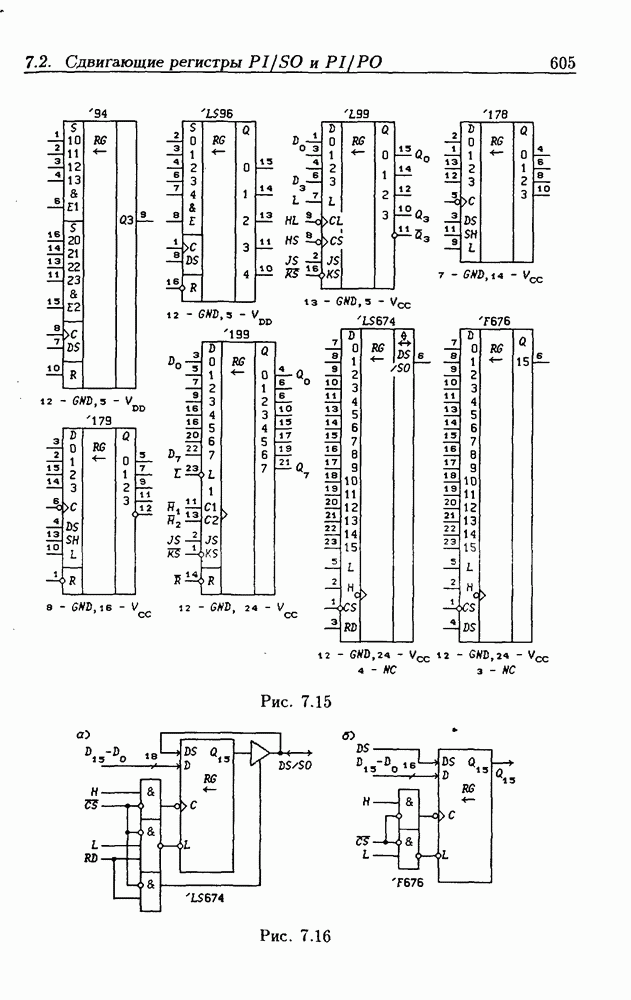
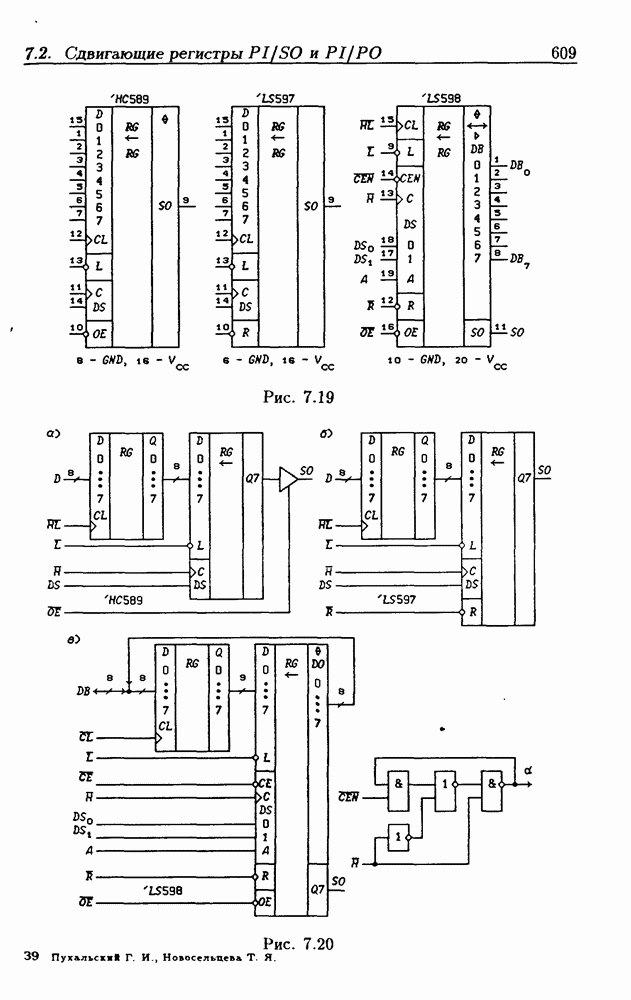
- 7.2. Сдвигающие регистры с параллельной записью данных
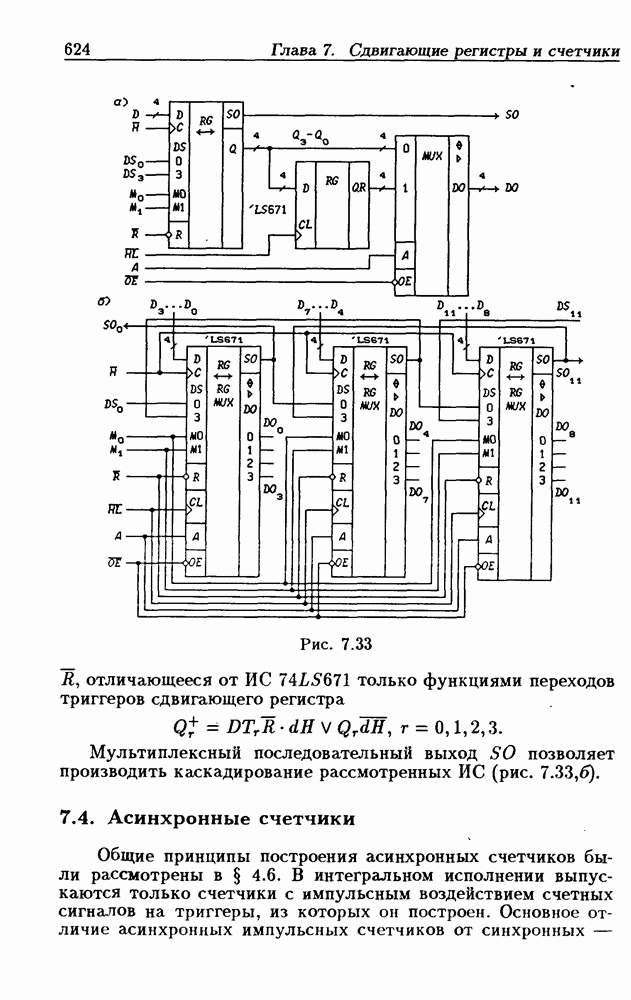
- Сдвигающие регистры с расширением знака.
- Сдвигающие регистры с входным регистром памяти.
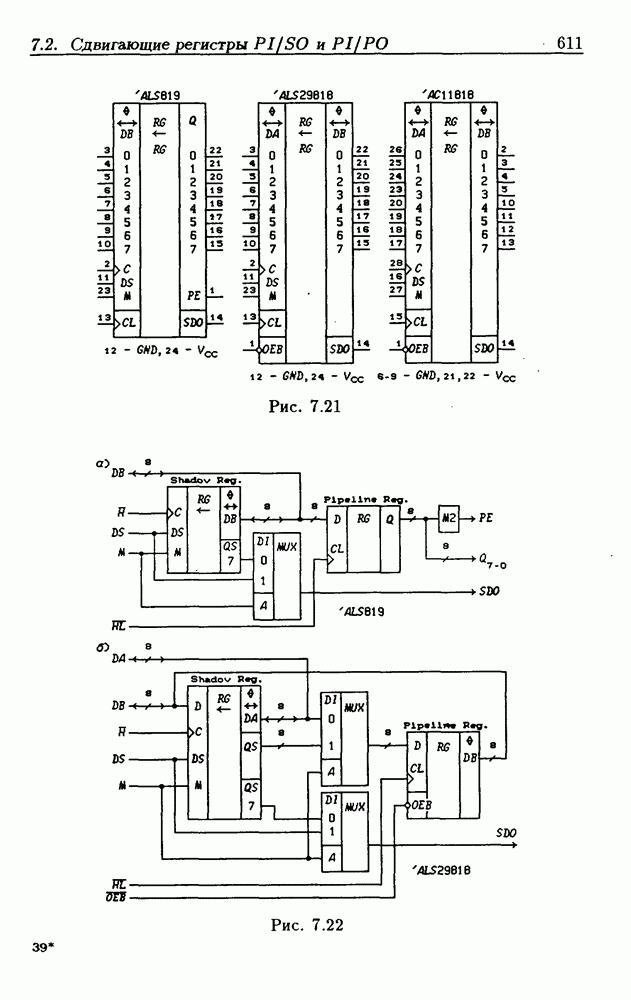
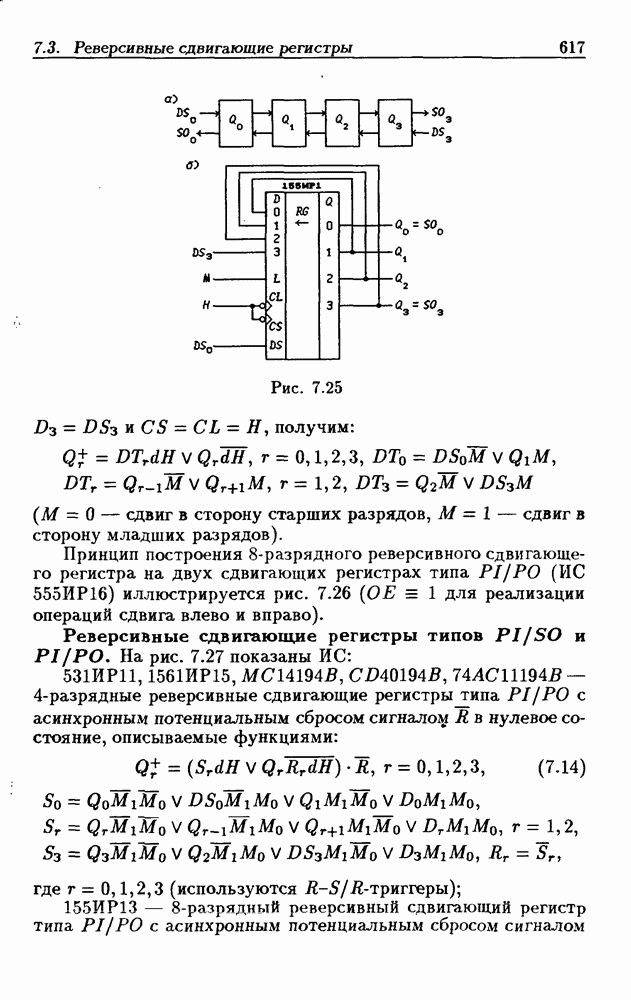
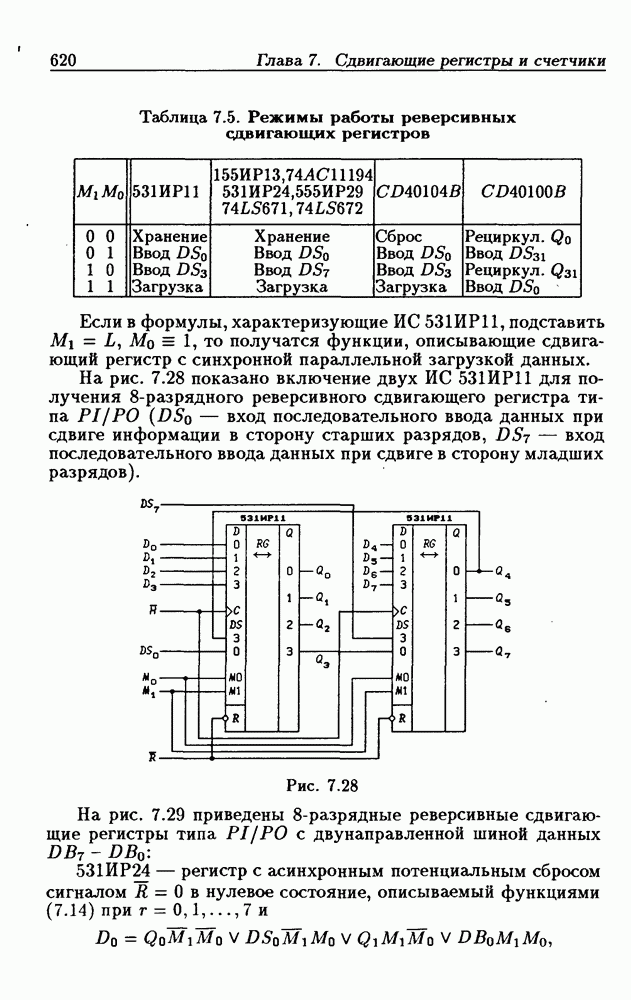
- 7.3. Реверсивные сдвигающие регистры
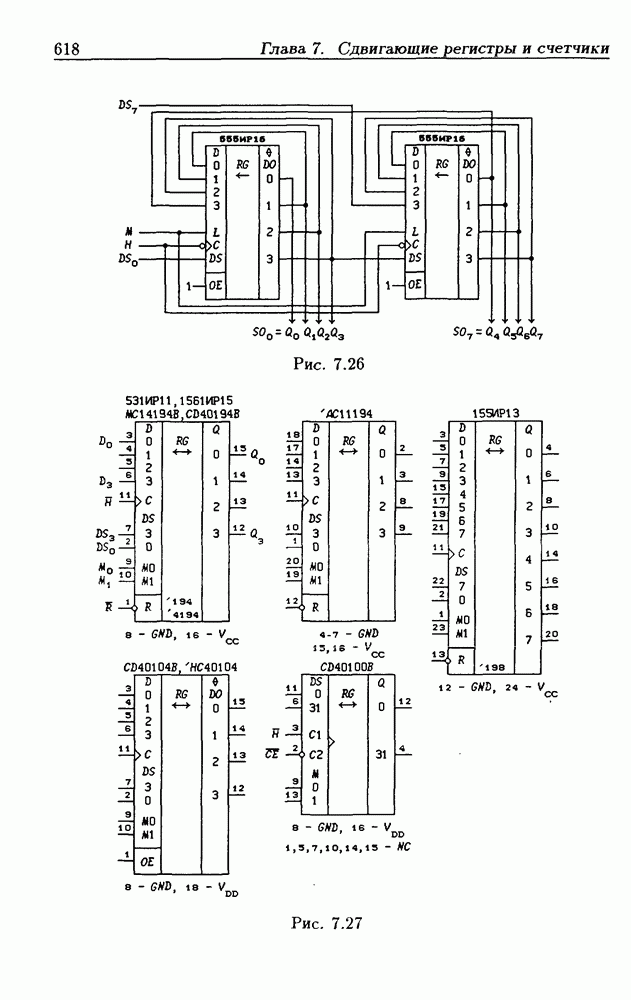
- Реверсивные сдвигающие регистры типов PI/SO и PI/PO.
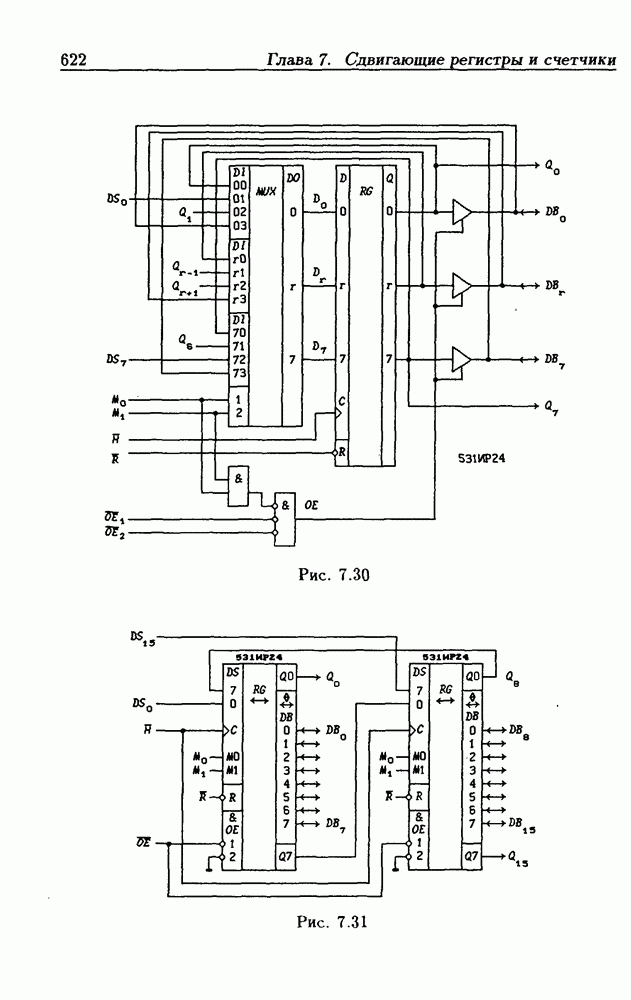
- Многофункциональные устройства на основе реверсивных сдвигающих регистров.
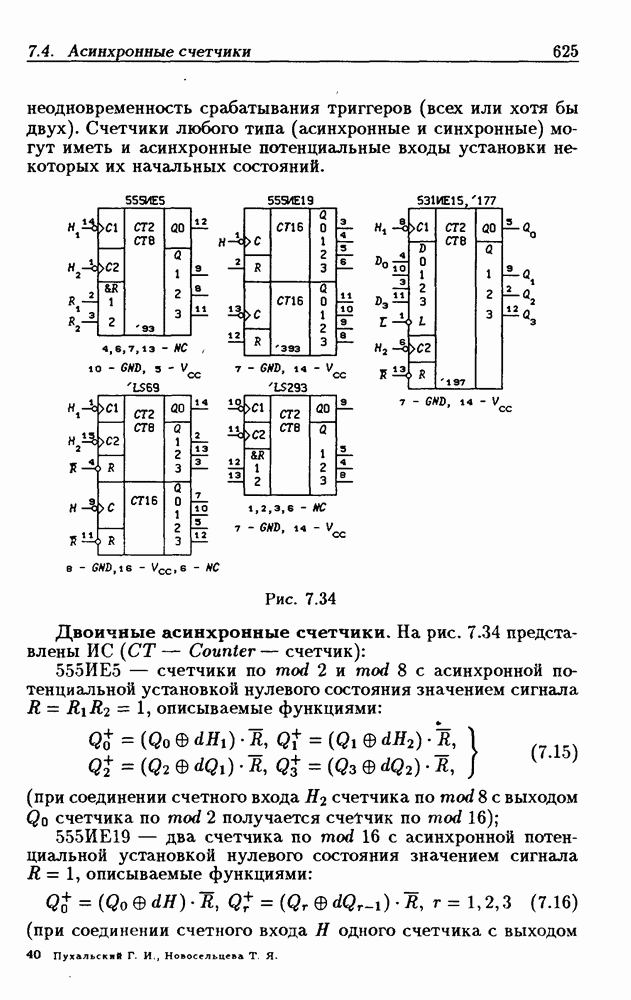
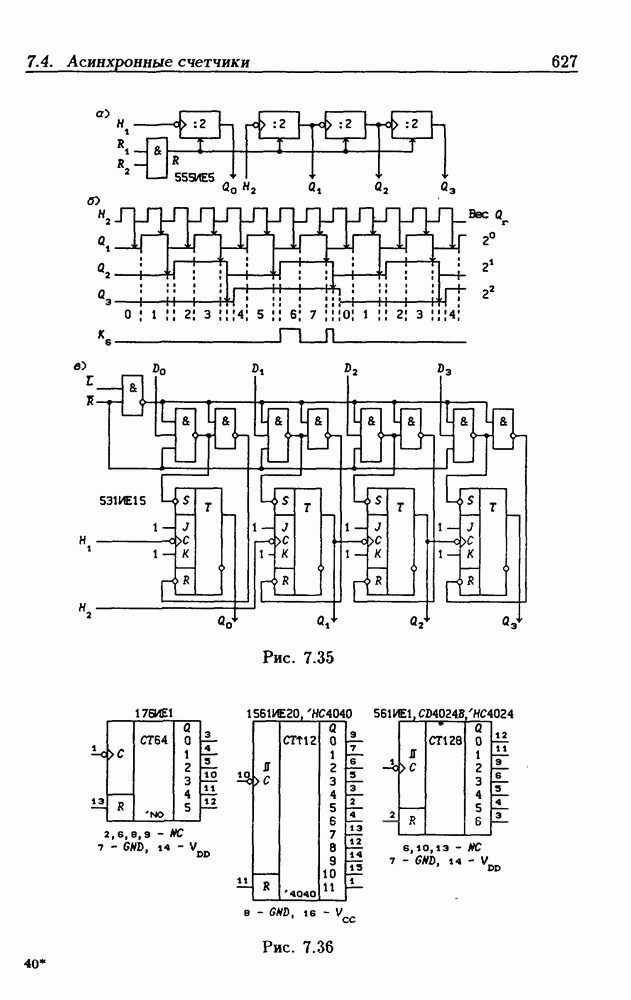
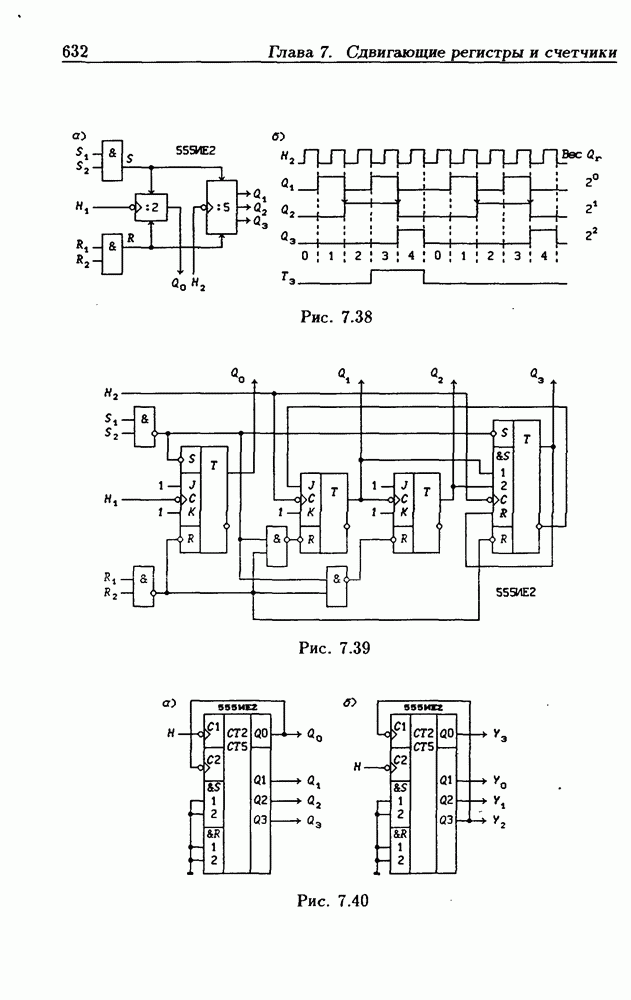
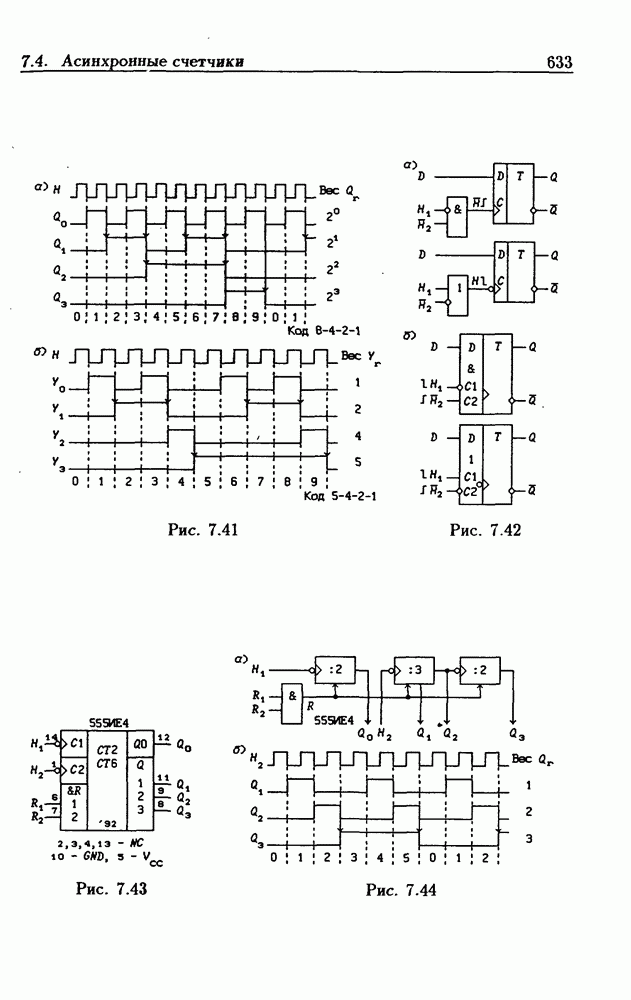
- 7.4. Асинхронные счетчики
- Двоично-десятичные асинхронные счетчики.
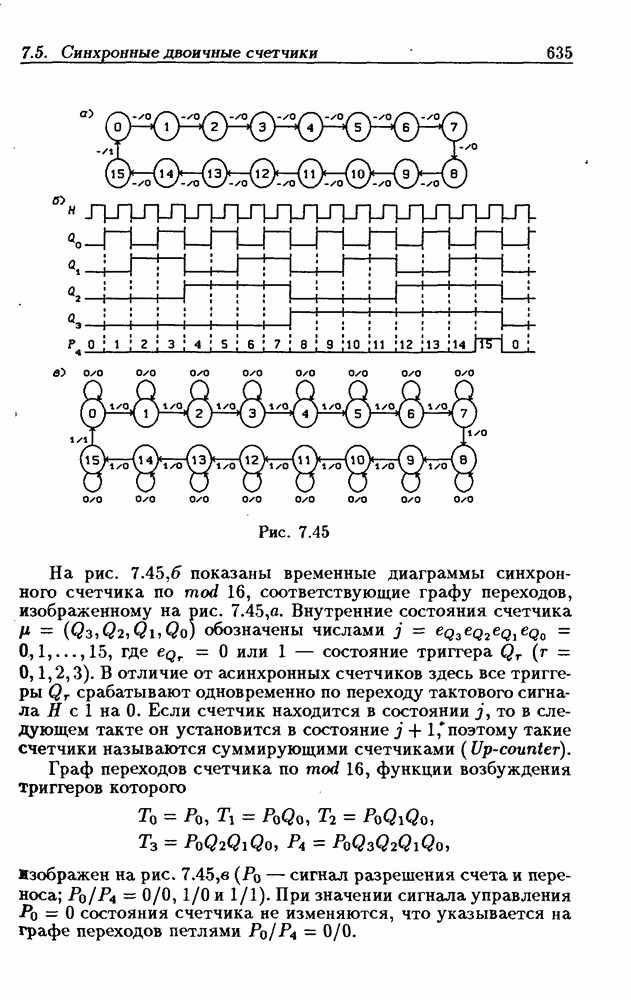
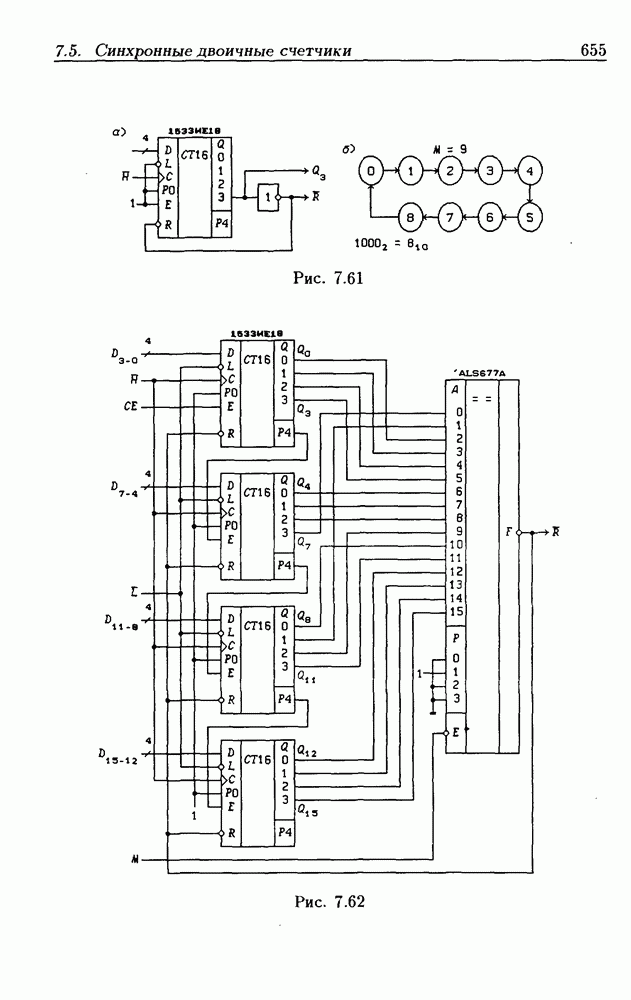
- 7.5. Синхронные двоичные счетчики
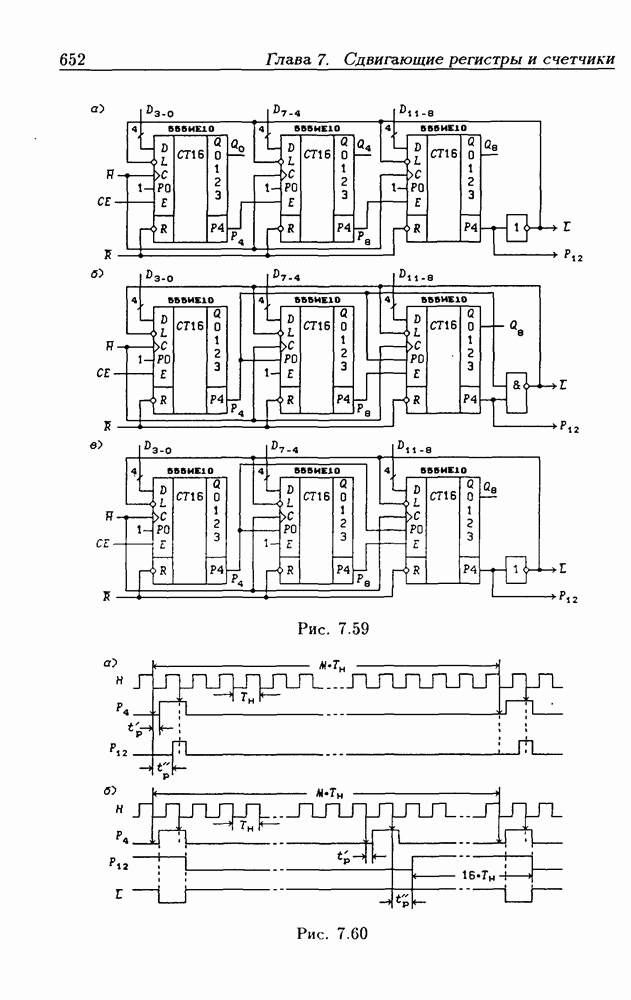
- Программирование модуля пересчета двоичных счетчиков.
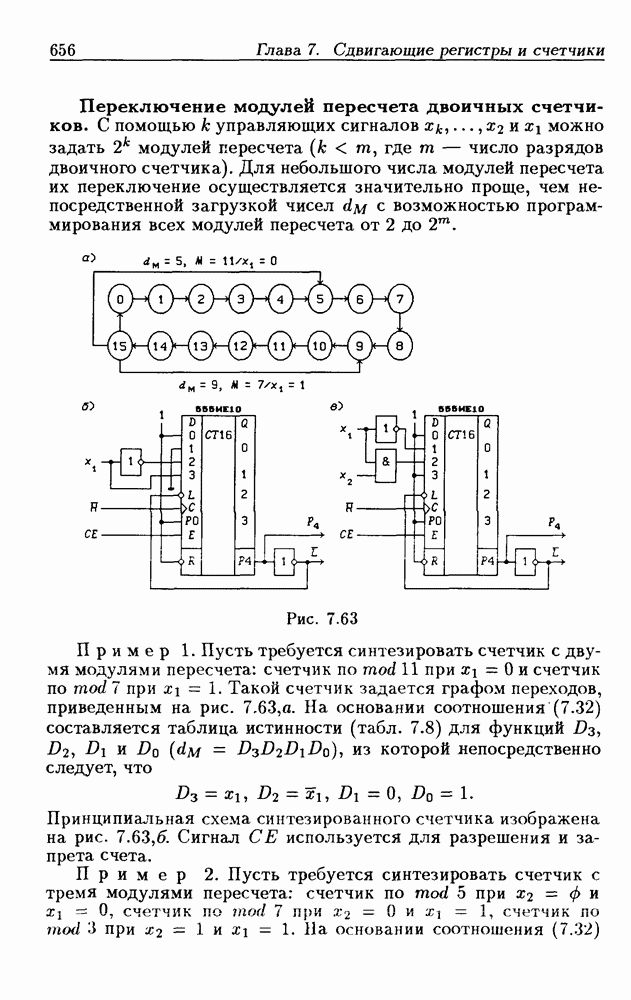
- Переключение модулей пересчета двоичных счетчиков.
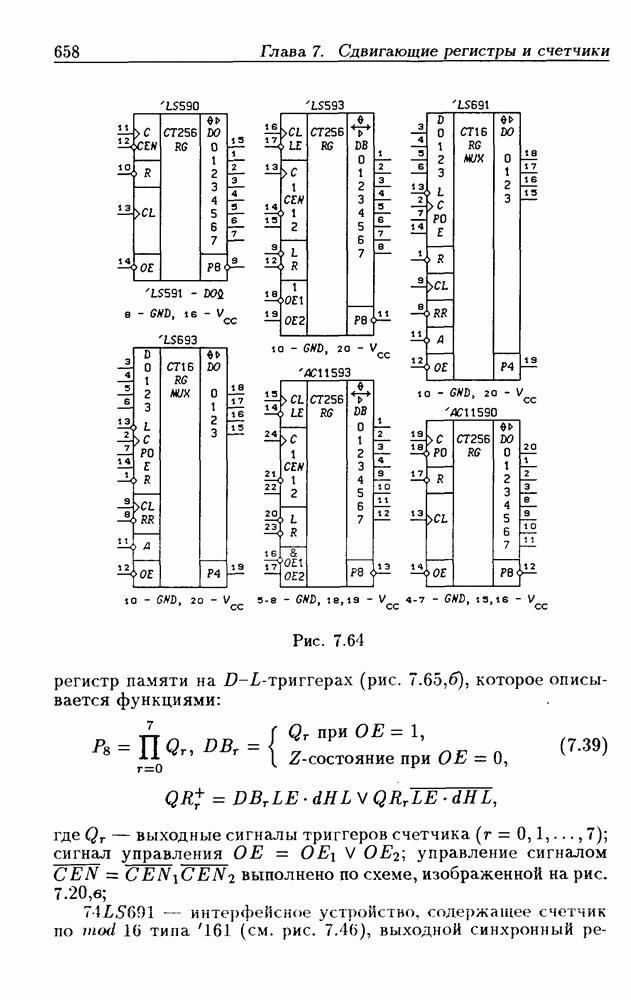
- Функциональные устройства на основе двоичных счетчиков.
- 7.6. Синхронные двоично-десятичные счетчики
- 7.7. Синхронные реверсивные счетчики
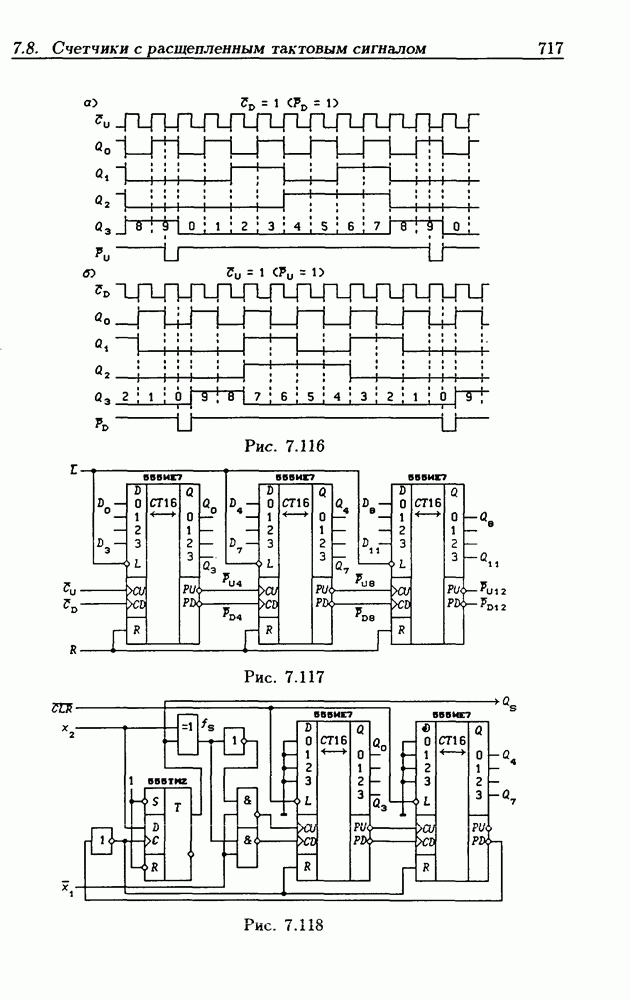
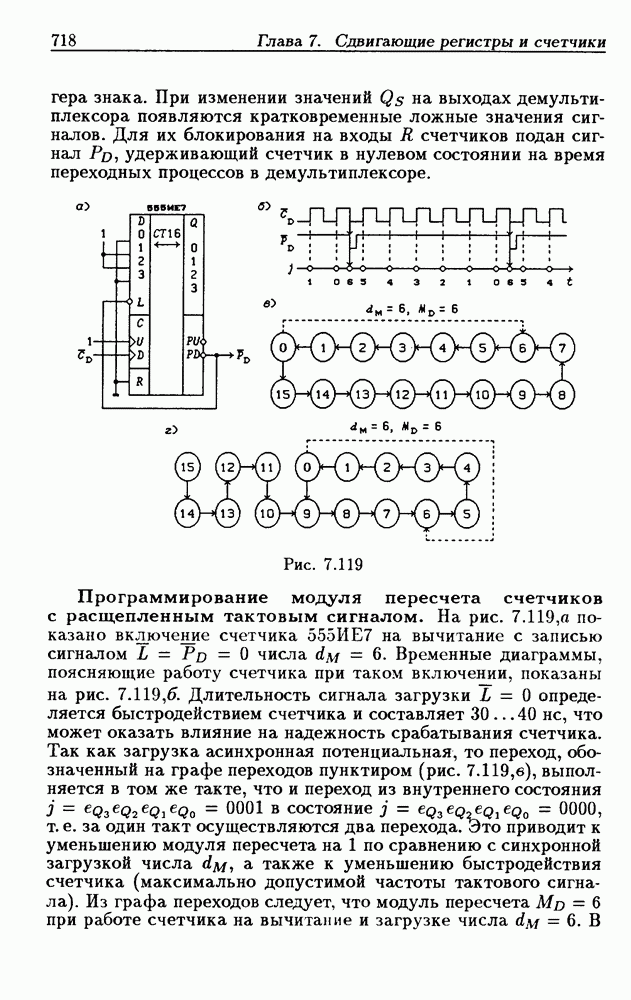
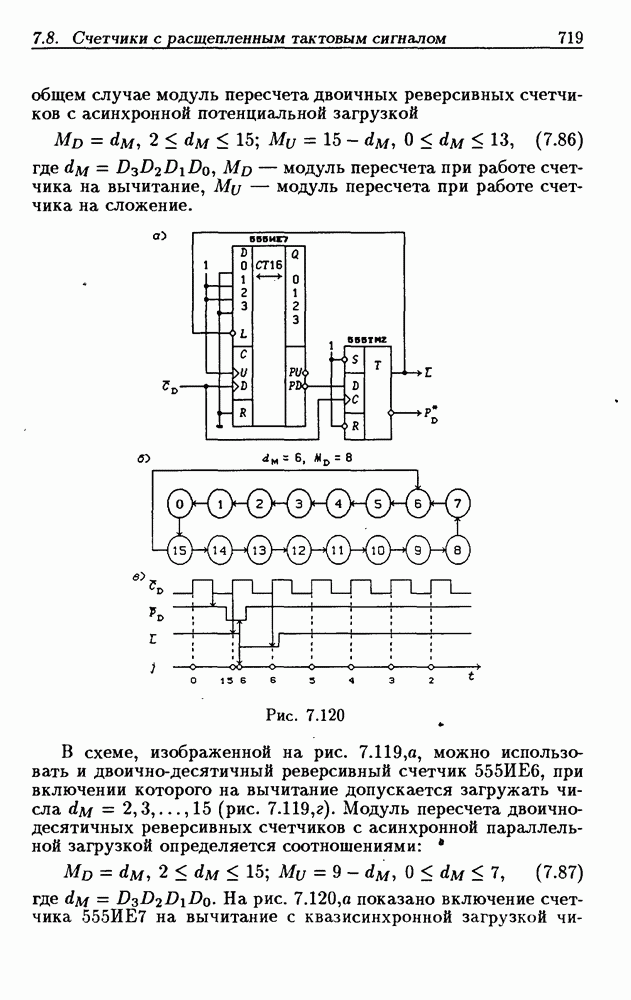
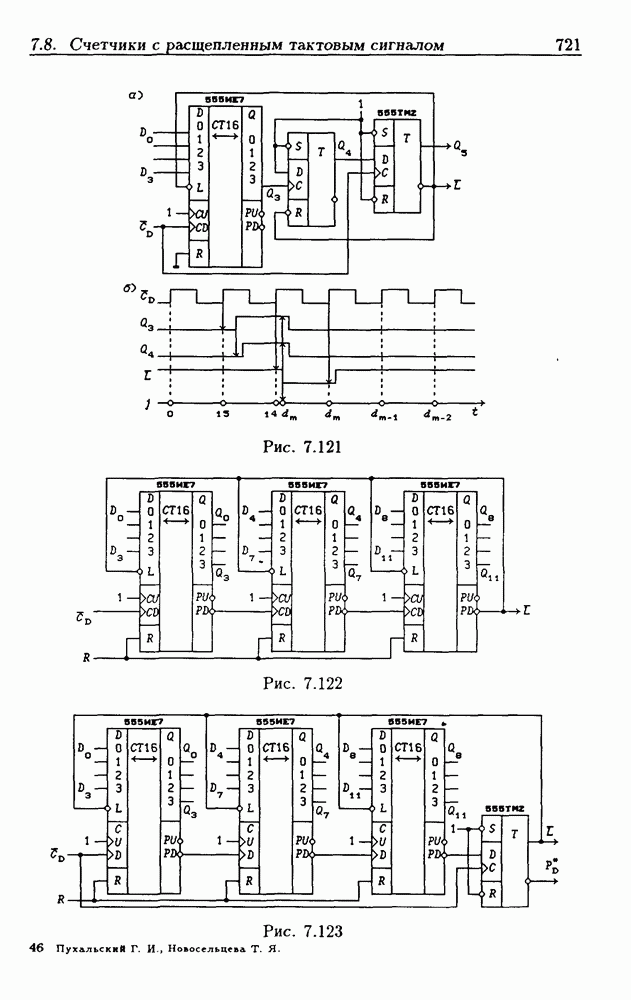
- 7.8. Счетчики с расщепленным тактовым сигналом
- 7.9. Счетчики на сдвигающих регистрах
- 7.10. Кольцевые счетчики
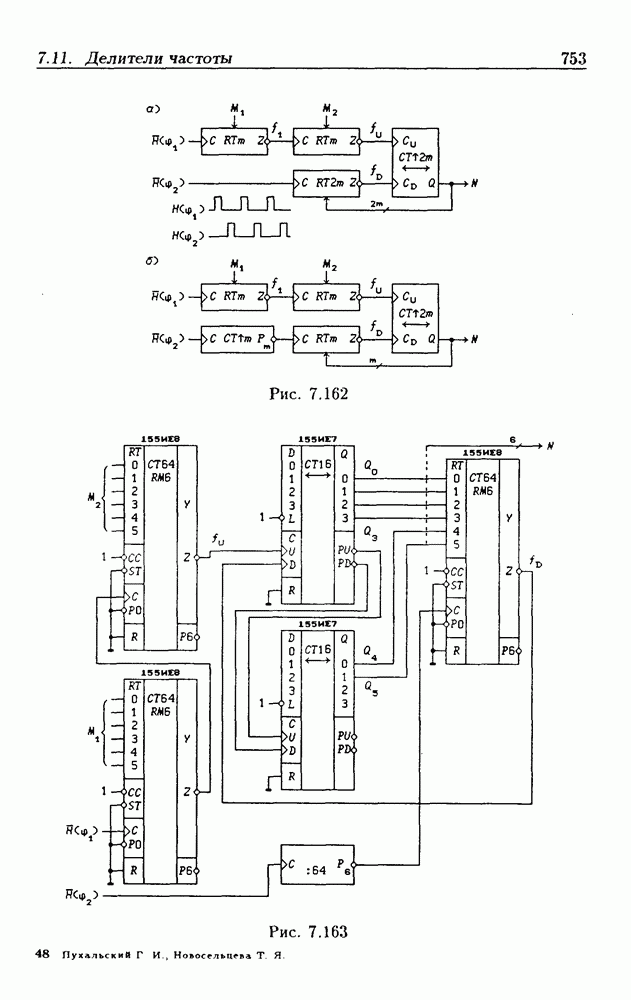
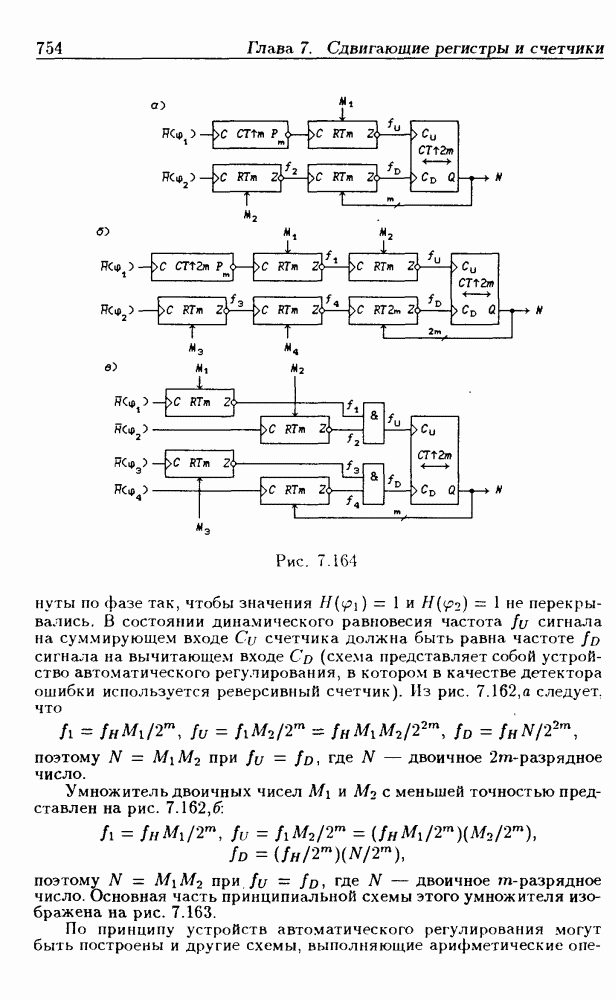
- 7.11. Делители частоты
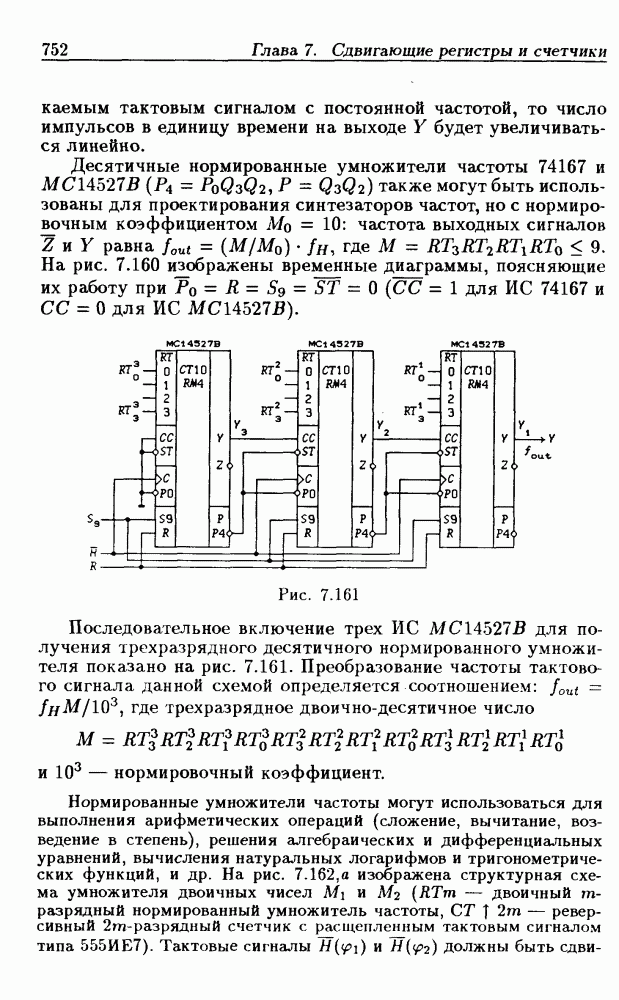
- Нормированные умножители частоты.
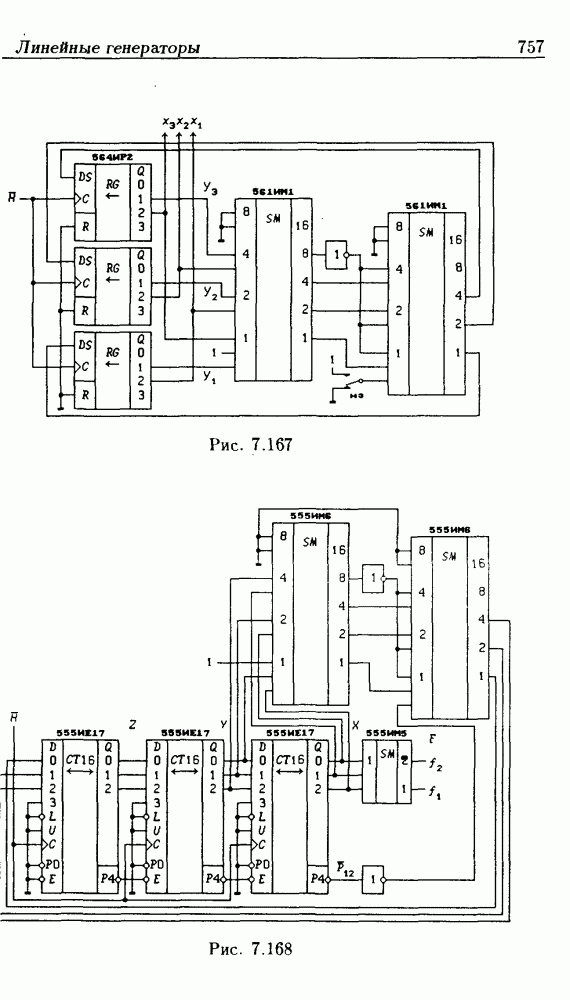
- 7.12. Линейные генераторы
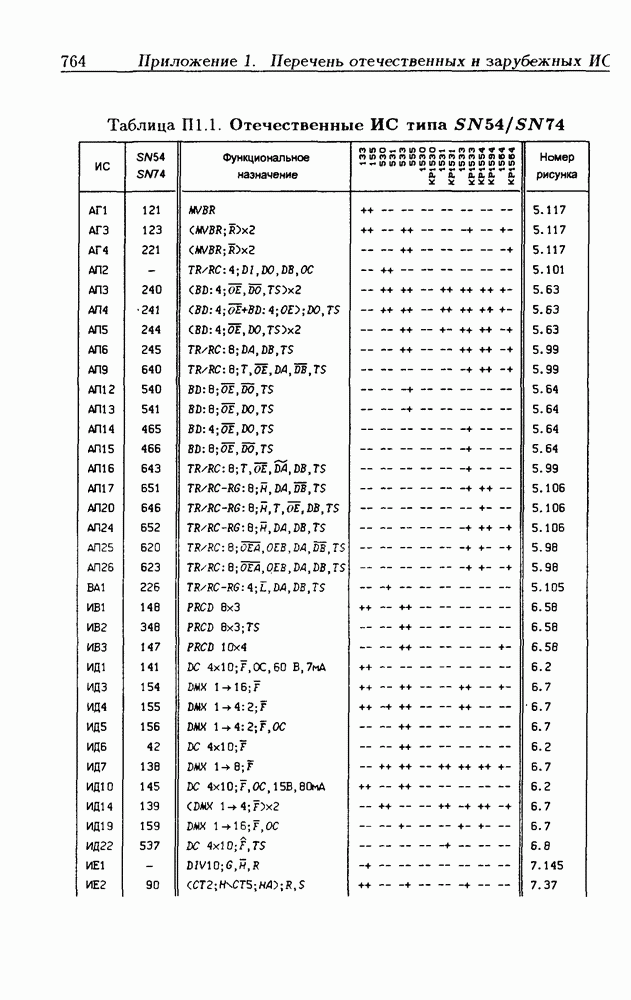
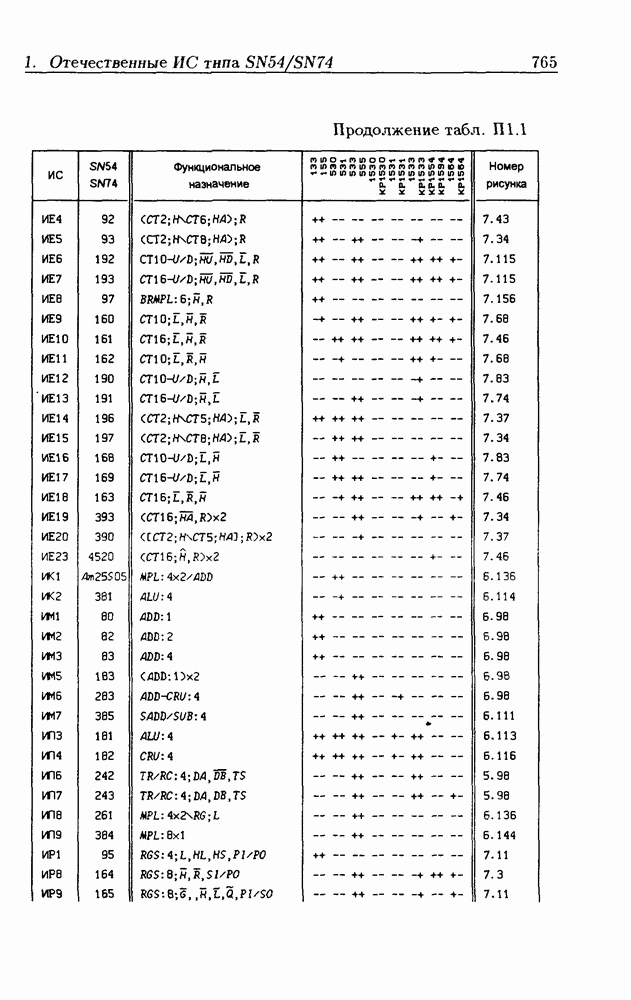
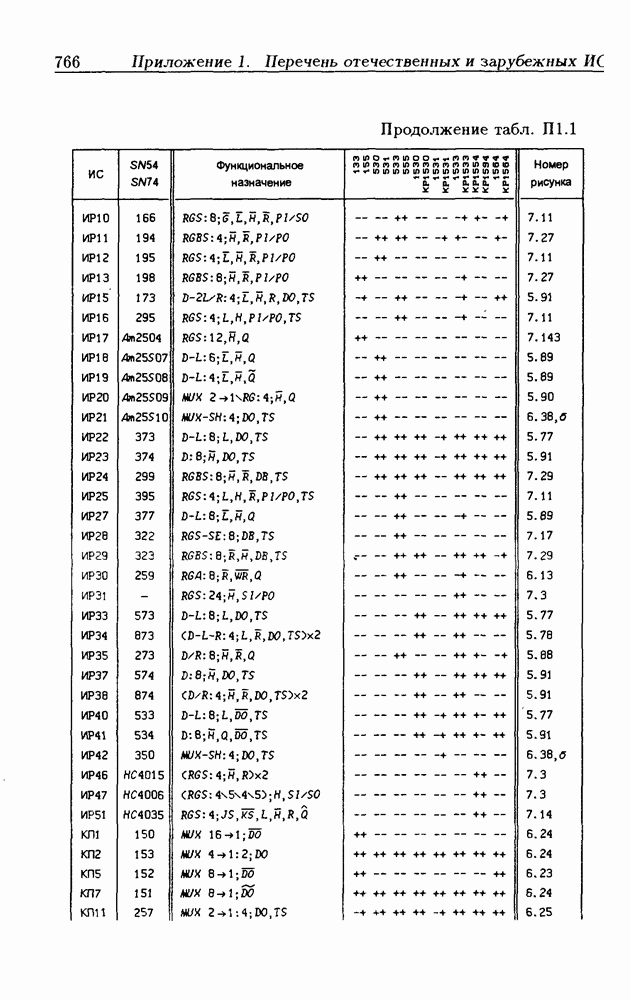
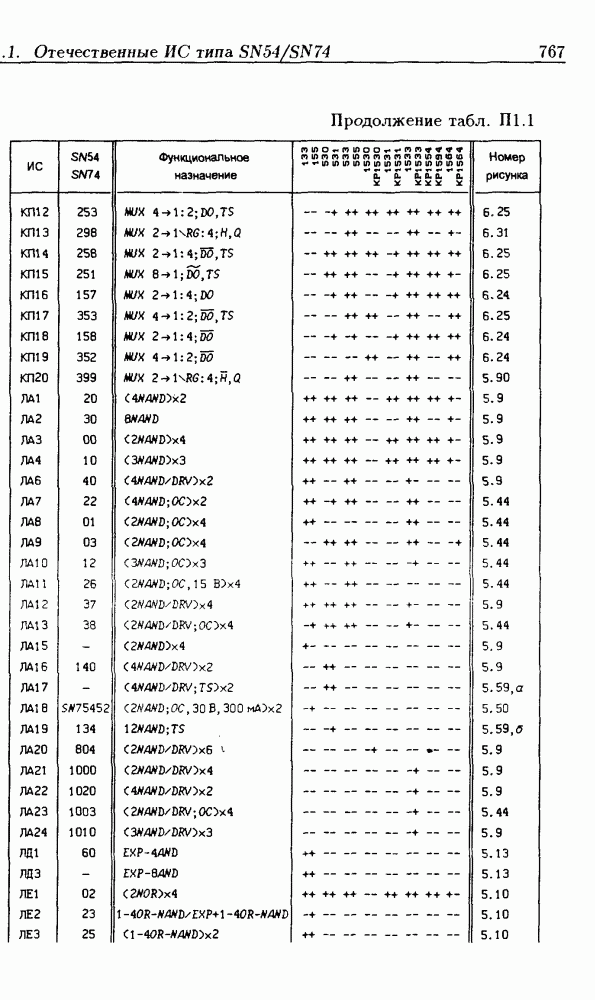
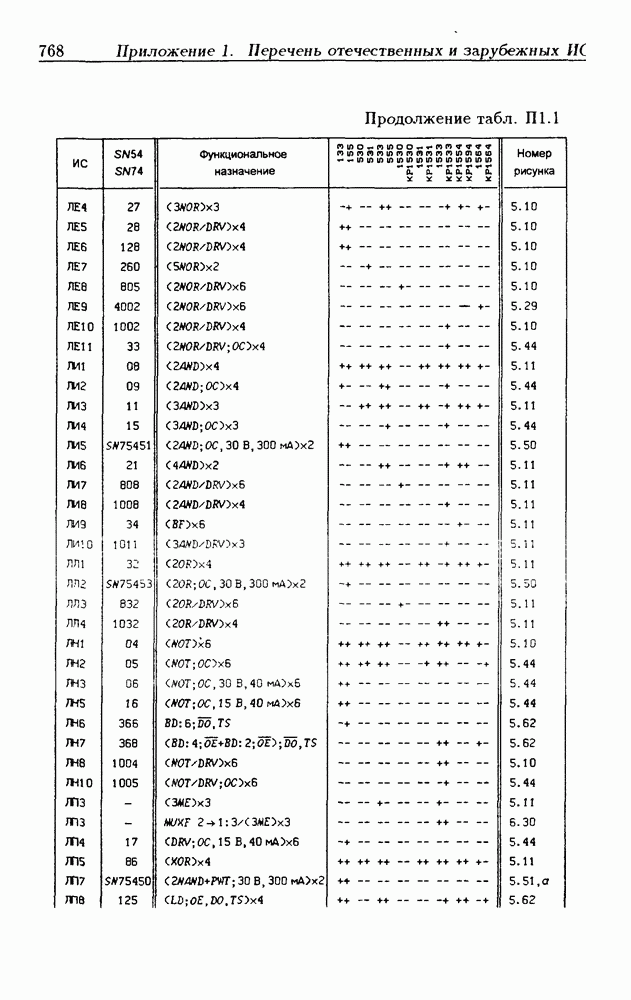
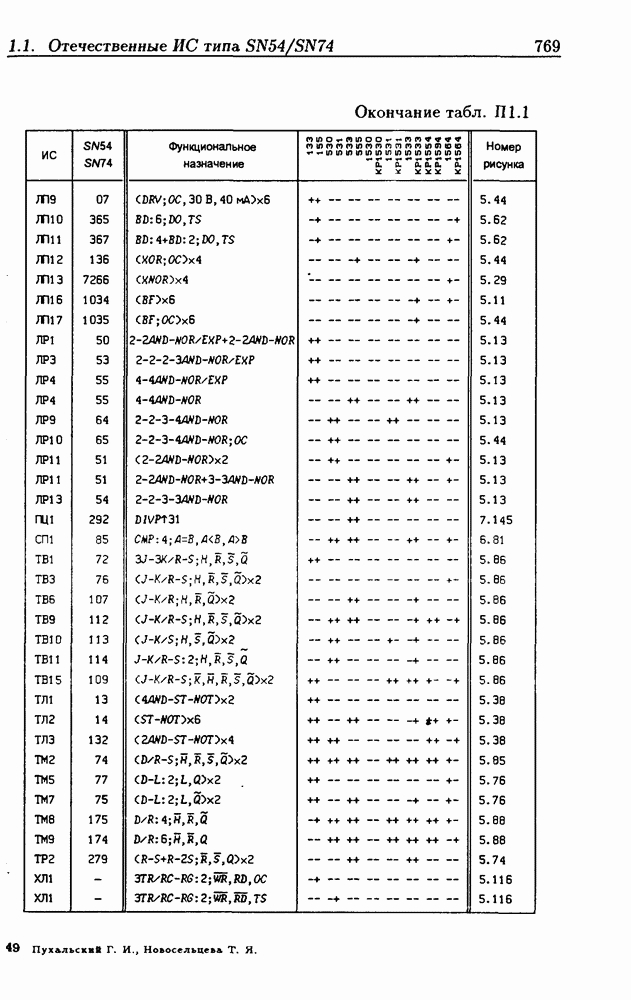
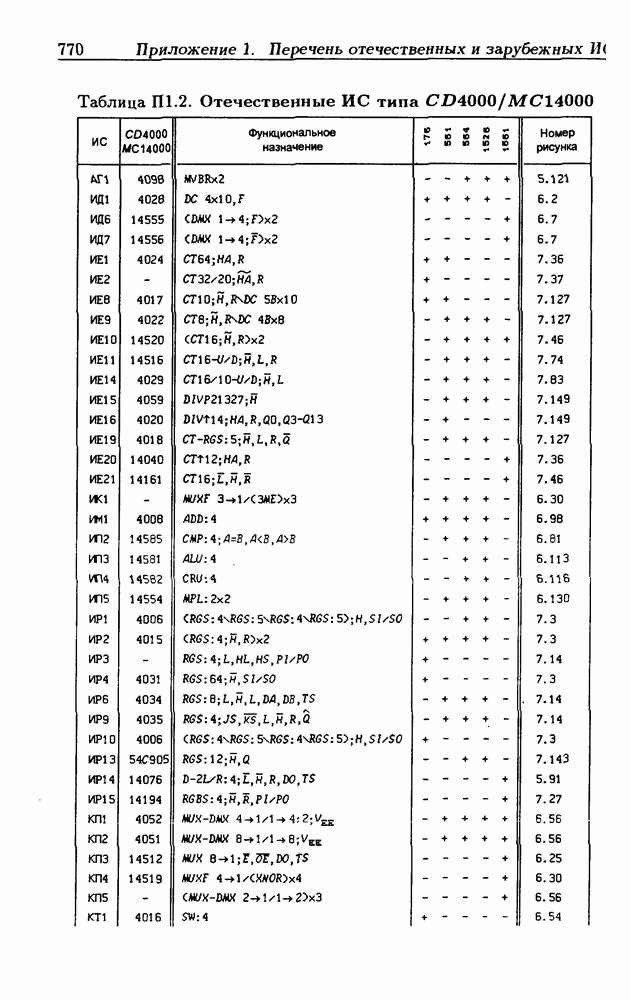
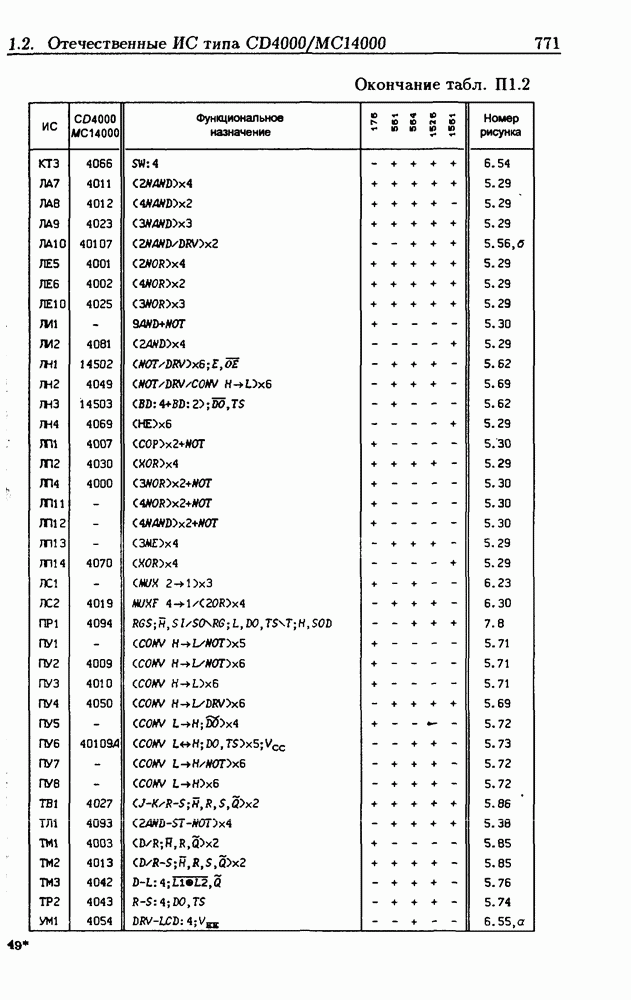
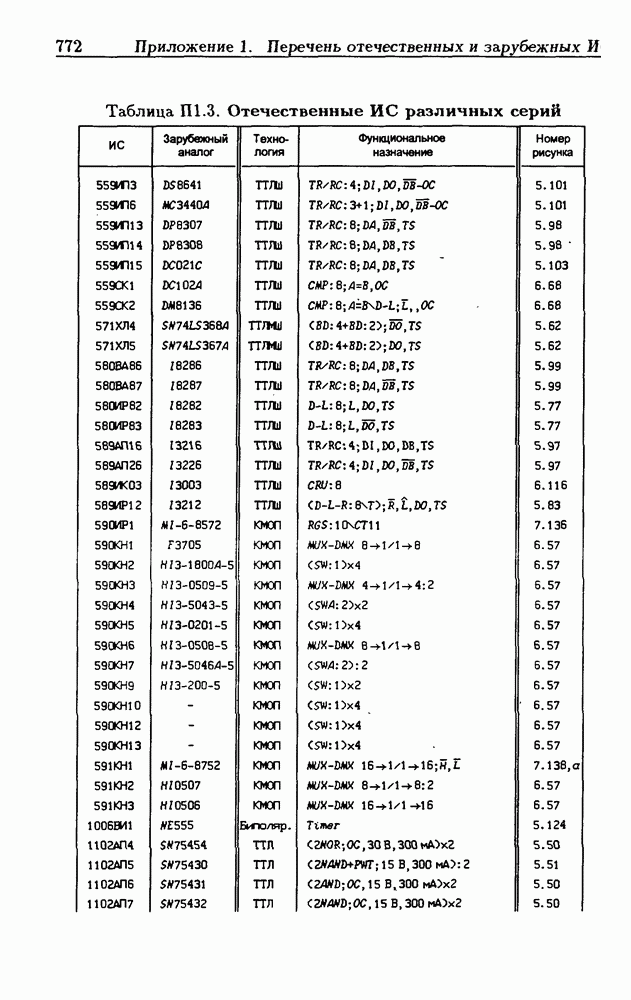
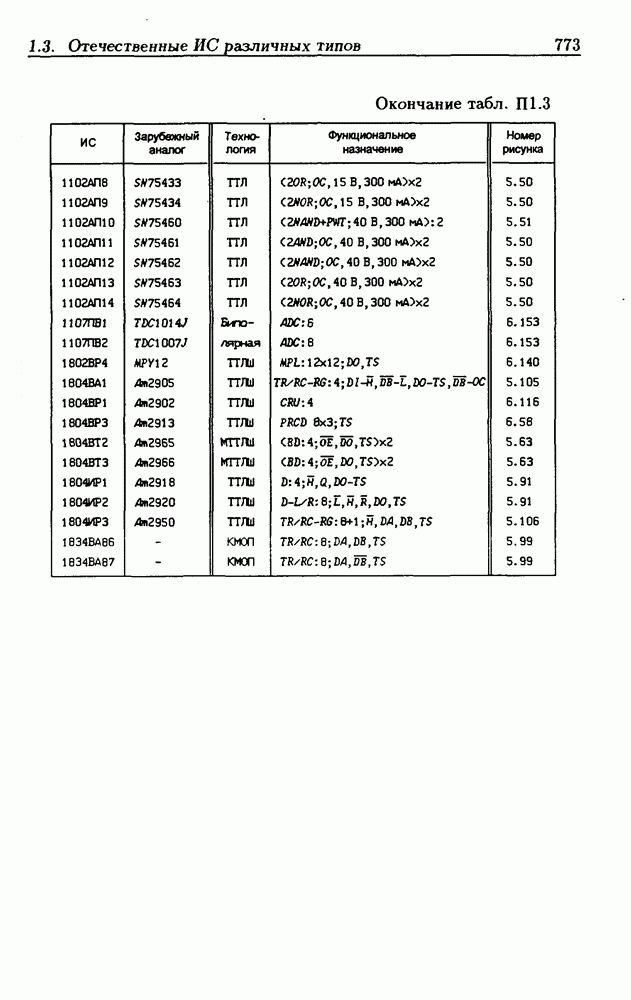
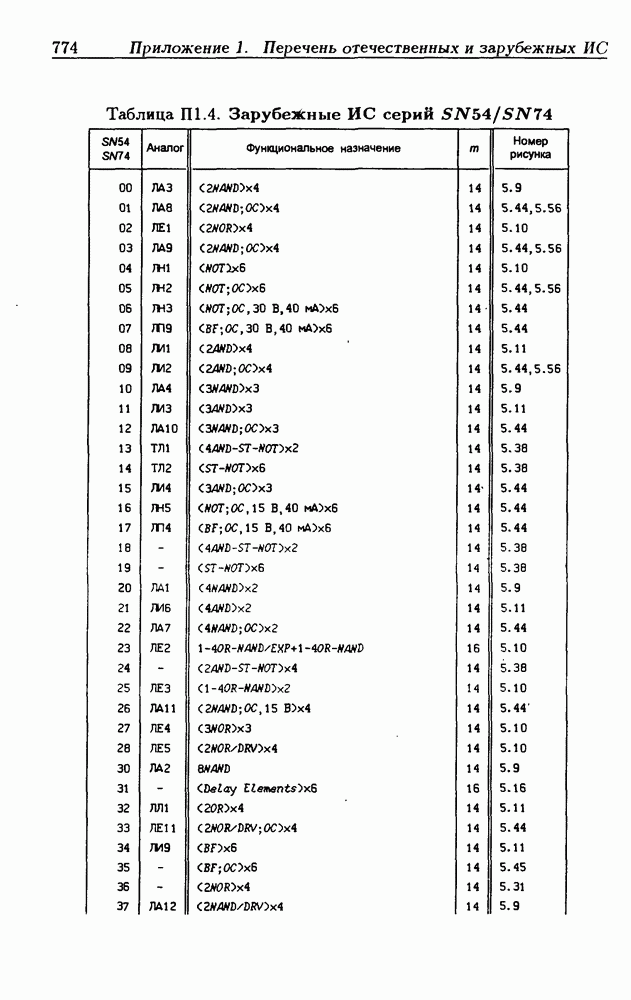
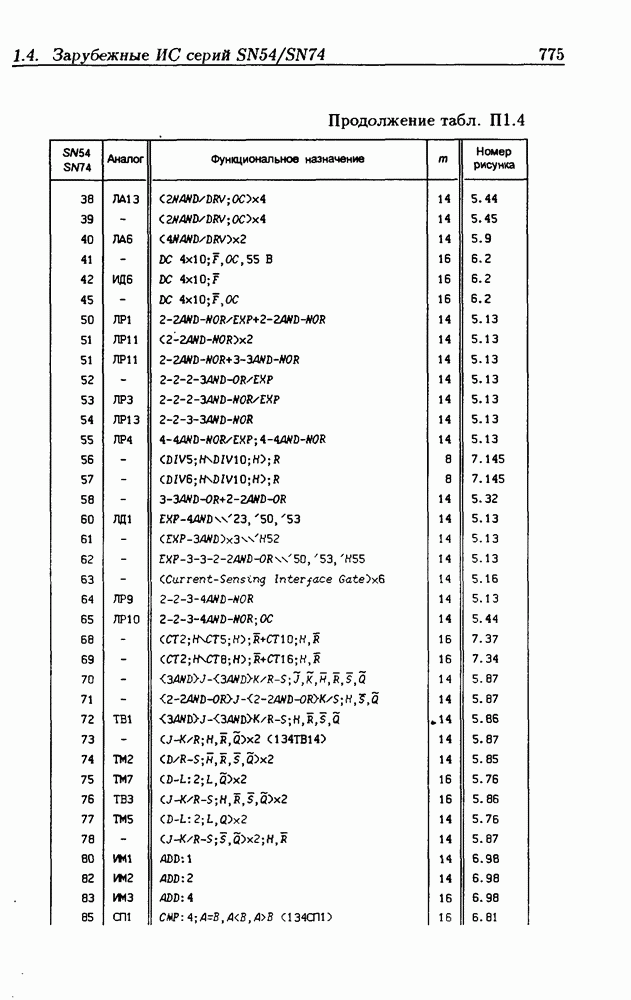
- Приложение 1. Перечень отечественных и зарубежных ИС
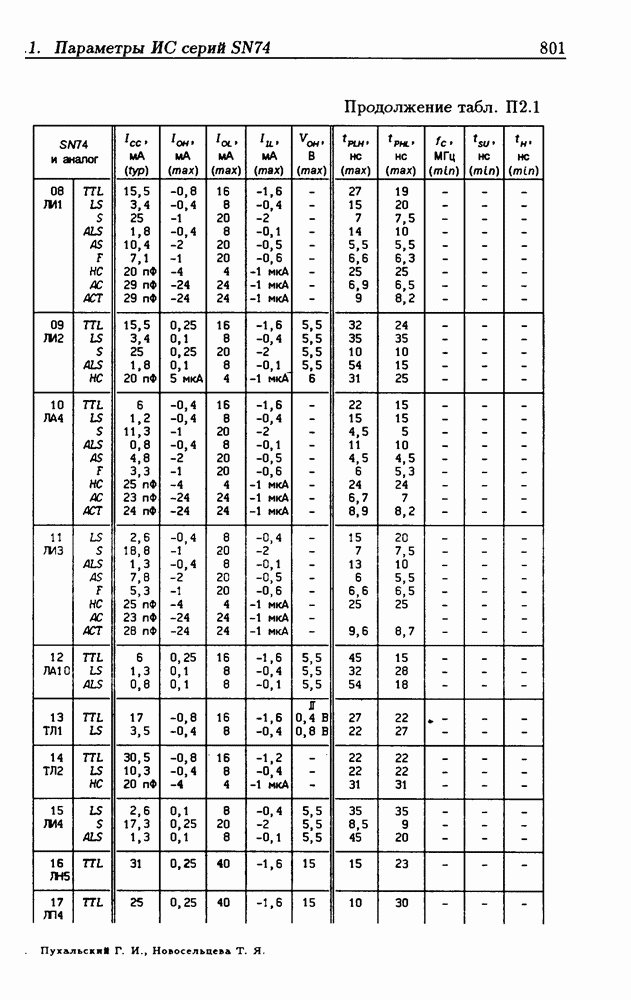
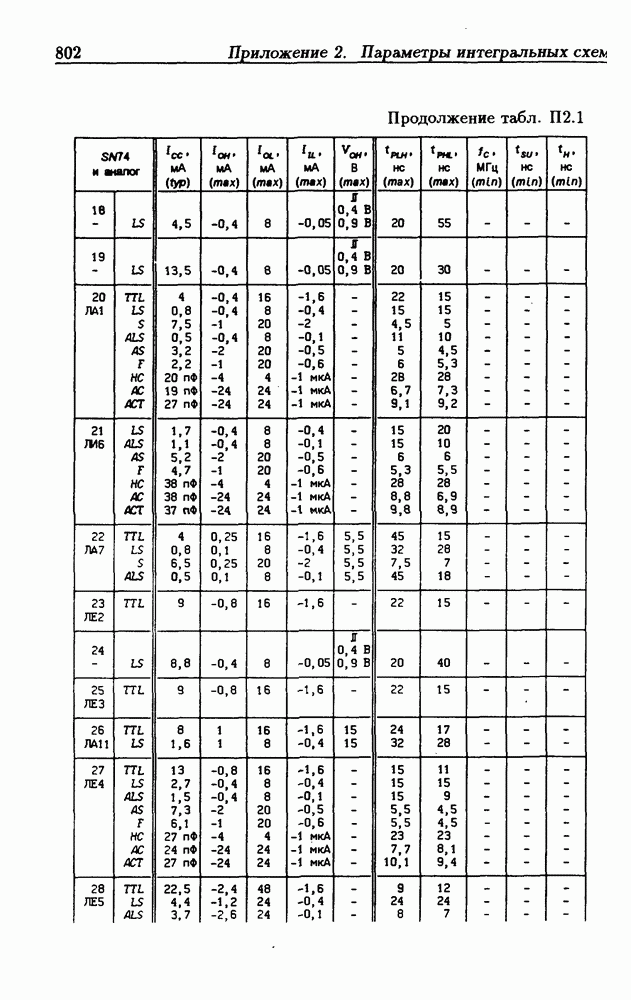
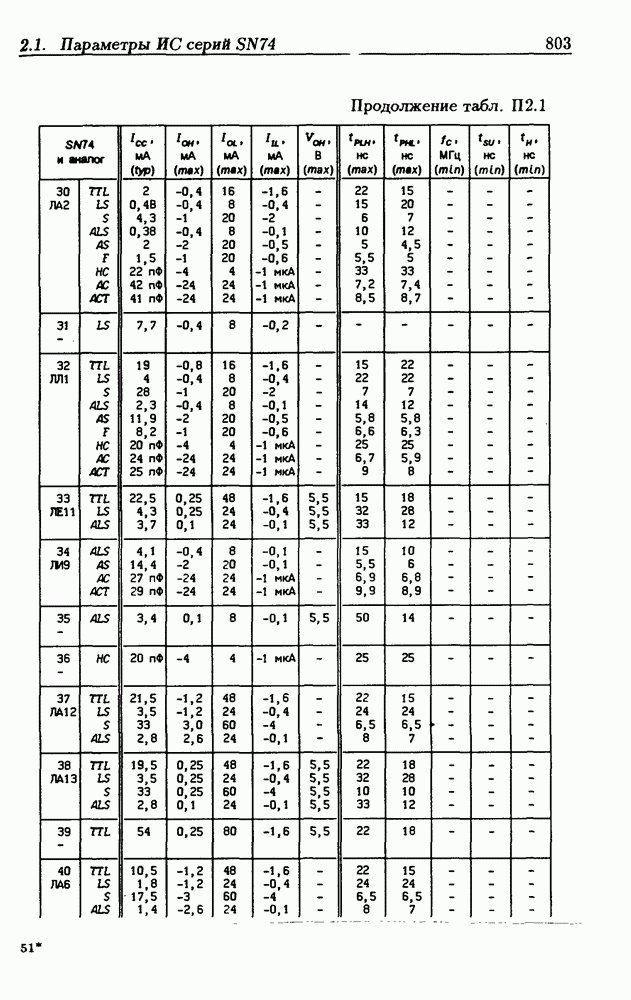
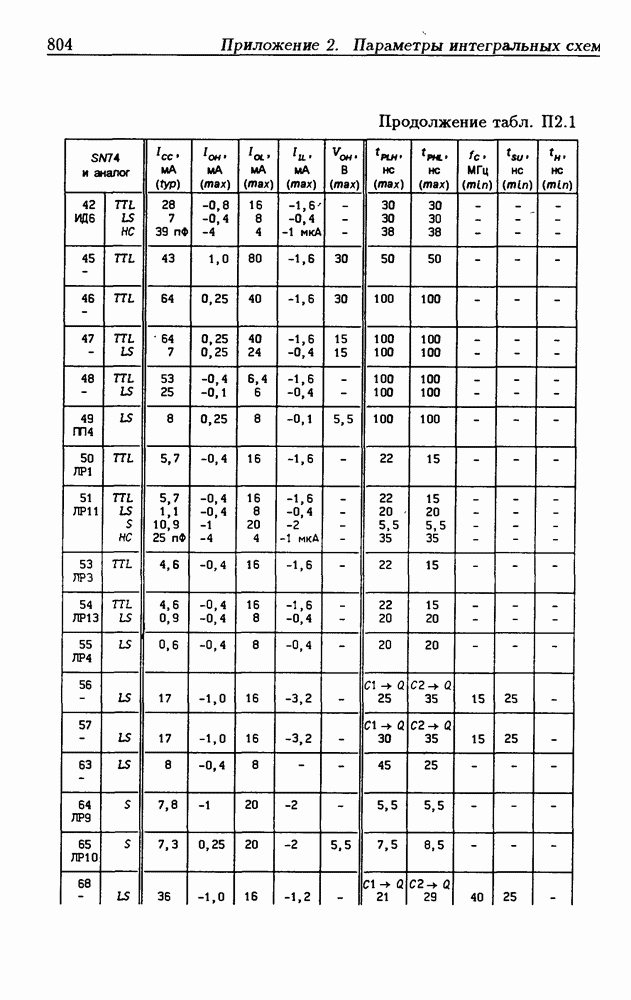
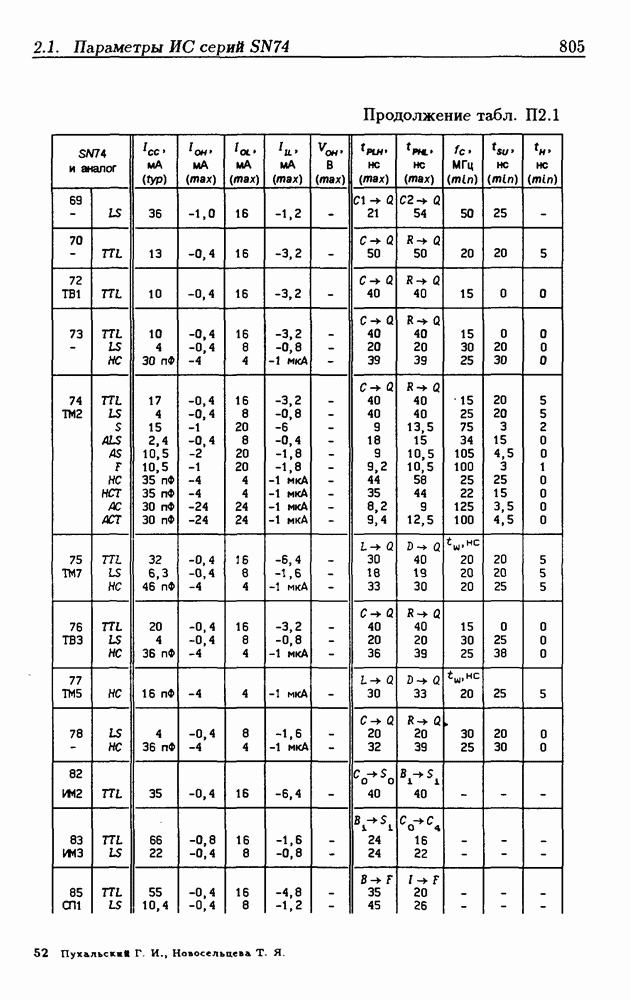
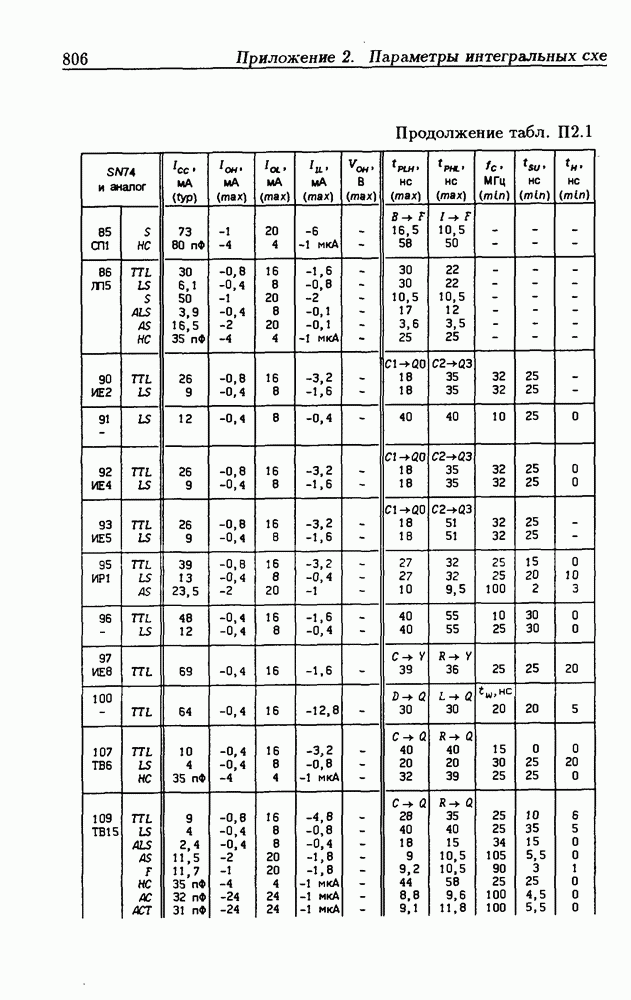
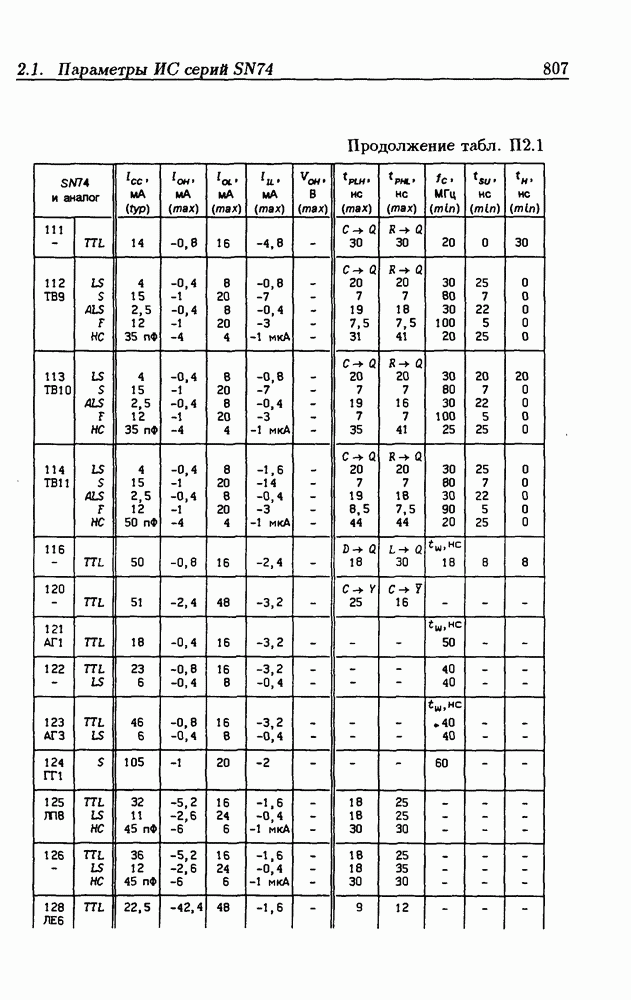
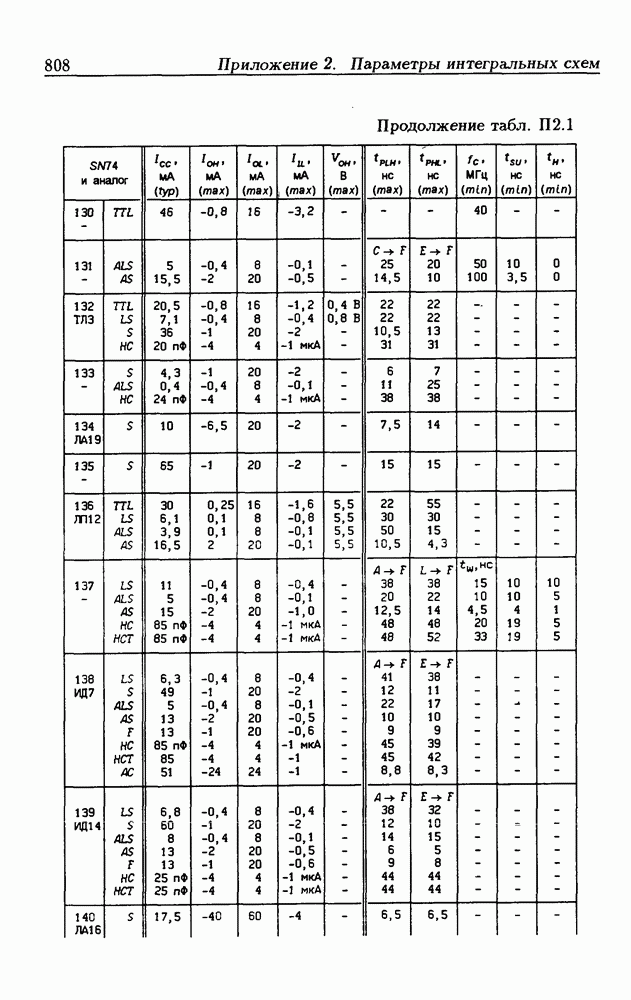
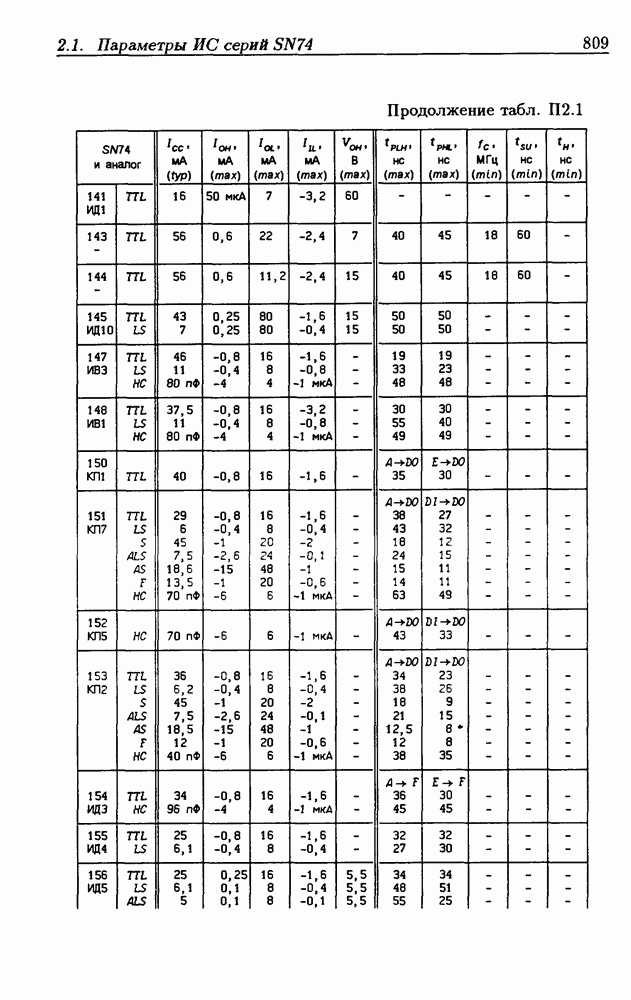
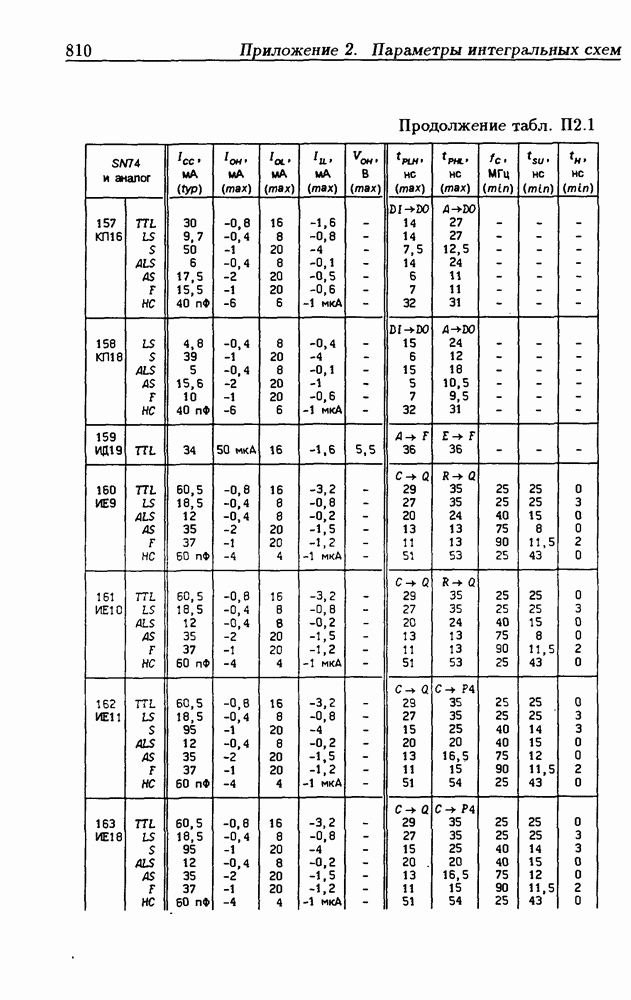
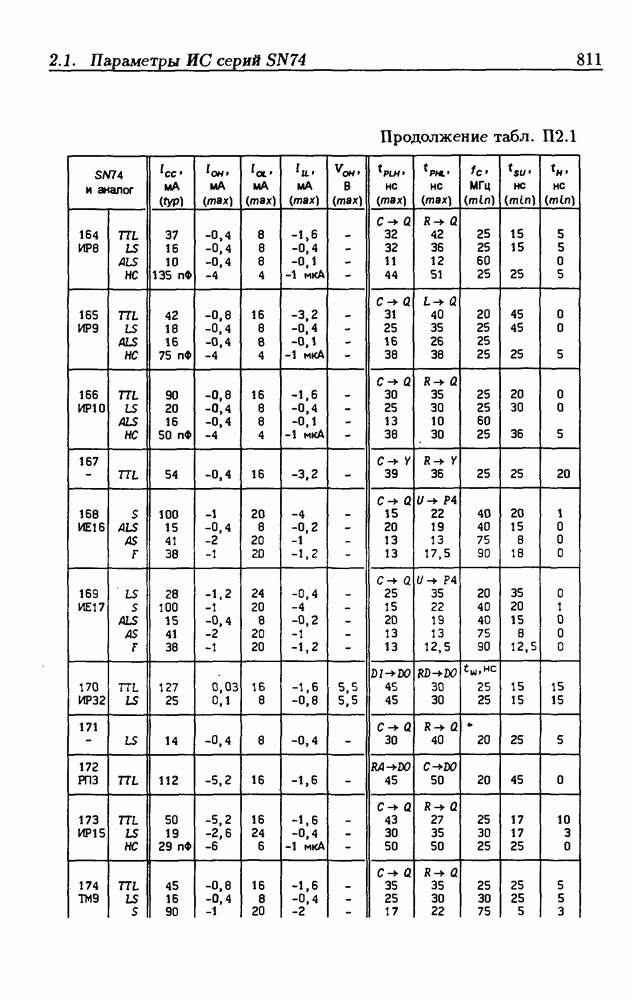
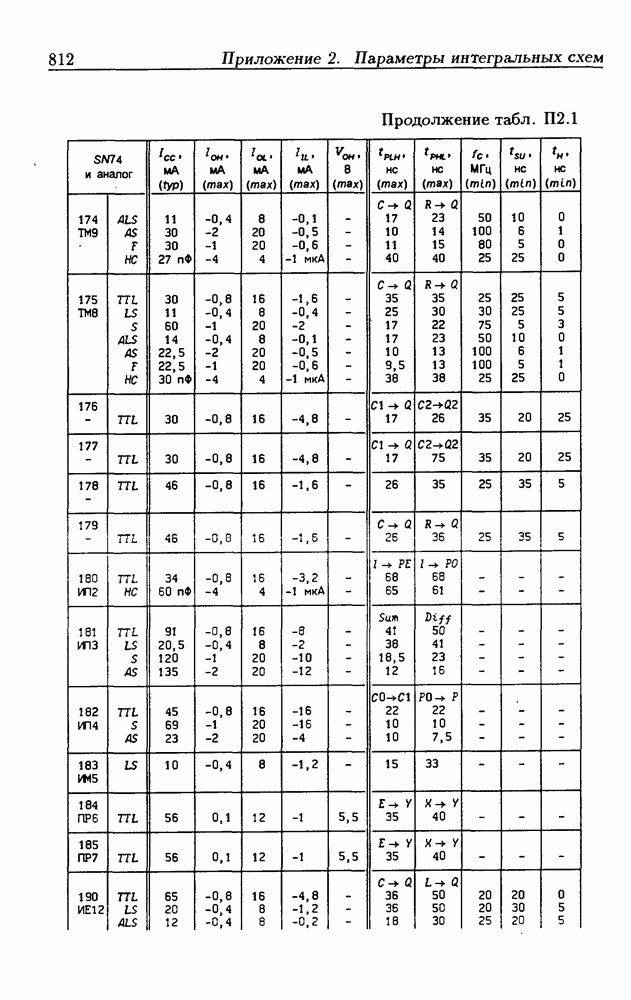
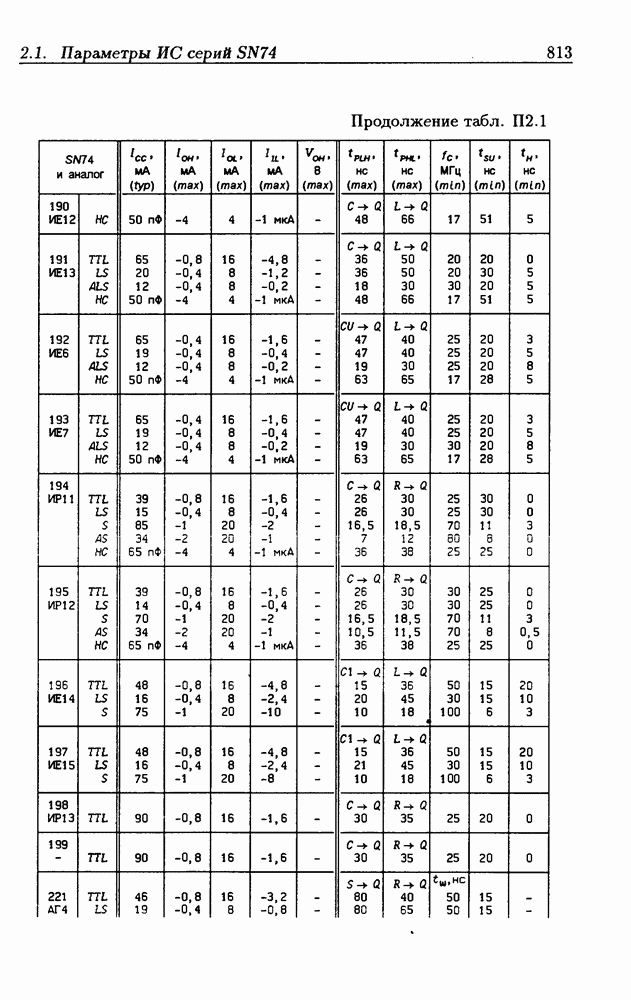
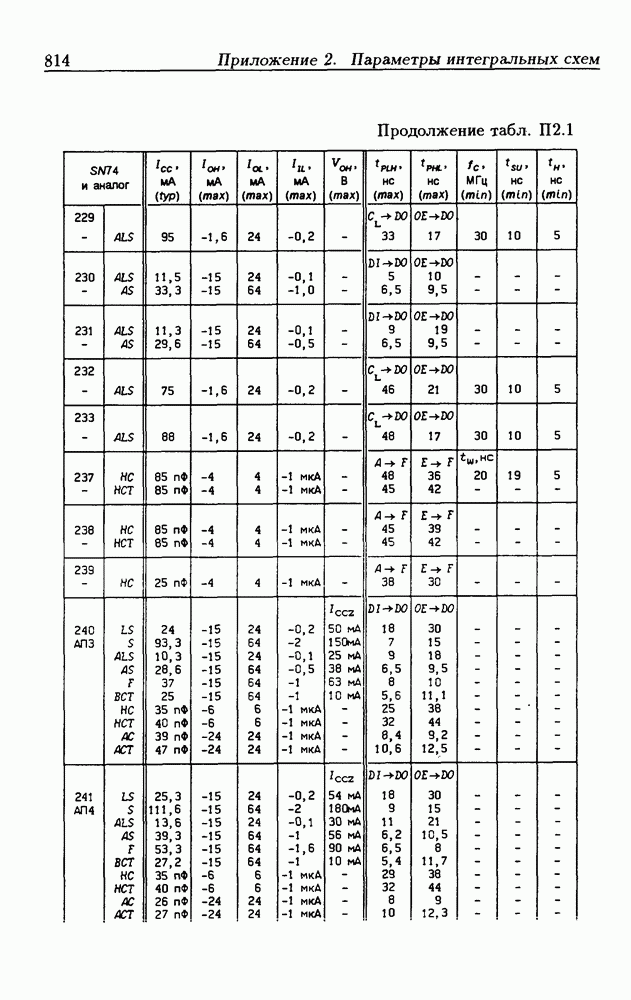
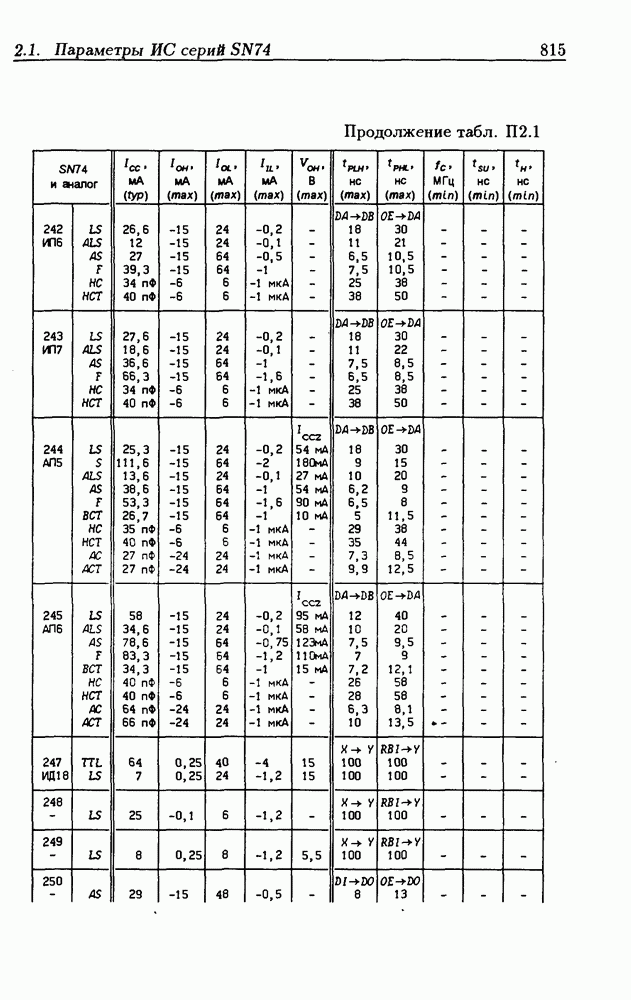
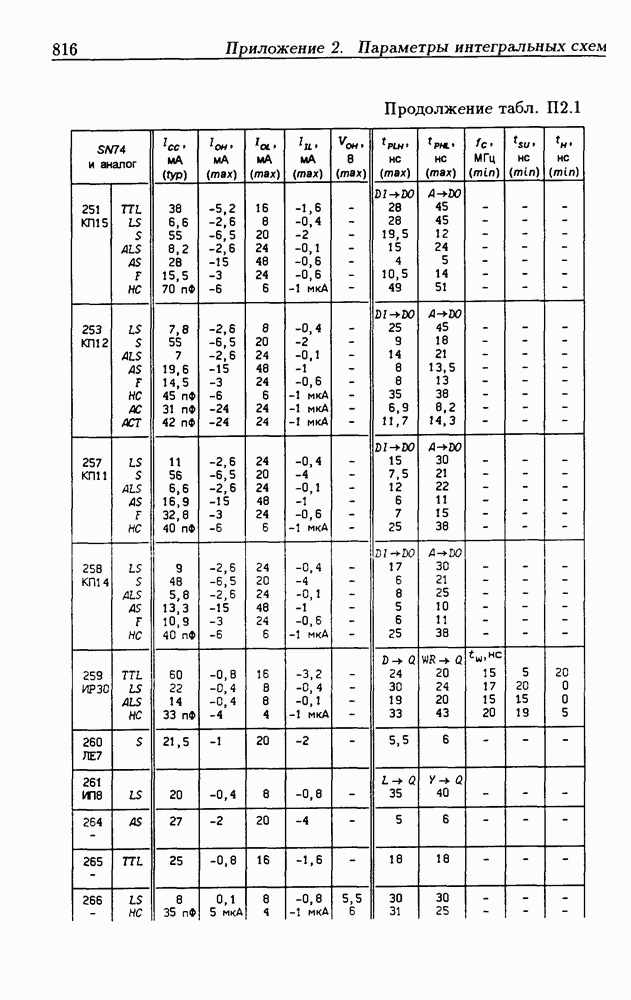
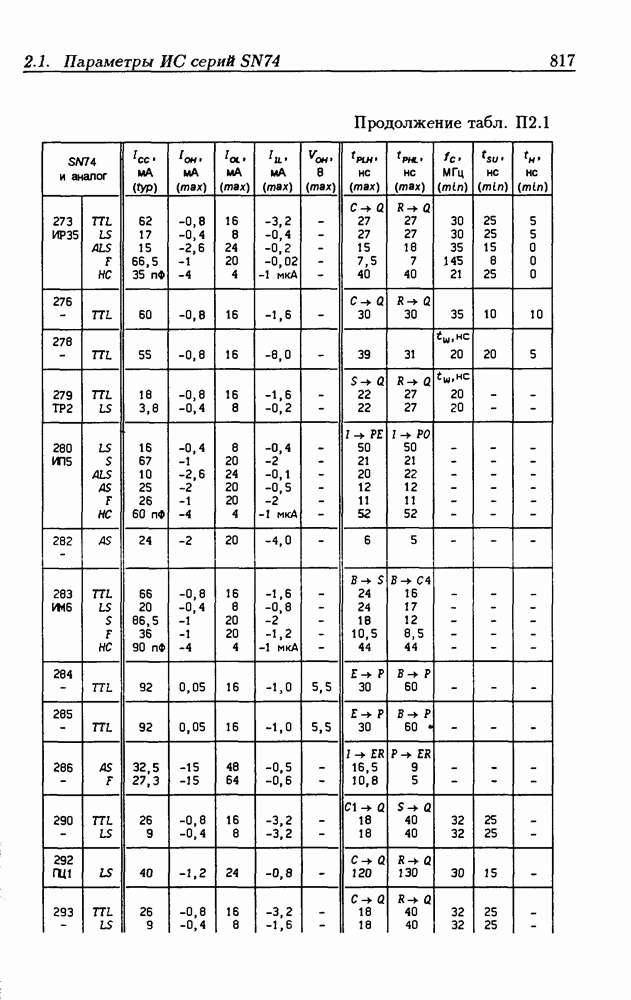
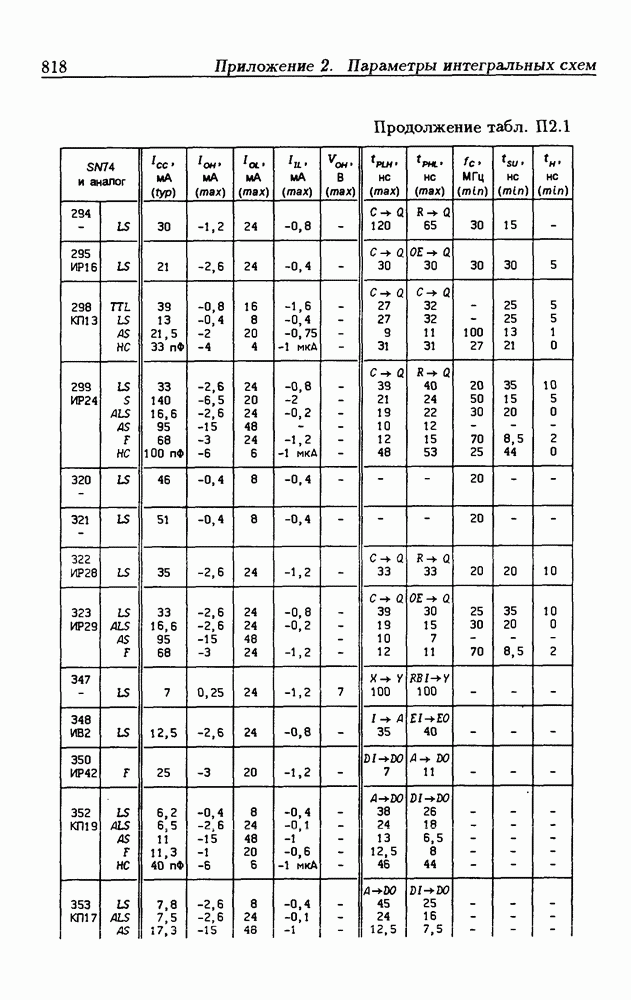
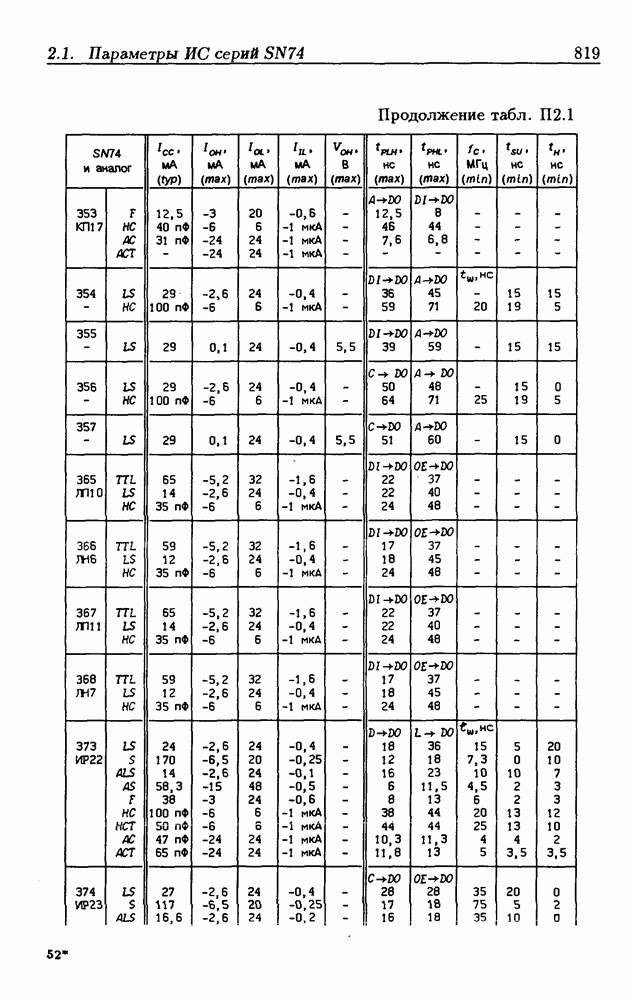
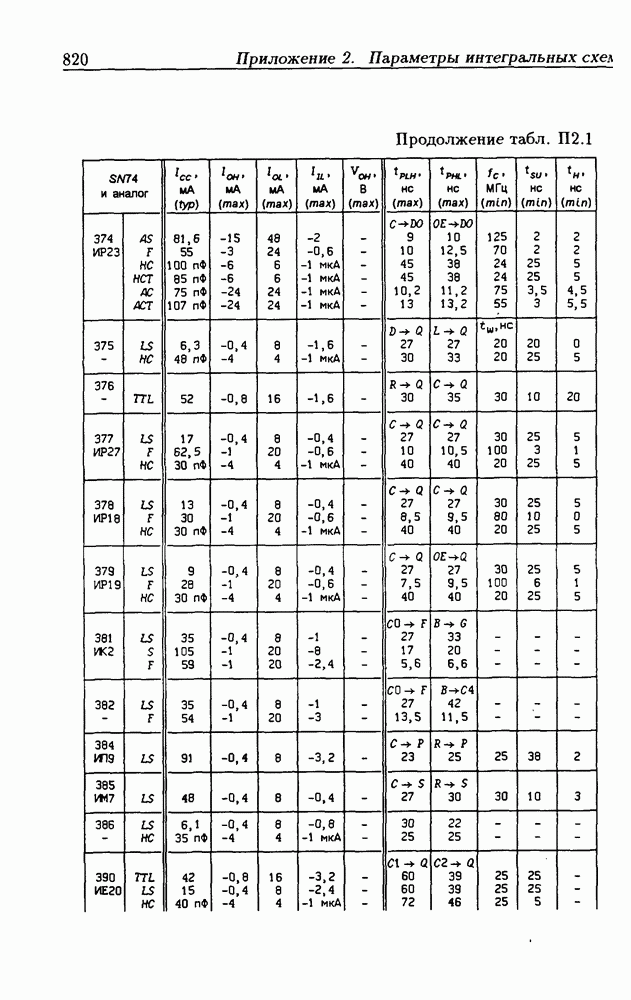
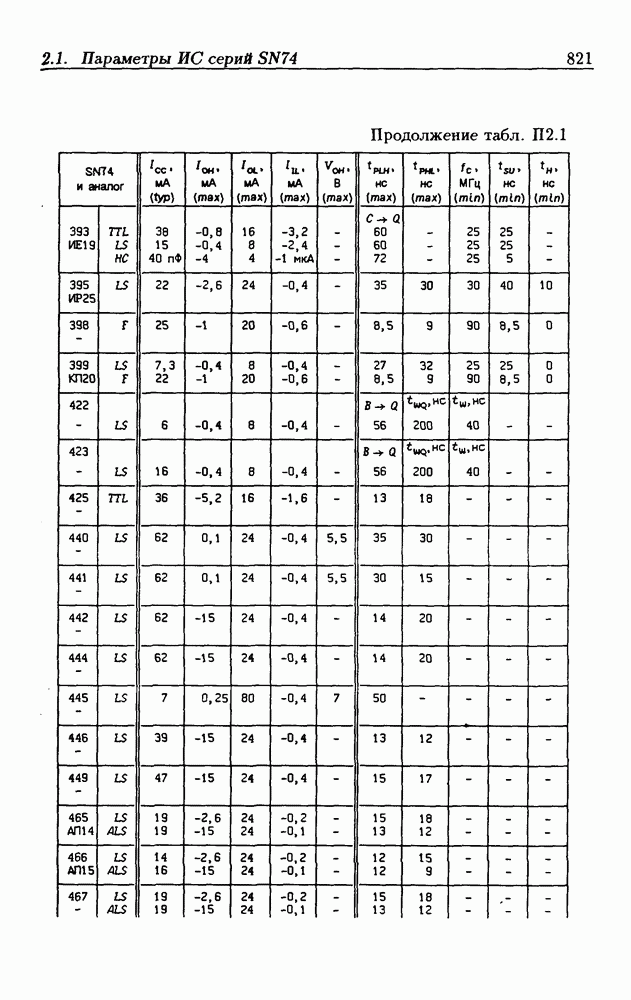
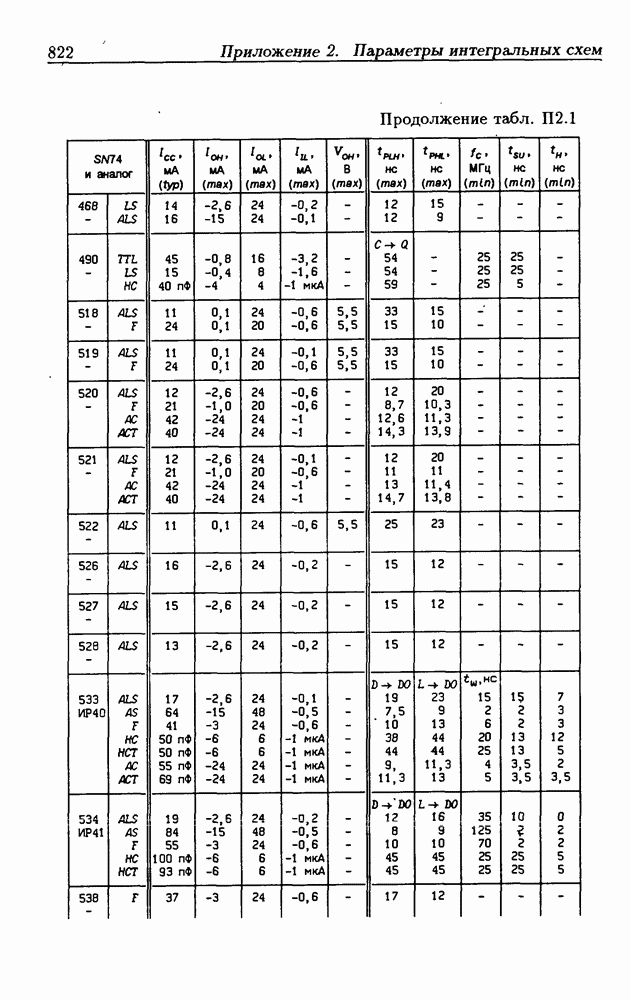
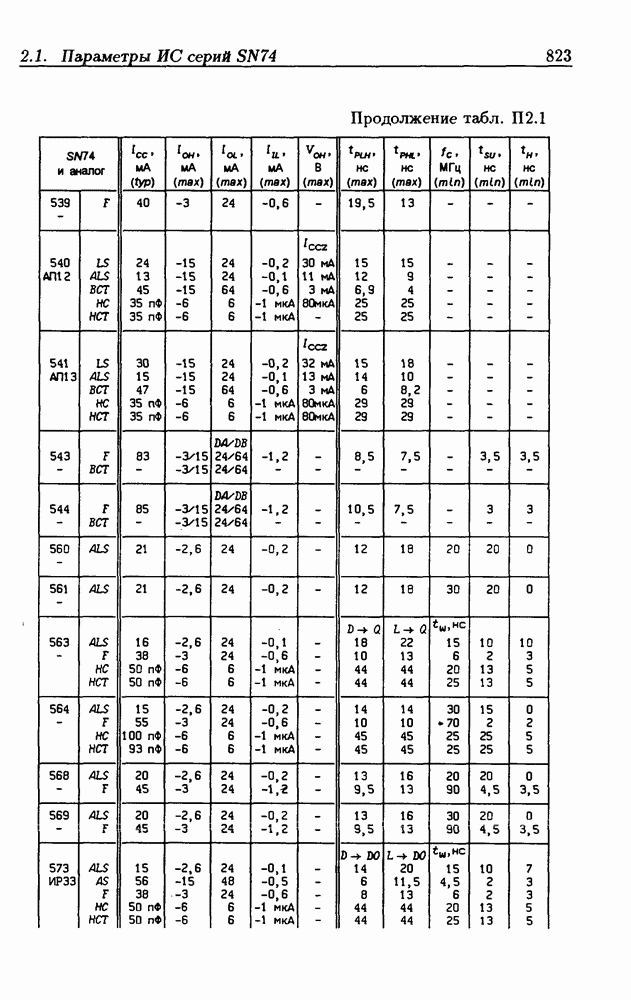
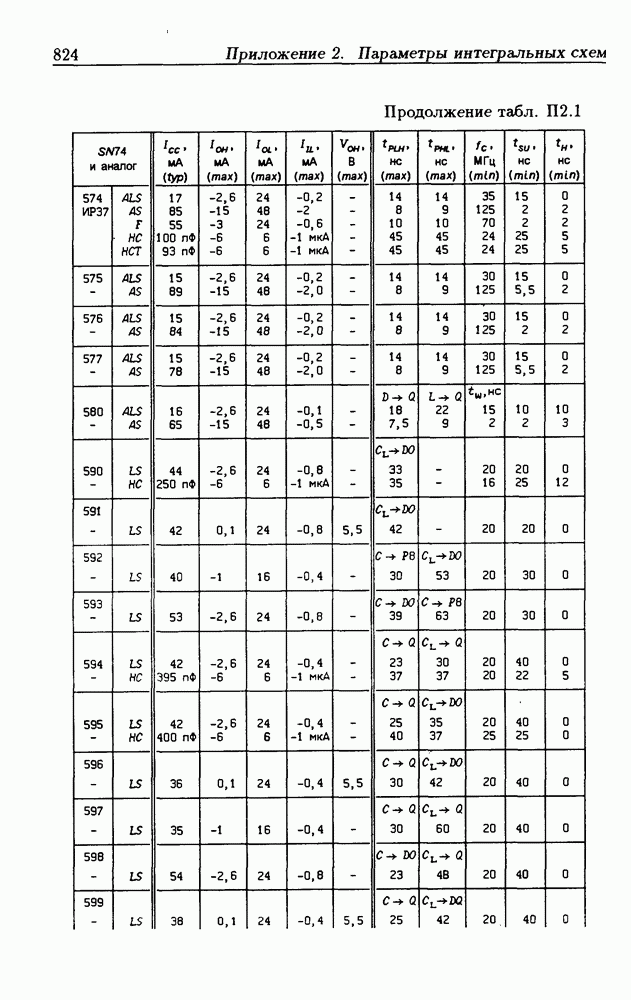
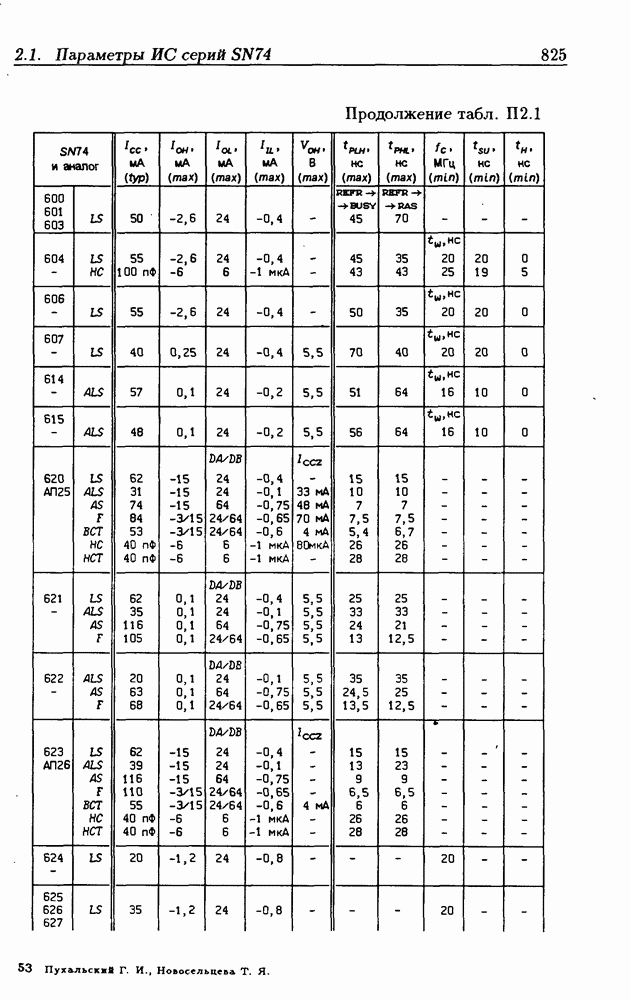
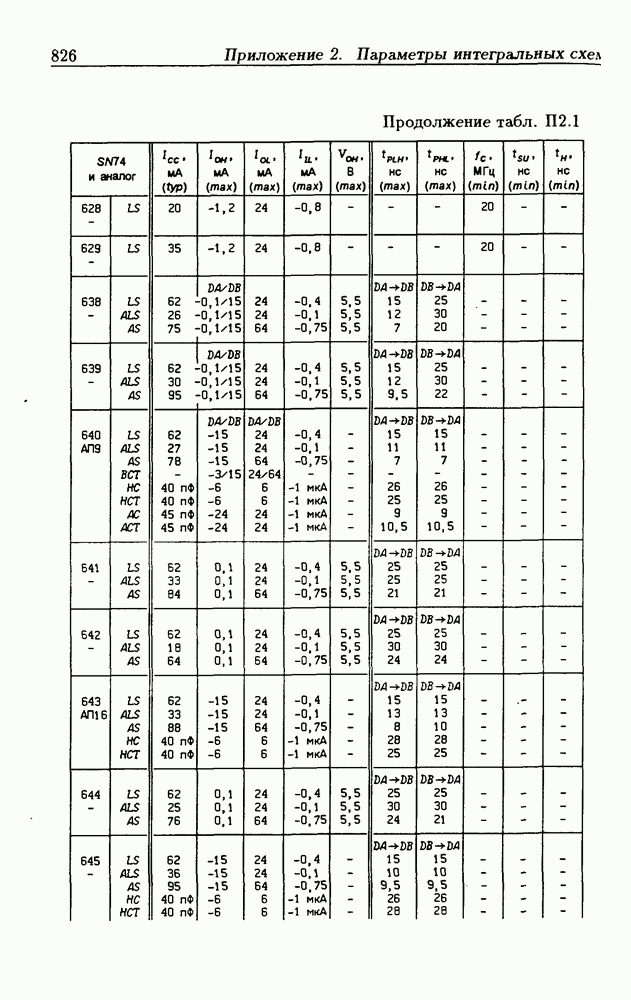
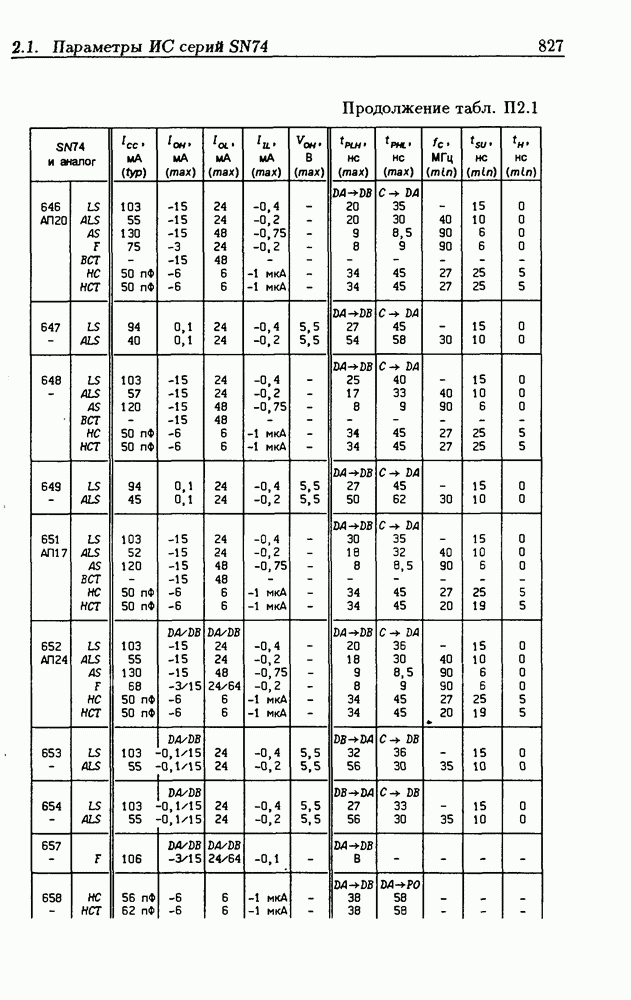
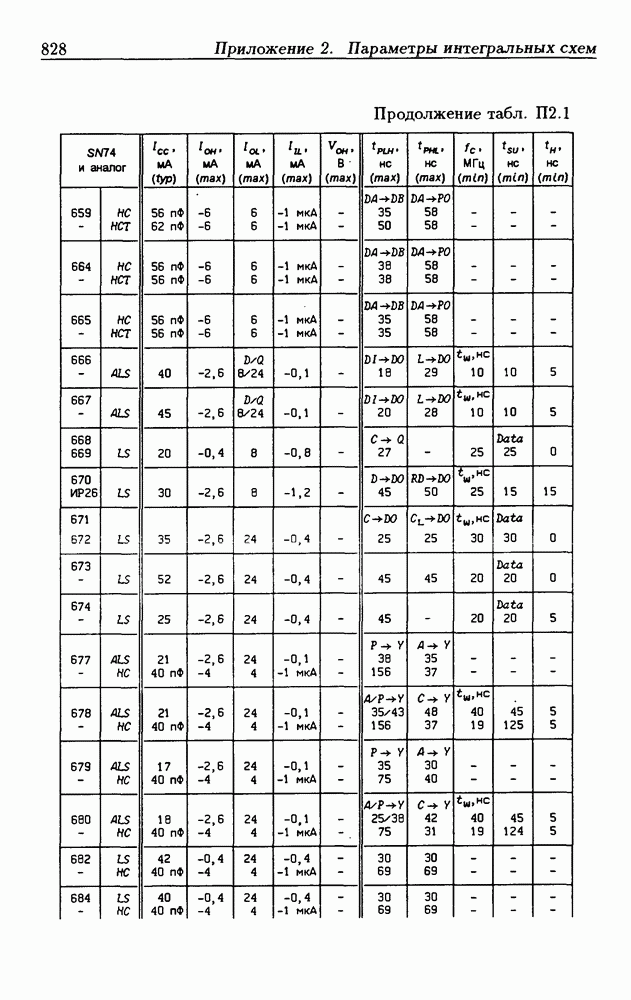
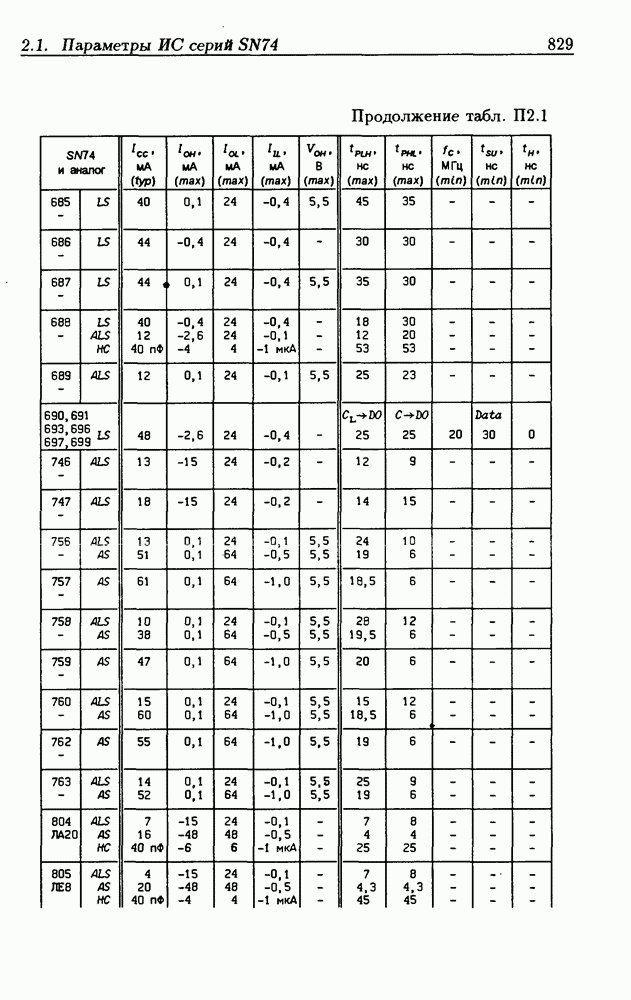
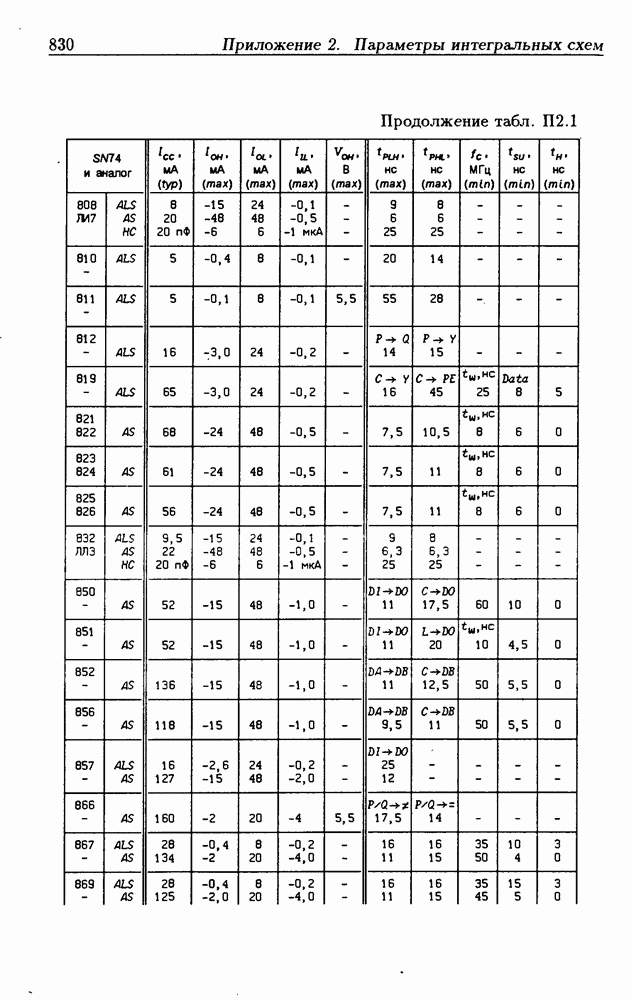
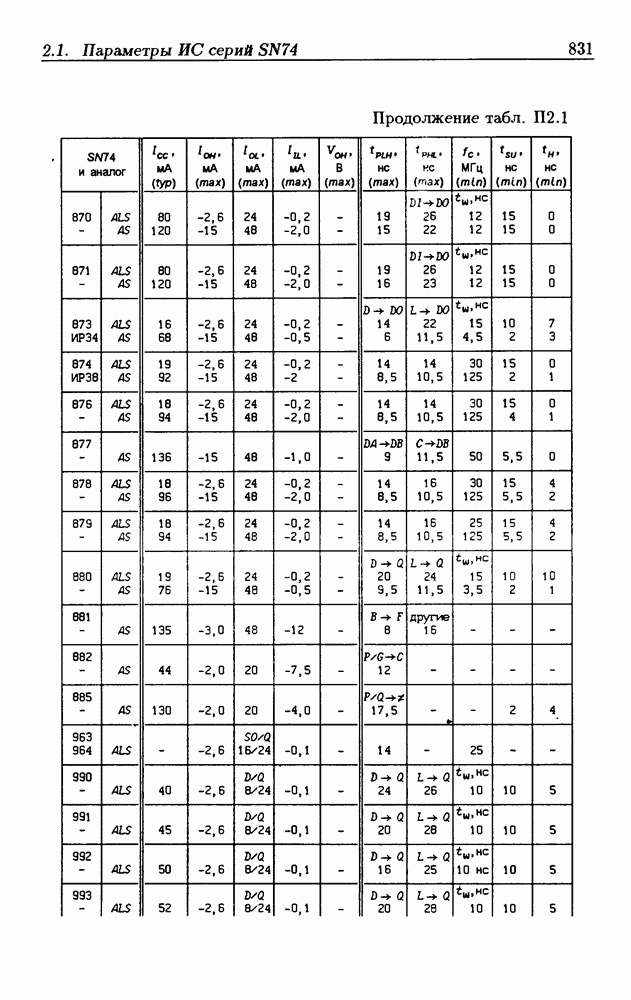
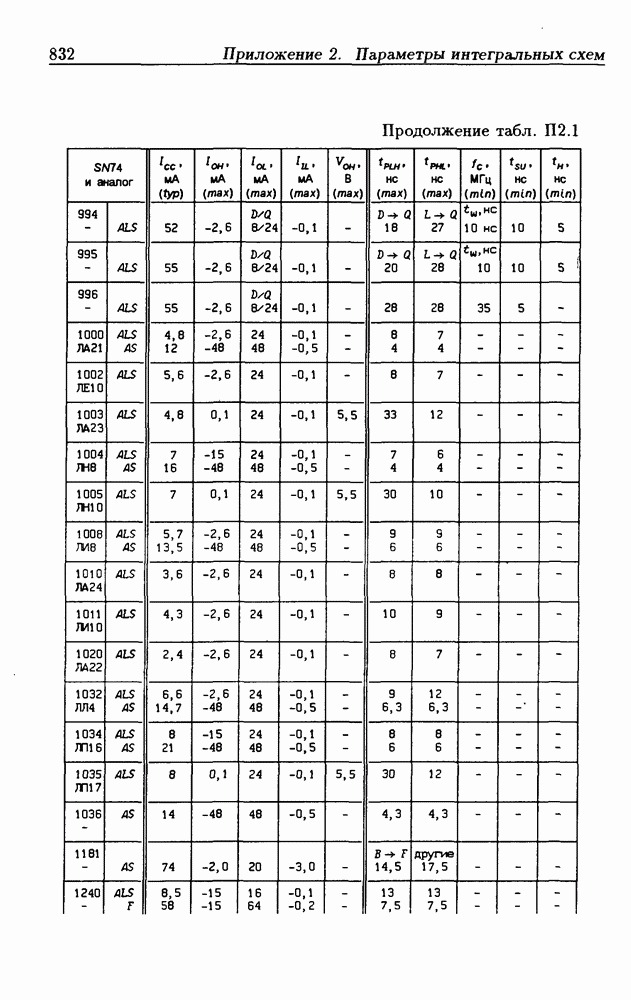
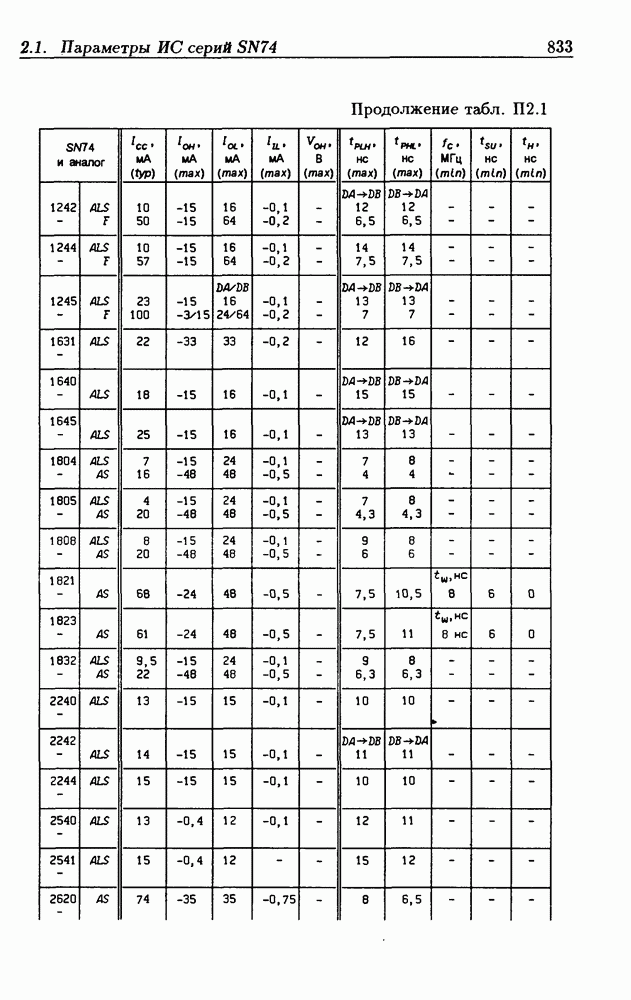
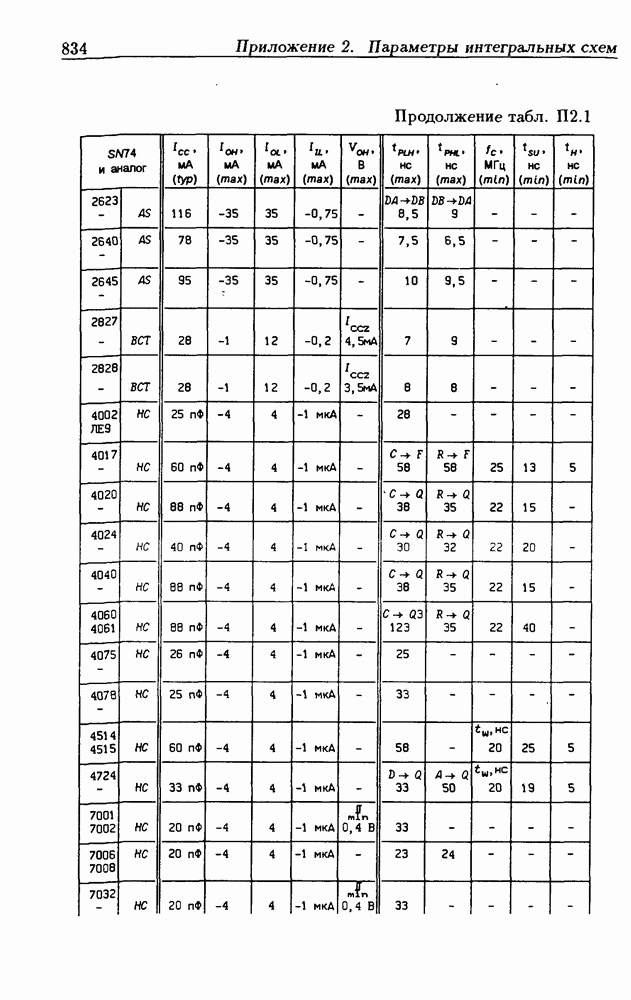
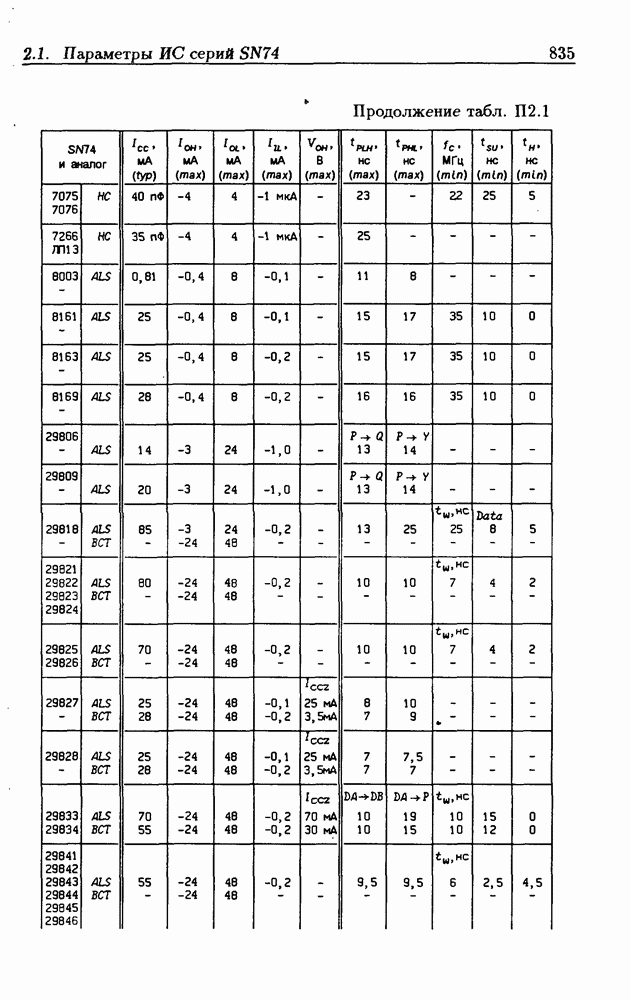
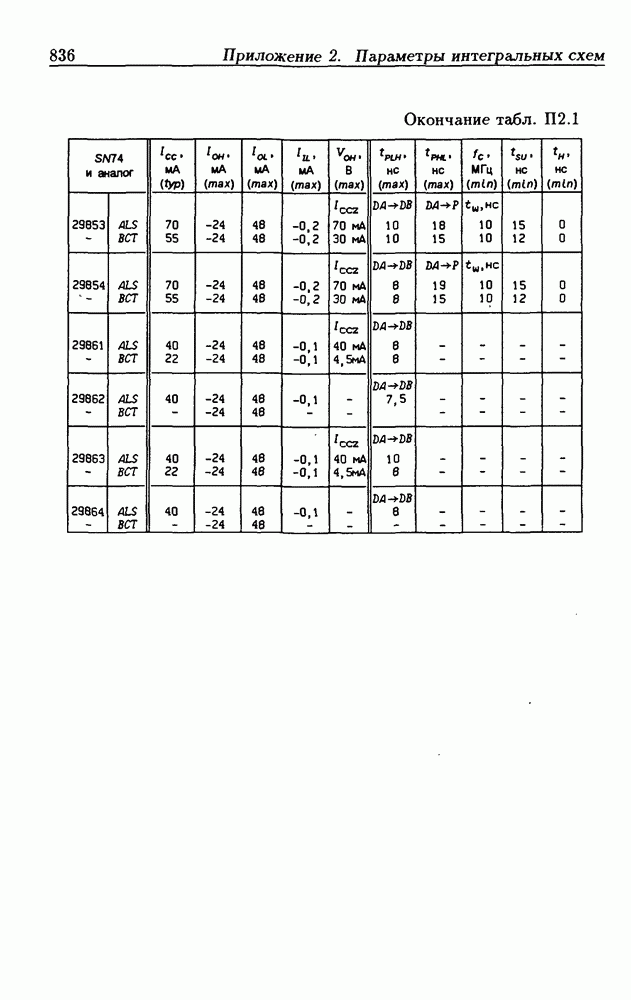
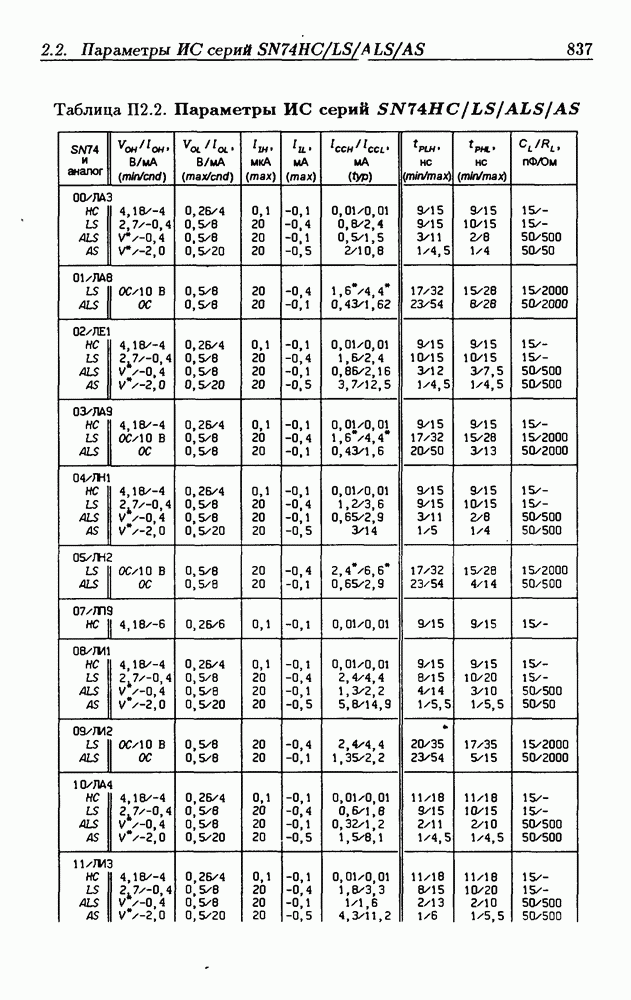
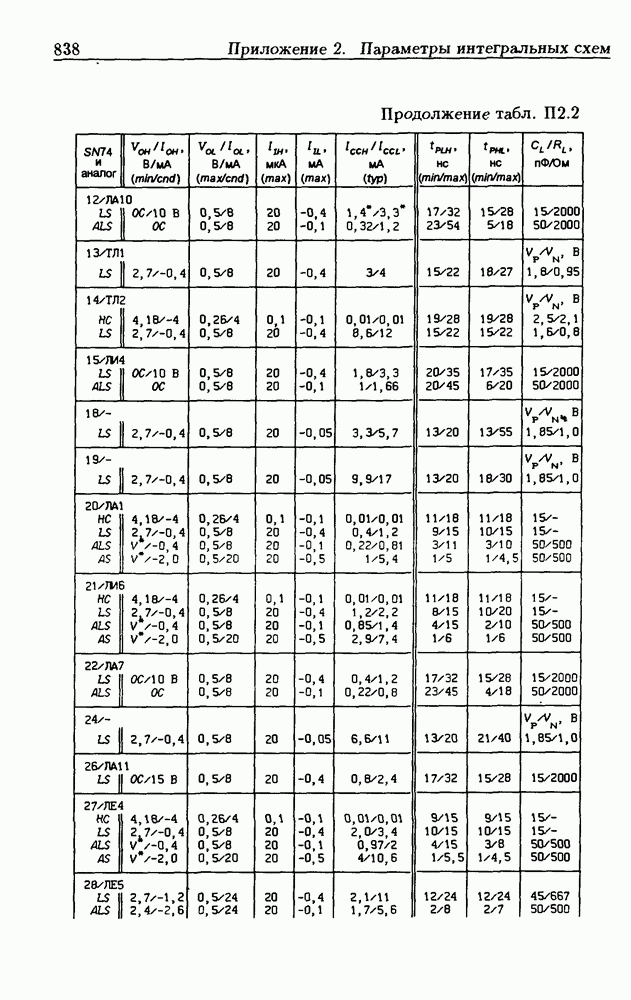
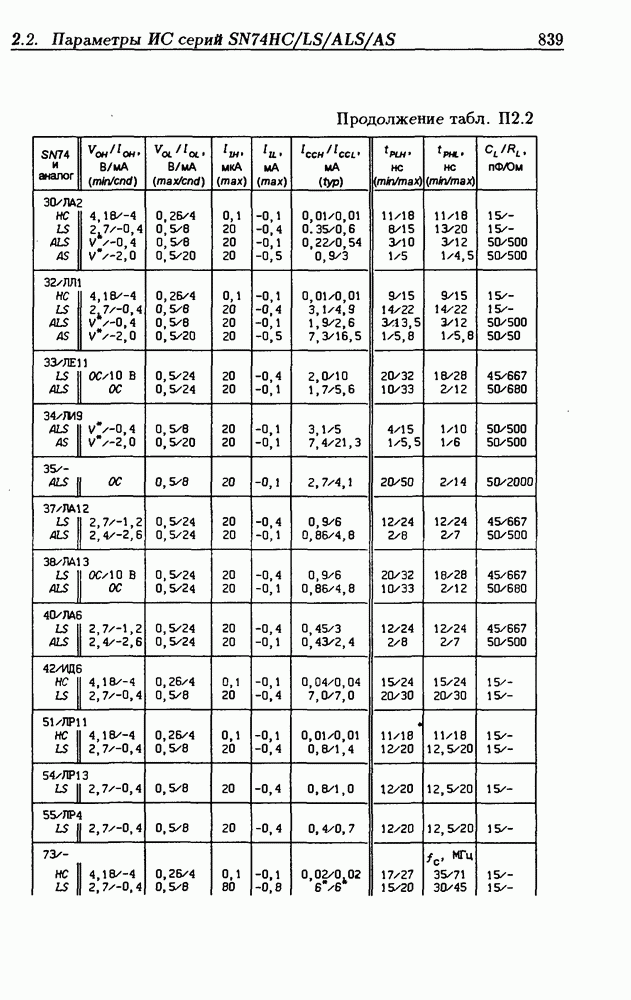
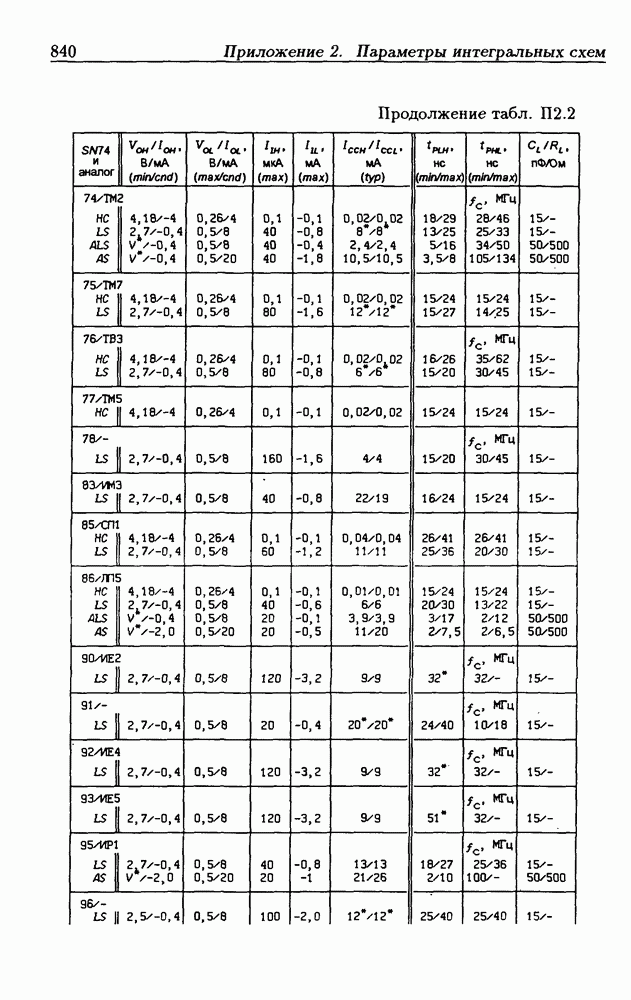
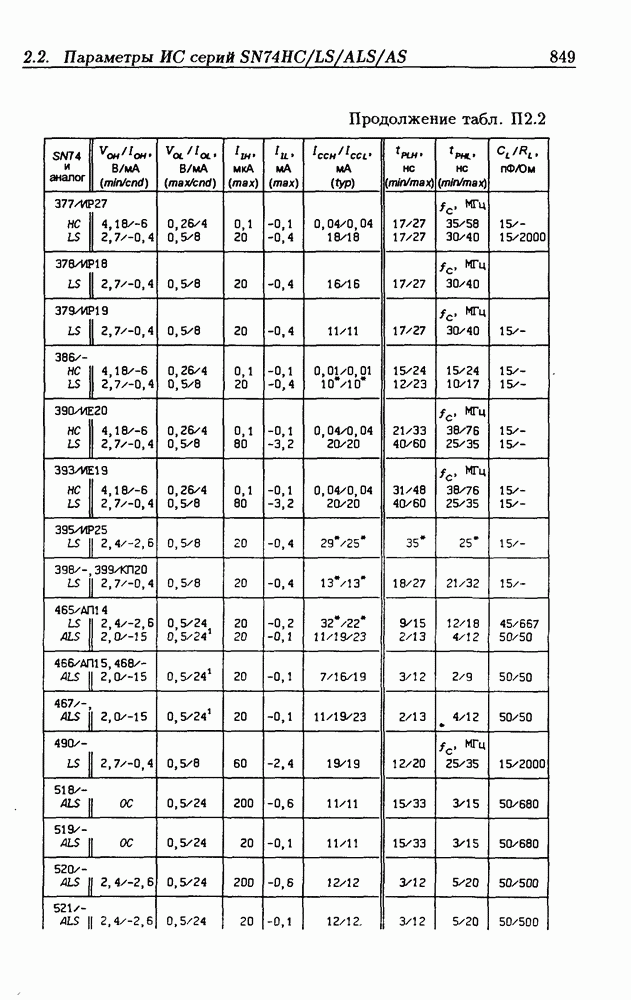
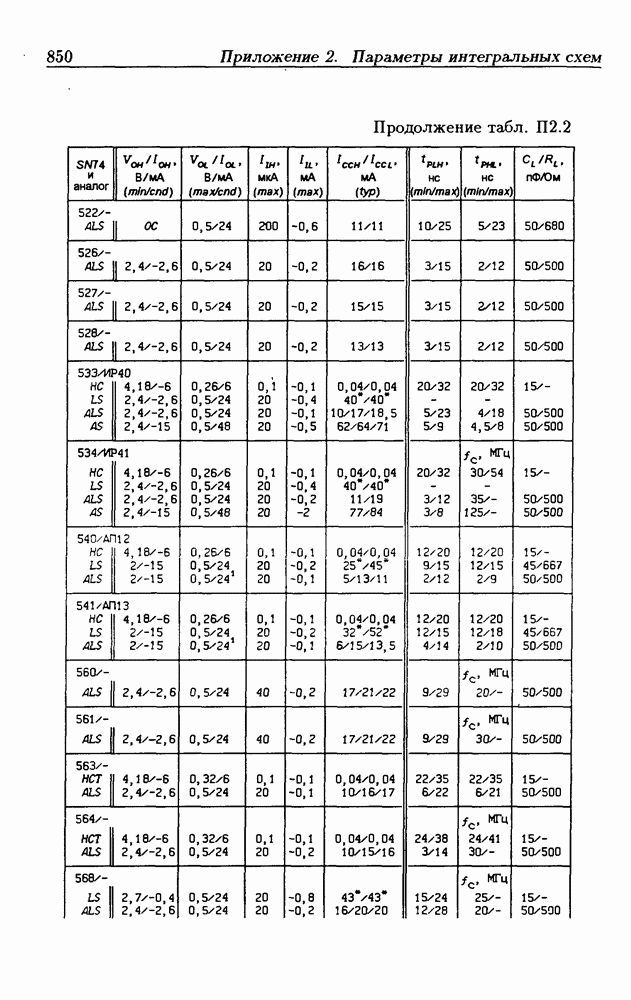
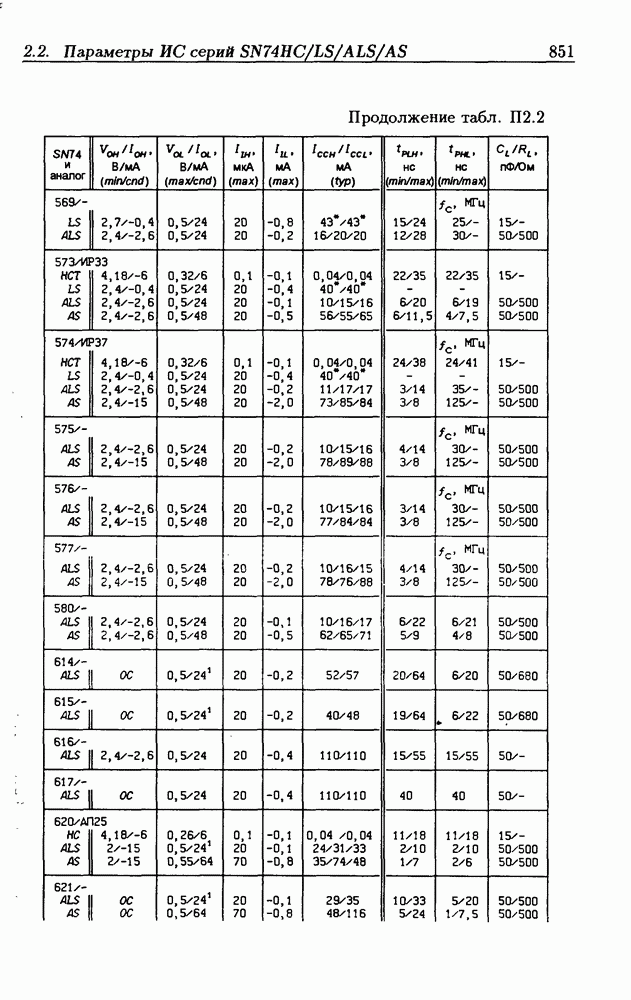
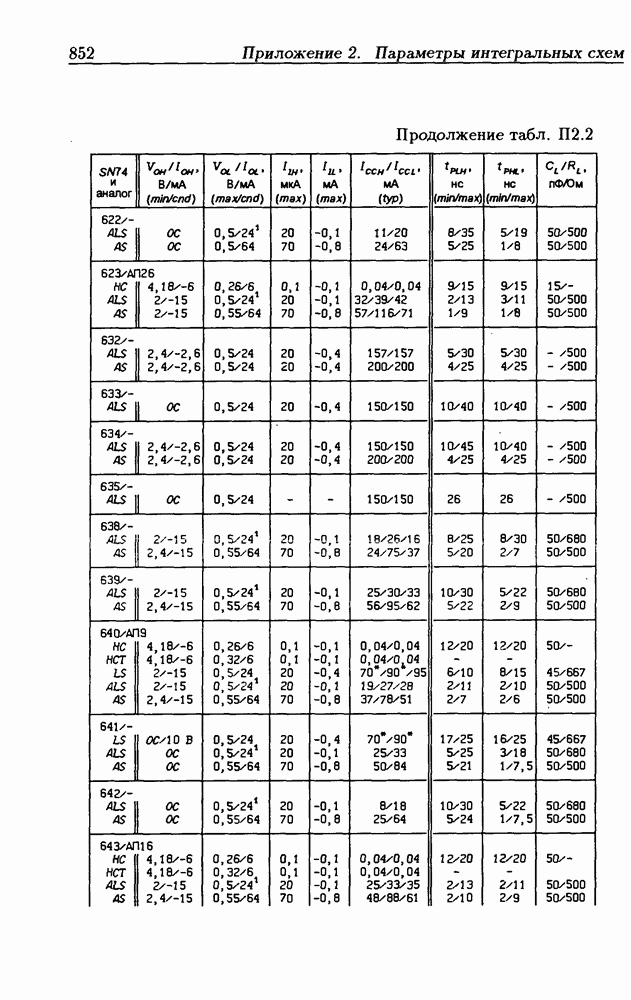
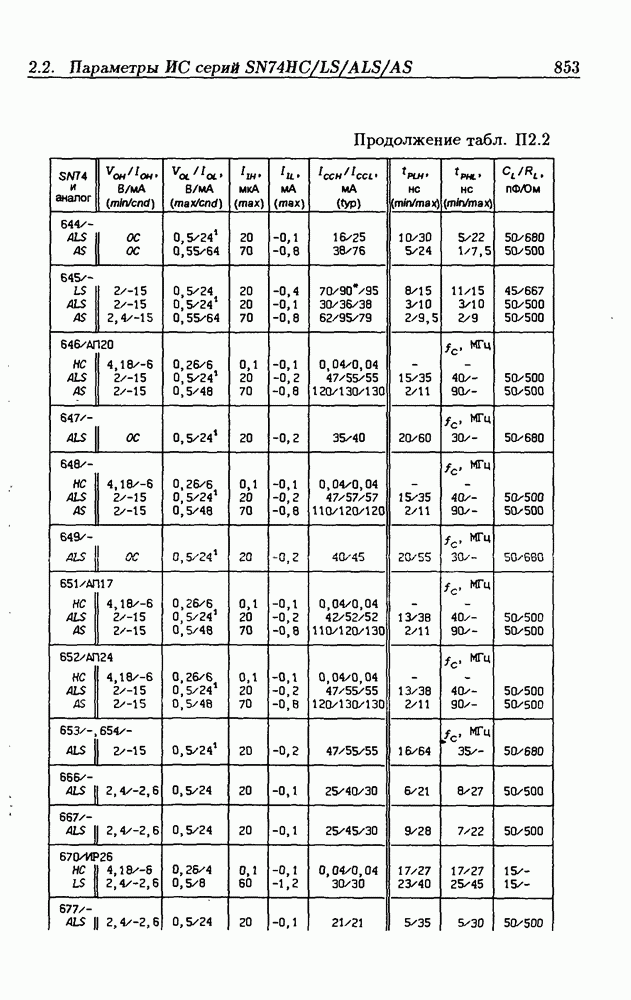
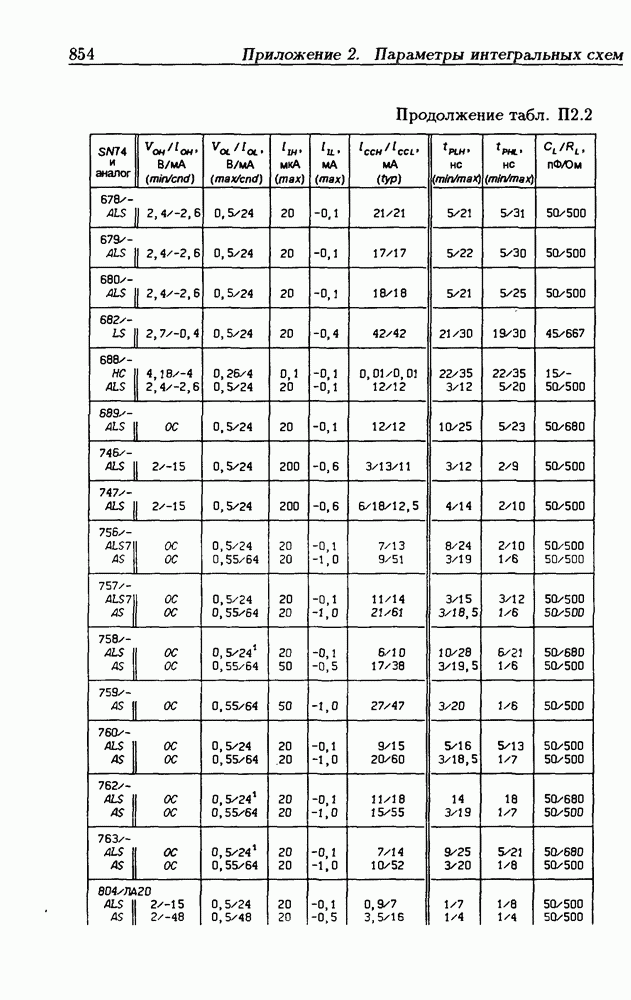
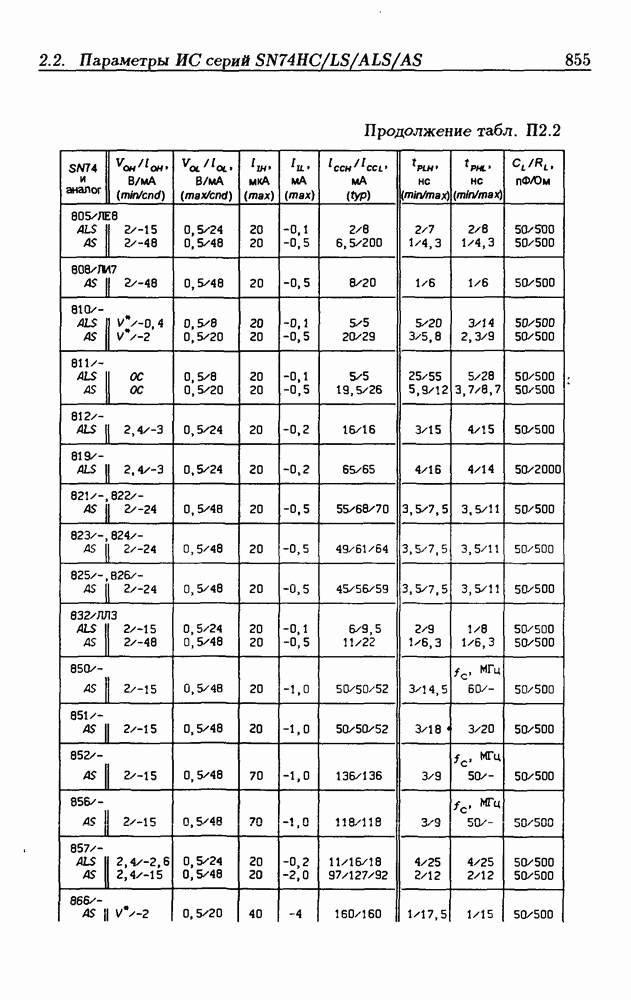
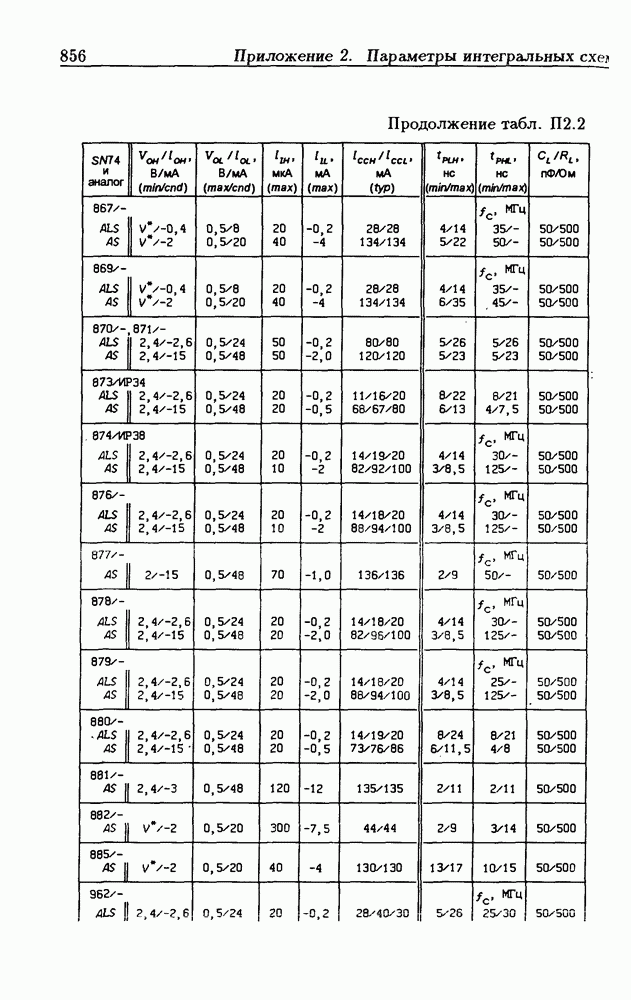
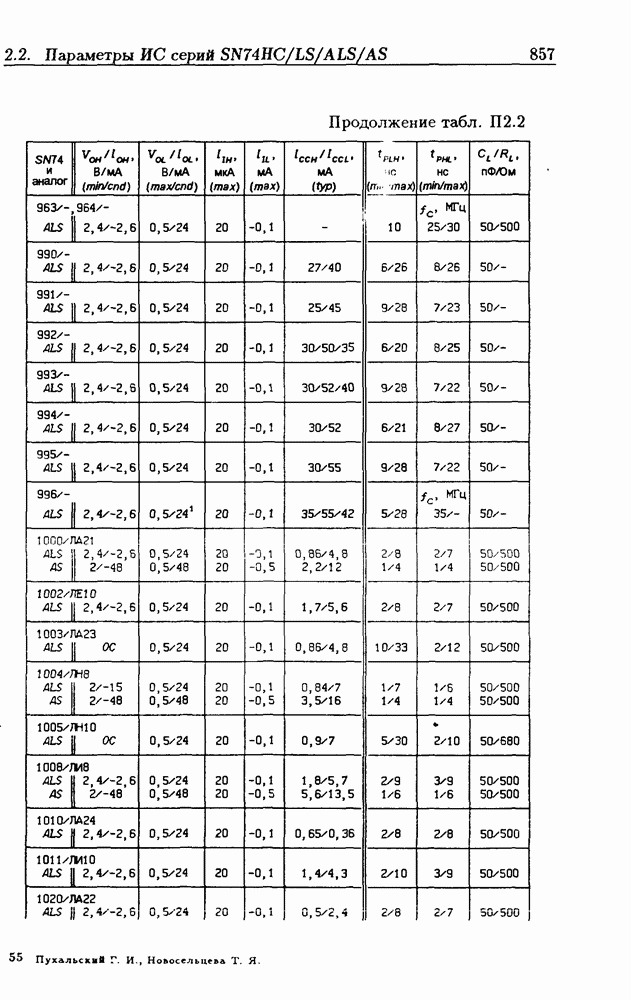
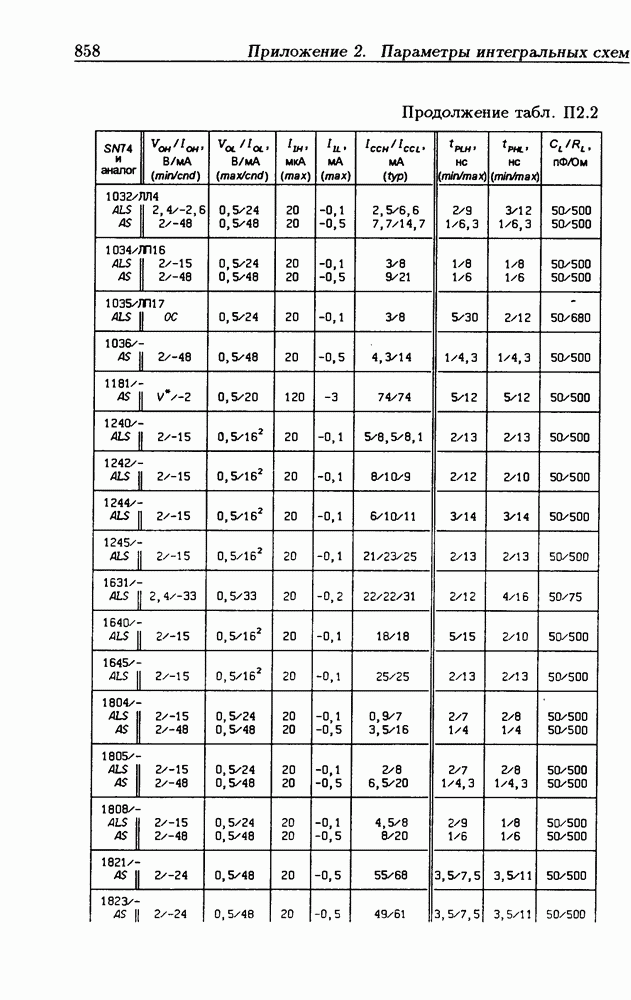
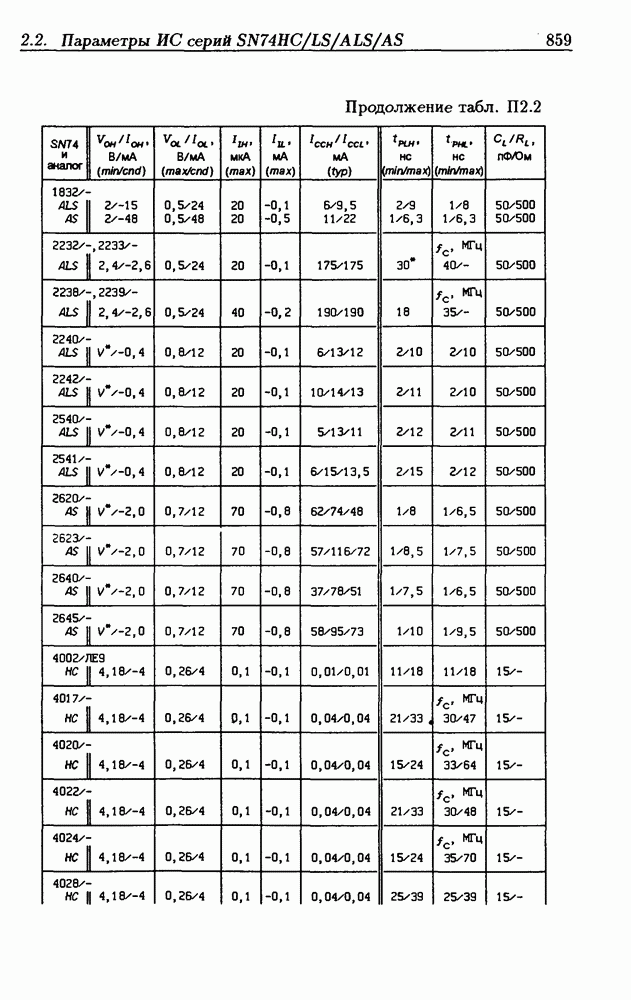
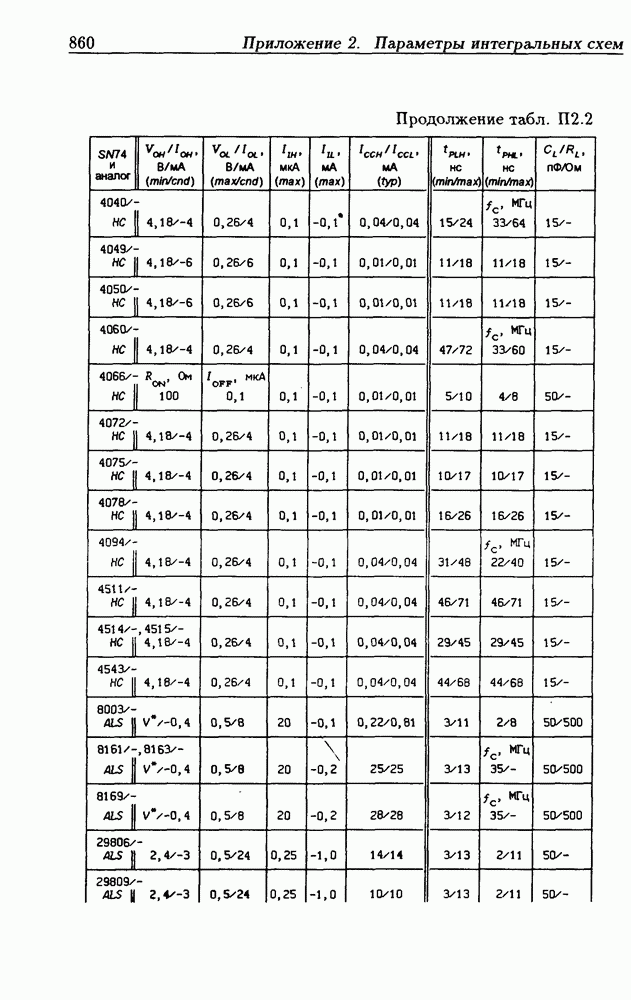
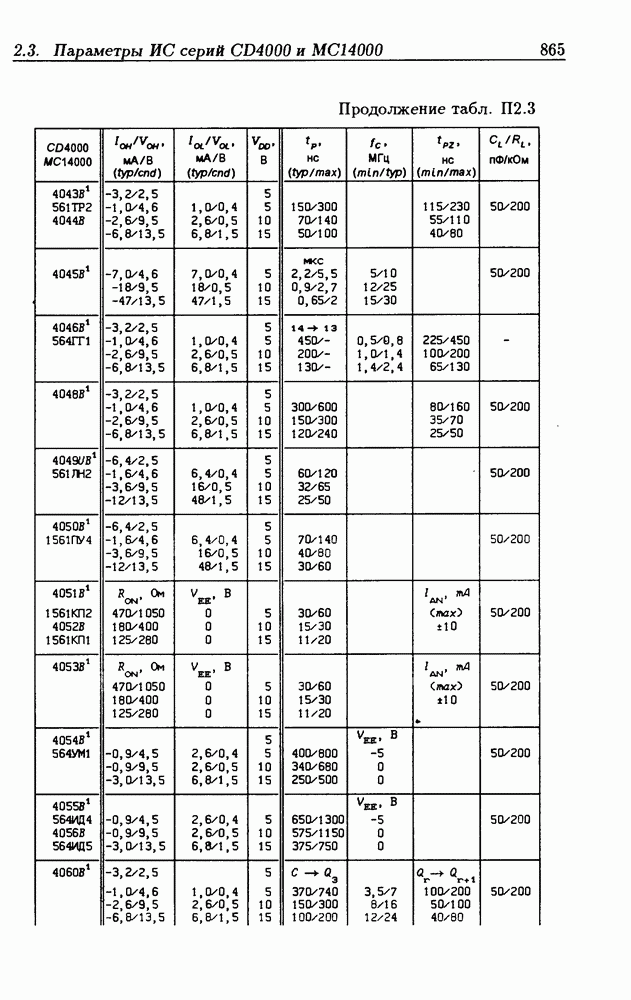
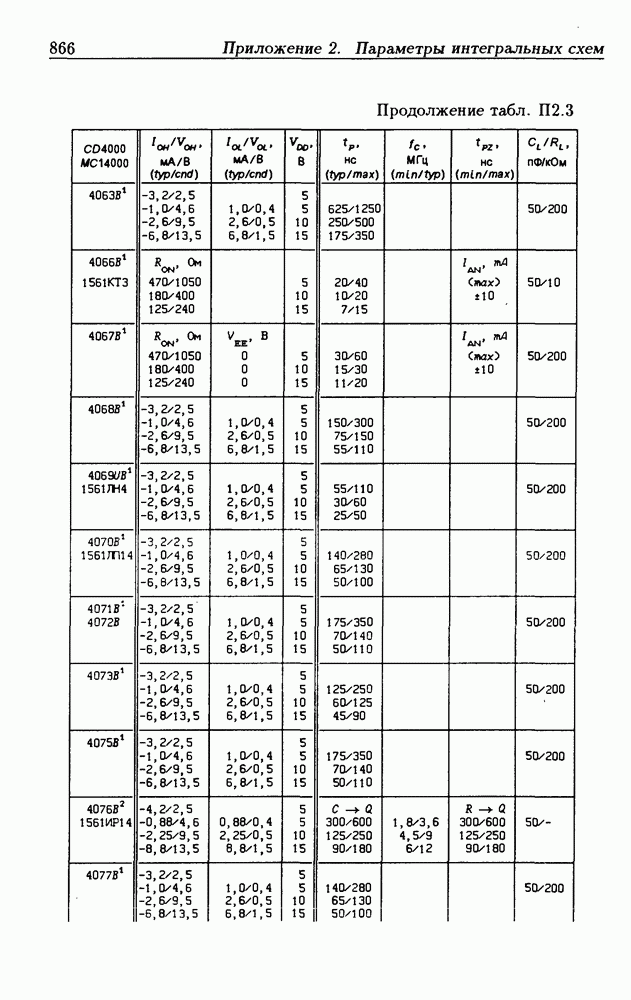
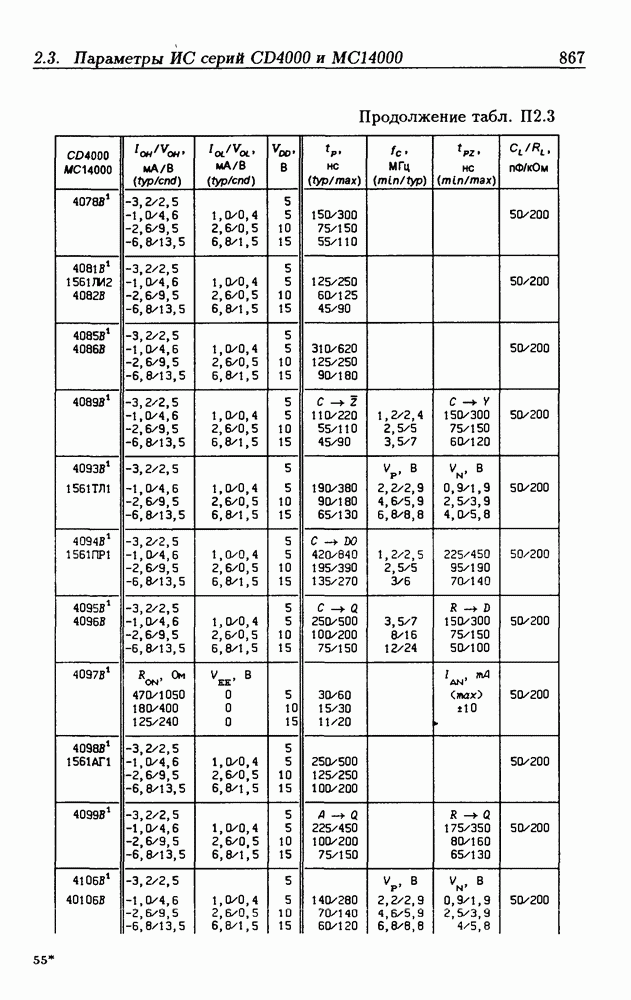
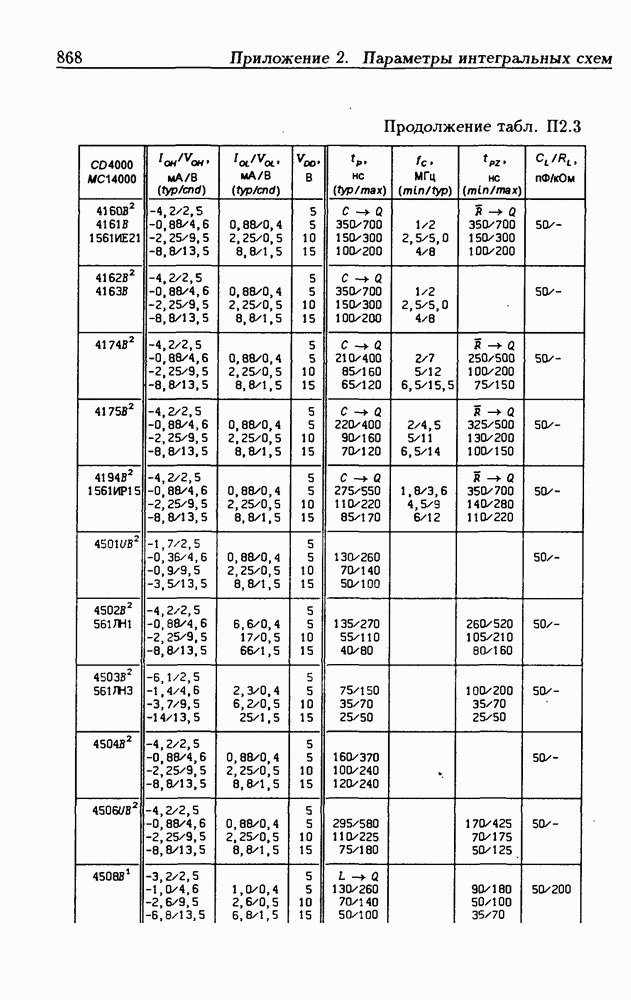
- Приложение 2. Параметры интегральных схем