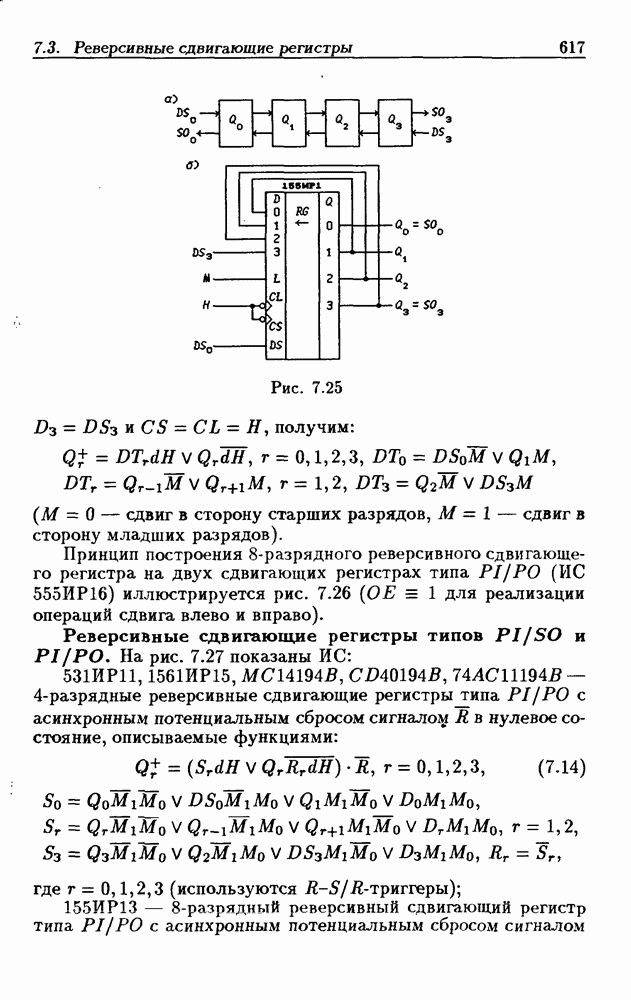
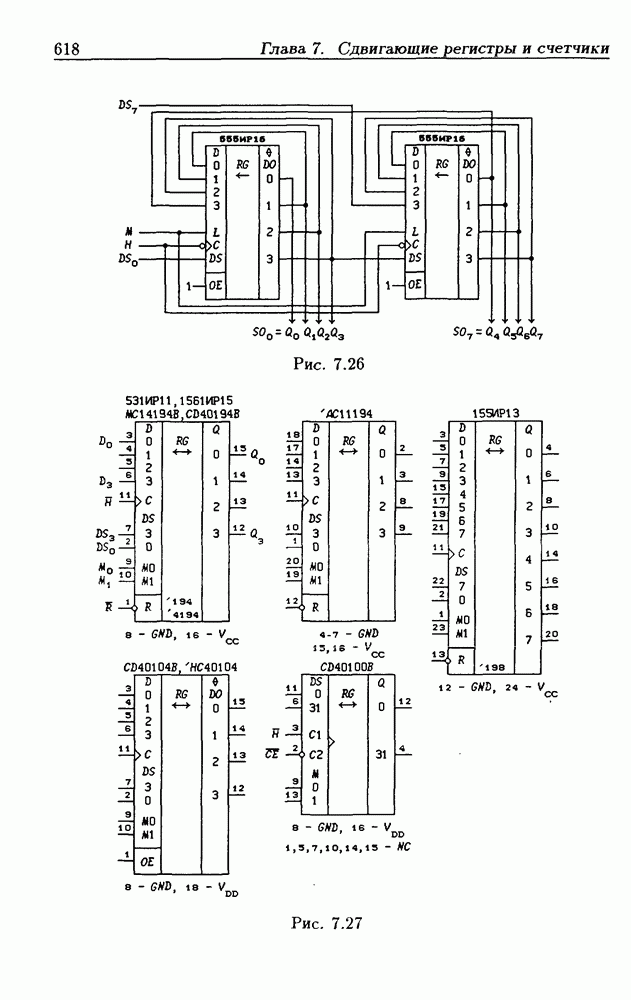
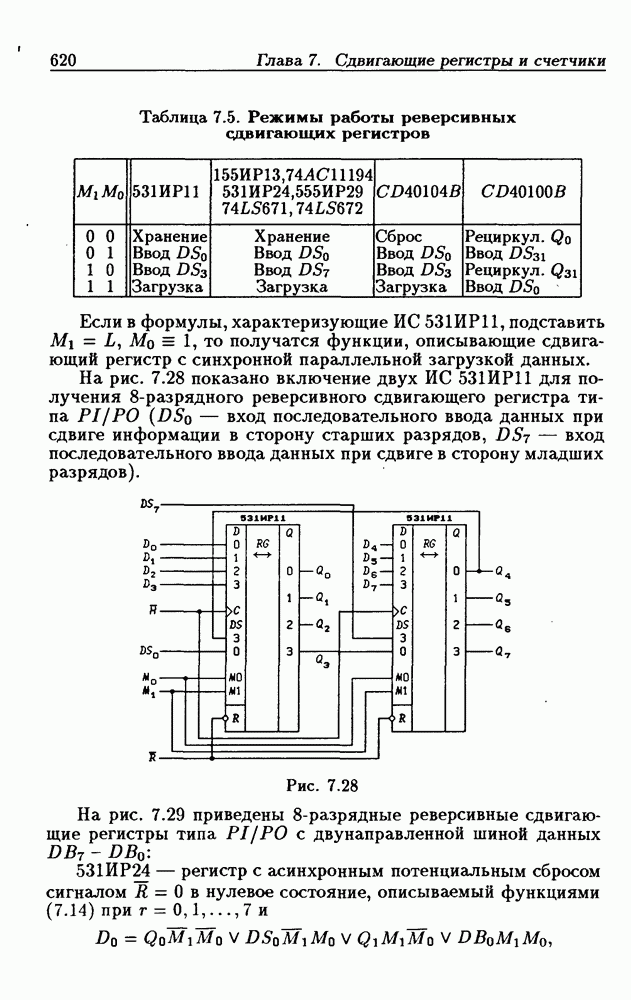
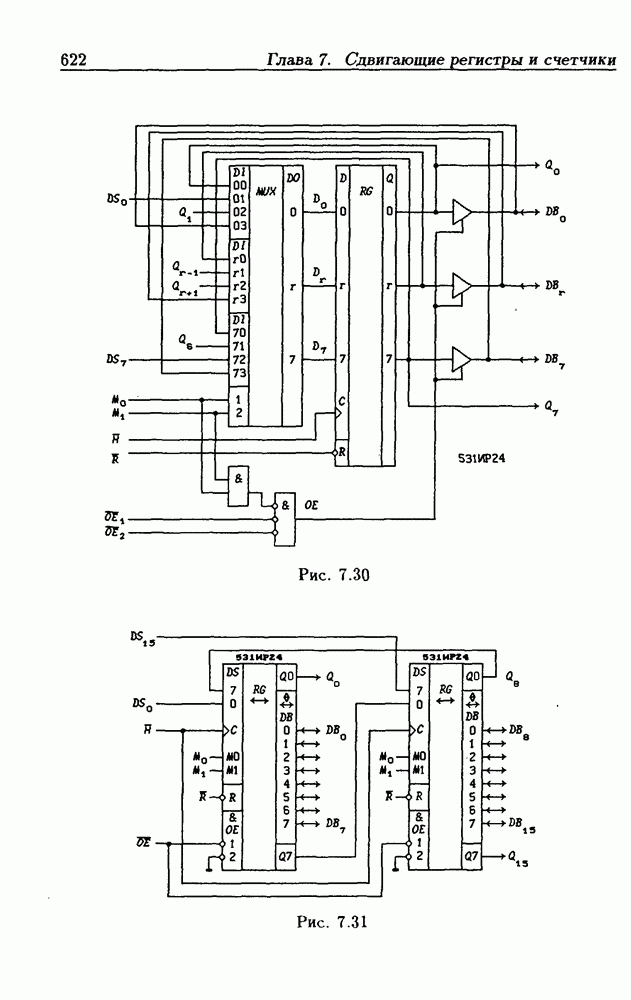
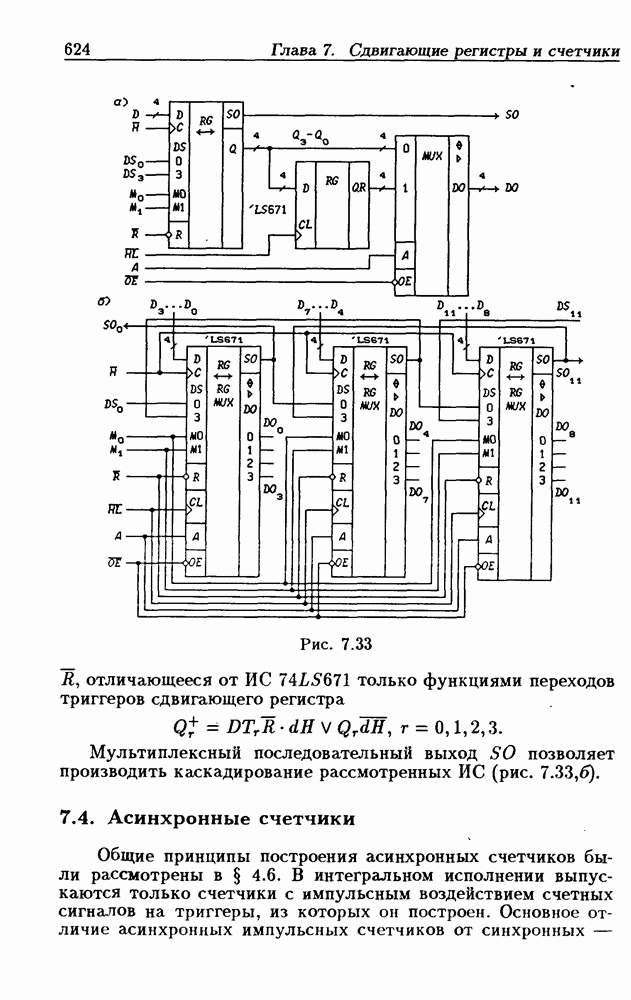
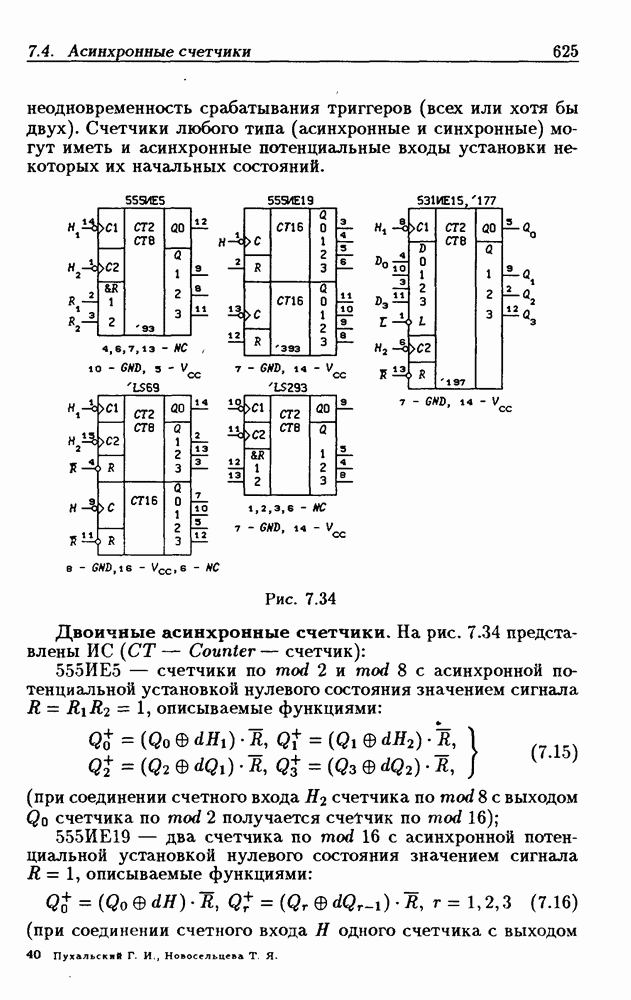
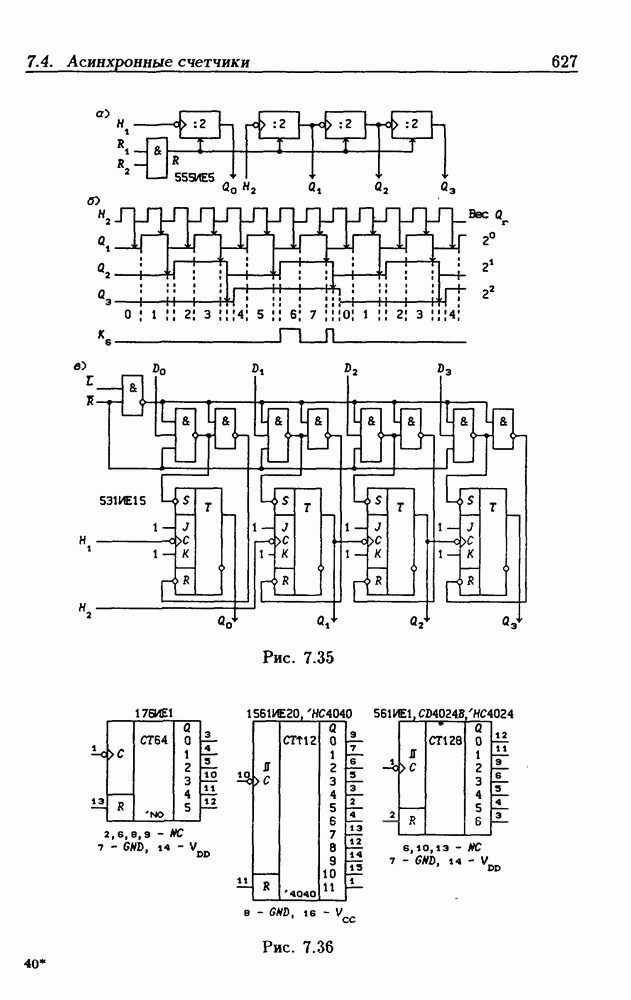
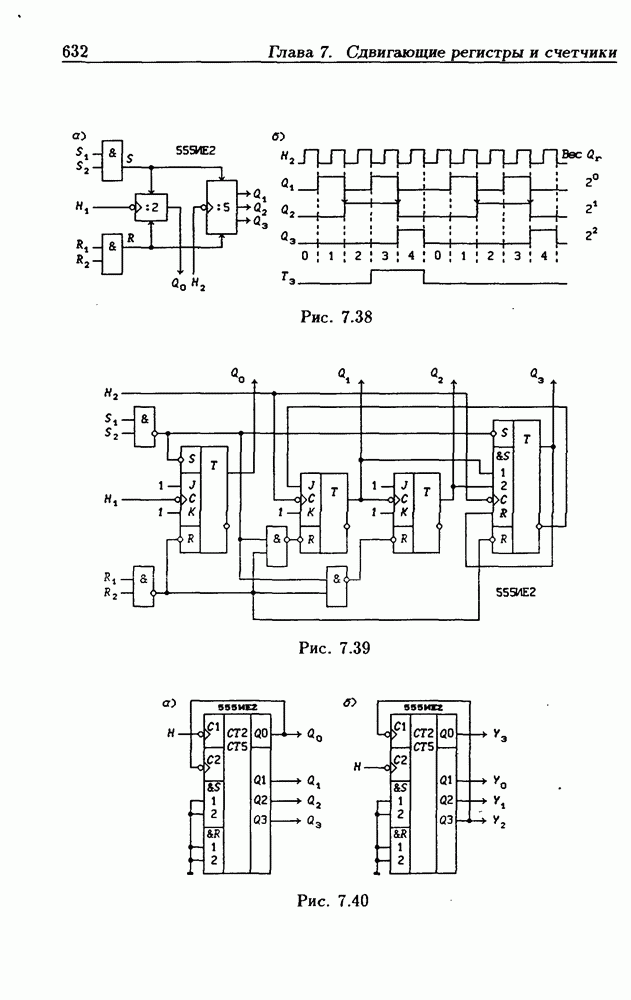
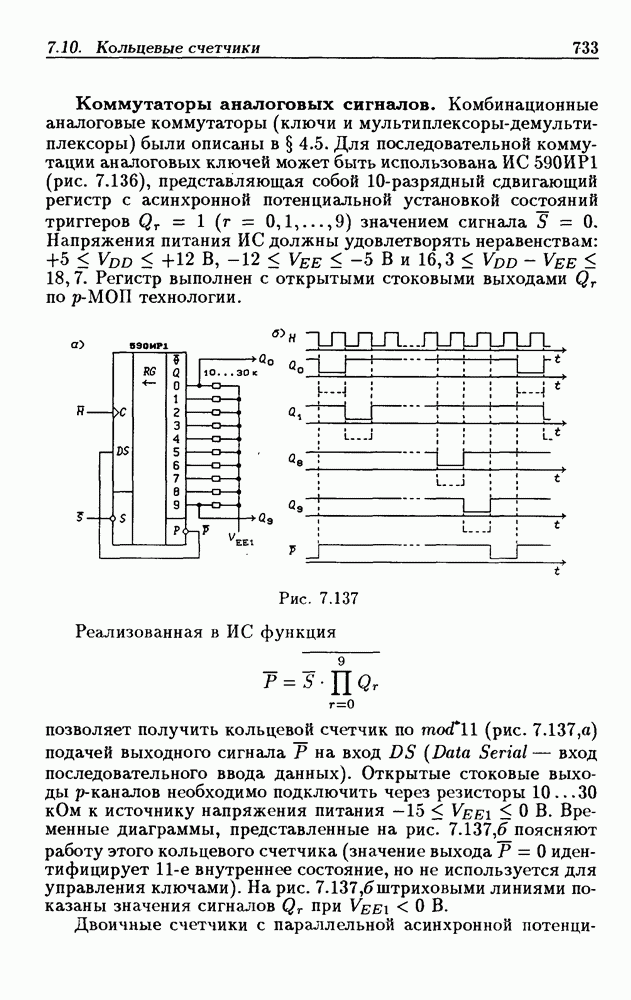
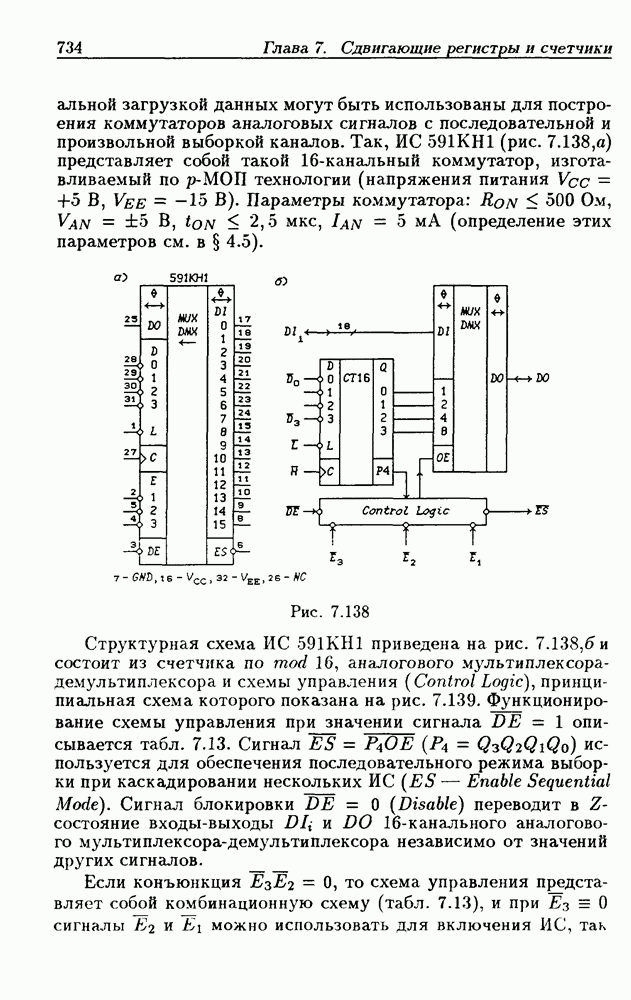
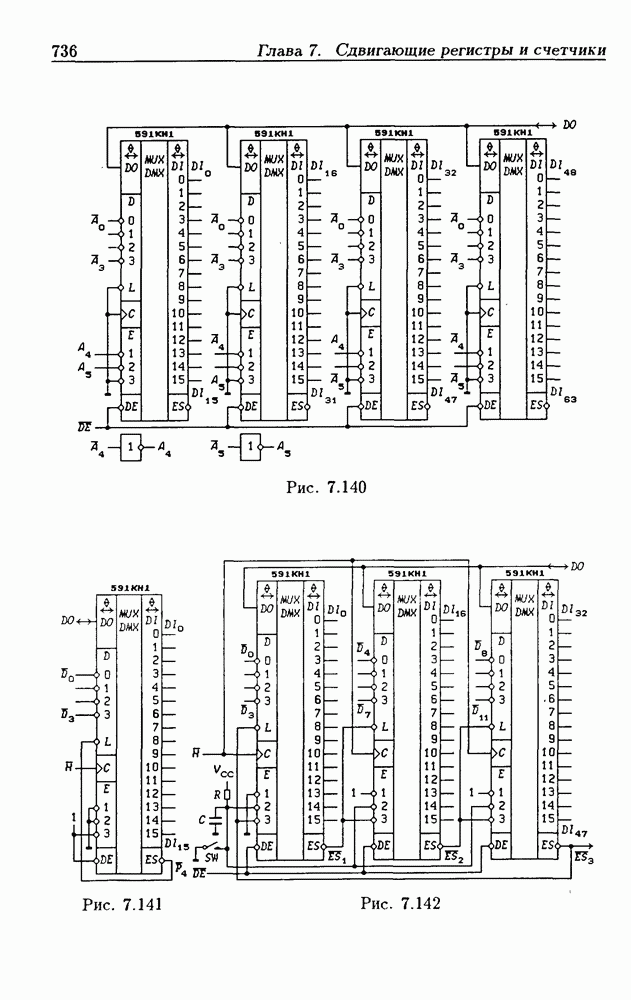
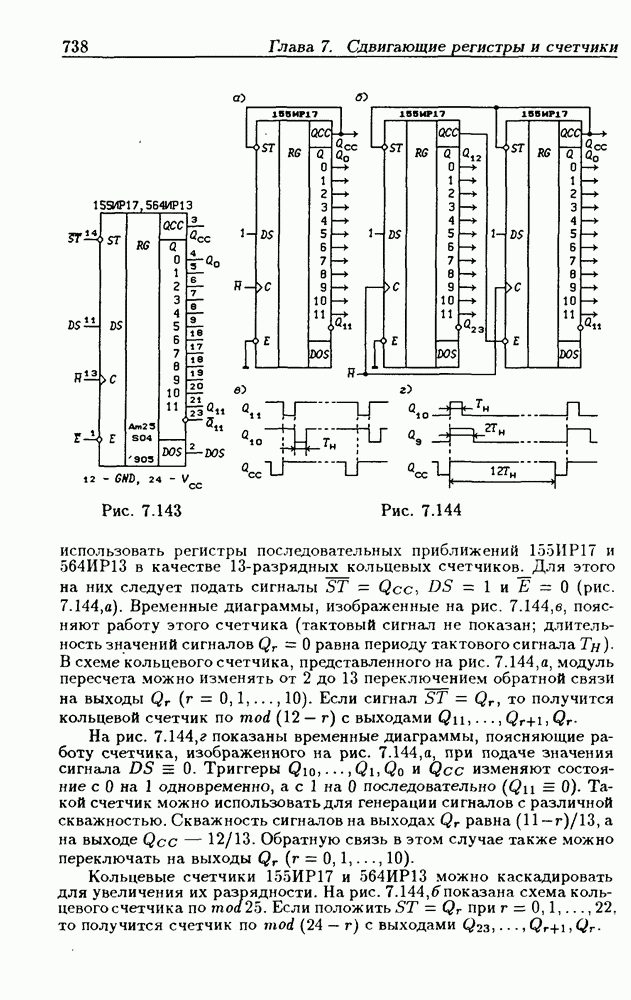
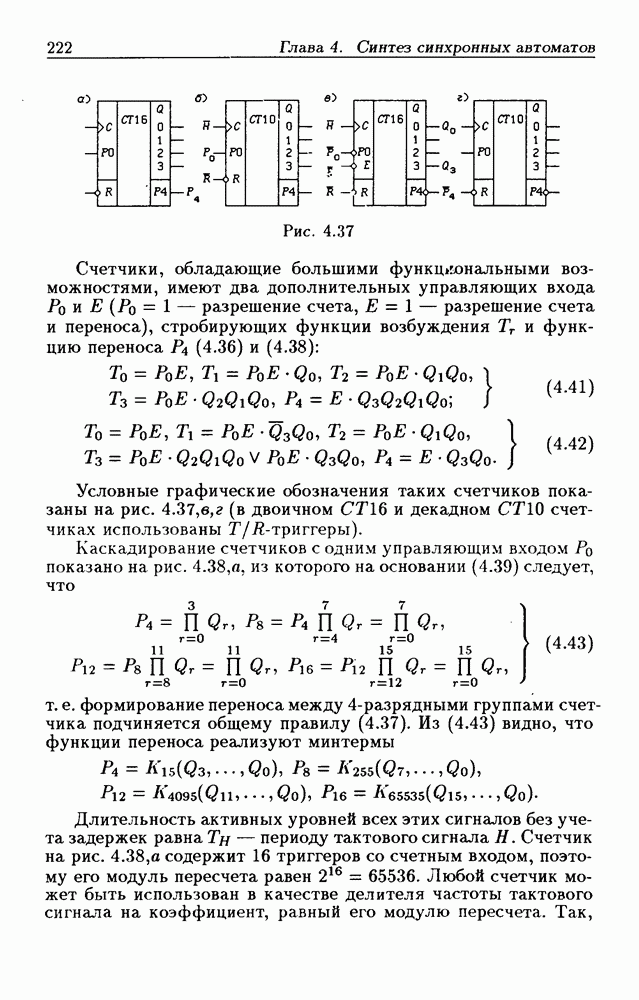| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
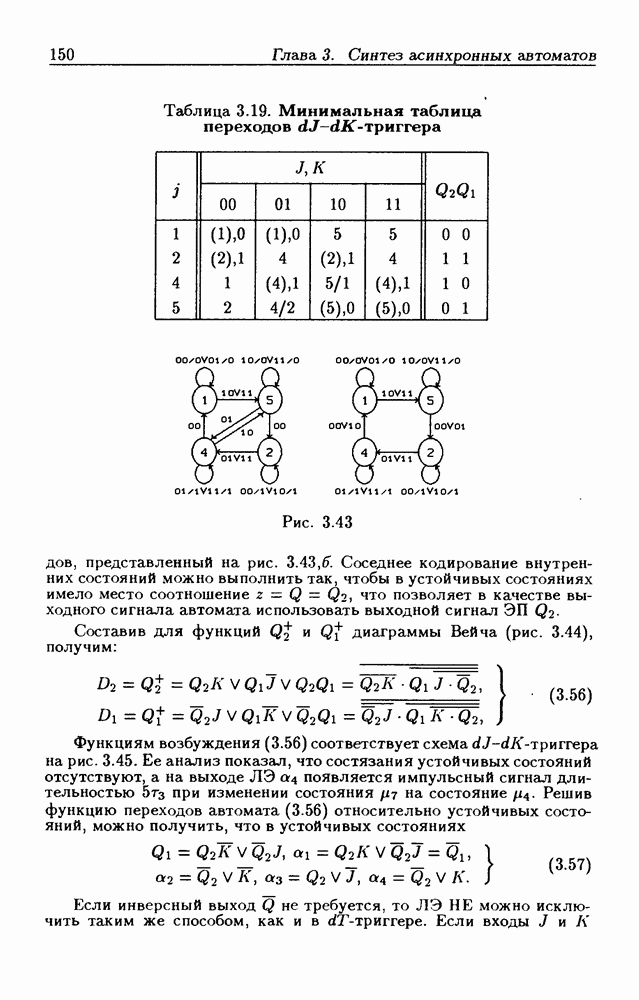
4.3. Примеры синтеза синхронных автоматов
Процесс проектирования синхронных цифровых устройств разделяется на несколько относительно независимых этапов. Первый этап состоит в словесной постановке задачи проектирования самим исполнителем или заказчиком, который может и не владеть аппаратом формального синтеза. Наиболее важным
этапом проектирования является второй — переход от словесного описания устройства к одному из формальных способов его задания, например графом переходов. На последнем, третьем, этапе используются единые для всех синхронных автоматов формальные методы получения функций возбуждения триггеров и минимальных форм переключательных функций, описывающих его физические выходы.
Последовательный сумматор.
Рассмотрим устройства суммирования целых положительных n-разрядных двоичных чисел

для которых при логическом проектировании схем удобнее использовать векторное представление

где  старшие разряды.
старшие разряды.
Операция сложения положительных двоичных чисел определяется правилами двоичной арифметики:
значение переноса  разряд равно 1, если не менее двух величин из
разряд равно 1, если не менее двух величин из  равны 1, где
равны 1, где  разряды чисел
разряды чисел  а
а  перенос из
перенос из  -го разряда;
-го разряда;
значение разряда суммы  чисел
чисел  равно 1, если нечетное число величин
равно 1, если нечетное число величин  равно 1. Для наглядности поясним эти правила примером:
равно 1. Для наглядности поясним эти правила примером:

Понятно, что значение переноса в первый разряд  Если при сложении разрядная сетка не переполняется, то перенос
Если при сложении разрядная сетка не переполняется, то перенос  в старший
в старший  разряд отсутствует
разряд отсутствует  и
и

В общем случае перенос  Разряды чисел
Разряды чисел  можно подавать на суммирующее устройство последовательно или парллельно. В соответствии с этим они подразделяются на последовательные и параллельные сумматоры.
можно подавать на суммирующее устройство последовательно или парллельно. В соответствии с этим они подразделяются на последовательные и параллельные сумматоры.
Рассмотрим последовательный двоичный сумматор, который должен производить сложение двух чисел, поступающих на его входы, начиная с младших разрядов. Числа вводятся в сумматор последовательно, разряд за разрядом, синхронно с тактовым сигналом. Сумматор в каждом такте должен вычислять значение разряда  суммы
суммы

при поступлении на его входы соответствующих разрядов слагаемых  с учетом переноса
с учетом переноса  из предыдущего разряда. При этом в сумматоре должен запоминаться (задерживаться на один такт) перенос
из предыдущего разряда. При этом в сумматоре должен запоминаться (задерживаться на один такт) перенос  в следующий разряд.
в следующий разряд.
Таким образом, синхронный автомат, выполняющий функцию последовательного сумматора, должен иметь два информационных входа для подачи разрядов чисел  и один выход, на который автомат последовательно выдает разряды
и один выход, на который автомат последовательно выдает разряды  суммы этих чисел. С точки зрения автомата разряды чисел
суммы этих чисел. С точки зрения автомата разряды чисел  неразличимы, т. е.
неразличимы, т. е.

Автомат должен иметь один элемент памяти (триггер)  для запоминания переноса
для запоминания переноса  в следующий разряд
в следующий разряд  Перед началом сложения чисел триггер
Перед началом сложения чисел триггер  необходимо устанавливать в 0, так как перенос
необходимо устанавливать в 0, так как перенос  Для этого можно использовать асинхронный потенциальный вход триггера
Для этого можно использовать асинхронный потенциальный вход триггера  Из сказанного следует, что автомат может быть задан графом переходов, изображенным на рис. 4.16 (ветви подписаны значениями сигналов
Из сказанного следует, что автомат может быть задан графом переходов, изображенным на рис. 4.16 (ветви подписаны значениями сигналов  а узлы — значением сигнала
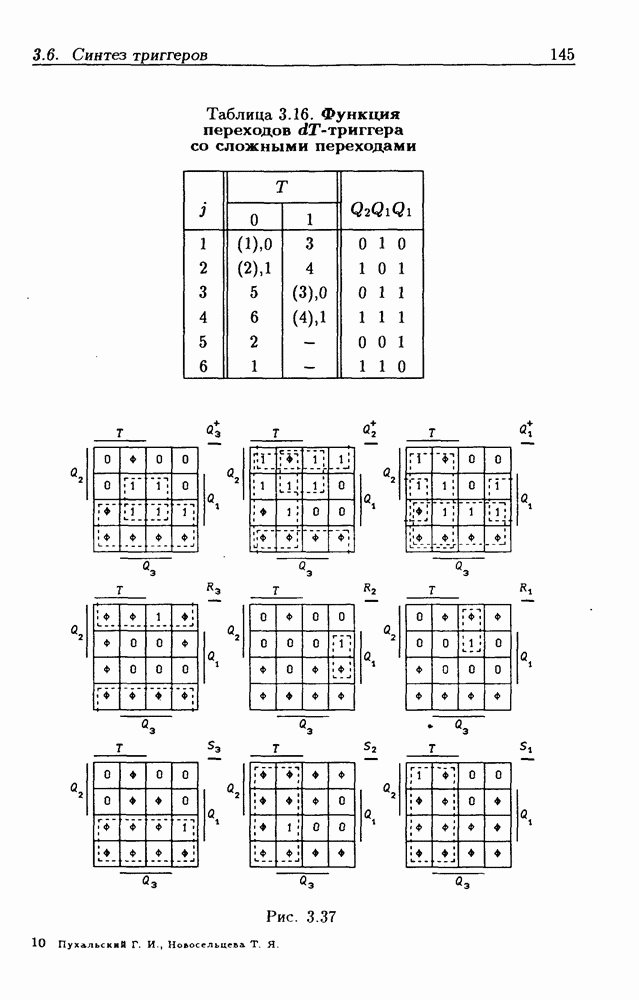
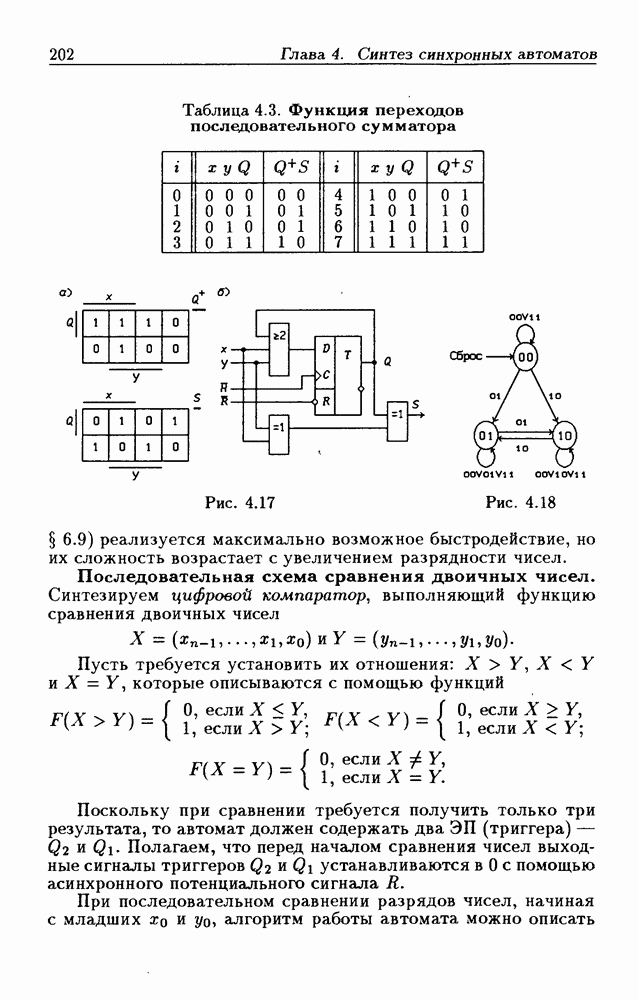
а узлы — значением сигнала  По графу переходов составляется таблица истинности (табл. 4.3), а затем диаграммы Вейча для функций
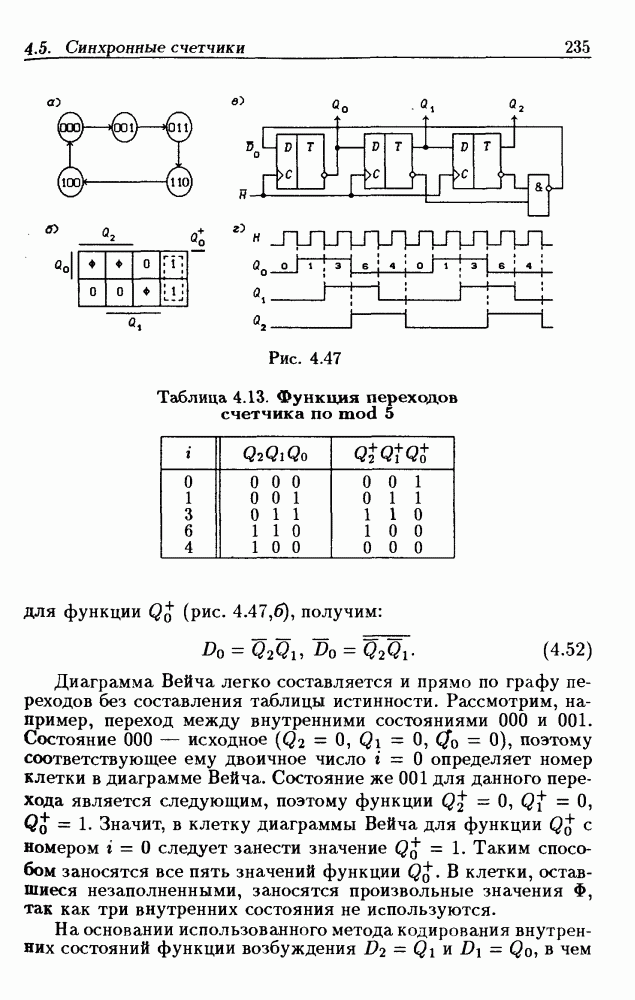
По графу переходов составляется таблица истинности (табл. 4.3), а затем диаграммы Вейча для функций  (рис. 4.17,а), из которых следует:
(рис. 4.17,а), из которых следует:


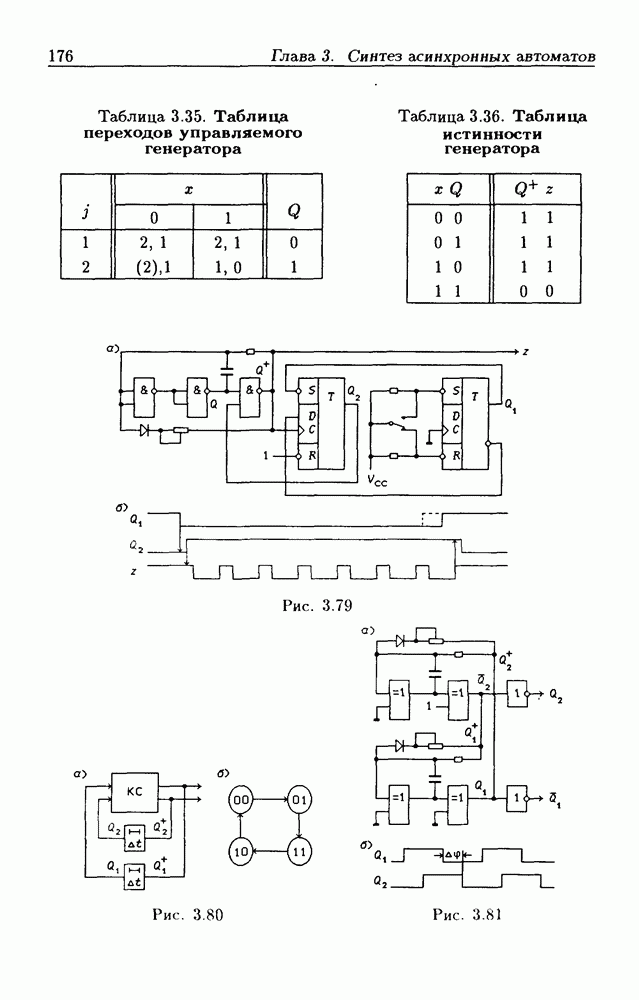
Рис. 4.16
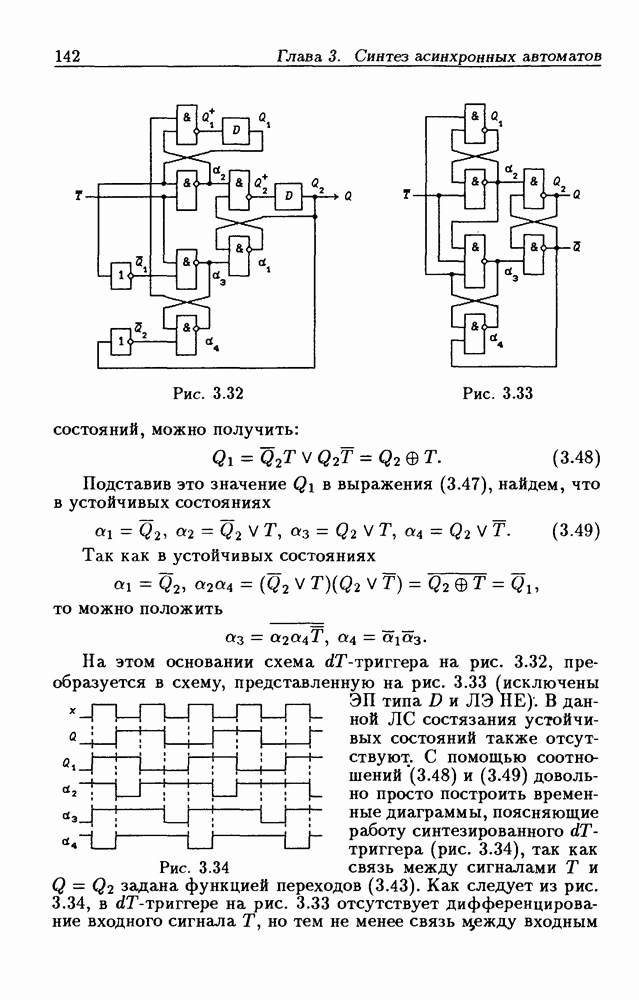
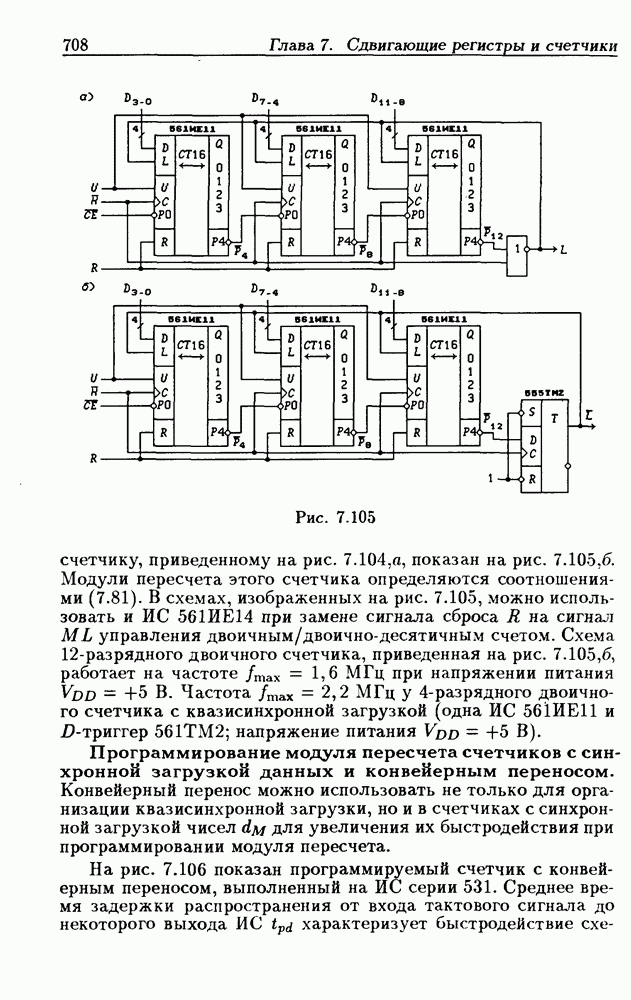
На рис.  показана схема последовательного двоичного сумматора, выполненная на
показана схема последовательного двоичного сумматора, выполненная на  -триггере, функция возбуждения
-триггере, функция возбуждения  которого реализована на трехвходовом мажоритарном элементе.
которого реализована на трехвходовом мажоритарном элементе.
Сложность (стоимость) последовательных сумматоров не зависит от разрядности чисел  время же их сложения пропорционально числу разрядов, что является существенным недостатком этих сумматоров. В параллельных сумматорах
время же их сложения пропорционально числу разрядов, что является существенным недостатком этих сумматоров. В параллельных сумматорах
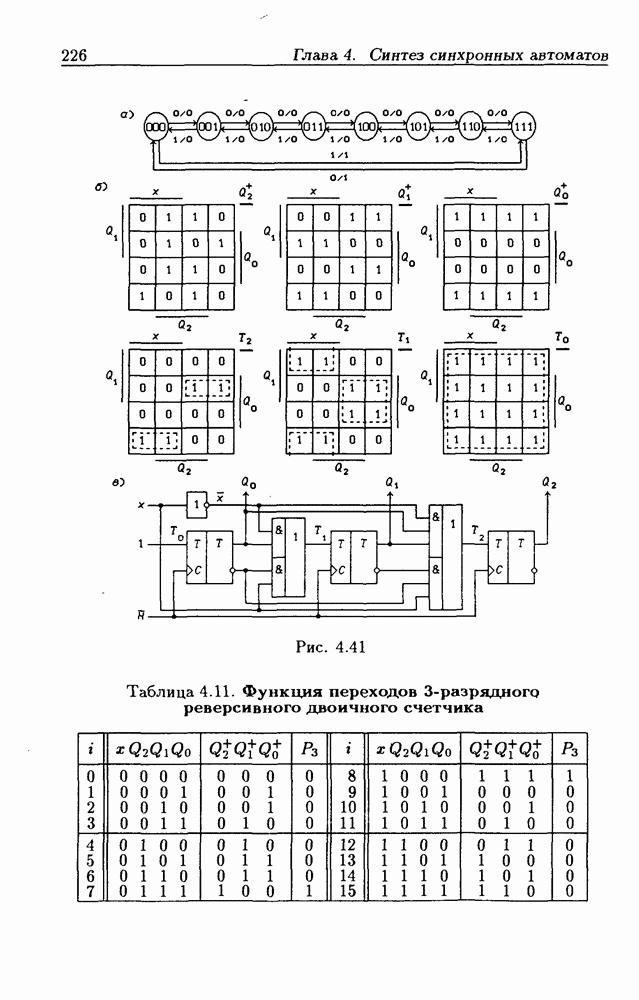
Таблица 4.3. (см. скан) Функция переходов последовательного сумматора

Рис. 4.17

Рис. 4.18
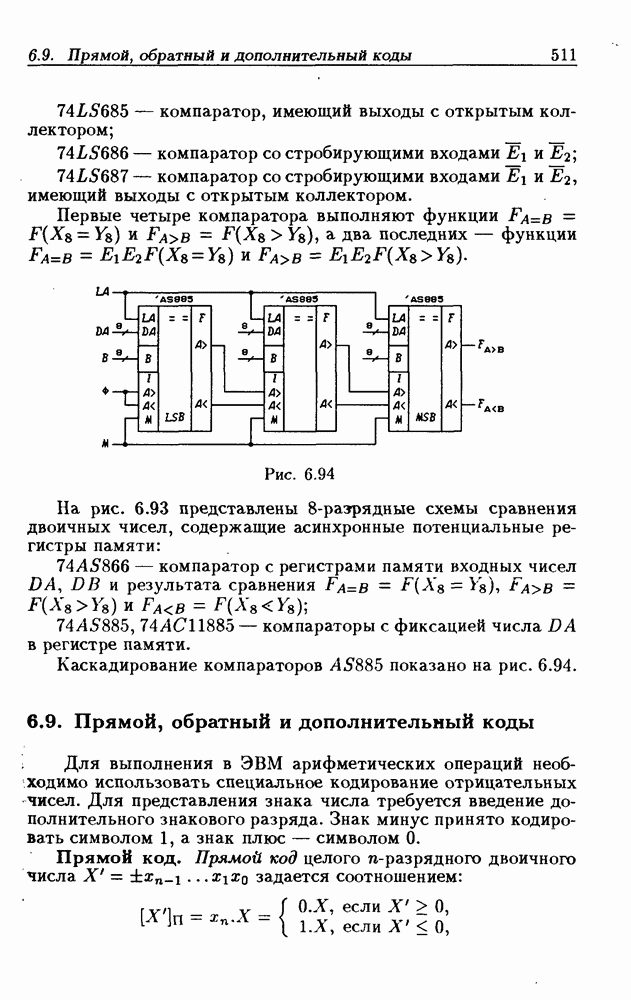
(см. § 6.9) реализуется максимально возможное быстродействие, но их сложность возрастает с увеличением разрядности чисел.
Последовательная схема сравнения двоичных чисел.
Синтезируем цифровой компаратор, выполняющий функцию сравнения двоичных чисел

Пусть требуется установить их отношения:  которые описываются с помощью функций
которые описываются с помощью функций

Поскольку при сравнении требуется получить только три результата, то автомат должен содержать два ЭП (триггера) —  Полагаем, что перед началом сравнения чисел выходные сигналы триггеров
Полагаем, что перед началом сравнения чисел выходные сигналы триггеров  устанавливаются в 0 с помощью асинхронного потенциального сигнала
устанавливаются в 0 с помощью асинхронного потенциального сигнала 
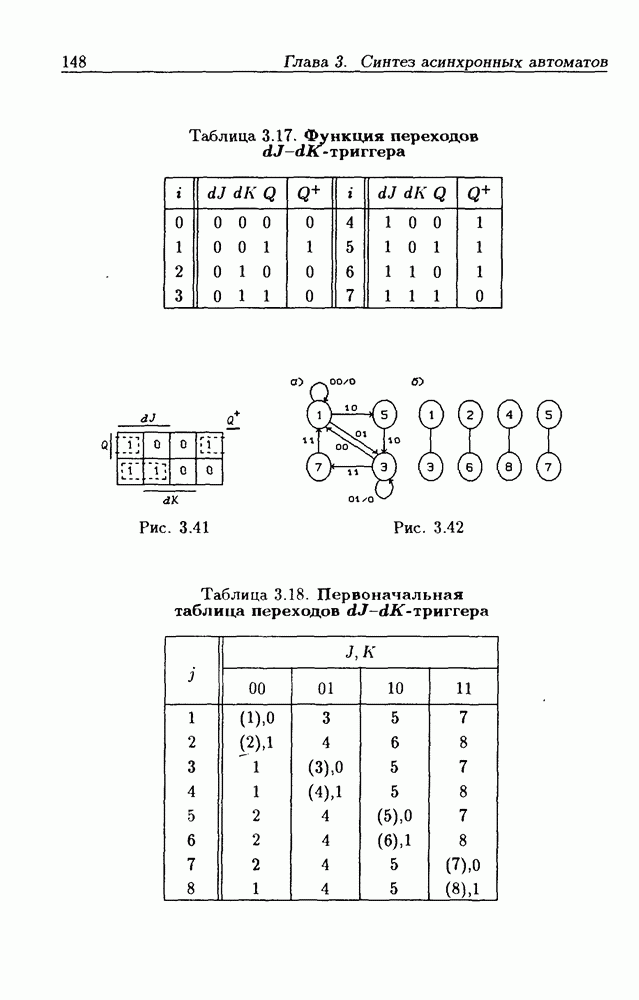
При последовательном сравнении разрядов чисел, начиная с младших  алгоритм работы автомата можно описать
алгоритм работы автомата можно описать
(см. скан)
следующим образом:
автомат находится в состоянии  до тех пор, пока значения разрядов х и у двоичных чисел
до тех пор, пока значения разрядов х и у двоичных чисел  совпадают; автомат переходит в состояние
совпадают; автомат переходит в состояние  если
если 
автомат переходит в состояние  если
если  Из данного алгоритма следует, что
Из данного алгоритма следует, что

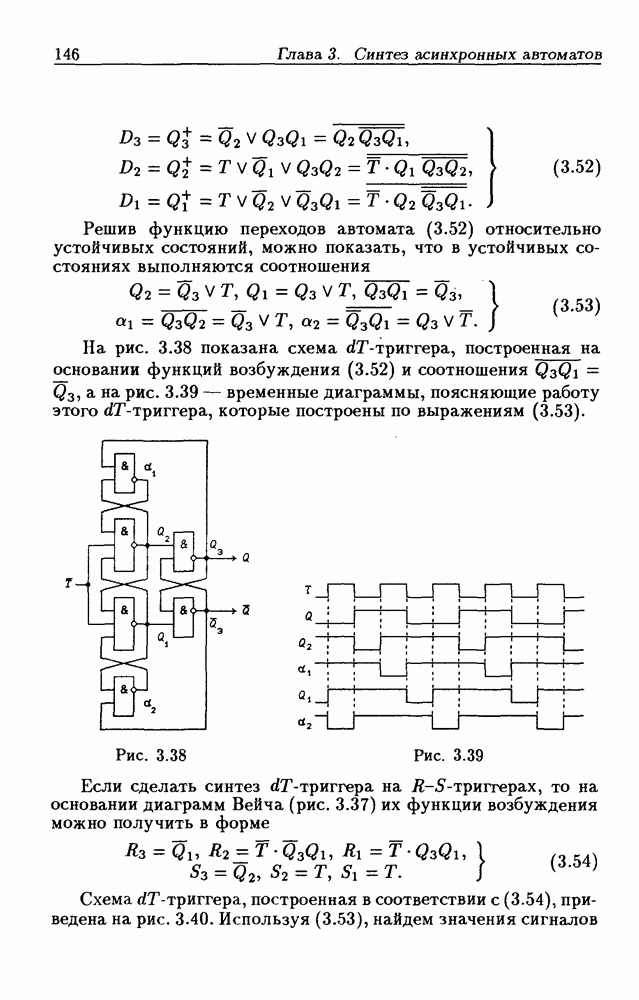
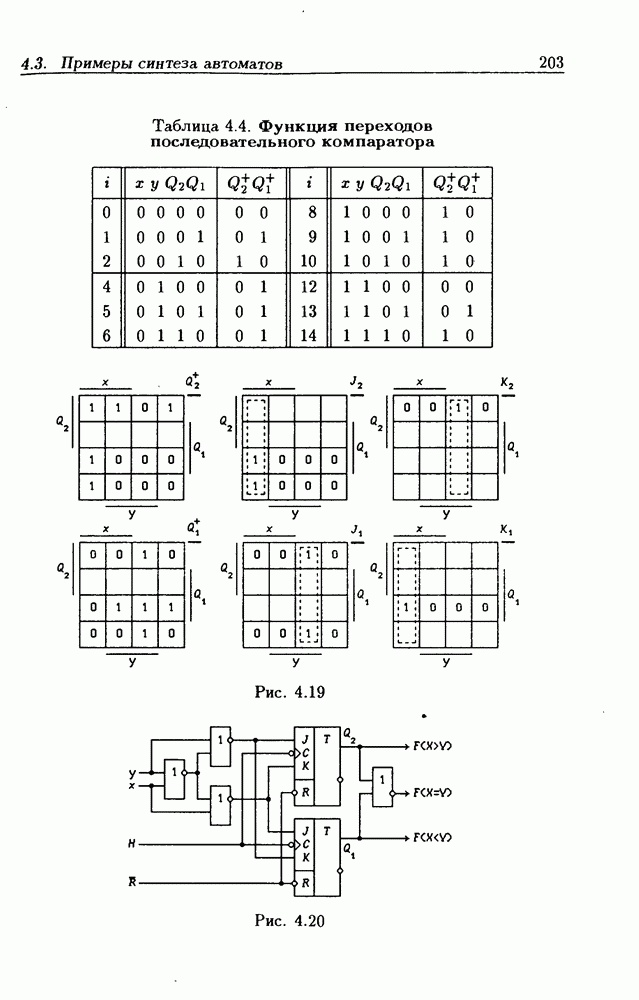
и автомат задается графом переходов, показанным на рис. 4.18 (ветви подписаны значениями только входных сигналов  так как выходные сигналы полностью определяются внутренним состоянием автомата). Составив по графу переходов таблицу истинности для функций
так как выходные сигналы полностью определяются внутренним состоянием автомата). Составив по графу переходов таблицу истинности для функций  (табл. 4.4), а затем диаграммы Вейча (рис. 4.19; пустым клеткам соответствуют неопределенные значения) для функций возбуждения
(табл. 4.4), а затем диаграммы Вейча (рис. 4.19; пустым клеткам соответствуют неопределенные значения) для функций возбуждения  -триггеров, получим:
-триггеров, получим:

На рис. 4.20 показана последовательная схема сравнения двоичных чисел, выполненная на  -триггерах в соответствии с полученными формами функций. Сложность последовательных компараторов не зависит от разрядности чисел
-триггерах в соответствии с полученными формами функций. Сложность последовательных компараторов не зависит от разрядности чисел  время же сравнения чисел пропорционально числу разрядов, что является их существенным недостатком. Понятно, что синтезированный компаратор может быть использован и для сравнения десятичных чисел, представленных в двоично-десятичном коде 8-4-2-1.
время же сравнения чисел пропорционально числу разрядов, что является их существенным недостатком. Понятно, что синтезированный компаратор может быть использован и для сравнения десятичных чисел, представленных в двоично-десятичном коде 8-4-2-1.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Глава 1. Основы теории переключательных функций
- 1.2. Позиционные системы счисления
- 1.3. Переключательные функции
- 1.4. Принцип и закон двойственности
- 1.5. Теоремы разложения
- 1.6. Решение систем логических уравнений
- 1.7. Первичные термы, минтермы и макстермы
- 1.8. Совершенные нормальные формы представления функций
- 1.9. Конъюнктивные и дизъюнктивные термы
- 1.10. Минимизация переключательных функций
- 1.11. Диаграммы Вейча
- 1.12. Минимизация неполностью определенных функций, совместная минимизация нескольких функций
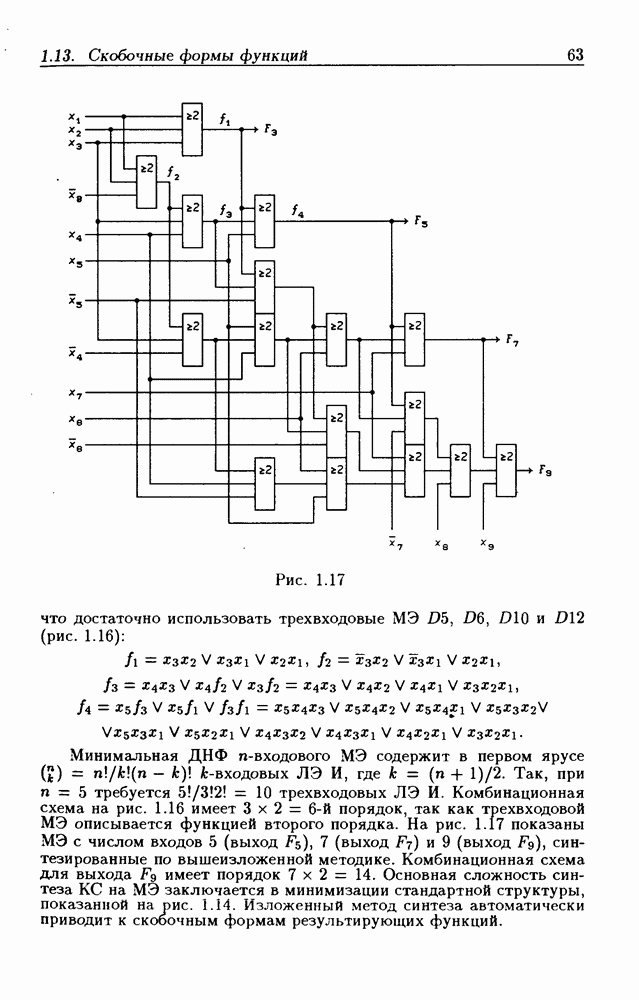
- 1.13. Скобочные формы функций
- 1.14. Закон двойственности для логических схем
- 1.15. Линейные функции
- Глава 2. Анализ и синтез логических схем
- 2.2. Модели логических элементов
- 2.3. Модели логических схем
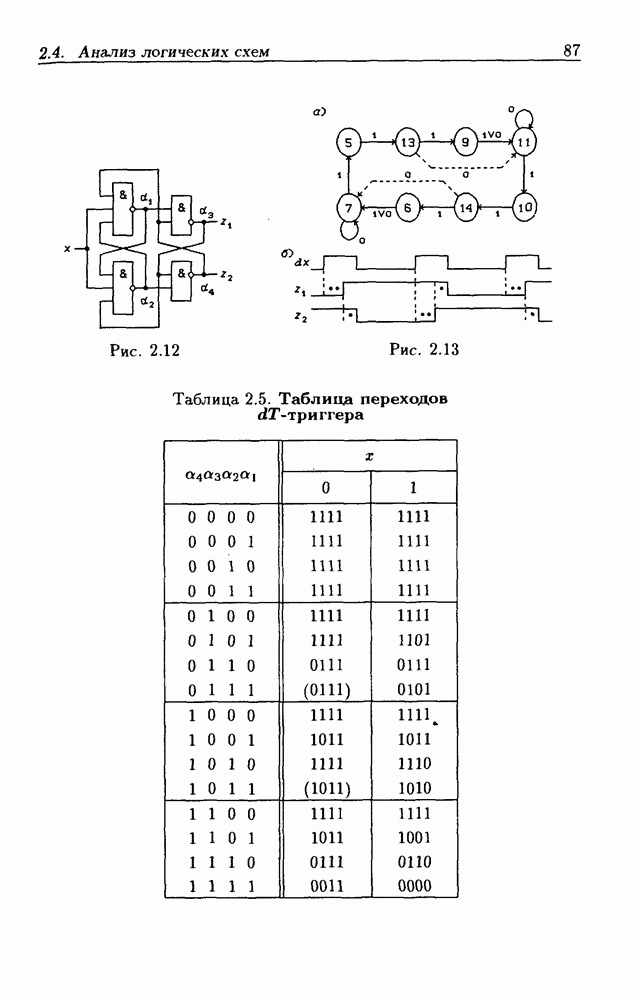
- 2.4. Анализ логических схем
- 2.5. Синтез комбинационных схем, свободных от состязаний
- Глава 3. Синтез асинхронных потенциальных автоматов
- 3.2. Асинхронные потенциальные автоматы
- 3.3. Асинхронные потенциальные триггеры и элементы памяти
- Триггеры типа R-S
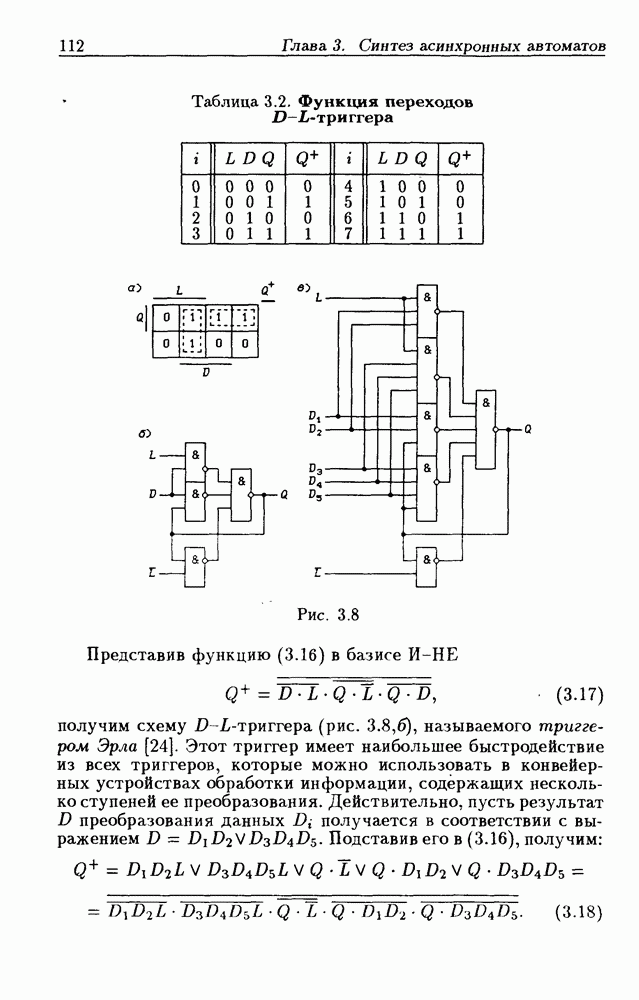
- Триггеры типа D-L
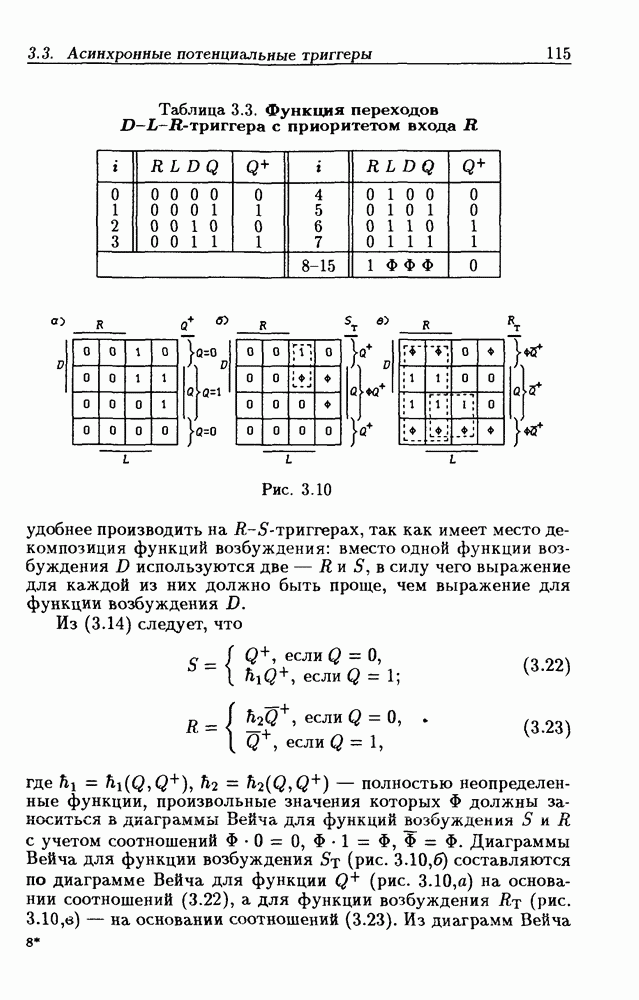
- Триггеры типа D-L-R с приоритетом входа R.
- Триггеры типа D-L-R с приоритетом входа L.
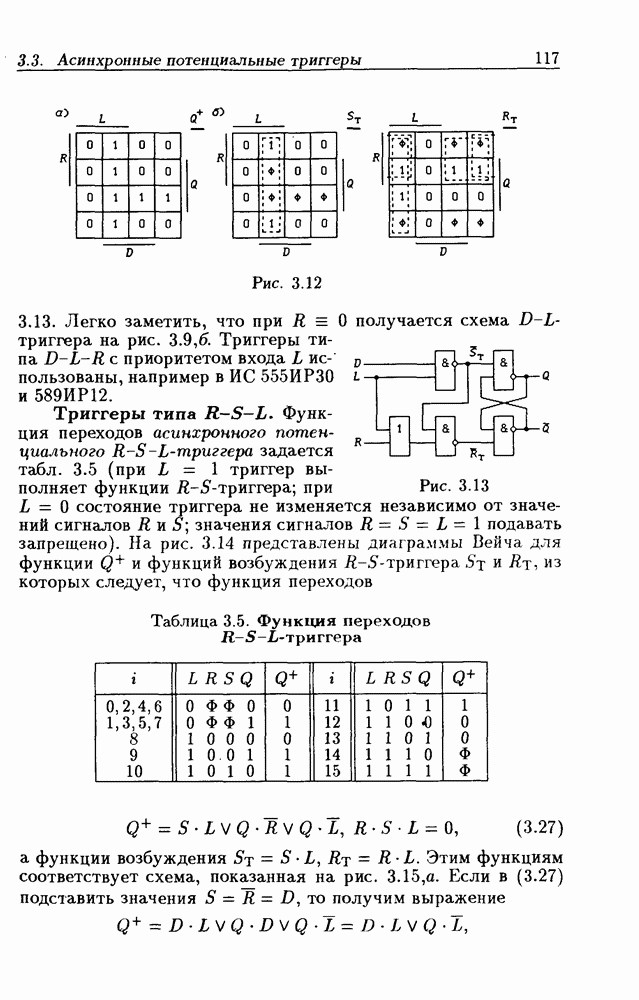
- Триггеры типа R-S-L.
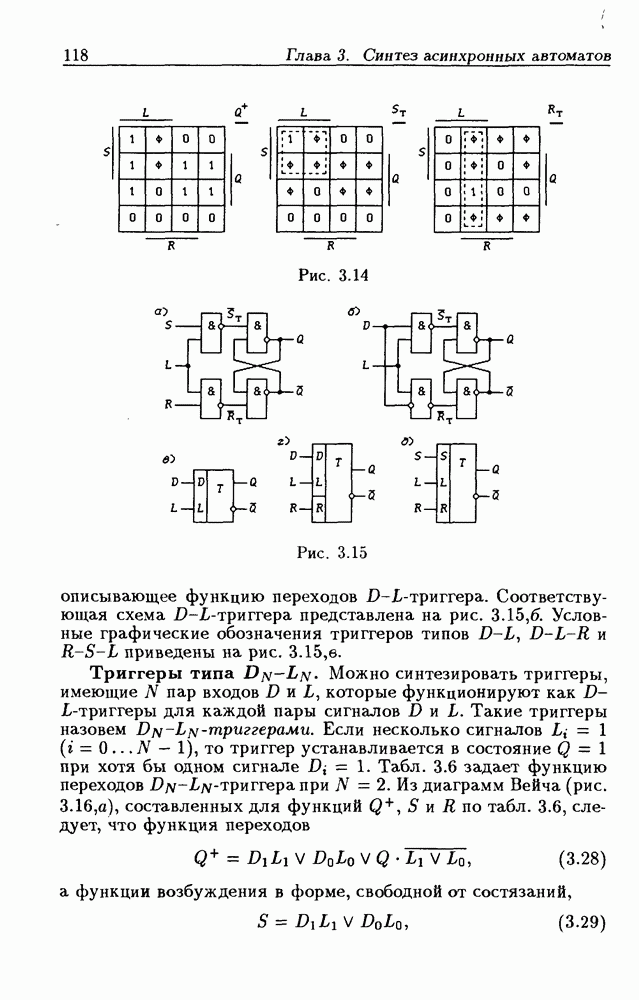
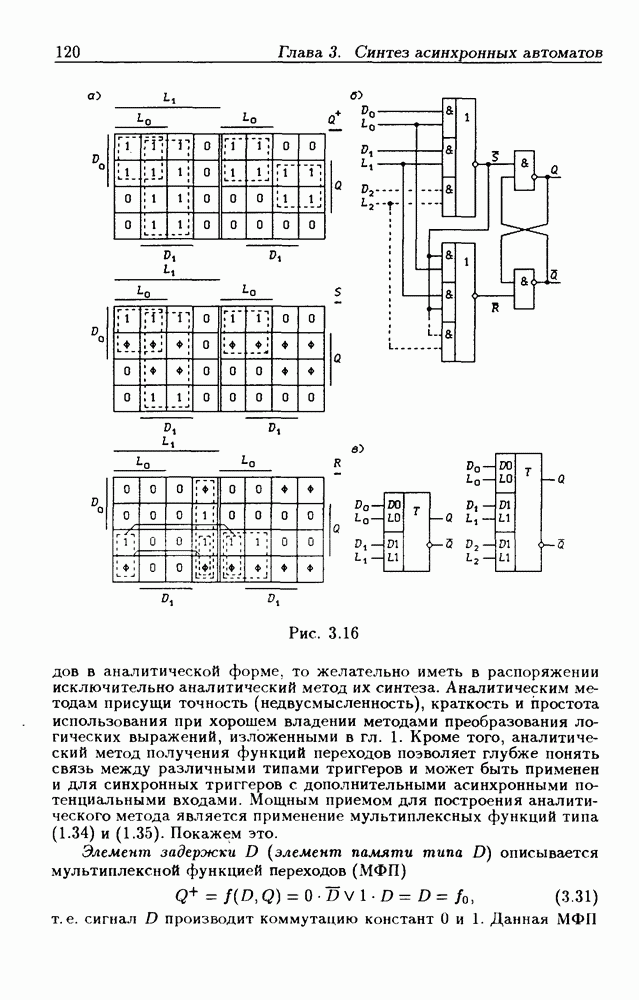
- Триггеры типа DN-LN
- Аналитический метод синтеза и анализа триггеров.
- 3.4. Задание асинхронных потенциальных автоматов таблицами и графами переходов
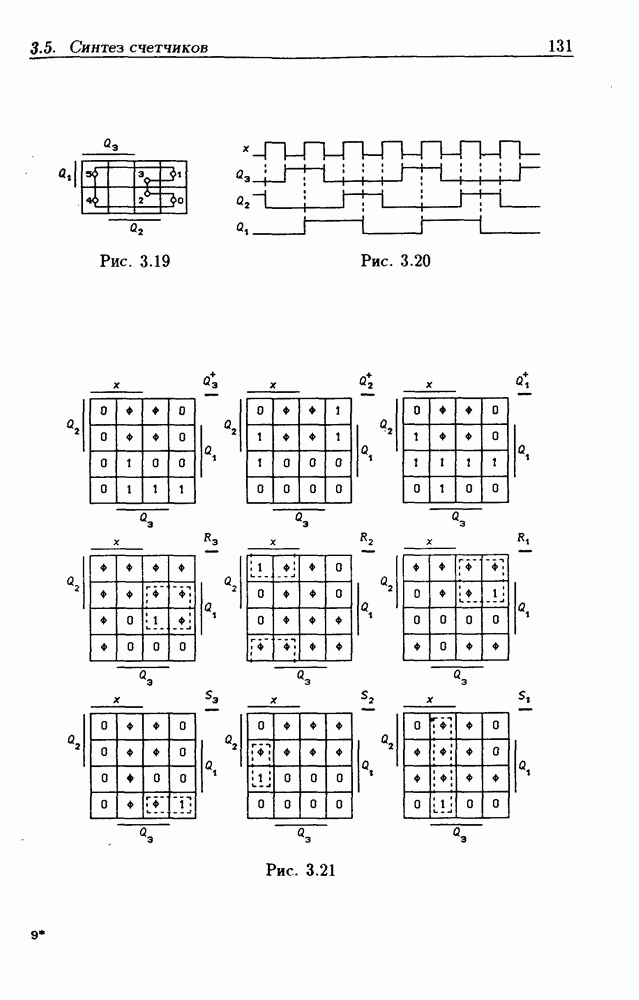
- 3.5. Синтез асинхронных потенциальных счетчиков
- 3.6. Синтез асинхронных импульсных триггеров
- Триггеры типа dJ-dK.
- Классификация триггеров.
- 3.7. Синтез синхронных триггеров
- Триггеры типа J-K
- Синхронно-асинхронные триггеры.
- 3.8. Примеры синтеза асинхронных потенциальных автоматов
- Цифровые фазочастотные детекторы.
- Квантизатор временных интервалов.
- 3.9. Генераторы сигналов
- Автогенераторы.
- Управляемые автогенераторы.
- Глава 4. Синтез синхронных автоматов
- 4.2. Синхронные триггеры
- Триггеры типов D и R-S с импульсным тактовым сигналом.
- Синхронные триггеры типов R-S и D-L
- Синхронно-асинхронные триггеры.
- Синхронные триггеры типа J-K
- Триггеры типа Т.
- Классификация синхронных триггеров.
- Преобразования типов синхронных триггеров.
- Триггеры типов D-T-L и D-T-L/R
- Функции переходов синхронно-асинхронных триггеров.
- 4.3. Примеры синтеза синхронных автоматов
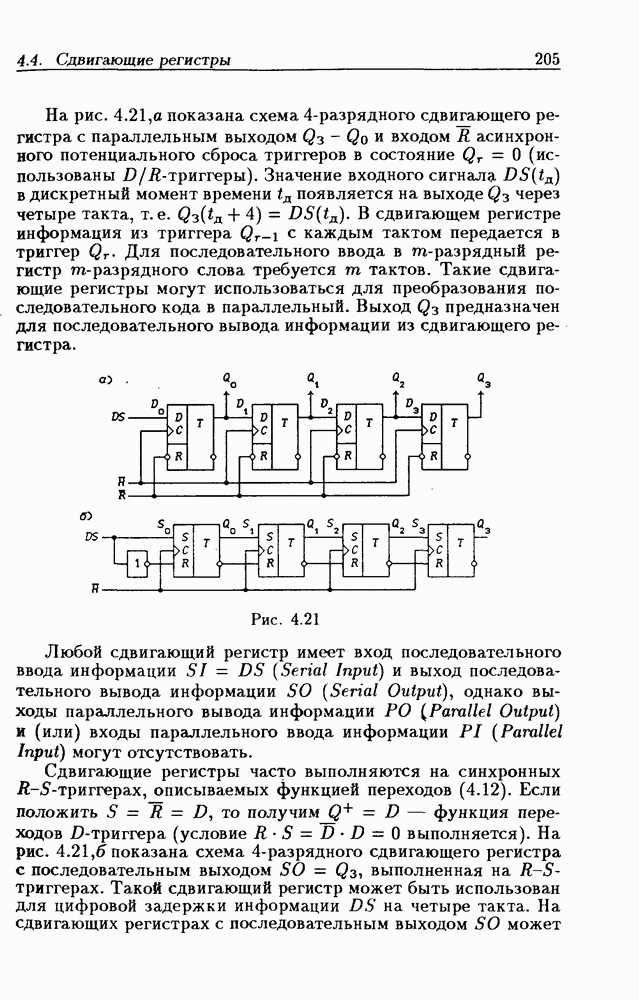
- 4.4. Сдвигающие регистры
- Синтез счетчиков на сдвигающих регистрах.
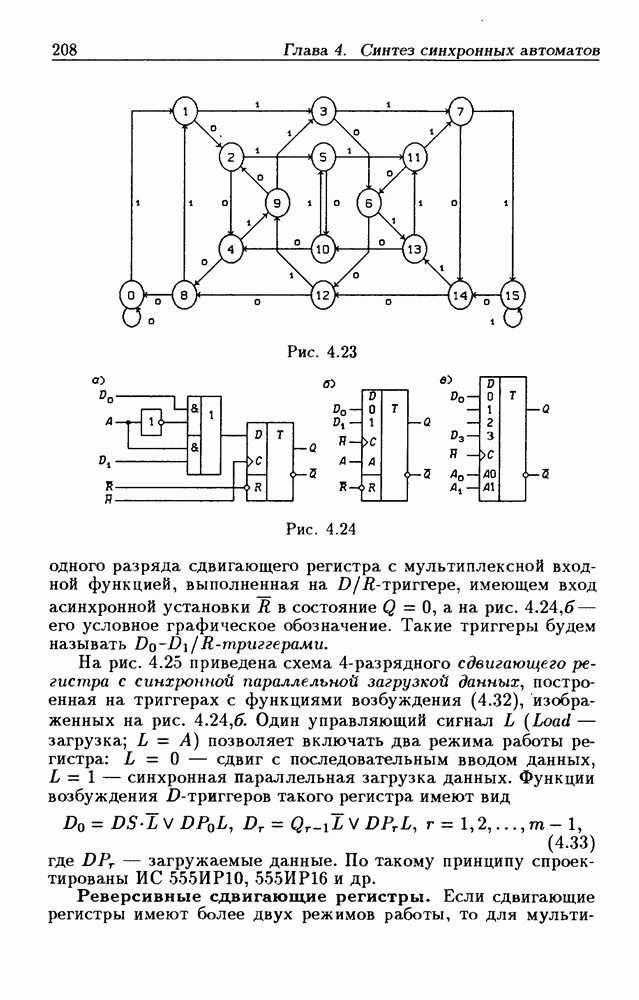
- Сдвигающие регистры с загрузкой данных.
- Реверсивные сдвигающие регистры.
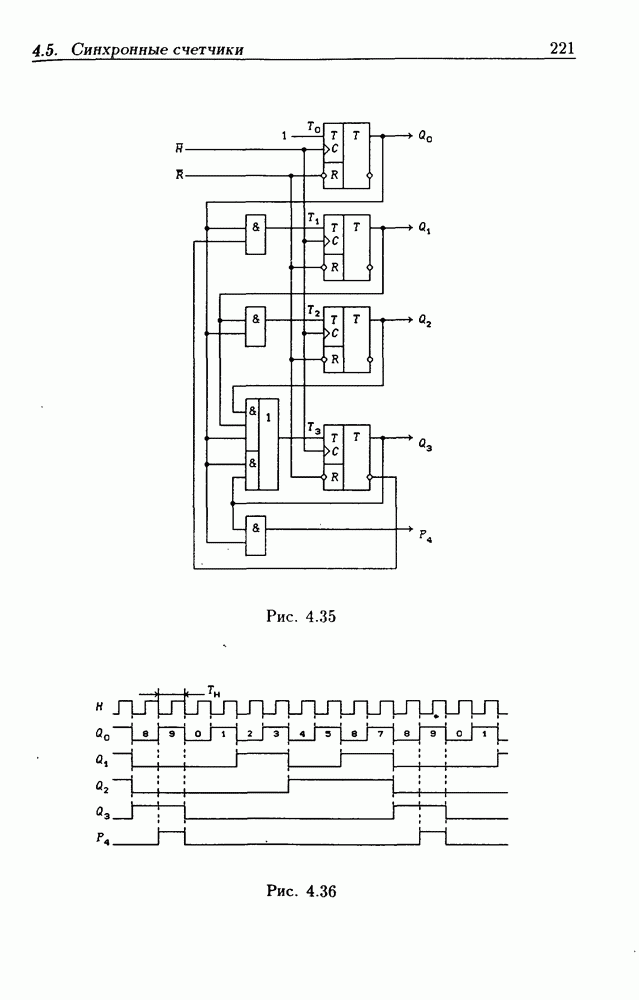
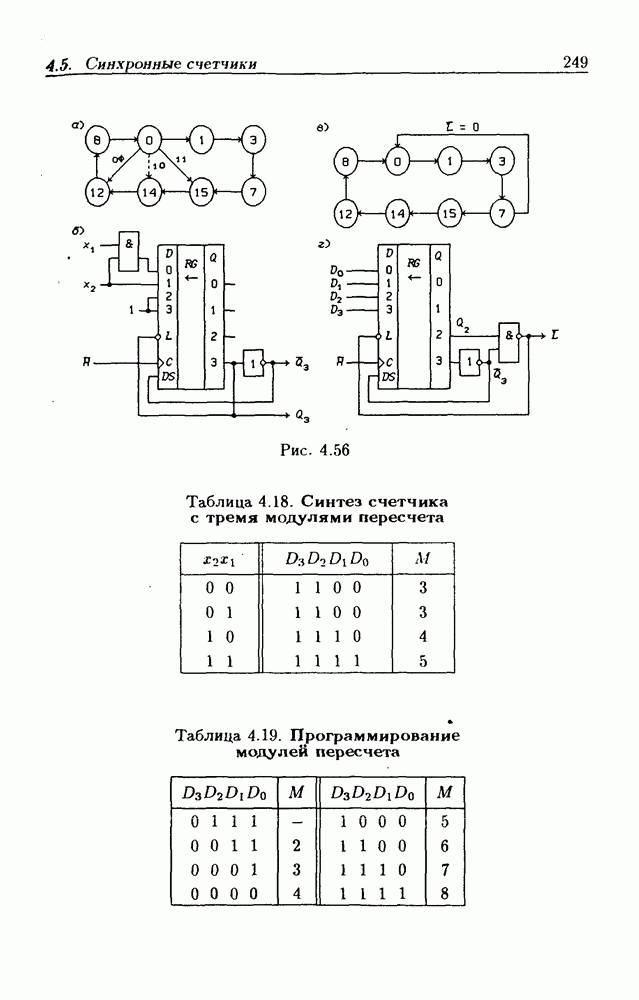
- 4.5. Синхронные счетчики
- Синхронные двоичные счетчики.
- Синхронные двоично-десятичные счетчики.
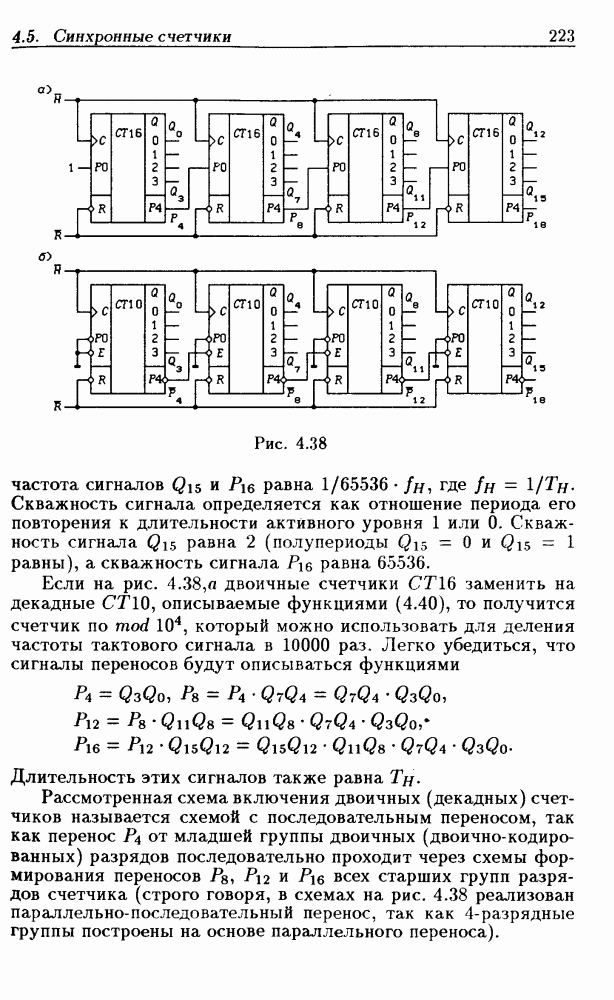
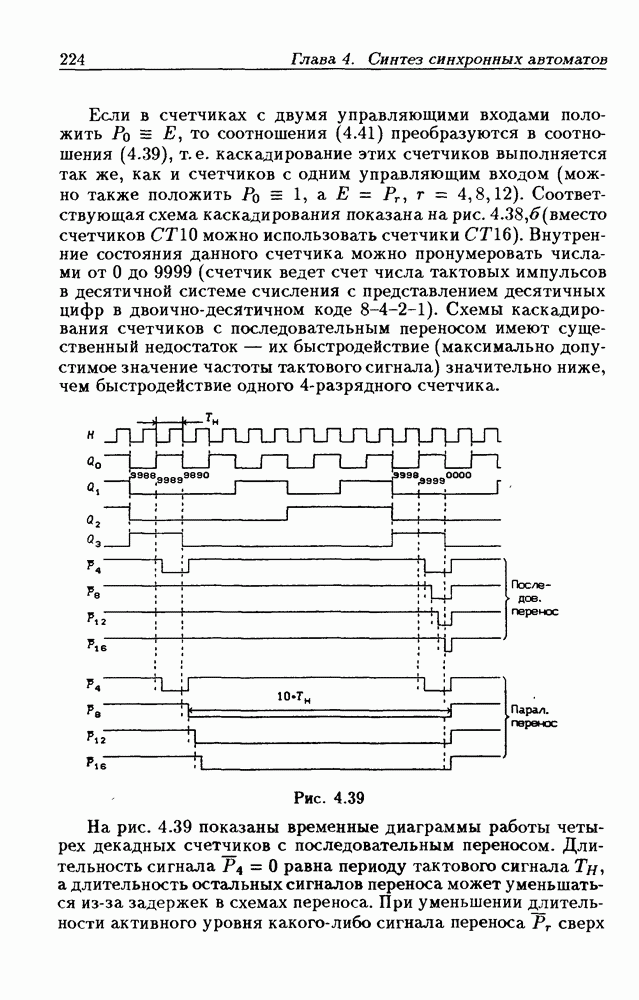
- Каскадирование двоичных и двоично-десятичных счетчиков.
- Синхронные двоичные реверсивные счетчики.
- Реверсивные двоично-десятичные счетчики.
- Каскадирование реверсивных счетчиков.
- Счетчики на сдвигающих регистрах.
- Кольцевые счетчики.
- Линейные счетчики.
- Программируемые счетчики.
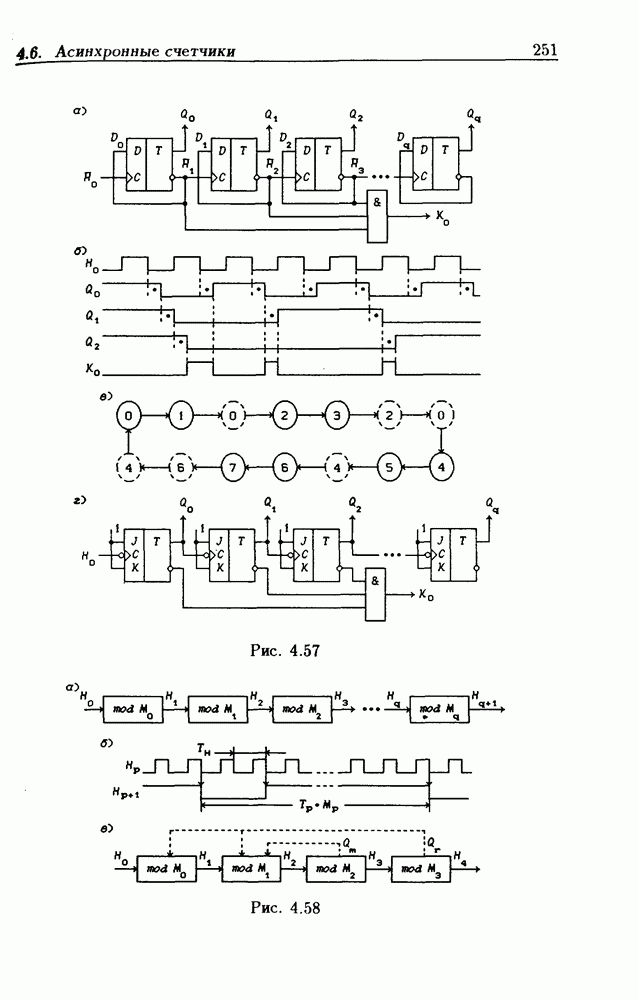
- 4.6. Асинхронные счетчики
- Асинхронные счетчики с умножением частоты счетного сигнала.
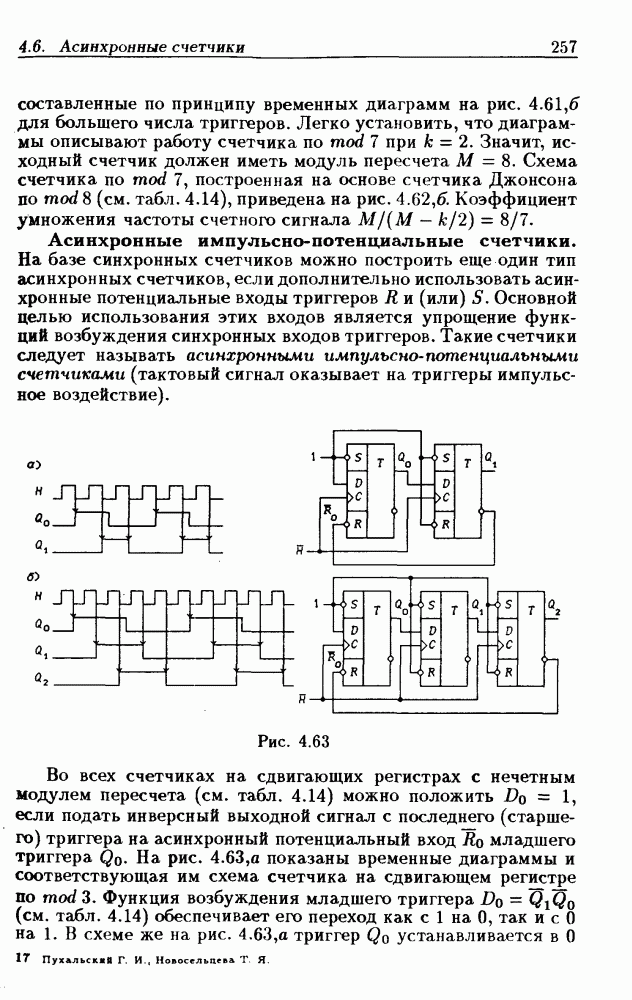
- Асинхронные импульсно-потенциальные счетчики.
- Асинхронное программирование модуля пересчета счетчиков.
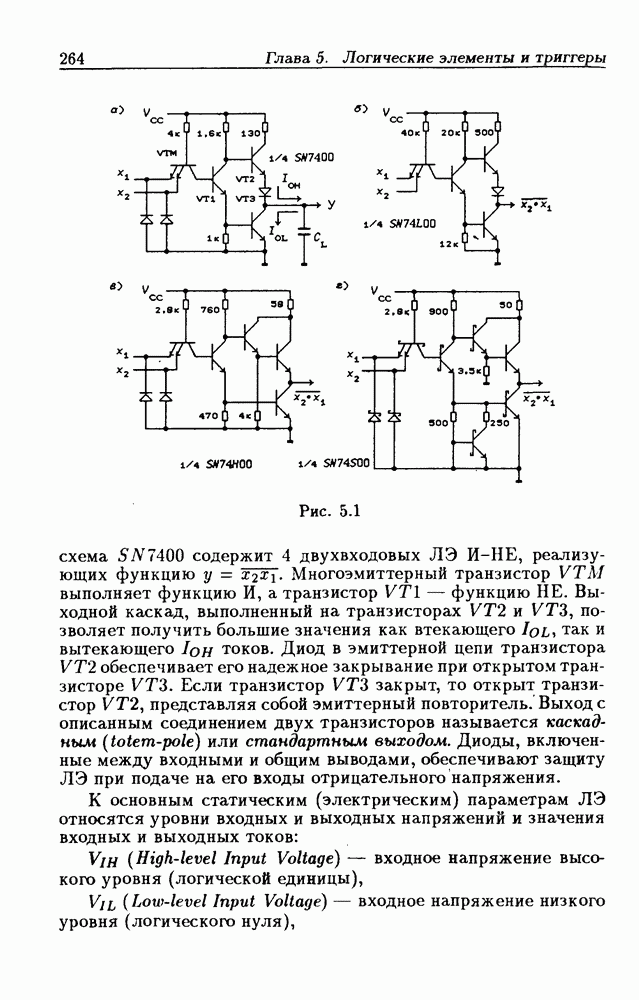
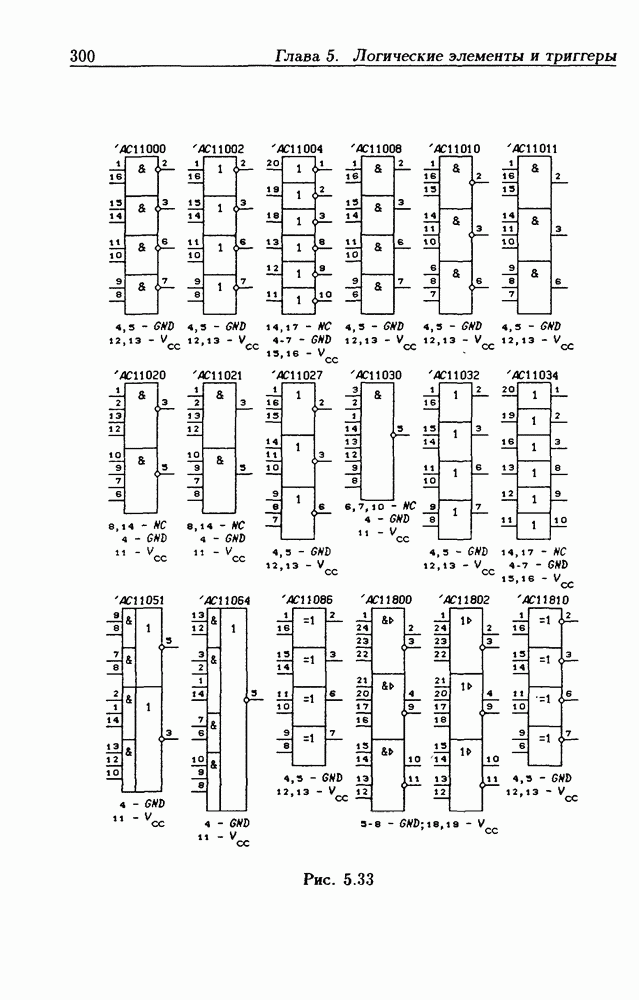
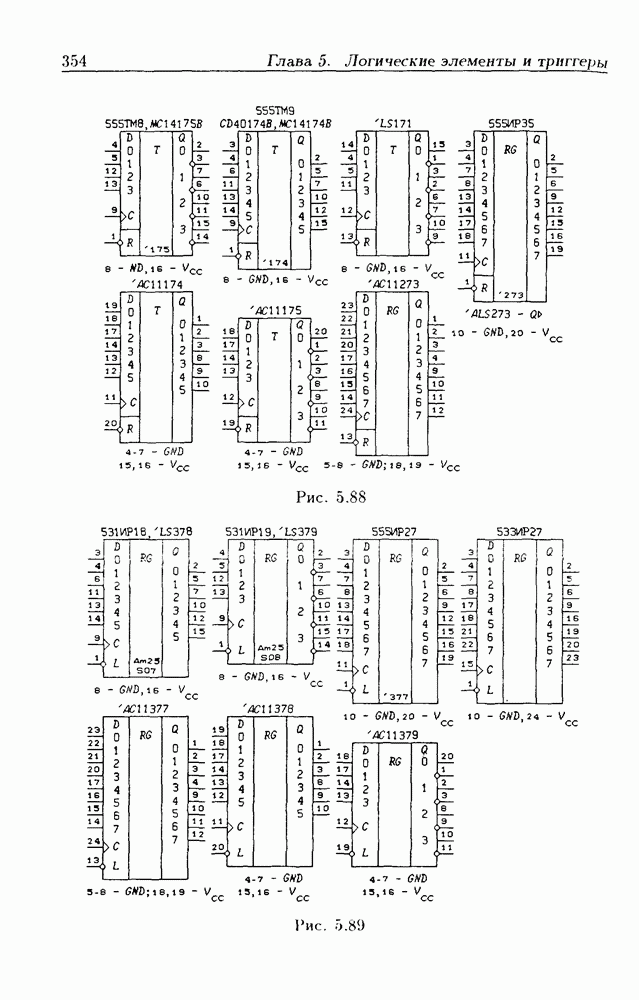
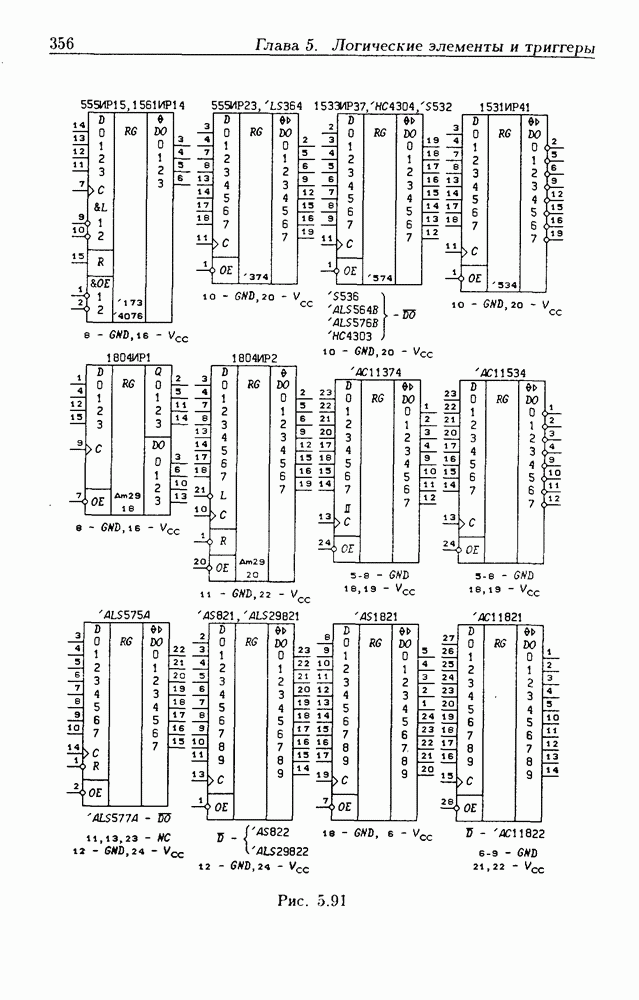
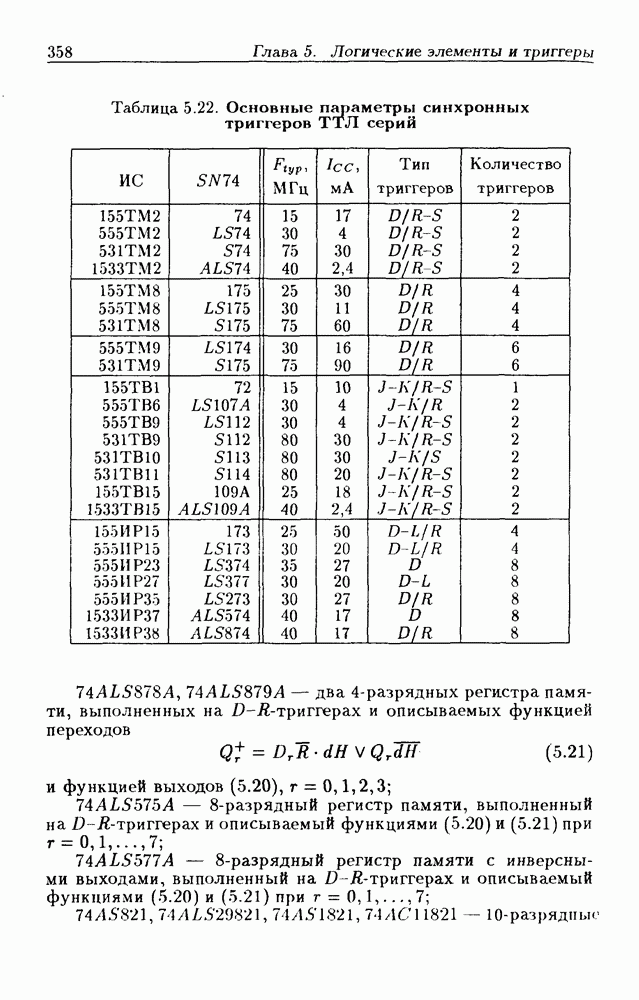
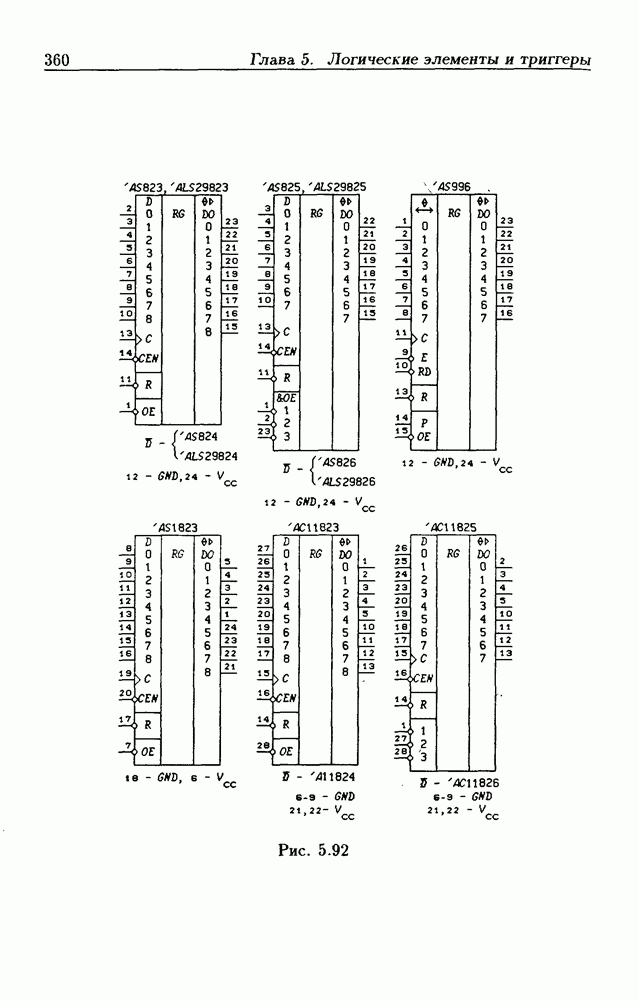
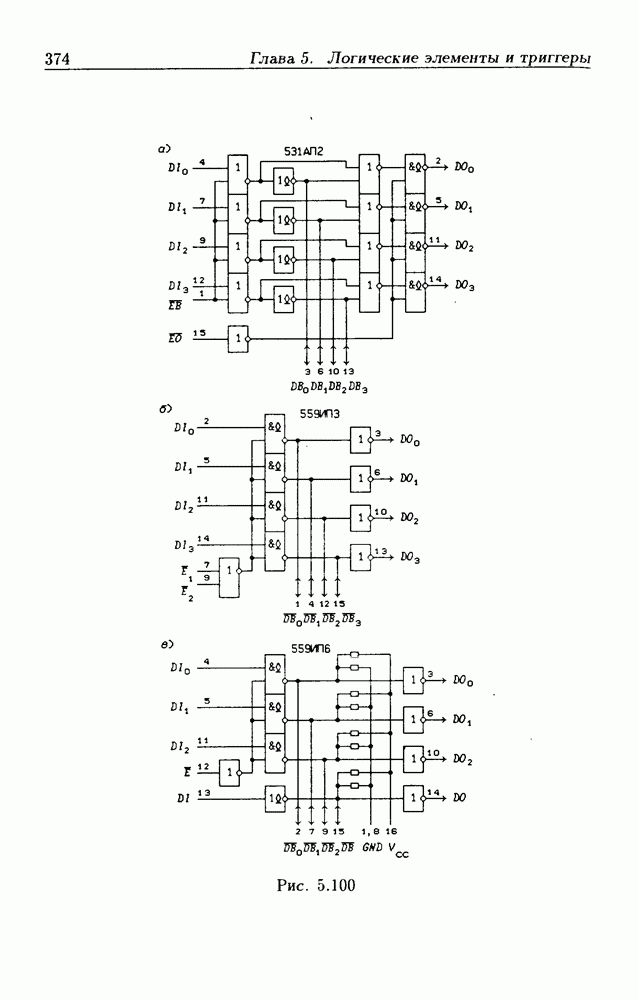
- Глава 5. Логические элементы и триггеры
- Логические элементы.
- Классификация ИС по степени интеграции.
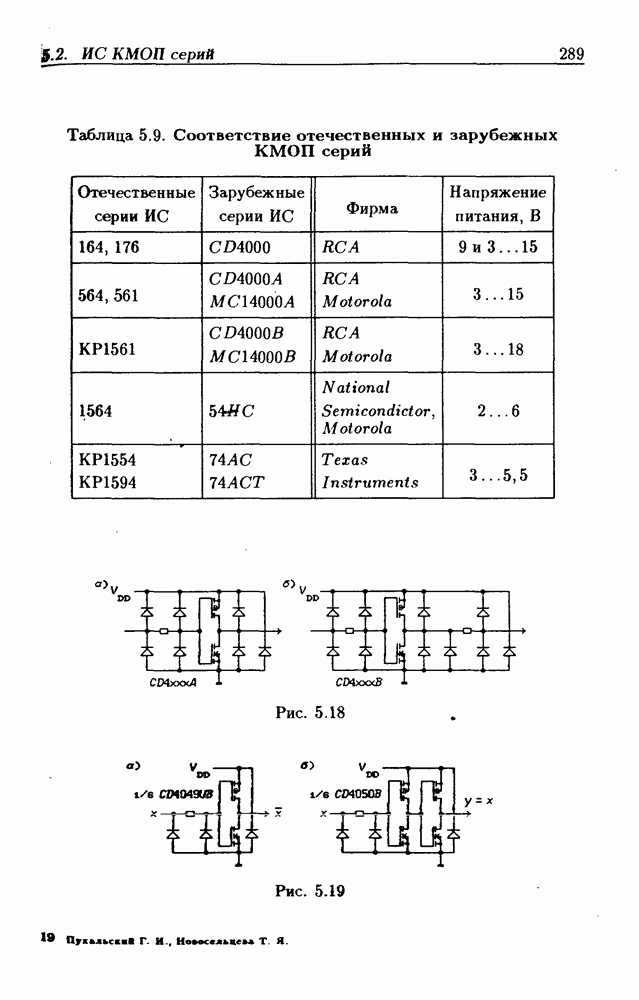
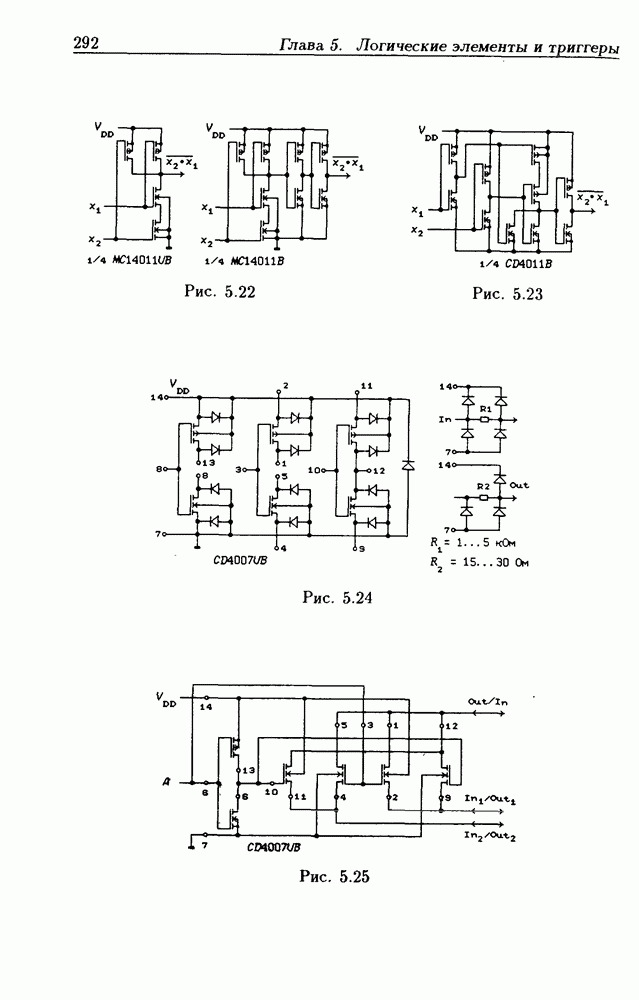
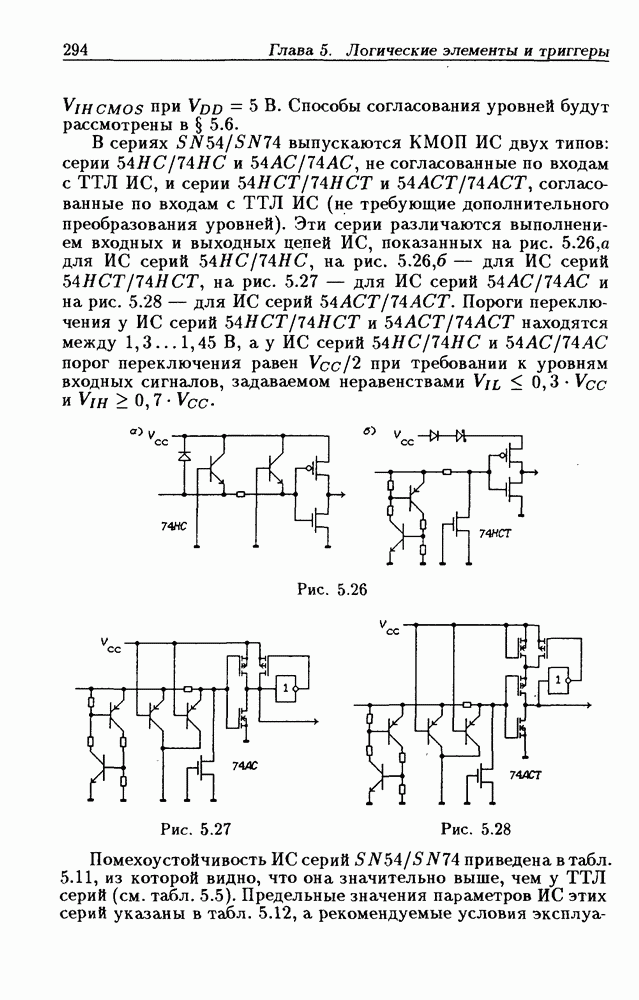
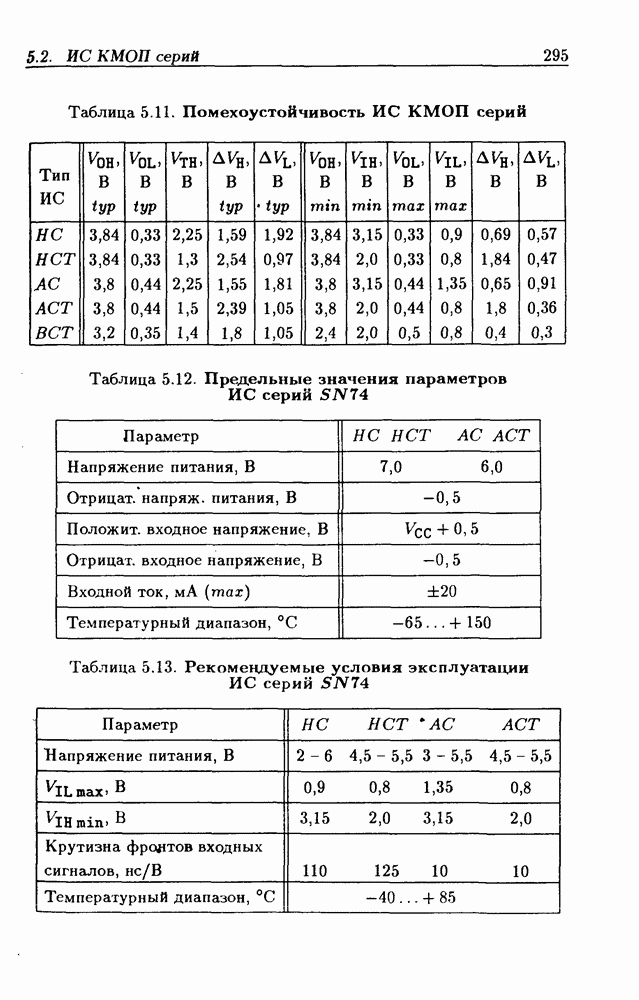
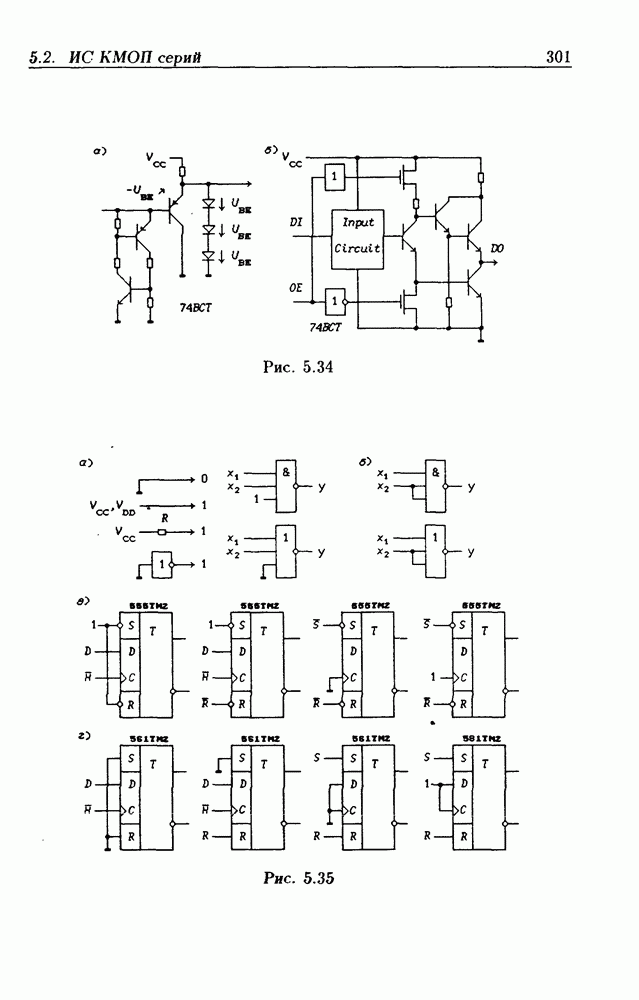
- 5.2. Интегральные схемы КМОП серий
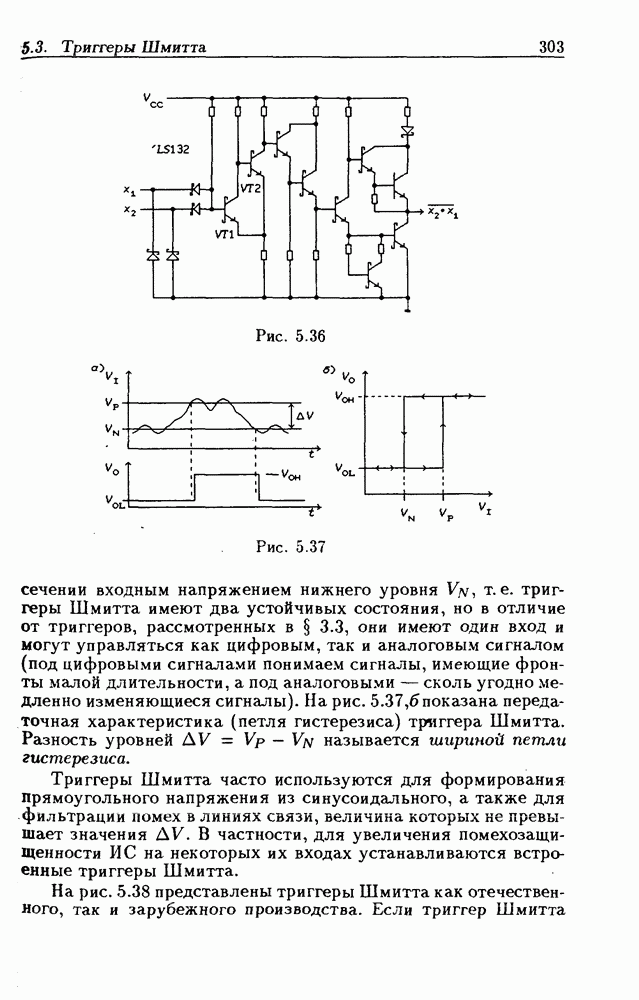
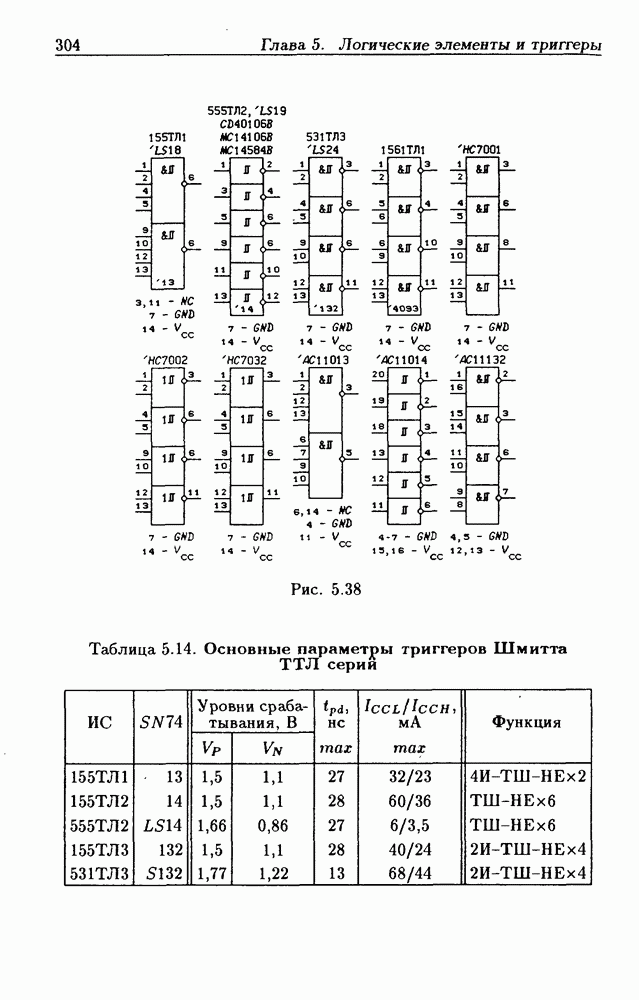
- 5.3. Триггеры Шмитта
- 5.4. Логические элементы с открытым коллекторным выходом
- Логические элементы с открытым коллекторным выходом.
- Применения ЛЭ с открытым коллекторным выходом.
- Интерфейсные ЛЭ с открытым коллекторным выходом.
- Логические элементы с открытым стоковым выходом.
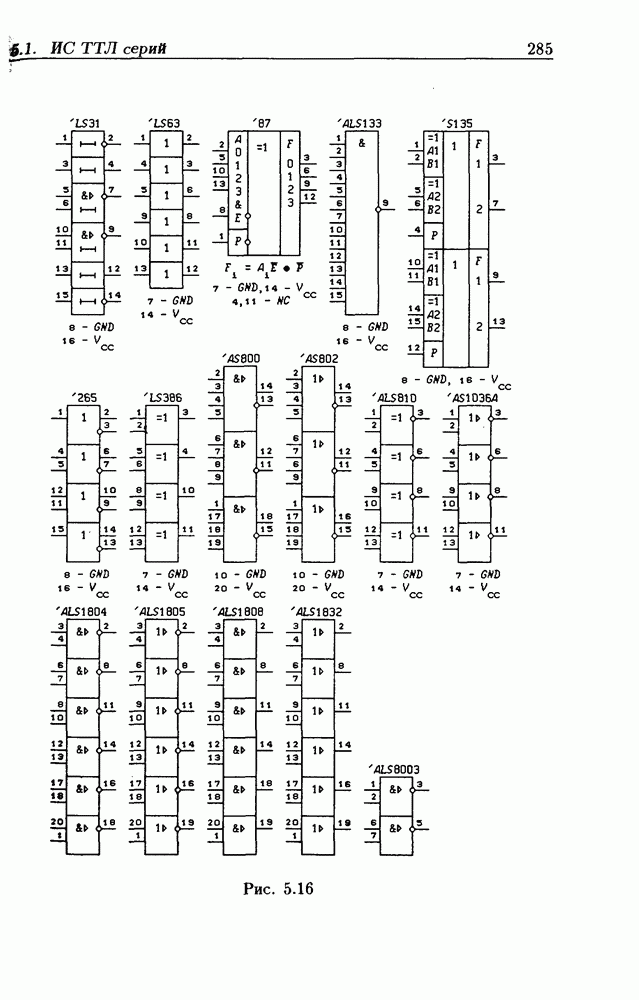
- Типовые цоколевки ИС.
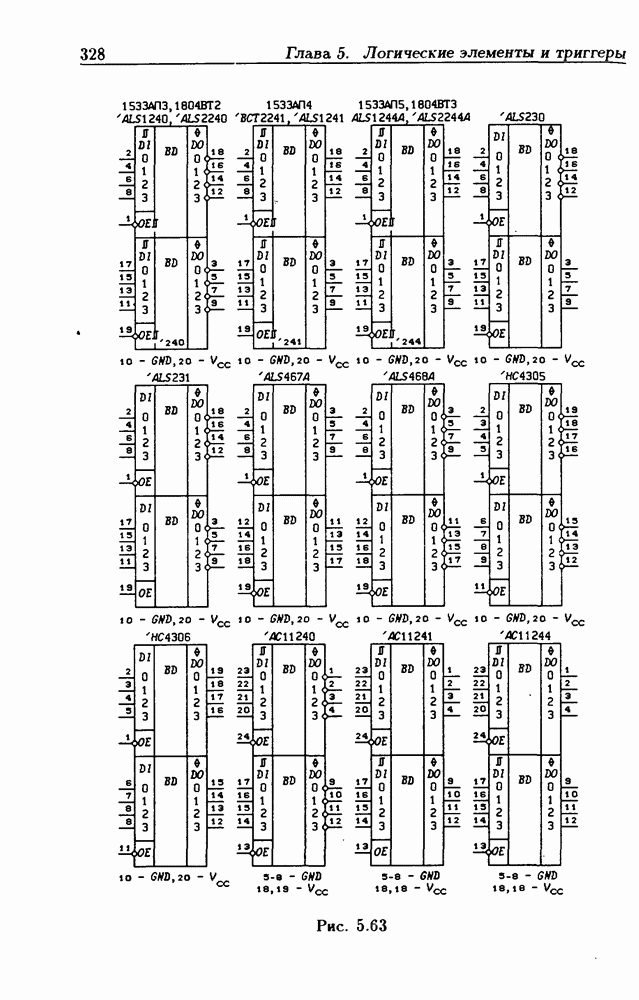
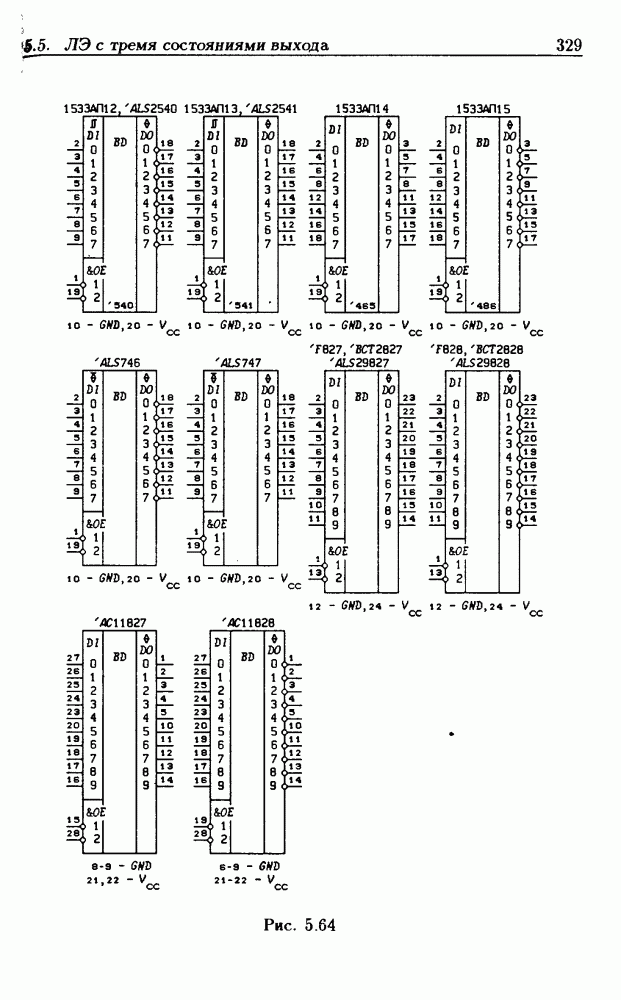
- 5.5. Логические элементы с тремя состояниями выхода
- Шинные драйверы с Z-состоянием выхода.
- Основные правила графического изображения ИС.
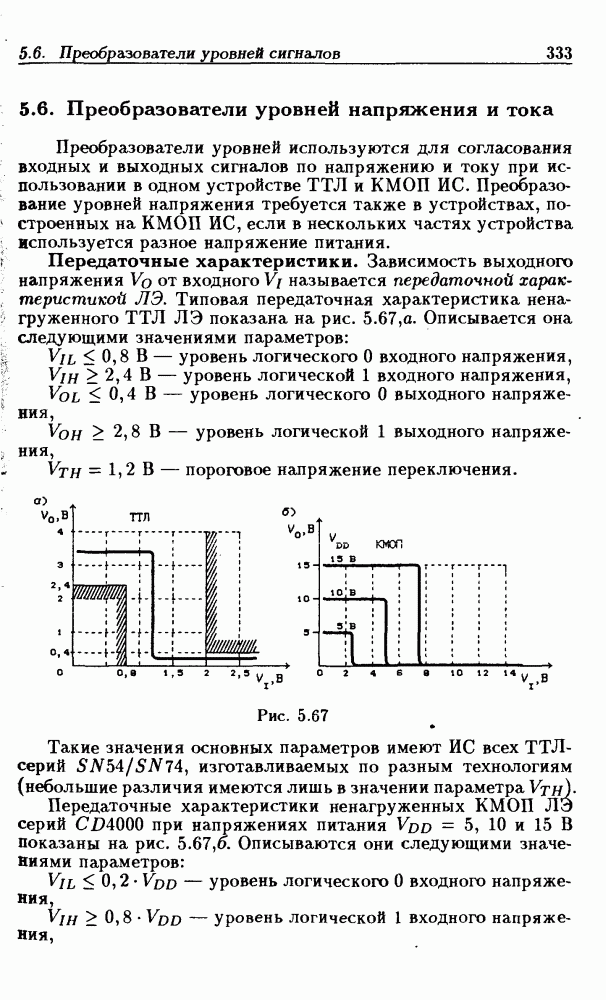
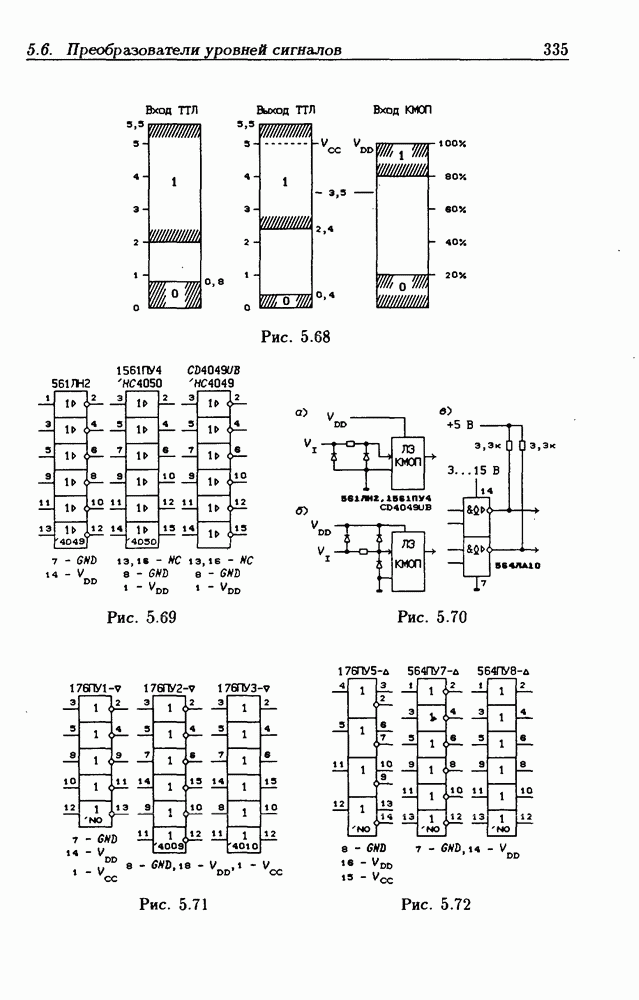
- 5.6. Преобразователи уровней напряжения и тока
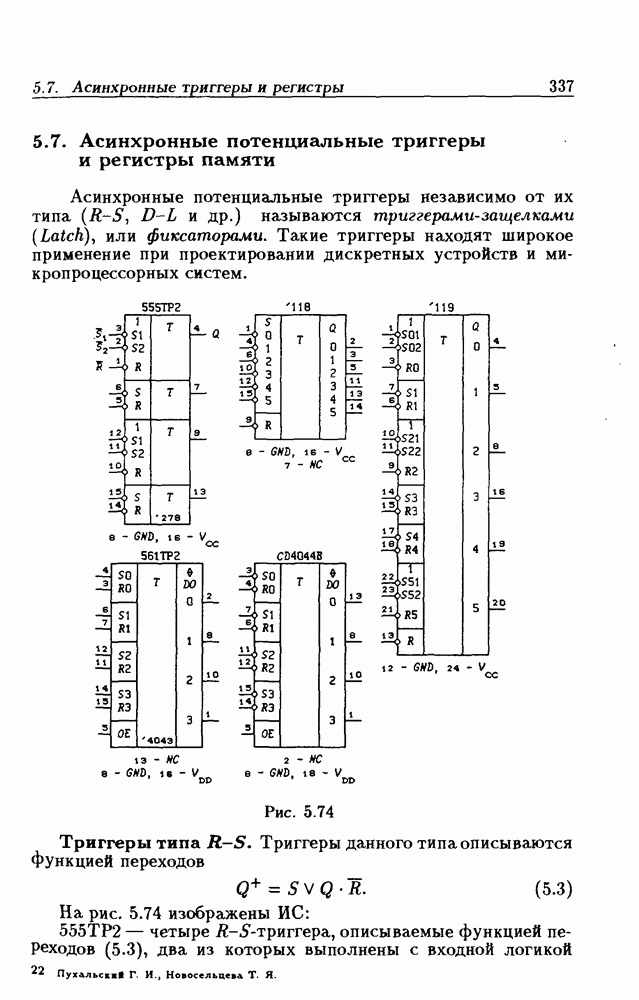
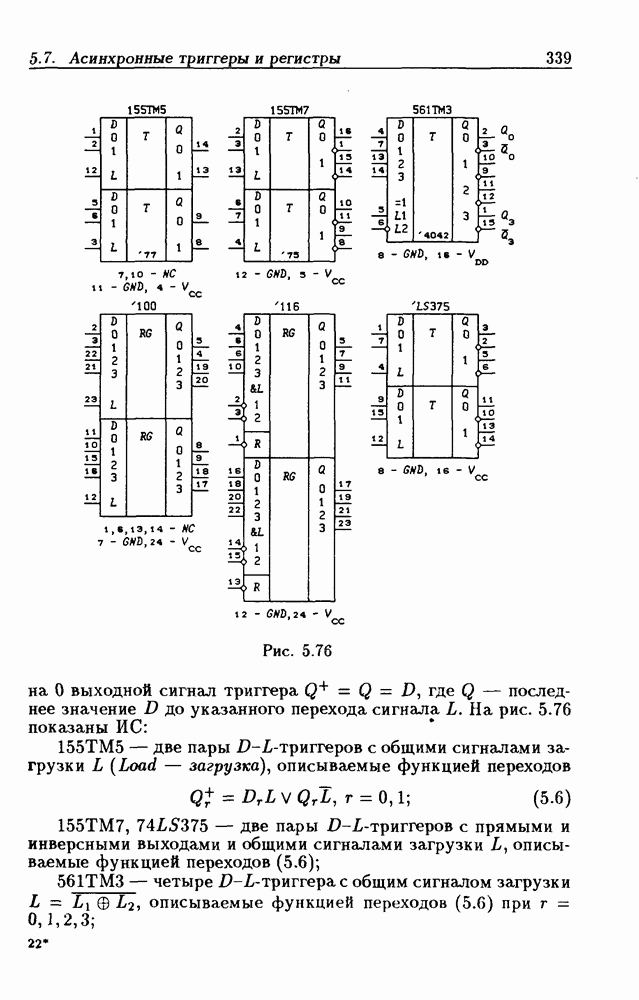
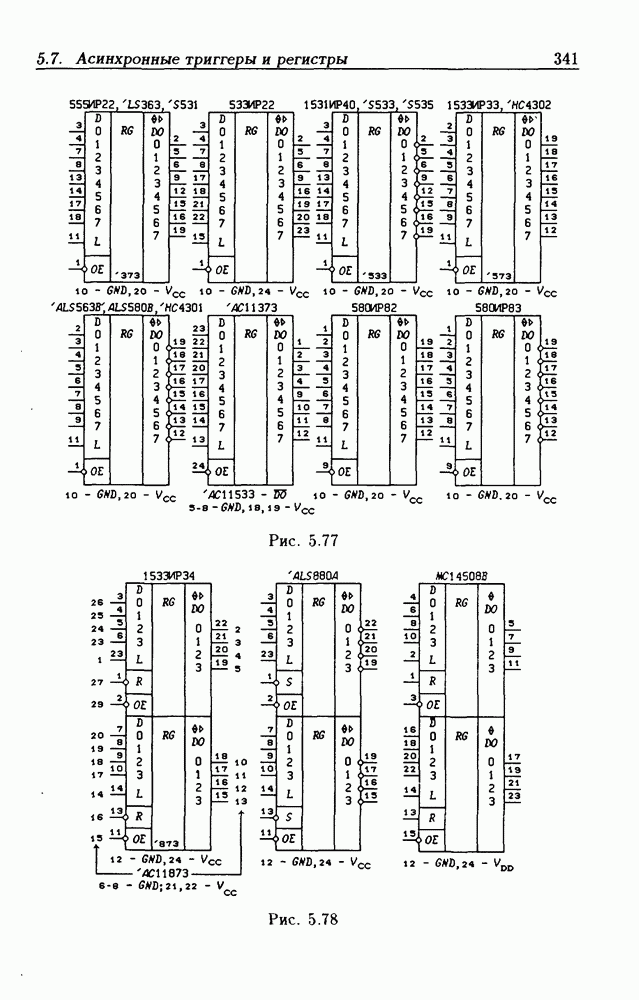
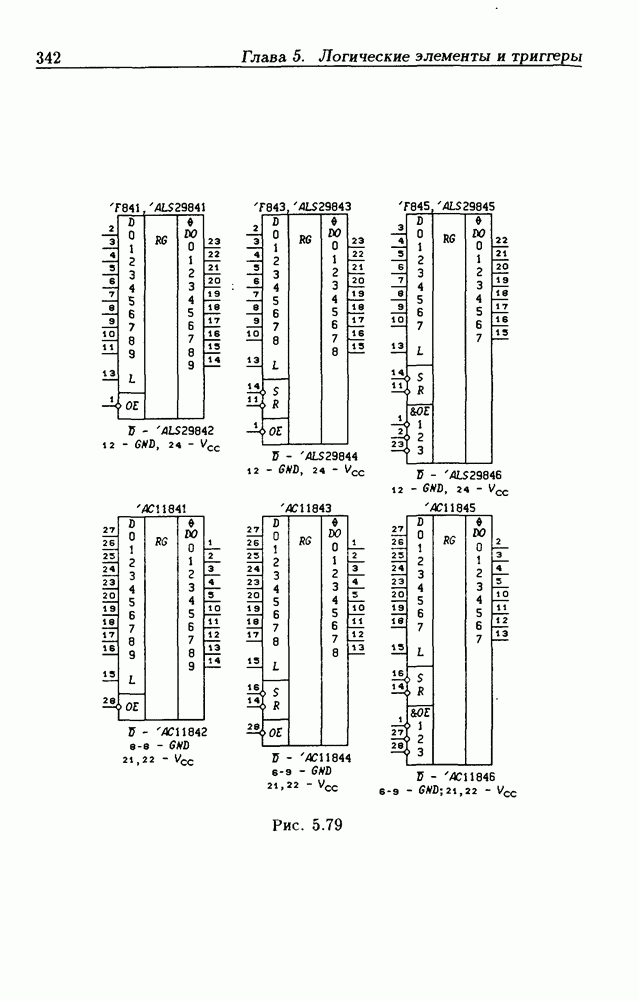
- 5.7. Асинхронные потенциальные триггеры и регистры памяти
- 5.8. Синхронные триггеры и регистры памяти
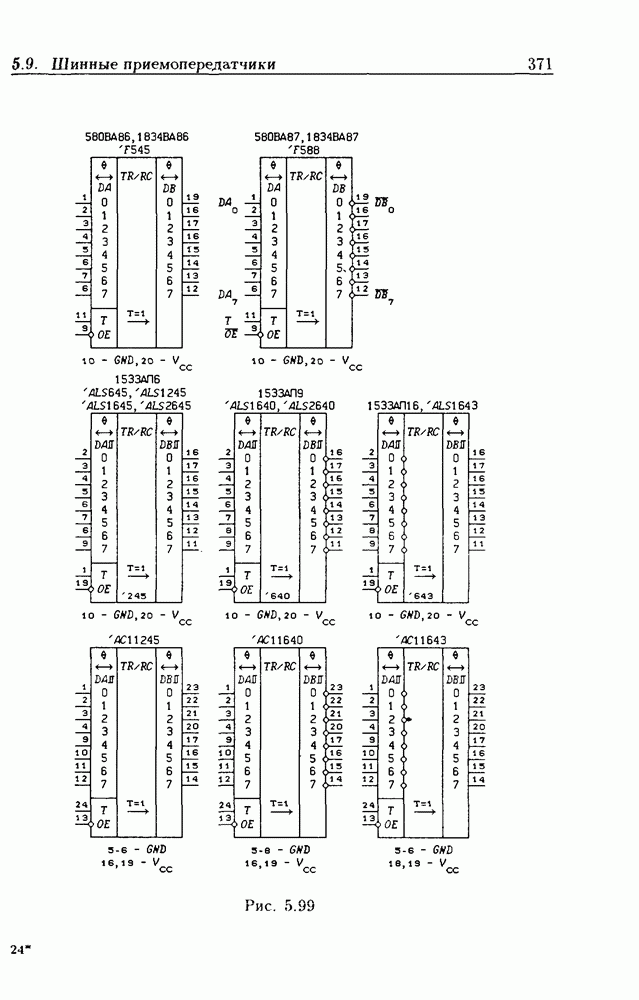
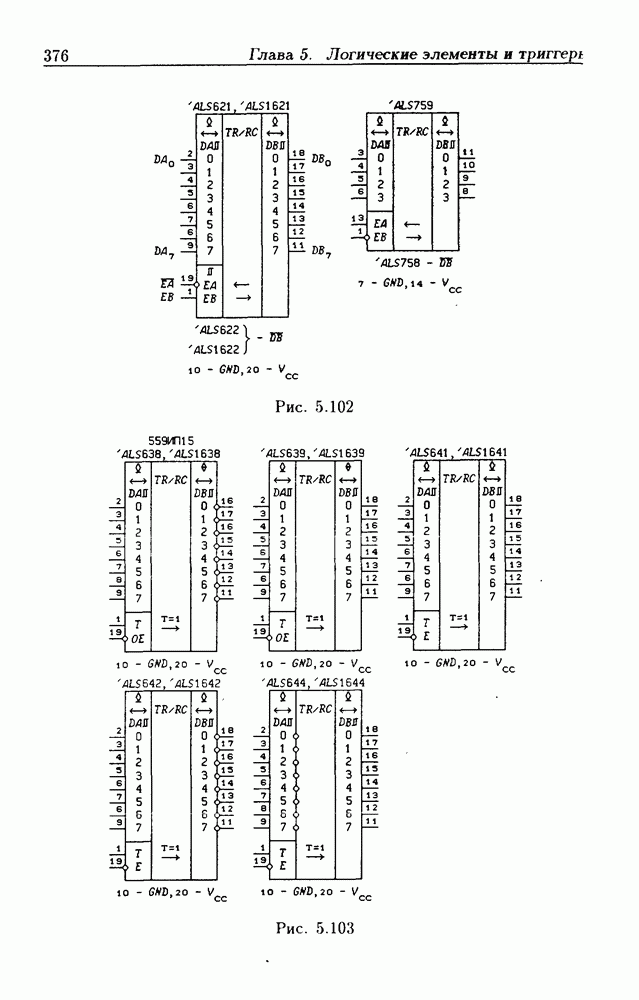
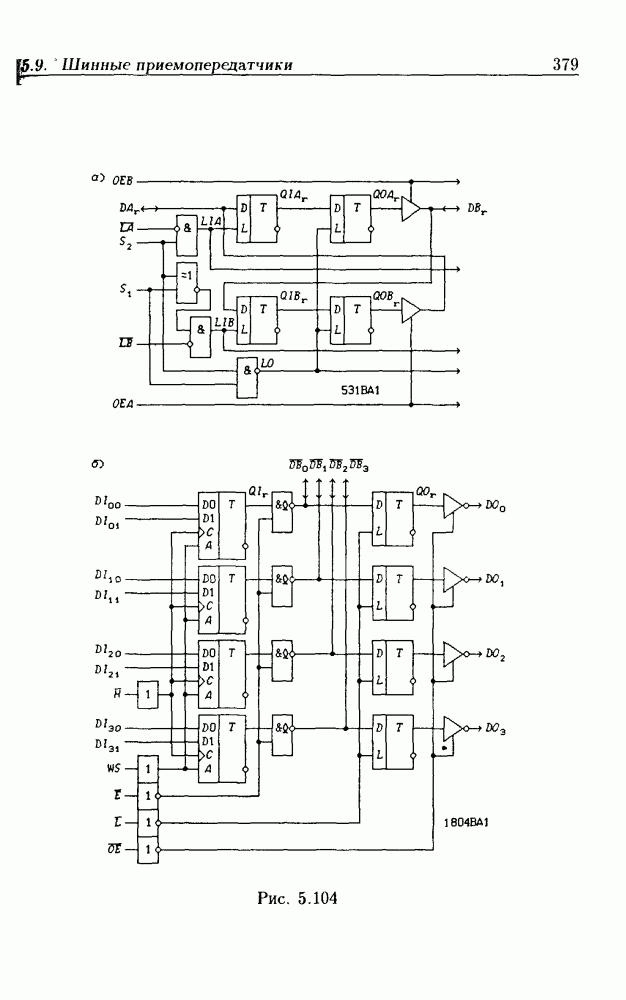
- 5.9. Шинные приемопередатчики
- Шинные приемопередатчики с Z-состоянием выхода.
- Шинные приемопередатчики с открытым коллекторным выходом.
- Шинные приемопередатчики с регистрами памяти.
- Шинные приемопередатчики со сдвигающим регистром.
- Шинные трехнаправленные приемопередатчики.
- 5.10. Мультивибраторы
- 5.11. Генераторы
- Схемы устранения «дребезга» механических контактов.
- Автогенераторы периодических сигналов.
- 5.12. Рекомендации по выбору серий ИС
- Глава 6. Коммутаторы и арифметические устройства
- 6.1. Дешифраторы
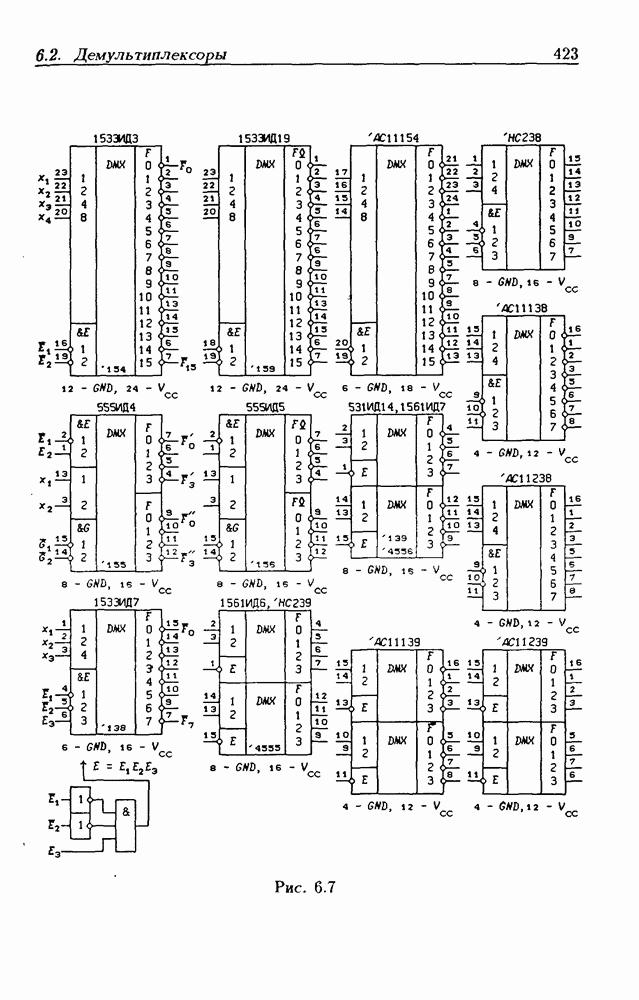
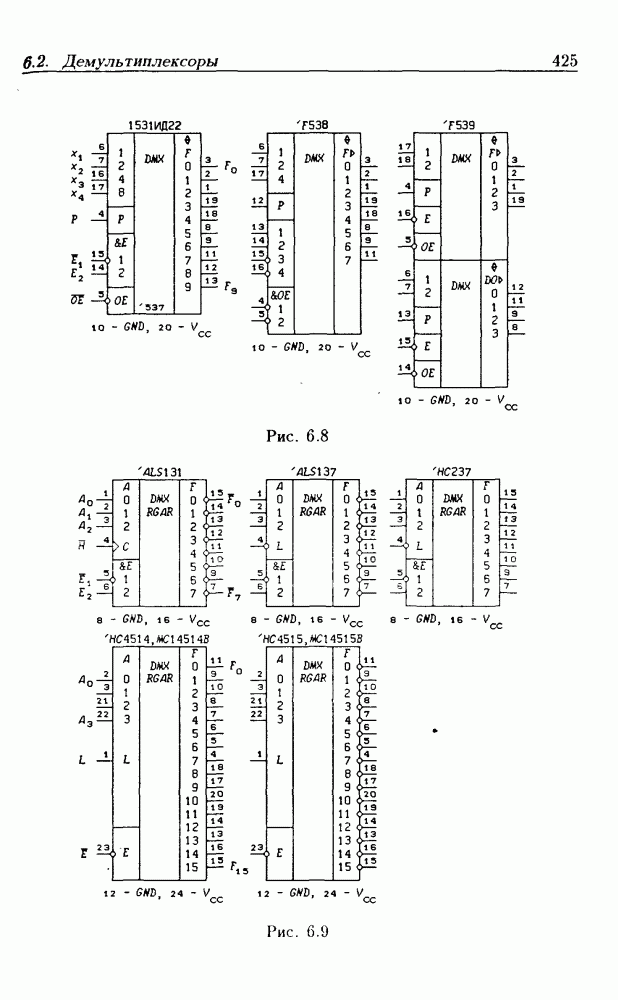
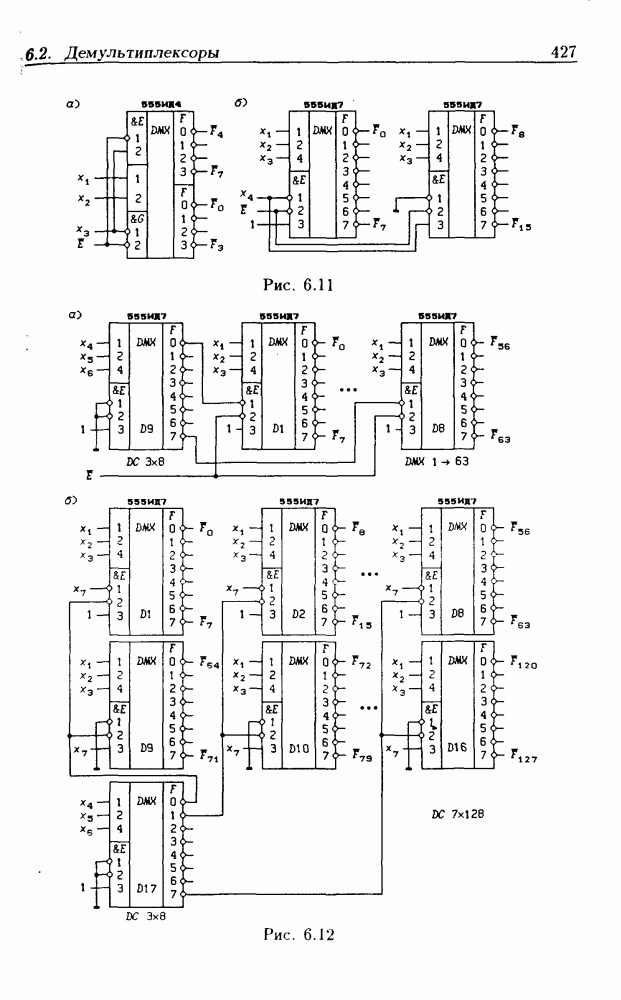
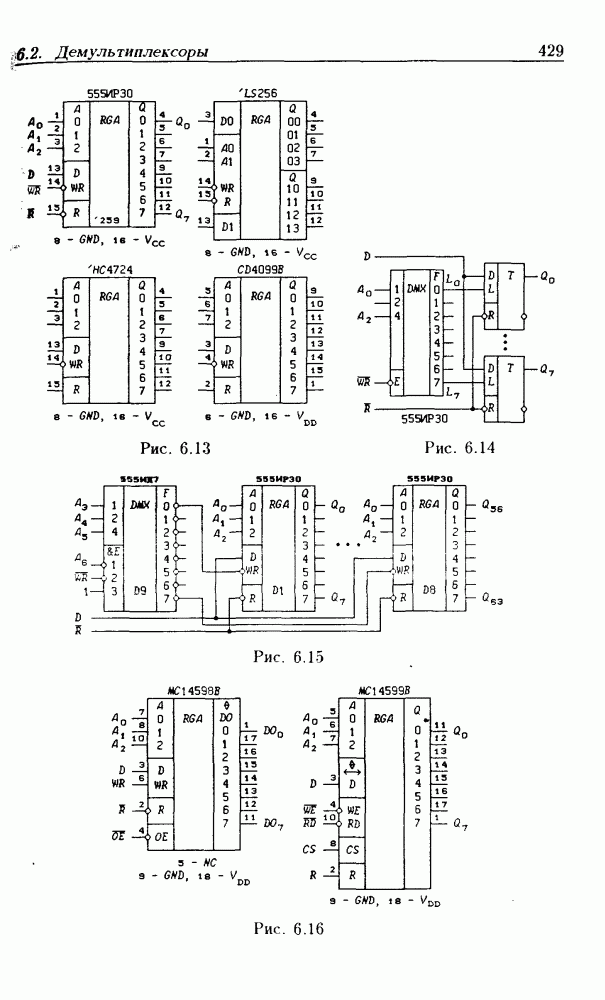
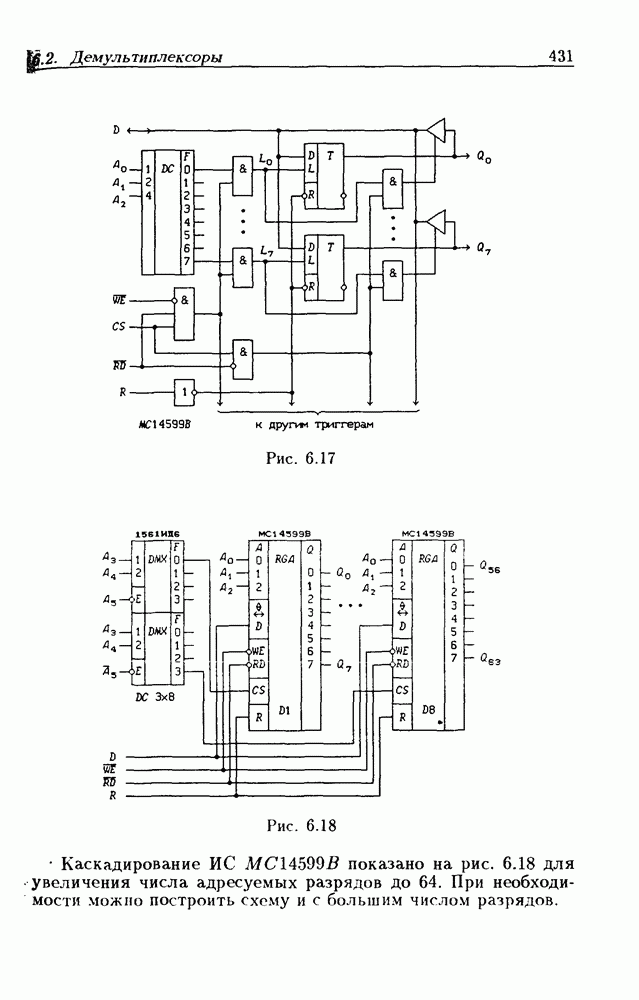
- 6.2. Демультиплексоры
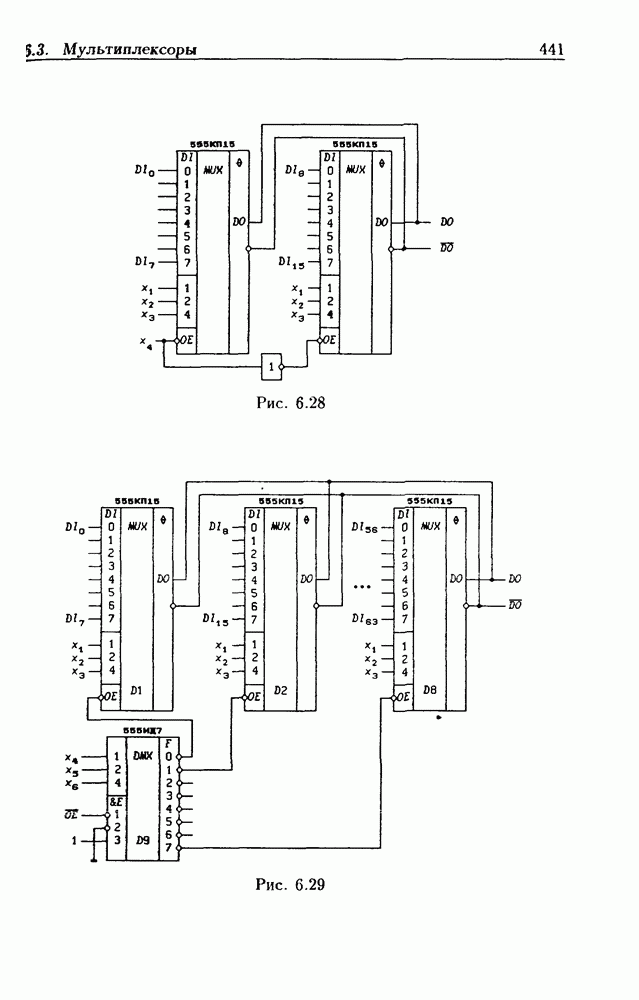
- 6.3. Мультиплексоры
- Мультиплексоры без стробирования.
- Мультиплексоры со стробированием.
- Мультиплексоры с Z-состоянием выхода.
- Каскадирование мультиплексоров.
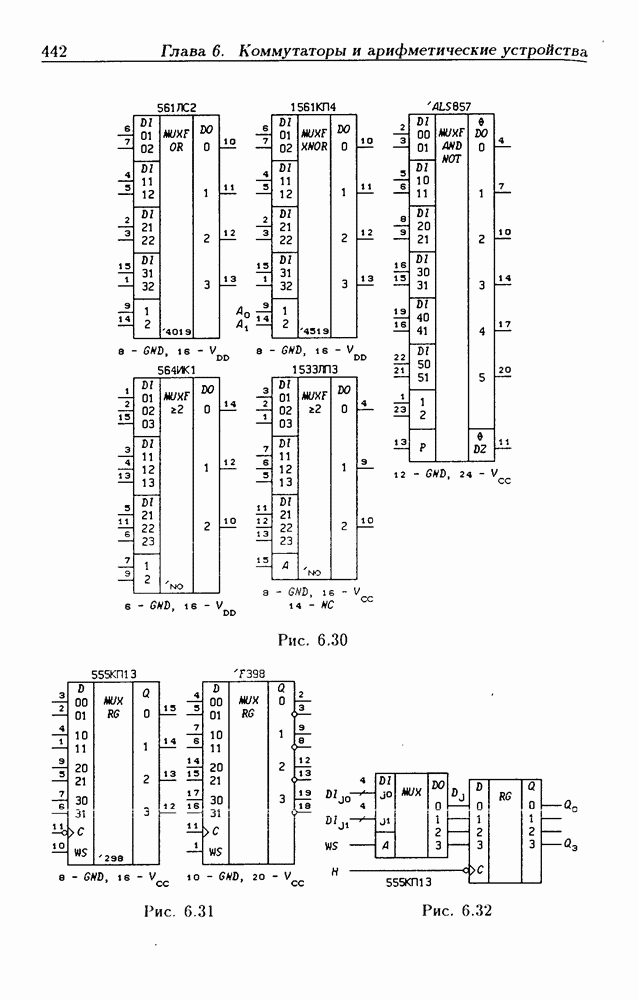
- Функциональные мультиплексоры.
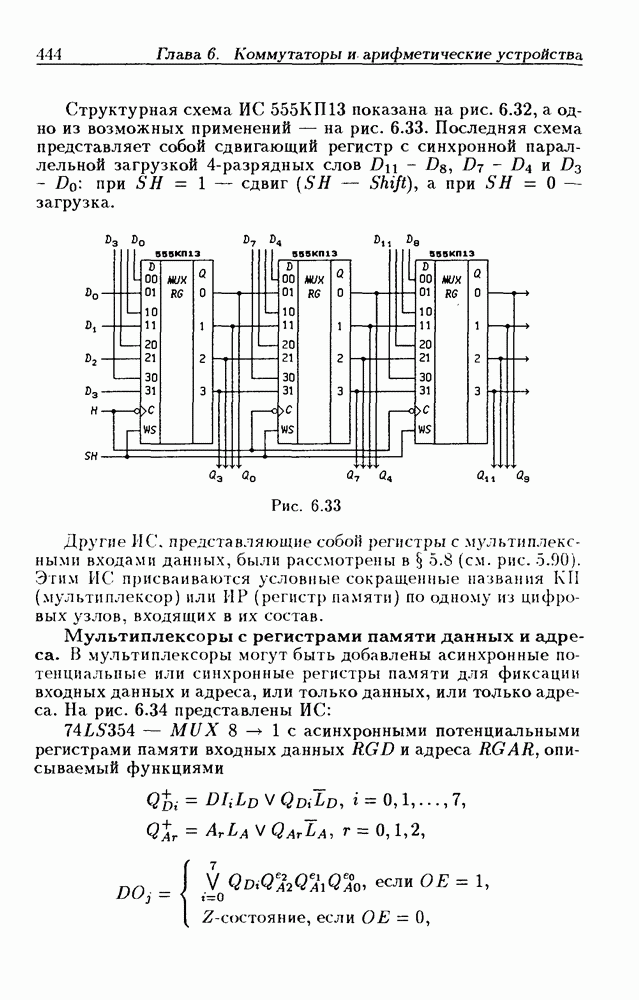
- Регистры памяти с мультиплексными входами данных.
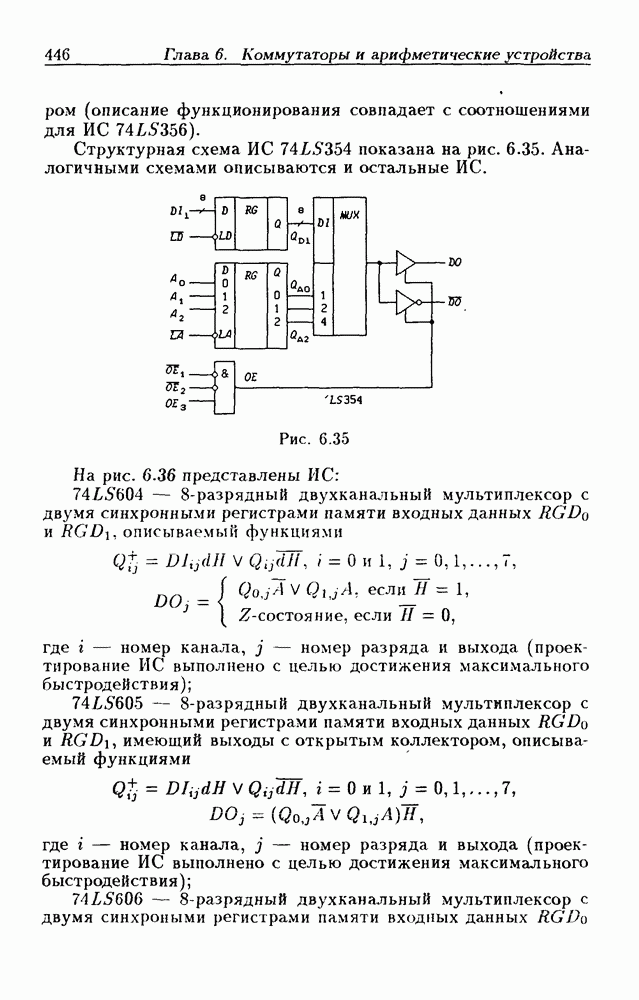
- Мультиплексоры с регистрами памяти данных и адреса.
- Сдвигающие мультиплексоры.
- 6.4. Синтез комбинационных схем и цифровых автоматов на мультиплексорах
- Синтез схем на 8-канальных мультиплексорах.
- Синтез на двухразрядных 4-канальных мультиплексорах.
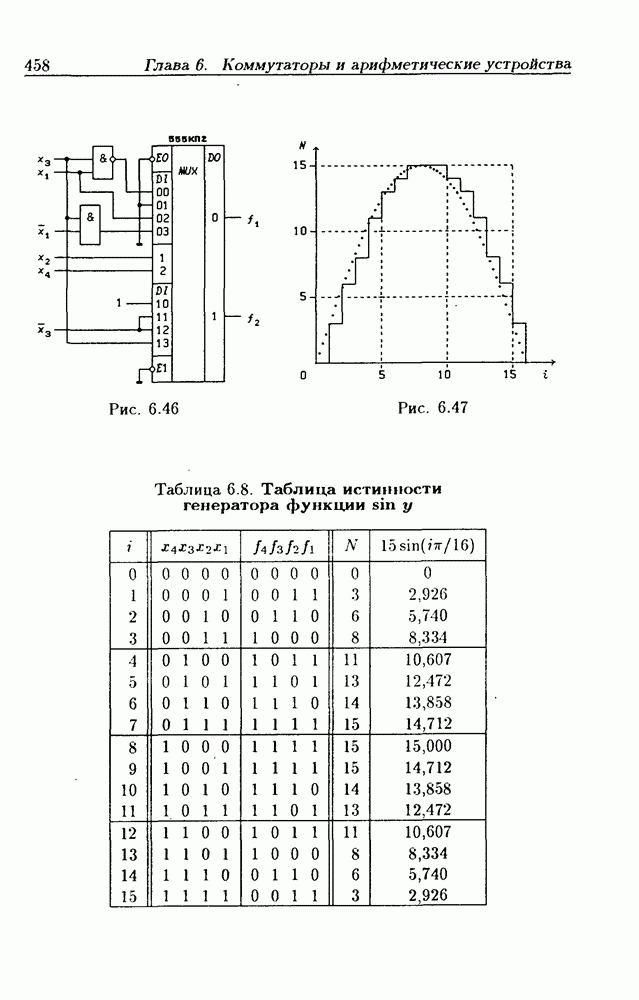
- Синтез генератора синусоидальной функции на мультиплексорах.
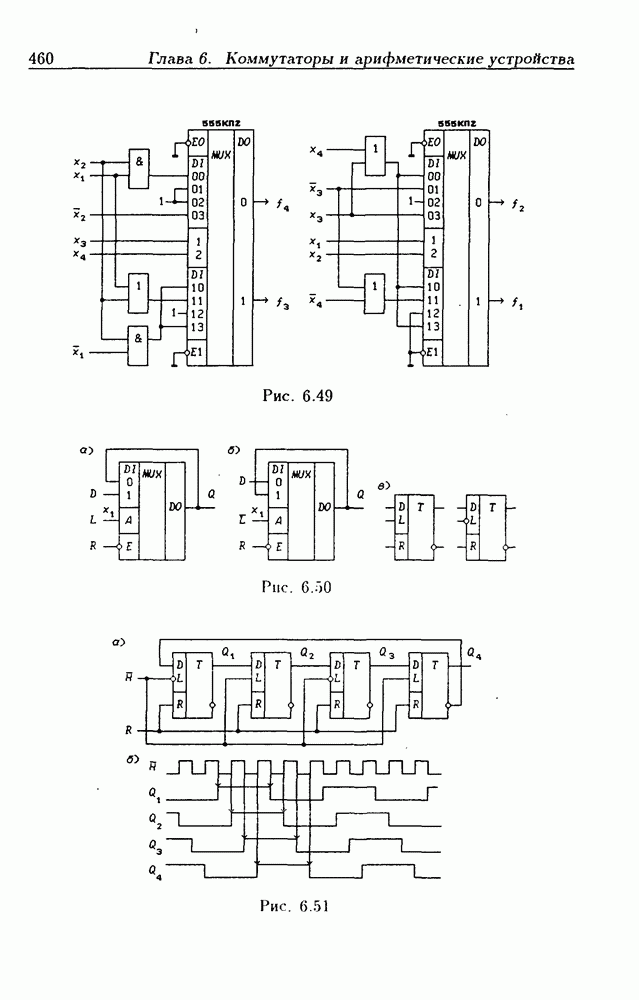
- Синтез триггеров на мультиплексорах.
- Синтез счетчиков на мультиплексорах.
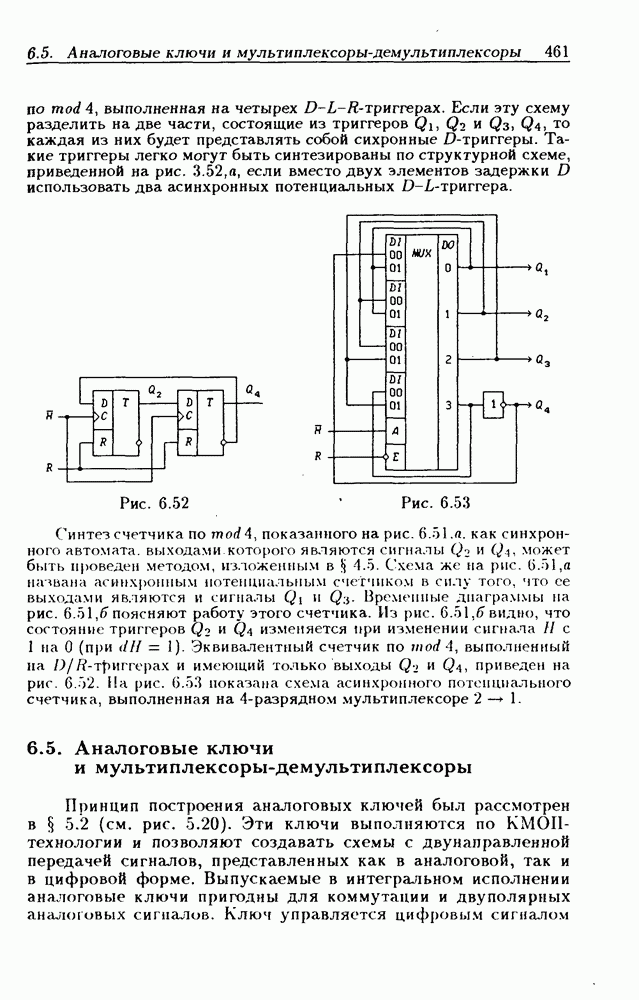
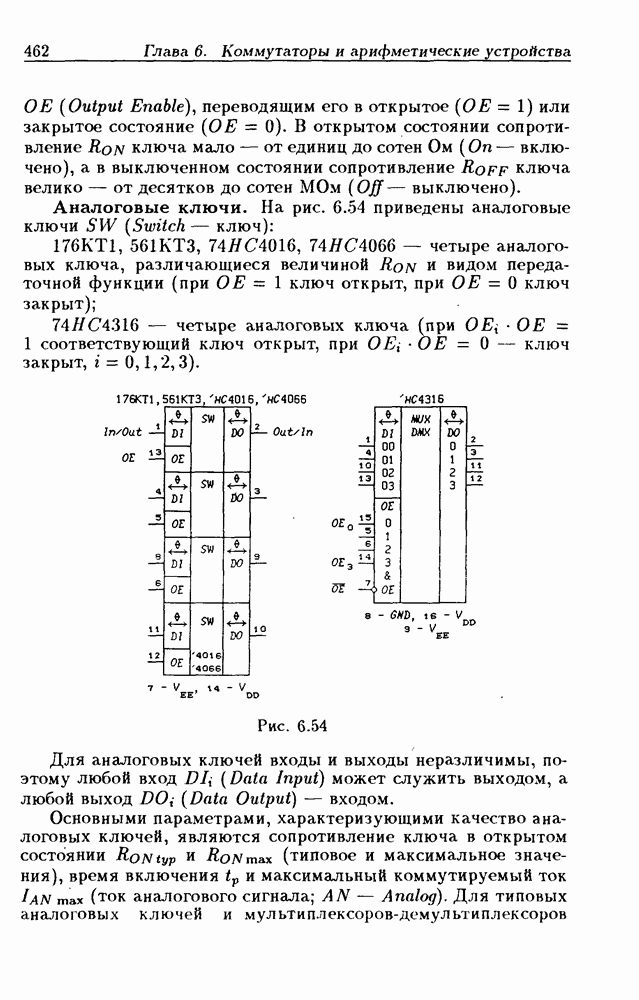
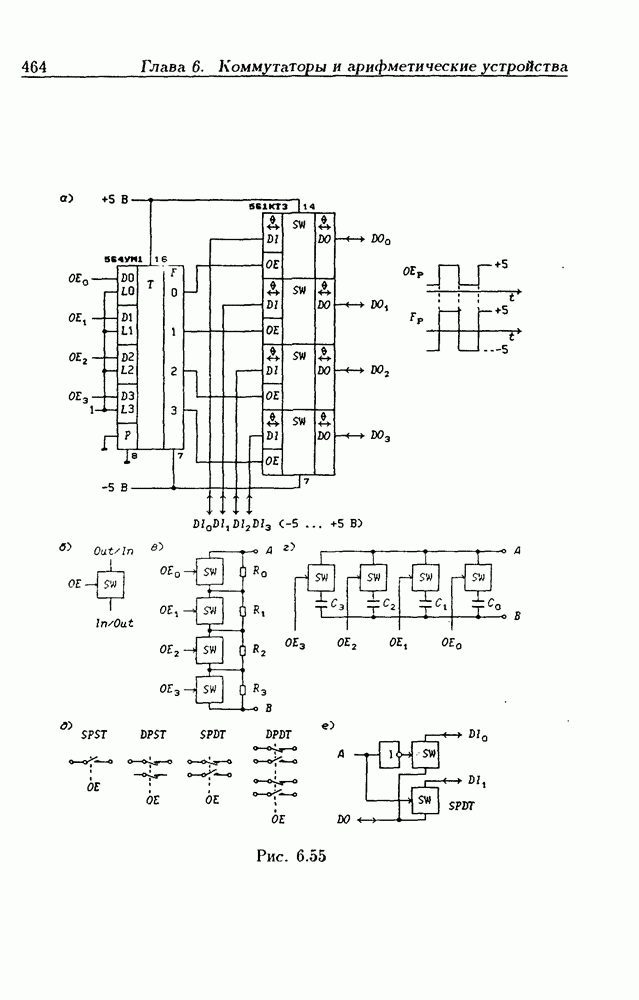
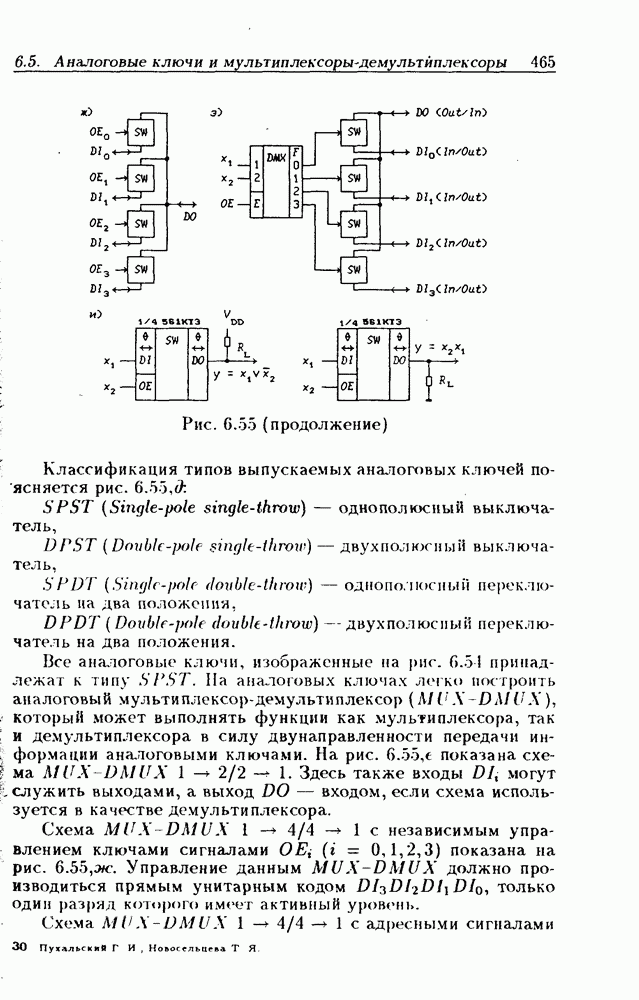
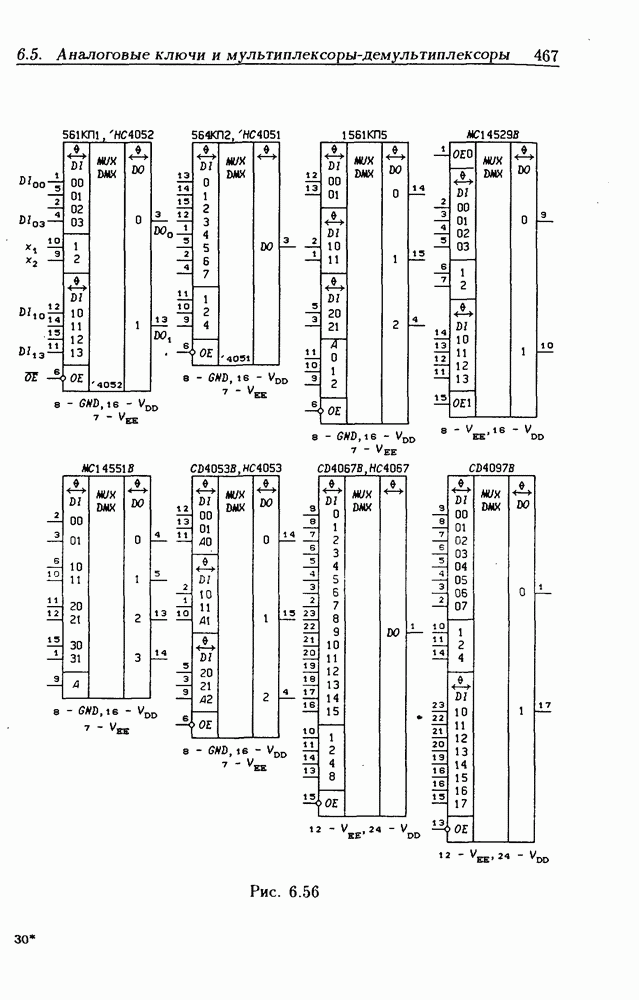
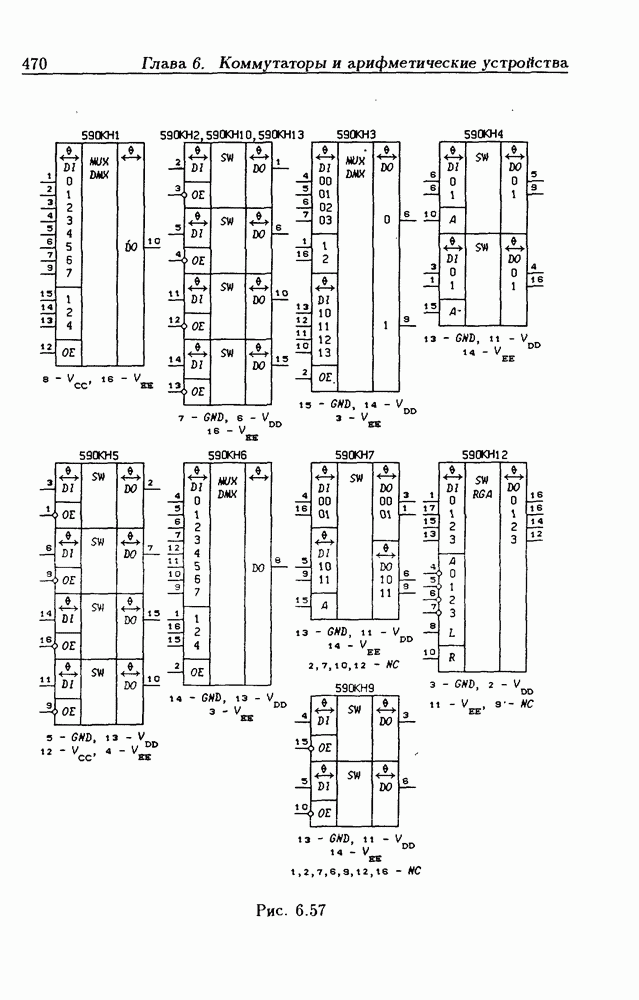
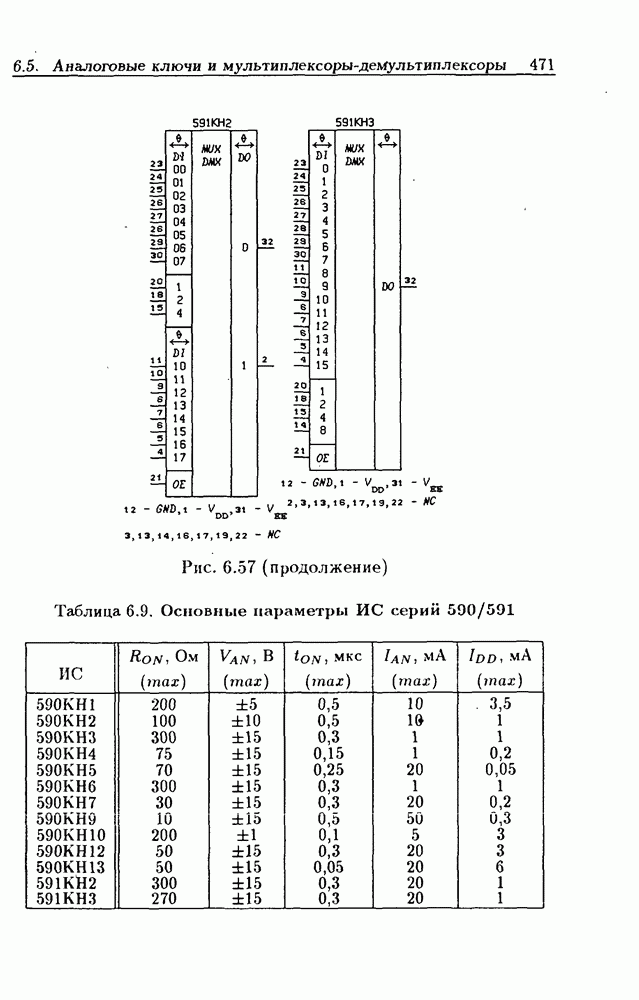
- 6.5. Аналоговые ключи и мультиплексоры-демультиплексоры
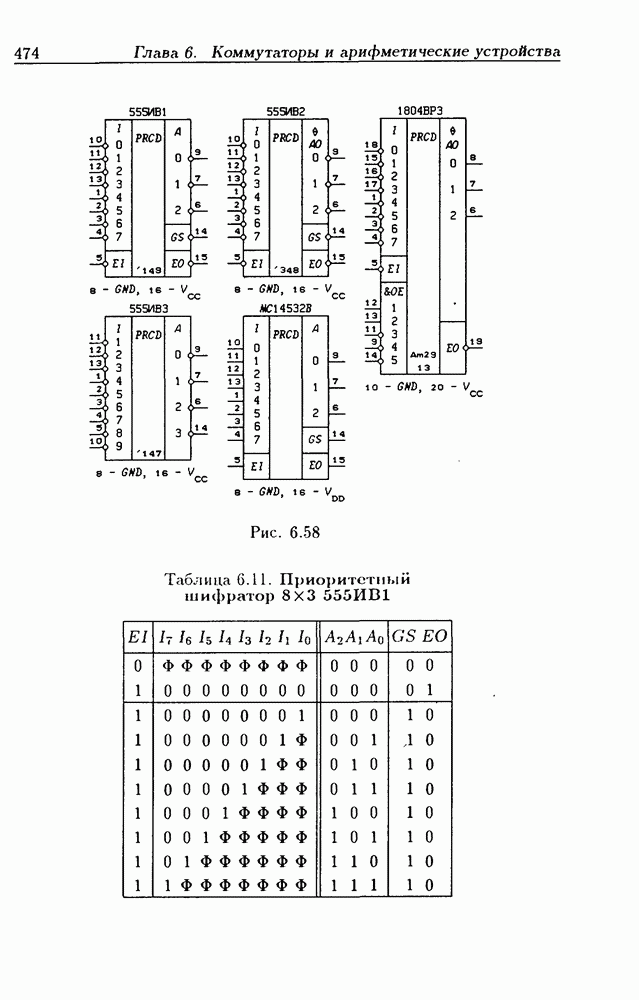
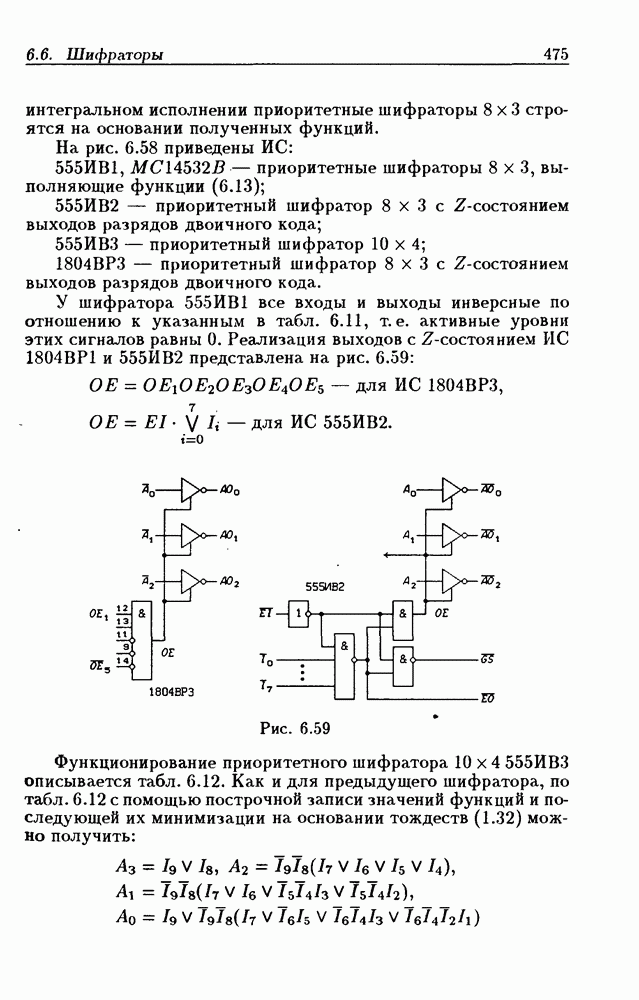
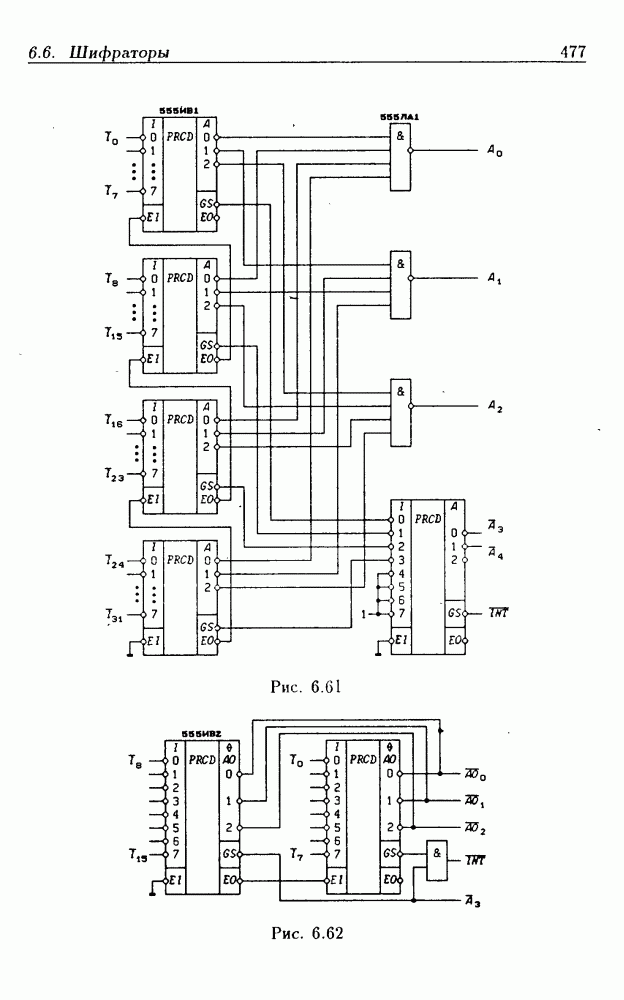
- 6.6. Шифраторы
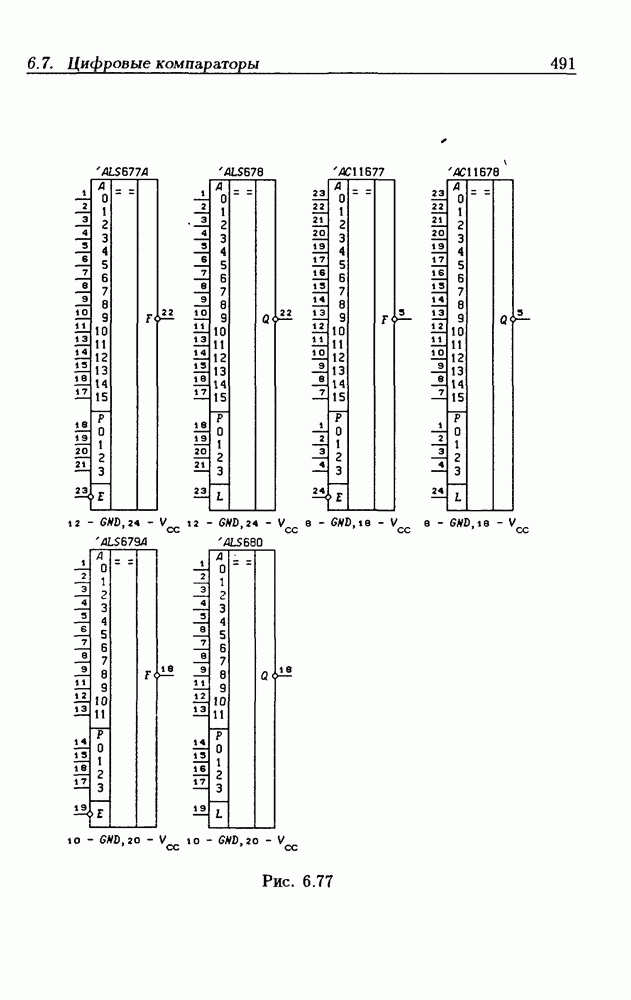
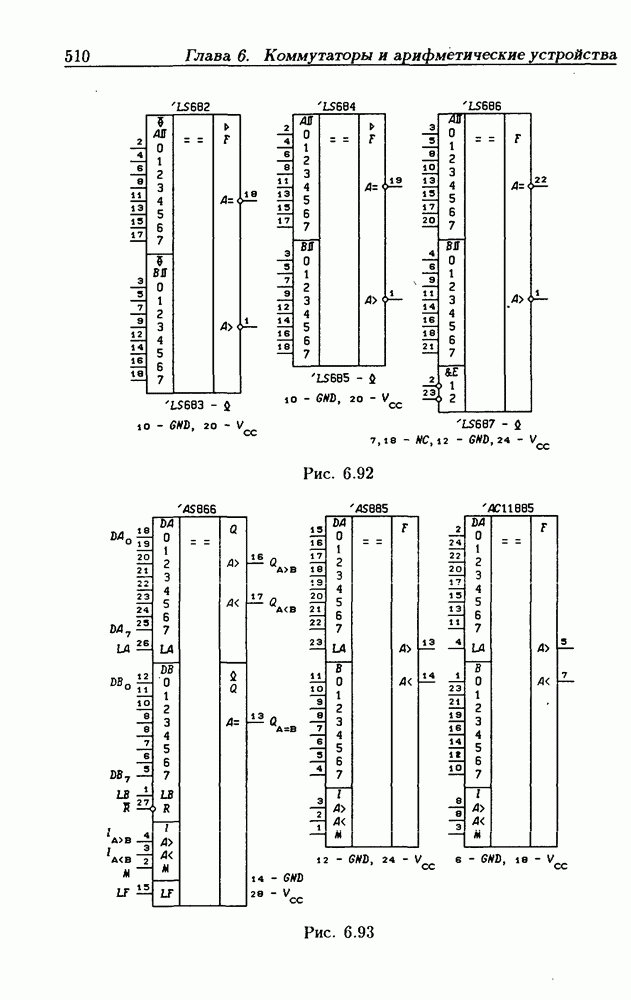
- 6.7. Цифровые компараторы
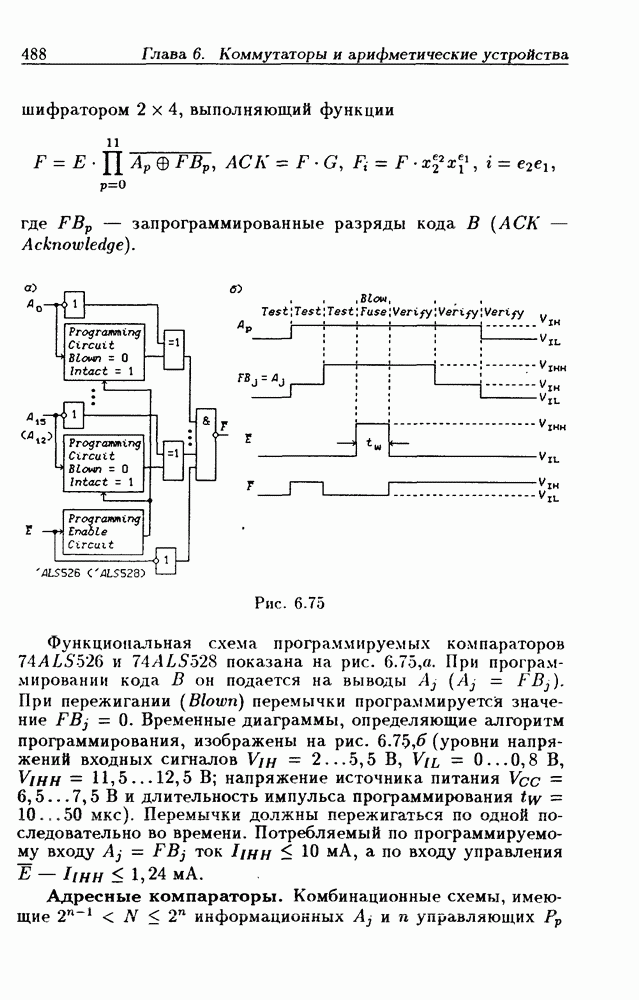
- Программируемые цифровые компараторы.
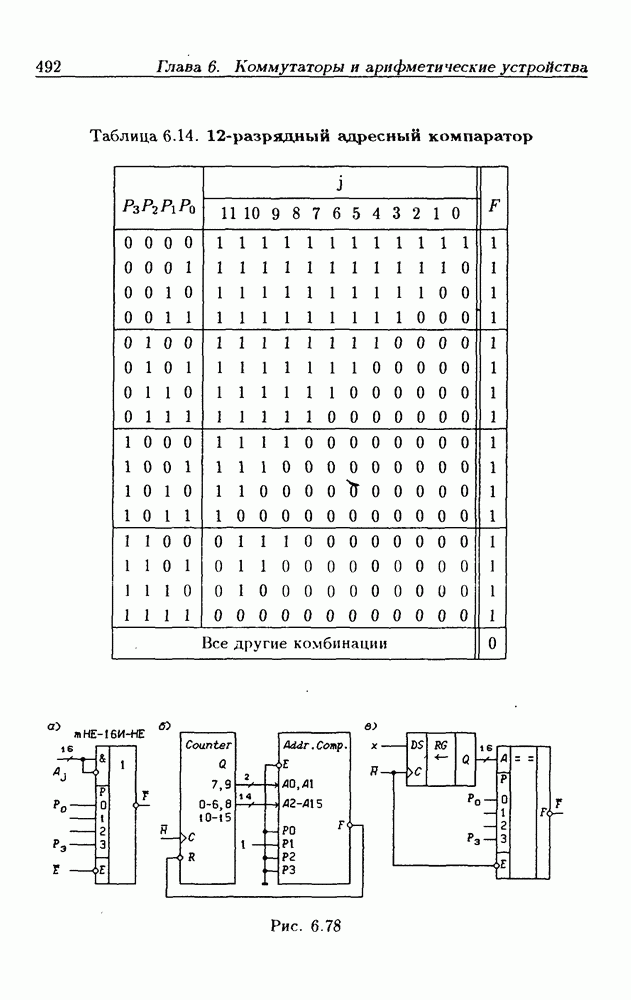
- Адресные компараторы.
- Применения адресных компараторов.
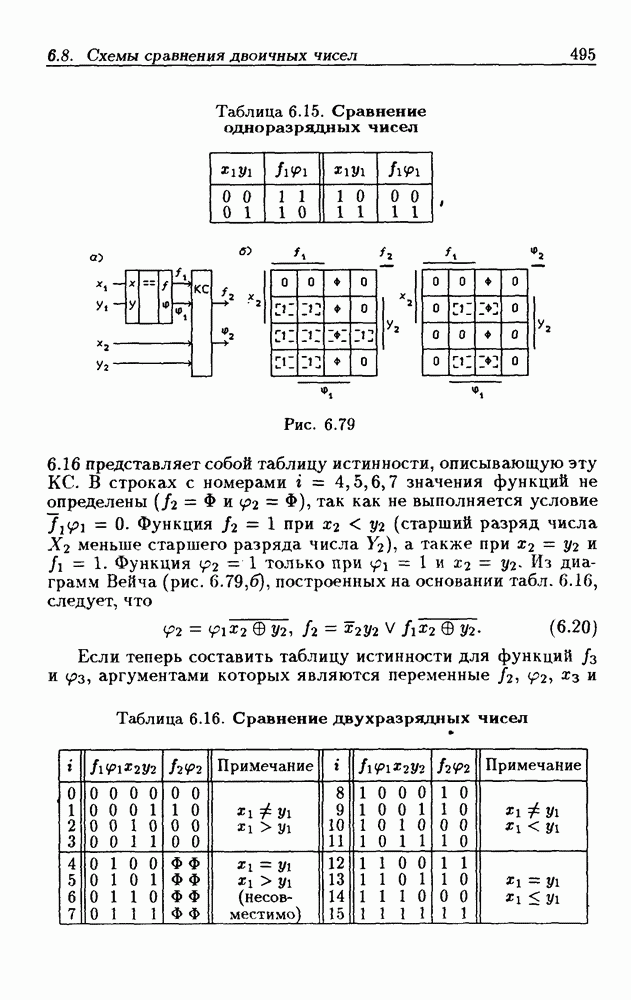
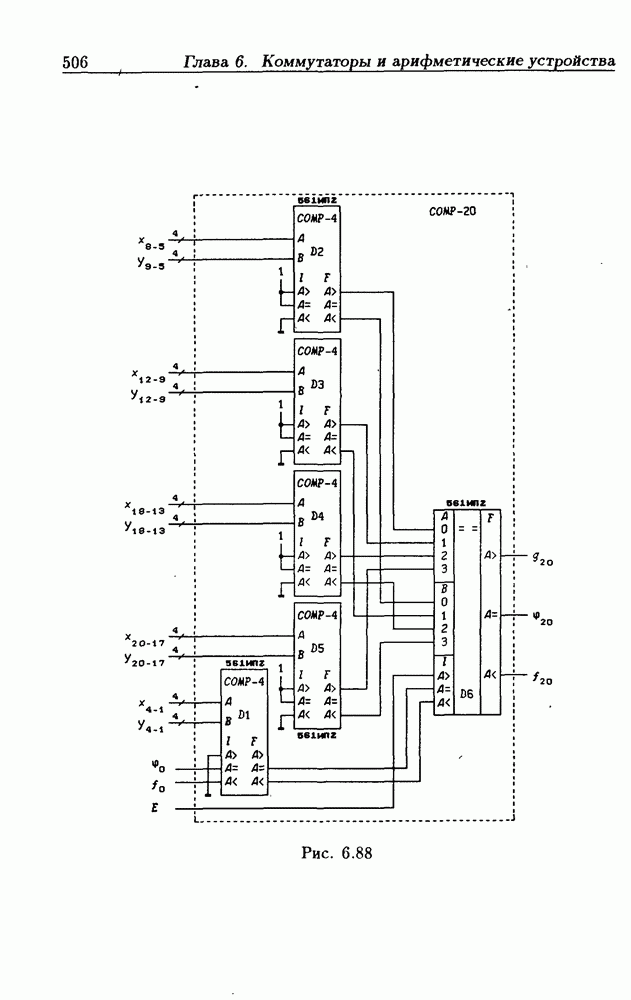
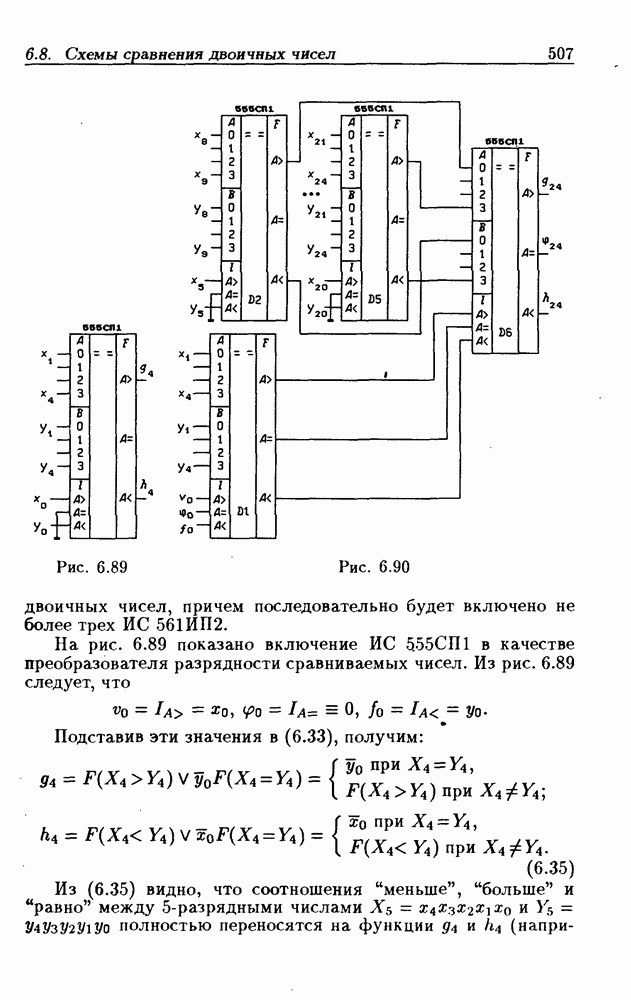
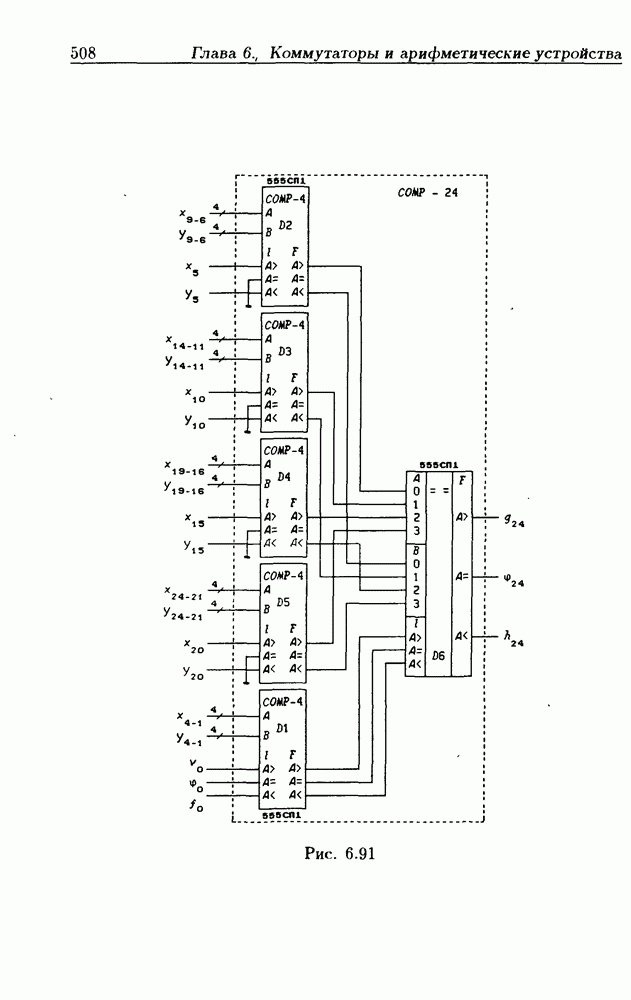
- 6.8. Схемы сравнения двоичных чисел
- 8-разрядные схемы сравнения двоичных чисел.
- 6.9. Прямой, обратный и дополнительный коды
- Дополнительный код.
- Сложение чисел в обратном коде.
- Код с избытком 3.
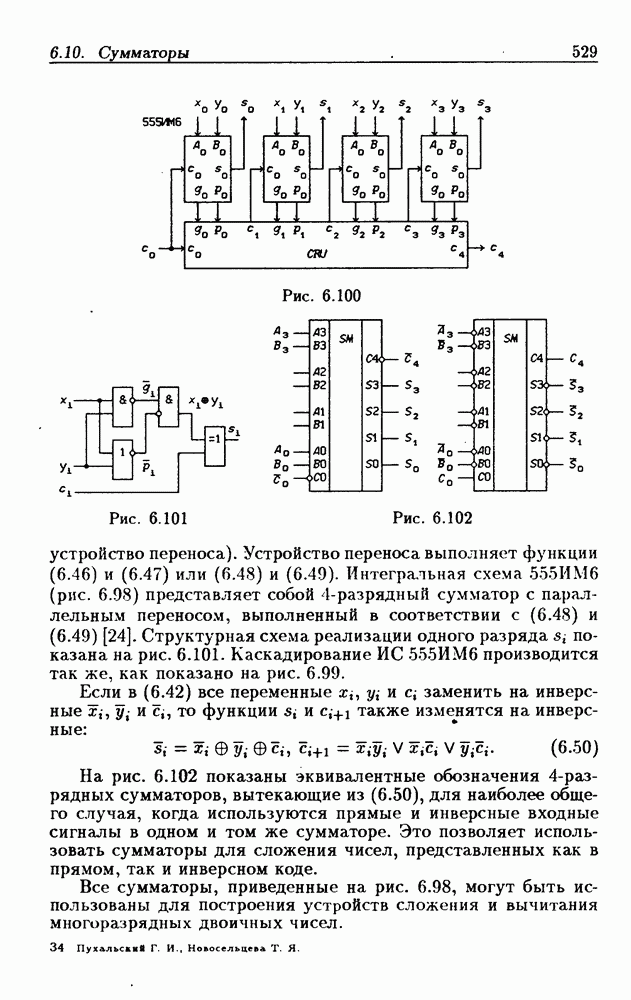
- 6.10. Сумматоры
- Двоичные параллельные сумматоры с последовательным переносом.
- Двоичные сумматоры с параллельным переносом.
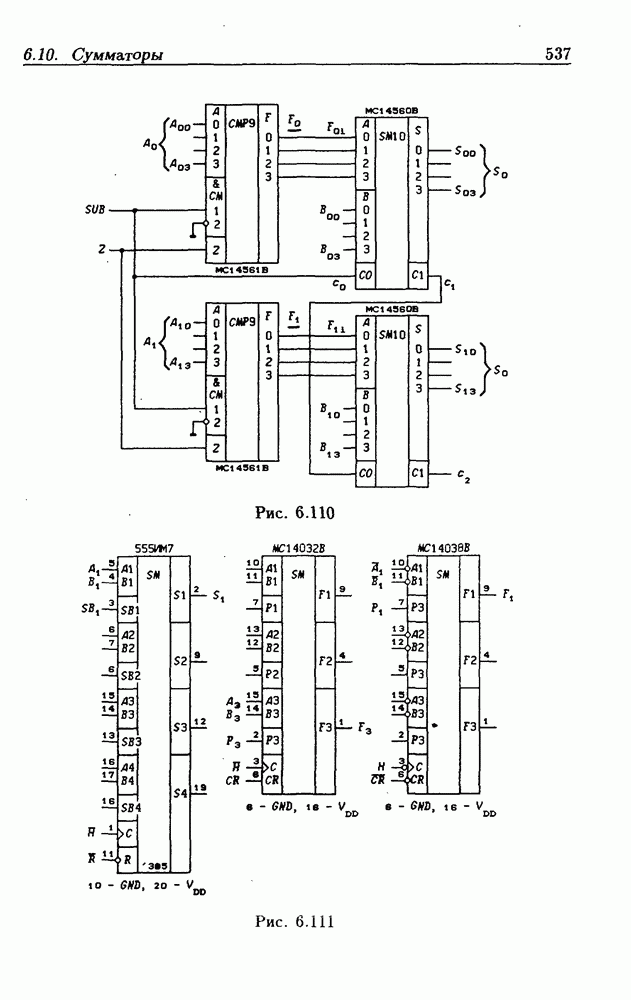
- Применения сумматоров.
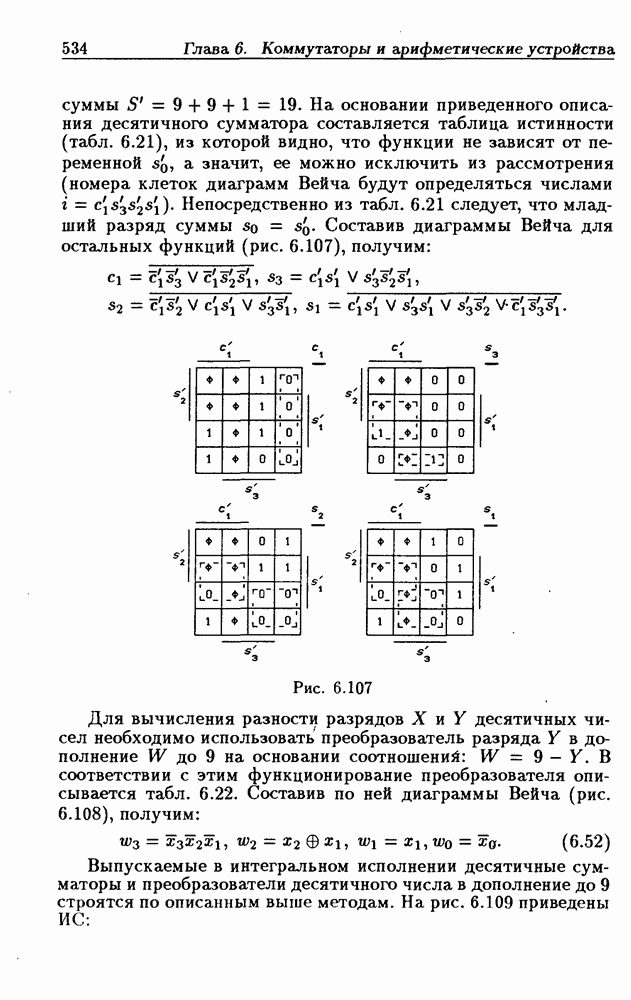
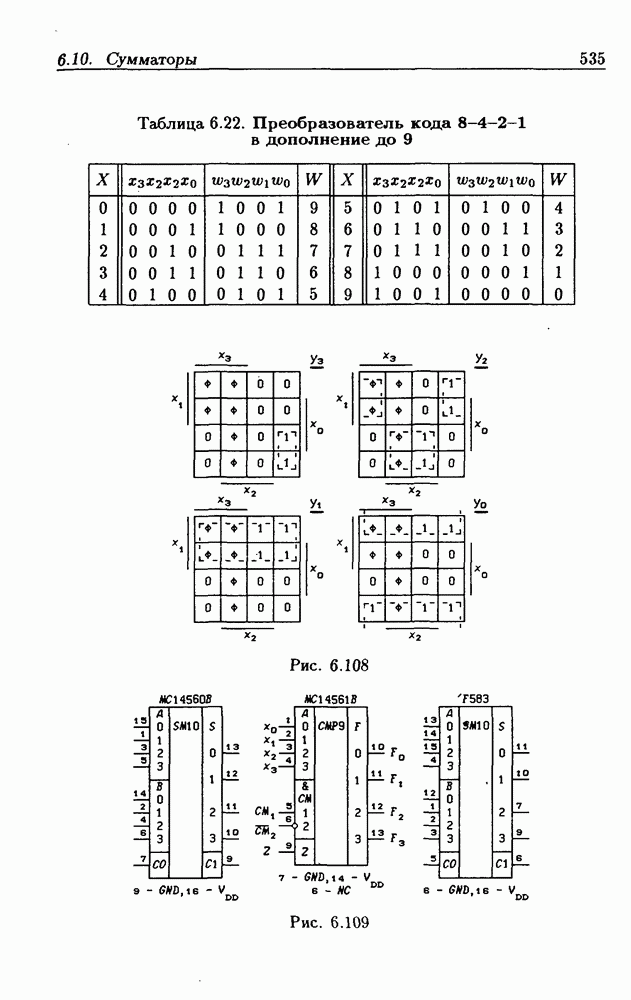
- Десятичные сумматоры.
- Последовательные двоичные сумматоры.
- 6.11. Арифметическо-логические устройства
- 6.12. Пороговые схемы и мажоритарные элементы
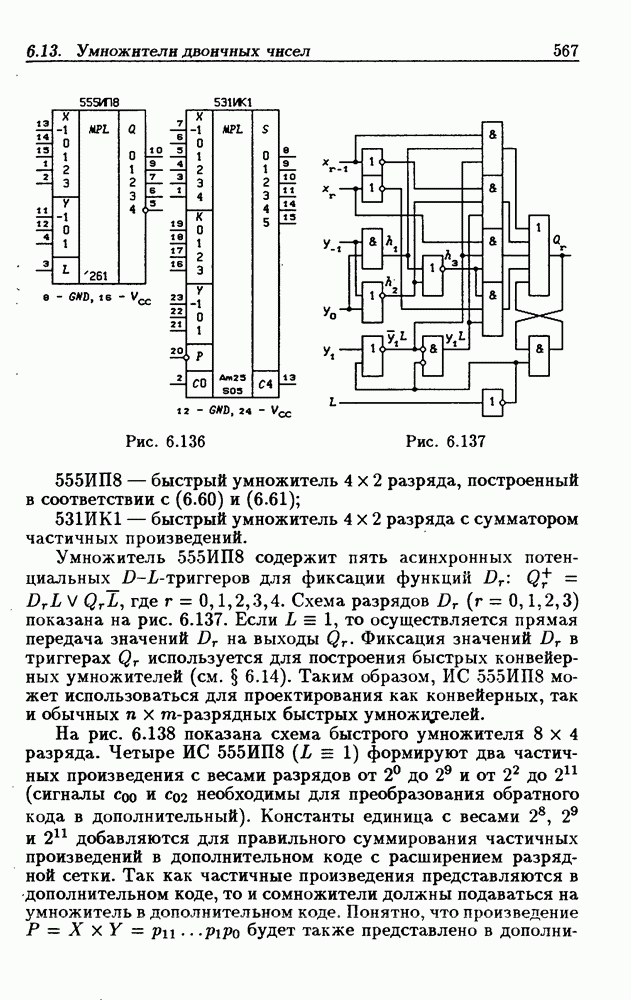
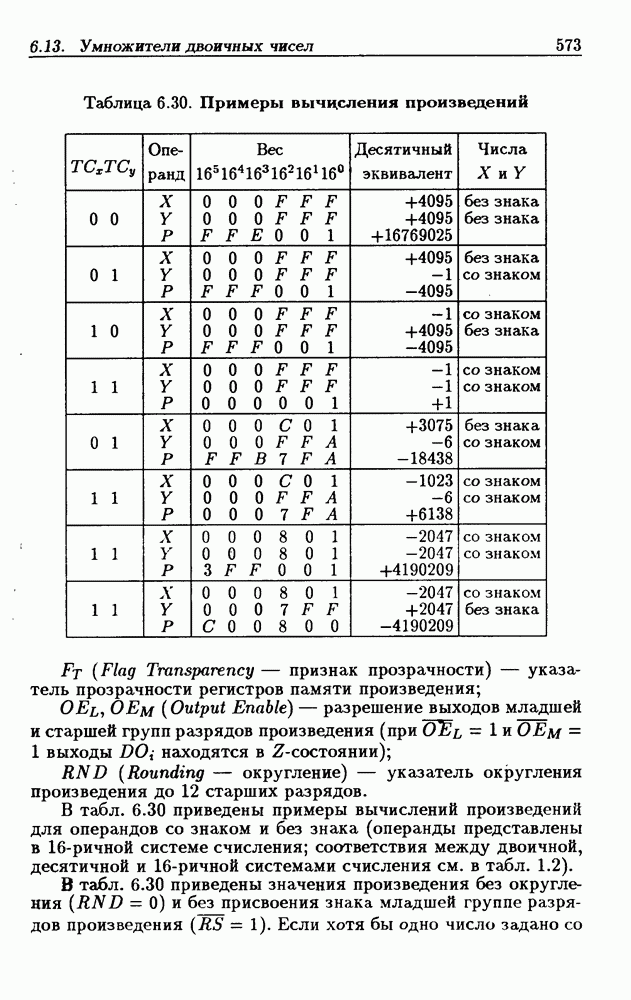
- 6.13. Умножители двоичных чисел
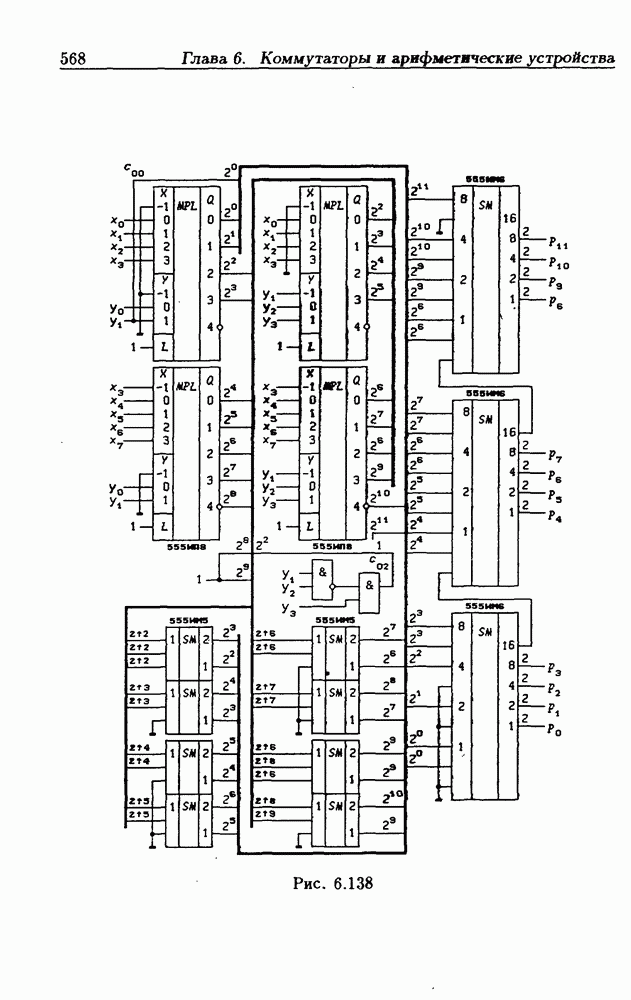
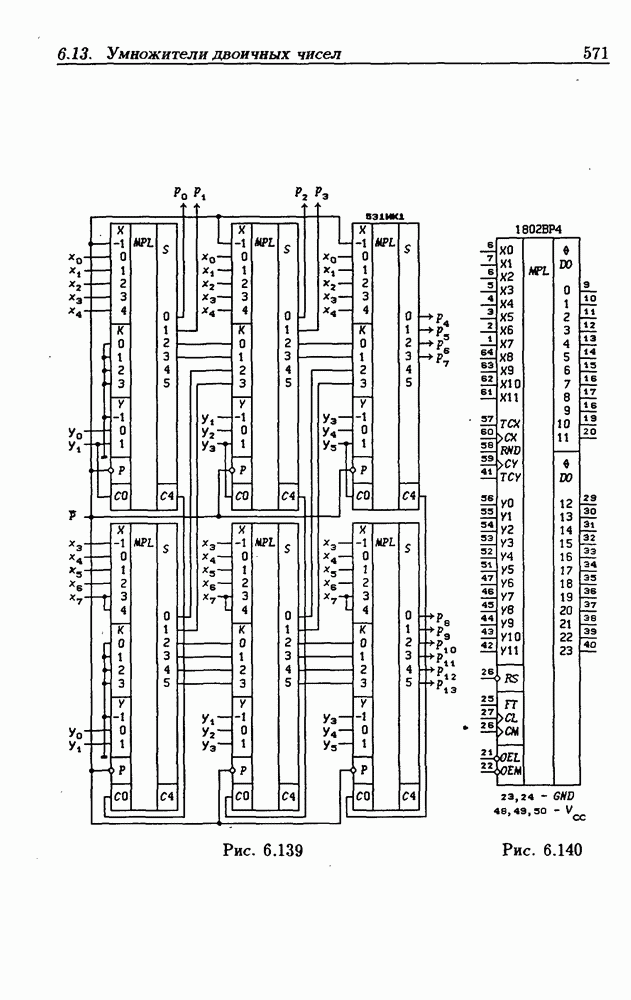
- Быстрые умножители.
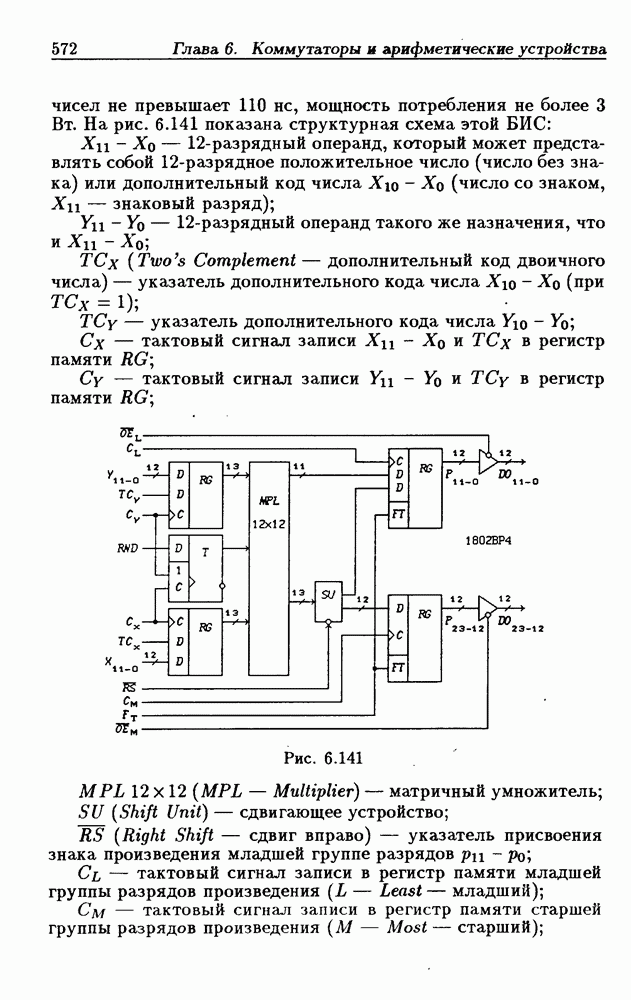
- БИС умножителя 12×12 разрядов 1802ВР4.
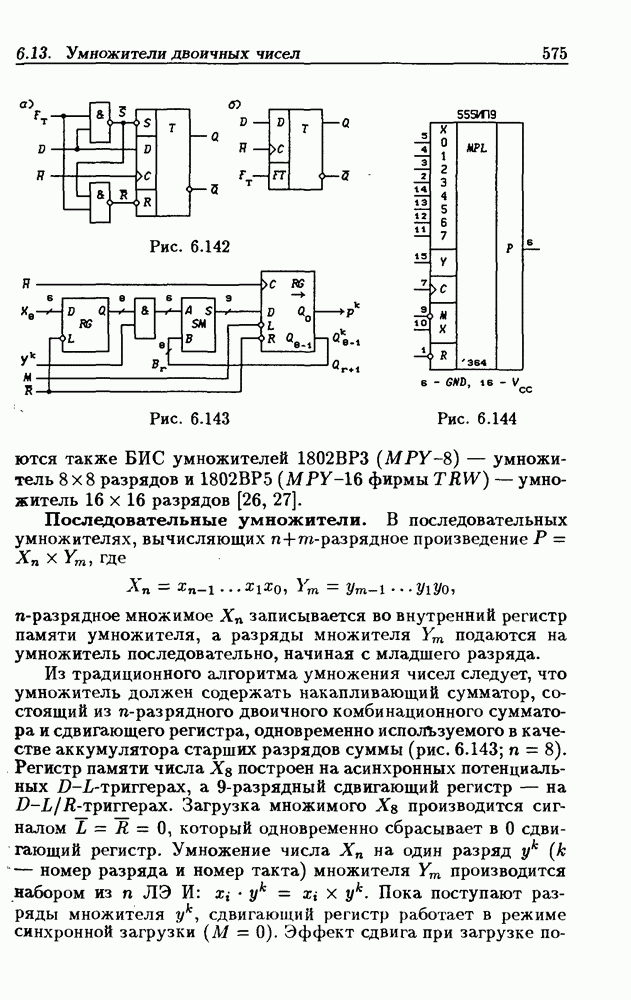
- Последовательные умножители.
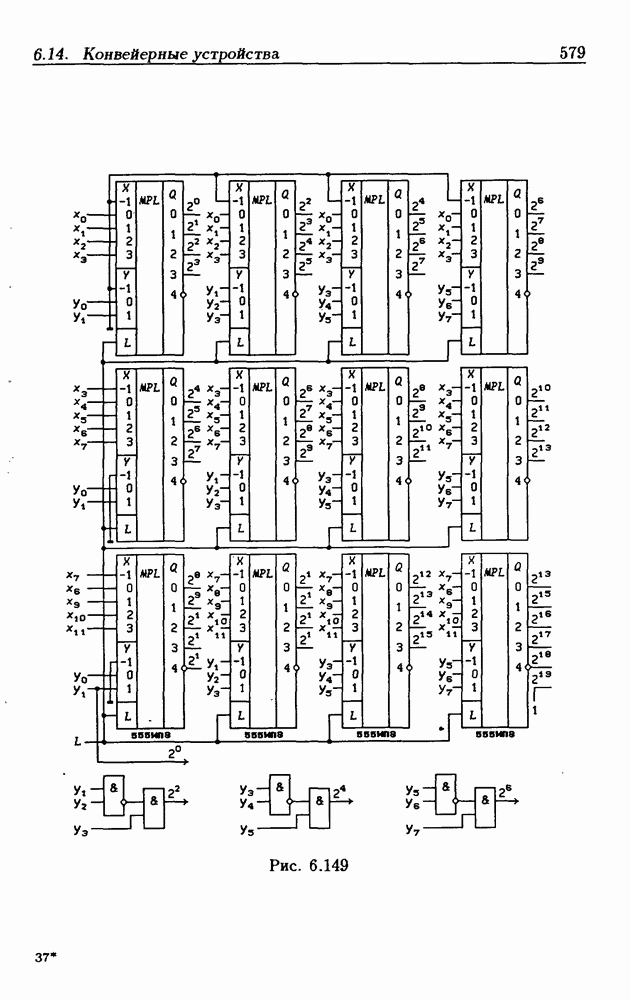
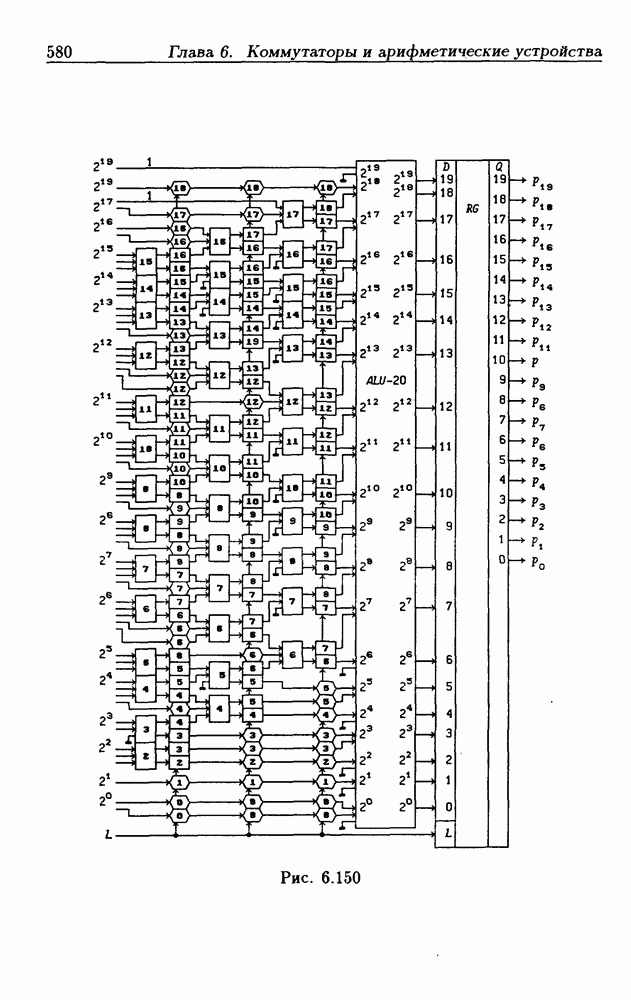
- 6.14. Конвейерные устройства
- Конвейерный быстрый умножитель.
- Конвейерные АЦП.
- 6.15. Синтез линейных комбинационных схем
- Сумматор по модулю q.
- Умножитель по модулю q.
- Глава 7. Сдвигающие регистры и счетчики
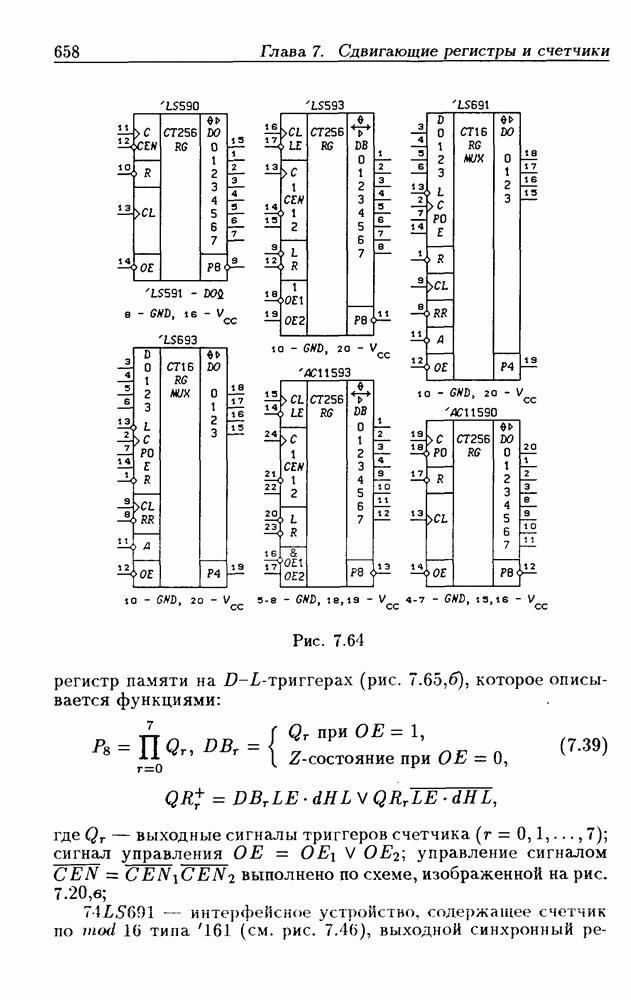
- 7.1. Сдвигающие регистры без параллельной записи данных
- Сдвигающие устройства с выходными регистрами памяти.
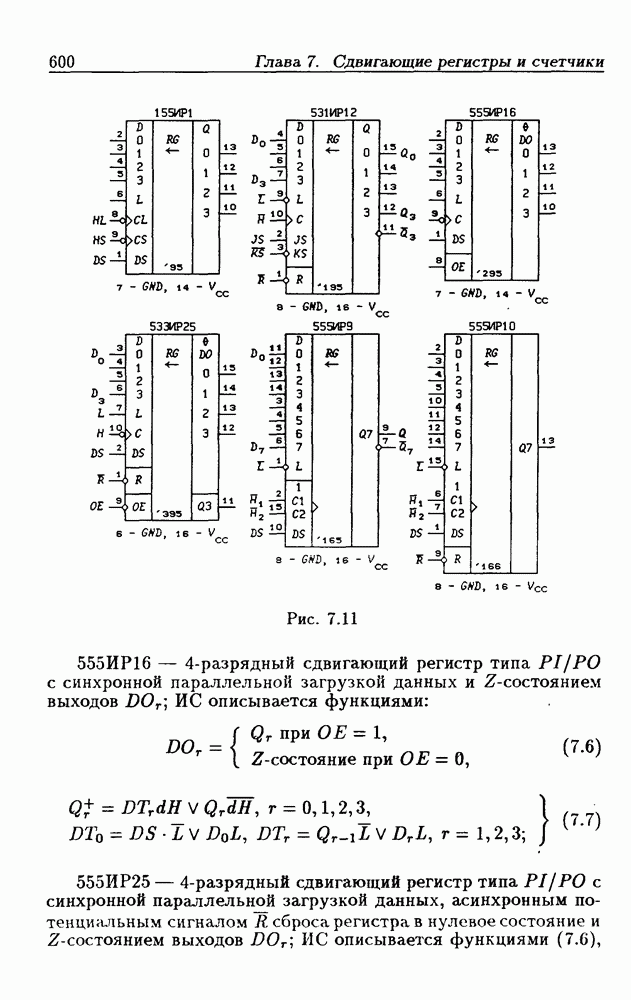
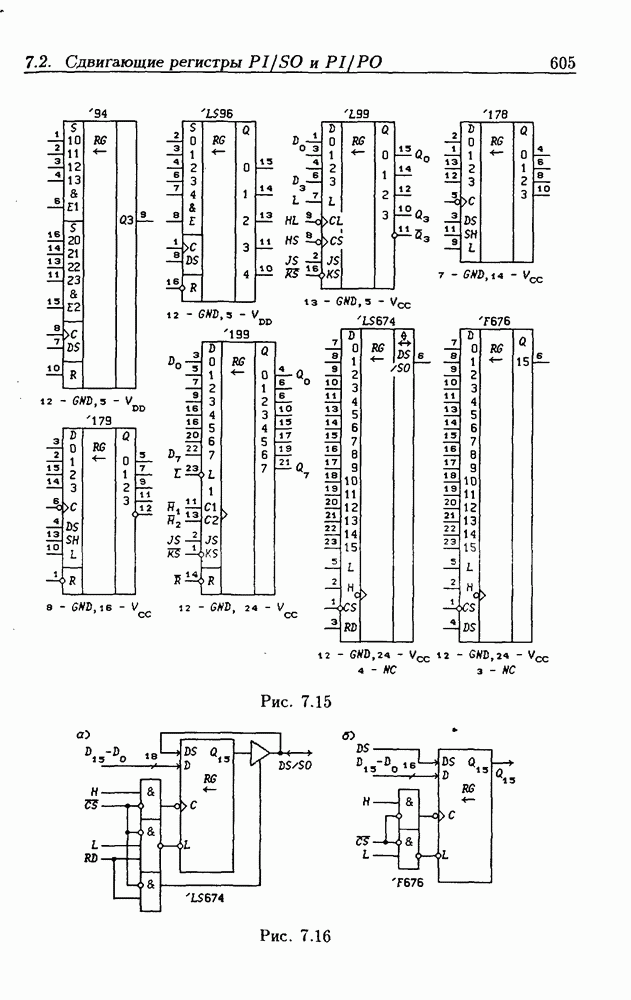
- 7.2. Сдвигающие регистры с параллельной записью данных
- Сдвигающие регистры с расширением знака.
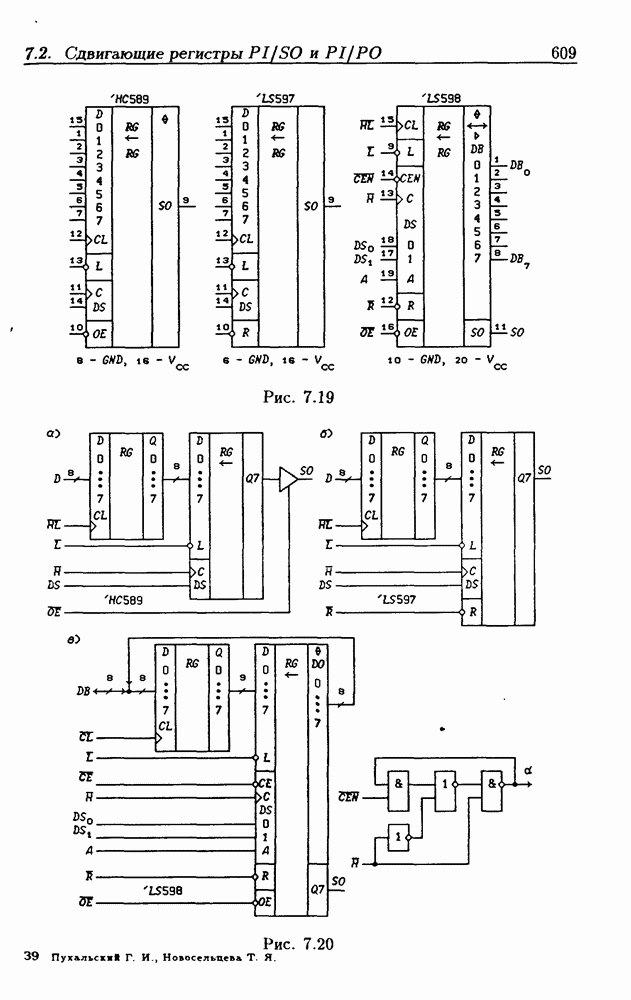
- Сдвигающие регистры с входным регистром памяти.
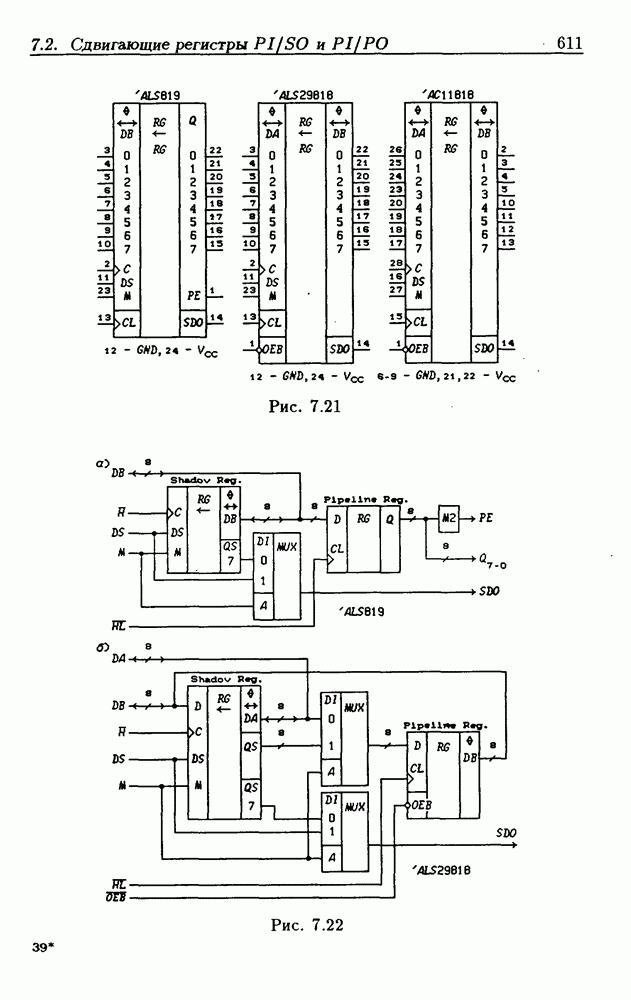
- 7.3. Реверсивные сдвигающие регистры
- Реверсивные сдвигающие регистры типов PI/SO и PI/PO.
- Многофункциональные устройства на основе реверсивных сдвигающих регистров.
- 7.4. Асинхронные счетчики
- Двоично-десятичные асинхронные счетчики.
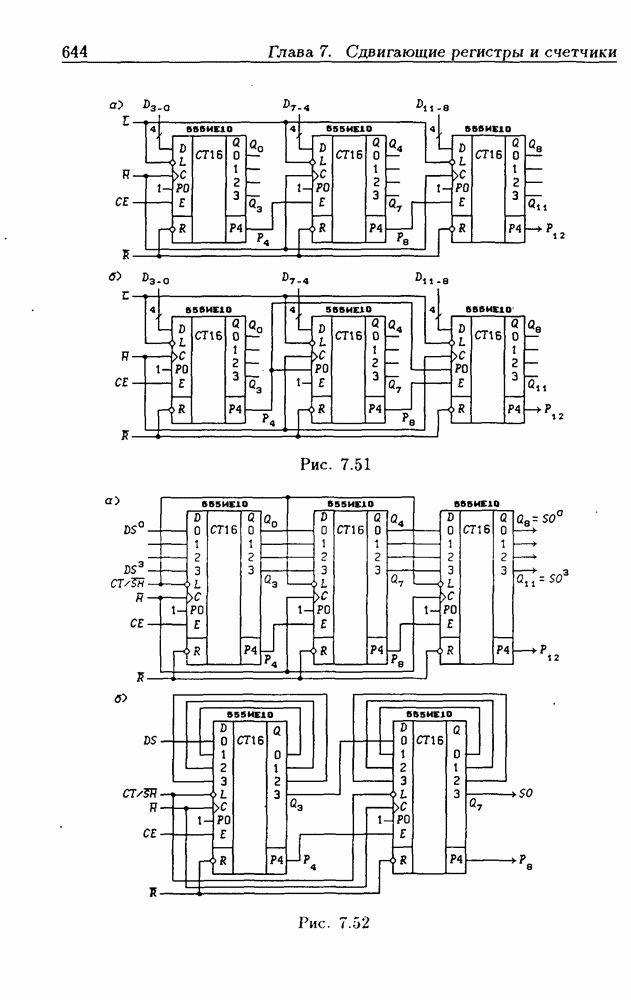
- 7.5. Синхронные двоичные счетчики
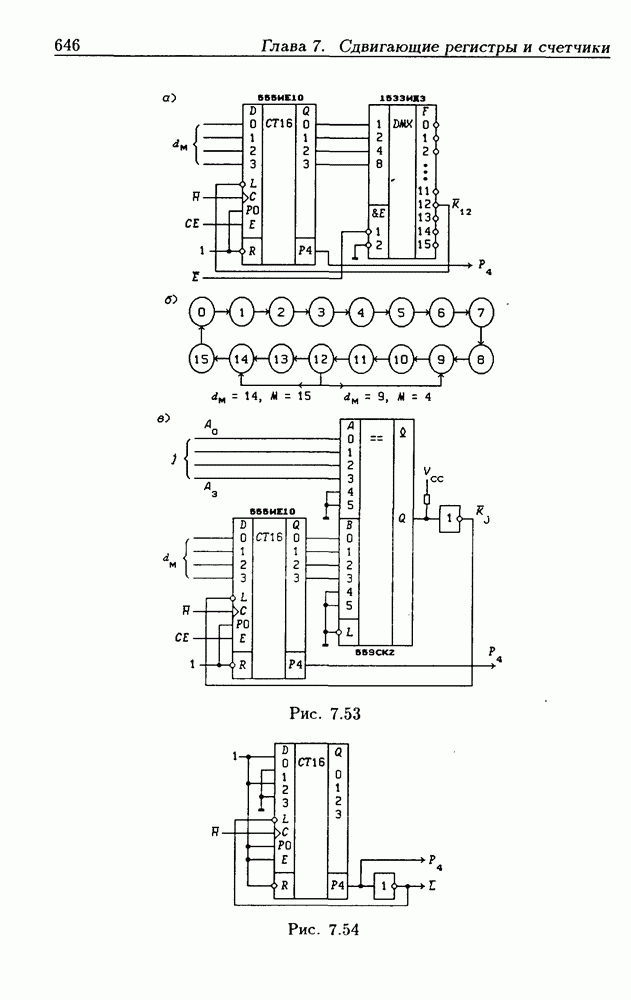
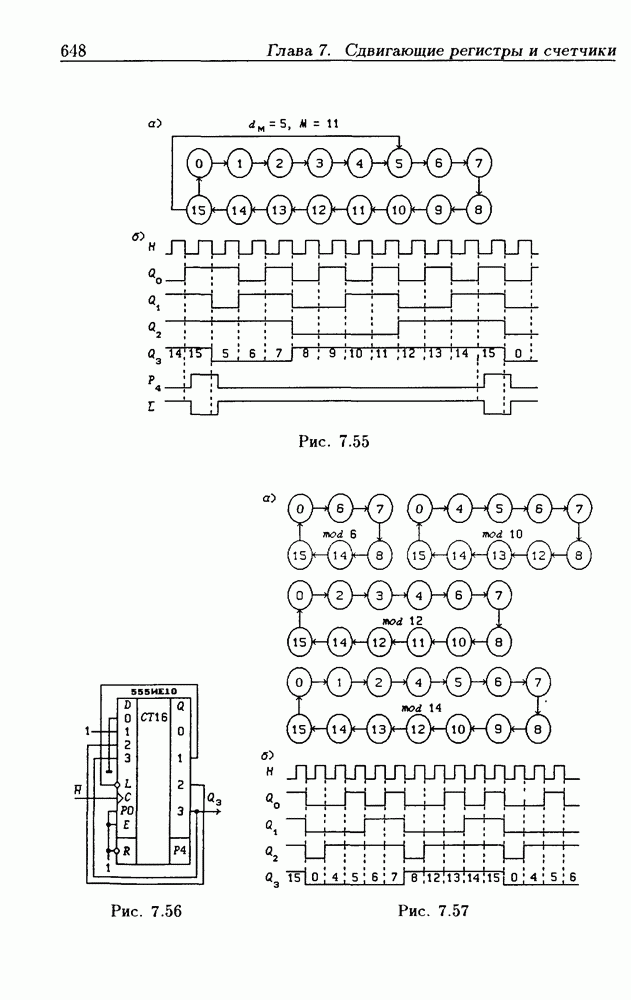
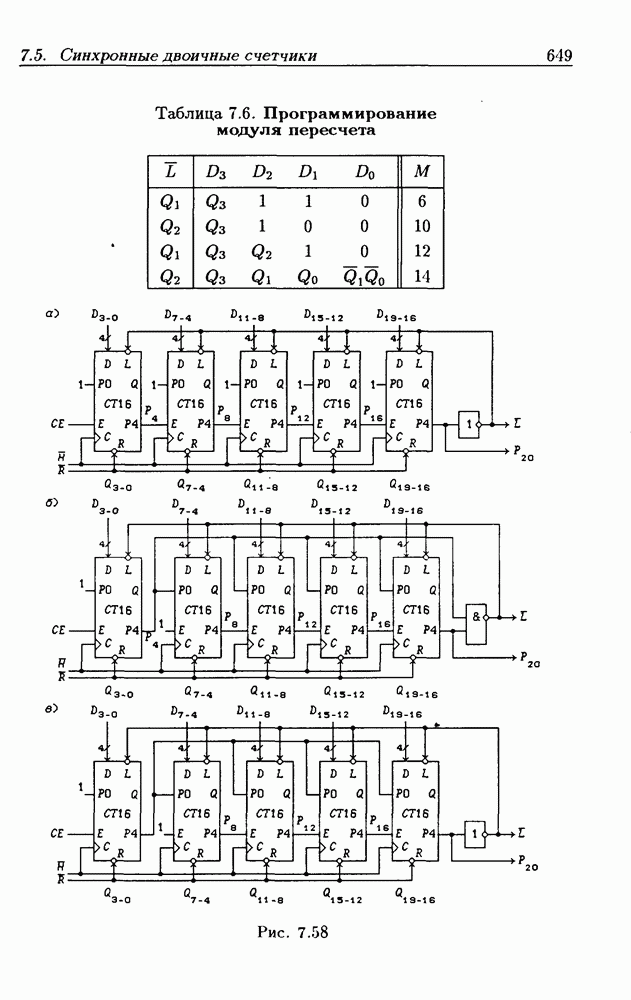
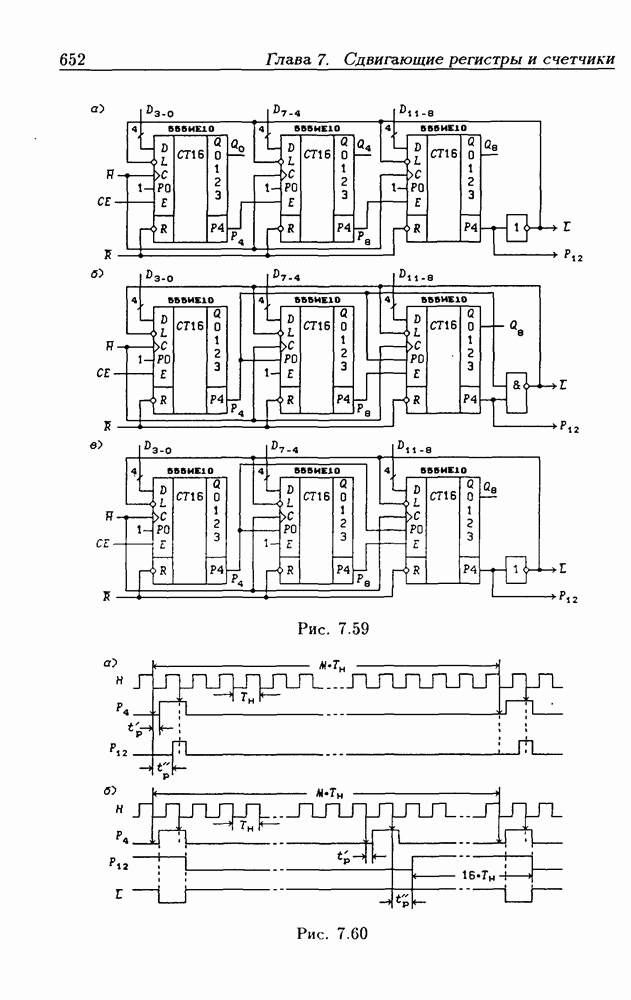
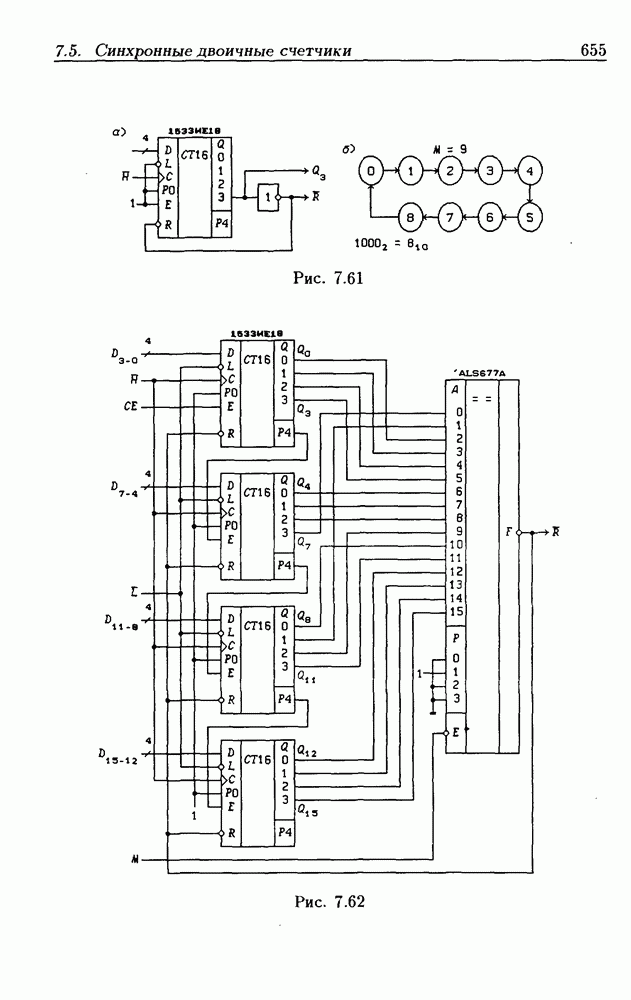
- Программирование модуля пересчета двоичных счетчиков.
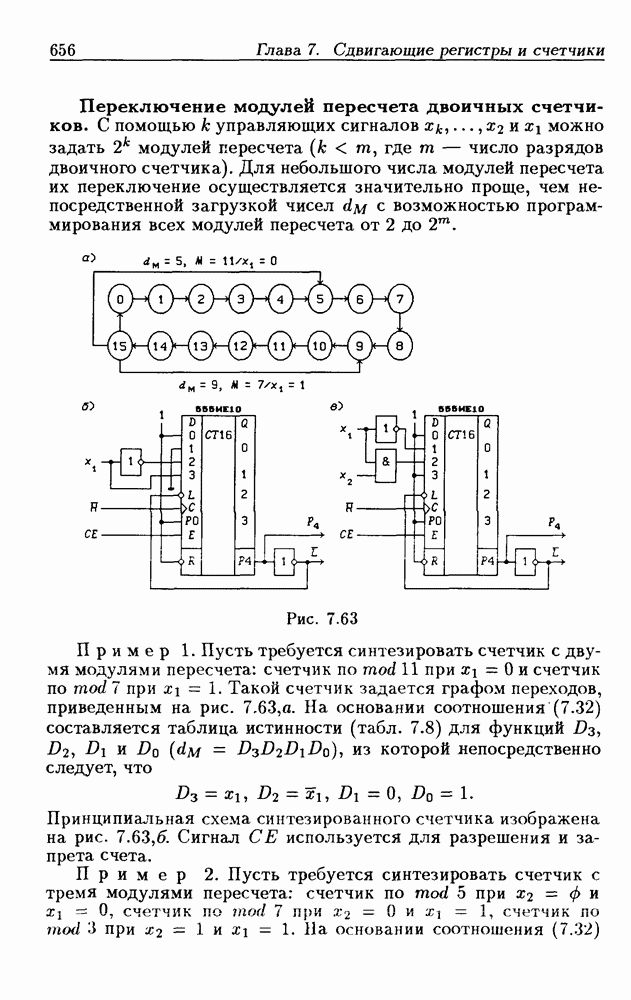
- Переключение модулей пересчета двоичных счетчиков.
- Функциональные устройства на основе двоичных счетчиков.
- 7.6. Синхронные двоично-десятичные счетчики
- 7.7. Синхронные реверсивные счетчики
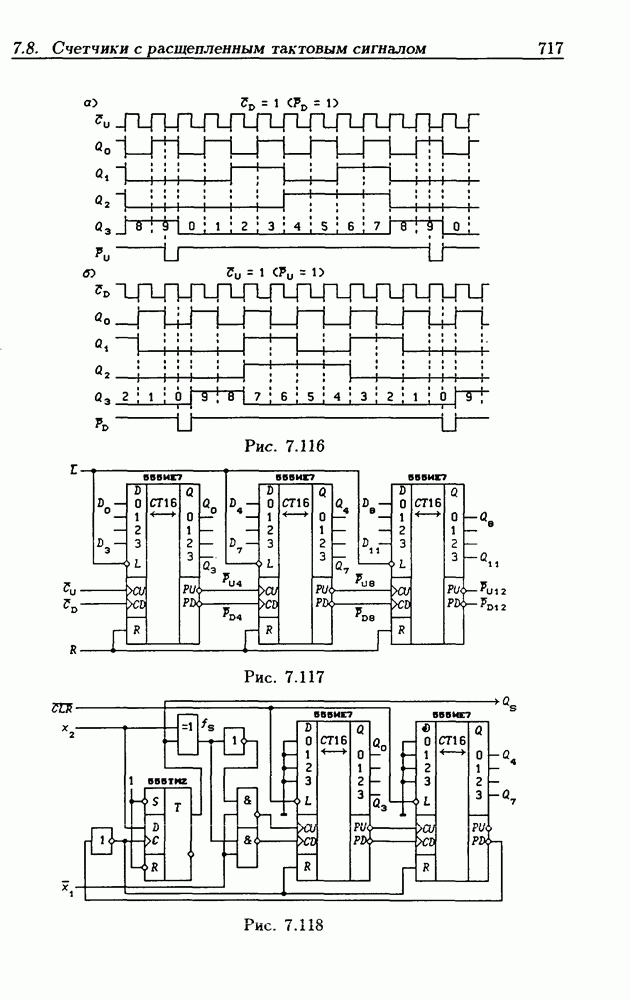
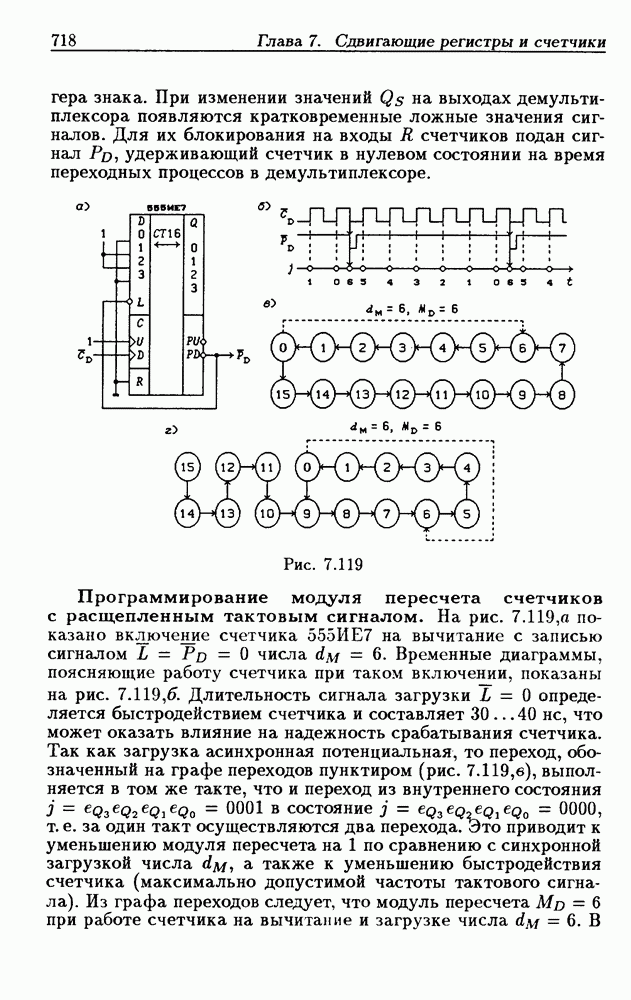
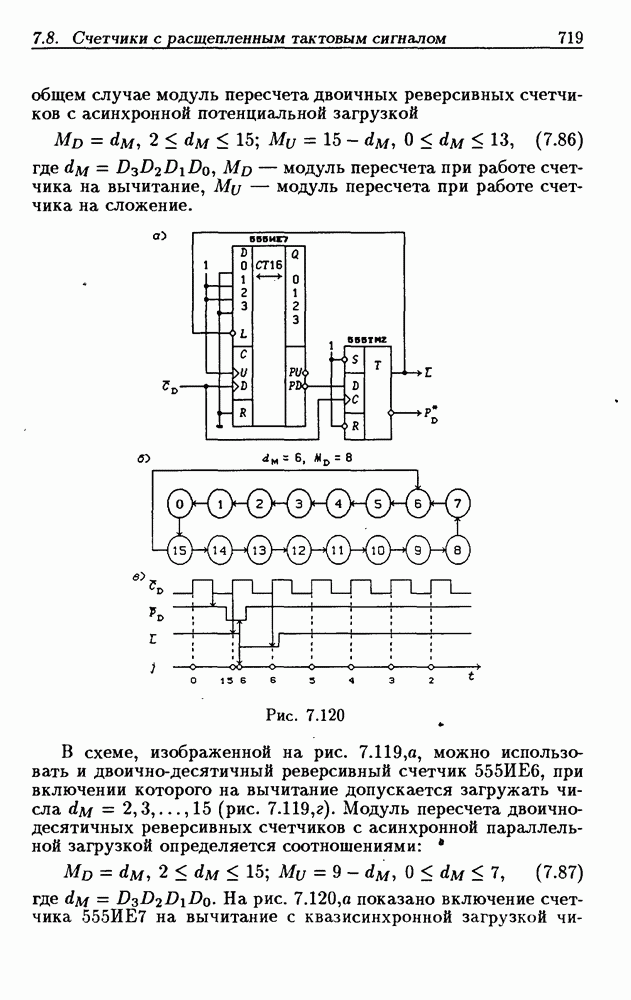
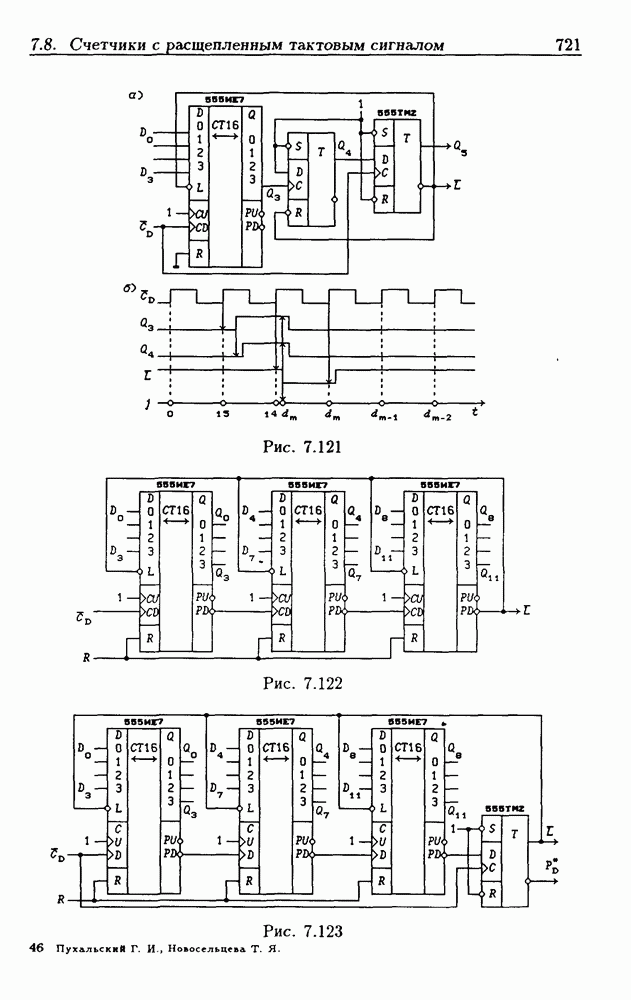
- 7.8. Счетчики с расщепленным тактовым сигналом
- 7.9. Счетчики на сдвигающих регистрах
- 7.10. Кольцевые счетчики
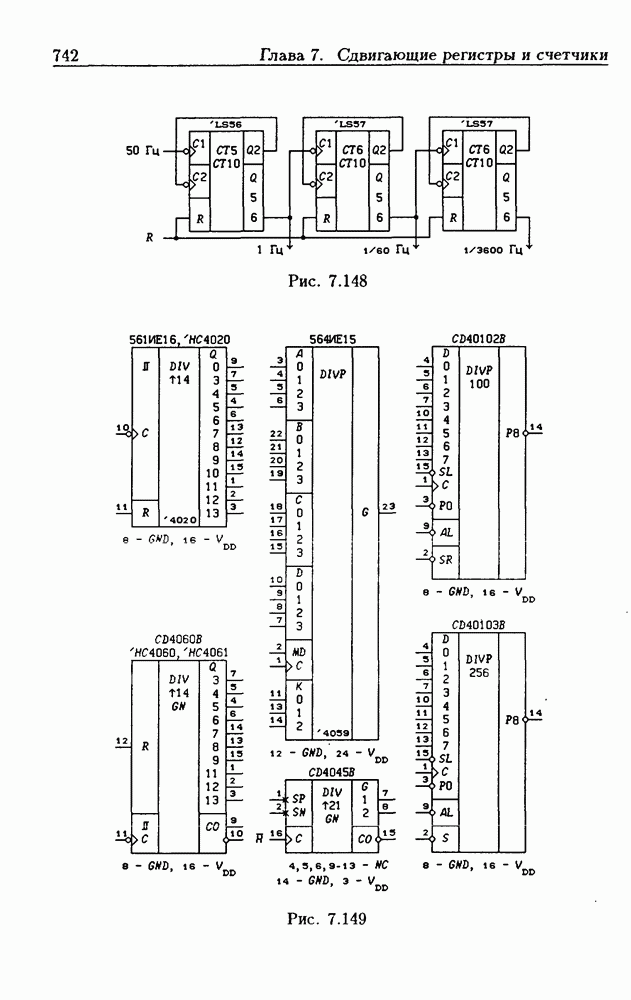
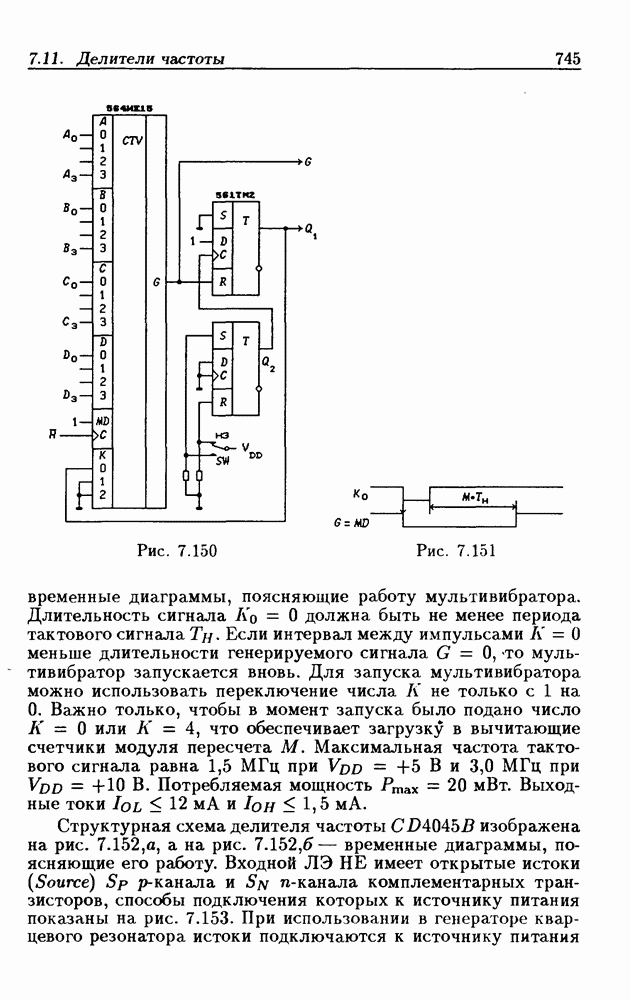
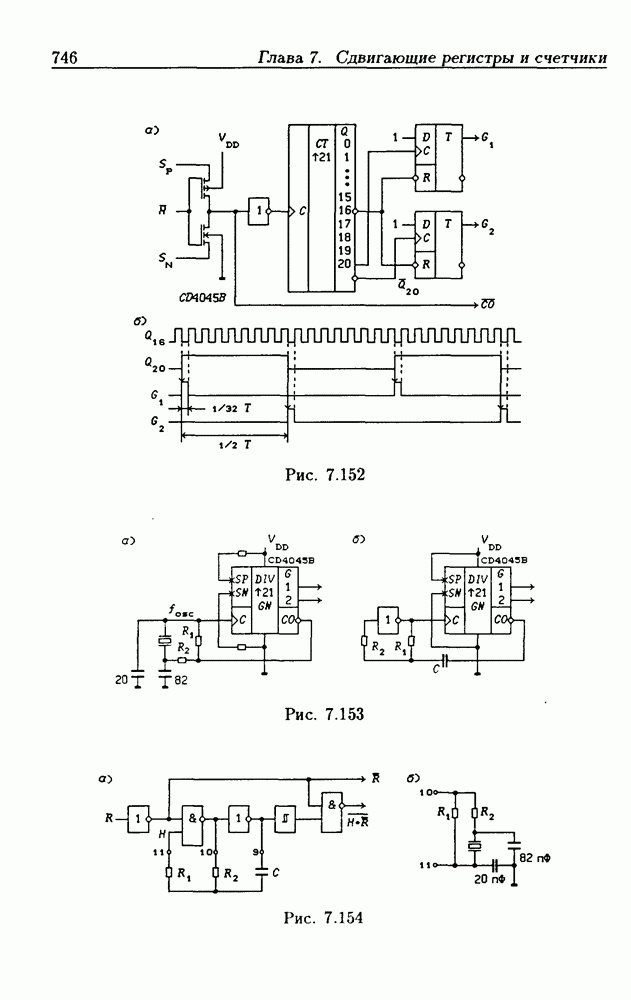
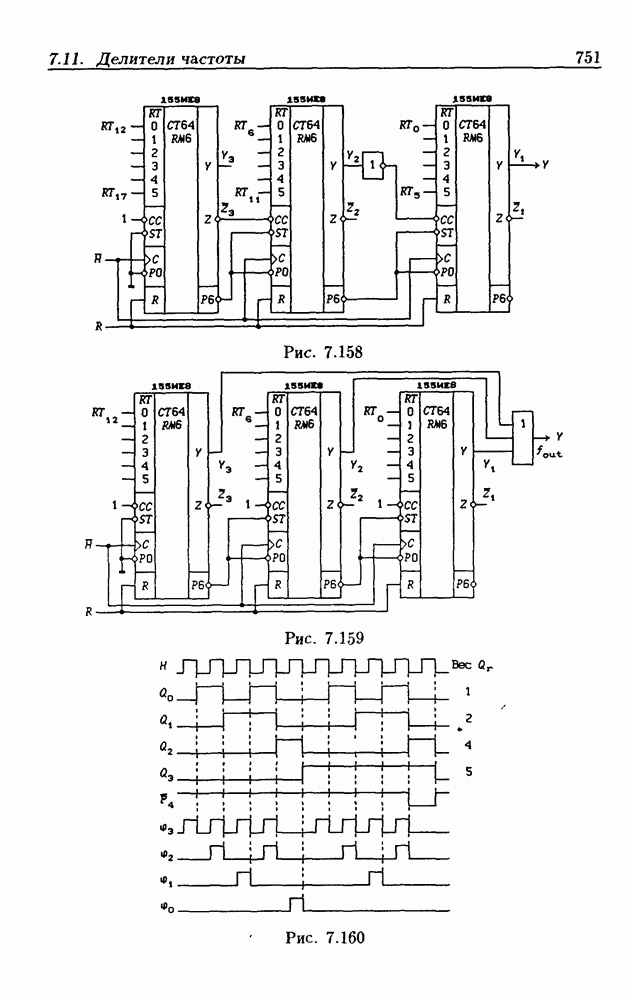
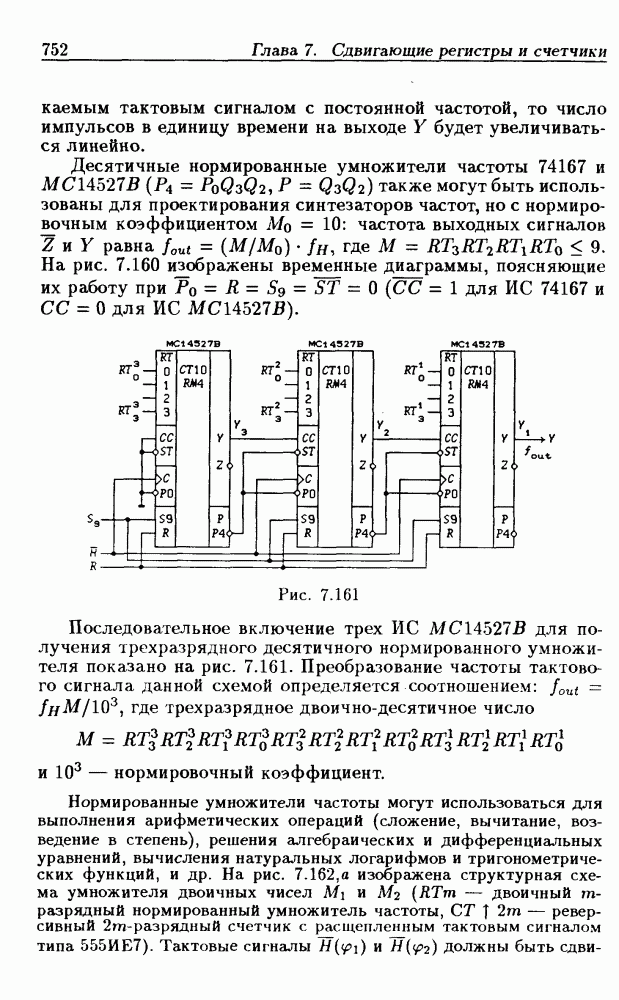
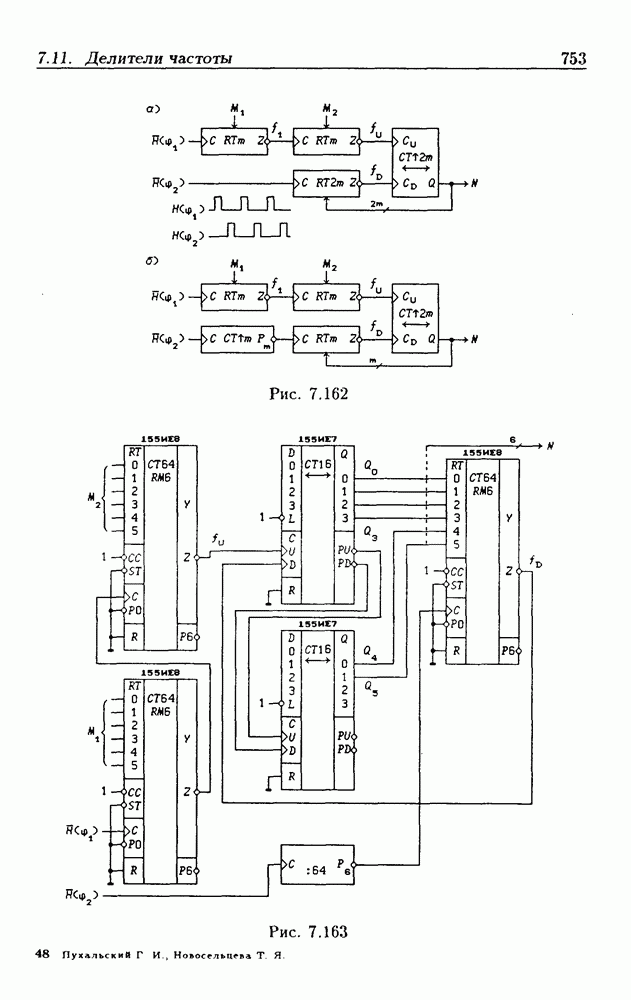
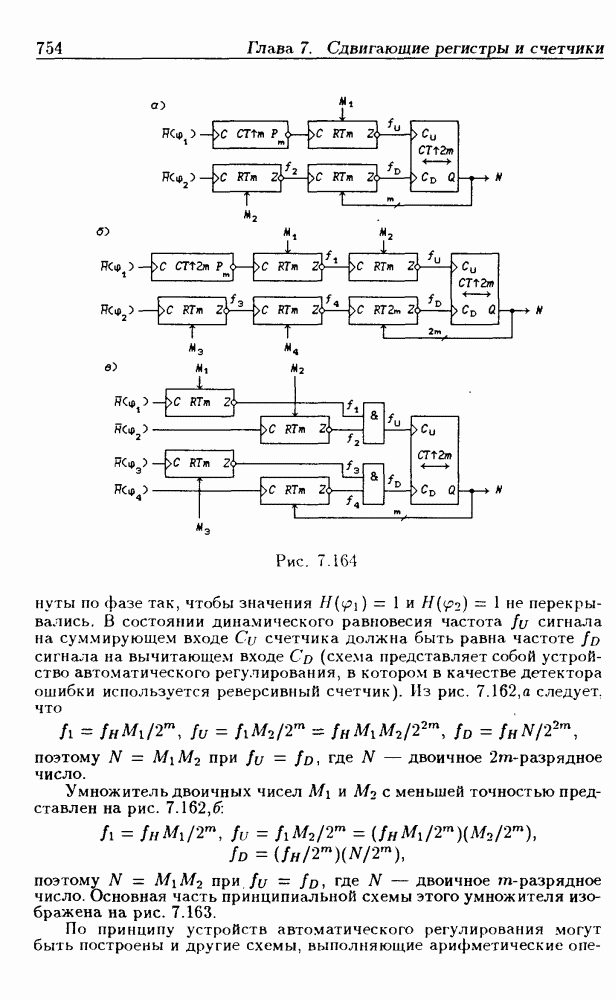
- 7.11. Делители частоты
- Нормированные умножители частоты.
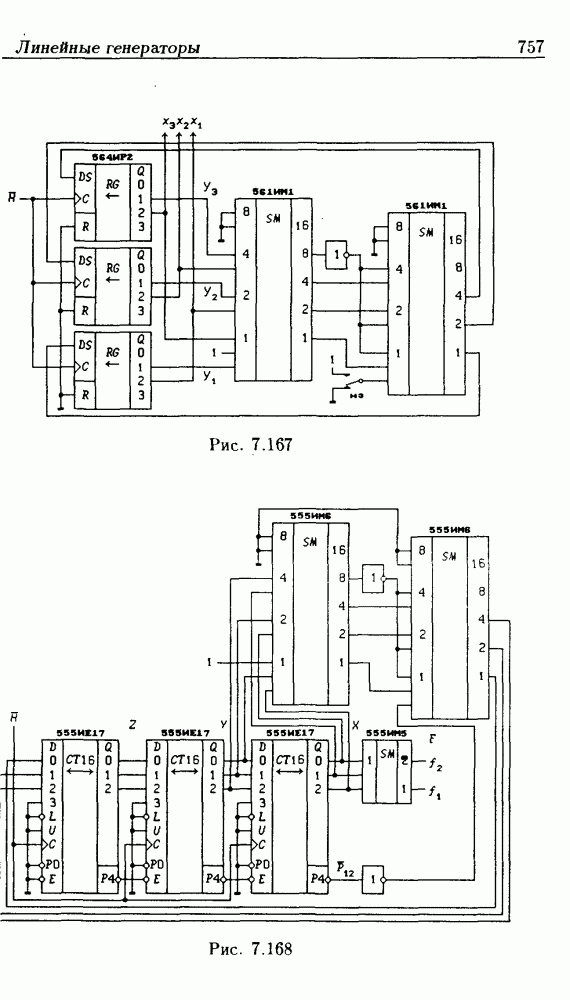
- 7.12. Линейные генераторы
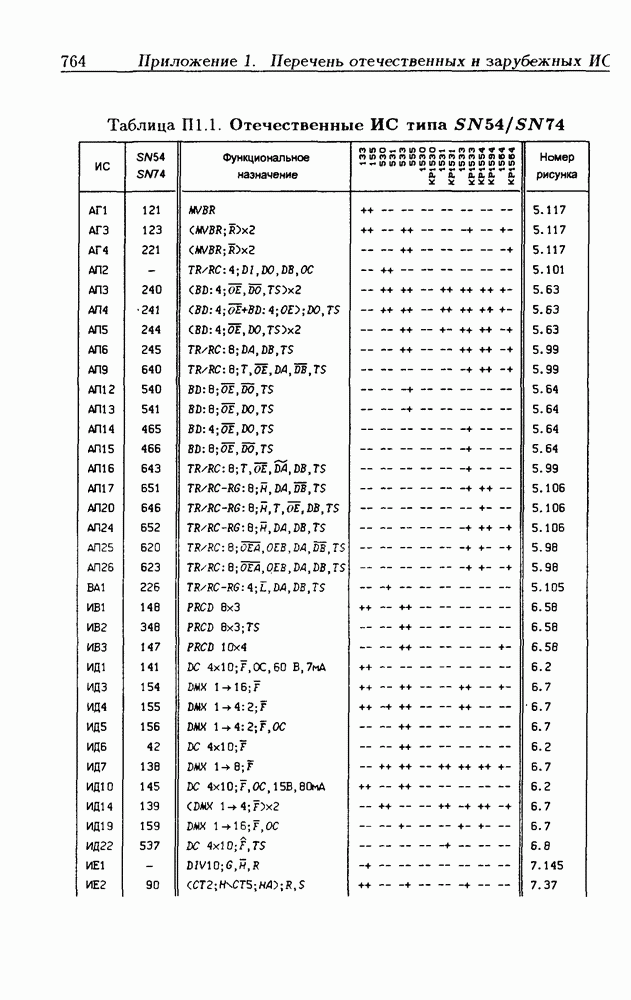
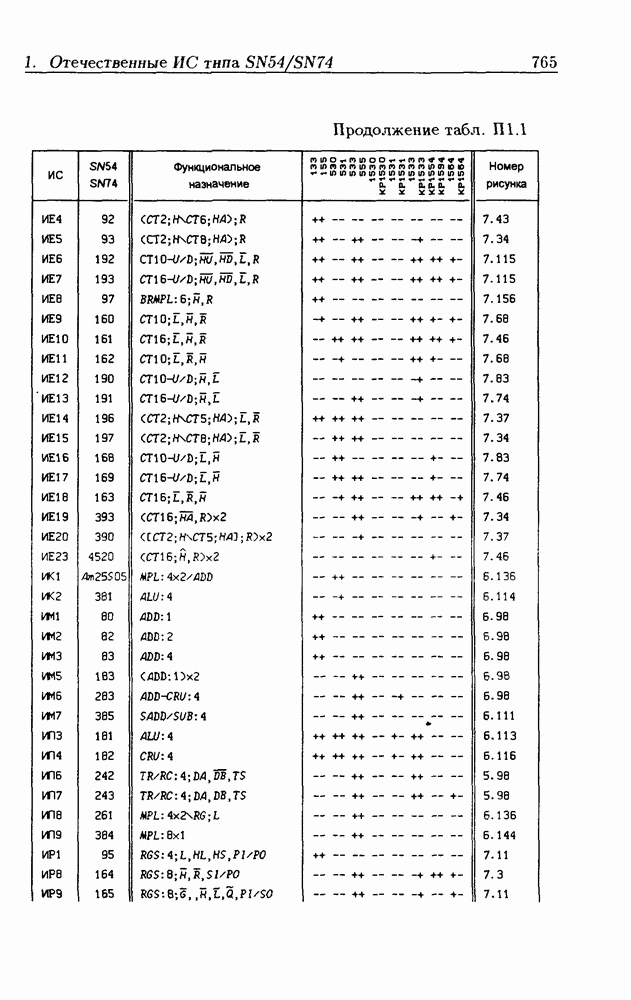
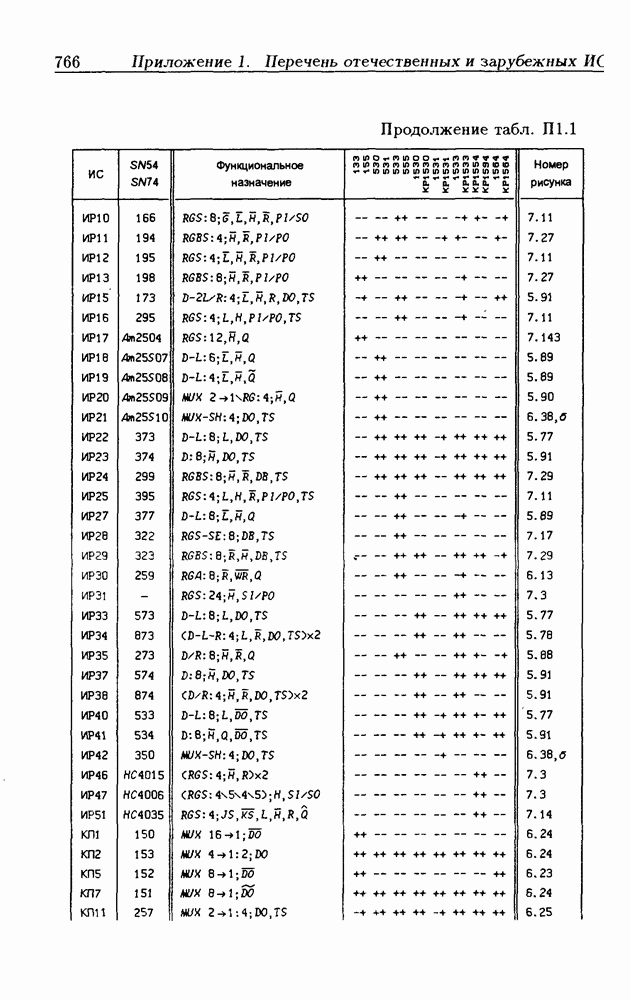
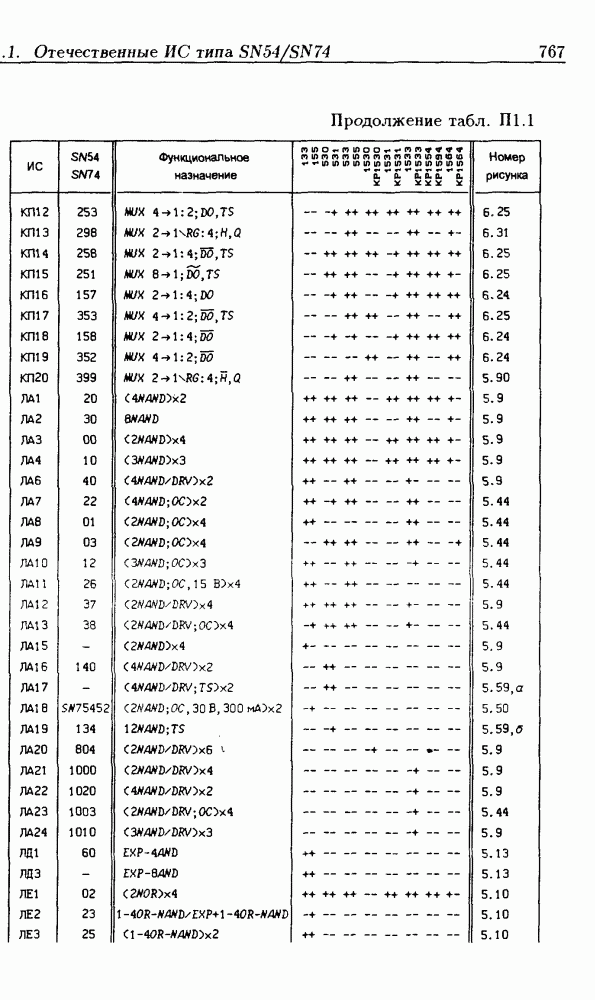
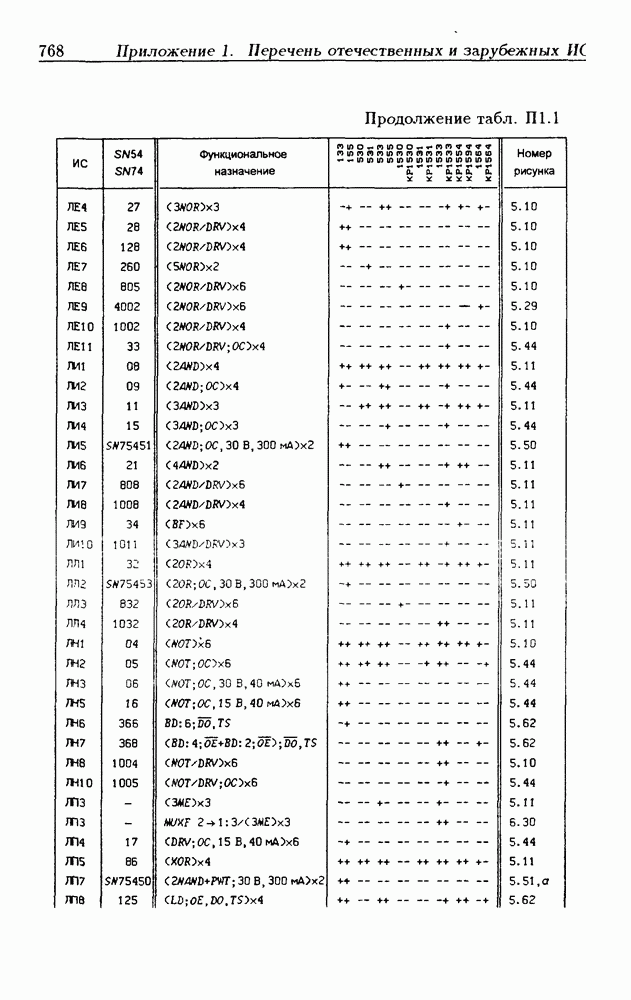
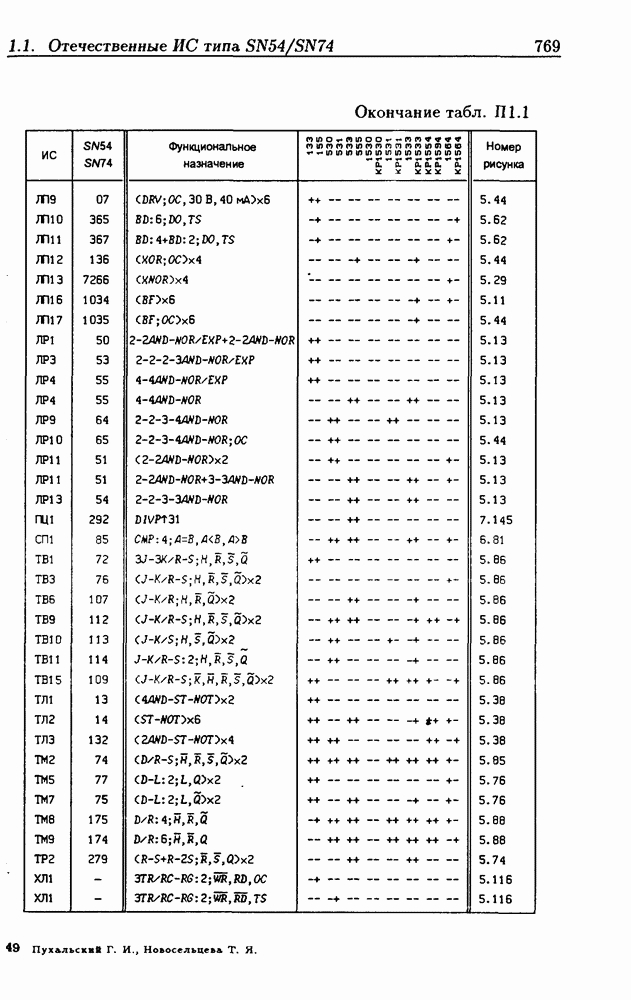
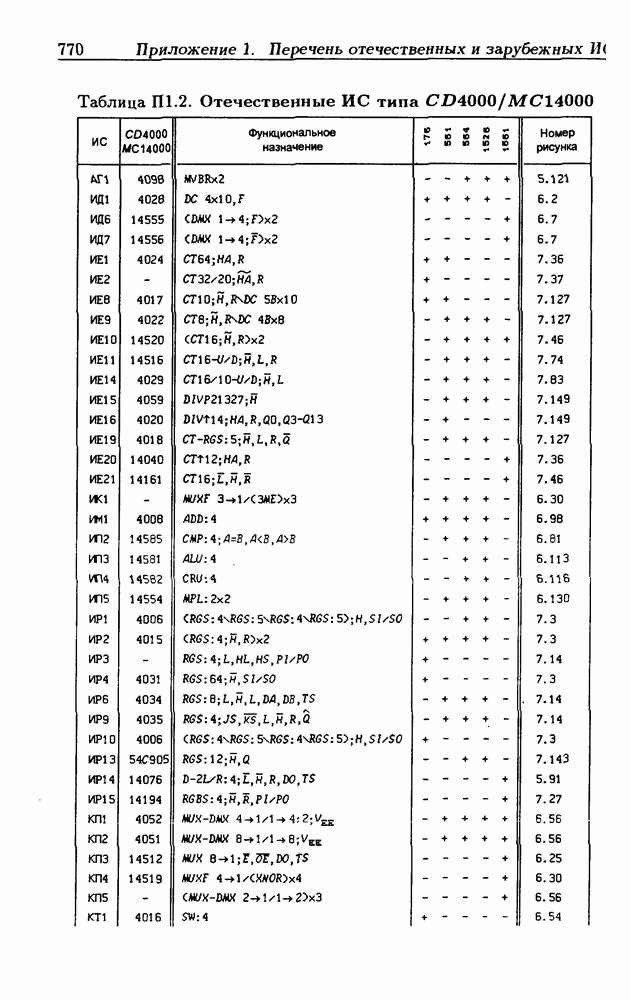
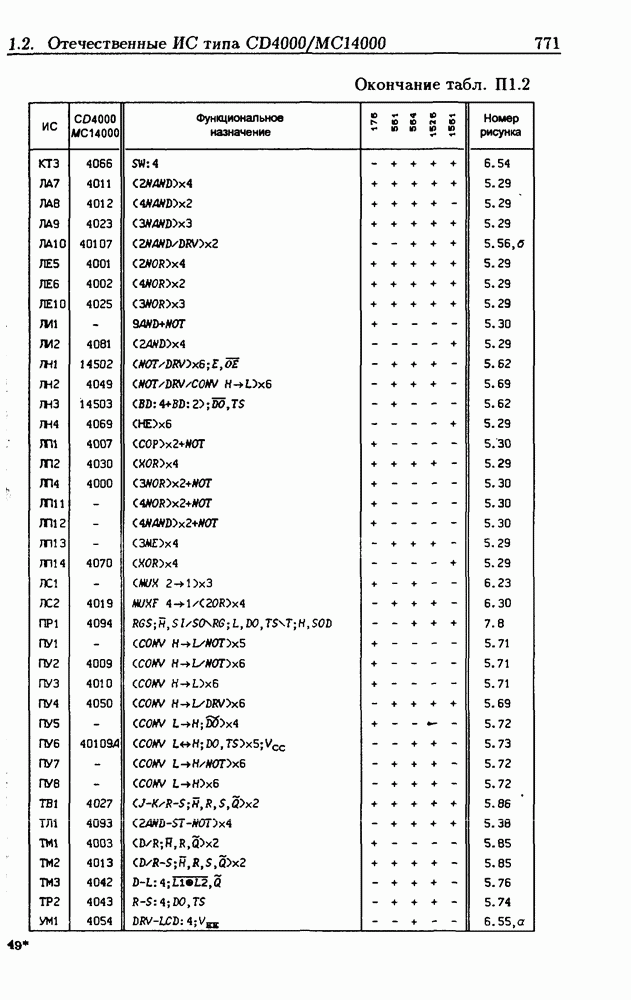
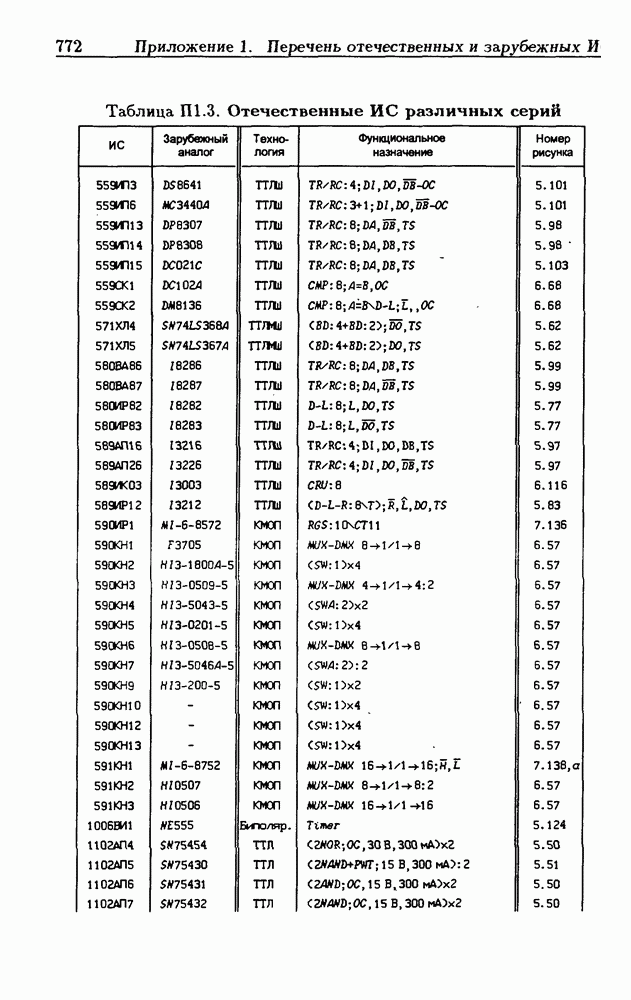
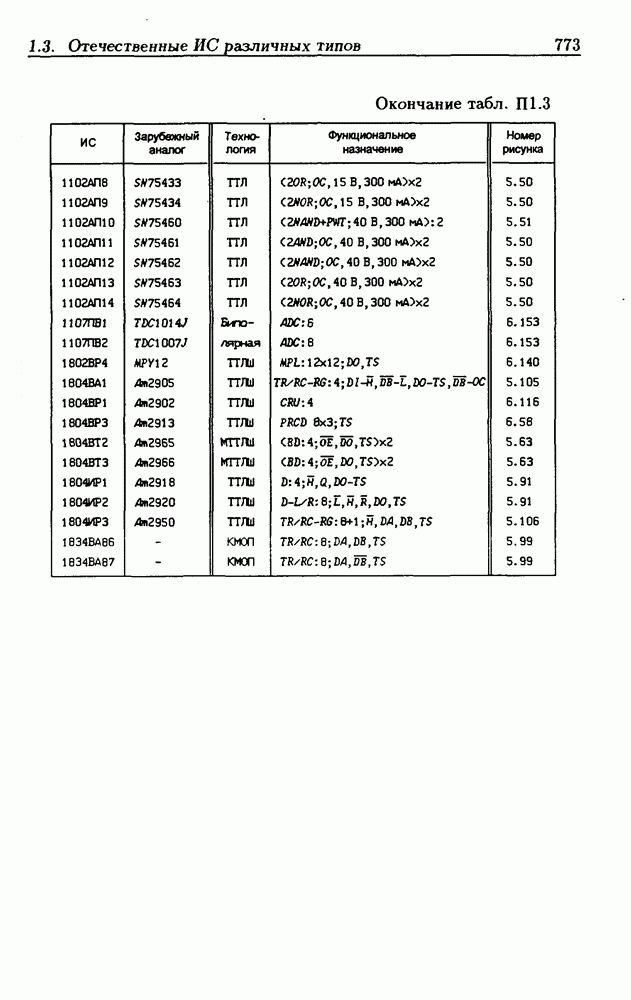
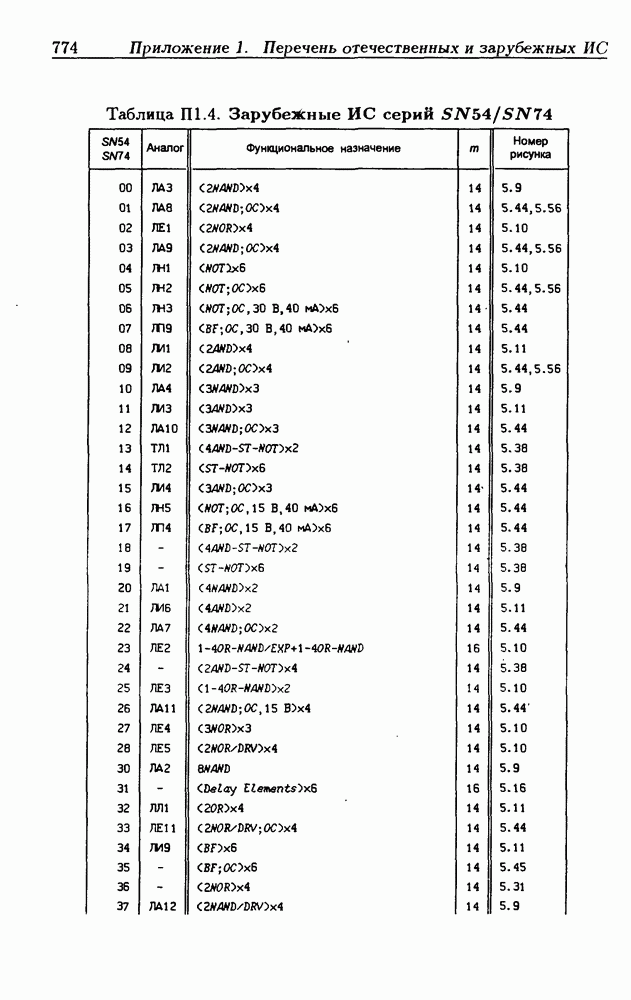
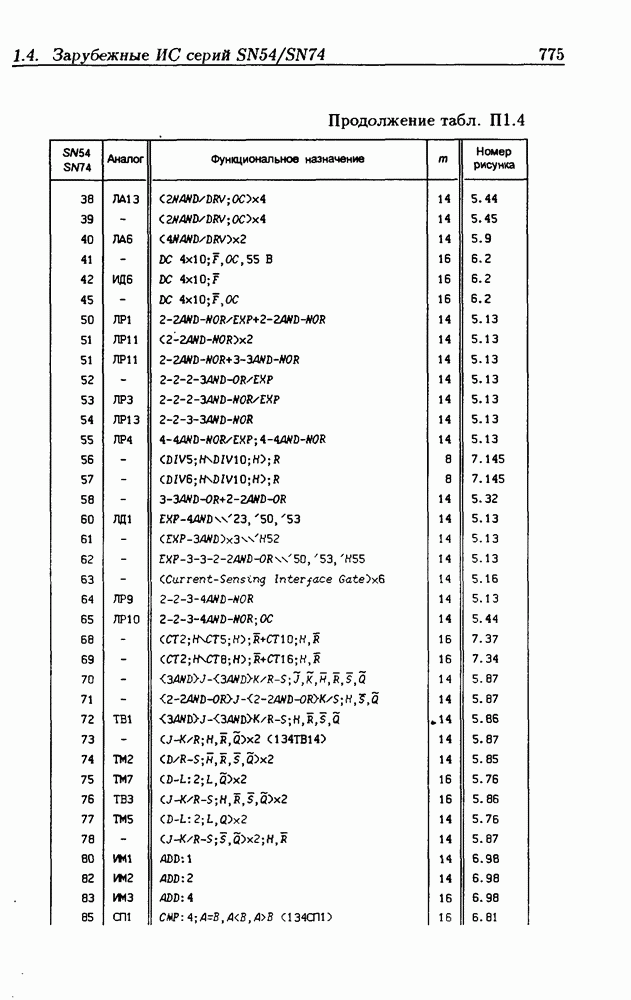
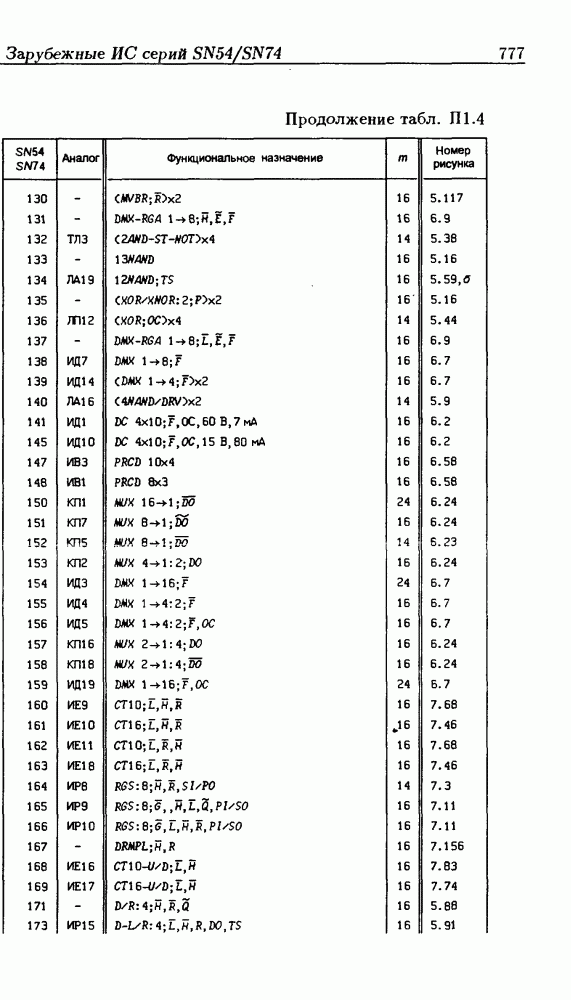
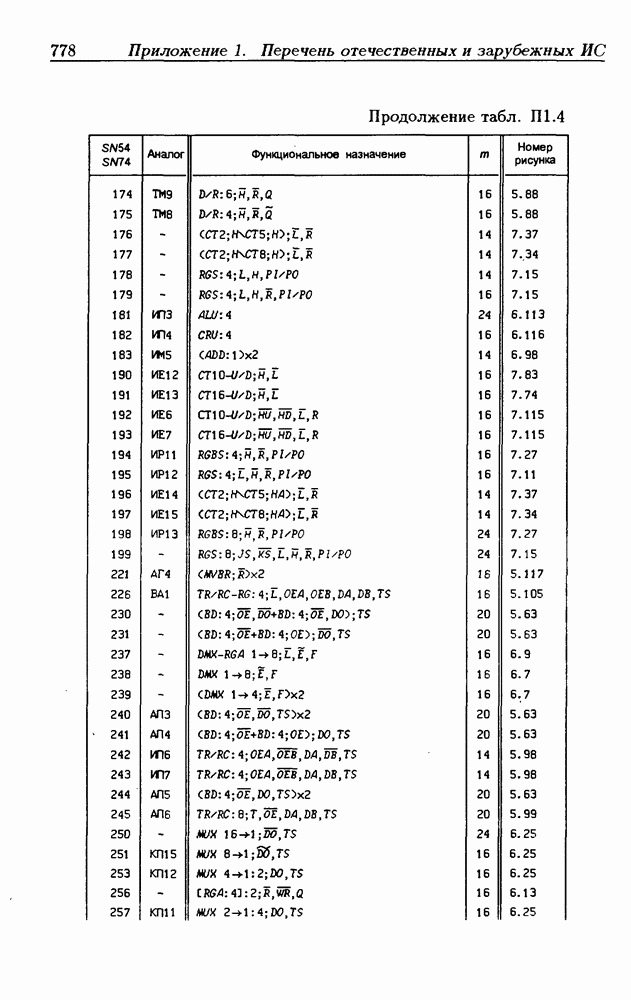
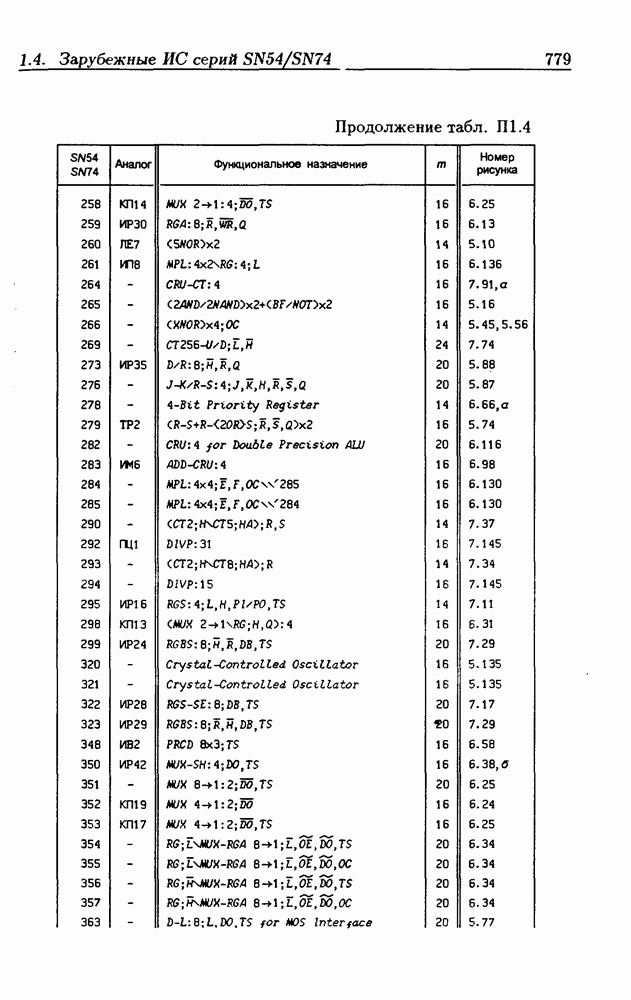
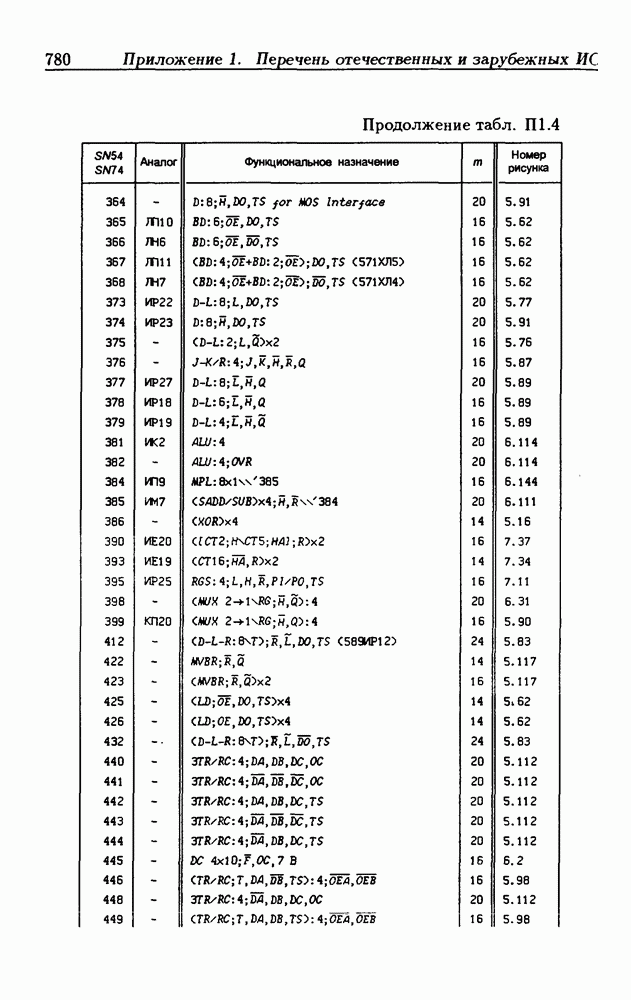
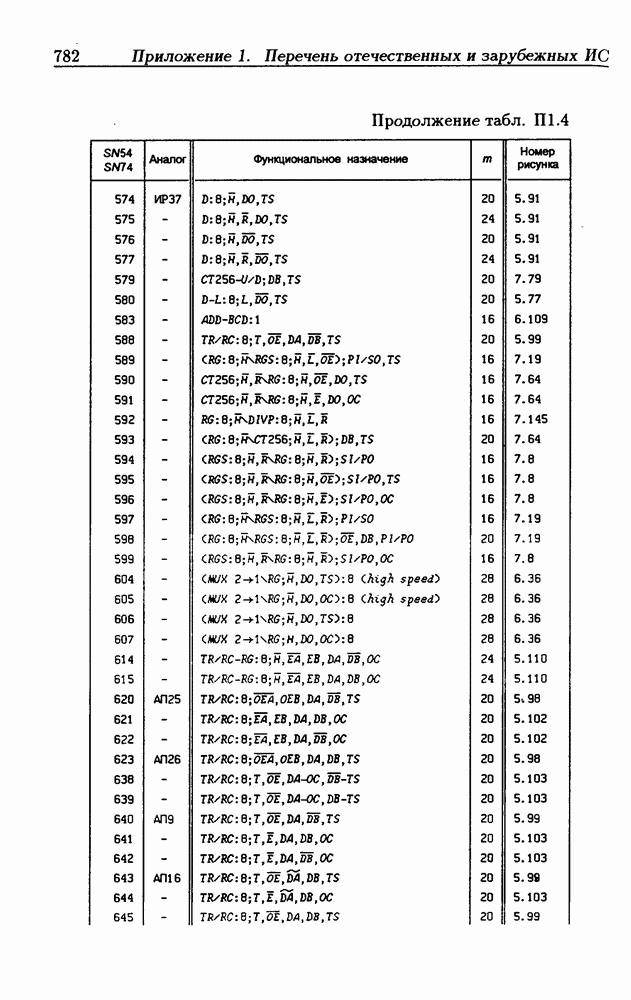
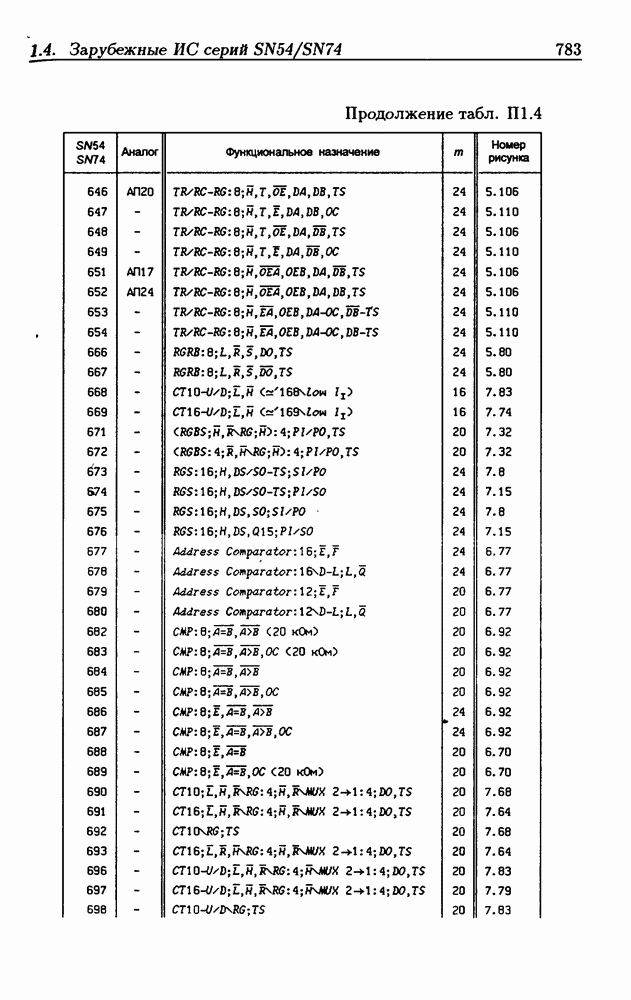
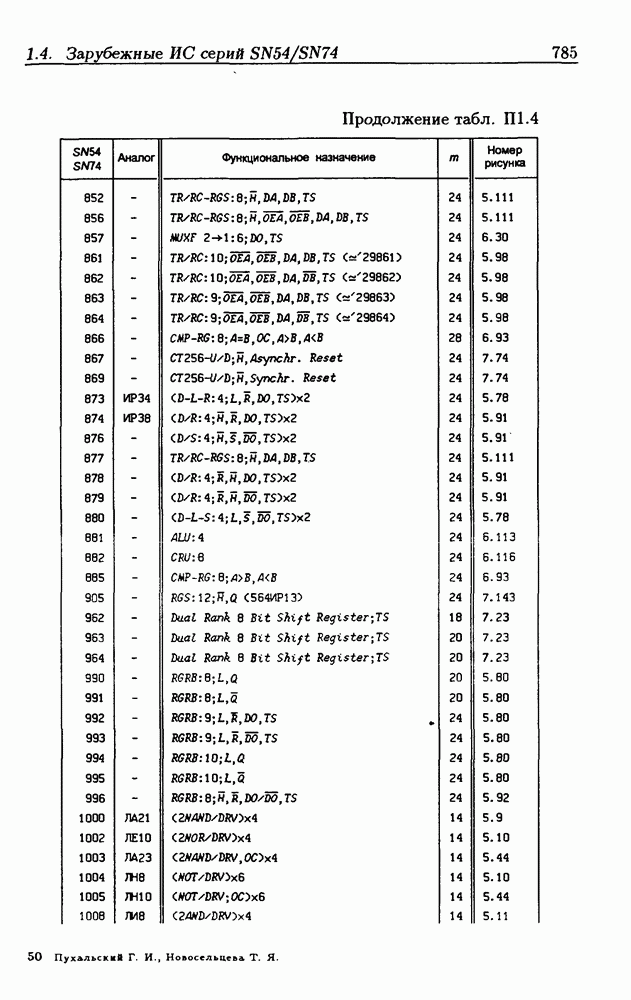
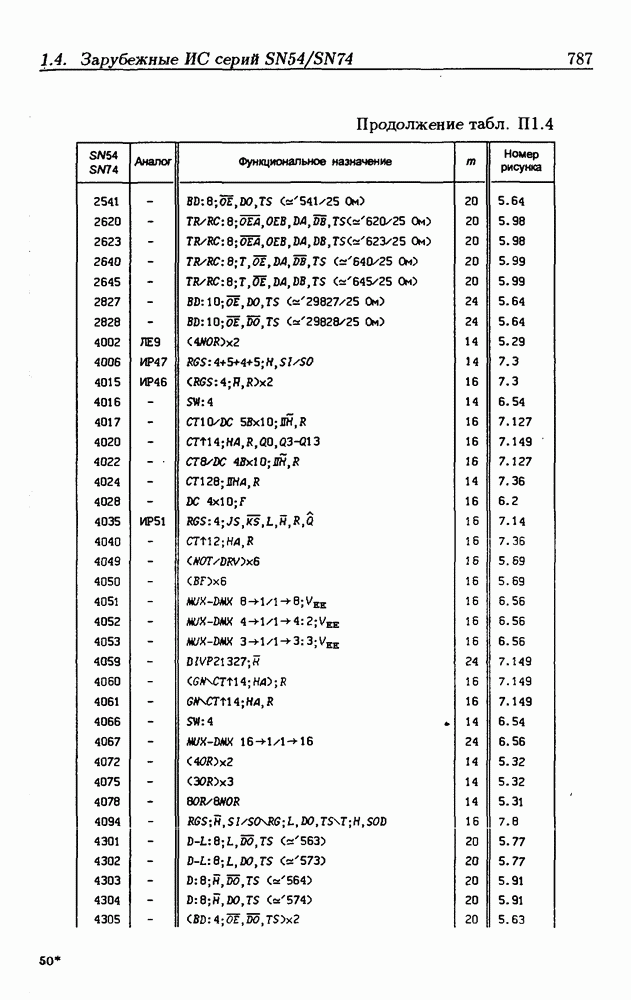
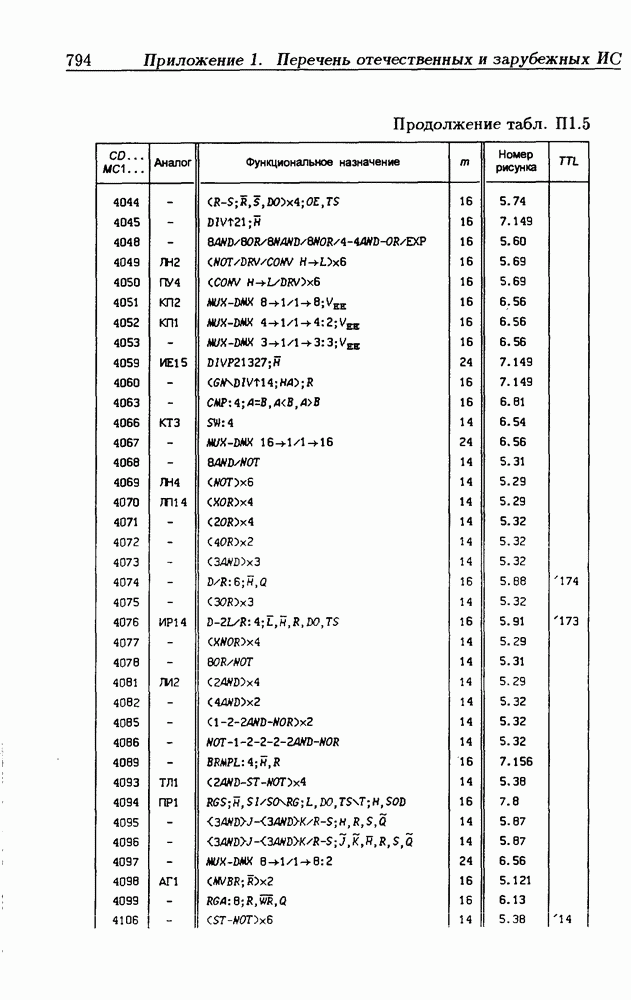
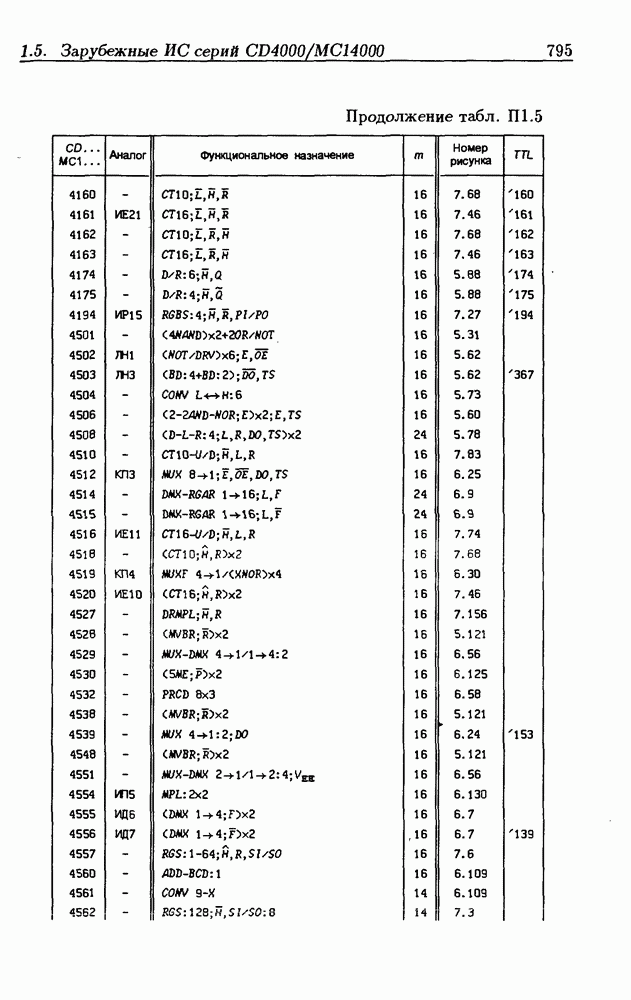
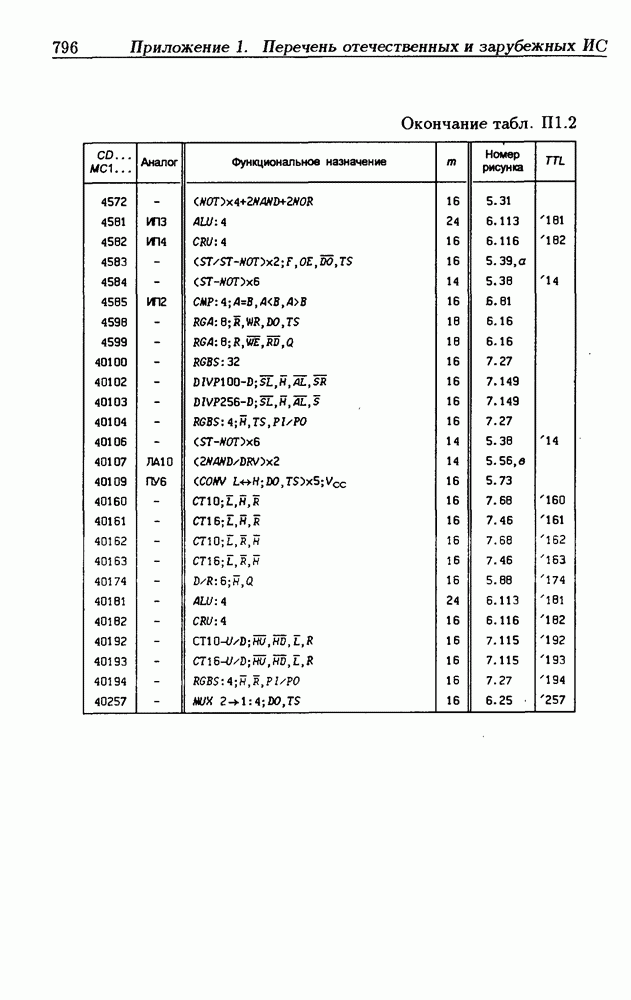
- Приложение 1. Перечень отечественных и зарубежных ИС
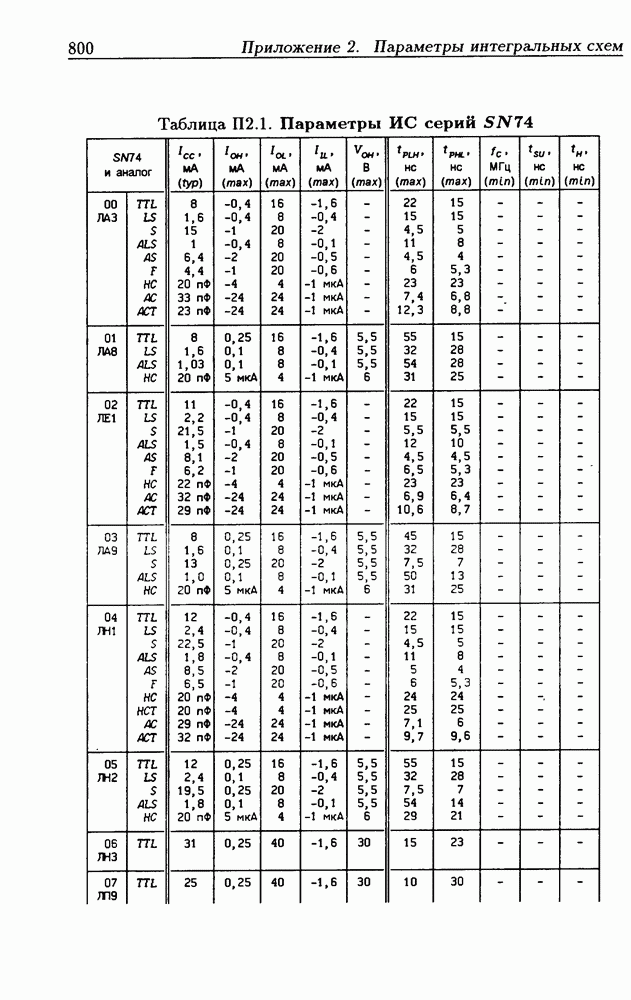
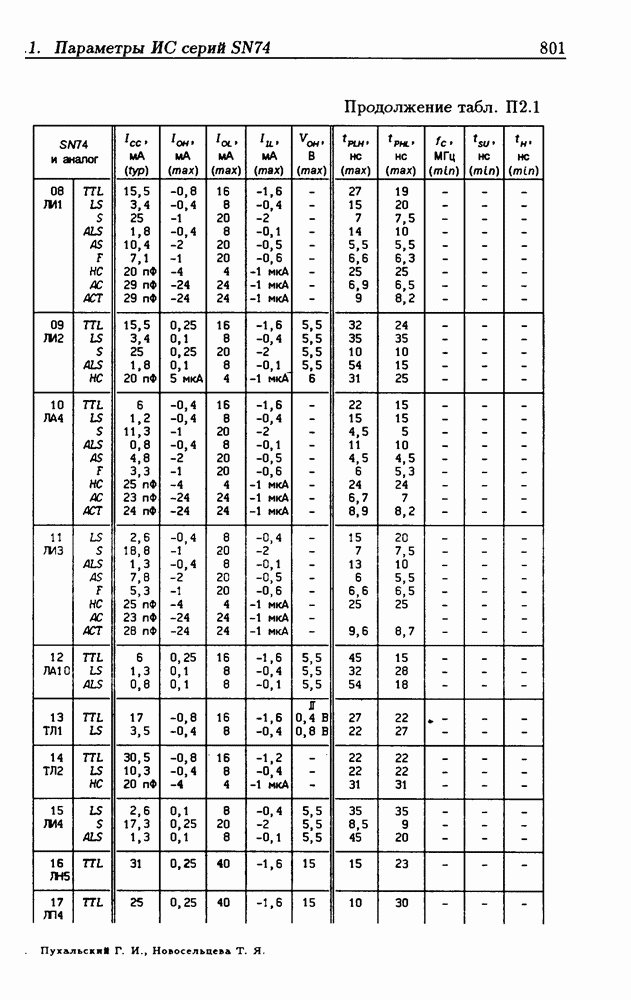
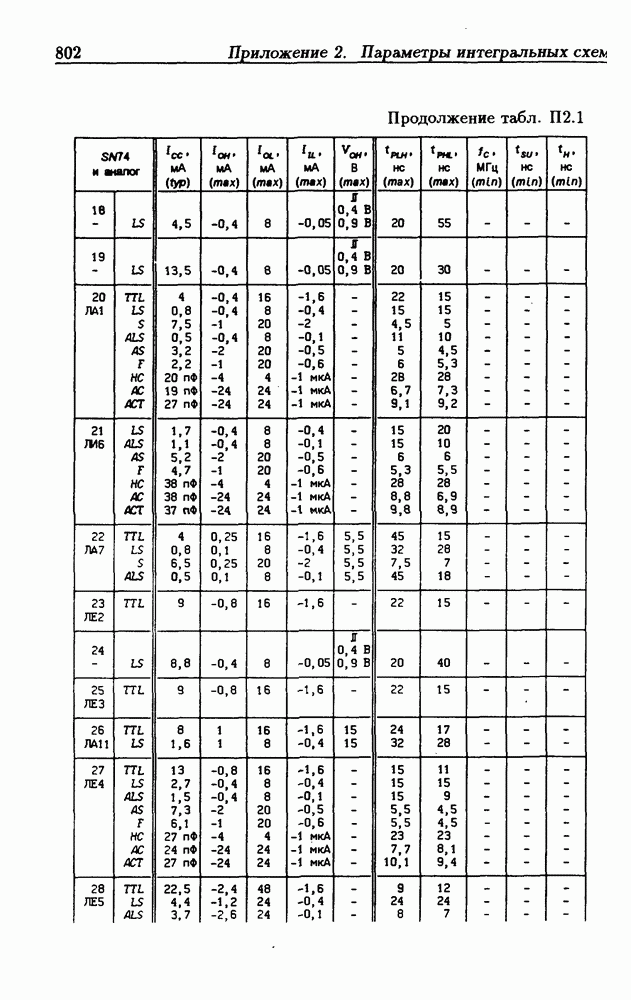
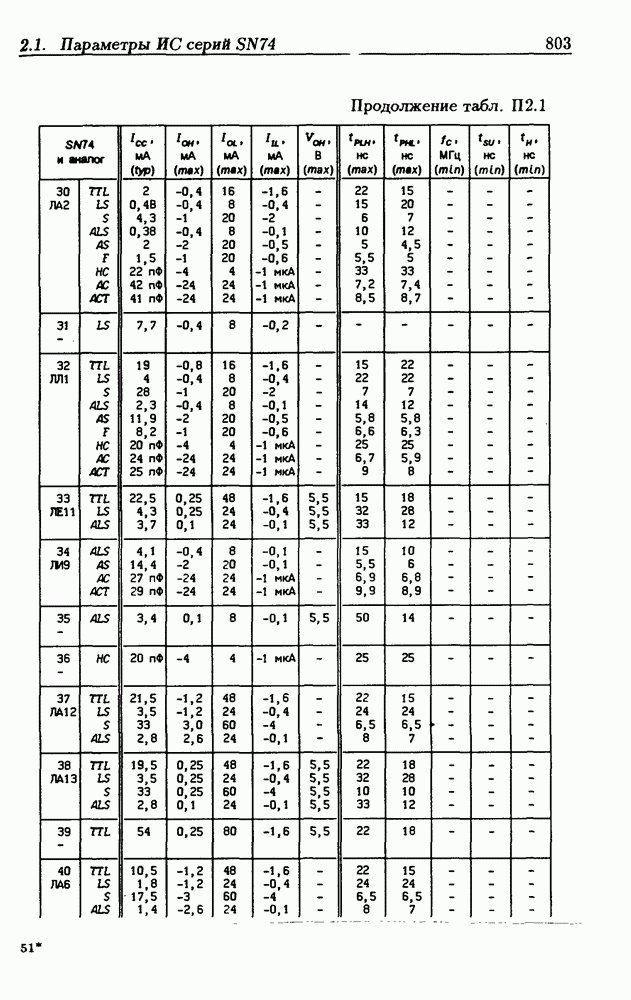
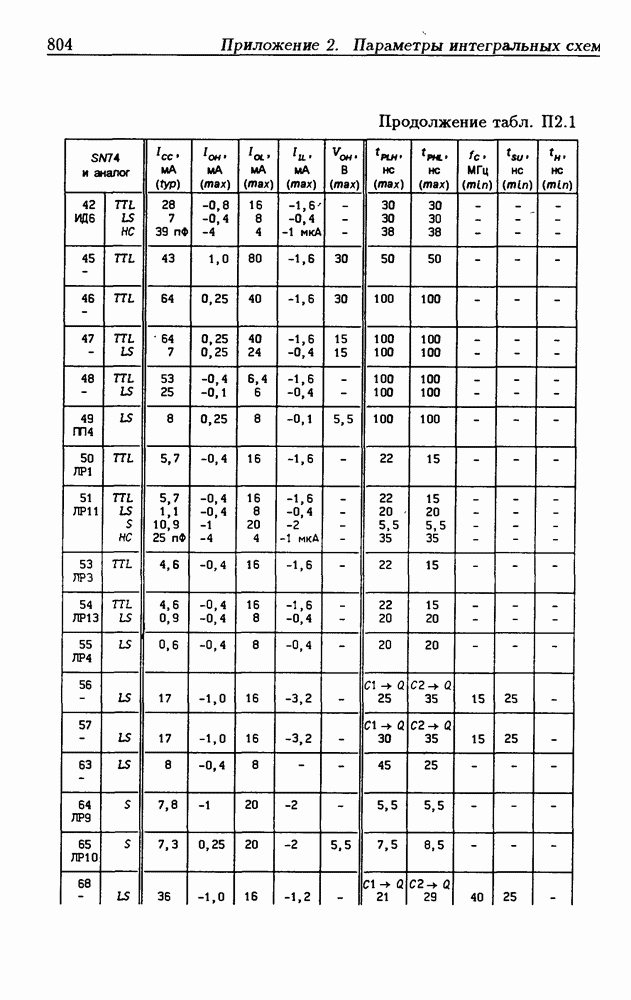
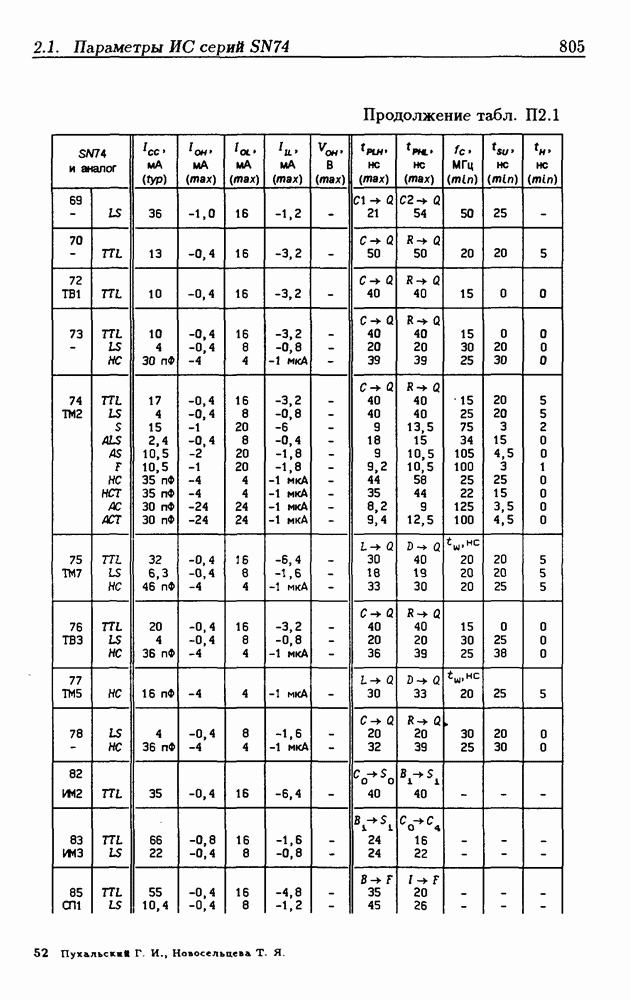
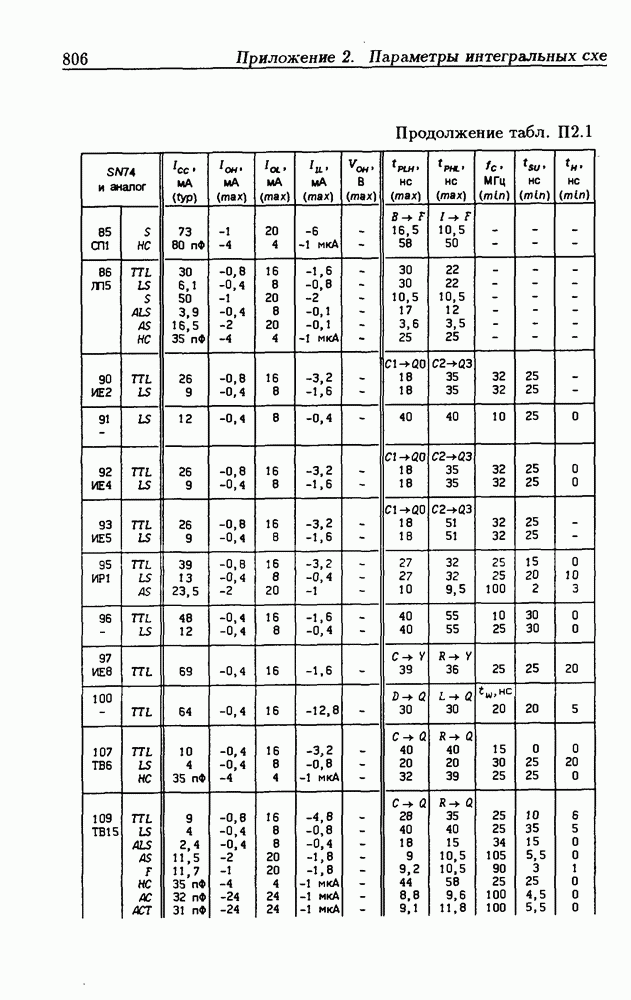
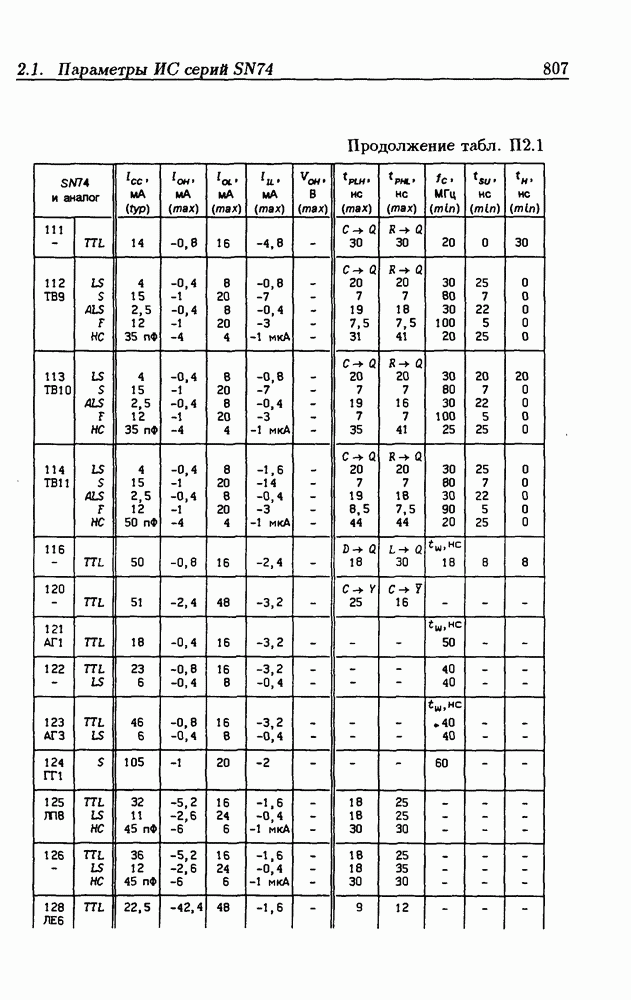
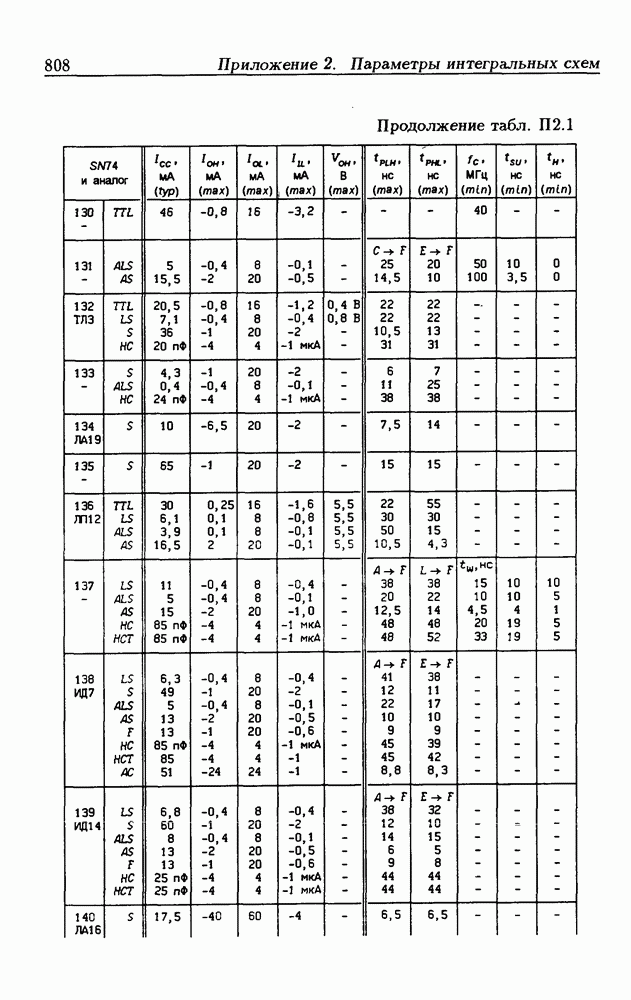
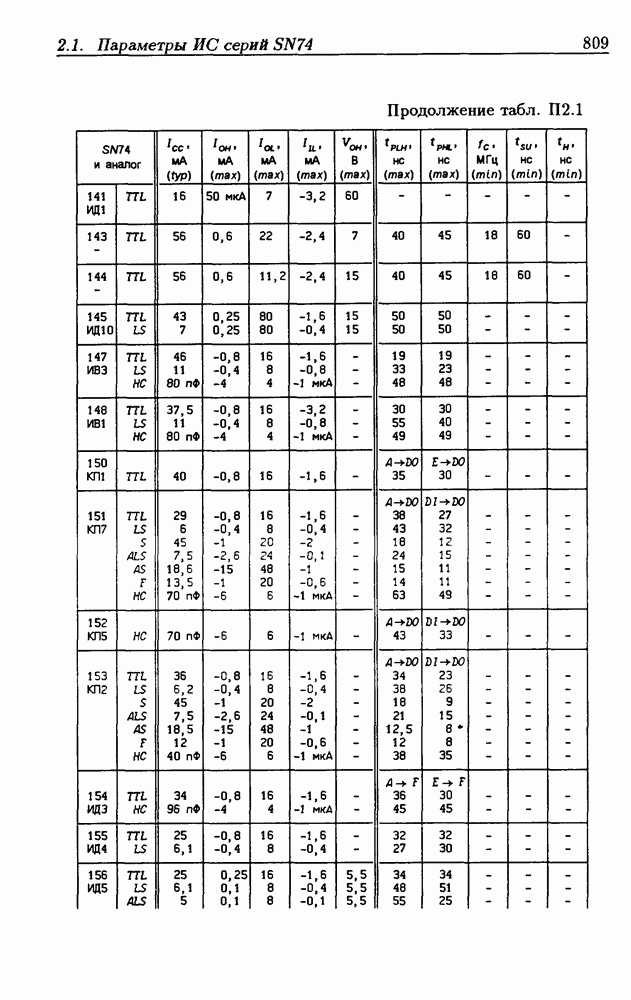
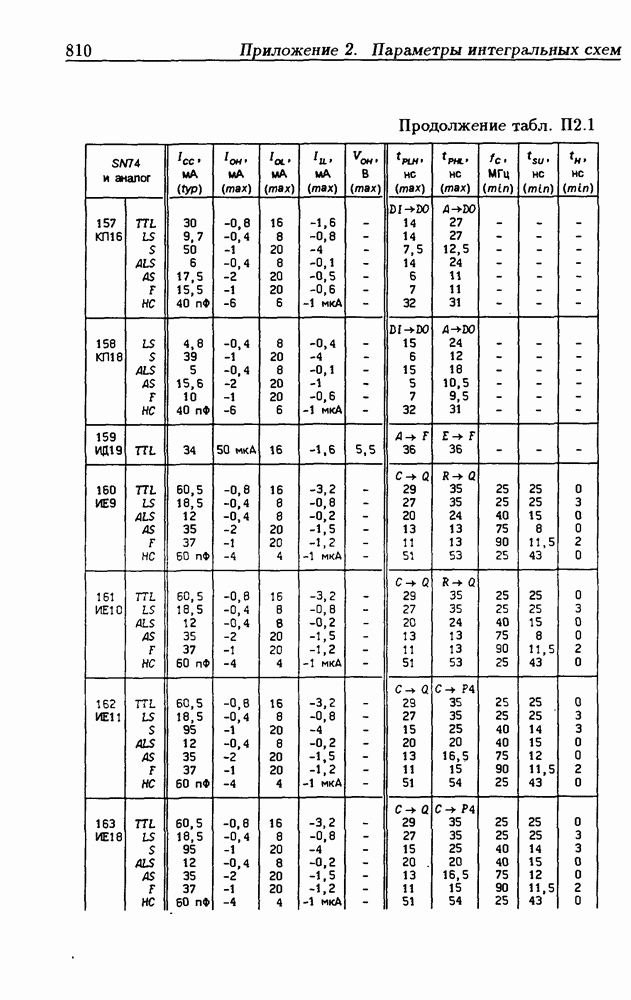
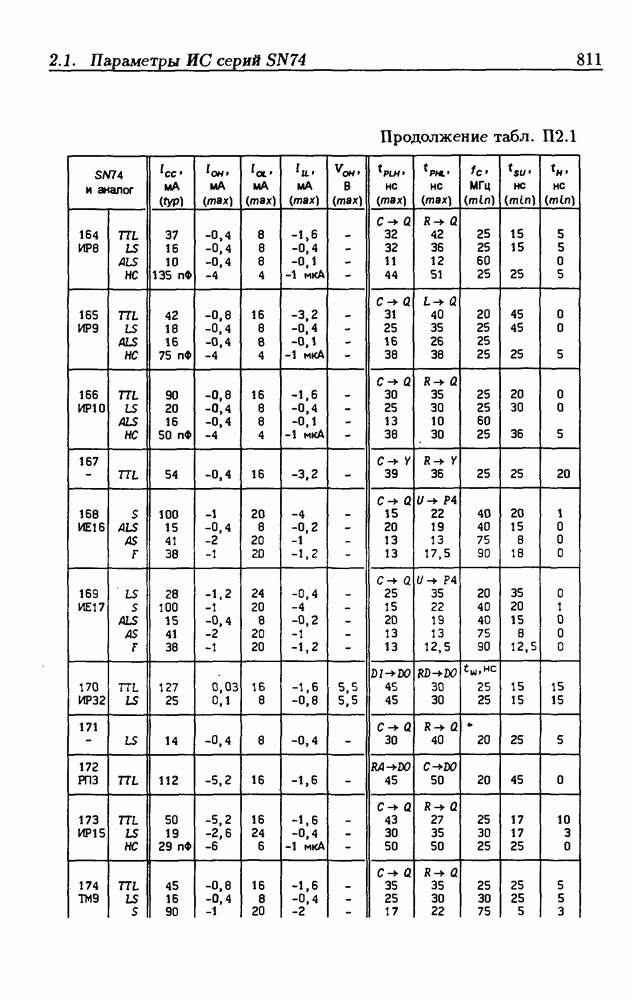
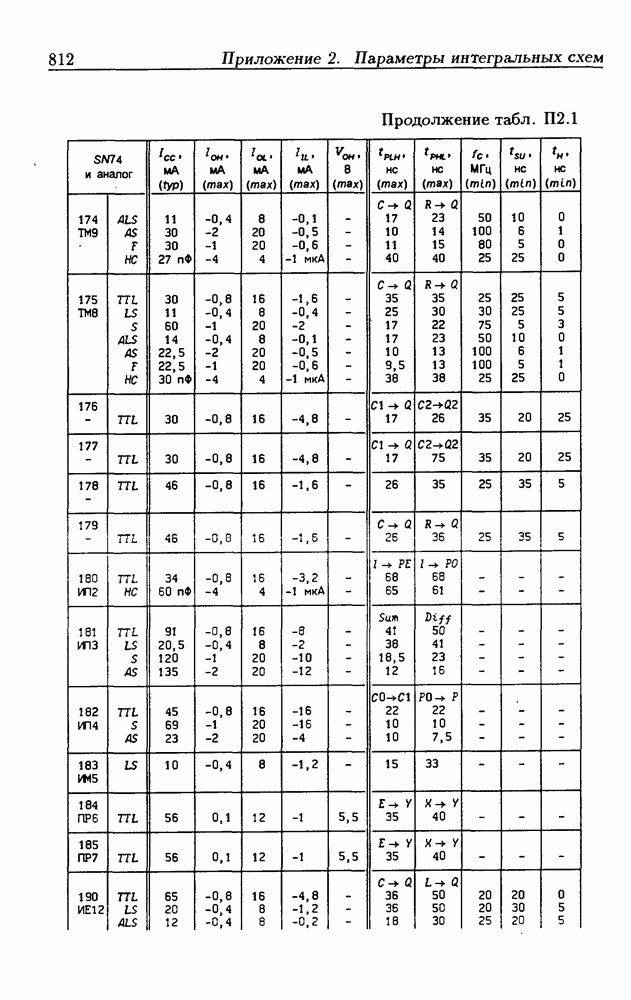
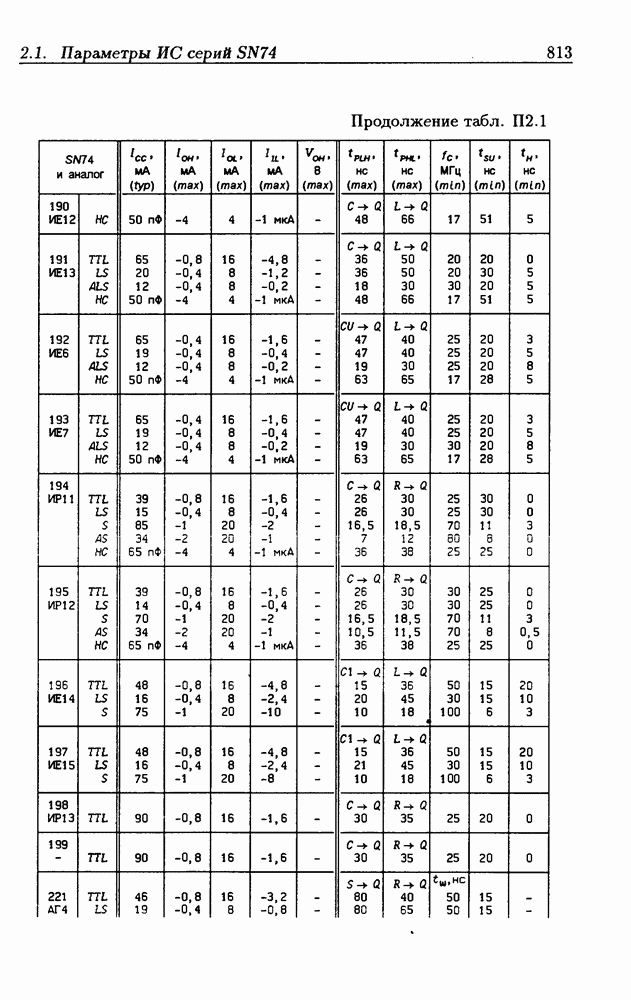
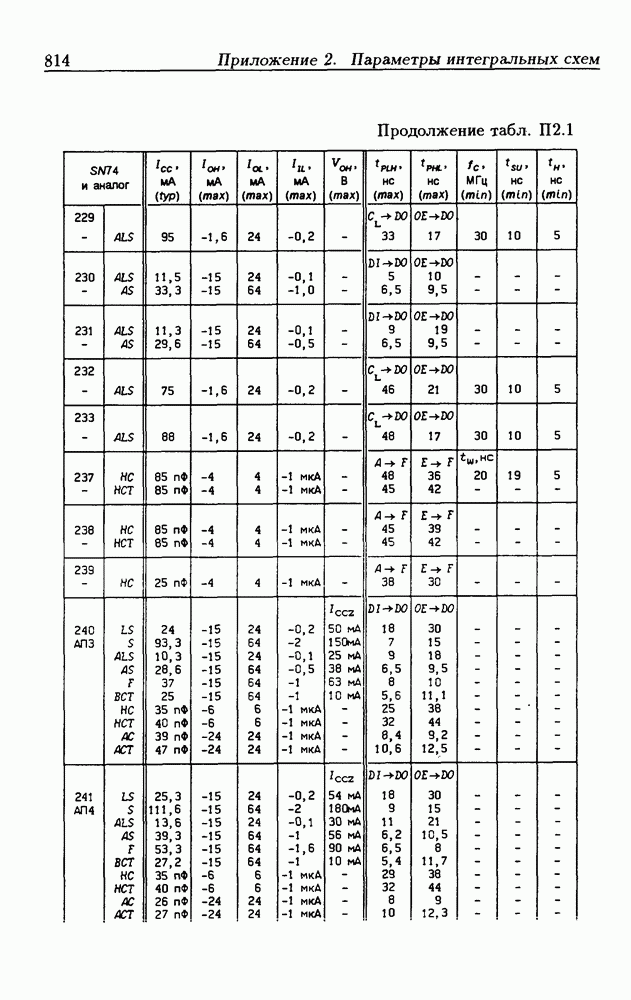
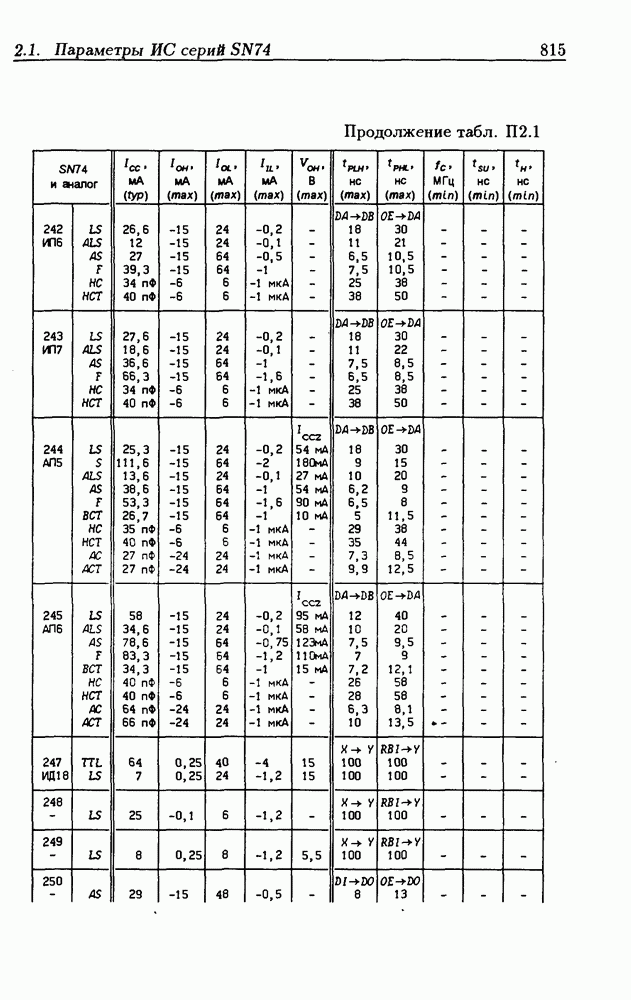
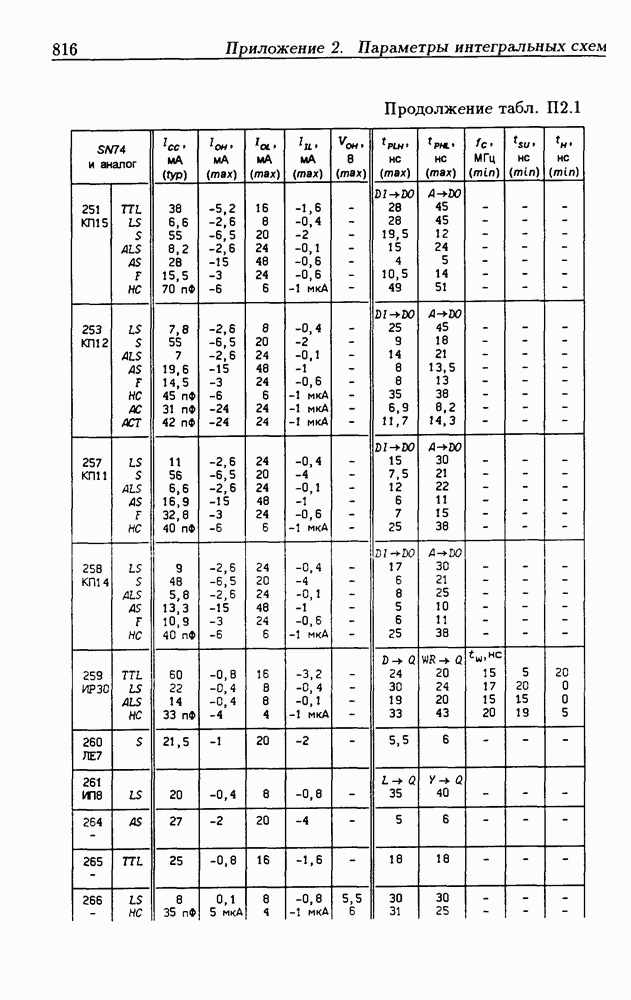
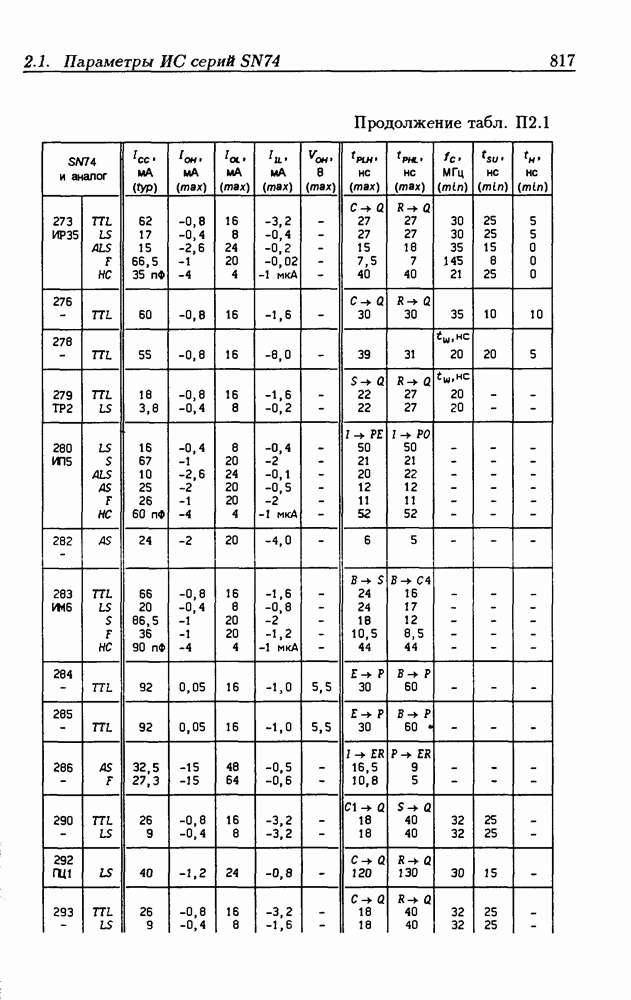
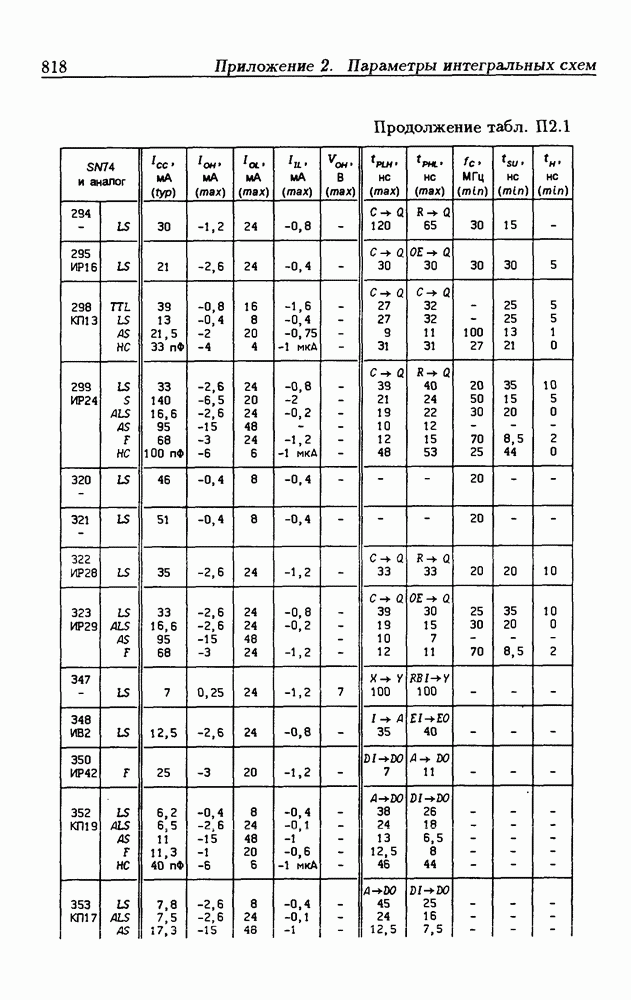
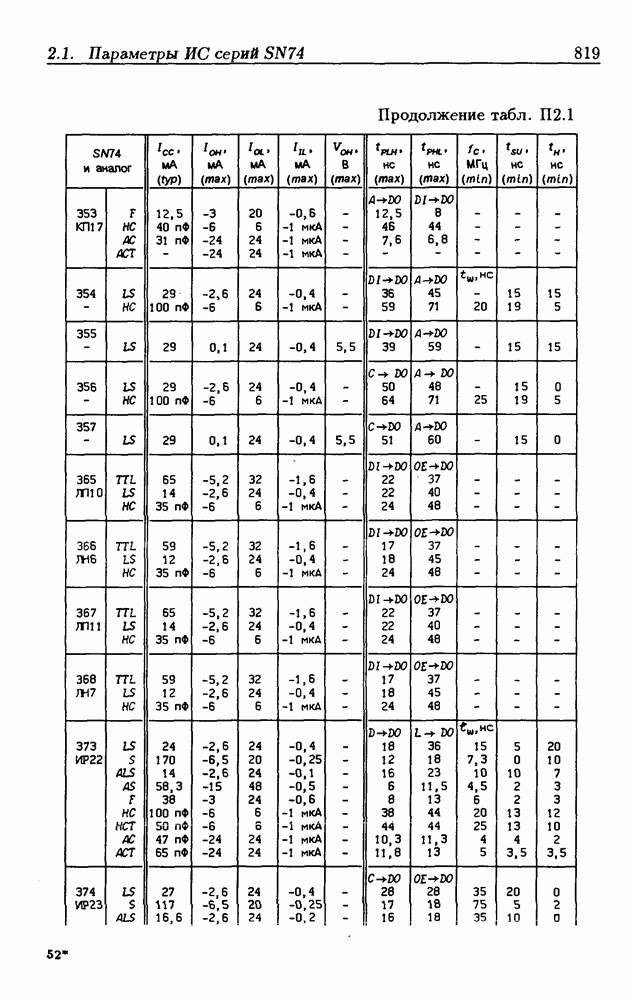
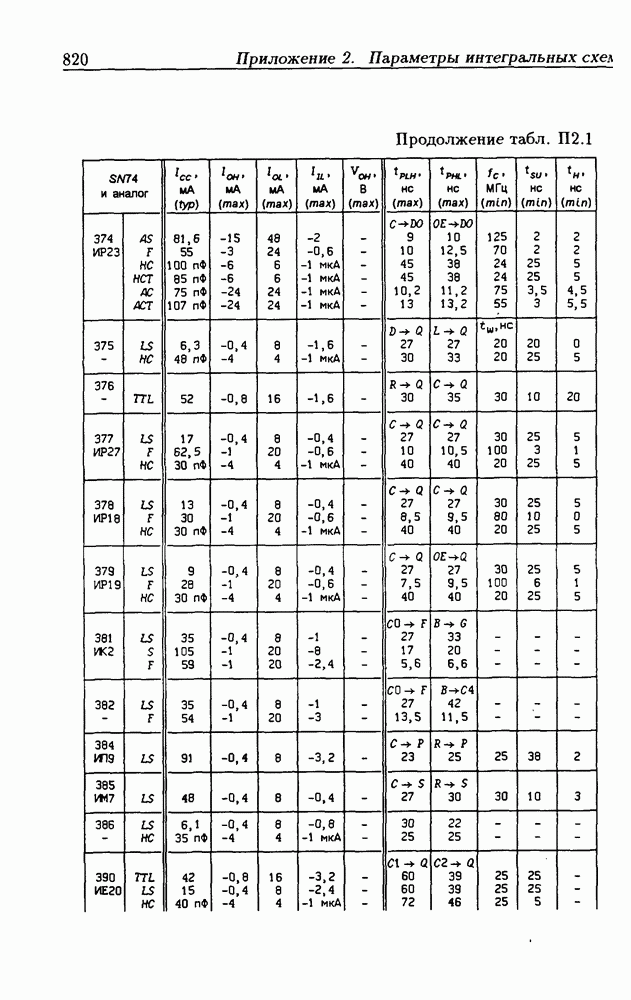
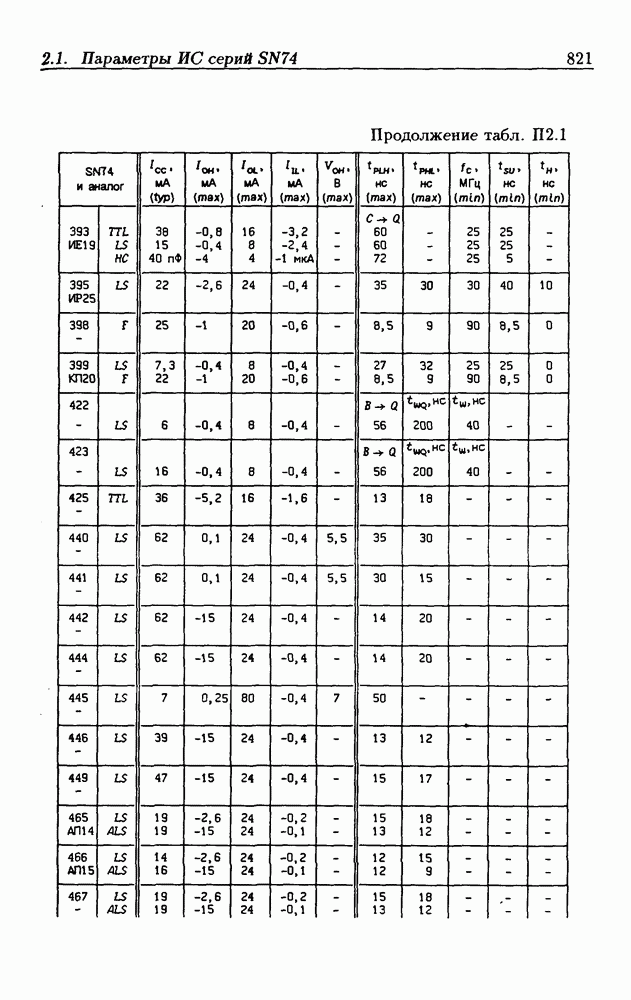
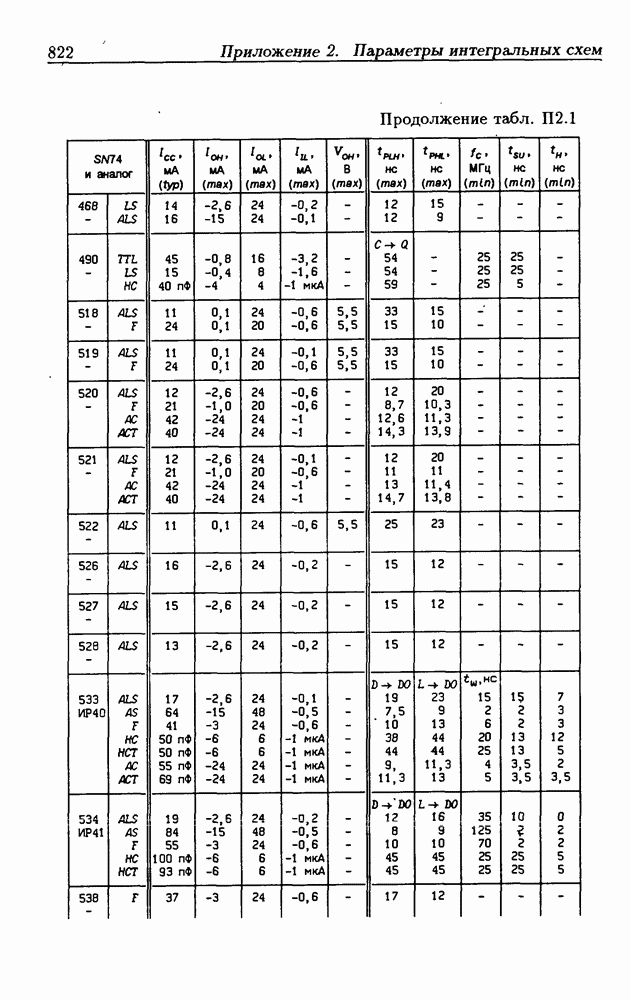
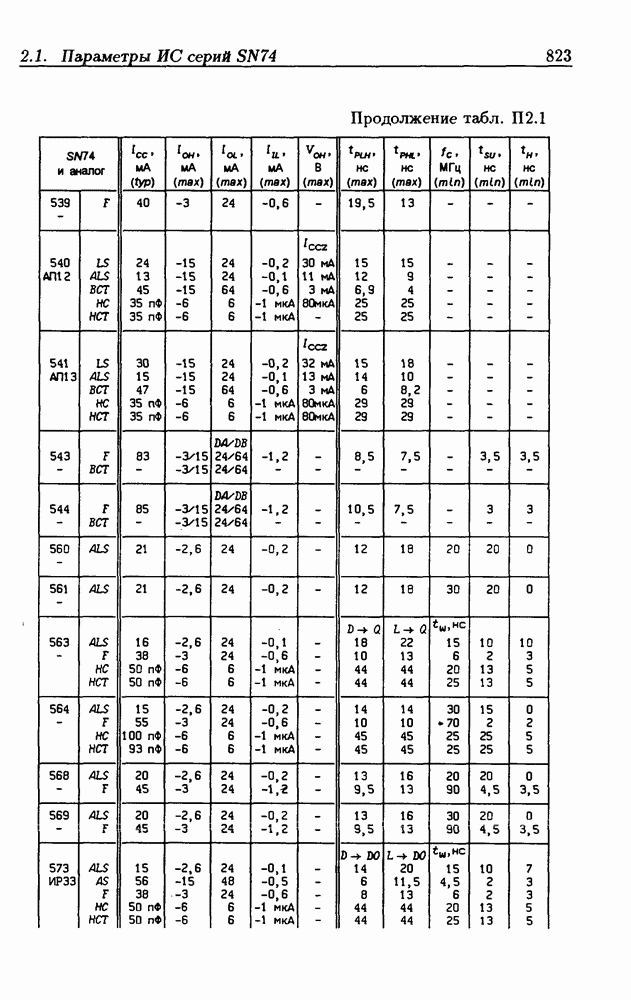
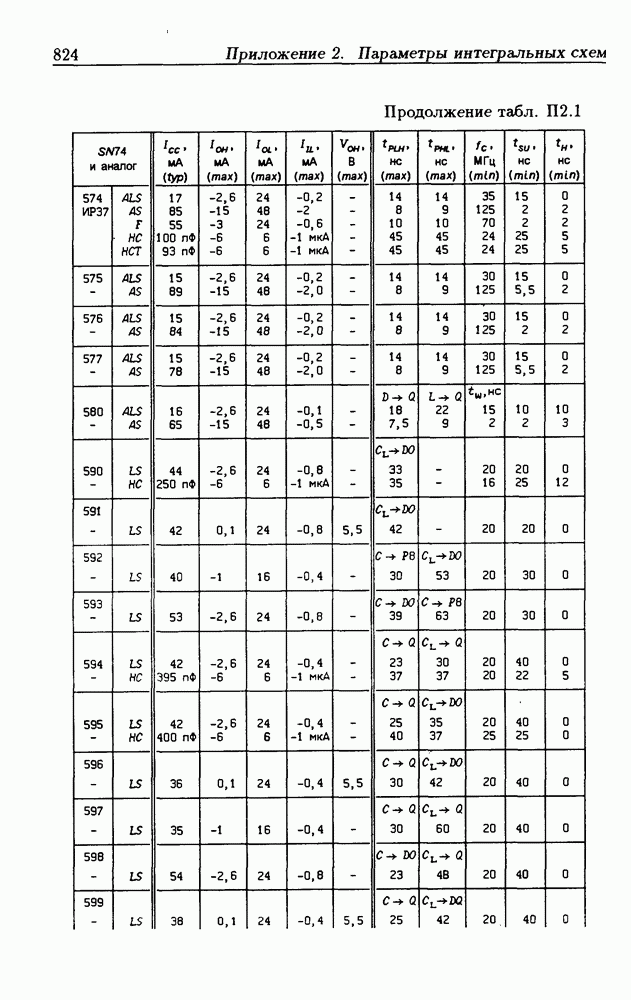
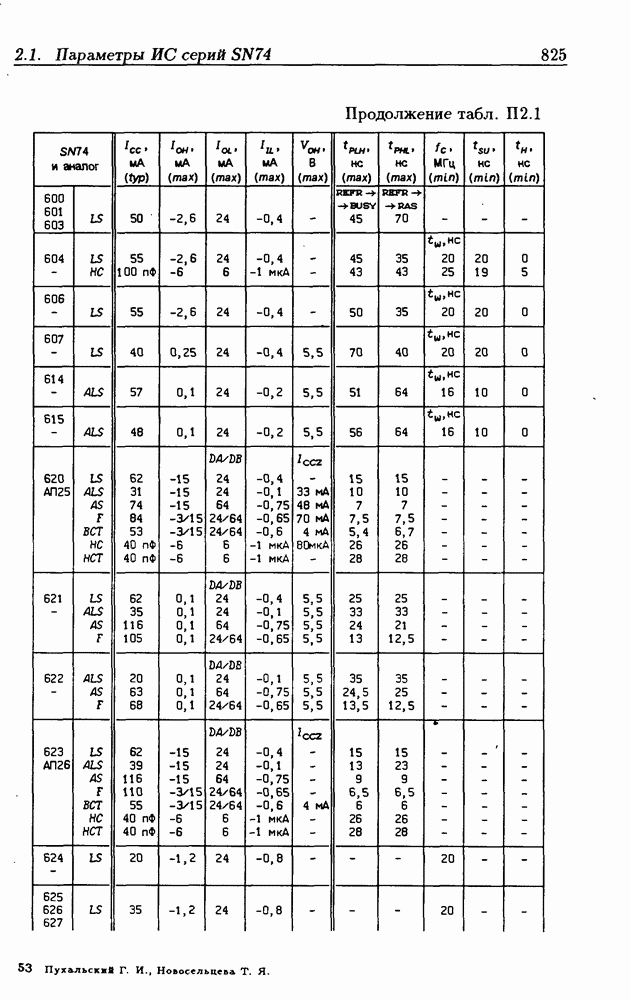
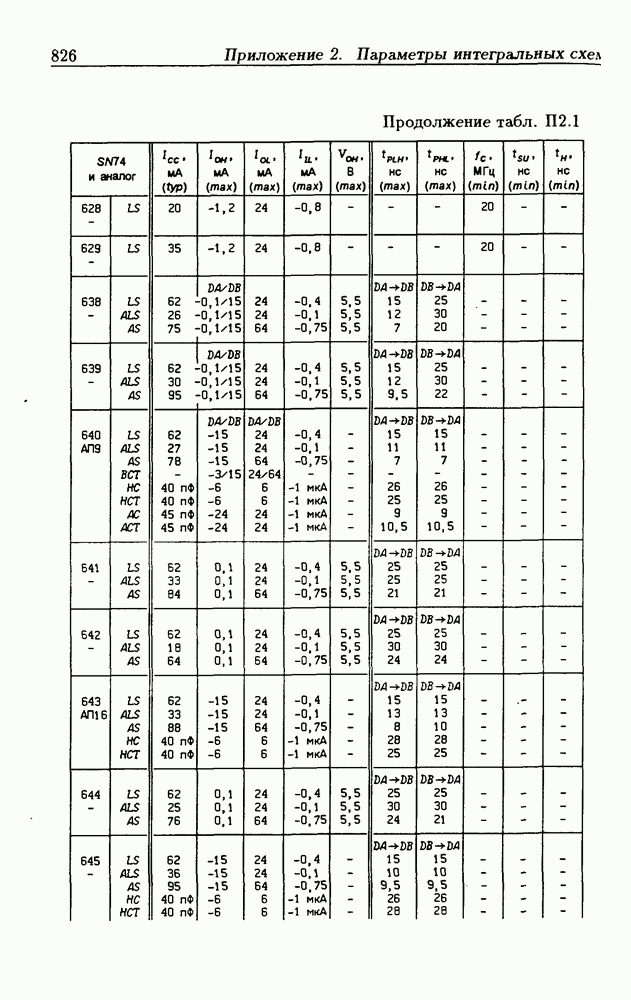
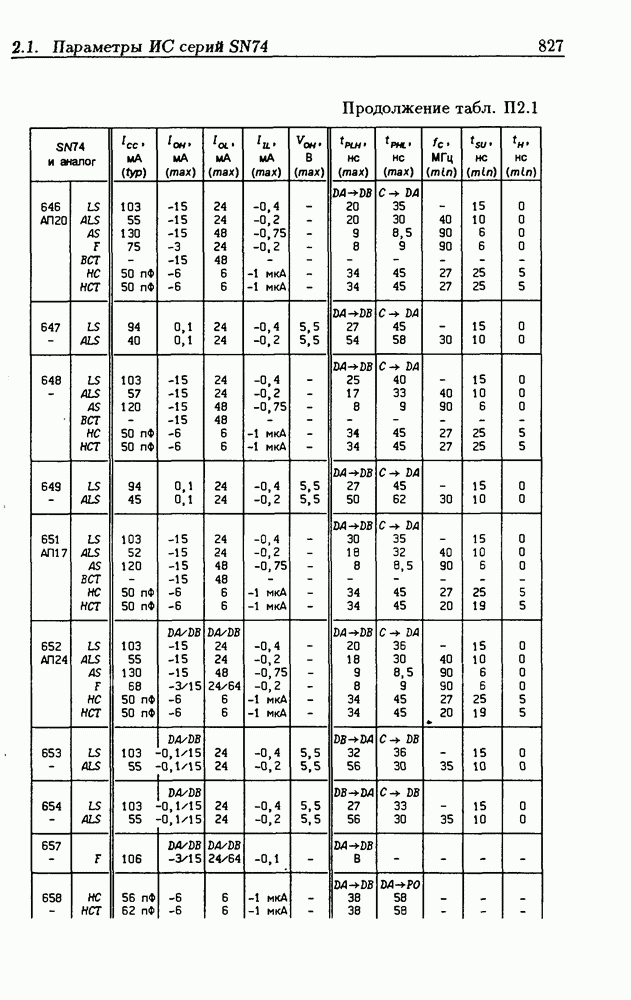
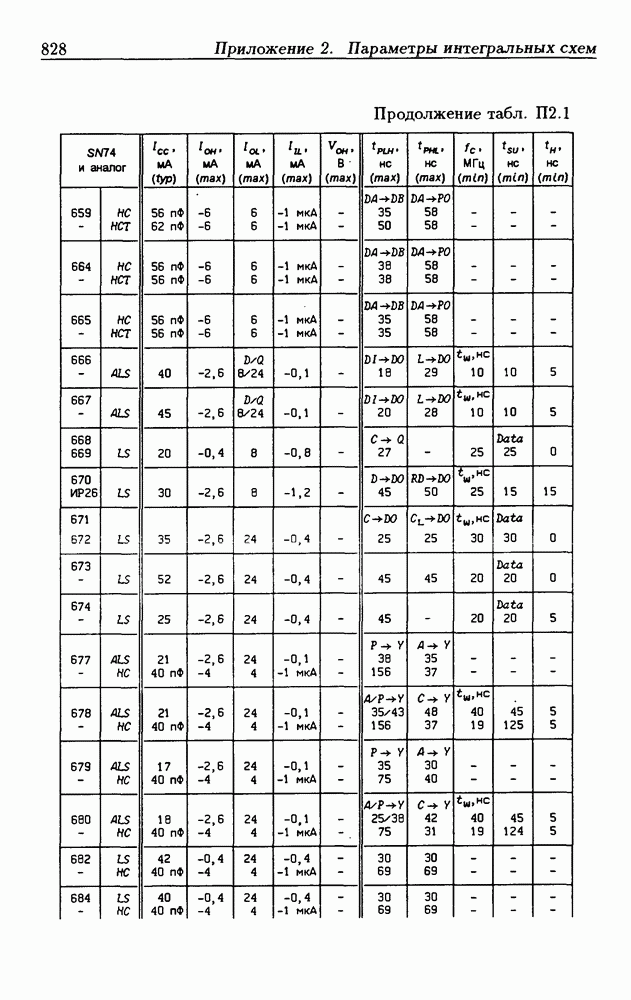
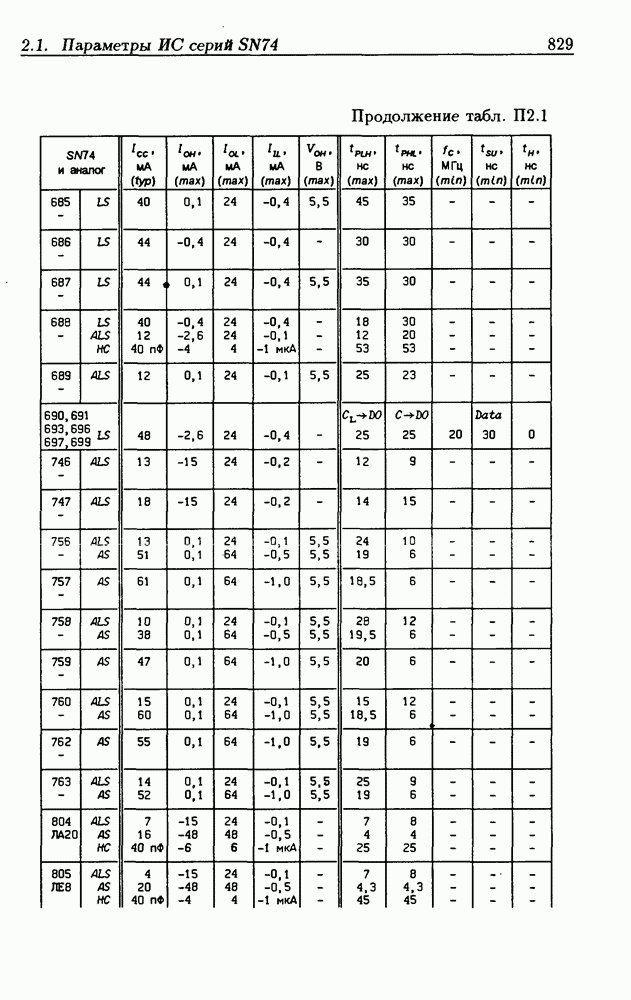
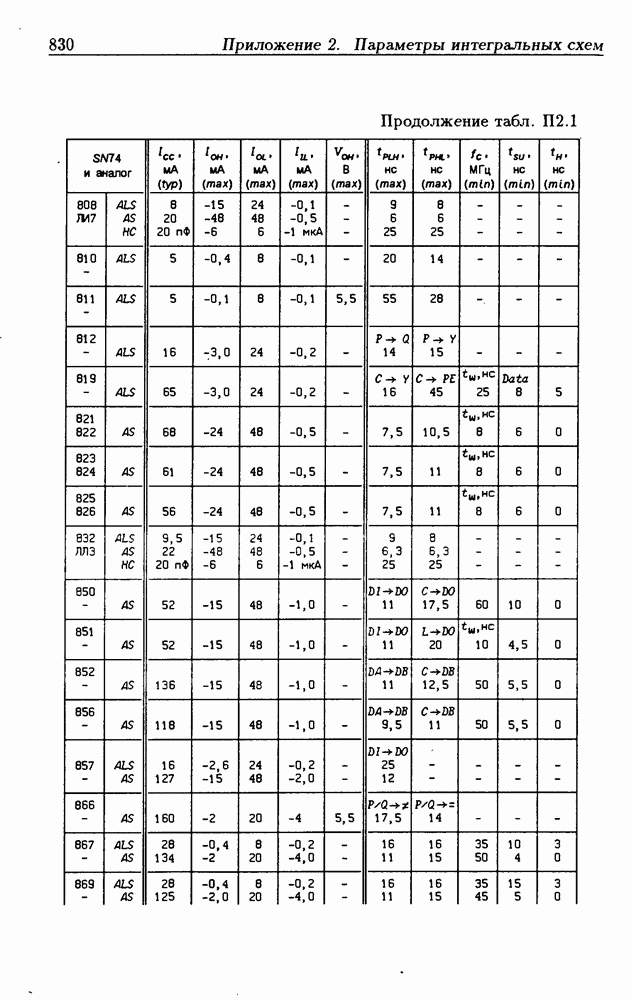
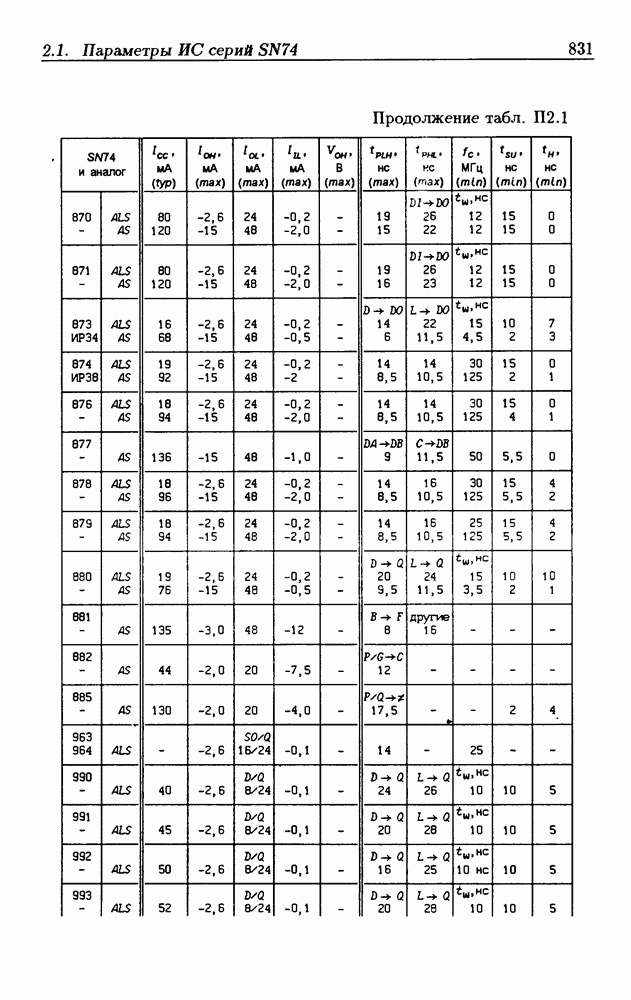
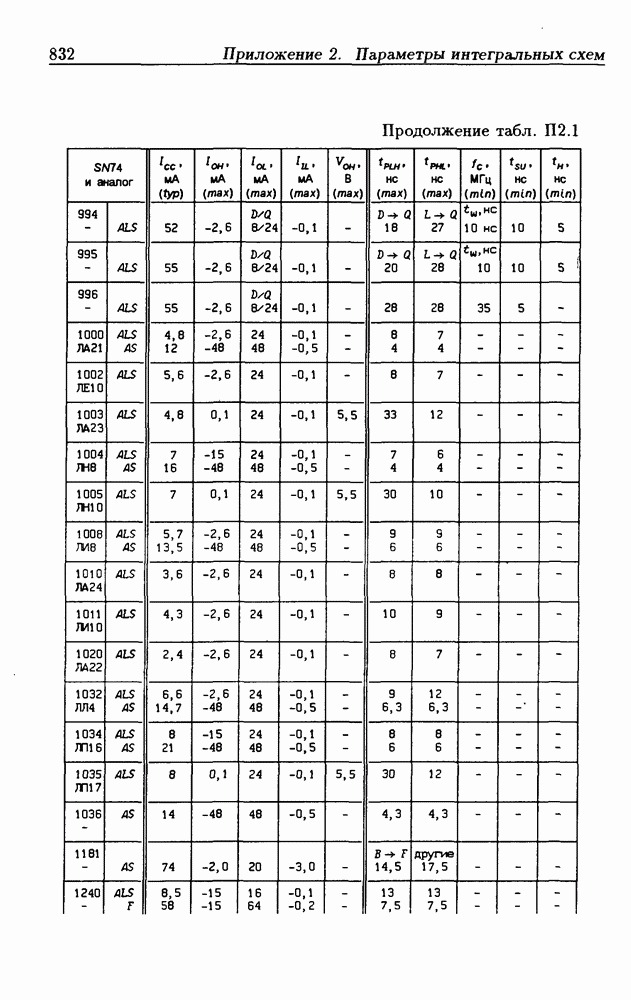
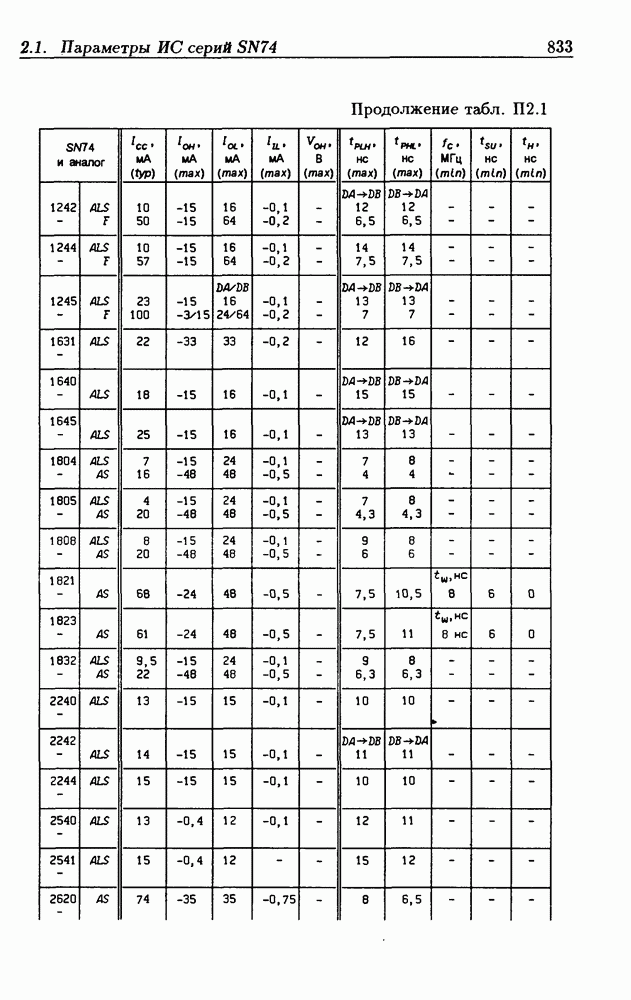
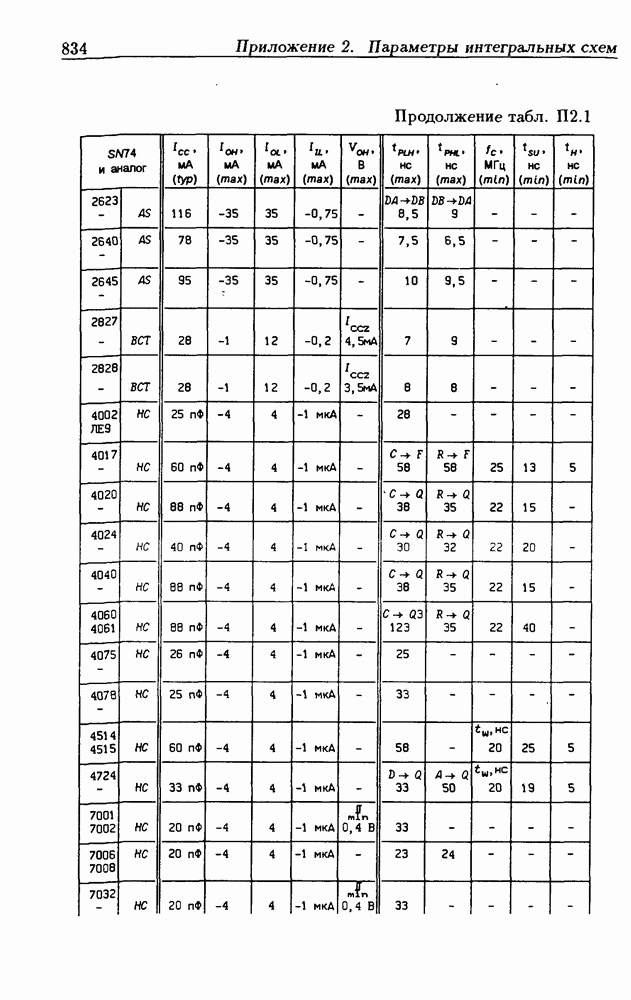
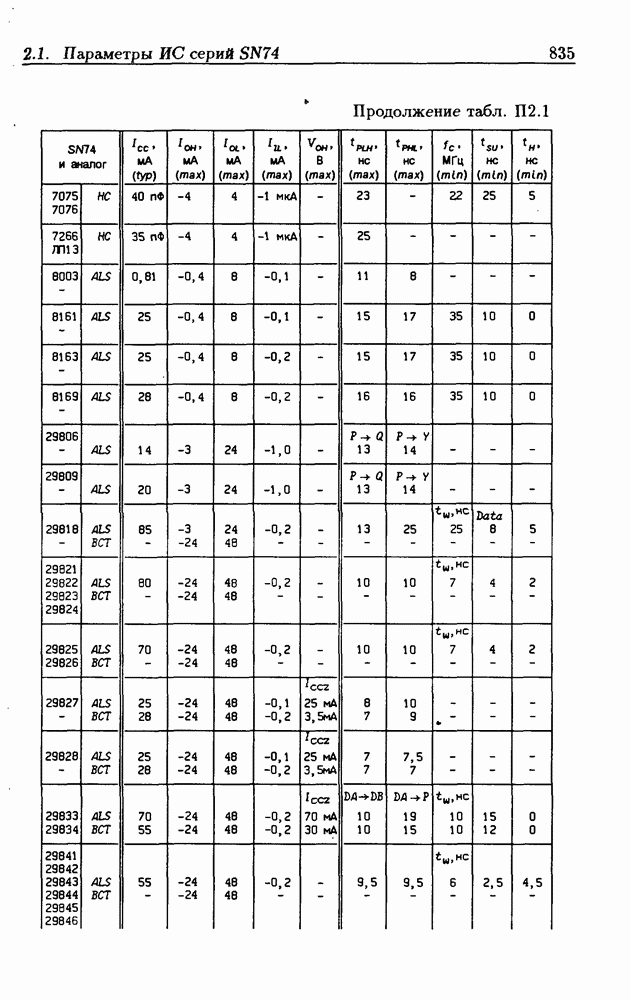
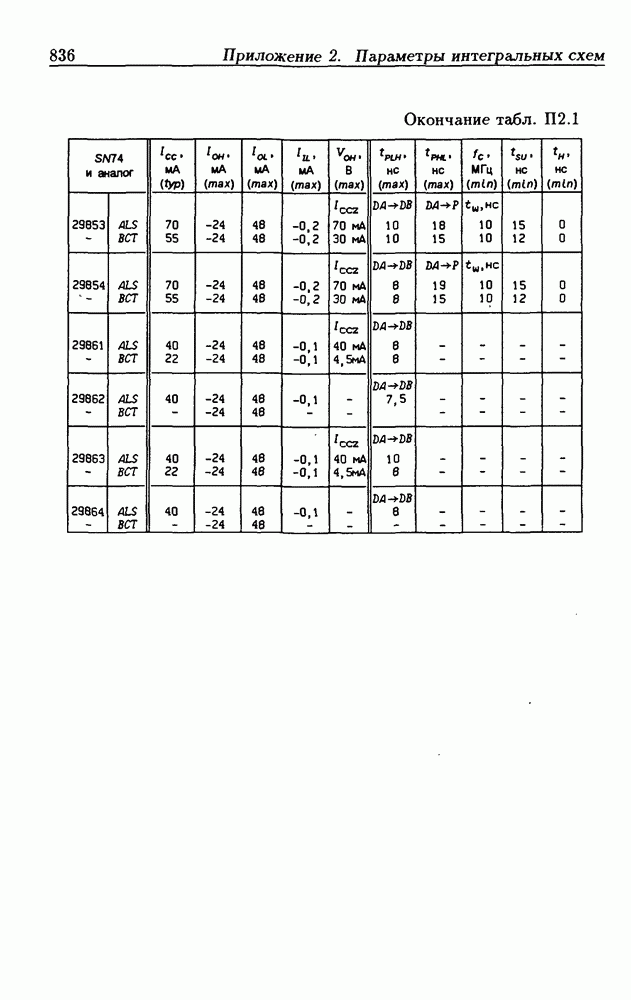
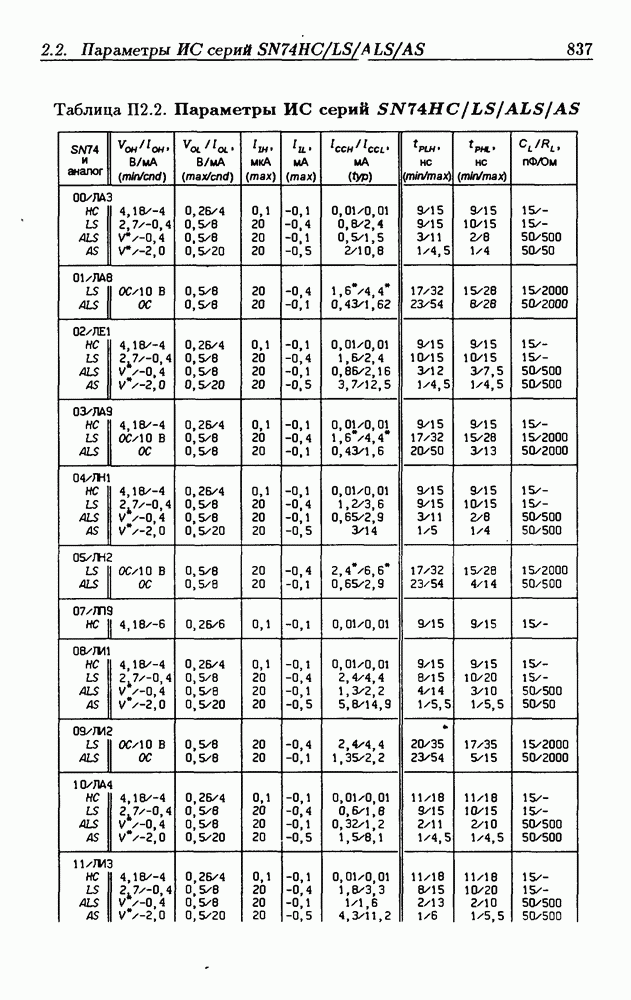
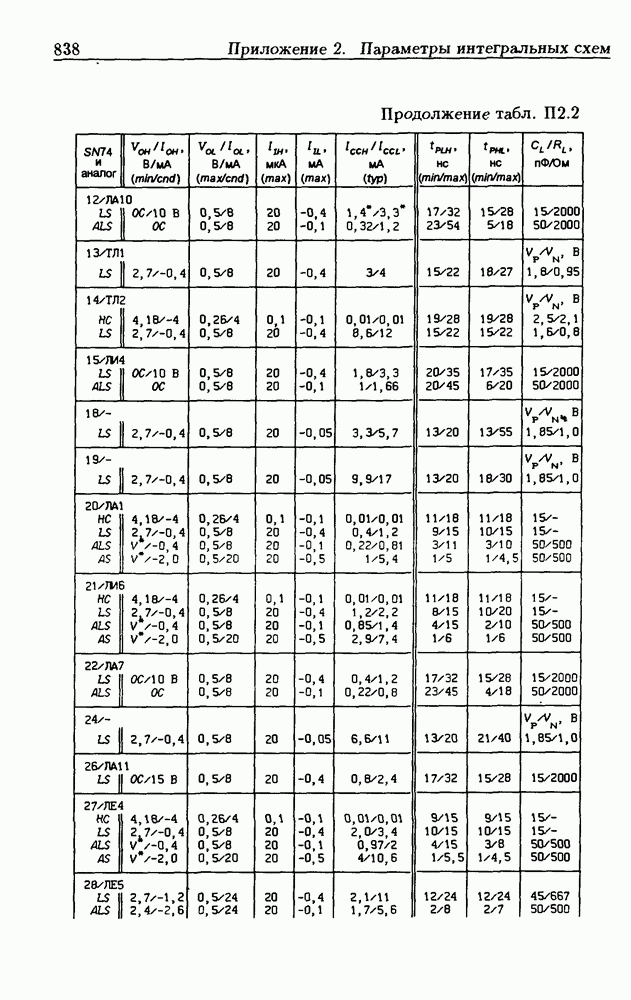
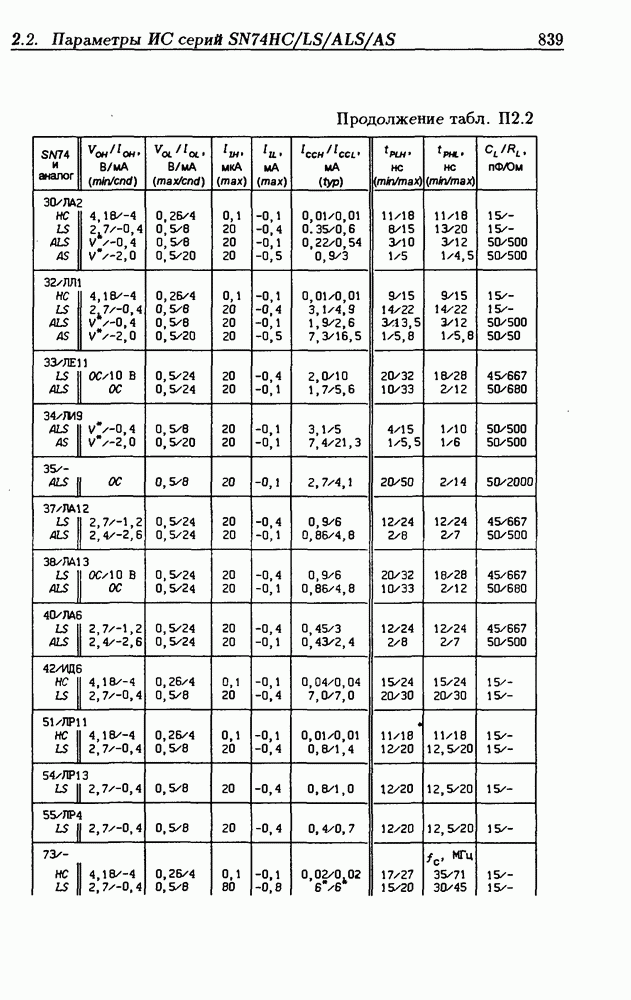
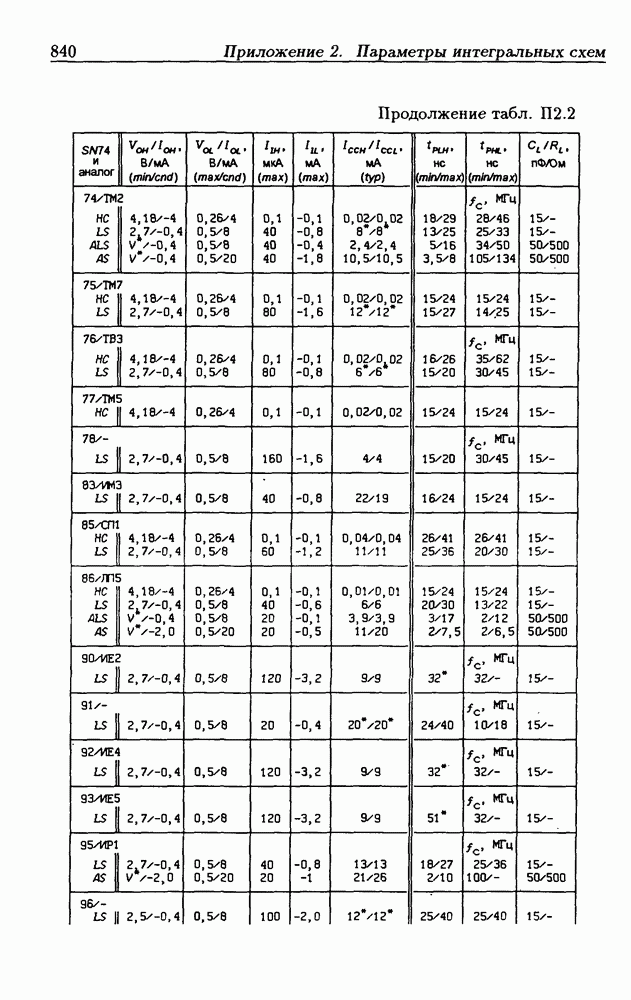
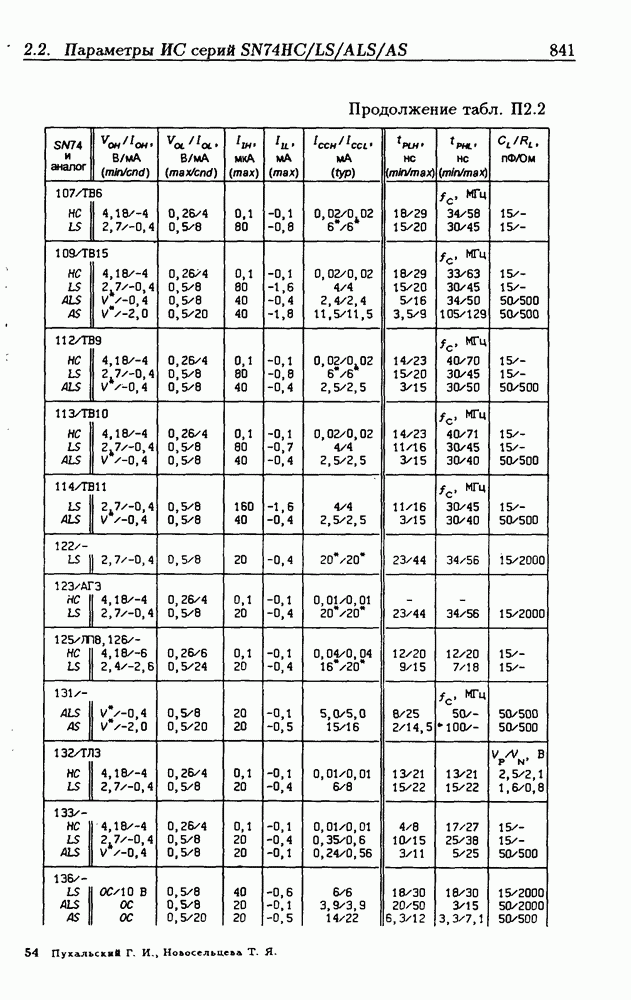
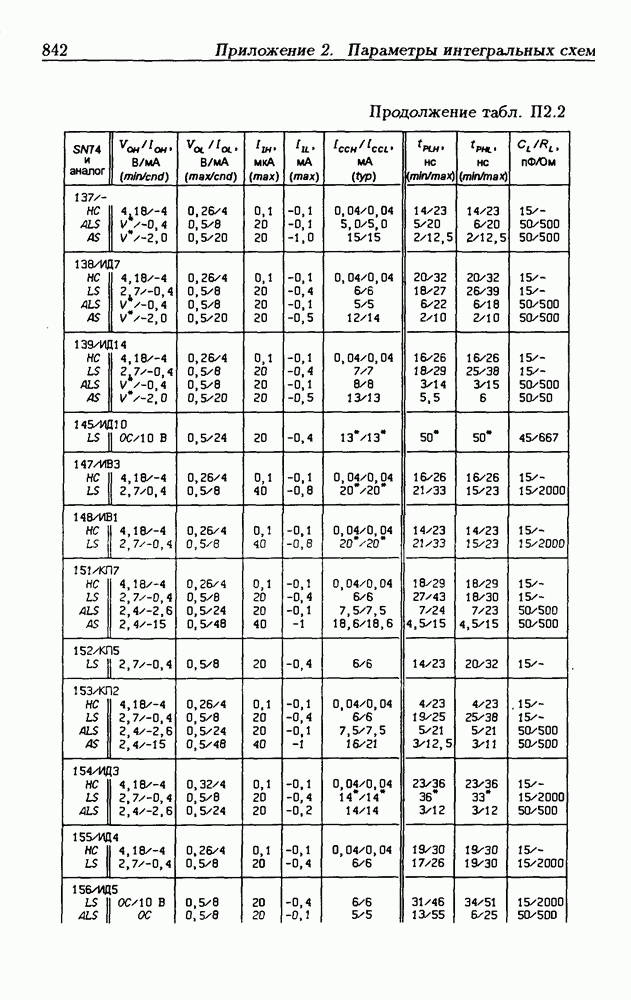
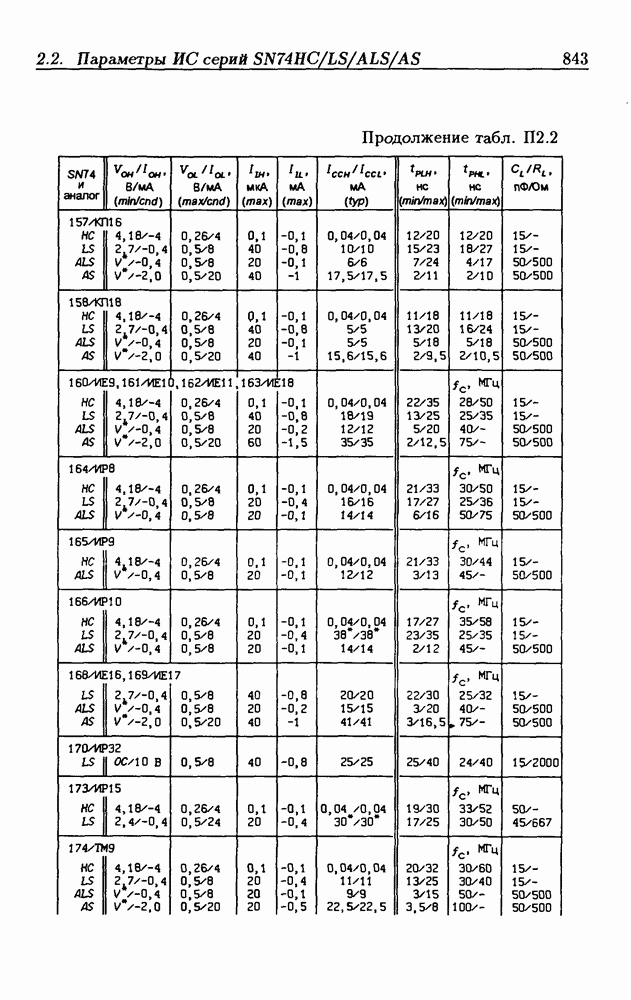
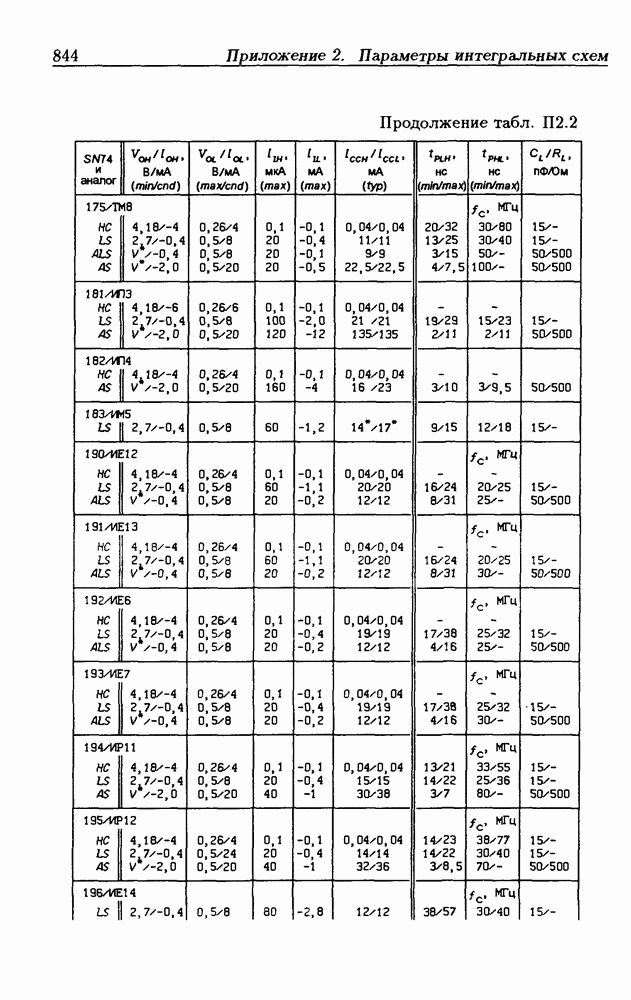
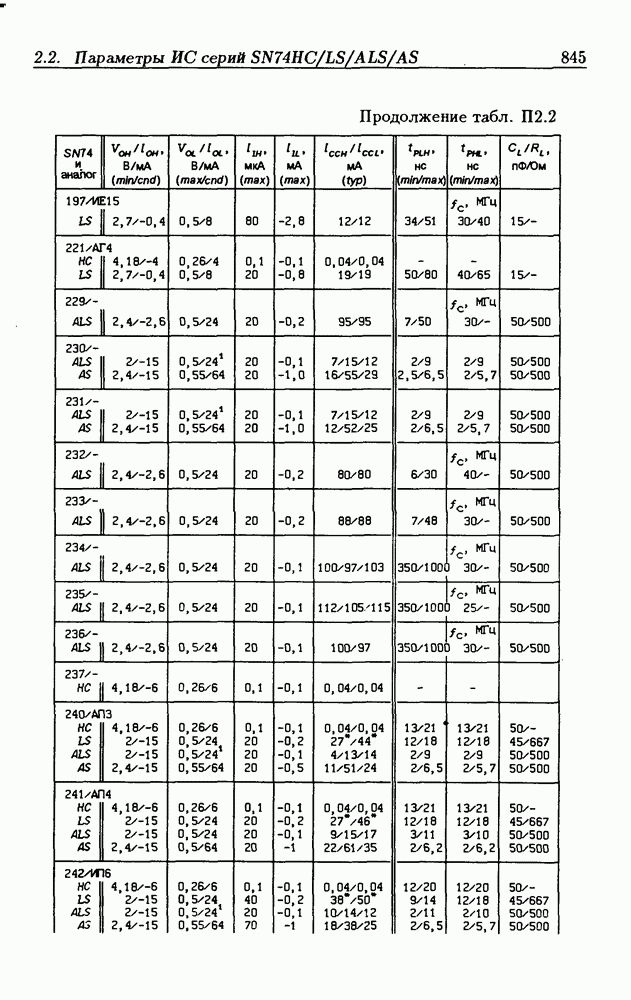
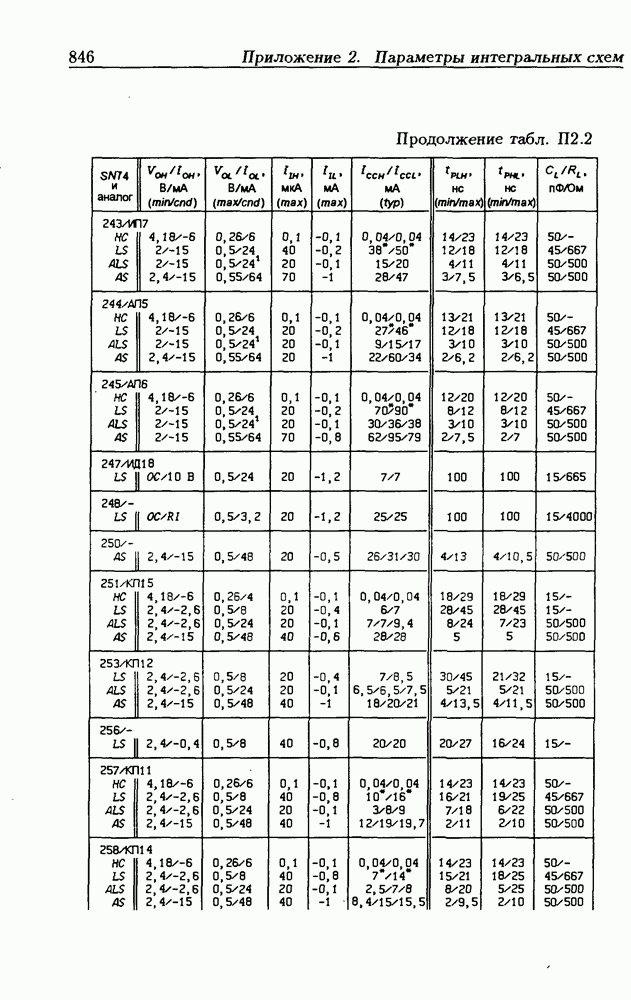
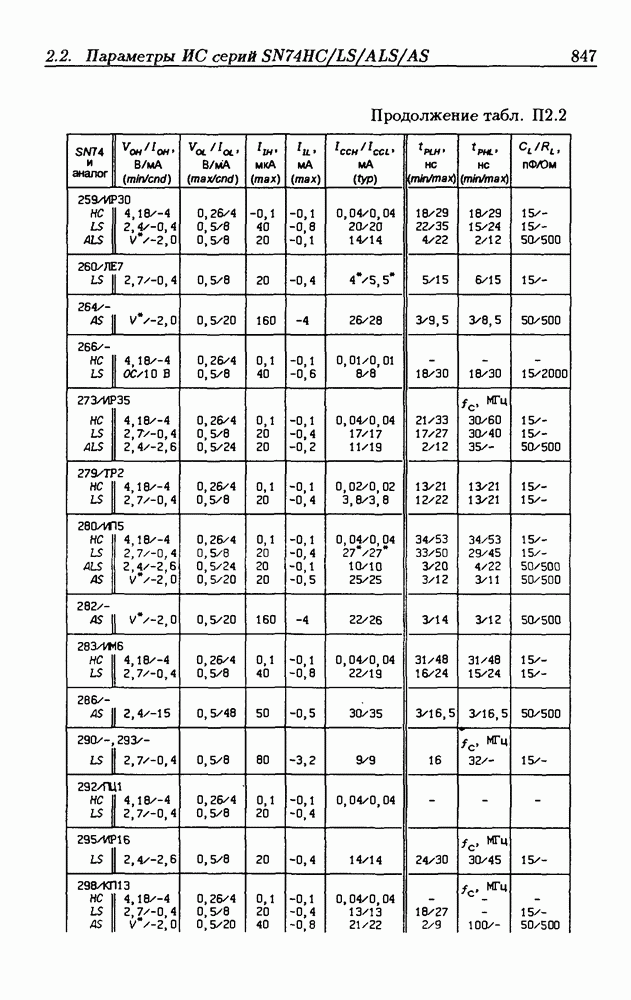
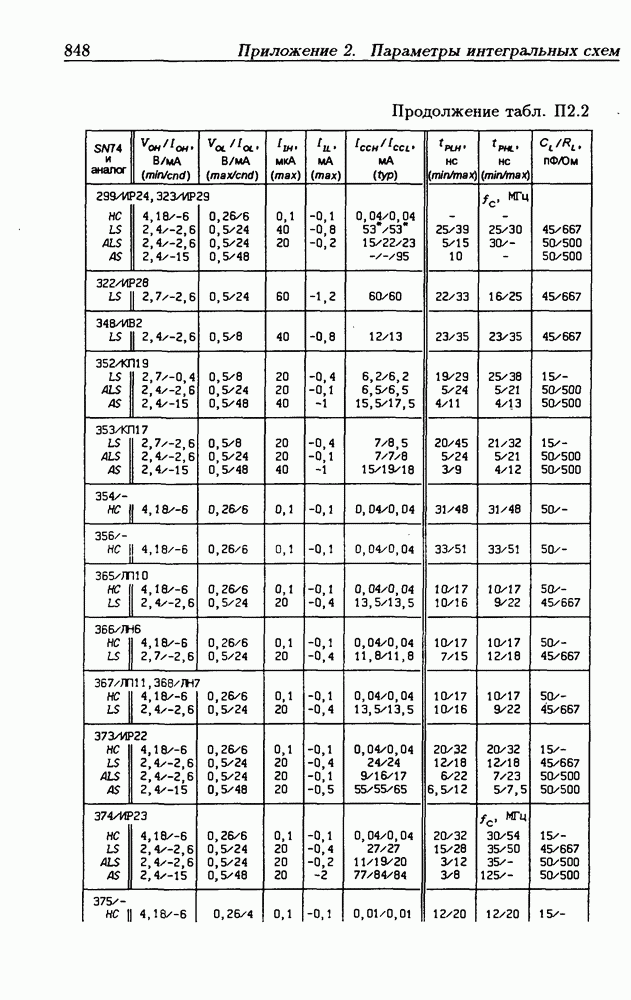
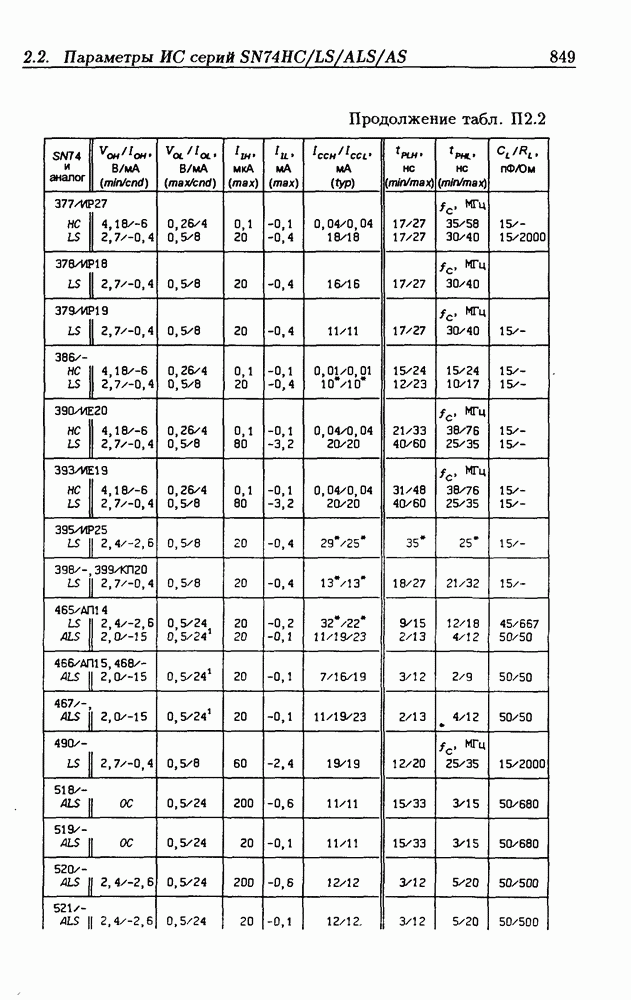
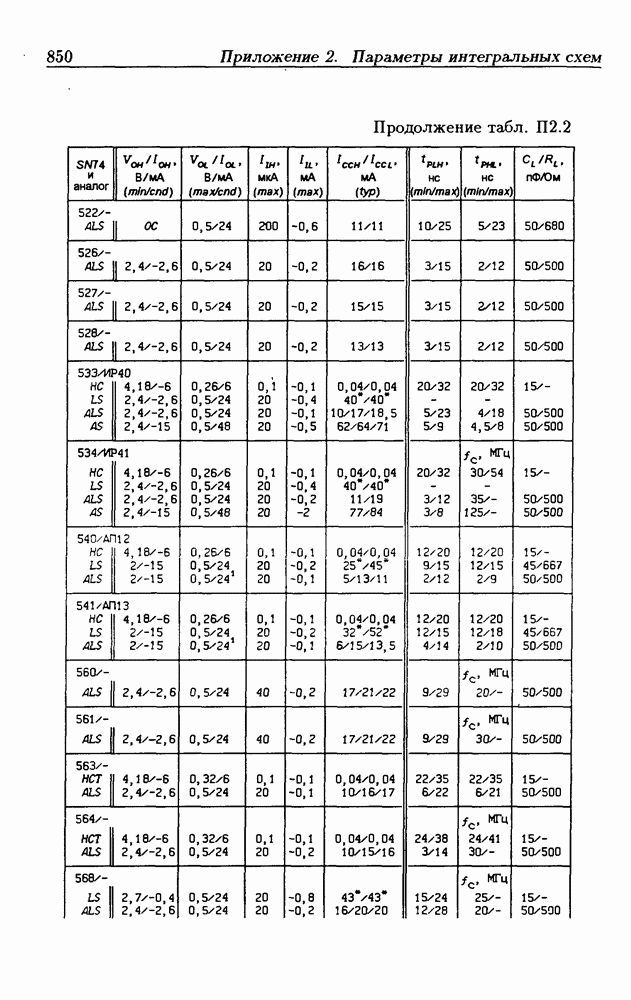
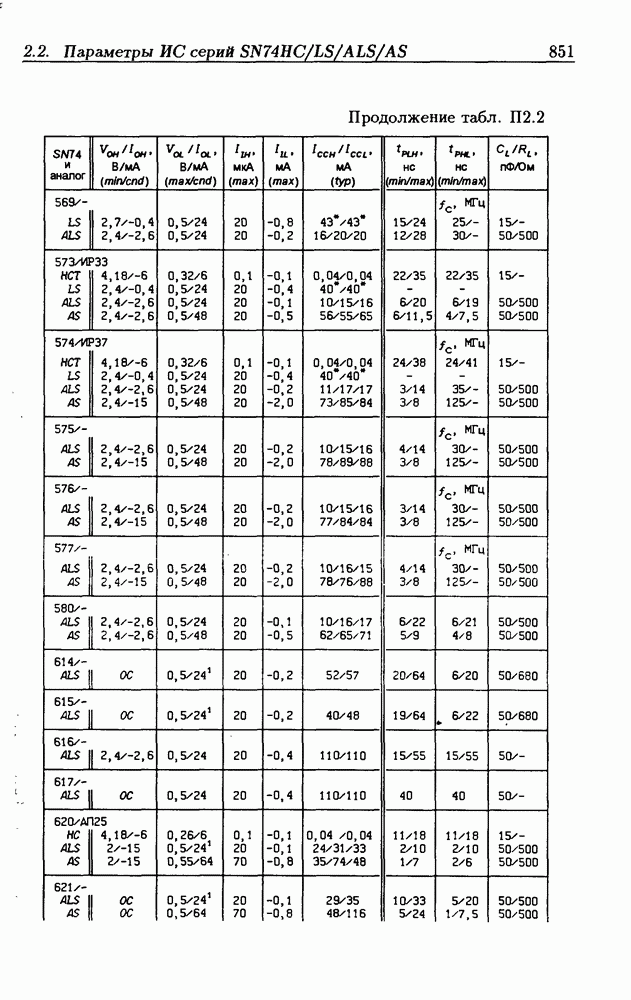
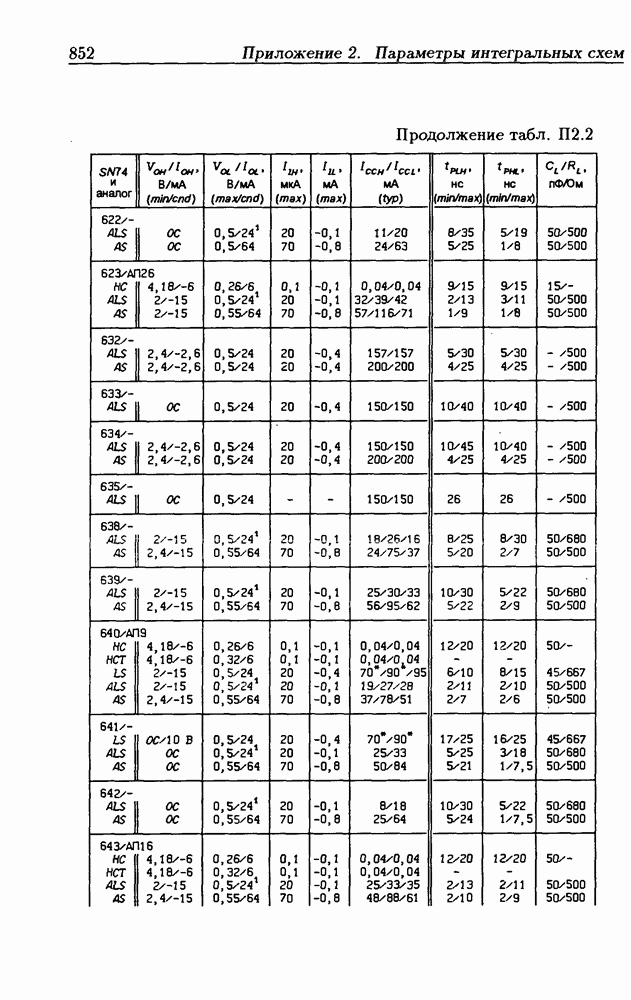
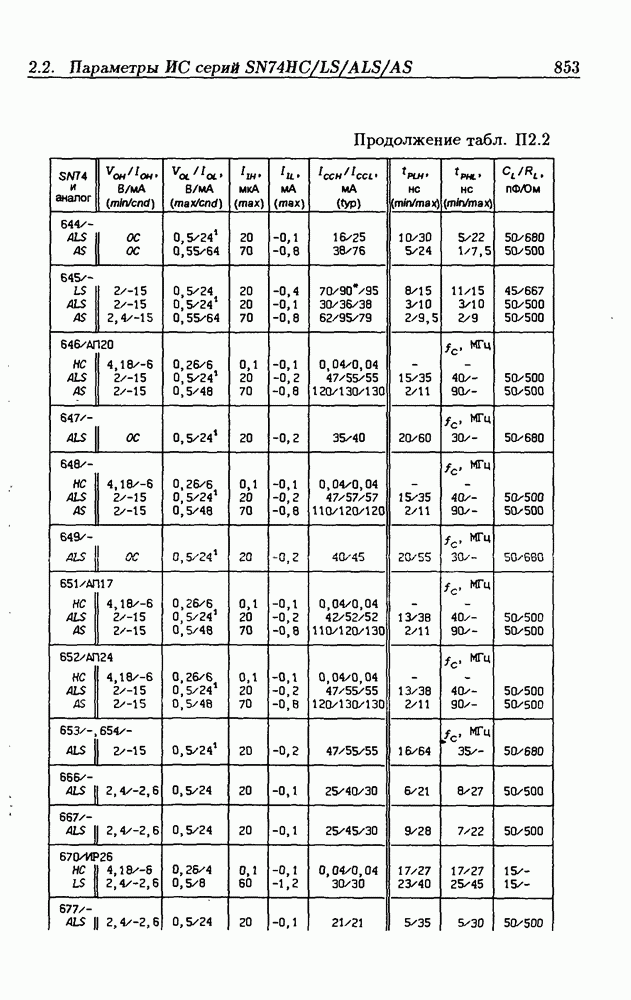
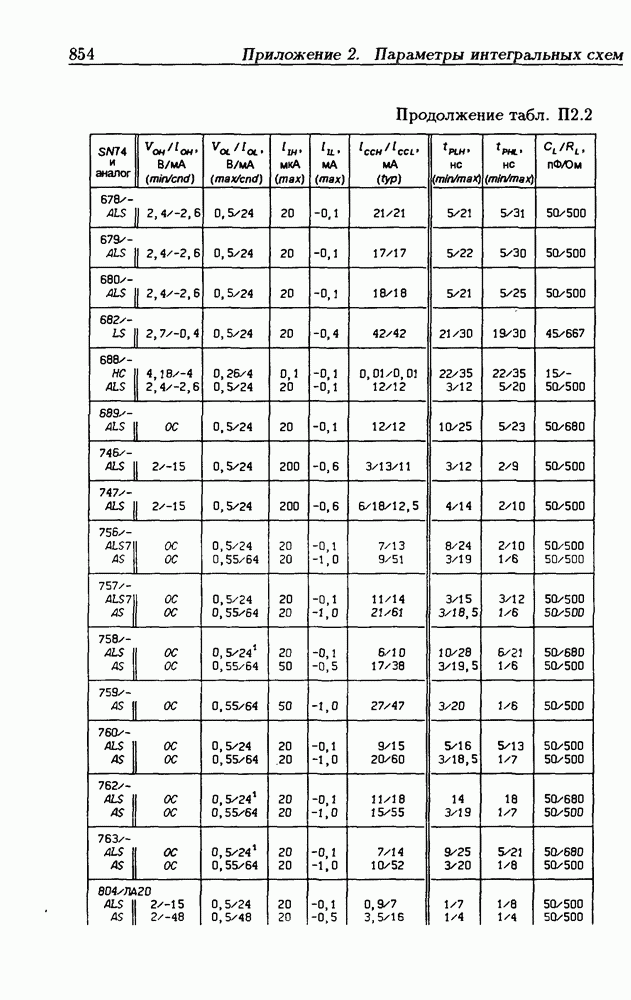
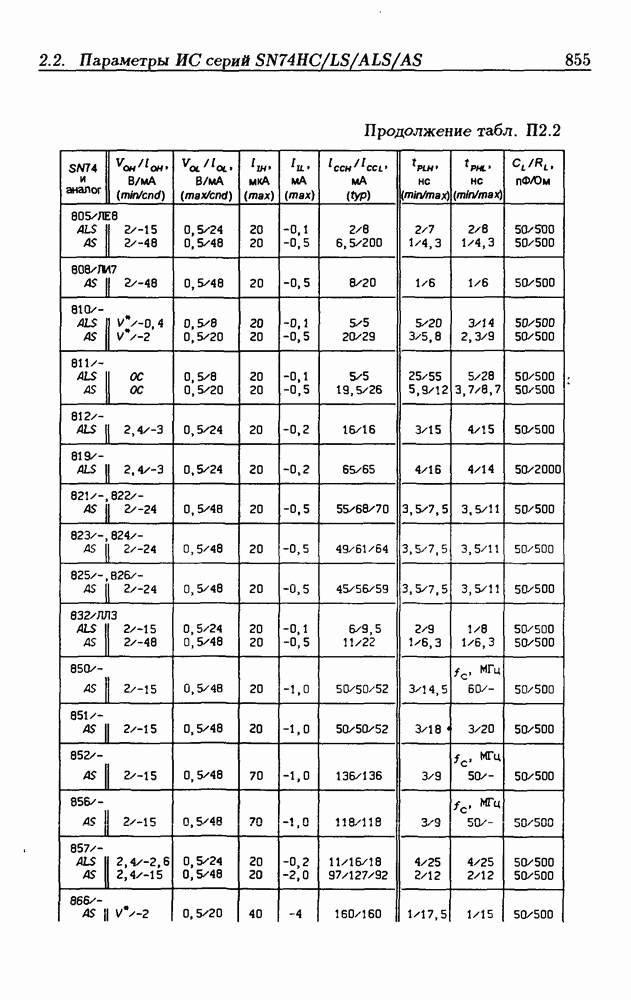
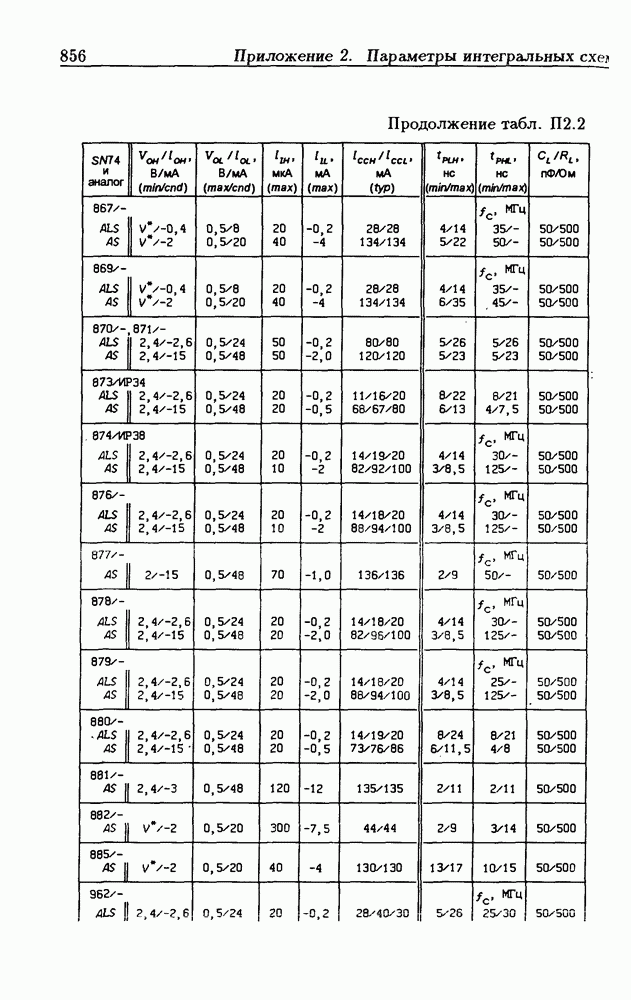
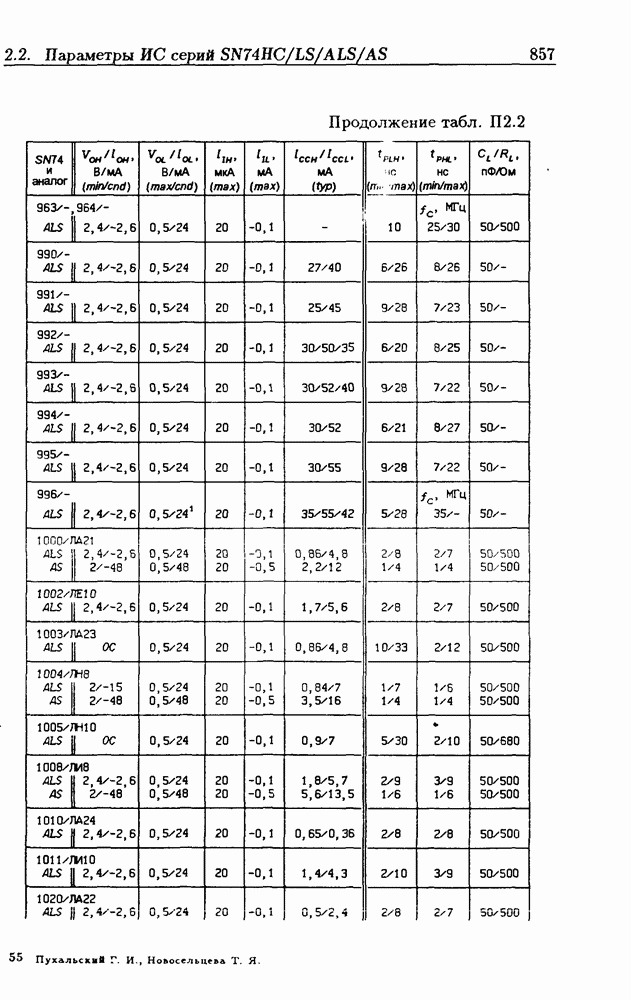
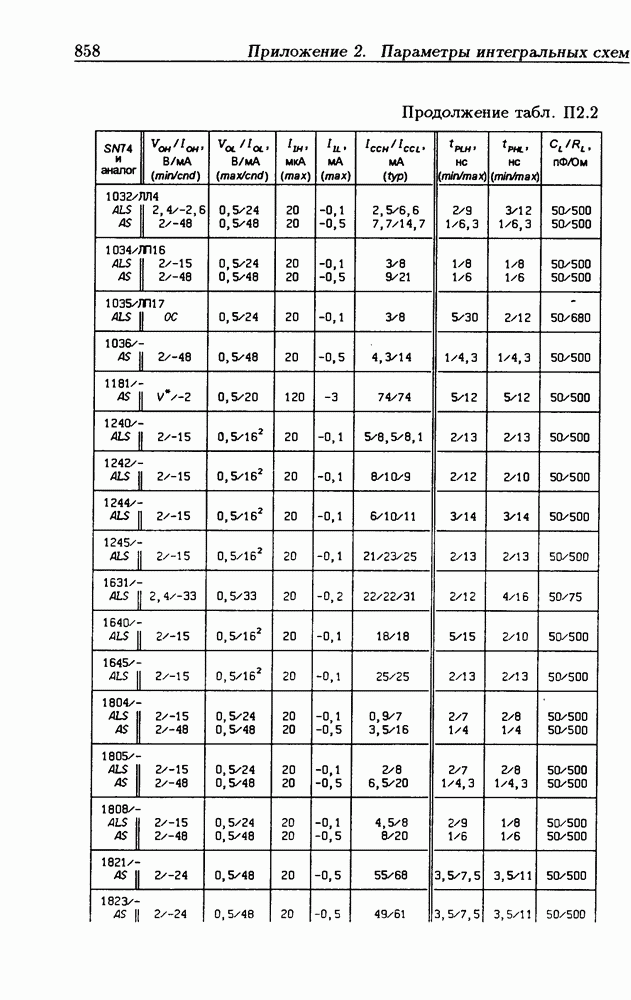
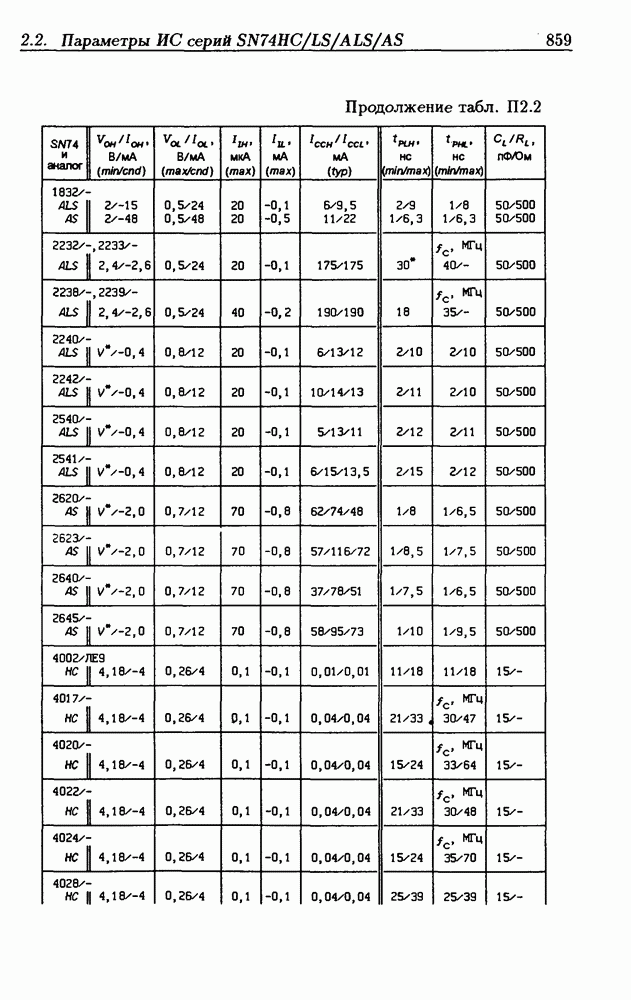
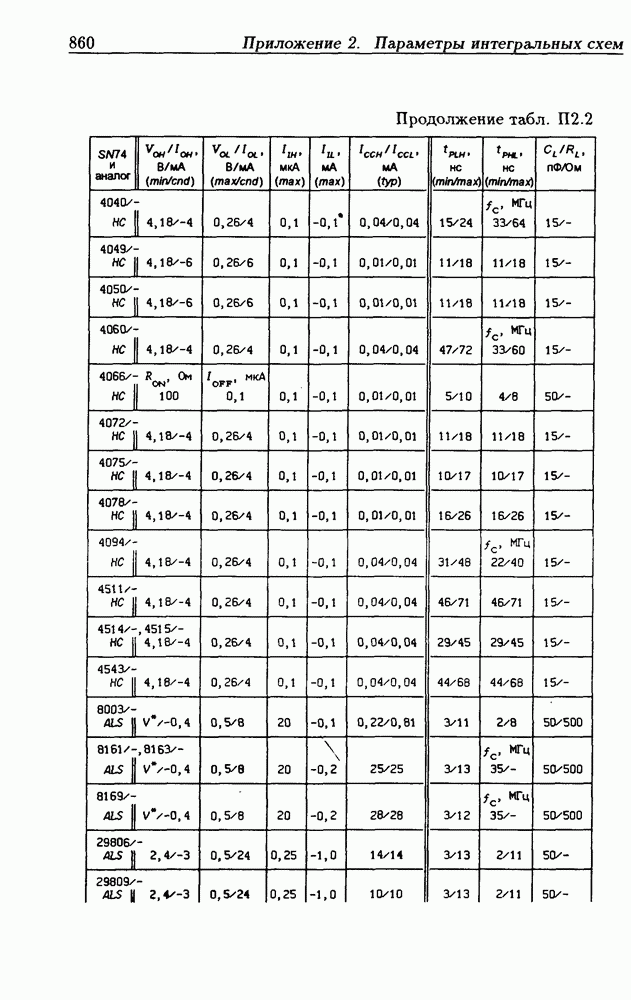
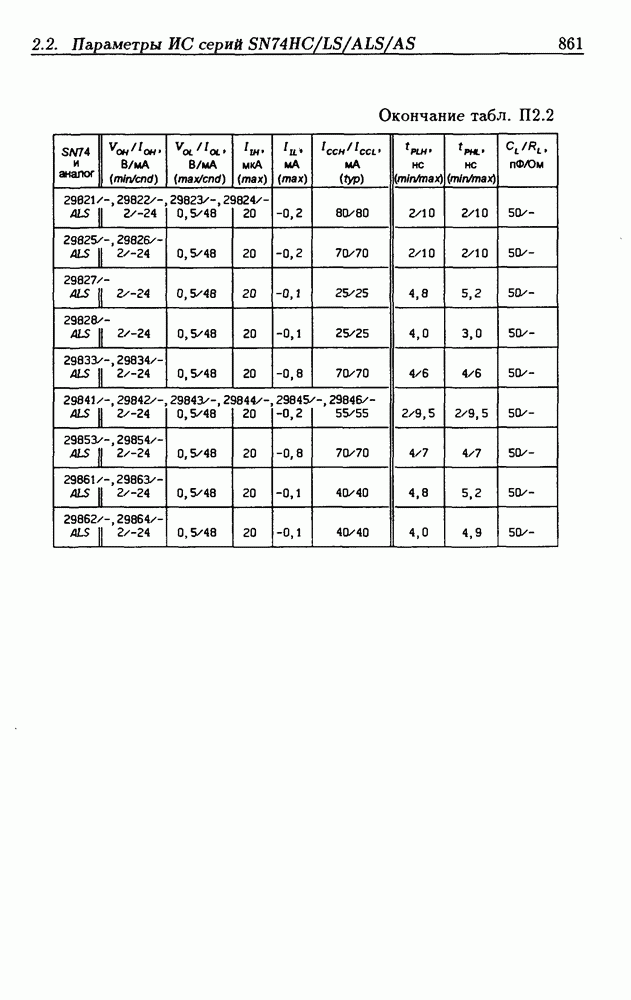
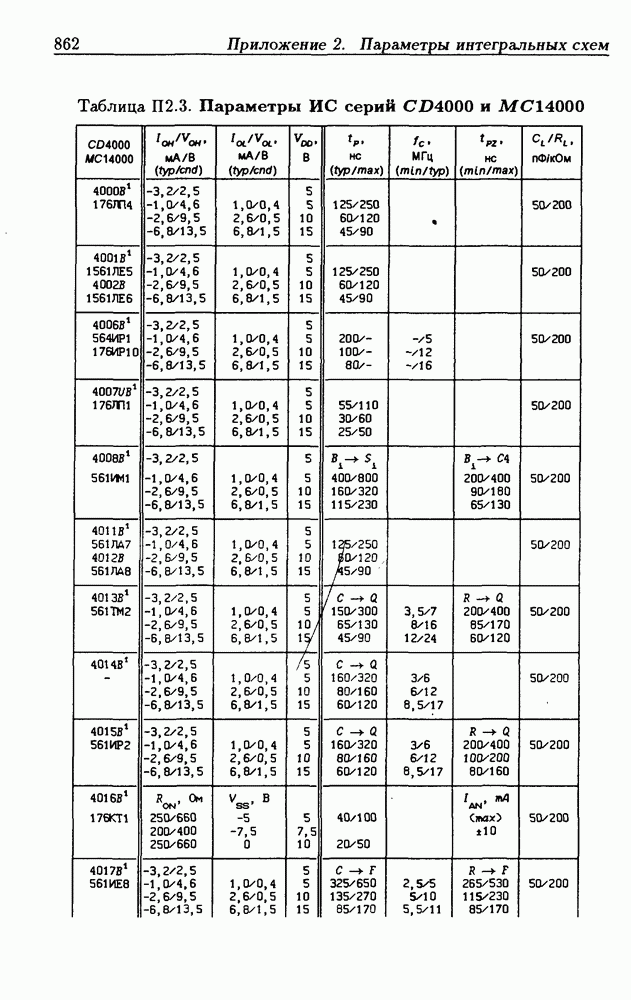
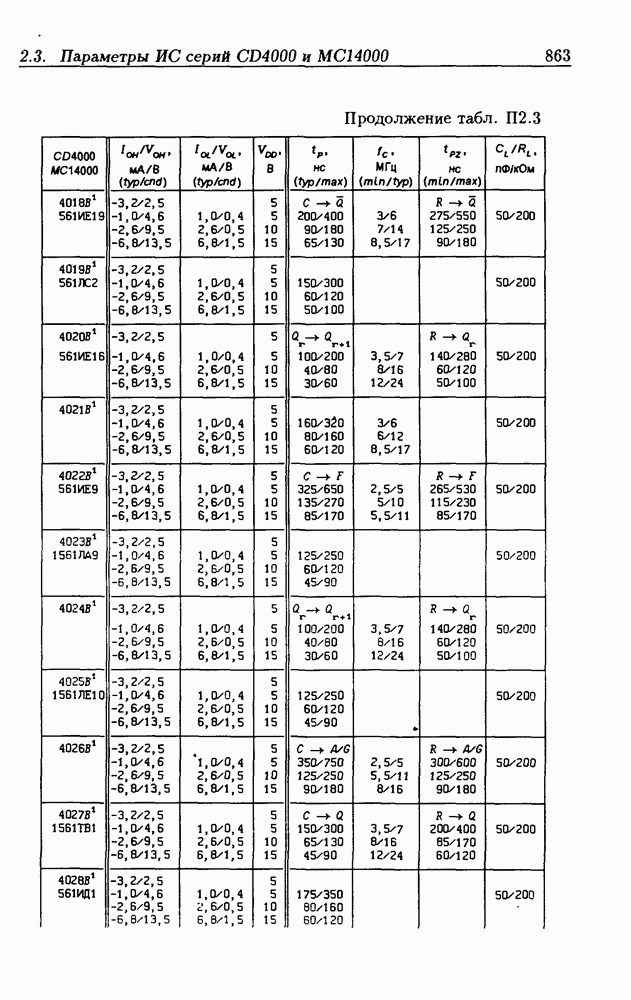
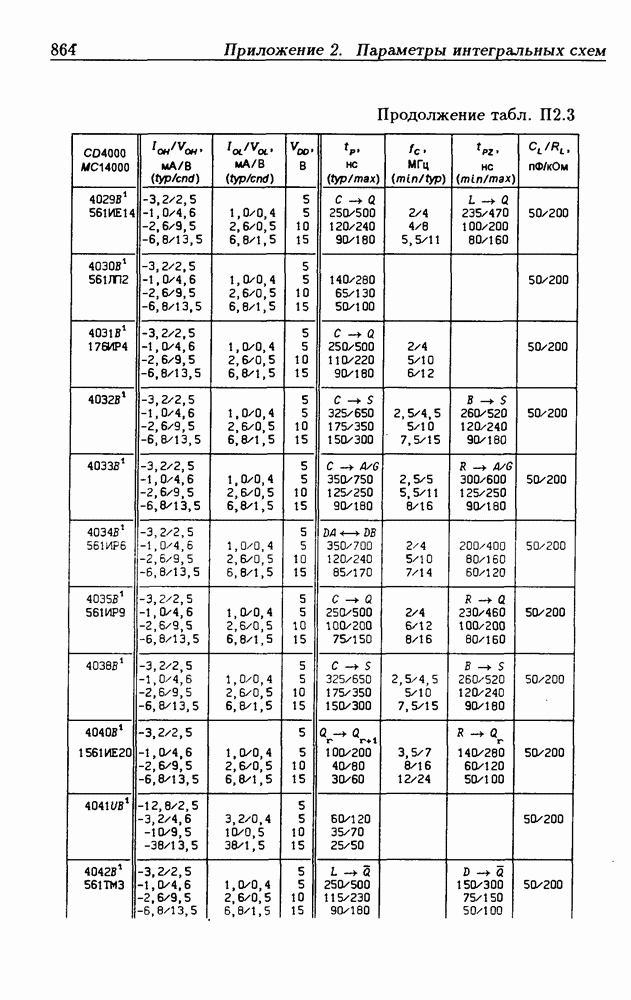
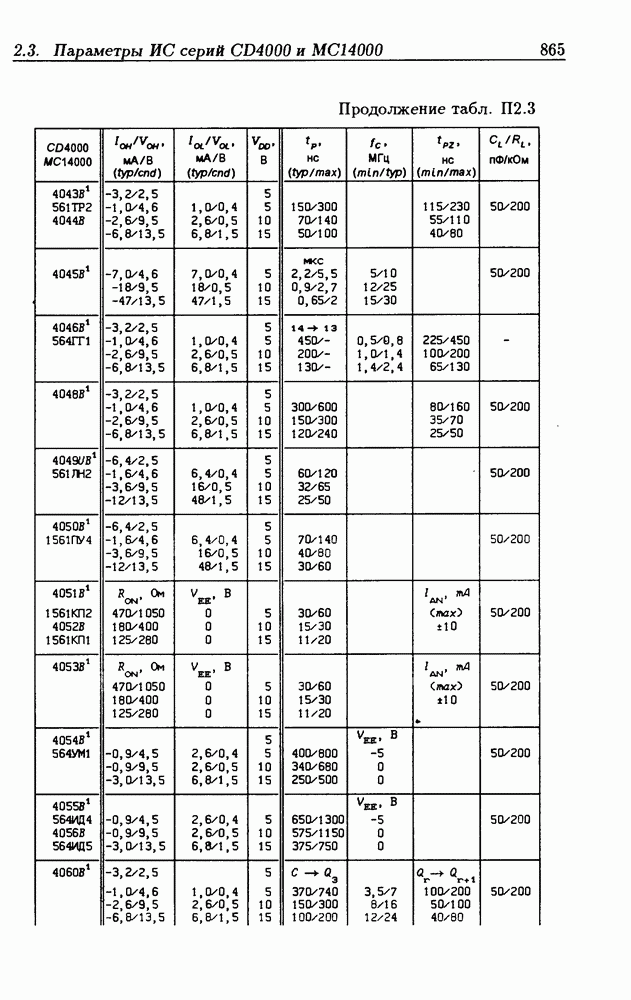
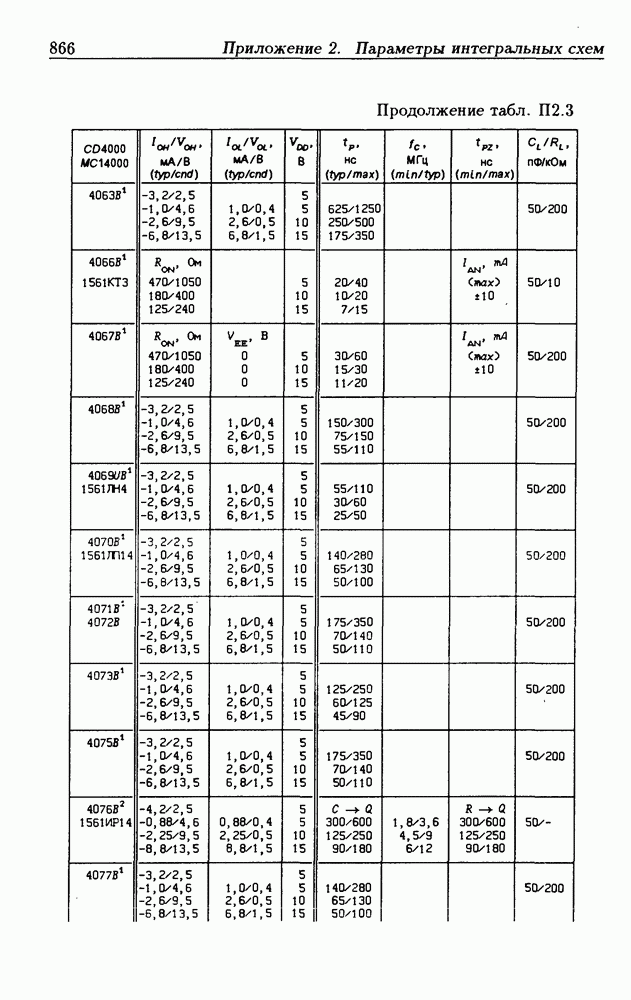
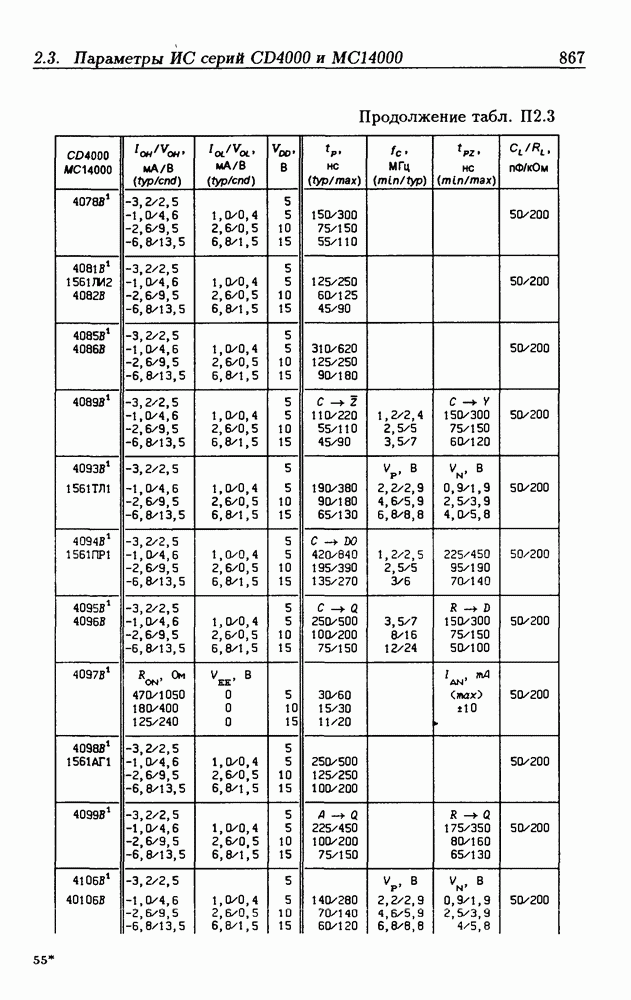
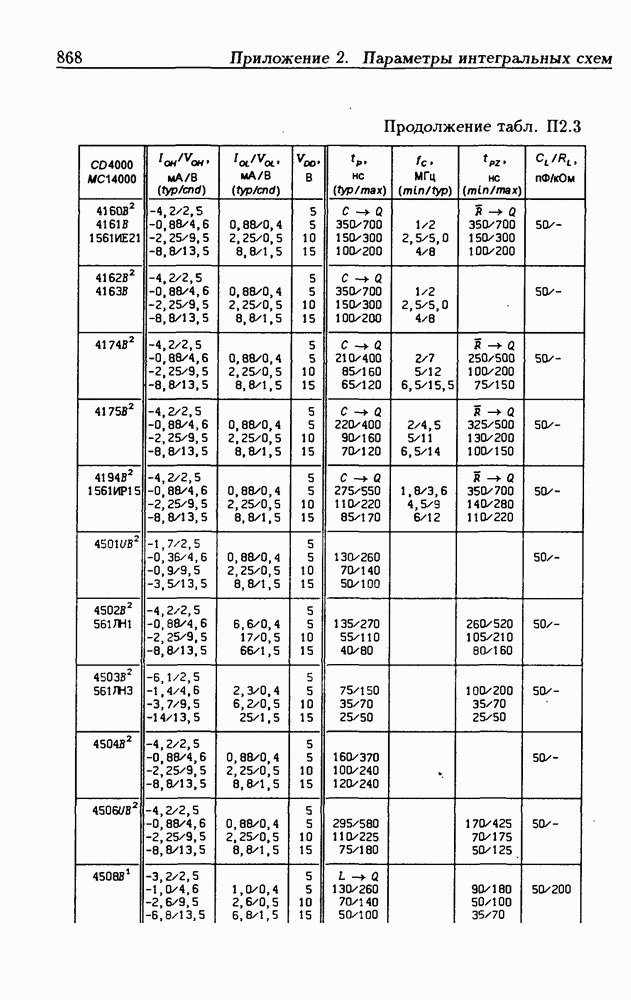
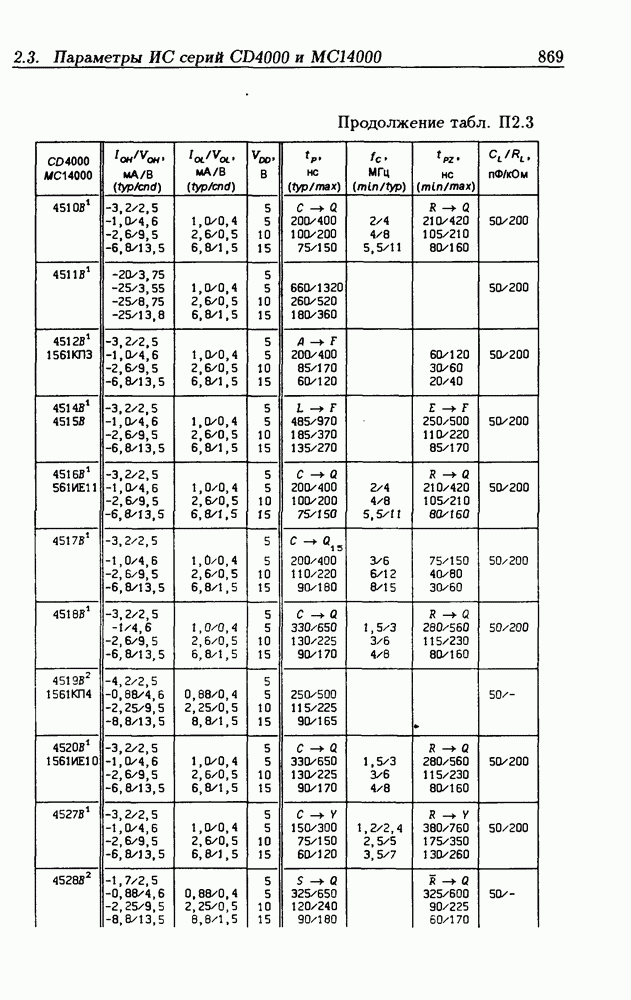
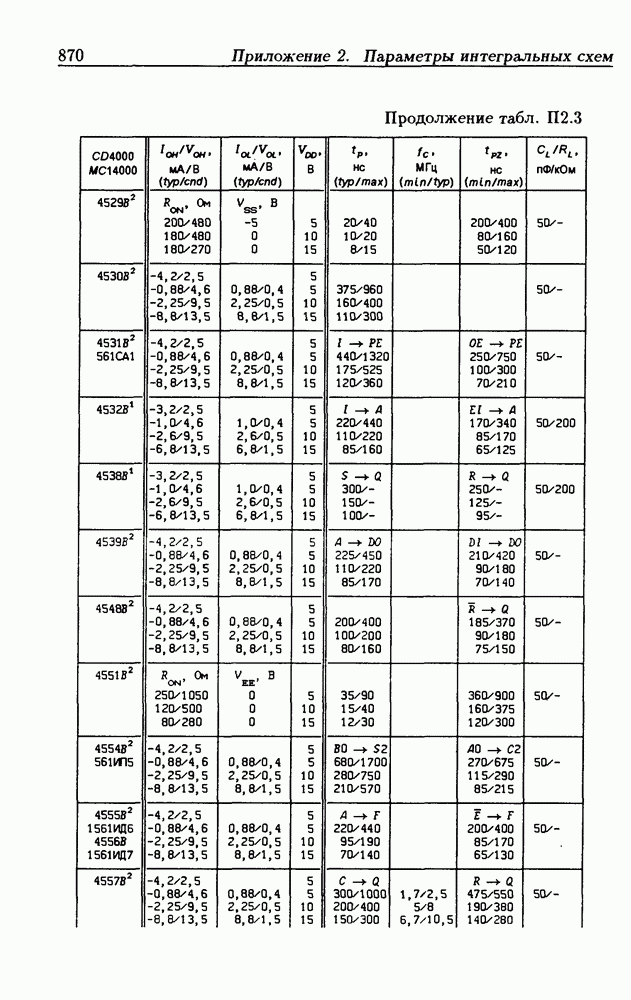
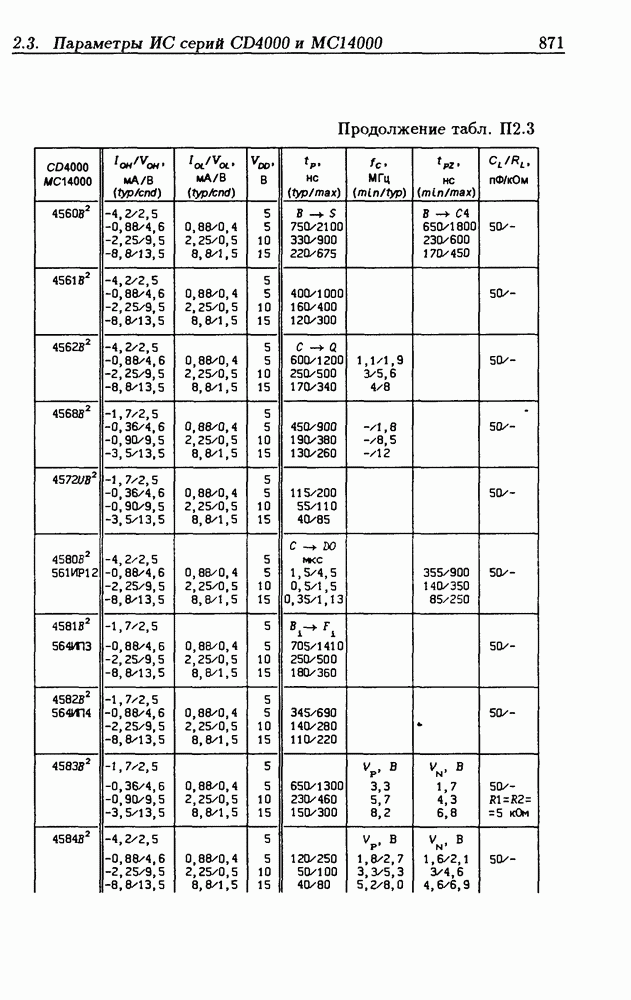
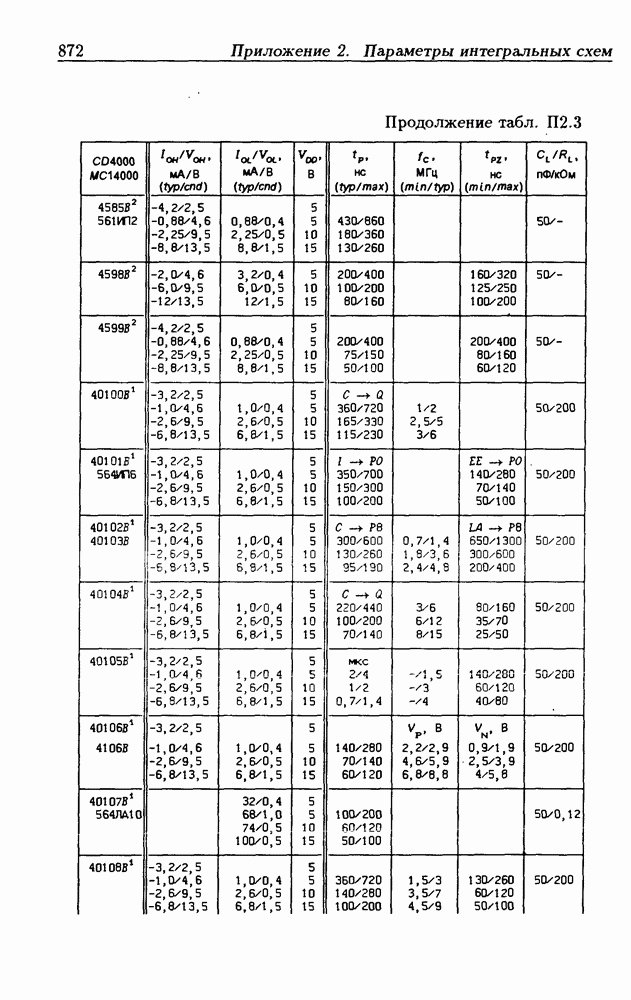
- Приложение 2. Параметры интегральных схем