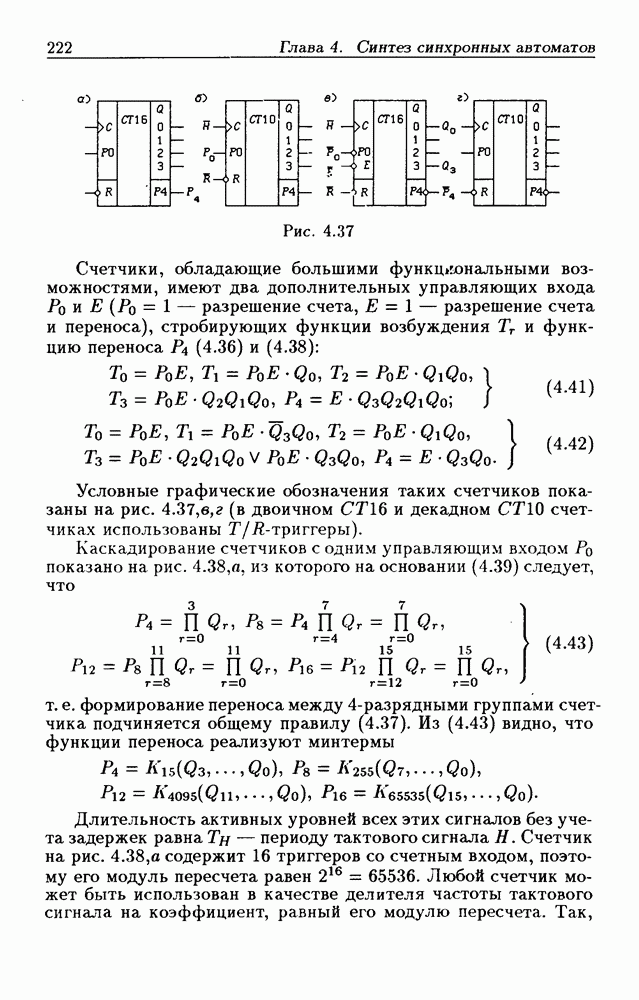| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.2. Асинхронные потенциальные автоматы
В основной модели автомата (см. рис. 3.1) используются асинхронные потенциальные элементы задержки (ЭП типа  Точные значения величин задержек
Точные значения величин задержек  в принципе неизвестны, так как они могут со временем изменяться под воздействием многих факторов. Поэтому даже при одновременном изменении входных сигналов нескольких элементов задержки их выходные сигналы могут изменяться неодновременно, причем порядок изменения выходных сигналов может быть самым различным.
в принципе неизвестны, так как они могут со временем изменяться под воздействием многих факторов. Поэтому даже при одновременном изменении входных сигналов нескольких элементов задержки их выходные сигналы могут изменяться неодновременно, причем порядок изменения выходных сигналов может быть самым различным.
Из основной модели асинхронного потенциального автомата следует, что  и
и

где  входные информационные сигналы ЭП. Функция (3.4) называется функцией переходов ЭП типа
входные информационные сигналы ЭП. Функция (3.4) называется функцией переходов ЭП типа  а функцию
а функцию

принято называть функцией возбуждения ЭП типа 
Элемент памяти  находится в устойчивом состоянии, если выполняется соотношение
находится в устойчивом состоянии, если выполняется соотношение  т.е., если значение выходного сигнала ЭП совпадает со значением его входного сигнала. Если же
т.е., если значение выходного сигнала ЭП совпадает со значением его входного сигнала. Если же  то ЭП находится в неустойчивом состоянии, так как значение его выходного сигнала должно в этом случае измениться через время, не большее чем
то ЭП находится в неустойчивом состоянии, так как значение его выходного сигнала должно в этом случае измениться через время, не большее чем 
Автомат находится в устойчивом состоянии, если  для всех
для всех  т. е., если все ЭП находятся в устойчивом состоянии. В векторной форме условие устойчивости состояния автомата можно записать так:
т. е., если все ЭП находятся в устойчивом состоянии. В векторной форме условие устойчивости состояния автомата можно записать так:

Автомат находится в неустойчивом состоянии, если хотя бы один ЭП находится в неустойчивом состоянии, т. е., если

Если при изменении состояния входа  на
на  автомат в зависимости от некоторых условий может перейти в любое из двух или большего числа устойчивых состояний, то в автомате имеют место состязания устойчивых состояний. Состязания устойчивых состояний недопустимы, так как нарушается детерминированность переходов.
автомат в зависимости от некоторых условий может перейти в любое из двух или большего числа устойчивых состояний, то в автомате имеют место состязания устойчивых состояний. Состязания устойчивых состояний недопустимы, так как нарушается детерминированность переходов.
Пусть автомат при некотором состоянии входа  находится в устойчивом состоянии
находится в устойчивом состоянии  что будем символически записывать в виде
что будем символически записывать в виде  Затем состояние входа изменяется на некоторое состояние
Затем состояние входа изменяется на некоторое состояние  при котором изменяются входные сигналы одного или нескольких ЭП. Автомат в этом случае переходит в неустойчивое состояние
при котором изменяются входные сигналы одного или нескольких ЭП. Автомат в этом случае переходит в неустойчивое состояние  Через время
Через время  на входах КС появятся новые значения выходных сигналов некоторых ЭП
на входах КС появятся новые значения выходных сигналов некоторых ЭП  При этом оказываются возможными три варианта дальнейшего поведения автомата.
При этом оказываются возможными три варианта дальнейшего поведения автомата.
1. Новые значения сигналов  не изменяют входных сигна-лов ни одного ЭП, а значит, в этом случае переходный процесс заканчивается через время
не изменяют входных сигна-лов ни одного ЭП, а значит, в этом случае переходный процесс заканчивается через время  устойчивое состояние изменяется на некоторое новое устойчивое состояние
устойчивое состояние изменяется на некоторое новое устойчивое состояние  Символически такие переходы можно представить в виде
Символически такие переходы можно представить в виде

и называются они простыми. Автоматы, имеющие только простые переходы, будем называть автоматами с простыми переходами.
2. Новые значения сигналов  (новое внутреннее состояние) в свою очередь изменяют входные сигналы одного или нескольких ЭП. В этом случае переходный процесс не заканчивается через время
(новое внутреннее состояние) в свою очередь изменяют входные сигналы одного или нескольких ЭП. В этом случае переходный процесс не заканчивается через время  так как состояние
так как состояние  не является устойчивым для состояния входа
не является устойчивым для состояния входа  и должно измениться на некоторое другое состояние
и должно измениться на некоторое другое состояние  которое в свою очередь может быть как устойчивым, так и неустойчивым. Таким образом, изменение состояния входа
которое в свою очередь может быть как устойчивым, так и неустойчивым. Таким образом, изменение состояния входа  на
на  может вызвать неоднократное изменение внутренних состояний, пока автомат не придет в устойчивое состояние. Символически такие переходы можно представить в виде
может вызвать неоднократное изменение внутренних состояний, пока автомат не придет в устойчивое состояние. Символически такие переходы можно представить в виде

(круглыми скобками отмечены устойчивые полные состояния автомата). В первом случае длительность переходного процесса равна  во втором -
во втором -  (задержками сигналов в КС пренебрегли). Автоматы, в которых хотя бы при одном изменении состояния входа возможно неоднократное изменение внутренних состояний, будем называть автоматами со сложными переходами. Внутреннее состояние
(задержками сигналов в КС пренебрегли). Автоматы, в которых хотя бы при одном изменении состояния входа возможно неоднократное изменение внутренних состояний, будем называть автоматами со сложными переходами. Внутреннее состояние  будем называть переходным, если
будем называть переходным, если

т. е., если состояние  не является устойчивым для состояния входа
не является устойчивым для состояния входа  вызывающего изменение состояния
вызывающего изменение состояния  на
на  В рассмотренных выше двух случаях переходов между устойчивыми состояниями имеются соответственно одно и
В рассмотренных выше двух случаях переходов между устойчивыми состояниями имеются соответственно одно и  переходных внутренних состояний.
переходных внутренних состояний.
3. Новые значения сигналов  возникающие в результате изменения состояния входа
возникающие в результате изменения состояния входа  на вызывают бесконечную последовательность смены внутренних состояний. Так как число этих состояний конечно
на вызывают бесконечную последовательность смены внутренних состояний. Так как число этих состояний конечно  то последовательность должна быть периодической, например:
то последовательность должна быть периодической, например:

В этом случае имеет место автоколебательный процесс (переходный процесс длится бесконечно долго). Такие процессы в автомате недопустимы ни при одном состоянии входа  так как неизвестно, в каком внутреннем состоянии
так как неизвестно, в каком внутреннем состоянии  он окажется к моменту следующего изменения состояния входа (нарушается детерминированность переходов).
он окажется к моменту следующего изменения состояния входа (нарушается детерминированность переходов).
Рассмотрим теперь ограничения, которые необходимо наложить на частоту изменения состояний входа, чтобы обеспечить правильную работу автомата. Пусть состояние входа  изменяется на
изменяется на  и при этом происходит изменение внутреннего состояния автомата. Если автомат не успеет достигнуть устойчивого состояния к моменту изменения состояния входа
и при этом происходит изменение внутреннего состояния автомата. Если автомат не успеет достигнуть устойчивого состояния к моменту изменения состояния входа  на некоторое новое состояние то нельзя сказать ничего определенного о дальнейшем поведении автомата, а значит, это может привести к недетерминированности переходов. Поэтому для автоматов с простыми переходами должно выполняться условие
на некоторое новое состояние то нельзя сказать ничего определенного о дальнейшем поведении автомата, а значит, это может привести к недетерминированности переходов. Поэтому для автоматов с простыми переходами должно выполняться условие  для автоматов со сложными переходами — условие
для автоматов со сложными переходами — условие  где
где  максимально допустимая частота изменений состояний входа, которая характеризует быстродействие автомата. Данные условия справедливы только при
максимально допустимая частота изменений состояний входа, которая характеризует быстродействие автомата. Данные условия справедливы только при  где ттах — максимальное время протекания
где ттах — максимальное время протекания
переходных процессов в КС. Эти же условия с учетом величины  будут приведены ниже. Очевидно, что быстродействие автоматов со сложными переходами значительно ниже быстродействия автоматов с простыми переходами.
будут приведены ниже. Очевидно, что быстродействие автоматов со сложными переходами значительно ниже быстродействия автоматов с простыми переходами.
В § 2.2 было показано, что в результате состязаний ЛЭ на выходах КС могут появляться ложные сигналы малой длительности. Так как в автомате имеются обратные связи, то ложные сигналы, поступив через ЭП на входы КС, могут привести к неправильному срабатыванию других ЭП, что может вызвать переход автомата в непредусмотренное функцией переходов внутреннее состояние — возникают состязания устойчивых состояний. Из этого следует, что КС необходимо синтезировать свободной от состязаний и что нельзя допускать несоседние изменения состояний входа.
После изменения состояния входа в КС начинает протекать переходный процесс, при этом входные сигналы одного или нескольких ЭП могут измениться раньше, чем он полностью закончится, т. е. прежде, чем КС придет в устойчивое состояние. Выходные сигналы указанных ЭП изменятся только через время  и если к этому времени переходный процесс в КС не закончится, то появление новых значений сигналов
и если к этому времени переходный процесс в КС не закончится, то появление новых значений сигналов  на входах КС может привести к нарушению правильности ее работы. Поэтому необходимо, чтобы время задержки
на входах КС может привести к нарушению правильности ее работы. Поэтому необходимо, чтобы время задержки  сигналов в ЭП было бы больше, чем максимально возможное время протекания переходных процессов в КС.
сигналов в ЭП было бы больше, чем максимально возможное время протекания переходных процессов в КС.
Таким образом, основным назначением ЭП является задержка сигналов, задающая время, отводимое в автомате на переходные процессы в КС. Чем большее требуется время  тем меньшее быстродействие будет иметь автомат. Точные значения величины
тем меньшее быстродействие будет иметь автомат. Точные значения величины  времени протекания в КС переходных процессов
времени протекания в КС переходных процессов  неизвестны, но всегда можно указать некоторые пределы, в которых они заключены:
неизвестны, но всегда можно указать некоторые пределы, в которых они заключены:

Тогда для гарантии правильной работы автомата должно выполняться соотношение

Если положить, что  то необходимо выполнение условия
то необходимо выполнение условия

С учетом этих соотношений для автоматов с простыми переходами необходимо соблюдать условие

а для автоматов со сложными переходами — условие

где  максимально допустимая частота изменения состояний входа,
максимально допустимая частота изменения состояний входа,  число переходных состояний.
число переходных состояний.
Если одновременно изменяются входные сигналы хотя бы двух ЭП, то их выходные сигналы не обязательно изменятся одновременно. Так как величины задержек для разных ЭП могут быть различными, то в автомате возникают состязания ЭП. Ввиду того, что точные значения величин задержек  неизвестны, ничего нельзя сказать о том, в какой последовательности изменяются выходные сигналы ЭП. Автомат может вести себя совершенно по-разному в зависимости от того, в какой последовательности они изменяются.
неизвестны, ничего нельзя сказать о том, в какой последовательности изменяются выходные сигналы ЭП. Автомат может вести себя совершенно по-разному в зависимости от того, в какой последовательности они изменяются.
Состязания ЭП могут быть критическими и некритическими. Если автомат в результате состязаний переходит в устойчивое состояние, задаваемое функцией переходов (3.1), независимо от соотношений величин задержек  то состязания называются некритическими, или допустимыми. Если же автомат в результате состязаний ЭП может перейти в какое-либо устойчивое состояние, не предусмотренное функцией переходов, то состязания называются критическими, или недопустимыми, так как состязания ЭП приводят к состязаниям устойчивых состояний, а значит, нарушается детерминированность переходов.
то состязания называются некритическими, или допустимыми. Если же автомат в результате состязаний ЭП может перейти в какое-либо устойчивое состояние, не предусмотренное функцией переходов, то состязания называются критическими, или недопустимыми, так как состязания ЭП приводят к состязаниям устойчивых состояний, а значит, нарушается детерминированность переходов.
Состязаний ЭП можно избежать с помощью специального кодирования внутренних состояний автомата, которое исключает возможность одновременного изменения входных сигналов двух или большего числа ЭП. Такое кодирование заключается в приписывании каждым двум состояниям  между которыми есть переход, соседних кодовых комбинаций
между которыми есть переход, соседних кодовых комбинаций

отличающихся значением только одного сигнала  Данное кодирование называется соседним кодированием внутренних состояний автомата. Очевидно, что при выполнении соседнего кодирования внутренних состояний в каждый момент времени будет изменяться выходной сигнал только одного ЭП.
Данное кодирование называется соседним кодированием внутренних состояний автомата. Очевидно, что при выполнении соседнего кодирования внутренних состояний в каждый момент времени будет изменяться выходной сигнал только одного ЭП.
Если бы даже величины задержек  сигналов во всех ЭП были одинаковы, то и тогда нельзя было бы допускать одновременного изменения выходных сигналов двух или большего числа ЭП. Это объясняется тем, что при одновременном изменении нескольких входных сигналов КС в ней могли бы возникнуть критические состязания ЛЭ, вызывающие появление ложных сигналов на выходах КС.
сигналов во всех ЭП были одинаковы, то и тогда нельзя было бы допускать одновременного изменения выходных сигналов двух или большего числа ЭП. Это объясняется тем, что при одновременном изменении нескольких входных сигналов КС в ней могли бы возникнуть критические состязания ЛЭ, вызывающие появление ложных сигналов на выходах КС.
Итак, чтобы иметь полную уверенность в том, что полученный в результате синтеза автомат будет выполнять заданные функции, следует потребовать выполнения шести условий:
1. При переходах не должны возникать автоколебательные процессы.
2. КС должна синтезироваться свободной от состязаний.
3. Состояния входа должны изменяться только на соседние.
4. Величина задержки сигналов в ЭП должна быть больше максимальной длительности переходных процессов в КС.
5. Частота изменения состояний входа должна быть ограничена некоторой величиной  при которой в автомате успевают заканчиваться все переходные процессы в интервале между двумя последовательными изменениями состояний входа.
при которой в автомате успевают заканчиваться все переходные процессы в интервале между двумя последовательными изменениями состояний входа.
6. Должны отсутствовать критические состязания ЭП.
Первое и последнее условия являются необходимыми, так как невыполнение их всегда приводит к недетерминированности переходов. Первое условие следует даже ввести в определение асинхронных потенциальных автоматов. Остальные условия являются достаточными, но не необходимыми, т.е. при их соблюдении автомат всегда будет функционировать в соответствии с заданным законом, а при несоблюдении некоторых из них может работать все-таки правильно. Однако следует иметь в виду, что при несоблюдении хотя бы одного достаточного условия не может быть никакой гарантии в том, что автомат будет работать правильно, а значит, в этих случаях после синтеза необходимо производить анализ на соответствие его работы заданному закону функционирования.
В качестве ЭП могут быть использованы линии задержки любого типа. При синтезе автоматов на интегральных микросхемах требуемую величину задержки можно получить с помощью некоторого числа последовательно включенных ЛЭ.
Будем считать, что сигналы  или
или  или
или  изменяются одновременно, если моменты их изменения разделены интервалом, меньшим чем
изменяются одновременно, если моменты их изменения разделены интервалом, меньшим чем  где
где  — максимально возможное время переходных процессов в КС. Если никакие два сигнала из
— максимально возможное время переходных процессов в КС. Если никакие два сигнала из  не изменяются одновременно, то для КС можно использовать модель, показанную на рис. 2.14. В этом случае основную модель автомата можно преобразовать к виду, приведенному на рис. 3.2,a (
не изменяются одновременно, то для КС можно использовать модель, показанную на рис. 2.14. В этом случае основную модель автомата можно преобразовать к виду, приведенному на рис. 3.2,a ( - паразитные элементы задержки с виртуальной и постоянной задержками соответственно). Паразитные элементы задержки на входах
- паразитные элементы задержки с виртуальной и постоянной задержками соответственно). Паразитные элементы задержки на входах  и выходах
и выходах  не показаны, так как они, находясь вне цепей обратных связей, не могут оказать сколько-нибудь существенного влияния на работу автомата.
не показаны, так как они, находясь вне цепей обратных связей, не могут оказать сколько-нибудь существенного влияния на работу автомата.

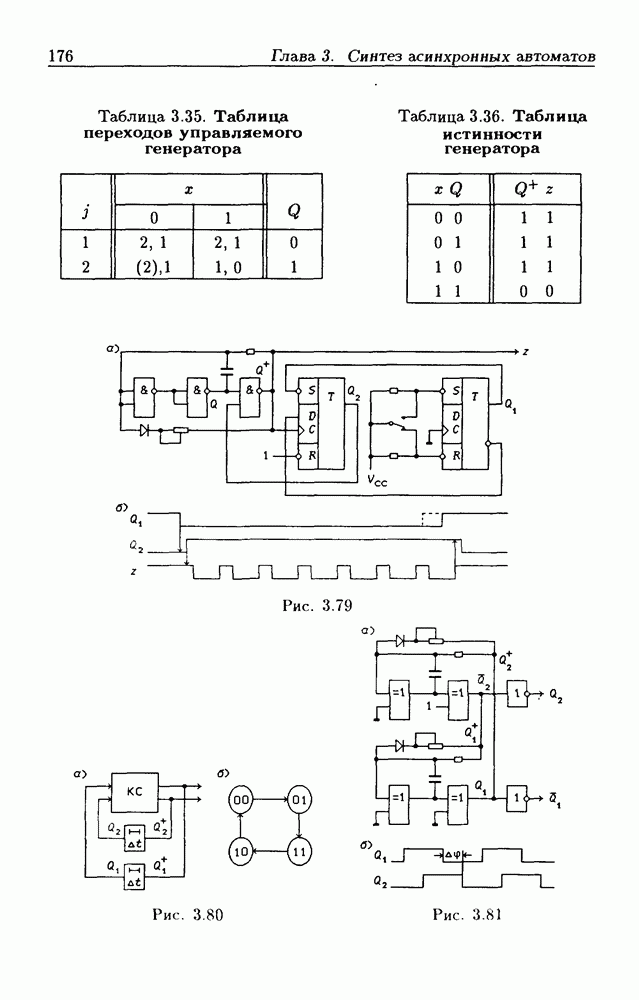
Рис. 3.2
Комбинационная схема в данной модели автомата является безынерционной, а значит, можно исключить из рассмотрения протекающие в ней переходные процессы. На этом основании часть КС, реализующую функции  можно рассматривать как совокупность
можно рассматривать как совокупность  гипотетических безинерционных ЛЭ, на выходах которых включены элементы задержки. Из этого следует, что все понятия, введенные в §§ 2.2 - 2.4, можно использовать и для асинхронных потенциальных автоматов с той лишь разницей, что внутреннее состояние автомата определяется как набор значений выходных сигналов ЭП, а не набор значений выходных сигналов всех ЛЭ, входящих в состав ЛС. В частности, таблицы и графы переходов автоматов по своей структуре должны быть аналогичны таблицам и графам переходов ЛС.
гипотетических безинерционных ЛЭ, на выходах которых включены элементы задержки. Из этого следует, что все понятия, введенные в §§ 2.2 - 2.4, можно использовать и для асинхронных потенциальных автоматов с той лишь разницей, что внутреннее состояние автомата определяется как набор значений выходных сигналов ЭП, а не набор значений выходных сигналов всех ЛЭ, входящих в состав ЛС. В частности, таблицы и графы переходов автоматов по своей структуре должны быть аналогичны таблицам и графам переходов ЛС.
Для анализа автоматов, так же как и для анализа ЛС, можно использовать решение функции переходов относительно устойчивых состояний. Отсутствие решения будет означать, что функция переходов задает некоторый генератор сигналов. Значит, не любая система функций (3.1) является функцией переходов асинхронного потенциального автомата.
При синтезе асинхронных потенциальных автоматов наиболее часто не выполняются третье и четвертое условия, что в ряде случаев может привести к возникновению состязаний устойчивых состояний. Так как все входные сигналы или хотя бы их часть могут поступать от независимого внешнего источника, то проектировщик автомата не может не допустить несоседние изменения состояний входа. Четвертое же условие часто не выполняется умышленно, так как с целью повышения быстродействия и упрощения реализации автомата желательно ЭП вообще не использовать, заменив их триггерами или непосредственными обратными связями. Если ЭП исключить из автомата, то его модель примет вид, показанный на рис. 3.2, б. Отметим, что во многих практических случаях для правильной работы автомата оказывается достаточным наличие паразитных элементов задержки.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Основы теории переключательных функций
- 1.2. Позиционные системы счисления
- 1.3. Переключательные функции
- 1.4. Принцип и закон двойственности
- 1.5. Теоремы разложения
- 1.6. Решение систем логических уравнений
- 1.7. Первичные термы, минтермы и макстермы
- 1.8. Совершенные нормальные формы представления функций
- 1.9. Конъюнктивные и дизъюнктивные термы
- 1.10. Минимизация переключательных функций
- 1.11. Диаграммы Вейча
- 1.12. Минимизация неполностью определенных функций, совместная минимизация нескольких функций
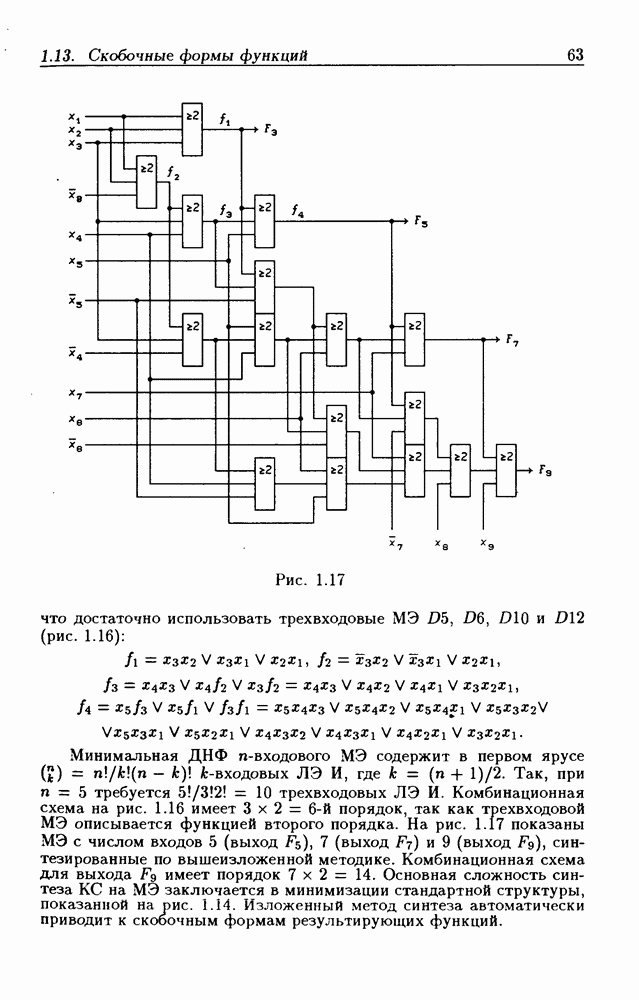
- 1.13. Скобочные формы функций
- 1.14. Закон двойственности для логических схем
- 1.15. Линейные функции
- Глава 2. Анализ и синтез логических схем
- 2.2. Модели логических элементов
- 2.3. Модели логических схем
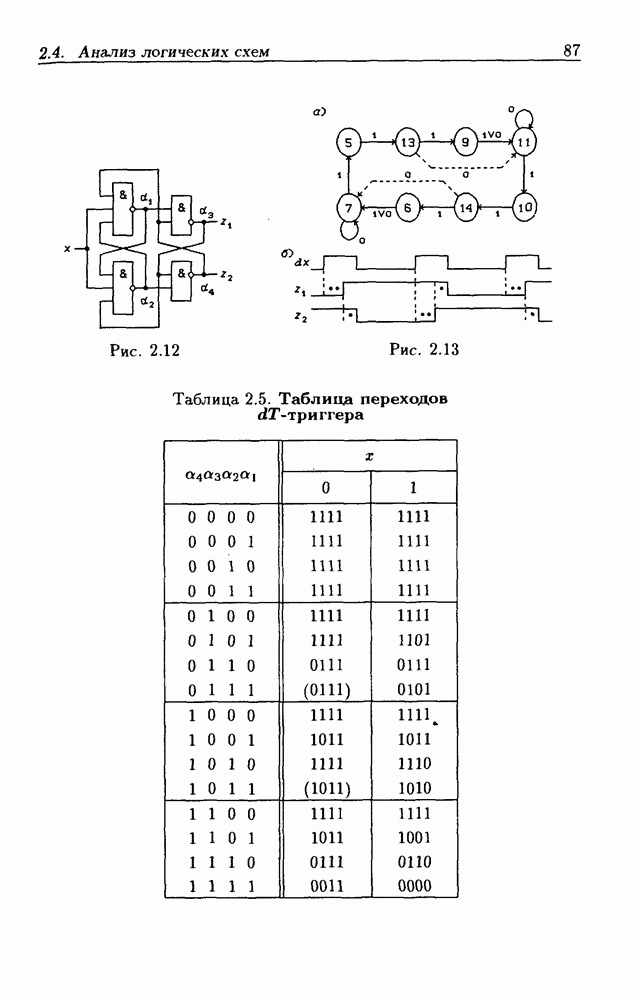
- 2.4. Анализ логических схем
- 2.5. Синтез комбинационных схем, свободных от состязаний
- Глава 3. Синтез асинхронных потенциальных автоматов
- 3.2. Асинхронные потенциальные автоматы
- 3.3. Асинхронные потенциальные триггеры и элементы памяти
- Триггеры типа R-S
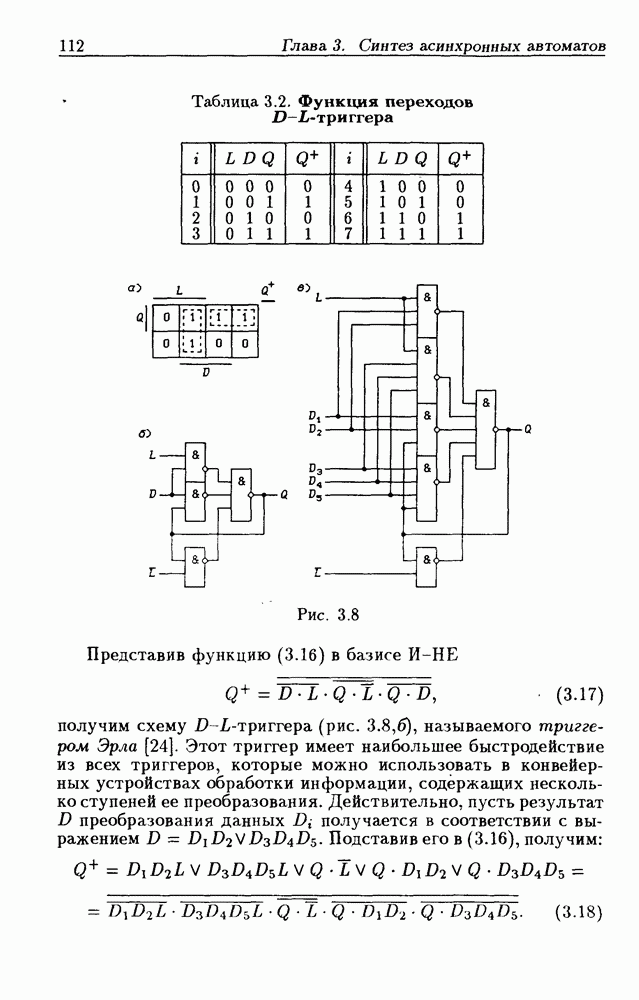
- Триггеры типа D-L
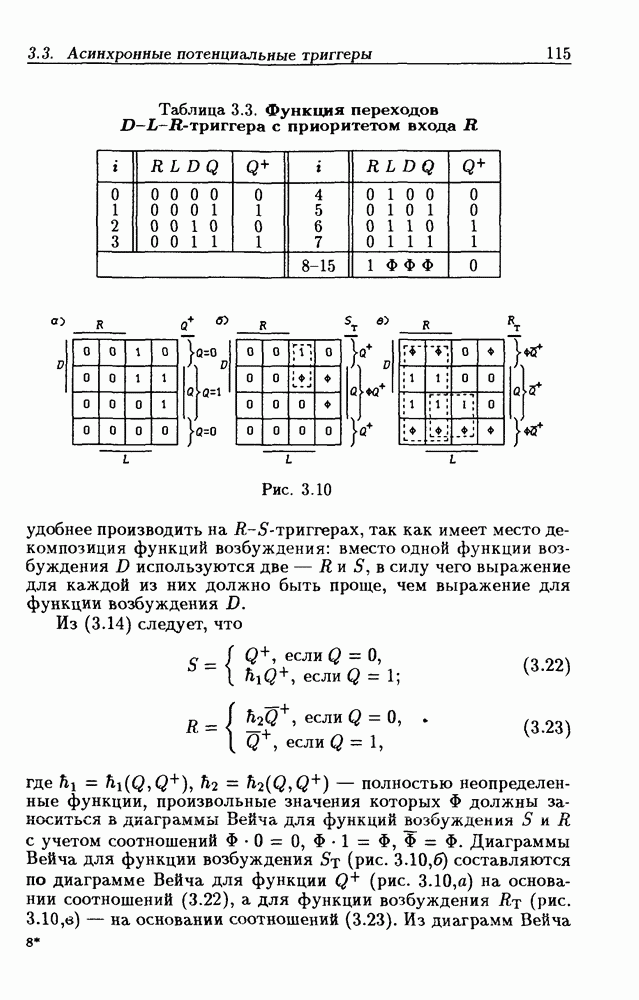
- Триггеры типа D-L-R с приоритетом входа R.
- Триггеры типа D-L-R с приоритетом входа L.
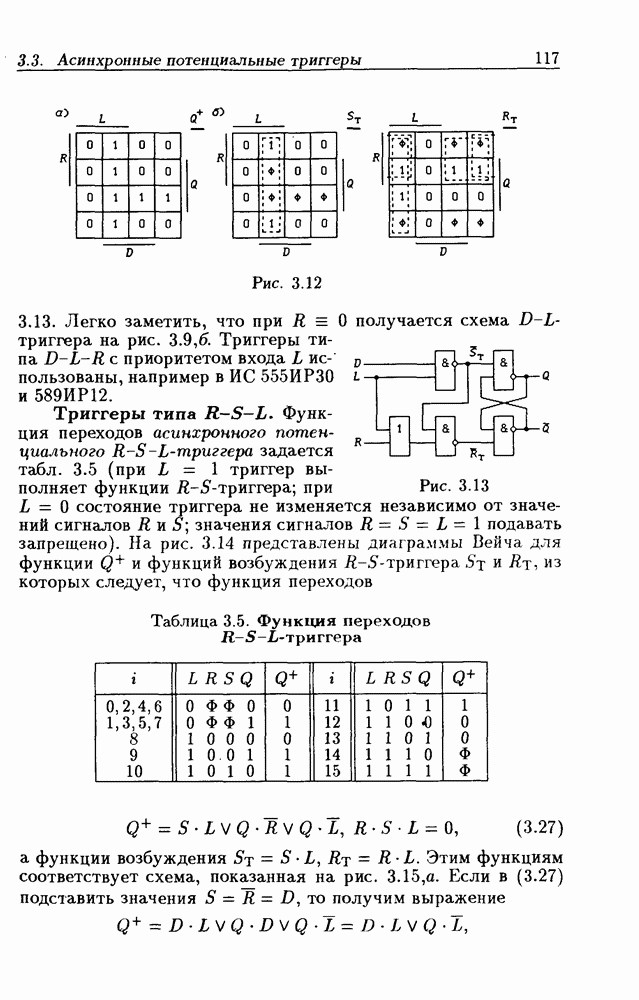
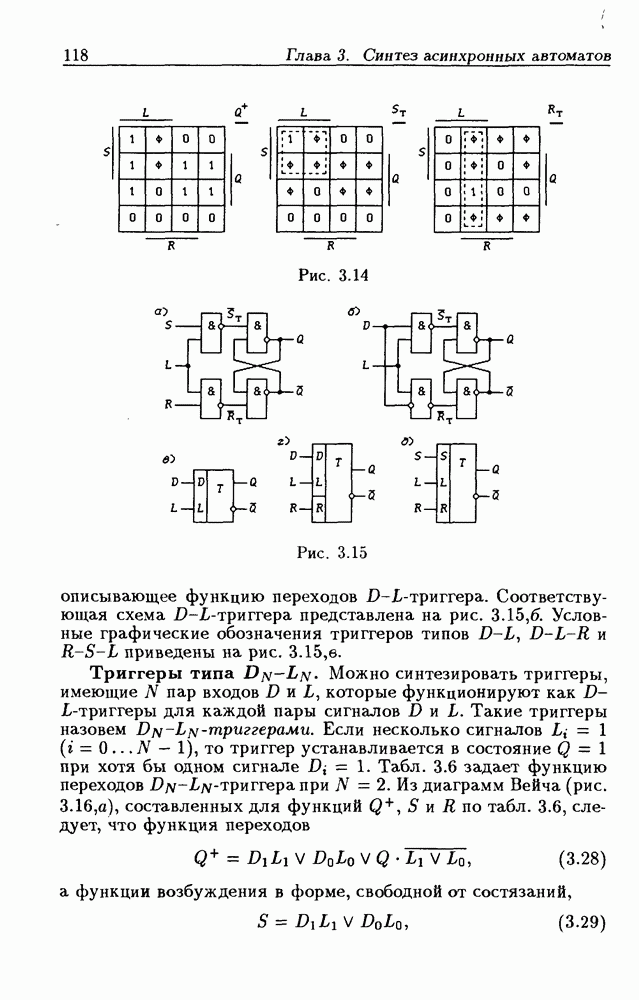
- Триггеры типа R-S-L.
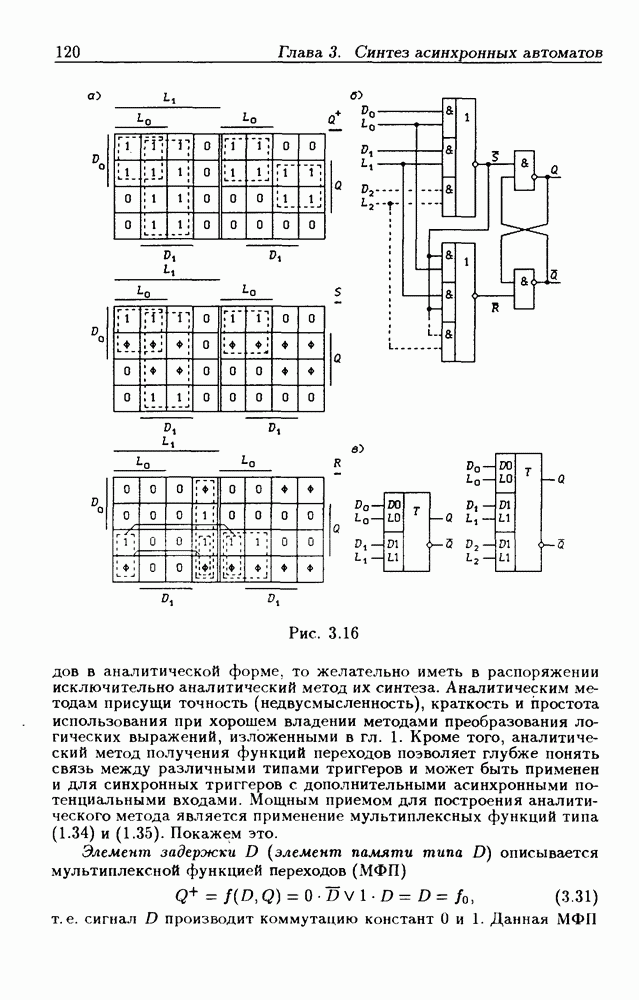
- Триггеры типа DN-LN
- Аналитический метод синтеза и анализа триггеров.
- 3.4. Задание асинхронных потенциальных автоматов таблицами и графами переходов
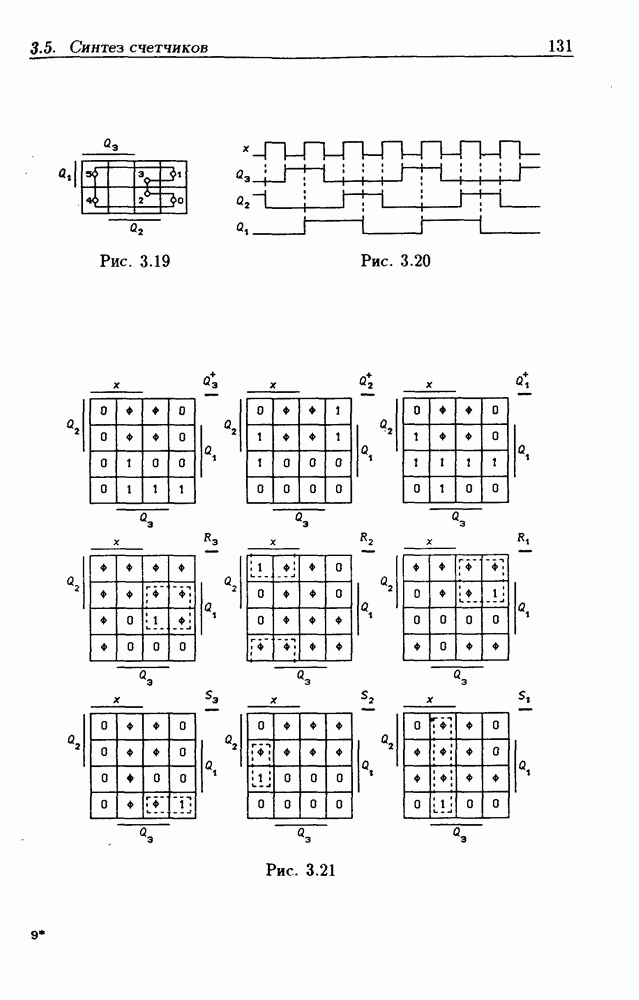
- 3.5. Синтез асинхронных потенциальных счетчиков
- 3.6. Синтез асинхронных импульсных триггеров
- Триггеры типа dJ-dK.
- Классификация триггеров.
- 3.7. Синтез синхронных триггеров
- Триггеры типа J-K
- Синхронно-асинхронные триггеры.
- 3.8. Примеры синтеза асинхронных потенциальных автоматов
- Цифровые фазочастотные детекторы.
- Квантизатор временных интервалов.
- 3.9. Генераторы сигналов
- Автогенераторы.
- Управляемые автогенераторы.
- Глава 4. Синтез синхронных автоматов
- 4.2. Синхронные триггеры
- Триггеры типов D и R-S с импульсным тактовым сигналом.
- Синхронные триггеры типов R-S и D-L
- Синхронно-асинхронные триггеры.
- Синхронные триггеры типа J-K
- Триггеры типа Т.
- Классификация синхронных триггеров.
- Преобразования типов синхронных триггеров.
- Триггеры типов D-T-L и D-T-L/R
- Функции переходов синхронно-асинхронных триггеров.
- 4.3. Примеры синтеза синхронных автоматов
- 4.4. Сдвигающие регистры
- Синтез счетчиков на сдвигающих регистрах.
- Сдвигающие регистры с загрузкой данных.
- Реверсивные сдвигающие регистры.
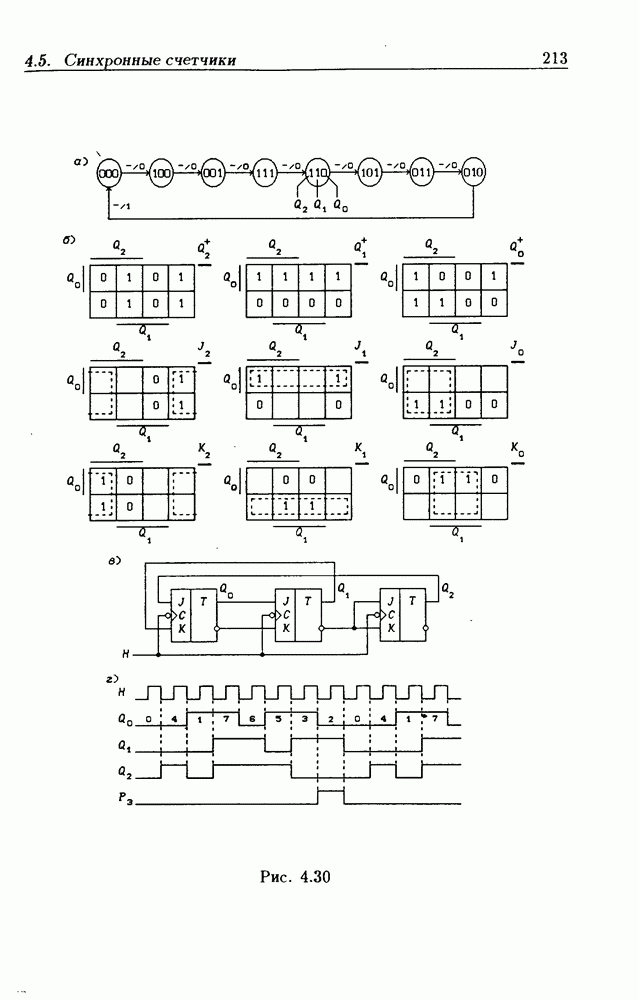
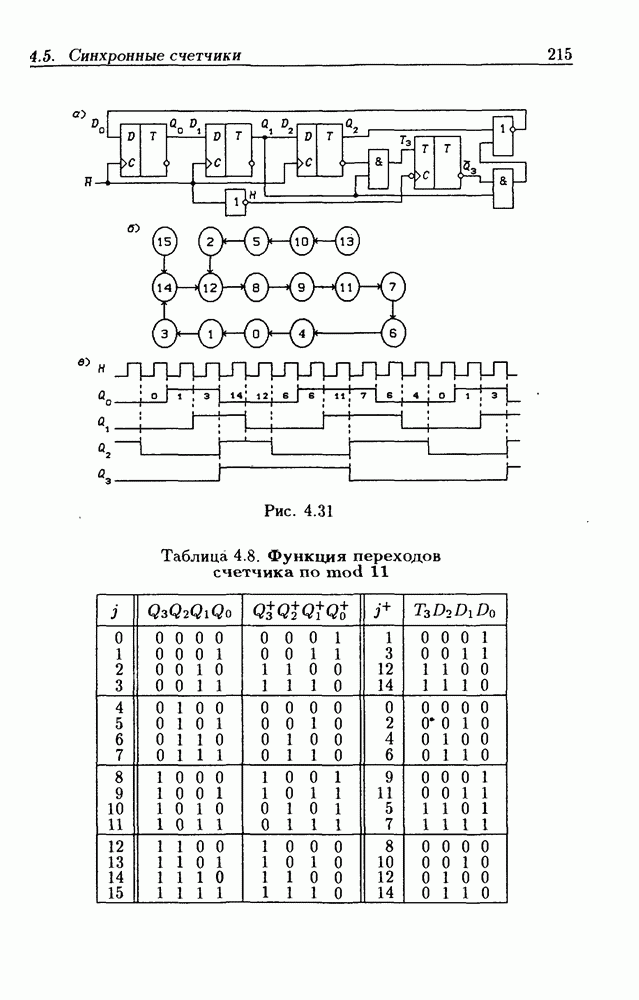
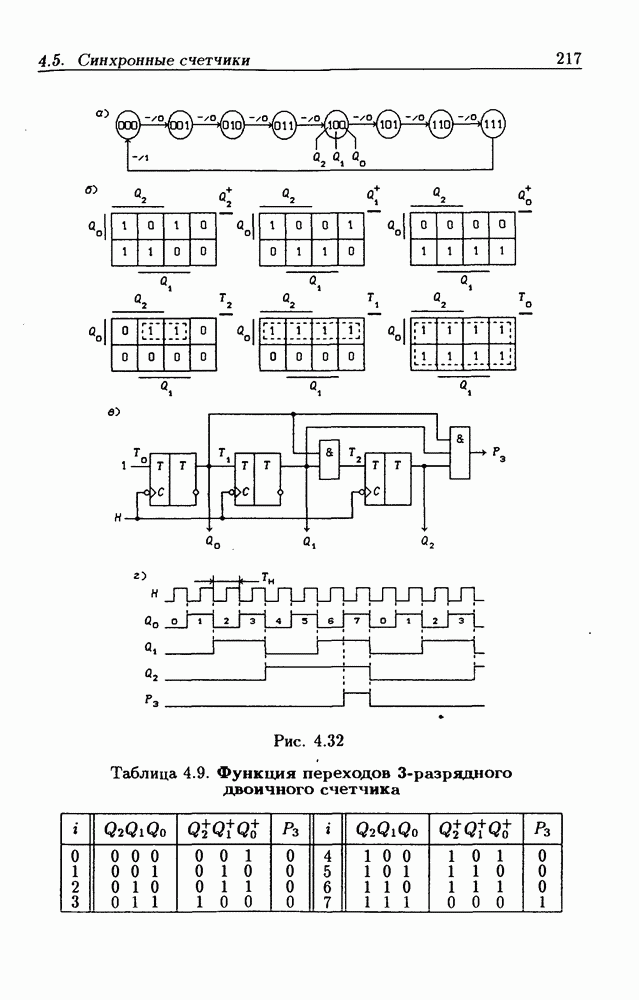
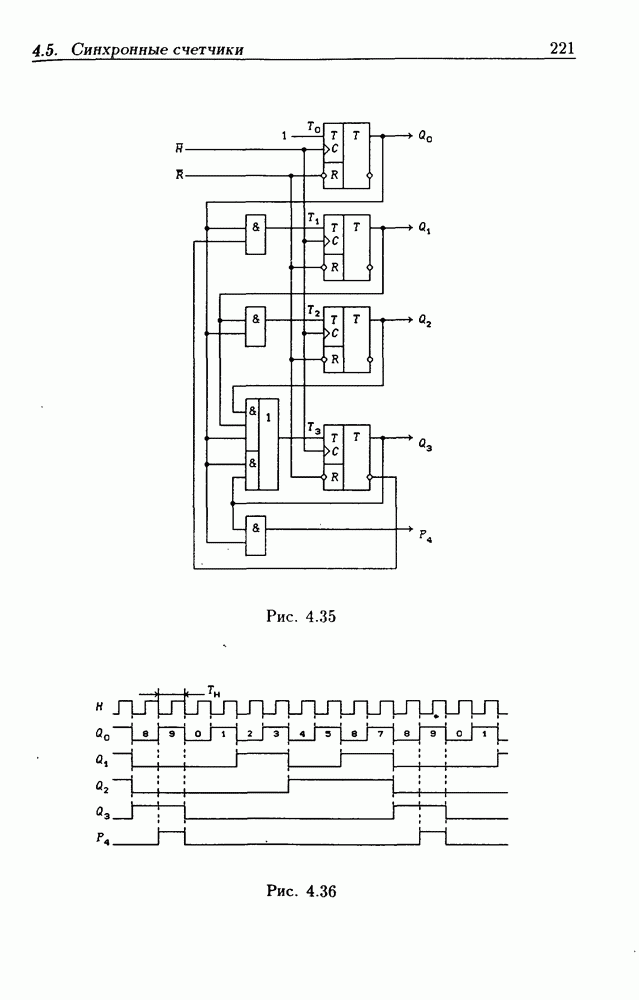
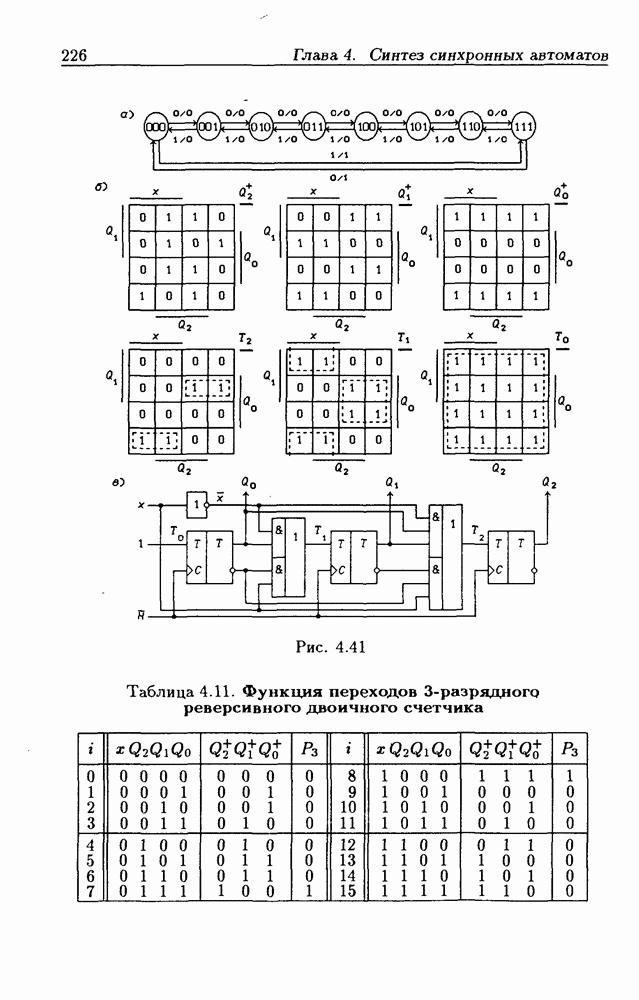
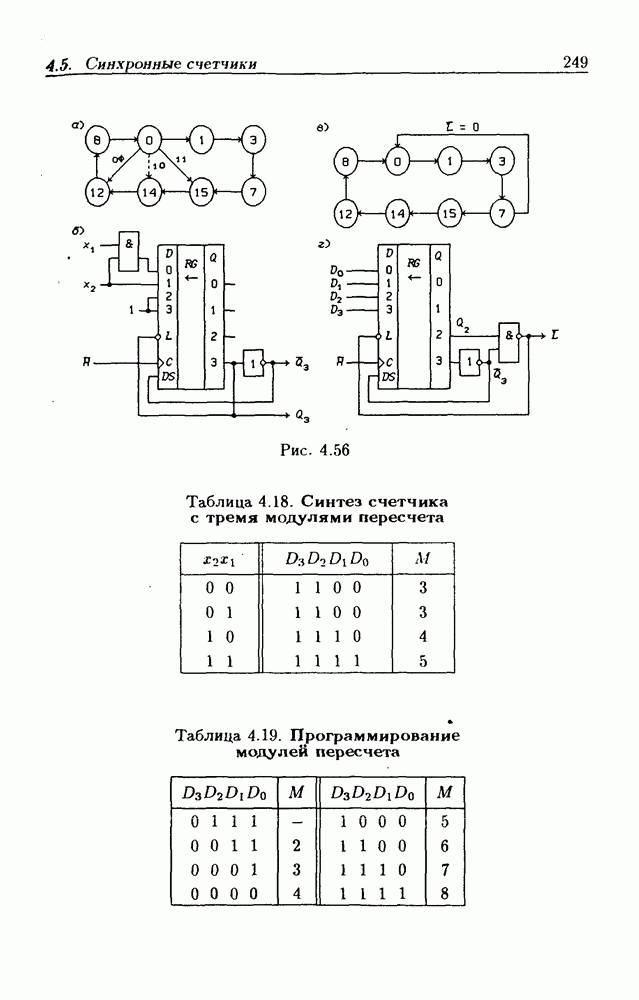
- 4.5. Синхронные счетчики
- Синхронные двоичные счетчики.
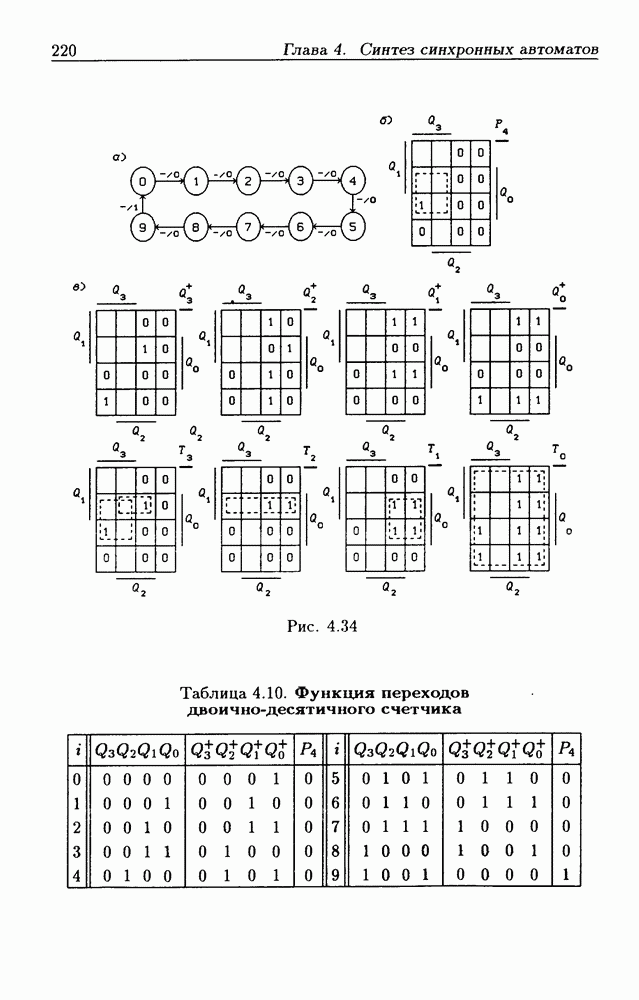
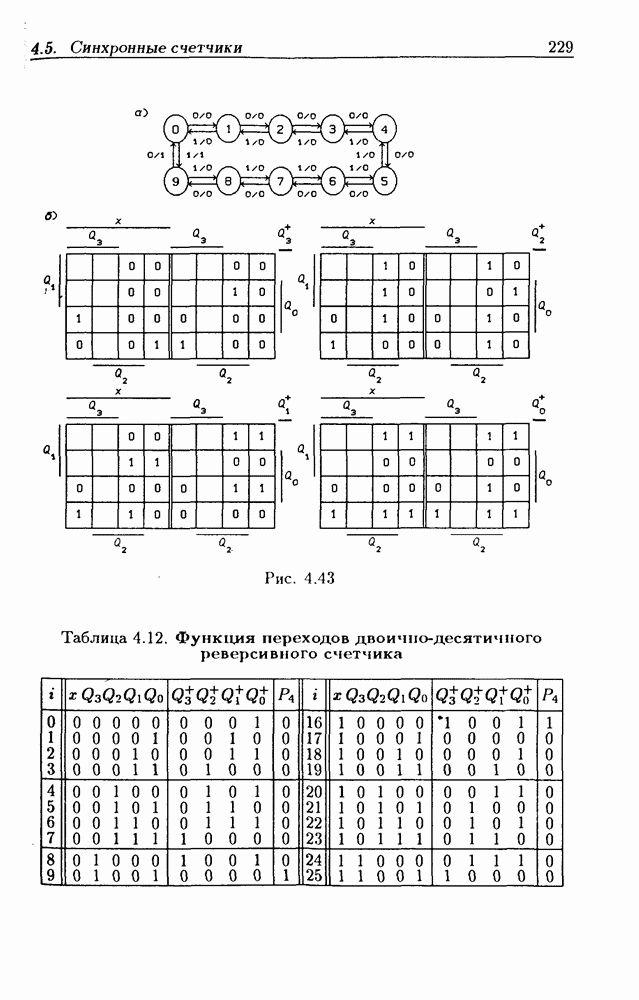
- Синхронные двоично-десятичные счетчики.
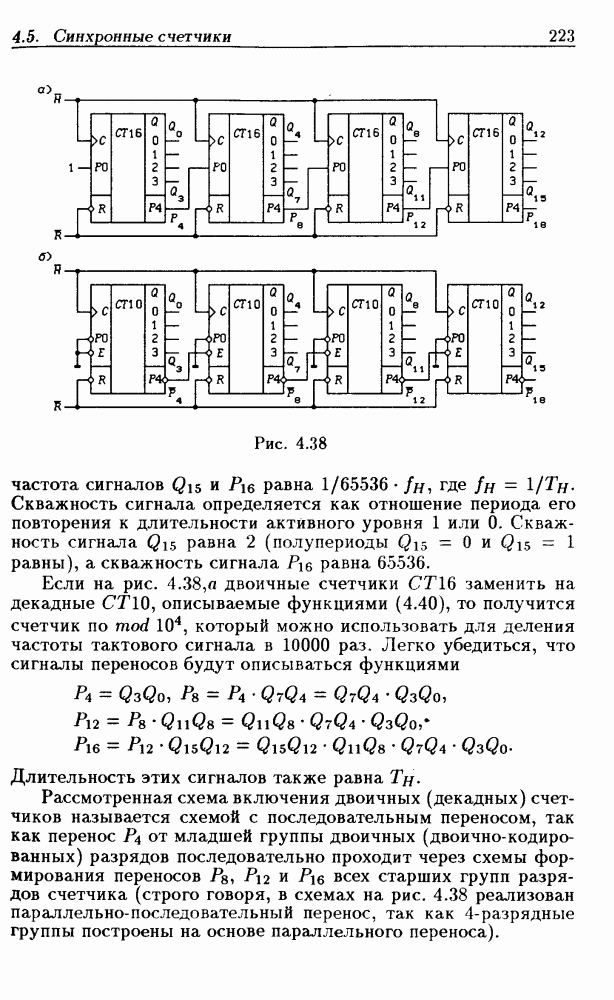
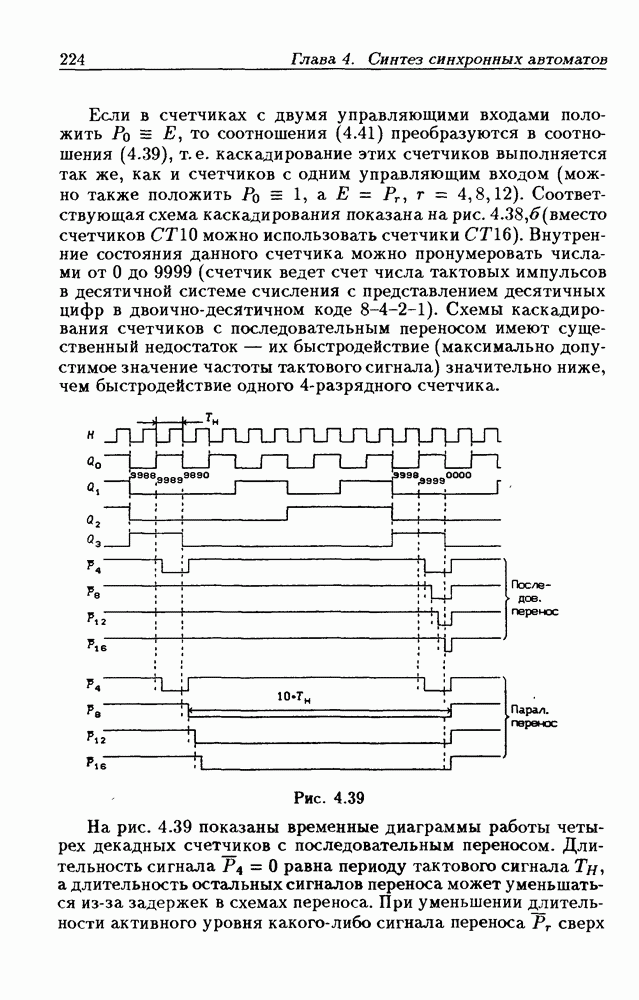
- Каскадирование двоичных и двоично-десятичных счетчиков.
- Синхронные двоичные реверсивные счетчики.
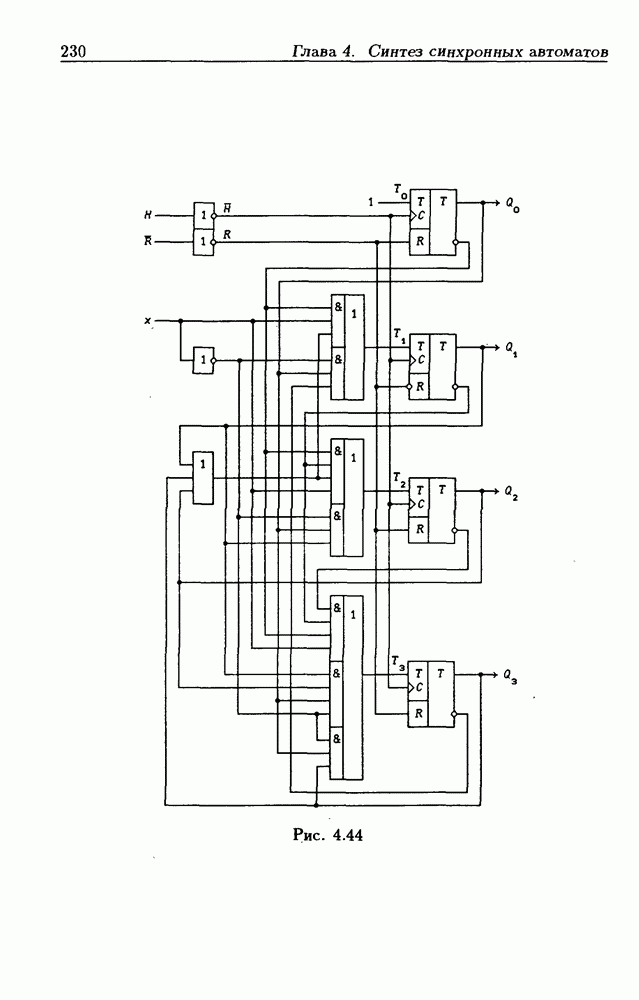
- Реверсивные двоично-десятичные счетчики.
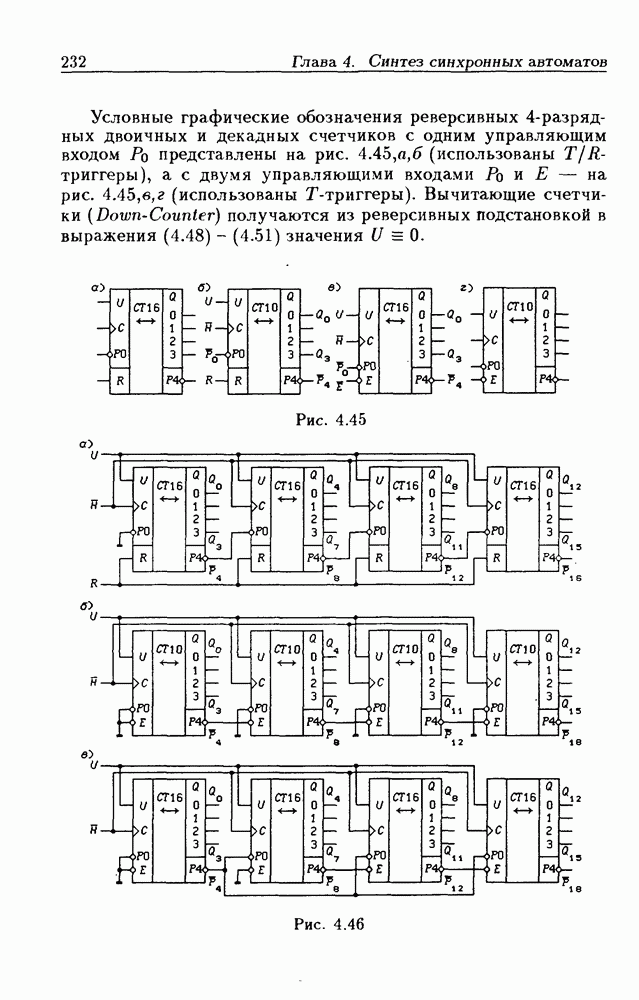
- Каскадирование реверсивных счетчиков.
- Счетчики на сдвигающих регистрах.
- Кольцевые счетчики.
- Линейные счетчики.
- Программируемые счетчики.
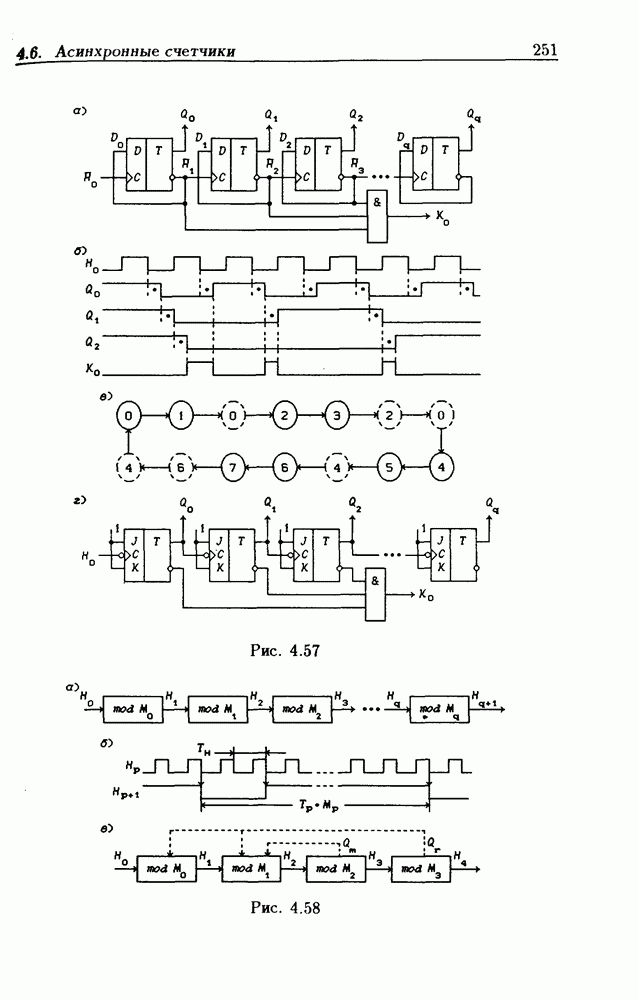
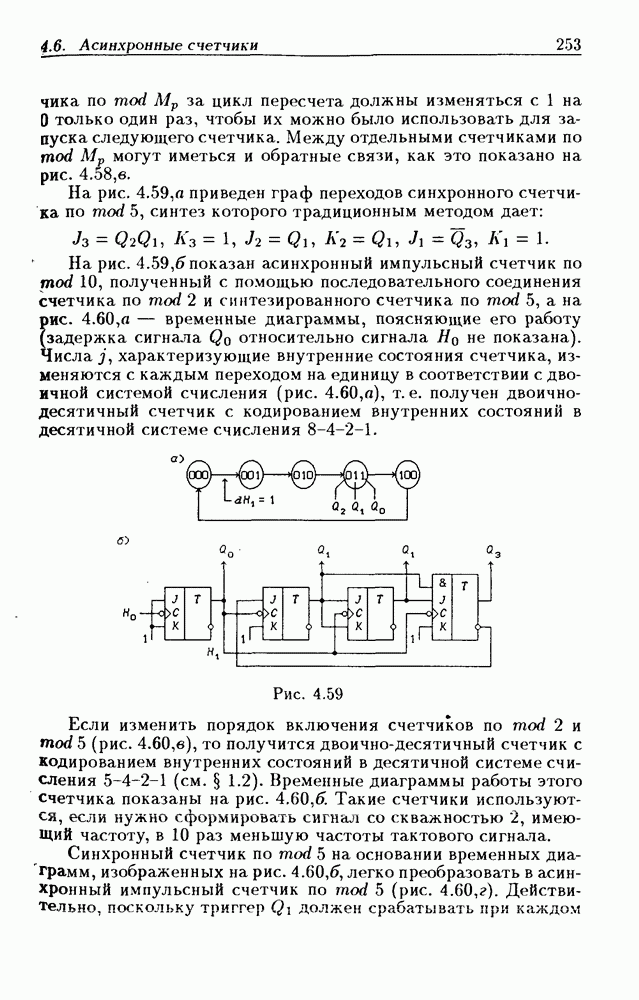
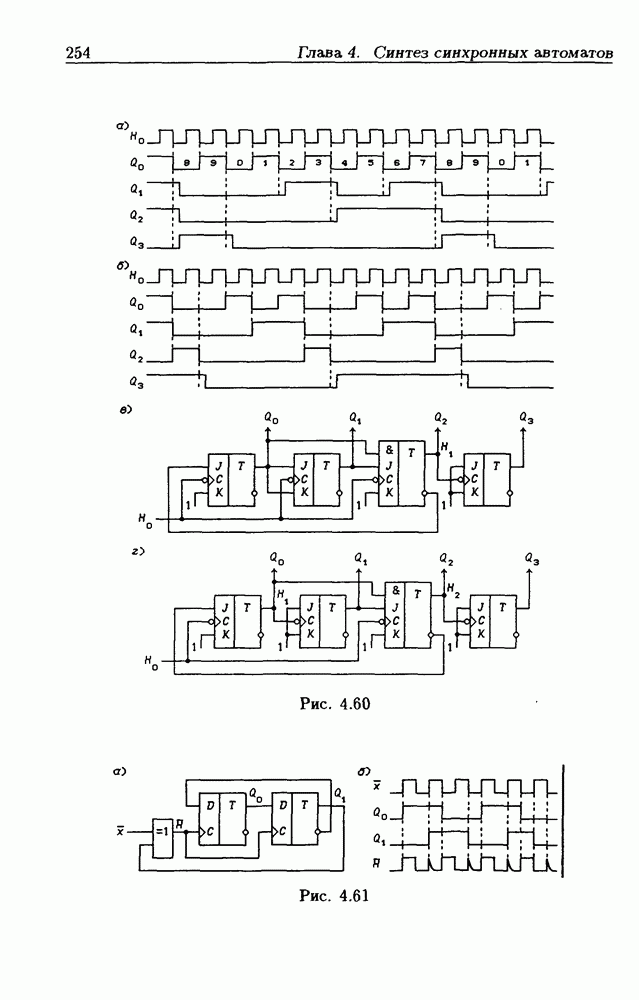
- 4.6. Асинхронные счетчики
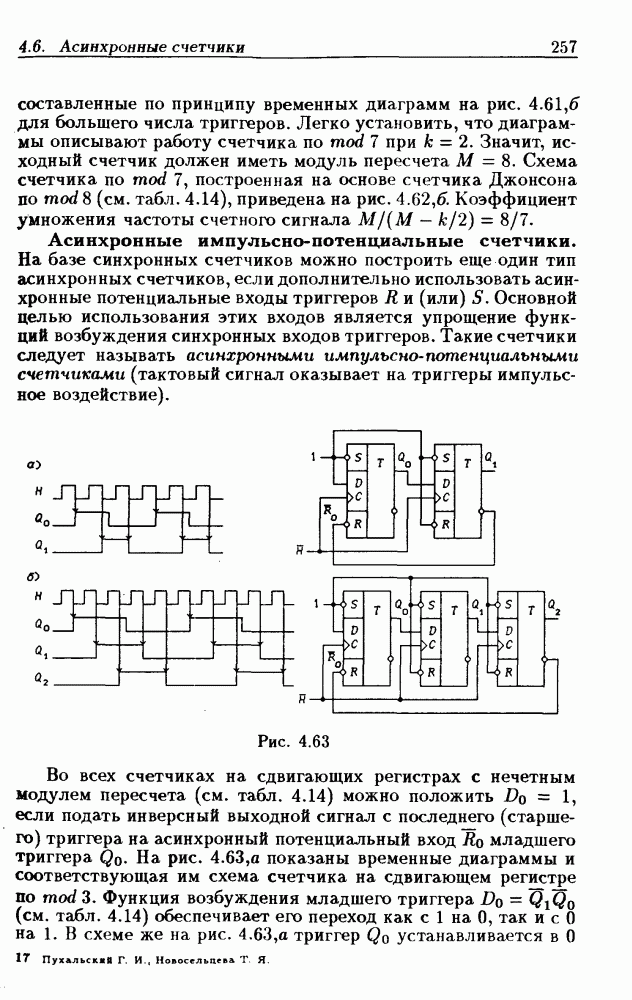
- Асинхронные счетчики с умножением частоты счетного сигнала.
- Асинхронные импульсно-потенциальные счетчики.
- Асинхронное программирование модуля пересчета счетчиков.
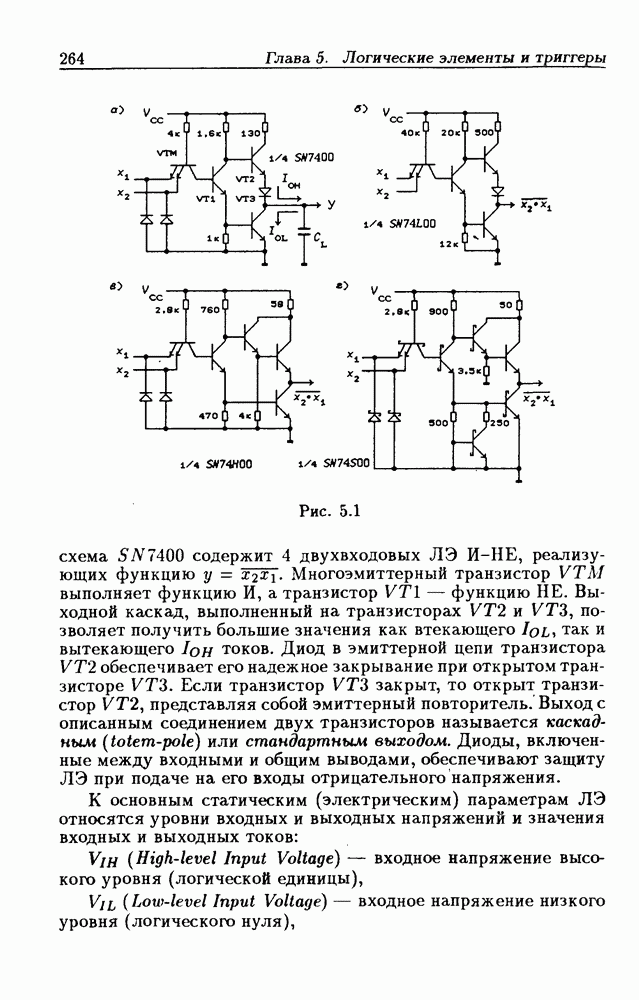
- Глава 5. Логические элементы и триггеры
- Логические элементы.
- Классификация ИС по степени интеграции.
- 5.2. Интегральные схемы КМОП серий
- 5.3. Триггеры Шмитта
- 5.4. Логические элементы с открытым коллекторным выходом
- Логические элементы с открытым коллекторным выходом.
- Применения ЛЭ с открытым коллекторным выходом.
- Интерфейсные ЛЭ с открытым коллекторным выходом.
- Логические элементы с открытым стоковым выходом.
- Типовые цоколевки ИС.
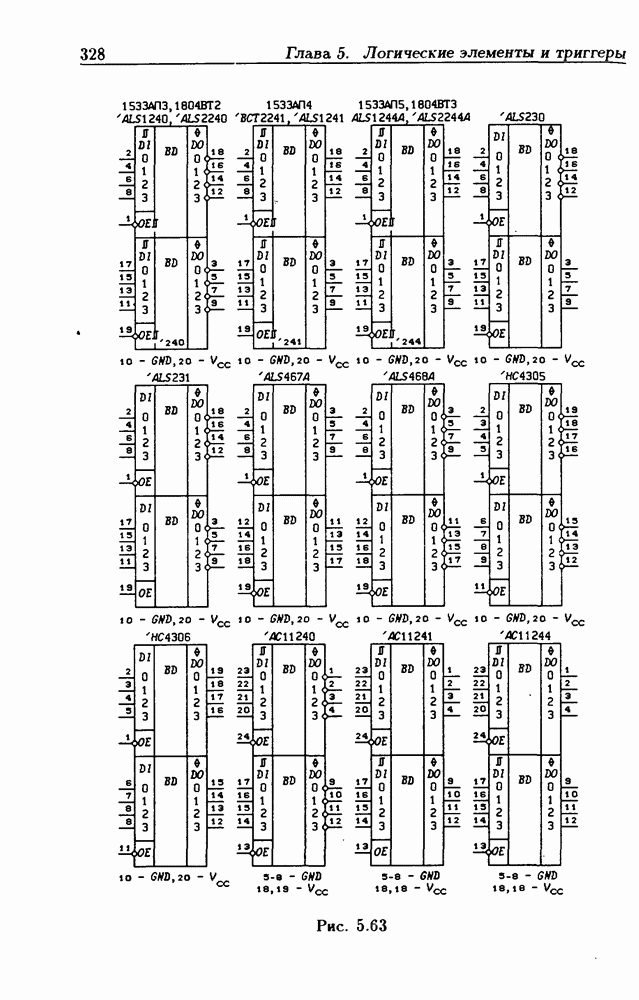
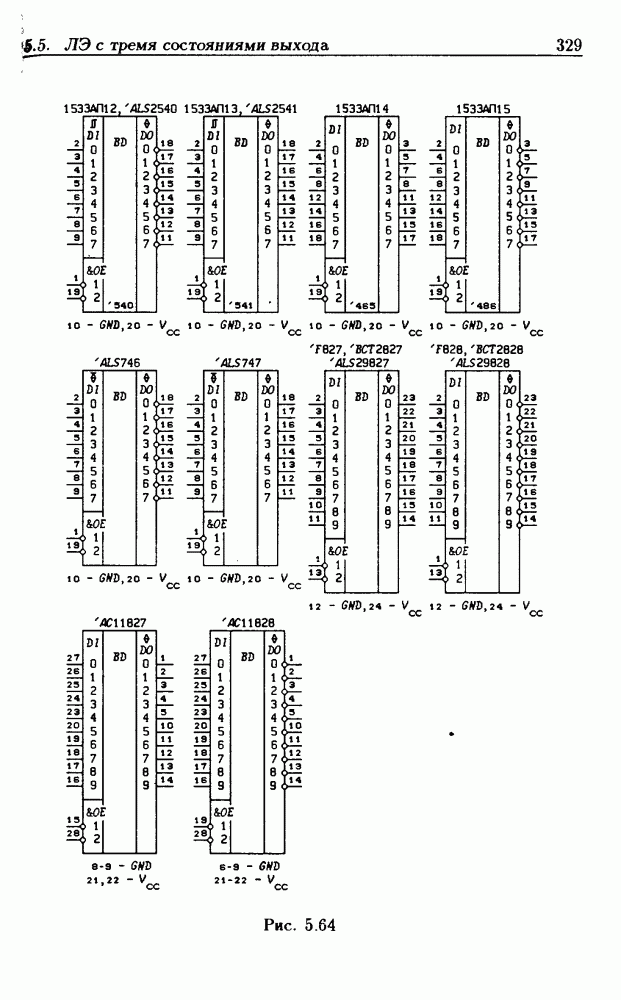
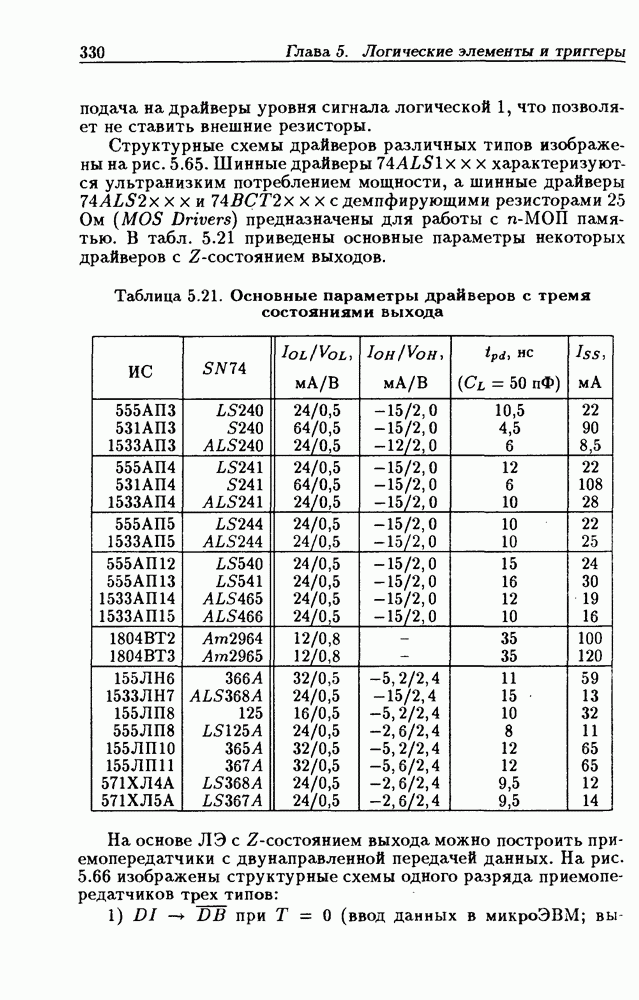
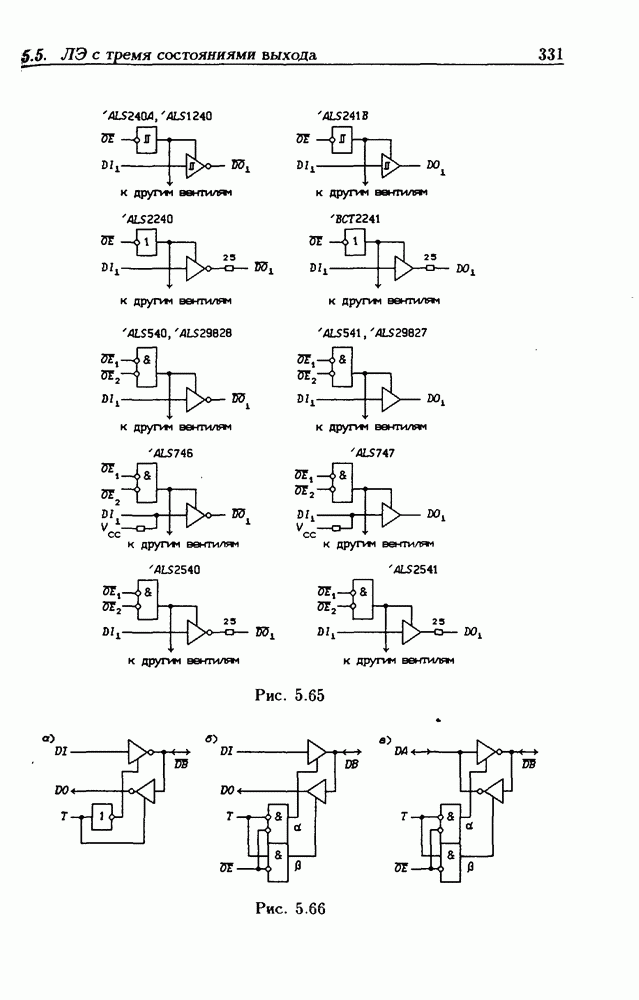
- 5.5. Логические элементы с тремя состояниями выхода
- Шинные драйверы с Z-состоянием выхода.
- Основные правила графического изображения ИС.
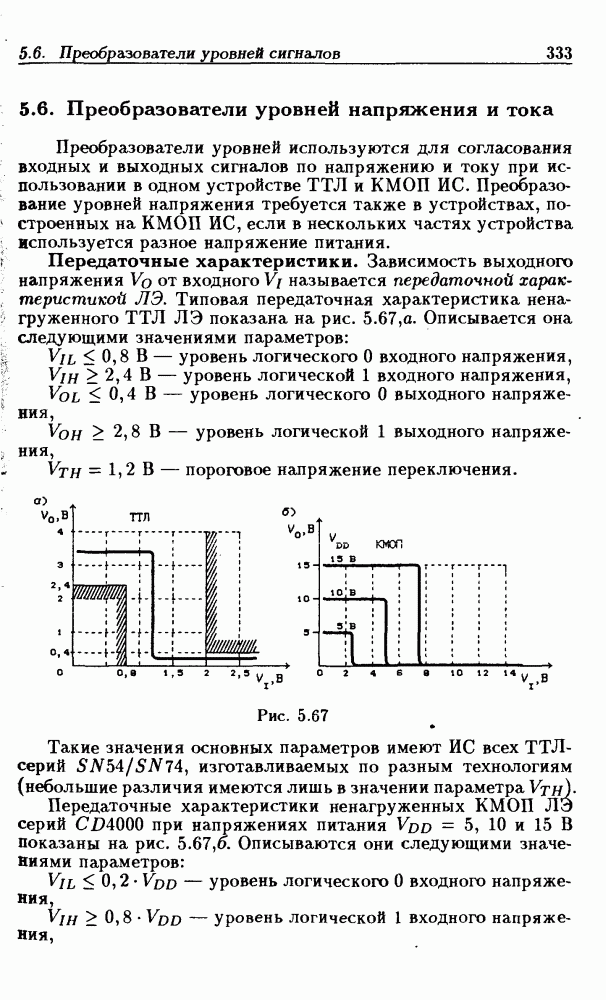
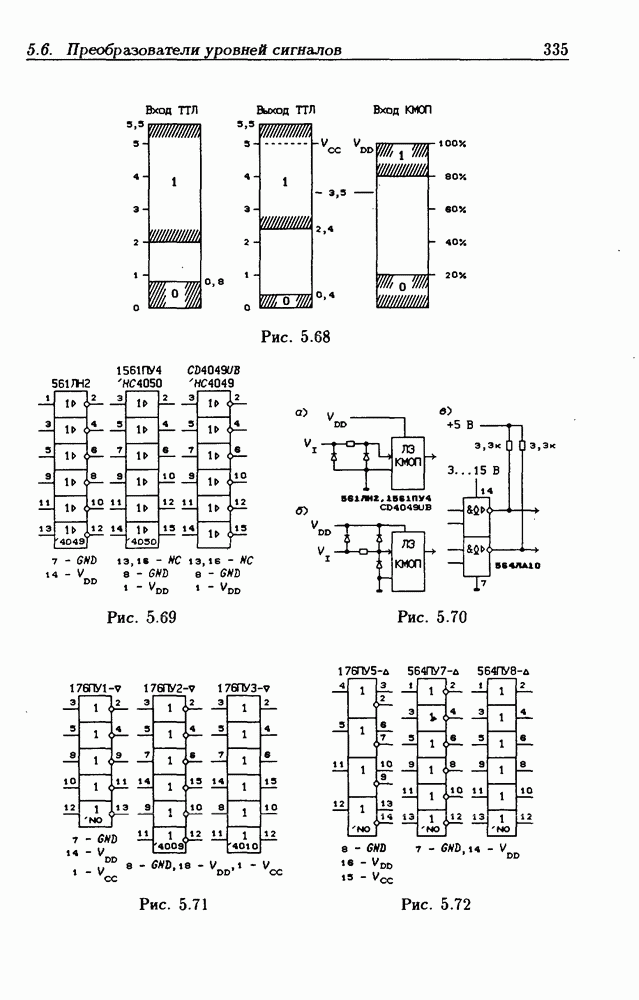
- 5.6. Преобразователи уровней напряжения и тока
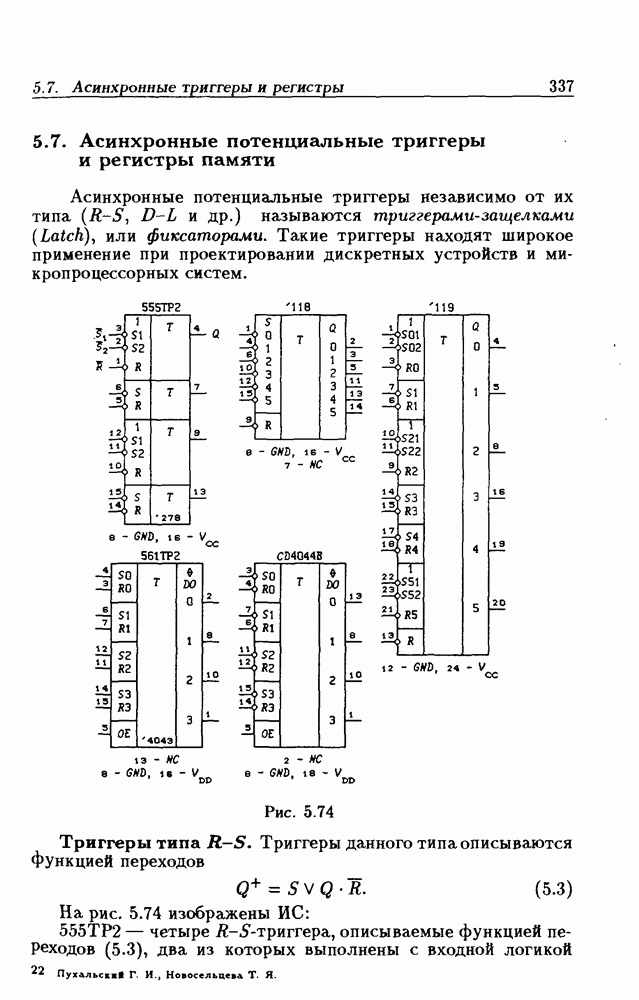
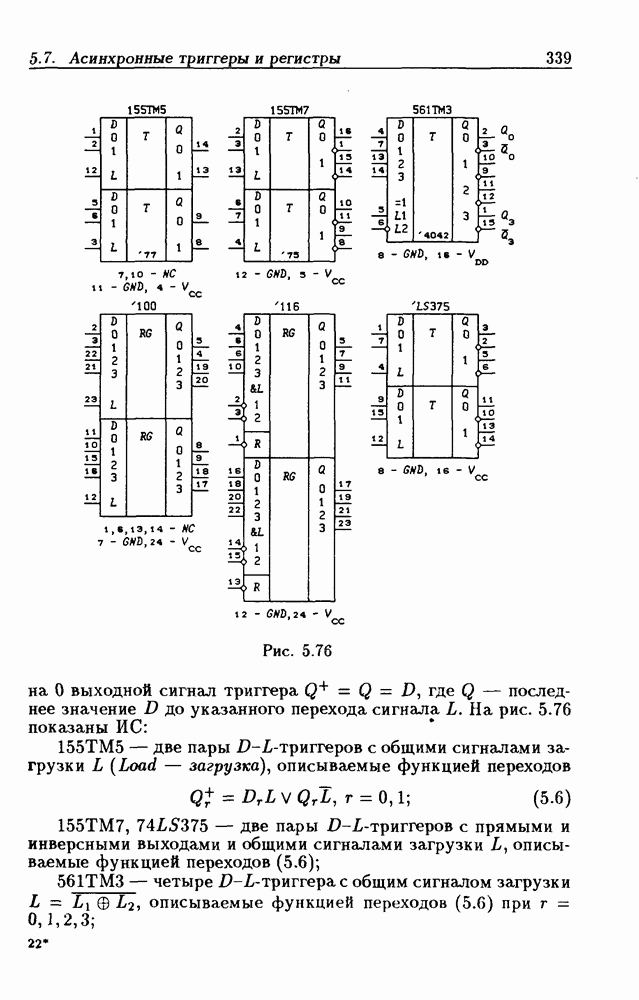
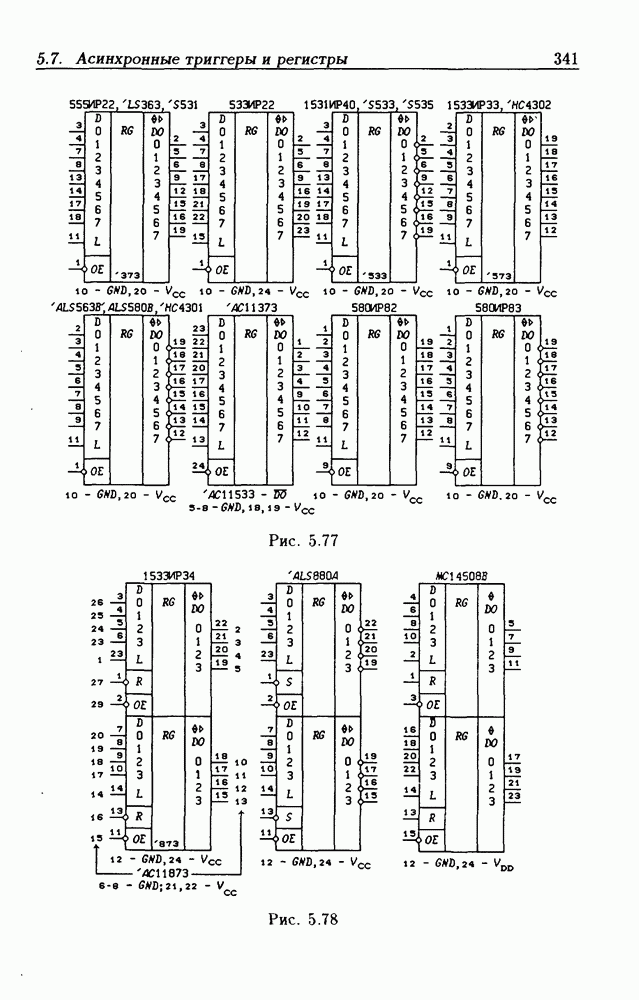
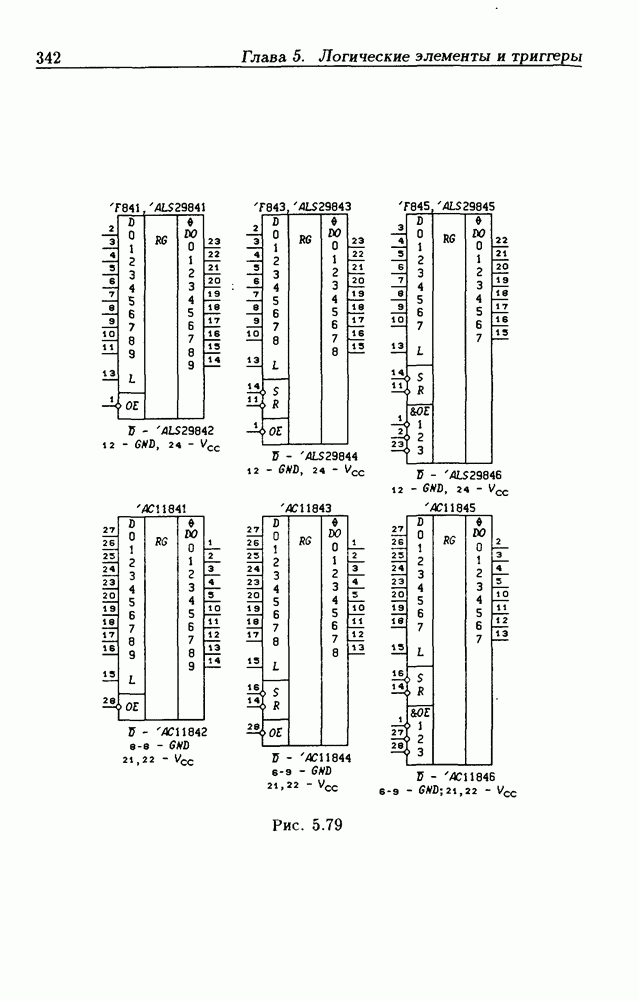
- 5.7. Асинхронные потенциальные триггеры и регистры памяти
- 5.8. Синхронные триггеры и регистры памяти
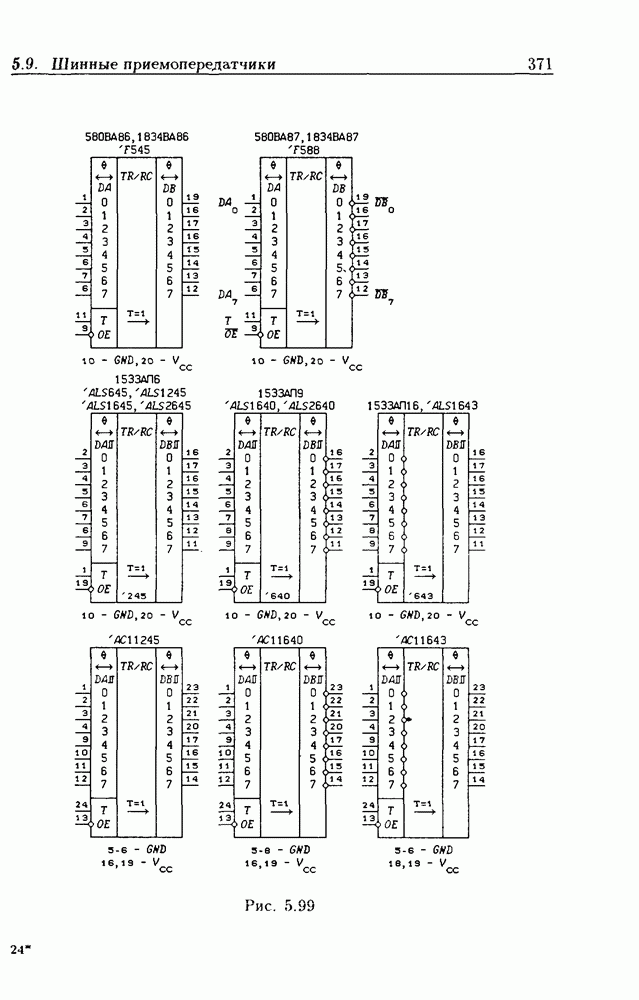
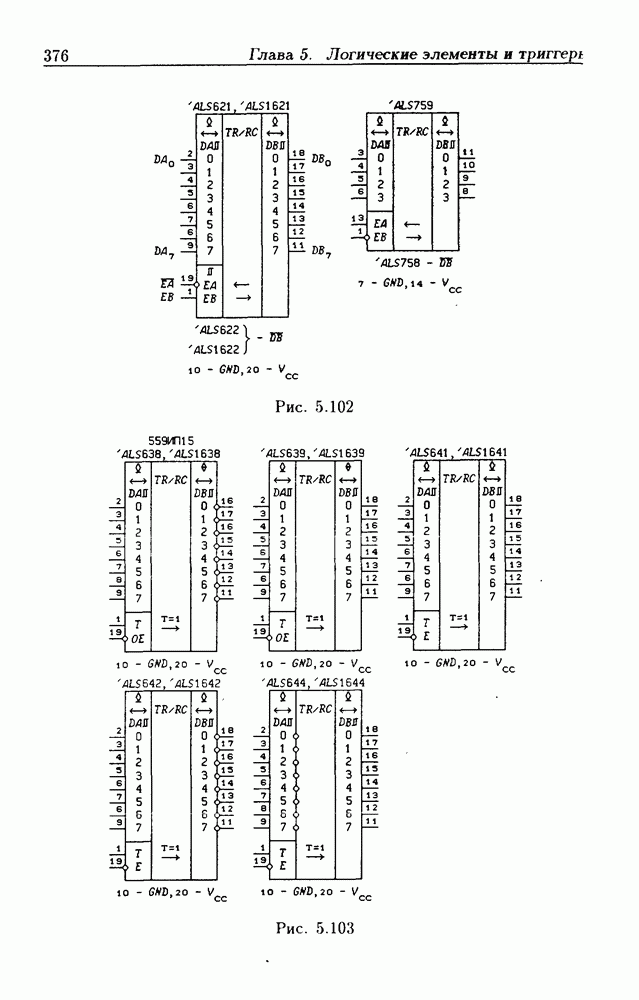
- 5.9. Шинные приемопередатчики
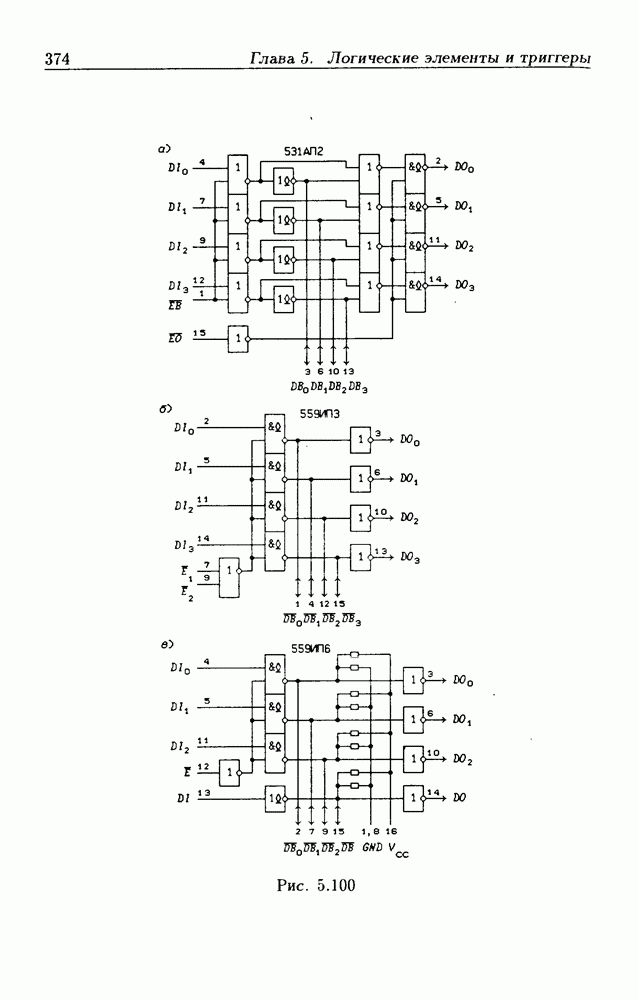
- Шинные приемопередатчики с Z-состоянием выхода.
- Шинные приемопередатчики с открытым коллекторным выходом.
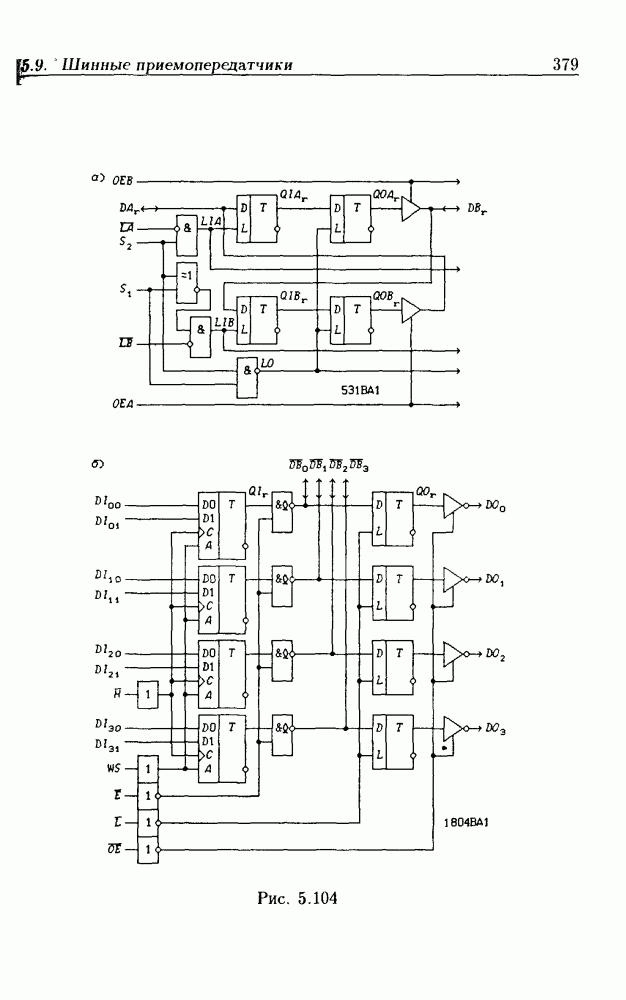
- Шинные приемопередатчики с регистрами памяти.
- Шинные приемопередатчики со сдвигающим регистром.
- Шинные трехнаправленные приемопередатчики.
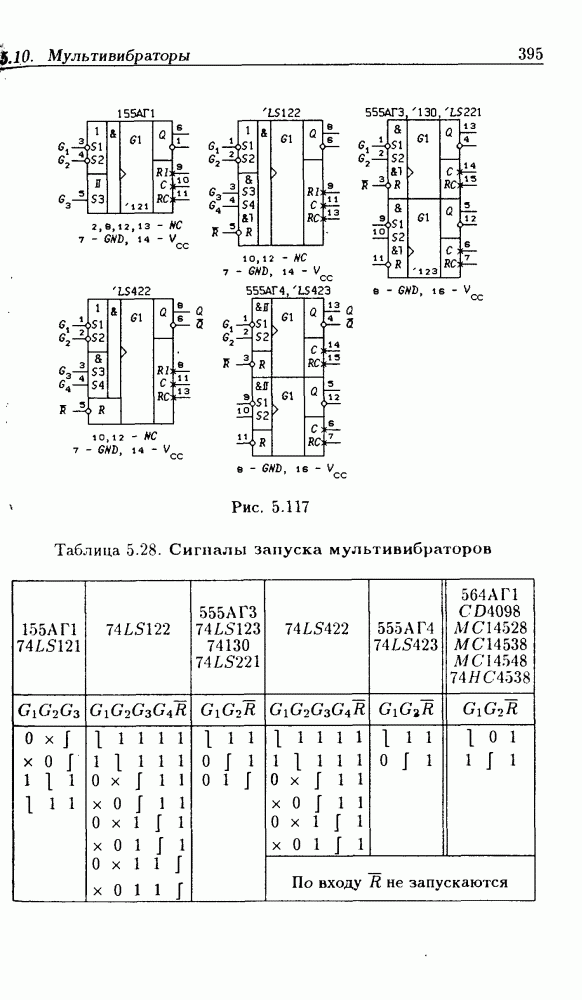
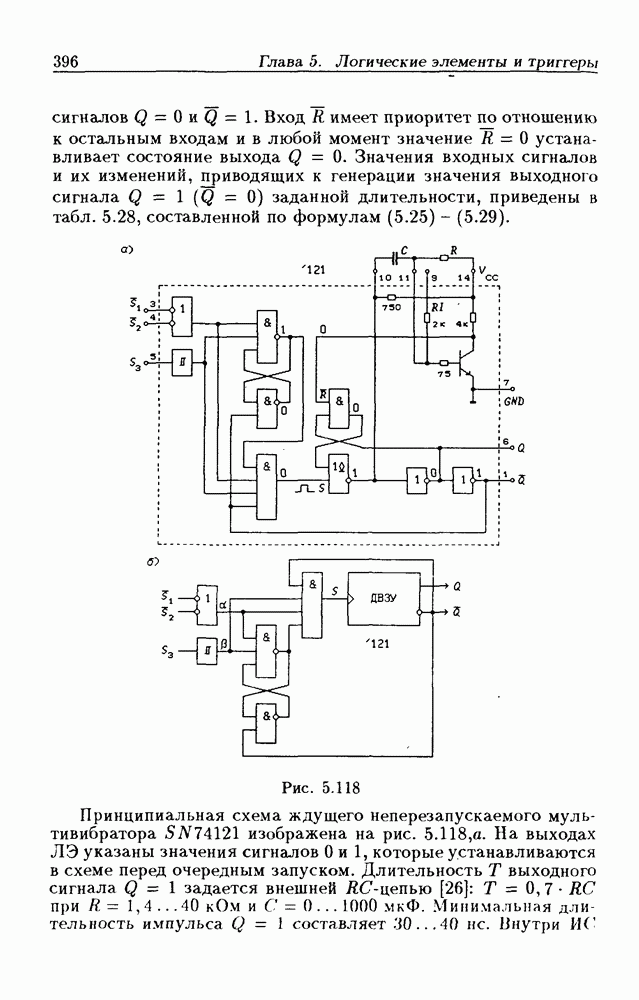
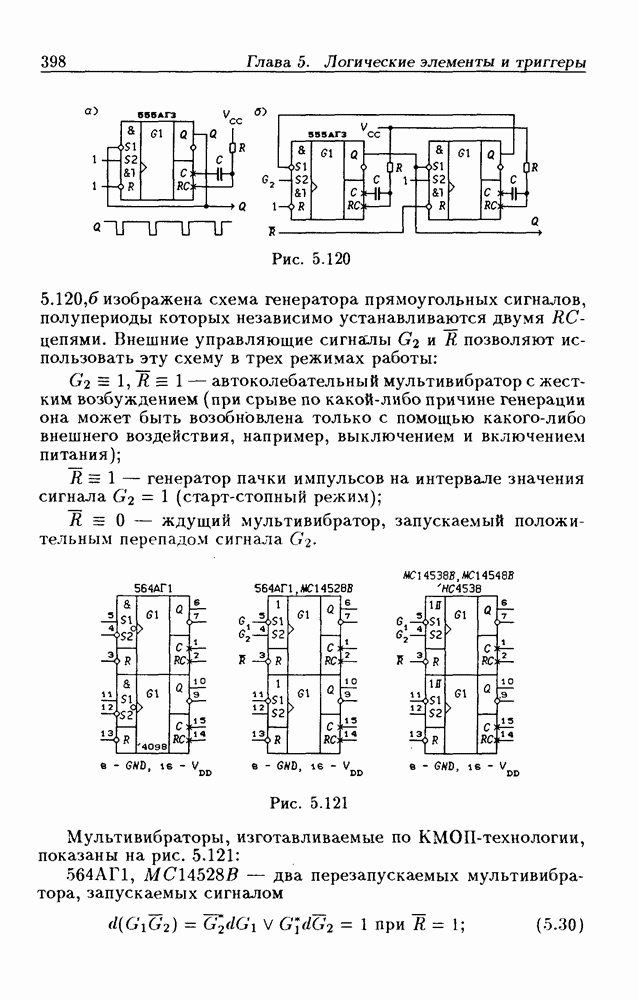
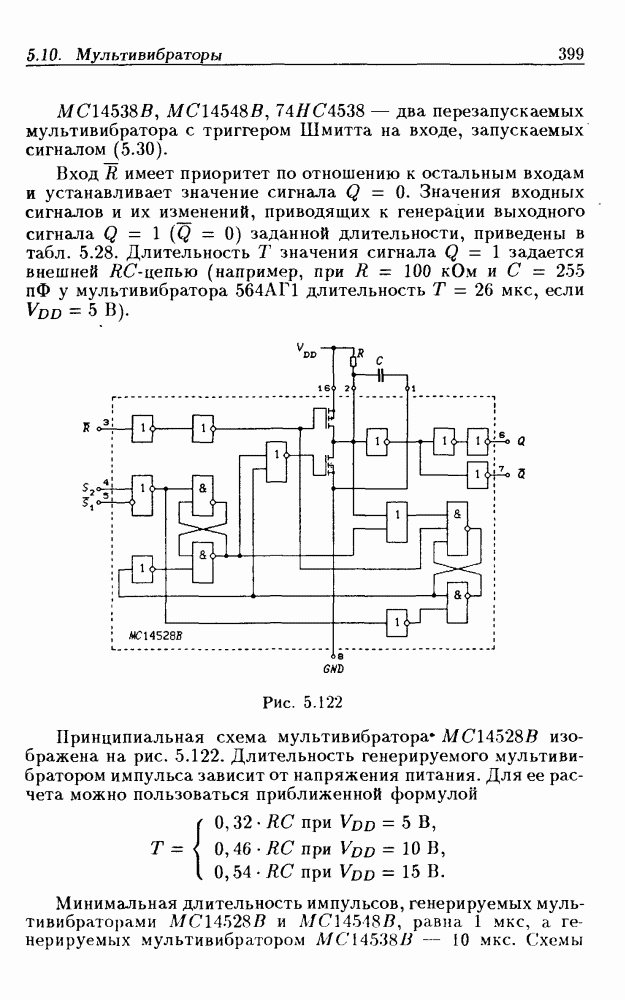
- 5.10. Мультивибраторы
- 5.11. Генераторы
- Схемы устранения «дребезга» механических контактов.
- Автогенераторы периодических сигналов.
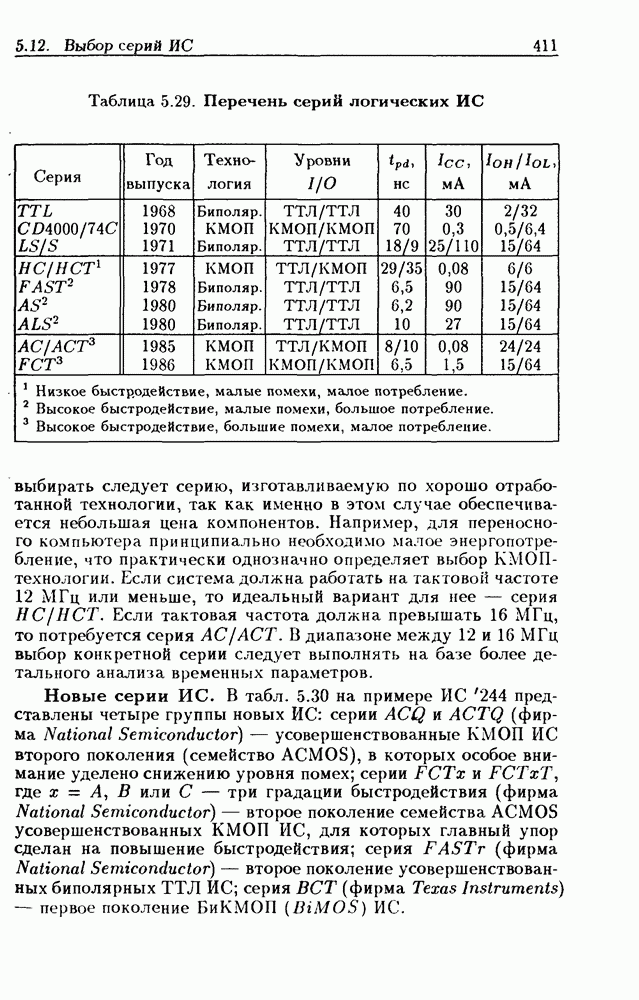
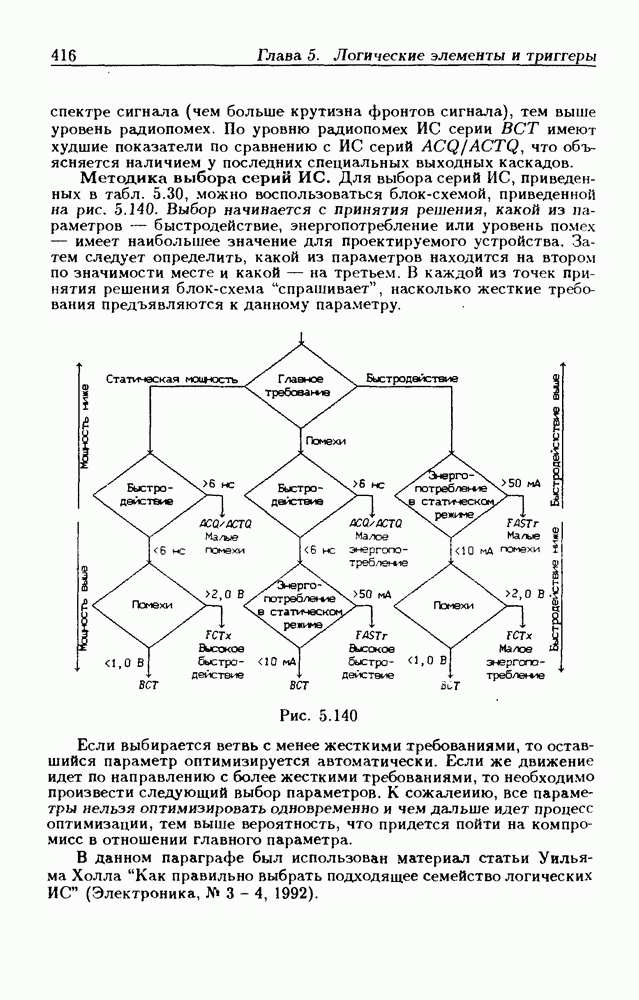
- 5.12. Рекомендации по выбору серий ИС
- Глава 6. Коммутаторы и арифметические устройства
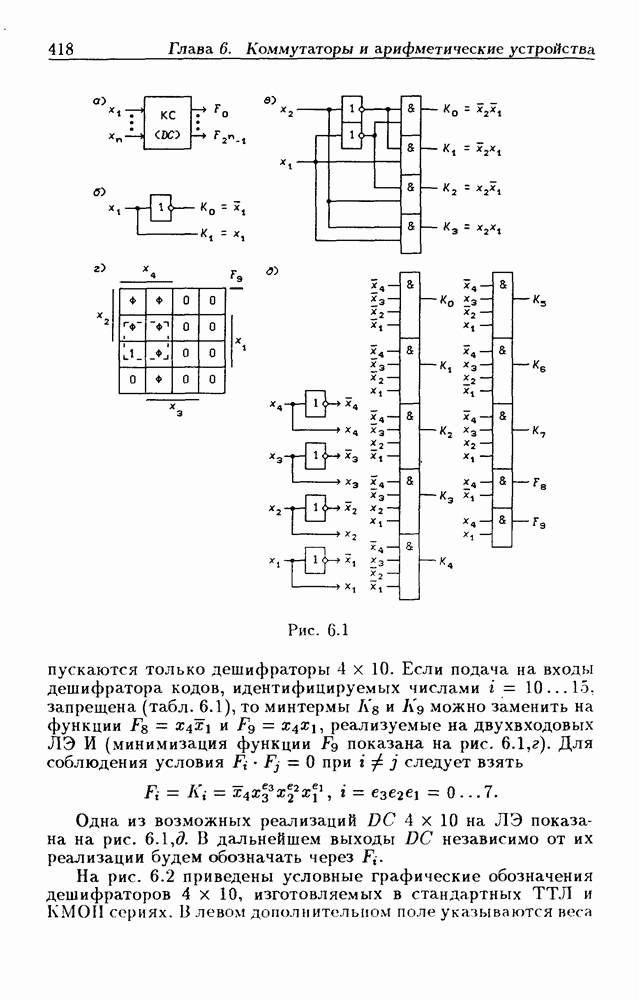
- 6.1. Дешифраторы
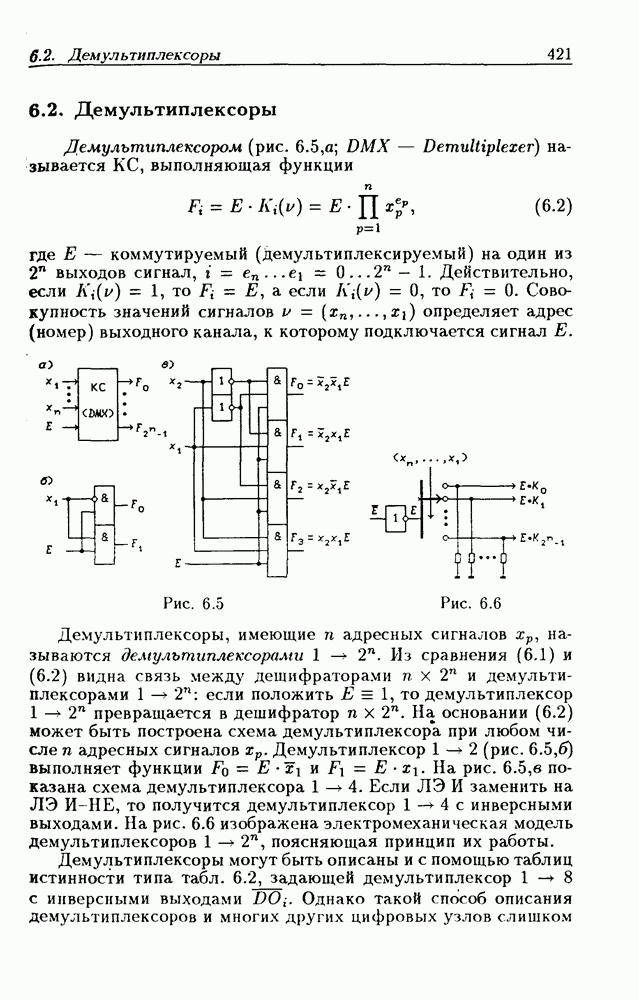
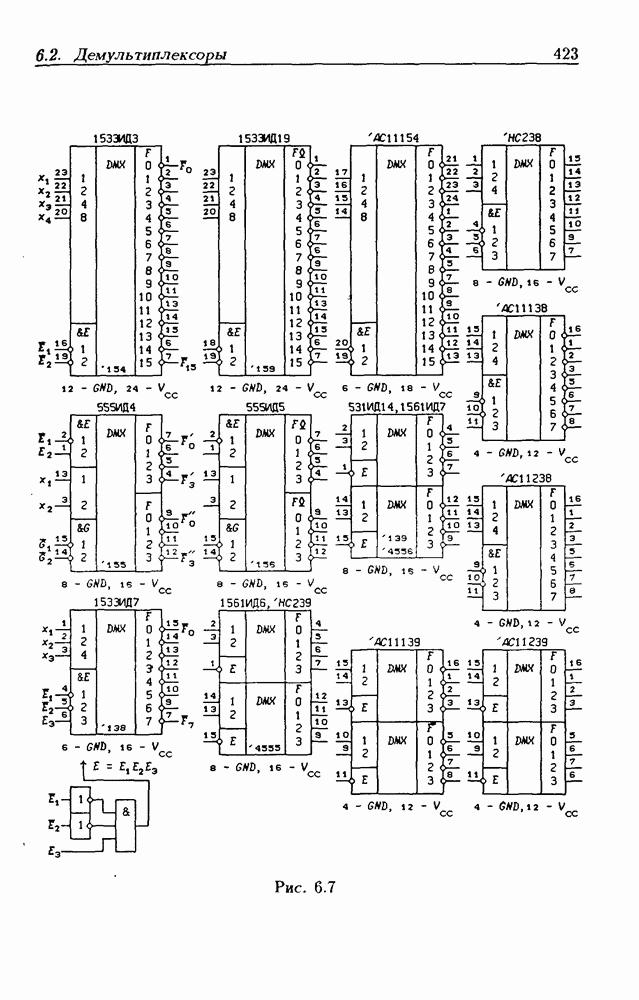
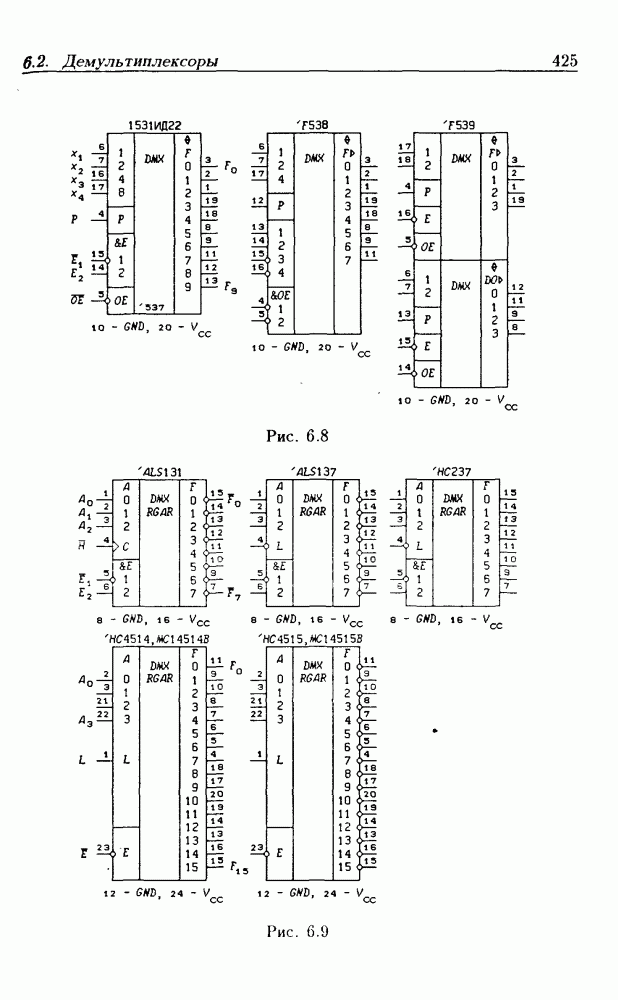
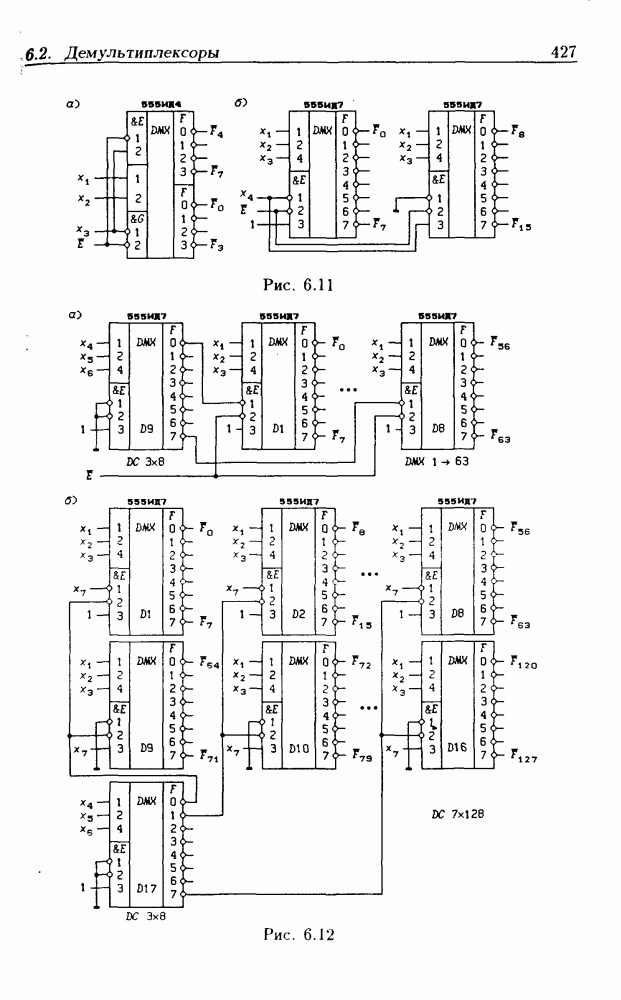
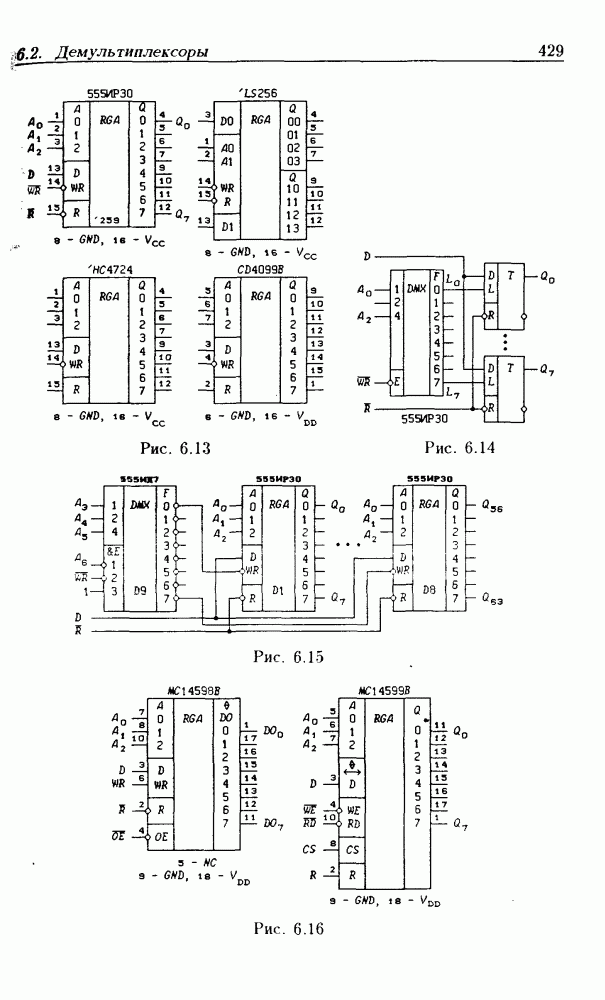
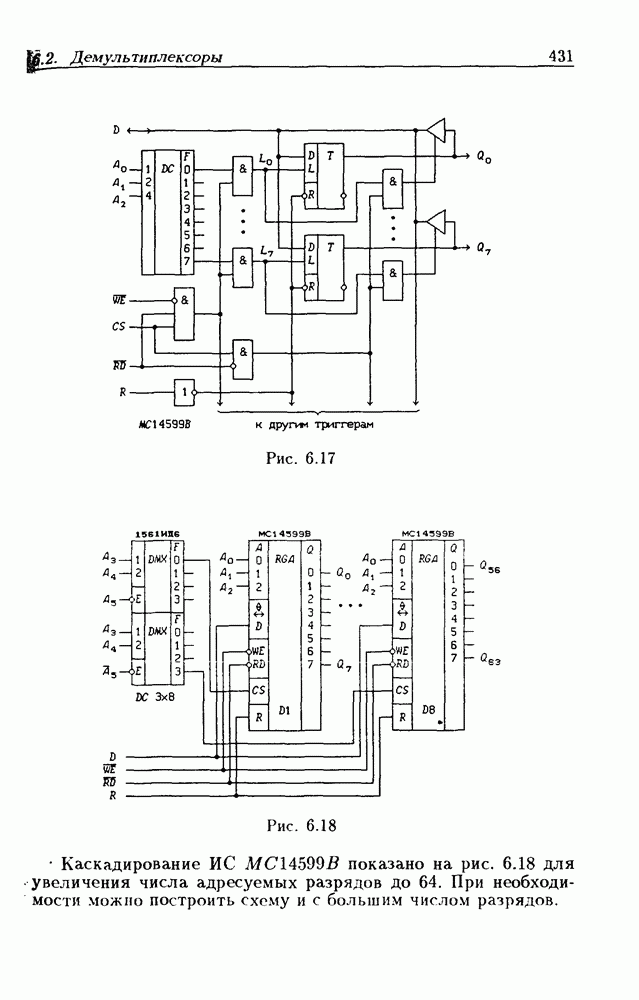
- 6.2. Демультиплексоры
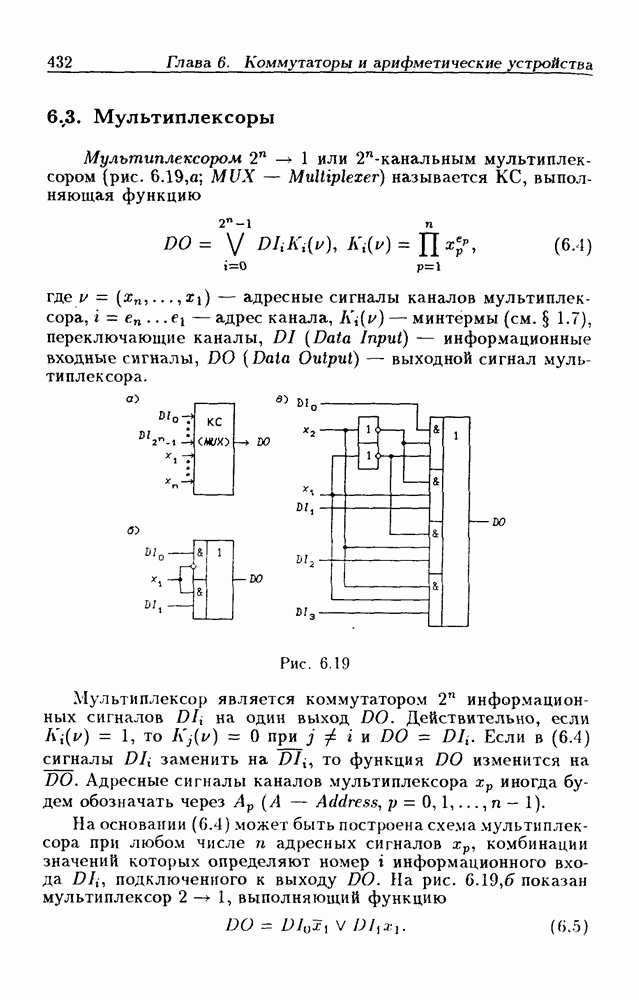
- 6.3. Мультиплексоры
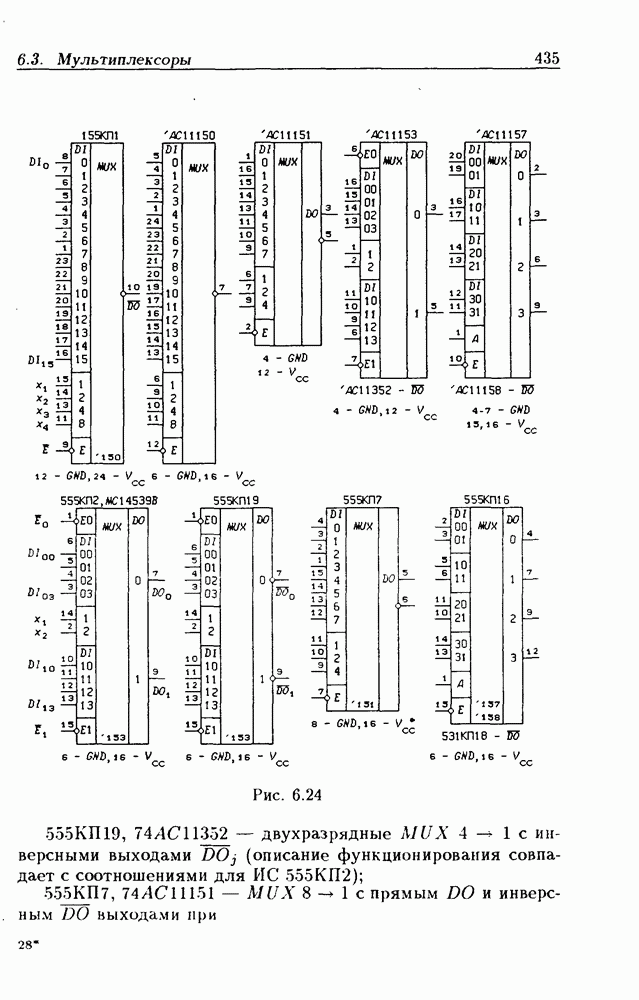
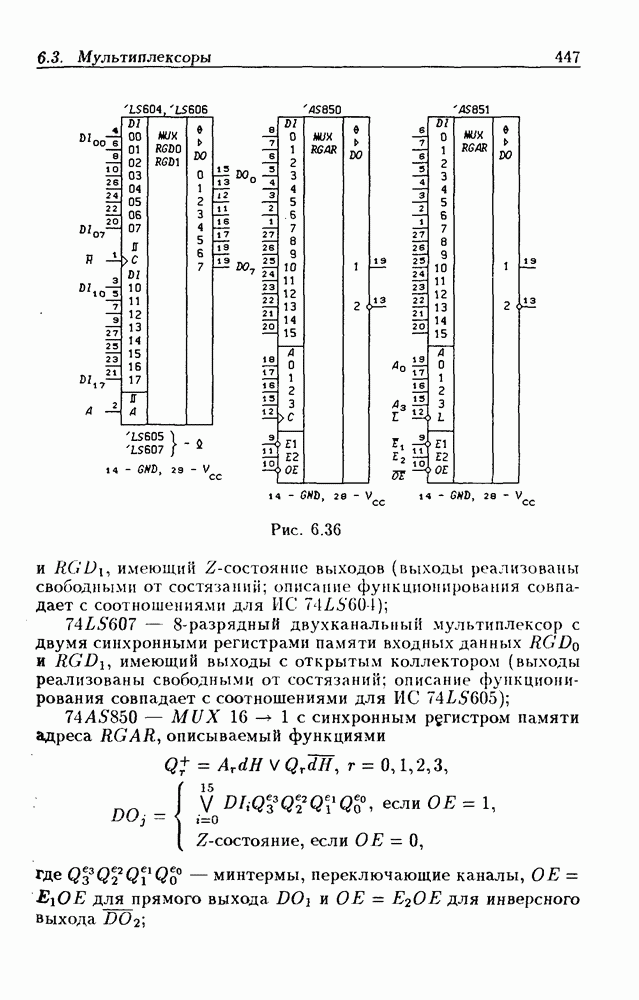
- Мультиплексоры без стробирования.
- Мультиплексоры со стробированием.
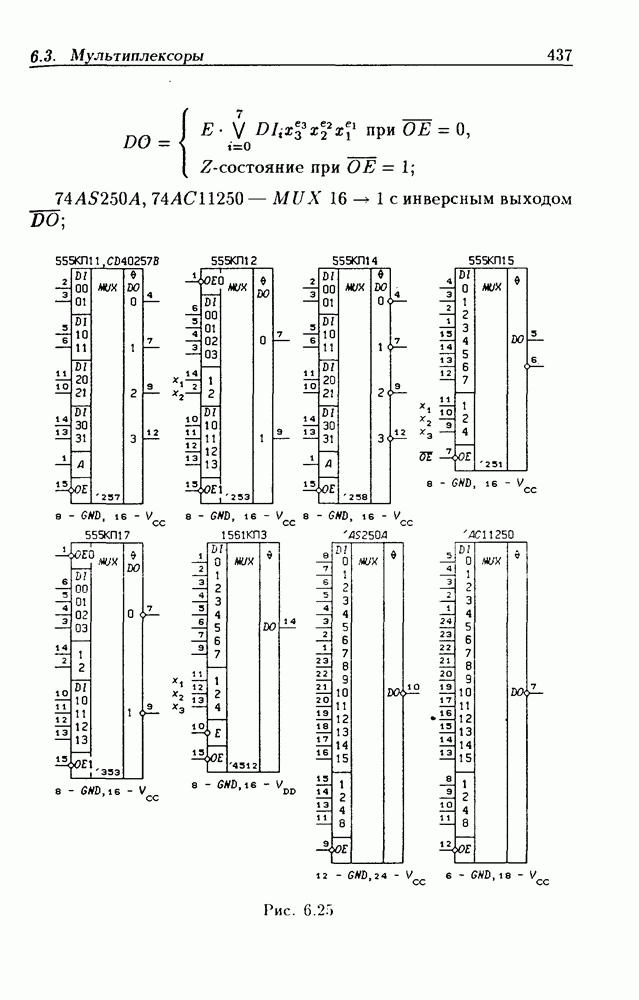
- Мультиплексоры с Z-состоянием выхода.
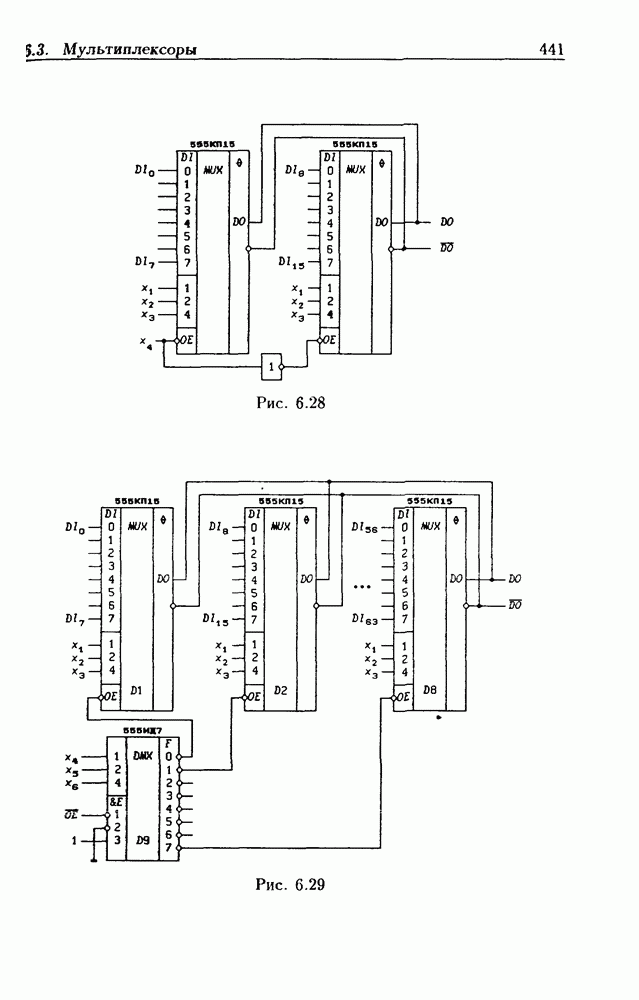
- Каскадирование мультиплексоров.
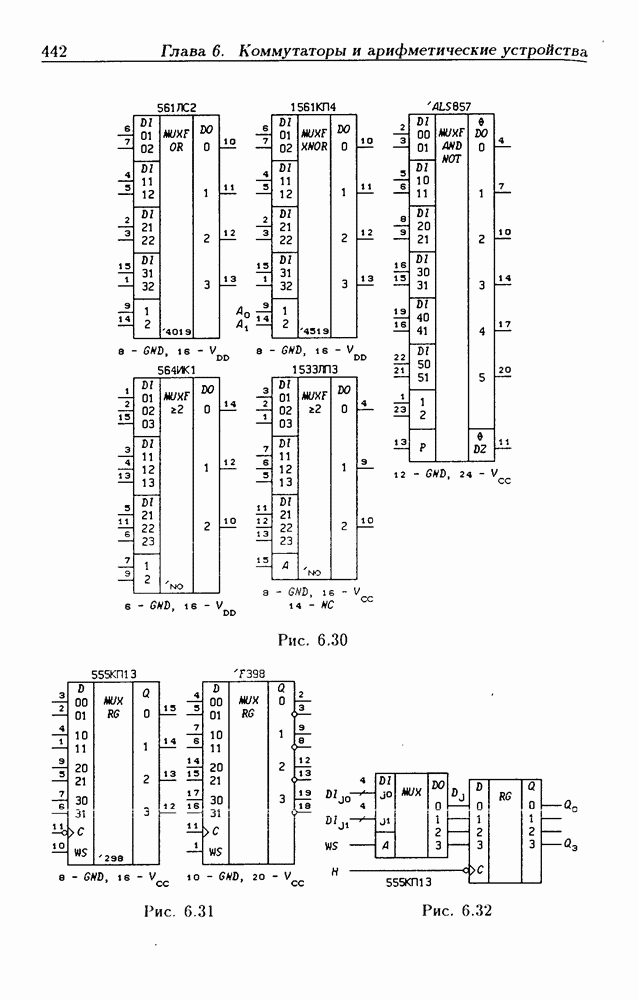
- Функциональные мультиплексоры.
- Регистры памяти с мультиплексными входами данных.
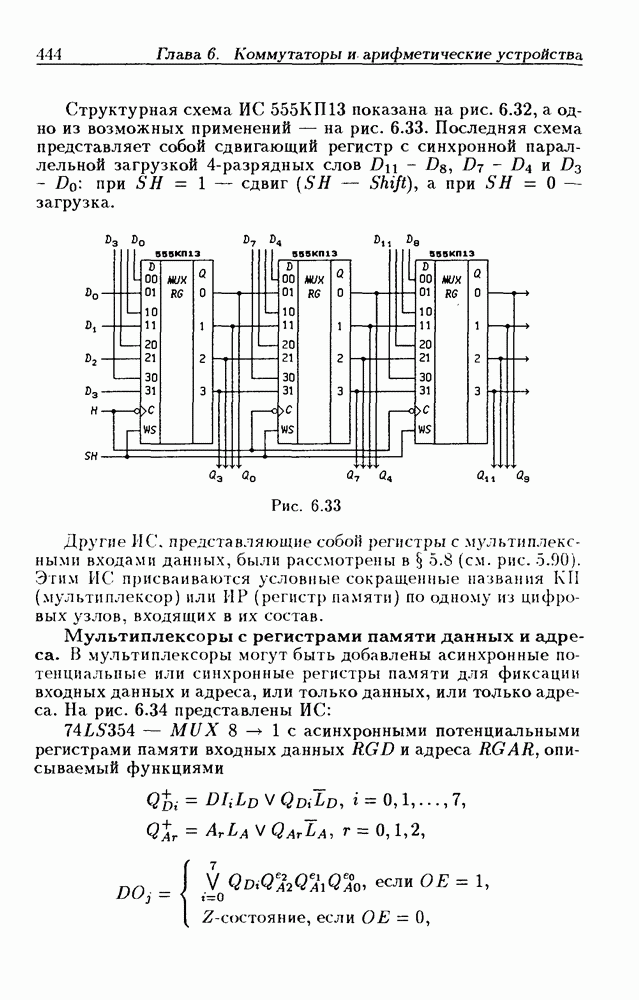
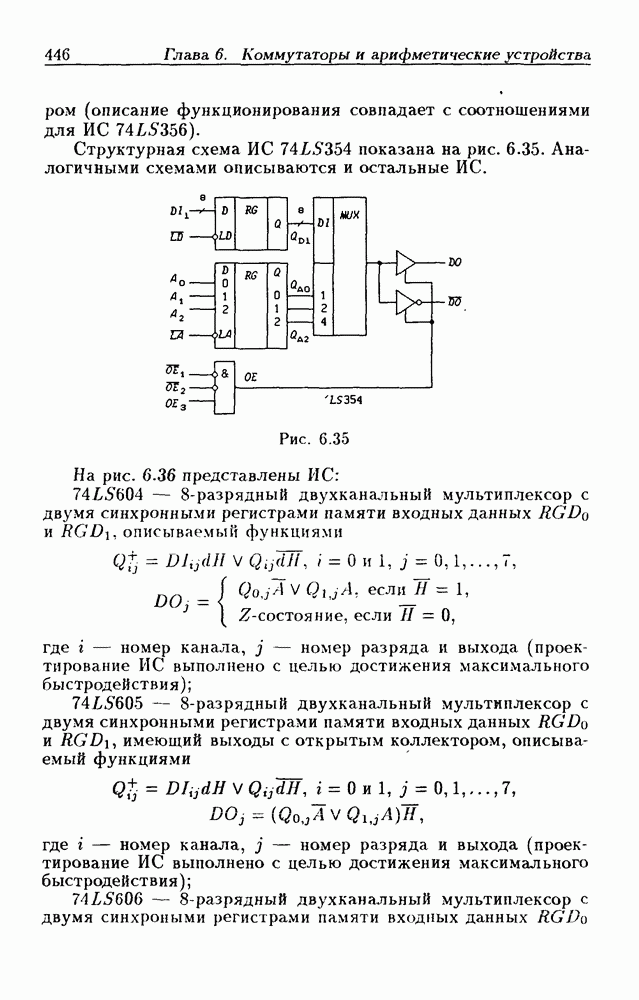
- Мультиплексоры с регистрами памяти данных и адреса.
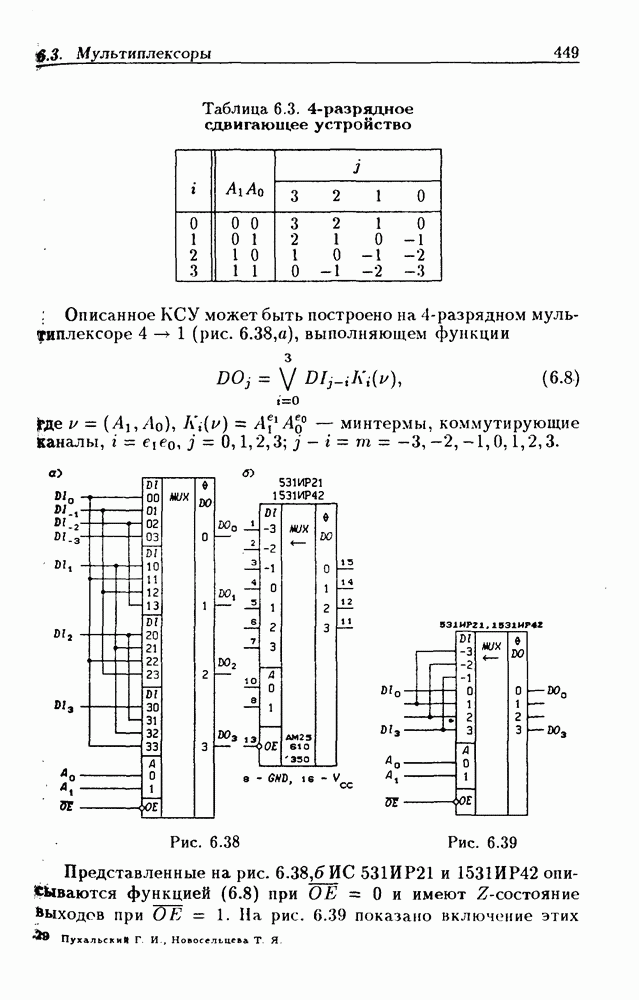
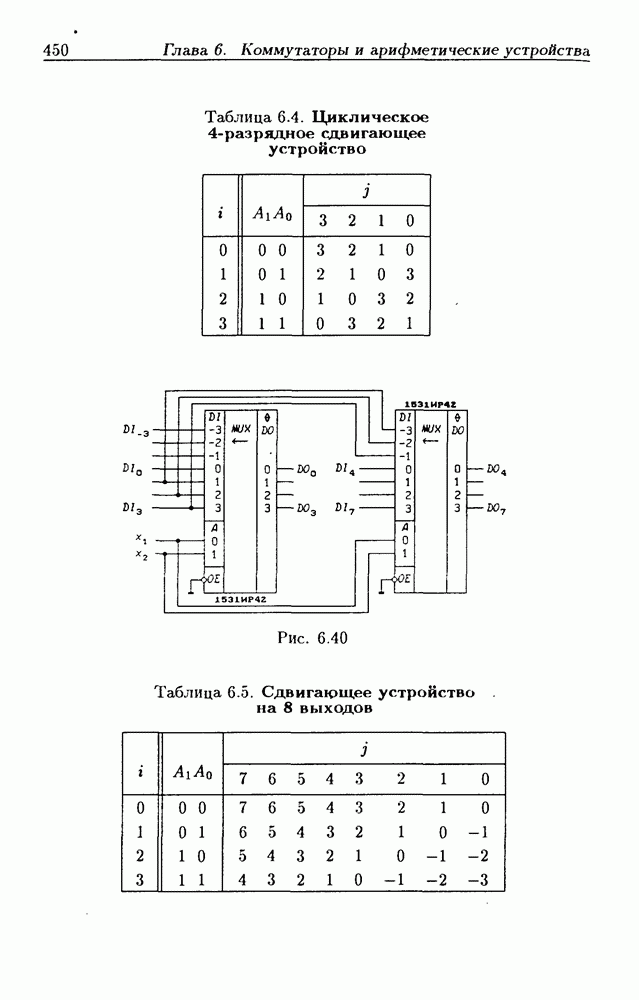
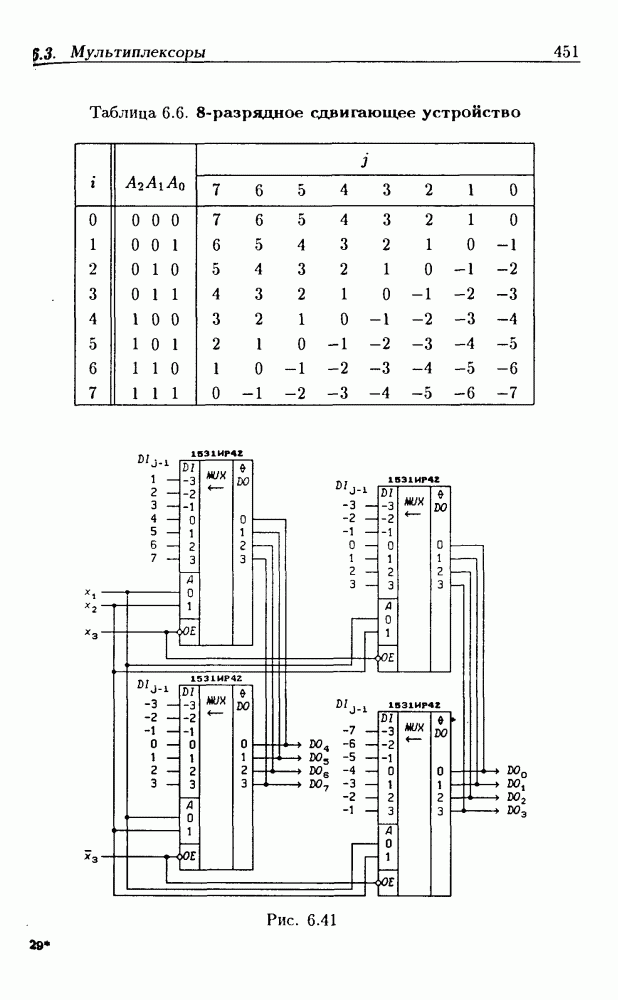
- Сдвигающие мультиплексоры.
- 6.4. Синтез комбинационных схем и цифровых автоматов на мультиплексорах
- Синтез схем на 8-канальных мультиплексорах.
- Синтез на двухразрядных 4-канальных мультиплексорах.
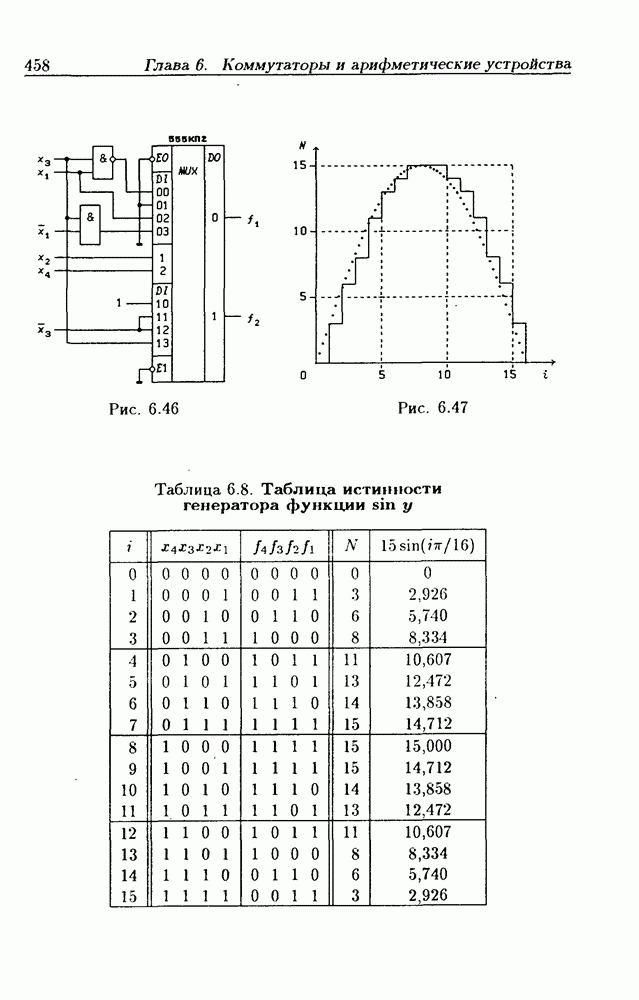
- Синтез генератора синусоидальной функции на мультиплексорах.
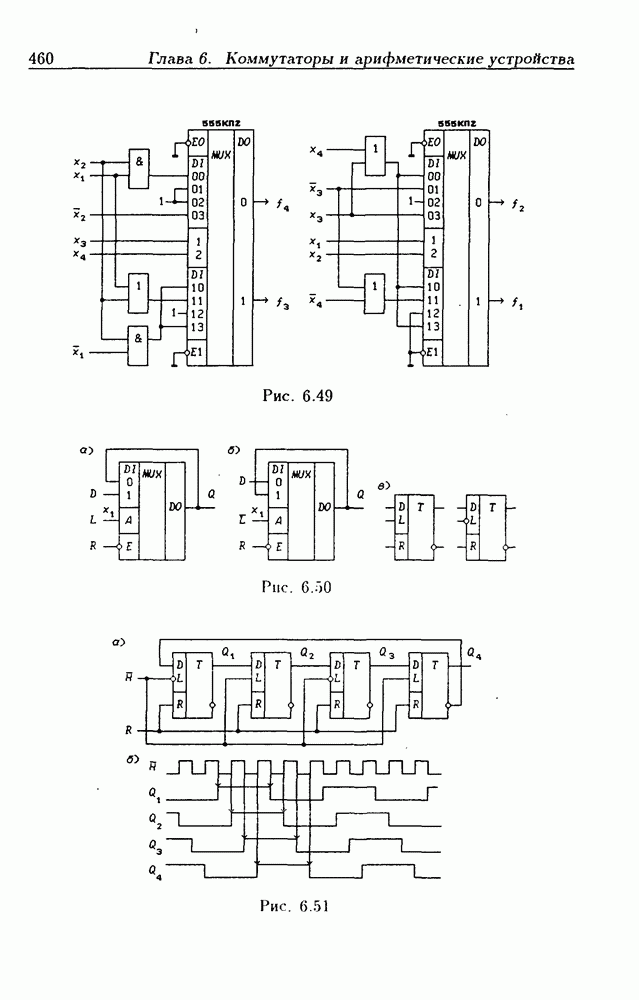
- Синтез триггеров на мультиплексорах.
- Синтез счетчиков на мультиплексорах.
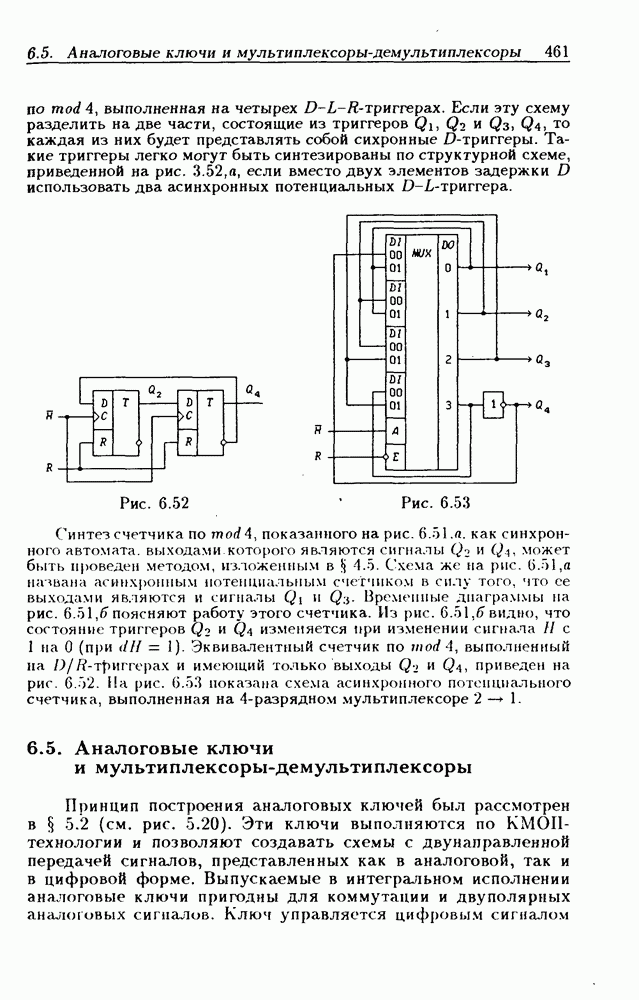
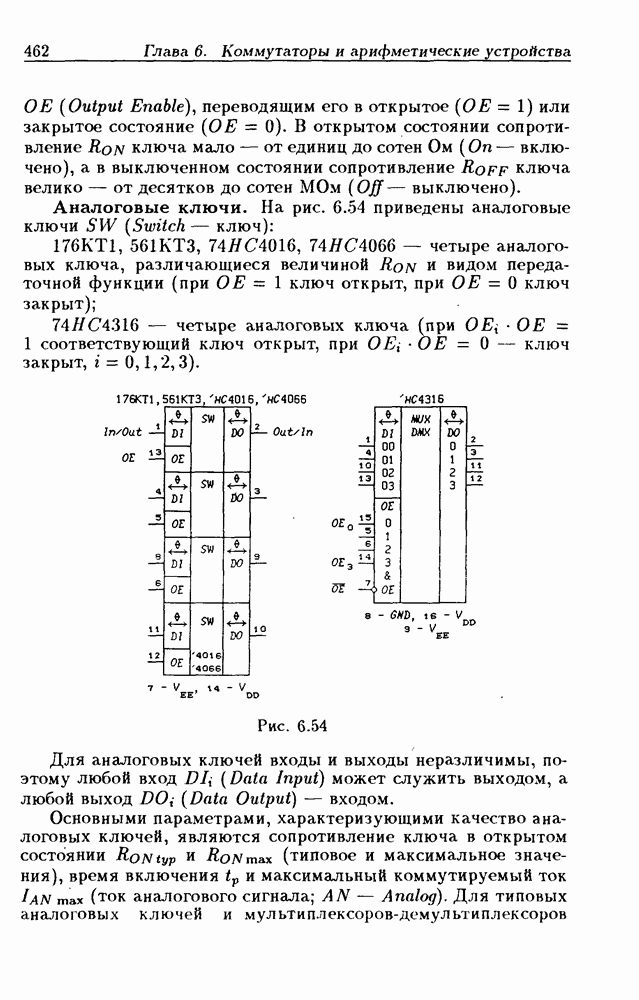
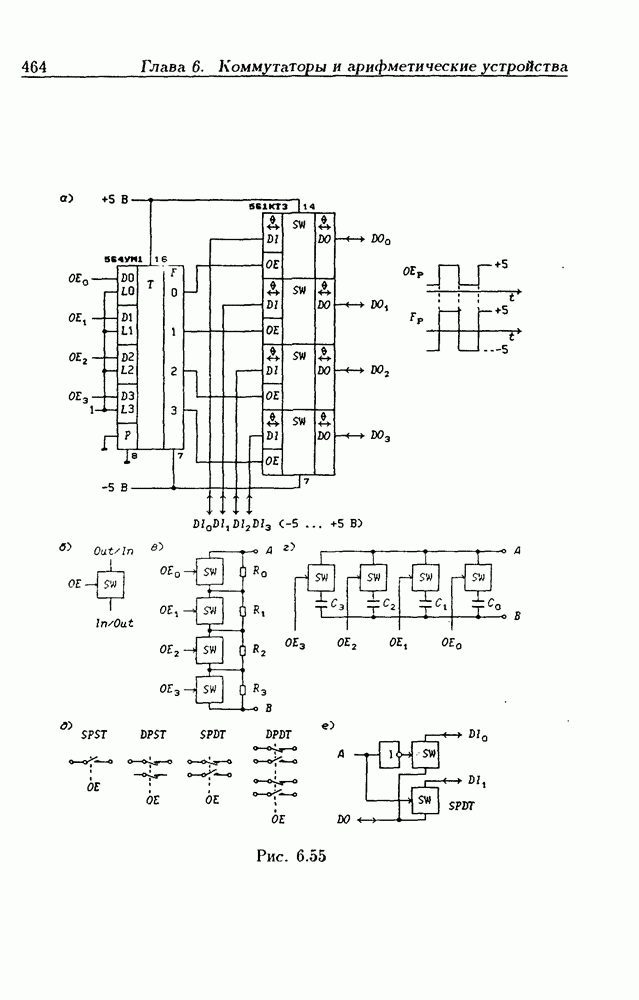
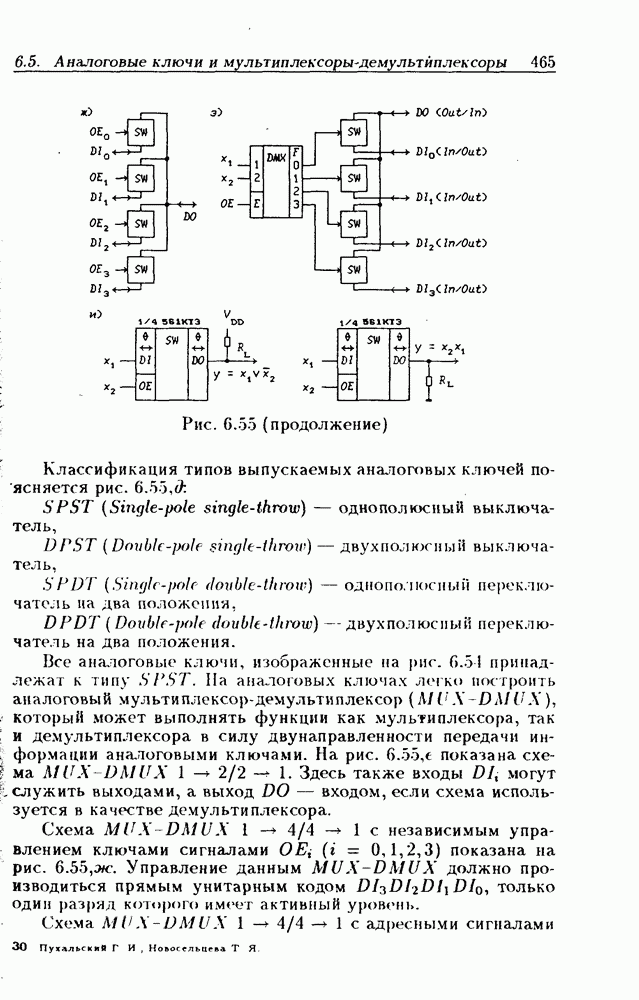
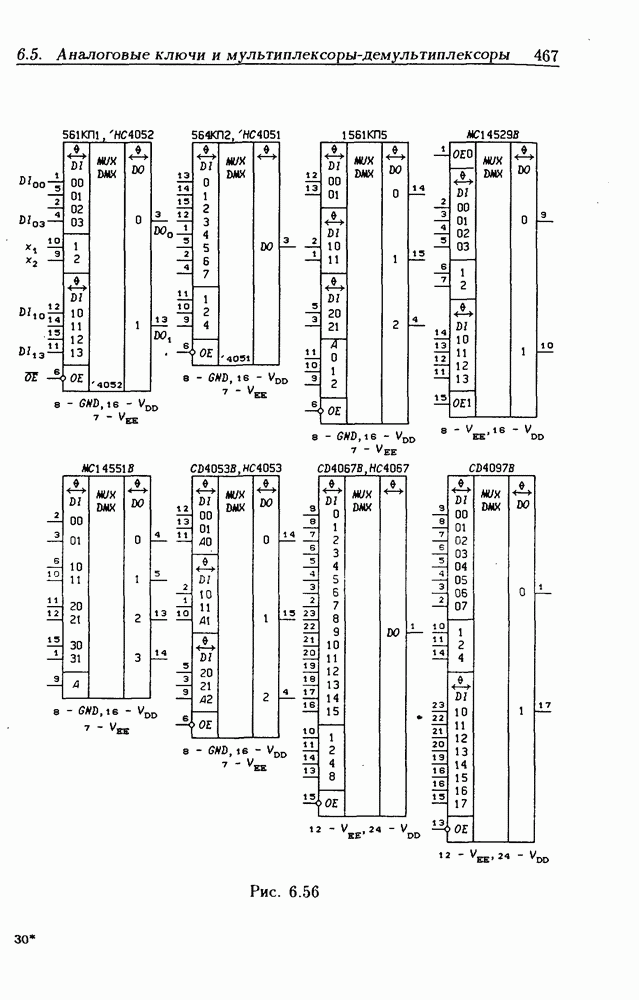
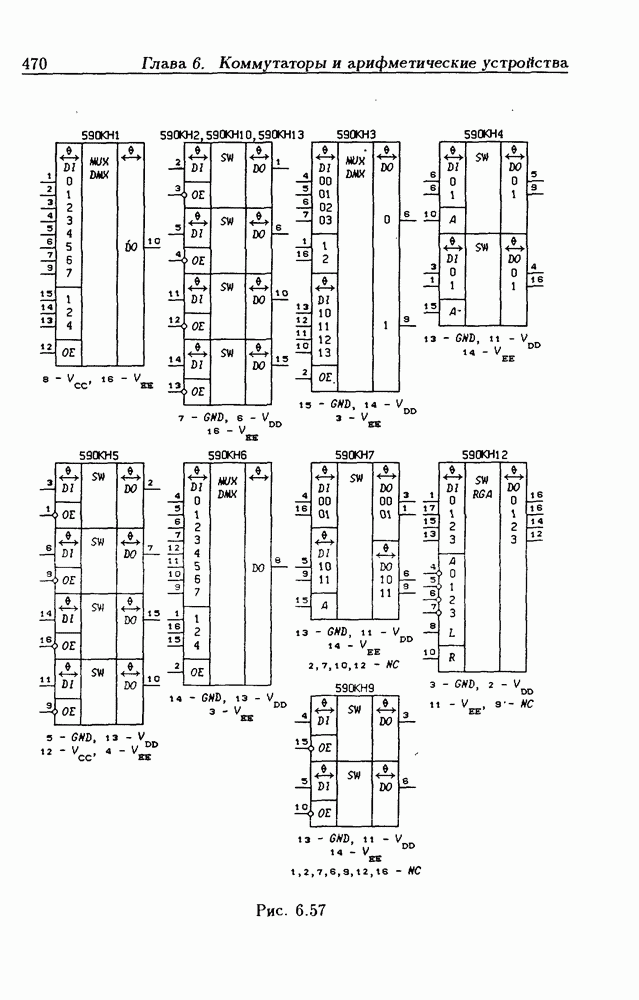
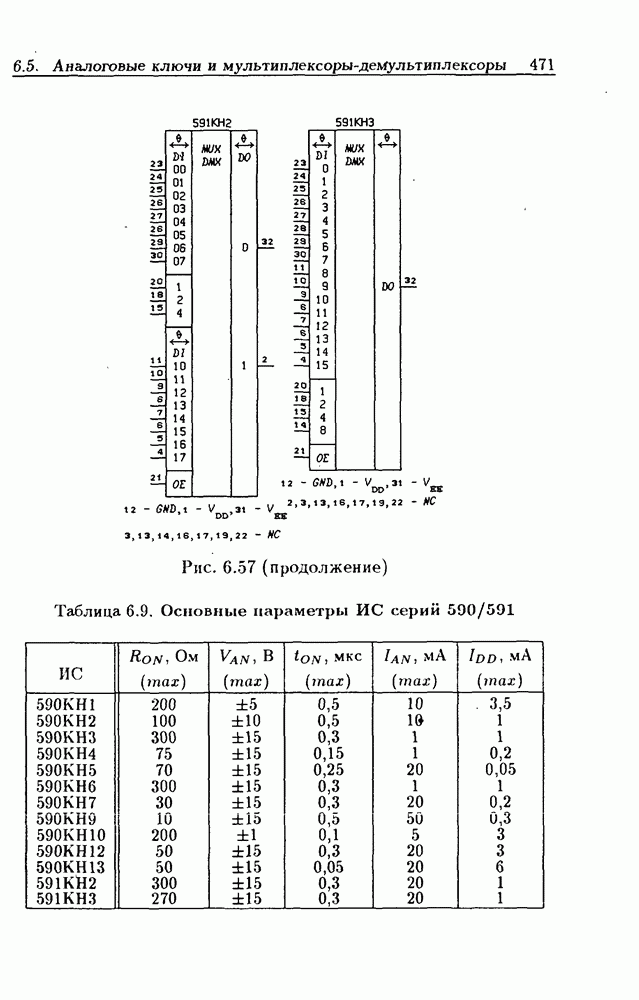
- 6.5. Аналоговые ключи и мультиплексоры-демультиплексоры
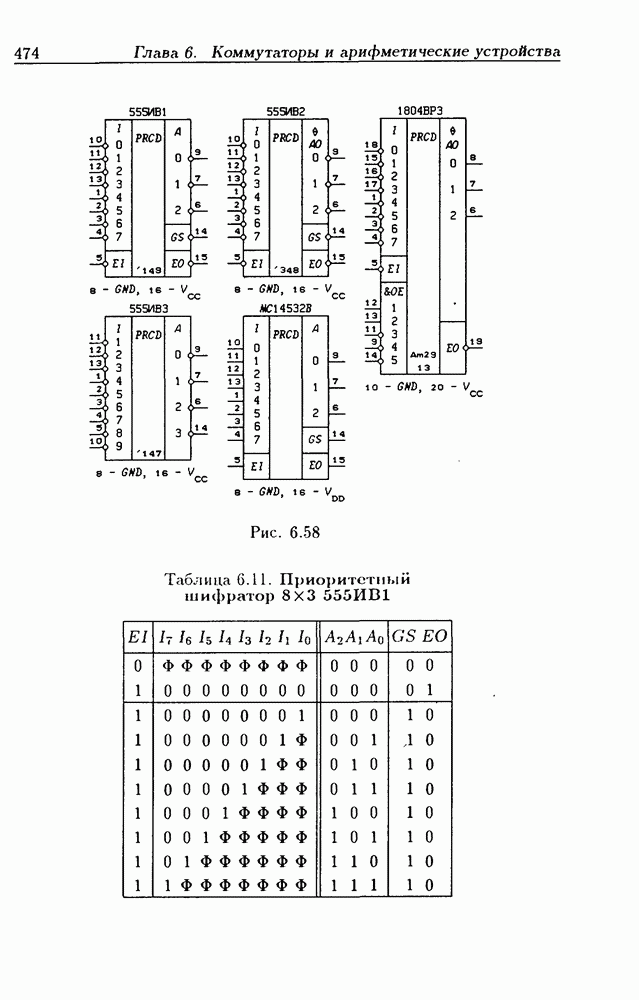
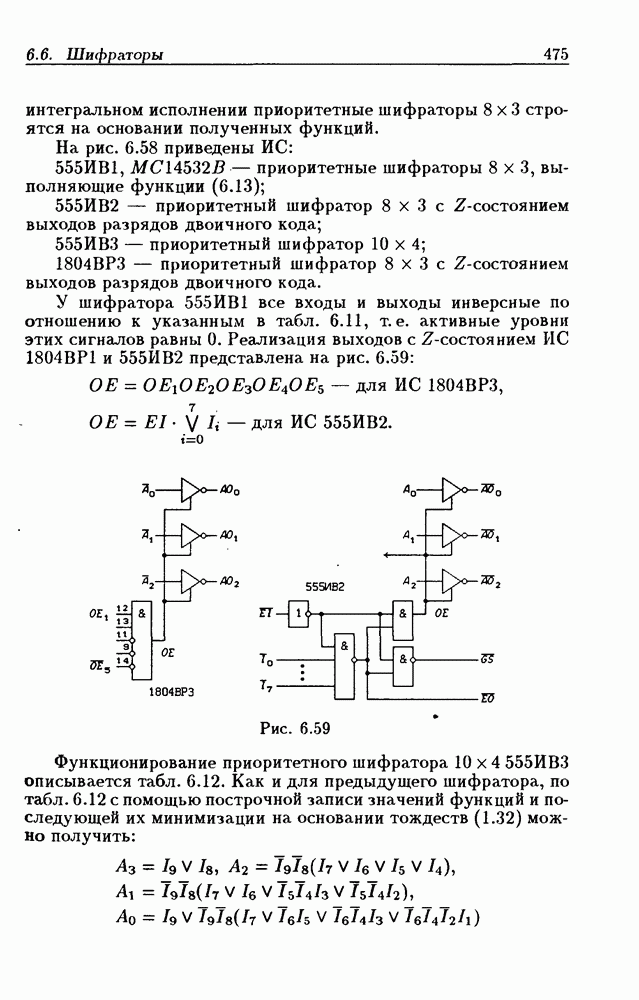
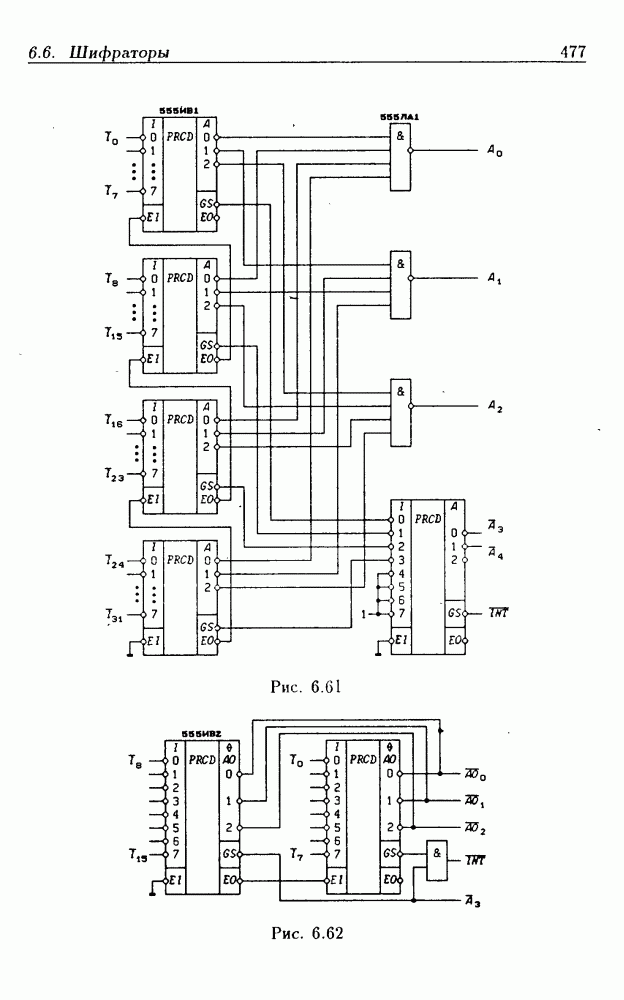
- 6.6. Шифраторы
- 6.7. Цифровые компараторы
- Программируемые цифровые компараторы.
- Адресные компараторы.
- Применения адресных компараторов.
- 6.8. Схемы сравнения двоичных чисел
- 8-разрядные схемы сравнения двоичных чисел.
- 6.9. Прямой, обратный и дополнительный коды
- Дополнительный код.
- Сложение чисел в обратном коде.
- Код с избытком 3.
- 6.10. Сумматоры
- Двоичные параллельные сумматоры с последовательным переносом.
- Двоичные сумматоры с параллельным переносом.
- Применения сумматоров.
- Десятичные сумматоры.
- Последовательные двоичные сумматоры.
- 6.11. Арифметическо-логические устройства
- 6.12. Пороговые схемы и мажоритарные элементы
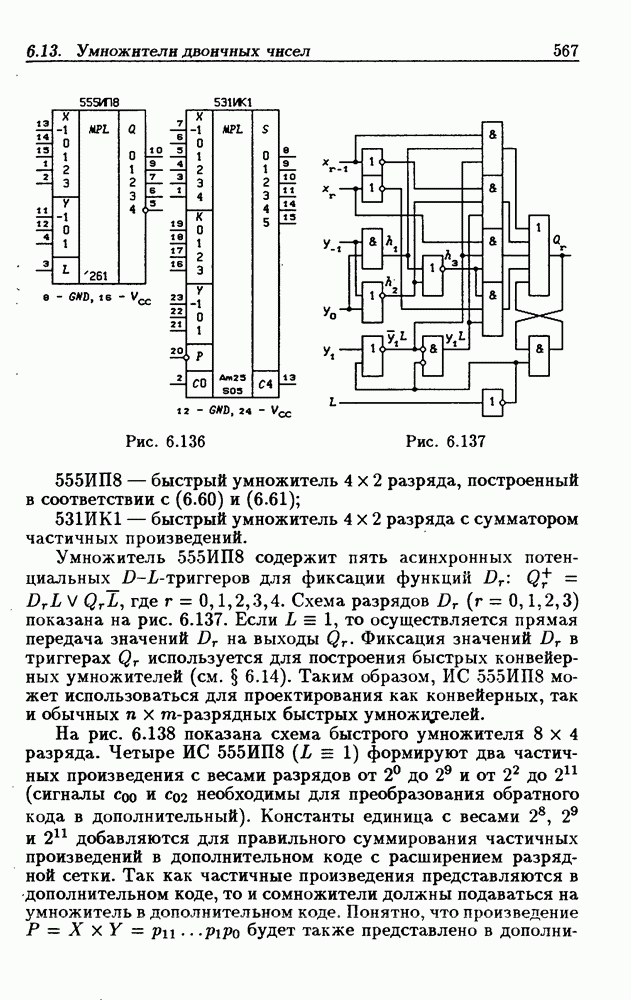
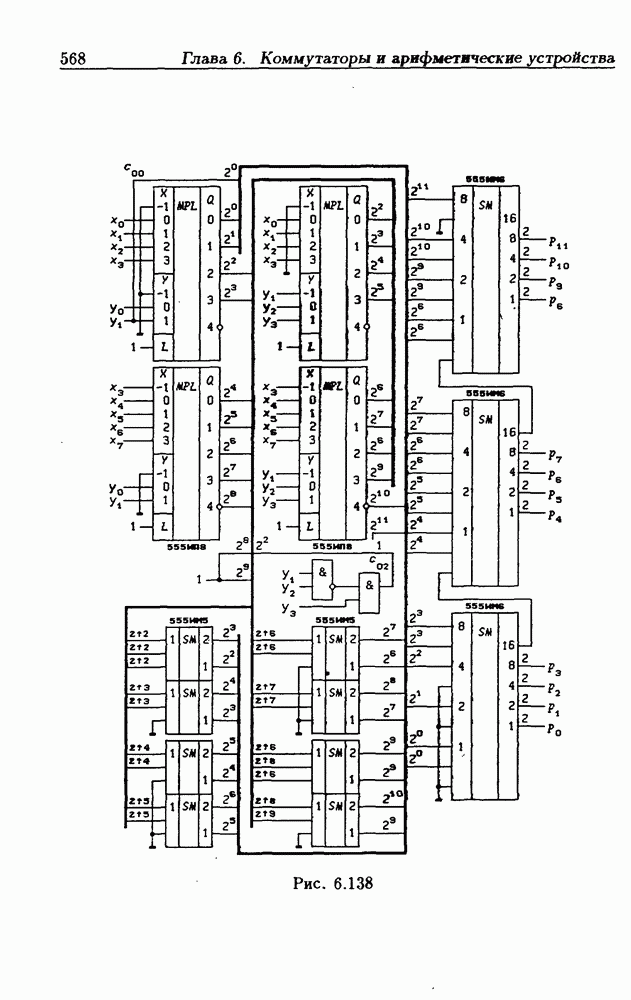
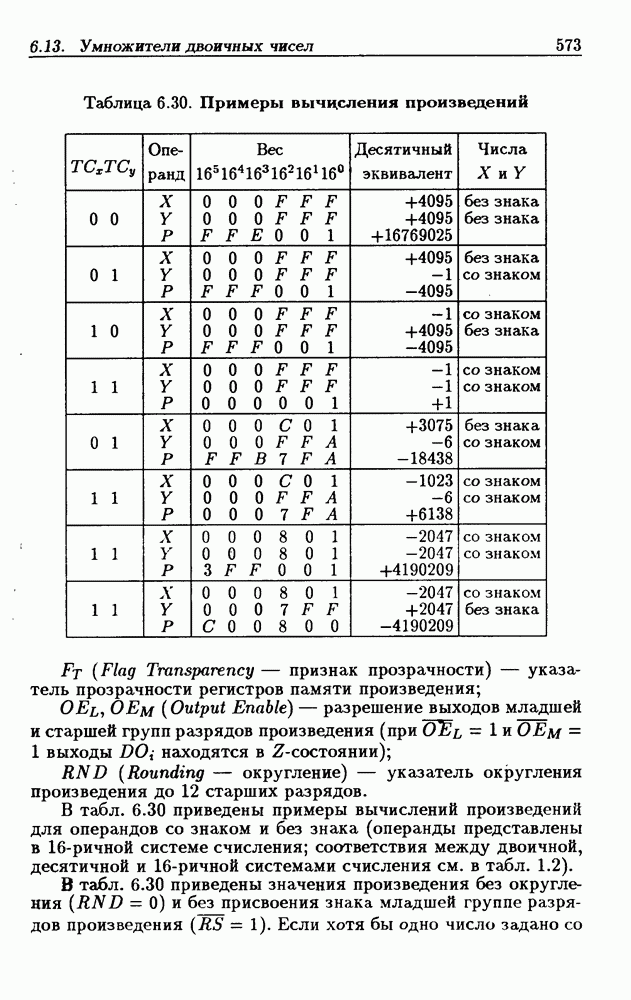
- 6.13. Умножители двоичных чисел
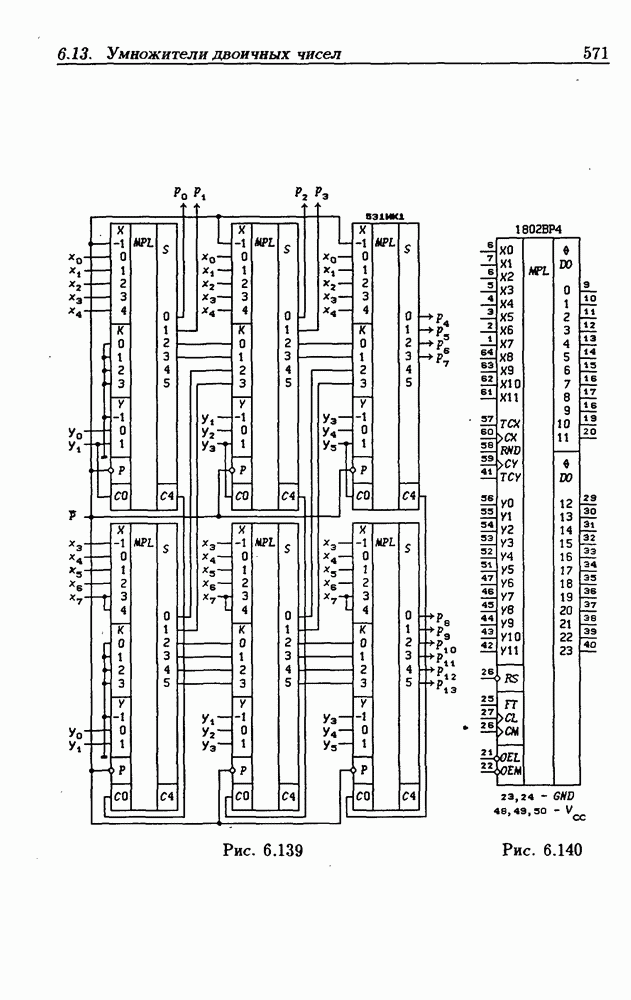
- Быстрые умножители.
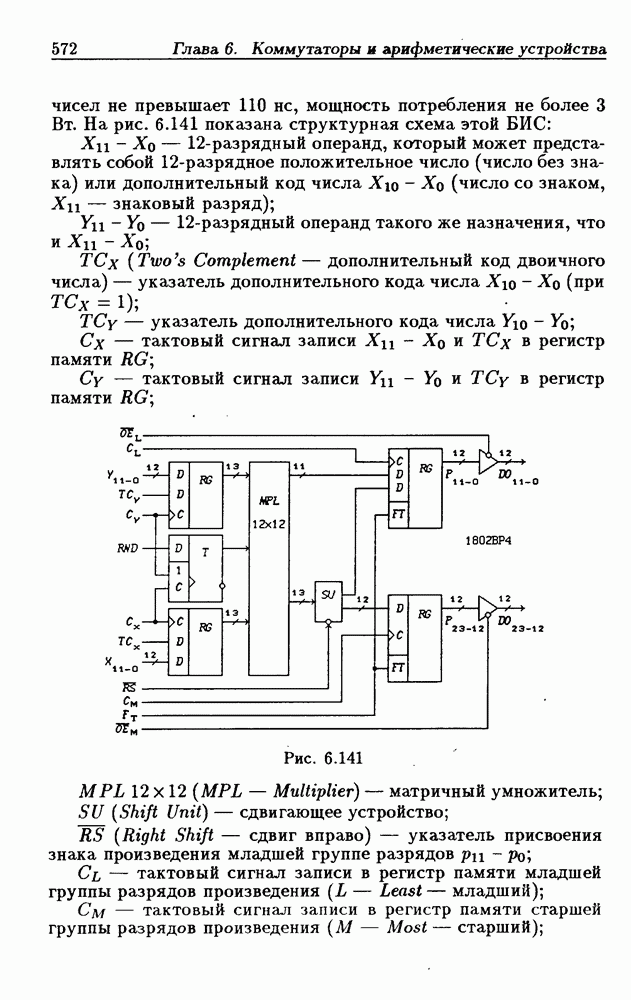
- БИС умножителя 12×12 разрядов 1802ВР4.
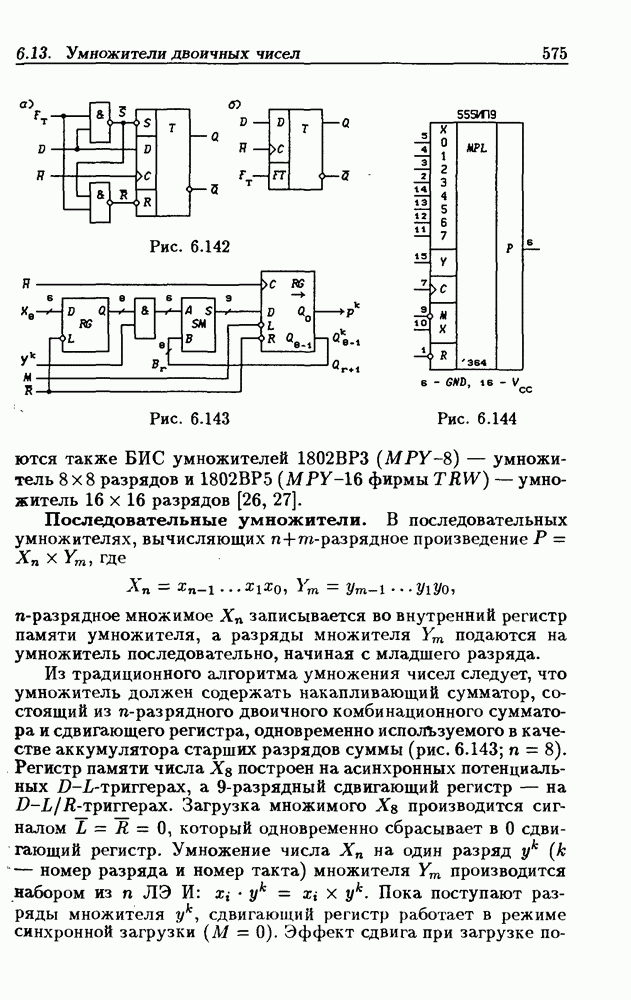
- Последовательные умножители.
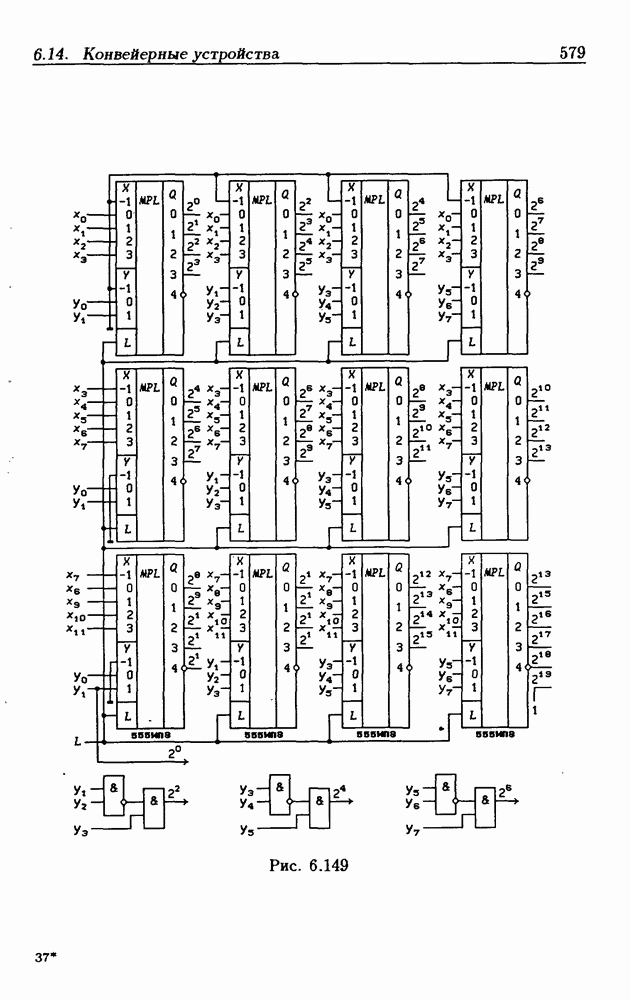
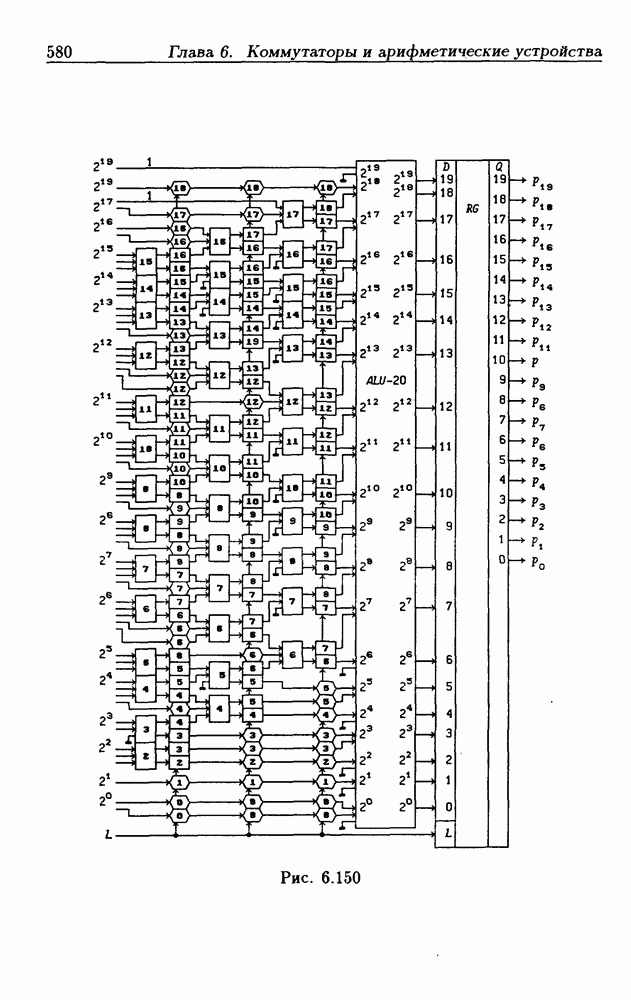
- 6.14. Конвейерные устройства
- Конвейерный быстрый умножитель.
- Конвейерные АЦП.
- 6.15. Синтез линейных комбинационных схем
- Сумматор по модулю q.
- Умножитель по модулю q.
- Глава 7. Сдвигающие регистры и счетчики
- 7.1. Сдвигающие регистры без параллельной записи данных
- Сдвигающие устройства с выходными регистрами памяти.
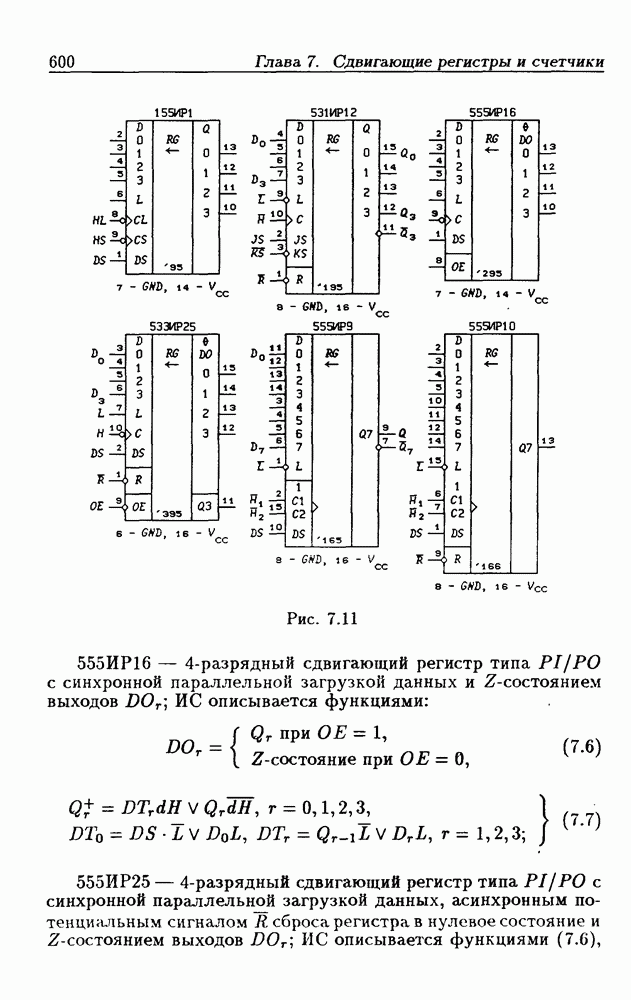
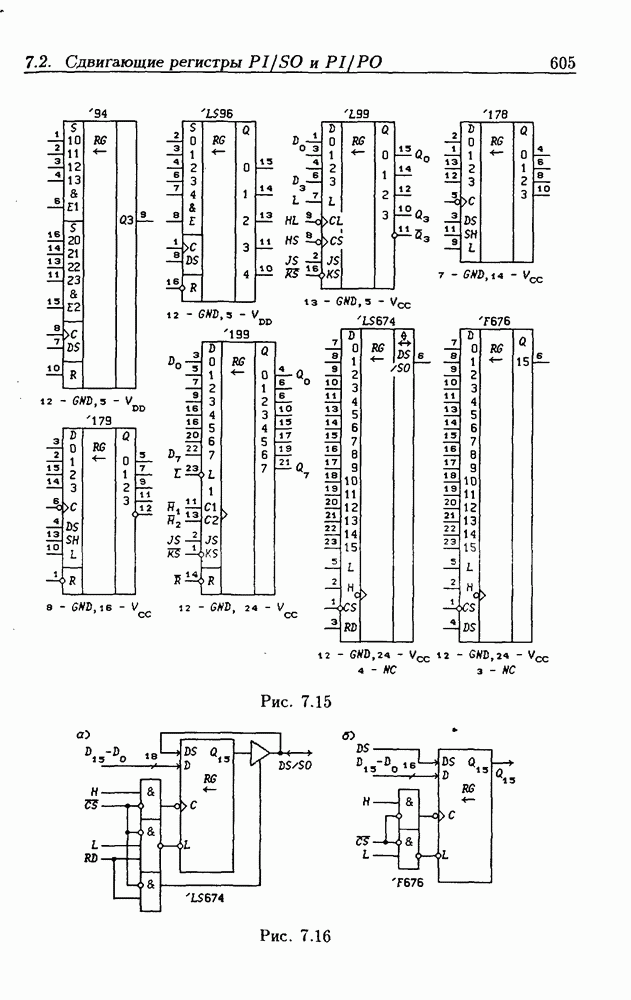
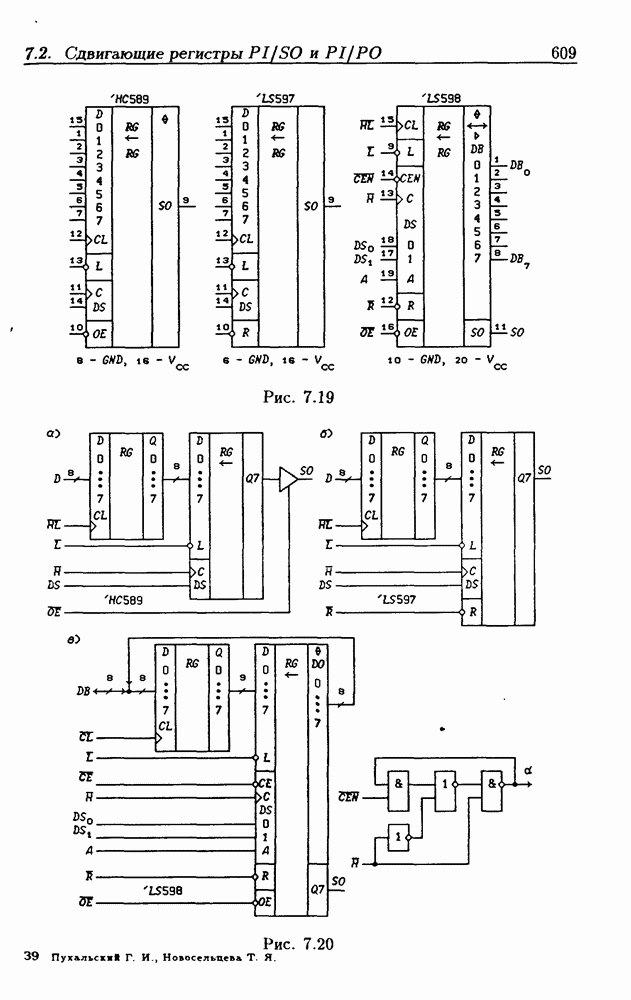
- 7.2. Сдвигающие регистры с параллельной записью данных
- Сдвигающие регистры с расширением знака.
- Сдвигающие регистры с входным регистром памяти.
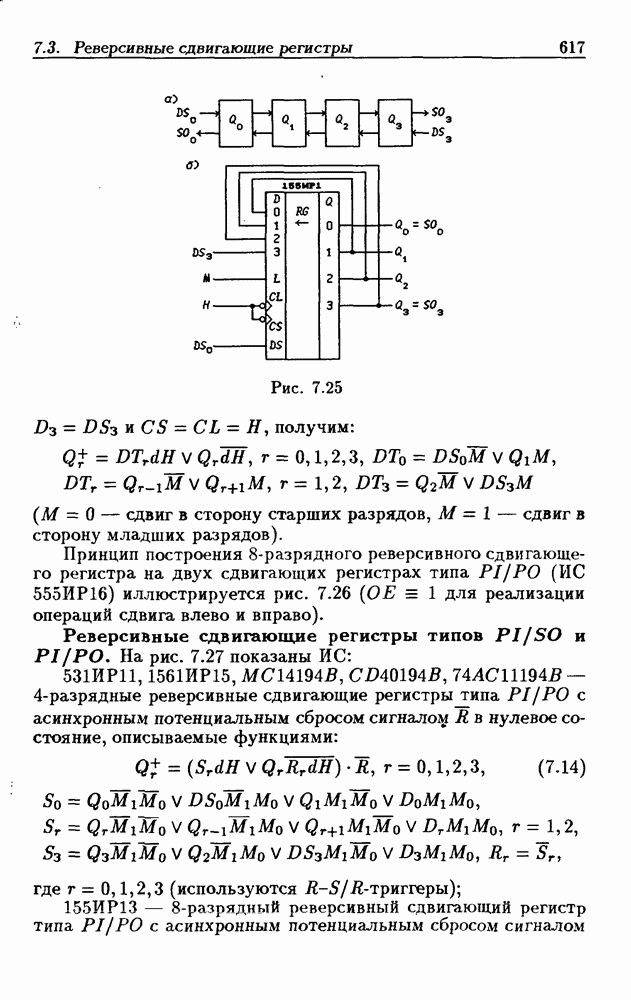
- 7.3. Реверсивные сдвигающие регистры
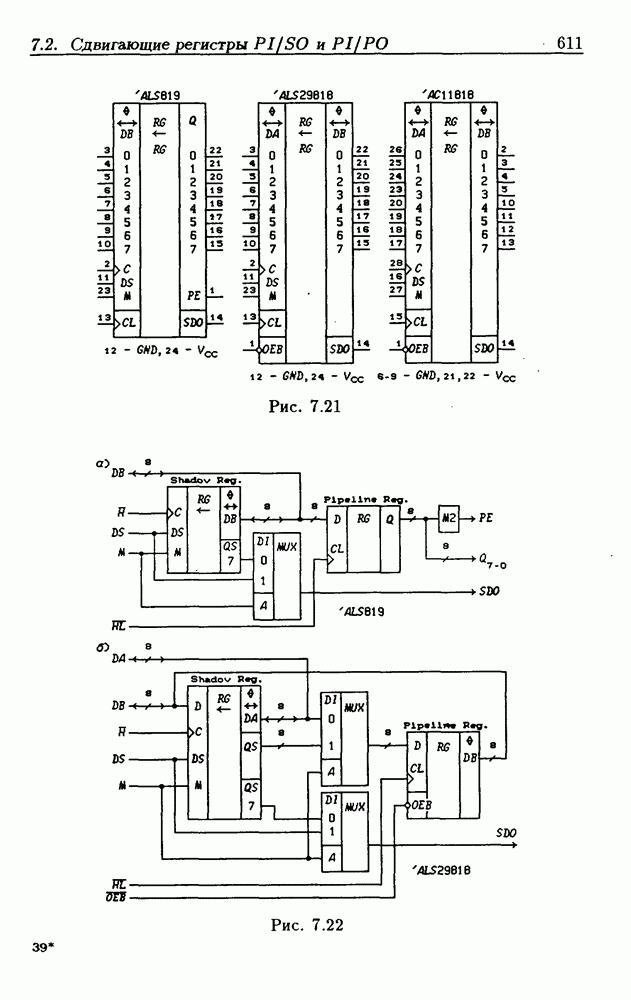
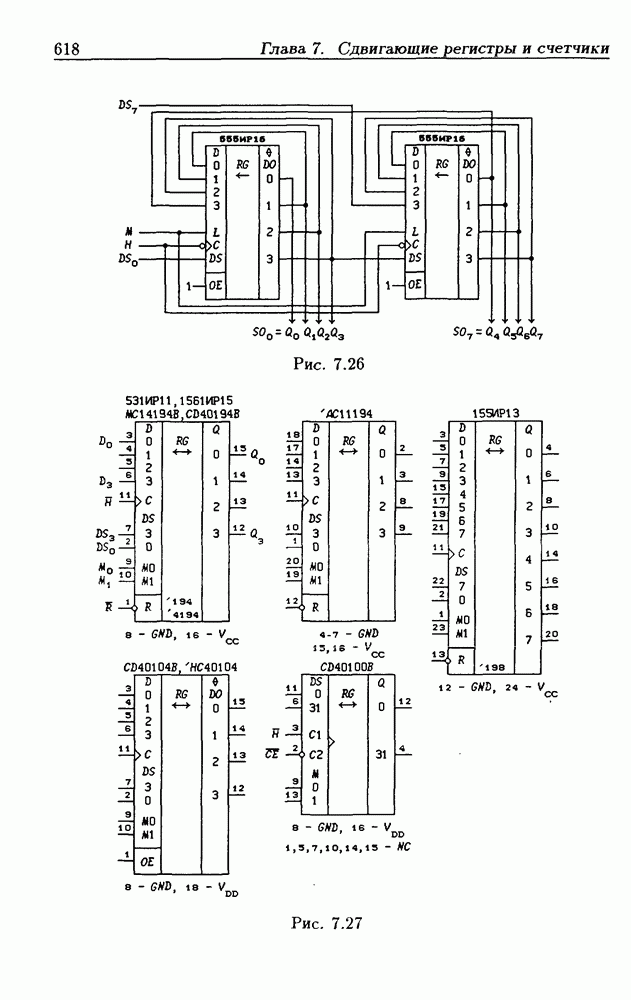
- Реверсивные сдвигающие регистры типов PI/SO и PI/PO.
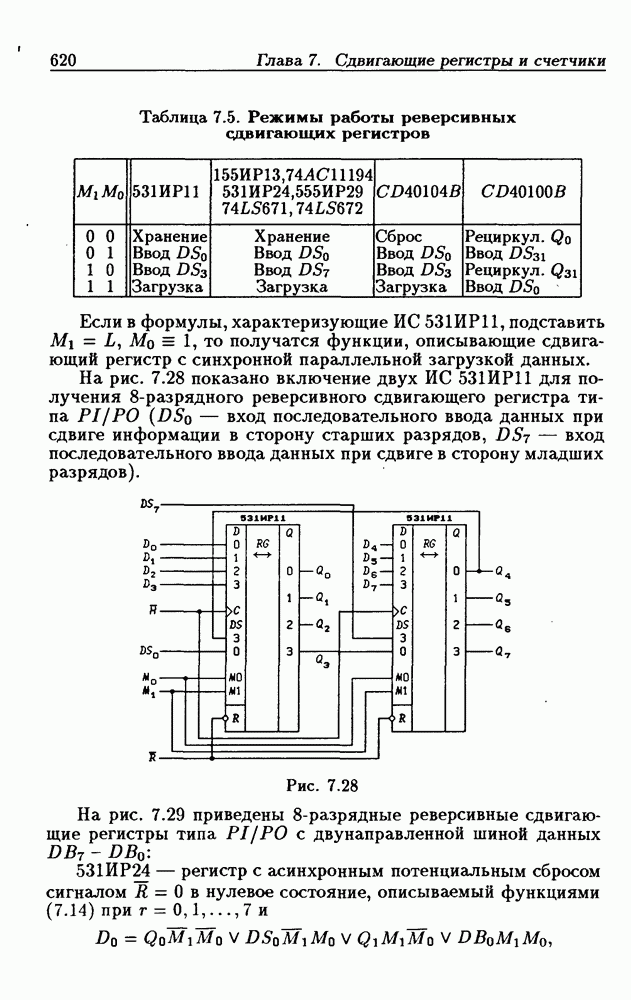
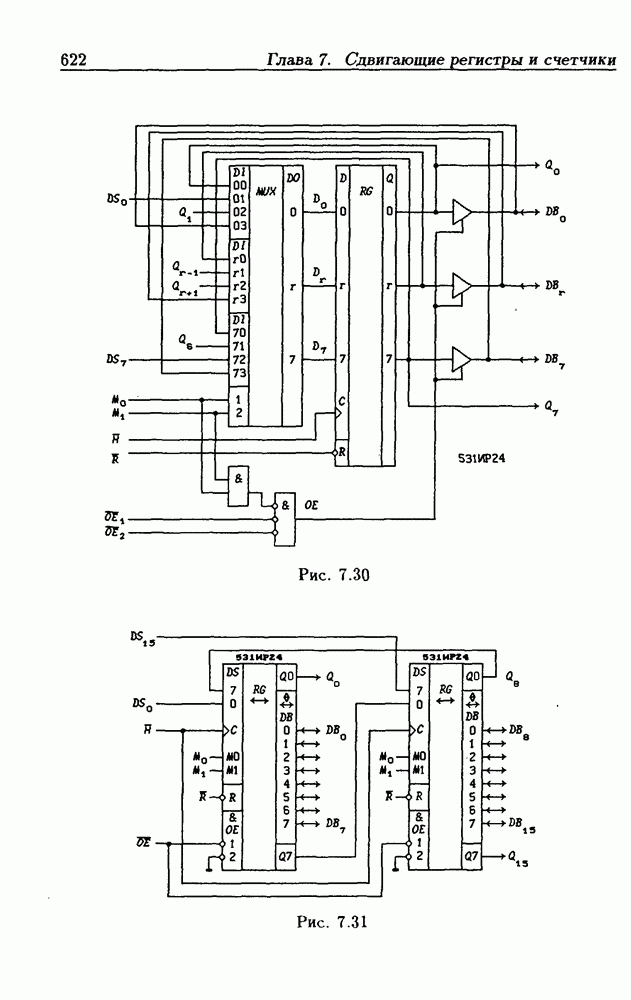
- Многофункциональные устройства на основе реверсивных сдвигающих регистров.
- 7.4. Асинхронные счетчики
- Двоично-десятичные асинхронные счетчики.
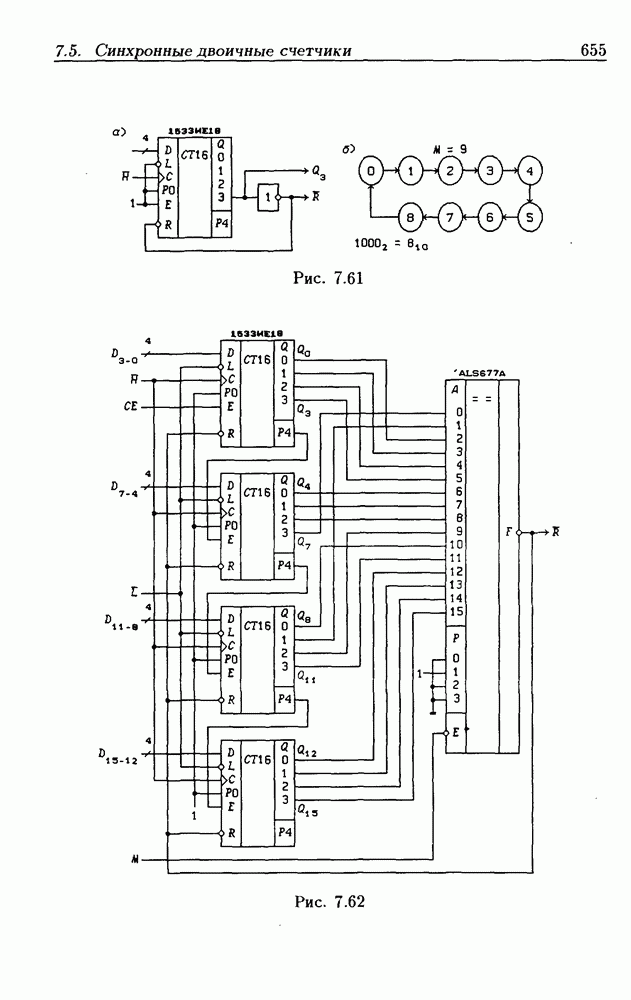
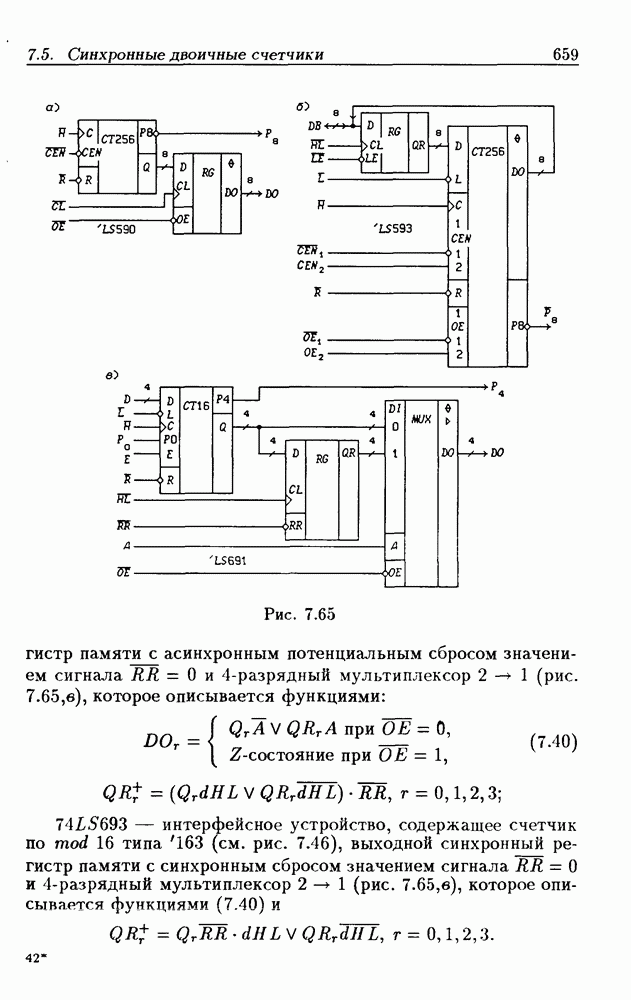
- 7.5. Синхронные двоичные счетчики
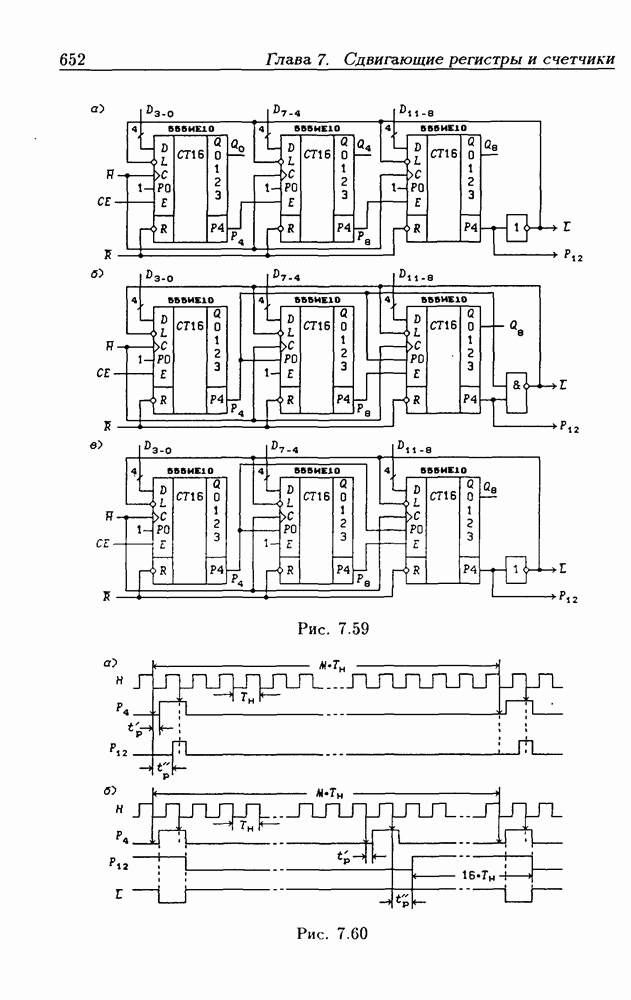
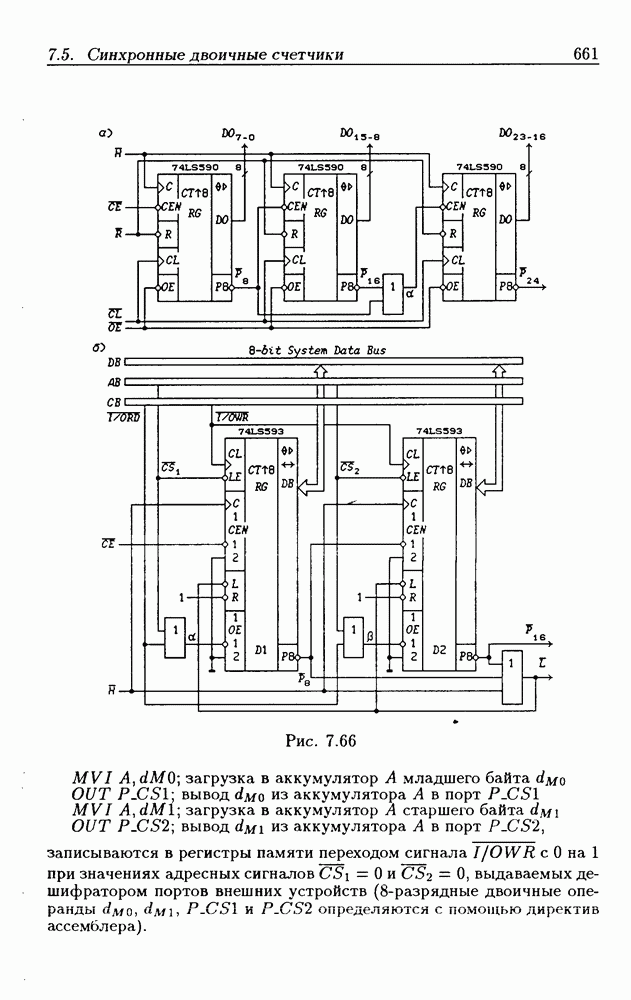
- Программирование модуля пересчета двоичных счетчиков.
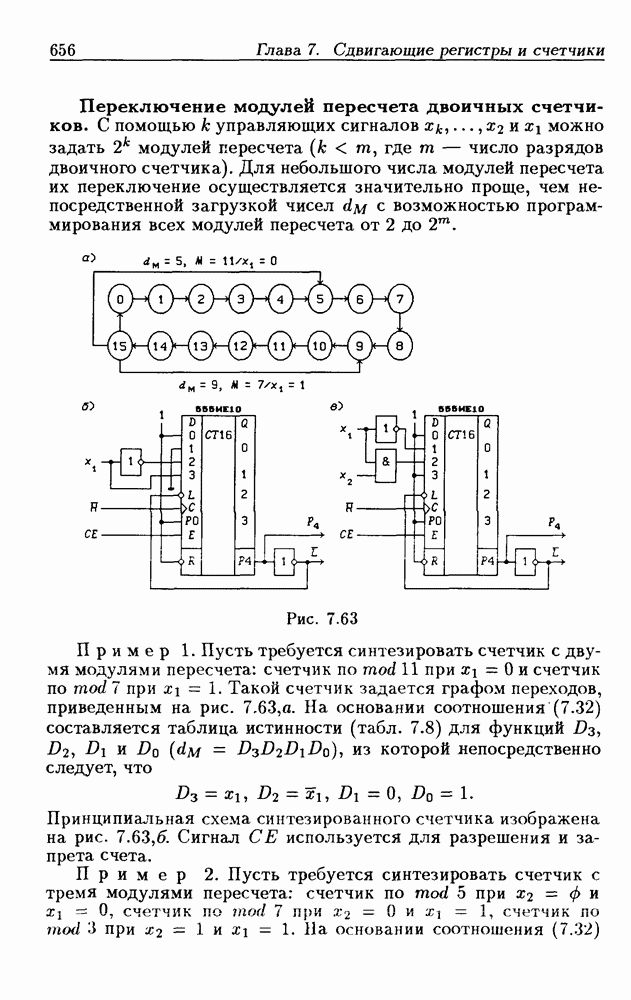
- Переключение модулей пересчета двоичных счетчиков.
- Функциональные устройства на основе двоичных счетчиков.
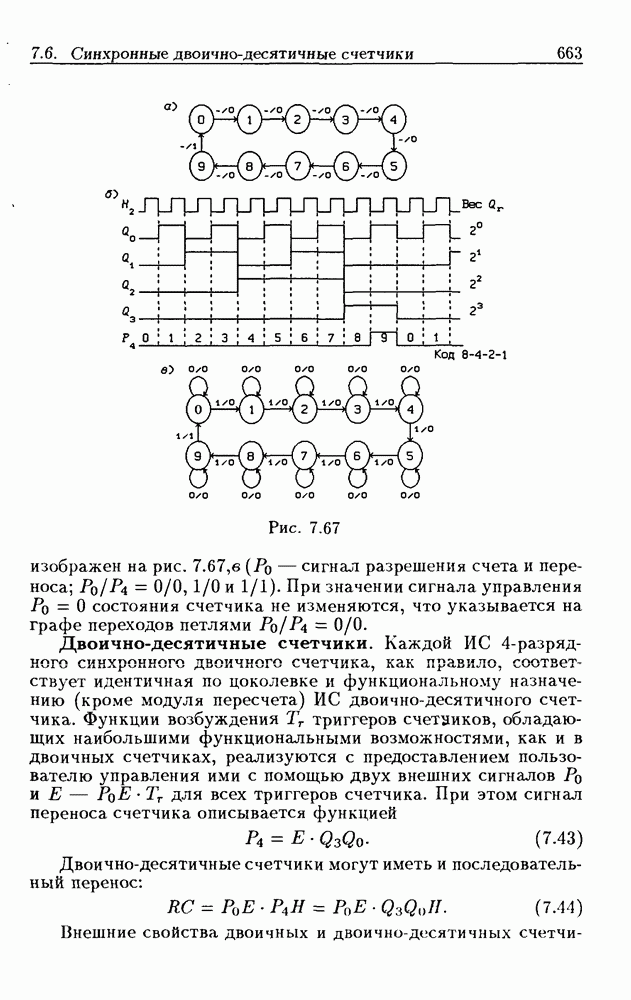
- 7.6. Синхронные двоично-десятичные счетчики
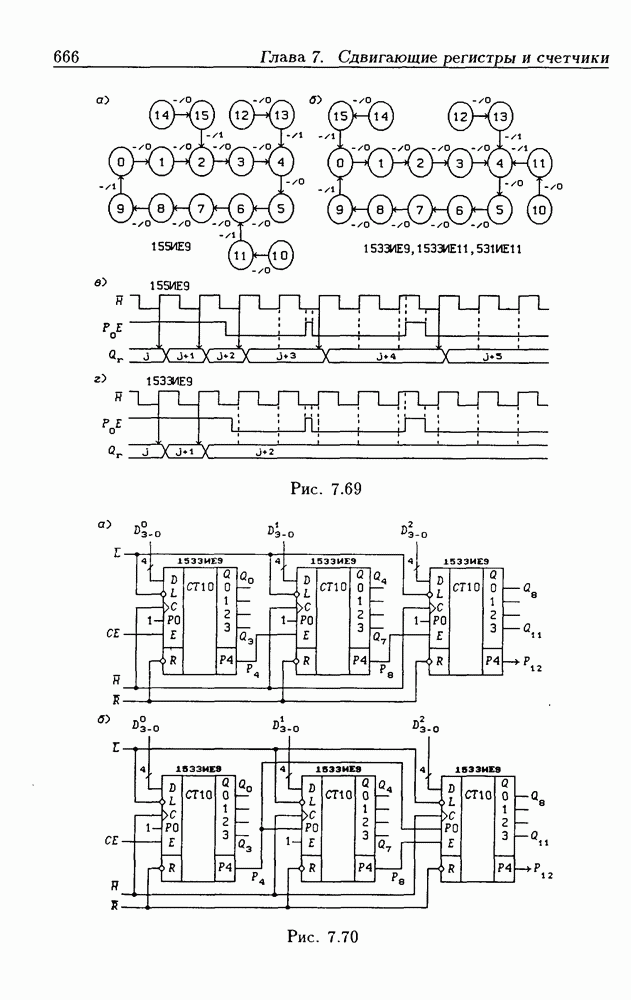
- 7.7. Синхронные реверсивные счетчики
- 7.8. Счетчики с расщепленным тактовым сигналом
- 7.9. Счетчики на сдвигающих регистрах
- 7.10. Кольцевые счетчики
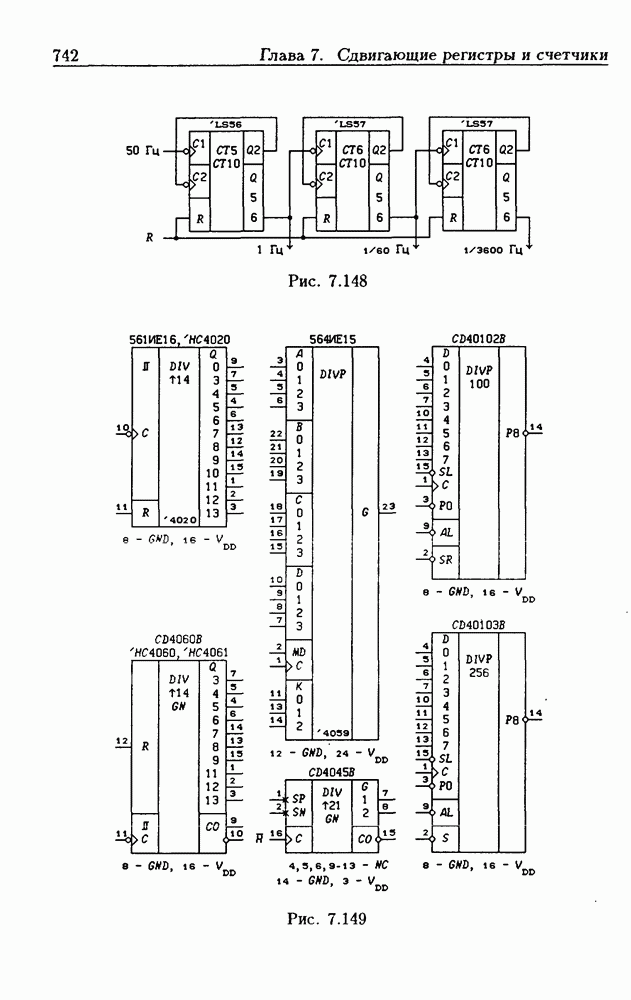
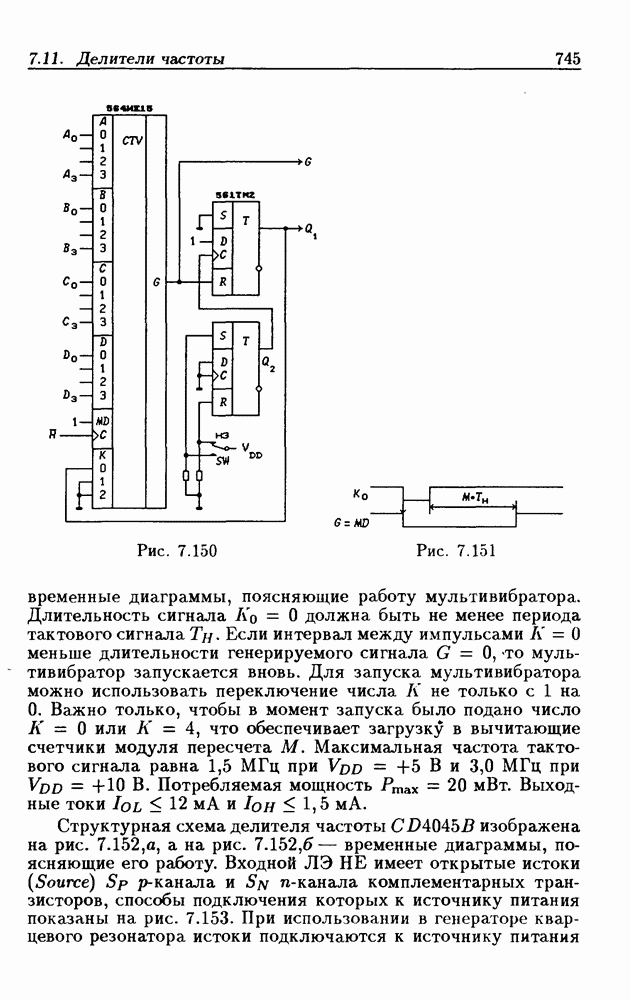
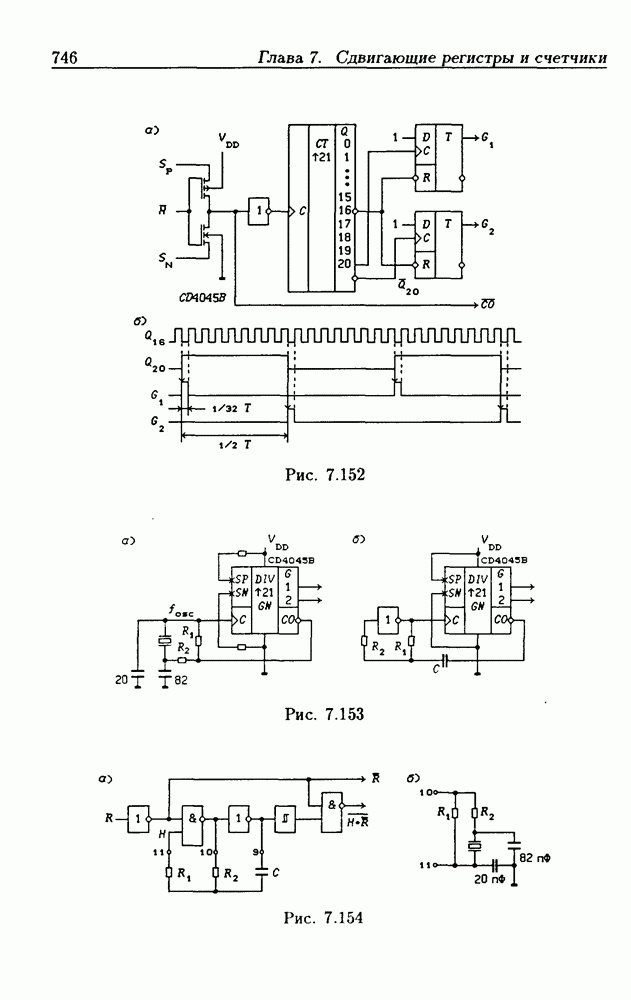
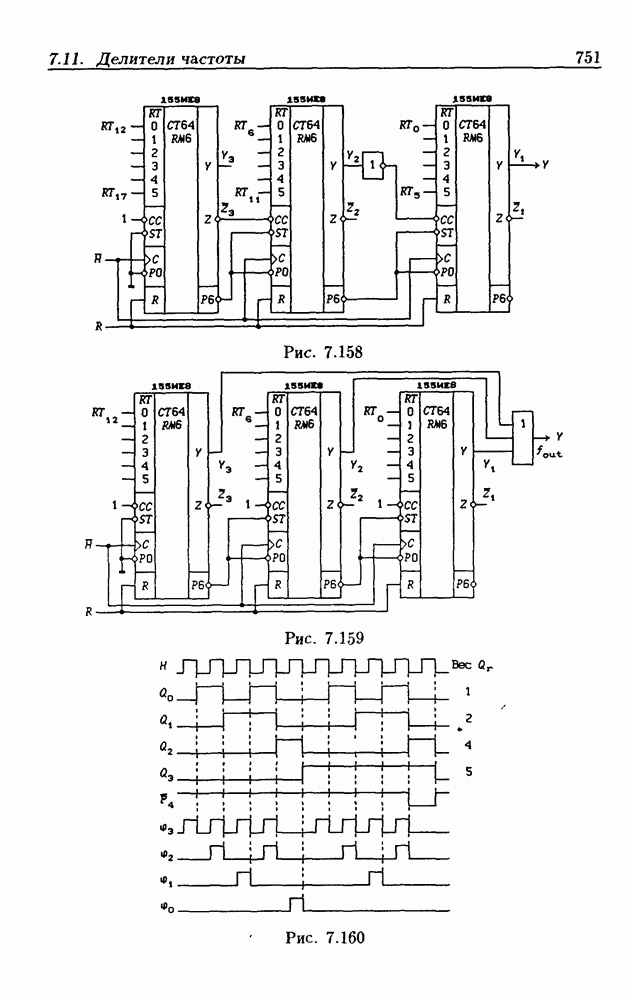
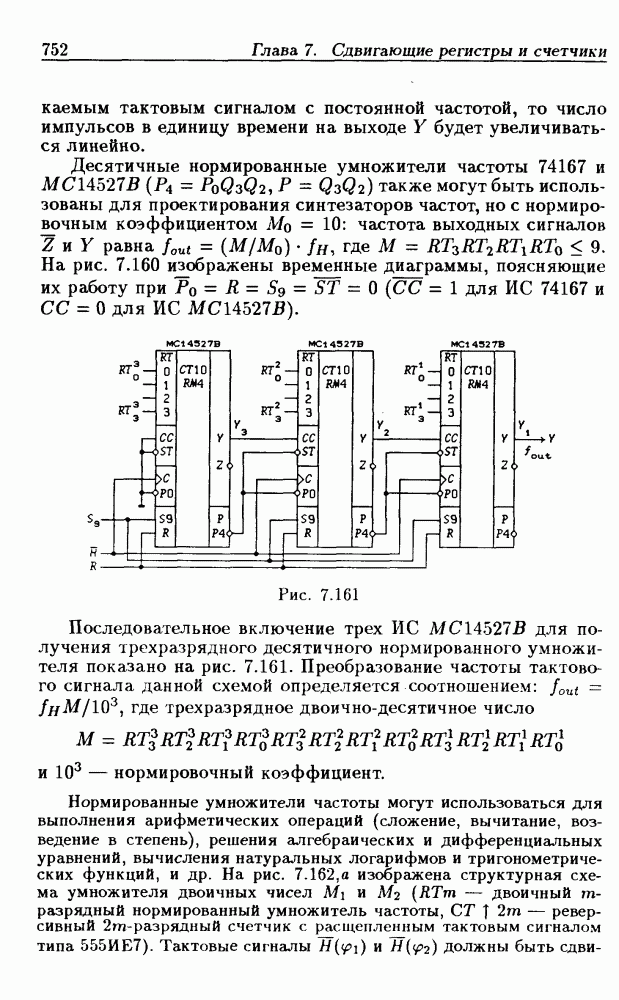
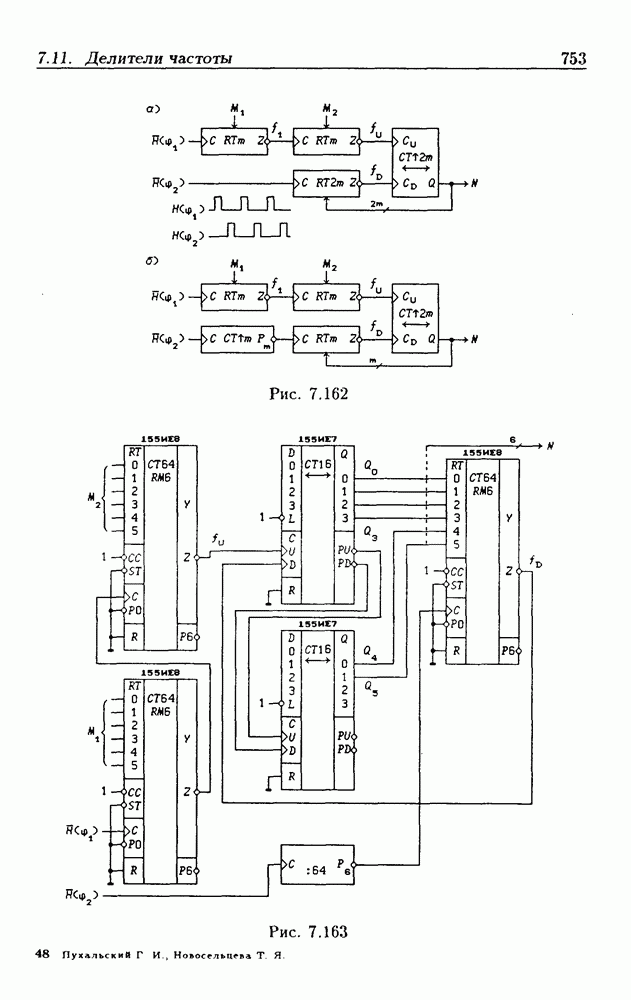
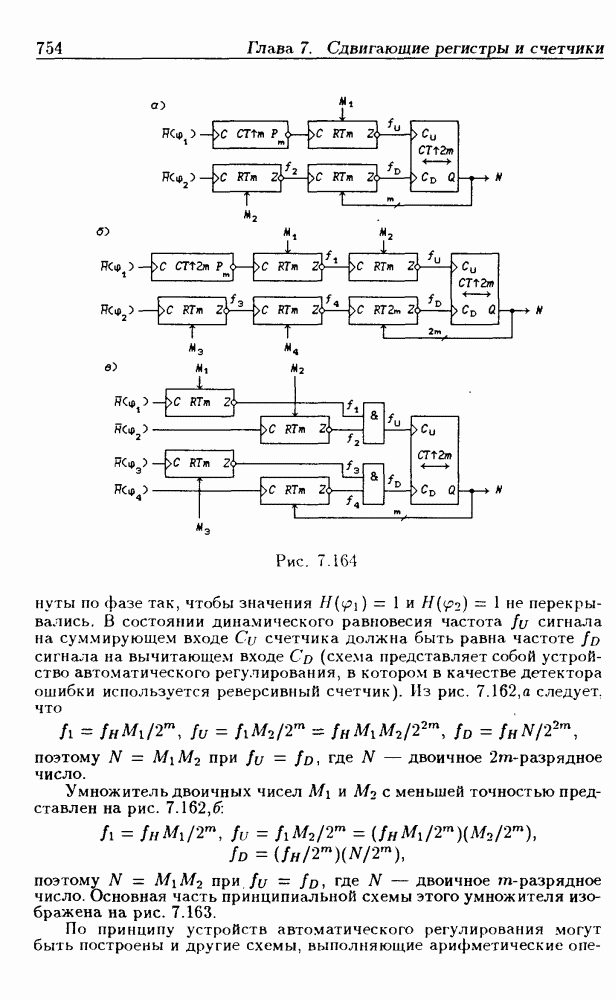
- 7.11. Делители частоты
- Нормированные умножители частоты.
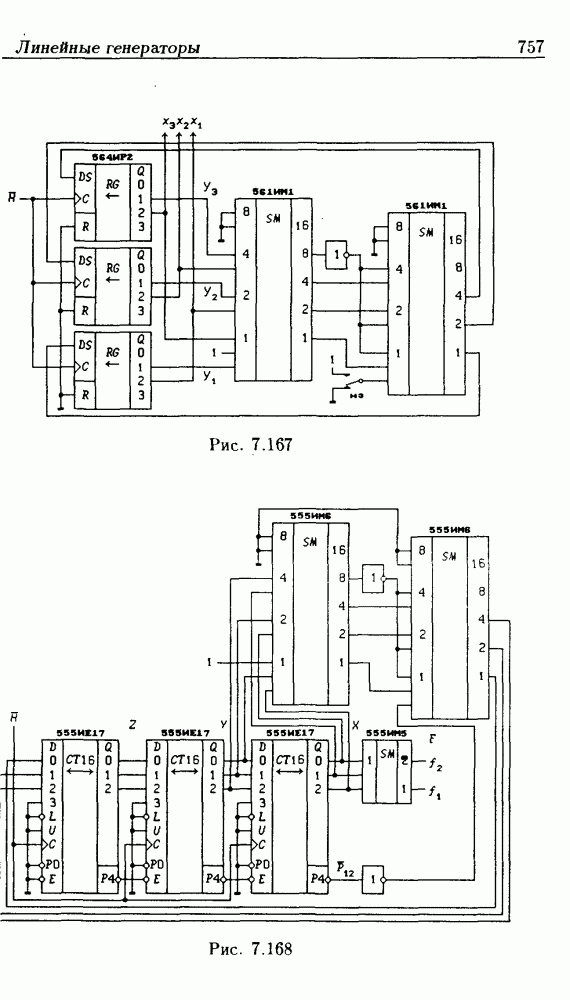
- 7.12. Линейные генераторы
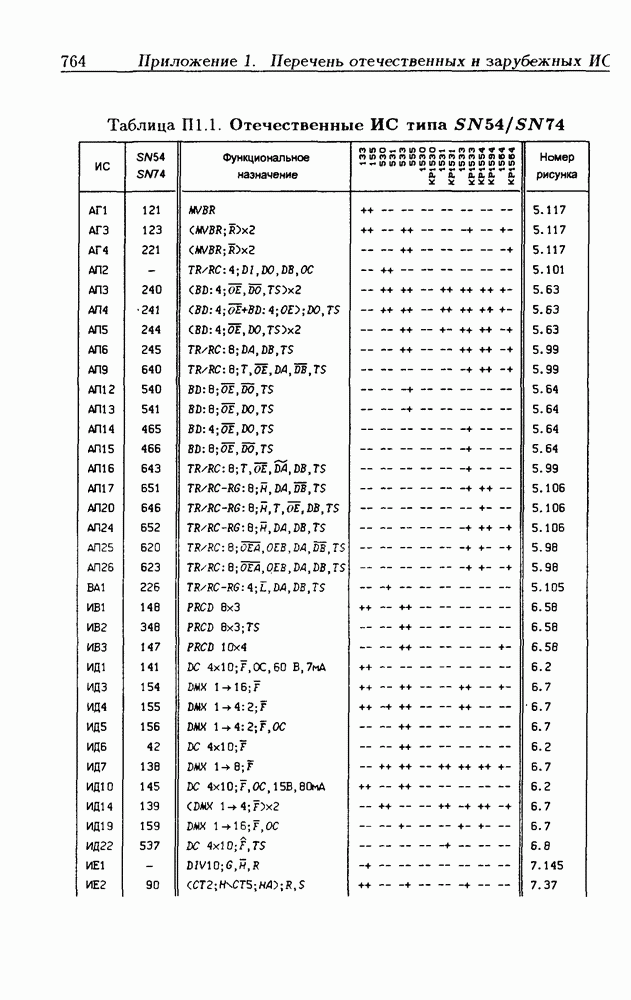
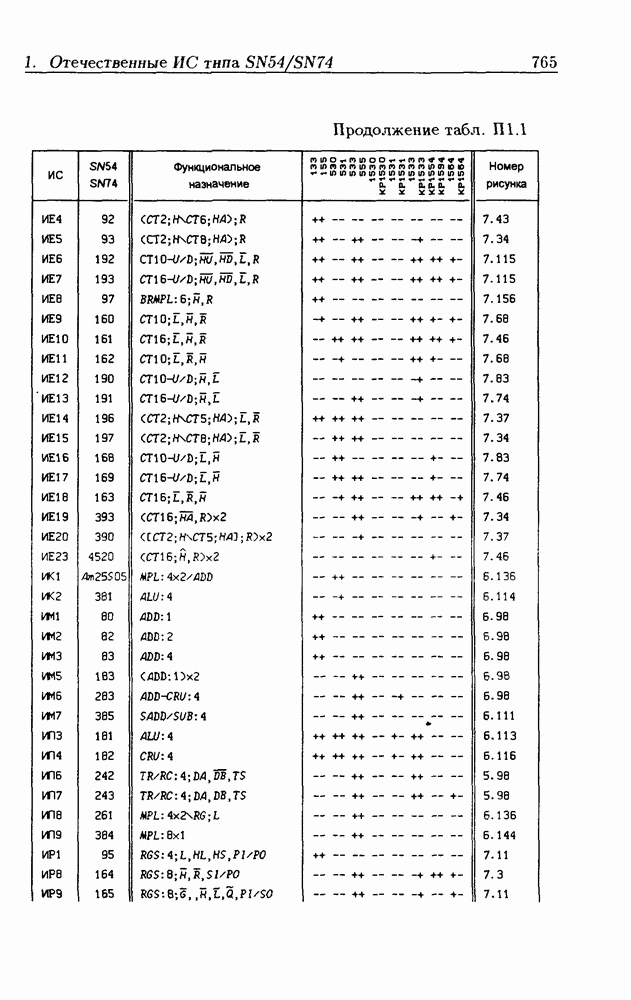
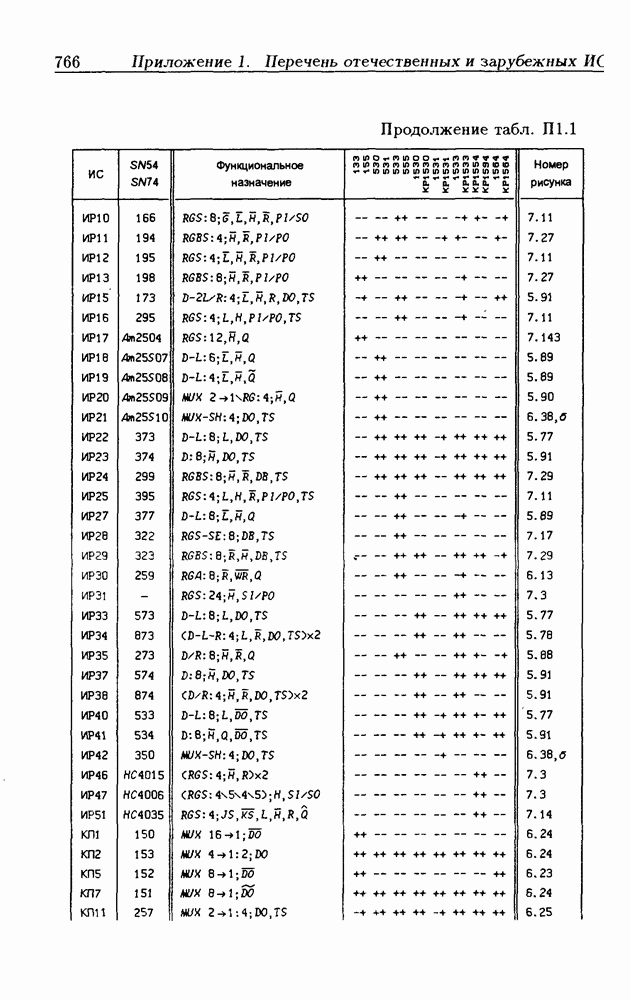
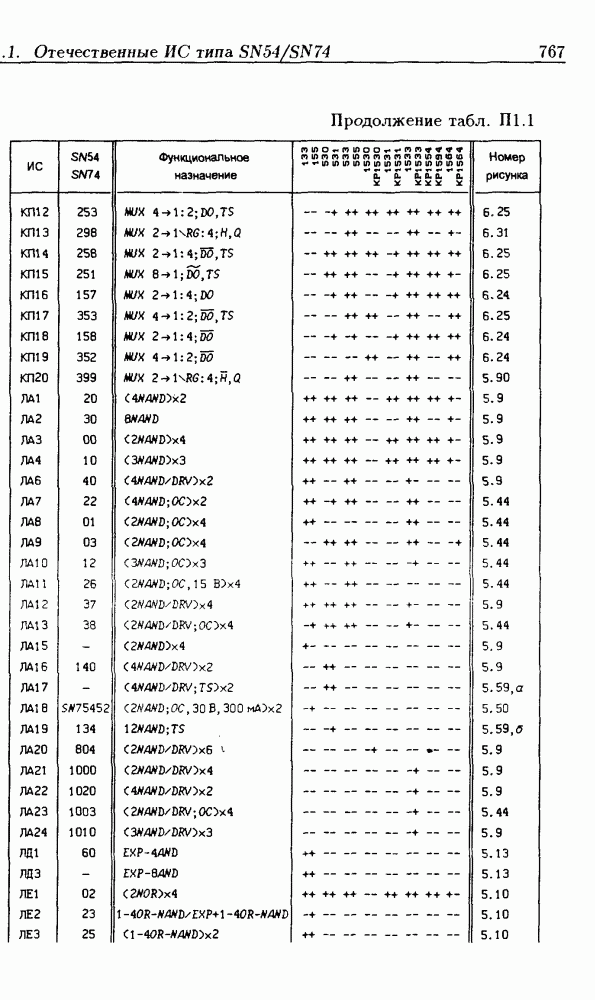
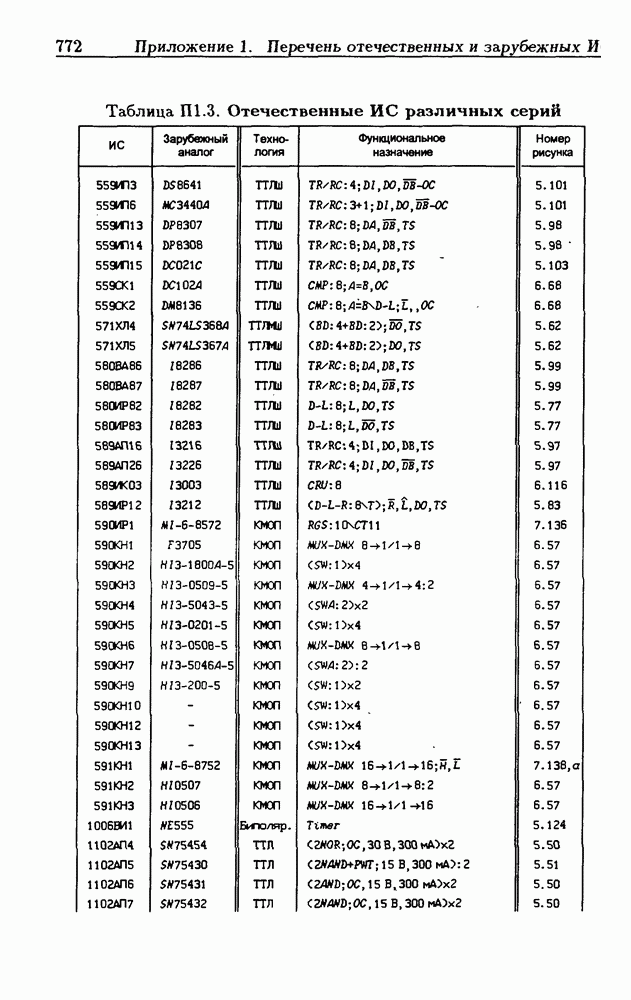
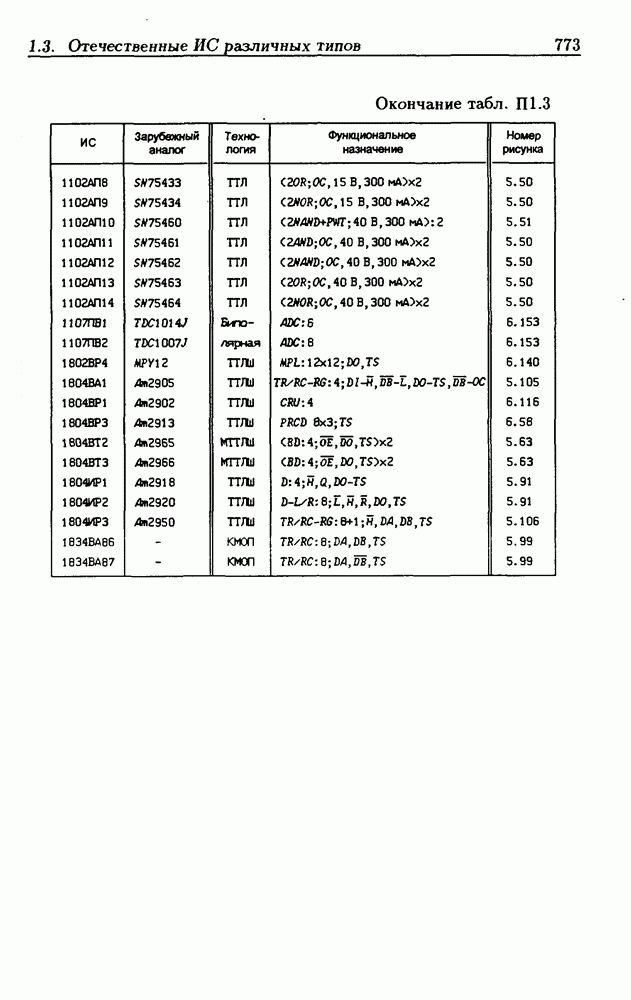
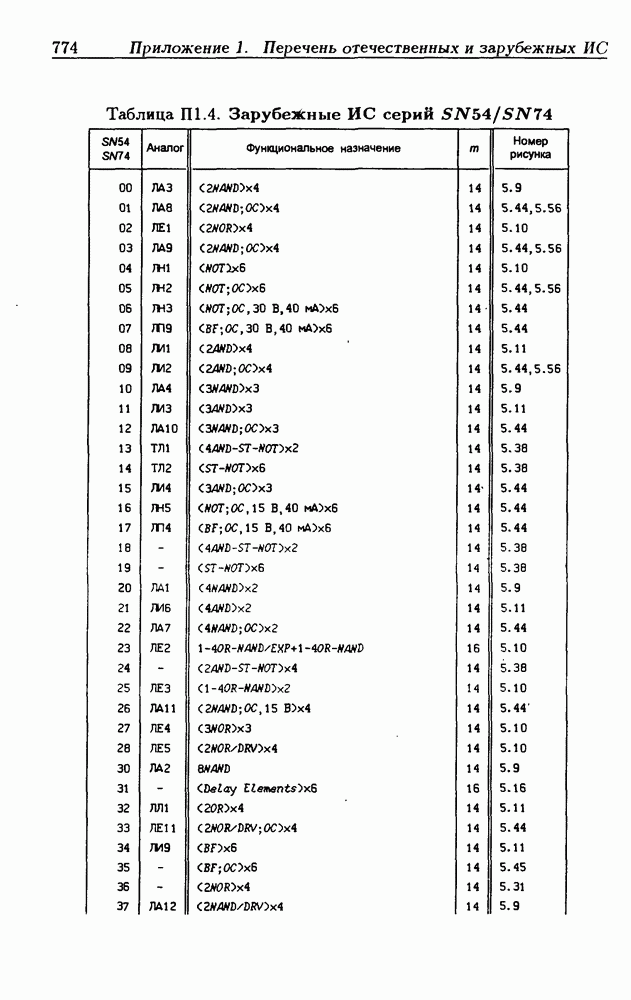
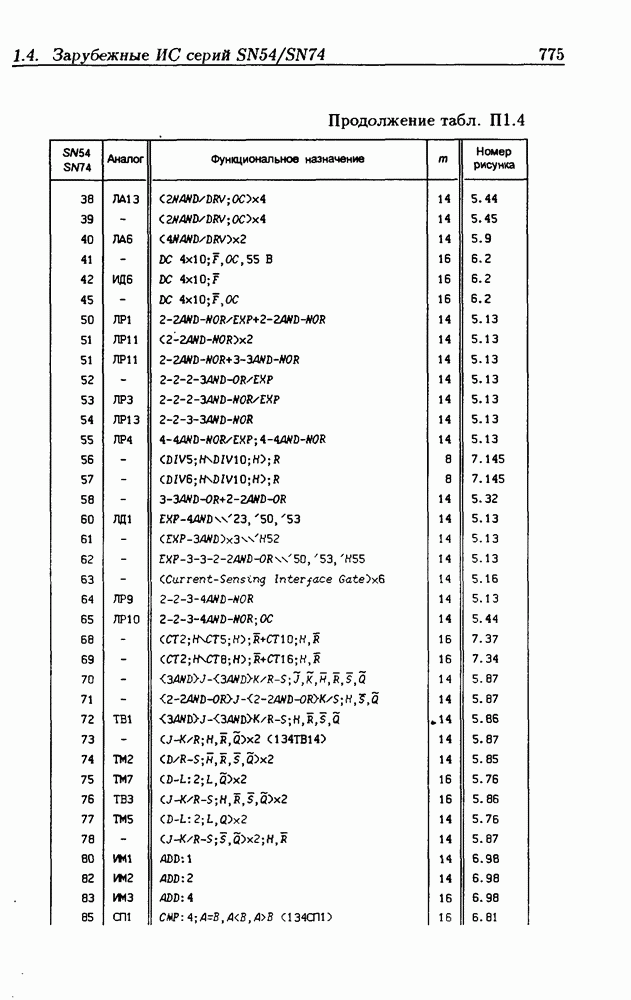
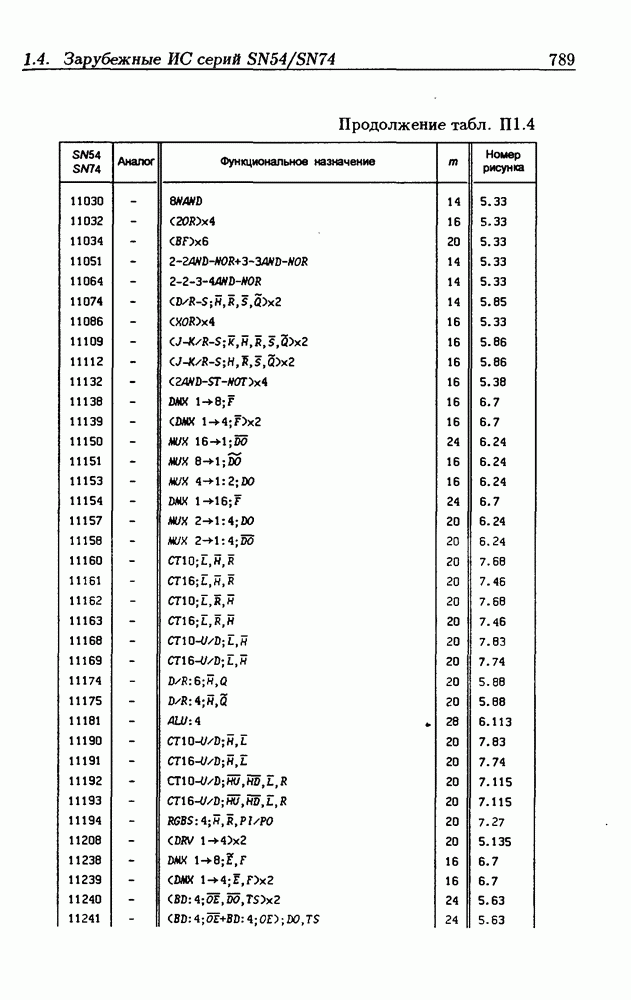
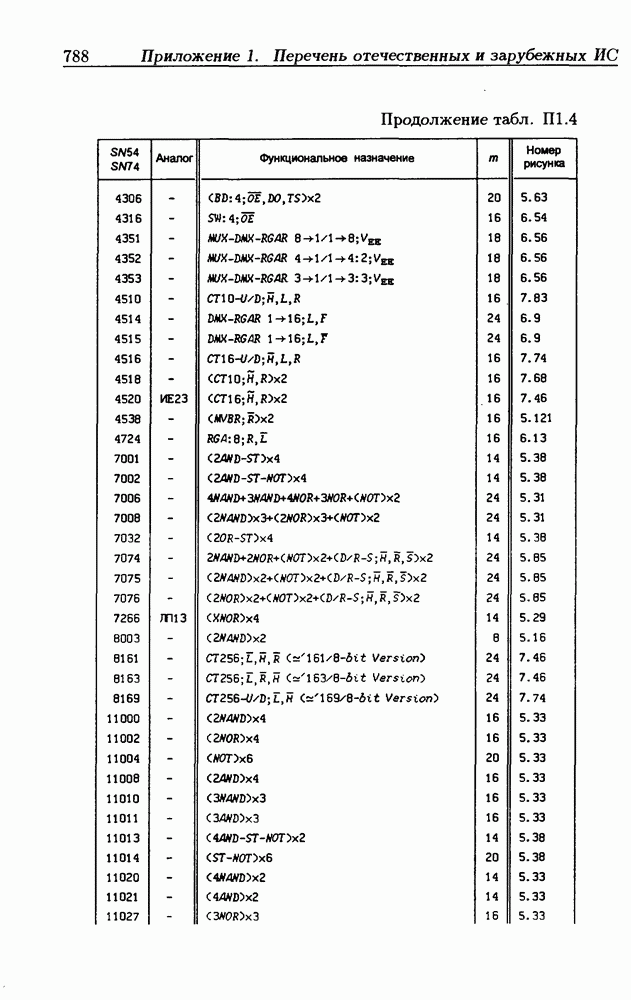
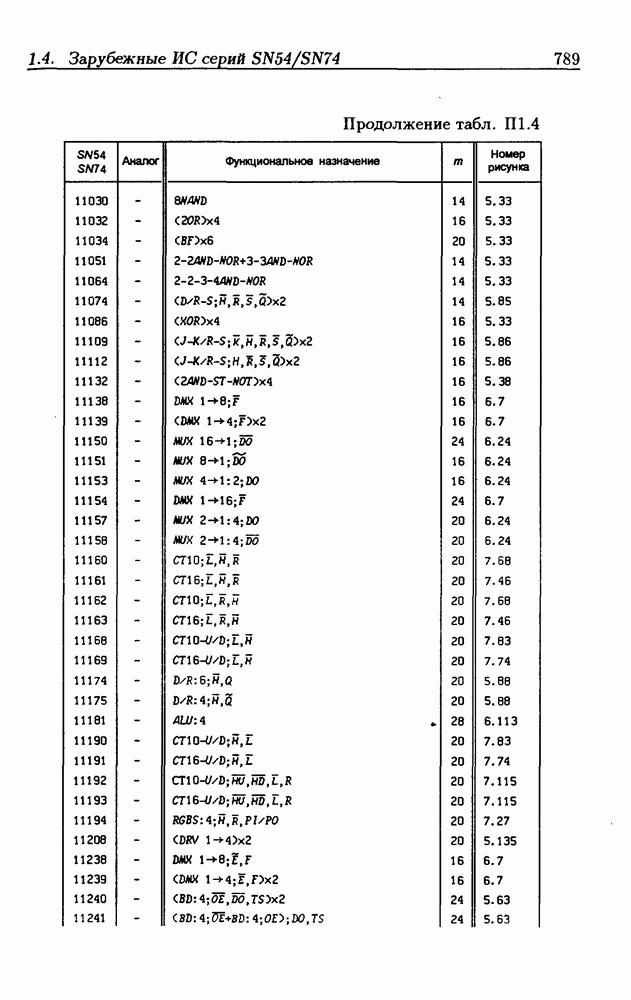
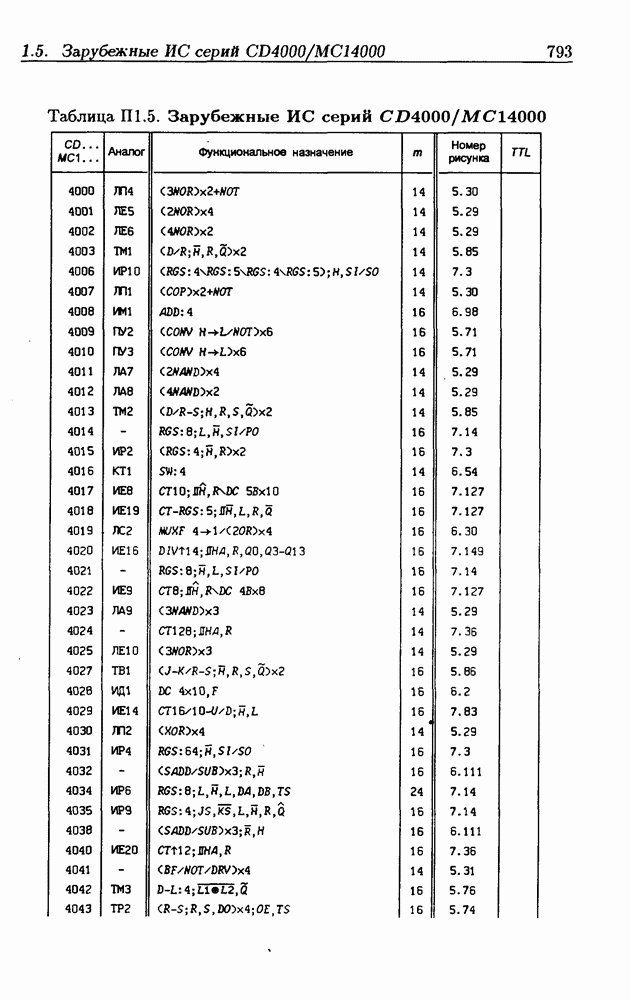
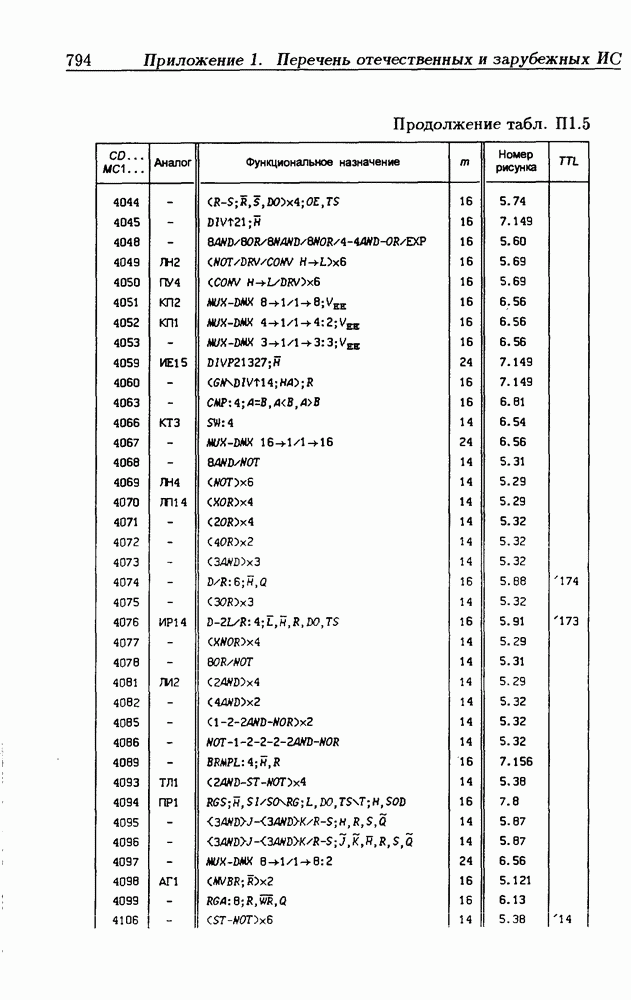
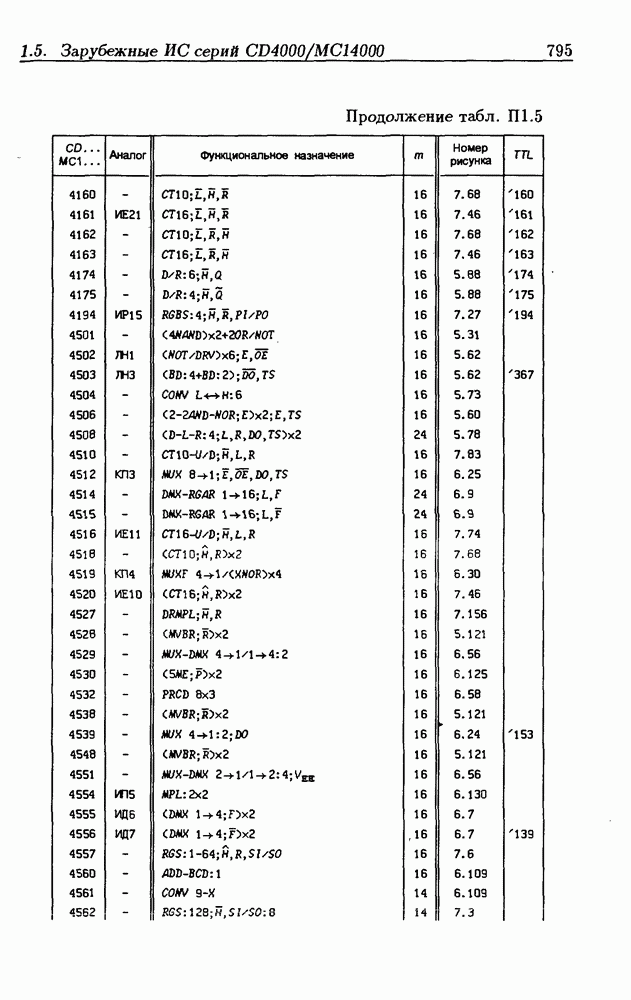
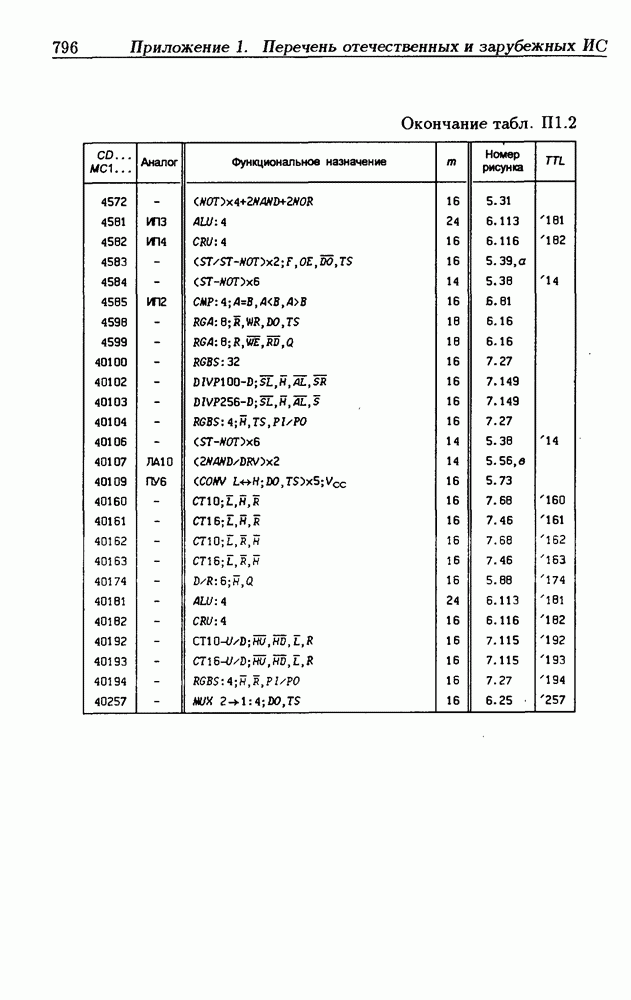
- Приложение 1. Перечень отечественных и зарубежных ИС
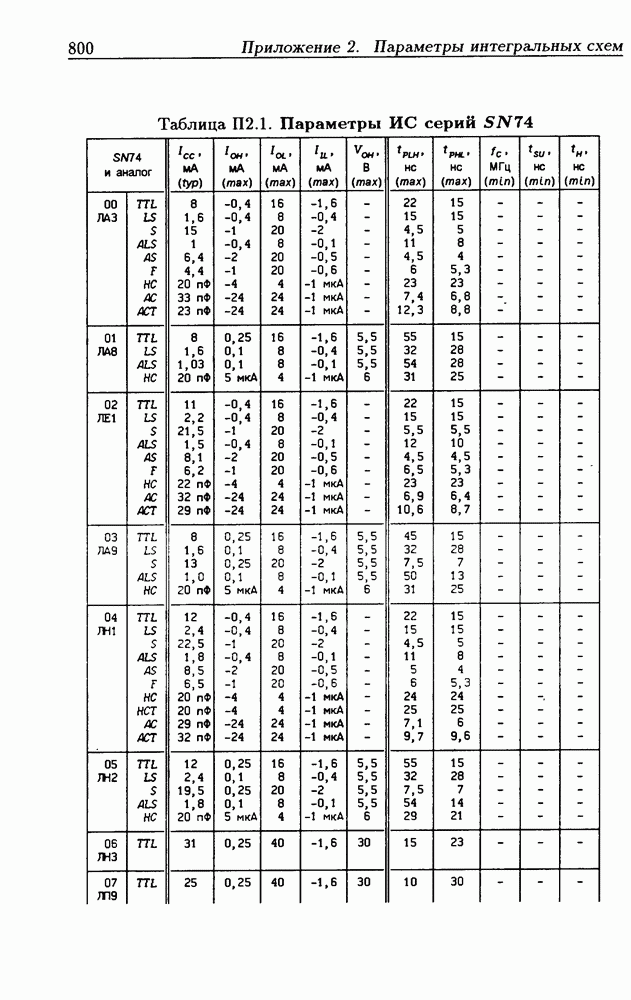
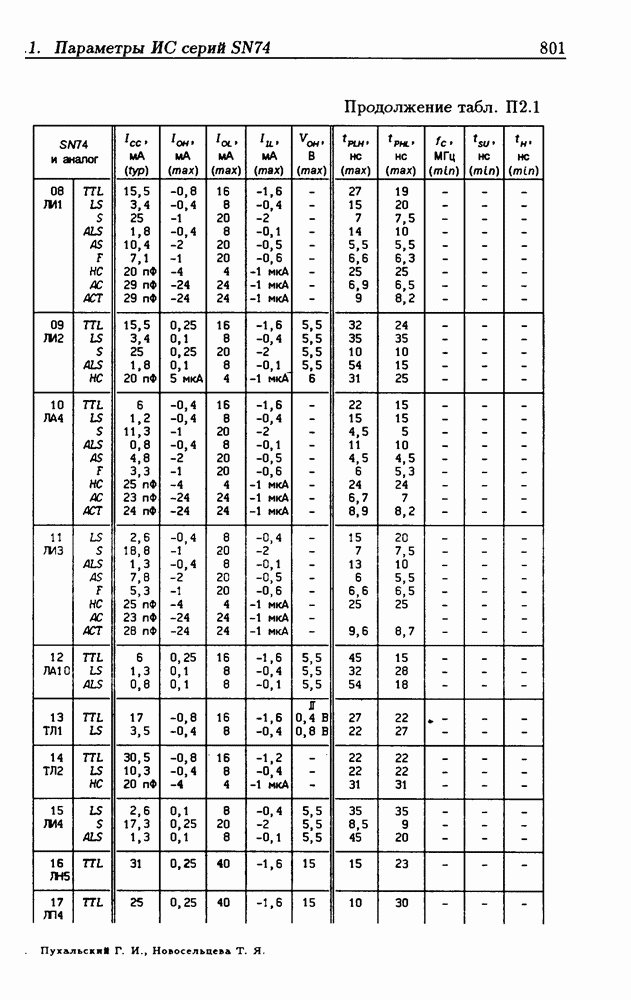
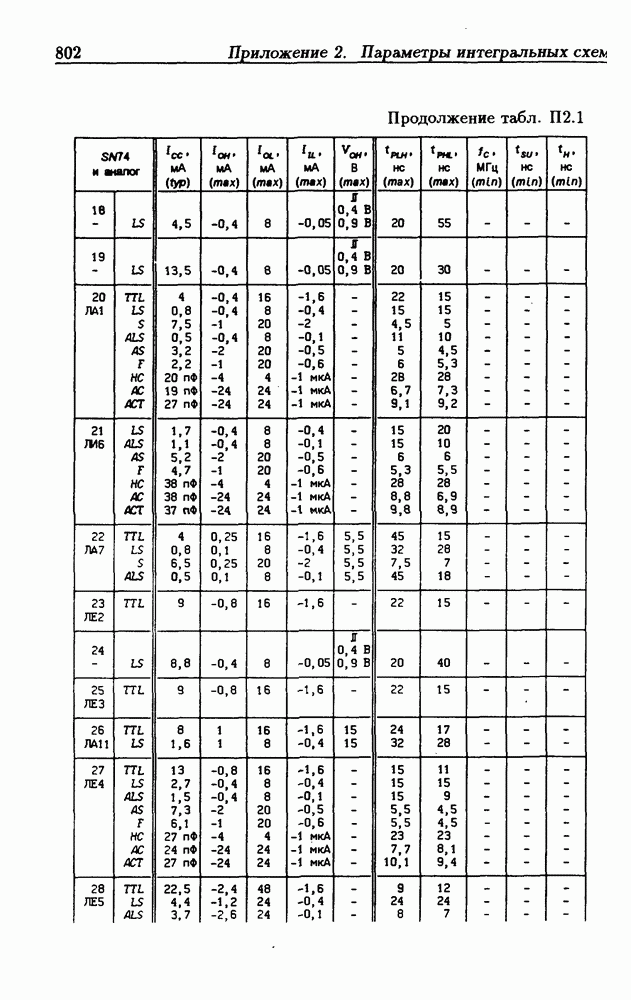
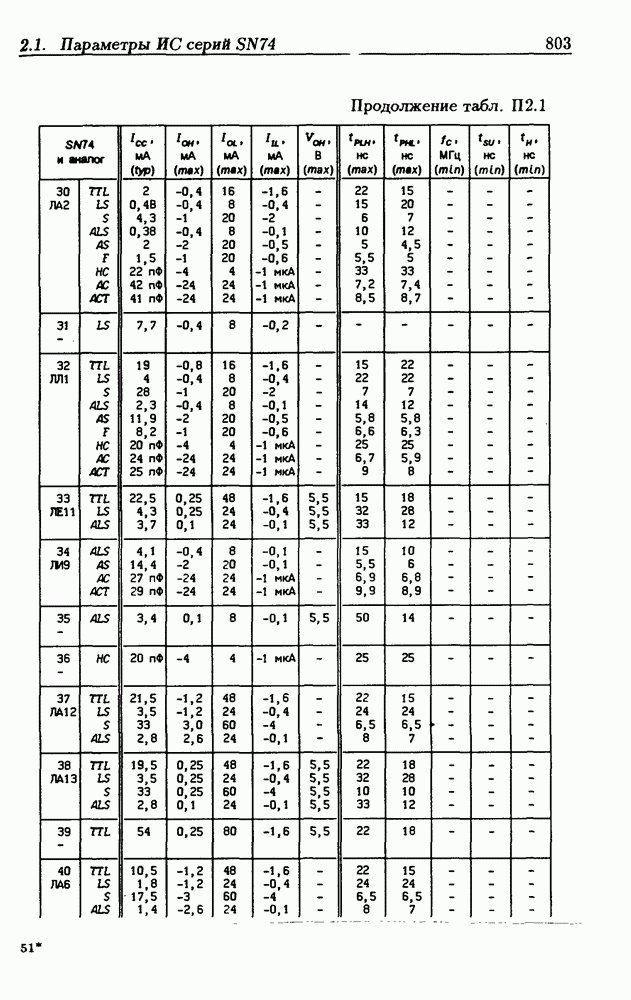
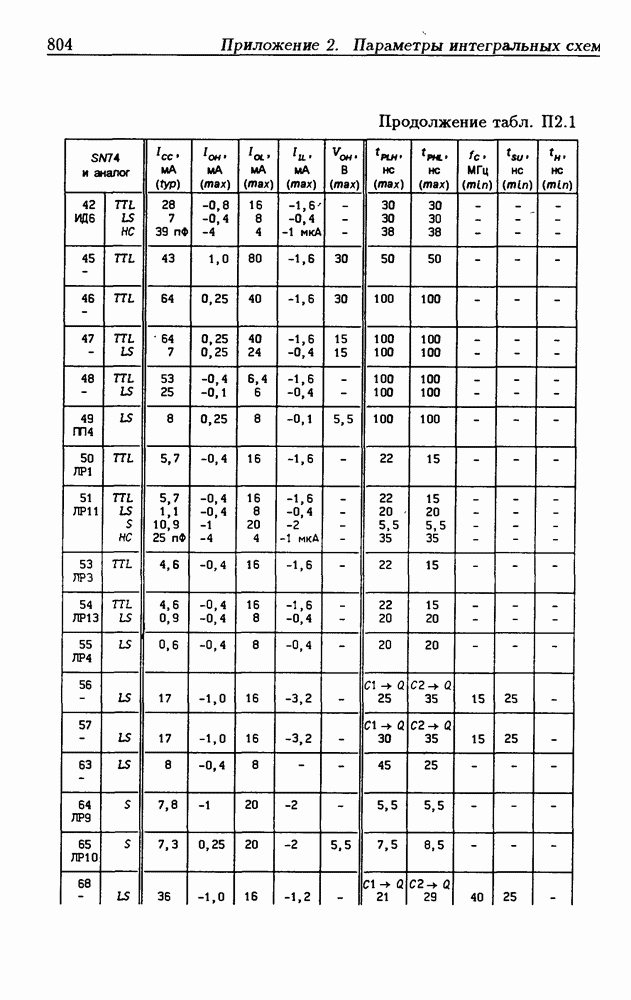
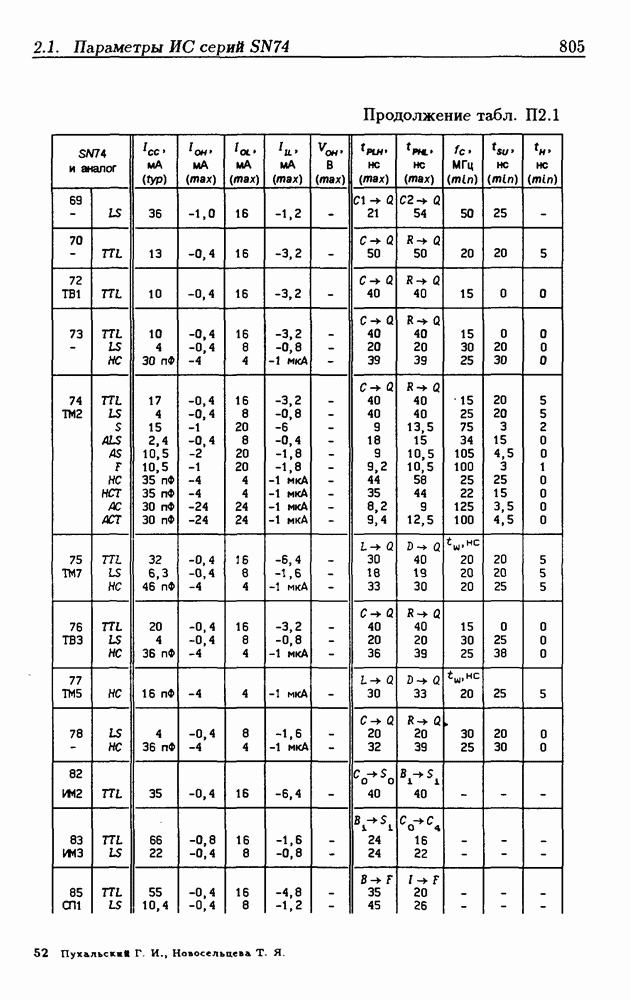
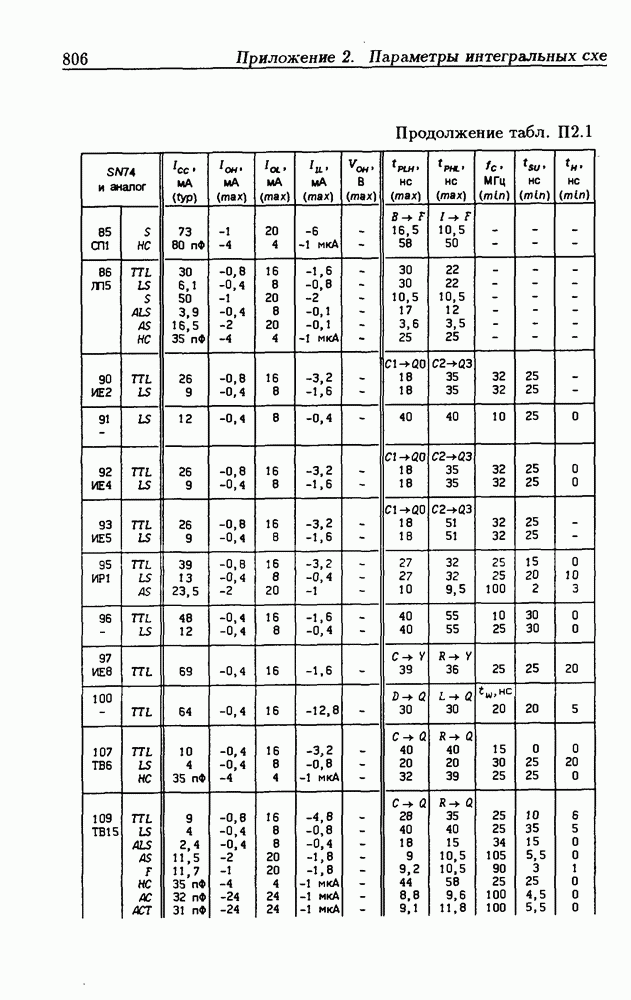
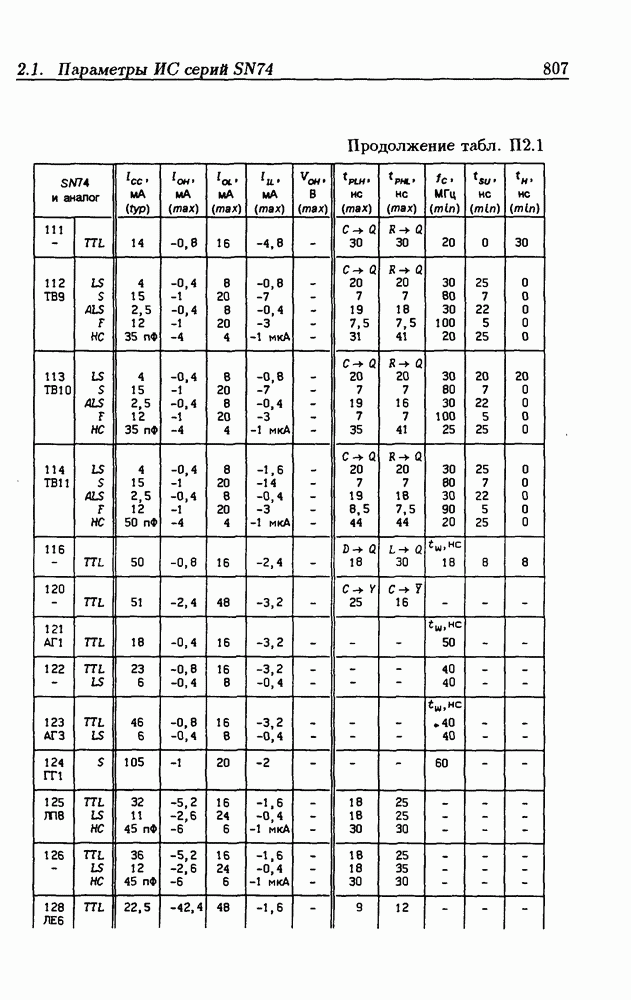
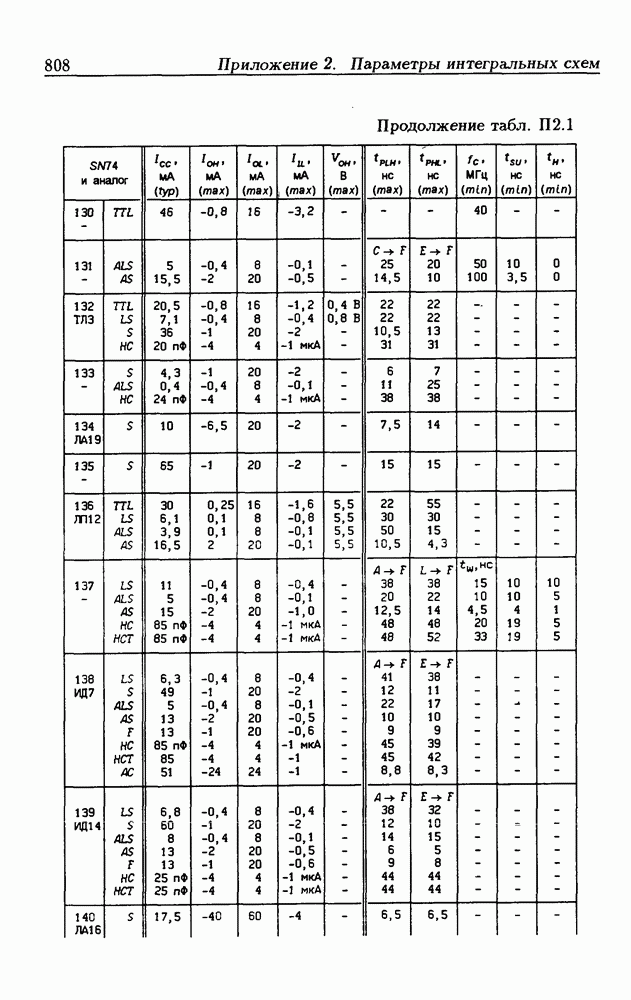
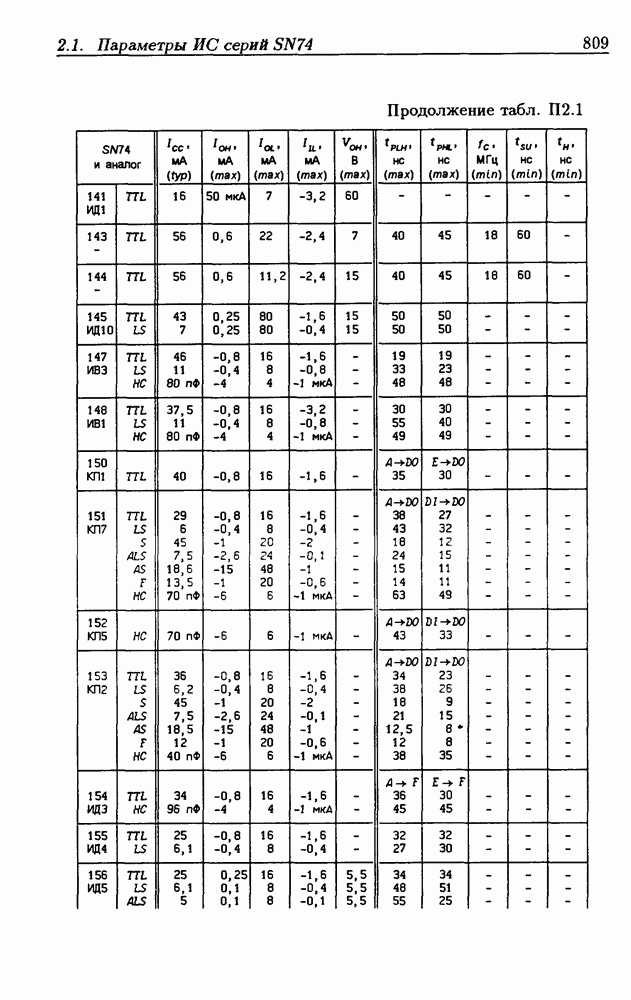
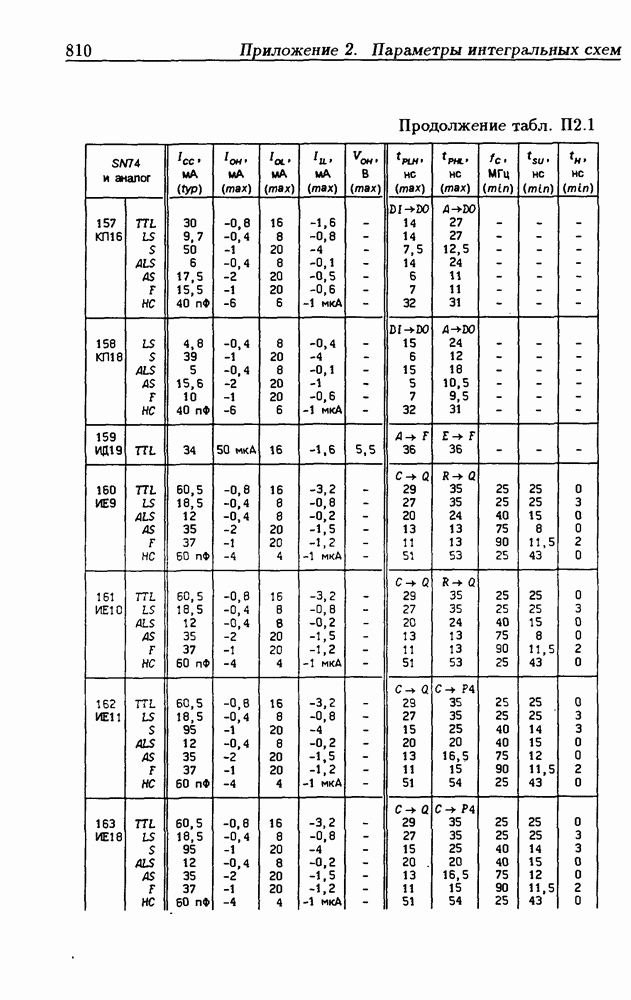
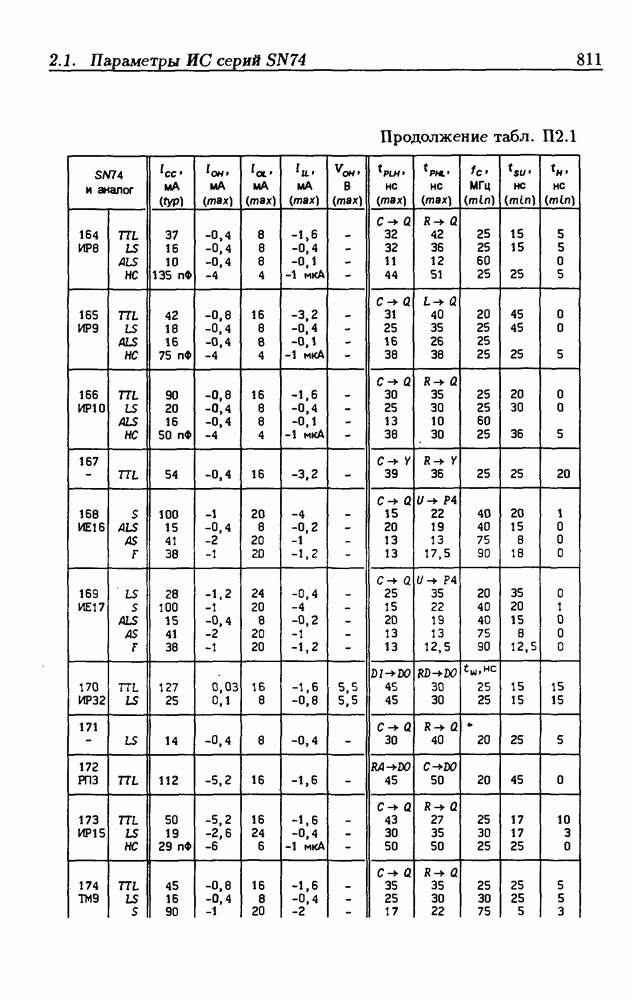
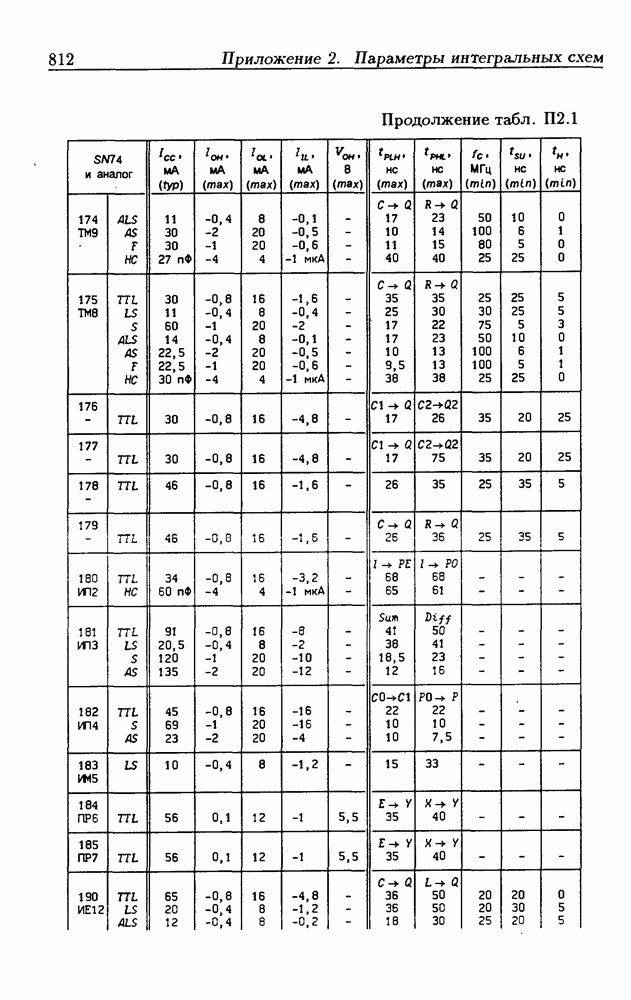
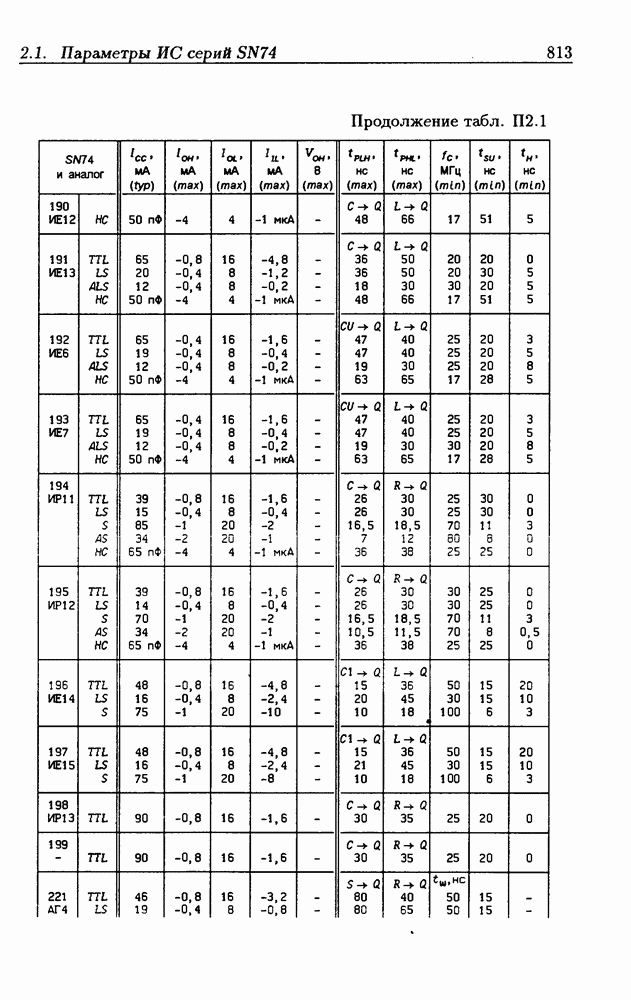
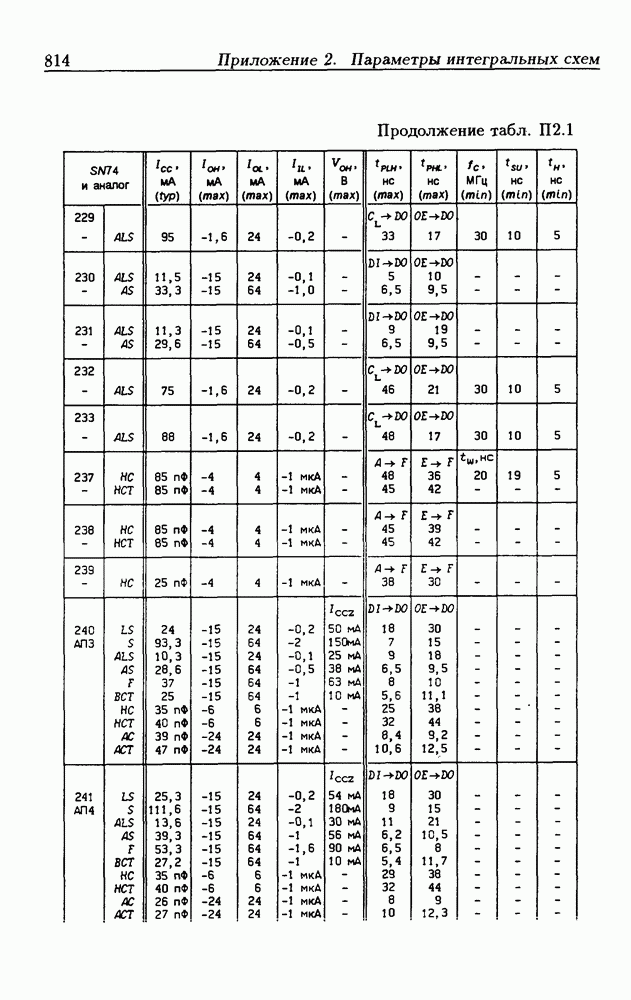
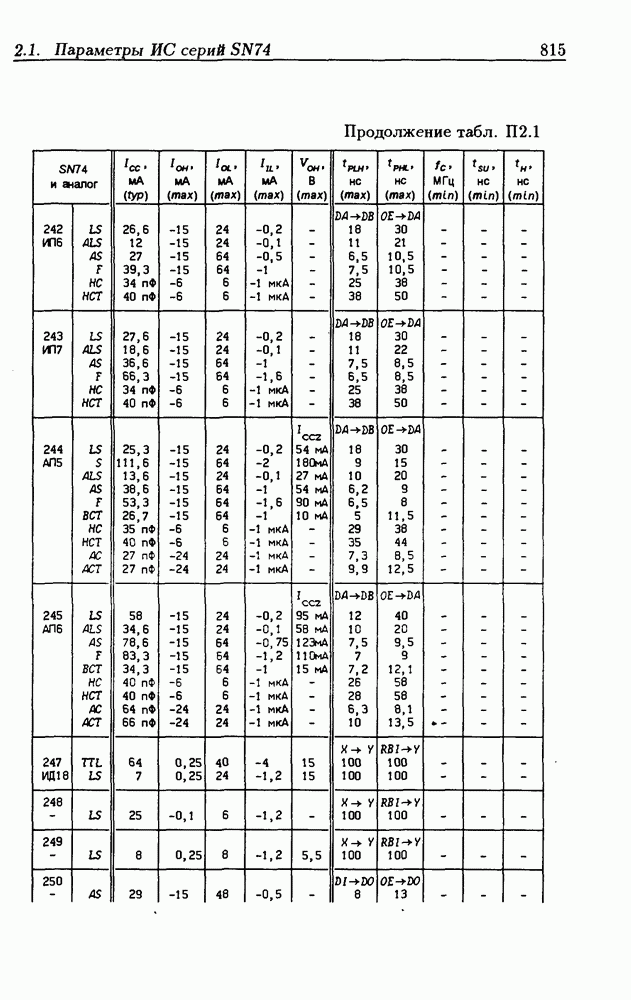
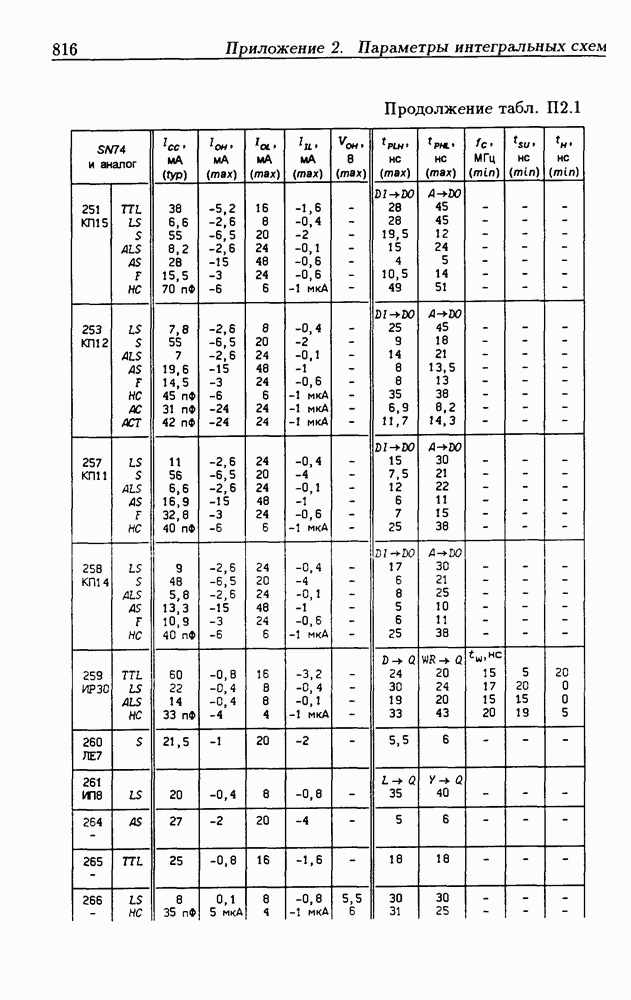
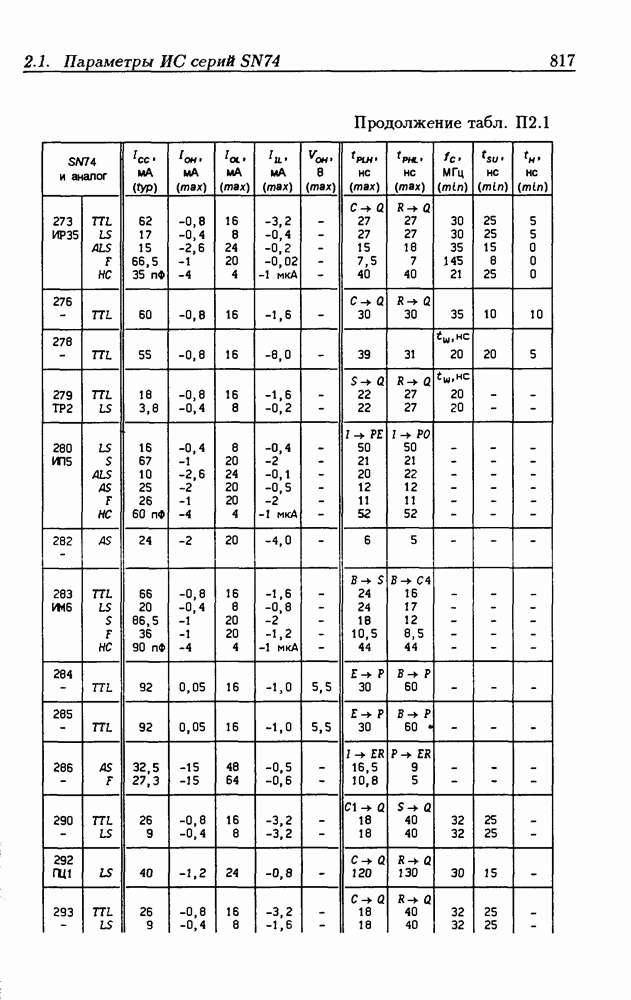
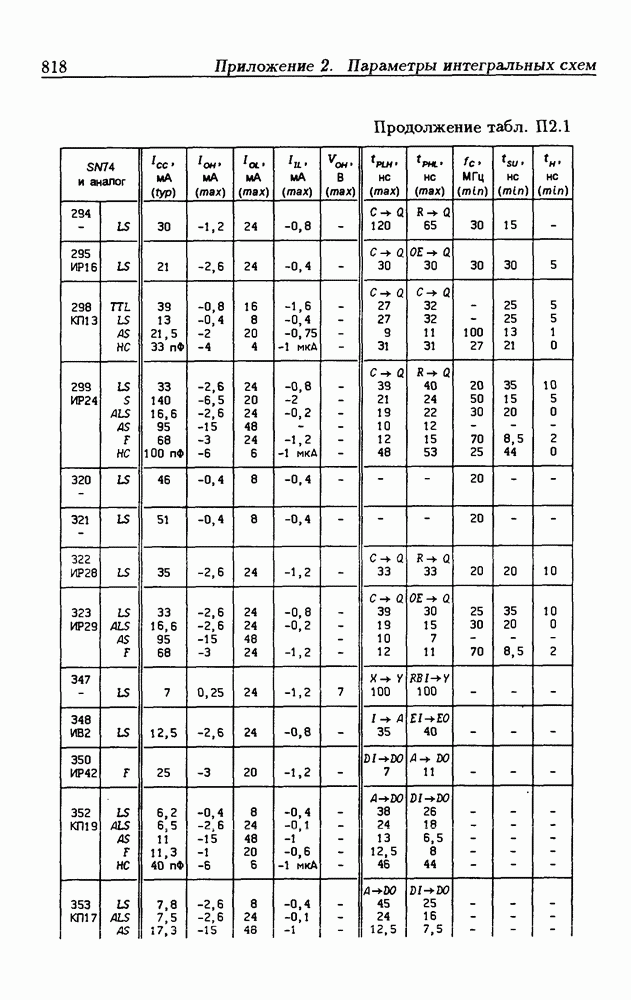
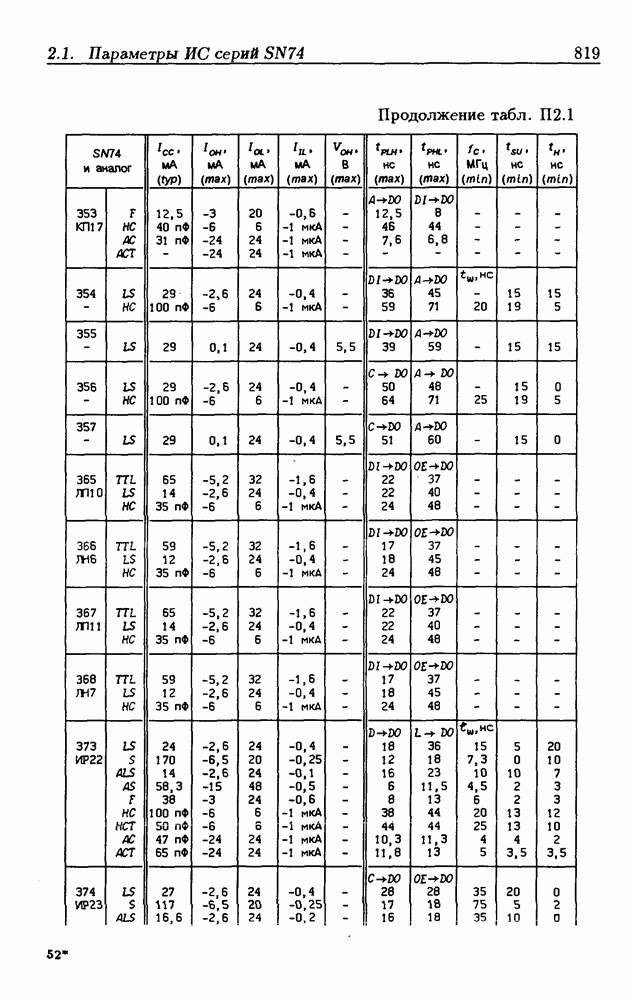
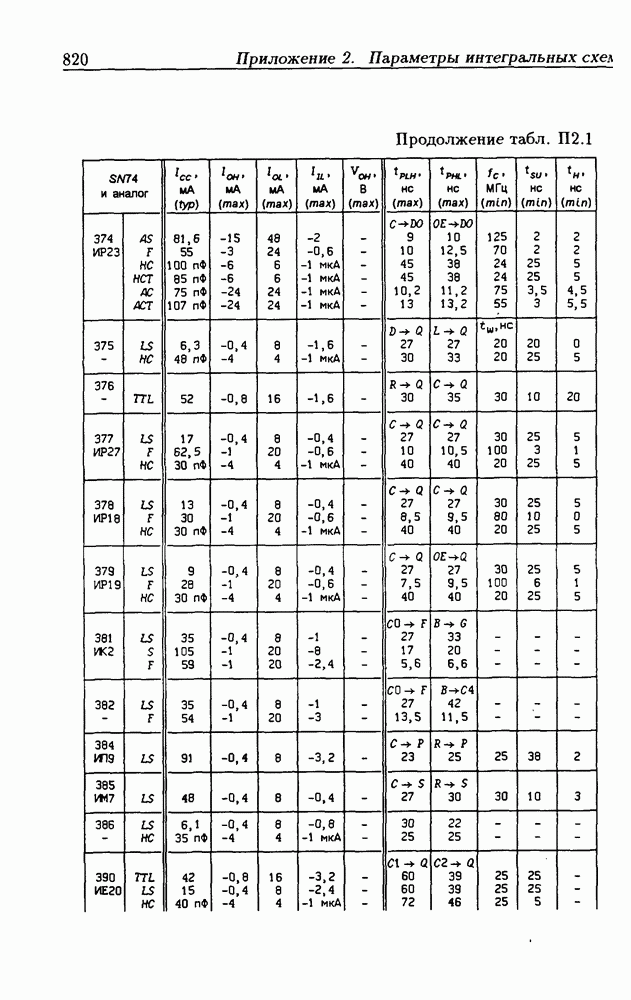
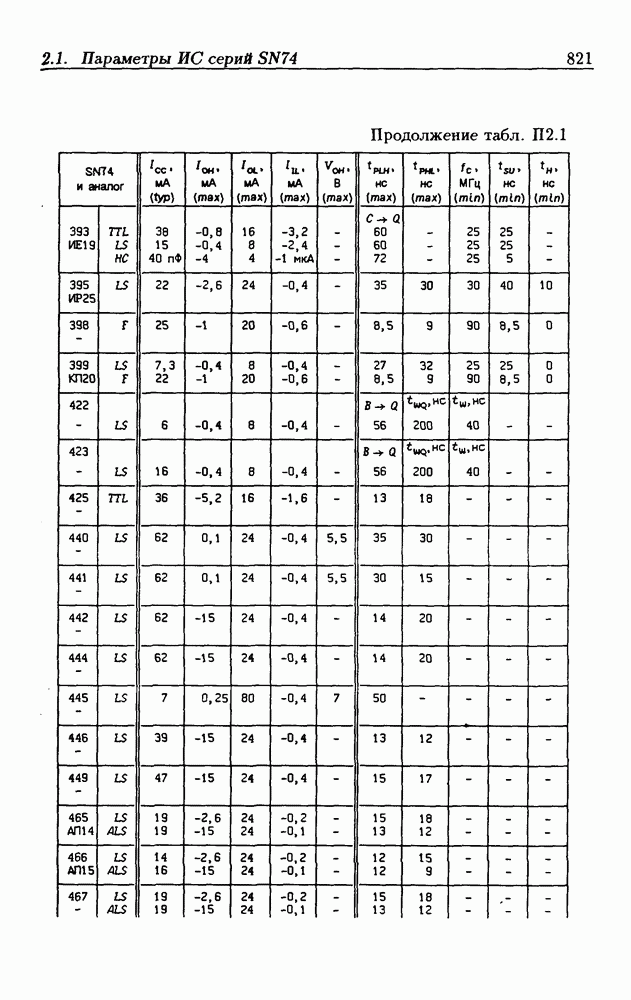
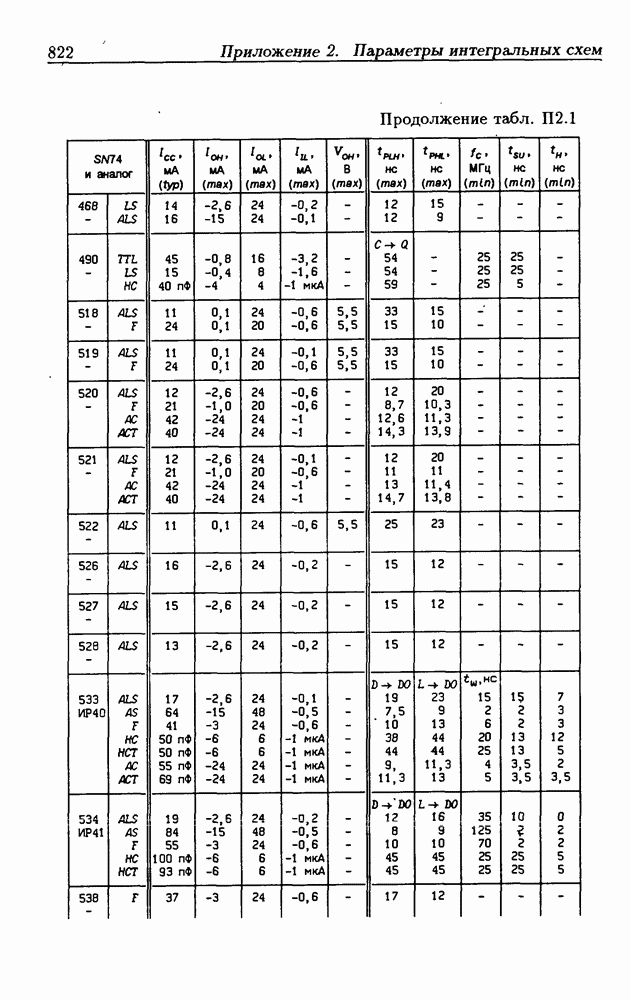
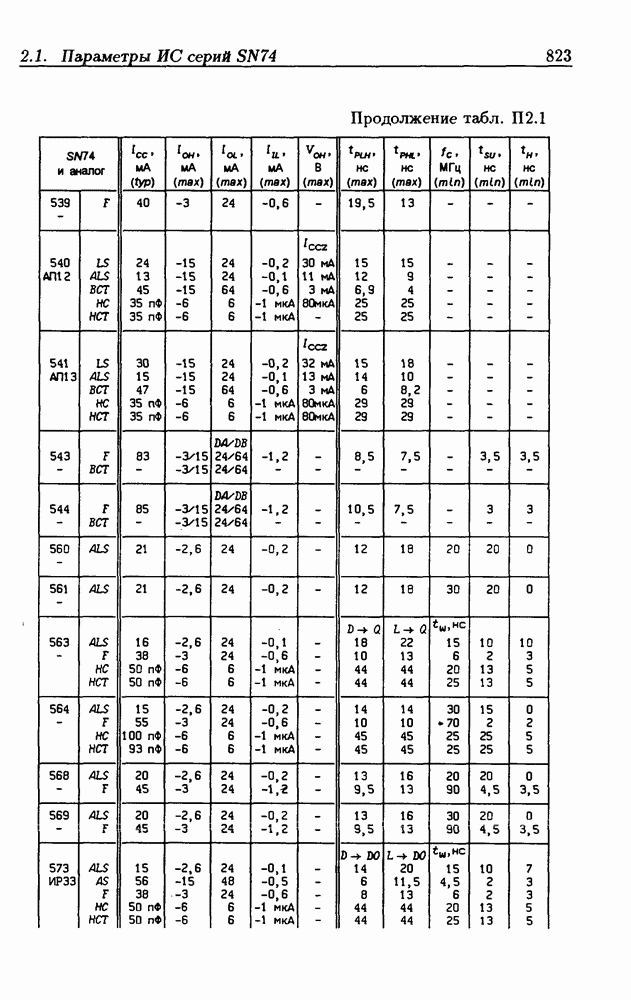
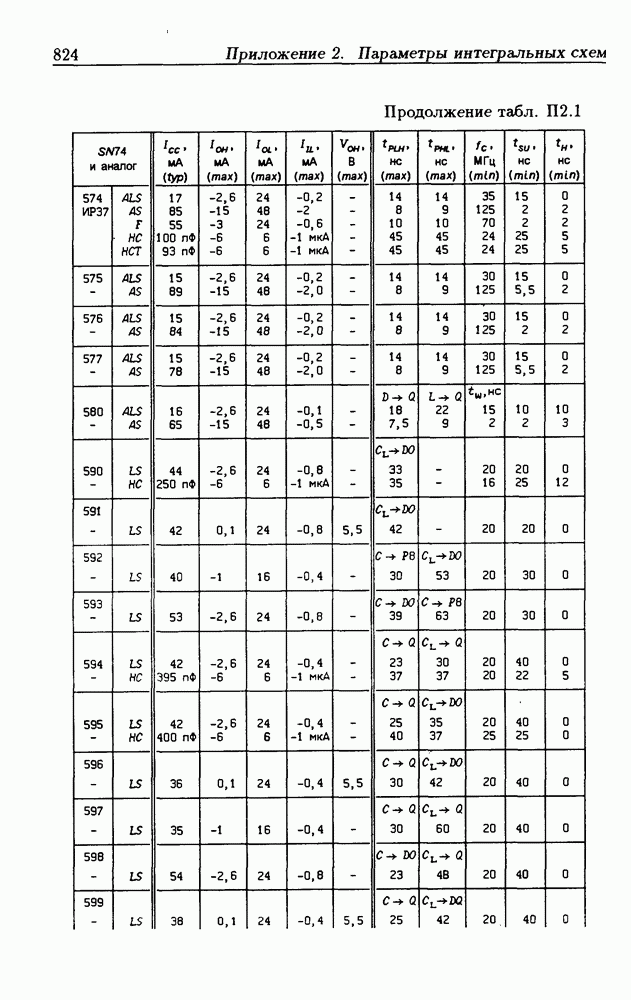
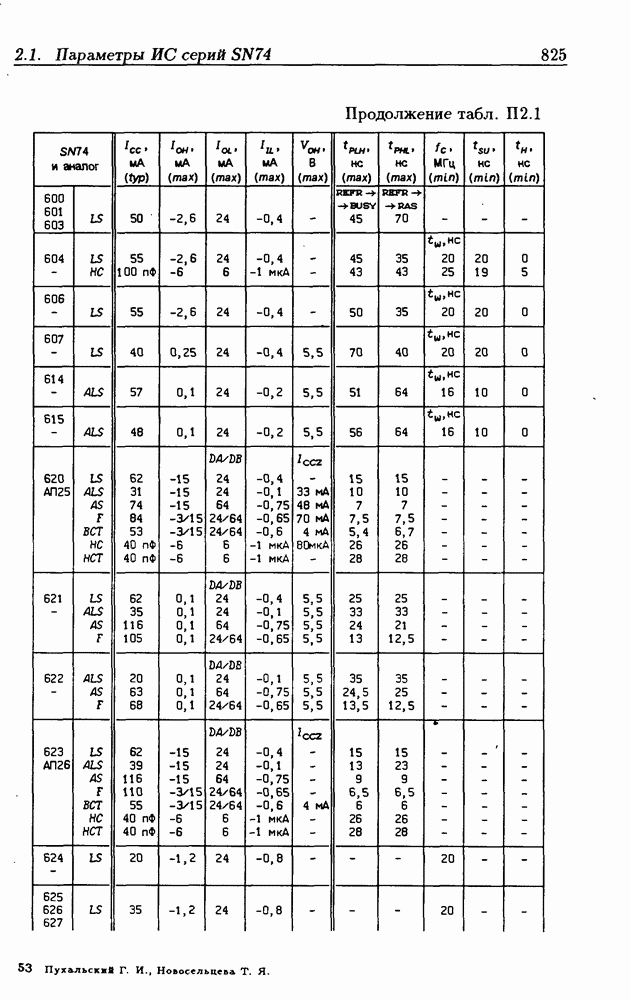
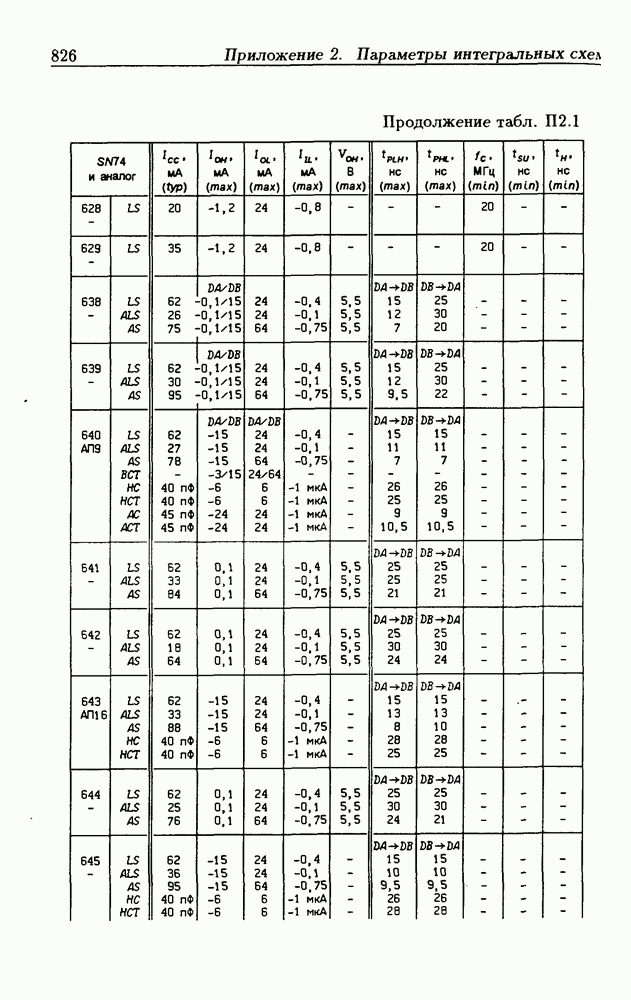
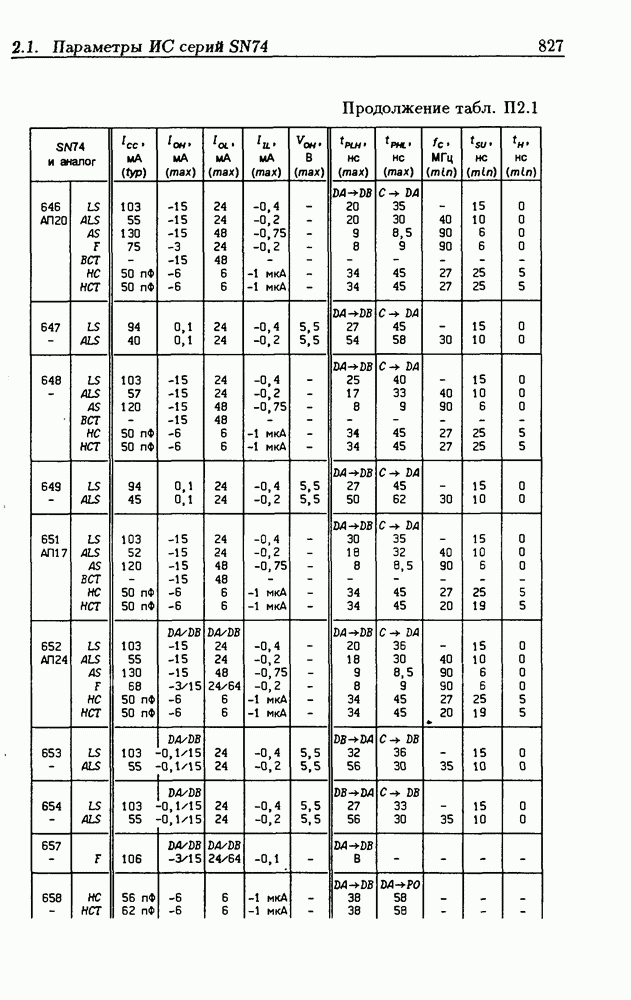
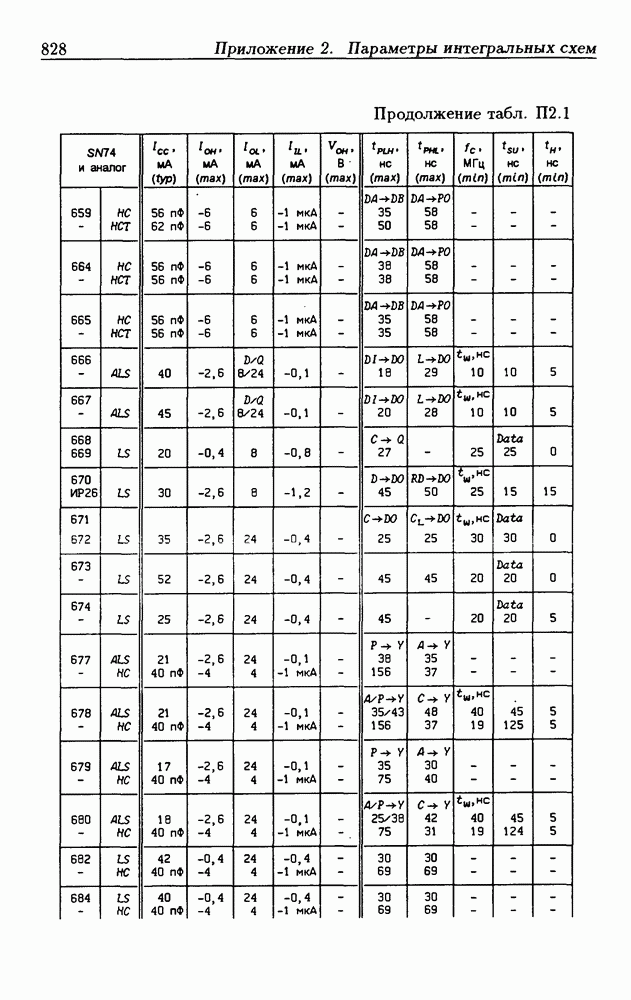
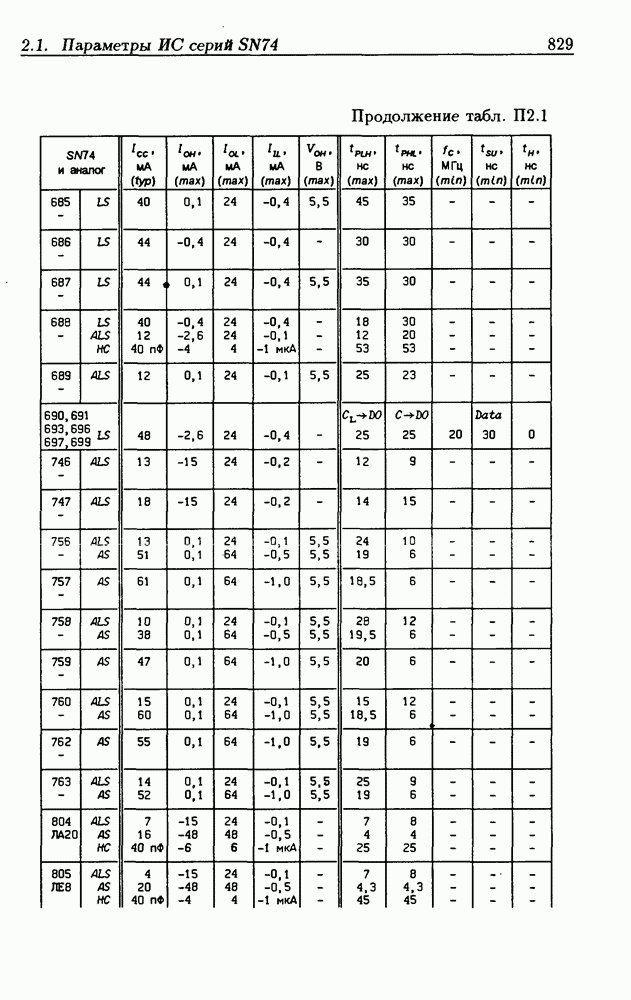
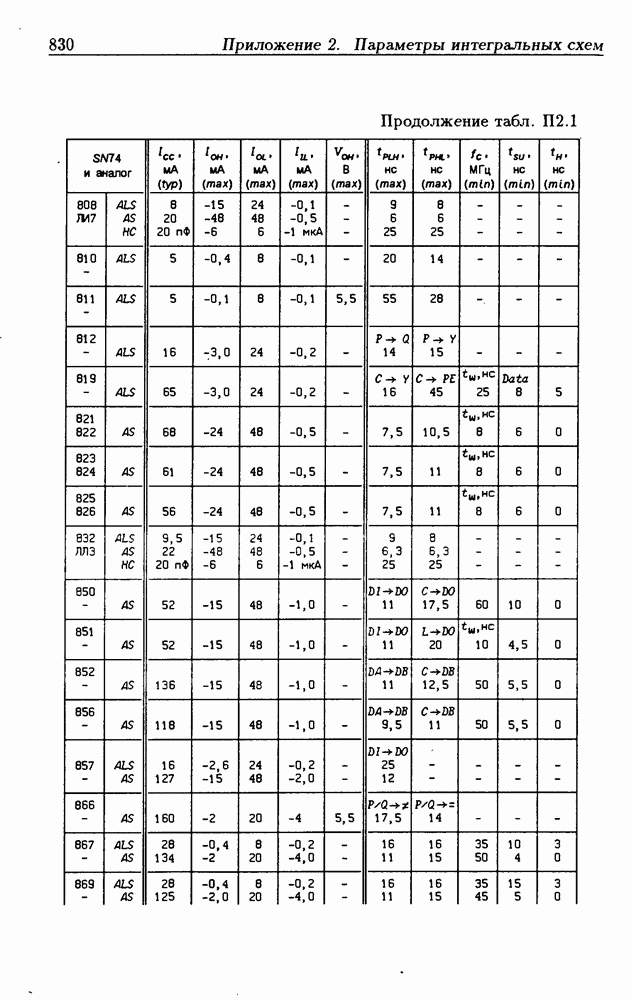
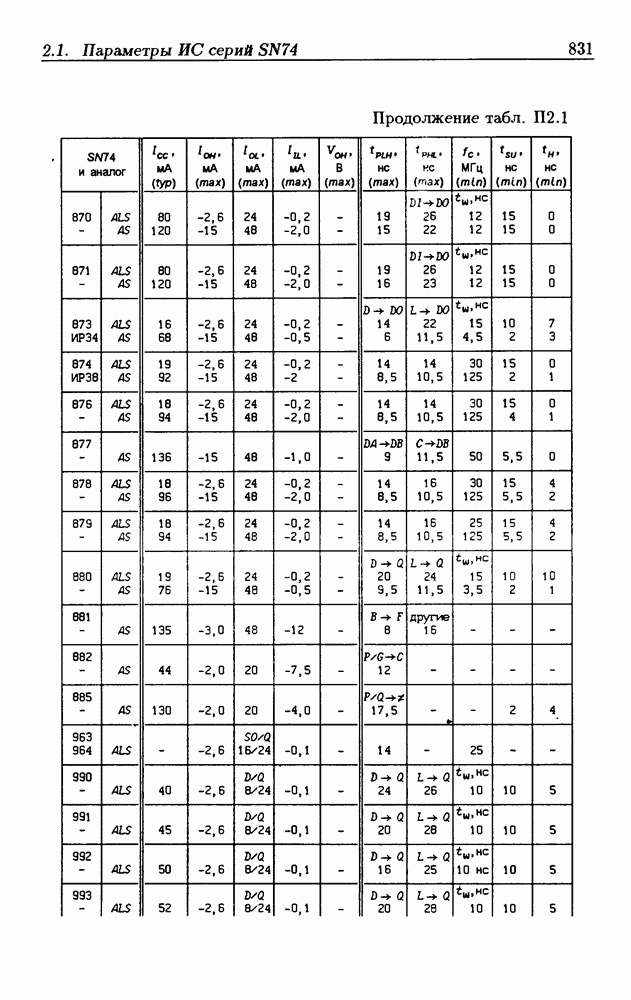
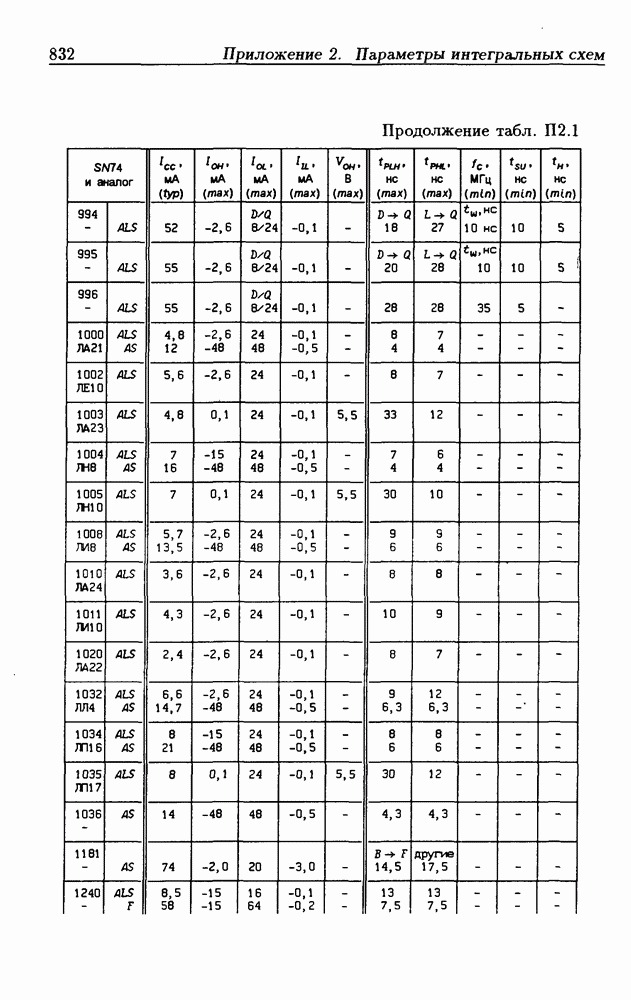
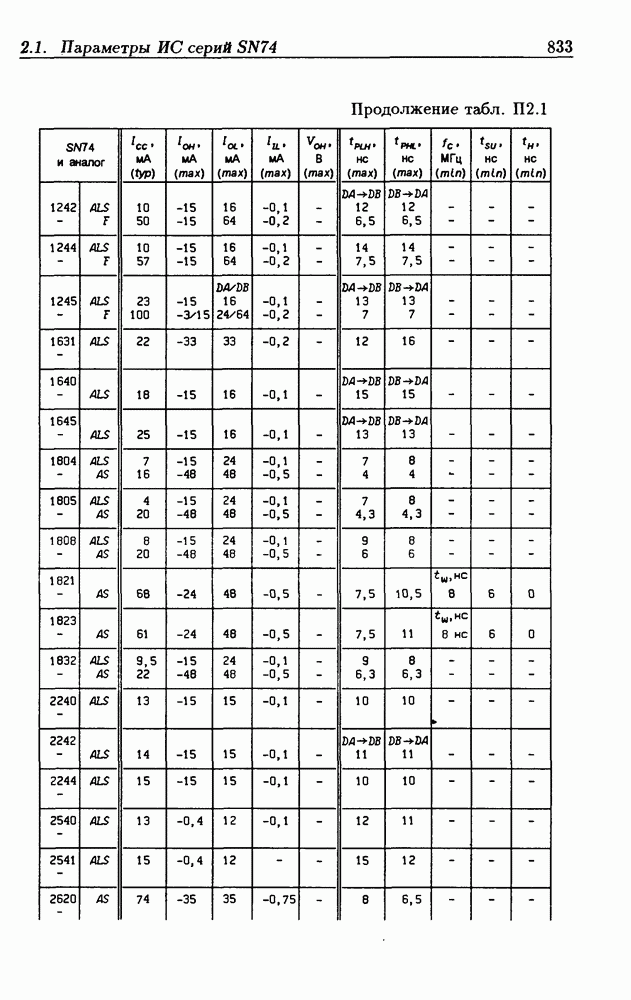
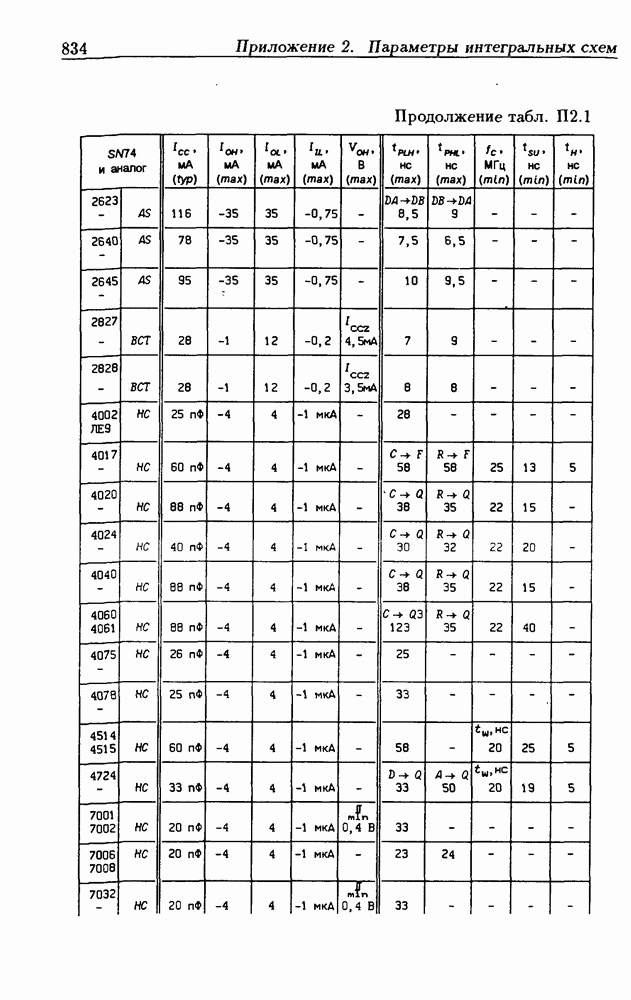
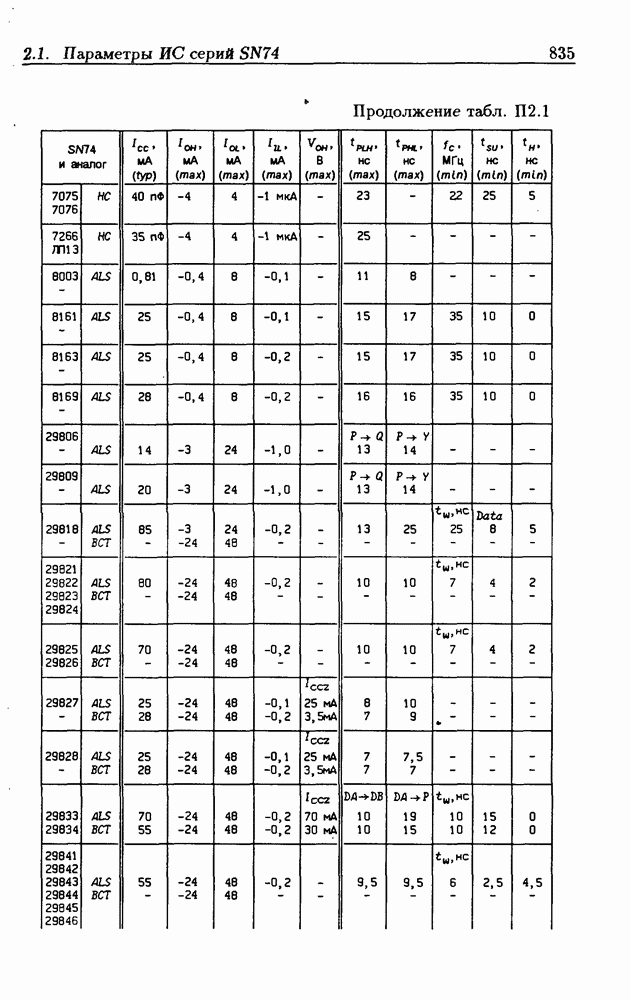
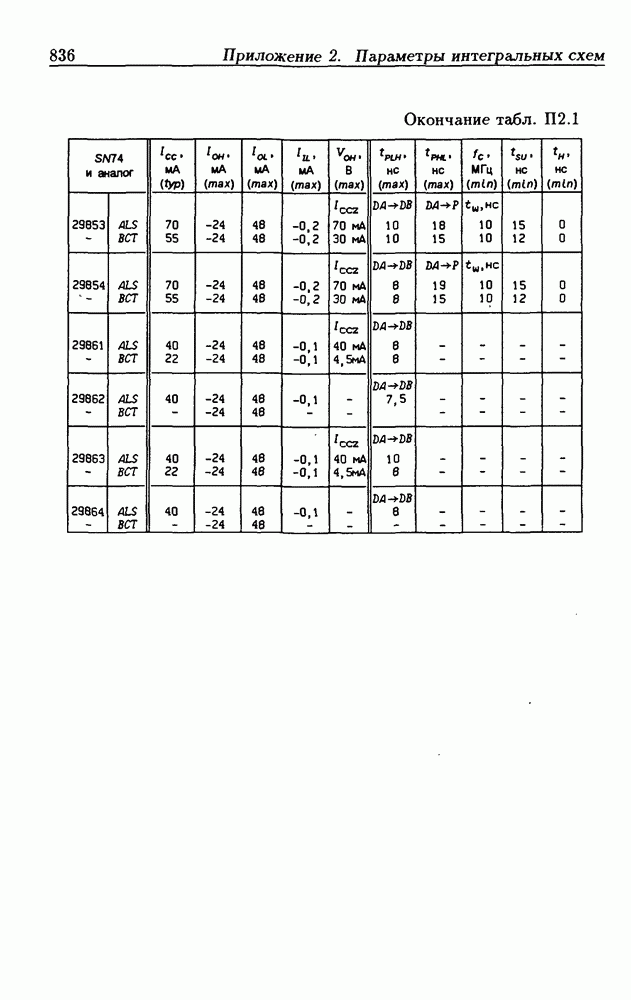
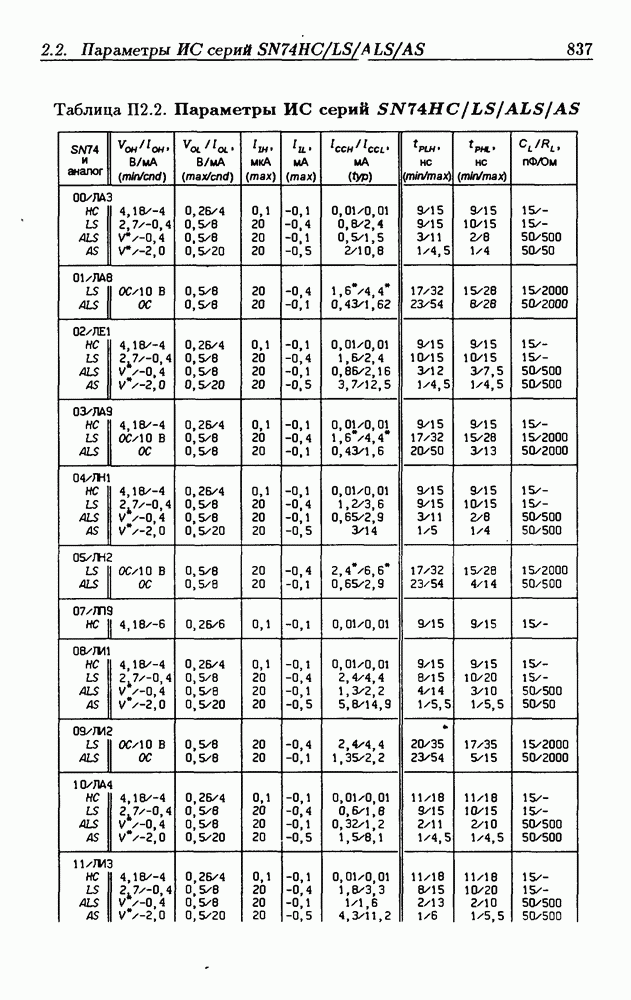
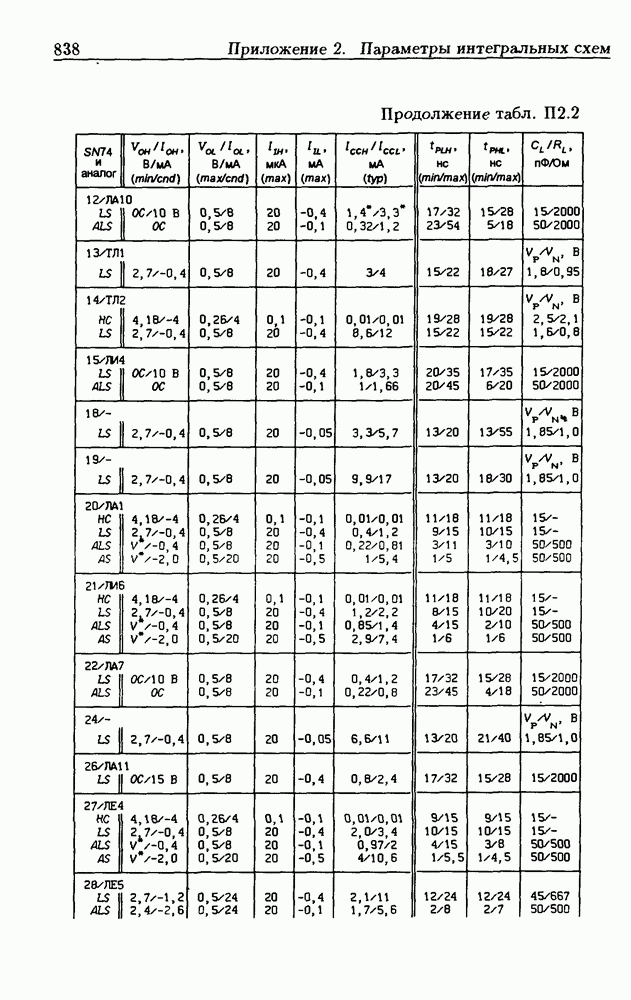
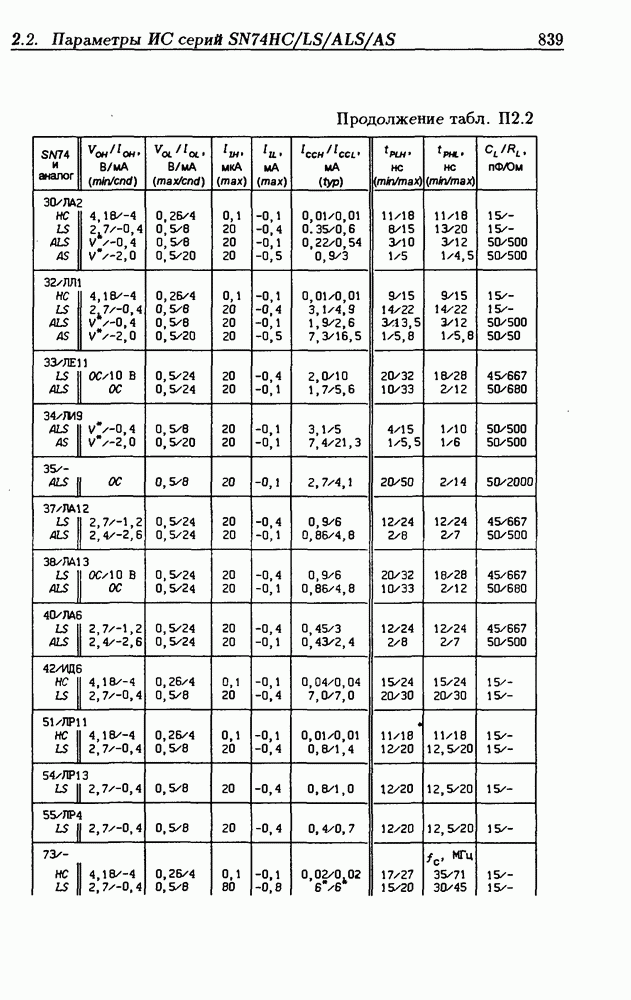
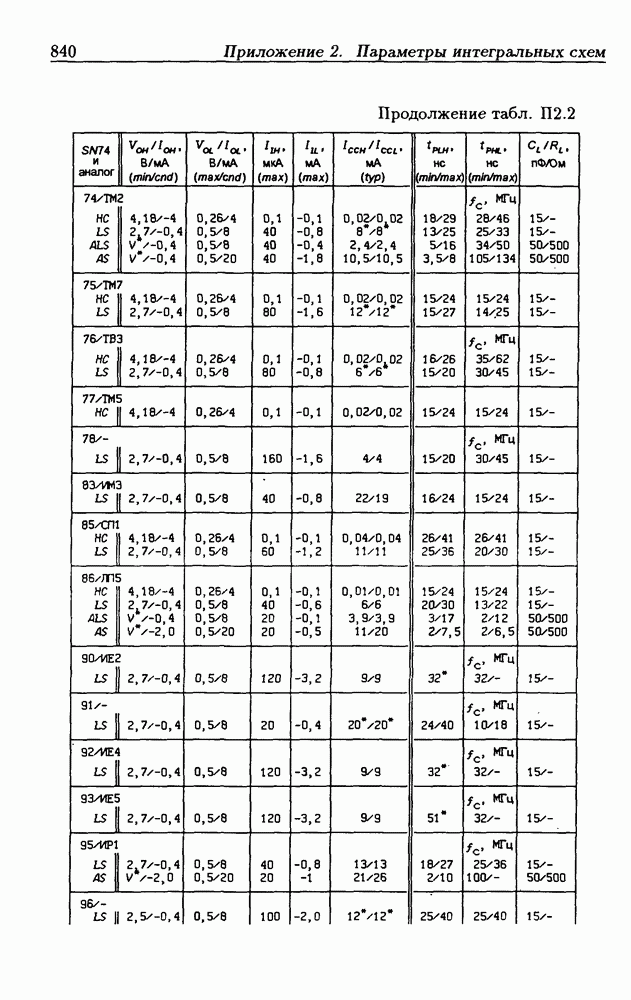
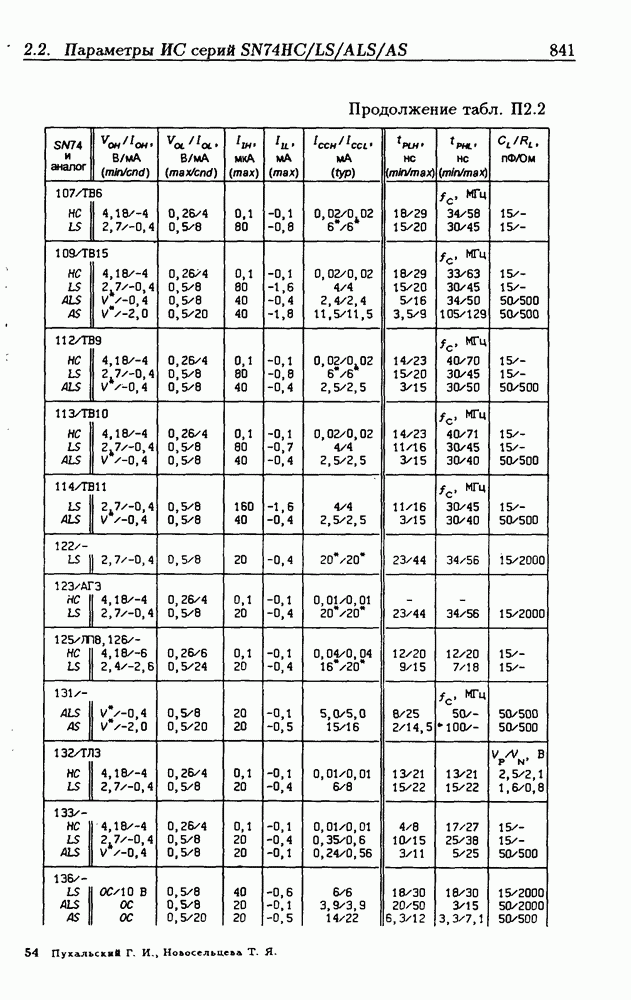
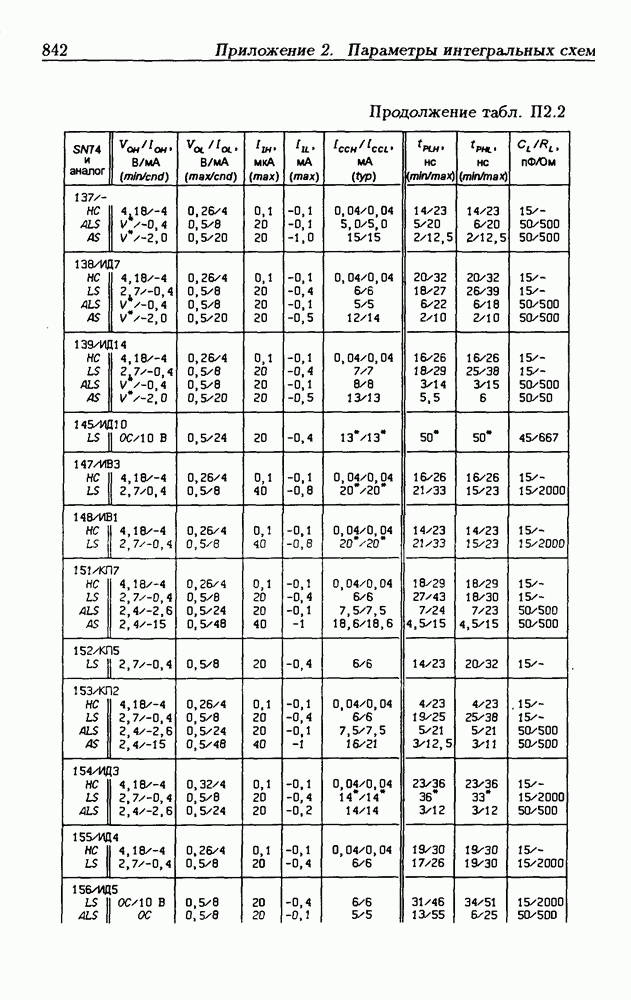
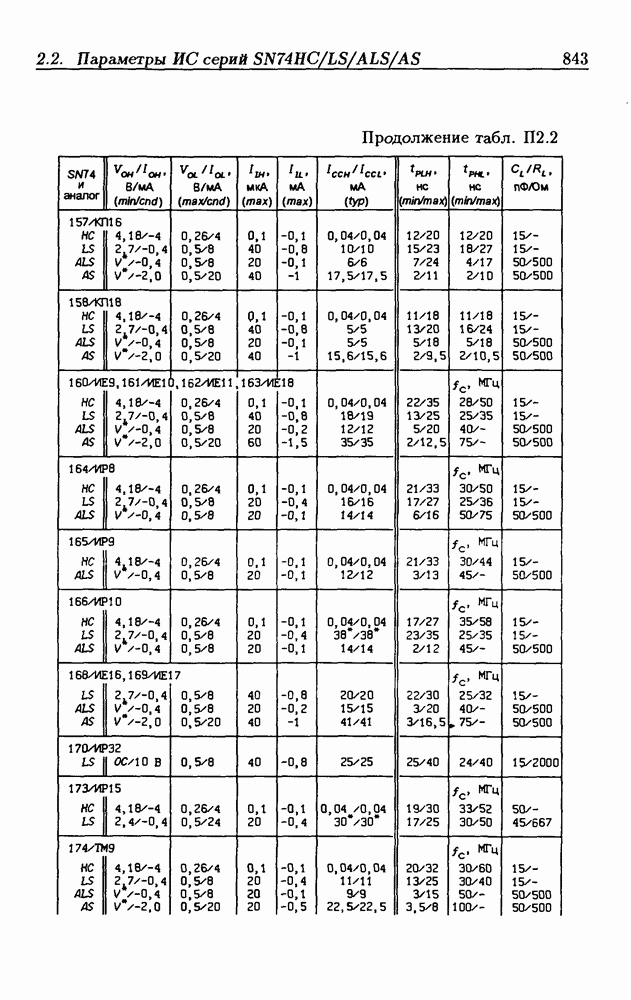
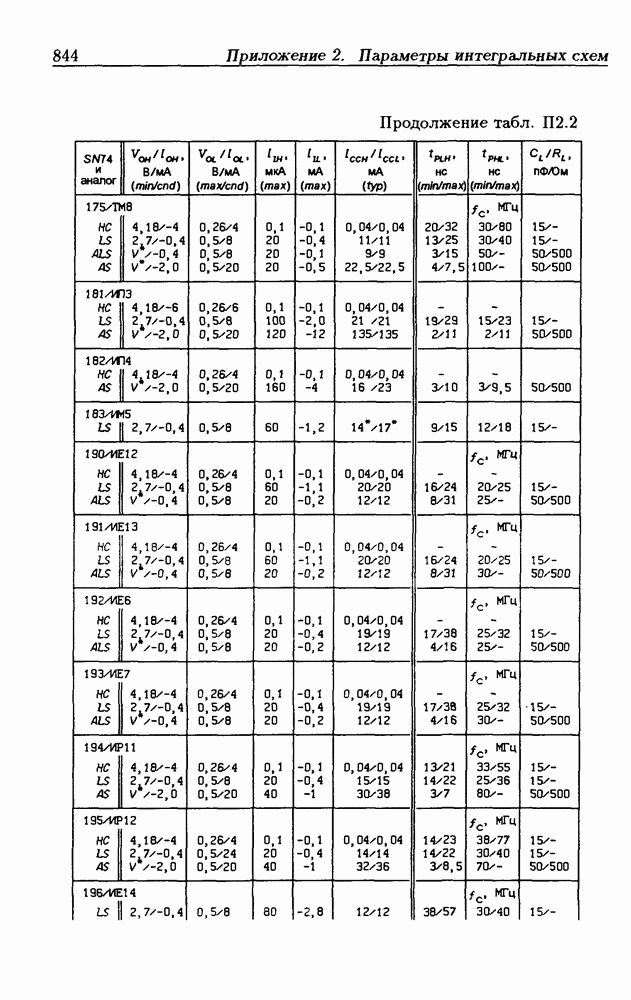
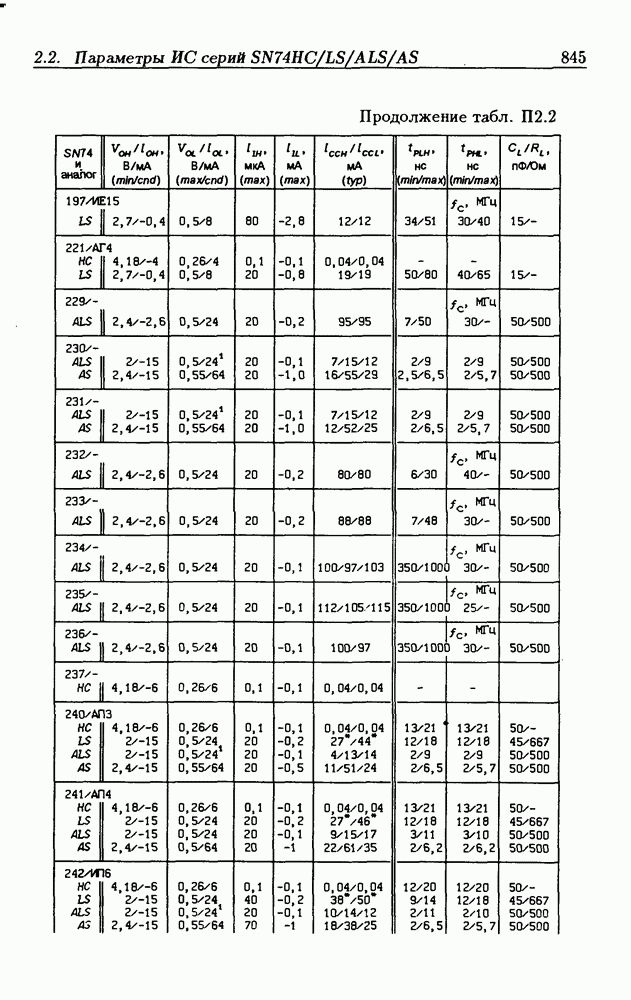
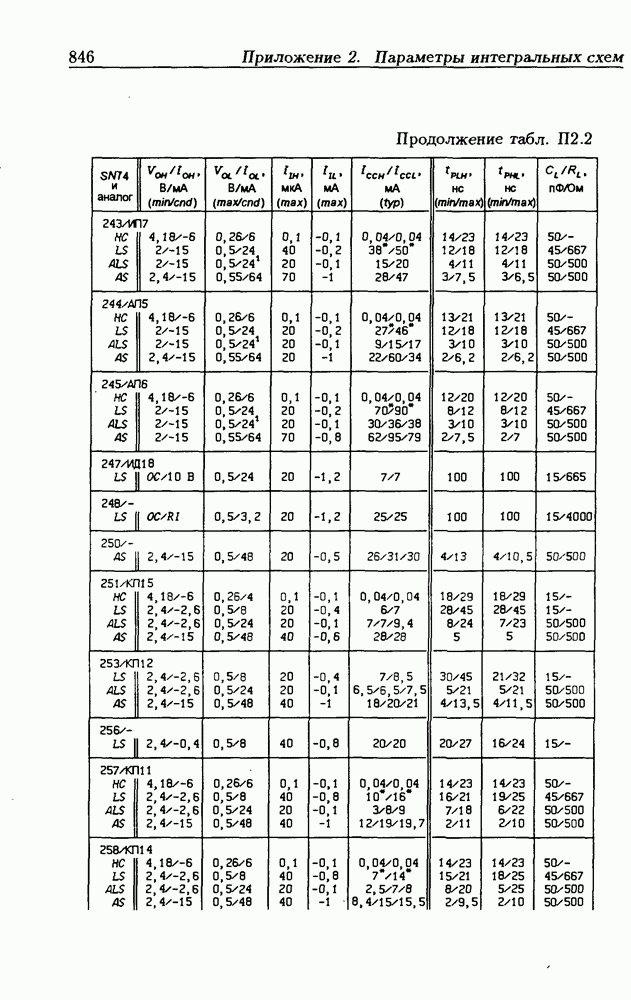
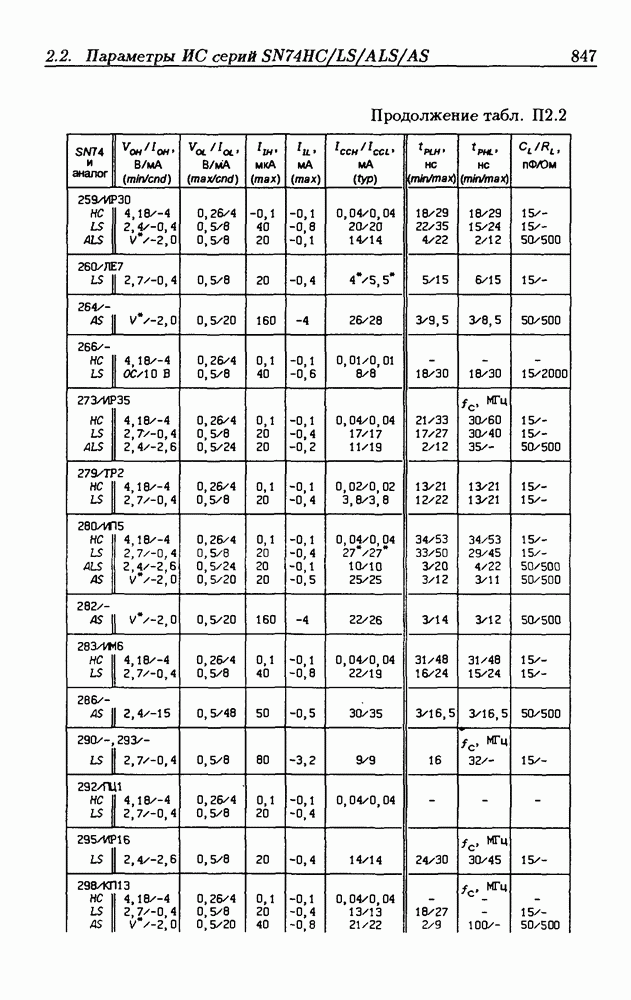
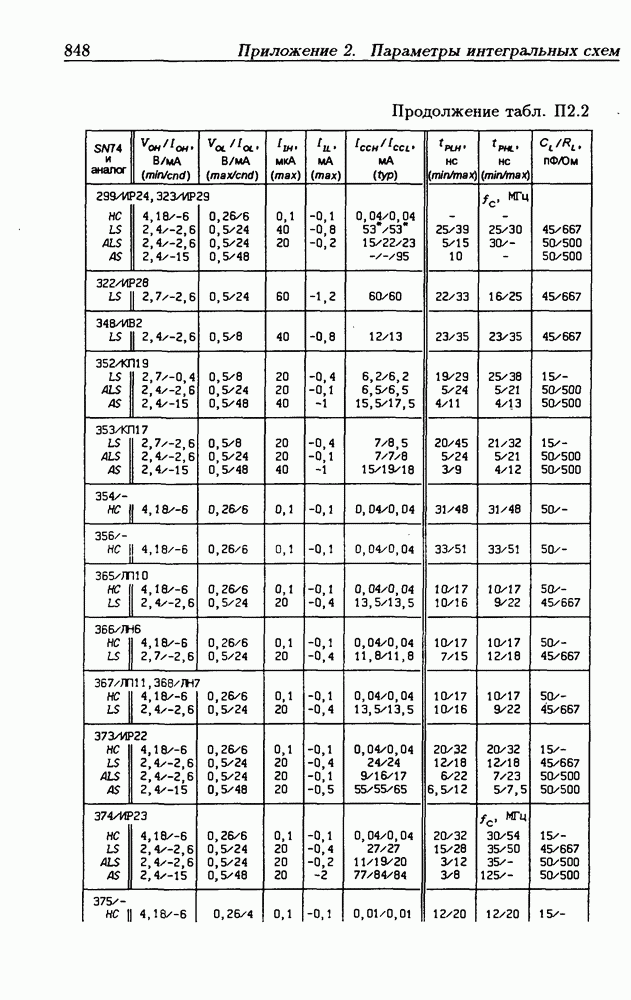
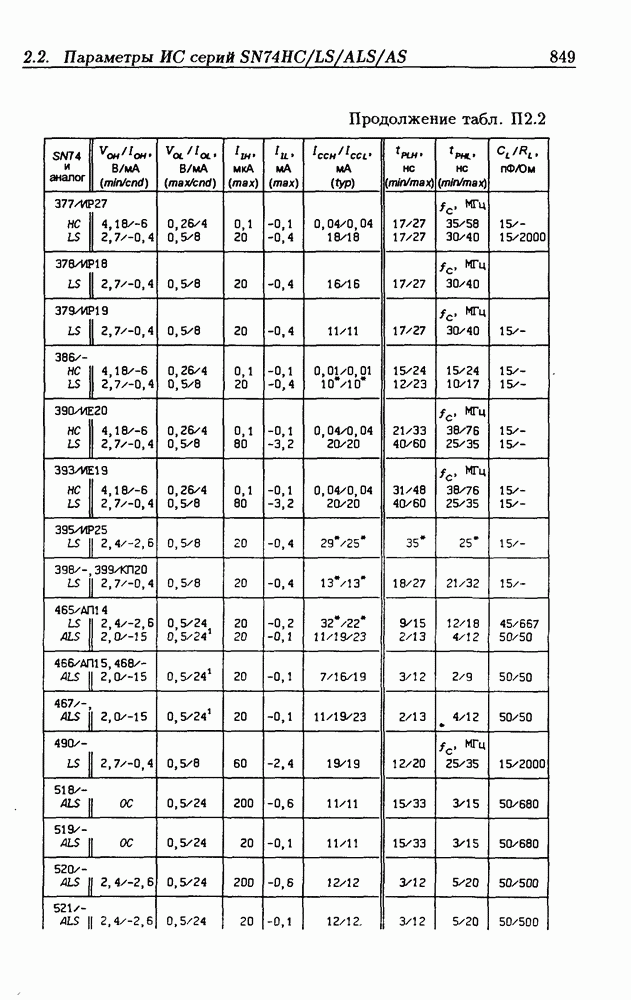
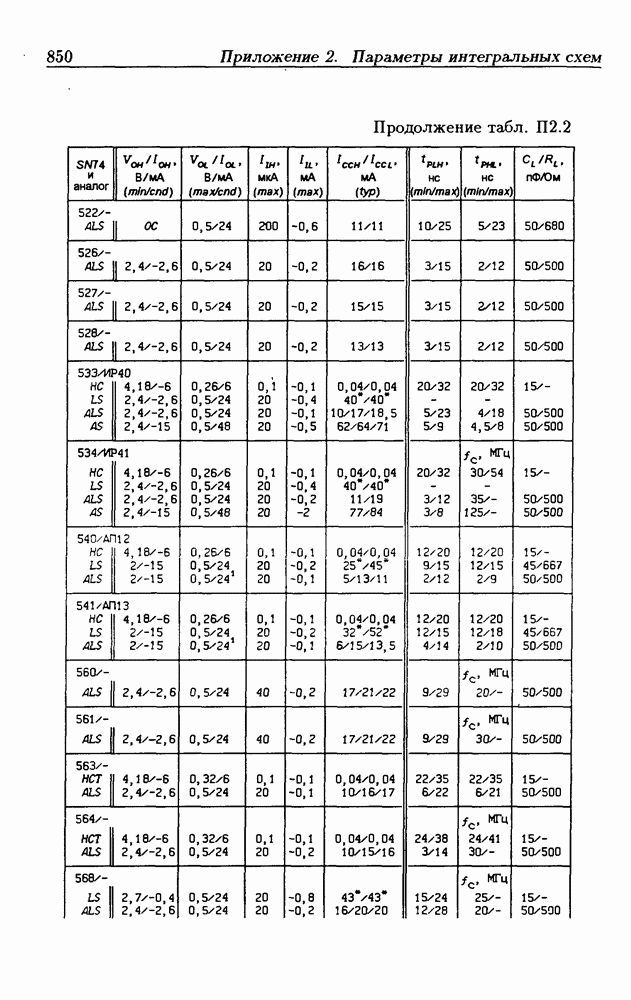
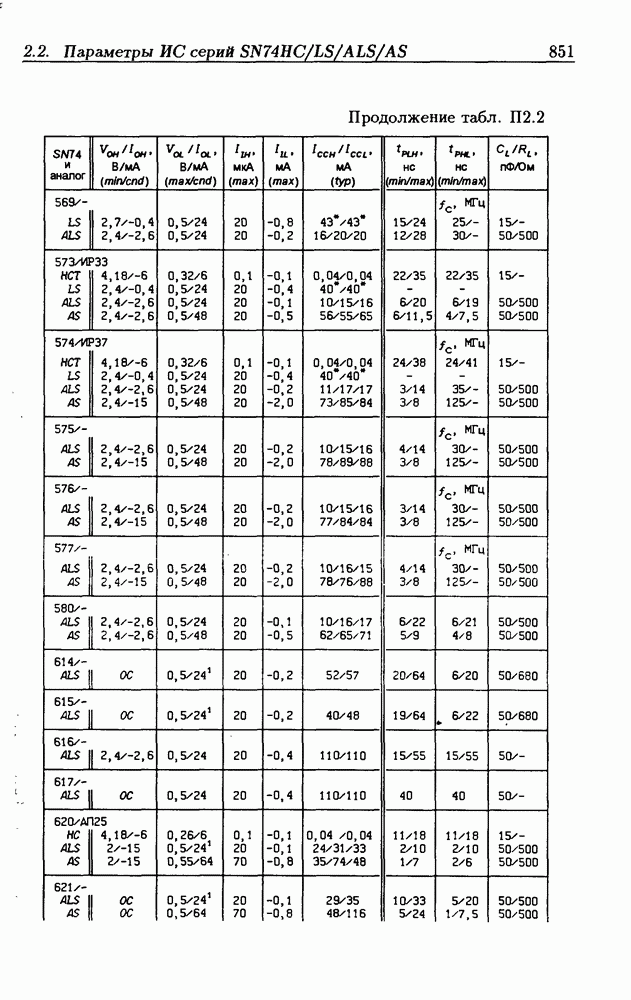
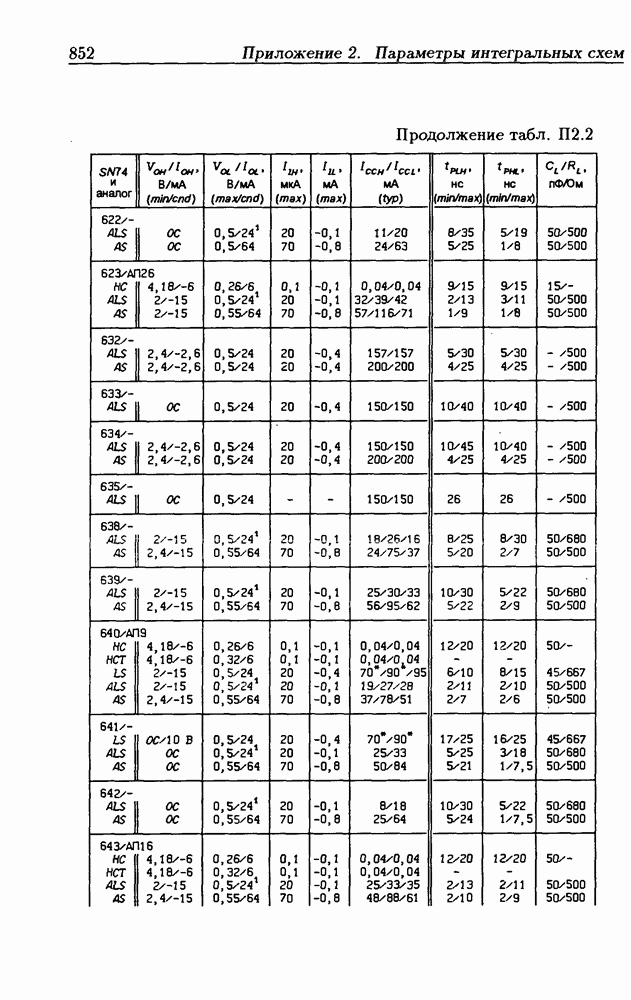
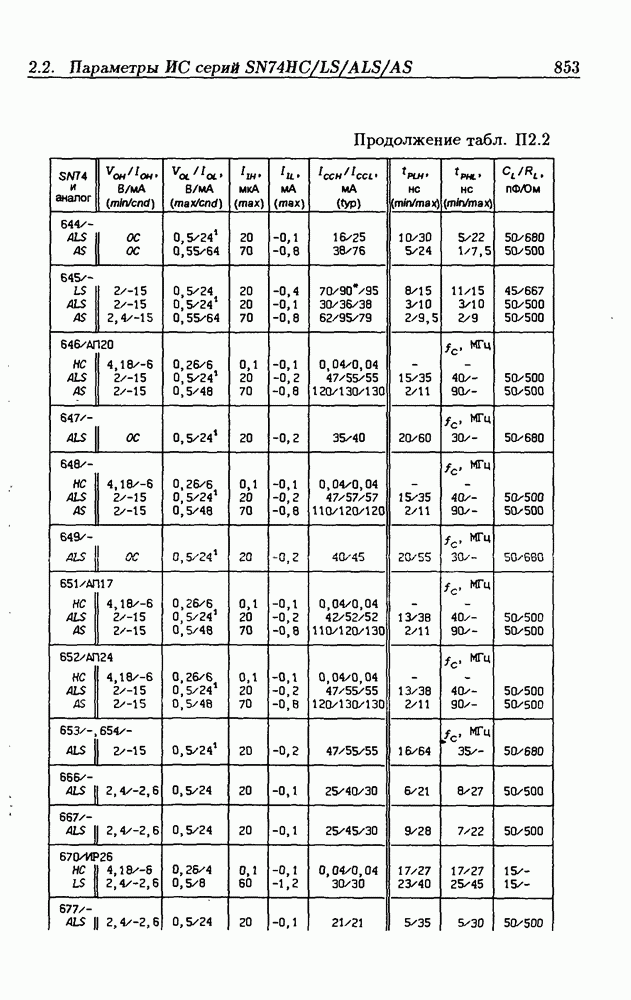
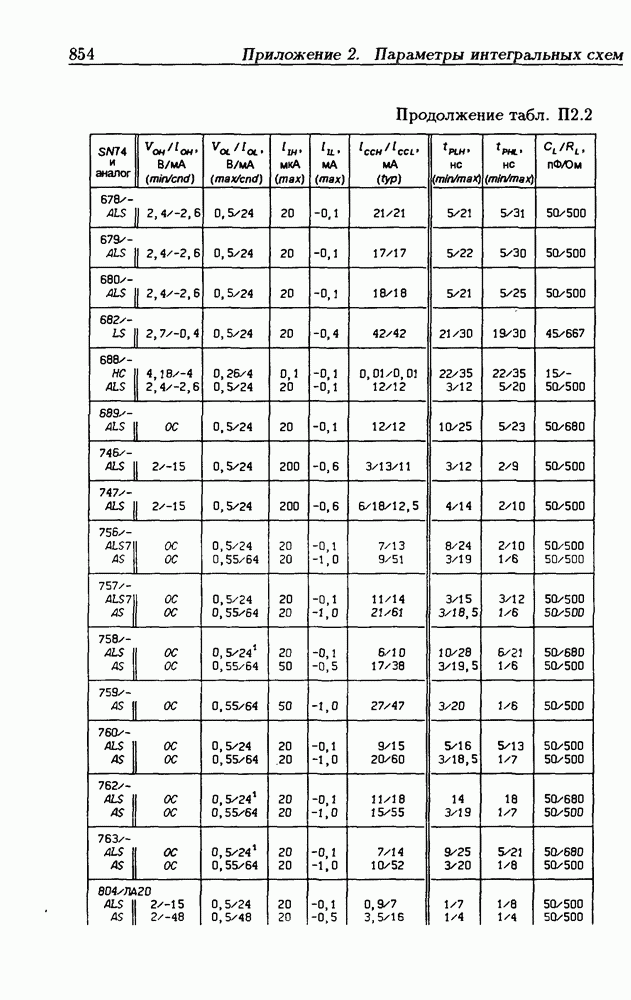
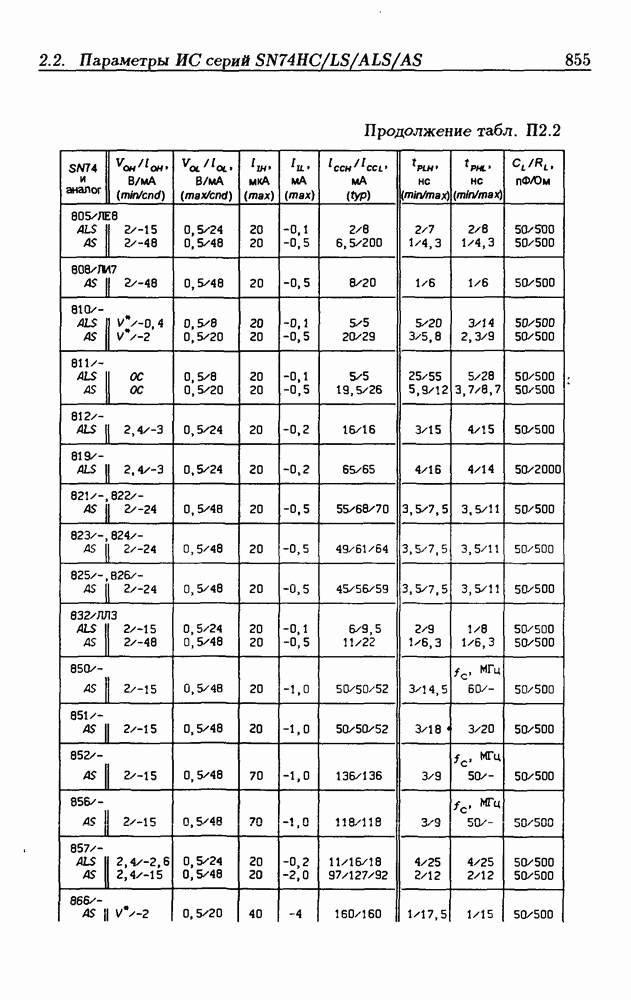
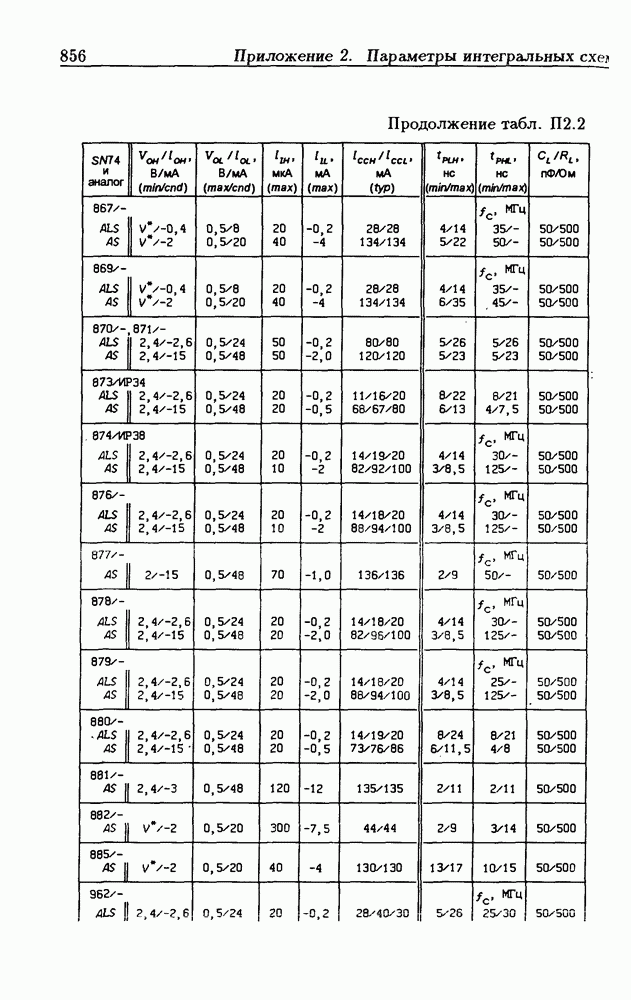
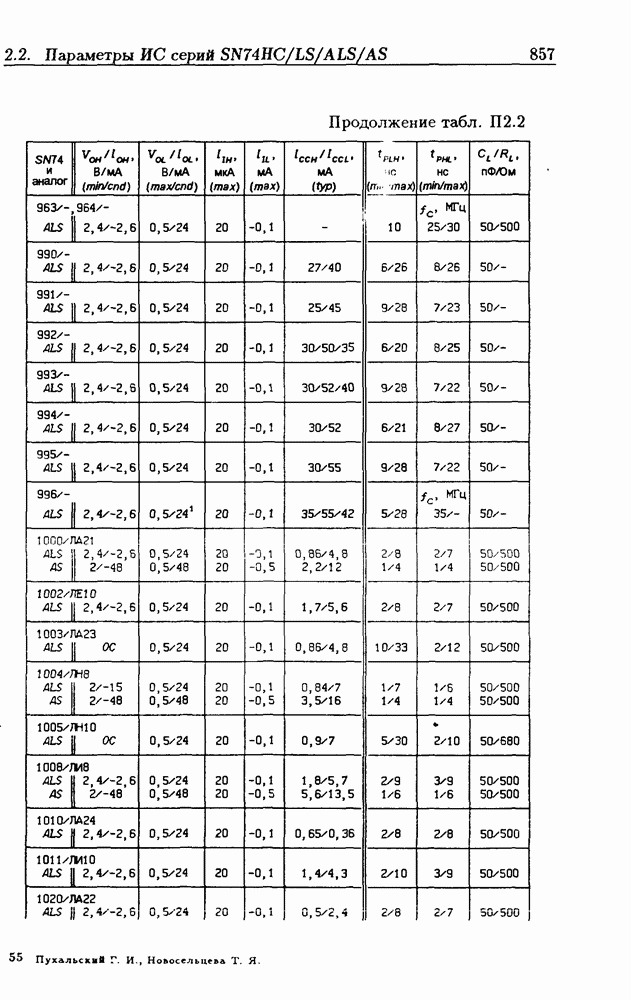
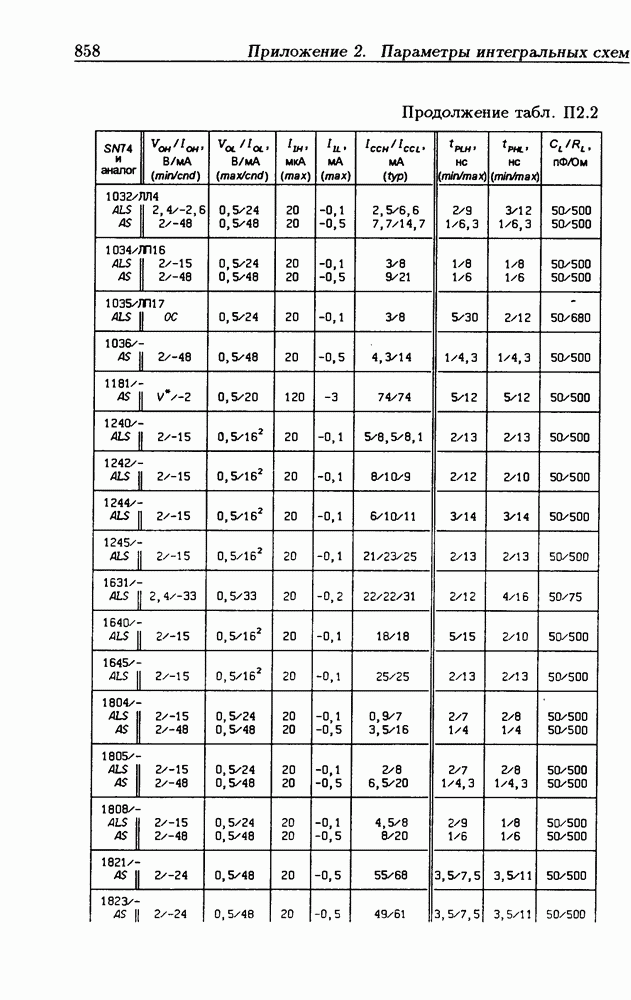
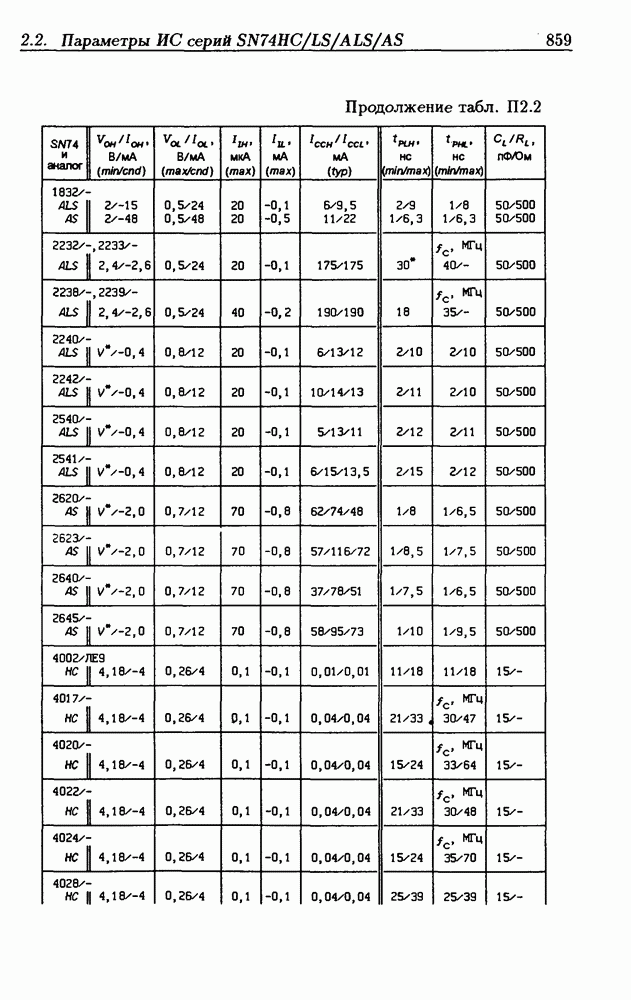
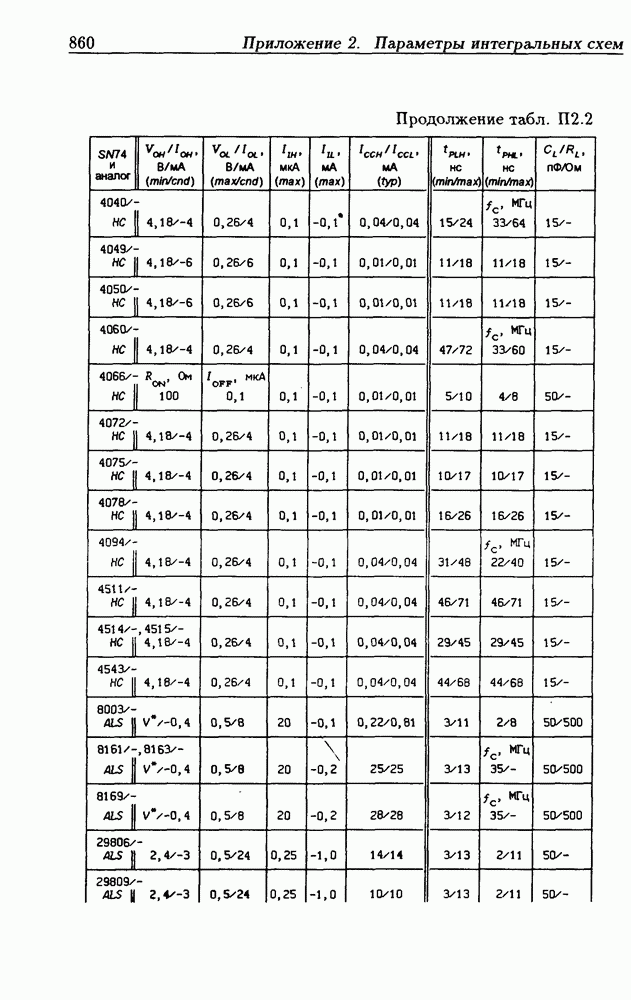
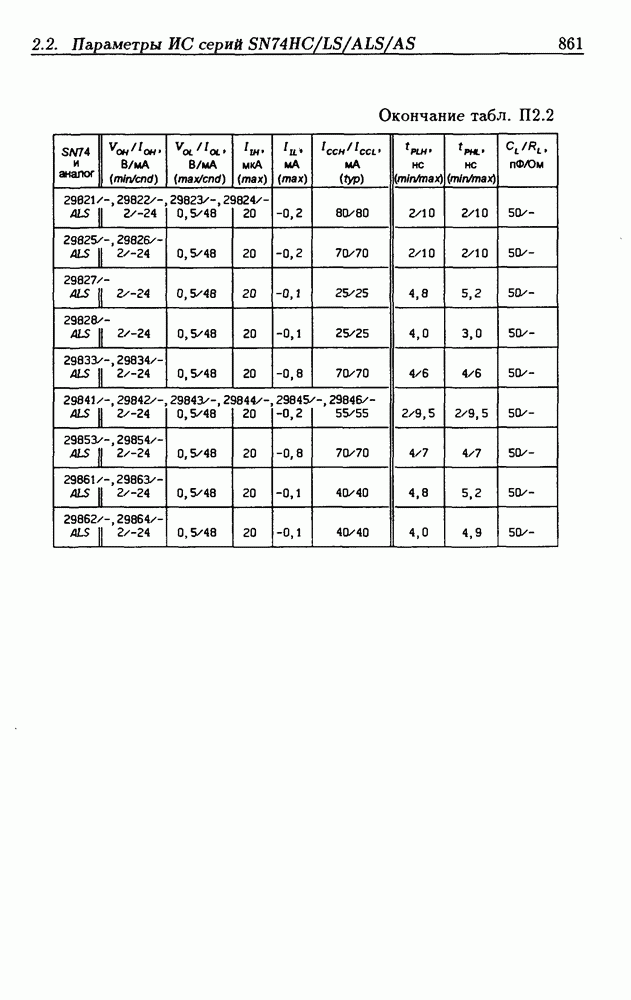
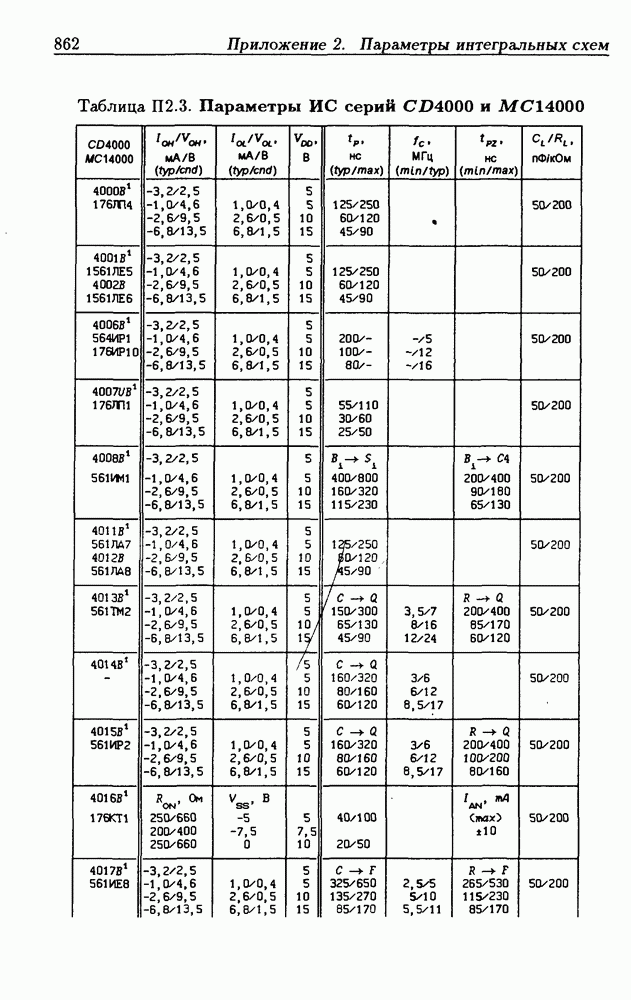
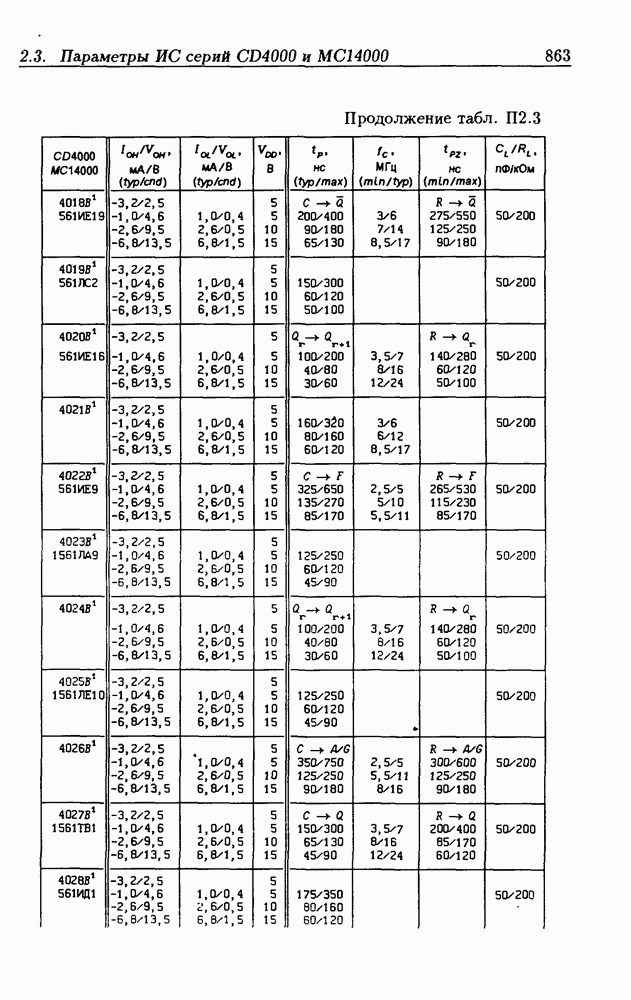
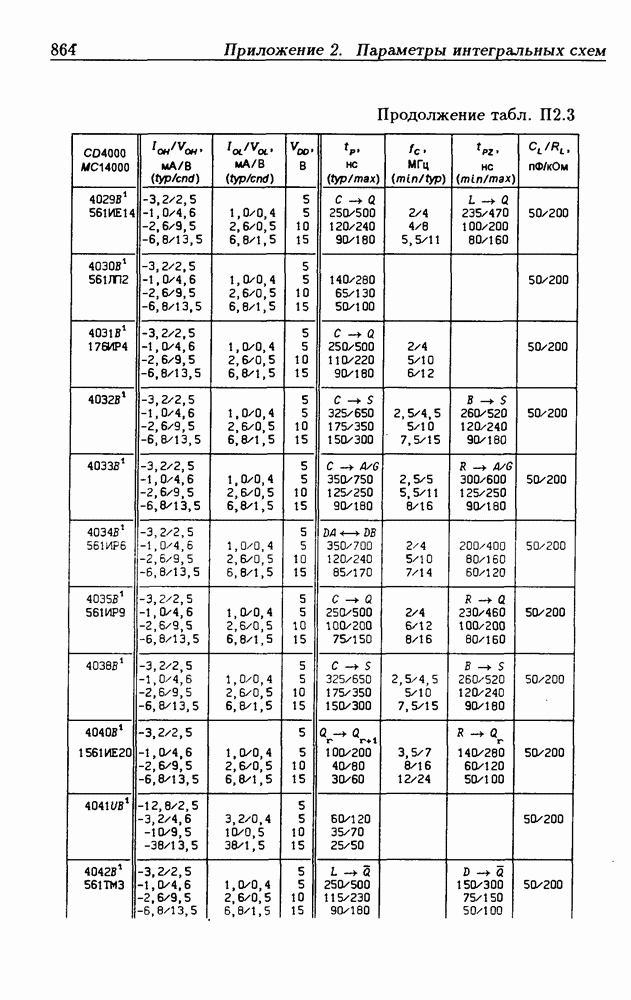
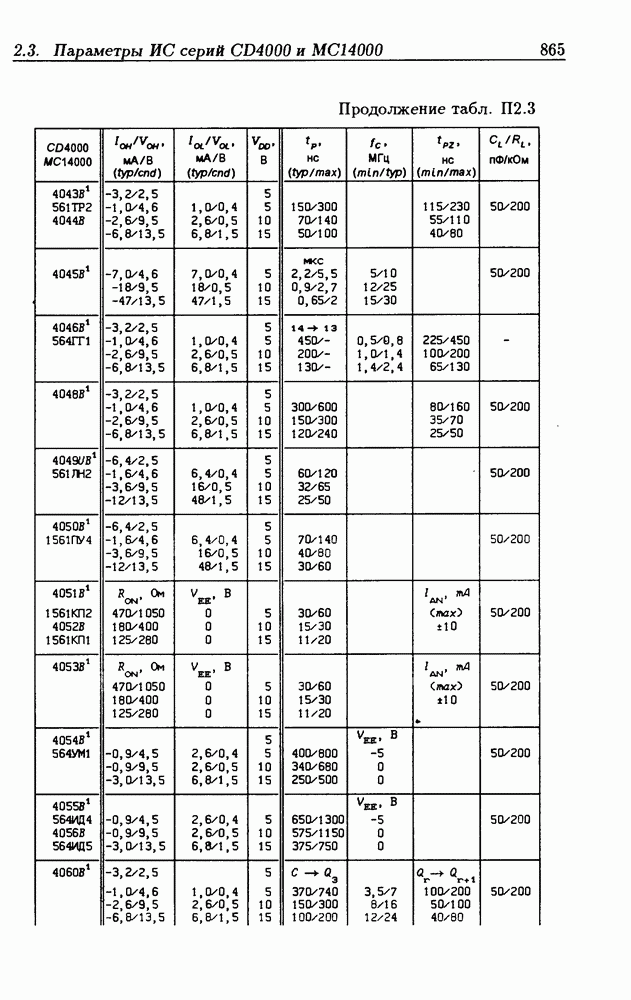
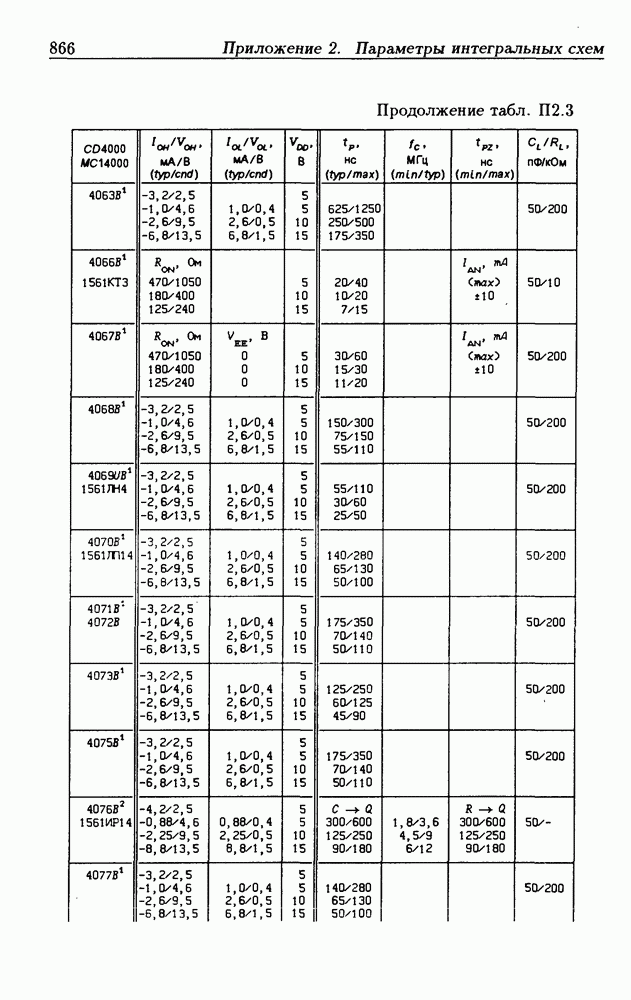
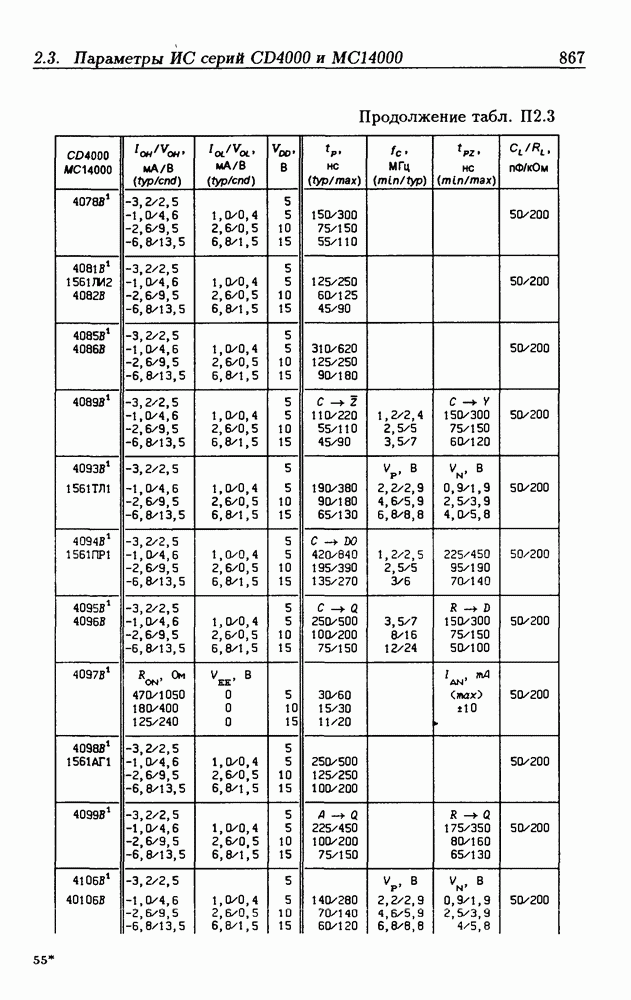
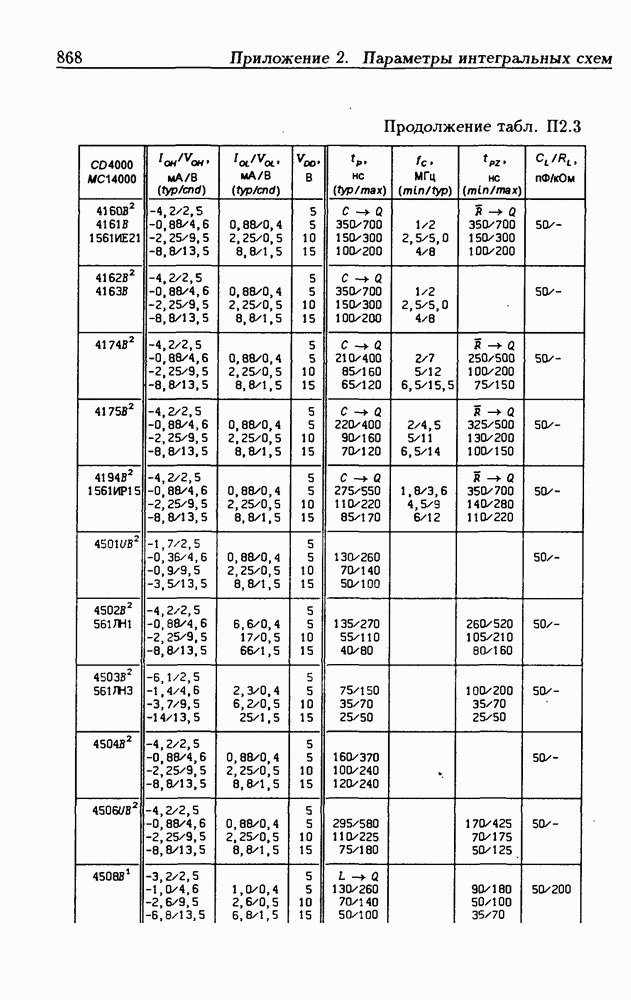
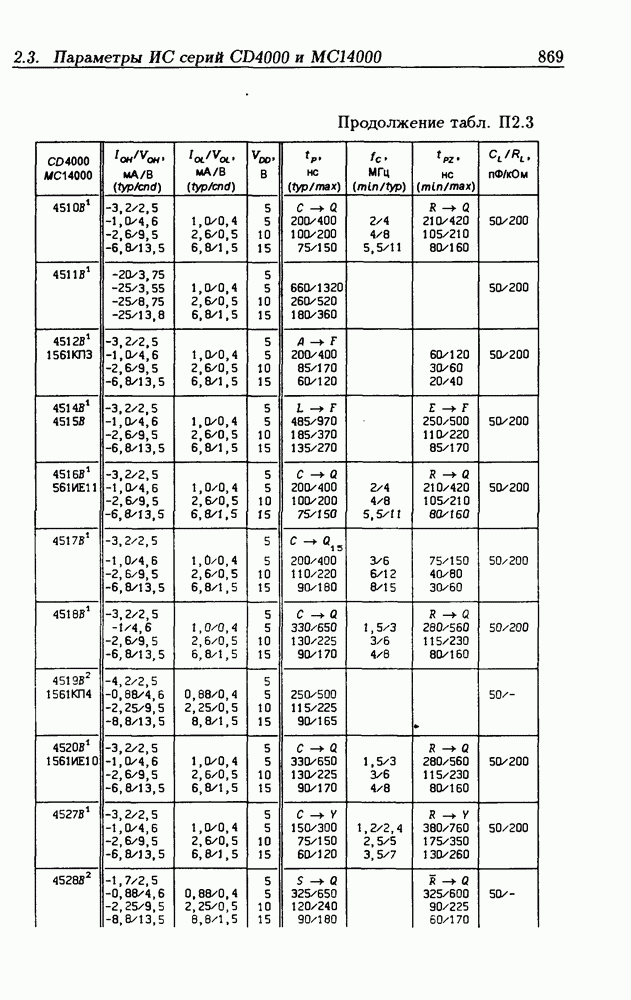
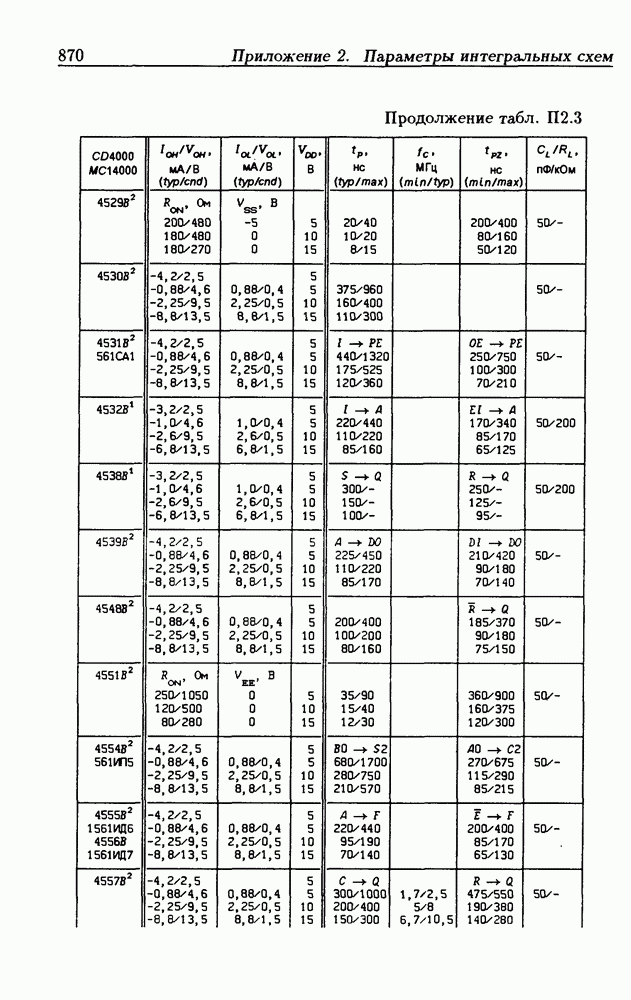
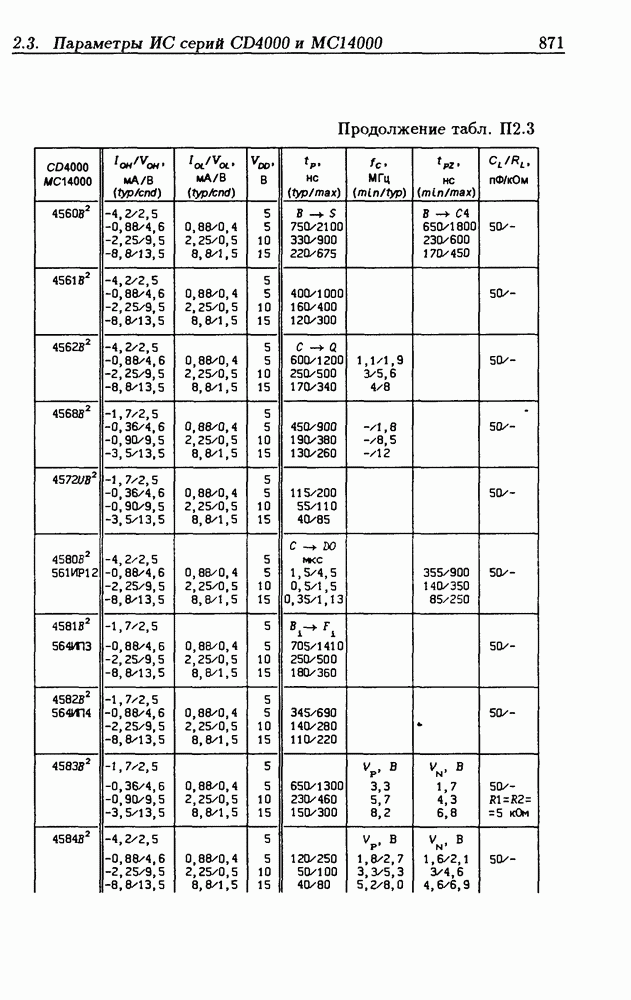
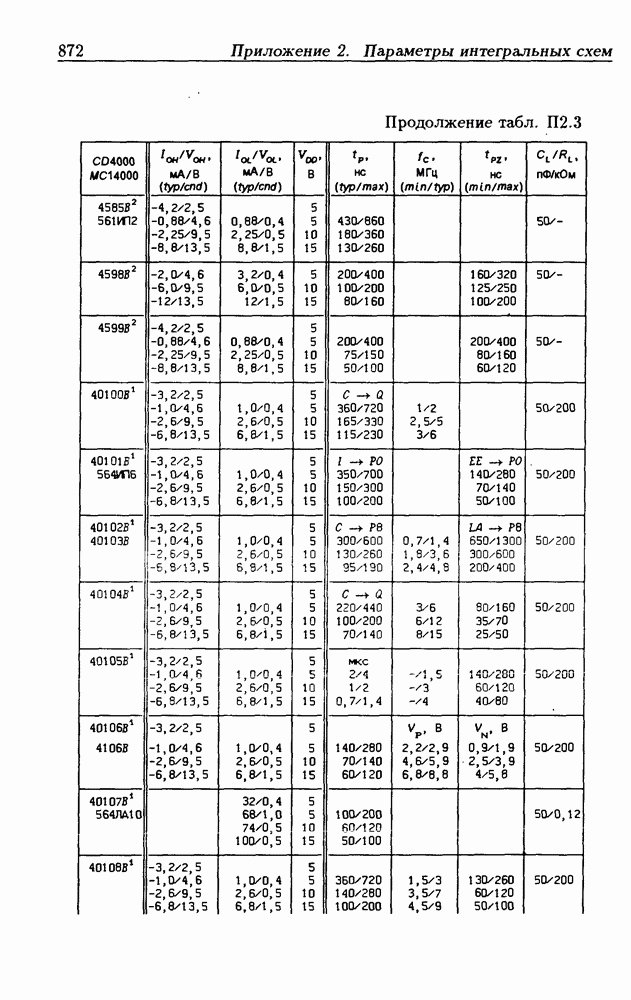
- Приложение 2. Параметры интегральных схем