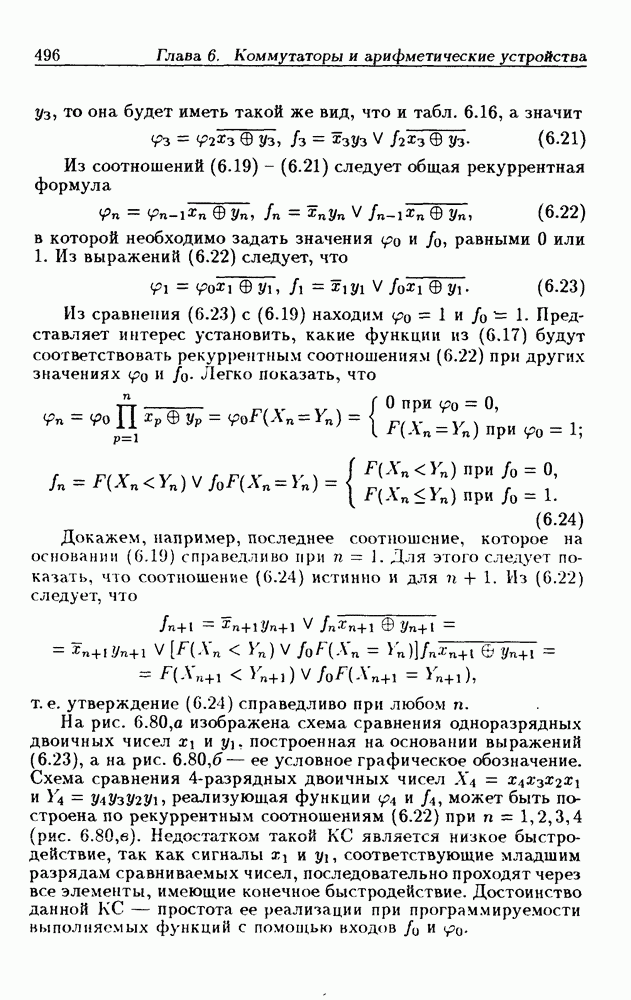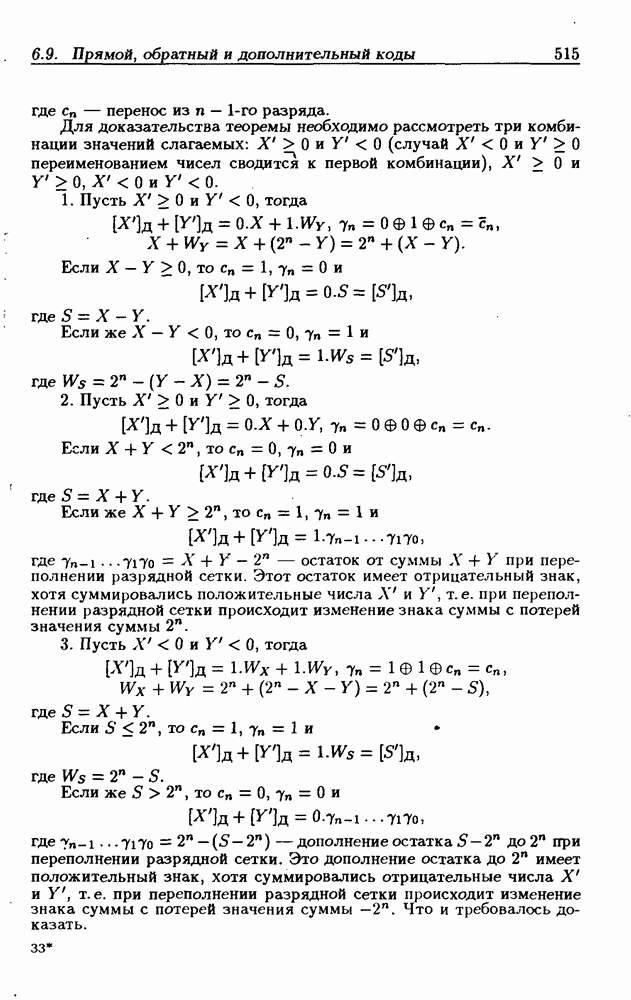| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.8. Схемы сравнения двоичных чисел
Пусть заданы два  -разрядных двоичных числа
-разрядных двоичных числа

где  старшие разряды этих чисел. Соотношения между числами
старшие разряды этих чисел. Соотношения между числами  описываются пятью функциями:
описываются пятью функциями:


Легко заметить, что можно рассматривать только две функции, например,  так как остальные достаточно просто выражаются через них:
так как остальные достаточно просто выражаются через них:

Схемы, реализующие все соотношения (6.17) или несколько из них, называются схемами сравнения чисел (Magnitude Comparator).
Соотношения (6.17) между числами в позиционных системах счисления, в которых вес любого старшего разряда больше веса любого младшего разряда, довольно просто могут быть установлены на основании последовательного сравнения их одноименных разрядов. Сравнение чисел можно производить, начиная или с младшего или со старшего разряда. Предпочтительнее первый вариант сравнения, так как он допускает более естественный способ наращивания разрядности чисел.
Схемы сравнения чисел.
Для описания схем сравнения двоичных чисел введем в рассмотрение переключательные функции  переменных:
переменных:

Сравнение чисел будем производить, начиная с младшего разряда. Из соотношений (6.18) следует, что

Табл. 6.15 задает функции  для одноразрядных двоичных чисел
для одноразрядных двоичных чисел  Из нее следует, что
Из нее следует, что

Пусть теперь имеются функции  для младших разрядов
для младших разрядов  а числа двухразрядные, т. е.
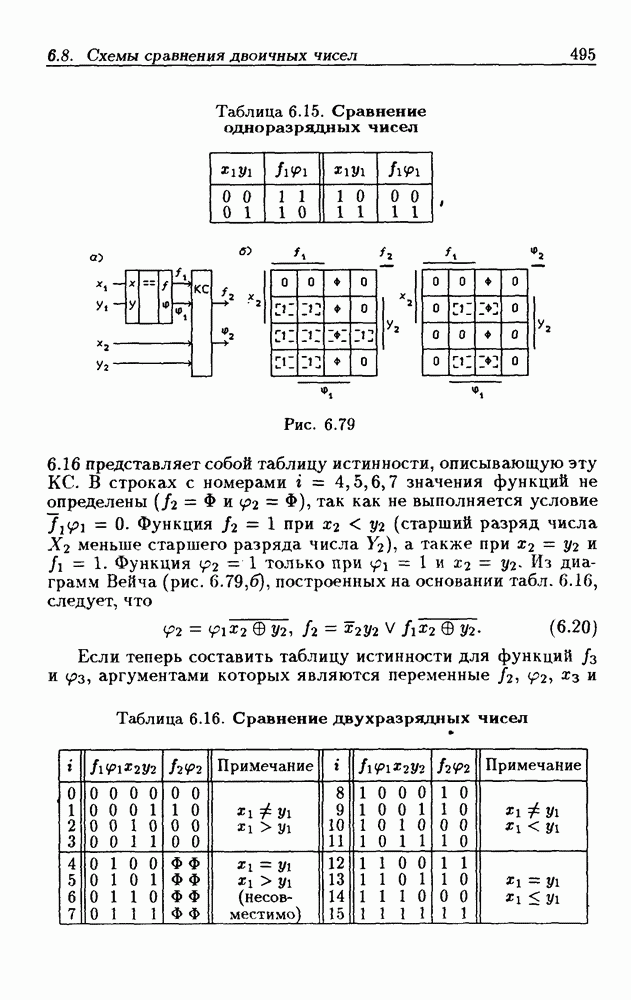
а числа двухразрядные, т. е.  Структурная схема сравнения этих чисел изображена на рис. 6.79,а. Требуется синтезировать КС для функций
Структурная схема сравнения этих чисел изображена на рис. 6.79,а. Требуется синтезировать КС для функций  аргументами которых являются переменные
аргументами которых являются переменные  Табл. 6.16
Табл. 6.16
Таблица 6.15. (см. скан) Сравнение одноразрядных чисел

Рис. 6.79
представляет собой таблицу истинности, описывающую эту КС. В строках с номерами  значения функций не определены
значения функций не определены  так как не выполняется условие
так как не выполняется условие  Функция
Функция  при
при  (старший разряд числа
(старший разряд числа  меньше старшего разряда числа
меньше старшего разряда числа  а также при
а также при  Функция
Функция  только при
только при  Из диаграмм Вейча (рис. 6.79,б), построенных на основании табл. 6.16, следует, что
Из диаграмм Вейча (рис. 6.79,б), построенных на основании табл. 6.16, следует, что

Если теперь составить таблицу истинности для функций  аргументами которых являются переменные
аргументами которых являются переменные  и
и
Таблица 6.16. (см. скан) Сравнение двухразрядных чисел
 то она будет иметь такой же вид, что и табл. 6.16, а значит
то она будет иметь такой же вид, что и табл. 6.16, а значит

Из соотношений (6.19) - (6.21) следует общая рекуррентная формула

в которой необходимо задать значения  равными 0 или 1. Из выражений (6.22) следует, что
равными 0 или 1. Из выражений (6.22) следует, что

Из сравнения (6.23) с (6.19) находим  Представляет интерес установить, какие функции из (6.17) будут соответствовать рекуррентным соотношениям (6.22) при других значениях
Представляет интерес установить, какие функции из (6.17) будут соответствовать рекуррентным соотношениям (6.22) при других значениях  Легко показать, что
Легко показать, что

Докажем, например, последнее соотношение, которое на основании (6.19) справедливо при  Для этого следует показать, что соотношение (6.24) истинно и для
Для этого следует показать, что соотношение (6.24) истинно и для  Из (6.22) следует, что
Из (6.22) следует, что

т.е. утверждение (6.24) справедливо при любом 
На рис. 6.80,а изображена схема сравнения одноразрядных двоичных чисел  построенная на основании выражений (6.23), а на рис. 6.80, б - ее условное графическое обозначение. Схема сравнения 4-разрядных двоичных чисел
построенная на основании выражений (6.23), а на рис. 6.80, б - ее условное графическое обозначение. Схема сравнения 4-разрядных двоичных чисел  реализующая функции
реализующая функции  может быть построена по рекуррентным соотношениям (6.22) при
может быть построена по рекуррентным соотношениям (6.22) при  (рис. 6.80,в). Недостатком такой КС является низкое быстродействие, так как сигналы
(рис. 6.80,в). Недостатком такой КС является низкое быстродействие, так как сигналы  соответствующие младшим разрядам сравниваемых чисел, последовательно проходят через все элементы, имеющие конечное быстродействие. Достоинство данной
соответствующие младшим разрядам сравниваемых чисел, последовательно проходят через все элементы, имеющие конечное быстродействие. Достоинство данной  простота ее реализации при программируемости выполняемых функций с помощью входов
простота ее реализации при программируемости выполняемых функций с помощью входов 

Рис. 6.80
Если последовательными подстановками значений  развернуть соотношения (6.22) при
развернуть соотношения (6.22) при  то можно получить:
то можно получить:

Схема, реализованная в соответствии с этими функциями, будет иметь значительно большее быстродействие, чем схема, показанная на рис. 6.80, так как раскрытие скобок при развертывании соотношений (6.22) уменьшило порядок переключательных функций 
Из (6.24) следует, что

Рассмотрим функцию

Докажем это соотношение, используя закон двойственности и другие тождества алгебры логики:


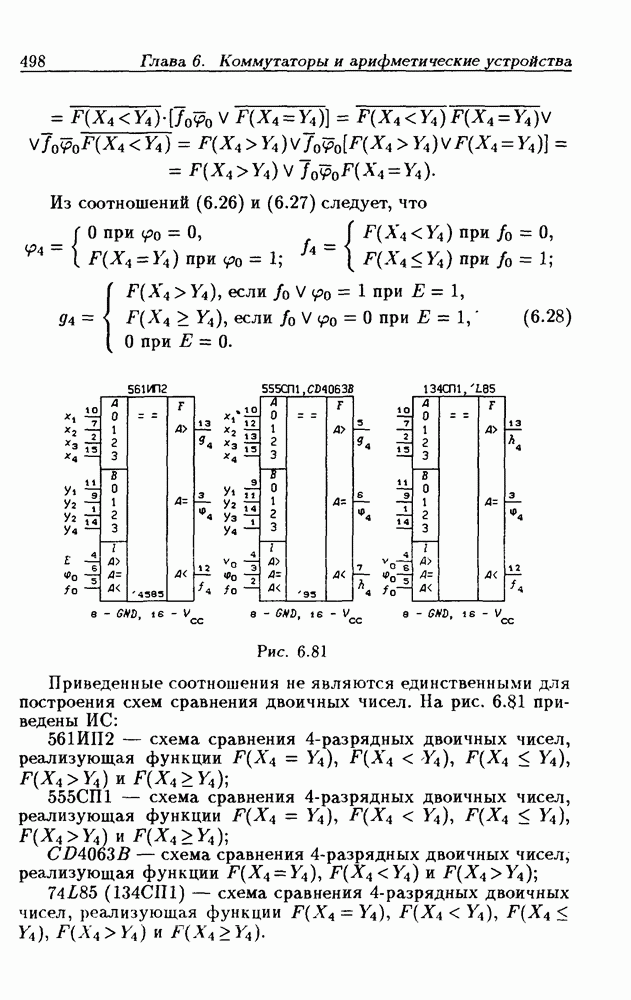
Из соотношений (6.26) и (6.27) следует, что


Рис. 6.81
Приведенные соотношения не являются единственными для построения схем сравнения двоичных чисел. На рис. 6.81 приведены ИС:
561ИП2 — схема сравнения  -разрядных двоичных чисел, реализующая функции
-разрядных двоичных чисел, реализующая функции  ;
;
555СП1 — схема сравнения  -разрядных двоичных чисел, реализующая функции
-разрядных двоичных чисел, реализующая функции  ;
;
CD4063В — схема сравнения  -разрядных двоичных чисел, реализующая функции
-разрядных двоичных чисел, реализующая функции  ;
;
74L85 (134СП1) — схема сравнения  -разрядных двоичных чисел, реализующая функции
-разрядных двоичных чисел, реализующая функции 
Схема сравнения 561ИП2 спроектирована в соответствии с соотношениями (6.25) и (6.27). Функции, выполняемые  программируются с помощью входов
программируются с помощью входов  что видно из табл. 6.17, составленной на основании выражений
что видно из табл. 6.17, составленной на основании выражений  На рис. 6.81 для ИС 561ИП2 введены обозначения:
На рис. 6.81 для ИС 561ИП2 введены обозначения:

(входные управляющие сигналы, использующиеся для каскадирования ИС и программирования выполняемых функций),

(выходные сигналы  Аналогичные обозначения введены и для остальных ИС, представленных на рис. 6.81.
Аналогичные обозначения введены и для остальных ИС, представленных на рис. 6.81.
Таблица 6.17. (см. скан) Функционирование ИС 561ИП2
Интегральные схемы, имеющие одинаковые номера (например,  всегда имеют одно и то же функциональное назначение, но могут выполнять несколько различающиеся функции. Это вызвано тем, что при совершенствовании технологии изготовления ИС вводились и усовершенствования схемотехнических решений функциональных узлов. Для построения 4-разрядных ИС сравнения двоичных чисел можно использовать самые различные преобразования функций
всегда имеют одно и то же функциональное назначение, но могут выполнять несколько различающиеся функции. Это вызвано тем, что при совершенствовании технологии изготовления ИС вводились и усовершенствования схемотехнических решений функциональных узлов. Для построения 4-разрядных ИС сравнения двоичных чисел можно использовать самые различные преобразования функций  а также и другие функции. Введем функцию
а также и другие функции. Введем функцию

Из сравнения соотношения (6.29) с (6.18) следует, что функция  может быть получена из выражения (6.22) для функции
может быть получена из выражения (6.22) для функции
 взаимной заменой
взаимной заменой  :
:

а функция  из выражения (6.25) для
из выражения (6.25) для  взаимной заменой переменных
взаимной заменой переменных 

Реализация функций  позволяет получить полностью симметричную схему относительно операций "меньше" и "больше". Интегральная схема
позволяет получить полностью симметричную схему относительно операций "меньше" и "больше". Интегральная схема  (рис. 6.81) выполняет функции сравнения 4-разрядных двоичных чисел:
(рис. 6.81) выполняет функции сравнения 4-разрядных двоичных чисел:

где переключательные функции  определяются соотношениями (6.25) и (6.30). Как видно из (6.31), функции, выполняемые
определяются соотношениями (6.25) и (6.30). Как видно из (6.31), функции, выполняемые  могут программироваться сигналами
могут программироваться сигналами  (табл. 6.18).
(табл. 6.18).
Таблица 6.18. (см. скан) Функционирование ИС 555СП1
Третий вариант схемы сравнения реализован в  которая выполняет функции
которая выполняет функции  где
где

а функция  получается из функции
получается из функции  взаимной заменой переменных
взаимной заменой переменных  и заменой
и заменой  на
на  Легко убедиться, что при
Легко убедиться, что при  схема выполняет функции
схема выполняет функции

Четвертый вариант схемы сравнения реализован в ИС 74L85, которая выполняет функции

Из этих соотношений следует, что

Каскадирование схем сравнения двоичных чисел. На рис. 6.82 показана  -разрядная схема сравнения двоичных чисел, построенная на трех 4-разрядных ИС 561ИП2 (символ
-разрядная схема сравнения двоичных чисел, построенная на трех 4-разрядных ИС 561ИП2 (символ  означает, что вход
означает, что вход  следует подключить либо к корпусу, либо к источнику питания) Из рис. 6.82 и соотношений (6.26) и (6.27) следует, что функции
следует подключить либо к корпусу, либо к источнику питания) Из рис. 6.82 и соотношений (6.26) и (6.27) следует, что функции

где  Подставив (6.26) в (6.32), получим:
Подставив (6.26) в (6.32), получим:

Аналогично на основании рис. 6.82 можно получить:

Из этих соотношений видно, что функции, выполняемые схемой на рис. 6.82, также задаются табл. 6.17 (индексы  следует просто заменить на индексы
следует просто заменить на индексы  и
и  Сигналы и
Сигналы и  подаются на младшую ИС, а сигнал
подаются на младшую ИС, а сигнал  на старшую ИС (деление на младшие и старшие ИС производится в соответствии
на старшую ИС (деление на младшие и старшие ИС производится в соответствии

Рис. 6.82
с младшими и старшими разрядами сравниваемых чисел). На входы  всех остальных ИС подаются значения
всех остальных ИС подаются значения  (либо 0 В, либо
(либо 0 В, либо  ).
).
Можно построить схему последовательного включения и большего числа ИС 561ИП2 для сравнения  -разрядных чисел, где
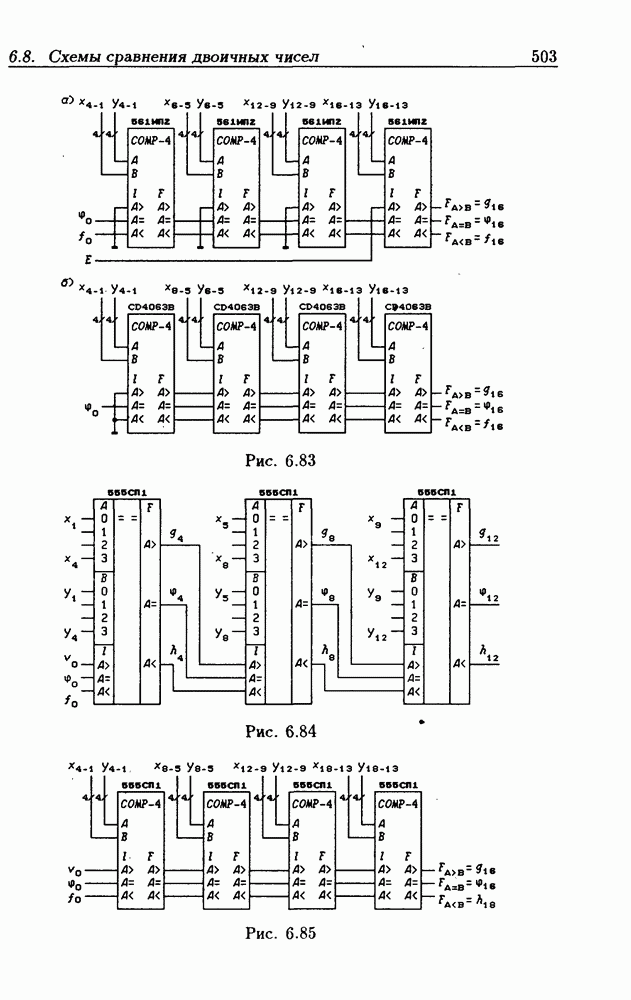
-разрядных чисел, где  число ИС. На рис. 6.83,а показана структурная схема сравнения 16-разрядных чисел при последовательном включении ИС 561ИП2. Каскадирование схем сравнения CD4063B при последовательном их включении представлено на рис. 6.83, б.
число ИС. На рис. 6.83,а показана структурная схема сравнения 16-разрядных чисел при последовательном включении ИС 561ИП2. Каскадирование схем сравнения CD4063B при последовательном их включении представлено на рис. 6.83, б.
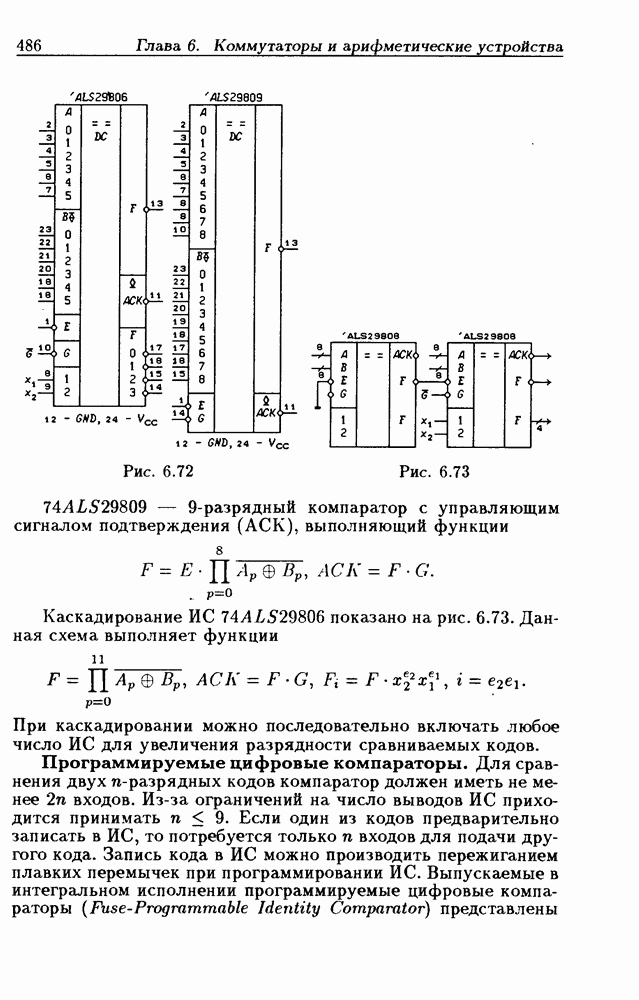
На рис. 6.84 показана схема сравнения  -разрядных двоичных чисел, построенная на трех ИС 555СП1. Из рис. 6.84 на основании (6.31) следует, что
-разрядных двоичных чисел, построенная на трех ИС 555СП1. Из рис. 6.84 на основании (6.31) следует, что

где  Подставив в (6.33) значения (6.31) функций
Подставив в (6.33) значения (6.31) функций  получим:
получим:


(кликните для просмотра скана)
Аналогично можно получить и функции

т.е. функции, выполняемые схемой на рис. 6.84, программируются сигналами  (табл. 6.18).
(табл. 6.18).
Аналогично схеме на рис. 6.84 можно построить схему сравнения  -разрядных чисел с последовательным включением
-разрядных чисел с последовательным включением  На рис. 6.85 изображена структурная схема для сравнения 16-разрядных двоичных чисел. Программирование функций при последовательном включении
На рис. 6.85 изображена структурная схема для сравнения 16-разрядных двоичных чисел. Программирование функций при последовательном включении  сигналами
сигналами  будет определяться табл. 6.18:
будет определяться табл. 6.18:  при нечетном
при нечетном  при четном
при четном  При последовательном включении ИС значительно снижается быстродействие схем сравнения многоразрядных чисел.
При последовательном включении ИС значительно снижается быстродействие схем сравнения многоразрядных чисел.
Каскадирование ИС сравнения двоичных чисел можно производить и при параллельном их включении. На рис.  показано включение ИС 561ИП2 в качестве преобразователя разрядности сравниваемых чисел. Из рис.
показано включение ИС 561ИП2 в качестве преобразователя разрядности сравниваемых чисел. Из рис.  следует, что
следует, что  Подставив эти значения в (6.26) и (6.27), получим:
Подставив эти значения в (6.26) и (6.27), получим:

 функция
функция  Из (6.34) видно, что соотношения "меньше", "больше" и "равно" между 4-разрядными числами
Из (6.34) видно, что соотношения "меньше", "больше" и "равно" между 4-разрядными числами  полностью переносятся на функции
полностью переносятся на функции  (например, если
(например, если  то и
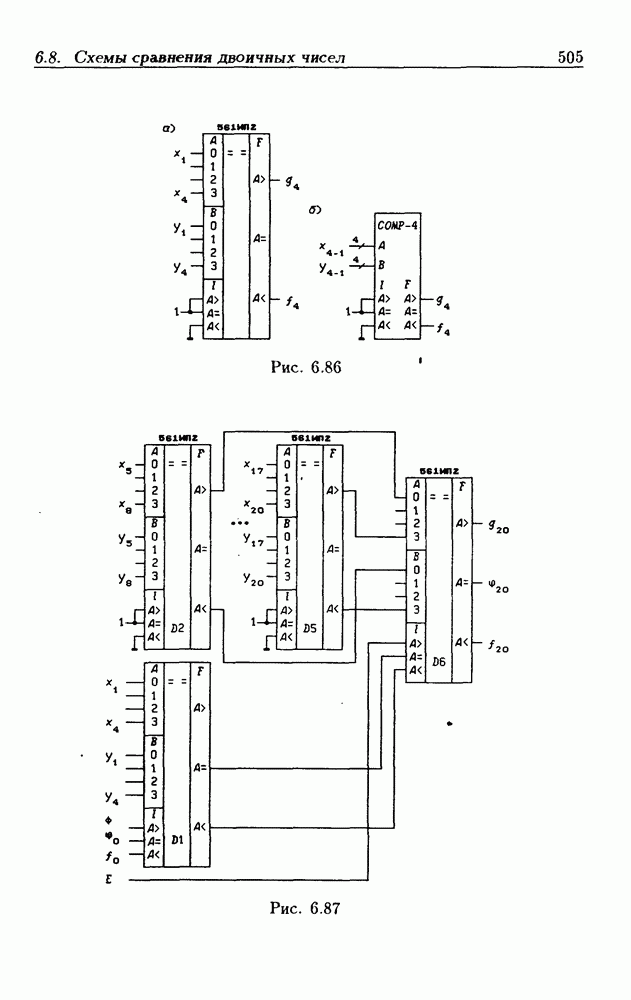
то и  которые можно рассматривать, как одноразрядные числа. На рис. 6.86,б приведено упрощенное обозначение этого преобразователя.
которые можно рассматривать, как одноразрядные числа. На рис. 6.86,б приведено упрощенное обозначение этого преобразователя.
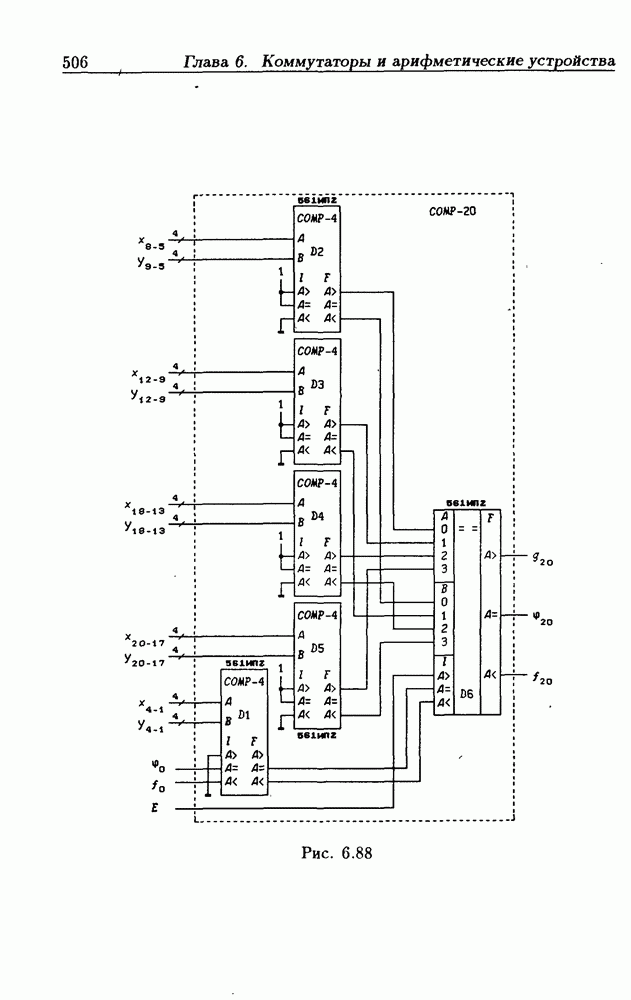
Схема сравнения  -разрядных двоичных чисел при параллельном включении ИС 561ИП2 показана на рис. 6.87, а полная ее структурная схема — на рис. 6.88 (все входные сигналы последовательно проходят только через две
-разрядных двоичных чисел при параллельном включении ИС 561ИП2 показана на рис. 6.87, а полная ее структурная схема — на рис. 6.88 (все входные сигналы последовательно проходят только через две  Интегральные схемы
Интегральные схемы  включены в качестве преобразователей разрядности сравниваемых чисел. Программирование выполняемых схемой функций осуществляется сигналами
включены в качестве преобразователей разрядности сравниваемых чисел. Программирование выполняемых схемой функций осуществляется сигналами  в соответствии с табл. 6.17. Если в схеме на рис. 6.87 положить
в соответствии с табл. 6.17. Если в схеме на рис. 6.87 положить  то ее можно использовать в качестве преобразователя
то ее можно использовать в качестве преобразователя  -разрядных чисел в одноразрядные числа
-разрядных чисел в одноразрядные числа  с сохранением соотношений "меньше", "больше" и "равно". Тогда вместо
с сохранением соотношений "меньше", "больше" и "равно". Тогда вместо  можно включить такие
можно включить такие  -разрядные преобразователи, а
-разрядные преобразователи, а  можно заменить на схему из
можно заменить на схему из  результате получится схема сравнения 100-разрядных
результате получится схема сравнения 100-разрядных

(кликните для просмотра скана)

(кликните для просмотра скана)

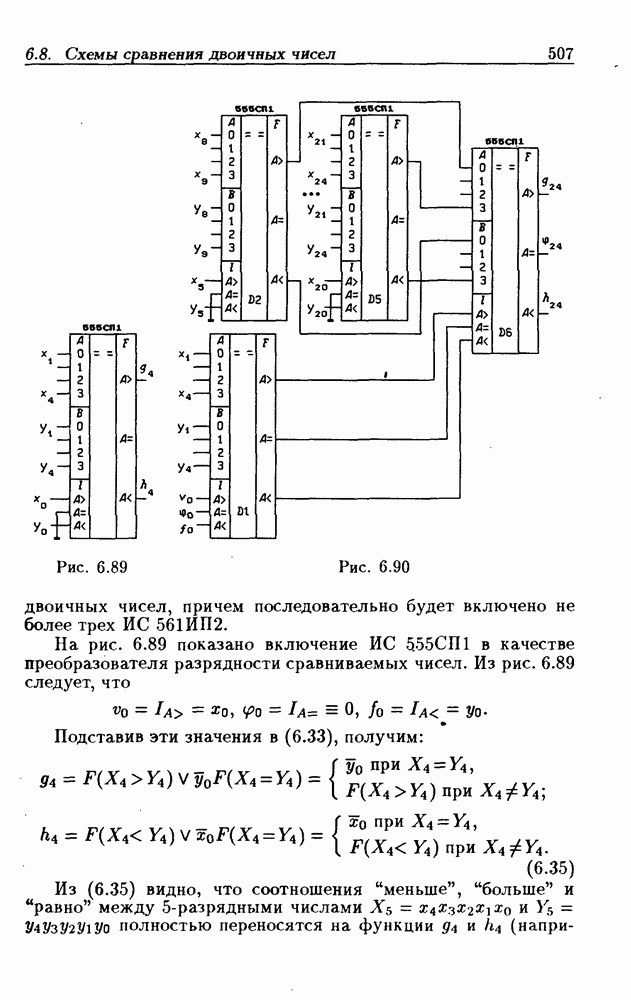
Рис. 6.89

Рис. 6.90
двоичных чисел, причем последовательно будет включено не более трех ИС 561ИП2.
На рис. 6.89 показано включение ИС 555СП1 в качестве преобразователя разрядности сравниваемых чисел. Из рис. 6.89 следует, что

Подставив эти значения в (6.33), получим:

Из (6.35) видно, что соотношения "меньше", "больше" и "равно" между  -разрядными числами
-разрядными числами  полностью переносятся на функции
полностью переносятся на функции  (например,
(например,

(кликните для просмотра скана)
если  то
то  которые можно рассматривать, как одноразрядные числа.
которые можно рассматривать, как одноразрядные числа.
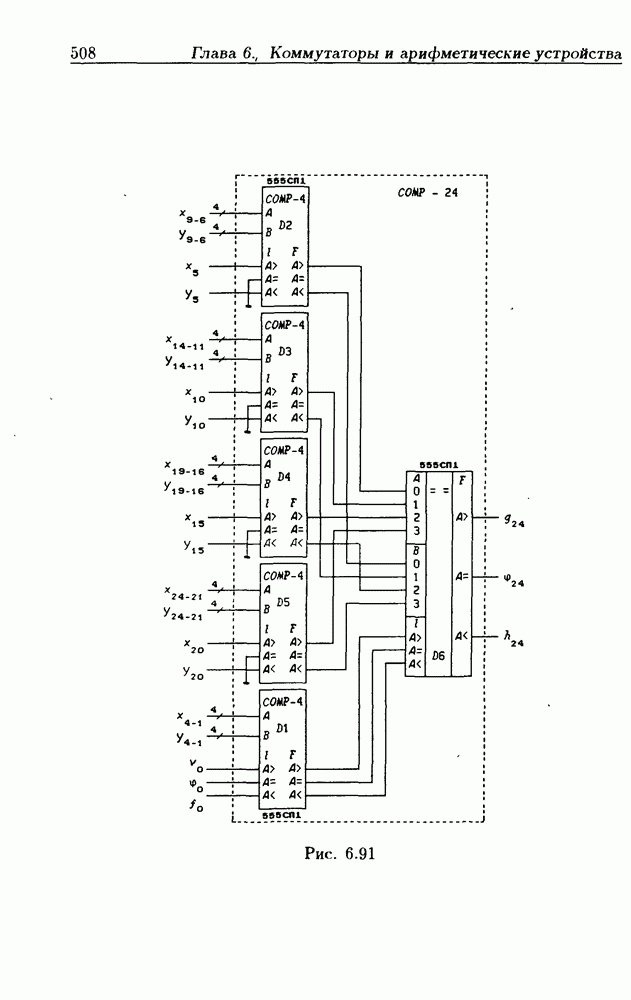
Схема сравнения  -разрядных двоичных чисел при параллельном включении ИС 555СП1 показана на рис. 6.90, а полная ее структурная схема — на рис. 6.91 (все входные сигналы последовательно проходят только через две
-разрядных двоичных чисел при параллельном включении ИС 555СП1 показана на рис. 6.90, а полная ее структурная схема — на рис. 6.91 (все входные сигналы последовательно проходят только через две  Интегральные схемы
Интегральные схемы  используются в качестве преобразователей разрядности сравниваемых чисел. Программирование выполняемых схемой функций осуществляется сигналами
используются в качестве преобразователей разрядности сравниваемых чисел. Программирование выполняемых схемой функций осуществляется сигналами  в соответствии с табл. 6.18 для функций
в соответствии с табл. 6.18 для функций  Если в схеме на рис. 6.90 положить
Если в схеме на рис. 6.90 положить  то ее можно использовать в качестве преобразователя
то ее можно использовать в качестве преобразователя  -разрядных чисел в одноразрядные числа
-разрядных чисел в одноразрядные числа  с сохранением соотношений "меньше", "больше" и "равно". Тогда вместо
с сохранением соотношений "меньше", "больше" и "равно". Тогда вместо  можно включить такие
можно включить такие  -разрядные преобразователи, а
-разрядные преобразователи, а  можно заменить на схему из
можно заменить на схему из  В результате получится схема сравнения
В результате получится схема сравнения  -разрядных двоичных чисел, причем последовательно будет включено не более трех ИС 555СП1.
-разрядных двоичных чисел, причем последовательно будет включено не более трех ИС 555СП1.
В табл. 6.19 приведены основные характеристики различных схем сравнения двоичных чисел [23] при параллельном включении ИС.
Таблица 6.19. (см. скан) Основные характеристики схем сравнения
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Основы теории переключательных функций
- 1.2. Позиционные системы счисления
- 1.3. Переключательные функции
- 1.4. Принцип и закон двойственности
- 1.5. Теоремы разложения
- 1.6. Решение систем логических уравнений
- 1.7. Первичные термы, минтермы и макстермы
- 1.8. Совершенные нормальные формы представления функций
- 1.9. Конъюнктивные и дизъюнктивные термы
- 1.10. Минимизация переключательных функций
- 1.11. Диаграммы Вейча
- 1.12. Минимизация неполностью определенных функций, совместная минимизация нескольких функций
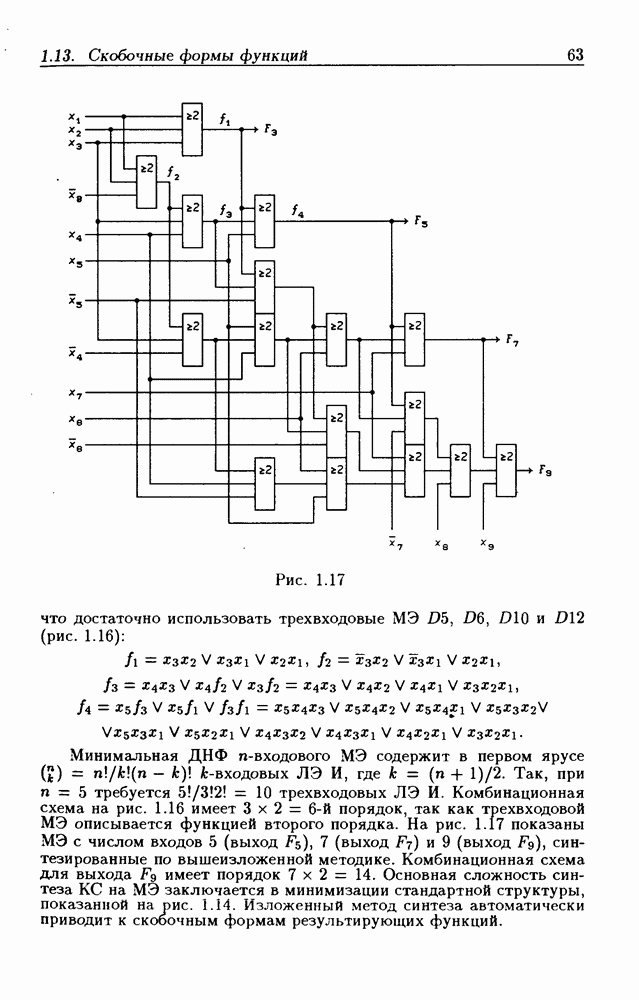
- 1.13. Скобочные формы функций
- 1.14. Закон двойственности для логических схем
- 1.15. Линейные функции
- Глава 2. Анализ и синтез логических схем
- 2.2. Модели логических элементов
- 2.3. Модели логических схем
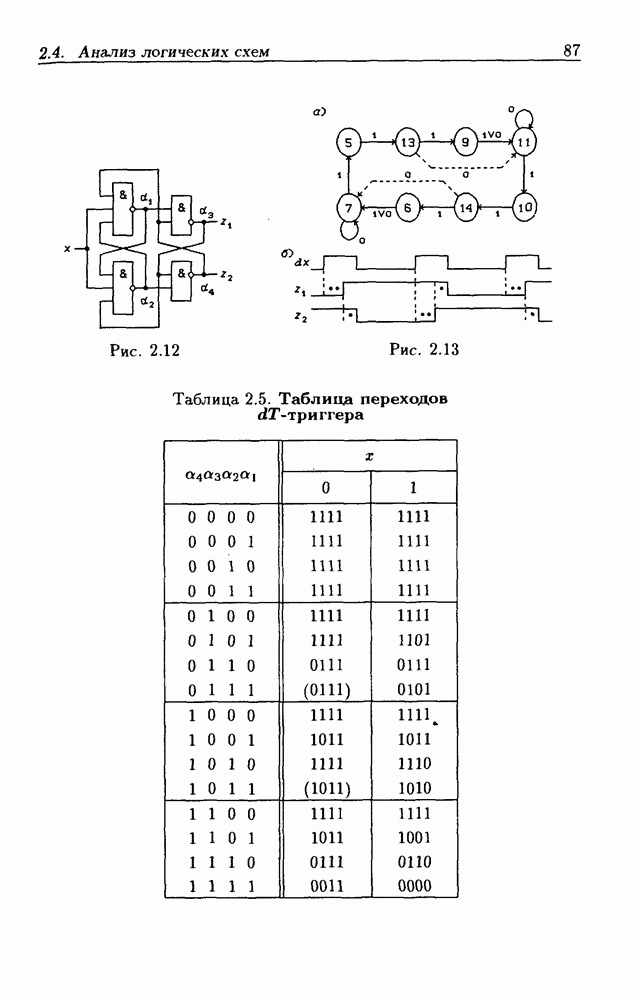
- 2.4. Анализ логических схем
- 2.5. Синтез комбинационных схем, свободных от состязаний
- Глава 3. Синтез асинхронных потенциальных автоматов
- 3.2. Асинхронные потенциальные автоматы
- 3.3. Асинхронные потенциальные триггеры и элементы памяти
- Триггеры типа R-S
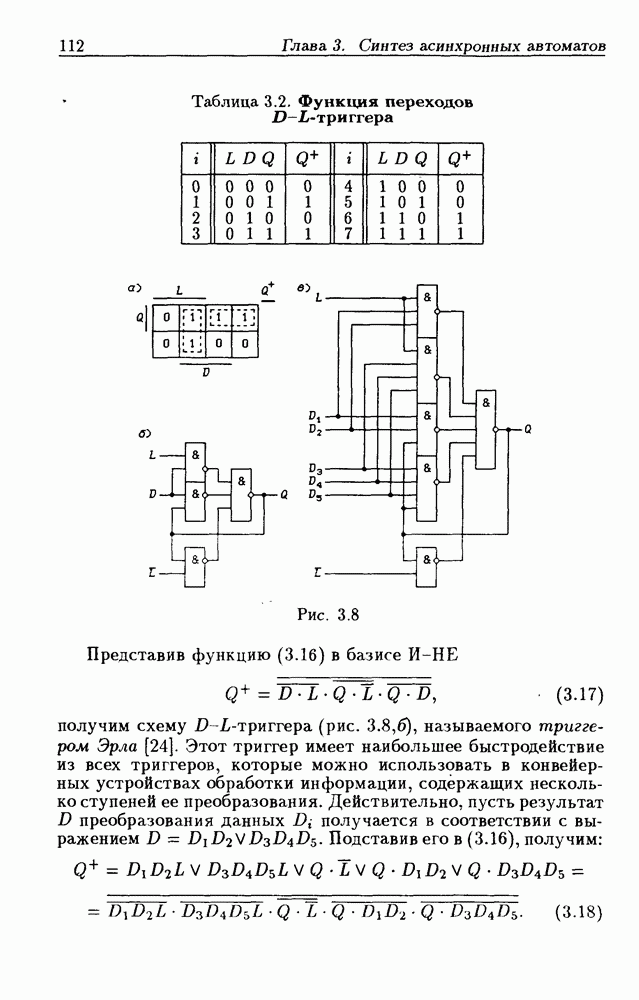
- Триггеры типа D-L
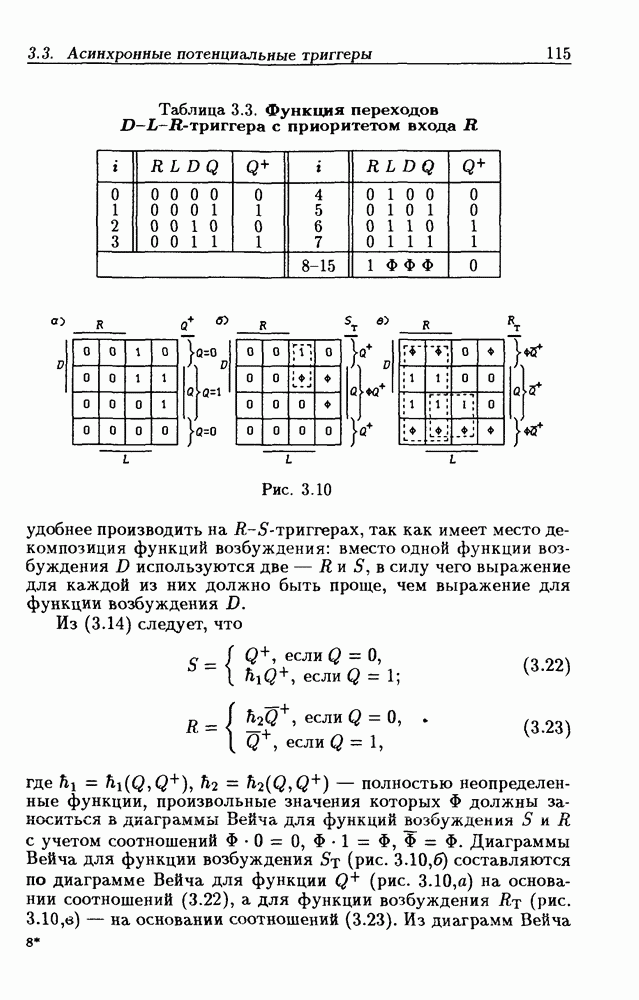
- Триггеры типа D-L-R с приоритетом входа R.
- Триггеры типа D-L-R с приоритетом входа L.
- Триггеры типа R-S-L.
- Триггеры типа DN-LN
- Аналитический метод синтеза и анализа триггеров.
- 3.4. Задание асинхронных потенциальных автоматов таблицами и графами переходов
- 3.5. Синтез асинхронных потенциальных счетчиков
- 3.6. Синтез асинхронных импульсных триггеров
- Триггеры типа dJ-dK.
- Классификация триггеров.
- 3.7. Синтез синхронных триггеров
- Триггеры типа J-K
- Синхронно-асинхронные триггеры.
- 3.8. Примеры синтеза асинхронных потенциальных автоматов
- Цифровые фазочастотные детекторы.
- Квантизатор временных интервалов.
- 3.9. Генераторы сигналов
- Автогенераторы.
- Управляемые автогенераторы.
- Глава 4. Синтез синхронных автоматов
- 4.2. Синхронные триггеры
- Триггеры типов D и R-S с импульсным тактовым сигналом.
- Синхронные триггеры типов R-S и D-L
- Синхронно-асинхронные триггеры.
- Синхронные триггеры типа J-K
- Триггеры типа Т.
- Классификация синхронных триггеров.
- Преобразования типов синхронных триггеров.
- Триггеры типов D-T-L и D-T-L/R
- Функции переходов синхронно-асинхронных триггеров.
- 4.3. Примеры синтеза синхронных автоматов
- 4.4. Сдвигающие регистры
- Синтез счетчиков на сдвигающих регистрах.
- Сдвигающие регистры с загрузкой данных.
- Реверсивные сдвигающие регистры.
- 4.5. Синхронные счетчики
- Синхронные двоичные счетчики.
- Синхронные двоично-десятичные счетчики.
- Каскадирование двоичных и двоично-десятичных счетчиков.
- Синхронные двоичные реверсивные счетчики.
- Реверсивные двоично-десятичные счетчики.
- Каскадирование реверсивных счетчиков.
- Счетчики на сдвигающих регистрах.
- Кольцевые счетчики.
- Линейные счетчики.
- Программируемые счетчики.
- 4.6. Асинхронные счетчики
- Асинхронные счетчики с умножением частоты счетного сигнала.
- Асинхронные импульсно-потенциальные счетчики.
- Асинхронное программирование модуля пересчета счетчиков.
- Глава 5. Логические элементы и триггеры
- Логические элементы.
- Классификация ИС по степени интеграции.
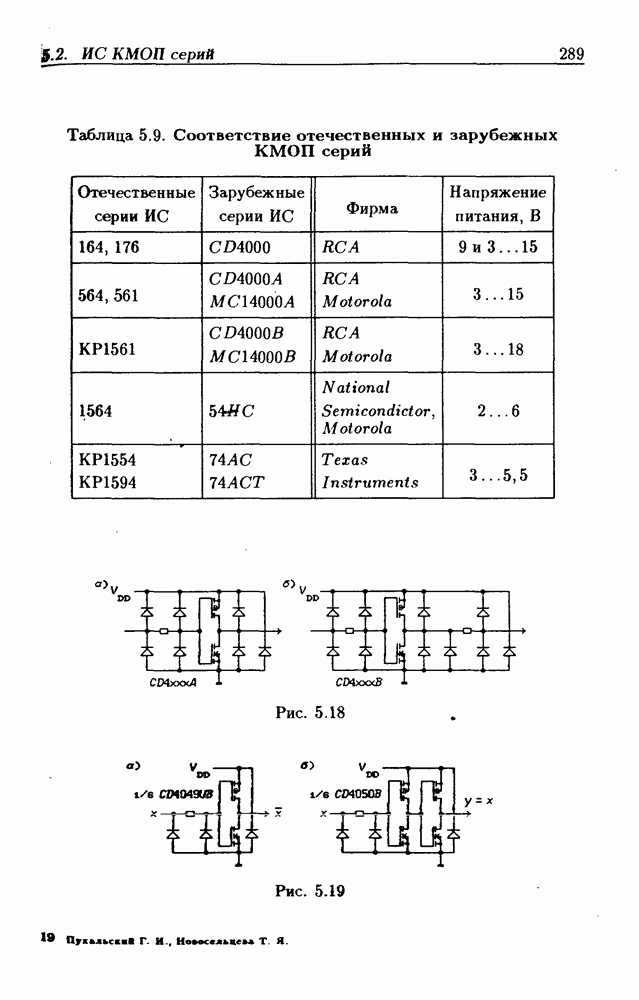
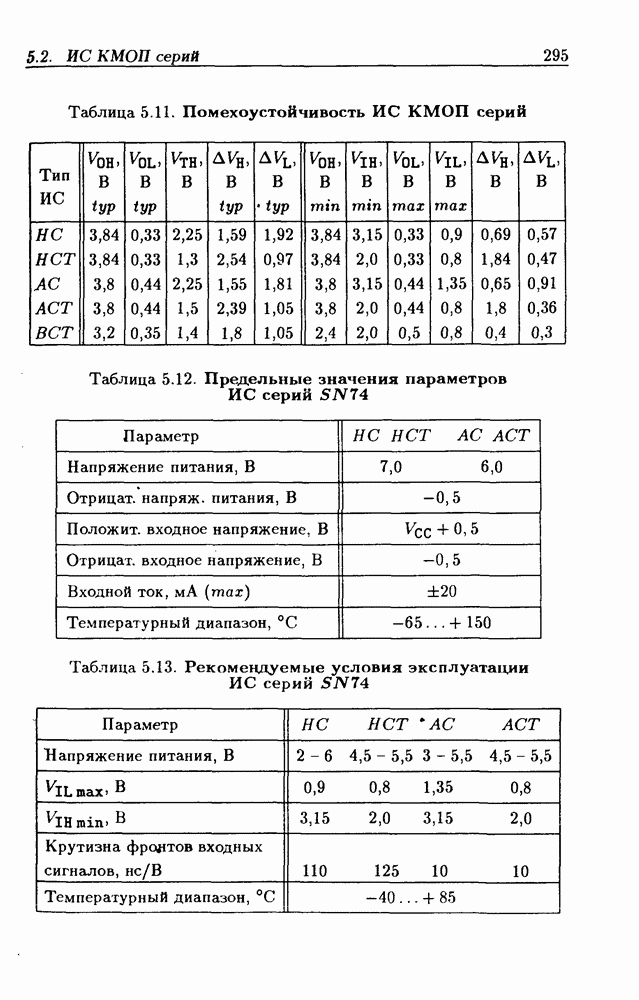
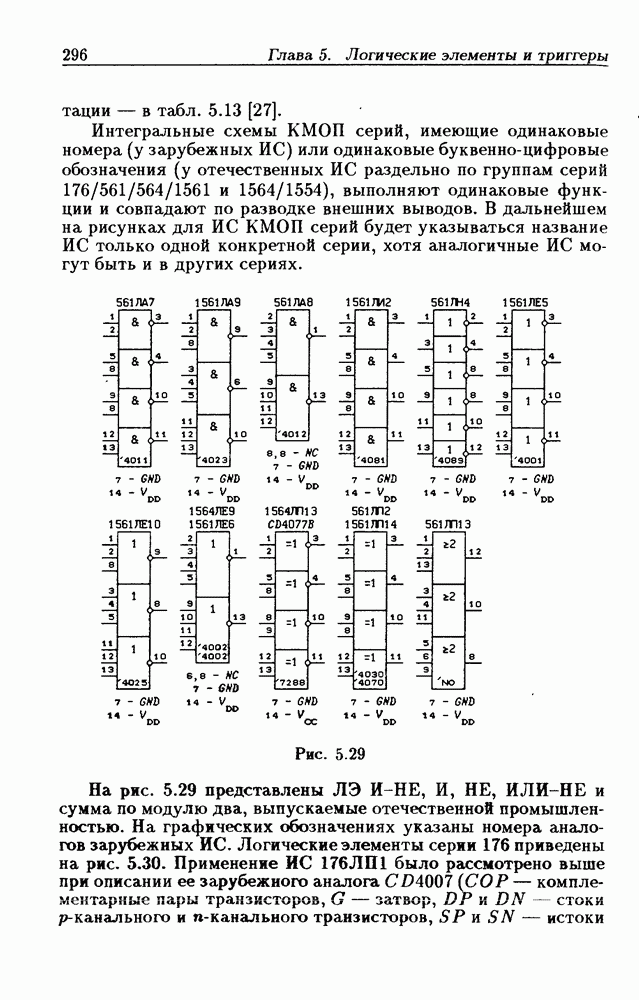
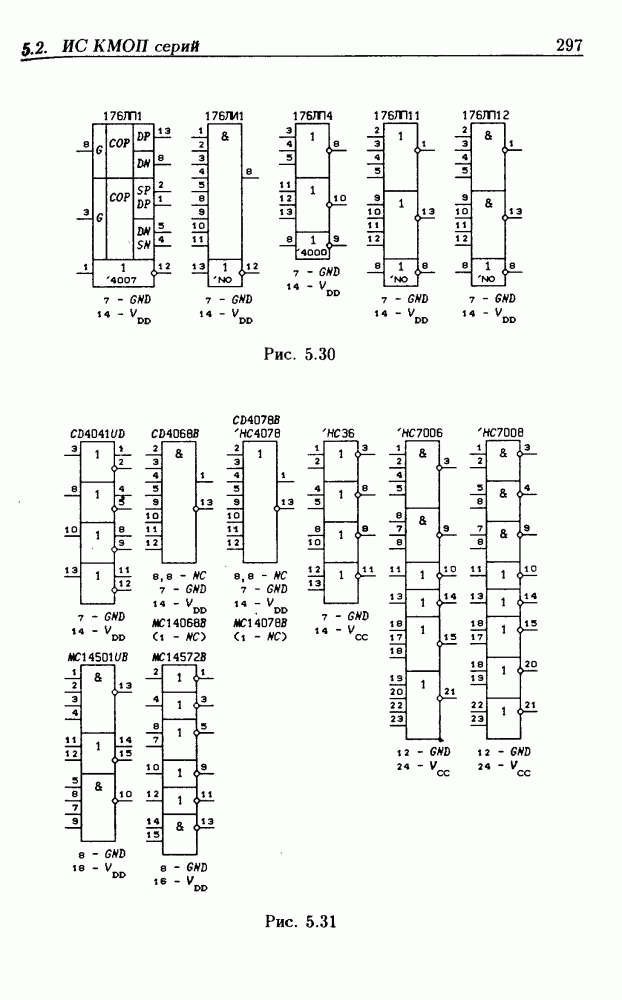
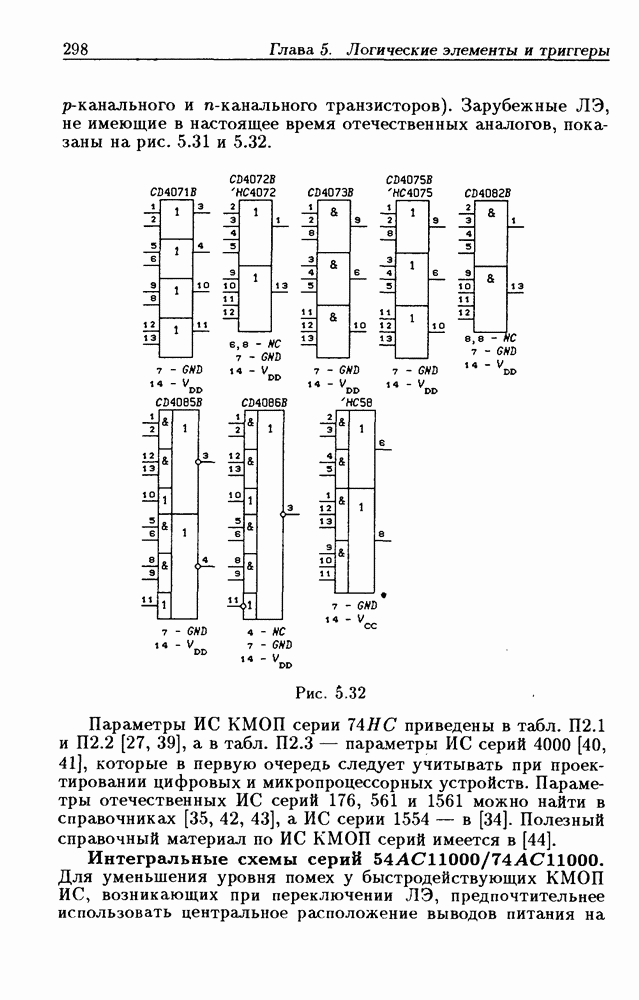
- 5.2. Интегральные схемы КМОП серий
- 5.3. Триггеры Шмитта
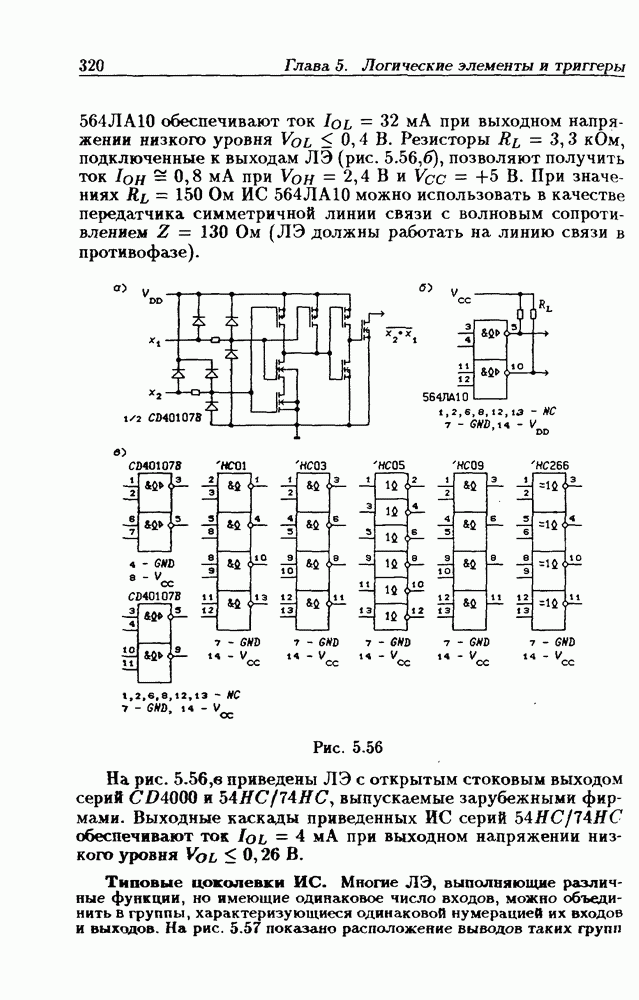
- 5.4. Логические элементы с открытым коллекторным выходом
- Логические элементы с открытым коллекторным выходом.
- Применения ЛЭ с открытым коллекторным выходом.
- Интерфейсные ЛЭ с открытым коллекторным выходом.
- Логические элементы с открытым стоковым выходом.
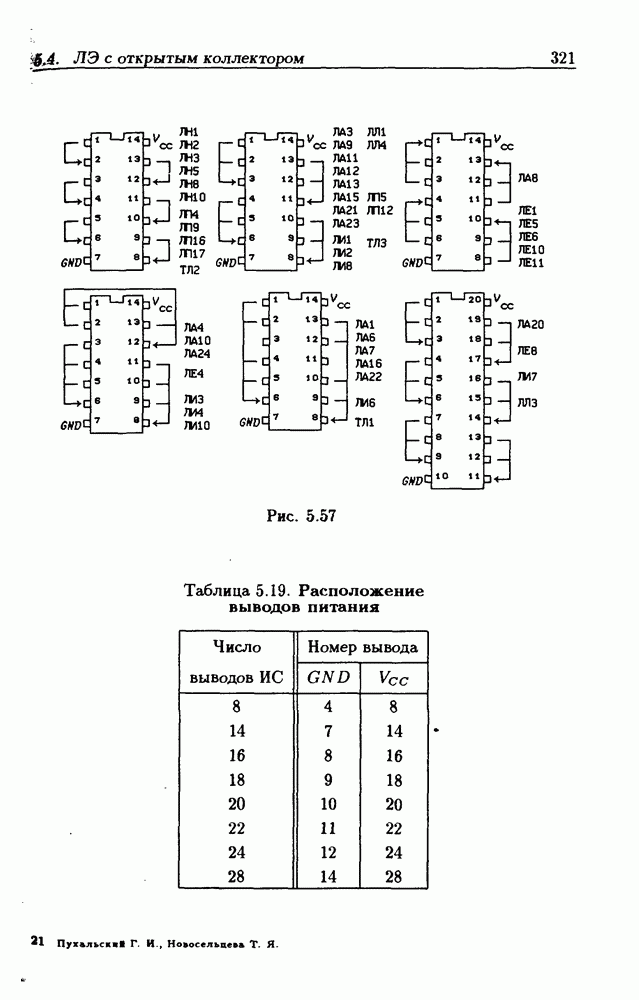
- Типовые цоколевки ИС.
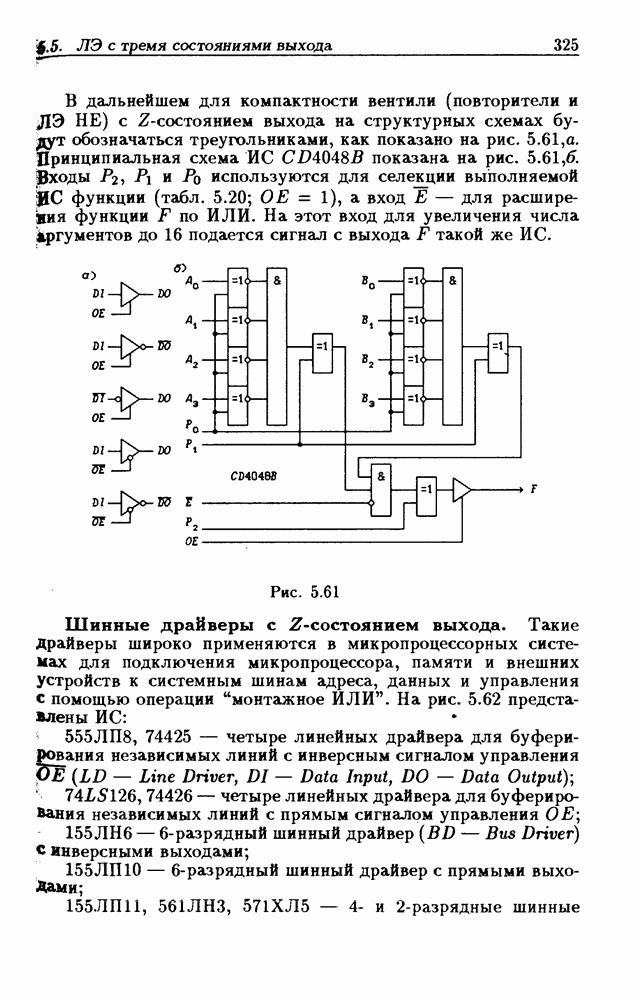
- 5.5. Логические элементы с тремя состояниями выхода
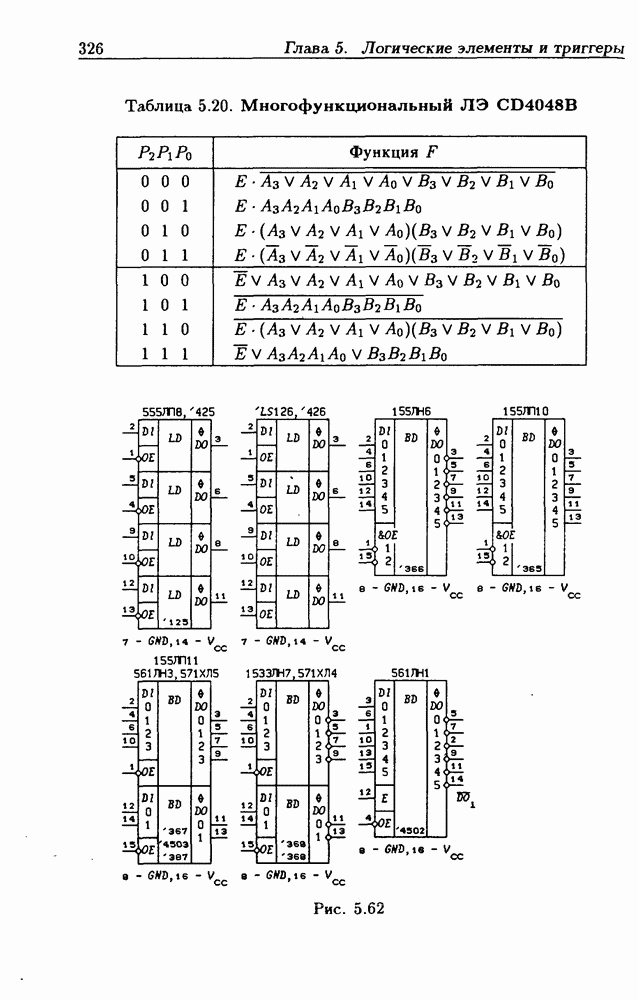
- Шинные драйверы с Z-состоянием выхода.
- Основные правила графического изображения ИС.
- 5.6. Преобразователи уровней напряжения и тока
- 5.7. Асинхронные потенциальные триггеры и регистры памяти
- 5.8. Синхронные триггеры и регистры памяти
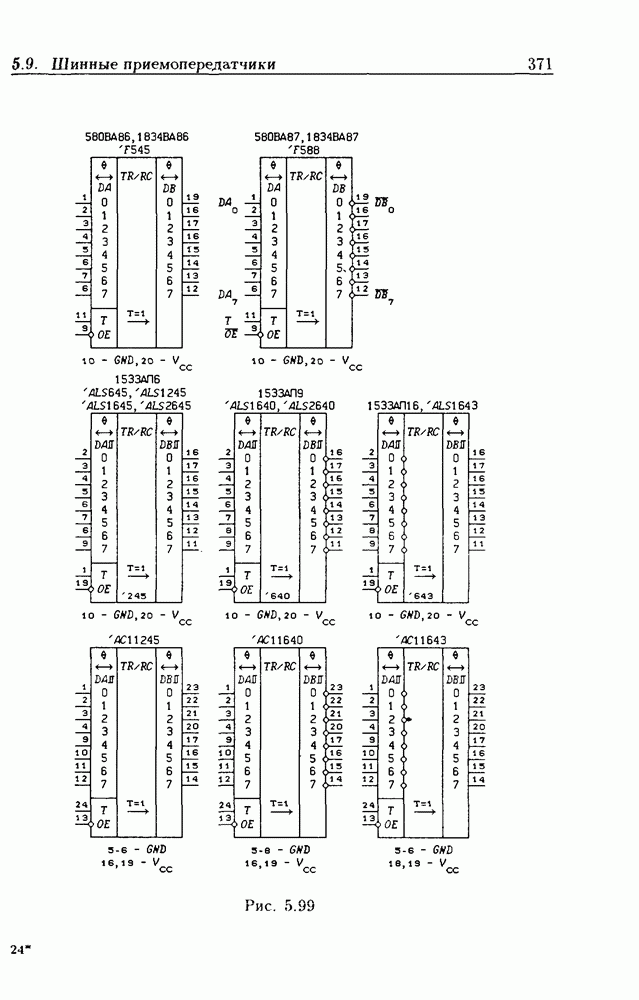
- 5.9. Шинные приемопередатчики
- Шинные приемопередатчики с Z-состоянием выхода.
- Шинные приемопередатчики с открытым коллекторным выходом.
- Шинные приемопередатчики с регистрами памяти.
- Шинные приемопередатчики со сдвигающим регистром.
- Шинные трехнаправленные приемопередатчики.
- 5.10. Мультивибраторы
- 5.11. Генераторы
- Схемы устранения «дребезга» механических контактов.
- Автогенераторы периодических сигналов.
- 5.12. Рекомендации по выбору серий ИС
- Глава 6. Коммутаторы и арифметические устройства
- 6.1. Дешифраторы
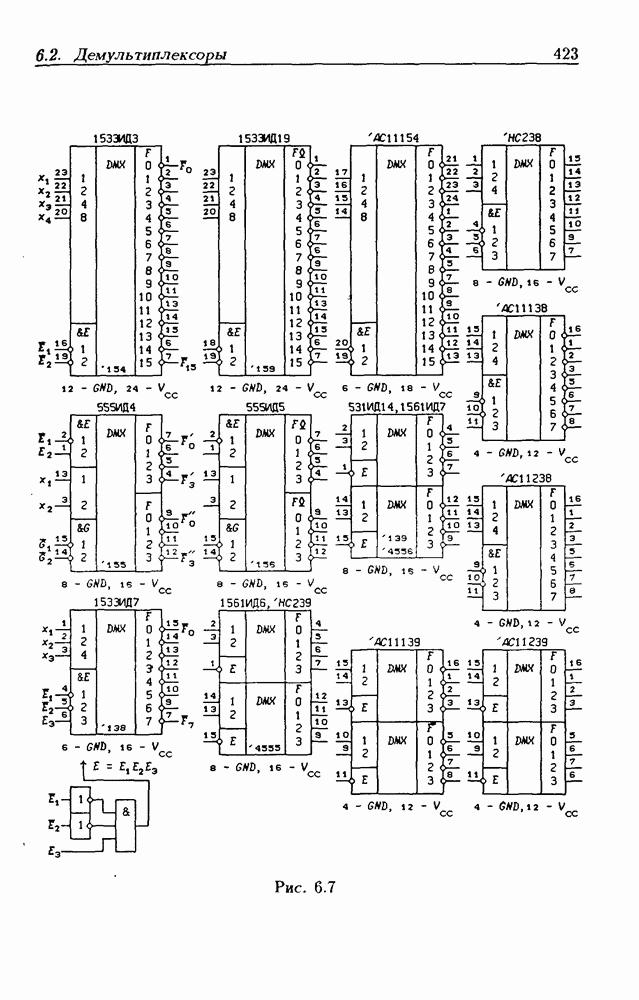
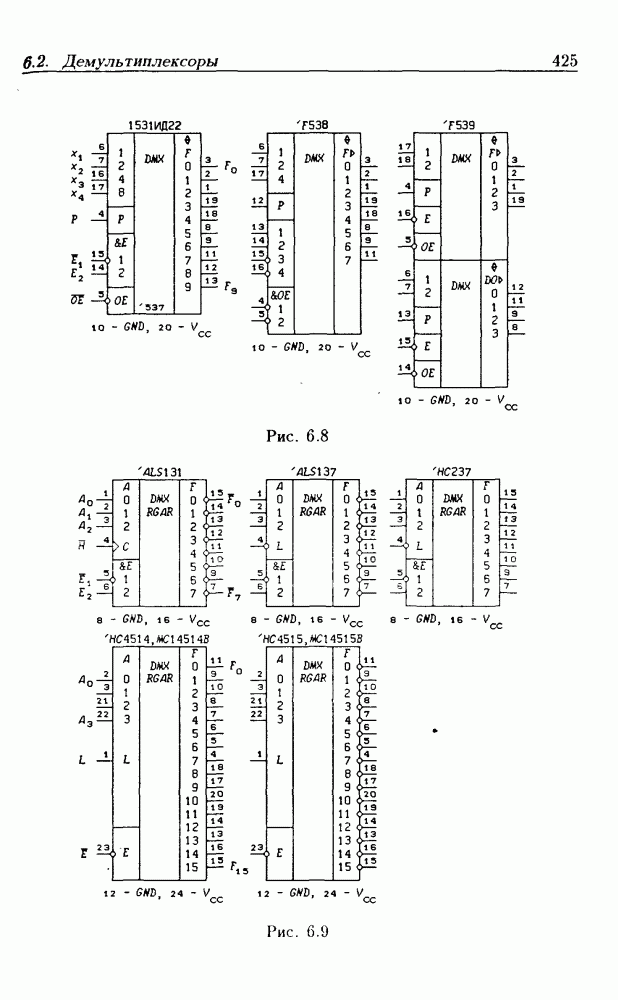
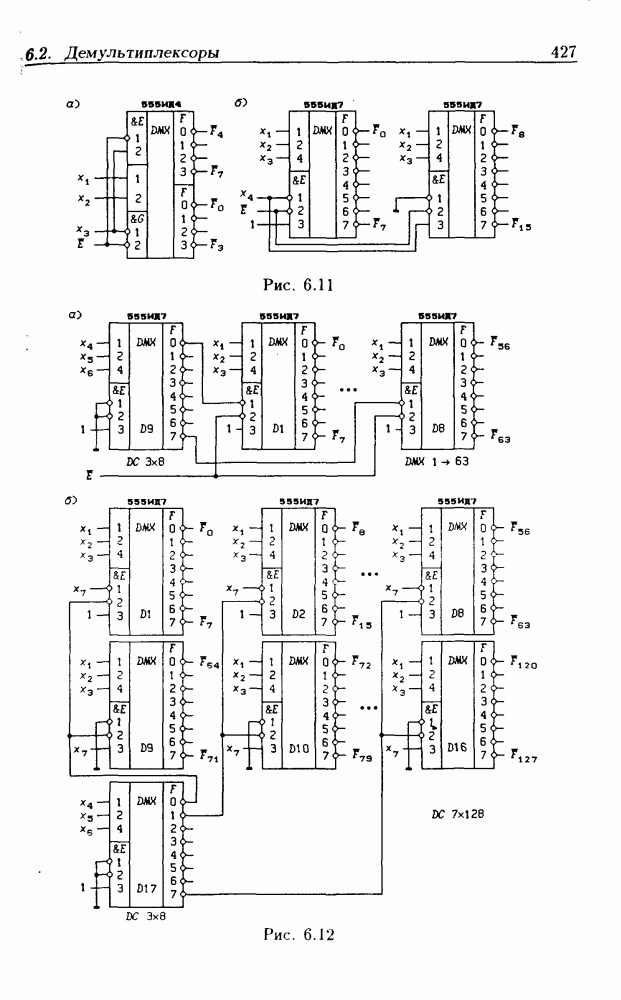
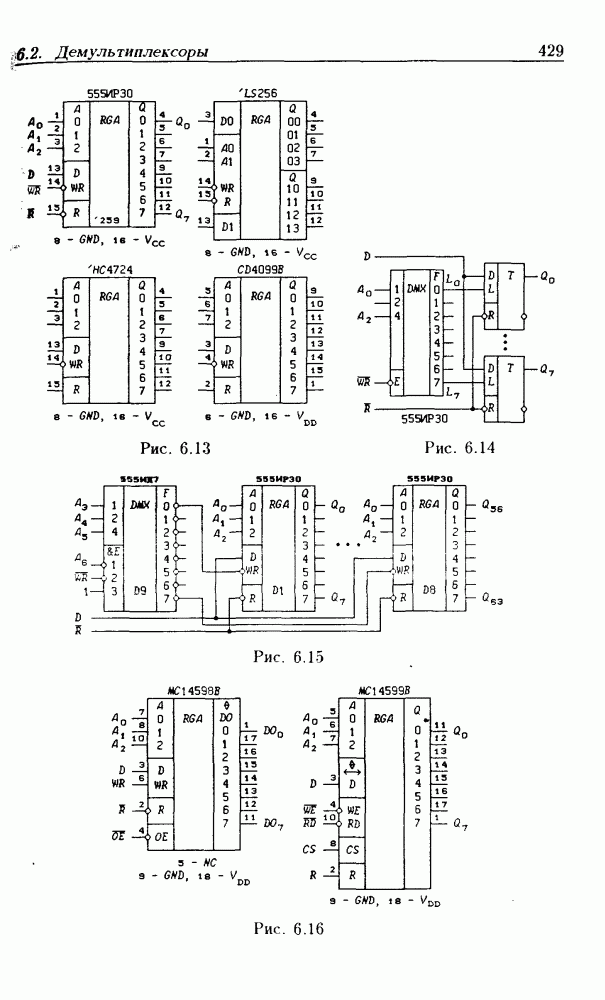
- 6.2. Демультиплексоры
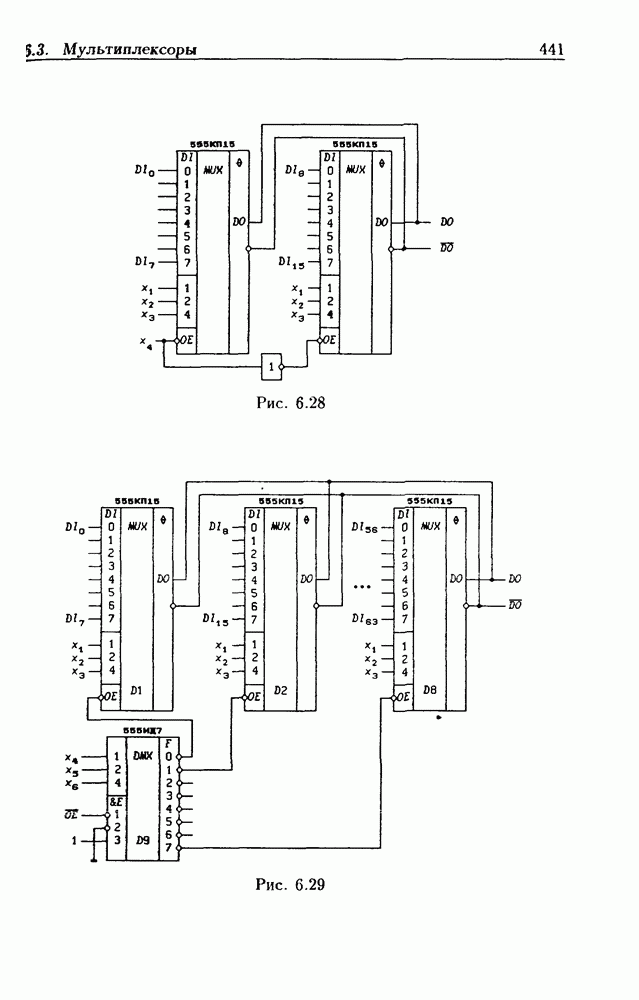
- 6.3. Мультиплексоры
- Мультиплексоры без стробирования.
- Мультиплексоры со стробированием.
- Мультиплексоры с Z-состоянием выхода.
- Каскадирование мультиплексоров.
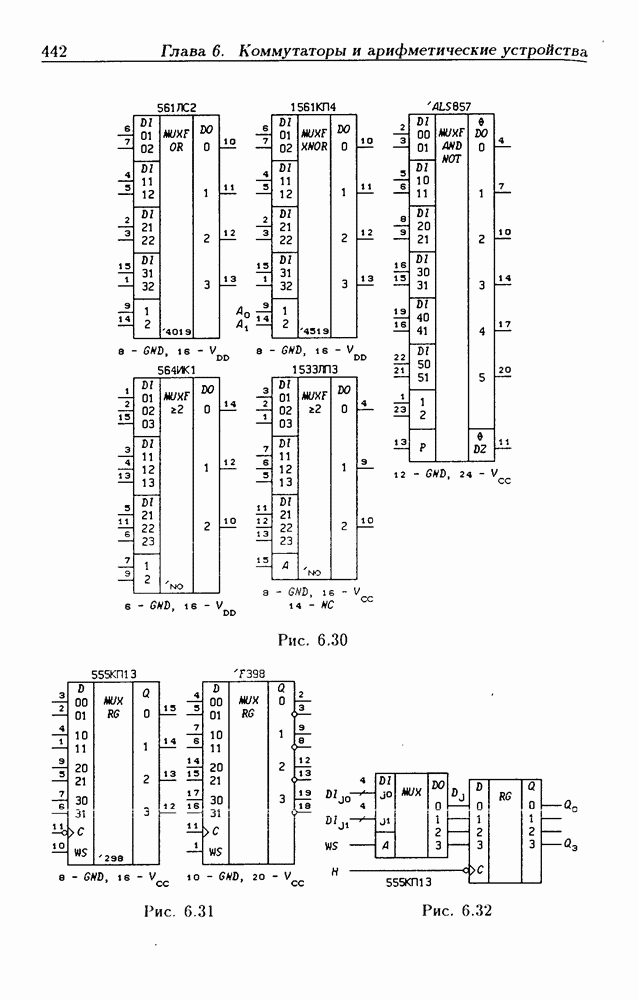
- Функциональные мультиплексоры.
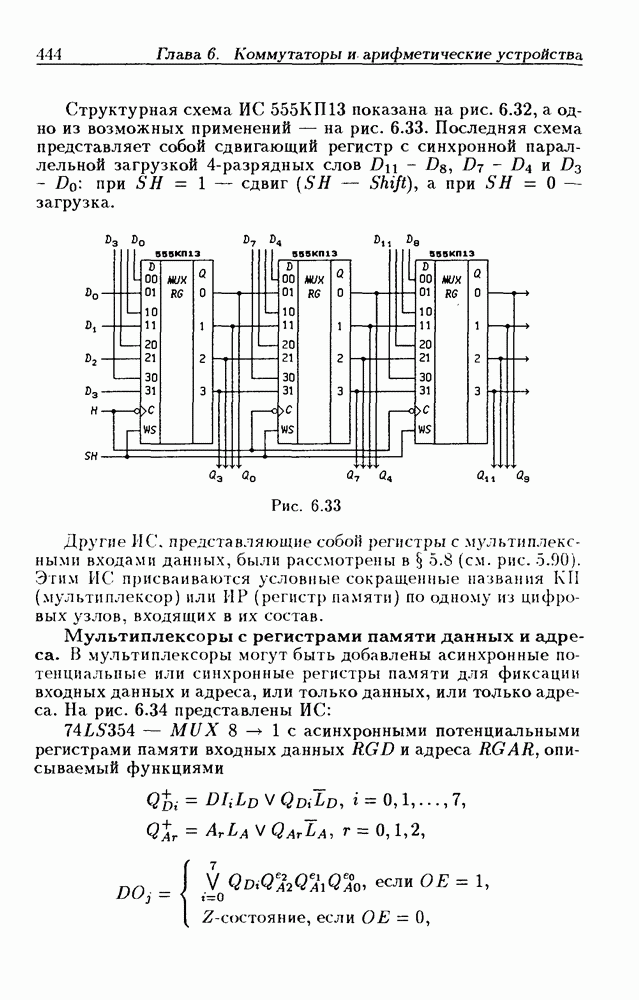
- Регистры памяти с мультиплексными входами данных.
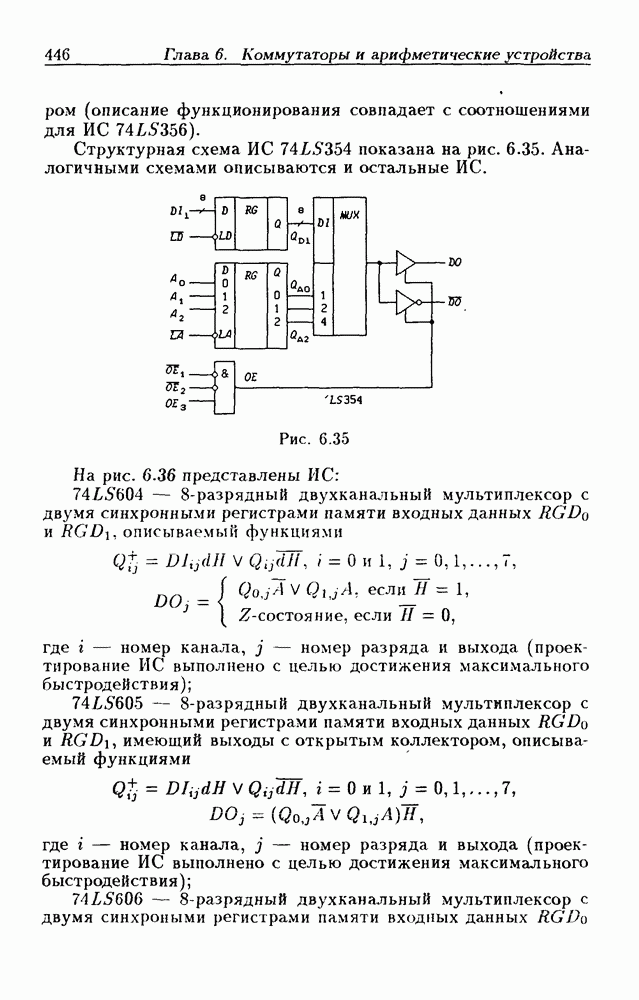
- Мультиплексоры с регистрами памяти данных и адреса.
- Сдвигающие мультиплексоры.
- 6.4. Синтез комбинационных схем и цифровых автоматов на мультиплексорах
- Синтез схем на 8-канальных мультиплексорах.
- Синтез на двухразрядных 4-канальных мультиплексорах.
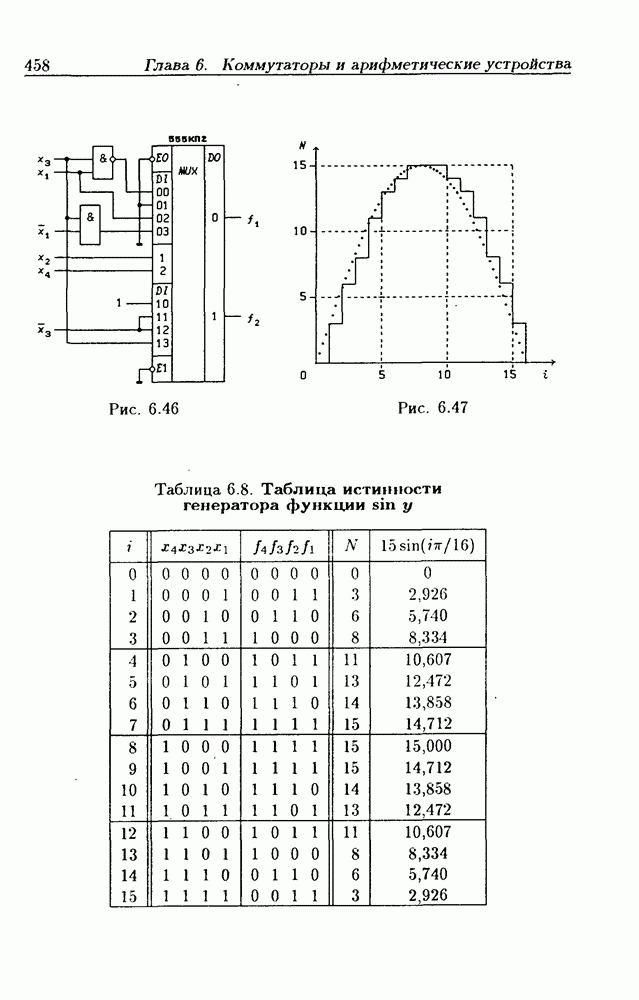
- Синтез генератора синусоидальной функции на мультиплексорах.
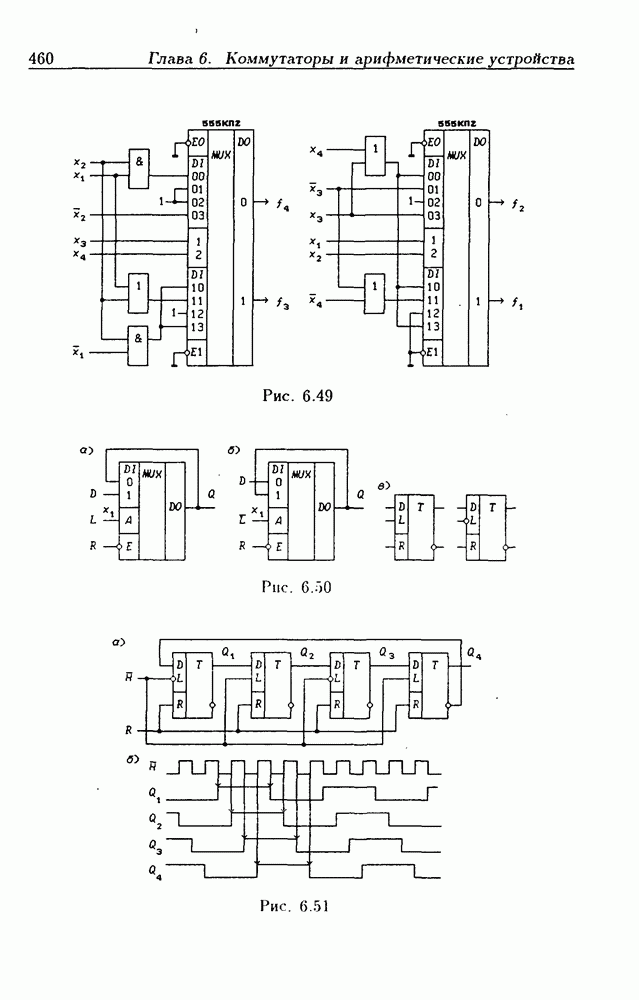
- Синтез триггеров на мультиплексорах.
- Синтез счетчиков на мультиплексорах.
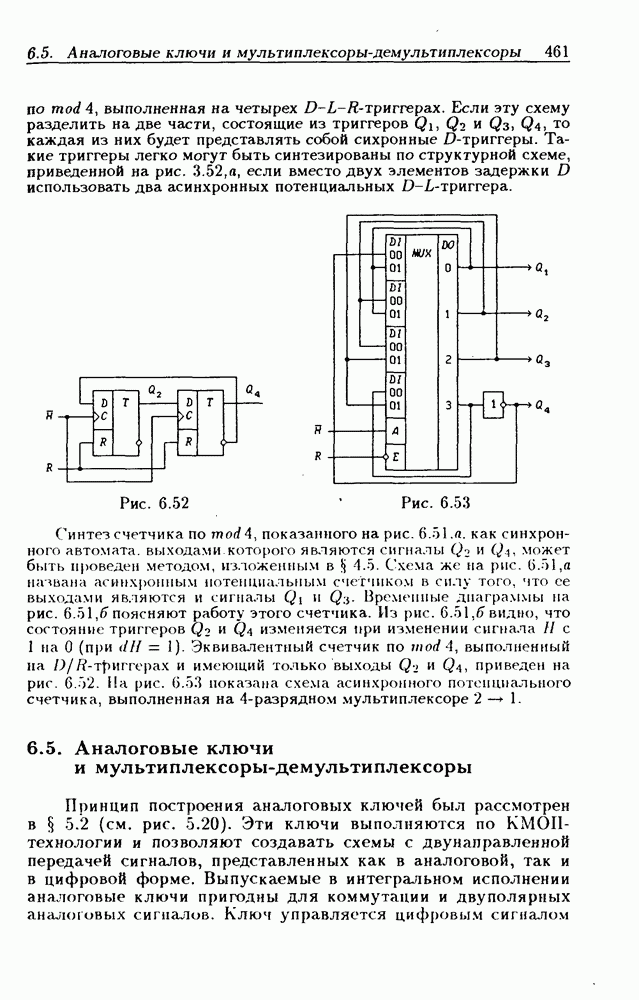
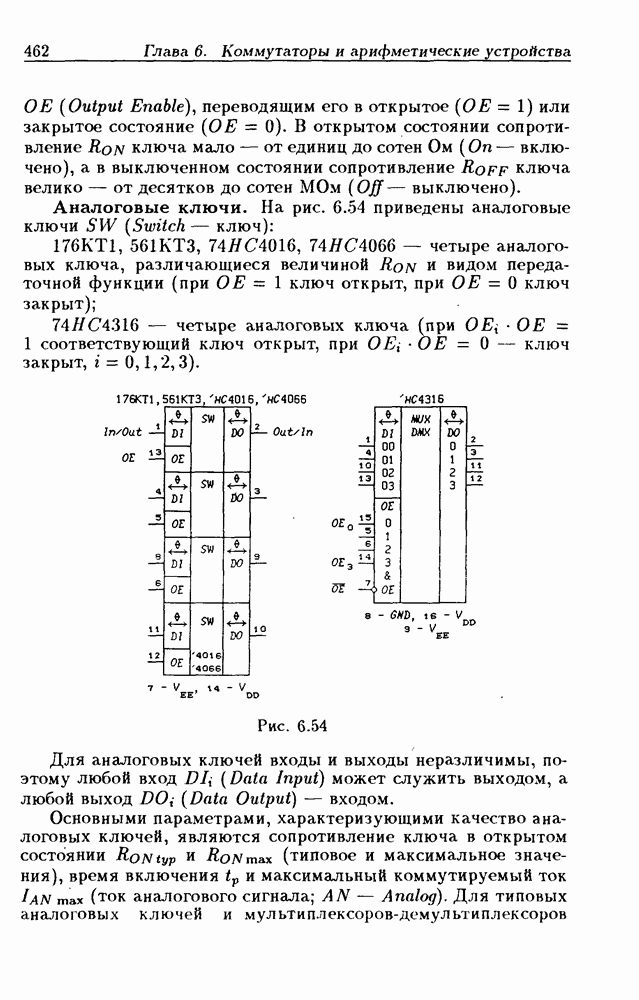
- 6.5. Аналоговые ключи и мультиплексоры-демультиплексоры
- 6.6. Шифраторы
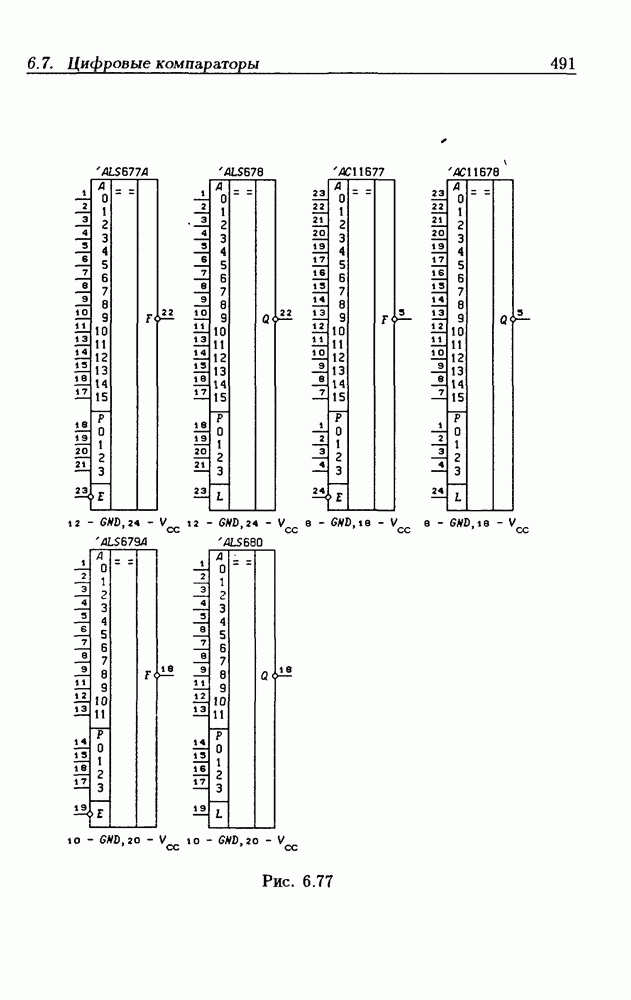
- 6.7. Цифровые компараторы
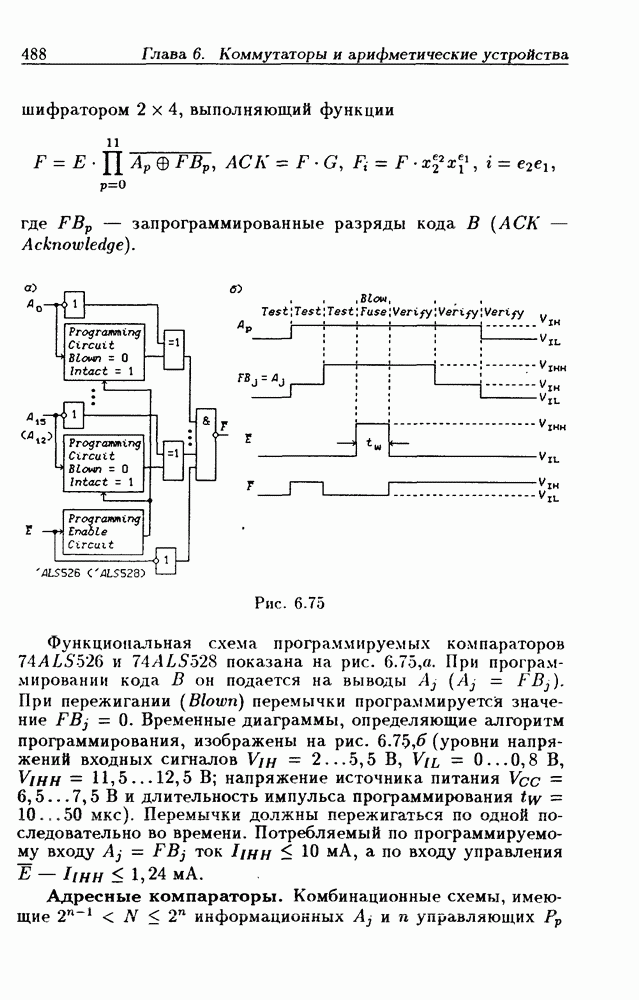
- Программируемые цифровые компараторы.
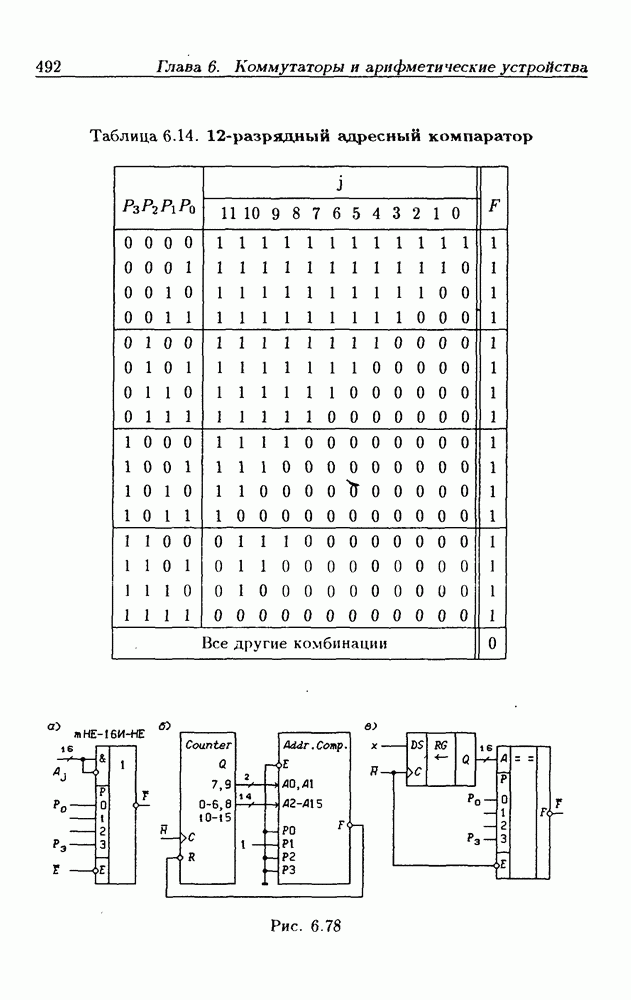
- Адресные компараторы.
- Применения адресных компараторов.
- 6.8. Схемы сравнения двоичных чисел
- 8-разрядные схемы сравнения двоичных чисел.
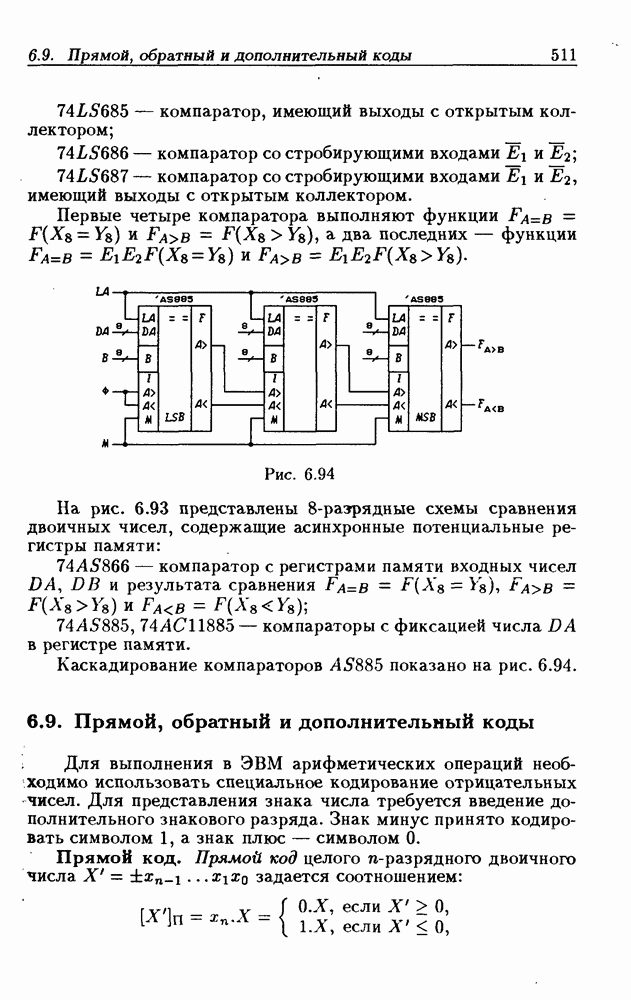
- 6.9. Прямой, обратный и дополнительный коды
- Дополнительный код.
- Сложение чисел в обратном коде.
- Код с избытком 3.
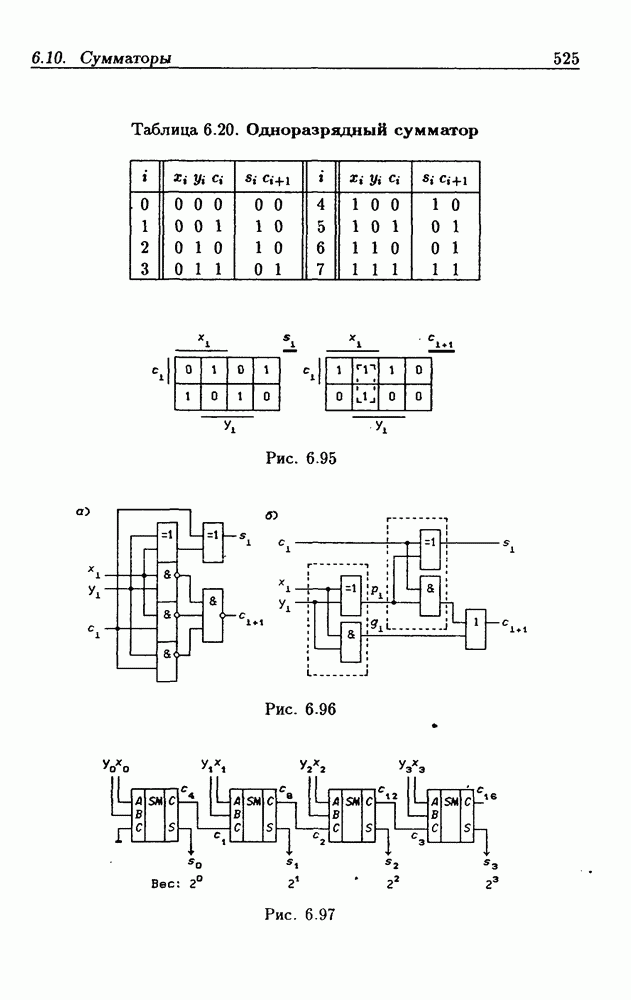
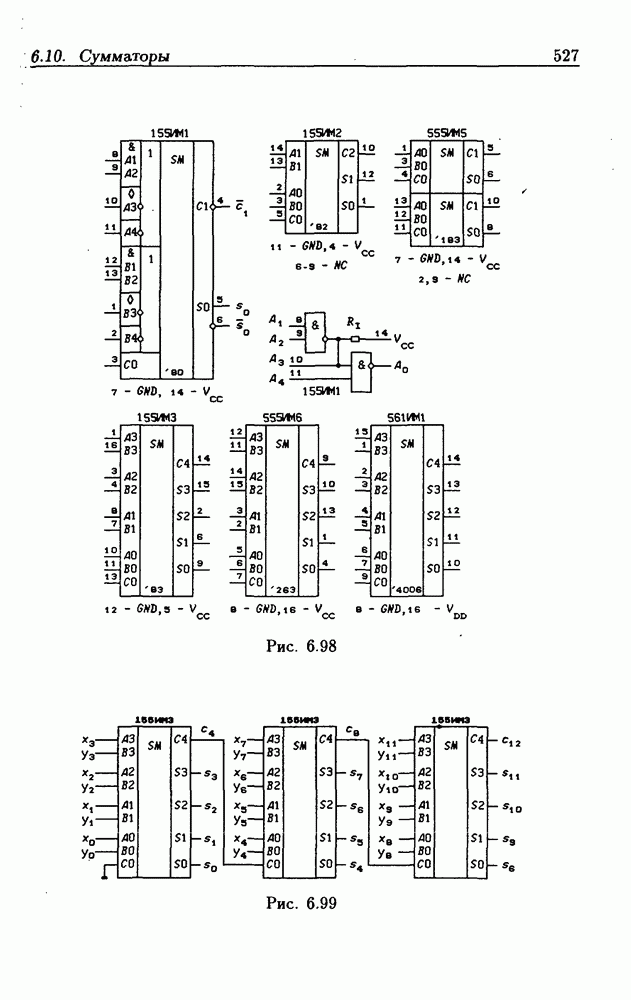
- 6.10. Сумматоры
- Двоичные параллельные сумматоры с последовательным переносом.
- Двоичные сумматоры с параллельным переносом.
- Применения сумматоров.
- Десятичные сумматоры.
- Последовательные двоичные сумматоры.
- 6.11. Арифметическо-логические устройства
- 6.12. Пороговые схемы и мажоритарные элементы
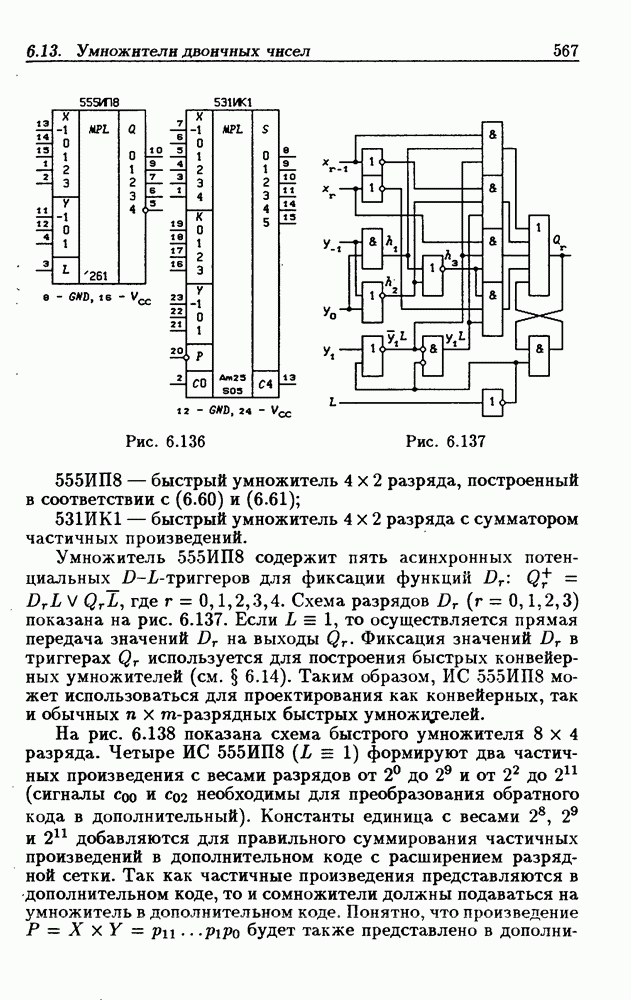
- 6.13. Умножители двоичных чисел
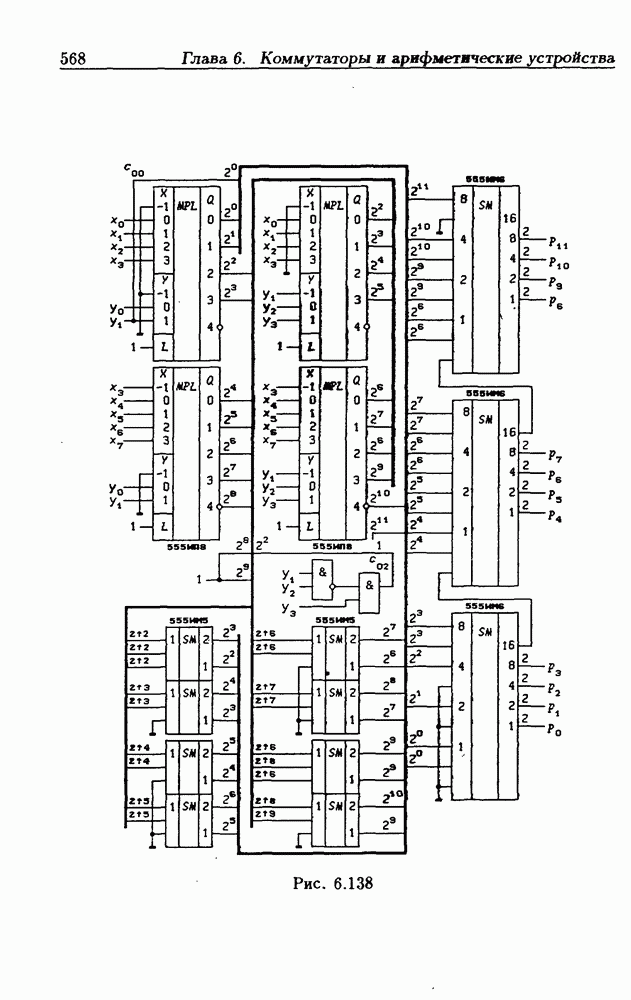
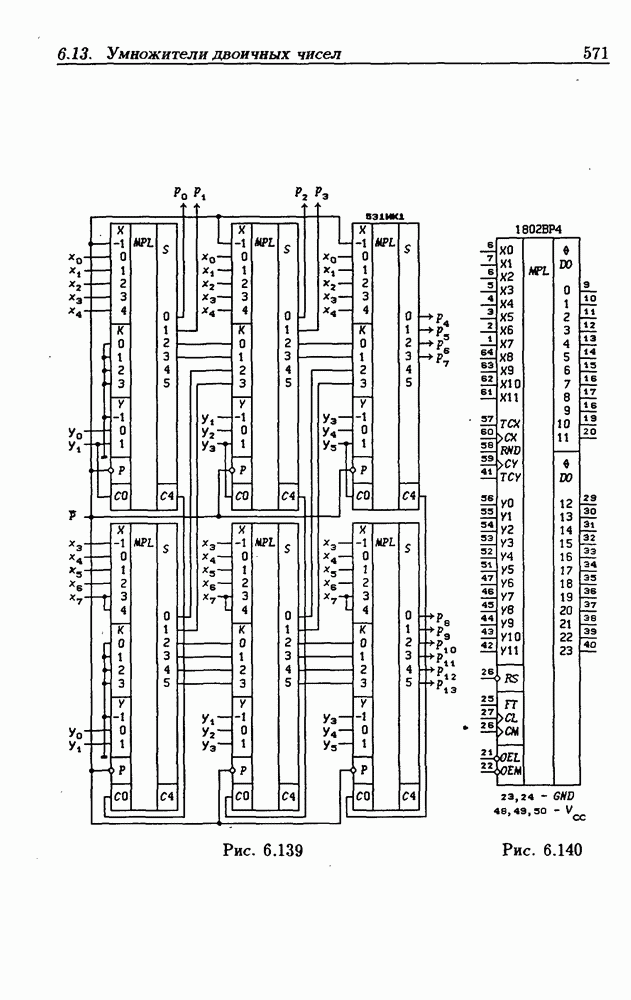
- Быстрые умножители.
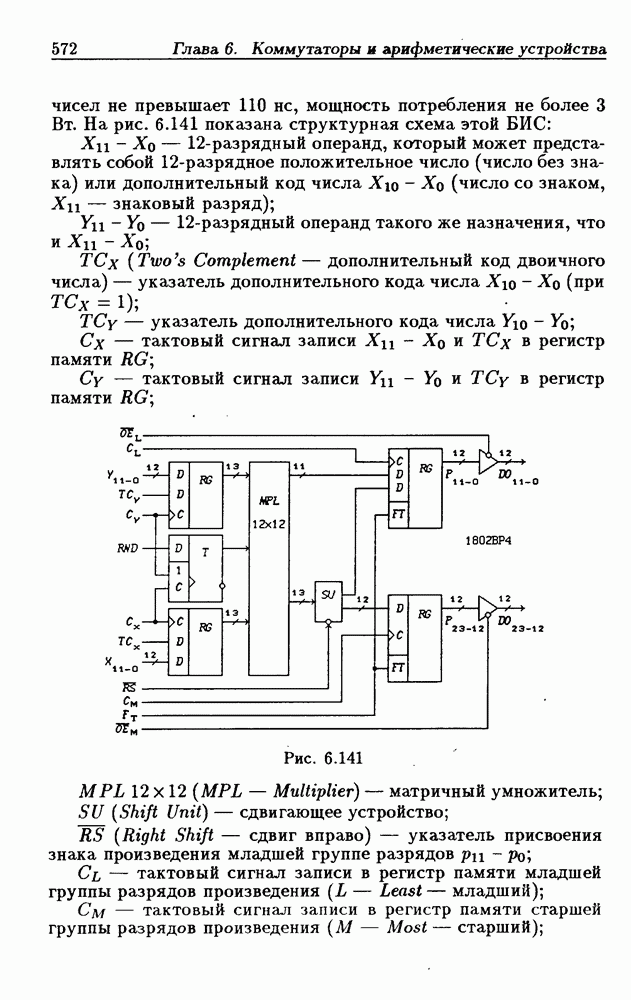
- БИС умножителя 12×12 разрядов 1802ВР4.
- Последовательные умножители.
- 6.14. Конвейерные устройства
- Конвейерный быстрый умножитель.
- Конвейерные АЦП.
- 6.15. Синтез линейных комбинационных схем
- Сумматор по модулю q.
- Умножитель по модулю q.
- Глава 7. Сдвигающие регистры и счетчики
- 7.1. Сдвигающие регистры без параллельной записи данных
- Сдвигающие устройства с выходными регистрами памяти.
- 7.2. Сдвигающие регистры с параллельной записью данных
- Сдвигающие регистры с расширением знака.
- Сдвигающие регистры с входным регистром памяти.
- 7.3. Реверсивные сдвигающие регистры
- Реверсивные сдвигающие регистры типов PI/SO и PI/PO.
- Многофункциональные устройства на основе реверсивных сдвигающих регистров.
- 7.4. Асинхронные счетчики
- Двоично-десятичные асинхронные счетчики.
- 7.5. Синхронные двоичные счетчики
- Программирование модуля пересчета двоичных счетчиков.
- Переключение модулей пересчета двоичных счетчиков.
- Функциональные устройства на основе двоичных счетчиков.
- 7.6. Синхронные двоично-десятичные счетчики
- 7.7. Синхронные реверсивные счетчики
- 7.8. Счетчики с расщепленным тактовым сигналом
- 7.9. Счетчики на сдвигающих регистрах
- 7.10. Кольцевые счетчики
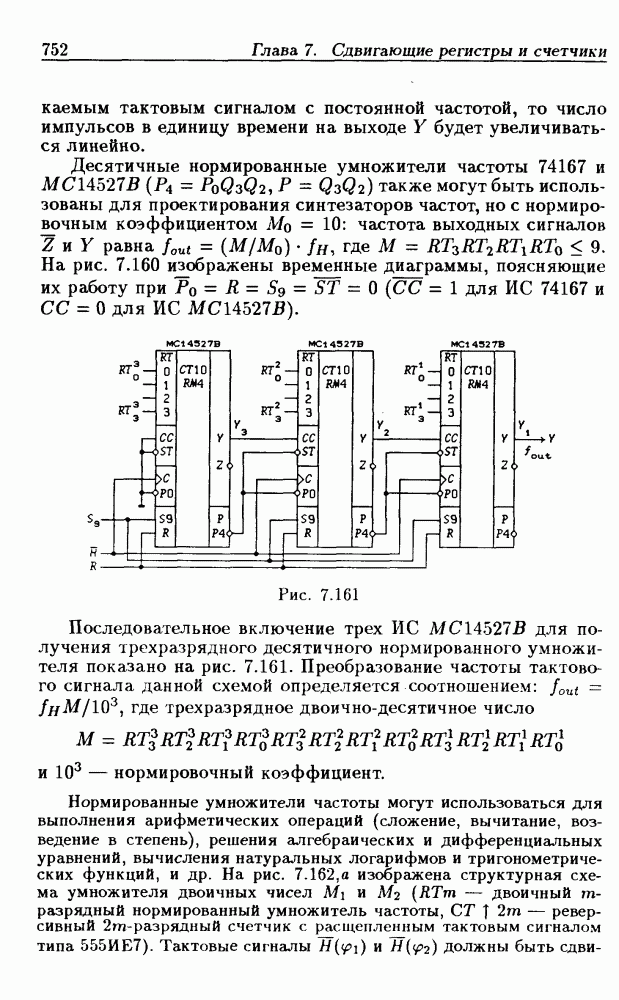
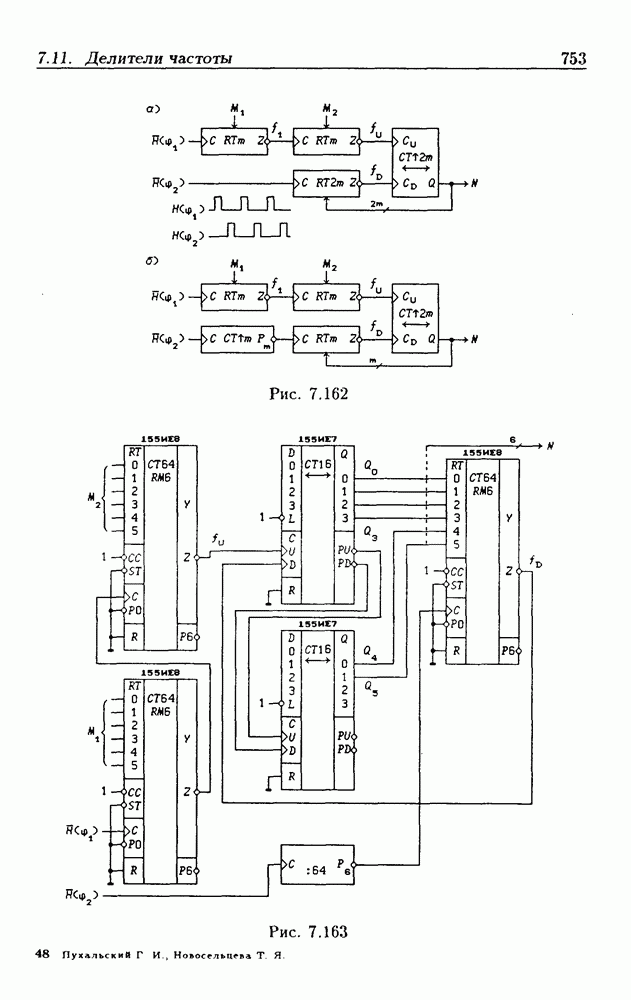
- 7.11. Делители частоты
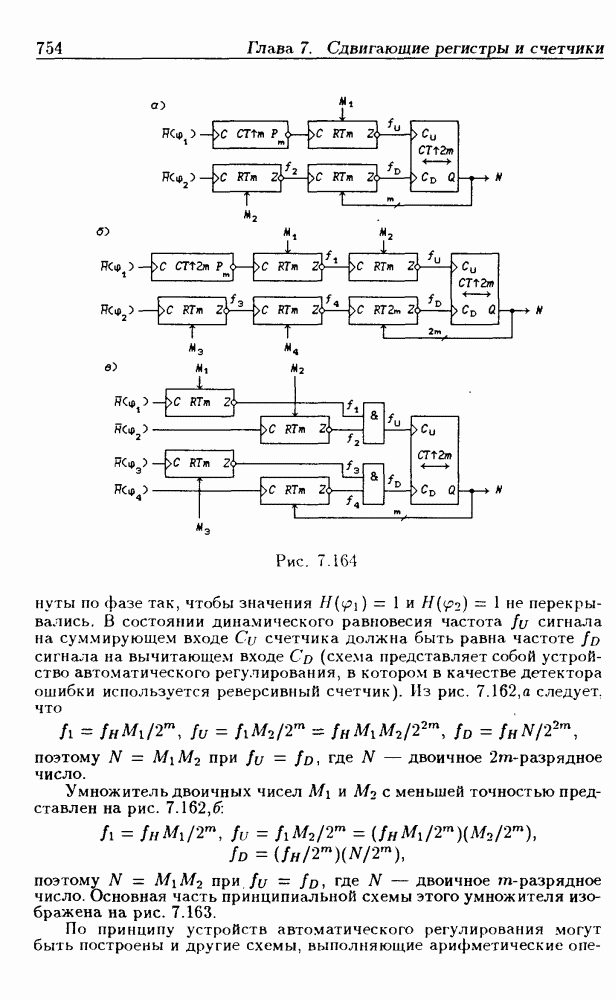
- Нормированные умножители частоты.
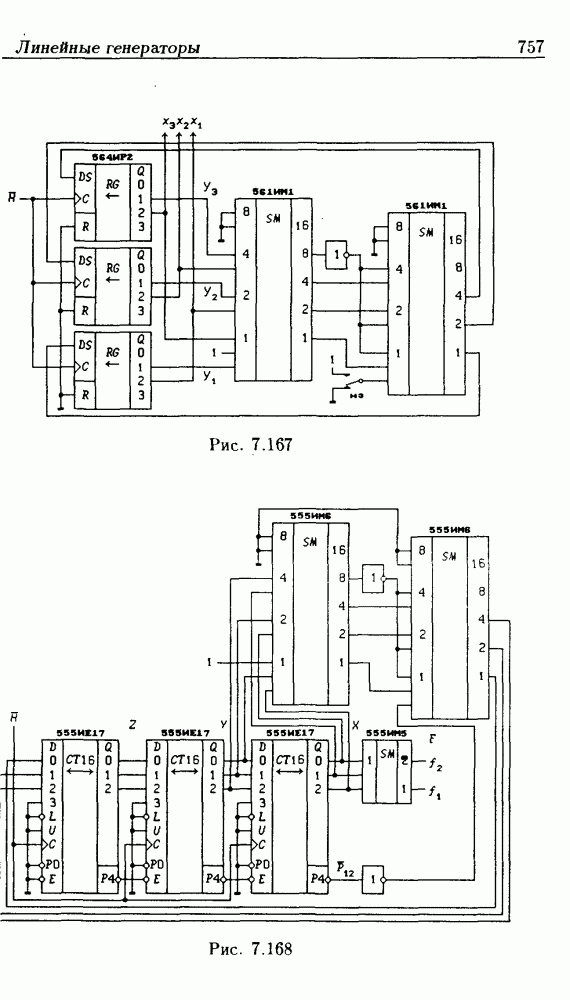
- 7.12. Линейные генераторы
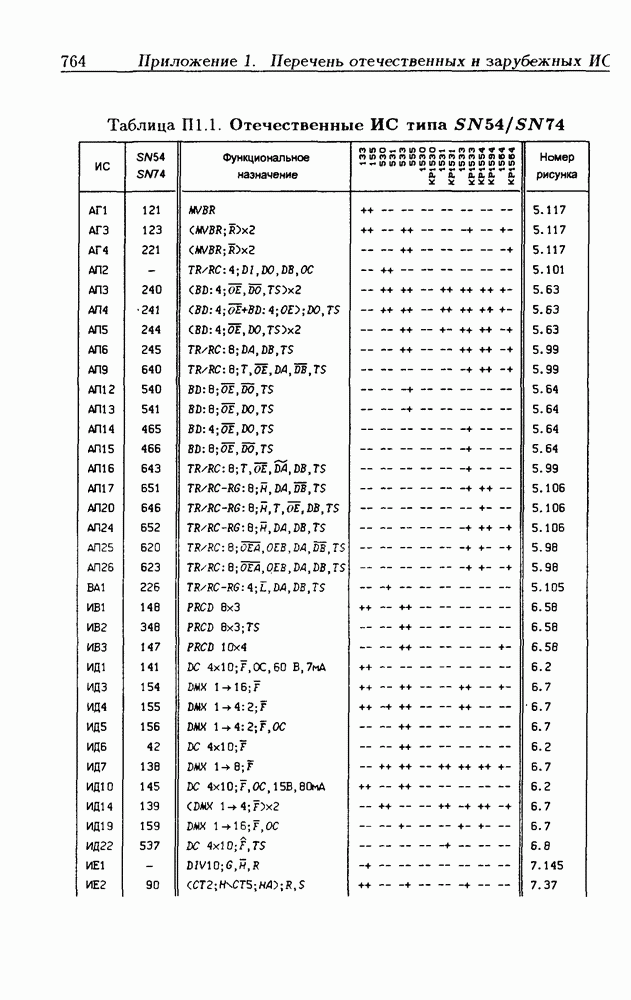
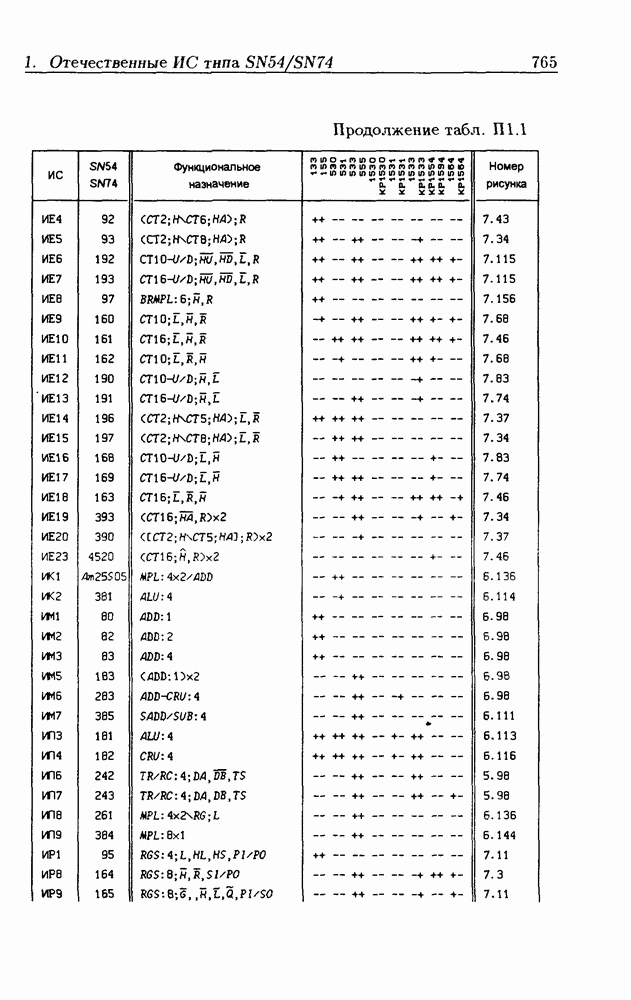
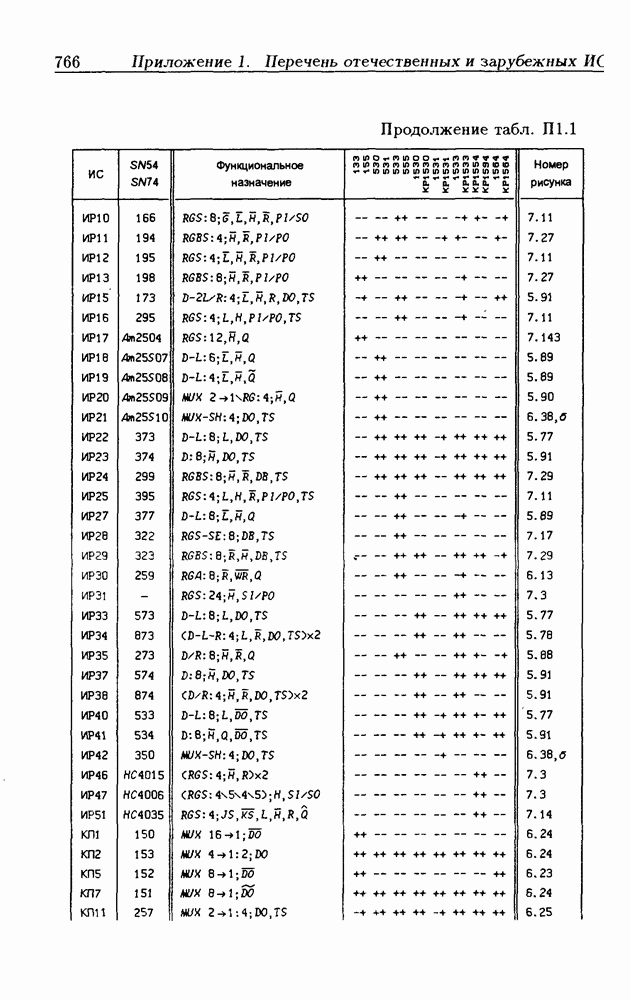
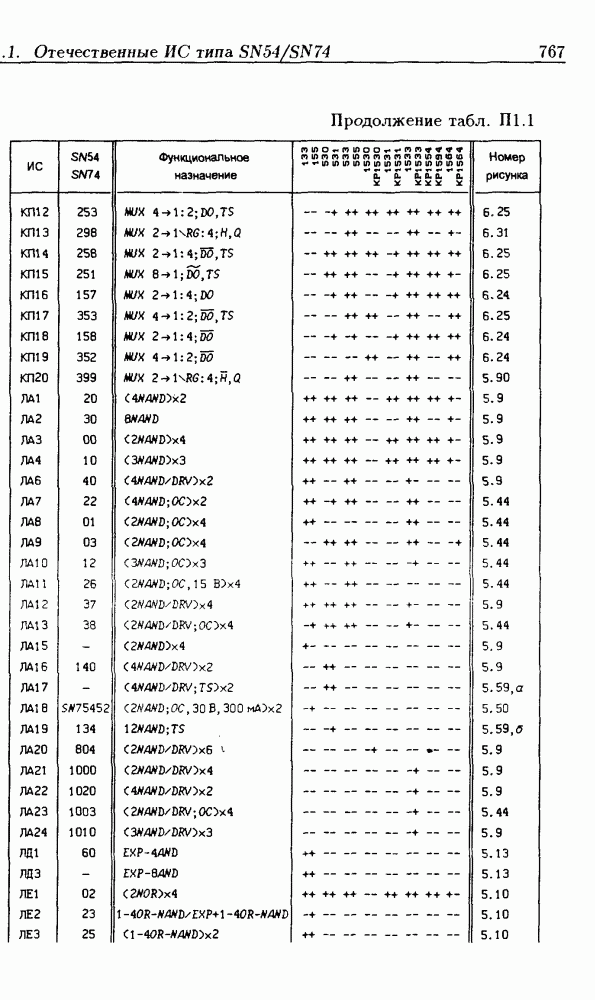
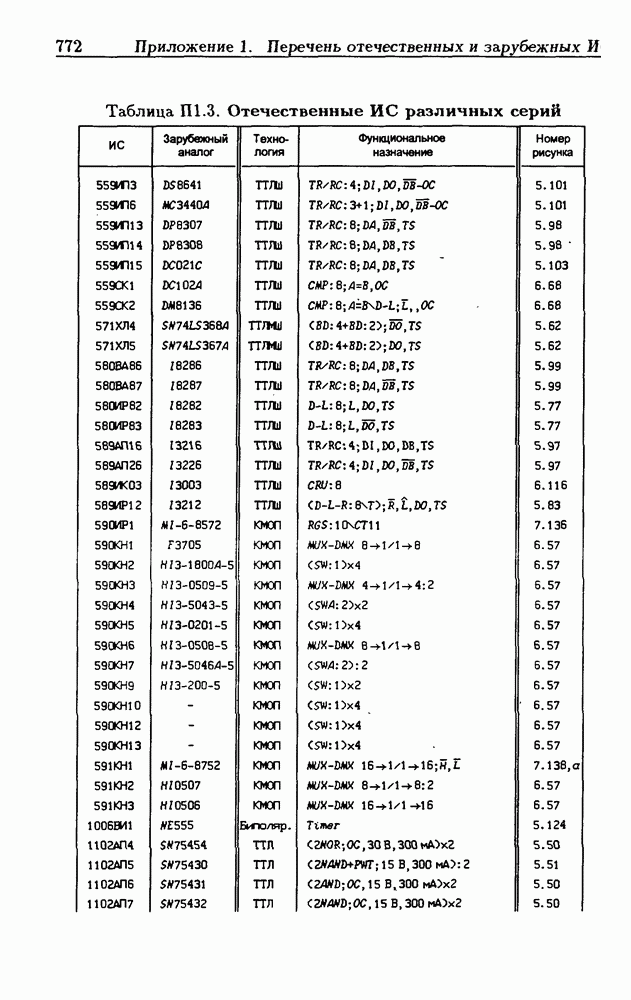
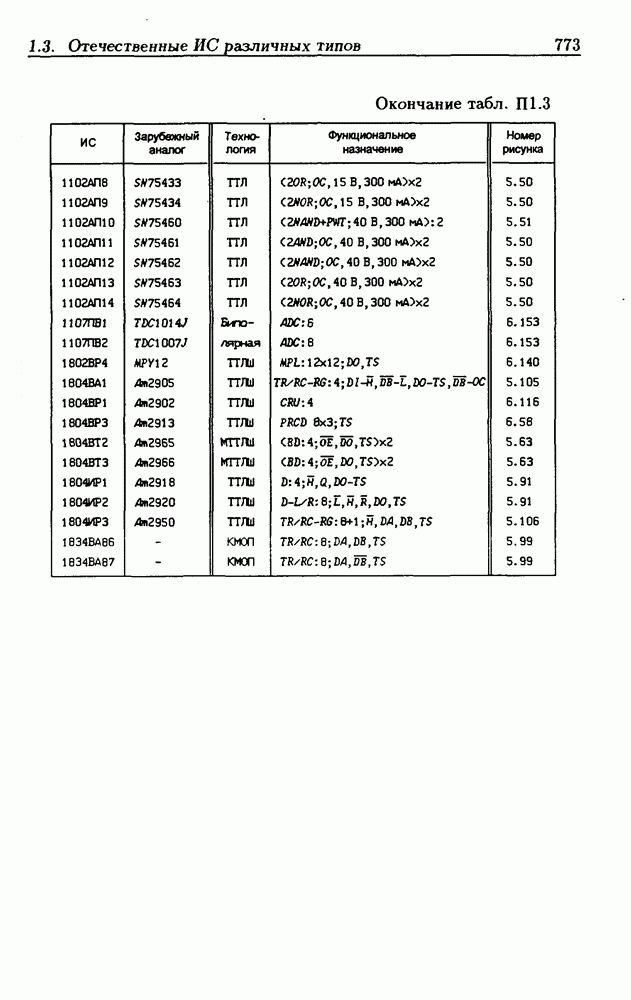
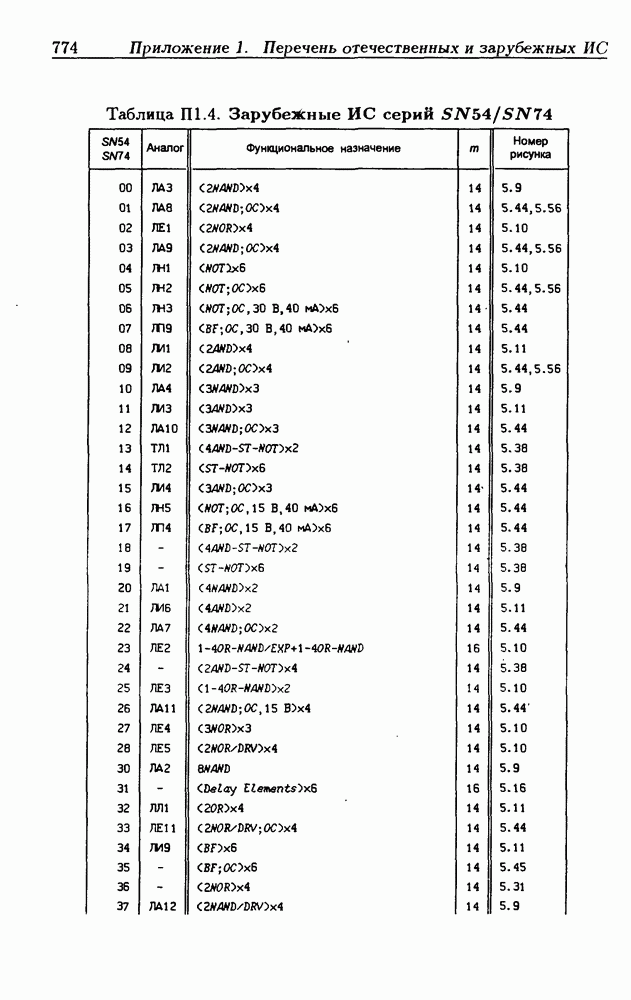
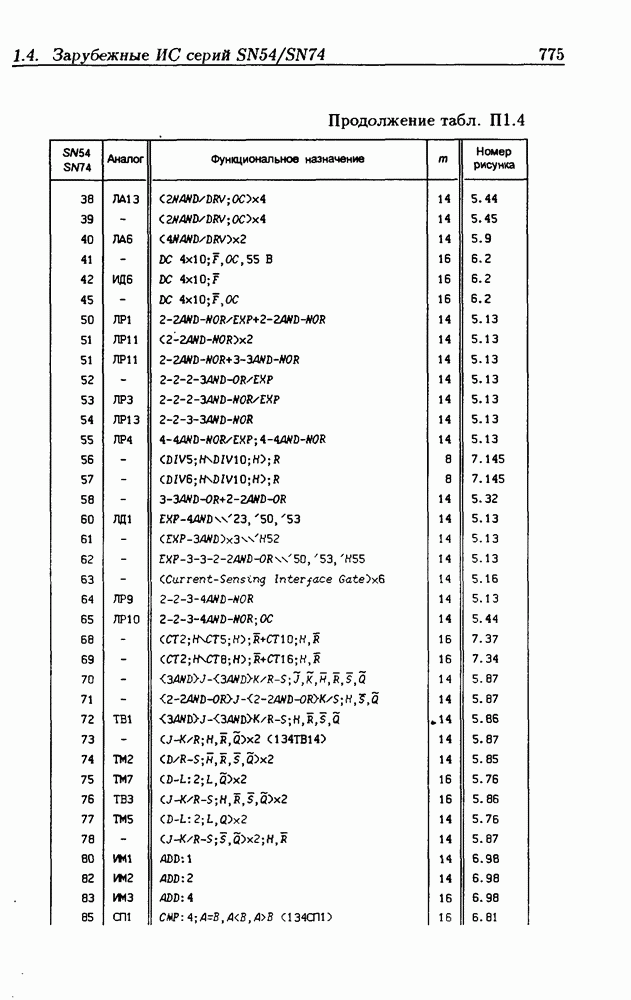
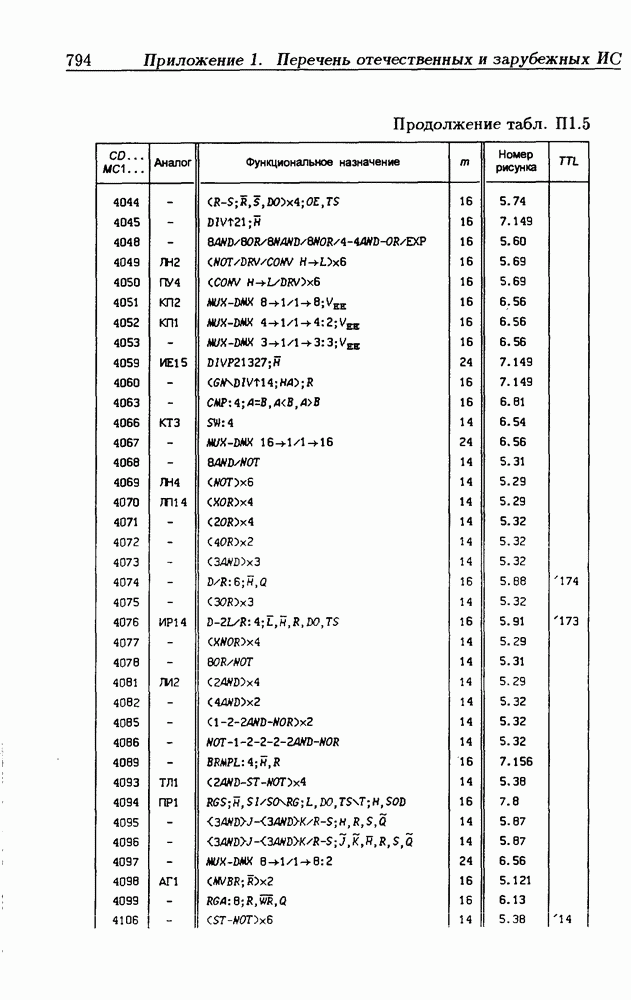
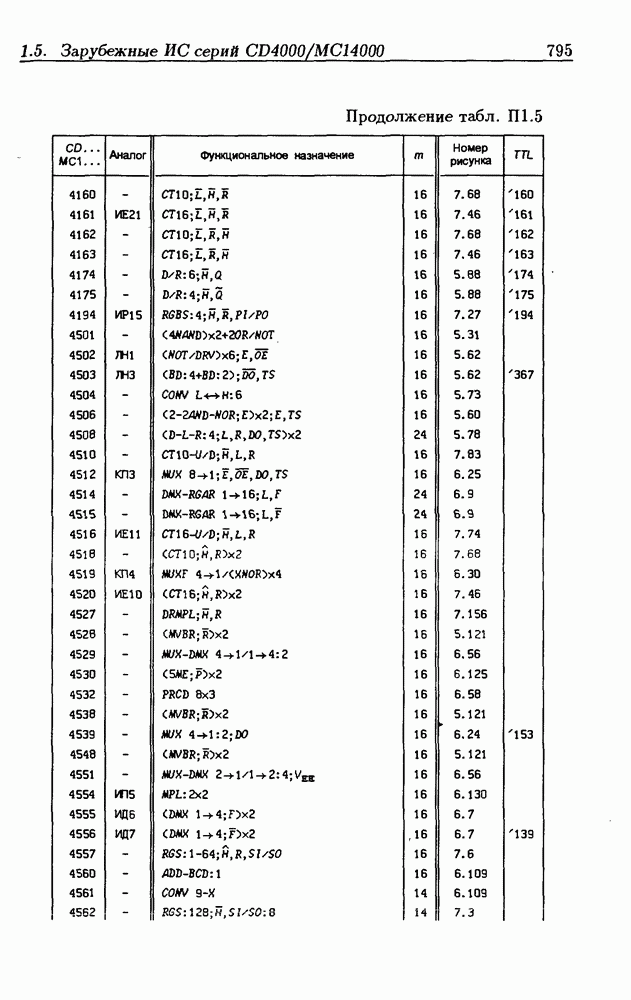
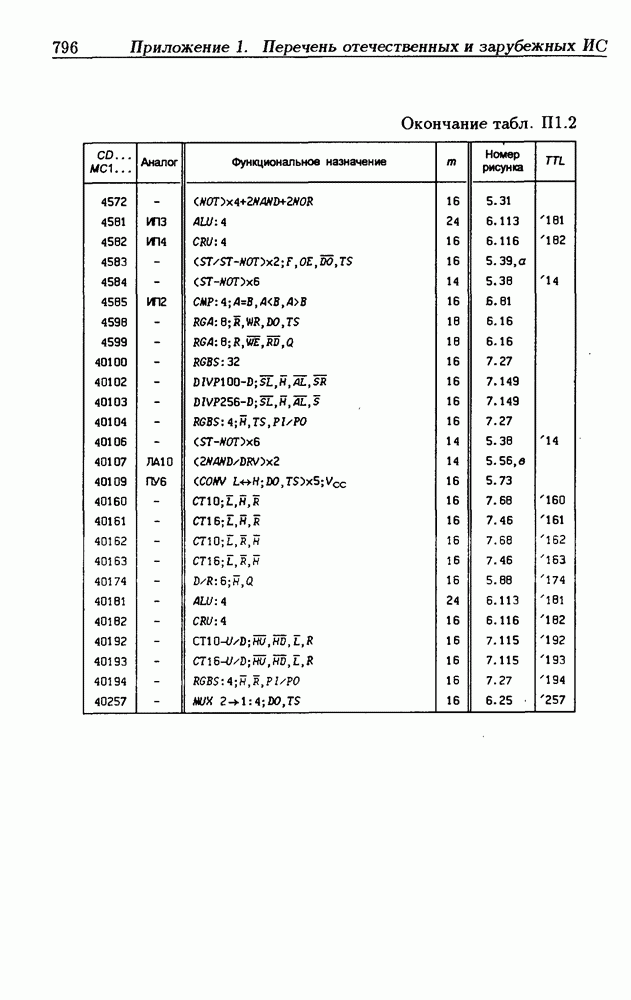
- Приложение 1. Перечень отечественных и зарубежных ИС
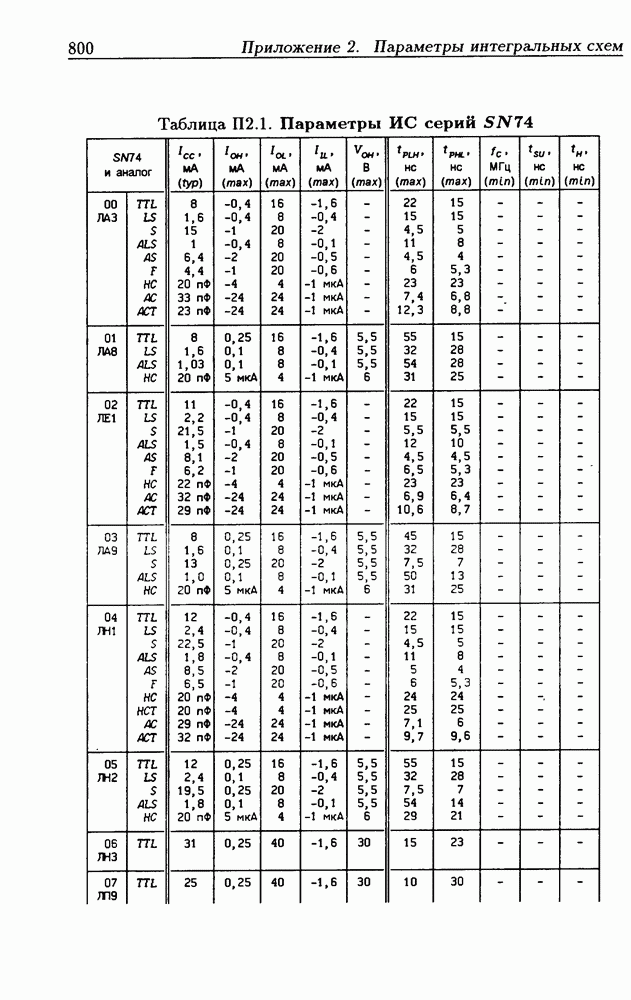
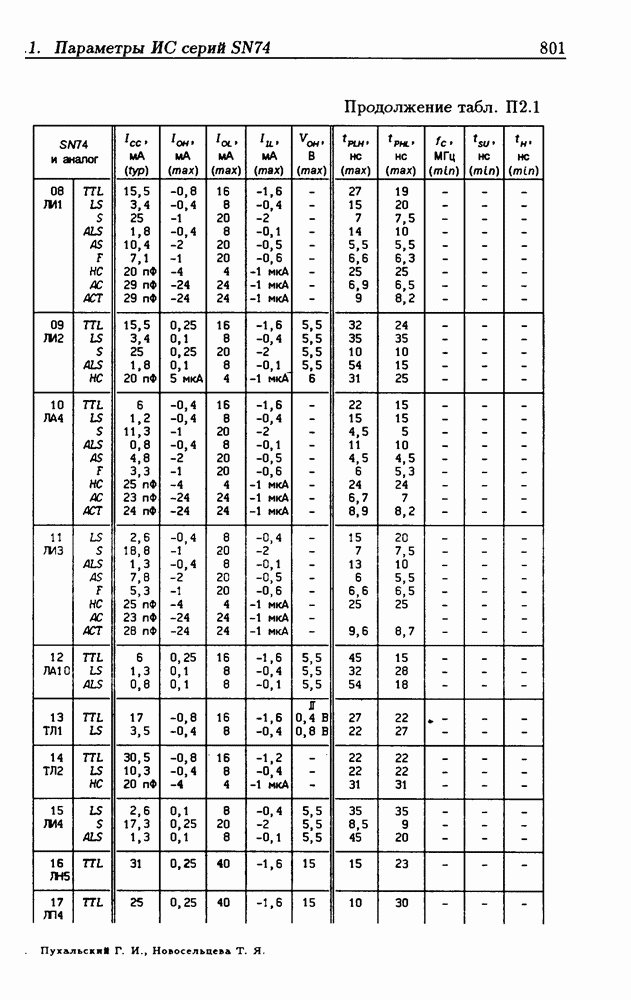
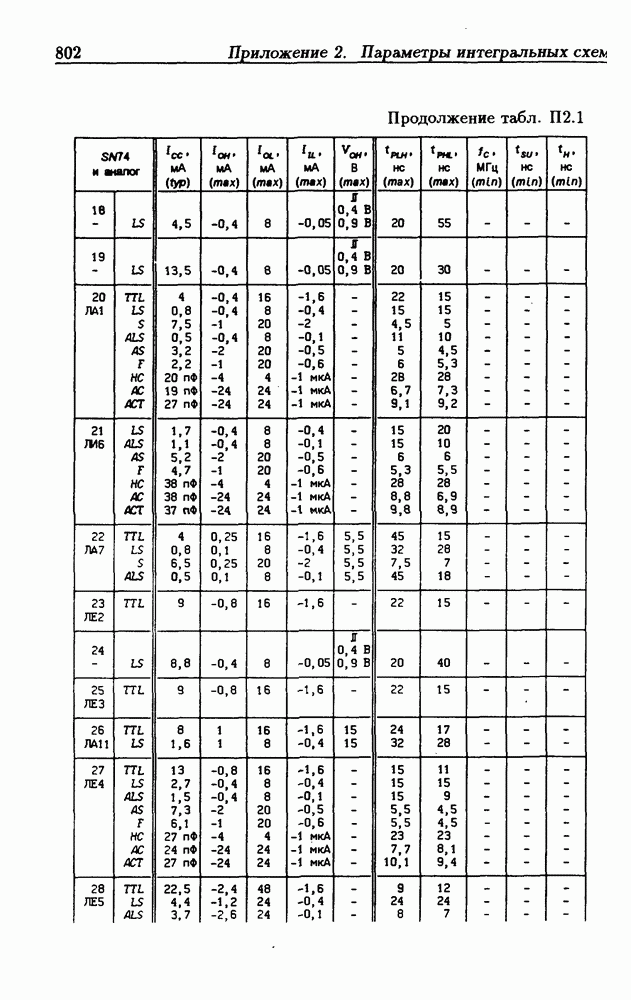
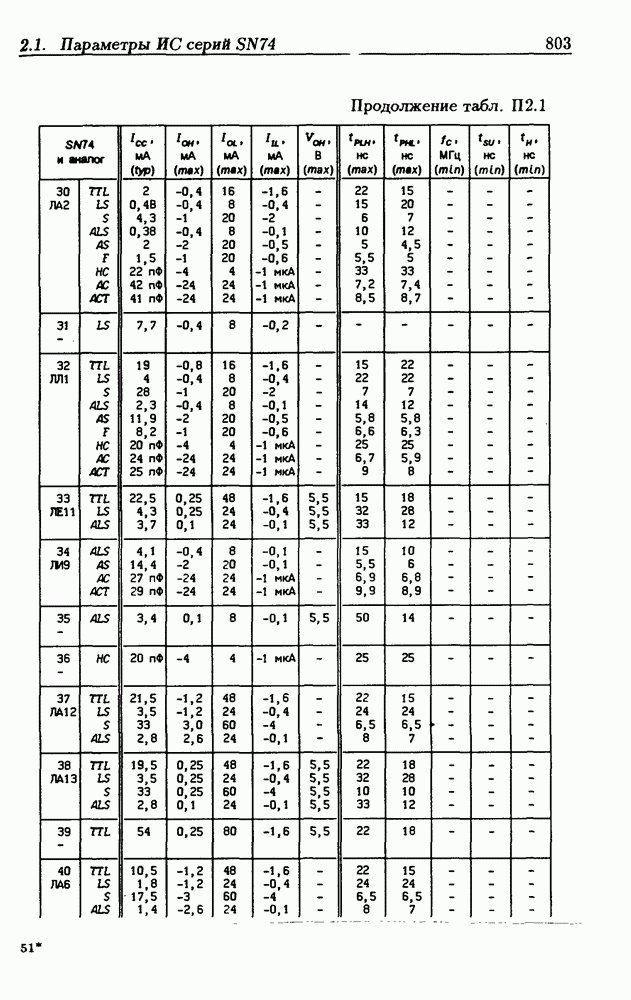
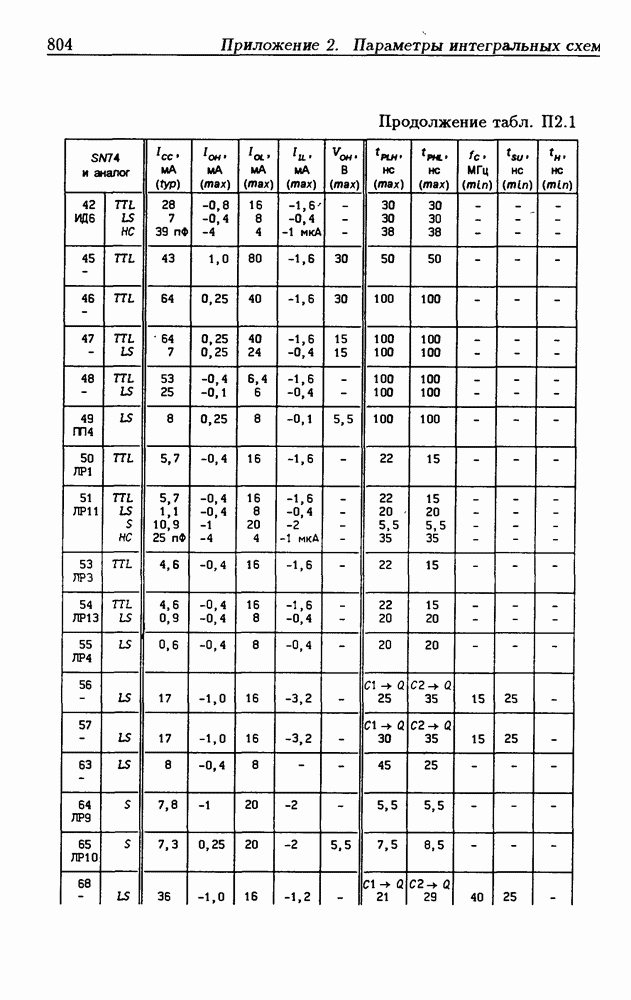
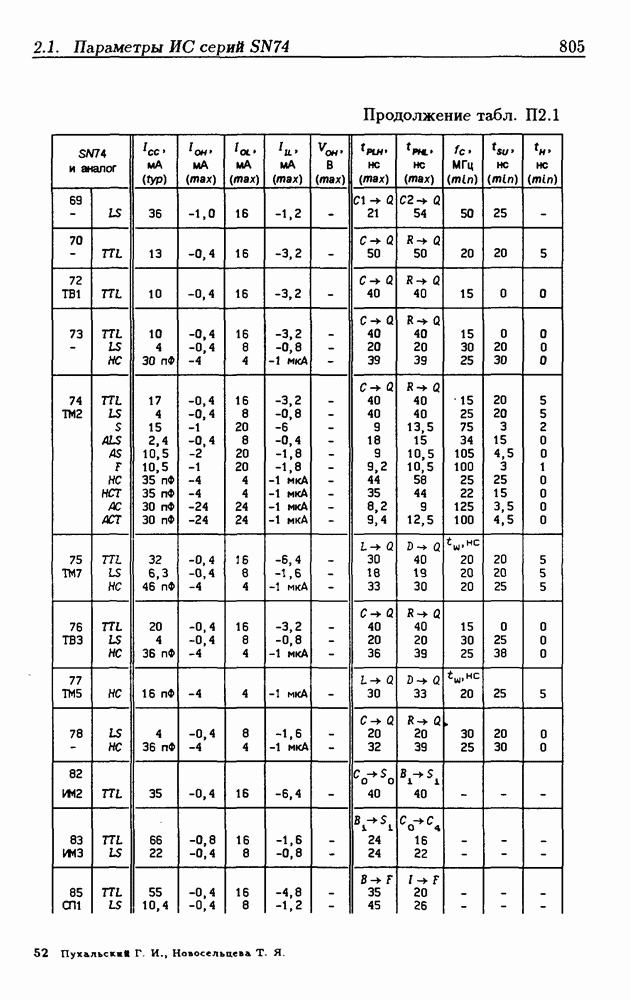
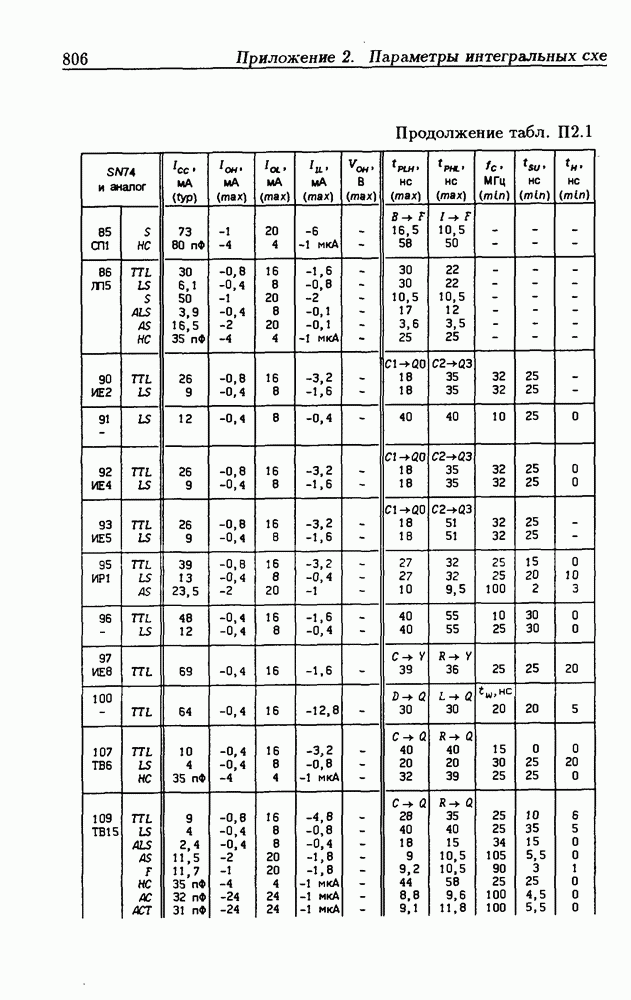
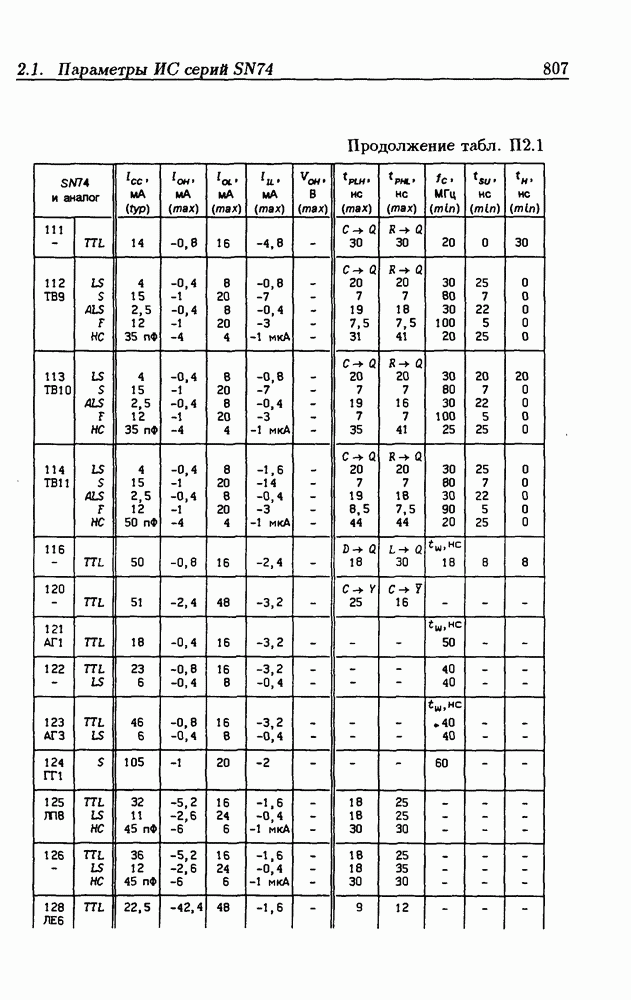
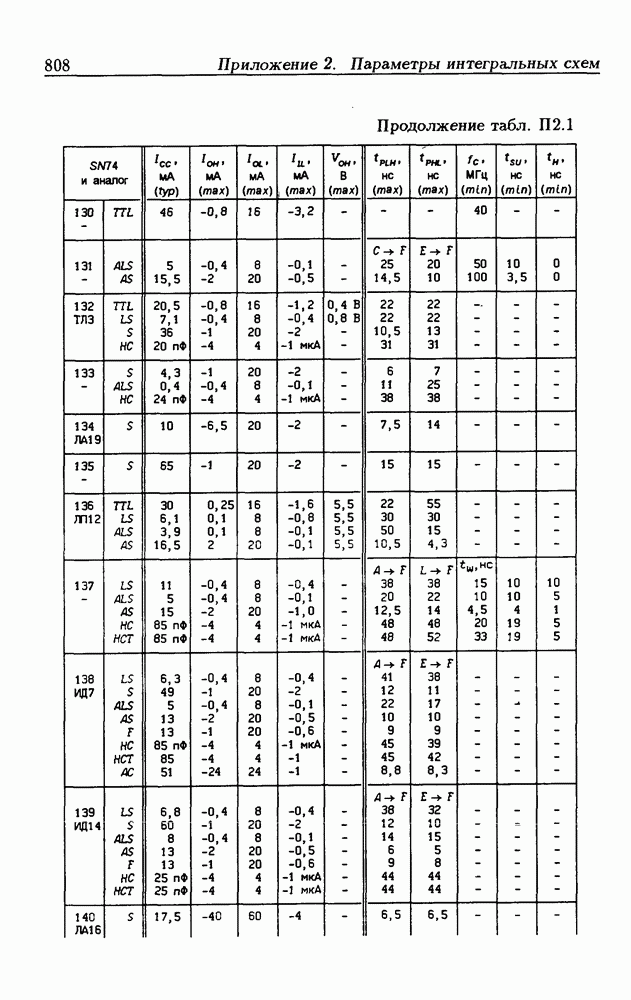
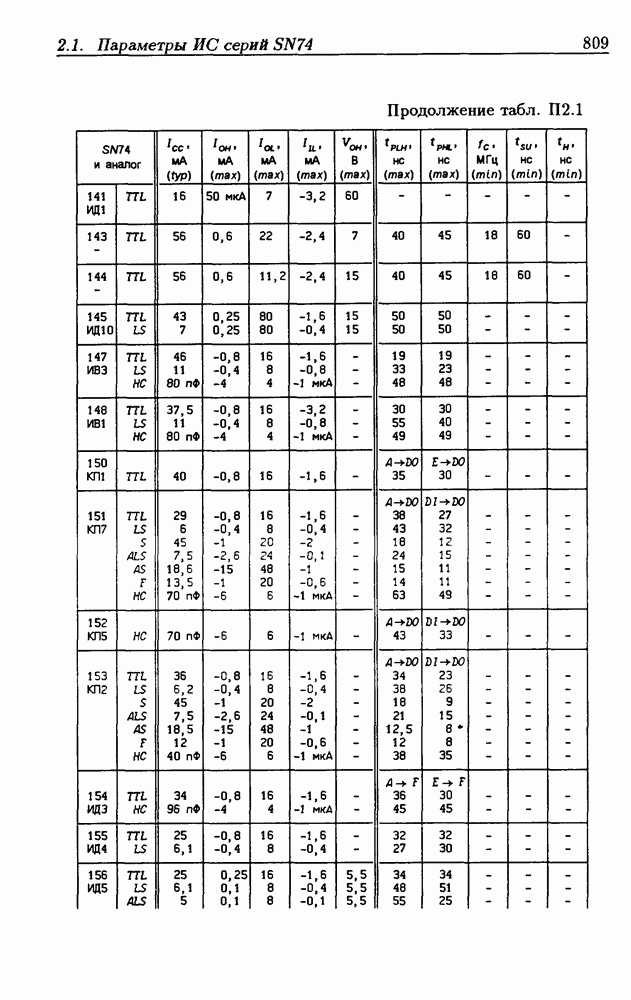
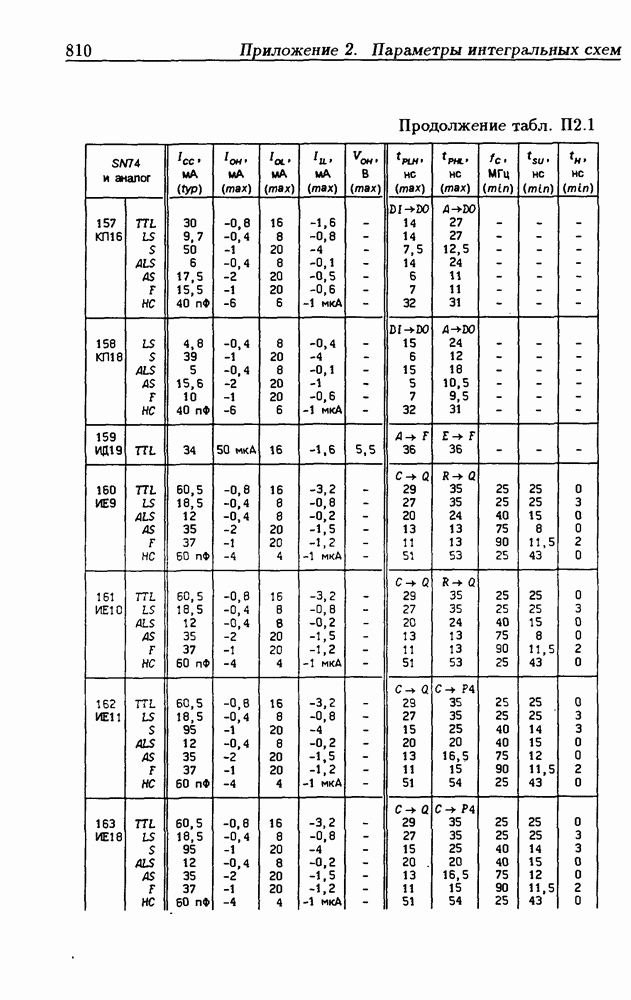
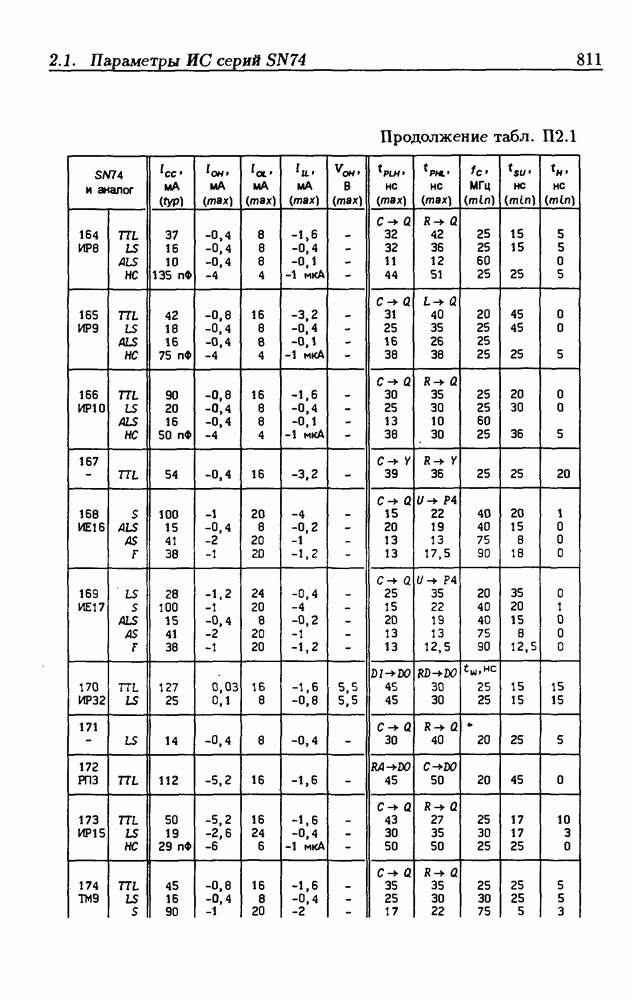
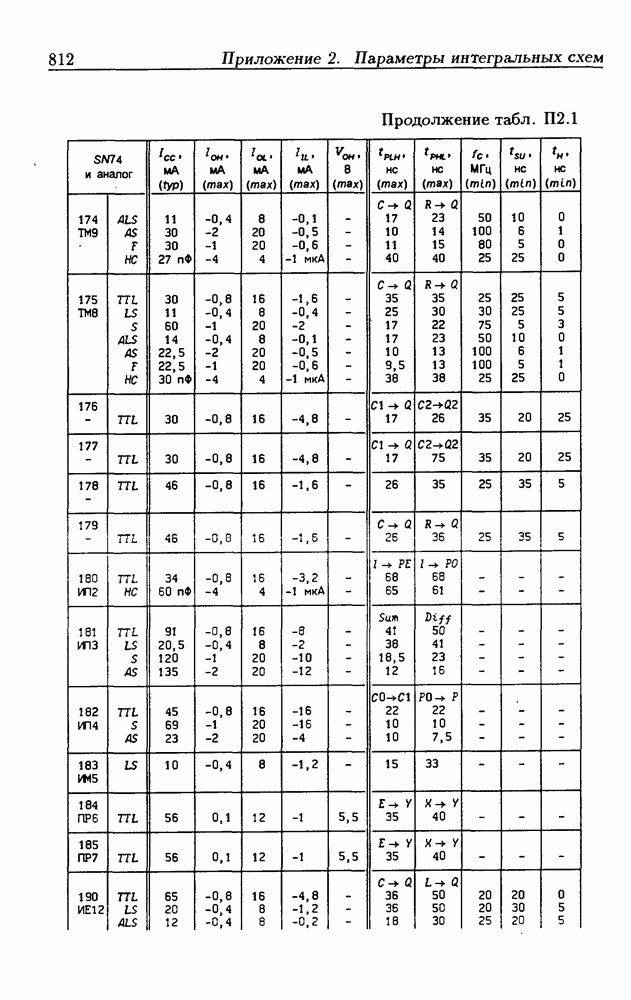
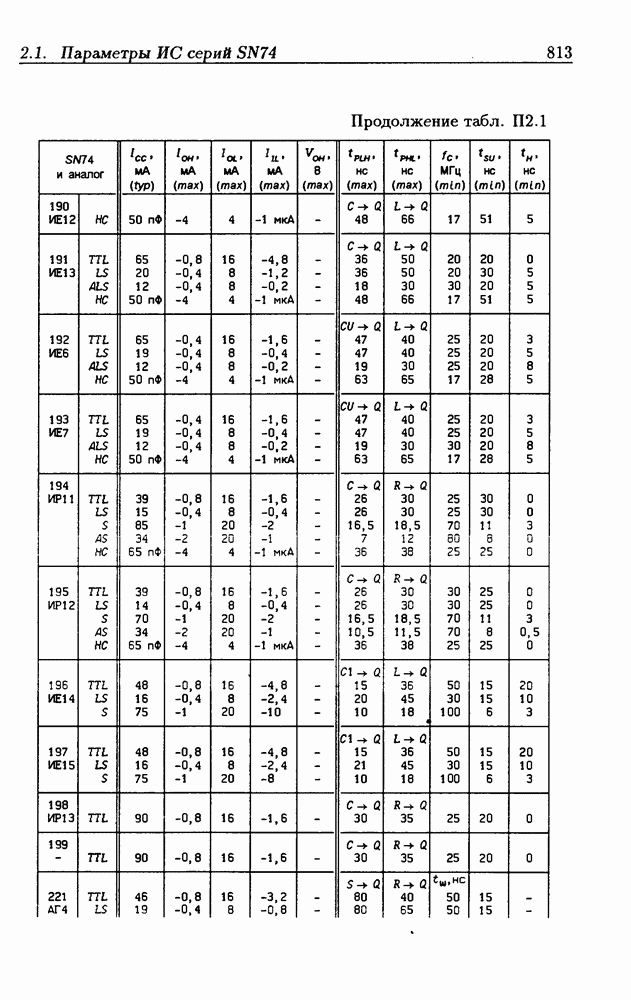
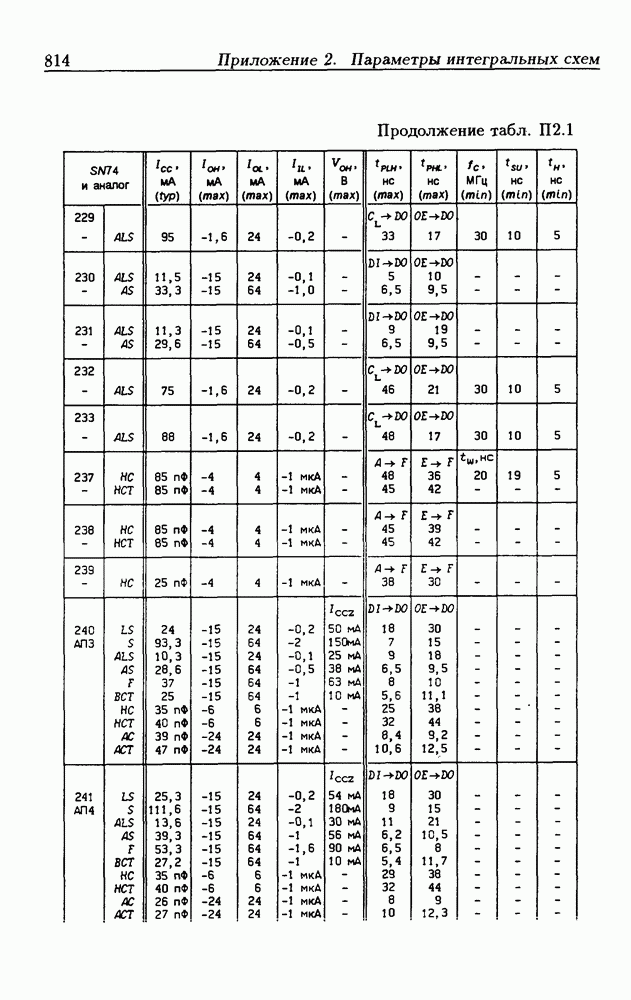
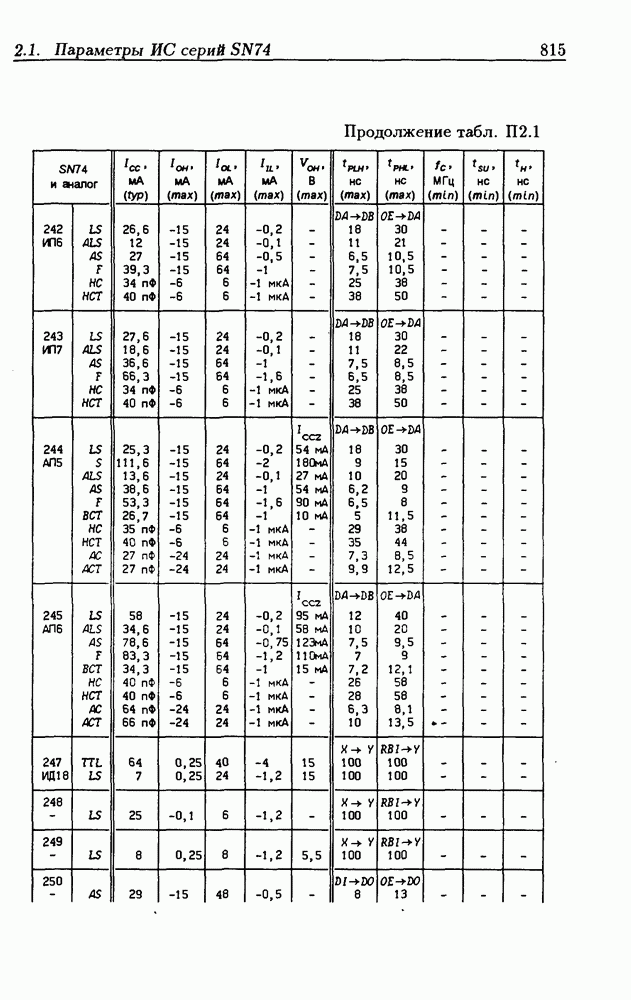
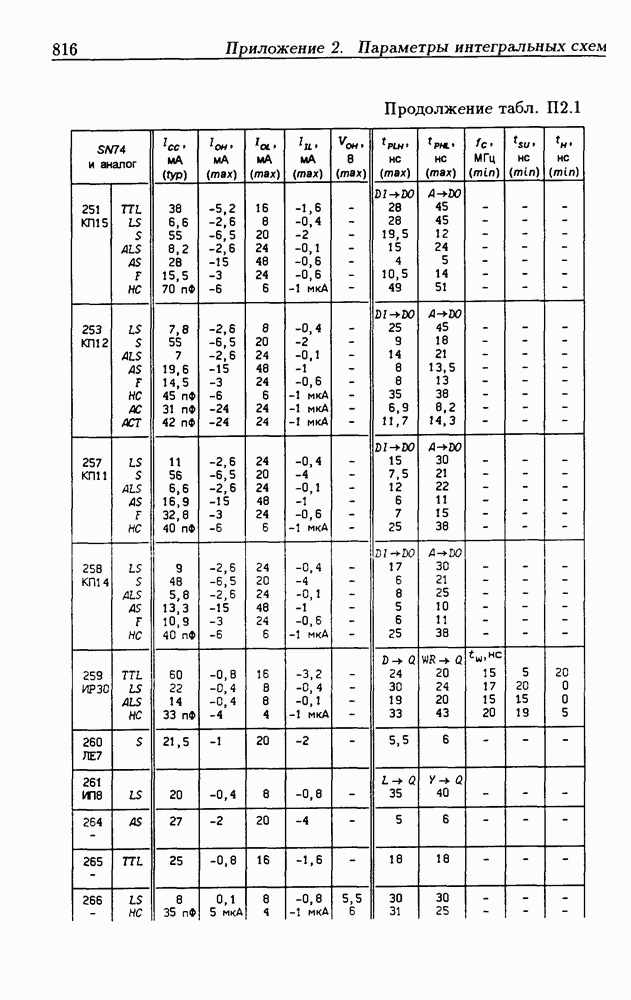
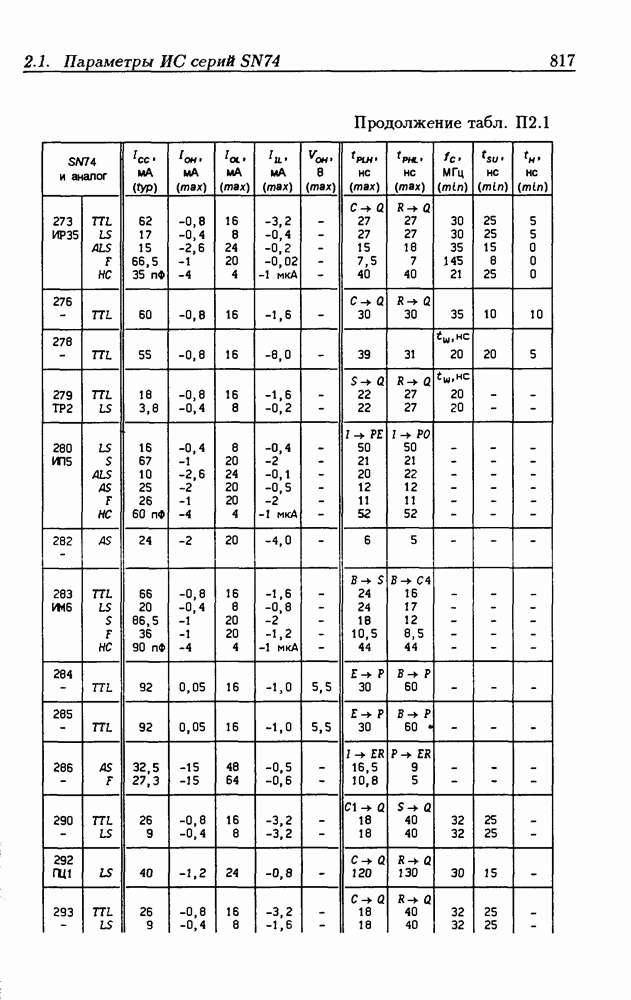
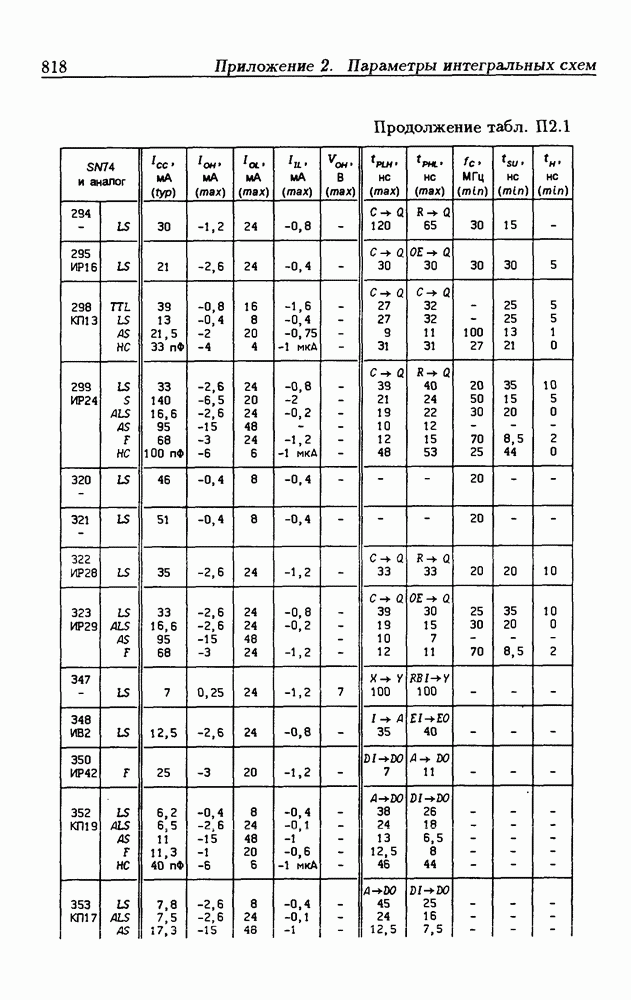
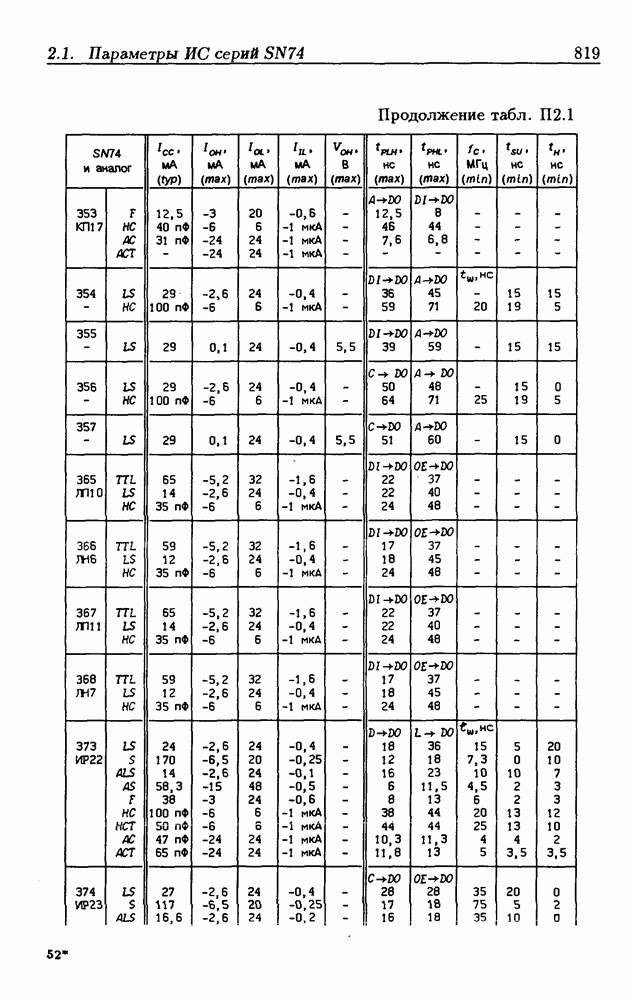
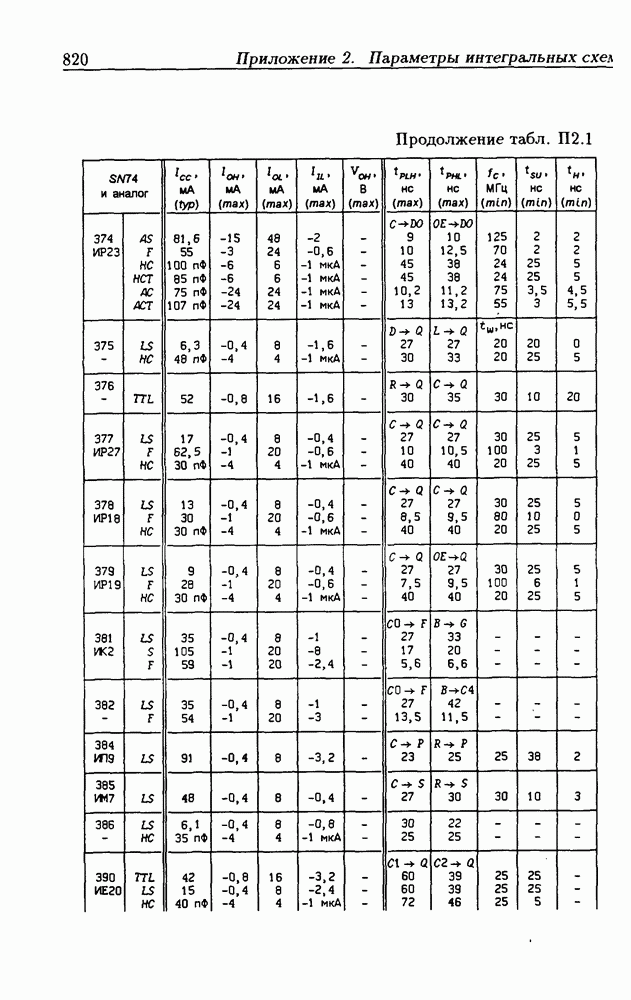
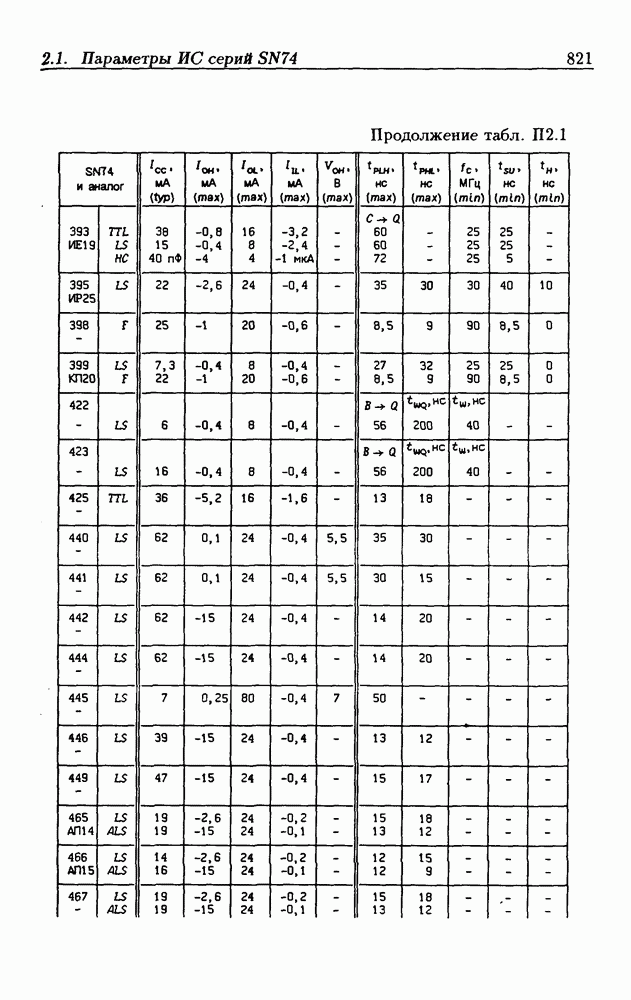
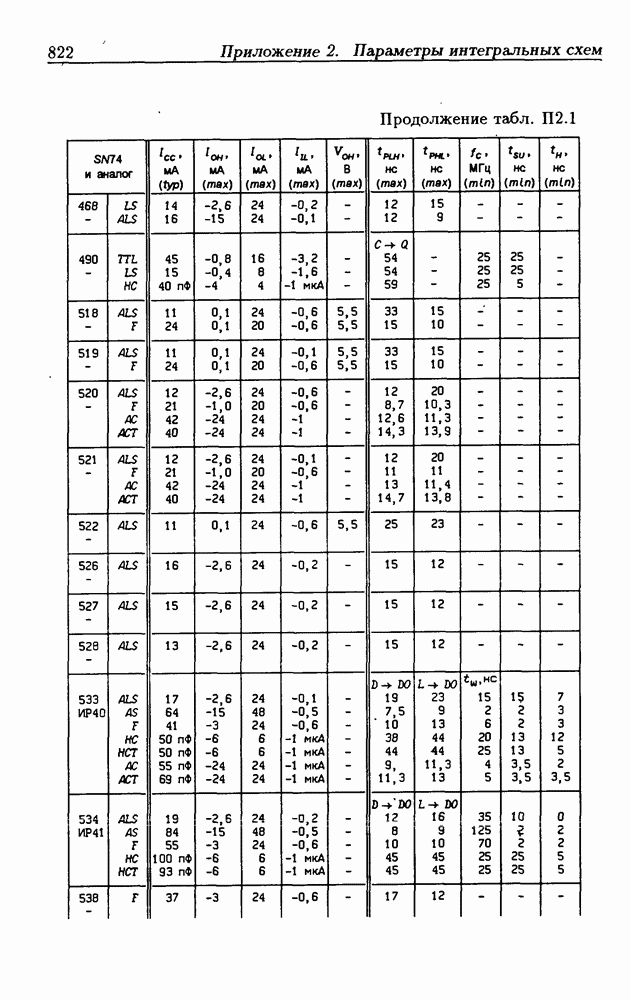
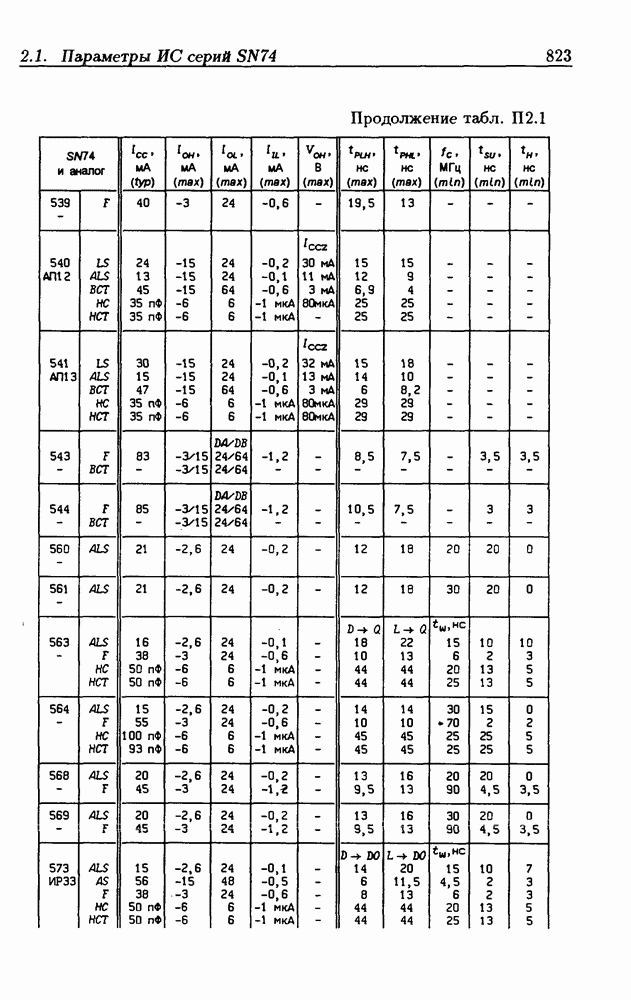
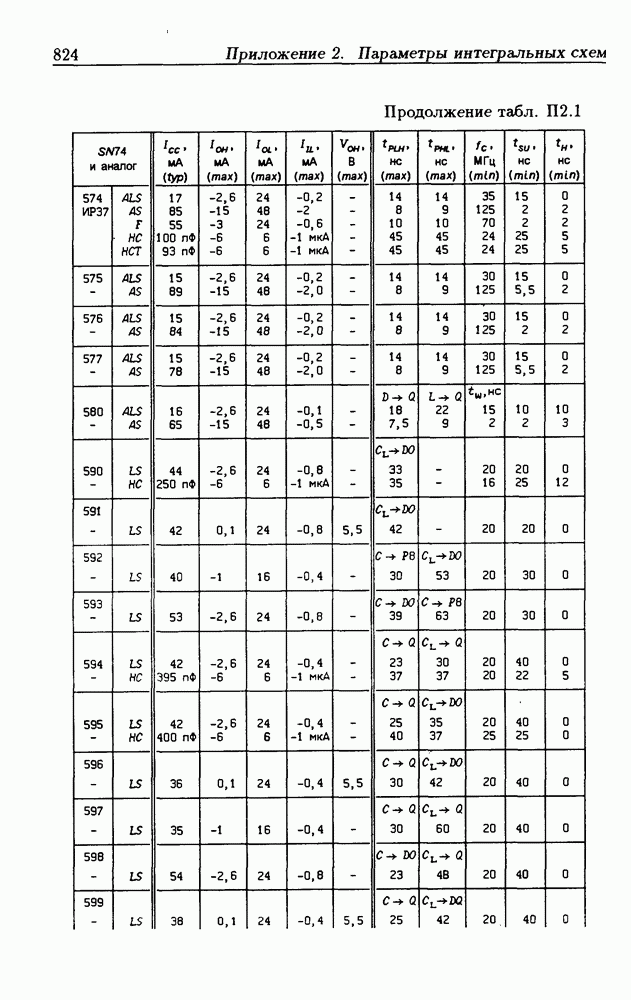
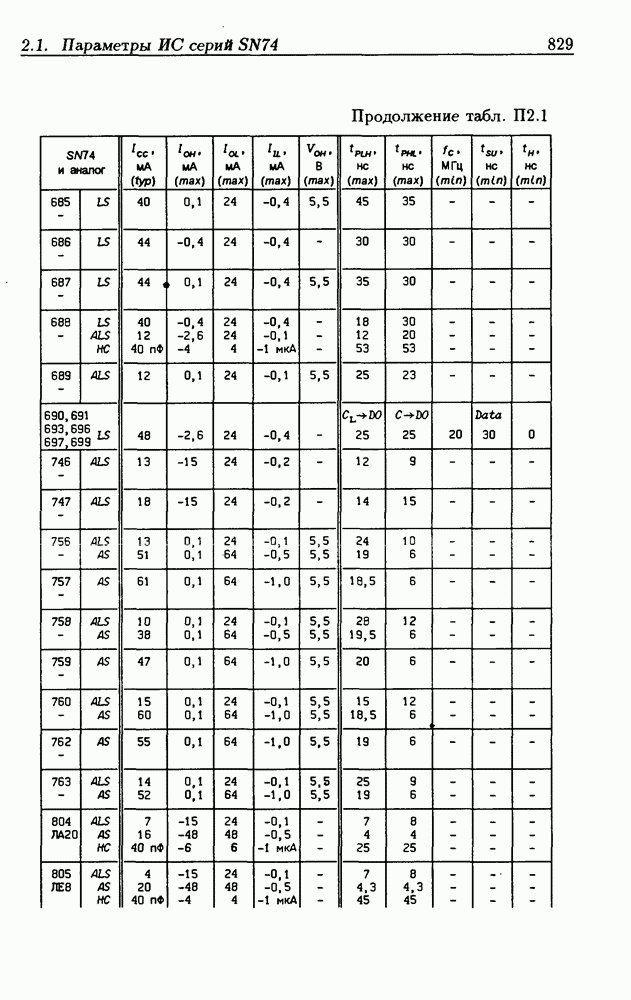
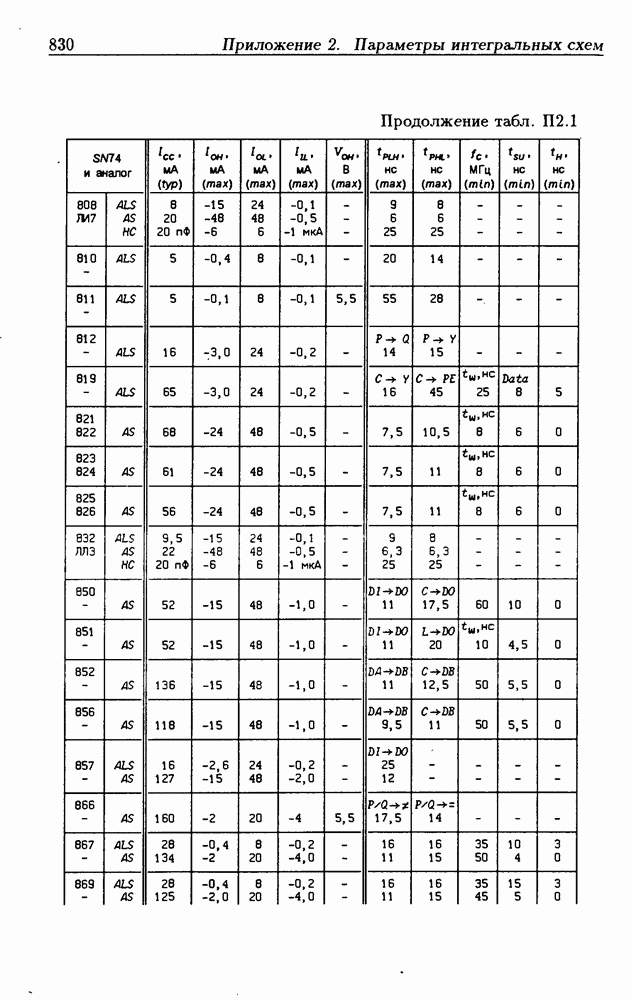
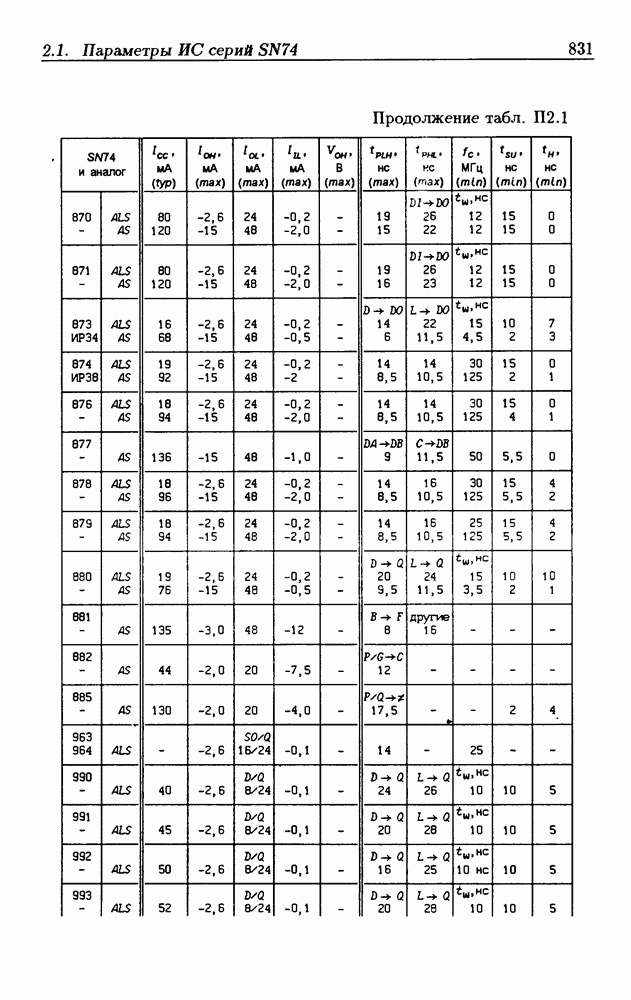
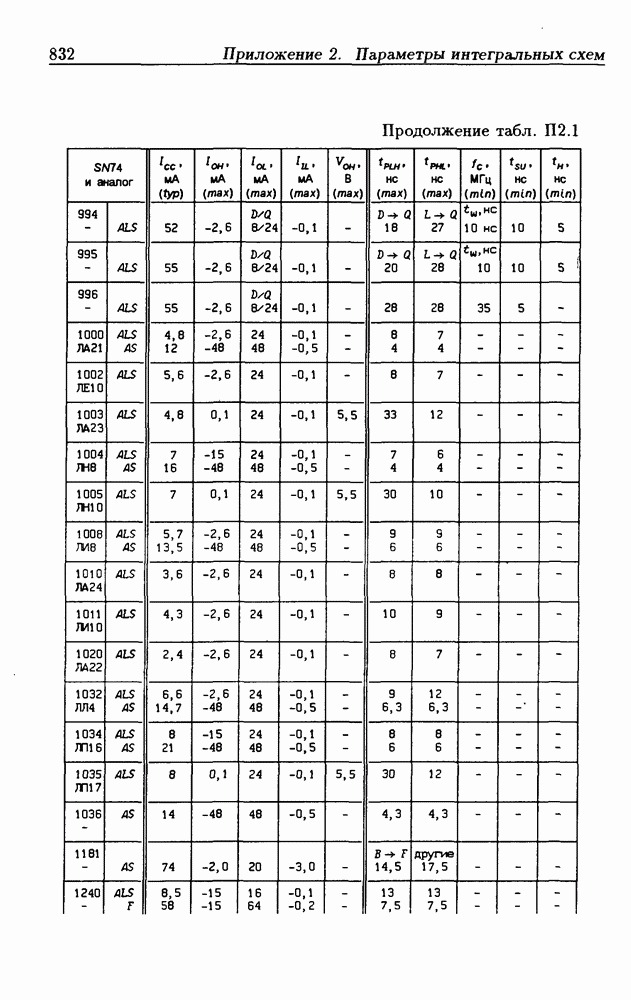
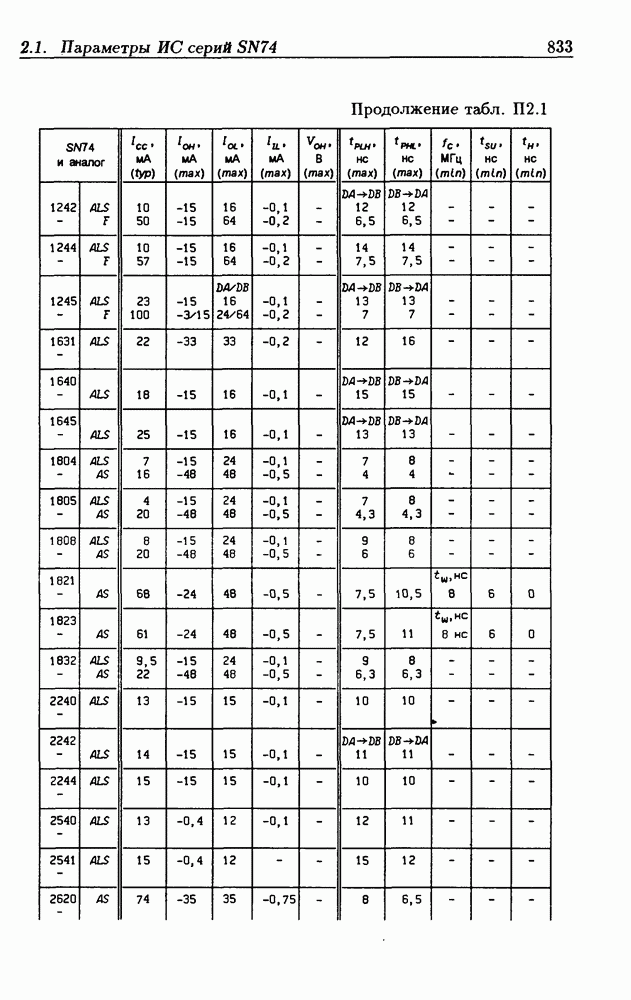
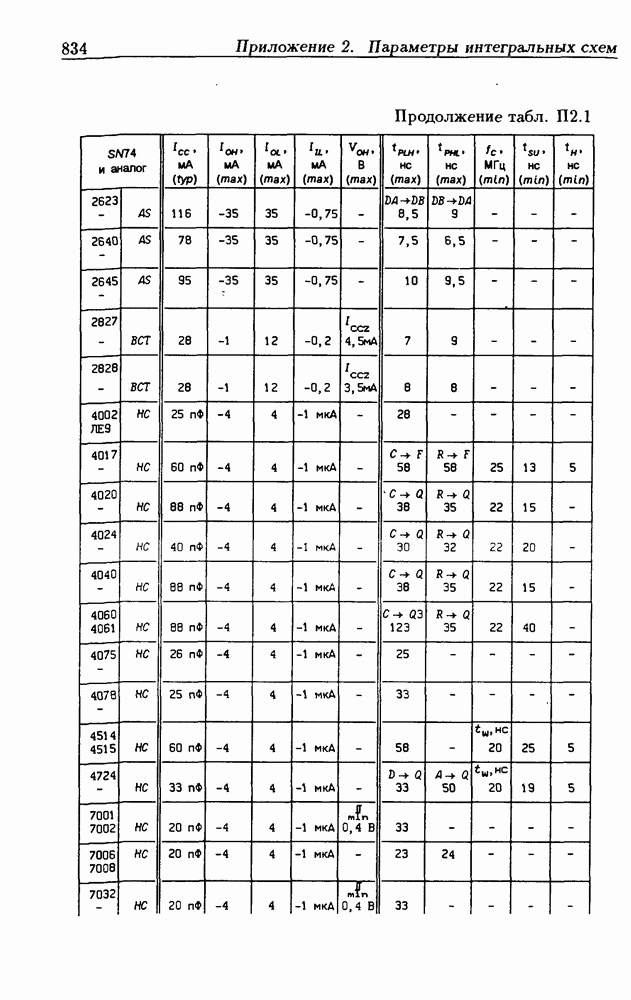
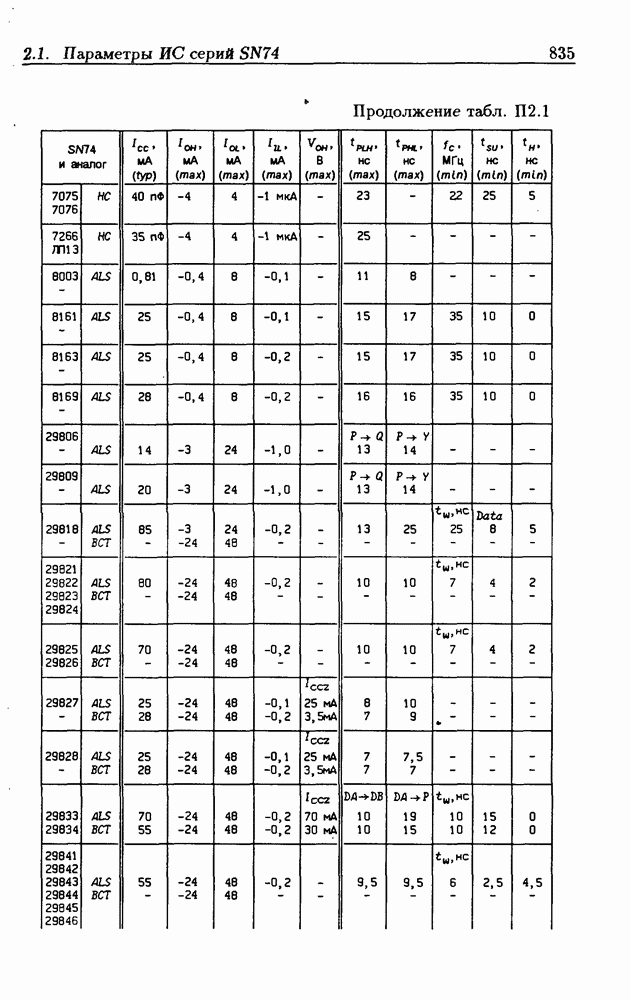
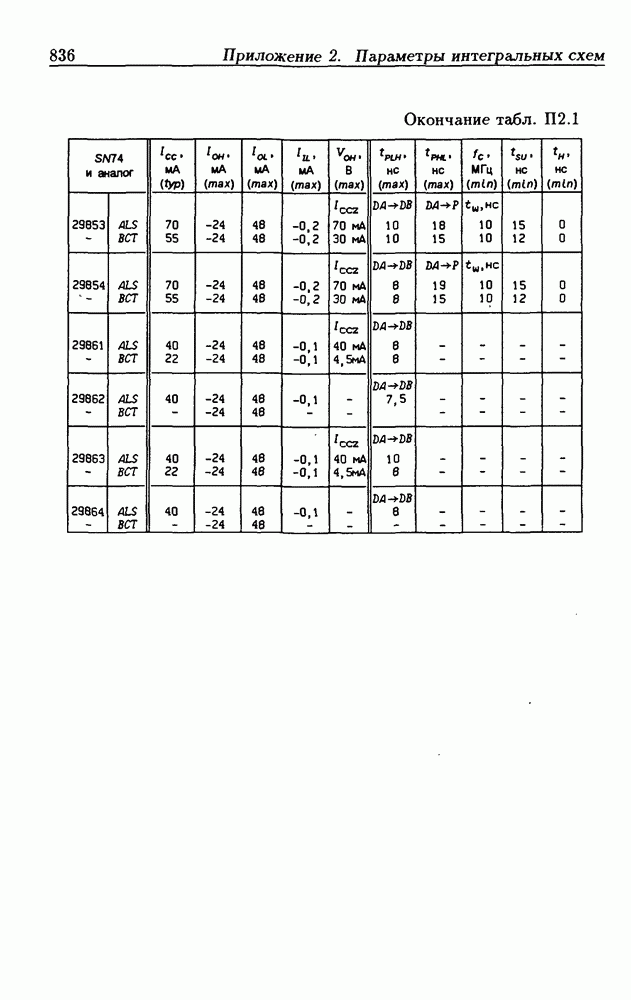
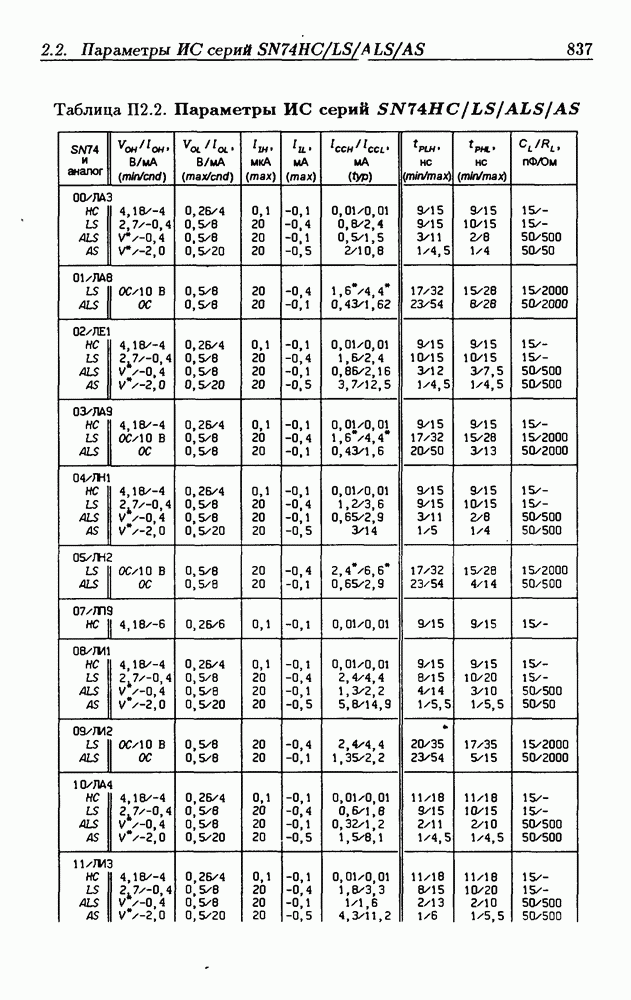
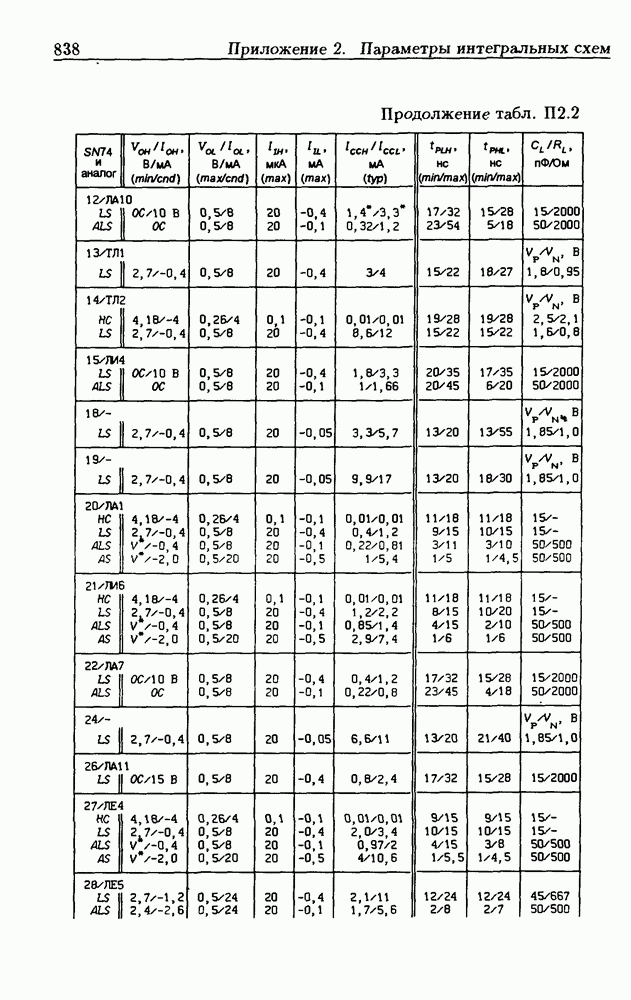
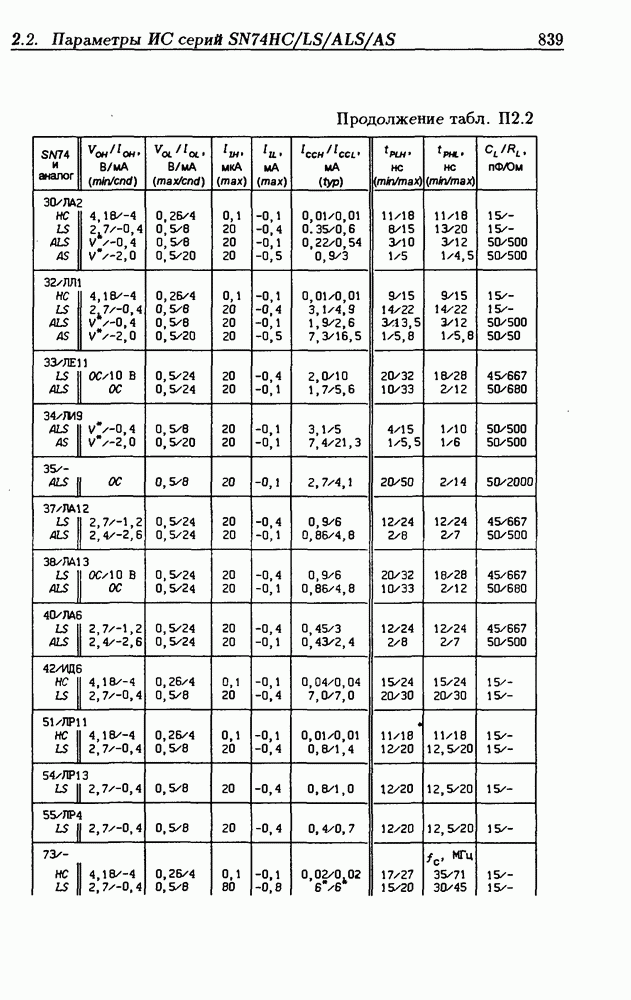
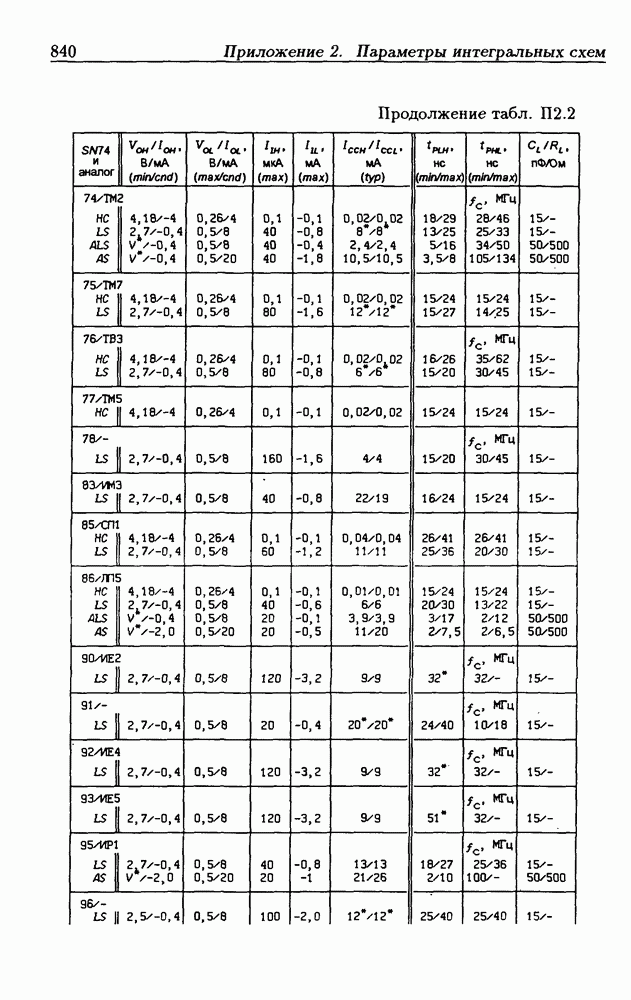
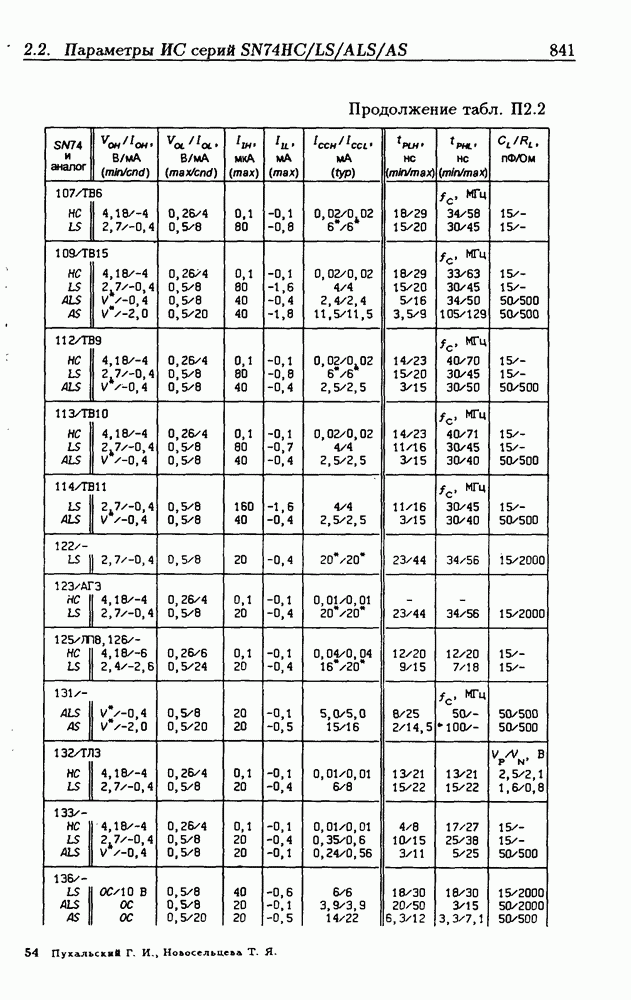
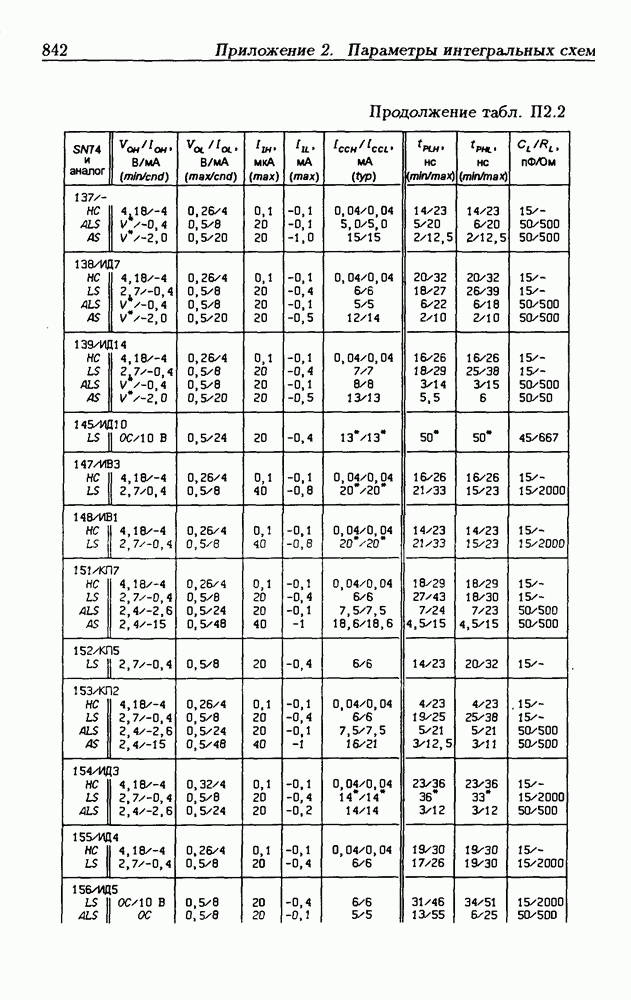
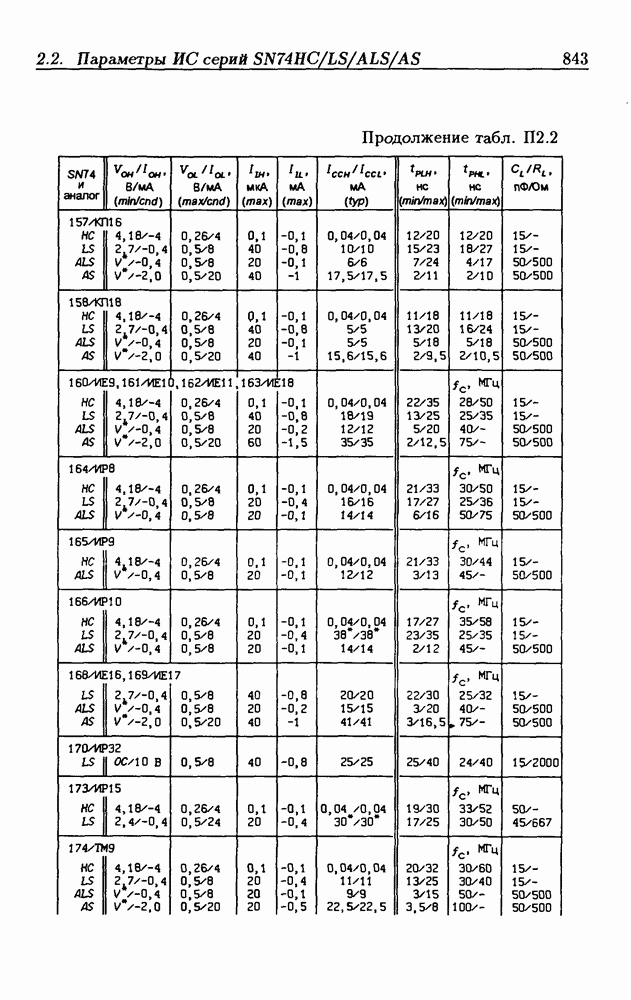
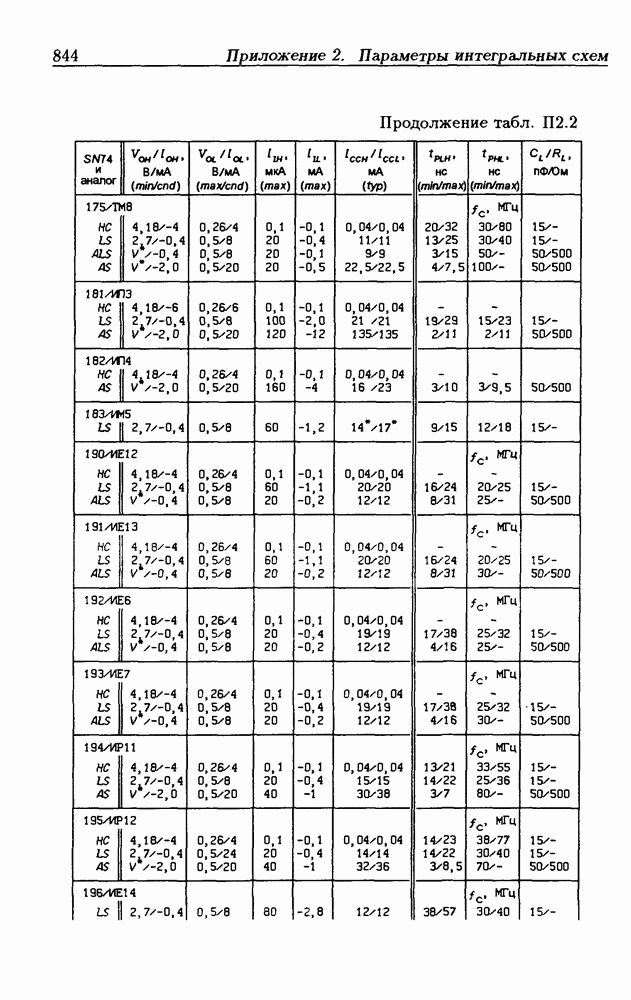
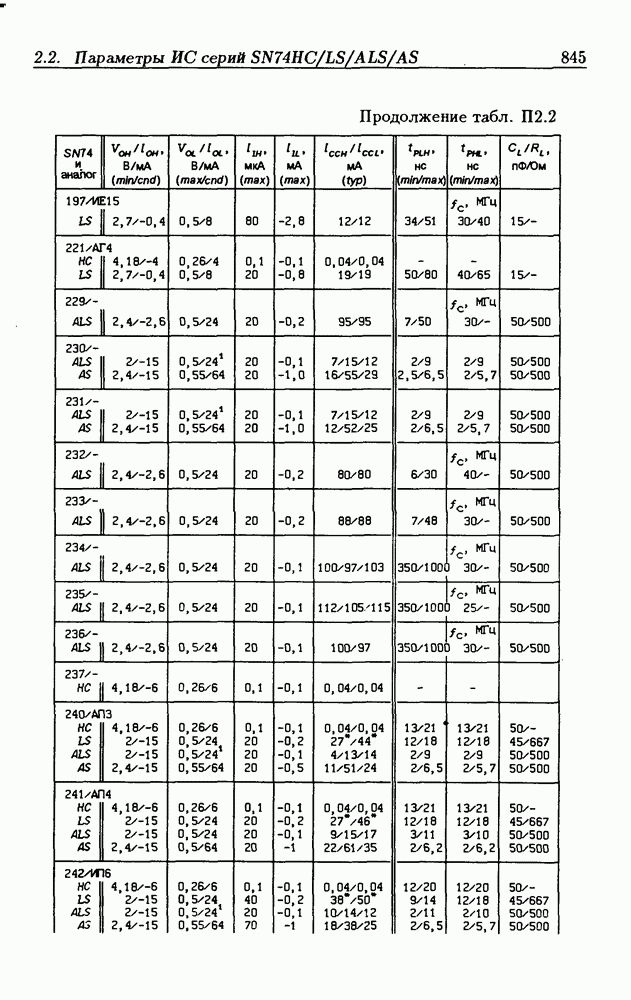
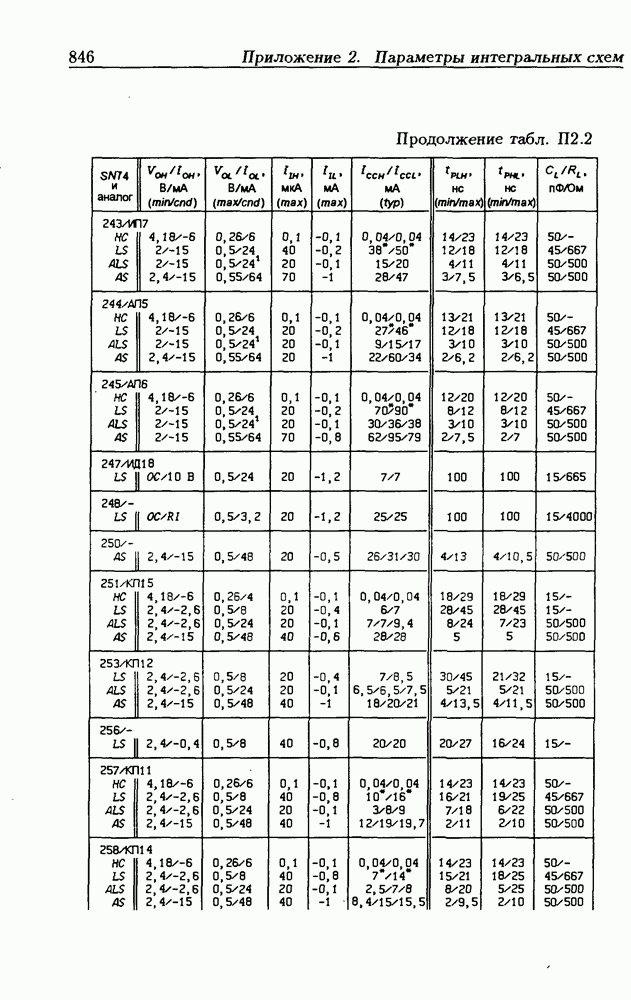
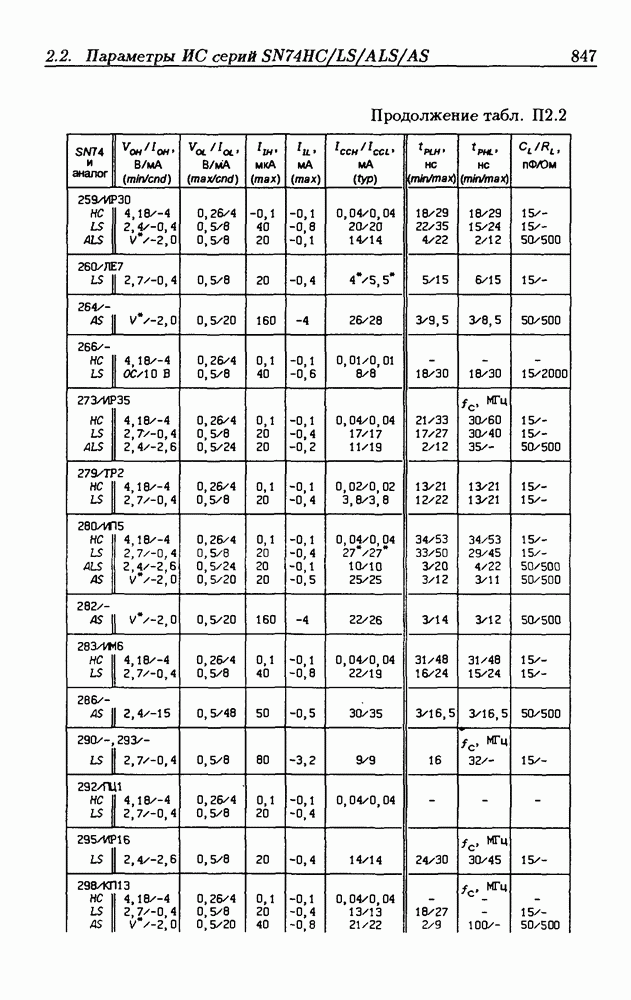
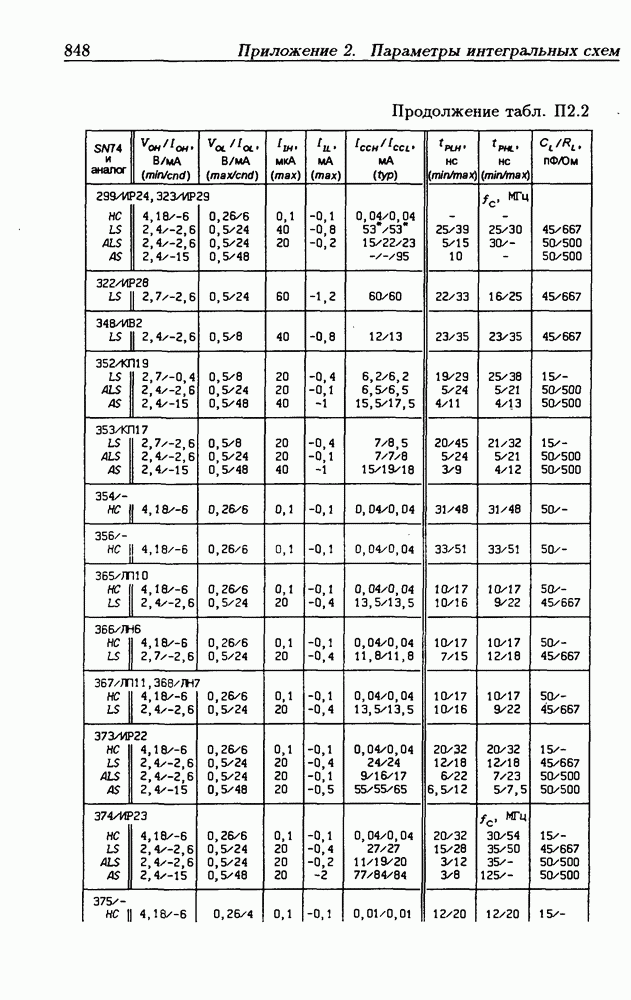
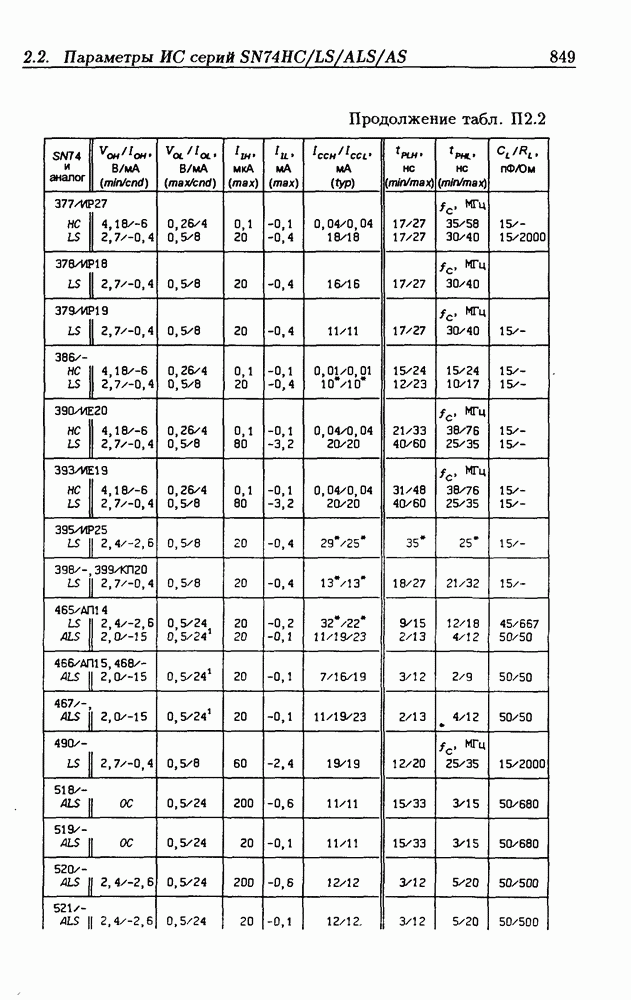
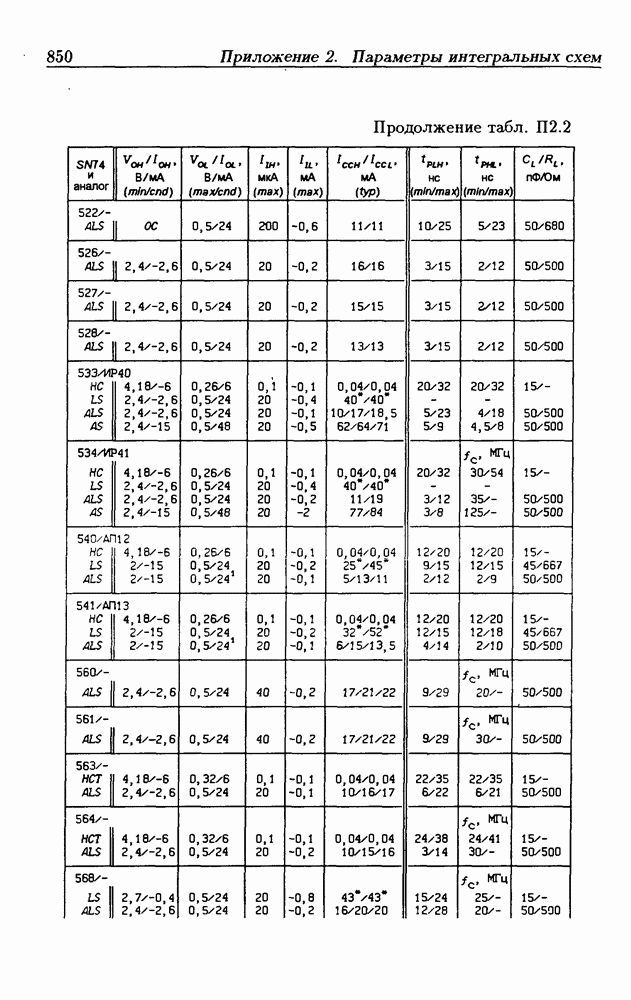
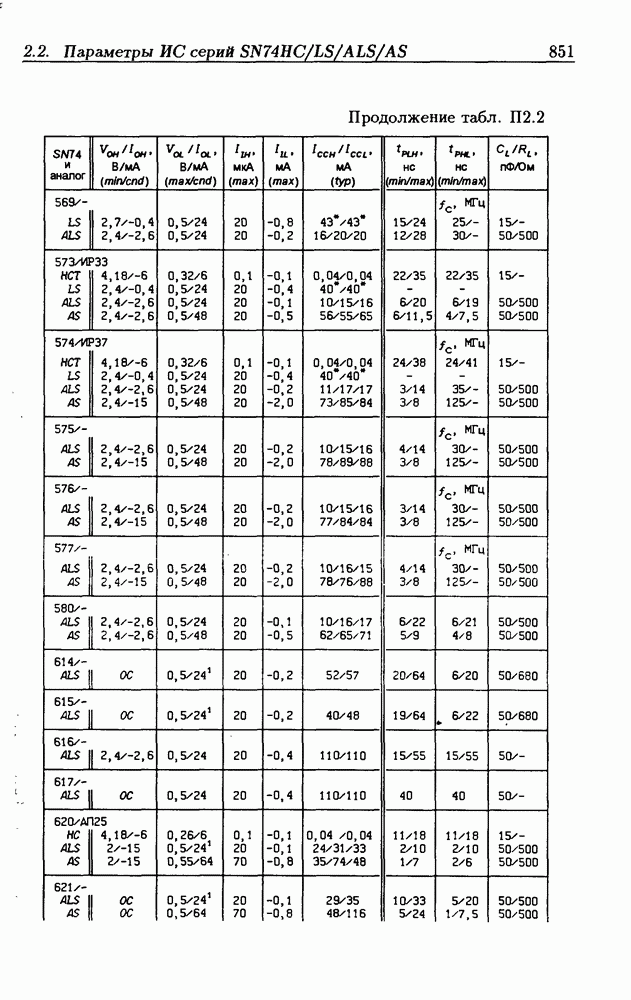
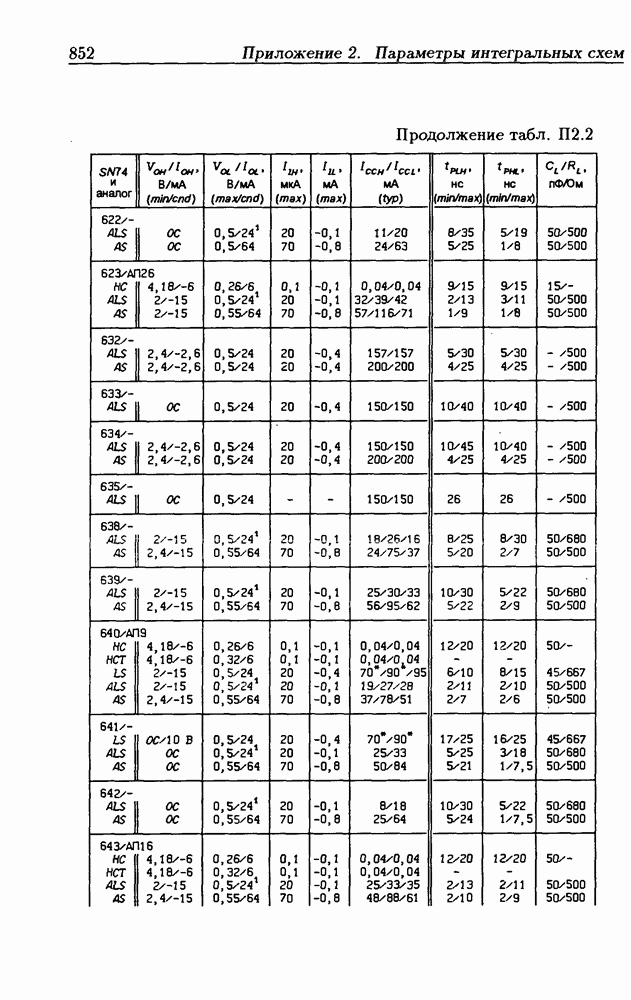
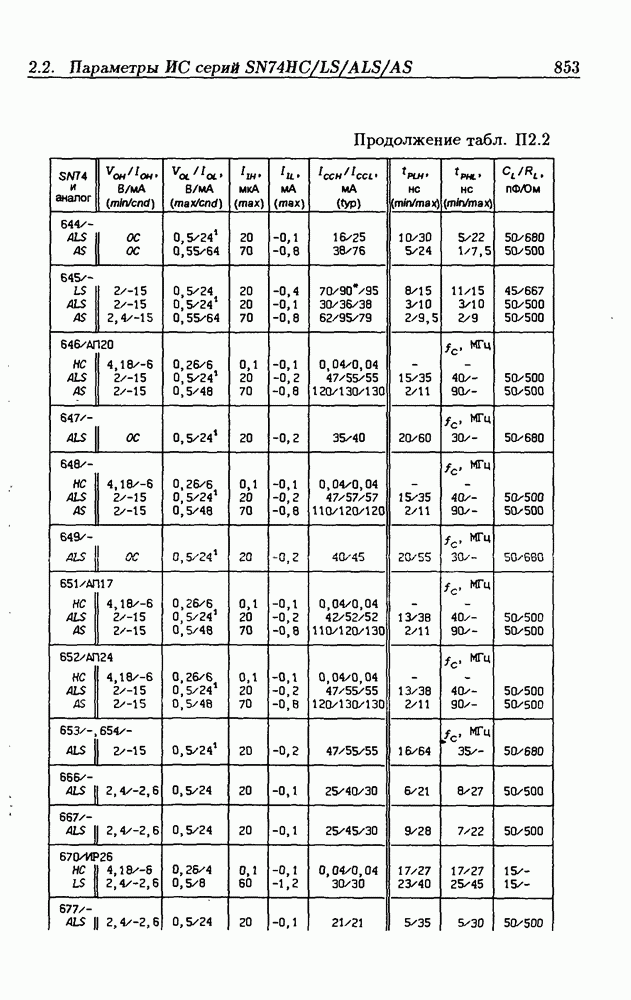
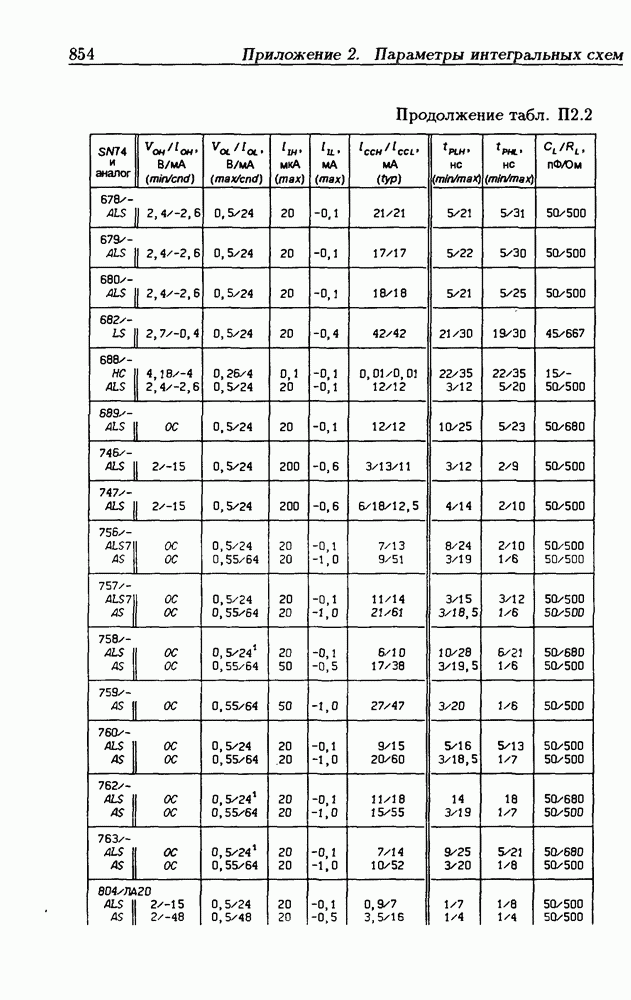
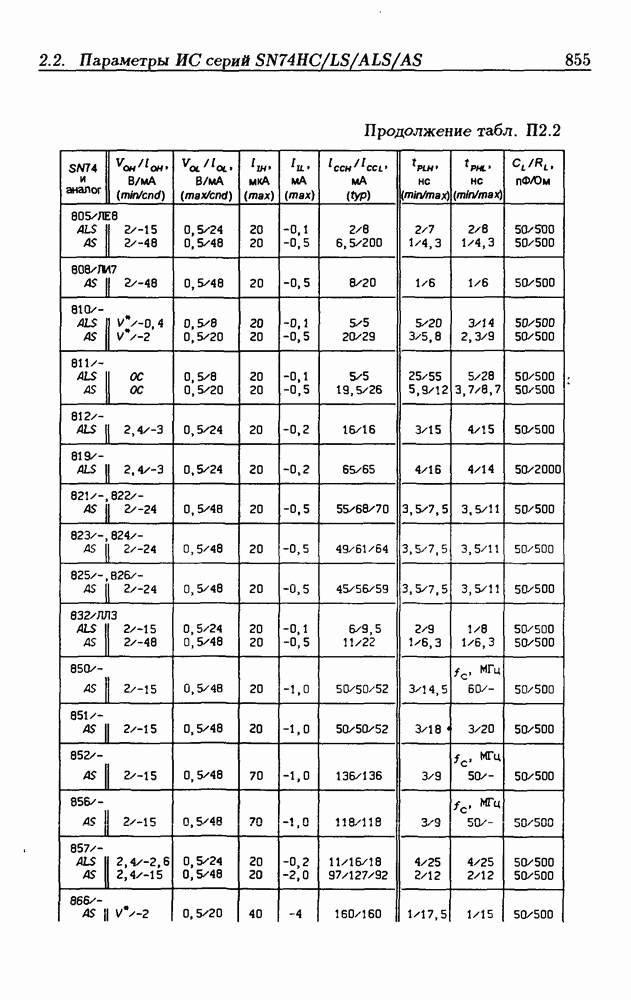
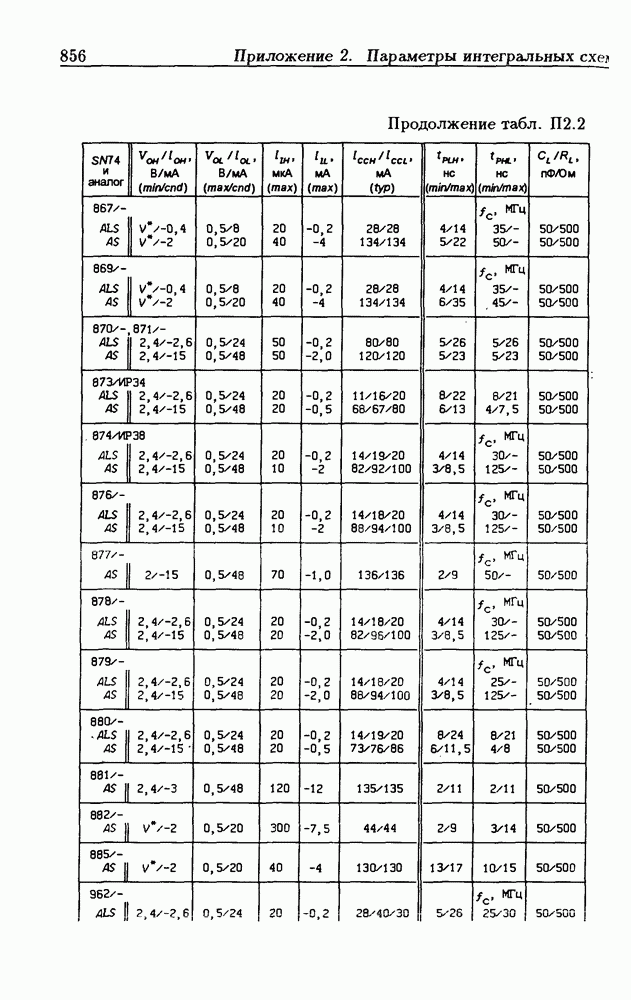
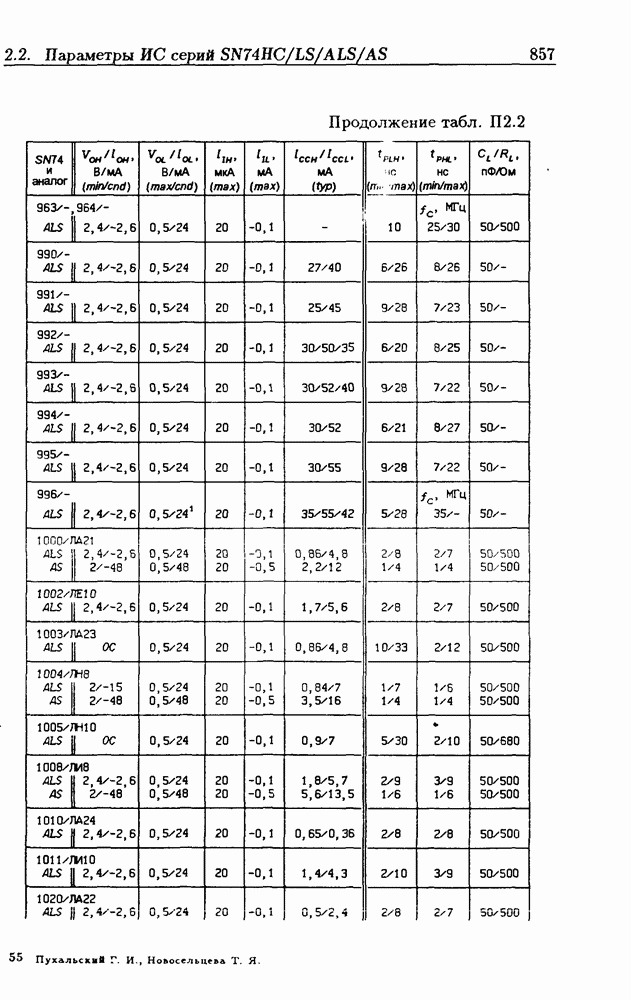
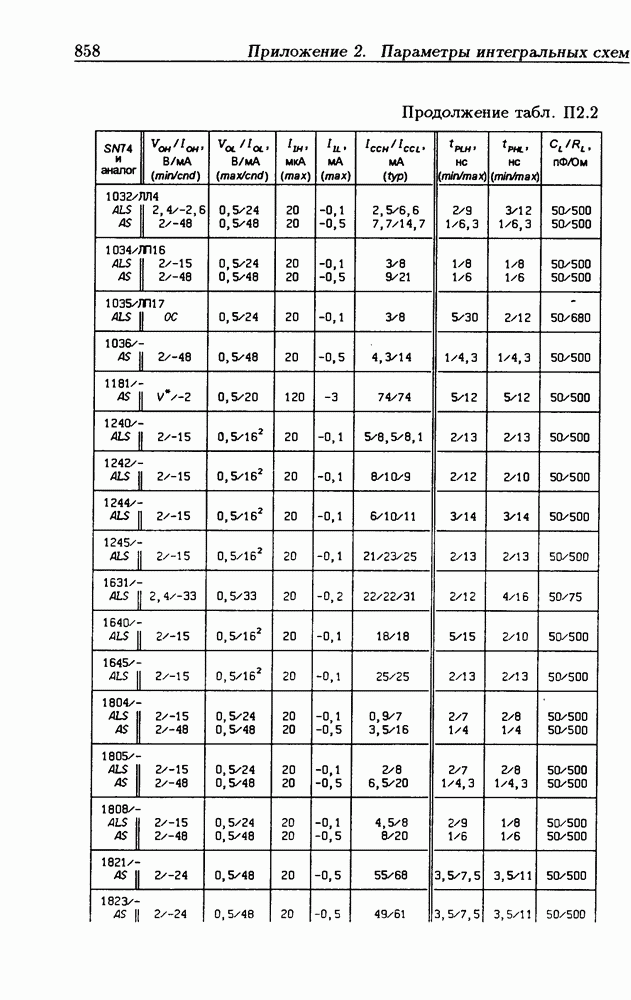
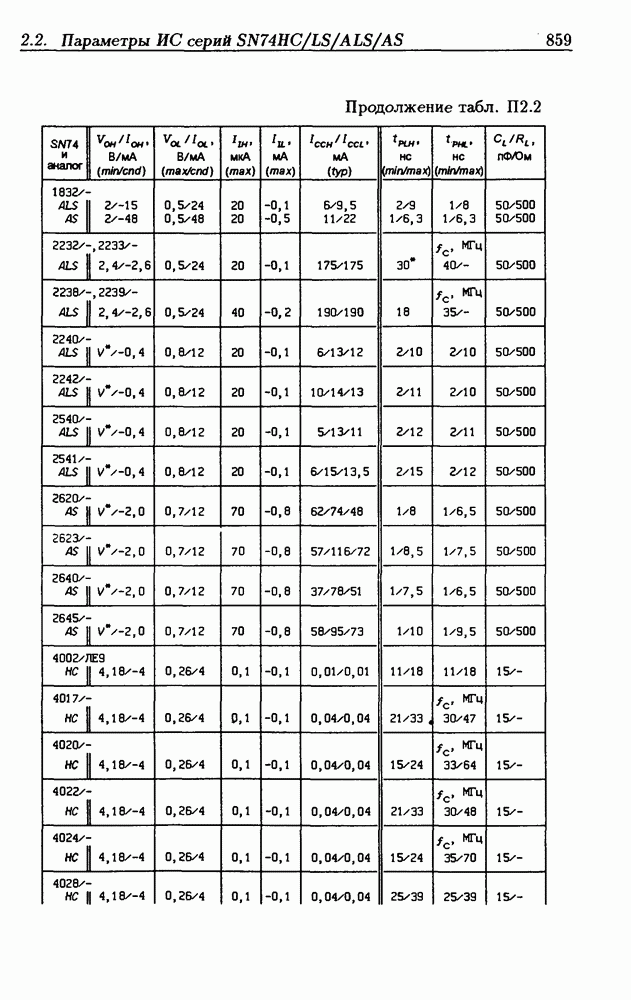
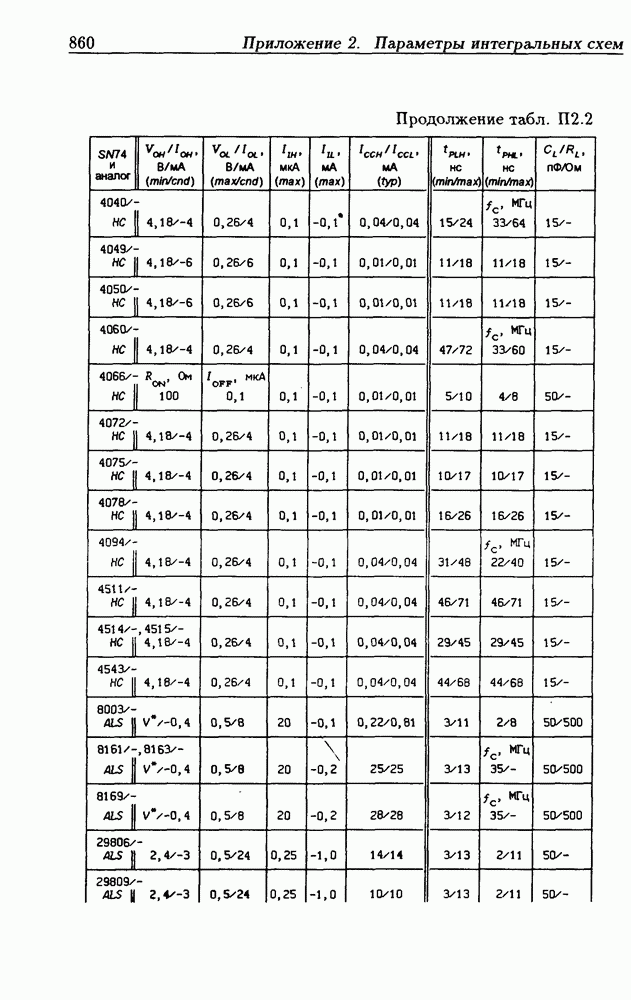
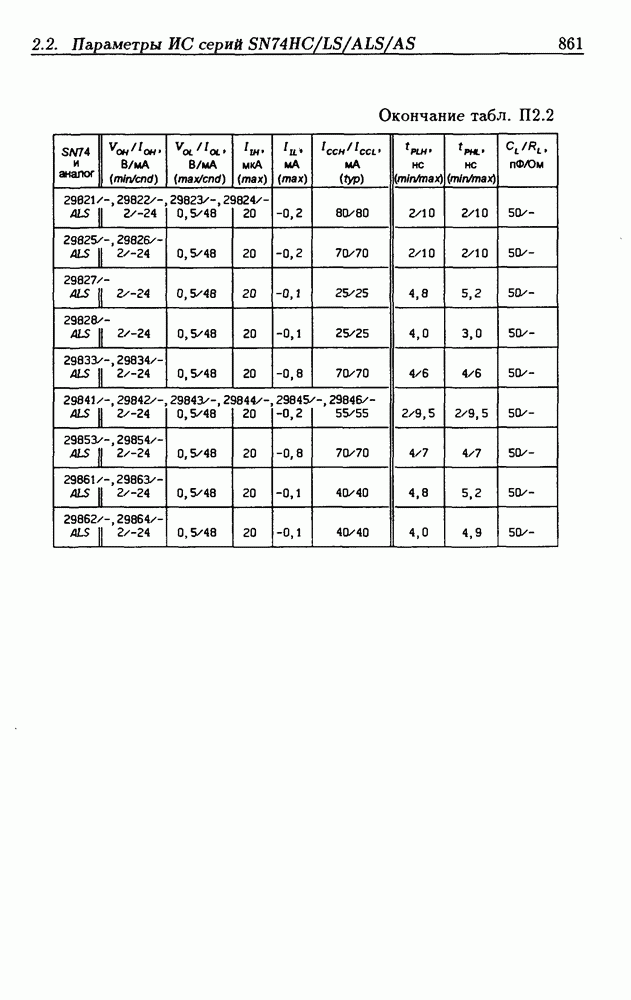
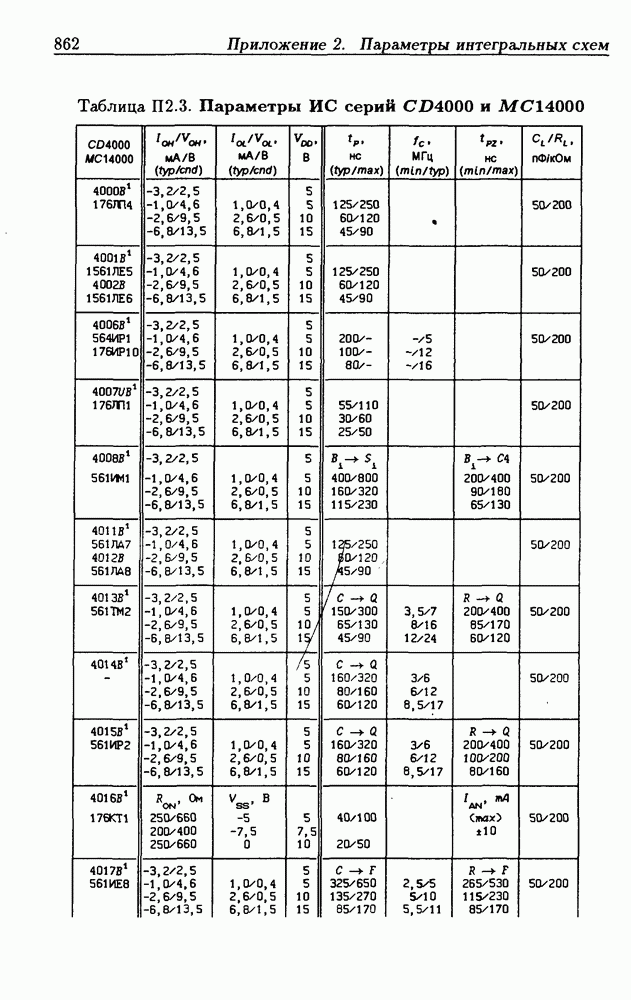
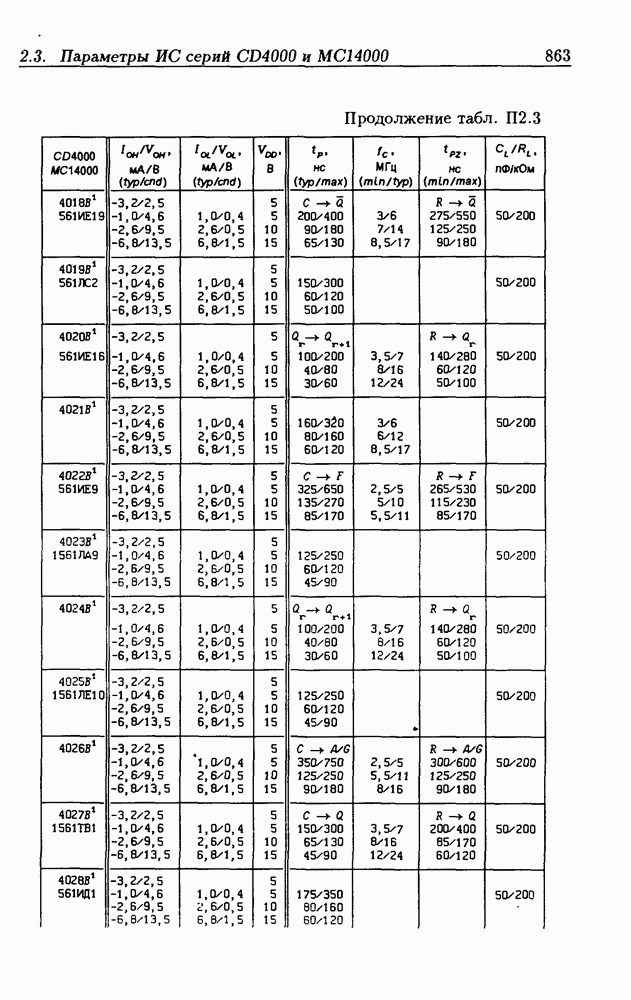
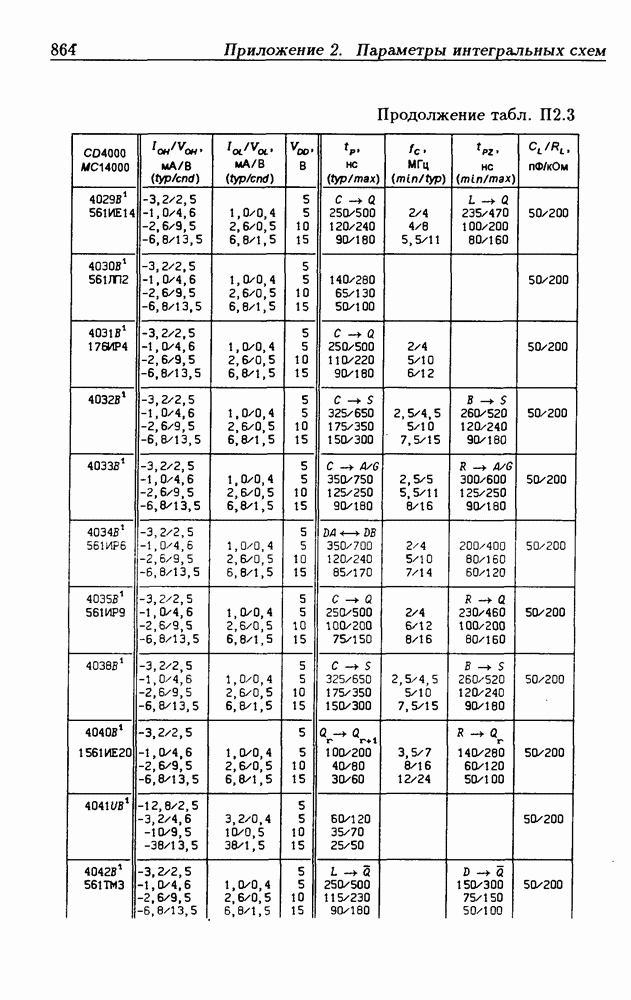
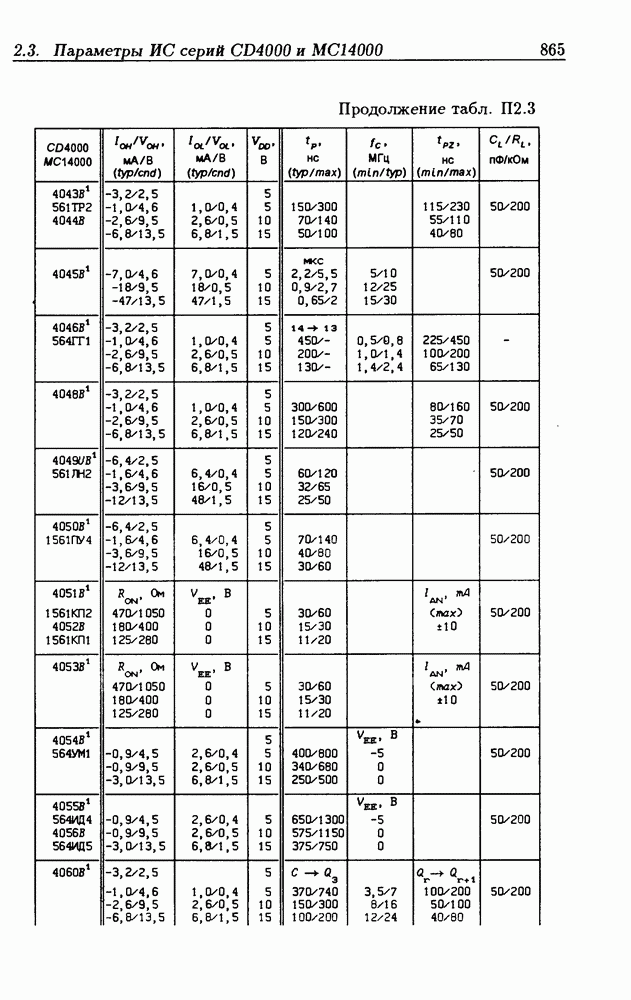
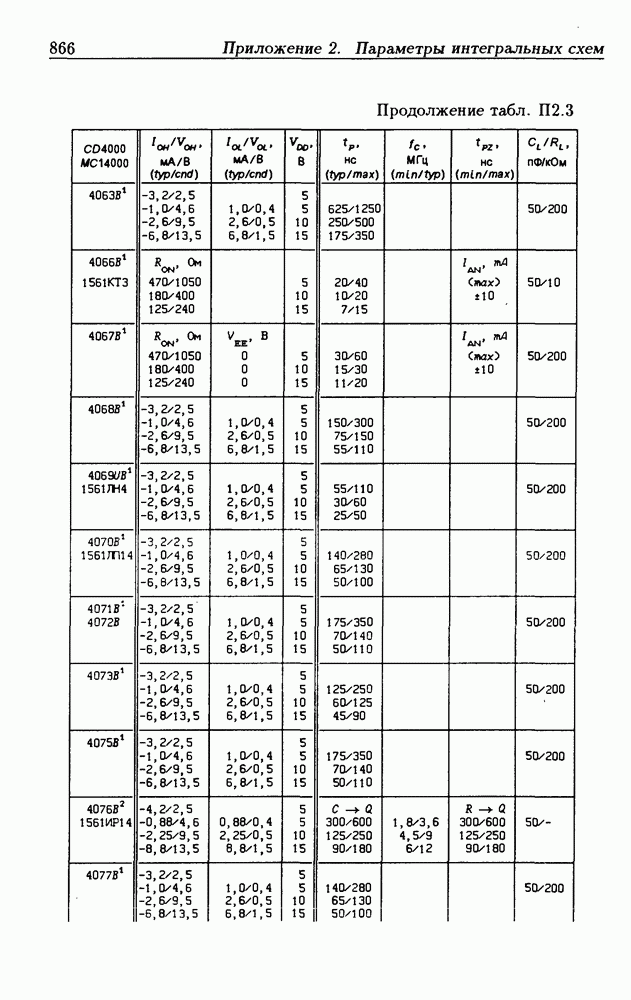
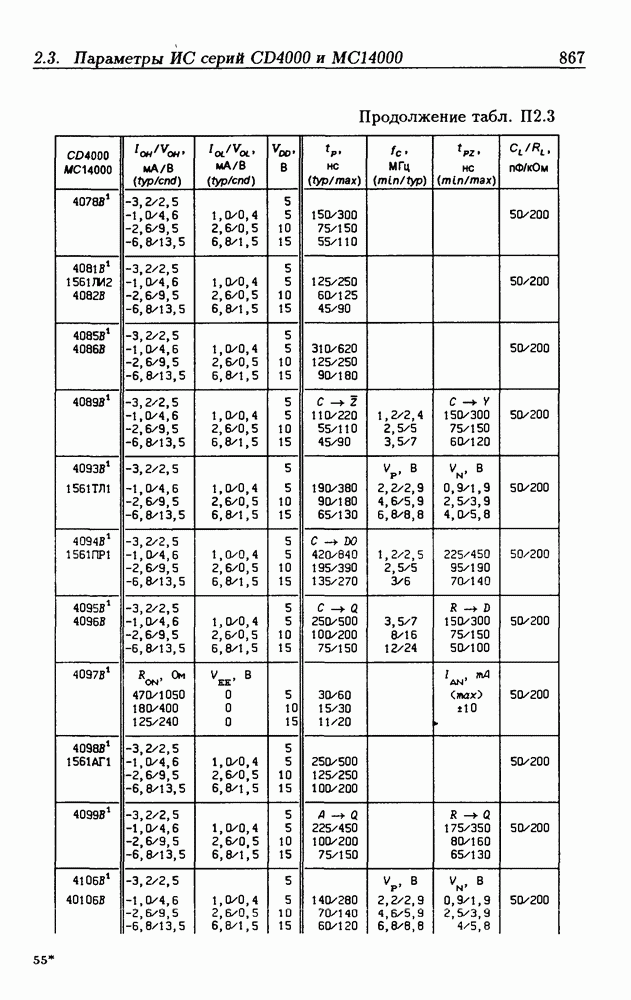
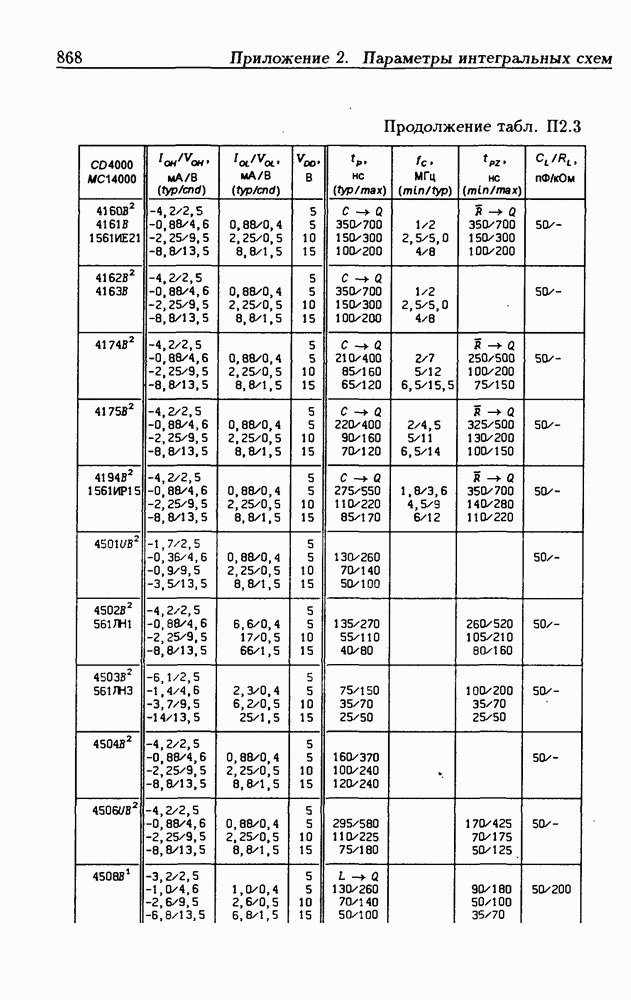
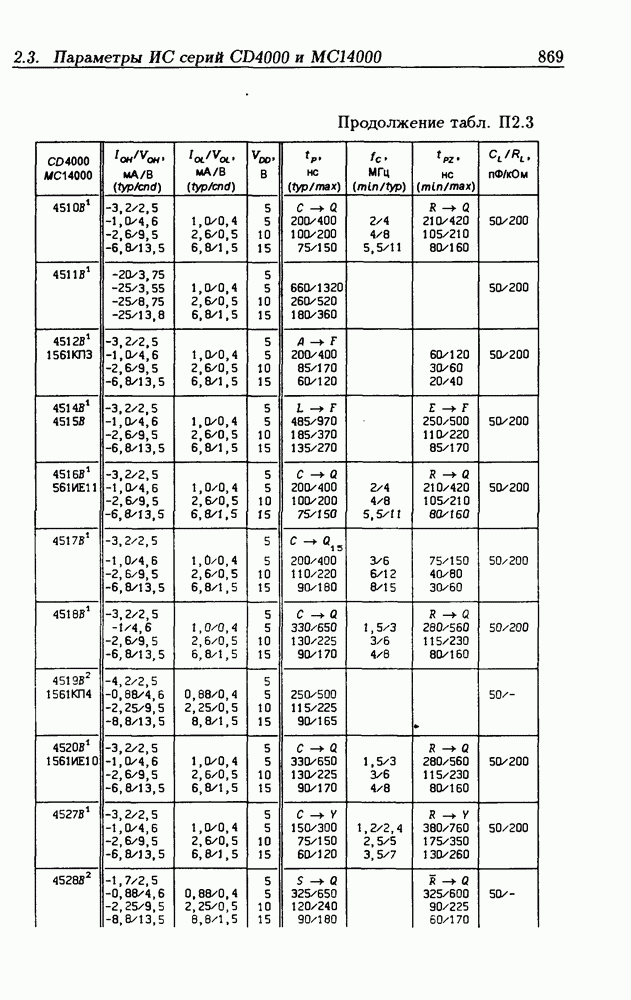
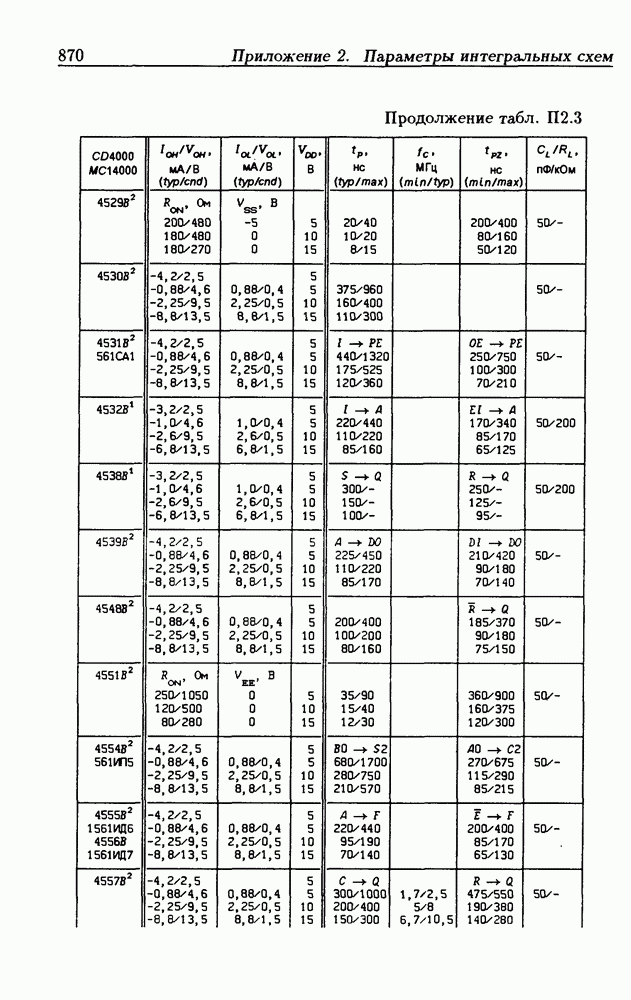
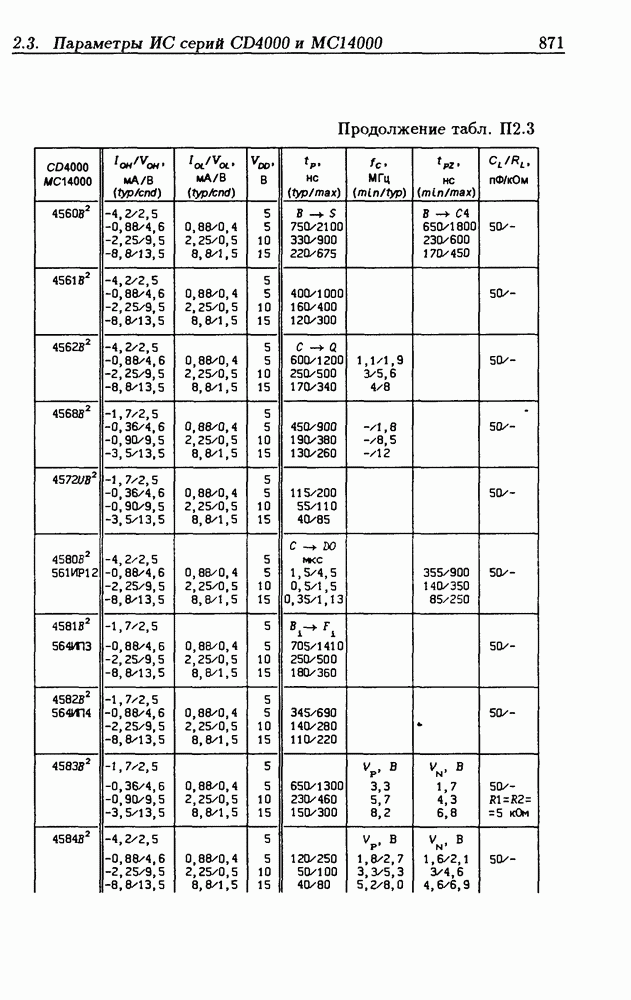
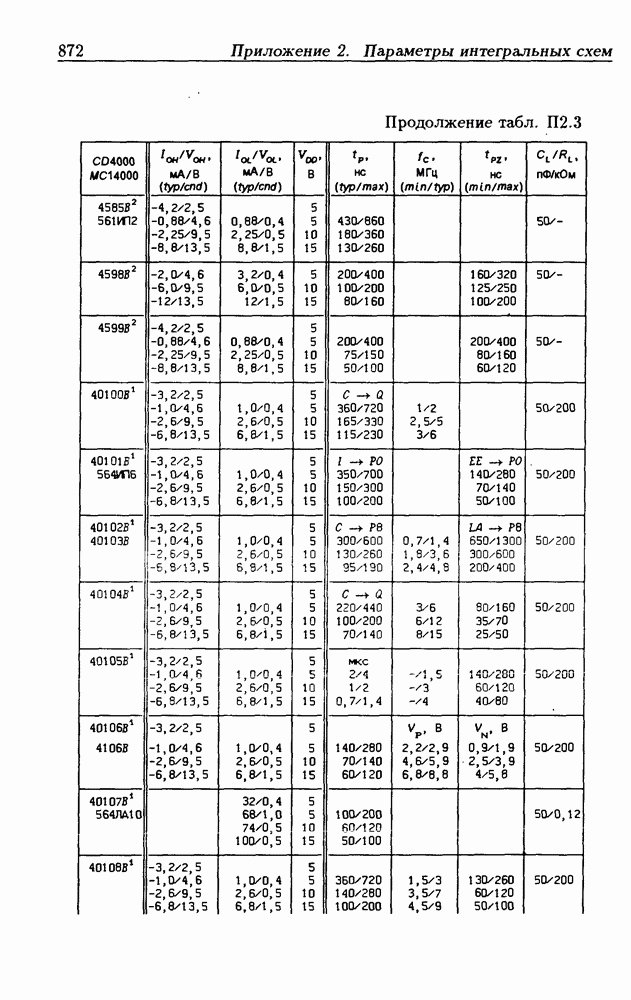
- Приложение 2. Параметры интегральных схем