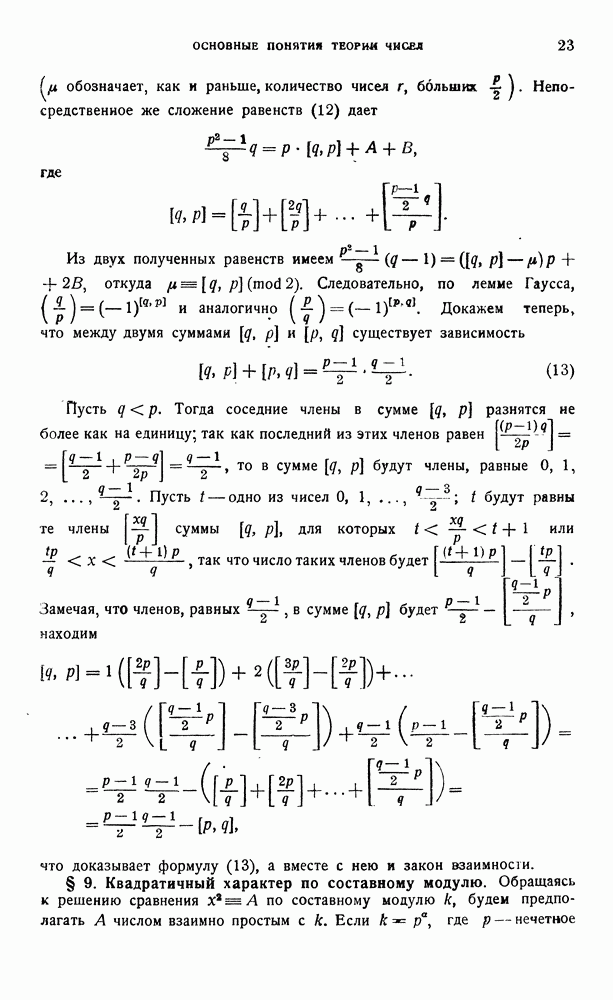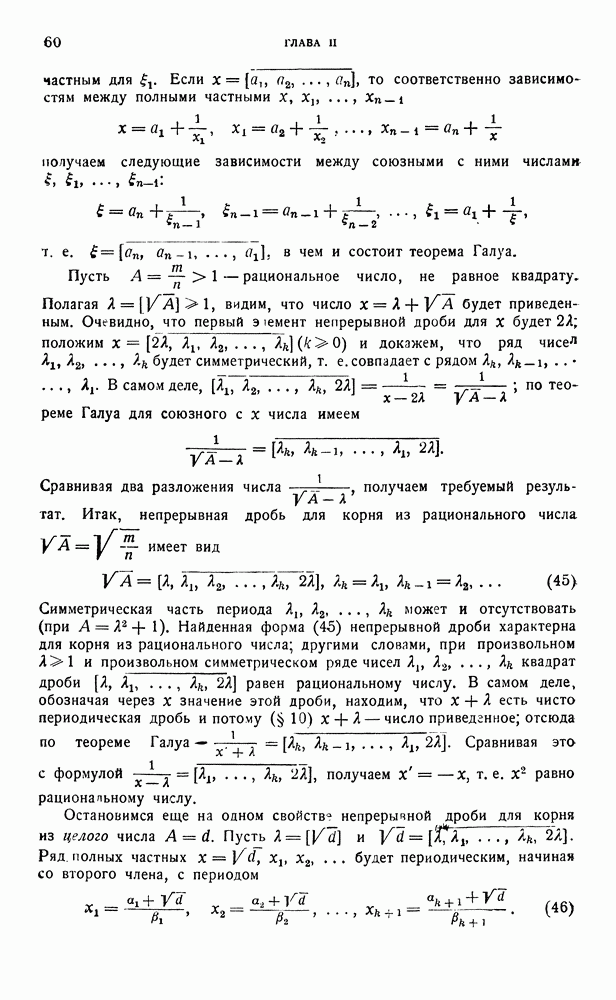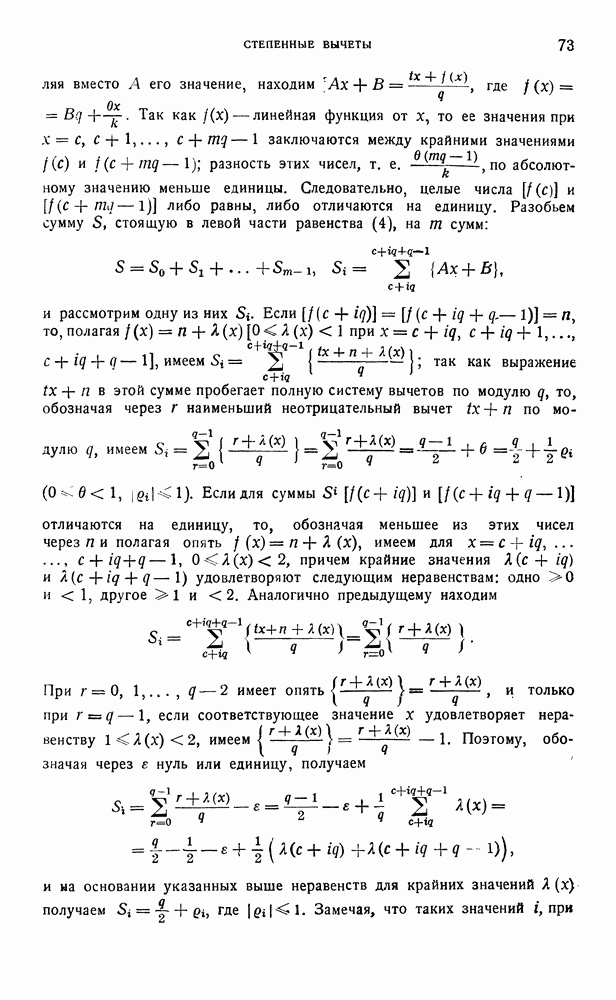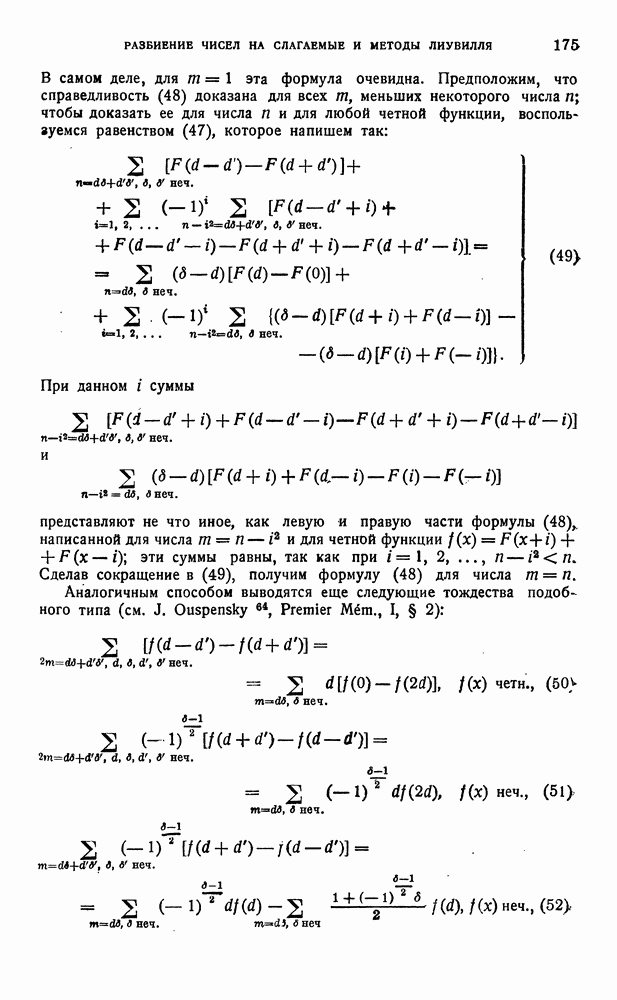| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Формы положительного определителя.
Переходя к формам положительного определителя, будем считать в этом параграфе коэфициенты рассматриваемых форм произвольными вещественными числами. Кроме того, будем предполагать, что форма  не обращается в нуль при целых
не обращается в нуль при целых  не равных одновременно нулю; тогда а и с отличны от нуля, и корни уравнения а
не равных одновременно нулю; тогда а и с отличны от нуля, и корни уравнения а  вещественны, различны и иррациональны. Назовем корень
вещественны, различны и иррациональны. Назовем корень  этого уравнения первым, а
этого уравнения первым, а  вторым корнем формы
вторым корнем формы 
(L.-Dirichlet 14, § 72), причем  есть определитель формы
есть определитель формы  Если
Если  переводится в форму
переводится в форму  подстановкой определителя
подстановкой определителя  то
то  и выражения и равны, очевидно, корням формы
и выражения и равны, очевидно, корням формы  Подставляя в
Подставляя в  величину
величину  и освобождаясь от
и освобождаясь от  в знаменателе дроби, найдем, что равно первому корню формы
в знаменателе дроби, найдем, что равно первому корню формы  при
при  и второму корню при
и второму корню при  Итак, если форма
Итак, если форма  подстановкою определителя
подстановкою определителя  переводится в форму
переводится в форму  с корнями
с корнями  то одноименные корни этих форм связаны соотношениями
то одноименные корни этих форм связаны соотношениями

Назовем форму  с корнями
с корнями  приведенного если
приведенного если  Определение это имеет большое сходство с данным в § 10 гл. II определением приведенных квадратных иррациональностей. Так же, как и там, найдем, что у приведенной формы
Определение это имеет большое сходство с данным в § 10 гл. II определением приведенных квадратных иррациональностей. Так же, как и там, найдем, что у приведенной формы  заключаются между
заключаются между  обратно, система неравенств
обратно, система неравенств  или
или  характеризует приведенность формы
характеризует приведенность формы  Каждая форма определителя
Каждая форма определителя  собственно эквивалентна приведенной форме. Пусть
собственно эквивалентна приведенной форме. Пусть  данная форма с корнями
данная форма с корнями  разложим
разложим  в обыкновенную непрерывную дробь:
в обыкновенную непрерывную дробь:  от
от  где
где  есть полное частное, и определим для каждого
есть полное частное, и определим для каждого  иррациональное число
иррациональное число  из уравнения
из уравнения  не может быть больше единицы для каждого
не может быть больше единицы для каждого  , так как тогда мы имели бы
, так как тогда мы имели бы  следовательно, найдется номер и, для которого
следовательно, найдется номер и, для которого  и тогда
и тогда  Таким образом видим, что можно выбрать четное число
Таким образом видим, что можно выбрать четное число  так, чтобы в равенствах
так, чтобы в равенствах

было  обозначает подходящую к дробь
обозначает подходящую к дробь  Преобразовывая
Преобразовывая  подстановкой
подстановкой  определителя
определителя  получаем форму с корнями
получаем форму с корнями  т. е. приведенную форму, что и требовалось доказать.
т. е. приведенную форму, что и требовалось доказать.
Припоминая данное в § 3 гл. II определение соседних форм, докажем теперь, что для приведенной формы  существует одна и только одна соседняя с нею справа приведенная форма. Пусть
существует одна и только одна соседняя с нею справа приведенная форма. Пусть 
подстановкой (k — целое число) переводится в соседнюю форму  Обозначим через
Обозначим через  корни форм
корни форм  тогда
тогда  Если
Если  приведенные формы, то
приведенные формы, то  из равенства
из равенства  видно, что к
видно, что к  и так как имеет знак
и так как имеет знак  то
то  Далее
Далее  следовательно,
следовательно,  так что
так что  Условиями
Условиями  целое число к определяется вполне при данной форме
целое число к определяется вполне при данной форме  обратно, определив к по этим условиям и переведя
обратно, определив к по этим условиям и переведя  подстановкою
подстановкою  в форму
в форму  с корнями
с корнями  из соотношений
из соотношений  легко найдем, что
легко найдем, что  т. е. форма
т. е. форма  приведенная. Замечая, что из соотношения
приведенная. Замечая, что из соотношения  вытекает
вытекает  и что форма
и что форма  будет приведенной одновременно с
будет приведенной одновременно с  находим, что для данной приведенной формы
находим, что для данной приведенной формы  существует одна и только одна соседняя с ней слева и также приведенная форма.
существует одна и только одна соседняя с ней слева и также приведенная форма.
Пусть дана любая приведенная форма  найдем соседнюю с
найдем соседнюю с  справа приведению форму
справа приведению форму  затем соседнюю с
затем соседнюю с  справа приведенную форму
справа приведенную форму  д. Точно так же найдем соседнюю с
д. Точно так же найдем соседнюю с  слева приведенную форму
слева приведенную форму  д. Получим ряд форм
д. Получим ряд форм

Ввиду иррациональности корней формы  этот ряд приведенных форм продолжается бесконечно как вправо, так и влево; он называется периодом формы
этот ряд приведенных форм продолжается бесконечно как вправо, так и влево; он называется периодом формы  (ср. А. А. Марков 54, стр. 4). Обозначая через
(ср. А. А. Марков 54, стр. 4). Обозначая через  корни формы
корни формы  имеем соотношения
имеем соотношения

Из этих соотношений, обозначая через абсолютное значение  получаем разложения в непрерывную дробь чисел
получаем разложения в непрерывную дробь чисел  для всякого
для всякого 

Пользуясь свойствами приведенных форм, нетрулно доказать формулированную раньше (конец § 3 гл. II) теорему Коркина о минимуме формы положительного определителя  Пусть дана приведенная форма
Пусть дана приведенная форма  определителя
определителя  построим соответствующий ей период (9) приведенных форм. Так как разность
построим соответствующий ей период (9) приведенных форм. Так как разность  корней формы
корней формы  равна
равна  эти корни разных знаков, то при помощи (12) получаем для всякого
эти корни разных знаков, то при помощи (12) получаем для всякого 

Покажем, что номер  можно выбрать так, что выражение в правой части равенства (13) будет больше или равно
можно выбрать так, что выражение в правой части равенства (13) будет больше или равно  . Действительно, рассмотрим ряд целых положительных чисел
. Действительно, рассмотрим ряд целых положительных чисел  Если в этом ряде есть хоть оаин элемент, бопьший или равный 3, например то мы достигнем цели, положив в
Если в этом ряде есть хоть оаин элемент, бопьший или равный 3, например то мы достигнем цели, положив в  Если этот ряд составлен исключительно из двоек и единиц, но содержит хоть одну двойку, например
Если этот ряд составлен исключительно из двоек и единиц, но содержит хоть одну двойку, например  то при
то при  правая часть (13) будет больше
правая часть (13) будет больше  Наконец, если все числа
Наконец, если все числа  то правая часть (13) при всяком
то правая часть (13) при всяком  равна
равна  Таким образом всегда найдется номер
Таким образом всегда найдется номер  при котором
при котором  а так как
а так как  равно значению формы
равно значению формы  при некоторых целых
при некоторых целых  то видим, что во всякой приведенной форме
то видим, что во всякой приведенной форме  можно дать переменным х, у такие целые, не равные одновременно нулю значения, при которых
можно дать переменным х, у такие целые, не равные одновременно нулю значения, при которых  эта теорема справедлива не только для приведенной, но для любой формы определителя
эта теорема справедлива не только для приведенной, но для любой формы определителя  так как было доказано, что всякая форма эквивалентна приведенной. Уже было замечено (§ 3 гл. II), что предел
так как было доказано, что всякая форма эквивалентна приведенной. Уже было замечено (§ 3 гл. II), что предел  у не может быть понижен, так как форма
у не может быть понижен, так как форма  (и все формы, эквивалентные ей собственно или несобственно) не может быть сделана меньше
(и все формы, эквивалентные ей собственно или несобственно) не может быть сделана меньше  целыми значениями
целыми значениями  не равными одновременно нулю. Предположим теперь, что данная форма определителя
не равными одновременно нулю. Предположим теперь, что данная форма определителя  не эквивалентна
не эквивалентна  Преобразовав ее в приведенную форму
Преобразовав ее в приведенную форму  и
и
построив период (9), убедимся, что ряд  не может состоять из одних единиц, и тогда аналогично предыдущему покажем, что номер
не может состоять из одних единиц, и тогда аналогично предыдущему покажем, что номер  в равенстве (13) можно выбрать так, что правая часть его будет больше или равна
в равенстве (13) можно выбрать так, что правая часть его будет больше или равна  получаем теорему: во всякой форме
получаем теорему: во всякой форме  определителя
определителя  не эквивалентной
не эквивалентной  переменным х, у можно дать такие целые, не равные одновременно нулю значения, при которых
переменным х, у можно дать такие целые, не равные одновременно нулю значения, при которых  причем этот предел опять оказывается точным для формы
причем этот предел опять оказывается точным для формы  и форм, ей эквивалентных. Развивая дальше эти соображения, А. А. Марков в своей диссертации 54 получил неограниченный ряд таких пределов, причем обнаружилась замечательная связь между этими пределами и решениями в целых числах
и форм, ей эквивалентных. Развивая дальше эти соображения, А. А. Марков в своей диссертации 54 получил неограниченный ряд таких пределов, причем обнаружилась замечательная связь между этими пределами и решениями в целых числах  неопределенного уравнения
неопределенного уравнения  примечания к этой главе).
примечания к этой главе).
Докажем теперь, что если две приведенные формы  собственно эквивалентны, то одна из них встречается в периоде другой. Пусть
собственно эквивалентны, то одна из них встречается в периоде другой. Пусть  переводится в
переводится в  подстановкой
подстановкой  Так как при переходе от приведенной формы к соседней с ней справа или слева приведенной форме меняется знак первого коэфициента, то можно предполагать, что в формах
Так как при переходе от приведенной формы к соседней с ней справа или слева приведенной форме меняется знак первого коэфициента, то можно предполагать, что в формах  числа
числа  Обозначая тогда через
Обозначая тогда через  корни форм
корни форм  имеем
имеем

Предположим сначала, что все числа  Рассмотрим случай
Рассмотрим случай  Так как у всех чисел
Так как у всех чисел  можно переменить знаки, то можем считать
можно переменить знаки, то можем считать  из равенства
из равенства  вытекает а
вытекает а  следовательно,
следовательно,  и так как
и так как  то первое из равенств (14) дает
то первое из равенств (14) дает  Если а
Если а  если же а
если же а  то второе равенство (14) показывает, что
то второе равенство (14) показывает, что  откуда
откуда  Неравенство
Неравенство  в связи с соотношением
в связи с соотношением  опять позволяет заключить, что
опять позволяет заключить, что  в самом деле, при
в самом деле, при  имеем
имеем  что невозможно. Итак, во всех случаях
что невозможно. Итак, во всех случаях  Разложим
Разложим  в непрерывную дробь с четным числом неполных частных:
в непрерывную дробь с четным числом неполных частных:  и положим
и положим  Тогда из равенств
Тогда из равенств  в соединении с неравенствами
в соединении с неравенствами  выведем
выведем  т. е.
т. е.  Построим теперь для формы
Построим теперь для формы  период приведенных форм; пусть это будет (9). Обозначая, как и раньше, через
период приведенных форм; пусть это будет (9). Обозначая, как и раньше, через  корни формы
корни формы  , ввиду
, ввиду
положительности  получаем из
получаем из  Сравнивая это с
Сравнивая это с  находим в силу единственности разложения
находим в силу единственности разложения  в непрерывную дробь
в непрерывную дробь  Отсюда, так как
Отсюда, так как  вытекает, что
вытекает, что  и тогда равенства (11) дают
и тогда равенства (11) дают  сравнивая это с
сравнивая это с  получаем
получаем  Итак, корни
Итак, корни  формы
формы  совпадают с корнями
совпадают с корнями  формы
формы  и так как эти формы
и так как эти формы  имеют одинаковый определитель и первые коэфициенты их больше нуля, то имеем тождественно
имеют одинаковый определитель и первые коэфициенты их больше нуля, то имеем тождественно  что и доказывает теорему для случая
что и доказывает теорему для случая  При
При  можем считать
можем считать  из равенства
из равенства  имеем
имеем  Так как
Так как  то второе равенство (14) дает
то второе равенство (14) дает  но у и
но у и  одного знака, следовательно,
одного знака, следовательно,  Замечая, что форма
Замечая, что форма  переводится в обратной подстановкой
переводится в обратной подстановкой  все коэфициенты которой положительны, заключаем на основании рассмотренного уже случая, что
все коэфициенты которой положительны, заключаем на основании рассмотренного уже случая, что  находится в правой части периода формы
находится в правой части периода формы  следовательно,
следовательно,  находится в левой части периода
находится в левой части периода  Остается рассмотреть случай, когда среди коэфициентов
Остается рассмотреть случай, когда среди коэфициентов  могут быть нули. При
могут быть нули. При  число
число  и первый коэфициент
и первый коэфициент  равен третьему коэфициенту с формы
равен третьему коэфициенту с формы  невозможно, так как предполагается, что в форме
невозможно, так как предполагается, что в форме  число
число  аналогично покажем, что
аналогично покажем, что  При
При  можно считать
можно считать  и вторая формула (14) дает
и вторая формула (14) дает  откуда, так как
откуда, так как  вытекает
вытекает  Тот же результат получим и при
Тот же результат получим и при  Теорема доказана.
Теорема доказана.
| << Предыдущий параграф | Следующий параграф >> |
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ЧИСЕЛ
- § 2. Простейшие арифметические функции.
- § 3. Теоремы о делимости факториалов.
- § 4. Теоремы Эйлера и Ферма; сравнения первой степени.
- § 5. Теоремы Лагранжа и Вильсона.
- § 6. Первообразные корни, индексы, двучленные сравнения.
- § 7. Числа Бернулли.
- § 8. Квадратичные вычеты; третье гауссово доказательство закона взаимности.
- § 9. Квадратичный характер по составному модулю.
- § 10. Обобщения сравнений.
- ГЛАВА II. НЕПРЕРЫВНЫЕ ДРОБИ И ДИОФАНТОВЫ ПРИБЛИЖЕНИЯ
- § 1. Ряды Фарея.
- § 2. Принцип Дирихле; теоремы Кронекера и Минковского.
- § 3. Теорема Эрмита.
- § 4. Непрерывные дроби; перечисление свойств подходящих дробей.
- § 5. Критерий Лежандра; теоремы Валена и Бореля.
- § 6. Эквивалентные числа.
- § 7. Относительные минимумы формы x — wy
- § 8. Арифметические приложения неравенства Дирихле.
- § 9. Симметрические непрерывные дроби.
- § 10. Разложение квадратных иррациональностей в непрерывную дробь.
- § 11. Союзные числа.
- § 12. Уравнение Пелля.
- § 13. Вопрос Ивана Бернулли.
- ГЛАВА III. СТЕПЕННЫЕ ВЫЧЕТЫ
- § 1. Первое гауссово доказательство квадратичного закона вэаимности.
- § 2. Распределение степенных вычетов в прогрессии.
- § 3. Биквадратичные вычеты; критерии принадлежности чисел к классам биквадратичного распределения.
- § 4. Кубические вычеты; метод Гаусса.
- § 5. Теорема о вычете числа а в разложении p = a^2+4b^2
- ГЛАВА IV. ГАУССОВА ТЕОРИЯ КВАДРАТИЧНЫХ ФОРМ
- § 1. О представлении целого числа бинарной квадратичной формой.
- § 2. Преобразование бинарной формы в себя.
- § 3. Приведение форм отрицательного определителя.
- § 4. Формы положительного определителя.
- § 5. Периоды целочисленных форм.
- § 6. Формы с определителем, равным квадрату.
- § 7. Решение общего уравнения второй степени с двумя неизвестными.
- § 8. Порядки форм; представление чисел полной системой неэквивалентных форм данного порядка
- § 9. Формы и классы anceps; некоторые специальные исследования о периодах неопределенных форм.
- § 10. Композиция бинарных форм.
- § 11. Сравнение чисел классов для определителей, отличающихся на квадрат.
- § 12. Распределение бинарных форм на роды.
- § 13. Тройничные формы, конечность числа классов, основные задачи теории.
- § 14. Представление чисел и бинарных форм тройничными формами.
- § 15. Приложение к бинарным формам, теорема Редея.
- § 16. Разложение чисел и бинарных форм на сумму трех квадратов.
- ГЛАВА V. РАЗБИЕНИЕ ЧИСЕЛ НА СЛАГАЕМЫЕ И МЕТОДЫ ЛИУВИЛЛЯ
- § 1. Точечные диаграммы, теорема Эйлера-Лежандра.
- § 2. Двойные разбиения, рекуррентные соотношения для аддитивных функций.
- § 3. Теорема Раманужана.
- § 4. Методы Лиувилля; вывод основных тождеств.
- § 5. О представлении чисел формами с двумя, тремя и четырьмя переменными.
- § 6. Количество представлений чисел суммою 2, 4, 6, 8 и 10 квадратов.
- ГЛАВА VI. ЧИСЛО КЛАССОВ БИНАРНЫХ КВАДРАТИЧНЫХ ФОРМ
- § 1. Табличные сведения о числе классов; регулярные определители.
- § 2. Соотношения Кронекера между числами классов.
- § 3. Формулы Дирихле.
- § 4. Доказательство формул Дирихле для чисто коренного случая отрицательного определителя.
- БИБЛИОГРАФИЧЕСКИЙ УКАЗАТЕЛЬ