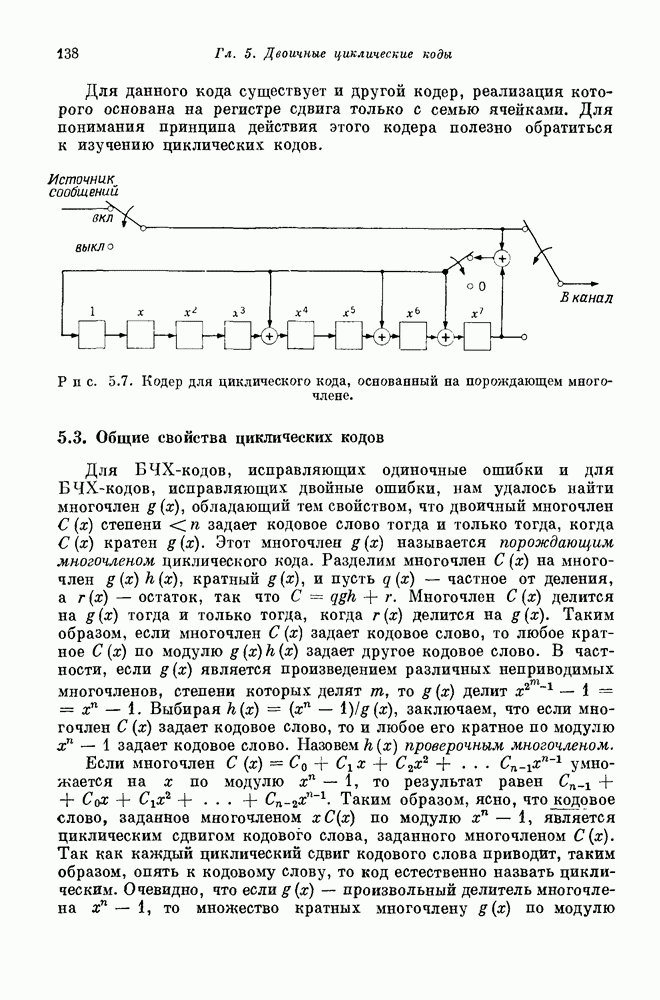
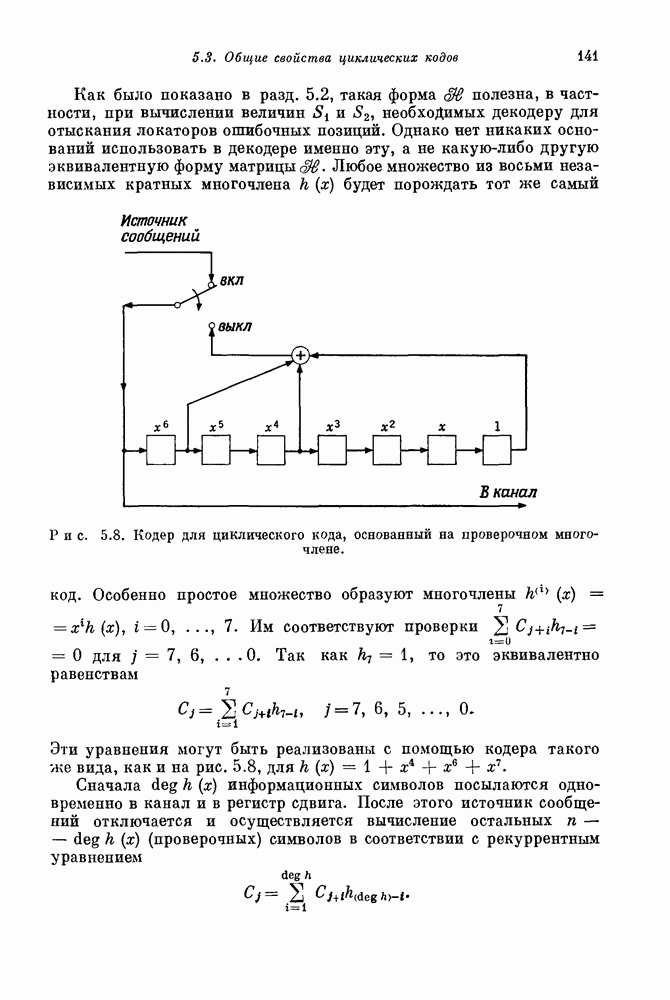
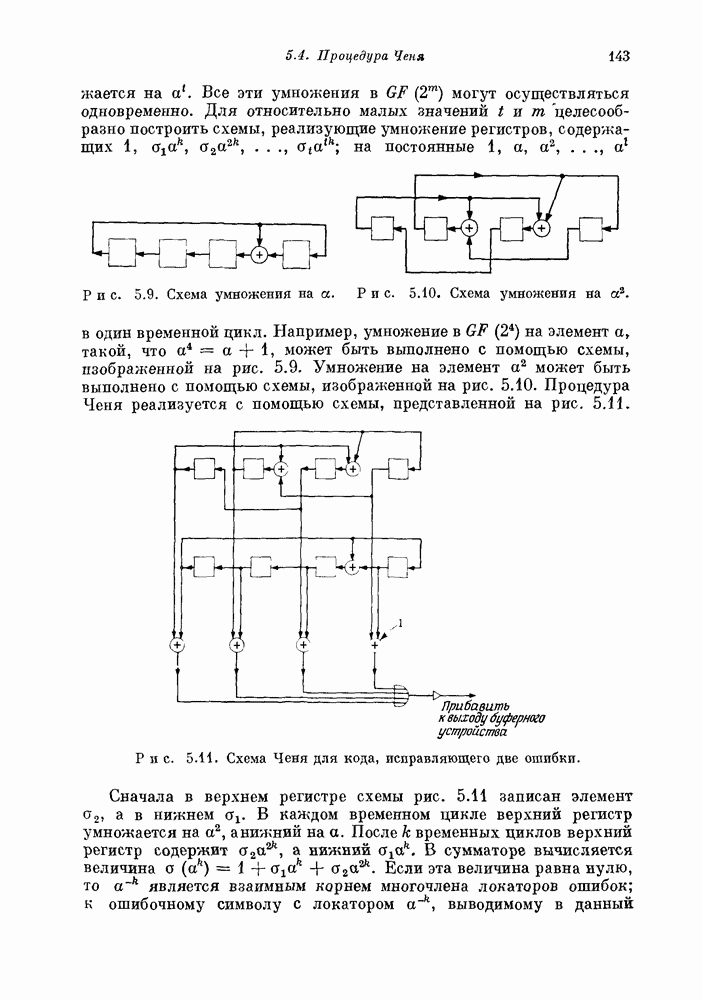
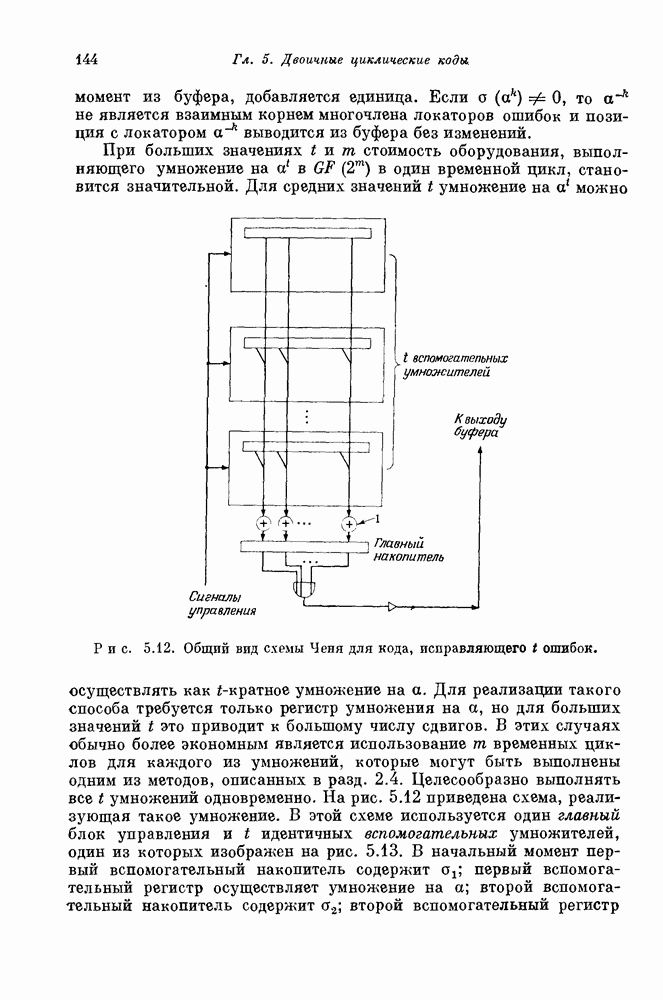
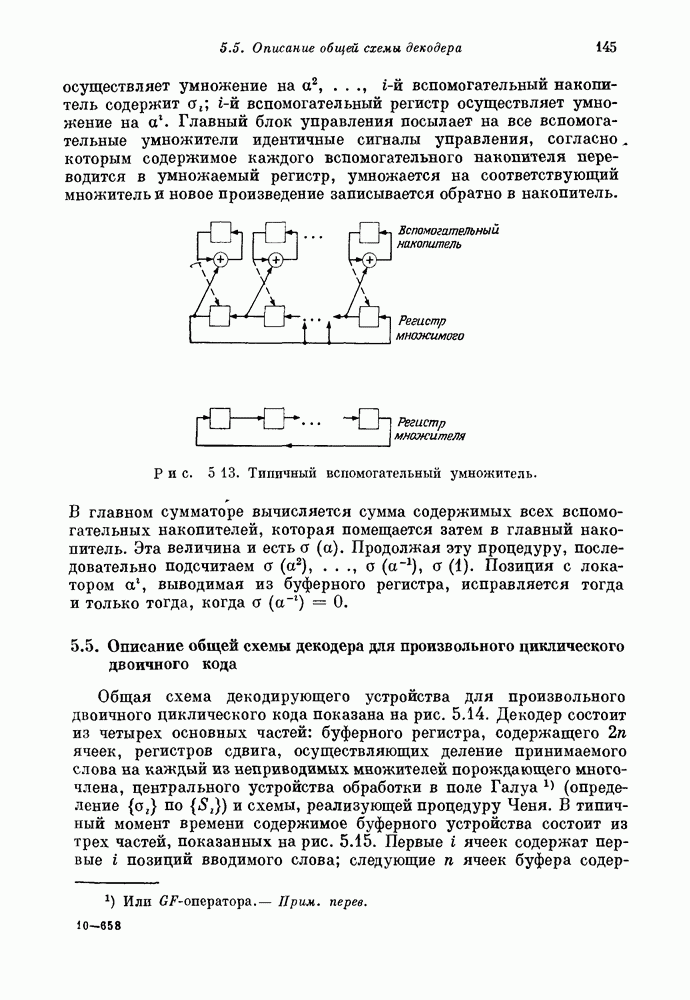
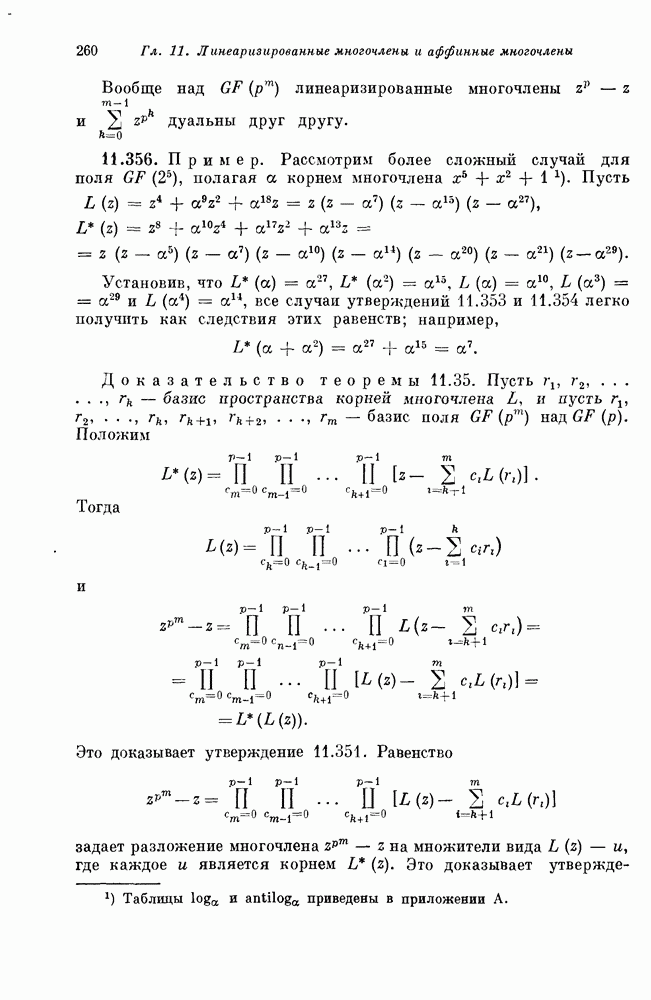| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
11.3. Общие свойства линеаризированных и аффинных многочленов
В этом разделе мы докажем общие свойства аффинных многочленов. В последующих разделах настоящей главы будут даны приложения этих результатов к некоторым вопросам теории кодирования. Основные идеи всех результатов данного раздела принадлежат Оре [1933, 1934], хотя многие из этих теорем были недавно независимо передоказаны несколькими специалистами по теории кодирования.
11.31. Теорема. Многочлен  является линеаризированным тогда и только тогда, когда его корни образуют линейное пространство над
является линеаризированным тогда и только тогда, когда его корни образуют линейное пространство над  и все имеют одну и ту же кратность, равную степени числа
и все имеют одну и ту же кратность, равную степени числа 
Замечание. Корни многочлена  не обязательно лежат в
не обязательно лежат в  они могут лежать в некотором расширении этого поля.
они могут лежать в некотором расширении этого поля.
Доказательство. Необходимость. Пусть  линеаризированный многочлен,
линеаризированный многочлен,  его корни, а
его корни, а  Тогда
Тогда  следовательно,
следовательно,  также корень
также корень  Значит, корни
Значит, корни  образуют линейное пространство над
образуют линейное пространство над 
Производная многочлена  равна
равна  Если
Если  то
то  не имеет кратных корней. С другой стороны, если
не имеет кратных корней. С другой стороны, если  но
но  то
то

является  степенью линеаризированного многочлена без кратных корней. В этом случае кратность каждого корня многочлена
степенью линеаризированного многочлена без кратных корней. В этом случае кратность каждого корня многочлена  равна
равна 
Заметим, что если  то
то 
Достаточность. Пусть корни многочлена  образуют линейное пространство над
образуют линейное пространство над  выберем в нем базис
выберем в нем базис  Каждый корень многочлена
Каждый корень многочлена  может быть однозначно записан в виде
может быть однозначно записан в виде  Для некоторого подходящего набора коэффициентов
Для некоторого подходящего набора коэффициентов  Не ограничивая общности рассуждений, можно считать многочлен
Не ограничивая общности рассуждений, можно считать многочлен  нормированным. Тогда
нормированным. Тогда

Положим

Докажем теперь индукцией по  что
что  линеаризированный многочлен. Это утверждение очевидно для
линеаризированный многочлен. Это утверждение очевидно для  Пусть
Пусть  линеаризированный многочлен. Тогда
линеаризированный многочлен. Тогда

и

Так как  линеаризированный многочлен, то его скалярное кратное
линеаризированный многочлен, то его скалярное кратное  и его
и его  степень
степень  также линеаризированные многочлены. Разность двух линеаризированных многочленов является линеаризированным многочленом, поэтому
также линеаризированные многочлены. Разность двух линеаризированных многочленов является линеаризированным многочленом, поэтому  линеаризирован. Следовательно,
линеаризирован. Следовательно,  линеаризированный многочлен и потому линеаризирована и его
линеаризированный многочлен и потому линеаризирована и его  степень
степень 
Аналогичный результат для аффинных многочленов содержится в следующей теореме:
11.32. Теорема. Многочлен  является аффинным тогда и только тогда, когда его корни образуют аффинное пространство над
является аффинным тогда и только тогда, когда его корни образуют аффинное пространство над  [т. е. если
[т. е. если  — его корни, то и
— его корни, то и  также его корень для любых
также его корень для любых  ] и все имеют одну и ту же кратность, равную степени числа
] и все имеют одну и ту же кратность, равную степени числа 
Доказательство. Пусть  — аффинный многочлен. Если
— аффинный многочлен. Если  корни
корни  то
то  корень
корень  для каждого
для каждого  Следовательно,
Следовательно,  значит,
значит,  корень многочлена
корень многочлена  Это означает, что корни аффинного многочлена образуют аффинное пространство.
Это означает, что корни аффинного многочлена образуют аффинное пространство.
Производная аффинного многочлена  и равна коэффициенту
и равна коэффициенту  . Если
. Если  то все корни
то все корни  различны. Если же
различны. Если же  то
то  есть
есть  степень аффинного многочлена с различными корнями, и, следовательно, каждый корень
степень аффинного многочлена с различными корнями, и, следовательно, каждый корень  имеет кратность
имеет кратность 
С другой стороны, если корни некоторого многочлена образуют аффинное пространство, то разности этих корней образуют линейное пространство. Согласно теореме 11.31, многочлен, корнями которого служат различные элементы этого линейного пространства, есть линеаризированный многочлен  Если
Если  произвольный корень
произвольный корень  то
то  или
или  где
где  Следовательно, корни
Следовательно, корни  суть корни многочлена
суть корни многочлена  , и так как
, и так как
кратность каждого корня  равна
равна  то
то  скалярное кратное многочлена
скалярное кратное многочлена  аффинный многочлен,
аффинный многочлен,
Различные корни произвольного аффинного многочлена образуют аффинное пространство. Пересечение любых двух аффинных пространств снова является аффинным пространством. Так как общие корни любых двух многочленов являются корнями их наибольшего общего делителя, то н. о. д. двух аффинных многочленов с различными корнями является аффинным многочленом с различными корнями. Более того, н. о. д. многочленов  равен н. о. д. многочленов
равен н. о. д. многочленов  возведенному в наименьшую из степеней
возведенному в наименьшую из степеней  или
или  Отсюда, в частности, вытекает теорема 11.331.
Отсюда, в частности, вытекает теорема 11.331.
11.331. Теорема. Н. о. д. двух аффинных многочленов является аффинным многочленом.
Если нуль — корень двух аффинных многочленов, то нуль является также корнем их н. о. д. Поэтому справедливо следующее утверждение.
11.332. Теорема. Н. о. д. двух линеаризированных многочленов является линеаризированным многочленом.
Если  два аффинных многочлена и А делит В, то корни многочлена А образуют подмножество множества корней В. Аффинное пространство корней А является, таким образом, аффинным подпространством пространства корней В. Множество всевозможных разностей корней А (т. е. совокупность всех корней линеаризированной части А) есть подмножество множества всевозможных разностей корней В — т. е. совокупности корней линеаризированной части В (см. доказательство теоремы 11.32). Так как кратность любого корня линеаризированной части аффинного многочлена совпадает с кратностью корней исходного аффинного многочлена, то получаем следующий результат.
два аффинных многочлена и А делит В, то корни многочлена А образуют подмножество множества корней В. Аффинное пространство корней А является, таким образом, аффинным подпространством пространства корней В. Множество всевозможных разностей корней А (т. е. совокупность всех корней линеаризированной части А) есть подмножество множества всевозможных разностей корней В — т. е. совокупности корней линеаризированной части В (см. доказательство теоремы 11.32). Так как кратность любого корня линеаризированной части аффинного многочлена совпадает с кратностью корней исходного аффинного многочлена, то получаем следующий результат.
11.34. Теорема. Если  аффинные многочлены и А делит В, то линеаризированная часть А делит линеаризированную часть В. Обратно если
аффинные многочлены и А делит В, то линеаризированная часть А делит линеаризированную часть В. Обратно если  линеаризированные многочлены от
линеаризированные многочлены от  делит
делит  то
то  делит
делит  для любого
для любого  лежащего в поле коэффициентов
лежащего в поле коэффициентов 
Часто необходимо знать, лежат ли в поле  все корни заданного аффинного многочлена
все корни заданного аффинного многочлена  . Если
. Если  делит
делит  то все корни
то все корни  лежат в
лежат в  но если
но если  не делит
не делит  то часть корней
то часть корней  лежит вне
лежит вне  Согласно
Согласно
теореме  делит
делит  только если
только если  делит
делит  Если же
Если же  делит
делит  то
то  и делит
и делит  тогда и только тогда, когда существует такой элемент
тогда и только тогда, когда существует такой элемент  что
что  Ясно, что для некоторых и существуют такие элементы
Ясно, что для некоторых и существуют такие элементы  что
что  Такие и образуют линейное пространство, называемое ранговым пространством линеаризированного многочлена
Такие и образуют линейное пространство, называемое ранговым пространством линеаризированного многочлена  Если и принадлежит ранговому пространству, то
Если и принадлежит ранговому пространству, то  и делит
и делит  и все корни многочлена
и все корни многочлена  и лежат в
и лежат в  Если же и не принадлежит ранговому пространству, то не существует такого
Если же и не принадлежит ранговому пространству, то не существует такого  что
что  и все корни многочлена
и все корни многочлена  и лежат вне
и лежат вне  Вопрос о принадлежности элементов из
Вопрос о принадлежности элементов из  ранговому пространству заданного линеаризированного многочлена
ранговому пространству заданного линеаризированного многочлена  полностью решается следующей теоремой.
полностью решается следующей теоремой.
11.35. Теорема. Пусть  произвольный нормированный линеаризированный многочлен над
произвольный нормированный линеаризированный многочлен над  делящий
делящий  Тогда существует единственный нормированный линеаризированный многочлен
Тогда существует единственный нормированный линеаризированный многочлен  делящий
делящий  и такой, что:
и такой, что:

11.353. Корни  лежат в
лежат в  тогда и только тогда, когда
тогда и только тогда, когда 
11.354. Корни  лежат в
лежат в  тогда и только тогда, когда
тогда и только тогда, когда 
Многочлены  и
и  будем называть дуальными.
будем называть дуальными.
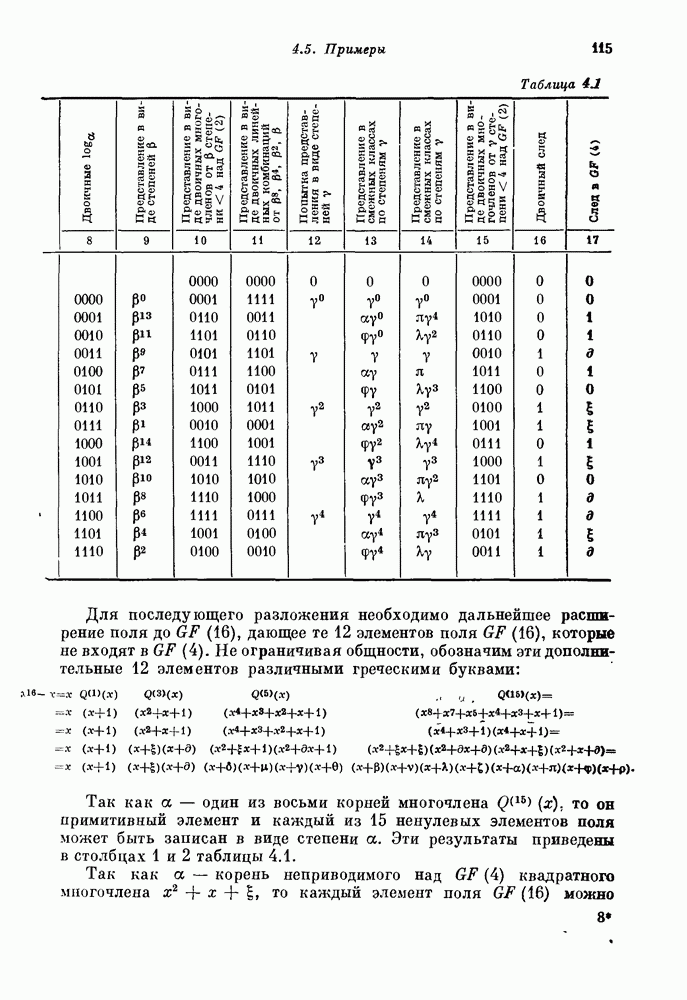
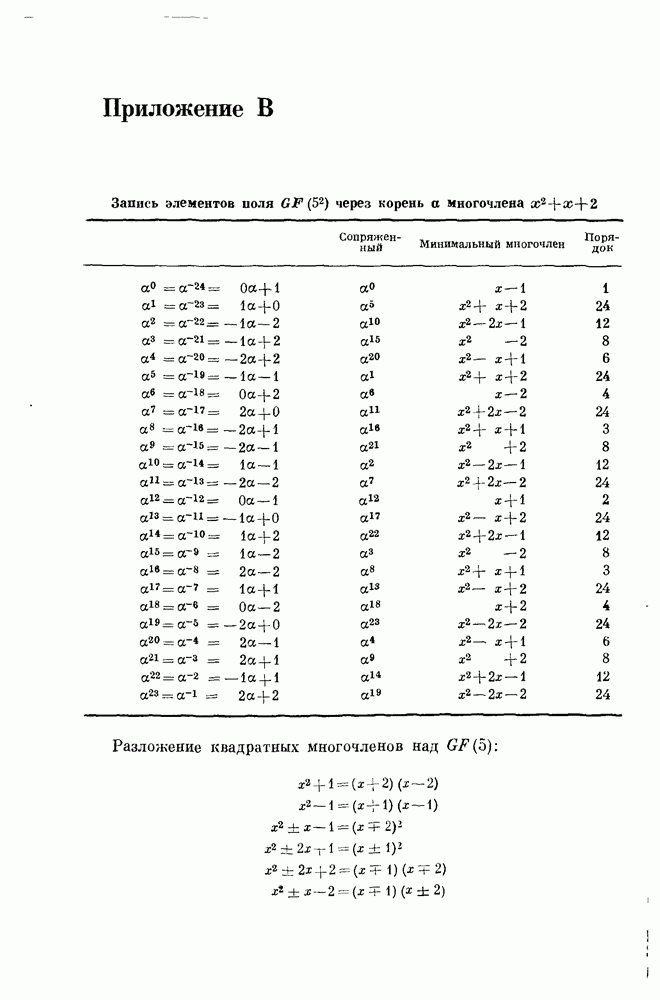
11.355. Пример. Пусть  над
над  Тогда
Тогда

и можно проверить, что

Корни уравнения  лежат в
лежат в  тогда и только тогда, когда
тогда и только тогда, когда  т. е. когда
т. е. когда  Корни уравнения
Корни уравнения  лежат в
лежат в  тогда и только тогда, когда
тогда и только тогда, когда  т. е. когда и
т. е. когда и 
Вообще над  линеаризированные многочлены
линеаризированные многочлены  дуальны друг другу.
дуальны друг другу.
11.356. Пример. Рассмотрим более сложный случай для поля  полагая а корнем многочлена
полагая а корнем многочлена  . Пусть
. Пусть

Установив, что  все случаи утверждений 11.353 и 11.354 легко получить как следствия этих равенств; например,
все случаи утверждений 11.353 и 11.354 легко получить как следствия этих равенств; например,

Доказательство теоремы 11.35. Пусть  базис пространства корней многочлена
базис пространства корней многочлена  и пусть
и пусть  базис поля
базис поля  над
над  Положим
Положим

Тогда

и

Это доказывает утверждение 11.351. Равенство

задает разложение многочлена  на множители вида
на множители вида  и, где каждое и является корнем
и, где каждое и является корнем  Это доказывает
Это доказывает
утверждение 11.353, а также единственность многочлена, дуального к многочлену  так как корневое пространство многочлена, дуального многочлену
так как корневое пространство многочлена, дуального многочлену  должно быть ранговым пространством
должно быть ранговым пространством 
Для доказательства утверждения 11.352 подсчитаем  Так как
Так как  линеаризированный многочлен над
линеаризированный многочлен над  то
то  следовательно,
следовательно,  Полагая
Полагая  получаем, что
получаем, что  . Это равенство должно быть тождеством относительно у и потому
. Это равенство должно быть тождеством относительно у и потому  что доказывает утверждение 11.352.
что доказывает утверждение 11.352.
Для доказательства утверждения 11.354 выберем базис  в корневом пространстве многочлена
в корневом пространстве многочлена  и базис
и базис  Остальная часть доказательства является двойственной к доказательству утверждения 11.353.
Остальная часть доказательства является двойственной к доказательству утверждения 11.353.
Если все коэффициенты линеаризированного многочлена лежат в основном поле  то на некоторые вопросы о его свойствах можно ответить с помощью рассмотрения ассоциированного с ним многочлена, определяемого следующим образом.
то на некоторые вопросы о его свойствах можно ответить с помощью рассмотрения ассоциированного с ним многочлена, определяемого следующим образом.
11.36. Определение. Если  для всех
для всех  , то многочлены
, то многочлены  называются ассоциированными;
называются ассоциированными;  линеаризированно ассоциированный с
линеаризированно ассоциированный с  стандартно ассоциированный с
стандартно ассоциированный с 
Плодотворность этого определения видна из следующей теоремы:
11.37. Теорема. Если  линеаризированные многочлены над
линеаризированные многочлены над  стандартно ассоциированные с ними многочлены, то
стандартно ассоциированные с ними многочлены, то  делит
делит  тогда и только тогда, когда
тогда и только тогда, когда  делит
делит  Если
Если  то
то  где
где  линеаризированно ассоциированный с
линеаризированно ассоциированный с 
Доказательство. Каждое из равенств

и

справедливо тогда и только тогда, когда  Для всех к.
Для всех к.
11.38. Следствие. Если  линеаризированный многочлен над
линеаризированный многочлен над  то
то  делит
делит  тогда и только тогда, когда
тогда и только тогда, когда
стандартно ассоциированный с ним многочлен  делит
делит  Если
Если  делит
делит  то стандартно ассоциированный с L (дуальным к L) многочлен задается равенством
то стандартно ассоциированный с L (дуальным к L) многочлен задается равенством

11.381. Пример. В соответствии с разложением  можно записать разложение для линеаризированно ассоциированного многочлена
можно записать разложение для линеаризированно ассоциированного многочлена  Эти разложения дуальны друг другу.
Эти разложения дуальны друг другу.
Используя последнее следствие, можно определить число элементов поля  обладающих
обладающих  линейно независимыми сопряженными относительно
линейно независимыми сопряженными относительно  элементами
элементами  Если
Если  то
то  линейно зависимы тогда и только тогда, когда существуют такие элементы
линейно зависимы тогда и только тогда, когда существуют такие элементы  не равные одновременно нулю, что
не равные одновременно нулю, что  Так как и — корень многочленов
Так как и — корень многочленов  и
и  то он является также корнем их н. о. д.
то он является также корнем их н. о. д.
Н. о. д. этих двух линеаризированных многочленов также линеаризирован. Таким образом, все сопряженные с и элементы линейно зависимы тогда и только тогда, когда и является корнем некоторого многочлена  делящего
делящего 
Пусть  и н. о. д.
и н. о. д.  , так что
, так что  различные неприводимые делители многочлена
различные неприводимые делители многочлена  Обозначим через
Обозначим через  степень многочлена
степень многочлена 
Ясно, что  Максимальный собственный делитель многочлена
Максимальный собственный делитель многочлена  имеет вид
имеет вид  Каждый собственный делитель многочлена
Каждый собственный делитель многочлена  делит по меньшей мере один из этих максимальных делителей. Каждому максимальному делителю многочлена
делит по меньшей мере один из этих максимальных делителей. Каждому максимальному делителю многочлена  соответствует максимальный линеаризированный делитель многочлена
соответствует максимальный линеаризированный делитель многочлена  а именно
а именно  Элемент
Элемент  имеет
имеет  линейно независимых
линейно независимых
сопряженных тогда и только тогда, когда он не является корнем ни одного из этих многочленов  .
.
Н. о. д. нескольких максимальных делителей многочлена  скажем,
скажем,  равен
равен  и имеет степень
и имеет степень  Соответственно н. о. д. многочленов
Соответственно н. о. д. многочленов  Ни
Ни  является линеаризированным многочленом степени
является линеаризированным многочленом степени  Если случайным образом выбирается элемент поля
Если случайным образом выбирается элемент поля  то вероятность того, что он есть корень равна
то вероятность того, что он есть корень равна  вероятность того, что он является корнем
вероятность того, что он является корнем  равна
равна  а вероятность того, что он одновременно является корнем
а вероятность того, что он одновременно является корнем  равна
равна  Таким образом, вхождение элемента в качестве корня в
Таким образом, вхождение элемента в качестве корня в  независимые события. То же самое можно сказать о
независимые события. То же самое можно сказать о  д. Вероятность того, что случайно выбранный элемент поля
д. Вероятность того, что случайно выбранный элемент поля  не есть корень
не есть корень  равна
равна  Применяя теорему умножения вероятностей, заключаем, что вероятность того, что случайно выбранный элемент поля
Применяя теорему умножения вероятностей, заключаем, что вероятность того, что случайно выбранный элемент поля  не является корнем ни одного из многочленов
не является корнем ни одного из многочленов  равна
равна  Это дает теорему 11.39.
Это дает теорему 11.39.
11.39. Теорема. Число элементов поля  обладающих
обладающих  линейно независимыми сопряженными относительно поля
линейно независимыми сопряженными относительно поля  равно
равно

где  степени различных неприводимых делителей многочлена
степени различных неприводимых делителей многочлена  над
над 
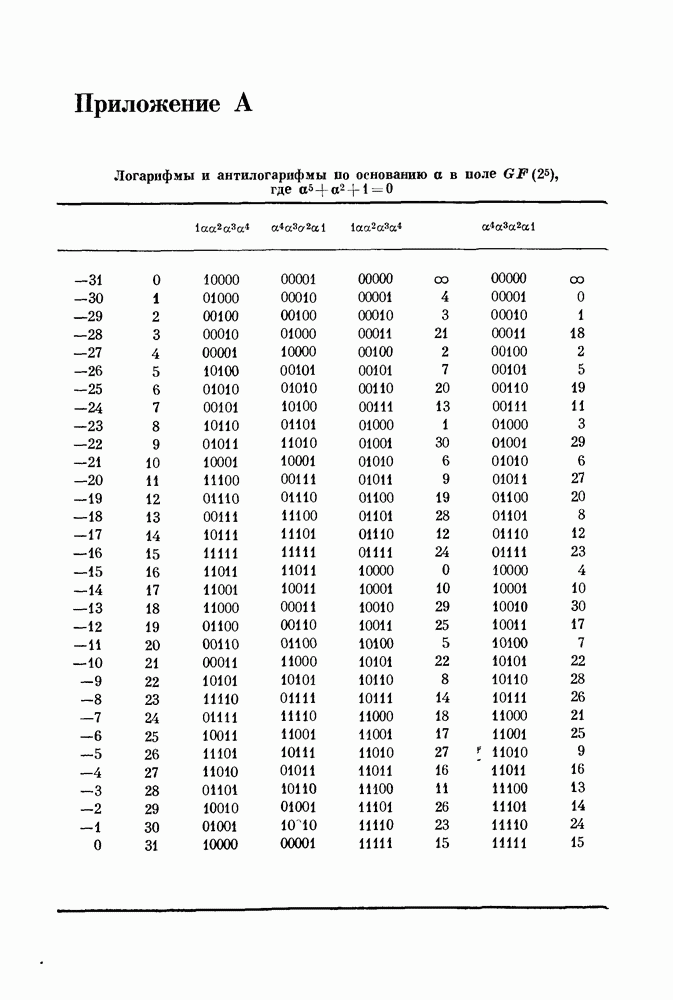
11.391. Пример. Рассмотрим поле  Над
Над 

где 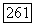 неприводимый многочлен степени
неприводимый многочлен степени 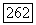 произведение двух неприводимых кубических многочленов. Итак,
произведение двух неприводимых кубических многочленов. Итак, 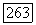 и число элементов поля
и число элементов поля 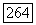 имеющих 14 линейно независимых сопряженных относительно
имеющих 14 линейно независимых сопряженных относительно 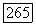 элементов, равно
элементов, равно 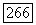 Эти элементы лежат в
Эти элементы лежат в 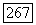 классах сопряженных (над GF(2)) элементов. Существует 448 неприводимых двоичных многочленов 14-й степени, корни которых линейно независимы.
классах сопряженных (над GF(2)) элементов. Существует 448 неприводимых двоичных многочленов 14-й степени, корни которых линейно независимы.
Читатели, относящиеся с недоверием к вероятностной аргументации, использованной в предыдущем доказательстве, могут доказать этот же результат с помощью комбинаторных методов. С нашей точки зрения вероятностный подход делает результат более прозрачным.
Как указал Кац [1959], вероятностный подход к вопросам перечисления нашел широкое применение во многих различных задачах.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. Основные двоичные коды
- 1.1. Коды с повторением и коды с одной проверкой на четность
- 1.2. Линейные коды
- 1.3. Коды Хэмминга
- 1.4. Конструктивное введение в теорию БЧХ-кодов, исправляющих двойные ошибки
- Глава 2. Арифметические операции по модулю неприводимого двоичного многочлена
- 2.1. Более подробно об алгоритме Евклида
- 2.2. Логические цепи
- 2.3. Мультипликативное обращение
- 2.4. Умножение
- 2.5. Решение систем линейных уравнений
- 2.6. Специальныё метод решения систем уравнениё, матрицы которых состоят почти сплошь из нулей
- Глава 3. Число неприводимых q-ичных многочленов заданной степени
- 3.2. Производящие функции
- 3.3. Число неприводимых нормированных q-ичных многочленов заданной степени
- 3.4. Формула обращения Мёбиуса
- Глава 4. Структура конечных полей
- 4.2. Мультипликативная структура конечных полей
- 4.3. Круговые многочлены
- 4.4. Алгебраическая структура конечных полей
- 4.5. Примеры
- 4.6. Алгебраическое замыкание
- 4.7. Определение минимальных многочленов
- Глава 5. Двоичные циклические коды
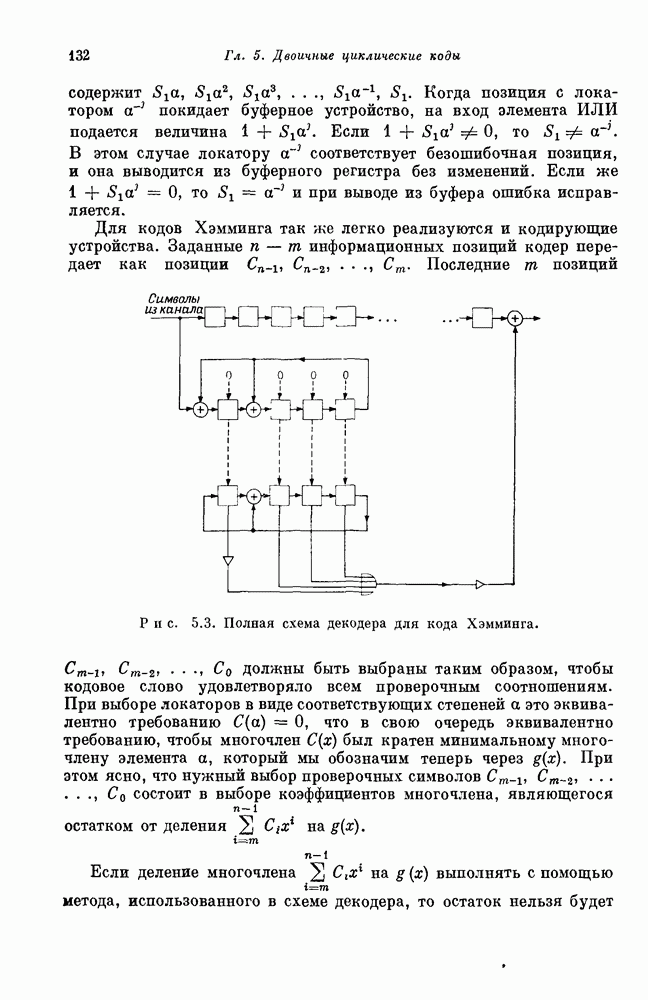
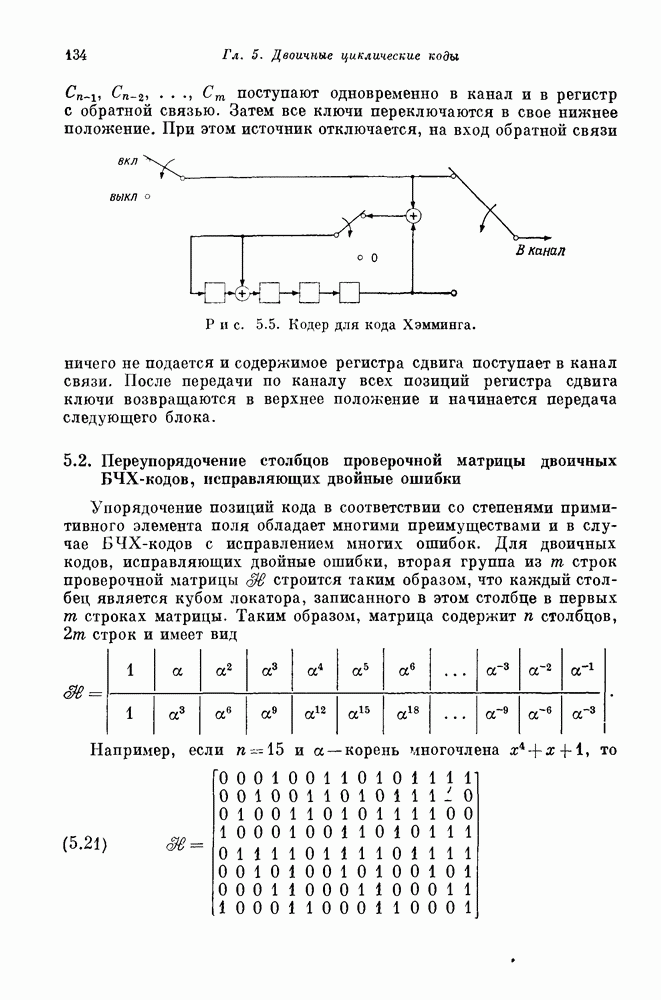
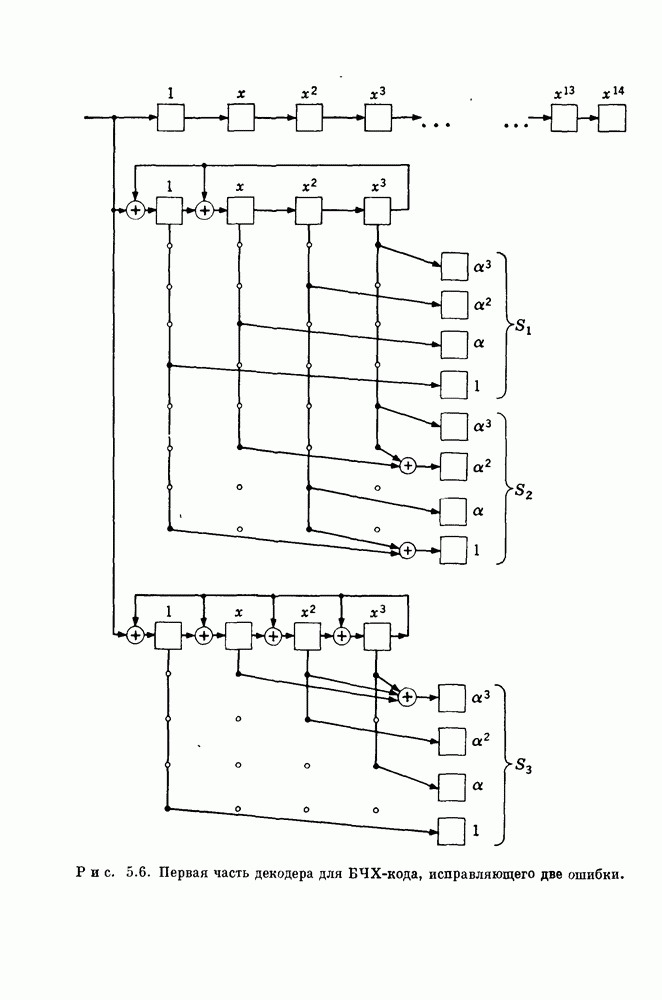
- 5.2. Переупорядочение столбцов проверочной матрицы двоичных БЧХ-кодов, исправляющих двойные ошибки
- 5.3. Общие свойства циклических кодов
- 5.4. Процедура Ченя
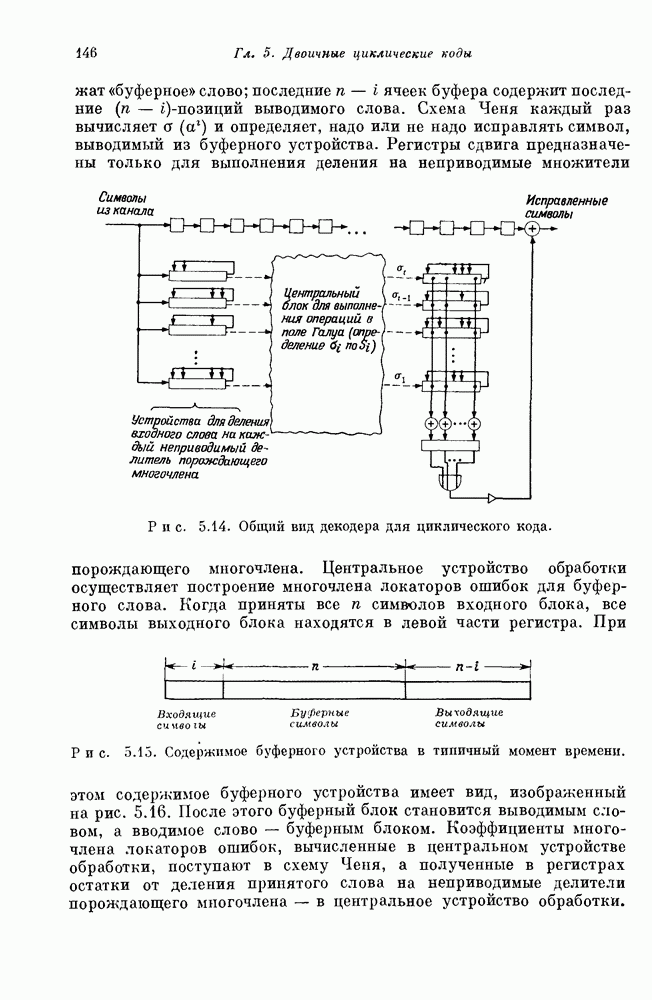
- 5.5. Описание общей схемы декодера для произвольного циклического двоичного кода
- 5.6. Пример
- 5.7. Пример
- 5.8. Эквивалентность определений циклических кодов при помощи различных примитивных корней n-степени из единицы
- Глава 6. Разложение многочленов над конечными полями
- 6.2. Определение периода многочлена
- 6.3. Трехчлены над GF(2)
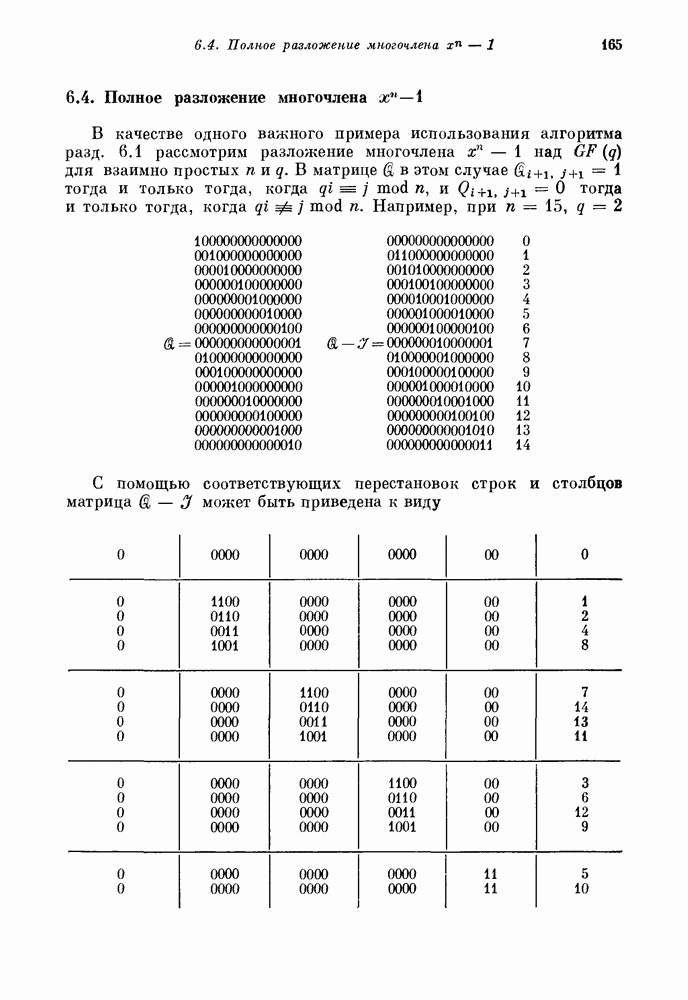
- 6.4. Полное разложение многочлена x^n-1
- 6.5. Определение степеней неприводимых делителей круговых многочленов
- 6.6. Четно или нечетно число неприводимых делителей f(x) над GF(q)?
- 6.7. Квадратичный закон взаимности
- Глава 7. Двоичные БЧХ-коды, исправляющие многократные ошибки
- 7.2. Ключевое уравнение для декодирования двоичных БЧХ-кодов
- 7.3. Эвристическое решение ключевого уравнения
- 7.4. Алгоритм решения ключевого уравнения над произвольным полем
- 7.5. Связь с матричными методами декодирования
- 7.6. Упрощение алгоритма 7.4 для двоичных БЧХ-кодов
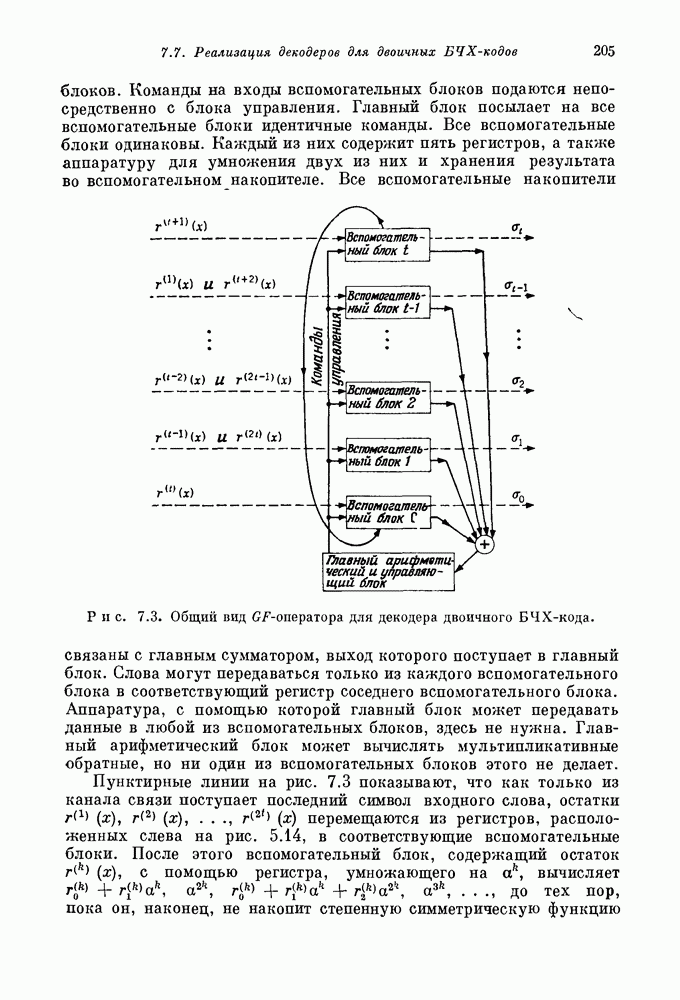
- 7.7. Реализация декодеров для двоичных БЧХ-кодов
- Глава 8. Недвоичное кодирование
- 8.2. Весовые функции
- Глава 9. Негациклические коды для метрики Ли
- 9.2. Коды, исправляющие две ошибки
- 9.3. Негациклические коды
- Глава 10. Недвоичное обобщение Горенстейна-Цирлера БЧХ-кодов в случае метрики Хэмминга
- 10.2. Примеры
- 10.3. БЧХ-коды общего типа и 1-удлиненные БЧХ-коды
- 10.4. Совместное декодирование стираний и ошибок
- 10.5. Декодирование более чем t ошибок
- 10.6. Примеры
- Глава 11. Линеаризированные многочлены и аффинные многочлены
- 11.2. Наименьшее аффинное кратное
- 11.3. Общие свойства линеаризированных и аффинных многочленов
- 11.4. Преобразования функции f(z)
- 11.5. Подсчет корней
- 11.6. Кодовые слова с малым весом в некоторых кодах
- Глава 12. Нахождение числа информационных символов в БЧХ-кодах
- 12.2. Сведение задачи для случая примитивных БЧХ-кодов к перечислению некоторых q-ичных последовательностей
- 12.3. Теоремы о числе последовательностей
- 12.4. Примеры
- 12.5. Определение числа информационных символов в непримитивных БЧХ-кодах
- 12.6. Асимптотические результаты
- 12.7. Истинные расстояния
- Глава 13. Скорость передачи информации для оптимальных кодов
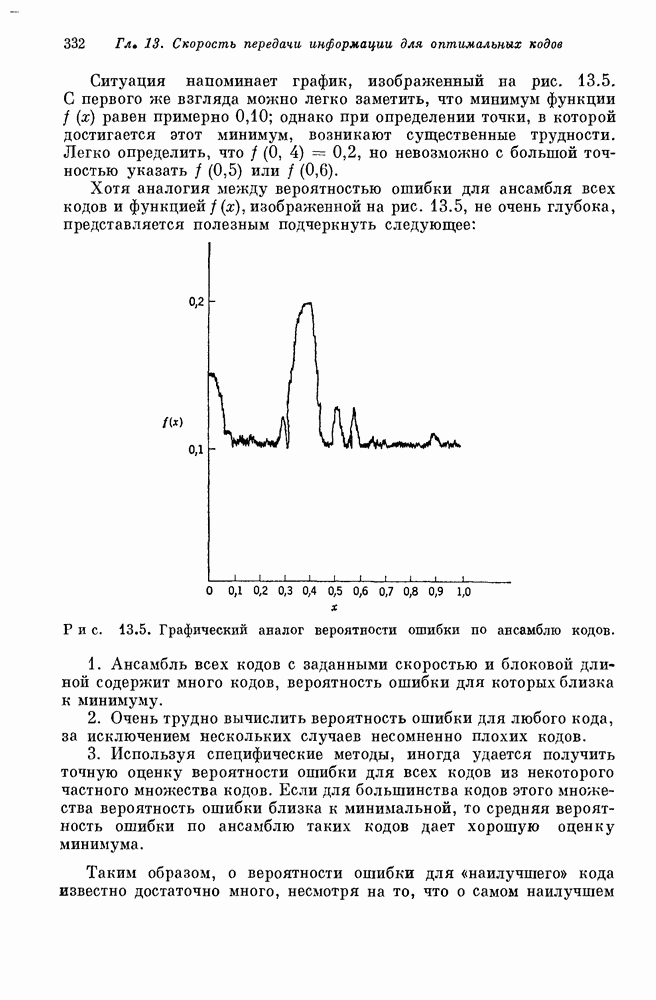
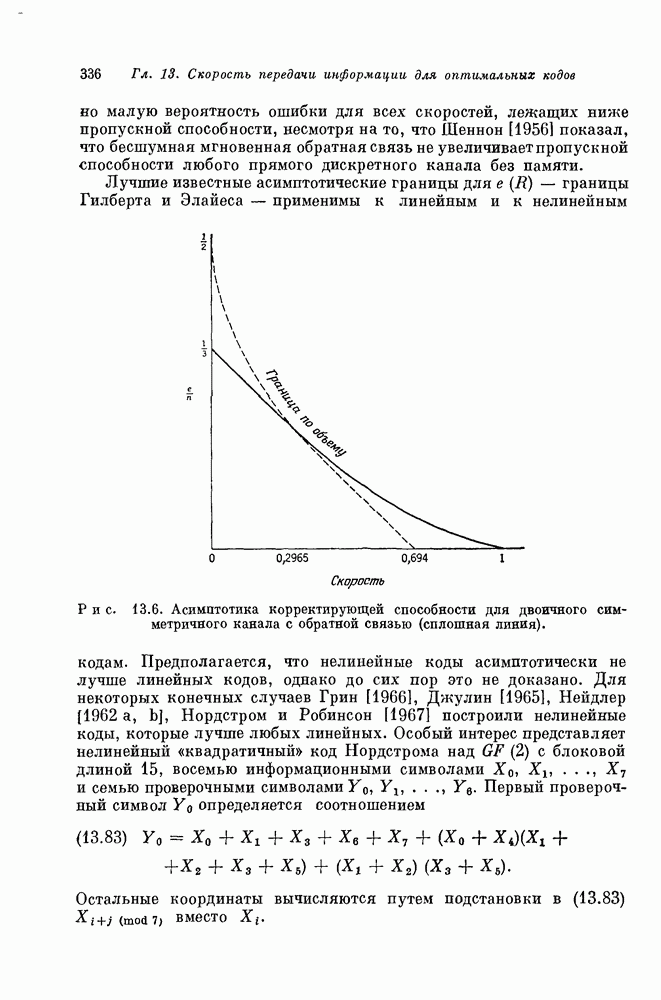
- 13.1. Граница сферической упаковки Хэминга — Рао для больших скоростей
- 13.2. Совершенные коды
- 13.3. Границы d <= n+1-k
- 13.4. Граница Плоткина для малых скоростей (граница среднего расстояния)
- 13.5. Эквидистантные коды
- 13.6. Граница Элайеса
- 13.7. Граница Гилберта
- 13.8. Асимптотические границы для вероятности ошибки и конечные частные случаи
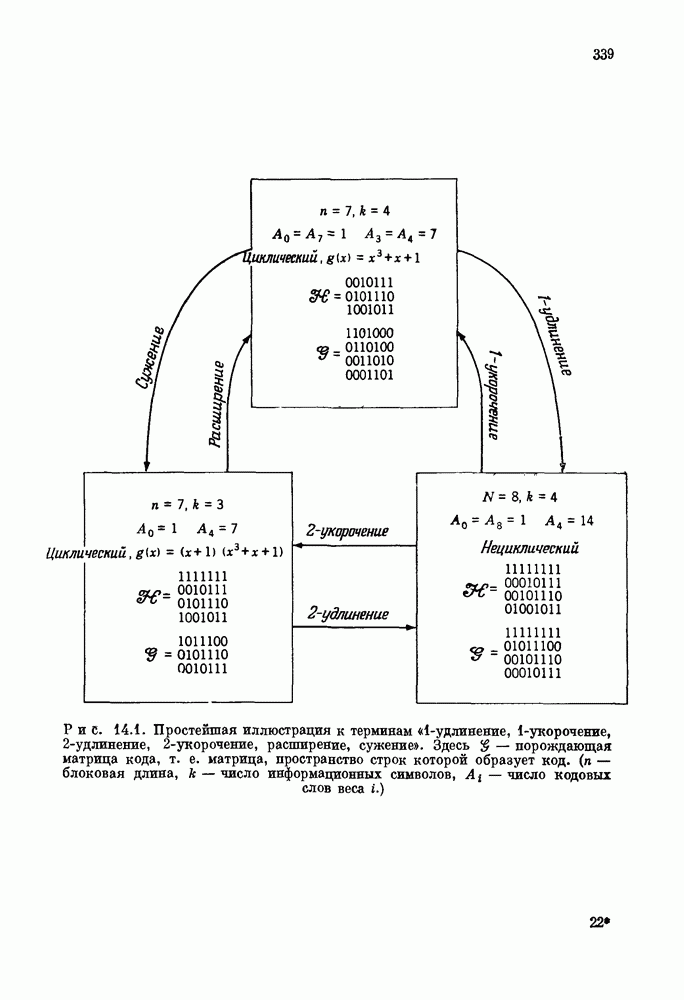
- Глава 14. Коды, полученные путем модификации и сочетания других кодов
- 14.2. 1-укорочение кода (выбрасывание проверочных символов)
- 14.3. Присоединение дополнительных кодовых слов
- 14.4. Выбрасывание кодовых слов
- 14.5. 2-удлинение кодов (добавление информационных символов)
- 14.6. 2-укорочение кода (вычеркивание информационных символов)
- 14.7. Подкоды над подполями
- 14.8. Прямое произведение кодов и его свойства
- 14.9. Каскадные коды
- Глава 15. Другие основные методы кодирования и декодирования
- 15.1. Коды Сривэставы — нециклические коды с алгебраическим алгоритмом декодирования
- 15.2. Вычетные коды — хорошие коды с трудным декодированием
- 15.3. Коды Рида — Маллера — слабые коды с легким декодированием
- 15.4. Пороговое декодирование — лучший из известных алгоритмов декодирования некоторых кодов
- 15.5. Ортогонализируемые коды, основанные на конечных геометриях
- 15.6. Сверточные коды — обзор
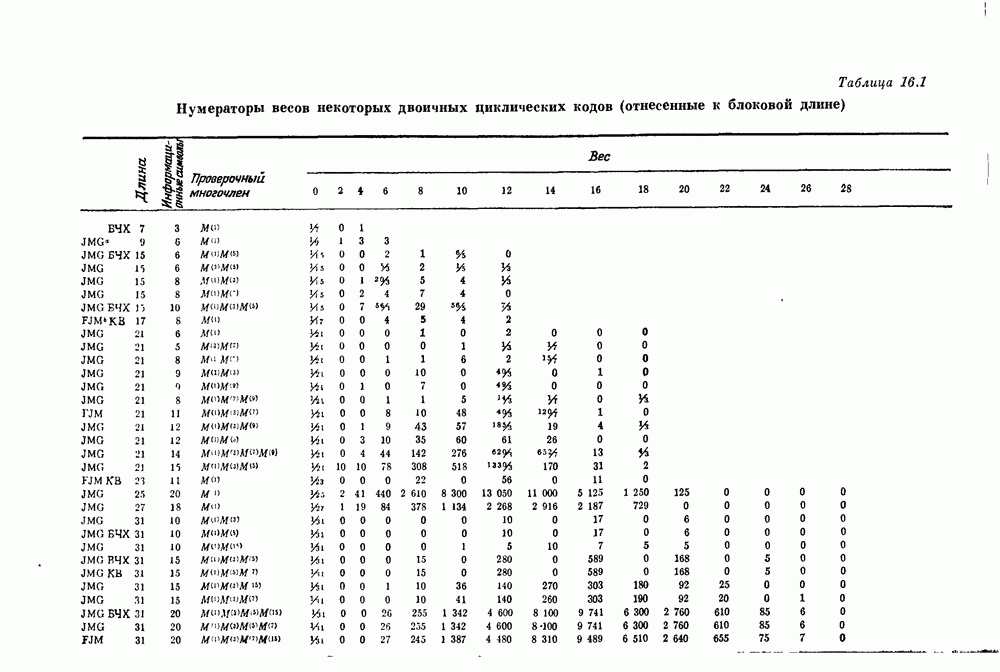
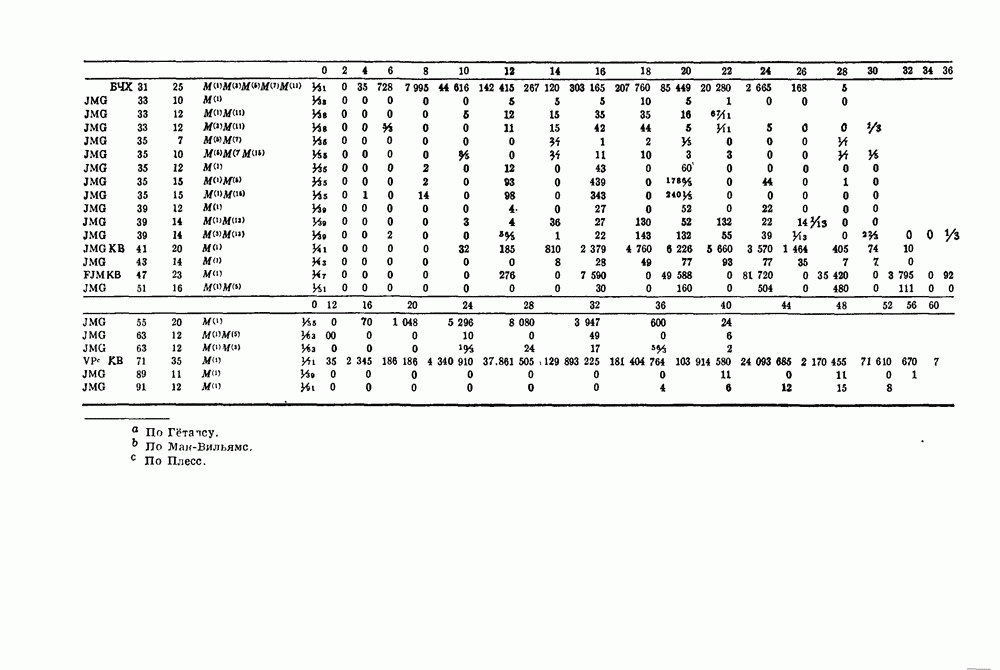
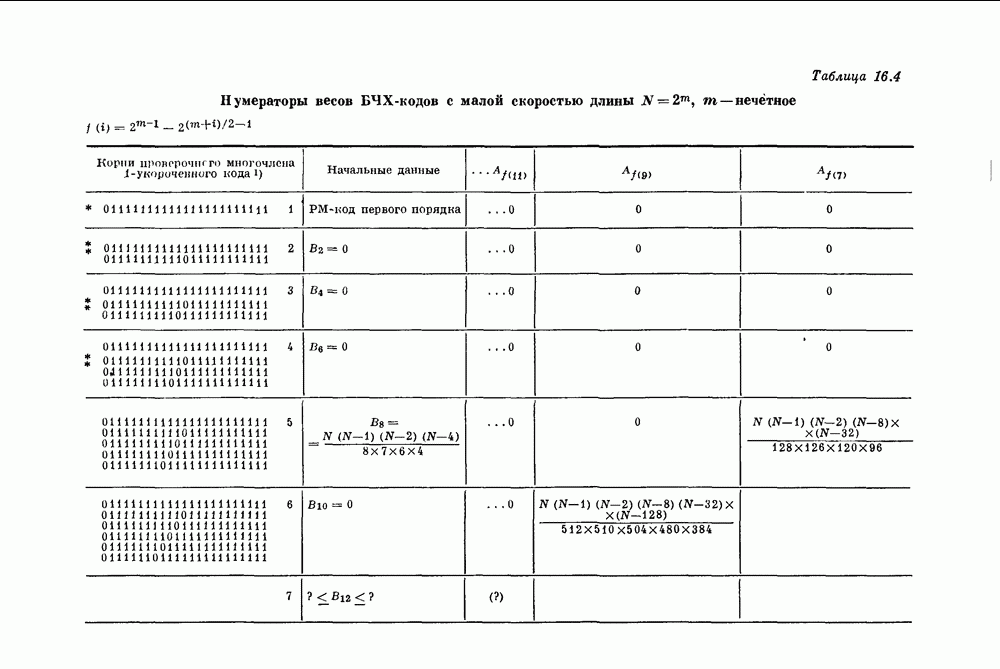
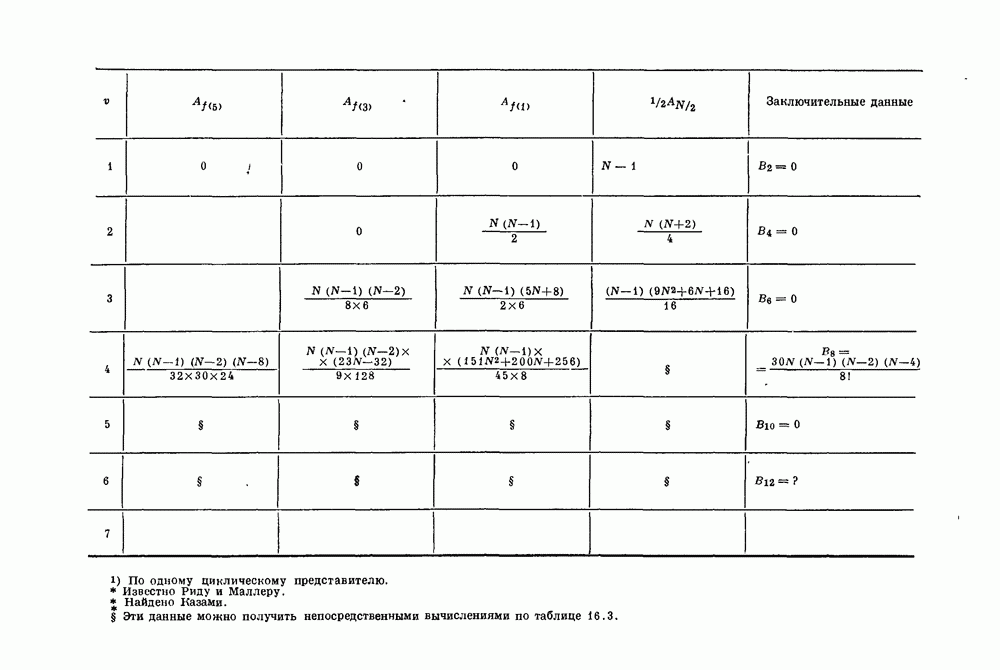
- Глава 16. Нумераторы весов
- 16.1. Соотношения между нумераторами весов и вероятностью отказа от декодирования
- 16.2. Уравнения Мак-Вильямс — Плесс для нумераторов весов дуальных кодов
- 16.3. Ограничения весов
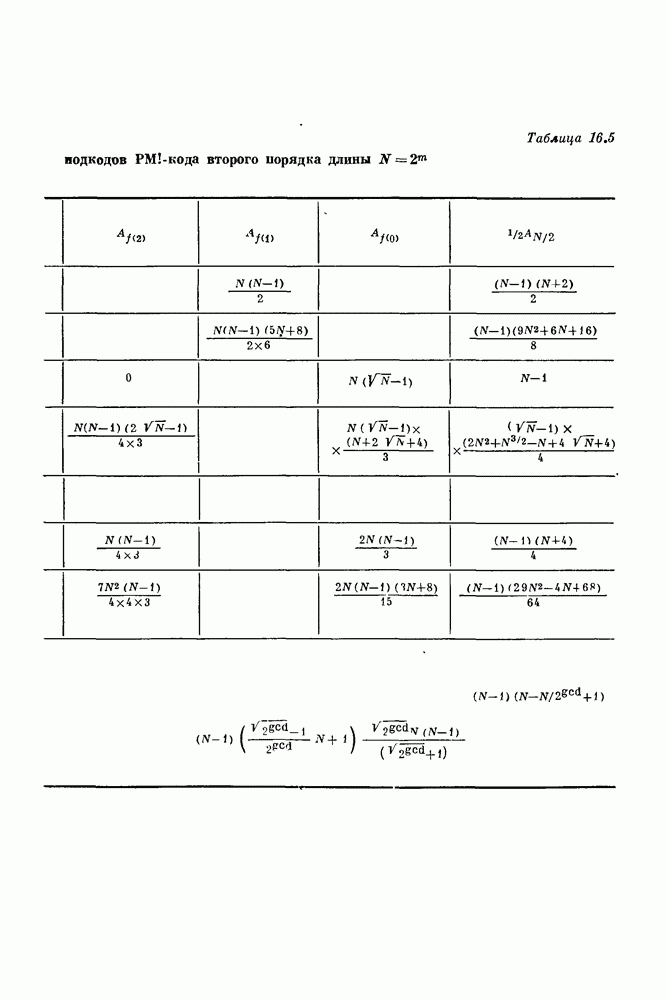
- 16.4. Нумераторы весов Казами для некоторых подкодов РМ-кода второго порядка
- 16.5. Нумераторы весов для кодов Рида — Соломона
- ЛИТЕРАТУРА