| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
10.2. Шкалы измерений
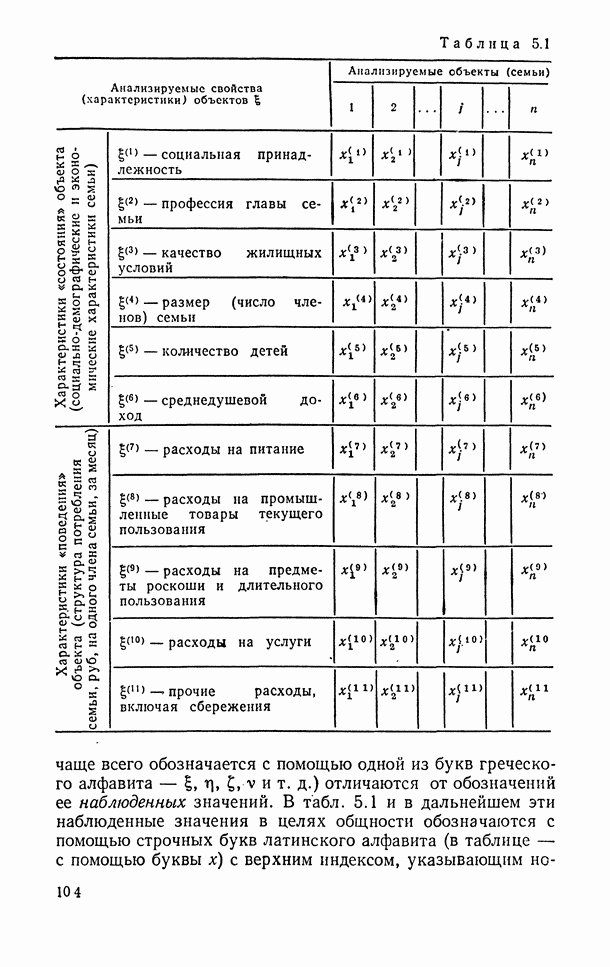
Каждое измерение над объектом производится в определенной шкале. Различные координаты одного вектора наблюдений могут быть выражены в разных шкалах. Так, в § 5.1 приведен пример вектора наблюдений (табл. 5.1), у которого первые координаты носят характер условных меток (социальная принадлежность семьи, пол и профессия главы семьи, качество жилищных условий), в то время как остальные выражаются числами (число членов семьи, количество детей, среднегодовой доход и т. п.). Свойства этих шкал сильно различаются между собой. Так, про пол главы семьи можно сказать только, что он или мужской или женский и что пол мужской отличается от пола женского; про жилищные условия — что они совпадают или отличаются и что в отдельных случаях одни жилищные условия лучше других; про расходы можно сказать, что расходы на питание одной семьи меньше, равны, больше расходов другой, можно оценить разность в расходах между семьями и подсчитать, во сколько раз расходы одной семьи отличаются от расходов другой.
Ниже описываются основные типы шкал и математические приемы унификации данных, выраженных в разных шкалах, которые обычно предшествуют применению методов многомерного анализа.
10.2.1. Номинальная шкала.
Эта шкала используется только для того, чтобы отнести индивидуум, объект в определенный класс. Если описаны заранее возможные классы и правила отнесения объекта в них, то говорят о категоризованной шкале, если нет, то о некатегоризованной. Примером категоризованной шкалы является пол. В исследовании индивидууму приписывается одно из двух значений: буква М или Ж, специальный знак или число 1 или 2. В принципе можно было бы приписывать и другие буквы и цифры, важно только, чтобы сохранялось взаимно-однозначное соответствие между кодами. Для ввода категоризованных данных удобно использовать «меню», т. е. перечень возможных категорий с их кодами. Примерами некатегоризованных номинальных переменных являются имя, фамилия, место рождения.
Другой важный источник некатегоризованных номинальных данных указан в § 5.3. Это случай, когда наблюдение задается над парой объектов, и переменная указывает только, принадлежат ли объекты, к одному классу или нет, и не указывает, к каким классам они принадлежат.
Последнее обстоятельство не надо рассматривать в качестве курьеза. Конечно, если классы заранее определены и нетрудно каждый объект отнести в определенный класс, то это следует сделать и записать, к какому классу объект принадлежит. Но иногда классы заранее не описаны, создание их полной классификации как раз и является целью работы, а вместе с тем оценить принадлежность объектов одному классу можно. Например, можно говорить о «близком», «похожем» течении болезни у двух больных, хотя все варианты течения заболевания и не описаны. Более того, выделение эмпирически близких вариантов течения болезни может служить отправным пунктом для выделения и описания всех возможных вариантов развития патологического процесса. То же относится к выделению социально-экономических групп и т. п.
Одна и та же переменная может в зависимости от цели использования выступать в разных качествах. Так, например, некатегоризованная номинальная переменная — имя программы — служит только для индивидуализации программы и, если программ немного, может быть найдена прямым просмотром списка программ. Вместе с тем если имена программ в списке каким-либо образом упорядочить (например, в алфавитно-цифровом порядке), то имя программы как поисковый образ несет в себе элементы порядковой величины. Про каждые два имени можно сказать, что они или совпадают, или одно из них предшествует другому при принятом способе упорядочивания. При изменении способа упорядочивания меняется и отношение следования.
Арифметические операции над величинами, измеренными в номинальной шкале, лишены смысла. Следовательно, и медиана, и среднее арифметическое не могут быть использованы в качестве осмысленной меры центральной тенденции. Более подходящая статистика здесь мода.
10.2.2. Порядковая (ординальная) шкала.
В дополнение к функции отнесения объектов в определенный класс эта шкала также упорядочивает классы по степени выраженности заданного свойства. Каждому классу приписывается свой собственный символ таким образом, чтобы заранее установленный порядок символов соответствовал порядку классов. Так, если классам будут приписаны числовые значения, то классы будут упорядочены согласно числовой последовательности; если буквы, то классы будут упорядочены в алфавитном порядке, а если слова, то классы будут упорядочены согласно значениям  слов.
слов.
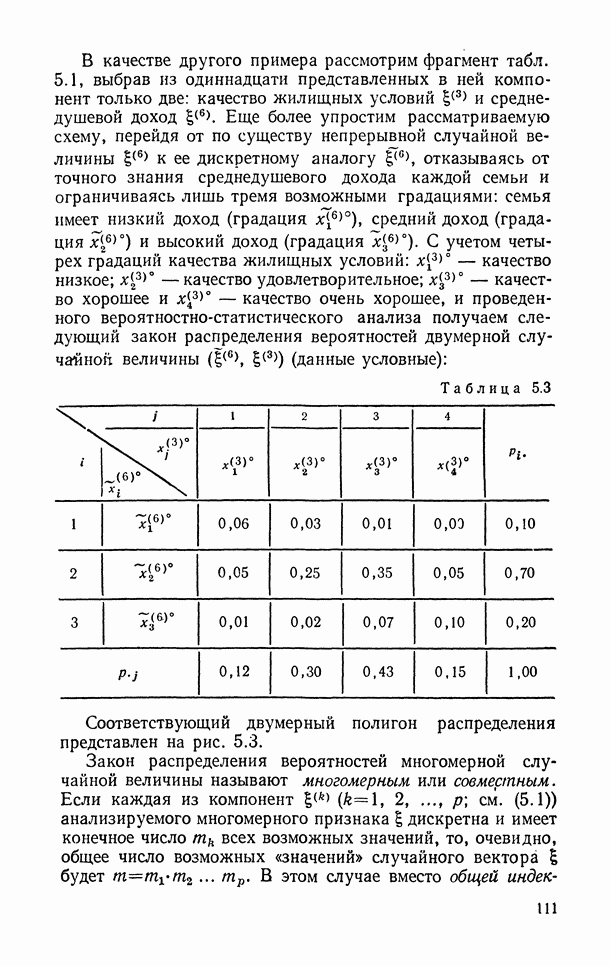
Например, в § 5.3 приводится пример порядковой шкалы для описания качества жилищных условий с четырьмя градациями (классами): «плохое», «удовлетворительное», «хорошее», «очень хорошее». Естественно, что эти классы могли бы быть занумерованы числами 1,2,3,4, или 4,3,2,1, или буквами а,б,в,г и т. п.
Другими известными примерами порядковых шкал являются: в медицине — шкала стадий гипертонической болезни по Мясникову, шкала степеней сердечной недостаточности по Стражеско — Василенко — Лангу, шкала степени выраженности коронарной недостаточности по Фогельсону; в минералогии — шкала Мооса (тальк —1, гипс — 2, кальцит — 3, флюорит — 4, апатит — 5, ортоклаз — 6, кварц — 7, топаз — 8, корунд — 9, алмаз — 10), по которой минералы классифицируются согласно критерию твердости; в географии — бофортова шкала ветров («штиль», «слабый ветер», «умеренный ветер» и т. д.).
Структура порядковой шкалы не разрушается при любом взаимно-однозначном преобразовании кодов, которое сохраняет порядок. Так же, как и в случае номинальной шкалы, арифметические операции не сохраняют своего смысла при преобразовании порядковых шкал, поэтому желательно ими не пользоваться. Нетрудно показать, что если опираться только на свойства шкал и не привлекать дополнительных, внешних по отношению к шкалам соображений, то единственными разрешенными статистиками при использовании порядковых шкал являются члены вариационного ряда [65].
10.2.3. Количественные шкалы.
Шкала, в которой можно отразить, на сколько по степени выраженности заданного свойства один из объектов отличается от другого, называется интервальной. Для того чтобы задать интервальную шкалу, надо определить объекты, соответствующие начальной точке и единице измерения. И далее при измерении ставить в соответствие каждому объекту число, показывающее, на сколько единиц измерения этот объект отличается от объекта, принятого за начальную точку. Простейшим примером интервальной шкалы является температура в градусах Цельсия, где 0° — начальная точка и 1° — единица измерения.
Структура интервальной шкалы не меняется при линейных преобразованиях вида  Эффект такого преобразования заключается в сдвиге начальной точки на b единиц и умножении единицы измерения на а.
Эффект такого преобразования заключается в сдвиге начальной точки на b единиц и умножении единицы измерения на а.
Например, путем преобразования  , где
, где  — температура в
— температура в  можно перейти к температуре в градусах Фаренгейта.
можно перейти к температуре в градусах Фаренгейта.
Если начало в интервальной шкале является абсолютной нулевой точкой, то возникает возможность отразить в шкале, во сколько раз одно измерение отличается от другого. Соответствующая шкала называется шкалой отношений. Шкала отношений допускает преобразования вида  . Большинство шкал, используемых в физике, являются либо интервальными (для измерения температуры, потенциальной энергии), либо шкалами отношений (для измерения времени, массы тела, заряда, расстояния).
. Большинство шкал, используемых в физике, являются либо интервальными (для измерения температуры, потенциальной энергии), либо шкалами отношений (для измерения времени, массы тела, заряда, расстояния).
Поскольку количественные шкалы допускают арифметические преобразования, среднее арифметическое может использоваться для описания интегральной тенденции в группировке данных.
10.2.4. Унифицированное представление разнотипных данных.
Каждому типу шкалы соответствует своя статистическая техника. Так, для переменных, измеренных в номинальной шкале, можно использовать  -критерий для полиномиальных распределений,
-критерий для полиномиальных распределений,  -критерий для проверки отсутствия ассоциаций в таблицах сопряженности, критерии для проверки гипотез о вероятности в биномиальном распределении. Порядковой шкале отвечают методы, основанные на использовании рангов (ранговая корреляция, непараметрические критерии для проверки гипотез типа
-критерий для проверки отсутствия ассоциаций в таблицах сопряженности, критерии для проверки гипотез о вероятности в биномиальном распределении. Порядковой шкале отвечают методы, основанные на использовании рангов (ранговая корреляция, непараметрические критерии для проверки гипотез типа  ) и т. п.). При интервальной шкале может быть использован весь арсенал статистических методов.
) и т. п.). При интервальной шкале может быть использован весь арсенал статистических методов.
Более того, разработаны статистические процедуры для случаев, когда наблюдаются векторы, одни координаты которых измерены в одной шкале, а другие — в другой. Типичным примером является обычный дисперсионный анализ (см. § 3.5), в котором факторы измеряются в номинальной шкале, а соответствующие их комбинациям отклики — в интервальной.
Тем не менее в целом ряде статистических методов, особенно в современных методах многомерного анализа, предполагается, что данные измерены в однотипных шкалах. Чтобы иметь возможность применять эти методы в общем случае разнотипных данных, были предложены различные приемы унификации данных. Познакомимся с важнейшими из них.
Сведение к двоичным переменным. В основе этого метода лежит введение вместо каждой исходной случайной переменной серии случайных величин, принимающих только два значения: 0 и 1.
Для номинальной величины  имеющей k градаций
имеющей k градаций  вводится k таких величин
вводится k таких величин  что
что  когда
когда  когда
когда 
Этот же прием иногда используют и при сведении к двоичным переменным случайной величины, измеренной в порядковой шкале. Однако в ряде случаев оказывается удобным выделять не событие  , а событие
, а событие  Для сравнения относительных достоинств этих двух способов рассмотрим следующую модельную задачу. Пусть
Для сравнения относительных достоинств этих двух способов рассмотрим следующую модельную задачу. Пусть  — равномерно распределенная на отрезке [0, 1] случайная величина,
— равномерно распределенная на отрезке [0, 1] случайная величина,  — малое число;
— малое число;

Функция  моделирует, очевидно, первый способ перехода к двоичным переменным, а функция
моделирует, очевидно, первый способ перехода к двоичным переменным, а функция  — второй. После несложных подсчетов получаем:
— второй. После несложных подсчетов получаем:

Из формул (10.1), (10.2) следует, что корреляция между  и
и  зависит от величины
зависит от величины  Коэффициент корреляции имеет разный знак в левой и правой половинах отрезка [0, 1], а при
Коэффициент корреляции имеет разный знак в левой и правой половинах отрезка [0, 1], а при  обращается в нуль. Корреляция между
обращается в нуль. Корреляция между  не зависит от взаимного расположения х и у. При втором способе перехода к двоичным переменным знак корреляции между
не зависит от взаимного расположения х и у. При втором способе перехода к двоичным переменным знак корреляции между  неизменен на всем отрезке и корреляция наибольшая при
неизменен на всем отрезке и корреляция наибольшая при  (формула (10.3)). Корреляция между
(формула (10.3)). Корреляция между  всегда положительна и тем больше, чем х ближе к у (формула(10.4)), что весьма естественно. Таким образом, при втором способе перехода к двоичным переменным в большей степени сохраняется интерпретация корреляционных связей.
всегда положительна и тем больше, чем х ближе к у (формула(10.4)), что весьма естественно. Таким образом, при втором способе перехода к двоичным переменным в большей степени сохраняется интерпретация корреляционных связей.
В том случае, когда имеют дело с непрерывной количественной переменной, ее значения сначала квантуют, объединяют в несколько градаций и далее поступают так же, как в случае порядковой шкалы.
Основной недостаток изложенной техники — это введение большого числа новых переменных и частичная потеря информации, содержащейся в данных, как из-за квантования, так и из-за искусственного снижения уровня используемой шкалы.
Оцифровка номинальных и порядковых переменных. Этот метод прямо противоположен только что изложенному, в нем все переменные поднимаются, подтягиваются до уровня количественных путем приписывания их градациям числовых значений. Иногда приписываемые значения называют метками.
Выбор меток существенно зависит от цели, с которой производится оцифровка. Так, если изучается величина связи между двумя номинальными признаками, то метки можно выбрать из условия максимизации коэффициента корреляции между ними [33], [123]. Если речь идет об отнесении наблюдений к одному из заранее определенных классов (дискриминантный анализ), то выбор меток можно связать с условием максимизации нормированного расстояния в многомерном выборочном пространстве между центрами изучаемых популяций (расстояния Махаланобиса). Иногда эту задачу упрощают и метки приписываются покоординатно так, чтобы максимизировать только нормированное расстояние между средними значениями данной координаты. Статистическое сравнение на примере одной частной задачи эффективности глобального и покоординатного подхода к оцифровке в дискриминантном анализе может быть найдено в [57, 59].
Изложенные приемы оцифровки, когда метки выбираются из условия максимизации соответствующим образом подобранного функционала, укладываются в рамки упомянутого в § 1.2 экстремального подхода к формулировке основных проблем математической статистики.
В целом оцифровка качественных переменных является задачей сложной как в вычислительном, так и в чисто статистическом плане. Отдельные аспекты этой проблемы обсуждаются в работах [31, 33, 40, 47, 123].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Раздел I. ПРИКЛАДНАЯ СТАТИСТИКА: ЕЕ СУЩНОСТЬ И НАЗНАЧЕНИЕ (общие методические принципы)
- Глава 1. ПРИКЛАДНАЯ СТАТИСТИКА КАК САМОСТОЯТЕЛЬНАЯ НАУЧНАЯ ДИСЦИПЛИНА
- 1.2. Оптимизационная формулировка основных задач прикладной статистики и проблема устойчивости статистического вывода
- 1.2.1. Связь между оптимизационной формулировкой основных задач прикладной статистики и проблемой устойчивости статистического вывода.
- 1.2.2. Проблема статистического исследования зависимостей между анализируемыми показателями.
- 1.2.3. Проблема классификации объектов или признаков.
- 1.2.4. Снижение размерности исследуемого факторного пространства и отбор наиболее информативных признаков.
- Выводы
- Глаза 2. ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 2.1.1. Статистический ансамбль и «игра случая».
- 2.1.2. Теория вероятностей и условия статистического ансамбля.
- 2.1.3. Основные типы реальных ситуаций с позиций соблюдения условий статистического ансамбля.
- 2.2. «Взаимоотношения» теории вероятностей и математической статистики
- 2.2.2. Теоретико-вероятностный способ решения.
- 2.2.3. Вероятностно-статистический (или математико-статистический) способ принятия решения.
- ВЫВОДЫ
- Глава 3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 3.1.1. О двух подходах к статистическому моделированию.
- 3.1.2. Понятие математической модели.
- 3.2. Общая логическая схема и основные этапы содержательного математического моделирования
- 3.2.2. Моделирование механизма явления вместо формальной статистической фотографии.
- 3.3. Понятие о статистическом моделировании
- 3.4. Возражения против математических моделей
- 3.5. Наиболее распространенные типы математических моделей, используемых в прикладной статистике
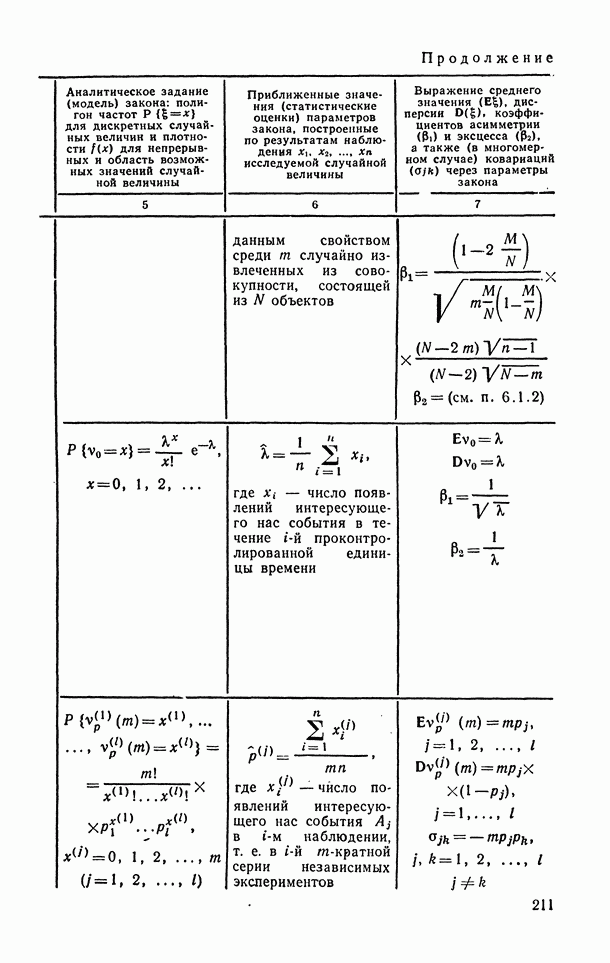
- 3.5.1. Модели законов распределения вероятностей случайных величин.
- 3.5.2. Линейные вероятностные модели.
- 3.5.3. Обобщение линейных моделей.
- 3.5.4. Геометрические модели.
- 3.5.5. Модели марковского типа.
- Выводы
- Раздел II. ОСНОВЫ ТЕОРЕТИКО-ВЕРОЯТНОСТНОГО МАТЕМАТИЧЕСКОГО АППАРАТА
- 4.1.1. Наблюдение, зафиксированное на объекте исследуемой совокупности (случайный эксперимент).
- 4.1.2. Случайные события и правила действий с ними.
- 4.1.3. Вероятностное пространство. Вероятности и правила действия с ними.
- 4.2. Непрерывное вероятностное пространство (аксиоматика А. Н. Колмогорова)
- 4.2.1. Специфика общего (непрерывного) случая вероятностного пространства.
- 4.2.2. Случайные события, их вероятности и правила действий с ними (аксиоматический подход А. Н. Колмогорова).
- Выводы
- Глава 5. случайные величины (исследуемые признаки)
- 5.1. Определение и примеры случайных величин
- 5.2. Возможные и наблюденные значения случайной величины
- 5.3. Типы случайных величин
- 5.4. Закон распределения вероятностей случайной величины. Генеральная совокупность и выборка из нее
- 5.4.1. Закон распределения вероятностей.
- 5.4.2. Генеральная совокупность и выборка из нее.
- 5.4.3. Основные способы организации выборки.
- 5.5. Способы задания закона распределения: функция распределения, функция плотности и их выборочные (эмпирические аналоги)
- 5.5.1. Функция распределения вероятностей одномерной случайной величины.
- 5.5.2. Функция плотности вероятности одномерной случайной величины.
- 5.5.3. Многомерные функции распределения и плотности. Статистическая независимость случайных величин.
- 5.6. Основные числовые характеристики случайных величин и их выборочные аналоги
- 5.6.1. Понятие о математических ожиданиях и моментах.
- 5.6.2. Характеристики центра группирования значений случайной величины.
- 5.6.3. Характеристики степени рассеяния случайной величины.
- 5.6.4. Вариационный ряд и порядковые статистики.
- 5.6.5. Квантили и процентные точки распределения.
- 5.6.6. Асимметрия и эксцесс.
- 5.6.7. Основные характеристики многомерных распределений (ковариации, корреляции, обобщенная дисперсия и др.).
- Выводы
- Глава 6. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ, НАИБОЛЕЕ РАСПРОСТРАНЕННЫЕ В ПРАКТИКЕ СТАТИСТИЧЕСКИХ ИССЛЕДОВАНИИ
- 6.1. Законы распределения, используемые для описания механизмов реальных процессов или систем
- 6.1.2. Гипергеометрическое распределение.
- 6.1.3. Распределение Пуассона.
- 6.1.4. Полиномиальное (мультиномиальное) распределение.
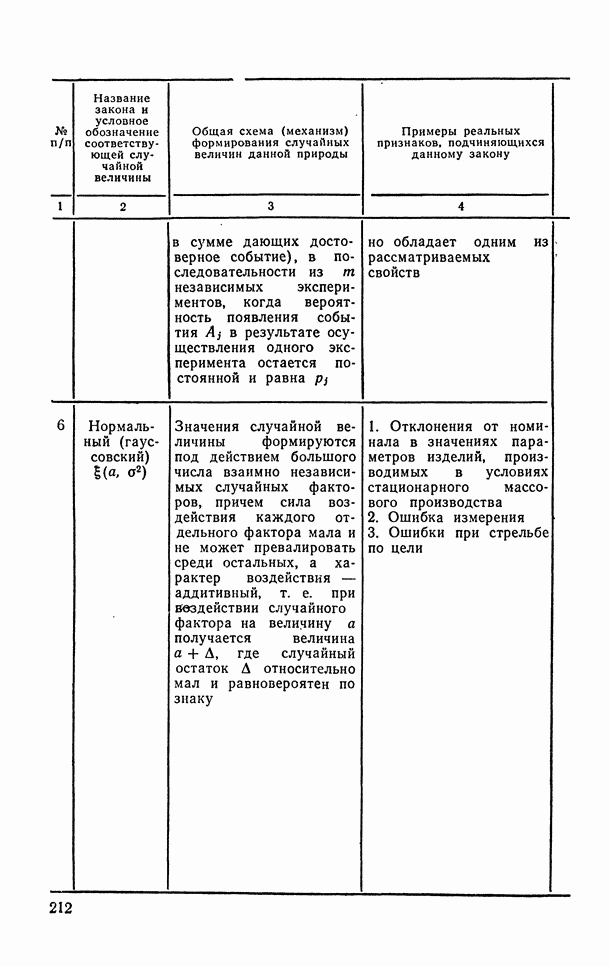
- 6.1.5. Нормальное (гауссовское) распределение.
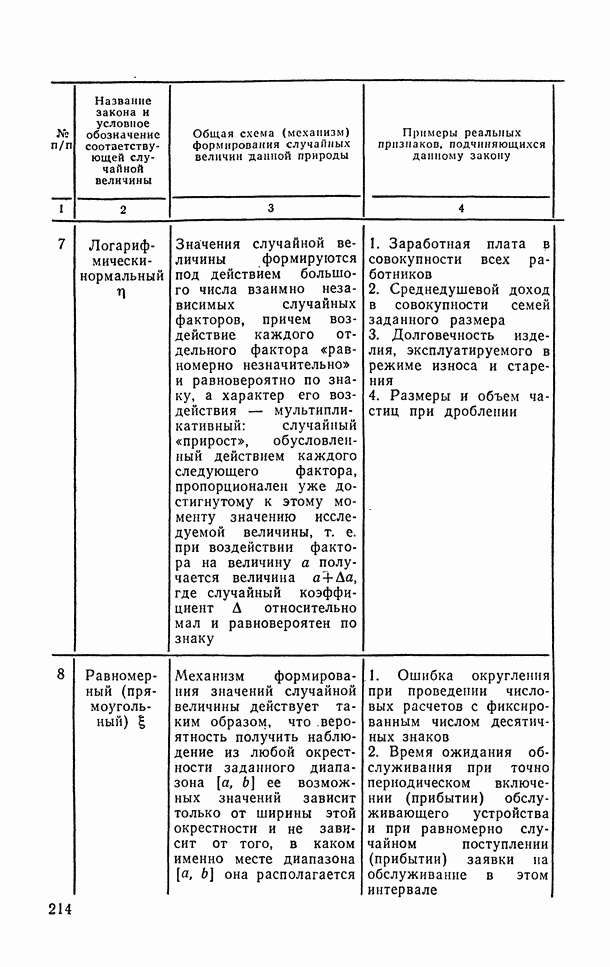
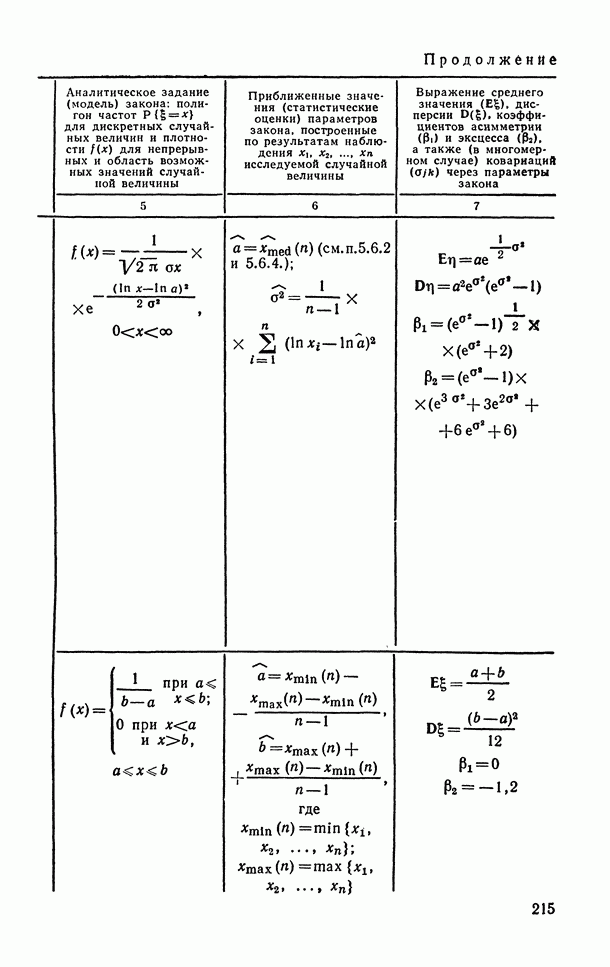
- 6.1.6. Логарифмически-нормальное распределение.
- 6.1.7. Равномерное (прямоугольное) распределение.
- 6.1.8. Распределение Вейбулла и экспоненциальное (показательное).
- 6.1.9. Распределение Парето.
- 6.1.10. Распределение Коши.
- 6.1.11. Некоторые комбинации основных модельных распределений, используемые в прикладной статистике.
- 6.2. Законы распределений вероятностей, используемые при реализации техники статистических вычислений
- 6.2.1. «хи квадрат»-распределение.
- 6.2.2. Распределение Стьюдента (t-распределение).
- 6.2.3. F-распределение (распределение дисперсионного отношения).
- 6.2.4. Замечание о нецентральных «хи-квадрат» и F- и t-распределениях.
- 6.2.5. Г-распределение.
- 6.2.6. В-распределение.
- 6.3. Техника статистического моделирования наблюдений, подчиняющихся заданному распределению
- 6.3.1. Получение равномерно распределенных на отрезке [0, 1] случайных чисел.
- 6.3.2. Моделирование дискретных случайных величин.
- Выводы
- Глава 7. ОСНОВНЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 7.1. Неравенство Чебышева
- 7.2. Свойство статистической устойчивости выборочных характеристик: закон больших чисел и его следствия
- 7.2.1. Закон больших чисел.
- 7.2.2. Теорема Я. Бернулли.
- 7.2.3 Статистическая устойчивость выборочных характеристик.
- 7.3. Особая роль нормального распределения: центральная предельная теорема
- 7.3.1. Центральная предельная теорема.
- 7.3.2. Многомерная центральная предельная теорема.
- 7.4. Закон распределения вероятностей случайных признаков, являющихся функциями от известных случайных величин
- Выводы
- Раздел III. ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- Глава 8. СТАТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- 8.1. Начальные сведения о задаче статистического оценивания параметров
- 8.1.2. Статистики, статистические оценки, их основные свойства.
- 8.1.3. Состоятельность.
- 8.1.4. Несмещенность.
- 8.1.5. Эффективность.
- 8.2. Функция правдоподобия. Количество информации, содержащееся в n независимых наблюдениях относительно неизвестного значения параметра
- 8.3. Неравенство Рао—Крамера—Фреше и измерение эффективности оценок
- 8.4. Асимптотические свойства оценок
- 8.5. Понятие об интервальном оценивании. Построение доверительных областей
- 8.6. Методы статистического оценивания неизвестных параметров
- 8.6.1. Метод максимального (наибольшего) правдоподобия.
- 8.6.2. Метод моментов.
- 8.6.3. Метод наименьших квадратов.
- 8.6.4. Оценивание с помощью «взвешенных» статистик; цензурирование, урезание выборок и порядковые статистики как частный случай взвешивания.
- 8.6.5. Построение интервальных оценок (доверительных областей).
- 8.6.6. Байесовский подход к статистическому оцениванию.
- Выводы
- Глава 9. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ (статистические критерии)
- 9.1. Основные типы гипотез, проверяемых в ходе статистической обработки данных
- 9.1.1. Гипотезы о типе закона распределения исследуемой случайной величины.
- 9.1.2. Гипотезы об однородности двух или нескольких обрабатываемых выборок или некоторых характеристик анализируемых совокупностей.
- 9.1.3. Гипотезы о числовых значениях параметров исследуемой генеральной совокупности.
- 9.1.4. Гипотезы о типе зависимости между компонентами исследуемого многомерного признака.
- 9.1.5. Гипотезы независимости и стационарности обрабатываемого ряда наблюдений.
- 9.2. Общая логическая схема статистического критерия
- 9.3. Построение статистического критерия; принцип отношения правдоподобия
- 9.3.1. Сущность принципа отношения правдоподобия.
- 9.3.2. Проверка простой гипотезы с помощью критерия логарифма отношения правдоподобия.
- 9.3.3. Проверка сложной гипотезы.
- 9.4. Характеристики «качества» статистического критерия
- 9.5. Последовательная схема принятия решения (последовательные критерии)
- 9.5.1. Последовательная схема наблюдений.
- 9.5.2. Последовательный критерий отношения правдоподобия (критерий Вальда) и его свойства.
- 9.5.3. Различение сложных гипотез в схеме обобщенного последовательного критерия.
- Выводы
- Раздел IV. ПЕРВИЧНАЯ СТАТИСТИЧЕСКАЯ ОБРАБОТКА ДАННЫХ
- 10.1. Документирование исследования; организация ввода и хранения данных в ЭВМ; просмотр данных
- 10.1.2. Ввод и хранение данных.
- 10.1.3. Просмотр данных.
- 10.2. Шкалы измерений
- 10.3. Изучение эмпирических распределений
- 10.3.1. Гистограмма.
- 10.3.2. Непараметрические оценки плотности.
- 10.3.3. Оценки функции распределения.
- 10.3.4. Преобразование переменных.
- 10.3.5. Таблицы сопряженности.
- 10.4. Оценивание параметров сдвига и масштаба
- 10.4.2. Оценивание параметров нормального закона.
- 10.4.3. Графический метод оценивания.
- 10.4.4. Проблема устойчивости оценок при небольших отклонениях распределения от нормального.
- 10.4.5. Оценивание положения центра симметричных распределений.
- 10.4.6. Параметризация с помощью экспоненциально взвешенных оценок (ЭВ-оценки).
- 10.5. Визуализация многомерных данных
- 10.5.2. Главные компоненты.
- 10.5.3. Свойства наименьшего искажения геометрической структуры для главных компонент.
- 10.5.4, Нелинейные отображения в пространство малой размерности.
- 10.5.5. Многомерное метрическое шкалирование.
- Выводы
- Глава 11. ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ ПРИРОДЫ ДАННЫХ
- 11.1. Проверка соответствия выбранной модели распределения исходным данным (критерии согласия)
- 11.1.1. Критерий «хи-квадрат» Пирсона.
- 11.1.2. Проверка нормального характера распределения по асимметрии, эксцессу и средним отклонениям.
- 11.1.3. Критерий Колмогорова — Смирнова и его применение к построению доверительных границ для неизвестной функции распределения.
- 11.1.4. Критерий Крамера — Мизеса — Смирнова.
- 11.1.5. Модификация статистик критериев Колмогорова — Смирнова и для выборок небольшого объема.
- 11.1.6. Статистическая техника практической реализации непараметрических критериев согласия.
- ll.1.7. Использование критериев согласия Колмогорова и «w-квадрат» в случае неизвестных параметров для проверки гипотезы о нормальном характере распределения.
- 11.2. Проверка гипотез однородности и симметрии распределения
- 11.2.1. Критерии однородности, основанные на эмпирических функциях распределения.
- 11.2.2. Критерий однородности «хи-квадрат»
- 11.2.3. Ранговые критерии однородности.
- 11.2.4. Непараметрическая проверка гипотезы равенства дисперсий.
- 11.2.5. Ранговые критерии для случая k > 2 классов.
- 11.2.6. Критерии проверки симметрии распределений.
- 11.2.7. Обработка совпадений.
- 11.2.8. Критерии однородности нормальных совокупностей (одномерный случай).
- 11.2.9. Критерии однородности многомерных нормальных совокупностей.
- 11.3. Проверка независимости и стационарности ряда наблюдений
- 11.3.1. Критерий серий, основанный на медиане выборки.
- 11.3.2. Критерий «восходящих» и «нисходящих» серий.
- 11.3.3. Критерий квадратов последовательных разностей (критерий Аббе).
- 11.4. Методы статистической обработки при наличии «стертых» (пропущенных) наблюдений
- 11.4.1. Оценивание неизвестных параметров при наличии пропущенных данных.
- 11.4.2. Использование главных компонент.
- 11.4.3. Заполнение «пропусков» и оценивание параметров с помощью метода максимального правдоподобия. Оценки «неподвижной точки».
- 11.4.4. Непараметрический подход к оценке пропусков в матрице данных.
- 11.5. Анализ резко выделяющихся наблюдений
- 11.5.2 Графические методы.
- 11.5.3. Аналитический метод исключения одного экстремального наблюдения.
- 11.5.4. Аналитический критерий одновременного исключения нескольких экстремальных наблюдений.
- Выводы
- Глава 12. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ И НЕКОТОРЫЕ ВОПРОСЫ ТЕХНИКИ ВЫЧИСЛЕНИЙ
- 12.1. Программное обеспечение прикладной статистики
- 12.1.1. Организация пакетов программ.
- 12.1.2. Вопросы организации возможности ведения данных.
- 12.1.3. Средства предварительной обработки (манипуляции) данных.
- 12.1.4. Возможности обработки данных при наличии пропущенных значений.
- 12.1.5. Первичная обработка неколичественных данных.
- 12.1.6. Средства визуализации данных.
- 12.1.7. Оценивание параметров и выделение аномальных наблюдений.
- 12.2. Вычисление функций распределения и обратных к ним
- 12.2.1. Нормальное распределение.
- 12.2.2. Распределение «хи-квадрат».
- 12.2.3. Бета-распределение.
- 12.2.4. F-распределение.
- 12.2.5. t-распределение Стьюдента.
- 12.2.6. Нецентральные распределения.
- 12.2.7. Аппроксимация «хвостов» распределений типа «w-квадрат»
- 12.2.8. Многомерное нормальное распределение.
- 12.2.9. Дискретные распределения.
- 12.2.10. Вычисление математического ожидания порядковых статистик.
- Выводы
- ИСПОЛЬЗУЕМЫЕ В КНИГЕ ОБОЗНАЧЕНИЯ
- СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ