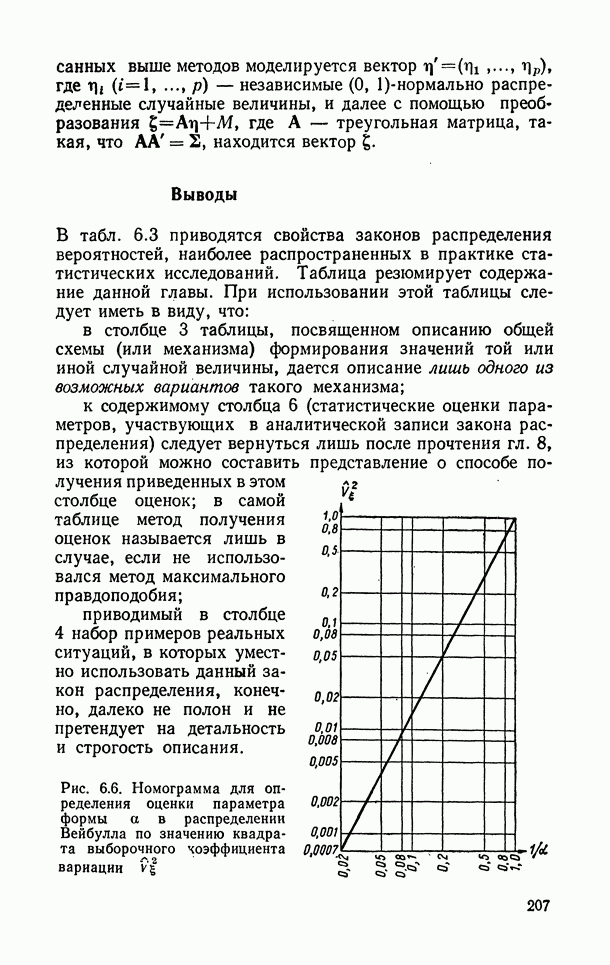
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
12.1.4. Возможности обработки данных при наличии пропущенных значений.
Рассмотрим возможности пакетов программ для обработки данных с пропусками. Соответствующие методы, на которые мы будем ссылаться, в основном описаны в § 11.4. Рассмотрим следующие способы и средства работы с пропущенными данными:
1. Кодирование пропусков с помощью специальных числовых «кодов пропущенных значений».
2. Удаление объектов с пропущенными значениями.
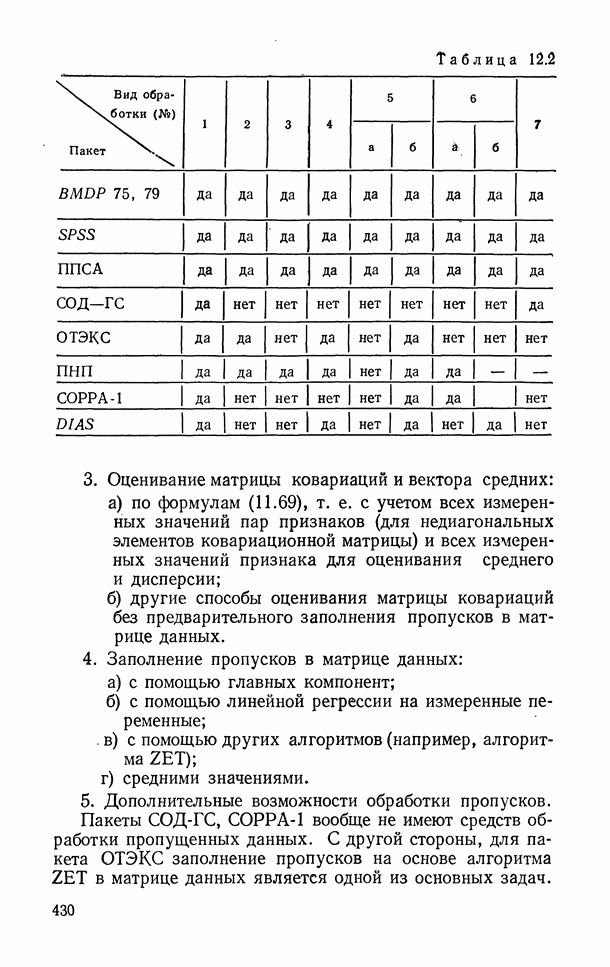
Таблица 12.2

3. Оценивание матрицы ковариаций и вектора средних:
а) по формулам (11.69), т. е. с учетом всех измеренных значений пар признаков (для недиагональных элементов ковариационной матрицы) и всех измеренных значений признака для оценивания среднего и дисперсии;
б) другие способы оценивания матрицы ковариаций без предварительного заполнения пропусков в матрице данных.
4. Заполнение пропусков в матрице данных:
а) с помощью главных компонент;
б) с помощью линейной регрессии на измеренные переменные;
в) с помощью других алгоритмов (например, алгоритма ZET);
г) средними значениями.
5. Дополнительные возможности обработки пропусков.
Пакеты СОД-ГС, СОРРА-1 вообще не имеют средств обработки пропущенных данных. С другой стороны, для пакета ОТЭКС заполнение пропусков на основе алгоритма ZET в матрице данных является одной из основных задач.
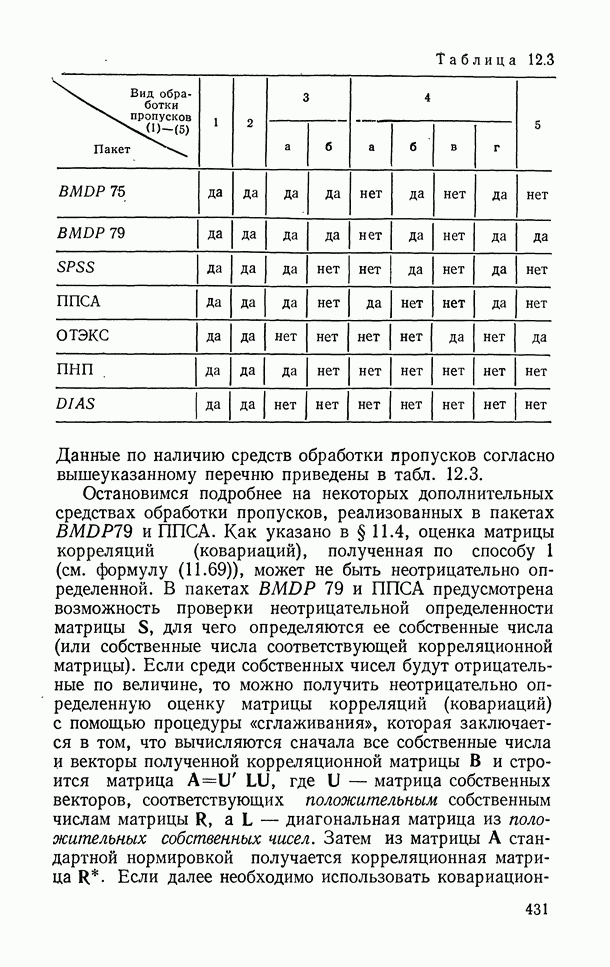
Таблица 12.3

Данные по наличию средств обработки пропусков согласно вышеуказанному перечню приведены в табл. 12.3.
Остановимся подробнее на некоторых дополнительных средствах обработки пропусков, реализованных в пакетах BMDP79 и ППСА. Как указано в § 11.4, оценка матрицы корреляций (ковариаций), полученная по способу 1 (см. формулу (11.69)), может не быть неотрицательно определенной. В пакетах BMDP 79 и ППСА предусмотрена возможность проверки неотрицательной определенности матрицы S, для чего определяются ее собственные числа (или собственные числа соответствующей корреляционной матрицы). Если среди собственных чисел будут отрицательные по величине, то можно получить неотрицательно определенную оценку матрицы корреляций (ковариаций) с помощью процедуры «сглаживания», которая заключается в том, что вычисляются сначала все собственные числа и векторы полученной корреляционной матрицы В и строится матрица  , где U — матрица собственных векторов, соответствующих положительным собственным числам матрицы R, a L — диагональная матрица из положительных собственных чисел. Затем из матрицы А стандартной нормировкой получается корреляционная матрица R.
, где U — матрица собственных векторов, соответствующих положительным собственным числам матрицы R, a L — диагональная матрица из положительных собственных чисел. Затем из матрицы А стандартной нормировкой получается корреляционная матрица R.
Если далее необходимо использовать ковариационную матрицу S, то она получается из R умножеййем столбцов и строк на оценки стандартных отклонений. Очевидно, как матрица R, так и матрица S будут неотрицательно определенными, но могут быть матрицами неполного ранга. Так как, однако, ранг этих матриц, а также собственные числа и векторы матрицы R известны, нетрудно получить, при необходимости, обобщенную обратную матрицу (см. [73]) для целей регрессионного и дискриминантного анализа.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Раздел I. ПРИКЛАДНАЯ СТАТИСТИКА: ЕЕ СУЩНОСТЬ И НАЗНАЧЕНИЕ (общие методические принципы)
- Глава 1. ПРИКЛАДНАЯ СТАТИСТИКА КАК САМОСТОЯТЕЛЬНАЯ НАУЧНАЯ ДИСЦИПЛИНА
- 1.2. Оптимизационная формулировка основных задач прикладной статистики и проблема устойчивости статистического вывода
- 1.2.1. Связь между оптимизационной формулировкой основных задач прикладной статистики и проблемой устойчивости статистического вывода.
- 1.2.2. Проблема статистического исследования зависимостей между анализируемыми показателями.
- 1.2.3. Проблема классификации объектов или признаков.
- 1.2.4. Снижение размерности исследуемого факторного пространства и отбор наиболее информативных признаков.
- Выводы
- Глаза 2. ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 2.1.1. Статистический ансамбль и «игра случая».
- 2.1.2. Теория вероятностей и условия статистического ансамбля.
- 2.1.3. Основные типы реальных ситуаций с позиций соблюдения условий статистического ансамбля.
- 2.2. «Взаимоотношения» теории вероятностей и математической статистики
- 2.2.2. Теоретико-вероятностный способ решения.
- 2.2.3. Вероятностно-статистический (или математико-статистический) способ принятия решения.
- ВЫВОДЫ
- Глава 3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 3.1.1. О двух подходах к статистическому моделированию.
- 3.1.2. Понятие математической модели.
- 3.2. Общая логическая схема и основные этапы содержательного математического моделирования
- 3.2.2. Моделирование механизма явления вместо формальной статистической фотографии.
- 3.3. Понятие о статистическом моделировании
- 3.4. Возражения против математических моделей
- 3.5. Наиболее распространенные типы математических моделей, используемых в прикладной статистике
- 3.5.1. Модели законов распределения вероятностей случайных величин.
- 3.5.2. Линейные вероятностные модели.
- 3.5.3. Обобщение линейных моделей.
- 3.5.4. Геометрические модели.
- 3.5.5. Модели марковского типа.
- Выводы
- Раздел II. ОСНОВЫ ТЕОРЕТИКО-ВЕРОЯТНОСТНОГО МАТЕМАТИЧЕСКОГО АППАРАТА
- 4.1.1. Наблюдение, зафиксированное на объекте исследуемой совокупности (случайный эксперимент).
- 4.1.2. Случайные события и правила действий с ними.
- 4.1.3. Вероятностное пространство. Вероятности и правила действия с ними.
- 4.2. Непрерывное вероятностное пространство (аксиоматика А. Н. Колмогорова)
- 4.2.1. Специфика общего (непрерывного) случая вероятностного пространства.
- 4.2.2. Случайные события, их вероятности и правила действий с ними (аксиоматический подход А. Н. Колмогорова).
- Выводы
- Глава 5. случайные величины (исследуемые признаки)
- 5.1. Определение и примеры случайных величин
- 5.2. Возможные и наблюденные значения случайной величины
- 5.3. Типы случайных величин
- 5.4. Закон распределения вероятностей случайной величины. Генеральная совокупность и выборка из нее
- 5.4.1. Закон распределения вероятностей.
- 5.4.2. Генеральная совокупность и выборка из нее.
- 5.4.3. Основные способы организации выборки.
- 5.5. Способы задания закона распределения: функция распределения, функция плотности и их выборочные (эмпирические аналоги)
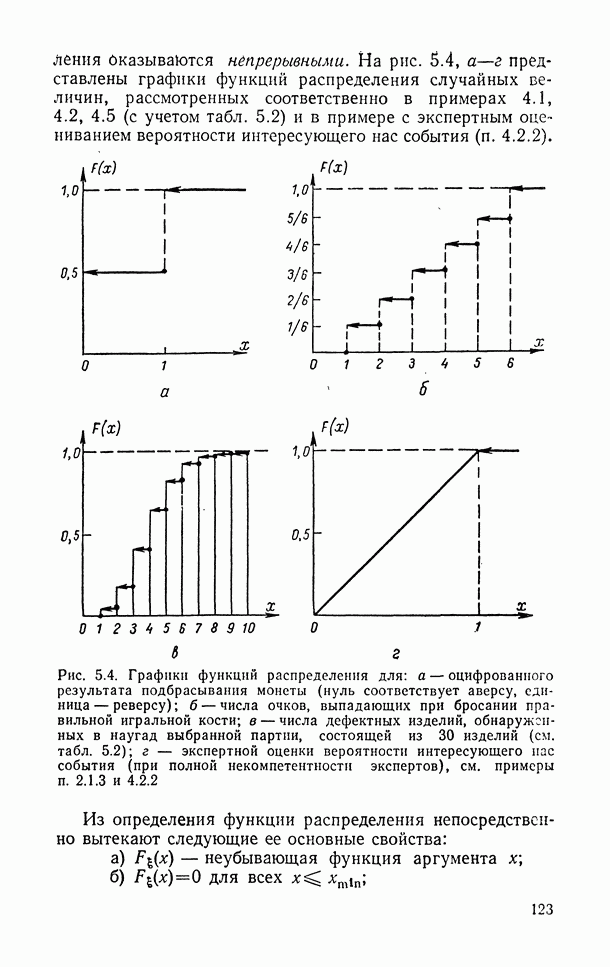
- 5.5.1. Функция распределения вероятностей одномерной случайной величины.
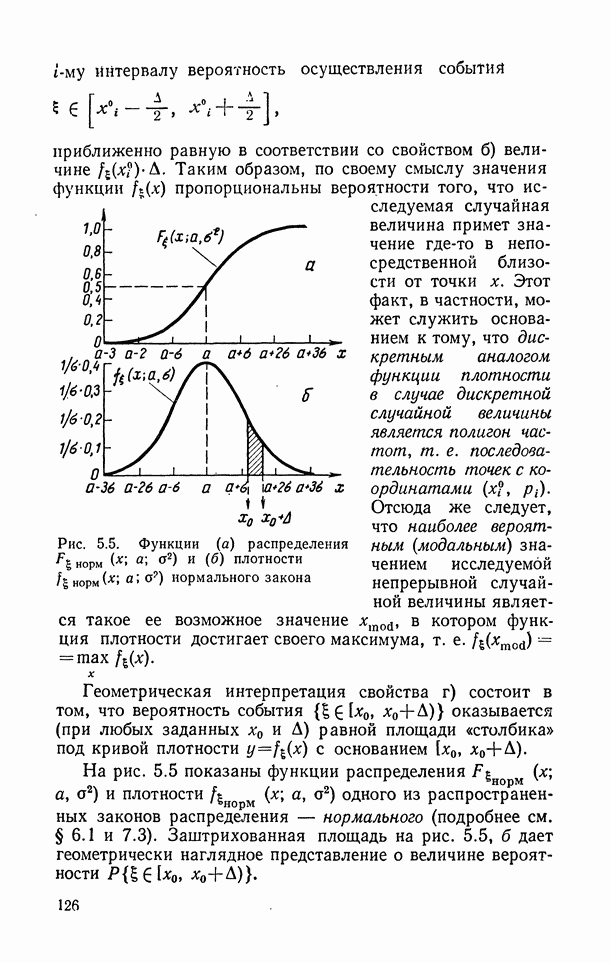
- 5.5.2. Функция плотности вероятности одномерной случайной величины.
- 5.5.3. Многомерные функции распределения и плотности. Статистическая независимость случайных величин.
- 5.6. Основные числовые характеристики случайных величин и их выборочные аналоги
- 5.6.1. Понятие о математических ожиданиях и моментах.
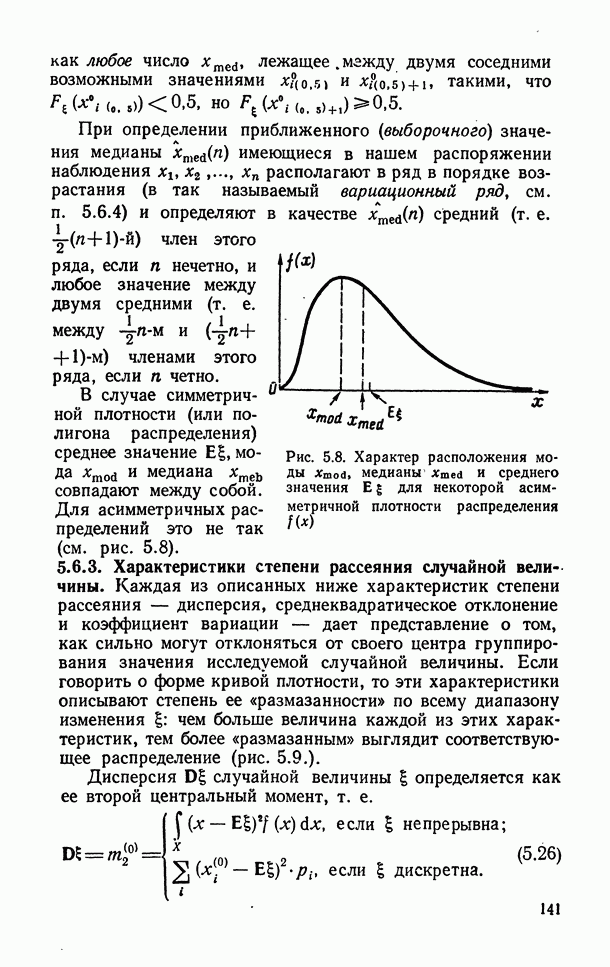
- 5.6.2. Характеристики центра группирования значений случайной величины.
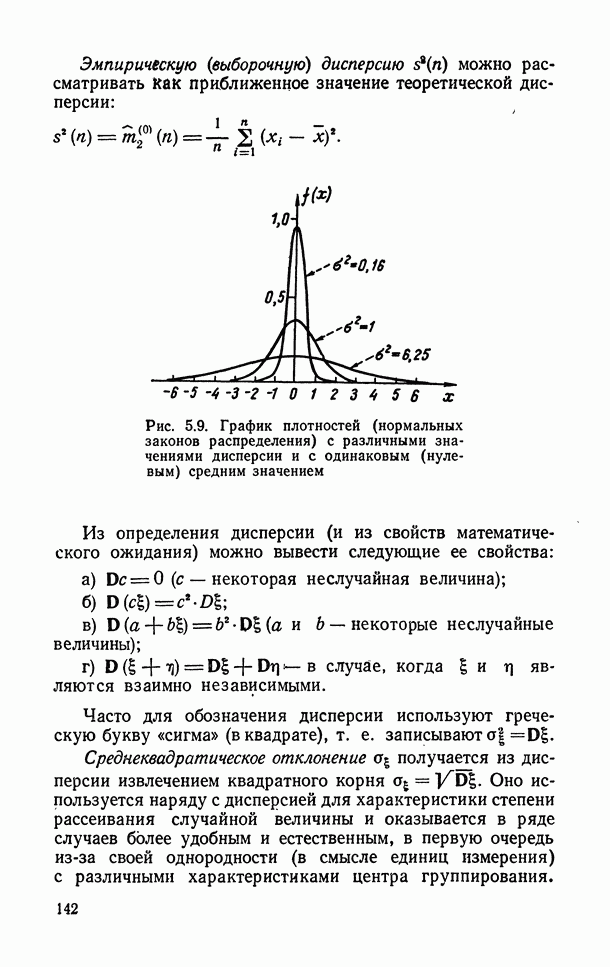
- 5.6.3. Характеристики степени рассеяния случайной величины.
- 5.6.4. Вариационный ряд и порядковые статистики.
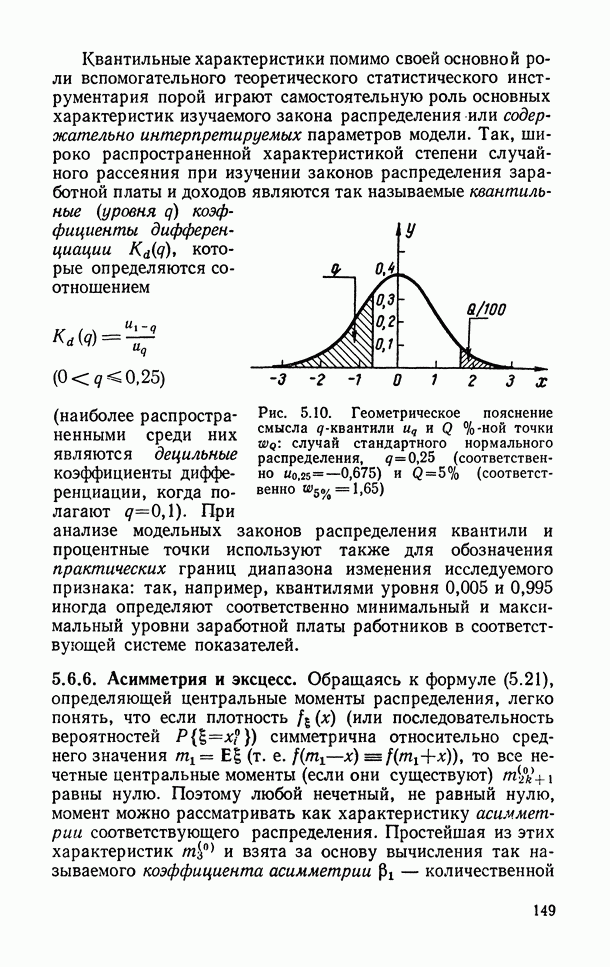
- 5.6.5. Квантили и процентные точки распределения.
- 5.6.6. Асимметрия и эксцесс.
- 5.6.7. Основные характеристики многомерных распределений (ковариации, корреляции, обобщенная дисперсия и др.).
- Выводы
- Глава 6. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ, НАИБОЛЕЕ РАСПРОСТРАНЕННЫЕ В ПРАКТИКЕ СТАТИСТИЧЕСКИХ ИССЛЕДОВАНИИ
- 6.1. Законы распределения, используемые для описания механизмов реальных процессов или систем
- 6.1.2. Гипергеометрическое распределение.
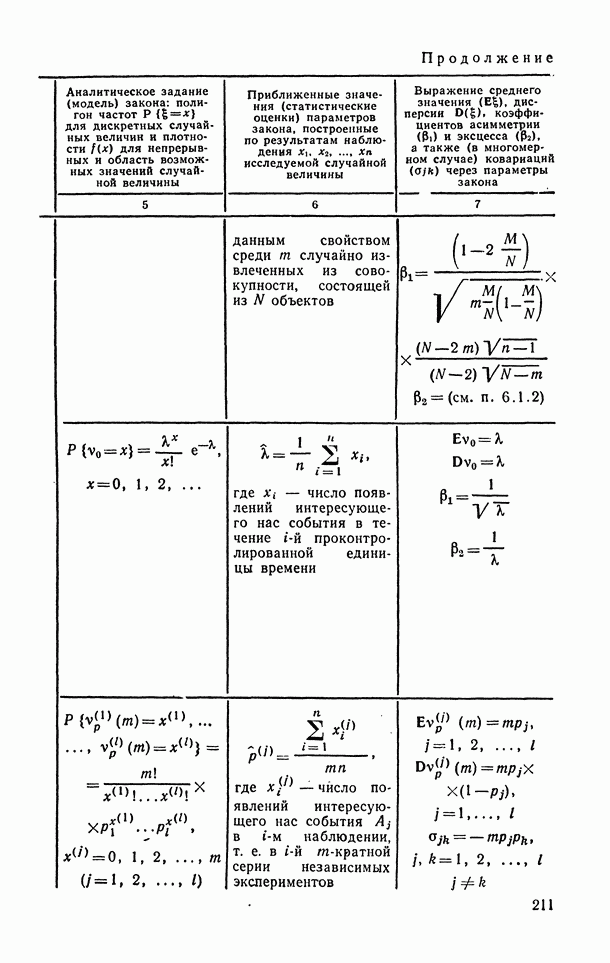
- 6.1.3. Распределение Пуассона.
- 6.1.4. Полиномиальное (мультиномиальное) распределение.
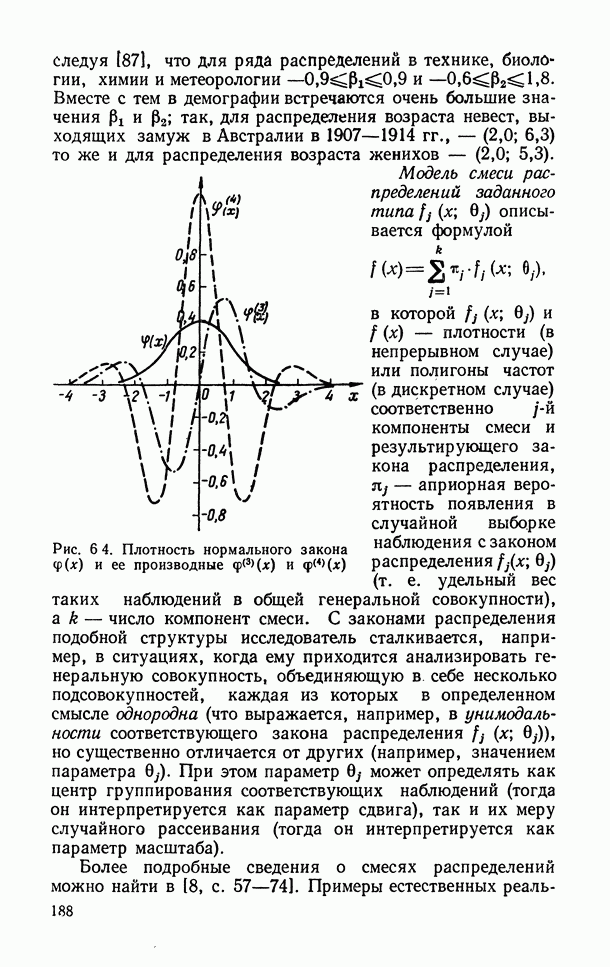
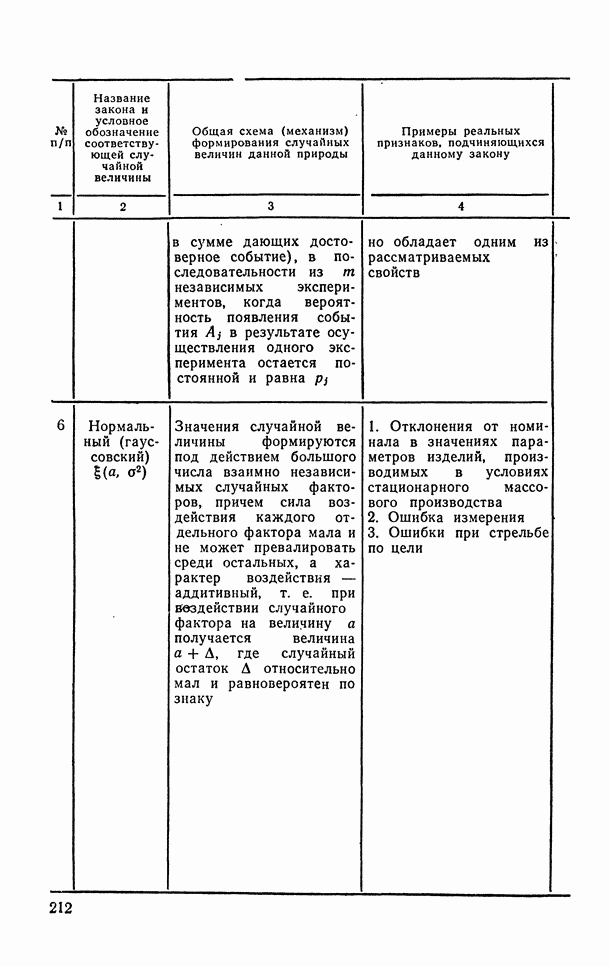
- 6.1.5. Нормальное (гауссовское) распределение.
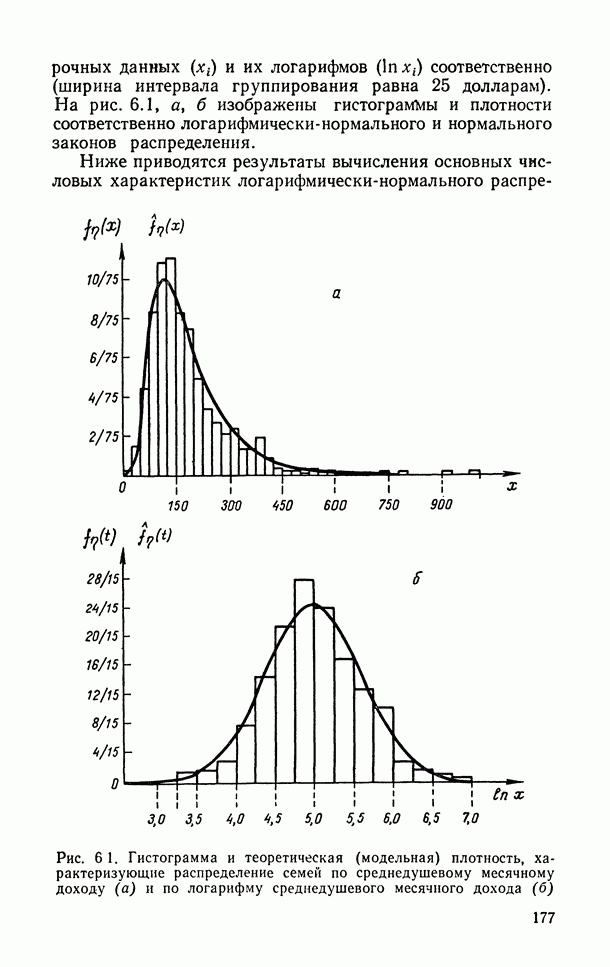
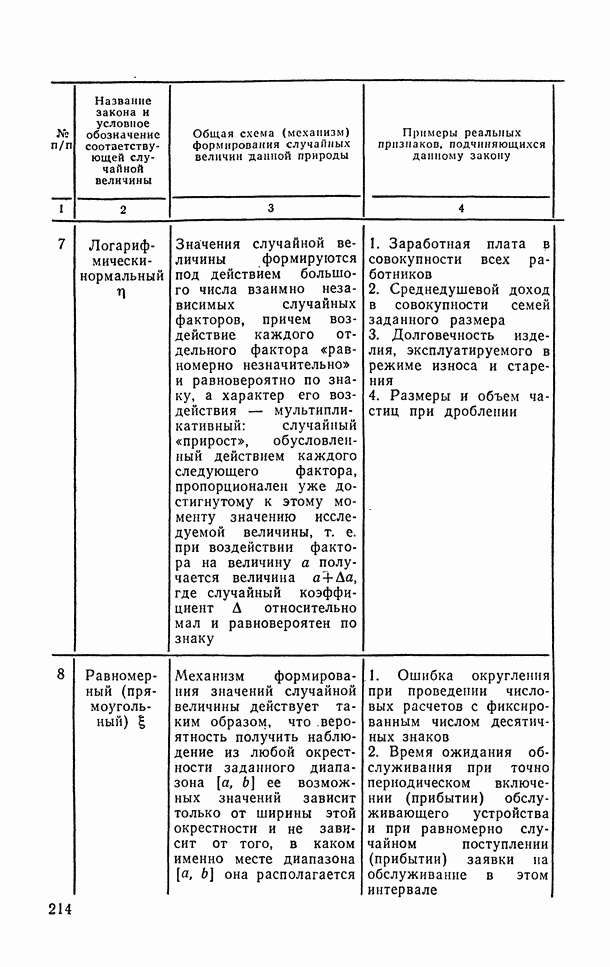
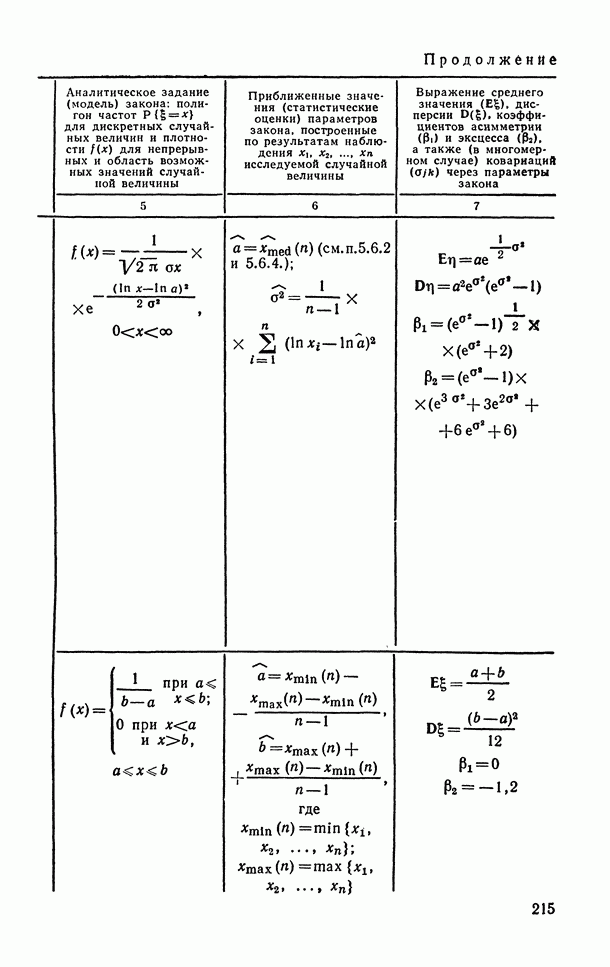
- 6.1.6. Логарифмически-нормальное распределение.
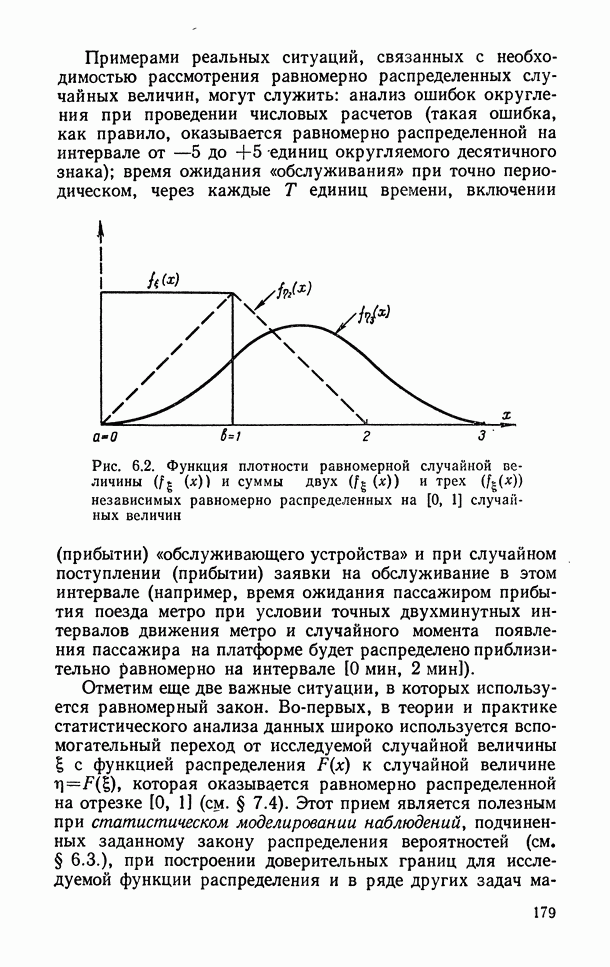
- 6.1.7. Равномерное (прямоугольное) распределение.
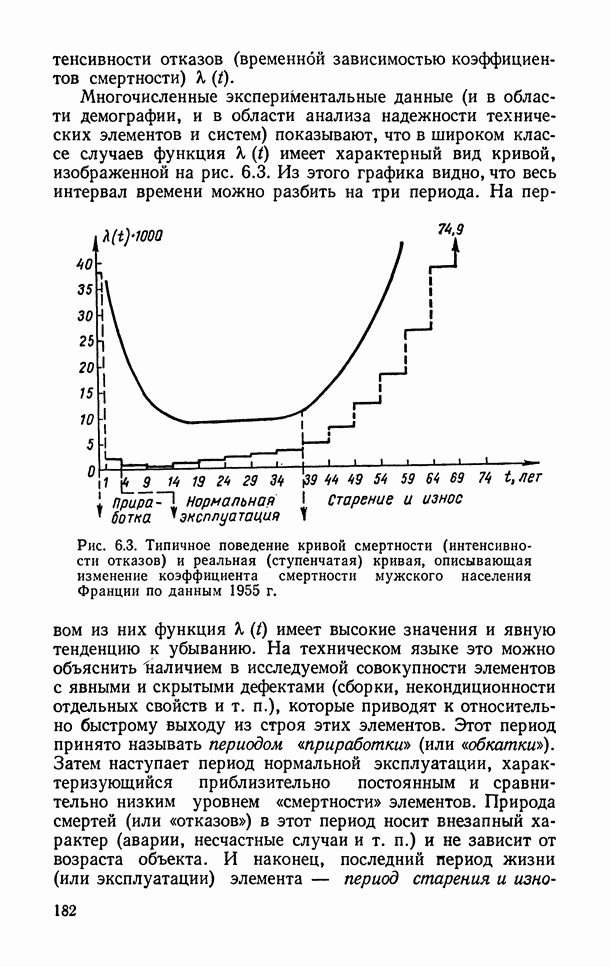
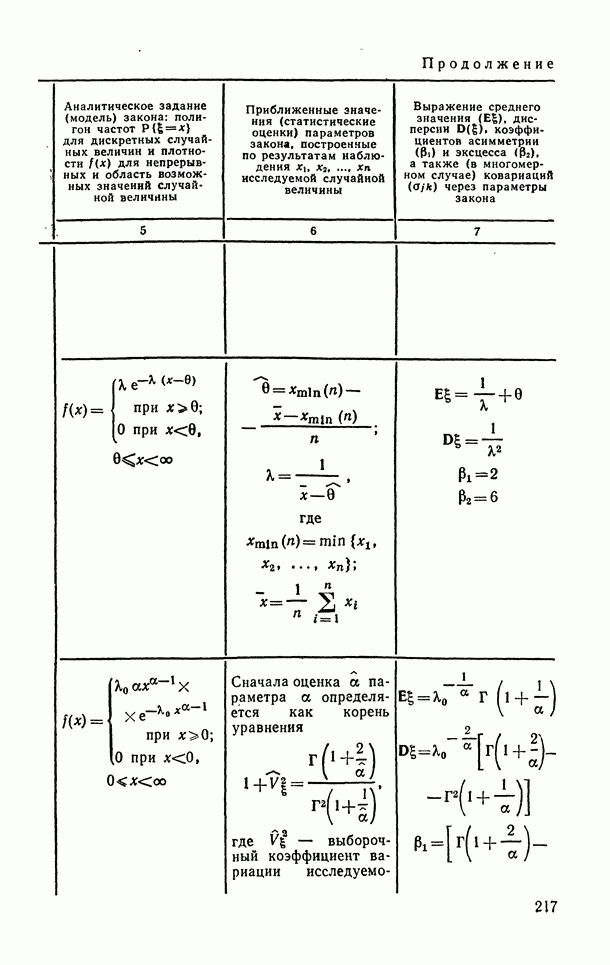
- 6.1.8. Распределение Вейбулла и экспоненциальное (показательное).
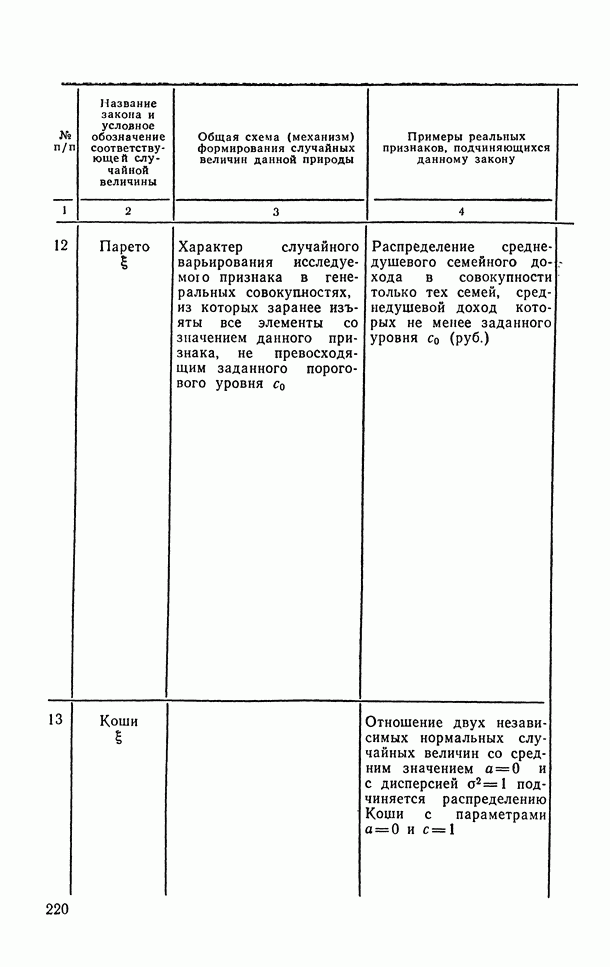
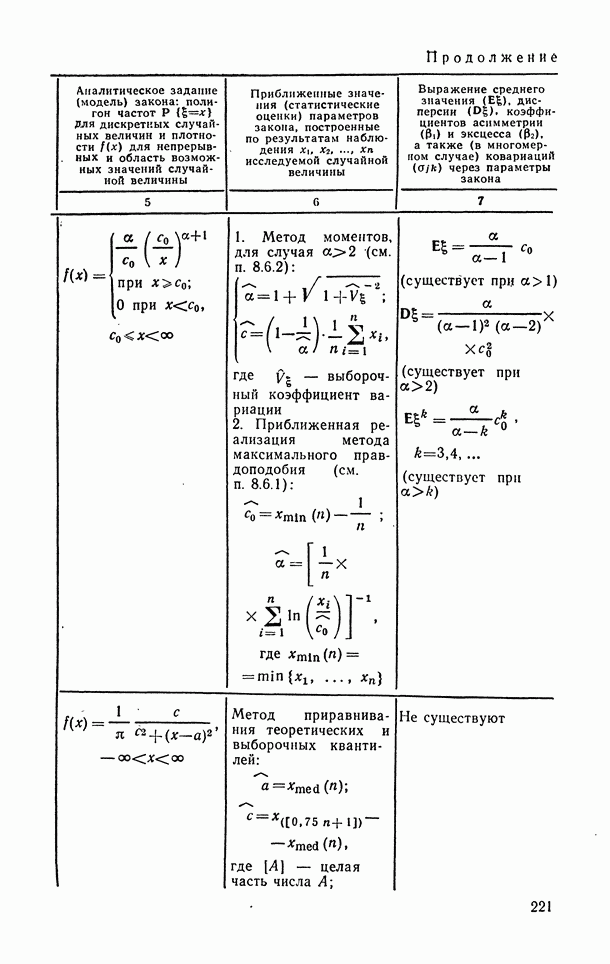
- 6.1.9. Распределение Парето.
- 6.1.10. Распределение Коши.
- 6.1.11. Некоторые комбинации основных модельных распределений, используемые в прикладной статистике.
- 6.2. Законы распределений вероятностей, используемые при реализации техники статистических вычислений
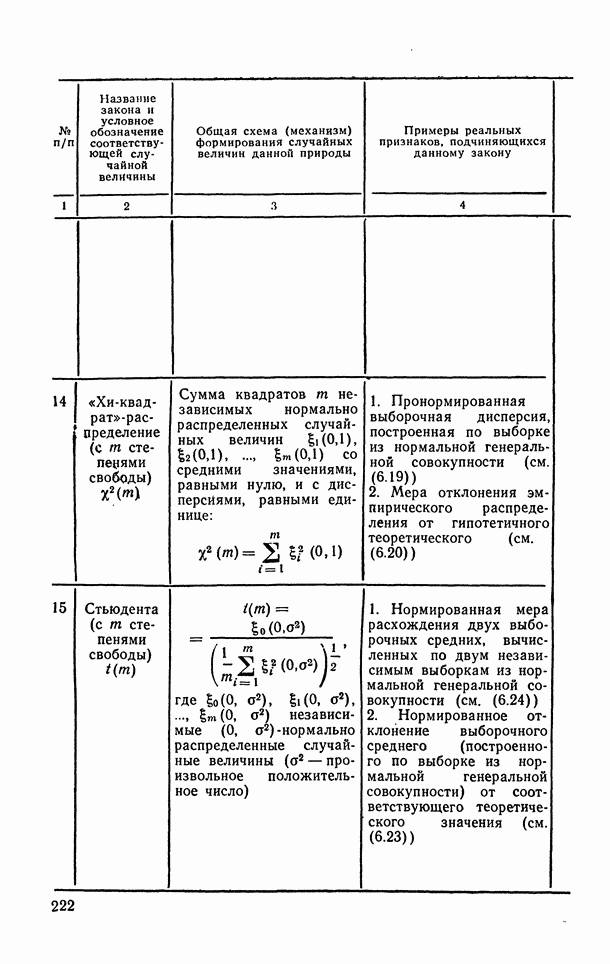
- 6.2.1. «хи квадрат»-распределение.
- 6.2.2. Распределение Стьюдента (t-распределение).
- 6.2.3. F-распределение (распределение дисперсионного отношения).
- 6.2.4. Замечание о нецентральных «хи-квадрат» и F- и t-распределениях.
- 6.2.5. Г-распределение.
- 6.2.6. В-распределение.
- 6.3. Техника статистического моделирования наблюдений, подчиняющихся заданному распределению
- 6.3.1. Получение равномерно распределенных на отрезке [0, 1] случайных чисел.
- 6.3.2. Моделирование дискретных случайных величин.
- Выводы
- Глава 7. ОСНОВНЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 7.1. Неравенство Чебышева
- 7.2. Свойство статистической устойчивости выборочных характеристик: закон больших чисел и его следствия
- 7.2.1. Закон больших чисел.
- 7.2.2. Теорема Я. Бернулли.
- 7.2.3 Статистическая устойчивость выборочных характеристик.
- 7.3. Особая роль нормального распределения: центральная предельная теорема
- 7.3.1. Центральная предельная теорема.
- 7.3.2. Многомерная центральная предельная теорема.
- 7.4. Закон распределения вероятностей случайных признаков, являющихся функциями от известных случайных величин
- Выводы
- Раздел III. ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- Глава 8. СТАТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- 8.1. Начальные сведения о задаче статистического оценивания параметров
- 8.1.2. Статистики, статистические оценки, их основные свойства.
- 8.1.3. Состоятельность.
- 8.1.4. Несмещенность.
- 8.1.5. Эффективность.
- 8.2. Функция правдоподобия. Количество информации, содержащееся в n независимых наблюдениях относительно неизвестного значения параметра
- 8.3. Неравенство Рао—Крамера—Фреше и измерение эффективности оценок
- 8.4. Асимптотические свойства оценок
- 8.5. Понятие об интервальном оценивании. Построение доверительных областей
- 8.6. Методы статистического оценивания неизвестных параметров
- 8.6.1. Метод максимального (наибольшего) правдоподобия.
- 8.6.2. Метод моментов.
- 8.6.3. Метод наименьших квадратов.
- 8.6.4. Оценивание с помощью «взвешенных» статистик; цензурирование, урезание выборок и порядковые статистики как частный случай взвешивания.
- 8.6.5. Построение интервальных оценок (доверительных областей).
- 8.6.6. Байесовский подход к статистическому оцениванию.
- Выводы
- Глава 9. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ (статистические критерии)
- 9.1. Основные типы гипотез, проверяемых в ходе статистической обработки данных
- 9.1.1. Гипотезы о типе закона распределения исследуемой случайной величины.
- 9.1.2. Гипотезы об однородности двух или нескольких обрабатываемых выборок или некоторых характеристик анализируемых совокупностей.
- 9.1.3. Гипотезы о числовых значениях параметров исследуемой генеральной совокупности.
- 9.1.4. Гипотезы о типе зависимости между компонентами исследуемого многомерного признака.
- 9.1.5. Гипотезы независимости и стационарности обрабатываемого ряда наблюдений.
- 9.2. Общая логическая схема статистического критерия
- 9.3. Построение статистического критерия; принцип отношения правдоподобия
- 9.3.1. Сущность принципа отношения правдоподобия.
- 9.3.2. Проверка простой гипотезы с помощью критерия логарифма отношения правдоподобия.
- 9.3.3. Проверка сложной гипотезы.
- 9.4. Характеристики «качества» статистического критерия
- 9.5. Последовательная схема принятия решения (последовательные критерии)
- 9.5.1. Последовательная схема наблюдений.
- 9.5.2. Последовательный критерий отношения правдоподобия (критерий Вальда) и его свойства.
- 9.5.3. Различение сложных гипотез в схеме обобщенного последовательного критерия.
- Выводы
- Раздел IV. ПЕРВИЧНАЯ СТАТИСТИЧЕСКАЯ ОБРАБОТКА ДАННЫХ
- 10.1. Документирование исследования; организация ввода и хранения данных в ЭВМ; просмотр данных
- 10.1.2. Ввод и хранение данных.
- 10.1.3. Просмотр данных.
- 10.2. Шкалы измерений
- 10.3. Изучение эмпирических распределений
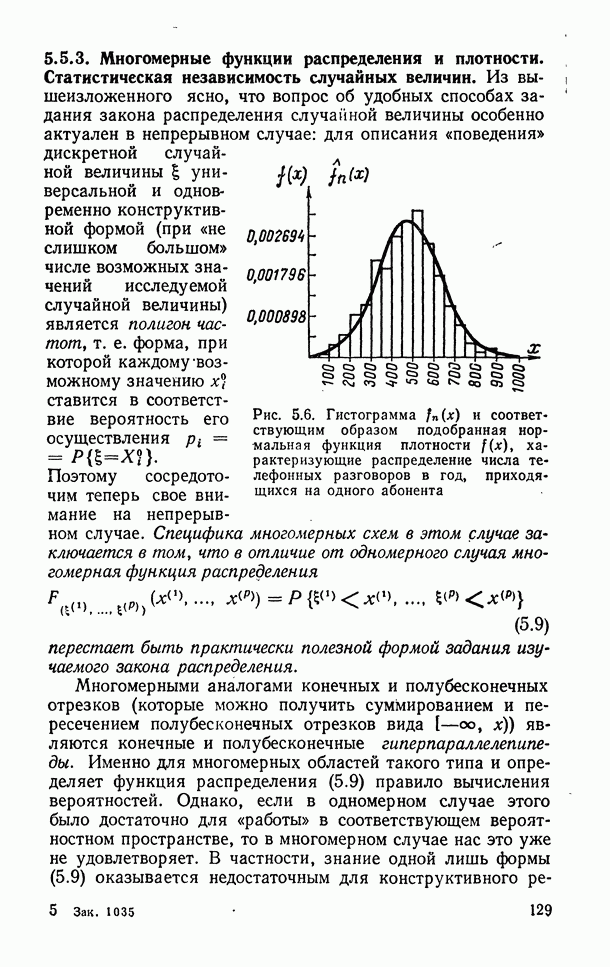
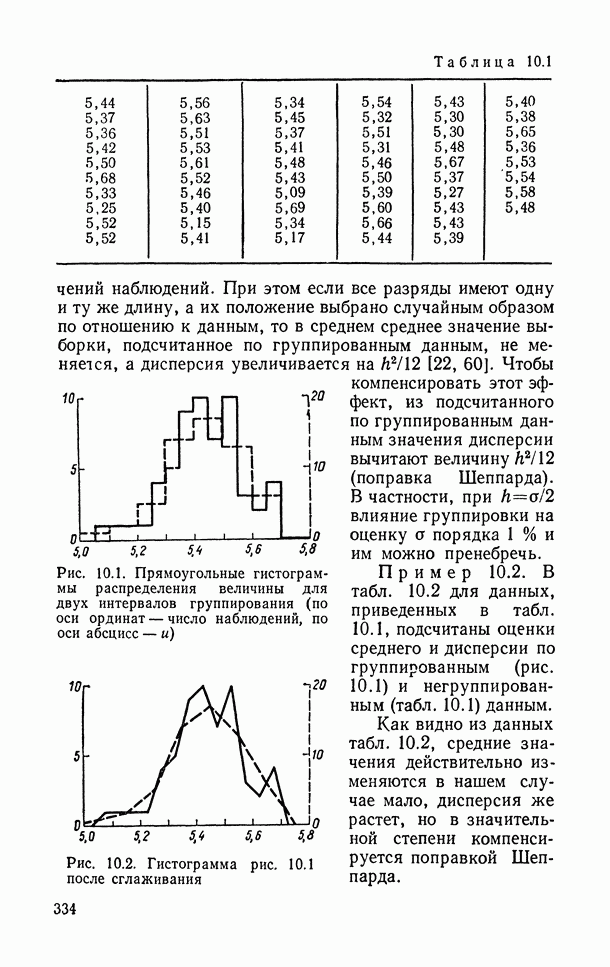
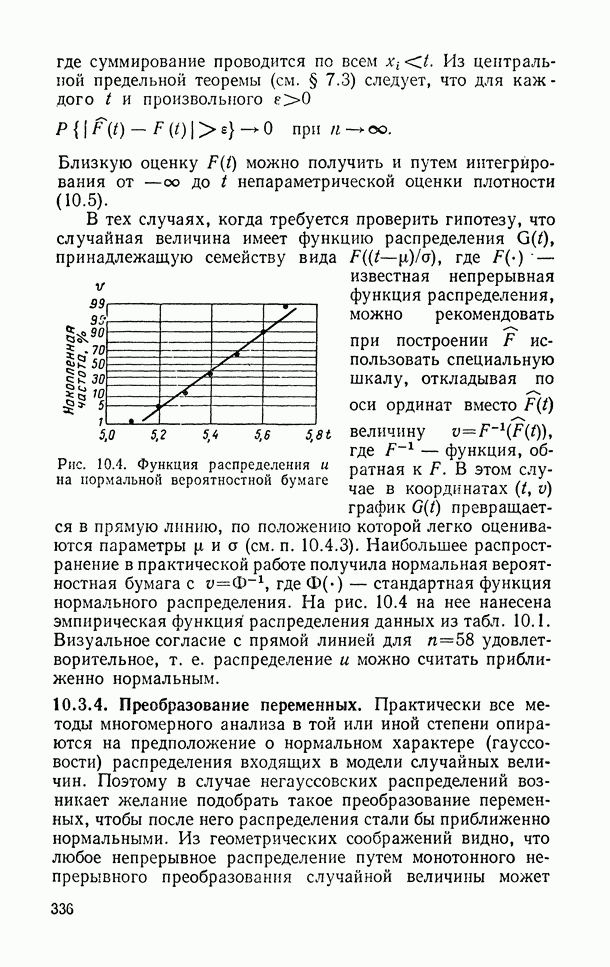
- 10.3.1. Гистограмма.
- 10.3.2. Непараметрические оценки плотности.
- 10.3.3. Оценки функции распределения.
- 10.3.4. Преобразование переменных.
- 10.3.5. Таблицы сопряженности.
- 10.4. Оценивание параметров сдвига и масштаба
- 10.4.2. Оценивание параметров нормального закона.
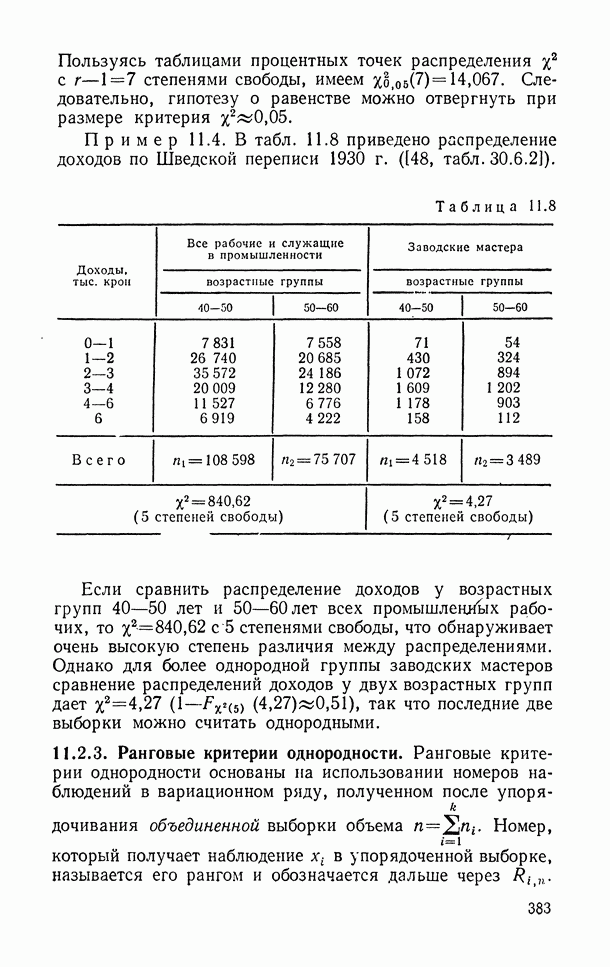
- 10.4.3. Графический метод оценивания.
- 10.4.4. Проблема устойчивости оценок при небольших отклонениях распределения от нормального.
- 10.4.5. Оценивание положения центра симметричных распределений.
- 10.4.6. Параметризация с помощью экспоненциально взвешенных оценок (ЭВ-оценки).
- 10.5. Визуализация многомерных данных
- 10.5.2. Главные компоненты.
- 10.5.3. Свойства наименьшего искажения геометрической структуры для главных компонент.
- 10.5.4, Нелинейные отображения в пространство малой размерности.
- 10.5.5. Многомерное метрическое шкалирование.
- Выводы
- Глава 11. ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ ПРИРОДЫ ДАННЫХ
- 11.1. Проверка соответствия выбранной модели распределения исходным данным (критерии согласия)
- 11.1.1. Критерий «хи-квадрат» Пирсона.
- 11.1.2. Проверка нормального характера распределения по асимметрии, эксцессу и средним отклонениям.
- 11.1.3. Критерий Колмогорова — Смирнова и его применение к построению доверительных границ для неизвестной функции распределения.
- 11.1.4. Критерий Крамера — Мизеса — Смирнова.
- 11.1.5. Модификация статистик критериев Колмогорова — Смирнова и для выборок небольшого объема.
- 11.1.6. Статистическая техника практической реализации непараметрических критериев согласия.
- ll.1.7. Использование критериев согласия Колмогорова и «w-квадрат» в случае неизвестных параметров для проверки гипотезы о нормальном характере распределения.
- 11.2. Проверка гипотез однородности и симметрии распределения
- 11.2.1. Критерии однородности, основанные на эмпирических функциях распределения.
- 11.2.2. Критерий однородности «хи-квадрат»
- 11.2.3. Ранговые критерии однородности.
- 11.2.4. Непараметрическая проверка гипотезы равенства дисперсий.
- 11.2.5. Ранговые критерии для случая k > 2 классов.
- 11.2.6. Критерии проверки симметрии распределений.
- 11.2.7. Обработка совпадений.
- 11.2.8. Критерии однородности нормальных совокупностей (одномерный случай).
- 11.2.9. Критерии однородности многомерных нормальных совокупностей.
- 11.3. Проверка независимости и стационарности ряда наблюдений
- 11.3.1. Критерий серий, основанный на медиане выборки.
- 11.3.2. Критерий «восходящих» и «нисходящих» серий.
- 11.3.3. Критерий квадратов последовательных разностей (критерий Аббе).
- 11.4. Методы статистической обработки при наличии «стертых» (пропущенных) наблюдений
- 11.4.1. Оценивание неизвестных параметров при наличии пропущенных данных.
- 11.4.2. Использование главных компонент.
- 11.4.3. Заполнение «пропусков» и оценивание параметров с помощью метода максимального правдоподобия. Оценки «неподвижной точки».
- 11.4.4. Непараметрический подход к оценке пропусков в матрице данных.
- 11.5. Анализ резко выделяющихся наблюдений
- 11.5.2 Графические методы.
- 11.5.3. Аналитический метод исключения одного экстремального наблюдения.
- 11.5.4. Аналитический критерий одновременного исключения нескольких экстремальных наблюдений.
- Выводы
- Глава 12. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ И НЕКОТОРЫЕ ВОПРОСЫ ТЕХНИКИ ВЫЧИСЛЕНИЙ
- 12.1. Программное обеспечение прикладной статистики
- 12.1.1. Организация пакетов программ.
- 12.1.2. Вопросы организации возможности ведения данных.
- 12.1.3. Средства предварительной обработки (манипуляции) данных.
- 12.1.4. Возможности обработки данных при наличии пропущенных значений.
- 12.1.5. Первичная обработка неколичественных данных.
- 12.1.6. Средства визуализации данных.
- 12.1.7. Оценивание параметров и выделение аномальных наблюдений.
- 12.2. Вычисление функций распределения и обратных к ним
- 12.2.1. Нормальное распределение.
- 12.2.2. Распределение «хи-квадрат».
- 12.2.3. Бета-распределение.
- 12.2.4. F-распределение.
- 12.2.5. t-распределение Стьюдента.
- 12.2.6. Нецентральные распределения.
- 12.2.7. Аппроксимация «хвостов» распределений типа «w-квадрат»
- 12.2.8. Многомерное нормальное распределение.
- 12.2.9. Дискретные распределения.
- 12.2.10. Вычисление математического ожидания порядковых статистик.
- Выводы
- ИСПОЛЬЗУЕМЫЕ В КНИГЕ ОБОЗНАЧЕНИЯ
- СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ