| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
4.1.2. Случайные события и правила действий с ними.
Как уже упоминалось, с каждым случайным экспериментом связано понятие совокупности всех возможных его исходов. Каждый из этих возможных исходов будем называть элементарным (неразложимым) событием (или элементарным исходом), а совокупность всех таких возможных исходов — пространством элементарных событий (исходов). Таким образом, в результате анализируемого случайного эксперимента обязательно происходит одно из элементарных событий, причем одновременно с ним не может произойти ни одно из остальных элементарных событий (о событиях, обладающих последним свойством, говорят, что они являются несовместными, см. ниже).
Рассмотрим пока лишь дискретный случай, т. е. только те ситуации, когда все элементарные события можно занумеровать числами 
Иначе говоря, рассматриваемое пространство элементарных событий (обозначим его  ) состоит лишь из конечного или счетного числа элементарных событий (обозначим их
) состоит лишь из конечного или счетного числа элементарных событий (обозначим их  ), а сам факт «пространство
), а сам факт «пространство  состоит из элементарных событий
состоит из элементарных событий  кратко обозначим
кратко обозначим

или

Рассмотрим несколько примеров случайных экспериментов и соответствующих им пространств элементарных событий.
Пример 4.1. Подбрасывание монеты:

Пример 4.2. Выбрасывание одной игральной кости:

Пример 4.3. Четырехкратное бросание игральной кости.

Пример 4.4. Проверка (по альтернативному признаку) одного изделия, случайно отобранного из продукции массового производства:

Пример 4.5. Проверка (по альтернативному признаку) N изделий, случайно отобранных из продукции массового производства:

где  — число обнаруженных изделий.
— число обнаруженных изделий.
Пример 4.6. Проверка (по альтернативному признаку) двух выборок, состоящих соответственно из  изделий, случайно отобранных из продукции массового производства:
изделий, случайно отобранных из продукции массового производства:

Пример 4.7. Определение  — числа сбоев станков автоматической линии за наугад выбранную смену:
— числа сбоев станков автоматической линии за наугад выбранную смену:

Кроме элементарных событий исследователю приходится иметь дело с так называемыми составными (или разложимыми) событиями.
Событие С называется составным (разложимым), если можно указать по меньшей мере два таких элементарных события  что из осуществления каждого из них в отдельности следует факт осуществления события С. Этот факт коротко формулируют: «событие С состоит из элементарных событий
что из осуществления каждого из них в отдельности следует факт осуществления события С. Этот факт коротко формулируют: «событие С состоит из элементарных событий  и записывают символически в виде
и записывают символически в виде 
Пользуясь такой терминологией, случайным событием А называют любое помножество  пространства элементарных событий (4.1), т. е.
пространства элементарных событий (4.1), т. е.

что следует понимать так: осуществление любого из элементарных событий  «входящих в А», влечет за собой осуществление события А.
«входящих в А», влечет за собой осуществление события А.
Поясним эту терминологию на некоторых из примеров 4.1-4.7.
В примере 4.2 события  = {выпадет четное число очков} и
= {выпадет четное число очков} и  = {выпавшее число очков не превзойдет 3} запишутся соответственно
= {выпавшее число очков не превзойдет 3} запишутся соответственно  .
.
В примере 4.3 интересовавшее нас в предыдущем параграфе событие А = {хотя бы один раз при четырехкратном бросании кости появится шестерка} будет состоять из всех тех четырехмерных векторов  в которых хотя бы одна из компонент равна шести (можно подсчитать, что число таких векторов равно 671).
в которых хотя бы одна из компонент равна шести (можно подсчитать, что число таких векторов равно 671).
В примере 4.5 событие А = {число обнаруженных дефектных изделий не более 4}, очевидно, может быть записано  .
.
В примере 4.7 событие А = {число зафиксированных за смену сбоев станков автоматической линии меньше 3} можно представить в виде  .
.
Из определения теории вероятностей (см. § 2.1) следует, что в первую очередь надо запастись определенной структурой всех возможных связей между случайными событиями или, другими словами, определенными правилами действий с событиями и соответствующей терминологией.
Сумма (объединение) событий
 — это такое событие
— это такое событие  , которое заключается в наступлении хотя бы одного из событий
, которое заключается в наступлении хотя бы одного из событий  На языке элементарных событий, следовательно, сумма событий
На языке элементарных событий, следовательно, сумма событий  определяется как событие
определяется как событие  , состоящее из всех различных элементарных событий, составляющих события
, состоящее из всех различных элементарных событий, составляющих события  Таким образом, если нас интересует, например, сумма А событий А (число обнаруженных дефектных изделий не более
Таким образом, если нас интересует, например, сумма А событий А (число обнаруженных дефектных изделий не более  (см. пример 4.5) и
(см. пример 4.5) и  = {число обнаруженных дефектных изделий заключено между 2 и 6 включительно} =
= {число обнаруженных дефектных изделий заключено между 2 и 6 включительно} =  , то, очевидно,
, то, очевидно,  так как о том, что событие А произошло, будет сигнализировать реализация любого из элементарных событий
так как о том, что событие А произошло, будет сигнализировать реализация любого из элементарных событий 
Произведение (пересечение) событий
 — это такое событие
— это такое событие  , которое заключается в обязательном наступлении всех событий
, которое заключается в обязательном наступлении всех событий  На языке элементарных событий, следовательно, произведение событий
На языке элементарных событий, следовательно, произведение событий  определяется как событие
определяется как событие  , состоящее лишь из тех элементарных событий, которые одновременно входят во все рассматриваемые события
, состоящее лишь из тех элементарных событий, которые одновременно входят во все рассматриваемые события  Так, что произведением упомянутых выше событий
Так, что произведением упомянутых выше событий  (см. пример 4.5) будет, очевидно, событие
(см. пример 4.5) будет, очевидно, событие  так как реализация каждого из элементарных событий
так как реализация каждого из элементарных событий  в отдельности означает, как легко видеть одновременное наступление событий
в отдельности означает, как легко видеть одновременное наступление событий 
Разность событий
 — это такое событие
— это такое событие  , которое заключается в одновременном осуществлении двух фактов: событие
, которое заключается в одновременном осуществлении двух фактов: событие  произошло, а событие
произошло, а событие  не произошло. На языке элементарных событий, следовательно, разность
не произошло. На языке элементарных событий, следовательно, разность  определяется как событие, состоящее из всех тех элементарных событий, которые входят в
определяется как событие, состоящее из всех тех элементарных событий, которые входят в  но не входят в
но не входят в  Так что разностью рассмотренных выше в схеме примера 4.5 событий
Так что разностью рассмотренных выше в схеме примера 4.5 событий  будет, очевидно, событие
будет, очевидно, событие  т. е. событие, заключающееся в том, что число обнаруженных в партии дефектных изделий окажется не превосходящим единицы.
т. е. событие, заключающееся в том, что число обнаруженных в партии дефектных изделий окажется не превосходящим единицы.
Противоположное (дополнительное) событие
(к событию А) — это такое событие  , которое состоит в ненаступлении события А. На языке элементарных событий, следовательно, А определяется как событие, состоящее из всех возможных элементарных событий, не входящих в А. Поэтому, используя понятие разности событий, можно записать
, которое состоит в ненаступлении события А. На языке элементарных событий, следовательно, А определяется как событие, состоящее из всех возможных элементарных событий, не входящих в А. Поэтому, используя понятие разности событий, можно записать  . Так, например, событием, противоположным к событию
. Так, например, событием, противоположным к событию  из примера 4.5, очевидно, будет событие, заключающееся в том, что число обнаруженных в партии объема N дефектных изделий окажется большим 4, т. е.
из примера 4.5, очевидно, будет событие, заключающееся в том, что число обнаруженных в партии объема N дефектных изделий окажется большим 4, т. е.  .
.
Достоверное событие
определяется как событие, состоящее из всех возможных элементарных событий, т. е. это событие  (см. (4.1)). Название этого события оправдано тем обстоятельством, что пространство элементарных событий состоит из всех возможных исходов, т. е. в результате анализируемого случайного эксперимента обязательно произойдет одно из элементарных событий
(см. (4.1)). Название этого события оправдано тем обстоятельством, что пространство элементарных событий состоит из всех возможных исходов, т. е. в результате анализируемого случайного эксперимента обязательно произойдет одно из элементарных событий  а следовательно, тот факт, что событие
а следовательно, тот факт, что событие  произойдет, достоверен.
произойдет, достоверен.
Невозможное (пустое) событие
 — это событие, противоположное достоверному, т. е.
— это событие, противоположное достоверному, т. е.  . Из определения непосредственно следует объяснение названия этого события: оно не содержит ни одного элементарного события
. Из определения непосредственно следует объяснение названия этого события: оно не содержит ни одного элементарного события  , и, следовательно, при реализации исследуемого случайного эксперимента его осуществление невозможно.
, и, следовательно, при реализации исследуемого случайного эксперимента его осуществление невозможно.
Несовместными
называются события  если в результате исследуемого случайного эксперимента никакие два из них не могут произойти одновременно. На языке элементарных событий это означает, что среди событий
если в результате исследуемого случайного эксперимента никакие два из них не могут произойти одновременно. На языке элементарных событий это означает, что среди событий  нельзя найти такую пару событий
нельзя найти такую пару событий  в которой обнаружилось бы хотя бы по одному общему элементарному событию. Используя понятия произведения событий и невозможного события, можно определить несовместные события как такую последовательность событий
в которой обнаружилось бы хотя бы по одному общему элементарному событию. Используя понятия произведения событий и невозможного события, можно определить несовместные события как такую последовательность событий  для любой пары которой
для любой пары которой  справедливо соотношение
справедливо соотношение  . Очевидно, любые пары
. Очевидно, любые пары  противоположных событий являются несовместными. Таковыми же являются (по определению) и все элементарные события.
противоположных событий являются несовместными. Таковыми же являются (по определению) и все элементарные события.
Полная система событий
— это такой набор несовместных событий  который в сумме исчерпывает все пространство элементарных событий, т. е.
который в сумме исчерпывает все пространство элементарных событий, т. е.

Очевидно, набор всех элементарных событий можно рассматривать как частный случай полной системы событий. И вообще любое разбиение множества элементарных событий  на непересекающиеся классы дает полную систему событий, в которой каждое из событий задается соответствующим классом разбиения. Так, обратившись вновь к примеру 4.5, положив в нем для определенности N=100 и обозначив букзой d число дефектных изделий, обнаруженных в партии, состоящей из 100 йаугад извлеченных изделий, отобранных от стационарно действующего массового производства, определим систему событий следующим образом.
на непересекающиеся классы дает полную систему событий, в которой каждое из событий задается соответствующим классом разбиения. Так, обратившись вновь к примеру 4.5, положив в нем для определенности N=100 и обозначив букзой d число дефектных изделий, обнаруженных в партии, состоящей из 100 йаугад извлеченных изделий, отобранных от стационарно действующего массового производства, определим систему событий следующим образом.

— партия отличного качества;

— брак в пределах допустимой нормы (партия принимается);

— брак выше допустимой нормы (партия принимается по сниженным расценкам);

— партия целиком возвращается.
Очевидно, события  образуют полную систему событий.
образуют полную систему событий.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Раздел I. ПРИКЛАДНАЯ СТАТИСТИКА: ЕЕ СУЩНОСТЬ И НАЗНАЧЕНИЕ (общие методические принципы)
- Глава 1. ПРИКЛАДНАЯ СТАТИСТИКА КАК САМОСТОЯТЕЛЬНАЯ НАУЧНАЯ ДИСЦИПЛИНА
- 1.2. Оптимизационная формулировка основных задач прикладной статистики и проблема устойчивости статистического вывода
- 1.2.1. Связь между оптимизационной формулировкой основных задач прикладной статистики и проблемой устойчивости статистического вывода.
- 1.2.2. Проблема статистического исследования зависимостей между анализируемыми показателями.
- 1.2.3. Проблема классификации объектов или признаков.
- 1.2.4. Снижение размерности исследуемого факторного пространства и отбор наиболее информативных признаков.
- Выводы
- Глаза 2. ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 2.1.1. Статистический ансамбль и «игра случая».
- 2.1.2. Теория вероятностей и условия статистического ансамбля.
- 2.1.3. Основные типы реальных ситуаций с позиций соблюдения условий статистического ансамбля.
- 2.2. «Взаимоотношения» теории вероятностей и математической статистики
- 2.2.2. Теоретико-вероятностный способ решения.
- 2.2.3. Вероятностно-статистический (или математико-статистический) способ принятия решения.
- ВЫВОДЫ
- Глава 3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 3.1.1. О двух подходах к статистическому моделированию.
- 3.1.2. Понятие математической модели.
- 3.2. Общая логическая схема и основные этапы содержательного математического моделирования
- 3.2.2. Моделирование механизма явления вместо формальной статистической фотографии.
- 3.3. Понятие о статистическом моделировании
- 3.4. Возражения против математических моделей
- 3.5. Наиболее распространенные типы математических моделей, используемых в прикладной статистике
- 3.5.1. Модели законов распределения вероятностей случайных величин.
- 3.5.2. Линейные вероятностные модели.
- 3.5.3. Обобщение линейных моделей.
- 3.5.4. Геометрические модели.
- 3.5.5. Модели марковского типа.
- Выводы
- Раздел II. ОСНОВЫ ТЕОРЕТИКО-ВЕРОЯТНОСТНОГО МАТЕМАТИЧЕСКОГО АППАРАТА
- 4.1.1. Наблюдение, зафиксированное на объекте исследуемой совокупности (случайный эксперимент).
- 4.1.2. Случайные события и правила действий с ними.
- 4.1.3. Вероятностное пространство. Вероятности и правила действия с ними.
- 4.2. Непрерывное вероятностное пространство (аксиоматика А. Н. Колмогорова)
- 4.2.1. Специфика общего (непрерывного) случая вероятностного пространства.
- 4.2.2. Случайные события, их вероятности и правила действий с ними (аксиоматический подход А. Н. Колмогорова).
- Выводы
- Глава 5. случайные величины (исследуемые признаки)
- 5.1. Определение и примеры случайных величин
- 5.2. Возможные и наблюденные значения случайной величины
- 5.3. Типы случайных величин
- 5.4. Закон распределения вероятностей случайной величины. Генеральная совокупность и выборка из нее
- 5.4.1. Закон распределения вероятностей.
- 5.4.2. Генеральная совокупность и выборка из нее.
- 5.4.3. Основные способы организации выборки.
- 5.5. Способы задания закона распределения: функция распределения, функция плотности и их выборочные (эмпирические аналоги)
- 5.5.1. Функция распределения вероятностей одномерной случайной величины.
- 5.5.2. Функция плотности вероятности одномерной случайной величины.
- 5.5.3. Многомерные функции распределения и плотности. Статистическая независимость случайных величин.
- 5.6. Основные числовые характеристики случайных величин и их выборочные аналоги
- 5.6.1. Понятие о математических ожиданиях и моментах.
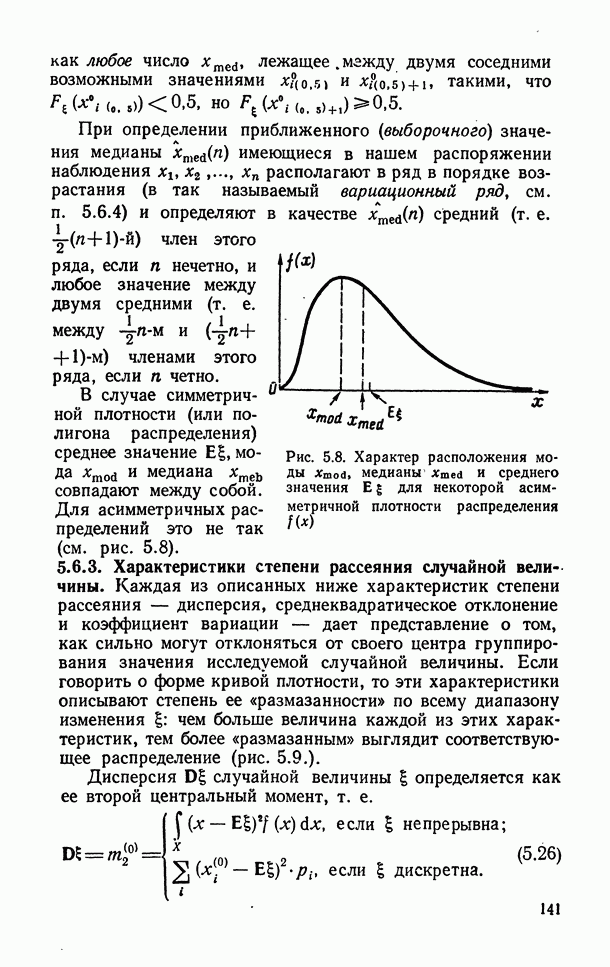
- 5.6.2. Характеристики центра группирования значений случайной величины.
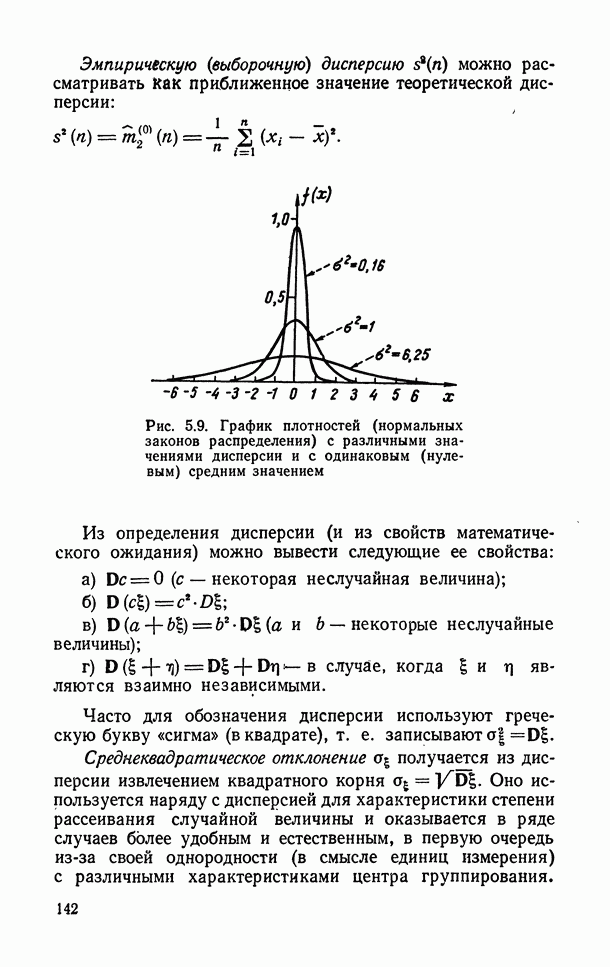
- 5.6.3. Характеристики степени рассеяния случайной величины.
- 5.6.4. Вариационный ряд и порядковые статистики.
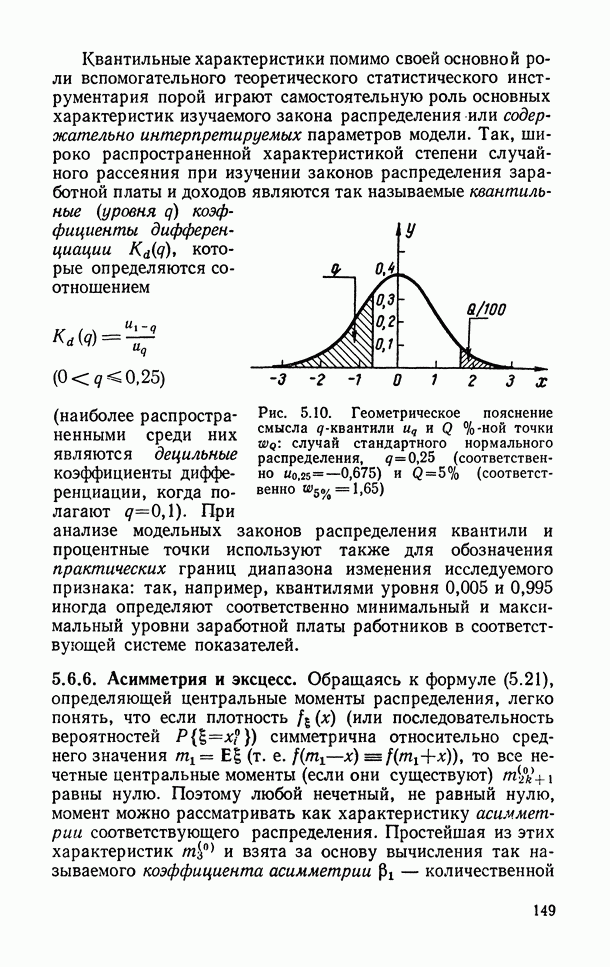
- 5.6.5. Квантили и процентные точки распределения.
- 5.6.6. Асимметрия и эксцесс.
- 5.6.7. Основные характеристики многомерных распределений (ковариации, корреляции, обобщенная дисперсия и др.).
- Выводы
- Глава 6. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ, НАИБОЛЕЕ РАСПРОСТРАНЕННЫЕ В ПРАКТИКЕ СТАТИСТИЧЕСКИХ ИССЛЕДОВАНИИ
- 6.1. Законы распределения, используемые для описания механизмов реальных процессов или систем
- 6.1.2. Гипергеометрическое распределение.
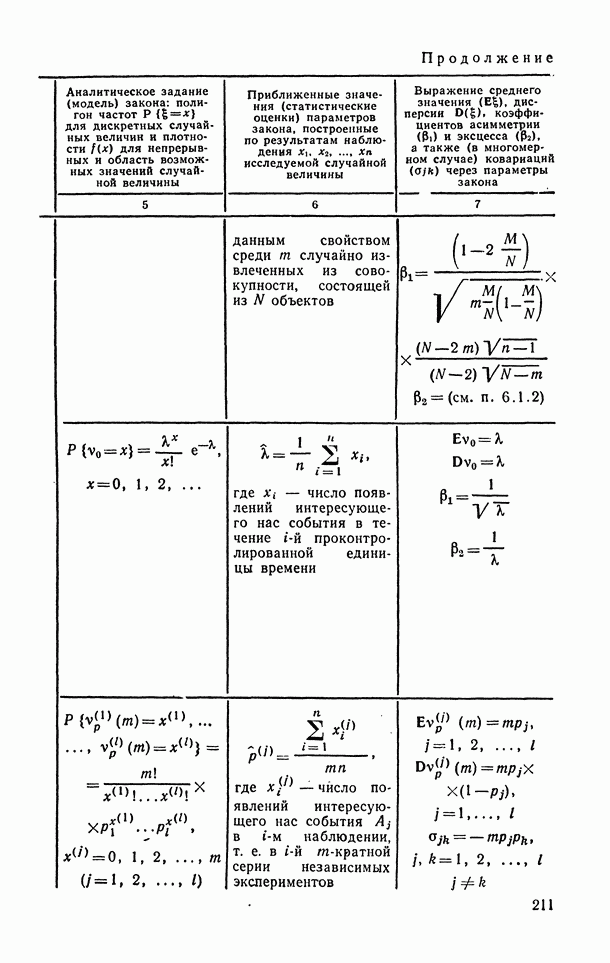
- 6.1.3. Распределение Пуассона.
- 6.1.4. Полиномиальное (мультиномиальное) распределение.
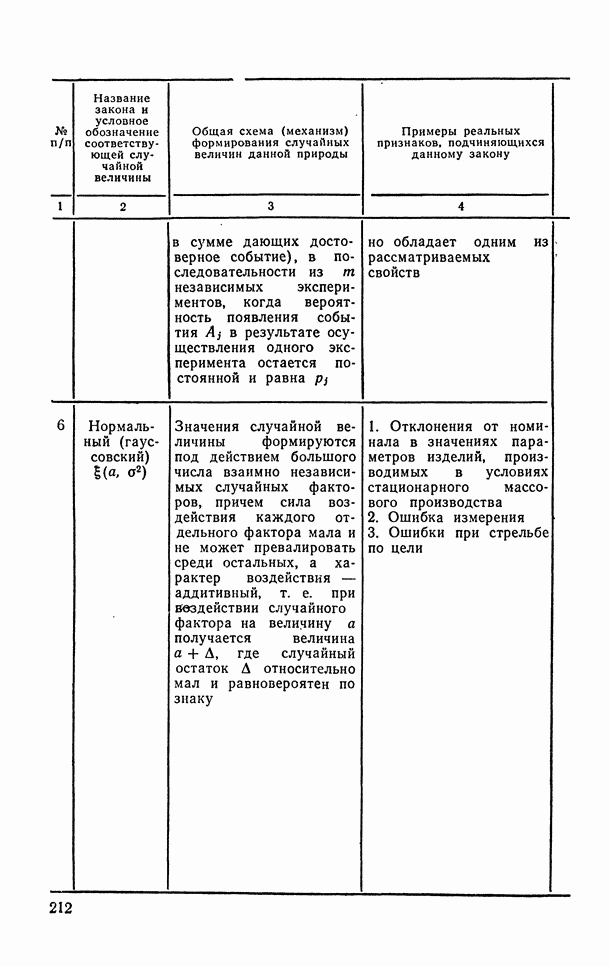
- 6.1.5. Нормальное (гауссовское) распределение.
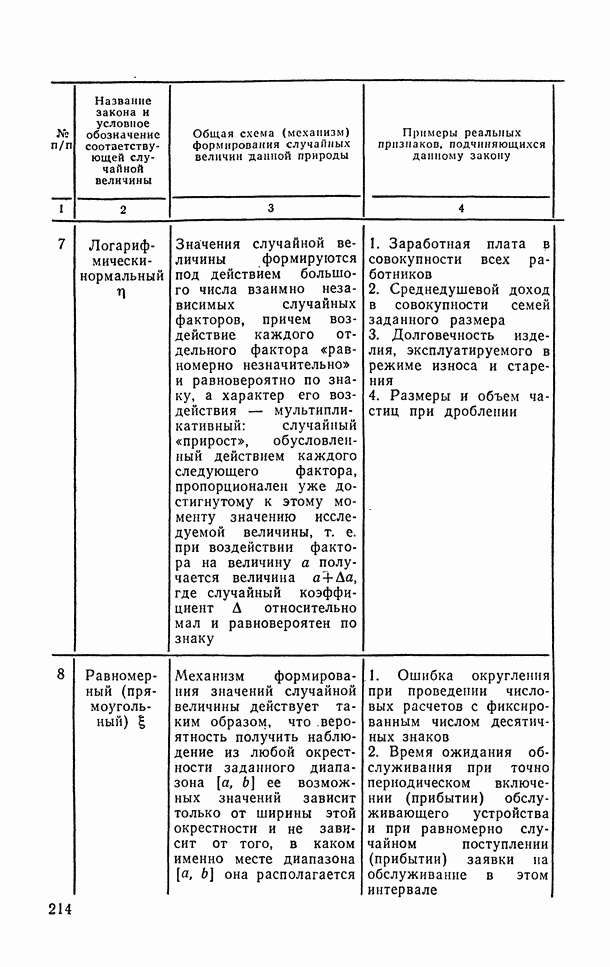
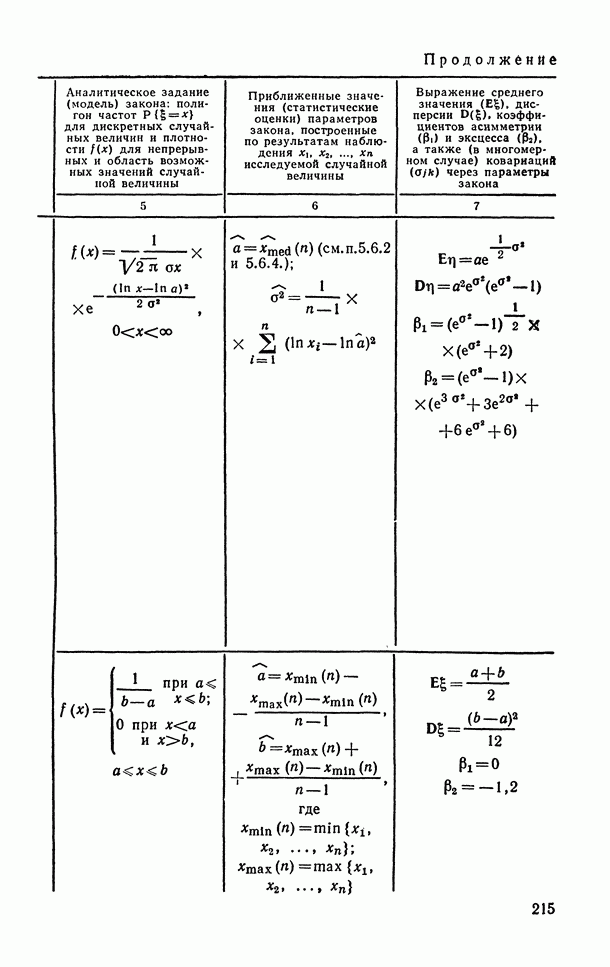
- 6.1.6. Логарифмически-нормальное распределение.
- 6.1.7. Равномерное (прямоугольное) распределение.
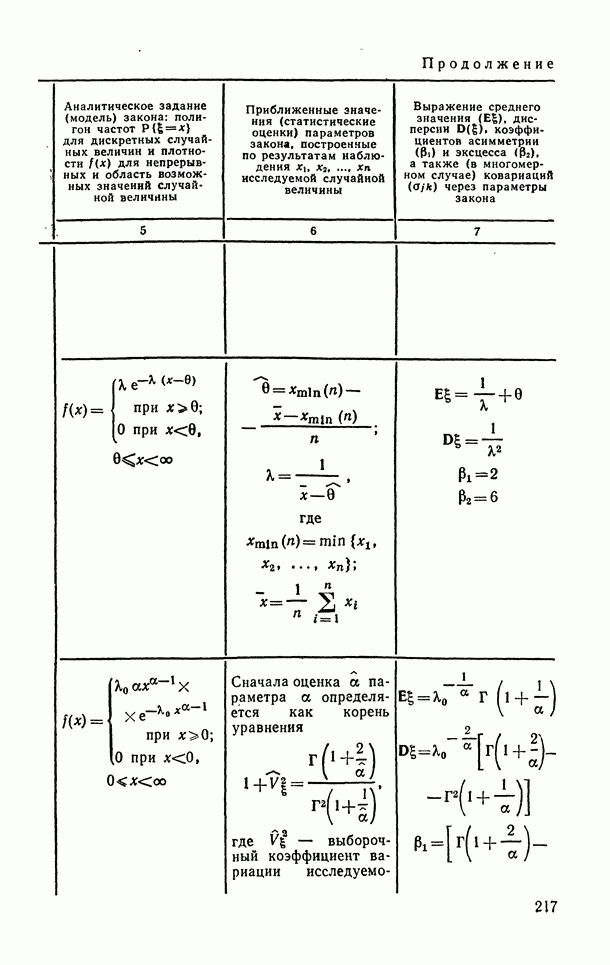
- 6.1.8. Распределение Вейбулла и экспоненциальное (показательное).
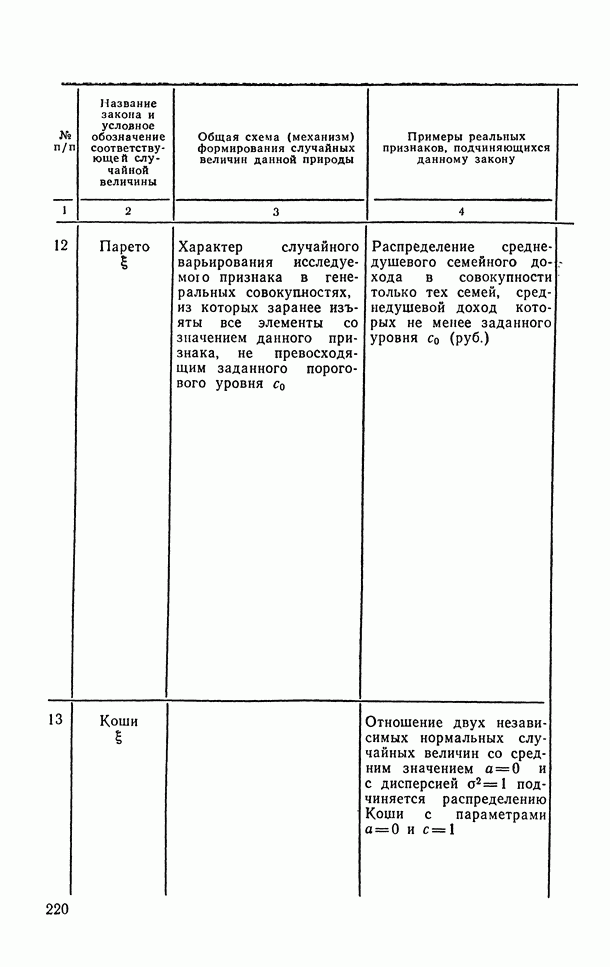
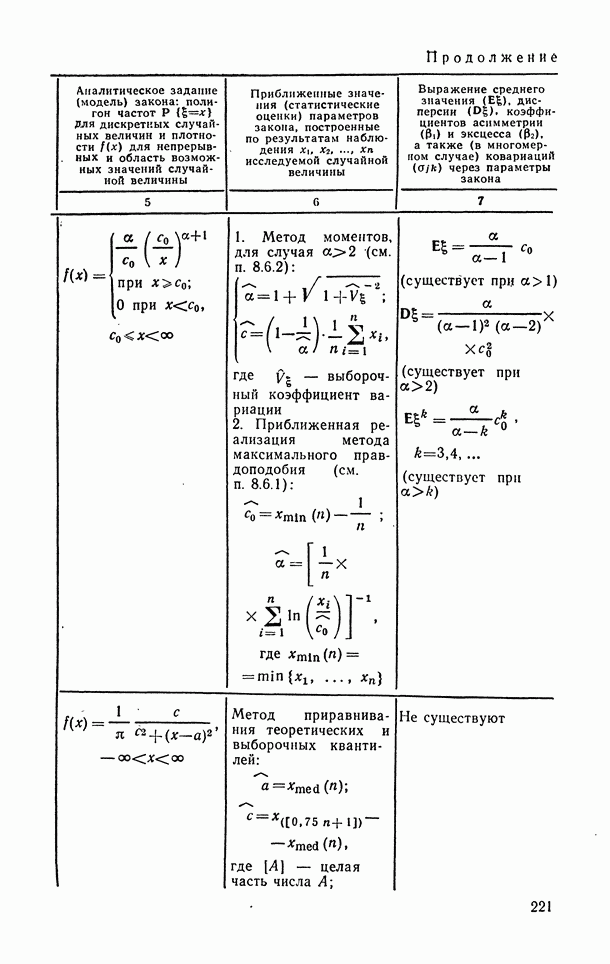
- 6.1.9. Распределение Парето.
- 6.1.10. Распределение Коши.
- 6.1.11. Некоторые комбинации основных модельных распределений, используемые в прикладной статистике.
- 6.2. Законы распределений вероятностей, используемые при реализации техники статистических вычислений
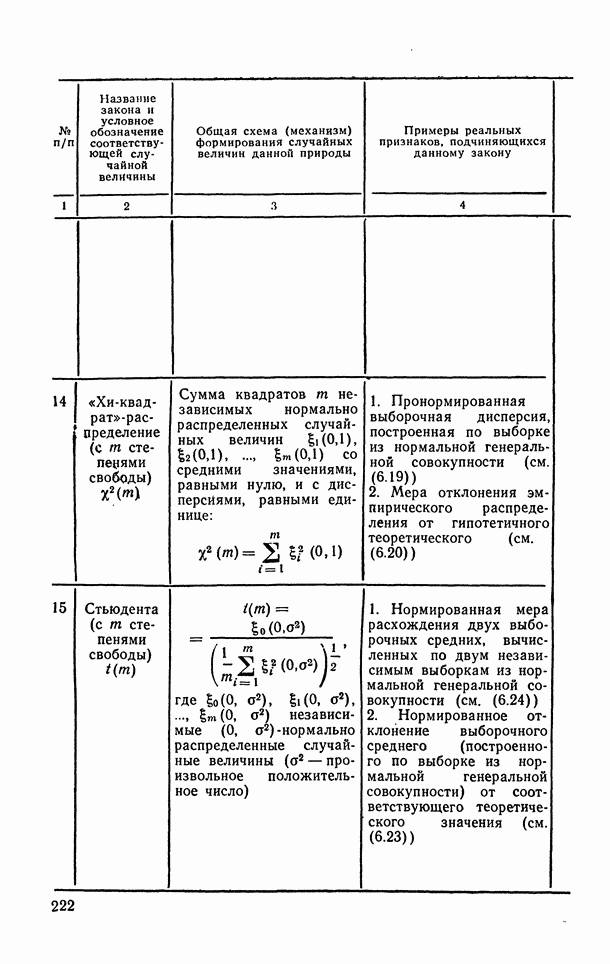
- 6.2.1. «хи квадрат»-распределение.
- 6.2.2. Распределение Стьюдента (t-распределение).
- 6.2.3. F-распределение (распределение дисперсионного отношения).
- 6.2.4. Замечание о нецентральных «хи-квадрат» и F- и t-распределениях.
- 6.2.5. Г-распределение.
- 6.2.6. В-распределение.
- 6.3. Техника статистического моделирования наблюдений, подчиняющихся заданному распределению
- 6.3.1. Получение равномерно распределенных на отрезке [0, 1] случайных чисел.
- 6.3.2. Моделирование дискретных случайных величин.
- Выводы
- Глава 7. ОСНОВНЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 7.1. Неравенство Чебышева
- 7.2. Свойство статистической устойчивости выборочных характеристик: закон больших чисел и его следствия
- 7.2.1. Закон больших чисел.
- 7.2.2. Теорема Я. Бернулли.
- 7.2.3 Статистическая устойчивость выборочных характеристик.
- 7.3. Особая роль нормального распределения: центральная предельная теорема
- 7.3.1. Центральная предельная теорема.
- 7.3.2. Многомерная центральная предельная теорема.
- 7.4. Закон распределения вероятностей случайных признаков, являющихся функциями от известных случайных величин
- Выводы
- Раздел III. ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- Глава 8. СТАТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- 8.1. Начальные сведения о задаче статистического оценивания параметров
- 8.1.2. Статистики, статистические оценки, их основные свойства.
- 8.1.3. Состоятельность.
- 8.1.4. Несмещенность.
- 8.1.5. Эффективность.
- 8.2. Функция правдоподобия. Количество информации, содержащееся в n независимых наблюдениях относительно неизвестного значения параметра
- 8.3. Неравенство Рао—Крамера—Фреше и измерение эффективности оценок
- 8.4. Асимптотические свойства оценок
- 8.5. Понятие об интервальном оценивании. Построение доверительных областей
- 8.6. Методы статистического оценивания неизвестных параметров
- 8.6.1. Метод максимального (наибольшего) правдоподобия.
- 8.6.2. Метод моментов.
- 8.6.3. Метод наименьших квадратов.
- 8.6.4. Оценивание с помощью «взвешенных» статистик; цензурирование, урезание выборок и порядковые статистики как частный случай взвешивания.
- 8.6.5. Построение интервальных оценок (доверительных областей).
- 8.6.6. Байесовский подход к статистическому оцениванию.
- Выводы
- Глава 9. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ (статистические критерии)
- 9.1. Основные типы гипотез, проверяемых в ходе статистической обработки данных
- 9.1.1. Гипотезы о типе закона распределения исследуемой случайной величины.
- 9.1.2. Гипотезы об однородности двух или нескольких обрабатываемых выборок или некоторых характеристик анализируемых совокупностей.
- 9.1.3. Гипотезы о числовых значениях параметров исследуемой генеральной совокупности.
- 9.1.4. Гипотезы о типе зависимости между компонентами исследуемого многомерного признака.
- 9.1.5. Гипотезы независимости и стационарности обрабатываемого ряда наблюдений.
- 9.2. Общая логическая схема статистического критерия
- 9.3. Построение статистического критерия; принцип отношения правдоподобия
- 9.3.1. Сущность принципа отношения правдоподобия.
- 9.3.2. Проверка простой гипотезы с помощью критерия логарифма отношения правдоподобия.
- 9.3.3. Проверка сложной гипотезы.
- 9.4. Характеристики «качества» статистического критерия
- 9.5. Последовательная схема принятия решения (последовательные критерии)
- 9.5.1. Последовательная схема наблюдений.
- 9.5.2. Последовательный критерий отношения правдоподобия (критерий Вальда) и его свойства.
- 9.5.3. Различение сложных гипотез в схеме обобщенного последовательного критерия.
- Выводы
- Раздел IV. ПЕРВИЧНАЯ СТАТИСТИЧЕСКАЯ ОБРАБОТКА ДАННЫХ
- 10.1. Документирование исследования; организация ввода и хранения данных в ЭВМ; просмотр данных
- 10.1.2. Ввод и хранение данных.
- 10.1.3. Просмотр данных.
- 10.2. Шкалы измерений
- 10.3. Изучение эмпирических распределений
- 10.3.1. Гистограмма.
- 10.3.2. Непараметрические оценки плотности.
- 10.3.3. Оценки функции распределения.
- 10.3.4. Преобразование переменных.
- 10.3.5. Таблицы сопряженности.
- 10.4. Оценивание параметров сдвига и масштаба
- 10.4.2. Оценивание параметров нормального закона.
- 10.4.3. Графический метод оценивания.
- 10.4.4. Проблема устойчивости оценок при небольших отклонениях распределения от нормального.
- 10.4.5. Оценивание положения центра симметричных распределений.
- 10.4.6. Параметризация с помощью экспоненциально взвешенных оценок (ЭВ-оценки).
- 10.5. Визуализация многомерных данных
- 10.5.2. Главные компоненты.
- 10.5.3. Свойства наименьшего искажения геометрической структуры для главных компонент.
- 10.5.4, Нелинейные отображения в пространство малой размерности.
- 10.5.5. Многомерное метрическое шкалирование.
- Выводы
- Глава 11. ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ ПРИРОДЫ ДАННЫХ
- 11.1. Проверка соответствия выбранной модели распределения исходным данным (критерии согласия)
- 11.1.1. Критерий «хи-квадрат» Пирсона.
- 11.1.2. Проверка нормального характера распределения по асимметрии, эксцессу и средним отклонениям.
- 11.1.3. Критерий Колмогорова — Смирнова и его применение к построению доверительных границ для неизвестной функции распределения.
- 11.1.4. Критерий Крамера — Мизеса — Смирнова.
- 11.1.5. Модификация статистик критериев Колмогорова — Смирнова и для выборок небольшого объема.
- 11.1.6. Статистическая техника практической реализации непараметрических критериев согласия.
- ll.1.7. Использование критериев согласия Колмогорова и «w-квадрат» в случае неизвестных параметров для проверки гипотезы о нормальном характере распределения.
- 11.2. Проверка гипотез однородности и симметрии распределения
- 11.2.1. Критерии однородности, основанные на эмпирических функциях распределения.
- 11.2.2. Критерий однородности «хи-квадрат»
- 11.2.3. Ранговые критерии однородности.
- 11.2.4. Непараметрическая проверка гипотезы равенства дисперсий.
- 11.2.5. Ранговые критерии для случая k > 2 классов.
- 11.2.6. Критерии проверки симметрии распределений.
- 11.2.7. Обработка совпадений.
- 11.2.8. Критерии однородности нормальных совокупностей (одномерный случай).
- 11.2.9. Критерии однородности многомерных нормальных совокупностей.
- 11.3. Проверка независимости и стационарности ряда наблюдений
- 11.3.1. Критерий серий, основанный на медиане выборки.
- 11.3.2. Критерий «восходящих» и «нисходящих» серий.
- 11.3.3. Критерий квадратов последовательных разностей (критерий Аббе).
- 11.4. Методы статистической обработки при наличии «стертых» (пропущенных) наблюдений
- 11.4.1. Оценивание неизвестных параметров при наличии пропущенных данных.
- 11.4.2. Использование главных компонент.
- 11.4.3. Заполнение «пропусков» и оценивание параметров с помощью метода максимального правдоподобия. Оценки «неподвижной точки».
- 11.4.4. Непараметрический подход к оценке пропусков в матрице данных.
- 11.5. Анализ резко выделяющихся наблюдений
- 11.5.2 Графические методы.
- 11.5.3. Аналитический метод исключения одного экстремального наблюдения.
- 11.5.4. Аналитический критерий одновременного исключения нескольких экстремальных наблюдений.
- Выводы
- Глава 12. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ И НЕКОТОРЫЕ ВОПРОСЫ ТЕХНИКИ ВЫЧИСЛЕНИЙ
- 12.1. Программное обеспечение прикладной статистики
- 12.1.1. Организация пакетов программ.
- 12.1.2. Вопросы организации возможности ведения данных.
- 12.1.3. Средства предварительной обработки (манипуляции) данных.
- 12.1.4. Возможности обработки данных при наличии пропущенных значений.
- 12.1.5. Первичная обработка неколичественных данных.
- 12.1.6. Средства визуализации данных.
- 12.1.7. Оценивание параметров и выделение аномальных наблюдений.
- 12.2. Вычисление функций распределения и обратных к ним
- 12.2.1. Нормальное распределение.
- 12.2.2. Распределение «хи-квадрат».
- 12.2.3. Бета-распределение.
- 12.2.4. F-распределение.
- 12.2.5. t-распределение Стьюдента.
- 12.2.6. Нецентральные распределения.
- 12.2.7. Аппроксимация «хвостов» распределений типа «w-квадрат»
- 12.2.8. Многомерное нормальное распределение.
- 12.2.9. Дискретные распределения.
- 12.2.10. Вычисление математического ожидания порядковых статистик.
- Выводы
- ИСПОЛЬЗУЕМЫЕ В КНИГЕ ОБОЗНАЧЕНИЯ
- СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ