| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
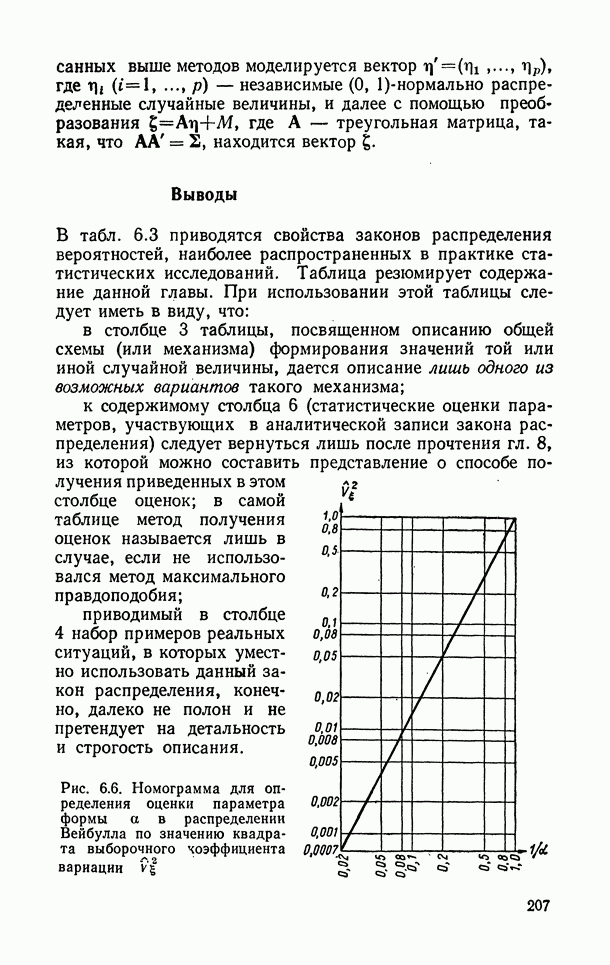
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
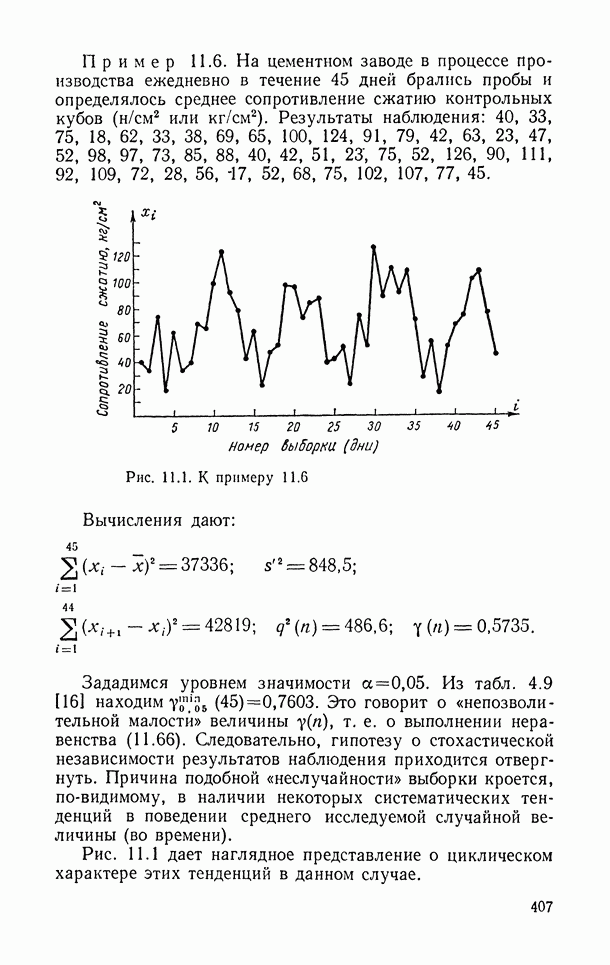
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
7.3. Особая роль нормального распределения: центральная предельная теорема
Смысл результатов § 7.2 заключается, грубо говоря, в том, что при осреднении большого числа  случайных слагаемых все менее ощущается характерный для случайных величин неконтролируемый разброс в их значениях, так что в пределе по
случайных слагаемых все менее ощущается характерный для случайных величин неконтролируемый разброс в их значениях, так что в пределе по  этот разброс исчезает вовсе или, как принято говорить, случайная величина вырождается в неслучайную. Однако при любом конечном числе слагаемых
этот разброс исчезает вовсе или, как принято говорить, случайная величина вырождается в неслучайную. Однако при любом конечном числе слагаемых  случайный разброс у среднего арифметического этих слагаемых остается. Поэтому возникает вопрос исследования (опять-таки асимптотического по
случайный разброс у среднего арифметического этих слагаемых остается. Поэтому возникает вопрос исследования (опять-таки асимптотического по  ) характера этого разброса. Фундаментальный результат в этом направлении (известный как «центральная предельная теорема») был рпервые сформулирован в упомянутом выше труде Лапласа (1812 г.), и заключался он в том, что для широкого класса независимых случайных величин
) характера этого разброса. Фундаментальный результат в этом направлении (известный как «центральная предельная теорема») был рпервые сформулирован в упомянутом выше труде Лапласа (1812 г.), и заключался он в том, что для широкого класса независимых случайных величин  предельный (по
предельный (по  ) закон распределения их нормированной суммы вне зависимости от типа распределения слагаемых стремится к нормальному закону распределения.
) закон распределения их нормированной суммы вне зависимости от типа распределения слагаемых стремится к нормальному закону распределения.
Однако эта формулировка нуждается в уточнениях: что значит «нормированная» сумма случайных величин и в каком именно смысле закон распределения одной случайной величины стремится к закону распределения другой? Существует несколько вариантов точных формулировок центральной предельной теоремы, отличающихся друг от друга степенью общности и видом постулируемых ограничительных условий. Мы приведем здесь формулировку Линдеберга и Леви.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Раздел I. ПРИКЛАДНАЯ СТАТИСТИКА: ЕЕ СУЩНОСТЬ И НАЗНАЧЕНИЕ (общие методические принципы)
- Глава 1. ПРИКЛАДНАЯ СТАТИСТИКА КАК САМОСТОЯТЕЛЬНАЯ НАУЧНАЯ ДИСЦИПЛИНА
- 1.2. Оптимизационная формулировка основных задач прикладной статистики и проблема устойчивости статистического вывода
- 1.2.1. Связь между оптимизационной формулировкой основных задач прикладной статистики и проблемой устойчивости статистического вывода.
- 1.2.2. Проблема статистического исследования зависимостей между анализируемыми показателями.
- 1.2.3. Проблема классификации объектов или признаков.
- 1.2.4. Снижение размерности исследуемого факторного пространства и отбор наиболее информативных признаков.
- Выводы
- Глаза 2. ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 2.1.1. Статистический ансамбль и «игра случая».
- 2.1.2. Теория вероятностей и условия статистического ансамбля.
- 2.1.3. Основные типы реальных ситуаций с позиций соблюдения условий статистического ансамбля.
- 2.2. «Взаимоотношения» теории вероятностей и математической статистики
- 2.2.2. Теоретико-вероятностный способ решения.
- 2.2.3. Вероятностно-статистический (или математико-статистический) способ принятия решения.
- ВЫВОДЫ
- Глава 3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 3.1.1. О двух подходах к статистическому моделированию.
- 3.1.2. Понятие математической модели.
- 3.2. Общая логическая схема и основные этапы содержательного математического моделирования
- 3.2.2. Моделирование механизма явления вместо формальной статистической фотографии.
- 3.3. Понятие о статистическом моделировании
- 3.4. Возражения против математических моделей
- 3.5. Наиболее распространенные типы математических моделей, используемых в прикладной статистике
- 3.5.1. Модели законов распределения вероятностей случайных величин.
- 3.5.2. Линейные вероятностные модели.
- 3.5.3. Обобщение линейных моделей.
- 3.5.4. Геометрические модели.
- 3.5.5. Модели марковского типа.
- Выводы
- Раздел II. ОСНОВЫ ТЕОРЕТИКО-ВЕРОЯТНОСТНОГО МАТЕМАТИЧЕСКОГО АППАРАТА
- 4.1.1. Наблюдение, зафиксированное на объекте исследуемой совокупности (случайный эксперимент).
- 4.1.2. Случайные события и правила действий с ними.
- 4.1.3. Вероятностное пространство. Вероятности и правила действия с ними.
- 4.2. Непрерывное вероятностное пространство (аксиоматика А. Н. Колмогорова)
- 4.2.1. Специфика общего (непрерывного) случая вероятностного пространства.
- 4.2.2. Случайные события, их вероятности и правила действий с ними (аксиоматический подход А. Н. Колмогорова).
- Выводы
- Глава 5. случайные величины (исследуемые признаки)
- 5.1. Определение и примеры случайных величин
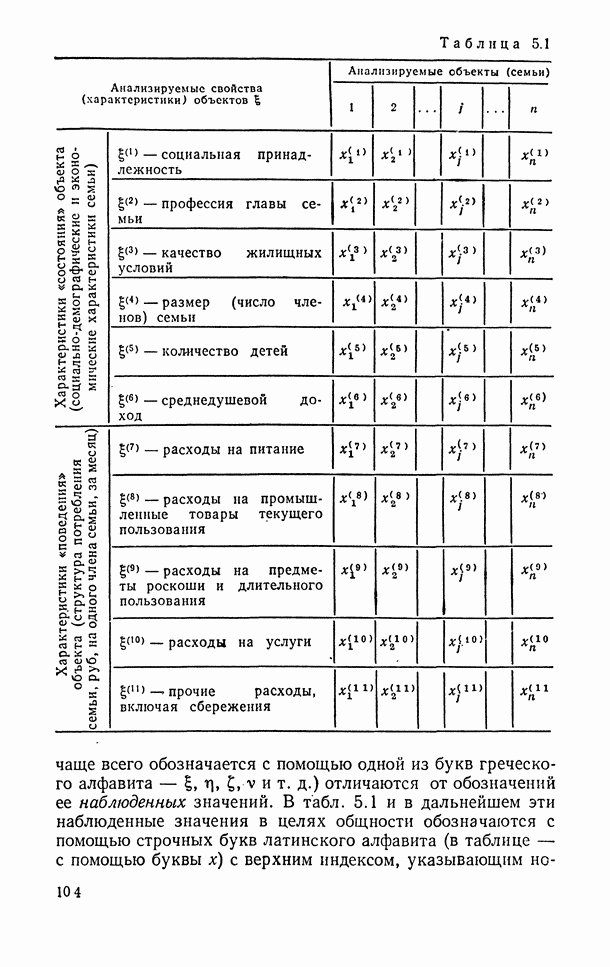
- 5.2. Возможные и наблюденные значения случайной величины
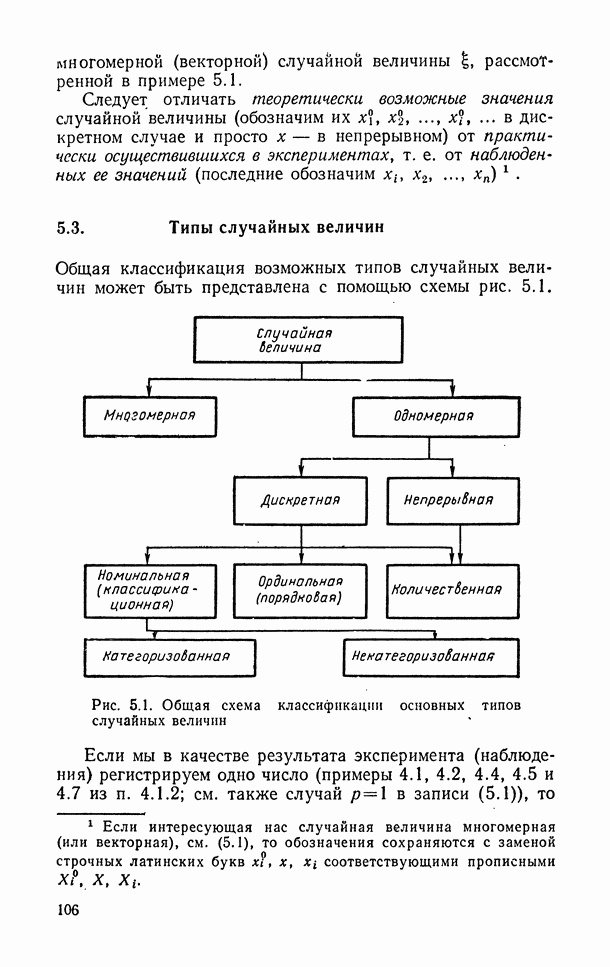
- 5.3. Типы случайных величин
- 5.4. Закон распределения вероятностей случайной величины. Генеральная совокупность и выборка из нее
- 5.4.1. Закон распределения вероятностей.
- 5.4.2. Генеральная совокупность и выборка из нее.
- 5.4.3. Основные способы организации выборки.
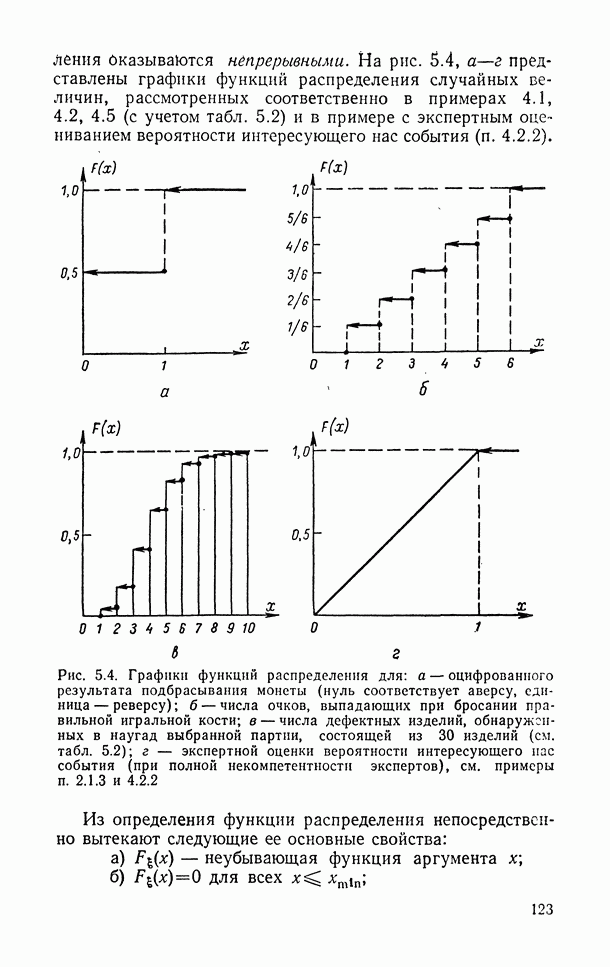
- 5.5. Способы задания закона распределения: функция распределения, функция плотности и их выборочные (эмпирические аналоги)
- 5.5.1. Функция распределения вероятностей одномерной случайной величины.
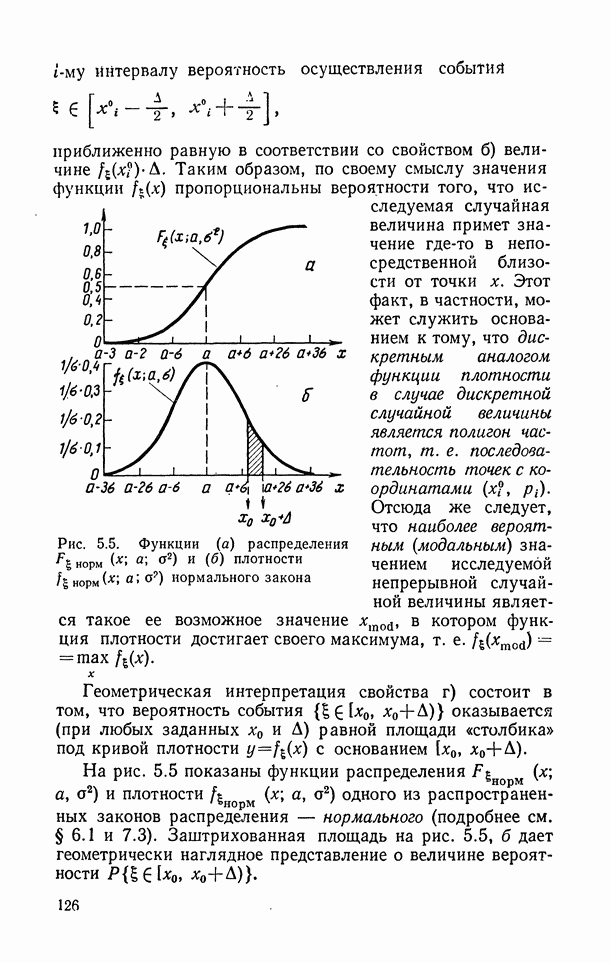
- 5.5.2. Функция плотности вероятности одномерной случайной величины.
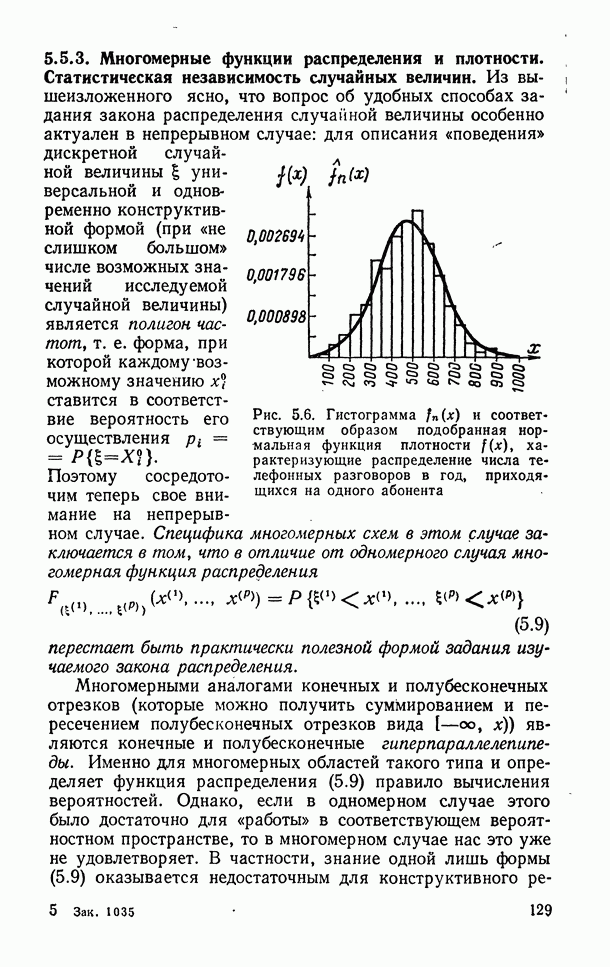
- 5.5.3. Многомерные функции распределения и плотности. Статистическая независимость случайных величин.
- 5.6. Основные числовые характеристики случайных величин и их выборочные аналоги
- 5.6.1. Понятие о математических ожиданиях и моментах.
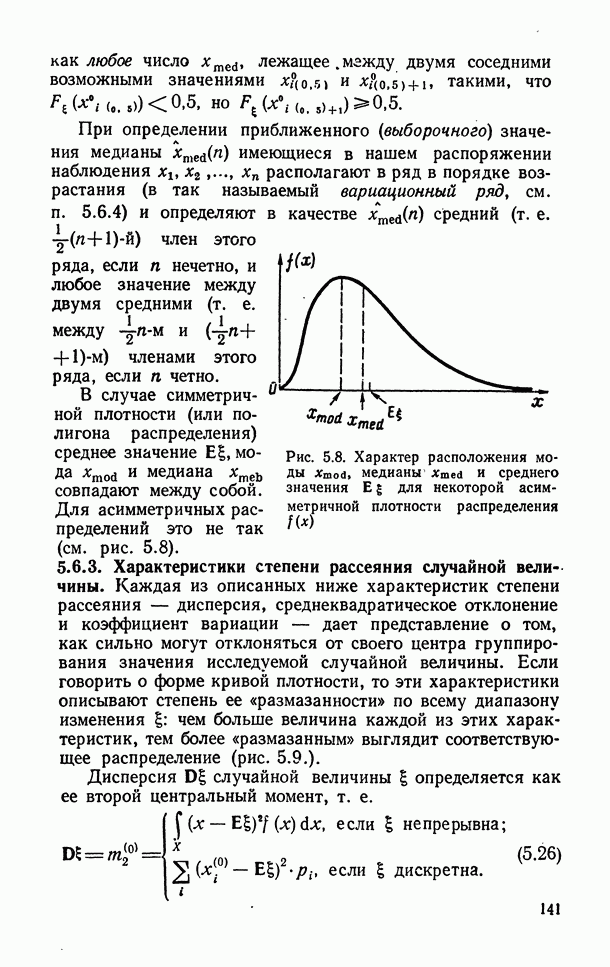
- 5.6.2. Характеристики центра группирования значений случайной величины.
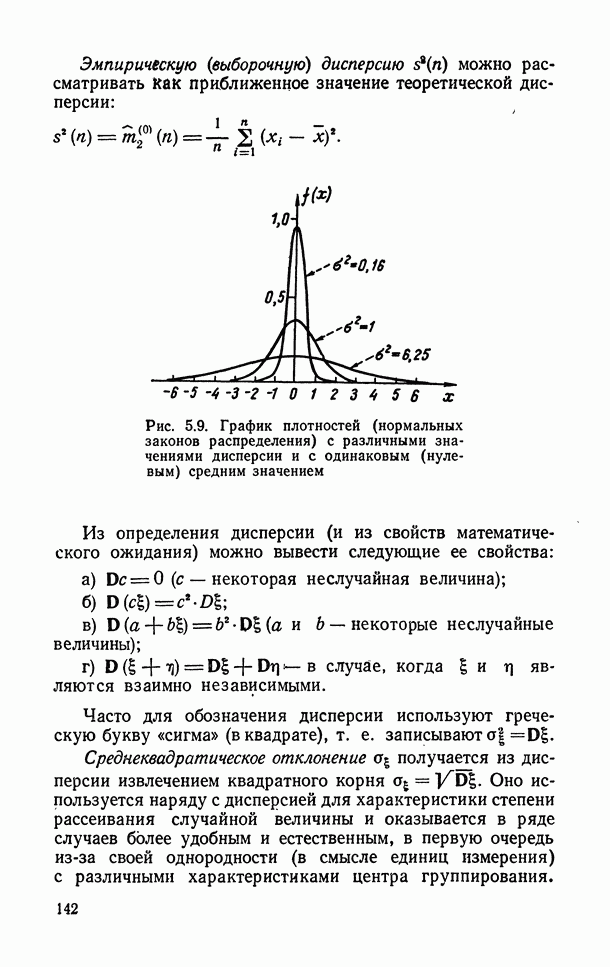
- 5.6.3. Характеристики степени рассеяния случайной величины.
- 5.6.4. Вариационный ряд и порядковые статистики.
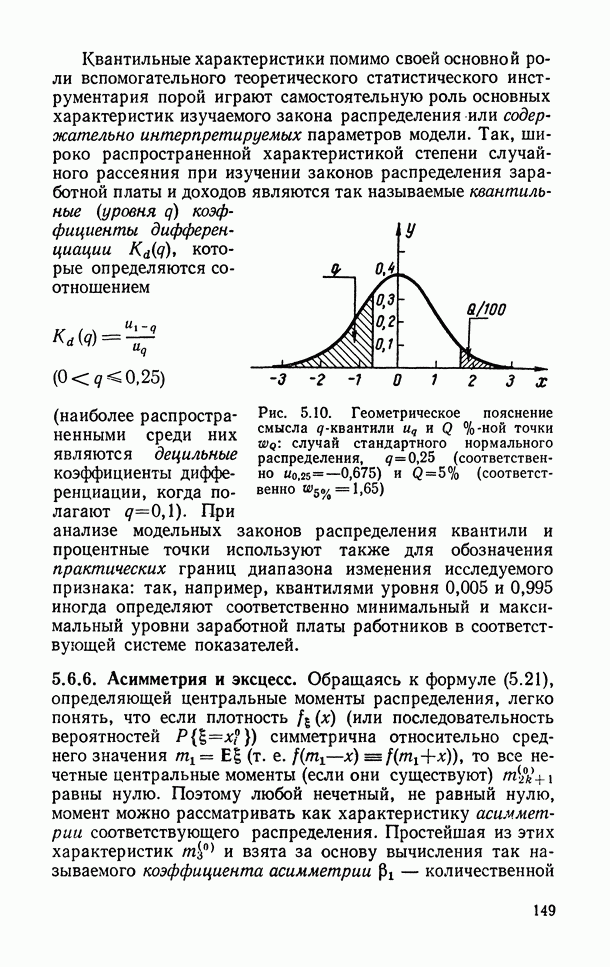
- 5.6.5. Квантили и процентные точки распределения.
- 5.6.6. Асимметрия и эксцесс.
- 5.6.7. Основные характеристики многомерных распределений (ковариации, корреляции, обобщенная дисперсия и др.).
- Выводы
- Глава 6. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ, НАИБОЛЕЕ РАСПРОСТРАНЕННЫЕ В ПРАКТИКЕ СТАТИСТИЧЕСКИХ ИССЛЕДОВАНИИ
- 6.1. Законы распределения, используемые для описания механизмов реальных процессов или систем
- 6.1.2. Гипергеометрическое распределение.
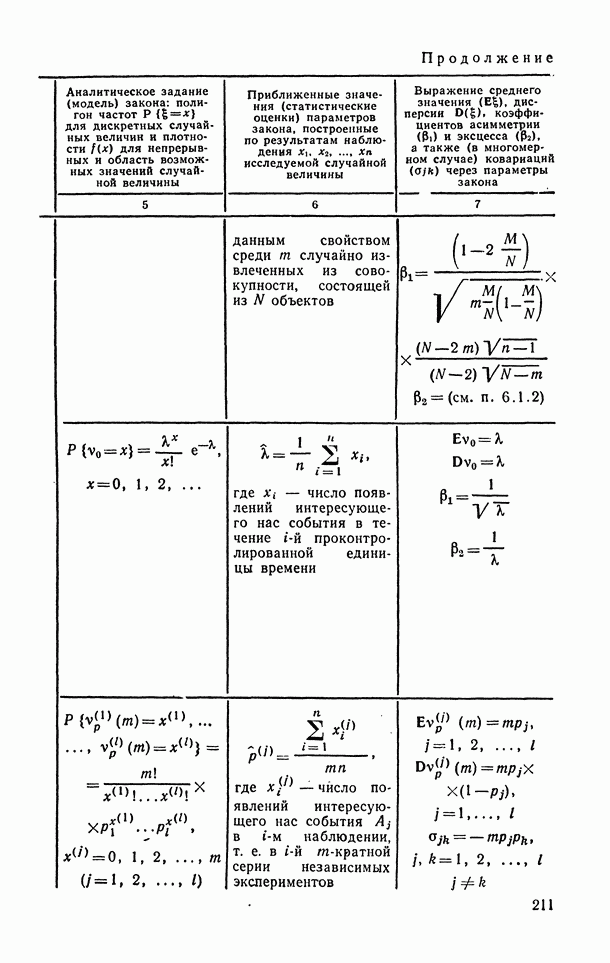
- 6.1.3. Распределение Пуассона.
- 6.1.4. Полиномиальное (мультиномиальное) распределение.
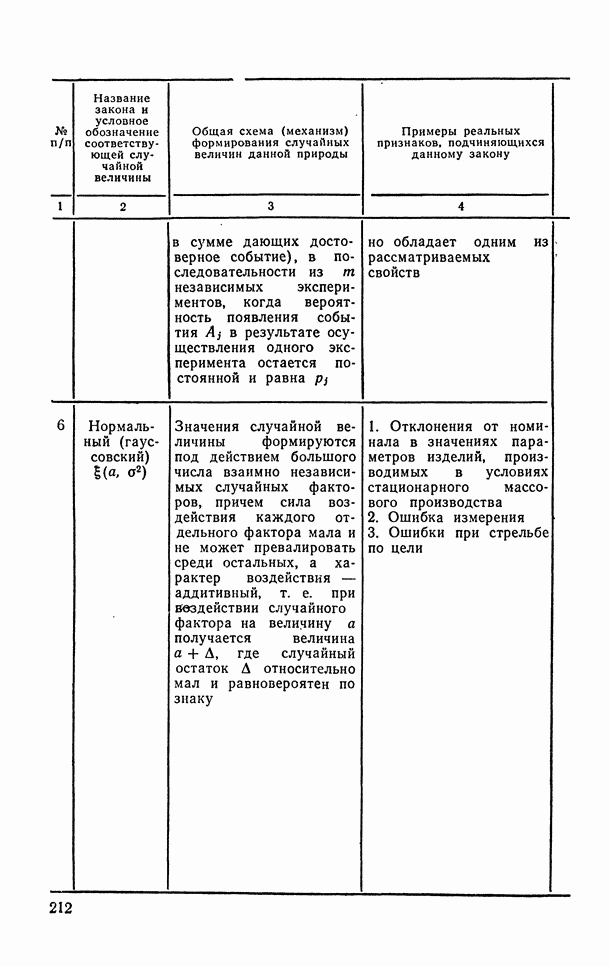
- 6.1.5. Нормальное (гауссовское) распределение.
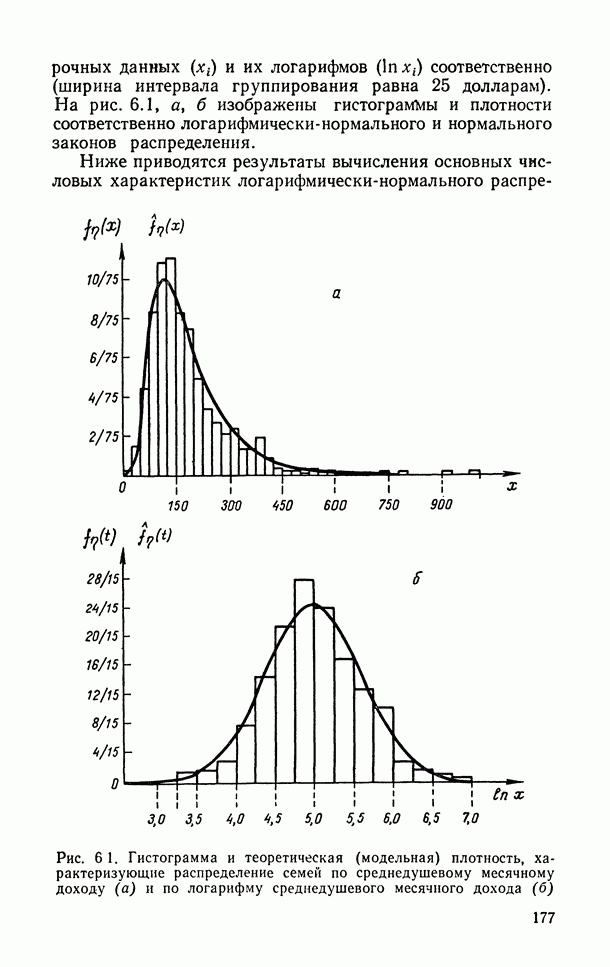
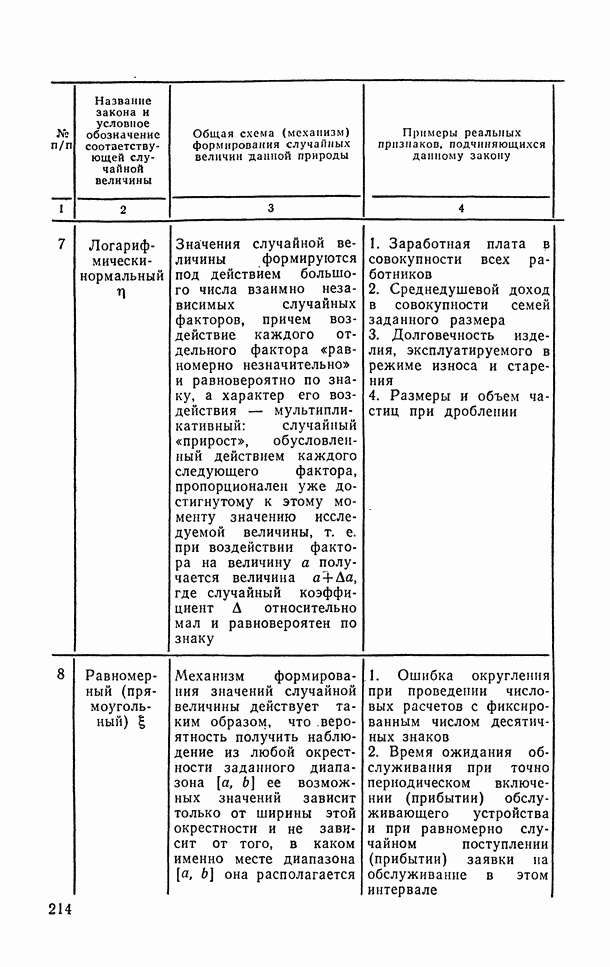
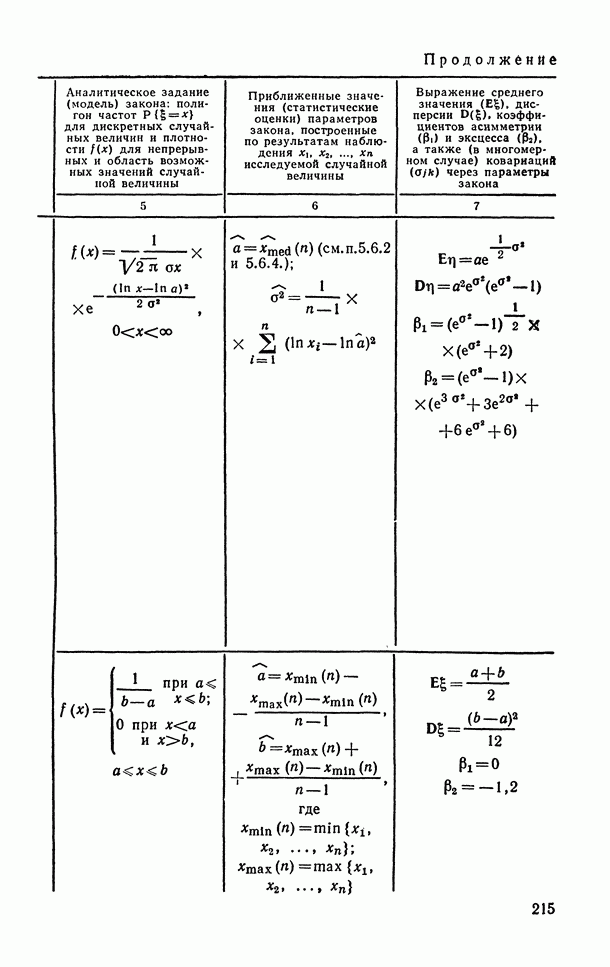
- 6.1.6. Логарифмически-нормальное распределение.
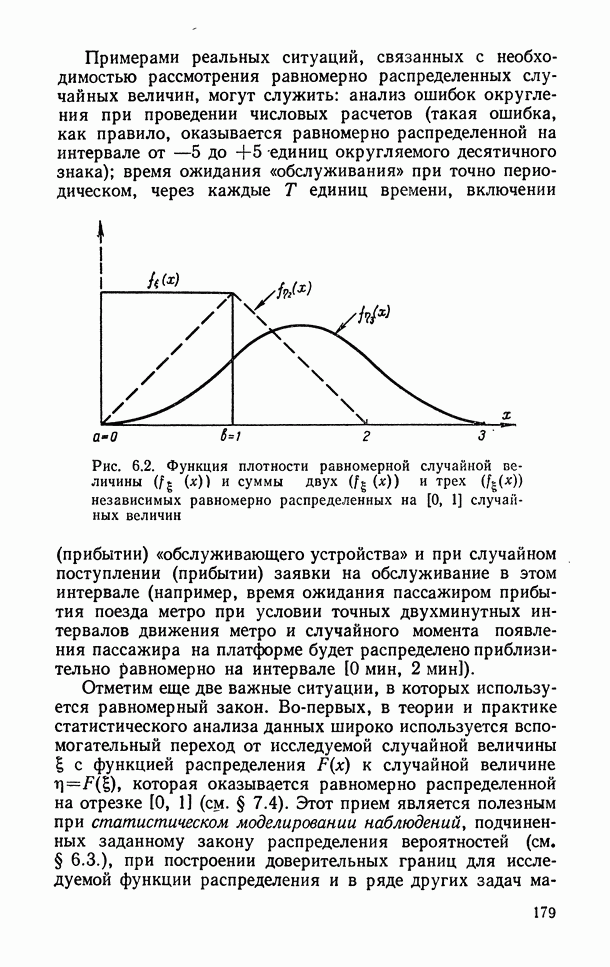
- 6.1.7. Равномерное (прямоугольное) распределение.
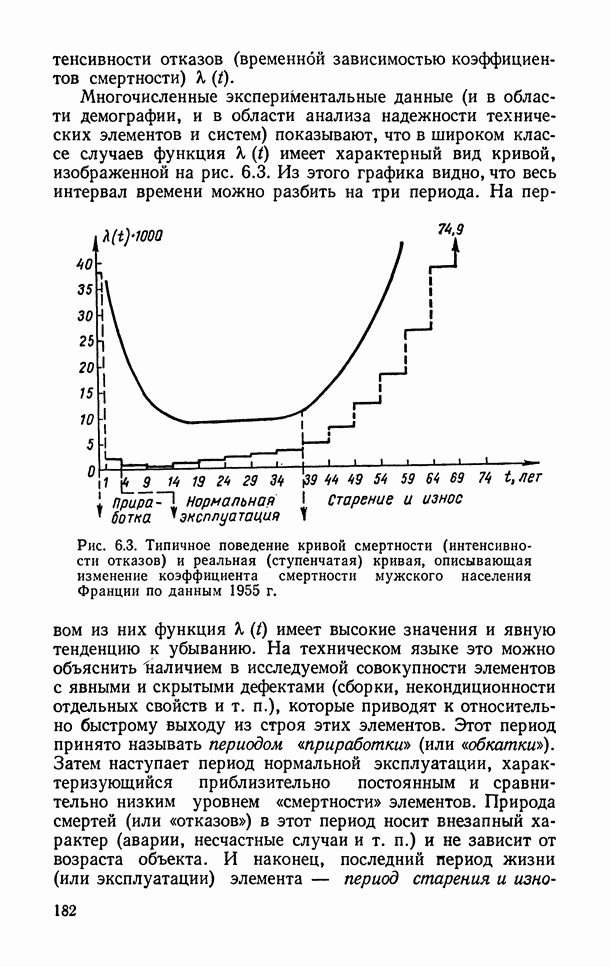
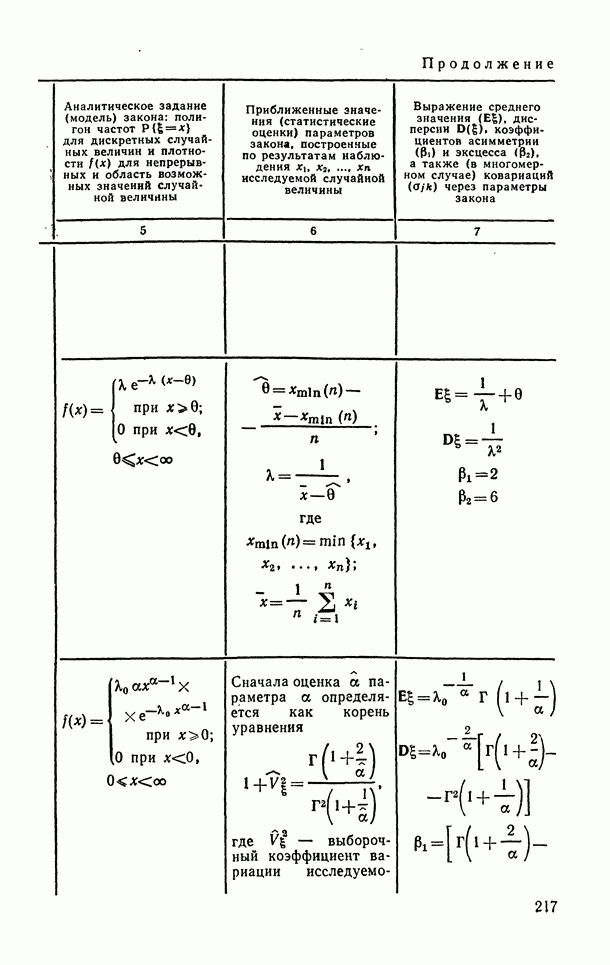
- 6.1.8. Распределение Вейбулла и экспоненциальное (показательное).
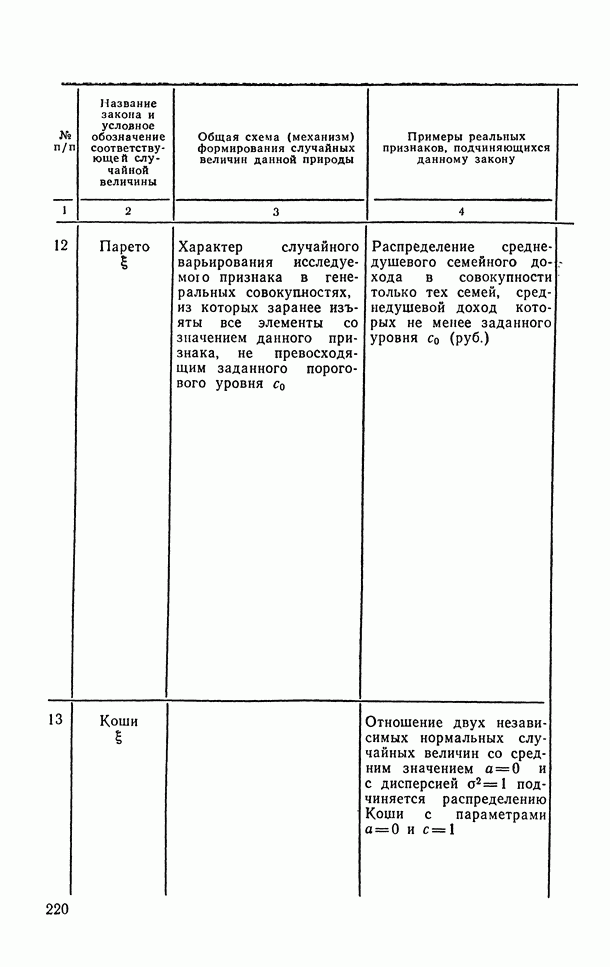
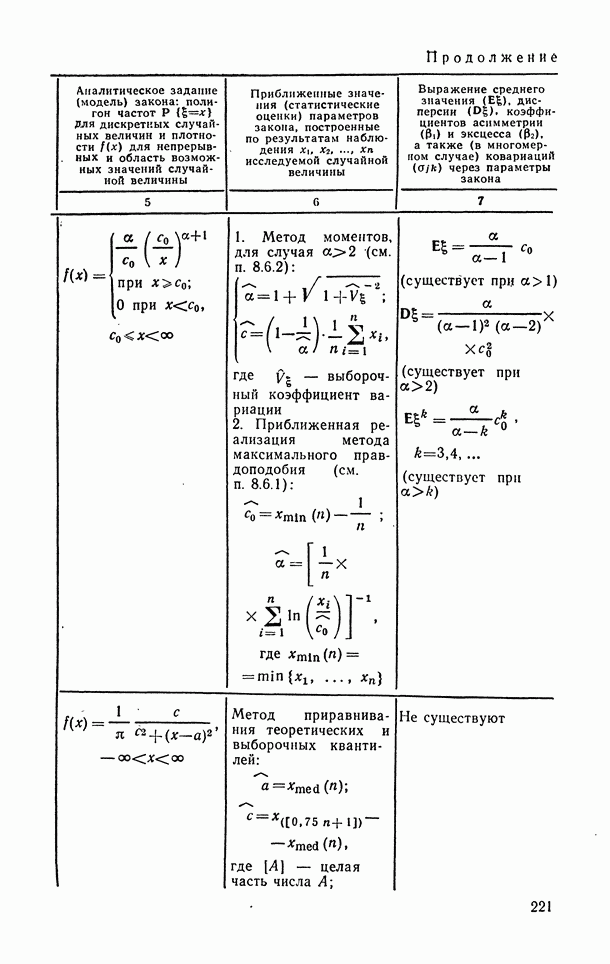
- 6.1.9. Распределение Парето.
- 6.1.10. Распределение Коши.
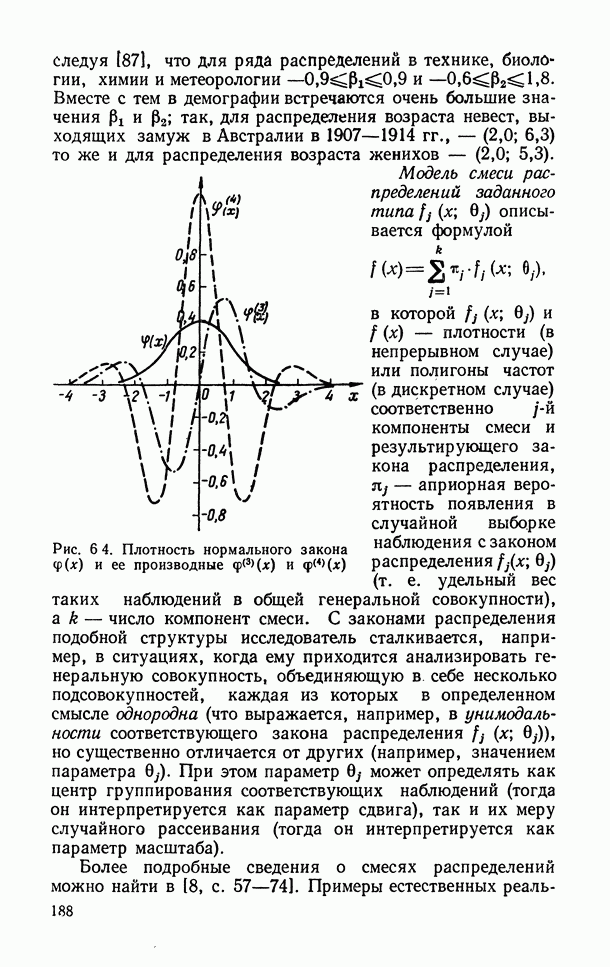
- 6.1.11. Некоторые комбинации основных модельных распределений, используемые в прикладной статистике.
- 6.2. Законы распределений вероятностей, используемые при реализации техники статистических вычислений
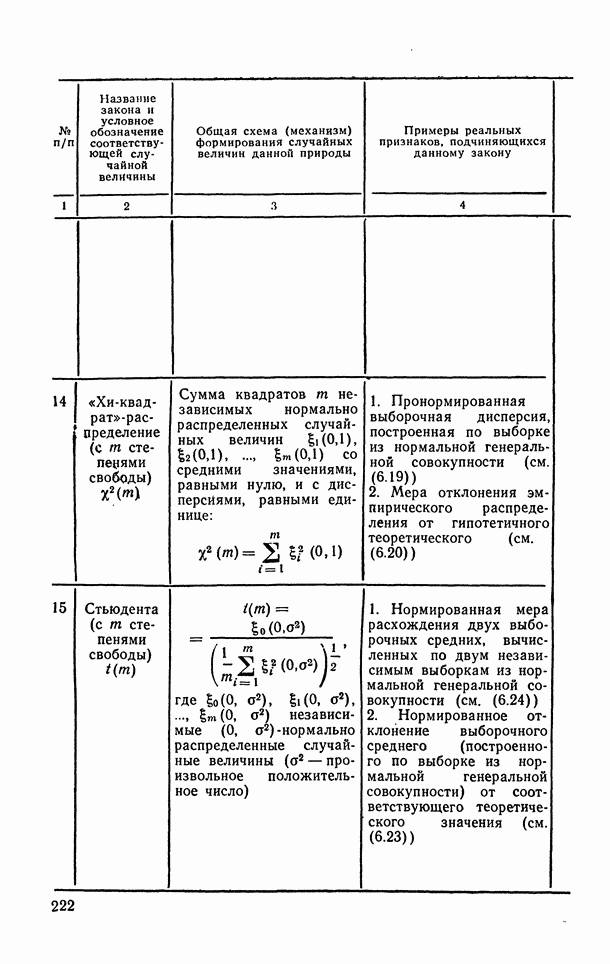
- 6.2.1. «хи квадрат»-распределение.
- 6.2.2. Распределение Стьюдента (t-распределение).
- 6.2.3. F-распределение (распределение дисперсионного отношения).
- 6.2.4. Замечание о нецентральных «хи-квадрат» и F- и t-распределениях.
- 6.2.5. Г-распределение.
- 6.2.6. В-распределение.
- 6.3. Техника статистического моделирования наблюдений, подчиняющихся заданному распределению
- 6.3.1. Получение равномерно распределенных на отрезке [0, 1] случайных чисел.
- 6.3.2. Моделирование дискретных случайных величин.
- Выводы
- Глава 7. ОСНОВНЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 7.1. Неравенство Чебышева
- 7.2. Свойство статистической устойчивости выборочных характеристик: закон больших чисел и его следствия
- 7.2.1. Закон больших чисел.
- 7.2.2. Теорема Я. Бернулли.
- 7.2.3 Статистическая устойчивость выборочных характеристик.
- 7.3. Особая роль нормального распределения: центральная предельная теорема
- 7.3.1. Центральная предельная теорема.
- 7.3.2. Многомерная центральная предельная теорема.
- 7.4. Закон распределения вероятностей случайных признаков, являющихся функциями от известных случайных величин
- Выводы
- Раздел III. ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- Глава 8. СТАТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- 8.1. Начальные сведения о задаче статистического оценивания параметров
- 8.1.2. Статистики, статистические оценки, их основные свойства.
- 8.1.3. Состоятельность.
- 8.1.4. Несмещенность.
- 8.1.5. Эффективность.
- 8.2. Функция правдоподобия. Количество информации, содержащееся в n независимых наблюдениях относительно неизвестного значения параметра
- 8.3. Неравенство Рао—Крамера—Фреше и измерение эффективности оценок
- 8.4. Асимптотические свойства оценок
- 8.5. Понятие об интервальном оценивании. Построение доверительных областей
- 8.6. Методы статистического оценивания неизвестных параметров
- 8.6.1. Метод максимального (наибольшего) правдоподобия.
- 8.6.2. Метод моментов.
- 8.6.3. Метод наименьших квадратов.
- 8.6.4. Оценивание с помощью «взвешенных» статистик; цензурирование, урезание выборок и порядковые статистики как частный случай взвешивания.
- 8.6.5. Построение интервальных оценок (доверительных областей).
- 8.6.6. Байесовский подход к статистическому оцениванию.
- Выводы
- Глава 9. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ (статистические критерии)
- 9.1. Основные типы гипотез, проверяемых в ходе статистической обработки данных
- 9.1.1. Гипотезы о типе закона распределения исследуемой случайной величины.
- 9.1.2. Гипотезы об однородности двух или нескольких обрабатываемых выборок или некоторых характеристик анализируемых совокупностей.
- 9.1.3. Гипотезы о числовых значениях параметров исследуемой генеральной совокупности.
- 9.1.4. Гипотезы о типе зависимости между компонентами исследуемого многомерного признака.
- 9.1.5. Гипотезы независимости и стационарности обрабатываемого ряда наблюдений.
- 9.2. Общая логическая схема статистического критерия
- 9.3. Построение статистического критерия; принцип отношения правдоподобия
- 9.3.1. Сущность принципа отношения правдоподобия.
- 9.3.2. Проверка простой гипотезы с помощью критерия логарифма отношения правдоподобия.
- 9.3.3. Проверка сложной гипотезы.
- 9.4. Характеристики «качества» статистического критерия
- 9.5. Последовательная схема принятия решения (последовательные критерии)
- 9.5.1. Последовательная схема наблюдений.
- 9.5.2. Последовательный критерий отношения правдоподобия (критерий Вальда) и его свойства.
- 9.5.3. Различение сложных гипотез в схеме обобщенного последовательного критерия.
- Выводы
- Раздел IV. ПЕРВИЧНАЯ СТАТИСТИЧЕСКАЯ ОБРАБОТКА ДАННЫХ
- 10.1. Документирование исследования; организация ввода и хранения данных в ЭВМ; просмотр данных
- 10.1.2. Ввод и хранение данных.
- 10.1.3. Просмотр данных.
- 10.2. Шкалы измерений
- 10.3. Изучение эмпирических распределений
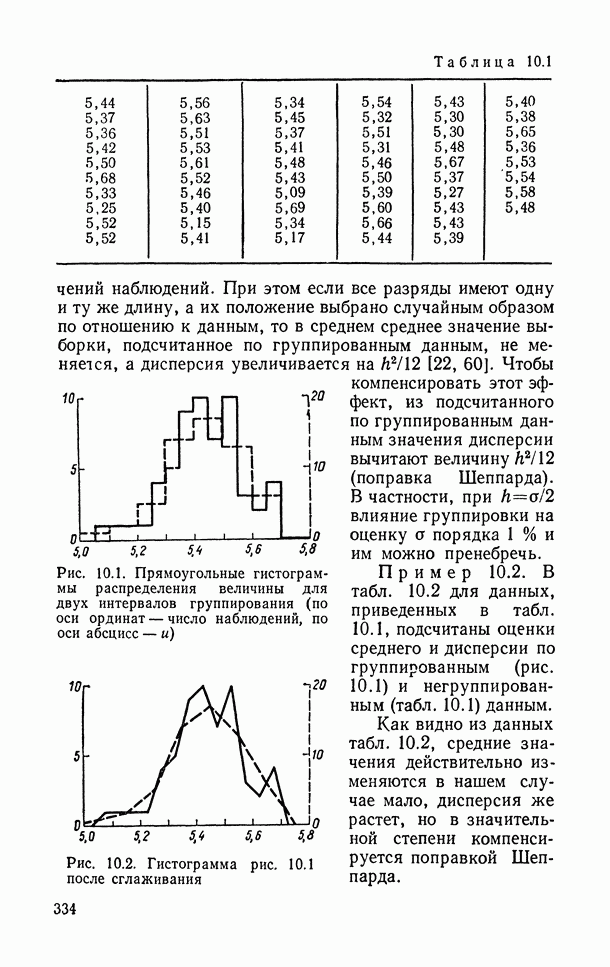
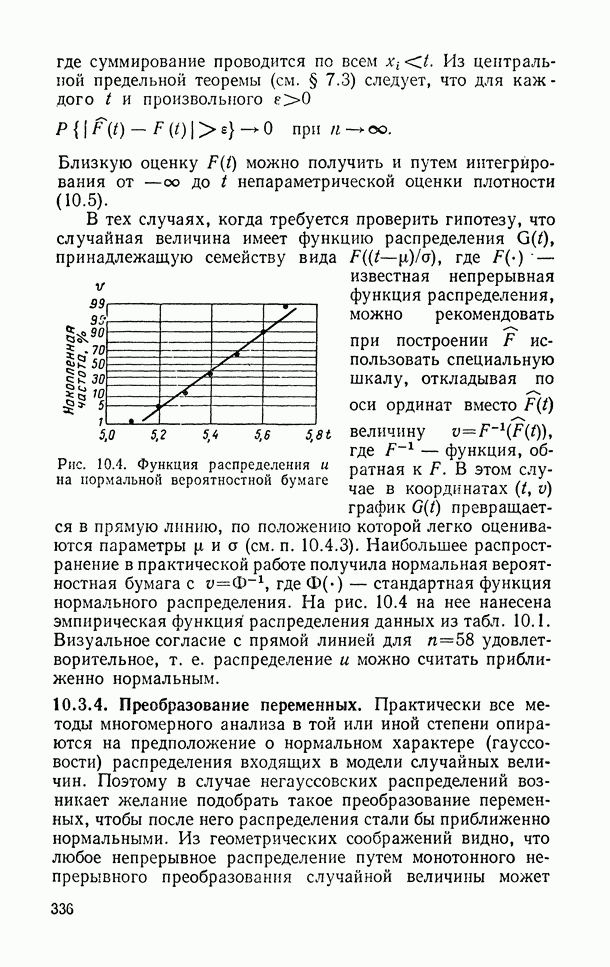
- 10.3.1. Гистограмма.
- 10.3.2. Непараметрические оценки плотности.
- 10.3.3. Оценки функции распределения.
- 10.3.4. Преобразование переменных.
- 10.3.5. Таблицы сопряженности.
- 10.4. Оценивание параметров сдвига и масштаба
- 10.4.2. Оценивание параметров нормального закона.
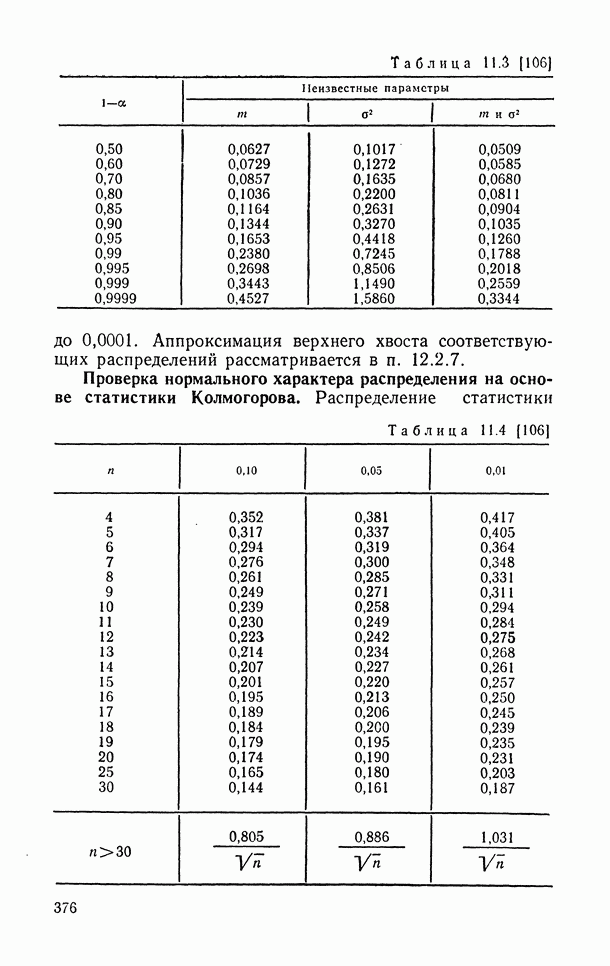
- 10.4.3. Графический метод оценивания.
- 10.4.4. Проблема устойчивости оценок при небольших отклонениях распределения от нормального.
- 10.4.5. Оценивание положения центра симметричных распределений.
- 10.4.6. Параметризация с помощью экспоненциально взвешенных оценок (ЭВ-оценки).
- 10.5. Визуализация многомерных данных
- 10.5.2. Главные компоненты.
- 10.5.3. Свойства наименьшего искажения геометрической структуры для главных компонент.
- 10.5.4, Нелинейные отображения в пространство малой размерности.
- 10.5.5. Многомерное метрическое шкалирование.
- Выводы
- Глава 11. ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ ПРИРОДЫ ДАННЫХ
- 11.1. Проверка соответствия выбранной модели распределения исходным данным (критерии согласия)
- 11.1.1. Критерий «хи-квадрат» Пирсона.
- 11.1.2. Проверка нормального характера распределения по асимметрии, эксцессу и средним отклонениям.
- 11.1.3. Критерий Колмогорова — Смирнова и его применение к построению доверительных границ для неизвестной функции распределения.
- 11.1.4. Критерий Крамера — Мизеса — Смирнова.
- 11.1.5. Модификация статистик критериев Колмогорова — Смирнова и для выборок небольшого объема.
- 11.1.6. Статистическая техника практической реализации непараметрических критериев согласия.
- ll.1.7. Использование критериев согласия Колмогорова и «w-квадрат» в случае неизвестных параметров для проверки гипотезы о нормальном характере распределения.
- 11.2. Проверка гипотез однородности и симметрии распределения
- 11.2.1. Критерии однородности, основанные на эмпирических функциях распределения.
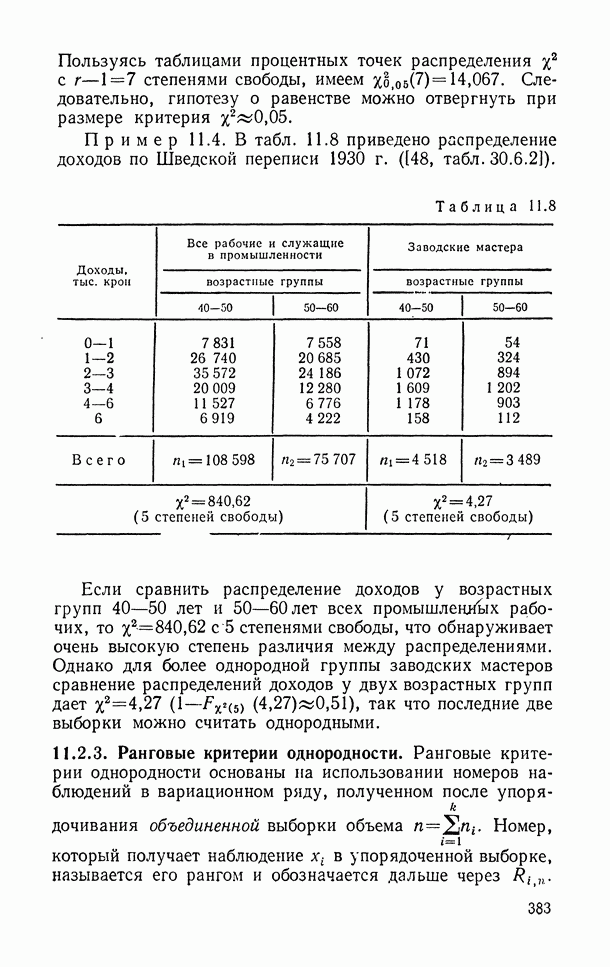
- 11.2.2. Критерий однородности «хи-квадрат»
- 11.2.3. Ранговые критерии однородности.
- 11.2.4. Непараметрическая проверка гипотезы равенства дисперсий.
- 11.2.5. Ранговые критерии для случая k > 2 классов.
- 11.2.6. Критерии проверки симметрии распределений.
- 11.2.7. Обработка совпадений.
- 11.2.8. Критерии однородности нормальных совокупностей (одномерный случай).
- 11.2.9. Критерии однородности многомерных нормальных совокупностей.
- 11.3. Проверка независимости и стационарности ряда наблюдений
- 11.3.1. Критерий серий, основанный на медиане выборки.
- 11.3.2. Критерий «восходящих» и «нисходящих» серий.
- 11.3.3. Критерий квадратов последовательных разностей (критерий Аббе).
- 11.4. Методы статистической обработки при наличии «стертых» (пропущенных) наблюдений
- 11.4.1. Оценивание неизвестных параметров при наличии пропущенных данных.
- 11.4.2. Использование главных компонент.
- 11.4.3. Заполнение «пропусков» и оценивание параметров с помощью метода максимального правдоподобия. Оценки «неподвижной точки».
- 11.4.4. Непараметрический подход к оценке пропусков в матрице данных.
- 11.5. Анализ резко выделяющихся наблюдений
- 11.5.2 Графические методы.
- 11.5.3. Аналитический метод исключения одного экстремального наблюдения.
- 11.5.4. Аналитический критерий одновременного исключения нескольких экстремальных наблюдений.
- Выводы
- Глава 12. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ И НЕКОТОРЫЕ ВОПРОСЫ ТЕХНИКИ ВЫЧИСЛЕНИЙ
- 12.1. Программное обеспечение прикладной статистики
- 12.1.1. Организация пакетов программ.
- 12.1.2. Вопросы организации возможности ведения данных.
- 12.1.3. Средства предварительной обработки (манипуляции) данных.
- 12.1.4. Возможности обработки данных при наличии пропущенных значений.
- 12.1.5. Первичная обработка неколичественных данных.
- 12.1.6. Средства визуализации данных.
- 12.1.7. Оценивание параметров и выделение аномальных наблюдений.
- 12.2. Вычисление функций распределения и обратных к ним
- 12.2.1. Нормальное распределение.
- 12.2.2. Распределение «хи-квадрат».
- 12.2.3. Бета-распределение.
- 12.2.4. F-распределение.
- 12.2.5. t-распределение Стьюдента.
- 12.2.6. Нецентральные распределения.
- 12.2.7. Аппроксимация «хвостов» распределений типа «w-квадрат»
- 12.2.8. Многомерное нормальное распределение.
- 12.2.9. Дискретные распределения.
- 12.2.10. Вычисление математического ожидания порядковых статистик.
- Выводы
- ИСПОЛЬЗУЕМЫЕ В КНИГЕ ОБОЗНАЧЕНИЯ
- СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ