| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.1.3. Вероятностное пространство. Вероятности и правила действия с ними.
Для полного описания механизма исследуемого случайного эксперимента недостаточно задать лишь пространство элементарных событий. Очевидно, наряду с перечислением всех возможных исходов исследуемого случайного эксперимента мы должны также знать, как часто в длинной серии таких экспериментов могут происходить те или другие элементарные события. Действительно, возвращаясь, скажем, к примерам 4.1-4.7, легко представить себе, что в рамках каждого из описанных в них пространств элементарных событий можно рассмотреть бесчисленное множество случайных экспериментов, существенно различающихся по своему механизму.
Так, в примерах 4.1-4.3 мы будем иметь существенно различающиеся относительные частоты появления одних и тех же элементарных исходов, если будем пользоваться различными моментами и игральными костями (симметричными, со слегка смещенным центром тяжести, с сильно смещенным центром тяжести и т. п.) В примерах 4.4-4.7 частота появления дефектных изделий, характер засоренности дефектными изделиями проконтролированных партий и частоты появления определенного числа сбоев станков автоматической линии будут зависеть от уровня технологической оснащенности изучаемого производства: при одном и том же пространстве элементарных событий частота появления «хороших» элементарных исходов будет выше в производстве с более высоким уровнем технологии.
Для построения (в дискретном случае) полной и законченной математической теории случайного эксперимента — теории вероятностей помимо уже введенных исходных понятий случайного эксперимента, элементарного исхода и случайного события необходимо запастись еще одним исходным допущением (аксиомой), постулирующим существование вероятностей элементарных событий (удовлетворяющих определенной нормировке), и определением вероятности любого случайного события.
Аксиома.
Каждому элементу пространства элементарных событий
пространства элементарных событий  соответствует некоторая неотрицательная числовая характеристика
соответствует некоторая неотрицательная числовая характеристика  шансов его появления, называемая вероятностью события
шансов его появления, называемая вероятностью события  , причем
, причем

(отсюда, в частности, следует, что  для всех
для всех  ).
).
Определение вероятности события.
Вероятность любого события А определяется как сумма вероятностей всех элементарных событий, составляющих событие А, т. е. если использовать символику для обозначения «вероятности события А», то
для обозначения «вероятности события А», то

Отсюда и из (4.2) непосредственно следует, что всегда  причем вероятность достоверного события равна единице, а вероятность невозможного события равна нулю.
причем вероятность достоверного события равна единице, а вероятность невозможного события равна нулю.
Все остальные понятия и правила действий с вероятностями и событиями будут уже производными от введенных выше четырех исходных определений (случайного эксперимента, элементарного исхода, случайного события и его вероятности) и одной аксиомы.
Таким образом, для исчерпывающего описания механизма исследуемого случайного эксперимента (в дискретном случае) необходимо задать конечное или счетное множество всех возможных элементарных исходов  и каждому элементарному исходу
и каждому элементарному исходу  поставить в соответствие некоторую неотрицательную (не превосходящую единицы) числовую характеристику
поставить в соответствие некоторую неотрицательную (не превосходящую единицы) числовую характеристику  интерпретируемую как вероятность появления исхода
интерпретируемую как вероятность появления исхода  причем установленное соответствие типа
причем установленное соответствие типа  должно удовлетворять требованию нормировки (4.2).
должно удовлетворять требованию нормировки (4.2).
Вероятностное пространство как раз и является понятием, формализующим такое описание механизма случайного эксперимента. Задать вероятностное пространство — это значит задать пространство элементарных событий Q и определить в нем вышеуказанное соответствие типа

Очевидно, соответствие типа (4.4) может быть задано различными способами: с помощью таблиц, графиков, аналитических формул, наконец, алгоритмически.
Как же построить вероятностное пространство, соответствующее исследуемому реальному комплексу условий? С наполнением конкретным содержанием понятий случайного эксперимента, элементарного события, пространства элементарных событий, а в дискретном случае — и любого разложимого случайного события затруднений, как правило, не бывает. А вот определить из конкретных условий решаемой задачи вероятности  отдельных элементарных событий не так-то просто! С этой целью используется один из следующих трех подходов.
отдельных элементарных событий не так-то просто! С этой целью используется один из следующих трех подходов.
Априорный подход к вычислению вероятностей  заключается в теоретическом, умозрительном анализе специфических условий данного конкретного случайного эксперимента (до проведения самого эксперимента). В ряде ситуаций этот предопытный анализ позволяет теоретически обосновать способ определения искомых вероятностей.
заключается в теоретическом, умозрительном анализе специфических условий данного конкретного случайного эксперимента (до проведения самого эксперимента). В ряде ситуаций этот предопытный анализ позволяет теоретически обосновать способ определения искомых вероятностей.
Например, возможен случай, когда пространство всех возможных элементарных исходов состоит из конечного числа N элементов, причем условия производства исследуемого случайного эксперимента таковы, что вероятности осуществления каждого из этих N элементарных исходов нам представляются равными (именно в такой ситуации мы находимся при подбрасывании симметричной монеты, бросании правильной игральной кости, случайном извлечении игральной карты из хорошо перемешанной колоды и т. п.). В силу аксиомы (4.2) вероятность каждого элементарного события равна в этом случае MN. Это позволяет получить простой рецепт и для подсчета вероятности любого события: если событие А содержит NA элементарных событий, то в соответствии с определением (4.3)

Смысл формулы (4.3) состоит в том, что вероятность события в данном классе ситуаций может быть определена как отношение числа благоприятных исходов (т. е. элементарных исходов, входящих в это событие) к числу всех возможных исходов (так называемое классическое определение вероятности). В современной трактовке формула (4.3) не является определением вероятности: она применима лишь в том частном случае, когда все элементарные исходы равновероятны.
Апостериорно-частотный подход к вычислению вероятностей  отталкивается, по существу, от определения вероятности, принятого так называемой частотной концепцией вероятности (подробнее об этой концепции см., например, в [48], [51]). В соответствии с этой концепцией вероятность
отталкивается, по существу, от определения вероятности, принятого так называемой частотной концепцией вероятности (подробнее об этой концепции см., например, в [48], [51]). В соответствии с этой концепцией вероятность  определяется как предел относительной частоты появления исхода
определяется как предел относительной частоты появления исхода  в процессе неограниченного увеличения общего числа случайных экспериментов
в процессе неограниченного увеличения общего числа случайных экспериментов  т. е.
т. е.
 (4.5)
(4.5)
где  — число случайных экспериментов (из общего числа
— число случайных экспериментов (из общего числа  произведенных случайных экспериментов), в которых зарегистрировано появление элементарного события
произведенных случайных экспериментов), в которых зарегистрировано появление элементарного события  Соответственно для практического (приближенного) определения вероятностей
Соответственно для практического (приближенного) определения вероятностей  предлагается брать относительные частоты появления события
предлагается брать относительные частоты появления события  в достаточно длинном ряду случайных экспериментов
в достаточно длинном ряду случайных экспериментов
Подобный способ вычисления вероятностей  не противоречит современной (аксиоматической) концепции теории вероятностей, поскольку последняя построена таким образом, что эмпирическим (или выборочным) аналогом объективно существующей вероятности
не противоречит современной (аксиоматической) концепции теории вероятностей, поскольку последняя построена таким образом, что эмпирическим (или выборочным) аналогом объективно существующей вероятности  любого события А является относительная частота осуществления этого события в ряду из
любого события А является относительная частота осуществления этого события в ряду из  независимых испытаний. Разными в этих двух концепциях оказываются определения вероятностей: в соответствии с частотной концепцией вероятность не является объективным, существующим до опыта, свойством изучаемого явления, а появляется только в связи с проведением опыта или наблюдения; это приводит к смешению теоретических (истинных, обусловленных реальным комплексом условий «существования» исследуемого явления) вероятностных характеристик и их эмпирических (выборочных) аналогов. Как пишет Г. Крамер, «указанное определение вероятности можно сравнить, например, с определением геометрической точки как предела пятен мела неограниченно убывающих размеров, но подобного определения современная аксиоматическая геометрия не вводит» ([48, с. 172]). Мы не будем здесь останавливаться на математических изъянах частотной концепции вероятности. Отметим лишь принципиальные сложности реализации вычислительного приема получения приближенных значений
независимых испытаний. Разными в этих двух концепциях оказываются определения вероятностей: в соответствии с частотной концепцией вероятность не является объективным, существующим до опыта, свойством изучаемого явления, а появляется только в связи с проведением опыта или наблюдения; это приводит к смешению теоретических (истинных, обусловленных реальным комплексом условий «существования» исследуемого явления) вероятностных характеристик и их эмпирических (выборочных) аналогов. Как пишет Г. Крамер, «указанное определение вероятности можно сравнить, например, с определением геометрической точки как предела пятен мела неограниченно убывающих размеров, но подобного определения современная аксиоматическая геометрия не вводит» ([48, с. 172]). Мы не будем здесь останавливаться на математических изъянах частотной концепции вероятности. Отметим лишь принципиальные сложности реализации вычислительного приема получения приближенных значений  с помощью относительных частот
с помощью относительных частот  . Во-первых, сохранение неизменными условий случайного эксперимента (т. е. сохранение условий статистического ансамбля), при котором оказывается справедливым допущение о тенденции относительных частот группироваться вокруг постоянного значения, не может поддерживаться неограниченно долго и с высокой точностью. Поэтому для оценки вероятностей
. Во-первых, сохранение неизменными условий случайного эксперимента (т. е. сохранение условий статистического ансамбля), при котором оказывается справедливым допущение о тенденции относительных частот группироваться вокруг постоянного значения, не может поддерживаться неограниченно долго и с высокой точностью. Поэтому для оценки вероятностей  с помощью относительных частот
с помощью относительных частот  не имеет смысла брать слишком длинные ряды (т. е. слишком большие
не имеет смысла брать слишком длинные ряды (т. е. слишком большие  ) и потому же, кстати, точный переход к пределу (4.5) не может иметь реального смысла.
) и потому же, кстати, точный переход к пределу (4.5) не может иметь реального смысла.
Во-вторых, в ситуациях, когда мы имеем достаточно большое число возможных элементарных исходов (а они могут образовывать и бесконечное, и даже, как это было уже отмечено в § 4.1, континуальное множество), даже в сколь угодно длинном ряду случайных экспериментов мы будем иметь возможные исходы  ни разу не осуществившиеся в ходе нашего эксперимента; да и по остальным возможным исходам полученные с помощью относительных частот приближенные значения вероятностей будут в этих условиях крайне мало надежными.
ни разу не осуществившиеся в ходе нашего эксперимента; да и по остальным возможным исходам полученные с помощью относительных частот приближенные значения вероятностей будут в этих условиях крайне мало надежными.
Апостериорно-модельный подход к заданию вероятностей  отвечающему конкретно исследуемому реальному комплексу условий, является в настоящее время, пожалуй, наиболее распространенным и наиболее практически удобным. Логика этого подхода следующая. С одной стороны, в рамках априорного подхода, т. е. в рамках теоретического, умозрительного анализа возможных вариантов специфики гипотетичных реальных комплексов условий разработан и исследован набор модельных вероятностных пространств (биномиальное, пуассоновское, нормальное, показательное и т. п., см. § 6.1). С другой стороны, исследователь располагает результатами ограниченного ряда случайных экспериментов. Далее с помощью специальных математико-статистических приемов (основанных на методах статистического оценивания неизвестных параметров и статистической проверки гипотез, см. гл. 8 и 9) исследователь как бы «прилаживает» гипотетичные модели вероятностных пространств к имеющимся у него результатам наблюдения (отражающим специфику изучаемой реальной действительности) и оставляет для дальнейшего использования лишь ту модель или те модели, которые не противоречат этим результатам и в некотором смысле наилучшим образом им соответствуют.
отвечающему конкретно исследуемому реальному комплексу условий, является в настоящее время, пожалуй, наиболее распространенным и наиболее практически удобным. Логика этого подхода следующая. С одной стороны, в рамках априорного подхода, т. е. в рамках теоретического, умозрительного анализа возможных вариантов специфики гипотетичных реальных комплексов условий разработан и исследован набор модельных вероятностных пространств (биномиальное, пуассоновское, нормальное, показательное и т. п., см. § 6.1). С другой стороны, исследователь располагает результатами ограниченного ряда случайных экспериментов. Далее с помощью специальных математико-статистических приемов (основанных на методах статистического оценивания неизвестных параметров и статистической проверки гипотез, см. гл. 8 и 9) исследователь как бы «прилаживает» гипотетичные модели вероятностных пространств к имеющимся у него результатам наблюдения (отражающим специфику изучаемой реальной действительности) и оставляет для дальнейшего использования лишь ту модель или те модели, которые не противоречат этим результатам и в некотором смысле наилучшим образом им соответствуют.
Опишем теперь основные правила действий с вероятностями событий, являющиеся следствиями принятых выше определений и аксиомы.
Вероятность суммы событий (теорема сложения вероятностей).
Сформулируем и докажем правило вычисления вероятности суммы двух событий  .
.
Для этого разобьем каждое из множеств элементарных событий, составляющих события  на две части:
на две части:

где  объединяет все элементарные события со, входящие в
объединяет все элементарные события со, входящие в  но не входящие в
но не входящие в  состоит из всех тех элементарных событий, которые одновременно входят и в
состоит из всех тех элементарных событий, которые одновременно входят и в  Пользуясь определением (4.3) и определением произведения событий
Пользуясь определением (4.3) и определением произведения событий  имеем:
имеем:

В то же время в соответствии с определением суммы событий  и с (4.3) имеем
и с (4.3) имеем

Из (4.6), (4.7) и (4.8) получаем формулу сложения вероятностей (для двух событий):

Формула (4.9) сложения вероятностей может быть обобщена на случай произвольного числа слагаемых (см., например, [83, с. 105]):

где «добавки»  вычисляются в форме суммы вероятностей вида
вычисляются в форме суммы вероятностей вида

причем суммирование в правой части производится, очевидно, при условии, что все  различны, a
различны, a  .
.
В частном случае, когда интересующая нас система  состоит лишь из несовместных событии, все произведения вида
состоит лишь из несовместных событии, все произведения вида  будут пустыми (или невозможными) событиями и соответственно формула (4.9) дает
будут пустыми (или невозможными) событиями и соответственно формула (4.9) дает

Вероятность произведения событий (теорема умножения вероятностей). Условная вероятность.
Рассмотрим ситуации, когда заранее поставленное условие или фиксация некоторого уже осуществившего события исключают из числа возможных часть элементарных событий анализируемого вероятностного пространства. Так, анализируя совокупность из N изделий массового производства, содержащую  изделий первого,
изделий первого,  — второго,
— второго,  — третьего и
— третьего и  — четвертого сорта
— четвертого сорта  мы рассматриваем вероятностное пространство с элементарными исходами
мы рассматриваем вероятностное пространство с элементарными исходами  и их вероятностями — соответственно
и их вероятностями — соответственно  (здесь
(здесь  означает событие, заключающееся в том, что наугад извлеченное из совокупности изделие оказалось
означает событие, заключающееся в том, что наугад извлеченное из совокупности изделие оказалось  сорта). Предположим, условия сортировки изделий таковы, что на каком-то этапе изделия первого сорта отделяются от общей совокупности и все вероятностные выводы
сорта). Предположим, условия сортировки изделий таковы, что на каком-то этапе изделия первого сорта отделяются от общей совокупности и все вероятностные выводы  в частности, подсчет вероятностей различных событий) нам предстоит строить применительно к урезанной совокупности, состоящей только из изделий второго, третьего и четвертого сорта. В таких случаях принято говорить об условных вероятностях, т. е. о вероятностях, вычисленных при условии уже осуществленного некоторого события. В данном случае таким осуществленным событием является событие
в частности, подсчет вероятностей различных событий) нам предстоит строить применительно к урезанной совокупности, состоящей только из изделий второго, третьего и четвертого сорта. В таких случаях принято говорить об условных вероятностях, т. е. о вероятностях, вычисленных при условии уже осуществленного некоторого события. В данном случае таким осуществленным событием является событие  , т. е. событие, заключающееся в
, т. е. событие, заключающееся в  любое наугад извлеченное изделие является либо второго, либо третьего, либо четвертого сорта. Поэтому, если нас интересует подсчет условной вероятности события А (при условии, что событие В уже имеет место), заключающегося, например, в том, что наугад извлеченное изделие окажется второго или третьего сорта, то, очевидно, эта условная вероятность (обозначим ее
любое наугад извлеченное изделие является либо второго, либо третьего, либо четвертого сорта. Поэтому, если нас интересует подсчет условной вероятности события А (при условии, что событие В уже имеет место), заключающегося, например, в том, что наугад извлеченное изделие окажется второго или третьего сорта, то, очевидно, эта условная вероятность (обозначим ее  ) может быть определена следующим соотношением:
) может быть определена следующим соотношением:

Как легко понять из этого примера, подсчет условных вероятностей — это, по существу, переход в другое, урезанное заданным условием В пространство элементарных событий, когда соотношение вероятностей элементарных событий в урезанном пространстве остается тем же, что и в исходном (более широком), но все они нормируются (делятся на  ) для того, чтобы и в новом вероятностном пространстве выполнялось требование нормировки (4.2). Конечно, можно было бы не вводить терминологии с условными вероятностями, а просто использовать аппарат обычных («безусловных») вероятностей в новом пространстве. Запись в терминах вероятностей «старого» пространства бывает полезной в тех случаях, когда по условиям конкретной задачи мы должны все время помнить о существовании исходного, более широкого пространства элементарных событий.
) для того, чтобы и в новом вероятностном пространстве выполнялось требование нормировки (4.2). Конечно, можно было бы не вводить терминологии с условными вероятностями, а просто использовать аппарат обычных («безусловных») вероятностей в новом пространстве. Запись в терминах вероятностей «старого» пространства бывает полезной в тех случаях, когда по условиям конкретной задачи мы должны все время помнить о существовании исходного, более широкого пространства элементарных событий.
Получим формулу условной вероятности в общем случае. Пусть В — событие (непустое), считающееся уже состоявшимся («условие»), а А — событие, условную вероятность которого Р(А|В) требуется вычислить. Новое (урезанное) пространство элементарных событий  состоит только из элементарных событий, входящих в В, и, следовательно, их вероятности (с условием нормировки (4.2)) определяются соотношениями
состоит только из элементарных событий, входящих в В, и, следовательно, их вероятности (с условием нормировки (4.2)) определяются соотношениями

По определению, вероятность Р(А|В) — это вероятность события А в «урезанном» вероятностном пространстве  , и, следовательно, в соответствии с (4.3) и (4.10)
, и, следовательно, в соответствии с (4.3) и (4.10)

т. е.

или, что то же,

Эквивалентные формулы (4.11) и (4.11') принято называть соответственно формулой условной вероятности и правилом умножения вероятностей.
Еще раз подчеркнем, что рассмотрение условных вероятностей различных событий при одном и том же условии В равносильно рассмотрению обычных вероятностей в другом (урезайном) пространстве элементарных событий  пересчетом соответствующих вероятностей элементарных событий по формуле (4.10). Поэтому все общие теоремы и правила действий с вероятностями остаются в силе и для условных вероятностей, если эти условные вероятности берутся при одном и том же условии.
пересчетом соответствующих вероятностей элементарных событий по формуле (4.10). Поэтому все общие теоремы и правила действий с вероятностями остаются в силе и для условных вероятностей, если эти условные вероятности берутся при одном и том же условии.
Независимость событий. Два события А и В называют независимыми, если

Для пояснения естественности такого определения вернемт. е.ся к теореме умножения вероятностей (4.11) и посмотрим, в каких ситуациях из нее следует (4.12). Очевидно, это может быть тогда, когда условная вероятность  равна соответствующей безусловной вероятности
равна соответствующей безусловной вероятности  , т.е., грубо говоря, тогда, когда знание того, что произошло событие
, т.е., грубо говоря, тогда, когда знание того, что произошло событие  никак не влияет на оценку шансов появления события А.
никак не влияет на оценку шансов появления события А.
Распространение определения независимости на систему более чем двух событий выглядит следующим образом. События  называются взаимно независимыми, если для любых пар, троек, четверок и т.д. событий, отобранных от этого набора событий, справедливы следующие правила умножения:
называются взаимно независимыми, если для любых пар, троек, четверок и т.д. событий, отобранных от этого набора событий, справедливы следующие правила умножения:

Очевидно, в первой строке подразумевается

(число сочетаний из k по два) уравнений, во второй —  и т. д. Всего, следовательно, (4.13) объединяет
и т. д. Всего, следовательно, (4.13) объединяет  условий. В то же время
условий. В то же время  условий первой строки достаточно для обеспечения попарной независимости этих событий. И хотя попарная и взаимная независимость системы событий, строго говоря, не одно и то же, их различие представляет скорее теоретический, чем практический интерес: практически важных примеров попарно независимых событий, не являющихся взаимно независимыми, по-видимому, не существует.
условий первой строки достаточно для обеспечения попарной независимости этих событий. И хотя попарная и взаимная независимость системы событий, строго говоря, не одно и то же, их различие представляет скорее теоретический, чем практический интерес: практически важных примеров попарно независимых событий, не являющихся взаимно независимыми, по-видимому, не существует.
Свойство независимости событий сильно облегчает анализ различных вероятностей, связанных с исследуемой системой событий. Достаточно сказать, что если в общем случае для описания вероятностей всевозможных комбинаций событий системы  нужно задать 2 вероятностей, то в случае взаимной независимости этих событий достаточно лишь k вероятностей
нужно задать 2 вероятностей, то в случае взаимной независимости этих событий достаточно лишь k вероятностей 
Независимые события весьма часто встречаются в изучаемой реальной действительности они осуществляются в экспериментах (наблюдениях), проводимых независимо друг от друга в обычном физическом смысле.
Именно свойство независимости исходов четырех последовательных бросаний игральной кости позволило (с помощью  ) легко подсчитать вероятность невыпадения (ни при одном из этих бросаний) шестерки в задаче п. 2.2.1. Действительно, обозначив
) легко подсчитать вероятность невыпадения (ни при одном из этих бросаний) шестерки в задаче п. 2.2.1. Действительно, обозначив  событие, заключающееся в невыпадении шестерки в
событие, заключающееся в невыпадении шестерки в  бросании
бросании  , и учитывая, что
, и учитывая, что  для всех
для всех  получаем
получаем

Формула полной вероятности.
При решении многих практических задач зачастую сталкиваются с ситуацией, когда прямое вычисление вероятности интересующего нас события А трудно или невозможно, в то время как вполне доступно вычисление (или задание) условных вероятностей того же события (при различных условиях).
В случае, когда условия  при которых известны (или легко вычисляемы) условные вероятности события А, образуют полную систему событий (см. п. 4.1.2), для подсчета вероятности
при которых известны (или легко вычисляемы) условные вероятности события А, образуют полную систему событий (см. п. 4.1.2), для подсчета вероятности  можно использовать соотношение
можно использовать соотношение

которое принято называть формулой полной вероятности.
Для доказательства формулы (4.14) заметим, что элементарные события, составляющие событие А, можно разбить на k непересекающихся групп, каждая из которых является общей частью (пересечением) события А с одним из событий  (эта возможность непосредственно вытекает из того, что события
(эта возможность непосредственно вытекает из того, что события  исчерпывают в сумме все пространство элементарных событий и попарно не пересекаются), т. е.
исчерпывают в сумме все пространство элементарных событий и попарно не пересекаются), т. е.

Далее, воспользовавшись теоремой сложения вероятностей  (применительно к несовместным событиям, каковыми являются события
(применительно к несовместным событиям, каковыми являются события  ) и вычислив вероятность каждого из произведений
) и вычислив вероятность каждого из произведений  по формуле произведения вероятностей (4.11'), мы и получаем (4.14).
по формуле произведения вероятностей (4.11'), мы и получаем (4.14).
Формула Байеса.
Обратимся вначале к следующей задаче. На складе имеются приборы, изготовленные тремя заводами: 20 % приборов, имеющихся на складе, изготовлено заводом № 1, 50 % — заводом № 2 и 30 % — заводом № 3. Вероятности того, что в течение гарантийного срока прибору потребуется ремонт, для продукции каждого из заводов равны соответственно 0,2; 0,1; 0,3. Взятый со склада прибор не имел заводской маркировки и потребовал ремонта (в течение гарантийного срока). Каким заводом вероятнее всего был изготовлен этот прибор? Какова эта вероятность? Если обозначить  событие, заключающееся в том, что случайно взятый со склада прибор оказался изготовленным на
событие, заключающееся в том, что случайно взятый со склада прибор оказался изготовленным на  заводе
заводе  , а В — событие, заключающееся в том, что наугад отобранный от продукции всех трех заводов прибора оказался дефектным (потребовал ремонта), то сформулированная выше задача, очевидно, сводится к вычислению условных вероятностей
, а В — событие, заключающееся в том, что наугад отобранный от продукции всех трех заводов прибора оказался дефектным (потребовал ремонта), то сформулированная выше задача, очевидно, сводится к вычислению условных вероятностей  по заданным вероятностям
по заданным вероятностям  Поскольку события
Поскольку события  образуют полную систему, воспользуемся для выражения искомых вероятностей
образуют полную систему, воспользуемся для выражения искомых вероятностей  известными нам основными правилами действий с вероятностями.
известными нам основными правилами действий с вероятностями.
По формуле условной вероятности (4.11)

Числитель этой дроби по теореме умножения вероятностей (4.11) может быть представлен в виде

а знаменатель  выражается с помощью формулы полной вероятности (4.14):
выражается с помощью формулы полной вероятности (4.14):

Подставляя (4.16) и (4.17) в (4.15), получаем

Воспользовавшись этой формулой, нетрудно подсчитать искомые вероятности:

Следовательно, вероятнее всего некондиционный прибор был изготовлен на заводе № 3.
Доказательство формулы (4.18) в случае полной системы событий, состоящей из произвольного числа k событий, в точности повторяет доказательство формулы (4.18). В таком общем виде формулу

принято называть формулой Байеса.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Раздел I. ПРИКЛАДНАЯ СТАТИСТИКА: ЕЕ СУЩНОСТЬ И НАЗНАЧЕНИЕ (общие методические принципы)
- Глава 1. ПРИКЛАДНАЯ СТАТИСТИКА КАК САМОСТОЯТЕЛЬНАЯ НАУЧНАЯ ДИСЦИПЛИНА
- 1.2. Оптимизационная формулировка основных задач прикладной статистики и проблема устойчивости статистического вывода
- 1.2.1. Связь между оптимизационной формулировкой основных задач прикладной статистики и проблемой устойчивости статистического вывода.
- 1.2.2. Проблема статистического исследования зависимостей между анализируемыми показателями.
- 1.2.3. Проблема классификации объектов или признаков.
- 1.2.4. Снижение размерности исследуемого факторного пространства и отбор наиболее информативных признаков.
- Выводы
- Глаза 2. ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 2.1.1. Статистический ансамбль и «игра случая».
- 2.1.2. Теория вероятностей и условия статистического ансамбля.
- 2.1.3. Основные типы реальных ситуаций с позиций соблюдения условий статистического ансамбля.
- 2.2. «Взаимоотношения» теории вероятностей и математической статистики
- 2.2.2. Теоретико-вероятностный способ решения.
- 2.2.3. Вероятностно-статистический (или математико-статистический) способ принятия решения.
- ВЫВОДЫ
- Глава 3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ПРИКЛАДНОЙ СТАТИСТИКЕ
- 3.1.1. О двух подходах к статистическому моделированию.
- 3.1.2. Понятие математической модели.
- 3.2. Общая логическая схема и основные этапы содержательного математического моделирования
- 3.2.2. Моделирование механизма явления вместо формальной статистической фотографии.
- 3.3. Понятие о статистическом моделировании
- 3.4. Возражения против математических моделей
- 3.5. Наиболее распространенные типы математических моделей, используемых в прикладной статистике
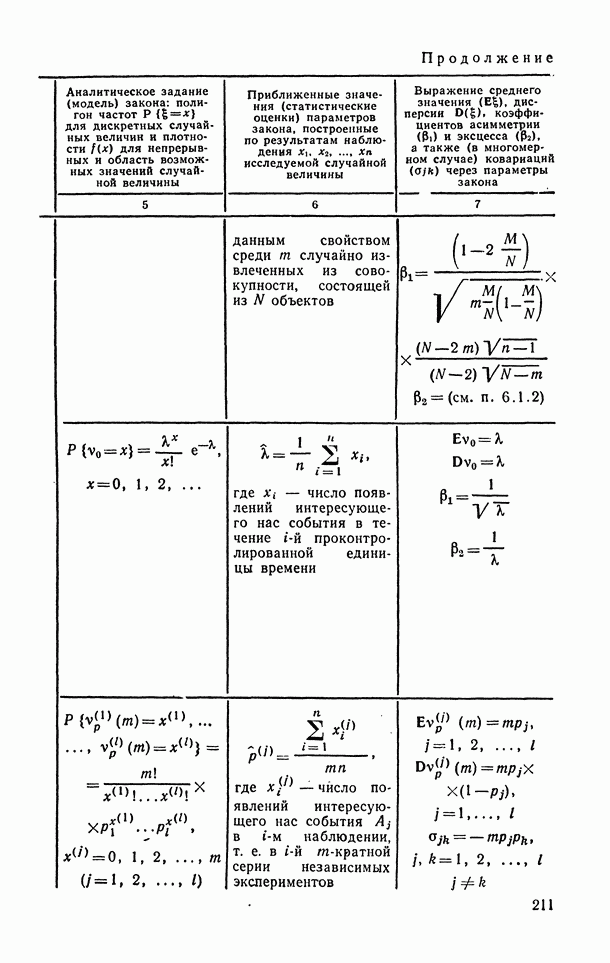
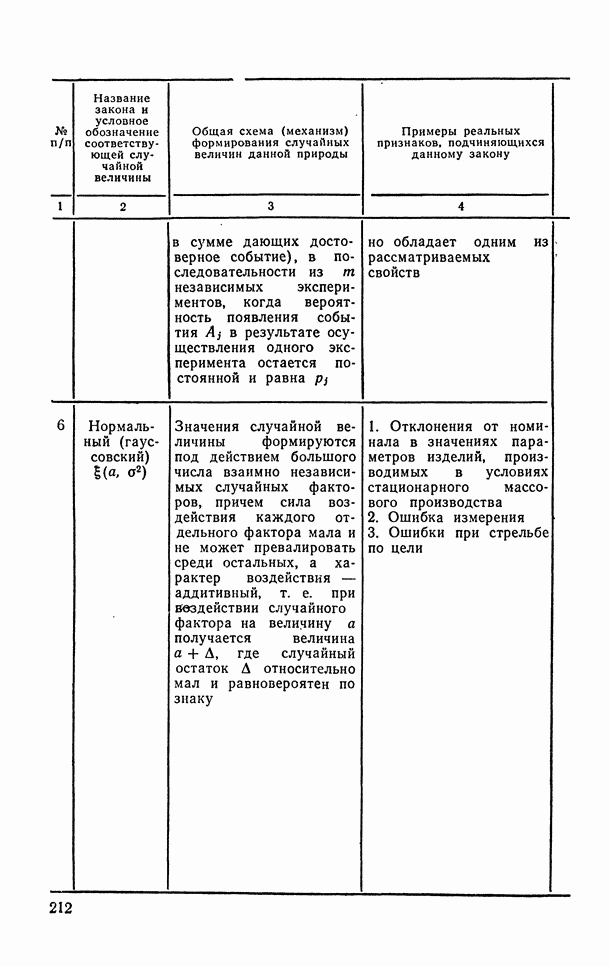
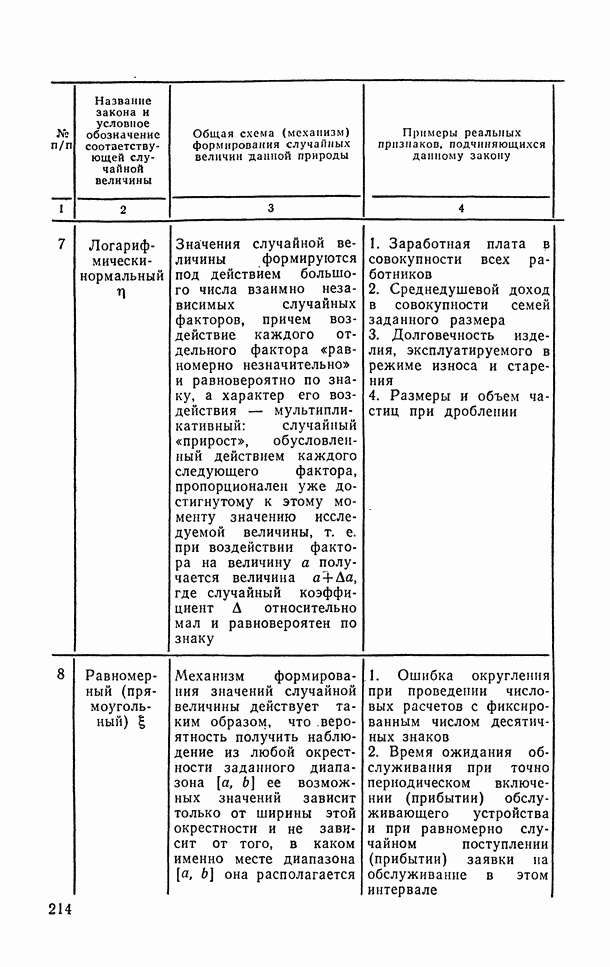
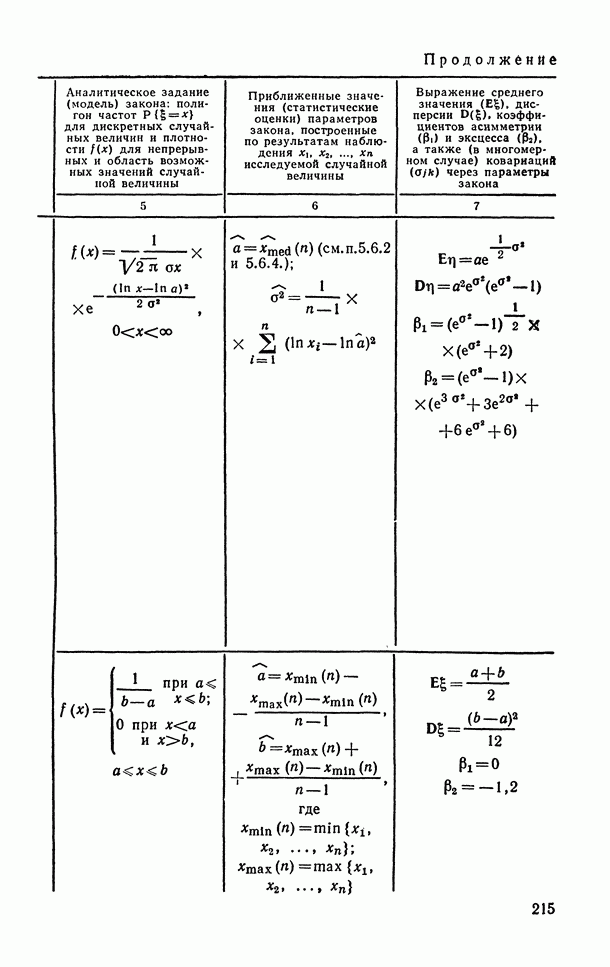
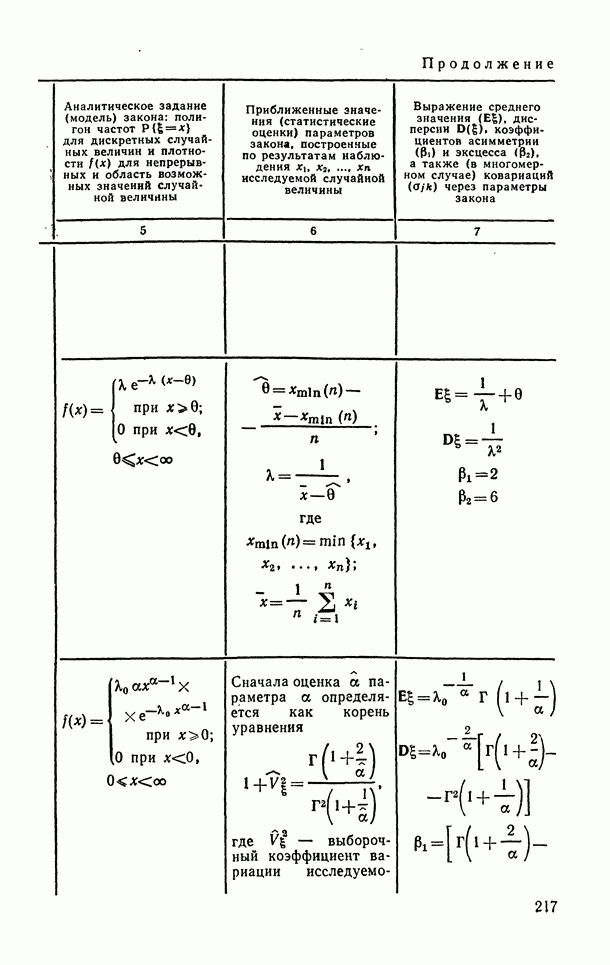
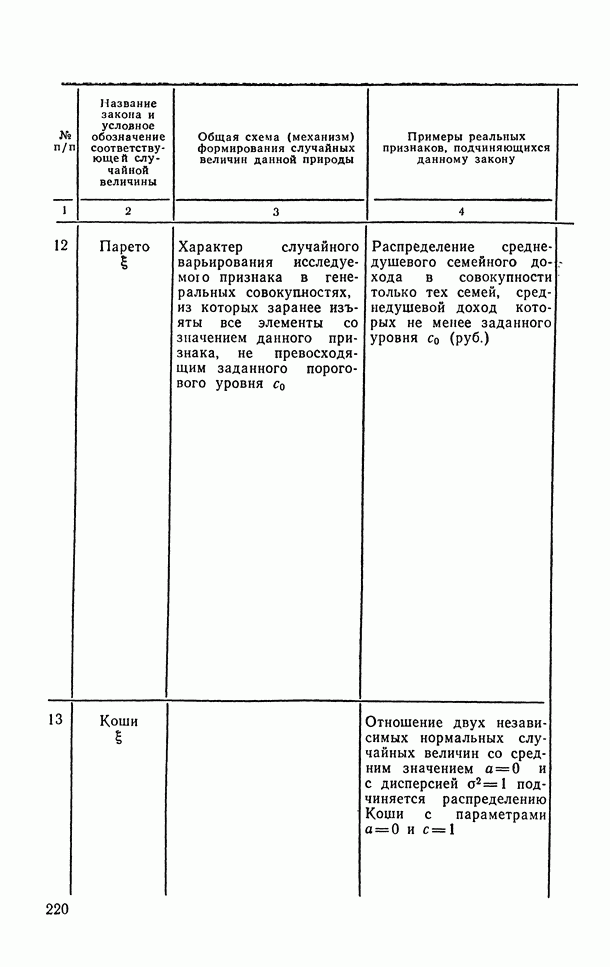
- 3.5.1. Модели законов распределения вероятностей случайных величин.
- 3.5.2. Линейные вероятностные модели.
- 3.5.3. Обобщение линейных моделей.
- 3.5.4. Геометрические модели.
- 3.5.5. Модели марковского типа.
- Выводы
- Раздел II. ОСНОВЫ ТЕОРЕТИКО-ВЕРОЯТНОСТНОГО МАТЕМАТИЧЕСКОГО АППАРАТА
- 4.1.1. Наблюдение, зафиксированное на объекте исследуемой совокупности (случайный эксперимент).
- 4.1.2. Случайные события и правила действий с ними.
- 4.1.3. Вероятностное пространство. Вероятности и правила действия с ними.
- 4.2. Непрерывное вероятностное пространство (аксиоматика А. Н. Колмогорова)
- 4.2.1. Специфика общего (непрерывного) случая вероятностного пространства.
- 4.2.2. Случайные события, их вероятности и правила действий с ними (аксиоматический подход А. Н. Колмогорова).
- Выводы
- Глава 5. случайные величины (исследуемые признаки)
- 5.1. Определение и примеры случайных величин
- 5.2. Возможные и наблюденные значения случайной величины
- 5.3. Типы случайных величин
- 5.4. Закон распределения вероятностей случайной величины. Генеральная совокупность и выборка из нее
- 5.4.1. Закон распределения вероятностей.
- 5.4.2. Генеральная совокупность и выборка из нее.
- 5.4.3. Основные способы организации выборки.
- 5.5. Способы задания закона распределения: функция распределения, функция плотности и их выборочные (эмпирические аналоги)
- 5.5.1. Функция распределения вероятностей одномерной случайной величины.
- 5.5.2. Функция плотности вероятности одномерной случайной величины.
- 5.5.3. Многомерные функции распределения и плотности. Статистическая независимость случайных величин.
- 5.6. Основные числовые характеристики случайных величин и их выборочные аналоги
- 5.6.1. Понятие о математических ожиданиях и моментах.
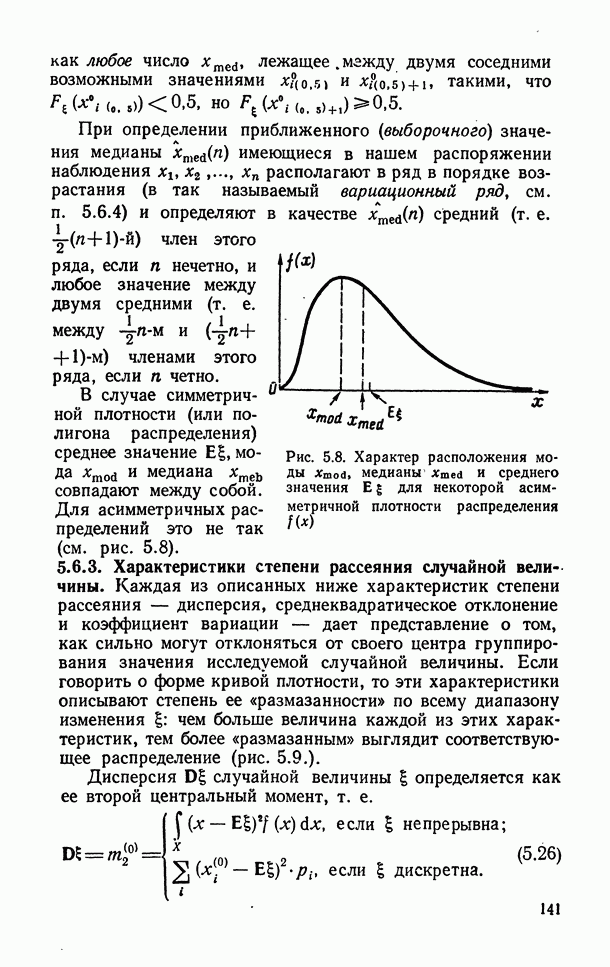
- 5.6.2. Характеристики центра группирования значений случайной величины.
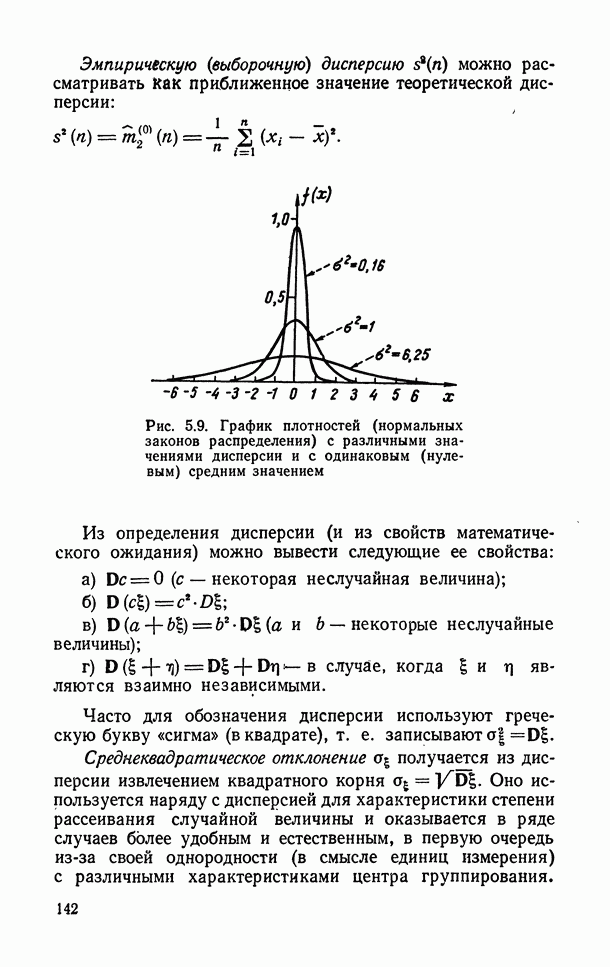
- 5.6.3. Характеристики степени рассеяния случайной величины.
- 5.6.4. Вариационный ряд и порядковые статистики.
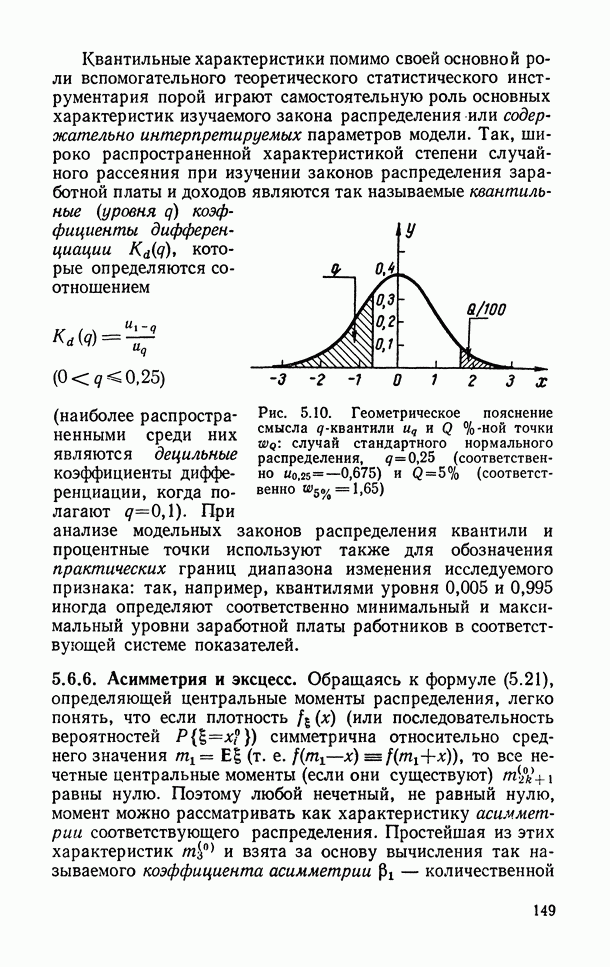
- 5.6.5. Квантили и процентные точки распределения.
- 5.6.6. Асимметрия и эксцесс.
- 5.6.7. Основные характеристики многомерных распределений (ковариации, корреляции, обобщенная дисперсия и др.).
- Выводы
- Глава 6. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ, НАИБОЛЕЕ РАСПРОСТРАНЕННЫЕ В ПРАКТИКЕ СТАТИСТИЧЕСКИХ ИССЛЕДОВАНИИ
- 6.1. Законы распределения, используемые для описания механизмов реальных процессов или систем
- 6.1.2. Гипергеометрическое распределение.
- 6.1.3. Распределение Пуассона.
- 6.1.4. Полиномиальное (мультиномиальное) распределение.
- 6.1.5. Нормальное (гауссовское) распределение.
- 6.1.6. Логарифмически-нормальное распределение.
- 6.1.7. Равномерное (прямоугольное) распределение.
- 6.1.8. Распределение Вейбулла и экспоненциальное (показательное).
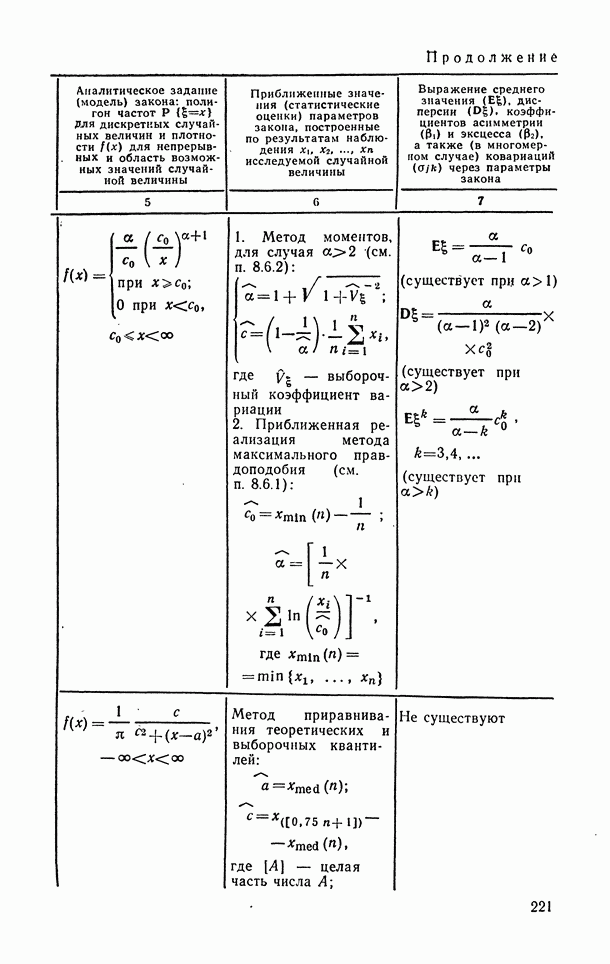
- 6.1.9. Распределение Парето.
- 6.1.10. Распределение Коши.
- 6.1.11. Некоторые комбинации основных модельных распределений, используемые в прикладной статистике.
- 6.2. Законы распределений вероятностей, используемые при реализации техники статистических вычислений
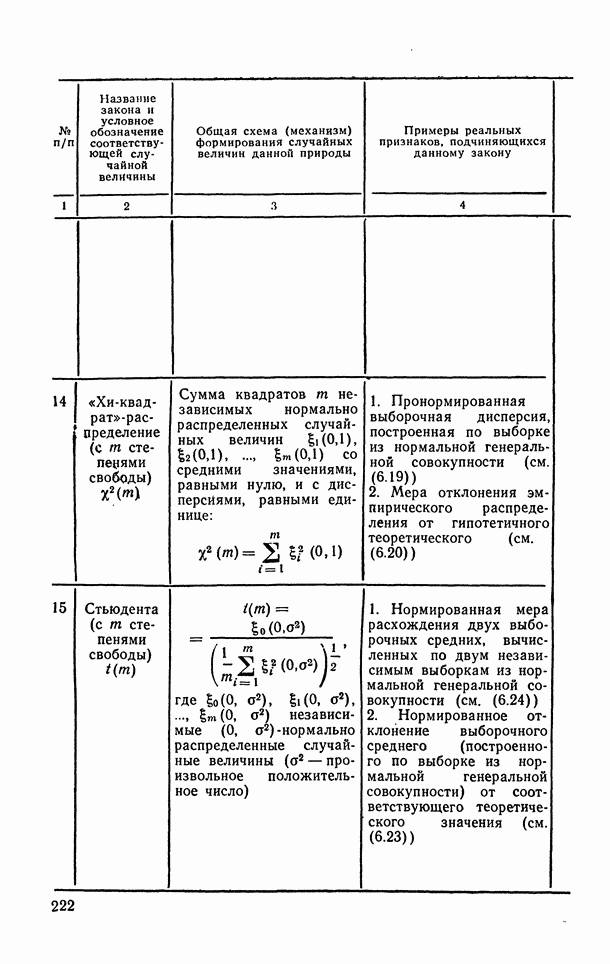
- 6.2.1. «хи квадрат»-распределение.
- 6.2.2. Распределение Стьюдента (t-распределение).
- 6.2.3. F-распределение (распределение дисперсионного отношения).
- 6.2.4. Замечание о нецентральных «хи-квадрат» и F- и t-распределениях.
- 6.2.5. Г-распределение.
- 6.2.6. В-распределение.
- 6.3. Техника статистического моделирования наблюдений, подчиняющихся заданному распределению
- 6.3.1. Получение равномерно распределенных на отрезке [0, 1] случайных чисел.
- 6.3.2. Моделирование дискретных случайных величин.
- Выводы
- Глава 7. ОСНОВНЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 7.1. Неравенство Чебышева
- 7.2. Свойство статистической устойчивости выборочных характеристик: закон больших чисел и его следствия
- 7.2.1. Закон больших чисел.
- 7.2.2. Теорема Я. Бернулли.
- 7.2.3 Статистическая устойчивость выборочных характеристик.
- 7.3. Особая роль нормального распределения: центральная предельная теорема
- 7.3.1. Центральная предельная теорема.
- 7.3.2. Многомерная центральная предельная теорема.
- 7.4. Закон распределения вероятностей случайных признаков, являющихся функциями от известных случайных величин
- Выводы
- Раздел III. ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- Глава 8. СТАТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ
- 8.1. Начальные сведения о задаче статистического оценивания параметров
- 8.1.2. Статистики, статистические оценки, их основные свойства.
- 8.1.3. Состоятельность.
- 8.1.4. Несмещенность.
- 8.1.5. Эффективность.
- 8.2. Функция правдоподобия. Количество информации, содержащееся в n независимых наблюдениях относительно неизвестного значения параметра
- 8.3. Неравенство Рао—Крамера—Фреше и измерение эффективности оценок
- 8.4. Асимптотические свойства оценок
- 8.5. Понятие об интервальном оценивании. Построение доверительных областей
- 8.6. Методы статистического оценивания неизвестных параметров
- 8.6.1. Метод максимального (наибольшего) правдоподобия.
- 8.6.2. Метод моментов.
- 8.6.3. Метод наименьших квадратов.
- 8.6.4. Оценивание с помощью «взвешенных» статистик; цензурирование, урезание выборок и порядковые статистики как частный случай взвешивания.
- 8.6.5. Построение интервальных оценок (доверительных областей).
- 8.6.6. Байесовский подход к статистическому оцениванию.
- Выводы
- Глава 9. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ (статистические критерии)
- 9.1. Основные типы гипотез, проверяемых в ходе статистической обработки данных
- 9.1.1. Гипотезы о типе закона распределения исследуемой случайной величины.
- 9.1.2. Гипотезы об однородности двух или нескольких обрабатываемых выборок или некоторых характеристик анализируемых совокупностей.
- 9.1.3. Гипотезы о числовых значениях параметров исследуемой генеральной совокупности.
- 9.1.4. Гипотезы о типе зависимости между компонентами исследуемого многомерного признака.
- 9.1.5. Гипотезы независимости и стационарности обрабатываемого ряда наблюдений.
- 9.2. Общая логическая схема статистического критерия
- 9.3. Построение статистического критерия; принцип отношения правдоподобия
- 9.3.1. Сущность принципа отношения правдоподобия.
- 9.3.2. Проверка простой гипотезы с помощью критерия логарифма отношения правдоподобия.
- 9.3.3. Проверка сложной гипотезы.
- 9.4. Характеристики «качества» статистического критерия
- 9.5. Последовательная схема принятия решения (последовательные критерии)
- 9.5.1. Последовательная схема наблюдений.
- 9.5.2. Последовательный критерий отношения правдоподобия (критерий Вальда) и его свойства.
- 9.5.3. Различение сложных гипотез в схеме обобщенного последовательного критерия.
- Выводы
- Раздел IV. ПЕРВИЧНАЯ СТАТИСТИЧЕСКАЯ ОБРАБОТКА ДАННЫХ
- 10.1. Документирование исследования; организация ввода и хранения данных в ЭВМ; просмотр данных
- 10.1.2. Ввод и хранение данных.
- 10.1.3. Просмотр данных.
- 10.2. Шкалы измерений
- 10.3. Изучение эмпирических распределений
- 10.3.1. Гистограмма.
- 10.3.2. Непараметрические оценки плотности.
- 10.3.3. Оценки функции распределения.
- 10.3.4. Преобразование переменных.
- 10.3.5. Таблицы сопряженности.
- 10.4. Оценивание параметров сдвига и масштаба
- 10.4.2. Оценивание параметров нормального закона.
- 10.4.3. Графический метод оценивания.
- 10.4.4. Проблема устойчивости оценок при небольших отклонениях распределения от нормального.
- 10.4.5. Оценивание положения центра симметричных распределений.
- 10.4.6. Параметризация с помощью экспоненциально взвешенных оценок (ЭВ-оценки).
- 10.5. Визуализация многомерных данных
- 10.5.2. Главные компоненты.
- 10.5.3. Свойства наименьшего искажения геометрической структуры для главных компонент.
- 10.5.4, Нелинейные отображения в пространство малой размерности.
- 10.5.5. Многомерное метрическое шкалирование.
- Выводы
- Глава 11. ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ ПРИРОДЫ ДАННЫХ
- 11.1. Проверка соответствия выбранной модели распределения исходным данным (критерии согласия)
- 11.1.1. Критерий «хи-квадрат» Пирсона.
- 11.1.2. Проверка нормального характера распределения по асимметрии, эксцессу и средним отклонениям.
- 11.1.3. Критерий Колмогорова — Смирнова и его применение к построению доверительных границ для неизвестной функции распределения.
- 11.1.4. Критерий Крамера — Мизеса — Смирнова.
- 11.1.5. Модификация статистик критериев Колмогорова — Смирнова и для выборок небольшого объема.
- 11.1.6. Статистическая техника практической реализации непараметрических критериев согласия.
- ll.1.7. Использование критериев согласия Колмогорова и «w-квадрат» в случае неизвестных параметров для проверки гипотезы о нормальном характере распределения.
- 11.2. Проверка гипотез однородности и симметрии распределения
- 11.2.1. Критерии однородности, основанные на эмпирических функциях распределения.
- 11.2.2. Критерий однородности «хи-квадрат»
- 11.2.3. Ранговые критерии однородности.
- 11.2.4. Непараметрическая проверка гипотезы равенства дисперсий.
- 11.2.5. Ранговые критерии для случая k > 2 классов.
- 11.2.6. Критерии проверки симметрии распределений.
- 11.2.7. Обработка совпадений.
- 11.2.8. Критерии однородности нормальных совокупностей (одномерный случай).
- 11.2.9. Критерии однородности многомерных нормальных совокупностей.
- 11.3. Проверка независимости и стационарности ряда наблюдений
- 11.3.1. Критерий серий, основанный на медиане выборки.
- 11.3.2. Критерий «восходящих» и «нисходящих» серий.
- 11.3.3. Критерий квадратов последовательных разностей (критерий Аббе).
- 11.4. Методы статистической обработки при наличии «стертых» (пропущенных) наблюдений
- 11.4.1. Оценивание неизвестных параметров при наличии пропущенных данных.
- 11.4.2. Использование главных компонент.
- 11.4.3. Заполнение «пропусков» и оценивание параметров с помощью метода максимального правдоподобия. Оценки «неподвижной точки».
- 11.4.4. Непараметрический подход к оценке пропусков в матрице данных.
- 11.5. Анализ резко выделяющихся наблюдений
- 11.5.2 Графические методы.
- 11.5.3. Аналитический метод исключения одного экстремального наблюдения.
- 11.5.4. Аналитический критерий одновременного исключения нескольких экстремальных наблюдений.
- Выводы
- Глава 12. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ И НЕКОТОРЫЕ ВОПРОСЫ ТЕХНИКИ ВЫЧИСЛЕНИЙ
- 12.1. Программное обеспечение прикладной статистики
- 12.1.1. Организация пакетов программ.
- 12.1.2. Вопросы организации возможности ведения данных.
- 12.1.3. Средства предварительной обработки (манипуляции) данных.
- 12.1.4. Возможности обработки данных при наличии пропущенных значений.
- 12.1.5. Первичная обработка неколичественных данных.
- 12.1.6. Средства визуализации данных.
- 12.1.7. Оценивание параметров и выделение аномальных наблюдений.
- 12.2. Вычисление функций распределения и обратных к ним
- 12.2.1. Нормальное распределение.
- 12.2.2. Распределение «хи-квадрат».
- 12.2.3. Бета-распределение.
- 12.2.4. F-распределение.
- 12.2.5. t-распределение Стьюдента.
- 12.2.6. Нецентральные распределения.
- 12.2.7. Аппроксимация «хвостов» распределений типа «w-квадрат»
- 12.2.8. Многомерное нормальное распределение.
- 12.2.9. Дискретные распределения.
- 12.2.10. Вычисление математического ожидания порядковых статистик.
- Выводы
- ИСПОЛЬЗУЕМЫЕ В КНИГЕ ОБОЗНАЧЕНИЯ
- СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ